Hydrodynamical transport structure and lagrangian connectivity of circulations in the Pearl River Estuary

Using a three-dimensional (3D) hydrodynamic model, this study explored the seasonal hydrodynamic transport structure in the Pearl River Estuary and illustrated the intrinsic connectivity under multiscale motions from a Lagrangian perspective. Generally, the surface Lagrangian residual current (U_L) is uniformly southwestward/southeastward in summer/winter, with a stronger intensity in the lower estuary. The bottom U_L features in the southeastward direction in the upper estuary and northwest direction in the lower estuary. The fluvial–tide interaction line advances southeastward and northwestward in summer and winter, respectively. The U_L captured the major transport processes and was in good agreement with the mean surface sediment transport patterns. In the transition region between Lantau Island and Neilingding Island, where it is largely affected by the interaction between the periodic tidal current and river discharge, the spatially averaged U_L showed intensified intratidal variations and had a larger difference with the locally temporally averaged Eulerian residual current. The remarkable Lagrangian coherent structures that illustrated the transport paths and transport convergence regions were identified, which are generally consistent with the bottom sediment depocenters. Based on the Lagrangian connectivity analysis, it was revealed that a barrier between the western and eastern estuaries existed, which was weakened by the strong river discharge during summer. Two convergence regions near the Macau and Hong Kong waters were identified, where the sediment and pollutants easily settled. The study demonstrated the importance of the Lagrangian view in understanding the hydrodynamic process and transport structure in the estuary–shelf regions.

Introduction

Estuaries, as key locations between the open sea and rivers, often sustain large populations, economies, and valuable ecosystems (Gill et al., 2001; Gillanders et al., 2003; Wang et al., 2015). The water motion inside estuaries and the associated mass transport have a great influence on estuarine and marine ecosystems. Because they are jointly driven by atmospheric forcings, tides, riverine discharge, and coastal currents over the adjacent shelf circulation, the hydrodynamic structure and transport pattern in the estuary–shelf system are naturally complicated. Given the multiscale motion in coastal estuaries, the residual current usually ultimately determines the long-term transport patterns of materials such as sediments, phytoplankton, and pollutants in estuarine areas (Stacey et al., 2001; Xing et al., 2012; Li et al., 2014; Xuan et al., 2016).

The Pearl River Estuary (PRE) is located in southern China (112°45′–113°50′E, 21°31′–23°10′N) and links the Pearl River, the second largest river in China in terms of discharge (annual average discharge: 10,000 m³/s), and the northern South China Sea (NSCS). The triangle-shaped PRE narrows northward in the upper estuary, and the width of the PRE gradually increases to approximately 60 km at the lower estuary, where the shelf is connected (Figure 1). Water motion inside the estuary is jointly driven by winds, tides, and riverine discharges (Lai et al., 2018; Liu et al., 2020). Moreover, the circulation in the lower estuary can be directly modulated by the strong shelf current in the NSCS. The multiscale motion determines the mass transport, alters its connectivity with the adjacent shelf waters, and plays a critical role in determining the water renewal and biogeochemical processes inside the estuary (Li et al., 2020; Li et al., 2021). Thus, the PRE is a valuable model site for providing new knowledge on residual current and mass transport in a complex environment. However, previous studies have primarily focused on the mean Eulerian current. The intrinsic mass transport structure may be blurred by oceanic currents and how different regions are connected by complicated physical motions, as well as the associated timescales and mass transports remain less understood.

FIGURE 1

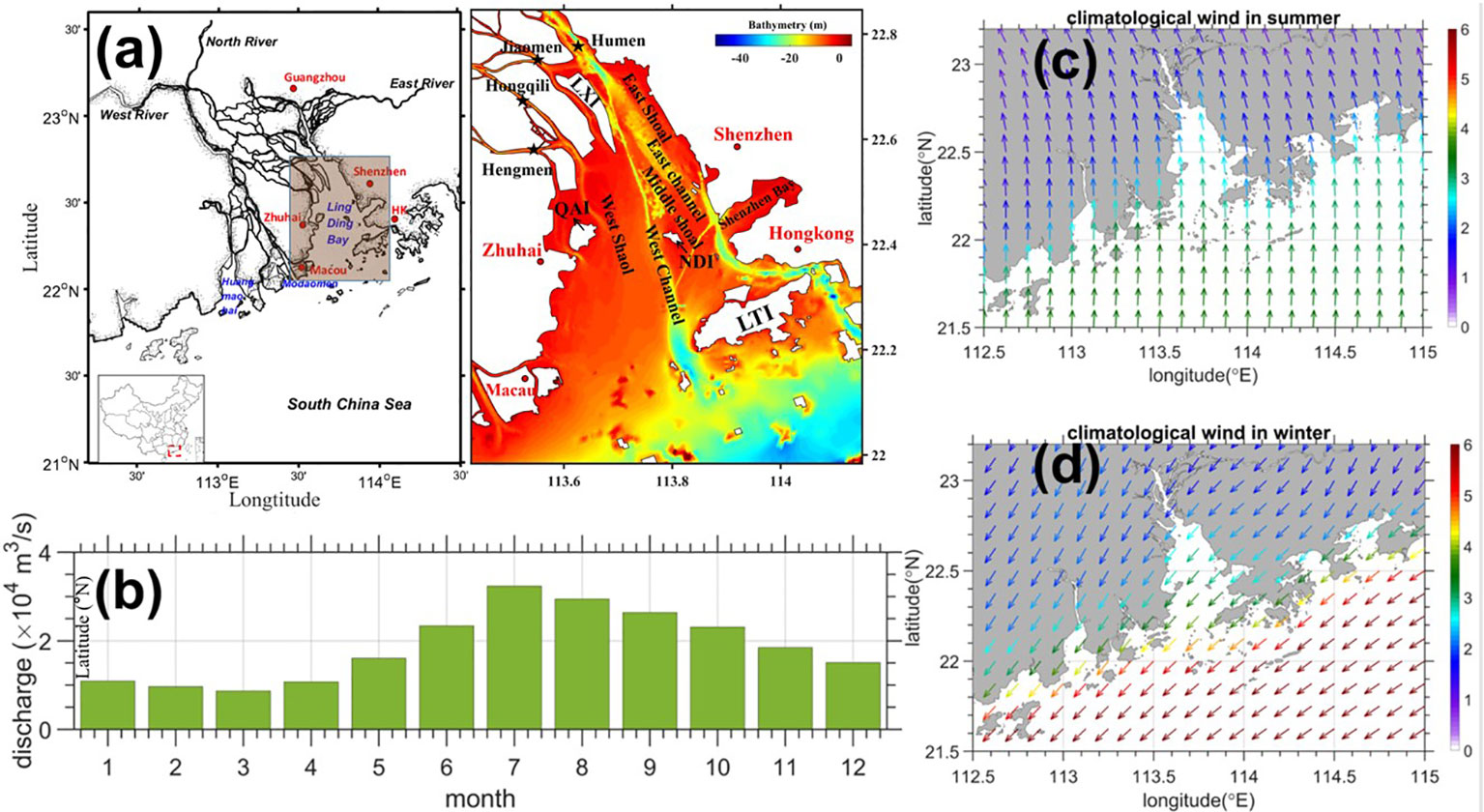
Figure 1 (A) Location and topography of the Pearl River Estuary (PRE). QAI: Qi’ao Island, NLI: Neilingding Island, LTI: Lantou Island, LXI: Longxue Island. (B) The monthly PRE river discharge (10⁴ m³/s). (C, D) The seasonal mean wind speed (m/s) during summer (June–August) and winter (December–February). Atmospheric forcing data were provided by the ERA5 atmospheric reanalysis data from the European Center for Medium-Range Weather Forecasts (ECMWF), and the monthly averaged riverine discharge data were provided by Chu et al. (2022).

Lagrangian tracking is an effective way to analyze the transport processes in estuaries, which helps to determine the origin and fate of specific water masses (Feng et al., 1986; Jonsson et al., 2004; Ju et al., 2009; Muller et al., 2009; Liu and Chua, 2016). As a combination of the Lagrangian and Eulerian methods, Lagrangian coherent structures (LCSs) can be identified from fluid motions, which represent the strongest repelling or attracting material lines, thus distinguishing water masses with different motion characteristics and the barriers between different circulation regions. It has proven to be a valuable and appropriate tool for simplifying the transport and mixing in fluid flows and diagnosing the transport properties of materials (Branicki and Wiggins, 2010; Wei et al., 2013). Many methods have been proposed to identify LCSs, and finite-time Lyapunov exponents (FTLEs) are widely used (Wei et al., 2013; Berta et al., 2014; Wei et al., 2018). The ridges in the FTLE fields can be used as barriers to mass transport and identify the LCSs in the flow field (Haller and Yuan, 2000; Haller, 2015; Wei et al., 2018).

To illustrate the transport structure and further understand the hydrodynamic intrinsic connectivity among different subregions in the PRE and the adjacent shelf region, the Lagrangian investigations were conducted in this study using the results from a climatological three-dimensional (3D) hydrodynamic model. The remainder of this paper is organized as follows. Section 2 introduces the numerical model and methodology for particle tracking. In Section 3, the seasonal hydrodynamic transport structure is revealed and compared with the net mean surface sediment transport pattern. Then, the intrinsic connectivity among the various subdomains of the PRE is illustrated based on the Lagrangian coherent structures (LCSs) and transport proportion matrix. This paper is summarized in Section 4.

Methodology

Numerical model

The Regional Ocean Modeling System (ROMS) (Shchepetkin and McWilliams, 2005) was used to simulate hydrodynamics in the study area. The model domain was bounded by the latitudes of 18.67°N and 24.66°N and the longitudes of 110.19°E and 120.45°E, which covers the PRE and the shelf region of the NSCS to resolve the multiscale interactive processes in the PRE and the adjacent shelf. The horizontal grid spacing was approximately 400 m. We used the terrain-following s-ordinate (Song and Haidvogel, 1994) to discretize the water column into 30 levels, and a higher resolution was used in both the surface and bottom boundary layers. To better illustrate the representative characteristics of the multiscale motions, we conducted process-oriented studies with climatologically averaged monthly atmospheric forcing and river discharges (Figures 1B–D). Atmospheric forcing data, including wind, heat flux, and precipitation, were provided by the ERA5 atmospheric reanalysis data from the European Center for Medium-Range Weather Forecasts (ECMWF) and applied to force ocean circulation using the bulk flux computation algorithm (Fairall et al., 2003). Monthly averaged riverine discharge data were provided by Chu et al. (2022). The subtidal flows and hydrographic properties were extracted from the numerical simulation of the Northern South China Sea, which has been used successfully in the water exchange and interannual variability of shelf circulation (Cai et al., 2022; Deng et al., 2022). To better represent the climatological seasonality of the shelf circulation, we applied the monthly averaged shelf circulation as the subtidal forcing along the southern, western, and eastern open boundaries of the computational domain. The harmonic constants of tides in the computational domain were computed and validated by Zu et al. (2008) using Oregon Tide Inverse Software (Egbert and Erofeeva, 2002). The tidal current was included along the open boundaries using the advanced dual-wave transmission-permitting algorithm proposed by Liu and Gan (2016; 2020). The major constituents of the semidiurnal (M₂, S₂, K₂, and N₂) and diurnal (K₁, O₁, P₁, and Q₁) tides and the M₄ tide were applied along the open boundary to impose tidal forcing in the computational domain. The simulation well captured the hydrodynamic and circulation featured in this region as illustrated in previous investigations and observed data. We exported the ocean current data with an interval of 20 min in summer (June–August) and winter (December–February) to better resolve the motions determined by complicated forcings. The saved data will be used in the off-line Lagrangian tracking and following analysis.

Lagrangian particle tracking

In this study, the net residual current in the PRE regions was examined based on off-line particle tracking using the Lagrangian TRANSport model (LTRANS v.2b), which is a popular off-line three-dimensional particle tracking module (e.g., North et al., 2011; Henry et al., 2018; Pearson et al., 2019; Liang et al., 2021). Using the high-frequency ocean current data retrieved from the validated hydrodynamic model, it was developed to simulate the movement of passive tracers, particles with sinking or floating behavior, such as sediment or oil droplets, and planktonic organisms, such as oyster larvae. It includes the fourth-order Runge–Kutta scheme for particle advection and reflective boundary conditions on solid walls, specific particle behavior routines, and settlement algorithms.

From the Lagrangian perspective, the transport processes are tracked by following fluid particles to identify the trajectories starting from or arriving at a given point. The transport equations were discretized along a moving frame of reference, and the particle positions and velocities were also considered between the Eulerian grid points. The Lagrangian residual velocity (Zimmerman, 1979; Feng et al., 2008) is expressed as

$\begin{array}{ll}{\stackrel{\rightharpoonup }{U}}_L\left({\stackrel{\rightharpoonup }{x}}_0,t_0;\tau \right)=\frac{\stackrel{\rightharpoonup }{x}\left(t_0+\tau \right)-\stackrel{\rightharpoonup }{x}\left(t_0\right)}{\tau }& (1)\end{array}$

where$\stackrel{\rightharpoonup }{x}\left(x,y,z\right)$ is a three-dimensional position vector in the Cartesian coordinate system, t₀ is the initial time for an arbitrary water parcel to be tracked, ${\stackrel{\rightharpoonup }{x}}_0$ is the initial position vector, and τ is the tracking period. In this study, the particles were released at each grid inside the PRE and tracked for 25 h to indicate the net motion after approximately one diurnal tidal cycle. The movement pattern over a longer period can be understood by the accumulation of the ${\stackrel{\rightharpoonup }{U}}_L\left(\stackrel{\rightharpoonup }{x},\text{τ};t_0\right)$. The numerical experiments also indicated that a longer tracking period did not change the major transport pattern (figure not shown). As illustrated in the previous numerical and theoretical investigations (e.g., Feng et al., 1986; Feng et al., 2008; Muller et al., 2009; Liu et al., 2012; Liu et al., 2021), ${\stackrel{\rightharpoonup }{U}}_L$ in the generally non-linear system highly depended on the initial time, even in a purely periodic, single tidal constituent–driven barotropic system. To remove the dependence of the residual current on the initial release time and illustrate the mean seasonal transport pattern, the particles were released every 2 h within 3 months of summer and winter.

Lagrangian coherent structures

To identify LCSs, the FTLE was calculated, which involved the simulation of the particle paths in an advection flow. FTLE fields represent the finite time average of the maximum expansion or contraction rate of a pair of passive advection fluid materials. It can be calculated as (e.g., Wei et al., 2018)

$\begin{array}{ll}{\sigma }_{t_0}^{\tau }(x_0):={\left|\tau \right|}^{-1}In║{\partial }_{x_0}x(t_0+\tau ;t_0,x_0)║& (2)\end{array}$

where║ ║ denotes the spectral norm. Consider an arbitrary fluid particle located at x₀ in the study area at time t₀ after being transported by the flow for a time interval τ , the particle is moved to x(t₀+τ;t₀,x₀) at time t=t₀+τ . The latter is obtained by integrating the particle trajectory equation (1). Repelling and attracting LCSs are then defined (Haller and Yuan, 2000; Shadden et al., 2005; Haller, 2011) as maximizing the ridges of the FTLE field computed forward (t > 0) and backward (t < 0) in time, respectively.

The high values in FTLE fields are associated with the LCSs that are defined as the ridges of the FTLE field. In the region where the FTLE < 0, fluid particles tend to converge, and pollutants converge here. In the region where the FTLE > 0, a higher value means a higher separation rate between two neighboring particles; the positive line in the FTLE can be regarded as the material transport path (e.g., Shadden et al., 2005; Liang et al., 2014).

Results and discussion

Estuarine circulation

The seasonally averaged features of the representative hydrodynamic conditions revealed in the simulation during summer and winter were examined in the study area, which captured the mean features of circulations neighboring the PRE, as illustrated in previous studies (e.g., Zu and Gan, 2015; Liu and Gan, 2020; Cai et al., 2022). In summer, strong gravity circulation was observed in the lower estuary, where the surface current flowed southeastward and the bottom current flowed northwestward (Figures 2A, C). In the upper estuary, induced by strong river discharge in the wet season, both the surface and bottom currents flowed seaward. Driven by the southwesterly monsoon, coastal upwelling with northeastward along-shore currents formed over the NSCS shelf. Sea surface temperature and salinity generally showed the characteristics of shelf upwelling, forming a northeastward-extending belt of cold salty water in the coastal seas to the east of the PRE (Figures 3A, C). In winter, when weaker discharges occur, the gravitational circulation was generally preserved but with weakened intensity (Figures 2B, D). Compared with summer conditions, bottom waters invaded further landward in the estuary, while the seaward flow was still observed in the surface layers. Because of the extensive northeasterly wind, the shelf current flowed southwestward with a larger magnitude than that in the summer (Figures 2B, D). Affected by the monsoon, buoyant water flowed southwestward in the estuary and was arrested by the southwestward shelf current after leaving the estuary, forming a cold salt wedge estuary (Figures 3B, D).

FIGURE 2

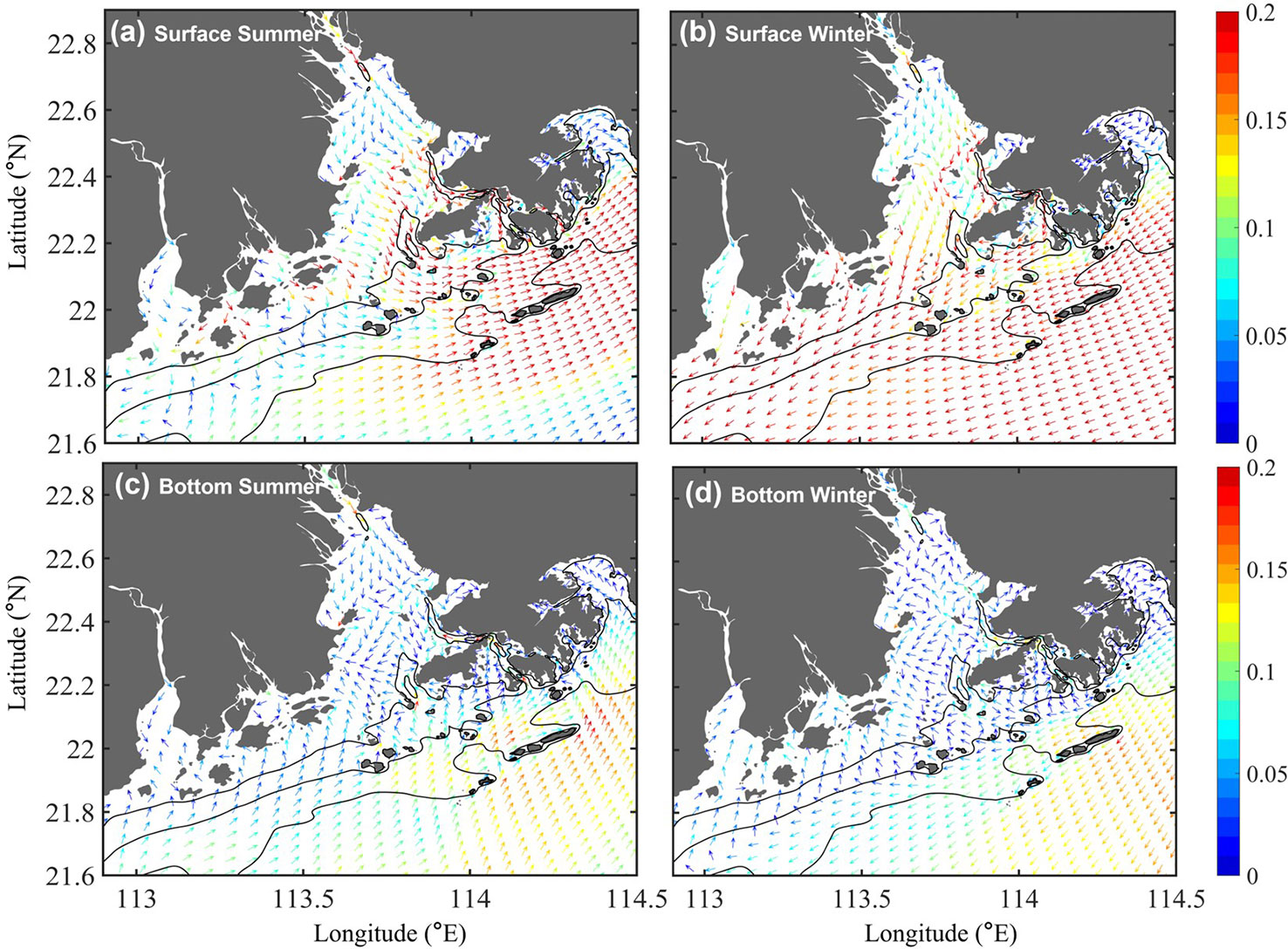
Figure 2 (A, C) Horizontal map of the seasonally averaged surface and bottom currents in summer calculated by the numerical model in this study; the arrow and color represent the direction and magnitude (m/s) of the velocity, respectively. (B, D) Same as (A, C), except that they represent winter conditions. The black lines are 10–30 m isobaths.

FIGURE 3

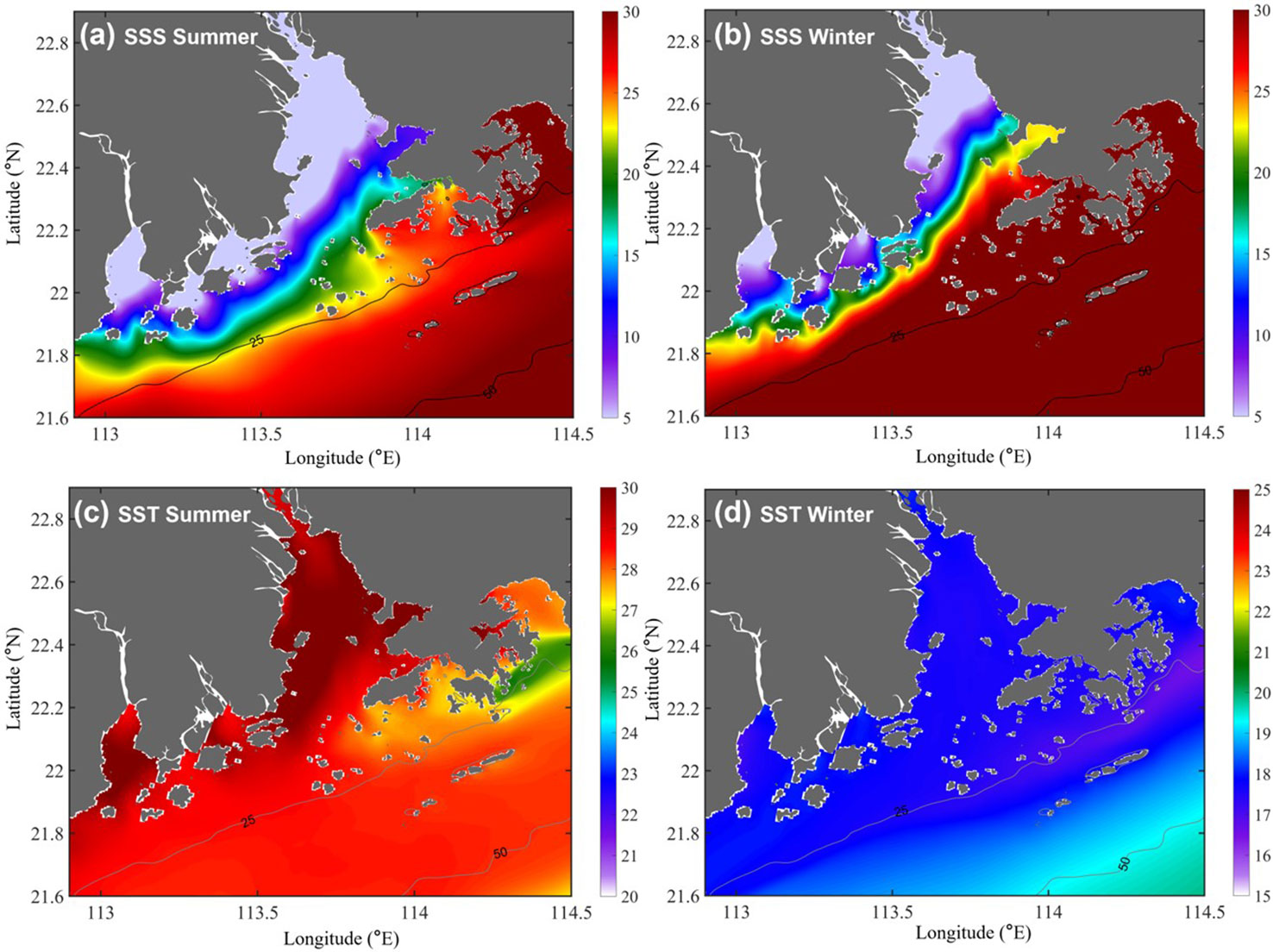
Figure 3 (A, B) Horizontal maps of the sea surface salinity (SSS, PSU) in summer and winter calculated by the numerical model in this study, respectively. (C, D) Same as (A, B), except for the sea surface temperature (SST, °C).

Seasonal Lagrangian transport structure

For simplicity, we first checked the seasonally averaged U_L with a different release time at the surface and bottom layers (Figures 4A–D). In general, the surface U_L inside the PRE was uniformly southwestward/southeastward in summer/winter (Figures 4A, B) and stronger (approximately 20 cm/s) in the lower PRE than that in the upper PRE. Over the shelf, owing to the different monsoon directions, the surface U_L flowed in a northwest/southeast direction (Figures 4A, B). Unlike the surface residual current, the bottom residual currents exhibited more complicated distributions. In summer, intensified fluvial dynamics occupied the region from the northwestern estuary to the northwest of Neilingding Island. The runoff from the northwest was transported southward along the west bank of the estuary and to the east of Qi’ao Island, forming a weak clockwise pattern around Qi’ao Island (Figure 4C). In winter, buoyant waters mainly rushed out of the estuary along the western bank of the PRE due to the reduced runoff and changes of wind direction (Lai et al., 2015), whereas saline shelf water occupied the lower estuary neighboring the eastern bank (Zheng et al., 2014), and the fluvial–tide interaction line advanced northwest. Then, the residual currents from the lower east channel resulted in a significant northwestward bottom residual current until it reached the north of Qi’ao Island and deflected southward by the plume, forming a counterclockwise pattern around Qi’ao Island (Figure 4D). In the lower PRE, the bottom U_L tended to flow northwestward (Figures 4C, D). Because the U_L indicates the averaged motions of different spatial locations on the trajectory, compared with the time-averaged Eulerian residual current at fixed location (U_E ) the upper U_L had a similar pattern but was not locally intensified over the deep channels (Figure 2), and the magnitude of the upper layer U_L was weaker than that of U_E . In the bottom layer, the discrepancies mainly occurred in the region to the north of Lantau Island, where the U_L featured onshore intrusion, which is opposite to Eulerian one. In the upper and lower estuaries, where the deep layer motions were dominated by relatively stable river discharge and shelf current, the U_L and U_E shared a similar pattern.

FIGURE 4

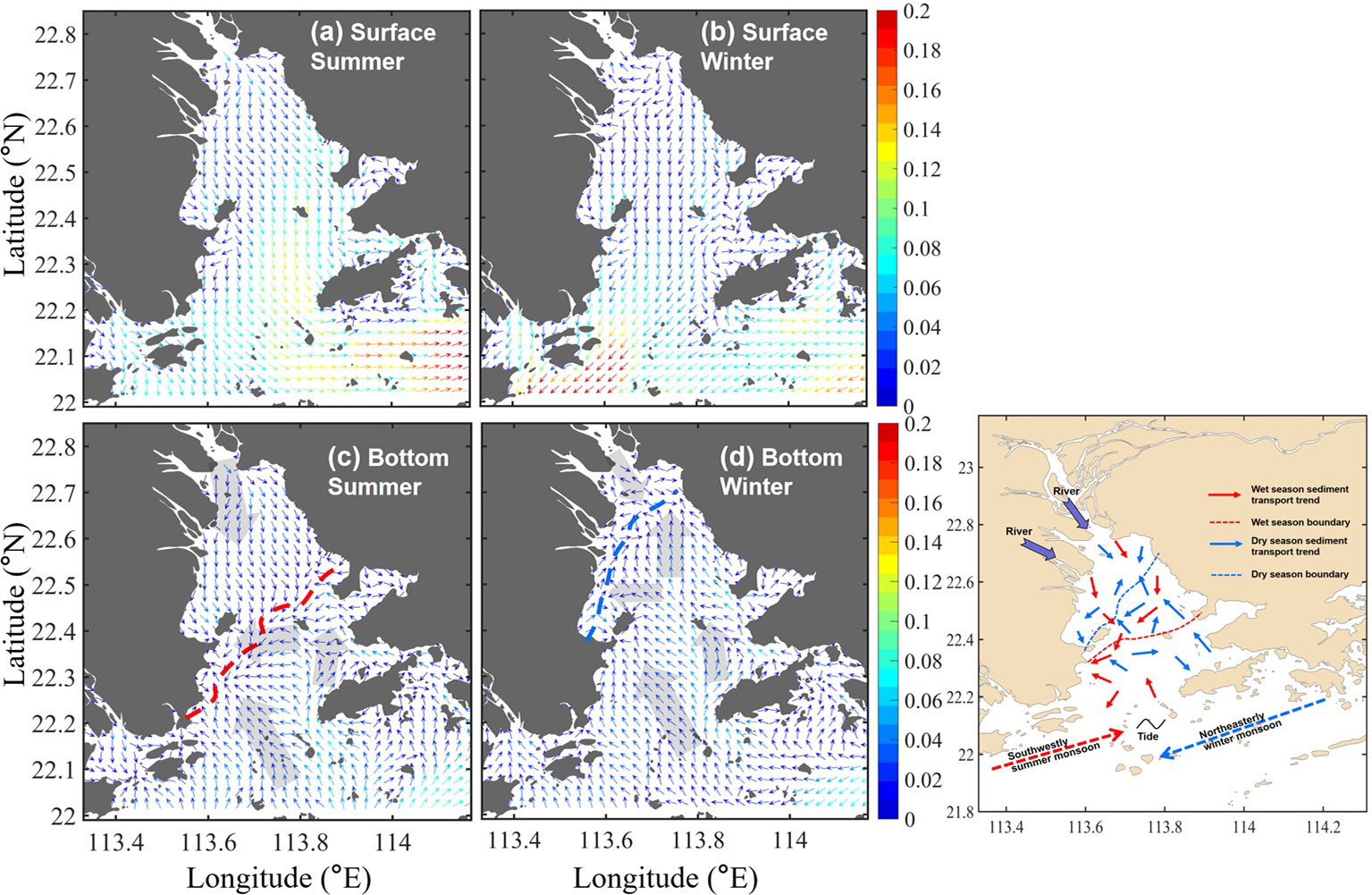
Figure 4 (A, B) The surface U_L (m/s) averaged in the summer (June–August) and winter (December–February). The colors indicate the magnitude, and the arrows indicate the direction. (C, D) Same as (A, B), except for the bottom U_L . The transparent arrows indicate the mean pattern of the U_L the Schematic map of the core transport path of the surface of the PRE sediment in summer and winter; the direction of coastal current is summarized by Xiao (2012); Li et al. (2014); Shi et al. (2015); Li and Li (2018); Zhang et al. (2019); Chu et al. (2020), and Wei et al. (2021).

The U_L represented the mean transport pattern of particles driven by the hydrodynamical motions, and as illustrated in previous investigations, the mean bottom residual currents can explain the major surficial sediment transport pattern (STP) over the estuary (Liu et al., 2012; Zhang et al., 2013). Thus, the STP in the PRE from various published papers (Xiao, 2012; Shi et al., 2015; Li and Li, 2018; Zhang et al., 2019; Chu et al., 2020; Wei et al., 2021) were combined to give the long-term mean transport pattern and to validate the transport pattern of the bottom U_L (Figure 4E). Although the calculated U_L ignored the sedimentation and resuspension processes, it was in good agreement with the mean STP, which also proved that the model and simulated U_L captured the major transport processes in the PRE. Being similar to the bottom U_L , the sediments were transported southward in the upper PRE and northward in the lower PRE in both summer and winter. Seasonally, the STP varied in spatial ranges that sediment transported further southward/northward in summer/winter. In the middle of the estuary, with fluvial–tide interactions, the STP showed a complicated structure. As also shown in the bottom U_L , the STP near Qi’ao Island was counterclockwise in winter and clockwise in summer (Zhang et al., 2013; Wei et al., 2021). Around the west bank of the lower PRE, which was reported to be a depositional center (Yang et al., 2019), both the U_L and STP had an overall westward transport trend and convergence pattern. However, it was also noted that the bottom U_L showed a relatively large difference with the STP around the northeast of Neilingding Island, possibly due to the sand mining activities that were declared in our previous study (Chu et al., 2020).

To further illustrate the intraseasonal variability of the U_L , the depth-averaged temporal standard deviation (STD) of the residual current in the zonal and meridional directions was calculated for summer and winter as follows (Liu et al., 2012):

$ST{D}_u=\sqrt{\frac{1}{n-1}\sum _{i=1}^n{\left(u_{Li}-\overline{u_L}\right)}^2}$ and

$\begin{array}{ll}ST{D}_v=\sqrt{\frac{1}{n-1}\sum _{i=1}^n{\left(v_{Li}-\overline{v_L}\right)}^2}& (3)\end{array}$

where u_L and v_L are the U_L in the zonal and meridional directions, respectively, and n is the number of U_L obtained from tracking using Equation 1. The high STD_v /STD_u values represent regions where the u_L /v_L is sensitive to the initial time. Inside the estuary, the temporal variability of the U_L is dominated by motions in the north–south direction with high STD_v Figures 5C, D). The high STD_v occurred mainly in the region between Lantau Island and Neilingding Island in both summer and winter, where strong fluvial–tide interactions and U_L featured opposite directions to the U_E (Figure 4). The time series of the U_L and the sea level illustrated that the high STD is mainly induced by the intratidal (period of ~25 h) and spring–neap tidal variabilities (not shown). A larger STD_v also existed along the western coast of the estuary near Macau in winter, where buoyant water was arrested. Over the shelf, the current has a larger component in the west–east direction, and the temporal variability is mainly controlled by the STD_u (Figures 5A, B).

FIGURE 5

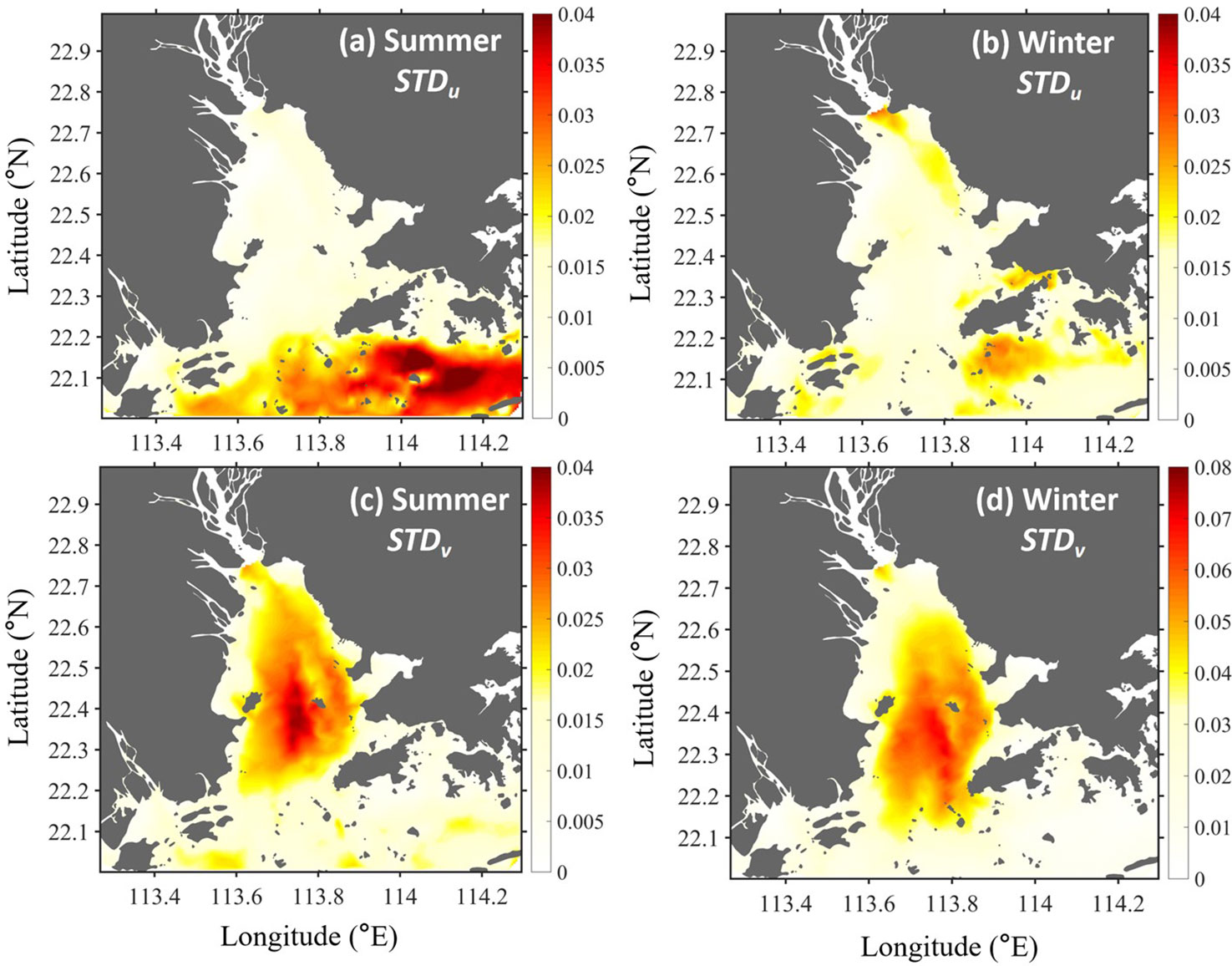
Figure 5 (A, B) The distribution of STD_u n summer and winter, respectively; (C, D) are same as (A, B) but for STD_v .

The bottom U_L was used as an example to illustrate its intratidal variability and dependence on initial time. The surface U_L showed a similar dependence on the initial time. In summer, the U_L with the initial time (t₀ ) at high tide generally moved southward in the PRE, with a high magnitude of approximately 0.1 m/s (Figure 6A). For the U_L at low tide, the U_L changed to the northward direction in the lower estuary, but in the upper estuary, it remained in the southward direction due to the strong river discharge (Figure 6C). To the north of Qi’ao Island and Neilingding Island, the eastward U_L occurs associated with the convergence of the southward U_L from the upper estuary and northward U_L from the lower estuary. Given the reduced fluvial dynamics in winter, when water parcels are released at high tide, the bottom U_L is transported northward in most areas of the PRE, except for the convergence pattern near Qi’ao Island (Figure 6B). In contrast, the bottom U_L at low tide features a stronger intrusion over the entire estuary with a magnitude larger than 0.1 m/s (Figure 6D).

FIGURE 6

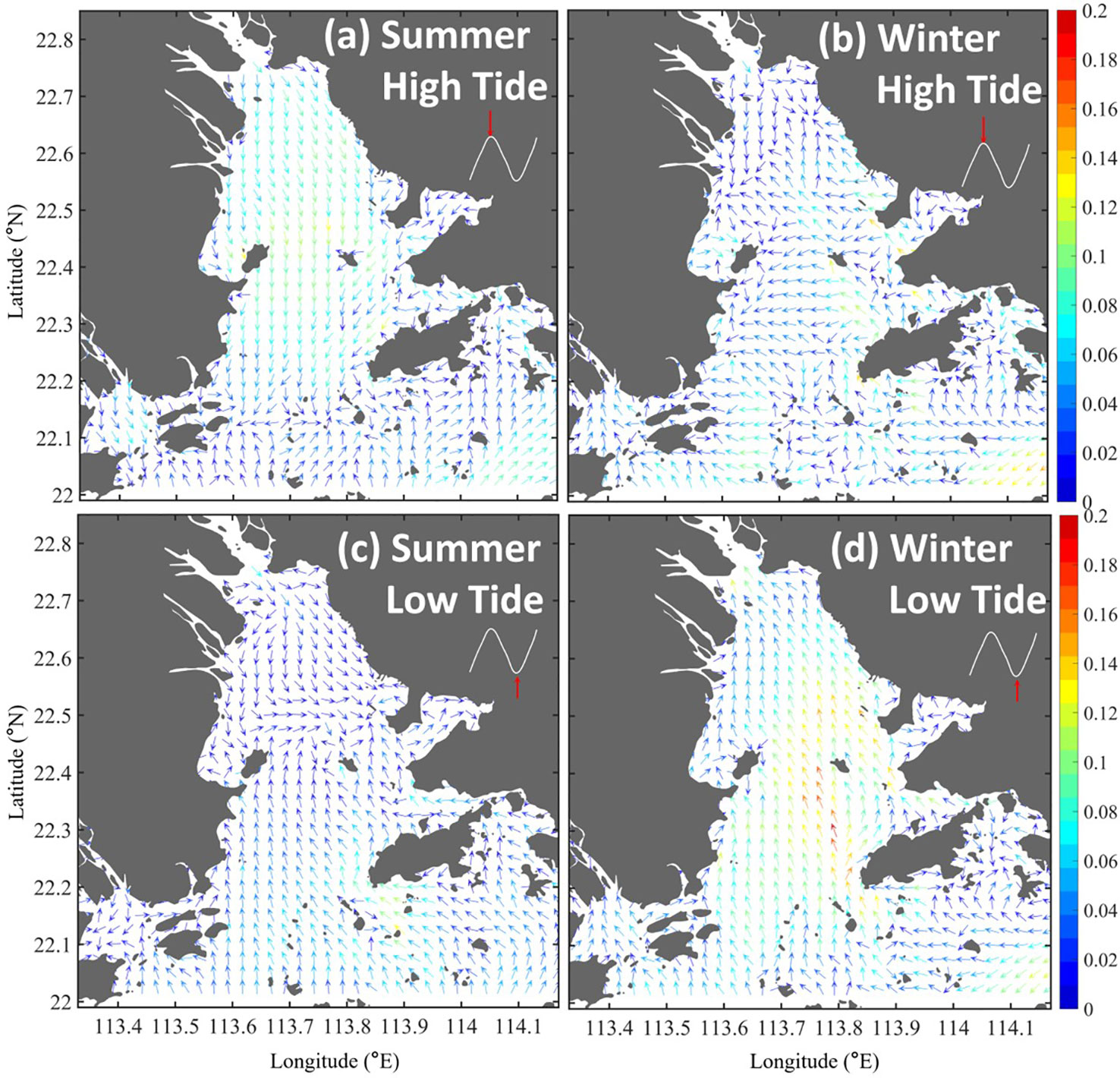
Figure 6 The bottom U_L (in m/s) corresponding to the initial tidal phases when the water parcels were released at spring high tide in summer (A) and winter (B); (C, D) are same as (A, B) but for U_L at low tide.

The background colors indicate the U_L magnitude.

Lagrangian coherent structures and transport connectivity

To explore the intrinsic transport structure and how different regions are connected, the LCSs were examined based on the FTLE in the bottom layer, where they had a more complicated structure and explained the major transport pattern, such as for sediment in the PRE regions. It was calculated following the methods of Onu et al. (2015) and Wei et al. (2018). The high-value ridge lines of the FTLE generally act as transport barriers and can be used to identify LCSs in the flow field.

In summer, high freshwater discharge enters the estuary through the four northwest outlets, and the associated sediment input accounts for the majority of the annual riverine sediment supply. The northwest forms the main transport path for materials, corresponding to the patches of highly positive FTLE values (L1, Figure 7A). An obvious highly positive FTLE can also be found in the southwest of Shenzhen Bay to the south of Middle Shoal (L2, Figure 8A). Along these ridge lines, fluid particles with high dispersion are the main material transport barriers. The negative FTLE regions present the convergence of residual currents, mainly around the southeast of Qi’ao Island, southeast of Macau, and northeast of Shenzhen Bay. These regions indicate fluid particle consolidation, such that the material tends to deposit under weak hydrodynamic conditions. It is interesting to note that the negative FTLE regions correspond well to the depocenters of the PRE revealed in previous investigations (Figure 7C). The riverine sediments from the three western outlets (i.e., Jiaomen, Hongqili, and Hengmen outlets) were trapped at the west shoals due to low bottom shear stress (Zhang et al., 2019), forming two depocenters around the northwest of Qi’ao Island and east of Macau water (Figure 7C). Meanwhile, the sediments released near the tidal channel (Humen outlet) were more deposited at the east shoal, i.e., the northwest of Shenzhen Bay (Figure 7C).

FIGURE 7

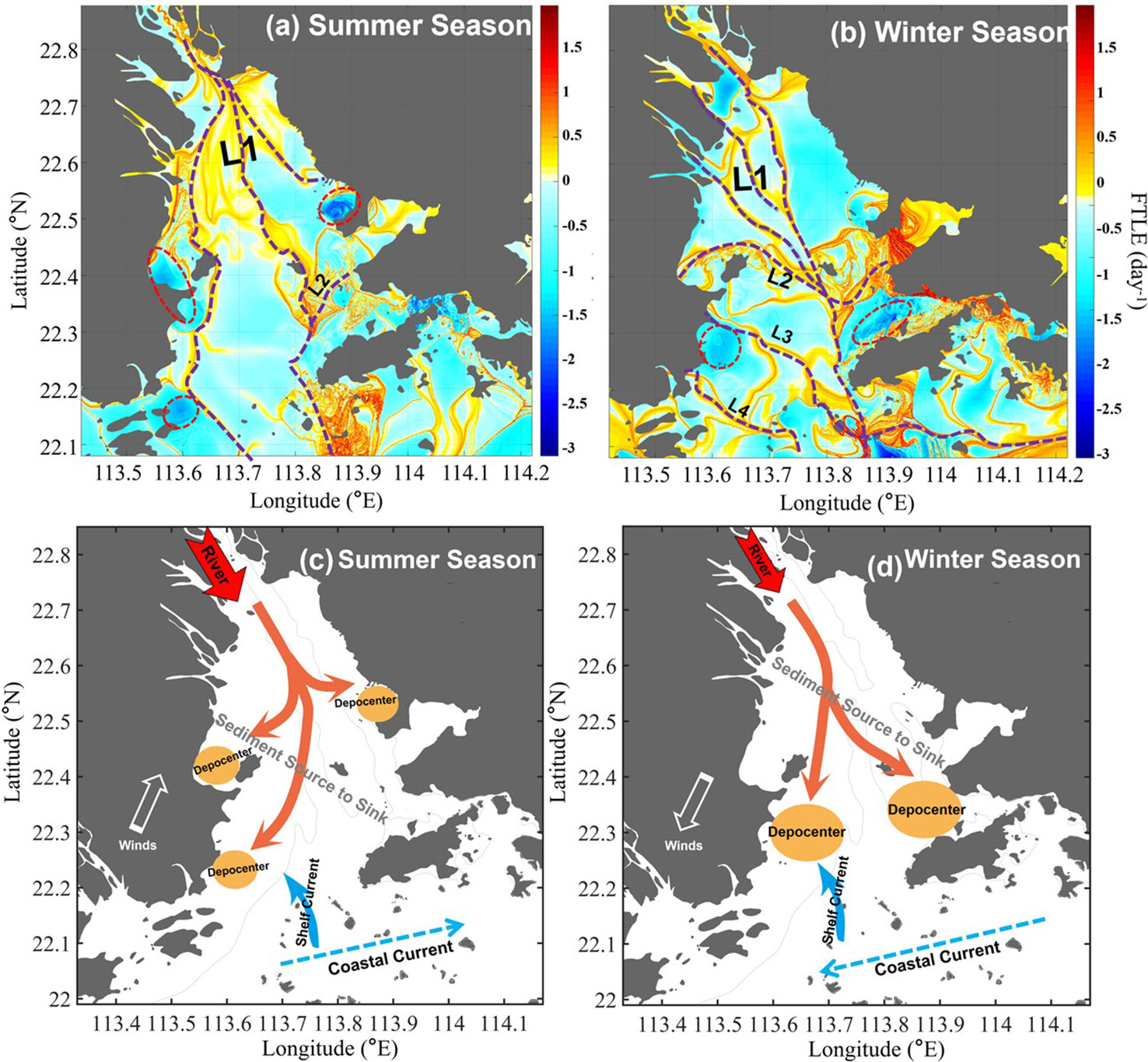
Figure 7 (A, B) Bottom FTLE structure in summer and winter, the dashed lines denote the main transport paths. (C, D) Schematic maps of the core transportation path of surface sediment and depocenters in the PRE in summer and winter; the gray lines are 5 m isobaths. The conceptual patterns of sediment source to sink are summarized from Zhang et al. (2019); Chen et al. (2020), and Chu et al. (2020).

FIGURE 8

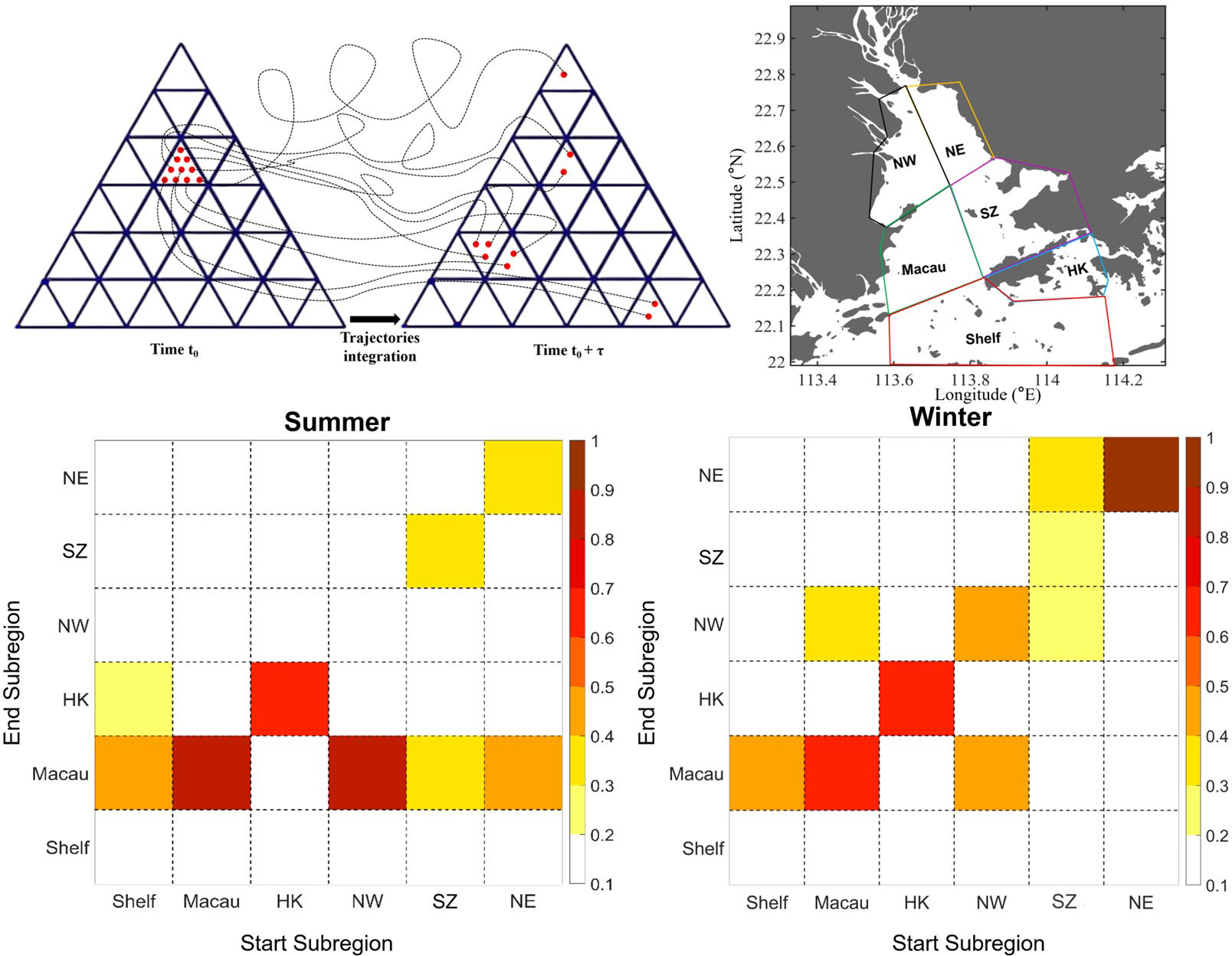
Figure 8 (A) Schematic figure showing the starting and ending subregions to conduct the connectivity matrix. (B) The six subregions in the PRE. (C, D) show the connectivity among six subregions in summer and winter, respectively.

Similarly, during the winter, the positive FTLE values in the upper PRE correspond to river outlet channels (L1). In the middle estuary, a belt of the FTLE ridge existed from the west of Qi’ao Island to Shenzhen Bay in the eastern part (Figure 7B). In the lower estuary, L3 and L4 from the continental shelf to the west coast of the estuary (Figure 7B) indicated the possible material transport from the shelf to the estuary. The negative FTLE value is mainly around the east shoal, south of the west shoal, and northwest of Lantau Island in winter. In contrast to summer, the freshwater discharges and sediment loads decrease sharply in winter seasons in the PRE; thus, salt intrusion is enhanced and brings more marine sediments into the estuary, and the estuarine turbidity maximum zones will shift, as well as the depocenters. Sediments from the open sea via the southwest of Lantau Island, forming two major depocenters around Macau and the north of Lantou Island, consisting of fluvial and marine sediments (Figure 7D).

Generally, the sediment source-to-sink process in the PRE corresponded well with the spatial distribution of the FTLE. Following its distribution, the sediment mainly enters the PRE from the northwest outlets and the south open sea, supplying the sediment source to the PRE, which consists of the fact that the sediment in the PRE is composed of terrestrial sources and marine sources (Wu and Zhao, 1982; Liu et al., 2007; Li et al., 2016; Wu et al., 2018; Chu et al., 2020). The terrestrial sediments were mainly derived from the Pearl River basin and drained through the three river-dominated outlets in the west. Due to the decline of the elevation slope and the backwater effect of the tidal current, the coarser sediment deposited around the west shoal and the finer particles continued to move toward the southeast through the west channel, eventually entered the adjacent shelf, or were intercepted around Lantou Island. The “source-to-sink” process of these terrestrial sediments can be consistent from the FTLE ridge, i.e., L1 (Figures 7A, B) to the negative FTLE center in the upper PRE region. For the marine sediments, they mainly entered the estuary through the east channel and the south of west channel. Some of them stayed close to the bay mouth under the control of shelf current, while some moved northwestward and were deposited in the west shoal when they encountered runoff (Li, 2017; Chu et al., 2020). This can be demonstrated from the FTLE ridge of L2–L4 (Figure 7) and the negative FTLE regions near Macau and Hong Kong waters.

The summer and winter results are consistent with previous predictions from a large number of complex sediment analyses (Wu and Zhao, 1982; Li, 2017; Yang et al., 2019; Chu et al., 2020), but Lagrangian analysis provides a similar answer in a more concise manner, thus providing a very useful method for interpreting predicted surface sediment transport and detecting the “source-to-sink” processes of estuarine sediments.

The FTLE field showed the different transport pattern between the east and west sides of PRE with reduced the exchanges. The zonal FTLE ridge (e.g., L2) separated the upper and middle estuary, and the lower estuary can be directly modulated by the strong shelf current. Thus, based on the structure illustrated from the FTLE, we divided the PRE into six subregions (R_i, i=1,2,…,6), including the shelf (Shelf), Macau water (Macau), Hong Kong water (HK), northwestern estuary (NW), Shenzhen water (SZ), and northeastern estuary (NE) (Figure 8B). These regions were generally separated by the ridges of the bottom FTLE. To quantitatively explore connectivity, the fluid transport proportions were established between these subregions (i.e., boxes in the fluid domain) within a given time interval. This transport ratio could be obtained from a Lagrangian perspective by following the trajectories of fluid particles and recording their initial and final positions (i.e., starting and ending subregions, Figure 8A). In this study, the particles were released uniformly inside each subregion and tracked for 30 days. The calculation with a different tracking time showed that it generally provided a reasonable and relatively stable connection pattern in the PRE, which was consistent with the basic transport pattern in the FTLE and U_L.

For each subregion (R_i), the flow proportion among these subregions can be given by the percentage (P_ij) of particles transported from the starting subregion R_i to the ending subregion R_j (N_Ri→Rj to the total number of particles released (N_Ri )as follows:

$\begin{array}{ll}{P}_{ij}=\frac{N_{Ri-Rj}}{N_{Ri}}\times 100\%(N_{Ri-Rj}\le N_{Ri})& (4)\end{array}$

Since the PRE was divided into six subregions, a 6 × 6 transport matrix P_ij was defined to represent the connectivity between them. The results are illustrated in (Figures 8C, D), where the x-axis represents the subregions that release the particles, and the y-axis indicates the subregions that receive the particles. Thus, the value of P_ij indicates the distribution of particles in ending subregions (region j on y-axis) after leaving the releasing subregion (region i on x-axis).

During winter, the majority of the shelf water was trapped by the strong shelf current, while part of it (~40%) intruded into the estuary and mainly stayed within the Macau region (Figure 8D). Inside the estuary, there was a transport barrier, from a Lagrangian perspective, between the western and eastern sides of the PRE, particularly in the upper estuary, although they were spatially close. The NW and Macau particles moved predominantly on the western side without entering the eastern side. Similarly, the particles released from the eastern side (SZ and NE) mainly remained within the eastern estuary, and only a small part (~20%) of SZ water enters the NW region (Figure 8D). This is consistent with the fact that the east and west sides of the PRE are controlled by different dynamics (Mao et al., 2004). In addition, the two subregions, HK and Macau, appear to be convergence zones, which have low FTLE values and weak connections with other subregions. Although they were directly adjacent to the strong shelf current, most (~60%) of the water remained inside the original region after 1 month. Consistent with previous studies, sediment and pollutants settled easily in these areas and have previously been reported as depocenters in the PRE (Figure 7, Yang et al., 2019; Chu et al., 2020).

During the summer, intrusive particles/water from the shelf region can be transported to the HK and Macau regions and affected by the bottom intrusion; the majority of the particles released from Macau (~80%), HK (~60%), and NW (~80%) remained in the original region. Associated with the intensified river discharge, the barriers between the western and eastern estuaries still existed but were reduced so that a higher proportion of particles from SZ (~30%) and NE (~40%) regions were able to move to the Macau waters than winter time. Similar to winter, HK and Macau are two distinct convergence zones that the waters from other subregions have a high possibility to accumulate in those two regions. This is consistent with the previous investigation that the western region near Macau and the eastern region near HK were reported to have a significant hypoxia and low dissolved oxygen in summer, mainly because of the convergence of water (Li et al., 2020).

Conclusions

Using a 3D hydrodynamic model and Lagrangian investigation, this study explored the seasonal hydrodynamic transport structure in the PRE and illustrated the intrinsic connectivity under multiscale motions from a Lagrangian perspective.

The transport structure was obtained based on Lagrangian tracking. Generally, the surface U_L was uniformly southwestward/southeastward in summer/winter and relatively stronger in the lower PRE than in the upper PRE. The bottom residual currents exhibited more complex distributions. In summer, the intensified fluvial dynamics occupies the region from the northwestern estuary to the northwest of Neilingding Island, where the U_L flowed in a southeastward direction in the upper estuary and northwestward in the lower direction. In winter, buoyant waters mainly rush out of the estuary along the western bank, and the fluvial–tide interaction line advances further to the northwest. The difference between the spatially averaged U_L and local temporally averaged U_E mainly occurred between Lantau Island and Neilingding Island, a transition region largely affected by the interaction between the periodic tidal current and river discharge. In this region, the U_L features an onshore intrusion, whereas the U_E exhibits a convergence pattern. Although the calculated U_L ignored the sedimentation and resuspension processes, it captured the major transport processes and was in good agreement with the mean STP.

Remarkable LCSs exist in the PRE that generally define the transport paths and convergence regions. The highly positive FTLE values are the river outlets and channels in the PRE, where the fluid particles with high dispersion are the main material transport paths; the regions with strongly negative FTLE values present a convergence of residual currents, mainly concentrated in the south of the west shoal and northwest of Lantau Island, where they are reported as depocenters in the PRE. Based on the FTLE structure, a connectivity analysis was conducted among the subregions of the PRE. There was a distinct barrier between the northwest and northeast sides of the estuary during the winter and summer. In addition, two convergence regions near the Macau and Hong Kong waters were identified in both the summer and winter seasons, which is consistent with the results from the LCSs and sediment analysis. Sediment and pollutants easily settle in regions that were also previously reported as the depocenters of the PRE and regions experiencing strong hypoxia. Lagrangian analysis provides a way to extract the spatial geometry of hydrodynamics by providing the sketches of the major circulation in estuaries. It proved to be a useful diagnostic method for understanding the hydrodynamic process and transport structure in the estuary–shelf regions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

ZC and ZL contributed to conception and design of the study. NC, GL, and PY conducted the data analysis and developed the method. ZC and ZL validated the results. NC wrote the first draft of the manuscript. GL, YD, and JX contributed to the manuscript revision. All authors contributed to read and approved the submitted version.

Acknowledgments

This study was funded by the Science and Technology Development Fund of Macau SAR (File/Project no. 0093/2020/A2 and SKL-IOTSC(UM)-2021-2023), CORE (EF007/IOTSCCZY/2022/HKUST), China Postdoctoral Science Foundation (2021M703788), Science, Technology and Innovation Commission of Shenzhen Municipality (JCYJ20210324105401004), and Special Fund of Shandong Province for PilotNational Laboratory for Marine Science and Technology (Qingdao) (2022QNLM010203- 1), Guangdong Basic and Applied Basic Research Foundation (2021B1515120080) and the National Natural Science Foundation of China (42276004). CORE is a joint research center for ocean research between QNLM and HKUST. This work was performed in part at the SICC, which is supported by the SKL-IOTSC, University of Macau.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Berta M., Ursella L., Nencioli F., Doglioli A. M., Petrenko A. A., Cosoli S. (2014). Surface transport in the northeastern Adriatic Sea from FSLE analysis of HF radar measurements. Cont. Shelf Res. 77, 14–23. doi: 10.1016/j.csr.2014.01.016

CrossRef Full Text | Google Scholar

Branicki M., Wiggins S. (2010). Finite-time Lagrangian transport analysis: stable and unstable manifolds of hyperbolic trajectories and finite-time lyapunov exponents. Nonlinear Process. Geophys. 17, 1–36. doi: 10.5194/npg-17-1-2010

CrossRef Full Text | Google Scholar

Cai Z., Liu G., Liu Z., Gan J. (2022). Spatiotemporal variability of water exchanges in the pearl river estuary by interactive multiscale currents. Estuar. Coast. Shelf Sci. 265, 107730. doi: 10.1016/j.ecss.2021.107730

CrossRef Full Text | Google Scholar

Chen K., Dong H., Jia L., He Z. (2020). Depocentre transfer in the lingdingyang estuary: Interferences from natural and anthropogenic forcings. Ocean Coast. Manage. 185, 105064. doi: 10.1016/j.ocecoaman.2019.105064

CrossRef Full Text | Google Scholar

Chu N., Yang Q., Liu F., Luo X., Cai H., Yuan L., et al. (2020). Distribution of magnetic properties of surface sediment and its implications on sediment provenance and transport in pearl river estuary. Mar. Geol. 424, 106162. doi: 10.1016/j.margeo.2020.106162

CrossRef Full Text | Google Scholar

Chu N., Yao P., Ou S., Wang H., Yang H., Yang Q. (2022). Response of tidal dynamics to successive land reclamation in the lingding bay over the last century. Coast. Eng. 173, 104095. doi: 10.1016/j.coastaleng.2022.104095

CrossRef Full Text | Google Scholar

Deng Y. F., Liu Z., Zu T., Hu J., Gan J., Lin Y., et al. (2022). Climatic controls on the interannual variability of shelf circulation in the northern south China Sea. J. Geophys. Res. doi: 10.1029/2022JC018419

CrossRef Full Text | Google Scholar

Egbert G. D., Erofeeva S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmospheric Ocean. Technol. 19, 183–204. doi: 10.1175/1520-0426(2002)019<0183:EIMOBO>2.0.CO;2

CrossRef Full Text | Google Scholar

Fairall C. W., Bradley E. F., Hare J. E., Grachev A. A., Edson J. B. (2003). Bulk parameterization of air–Sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 16, 571–591. doi: 10.1175/1520-0442(2003)016<0571:BPOASF>2.0.CO;2

CrossRef Full Text | Google Scholar

Feng S. Z., Cheng R. T., Xi P. G. (1986). On tide-induced lagrangian residual current and residual transport: 1. Lagrangian residual current. Water Resour Res. 22 (12), 1623–1634. doi: 10.1029/WR022i012p01623

CrossRef Full Text | Google Scholar

Feng S. Z., Ju L., Jiang W. S. (2008). A Lagrangian mean theory on coastal sea circulation with inter-tidal transports I. Fundamentals Acta Oceanol. Sin. 27 (6), 1–16. doi: 10.3969/j.issn.0253-505X.2008.06.001

CrossRef Full Text | Google Scholar

Gillanders B. M., Able K. W., Brown J. A., Eggleston D. B., Sheridan P. F. (2003). Evidence of connectivity between juvenile and adult habitats for mobile marine fauna: an important component of nurseries. Mar. Ecol. Prog. Ser. 247, 281–295. doi: 10.3354/meps247281

CrossRef Full Text | Google Scholar

Gill J. A., Norris K., Potts P. M., Gunnarsson T. G., Atkinson P. W., Sutherland W. J. (2001). The buffer effect and large-scale population regulation in migratory birds. Nature 412, 436–438. doi: 10.1038/35086568

PubMed Abstract | CrossRef Full Text | Google Scholar

Haller G. (2015). Lagrangian Coherent structures. Annu. Rev. Fluid Mech. 47, 137–162. doi: 10.1146/annurev-fluid-010313-141322

CrossRef Full Text | Google Scholar

Haller G. (2011). A variational theory of hyperbolic Lagrangian Coherent Structures. Physica D: Nonlinear Phenomena. 240 (7), 574–98. doi: 10.1016/j.physd.2010.11.010

CrossRef Full Text | Google Scholar

Haller G., Yuan G. (2000). Lagrangian Coherent structures and mixing in two-dimensional turbulence. Phys. D 147, 352–370. doi: 10.1016/S0167-2789(00)00142-1

CrossRef Full Text | Google Scholar

Henry L. A., Mayorga-Adame C. G., Fox A. D., Polton J. A., Ferris J. S., McLellan F., et al. (2018). Ocean sprawl facilitates dispersal and connectivity of protected species. Sci. Rep. 8, 11346. doi: 10.1038/s41598-018-29575-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Jonsson B., Lundberg P. A., Doos K. (2004). Baltic Sub-basin turnover times examined using the rossby centre ocean model. Ambio 33, 257–260. doi: 10.1639/0044-7447(2004)033[0257:BSTTEU]2.0.CO;2

PubMed Abstract | CrossRef Full Text | Google Scholar

Ju L., Jiang W. S., Feng S. Z. (2009). A Lagrangian mean theory on coastal sea circulation with inter-tidal transports II. numerical experiments. Acta Oceanol. Sin. 28 (1), 1–14. doi: CNKI:SUN:SEAE.0.2009-01-001

Google Scholar

Lai Z., Ma R., Gao G., Chen C., Beardsley R. C. (2015). Impact of multichannel river network on the plume dynamics in the pearl river estuary. J. Geophys. Res.-Oceans 120, 5766–5789. doi: 10.1002/2014JC010490

CrossRef Full Text | Google Scholar

Lai W., Pan J., Devlin A. T. (2018). Impact of tides and winds on estuarine circulation in the pearl river estuary. Cont. Shelf Res. 168, 68–82. doi: 10.1016/j.csr.2018.09.004

CrossRef Full Text | Google Scholar

Li T. J. (2017). Analysis of lingding bay landform stage evolution and trends. ph. d. thesis (China: China University of Geosciences).

Google Scholar

Liang S. X., Han S. L., Sun Z. C. (2014). Lagrangian Methods for water transport processes in a long-narrow bay-xiangshan bay, china. J. Hydrodynamics 26 (4), 558–567. doi: CNKI:SUN:SDYW.0.2014-04-007

Google Scholar

Liang J.-H., Liu J., Benfield M., Justic D., Holstein D., Liu B., et al. (2021). Including the effects of subsurface currents on buoyant particles in Lagrangian particle tracking models: Model development and its application to the study of riverborne plastics over the Louisiana/Texas shelf, ocean modelling. 167, 101879. doi: 10.1016/j.ocemod.2021.101879

CrossRef Full Text | Google Scholar

Li D., Gan J., Hui R., Liu Z., Yu L., Lu Z., et al. (2020). Vortex and biogeochemical dynamics for the hypoxia formation within the coastal transition zone off the pearl river estuary. J. Geophys. Res.-Oceans 125, e2020JC016178. doi: 10.1029/2020JC016178

CrossRef Full Text | Google Scholar

Li D., Gan J., Hui C., Yu L., Liu Z., Lu Z., et al. (2021). Spatiotemporal development and dissipation of hypoxia induced by variable wind-driven shelf circulation off the pearl river estuary: Observational and modeling studies. J. Geophys. Res.-Oceans 126, e2020JC016700. doi: 10.1029/2020JC016700

CrossRef Full Text | Google Scholar

Li T., Li T.-J. (2018). Sediment transport processes in the pearl river estuary as revealed by grain-size end-member modeling and sediment trend analysis. Geo-Mar. Lett. 38, 167–178. doi: 10.1007/s00367-017-0518-2

CrossRef Full Text | Google Scholar

Liu G. L., Chua V. P. (2016). A SUNTANS-based unstructured grid local exact particle tracking model. Ocean Dynam 66, 811–821. doi: 10.1007/s10236-016-0952-0

CrossRef Full Text | Google Scholar

Liu Z. F., Colin C., Huang W., Chen Z., Trentesaux A., Chen J. F. (2007). Clay minerals in surface sediments of the pearl river drainage basin and their contribution to the south China Sea. Chin. Sci. Bull. 52, 1101–1111. doi: CNKI:SUN:JXTW.0.2007-08-013

Google Scholar

Liu Z., Gan J. (2016). Open boundary conditions for tidally and subtidally forced circulation in a limited-area coastal model using the regional ocean modeling system (ROMS). J. Geophys. Res.-Oceans 121, 6184–6203. doi: 10.1002/2016JC011975

CrossRef Full Text | Google Scholar

Liu Z., Gan J. (2020). A modeling study of estuarine-shelf circulation using a composite tidal and subtidal open boundary condition. Ocean Model. 147, 101563. doi: 10.1016/j.ocemod.2019.101563

CrossRef Full Text | Google Scholar

Liu G., Liu Z., Gao H., Feng S. (2021). Initial time dependence of wind- and density-driven Lagrangian residual velocity in a tide-dominated bay. Ocean Dynamics 71 (3), 447–469. doi: 10.1007/s10236-021-01447-y

CrossRef Full Text | Google Scholar

Liu G., Liu Z., Gao H., Gao Z., Feng S. (2012). Simulation of the Lagrangian tide-induced residual velocity in a tide-dominated coastal system: a case study of jiaozhou bay, China. Ocean Dyn. 62, 1443–1456. doi: 10.1007/s10236-012-0577-x

CrossRef Full Text | Google Scholar

Liu Z., Zu T., Gan J. (2020). Dynamics of cross-shelf water exchanges off pearl river estuary in summer. Prog. Oceanogr. 189, 102465. doi: 10.1016/j.pocean.2020.102465

CrossRef Full Text | Google Scholar

Li T., Xiang R., Li T. J. (2014). Influence of trace metals in recent benthic foraminifera distribution in the pearl river estuary. Mar. Micropaleontol. 108 (1), 13–27. doi: 10.1016/j.marmicro.2014.02.003

CrossRef Full Text | Google Scholar

Li G., Yan W., Zhong L. (2016). Element geochemistry of offshore sediments in the northwestern south China Sea and the dispersal of pearl river sediments. Prog. Oceanogr. 141, 17–29. doi: 10.1016/j.pocean.2015.11.005

Google Scholar

Mao Q., Shi P., Yin K., Gan J., Qi Y. (2004). Tides and tidal currents in the pearl river estuary. Continental Shelf Res. 24 (16), 1797–1808. doi: 10.1016/j.csr.2004.06.008

CrossRef Full Text | Google Scholar

Muller H., Blanke B., Dumas F., Lekien F., Mariette V. (2009). Estimating the Lagrangian residual circulation in the iroise Sea. J. Mar. Syst. 78, S17–S36. doi: 10.1016/j.jmarsys.2009.01.008

CrossRef Full Text | Google Scholar

North E. W., Adams E. E., Schlag S., Sherwood C. R., He R., Socolofsky S. (2011). Simulating oil droplet dispersal from the deepwater horizon spill with a Lagrangian approach. Geophysical Monograph Series. 195, 217–226. doi: 10.1029/2011GM001102

CrossRef Full Text | Google Scholar

Onu K., Huhn F., Haller G. (2015). LCS tool: A computational platform for Lagrangian coherent structures. J. Comput. Sci. 7, 26–36. doi: 10.1016/j.jocs.2014.12.002

CrossRef Full Text | Google Scholar

Pearson J., Fox-Kemper B., Barkan R., Choi J., Bracco A., McWilliams J. C. (2019). Impacts of convergence on structure functions from surface drifters in the gulf of Mexico. J. Phys. Oceanogr. 49 (3), 675–690. doi: 10.1175/JPO-D-18-0029.1

CrossRef Full Text | Google Scholar

Shadden S. C., Lekien F., Marsden J. E. (2005). Definition and properties of Lagrangian coherent structures from finite-time lyapunov exponents in two-dimensional aperiodic flows. Physica D: Nonlinear Phenomena 212 (3), 271–304. doi: 10.1016/j.physd.2005.10.007

CrossRef Full Text | Google Scholar

Shchepetkin A. F., McWilliams J. C. (2005). The regional oceanic modeling system (ROMS): a split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 9, 347–404. doi: 10.1016/j.ocemod.2004.08.002

CrossRef Full Text | Google Scholar

Shi C., Gan H. Y., Xia Z., Lin J. Q. (2015). Characteristics and transport trend of surface sediment in inner lingdingyang firth of the pearl river estuary. Mar. Geology Quaternary Geology 35 (1), 13–20. doi: CNKI:SUN:HYDZ.0.2015-01-003

Google Scholar

Song Y., Haidvogel D. (1994). A semi-implicit ocean circulation model using a generalized topography-following coordinate system. J. Comput. Phys. 115, 228–244. doi: 10.1006/jcph.1994.1189

CrossRef Full Text | Google Scholar

Stacey M. T., Burau J. R., Monismith S. G. (2001). Creation of residual flows in a partially stratified estuary. J. Geophys. Res. 106 (C8), 17013–17037. doi: 10.1029/2000JC000576

CrossRef Full Text | Google Scholar

Wang Z. B., Van Maren D. S., Ding P. X., Yang S. L., Van Prooijen B. C., De Vet P. L. M., et al. (2015). Human impacts on morphodynamic thresholds in estuarine systems. Cont. Shelf Res. 111, 174–183. doi: 10.1016/j.csr.2015.08.009

CrossRef Full Text | Google Scholar

Wei X., Cai S., Zhan W., Li Y. (2021). Changes in the distribution of surface sediment in pearl river estuary 1975-2017, largely due to human activity. Cont. Shelf Res. 228, 104538. doi: 10.1016/j.csr.2021.104538

CrossRef Full Text | Google Scholar

Wei X., Ni P., Zhan H. (2013). Monitoring cooling water discharge using Lagrangian coherent structures: A case study in daya bay, China. Mar. pollut. Bull. 75, 105–113. doi: 10.1016/j.marpolbul.2013.07.056

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei X., Zhan H., Cai S., Zhan W., Ni P. (2018). Detecting the transport barriers in the pearl river estuary, southern China with the aid of Lagrangian coherent structures. Estuar. Coast. Shelf Sci. 205, 10–20. doi: 10.1016/j.ecss.2018.03.010

CrossRef Full Text | Google Scholar

Wu Z. Y., Milliman J. D., Zhao D. N., Cao Z., Zhou J., Zhou C. (2018). Geomorphologic changes in the lower pearl river delta 1850–2015, largely due to human activity. Geomorphology 314, 42–54. doi: 10.1016/j.geomorph.2018.05.001

CrossRef Full Text | Google Scholar

Wu W. Z., Zhao H. T. (1982). On silt sources of lingdingyang of the zhujiang (Pearl river) estuary by means of mineralogical analyses of the sediments. Tropic Oceanol. 1, 2.

Google Scholar

Xiao Z. J. (2012). Surface sediment characteristics and sediment transport trend of the zhujiang river estuary and adjacent sea area. Mar. Sci. Vulletin 5 (31), 481–488. doi: CNKI:SUN:HUTB.0.2012-05-000

Google Scholar

Xing F., Wang Y. P., Wang H. V. (2012). Tidal hydrodynamics and fine-grained sediment transport on the radial sand ridge system in the southern yellow Sea. Mar. Geology 291-294, 192–210. doi: 10.1016/j.margeo.2011.06.006

CrossRef Full Text | Google Scholar

Xuan J., Yang Z., Huang D., Wang T., Zhou F. (2016). Tidal residual current and its role in the mean flow on the changjiang bank. J. Mar. Syst. 154, 66–81. doi: 10.1016/j.jmarsys.2015.04.005

CrossRef Full Text | Google Scholar

Yang L., Liu F., Gong W., Cai H., Yu F., Pan H. (2019). Morphological response of lingding bay in the pearl river estuary to human intervention in recent decades. Ocean Coast. Manage. 176, 1–10. doi: 10.1016/j.ocecoaman.2019.04.011

CrossRef Full Text | Google Scholar

Zhang G., Cheng W., Chen L., Zhang H., Gong W. (2019). Transport of riverine sediment from different outlets in the pearl river estuary during the wet season. Mar. Geol. 415, 105957. doi: 10.1016/j.margeo.2019.06.002

CrossRef Full Text | Google Scholar

Zhang W., Zheng J., Ji X., Hoitink A. J. F., van der Vegt M., Zhu Y. (2013). Surficial sediment distribution and the associated net sediment transport pattern in the pearl river estuary, south China. Cont. Shelf Res. 61–62, 41–51. doi: 10.1016/j.csr.2013.04.011

CrossRef Full Text | Google Scholar

Zheng S., Guan W., Cai S., Wei X., Huang D. (2014). A model study of the effects of river discharges and interannual variation of winds on the plume front in winter in pearl river estuary. Cont. Shelf Res. 73, 31–40. doi: 10.1016/j.csr.2013.11.019

CrossRef Full Text | Google Scholar

Zimmerman J. T. F. (1979). On the Euler-Lagrange transformation and the stokes’ drift in the presence of oscillatory and residual currents. Deep Sea Res. Part Oceanogr. Res. Pap. 26, 505–520. doi: 10.1016/0198-0149(79)90093-1

CrossRef Full Text | Google Scholar

Zu T., Gan J. (2015). A numerical study of coupled estuary-shelf circulation around the pearl river estuary during summer: responses to variable winds, tides and river discharge. Deep-Sea Res. II. 117, 53–64 doi: 10.1016/j.dsr2.2013.12.010

CrossRef Full Text | Google Scholar

Zu T., Gan H., Erofeeva S. Y. (2008). Numerical study of the tide and tidal dynamics in the south China Sea. Deep-Sea Res. Part -Oceanogr. Res. Pap. 55, 137–154. doi: 10.1016/j.dsr.2007.10.007

CrossRef Full Text | Google Scholar