- 1Department of Earth, Ocean, and Atmospheric Sciences, University of British Columbia, Vancouver, BC, Canada
- 2School of Earth and Ocean Sciences, University of Victoria, Victoria, BC, Canada
The Strait of Georgia (SoG) is a semi-enclosed, urban basin with seasonally dependent estuarine water circulation, dominantly influenced by Northeast Pacific waters and the Fraser River. To establish a baseline and understand the fate and potential toxicity of Cu in the SoG, we determined seasonal and spatial depth profiles of dissolved Cu (dCu) speciation, leading to estimates of the free hydrated copper (Cu2+) concentrations, as a proxy for Cu toxicity. The concentration of dCu was largely controlled by conservative mixing of the ocean and freshwater endmembers in the SoG. In all samples, ligand concentrations exceeded dCu, by a ratio greater than 1.5, resulting in the complexation of 99.98% of the dCu by strong binding organic ligands. The concentrations of Cu2+ were less than 10-13.2 M, significantly lower than the well-established Cu toxicity threshold (10-12 M Cu2+) for microorganisms. Our results indicate that ambient Cu-binding ligands effectively buffer Cu2+ concentrations within the Strait of Georgia, posing no threat to marine life. In almost 90% of the samples, the ligands were best classified as a single ligand class, with a log between 12.5 and 14.1. The concentrations of these single class ligands were greatest in warm, low salinity, nutrient depleted waters, suggesting that either terrestrially sourced ligands dominate dCu speciation in the SoG, or freshwater sources in the SoG establish the conditions that promote the production of Cu binding ligands in its surface waters. The remaining 10% of the samples were from the euphotic zone, where we detected a stronger ligand class, L1, of log between 13.5 and 14.3, and a weaker ligand class, L2, of log between 11.5 and 12.3. In these surface samples, log and log were positively correlated with temperature, while L2 concentrations were positively correlated with chromophoric dissolved organic matter of terrestrial origin. This study is the first to perform hierarchal clustering of a trace metal speciation dataset and enabled the distinction of 6 clusters across season, depth, and region of the SoG, highlighting the influence of freshwater and open ocean ligand sources, conservative mixing dynamics, and particulate Cu concentrations on dCu speciation within estuarine basins.
Introduction
While copper (Cu) is a metabolically essential micronutrient to marine biota, facilitating electron transfer in many biological processes (Manahan and Smith, 1973; Palenik and Morel, 1991; Peers et al., 2005; Maldonado et al., 2006; Peers and Price, 2006; Guo et al., 2010; Glass and Orphan, 2012), Cu can also become toxic at relatively low concentrations. Elevated Cu concentrations have been shown to influence marine food webs by inhibiting algae growth (Brand et al., 1986), increasing domoic acid production (Maldonado et al., 2002), bioaccumulating (DeForest et al., 2007), biomagnifying (Cardwell et al., 2013), and promoting stress responses in certain vertebrates (Ransberry et al., 2015) and other marine biota (Sunda et al., 1987). Copper toxicity depends not on total dissolved Cu concentrations (dCu), but rather the concentration of the most bioavailable Cu species, free hydrated Cu2+. Toxicity thresholds for Cu2+ vary between phytoplankton species and between coastal and oceanic strains of the same genus (Brand et al., 1986); however, Cu2+ concentrations greater than 10-12 M, or a pCu2+ (i.e. pCu2+ = - log[Cu2+]) less than 12, are considered toxic to marine food webs, as these concentrations can inhibit cyanobacteria growth rates (Mann et al., 2002), decrease the viability of other phytoplankton species (Brand et al., 1986; Croot et al., 2000), and inhibit the reproduction of copepods (Sunda et al., 1987).
Presumably, more than 99% of dCu in the marine environment is complexed by a heterogeneous pool of natural organic ligands, which form stable, less bioavailable organic complexes that buffer against Cu toxicity (Barber and Ryther, 1969; van den Berg et al., 1987; Buck et al., 2007). Complexation depends on the concentration (Li) and conditional stability constants () of the ligand pool, typically subdivided into two ligand classes (L1 and L2), where the stronger ligand class, L1, has a log between approximately 13 and 16 and the weaker ligand class, L2, has a log between approximately 10 and 13 (Buck and Bruland, 2005; Bundy et al., 2013; Whitby, 2016). Cu binding ligands are often produced by phytoplankton, in response to toxic Cu concentrations (Moffett and Brand, 1996; Dupont et al., 2004), Cu limitation (Kim et al., 2005; Walsh et al., 2015), or are of terrestrial origin, such as humic substances in river water (Kogut and Voelker, 2001; Voelker and Kogut, 2001; Whitby and van den Berg, 2015) and biological macromolecules carried by municipal wastewater (Sedlak et al., 1997).
The Strait of Georgia (SoG) is a coastal seawater basin between the British Columbia (BC) mainland and Vancouver Island and is part of the network of coastal waters within the Salish Sea. The estuarine circulation of the SoG is driven by surface freshwater that flows toward the ocean from the BC mainland and intermediate NE Pacific water that enters the SoG at depth via Juan de Fuca and Haro Strait (Li et al., 2000). During the summer, prevailing wind-driven coastal upwelling brings high nutrient Pacific water, with a dCu concentration of 1.4 nM (Whitby et al., 2018), into the Juan de Fuca’s deep basin, where a fraction is brought to the surface via tidal mixing within Haro Strait. The bulk of upwelled Pacific seawater remains in the SoG’s intermediate (50-200 meters) and deep waters (>200 meters) (Li et al., 2000; Pawlowicz et al., 2019). Within the SoG, estuarine circulation allows nutrients in intermediate depths to be entrained into surface waters, where high primary productivity supports a diverse ecosystem (Yin et al., 1997; Masson and Perry, 2013). The SoG’s main freshwater source is the Fraser River, with seasonal variability in dCu concentration, between 29.7 nM during April to 12.5 nM during February (Buoy BC08MH0453: Government of Canada, 2022), and peak freshet―or spring thaw―flows in early June (Halverson and Pawlowicz, 2008), which discharges into the southern SoG and forms a thin plume over surface waters (Wang et al., 2019).
Copper toxicity is an important concern in coastal regions, such as the SoG, as anthropogenic Cu inputs, from municipal effluents (Johannessen et al., 2015), mining (Chretien, 1997), antifouling agent-coated ships (Carić et al., 2021), and urban stormwater (Barałkiewicz et al., 2014), can elevate local dCu to concentrations possibly toxic to the biota (Moffett et al., 1997). Near the SoG is Metro Vancouver, which discharges approximately 4.5 x 1011 L of municipal wastewater into the SoG annually, over 50% of which only receives primary treatment (Metro Vancouver, 2018). Metro Vancouver’s municipal wastewater may act as a point source for heavy metals, such as Pb, Cr, Cd, Ni, Ag, and Cu (Sedlak et al., 1997; Karvelas et al., 2003; Johannessen et al., 2015; Metro Vancouver, 2018), as well as metal binding ligands, within wastewater organic matter (WWOM) (Kunz and Jardim, 2000; Buck et al., 2007; Katsoyiannis and Samara, 2007). Currently, BC-approved water quality guidelines have thresholds for short-term maximum and long-term average total dCu concentrations in estuarine environments, 47.2 nM and 31.5 nM, respectively (Government of Canada, Ministry of Environment & Climate Change -Water Protection & Sustainability Branch Strategy, 2019). However, total dissolved metal concentrations do not provide sufficient information into the bioavailability of heavy metal species; the complexation capacity of the receiving SoG water body is required to understand the speciation, bioavailability, and toxicity of dissolved heavy metals.
In collaboration with Metro Vancouver’s Georgia Strait Ambient Monitoring Program, here we attempt to understand the seasonal and spatial speciation of dCu in the SoG. To do so, we characterized some of the ligands governing Cu speciation in the SoG by determining depth profiles of Li and log at 4 stations in August 2018. Additionally, this work considered seasonal variability of depth profiles of Li and log at the time series station S4-1.5 in the Southern SoG (SG), by measuring Cu speciation in September (i.e., during a fall bloom), December (i.e., winter baseline conditions), April (i.e., during a spring bloom), and June (i.e., the peak of the Fraser River freshet). To shed light on the biological, chemical, and physical processes that influence the coastal Cu binding ligand pool, Cu speciation results were compared with salinity, density, temperature, irradiance, percent surface irradiance (light level), chromophoric dissolved organic matter (CDOM), CDOM spectral slope (Sλ), phytoplankton composition and abundance, nutrients, and chlorophyll a (Chl a). In addition to relating dCu speciation to the seasonal water circulation within the SoG, the dataset underwent principal component analysis (PCA) and was clustered to define distinct patterns of dCu speciation between seasons and regions. This dataset can be used as a baseline and to understand the fate and potential toxicity of inorganic Cu in the SoG in the future.
Materials and methods
Sample collection
Samples were collected in the Strait of Georgia, B.C. (Figure 1) during five cruises (Supplementary Table 1) and, for the purpose of this study and discussion, are divided into two sets of depth profiles: seasonal and spatial. Seasonal samples were collected at the Southern SoG (SG) time series station S4-1.5 (Pawlowicz et al., 2007), in September 2017, December 2017, April 2018, and June 2018 on board the Canadian Coast Guard (CCG) Hovercrafts (Siyay and Moytel). Spatial samples were collected, from the CCG Ship Vector, in August 2018 at station SG, as well as three additional stations: a) the Northern SoG (NG); b) the tidal mixing region, Haro Strait (HS); and c) the NE Pacific water entryway, Juan de Fuca Strait (JF).
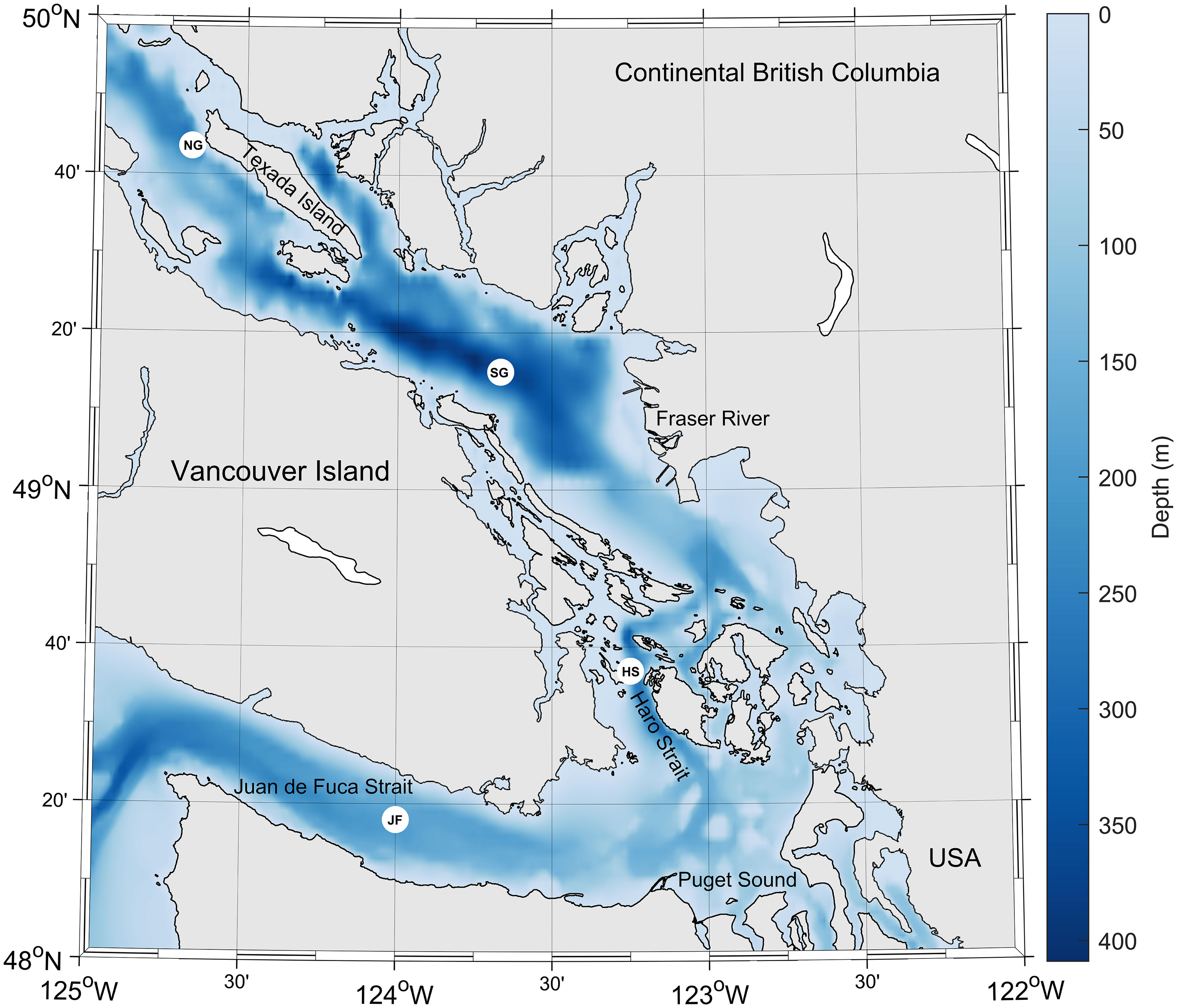
Figure 1 Map of the Salish Sea, with sampling locations as white markers, Southern SoG (SG), Northern SoG (NG), Haro Strait (HS), and Juan de Fuca Strait (JF). The bathymetry of the Salish Sea is shown in blue tones. Figure generated using Matlab script m_map (Pawlowicz, 2020).
Water for Cu speciation samples were collected into 12 L Teflon-coated GO-FLO (General Oceanics, FL, USA) bottles, deployed from a synthetic Amsteel-Blue line triggered with Teflon messengers. Cu speciation samples were gravity-filtered through trace metal clean 0.2 μm AcroPak polyethersulfone membrane filters (Pall Corporation), into trace metal clean (i.e., following section 1.3.1 of GEOTRACES (2017)) 500 mL fluorinated linear polyethylene (FLPE) bottles and immediately frozen at -20°C until analysis. Samples were thawed overnight at 4°C, in the dark, before the analyses. Most samples were analyzed within 1 or 2 days after defrosting, but a handful were measured within 6 days after thawing. dCu samples were gravity filtered through the 0.2 μm AcroPak into 250 mL trace metal clean HDPE bottles and acidified with 250 μL of ultrapure concentrated HCl (Aristar Ultra grade, VWR Chemicals BDH) to a pH of ~1.8 within 24 hours.
Supporting chemical and biological parameters
Water properties (i.e., temperature, salinity, density, dissolved oxygen concentrations, irradiance, transmissivity, conductivity, and fluorescence) were measured using a Seabird SBE25 conductivity-temperature-depth (CTD) instrument, equipped with a SBE 43 dissolved oxygen sensor and a Biospherical scalar irradiance sensor for photosynthetically active radiation (PAR). Densities, calculated from pressure, temperature and conductivity are accurate to 0.01 kg·m-3. CTD measured oxygen concentrations were calibrated against periodic Winkler titration analyses with bottle field samples and with the sensor being accurate to better than 1 ml/L in absolute terms, but better than 0.1 ml/L relative to each other. The PAR sensor is uncalibrated but provided stable readings over the course of the program, in μE m2 s-1. PAR was used to calculate percent light level, as percent of PAR from 0m depth, and the euphotic zone depth was defined as the depth of 1% surface irradiance.
Nutrients were sampled into pre-cleaned 15 mL polypropylene Falcon® tubes by filtering seawater through 0.45 µm Acrodisk nylon membrane syringe filters and analyzed using a Lachat QuikChem 8500 Series 2 Flow Injection Analysis System. Nitrate () and nitrite () concentrations were measured following the protocol in Smith and Bogren (2003), while for phosphate () and silicate (SiO2) determinations, we followed the protocols in Knepel and Bogren (2008), and Tucker (2010), respectively.
Chromophoric dissolved organic matter (CDOM) was measured on a subset of Cu speciation sample bottles, which were refrozen at -20°C following speciation measurements and thawed to room temperature in the dark prior to CDOM analysis. Sample absorption spectra were measured, between 325 to 1100 nm, on a Genesys 30 Visible spectrophotometer with a 100 mm path length special optical glass cell (Fisherbrand). As in Osburn et al. (2016), CDOM is measured as napierian absorption coefficients at 350 nm (a350), calculated from sample absorption spectra [aλ=2.303 · λ · pathlength-1] (Kirk, 1994), compared with Milli-Q water blanks and drift corrected against absorption at 700 nm (Bricaud et al., 1981). The spectral slope (Sλ) was calculated by the standard slope equation (Bricaud et al., 1981), over a 20 nm wavelength interval, between 380 and 399 nm (S390) (Loiselle et al., 2009). This spectral range was chosen because humic acid and fulvic acid CDOM Sλ spectra peak at 390 nm and Sλ between 380 and 399 nm is sensitive to changes in humic acid CDOM due to photobleaching (Loiselle et al., 2009). On the Genesys 30 spectrophotometer, the CDOM a350, a380, and a399 limit of detection are 0.032 m-1, 0.032 m-1, and 0.064 m-1, respectively.
Chl a, eukaryotic phytoplankton abundance, and HPLC-pigments derived phytoplankton community composition were measured in surface water samples (< 40 m). The Chl a concentrations were determined in 250 mL of seawater filtered onto 47 mm Whatman GF/F filters (0.7 μm nominal pore size). The Chl a on the filters was extracted at -20oC, in the dark for 24 h, using ice-cold 90% acetone. After extraction, the concentrations of Chl a were determined with a Turner Designs 10 AUTM fluorometer. Eukaryotic phytoplankton abundance was measured by concentrating the water samples (preserved in 4% formalin) ten times and counting cells under a light microscope in a Sedgewick Rafter counting chamber. Note that cell density measurements under microscope do not include picoplankton. Phytoplankton community composition was estimated from HPLC pigment analysis. HPLC samples were collected by filtering 1000 mL water samples onto pre-combusted 47 mm Whatman GF/F filters, which were then folded in half, blotted dry, and flash-frozen in liquid nitrogen on board the vessel and stored at -80oC until further analyses. The sample filters were sent to the Estuarine Ecology Lab, affiliated with the Marine Science Division of the School of the Earth, Ocean, and Environment at the University of South Carolina, for phytoplankton pigment HPLC analysis. Phytoplankton HPLC pigment results were then analyzed using a factorization matrix program (CHEMTAX v1.95) to estimate the contribution of the main phytoplankton taxonomic groups to total Chl a (Mackey et al., 1996; Taylor et al., 2016). The chemotaxonomic analysis clustered algal groups as Diatoms, Dinoflagellates, Chlorophytes, Cyanobacteria, Prasinophytes, Cryptophytes, Pelagophytes, Haptophytes, and Raphidophytes. Pigment ratios were kept fixed per season and station. Initial pigment ratios (pigment: Chl a) for each algal group were obtained from Higgins et al. (2011) and the final pigment ratio matrix was an average of the best 6 iterative matrices of the initial pigment ratio matrix for each analyzed sample (Supplementary Table 2).
Dissolved copper complexation
Dissolved Cu concentrations were determined using an automated seawater preconcentration system, seaFAST-picoTM; Elemental Scientific, followed by ICP-MS, at the University of Victoria, as described in Lagerström et al. (2013). The seaFAST-picoTM system buffers acidified seawater inline before loading onto a column, containing a high-affinity resin with carboxymethylated polyethylenimine as the chelating ligand to retain transition metals while allowing the bulk seawater major ion matrix to pass through. Concentrated samples are eluted into clean collection vials (Kagaya and Inoue, 2014) and trace metal concentrations are determined in the eluent by triple quadrupole ICP-MS/MS (Jackson et al., 2018). Procedural blank solution was prepared fresh for each batch of samples following Lagerström et al. (2013). Multiple blanks were processed at the beginning of each preconcentration run and then monitored every 6 samples throughout the sample extraction sequence. The average dissolved Cu concentration measured in blank solutions was 0.02 ± 0.01 nM (n=15). The accuracy of our dissolved Cu measurements was validated by analysis of nearshore seawater certified reference material CASS-6, where we measured a concentration of 8.07 ± 0.15 nM, which compared favorably with the certified value of 8.34 ± 0.50 nM total Cu.
Competitive ligand exchange, adsorptive cathodic stripping voltammetry (CLE-ACSV) is a widely used assay for the complexation of metal ions in seawater. In CLE-ACSV, a known concentration of an organic ligand (AL), which forms electroactive metal complexes with known conditional stability constants, is added to buffered seawater, to compete for the inorganic metal of interest (Me) with the sample’s ambient organic ligands, across a titration concentration gradient of the metal (dMe), designed to saturate the ambient ligand pool. Following equilibration, the concentration of the resulting Me(AL)x complexes are determined with cathodic stripping voltammetry (CSV). In CSV, the Me(AL)x complex is adsorbed to the surface of a working electrode at a set voltage potential and subsequently reduced, as the potential at the working electrode is scanned in the negative direction and the reductive current response is measured (Buck et al., 2012). The metal’s reduction potential presents itself as a current peak, which is plotted for each metal addition in the titration. From the peak height, the concentration of the Me(AL)x complex is measured proportionally by assay sensitivity, which is internally calibrated as the slope of the ligand-saturated data points (Buck and Bruland, 2005). From this titration, the complexation parameters of a seawater sample’s ambient metal binding ligands, as concentration (Li) and conditional stability constant (), can be determined by interpretation of linear and non-linear transformations (Scatchard, 1949; Mantoura and Riley, 1975; Ružić, 1982; van den Berg, 1982; Gerringa et al., 1995). Copper speciation determined via CLE-ACSV, with salicylaldoxime (SA) as the added competitive ligand, was initially detailed in Campos and van den Berg (1994). SA is widely used in Cu speciation studies, given its high sensitivity for Cu (Campos and van den Berg, 1994; Buck et al., 2012).
Copper standards were prepared by dilution of copper (II) chloride (99.999% trace metal basis, Sigma-Aldrich) in 0.024 M HCl (Aristar Ultra grade, VWR Chemicals BDH). A series of Cu standards were prepared, from 10 mM to 0.1 μM for Cu additions. A stock solution of 25 mM SA (ACROS Organics) was prepared in methanol (OmniSolv® LC-MS) and sub-stock solutions of 2.5 mM and 10 mM SA in Milli-Q water were prepared monthly. Samples were equilibrated at a pH of 8.2 by a borate/ammonia pH buffer, prepared using 1 M boric acid (99.99% metal basis, Alfa Aesar) and 0.35 M ammonium hydroxide (Aristar Plus grade, VWR Chemicals BDH), which was then chelated to remove contaminating metals and UV-digested to remove contaminating organic matter, using a UV oxidation apparatus built by Achterberg and van den Berg (1994).
The voltammetric equipment used was a BioAnalytical Systems (BASi) controlled growth mercury electrode (CGME), set to a static mercury drop, and interfaced with a BASi Epsilon ϵ2 voltammetric analyzer. The reference electrode was Ag/AgCl with a 3 M NaCl salt bridge and a platinum wire counter electrode. Polytetrafluoroethylene (PTFE) voltammetry cells were used during analysis, with a rotating PTFE rod for stirring. Samples were equilibrated in 15 mL Teflon vials (Savillex). Sample vials and voltammetry cells were treated with 1 N HCl (trace metal grade) for at least one week at 60oC, followed by 0.1 N HCl (Aristar Ultra grade, VWR Chemicals BDH) for at least one month, and rinsed with Milli-Q. Sample Teflon vials were preconditioned using Ocean Station Papa seawater (Whitby et al., 2018), with buffer, SA, and the set Cu addition for each individual vial. These conditioned Teflon sample vials were never treated with HCl for the remainder of the study. However, between titrations, the voltammetry cells were quickly rinsed with 0.01 N HCl (Aristar Ultra grade, VWR Chemicals BDH) and Milli-Q, followed by sample with buffer and SA.
The concentration and conditional stability constants for each sample’s ambient Cu-complexing ligands were estimated via CLE-ACSV. Sample aliquots of 10 mL, treated with 0.01 M ammonia/borate buffer, were pipetted into 22 conditioned Teflon sample vials where CuCl2 was added to each vial in order of increasing concentration. Usual Cu additions were 0, 0.5, 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 17, 20, 22, 25, 30, 40, 50, 80, and 100 nM Cu. For samples at surface depths (i.e., above 20 meters), 120 and 150 nM Cu additions were chosen instead of 0.5 and 1 nM Cu to ensure ambient ligand saturation. The vials were then allowed to equilibrate in the dark for 1 hour. Following equilibration, 2.5 μM SA was added to each vial and allowed to equilibrate overnight (>12 h), in the dark, at 4oC. Following this second equilibration, samples were left to warm to room temperature for 30 minutes and each sample was purged with 0.22 μm filtered high purity N2 gas for 2 minutes before analysis. To compare complexation results against a higher analytical window, duplicates, at 0, 5, and 100 m depth in the SG September cruise, were equilibrated with 10 μM SA.
At an applied potential of -150 mV, a deposition time of 180 seconds, and stir rate of 600 rpm, the Cu addition samples’ electroactive Cu(SA)x complexes were adsorbed to the surface of a fresh mercury drop (size “14”). Following deposition, a quiet time of 10 seconds took place, in which the sample is no longer stirred. Subsequently, the samples were scanned in differential pulse mode from -150 mV to -600 mV, at a rate of 4 mV/s (pulse width 35 ms, pulse period 200 ms, pulse amplitude 50 mV, and analyzer sensitivity 10 μA/V) to measure the Cu(SA)x reduction peak. Each sample was triple scanned. The height of each Cu addition current peak, occurring near -300 mV, was measured using ECDSOFT and the average amongst the three scans was plotted with respect to total dCu. Data points in which peak heights were below the limit of detection (7.98 nA) or above the linear threshold (800 nA; Buck and Bruland, 2005) were excluded from titration data. For examples of Cu complexation titration curves, see Supplementary Figure 1. The two titrations measured per sample, along with the added ligand side reaction coefficient (αCuAL) for CuSAx (Campos and van den Berg, 1994) and inorganic Cu (Cu’) concentrations determined for each individual sample, based on salinity and temperature (van den Berg, C. M. G. Speciation.xls), were each fitted via the Langmuir/Gerringa non-linear transformation, initially discussed in Gerringa et al. (1995) and preferred to linear transformations when determining a multi-ligand class model, within ProMCC software (Omanović et al., 2015). Depending on the salinity of the sample, logαCuAL was 4.2 - 4.3 and 5.1 - 5.2, for 2.5 μM SA and 10 μM SA, respectively. Sensitivity was measured following Omanović et al.’s (2015) recommendation for finding the true sensitivity. The slope from the last 3 titration points (below the linear threshold of 800 nA) was used as the initial sensitivity, and then ProMCC’s Auto Adjust function selected the sensitivity with the lowest AVG error (average value of relative errors between experimental and fitted values [([M]meas − [M]FIT)/[M]FIT x100%]. We determined the sensitivity within ProMCC for each titration, with duplicate titrations per sample. The average sensitivity amongst all sample titrations was 4.6 ± 0.9 nA nM-1 min-1. The average initial sensitivity and the average final, internally-calibrated sensitivity chosen for each sample’s duplicate titrations are found within this manuscript’s data repository (https://doi.org/10.5683/SP3/6AB0JI).
To determine whether a single or two ligand model best represents the titration curve of a sample, titration data, in the linear Scatchard transformation and the logarithmic Langmuir transformation, were compared to Figure 1 in Omanović et al. (2015). In all samples, both duplicate titration curves were best represented by the same number of ligands. Single ligand model parameters are denoted as L and log, two ligand model parameters are denoted with a subscript (i.e., L1 and log or L2 and log). Complexation stability constants were calculated with respect to Cu2+ and free ligand (L’), as conditional constants for experimental salinity and pH. For the September samples, which underwent Cu complexation analysis at two analytical windows, all four titrations (two via 10 μM SA and two via 2.5 μM SA) were calibrated with the sensitivity predetermined per titration as described above and then combined into a unified dataset. This dataset was introduced into ProMCC and underwent the multiwindow detection (MWD) analysis, following the complete complexation model protocol described in Omanović et al. (2015). For each sample, multiple MWD runs were taken (i.e. both the single ligand model and the two ligand model and using the initial Cu ligand parameters from the results of both the 10 μM SA and 2.5 μM SA Langmuir/Gerringa non-linear transformations of each of the four titrations) and the run with the lowest AVG error was considered the best result.
Correlations and hierarchical cluster analysis
An empirical approach was applied to identify different potential ligand sources within the SoG. We first generated a heatmap of the Pearson correlation coefficients between Cu speciation parameters and parameters characteristic of water mass endmembers, seasonality, and biota (i.e., dCu, depth, density, temperature, salinity, irradiance, light level, CDOM a350, S390, dissolved oxygen, nutrients, Chl a, eukaryotic phytoplankton density, and phytoplankton community composition). While all 65 samples with Cu speciation data were used for the correlations, the number of observations (i.e., n) used for each individual correlation varied, depending on the data available for the parameters characteristic of water mass endmembers, seasonality, and biota (see Discussion section for specific n).
Cu speciation parameters associated with the single ligand class then underwent hierarchical clustering (Wishart, 1969; Wilks, 2019) to signify how differences in water masses, depth, and/or seasons of the SoG estuarine circulation system influence SoG Cu speciation profiles. The data were first preprocessed by selecting all single ligand class observations for salinity, dCu, L, and log (57 observations) and then normalizing and standardizing the data (Supplementary Figure 2) to allow consistent comparisons across the dataset, which includes variables of different units and magnitudes. Then, the normalized and standardized data underwent PCA (Jolliffe, 1990), using MATLAB’s function “pca”, to identify the key modes of variability within the dataset (Supplementary Figure 3). The first three modes, describing 95% of the total variance in the dataset, were then clustered, using Ward’s method (Ward, 1963) of hierarchical clustering, via MATLAB’s functions “linkage” and “cluster”. In Ward’s method, underlying dataset structure is revealed by an unsupervised grouping of similar data points together, while minimizing the intracluster variance, or “loss of information”, as data points merge into groups, or clusters (Wishart, 1969). Compared to other hierarchical clustering methods, Ward’s method is favorable in identifying structure in known clusters (Mangiameli et al., 1996). For our data, the number of clusters observed using objective-function based clustering―in which the change in dendrogram distance between cluster numbers is maximized―was only two clusters (n = 2) (Supplementary Figure 4). Thus, our approach was a clustering framework based on subjective validity criteria. In essence, we visualize several possible clustering outputs, with the number of clusters ranging between 2 and 6; considering that the latter is the number of boxes included in the Salish Sea Box Model described in Wang et al. (2019). At the end, 6 clusters (n = 6) were chosen, as this clustering enabled the surface waters of SG during the June freshet to become a distinct cluster.
Results
Supporting chemical and biological parameters
The seasonal SoG depth profiles of a series of physical, biological, and chemical parameters (Supplementary Figures 5-7) clearly show that SoG surface waters experience the most variability. Due to the Fraser River discharge, which is at its maximum in the summer, surface waters in SoG in June exhibit low density, warm temperatures, salinity below 20 PSU (Supplementary Figure 7), low nitrate and phosphate concentrations (Supplementary Figure 6), but high CDOM content (Supplementary Figure 5), and are distinctly different from the denser waters found throughout the rest of the year. In December, freshwater runoff lowered surface water density, deepening the pycnocline to 20 m, and dropping surface water temperatures. August spatial profiles highlighted the N. Pacific end member, where cold, salty water, with a density greater than 1026 kg·m-3 and dissolved oxygen concentrations less than 100 μM, is seen in JF deep waters (Supplementary Figure 7). The euphotic zone depth was deepest in June, at 44 m, and shallowest in April, at 12 m (Supplementary Table 1). CDOM S390 (Supplementary Figure 5) depth profiles have a lack of clear structure, potentially due to the wide variation in CDOM composition and possibly photobleaching in some samples (Loiselle et al., 2009). CDOM S390nm had a maximum value of 0.0247 nm-1 at NG 0 m, and a minimum value of 0.0048 nm-1 at HS 0 m.
The seasonal depth profiles in SG show that the phytoplankton biomass in this temperate region was greatest during the April spring bloom, with 5.91 μg Chl a·L−1 at 5 m, decreasing to 0.22 μg Chl a·L−1 by 30 m (Supplementary Figure 5). The eukaryotic phytoplankton abundance in April was 1.39 x 106 cells·L−1 at 5 m, decreasing to 4.60 x 104 cells·L−1 by 30 m (Supplementary Figure 5), and diatoms accounted for 96% of the HPLC-pigment derived phytoplankton composition (Supplementary Table 3). April and September experienced the most variation in Chl a with depth, due to spring and fall phytoplankton blooms, respectively, while December experienced the least. In September, a fall bloom was observed with a maximum chlorophyll of 2.65 μg Chl a·L−1 at 0 m, and eukaryotic phytoplankton cell densities of 7.80 x103 cells·L−1 at 2.5 m (Supplementary Figure 5). In December, maximum chlorophyll was 0.44 μg Chl a ·L−1 at 0 m, with eukaryotic phytoplankton abundances of 2.66 x104 cells·L−1 and with a community composition dominated by diatoms and prasinophytes (Supplementary Table 3). In June, maximum Chl a (i.e., ~ 0.94 μg Chl a·L−1) was observed between 5 and 10 m, with a maximum eukaryotic phytoplankton abundance (i.e., 1.94 x105 cells·L−1) at 0 m, and a dominance of diatoms, cyanobacteria and raphidophytes (Supplementary Table 3).
Among the four SoG stations sampled in August 2018, phytoplankton biomass (i.e., 3.22 μg Chl a ·L−1) and eukaryotic phytoplankton abundance (5.83 x104 cells·L−1) were greatest at HS (Supplementary Figure 5), and were dominated by diatoms (Supplementary Table 3). At the JF station, the phytoplankton community was also dominated by diatoms, with maximum Chl a and eukaryotic phytoplankton abundance at 10 m depth (i.e., 1.37 μg Chl a ·L−1 and 4.43 x104 cells·L−1, respectively). Both SG and NG experienced maximum chlorophyll at 5 m, with 3.06 and 1.68 μg Chl a ·L−1, respectively (Supplementary Figure 5). At SG, eukaryotic phytoplankton abundance was maximum at 0 m, with 5.21 x104 cells·L−1, with a community composition that was dominated by diatom, dinoflagellate, and cyanobacteria in surface waters. The Northern SoG station, NG, had a eukaryotic phytoplankton abundance of 2.24 x104 cells·L−1 at 5 m, where prasinophytes dominated (Supplementary Table 3). The spatial summer algal group variability in the SoG aligns with the interannually consistent biological zones and associated physical drivers identified by Jarníková et al. (2022), where Juan de Fuca Strait, with episodic summer mixing, enables higher summer diatom abundance and the central SoG, with shallower haloclines and stronger summer stratification, enables a higher summer flagellate abundance (i.e., prasinophytes, and dinoflagellates).
Spatial dissolved copper speciation
In August 2018, dCu and organic Cu binding ligand concentration depth profiles (Figure 2) vary among SoG stations, where dCu is inversely correlated with salinity depth profiles (Pearson r = -0.84, p value< 0.001, n = 41) with the NE Pacific water as the high salinity endmember, in the deep waters of Juan de Fuca Strait (JF), and the Fraser River as the freshwater endmember, nearest SG. In the vast majority of the samples, only one ligand class was detected, with concentrations ranging between 4.2 and 30.1 nM, and a log between 12.5 and 14.1. The exception was the 30 m sample at HS, where two ligand classes, L1 and L2, were detected (see below).
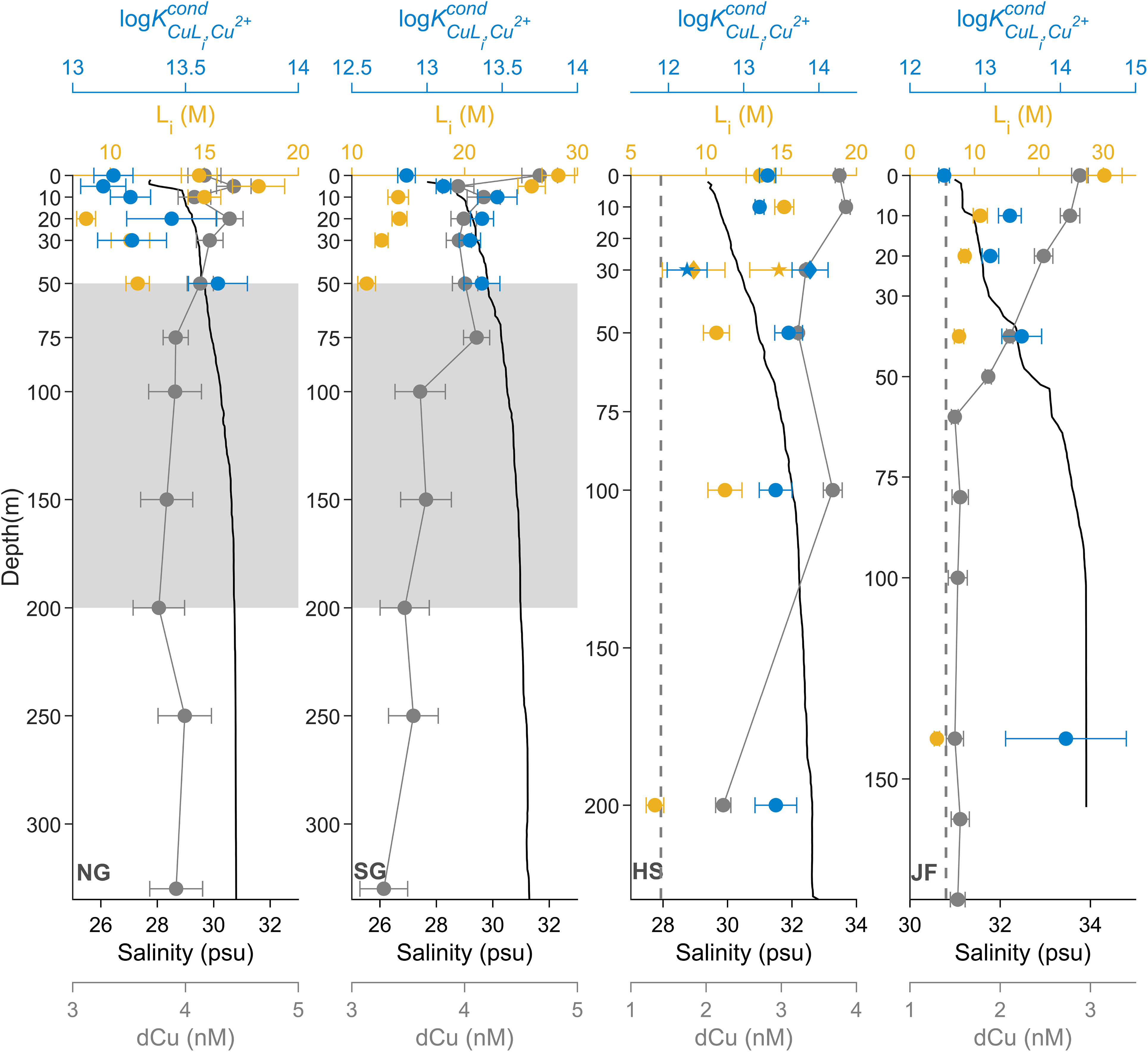
Figure 2 Spatial dCu concentrations (grey) and Cu speciation depth profiles of Li (yellow-orange) and log (blue) for stations NG, SG, HS, and JF, in August 2018, plotted with salinity depth profiles (black). Speciation parameters related to single ligand class L, two ligand class L1, and two ligand class L2 are represented as circle (●), diamond (♦), and star (★), respectively. Grey boxes, between 50 and 200 m, in NG and SG represent SoG intermediate waters. Black dashed lines in HS and JF correspond to dCu averaged between 100 m to 200 m at Line P4 (Whitby et al., 2018). Speciation parameter error bars represent average 95% confidence intervals of two replicate titrations of the same sample and dCu error bars represent one standard deviation.
Farthest from the Pacific water endmember, the NG dCu depth profile (Figure 2) averaged 4.06 ± 0.21 nM and was uniform with depth. Within the Northern SoG, tidal currents can be extremely fast, resulting in a well-mixed water column (Pawlowicz et al., 2007), which can explain the lack of structure in L concentrations with depth, averaging at 13.14 ± 3.32 nM across the water column. However, there is an increase in log profiles with depth, from 13.2 ± 0.1 at 0 m to 13.6 ± 0.1 at the 50 m depth.
In the southern SoG, SG (Figure 2), the surface 0 m sample had the greatest dCu, at 4.67 ± 0.16 nM, where salinity was lowest, at 27.7 psu. dCu averages 3.67 ± 0.29 nM below 50 m. Ligand concentrations were greatest in surface waters, with 28.3 ± 1.44 nM at 0 m and 25.9 ± 1.2 nM at 5 m, and decreasing between 5 and 10 m, to an average of 13.1 ± 1.4 nM between 10 and 50 m. Likewise, log is lowest in the surface, at 12.86 ± 0.06, and increasing between 5 m and 10 m to an average of 13.4 ± 0.1, between 10 and 50 m. This suggests an influx of weak ligands to the surface waters of SG, where both the Fraser River and Metro Vancouver are in proximity. Meanwhile, the average log at SG below 10 m is the same as the average log across the water column in HS, where SG’s intermediate waters are sourced.
Within HS (Figure 2), dCu averages at 3.57 ± 0.28 nM above 100 m, dropping to a value of 2.23 ± 0.10 nM at 200 m depth. The same trend occurs in L concentrations which average 12.7 ± 2.1 nM above 100 m, dropping to a value of 6.6 ± 0.6 nM at 200 m depth. However, log remains relatively constant with depth, averaging at 13.4 ± 0.2. Within the Haro Strait basin, Pacific water from Juan de Fuca enters at depth, where strong tidal currents vigorously mix the entire water column, explaining the decrease in dCu concentrations and the presence of fewer ligands, from surface to deep (Thomson, 1981; Pawlowicz et al., 2019). At 30 m in HS, two distinct ligand classes were identified, with an L1 of 9.2 ± 2.1 nM, log of 13.9 ± 0.2, and an L2 of 14.9 ± 1.9 nM, log of 12.3 ± 0.3. Given log at 30 m is similar to log across depths (13.4 ± 0.2) and log is objectively less than log across depths (13.4 ± 0.2), input of L2 may be possibly the cause of the detection of two ligands. While Haro Strait is only weakly stratified, a small pycnocline is observed between 30 and 50 m depth, with a density change of 0.7 kg·m-3 (Supplementary Figure 7).
In JF (Figure 2), dCu was maximum in surface waters, at 2.88 ± 0.09 nM, converging to an average of 1.53 ± 0.03 nM below 60 m, with a salinity of 33.9 psu. This is consistent with NE Pacific Line P dCu concentrations, at the continental shelf station (P4) with a salinity of 33.9 psu, where dCu concentrations, between 200 and 300 m, was between 1.4 to 1.6 nM in August 2012 (Whitby et al., 2018), averaging at 2.6 nM in August 2011, between 200 and 300 m (Posacka et al., 2017). Within JF, ligand concentrations were highest in the surface, at 30.2 ± 2.7 nM, decreasing to 7.6 ± 0.7 nM by 40 m, while JF log increases from 12.5 ± 0.1, in the surface, to 13.5 ± 0.3 by 50 m. Interestingly, at 140 m, ligand concentration is only 4.2 ± 0.4 nM, with a log of 14.1 ± 0.8. This indicates that very strong Cu binding ligands, at low concentrations, enter the deep Juan de Fuca Strait. Whitby et al. (2018) also detected a low concentration of very strong ligands, with log of 16, at 200 m in station P4, using an analytical window set to 10 μM SA. While the Cu speciation analytical strengths differ between methods, making the intercomparison of results difficult, similarities in dCu concentrations and evidence of strong binding organic Cu ligands between the deep Juan de Fuca Strait and the continental shelf of the NE Pacific aligns with our understanding that NE Pacific intermediate water enters Juan de Fuca Strait at depth (Pawlowicz et al., 2007).
Seasonal dissolved copper speciation
The seasonal profiles of dCu concentrations (Figure 3) show variations that relate to salinity (Pearson r = -0.71, p value< 0.001, n = 48). Cu speciation parameters follow salinity trends as well (L: Pearson r = -0.87, p value< 0.001, n = 35; log: Pearson r = 0.57, p value< 0.001, n = 35). The greatest Cu speciation variations between seasons in SG were at depths< 50 m, where two distinct ligand classes were often detected at depths shallower than 10 m (Supplementary Figure 8), and above the pycnocline (Supplementary Figure 7) and the euphotic zone depths (Supplementary Table 1). Within surface depths, the stronger binding L1 concentrations ranged between 10.5 to 15.7 nM, with log values between 13.5 and 14.3 (Supplementary Figure 8). The weaker binding L2 concentrations ranged between 30.9 and 107.7 nM, with log values between 11.5 and 12.3.
In September, average dCu, L, and log below 50 m were 3.85 ± 0.42 nM, 11.0 ± 2.6 nM, and 13.2 ± 0.2, respectively. At the surface, dCu and L increased to 4.85 ± 0.05 nM and 24.4 ± 1.5 nM, respectively, while log decreased to 12.8 ± 0.1. At 5 m depth, two ligand classes were detected, with a log of 13.8 ± 0.2 and log of 12.2 ± 0.1. This suggests a potential input of both L1 and L2 ligands near the surface during the fall bloom, as both log and log differ from log near surface (12.8 ± 0.1).
In December, average dCu, L, and log below 50 m were 4.22 ± 1.15 nM, 11.6 ± 4.07 nM, and 13.2 ± 0.1, respectively. At the surface, dCu and L increased to 7.9 ± 0.05 nM and two ligand classes were detected, with a log of 13.6 ± 0.3 and log of 12.0 ± 0.2. This indicates a potential input of L2, given surface log and deep log (13.2 ± 0.1) are indistinguishable, at the same time as cold, freshwater input mixes in surface waters.
In April, average dCu, L, and log below 50 m were 4.76 ± 0.92 nM, 10.1 ± 2.5 nM, and 13.4 ± 0.2, respectively. At surface, L increased to 20.4 ± 1.4 nM, while log remains relatively unchanged, at 13.1 ± 0.1. Between 0 and 50 m, there is a spike in dCu concentrations, averaging at 8.06 ± 0.48 nM, near which springtime snow melt input in the Fraser River mixes into the upper 50 m of the SoG. There is another spike in dCu concentrations at 200 m depth, with a dCu concentration of 6.51 ± 0.14 nM. Furthermore, at 5 m, two ligand classes were detected, with a log of 13.7 ± 0.1 and log of 12.0 ± 0.2. This suggests a potential input of L2, given that the surface log and the deep log (13.4 ± 0.2) are indistinguishable.
In June, average dCu, L, and log at 50 m were 3.78 ± 0.13 nM, 10.1 ± 0.6 nM, and 13.1 ± 0.1, respectively. Meanwhile, the maximum dCu concentration of all seasonal SG data is at the very surface in June, at 9.76 ± 0.15 nM. During June, the Fraser River freshet is at its maximum, due to snowpack melting, which results in high freshwater discharge into the SoG, near the SG station (Pawlowicz et al., 2007; Halverson and Pawlowicz, 2008). In June surface waters, two ligand classes were detected, with a log of 14.3 ± 0.6 and log of 12.3 ± 0.1. This indicates a potential input of L1, given that surface log is objectively greater than deeper values of log (13.1 ± 0.1). However, L1 concentration in surface waters (i.e., 11.9 ± 2.7 nM) is indistinguishable from L concentration at 50 m (10. 1 ± 0.6 nM). An input of L2 is also plausible, given log is objectively lower than deeper values of log (13.1 ± 0.1) and L2 concentrations spike in June surface waters, to 56.3 ± 3.4 nM at 0 m and 107.7 ± 6.2 nM at 5 m depth. During June, 56% of river discharge comes from the Fraser River, whereas Fraser River input only accounts for 35% in other seasons (Pawlowicz et al., 2019).
Below 50 m, dCu and salinity remain uniform with depth and seasons, averaging 4.20 ± 0.81 nM and 30.1 ± 1.77 psu, respectively (Figure 3). This is consistent with the upper 100 m of the August HS, averaging 3.57 ± 0.28 nM dCu and 30.48 ± 1.04 psu (Figure 2), the source of the intermediate and deep waters of the Strait of Georgia, SG station. In intermediate depths, between 50 m and 200 m, ligand concentrations and binding strengths are also relatively constant between depths and seasons, with average L concentration of 11.3 ± 1.7 nM and log of 13.2 ± 0.1, similar to the L found in August at HS (Figure 2). This nicely agrees with the SoG estuarine circulation pattern, where the intermediate layer (between 50 to 200 m) receives water from Haro Strait year-round (Pawlowicz et al., 2019).
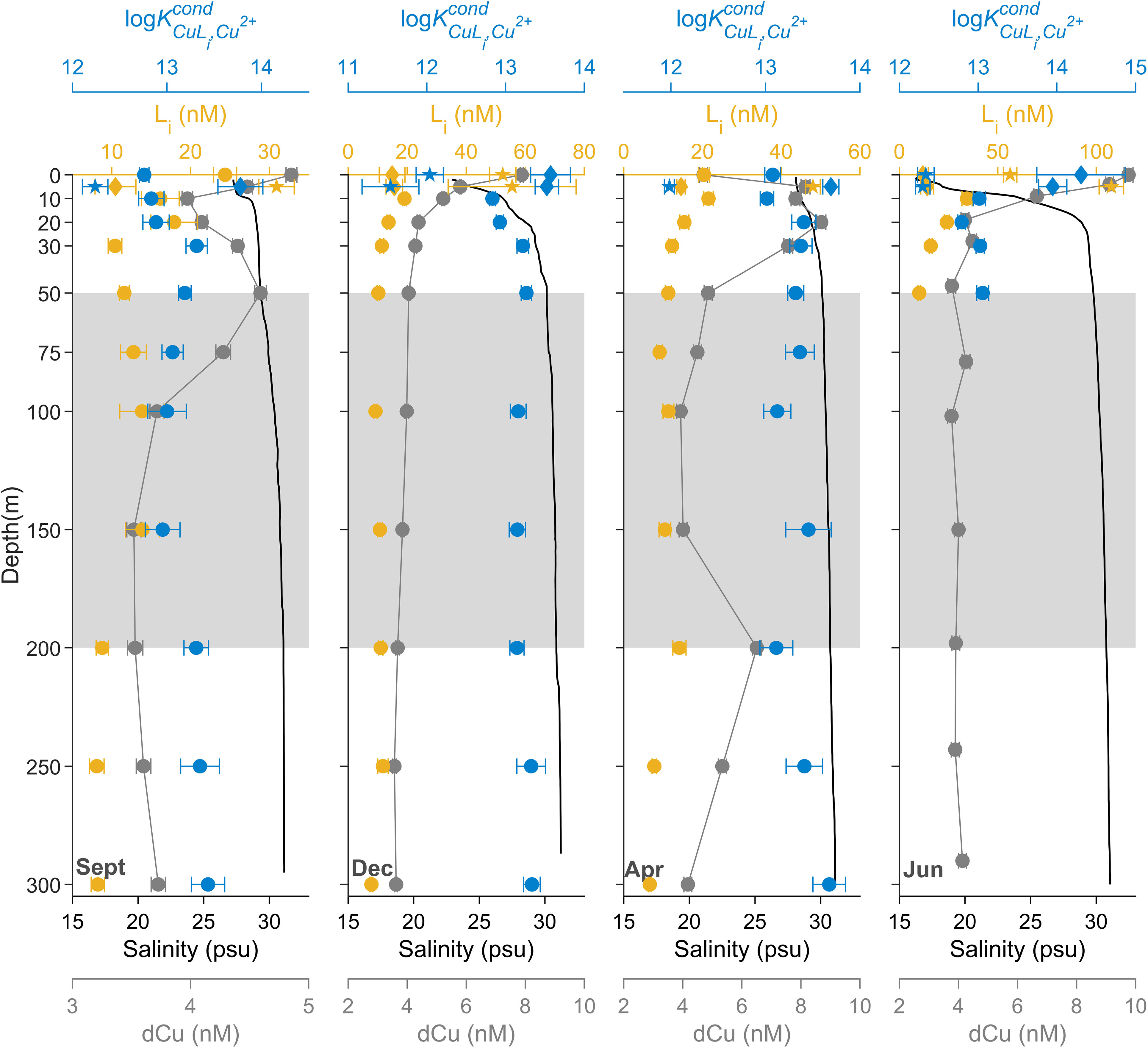
Figure 3 Seasonal 2017-2018 dCu concentrations (grey) and speciation depth profiles of Li (yellow-orange) and log (blue) for station SG, plotted with salinity depth profiles (black). Speciation parameters related to single ligand class L, two ligand class L1, and two ligand class L2 are represented as circle (●), diamond (♦), and star (★), symbols respectively. Grey boxes, between 50 and 200m, represent SoG intermediate waters. Speciation parameter error bars represent average 95% confidence intervals of two replicate titrations of the same sample and dCu error bars represent one standard deviation.
Discussion
Dissolved copper endpoints between NE Pacific and Fraser River
Dissolved Cu is known to act both conservatively and non-conservatively within estuary environments (Cutter, 1991). Whether dCu behaves conservatively within the SoG, between 16.3 to 33.9 psu, appears seasonally dependent. For most of the year, the dominant control on dCu in the SoG estuary system is conservative mixing of N. Pacific and Fraser River endmembers, as indicated by the linear relationship between dCu and salinity (Figure 4). For non-April samples, regression of all dCu observations against salinity yields a strong and significant correlation (Figure 4), which aligns with the conservative mixing line between NE Pacific incoming waters and the Fraser River (Figure 4). This indicates that the dominant source of dCu within the SoG is the Fraser River plume.
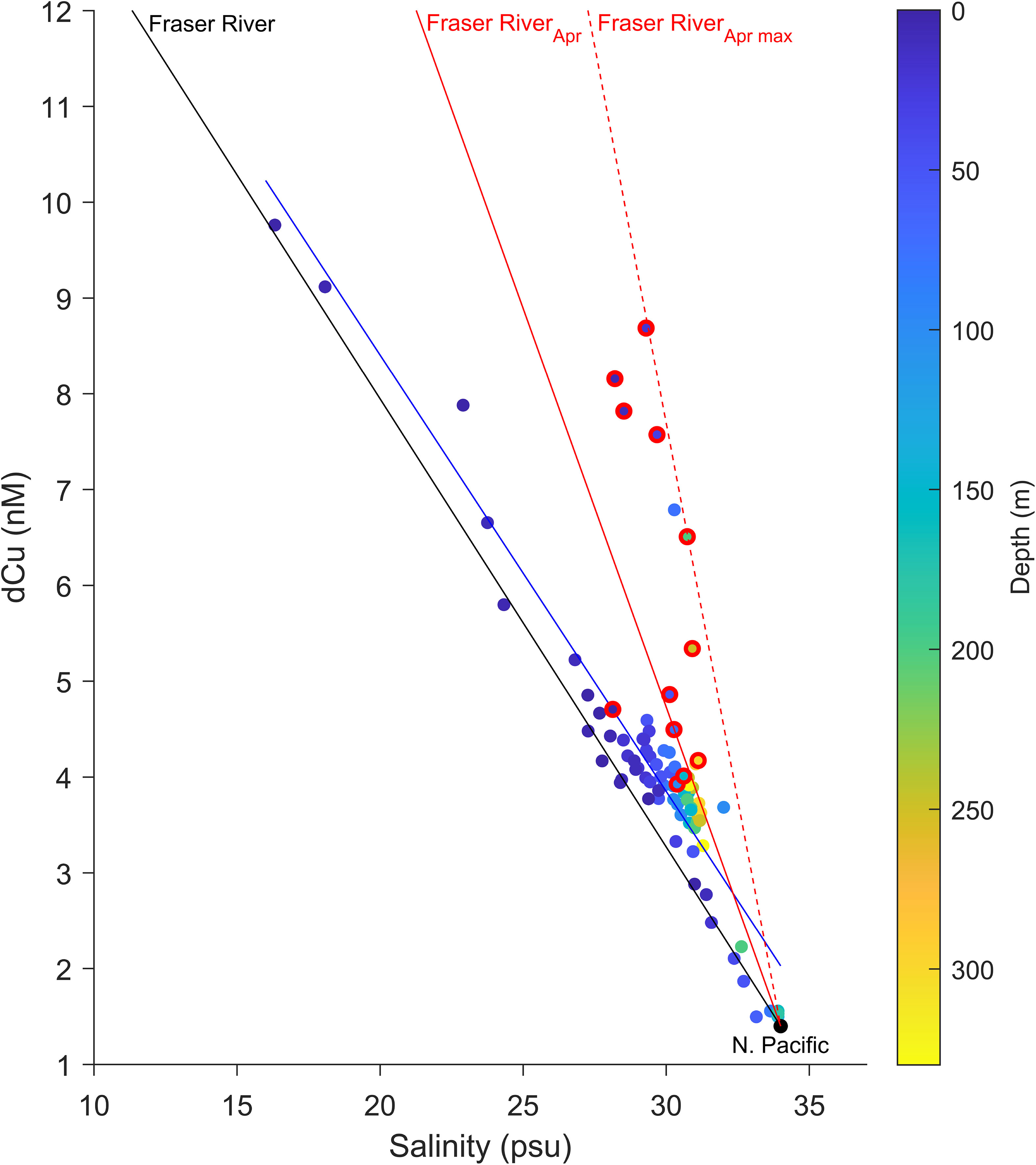
Figure 4 Dissolved Cu (dCu) concentrations, encompassing the entire dataset (n = 89), along the salinity gradient between the N. Pacific (34 psu) lower dCu baseline input, 1.4 nM dCu (Whitby et al., 2018) and the Fraser River (0 psu) at Gravesend Reach (Buoy BC08MH0453: Government of Canada, 2022). Red outlined points represent the April SG depth profile. The red line indicates the average (from all April measurements between 2010-2020) gradient of conservative mixing during April [y = -0.83 x + 29.7], where the average Fraser River concentration is 29.7 nM. The red dashed (- - -) line indicates the steepest conservative mixing gradient measured during April [y = -1.57 x + 54.9], between 2010-2020, where the Fraser River concentration is 54.9 nM. The continuous black line indicates the 2010-2020 average gradient of conservative mixing during the rest of the year [y =-0.47 x + 17.30], with an average Fraser River concentration of 17.3 nM. The blue line indicates regression [y = -0.46 x + 17.52, p value< 0.001, Pearson r = -0.93, n = 77] across non-April dCu concentrations with respect to salinity.
In contrast, the April samples, particularly those in surface waters, do not strongly follow linearly with salinity (Pearson r = 0.56, p value = 0.058, n = 12), nor does the regression align particularly well with the conservative mixing line between NE Pacific incoming waters and the Fraser River. One possible explanation is that, while the Fraser River discharge is greatest in June, the greatest dCu concentrations in the Fraser River are seen in the spring, when the first snow melt washes off winter-accumulated lithogenic matter into the Fraser River (Kuang, 2019), thus a second conservative mixing line is required to understand the conservative mixing in the April SG dataset.
To determine the Fraser River plume dCu concentration in April, an average of seven measurements, taken between 2010 and 2020 at the Fraser River Gravesend Reach (Buoy BC08MH0453: Government of Canada, 2022), was used (i.e., average = 29.7 nM; range 18.4 and 54.9 nM dCu). Since we did not measure dCu in the Fraser River during April 2018, the average and maximum mixing line we calculated were used to examine our April dataset (Figure 4). Given that April surface waters more closely aligns with the mixing line associated with the maximum Fraser River concentration [y = -1.57 x + 54.9], it is likely that the Fraser River dCu concentration in April 2018 was near 54.9nM. Conservative mixing trends are often observed for dCu in estuary environments, and most variation is often detected closer to the freshwater endpoint (Illuminati et al., 2019; Hollister et al., 2021). Thus, these higher and more variable concentrations of dCu during spring, associated with the first snow melt, may explain the deviation observed in April.
Another possible explanation for the April dCu data is that dCu behaves non-conservatively in spring due to sediment fluxes (Cutter, 1991; Laglera and van den Berg, 2003). Thomas and Grill (1977) measured dCu close to the mouth of the Fraser River, in May, and found that dCu concentrations peak in waters between 25 and 28 psu, which are located adjacent to the sloping banks near the Fraser River delta. They suggested that sediments escaping deposition on the delta flats were responsible for the release of dCu via adsorptive exchange equilibrium. Thus, it is possible that the elevated dCu concentrations in April are due to suspended sediment, which peaked in the Fraser River during April (Buoy BC08MH0453: Government of Canada, 2022), and released dCu into the SoG. While this was not observed in non-spring samples, the SoG dataset only comprises salinities as low as 16.3 psu, with only two measurements below 20 psu. Thus, we are unable to detect any non-conservative dCu behavior at salinities below 20 psu, in contrast to other studies (Byrd et al., 1990; Laglera and van den Berg, 2003).
Copper complexation on bioavailable Cu2+
In all samples, ligand concentrations exceed dCu by a ratio greater than 1.5, 4.0 on average, indicating that the complexation capacity of organic Cu binding ligands in the SoG is greater than required to buffer [Cu2+] below toxic levels (i.e., 10-12 M). With dCu concentrations in the range of 1.49 to 9.76 nM, pCu2+ (i.e., pCu2+ = -log[Cu2+]) would fall between 9.2 and 10.0 in the absence of organic ligands, greatly exceeding the traditional toxicity pCu2+ threshold of 12 (Brand et al., 1986). However, across all depths and seasons sampled during our SoG study, pCu2+ was well below the toxicity threshold, with an average, maximum, and minimum of 13.6, 14.3, and 13.2, respectively (Data Repository: https://doi.org/10.5683/SP3/6AB0JI). Ambient organic Cu complexing ligands, given their concentration and binding affinity, are complexing more than 99.98% of the dCu in SoG, preventing toxic conditions. Especially considering that coastal phytoplankton are more tolerant to Cu2+ than the traditional toxicity pCu2+ threshold suggests; studies observing the reduction in growth and motility of coastal species of dinoflagellates (Anderson and Morel, 1978), cyanobacteria (Stuart et al., 2009), and diatoms (Miao et al., 2005) report toxic pCu2+ values of 9.7, 10, and 9.2, respectively. Important to note is that, while the organic complexation of Cu in the SoG reduces Cu toxicity for Cu-sensitive phytoplankton, some eukaryotic marine phytoplankton can assimilate organically complexed Cu (Quigg et al., 2006; Guo et al., 2010; Semeniuk et al., 2015) and whether organically complexed Cu in SoG is bioavailable remains to be determined. Furthermore, even though some studies have measured pCu2+ concentrations (pCu2+ = 15) in the North Pacific that could potentially limit phytoplankton growth (Peers et al., 2005), the pCu2+ levels we determined (average of 13.6) for SoG are optimal for phytoplankton growth.
Analytical window comparison
Copper complexation results must be operationally defined by the selected analytical window. For example, in estuaries, the heterogeneity of the samples―which contain a variety of organic ligands that may complex Cu with a range of binding strengths― results in a range of stability constants of Cu ligands that may need to be resolved using a variety of detection windows (van den Berg and Donat, 1992; Gerringa et al., 2014). Thus, in addition to the seasonal and spatial depth profiles of SoG ligand data that we measured using 2.5 µM SA, three September SG depths were measured at a 10 μM SA competition strength (Table 1). Changing the competition strength of the added ligand from 2.5 μM to 10 μM SA increases the binding strength of the detected ligand class, as observed in Buck and Bruland (2005); Bundy et al. (2013), and Wong et al. (2018). Higher competitive ligand concentrations are best to detect the strongest L1 class; however, can fail to resolve the weaker L2 class, which is important when considering the partitioning of dCu between inorganic and organic complexes (Buck and Bruland, 2005).
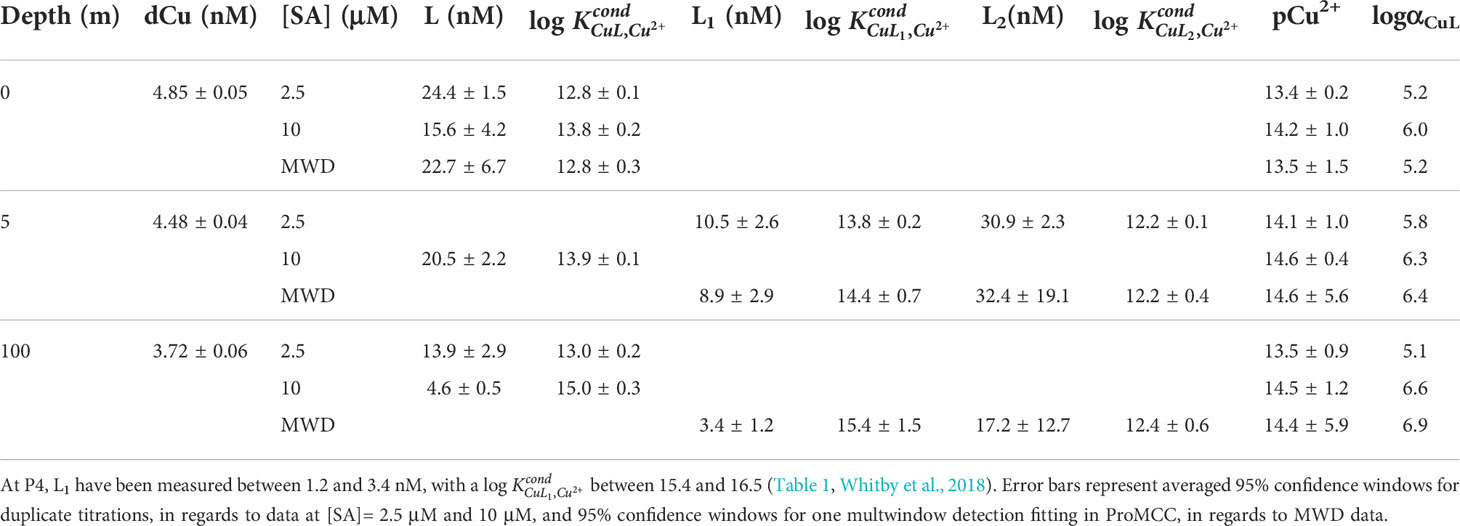
Table 1 Copper binding ligand concentrations (Li), conditional stability constants (), pCu2+, and the ligand side reaction coefficient (αCuL= ) from two analytical windows ([SA]= 2.5 μM as logαCuAL =4.2 - 4.3; [SA]= 10 μM as logαCuAL =5.1 – 5.2), and the multiwindow detection (MWD) using titrations from both analytical windows, for September 2017 SG samples.
To focus on the high terrestrial input of weaker ligands within estuary samples, a lower competition strength, like 2.5 μM, increases the likelihood of detecting two ligand classes (Buck and Bruland, 2005). Even when using 2.5 μM SA, for many of the SoG samples, we were only able to fit a single ligand class to the titration data. Therefore, if we were to use a 10 μM SA competition strength for all SoG samples, we would have likely detected two distinct ligand classes in even fewer samples. Furthermore, choosing a 10 μM SA analytical window for estuary samples can result in insufficient curvature in the titration data and prevent fitting data in ProMCC, as experimental error is weighed more heavily in the model as the analytical window increases (Hollister et al., 2021). For example, when sampling the Amazon River estuary for Cu binding organic ligands, Hollister et al. (2021) found that, with a 10 μM SA analytical window, 20% of their titrations could not successfully determine ligand concentration and strength, due to fitting data challenges in ProMCC. Thus, even though an underestimation of the strongest Cu binding organic ligands may occur, choosing a lower analytical window is prudent for Cu speciation in estuarine environments. In addition, certain ligand classes may not be detected within CLE-ACSV when a) strong ligand concentrations are below that of dCu (L1< dCu) (Ndungu, 2012); b) multiple ligands with similar side reaction coefficients (αCuL) combine into one detectable ligand class; or c) when ligands are too similar in strength to- or weaker than-the added ligand (when αCuL approaches αCuAL), resulting in an insufficient analytical signal (van den Berg, 1995; Laglera and van den Berg, 2003; Gerringa et al., 2014).
We combined titrations from both analytical windows, 2.5 and 10 μM SA, enabled MWD analysis, and provided some insight into the distribution of the Cu ligand pool (Table 1). For example, the 0 m and 5 m September samples’ MWD analysis aligns with the Cu complexation results using the single window detection of 2.5 μM SA. However, the 100 m September sample’s MWD results suggest that separate classes of ligands are detected, depending on the analytical window; strong L1 ligands are detected at 10 μM SA, weaker L2 ligands are detected at 2.5 μM SA, and unifying the titrations with MWD detects both ligand classes―with concentrations not unlike the concentrations determined in single window detection results. This finding supports the results of an intercomparison between CLE-ACSV data analysis methods, which found that the most accurate results arise from a unified analysis of MWD titration curves, including a better estimate of the true pCu2+ value, which is sensitive to methods bias on the binding strength detected (Pižeta et al., 2015). Using multiple analytical windows also enables us to predict the impact of increasing dCu concentrations and allows a more comprehensive interrogation of the Cu ligand pool (Moffett et al., 1997; Croot, 2003; Buck and Bruland, 2005; Ndungu, 2012; Bundy et al., 2013).
However, when sample volumes may limit the number of analytical windows for the measurements, 5 μM SA may prove the best choice for CLE-ACSV in estuarine samples, enabling the detection of strong L1 ligands without preventing fit in ProMCC (Wong et al., 2018). Alternatively, one could focus on one analytical window (i.e., 2.5 or 5 μM SA) and select some representative samples to be analyzed in a second analytical window (i.e.,10 μM SA), as done in this study and that of Santos-Echeandía et al. (2013).
Typically, the guiding distinction between L1 and L2 is a log of 13. However, an absolute threshold fails to consider that the ambient Cu binding ligand pool is characterized by a continuum of binding strengths, comprising a heterogeneous ligand pool that may have multiple binding sites and a variety of Cu binding functional groups (Moffett and Brand, 1996; Boiteau et al., 2016). Regardless of competition strengths, pCu values should remain relatively consistent, given its dependence on the ambient ligand side reaction coefficient, which remains balanced between decreasing Li and increasing as SA concentration increases (Bruland et al., 2000).
By including Cu speciation measurements under a competition strength of 10 μM SA in our study (Table 1), SoG ligand parameters are made analytically comparable to other data, such as those from P4, a continental shelf station within the NE Pacific Line P transect (Whitby et al., 2018). For P4, Whitby et al. (2018) measured relatively low L1 concentrations (i.e., ranging between 3.4 and 1.2 nM), with a strong binding capacity, log, (i.e., ranging between 15.4 and 16.5; see Table 1 in Whitby et al., 2018). While these high log values could be partially attributed to inert colloidal Cu fractions (Kogut and Voelker, 2003), or Cu adsorption to Sterilin (polystyrene) vessels during equilibration with SA (Barus et al., 2021), the detection of a low concentration of strong ligands at intermediate depths of the NE Pacific is supported by the Cu complexation results of the 100m September SG sample, measured at 10 μM SA. In this September samples, we detected a strong ligand concentration of 4.6 nM and a strong binding capacity, log, of 15.0, supporting current understanding of SoG estuarine circulation, where offshore NE Pacific water between 100 and 200 m travels into the SoG’s intermediate water year-round through Juan de Fuca and Haro Strait. While variations in salinity and equilibration times can impact comparisons between trace metal speciation studies (Buck and Bruland, 2005; Genovese et al., 2022), deep SoG waters and P4 have comparable salinities (ie., 31.8-34.5 psu for P4 and 30.4 in 100 m Sept) and equilibration times (i.e., > 8 hours for P4 and >12 hours for 100 m Sept).
Possible ligand sources in SoG
In almost 90% of the samples, the ligands were best classified as a single ligand class, with log between 12.5-14.1, average 13.2. The strong and significant anticorrelation (i.e., p< 0.001, n = 57; Figure 5) between single ligand class L concentrations and nutrient concentrations (i.e., Pearson r = -0.75, -0.62, and -0.79 for , SiO2, and NO2 + NO3, respectively), density (Pearson r = -0.76) and salinity (Pearson r = -0.73); as well as the positive and significant correlation between single ligand class L concentrations and dissolved oxygen (i.e., Pearson r = 0.67, p< 0.001, n = 57; Figure 5) suggest that Cu binding ligands are most abundant in the nutrient depleted, fresher, and less dense waters of the SoG, where dissolved oxygen concentrations are highest. These environmental conditions are satisfied best in spring and summer surface waters, during the Fraser River freshet and indicates that freshwater sources in the SoG input, and/or establish the conditions for production of, Cu binding ligands in the surface waters of SoG.
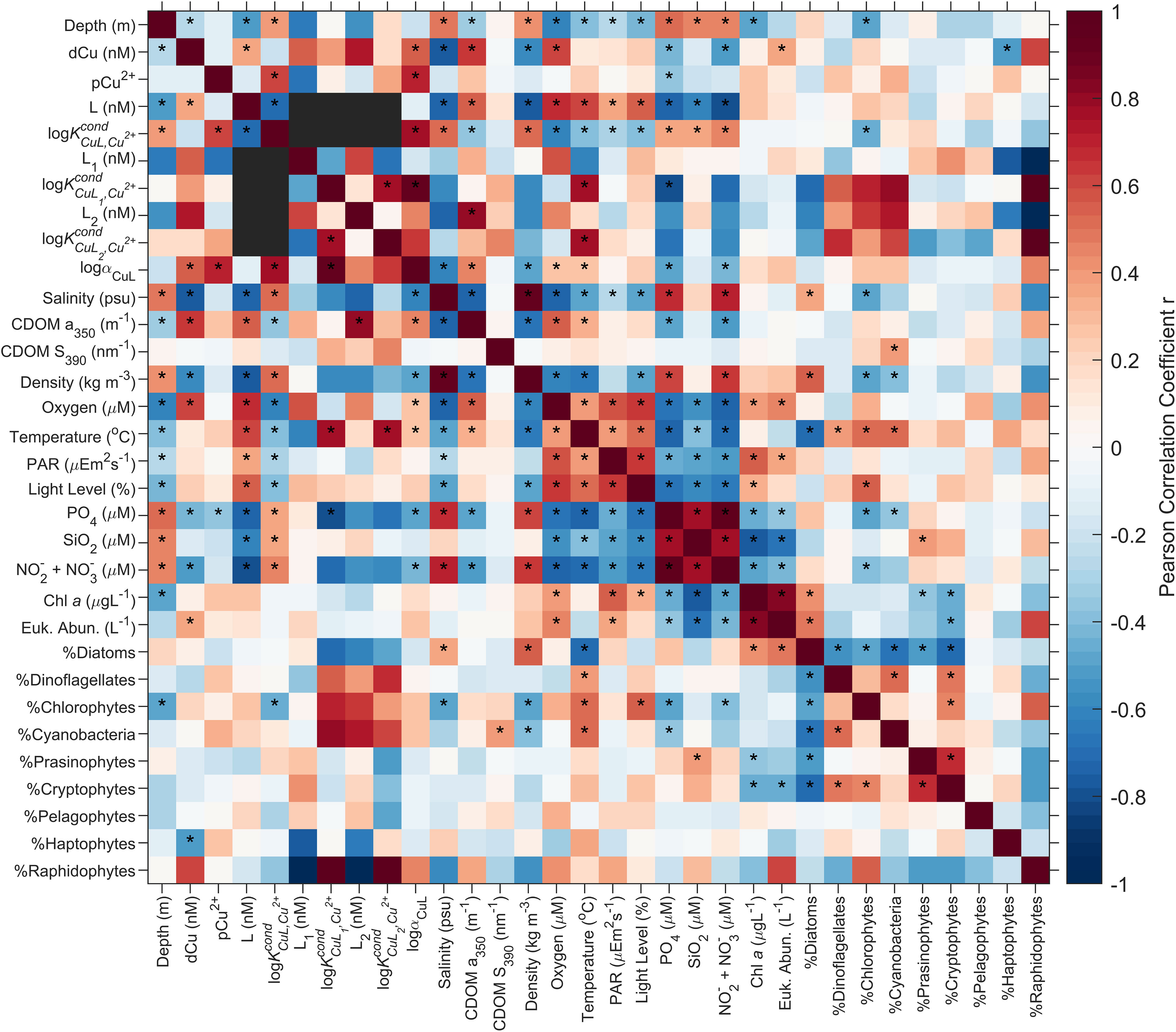
Figure 5 Heatmap of the Pearson correlation coefficient, r, across ligand parameters and salinity, CDOM a350, CDOM S390, density, dissolved oxygen concentrations, temperature, PAR irradiance, light level, nutrient concentrations, Chl a, eukaryotic phytoplankton abundance (Euk. Abun.), and HPLC phytoplankton community composition. Correlations deemed statistically significant, with a p value less than 0.05 are indicated with *. αCuL is equal to . Black boxes represent comparisons with no data for correlations. n varies between correlation, depending on data available for the parameters characteristic of water mass endmembers, seasonality, and biota (see Discussion section for specific n).
In only 7 of the 64 measured samples were we able to determine two distinct classes of ligand, with a stronger ligand class, L1, of log between 13.5-14.3, and an average of 13.8, and a weaker ligand class, L2, of log between 11.5-12.3, and an average of 12.1 (Figures 2, 3, and Supplementary Figure 8). Six of these 7 two ligand class samples were collected in the euphotic zone, suggesting that the surface waters are a source of ligands to the ligand pool, L1 in June and L2 in September, December, and April (see section 3.3). However, we were unable to determine two classes of ligands in 15 measured samples which were collected at depths shallower than 10 m. Another apparent commonality amongst all two ligand class samples is their presence above the pycnocline, suggesting that stratification mediates the accumulation of a ligand pool with two distinct classes. Identifying the sources of the SoG Cu binding ligands in the two-ligand model dataset and comparing parameters related to these sources with the single ligand class samples may explain when and where in the SoG two ligand classes are detectable. Possible sources of ligands within the SoG include WWOM (Sedlak et al., 1997), terrestrial and marine-derived humic substances (Laglera et al., 2007; Whitby and van den Berg, 2015), and phytoplankton exudates (Moffett and Brand, 1996; Dupont et al., 2004; Kim et al., 2005; Walsh et al., 2015).
Wastewater, discharged from urban cities, may contain non-biodegradable DOC, anthropogenic ligands like EDTA, and biopolymers from activated sludge (Buck et al., 2007; Katsoyiannis and Samara, 2007). This WWOM can have a log of up to 14.5 (e.g., 13 for EDTA; Sedlak et al., 1997), on par with single ligand class log at 50 m in SG, across seasons (13.2 ± 0.1). In SoG, the Iona Outfall (a discharge point from a primary wastewater treatment plant) accounts for ~ 45% of the total wastewater discharge in Metro Vancouver, with its terminus located at 100 m depth, ~20 km west of station SG (Metro Vancouver, 2018; Kuang, 2019). Once released, the wastewater discharge rises to 50 m depth (i.e., where it reaches neutral buoyancy), and by the time it reaches station SG, it has been diluted more than 5000x with ambient seawater (Kuang, 2019). However, given that Cu ligand concentrations at 50 m (Figure 3) are not significantly different from the ligand concentrations throughout the entire intermediate layer (50 m to 200 m), the contribution to the Cu ligand pool from WWOM must be negligible.
The concentration of L2 ligand class and CDOM significantly correlate (e.g., Pearson r = 0.81, p value = 0.028, n=7; Figure 5). Much of the CDOM in estuaries is sourced from terrestrial runoff and is often used as a proxy for terrestrial dissolved organic matter (DOM) (Coble, 2007; Bowers and Brett, 2008; Osburn et al., 2016). Strong correlations between dCu binding ligand parameters and terrestrial DOM have been documented in other estuaries (Tang et al., 2001; Shank et al., 2004; Muller and Batchelli, 2013; Dulaquais et al., 2020), specifically DOC derived from humic substances (Shank et al., 2004). The link between humic substances and Cu binding ligands, as both L1 and L2 ligands (Xue and Sunda, 1997; Kogut and Voelker, 2001; Voelker and Kogut, 2001; Whitby and van den Berg, 2015; Dulaquais et al., 2020), suggests that the correlation between L2 concentrations and CDOM may be due to the incorporation of Fraser River derived humic substances into the Cu ligand pool of the SoG, decreasing the overall log, with decreasing salinity. In addition, there is a significant negative correlation between single ligand class concentrations and salinity (i.e., Pearson r = -0.73, p value< 0.001, n = 57), and a significant positive correlation between single ligand log and salinity (i.e., Pearson r = 0.50, p value< 0.001, n = 57), suggesting that freshwater adds weaker ligands―on par with humic substances and L2 within the two ligand class observations―to the Cu ligand pool, decreasing the log, when ligand parameters are observed as a single ligand class. However, without complementary concentrations of humic substances, DOM, and perhaps a wider wavelength range of CDOM (i.e., between 280-320 nm can enable an assessment of CDOM quality; Helms et al., 2013; Heller et al., 2016), it is difficult to confirm whether terrestrially derived humic substances are a significant source of ligands within the SoG.
Strong Cu binding ligands are extensively described and documented to be of biological origin (Gonzalez-Davila et al., 1995; Moffett and Brand, 1996; Gledhill et al., 1999; Croot et al., 2000; Gordon et al., 2000; Rijstenbil and Gerringa, 2002; Dupont et al., 2004; Dupont and Ahner, 2005; Kim et al., 2005), with thiols, in particular, acting as strong Cu binding ligands, as both L1 and L2 (Laglera and van den Berg, 2003). Previous work, characterizing Cu binding ligands within the SoG, isolated and identified thiol functional groups (Ross et al., 2003), indicating the presence of thiol Cu binding ligands within the SoG. As well, within our voltammograms, a broad peak (i.e., peaked at -520 to -530 mV, depending on the sample and Cu addition) was prevalent amongst most samples; such peaks are often associated with thiols, such as glutathione (Laglera and Tovar-Sánchez, 2012; Whitby et al., 2018). While L and L1 concentrations do not strongly correlate to any of the biological complementary parameters, log correlates positively with temperature (i.e., Pearson r = 0.77; p value = 0.044, n=7) and negatively with phosphate concentrations (i.e., Pearson r = -0.80, p value = 0.032, n = 7), indicating that a stronger L1 ligand pool is found in warm, phosphorus deficient waters, from either direct inputs of the Fraser River (i.e., 0.5 μM and 0.05 μM for total dissolved phosphorus and orthophosphate, respectively, Buoy BC08MH0453: Government of Canada, 2022) or low salinity, stratified surface waters in SoG during spring or summer, which may promote the production of Cu binding ligands by phytoplankton (Croot et al., 2000; Dryden et al., 2007). The inability to find a correlation between biological parameters and ligand parameters (Figure 5) is possibly due to time lags between changes in the phytoplankton community and the Cu binding ligand pool, on time scale of days (Leal et al., 1999) to weeks (Dryden et al., 2007).
Because the CLE-ACSV assay is unable to characterize ligands by chemical structure, ligand source discussions are based on the reported average log values for Cu binding ligands in the SoG and correlations between complexation parameters and other physical, chemical, and biological parameters from the stations. These comparisons are heavily impacted by analytical window bias, as well as experimental error, in which case the variability within ligand concentrations and binding strengths may be attributed to the environment sampled, or experimental error (Gerringa et al., 2014). Furthermore, given the small range in log, log, and log in our study (i.e., 12.5- 14.0, 13.5- 14.3, and 11.5-12.3, respectively), it is challenging to attribute a correlation in the SoG Cu speciation dataset to specific sources. Nor are we able to decouple the conditionality effect that salinity has on log from changes to ligand species between water masses of different salinities. Additionally, CLE-ACSV does not take into consideration inert colloid complexes, which can inadvertently result in elevated log values, given these inert species are unexchangeable between the natural Cu pool and SA within the timescales that CLE-ACSV samples are equilibrated (Kogut and Voelker, 2003; Moriyasu and Moffett, 2022). The low correlation between dCu and L concentrations (Figure 5), yet strong correlations individually to the same parameters (i.e., CDOM a350, oxygen, , and + ), suggests that some ligand pool variability may be due to loss of ligands via photodegradation, while dCu remains. While there is no strong correlation between ligand parameters and light level or CDOM S390 to support photodegradation of ligands (Loiselle et al., 2009) within the SoG, photooxidation occurs in timescales of hours to days, which is not captured by our one-day sampling per season (Laglera and van den Berg, 2006; Brooks et al., 2007).
To structurally characterize and confirm potential sources of Cu binding organic ligands in the SoG, CLE-ACSV (i.e., under multiple detection windows) should be combined with other techniques, such as HPLC-ESI-MS (McCormack et al., 2003; Ross et al., 2003; Nixon and Ross, 2016), allowing comparisons of speciation data from field samples and those from phytoplankton and bacteria cultures (Whitby et al., 2018). Additionally, ligand parameters should be complemented with concentrations of potential ligands, such as thiols and humic substances (Laglera and Tovar-Sánchez, 2012; Whitby et al., 2018), as well as DOC, CDOM across a wider range of wavelengths, suspended particulate matter, colloidal trace metal fractions (Bertine and VernonClark, 1996; Kogut and Voelker, 2003; Moriyasu and Moffett, 2022) and other proxies, while considering time delays between biological parameters and Cu ligand parameters (Dryden et al., 2007), informed by cell cultures (Leal et al., 1999; Gordon et al., 2000).
Cu speciation clusters for the single-ligand class within the SoG
Performing hierarchal clustering on the single ligand dataset and identifying the spatial and seasonal characteristics of the clusters may hint at reasonable assignation of reservoirs for a Salish Sea Cu speciation box model and identify how differences in the water masses of the SoG estuarine circulation system, involving region, season, and depth, can influence SoG Cu ligand pools. In recent years, the hierarchal clustering of physical and biogeochemical ocean models and datasets has become more common (e.g., Follows et al., 2007; Sonnewald et al., 2020; Sun et al., 2021), including within the SoG (Jarníková et al., 2022). However, this approach has never been applied to trace metal speciation data, because these datasets are often not large enough to warrant clustering (Buck et al., 2007; Boiteau et al., 2016; Whitby et al., 2018) or trends in large datasets are simplified by water masses (Buck et al., 2015; Ruacho et al., 2020). However, trace metal speciation dynamics in estuary systems are particularly challenging to interpret by water bodies alone, given the closely adjacent sources of terrestrially- and anthropogenically-derived ligands, such as wastewater treatment plants, mixing with the open ocean ligand pool occurring in tandem with large seasonal variability in biological productivity and algal groups within the estuary (Buck et al., 2007).
Given that single ligand class concentrations vary with parameters that follow seasonal SoG water circulation patterns (e.g., density, salinity, temperature, nutrients, and dissolved oxygen), the Cu binding ligand pool may follow similar trends as those accounted for in the Salish Sea Box Model described in Wang et al. (2019). The model divides the SoG into 6 boxes of 3 locations: Strait of Georgia, Haro Strait, and Juan de Fuca Strait, which are further divided into two depths: upper, as the top 50 m depths, and lower, as all depths below 50 m. But, grouping SoG Cu speciation parameters by water body, according to the 6 boxes outlined in Wang et al. (2019) only accounts for conservative mixing between regions of the SoG and ignores changes in biological production across depth and season, Cu transfer between dissolved and particulate phases, particulate resuspension, and Cu binding ligand stability across the salinity gradient. Thus, given the extent of seasons (4), depths (12), and regions (4) included in this study, encompassed in 64 samples, 57 of which are described as single ligand complexation, performing hierarchical clustering is warranted.
Before hierarchical clustering, PCA was performed to determine the most efficient set of statistical modes representing the seasonal and spatial variability of the single ligand class Cu complexation dataset (i.e., dCu, salinity, L, and single log) with 57 observations (Supplementary Figure 3). Within the PC results, mode 1 follows decreasing salinity, increasing dCu concentrations, increasing ligand concentrations, and decreasing log, where the greatest PC score is in June surface waters―when the Fraser river’s freshwater contribution to the SoG is the greatest―and the greatest negative PC score is in Juan de Fuca, at 140 m depth. This suggests that mode 1 explains the variability between a high concentration of weaker ligands from a freshwater source and a low concentration of stronger ligands from seawater sourced from the NE Pacific into SoG. Mode 2 follows increasing dCu and log, where PC scores are elevated in April surface waters, suggesting a seasonal presence of stronger ligands during the springtime phytoplankton bloom. In mode 3, eigenvectors follow increasing salinity and decreasing log, where the PC scores are greatest in depths below 200 m in April, suggesting an input of stronger ligands from N. Pacific waters during summer deep water renewal (Masson, 2002).
Hierarchical clustering of the first three PCA modes resulted in 6 distinct clusters, projected in Supplementary Figure 4. Projecting these clusters over depth profiles from all 8 cruises (Supplementary Figure 9) results in a harmonized schematic of the SoG ligand pool, shown in Figure 6. Determining the Cu speciation characteristics of each cluster (Figure 7) enables us to decipher sources of Cu binding ligands into the SoG and how these various ligand pools behave as water circulates in the SoG.
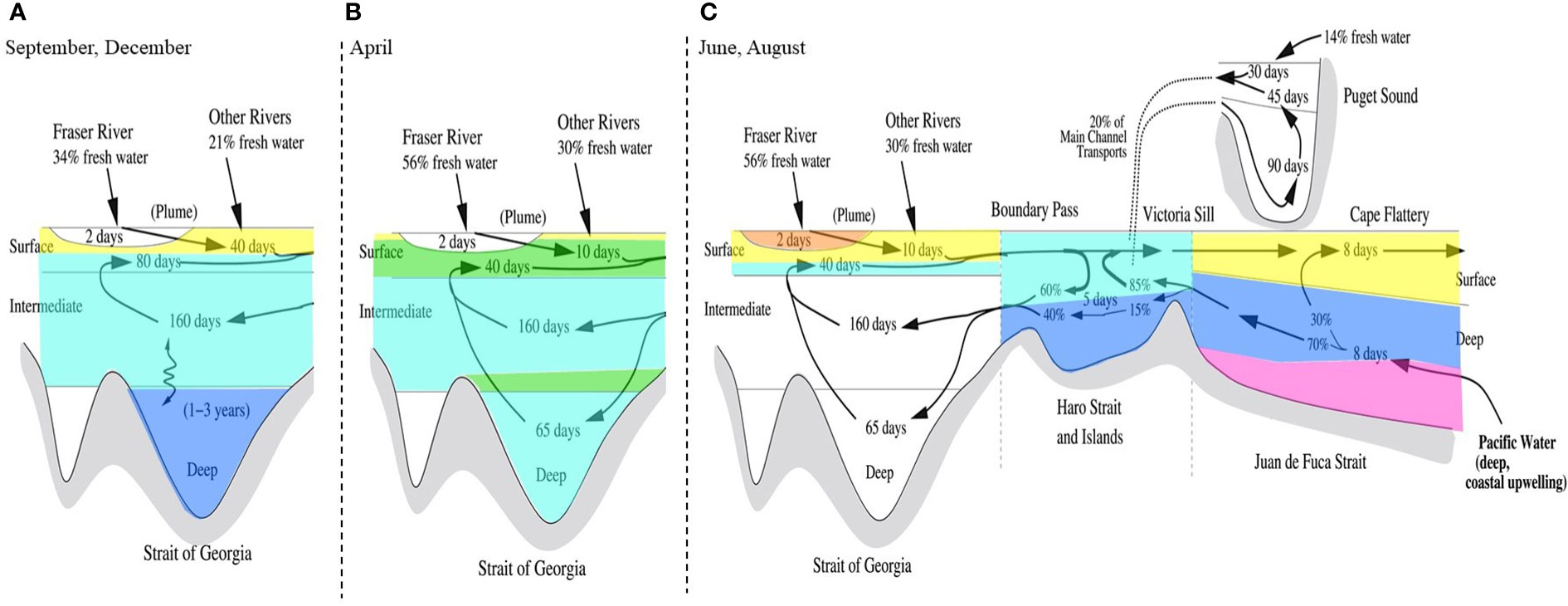
Figure 6 Schematic water circulation diagram of the Salish Sea, adapted from Pawlowicz et al. (2019), showcasing hierarchical clustering on single ligand class dissolved Cu speciation parameters (i.e. salinity, dCu, L, and log ) into 6 clusters, 1 (magenta), 2 (blue), 3 (teal), 4 (green), 5 (yellow), and 6 (orange). This diagram is complementary to Figure 7, and the clustered depth profiles in Supplementary Figure 9. Clusters describing the September and December SG cruises (A) are shown over the schematic of Salish Sea water circulation during non-summer conditions, when the SoG’s deep water is stagnant. Clusters describing the April SG (B), June SG (C), August SG (C), August NG (C), August HS (C), and August JF (C) cruises are shown over the schematic of Salish Sea water circulation during summer conditions, when the deep water of the SoG is actively renewed.
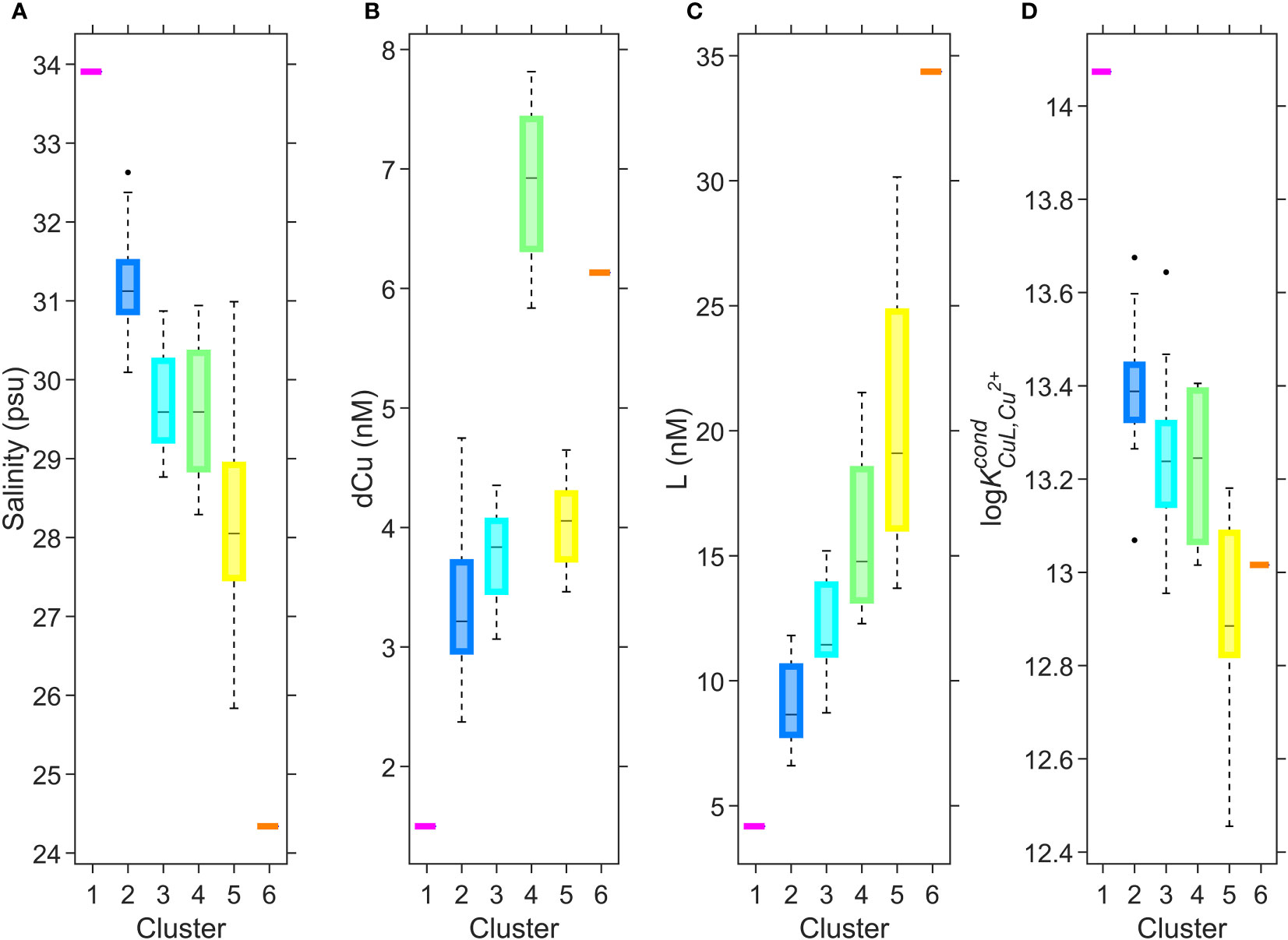
Figure 7 Boxplots of salinity (A), dCu concentration (B), L concentration (C), and log (D) for 6 clusters; 1 (n=1), 2 (n=10), 3 (n=28), 4 (n=4), 5 (n=13), and 6 (n=1). This diagram is complementary to Figure 6, and the clustered depth profiles in Supplementary Figure 9. On each box, the central black mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The dashed whiskers extend to the most extreme data points not considered outliers, and the black markers are outliers.
Cluster 1 (magenta, Figures 6, 7), consisting of a single data point, defines the behavior of the incoming intermediate NE Pacific water into deep Juan de Fuca, with a low concentration of dCu and the strongest Cu binding ligands in the SoG. Cluster 2 (blue, Figures 6, 7) encompasses the ligands carried to the deep SoG during summer deep water renewal. Cluster 3 (teal, Figures 6, 7) includes SoG intermediate water, received from well mixed Haro Strait surface waters. Cluster 4 (green, Figures 6, 7) specifies April SG surface and intermediate water, where elevated dCu concentrations are evident, and which would not have been accounted for by a conservative mixing model between Fraser River freshwater and the NE Pacific waters within Juan de Fuca. Instead, cluster 4 aligns with regions of high particulate Cu concentrations in spring SG waters, near surface and 200 m depth (see Figure 22b in Flores Ruiz, 2020). The high Cu particulate load in April in surface waters may be attributed to higher concentrations of particulate Cu within the Fraser River plume, due to the springtime snow melt washing off winter accumulated lithogenic matter into the Fraser River (Kuang, 2019). Similarly, the elevated particulate Cu concentrations at 200 m depth (see Figure 22b in Flores Ruiz, 2020) may be due to scavenging of remineralized Cu onto sinking particles (Bruland, 1980; Little et al., 2013). However, since Haro Strait water, high in particulate matter, discharges into the SoG between 100 to 200 m, these local particulate Cu maxima in SoG may also reflect lateral transport of HS particulate matter (Johannessen et al., 2006; Kuang, 2019). While Cu2+ concentrations fall below the toxicity threshold throughout all SoG samples, dCu concentrations most closely approach L concentrations within cluster 4, suggesting that April surface and intermediate waters are at most risk of Cu toxicity.
Cluster 5 (yellow, Figures 6, 7) includes Juan de Fuca Strait surface water, as well as SG and NG surface water samples (ie., above 30 m) other than high particulate Cu April waters and samples taken directly within the Fraser River plume. The distinction of cluster 5 is possibly due to either biologically derived ligands in sunlit depths, or the addition of terrestrial ligands from freshwater inputs. Cluster 6 (orange, Figures 6, 7) is comprised of the single freshest sample in our dataset, as the strongest Fraser River plume signal, signifying the highest contribution of Cu binding ligands, with a log value of 13.0. These 6 clusters enable key regional and temporal distinctions between ligand concentrations and stability constants, allowing resolved values for Cu speciation for seasons and SoG regions. For example, if modelling Cu bioavailability within the coastal NE Pacific, the ligand parameters of cluster 5 are more applicable than those calculated by averaging across the entire SoG ligand dataset.
Conclusion
Conservative mixing between freshwater sources and the N. Pacific largely controls the seasonal and spatial distributions of dCu within the Salish Sea. In the SoG, Cu speciation is dominated by Cu complexing organic ligands, which complex greater than 99.98% of dCu, resulting in Cu2+ concentrations suitable for the growth of healthy and robust phytoplankton communities, regardless of season or location within the SoG.
Possible ligand sources were discussed via correlation with supporting physical, chemical, and biological parameters, where a strong correlation was found between high concentration of single ligand class L and warm, low salinity, high dissolved oxygen, and nutrient-depleted waters. A stronger ligand class, L1, of log between 13.5 and 14.3, and a weaker ligand class, L2, of log between 11.5 and 12.3, were detected in surface waters of the Southern SoG, but only in 7 samples out of our 64 sample dataset. The two-ligand model dataset was used to isolate specific sources of the SoG Cu binding ligands. A relationship was found for two-ligand class log and log with temperature, in the absence of correlation with Chl a and eukaryotic phytoplankton density, while a correlation was found between two-ligand class L2 concentrations and CDOM. This suggests that a warm freshwater terrestrial source to the Cu binding ligand pool dominates any possible biological source signal. Future studies should measure DOC and humic substance concentrations, include more phytoplankton composition observations within the Cu binding ligand dataset, characterize ligands using HPLC-ESI-MS concentrations, and utilize multiple analytical windows within CLE-ACSV to corroborate conclusions surrounding the dominant source of the SoG’s ligand pool.
Spatial ligand and dCu depth profiles support the current understanding of the water circulation pattern within the SoG, detecting traces of NE Pacific water along the depths of Juan de Fuca Strait, Haro Strait, and the Southern SoG. Furthermore, hierarchal clustering enables us to distinguish unique features of surface waters, affected by strong seasonality, and identifying changes in Cu speciation in regions and depths with high particulate Cu concentrations and that ligand parameters require a shallower distinction for surface water than the currently described 50 m shallow-intermediate depth. This study is the first to perform hierarchal clustering analysis on a trace metal speciation dataset to describe the dynamics of the Cu ligand pool within an estuary environment. Future studies should expand the SoG ligand pool dataset to test the clusters established in this study, as well as investigate particulate Cu speciation and changes in the phase of total Cu within Spring SoG waters to better understand how freshwater lithogenic input affects dCu speciation.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Borealis, the Canadian Dataverse Repository, under Seasonal and Spatial Depth Profiles of Dissolved Copper Speciation in the Strait of Georgia. https://doi.org/10.5683/SP3/6AB0JI.
Author contributions
The experimental design was carried out by IF-R and MM. Sample collection was performed by IF-R, CK, and JG. Biological parameter analysis was performed by IF-R and JG. Dissolved Cu analysis was performed by IF-R and CK, led by JC. Copper speciation analysis was performed by L-JW. Data interpretation was performed by IF-R, MM, and L-JW. The manuscript was primarily written by L-JW and edited by MM, and JC. All authors contributed to the article and approved the submitted version.
Funding
We thank Metro Vancouver, and the Natural Sciences and Engineering Research Council of Canada under grant CRDPJ 486139-15 for funding.
Acknowledgments
We must thank the captain and crew of the CCGH Siyay and CCGS Vector, as well as Maureen Soon, Yuanji J. Sun, Ryan Gan, Alix Rommel, Chris Payne, and Larysa Pakhomova for help in sampling. We also thank Jody Spence for the technical support in QQQ-ICP-MS/MS analysis and Hannah Whitby, Kristen N. Buck, and Randelle M. Bundy for their insights into Cu speciation method development and data interpretation.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.983763/full#supplementary-material
References
Achterberg E. P., van den Berg C. M. (1994). In-line ultraviolet-digestion of natural water samples for trace metal determination using an automated voltammetric system. Analytica Chimica Acta 291 (3), 213–232. doi: 10.1016/0003-2670(94)80017-0
Anderson D. M., Morel F. M. (1978). Copper sensitivity of gonyaulax tamarensis 1. Limnol. Oceanogr. 23 (2), 283–295. doi: 10.4319/lo.1978.23.2.0283
Barałkiewicz D., Chudzińska M., Szpakowska B., Świerk D., Gołdyn R., Dondajewska R. (2014). Storm water contamination and its effect on the quality of urban surface waters. Environ. Monit. Assess. 186 (10), 6789–6803. doi: 10.1007/s10661-014-3889-0
Barber R. T., Ryther J. H. (1969). Organic chelators: factors affecting primary production in the Cromwell current upwelling. J. Exp. Mar. Biol. Ecol. 3 (2), 191–199. doi: 10.1016/0022-0981(69)90017-3
Barus B. S., Chen K., Cai M., Li R., Chen H., Li C., et al. (2021). Heavy metal adsorption and release on polystyrene particles at various salinities. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.671802
Bertine K. K., VernonClark R. (1996). Elemental composition of the colloidal phase isolated by cross-flow filtration from coastal seawater samples. Mar. Chem. 55 (1-2), 189–204. doi: 10.1016/S0304-4203(96)00056-4
Boiteau R. M., Till C. P., Ruacho A., Bundy R. M., Hawco N. J., McKenna A. M., et al. (2016). Structural characterization of natural nickel and copper binding ligands along the US GEOTRACES Eastern pacific zonal transect. Front. Mar. Sci. 3. doi: 10.3389/fmars.2016.00243
Bowers D. G., Brett H. L. (2008). The relationship between CDOM and salinity in estuaries: An analytical and graphical solution. J. Mar. Syst. 73 (1-2), 1–7. doi: 10.1016/j.jmarsys.2007.07.001
Brand L. E., Sunda W. G., Guillard R. R. (1986). Reduction of marine phytoplankton reproduction rates by copper and cadmium. J. Exp. Mar. Biol. Ecol. 96 (3), 225–250. doi: 10.1016/0022-0981(86)90205-4
Bricaud A., Morel A., Prieur L. (1981). Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnol. Oceanogr. 26 (1), 43–53. doi: 10.4319/lo.1981.26.1.0043
Brooks M. L., Meyer J. S., McKnight D. M. (2007). Photooxidation of wetland and riverine dissolved organic matter: altered copper complexation and organic composition. Hydrobiologia 579 (1), 95–113. doi: 10.1007/s10750-006-0387-6
Bruland K. W. (1980). Oceanographic distributions of cadmium, zinc, nickel, and copper in the north pacific. Earth Planetary Sci. Lett. 47 (2), 176–198. doi: 10.1016/0012-821X(80)90035-7
Bruland K. W., Rue E. L., Donat J. R., Skrabal S. A., Moffett J. W. (2000). Intercomparison of voltammetric techniques to determine the chemical speciation of dissolved copper in a coastal seawater sample. Analytica Chimica Acta 405 (1-2), 99–113. doi: 10.1016/S0003-2670(99)00675-3
Buck K. N., Bruland K. W. (2005). Copper speciation in San Francisco bay: a novel approach using multiple analytical windows. Mar. Chem. 96 (1-2), 185–198. doi: 10.1016/j.marchem.2005.01.001
Buck K. N., Moffett J., Barbeau K. A., Bundy R. M., Kondo Y., Wu J. (2012). The organic complexation of iron and copper: an intercomparison of competitive ligand exchange-adsorptive cathodic stripping voltammetry (CLE-ACSV) techniques. Limnol. Oceanogr.: Methods 10 (7), 496–515. doi: 10.4319/lom.2012.10.496
Buck K. N., Ross J. R., Flegal A. R., Bruland K. W. (2007). A review of total dissolved copper and its chemical speciation in San Francisco bay, California. Environ. Res. 105 (1), 5–19. doi: 10.1016/j.envres.2006.07.006
Buck K. N., Sohst B., Sedwick P. N. (2015). The organic complexation of dissolved iron along the US GEOTRACES (GA03) north Atlantic section. Deep Sea Res. Part II: Topical Stud. Oceanogr. 116, 152–165. doi: 10.1016/j.dsr2.2014.11.016
Bundy R. M., Barbeau K. A., Buck K. N. (2013). Sources of strong copper-binding ligands in Antarctic peninsula surface waters. Deep Sea Res. Part II: Topical Stud. Oceanogr. 90, 134–146. doi: 10.1016/j.dsr2.2012.07.023
Byrd J. T., Lee K. W., Lee D. S., Smith R. G., Windom H. L. (1990). The behavior of trace metals in the geum estuary, Korea. Estuaries 13 (1), 8–13. doi: 10.2307/1351426
Campos M. L. A. M., van den Berg C. M. G. (1994). Determination of copper complexation in sea water by cathodic stripping voltammetry and ligand competition with salicylaldoxime. Analytica Chimica Acta 284 (3), 481–496. doi: 10.1016/0003-2670(94)85055-0
Cardwell R. D., DeForest D. K., Brix K. V., Adams W. J. (2013). Do cd, Cu, Ni, Pb, and zn biomagnify in aquatic ecosystems? Rev. Environ. Contamination Toxicol. 226, 101–122. doi: 10.1007/978-1-4614-6898-1_4
Carić H., Cukrov N., Omanović D. (2021). Nautical tourism in marine protected areas (MPAs): Evaluating an impact of copper emission from antifouling coating. Sustainability 13 (21), 11897. doi: 10.3390/su132111897
Chretien A. R. N. (1997). Geochemical behaviour, fate and impacts of Cu, cd and zn from mine effluent discharges in Howe sound (Vancouver (BC: University of British Columbia). doi: 10.14288/1.0053151
Coble P. G. (2007). Marine optical biogeochemistry: the chemistry of ocean color. Chem. Rev. 107 (2), 402–418. doi: 10.1021/cr050350+
Croot P. L. (2003). Seasonal cycle of copper speciation in gullmar fjord, Sweden. Limnol. Oceanogr. 48 (2), 764–776. doi: 10.4319/lo.2003.48.2.0764
Croot P. L., Moffett J. W., Brand L. E. (2000). Production of extracellular Cu complexing ligands by eucaryotic phytoplankton in response to Cu stress. Limnol. Oceanogr. 45 (3), 619–627. doi: 10.4319/lo.2000.45.3.0619
Cutter G. A. (1991). Trace elements in estuarine and coastal waters-US studies from 1986–1990. Rev. Geophys. 29 (S2), 639–644. doi: 10.1002/rog.1991.29.s2.639
DeForest D. K., Brix K. V., Adams W. J. (2007). Assessing metal bioaccumulation in aquatic environments: the inverse relationship between bioaccumulation factors, trophic transfer factors and exposure concentration. Aquat. Toxicol. 84 (2), 236–246. doi: 10.1016/j.aquatox.2007.02.022
Dryden C. L., Gordon A. S., Donat J. R. (2007). Seasonal survey of copper-complexing ligands and thiol compounds in a heavily utilized, urban estuary: Elizabeth river, Virginia. Mar. Chem. 103 (3-4), 276–288. doi: 10.1016/j.marchem.2006.09.003
Dulaquais G., Waeles M., Breitenstein J., Knoery J., Riso R. (2020). Links between size fractionation, chemical speciation of dissolved copper and chemical speciation of dissolved organic matter in the Loire estuary. Environ. Chem. 17 (5), 385–399. doi: 10.1071/EN19137
Dupont C. L., Ahner B. A. (2005). Effects of copper, cadmium, and zinc on the production and exudation of thiols by emiliania huxleyi. Limnol. Oceanogr. 50 (2), 508–515. doi: 10.4319/lo.2005.50.2.0508
Dupont C. L., Nelson R. K., Bashir S., Moffett J. W., Ahner B. A. (2004). Novel copper-binding and nitrogen-rich thiols produced and exuded by emiliania huxleyi. Limnol. Oceanogr. 49 (5), 1754–1762. doi: 10.4319/lo.2004.49.5.1754
Flores Ruiz B. I. (2020). Zooplankton trace metal accumulation in the strait of Georgia: Trends, sources and insight (Vancouver (BC: University of British Columbia). doi: 10.14288/1.0394582
Follows M. J., Dutkiewicz S., Grant S., Chisholm S. W. (2007). Emergent biogeography of microbial communities in a model ocean. science 315 (5820), 1843–1846. doi: 10.1126/science.1138544
Genovese C., Grotti M., Ardini F., Wuttig K., Vivado D., Cabanes D., et al. (2022). Effect of salinity and temperature on the determination of dissolved iron-binding organic ligands in the polar marine environment. Mar. Chem. 238, 104051. doi: 10.1016/j.marchem.2021.104051
GEOTRACES (2017) Sampling and sample-handling protocols for GEOTRACES cruises cookbook, version 3.0. Available at: https://www.geotraces.org/methods-cookbook/ (Accessed August 2017).
Gerringa L. J. A., Herman P. M. J., Poortvliet T. C. W. (1995). Comparison of the linear van den Berg/Ružić transformation and a non-linear fit of the langmuir isotherm applied to Cu speciation data in the estuarine environment. Mar. Chem. 48 (2), 131–142. doi: 10.1016/0304-4203(94)00041-B
Gerringa L. J., Rijkenberg M. J., Thuróczy C. E., Maas L. R. (2014). A critical look at the calculation of the binding characteristics and concentration of iron complexing ligands in seawater with suggested improvements. Environ. Chem. 11 (2), 114–136. doi: 10.1071/EN13072
Glass J. B., Orphan V. J. (2012). Trace metal requirements for microbial enzymes involved in the production and consumption of methane and nitrous oxide. Front. Microbiol. 3. doi: 10.3389/fmicb.2012.00061
Gledhill M., Nimmo M., Hill S. J., Brown M. T. (1999). The release of copper-complexing ligands by the brown alga fucus vesiculosus (Phaeophyceae) in response to increasing total copper levels. J. Phycol. 35 (3), 501–509. doi: 10.1046/j.1529-8817.1999.3530501.x
Gonzalez-Davila M., Santana-Casiano J. M., Perez-Pena J., Millero F. J. (1995). Binding of Cu (II) to the surface and exudates of the alga dunaliella tertiolecta in seawater. Environ. Sci. Technol. 29 (2), 289–301. doi: 10.1021/es00002a004
Gordon A. S., Donat J. R., Kango R. A., Dyer B. J., Stuart L. M. (2000). Dissolved copper-complexing ligands in cultures of marine bacteria and estuarine water. Mar. Chem. 70 (1-3), 149–160. doi: 10.1016/S0304-4203(00)00019-0
Government of Canada (2022) Fraser River (Main arm) at Gravesend reach - buoy (BC08MH0453). Available at: https://aquatic.pyr.ec.gc.ca/WQMSDOnlineNationalData2019/en/Variables/Index/BC08MH0453 (Accessed May 1, 2022).
Government of Canada, Ministry of Environment & Climate Change -Water Protection & Sustainability Branch Strategy (2019) The British Columbia approved water quality guidelines: Aquatic life, wildlife & agriculture. Available at: https://www2.gov.bc.ca/assets/gov/environment/air-land-water/water/waterquality/water-quality-guidelines/approved-wqgs/wqg_summary_aquaticlife_wildlife_agri.pdf (Accessed April 10, 2020).
Guo J., Annett A. L., Taylor R. L., Lapi S., Ruth T. J., Maldonado M. T. (2010). Copper-uptake kinetics of coastal and oceanic diatoms 1. J. Phycol. 46 (6), 1218–1228. doi: 10.1111/j.1529-8817.2010.00911.x
Halverson M. J., Pawlowicz R. (2008). Estuarine forcing of a river plume by river flow and tides. J. Geophys. Res.: Oceans 113, C9. doi: 10.1029/2008JC004844
Heller M. I., Wuttig K., Croot P. L. (2016). Identifying the sources and sinks of CDOM/FDOM across the Mauritanian shelf and their potential role in the decomposition of superoxide (O 2-). Front. Mar. Sci. 3. doi: 10.3389/fmars.2016.00132
Helms J. R., Stubbins A., Perdue E. M., Green N. W., Chen H., Mopper K. (2013). Photochemical bleaching of oceanic dissolved organic matter and its effect on absorption spectral slope and fluorescence. Mar. Chem. 155, 81–91. doi: 10.1016/j.marchem.2013.05.015
Higgins H. W., Wright S. W., Schluter L. (2011). “Quantitative interpretation of chemotaxonomic pigment data, phytoplankton pigments: Characterization, chemotaxonomy and applications,” in Phytoplankton pigments: characterization, chemotaxonomy and applications in oceanography. Eds. Roy S., Llewellyn C. A., Egeland E. S., Johnsen G. (New York: Cambridge University Press), 257–313. doi: 10.1017/CBO9780511732263
Hollister A. P., Whitby H., Seidel M., Lodeiro P., Gledhill M., Koschinsky A. (2021). Dissolved concentrations and organic speciation of copper in the Amazon river estuary and mixing plume. Mar. Chem. 234, 104005. doi: 10.1016/j.marchem.2021.104005
Illuminati S., Annibaldi A., Truzzi C., Tercier-Waeber M. L., Nöel S., Braungardt C. B., et al. (2019). In-situ trace metal (Cd, Pb, Cu) speciation along the po river plume (Northern Adriatic Sea) using submersible systems. Mar. Chem. 212, 47–63. doi: 10.1016/j.marchem.2019.04.001
Jackson S. L., Spence J., Janssen D. J., Ross A. R. S., Cullen J. T. (2018). Determination of Mn, fe, Ni, Cu, zn, cd and Pb in seawater using offline extraction and triple quadrupole ICP-MS/MS. J. Anal. Atomic Spectrom. 33 (2), 304–313. doi: 10.1039/C7JA00237H
Jarníková T., Olson E. M., Allen S. E., Ianson D., Suchy K. D. (2022). A clustering approach to determine biophysical provinces and physical drivers of productivity dynamics in a complex coastal sea. Ocean Sci., 18, 1451–1475. doi: 10.5194/os-18-1451-2022
Johannessen S. C., Masson D., Macdonald R. W. (2006). Distribution and cycling of suspended particles inferred from transmissivity in the strait of Georgia, haro strait and Juan de fuca strait. Atmosphere-Ocean 44 (1), 17–27. doi: 10.3137/ao.440102
Johannessen S. C., Macdonald R. W., Burd B., van Roodselaar A., Bertold S. (2015). Local environmental conditions determine the footprint of municipal effluent in coastal waters: A case study in the strait of Georgia, British Columbia. Sci. Total Environ. 508, 228–239. doi: 10.1016/j.scitotenv.2014.11.096
Jolliffe I. T. (1990). Principal component analysis: a beginner's guide–i. introduction and application. Weather 45 (10), 375–382. doi: 10.1002/j.1477-8696.1990.tb05558.x
Kagaya S., Inoue Y. (2014). Chelating materials immobilizing carboxymethylated pentaethylenehexamine and polyethyleneimine as ligands. Anal. Sci. 30 (1), 35–42. doi: 10.2116/analsci.30.35
Karvelas M., Katsoyiannis A., Samara C. (2003). Occurrence and fate of heavy metals in the wastewater treatment process. Chemosphere 53 (10), 1201–1210. doi: 10.1016/S0045-6535(03)00591-5
Katsoyiannis A., Samara C. (2007). The fate of dissolved organic carbon (DOC) in the wastewater treatment process and its importance in the removal of wastewater contaminants. Environ. Sci. pollut. Res International 14 (5), 284–292. doi: 10.1065/espr2006.05.302
Kim H. J., Galeva N., Larive C. K., Alterman M., Graham D. W. (2005). Purification and physical– chemical properties of methanobactin: A chalkophore from methylosinus trichosporium OB3b. Biochemistry 44 (13), 5140–5148. doi: 10.1021/bi047367r
Kirk J. T. (1994). Light and photosynthesis in aquatic ecosystems (United Kingdom: Cambridge University Press).
Knepel K., Bogren K. (2008). Determination of orthophosphate by flow injection analysis. QuikChem method 31-115-01-1-H (Loveland, Colorado: Lachat Instruments).
Kogut M. B., Voelker B. M. (2001). Strong copper-binding behavior of terrestrial humic substances in seawater. Environ. Sci. Technol. 35 (6), 1149–1156. doi: 10.1021/es0014584
Kogut M. B., Voelker B. M. (2003). Kinetically inert Cu in coastal waters. Environ. Sci. Technol. 37 (3), 509–518. doi: 10.1021/es020723d
Kuang C. (2019). The biogeochemical cycling and anthropogenic inputs of cadmium and silver in the strait of Georgia, British Columbia (Vancouver (BC: University of British Columbia). doi: 10.14288/1.0387034
Kunz A., Jardim W. F. (2000). Complexation and adsorption of copper in raw sewage. Water Res. 34 (7), 2061–2068. doi: 10.1016/S0043-1354(99)00347-4
Lagerström M. E., Field M. P., Séguret M., Fischer L., Hann S., Sherrell R. M. (2013). Automated on-line flow-injection ICP-MS determination of trace metals (Mn, fe, Co, Ni, Cu and zn) in open ocean seawater: Application to the GEOTRACES program. Mar. Chem. 155, 71–80. doi: 10.1016/j.marchem.2013.06.001
Laglera L. M., Battaglia G., van den Berg C. M. (2007). Determination of humic substances in natural waters by cathodic stripping voltammetry of their complexes with iron. Analytica Chimica Acta 599 (1), 58–66. doi: 10.1016/j.aca.2007.07.059
Laglera L. M., Tovar-Sánchez A. (2012). Direct recognition and quantification by voltammetry of thiol/thioamide mixes in seawater. Talanta 89, 496–504. doi: 10.1016/j.talanta.2011.12.075
Laglera L. M., van den Berg C. M. (2003). Copper complexation by thiol compounds in estuarine waters. Mar. Chem. 82 (1-2), 71–89. doi: 10.1016/S0304-4203(03)00053-7
Laglera L. M., van den Berg C. M. (2006). Photochemical oxidation of thiols and copper complexing ligands in estuarine waters. Mar. Chem. 101 (1-2), 130–140. doi: 10.1016/j.marchem.2006.01.006
Leal M. F. C., Vasconcelos M. T. S., van den Berg C. M. (1999). Copper-induced release of complexing ligands similar to thiols by emiliania huxleyi in seawater cultures. Limnol. Oceanogr. 44 (7), 1750–1762. doi: 10.4319/lo.1999.44.7.1750
Li M., Gargett A., Denman K. (2000). What determines seasonal and interannual variability of phytoplankton and zooplankton in strongly estuarine systems? application to the semienclosed estuary of strait of Georgia and Juan de fuca strait. Estuarine Coast. Shelf Sci. 50 (4), 467–488. doi: 10.1006/ecss.2000.0593
Little S. H., Vance D., Siddall M., Gasson E. (2013). A modeling assessment of the role of reversible scavenging in controlling oceanic dissolved Cu and zn distributions. Global Biogeochem. Cycles 27 (3), 780–791. doi: 10.1002/gbc.20073
Loiselle S. A., Bracchini L., Dattilo A. M., Ricci M., Tognazzi A., Cózar A., et al. (2009). The optical characterization of chromophoric dissolved organic matter using wavelength distribution of absorption spectral slopes. Limnol. Oceanogr. 54 (2), 590–597. doi: 10.4319/lo.2009.54.2.0590
Mackey M. D., Mackey D. J., Higgins H. W., Wright S. W. (1996). CHEMTAX-a program for estimating class abundances from chemical markers: application to HPLC measurements of phytoplankton. Mar. Ecol. Prog. Ser. 144, 265–283. doi: 10.3354/meps144265
Maldonado M. T., Allen A. E., Chong J. S., Lin K., Leus D., Karpenko N., et al. (2006). Copper-dependent iron transport in coastal and oceanic diatoms. Limnol. Oceanogr. 51 (4), 1729–1743. doi: 10.4319/lo.2006.51.4.1729
Maldonado M. T., Hughes M. P., Rue E. L., Wells M. L. (2002). The effect of fe and Cu on growth and domoic acid production by pseudo-nitzschia multiseries and pseudo-nitzschia australis. Limnol. Oceanogr. 47 (2), 515–526. doi: 10.4319/lo.2002.47.2.0515
Manahan S. E., Smith M. J. (1973). Copper micronutrient requirement for algae. Environ. Sci. Technol. 7 (9), 829–833. doi: 10.1021/es60081a013
Mangiameli P., Chen S. K., West D. (1996). A comparison of SOM neural network and hierarchical clustering methods. Eur. J. Operational Res. 93 (2), 402–417. doi: 10.1016/0377-2217(96)00038-0
Mann E. L., Ahlgren N., Moffett J. W., Chisholm S. W. (2002). Copper toxicity and cyanobacteria ecology in the Sargasso Sea. Limnol. Oceanogr. 47 (4), 976–988. doi: 10.4319/lo.2002.47.4.0976
Mantoura R. F. C., Riley J. P. (1975). The use of gel filtration in the study of metal binding by humic acids and related compounds. Analytica Chimica Acta 78 (1), 193–200. doi: 10.1016/S0003-2670(01)84765-6
Masson D. (2002). Deep water renewal in the strait of Georgia. Estuarine Coast. Shelf Sci. 54 (1), 115–126. doi: 10.1006/ecss.2001.0833
Masson D., Perry R. I. (2013). The strait of Georgia ecosystem research initiative: an overview. Prog. Oceanogr. 115, 1–5. doi: 10.1016/j.pocean.2013.05.009
McCormack P., Worsfold P. J., Gledhill M. (2003). Separation and detection of siderophores produced by marine bacterioplankton using high-performance liquid chromatography with electrospray ionization mass spectrometry. Anal. Chem. 75 (11), 2647–2652. doi: 10.1021/ac0340105
Metro Vancouver (2018) The 2018 greater Vancouver sewerage and drainage district environmental management and quality control annual report. Available at: http://www.metrovancouver.org/services/liquid-waste/LiquidWastePublications/2018GVSDD-EMQCAnnualReport.pdf (Accessed April 10, 2020).
Miao A. J., Wang W. X., Juneau P. (2005). Comparison of cd, Cu, and zn toxic effects on four marine phytoplankton by pulse-amplitude-modulated fluorometry. Environ. Toxicol. Chemistry: Int. J. 24 (10), 2603–2611. doi: 10.1897/05-009R.1
Moffett J. W., Brand L. E. (1996). Production of strong, extracellular Cu chelators by marine cyanobacteria in response to Cu stress. Limnol. Oceanogr. 41 (3), 388–395. doi: 10.4319/lo.1996.41.3.0388
Moffett J. W., Brand L. E., Croot P. L., Barbeau K. A. (1997). Cu Speciation and cyanobacterial distribution in harbors subject to anthropogenic Cu inputs. Limnol. Oceanogr. 42, 789–799. doi: 10.4319/lo.1997.42.5.0789
Moriyasu R., Moffett J. W. (2022). Determination of inert and labile copper on GEOTRACES samples using a novel solvent extraction method. Mar. Chem. 239, 104073. doi: 10.1016/j.marchem.2021.104073
Muller F. L., Batchelli S. (2013). Copper binding by terrestrial versus marine organic ligands in the coastal plume of river thurso, north Scotland. Estuar. Coast. Shelf Sci. 133, 137–146. doi: 10.1016/j.ecss.2013.08.024
Ndungu K. (2012). Model predictions of copper speciation in coastal water compared to measurements by analytical voltammetry. Environ. Sci. Technol. 46 (14), 7644–7652. doi: 10.1021/es301017x
Nixon R. L., Ross A. R. (2016). Evaluation of immobilized metal-ion affinity chromatography and electrospray ionization tandem mass spectrometry for recovery and identification of copper (II)-binding ligands in seawater using the model ligand 8-hydroxyquinoline. Front. Mar. Sci. 3. doi: 10.3389/fmars.2016.00246
Omanović D., Garnier C., Pižeta I. (2015). ProMCC: an all-in-one tool for trace metal complexation studies. Mar. Chem. 173, 25–39. doi: 10.1016/j.marchem.2014.10.011
Osburn C. L., Boyd T. J., Montgomery M. T., Bianchi T. S., Coffin R. B., Paerl H. W. (2016). Optical proxies for terrestrial dissolved organic matter in estuaries and coastal waters. Front. Mar. Sci. 2. doi: 10.3389/fmars.2015.00127
Palenik B., Morel F. M. (1991). Amine oxidases of marine phytoplankton. Appl. Environ. Microbiol. 57 (8), 2440–2443. doi: 10.1128/aem.57.8.2440-2443.1991
Pawlowicz R. (2020) M_Map: A mapping package for MATLAB", version 1.4m. Available at: https://www.eoas.ubc.ca/~rich/map.html (Accessed March 12, 2020).
Pawlowicz R., Hannah C., Rosenberger A. (2019). Lagrangian Observations of estuarine residence times, dispersion, and trapping in the salish Sea. Estuar. Coast. Shelf Sci. 225, 106246. doi: 10.1016/j.ecss.2019.106246
Pawlowicz R., Riche O., Halverson M. (2007). The circulation and residence time of the strait of Georgia using a simple mixing-box approach. Atmosphere-Ocean 45 (4), 173–193. doi: 10.3137/ao.450401
Peers G., Price N. M. (2006). Copper-containing plastocyanin used for electron transport by an oceanic diatom. Nature 441 (7091), 341–344. doi: 10.1038/nature04630
Peers G., Quesnel S. A., Price N. M. (2005). Copper requirements for iron acquisition and growth of coastal and oceanic diatoms. Limnol. Oceanogr. 50 (4), 1149–1158. doi: 10.4319/lo.2005.50.4.1149
Pižeta I., Sander S. G., Hudson R. J. M., Omanović D., Baars O., Barbeau K. A., et al. (2015). Interpretation of complexometric titration data: An intercomparison of methods for estimating models of trace metal complexation by natural organic ligands. Mar. Chem. 173, 3–24. doi: 10.1016/j.marchem.2015.03.006
Posacka A. M., Semeniuk D. M., Whitby H., van den Berg C. M., Cullen J. T., Orians K., et al. (2017). Dissolved copper (dCu) biogeochemical cycling in the subarctic northeast pacific and a call for improving methodologies. Mar. Chem. 196, 47–61. doi: 10.1016/j.marchem.2017.05.007
Quigg A., Reinfelder J. R., Fisher N. S. (2006). Copper uptake kinetics in diverse marine phytoplankton. Limnol. Oceanogr. 51 (2), 893–899. doi: 10.4319/lo.2006.51.2.0893
Ransberry V. E., Morash A. J., Blewett T. A., Wood C. M., McClelland G. B. (2015). Oxidative stress and metabolic responses to copper in freshwater-and seawater-acclimated killifish, fundulus heteroclitus. Aquat. Toxicol. 161, 242–252. doi: 10.1016/j.aquatox.2015.02.013
Rijstenbil J. W., Gerringa L. J. A. (2002). Interactions of algal ligands, metal complexation and availability, and cell responses of the diatom ditylum brightwellii with a gradual increase in copper. Aquat. Toxicol. 56 (2), 115–131. doi: 10.1016/S0166-445X(01)00188-6
Ross A. R., Ikonomou M. G., Orians K. J. (2003). Characterization of copper-complexing ligands in seawater using immobilized copper (II)-ion affinity chromatography and electrospray ionization mass spectrometry. Mar. Chem. 83 (1-2), 47–58. doi: 10.1016/S0304-4203(03)00095-1
Ruacho A., Bundy R. M., Till C. P., Roshan S., Wu J., Barbeau K. A. (2020). Organic dissolved copper speciation across the US GEOTRACES equatorial pacific zonal transect GP16. Mar. Chem. 225, 103841. doi: 10.1016/j.marchem.2020.103841
Ružić I. (1982). Theoretical aspects of the direct titration of natural waters and its information yield for trace metal speciation. Analytica Chimica Acta 140 (1), 99–113. doi: 10.1016/S0003-2670(01)95456-X
Santos-Echeandía J., Caetano M., Laglera L. M., Vale C. (2013). Salt-marsh areas as copper complexing ligand sources to estuarine and coastal systems. Chemosphere 90 (2), 772–781. doi: 10.1016/j.chemosphere.2012.09.074
Scatchard G. (1949). The attractions of proteins for small molecules and ions. Ann. New York Acad. Sci. 51 (4), 660–672. doi: 10.1111/j.1749-6632.1949.tb27297.x
Sedlak D. L., Phinney J. T., Bedsworth W. W. (1997). Strongly complexed Cu and Ni in wastewater effluents and surface runoff. Environ. Sci. Technol. 31 (10), 3010–3016. doi: 10.1021/es970271i
Semeniuk D. M., Bundy R. M., Payne C. D., Barbeau K. A., Maldonado M. T. (2015). Acquisition of organically complexed copper by marine phytoplankton and bacteria in the northeast subarctic pacific ocean. Mar. Chem. 173, 222–233. doi: 10.1016/j.marchem.2015.01.005
Shank G. C., Skrabal S. A., Whitehead R. F., Kieber R. J. (2004). Strong copper complexation in an organic-rich estuary: the importance of allochthonous dissolved organic matter. Mar. Chem. 88 (1-2), 21–39. doi: 10.1016/j.marchem.2004.03
Smith P., Bogren K. (2003). Determination of nitrate and/or nitrite in brackish or seawater by flow injection analysis colorimetry. QuikChem method 31-107-04-1-E (Loveland, Colorado: Lachat Instruments).
Sonnewald M., Dutkiewicz S., Hill C., Forget G. (2020). Elucidating ecological complexity: Unsupervised learning determines global marine eco-provinces. Sci. Adv. 6 (22), eaay4740. doi: 10.1126/sciadv.aay4740
Stuart R. K., Dupont C. L., Johnson D. A., Paulsen I. T., Palenik B. (2009). Coastal strains of marine synechococcus species exhibit increased tolerance to copper shock and a distinctive transcriptional response relative to those of open-ocean strains. Appl. Environ. Microbiol. 75 (15), 5047–5057. doi: 10.1128/AEM.00271-09
Sunda W. G., Tester P. A., Huntsman S. A. (1987). Effects of cupric and zinc ion activities on the survival and reproduction of marine copepods. Mar. Biol. 94 (2), 203–210. doi: 10.1007/BF00392932
Sun Q., Little C. M., Barthel A. M., Padman L. (2021). A clustering-based approach to ocean model–data comparison around Antarctica. Ocean Sci. 17 (1), 131–145. doi: 10.5194/os-17-131-2021
Tang D., Warnken K. W., Santschi P. H. (2001). Organic complexation of copper in surface waters of Galveston bay. Limnol. Oceanogr. 46 (2), 321–330. doi: 10.4319/lo.2001.46.2.0321
Taylor A. G., Landry M. R., Freibott A., Selph K. E., Gutiérrez-Rodríguez A. (2016). Patterns of microbial community biomass, composition and HPLC diagnostic pigments in the Costa Rica upwelling dome. J. Plankton Res. 38 (2), 183–198. doi: 10.1093/plankt/fbv086
Thomas D. J., Grill E. V. (1977). The effect of exchange reactions between Fraser river sediment and seawater on dissolved Cu and zn concentrations in the strait of Georgia. Estuar. Coast. Mar. Sci. 5 (3), 421–427. doi: 10.1016/0302-3524(77)90066-4
Thomson R. E. (1981). Oceanography of the British Columbia coast: Canadian special publication of fisheries and oceans 56 (Ottawa: Department of Fisheries and Oceans).
Tucker S. (2010). Determination of silicate in brackish or seawater by flow injection analysis. QuikChem method 31-114-27-2-A (Loveland, Colorado: Lachat Instruments).
van den Berg C. M. G. Speciation.xls (Liverpool University). Available at: https://www.liverpool.ac.uk/~sn35/Documents/Speciation.xls (Accessed May 2017).
van den Berg C. M. G. (1982). Determination of copper complexation with natural organic ligands in seawater by equilibration with MnO2 i. theory. Mar. Chem. 11 (4), 307–322. doi: 10.1016/0304-4203(82)90028-7
van den Berg C. M. (1995). Evidence for organic complexation of iron in seawater. Mar. Chem. 50 (1-4), 139–157. doi: 10.1016/0304-4203(95)00032-M
van den Berg C. M., Donat J. R. (1992). Determination and data evaluation of copper complexation by organic ligands in sea water using cathodic stripping voltammetry at varying detection windows. Analytica Chimica Acta 257 (2), 281–291. doi: 10.1016/0003-2670(92)85181-5
van den Berg C. M., Merks A. G., Duursma E. K. (1987). Organic complexation and its control of the dissolved concentrations of copper and zinc in the scheldt estuary. Estuarine Coast. Shelf Sci. 24 (6), 785–797. doi: 10.1016/0272-7714(87)90152-1
Voelker B. M., Kogut M. B. (2001). Interpretation of metal speciation data in coastal waters: the effects of humic substances on copper binding as a test case. Mar. Chem. 74 (4), 303–318. doi: 10.1016/S0304-4203(01)00022-6
Walsh M. J., Goodnow S. D., Vezeau G. E., Richter L. V., Ahner B. A. (2015). Cysteine enhances bioavailability of copper to marine phytoplankton. Environ. Sci. Technol. 49 (20), 12145–12152. doi: 10.1021/acs.est.5b02112
Wang C., Pawlowicz R., Sastri A. R. (2019). Diurnal and seasonal variability of near-surface oxygen in the strait of Georgia. J. Geophys. Res.: Oceans 124 (4), 2418–2439. doi: 10.1029/2018JC014766
Ward J. H. Jr. (1963). Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 58 (301), 236–244. doi: 10.1080/01621459.1963.10500845
Whitby H. (2016). Identifying the factors affecting copper speciation in estuarine, coastal, and open ocean waters (Liverpool (England: University of Liverpool). doi: 10.17638/03003336
Whitby H., Posacka A. M., Maldonado M. T., van den Berg C. M. (2018). Copper-binding ligands in the NE pacific. Mar. Chem. 204, 36–48. doi: 10.1016/j.marchem.2018.05.008
Whitby H., van den Berg C. M. (2015). Evidence for copper-binding humic substances in seawater. Mar. Chem. 173, 282–290. doi: 10.1016/j.marchem.2014.09.011
Wilks D. S. (2019). “Chapter 16–cluster analysis,” in Statistical methods in the atmospheric sciences (Fourth edition) (Amsterdam, Netherlands: Elsevier), 721–738. doi: 10.1016/C2017-0-03921-6
Wishart D. (1969). Note: An algorithm for hierarchical classifications. Biometrics 25, 165–170. doi: 10.2307/2528688
Wong K. H., Obata H., Kim T., Mashio A. S., Fukuda H., Ogawa H. (2018). Organic complexation of copper in estuarine waters: An assessment of the multi-detection window approach. Mar. Chem. 204, 144–151. doi: 10.1016/j.marchem.2018.07.001
Xue H., Sunda W. G. (1997). Comparison of [Cu2+] measurements in lake water determined by ligand exchange and cathodic stripping voltammetry and by ion-selective electrode. Environ. Sci. Technol. 31 (7), 1902–1909. doi: 10.1021/es960551i
Keywords: copper speciation, trace metals, organic ligands, estuary, Strait of Georgia, hierarchical clustering, copper
Citation: Waugh L-jC, Flores Ruiz I, Kuang C, Guo J, Cullen JT and Maldonado MT (2022) Seasonal dissolved copper speciation in the Strait of Georgia, British Columbia, Canada. Front. Mar. Sci. 9:983763. doi: 10.3389/fmars.2022.983763
Received: 01 July 2022; Accepted: 04 October 2022;
Published: 03 November 2022.
Edited by:
Johan Schijf, University of Maryland, College ParkReviewed by:
Luis Miguel Laglera, University of the Balearic Islands, SpainPeter Leslie Croot, National University of Ireland Galway, Ireland
Darlo Omanović, Rudjer Boskovic Institute, Croatia
Copyright © 2022 Waugh, Flores Ruiz, Kuang, Guo, Cullen and Maldonado. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lori-jon C. Waugh, bHdhdWdoQGVvYXMudWJjLmNh
 Lori-jon C. Waugh
Lori-jon C. Waugh Iselle Flores Ruiz
Iselle Flores Ruiz Cheng Kuang
Cheng Kuang Jian Guo
Jian Guo Jay T. Cullen
Jay T. Cullen Maria T. Maldonado
Maria T. Maldonado