- 1Department of Marine Environment and Engineering, The Center for Water Resources Studies, National Sun Yat-Sen University, Kaohsiung, Taiwan
- 2Marine Science and Information Research Center, National Academy of Marine Research, Kaohsiung, Taiwan
In this paper, we study the particle dynamics of nonlinear flexural-gravity waves propagating in a finite water depth, which is the interaction between ice sheets and water flows. The nonlinear deformation of a floating elastic sheet is modeled by the Cosserat shell theory. The theoretical analysis is performed by a uniform asymptotic perturbation expansion. A third-order explicit parametric solution of particle trajectories in Lagrangian coordinates is presented. Taking the time average of particle motion, the mass transport velocity and the Lagrangian surface setup are also derived. Numerical simulations are computed. The influences of flexural rigidity on the water particle orbits and the mass transport velocity of nonlinear flexural-gravity waves are first discussed.
Introduction
The study of the flexural-gravity wave problem has important contributions to floating ice sheet, climate change, and engineering applications such as manmade floating structures in polar oceans. Such hydroelastic waves have been measured in many cold regions of the Arctic (Squire and Moore, 1980; Wadhams and Holt, 1991; Squire et al., 1995). A variety of linear and nonlinear elastic sheet models are used according to the proposed linear equation (Greenhill, 1886), the Kirchhoff–Love plate theory or Cosserat theory (Toland, 2007). Previously, the linear and nonlinear theoretical solutions as well as numerical simulations were developed to study the propagation of flexural-gravity waves and were compared with field investigations (Greenhill, 1916; Forbes, 1986; Marko, 2003; Vanden-Broeck and Părău, 2011; Gao et al., 2016; Gao et al., 2019). Toland (2008) further proved the existence of progressive flexural-gravity waves using a Lagrangian method.
There are fewer studies of the particle trajectories beneath the flexural-gravity waves. It is important to understand the transport mechanism of nonlinear water waves. Linearized solution patterns of flexural-gravity waves with uniform current have been presented in Ref (Bhattacharjee and Sahoo, 2007).. Wang et al. (Wang et al., 2020) calculated particle paths numerically for the fully nonlinear equations of flexural-gravity waves with constant vorticity. They studied the fluid particle motion based on integrating the water particle velocity derived by the Eulerian coordinates. This method was often used to trace the particle path and the steady streaming velocity on water waves (Stokes, 1847; Longuet-Higgins, 1953). However, the above studies cannot show some important properties of particle dynamics such as the Lagrangian wave period, a Lagrangian setup that is different from the wave properties in the Eulerian frameworks (Longuet-Higgins, 1986; Ng, 2004).
The first linear Lagrangian exact solution describing a flow of non-constant vorticity in water of infinite depth was presented by Gerstner (1802). Using a rigorous mathematical analysis, Constantin (2006) showed that the exact solution by Gerstner is dynamically possible. He then successfully extended Gerstner’s solution to the problem of edge and geophysical waves (Constantin, 2012a; Constantin, 2013). Chen and Hsu (2009) provided a method of modified Euler–Lagrange transformation to obtain the third-order approximation for the particle motion in nonlinear Stokes waves. Some asymptotic solutions for the nonlinear progressive or short-crested waves in the Lagrangian approach have been developed (Pierson, 1962; Buldakov et al., 2006; Clamond, 2007; Hsu et al., 2010; Chen et al., 2010; Chen and Chen, 2014). More recently, analytical solutions that provide a detailed mechanism of the water particle orbits for water waves were presented in Refs (Constantin and Villari, 2008; Constantin and Escher, 2011; Constantin, 2012b). These works proved that there exist open orbits in two-dimensional nonlinear irrotational and inviscid flows.
The focus of this work is to describe the particle dynamics in flexural-gravity waves in Lagrangian coordinates. To our knowledge, it has not been studied yet. We introduce the equations of motion together with their boundary conditions in Section 2. A Lindstedt–Poincare perturbation method used to obtain a third-order asymptotic parametric solution for the particle trajectories in the Lagrangian framework will be discussed in Section 3. In Section 4, we will analyze the particle trajectory, drift velocity, and Lagrangian surface setup of flexural-gravity waves under the influences of ice sheet thickness, water depth, and wave steepness. Finally, in Section 5, we give a short conclusion.
Formulations
We consider a two-dimensional irrotational, inviscid, and incompressible fluid for the steady finite-amplitude progressive flexural-gravity waves. The water depth h is finite with an impermeable bottom. The Cartesian coordinates are introduced where the x-axis is taken at the undisturbed ice sheet, and y is the upward positive vertical axis. The wave is periodic with the wave number k = 2π / L and wave frequency σw = 2π / Tw . Following Toland (Toland, 2007; Toland, 2008) and Wang et al. (2020), the nonlinear Cosserat model of hyperelastic sheets is used to express the deformation of floating ice sheets, which is assumed as
where p is the pressure across the elastic sheet, is the flexural rigidity, E is Young’s modulus, ν is Poisson’s ratio, d is the thickness of the ice sheet, κ is the curvature of the sheet, and s is the arc length. Since the thickness of the elastic sheet is small compared with the wavelength of the flexural wave, the sheet density is neglected in this paper.
In the Lagrangian coordinates, the mathematical description of fluid particle motion (x(a,b,t), y(a,b,t)) is expressed in two horizontal and vertical variables a and b labeling individual fluid particles at time t = 0, where the vertical label b = 0 corresponding to the free surface η and b = -h is on the impermeable sea bottom. For an incompressible and inviscid fluid, the continuity equation that sets the invariant condition on the total volume variation of a water particle in the Lagrangian framework is
Taking the partial differentiating Eq. (2.3) with respect to t yields
and the irrotational flow conditions are (Chen et al., 2010; Chen and Chen, 2014)
The Bernoulli equation (Chen et al., 2010; Chen and Chen, 2014) including the term of flexural rigidity of the elastic ice sheet in the Lagrangian description can be written as
where and κ = (xayaa − xaaya)/J3/2 .
The boundary conditions of zero pressure at the upper boundary and zero vertical velocity at the rigid and impermeable sea bed for water particles are
where the subscripts a, b, and t denote partial differentiation with respect to the specified variable; g is the constant gravitational acceleration; and ϕ (a, b, t) is a Lagrangian velocity potential function introduced by (2.4). Therefore, the governing equations and boundary conditions of two-dimensional irrotational progressive flexural-gravity water waves in the Lagrangian coordinates are established, which consist of the continuity equations (2.2) and (2.3), vorticity conservation equation (2.4), energy equation (2.5), dynamic boundary condition (2.6) under the sheet, and condition (2.8) at the bottom.
Asymptotic solutions
We used the Lindstedt–Poincare technique to solve the nonlinear boundary value equations (2.2)–(2.5) with boundary conditions (2.6) and (2.7) in the Lagrangian coordinates. Following Chen and Hsu (Chen et al., 2010) and Chen and Chen (2014), the solutions of the particle displacements x and y, the potential function ϕ , and the pressure p are sought in the power series as
where ϵ is an ordering parameter that is used to identify the order of the perturbation expansion. In these expressions, fn, gn, ϕn , and pn are the nth-order periodic harmonic function solutions. and are the non-periodic functions that are a function of time t. is related to the Lagrangian wave mean level and is a function of the vertical label b. σ = 2π / TL is the Lagrangian angular frequency of a particle reappearing at the same elevation where TL is the particle motion period. Substituting the power series functions (3.1)–(3.5) into (2.3)–(2.8), and equating the equal order terms of ϵ up to the third order, we obtain a recursive series of nonhomogeneous linear partial differential equations that can be solved successively.
First-order solution
At the first order ϵ , the governing equations (2.3)–(2.6) yield
Also, the dynamic free surface boundary condition and the bottom boundary condition give
From the continuity equation (3.6a) and the bottom boundary condition (3.6g), the first-order periodic solution can be obtained by the separation of variables. From (3.6b) to (3.6d) and avoiding the secular terms, the first-order analytical solution can be easily written in the form
where the parameter A represents the linear amplitude. Substituting (3.7)–(3.9) into (3.6e), we can get the wavenumber k satisfying the linear dispersion equation at the leading order
The linear dispersion relation in the Lagrangian coordinates is the same as that of the leading-order progressive flexural-gravity wave in the Eulerian approach (Wang et al., 2020). By setting b = 0 in (3.8), we can get the first-order free surface function in the Lagrangian coordinates.
Second-order solution
At the second order ϵ2 , we have the following set of governing equations:
and the boundary conditions are
eliminating the secular term yields σ1b = 0 and, hence, σ1 = w1 = constant . Solving for the other modes that satisfy the mass conservation equation (3.11a)–(3.11b) and the bottom boundary condition (3.11g), the second-order parametric equations of water particle trajectory can be expressed as periodic harmonic functions f2 and g2 in the horizontal and vertical coordinates
and non-periodic function and
Inserting the first-order solutions into the irrotational conditions (3.11c) and (3.11d) and eliminating the secular term, we can get αw1 + σ0β2111 = 0 . By integrating over the Lagrangian variables a or b to (3.11c) and (3.11d), the second-order Lagrangian velocity potential ϕ2 is obtained as
Substituting (3.16) and the first-order solution into the Bernoulli equation (3.11e) and applying (3.11f), we find the coefficients as
From the obtained asymptotic solution at the second-order approximation, the perturbation scheme is valid except for the singularity condition that the denominator β2 is zero. The second-order approximation is found to break down at and near the critical value, where this singularity condition occurs. It was first pointed out by Wilton (1915) for capillary waves.
Third-order solution
The continuity, irrotational, and energy equations up to order ϵ3 are as follows:
and the boundary conditions are
On substituting the first- and second-order solutions into (3.27a–e), the third-order analytical solutions of the particle trajectory and potential function can be assumed to have the following forms:
Using the dynamic boundary condition (3.27f) and neglecting the secular terms that grow with time, we can obtain the second-order correction of the Lagrangian wave frequency, which is
and two unknown coefficients β3 and γ3 , which are
The second-order correction term that only appears in the odd order asymptotic solution is different from the second-order wave frequency in the Eulerian coordinates obtained in Refs (Greenhill, 1886; Wang et al., 2020).. In Equation (3.31), the first term varies exponentially with the vertical particle label b and relative water depth, and the second term is the second-order Stokes wave frequency. Equations (3.28)–(3.33) are exactly the same as those of Chen et al. (2010) as flexural rigidity is neglected. The third-order approximation is found to break down as the denominator of β3 is zero.
Dinvay et al. (2019) discussed the dispersion relation for moving loads on ice sheets. In Figure 1, the variation of flexural-gravity wavenumber k with the Lagrangian wave frequency from the nonlinear dispersion relation (3.31) for different values of ice sheet thickness d is presented. It is shown that for constant ice sheet thickness, the wavenumber increases with a decreasing Lagrangian wave period. Furthermore, the wavenumber decreases with an increasing thickness of ice sheet.
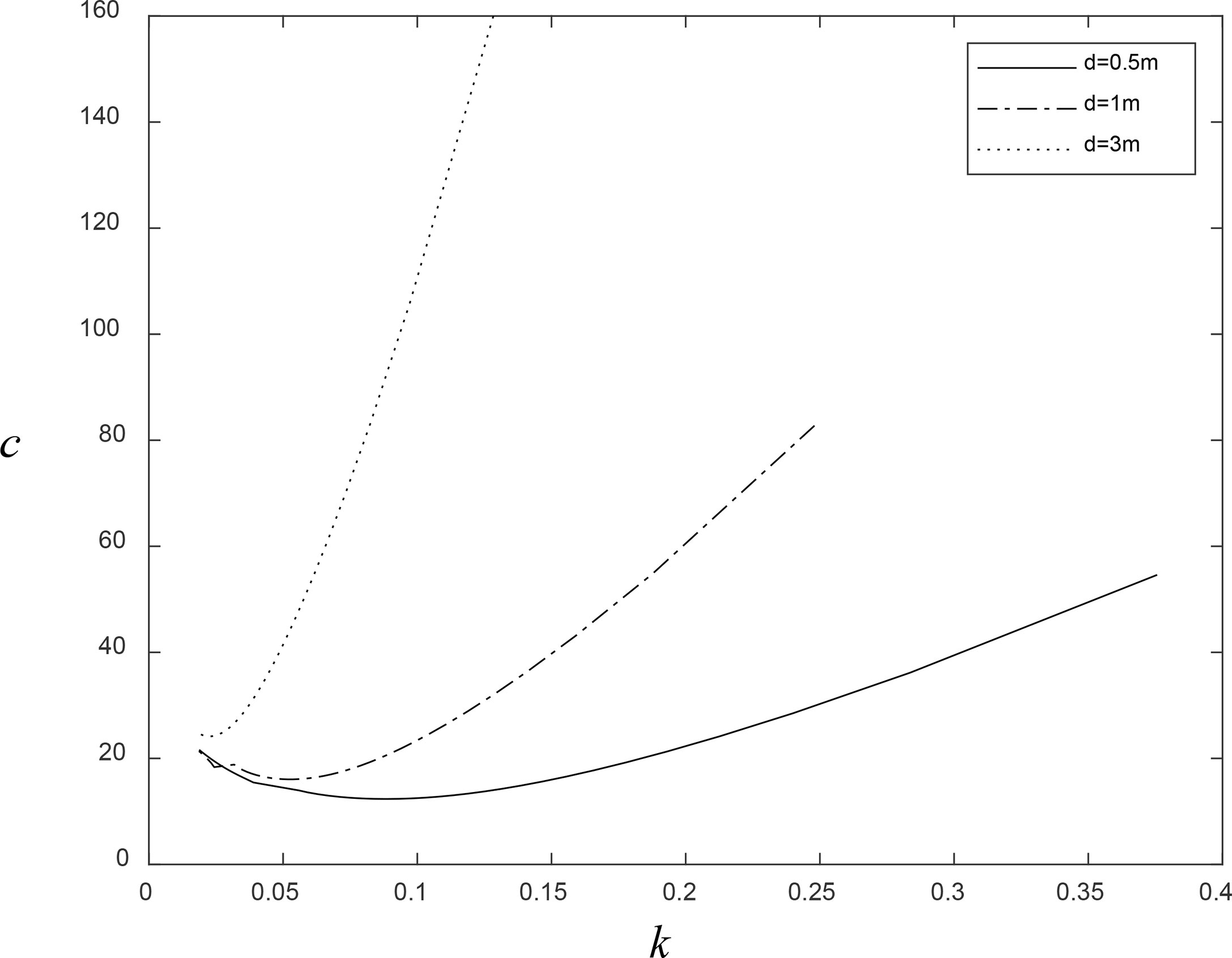
Figure 1 Nonlinear dispersion curve under various thicknesses of the ice sheet d = 0.5, 1, 3 m for water depth h = 100 m.
Computational results and discussion
The trajectory of water particles
The trajectories of particles can be directly derived from third-order parametric equations in the Lagrangian coordinates. In Figures 2A–D, the particle trajectories for progressive flexural-gravity waves are plotted at five vertical levels for two Lagrangian wave frequencies under various water depths and vertical levels b for the ice sheet thickness d = 1 m and wave period Tw = 10 s. It can be seen that the horizontal and vertical displacements of water particle trajectory are larger with the shallower water depth. The vertical excursion is larger than the horizontal counterpart for the particle orbit near the free surface for the shallow water depth. The particle trajectories show an open and spiraling curve in the direction of the wave propagation.
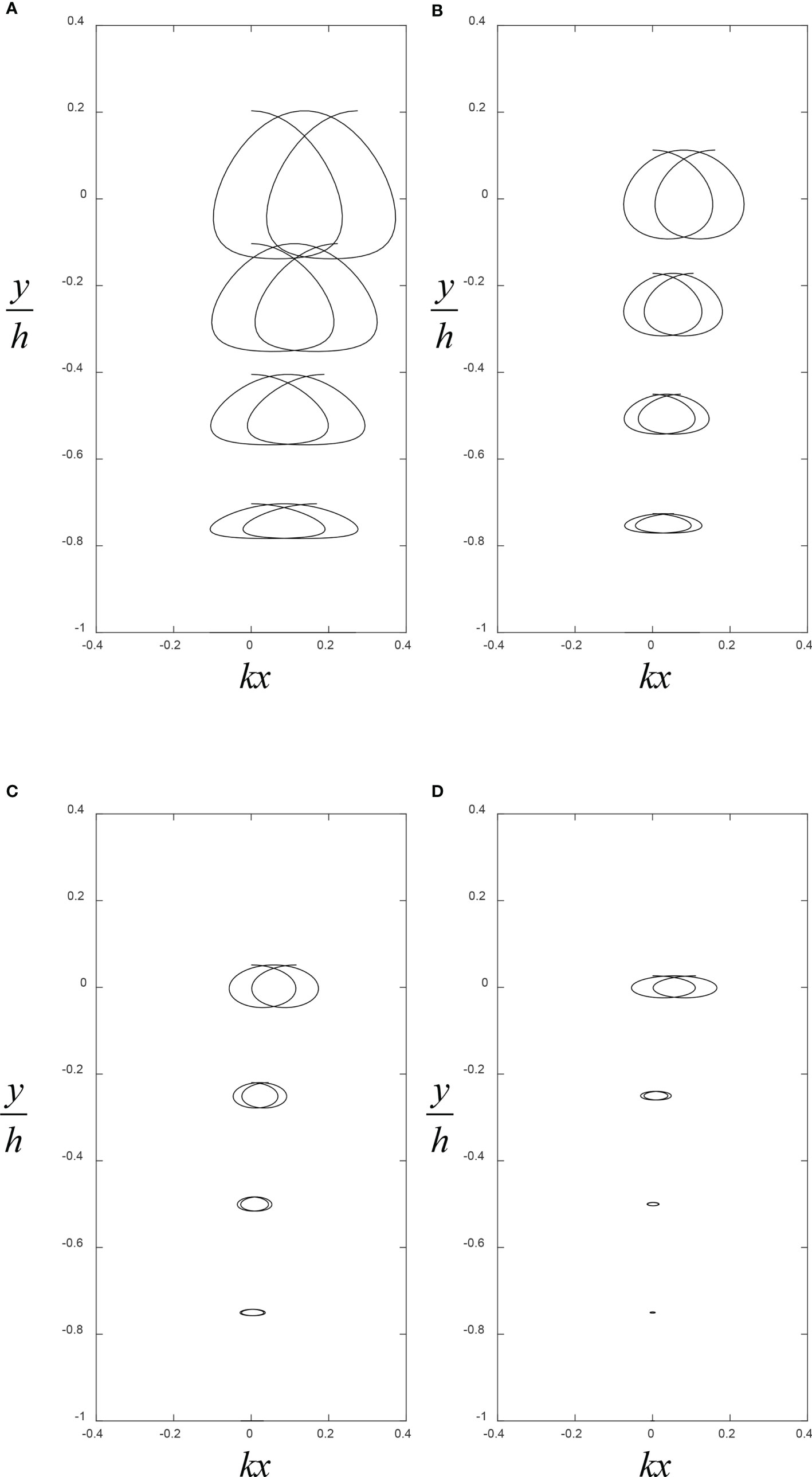
Figure 2 (A–D) The variation of third-order water particle trajectories at different vertical labels b for the thickness of the ice sheet d = 1 m under various water depths h = 10, 20, 50, 100 m.
In Figures 3A–D, the particle trajectories for nonlinear flexural-gravity waves in water depth h (=50 m) are plotted for various ice sheet thicknesses (d = 0,0.5,1,3 m) and vertical positions b. Figures 3A–D show the larger displacement amplitude of particle trajectories for the larger thickness (d = 3 m) of the ice sheet than the pure progressive gravity wave with d = 0. Increasing the thickness of the ice sheet is to increase the horizontal and vertical excursions traveled by water particles due to increasing the drift velocity. Overall, an increase in the thickness of the ice sheet and the material rigidity tends to increase the particle that moves along the orbit.
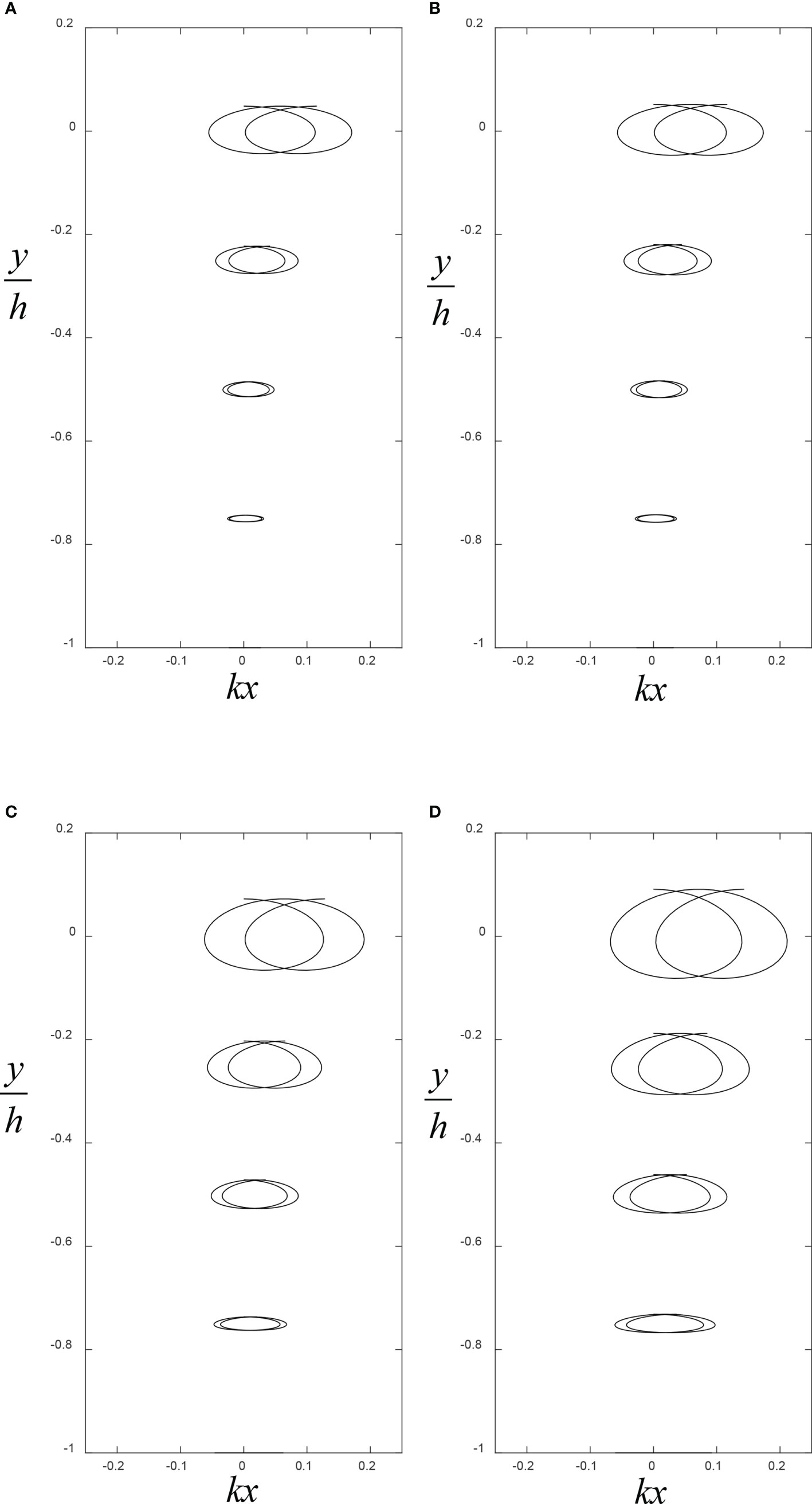
Figure 3 (A–D) The variation of third-order water particle trajectories at different vertical labels b for water depth h = 50 m under various thicknesses of the ice sheet d = 0, 0.5, 1, 3 m.
The drift velocity
In Section 3.2, we found that the mass transport velocity and the Lagrangian wave setup could be derived by taking the time average over one Lagrangian wave period to the horizontal and vertical parametric equations of the water particle that appears in the even order of our analytical solution. Taking the time average of the third-order approximation solution, the drift velocity and Lagrangian mean wave level over the whole range of depths can be obtained as follows:
Figure 4 shows the second-order drift velocity versus the water depth and vertical label b for the ice sheet thickness d = 1 m and the wave steepness kA = 0.03π . Figure 5 shows the variation of the mass transport velocity against various ice sheet thicknesses and the vertical label b for the water depth h = 50 m and the wave steepness kA = 0.03π . From Figures 4 and 5, we can find that the mass transport velocity decays with dimensionless vertical depth for all thicknesses of the ice sheet. In Figure 5, the case d = 0 shows that the mass transport velocity is the same as that of Chen et al. (2010).
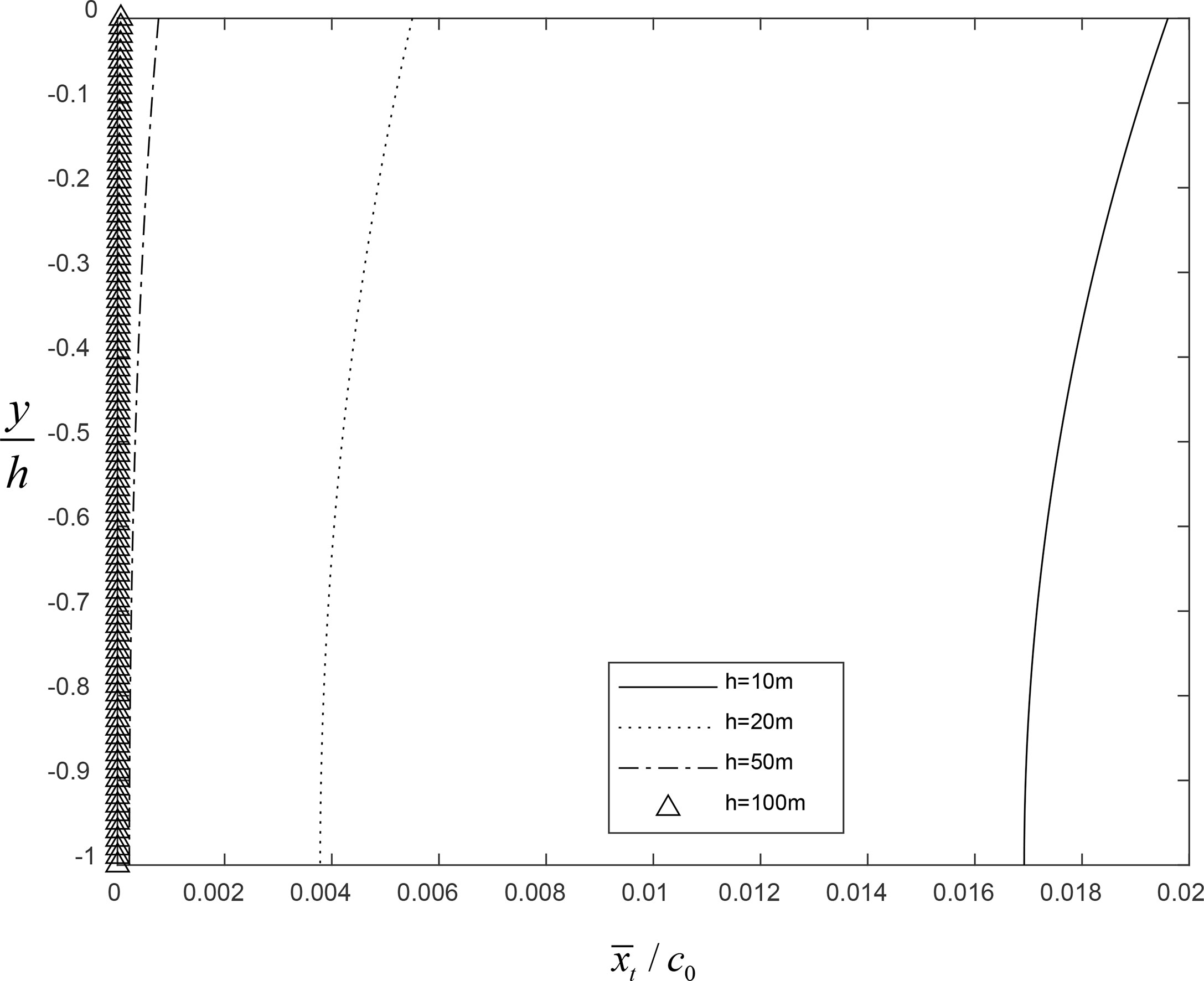
Figure 4 Dimensionless mass transport velocity versus vertical labels b for the thickness of the ice sheet d = 1 m under various water depths h = 10, 20, 50, 100 m.
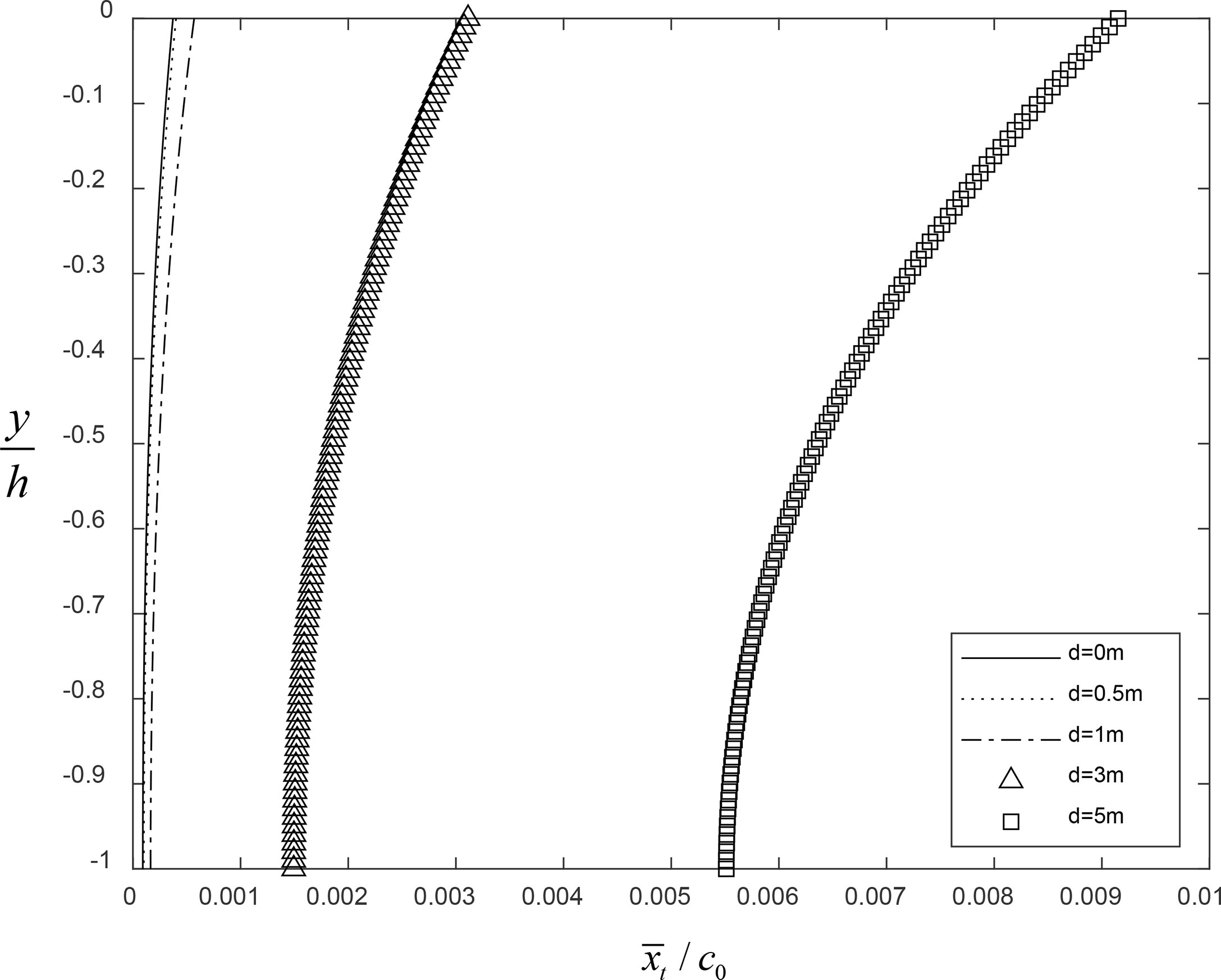
Figure 5 Dimensionless mass transport velocity versus vertical labels b for water depth h = 50 m under various thicknesses of the ice sheet d = 0, 0.5, 1, 3, 5 m.
Conclusions
We extended the work of Chen et al. (2010) to include the elastic sheet effect to derive the third-order analytical parametric solution for nonlinear progressive flexural-gravity water waves in Lagrangian coordinates. The particle trajectories could directly be determined by the third-order Lagrangian approximation. Through the numerical simulations, the effect of the rigidity of the ice sheet on the particle dynamics of the nonlinear flexural-gravity waves was discussed. The properties of particle motion for the flexural-gravity waves are similar to the gravity-capillary waves (Hsu et al., 2016).
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
H-CH: Conceptualization, Methodology, Formal analysis, Investigation, Writing-original. M-SL: software. visualization, formal analysis. All authors contributed to the article and approved the submitted version.
Funding
The work was supported by the Research Grant of the National Science andTechnology Council, Taiwan through Project No. 110-2221-E-110-016-MY3.
Acknowledgments
The authors would like to acknowledge the referees for helpful comments.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bhattacharjee J., Sahoo T. (2007). Interaction of current and flexural gravity waves. Ocean Eng. 34 (11–12), 1505–1515. doi: 10.1016/j.oceaneng.2007.01.004
Buldakov E. V., Taylor P. H., Eatock-Taylor R. (2006). New asymptotic description of nonlinear water waves in Lagrangian coordinates. J. Fluid Mech. 562, 431–444. doi: 10.1017/S0022112006001443
Chen Y. Y., Chen H. S. (2014). Lagrangian Solution for irrotational progressive water waves propagating on a uniform current: Part 1. fifth-order analysis. Ocean Eng. 88, 546–567. doi: 10.1016/j.oceaneng.2014.03.011
Chen Y. Y., Hsu H. C. (2009). A modified Euler–Lagrange transformation for particle orbits in nonlinear progressive waves. Ocean Eng. 36, 747–775. doi: 10.1016/j.oceaneng.2009.04.003
Chen Y. Y., Hsu H. C., Chen G. Y. (2010). Lagrangian Experiment and solution for irrotational finite-amplitude progressive gravity waves at uniform depth. Fluid Dyn. Res. 42, 045511. doi: 10.1088/0169-5983/42/4/045511
Clamond D. (2007). On the Lagrangian description of steady surface gravity waves. J. Fluid Mech. 589, 433–454. doi: 10.1017/S0022112007007811
Constantin A. (2006). The trajectories of particles in stokes waves. Invent. Math 166, 523–535. doi: 10.1007/s00222-006-0002-5
Constantin A. (2012a). An exact solution for equatorially trapped waves. J. Geophys. Res. Oceans 117, C05029. doi: 10.1029/2012JC007879
Constantin A. (2012b). Particle trajectories in extreme stokes waves. IMA J. Appl. Math. 77, 293–307. doi: 10.1093/imamat/hxs033
Constantin A. (2013). Some three-dimensional nonlinear equatorial flows. J. Phys. Oceanogr. 43, 165–175. doi: 10.1175/JPO-D-12-062.1
Constantin A., Escher J. (2011). Analyticity of periodic traveling free surface water waves with vorticity. Ann. Math 173, 559–568. doi: 10.4007/annals.2011.173.1.12
Constantin A., Villari G. (2008). Particle trajectories in linear water waves. J. Math. Fluid Mech. 10, 1–18. doi: 10.1007/s00021-005-0214-2
Dinvay E., Kalisch H., Parau E. I. (2019). Fully dispersive models for moving loads on ice sheets. J. Fluid Mech. 876, 122–149. doi: 10.1017/jfm.2019.530
Forbes L. K. (1986). Surface waves of large amplitude beneath an elastic sheet. part 1. high-order series solution. J. Fluid Mech. 169, 409–428. doi: 10.1017/S0022112086000708
Gao T., Wang Z., Milewski P. A. (2019). Nonlinear hydroelastic waves on a linear shear current at finite depth. J. Fluid Mech. 876, 55–86. doi: 10.1017/jfm.2019.528
Gao T., Wang Z., Vanden-Broeck J.-M. (2016). New hydroelastic solitary waves in deep water and their dynamics. J. Fluid Mech. 788, 469–491. doi: 10.1017/jfm.2015.695
Gerstner F. J. (1802). Theorie de wellen, abh. d. k. bohm. ges. wiss. Ann. Der Phys. 32, 412–440. doi: 10.1002/andp.18090320808
Greenhill A. G. (1886). Wave motion in hydrodynamics. Am. J. Math 9 (1), 62–96. doi: 10.2307/2369499
Hsu H. C., Chen Y. Y., Wang C. F. (2010). Perturbation analysis of the short-crested waves in Lagrangian coordinates, nonlinear anal. Real World Appl. 11, 1522–1536. doi: 10.1016/j.nonrwa.2009.03.014
Hsu H. C., Francius M., Montalvo P., Kharif C. (2016). Gravity-capillary waves in finite depth on flows of conatsnt vorticity. Proc. R. London A: Math. Phys. Eng. Sci. 472, 20160363. doi: 10.1098/rspa.2016.0363
Longuet-Higgins M. S. (1953). Mass transport in water waves. Phil. Trans. R. Soc Lond. A 245, 535–581. doi: 10.1098/rsta.1953.0006
Longuet-Higgins M. S. (1986). Eulerian and Lagrangian aspects of surface waves. J. Fluid Mech. 173, 683–707. doi: 10.1017/S0022112086001325
Marko J. R. (2003). Observations and analyses of an intense waves-in-ice event in the Sea of Okhotsk. J. Geophys. Res. 108, 3296. doi: 10.1029/2001JC001214
Ng C. O. (2004). Mass transport in gravity waves revisited. J. Geophys. Res. 109, C04012. doi: 10.1029/2003JC002121
Pierson W. J. (1962). Perturbation analysis of the navier–stokes equations in Lagrangian form with selected linear solution. J. Geophys. Res. 67 (8), 3151–3160. doi: 10.1029/JZ067i008p03151
Squire V. A., Dugan J. P., Wadhams P., Rottier P. J., Liu A. K. (1995). Of ocean waves and sea ice. Annu. Rev. Fluid Mech. 27, 115–168. doi: 10.1146/annurev.fl.27.010195.000555
Squire V. A., Moore S. C. (1980). Direct measurement of the attenuation of ocean waves by pack ice. Nature 283 (5745), 365–368. doi: 10.1038/283365a0
Toland J. F. (2007). Heavy hydroelastic travelling waves. Proc. R. Soc A 463, 2371–2397. doi: 10.1098/rspa.2007.1883
Toland J. F. (2008). Steady periodic hydroelastic waves. Arch. Ration. Mech. Anal. 189, 325–362. doi: 10.1007/s00205-007-0104-2
Vanden-Broeck J.-M., Părău E. I. (2011). Two-dimensional generalized solitary waves and periodic waves under an ice sheet. Phil. Trans. R. Soc Lond. A 369, 2957–2972. doi: 10.1098/rsta.2011.0108
Wadhams P., Holt B. (1991). Waves in frazil and pancake ice and their detection on seasat synthetic aperture radar imagery. J. Geophys. Res. 96, 8835–8852. doi: 10.1029/91JC00457
Wang Z., Guan X., Vanden-Broeck J. M. (2020). Progressive flexural-gravity waves with constant vorticity. J. Fluid Mech. 905, A12–A28. doi: 10.1017/jfm.2020.750
Keywords: lagrangian, flexural wave, particle trajectory, mass transport, perturbation
Citation: Hsu H-C and Li M-S (2022) Particle trajectory of nonlinear progressive flexural-gravity waves in Lagrangian coordinates. Front. Mar. Sci. 9:982333. doi: 10.3389/fmars.2022.982333
Received: 30 June 2022; Accepted: 07 October 2022;
Published: 27 October 2022.
Edited by:
Henrik Kalisch, University of Bergen, NorwayReviewed by:
Evgueni Dinvay, Inria Rennes - Bretagne Atlantique Research Centre, FranceSergey Gavrilyuk, Aix-Marseille Université, France
Copyright © 2022 Hsu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hung-Chu Hsu, aGNoc3VAbWFpbC5uc3lzdS5lZHUudHc=
 Hung-Chu Hsu
Hung-Chu Hsu Meng-Syue Li
Meng-Syue Li