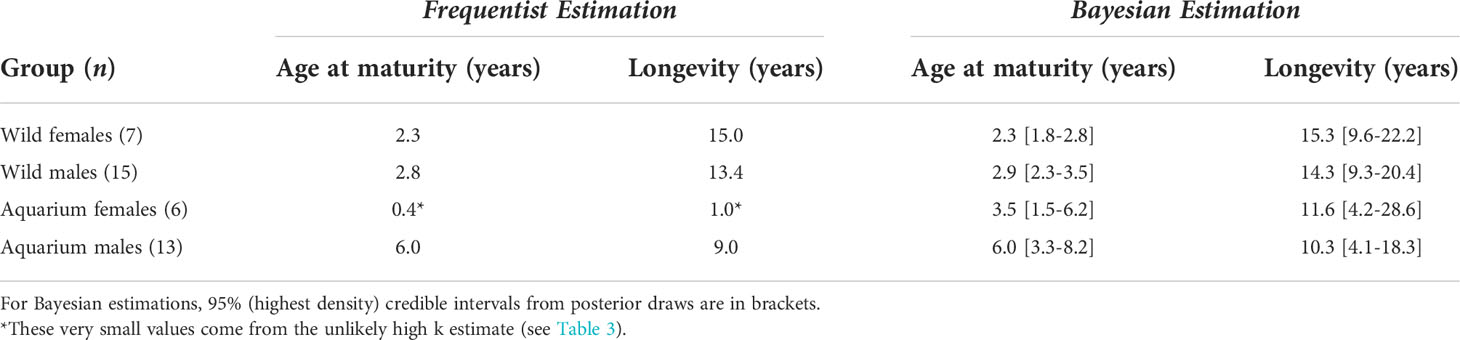Whitespotted eagle ray (Aetobatus narinari) age and growth in wild (in situ) versus aquarium-housed (ex situ) individuals: Implications for conservation and management

Elasmobranchs typically display slow growth, late maturity and low fecundity life history characteristics, making them vulnerable to fishing pressures and environmental perturbations. The whitespotted eagle ray (Aetobatus narinari), a large pelagic migratory ray with an endangered status on the IUCN Red List, fits this pattern based on available literature. Historically, age and growth parameters for this ray have been reported through vertebral ageing methods. However, the periodicity of vertebrate band pair formation, which is used for ageing, has not been validated for this species, making ageing accuracy and thus the resulting growth parameters uncertain. In this study, we used both a frequentist and Bayesian method of estimating sex-specific von Bertalanffy growth parameters (DW_∞, k) in wild recaptured versus aquarium-housed rays. Additionally, we estimated growth from repeated measurement data collected from aquarium-housed rays, as an alternative approach to obtain growth parameters while allowing for individual variability. Between 2009 and 2020, 589 whitespotted eagle rays were caught, measured, tagged and released along the southwest coast of Florida. Of these rays, 34 were recaptured between 5–1413 days at liberty. Nineteen additional rays were collected during the same period, transported and maintained at Georgia Aquarium, Atlanta, where they were regularly weighted and measured. Data from Association of Zoos and Aquariums accredited facilities provided prior information on maximum size for the Bayesian estimations, and size at birth, size at maturity, and maximum life span. These data were used to plot and interpret von Bertalanffy growth curves. Wild whitespotted eagle rays were found to grow faster and mature earlier than previously thought, with Bayesian estimates of k = 0.28 year^-1 in females, and k = 0.30 year^-1 in males. Aquarium-housed individuals seemed to grow slower and reach smaller sizes, although data provided by the aquariums showed variable growth patterns depending on the facility. Longevity was estimated at 14-15 years in wild rays while maximum lifespan observed in aquariums was 19-20+ years. Life history parameters and growth trajectories generated from this study offer valuable information to aid with future conservation management strategies of this endangered species.

Introduction

Life history traits (e.g., growth patterns, age at maturity or longevity) determine how populations will change in time and respond to exploitation pressure, making them key aspects in species management and conservation. Many elasmobranch (shark, ray and skate) species are particularly vulnerable to overexploitation (Frisk et al., 2005; Dulvy et al., 2014) and are among the latest-maturing and longest-living vertebrates (Hoenig & Gruber, 1990; Cortés, 1998; Cortés, 2002). Estimating age at maturity or longevity requires accurate age information, which is often difficult to obtain reliably in sharks and rays. The most widely used ageing technique in elasmobranchs consists of counting growth zones in calcified structures, such as band pairs in vertebral centra, assuming periodic deposition (Cailliet & Goldman, 2004). However, only a few studies have rigorously validated this temporal periodicity for particular species and commonly only for some portion of lifespan (see review by Cailliet, 2015). To further complicate this, recent studies suggest that growth zone deposition (i.e., vertebral band pairs) in sharks and batoids is closely related to somatic growth and body shape, rather than time (Natanson et al., 2018; James & Natanson, 2020). As an alternative, theoretical ages may be obtained indirectly from length via growth models, such as the von Bertalanffy growth model, which is the most common growth model utilized for fishes. Mark-recapture data can provide information on size increments over time, which are used as inputs to these growth models. Rearing in research laboratories or public aquariums such as Association of Zoos and Aquariums (AZA) accredited institutions also provides the invaluable opportunity to advance scientific knowledge of the animals in their care and enhance the conservation of wild populations (Association of Zoos and Aquariums, 2022a). Carefully and regularly taken morphometric data from participating aquariums can help fill critical data gaps in our understanding of age and growth, especially of shark and ray species for which band pair formation periodicity has been difficult to validate.

The whitespotted eagle ray is a durophagous mesopredator feeding mainly on benthic invertebrates (Ajemian et al., 2012; Serrano-Flores et al., 2018) and is often found near coral reefs, along beaches and coastal inlets, and in estuarine seagrass habitats (Silliman & Gruber, 1999; Ajemian et al., 2012; Bassos-Hull et al., 2014; Flowers et al., 2017; Cerutti-Pereyra et al., 2018; DeGroot et al., 2020). Previously thought to be a single, globally distributed species in warm and tropical waters (Bigelow and Schroeder, 1953; Last et al., 2016) and the only species of its genus, A. narinari has been recently identified as a complex of several cryptic lineages: the genus Aetobatus (Blainville, 1816) currently comprises at least five known species, based on genetic and morphologic evidence (Richards et al., 2009; White, 2014; White & Naylor, 2016; Sales et al., 2019), with the “true” A. narinari now restricted to the tropical Atlantic Ocean (Sales et al., 2019; Fricke et al., 2022). The conservation status of each member of this species complex thus needs to be assessed accounting for their geographic range and regionalized threats. While A. narinari is protected in Florida state waters, Bermuda and the Bahamas, this protection might be insufficient as the species is capable of long-distance migrations over hundreds of kilometers (see Sellas et al., 2015, DeGroot et al., 2021 and Friess et al., 2021) and is exposed to intensive and unregulated inshore fisheries throughout most of its range, including for consumption in parts of Central and South America (Cuevas-Zimbrón et al., 2011; Tagliafico et al., 2012; Cordovés et al., 2013; Cuevas et al., 2013; Cuban Ministry of the Food Industry, 2015). Females bear one to five pups after a gestation period of approximately one year (Swider et al., 2017). Due to its low fecundity, association with near-shore coral reef, beach, and seagrass habitats, and its exposure to fishing pressure, A. narinari was recently classified as “Endangered” by the IUCN Red List (Dulvy et al., 2021).

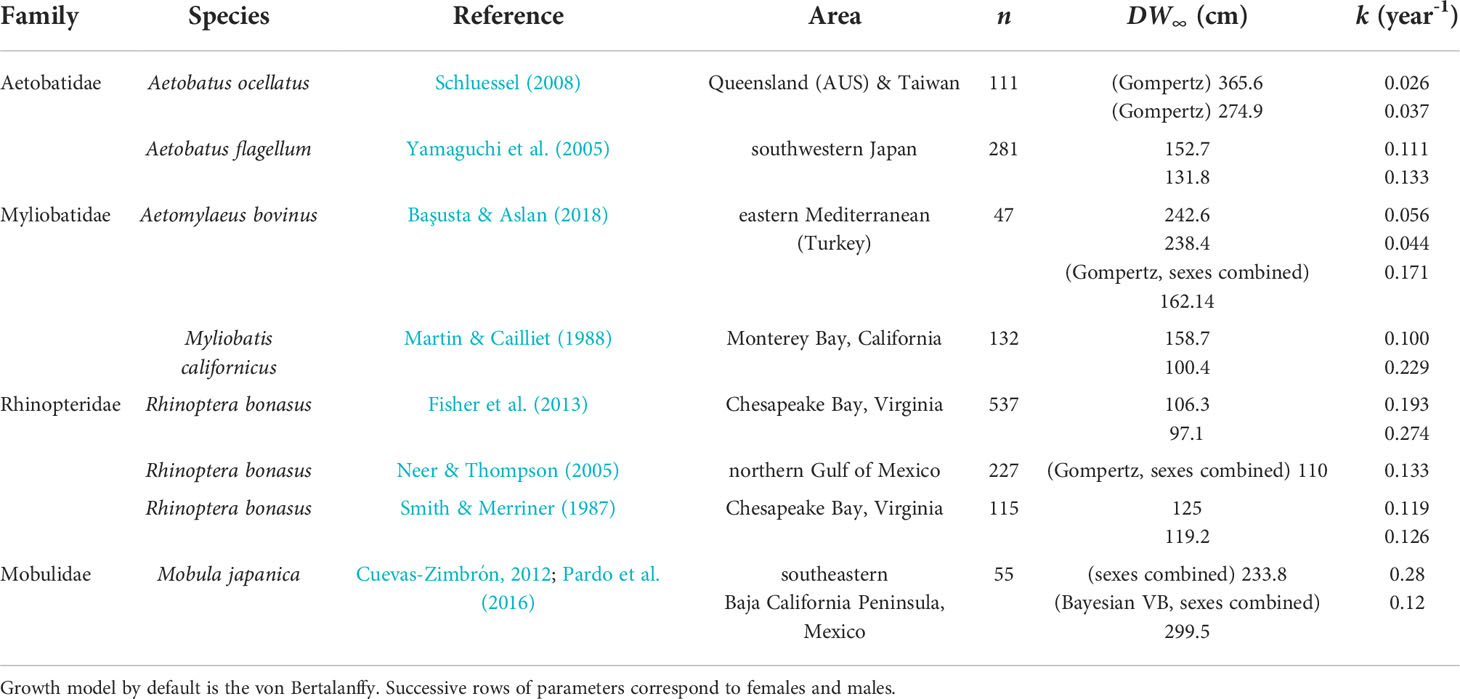
Current knowledge on A. narinari life history (Table 1) is limited and derived from a few fisheries-dependent studies (Dubick, 2000; Yokota & Lessa, 2006; Tagliafico et al., 2012; Utrera-López, 2015; Araújo, 2020) and one tagging study (Bassos-Hull et al., 2014). Dubick (2000), Utrera-López (2015) and Araújo (2020) used calcified vertebrae to visualize band pairs and estimate growth parameters in Puerto Rico, Mexico and Brazil respectively. However, they were not able to reliably validate the band pair formation periodicity. Bassos-Hull et al. (2014) was the first tagging study on wild, free-swimming A. narinari in US coastal waters, investigating life history and seasonality of the species along the southwest Florida coast (i.e., Gulf of Mexico). Using the Fabens method (Fabens, 1965), von Bertalanffy growth parameters were estimated from recaptured rays’ disc width increments during time at liberty, but the sample size (n=22) was small and included some biologically questionable (e.g., null and negative) growth rates. As for ex situ studies, little research has been done on A. narinari in managed care due to the relatively few individuals represented in zoo and aquarium collections. Although there are only 53 A. narinari currently housed in 16 different AZA-accredited facilities (Swider et al., 2021), the species is becoming increasingly common in public aquariums due to their visually appealing spot pattern and graceful swimming motions (Swider et al., 2017).

TABLE 1

Table 1 Literature summary of Aetobatus narinari life history traits.

The typically small sample sizes available for both wild and aquarium populations, combined with the possibility of measurement errors and non-negligible individual growth variability, imply that simple growth estimation methods such as the (frequentist) Fabens method can yield unrealistic growth parameters (see Bassos-Hull et al., 2014). Incorporating auxiliary information on growth parameters, even basic information such as a biologically feasible range for the disc width, can help the estimation process in such situations (e.g. Dureuil et al., 2022). Building on previously published work by Bassos-Hull et al. (2014) and incorporating data from individuals housed in aquarium and zoo facilities, this study re-estimated growth parameters in this endangered ray species using both a frequentist and Bayesian modeling framework. In the latter, auxiliary information was formalized in prior distributions assigned to growth parameters. In addition, important life history parameters such as size at birth, age at maturity, growth, maximum size and longevity of wild and aquarium-housed A. narinari were examined and compared. We propose that using a combination of information obtained through in situ and ex situ studies will improve these life history and growth parameter estimates, which is critically important to stock assessments and management agencies and will help aquarium facilities enhance their husbandry methods for the species.

Materials and methods

The study area, the sampling process, and the animal captures and handling for the wild rays are exactly the same as described in Bassos-Hull et al. (2014), except only boat-based surveys are considered in this study. The following two paragraphs summarize the adopted field methodology. Please refer to the Methods section of Bassos-Hull et al. (2014) for further detailed information.

Study area and sampling surveys

A. narinari individuals were captured in the eastern Gulf of Mexico (“Gulf”) through boat-based surveys (n=321) conducted between July 2009 and November 2019 along the southwest Florida coast (Figure 1A). This area consists mostly of fringing barrier islands and shallow passes and inlets (200–2,500 m wide,< 20 m deep), which shelter various invertebrates that are potential prey for A. narinari: macrogastropods such as whelks and conch, and bivalves such as scallops and clams (Ajemian et al., 2012; Serrano-Flores et al., 2018). Sampling occurred primarily between north Longboat Key (latitude 27.4°N, longitude −82.7°W) and south Siesta Key (latitude 27.2°N, longitude −82.5°W) (Figure 1B), predominantly April through November each year.

FIGURE 1

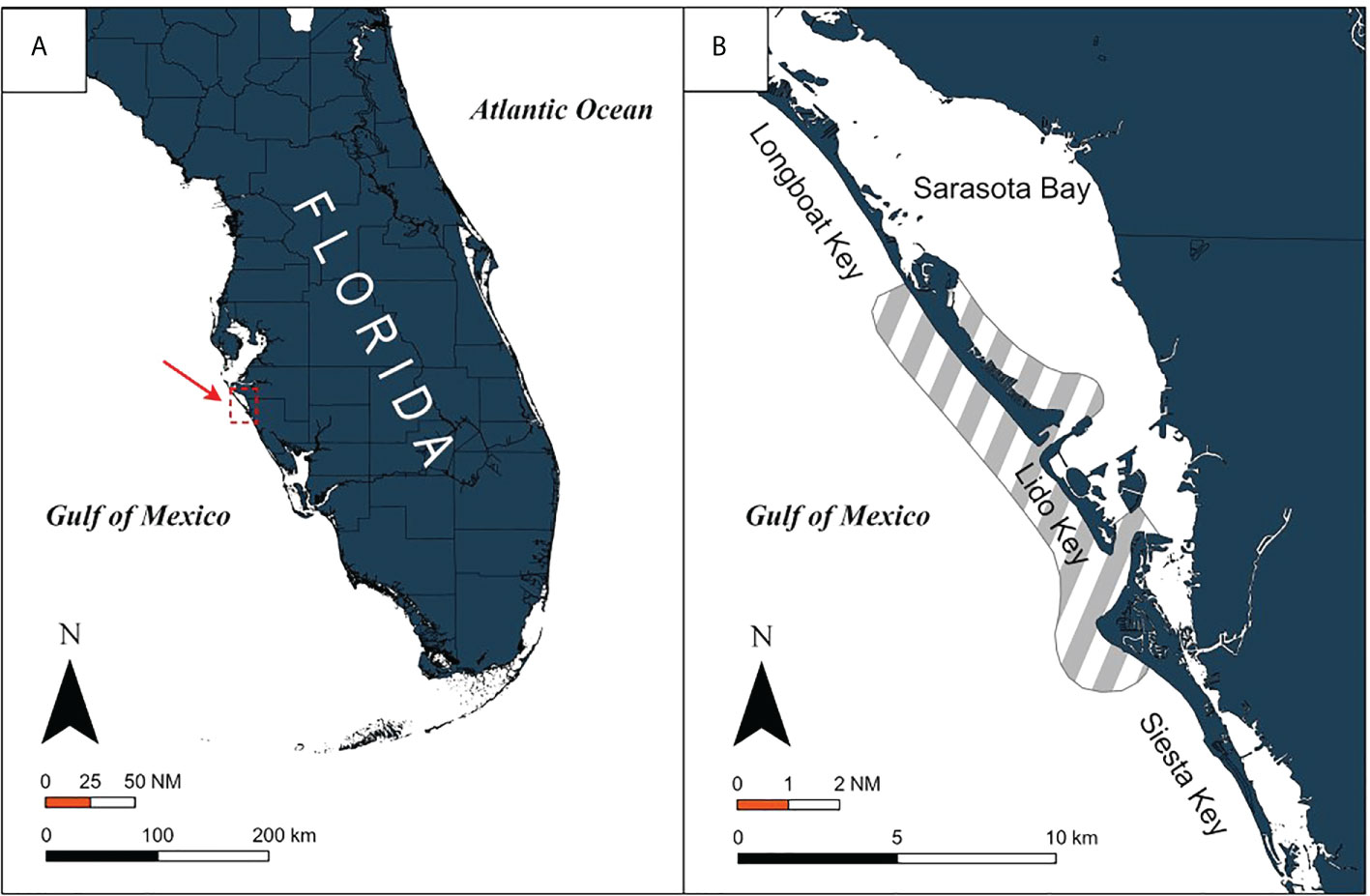
Figure 1 Location of (A) the study area on the southwest Florida coast and (B) the boat-based survey coverage (shaded area) in the vicinity of Sarasota Bay.

Animal captures, tagging and measurement

When rays were encountered in workable conditions of depth and current, they were captured with a nylon seine net for medium to large rays or a cast net for small rays (<80 cm disc width, DW), with in-water assistance provided by one or two snorkelers to transfer them to the vessel’s live well. Very large rays (>180 cm DW) were examined in a floating net pen (2.5 m diameter) off the side of the boat. Once a ray was restrained, a series of measurements and samples were taken. Males were identified by the presence of claspers, which were classified as noncalcified (soft and flexible claspers, immature), partially calcified (harder but partially flexible claspers, maturing), or fully calcified (large and rigid claspers, mature). DW and total length (TL) were measured to the nearest mm, and WT was measured to the nearest 0.1 kg using a hoop net attached to a calibrated digital scale on a davit. Each ray was injected with a passive integrated transponder (PIT), unless a previously applied PIT tag was detected; in this case it was used to identify the individual and the event was recorded as a recapture. All captures and recaptures were performed by trained researchers following this protocol.

A subset (n=19) of the animals captured for the wild study were retained for eventual display at Georgia Aquarium (GAI). Three of these individuals were collected in March 2009 prior to the initiation of the field research study and 16 were collected between 2012-2015 during the field research study. All animals collected and sampled for projects were conducted under Florida Protected Species permit #s SAL-(09-19)-1140-SRP approved protocols. All animal handling procedures were approved through Mote Marine Laboratory’s IACUC permits #10-03-PH1 and 13-02-PH1.

Animal housing and monitoring in the study aquarium

Current and historical morphometric data from these 19 aquarium-housed A. narinari were included in this study. All A. narinari at GAI were housed in the Ocean Voyager exhibit, in a 24-million-liter saltwater habitat containing about 8000 individuals of 60 other species of sharks, rays, and teleost fishes. Water temperature in the exhibit was maintained between 24-25°C year-round. Juvenile and adult rays were target fed a daily ration between 1.5-3% of their body weight (BW), with pups receiving higher rations (3-5% of BW/d). Current diets consist of surf clam (Spisula solidissima), hard-shell clam (Mercenaria mercenaria), Jonah crab (Cancer borealis), knobbed whelk (Busycon carica), Atlantic sea scallops (Placopecten magellanicus), whiteleg shrimp (Litopenaeus vannamei) and blue mussels (Mytilus edulis), but have varied historically. Animals were handled at least once a year for routine veterinary examination including morphometrics (DW and WT) and more frequently as veterinary or husbandry needs dictated. For these examinations, animals were captured by divers and transferred from the main exhibit into a small holding pool with oxygenated water. DW was measured to the nearest 0.1 cm using a soft measuring tape. WT was recorded to the nearest 0.1 kg using a hanging scale. After examination, A. narinari individuals were released into the main exhibit and resumed normal behavior.

Aquarium survey

Aetobatus narinari is managed in public aquariums through the Species Survival Plan^® (SSP) of the Association of Zoos and Aquariums. The cooperatively-managed SSP programs oversee the population management and enhance conservation of select species in AZA member institutions. SSP programs are led by AZA member volunteers who work collaboratively with AZA committees, Scientific Advisory Groups, and AZA-accredited institutions to maintain healthy, genetically diverse, and demographically varied populations through strategic management and planning (Association of Zoos and Aquariums, 2022b). To collect data for this study, a survey was sent to the AZA A. narinari stakeholders. In the survey, institutions were asked to provide the following information, as available, regarding animals of each sex in their collection: maximum size (DW in cm) recorded with corresponding age, maximum lifespan recorded and corresponding size, all sizes at birth recorded and ages at first reproduction recorded for sexually mature rays. Participants were asked to indicate how age was determined, e.g. based on the size at capture and the time spent in the aquarium facility, or exact age if the ray was born in an ex situ setting.

Growth analysis

As basis for our growth model we considered the von Bertalanffy (vB) equation (von Bertalanffy, 1938):

$\begin{array}{ll}D{W}_t=D{W}_{\infty }-(D{W}_{\infty }-D{W}_0)e^{-kt}& (1)\end{array}$

where DW_t is the length at age t, DW₀ is the length at birth (t = 0), DW_∞ is a parameter representing the (asymptotic) maximum length expressed in the same units as DW_t and, DW₀ and k is a parameter known as the Brody coefficient describing how fast DW gets to DW_∞ as t nears ∞, expressed in the reciprocal of the time units (e.g., year^-1). The original vB equation implicitly takes birth as a reference point and defines a growth increment from t = 0 to an arbitrary age t (one can subtract DW₀ on both sides of Equation (1) to make this apparent). A more general form of the vB equation is given by Fabens (1965) for two arbitrary time points T₁ and T₂, with T₁ ≤ T₂, and the corresponding lengths D>W_T1 and DW_T2

$\begin{array}{ll}D{W}_{T_2}=D{W}_{\infty }-(D{W}_{\infty }-D{W}_{T_1}){\text{e}}^{-k\Delta T}& \text{,(2)}\end{array}$

where ΔT = T₂ – T₁. This formulation is therefore suitable to examine growth from the present A. narinari data. T₁ then denotes the time of first capture and T₂ is the time at recapture. The absolute times themselves do not matter, only the time difference ΔT (i.e., the time at liberty) enters the growth model.

Equation (2) represents merely an idealized growth trajectory. As such, it can only be expected to hold on average for growth measurements, assumed collected with some random errors. This yields the following Fabens (1965) equation formulated as a statistical model (see e.g. James, 1991), which we will simply refer to as the Fabens model:

$\begin{array}{ll}D{W}_{T_2,i}=E[D{W}_{T_2,i}]+{ϵ}_i=D{W}_{\infty }-(D{W}_{\infty }-D{W}_{T_1,i}){\text{e}}^{-k\Delta T_i}+{ϵ}_i,& (3)\end{array}$

where the i index identifies an individual among n in a given sample (n being the sample size), E[DW_T2,i] denotes the mean of a random variable (mathematical expectation), and ϵ_i is an error term with mean 0 and a constant variance denoted by σ². In addition, the error terms are assumed independent. This means that the way the measurement DW_T2,i differs from its mean E[DW_T2,i] cannot be predicted from how the length measurement of another individual measurement DW_T2,j differs from its respective E[DW_{T2 ,j}] , for i ≠ j. Under these assumptions, Equation (3) closely resembles to a non-linear regression model where the lengths at recapture DW_{T2 ,i} form the response variable while the lengths at capture DW_{T1 ,i} and the times at liberty ΔT_i are covariates (explanatory variables) considered fixed. The unknown parameters to estimate are DW_∞, k, and the error variance σ².

Frequentist estimation of DW_∞ and k can be carried out by least squares, i.e., the estimates $\widehat{D{W}_{\infty }}$ and $\widehat{k}$ jointly minimize the sum of squared residuals which is equivalent to maximizing a likelihood function based on assuming all ϵ_i’s are identically distributed as Gaussian. No closed form expressions exist (Fabens, 1965), these have to be found numerically for instance through a Newton-Raphson algorithm. Given these estimates, the error variance σ² is typically estimated from the mean squared residuals corrected for the lost degrees of freedom:

$${\widehat{\sigma }}^2=\frac{1}{n-2} \sum _{i=1}^n{(D{W}_{T_2,i}(\widehat{D{W}_{\infty }}-(\widehat{D{W}_{\infty }}-D{W}_{T_1,i}){\text{e}}^{-\widehat{k}\Delta T_i}))}^2$$

The maximum likelihood estimator (MLE) for σ² is given by ${\widehat{\sigma }}^2(n-2)/n$. Standard errors can then be computed from the asymptotic approximation given by the inverse Fisher information matrix. The latter also indicates that $\widehat{D{W}_{\infty }}$ and $\widehat{k}$ are always negatively correlated.

A likelihood ratio test (LRT) was constructed to compare growth parameters between wild and aquarium rays. LRT p-values were computed two different ways, using the asymptotic χ² distribution and through a parametric bootstrap scheme (see Supplementary Material 1 for detailed methodology).

In addition to the frequentist estimation and inference described above, we also applied a Bayesian approach. We refer to Gelman et al. (2014) for a general background on Bayesian statistics. The main addition here is that the data analyst incorporates subjective knowledge and uncertainty about the Fabens model parameters DW_∞, k, σ² and in the form of probability distributions that do not depend on the data at hand, referred to as prior distributions. Following Dureuil et al. (2022), we constructed a lognormal prior for DW_∞ based on published studies (Silliman and Gruber, 1999; Dubick, 2000; Cuevas-Zimbrón et al., 2011; Ajemian et al., 2012; Tagliafico et al., 2012; Utrera-López, 2015; Briones Bell-lloch, 2016; DeGroot et al., 2021; Araújo et al., 2022) and on our aquarium survey results for the wild and aquarium populations, respectively. For both populations, we used the largest reported length DW_max, for both females and males, to set the lognormal prior mean and variance (on the natural logarithm scale) parameters: the lognormal median is set as DW_max /0.99 so that the mean parameter is log (DW_max/0.99) while, given the mean, the variance is found numerically such that the 99^th lognormal percentile matches 1.2 times the median. The 1.2 coefficient ensures a reasonably wide distribution with some inherent right-skewness that is meaningful for an asymptotic parameter like DW_∞ for which more uncertainty exists for higher values than for smaller ones; see Supplementary Material 2, for the lognormal prior distributions we thus specified for wild and aquarium, and for female and male, A. narinari individuals. Regarding the other two parameters, k and σ², we had little prior information which could be directly represented by a probability distribution. We followed Dureuil et al. (2022) in specifying uniform prior distributions for both parameters, with lower and upper bounds defining a realistic range of values: [0.01, 1] for k and [10^-5, 50] for σ. These bounds are the same for females and males, as well as for aquarium and wild individuals.

Based on our priors and a Gaussian distribution assumed for the ϵ_i error terms, i.e., a Gaussian likelihood for the data given the parameters, Bayesian estimates are based on the posterior distribution of the parameters given the data. This posterior distribution is not available in a closed form here, thus we relied on the No-U-Turn Sampling (NUTS) algorithm (Hoffman and Gelman, 2014) which can be considered as an advanced Markov chain Monte Carlo (MCMC) method. Running five chains in parallel, we retained the last 10,000 draws after a burn-in period of 10,000 iterations. This means we had 50,000 draws from the posterior distributions from which we derived summary statistics and graphical representations like histograms (see Supplementary Figures 3.1–3.4). To ease the comparison of estimates between frequentist and Bayesian estimation, we considered a Bayesian point estimate computed as the median of the posterior draws. Using a posterior median rather than, say, a posterior mean, is meaningful here due to the high right-skewness we regularly notice in the posterior distributions, notably in that of DW_∞ with small sample sizes. We computed credible intervals following the highest density interval approach; a 95% credible interval consists of the narrowest interval which contains 0.95 probability around the posterior mode.

A formal comparison of growth parameters between wild versus aquarium populations was carried out by computing Bayes factors (BFs; Kass & Raftery, 1995). The exact methodology is available in Supplementary Material 4.

The wild versus aquarium population comparison requires the same model to be fitted to both samples, which is the Fabens model in Equation (3) above with lengths at a single recapture modeled given the lengths measured at the initial capture. But each individual of our aquarium population was measured multiple times, at their capture and throughout their lives at the aquarium. This extra information was leveraged in a secondary analysis: having repeated measurements for each aquarium individual allowed us to specify a random effect, say on DW_∞, which represents individual growth variability. The Fabens model with random intercept on DW_∞ is thus:

$\begin{array}{ll}D{W}_{T_{\text{j}},i}=D{W}_{\infty ,i}-(D{W}_{\infty ,i}-D{W}_{T_1,i}){\text{e}}^{-k\Delta T_{j,i}}+{ϵ}_{i,j}& (4)\end{array}$

where j = 2,3,…,n_i identifies the recapture among the n_i repeated measurements for individual i, ΔT_j,i = T_j – T₁ for individual i, the ϵ_i,j error terms are independent Gaussian with mean zero and variance σ², and the DW_∞,i ‘s are now random too with a Gaussian distribution with mean μ_∞ and variance ${\sigma }_{\infty }^2$. As compared to the previous Fabens model, this model has one extra parameter: the random intercept variance ${\sigma }_{\infty }^2$ which represents how different the individual-specific vB curves are. Thus, a ${\sigma }_{\infty }^2$ value close to zero means the individuals are relatively similar to each other in terms of growth trajectories, while a large ${\sigma }_{\infty }^2$ value (relative to σ²) means the individual vB curves differ markedly from the population average vB curve parametrized by μ_∞ . We fitted such a random effects model by maximizing the marginal log-likelihood of the data after having integrated out the (unobserved) DW_∞,i ‘s; we again made use of the Laplace approximation for these integrals. Given parameter estimates, the random intercepts can then be predicted by the maximizers of the joint log-likelihood (equivalent to posterior modes if we were to view the random effect distribution as a Bayesian prior) as these are anyway computed in the Laplace approximation scheme.

All the model estimation and inference described above were implemented in R version 4.0.2 (R Core Team, 2022). We made use of the R package Template Model Builder (TMB; Kristensen et al., 2016) to code the joint likelihood of the Bayesian Fabens estimation and of the Fabens model with random intercept. For the former, we used the R packages tmbstan (Monnahan & Kristensen, 2018) and rstan (Stan Development Team, 2020) to link to the Stan Stan Development Team, 2022 statistical libraries which include the NUTS algorithm. We used TMB’s efficient implementation of the Laplace approximation for integrating random effects both to evaluate the marginal log-likelihood in the random effects model and to evaluate the marginal densities in the BF computations. Our code is readily available on the GitHub page of the third author (Aeberhard, 2022).

Data preparation

In the wild population, only recaptures with times at liberty longer than 90 days were included in the growth analysis because of the large variability and influence on errors for shorter time periods (Simpfendorfer, 2000; McAuley et al., 2006). Successive recaptures of the same individual were merged into a single capture-recapture event to maximize the time at liberty and thus the observed growth. Two methods were then used to identify potential outliers, the influence plot (Dureuil & Worm, 2015) and the interquartile range (Dureuil et al., 2022). Any data point identified by both of these methods was considered an outlier. To estimate growth parameters in the aquarium population, we considered the first and the last measurement of each individual in order to maximize the observed growth.

Life history characteristics

Following Equation (1), growth parameters estimated by frequentist and Bayesian approaches were used to plot von Bertalanffy growth trajectories of each population. DW₀ was defined for each sex as the average size at birth based on sizes reported in the aquarium survey. Size at sexual maturity, i.e., the disc width at which 50% of the individuals are mature, was determined from clasper rigidity in males (see methodology of Bassos-Hull et al., 2014) and from literature (Tagliafico et al., 2012) in females. Longevity was calculated as the age at size corresponding to 99% of DW_∞ (Dureuil et al., 2021). The disc width-weight relationship in wild versus aquarium rays was also assessed and can be reviewed in Supplementary Material 5.

Results

Morphometrics of captured and recaptured wild rays

A total of 609 individual rays (347 males, 261 females, and 1 unrecorded sex) were captured between July 2009 and January 2020. The sex ratio of our sample was significantly skewed toward males (male:female ratio = 0.75, χ² = 12.5, df = 1, p< 0.001). Although female maximum size (205 cm DW) and weight (119.2 kg) exceeded those of males (191.2 cm DW, 108.4 kg), there were no significant differences between average DW and WT of males vs. females (DW: t-test, t = 0.88, df = 536.5, p = 0.380; WT: t = −0.004, df = 443.56, p = 0.996). Of 346 males and 259 females measured, male DW ranged 42–191.2 cm while females ranged 41.4–205 cm. Male WT ranged 1.1–108.4 kg and females ranged 1.3–119.2 kg. The normalized size distribution of all captured rays was plotted in Figure 2.

FIGURE 2

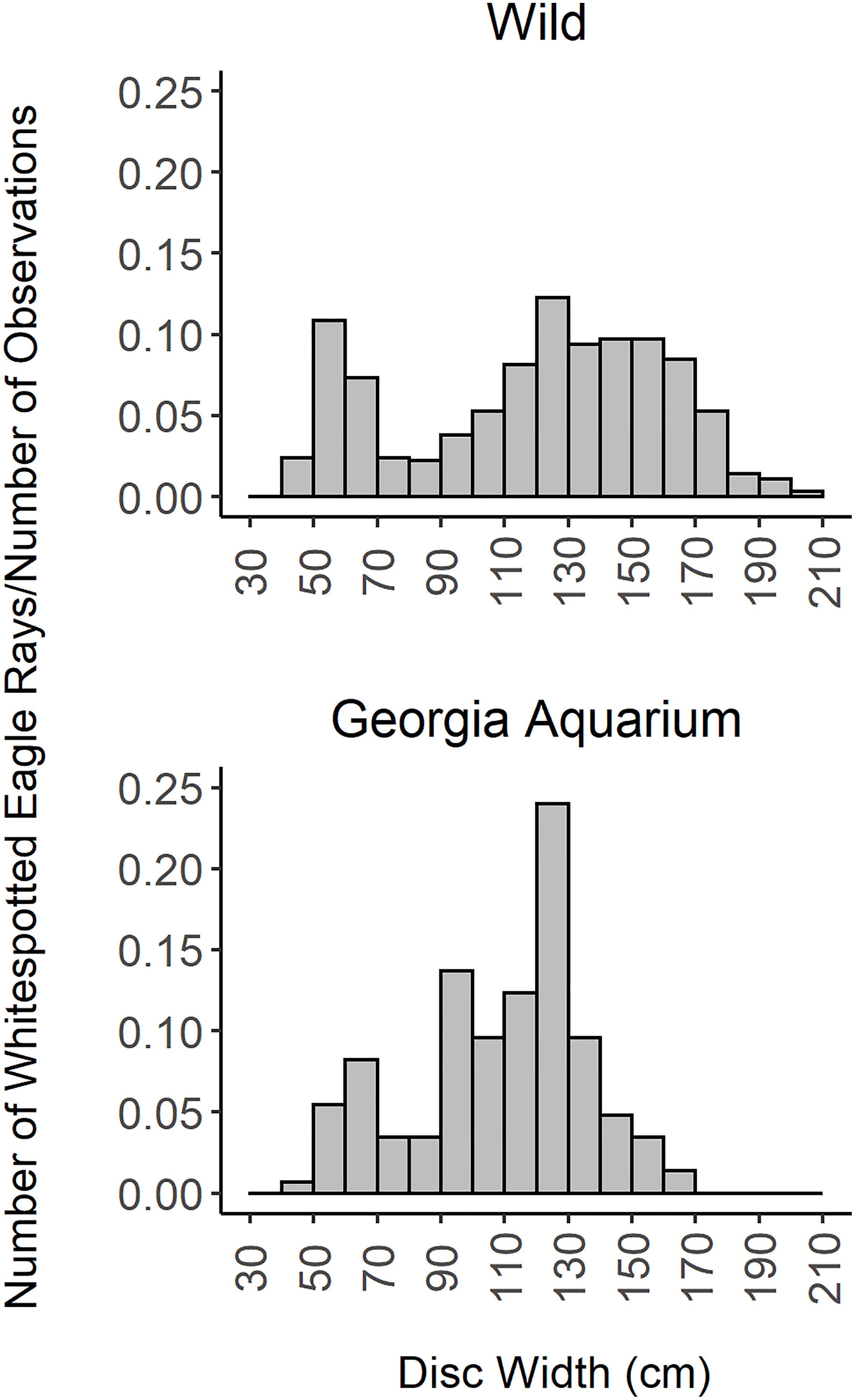
Figure 2 Normalized size histogram of wild and aquarium-housed Aetobatus narinari. Wild sample consists of 628 measurements from 589 individuals, with 1-3 measurements per individual. Aquarium sample consists of 146 measurements from 19 individuals, with 5-11 measurements per individual.

Of the 589 A. narinari individuals tagged and released during the field research study (excluding the 16 rays transferred to GAI and utilized to examine growth in the aquarium), 34 (5.8%) were recaptured on one-two occasions, including 20 males and 14 females. For recaptured rays, size at capture ranged from 51 to 159 cm DW in males and 56 to 188.4 cm DW in females. Size at recapture ranged from 59.2 to 169.5 cm DW in males and 57 to 185.2 cm DW in females. Time at liberty ranged from 5 to 1413 days (mean = 316 days) in males, and 7 to 995 days (mean = 333 days) in females.

Morphometrics and growth of aquarium-housed rays

Nineteen rays, including 13 males and six females, were monitored at GAI after being captured in the study area (Supplementary Material 6). Size at first measurement ranged 48.3-120 cm DW in males and 64-108 cm DW in females, and size at last measurement ranged 118-143 cm DW in males and 144-162 cm DW in females. Males were monitored during 3.3 to 10.9 years and grew 11 to 81 cm, while females were monitored during 4.4 to 7.4 years and grew 40 to 97 cm.

AZA - SSP survey results

Information was provided from nine institutions representing 75 individual animals (Table 2). Due to lack of regular morphometric measurements taken on many animals managed in the SSP, not all participating facilities were able to fully provide answers to all questions with accuracy. One newborn female of 35.5 cm DW considered abnormally small its whole life was not included in the average size at birth calculation.

TABLE 2

Table 2 Summary of the participating AZA aquariums’ data.

Estimation and comparison of growth parameters

Estimation of von Bertalanffy growth parameters in wild versus aquarium rays

In the wild group, none of the eligible data points were considered an outlier using the methods previously described (influence plot and IQR). However, a single recapture of a small male (74 cm DW) showing null growth over five months (166 days) was removed from the dataset. The selection of recaptures with times at liberty longer than 90 days resulted in a final data set of 22 recaptures (15 males and seven females) used for growth analysis (Supplementary Material 7). Size at capture ranged from 60 to 155 cm in females, and from 51 to 159 cm DW in males. Size at recapture ranged from 134 to 185.2 cm DW in females, and from 84 to 169.5 cm DW in males. Time at liberty ranged 1.1–2.72 years (403–995 days) in females and 0.37–3.87 years (134–1413 days) in males.

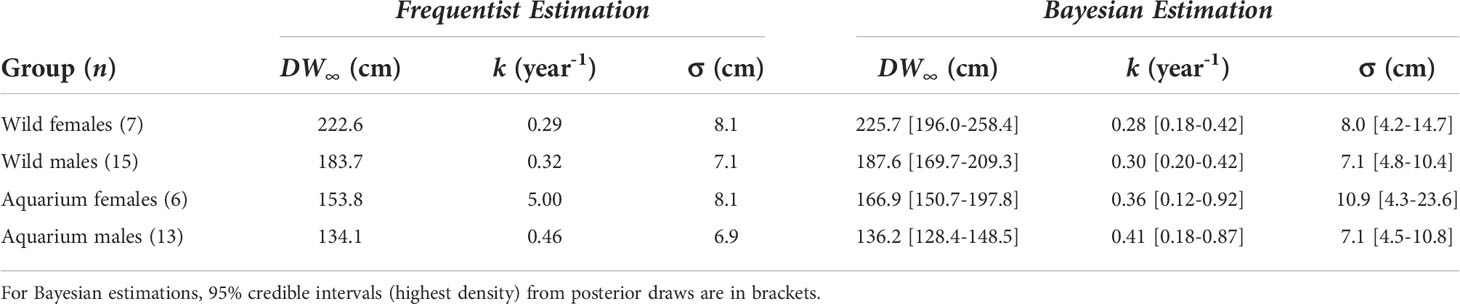
The frequentist and the Bayesian approaches produced consistent, plausible growth parameter estimates for all groups of rays, except an unlikely high frequentist estimate of k in the aquarium females (Table 3). We note that this large value for k implies a likely underestimated DW_∞, since these two parameter estimates are negatively correlated. This explains the discrepancy between frequentist and Bayesian estimates of DW_∞ for the aquarium females. Females were estimated to have a larger DW_∞ than males, this sexual dimorphism being more pronounced in the wild population (ΔDW_∞ ~ 39 cm) than in the aquarium population (ΔDW_∞ ~ 31 cm). k estimated values ranged between 0.28 and 0.32 year^-1 in the wild rays, while ranging 0.36–0.46 year^-1 in the aquarium rays.

TABLE 3

Table 3 von Bertalanffy growth parameter estimates.

Comparison of growth parameters between groups: Varying by sex and condition

(wild/aquarium)

All the p-values computed using the asymptotic χ² distribution were well under the 0.05 threshold, meaning the growth parameters (DW_∞, k) were significantly different between groups in the four comparisons (Table 4). The (more reliable) bootstrapped p-values were also under the 0.05 threshold but weaker, with some values close to 0.02–0.03.

TABLE 4

Table 4 Comparison of growth parameters between groups.

The Bayes factors only indicated substantial evidence for different growth parameters between wild and aquarium males (BF>>3.2). Simulations (not presented here), however, revealed that on average only 57% of BF values were >3.2 when the growth parameters were indeed different (with simulation parameters set to the Bayesian estimates in Table 3 so as to mimic the real data), suggesting a lack of test power.

Estimation of individual variability in DW_∞

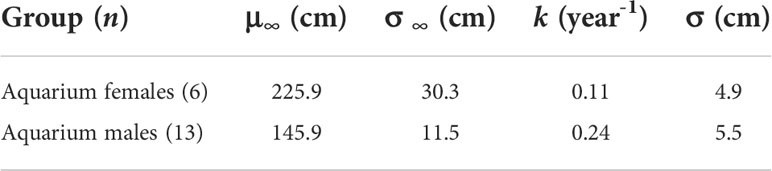
Repeated measurements of aquarium rays were used to investigate the individual variability in DW_∞ while keeping k constant across individuals. Each ray counted 4–10 measurements along their lifespan at the GAI, 4–6 in females and 4–10 in males. We found a high variability in DW_∞ (σ_∞ = 30.3 cm) for the females (Table 5). In comparison, males yielded more consistent results with a moderate variability in DW_∞ (σ_∞ = 11.5 cm). Individual-specific von Bertalanffy growth curves were then plotted using these parameter estimates (Figure 3).

TABLE 5

Table 5 Estimated growth parameters with individual variability in DW_∞.

FIGURE 3

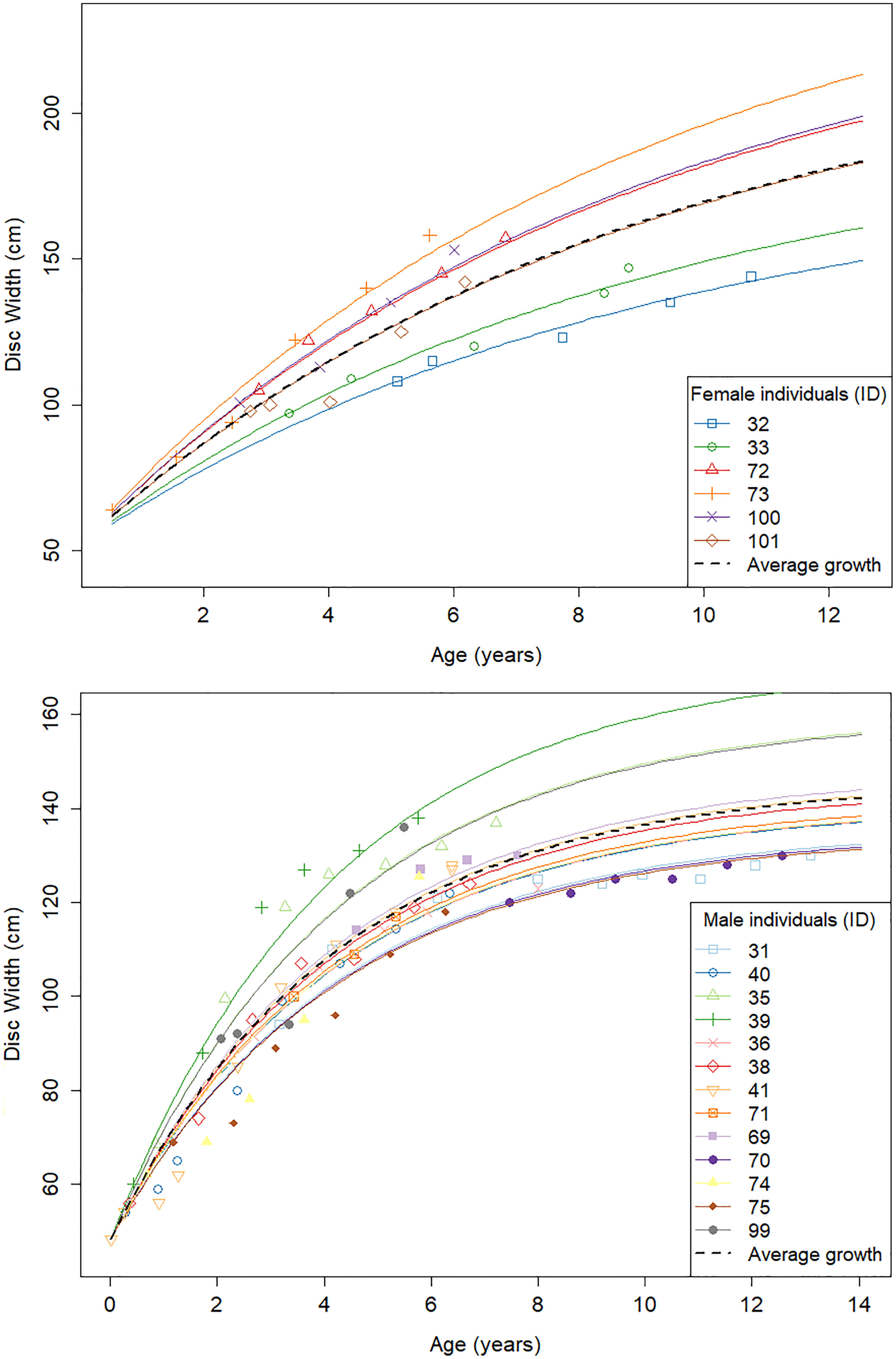
Figure 3 Individual von Bertalanffy growth curves for aquarium males (top) and females (bottom) from repeated DW measurements of the same individual.

Growth trajectories and life history characteristics

Growth parameter estimates from Table 3 were used to plot average von Bertalanffy growth trajectories for each population (Figure 4). For plotting purposes, size at birth DW₀ is required, which was determined from the average reported in the aquarium survey: 51.5 cm in females and 48.1 cm in males (Table 2).

FIGURE 4

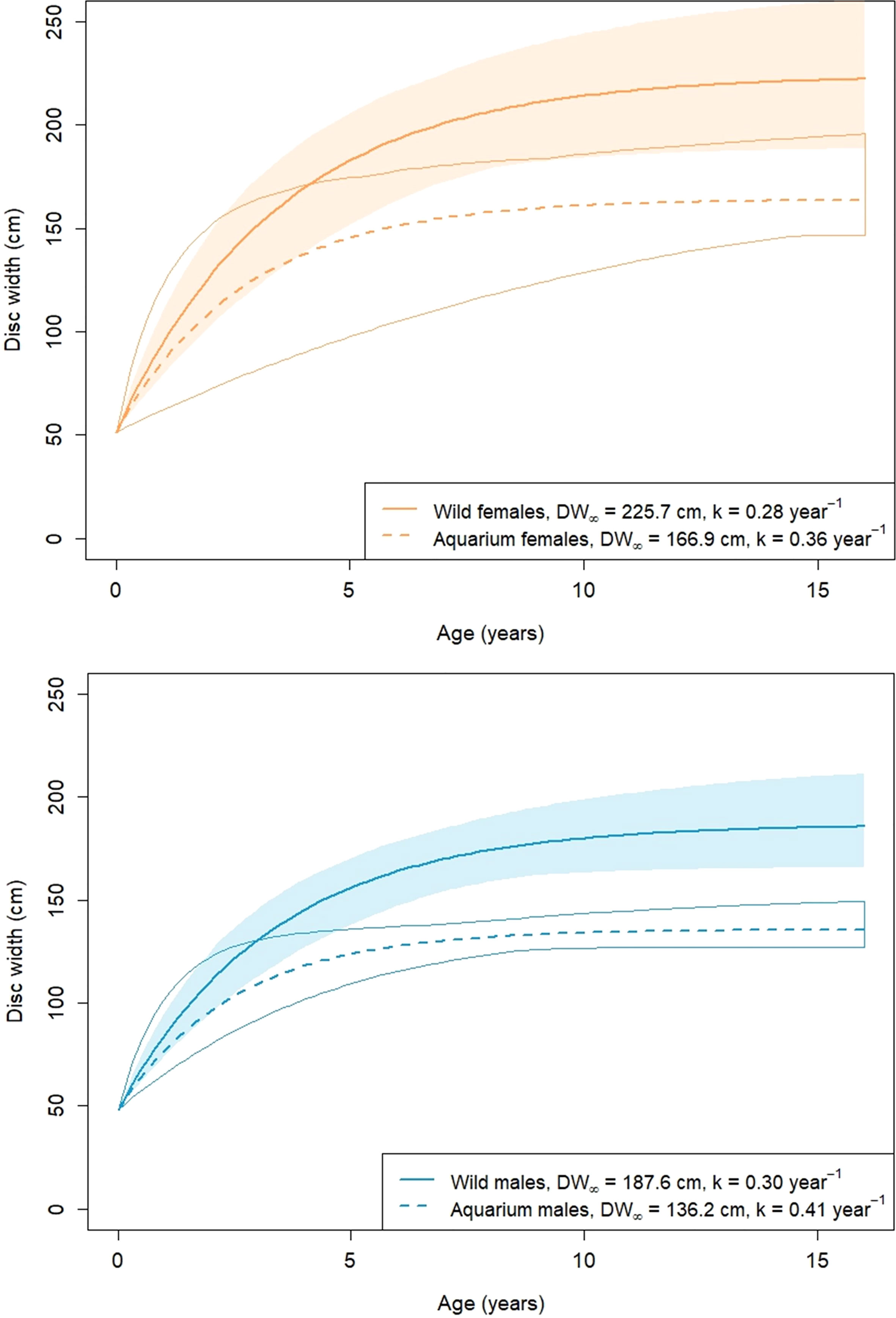
Figure 4 A. narinari von Bertalanffy growth curves inferred from Bayesian estimates (posterior medians). The envelope around each curve represents 95% credible intervals from posterior draws.

Size at sexual maturity (i.e., the disc width at which 50% of the males are mature) was calculated from the rigidity of claspers in the wild capture data set (Clark and von Schmidt, 1965). With 288 males examined, the logistic regression produced an estimate of 128.6 cm. The disc width at which 50% of the females are mature was estimated by Tagliafico et al. (2012) as 134.9 cm. From this, age at maturity was estimated between two and three years old in wild rays, and up to six years old in aquarium males (Table 6). Longevity estimates ranged from 10 to 15 years, with credible intervals overlapping between aquarium and wild rays.

TABLE 6

Table 6 Life history characteristics inferred from von Bertalanffy growth curves.

Discussion

Comparison of our results with vertebral age/growth studies

Our results suggest wild A. narinari grows considerably faster (Figure 5) than previously published (Table 1). For example, on average, a ray of 100 cm DW was previously estimated to grow 20 cm in 1.7 year (female growth in Utrera-López, 2015) to 6.4 years (male growth in Dubick, 2000), whereas such growth seems to occur in 7 to 11 months on average based on our analysis. Although inherent differences between growth curves calculated from age-length and length-increment data prevent a direct comparison from being made (Francis, 1988), growth rates estimated here substantially exceed those from previous vertebral ageing studies on the species. Only few published studies investigating age and growth in elasmobranch species have successfully validated an annual deposition periodicity in vertebral centra (reviewed by Cailliet, 2015), and while a lack of validation does not invalidate deposition periodicity in one species, unvalidated age estimates resulting from vertebral readings must be carefully considered. Recent studies have highlighted several limitations when using calcified growth zones to determine age, including systemic age underestimation in larger and older individuals (Harry, 2017), and correlation of vertebral band pairs with somatic growth rather than time (Natanson et al., 2018; James & Natanson, 2020). Further investigation is therefore needed to elucidate vertebral band pair deposition and age determination in elasmobranch species such as A. narinari, and indirect, complementary approaches such as mark-recapture and aquarium rearing combined with chemical markers (e.g., oxytetracycline) will certainly help answer this critical biology question.

FIGURE 5

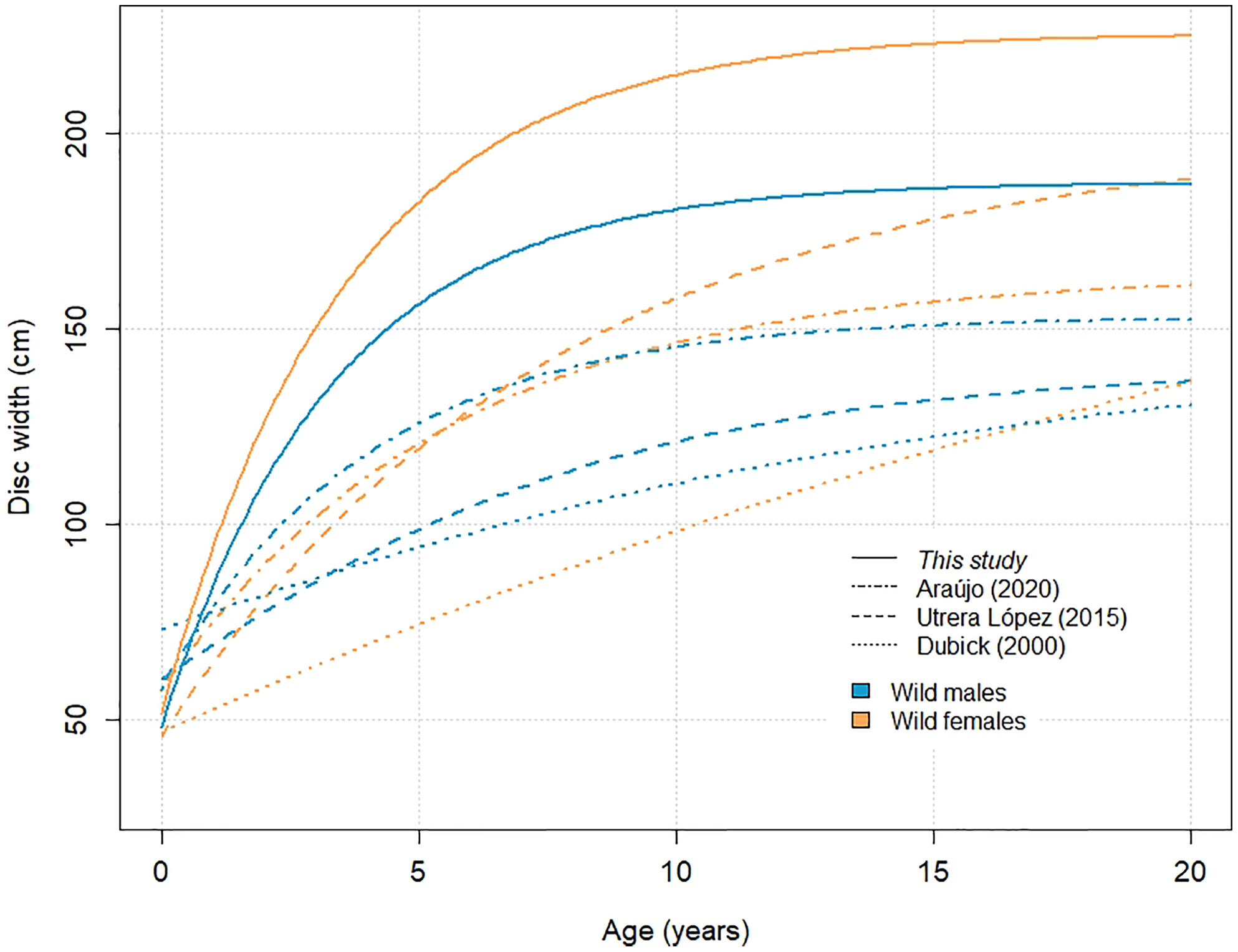
Figure 5 Von Bertalanffy growth curves generated for wild A. narinari. Parameters for female curves: DW_∞ = 225.7 cm, k = 0.28 year^-1 (this study); DW_∞= 164.2 cm, k = 0.18 year^-1 (Araújo, 2020); DW_∞ = 200.0 cm, k = 0.13 year^-1 (Utrera-López, 2015); DW_∞ = 245.9 cm, k = 0.03 year^-1 (Dubick, 2000). Parameters for male curves: DW_∞ = 187.6 cm, k = 0.30 year^-1 (this study); DW_∞ = 153.3 cm, k = 0.25 year^-1 (Araújo, 2020); DW_∞ = 140.0 cm, k = 0.18 year^-1 (Utrera-López, 2015); DW_∞ = 146.5 cm, k = 0.09 year^-1 (Dubick, 2000).

Life history profile and implications for species management

Size increments from mark-recaptured individuals produced plausible growth parameters with the Bayesian methodology adopted. DW_∞ estimates for both sexes (225.7 cm in females and 187.6 cm in males) are compatible with observed maximum sizes in the region: 195.2 cm and 140 cm in the Bahamas (Silliman & Gruber, 1999) and 202 cm and 150 cm in the southern Gulf of Mexico (Cuevas-Zimbrón et al., 2011) for females and males, respectively. The largest male observed in this study (DW = 191.2 cm) is the largest male recorded in the Atlantic Ocean. In both wild and aquarium rays, females were estimated to reach larger sizes and grow faster than males. This sexual dimorphism in A. narinari was reported in fishery-dependent studies (Cuevas-Zimbrón et al., 2011; Tagliafico et al., 2012) and is typical in myliobatiform rays (Capapé et al., 2007; Schluessel et al., 2010; Setyawan et al., 2022). Larger size of females may be attributed to the accommodation of developing young, as this feature is also common for many viviparous shark species (Cortés, 2000). k estimates (0.30 year^-1 in females and 0.28 year^-1 in males) fall within the 0.2–0.3 range theorized for rays by Holden (1974) but are relatively high compared to other myliobatiform ray species (Table 7). However, all these studies used vertebral ageing methodology with the possible limitations mentioned previously in band pair periodicity validation; thus, the resulting growth parameters of these previous studies should be carefully considered. All other things being equal, a higher k means that on average, the individuals approach their DW_∞ relatively faster, resulting in earlier age at maturity and shorter theoretical longevity. Our results suggest A. narinari matures at 2–3 years old, which is half the age previously proposed (4–6 years old) in the previous IUCN assessment (Kyne et al., 2006). However, this previous estimate was based on A. ocellatus in Australian waters (Last & Stevens, 2009) which has since been re-described as a distinct species from A. narinari (White et al., 2010) and is known to reach larger sizes (Kyne et al., 2016). Likewise, theoretical longevity appears to be shorter than previously thought, 14–15 years instead of 20–25 years estimated by Dubick (2000). Such life history parameters might be beneficial to the species’ resilience since fast-growing species are theoretically less susceptible to overfishing. Nevertheless, A. narinari is still characterized by a low reproductive potential with a long gestation and small litters (Swider et al., 2017).

TABLE 7

Table 7 Von Bertalanffy growth parameters estimated in Myliobatiformes using vertebral ageing.

As highlighted in the recent IUCN assessment (Dulvy et al., 2021), A. narinari population trends are inferred from limited landings data and remain uncertain in many parts of its range. Stock assessments ideally rely on both fisheries and biological data related to survival and reproduction of the species. The parameters estimated in this study (i.e., DW_∞, k, size at birth, age at sexual maturity and longevity) contribute to refine our current knowledge of A. narinari life history (Table 1) and constitute helpful data to fisheries stock assessments as they can be utilized to compute essential demographic parameters, such as natural mortality (Dureuil & Froese, 2021; Dureuil et al., 2021). As regional variability may exist between distinct populations (King & McFarlane, 2010; Bradley et al., 2017), life history parameters estimated in this study are thought to be relevant at least to the Gulf of Mexico and the Caribbean Sea regions where targeted, intensive, and unregulated inshore fisheries occur (Cuevas-Zimbrón et al., 2011; Tagliafico et al., 2012; Cuevas et al., 2013).

Differences observed between aquarium and wild rays

With Bayesian estimates of DW_∞ = 166.9 cm and DW_∞ = 136.2 cm for females and males respectively, aquarium rays in this study were characterized by smaller asymptotic sizes than wild rays (DW_∞ = 225.7 cm and DW_∞ = 187.6 cm). The complementary growth analysis using multiple measurements for each ray yielded mean DW_∞ estimates (μ_∞  = 225.9 cm and μ_∞  = 145.9 cm) falling closer to those estimated in wild rays, but indicated a substantial individual variability in growth trajectory, especially in females. However, a potential limitation in this analysis lies in the k parameter which is assumed to be constant across all rays, whereas DW_∞ and k are inherently negatively correlated. Considering the high variability in the small female sample, the potential limitation of a constant k parameter with variable individual DW_∞, and ease of comparison between A. narinari populations, we used the Bayesian estimates to derive the von Bertalanffy growth curves and the life history traits of the aquarium population. While these suggest a slower growth trajectory compared to wild rays, information communicated by the AZA facilities indicated growth variability across the aquariums, with some individuals demonstrating similar maximum sizes and growth rates (Swider, unpublished data) to wild rays. Data from the AZA survey and GAI rays also indicated similar sizes at maturity for both sexes compared to wild rays, suggesting A. narinari maturation is dependent on size rather than age. The same observation was made by Henningsen & Leaf (2010) who studied Hypanus americanus in captivity and found sizes at maturity similar to those reported in the wild. In the present study, this means GAI rays reach maturity later than wild rays.

It is well documented that animals managed under human care, sharks and rays included, can exhibit different life history traits compared to their wild counterparts (e.g., Cailliet et al., 1992; Kusher et al., 1992; Mollet et al., 2002; Braccini et al., 2010; Ezcurra et al., 2012). Growth rates in ectotherms are highly plastic in response to changes in temperature, resource availability, or density and life history trade-offs are expected in stable versus stochastic environments (Gotthard, 2001; Audzijonyte et al., 2016). The most likely explanation for the lower growth rates in aquarium A. narinari in this study is the year-round lower water temperatures maintained in the GAI Ocean Voyager exhibit (24-25°C). Along the Gulf coast of Florida, A. narinari has been shown to use only a portion (18-34°C) of the available thermal regime available (8-34°C), and rays were mostly observed when sea temperature was above 25°C, suggesting a preference for warm waters (DeGroot et al., 2021).

Food availability can be a limiting factor for ectotherms needing to invest energy into growth, although it should be noted that optimal growth is not the same as maximal growth (Gotthard, 2001). While consumption rates for this species are unknown in the wild, daily rations for aquarium A. narinari (1.5-5% BW/d) exceeded recommendations (0.6-0.9% BW/d for adults) based on data for other species of elasmobranchs (Janse et al., 2004). Similarly, the diets of the aquarium rays were formulated to closely approximate the nutrient composition and energy density of A. narinari prey sampled in Sarasota Bay (L. Hoopes, unpublished data). Daily, stable, year-round targeted feeding of rays at GAI suggest that food availability is not limiting adequate growth as animals are reaching maturation at similar sizes to wild cohorts. In the wild, density or animal abundance can impact resource acquisition through competition for resources, shaping growth rates among fishes (e.g., Huntsmann et al., 2021), although it is difficult to empirically identify density dependent factors as a specific drivers of growth or other life-history characteristics (Audzijonyte et al., 2016). Invertebrate prey availability in Sarasota Bay is abundant and individuals can consume up to 12 different species of gastropod and bivalve prey based on stomach content analysis (K. Bassos-Hull, unpublished data), making Sarasota Bay a productive seasonal habitat for foraging. A more comprehensive understanding of the diet, feeding ecology, and energetic requirements of A. narinari would help discern the role of food intake on growth.

Bayesian growth estimates suggest a decreased longevity for aquarium rays compared with wild animals, which is a direct result of lower asymptotic sizes. However, longevity estimates based on the von Bertalanffy parameters reflect a mean maximum age in the population, and here credible intervals considerably overlap between aquarium and wild rays (Table 6). Some studies, both in wild and aquarium contexts, have reported older rays than the longevity estimated from their von Bertalanffy parameters (Henningsen & Leaf, 2010; Vaudo et al., 2018). Likewise, several A. narinari managed under human care have lived upwards of 20 years of age (Table 2; D. Swider, personal communication), even exceeding the longevity estimated in the wild. Many animals, including elasmobranchs, have longer lifespans under human care due to readily available veterinary care, a constant supply of quality food, and freedom from predators, diseases and other pressures (Tidière et al., 2016; Grassmann et al., 2017). Conversely, elasmobranchs may also be exposed to a variety of stress-inducing variables in aquaria which may affect their health. A. narinari populations in aquarium settings have been plagued by gill parasites which can cause premature mortality (Nolan et al., 2016). As aquarium facilities perfect ideal habitat conditions and successful reproduction continues to occur in A. narinari housed in aquaria, more definitive maximum longevity for this species may be determined in the future.

Potential limitations in this study

The methods and data we used in this study have some limitations. We filtered out observations with times at liberty smaller than 90 days and one ray which displayed no growth in five months. This was out of concern of the undue impact on the estimations such zero, or even potential negative, observed growth data points can have. These would indeed bias the fitted von Bertalanffy curves downwards, especially given the small sample sizes. This filtration was a simple device to somewhat address this robustness issue. Methods which can accommodate such observations should be explored in future work.

More importantly, the estimated growth trajectories and population comparisons rely on the validity of the von Bertalanffy model itself. While we did not find any particular departures from this assumed model in our data, other more flexible models such as Gompertz or Richards growth functions (Richards, 1959; Baker et al., 1991) would be worth exploring in future analyses. Another important limitation is the Gaussian distribution assumption for all error terms (likelihood) and for the random effect on DW_∞ for aquarium rays. Admittedly, such an assumption is often made out of convenience for ease of implementation, computation, and interpretation. However, we found model residuals to be roughly symmetrically distributed around 0 with no concerning values, and the Gaussian random effect on DW_∞ does yield individual-specific von Bertalanffy curves which cover well the range of observed lengths (Figure 2).

Perhaps the most important limitation in this study lies in the small sample sizes. This affects both frequentist and Bayesian approaches, albeit in different ways. For the former, as noted by Dureuil et al. (2022), maximum likelihood estimates can become unreliable with extremely small samples. This is likely the case with the unrealistically large k we obtained for aquarium females (with n=6). Another direct impact of small sample sizes is a potentially low test power when comparing populations. Here, all LRTs pointed to significant differences, even when using a parametric bootstrap for computing p-values. Thus, we have some confidence that differences at the population level are strong enough to be reflected in our small samples here. For the Bayesian approach, the impact of the sample size is to be balanced with the amount of information supplied by the prior distributions. The specification of meaningful priors is always delicate, but even more so when the sample is small as there is a risk that the prior may be too concentrated relative to the likelihood and thus may contribute to estimation and inference more than intended. Even though our prior distributions are somewhat informative, we believe we avoided such a problem. The AZA-SSP survey supplied reliable information, in particular about the maximum observed lengths, on which we based our priors following Dureuil et al. (2022). The resulting lognormal distributions for DW_∞ cover a realistic range of values while being adequately wide given our uncertainty. In addition, the comparison of prior densities and posterior histograms (Supplementary Figures 3.1–3.4) confirms that our priors generally do not drive estimation and inference too much. A good illustration of this sample-prior balance is the realistic k Bayesian estimate we obtained for aquarium females, where frequentist estimation seemed to break down as noted above. This sample-prior balance does however come with drawbacks, here manifested in the BF values (Table 4). With priors specified under equality of growth parameters (model M₀) reasonably wide to reflect our uncertainty, for all comparisons except the wild versus aquarium males, there is likely not enough evidence in the data, with such small sample sizes, to warrant the more complex model M₁. In other words, when comparing with the LRT values, the differences between populations appear not strong enough to counteract the uncertainty embedded in our priors in M₀ and M₁. The fact that the only large BF value happens for the wild versus aquarium males comparison, where the group sizes are largest here, hints that this is most likely an issue of low test power.

Conclusion

Globally, the spotted eagle ray species complex (White, 2014) have come under increased threats from targeted fisheries and bycatch as well as habitat loss and range reduction which resulted in upgrading their IUCN Red List status, in the case of A. narinari, to “Endangered” (Dulvy et al., 2021). The evaluation assessments to categorize the IUCN Red List threat level requires reliable life history metrics such as age at sexual maturity and longevity which we were able to present. A. narinari likely grows faster and matures earlier than previously thought when comparing mark-recapture growth to vertebral banding estimates. While this may benefit the species from a fishery take perspective, other parameters such as longevity are more complicated to measure. Longevity estimates can take decades to evaluate and highlights one benefit of long term tagging studies and monitoring animals in aquariums to arrive at these estimates. The research presented in this study highlights the positive outcomes of collaborating with aquariums and how comparing in situ and ex situ individuals benefits conservation research.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics statement

The animal study was reviewed and approved by Florida state laws and regulations for work on protected marine species (FWC SAL-(09-19)-1140-SRP). IACUC protocols were approved by Mote Marine Laboratory (#10-03-PH1 and #13-02-PH1).

Author contributions

KB-H conceived the study. KB-H and LH obtained funding. KB-H and KW conducted fieldwork. LH and DS provided aquarium data. AB-P, WA, KW, and MD designed the analysis methodology. AB-P, WA, and KW conducted analysis. AB-P, KB-H, WA, LH, DS, and KW helped to write the manuscript. All authors contributed to the article and approved the submitted version.

Funding

Funding for this project was provided by National Aquarium, Save Our Seas Foundation, Disney Conservation Fund, Mote Scientific Foundation and Georgia Aquarium.

Acknowledgments

We thank Mote Marine Laboratory’s Marine Operations Team (P. Hull, D. Dougherty, G. Byrd and C. Cole) and several field operations graduate students and interns (especially Breanna DeGroot and Brianna Cahill). We wish to thank the Animal Health and Zoological Operations teams at Georgia Aquarium, and the AZA Spotted Eagle Ray SSP stakeholders who provided valuable growth and life history data. We are grateful to Matthew Ajemian and Juan Carlos Pérez-Jiménez for their helpful comments and constructive suggestions for improving the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.960822/full#supplementary-material

References

Aeberhard W. H. (2022) Eagle ray growth. Available at: https://github.com/williamaeberhard/EagleRayGrowth.

Google Scholar

Ajemian M. J., Powers S. P., Murdoch T. J. T. (2012). Estimating the potential impacts of Large mesopredators on benthic resources: Integrative assessment of spotted eagle ray foraging ecology in Bermuda. PloS One 7 (7), e40227. doi: 10.1371/journal.pone.0040227

PubMed Abstract | CrossRef Full Text | Google Scholar

Araújo P. R. V. (2020). História de vida de aetobatus narinari (Myliobatiformes) capturada pela pesca artesanal no litoral da paraíba e pernambuco, brasil (Dos Irmãos, Recife:Universidade Federal Rural de Pernambuco).

Google Scholar

Araújo P. R. V., Oddone M. C., Evêncio-Neto J., Lessa R. (2022). Reproductive biology of the whitespotted eagle ray aetobatus narinari (Myliobatiformes) captured in the coast of paraíba and pernambuco, Brazil. J. Fish Biol. 100 (4), 944–957. doi: 10.1111/jfb.15026

PubMed Abstract | CrossRef Full Text | Google Scholar

Association of Zoos & Aquariums (2022a) Strategic plan. Available at: https://www.aza.org/strategic-plan (Accessed May 18, 2022).

Google Scholar

Association of Zoos & Aquariums (2022b) Species survival plan. Available at: https://www.aza.org/species-survival-plan-programs (Accessed May 18, 2022).

Google Scholar

Audzijonyte A., Fulton E., Haddon M., Helidoniotis F., Hobday A. J., Kuparinen A., et al. (2016). Trends and management implications of human-influenced life-history changes in marine ectotherms. Fish Fish. 17 (4), 1005–1028. doi: 10.1111/faf.12156

CrossRef Full Text | Google Scholar

Baker T. T., Lafferty R., Quinn T. J. (1991). A general growth model for mark-recapture data. Fish. Res. 11 (34), 257.–281 doi: 10.1016/0165-7836(91)90005-Z

CrossRef Full Text | Google Scholar

Başusta N., Aslan E. (2018). Age and growth of bull ray aetomylaeus bovinus (Chondrichthyes: Myliobatidae) from the northeastern Mediterranean coast of Turkey. Cahiers de Biologie Marine 59, 107–114. doi: 10.21411/CBM.A.5F77152Es

CrossRef Full Text | Google Scholar

Bassos-Hull K., Wilkinson K. A., Hull P. T., Dougherty D. A., Omori K. L., Ailloud L. E., et al. (2014). Life history and seasonal occurrence of the spotted eagle ray, aetobatus narinari, in the eastern gulf of Mexico. Environ. Biol. Fish. 97 (9), 1039–1056. doi: 10.1007/s10641-014-0294-z

CrossRef Full Text | Google Scholar

Blainville H. de.. (1816). Prodrome d'une nouvelle distribution systématique du règne animal. Bulletin de la Société Philomathique de Paris 8, 105–112

Google Scholar

Bigelow H. G., Schroeder W. C. (1953). “Sawfishes, guitarfishes, skates, and rays,” in Fishes of the western north Atlantic. Ed. Tee-Van J. (New Haven: Memorial Sears Foundation for Marine Research, Yale University), p 464–p 465.

Google Scholar

Braccini J., Troynikov V., Walker T., Mollet H., Ebert D., Barnett A., et al. (2010). Incorporating heterogeneity into growth analyses of wild and captive broadnose sevengill sharks notorynchus cepedianus. Aquat. Biol. 9 (2), 131–138. doi: 10.3354/ab00246

CrossRef Full Text | Google Scholar

Bradley D., Conklin E., Papastamatiou Y. P., McCauley D. J., Pollock K., Kendall B. E., et al. (2017). Growth and life history variability of the grey reef shark (Carcharhinus amblyrhynchos) across its range. PloS One 12 (2), e0172370. doi: 10.1371/journal.pone.0172370

PubMed Abstract | CrossRef Full Text | Google Scholar

Cailliet G. M. (2015). Perspectives on elasmobranch life-history studies: a focus on age validation and relevance to fishery management: chondrichthyan age validation and management. J. Fish Biol. 87 (6), 1271–1292. doi: 10.1111/jfb.12829

PubMed Abstract | CrossRef Full Text | Google Scholar

Cailliet G., Goldman K. (2004). “Age determination and validation in chondrichthyan fishes,” in Biology of sharks and their relatives. Eds. Musick J., Carrier J., Heithaus M. (Boca Raton, FL:CRC Press), 399–447.

Google Scholar

Cailliet G. M., Mollet H. F., Pittenger G. G., Bedford D., Natanson L. J. (1992). Growth and demography of the pacific angel shark (Squatina californica), based upon tag returns off California. Aust. J. Mar. Freshw. Res. 43, 1313–1330. doi: 10.1071/MF9921313

CrossRef Full Text | Google Scholar

Capapé C., Guélorget O., Vergne Y., Quignard J. P. (2007). Reproductive biology of the common eagle ray myliobatis aquila (Chondrichthyes: Myliobatidae) from the coast of languedoc (Southern France, northern Mediterranean). Vie Milieu 57 (3), 6.

Google Scholar

Cerutti-Pereyra F., Bassos-Hull K., Arvizu-Torres X., Wilkinson K. A., García-Carrillo I., Pérez-Jiménez J. C., et al. (2018). Observations of spotted eagle rays (Aetobatus narinari) in the Mexican Caribbean using photo-ID. Environ. Biol. Fish. 101 (2), 237–244. doi: 10.1007/s10641-017-0694-y

CrossRef Full Text | Google Scholar

Clark E., von Schmidt K. (1965). Sharks of the central gulf coast of Florida. Bull. Mar. Sci. 15, 13–83.

Google Scholar

Cordovés M., Ron E., Cordovés P., Tavares R. (2013). Caracterización de las capturas comerciales del chucho pintado, aetobatus narinari (Elasmobranchii: Myliobatidae), procedentes del archipiélago de Los frailes, región nororiental de Venezuela. Anartia 25, 47–63.

Google Scholar

Cortés E. (1998). Demographic analysis as an aid in shark stock assessment and management. Fish. Res. 39 (2), 199–208. doi: 10.1016/S0165-7836(98)00183-0

CrossRef Full Text | Google Scholar

Cortés E. (2000). Life history patterns and correlations in sharks. Rev. Fish. Sci. 8 (4), 299–344. doi: 10.1080/10408340308951115

CrossRef Full Text | Google Scholar

Cortés E. (2002). Incorporating uncertainty into demographic modeling: Application to shark populations and their conservation. Conserv. Biol. 16 (4), 1048–1062. doi: 10.1046/j.1523-1739.2002.00423.x

CrossRef Full Text | Google Scholar

Cuban Ministry of the Food Industry (2015). National plan of action for the conservation and management of Chondrichthyes in the republic of Cuba (Havana, Cuba:Cuban Ministry of the Food Industry), 48 p.

Google Scholar

Cuevas E., Pérez-Jiménez J. C., Méndez I. (2013). Efecto de factores ambientales y la asignación del esfuerzo pesquero sobre las capturas de la raya aetobatus narinari (Rajiformes: Myliobatidae) en el sur del golfo de méxico. Rev. Biología Trop. 61 (3), 1341–1349. doi: 10.15517/rbt.v61i3.11963

CrossRef Full Text | Google Scholar

Cuevas-Zimbrón E., Pérez-Jiménez J. C., Méndez-Loeza I. (2011). Spatial and seasonal variation in a target fishery for spotted eagle ray aetobatus narinari in the southern gulf of Mexico. Fish. Sci. 77 (5), 723–730. doi: 10.1007/s12562-011-0389-9

CrossRef Full Text | Google Scholar

Cuevas-Zimbrón E., Sosa-Nishizaki O., Pérez-Jiménez J. C., O’Sullivan J. B. (2012). An analysis of the feasibility of using caudal vertebrae for ageing the spinetail devilray, mobula japanica (Müller and henle 1841). Environ. Biol. Fish. 96 (8), 907.–914 doi: 10.1007/s10641-012-0086-2

CrossRef Full Text | Google Scholar

DeGroot B. C., Bassos-Hull K., Wilkinson K. A., Lowerre-Barbieri S., Poulakis G. R., Ajemian M. J. (2021). Variable migration patterns of whitespotted eagle rays aetobatus narinari along florida’s coastlines. Mar. Biol. 168 (2), 18. doi: 10.1007/s00227-021-03821-2

CrossRef Full Text | Google Scholar

DeGroot B., Roskar G., Brewster L., Ajemian M. (2020). Fine-scale movement and habitat use of whitespotted eagle rays aetobatus narinari in the Indian river lagoon, Florida, USA. Endangered Species Res. 42, 109–124. doi: 10.3354/esr01047)

CrossRef Full Text | Google Scholar

Dubick J. D. (2000). Age and growth of the spotted eagle ray, aetobatus narinari (Euphrase), from southwest Puerto Rico with notes on its biology and life history (Mayagüez:University of Puerto Rico).

Google Scholar

Dulvy N. K., Carlson J., Charvet P., Bassos-Hull K., Blanco-Parra M. P., Chartrain E., et al. (2021). Aetobatus narinari. The IUCN red list of threatened species 2021, : e.T42564343A2924463 doi: 10.2305/IUCN.UK.2021-1.RLTS.T42564343A2924463.en

CrossRef Full Text | Google Scholar

Dulvy N. K., Pardo S. A., Simpfendorfer C. A., Carlson J. K. (2014). Diagnosing the dangerous demography of manta rays using life history theory. PeerJ 2, e400. doi: 10.7717/peerj.400

PubMed Abstract | CrossRef Full Text | Google Scholar

Dureuil M., Aeberhard W., Burnett K., Hueter R., Tyminski J., Worm B. (2021). Unified natural mortality estimation for teleosts and elasmobranchs. Mar. Ecol. Prog. Ser. 667, 113–129. doi: 10.3354/meps13704

CrossRef Full Text | Google Scholar

Dureuil M., Aeberhard W. H., Dowd M., Pardo S. A., Whoriskey F. G., Worm B. (2022). Reliable growth estimation from mark–recapture tagging data in elasmobranchs. Fisheries Research 256, 106488. doi: 10.1016/j.fishres.2022.106488

CrossRef Full Text | Google Scholar

Dureuil M., Froese R. (2021). A natural constant predicts survival to maximum age. Commun. Biol. 4 (1), 641. doi: 10.1038/s42003-021-02172-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Dureuil M., Worm B. (2015). Estimating growth from tagging data: an application to north-east Atlantic tope shark galeorhinus galeus. J. Fish Biol. 87 (6), 1389–1410. doi: 10.1111/jfb.12830

PubMed Abstract | CrossRef Full Text | Google Scholar

Ezcurra J., Lowe C., Mollet H., Ferry L., O’Sullivan J. (2012). “Captive feeding and growth of young-of-the-Year white sharks, carcharodon carcharias, at the Monterey bay aquarium,” in Global perspectives on the biology and life history of the white shark (Boca Raton, FL:CRC Press), 316.

Google Scholar

Fabens A. J. (1965). Properties and fitting of the von bertalanffy growth curve. Growth 29, 265–289.

PubMed Abstract | Google Scholar

Fisher R. A., Call G. C., Grubbs R. D. (2013). Age, growth, and reproductive biology of cownose rays in Chesapeake bay. Mar. Coast. Fish. 5 (1), 224–235. doi: 10.1080/19425120.2013.812587

CrossRef Full Text | Google Scholar

Flowers K. I., Henderson A. C., Lupton J. L., Chapman D. D. (2017). Site affinity of whitespotted eagle rays aetobatus narinari assessed using photographic identification. J. Fish Biol. 91 (5), 1337–1349. doi: 10.1111/jfb.13452

PubMed Abstract | CrossRef Full Text | Google Scholar

Francis R. I. C. C. (1988). Are growth parameters estimated from tagging and age–length data comparable? Can. J. Fish. Aquat. Sci. 45 (6), 936–942. doi: 10.1139/f88-115

CrossRef Full Text | Google Scholar

Fricke R., Eschmeyer W. N., van der Laan R. (2022) Eschmeyer’s catalog of fishes: genera, species, references. Available at:http://researcharchive.calacademy.org/researh/ichthyology/catalog/fishcatmain.asp(Accessed May 18, 2022).

Google Scholar

Friess C., Lowerre-Barbieri S., Poulakis G., Hammerschlag N., Gardiner J., Kroetz A., et al. (2021). Regional-scale variability in the movement ecology of marine fishes revealed by an integrative acoustic tracking network. Mar. Ecol. Prog. Ser. 663, 157–177. doi: 10.3354/meps13637

CrossRef Full Text | Google Scholar

Frisk M. G., Miller T. J., Dulvy N. K. (2005). Life histories and vulnerability to exploitation of elasmobranchs: Inferences from elasticity, perturbation and phylogenetic analyses. J. Northwest Atlantic Fish. Sci. 35, 27–45. doi: 10.2960/J.v35.m514

CrossRef Full Text | Google Scholar

Gelman A., Hwang J., Vehtari A. (2014). Understanding predictive information criteria for Bayesian models. Stat Comput. 24 (6), 997–1016. doi: 10.1007/s11222-013-9416-2

CrossRef Full Text | Google Scholar

Gotthard K. (2001). “Chapter 15: Growth strategies of ectothermic animals intemperate environments,” in Animal developmental ecology. Eds. Atkinson D., Thorndyke M. (Oxford: BIOS Scientific Publishers Ltd).

Google Scholar

Grassmann M., McNeil B., Wharton J. (2017). Sharks in captivity: The role of husbandry, breeding, education, and citizen science in shark conservation. Adv. Mar. Biol. 78, 89–119. doi: 10.1016/bs.amb.2017.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Harry A. V. (2017). Evidence for systemic age underestimation in shark and ray ageing studies. Fish Fish. 19 (2), 185–200. doi: 10.1111/faf.12243

CrossRef Full Text | Google Scholar

Henningsen A. D., Leaf R. T. (2010). Observations on the captive biology of the southern stingray. Trans. Am. Fish. Soc. 139 (3), 783–791. doi: 10.1577/T09-124.1

CrossRef Full Text | Google Scholar

Hoffman M. D., Gelman A. (2014). The no-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623.

Google Scholar

Hoenig J. M., Gruber S. H. (1990). Life-history patterns in the elasmobranchs: Implications for fisheries management. NOAA Technical Report. NMFS 90, 1–16

Google Scholar

Holden M. J. (1974). ““Problems in the rational exploitation of elasmobranch populations and some suggested solutions”,” in Sea Fisheries research. Ed. Harden–Jones F. R. (London, UK: Elek Science), 117–138.

Google Scholar

Huntsmann B. M., Lynch A. J., Caldwell C. A. (2021). Interacting effects of density-dependent and density-independent factors on growth rates in southwestern cutthroat trout populations. Trans. Am. Fish. Soc. 150 (5), 651–664. doi: 10.1002/TAFS.10319

CrossRef Full Text | Google Scholar

James I. R. (1991). Estimation of von bertalanffy growth curve parameters from recapture data. Biometrics 47 (4), 1519. doi: 10.2307/2532403

CrossRef Full Text | Google Scholar

James K., Natanson L. (2020). Positional and ontogenetic variation in vertebral centra morphology in five batoid species. Mar. Freshw. Res. 72 (6), 887–898. doi: 10.1071/MF20183

CrossRef Full Text | Google Scholar

Janse M., Firchau B., Mohan P. J. (2004). “Chapter 14 elasmobranch nutrition, food handling, and feeding techniques,” in The elasmobranch husbandry manual: Captive care of sharks, rays and their relatives. Eds. Smith M., Warmolts D., Thoney D., Hueter R.. (Special Publication of the Ohio Biological Survey), Pages 183–200.

Google Scholar

Kass R. E., Raftery A. E. (1995). Bayes factors. J. Am. Stat. Assoc. 90 (430), 773–795. doi: 10.2307/2291091

CrossRef Full Text | Google Scholar

King J. R., McFarlane G. A. (2010). Movement patterns and growth estimates of big skate (Raja binoculata) based on tag-recapture data. Fish. Res. 101 (12), 50–59. doi: 10.1016/j.fishres.2009.09.006

CrossRef Full Text | Google Scholar

Kusher D. I., Smith S. E., Cailliet G. M. (1992). Validated age and growth of the leopard shark, triakis semifasciata, with comments on reproduction. Environ. Biol. Fish. 35 (2), 187–203. doi: 10.1007/BF00002193

CrossRef Full Text | Google Scholar

Kristensen K., Nielsen A., Berg C. W., Skaug H. J., Bell B (2016). TMB: automatic differentiation and Laplace approximation. J Stat Soft. 70, 1–21. doi: 10.18637/jss.v070.i05

CrossRef Full Text | Google Scholar

Kyne P. M., Ishihara H., Dudley S. F. J., White W. T. (2016). Aetobatus narinari. The IUCN red list of threatened species, e.T39415A10231645. doi: 10.2305/IUCN.UK.2006.RLTS.T39415A10231645.en

CrossRef Full Text | Google Scholar

Kyne P. M., Dudgeon C. L., Ishihara H., Dudley S. F.J., White W. T. (2016). Atobatus ocellatus. The IUCN Red List of Threatened Species, e.T42566169A42566212. doi: 305/IUCN.UK.2016-1.RLTS.T42566169A42566212.en

Google Scholar

Last P., Naylor G., Séret B., White W., de Carvalho M., Stehmann M. (2016). Rays of the world (Ithaca, NY:Cornell University Press (Comstock Publishing Associates); Clayton (Australia): CSIRO Publishing).

Google Scholar

Last P. R., Stevens J. D. (2009). Sharks and rays of australia. second edition (Collingwood: CSIRO Publishing).

Google Scholar

Martin L. K., Cailliet G. M. (1988). Age and growth determination of the bat ray, myliobatis californica gill, in central California. Copeia 1988 (3), 762–773. doi: 10.2307/1445399

CrossRef Full Text | Google Scholar

McAuley R. B., Simpfendorfer C. A., Hyndes G. A., Allison R. R., Chidlow J. A., Newman S. J., et al. (2006). “Validated age and growth of the sandbar shark, carcharhinus plumbeus (Nardo 1827) in the waters off Western Australia,” in Special issue: Age and growth of chondrichthyan fishes: New methods, techniques and analysis. Eds. Carlson J. K., Goldman K. J. (Dordrecht: Springer Netherlands), 385–400.

Google Scholar

Mollet H. F., Ezcurra J. M., O’Sullivan J. B. (2002). Captive biology of the pelagic stingray, dasyatis violacea (Bonaparte 1832). Mar. Freshw. Res. 53 (2), 531–541. doi: 10.1071/MF01074

CrossRef Full Text | Google Scholar

Monnahan C. C., Kristensen K. (2018). No-u-turn sampling for fast Bayesian inference in ADMB and TMB: Introducing the adnuts and tmbstan r packages. PloS One 13 (5), e0197954. doi: 10.1371/journal.pone.0197954

PubMed Abstract | CrossRef Full Text | Google Scholar

Natanson L. J., Skomal G. B., Hoffmann S. L., Porter M. E., Goldman K. J., Serra D. (2018). Age and growth of sharks: do vertebral band pairs record age? Mar. Freshw. Res. 69 (9), 1440–1452. doi: 10.1071/MF17279

CrossRef Full Text | Google Scholar

Neer J. A., Thompson B. A. (2005). Life history of the cownose ray, rhinoptera bonasus, in the northern gulf of Mexico, with comments on geographic variability in life history traits. Environ. Biol. Fish. 73 (3), 321–331. doi: 10.1007/s10641-005-2136-5

CrossRef Full Text | Google Scholar

Nolan E. C., Mylniczenko N. D., Steinmetz J., Corwin A., Thomas A., Stamper M. A. (2016) in Oral Praziquantel Pharmacokinetics in Spotted Eagle Rays (Aetobatus narinari) [Conference presentation]. IAAAM 2016 Meeting and Conference, Virginia Beach, VA, United States, May 21-26.

Google Scholar

Pardo S. A., Kindsvater H. K., Cuevas-Zimbrón E., Sosa-Nishizaki O., Pérez-Jiménez J. C., Dulvy N. K., et al (2016). Growth, productivity and relative extinction risk of a data-sparse devil ray. Sci. Rep. 6 (1), 33745. doi: 10.1038/srep33745

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2022) R: A language and environment for statistical computing (Vienna, Austria: R Foundation for Statistical Computing). Available at: https://www.R-project.org/ (Accessed May 18, 2022).

Google Scholar

Richards F. J. (1959). A flexible growth function for empirical use. J. Exp. Bot. 10 (2), 290–301. doi: 10.1093/jxb/10.2.290

CrossRef Full Text | Google Scholar

Richards V. P., Henning M., Witzell W., Shivji M. S. (2009). Species delineation and evolutionary history of the globally distributed spotted eagle ray (Aetobatus narinari). J. Heredity 100 (3), 273–283. doi: 10.1093/jhered/esp005

CrossRef Full Text | Google Scholar

Sales J. B. L., de Oliveira C. N., dos Santos W. C. R., Rotundo M. M., Ferreira Y., Ready J., et al. (2019). Phylogeography of eagle rays of the genus aetobatus: Aetobatus narinari is restricted to the continental western Atlantic ocean. Hydrobiologia 836 (1), 169–183. doi: 10.1007/s10750-019-3949-0

CrossRef Full Text | Google Scholar

Schluessel V. (2008). Life history, population genetics and sensory biology of the white spotted eagle ray aetobatus narinari (Euphrasen 1790) with emphasis on the relative importance of olfaction (Saint Lucia (QLD: University of Queensland).

Google Scholar

Schluessel V., Bennett M. B., Collin S. P. (2010). Diet and reproduction in the white-spotted eagle ray aetobatus narinari from Queensland, Australia and the penghu islands, Taiwan. Mar. Freshw. Res. 61 (11), 1278–1289. doi: 10.1071/MF09261

CrossRef Full Text | Google Scholar

Sellas A. B., Bassos-Hull K., Pérez-Jiménez J. C., Angulo-Valdes J. A., Bernal M. A., Hueter R. E. (2015). Population structure and seasonal migration of the spotted eagle ray, aetobatus narinari. J. Heredity 106 (3), 266–275. doi: 10.1093/jhered/esv011

CrossRef Full Text | Google Scholar

Serrano-Flores F., Pérez-Jiménez J. C., Méndez-Loeza I., Bassos-Hull K., Ajemian M. J. (2018). Comparison between the feeding habits of spotted eagle ray ( aetobatus narinari ) and their potential prey in the southern gulf of Mexico. J. Mar. Biol. Assoc. United Kingdom 99 (3), 661–672. doi: 10.1017/S0025315418000450

CrossRef Full Text | Google Scholar

Setyawan E., Stevenson B. C., Izuan M., Constantine R., Erdmann M. V. (2022). How big is that manta ray? a novel and non-invasive method for measuring reef manta rays using small drones. Drones 6 (3), 63. doi: 10.3390/drones6030063

CrossRef Full Text | Google Scholar

Silliman W. R., Gruber S. H. (1999). Behavioral biology of the spotted eagle ray, aetobatus narinari. Bahamas J. Sci. 11, 13–20.

Google Scholar

Simpfendorfer C. A. (2000). Growth rates of juvenile dusky sharks carcharhinus obscurus (Lesueur 1818) from southwestern Australia estimated from tag-recapture data. Fish. Bull. 98 (4), 811–822.

Google Scholar

Smith J. W., Merriner J. V. (1987). Age and growth, movements and distribution of the cownose ray, rhinoptera bonasus, in Chesapeake bay. Estuaries 10 (2), 153–164. doi: 10.2307/1352180

CrossRef Full Text | Google Scholar

Stan Development Team (2020) RStan: the R interface to Stan. Available at: https://mc-stan.org/.

Google Scholar

Stan Development Team (2022) RStan: the r interface to stan. r package version 2.21.5. Available at: https://mc-stan.org/.

Google Scholar

Swider D. A., Corwin A. L., Kamerman T. Y., Zimmerman S. L., Violetta G. C., Davis J., et al. (2017). ““Reproduction of spotted eagle rays, aetobatus narinari, in aquaria”,” in Elasmobranch husbandry manual II: Recent advances in the care of sharks, rays and their relatives. Eds. Smith M., Warmolts D., Thoney D., Hueter R., Murray M., Ezcurra J. (Colombus, OH: Ohio Biological Survey), 433–442.

Google Scholar

Swider D. A., Thomas R., Lawless A. (2021). Population analysis & breeding and transfer plan, spotted eagle ray (Aetobatus narinari) AZA species survival plan® yellow program (Chicago: AZA Population Management Center).

Google Scholar

Tagliafico A., Rago N., Rangel S., Mendoza J. (2012). Exploitation and reproduction of the spotted eagle ray (Aetobatus narinari) in Los frailes archipelago, Venezuela. Fish. Bull. 110 (3), 307–316.

Google Scholar

Tidière M., Gaillard J.-M., Berger V., Müller D. W. H., Bingaman Lackey L., Gimenez O., et al. (2016). Comparative analyses of longevity and senescence reveal variable survival benefits of living in zoos across mammals. Sci. Rep. 6 (1), 36361. doi: 10.1038/srep36361

PubMed Abstract | CrossRef Full Text | Google Scholar

Utrera-López N. (2015). Estimación de la edad y crecimiento de la raya águila aetobatus narinari (Euphrasen 1790) en el sur del golfo de méxico (La Paz, Mexico: Universidad autónoma de Baja California Sur).

Google Scholar

Vaudo J. J., Wetherbee B. M., Harvey G. C. M., Harvey J. C., Prebble A. J. F., Corcoran M. J., et al. (2017). Characterisation and monitoring of one of the world’s most valuable ecotourism animals, the southern stingray at stingray city, grand Cayman. Mar. Freshw. Res. 69 (1), 144–154. doi: 10.1071/MF17030

CrossRef Full Text | Google Scholar

von Bertalanffy L.. (1938). A quantitative theory of organic growth. Hum. Biol. 10, 181–213

Google Scholar

White W., Last P., Naylor G., Jensen K., Caira J. N. (2010). Clarification of Aetobatus ocellatus (Kuhl, 1823) as a valid species, and a comparison with Aetobatus narinari (Euphrasen, 1790) (Rajiformes: Myliobatidae). Descriptions of New Sharks and Rays from Borneo, 141–164

Google Scholar

White W. T. (2014). A revised generic arrangement for the eagle ray family myliobatidae, with definitions for the valid genera. Zootaxa 3860 (2), 149. doi: 10.11646/zootaxa.3860.2.3

PubMed Abstract | CrossRef Full Text | Google Scholar

White W. T., Naylor G. J. P. (2016). Resurrection of the family aetobatidae (Myliobatiformes) for the pelagic eagle rays, genus aetobatus. Zootaxa 4139 (3), 435. doi: 10.11646/zootaxa.4139.3.10

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamaguchi A., Kawahara I., Ito S. (2005). Occurrence, growth and food of longheaded eagle ray, aetobatus flagellum, in ariake sound, Kyushu, Japan. Environ. Biol. Fish. 74 (2), 229–238. doi: 10.1007/s10641-005-0217-0

CrossRef Full Text | Google Scholar

Yokota L., Lessa R. P. (2006). A nursery area for sharks and rays in northeastern Brazil. Environ. Biol. Fish. 75 (3), 349–360. doi: 10.1007/s10641-006-0038-9

CrossRef Full Text | Google Scholar