- 1Frontier Science Center for Deep Ocean Multispheres and Earth System (FDOMES) and Physical Oceanography Laboratory, Ocean University of China, Qingdao, China
- 2Qingdao National Laboratory for Marine Science and Technology, Qingdao, China
In this study, we examine the regulation of wind-powered near-inertial internal waves (NIWs) in the ocean interior by mesoscale eddies, using an eddy-resolving global climate model. There is an enhancement (weakening) of NIW activity within anticyclonic (cyclonic) eddies from the surface boundary layer (SBL) base down to ~4,000 m, associated with a decreased (increased) wave vertical scale. The influence of anticyclonic eddies on NIW activity is more pronounced than that of cyclonic eddies, suggesting that the net effect of mesoscale eddies is to intensify the NIWs in the ocean interior. The enhanced (weakened) NIW activity under the SBL in anticyclonic (cyclonic) eddies is ascribed to both horizontal convergence (divergence) of NIW energy flux under the SBL and increased (decreased) downward NIW energy flux from the SBL base. The former is only confined to a layer within several hundred meters under the SBL, whereas the latter becomes dominant in the deeper ocean.
Introduction
Turbulent diapycnal mixing affects a variety of oceanic processes and plays a significant role in regulating large-scale ocean circulations and global climate (Gregory, 2000; Wunsch and Ferrari, 2004; Saenko and Merryfield, 2005). In the ocean interior, diapycnal mixing is mainly driven by internal wave breaking with winds and tides being two major sources of energy input to the internal wave field (Munk and Wunsch, 1998; Wunsch and Ferrari, 2004). As omnipresent features in the global ocean, wind-powered near-inertial internal waves (NIWs) are suggested to play a crucial role in furnishing the diapycnal mixing in the ocean interior, accounting for its distinctive seasonal cycle (Jing and Wu, 2010; Wu et al., 2011; Whalen et al., 2012; Jing and Wu, 2014; Whalen et al., 2015).
The wind power exerted on NIWs (denoted as WI) mainly occurs during the passage of synoptic storms with a horizontal scale of O(1,000 km) (D’Asaro, 1985; Alford et al., 2016). If the ocean were horizontally homogeneous, most of the excited NIWs would dissipate inside the surface boundary layer (SBL) with little energy radiating into the deep ocean to power the diapycnal mixing there, due to their small vertical group velocity. Theoretical studies suggest that the downward radiation of NIWs is strongly affected by mesoscale eddies (Kunze, 1985; Young and Ben Jelloul, 1997; Balmforth et al., 1998; Klein et al., 2004; Danioux et al., 2015). Using the WKB approximation, Kunze (1985) showed that the lower bound of the internal wave frequency band is shifted from the local Coriolis frequency (f) by half the background relative vorticity (ζ / 2) to a so-called effective Coriolis frequency, , despite the fact that NIWs can have a horizontal scale similar to that of mesoscale eddies. Young and Ben Jelloul (1997) relaxed the horizontal scale assumption implicit in the WKB approach and proposed a complementary framework (referred to as the YBJ model hereafter). However, the YBJ model relies on a strong dispersion approximation that is invalid for high-vertical modes. Recently, Danioux et al. (2015) pointed out that the trapping of NIWs in anticyclonic eddies (AEs) associated with a reducing spatial scale of the wave field can be understood as a direct consequence of a conservation law associated with the YBJ model, without making assumptions about the smallness of the horizontal scales of NIWs relative to mesoscale eddies (Kunze, 1985), the short evolution time of NIWs and the nature of the vorticity field (Klein et al., 2004), or the relative importance of dispersion (Young and Ben Jelloul, 1997).
Although observational and numerical studies confirm the important role of mesoscale eddies in promoting NIW activity in the stratified ocean interior (Kunze, 1985; Balmforth et al., 1998; Lee & Niiler, 1998; Zhai et al., 2005; Zhai et al., 2007; Jing & Wu, 2014; Lelong et al., 2020), several questions remain to be answered. First, AEs are well recognized as an energy conduit for NIW radiation (Lee and Niiler, 1998), yet the effects of cyclonic eddies (CEs) remain unclear and different studies do not reach a consensus (Kunze, 1985; Balmforth et al., 1998). Kunze (1985) suggests that the NIWs should be repelled from CEs due to their higher feff value than the surrounding region, resulting in reduced NIW activity in the ocean interior within CEs. In contrast, by applying the YBJ model to an idealized setting, Balmforth et al. (1998) showed that NIW activity in the ocean interior is enhanced in both AEs and CEs. Second, existing studies chiefly focus on NIW’s energy rather than its energy flux. It is yet unknown to what extent the effects of mesoscale eddies on NIW energy can be used to infer their effects on NIW energy flux. In particular, is the regulation of NIW energy under the SBL by mesoscale eddies due to the downward NIW energy flux at the SBL base or the horizontal NIW energy flux convergence/divergence under the SBL?
Currently, in situ observations are only available at a few sites, making them too sparse to be useful for evaluating the influences of mesoscale eddies on NIWs on global scale. Owing to the rapid increase of computational capacity, present-day state-of-the-art global ocean numerical simulations are capable of resolving mesoscale eddies, NIWs, as well as their interactions (Sun et al., 2021; Yuan et al., 2021). In this study, we systematically investigate the effects of AEs and CEs on the characteristics of NIWs (kinetic energy, shear variance, and three-dimensional energy flux) in the global ocean using an eddy-resolving Community Earth System Model (CESM). The manuscript is organized as follows. Data and methodology are described in Section 2. In Section 3, global and regional composites of NIW characteristics in AEs and CEs are presented. In Section 4, implications on the diapycnal mixing are discussed. Conclusions are given in Section 5.
Methodology
An eddy-resolving CESM
We perform the numerical simulation using an eddy-resolving CESM version 1.3 (Chang et al., 2020). The atmospheric model is on a 0.25° horizontal grid with 30 levels in the vertical, fine enough to resolve the mesoscale winds that contribute significantly to WI (Rimac et al., 2013; Jing et al., 2016). The oceanic model is on a horizontal grid of 0.1° nominal resolution with 62 vertical levels, where the layer thickness increases gradually from 5 m at the sea surface to 250 m near the topography. The horizontal grids for the sea ice and land components are identical with those of the oceanic and atmospheric models, respectively. The diapycnal mixing for tracer and momentum is represented using a K-profile parameterization scheme (Large et al., 1994) except that the tracer mixing outside the SBL induced by internal wave breaking is replaced from the constant 10-5m2s-1 by that derived from the modified finescale parameterization (MFP) that parameterizes the NIW-driven diapycnal mixing in the ocean interior (Jing et al., 2016; Yuan et al., 2021).
We initialize the oceanic model of CESM using the January-mean climatology from the World Ocean Atlas (WOA; Levitus et al., 2015). The climate forcings are set as the present-day (the year 2000) conditions and repeated every year. After a spin-up of 2 years, the global kinetic energy in the upper 1,000 m shows no notable tendency, suggesting a quasi-equilibrium state for mesoscale eddies. We then integrate the model for ten more years. During the 7th model year, snapshots of the ocean velocity, potential density, wind stress, surface air pressure, SBL depth, sea surface height (SSH), and turbulent dissipation rate parameterized by the MFP are output every 3 h for analyzing the interactions between mesoscale eddies and NIWs.
As detailed by Yuan et al. (2021), the CESM has fidelity in reproducing the observed sea surface geostrophic kinetic energy, near-inertial current amplitude, and WI (Chaigneau et al., 2008; Liu et al., 2019 ). Moreover, the statistics of CESM-simulated AEs and CEs show good agreement with the observed ones (Section 3.1). Finally, the parameterized NIW-induced turbulent dissipation rate is qualitatively consistent with that inferred from finestructure measurements of Argo data, reproducing the enhancement in the Kuroshio Extension, Gulf Stream extension, and the Southern Ocean where winds input considerable amount of energy to the NIWs (Yuan et al, 2021). These consistencies lend support to the realism of CESM in simulating the interaction between NIWs and mesoscale eddies as well as its effect on diapycnal mixing.
Computation of NIW characteristics
To extract the near-inertial velocity , we apply a 4th-order Butterworth bandpass filter that retains the velocity components within the near-inertial band (between 0.75f and 1.25f, f being the local Coriolis frequency) to the 3-h ocean velocity. Domain within 5° S– 5° N is discarded for analysis to avoid the influence of the vanishing f near the equator on the results. The kinetic energy of NIWs is computed as
The vertical NIW shear variance is calculated as
The downward NIW energy flux is computed as
where pI is the pressure perturbation in the near-inertial band estimated based on the hydrostatic approximation. The horizontal NIW energy flux convergence is computed as
Mesoscale eddy detection and composite analysis
In this study, mesoscale eddies are detected by analyzing the 3-h snapshots of the CESM-simulated SSH from the seventh model year following Faghmous et al. (2013). Supplementary Figure 1 shows a snapshot of detected eddies, illustrating their centroids and edges. The eddy radius R is defined as the radius of the circle that has an identical area with the eddy. As the method proposed by Faghmous et al. (2013) can only identify eddy structures at the sea surface, we assume that eddies do not tilt or only tilt slightly in the vertical. The composite analysis of some variable s is performed based on Chaigneau et al. (2011) as follows: For each eddy, we first transform s to a horizontal coordinate system in which the zonal and meridional axes are normalized by R and the origin is located at the eddy center. Then, we interpolate s onto a vertical coordinate system whose origin is located at the SBL base. The SBL depth is derived from the K-profile parameterization scheme and available in the model output (Large et al., 1994; Smith et al., 2010). The SBL depth for each eddy is set as the mean SBL depth within R from the eddy center. Sensitivity tests suggest that allowing for a spatially varying SBL depth has no noticeable influence on the results.
In the following analysis, we denote the mean value of s within R from the eddy center as . The background level of s in absence of eddies (denoted as ) is defined as the mean value of s outside 2R from the eddy center but within the square centered on the eddy center (the area occupied by any other detected eddies is excluded before calculating ). The effects of eddies on s are estimated via . The statistical uncertainties in Δs for AEs and CEs and influences of eddy detection methodology are evaluated in Supplementary Figures 2–5.
Results
Characteristics of the detected eddies
Figure 1 shows the characteristics of the AEs and CEs detected in the CESM simulation and those obtained from the merged altimetric sea level anomaly data provided by the Copernicus Marine Environmental Monitoring Service (CMEMS; https://marine.copernicus.eu) using the eddy detection method proposed by Faghmous et al. (2013). There are in total 12,387,430 3-h AE snapshots detected in the CESM during the seventh model year, very close to 13,033,066 for the 3-h CE snapshots.
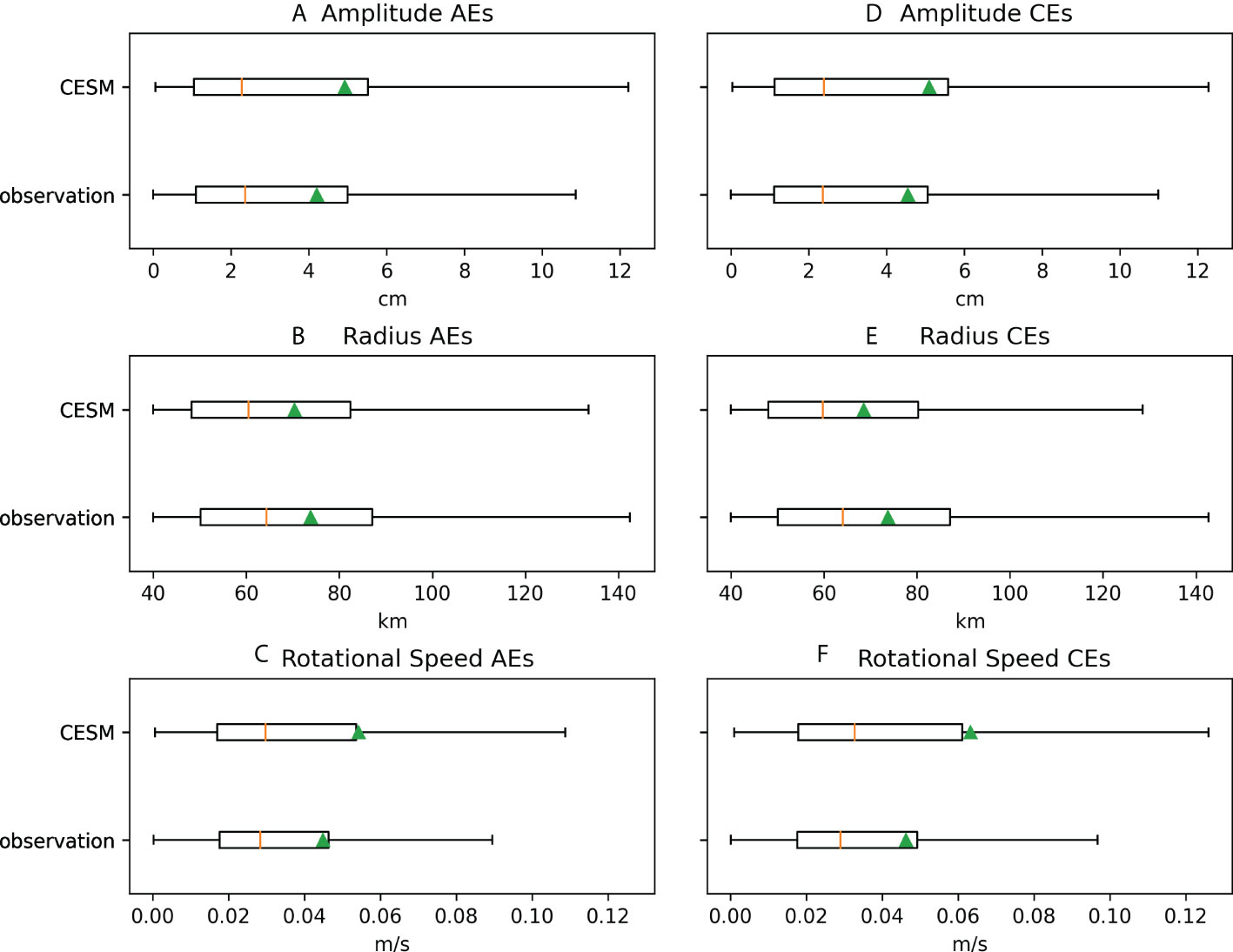
Figure 1 Boxplots of the (A, D) amplitude, (B, E) radius, and (C, F) rotational speed of AEs and CEs in the CESM and observations, respectively. Orange lines denote the median values, whereas green triangles denote the mean values.
The eddy amplitude is defined as the magnitude of the difference between the SSH extrema of the eddy and the mean SSH of the eddy’s boundary. The median eddy amplitude in the CESM is about 2.3 (2.4) cm for AEs (CEs) in the global ocean, very close to 2.4 (2.4) cm obtained from the observations. The median R of AEs (CEs) in the CESM is about 60.4 (59.8) km, slightly smaller than 64.3 (64.0) km in the observations. The rotational speed of an eddy is defined as the mean geostrophic speed inside the eddy. It is found that both AEs and CEs in the CESM rotate slightly faster than their observed counterparts. The median rotational speed is 3.0 cm/s for AEs and 3.3 cm/s for CEs in the CESM, whereas the median rotational speeds for AEs and CEs in the observations are about 2.8 cm/s and 2.9 cm/s, respectively. In conclusion, the simulated AEs and CEs in the CESM are qualitatively consistent with the observed ones.
NIW activities in AEs and CEs
Figures 2A–C show the composites of KEI, , and squared buoyancy frequency N2 for AEs in the global ocean, respectively. Under the SBL, KEI is enhanced around the centers of AEs. The enhancement is noticeable from the SBL base down to at least 4,000 m but is most evident between 400 and 700 m, where is about 60% of . According to the WKB theory, the refraction effect due to the changing N2 alone makes KEI and scaled as N2 and N3, respectively. Therefore, the elevated KEI in AEs cannot be explained by the refraction effect due to the spatially inhomogeneous N2, as the is only 5% of between 400 and 700 m. Such finding lends support to the argument that AEs can pipe NIW energy down to great depth via NIW-mean flow interactions (the so-called “chimney effect”; Lee & Niiler, 1998). The spatial structure of in AEs is qualitatively similar to that of KEI. However, the enhancement of within AEs is more pronounced than that of KEI, with a about 125% of between 400 and 700 m. The differed extent of the enhancement of KEI and means that the vertical scale of NIWs shrinks in AEs. Such a shrinkage of NIW vertical scale in AEs cannot be ascribed to the refraction by the changing N2, either. However, it is consistent with the theoretical finding derived from the ray tracing of NIWs in an idealized AE where the vertical scale shrinkage is caused by the refraction due to the spatial inhomogeneity in feff (Kunze, 1985).
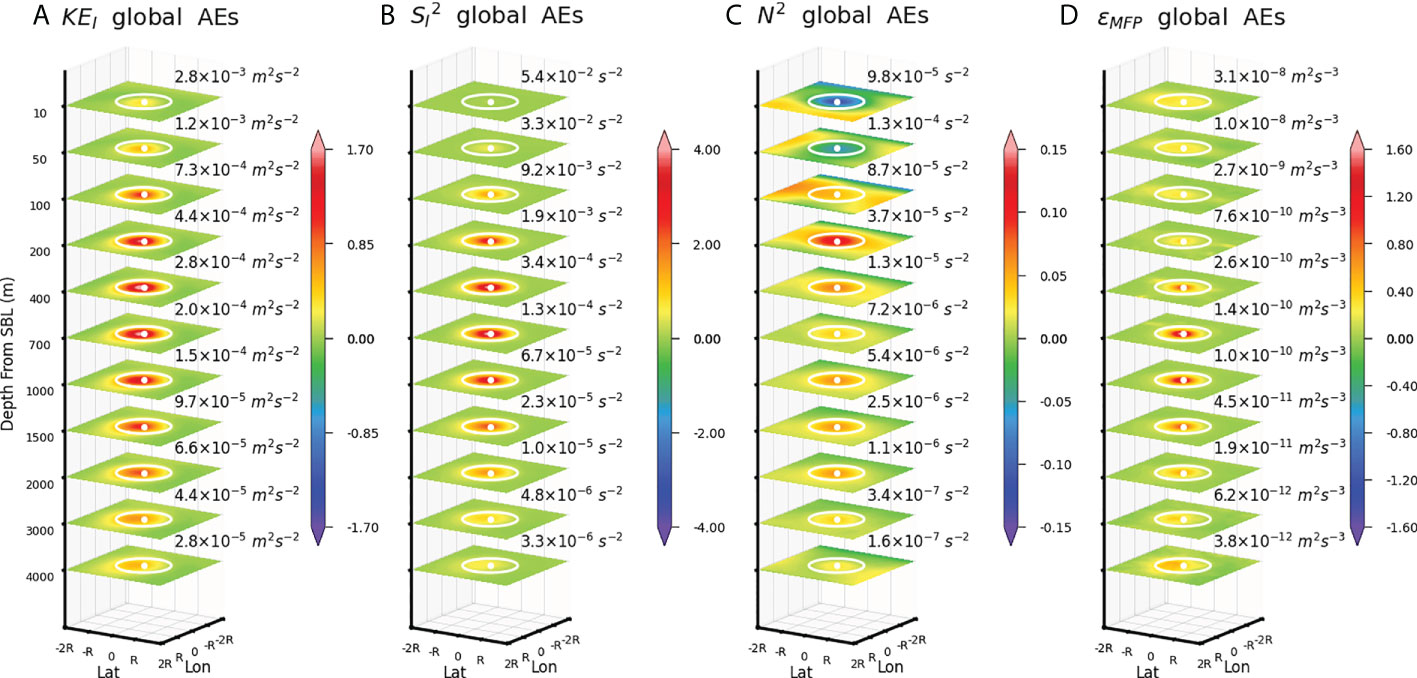
Figure 2 (A) Relative difference of the composite KEI with respect to its background value, , for AEs in the global ocean. The value of is denoted above each horizontal slice. (B–D) Same as (A) but for , N2, and ϵMFP.
On the contrary, KEI is reduced around the centers of CEs compared with the background level (Figure 3A). The weakening is evident from the SBL base down to at least 4,000 m. The ΔN2 is too small to account for the reduced KEI in CEs (Figure 3C), providing evidence that the weakened NIW activity under the SBL in the CEs is due to the NIW-mean flow interactions. The in CEs shares a similar spatial structure as KEI but shows a more pronounced reduction than that of KEI. For instance, is about -40% of at 400 m, whereas the ratio is only about -29% for KEI at the same depth, suggesting an expanded vertical scale of NIWs in CEs. Again, the expanded vertical scale of NIWs in CEs cannot be attributed to the refraction by the changing N2 (Figure 3C) but is probably due to the changes in feff. Finally, we remark that there is asymmetry between the strengthening effect of AEs and the weakening effect of CEs on NIW activity, with the former more pronounced than the latter. Accordingly, the net effect of mesoscale eddies is to promote the NIW activity in the ocean interior.
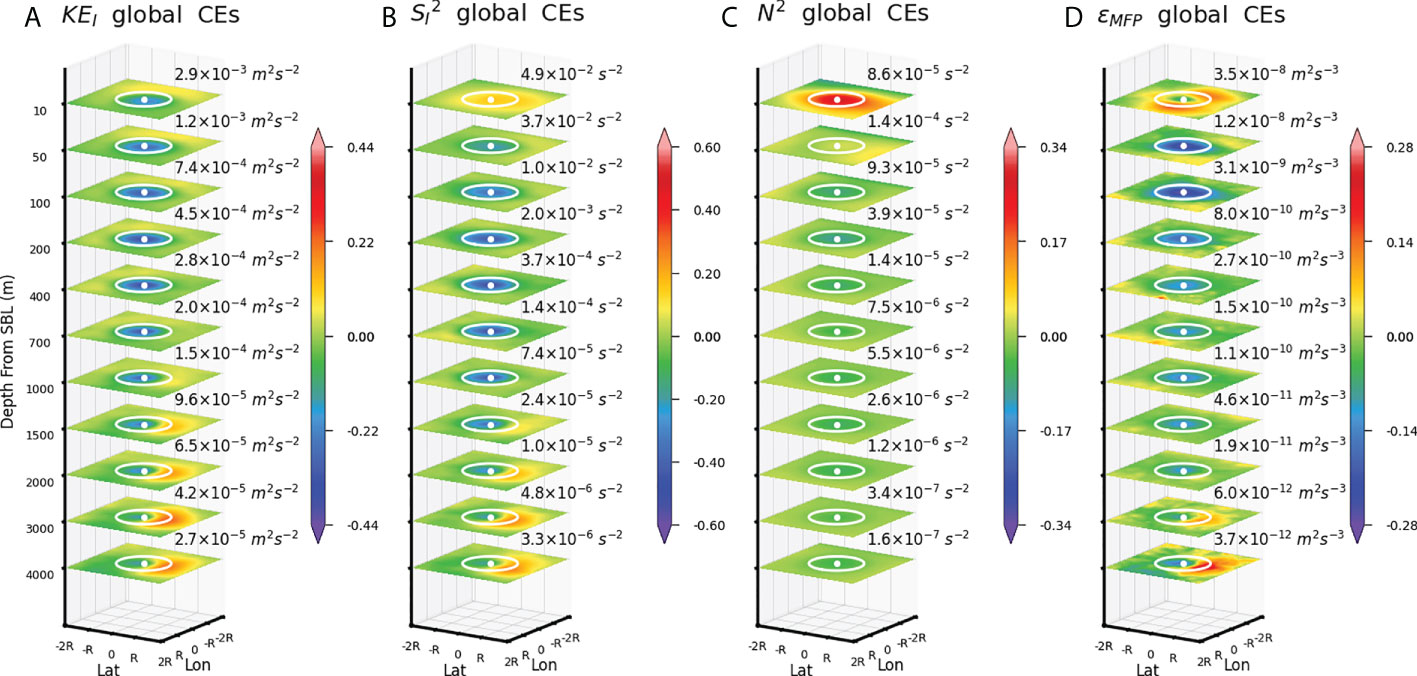
Figure 3 Same as Figure 2 but for CEs.
We next examine the regulation of NIW activity under the SBL by AEs and CEs in different regions including the Kuroshio Extension (KE), Gulf Stream (GS), subtropical countercurrent (STCC), and the Southern Ocean (SO) (Figures 4, 5). The vertical structures of the mesoscale eddies in these regions differ significantly (Supplementary Figure 6). The enstrophy (ζ2) of mesoscale eddies in the SO has an e-folding vertical scale of 566.5 m, whereas this value is reduced to 403.8 m, 273.5 m, and 145.4 m in the GS, KE, and STCC, respectively. There is a universal enhancement of KEI around the center of AEs in different regions. However, the peaking depth and the downward penetration of this enhancement differ evidently among different regions. The enhancement of KEI peaks at a greater depth and penetrates deeper for AEs with a larger e-folding vertical scale, suggesting that the more barotropic the AEs are, the more efficient they are to drain the NIW energy into the abyssal ocean. As for CEs, the KEI around the eddy center is universally weakened in different regions. In general, this weakening effect penetrates into a deeper region as the vertical e-folding scale of ζ2 increases.
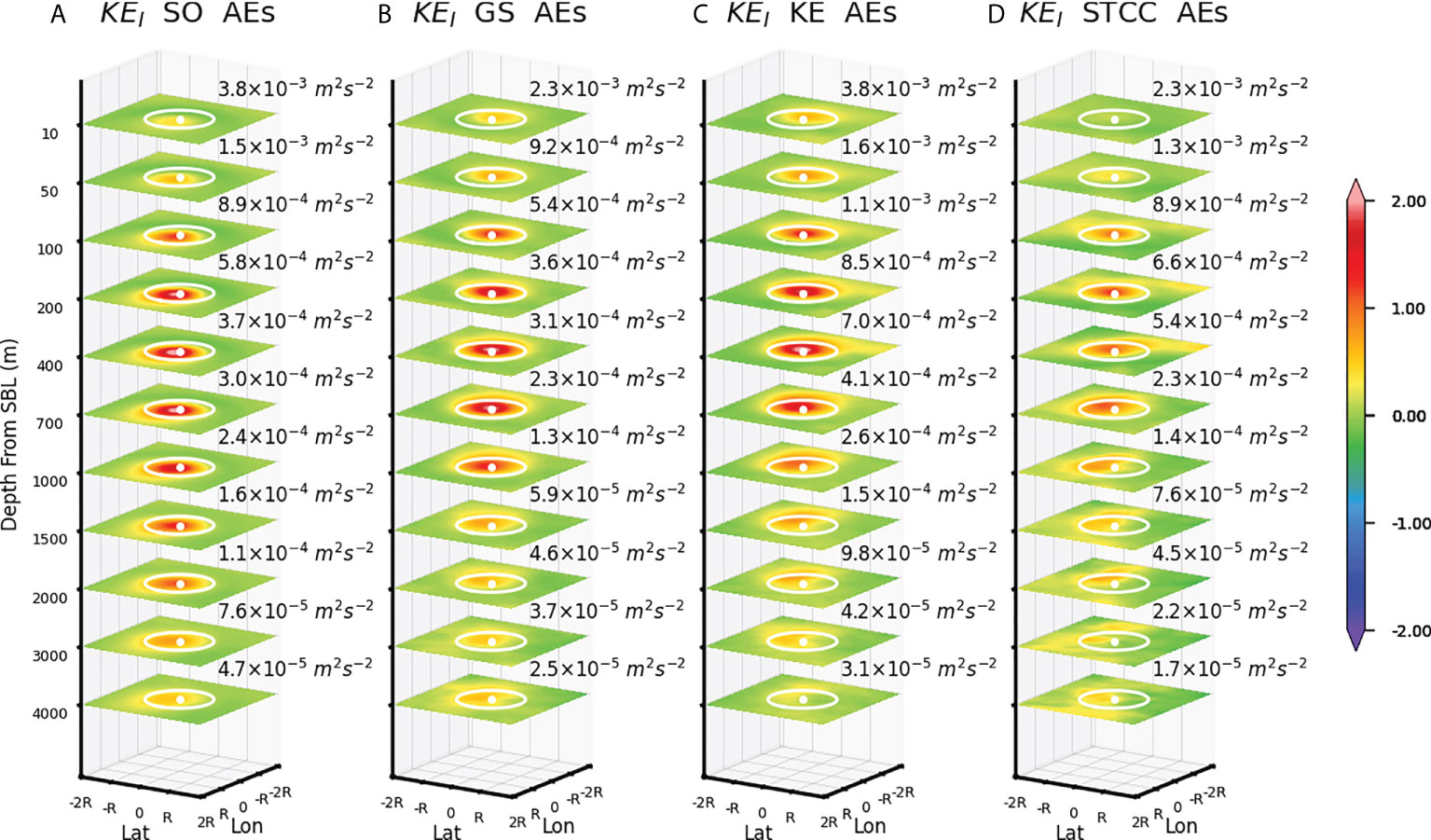
Figure 4 Same as Figure 2A but for AEs in the (A) Southern Ocean (SO), (B) Gulf Stream (GS), (C) Kuroshio extension (KE), and (D) subtropical countercurrent (STCC), respectively.
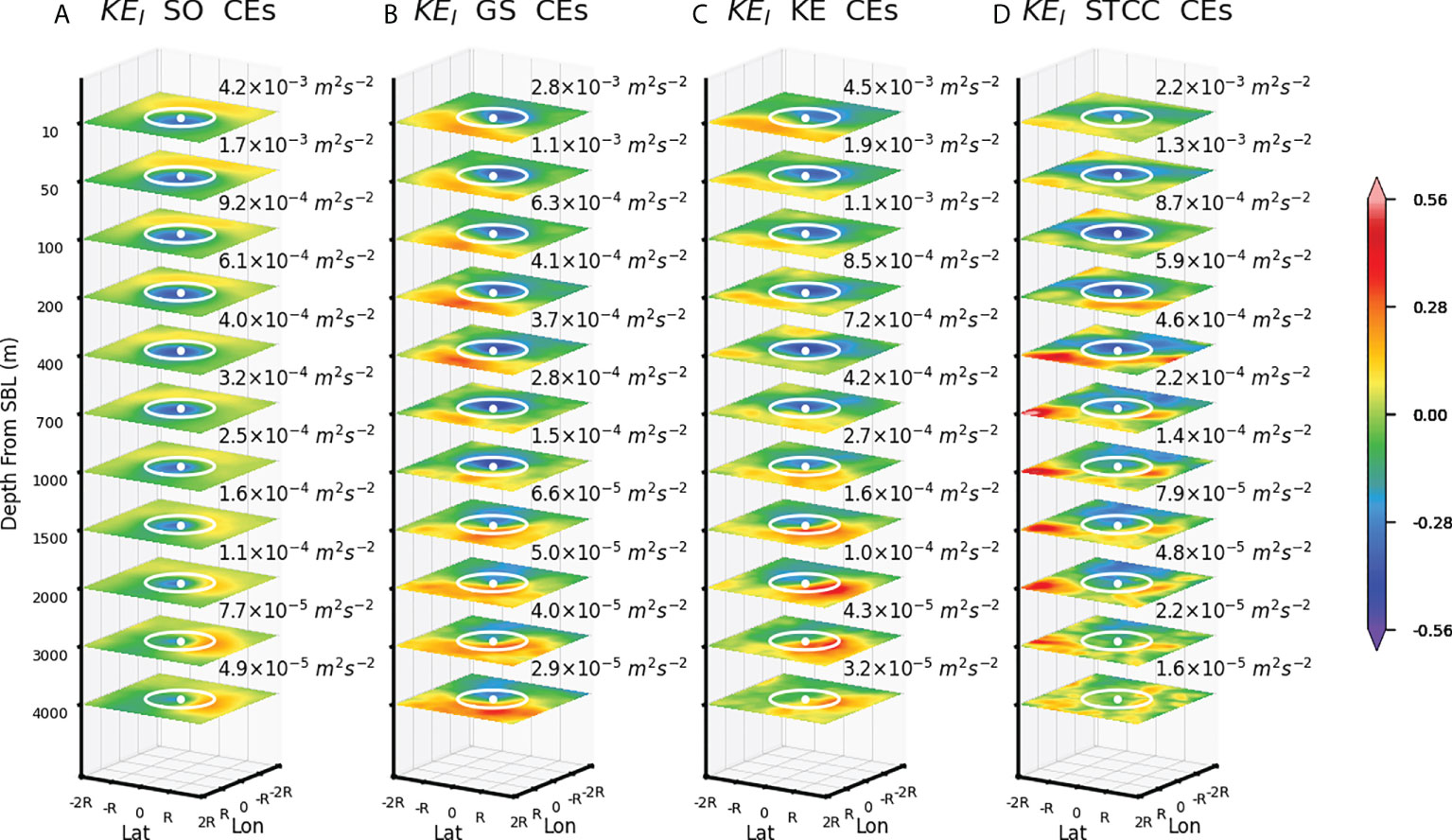
Figure 5 Same as Figure 4 but for CEs.
Underlying dynamics
The enhanced NIW activity under the SBL in AEs implies an increased NIW energy flux into this region. This enhancement could result from the elevated downward NIW energy flux from the SBL base into the deep ocean (measured by ) or/and the horizontal convergence of NIW energy flux under the SBL (measured by ). Here, rather than is used for comparison, because the latter contains the background downward NIW energy flux in absence of the eddies. It is found that dominates over in enhancing NIW activity from the SBL to the sea floor. In terms of the global average, the value of at the SBL base peaks around the AE center with a positive of 0.17 mWm-2 (Figure 6A and Supplementary Figure 7), whereas the value of integrated from the SBL base to ~4,000 m is only about 0.06 mWm-2. However, a large fraction of is concentrated within a few hundred meters under the SBL base, suggesting that the horizontal convergence of NIW energy flux may contribute importantly to powering NIWs in this layer. This is confirmed by the vertical profile of that does not peak at the SBL base but ~150 m further downward where the value of decays to a negligible level. In the deeper ocean, the enhanced NIW activity in AEs is mostly ascribed to the increased downward NIW energy flux with the horizontal NIW energy flux convergence playing a negligible role. The vertical profiles of and for AEs in different regions are qualitatively similar to their global mean profiles (Figures 6B–E), suggesting the universality of underlying dynamics for the enhanced NIW activity in AEs across the global ocean.
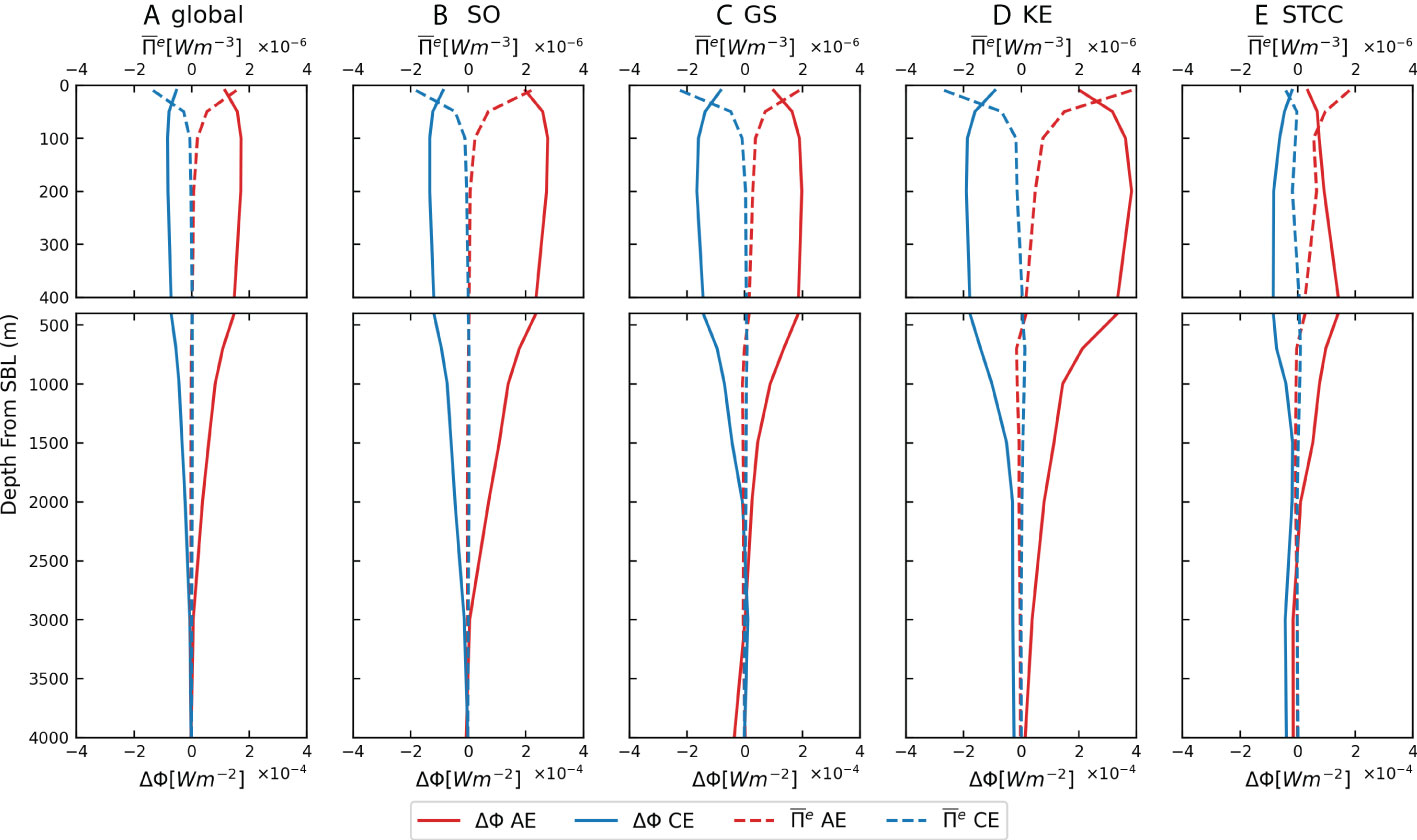
Figure 6 Composites of (solid lines) and Πe (dashed lines) in AEs (red lines) and CEs (blue lines) in the (A) global ocean, (B) SO, (C) GS, (D) KE, and (E) STCC, respectively.
The vertical profiles of and in CEs generally resemble those in AEs but are in opposite signs. Accordingly, the reduced NIW activity under the SBL in CEs is due to both the suppressed downward NIW energy flux from the SBL base and the horizontal divergence of NIW energy flux under the SBL. The negative in CEs in combination with the positive in AEs suggests a NIW energy radiation from CEs to AEs under the SBL, consistent with the theoretical prediction from Kunze (1985). Moreover, the vertical profiles of and for CEs in different regions share similar features as their global mean counterparts. Finally, we note that the magnitude of in CEs is systematically smaller than that in AEs. This may account for the weaker effect of CEs than AEs on NIW activity.
Discussion
The motivation for understanding the regulation of NIWs by mesoscale eddies roots largely from its effect on the diapycnal mixing in the ocean interior. In this section, we estimate the influences of AEs and CEs on the NIW-induced turbulent dissipation rate ϵ under the SBL. Here, the value of ϵ is derived from the MFP (Jing et al., 2016; Yuan et al., 2021), denoted as ϵMFP henceforth. The MFP relates ϵMFP to the model-simulated and N2, parameterizing the NIW-induced diapycnal mixing using a finescale parameterization (Polzin et al., 2014) modified to remedy the underestimation of induced by model’s vertical resolution. Figures 2D, 3D display the composites of ϵMFP in AEs and CEs in the global ocean, respectively. The spatial structures of ϵMFP resemble those of , being enhanced (weakened) around the center of AEs (CEs) from the SBL base down to at least 4,000 m. Similar to , the effect of AEs on ϵMFP is more evident than that of CEs, suggesting a net contribution of mesoscale eddies to intensifying the diapycnal mixing in the ocean interior.
Application of the MFP requires resolving both the mesoscale eddies and NIWs, which is possible for the eddy-resolving CESM but beyond the capacity of coarse-resolution coupled global climate models (CGCMs). Currently, the parameterizations applied to coarse-resolution CGCMs typically assume a constant fraction of WI radiating downward into the stratified ocean interior (e.g., Jochum et al., 2013; Olbers and Eden, 2013, 2017; Eden and Olbers, 2014; Pollmann et al., 2017). However, observations and modeling studies suggest that this fraction is not a constant in global range (Furuichi et al., 2008; Zhai et al., 2009; Alford et al., 2012; Jing and Wu, 2014; Voelker et al., 2020; Sun et al., 2021). The composite , maximum downward NIW energy flux under the SBL base , and their ratio for AEs and CEs in the global ocean and different regions are summarized in Table 1. We find that the value of r differs substantially between AEs and CEs. In terms of the global average, the value of r for AEs is about 43.2%, more than twice of 20.8% for CEs. Similar is the case for eddies over different regions. It thus suggests that the diapycnal mixing should be different between AEs and CEs. Moreover, our analysis suggests that the mesoscale eddy-induced horizontal NIW energy flux convergence/divergence under the SBL base plays a key role in regulating NIW activity in the ocean interior. Such an effect is overlooked in previous studies but needs further consideration to improve the parameterization of NIW-induced diapycnal mixing in coarse-resolution CGCMs.
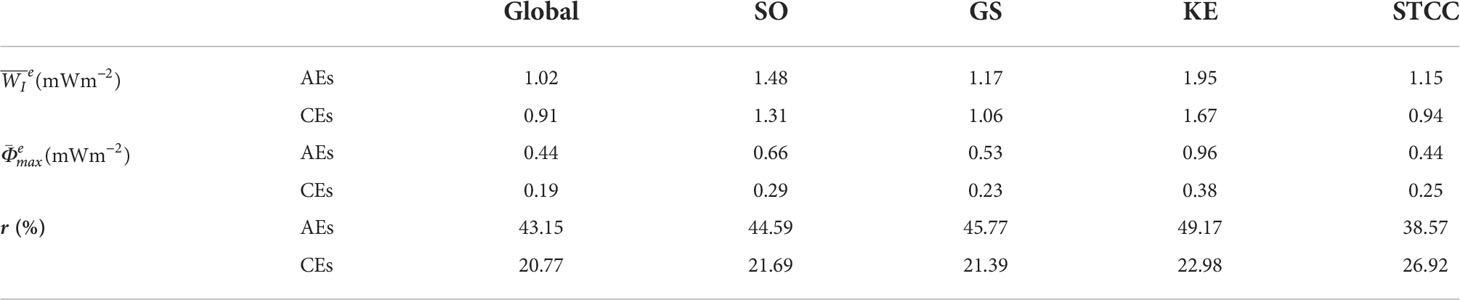
Table 1 Composites of , maximum downward NIW energy flux under the SBL base, and their ratio for AEs and CEs in the global ocean and different regions.
Conclusions
In this study, we evaluate the effects of CEs and AEs on NIW characteristics under the SBL in the global ocean, using an eddy-resolving CESM. The main conclusions are as follows:
1. In terms of the global average, KEI is increased (decreased) and the vertical scale of NIWs is shrunk (enlarged) within AEs (CEs) probably due to the NIW-mean flow interactions. The enhanced (weakened) NIW activity in AEs (CEs) is noticeable from the SBL base down to at least 4,000 m but is most prominent between 400 and 700 m under the SBL. The effect of AEs on NIW activity is more evident than that of CEs, indicating a net strengthening of NIWs in the ocean interior by mesoscale eddies.
2. The enhanced (weakened) NIW activity under the SBL in AEs (CEs) is due to both the horizontal convergence (divergence) of NIW energy flux under the SBL and the increased (decreased) downward NIW energy flux from the SBL base into the ocean interior. The former effect attenuates rapidly with the increasing depth, confined to a layer several hundred meters under the SBL, whereas the latter’s effect becomes dominant in the deeper ocean.
3. The regulations of NIWs by AEs (CEs) are qualitatively similar in different regions, suggesting a universal enhancement (weakening) of NIWs in the ocean interior by AEs (CEs) across the global ocean.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This research was supported by the National Science Foundation of China (NSFC 42006014, NSFC 41822601, and NSFC 41776006) and Taishan Scholar Funds (tsqn201909052).
Acknowledgments
The authors are grateful to the High Performance Computing Center of Qingdao National Laboratory for Marine Science and Technology for supporting the conduction of the model simulation and much of the numerical analysis.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.949610/full#supplementary-material
References
Alford M. H., Cronin M. F., Klymak J. M. (2012). Annual cycle and depth penetration of wind-generated near-inertial internal waves at ocean station papa in the northeast pacific. J. Phys. Oceanogr. 42, 889–909. doi: 10.1175/JPO-D-11-092.1
Alford M. H., MacKinnon J. A., Simmons H. L., Nash J. D. (2016). Near-inertial internal gravity waves in the ocean. Ann. Rev. Mar. Sci. 8, 95–123. doi: 10.1146/annurev-marine-010814-015746
Balmforth N. J., Llewellyn Smith S. G., Young W. R. (1998). Enhanced dispersion of near-inertial waves in an idealized geostrophic flow. J. Mar. Res. 56, 1–40. doi: 10.1357/002224098321836091
Chaigneau A., Le Texier M., Eldin G., Grados C., Pizarro O. (2011). Vertical structure of mesoscale eddies in the eastern south pacific ocean: A composite analysis from altimetry and argo profiling floats. J. Geophys. Res. Ocean. 116, 1–16. doi: 10.1029/2011JC007134
Chaigneau A., Pizarro O., Rojas W. (2008). Global climatology of near-inertial current characteristics from Lagrangian observations. Geophys. Res. Lett. 35, 1–5. doi: 10.1029/2008GL034060
Chang P., Zhang S., Danabasoglu G., Yeager S. G., Fu H., Wang H., et al. (2020). An unprecedented set of high-resolution earth system simulations for understanding multiscale interactions in climate variability and change. J. Adv. Model. Earth Syst. 12, 1–52. doi: 10.1029/2020MS002298
Danioux E., Vanneste J., Bühler O. (2015). On the concentration of near-inertial waves in anticyclones. J. Fluid Mech. 773, R21–R212. doi: 10.1017/jfm.2015.252
D’Asaro E. A. (1985). The energy flux from the wind to near-inertial motions in the surface mixed layer. J. Phys. Oceanogr. 15, 1043–1059. doi: 10.1175/1520-0485(1985)015<1043:TEFFTW>2.0.CO;2
Eden C., Olbers D. J. (2014). An energy compartment model for propagation, nonlinear interaction, and dissipation of internal gravity waves. J. Phys. Oceanogr. 44, 2093–2106. doi: 10.1175/JPO-D-13-0224.1
Faghmous J. H., Le M., Uluyol M., Kumar V., Chatterjee S. (2013). “A parameter-free spatio-temporal pattern mining model to catalog global ocean dynamics,” in 2013 IEEE 13th international conference on data mining (Dallas, TX, United States:IEEE), 151–160. doi: 10.1109/ICDM.2013.162
Furuichi N., Hibiya T., Niwa Y. (2008). Model-predicted distribution of wind-induced internal wave energy in the world’s oceans. J. Geophys. Res. Ocean 113, 1–13. doi: 10.1029/2008JC004768
Gregory J. M. (2000). Vertical heat transports in the ocean and their effect on time-dependent climate change. Clim. Dyn. 16, 501–515. doi: 10.1007/s003820000059
Jing Z., Wu L. (2010). Seasonal variation of turbulent diapycnal mixing in the northwestern pacific stirred by wind stress. Geophys. Res. Lett. 37, 1–5. doi: 10.1029/2010GL045418
Jing Z., Wu L. (2014). Intensified diapycnal mixing in the midlatitude western boundary currents. Sci. Rep. 4, 1–6. doi: 10.1038/srep07412
Jing Z., Wu L., Ma X., Chang P. (2016). Overlooked role of mesoscale winds in powering ocean diapycnal mixing. Sci. Rep. 6, 1–7. doi: 10.1038/srep37180
Jochum M., Briegleb B. P., Danabasoglu G., Large W. G., Norton N. J., Jayne S. R., et al. (2013). The impact of oceanic near-inertial waves on climate. J. Clim. 26, 2833–2844. doi: 10.1175/JCLI-D-12-00181.1
Klein P., Smith S. L., Lapeyre G. (2004). Organization of near-inertial energy by an eddy field. Q. J. R. Meteorol. Soc 130, 1153–1166. doi: 10.1256/qj.02.231
Kunze E. (1985). Near-inertial wave propagation in geostrophic shear. J. Phys. Oceanogr. 15, 544–565. doi: 10.1175/1520-0485(1985)015<0544:NIWPIG>2.0.CO;2
Large W. G., McWilliams J. C., Doney S. C. (1994). Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32, 363–403. doi: 10.1029/94RG01872
Lee D.-K., Niiler P. P. (1998). The inertial chimney: The near-inertial energy drainage from the ocean surface to the deep layer. J. Geophys. Res. Ocean. 103, 7579–7591. doi: 10.1029/97JC03200
Lelong M. P., Cuypers Y., Bouruet-Aubertot P. (2020). Near-inertial energy propagation inside a mediterranean anticyclonic eddy. J. Phys. Oceanogr. 50, 2271–2288. doi: 10.1175/JPO-D-19-0211.1
Levitus S., Boyer T. P., Garcia H. E., Locarnini R. A., Zweng M. M., Mishonov A. V., et al. (2015). “World ocean atlas 2013,” in NOAA Natl. centers environ. inf. Boulder, Colorado, United States: NOAA National Centers for Environmental Information. doi: 10.7289/v5f769gt
Liu Y., Jing Z., Wu L. (2019). Wind power on oceanic near-inertial oscillations in the global ocean estimated from surface drifters. Geophys. Res. Lett. 46, 2647–2653. doi: 10.1029/2018GL081712
Munk W. H., Wunsch C. (1998). Abyssal recipes II: Energetics of tidal and wind mixing. Deep. Res. Part I Oceanogr. Res. Pap. 45, 1977–2010. doi: 10.1016/S0967-0637(98)00070-3
Olbers D. J., Eden C. (2013). A global model for the diapycnal diffusivity induced by internal gravity waves. J. Phys. Oceanogr. 43, 1759–1779. doi: 10.1175/JPO-D-12-0207.1
Olbers D. J., Eden C. (2017). A closure for internal wave–mean flow interaction. part I: Energy conversion. J. Phys. Oceanogr. 47, 1389–1401. doi: 10.1175/JPO-D-16-0054.1
Pollmann F., Eden C., Olbers D. J. (2017). Evaluating the global internal wave model IDEMIX using finestructure methods. J. Phys. Oceanogr. 47, 2267–2289. doi: 10.1175/JPO-D-16-0204.1
Polzin K. L., Naveira-Garabato A. C., Huussen T. N., Sloyan B. M., Waterman S. (2014). Finescale parameterizations of turbulent dissipation. J. Geophys. Res. Ocean, 119, 1383–1419. doi: 10.1002/2013JC008979
Rimac A., von Storch J.-S., Eden C., Haak H. (2013). The influence of high-resolution wind stress field on the power input to near-inertial motions in the ocean. Geophys. Res. Lett. 40, 4882–4886. doi: 10.1002/grl.50929
Saenko O. A., Merryfield W. J. (2005). On the effect of topographically enhanced mixing on the global ocean circulation. J. Phys. Oceanogr. 35, 826–834. doi: 10.1175/jpo2722.1
Smith R., Jones P. W., Briegleb B. P., Bryan F. O., Danabasoglu G., Dennis J. M., et al. (2010). The parallel ocean program (POP) reference manual ocean component of the community climate system model (CCSM) and community earth system model (CESM). LAUR-01853 141, 1–140. Available at: http://n2t.net/ark:/85065/d70g3j4h.
Sun B., Wang S., Yuan M., Wang H., Jing Z., Chen Z., et al. (2021). Energy flux into near-inertial internal waves below the surface boundary layer in the global ocean. J. Phys. Oceanogr. 51, 2315–2328. doi: 10.1175/JPO-D-20-0276.1
Voelker G. S., Olbers D. J., Walter M., Mertens C., Myers P. G. (2020). Estimates of wind power and radiative near-inertial internal wave flux: The hybrid slab model and its application to the north Atlantic. Ocean Dyn. 70, 1357–1376. doi: 10.1007/s10236-020-01388-y
Whalen C. B., MacKinnon J. A., Talley L. D., Waterhouse A. F. (2015). Estimating the mean diapycnal mixing using a finescale strain parameterization. J. Phys. Oceanogr. 45, 1174–1188. doi: 10.1175/JPO-D-14-0167.1
Whalen C. B., Talley L. D., MacKinnon J. A. (2012). Spatial and temporal variability of global ocean mixing inferred from argo profiles. Geophys. Res. Lett. 39, 1–9. doi: 10.1029/2012GL053196
Wu L., Jing Z., Riser S., Visbeck M. (2011). Seasonal and spatial variations of southern ocean diapycnal mixing from argo profiling floats. Nat. Geosci. 4, 363–366. doi: 10.1038/ngeo1156
Wunsch C., Ferrari R. (2004). Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314. doi: 10.1146/annurev.fluid.36.050802.122121
Young W. R., Ben Jelloul M. (1997). Propagation of near-inertial oscillations through a geostrophic flow. J. Mar. Res. 55, 735–766. doi: 10.1357/0022240973224283
Yuan M., Song Z., Li Z., Jing Z., Chang P., Sun B., et al. (2021). An improved parameterization of wind-driven turbulent vertical mixing based on an eddy-resolving climate model. J. Adv. Model. Earth Syst. 13, 1–20. doi: 10.1029/2021MS002630
Zhai X., Greatbatch R. J., Eden C. (2007). Spreading of near-inertial energy in a 1/12° model of the north Atlantic ocean. Geophys. Res. Lett. 34, 1–5. doi: 10.1029/2007GL029895
Zhai X., Greatbatch R. J., Eden C., Hibiya T. (2009). On the loss of wind-induced near-inertial energy to turbulent mixing in the upper ocean. J. Phys. Oceanogr. 39, 3040–3045. doi: 10.1175/2009JPO4259.1
Keywords: mesoscale eddies, near-inertial internal waves, turbulent vertical mixing, coupled global climate models, community earth system model
Citation: Yuan M, Song Z, Jing Z, Li Z and Wu L (2022) Distinct roles of global cyclonic and anticyclonic eddies in regulating near-inertial internal waves in the ocean interior. Front. Mar. Sci. 9:949610. doi: 10.3389/fmars.2022.949610
Received: 21 May 2022; Accepted: 05 August 2022;
Published: 02 September 2022.
Edited by:
Chunyan Li, Louisiana State University, United StatesReviewed by:
Haosheng Huang, Louisiana State University, United StatesEnric Pallàs-Sanz, Center for Scientific Research and Higher Education in Ensenada (CICESE), Mexico
Quanan Zheng, University of Maryland, College Park, United States
Copyright © 2022 Yuan, Song, Jing, Li and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhuo Song, c29uZ3podW9Ab3VjLmVkdS5jbg==
 Man Yuan
Man Yuan Zhuo Song
Zhuo Song Zhao Jing
Zhao Jing Zhuoran Li1,2
Zhuoran Li1,2