The Fourth-Order Nonlinear Schrödinger Equation and Stability Analysis for Stokes Waves on Slowly Varying Topography

Introduction

The interactions among wave packets with narrowband range frequencies and wavelengths received considerable attention. Benjamin and Feir (1967) theoretically proved that wave packets were unstable when kh is larger than 1.363, where k is the dominant wavenumber, and h is the water depth. Whitham (1967) identified and explained the Benjamin–Feir instability by theoretical analysis. Benney and Roskes (1969) complemented Whitham’s theory. With a pair of nonlinear conservation equations introduced by Whitham, Lighthill (1967) analyzed the nonlinear wave evolution process after the initial stable stage of a single wave packet. Chu and Mei (1971) added the modulation rate term to Whitham’s equation for long-term wave packet evolution processes to interpret the high-order dispersion effect.

The wave packet evolution process can be studied by the cubic nonlinear Schrödinger (NLS) equation [Zakharov (1968); Benney and Roskes (1969)], which is equal to the conservation equation proposed by Chu and Mei (Hasimoto and Ono, 1972). Zakharov and Shabat (Davey, 1972) solved the analytical NLS solution. Hasimoto and Ono (Zakharov and Shabat, 1972) obtained a one-dimensional NLS for the wave packet envelope from multiple scale expansions for finite depth. Davey and Stewartson (1974) investigated the transformation of slowly varying wave packets in a three-dimensional finite depth, concluding that the wave packet envelope is confined to two nonlinear partial differential equations, similar to NLS in form. Lo and Mei (1985) highlighted the simulation value with NLS’s preferably approached measured value if ε < 0.1, while the departure between the simulation and measured values was larger when ε > 0.1. Martin (Martin H. Yuen, 1980) found that the simulated wave energy with NLS does not satisfy the conservation law due to energy attenuation. Besides the confined condition of small wave steepness, NLS showed Benjamin–Feir instability in an unbounded region by two-dimensional sideband perturbation, resulting in leaking energy from low wavenumber components to high wavenumber components (Dysthe, 1979).

The NLS has been modified to overcome these defects above. By expanding the equation to the fourth order on finite depth, Dysthe (1979) established the modified nonlinear Schrödinger equation (MNLS) to improve wave packets’ instability properties. Lo and Mei (1987) numerically solved and transformed MNLS in moving coordinates, showing poor long-time wave packet evolution reproducibility on infinite depth and asymmetry of sideband perturbation evolution. By considering that the wave spectrum in a realistic ocean is not narrowband, Trulsen and Dysthe (1996) developed a broader band modified nonlinear Schrödinger equation (BMNLS) by extending the bandwidth to the ${\epsilon }^{\frac{1}{2}}$ order. It showed the same precision as MNLS in nonlinear terms but higher precision in linear dispersive terms than MNLS. In deep water, to compute the dispersive relation efficiently using the pseudo-spectrum method and keep the simple structure of the Dysthe equation, Trulsen et al. (2000) used cubic nonlinear terms to modify linear dispersive relations, improving wave packets’ instability property by comparing the result with that from the Stokes wave analytic solution of Mclean (McLean, 1982), ensuring the boundness of Benjamin–Feir instability and stopping the wave energy leaking to high wavenumber components. Craig et al. (2012) proposed that NLS is not a Hamilton partial differential equation but an approximation to the Euler equation. Craig et al. (Craig et al., 2010; Craig et al., 2011) adopted Hamilton’s method to solve the nonlinear wave modulation process and provided a Hamilton structure of the Dysthe equation (Dysthe, 1979) to describe the gravity wave evolution process on finite and infinite depth. Craig et al. (2012) developed the Hamilton method by introducing the Hamilton pair to the equations proposed by Trulsen et al. (Trulsen and Dysthe, 1996; Trulsen et al., 2000). The equations developed using this method were compatible with water wave equations. Zhang and Li (2012) modified the pseudo-spectrum method by splitting the technique to make the MNLS equation suitable for nonperiodic boundary conditions. The method can efficiently solve nonlinear wave equations through numerical examples by nonlinear parabolic and MNLS equations.

The topography under nature waters is complicated and a crucial factor affecting the propagation process of surface gravity waves in coastal areas. Mei (2005) solved the weakly nonlinear narrowband wave packet equation on a finite flat bottom, indicating the effect of a three-order nonlinearity on the first-order wave height when the time scale is longer than ε^-2 of the dominant wave period or space scale is larger than ε^-2 of the dominant wave length. Brinch-Nielsen and Jonsson (1986) extended the nonlinear Schrödinger equation to the fourth order in three dimensions on an arbitrary constant depth, concluding that water depth can affect the applicability of wave instability expressions in deep water. Mild slope equations (Berkhoff, 1972; Lozano and Meyer, 1976) and their extensions (Kirby, 1986; Chamberlain and Porter, 1995; Miles and Chamberlain, 1998; Agnon and Pelinovsky, 2001) are powerful tools, aiming either at steeper slopes on large length scales or shorter irregularities, primarily used for calculating wave fields on the background of ocean engineering. According to Yue and Mei (1980), restricting ∇_hh to O (ε²), Kirby (Kirby and Dalrymple, 1983) introduced two variable x scales and one variable y scale. A parabolic equation with time independence was developed, avoiding the caustics and irregular focusing on the ray approximation while precluding wave instability analysis (Kirby and Dalrymple, 1983). Xiao and Lo (Xiao and Lo 2004) introduced the first-order depth variation terms to NLS by expanding the equation to the third-order to allow $\frac{\Delta \omega }{\omega }=\frac{\Delta k}{k}=\text{O}\left({\epsilon }^{\frac{2}{3}}\right)$ and depth variation $\frac{\Delta h}{h}=O\left({\epsilon }^{\frac{4}{3}}\right)$. No stable region exists for a uniform Stokes wave on varying bottoms, and a higher order instability beyond the Benjamin-Feir type is introduced by depth variation (Xiao and Lo 2004). Combined with experimental results and numerical analysis, Li et al. (Li et al., 2021; Li et al., 2021) found additional wave packets propagating freely and arising at first and second orders in wave steepness in a Stokes expansion as the wave packet travels over a sudden depth transition area. Free and bound waves coexisting with different phases at the second-order wave steepness indicated that the combination of the local transient peak and the magnitude of the linear free waves explained the rogue waves observed after a sudden depth transition. Zhang and Benoit (2021) proposed that the wave-bottom interaction in coastal areas forms rogue waves and increases the possibility of big waves occurring.

Neither MNLS nor BMNLS can describe the wave packet evolution process on varying bottoms. Considering the extensive application of NLS, the wave evolution process and its instability features in realistic situations can be evaluated by improving NLS to the fourth order for variable depths. Based on a mathematical technique introduced by Mei (Chu and Mei, 1970) and a boundary condition adopted by Kirby (Kirby and Dalrymple, 1983), the narrowband wave packet evolution equation was expanded to the fourth-order wave steepness. A topographic modified nonlinear Schrödinger (TMNLS) equation is obtained and investigated for the instability of a uniform Stokes wave train.

Evolution Equation for Narrowband Wave Packets on the Finite Depth

We assign (x, y, z) as spatial coordinates with z pointing vertically upward and assume that the water depth h (x, y) is slowly varying and finite at $\frac{\pi }{10}<kh<\pi$. In the irrotational current field of inviscid and incompressible fluids, velocity potential Ф (x, y, z, t) and free surface displacement ς (x, y, t) describe surface wave propagation.

P_a is the local atmospheric pressure, and the equations to describe waves are as follows.

Laplace equation:

$\begin{array}{ll}\Delta \Phi =0& (1)\end{array}$

Kinematic boundary condition on the bottom:

$\begin{array}{ll}\begin{array}{cc}\frac{\partial \Phi }{\partial x}\frac{\partial h}{\partial x}\text{+ }\frac{\partial \Phi }{\partial y}\frac{\partial h}{\partial y}=-\frac{\partial \Phi }{\partial z}& \left(z=-h\right)\end{array}& (2)\end{array}$

Dynamic boundary condition on the surface:

$\begin{array}{ll}\begin{array}{cc}-\frac{p_a}{\rho }=g\varsigma +\frac{\partial \Phi }{\partial t}+\frac{1}{2}{\left|\nabla \Phi \right|}^2& \left(z=\varsigma \right)\end{array}& (3)\end{array}$

Kinematic boundary condition on the surface:

$\begin{array}{ll}\begin{array}{cc}\frac{\partial \varsigma }{\partial t}\text{+ }\frac{\partial \Phi }{\partial x}\frac{\partial \varsigma }{\partial x}\text{+ }\frac{\partial \Phi }{\partial y}\frac{\partial \varsigma }{\partial y}=\frac{\partial \Phi }{\partial z}& \left(z=\varsigma \right)\end{array}& (4)\end{array}$

We act the operator $\frac{\partial }{\partial t}+\overrightarrow{u}·\nabla$ on two sides of Equation (3). p_a is a constant. Equation (3) can be given as

$\begin{array}{ll}\begin{array}{cc}\frac{{\partial }^2\Phi }{\partial t^2}+g\frac{\partial \Phi }{\partial z}+\frac{\partial }{\partial t}\left({\left|\overrightarrow{u}\right|}^2\right)+\frac{1}{2}\overrightarrow{u}·\nabla {\left|u\right|}^2\mathrm{=0}& \left(z=\varsigma \right)\end{array}& (5)\end{array}$

The variable of Equation (5) is expanded into the Taylor series about (z = 0) to the fourth order, yielding

$\begin{array}{ll}\begin{array}{l}{\left[\frac{{\partial }^2\Phi }{\partial t^2}+g\frac{\partial \Phi }{\partial z}\right]}_{z=0}+\varsigma {\left[\frac{\partial }{\partial z}\left(\frac{{\partial }^2\Phi }{\partial t^2}+g\frac{\partial \Phi }{\partial z}\right)\right]}_{z=0}+{\left[\frac{\partial }{\partial t}\left({\left|\overrightarrow{u}\right|}^2\right)\right]}_{z=0}\\ +\frac{{\varsigma }^2}{2}{\left[\frac{{\partial }^2}{\partial z^2}\left(\frac{{\partial }^2\Phi }{\partial t^2}+g\frac{\partial \Phi }{\partial z}\right)\right]}_{z=0}+\varsigma {\left[\frac{{\partial }^2}{\partial t\partial z}\left({\left|\overrightarrow{u}\right|}^2\right)\right]}_{z=0}+\frac{1}{2}{\left[\overrightarrow{u}·\nabla \left({\left|\overrightarrow{u}\right|}^2\right)\right]}_{z=0}\\ +\frac{1}{6}{\varsigma }^3\frac{{\partial }^3}{\partial z^3}\left(\frac{{\partial }^2\Phi }{\partial t^2}\right){|}_{z=0}+\frac{1}{6}g{\varsigma }^3\frac{{\partial }^3}{\partial z^3}\left(\frac{\partial \Phi }{\partial z}\right){|}_{z=0}\\ +\frac{1}{2}{\varsigma }^2\frac{{\partial }^2}{\partial z^2}\left(\frac{\partial \left({\left|\overrightarrow{u}\right|}^2\right)}{\partial t}\right){|}_{z=0}+\frac{1}{2}\varsigma \frac{\partial }{\partial z}\left(\overrightarrow{u}·\nabla \left({\left|\overrightarrow{u}\right|}^2\right)\right){|}_{z=0}=0\end{array}& (6)\end{array}$

Incorporating p_a into Ф in Equation (3) yields

$\begin{array}{ll}\begin{array}{cc}g\varsigma +\frac{\partial \Phi }{\partial t}+\frac{1}{2}{\left|\nabla \Phi \right|}^2\mathrm{ =0}& \left(z=\varsigma \right)\end{array}& (7)\end{array}$

The variable of Equation (7) is expanded into the Taylor series about (z = 0) to the fourth order, yielding

$\begin{array}{ll}\begin{array}{l}-g\varsigma ={\left[\frac{\partial \Phi }{\partial t}\right]}_{z=0}+\varsigma {\left[\frac{{\partial }^2\Phi }{\partial z\partial t}\right]}_{z=0}+\frac{1}{2}{\left[{\left|\overrightarrow{u}\right|}^2\right]}_{z=0}+\frac{{\varsigma }^2}{2}{\left[\frac{{\partial }^2}{\partial z^2}\left(\frac{\partial \Phi }{\partial t}\right)\right]}_{z=0}\\ +\frac{\varsigma }{2}{\left[\frac{\partial }{\partial z}\left({\left|\overrightarrow{u}\right|}^2\right)\right]}_{z=0}+\frac{{\varsigma }^3}{6}{\left[\frac{{\partial }^3}{\partial z^3}\left(\frac{\partial \Phi }{\partial t}\right)\right]}_{z=0}+\frac{{\varsigma }^2}{4}{\left[\frac{{\partial }^2}{\partial z^2}\left({\left|\overrightarrow{u}\right|}^2\right)\right]}_{z=0}\end{array}& (8)\end{array}$

Thus Equations (6) and (8) are the (ka)⁴ order. k is the dominant wavenumber, and a is the dominant wave’s amplitude. It is supposed that k a=ε≪1.

It is supposed that the dominant wave direction is along the x-axis, and the wave packet is slowly modulated. The multiscale variables are

$\begin{array}{ll}\begin{array}{l}x,x_1=\epsilon x,x_2={\epsilon }^{2}x,\dots \text{..},\\ y_1=\epsilon y,y_2={\epsilon }^{2}y,\dots \text{..},\\ t,t_1=\epsilon t,t_2={\epsilon }^{2}t,\dots \text{..},\end{array}& (9)\end{array}$

We expand the velocity potential and wave displacement into a perturbation series

$\begin{array}{ll}\begin{array}{cc}\Phi ={\displaystyle \sum _{n=1}^{\infty }{\epsilon }^n{\varphi }_n}& \varsigma ={\displaystyle \sum _{n=1}^{\infty }{\epsilon }^n{\varsigma }_n}\end{array}& (10)\end{array}$

Where

$\begin{array}{ll}\begin{array}{l}{\varphi }_n={\varphi }_n\left(x,x_1,x_2,\dots ;y_1,y_2,\dots ;z;t,t_1,t_2,\dots \right)\\ {\varsigma }_n={\varsigma }_n\left(x,x_1,x_2,\dots ;y_1,y_2,\dots ;t,t_1,t_2,\dots \right) \end{array}& \text{(10-1)}\end{array}$

$\begin{array}{ll}\frac{\partial }{\partial x}\to \frac{\partial }{\partial x}+\epsilon \frac{\partial }{\partial x_1}+{\epsilon }^2\frac{\partial }{\partial x_2}+\dots +{\epsilon }^n\frac{\partial }{\partial x_n}+\dots & \text{(10-2)}\end{array}$

$\begin{array}{ll}\frac{\partial }{\partial y}\to \epsilon \frac{\partial }{\partial y_1}+{\epsilon }^2\frac{\partial }{\partial y_2}+\dots +{\epsilon }^n\frac{\partial }{\partial y_n}+\dots & \text{(10-3)}\end{array}$

The variable of Laplace Equation (1) is expanded into a perturbation series to the fourth order, yielding

$\begin{array}{ll}\frac{{\partial }^2{\varphi }_n}{\partial x^2}+\frac{{\partial }^2{\varphi }_n}{\partial z^2}=F_n,\left(n=1,2,3,4\right)& (11)\end{array}$

$\begin{array}{ll}\begin{array}{l}(F_1=0,F_2=-2\frac{{\partial }^2{\varphi }_1}{\partial x\partial x_1},F_3=-\left(\frac{{\partial }^2{\varphi }_1}{\partial x_1^2}+\frac{{\partial }^2{\varphi }_1}{\partial y_1^2}+2\frac{{\partial }^2{\varphi }_1}{\partial x\partial x_2}+2\frac{{\partial }^2{\varphi }_2}{\partial x\partial x_1}\right),\\ F_4=-\left(\frac{{\partial }^2{\varphi }_2}{\partial x_1^2}+\frac{{\partial }^2{\varphi }_2}{\partial y_1^2}+2\frac{{\partial }^2{\varphi }_2}{\partial x\partial x_2}+2\frac{{\partial }^2{\varphi }_3}{\partial x\partial x_1}+2\frac{{\partial }^2{\varphi }_1}{\partial x_1\partial x_2}+2\frac{{\partial }^2{\varphi }_1}{\partial x\partial x_3}+2\frac{{\partial }^2{\varphi }_1}{\partial y_1\partial y_2}\right))\end{array}& \text{(11-1)}\end{array}$

The variable of Equation (6) is expanded into a perturbation series to the fourth order, yielding

$\begin{array}{ll}\Gamma {\varphi }_n=G_n\left(z=0\right),\Gamma =g\frac{\partial }{\partial z}+\frac{{\partial }^2}{\partial t^2}& (12)\end{array}$

$\begin{array}{ll}{G}_1\mathrm{=0, }{G}_2=-[2\frac{{\partial }^2{\varphi }_1}{\partial t\partial t_1}+{\varsigma }_1\left(\frac{{\partial }^3{\varphi }_1}{\partial z\partial t^2}+g\frac{{\partial }^2{\varphi }_1}{\partial z^2}\right)+2\left[\frac{\partial {\varphi }_1}{\partial x}\frac{{\partial }^2{\varphi }_1}{\partial x\partial t}+\frac{\partial {\varphi }_1}{\partial z}\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}\right]]& \text{(12-1)}\end{array}$

$\begin{array}{ll}\begin{array}{l}{G}_3=-\{2\frac{{\partial }^2{\varphi }_2}{\partial t\partial t_1}+2\frac{{\partial }^2{\varphi }_1}{\partial t\partial t_2}+\frac{{\partial }^2{\varphi }_1}{\partial t_1^2}+{\varsigma }_2\frac{\partial }{\partial z}\left(\frac{{\partial }^2}{\partial t^2}+g\frac{\partial }{\partial z}\right){\varphi }_1+{\varsigma }_1\frac{\partial }{\partial z}\left(\frac{{\partial }^2}{\partial t^2}+g\frac{\partial }{\partial z}\right){\varphi }_2\\ +{\varsigma }_1\left(2\frac{{\partial }^3{\varphi }_1}{\partial z\partial t\partial t_1}+2\frac{\partial }{\partial z}\left[\frac{\partial {\varphi }_1}{\partial x}\frac{{\partial }^2{\varphi }_1}{\partial x\partial t}+\frac{\partial {\varphi }_1}{\partial z}\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}\right]\right)+\frac{{\varsigma }_1^2}{2}\frac{{\partial }^2}{\partial z^2}\left(\frac{{\partial }^2}{\partial t^2}+g\frac{\partial }{\partial z}\right){\varphi }_1\\ +2[\frac{\partial {\varphi }_1}{\partial x}\frac{{\partial }^2{\varphi }_2}{\partial x\partial t}+\frac{{\partial }^2{\varphi }_1}{\partial x\partial t}\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial z}\frac{{\partial }^2{\varphi }_2}{\partial z\partial t}+\frac{\partial {\varphi }_2}{\partial z}\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}+\frac{\partial {\varphi }_1}{\partial x}\frac{{\partial }^2{\varphi }_1}{\partial x_1\partial t}+\frac{\partial {\varphi }_1}{\partial x}\frac{{\partial }^2{\varphi }_1}{\partial x\partial t_1}\\ +\frac{{\partial }^2{\varphi }_1}{\partial x\partial t}\frac{\partial {\varphi }_1}{\partial x_1}+\frac{\partial {\varphi }_1}{\partial z}\frac{{\partial }^2{\varphi }_1}{\partial z\partial t_1}]+\frac{1}{2}\left[{\left({\varphi }_1\right)}_x\frac{\partial }{\partial x}+{\left({\varphi }_1\right)}_z\frac{\partial }{\partial z}\right]\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]\}\end{array}& \text{(12-2)}\end{array}$

$\begin{array}{ll}\begin{array}{l}{G}_4=-\{2\frac{{\partial }^2{\varphi }_3}{\partial t\partial t_1}+2\frac{{\partial }^2{\varphi }_2}{\partial t\partial t_2}+2\frac{{\partial }^2{\varphi }_1}{\partial t\partial t_3}+\frac{{\partial }^2{\varphi }_2}{\partial t_1^2}+2\frac{{\partial }^2{\varphi }_1}{\partial t_1\partial t_2}\\ +2\{\frac{\partial {\varphi }_1}{\partial x}\left(\frac{{\partial }^2{\varphi }_3}{\partial x\partial t}+\frac{{\partial }^2{\varphi }_2}{\partial x_1\partial t}+\frac{{\partial }^2{\varphi }_1}{\partial x_2\partial t}+\frac{{\partial }^2{\varphi }_2}{\partial x\partial t_1}+\frac{{\partial }^2{\varphi }_1}{\partial x_1\partial t_1}+\frac{{\partial }^2{\varphi }_1}{\partial x\partial t_2}\right)\\ +\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right)\left(\frac{{\partial }^2{\varphi }_2}{\partial x\partial t}+\frac{{\partial }^2{\varphi }_1}{\partial x_1\partial t}\right)+\left(\frac{\partial {\varphi }_3}{\partial x}+\frac{\partial {\varphi }_2}{\partial x_1}+\frac{\partial {\varphi }_1}{\partial x_2}\right)\frac{{\partial }^2{\varphi }_1}{\partial x\partial t}+\frac{\partial {\varphi }_1}{\partial y_1}\frac{{\partial }^2{\varphi }_1}{\partial y_1\partial t}\\ +\frac{\partial {\varphi }_1}{\partial z}\left(\frac{{\partial }^2{\varphi }_3}{\partial z\partial t}+\frac{{\partial }^2{\varphi }_2}{\partial z\partial t_1}+\frac{{\partial }^2{\varphi }_1}{\partial z\partial t_2}\right)+\frac{\partial {\varphi }_2}{\partial z}\left(\frac{{\partial }^2{\varphi }_2}{\partial z\partial t}+\frac{{\partial }^2{\varphi }_1}{\partial z\partial t_1}\right)\\ +\frac{\partial {\varphi }_3}{\partial z}\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}+\frac{{\partial }^2{\varphi }_1}{\partial x\partial t_1}\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right)\}\\ +\frac{\partial {\varphi }_1}{\partial x}\left\{\frac{\partial }{\partial x}\left[\frac{\partial {\varphi }_1}{\partial x}\frac{\partial {\varphi }_1}{\partial x_1}+\frac{\partial {\varphi }_1}{\partial x}\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial {\varphi }_2}{\partial z}\right]+\frac{1}{2}\frac{\partial }{\partial x_1}\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]\right\}\\ +\frac{1}{2}\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right)\frac{\partial }{\partial x}\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]\\ +\frac{\partial {\varphi }_1}{\partial z}\frac{\partial }{\partial z}\left(\frac{\partial {\varphi }_1}{\partial x}\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x}\frac{\partial {\varphi }_1}{\partial x_1}+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial {\varphi }_2}{\partial z}\right)+\frac{1}{2}\frac{\partial {\varphi }_2}{\partial z}\frac{\partial }{\partial z}\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]\\ +{\varsigma }_1[\frac{\partial }{\partial z}\left(\frac{{\partial }^2{\varphi }_3}{\partial t^2}+2\frac{{\partial }^2{\varphi }_2}{\partial t\partial t_1}+2\frac{{\partial }^2{\varphi }_1}{\partial t\partial t_2}+\frac{{\partial }^2{\varphi }_1}{\partial t_1^2}\right)+g\frac{{\partial }^2{\varphi }_3}{\partial z^2}\\ +2\frac{\partial }{\partial z}[\frac{\partial {\varphi }_1}{\partial x}\frac{\partial }{\partial t}\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right)+\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right)\frac{\partial }{\partial t}\left(\frac{\partial {\varphi }_1}{\partial x}\right)\\ +\frac{\partial {\varphi }_1}{\partial z}\frac{\partial }{\partial t}\left(\frac{\partial {\varphi }_2}{\partial z}\right)+\frac{\partial {\varphi }_2}{\partial z}\frac{\partial }{\partial t}\left(\frac{\partial {\varphi }_1}{\partial z}\right)+\frac{\partial {\varphi }_1}{\partial x}\frac{\partial }{\partial t_1}\left(\frac{\partial {\varphi }_1}{\partial x}\right)+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial }{\partial t_1}\left(\frac{\partial {\varphi }_1}{\partial z}\right)]\\ +\frac{1}{2}\frac{\partial }{\partial z}\{\frac{\partial {\varphi }_1}{\partial x}[\frac{\partial }{\partial x}\left({\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right)]+\frac{\partial {\varphi }_1}{\partial z}[\frac{\partial }{\partial z}\left({\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right)]\}]\\ +{\varsigma }_2\{\frac{\partial }{\partial z}(\frac{{\partial }^2{\varphi }_2}{\partial t^2}+2\frac{{\partial }^2{\varphi }_1}{\partial t\partial t_1})+g\frac{{\partial }^2{\varphi }_2}{\partial z^2}+2\frac{\partial }{\partial z}[\frac{\partial {\varphi }_1}{\partial x}\frac{\partial }{\partial t}(\frac{\partial {\varphi }_1}{\partial x})+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial }{\partial t}(\frac{\partial {\varphi }_1}{\partial z})]\}\\ +{\varsigma }_3\left[\frac{\partial }{\partial z}\left(\frac{{\partial }^2{\varphi }_1}{\partial t^2}\right)+g\frac{{\partial }^2{\varphi }_1}{\partial z^2}\right]\\ +{\varsigma }_1^2[\frac{1}{2}\frac{{\partial }^2}{\partial z^2}(\frac{{\partial }^2{\varphi }_2}{\partial t^2}+2\frac{{\partial }^2{\varphi }_1}{\partial t\partial t_1})+\frac{g}{2}\frac{{\partial }^3{\varphi }_2}{\partial z^3}+\frac{{\partial }^2}{\partial z^2}[\frac{\partial {\varphi }_1}{\partial x}\frac{\partial }{\partial t}(\frac{\partial {\varphi }_1}{\partial x})+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial }{\partial t}(\frac{\partial {\varphi }_1}{\partial z})]]\\ +{\varsigma }_1{\varsigma }_2\left[\frac{{\partial }^2}{\partial z^2}\left(\frac{{\partial }^2{\varphi }_1}{\partial t^2}\right)+g\frac{{\partial }^3{\varphi }_1}{\partial z^3}\right]+\frac{1}{6}{\varsigma }_1^3\left[\frac{{\partial }^3}{\partial z^3}\left(\frac{{\partial }^2{\varphi }_1}{\partial t^2}\right)+g\frac{{\partial }^4{\varphi }_1}{\partial z^4}\right]\}\end{array}& \text{(12-3)}\end{array}$

The variable of boundary condition (8) is expanded into a perturbation series to the fourth order, yielding

$\begin{array}{ll}\begin{array}{cc}-g{\varsigma }_n=H_n& \left(z=0\right)\end{array}& (13)\end{array}$

$\begin{array}{ll}{H}_1=\frac{\partial {\varphi }_1}{\partial t},H_2=\frac{\partial {\varphi }_2}{\partial t}+\frac{\partial {\varphi }_1}{\partial t_1}+{\varsigma }_1\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}+\frac{1}{2}\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]& \text{(13-1)}\end{array}$

$\begin{array}{ll}\begin{array}{l}{H}_3=\frac{\partial {\varphi }_3}{\partial t}+\frac{\partial {\varphi }_2}{\partial t_1}+\frac{\partial {\varphi }_1}{\partial t_2}+{\varsigma }_1\left[\frac{{\partial }^2{\varphi }_2}{\partial z\partial t}+\frac{{\partial }^2{\varphi }_1}{\partial z\partial t_1}\right]+{\varsigma }_2\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}\\ +\frac{1}{2}\left[2\frac{\partial {\varphi }_1}{\partial x}\frac{\partial {\varphi }_2}{\partial x}+2\frac{\partial {\varphi }_1}{\partial x}\frac{\partial {\varphi }_1}{\partial x_1}+2\frac{\partial {\varphi }_1}{\partial z}\frac{\partial {\varphi }_2}{\partial z}\right]+\frac{{\varsigma }_1^2}{2}\frac{{\partial }^2}{\partial z^2}\left(\frac{\partial {\varphi }_1}{\partial t}\right)+\frac{{\varsigma }_1}{2}\frac{\partial }{\partial z}\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]\end{array}& \text{(13-2)}\end{array}$

$\begin{array}{ll}\begin{array}{l}{H}_4=\frac{\partial {\varphi }_4}{\partial t}+\frac{\partial {\varphi }_3}{\partial t_1}+\frac{\partial {\varphi }_2}{\partial t_2}+\frac{\partial {\varphi }_1}{\partial t_3}+{\varsigma }_3\frac{{\partial }^2{\varphi }_1}{\partial z\partial t}+{\varsigma }_2\left[\frac{\partial }{\partial z}\left(\frac{\partial {\varphi }_2}{\partial t}+\frac{\partial {\varphi }_1}{\partial t_1}\right)\right]\\ +{\varsigma }_1\left[\frac{\partial }{\partial z}\left(\frac{\partial {\varphi }_3}{\partial t}+\frac{\partial {\varphi }_2}{\partial t_1}+\frac{\partial {\varphi }_1}{\partial t_2}\right)\right]+{\varsigma }_1{\varsigma }_2\frac{{\partial }^2}{\partial z^2}\left(\frac{\partial {\varphi }_1}{\partial t}\right)+\frac{{\varsigma }_1^2}{2}\frac{{\partial }^2}{\partial z^2}\left(\frac{\partial {\varphi }_2}{\partial t}+\frac{\partial {\varphi }_1}{\partial t_1}\right)\\ +\frac{{\varsigma }_1^3}{6}\frac{{\partial }^3}{\partial z^3}\left(\frac{\partial {\varphi }_1}{\partial t}\right)+\frac{1}{2}\left[{\left(\frac{\partial {\varphi }_2}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial x_1}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial y_1}\right)}^2+{\left(\frac{\partial {\varphi }_2}{\partial z}\right)}^2\right]\\ +\frac{\partial {\varphi }_2}{\partial x}\frac{\partial {\varphi }_1}{\partial x_1}+\frac{\partial {\varphi }_1}{\partial x}(\frac{\partial {\varphi }_3}{\partial x}+\frac{\partial {\varphi }_2}{\partial x_1}+\frac{\partial {\varphi }_1}{\partial x_2})+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial {\varphi }_3}{\partial z}+\frac{{\varsigma }_2}{2}\frac{\partial }{\partial z}[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2]\\ +{\varsigma }_1\frac{\partial }{\partial z}\left[\frac{\partial {\varphi }_1}{\partial x}\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right)+\frac{\partial {\varphi }_1}{\partial z}\frac{\partial {\varphi }_2}{\partial z}\right]+\frac{{\varsigma }_1^2}{4}\frac{{\partial }^2}{\partial z^2}\left[{\left(\frac{\partial {\varphi }_1}{\partial x}\right)}^2+{\left(\frac{\partial {\varphi }_1}{\partial z}\right)}^2\right]\end{array}& \text{(13-3)}\end{array}$

ϕ_n, F_n, and G_n are expanded as

$\begin{array}{ll}\left\{{\varphi }_n,F_n,G_n\right\}={\displaystyle \sum _{m=-n}^n\left[e^{im\left(kx-\omega t\right)}\left\{{\varphi }_{nm},F_{nm},G_{nm}\right\}\right]}& (14)\end{array}$

ϕ_n-m = (ϕ_{n, m})^*, ()^*, and c.c. are complex conjugate numbers.

According to the boundary condition introduced by Kirby (Kirby and Dalrymple, 1983), depth h is modulated at the x and y directions as

$\begin{array}{ll}\frac{\partial h}{\partial x}={\epsilon }^2\frac{\partial h}{\partial x_2}+{\epsilon }^3\frac{\partial h}{\partial x_3}+\dots ,\frac{\partial h}{\partial y}=\epsilon \frac{\partial h}{\partial y_1}+{\epsilon }^2\frac{\partial h}{\partial y_2}+\dots & (15)\end{array}$

The variable of the bottom boundary condition (2) is expanded into a perturbation series to the fourth order, yielding

$\begin{array}{ll}\begin{array}{cc}\frac{\partial {\varphi }_n}{\partial z}{|}_{z=-h}=B_n& \left(n=1,2,3,4\right)\end{array}& (16)\end{array}$

$\begin{array}{ll}{B}_1=B_2=0,B_3=-\frac{\partial {\varphi }_1}{\partial x}{|}_{z=-h}\frac{\partial h}{\partial x_2}-\frac{\partial {\varphi }_1}{\partial y_1}{|}_{z=-h}\frac{\partial h}{\partial y_1}& \text{(16-1)}\end{array}$

$\begin{array}{ll}\begin{array}{l}{B}_4=\frac{\partial {\varphi }_4}{\partial z}{|}_{z=-h}=-\left(\frac{\partial {\varphi }_2}{\partial x}+\frac{\partial {\varphi }_1}{\partial x_1}\right){|}_{z=-h}\frac{\partial h}{\partial x_2}-\frac{\partial {\varphi }_1}{\partial x}{|}_{z=-h}\frac{\partial h}{\partial x_3}\\ -\left(\frac{\partial {\varphi }_1}{\partial y_2}+\frac{\partial {\varphi }_2}{\partial y_1}\right){|}_{z=-h}\frac{\partial h}{\partial y_1}-\frac{\partial {\varphi }_1}{\partial y_1}{|}_{z=-h}\frac{\partial h}{\partial y_2}\end{array}& \text{(16-2)}\end{array}$

Equations (11), (12), (13), (14), and the bottom boundary condition (16) constitute definition conditions.

The free surface’s leading-order displacement is

$\begin{array}{ll}\varsigma =\frac{1}{2}\left(A{e}^{i\left(kx-\omega t\right)}+*\right)& \text{(16-3)}\end{array}$

A is the free surface leading-order displacement amplitude. Under third and fourth-order definition conditions, the first-order wave height’s dimensionless equation are

$\begin{array}{ll}\begin{array}{l}\frac{\partial A}{\partial t}+{C^{\prime }}_g\frac{\partial A}{\partial x}-\frac{i{C^{\prime }}_g}{2}\frac{{\partial }^{2}A}{\partial y^2}-\frac{i}{2}\frac{\partial {C^{\prime }}_g}{\partial y}\frac{\partial A}{\partial y}-\frac{i}{2}{\left(\frac{{\partial }^2\omega }{\partial k^2}\right)}^{\prime }\frac{{\partial }^{2}A}{\partial x^2}\\ +\frac{1}{16s{h}^{4}kh}\left[8+ch4kh-2t{h}^{2}kh\right]i{A}^2{A}^{*}\\ +[\frac{1}{2}\frac{\partial {C^{\prime }}_g}{\partial x}+\frac{i}{4}{K}_2\frac{{\partial }^{2}h}{\partial y^2}-\frac{i}{4}{K}_3{(\frac{\partial h}{\partial y})}^2-\frac{1}{2c{h}^{2}kh}i(\frac{\partial {\varphi }_{10}}{\partial t}-2c{h}^{2}kh\frac{\partial {\varphi }_{10}}{\partial x})]A=0\end{array}& (17)\end{array}$

$\begin{array}{ll}\begin{array}{l}\frac{\partial A}{\partial t}+\left({C^{\prime }}_g+i{N}_3\frac{\partial h}{\partial x}+\frac{1}{16}{N}_6\frac{{\partial }^{2}h}{\partial y^2}+\frac{1}{8}{N}_9{\left(\frac{\partial h}{\partial y}\right)}^2+\frac{\partial {\varphi }_{10}}{\partial x}+N_7\frac{\partial {\varphi }_{10}}{\partial t}\right)\frac{\partial A}{\partial x}\\ -\frac{i{C^{\prime }}_g}{2}\frac{{\partial }^{2}A}{\partial y^2}+\left(\frac{\partial {\varphi }_{10}}{\partial y}-\frac{i}{2}\frac{\partial {C^{\prime }}_g}{\partial y}\right)\frac{\partial A}{\partial y}-\frac{i}{2}{\left(\frac{{\partial }^2\omega }{\partial k^2}\right)}^{\prime }\frac{{\partial }^{2}A}{\partial x^2}+\frac{1}{8}{N}_1\frac{{\partial }^{3}A}{\partial x\partial y^2}-\frac{1}{6}{\left(\frac{{\partial }^3\omega }{\partial k^3}\right)}^{\prime }\frac{{\partial }^{3}A}{\partial x^3}\\ +N_2\frac{\partial h}{\partial y}\frac{{\partial }^{2}A}{\partial x\partial y}+\frac{1}{16s{h}^{4}kh}\left[8+ch4kh-2t{h}^{2}kh\right]i{A}^2{A}^{*}+N_4{A}^2\frac{\partial A^{*}}{\partial x}+N_{5}A{A}^{*}\frac{\partial A}{\partial x}\\ +[\frac{1}{2}\frac{\partial {C^{\prime }}_g}{\partial x}+\frac{i}{4}{K}_2\frac{{\partial }^{2}h}{\partial y^2}-\frac{i}{4}{K}_3{\left(\frac{\partial h}{\partial y}\right)}^2-\frac{1}{2c{h}^{2}kh}i\left(\frac{\partial {\varphi }_{10}}{\partial t}-2c{h}^{2}kh\frac{\partial {\varphi }_{10}}{\partial x}\right)\\ -\left(\frac{kh}{sh2kh}+\frac{khshkh}{chkh}\right)\frac{{\partial }^2{\varphi }_{10}}{\partial x^2}+\frac{1}{2}\frac{{\partial }^2{\varphi }_{10}}{\partial y^2}-N_8\frac{{\partial }^2{\varphi }_{10}}{\partial x\partial t}-\frac{s{h}^{2}kh}{c{h}^{2}kh}\frac{{\partial }^2{\varphi }_{10}}{\partial t^2}]A=0\end{array}& (18)\end{array}$

The coefficients in Equations (17) and (18) are

$${C^{\prime }}_g=\frac{1}{2}\left(1+\frac{2kh}{sh2kh}\right)$$

$${\left(\frac{{\partial }^2\omega }{\partial k^2}\right)}^{\prime }=-\frac{1}{4}\left[\left(\frac{4}{c{h}^{2}kh}+\frac{4}{s{h}^{2}2kh}\right)k^2{h}^2-\frac{2kh}{shkhchkh}+1\right]$$

$${\left(\frac{{\partial }^3\omega }{\partial k^3}\right)}^{\prime }=-6\left(\frac{kh}{8sh2kh}+\frac{k^2{h}^2}{4s{h}^{2}kh}-\frac{1}{16}-\frac{3k^2{h}^2}{4s{h}^{2}2kh}-\frac{k^3{h}^3}{2s{h}^{3}2kh}-\frac{k^3{h}^3}{6sh2kh}-\frac{k^3{h}^{3}shkh}{4c{h}^{3}kh}\right)$$

$$K_1=\frac{sh2kh-2khch2kh}{s{h}^{2}2kh},K_2=\frac{1}{sh2kh}+\frac{2khch2kh}{s{h}^{2}2kh}$$

$$K_3=\frac{1}{c{h}^{2}kh}-\frac{4ch2kh}{s{h}^{2}2kh}+\left(\frac{8c{h}^{2}2kh}{s{h}^{3}2kh}+\frac{1}{shkhc{h}^{3}kh}-\frac{4}{sh2kh}\right)kh$$

$$\frac{\partial {C^{\prime }}_g}{\partial x}=K_1\frac{\partial h}{\partial x},\frac{\partial {C^{\prime }}_g}{\partial y}=K_1\frac{\partial h}{\partial y}$$

$$N_1=\left(3+\frac{4k^2{h}^2}{s{h}^{2}2kh}+\frac{4k^2{h}^2}{c{h}^{2}kh}\right)$$

$$\begin{array}{l}{N}_2=\frac{1}{4sh2kh}-\frac{ch2kh}{2sh2kh}+\left(\frac{1}{c{h}^{2}kh}+\frac{3}{2s{h}^{2}2kh}-\frac{ch2kh}{2s{h}^{2}2kh}\right)kh\\ -\left(\frac{ch2kh}{4shkhc{h}^{3}kh}+\frac{shkh}{c{h}^{3}kh}+\frac{1}{2shkhchkh}+\frac{ch2kh}{s{h}^{3}2kh}\right)k^2{h}^2\end{array}$$

$$\begin{array}{l}{N}_3=\left(\frac{1}{c{h}^{2}khsh2kh}-\frac{1}{2shkhchkh}-\frac{3ch2kh}{4shkhc{h}^{3}kh}-\frac{ch2kh}{s{h}^{3}2kh}\right)k^2{h}^2\\ +\left(\frac{3}{2s{h}^{2}2kh}+\frac{5}{4c{h}^{2}kh}+\frac{ch2kh}{2s{h}^{2}2kh}\right)kh-\frac{1}{4sh2kh}-\frac{ch2kh}{2sh2kh}\end{array}$$

$$\begin{array}{l}{N}_4=\frac{1}{2}\{\frac{1}{2}-\frac{c{h}^{2}kh}{2s{h}^{2}kh}+\frac{c{h}^{4}kh}{2s{h}^{4}kh}-\frac{ch4kh}{16s{h}^{4}kh}-\frac{ch2kh}{4s{h}^{2}kh}+\frac{1}{s{h}^{2}kh}-\frac{3ch2kh}{4s{h}^{4}kh}+\frac{c{h}^{2}kh}{4s{h}^{4}kh}\\ -\frac{1}{2s{h}^{4}kh}+\frac{1}{8s{h}^{2}khc{h}^{2}kh}+(\frac{17}{8s{h}^{3}khchkh}+\frac{17}{4shkhchkh}-\frac{7chkh}{4s{h}^{3}kh}-\frac{3ch2kh}{2s{h}^{3}khchkh}\\ -\frac{chkhch2kh}{8s{h}^{4}kh}+\frac{1}{2shkhc{h}^{3}kh}+\frac{ch2kh}{2shkhchkh}-\frac{ch2kh}{2s{h}^{5}khchkh}+\frac{ch2kh}{8s{h}^{3}khc{h}^{3}kh}-\frac{ch2khch4kh}{16s{h}^{5}khchkh})kh\}\end{array}$$

$$\begin{array}{l}{N}_5=\frac{1}{2}\{\frac{21ch2kh}{4s{h}^{4}kh}+4-\frac{3ch2kh}{4s{h}^{4}khc{h}^{2}kh}-\frac{27}{4s{h}^{2}kh}+\frac{1}{4c{h}^{2}kh}-\frac{1}{s{h}^{4}kh}-\frac{ch4kh}{8s{h}^{4}kh}+\frac{1}{4s{h}^{2}khc{h}^{2}kh}\\ +kh[\frac{1}{c{h}^{2}khsh2kh}+\frac{2ch2kh}{4s{h}^{5}khchkh}-\frac{9ch2kh}{4s{h}^{5}khchkh}+\frac{3ch2kh}{8s{h}^{5}khc{h}^{3}kh}+\frac{3}{4s{h}^{3}khchkh}+\frac{6chkh}{s{h}^{3}kh}\\ +\frac{2chkh}{shkh}-\frac{ch2khch4kh}{8s{h}^{5}khchkh}+\frac{ch2kh}{4s{h}^{3}khc{h}^{3}kh}+\frac{3}{2s{h}^{5}khchkh}-\frac{3chkh}{2s{h}^{5}kh}\\ +\frac{3ch2kh}{8s{h}^{7}khc{h}^{3}kh}-\frac{15ch2kh}{8s{h}^{7}khchkh}-\frac{3chkhch2kh}{s{h}^{5}kh}+\frac{3chkhch2kh}{2s{h}^{7}kh}]\}\end{array}$$

$$\begin{array}{l}{N}_6=\left(\frac{8}{sh2khc{h}^{2}kh}-\frac{8ch2kh}{s{h}^{3}2kh}-\frac{4}{shkhchkh}-\frac{6ch2kh}{shkhc{h}^{3}kh}\right)k^2{h}^2\\ +\left(\frac{2}{s{h}^{2}kh}-\frac{1}{s{h}^{2}khc{h}^{2}kh}-\frac{4ch2kh}{s{h}^{2}2kh}\right)kh-\frac{2ch2kh}{shkhchkh}-\frac{1}{shkhchkh}\end{array}$$

$$N_7=(\frac{1}{2c{h}^{2}khsh2kh}+\frac{s{h}^{2}kh}{c{h}^{2}khsh2kh}+\frac{shkh}{2c{h}^{3}kh})kh-\frac{3}{4c{h}^{2}kh}$$

$$N_8=1-\frac{1}{4c{h}^{2}kh}-(\frac{kh}{sh2kh}+\frac{khshkh}{chkh})$$

$$\begin{array}{l}{N}_9=-\frac{4s{h}^{2}kh-1}{s{h}^{2}kh}+\frac{2}{c{h}^{2}kh}+\frac{c{h}^{2}khch2kh+s{h}^{2}khch2kh}{s{h}^{2}khc{h}^{2}kh}\\ +\left(\frac{2shkh}{c{h}^{3}kh}-\frac{2}{shkhchkh}-\frac{chkh}{s{h}^{3}kh}+\frac{1}{shkhc{h}^{3}kh}\right)2kh\\ +\left[\frac{1}{s{h}^{2}kh}+\frac{3}{c{h}^{2}kh}+\frac{1}{s{h}^{2}khc{h}^{2}kh}+\frac{2}{shkhc{h}^{3}kh}\left(\frac{1}{sh2kh}+\frac{shkh}{chkh}\right)\right]k^2{h}^2\end{array}$$

ϕ₁₀ is the velocity potential of wave-induced current in equation (17) and (18). Equation (17) indicates that the water depth’s second derivative and the square of the water depth’s first derivative affect the first-order wave amplitude when the time scale is longer than ε^-2 times of the dominant wave period or the space scale is larger than ε^-2 of the dominant wavelength. Equation (18) is more complicated than Equation (17). Equation (18) improves the coefficient of Equation (17) by incorporating depth variation and wave-induced current terms. In Equation (18), higher-order dispersive and nonlinear terms are added. Equation (18) indicates that when the time scale is longer than ε^-3 times of the dominant wave period or the space scale is larger than ε^-3 times the dominant wavelength, the second water depth derivative and the square of the water depth’s first derivative affect the first-order wave amplitude.

When $\frac{\partial A}{\partial t},{\left(\frac{\partial h}{\partial y}\right)}^2,\frac{{\partial }^{2}h}{\partial y^2},-\frac{i}{2}{\left(\frac{{\partial }^2\omega }{\partial k^2}\right)}^{\prime }\frac{{\partial }^{2}A}{\partial x^2}\text{and}\frac{\partial {\varphi }_{10}}{\partial t_1}-2c{h}^{2}kh\frac{\partial {\varphi }_{10}}{\partial x_1}\text{are}$ neglected, Equation(17)is transformed to be

$\begin{array}{ll}{C^{\prime }}_g\frac{\partial A}{\partial x}-\frac{i{C^{\prime }}_g}{2}\frac{{\partial }^{2}A}{\partial y^2}-\frac{i}{2}\frac{\partial {C^{\prime }}_g}{\partial y}\frac{\partial A}{\partial y}+\frac{1}{2}\frac{\partial {C^{\prime }}_g}{\partial x}A+\frac{1}{16s{h}^{4}kh}\left[8+ch4kh-2t{h}^{2}kh\right]i{A}^2{A}^{*}=0& (19)\end{array}$

Equation (19) is the same as Equation (2.18) of reference (Kirby and Dalrymple, 1983). It cannot analyze wave instability properties because the equation is steady.

When kh limits to infinite, the coefficients of Equation (18) are transformed to

$$\begin{array}{l}-\frac{1}{6}{\left(\frac{{\partial }^3\omega }{\partial k^3}\right)}^{\prime }=-\frac{1}{16},-\frac{1}{2}{\left(\frac{{\partial }^2\omega }{\partial k^2}\right)}^{\prime }=\frac{1}{8},{C^{\prime }}_g=\frac{1}{2},\frac{\partial \mathrm{l}{C^{\prime }}_g}{\partial y}=\frac{\partial {C^{\prime }}_g}{\partial x}=0,\\ N_1=3,N_2=-\frac{1}{2},N_3=-\frac{1}{2},N_4=-\frac{1}{4},N_5=\frac{3}{2},N_6=-4,N_7=0,N_9=0\end{array}$$

Omitting the terms about ϕ₁₀, except for $\frac{\partial {\varphi }_{10}}{\partial x}$ before A, Equation (18) is transformed to

$\begin{array}{ll}\begin{array}{l}\frac{\partial A}{\partial t}+\left(\frac{1}{2}-\frac{1}{2}i\frac{\partial h}{\partial x}-\frac{1}{4}\frac{{\partial }^{2}h}{\partial y^2}\right)\frac{\partial A}{\partial x}-\frac{i}{4}\frac{{\partial }^{2}A}{\partial y^2}+\frac{i}{8}\frac{{\partial }^{2}A}{\partial x^2}+\frac{3}{8}\frac{{\partial }^{3}A}{\partial x\partial y^2}-\frac{1}{16}\frac{{\partial }^{3}A}{\partial x^3}-\frac{1}{2}\frac{\partial h}{\partial y}\frac{{\partial }^{2}A}{\partial x\partial y}\\ +\frac{1}{2}i{A}^2{A}^{*}-\frac{1}{4}{A}^2\frac{\partial A^{*}}{\partial x}+\frac{3}{2}A{A}^{*}\frac{\partial A}{\partial x}+iA\frac{\partial {\varphi }_{10}}{\partial x}=0\end{array}& (20)\end{array}$

$\begin{array}{ll}{\nabla }^2{\varphi }_{10}=0\text{ (}-h<z<0)& (21)\end{array}$

$\begin{array}{ll}\begin{array}{cc}\frac{\partial {\varphi }_{10}}{\partial z}=\frac{1}{2}\frac{\partial }{\partial x}{\left|A\right|}^2& (z=0)\end{array}& (22)\end{array}$

$\begin{array}{ll}\begin{array}{cc}\frac{\partial {\varphi }_{10}}{\partial z}=0& (z=-h)\end{array}& (23)\end{array}$

In contrast with the MNLS (Trulsen and Dysthe, 1996), Equation (20) is added by topography variation terms of$\left(-\frac{1}{2}i\frac{\partial h}{\partial x}-\frac{1}{4}\frac{{\partial }^{2}h}{\partial y^2}\right)\frac{\partial A}{\partial x}-\frac{1}{2}\frac{\partial h}{\partial y}\frac{{\partial }^{2}A}{\partial x\partial y}$. The first and second-order water depth derivatives affect the first-order wave amplitude on infinite depth. Equation (20) can be called a topographic modified nonlinear Schrödinger equation (TMNLS).

Instability of a Uniform Stokes Wave Train

It is supposed that the Stoke wave solution is.$A=a_0{e}^{-\frac{i}{2}{a}_0^{2}t}$Its instability can be evaluated by assuming small perturbations in amplitude and phase. μ and λ are the wavenumbers of small perturbations in x and y direction.

$\begin{array}{ll}A=a_0{a}^{\prime }{e}^{i\left(-\frac{1}{2}{a}_0^{2}t\right)}+a_0{e}^{i\left({\theta }^{\prime }-\frac{1}{2}{a}_0^{2}t\right)}=a_0\left[a^{\prime }+1+i{\theta }^{\prime }\right]e^{-\frac{i}{2}{a}_0^{2}t}& (24)\end{array}$

It is supposed that small perturbations have the plane wave solution

$\begin{array}{ll}\left(\begin{array}{l}{a}^{\prime }\\ {\theta }^{\prime }\\ \overline{\varphi }\end{array}\right)=\left(\begin{array}{l}\widehat{a}\\ \widehat{\theta }\\ \widehat{\varphi }\end{array}\right)e^{i\left(\lambda x+\mu y-\Omega t\right)}+c.c.& (25)\end{array}$

According to Equation (20), the dispersion relation for perturbation is

$\begin{array}{ll}\Omega =\frac{1}{2}\left[\frac{1}{8}{\lambda }^3-\frac{3}{4}\lambda {\mu }^2+\left(1-\frac{1}{2}\frac{{\partial }^{2}h}{\partial y^2}\right)\lambda +3a_0^2\lambda \right]\pm \frac{1}{2}\left(p+iq\right)-\frac{1}{2}\frac{\partial h}{\partial y}\mu \lambda i& (26)\end{array}$

$\begin{array}{ll}\begin{array}{l}q=\left\{\frac{1}{2}\right\{[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)\\ -{\lambda }^2{\left(\frac{\partial h}{\partial x}\right)}^2{]}^2+{\left(\frac{1}{2}{\lambda }^2-{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)}^2{\left(\frac{\partial h}{\partial x}\right)}^2{\lambda }^2{\}}^{\frac{1}{2}}\\ -\frac{1}{2}[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)-{\lambda }^2{\left(\frac{\partial h}{\partial x}\right)}^2]{\}}^{\frac{1}{2}}\end{array}& \text{(26-1)}\end{array}$

$\begin{array}{ll}p=\frac{1}{2q}\left(\frac{1}{2}{\lambda }^2-{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)\frac{\partial h}{\partial x}\lambda & \text{(26-2)}\end{array}$

$\begin{array}{ll}K=\sqrt{{\mu }^2+{\lambda }^2}& \text{(26-3)}\end{array}$

Thus,

$\begin{array}{ll}\begin{array}{l}\mathrm{Im}\Omega =-\frac{1}{2}\frac{\partial h}{\partial y}\mu \lambda \pm \frac{1}{2}\left\{\frac{1}{2}\right\{[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)\\ -{\lambda }^2{\left(\frac{\partial h}{\partial x}\right)}^2{]}^2+{\left(\frac{1}{2}{\lambda }^2-{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)}^2{\left(\frac{\partial h}{\partial x}\right)}^2{\lambda }^2{\}}^{\frac{1}{2}}\\ -\frac{1}{2}[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)-{\lambda }^2{\left(\frac{\partial h}{\partial x}\right)}^2]{\}}^{\frac{1}{2}}\end{array}& (27)\end{array}$

As shown in Equation (26),$\frac{{\partial }^{2}h}{\partial y^2}$ influences the perturbation phase without affecting the perturbation amplitude. Equation (27) demonstrates that $\frac{\partial h}{\partial y}$ and $\frac{\partial h}{\partial x}$affect the small perturbation’s amplitude. ImΩ is defined as growth rate of Stokes wave disturbed by perturbation by Lo and Mei (1987). To ensure the ungrowth of perturbations, ImΩ = 0, meaning

$\begin{array}{ll}\begin{array}{l}\left|\mathrm{Im}\Omega \right|=\mid \frac{1}{2}\frac{\partial h}{\partial y}\mu \lambda -\frac{1}{2}\left\{\frac{1}{2}\right\{[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)\\ -{\lambda }^2{\left(\frac{\partial h}{\partial x}\right)}^2{]}^2+{\left(\frac{1}{2}{\lambda }^2-{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)}^2{\left(\frac{\partial h}{\partial x}\right)}^2{\lambda }^2{\}}^{\frac{1}{2}}\\ -\frac{1}{2}[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)-{\lambda }^2{\left(\frac{\partial h}{\partial x}\right)}^2]{\}}^{\frac{1}{2}}\mid =0\end{array}& (28)\end{array}$

A uniform Stokes wave disturbed by small perturbations is stable only when Equation (28) is satisfied. Therefore, the small perturbation’s instability area is the entire perturbation wavenumber space, except for the curve satisfying Equation (28). It is shown that there are solutions for ImΩ = 0 when Equation (28) is satisfied.

When $\frac{\partial h}{\partial x}$ is a higher order of magnitude than $\frac{\partial h}{\partial y}$, ${\left(\frac{\partial h}{\partial x}\right)}^2$ is neglected. Then,

$\begin{array}{ll}\mathrm{Im}\Omega =-\frac{1}{2}\frac{\partial h}{\partial y}\mu \lambda \pm \frac{1}{2}{\{-[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)]\}}^{\frac{1}{2}}& (29)\end{array}$

The first depth derivative perpendicular to the dominant wave packet imposes on the wave instability disturbed by small perturbations when$\frac{\partial h}{\partial x}$is a higher order of magnitude than$\frac{\partial h}{\partial y}$.

Without regard to the bottom slope,$\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}=0$, then

$\begin{array}{ll}\mathrm{Im}\Omega =\pm \frac{1}{2}{\{-[\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)]\}}^{\frac{1}{2}}& (30)\end{array}$

ImΩ must have a real root, then

$\begin{array}{ll}\frac{1}{4}{a}_0^4{\lambda }^2+\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2\right)\left(\frac{1}{4}{\lambda }^2-\frac{1}{2}{\mu }^2-2a_0^2+2\frac{{\lambda }^2}{K}{a}_0^2\right)<0& (31)\end{array}$

The left-hand of Inequality (31) is the same as the right-hand of Equation (18) in reference (Trulsen and Dysthe, 1996) when kh limits to infinite. Inequality (31) stands for the Stokes wave instability area disturbed by the MNLS perturbation on a flat bottom.

A uniform Stokes wave train is unstable disturbed by small perturbations on infinite and slowly varying depth, except for the curve satisfying Equation (28). Compared with the MNLS perturbation analysis on the flat bottom when h_x= h_y = 0, the small perturbation’s instability area is the entire wavenumber space, except for the curve satisfying Equation (28) on a slowly varying bottom.

Discussions

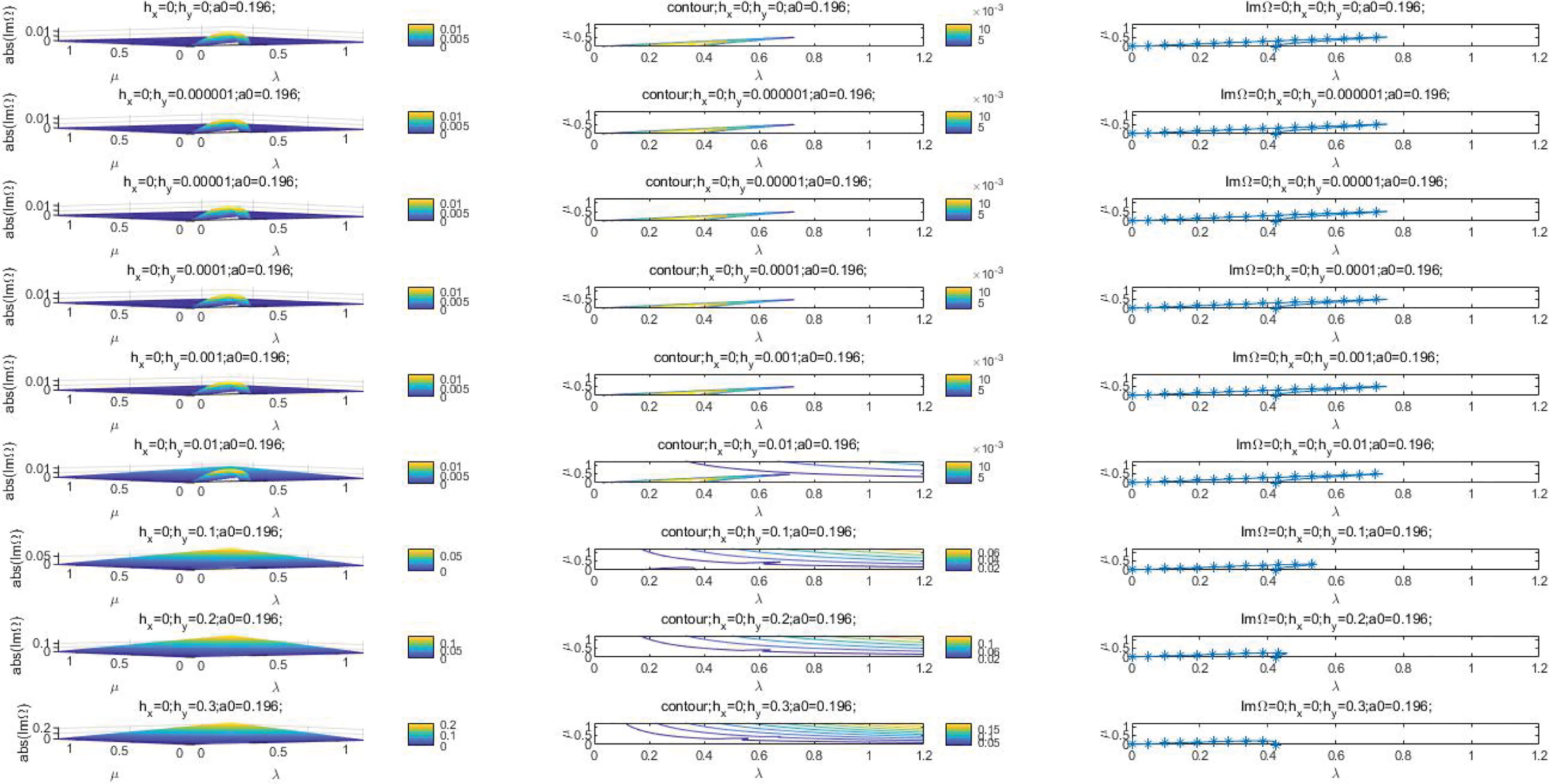
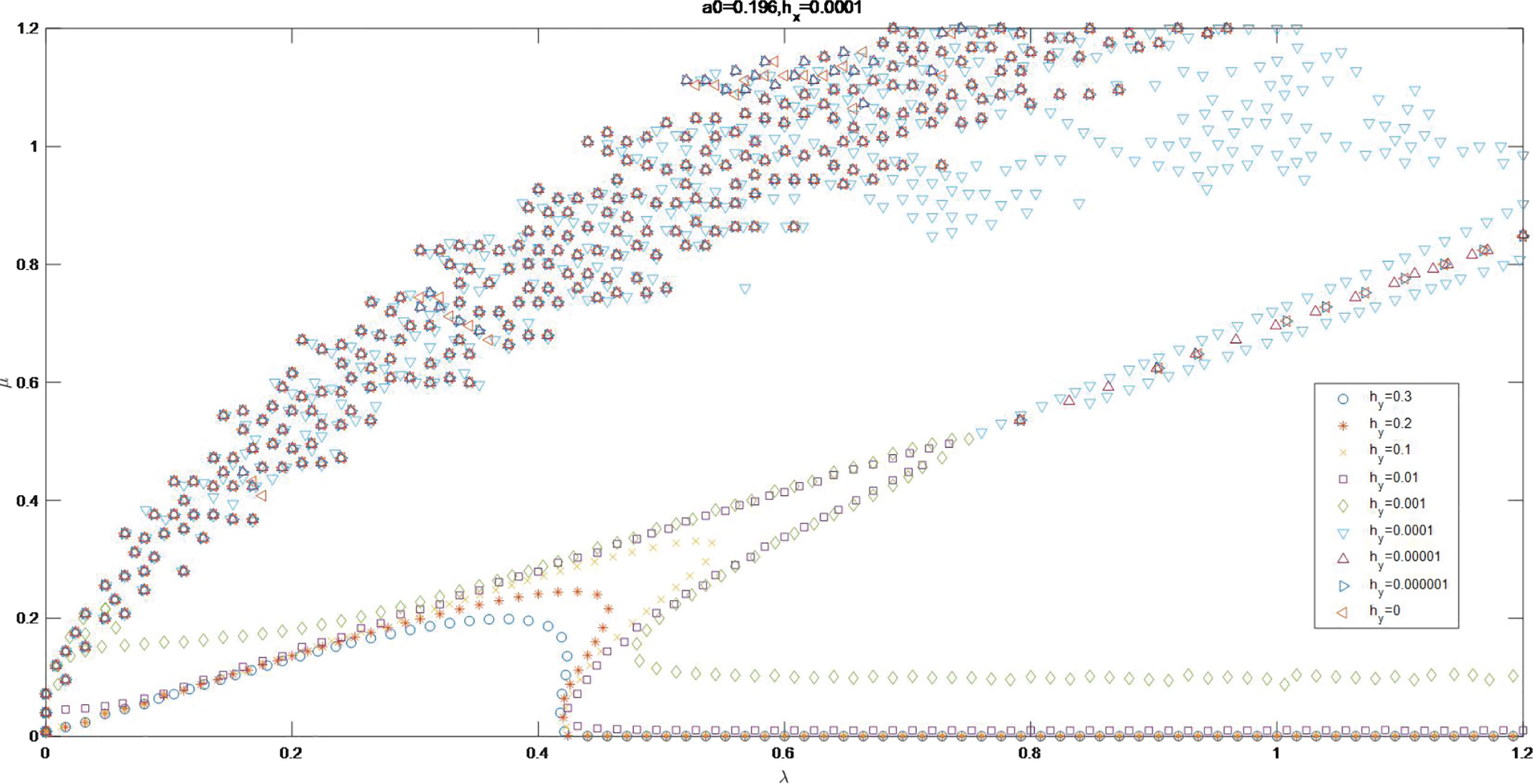
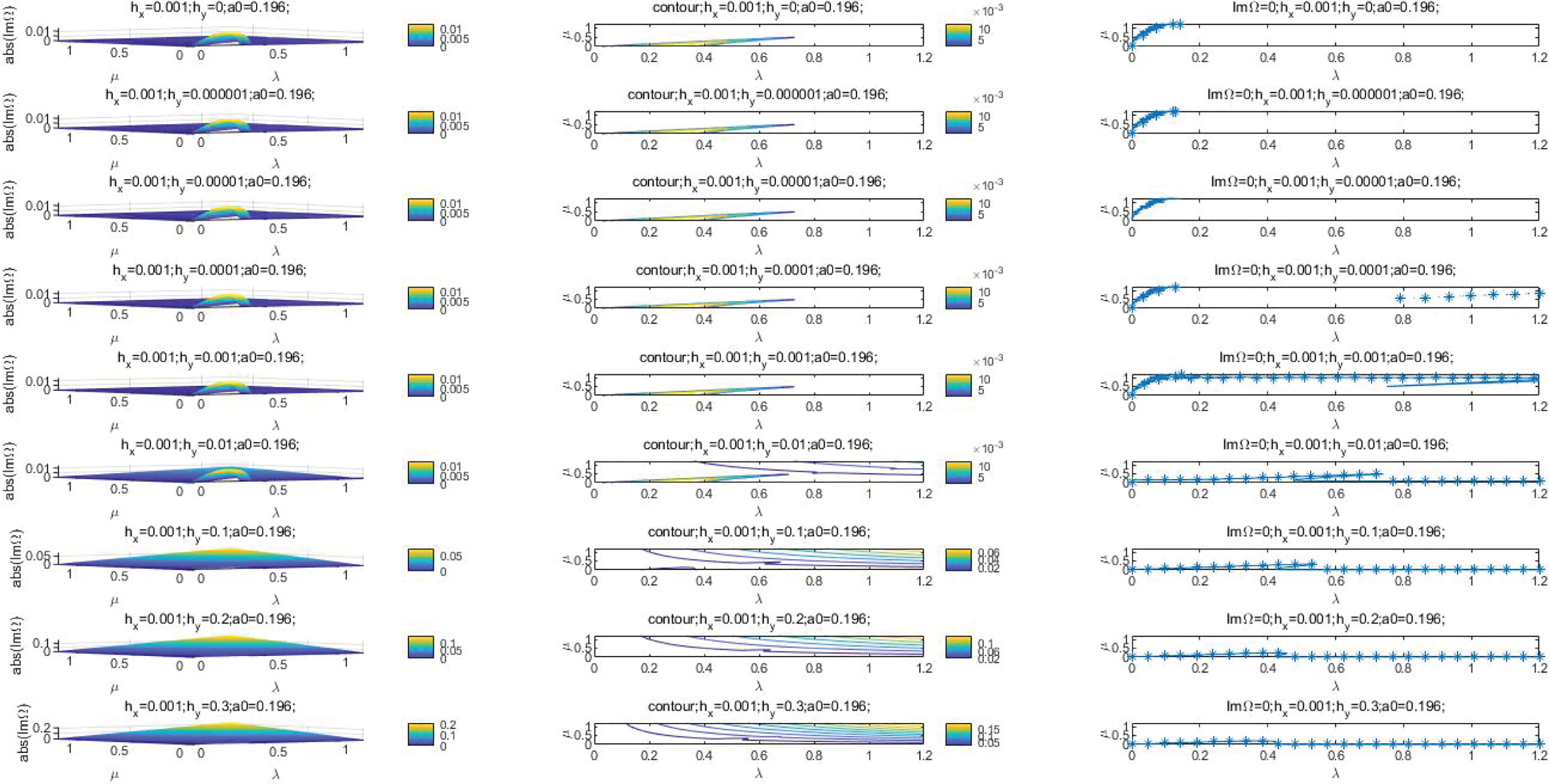
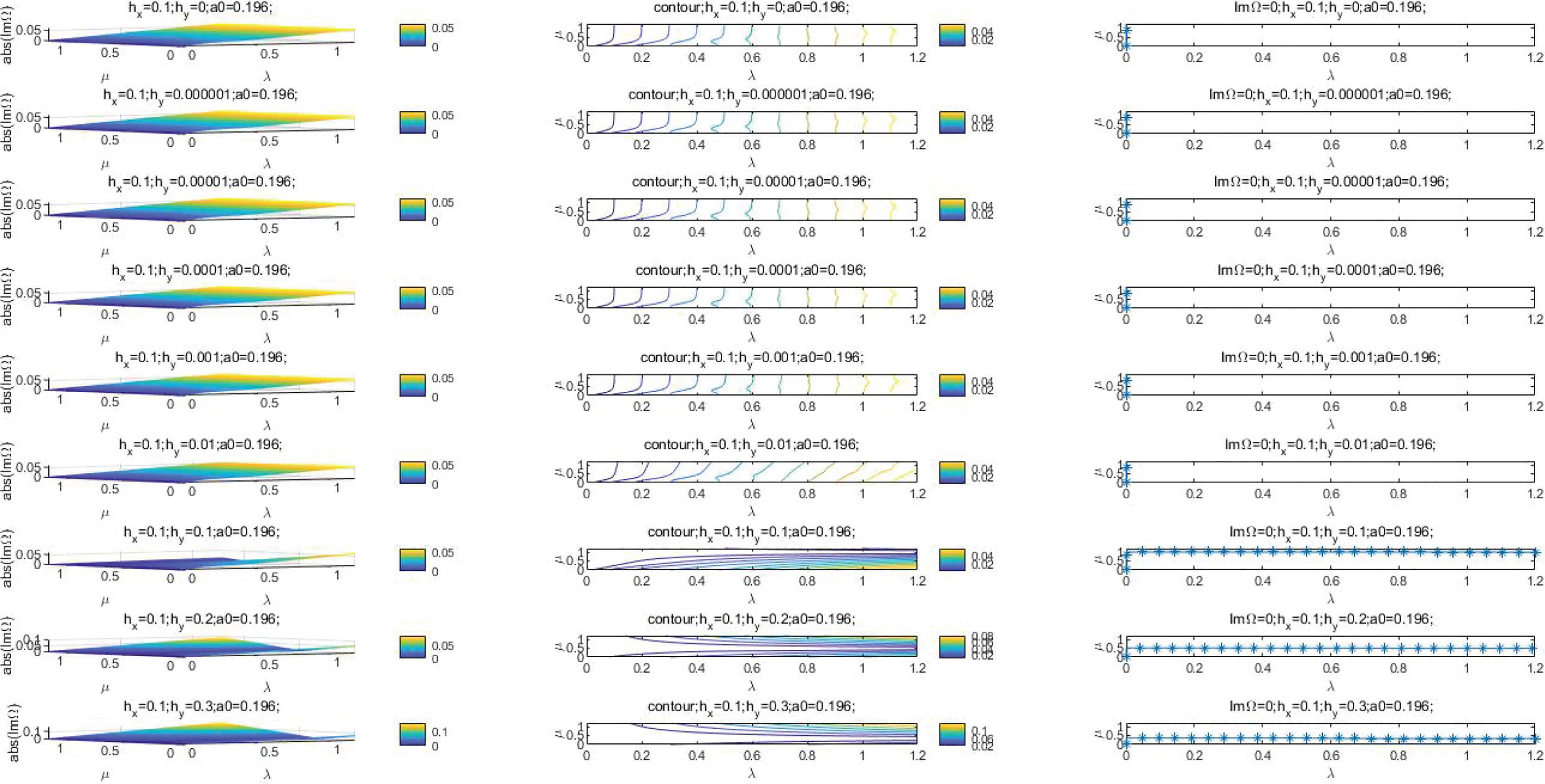
According to the results of Mclean (McLean, 1982) and Trulsen (Trulsen and Dysthe, 1996), we choose a₀ = 0.0995 and a₀ = 0.196 to plot the stability curves for ǀIm Ωǀ and Im Ω = 0, corresponding to ε = 0.1 and ε = 0.2. ǀIm Ωǀ is the growth rate of Stokes wave disturbed by perturbation and the curve of Im Ω = 0 is the stable curve for Stokes wave. Figures 1–12 and Figures 1–24 in the Supplementary Material show the curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0196, the value of $\frac{\partial h}{\partial x}$ and $\frac{\partial h}{\partial y}$ ranging from 0 to 0.3. Figure 25 to Figure 60 in the Supplementary Material show the curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.0995, the value of $\frac{\partial h}{\partial x}$ and $\frac{\partial h}{\partial y}$ varying from 0 to 0.3. To distinguish the influence of the orders of bottom variation, the selected orders of $\frac{\partial h}{\partial x}$ and $\frac{\partial h}{\partial y}$ are 0, 0.000001, 0.00001, 0.0001, 0.001, 0.01, 0.1, 0.2, and 0.3. In Figures 1–15, h_x and h_y are $\frac{\partial h}{\partial x}$ and $\frac{\partial h}{\partial y}$ respectively. In Figures 1, 13–15, h_x = h_y = 0 stands for the MNLS perturbation wave stability curve, neglecting the bottom slope and to compare with other curves.

FIGURE 1

Figure 1 Curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0$.

FIGURE 2

Figure 2 The magnified curves of Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0$.

FIGURE 3

Figure 3 Curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.00001$.

FIGURE 4

Figure 4 The magnified curves of Im Ω = 0 for a₀ = 0.196 and ∂ $\frac{\partial h}{\partial x}=0.00001$.

FIGURE 5

Figure 5 Curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.0001$.

FIGURE 6

Figure 6 The magnified curves of Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.0001$.

FIGURE 7

Figure 7 Curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.001$.

FIGURE 8

Figure 8 The magnified curves of Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.001$.

FIGURE 9

Figure 9 Curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.01$.

FIGURE 10

Figure 10 The magnified curves of Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.01$.

FIGURE 11

Figure 11 Curves of ǀIm Ωǀ and Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=$ 0.1.

FIGURE 12

Figure 12 The magnified curves of Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=0.1$.

FIGURE 13

Figure 13 Curves of Im Ω = 0 for a₀ = 0.0995 and a₀ = 0.196 as $\frac{\partial h}{\partial x}=0$.

FIGURE 14

Figure 14 Curves of Im Ω = 0 for a₀ = 0.0995 and $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}$.

FIGURE 15

Figure 15 Curves of Im Ω = 0 for a₀ = 0.196 and $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}$.

Figures 1–12 and Figures 1–6 in the Supplementary Material indicate curves of ǀIm Ωǀ and the corresponding scatter diagrams of Im Ω = 0 with the invariable value of $\frac{\partial h}{\partial x}$ and the variable value of $\frac{\partial h}{\partial y}$ from 0 to 0.3. The discussions are as follows:

1. As Figures 1–12 shown, for a₀ = 0.196 and the invariable value of $\frac{\partial h}{\partial x}$, the value of ǀIm Ωǀ increases as the value of $\frac{\partial h}{\partial y}$ rises. As the value of $\frac{\partial h}{\partial y}$ varying from 0 to 0.01, the value of ǀIm Ωǀ is maximum around the original point in wave number plane. As the value of $\frac{\partial h}{\partial y}$ is 0.1, 0.2 and 0.3, there is no maximum value of ǀIm Ωǀ around the original point in wave number plane. As the value of $\frac{\partial h}{\partial x}$ increasing from 0 to 0.001, the contours for ǀIm Ωǀ are similar. As $\frac{\partial h}{\partial x}=0.01$, the contours show obvious change by comparing with that As

$\frac{\partial h}{\partial x}=0.001$. There are no extra maximum value points of ǀIm Ωǀ beside that around the original point in wave number plane as the value of $\frac{\partial h}{\partial x}$ varying from 0 to 0.001. It is indicated, on the order of 0.01, $\frac{\partial h}{\partial x}$ begins to affect the curve of ǀIm Ωǀ.

2. For a0 = 0.196 and $\frac{\partial h}{\partial x}=0$, the shape of curves of Im Ω = 0 are similar for the value of $\frac{\partial h}{\partial y}$ ranging from 0 to 0.001. The curve is reduced to the MNLS equation instability curve as $\frac{\partial h}{\partial y}=0$. The curve for Im Ω = 0 approaches to original point more closely with larger value of $\frac{\partial h}{\partial y}$.

3. As $\frac{\partial h}{\partial x}=0.00001$, the curves of Im Ω = 0 for $\frac{\partial h}{\partial y}=0,0.000001$ and 0.00001 are not smooth lines, but scatter groups. The curves for $\frac{\partial h}{\partial x}=0.0001$, 0.001, 0.01, 0.1, 0.2, 0.3 are extended in λ axis. It is suggested that $\frac{\partial h}{\partial x}$ begins to influence the shape of curve for Im Ω = 0 on the order of 0.00001.

4. As $\frac{\partial h}{\partial x}=0.0001$, the curve of Im Ω = 0 for $\frac{\partial h}{\partial y}=0.0001$ is not a smooth curve, but is a scatter group. The scatter groups for $\frac{\partial h}{\partial y}=0,0.000001$ and 0.00001 are in the upper left of the map. The curves for $\frac{\partial h}{\partial x}=0.001$, 0.01, 0.2, 0.3 are extended along and in λ axis.

5. As $\frac{\partial h}{\partial x}=0.001$, the curve of Im Ω = 0 for $\frac{\partial h}{\partial y}=0.001$ is not a smooth line, but a scatter group, partially around the line of μ = 1. The scatter groups for $\frac{\partial h}{\partial y}=0,0.000001$, 0.00001 and 0.0001 are in the upper left of the map, partially distributed in μ axis. The curves for $\frac{\partial h}{\partial x}=0.01$, 0.1, 0.2, 0.3 are extended continuously along and in λ axis.

6. As $\frac{\partial h}{\partial x}=0.01$, the curve of Im Ω = 0 for $\frac{\partial h}{\partial y}=0.01$ is not a smooth line, but a scatter group, partially distributed around the line of μ = 1. The scatter groups for $\frac{\partial h}{\partial y}=0,0.000001$, 0.00001, 0.0001 and 0.001 almostly distribute in μ axis. The curves for $\frac{\partial h}{\partial x}=0.1$, 0.2, 0.3 are lifted from λ axis.

7. As $\frac{\partial h}{\partial x}=0.1$, the scatter groups of Im Ω = 0 for $\frac{\partial h}{\partial y}=0.1,0.2,0.3$ are partially in the lines of μ = 1, μ = 0.5 and μ = 0.333, with others in μ axis. The scatter groups for $\frac{\partial h}{\partial y}=0,0.000001$, 0.00001, 0.0001, 0.001 and 0.01 are in μ axis.

8. As $\frac{\partial h}{\partial x}=0.2$, the scatter groups of Im Ω = 0 for $\frac{\partial h}{\partial y}=0.2,0.3$ are partially in the lines of μ = 1 and μ = 0.667, with others in μ axis.The scatter groups for $\frac{\partial h}{\partial y}=0,0.000001$, 0.00001, 0.0001, 0.001, 0.01 and 0.1 are in μ axis.

9. As $\frac{\partial h}{\partial x}=0.3$, the scatter groups of Im Ω =0 for $\frac{\partial h}{\partial y}=0.3$ are partially in the line of μ = 1, with others in μ axis. The scatter groups for $\frac{\partial h}{\partial y}=0,0.000001$, 0.00001, 0.0001, 0.001, 0.01, 0.1 and 0.2 are in μ axis.

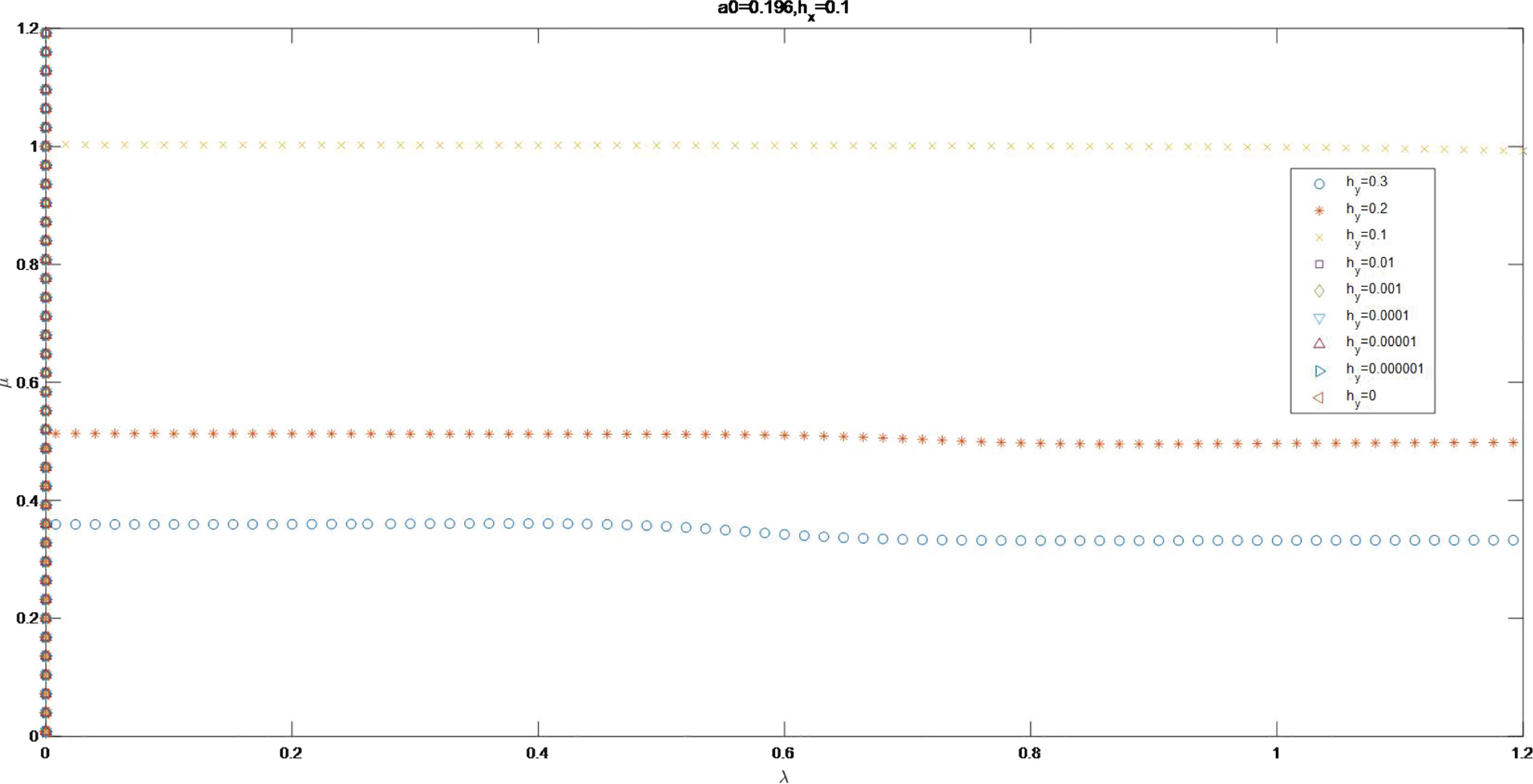
10. In conclusion, as the value of $\frac{\partial h}{\partial x}$ increases, the curve of Im Ω = 0 approximates to μ axis as $\frac{\partial h}{\partial y}<\frac{\partial h}{\partial x}$. The increment of depth variation in x direction contributes the the Stokes wave to be stable in or to parallel to y axis disturbed by small perturbation for $\frac{\partial h}{\partial y}<\frac{\partial h}{\partial x}$. The curve of Im Ω = 0 is the broken line composed by μ = 1 and μ axis for the value of $\frac{\partial h}{\partial y}=\frac{\partial h}{\partial x}$ from 0.01 to 0.1.

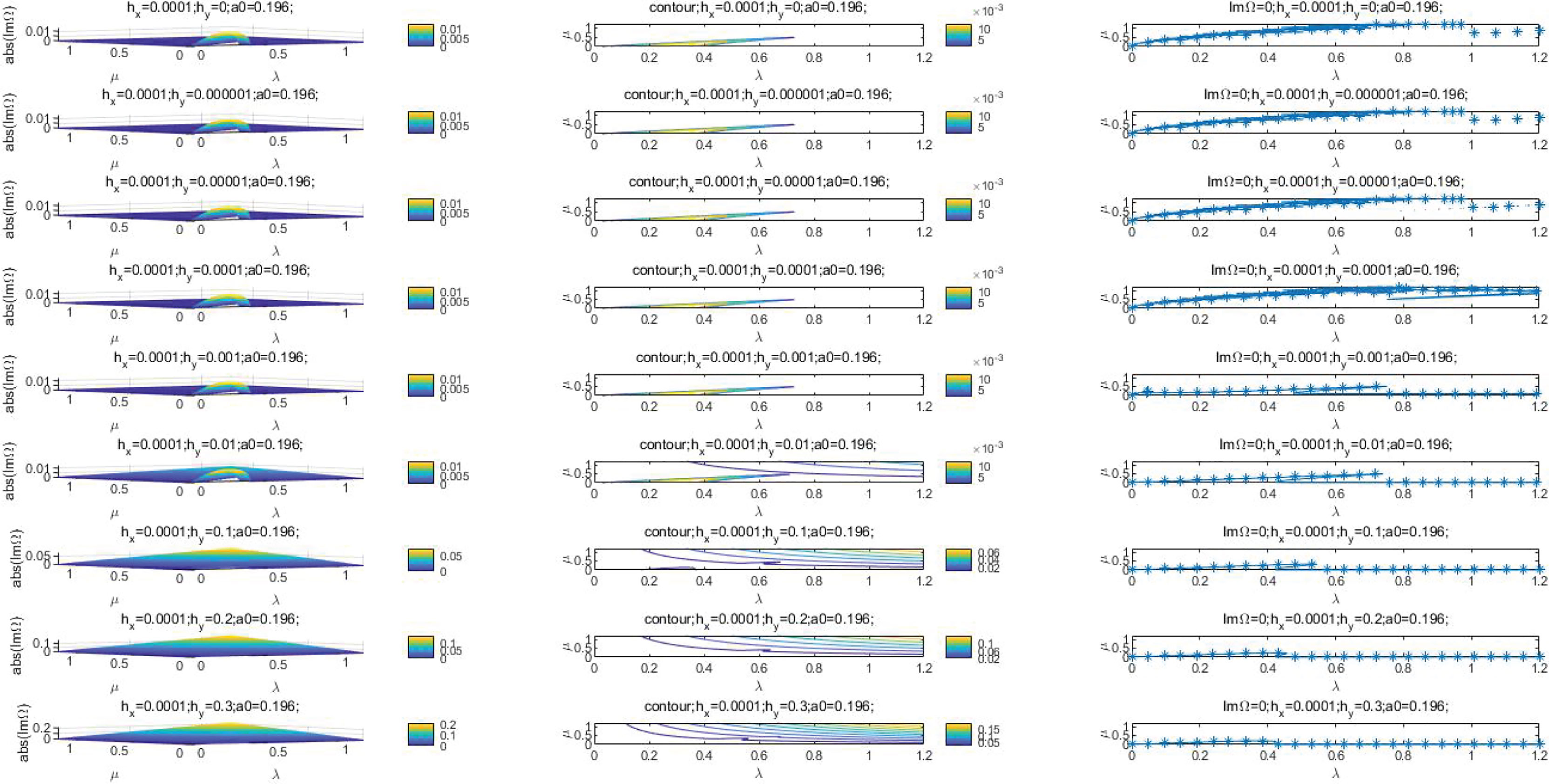
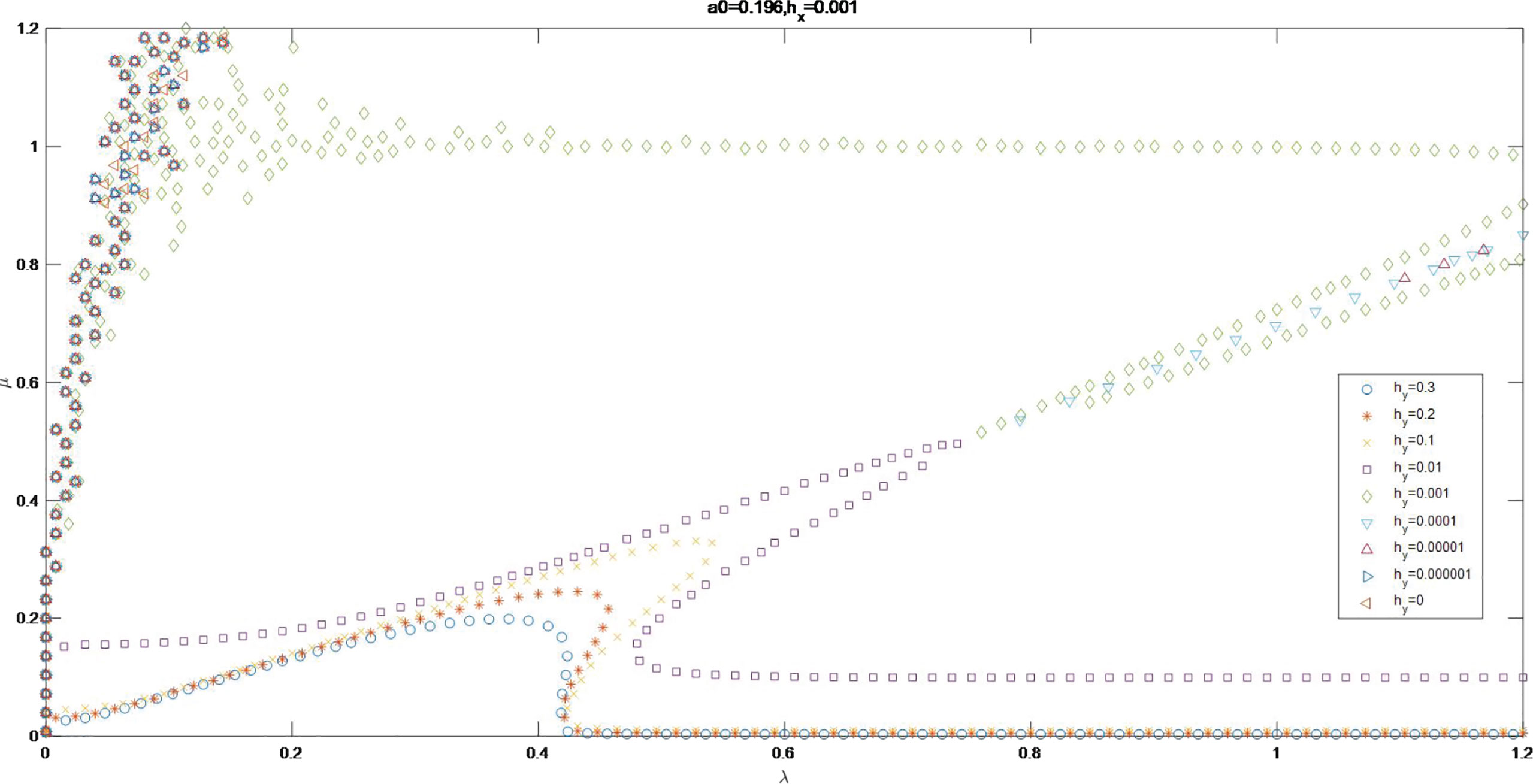
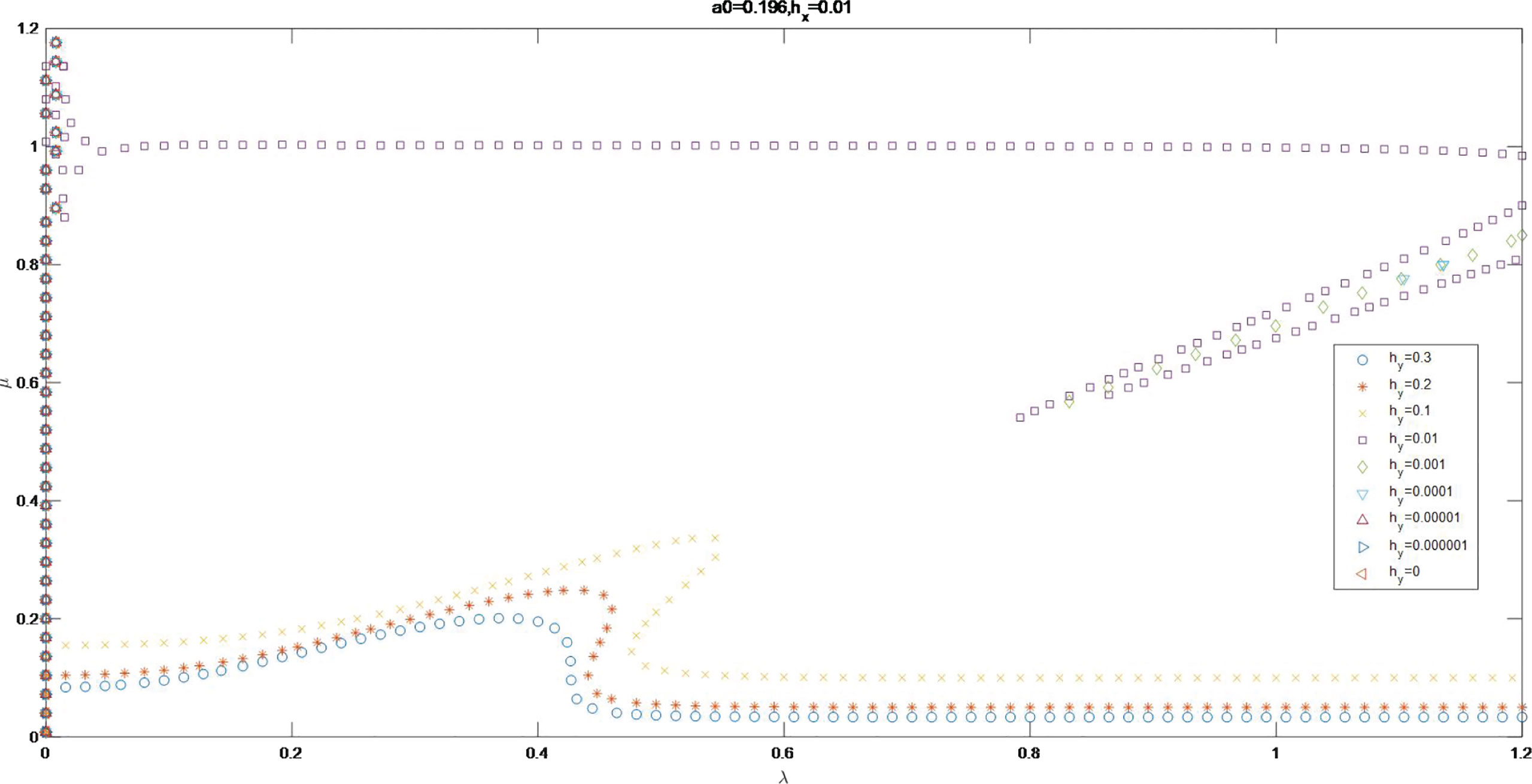
Figure 7 to Figure 24 in the Supplementary Material indicate curves and the corresponding scatter diagrams for the invariable value of $\frac{\partial h}{\partial y}$ and with the variable value of $\frac{\partial h}{\partial x}$ from 0 to 0.3.The discussions are as follows:

1. For a0 = 0.196 and the invariable value of $\frac{\partial h}{\partial y}$, the value of ǀIm Ωǀ increases as the value of $\frac{\partial h}{\partial x}$ rises. As the value of $\frac{\partial h}{\partial x}$ is from 0 to 0.01, the value of ǀIm Ωǀ is maximum around the original point in wave number plane. As the values of $\frac{\partial h}{\partial x}$ are 0.1, 0.2 and 0.3, there are no maximum value of ǀIm Ωǀ around the original point in wave number plane. As the value of $\frac{\partial h}{\partial y}$ varying from 0 to 0.00001, the curve for Im Ω = 0 as $\frac{\partial h}{\partial y}=0$ are similar to that as $\frac{\partial h}{\partial y}=0.000001$. As $\frac{\partial h}{\partial y}=0.0001$, the curve for Im Ω = 0 show obvious change as the contrast with that as $\frac{\partial h}{\partial y}=0.00001$. There is no maximum value points of ǀIm Ωǀ in wave number plane as the value of $\frac{\partial h}{\partial y}=0.1$. It is indicated, on the order of 0.01, $\frac{\partial h}{\partial y}$ begins to affect the curve of ǀIm Ωǀ.

2. The shape of curves for Im Ω = 0 as $\frac{\partial h}{\partial y}=0$ are similar to that as $\frac{\partial h}{\partial y}=0.00001$. The curve is reduced to the MNLS equation instability curve as $\frac{\partial h}{\partial x}=0$. The curves for $\frac{\partial h}{\partial x}=0.01,0.1,0.2\text{\hspace{0.17em}and\hspace{0.17em}}0.3$ are in μ axis.

3. As $\frac{\partial h}{\partial y}=0.0001$, the scatter groups of Im Ω =0 for $\frac{\partial h}{\partial x}=0.0001$, 0.001 and 0.01 are on the bottom right relative to that as $\frac{\partial h}{\partial y}=0.00001$. The scatter groups of Im Ω = 0 for $\frac{\partial h}{\partial x}=0.00001$ begin to be a smooth line with some scatters distributing along the line. The curves for $\frac{\partial h}{\partial x}=0.01,0.1,0.2,0.3$ are in μ axis. It is suggested that, $\frac{\partial h}{\partial y}$ begins to influence the shape of the curve of Im Ω =0 on the order of 0.0001.

4. As $\frac{\partial h}{\partial y}=0.001$, the scatter groups of Im Ω = 0 for

$\frac{\partial h}{\partial x}=0.0001,0.001\text{\hspace{0.17em}and\hspace{0.17em}}0.01$ are on the bottom right slightly compared with that as $\frac{\partial h}{\partial y}=0.0001$. Partial points for $\frac{\partial h}{\partial x}=0.001$ are in the line of μ = 1. The scatter groups of Im Ω = 0 for $\frac{\partial h}{\partial x}=0.00001,0.0001$ form smooth curves. The curves for $\frac{\partial h}{\partial x}=0.01,0.1,0.2\text{\hspace{0.17em}and\hspace{0.17em}}0.3$ are in μ axis. Part of scatters for

$\frac{\partial h}{\partial x}=0.01$ are outside of μ axis.

5. As $\frac{\partial h}{\partial y}=0.01$, the scatter groups of Im Ω = 0 for $\frac{\partial h}{\partial x}=0.01$ distribute along λ axis. The smooth lines of Im Ω = 0 for

$\frac{\partial h}{\partial x}=0.0001,0.001$ extend along and in λ axis. The scatter groups for

$\frac{\partial h}{\partial x}=0.001$ form smooth curves. The curves for $\frac{\partial h}{\partial x}=0.01,0.1\text{and\hspace{0.17em}}0.3$ are in μ axis. Part of scatters for $\frac{\partial h}{\partial x}=0.01$ are outside of μ axis.

6. As $\frac{\partial h}{\partial y}=0.1$, the scatter groups of Im Ω = 0 for $\frac{\partial h}{\partial x}=0.01$ form smooth curves. The curves for $\frac{\partial h}{\partial x}=0.2$ and 0.3 are in μ axis. Scatters for $\frac{\partial h}{\partial x}=0.1$ form a smooth line compose by μ = 1 and μ axis.

7. As $\frac{\partial h}{\partial y}=0.2$, part of the curves of Im Ω =0 for $\frac{\partial h}{\partial x}=0.2$ and 0.1 are approximate to the line of μ = 1 and μ = 0.5 with part of which are in μ axis. The scatters for $\frac{\partial h}{\partial x}=0.3$ are in μ axis.

8. As $\frac{\partial h}{\partial y}=0.3$, curves of Im Ω = 0 for $\frac{\partial h}{\partial x}=0.1,0.2\text{\hspace{0.17em}and}0.3$ are broken lines, partially in the lines of μ = 0.333, μ = 0.667 and μ = 1, others in μ axis.

n summary, as the value of $\frac{\partial h}{\partial y}$ increases, the curve of Im Ω = 0 approximates to λ axis for $\frac{\partial h}{\partial x}<\frac{\partial h}{\partial y}$. The increment of depth variation in y direction helps the Stokes wave to be stable in or to parallel to λ axis for $\frac{\partial h}{\partial x}<\frac{\partial h}{\partial y}$. The curve of Im Ω = 0 is a broken line comblined with μ = 1 and μ axis for the value of $\frac{\partial h}{\partial y}=\frac{\partial h}{\partial x}$ from 0.01 to 0.1.

For a₀ = 0.0995, Figure 25 to Figure 60 in Supplementary Material indicate curves of ǀIm Ωǀ and corresponding scatter diagrams of Im Ω = 0 for the value of $\frac{\partial h}{\partial x}$ and the value of $\frac{\partial h}{\partial y}$ both varying from 0 to 0.3. It is indicated that $\frac{\partial h}{\partial x}$ begins to influence the shape of curve for Im Ω = 0 on the order of 0.000001 and to affect the value of ǀIm Ωǀ on the order of 0.01. It is shown $\frac{\partial h}{\partial y}$ begins to influence the shape of curve for Im Ω = 0 on the order of 0.00001 and affect the value of ǀIm Ωǀ on the order of 0.01. They show similar properties to the curves and corresponding scatter diagrams for a₀ = 0.196, with little value of ǀIm Ωǀ than that for a₀ = 0.196.

It is concluded the curve for Im Ω = 0 is more sensitive to depth variation terms than the curve of ǀIm Ωǀ. The curve for Im Ω = 0 is more sensitive to depth variation terms as a₀ = 0.0995 than that as a₀ = 0.196. The curve for Im Ω = 0 is more sensitive to $\frac{\partial h}{\partial x}$ than that to $\frac{\partial h}{\partial y}$.

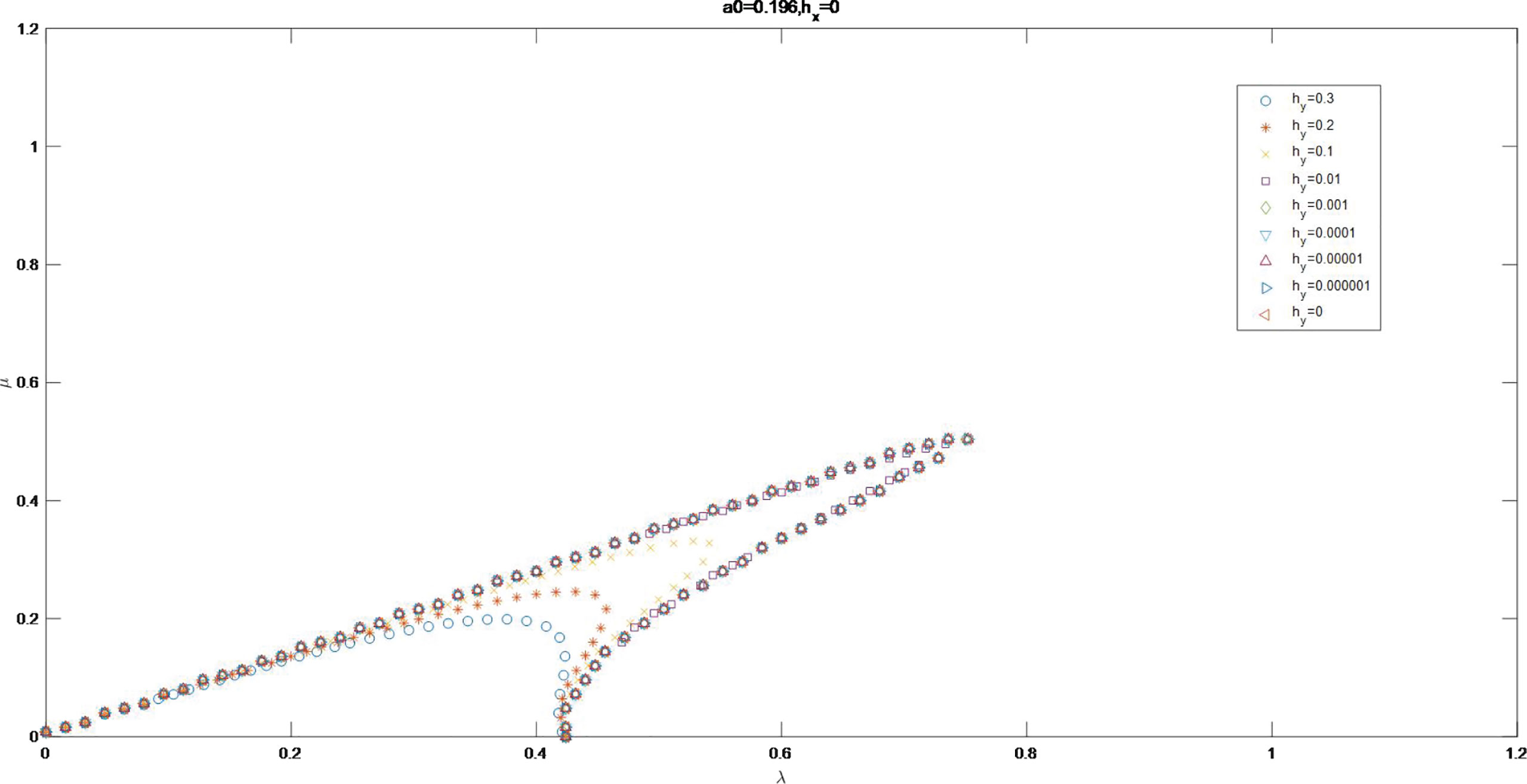
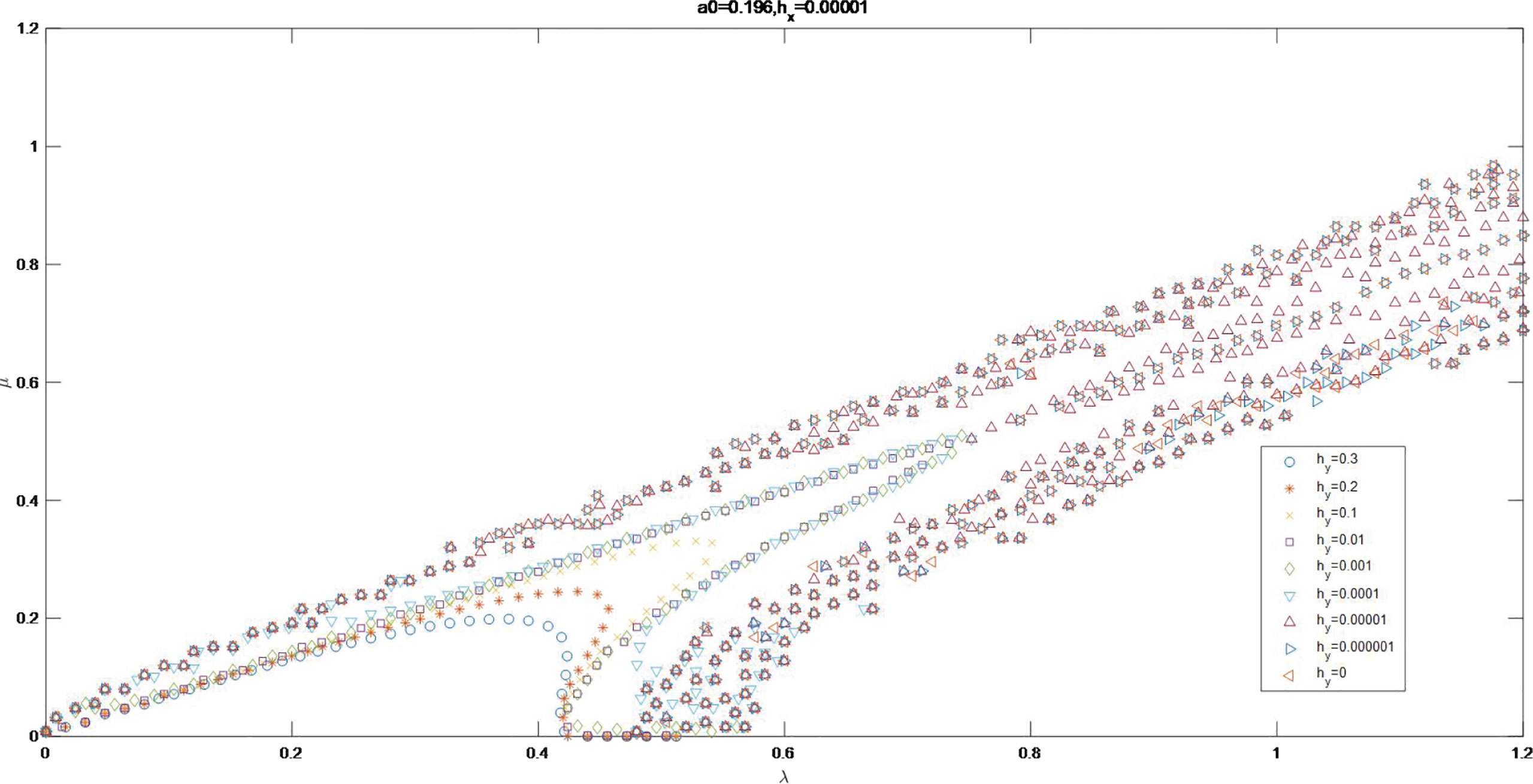
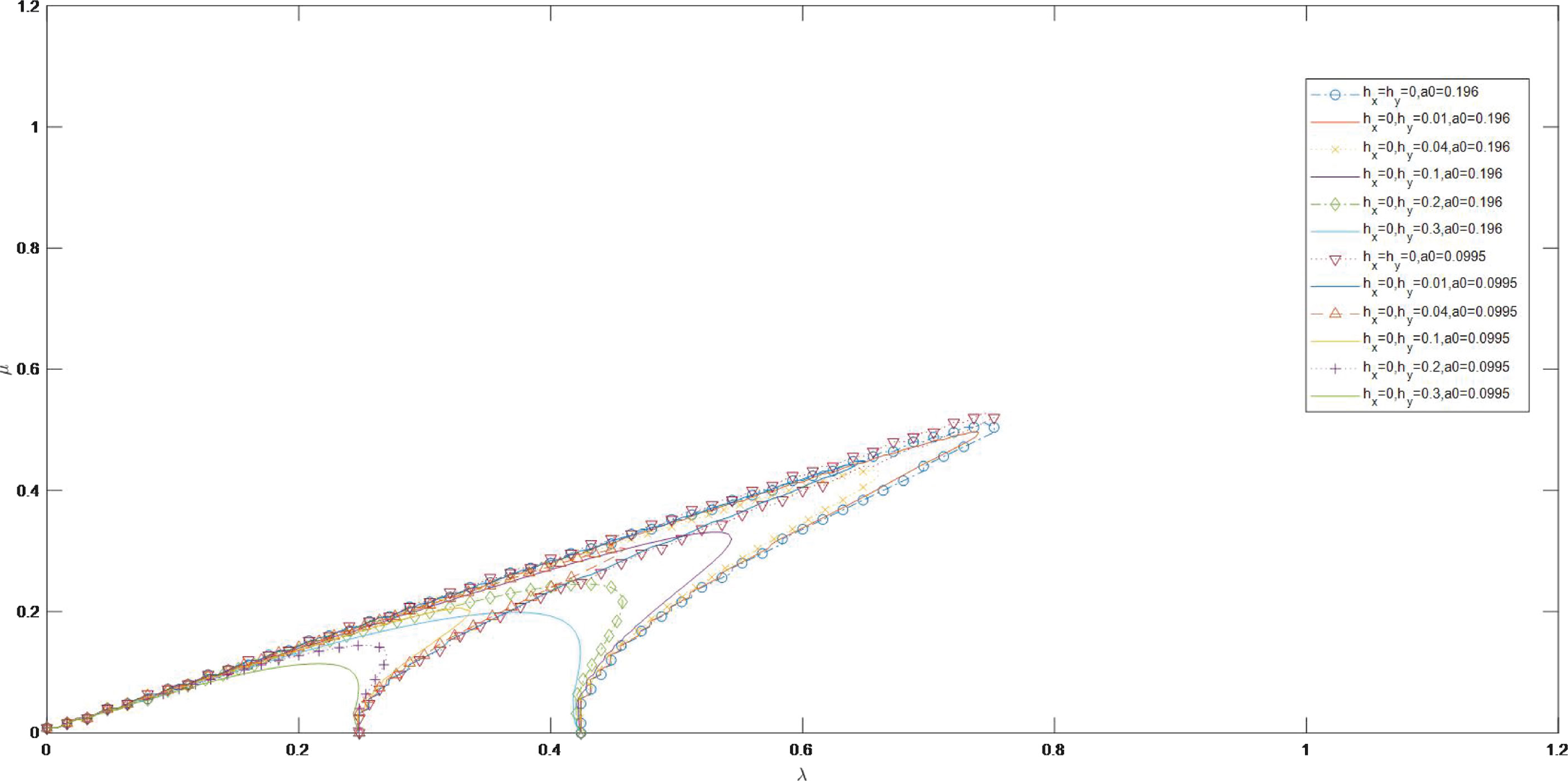
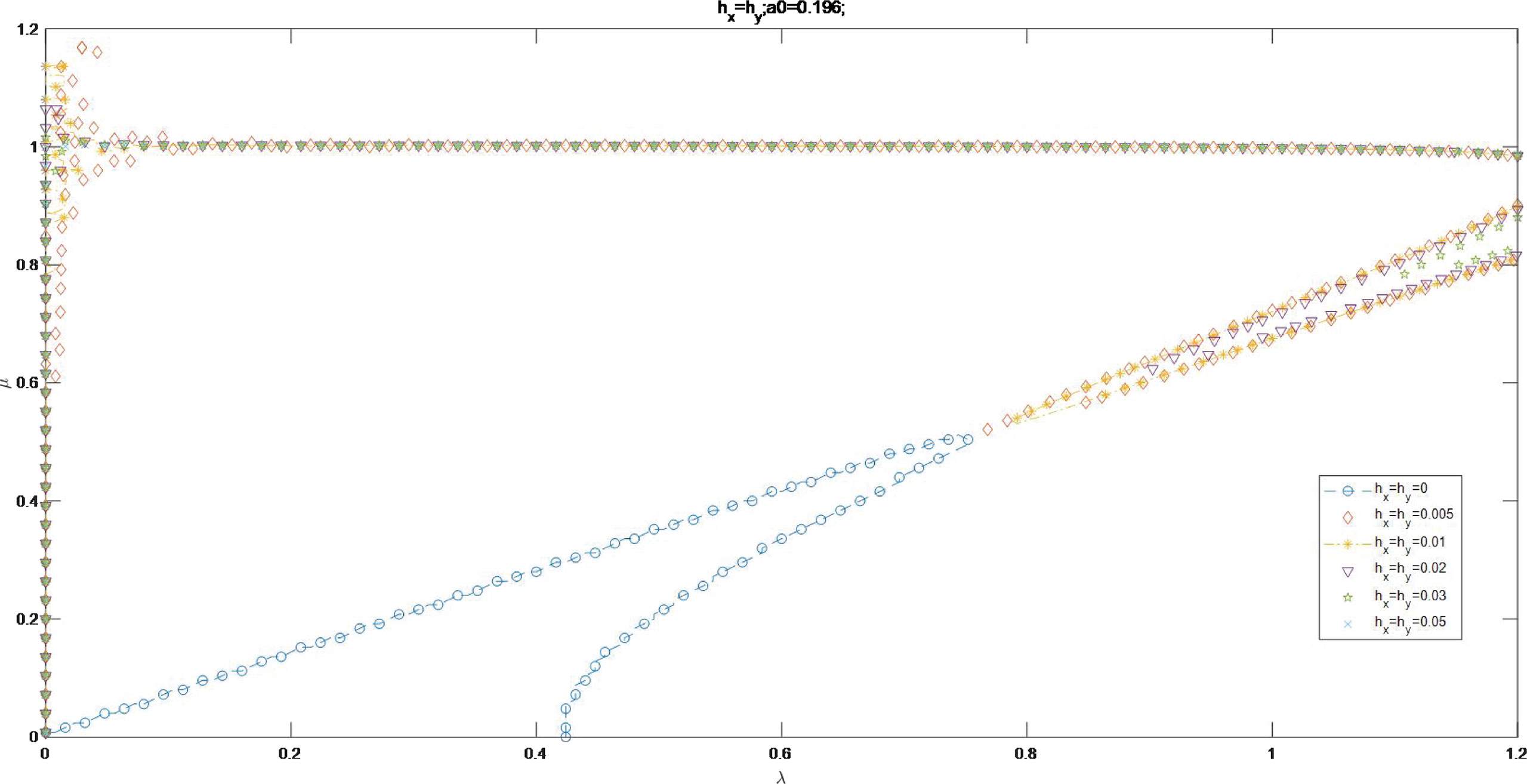
Scatter maps of Im Ω = 0 for a₀ = 0.0995, a₀ = 0.196 and $\frac{\partial h}{\partial x}=0$ are indicated in Figure 13. The values of a₀ and $\frac{\partial h}{\partial y}$ determine the characteristics of curves of Im Ω = 0. The value of a₀ determines the intercept in λ axis, with larger intercept for a₀ = 0.196 than for a₀ = 0.0995. The value of $\frac{\partial h}{\partial y}$ changes the amplitude of curve, with little amplitude for larger value of $\frac{\partial h}{\partial y}$.

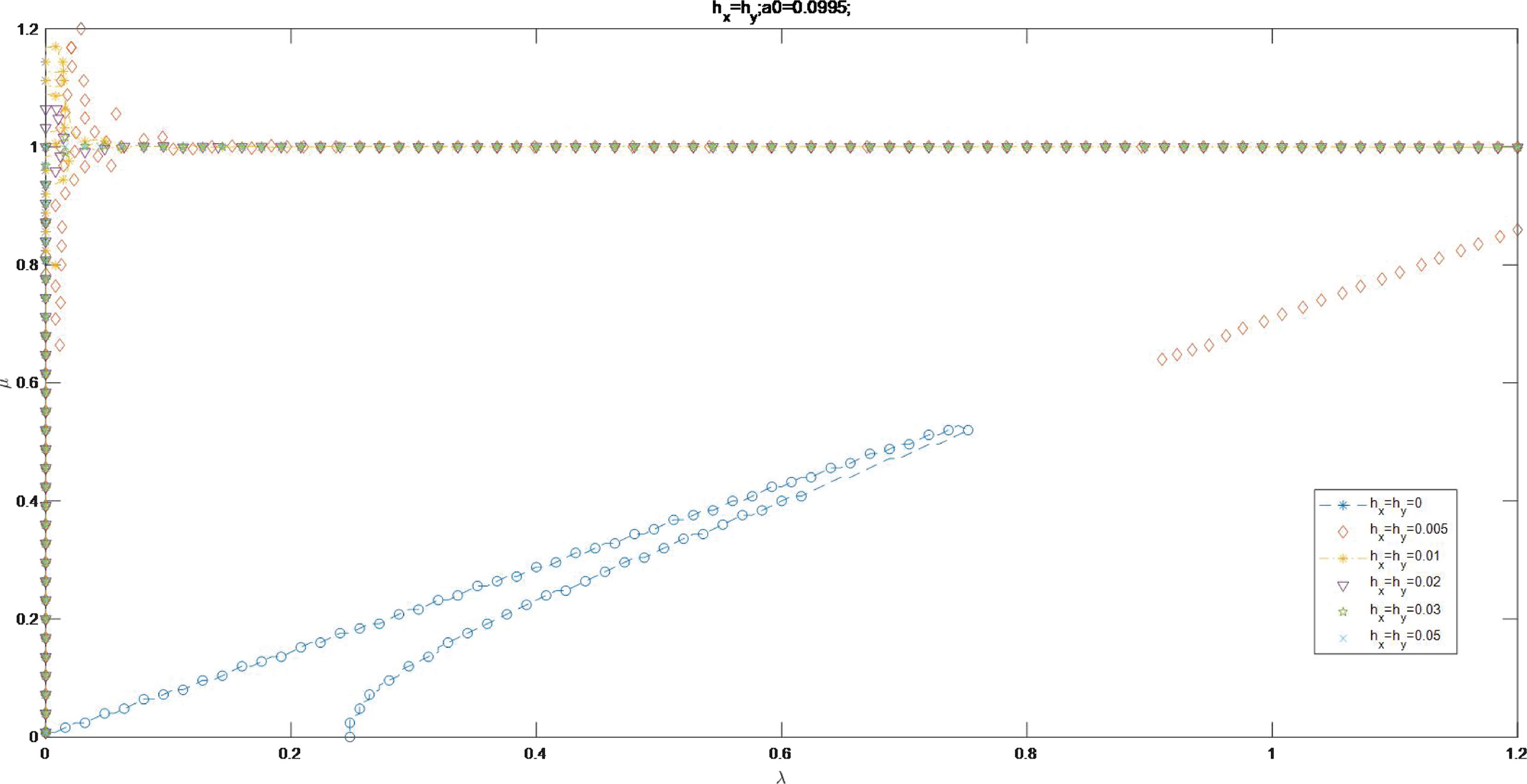
Figures 14, 15 show the curves of Im Ω = 0 as a₀ = 0.196 and a₀ = 0.0995 for the value of $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}$ varying from 0 to 0.05. The scatters of Im Ω = 0 form smooth curves for $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}=0$. The scatters gather to be groups for $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}\ne 0$. A broken line is formed as $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}=0.05$, in the line of μ = 1 and μ axis.

Conclusions

On a finite slowly varying depth, the surface gravity wave equation is expanded to the fourth order by multiscale expansion in the narrowband range, and the TMNLS equation is obtained. When the time scale is longer than ε^-3 times of the dominant wave period or the space scale is larger than ε^-3 times of the dominant wavelength, the second depth derivative and square of the first depth derivative influence on the first-order wave height.

Compared with the MNLS perturbation analysis results on the flat bottom when h_x = h_y = 0, the small perturbation’s instability area by TMNLS is the entire wavenumber space, except for the curve satisfying Equation (28), which means that TMNLS increases the small perturbation’s instability area by including depth variation terms to MNLS.

For a₀ = 0.196, $\frac{\partial h}{\partial x}$ starts to influence the shape of curve for Im Ω = 0 on the order of 0.00001 and to affect the curve of ǀIm Ωǀ on the order of 0.01. $\frac{\partial h}{\partial y}$ starts to influence the shape of curve for Im = 0 on the order of 0.0001 and affect the curve of ǀIm Ωǀ on the order of 0.01.

For a₀ = 0.0995, $\frac{\partial h}{\partial x}$ begins to influence the shape of curve for Im Ω = 0 on the order of 0.000001 and to affect the curve of ǀIm Ωǀ on the order of 0.01. $\frac{\partial h}{\partial y}$ begins to influence the shape of curve for Im Ω = 0 on the order of 0.00001 and affect the curve of ǀIm Ωǀ on the order of 0.01.

The curve for Im Ω = 0 is more sensitive to depth variation terms than the curve of ǀIm Ωǀ. The curve for Im Ω = 0 is more sensitive to depth variation terms as a₀ = 0.0995 than that as a₀ = 0.196. The curve for Im Ω = 0 is more sensitive to $\frac{\partial h}{\partial x}$ than that to $\frac{\partial h}{\partial y}$.

As the value of $\frac{\partial h}{\partial x}$ increases, the curve for Im Ω = 0 approximates to μ axis as $\frac{\partial h}{\partial y}<\frac{\partial h}{\partial x}$. The increment of the value for depth variation in x direction contributes the Stokes wave to be stable in or paralleling μ axis disturbed by small perturbation for $\frac{\partial h}{\partial y}<\frac{\partial h}{\partial x}$. The curve of Im Ω = 0 is the broken line composed by μ = 1 and μ axis for $\frac{\partial h}{\partial y}=\frac{\partial h}{\partial x}\ge 0.05$. As the value of $\frac{\partial h}{\partial y}$ increases, the curve approximates to λ axis for $\frac{\partial h}{\partial x}<\frac{\partial h}{\partial y}$. The increment of the value for depth variation in y direction contributes the Stokes wave to be stable in or paralleling λ axis for $\frac{\partial h}{\partial x}<\frac{\partial h}{\partial y}$. The curve of Im Ω = 0 is a broken line combined by μ = 1 and μ axis for $\frac{\partial h}{\partial x}=\frac{\partial h}{\partial y}\ge 0.05$.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author Contributions

XZ, YZ contributed to conception and design of the study. XZ performed the statistical analysis, wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.928096/full#supplementary-material

References

Agnon Y., Pelinovsky E. (2001). Accurate Refraction-Diffraction Equations for Water Waves on a Variable-Depth Rough Bottom. J. Fluid. Mech. 449, 301–411. doi: 10.1017/S0022112001006280

CrossRef Full Text | Google Scholar

Benjamin T. B., Feir J. E. (1967). The Disintegration of Wave Trains on Deep Water. J. Fluid. Mech. 27, 417–430. doi: 10.1017/S002211206700045X

CrossRef Full Text | Google Scholar

Benney D. J., Roskes G. J. (1969). Wave Instabilities. Stud. Appl. Math. 48, 377–385. doi: 10.1002/sapm1969484377

CrossRef Full Text | Google Scholar

Berkhoff J. C. W. (1972). “Computation of Combined Refraction-Diffraction,” in Proc. 13th Conf. Coastal Eng. ASCE, Vol. 1. 471–491. doi: 10.9753/icce.v13.23

CrossRef Full Text | Google Scholar

Brinch-Nielsen U., Jonsson I. G. (1986). Fourth Order Evolutions and Stability Analysis for Stokes Waves on Arbitrary Depth. Wave. Motion. 8, 455–472. doi: 10.1016/0165-2125(86)90030-2

CrossRef Full Text | Google Scholar

Chamberlain P. G., Porter D. (1995). The Modified Mild-Slope Equation. J. Fluid. Mech. 291, 393–407. doi: 10.1017/S0022112095002758

CrossRef Full Text | Google Scholar

Chu V. C., Mei C. C. (1970). On Slowly Varying Stokes Waves. J. Fluid. Mech. 41, 873–887. doi: 10.1017/S0022112070000988

CrossRef Full Text | Google Scholar

Chu V. C., Mei C. C. (1971). The Nonlinear Evolution of Stokes Waves in Deep Water. J. Fluid. Mech. 47, 337–352. doi: 10.1017/S0022112071001095

CrossRef Full Text | Google Scholar

Craig W., Guyenne P., Sulem C. (2010). A Hamiltonian Approach to Nonlinear Modulation of Surface Water Waves. Wave. Motion. 47, 552–563. doi: 10.1016/j.wavemoti.2010.04.002

CrossRef Full Text | Google Scholar

Craig W., Guyenne P., Sulem C. (2011). Coupling Between Internal and Surface Waves. Nat. Hazard. 57, 617–642. doi: 10.1007/s11069-010-9535-4

CrossRef Full Text | Google Scholar

Craig W., Guyenne P., Sulem C. (2012). Hamiltonian Higher-Order Nonlinear Schrödinger Equations for Broader-Banded Waves on Deep Water. Eur. J. Mechanics-B/Fluid. 32, 22–31. doi: 10.1016/j.euromechflu.2011.09.008

CrossRef Full Text | Google Scholar

Davey A. (1972). The Propagation of a Weak Nonlinear Wave. J. Fluid. Mech. 53, 769–781. doi: 10.1017/S0022112072000473

CrossRef Full Text | Google Scholar

Davey A., Stewartson K. (1974). On Three-Dimensional Packets of Surface Waves. Proc. R. Soc Lond. A338, 101–110. doi: 10.1098/rspa.1974.0076

CrossRef Full Text | Google Scholar

Dysthe K. B. (1979). Note on a Modification to the Nonlinear Schröedinger Equation for Application to Deep Water Waves. Proc. R. Soc. Lond. Ser. A-Math. Phys. Eng. Sci. Lond. 369, 105–114. doi: 10.2307/2398590

CrossRef Full Text | Google Scholar

Hasimoto H., Ono H. (1972). Nonlinear Modulation Gravity Waves. J.Phys.Soc.Jap. 33, 805–811. doi: 10.1143/JPSJ.33.805

CrossRef Full Text | Google Scholar

Kirby J. T. (1986). A General Wave Equation for Waves Over Ripple Beds. J. Fluid. Mech. 162, 171–186. doi: 10.1017/S0022112086001994

CrossRef Full Text | Google Scholar

Kirby J. T., Dalrymple R. A. (1983). A Parabolic Equation for the Combined Refraction–Diffraction of Stokes Waves by Mildly Varying Topography. J.Fluid. Mech. 136, 453–466. doi: 10.1017/S0022112083002232

CrossRef Full Text | Google Scholar

Li Y., Draycott S., Adcock T. A. A., van den Bremer T. S. (2021). Surface Wavepackets Subject to an Abrupt Depth Change. Part 2. Experimental Analysis. J. Fluid. Mech., 1–22. doi: 10.1017/jfm.2021.49

CrossRef Full Text | Google Scholar

Lighthill M. J. (1967). Some Special Cases by the Whitham Theory. Proc. R. Soc Lond.A. 299, 28–53. doi: 10.1098/rspa.1967.0121

CrossRef Full Text | Google Scholar

Li Y., Zheng Y., Lin Z., Adcock T. A. A., van den Bremer T. S. (2021). Surface Wavepackets Subject to an Abrupt Depth Change. Part 1. Second-Order Theory. J. Fluid. Mech. 915 (A72), 1–28. doi: 10.1017/jfm.2021.48

CrossRef Full Text | Google Scholar

Lo E., Mei C. C. (1985). A Numerical Study of Water-Wave Modulation Based on a Higher-Oder Nonlinear Schröedinger Equation. J. Fluid. Mechanic. 150, 395–416. doi: 10.1017/S0022112085000180

CrossRef Full Text | Google Scholar

Lo E., Mei C. C. (1987). Slow Evolution for Nonlinear Deep Water Waves in Two Horizontal Directions: A Numerical Study. Wave. Motion. 9, 245–259. doi: 10.1016/0165-2125(87)90014-X

CrossRef Full Text | Google Scholar

Lozano C. J., Meyer R. E. (1976). Leakage and Response of Waves Trapped Round Islands. Phys. Fluid. 19, 1075–1088. doi: 10.1063/1.861613

CrossRef Full Text | Google Scholar

Martin H. Yuen D. (1980). Quasi-Recurring Energy Leakage in the Two-Dimensional Nonlinear Schrödinger Equation. Phys.Fluids. 23, 881–883. doi: 10.1063/1.863075

CrossRef Full Text | Google Scholar

McLean J. W. (1982). Instabilities of Finite-Amplitude Water Waves. J.Fluid. Mech. 114, 315–330. doi: 10.1017/S0022112082000172

CrossRef Full Text | Google Scholar

Mei C. C. (2005). “Theory and Applications of Ocean Surfaces Waves,” in World Scientific Publishing (Singapore: World Scientific Publishing Co.Pte.Ltd), 23., 747–756.

Google Scholar

Miles J. W., Chamberlain P. G. (1998). Topographical Scattering of Gravity Waves. J. Fluid. Mech. 361, 175–188. doi: 10.1017/S002211209800857X

CrossRef Full Text | Google Scholar

Trulsen K., Dysthe K. B. (1996). A Modified Nonlinear Schröedinger Equation for Broader Bandwidth Gravity Waves on Deep Water. Wave. Motion. 24, 281–289. doi: 10.1016/S0165-2125(96)00020-0

CrossRef Full Text | Google Scholar

Trulsen K., Kliakhandler I., Dysthe K. B., Velarde M. G. (2000). On Weakly Nonlinear Modulation of Waves on Deep Water. Phys. Fluid. 12, 2432–2437. doi: 10.1063/1.1287856

CrossRef Full Text | Google Scholar

Whitham G. B. (1967). Nonlinear Dispersion of Water Waves. J. Fluid. Mech. 27, 399–412. doi: 10.1017/S0022112067000424

CrossRef Full Text | Google Scholar

Xiao R., Lo E. Y.M. (2004). On the Stability of Shoaling Stokes Waves Over a Slowly Varying Bottom. Appl. Ocean. Res. 26, 205–212. doi: 10.1016/j.apor.2005.03.003

CrossRef Full Text | Google Scholar

Yue D. K.-P., Mei C. C. (1980). Forward Diffraction of Stokes Waves by a Thin Wedge. J. Fluid. Mech. 99, 33–52. doi: 10.1017/S0022112080000481

CrossRef Full Text | Google Scholar

Zakharov V. E. (1968). Stability of Periodic Waves of Finite Amplitude on the Surface of a Deep Fluid. J.Appl.Mech.Tech.Phys. 2, 190–194.

Google Scholar

Zakharov V. E., Shabat A. B. (1972). Exact Theory of Two-Dimensional Shelf-Focusing and One-Dimensional Shelf Modulation of Waves in Nonlinear Media. Sov.Phys.JEPT. 34, 62–69. doi: 10.1007/bf00913182

CrossRef Full Text | Google Scholar

Zhang J., Benoit M. (2021). Wave–bottom Interaction and Extreme Wave Statistics Due to Shoaling and De-Shoaling of Irregular Long-Crested Wave Trains Over Steep Seabed Changes. J. Fluid. Mech. 912), 1–34. doi: 10.1017/jfm.2020.1125

CrossRef Full Text | Google Scholar

Zhang Y. F., Li R. J. (2012). Numerical Solutions for Two Nonlinear Wave Equations. Water Sci. Eng. 5 (4), 410–418. doi: 10.3882/j.issn.1674-2370.2012.04.005

CrossRef Full Text | Google Scholar