
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 04 May 2022
Sec. Marine Fisheries, Aquaculture and Living Resources
Volume 9 - 2022 | https://doi.org/10.3389/fmars.2022.891046
In this paper, a new type of bottom trawl was designed for target fishing vessels to use in deep-water fishing grounds. The trawl’s hydrodynamic performance was investigated using numerical simulation and physical modeling methods, and a numerical model based on the finite element method was proposed for estimating hydrodynamic forces and predicting performances. A series of physical model tests based on Tauti’s law were carried out in a towing tank to explore the hydrodynamic performance of the trawl and to assess the applicability of the numerical simulation method. The results showed that the working towing speed of the trawl was 3.5 kn. The drag force and the height of net opening were 50 kN and 5.62 m, respectively, and the swept area was 128 m2 at that speed. The simulated result was close to the experimental result, with a maximum relative error less than 20%, and an average relative error of 10%. The net shape and tension distribution of the trawl were analyzed using the numerical simulation method, and the hanging ratio in T-direction of the mesh of the codend was 0.25 at the working towing speed. The newly designed deep bottom trawl had a superior hydrodynamic performance for high catch efficiency and selectivity and may be applied to commercial fishing operations.
Trawling depends on the power of the fishing vessel and its ability to force fish, shrimp, and other organisms into the net. A trawl is a form of active fishing gear that operates flexibly to catch both middle and bottom commercial species. Evidence shows that bottom trawling and pelagic trawling jointly account for about 35% of all catch (Cashion et al., 2018). The trawl is an essential type of fishing gear for both coastal and pelagic fishing industries.
Fishery resource exhaustion and environmental deterioration are very serious issues in coastal waters (Shen and Heino, 2014). The scope of traditional fishing grounds has been greatly reduced over the last few decades, leading to a major decline in economic benefits. However, the deeper water in exclusive economic zones contains abundant resources with great harvest potential, like the hairtail and cephalopods that inhabit depths of about 200 m, and has gradually become the focus of attention by the fishing industry (Yu et al., 2008). It is increasingly necessary to develop new and more efficient fishing equipment for deep-water fishing. In China, fishermen used to design and improve fishing gears based on their own experiences. However, lax industry standards resulted in the abuse of inapplicable and prohibited fishing gears, which had a negative impact on the sustainable utilization and healthy development of fisheries. Consequently, the authors of this paper designed a new deep bottom trawl based on scientific research to promote the standardization of both bottom trawling fishing gear and deep-water fishing industry.
Trawls are “fuel-greedy” on account of their high drag forces. High energy consumption and rising fuel prices increase the cost of operations and impact the entire industry. In addition, the shape, the net opening spreading performance of the trawl, and the mesh opening performance of the codend are crucial for hydrodynamic performances (Wan et al., 2021). Better fishing gear design also promotes the sustainable utilization of resources, improves the utilization value of resources, and reduces the impact of fishing operations on the ecosystem (Wan et al., 2019). With these factors in mind, we set out to design a new deep bottom trawl and investigate its hydrodynamic performance.
The main methods for exploring the hydrodynamic performance of fishing gear are physical model tests in a water tank or wind tunnel facility (Mellibovsky et al., 2018), numerical modeling calculations, and full-scale measurements at sea (Fiorentini et al., 2004; Sala et al., 2009; Nguyen et al., 2015). Bessonneau and Marichal (1998) modeled the flexibility of the trawl structure using a set of rigid bars and investigated its dynamic behavior. Priour (1999) developed the process of modeling fishing gear based on the finite element method. The fishing net was model led by a triangular element, and the principle of virtual work was applied to determine the equation for the relationship between force and displacement. A numerical tool was used to reduce the drag per swept area of the trawl (Priour, 2009), and the catch weight influence on trawl behavior was studied using the numerical method and measurement at sea (Priour and Prada, 2015). Wan et al. (Wan et al 2002a; Wan et al 2002b; Wan et al., 2004; Wan et al., 2019) established the numerical model based on the finite element method and analyzed the hydrodynamic performance of fishing nets and ropes in a uniform current. The nonlinear equilibrium equation of the flexible gear structure was solved through the method of numerical iterative calculation. The shape and tension distribution of the longline, plane net, gillnet, and an Antarctic krill trawl were investigated using the numerical method. The accuracy of the numerical method was then verified through comparisons with flume tank experiments. Lee et al. (2005) presented a numerical model of a flexible system, which was composed of a network of masses and springs. The behaviors of netting and fishing gear systems (trawl and purse seine) were studied based on the fundamental law of dynamics. Balash and Sterling (Balash and Sterling, 2012; Balash and Sterling, 2014) investigated the innovations of prawn trawls based on model tests in flume tank and sea trials that include implementing high-strength netting, quantifying the effect of mesh orientation on netting drag, and enhancing the redirection of netting drag from the wings, to reduce drag and improve the energy efficiency of the trawl system. Khaled et al. (Khaled et al., 2012; Khaled et al., 2013) presented a mechanical model for trawls based on a finite element method, which was adapted to minimize the drag-to–mouth area ratio. The authors also explored the effect of cable length optimization on the ratio between the estimated trawl drag and the predicted catch efficiency. In addition, the effects of the catch, cutting ratio, and liners on the hydrodynamic performance of trawls were analyzed using physical model tests (Liu et al., 2021; Tang et al., 2022). The distribution characteristics of the flow field inside and around the trawl were also explored using numerical simulations and measurements in a flume tank (Thierry et al., 2021; Thierry et al., 2022). These works provide important foundations of both methods and guidelines for fishing gear designs and hydrodynamic performance investigations. However, there is a lack of comprehensive and integrated analysis on the hydrodynamic performance of deep bottom trawls, from forces (the total drag force and the tension of each part) to deformations (the spreading performance of net opening and the mesh opening performance of the codend).
The numerical simulation method has emerged as a powerful and popular tool for investigating the hydrodynamic performance of trawls because it is theoretically feasible and cost-effective, compared to expensive sea trials (Thierry et al., 2021). It is worth noting that a trawl is a flexible structure, which undergoes large deformations caused by the interaction with water. The equation of deformations is also nonlinear in most cases (Wan et al., 2002a; Wan et al., 2002b), which makes numerical simulations especially helpful for calculating structural deformations. In this paper, a new deep bottom trawl was designed based on a target fishing vessel with potential applications for deep-water fishing grounds. The hydrodynamic performance of the trawl was investigated by means of numerical simulations and physical model tests in a towing tank. The principle of minimum potential energy and Newton–Raphson iterative method were used to determine and solve the equilibrium equation, respectively. In addition, a series of physical model tests were conducted to investigate the hydrodynamic performance of the deep bottom trawl and assess the applicability of the numerical simulation method through comparison between the experimental and numerical simulation results.
A deep bottom trawl is a system of nets, cables, and other attached tools that is flexible and able to be deformed under pressure from currents. The fishing net can be regarded as a structure connected by a large number of mesh bars, whereas the cable is several straight segments. Both bars and segments can be considered as straight discrete elements (Figure 1). As a result, the deep bottom trawl is modeled as a discrete structure with finite elements. In the numerical model, elements are connected through their ends, i.e., nodes (Wan et al., 2002a; Wan et al., 2002b; Wan et al., 2004).
When the trawl moves in water at a constant speed, its elements will incur significant relative displacements from an initial state to the deformed, which is the equilibrium state (Wan et al., 2019). According to the above hypothesis, the total potential energy Π of the discrete trawl system can be expressed as follows (Wan et al., 2004):
Where Fi is the equivalent nodal load on the ith node; Di is the nodal displacement of the ith node; Tg is the axial force of the gth element; Lg0 is the initial length of the gth element; Lg(Di) is the length of the gth element after deformation; Ag is cross-sectional area of the gth element; E is the Young’s modulus of the material; f is the nodal degree of freedom; and m is the number of the element. On the right side of the equation, the first term represents the load potential energy of the structure, the second term represents the strain energy of the axial force, and the third term represents the work done by the axial force (Wan et al., 2019).
The equilibrium equation is determined by the principle of minimum potential energy, which states that the total potential energy of a system reaches an absolute minimum when the system is in a state of equilibrium (i.e. and ). Accordingly, the equilibrium equation of a deep bottom trawl can be obtained:
Obviously, these equilibrium equations include (f + m)degrees of freedom with unknown Di and Tg, which are nonlinear, and need to be solved by applying Newton–Raphson iterative method (Wan et al., 2004):
where and are the solution and correction of the rth step of the iteration. As a result, the solution of the (r + 1) th step is . As stated in the previous work a desired solution can be converged by such iterating calculations (Wan et al., 2019).
The deep bottom trawl system is subjected to many loads, including those resulting from gravity like weight and buoyancy, hydrodynamic loads caused by the interaction between the structure and water, and other kinds of external loads. The hydrodynamic load acting on the element is calculated by the truss model. As shown in Figure 2, the relative velocity V between the element and water is divided into two components: the normal component Vn and the tangential component Vt. The normal drag coefficient Cn and the tangential drag coefficient Ct are calculated by the following formulas (Choc and Casarella, 1971):
Cn and Ct are calculated according to Reynolds number Ren, where Ren=ρVnd/µ; d is the diameter of the element; and μ is the coefficient of fluid viscosity. The normal hydrodynamic load Fn of the element is calculated as follows:
where L is the length of the element. The tangential hydrodynamic load Ft is calculated similarly.
The mesh grouping method is used for reducing the number of calculations. A given number of actual meshes are modeled by a fictitious equivalent mesh, which has the same physical qualities as the actual meshes, like the shape (Figure 3), projected area of the netting, and volume (Li et al., 2006). Thus, the following equations are obtained:
where N is the grouping number. Subscripts 1 and 2 represent the actual mesh and fictitious mesh, respectively.
A new deep bottom trawl (79.9 × 66.26 m) was designed for the target trawler with the main engine power of about 1,000 HP. The trawl included four panels with diamond mesh. The mesh size was determined according to the minimum mesh size and the fishermen’s requirements. A 1:15 scale (λ=15), ratio of the total scale of the trawl) model of the bottom trawl was manufactured based on Tauti’s law (Tauti, 1934), with the small-scale ratio λ`=6 (ratio of the netting twine). The expanded view of the model trawl is shown in Figure 4. Main specifications and parameters of the full-scale trawl and the model trawl are provided in Table 1.
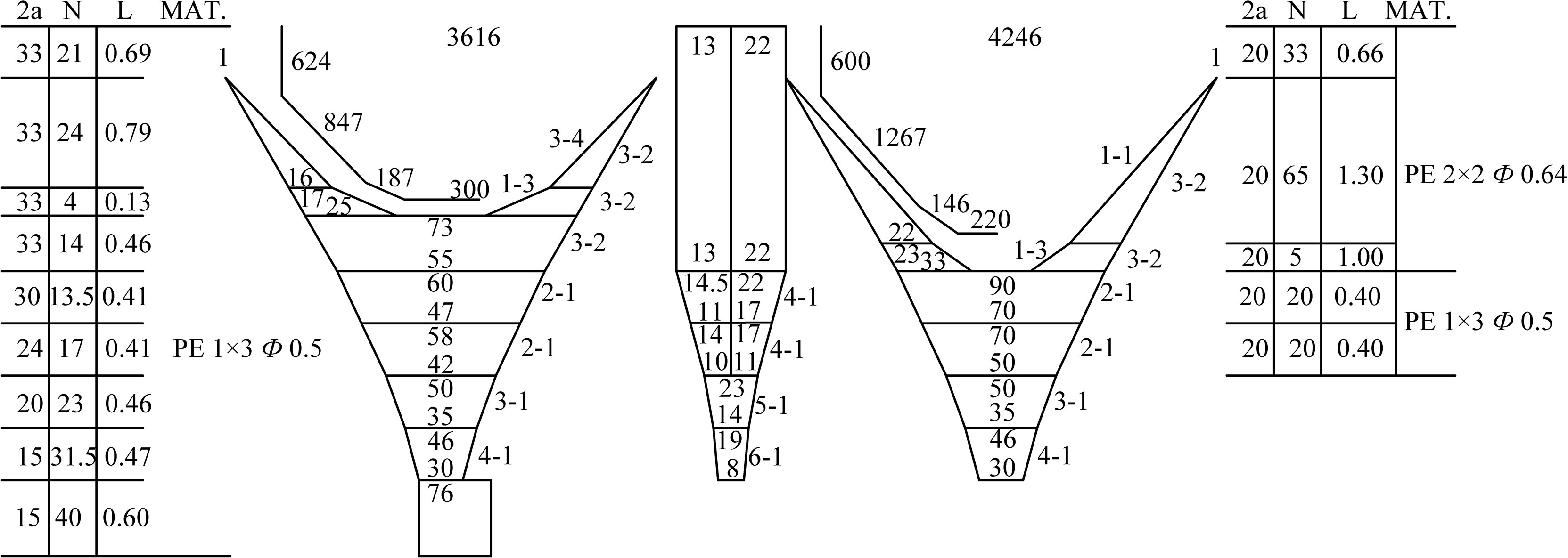
Figure 4 Schematic net plan of the model trawl. Unit of net length (L), m; unit of mesh size (2a) and twine diameter (Φ), mm; unit of cable length, mm.
A series of physical model tests were conducted in a towing tank at East China Sea Fisheries Research Institute, Chinese Academy of Fishery Sciences, China. The size of the tank was 90 m (length) × 6 m (width) × 3 m (height). The towing vehicle of the tank can be operated at a towing speed ranging between 0 and 4 m/s.
The basic setup of the physical model test is shown in Figure 5. The end of the leg was connected to a load cell, which was fixed on a supporting bar. The horizontal spreading ratio of the trawl (the ratio of the horizontal distance between wing-ends to the length of ground rope) was set to 0.4 by adjusting the horizontal distance between leg-ends. Floats were added to the headline to provide buoyancy for the headline height (height of net opening), which was measured by a structure scanner. The scanner with a 30-mm distance resolution was connected to the towing vehicle by a movable device. The full-scale towing speed of the trawl was set to 2.5–5.5 kn with a step of 0.5 kn, which was converted to the speed of the towing vehicle in physical model tests according to Tauti’s law (Tauti, 1934).
Drag forces (converted to full-scale values) from physical model tests and numerical simulations are shown in Figure 6. As the towing speed increased from 2.5 to 5.5 kn, the experimental drag force increased from 28.9 to 104.4 kN. At lower speeds, the measured drag force was greater than the calculated drag force, and the calculated drag force was greater than that from model tests when the towing speed was higher, with a difference of about 17.7%. The simulated value was generally close to the experimental value, with an average relative error of about 10.2%.
Figure 7 shows the experimental and simulated value of the height of net opening. As can be seen from the result, the height decreased from 7.5 to 3.9 m, with the towing speed increasing from 2.5 to 5.5 kn. The vertical spreading ratio (the ratio of the headline height to the circumference of net opening) decreased from 9.3% to 4.8% with the towing speed. The simulated value was greater than the experimental value in most cases with a maximum difference of about 15.7%. Overall, the mean difference was about 6.8%.
The power consumption was calculated by multiplying the drag force and the towing speed. As shown in Figure 8, the power consumption increased from 37.2 to 295.5 kW as the towing speed increased from 2.5 to 5.5 kn. It was worth noting that when the towing speed was equal to 3.5 kn, the power reached about 90 kW, accounting for about 10% of the main engine power of the target trawler. Therefore, the newly designed trawl could operate normally at a working towing speed of 3.5 kn. At lower speeds, the experimental power from model tests was greater than the simulated power. The higher the towing speed was, the larger the simulated power could be. The simulated power tracked closely to the experimental value, with an average relative error of about 10.2%.
The swept area of trawl is an important hydrodynamic performance index, which is generally considered to be directly proportional with the catch efficiency. However, the shape of the trawl mouth was irregular (Figure 9). Therefore, the swept area could only be roughly estimated. The experimental swept area was approximated by the product of the height of net opening and the horizontal distance between wing-ends and then multiplied by the shape coefficient. As for the numerical simulation, the swept area was calculated as the sum of the projection of the surrounding area formed by each element, which modeled the cable (headline and ground rope), on the plane perpendicular to the towing displacement. The swept area is shown in Figure 10. The higher the towing speed, the smaller the swept area. The area was about 128 m2 at the towing speed of 3.5 kn. When the shape coefficient was about 0.8 to 0.9, the estimation value from model tests was close to the calculated value from numerical simulations, with a mean difference of about 6%.
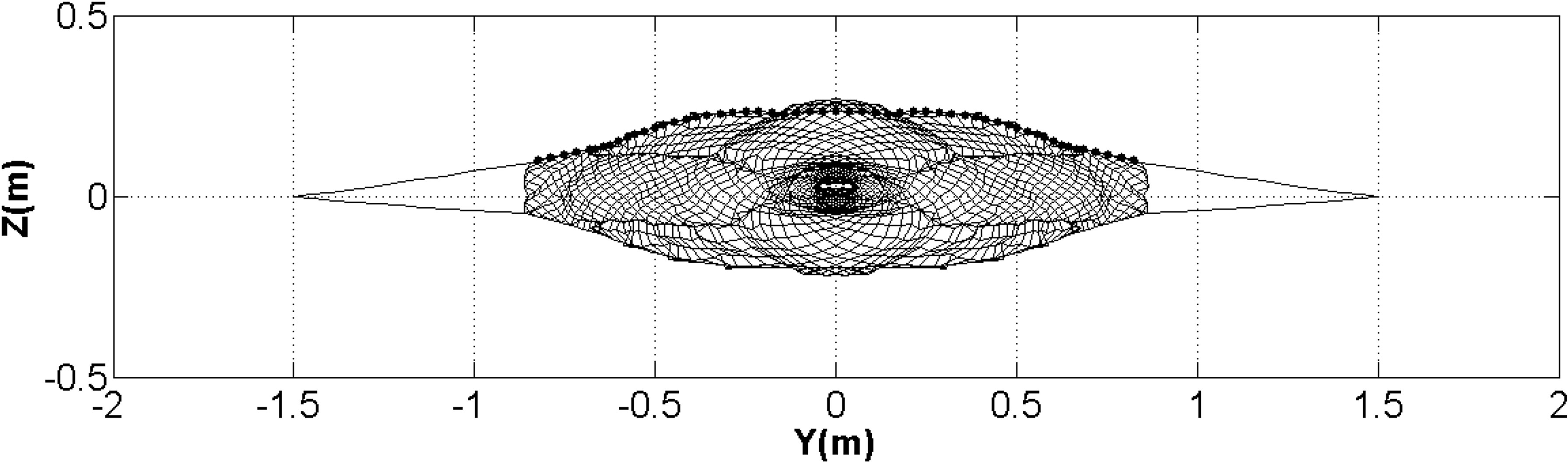
Figure 9 Shape of trawl mouth from the numerical simulation at the towing speed of 1.43 kn in model tests.
The shape and the tension distribution of the model trawl at different towing speeds were calculated using numerical simulations (Figure 11). The shape of the trawl was stable and smooth, with fine bottom sticking performance. The leg produced a straight line and the cable showed a catenary shape. The shape of trawl body was presented as a conical shape, whereas the codend was a cylindrical shape. The tension of the leg was the greatest with that of the bottom leg greater than the top leg. The tension of the ground rope and the headline was greater, whereas that of the front part of cables was greater than the back part. The tension of the trawl netting was smaller.
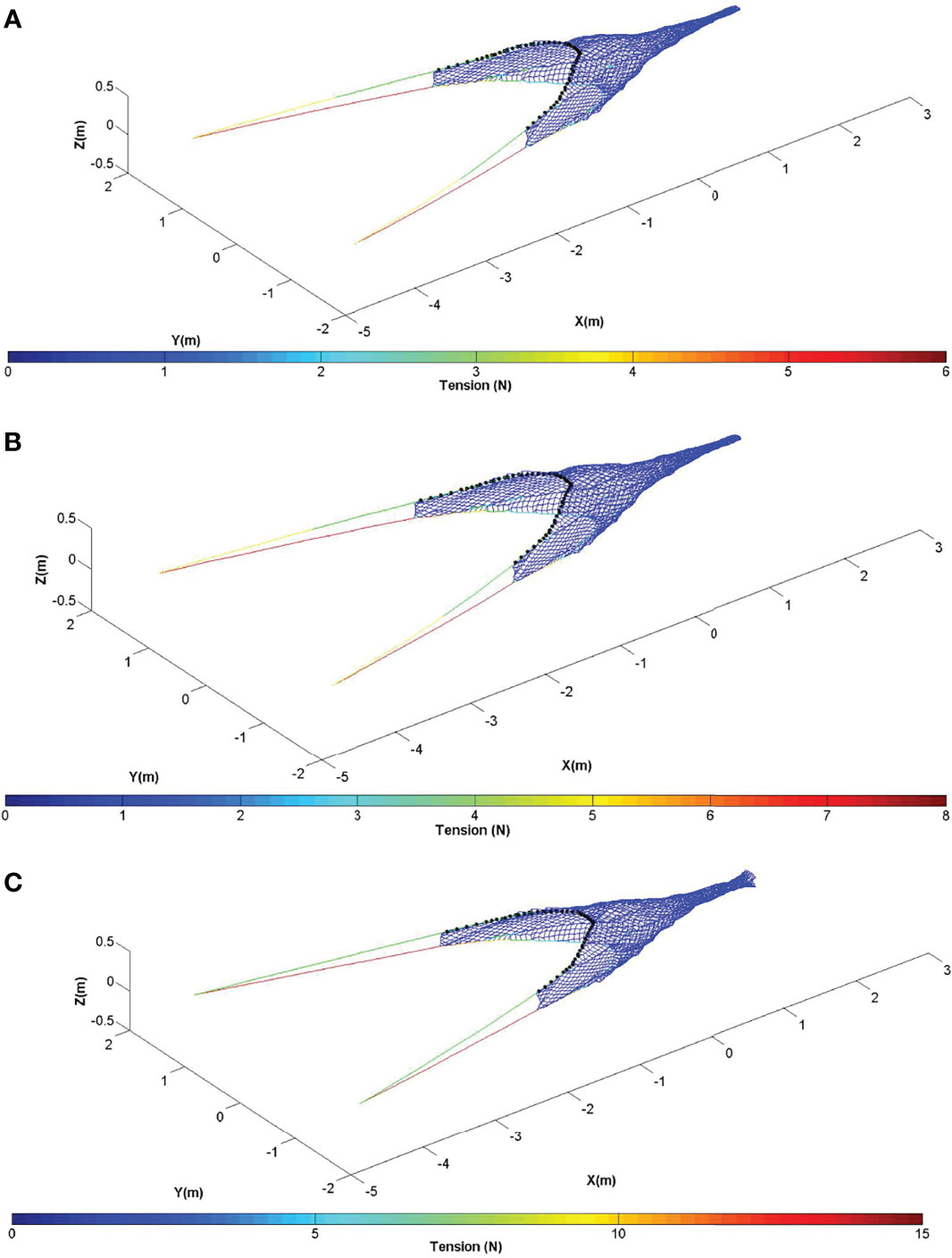
Figure 11 Shape and tension distribution from numerical simulations of the model trawl at different speeds. (A) 3 kn (full-scale); (B) 3.5 kn (full-scale); (C) 4 kn (full-scale).
The mesh opening performance of the codend is closely related to the selectivity of the fishing gear. In this paper, the mesh opening performance was expressed by the hanging ratio in T-direction and estimated using vector calculations in the numerical model. As shown in Figure 12, the hanging ratio in T-direction increased first and then decreased when the towing speed increased. When the towing speed was equal to 3.5 kn, the average hanging ratio was about 0.25. The maximum and the minimum ratio were 0.38 and 0.17, respectively. The greatest hanging ratio occurred at the front, end and middle of the codend, especially at the middle of the back net and belly net.
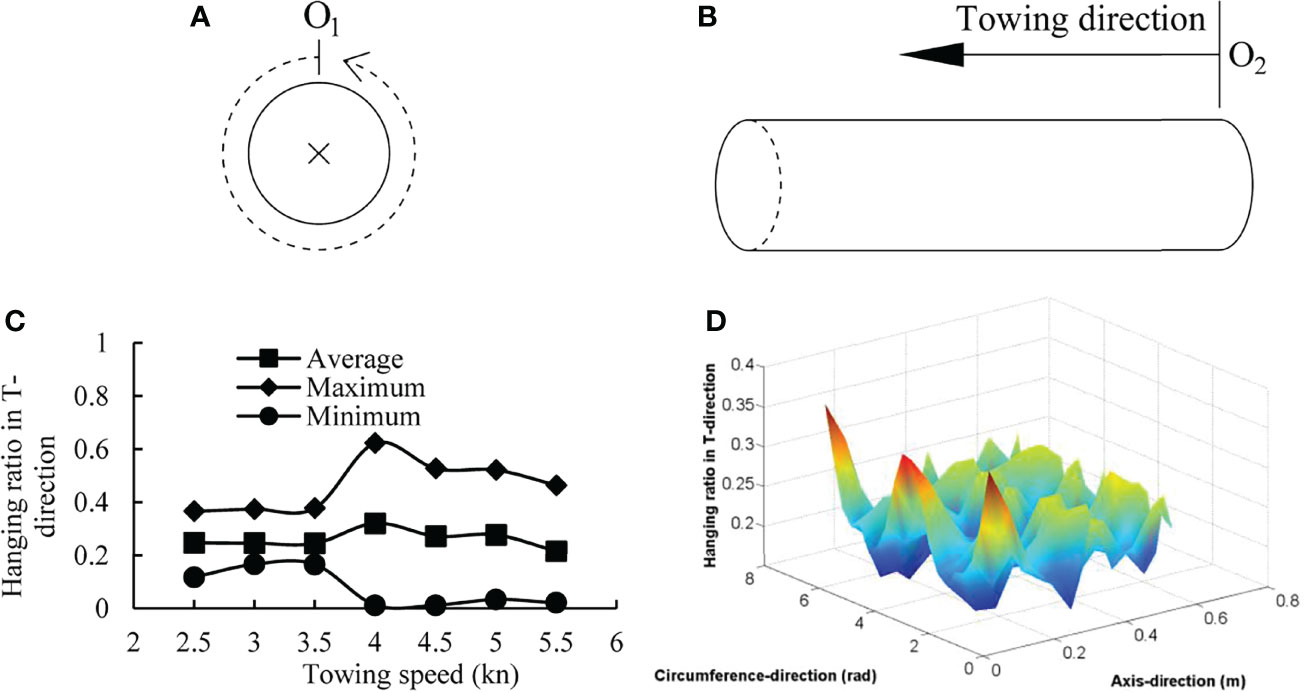
Figure 12 Mesh opening performance of the codend. (A) The origin O1 (midpoint of back net) and positive direction (anticlockwise) in the circumference-direction, ×: towing direction vertical inward; (B) the origin O2 (end of the codend) and positive direction (towing direction) in the axis direction; (C) the average, maximum, and minimum hanging ratio in T-direction at different towing speeds; (D) the hanging ratio in T-direction at the towing speed of 3.5 kn.
Deep-water fishing grounds are rich in resources, which makes them an important opportunity for the fishing industry and encourages the development of efficient gear to reduce impacts on coastal ecology. In this paper, a new bottom trawl was designed on the basis of target fishing vessel, and its hydrodynamic performance was investigated using numerical and physical model methods. The validity of the numerical simulation based on the finite element method was assessed by comparing the experimental result from physical model tests with the calculated result from numerical simulations.
The newly designed trawl can be applied at a working towing speed of 3.5 kn. Under this condition, the drag force was about 50 kN and the height of net opening was about 5.62 m, whereas the vertical spreading ratio was about 7.03%. The swept area was about 128 m2, and the drag per swept area was about 390.6 N/m2, which was related to the energy efficiency of the trawl (Priour, 2009). The trawl was designed to match the drag force with the towing force of the target trawler. The working towing speed of 3.5 kn would be suitable for harvesting the near-bottom economic species that we are concerned about, such as hairtail and cephalopods. The height of net opening is more crucial for pelagic trawls than bottom trawls, and the variation of the headline height with towing speeds was less than that of pelagic trawls (Wan et al., 2019). After investigating the hydrodynamic performance of the designed deep bottom trawl, we may further explore the effects of operation and characteristic parameters on the performance of the trawl, such as cable length (Khaled et al., 2013), the buoyancy-weight ratio (Feng et al., 2012), and the length proportion of each part of the trawl (Feng et al., 2017), to provide scientific guidance for practical operations. This study designed a deep bottom trawl based on characteristics of the target fishing vessel, species, and fishing grounds and carried out numerical simulations and physical model tests to explore its hydrodynamic performance. This work can enhance the standardization of fishing gear management (traceability and prevention of discarding) and may also contribute to the standardization of deep-water fisheries in China. In addition, its use would be conducive to energy conservation, emissions reduction from trawling operations, and mitigation of the fishing industry’s ecological impact.
The average relative error between drag forces from model tests and numerical simulations was about 10.2%, whereas that for the height of net opening was about 6.8%. Similarly, the average relative error between the power consumption from model tests and numerical simulations was about 10.2%. The numerical simulation result corresponded well with the result from physical model tests. Therefore, the use of the numerical simulation method proposed in this study to estimate the hydrodynamic performances of bottom trawl is feasible. Then, the hydrodynamic performances (swept area, shape, tension distribution, and mesh opening performance) of the trawl were then investigated using numerical simulations, which were difficult to carry out measurements underwater with the desired accuracy for both field experiments and model tests in practice (Wan et al., 2004). Through comparisons, it was found that the shape coefficient of 0.8 to 0.9 for estimating the swept area was appropriate. The shape and tension distribution of the trawl through the graphical display of numerical simulation results could help us examine the shape and tension of netting twines, cables, and other parts of the trawl system more carefully, such as net stacking, net deformation and tension concentration, which would lead to net and cable fractures and a decline in fishing efficiency (Wan et al., 2019). At the working towing speed, the net shape was smooth and the tension distribution was uniform, with no mutations, whereas the tensions of legs, ground ropes, and headlines were greater. Therefore, it is suggested that thicker cables and ropes are used for these components. The greater the hanging ratio in T-direction of the codend was, the more conducive the trawl was to releasing juvenile fish and improving the selectivity (Liu et al., 2021). The hanging ratio in T-direction of the codend was about 0.25 at the towing speed of 3.5 kn. Greater hanging ratios occurred at the front, end and middle of the codend, especially at the middle of the back net and belly net, which could provide scientific basis for the installation and application of a sorting device (Riedel and Dealteris, 1995; Eigaard and Holst, 2004; Larsen et al., 2018).
In this study, the interaction between the trawl and the bottom was not taken into consideration. In addition, the following hard-to-avoid factors might lead to differences between simulated and experimental results: (a) error caused by the difference between the hydrodynamic loading model (truss model) and the real netting twine; (b) slightly oblique placement of the experimental system; (c) instrument measurement error, and so on. However, numerical simulations can accurately estimate the hydrodynamic performance of fishing gear, and obtain results that cannot be measured by physical model tests and sea trials (Nguyen et al., 2015). The authors believe that numerical simulation technology will be more widely used in the early stage of fishing gear designs and the hydrodynamic performance investigations. This study provides the scientific basis and guidance for the design of a deep bottom trawl, with many future applications for deep-water fisheries.
We carried out investigations on the hydrodynamic performance of a new bottom trawl designed for a target fishing vessel for application in deep-water fishing grounds using numerical simulations and physical model tests. The main conclusions are as follows:
(1) The trawl that we designed operates with superior hydrodynamic performance at the towing speed of 3.5 kn. This would be practicable and beneficial for commercial fishing industries.
(2) The accuracy of the numerical simulation method proposed in this paper for hydrodynamic performances of the trawl was verified by comparing simulated and experimental results. This tool can be used to guide fishing gear design and carry out explorations of structural optimizations in the future.
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
QG: conceptualization, methodology, data curation, software, validation, writing original draft, and review and editing the original draft. WZ: funding, supervision and conceptualization. AZ and YW: investigation. WT: conceptualization, review the original draft. RW: conceptualization. All authors contributed to the article and approved the submitted version.
This research was supported by the National Key R&D Program of China (Grant No. 2019YFD0901505).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Balash C., Sterling D. (2012). “Prawn Trawl Drag Due to Material Properties-An Investigation of the Potential for Drag Reduction,” in Proceedings of the 2nd International Symposium on Fishing Vessel Energy Efficiency E-Fishing, Vigo, Spain, May 2012.
Balash C., Sterling D. (2014). “Australian Prawn-Trawling Innovations for Enhanced Energy Efficiency,” in Proceedings of the 3rd International Symposium on Fishing Vessel Energy Efficiency E-Fishing, Vigo, Spain, May 2014.
Bessonneau J. S., Marichal D. (1998). Study of the Dynamics of Submerged Supple Nets (Applications to Trawls). Ocean. Eng. 25, 563–583. doi: 10.1016/S0029-8018(97)00035-8
Cashion T., Al-Abdulrazzak D., Belhabib D., Derrick B., Divovich E., Moutopoulos D. K., et al. (2018). Reconstructing Global Marine Fishing Gear Use: Catches and Landed Values by Gear Type and Sector. Fish. Res. 206, 57–64. doi: 10.1016/j.fishres.2018.04.010
Choc Y. I., Casarella M. J. (1971). Hydrodynamic Resistance of Towed Cables. J. Hydronaut/ 5, 126–131. doi: 10.2514/3.62882
Eigaard O. R., Holst R. (2004). The Effective Selectivity of a Composite Gear for Industrial Fishing: A Sorting Grid in Combination With a Square Mesh Window. Fish. Res. 68, 99–112. doi: 10.1016/S0165-7836(04)00045-1
Feng C., Huang H., Zhou A., Zhang X., Liu J., Xu G., et al. (2012). Performance Optimization of a Trawl for Antarctic Krill. J. Fish. Sci. China 19, 662–670.
Feng C., Liu J., Zhang Y., Wang Y., Zhang X., Zhou A., et al. (2017). Structure Improvement Design and Performance Experiment of Antarctic Krill Trawl Net. Trans. Chin. Soc. Agric. Eng. 33, 75–81. doi: 10.11975/j.issn.1002-6819.2017.07.010
Fiorentini L., Sala A., Hansen K., Cosimi G., Palumbo V. (2004). Comparison Between Model Testing and Full-Scale Trials of New Trawl Design for Italian Bottom Fisheries. Fish. Sci. 70, 349–359. doi: 10.1111/j.1444-2906.2004.00813.x
Khaled R., Priour D., Billard J. Y. (2012). Numerical Optimization of Trawl Energy Efficiency Taking Into Account Fish Distribution. Ocean. Eng. 54, 34–45. doi: 10.1016/j.oceaneng.2012.07.014
Khaled R., Priour D., Billard J. Y. (2013). Cable Length Optimization for Trawl Fuel Consumption Reduction. Ocean. Eng. 58, 167–179. doi: 10.1016/j.oceaneng.2012.10.001
Larsen R. B., Herrmann B., Sistiaga M., Brinkhof J., Santos J. (2018). Catch and Release Patterns for Target and Bycatch Species in the Northeast Atlantic Deep-Water Shrimp Fishery: Effect of Using a Sieve Panel and a Nordmøre Grid. PloS One 13, e0209621. doi: 10.1371/journal.pone.0209621
Lee C. W., Lee J. H., Cha B. J., Kim H. Y., Lee J. H. (2005). Physical Modeling for Underwater Flexible Systems Dynamic Simulation. Ocean. Eng. 32, 331–347. doi: 10.1016/j.oceaneng.2004.08.007
Liu W., Tang H., You X., Dong S., Xu L., Hu F. (2021). Effect of Cutting Ratio and Catch on Drag Characteristics and Fluttering Motions of Midwater Trawl Codend. J. Mar. Sci. Eng. 9, 256. doi: 10.3390/jmse9030256
Li Y., Zhao Y., Gui F., Teng B. (2006). Numerical Simulation of the Hydrodynamic Behaviour of Submerged Plane Nets in Current. Ocean. Eng. 33, 2352–2368. doi: 10.1016/j.oceaneng.2005.11.013
Mellibovsky F., Prat J., Notti E., Sala A. (2018). Otterboard Hydrodynamic Performance Testing in Flume Tank and Wind Tunnel Facilities. Ocean. Eng. 149, 238–244. doi: 10.1016/j.oceaneng.2017.12.034
Nguyen T. X., Winger P. D., Orr D., Legge G., Delouche H., Gardner A. (2015). Computer Simulation and Flume Tank Testing of Scale Engineering Models: How Well do These Techniques Predict Full-Scale at-Sea Performance of Bottom Trawls? Fish. Res. 161, 217–225. doi: 10.1016/j.fishres.2014.08.007
Priour D. (1999). Calculation of Net Shapes by the Finite Element Method With Triangular Elements. Commun. Numer. Methods Eng. 15, 757–765. doi: 10.1002/(SICI)1099-0887(199910)15:10<755::AID-CNM299>3.0.CO;2-M
Priour D. (2009). Numerical Optimisation of Trawls Design to Improve Their Energy Efficiency. Fish. Res. 98, 40–50. doi: 10.1016/j.fishres.2009.03.015
Priour D., Prada A. D. L. (2015). An Experimental/Numerical Study of the Catch Weight Influence on Trawl Behavior. Ocean. Eng. 94, 94–102. doi: 10.1016/j.oceaneng.2014.11.016
Riedel R., Dealteris J. (1995). Factors Affecting Hydrodynamic Performance of the Nordmøre Grate System: A Bycatch Reduction Device Used in the Gulf of Maine Shrimp Fishery. Fish. Res. 24, 181–198. doi: 10.1016/0165-7836(95)00375-K
Sala A., Prat J., Antonijuan J., Lucchetti A. (2009). Performance and Impact on the Seabed of an Existing- and an Experimental-Otterboard: Comparison Between Model Testing and Full-Scale Sea Trials. Fish. Res. 100, 156–166. doi: 10.1016/j.fishres.2009.07.004
Shen G., Heino M. (2014). An Overview of Marine Fisheries Management in China. Mar. Policy 44, 265–272. doi: 10.1016/j.marpol.2013.09.012
Tang H., Thierry B. N. N., Achille N. P., He P., Xu L., Hu F. (2022). Flume Tank Evaluation on the Effect of Liners on the Physical Performance of the Antarctic Krill Trawl. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.829615
Tauti M. (1934). A Relation Between Experiments on Model and on Full Scale of Fishing Net. Nip. Suisan Gakkaishi. 3, 171–177. doi: 10.2331/suisan.3.171
Thierry B. N. N., Tang H., Achille N. P., Xu L., Hu F. (2022). Unsteady Turbulent Flow Developing Inside and Around Different Parts of Fluttering Trawl Net in Flume Tank. J. Fluid. Struct. 108, 103451. doi: 10.1007/s11802-021-4740-4741
Thierry B. N. N., Tang H., Xu L., Hu F., Dong S., Achille N. P., et al. (2021). Comparison Between Physical Model Testing and Numerical Simulation Using Two-Way Fluid-Structure Interaction Approach of New Trawl Design for Coastal Bottom Trawl Net. Ocean. Eng. 233, 109112. doi: 10.1016/j.oceaneng.2021.109112
Wan R., Guan Q., Huang L., Li Z., Zhou C., Wang L., et al. (2021). Effects of Otter Board and Cable Length on Hydrodynamic Performance of Antarctic Krill Trawl System. Ocean. Eng. 236, 109408. doi: 10.1016/j.oceaneng.2021.109408
Wan R., Huang W., Song X., Hu F., Tokai T. (2004). Statics of a Gillnet Placed in a Uniform Current. Ocean. Eng. 31, 1725–1740. doi: 10.1016/j.oceaneng.2004.02.005
Wan R., Hu F., Tokai T. (2002a). A Static Analysis of the Tension and Configuration of Submerged Plane Nets. Fish. Sci. 68, 815–823. doi: 10.1046/j.1444-2906.2002.00497.x
Wan R., Hu F., Tokai T., Matuda K. (2002b). A Method for Analyzing the Static Response of Submerged Rope Systems Based on a Finite Element Method. Fish. Sci. 68, 65–70. doi: 10.1046/j.1444-2906.2002.00390.x
Wan R., Jia M., Guan Q., Huang L., Cheng H., Zhao F., et al. (2019). Hydrodynamic Performance of a Newly-Designed Antarctic Krill Trawl Using Numerical Simulation and Physical Modeling Methods. Ocean. Eng. 179, 173–179. doi: 10.1016/j.oceaneng.2019.03.022
Keywords: deep bottom trawl, hydrodynamic performance, finite element method, numerical simulation, physical model test
Citation: Guan Q, Zhu W, Zhou A, Wang Y, Tang W and Wan R (2022) Numerical and Experimental Investigations on Hydrodynamic Performance of a Newly Designed Deep Bottom Trawl. Front. Mar. Sci. 9:891046. doi: 10.3389/fmars.2022.891046
Received: 07 March 2022; Accepted: 04 April 2022;
Published: 04 May 2022.
Edited by:
Wei-Bo Chen, National Science and Technology Center for Disaster Reduction (NCDR), TaiwanReviewed by:
Achille Njomoue Pandong, University of Douala, CameroonCopyright © 2022 Guan, Zhu, Zhou, Wang, Tang and Wan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenbin Zhu, d2VuYmluemh1QHpqb3UuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.