Synthesizing Empirical and Modelling Studies to Predict Past and Future Primary Production in the North Sea

Understanding change at the base of the marine foodwebs is fundamental to understanding how climate change can impact fisheries. However, there is a shortage of empirical measurements of primary productivity, and models estimates often disagree with each other by an order of magnitude or more. In this study we incorporate information from empirical studies and a suite of Earth system models statistically downscaled using an ensemble model to produce estimates of North Sea primary production with robust quantification of uncertainties under two different climate scenarios. The results give a synthesised estimate of primary production that can feed into regional fisheries models. We found that Earth system models describe the dynamics of primary production in the North Sea poorly, and therefore the effects of climate change on future primary production are uncertain. The methods demonstrated here can be applied to other geographical locations and are not limited in application to primary production.

1 Introduction

The resilience of marine ecosystems to future climate change and human activities is dependent on primary production. Understanding change at the base of the marine food web is fundamental to our understanding of how climate change impacts cascade through the ecosystem (Capuzzo et al., 2018).

The climate impacts on primary production can be simulated with Earth system models (ESMs). ESMs are increasingly being used in the context of fisheries management (Kearney et al., 2021). Outputs of primary production from ESMs are often used as boundary conditions in regional fisheries models (e.g. Barange et al., 2014; Bryndum-Buchholz et al., 2019; Lotze et al., 2019; Bryndum-Buchholz et al., 2020; Tittensor et al., 2021), which are often for a whole region and spatially implicit (e.g. North Sea multispecies size-spectrum model of Blanchard et al., 2014). There are common protocols for running these models with inputs from ESMs (e.g. Tittensor et al., 2018), something known as dynamic downscaling-child domain (see Drenkard et al., 2021). However, the ESMs all tend to say different things about primary production and there can be a number of complexities involved in connecting ESMs to regional fisheries models (Schrum et al., 2016; Kearney et al., 2021), which often require either statistical or dynamical downscaling (Drenkard et al., 2021), leading to uncertainty.

Some studies attempt to take account of uncertainty by using several different estimates of primary production from different ESMs (e.g. Tittensor et al., 2018; Pozo Buil et al., 2021) but in order to interpret the results, one must make judgements about which of the estimates are most likely to be right. In reality, no more than one can be right, and most probably all of them will be wrong. Despite this, they all give information about primary production level (Skogen et al., 2020) and therefore one would ideally synthesise the empirical and modelling studies to give a coherent estimate of primary production.

In this study we were interested in the primary production in the North Sea. Methods of weighting ESMs, such as Bayesian model averaging (Banner and Higgs, 2017), assume that one of the models gives the exact value of the primary production, which we do not feel is a reasonable assumption. Further, we did not assume that the model average would lead to the correct result, as we do not expect the ESMs to be centered on the truth (Knutti, 2010; Chandler, 2013; Rougier et al., 2013; Christiansen, 2021). Instead we use an empirical study and several ESMs to quantify the uncertainty in the true primary production both in the past and the future. We adopted the ensemble modelling approach of Spence et al. (2018), which has been applied to fisheries management (Spence et al., 2021), to statistically downscale ESMs’ estimates of primary production in the North Sea to give a coherent estimate for primary production under two future climate scenarios with quantifiable uncertainty. This approach characterises how the ESMs were wrong through time. Each ESM output plus a discrepancy term, specific to that ESM, is equal to the truth. The discrepancy terms and the truth are uncertain, so we used the empirical study of Capuzzo et al. (2018), a noisy incomplete observation of the truth, to learn these values. We present the empirical study and the ESMs in Section 2, show the results in Section 3 and briefly describe their possible uses of the results in Section 4. The projections of primary production for the two scenarios along with code from this study are available at https://github.com/michaelspence/EnsemblePP.

2 Methods

In this study we estimated the primary production in the North Sea under two future climate scenarios from 1984 until 2100 by combining projections from ESMs and an empirical study, whilst quantifying the uncertainty, using the ensemble model of Spence et al. (2018).

2.1 Scenarios

The Coupled Model Inter-comparison Project Phase 6 (CMIP6) projections make use of Shared Socioeconomic Pathways (SSP, O’Neill et al., 2016), which are designed to provide future scenarios of anthropogenic climate forcing spanning a range from a low emission scenario characterized by active mitigation (SSP126) to a high emission scenario (SSP585). Each SSP is associated with plausible combinations of projected population growth, economic activity, energy intensity, and socio-economic development.

The SSP scenarios were named based on their total radiative forcing by 2100, and one of five baseline societal pathways. In this study we choose two possible futures, one representing modest mitigation activity (SSP370), and one representing a continuation of historical fossil fuel-reliant development trends with no additional mitigation (SSP585), and investigated the primary production under both scenarios up until 2100.

2.2 Earth System Models

In this study we used 10 ESMs from CMIP6 (see Table 1 in Séférian et al., 2020) to project average annual North Sea primary production for both SSP370 and SSP585 climate scenarios. The ESMs were projected up to 2014 forced by historical emissions and then the two SSP scenarios began in 2015. We calculated annual mean primary production for each year over the whole of the North Sea for each ESM. Although the ESMs’ biogeochemical formulations are of varying complexity (Séférian et al., 2020) we included them all in the ensemble, as if they perform poorly the ensemble model discounts them.

2.3 Empirical Studies

Capuzzo et al. (2018) presented a time series of gross primary production in the North Sea from 1988 to 2013. Primary production was estimated using in situ measurements of chlorophyll, underwater light and the empirical model of Cole and Cloern (1987). The model was fitted to measurements of primary production using the ¹⁴C method with an R-squared value of 0.86. For more details see Capuzzo et al. (2018).

2.4 Ensemble Model

The primary production projections from the ESMs were combined with the empirical study using the ensemble model of Spence et al. (2018). We fitted two different ensemble models, one for each scenario. The ensemble model for each scenario is described below.

2.4.1 The Truth

At time t, the natural logarithm of the true primary production under each scenario, y^(t), evolved as a random walk,

$\begin{array}{ll}{y}^{\left(t\right)}\sim N\left(y^{\left(t-1\right)},{\sigma }_s^2\right),& (1)\end{array}$

where a ~ N (b,c) means that a is sampled from a Gaussian distribution with expectation b and variance c. The data from Capuzzo et al. (2018) was an indirect observation of the true primary production, $\text{exp}\left({\widehat{y}}^{\left(t\right)}\right)$, for t = (1988, … ,2013). As Capuzzo et al. (2018) reported an R-squared value of 0.86, we said that

$\begin{array}{ll}{\widehat{y}}^{\left(t\right)}\sim N\left(y^{\left(t\right)},{0.146}^2\right),& (2)\end{array}$

as the variance of ${\widehat{y}}^{\left(t\right)}$ was 0.131 (see Supplementary Material S1.2).

2.4.2 ESMs

For each scenario the primary production was projected by 10 ESMs, with the natural logarithm of ith ESM’s projection at time t being $x_i^{\left(t\right)}$. The relationship between the natural logarithm of truth and the ith ESM was

$\begin{array}{ll}{y}^{\left(t\right)}=x_i^{\left(t\right)}+{\zeta }_i^{\left(t\right)},& (3)\end{array}$

where ${\zeta }_i^{\left(t\right)}$ is the discrepancy of the ith ESM (Kennedy and O’Hagan, 2001). We split the discrepancy term between discrepancies that were shared by all of the ESMs, and discrepancies that were specific to the ith ESM. These two discrepancies were further split into fixed discrepancies, the long-term shared discrepancy, δ, and ESM i's long-term individual discrepancy, γ_i, and dynamic discrepancies, the short-term shared discrepancy, η^(t), and ESM i's short-term individual discrepancy, $z_i^{\left(t\right)}$, i.e.

$\begin{array}{ll}{\zeta }_i^{\left(t\right)}=\delta +{\eta }^{\left(t\right)}+{\gamma }_i+z_i^{\left(t\right)}& (4)\end{array}$

The ith ESM’s long-term individual discrepancy was a random effect (for more details see Chandler, 2013; Rougier et al., 2013),

$\begin{array}{ll}{\gamma }_i\sim N\left(0,{\varphi }^2\right).& (5)\end{array}$

We expect each of the shared and individual short-term discrepancy terms to be correlated in time, for example if $z_i^{\left(t\right)}$ was larger than 0 then we might expect $z_i^{\left(t+1\right)}$ to also be larger than 0. With this in mind, we let these terms follow a stationary auto-regressive processes of order one (AR1) (for more details see Spence et al., 2018),

$\begin{array}{ll}{\eta }^{\left(t\right)}\sim N\left({\rho }_{\eta }{\eta }_{\left(t-1\right)},{\lambda }_{\eta }^2\right)& (6)\end{array}$

and

$\begin{array}{ll}{z}_i^{\left(t\right)}\sim N\left({\rho }_i{z}_{\left(t-1\right)},{\lambda }_i^2\right)& (7)\end{array}$

respectively, with | ρ _η| < 1 and | ρ _i| < 1.

2.4.3 Initial Values

In 1984, at the beginning of the study, we said

$\begin{array}{ll}{y}^{\left(1984\right)}\sim N\left(5.4,2^2\right),& (8)\end{array}$

as 5.4 is the mean of the natural log of the observed primary production. As the short-term discrepancy terms are stationary AR1 processes, the initial distributions were

$\begin{array}{ll}{\eta }^{\left(1984\right)}\sim N\left(0,\frac{{\lambda }_{\eta }^2}{1-{\rho }_{\eta }^2}\right)& (9)\end{array}$

and

$\begin{array}{ll}{z}_i^{\left(1984\right)}\sim N\left(0,\frac{{\lambda }_i^2}{1-{\rho }_i^2}\right)& (10)\end{array}$

We used a Kalman filter to calculate the likelihood of the ensemble model (Chui and Chen, 2009), and then to estimate the truth (Durbin and Koopman, 2002; Strickland et al., 2009). As we were interested in the uncertainty of the estimates, we adopted a Bayesian framework (Bayes, 1763). Due to the high dimensionality and correlation of the uncertain parameter space, we fitted the ensemble model using the No U-turn Hamiltonian Monte Carlo (Hoffman and Gelman, 2011) in the package Stan (Stan Development Team, 2020). We ran the algorithm for 4000 iterations discarding the first 2000 as burn in. For more details see the Supplementary Material S2.

3 Results

The ESMs disagree with each other about the magnitude of primary productivity, but tend to agree with each other on there being little future trend and on SSP370 and SSP585 being similar. On the other hand, the empirical study showed a lot more inter-annual variation than the ESMs. The ESMs inability to capture inter-annual variability suggests that the ESMs are not good at describing primary production in the North Sea on the short-term (Figure 1) The ESMs project changes in future primary production that are smaller relative to the inter-annual variation implied by the empirical study.

FIGURE 1

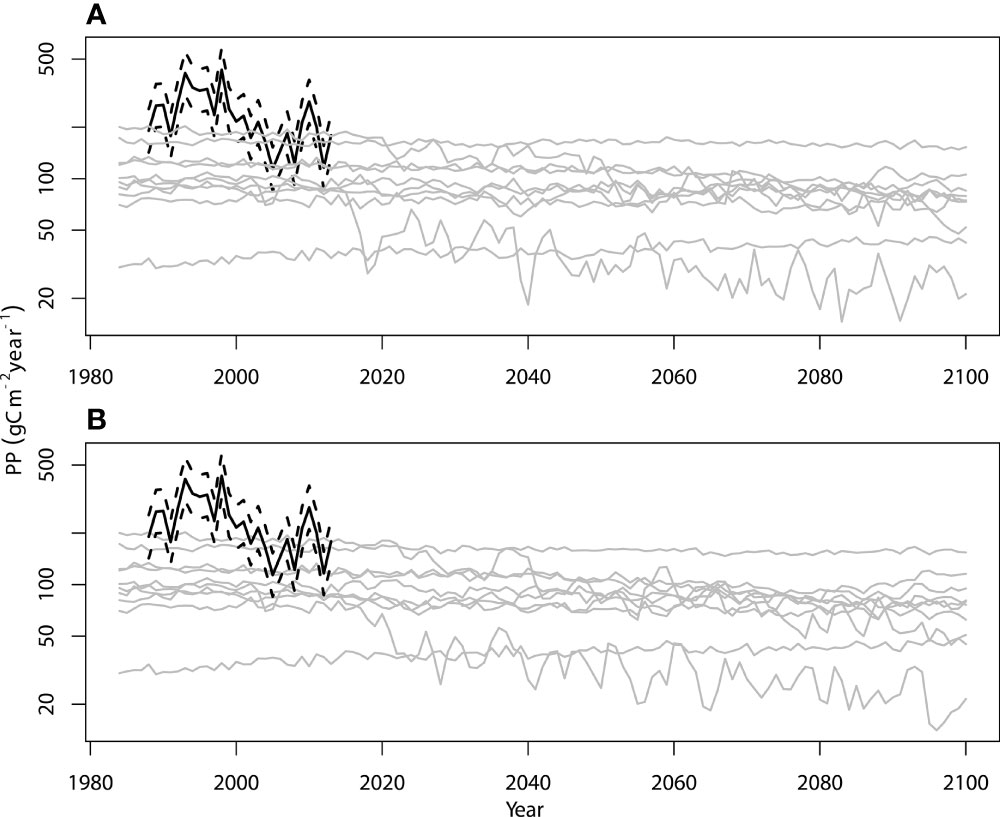
Figure 1 The ESMs’ projections in grey for a) SSP370 and b) SSP585. The empirical study from Capuzzo et al. (2018) is the black solid line with the 5th and 95th percentiles being the black dashed lines.

There was not a substantial difference in projections of primary production [exp (y^(t))] between the two scenarios from the ensemble model (Figure 2), with both scenarios predicting that the primary production in the North Sea in 2041-2050 will be lower than it was in 1991-2000 (with probability 0.996), but higher than in 2001-2010 and 2011-2020 (with probability 0.983 and 0.764 respectively under the SSP585). Table 1 shows comparisons of decades under SSP585. We found that there’s not enough evidence in the ESMs to make strong statements about which scenario would give a higher primary production in a given year (see Supplementary Material S3.1).

FIGURE 2

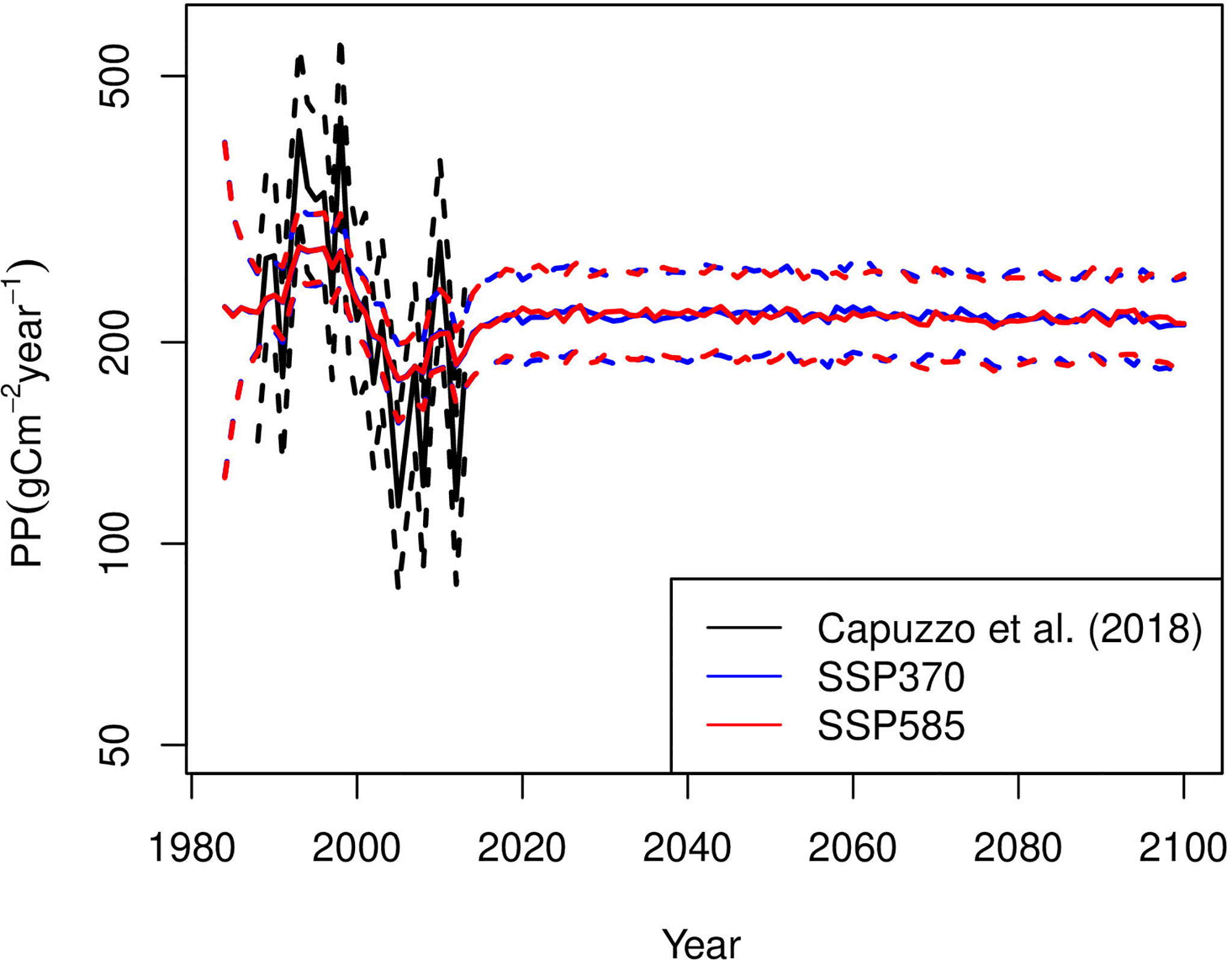
Figure 2 The empirical study from Capuzzo et al. (2018) in black and the ensemble model’s median projection of the true primary production [ exp ( y ^(t) ) ] for SSP370 and SSP585 in blue and red respectively. The dshed lines are the 5th and 95th percentiles.

TABLE 1

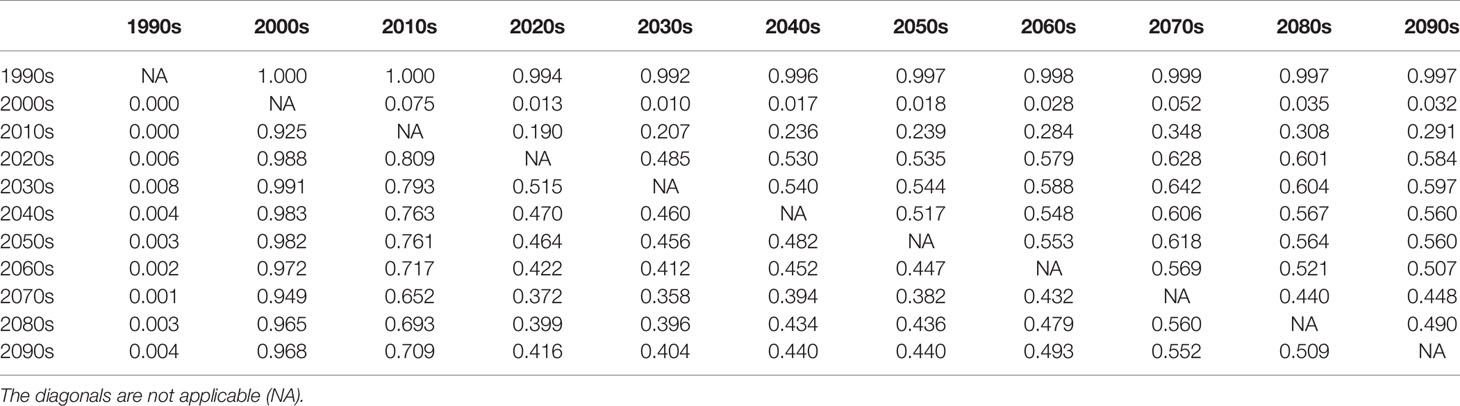
Table 1 Probability (to 3 decimal places) that the decade on the row will have a higher mean primary productivity than the decade on the column under future projection SSP585.

The median trajectories in Figure 2 masked inter-annual variability in individual samples from the ensemble model, which showed similar variability for each scenario (Figure 3). These represent integrated knowledge of a suite of models and empirical data that can be used as input to other studies, freeing them from dependence on a subset of models or data, and assisting with their quantification of uncertainty connected with primary productivity.

FIGURE 3

Figure 3 A single sample from the ensemble model’s projection of the true primary production [ exp ( y ^(t) ) ] for SSP370 and SSP585 scenarios in blue and red respectively.

4 Discussion

In this brief research report, projections of primary production in the North Sea from 10 ESMs for two future climate scenarios, SSP370 and SSP585, were statistically downscaled, using the ensemble model of Spence et al. (2018) and the empirical study of Capuzzo et al. (2018), with robust calculations of uncertainty.

The ensemble model exploits the strengths, while discounting the weaknesses, of the different sources of information (empirical study and the ESMs). In this study it learns about the short-term variability from the empirical study, but the long-term changes from the ESMs. Therefore the short-term dynamics in the future are quite uncertain, but we have more confidence in the future level of primary production being broadly similar to the past (Table 1 and Figure 2). Despite the summaries of the ensemble model giving relatively stable primary production in the future, samples of potential primary production levels do show inter-annual variability (Figure 3).

Alternative ways of combining the ESMs that assume that one of the ESMs is correct (e.g. Bayesian model averaging), or that the average of the ESMs is the truth, would fail to show this large uncertainty, despite it being clear that none of the ESMs are able to capture the inter-annual variability. We see this a positive of the ensemble model of Spence et al. (2018), as it does not force information when there is none, something that could result in the uncertainty being underestimated which could have bad consequences for management (Harwood and Stokes, 2003). More generally, this demonstrates that one does not have to decide whether to include specific modelling studies, something that that is seen as a ‘major crux’ of ensemble modelling (Jardim et al., 2021), as studies that do not give much information will simply be ignored.

Some of the ESMs are better than others at modelling primary production, possibly due to the aims of the individual ESMs, with some ESMs having more complex representations of primary production, however none of them seem able to capture the observed behaviour, even when allowing for observational errors. We chose the ESMs as they were the only models that were available to us, however the ensemble model framework allows additional models, and observations, to be included if they became available (Spence et al., 2021). To reduce the uncertainty in the effects of climate change on primary production in the North Sea, effort should be focused on developing regional models that can simulate primary production changes on shorter time scales (Schrum et al., 2016; Tittensor et al., 2018), as well as including regional models (Holt et al., 2014) and other empirical studies, such as satellite data (Tucker and Sellers, 1986) in the ensemble model, but this is beyond the scope of the study. In addition, future work could investigate the sensitivity of choices in how short-term discrepancies evolve in the ensemble model. Alternative models, such as auto-regressive models of higher orders or moving average models, could be used instead although we do not imagine the results would change much here.

Primary production projections for the North Sea under the two scenarios from the ensemble model and the code are available at https://github.com/michaelspence/EnsemblePP. We envisage that the primary production projections generated in this study could be used as inputs to other empirical and modelling studies. The approach demonstrated here provides an appropriate way to statistically downscale the ESMs, exploiting the information given in each ESM. The methods used in this study are applicable to other geographical locations and are not limited in application to primary production. This resource will benefit future studies by reducing their dependence on a single model or data scenario and facilitating the provision of robust estimates of the variables of interest, and their associated uncertainties.

Data Availability Statement

Primary production estimates for the North Sea under the two scenarios from the ensemble model and the code are available at https://github.com/michaelspence/EnsemblePP.

Author Contributions

MS, CL, RT, and PD designed the study, RH extracted the data and the model runs, MS analyzed the outputs and developed the methods. MS led the writing of the manuscript and all authors contributed during the editing process. All authors contributed to the article and approved the submitted version.

Funding

This work was funded by DEFRA via the ‘mixed-fisheries and multispecies modelling’ theme and EU’s Horizon 2020 research and innovation programme under Grant Agreement No 773713 (PANDORA). CPL was funded by EU’s Horizon 2020 Project ‘Climate Change and Future Marine Ecosystem Services and Biodiversity’ (FutureMARES, grant No 869300).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would also like to thank James Scott for help extracting the ESM runs in an earlier verison of this manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2022.828623/full#supplementary-material

References

Banner K. M., Higgs M. D. (2017). Considerations for Assessing Model Averaging of Regression Coefficients. Ecol. Appl. 27, 78–93. doi: 10.1002/eap.1419

PubMed Abstract | CrossRef Full Text | Google Scholar

Barange M., Merino G., Blanchard J. L., Scholtens J., Harle J., Allison E. H., et al. (2014). Impacts of Climate Change on Marine Ecosystem Production in Societies Dependent on Fisheries. Nat. Clim. Change 4, 211–216. doi: 10.1038/nclimate2119

CrossRef Full Text | Google Scholar

Bayes T. (1763). LII. An Essay Towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. s. Philos. Trans. 53, 370–418. doi: 10.1098/rstl.1763.0053

CrossRef Full Text | Google Scholar

Blanchard J. L., Andersen K. H., Scott F., Hintzen N. T., Piet G., Jennings S. (2014). Evaluating Targets and Trade-Offs Among Fisheries and Conservation Objectives Using a Multispecies Size Spectrum Model. J. Appl. Ecol. 51, 612–622. doi: 10.1111/1365-2664.12238

CrossRef Full Text | Google Scholar

Bryndum-Buchholz A., Prentice F., Tittensor D. P., Blanchard J. L., Cheung W. W., Christensen V., et al. (2020). Differing Marine Animal Biomass Shifts Under 21st Century Climate Change Between Canada’s Three Oceans. FACETS 5, 105–122. doi: 10.1139/facets-2019-0035

CrossRef Full Text | Google Scholar

Bryndum-Buchholz A., Tittensor D. P., Blanchard J. L., Cheung W. W. L., Coll M., Galbraith E. D., et al. (2019). Twenty-First-Century Climate Change Impacts on Marine Animal Biomass and Ecosystem Structure Across Ocean Basins. Global Change Biol. 25, 459–472. doi: 10.1111/gcb.14512

CrossRef Full Text | Google Scholar

Capuzzo E., Lynam C. P., Barry J., Stephens D., Forster R. M., Greenwood N., et al. (2018). A Decline in Primary Production in the North Sea Over 25 Years, Associated With Reductions in Zooplankton Abundance and Fish Stock Recruitment. Global Change Biol. 24, e352–e364. doi: 10.1111/gcb.13916

CrossRef Full Text | Google Scholar

Chandler R. E. (2013). Exploiting Strength, Discounting Weakness: Combining Information From Multiple Climate Simulators. Philos. Trans. R. Soc. A.: Math. Phys. Eng. Sci. 371, 20120388. doi: 10.1098/rsta.2012.0388

CrossRef Full Text | Google Scholar

Christiansen B. (2021). Understanding the Distribution of Multimodel Ensembles. J. Clim. 33, 9447–9465. doi: 10.1175/JCLI-D-20-0186.1

CrossRef Full Text | Google Scholar

Chui C. K., Chen G. (2009). Sequential and Square-Root Algorithms (Berlin, Heidelberg: Springer Berlin Heidelberg), 97–107. doi: 10.1007/978-3-540-87849-0_7

CrossRef Full Text | Google Scholar

Cole B., Cloern J. (1987). An Empirical Model for Estimating Phytoplankton Productivity in Estuaries. Mar. Ecol-Progr. Ser. - Mar. Ecol-Progr. Ser. 36, 299–305. doi: 10.3354/meps036299

CrossRef Full Text | Google Scholar

Drenkard E. J., Stock C., Ross A. C., Dixon K. W., Adcroft A., Alexander M., et al. (2021). Next-Generation Regional Ocean Projections for Living Marine Resource Management in a Changing Climate. ICES. J. Mar. Sci. 78, 1969–1987. doi: 10.1093/icesjms/fsab100

CrossRef Full Text | Google Scholar

Durbin J., Koopman S. J. (2002). A Simple and Efficient Simulation Smoother for State Space Time Series Analysis. Biometrika 89, 603–615. doi: 10.1093/biomet/89.3.603

CrossRef Full Text | Google Scholar

Harwood J., Stokes K. (2003). Coping With Uncertainty in Ecological Advice: Lessons From Fisheries. Trends Ecol. Evol. 18, 617–622. doi: 10.1016/j.tree.2003.08.001

CrossRef Full Text | Google Scholar

Hoffman M., Gelman A. (2011). The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo. J. Mach. Res. 15, 1593–1623. doi: 10.5555/2627435.2638586

CrossRef Full Text | Google Scholar

Holt J., Schrum C., Cannaby H., Daewel U., Allen I., Artioli Y., et al. (2014). Physical Processes Mediating Climate Change Impacts on Regional Sea Ecosystems. Biogeosci. Discuss. 11, 1909–1975. doi: 10.5194/bgd-11-1909-2014

CrossRef Full Text | Google Scholar

Jardim E., Azevedo M., Brodziak J., Brooks E. N., Johnson K. F., Klibansky N., et al. (2021). Operationalizing Ensemble Models for Scientific Advice to Fisheries Management. ICES. J. Mar. Sci. 78, 1209–1216. doi: 10.1093/icesjms/fsab010

CrossRef Full Text | Google Scholar

Kearney K. A., Bograd S. J., Drenkard E., Gomez F. A., Haltuch M., Hermann A. J., et al. (2021). Using Global-Scale Earth System Models for Regional Fisheries Applications. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.622206

CrossRef Full Text | Google Scholar

Kennedy M. C., O’Hagan A. (2001). Bayesian Calibration of Computer Models. J. R. Stat. Soc.: Ser. B. (Stat. Method. 63, 425–464. doi: 10.1111/1467-9868.00294

CrossRef Full Text | Google Scholar

Knutti R. (2010). The End of Model Democracy? Clim. Change 102, 395–404. doi: 10.1007/s10584-010-9800-2

CrossRef Full Text | Google Scholar

Lotze H. K., Tittensor D. P., Bryndum-Buchholz A., Eddy T. D., Cheung W. W. L., Galbraith E. D., et al. (2019). Global Ensemble Projections Reveal Trophic Amplification of Ocean Biomass Declines With Climate Change. Proc. Natl. Acad. Sci. 116, 12907–12912. doi: 10.1073/pnas.1900194116

CrossRef Full Text | Google Scholar

O’Neill B. C., Tebaldi C., van Vuuren D. P., Eyring V., Friedlingstein P., Hurtt G., et al. (2016). The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 9, 3461–3482. doi: 10.5194/gmd-9-3461-2016

CrossRef Full Text | Google Scholar

Pozo Buil M., Jacox M. G., Fiechter J., Alexander M. A., Bograd S. J., Curchitser E. N., et al. (2021). A Dynamically Downscaled Ensemble of Future Projections for the California Current System. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.612874

CrossRef Full Text | Google Scholar

Rougier J., Goldstein M., House L. (2013). Second-Order Exchangeability Analysis for Multimodel Ensembles. J. Am. Stat. Assoc. 108, 852–863. doi: 10.1080/01621459.2013.802963

CrossRef Full Text | Google Scholar

Schrum C., Lowe J., Meier H. E. M., Grabemann I., Holt J., Mathis M., et al. (2016). Projected Change—North Sea (Cham: Springer International Publishing), 175–217. doi: 10.1007/978-3-319-39745-0_6

CrossRef Full Text | Google Scholar

Séférian R., Berthet S., Yool A., Palmiéri J., Bopp L., Tagliabue A., et al. (2020). Tracking Improvement in Simulated Marine Biogeochemistry Between CMIP5 and CMIP6. Curr. Clim. Change Rep. 6, 95–119. doi: 10.1007/s40641-020-00160-0

CrossRef Full Text | Google Scholar

Skogen M., Ji R., Akimova A., Daewel U., Hansen C., Hjøllo S., et al. (2020). Disclosing the Truth: Are Models Better Than Observations? Mar. Ecol. Prog. Ser. 680, 7–13. doi: 10.3354/meps13574

CrossRef Full Text | Google Scholar

Spence M. A., Blanchard J. L., Rossberg A. G., Heath M. R., Heymans J. J., Mackinson S., et al. (2018). A General Framework for Combining Ecosystem Models. Fish. Fish. 19, 1031–1042. doi: 10.1111/faf.12310

CrossRef Full Text | Google Scholar

Spence M. A., Griffiths C. A., Waggitt J. J., Bannister H. J., Thorpe R. B., Rossberg A. G., et al. (2021). Sustainable Fishing can Lead to Improvements in Marine Ecosystem Status: An Ensemble-Model Forecast of the North Sea Ecosystem. Mar. Ecol. Prog. Ser. 680, 207–221. doi: 10.3354/meps13870

CrossRef Full Text | Google Scholar

Stan Development Team (2020). Stan Modeling Language Users Guide and Reference Manual, 2.19.3. Available at: https://mc-stan.org, https://mc-stan.org/users/citations/.

Google Scholar

Strickland C. M., Turner I. W., Denham R., Mengersen K. L. (2009). Efficient Bayesian Estimation of Multivariate State Space Models. Comput. Stat Data Anal. 53, 4116–4125. doi: 10.1016/j.csda.2009.04.019

CrossRef Full Text | Google Scholar

Tittensor D. P., Eddy T. D., Lotze H. K., Galbraith E. D., Cheung W., Barange M., et al. (2018). A Protocol for the Intercomparison of Marine Fishery and Ecosystem Models: Fish-MIP V1.0. Geosci. Model Dev. 11, 1421–1442. doi: 10.5194/gmd-11-1421-2018

CrossRef Full Text | Google Scholar

Tittensor D. P., Novaglio C., Harrison C. S., Heneghan R. F., Barrier N., Bianchi D., et al. (2021). Next-Generation Ensemble Projections Reveal Higher Climate Risks for Marine Ecosystems. Nat. Clim. Change. 11, 973–981. doi: 10.1038/s41558-021-01173-9

CrossRef Full Text | Google Scholar

Tucker C. J., Sellers P. J. (1986). Satellite Remote Sensing of Primary Production. Int. J. Remote Sens. 7, 1395–1416. doi: 10.1080/01431168608948944

CrossRef Full Text | Google Scholar