Single-channel blind source separation of underwater acoustic signals using improved NMF and FastICA

Introduction

As a floating automatic monitoring platform for monitoring the comprehensive marine environment, such as marine meteorological, hydrological and ecological parameters, ocean observation sonar buoy plays an important role in the monitoring and research of marine environment, and is the basis for caring about the ocean, understanding the ocean and managing the ocean. Maintaining and improving this capability is crucial to the protection of maritime and littoral waterways. With the development of marine resources and the strengthening of maritime trade, the identification and judgment of marine and underwater targets, based on underwater acoustic signals received by buoys, has gradually become an important direction to analyze the impact of the development of modern ship technology and the prosperity of maritime trade on marine ecology.

Underwater vessels (i.e., submarines) and surface vessels create and transmit acoustic signals with their screws (sometimes referred to as “propellers” by folks outside the field), which are transmitted over long distances through the water medium. So, when multi-target signals are received by single buoys, separating and processing them requires statistical blind source separation (BSS) techniques (Dianmant et al., 2019; Zhang et al., 2020) prior to any recognition, analysis, and localization efforts (Zhang and Yang, 2021). The number of signals, source and its proportion of each underwater acoustic target signal in the mixed signal received by a single passive sonar buoy is unknown, Hence, a single-channel statistical BSS framework is used (Wildeboer et al., 2020).

Although nonlinear signals are most often encountered in real maritime scenarios, it is incredibly difficult to deconstruct and process them, even with machine learning tools. Therefore, linear models are widely applied based on mathematical approximations (Huang et al., 2019). Notably, the powerful non-negative matrix factorization (NMF) method, which was the hotspot in the linear model, ingests a data structure that fits the linear mixed model reasonably well (Rathnayake et al., 2020). Thus, dependence on prior knowledge is reduced and the dimension of high-dimensional massive data is reduced (Zhang et al., 2022).. However, owing to the non-convexity of the NMF objective function, the globally optimal solution is difficult to guarantee. Therefore, various constraints must be imposed according to the signal characteristics to narrow the solution space. The remainder of the introduction leverages the extant literature to explain why NMF-type models are the only viable solutions to mixed-signal BSS tasks. Subsequently, Section 2 provides additional information from the literature to provide the current NMF machine learning advancements that illuminate the present capability gap while also explaining algorithmic methods.

A neighborhood spatial information constraint was added into NMF to improve its convergence and classification in Ref (Lu et al., 2013)., by analyzing the manifold structural features of the signal image; however, the sparse constraint of the method’s norm was vulnerable to noise and overly sensitive to the initial value. Hence, bias was unavoidable. Li (Li and Wang, 2019) applied a quadratic sparse constraint to the NMF based on manifold attributes to make better use of the sparse features of the NMF’s coefficient matrix. Wang (Wang et al., 2020) and Lu (Lu et al., 2020) used similar adjacent pixels to extract spatial structure information by clustering time-frequency images. The spatial similarity, strengthened by cluster labels, was then used to optimize the constraint of the NMF’s objective function, and the BSS efficacy was improved (Zhang et al., 2021). Similarly, the adaptive spectral local neighborhood information of pixels was extracted by Chen (Chen and Lv, 2021) and added to the NMF in the form of adaptive weights, and the blind unmixing performance was improved.

Advancements outside the maritime domain have contributed to the current operational capability. Wang et al. (2019) highlighted the local features and achieved the successful separation of multiple coupled fault signals by combining the variational mode decomposition optimized by energy convergence with local NMF whose optimal base matrix dimensionality was calculated by using the adjacent feature dominance method A deep-transduction NMF was later developed by Li (Yurong et al., 2020) to separate the mixed speech signals from multiple speakers, and Sriharsha (Sriharsha and Abhijit, 2018). integrated the homotopy optimisation with perturbation and ensemble and denoising autoencoder into an NMF for single-channel audio source separation. The objective speech quality was significantly improved (Zhang et al., 2022), and the techniques were useful for underwater target signal separation. Huang (Huang et al., 2019) fused the L₂₁ and L_1/2 norms and added the composite to the NMF model, improving the model’s anti-noise performance against band- and pixel-level noise.

From the examples annotated above, it is clear that NMF methods are essential to BSS applications in the fields of hyperspectral unmixing, composite fault signal separation, and multi-speaker voice separation (Huang et al., 2019), and it is clear that the NMF model is essential to the BSS of underwater acoustic multi-target signals. Hence, this article reports on the joint BSS algorithm based on our improved NMF and FastICA backbone. The main improvement of the proposed algorithm is to improve the NMF based on the features of underwater acoustic target signal, and then, the NMF base matrix is used as signal input of FastICA, realizing BSS. Simulated and empirical results show that, compared with state-of-the-art NMF and FastICA BSS models, our new method obtains better signal noise reduction and separation accuracy while maintaining superior target recognition signal characteristics. Hence, the verification of underwater targets and their statuses is improved for maritime targets detection and location.

Current application of NMF in multi-target underwater acoustic signals

NMF achieves part-to-whole representations using non-negative constraints on decomposed objects (Weiderer et al., 2020). For a non-negative data matrix, $V=\left[v_1,v_2,\cdots ,v_n\right]\in R_{+}^{m\times n}$, where v_i is a m-dimensional vector, the NMF algorithm decomposes it into two non-negative matrices, $W=\left[w_1,w_2,\cdots ,w_r\right]\in R_{+}^{m\times r}$ and $H=\left[h_1,h_2,\cdots ,h_n\right]\in R_{+}^{r\times n}$, via cyclic iterations, according to Eq. (1):

$\begin{array}{ll}{V}_{m\times n}\approx W_{m\times r}{H}_{r\times n}& (1)\end{array}$

Where W and H are the base and coefficient matrices, respectively, r is the dimensionality of the base vector (usually r≪n ). Obviously, the NMF method can obtain data dimension reduction at the same time. To measure the reconstruction effects of Eq. (1), many optimization improvements to the objective function have been proposed (Yurong et al., 2020), such as the Kullback–Leibler (KL) divergence:

$\begin{array}{ll}KL(V|WH)={\displaystyle \sum _{i,j}{V}_{i,j}log\frac{V_{i,j}}{{(WH)}_{ij}}-V_{i,j}+{(WH)}_{ij}}& (2)\end{array}$

The iterative solution of Eq. (2) can be found by using the multiplication criterion (Hien and Gillis, 2021).

When performing underwater acoustic multi-target BSS with the classical NMF method, the low-frequency analysis and range (LOFAR) spectrum, $V\in R_{+}^{F\times N}$, of the mixed signal is calculated first, where N indicate the frame numbers of received mixed signal and F is the FFT dimensions of signal frames. After estimating the optimal number r of base vectors, the base matrix, $W=\left\{{{\displaystyle {\sum }_i{W}_i\in R}}_{+}^{F\times r}\right\}$, can be calculated using Eq. (2), where W_i is the base matrix of the target i, and r reflects the description performance of the base vector to the original signal. And then, if the basis matrix W_i of each source signal is separated by using some BSS algorithm, such as FastICA, from the above W, the source signal spectrum will be constructed using the W_i and its corresponding coefficient matrix. In this way, the final separation of the mixed signals received by signal buoy is achieved. This process is shown in Figure 1, in which, the Feature Dictionary Set W is the whole base matrix calculated from the received mixed signals and W_I and e is the base matrix of target Iand target e

FIGURE 1

Figure 1 The NMF process of Underwater acoustic multi-target signal.

Obviously, the classical NMF algorithm is suitable for underwater acoustic multi-target signal decomposition; however, the algorithm itself is non-convex, often causing it to fall into local optimum (Li and Yang, 2016). Moreover, the characteristics of the underwater acoustic target signals also affect the decomposition effect. First, the base matrix obtained by NMF comprises an unordered array of base vectors, which makes it difficult to reconstruct the source signal directly. Second, the multi-source components cause a lot of interference, which quickly leads to data redundancy. Therefore, the performance of the NMF BSS algorithm needs to be improved by deeply mining the relevant features contained in the underwater acoustic target signals and establishing suitable constraints based on the actual signal features. To answer this need, our joint BSS algorithm for underwater acoustic multi-target signals based on an improved NMF with a FastICA backbone is proposed.

Improving NMF using signal features

Optimize the NMF base vector using signal features

Improving the adaptability of objective function to signal feature will significantly improve NMF decomposition performance (Li and Yang, 2016). Thus, when extracting the base vector of the received underwater acoustic multi-target signals, if the feature correlation between source signals is low, the local independence of the base vector improves, as does the efficacy of the NMF algorithm (Li et al., 2016; Zhang et al., 2022). However, underwater acoustic target signals show significant feature diversity within the same class and feature correlations between different classes. Notably, the line spectrum feature of underwater acoustic signals is an important characteristic for target recognition, leading to the limited use of that the traditional KL divergence, F-norm, Lp-norm, and other target functions that is easily influenced by high-energy line spectrum components within the LOFAR spectrum (Sadeghi et al., 2021). Therefore, the proposed algorithm improves the NMF objective function with dual constraints, that is determinant constraints and У β-divergence, to reduce the method’s dependence on the source signal structure. Hence, the uniqueness and independence of the base matrix are reinforced.

The formula of the β-divergence is

$\begin{array}{ll}{d}_{\beta }(y,x)=\{\begin{array}{l}\frac{y^{\beta }}{\beta (\beta -1)}+\frac{x^{\beta }}{\beta }-\frac{y{x}^{\beta -1}}{(\beta -1)},\beta \in R/\left\{0,1\right\}\\ y\ln \frac{y}{x}-y+x,\beta =1\\ \frac{y}{x}-\ln \frac{y}{x}-1,\beta =0\end{array}& (3)\end{array}$

Where R/{0,1} is the set of real numbers, excluding zero and one. It can be seen from Eq. (3) that the β-divergence satisfies

$\begin{array}{ll}{d}_{\beta }(\lambda y,\lambda x)={\lambda }^{\beta }d(y,x)& (4)\end{array}$

When the value of β is zero, the value of Eq. (4) is scale shift invariant. That is, it is unrelated to scale factor λ, indicating that when NMF is performed, the line spectrum components in the LOFAR image of mixed signal will have equal weight across the continuous spectrum components, so as to avoid the influence of high-energy line spectrum on the results,. However, when β ≠ 0, β-divergence will still be affected by the line spectrum components.

To improve the independence of the NMF base vectors and mitigate the impact of their feature redundancy on the signal reconstruction, determinant constraints are added. Let the volume of the space stretched by matrix $W=\left[w_1,w_2,\cdots ,w_r\right]\in R_{+}^{m\times r}$be expressed as

$\begin{array}{ll}vol(W)=\{\begin{array}{l}\sqrt{\det (W{W}^T)},m<r\\ \left|\det (W)\right|,m=r\\ \sqrt{\det (W^{T}W)},m>r\end{array}& (5)\end{array}$

When the volume, vol(W) , in Eq. (5) is smallest, each vector w_i∈W can be uniquely determined (Sadeghi et al., 2021). Thus, the improved NMF objective function based on β-divergence and determinant constraints can be expressed as

$\begin{array}{ll}\min (J)=d_{\beta =0}(V,WH)+\alpha ·vol(W)& (6)\end{array}$

Optimize the NMF coefficient matrix by spatial similarity

The radiated noise of underwater acoustic targets is the main source of passive buoy detection (Liu et al., 2021). The shape, displacement, structure, and other features of acoustic targets comprise the main factors of signal characteristics, that is, when the acoustic targets remains a relatively stable sailing state, the spectrum distribution of its radiated signal will show good short-term stability, as shown in Figure 2. Owing to the short interval between two adjacent frames, even if environmental noise exists, It still shows good short-term similarity by using of a fitted spectrum distribution and an interframe alias is useful (Li et al., 2016),.

FIGURE 2

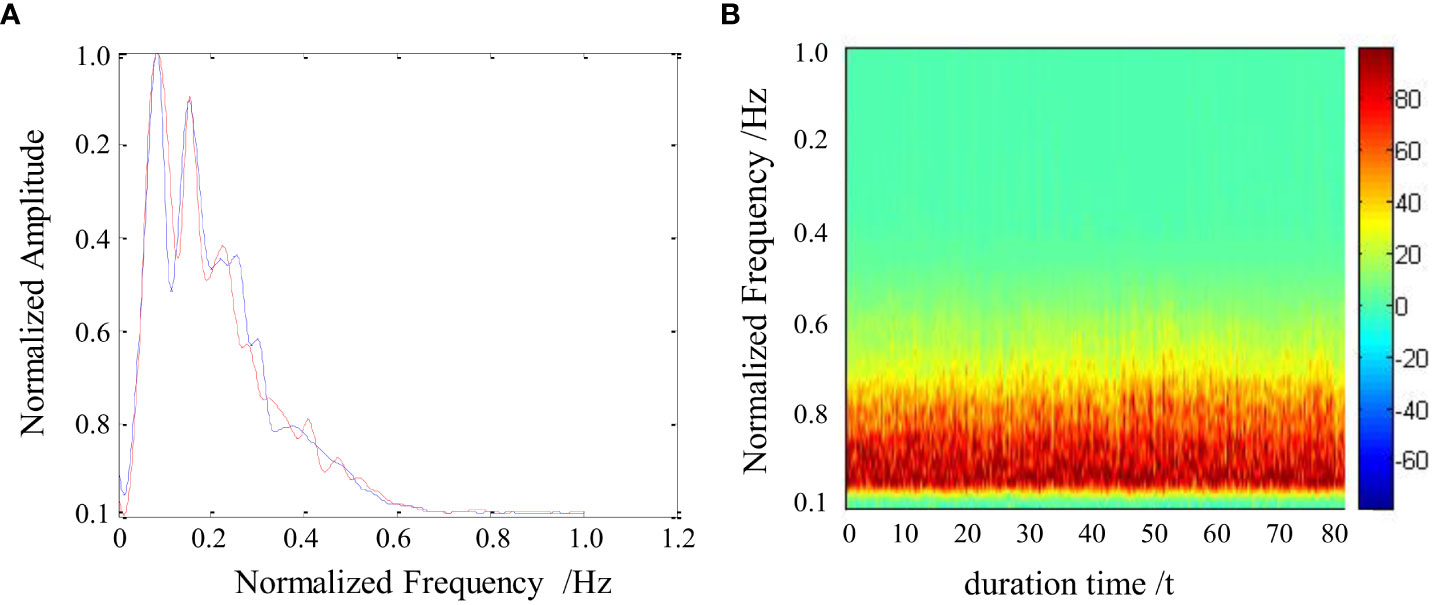
Figure 2 Spectrogram of radiated noise from a surface target: (A) trend diagram of two adjacent signals in a frame; (B) spectrum trend of the surface target.

Figure 2 shows the spectrum of multi-target mixed signals observed by a single marine environment monitoring buoy in a certain time period. Although the frequency spectrums of different targets under different working conditions are different, and the frequency spectrums of mixed signals formed by these signals are also diverse, it is usually difficult for each target to have a large change in a short period of time within the monitoring range of the marine environment monitoring buoy. Therefore, the mixed signals will also maintain a certain characteristic stability in a short time. Of course, the spectrum of the mixed signal is different for different periods of time or for different targets, the spectrum is relatively stable only in a short period of time.

When calculating the LOFAR spectrum of the received signal, fast Fourier transform (FFT) resolution inefficiencies will lead to a certain degree of spectral smoothness between adjacent frequencies. Therefore, in addition to the short-time similarity between the signal frames, as shown in Figure 2, the eight neighbors of the current pixel are taken as local neighborhood candidate regions. Then, adaptive local neighborhood weighting is used to analyze the similarity contributions of the neighboring candidate pixels to the current pixel to make full use of the spatial similarity between them for the benefit of the NMF model.

Within the eight-neighborhood range of the current pixel, the weight contribution of pixel y_j to y_i is expressed as

$\begin{array}{ll}{c}_{ij}={\Gamma }^{-1}+\rho & (7)\end{array}$

where Γ describes the neighborhood position of pixel y_j, and P reflects the similarity between two pixels. The calculation formula is

$\begin{array}{ll}\{\begin{array}{l}\Gamma =\left|x_i-x_j\right|+\left|y_i-y_j\right|\\ \rho =\langle H_i,H_j\rangle \end{array}& (8)\end{array}$

where 〈·〉 represents the inner product of the vector, and s_i is the coefficient vector corresponding to the pixel. Thus, when the spatial similarity of two pixels is high, their weight value, c_ij, is also large, and vice versa. Therefore, the weight contribution of the eight pixels in the neighborhood of the current pixel, y_i, can be expressed as

$\begin{array}{ll}{C}_i={\displaystyle \sum _{j\in N\left(i\right)}{c}_{ij}}& (9)\end{array}$

Thus, an adaptive calculation of the weight contribution of the pixels in the neighborhood can be realized. The improved NMF model that incorporates the adaptive weighted spatial similarity is

$\begin{array}{ll}\begin{array}{c}\min (J)=d_{\beta =0}(V,WH)+\frac{\alpha }{2}·(vol\left(W\right)+{\Vert \tilde{W}-W\Vert }^2)+\lambda \\ {\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j\in N\left(i\right)}^{}{c}_{ij}·{\Vert H_i-H_j\Vert }_2^2}}+\beta {\Vert H\Vert }_{1/2}\end{array}& (10)\end{array}$

where W ≥ 0, H ≥ 0, $1_r^{\text{T}}H=1_n^{\text{T}}$, α, β, and λ are regularization coefficients. ‖·‖_1/2 is the L_1/2-norm, which is used to add a sparse constraint to the coefficient matrix to prevent overfitting and noise residue. ${\Vert \tilde{W}-W\Vert }^2$ describes the smoothness of a single source signal, which is used to increase the separability between multi-targets, and $\tilde{W}$ is the moving average matrix of the calculated values of the previous iteration of W (Liu et al., 2021). The optimal solution of Eq. (10) can be achieved by the derivative of a variable or the least-squares method under the Karush–Kuhn–Tucker condition (Chen and Lv, 2021), that is:

$$W\leftarrow W\frac{\left[V{(WH)}^{-2}+\alpha \tilde{W}\right]H^{\text{T}}}{{(WH)}^{-1}{H}^{\text{T}}+\alpha W}$$

$\begin{array}{ll}H\leftarrow H\frac{W^{\text{T}}\left[V{(WH)}^{-2}+\lambda H_C\right]}{W^{\text{T}}{(WH)}^{-1}+\lambda CH+\frac{\beta }{2}{H}^{-\frac{1}{2}}}& (11)\end{array}$

The dimensionality of the base matrix is very important for NMF decomposition as it directly affects target feature extraction, especially for acoustic target signals. The noise interference of the receiving signal is large, and the signal features overlap to some extent. Hence, when the dimensionality is too large, the NMF decomposition base matrix introduces too much noise. However, if the dimensionality is too small, the decomposition fidelity of the base matrix will be reduced, leading to the non-uniqueness of the local expression characteristics and insufficient separation accuracy. Therefore, the nearest-neighbor eigenvalue dominance method (Wang et al., 2019) is used to estimate the dimensionality of the base matrix.

Joint blind separation using improved NMF and FastICA

The base matrix combines the base vector of all source signals in the mixed signal received by a single buoy. Because the base vectors are not ordered, it is difficult to determine which base vectors are from the same source signal. Therefore, the FastICA algorithm is used here to separate the base matrix into base vector groups based on their independent sources.

According to the central limit theorem (Krishna et al., 2020), the mixed signal obtained from independent source signals has a high Gaussian distribution. From information theory, the stronger the Gaussian property of the equivariance random variable, the greater its entropy. The FastICA algorithm was explicitly built to maximize the non-Gaussian property of mixed observation signals, and negative entropy is used as the parameter. When negative entropy reaches its maximum, the non-Gaussian property of each source signal also reaches its maximum, indicating that each independent component is well-separated (Krishna et al., 2020).

Let signal Y=B^T. v be the matrix of the source signal separated from the whitened observation signal, v. Its negative entropy can then be expressed by its differential entropy. However, for that the probability density of random variables is difficult to estimate, the calculation is simplified with a common approximation formula:

$\begin{array}{ll}J\left(Y\right)={(E(g(Y))-E(g(Y_{Gauss})))}^2=(E(g(B^T·v))-E(g(Y_{Gauss}))){)}^2& (12)\end{array}$

where B is the separation matrix, b_i∈B is a column vector in the matrix, and ‖b_i‖=1 . g(·) is an arbitrary non-quadratic function and its reasonable selection leads to a good approximation of the source signal (Abdalla and Alrufaiaat, 2021). When the y³ form is selected, it has already been proven to be optimal for separation performance, accuracy, and convergence when used by the FastICA model (Xiumin et al., 2020). To solve Eq. (12), the Lagrangian function is constructed as

$\begin{array}{ll}L(B,\beta )=J(B)-\beta ({\Vert B\Vert }^2-1)={(E(g(B^T·v))-E(g(Y_{Gauss})))}^2+\beta {\Vert B\Vert }^2& (13)\end{array}$

where β=E(B^Tvg^′(B^T·v)) , and g^′(·) is the derivative of g(·) . It can be seen that the maximization of Eq. (12) can be converted to the derivative of Eq. (13):

$\begin{array}{ll}E(v·g(B^T·v))-\beta B=0& (14)\end{array}$

As v is the whitened data, according to the third-order Newton iteration method, the iteration formula of the FastICA algorithm is

$\begin{array}{ll}\{\begin{array}{l}{B}^{*}=E(vg(B^{T}v))-E(g^{\prime }(B^{T}v))B\\ B=E(vg(B^{T}v))+E(vg(B^{*T}v)))-E(g^{\prime }(B^{T}v))B-\beta B^{*}\end{array}& (15)\end{array}$

where B^* is the intermediate value of the iterative calculation of new B. FastICA is the main model used for BSS tasks. However, the number of observed signals must be greater than or equal to the number of source signals. Although the multivariate LOFAR time-frequency spectrum can be obtained from the short-time Fourier transform, it cannot be directly applied to FastICA for BSS because all column vectors in the spectrum come from the same channel.

However, after NMF decomposition of the LOFAR spectrum, the characteristics of each independent source signal from the mixed signal can be reflected by NMF base vectors. Thus, the base matrix can be viewed as a combination of the base vectors of each independent source signal. Nevertheless, the order of the base vectors is messy, making it impossible to determine ownership.

Therefore, after improving the NMF method, we designate the base and coefficient matrices of the received observation signal, V, as W, and H, respectively, where W={w₁,w₂,⋯,w_r} , and r is the dimensionality of the base matrix. If the ownership of the base vectors in W={w₁,w₂,⋯,w_r} is obtained, then W can be expressed as W={W₁,W₂,⋯,W_i} , such that

$\begin{array}{ll}\begin{array}{l}{V}_j=\left\{W_1,W_2,\cdots ,W_i\right\}{\left\{h_{j1}^{\text{T}},h_{j2}^{\text{T}},\cdots ,h_{ji}^{\text{T}}\right\}}^{\text{T}}=W_1{h}_1+W_2{h}_2+\cdots +W_i{h}_i\\ =Y_1{b}_1+Y_2{b}_2+\cdots +Y_i{b}_i=bY=h_j{W}^{\text{T}}\end{array}& (16)\end{array}$

where Y is the source signal matrix, i is the number of source signals, and W_i is the base matrix of the source signal, which comprises the base vector belonging to the same independent source. It is, therefore, obvious that W_ihas disturbed the order of the original w_i in W. Thus, h_ji becomes the new column vector of the coefficient matrix, H, corresponding to the new order of w_i (i.e., corresponding to the order of W_i). $h_i=h_{ji}^{\text{T}}$ and its dimensionality is thus consistent with that of W_i, and b_i is a vector separated from h_i. Since there is a part value h_i′ in h_i, making W_ih_i^′=Y_i , the remaining part b_i of h_i after removing h_i^′ can be regarded as the contribution of Y_i when V_j is generated, Thus, we have the parameter of its corresponding mixed matrix.

Alongside the derivation process of FastICA (Abdalla and Alrufaiaat, 2021), it can be further deduced from Eq. (16) that

$\begin{array}{ll}Y=b^{-1}{h}_j{W}^{\text{T}}=B{W}^{\text{T}}& (17)\end{array}$

Accordingly, the source signal, Y, can be calculated from the base matrix, W (obtained from the improved NMF), and the unmixing matrix, B.

The input matrix, v, of the proposed algorithm from Eq. (14) can be obtained by recombining W and one column, V_i, of the LOFAR image of the observed mixed signal. Then, the unmixing matrix, B, in Eq. (17) can be obtained via iterative calculations, as shown in Eq. (14). Finally, the BSS of the acoustic multi-target signals received by the buoy can be achieved.

From the above analysis, the proposed BSS algorithm that joint improved NMF and FastICA is shown in Figure 3. Note that after signal separation, Y=Bv^T , because the dimensionality of the base matrix obtained by the improved NMF is greater than the number of source signals, there will be different sequences of the same source signal in the separated results. Thus, it will be necessary to further select and combine them using correlation analysis or other algorithms.

FIGURE 3

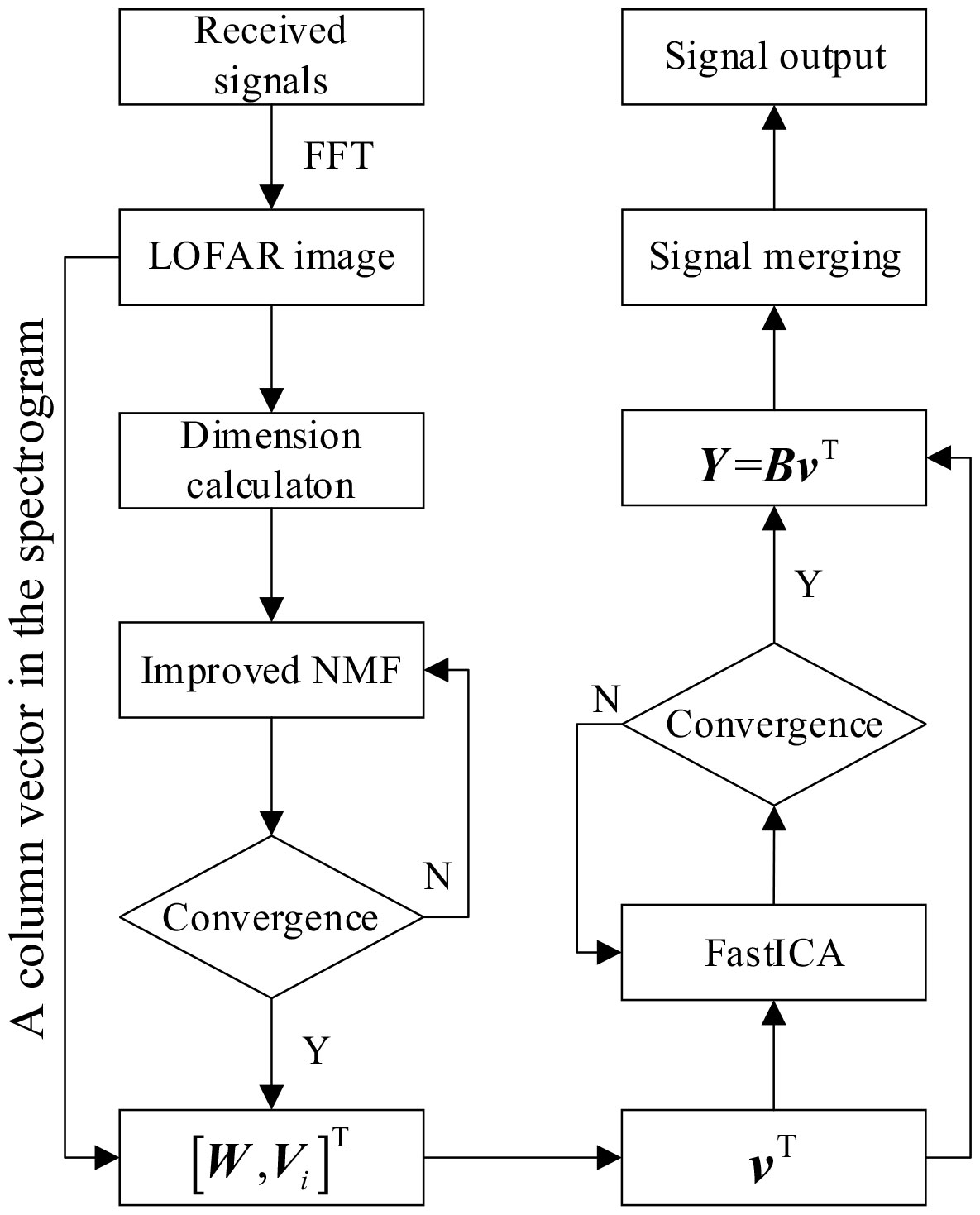
Figure 3 Application of the proposed improved non-negative matrix factorization (NMF) and FastICA for the blind source separation of underwater acoustic multi-target signals.

Experimental verification and analysis

To verify the efficacy of the proposed BSS algorithm used for underwater acoustic multi-target signal received by a single buoy, the normalized cross-correlation coefficient (NCC) and logarithmic spectral distance (LSD) are used as evaluation criteria. The larger the LSD value, the better the signal reconstruction performance (Li and Wang, 2019). The LSD formula is

$\begin{array}{ll}{f}_{\text{LSD}}=\sqrt{\frac{1}{N}{{\displaystyle \sum _{n=0}^{N/2-1}\left|L(S(l,n))-L(S_d(l,n))\right|}}^2}& (18)\end{array}$

where L(S(l,n)) is the logarithmic spectrum between two signals, and N is the number of data. The S and S_d indicate source signals and reconstructed signals respectively

The spectrum features of an acoustic target signal mainly include its line spectrum, continuous spectrum, and envelope modulation spectrum (Li et al., 2016). When the sailing speed of underwater acoustic target exceeds its critical speed, its propeller will periodically modulate it radiated signal, representing as envelope line spectrum. Therefore, the modulation line spectrum, which reflects the axial frequency and other information of targets, is an important feature for target recognition, that is why the modulated line spectrum is needed; and it can be obtained by extracting the envelope of the signal and performing FFT. Thus, the simulation signal model with periodic modulation is

$\begin{array}{ll}s\left(t\right)={\displaystyle \sum _i(1+A_m·\cos \left\{-2\pi f_0\left(t-{\tau }_i\right)\right\})\cos (2\pi f_c(t-iT-{\tau }_i)}& (19)\end{array}$

Where A_m is the modulation amplitude, and its cosine signal is used to simulate the screw modulation, in which f₀ is the modulation frequency reflecting the axial frequency. Because the main test feature is the axial frequency information of the underwater acoustic target, other signals (e.g., hydrodynamic) are simplified to cosine or sine signals with frequency f_c. In our experiment, the mixed signals of three simulation signals were used. The sampling rate, f_s=1/T, was 6,000, and so there were 4,096 sampling point. the values of f₀ and f_C in each simulation signal are listed in Table 1.

TABLE 1

Table 1 Simulated signal parameters for the experiment.

The mixed matrix, $\omega =\left[\begin{array}{ccc}0.756& 0.871& 0.559\end{array}\right]$, was generated randomly. n(t) was the superimposed noise, and i=20. The time-domain waveforms of all signals and mixed signals are shown in Figure 4.

FIGURE 4

Figure 4 Time domain waveform of the simulated signal for the experiment.

The demodulation line spectra of the mixed signal were calculated via FFT on the extracted envelope, S(t) , as shown in Figure 5. The spectrum information within 100 Hz is displayed for simplicity.

FIGURE 5

Figure 5 Envelope spectrum of the hybrid simulation signal.

In Figure 5, the modulation line spectrum and its octave harmonics reflect the screw frequency information of different acoustic targets, but they are interlaced. The proposed BSS algorithm based on the improved NMF and FastICA was used as described in the previous sections. The signals were divided into frames, and FFT was performed first with all 4,096 data points and a 50% overlap between the frames. Thus, the LOFAR spectrum of the experimental mixed signals was generated. Next, the improved NMF was used to decompose the LOFAR spectrum using an 18-dimensional base matrix with 300 iterations. FastICA was then used for the BSS. After that the obtained decomposed signals were analyzed for similarity, and those with high similarity were merged into the same source signal.

The time domain waveform and envelope spectrum of the decomposed source signal are shown in Figures 6 and 7, respectively. From Figure 7, owing to the β -divergence, the proposed algorithm better maintains the spectrum components of the mixed signal, and their three modulation components (i.e., 20, 35, and 45 Hz) and harmonic components were effectively separated. This verifies the efficacy of our proposed algorithm.

FIGURE 6

Figure 6 Time-domain waveform of separated signals.

FIGURE 7

Figure 7 Envelope spectrum of the separated signals.

The cross-correlation coefficient between the separated and source signals was calculated, as listed in Table 2. The cross-correlation between the separated signal and its source is large, but that of the separated signal and the other two source signals is small, indicating that the algorithm has good BSS accuracy.

TABLE 2

Table 2 Cross-correlation coefficient between separated and source signals.

To further understand the robustness of the proposed method, white noise was added at different signal-to-noise ratios to the simulated mixed source signals. The improved NMF with an Improved Crest Factor (ICF) ICF operator (NMF+ICF) (Li and Yang, 2016), improved FastICA (iFastICA) (Guotao et al., 2021), and the combined classical NMF and FastICA (NMF+FastICA) were compared. The NCC and LSD of each used were analyzed under different signal-to-noise ratios (Yurong et al., 2020), and the results are illustrated in Figures 8 and 9, where each value is the average of the three source signals from several experimental trials. The KL divergence is used as the objective function of classical NMF in this experiment.

FIGURE 8

Figure 8 Normalized cross-correlation coefficient under different signal-to-noise ratios.

FIGURE 9

Figure 9 Logarithmic spectral distance of each algorithm under different signal-to-noise ratios.

$\begin{array}{ll}{R}_{SNR}=10\lg \left(\frac{E\left(x^{\text{T}}x\right)}{E\left(n^{\text{T}}n\right)}\right)& (20)\end{array}$

From Figures 8 and 9, iFastICA’s BSS results were not ideal for all SNRs because its original FastICA component requires mixed signals in multiple channels. However, recall that the LOFAR spectrum is essentially one channel signal. Therefore, although the FastICA algorithm was improved in iFastICA, its blind separation effect is still not ideal.

Compared with iFastICA, the signal separation accuracy of NMF+ICF was improved to some extent, but it is still not ideal. On the one hand, the algorithm improved the NMF and its adaptability to modulated pulse signals. However, because there was no reasonable sparse constraint on the NMF coefficient matrix, the decomposed base matrix suffered an insufficient independent local expression ability for the source signal. On the other hand, NMF+ICF used the correlation-based ICF factor to select the base vector with the highest ICF value as the final separated signal, which easily causes the loss of important signal components.

NMF+FastICA combined the advantages of classical NMF and FastICA algorithms and achieved the best separation results. However, as the classic NMF is not optimized for underwater acoustic target signals, the local and dependent characteristics of the basis matrix affected the final BSS effect. The proposed algorithm (iNMF+FastICA) achieved the best separation effect under various SNRs; because of that, it better retains the separable characteristics of the via the improved NMF. Thus, the separated signal more approximated the source signal.

Conclusion

Based on the improved NMF and FastICA algorithm, this study addressed an important BSS problem used for mixed signals from underwater acoustic multi-targets are received by automatic monitoring buoys Our method was successful because it addressed the non-convex and feature correlation problems encountered by the classical NMF algorithm with spatial and spectral correlation optimization. This improved the adaptability of the classic NMF to handle the modulation characteristics of underwater acoustic target signals while improving the local expressability and independence of the NMF base matrix. Then, the advantages of the improved NMF and FastICA algorithms were combined to achieve superior BSS of underwater acoustic multi-target signals.

The simulation signal experiment results showed that compared with state-of-the-art BSS algorithms based on NMF and FastICA, the novel proposal achieves better signal separation accuracy while maintaining the modulation characteristics of the original signal. Furthermore, it reduces SNR and enhances signal separation, which leads to better feature interpretation and target recognition.

Presently, when the proposed method is applied to underwater acoustic target signals with obvious lines or modulation spectra, the BSS is good. However, with the advancement of noise reduction technologies, the radiated signals of underwater acoustic targets have become more difficult to detect. Therefore, Future work should further improve and optimize these methods by combining extant signal detection, feature extraction, noise reduction, and signal enhancement techniques to improve their applicability.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

LD, the first author of the paper, led most of the main work, such as algorithm design, theoretical derivation, experimental verification, and finally completed the writing of the paper. WM, the second author of the paper, mainly modified the algorithm and made great contributions to the reasonable integration based on NMF and FastICA. As the third author of the paper, YL is mainly involved in the design and modification of the algorithm in the paper. He has deep attainments in the research of NMF algorithm feature line spectrum maintenance, and has great guidance for algorithm design. HJ is the fourth author of the paper. He designed verification experiments based on the algorithm of the paper, collected and simulated relevant experimental data. ZH, the fifth author of the paper, participated in the collation of experimental data, the revision and correction of the paper. All authors contributed to the article and approved the submitted version.

Funding

This paper is funded by the University Civil Affairs Fund (I32102003).

Acknowledgments

We would like to thank Editage (www.editage.cn) for English language editing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdalla K., Alrufaiaat S. (2021). A new robust decoding technique of four transmitters MIMO STBC system based on FastICA algorithm. Int. J. Intelligent Eng. Systems. 14 (1), 181–191. doi: 10.22266/ijies2021.0228.18

CrossRef Full Text | Google Scholar

Chen S., Lv J. (2021). A nonnegative matrix factorization method based on adaptive local neighborhood weighted constraint and its application in hyperspectral unmixing. J. Signal Process. 37 (5), 804–813. doi: 10.16798/j.issn.1003-0530.2021.05.014

CrossRef Full Text | Google Scholar

Dianmant R., Kipnis D., Bigal E., Scheinin A., Dan T., Pinchasi A., et al. (2019). “An active acoustic track-before-detect approach for finding underwater mobile targets,” in IEEE Journal of Selected Topics in Signal Processing, (United States: IEEE) Vol. 13. 104–119. doi: 10.1109/JSTSP.2019.2899237

CrossRef Full Text | Google Scholar

Guotao W., Qiuxi J., Fangzheng L. (2021). An improved FastICA radar signal sorting method. J. Detection Control 43 (6), 43–49.

Google Scholar

Hien L., Gillis N. (2021). Algorithms for nonnegative matrix factorization with the kullback–leibler divergence. J. Sci. Computing. 87 (3), 417–439. doi: 10.1007/s10915-021-01504-0

CrossRef Full Text | Google Scholar

Huang R., Li X., Zhao L. (2019). “Spectral–spatial robust nonnegative matrix factorization for hyperspectral unmixing,” in IEEE Transactions on Geoscience and Remote Sensing, (United States: IEEE) Vol. 57. 8235–8254. doi: 10.1109/TGRS.2019.2919166

CrossRef Full Text | Google Scholar

Krishna A., Nimbal A., Makam A., Rao V. (2020). Implementation of fast independent component analysis on field-programmable gate array for resolving the slot collision issue in the space-based automatic identification system. Int. J. Satellite Commun. Networking. 38 (6), 480–498. doi: 10.1002/sat.1362

CrossRef Full Text | Google Scholar

Liu X., Wu M., Zheng X., Li D. W. (2021). Underwater acoustic target signal enhancement algorithm optimized by improved NMF. Electron. Optics Control. 28 (9), 6–5+53. doi: 10.3969/j.issn.1671-637X.2021.09.002

CrossRef Full Text | Google Scholar

Li D., Wang Z. (2019). Improved spatial information constrained nonnegative matrix factorization method for hyperspectral unmixing. Laser Optoelectronics Progress. 56 (11), 111006. doi: 10.3788/LOP56.111006

CrossRef Full Text | Google Scholar

Li D., Yang R. (2016). Detection of speech signal in strong ship-radiated noise based on spectrum entropy. J. Vibroengineering. 18 (1), 661–670. doi: 10.3969/j.issn.1001-2400.2016.05.024

CrossRef Full Text | Google Scholar

Li D., Yang R., Han J. (2016). Study of speech enhancement in the background of ship-radiated noise. J. Xidian University. 43 (5), 133–138.

Google Scholar

Lu X., Dong L., Yuan Y. (2020). “Subspace clustering constrained sparse NMF for hyperspectral unmixing,” in IEEE Transactions on Geoscience and Remote Sensing, (United States: IEEE) Vol. 58. 3007–3019.

Google Scholar

Lu X., Wu H., Yuan Y., Yan P., Li X. (2013). “Manifold regularized sparse NMF for hyperspectral unmixing,” in IEEE Transactions on Geoscience and Remote Sensing, (United States: IEEE) Vol. 51. 2815–2826.

Google Scholar

Rathnayake B., Ekanayake E., Weerakoon K., Godaliyadda G., Herath H. (2020). “Graph-based blind hyperspectral unmixing via nonnegative matrix factorization,” in IEEE Transactions on Geoscience and Remote Sensing, (United States: IEEE) Vol. 58. doi: 10.1109/TGRS.2020.2976799

CrossRef Full Text | Google Scholar

Sadeghi M., Behnia F., Amiri R. (2021). “Optimal geometry analysis for TDOA-based localization under communication constraints,” in IEEE Transactions on Aerospace and Electronic Systems, (United States: IEEE) Vol. 57. 3096–3106. doi: 10.1109/TAES.2021.3069269

CrossRef Full Text | Google Scholar

Sriharsha K., Abhijit K. (2018). Homotopy optimization based NMF for audio source separation. IET Signal Processing. 12, 1099–1106. doi: 10.1109/ACCESS.2020.2985842

CrossRef Full Text | Google Scholar

Wang W., Qian Y., Liu H. (2020). “Multiple clustering guided nonnegative matrix factorization for hyperspectral unmixing,” in IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, (United States: IEEE) Vol. 13. 5162–5179.

Google Scholar

Wang M., Wang H., Dong F., Ren B., Song L. (2019). A method of compound fault signal separation based on EVMD-LNMF. J. Vibration Shock. 38 (16), 146–152. doi: 10.13465/j.cnki.jvs.2019.16.021

CrossRef Full Text | Google Scholar

Weiderer P., Tomé A., Lang E. (2020). A NMF-based extraction of physically meaningful components from sensory data of metal casting processes. J. Manufacturing Systems. 54, 62–73. doi: 10.1016/j.jmsy.2019.09.013

CrossRef Full Text | Google Scholar

Wildeboer R., Schoot B., Wijkstra H., Mischi M., Salomon G. (2020). “Blind source separation for clutter and noise suppression in ultrasound imaging: Review for different applications,” in IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, (United States: IEEE) Vol. 67. 1497–1512.

Google Scholar

Xiumin C., Shanjun L., Xingjian D. (2020). Simulation. analysis of nonlinear function performance of FastICA algorithm. Comput. Appl. Software 37 (6), 277–282+333. doi: CNKI:SUN:JYRJ.0.2020-06-049

Google Scholar

Yurong L., Jie L., Lailin L., Gong C., Wang Y. (2020). Parallel algorithm of deep transductive non-negative matrix factorization for speech separation. Comput. Sci. 47 (8), 49–55. doi: 10.11896/jsjkx.190900202

CrossRef Full Text | Google Scholar

Zhang X., Wu H., Sun H., Ying W. (2021). “Multireceiver SAS imagery based on monostatic conversion,” in IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, (United States: IEEE) Vol. 14. 10835–10853.

Google Scholar

Zhang X., Yang P. (2021). An improved imaging algorithm for multi-receiver SAS system with wide-bandwidth signal. Remote Sensing. 13 (24), 5008. doi: 10.3390/rs13245008

CrossRef Full Text | Google Scholar

Zhang X., Yang P., Feng X., Sun H. (2022). Efficient imaging method for multireceiver SAS. IET Radar Sonar Navigation. 16 (9), 1470–1483.

Google Scholar

Zhang X., Yang P., Huang P., Huang P., Sun H., Ying W., et al. (2022). Wide-bandwidth signal-based multireceiver SAS imagery using extended chirp scaling algorithm. IET Radar Sonar Navigation 16 (3), 531–541.

Google Scholar

Zhang X., Yang P., Sun M. (2022). ). experiment results of a novel sub-bottom profiler using synthetic aperture technique. Curr. Science. 12 (4), 461–464.

Google Scholar

Zhang X., Ying W., Yang P., Sun M. (2020). Parameter estimation of underwater impulsive noise with the class b model. IET Radar Sonar Navigation. 14 (7), 1055–1060. doi: 10.1049/iet-rsn.2019.0477

CrossRef Full Text | Google Scholar