Second-order Stokes wave-induced dynamic response and instantaneous liquefaction in a transversely isotropic and multilayered poroelastic seabed

The ocean waves exhibit obvious non-linearity with asymmetric distribution of wave crests and troughs, which could induce significantly different effect on the seabed compared to the commonly used linear wave theory. In this paper, a semi-analytical solution for a transversely isotropic and multilayered poroelastic seabed under non-linear ocean wave is proposed by virtue of the dual variable and position (DVP) method. The ocean wave and seabed are, respectively, modelled using second-order Stokes theory and Biot’s complete poroelastodynamic theory. Then the established governing equations are decoupled and solved via the powerful scalar potential functions. Making use of the DVP scheme, the layered solutions are finally gained by combining the boundary conditions of the seabed. The developed solutions are verified by comparing with existing solutions. The selected numerical examples are presented to investigate the effect of main parameters on the dynamic response of the seabed and evaluate the corresponding liquefaction potential. The results show that the anisotropic stiffness and permeability, degree of saturation and stratification have remarkable influence on the dynamic response and liquefaction behavior of the seabed. The present solution is a useful tool to estimate the stability of transversely isotropic and layered seabed sediment in the range of non-linear ocean wave.

1. Introduction

With the increasing utilization of land-based resources, people have begun to turn their attention to the oceans and promote the development of offshore drilling rigs, offshore wind turbines, even the wind power generation in deep water environments (Jouffray et al., 2020; He et al., 2022a; He et al., 2022b). As the main deep foundation elements for marine structures, the vibration characteristics of monopiles under mechanical and seismic loads have received detailed investigations in recent years (Chen et al., 2022a; Chen et al., 2022b; Zhang et al., 2022). It should be pointed out that harbor oscillations induced by infragravity waves or transient wave groups (Gao et al., 2017; Gao et al., 2020; Gao et al., 2021) can interrupt the normal operation of docks, cause the extreme movements of moored ships, and even give rise to the break of mooring lines. Moreover, liquefaction of the seabed induced by sea wave (Jeng, 2015) can cause the destruction of offshore structures, which further affects the safety of human operations in ocean and even leads to accidents (e.g., oil spills) with a negative impact on the marine ecosystem (Soto et al., 2014; Joydas et al., 2017). The United Nations aimed to achieve considerable progress in science and technology areas to generate safe and clean oceans from 2021 to 2030 (Ryabinin et al., 2019). The seabed would liquefy when it is subjected to wave loadings or seismic loadings, and it was found that the liquefaction mechanism for the seabed under wave and earthquake actions is similar (Ye et al., 2018). Considering that the waves are the most frequent load over the seabed in the ocean environment, the dynamic response and liquefaction behavior of the seabed under wave loadings are the key factors in the design of marine structures.

Since the middle of the last century, scholars began to investigate the dynamic response of the seabed under wave load. Due to complexity of the problem, researchers attempted to present the explicit closed-form solution for the wave-induced seabed response based on the quasi-static (QS) governing equation, such as general consolidation equation of Biot (1941) or storage equation of Verruijt (1969). Yamamoto et al. (1978) and Madsen (1978) derived their analytical solutions for the dynamic response of poroelastic seabed under linear wave. Following the work by Yamamoto et al. (1978), Okusa (1985) further considered the effect of seabed saturation and obtained the analytical solution for unsaturated seabed. In addition, various waved-induced seabed response problems have been investigated in terms of the QS governing equation (Mei and Foda, 1981; Hsu et al., 1993; Tsai and Lee, 1995; Jeng and Seymour, 1997; Kitano and Mase, 2001). In view of QS governing equation disregarding the accelerations of the pore fluid and soil skeleton, the subsequent studies mainly based on the fully or partly poroelastodynamic theory by Biot (1956), Biot (1962) and Zienkiewicz et al. (1980). Sakai et al. (1988) considered the effects of the acceleration of pore fluid and solid and the gravity, and derived the analytical solution of the seabed response under small amplitude wave. Jeng et al. (1999); Jeng and Rahman (2000); Jeng and Zhang (2005) used a partly dynamic (PD) formulation in their study and found that the dynamic response of the seabed under certain combinations of different wave and seabed conditions differs significantly from that without considering inertial items. The similar conclusions about the contribution of inertial items can also be found in Yuhi and Ishida (1998) and Quiuqui et al. (2022), who employed the fully dynamic (FD) formulation to solve the related problem. To enhance the practicability of the simplified solutions in engineering, Ulker et al. (2009) presented the scope of application of FD, PD and QS formulations in the frame of linear wave theory. Besides, Le Méhauté (1976) provided the scope of application of different wave models corresponding to different types of ocean waves and seabed conditions. The dynamic response of the seabed under different types of wave loadings has been studied in detail, such as cnoidal wave (Hsu et al., 2019), second-order Stokes wave (Jeng and Cha, 2003) and the combination of wave and currents (Qi et al., 2020).

Seabed tends to exhibit anisotropy and stratification due to the long-time natural sediment process. The researchers gradually paid their effort to seek the influence mechanism of material anisotropy and stratification on the dynamic response of the seabed. Jeng and Seymour (1997) studied the influence of hydraulic anisotropy on the waved-induce seabed response, however the soil is limited to isotropic medium. Gatmiri (1992) carried out the numerical analysis of the dynamic response of sandy seabed considering material anisotropy, and found that the effect of anisotropic parameters on the dynamic response of seabed is significant. Hsu and Jeng (1994) developed an analytical solution for the wave-induced response of the seabed by modelling the seabed material as transversely isotropic (TI) medium. Subsequent study on TI seabed also showed the significant effect of anisotropy on the dynamic response of the seabed (Yuhi and Ishida, 2002). For the layered seabed, Yamamoto (1981) analytically studied the response of multilayered poroelastic seabed to wave and found that the instabilities can be prevented by covering the bed by a layer of concrete blocks or rubble. Ulker’s studies on two-layer seabed (Ulker, 2012a; Ulker, 2012b) indicated that material layering has great influence on the dynamic response of the seabed. However, the propagating matrix of the field quantities in his study is too cumbersome, hence the theoretical solution only models the seabed as a two-layer structure. Li et al. (2020) employed the DVP method to establish the propagating matrix among different layers, which greatly improved the computational efficiency. It is noted that DVP method is very powerful and stable, and has been applied in different study areas, such as geophysics (Zhou et al., 2021), time-harmonic load buried in layered poroelastic medium (Zhang and Pan, 2020), moving load over layered poroelastic medium (Liu et al., 2022), and rigid disc resting on layered subgrade (Zhang and Pan, 2023), etc. Besides, Chen et al. (2022) employed the global dynamic stiffness matrix method to handle the layered structure. The comparison among different propagating matrix methods was reviewed by Pan (2019), which could give better understanding for the researchers to attack the layered problem.

Researchers have found from observations of waves on the sea surface that climatic factors generally cause the wave to show the non-linearity (Lauton et al., 2021). Jeng and Cha (2003) derived the analytical solutions for the dynamic response of a homogeneous seabed to second-order Stokes wave. Zhou et al. (2011) obtained the solution for a two-layer isotropic seabed under the action of second-order Stokes wave. By modelling the seabed as an elasto-plastic material, Chen et al. (2019) numerically analyzed the dynamic characteristics of a homogeneous TI poroelastic seabed under second-order Stokes wave. From previous works, the dynamic response of TI multilayered poroelastic seabed under non-linear wave has not been reported yet. Hence, the objective of the present study is to develop a semi-analytical solution to systematically investigate the dynamic response and liquefaction potential of TI multilayered poroelastic seabed under second-order Stokes wave. To achieve this end, we decouple Biot’s complete dynamic equations for TI poroelastic medium using powerful scalar potential functions expressed in the (u, p) form and gain the general solution for any homogeneous layer. Then we utilize the DVP method to derive the semi-analytical solutions for the layered seabed. Finally, the influence of the main soil parameters on the dynamic response and liquefaction behavior of seabed under both non-linear and linear waves is analyzed in detail.

2. The boundary-value problem

As shown in Figure 1, the second-order Stokes waves propagating over a TI layered poroelastic seabed with a rigid impermeable bottom is considered in the present study. The layered seabed is arranged from the top surface to the bottom of the seabed in the order of layer 1 to layer n. Following Li et al. (2020), the coordinate z is vertically upwards with the negative value below the mudline, hence the thickness of layer j (1≤j≤n) can be denoted by h_j=z_j-1-z_j. Each layer is assumed to be composed of homogeneous TI poroelastic material and the interfaces between adjacent layers are perfectly connected. Moreover, the wave-height, wavelength and depth of sea water are denoted by H, L and d, respectively.

FIGURE 1

Figure 1 Interaction between the ocean wave and TI layered poroelastic seabed.

2.1. Governing equations

Following Biot (1962) and Zienkiewicz et al. (1980), the equations of motion for the poroelastic medium can be expressed in terms of Cartesian coordinate system as

$\begin{array}{ll}{\sigma }_{ij,j}=\rho {\ddot{u}}_i+{\rho }_f{\ddot{w}}_i& (1)\end{array}$

$\begin{array}{ll}-p_{,i}={\rho }_f{\ddot{u}}_i+\frac{{\rho }_f}{\varphi }{\ddot{w}}_i+\frac{{\rho }_{f}g}{k_i}{\dot{w}}_i& (2)\end{array}$

where the subscript index following a comma and dot above a symbol indicate the derivative with respect to a spatial coordinate and time, respectively; σ_ij is the total stress tensor; p is the fluid pressure; ϕ is the porosity; w_i=ϕ(U_i-u_i) is the average displacement component of the fluid relative to the solid in which u_i and U_i are the displacement components of the solid skeleton and pore fluid, respectively; ρ=(1-ϕ)ρ_s+ϕρ_f is the density of the solid-fluid mixture with ρ_f and ρ_s being the densities of fluid and solid, respectively; k_i is the permeability coefficient (or called hydraulic conductivity coefficient) in the ith direction; g indicates the acceleration of gravity.

Following generalized Hooke’s law, the stress-strain relationship under plane strain condition can be written as

$\begin{array}{ll}\left\{\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{zz}\\ {\sigma }_{xz}\\ p\end{array}\right\}=\left[\begin{array}{cccc}{A}_{11}& A_{12}& 0& M_{11}\\ A_{12}& A_{22}& 0& M_{33}\\ 0& 0& A_{33}& 0\\ M_{11}& M_{33}& 0& M\end{array}\right]\left\{\begin{array}{c}{u}_{x,x}\\ u_{z,z}\\ u_{x,z}\\ \zeta \end{array}\right\}& (3)\end{array}$

in which

$\begin{array}{ll}\begin{array}{l}{A}_{11}=C_{11}+{\alpha }_1^{2}M;A_{12}=C_{13}+{\alpha }_1{\alpha }_{3}M;A_{22}=C_{33}+{\alpha }_3^{2}M;A_{33}=C_{44};\\ M_{11}=-{\alpha }_{1}M;M_{33}=-{\alpha }_{3}M;\zeta =-\left(\partial w_x/\partial x+\partial w_z/\partial z\right)\end{array}& (4)\end{array}$

$\begin{array}{ll}\begin{array}{l}{\alpha }_1=1-\frac{C_{11}+C_{12}+C_{13}}{3K_s};{\alpha }_3=1-\frac{2C_{13}+C_{33}}{3K_s}\\ M={\left(\frac{1-\varphi }{K_s}+\frac{\varphi }{K_f}-\frac{2C_{11}+C_{33}+2C_{12}+4C_{13}}{9K_s^2}\right)}^{-1}\end{array}& (5)\end{array}$

where α_i (i=1, 3) and M are the Biot’s effective stress coefficients and Biot’s modulus, respectively; C₁₁, C₁₂, C₁₃, C₃₃, C₄₄ are the elastic constants, and the relation between the elastic constants and engineering parameters is listed in Appendix A; K_s and K_f are bulk moduli of solid skeleton and the pore fluid, respectively.

When seabed is in the unsaturated state with very small amount of gas, the following relation holds

$\begin{array}{ll}\frac{1}{K_f}=\frac{1}{K_w}+\frac{1-S_r}{P_{w0}}& (6)\end{array}$

where S_r is the degree of saturation; K_w is the true bulk modulus of elasticity of water which is generally selected as 2×10⁹Pa; P_w0=ρ_fgd is the absolute pore-fluid pressure with d being the depth of the sea water.

2.2. Continuity conditions

As already mentioned, we have assumed that any layer interface of the multilayered seabed is perfectly connected. Hence, the continuity conditions on z=z_f can be written as (i=x, z; j=x, z)

$\begin{array}{ll}\begin{array}{l}{u}_i(z_{f+})=u_i(z_{f-});{\sigma }_{ij}(z_{f+})={\sigma }_{ij}(z_{f-});\\ w_z(z_{f+})=w_z(z_{f-});p(z_{f+})=p(z_{f-})\end{array}& (7)\end{array}$

2.3. Boundary conditions

1) Boundary conditions at the seabed surface (z=0)

Based on the linear wave theory proposed by Wang (2017), it is known that the pressure on the seabed surface is maximum when the wave is at the crest and vice versa. According to the study by Jeng and Cha (2003), the dynamic wave pressure at the seabed surface (z=0) under the action of second-order Stokes wave can be expressed as

$\begin{array}{ll}{p}_b(x,t)=\mathrm{Re}{\displaystyle \sum _{m=1}^2{P}_m{\text{e}}^{\text{i}m\left(kx-\omega t\right)}}& (8)\end{array}$

in which

$\begin{array}{ll}{P}_1=\frac{{\rho }_{f}gH}{2\cosh \left(kd\right)}& (9)\end{array}$

$\begin{array}{ll}{P}_2=\frac{3}{4}{\gamma }_{w}H\left(\frac{\text{π}H}{L}\right)\frac{1}{\sinh \left(2kd\right)}\left[\frac{1}{{\sinh }^2\left(kd\right)}-\frac{1}{3}\right]& (10)\end{array}$

where i=(−1)^0.5 is an imaginary number; k=2π/L is the wavenumber (L=wavelength); ω=2π/T is the angular frequency of wave with period T. It is stated that we solve the problem in the complex variable domain to facilitate the derivation, hence we only take the real part of the complete solutions. Earlier study (Wang et al., 2005) has shown that the dispersion relation of second-order Stokes wave is consistent with linear wave, and ω can be calculated iteratively from the following equation

$\begin{array}{ll}{\omega }^2=gk\tanh \left(kd\right)& (11)\end{array}$

At the top surface of the seabed, the vertical effective stress and the shear stress are commonly assumed to be zero. Therefore, the boundary conditions on the top surface of the seabed can be written as

$\begin{array}{ll}{{\sigma }^{\prime }}_{zz}^{}={\tau }_{xz}=0;p=p_b(x,t) \text{at} z=z_0=0& (12)\end{array}$

2) Boundary conditions at the seabed bottom

For the seabed of finite thickness with a rigid and impermeable bottom, the boundary condition can be expressed as

$\begin{array}{ll}{u}_x=u_z=w_z=0\mathrm{ a}\mathrm{t }z=z_n=-h& (13)\end{array}$

3. Semi-analytical solution for the multilayered poroelastic seabed

3.1. General solution to the governing equations

Since the wave-induced response of the seabed is periodic, we express the field quantities in the form of complex variables as

$\begin{array}{ll}\left\{\begin{array}{c}{u}_x\left(x,z,t\right)\\ u_z\left(x,z,t\right)\\ w_x\left(x,z,t\right)\\ w_z\left(x,z,t\right)\\ p\left(x,z,t\right)\end{array}\right\}={\displaystyle \sum _{m=1}^2\left\{\begin{array}{c}{u}_x^{(m)}\left(x,z,t\right)\\ u_z^{(m)}\left(x,z,t\right)\\ w_x^{(m)}\left(x,z,t\right)\\ w_z^{(m)}\left(x,z,t\right)\\ p_{}^{(m)}\left(x,z,t\right)\end{array}\right\}}={\displaystyle \sum _{m=1}^2\mathrm{Re}}\left\{\begin{array}{c}{\overline{U}}_x^{(m)}\left(z\right)\\ {\overline{U}}_z^{(m)}\left(z\right)\\ {\overline{W}}_x^{(m)}\left(z\right)\\ {\overline{W}}_x^{(m)}\left(z\right)\\ {\overline{P}}_{}^{(m)}\left(z\right)\end{array}\right\}{\text{e}}^{\text{i}m(kx-\omega t)}& (14)\end{array}$

where m=1, 2 represents the response caused by the first-order and the second-order waves, respectively. ${\overline{U}}_x^{\left(m\right)}$, ${\overline{U}}_z^{\left(m\right)}$, ${\overline{W}}_x^{\left(m\right)}$, ${\overline{W}}_z^{\left(m\right)}$and ${\overline{P}}_{}^{\left(m\right)}$are the magnitudes of the dynamic response induced by the wave loading. To facilitate the derivation for the solution of the layered system in the following section, the stress components (e.g., σ_zz(x, z, t), τ_xz(x, z, t)) should also be expressed as the similar complex variable form. It is noted that the solution in the complex variables domain can be solved first, then taking the summation of the real part of each order results in the final solution.

Substituting Eq. (14) into Eq. (2), the following relations can be derived

$\begin{array}{ll}{\overline{W}}_x^{(m)}=\left(\text{i}km{\overline{P}}^{(m)}-{\rho }_f{m}^2{\omega }^2{\overline{U}}_x^{(m)}\right){\delta }_1^{(m)}& (15)\end{array}$

$\begin{array}{ll}{\overline{W}}_z^{(m)}=\left(\frac{\partial {\overline{P}}^{(m)}}{\partial z}-{\rho }_f{m}^2{\omega }^2{\overline{U}}_z^{(m)}\right){\delta }_3^{(m)}& (16)\end{array}$

where ${\delta }_1^{(m)}={\left({\rho }_f{m}^2{\omega }^2/\varphi +\text{i}m\omega {\rho }_{f}g/k_x\right)}^{-1}$;

$\begin{array}{ll}{\delta }_3^{(m)}={\left({\rho }_f{m}^2{\omega }^2/\varphi +\text{i}m\omega {\rho }_{f}g/k_z\right)}^{-1}& (17)\end{array}$

Combining Eqs. (1), (3), (14)-(16) and eliminating w_x and w_z, we have

$\begin{array}{ll}\left[\begin{array}{ccc}{a}_1^{(m)}+C_{44}{\text{D}}^2& \text{i}k{a}_2^{(m)}\text{D}& \text{i}k{a}_3^{(m)}\\ \text{i}k{a}_2^{(m)}\text{D}& a_4^{(m)}+C_{33}{\text{D}}^2& a_5^{(m)}\text{D}\\ \text{i}k{a}_3^{(m)}& a_5^{(m)}\text{D}& -a_6^{(m)}-{\delta }_3^{(m)}{\text{D}}^2\end{array}\right]\left[\begin{array}{c}{\overline{U}}_x^{(m)}(z)\\ {\overline{U}}_z^{(m)}(z)\\ {\overline{P}}^{(m)}(z)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]& (18)\end{array}$

where D is the differential operator (i.e., D=∂/∂z); $a_i^{(m)}$ (i=1-6) are the coefficients with being defined as

$\begin{array}{ll}\begin{array}{l}{a}_1^{(m)}=\rho m^2{\omega }^2-m^2{k}^2{C}_{11}-{\delta }_1^{(m)}{\rho }_f^2{m}^4{\omega }^4;\begin{array}{c}\end{array}{a}_2^{(m)}=m(C_{13}+C_{44});\begin{array}{c}\end{array}{a}_3^{(m)}={\delta }_1^{(m)}{\rho }_f{m}^3{\omega }^2-m{\alpha }_1;\\ a_4^{(m)}=\rho m^2{\omega }^2-m^2{k}^2{C}_{44}-{\delta }_3^{(m)}{\rho }_f^2{m}^4{\omega }^4;\begin{array}{c}\end{array}{a}_5^{(m)}={\delta }_3^{(m)}{\rho }_f{m}^2{\omega }^2-{\alpha }_3;\begin{array}{c}\end{array}{a}_6^{(m)}=\frac{1}{M}-{\delta }_1^{(m)}{m}^2{k}^2\end{array}& (19)\end{array}$

The potential function ${\overline{\Phi }}^{(m)}(z)$ is introduced, which has been successfully applied to the dynamic response of the seabed under linear wave (Li et al., 2020). The aforementioned field quantities can be expressed in terms of potential function as

$\begin{array}{ll}\begin{array}{l}{\overline{U}}_x^{(m)}(z)=-\text{i}k\left[a_2^{(m)}\left(a_6^{(m)}+{\delta }_3^{(m)}{\text{D}}^2\right)+a_3^{(m)}{a}_5^{(m)}\right]\text{D}{\overline{\Phi }}^{(m)}(z)\\ {\overline{U}}_z^{(m)}(z)=\left[\left(a_6^{(m)}+{\delta }_3^{(m)}{\text{D}}^2\right)\left(a_1^{(m)}+C_{44}{\text{D}}^2\right)-{\left(a_3^{(m)}\right)}^2{k}^2\right]{\overline{\Phi }}^{(m)}(z)\\ {\overline{P}}^{(m)}(z)=\left[a_5^{(m)}\left(a_1^{(m)}+C_{44}{\text{D}}^2\right)+a_2^{(m)}{a}_3^{(m)}{k}^2\right]\text{D}{\overline{\Phi }}^{(m)}(z)\end{array}& (20)\end{array}$

It is noted that the introduced potential function automatically satisfies the first and third equations in Eq. (18). Substituting Eq. (20) into Eq. (18), the final form of the governing equation can be written as

$\begin{array}{ll}{r}_1^{(m)}{\text{D}}^6{\overline{\Phi }}^{(m)}(z)+r_2^{(m)}{\text{D}}^4{\overline{\Phi }}^{(m)}(z)+r_3^{(m)}{\text{D}}^2{\overline{\Phi }}^{(m)}(z)+r_4^{(m)}{\overline{\Phi }}^{(m)}(z)=0& (21)\end{array}$

where $r_i^{(m)}$ (i=1-4) are coefficients, whose detailed expressions are given in Appendix B.

Through some algebraic calculations, the solution of Eq. (21) can be given as

$\begin{array}{ll}{\overline{\Phi }}^{(m)}(z)={\displaystyle \sum _{i=1}^3{A}_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}+}{B}_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}& (22)\end{array}$

where $\pm {\lambda }_i^{\left(m\right)}$(i=1-3) are given in Appendix C. The values of $A_i^{(m)}$and $B_i^{(m)}$(i=1-3) are to be determined by the boundary conditions.

Substituting Eq. (22) into Eq. (20) and performing some algebraic calculations, the general solutions of displacements, pore pressure and stresses in any homogeneous layer under the action of second-order Stokes wave can be expressed as

$\begin{array}{ll}\begin{array}{l}{u}_x^{(m)}(x,z,t)={\displaystyle \sum _{i=1}^3{\chi }_i^{(m)}\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}-B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\\ u_z^{(m)}(x,z,t)={\displaystyle \sum _{i=1}^3{\phi }_i^{(m)}\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}+B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\\ p^{(m)}(x,z,t)={\displaystyle \sum _{i=1}^3{\xi }_i^{(m)}\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}-B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\\ w_z^{(m)}(x,z,t)={\displaystyle \sum _{i=1}^3{\eta }_i^{(m)}\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}+B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\end{array}& (23)\end{array}$

$\begin{array}{ll}\begin{array}{l}{\sigma }_{xx}^{\left(m\right)}(x,z,t)={\displaystyle \sum _{i=1}^3\left(\text{i}km{C}_{11}{\chi }_i^{(m)}+C_{13}{\lambda }_i^{(m)}{\phi }_i^{(m)}-{\alpha }_1{\xi }_i^{(m)}\right)\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}-B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\\ {\sigma }_{zz}^{\left(m\right)}(x,z,t)={\displaystyle \sum _{i=1}^3\left(\text{i}km{C}_{13}{\chi }_i^{(m)}+C_{33}{\lambda }_i^{(m)}{\phi }_i^{(m)}-{\alpha }_3{\xi }_i^{(m)}\right)\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}-B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\\ {\tau }_{xz}^{\left(m\right)}(x,z,t)={\displaystyle \sum _{i=1}^3{C}_{44}\left(\text{i}km{\phi }_i^{(m)}+{\lambda }_i^{(m)}{\chi }_i^{(m)}\right)\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}+B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\end{array}& \text{(24a)}\end{array}$

$\begin{array}{ll}\begin{array}{l}{{\sigma }^{\prime }}_{xx}^{\left(m\right)}(x,z,t)={\displaystyle \sum _{i=1}^3\left(\text{i}km{C}_{11}{\chi }_i^{(m)}+C_{13}{\lambda }_i^{(m)}{\phi }_i^{(m)}\right)\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}-B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\\ {{\sigma }^{\prime }}_{zz}^{\left(m\right)}(x,z,t)={\displaystyle \sum _{i=1}^3\left(\text{i}km{C}_{13}{\chi }_i^{(m)}+C_{33}{\lambda }_i^{(m)}{\phi }_i^{(m)}\right)\left(A_i^{(m)}{\text{e}}^{{\lambda }_i^{(m)}z}-B_i^{(m)}{\text{e}}^{-{\lambda }_i^{(m)}z}\right){\text{e}}^{\text{i}m(kx-\omega t)}}\end{array}& \text{(24b)}\end{array}$

where ${\chi }_i^{(m)}$, ${\phi }_i^{(m)}$, ${\xi }_i^{(m)}$and ${\eta }_i^{(m)}$(i=1-3) are the coefficients given in Appendix D. It is noted that the effective stresses in Eq. (24b) are derived via the relations between total stress and pore pressure.

3.2.. Solution of multilayered seabed

We adopt the dual variable and position (DVP) method (Pan, 2019; Liu et al., 2022) to expand the single-layer solution to the multilayered solution. It is stated again that the layered solution corresponding to different m will be solved separately and then be superposed together to gain the complete solution. To facilitate the derivation, e^im(kx-ωt) is suppressed, and the vectors and diagonal matrices are defined as

$U^{(m)}(z)={\left[{\overline{U}}_x^{(m)}(z),{\overline{U}}_z^{(m)}(z),{\overline{W}}_z^{(m)}(z)\right]}^{\text{T}}$;

$\begin{array}{ll}{T}^{(m)}(z)={\left[{\overline{\tau }}_{xz}^{(m)}(z),{\overline{\sigma }}_{zz}^{(m)}(z),{\overline{P}}^{(m)}(z)\right]}^{\text{T}}& (25)\end{array}$

$E_1^{(m)}(z)=diag\left[{\text{e}}^{{\lambda }_1^{(m)}z},{\text{e}}^{{\lambda }_2^{(m)}z},{\text{e}}^{{\lambda }_3^{(m)}z}\right]$;

$\begin{array}{ll}{E}_2^{(m)}(z)=diag\left[{\text{e}}^{-{\lambda }_1^{(m)}z},{\text{e}}^{-{\lambda }_2^{(m)}z},{\text{e}}^{-{\lambda }_3^{(m)}z}\right]& (26)\end{array}$

where ${\overline{\tau }}_{xz}^{(m)}(z)$and ${\overline{\sigma }}_{zz}^{(m)}(z)$are the stress magnitudes.

Then the single-layer solution for jth layer can be rewritten in terms of matrix form as

$\begin{array}{ll}\left[\begin{array}{c}{U}^{(m)}(z)\\ T^{(m)}(z)\end{array}\right]=\left[\begin{array}{cc}{M}_{11}^{(m)}& M_{12}^{(m)}\\ M_{21}^{(m)}& M_{22}^{(m)}\end{array}\right]\left[\begin{array}{cc}{E}_1^{(m)}\left(z-z_{j-1}\right)& 0\\ 0& E_2^{(m)}\left(z-z_j\right)\end{array}\right]\left[\begin{array}{c}{K}_{+}^{(m)}\\ K_{-}^{(m)}\end{array}\right]& (27)\end{array}$

where $\left[M_{ij}^{(m)}\right]$ is the 3×3 submatrix of 6×6 matrix M^(m), the elements of which are given in Appendix E.

Substituting z=z_j−1 and z=z_j into Eq. (27), the solutions for the top and bottom interfaces of jth layer can be written as

$\begin{array}{ll}\left[\begin{array}{c}{U}^{(m)}\left(z_{j-1}\right)\\ T^{(m)}\left(z_{j-1}\right)\end{array}\right]=\left[\begin{array}{cc}{M}_{11}^{(m)}& M_{12}^{(m)}{E}_2^{(m)}\left(h_j\right)\\ M_{21}^{(m)}& M_{22}^{(m)}{E}_2^{(m)}\left(h_j\right)\end{array}\right]\left[\begin{array}{c}{K}_{+}^{(m)}\\ K_{-}^{(m)}\end{array}\right]& (28)\end{array}$

$\begin{array}{ll}\left[\begin{array}{c}{U}^{(m)}\left(z_j\right)\\ T^{(m)}\left(z_j\right)\end{array}\right]=\left[\begin{array}{cc}{M}_{11}^{(m)}{E}_1^{(m)}\left(-h_j\right)& M_{12}^{(m)}\\ M_{21}^{(m)}{E}_1^{(m)}\left(-h_j\right)& M_{22}^{(m)}\end{array}\right]\left[\begin{array}{c}{K}_{+}^{(m)}\\ K_{-}^{(m)}\end{array}\right]& (29)\end{array}$

By eliminating the unknown vectors $K_{+}^{(m)}$, $K_{-}^{(m)}$ and making use of DVP method, the relation for the layer j can be expressed as

$\begin{array}{ll}\left[\begin{array}{c}{U}^{(m)}(z_{j-1})\\ T^{(m)}(z_j)\end{array}\right]=\left[\begin{array}{cc}{N}_{11\left(j\right)}^{(m)}& N_{12\left(j\right)}^{(m)}\\ N_{21\left(j\right)}^{(m)}& N_{22\left(j\right)}^{(m)}\end{array}\right]\left[\begin{array}{c}{U}^{(m)}(z_j)\\ T^{(m)}(z_{j-1})\end{array}\right]& (30)\end{array}$

where

$\begin{array}{ll}\left[\begin{array}{cc}{N}_{11\left(j\right)}^{(m)}& N_{12\left(j\right)}^{(m)}\\ N_{21\left(j\right)}^{(m)}& N_{22\left(j\right)}^{(m)}\end{array}\right]=\left[\begin{array}{cc}{M}_{11}^{(m)}& M_{12}^{(m)}{E}_2^{(m)}\left(h_j\right)\\ M_{21}^{(m)}{E}_1^{(m)}\left(-h_j\right)& M_{22}^{(m)}\end{array}\right]{\left[\begin{array}{cc}{M}_{11}^{(m)}{E}_1^{(m)}\left(-h_j\right)& M_{12}^{(m)}\\ M_{21}^{(m)}& M_{22}^{(m)}{E}_2^{(m)}\left(h_j\right)\end{array}\right]}^{-1}& (31)\end{array}$

After gaining the layer-matrix relation for layer j+1, utilizing the continuity conditions Eq. (7) and making some algebraic operations leads to the recursive relationship from jth layer to (j+1)th layer

$\begin{array}{ll}\left[\begin{array}{c}{U}^{(m)}\left(z_{j-1}\right)\\ T^{(m)}\left(z_{j+1}\right)\end{array}\right]=\left[\begin{array}{cc}{N}_{11\left(j:j+1\right)}^{(m)}& N_{12\left(j:j+1\right)}^{(m)}\\ N_{21\left(j:j+1\right)}^{(m)}& N_{22\left(j:j+1\right)}^{(m)}\end{array}\right]\left[\begin{array}{c}{U}^{(m)}\left(z_{j+1}\right)\\ T^{(m)}\left(z_{j-1}\right)\end{array}\right]& (32)\end{array}$

in which

$\begin{array}{ll}\begin{array}{l}\left[N_{11\left(j:j+1\right)}^{(m)}\right]=\left[N_{11\left(j\right)}^{(m)}{N}_{11\left(j+1\right)}^{(m)}\right]+\left[N_{11\left(j\right)}^{(m)}{N}_{12\left(j+1\right)}^{(m)}\right]{\left[I-N_{21\left(j\right)}^{(m)}{N}_{12\left(j+1\right)}^{(m)}\right]}^{-1}\left[N_{21\left(j\right)}^{(m)}{N}_{11\left(j+1\right)}^{(m)}\right]\\ \left[N_{12\left(j:j+1\right)}^{(m)}\right]=\left[N_{12\left(j\right)}^{(m)}\right]+\left[N_{11\left(j\right)}^{(m)}{N}_{12\left(j+1\right)}^{(m)}\right]{\left[I-N_{21\left(j\right)}^{(m)}{N}_{12\left(j+1\right)}^{(m)}\right]}^{-1}\left[N_{22\left(j\right)}^{(m)}\right]\\ \left[N_{21\left(j:j+1\right)}^{(m)}\right]=\left[N_{21\left(j+1\right)}^{(m)}\right]+\left[N_{22\left(j+1\right)}^{(m)}\right]{\left[I-N_{21\left(j\right)}^{(m)}{N}_{12\left(j+1\right)}^{(m)}\right]}^{-1}\left[N_{21\left(j\right)}^{(m)}{N}_{11\left(j+1\right)}^{(m)}\right]\\ \left[N_{22\left(j:j+1\right)}^{(m)}\right]=\left[N_{22\left(j+1\right)}^{(m)}\right]{\left[I-N_{21\left(j\right)}^{(m)}{N}_{12\left(j+1\right)}^{(m)}\right]}^{-1}\left[N_{22\left(j\right)}^{(m)}\right]\end{array}& (33)\end{array}$

where I denotes the identity matrix.

After obtaining the recurrence relation Eq. (32), the dynamic response of the layered seabed can be solved according to the boundary conditions. For the seabed of finite thickness, the boundary conditions in Eqs. (12) and (13) can be rewritten as

$\begin{array}{ll}{T}^{(m)}(z_0)={[0,-{\alpha }_{31}{P}^{(m)},P^{(m)}]}^T\text{at\hspace{0.17em}}z=z_0=0& (34)\end{array}$

$\begin{array}{ll}{U}^{(m)}(z_n)=0\text{\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}\hspace{0.17em}}z=z_n=-h& (35)\end{array}$

where the subscript 1 in α₃₁ denotes the layer number; P⁽¹⁾=P₁ and P⁽²⁾=P₂.

In order to solve the dynamic response at arbitrary depth z=z_a (say in layer j, see Figure 1), we further divide the homogeneous layer j into two sublayers, i.e., sublayers a1 and a2 on the top and bottom parts, respectively. We propagate the recursive relation Eq. (32) from layer 1 to sublayer a1 and from sublayer a2 to layer n, which yields the global matrix as

$\begin{array}{ll}\left[\begin{array}{c}{U}^{(m)}\left(z_0\right)\\ U^{(m)}\left(z_a\right)\\ T^{(m)}\left(z_a\right)\\ T^{(m)}\left(z_n\right)\end{array}\right]={\left[\begin{array}{cccc}-I& N_{11\left(1:a1\right)}^{(m)}& 0& 0\\ 0& N_{21\left(1:a1\right)}^{(m)}& -I& 0\\ 0& -I& N_{12\left(a2:n\right)}^{(m)}& 0\\ 0& 0& N_{22\left(a2:n\right)}^{(m)}& -I\end{array}\right]}^{-1}\left[\begin{array}{c}-\left[N_{12\left(1:a1\right)}^{(m)}\right]T^{(m)}\left(z_0\right)\\ -\left[N_{22\left(1:a1\right)}^{(m)}\right]T^{(m)}\left(z_0\right)\\ 0\\ 0\end{array}\right]& (36)\end{array}$

Till here, the solutions for the filed quantities corresponding to different m are gained. Then taking the summation of solutions corresponding to m=1 and 2 yields the final solutions. It should be pointed out that for the homogeneous TI poroelastic seabed, the analytical solution can be easily derived by combining the boundary conditions in Eqs. (12) and (13), and general solution in Eqs. (23) and (24). In addition, if the seabed is actually a layered half-space, we only need set the nth layer with a very large thickness to gain the half-space results.

4. Numerical results and discussions

4.1. Verification of the present solution

In order to validate the reliability of the present solution, two cases corresponding to single-layer and multilayered seabed under linear wave are considered first. In the comparison, we take the amplitude of the pore pressure |p| and vertical effective stress |σ^′_zz| as the analyzed physical quantities. That is to say, |p| and |σ^′_zz| are the maximum value of p and σ^′_zz , respectively. The variable used for normalization is defined as p₀=ρ_fgH/(2cosh(kd)). For the single-layer seabed (e.g., graveled seabed), the solution of Jeng and Lee (2001) and the reduced one of the present study are compared with using the following parameters: T=15 s, d=20 m, H=2 m, h=20 m, v=1/3, ϕ=0.35, S_r=0.95-1.0, ρ_s=2650 kg/m³, ρ_f=1000 kg/m³, k_x=k_z=1×10^-1 m/s, G_h=G_v=5×10⁷ N/m². Moreover, the following poroelastic properties α₁=α₃ = 1 and M=K_f/ϕ are used in the present solution. Figure 2 shows the comparison of the present reduced solution with that by Jeng and Lee (2001) for a homogeneous isotropic and poroelastic seabed subjected to linear wave. In order to gain the reduced solution for linear wave, we need to fix P₂ = 0 and thus m=1. Notice that the complete Biot’s poroelastodynamic theory are considered in both studies. It is observed from Figure 2 that the solution of the present study is in good agreement with that of Jeng and Lee (2001).

FIGURE 2

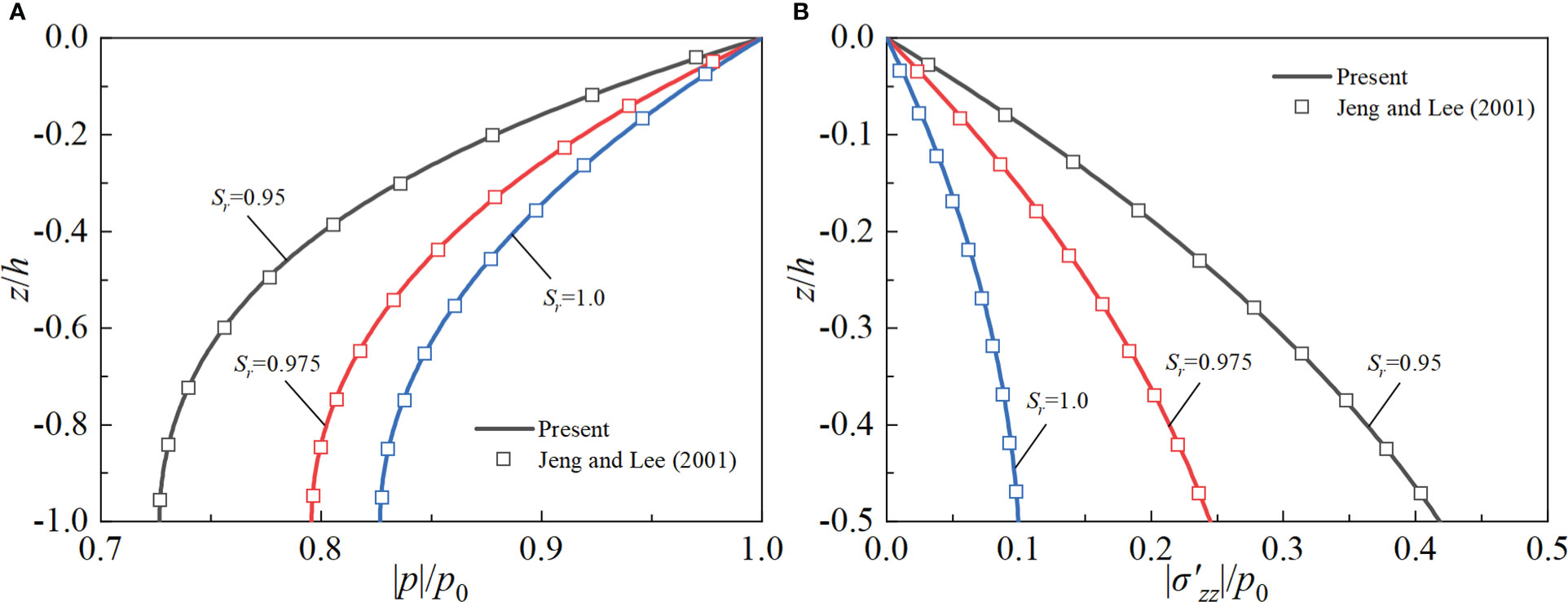
Figure 2 Comparison of the present solution with existing one for a homogeneous isotropic and poroelastic seabed under linear wave: (A) pore pressure; (B) vertical effective stress.

We further consider a two-layer seabed under linear wave and compare the reduced results from present study with those by Hsu et al. (1995) as shown in Figure 3. The parameters used for verification are: T=10 s, d=20 m, H=6 m, L=121.12 m, k_z2 = 10^-3 m/s, h₁ = 10 m and h₂ = 40 m. The remaining seabed parameters, except for permeability coefficient, are the same for both two layers and taken as v=1/3, ϕ=0.3, S_r=0.975, ρ_f=1000 kg/m³, ρ_s=2000 kg/m³, G_v=G_h=1×10⁷ N/m², α₁=α₃ = 1 and M=K_f/ϕ. It can be seen from Figure 3 that the results from the reduced solution of present study agree well with those of Hsu et al. (1995). It can be concluded from above two cases that the present solutions are applicable for both the single-layer and multilayered cases.

FIGURE 3

Figure 3 Comparison of pore pressure of a layered isotropic poroelastic seabed under linear wave.

The present solution is further compared with the existing one for a homogeneous, isotropic and poroelastic seabed under nonlinear wave. In the comparison, the parameters are: T=10 s, d=10 m, L=240 m, H=0.08tanh(kd) m, h=50 m, v=0.333, ϕ=0.3, ρ_s=2650 kg/m³, ρ_f=1000 kg/m³, k_x=k_z=1×10^-3 m/s, G_h=G_v=1×10⁷ N/m², α₁=α₃ = 1 and M=K_f/ϕ. Figure 4 shows the comparison of the present reduced solution with that by Zhou et al. (2011) for a homogeneous, isotropic and poroelastic seabed subjected to second-order Stokes wave. |u_z| in Figure 4 denotes the amplitude of u_z. It can be observed from Figure 4 that the results from the present study have good agreement with those from Zhou et al. (2011).

FIGURE 4

Figure 4 Comparison of the present solution with existing one for a homogeneous, isotropic and poroelastic seabed under second-order Stokes wave.

4.2. Numerical analysis

It has been mentioned in Li et al. (2020) that the linear wave-induced dynamic response of a finite-thickness seabed is dependent on the properties of the soil, and anisotropic stiffness and permeability have significant effect on the seabed response. However, the dynamic response of the anisotropic seabed under non-linear wave is still unknown. Therefore, in the subsequent study, we will analyze the dynamic response and liquefaction behavior of single-layer and multilayered anisotropic seabed with different anisotropic parameters and degree of saturation and subjected to non-linear wave. The basic poroelastic properties and wave conditions used in the following analysis are listed in Table 1, and it should be pointed out that all parameters are taken from this table if there is no further statement.

TABLE 1

Table 1 The basic poroelastic properties and wave conditions.

Figure 5 shows the comparison of the induced pressures induced by non-linear wave (i.e., second-order Stokes wave) and linear wave at the seabed surface. It can be observed that the wave loading by non-linear wave is different with that by linear wave. Compared to linear wave, the wave loading by non-linear wave shows higher/sharper wave crest and lower/flatter wave trough, and takes on more evident characteristics of asymmetric distribution. As a result, fully understanding the difference in the induced filed quantities (e.g., pore pressure, vertical effective stress) by linear and non-linear waves for different soil properties is of great importance. In the following parts, based on the input data given in Table 1, the influence of anisotropic stiffness, anisotropic permeability, degree of saturation and stratification on the vertical distribution of maximum pore pressure |p|, vertical effective stress |σ^′_zz| and shear stress |τ_xz| are analyzed for both linear and non-linear waves. Unless otherwise stated, the solid and dash line denote, respectively, the response of non-linear and line waves in Figures 6–14.

FIGURE 5

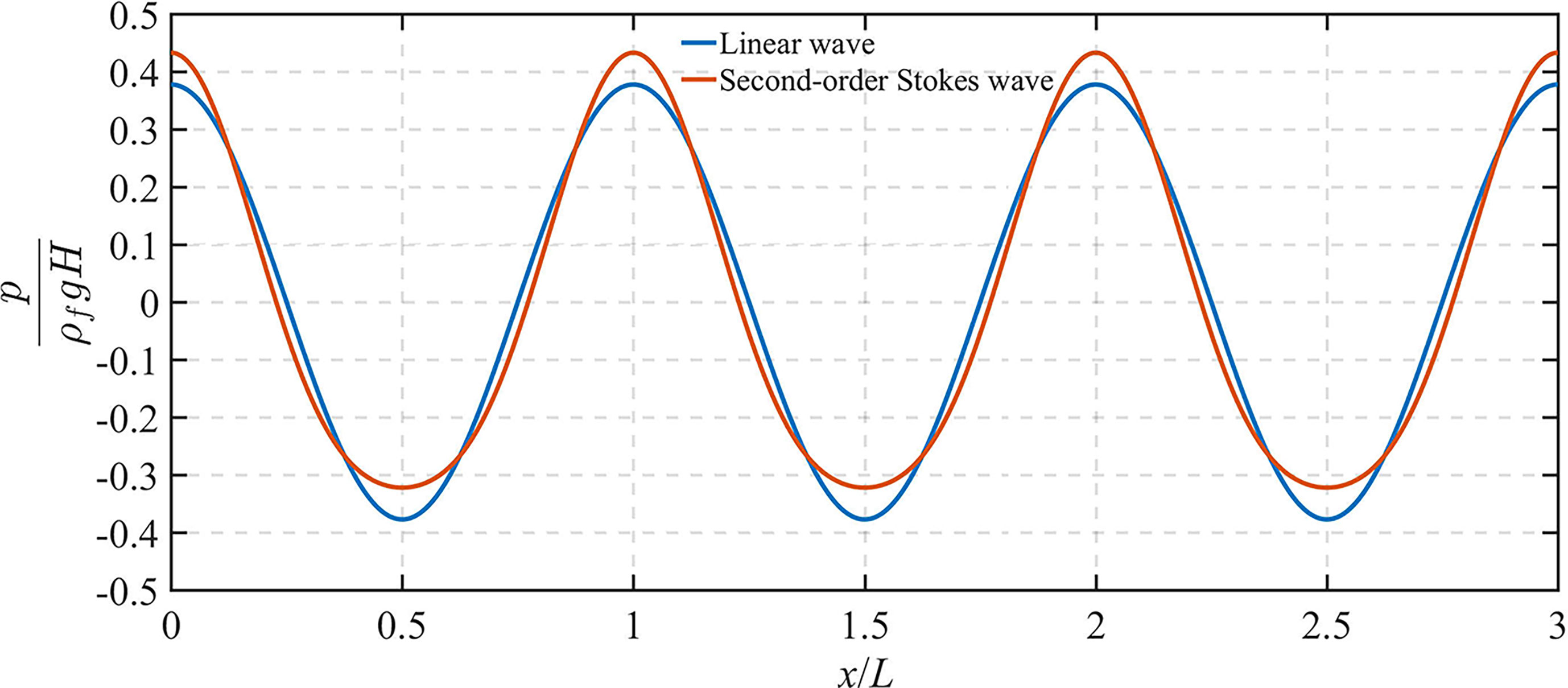
Figure 5 Comparison between the induced pressures by second-order Stokes wave and linear wave at the seabed surface.

FIGURE 6

Figure 6 Influence of anisotropic stiffness on the dynamic response of the seabed under non-linear and linear waves: anisotropic moduli ratios G_v/E_v in (A–C) and E_h/E_v in (D–F).

4.2.1. Influence of soil properties

Figure 6 illustrates the influence of anisotropic stiffness on the dynamic response of the seabed under non-linear and linear waves. The anisotropic stiffness is commonly portrayed by two anisotropic moduli ratios, i.e., E_h/E_v and G_v/E_v with reference modulus E_v. For non-linear wave, the maximum pore pressure |p| decreases (increases) with the increase of E_h/E_v (G_v/E_v), while the maximum vertical effective stress |σ^′_zz| shows the opposite changing trend. Moreover, the effect of G_v/E_v is more pronounced than that of E_h/E_v, especially for the influence on the maximum shear stress |τ_xz|. It can be also observed that, for both the non-linear and linear waves, the changing trend of field quantities is similar except for the different amplitude. That is to say, for fixed anisotropic moduli ratio, |p|, |σ^′_zz| and |τ_xz| by non-linear wave are greater than those by linear wave within the observed depth range.

As known to us, the marine sediments exhibit obvious anisotropic permeability in nature and a small amount of gas is common to be observed in those bulk materials. The anisotropic permeability ratio k_z/k_x is commonly introduced to characterize the anisotropic permeability, while the degree of saturation S_r is defined as the ratio of the volume of water to the total volume of void space to intuitively reflect the content of gas. To clearly reflect the influence of k_z/k_x and S_r, the seabed is assumed to be composed of isotropic poroelastic material. Figures 7, 8 depict the influence of anisotropic permeability and degree of saturation on the dynamic response of homogeneous isotropic poroelastic seabed, respectively. It can be seen from Figures 7, 8 that k_z/k_x and S_r have marked influence on the distribution of the pore pressure and vertical effective stress. Under the action of linear or non-linear wave, |p| (|σ^′_zz| ) increase (decreases) with increasing k_z/k_x or S_r. However, the effect of k_z/k_x and S_r on |τ_xz| is relatively small, particularly |τ_xz| is not very sensitive to S_r. Similar to the influence of anisotropic stiffness, |p|, |σ^′_zz| and |τ_xz| by the non-linear wave are greater than those by linear wave in the observed depth range.

FIGURE 7

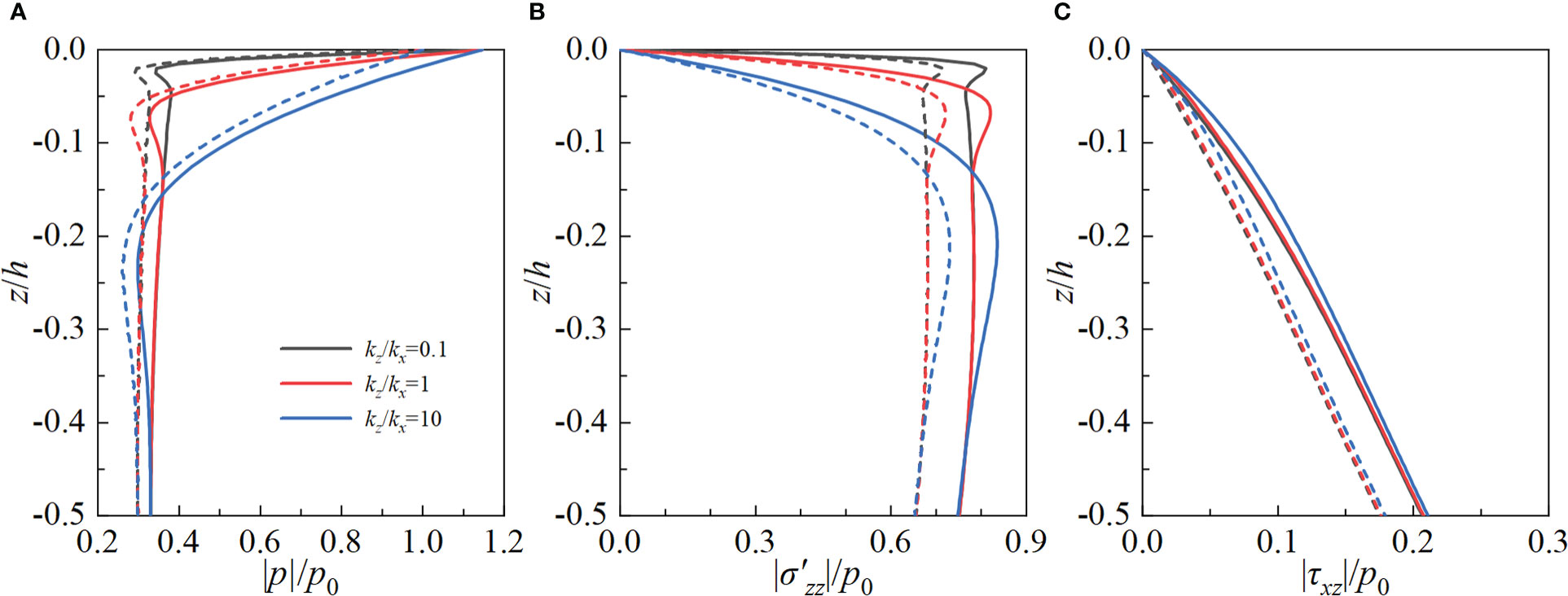
Figure 7 Influence of anisotropic permeability on the dynamic response of homogeneous isotropic seabed under non-linear and linear waves. (A) pore pressure; (B) vertical effective stress; (C) shear stress.

FIGURE 8

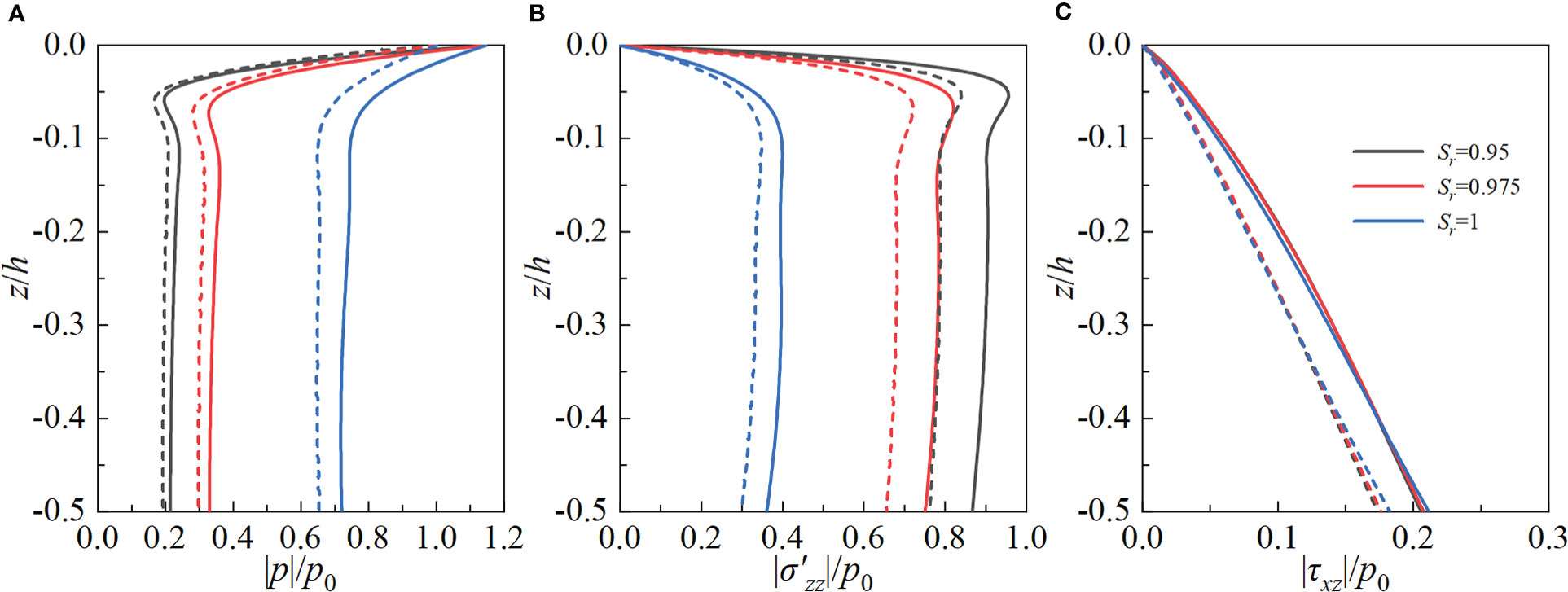
Figure 8 Influence of degree of saturation S_r on the dynamic response of homogeneous isotropic seabed under non-linear and linear waves. (A) pore pressure; (B) vertical effective stress; (C) shear stress.

In practical engineering, the stratification is the intrinsic behavior of the seabed due to the long-time sedimentation process of the soil. To study the effect of stratification, a typical two-layer TI poroelastic seabed with different stiffness is constructed. The thicknesses of two layers are fixed at h₁ = 8 m and h₂ = 16 m, respectively. The specific parameters used in calculation for plotting Figure 9 are E_hi/E_vi=0.8, G_vi/E_vi=0.6, k_zi/k_xi=1 and S_ri=0.975 (i=1, 2), and the left parameters are selected from Table 1. As shown in Figure 9, under the action of the non-linear wave, |p| (|σ^′_zz| ) decreases (increases) roughly with increasing E_v1/E_v2 above the layer interface, while they show the completely opposite changing trend below the layer interface. |τ_xz| decreases with increasing E_v1/E_v2, and there exists a difference in the changing rate above and below the layer interface. Moreover, the amplitude of induced field quantities by non-linear wave are still larger than that by the linear wave. Therefore, it could be concluded from Figures 6–9 that the maximum pore pressure, vertical effective stress and shear stress by non-linear wave are higher than those by linear wave due to the larger wave crest of non-linear wave.

FIGURE 9

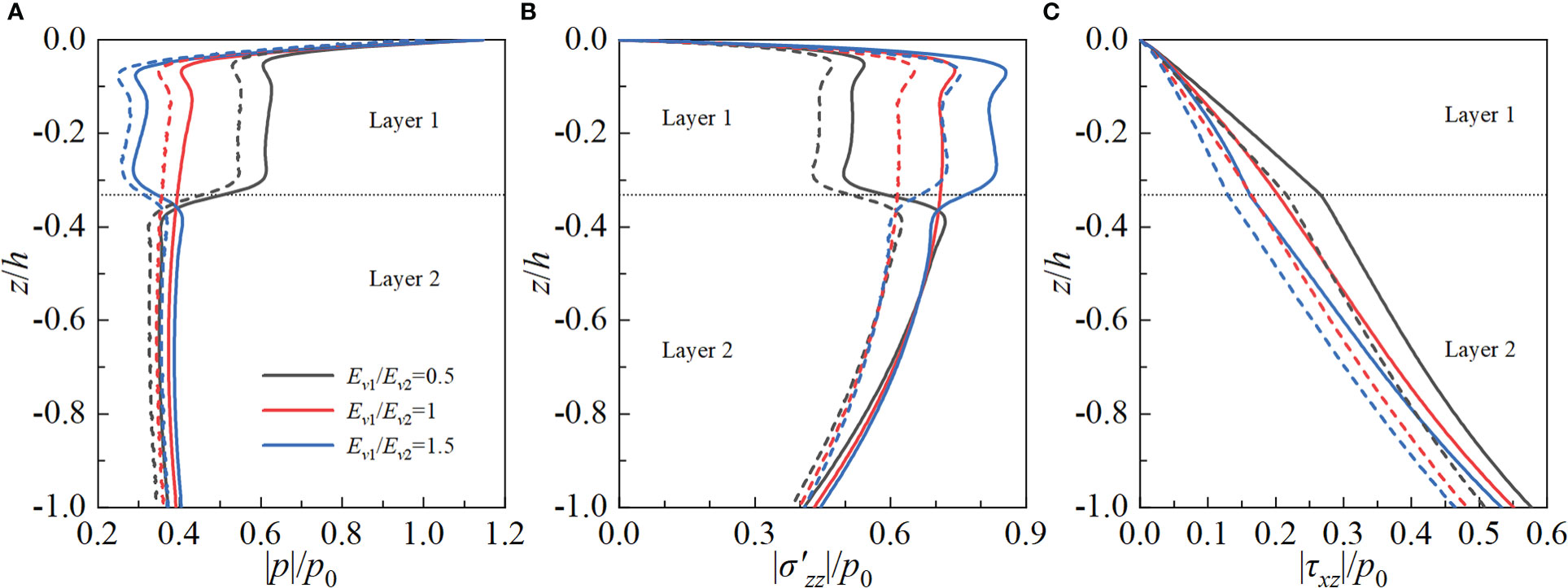
Figure 9 Influence of modulus ratio E_v1/E_v2 on the dynamic response of the TI poroelastic seabed under non-linear and linear waves. (A) pore pressure; (B) vertical effective stress; (C) shear stress.

4.2.2. Analysis of liquefaction

Hsu et al. (1995) reported that that the liquefaction criterion based on effective normal stress may not be valid when effective stress is low. Hence, the 3-D liquefaction criterion proposed by Hsu et al. (1995) is employed in the present study with being defined as

$\begin{array}{ll}-\frac{\left(1+2K_0\right)}{3}\left({\gamma }_s-{\gamma }_w\right)z\le -\left(p_b-p\right)& (37)\end{array}$

where K₀=v/(1−v) denotes the lateral earth pressure coefficient at rest. γ_s and γ_w denote the unit weights of the seabed soil and water, respectively. p_b and p denote the wave pressure at the surface of the seabed and the wave-induced pore pressure at depth z in the seabed, respectively. This calculation method considers the left and right sides of Eq. (37) as the initial vertical effective stress and the excess pore pressure, respectively. Eq. (37) indicates that when the excess pore pressure is greater than the initial vertical effective stress, liquefaction of the seabed will potentially occur. In the following part, the liquefaction zone for different parameters under both non-linear and linear waves are analyzed in detail.

The liquefied zone in a homogeneous TI poroelastic seabed for different anisotropic moduli ratios under both linear and non-linear waves is shown in Figure 10. The anisotropic ratios E_h/E_v and G_v/E_v have significant influence on the maximum potential liquefaction depth for two kind of waves. The maximum liquefaction depth increases with increasing E_h/E_v or decreasing G_v/E_v, which indicates that it is necessary to consider the anisotropy of the seabed to accurately judge the liquefaction potential. Moreover, for the same material parameters of the seabed, the maximum liquefaction depth induced by the non-linear wave is markedly lower than that by the linear wave. However, the liquefaction width by the non-linear wave is wider than that by the linear wave. This phenomenon could be due to the fact that the wave trough of the non-linear ocean wave is much lower and flatter than the linear wave.

FIGURE 10

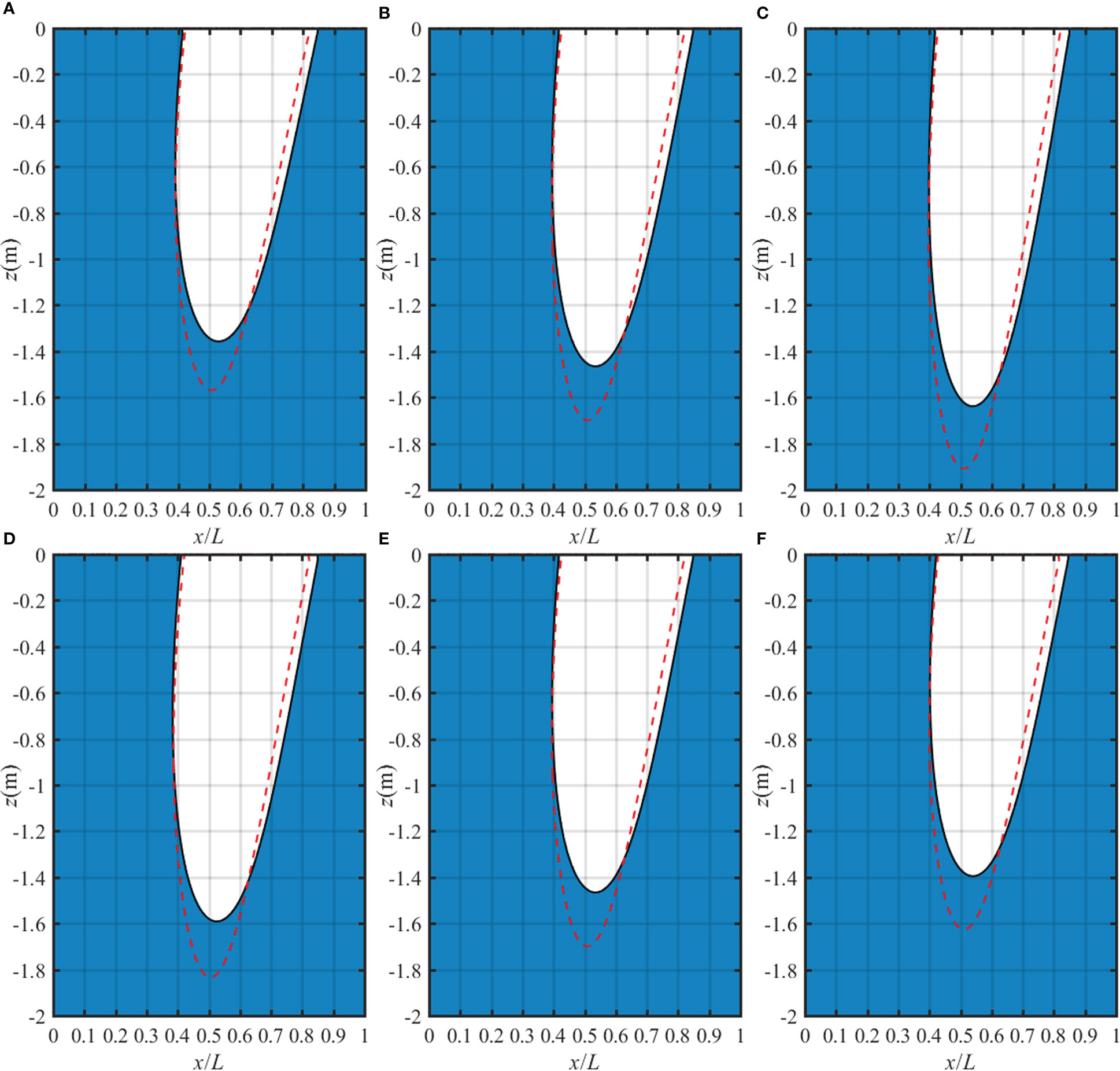
Figure 10 Liquefaction zone in a homogeneous TI poroelastic seabed for various anisotropic moduli ratio: (A) E_h/E_v=0.5, (B) E_h/E_v=1 and (C) E_h/E_v=1.5 with fixed G_v/E_v=1/2.8; (D) G_v/E_v=0.1, (E) G_v/E_v=1/2.8 and (F) G_v/E_v=0.6 with fixed E_h/E_v=1.

The liquefaction zone in a homogeneous isotropic poroelastic seabed for various anisotropic permeability ratio is shown in Figure 11. It can be seen from Figure 11 that the anisotropic permeability makes great contribution to the liquefaction potential. When k_z/k_x=1, the liquefaction depth in the seabed is the biggest. As k_z/k_x decreases (e.g., k_z/k_x<1), the liquefaction depth shows little decrease and liquefaction width shows obvious increase. Through detailed calculation, when k_z/k_x further decreases to 0.0001, the liquefaction depth shows negligible variation indicating there exists a critical value for k_z/k_x. However, when k_z/k_x increases (e.g., k_z/k_x>1), both liquefaction depth and liquefaction width markedly decrease. Through further calculation, when k_z/k_x=10 (the result is not given in the figure), the non-linear wave no longer produces liquefaction and the liquefaction zone produced by the linear wave tends to zero. This phenomenon may be due to the fact that the pore pressure is hard to develop in the soil with better permeability, thus the vertical effective stress makes the controlling contribution. It could be concluded that increasing the vertical permeability of the seabed will greatly reduce the probability of the occurrence of liquefaction.

FIGURE 11

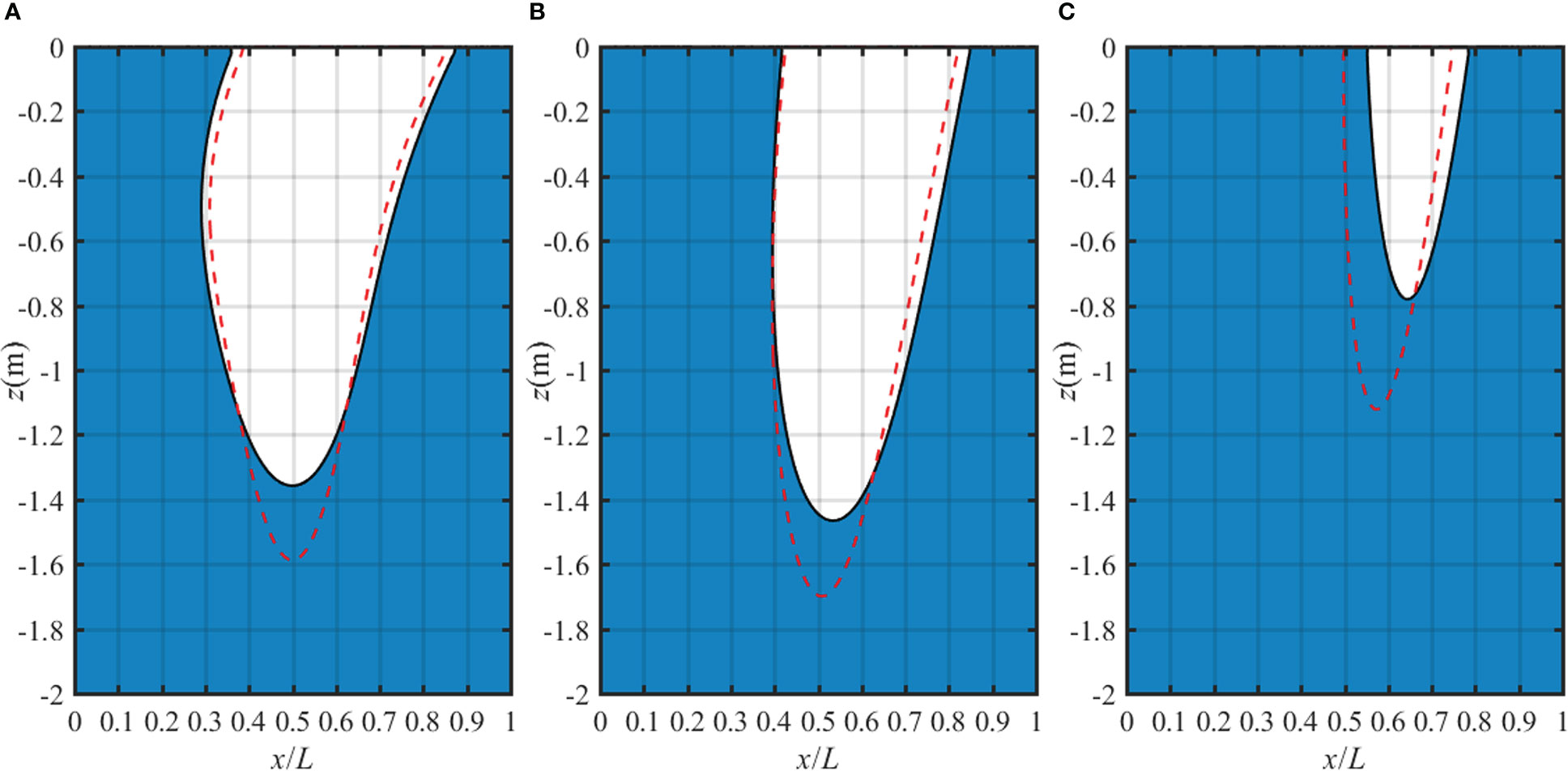
Figure 11 Liquefaction zone in a homogeneous isotropic poroelastic seabed for various anisotropic permeability ratio: (A) k_z/k_x=0.1, (B) k_z/k_x=1 and (C) k_z/k_x=5.

Figure 12 shows the liquefaction zone in a homogeneous isotropic poroelastic seabed for various degree of saturation. As reported in past studies, when S_r=1 the subgrade would not liquefy (Jeng, 1996), while the seabed could liquefy at certain soil properties conditions (Chen et al., 2022). Hence, we present the results corresponding to S_r=0.95, 0.975 and 0.99. It is found that the maximum liquefaction depth decreases significantly with increasing S_r. When the seabed tends to be completely saturated, the probability of seabed liquefaction will be greatly reduced.

FIGURE 12

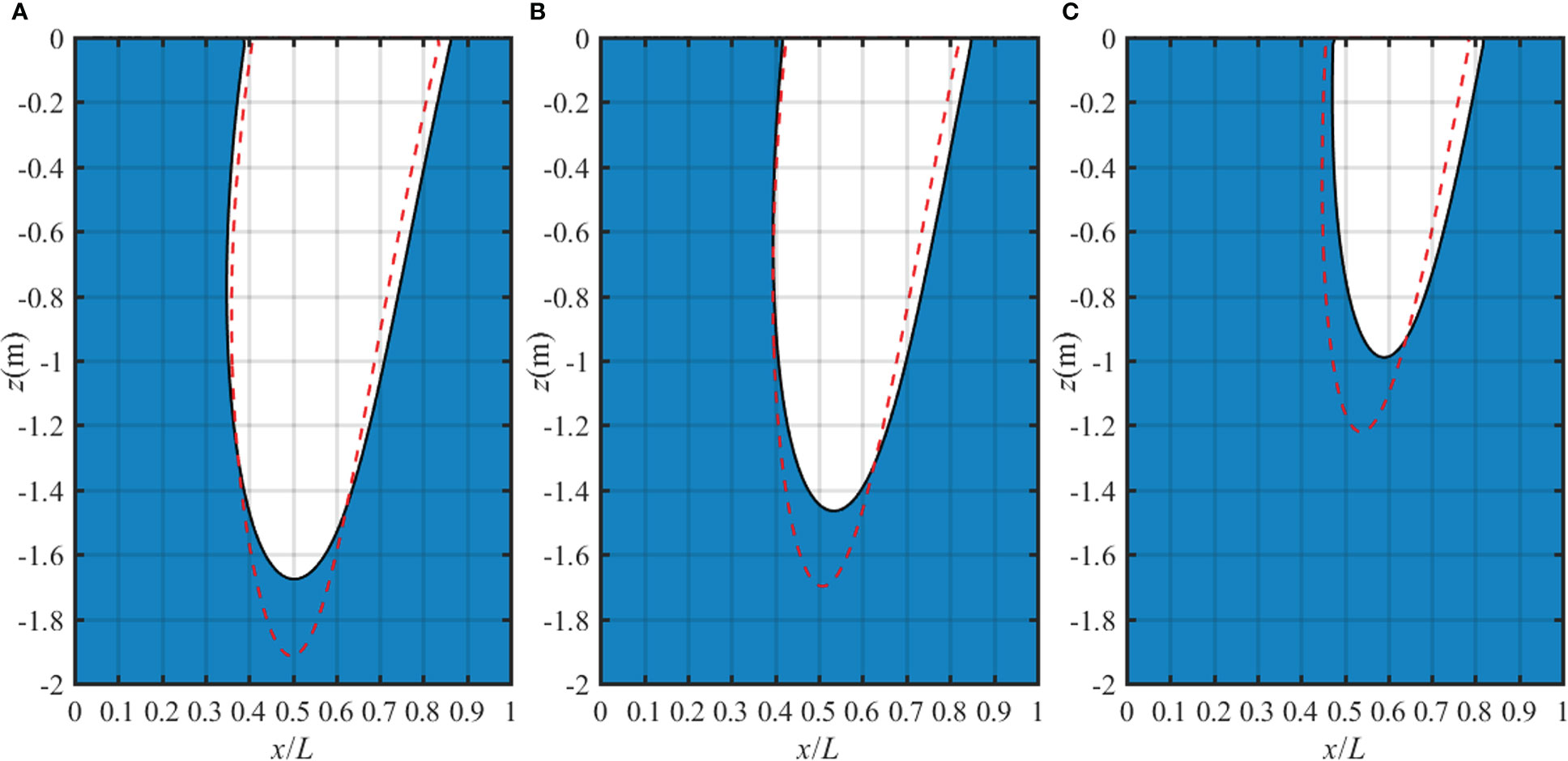
Figure 12 Liquefaction zone in a homogeneous isotropic poroelastic seabed for various degree of saturation: (A) S_r=0.95, (B) S_r=0.975 and (C) S_r=0.99.

The liquefaction zone in a two-layer anisotropic seabed for various moduli ratio E_v1/E_v2 is shown in Figure 13. The depth and width of the liquefaction zone in the seabed increase with the increase of E_v1/E_v2. In other words, when the other parameters are fixed, the stiff top layer makes the seabed much easier to liquefy. The liquefaction zone in a two-layer anisotropic seabed for various permeability ratio k_z1/k_z2 is shown in Figure 14. The effect of k_z1/k_z2 is similar to the effect of anisotropic permeability ratio k_z/k_x in the single-layer case. When the permeability of the first layer increases, the pore pressure is hard to accumulate, resulting in more vertical effective stress in the seabed and thus the lower liquefaction depth. Furthermore, it can be concluded from Figures 10–14 that the liquefaction depth and liquefaction width by the non-linear wave are lower than those by the linear wave for various soil properties. Hence, in order to accurately judge the liquefaction potential of the seabed, the anisotropic stiffness, anisotropic permeability, degree of saturation and stratification should be carefully considered.

FIGURE 13

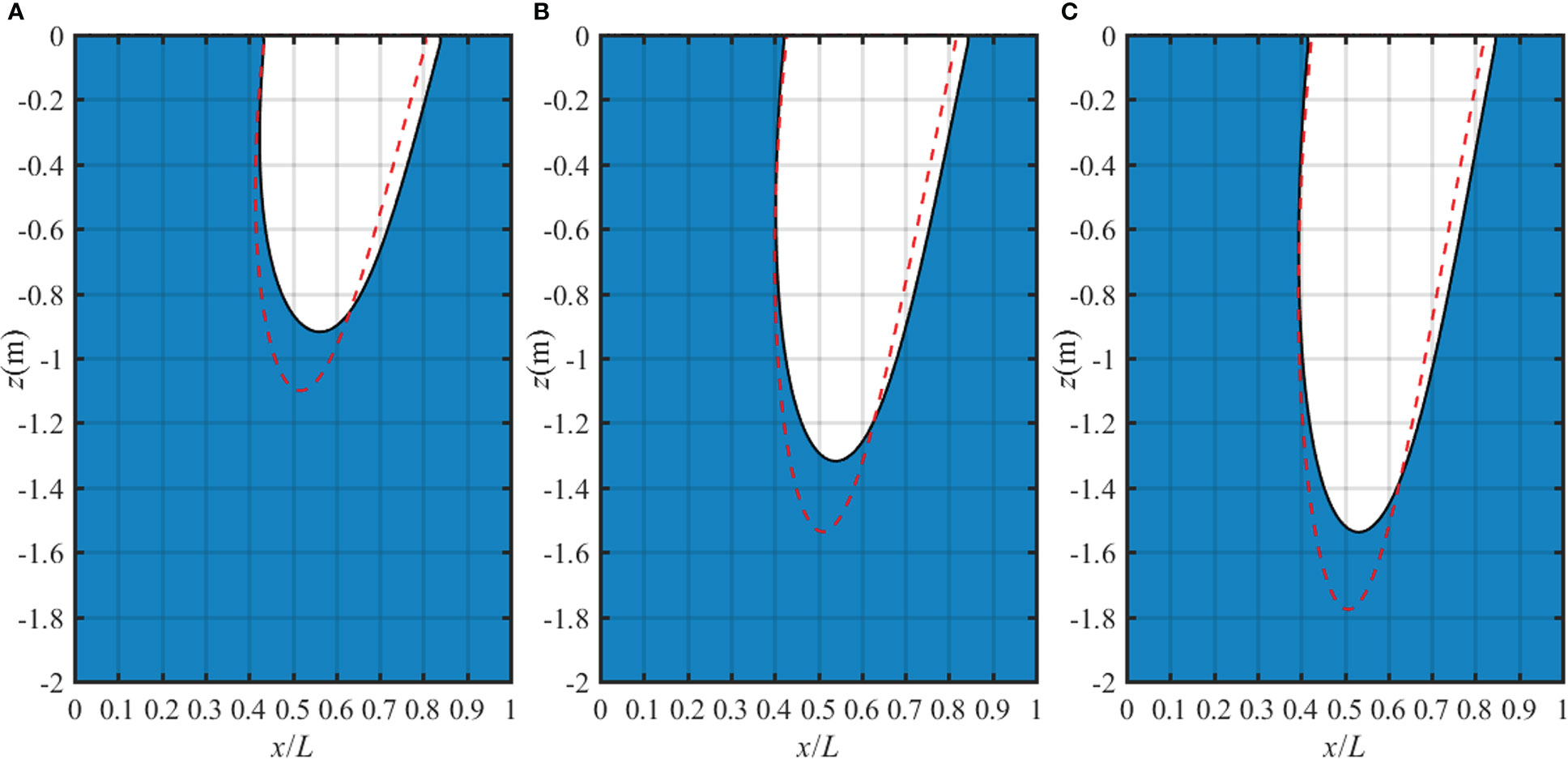
Figure 13 Liquefaction zone in a two-layer TI poroelastic seabed for various E_v1/E_v2: (A) E_v1/E_v2 = 0.5, (B) E_v1/E_v2 = 1 and (C) E_v1/E_v2 = 1.5 with fixed E_hi/E_vi=0.8, G_vi/E_vi=0.6, k_zi/k_xi=1, E_v2 = 1.4×10⁷ Pa.

FIGURE 14

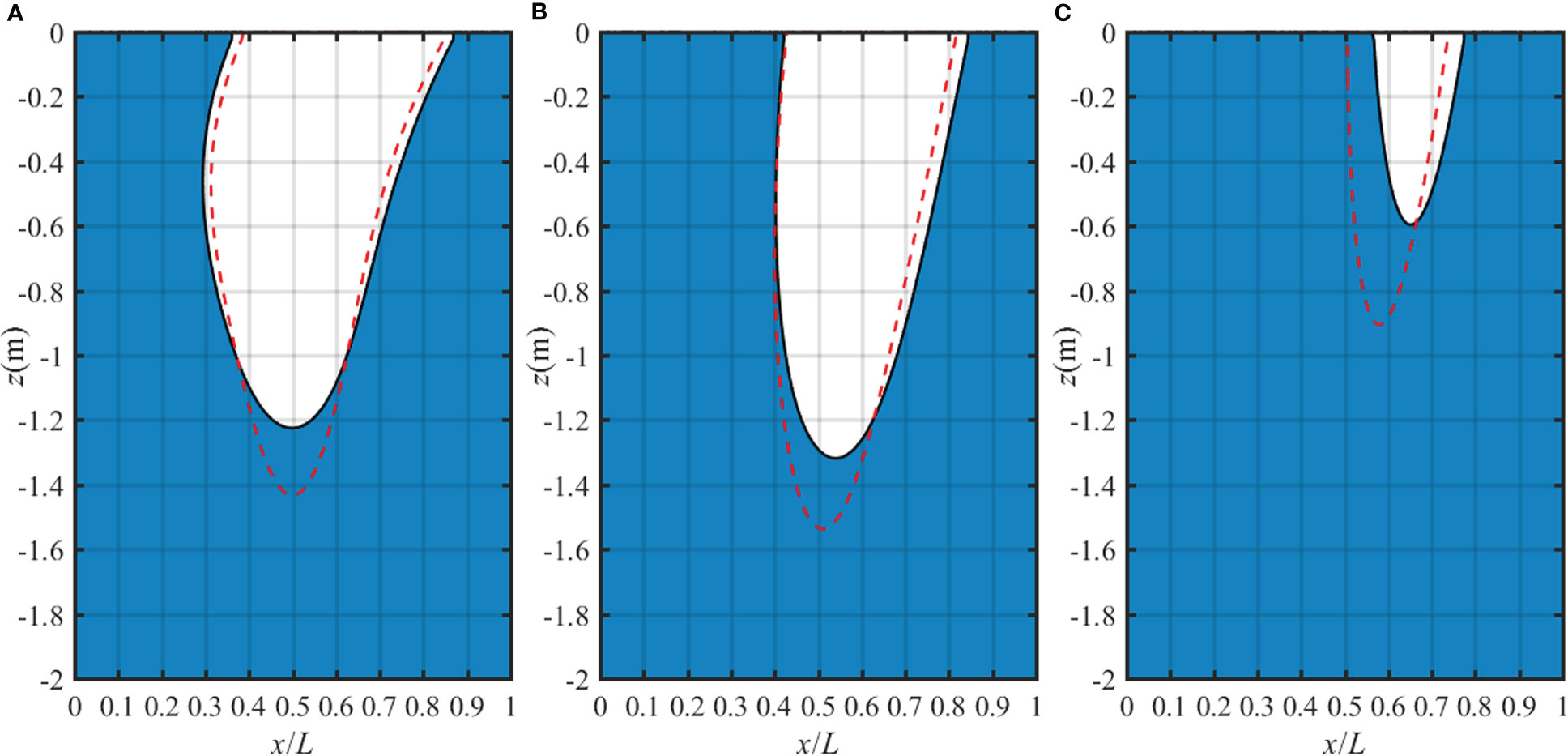
Figure 14 Liquefaction region in a two-layer TI poroelastic seabed for various k_z1/k_z2: (A) k_z1/k_z2 = 0.1, (B) k_z1/k_z2 = 1 and (C) k_z1/k_z2 = 5 with fixed E_hi/E_vi=0.8, G_vi/E_vi=0.6, k_zi/k_xi=1, k_z2 = 1×10^-4 m/s.

5. Conclusions

In this study, the dynamic response of a TI multilayered poroelastic seabed under non-linear wave is established based on Biot’s complete dynamic consolidation theory and second-order Stokes theory. The corresponding solution is derived by virtue of potential-function scheme and DVP method. After verifying the accuracy and reliability of the developed solution, the effects of main parameters on the dynamic response and liquefaction potential of single-layer and multilayered anisotropic poroelastic seabed are analyzed. The main conclusions can be summarized as follows:

1. Compared to the linear wave, the nonlinear wave shows higher/sharper wave crest and lower/flatter wave trough with the evident behavior of asymmetric distribution. The changing rule of pore pressure, normal effective stress and shear stress in the seabed induced by non-linear wave is similar with that by the linear wave, except for much higher induced amplitude by non-linear wave. For the liquefaction potential, the depth and width of liquefaction by the nonlinear wave are generally lower than those by linear wave for various soil properties.

2. Both anisotropic stiffness and permeability have significant influence on the dynamic response and liquefaction potential of the seabed to non-linear wave. The maximum liquefaction depth increases with increasing E_h/E_v or decreasing G_v/E_v, while the liquefaction zone by the nonlinear wave is wider than that by the linear wave. The influence of anisotropic permeability on the liquefaction depth is relatively complex.

3. The degree of saturation S_r of the seabed has a significant effect on the dynamic response and liquefaction potential of the seabed under non-linear wave. The maximum pore pressure (vertical effective stress) increase (decreases) with increasing S_r. The seabed soil is less susceptible to liquefy as the degree of saturation increases.

4. The stratification has remarkable influence on the dynamic response of the seabed subjected to non-linear wave. For a typical two-layer seabed, the depth and width of the liquefaction zone increase with increasing E_v1/E_v2 (i.e., increasing Young’s modulus in the top layer) and decrease with increasing k_z1/k_z2 (i.e., increasing vertical permeability coefficient in the top layer). That is to say, when the top layer is stiff or the corresponding permeability is poor, the seabed is much easier to liquefy.

Data availability statement

The raw data supporting the conclusions of this article will be available by the corresponding authors upon request.

Author contributions

ZZ: Software, Writing original draft. BZ: Formal analysis, Writing original draft. XL: Methodology, Writing-review and editing, Supervision. ZW: Conceptualization, Methodology. All authors contributed to the article and approved the submitted version.

Funding

This research is supported by National Natural Science Foundation of China (Grant Nos. 52178367, 52078467), Natural Science Foundation of Zhejiang Province (Grant No. LHZ21E090001), and Research and Development Fund of Zhejiang A & F University (Grant No. 2020FR052).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Biot M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164. doi: 10.1063/1.1712886

CrossRef Full Text | Google Scholar

Biot M. A. (1956). Theory of propagation of elastic waves in a fluid-saturated porous solid. i. low-frequency range. J. Acoust. Soc Am. 28, 168–178. doi: 10.1121/1.1908239

CrossRef Full Text | Google Scholar

Biot M. A. (1962). Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 33, 1482–1498. doi: 10.1063/1.1728759

CrossRef Full Text | Google Scholar

Chen W. Y., Chen G. X., Chen W., Liao C. C., Gao H. M. (2019). Numerical simulation of the non-linear wave-induced dynamic response of anisotropic poro-elastoplastic seabed. Mar. Georesour. Geotec. 37, 924–935. doi: 10.1080/1064119X.2018.1507064

CrossRef Full Text | Google Scholar

Cheng A. H. D. (1997). Material coefficients of anisotropic poroelasticity. Int. J. Rock Mech. Min. Sci. 34, 199–205. doi: 10.1016/S0148-9062(96)00055-1

CrossRef Full Text | Google Scholar

Chen L. B., Wu W. B., Liu H., El Naggar M. H., Wen M. J., Wang K. H. (2022a). Influence of defects on the lateral dynamic characteristics of offshore piles considering hydrodynamic pressure. Ocean Eng. 260, 111894. doi: 10.1016/j.oceaneng.2022.111894

CrossRef Full Text | Google Scholar

Chen L. B., Wu W. B., Liu H., Li J. X., Newson T., El Naggar M. H. (2022b). Analytical solution for kinematic response of offshore piles under vertically propagating s-waves. Ocean Eng. 262, 112018. doi: 10.1016/j.oceaneng.2022.112018

CrossRef Full Text | Google Scholar

Chen X., Zhang Q., Zheng X. Y., Lei Y. (2022). Dynamic responses of a multilayered transversely isotropic poroelastic seabed subjected to ocean waves and currents. J. Mar. Sci. Eng. 10, 73. doi: 10.3390/jmse10010073

CrossRef Full Text | Google Scholar

Gao J. L., Ji C. Y., Ma X. J., Liu Y. Y., Gaidai O. (2017). Numerical investigation of infragravity wave amplifications during harbor oscillations influenced by variable offshore topography. Ocean Dynam. 67, 1151–1162. doi: 10.1007/s10236-017-1081-0

CrossRef Full Text | Google Scholar

Gao J. L., Ma X. Z., Dong G. H., Chen H. Z., Liu Q., Zhang J. (2021). Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 170, 103977. doi: 10.1016/j.coastaleng.2021.103977

CrossRef Full Text | Google Scholar

Gao J. L., Ma X. Z., Zang J., Dong G. H., Ma X. J., Zhu Y. Z., et al. (2020). Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 158, 103670. doi: 10.1016/j.coastaleng.2020.103670

CrossRef Full Text | Google Scholar

Gatmiri B. (1992). Response of cross-anisotropic seabed to ocean waves. J. Geotech. Eng. 118, 1295–1314. doi: 10.1061/(ASCE)0733-9410(1992)118:9(1295

CrossRef Full Text | Google Scholar

He R., Kaynia A. M., Zheng J., Zhang J. (2022a). Effect of gap and scour on dynamic behavior of monopiles and offshore wind structures. Ocean Eng. 243, 110336. doi: 10.1016/j.oceaneng.2021.110336

CrossRef Full Text | Google Scholar

He R., Zhang J., Zheng J. (2022b). Vertical dynamic interaction factors for offshore thin-walled pipe piles. Comput. Geotech. 145, 104656. doi: 10.1016/j.compgeo.2022.104656

CrossRef Full Text | Google Scholar

Hsu C. J., Chen Y. Y., Tsai C. C. (2019). Wave-induced seabed response in shallow water. Appl. Ocean Res. 89, 211–223. doi: 10.1016/j.apor.2019.05.016

CrossRef Full Text | Google Scholar

Hsu J. R. C., Jeng D. S. (1994). Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness. Int. J. Numer. Anal. Methods Geomech. 18, 785–807. doi: 10.1002/nag.1610181104

CrossRef Full Text | Google Scholar

Hsu J. R. C., Jeng D. S., Lee C. P. (1995). Oscillatory soil response and liquefaction in an unsaturated layered seabed. Int. J. Numer. Anal. Methods Geomech. 19, 825–849. doi: 10.1002/nag.1610191202

CrossRef Full Text | Google Scholar

Hsu J. R. C., Jeng D. S., Tsai C. P. (1993). Short-crested wave-induced soil response in a porous seabed of infinite thickness. Int. J. Numer. Anal. Methods Geomech. 17, 553–576. doi: 10.1002/nag.1610170803

CrossRef Full Text | Google Scholar

Jeng D. S. (1996). Wave-induced liquefaction potential in a cross-anisotropic seabed. J. Chin. Institute Engineers 19, 59–70. doi: 10.1080/02533839.1996.9677765

CrossRef Full Text | Google Scholar

Jeng D. S. (2015). Review of liquefaction around marine structures by b. mutlu Sumer. J. Waterw. Port Coast. Ocean Eng. 141, 07515001. doi: 10.1061/(ASCE)WW.1943-5460.0000296

CrossRef Full Text | Google Scholar

Jeng D. S., Cha D. H. (2003). Effects of dynamic soil behavior and wave non-linearity on the wave-induced pore pressure and effective stresses in porous seabed. Ocean Eng. 30, 2065–2089. doi: 10.1016/S0029-8018(03)00070-2

CrossRef Full Text | Google Scholar

Jeng D. S., Lee T. L. (2001). Dynamic response of porous seabed to ocean waves. Comput. Geotech. 28, 99–128. doi: 10.1016/S0266-352X(00)00026-4

CrossRef Full Text | Google Scholar

Jeng D. S., Rahman M. S. (2000). Effective stresses in a porous seabed of finite thickness: inertia effects. Can. Geotech. J. 37, 1383–1392. doi: 10.1139/t00-063

CrossRef Full Text | Google Scholar

Jeng D. S., Rahman M. S., Lee T. L. (1999). Effects of inertia forces on wave-induced seabed response. Int. J. Offshore Polar Eng. 9, 307–313. Available at: https://www.scopus.com/record/display.uri?eid=2-s2.0-0033496335&origin=inward.

Google Scholar

Jeng D. S., Seymour B. R. (1997). Wave-induced pore pressure and effective stresses in a porous seabed with variable permeability. J. Offshore Mech. Arct. Eng. 119, 226–233. doi: 10.1115/1.2829100

CrossRef Full Text | Google Scholar

Jeng D. S., Zhang H. (2005). An integrated three-dimensional model of wave-induced pore pressure and effective stresses in a porous seabed: II. breaking waves. Ocean Eng. 32, 1950–1967. doi: 10.1016/j.oceaneng.2005.01.005

CrossRef Full Text | Google Scholar

Jouffray J.-B., Blasiak R., Norström A. V., Österblom H., Nyström M. (2020). The blue acceleration: The trajectory of human expansion into the ocean. One Earth 2, 43–54. doi: 10.1016/j.oneear.2019.12.016

CrossRef Full Text | Google Scholar

Joydas T. V., Qurban M. A., Borja A., Krishnakumar P. K., Al-Suwailem A. (2017). Macrobenthic community structure in the northwestern Arabian gulf, twelve years after the 1991 oil spill. Front. Mar. Sci. 4. doi: 10.3389/fmars.2017.00248

CrossRef Full Text | Google Scholar

Kitano T., Mase H. (2001). Wave-induced porewater pressure in a seabed with inhomogeneous permeability. Ocean Eng. 28, 279–296. doi: 10.1016/S0029-8018(00)00010-X

CrossRef Full Text | Google Scholar

Lauton G., Pattiaratchi C. B., Lentini C. A. D. (2021). Observations of breaking internal tides on the Australian north West shelf edge. Front. Mar. Sci. 8. doi: 10.3389/fmars.2021.629372

CrossRef Full Text | Google Scholar

Le Méhauté B. (1976). An introduction to hydrodynamics and water waves (Berlin Heidelberg: Springer). doi: 10.1007/978-3-642-85567-2

CrossRef Full Text | Google Scholar

Liu K. F., Zhang Z. Q., Pan E. (2022). Dynamic response of a transversely isotropic and multilayered poroelastic medium subjected to a moving load. Soil Dyn. Earthq. Eng. 155, 107154. doi: 10.1016/j.soildyn.2022.107154

CrossRef Full Text | Google Scholar

Li X. B., Zhang Z. Q., Pan E. (2020). Wave-induced dynamic response in a transversely isotropic and multilayered poroelastic seabed. Soil Dyn. Earthq. Eng. 139, 106365. doi: 10.1016/j.soildyn.2020.106365

CrossRef Full Text | Google Scholar

Madsen O. S. (1978). Wave-induced pore pressures and effective stresses in a porous bed. Géotechnique 28, 377–393. doi: 10.1680/geot.1978.28.4.377

CrossRef Full Text | Google Scholar

Mei C. C., Foda M. A. (1981). Wave-induced responses in a fluid-filled poro-elastic solid with a free surface — a boundary layer theory. Geophys. J. Int. 66, 597–631. doi: 10.1111/j.1365-246X.1981.tb04892.x

CrossRef Full Text | Google Scholar

Okusa S. (1985). Wave-induced stresses in unsaturated submarine sediments. Géotechnique 35, 517–532. doi: 10.1680/geot.1985.35.4.517

CrossRef Full Text | Google Scholar

Pan E. (2019). Green’s functions for geophysics: a review. Rep. Prog. Phys. 82, 106801. doi: 10.1088/1361-6633/ab1877

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi H. F., Chen Z. L., Li Y. C., Feng S. J., Chen H. X. (2020). Wave and current-induced dynamic response in a multilayered poroelastic seabed. Bull. Eng. Geol. Environ. 79, 11–26. doi: 10.1007/s10064-019-01553-8

CrossRef Full Text | Google Scholar

Quiuqui J. P. C., Tamayo J. P., Maghous S. (2022). Closed-form solutions for wave-induced poroelastic response in seabed under dynamic and quasi-static regimes. J. Braz. Soc Mech. Sci. Eng. 44, 16. doi: 10.1007/s40430–021-03300-1.

CrossRef Full Text | Google Scholar

Ryabinin V., Barbière J., Haugan P., Kullenberg G., Smith N., McLean C., et al. (2019). The UN decade of ocean science for sustainable development. Front. Mar. Sci. 6. doi: 10.3389/fmars.2019.00470

CrossRef Full Text | Google Scholar

Sakai T., Mase H., Matsumoto A. (1988). “Effects of inertia and gravity on seabed response to ocean waves,” in Modeling soil-Water-Structure interactions. Eds. Kolkman P. A., Linderberg J., Pilarczyk K., Rotterdam A., Balkema A., Rotterdam. 61–66.

Google Scholar

Soto L. A., Botello A. V., Licea-Durán S., Lizárraga-Partida M. L., Yáñez-Arancibia A. (2014). The environmental legacy of the ixtoc-I oil spill in campeche sound, southwestern gulf of Mexico. Front. Mar. Sci. 1. doi: 10.3389/fmars.2014.00057

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai C. P., Lee T. L. (1995). Standing wave induced pore pressures in a porous seabed. Ocean Eng. 22, 505–517. doi: 10.1016/0029-8018(95)00003-4

CrossRef Full Text | Google Scholar

Ulker M. B. C. (2012a). Dynamic pore pressure response of two-layer seabed under non-linear waves. AIP Conf. Proc. 1479, 1480–1483. doi: 10.1063/1.4756443

CrossRef Full Text | Google Scholar

Ulker M. B. C. (2012b). Pore pressure, stress distributions, and instantaneous liquefaction of two-layer soil under waves. J. Waterw. Port Coast. Ocean Eng. 138, 435–450. doi: 10.1061/(ASCE)WW.1943-5460.0000155

CrossRef Full Text | Google Scholar

Ulker M. B. C., Rahman M. S., Jeng D. S. (2009). Wave-induced response of seabed: Various formulations and their applicability. Appl. Ocean Res. 31, 12–24. doi: 10.1016/j.apor.2009.03.003

CrossRef Full Text | Google Scholar

Verruijt A. (1969). “Elastic storage of aquifers,” in Flow through porous media. Eds. De Weist R. J. M., Bear J. (New York: Academic Press), 331–376.

Google Scholar

Wang H. F. (2017). Theory of linear poroelasticity with applications to geomechanics and hydrogeology (New Jersey: Princeton University Press).

Google Scholar

Wang Z. T., Luan M. T., Liu T. G., Wang D. (2005). Studies on the effect of non-linear wave loading in shallow water region on dynamic response of sandy seabed. Ocean Eng. 23, 41–46.

Google Scholar

Yamamoto T. (1981). Wave-induced pore pressures and effective stresses in inhomogeneous seabed foundations. Ocean Eng. 8, 1–16. doi: 10.1016/0029-8018(81)90002-0

CrossRef Full Text | Google Scholar

Yamamoto T., Koning H. L., Sellmeijer H., Hijum E. V. (1978). On the response of a poro-elastic bed to water waves. J. Fluid Mech. 87, 193–206. doi: 10.1017/S0022112078003006

CrossRef Full Text | Google Scholar

Ye G. J., Leng J., Jeng D. S. (2018). Numerical testing on wave-induced seabed liquefaction with a poro-elastoplastic model. Soil Dyn. Earthq. Eng. 105, 150–159. doi: 10.1016/j.soildyn.2017.11.026

CrossRef Full Text | Google Scholar

Yuhi M., Ishida H. (1998). Analytical solution for wave-induced seabed response in a soil-water two-phase mixture. Coast. Eng. J. 40, 367–381. doi: 10.1142/S0578563498000212

CrossRef Full Text | Google Scholar

Yuhi M., Ishida H. (2002). Simplified solutions for wave-induced response of anisotropic seabed. J. Waterw. Port Coast. Ocean Eng. 128, 46–50. doi: 10.1061/(ASCE)0733-950X(2002)128:1(46

CrossRef Full Text | Google Scholar

Zhang Y. P., El Naggar M. H., Wu W. B., Wang Z. Q., Yang X. Y., Jiang G. S. (2022). Dynamic torsional impedance of large-diameter pipe pile for offshore engineering: 3D analytical solution. Appl. Math. Model. 111, 664–680. doi: 10.1016/j.apm.2022.07.017

CrossRef Full Text | Google Scholar

Zhang Z. Q., Pan E. (2020). Time-harmonic response of transversely isotropic and layered poroelastic half-spaces under general buried loads. Appl. Math. Model. 80, 426–453. doi: 10.1016/j.apm.2019.11.035

CrossRef Full Text | Google Scholar

Zhang Z. Q., Pan E. (2023). Coupled horizontal and rocking vibrations of a rigid circular disc on the surface of a transversely isotropic and layered poroelastic half-space. Appl. Math. Model. 114, 270–290. doi: 10.1016/j.apm.2022.10.005

CrossRef Full Text | Google Scholar

Zhou J. C., Pan E., Bevis M. (2021). Deformation due to surface temperature variation on a spherically layered, transversely isotropic and self-gravitating earth. Geophys. J. Int. 225, 1672–1688. doi: 10.1093/gji/ggab056

CrossRef Full Text | Google Scholar

Zhou X. L., Xu B., Wang J. H., Li Y. L. (2011). An analytical solution for wave-induced seabed response in a multi-layered poro-elastic seabed. Ocean Eng. 38, 119–129. doi: 10.1016/j.oceaneng.2010.10.003

CrossRef Full Text | Google Scholar

Zienkiewicz O. C., Chang C. T., Bettess P. (1980). Drained, undrained, consolidating and dynamic behaviour assumptions in soils. Géotechnique 30, 385–395. doi: 10.1680/geot.1980.30.4.385

CrossRef Full Text | Google Scholar

Appendix A The relation between elastic constants and engineering parameters

According to Cheng (1997), the between elastic constants and engineering parameters can be expressed as

$\begin{array}{ll}\begin{array}{l}{C}_{11}=\frac{E_h\left[1-(E_h/E_v)v_v^2\right]}{(1+v_h)\left[1-v_h-(2E_h/E_v)v_v^2\right]}\\ C_{12}=\frac{E_h\left[v_h+(E_h/E_v)v_v^2\right]}{(1+v_h)\left[1-v_h-(2E_h/E_v)v_v^2\right]}\\ C_{13}=\frac{E_h{v}_v}{1-v_h-(2E_h/E_v)v_v^2};C_{33}=\frac{E_v(1-v_h)}{1-v_h-(2E_h/E_v)v_v^2}\\ C_{44}=G_v;C_{66}\equiv \frac{C_{11}-C_{12}}{2}=\frac{E_h}{2(1+v_h)}=G_h\end{array}& \text{(A.1)}\end{array}$

where ν_h and ν_v are the Poisson’s ratio of the solid skeleton in horizontal and vertical directions, respectively.

Appendix B Coefficients $r_i^{(m)}$(i=1-4)

$\begin{array}{ll}\begin{array}{l}{r}_1^{(m)}=C_{33}{C}_{44}{\delta }_3^{(m)};\\ r_2^{(m)}=(a_4^{(m)}{C}_{44}+a_1^{(m)}{C}_{33}+a_2^{(m)}{a}_2^{(m)}{k}^2){\delta }_3^{(m)}+(a_6^{(m)}{C}_{33}+a_5^{(m)}{a}_5^{(m)})C_{44};\\ r_3^{(m)}=a_1^{(m)}{a}_4^{(m)}{\delta }_3^{(m)}+(a_4^{(m)}{C}_{44}+a_1^{(m)}{C}_{33}+a_2^{(m)}{a}_2^{(m)}{k}^2)a_6^{(m)}\\ +a_1^{(m)}{a}_5^{(m)}{a}_5^{(m)}+(2a_2^{(m)}{a}_3^{(m)}{a}_5^{(m)}-a_3^{(m)}{a}_3^{(m)}{C}_{33})k^2;\\ r_4^{(m)}=a_4^{(m)}(a_1^{(m)}{a}_6^{(m)}-a_3^{(m)}{a}_3^{(m)}{k}^2)\end{array}& \text{(B.1)}\end{array}$

Appendix C Coefficients ${\lambda }_i^{(m)}$ (i=1-3)

$\begin{array}{ll}\begin{array}{l}{\lambda }_1^{(m)}=\sqrt{{\Delta }_1^{(m)}-\frac{{\Delta }_2^{(m)}}{3{\Delta }_1^{(m)}}-\frac{r_2^{(m)}}{3r_1^{(m)}}};\begin{array}{c}\end{array}{\lambda }_2^{(m)}=\sqrt{{\Delta }_1^{(m)}{\Delta }_4^{(m)}-\frac{{\Delta }_2^{(m)}}{3{\Delta }_1^{(m)}{\Delta }_4^{(m)}}-\frac{r_2^{(m)}}{3r_1^{(m)}}};\begin{array}{c}\end{array}\\ {\lambda }_3^{(m)}=\sqrt{{\Delta }_1^{(m)}{\left({\Delta }_4^{(m)}\right)}^2-\frac{{\Delta }_2^{(m)}}{3{\Delta }_1^{(m)}{\left({\Delta }_4^{(m)}\right)}^2}-\frac{r_2^{(m)}}{3r_1^{(m)}}}\end{array}& \text{(C.1)}\end{array}$

where

$\begin{array}{ll}\begin{array}{l}{\Delta }_1^{(m)}={\left(-\frac{1}{2}{\Delta }_3^{(m)}+\frac{1}{2}\sqrt{{\left({\Delta }_3^{(m)}\right)}^2+4{\left({\Delta }_2^{(m)}\right)}^3/27}\right)}^{1/3};\begin{array}{c}\end{array}{\Delta }_2^{(m)}=-\frac{{\left(r_2^{(m)}\right)}^2}{3{\left(r_1^{(m)}\right)}^2}+\frac{r_3^{(m)}}{r_1^{(m)}}\\ {\Delta }_3^{(m)}=\frac{2{\left(r_2^{(m)}\right)}^3}{27{\left(r_1^{(m)}\right)}^3}-\frac{3r_2^{(m)}{r}_3^{(m)}}{9{\left(r_1^{(m)}\right)}^2}+\frac{r_4^{(m)}}{r_1^{(m)}};\begin{array}{c}\end{array}{\Delta }_4^{(m)}=\frac{-1+\sqrt{3}\text{i}}{2}\end{array}& \text{(C.2)}\end{array}$

Appendix D Coefficients ${\chi }_i^{(m)}$, ${\phi }_i^{(m)}$, ${\xi }_i^{(m)}$and ${\eta }_i^{(m)}$(i=1-3)

$\begin{array}{ll}\begin{array}{l}{\chi }_i^{(m)}=-\text{i}k{\lambda }_i^{(m)}\left[a_2^{(m)}\left(a_6^{(m)}+{\delta }_3^{(m)}{\lambda }_i^{(m)}{\lambda }_i^{(m)}\right)+a_3^{(m)}{a}_5^{(m)}\right]\\ {\phi }_i^{(m)}=\left(a_6^{(m)}+{\delta }_3^{(m)}{\lambda }_i^{(m)}{\lambda }_i^{(m)}\right)\left(a_1^{(m)}+C_{44}{\lambda }_i^{(m)}{\lambda }_i^{(m)}\right)-a_3^{(m)}{a}_3^{(m)}{k}^2\\ {\xi }_i^{(m)}={\lambda }_i^{(m)}\left[a_5^{(m)}\left(a_1^{(m)}+C_{44}{\lambda }_i^{(m)}{\lambda }_i^{(m)}\right)+a_2^{(m)}{a}_3^{(m)}{k}^2\right]\\ {\eta }_i^{(m)}={\delta }_3^{(m)}\left({\xi }_i^{(m)}{\lambda }_i^{(m)}-{\rho }_f{\omega }^2{\phi }_i^{(m)}\right)\end{array}& \text{(D.1)}\end{array}$

Appendix E Elements of constant coefficients $M_{}^{(m)}$(i=1-3)

$\begin{array}{ll}\begin{array}{l}{M}_{1i}^{(m)}={\chi }_i^{(m)};M_{1(i+3)}^{(m)}=-{\chi }_i^{(m)};\hfill \\ M_{2i}^{(m)}={\phi }_i^{(m)};M_{2(i+3)}^{(m)}={\phi }_i^{(m)};\hfill \\ M_{3i}^{(m)}={\eta }_i^{(m)};M_{3(i+3)}^{(m)}={\eta }_i^{(m)};\hfill \\ M_{4i}^{(m)}=C_{44}(ikm{\phi }_i^{(m)}+{\lambda }_i^m{\chi }_i^{(m)})M_{4(i+3)}^{(m)}=C_{44}(ikm{\phi }_i^{(m)}+{\lambda }_i^m{\chi }_i^{(m)});\hfill \\ M_{5i}^{(m)}=ikm{C}_{13}{\chi }_i^{(m)}+C_{33}{\lambda }_i^m{\phi }_i^{(m)}-{\alpha }_3{\xi }_i^{(m)};M_{5(i+3)}^{(m)}=-(ikm{C}_{13}{\chi }_i^{(m)}+C_{33}{\lambda }_i^m{\phi }_i^{(m)}-{\alpha }_3{\xi }_i^{(m)});\hfill \\ M_{6i}^{(m)}={\xi }_i^{(m)};M_{6(i+3)}^{(m)}=-{\xi }_i^{(m)}\hfill \end{array}& \text{(E.1)}\end{array}$