
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mar. Sci. , 10 November 2022
Sec. Ocean Observation
Volume 9 - 2022 | https://doi.org/10.3389/fmars.2022.1027830
This article is part of the Research Topic Ocean Observation based on Underwater Acoustic Technology View all 20 articles
In the marine environment, estimating the direction of arrival (DOA) is challenging because of the multipath signals and low signal-to-noise ratio (SNR). In this paper, we propose a convolutional recurrent neural network (CRNN)-based method for underwater DOA estimation using an acoustic array. The proposed CRNN takes the phase component of the short-time Fourier transform of the array signals as the input feature. The convolutional part of the CRNN extracts high-level features, while the recurrent component captures the temporal dependencies of the features. Moreover, we introduce a residual connection to further improve the performance of DOA estimation. We train the CRNN with multipath signals generated by the BELLHOP model and a uniform line array. Experimental results show that the proposed CRNN yields high-accuracy DOA estimation at different SNR levels, significantly outperforming existing methods. The proposed CRNN also exhibits a relatively short processing time for DOA estimation, extending its applicability.
Direction of arrival (DOA) estimation of an acoustic signal is of considerable interest in several applications, including environmental monitoring, defense, and information acquisition (Singer et al., 2009; Zhang et al., 2022; Kandimalla et al., 2022). Especially in the underwater environment, DOA estimation plays an important role in source tracking, coastal surveillance, and navigation. Underwater DOA estimation methods are based on the capability of sonar arrays to receive acoustic signals transmitted from the source. The use of sonar arrays has significant advantages, including a wide detection range, reduced power consumption, and increased safety. Such advantages are preferable in underwater target detection, recognition, and tracking (Han et al., 2019; Zhang and Yang, 2021).
Several effective methods for estimating DOAs in different complex scenarios have been developed, such as conventional beamforming (CBF), estimation of parameters via the rotational invariance technique (ESPRIT), minimum variance distortionless response (MVDR), multiple signal classification (MUSIC), and their variants (Li et al., 2019). However, the underwater environment has additional complexity in terms of changing time-space-frequency channels (Jia et al., 2012), which introduce signal attenuation during transmission, multipath effects, Doppler effects, and varying propagation delays (Yang, 2012). The multipath effects occur because underwater the signal propagates through multiple paths with an abundance of delay spreads that cause a lot of interference to the original signal. The resultant signal obtained at the sonar array is significantly faded and has the ambiguity of direction. Similarly, the complex time-variant nature of the ocean and the waves generated on the ocean surface result in a large Doppler spread that makes the estimation of DOAs a difficult task. Due to these challenging characteristics, the signals received by sonar arrays consist of anomalies that make it difficult for traditional algorithms to accurately determine the DOA of the source. Although several methodologies have been proposed for accurate DOA estimation in the underwater environment, their performance degrades in the presence of the above challenging characteristics. To improve the capability of sonar array systems in the challenging underwater environment, novel DOA estimation methodologies are required.
In recent years, the availability of big data has enabled machine learning and deep learning to be employed in research domains such as image processing, speech processing, and acoustic signal processing (Wang et al., 2019; Bai et al., 2019; Bai et al., 2021; Chen et al., 2022; Bai et al., 2022). Various methodologies based on deep learning have been highly effective in solving classification, localization, association, and functional approximation tasks (Ayub et al., 2021; Desai and Mehendale, 2022; Ayub et al., 2022). Deep learning has recently been applied to the estimation of various parameters from acoustic signals in an underwater environment using sonar array systems (Niu et al., 2017; Ferguson et al., 2017; Houégnigan et al., 2017; Wang and Peng, 2018; Bianco et al., 2019; Shen et al., 2020; Ozanich et al., 2020).These studies show that deep learning performs exceptionally well in comparison to traditional methods. Specifically, in the domain of DOA estimation in an underwater environment using sonar arrays, several methods based on convolutional neural networks (CNNs) have been developed (Liu et al., 2021; Cao et al., 2021). These methods take the DOA estimation task as a classification problem and employ a CNN to compute the DOA of the source. CNNs are good at modeling time and frequency invariances and have the capability to exploit temporal contexts. Nonetheless, they struggle to exploit longer temporal context information. To overcome this shortcoming, recurrent neural networks (RNNs) combine information from previous temporal windows, enabling theoretically unlimited contextual information to be incorporated (Sun et al., 2021). To combine the advantages of CNNs and RNNs, the two architectures can be employed together in the form of a single network with convolutional layers followed by recurrent layers. This structure is typically referred to as a convolutional recurrent neural network (CRNN).
To efficiently solve the underwater DOA estimation problem, this paper proposes a deep DOA estimation algorithm for underwater signals based on CRNNs. The model takes the phase components of the short-time Fourier transform (STFT) of the received signal at each sensor of the array. The CNN is used to efficiently extract high-level information, while the RNN is used to ensure that temporal context information is efficiently modeled to enable DOA estimation. To adopt challenging conditions like multipath propagation of high-frequency sound signals in a shallow water environment, the proposed method is validated on a synthetic dataset generated by BELLHOP Jing et al. (2018); Han et al. (2021); Li et al. (2022). Similarly, to validate the performance of the proposed methodology in actual complex underwater environmental effects we test it on real data obtained through experiments in the sea. The results show that our model obtains accurate DOA estimates for multipath signals using a sonar array, and is suitable for use in underdetermined scenarios that are overlooked by traditional methods.
The main contributions of the paper are listed as follows:
1. We propose to use deep learning-based method for underwater DOA estimation. The proposed method uses residual CNN to extract high-level information and RNN to model the temporal contexts of the received signals.
2. For data simulation, we use BELLHOP to simulate the array signals which are multipath signals and with low SNRs in the underwater environment.
3. We further conduct the proposed method on real sea data to validate the performance of DOA estimation.
4. The proposed method achieves a notable improvement in the performance of DOA estimation on simulated and real data as compared to traditional and deep learning-based methods
The remainder of this paper is organized as follows. Section 2 presents a review of existing traditional and learning-based methods for the problem of DOA estimation in underwater scenarios. In section 3, the signal model is formulated and the array formation, feature generation process, and proposed DOA estimation model are described. Section 4 presents experimental results and analysis to verify the effectiveness of the proposed methodology. Finally, this paper is concluded in section 5.
Since the breakthrough of sonar array systems, determining the DOA has been the most important task in underwater applications. The earliest method for estimating the DOA is beamforming (Singer et al., 2009). This method employs the array to define the directivity and searches through spatial regions to determine the direction. Although the limited processing and analysis power at the time meant this method had low accuracy and performed poorly in the presence of noise, it laid the foundations for the development of novel estimation methods. During the 1960s, a new methodology of maximum entropy spectral estimation (Ables, 1974; Berger et al., 1996) was presented, which is the basis of most modern estimation methods. This class of methodologies possesses high resolution but has significant computational requirements. Later, Capon presented the MVDR methodology based on the maximum SNR criterion (Capon, 1969). MVDR estimates the spatial wave number spectrum as a means of improving the resolution and collectively increasing the noise suppression. Nonetheless, the computational complexity of this methodology is still high.
A methodology based on the time difference of arrival was proposed by Knapp and Carter (1976). This focused on minimizing the calculation complexity while increasing the resolution, but the performance deteriorates significantly in the presence of noise and reverberation (Zhang et al., 2020; Zhang et al., 2021). A breakthrough was achieved in the 1970s when Schimt proposed a methodology based on the spatial subspace (Schmidt, 1986). This MUSIC method laid the foundation for a new direction of research in the field of DOA estimation. The concept of estimation gave birth to the expansion of subspace class estimation methodologies. In subsequent years, many enhanced variants of MUSIC were proposed, including the weighted MUSIC method (Stoica and Nehorai, 1990; Xu and Buckley, 1992), root MUSIC algorithm (Barabell, 1983; Rao and Hari, 1989; Ren and Willis, 1997), and several others. In the 1980s, the ESPRIT framework was presented (Roy and Kailath, 1989). This methodology employed the phenomenon of rotation-invariance among the subspaces to compute the DOA. The methodology was further enhanced to produce the MI-ESPRIT (Swindlehurst et al., 1992) and weighted ESPRIT (Eriksson and Stoica, 1994) methods.
In the 1990s, Ottersten and Viberg developed weighted subspace fitting (Viberg et al., 1991), which consists of a combined structure for minimizing the error in the estimation of the covariance matrix. This methodology can distinguish the sources accurately and has enhanced resolution. Nonetheless, the methodology is computationally expensive in terms of computing the set parameters and is prone to fail in the presence of small errors. In 2006, Candes et al. presented a new concept based on sparse signal acquisition and recovery, known as compressed sensing (Donoho, 2006; Candès et al., 2006). Their methodology is based on the sparsity of signals and can be employed without fulfilling the Nyquist sampling theorem.
Recently, there have been continuous improvements in deep learning theory and methodologies for DOA estimation (Hu et al., 2020). The use of deep learning for DOA estimation can be segregated into two broad domains. The first domain is based on supervised learning and employs the learned projective relationship among the input measurements to give the DOA output. A single-layer network model that learned the DOA using the input features for the first time was presented by Xiao et al. (2015). Similarly, a CNN was employed by Chakrabarty and Habets (2017) to learn the DOAs from the input features. This methodology enhanced the accuracy of estimation in noisy and reverberant environments. Xiang et al. (2020) presented a methodology that employs phase enhancement to increase the accuracy of DOA estimation. They later proposed an LSTM-based DOA estimation method for moving targets, which achieved high robustness to array imperfections (Xiang et al., 2021).
The second domain is based on unsupervised learning. For instance, Yuan et al. (2021) proposed an unsupervised learning strategy for DOA estimation using a novel loss function. Although methods based on deep learning provide significant improvements in the estimation results, they cannot be easily generalized to the underwater environment, which is complex and exhibits temporal and spatial variations. Several methods have been proposed to target these changing conditions. Liu et al. (2021) proposed a DOA estimation method based on CNNs using sonar arrays. Their methodology consists of a two-channel CNN that estimates the DOA using the real and imaginary covariance matrices. This approach outperforms MUSIC in terms of accuracy and estimation time. Similarly, a deep transfer learning methodology in which a CNN-based network adapts to new environments has been proposed (Cao et al., 2021). This methodology uses a single vector sensor as opposed to a sonar array. However, the above approaches cannot efficiently exploit the temporal context information, which is essential in the underwater environment. To solve this problem, we propose a DOA estimation method based on a CRNN that can capture the temporal context information in addition to the time-frequency invariance. The proposed methodology achieves accurate DOA estimation with relatively low time and space complexity.
In this section, we introduce the proposed method for underwater DOA estimation using an acoustic array. We first formulate the problem of underwater DOA estimation using a uniform sonar linear array. Secondly, we show the scheme overview of the proposed method. Then we introduce the feature extraction part of our method. Finally, we describe the proposed CRNN for underwater DOA estimation.
This paper presents a methodology based on an underwater sonar array. The methodology considers a uniform sonar linear array for the reception of acoustic signals. The assumption of narrowband conditions requires the time during which the signal passes through the complete array to be less than the coherence time of the generated signal. It is also assumed that the generating source and the receiving array lie on the same plane. Similarly, the far-field condition is imposed and it is assumed that the signal reaches the array as a plane wave. Consider a total of N narrowband signals, denoted by sn(t) , which are received by the sonar array consisting of M sensor elements with an inter-element distance of d . The wave path difference among the elements of the receiving array is denoted by Dm and can be expressed as:
The time difference of arrival among the elements of the array can be computed as:
In the above equation, v denotes the speed of signal propagation in the underwater environment. The phase-shift of the signals approaching the array can then be computed as:
This can be further elaborated by setting f=v/λ:
The signal received by the array can then be formulated as:
In the above equation, nm(k) denotes the interference at the m th sensor element. The objective is to estimate the DOA of the source using the acquired signal. The methodology divides the set of incident angles [−70∘,70∘] into 141 distinct classes and computes the probability among the classes to give the model output.
The overview of the proposed deep learning-based underwater DOA estimation method using CRNN is shown in Figure 1. Initially, we use the BELLHOP model to simulate the multipath array signals for the underwater marine environment. Then, we extract the acoustic features in the feature extraction stage. Next, we propose to use CRNN for modeling the local and temporal acoustic characteristics, and finally, the trained model is used to estimate the direction of the target source.
BELLHOP is a well-known model for ocean environment simulations, allowing acoustic ray tracing to be performed by configuring the ocean environmental files and predicting the acoustic pressure fields in the ocean (Porter and Bucker, 1987). As BELLHOP provides detailed modeling of the underwater environment, we used it in this study to generate underwater acoustic signals.
In the BELLHOP tool, the number of multipaths, incident angles, transmission losses, amplitudes, and delays are obtained by specifying the parameters of the channel geometry, velocity profile, submarine topography, and interface reflection loss (Porter, 2011).
Feature extraction aims to extract an acoustic representation that enables the acoustic model to learn the mapping from array signals to a set of DOA values via training. In this paper, we use the phase map of STFT as the input feature instead of applying explicit feature extraction to calculate the input acoustic features of the network.
We first transform the array signals into STFTs with an N -point Fourier transform. The STFT feature of the array signals is computed as:
where X∈ℂM×T×F is the STFT feature, T is the number of frames, F is the number of frequency bins, Xm(t,f) = Am(t,f)ejϕm(t,f) is the complex component of X at the m -th element for the t -th frame and f -th frequency bin, and Am(t,f) , ϕm(t,f) are the corresponding magnitude and phase, respectively. We directly use the phase part of the STFT as the input feature of our method, formulated as Y∈ℝM×T×F , where F=N/2+1 can be up to the Nyquist frequency. The phase of the STFT is denoted as the STFT phase in this paper.
CNNs have achieved significant success in computer vision tasks due to their feature extraction ability. CNNs have recently been used for audio pattern recognition tasks, such as speech recognition, environmental sound recognition, and DOA estimation. Conventional CNNs usually consist of convolution layers, downsampling layers, and fully connected layers. The CNNs adopted in the proposed CRNN are structured as follows.
We assume that the input to the proposed network is Y, which is fed to the convolutional layers. We employ three convolutional layers in the CRNN, each having the same kernel size of 3×3 . After each convolutional layer, we apply batch normalization to accelerate and stabilize the training. Next, we adopt the ReLU (Nair and Hinton, 2010) nonlinear activation function. The operations on the input feature Y are expressed as:
where O is the output feature, W is the kernel, b is the bias ⊗ represents the convolution, and σ(·) denotes the ReLU. We apply max-pooling in the downsampling layer to reduce the dimensionality of the feature. The first to third convolutional layers have channels of 32, 64, and 64. The kernels and filters of the convolutional layers are used to learn the local patterns of the input features. High-level features can be extracted by the stacked convolutional layers.
To further improve the performance and simplify the training process, we introduce a residual connection into the proposed CRNN. We assume that the input of the residual connection is O and express the operations of the residual connection as:
where O′ is the output of the residual connection.
CNNs sometimes struggle to capture the temporal dependency of the input features. Therefore, an RNN is used to model temporal sequences by storing historical information in the hidden states. As we are using the phase map of the STFT as the input feature, we adopt an RNN to model the STFT phase over the time dimension. The temporal information is useful for robust DOA estimation.
After the convolutional layers, we average the frequency dimension of the CNN output, denoted as Oc∈ℝT′×C , where T′ is the time dimension and C is the number of channels of the final convolutional layer. The temporal features from Oc are iteratively modeled by multiple RNN units, which output a hidden feature ot for each frame. The operations can be formulated as:
where ℱ and G represent the mapping functions of the RNN and l is the number of recurrent layers. In this paper, we use different RNN units, i.e., gated recurrent unit (GRU), bi-directional GRU (biGRU), long short-term memory (LSTM), and bi-directional LSTM (biLSTM).
The output of the final RNN layer is passed into a fully connected layer to predict the direction probabilities. Three different architectures used in this paper are shown in Figure 2.
The steps for generating the underwater acoustic signals using BELLHOP are elaborated here. We used a 1000 Hz sound source at a source depth of 75 m, with the receiver placed at a distance of 1.5 km and a depth of 75 m. The DOA varied from −70∘ to 70∘ . All other parameters are presented in Table 1. By setting the environmental parameters, the multipath signals (eigenrays) of the receiver were simulated. The received multipath signals consisted of impulse responses with different amplitudes and delays. The multipath signals are illustrated in Figure 3.
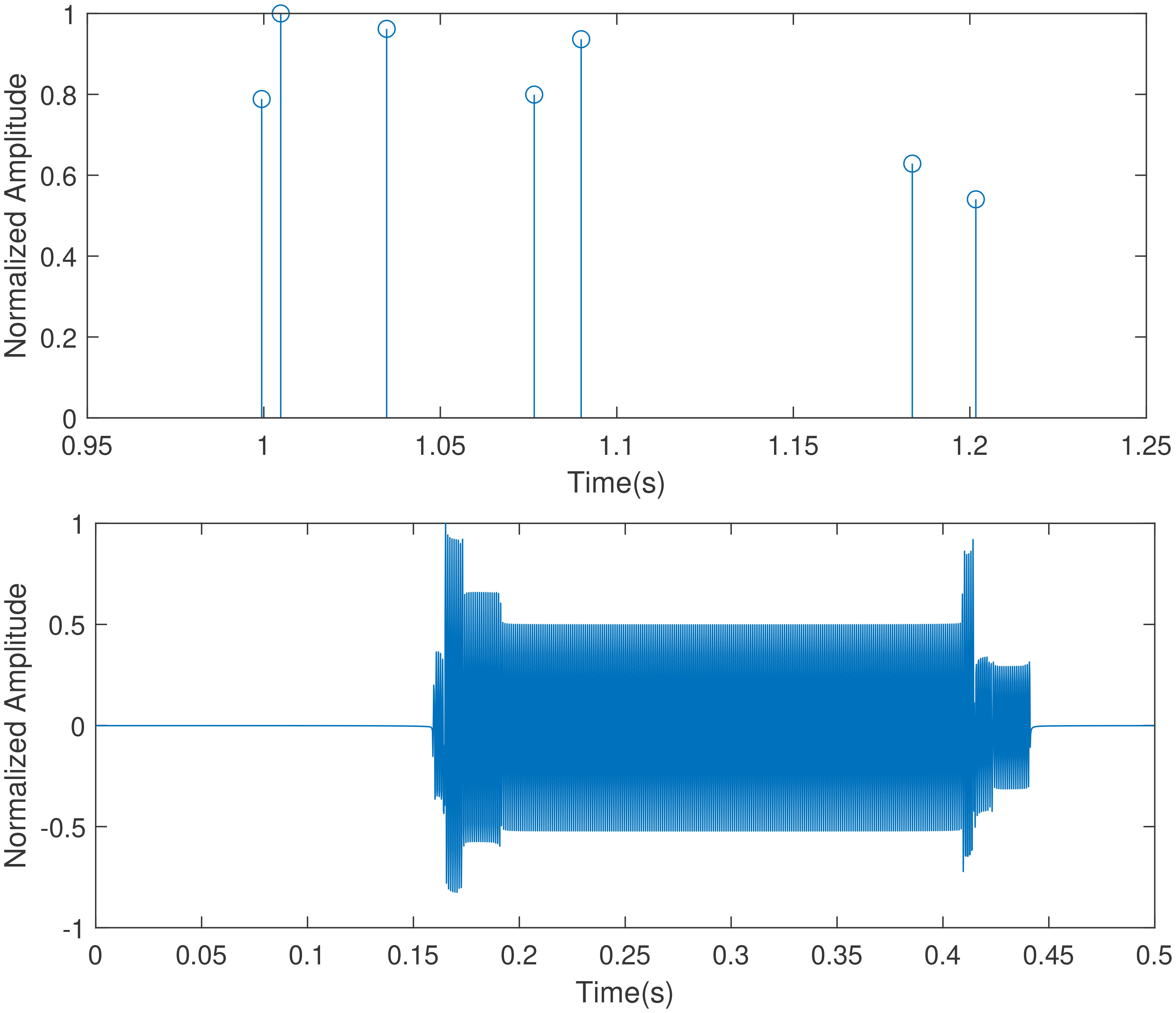
Figure 3 Multipath signals using BELLHOP. The picture above is underwater impulse responses with amplitudes and delays, and the picture below is received underwater multipath signals.
The dataset used to evaluate our proposed method was generated using the following procedures. We simulated the signal of the first element by applying the BELLHOP toolbox in MATLAB. Array signals were generated by delaying the signal of the first element in the uniform line array (ULA) with an inter-element distance of d = 0.75 m. The DOA angles ranged from −70∘ to 70∘ at intervals of 1∘ . We generated 500 samples for each direction, and so the total number of underwater ULA signals was 70,500. The samples were divided into training, validation, and test sets at a ratio of 7:2:1 . The training and validation sets were fed into the deep learning-based method, and the testing set was used to compare the performance of all methods.
We used the phase map of the STFT as the input acoustic features for the proposed CRNN. The duration of the underwater ULA signals was 0.5 s with a sampling rate of 5000 Hz. We calculated the STFT using a frame length of 26 ms and a hop length of 13 ms in a Hanning window. For each channel of the array signals, the size of the STFT-phase was 65×24 .
For training, we used the Adam optimizer with an initial learning rate of 0.001, which was reduced by a factor of 0.95 every two epochs. The batch size was set to 32. We trained the model for 50 epochs in all of the experiments.
We evaluated the performance of our proposed method for the DOA estimation of underwater array signals via the classification accuracy (ACC) and root mean square error (RMSE), which is formulated as:
where N is the number of test samples, θn is the true angle of the n -th sample, and is the estimated angle of the n -th sample. The RMSE is calculated as the averaged mean value of 500 samples for all angles from −70∘ to 70∘ at intervals of 1∘
In this section, we present results from various DOA estimation methods to evaluate the effectiveness of our proposed algorithm.
Table 2 compares the performance of different methods for DOA estimation. CBF and MUSIC are conventional DOA estimation algorithms. The grid interval of these methods was set to 1° for comparison. The two-channel CNN (Liu et al., 2021) for underwater DOA estimation uses real and imaginary covariance matrices as the two-channel inputs to the network. The deep transfer learning (DTL) CNN was proposed for the DOA estimation using a single vector sensor Cao et al. (2021). The authors also used KRAKEN to simulate the underwater array signals, which is similar to the research target of this paper. This method contains 8 convolutional layers and 4 fully connected layers. We used the phase map of the STFT as input instead of the real and imaginary parts of the cross-spectrum due to the difference between the two types of acoustic arrays. The Dense U-net was proposed for high-resolution DOA estimation using a DenseBlock-based U-net structure with the bearing-time record Sun et al. (2022). In our experiment, we only used the contracting path because we do not focus on reconstructing the input feature. And we also use the phase map of the STFT as the input feature to make a fair comparison.
In Table 2, the results from the different methods are compared in terms of ACC and RMSE under different SNRs with 10 array elements. For all methods, ACC increases and RMSE decreases with increasing SNR. Generally, deep learning-based methods achieve better DOA estimation performance than conventional methods. That is, the deep learning-based methods achieve higher ACCs and lower RMSEs than the conventional methods. Compared with different deep learning-based methods, the proposed CRNN achieves high ACCs of 99.9% (0 dB), 99.3 % (-5 dB), and 90.3 % (-10 dB), and low RMSEs of 0.024∘ (0 dB), 0.080° (-5 dB), and 0.313° (-10 dB), outperforming the other deep learning-based methods. Dense U-net outperforms two-channel CNN when SNR is -10 and -5 dB but achieves worse results when SNR is 0 dB. Moreover, the DTL CNN fails to achieve good performance for DOA estimation The parameters of CNN are too large, so we assume that the network is overfitting. The above observations indicate that the proposed CRNN outperforms conventional and deep learning-based methods, and achieves stable DOA estimation performance under different SNRs.
We conducted ablation experiments to compare the DOA estimation performance of different features and networks. In Table 3, we first analyze the proposed CNN using the covariance matrix as the input feature. The proposed CNN does not achieve better results when the STFT-phase is used as the input feature instead of the covariance matrix. We then introduced various RNNs (GRU, biGRU, LSTM, and biLSTM) into our CNN architecture. The RMSE can be further reduced by introducing the GRU into our CNN model, indicating that RNNs can exploit temporal information in the STFT phase. From the experimental results with the various RNNs, we can see that bi-directional architectures do not produce lower RMSEs. Moreover, the proposed CRNN adopts a residual connection to improve the performance of DOA estimation. It can be seen that the proposed residual-CNN-GRU achieves an ACC of 99.9% and an RMSE of 0.024∘ , outperforming the other networks.
For underwater DOA estimation in realistic conditions, the SNR is usually low. More array elements will enable more useful information to be obtained from the target signals. Therefore, we further explored the relationships between the number of array elements and the performance of deep learning-based DOA estimation at a low SNR of -10 dB. Table 4 presents the ACC and RMSE results of the proposed CRNN with 10, 16, and 20 array elements. The ACC increases and the RMSE decrease with the increasing number of array elements. This is because the STFT-phase channels increase with an increase in the number of array elements, and so more useful information is available for modeling between the directions and features.
The underwater acoustic environment is complex and dynamic. Therefore, the processing time is important for practical DOA estimation methods. We compared the processing time of conventional methods against that of the proposed CRNN using only the CPU. As deep learning-based methods usually transform underwater signals into acoustic features, we included the processing time for feature extraction to ensure a fair comparison. Figure 4 shows the mean DOA estimation times of different methods with 10 array elements. The experiments were repeated 7,050 times for each method. The proposed CRNN achieves the best DOA estimation time of 3.21 ms. MUSIC has a processing time of 3.29 ms, which is five times faster than that of CBF. This is because the matrix operations are optimized in MUSIC, leading to lower processing times. The proposed CRNN simultaneously achieves high accuracy and fast processing for DOA estimation, making it suitable for real-time applications.
In realistic conditions, there will be non-integer source directions. Conventional methods can calculate non-integer directions by changing the search grid, but this increases the computation time. However, the proposed deep learning-based DOA estimation method has been trained with defined integer angles. Therefore, we performed an experiment with three different non-integer angles to investigate whether these directions could be correctly estimated by the proposed method. The DOA estimation results of three different non-integer angles are shown in Figure 5. The proposed CRNN tends to classify 0.3∘ as 0∘ and 40.7∘ as 41∘ . That is, the non-integer angles are mostly classified as the nearest integer value. This indicates that the proposed CRNN can classify non-integer angles to the closest integer angle with the least error. Thus, the deep learning-based method can achieve stable and accurate DOA estimation performance in the case of non-integer directions.
In this section, we conduct experiments using the proposed method and the comparative deep learning-based methods on the actual data in the marine environment. The real marine underwater data was collected in January 2016 with a vertical ULA in the shallow water sea area around China Jiang et al. (2022). The target source is a real ship sailing on the sea. The ULA consists of 16 elements, the depth of the first element is about 205m, and the depth of the 16th element is about 303m. The GPS information of the ULA and the target ship is provided, so we can calculate the distance between the ULA and the target ship, and then calculate the direction of the target ship. The angle of the ship is ranged from 20° to 70°, and we divided the angles into 51 classes. We collected a total of 500 recordings each for a duration of 0.5s at a sampling rate of 17,067 Hz. We divided the dataset into training, validation, and test sets at a ratio of 7:2:1.
Table 5 compares the performance of different deep learning-based methods on the test set for DOA estimation in the real sea environment. The Dense U-net achieves an RMSE of 7.709°, which is higher than the other methods. While the DTL CNN performs better than the two-channel CNN, showing better DOA estimation performance than that on simulated data. And the proposed CRNN achieves an RMSE of 3.594°, outperforming the other methods on the real data.
Similarly, we calculate the RMSEs in different angle intervals for the deep learning-based methods, and the results are shown in Figure 6. It can be seen that the proposed CRNN achieves less than 2° RMSEs when the angle is in 20° - 30° and 40° - 50 and . The two-channel CNN achieves less than 2° RMSEs when the angle is in 20° - 30° and 30° - 40. Similarly, the DTL CNN has less than 2° RMSEs in 60° - 70°, however, the performance of this method degrades in other intervals. The Dense U-net achieves an RMSE of about 2° in 40° - 50 but fails to achieve robust performance in other intervals.
From the above observations, it is seen that the DOA estimation results in a real marine environment are not accurate as in simulation. Nevertheless, the proposed method can achieve robust performance for DOA estimation in different underwater environments, and deep learning-based methods can be applied to more complex underwater environments.
This paper has proposed a CRNN-based method for underwater DOA estimation employing an acoustic ULA. We used the phase component of the STFT as the input feature of the CRNN. The CRNN structure uses CNN layers to extract local invariant features and RNN layers to model the temporal dependencies of the input features. The method was validated on a dataset consisting of multipath signals, which was simulated using the BELLHOP model and a ULA. We compared the proposed CRNN with traditional and deep learning-based methods for DOA estimation. The simulations and experimental analysis at various SNRs indicate that the proposed method achieves high accuracy and low RMSEs compared with previous methods. We also experimented with different network architectures and found that the residual-CNN-GRU achieves the best DOA estimation performance. In a comparison of different array elements under a low SNR of -10 dB, it was observed that the DOA estimation could be improved by increasing the number of array elements. The proposed CRNN has a lower estimation time than other DOA methods. Similarly, experiments are also validated on real data captured from the sea. The observations and experimental results show that the proposed method is sufficiently robust and accurate for underwater DOA estimation in different underwater environments, and can be applied to various underwater monitoring tasks.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
XL wrote the data processing code, conducted the experiments, and wrote the first draft of the manuscript. JC designed the experiments and revised the draft of the manuscript. JB conducted the experiments and analysis and created the figures. AM, DZ, MSA, and QY conducted the experiments. All authors contributed to manuscript revision, read and approved the submitted version, and were involved in the conception and design of the study.
This work is supported by the National Natural Science Foundation of China (Grant No. 62071383) and the Key Research and Development Plan of Shaanxi Province (Grant No. 2021NY-036).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ayub M. S., Jianfeng C., Zaman A. (2021). “Multiple source data association for distributed acoustic sensor network in open environment,” in 2021 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC) (NEW YORK, USA: IEEE) 01–06.
Ayub M. S., Jianfeng C., Zaman A. (2022). Multiple acoustic source localization using deep data association. Appl. Acoust. 192, 108731. doi: 10.1016/j.apacoust.2022.108731
Bai J., Chen C., Chen J. (2019). “A multi-feature fusion based method for urban sound tagging,” in 2019 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC). 1313–1317 (NEW YORK, USA: IEEE).
Bai J., Chen J., Wang M. (2022). Multimodal urban sound tagging with spatiotemporal context. IEEE Trans. Cogn. Dev. Syst 1–1. doi: 10.1109/TCDS.2022.3160168
Bai J., Wang M., Chen J. (2021). “Dual-path transformer for machine condition monitoring,” in 2021 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), 1144–1148 (NEW YORK, USA: IEEE).
Barabell A. (1983). “Improving the resolution performance of eigenstructure-based direction-finding algorithms,” in ICASSP’83. IEEE International Conference on Acoustics, Speech, and Signal Processing, 8. 336–339 (NEW YORK, USA: IEEE).
Berger A., Della Pietra S. A., Della Pietra V. J. (1996). A maximum entropy approach to natural language processing. Comput. Linguist. 22, 39–71.
Bianco M. J., Gerstoft P., Traer J., Ozanich E., Roch M. A., Gannot S., et al. (2019). Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 146, 3590–3628. doi: 10.1121/1.5133944
Candès E. J., Baraniuk R. G., Candes E., Nowak R., Vetterli M.. (2006). “Compressive sampling,” in Proceedings of the International Congress of Mathematicians, Vol. 3. 1433–1452 (Citeseer).
Cao H., Wang W., Su L., Ni H., Gerstoft P., Ren Q., et al. (2021). Deep transfer learning for underwater direction of arrival using one vector sensor. J. Acoust. Soc Am. 149, 1699–1711. doi: 10.1121/10.0003645
Capon J. (1969). High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 57, 1408–1418. doi: 10.1109/PROC.1969.7278
Chakrabarty S., Habets E. A. (2017). “Broadband DOA estimation using convolutional neural networks trained with noise signals,” in 2017 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. 136–140 (NEW YORK, USA: IEEE).
Chen J., Wang M., Zhang X.-L., Huang Z., Rahardja S. (2022). “End-to-end multi-modal speech recognition with air and bone conducted speech,” in ICASSP 2022-2022 IEEE International Conference on Acoustics, Speech and Signal Processing. 6052–6056 (NEW YORK, USA: IEEE).
Desai D., Mehendale N. (2022). A review on sound source localization systems. Arch. Comput. Methods Eng., 1–12. doi: 10.1007/s11831-022-09747-2
Donoho D. L. (2006). Compressed sensing. IEEE Trans. Inf. Theory 52, 1289–1306. doi: 10.1109/TIT.2006.871582
Eriksson A., Stoica P. (1994). Optimally weighted ESPRIT for direction estimation. Signal Process 38, 223–229. doi: 10.1016/0165-1684(94)90141-4
Ferguson E. L., Ramakrishnan R., Williams S. B., Jin C. T. (2017). “Convolutional neural networks for passive monitoring of a shallow water environment using a single sensor,” in 2017 IEEE International Conference on Acoustics, Speech and Signal Processing. 2657–2661 (NEW YORK, USA: IEEE).
Han X., Liu M., Zhang S., Zhang Q. (2019). A multi-node cooperative bearing-only target passive tracking algorithm via UWSNs. IEEE Sens. J. 19, 10609–10623. doi: 10.1109/JSEN.2019.2931885
Han X., Liu M., Zhang S., Zheng R., Lan J. (2021). A passive doa estimation algorithm of underwater multipath signals via spatial time-frequency distributions. IEEE Trans. Veh. Technol. 70, 3439–3455. doi: 10.1109/TVT.2021.3064279
Houégnigan L., Safari P., Nadeu C., André M., van der Schaar M. (2017). “Machine and deep learning approaches to localization and range estimation of underwater acoustic sources,” in 2017 IEEE/OES Acoustics in Underwater Geosciences Symposium (RIO Acoustics). 1–6 (NEW YORK, USA: IEEE).
Hu B., Liu M., Yi F., Song H., Jiang F., Gong F., et al. (2020). DOA robust estimation of echo signals based on deep learning networks with multiple type illuminators of opportunity. IEEE Access 8, 14809–14819. doi: 10.1109/ACCESS.2020.2966653
Jia F., Cheng E., Yuan F. (2012). “The study on time-variant characteristics of under water acoustic channels,” in 2012 International Conference on Systems and Informatics. 1650–1654 (NEW YORK, USA: IEEE).
Jiang J., Wu Z., Huang M., Xiao ,. Z. (2022). Detection of underwater acoustic target using beamforming and neural network in shallow water. Appl. Acoust. 189, 108626. doi: 10.1016/j.apacoust.2021.108626
Jing H., Wang H., Liu Z., Shen X. (2018). Doa estimation for underwater target by active detection on virtual time reversal using a uniform linear array. Sensors 18, 2458. doi: 10.3390/s18082458
Kandimalla V., Richard M., Smith F., Quirion J., Torgo L., Whidden C. (2022). Automated detection, classification and counting of fish in fish passages with deep learning. Front. Mar. Sci 8, 2049. doi: 10.3389/fmars.2021.823173
Knapp C., Carter G. (1976). The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process 24, 320–327. doi: 10.1109/TASSP.1976.1162830
Li J., Tong F., Zhou Y., Yang Y., Hu Z. (2022). Small size array underwater acoustic doa estimation based on direction-dependent transmission response. IEEE Trans. Veh. Technol., 1–12. doi: 10.1109/TVT.2022.3197922
Liu Y., Chen H., Wang B. (2021). DOA estimation based on CNN for underwater acoustic array. Appl. Acoust. 172, 107594. doi: 10.1016/j.apacoust.2020.107594
Li J., Wang J., Wang X., Qiao G., Luo H., Gulliver T. A. (2019). Optimal beamforming design for underwater acoustic communication with multiple unsteady sub-Gaussian interferers. IEEE Trans. Veh. Technol. 68, 12381–12386. doi: 10.1109/TVT.2019.2945007
Nair V., Hinton G. E. (2010). “Rectified linear units improve restricted Boltzmann machines,” in ICML.
Niu H., Reeves E., Gerstoft P. (2017). Source localization in an ocean waveguide using supervised machine learning. J. Acoust. Soc Am. 142, 1176–1188. doi: 10.1121/1.5000165
Ozanich E., Gerstoft P., Niu H. (2020). A feedforward neural network for direction-of-arrival estimation. J. Acoust. Soc Am. 147, 2035–2048. doi: 10.1121/10.0000944
Porter M. B. (2011). The BELLHOP manual and user’s guide: Preliminary draft Vol. 260 (La Jolla, CA, USA: Heat, Light, and Sound Research, Inc.). Tech. Rep.
Porter M. B., Bucker H. P. (1987). Gaussian Beam tracing for computing ocean acoustic fields. J. Acoust. Soc Am. 82, 1349–1359. doi: 10.1121/1.395269
Rao B. D., Hari K. S. (1989). Performance analysis of root-MUSIC. IEEE Trans. Acoust. Speech Signal Process 37, 1939–1949. doi: 10.1109/29.45540
Ren Q., Willis A. (1997). Fast root MUSIC algorithm. Electron. Lett. 33, 450–451. doi: 10.1049/el:19970272
Roy R., Kailath T. (1989). ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process 37, 984–995. doi: 10.1109/29.32276
Schmidt R. (1986). Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 34, 276–280. doi: 10.1109/TAP.1986.1143830
Shen Y., Pan X., Zheng Z., Gerstoft P. (2020). Matched-field geoacoustic inversion based on radial basis function neural network. J. Acoust. Soc Am. 148, 3279–3290. doi: 10.1121/10.0002656
Singer A. C., Nelson J. K., Kozat S. S. (2009). Signal processing for underwater acoustic communications. IEEE Commun. Mag. 47, 90–96. doi: 10.1109/MCOM.2009.4752683
Stoica P., Nehorai A. (1990). MUSIC, maximum likelihood, and Cramer-rao bound: further results and comparisons. IEEE Trans. Acoust. Speech Signal Process 38, 2140–2150. doi: 10.1109/29.61541
Sun D., Jia Z., Teng T., Ma C. (2022). Robust high-resolution direction-of-arrival estimation method using denseblock-based u-net. J. Acoustic. Soc. America 151, 3426–3436. doi: 10.1121/10.0011470
Sun X., Jia X., Zheng Y., Wang Z. (2021). A data-driven method for estimating the target position of low-frequency sound sources in shallow seas. Front. Inf. Technol. Electron. Eng. 22, 1020–1030. doi: 10.1631/FITEE.2000181
Swindlehurst A. L., Ottersten B., Roy R., Kailath T. (1992). Multiple invariance ESPRIT. IEEE Trans. Signal Process 40, 867–881. doi: 10.1109/78.127959
Viberg M., Ottersten B., Kailath T. (1991). Detection and estimation in sensor arrays using weighted subspace fitting. IEEE Trans. Signal Process 39, 2436–2449. doi: 10.1109/78.97999
Wang Y., Peng H. (2018). Underwater acoustic source localization using generalized regression neural network. J. Acoust. Soc Am. 143, 2321–2331. doi: 10.1121/1.5032311
Wang M., Zhao M., Chen J., Rahardja S. (2019). Nonlinear unmixing of hyperspectral data via deep autoencoder networks. IEEE Geosci. Remote Sens. Lett. 16, 1467–1471. doi: 10.1109/LGRS.2019.2900733
Xiang H., Chen B., Yang T., Liu D. (2020). Phase enhancement model based on supervised convolutional neural network for coherent DOA estimation. Appl. Intell. 50, 2411–2422. doi: 10.1007/s10489-020-01678-4
Xiang H., Chen B., Yang M., Xu S., Li Z. (2021). Improved direction-of-arrival estimation method based on LSTM neural networks with robustness to array imperfections. Appl. Intell. 51, 4420–4433. doi: 10.1007/s10489-020-02124-1
Xiao X., Zhao S., Zhong X., Jones D. L., Chng E. S., Li H. (2015). “A learning-based approach to direction of arrival estimation in noisy and reverberant environments,” in 2015 IEEE International Conference on Acoustics, Speech and Signal Processing. 2814–2818 (NEW YORK, USA: IEEE).
Xu X.-L., Buckley K. M. (1992). Bias analysis of the MUSIC location estimator. IEEE Trans. Signal Process 40, 2559–2569. doi: 10.1109/78.157296
Yang T. (2012). Properties of underwater acoustic communication channels in shallow water. J. Acoust. Soc Am. 131, 129–145. doi: 10.1121/1.3664053
Yuan Y., Wu S., Wu M., Yuan N. (2021). Unsupervised learning strategy for direction-of-arrival estimation network. IEEE Signal Process Lett. 28, 1450–1454. doi: 10.1109/LSP.2021.3096117
Zhang X., Wu H., Sun H., Ying W. (2021). Multireceiver SAS imagery based on monostatic conversion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 14, 10835–10853. doi: 10.1109/JSTARS.2021.3121405
Zhang X., Yang P. (2021). An improved imaging algorithm for multi-receiver SAS system with wide-bandwidth signal. Remote Sens. 13, 5008. doi: 10.3390/rs13245008
Zhang X., Yang P., Huang P., Sun H., Ying W. (2022). Wide-bandwidth signal-based multireceiver SAS imagery using extended chirp scaling algorithm. IET Radar Sonar Nav. 16, 531–541. doi: 10.1049/rsn2.12200
Keywords: DOA estimation, array signal processing, underwater acoustic, convolutional recurrent neural network, deep learning
Citation: Li X, Chen J, Bai J, Ayub MS, Zhang D, Wang M and Yan Q (2022) Deep learning-based DOA estimation using CRNN for underwater acoustic arrays. Front. Mar. Sci. 9:1027830. doi: 10.3389/fmars.2022.1027830
Received: 25 August 2022; Accepted: 19 October 2022;
Published: 10 November 2022.
Edited by:
Haixin Sun, Xiamen University, ChinaCopyright © 2022 Li, Chen, Bai, Ayub, Zhang, Wang and Yan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jianfeng Chen, Y2hlbmpmQG53cHUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.