- 1Department of Electrical and Computer Engineering, Sungkyunkwan University, Suwon, South Korea
- 2Future Convergence Engineering, School of Computer Science and Engineering, Korea University of Technology and Education, Cheonan, South Korea
Restoration of underwater images plays a vital role in underwater target detection and recognition, underwater robots, underwater rescue, sea organism monitoring, marine geological survey, and real-time navigation. Mostly, physics-based optimization methods do not incorporate structural differences between the guidance and transmission maps (TMs) which affect the performance. In this paper, we propose a method for underwater image restoration by utilizing a robust regularization of coherent structures. The proposed method incorporates the potential structural differences between TM and the guidance map. The optimization of TM is modeled through a nonconvex energy function which consists of data and smoothness terms. The initial TM is taken as a data term whereas the smoothness term contains static and dynamic structural priors. Finally, the optimization problem is solved using majorize-minimize (MM) algorithm. The proposed method is tested on benchmark dataset and its performance is compared with the state-of-the-art methods. The results from the experiments indicate that the proposed regularization scheme adequately improves the TM, which results in high-quality restored images.
1 Introduction
Restoration of underwater images is a challenging task and it plays a vital role in underwater target detection and recognition, underwater robots, underwater rescue, sea organism monitoring, marine geological survey, and real-time navigation Jian et al. (2021). Underwater images suffer from strong light absorption, scattering, color distortion, and noise from the artificial light source. Image formation in the water is shown in Figure 1A. It can be observed that the image is formed through the three types of lights 1) the reflected light comes to the camera directly after striking the object, 2) the forward-scattered light that deviates from its way from the original direction after striking the object, 3) the back-scattering light comes to the camera after encountering particles Han et al. (2020); Islam et al. (2020).
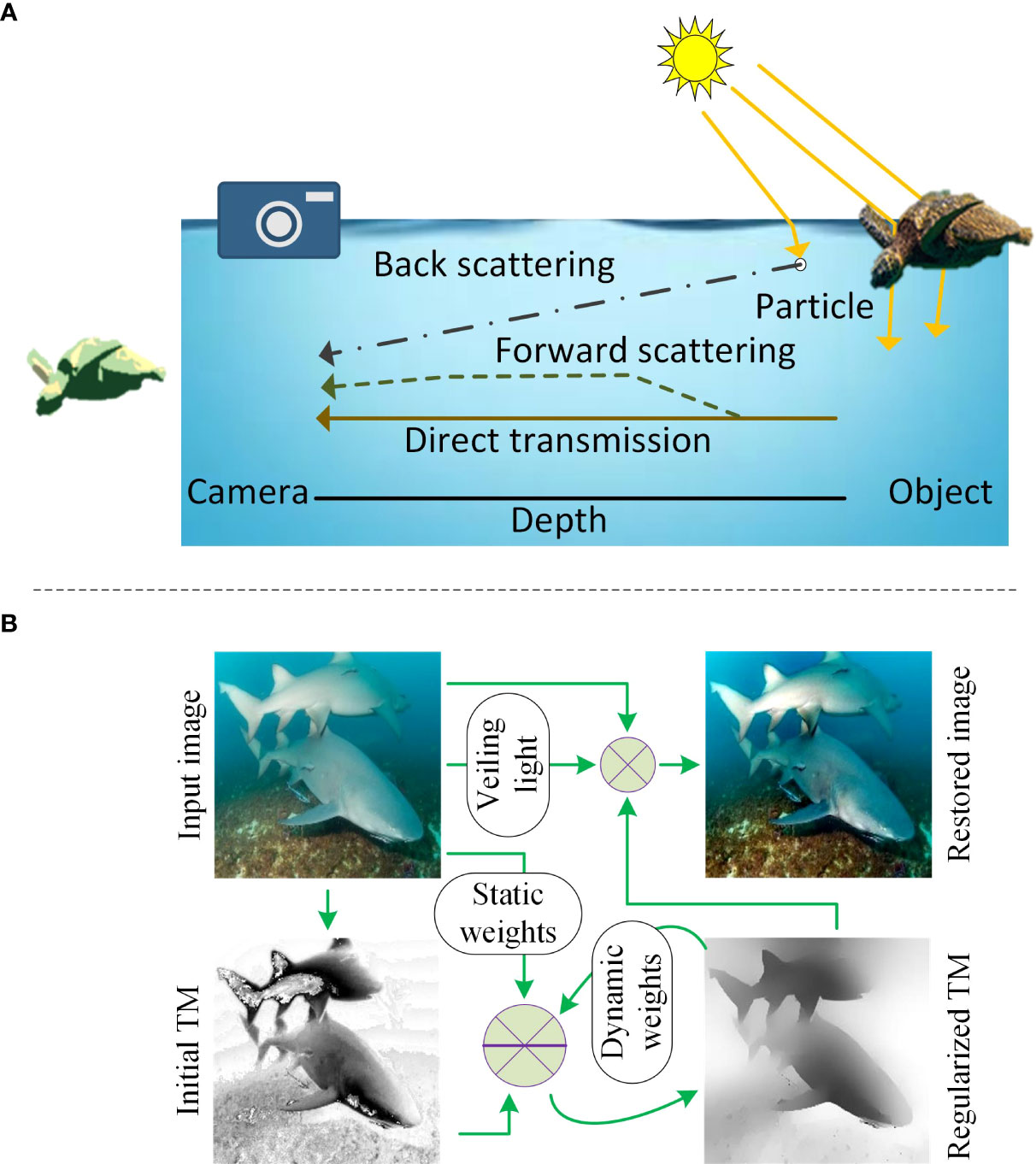
Figure 1 (A) Underwater image formation. Object signal is attenuated along the line of sight (direct transmission). Light scattered from the environment (e.g., particle) carries no information of the scene. Forward scattered light blurs the scene. (B) Proposed method. Firstly, following the physical scattering model, a transmission map (TM) and veiling light are computed from the input image. Then, the initial TM is improved by solving a robust energy function that utilizes a nonconvex regularizer and two types of regularization weights. Finally, an enhanced image is restored by using the regularized TM.
Underwater image restoration is well studied in terms of enhancement, noise reduction, defogging/dehazing, segmentation, saliency detection, color constancy, and color correction Jian et al. (2021). Methods for underwater images can be divided into physics and machine/deep learning-based methods Islam et al. (2020). A comprehensive survey on deep learning-based underwater image enhancement algorithms is done in the study Anwar and Li (2020). This study suggested that the algorithms can further be divided into several categories, e.g., encoder–decoder models, modular designs, multi-branch designs, depth-guided networks, and dual generator GANs. In a study, generative adversarial networks (GANs)-based method is proposed to improve the quality of visual underwater scenes Fabbri et al. (2018). As mostly, deep learning-based models are computationally expensive, so a convolutional neural network (CNN)-based diver detection model is suggested to balance the trade-offs between robustness and efficiency Islam et al. (2019). In another work, the authors employed the cycle-consistent adversarial networks to generate synthetic underwater images, and then a deep residual framework-based model is developed for image enhancement Liu et al. (2019). The deep learning approach has become the state-of-the-art solution and it has provided reasonable performance.
Physics-based methods usually restore the image by computing a transmission map (TM). The initial TM is improved using various techniques including guided filtering, statistical models, and matting algorithms Lu et al. (2013). For instance, in a work, guided trigonometric bilateral filters are applied for improving the TM and then a color correction algorithm is applied for enhancing the image visibility Lu et al. (2013). In another work, an underwater enhancement method is proposed that provided two versions of the restored image. This method is based on the minimum information loss principle and histogram distribution prior Li et al. (2016). In a recent work, the authors suggested methods for image restoration and color correction by taking into account the different optical water types. The revised model for image formation Akkaynak and Treibitz (2018) has been used and a depth map is also required as an input for their solutions Berman et al. (2021). Another recent work with improved results uses a locally adaptive color correction method using the minimum color loss principle and the maximum attenuation map-guided fusion strategy Zhang et al. (2022). In another study, an underwater normalized total variation (UNTV) model is suggested for underwater image dehazing and deblurring that uses sparse prior knowledge of blur kernel. The blur kennel is obtained by using an iterative reweighted least squares algorithm Xie et al. (2022). Mostly, physics-based optimization-based methods optimize TM by utilizing weights from some guidance map that depends on the input image. However, these methods do not incorporate structural differences between the guidance map and TM. Consequently, images recovered are of poor quality.
In this paper, we propose a method for underwater image restoration by utilizing a robust regularization of coherent structures in image and transmission map. The proposed method incorporates the potential structural differences between TM and the guidance map. The optimization of TM is modeled through a nonconvex energy function which consists of data and smoothness terms. The initial TM is taken as a data term whereas the smoothness term contains static and dynamic structural priors. Finally, the optimization problem is solved using majorize-minimize (MM) algorithm. The proposed method is tested on benchmark dataset and its performance is compared with the state-of-the-art methods. The results from the experiments indicate that the proposed regularization scheme adequately improves the TM, which results in high-quality restored images.
2 Proposed method
The proposed method for underwater image restoration can be divided into three steps as shown in Figure 1B. In the first step, the veiling light and initial TM are computed. In the second step, initial TM is regularized through the proposed nonconvex energy framework. During this step, static and dynamic weights are computed from the input image and iteratively regularized TM. In the last step, an image is restored using the underwater imaging model. These steps have been described in detail in the following sections.
2.1 Veiling light and initial transmission map
Based on the Koschmieder’s law Koschmieder (1924), only a small portion of the reflected light reaches the observer and it causes poor visibility. The formation of images underwater has been described in Figure 1A. Usually, a linear interpolation-based model is used to describe the image formation in scattering media like water Han et al. (2020); Islam et al. (2020). Recently, a refined image formation model has been proposed in Akkaynak and Treibitz (2018). This revised model tries to explain the instabilities of current models however it also has certain limitations Li et al. (2021). Contrarily, the widely used physical scattering model Han et al. (2020); Berman et al. (2021) that describes the formation of images underwater is as follows,
where x = (x,y) denotes the pixel coordinates, I is the observed intensity (i.e., underwater image), J is the scene radiance, V is the global veiling light, and n is the medium transmission map (TM). When the medium is homogeneous, TM can be expressed as n(x) = e-βd(x), where β is the medium extinction coefficient, and d(x) is the depth. Actually, this β is dependent on the color channel, however, for simplicity, we have used it same for all three channels. The main goal of underwater image restoration methods is to recover J, V, and n from I. Although the initial TM n can be obtained through any priors mentioned in the literature, in this work, veiling light V and initial TM n were computed using the haze-lines (HL) prior (Berman et al., 2020). The initial TM is computed per-pixel and is not spatially coherent. To improve this initial TM n, we propose to apply non-convex regularization. The improvement in TM ultimately leads to the restoration of images that are of better quality.
2.2 Model
This paper proposes optimizing the initial TM n by efficiently minimizing the following energy function
where is the regularized (target) TM, Ω is the 2D spatial domain of TM, λ controls the smoothness level by adjusting the significance of two terms on the right-hand side, Nx is a 2D neighborhood window centered at x. is the spatially varying weighting function computed from guidance s. The neighborhood coherence (smoothness) between pixels located at positions x and is enforced adaptively using spatially varying weights . To benefit from the advantages of guided filtering He et al. (2013); Shen et al. (2015), we have incorporated guidance signal s in our proposed framework. Specifically, the spatial regularization (smoothness) weights have been computed from s instead of n or . Gray-scale image computed from the input image I has been taken as the guidance s. The idea is that if s(x) is considerably different from (e.g., if x and are across an edge in the gray-scale input image), then should have a little effect in the regularization of . We define these weights using Gaussian distance in space and intensity as,
where the first term is the spatial filter that would decrease the weight if the distance between x and is large, second is the intensity range filter that would decrease the weight if the intensity difference between s(x) and is large. μ and v are the positive parameters defined by the user. These parameters control the decay rate of the spatial and intensity range filter, respectively, and thus adjust the regularization (smoothness) bandwidth. The proposed robust regularizer is the parameterized squared hyperbolic tangent function defined as
where ρ djusts the skewness of this function. This function maps any to the range [0 1] and can compresses large values to approach to 1. While observing this function, it can be inferred that this function ψρ(j) penalizes large gradients of less than L2 or L1 regularizer function during filtering. This results in better preservation of high-frequency features (e.g., edges and corners). In other words, our function restrains the large deviations to be fused together.
2.3 Regularization
In the literature, mostly, a convex energy function is minimized for regularization. Contrarily, we have proposed and solved a non-convex energy function (Eq. 2). For such non-convex energy functions, the optimization is non-trivial. To solve this optimization problem, we have used a sophisticated technique of majorize minimization (MM) algorithm. This algorithm performs two steps several times. In the first (i.e., majorization) step, a convex surrogate function for the objective function is created. In the second (i.e., minimization) step, a local minimum is found for the surrogate function. These two steps are followed interchangeably several times until the algorithm converges. While the iteration number k is increased, the values of corresponding to the set decrease monotonically.
At the majorization step, E(k) for ℰ is achieved by substituting the regularizer ψρ(j) with in (2) as follows
where is a surrogate function for ψρ(j). That is, stays above the ψρ(j), and they touch each other only at j = i. The convex function E(k) is easy to be minimized by taking its first derivative with respect to . The normal equation of (5) is
where,
The output is obtained through the vectorized form of (6) by iteratively solving the linear systems of the form, , where I is an identity matrix, n and denote the column vectors of n and , respectively, and L is a Laplacian matrix.
2.4 Recovered image
The goal of underwater image restoration is to recover the scene radiance J(x) from I(x) based on Eq. 1. Once the regularized TM is obtained, the scene radiance J(x) can be recovered by using,
3 Results and discussion
Our proposed regularization-based scheme (Eq. 2) involves a number of parameters. We firstly describe what are the values of these parameters and how these values are determined. We have performed extensive experiments on a variety of underwater images and empirically found the optimal values for these parameters. Those optimal values are λ = 200, ρ = 2.5, μ = 1, and v = 200. These same values have been used for all the images tested in this work. Now, we visually examine how our regularization scheme improves the initial TM. To do so, few underwater images have been taken from the EUVP dataset Islam et al. (2020). These images are named as jellyfish, shark, angel butterfly, coral leaf, snake eels, red snapper, mangrove, and yellow fish, and these images have been shown in the first row of Figure 4. Their initial TMs have been shown in the second row, where the color variation between black (dark) and white (bright) corresponds to the variation in the TM values. It can be seen that the initial TMs have abrupt variations even for the neighboring similar depth regions. Moreover, in these initial TMs, the object boundaries have mingled with the background. If these inaccurate TMs are used for image restoration, their inaccuracies cause degradation in the quality of restored images. This is indicated by the images shown in the third row. These images are obtained through Eq. 8 by using the initial TMs, i.e., . It can be seen that these images suffer from poor visibility. Further, these images have several glitches like, detail loss, color shift, and dimmed light. The inaccuracies of initial TMs need to be addressed for accurate image restoration. We have improved these initial TMs through our non-convex regularization scheme. Our regularized TMs have been displayed in the fourth row. These TMs are considerably better than the initial TMs in a number of ways. Like, our regularized TMs have retained the structures as well as edges of the objects in the scene. On the one hand, these regularized TMs are adequately smooth which ensures the consistency of structures in the spatial domain. On the other hand, sharp structural edges are retained which agrees with the depth discontinuities in the scene. These attributes of the regularized TMs characterize the geometry of the scene. The images restored by using these regularized TMs in Eq. 8 are shown in the last row. It can be observed that these images have higher visibility as compared to the images in the third row. In these images, the details and the natural appearance of the scene are well-preserved. These restored images have rich color information with no artifacts like color saturation. In short, we can also compare the quality of restored images in the third and fifth rows of Figure 2 on the likert scale. Accordingly, each of the images in the third row is of ‘poor’ quality as compared to the corresponding image in the fifth row which is of ‘good’ quality. This comparison indicates the necessity of improving the initial TM, and that the proposed regularization scheme is effective in improving the initial TM.

Figure 2 Improvement of initial TMs using the proposed regularization scheme. The images restored using the regularized TMs are of better quality as compared to the images restored using the initial TMs.
Next, we quantitatively evaluated the advantage gained by regularizing the initial TM. To do so, we computed the perception-based image quality evaluator (PIQE) Venkatanath et al. (2015) for the images, where lower values of this metric indicate better perception quality of the images. PIQE values (before applying regularization, after applying regularization) for the images shown in Figure 2 are jellyfish (42.76,36.20), shark (53.36,38.44), angel butterfly (49.26,24.96), coral leaf (44.07,22.27), snake eels (44.08,34.34), red snapper (50.71,30.55), mangrove (46.89,28.60), and yellow fish (48.46, 23.87). It can be observed that PIQE values of images restored from the initial TMs are worse as compared to the values of images restored from the regularized TMs. This indicates that the regularization of initial TM results in the restoration of better quality images.
Finally, we compared the performance of the proposed method with several state-of-the-art methods. Among the compared methods, eight are learning-based: (i) image enhancement based on generative adversarial network with paired (IE-GAN), and (ii) unpaired training (IE-GAN-UP) Islam et al. (2020), (iii) GAN with cycle-consistency loss (CycleGAN) Zhu et al. (2017), (iv) underwater GAN with gradient penalty (UGAN-P) Fabbri et al. (2018), (v) Pix2Pix Isola et al. (2017), (vi) least-squared GAN (LS-GAN) Mao et al. (2017), (vii) GAN with residual blocks in the generator (Res-GAN) Li et al. (2017), and (viii) Wasserstain residual GAN (Res-WGAN) Arjovsky et al. (2017). Two physics-based methods: (i) multi-band fusion-based enhancement (Mband-En) Cho et al. (2018), and (ii) underwater color restoration based on haze-lines (Uw-HL) Berman et al. (2021), are also included for comparison. The output restored images of these methods have been shown in Figure 4 for few underwater images from the EUVP dataset Islam et al. (2020). It can be seen that the IE-GAN and IE-GAN-UP have increased the visibility to some extent but shifted the colors. CycleGAN and LS-GAN exhibit poor visibility, and loose the object boundaries and texture details. UGAP-N, Pix2Pix, Res-GAN, Res-WGAN, Mband-En, and Uw-HL over saturate the objects. Pix2Pix and LS-GAN often fail to improve global brightness as well. Mband-En and Uw-HL have shifted the colors by a large extent. On the other hand, our proposed method provides good quality results which are free from the above mentioned artifacts of the compared methods. Our proposed method adequately enhances the visibility without any color-shifting artifacts. Further, the output images of our method retain the fine details. We also used the quantitative measures to evaluate the quality of the images of Figure 3. Two quantitative measures naturalness image quality evaluator (NIQE) Mittal et al. (2012), and perception-based image quality evaluator (PIQE) Venkatanath et al. (2015) have been computed and shown in the Figure 4. Lower values of these measures reflect better perceptual quality of the image. The eleven bars for each image respectively correspond to the images restored by approaches IE-GAN, IE-GAN-UP Islam et al. (2020), CycleGAN Zhu et al. (2017), UGAN-P Fabbri et al. (2018), Pix2Pix Isola et al. (2017), LS-GAN Mao et al. (2017), Res-GAN Li et al. (2017), Res-WGAN Arjovsky et al. (2017), Mband-En Cho et al. (2018), Uw-HL Berman et al. (2021), and our method. It can be seen that the proposed method attains the least values for both of these quantitative measures for almost all six images. These values suggest that the perception qualities of our restored images are better than the input images and the restored images by the compared methods. From this qualitative and quantitative comparison among the quality of restored images, it can be deduced that our proposed method outperforms the state-of-the-art methods.

Figure 3 Comparison of our method with other approaches IE-GAN, IE-GAN-UP Islam et al. (2020), CycleGAN Zhu et al. (2017), UGAN-P Fabbri et al. (2018), Pix2Pix Isola et al. (2017), LS-GAN Mao et al. (2017), Res-GAN Li et al. (2017), Res-WGAN Arjovsky et al. (2017), Mband-En Cho et al. (2018), and Uw-HL Berman et al. (2021).
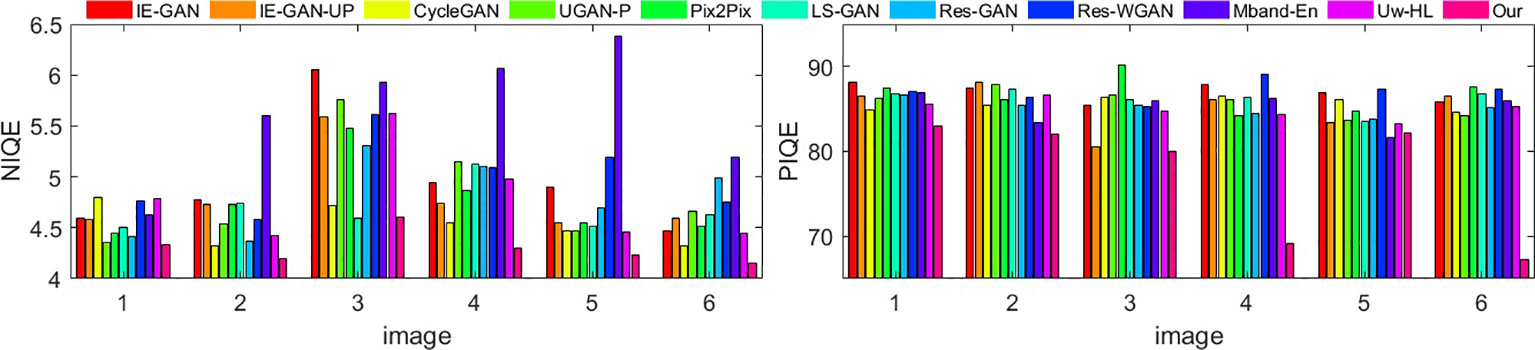
Figure 4 Quantitative measures NIQE Mittal et al. (2012) and PIQE Venkatanath et al. (2015) for the six images shown in Figure 3. The eleven bars for each image respectively correspond to the images restored by different compared approaches and our method.
4 Conclusion
In this paper, a robust regularization-based method has been proposed for the underwater image restoration. Usually, the TM suffers from several artifacts like, abrupt variations which are inconsistent with the scene, and object boundaries mingled with the background. These inaccuracies in TM lead to the image restoration of degraded quality. We have formulated a nonconvex energy function for the optimization of initial TM. As a result, the regularized TM is free from the artifacts; it is adequately smooth as well as retains the sharp boundaries. This improvement in TM results in image restoration of better quality. The experimental results demonstrated that the proposed method is remarkably effective for the restoration of underwater images and it outperforms the state-of-the-art methods.
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found here: https://irvlab.cs.umn.edu/resources/euvp-dataset.
Author contributions
UA and MM contributed to conception and design of the study. UA wrote the code for simulations and collected the data. MM performed the analysis. UA and MM wrote the draft of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported in parts by the Creative Challenge Research Program (2021R1I1A1A01052521), BK-21 FOUR Program funded by the Ministry of Education, by the Basic Research Program (2022R1F1A1071452) and Basic Science Research Program (2022R1A4A3033571) funded by the Korea government (MSIT: Ministry of Science and ICT), through the National Research Foundation of Korea (NRF).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akkaynak D., Treibitz T. (2018). “A revised underwater image formation model,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. 6723–6732. doi: 10.1109/CVPR.2018.00703
Anwar S., Li C. (2020). Diving deeper into underwater image enhancement: A survey. Signal Processing: Image Communication 89, 115978. doi: 10.1016/j.image.2020.115978
Arjovsky M., Chintala S., Bottou L. (2017). “Wasserstein generative adversarial networks,” in International conference on machine learning (PMLR). eds. Precup D., Yee Whye T.. Sydney, NSW, Australia: PMLR 70, 214–223. Available at: https://proceedings.mlr.press/v70/arjovsky17a.html
Berman D., Levy D., Avidan S., Treibitz T. (2021). “Underwater single image color restoration using haze-lines and a new quantitative dataset,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, 43 (8), 2822–2837. doi: 10.1109/TPAMI.2020.2977624
Berman D., Treibitz T., Avidan S. (2020). “Single image dehazing using haze-lines,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, 42 (3), 720–734. doi: 10.1109/TPAMI.2018.2882478
Cho Y., Jeong J., Kim A. (2018). “Model-assisted multiband fusion for single image enhancement and applications to robot vision,” in IEEE Robotics and Automation Letters 3 (4), 2822–2829. doi: 10.1109/LRA.2018.2843127
Fabbri C., Islam M. J., Sattar J. (2018). “Enhancing underwater imagery using generative adversarial networks,” in 2018 IEEE International Conference on Robotics and Automation (ICRA). 7159–7165. doi: 10.1109/ICRA.2018.8460552
Han M., Lyu Z., Qiu T., Xu M. (2020). “A review on intelligence dehazing and color restoration for underwater images,” in IEEE Transactions on Systems, Man, and Cybernetics: Systems, 50 (5), 1820–1832. doi: 10.1109/TSMC.2017.2788902
He K., Sun J., Tang X. (2013). “Guided image filtering,” in IEEE transactions on pattern analysis and machine intelligence, 35 (6), 1397–1409. doi: 10.1109/TPAMI.2012.213
Islam M. J., Fulton M., Sattar J. (2019). “Toward a generic diver-following algorithm: Balancing robustness and efficiency in deep visual detection,” in IEEE Robotics and Automation Letters, 4 (1), 113–120 8543168. doi: 10.1109/LRA.2018.2882856
Islam M. J., Xia Y., Sattar J. (2020). “Fast underwater image enhancement for improved visual perception,” in IEEE Robotics and Automation Letters, 5 (2), 3227–3234. doi: 10.1109/LRA.2020.2974710
Isola P., Zhu J.-Y., Zhou T., Efros A. A. (2017). “Image-to-image translation with conditional adversarial networks,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 5967–5976. doi: 10.1109/CVPR.2017.632
Jian M., Liu X., Luo H., Lu X., Yu H., Dong J. (2021). Underwater image processing and analysis: A review. Signal Processing: Image Communication 91, 116088. doi: 10.1016/j.image.2020.116088
Koschmieder H. (1924). Theorie der horizontalen Sichtweite. Beitrage zur Physik der freien Atmosphare 12, 33–53.
Li C., Anwar S., Hou J., Cong R., Guo C., Ren W. (2021). Underwater image enhancement via medium transmission-guided multi-color space embedding,” in IEEE Transactions on Image Processing 30, 4985–5000. doi: 10.1109/TIP.2021.3076367
Li C.-Y., Guo J.-C., Cong R.-M., Pang Y.-W., Wang B. (2016). “Underwater image enhancement by dehazing with minimum information loss and histogram distribution prior,” in IEEE Transactions on Image Processing, 25 (12), 5664–5677. doi: 10.1109/TIP.2016.2612882
Li J., Liang X., Wei Y., Xu T., Feng J., Yan S. (2017). “Perceptual generative adversarial networks for small object detection,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 1951–1959. doi: 10.1109/CVPR.2017.211
Liu P., Wang G., Qi H., Zhang C., Zheng H., Yu Z. (2019). “Underwater image enhancement with a deep residual framework,” in IEEE Access. 7, 94614–94629. doi: 10.1109/ACCESS.2019.2928976
Lu H., Li Y., Serikawa S. (2013). “Underwater image enhancement using guided trigonometric bilateral filter and fast automatic color correction,” in 2013 IEEE International Conference on Image Processing 3412–3416. doi: 10.1109/ICIP.2013.6738704
Mao X., Li Q., Xie H., Lau R. Y., Wang Z., Smolley S. P. (2017). “Least squares generative adversarial networks,” Proceedings of the IEEE International Conference on Computer Vision (ICCV). 2813–2821. doi: 10.1109/ICCV.2017.304
Mittal A., Soundararajan R., Bovik A. C. (2012). Making a “completely blind” image quality analyzer. IEEE Signal processing letters. 20 (3), 209–212. doi: 10.1109/LSP.2012.2227726
Shen X., Zhou C., Xu L., Jia J. (2015). “Mutual-structure for joint filtering,” in Proceedings of the IEEE International Conference on Computer Vision. 3406–3414. doi: 10.1109/ICCV.2015.389
Venkatanath N., Praneeth D., Bh M. C., Channappayya S. S., Medasani S. S. (2015). “Blind image quality evaluation using perception based features,” in 2015 Twenty First National Conference on Communications (NCC) (IEEE). 1–6. doi: 10.1109/NCC.2015.7084843
Xie J., Hou G., Wang G., Pan Z. (2022). “A variational framework for underwater image dehazing and deblurring,” in IEEE Transactions on Circuits and Systems for Video Technology, 32 (6), 3514–3526. doi: 10.1109/TCSVT.2021.3115791
Zhang W., Zhuang P., Sun H.-H., Li G., Kwong S., Li C. (2022). “Underwater image enhancement via minimal color loss and locally adaptive contrast enhancement,” in IEEE Transactions on Image Processing 31, 3997–4010. doi: 10.1109/TIP.2022.3177129
Keywords: underwater images, image restoration, robust regularization, coherent structures, optimization problem
Citation: Ali U and Mahmood MT (2022) Underwater image restoration through regularization of coherent structures. Front. Mar. Sci. 9:1024339. doi: 10.3389/fmars.2022.1024339
Received: 21 August 2022; Accepted: 23 September 2022;
Published: 13 October 2022.
Edited by:
Rizwan Ali Naqvi, Sejong University, South KoreaReviewed by:
Humaira Nisar, Tunku Abdul Rahman University, MalaysiaMuhammad Arsalan, Dongguk University Seoul, South Korea
Copyright © 2022 Ali and Mahmood. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Tariq Mahmood, dGFyaXFAa29yZWF0ZWNoLmFjLmty
 Usman Ali
Usman Ali Muhammad Tariq Mahmood
Muhammad Tariq Mahmood