Space-time statistics of extreme ocean waves in crossing sea states

The study of extreme ocean waves has gained considerable interest in recent years, due to their importance for offshore design and navigation safety, and several theoretical approaches have been developed for their statistical description. However, in the case of crossing seas, where two or more wave systems of different characteristics are present, a full understanding of the main physical mechanisms responsible for the occurrence of very high individual waves is still lacking. As a consequence, the prediction of extremes in such conditions currently relies on integrated parameters of the total sea state, such as the spectral wave steepness. In this study, to gain further insight into the role of the crossing wind sea and swell wave systems in producing extreme individual waves, we investigate realistic sea states during typhoon Kong-rey (2018) using an ensemble of numerical simulations obtained from a phase-resolving wave model based on the High-Order Spectral (HOS) method. The reliability of the numerical fields is assessed for the first time with stereo wave measurements of the sea surface elevation field collected from an offshore platform in the area of interest. We show that, in specific conditions, space-time extreme crest heights in crossing seas can be larger than in unimodal seas due to second-order bound wave interactions between the wind sea and the swell. To improve existing prediction capabilities, we propose a novel formulation for the wave steepness in crossing seas, which includes nonlinear effects up to the second order and accounts for the spectral parameters of the interacting wave systems.

1. Introduction

In recent years, significant advances have been made in the understanding of the physical mechanisms leading to abnormally high waves. In deep water conditions, several effects have been proposed to explain the formation of extreme waves, with the two main competing hypotheses being the directional and dispersive focusing enhanced by second-order nonlinear non-resonant or bound harmonic waves (Tayfun, 1980; Forristall, 2000) and the nonlinear focusing due to third-order nonlinear quasi-resonant free wave interactions, also called modulational instability (Benjamin and Feir, 1967; Zakharov and Filonenko, 1967). These effects cause the statistics of realistic gravity waves to differ significantly from the Gaussian model of linear seas, thus leading to unexpectedly high waves. To date, a consensus has not yet been reached on whether in typical oceanic seas second-order nonlinearities dominate the dynamics of extreme waves or if third-order nonlinear effects also play a significant role in the formation of the highest waves. The discussion on nonlinear instabilities active in rogue wave generation has often focused on the role of the modulational instability phenomenon, whose strength and influence are usually measured via the Benjamin-Feir Index (BFI), a parameter proposed by Janssen (2003). In general, this type of instability seems to be most effective in narrow-banded and directionally limited sea states, whereas its effect decreases as the spectrum broadens (Alber, 1978; Onorato et al., 2004). Typical oceanic wind seas are short-crested, directionally spread wave fields, so nonlinear focusing due to modulational effects seems to be reduced (Onorato et al., 2009; Waseda et al., 2009; Fedele, 2015), though it might still be significant if the wave steepness is large enough and the spectral bandwidth is sufficiently small (Mori et al., 2011; Waseda et al., 2011). On the other hand, the constructive interference of waves with random amplitudes and phases enhanced by second-order bound nonlinearities has proven to be the most effective mechanism for extreme wave generation in realistic seas (Tayfun and Fedele, 2007; Tayfun, 2008; Fedele, 2012; Benetazzo et al., 2015), so the role of third-order nonlinearities in the generation of extreme waves was recently questioned (see, e.g., Fedele et al., 2016; Brennan et al., 2018). These studies showed that the main parameters governing the occurrence of extreme waves are the steepness, the spectral bandwidth and the directional spreading, with the wave steepness being the most effective.

However, most of the theoretical approaches and numerical studies focused on unimodal sea states, for which the wave energy is concentrated around a single peak in the wave spectrum. On the other hand, bimodal conditions, where generally a wind sea mixes with a swell system, are not infrequent since they make up 15-25% of the ocean state at different locations around the world (Guedes Soares, 1984; Guedes Soares, 1991; Boukhanovsky et al., 2007; Rapizo et al., 2015). When a bimodal (also called crossing) sea state is present, the formation of extreme waves can also be influenced by the nonlinear interaction between the two wave systems, depending on additional factors such as the energy ratio between the constituent systems and their frequency and angular separations.

Most of the recent work on rogue wave occurrence in crossing seas has focused on the influence of the crossing angle in idealized, long-crested conditions. For example, Onorato et al. (2010) showed that, for similarly long-crested systems, freak waves may appear with a higher probability for angles between 10° and 30° and, similarly, Toffoli et al. (2011), taking the kurtosis as a proxy for the presence of extreme events (Janssen et al., 2003), showed that maximum values are obtained for two long-crested wave systems with an interaction angle between 40° and 60°. In more directionally spread conditions, Toffoli et al. (2006) showed that for small incidence angles the wave crest distribution differs from the one related to unimodal sea states, while Bitner-Gregersen and Toffoli (2014) found that systems with small crossing angles seem to possess somewhat larger kurtosis and skewness, all the more when a narrow directional distribution is present. A comprehensive study on the effect of the relative crossing angle was carried out by Gramstad et al. (2018) where, for both narrow-banded and realistic broadband and directionally spread conditions with the same peak frequency and energy, increased sea surface kurtosis was found for small and large crossing angles and a minimum in the kurtosis was found for crossing angles close to 90°. Interestingly, the maximum crest height distribution at a fixed point was almost independent of both the crossing angle and the spectral bandwidth. Similarly, Luxmoore et al. (2019) suggested that a greater role in the formation of extremes might be played by the component directional spreading rather than the crossing angle, whose influence was found to be weak in laboratory experiments. Conversely, the work by McAllister et al. (2018) showed that for a unimodal sea state with a very large directional spreading and for two wave groups with the same frequency and amplitude crossing with large relative angles, maximum crest heights over a spatial domain are further enhanced due to the presence of a set-up of the wave-averaged free surface.

The influence of the energy ratio and the peak frequency separation was only recently addressed by Wang et al. (2021) for the simplified case of two co-propagating long-crested waves. They found that for a fixed energy ratio the kurtosis is higher when the two systems have similar peak frequencies, whereas for a fixed peak frequency separation the kurtosis seems to be lower when they have the same energy content. Mild, weakly nonlinear extreme wave statistics were found also by Støle-Hentschel et al. (2020) for two co-propagating long-crested systems with similar energy, somewhat intermediate between those of a linear swell and a strongly nonlinear wind sea, highlighting the need to extend the analysis also to the single wave partitions separately as well as on the combined sea state to gain insight on the mechanisms at play. However, in realistic ocean conditions the wind sea contribution is usually short-crested and directionally spread, while the narrow-banded swell is usually less steep, so we expect the statistics of the single partitions and of the combined sea state to differ from the idealized case of two long-crested systems. To date, the investigation of the influence of energy ratio, frequency separation and crossing angle on extreme wave heights in such realistic conditions is still lacking.

Moreover, few studies have focused directly on the physical mechanisms leading to the formation of particularly high waves in realistic crossing seas. Støle-Hentschel et al. (2020), taking the results of numerical simulations for short-crested bimodal seas during the Prestige accident of Trulsen et al. (2015) and assuming the independence of the wind sea and swell systems, provided indirect evidence of nonlinear interactions between two crossing wave systems in addition to their simple linear superposition. In this context, the work by McAllister et al. (2018) represents an important step forwards in describing the second-order nonlinear interactions that may occur in a crossing sea state, which can lead to increased crest heights due to the set-up of the free surface. As regards the effects related to modulational instability, the work by Brennan et al. (2018) showed that, if the single partitions do not show signs of instability, then the phenomenon will unlikely arise in the crossing sea state, even over large temporal scales. Nevertheless, enhanced growth rates of the instabilities cannot be excluded in the particular case where the crossing of two steep, narrow-banded wave systems occurs.

Our still incomplete knowledge of the physics of crossing seas is also reflected in the statistical distributions used for the prediction of extreme waves in the case of bimodal sea states. Indeed, existing formulations rely on integrated parameters, such as the wave steepness, which are computed from the directional wave spectrum and therefore lack physical meaning when two or more systems are present (Portilla-Yandun et al., 2015), since they cannot be directly associated with the characteristics of any constituent wave systems and with their interactions.

The goal of the present work is therefore twofold. First, we aim at investigating the role of the concurrent wave systems in producing extreme individual waves for different energy ratios and crossing angles in realistic ocean conditions and test if they can be higher than in pure wind sea conditions. The second objective is to test how well currently used distributions relying on a unified steepness are able to predict extremes and we investigate alternative, more physically consistent formulations for the wave steepness in a crossing sea state, which rely on the characteristics of the two constituent wave systems and of the bimodal spectrum.

For the study of the interaction between different wave systems within a crossing sea state, we have focused on the wave field caused by particular atmospheric conditions such as tropical cyclones, where multiple crossing sea states can be identified within the same wave field (Wright et al., 2001; Black et al., 2007; Holthuijsen et al., 2012) and particularly interesting cases can be selected for extreme wave assessment. In particular, depending on the relative position with respect to the cyclone eye, several azimuthal sectors experiencing different types of mixed sea states (and wave spectra) have been identified within a cyclone (see also Hu and Chen, 2011; Liu et al., 2017). As a result of these combinations, it was suggested that long-crested, unidirectional extreme waves resulting from nonlinear instability have a greater potential of occurring south-east of the storm centre in the Northern Hemisphere, whereas in the south and west areas the nonlinear four-wave interactions are attenuated and the wave field is thought to exhibit a weakly nonlinear behaviour, though it might still be dangerous due to the presence of crossing sea states (Mori, 2012). Indeed, enhanced spatio-temporal probability of high waves due to bound-mode effects was found by Benetazzo et al. (2021a) to the south/south-west of the translating storm, whereas increased BFI values, possibly linked to extreme waves caused by modulational instability, were found in the south-east part of the cyclone. However, the role of crossing seas in the formation of such high waves is still an open question.

The tropical cyclone selected for this study is typhoon Kong-rey, a tropical storm that originated from a disturbance in the open Northwestern Pacific Ocean (Yellow Sea), in late September 2018 and made landfall in South Korea on 6 October 2018, where also 3D stereo measurements were available for the assessment of the numerical model used herein. For this event, high values of dimensionless crest heights were found by Benetazzo et al. (2021a) in regions of high steepness.

For the simulation of realistic crossing sea states during typhoon Kong-rey, we employ a phase-resolving wave model based on the High-Order Spectral method, which allows multiple realizations of spatio-temporal sea surface elevation fields with random phases for each case considered. Indeed, due to the recent advances in computing power, the study of extreme waves with very low probability levels with numerical phase-resolving simulations of long and short-crested sea states has gained popularity, since these models grant a large amount of statistically homogeneous data not always available from laboratory or in-situ measurements. For instance, even the most accurate instrument for spatio-temporal sea surface elevation fields presently available, namely the stereo system, can collect a limited number of space-time data due to the limited camera footprint, compared to the length of very high waves, and the limited duration of the recording, which often cannot be extended beyond the usual 20-30 minutes due to the required stationarity of the measured sea states. This limitation may prove to be challenging for the analysis of the nonlinearities at play because the sampling variability may dominate over such effects (Bitner-Gregersen et al., 2021). Of course, the stereo system still represents a unique source of space-time data that has the advantage of capturing all the physical processes involved (e.g. dissipation due to wave breaking) and provides an accurate quantification of their effects on maxima.

A distinctive feature of the analysis carried out is the use of two different statistical approaches for the extreme-value analysis at short-term/range, namely the conventional time approach at a fixed point, which may however be subject to sampling variability, and the space-time approach, where the statistics refer to a given sea surface area. Indeed, the latter approach has recently been envisaged as a more reliable approach for the analysis of extreme waves (Bitner-Gregersen et al., 2021; Kirezci et al., 2021) and it was shown that the statistical moments resulting from numerical simulations can vary significantly, depending on the size of the sea surface area considered for their computation (Kokina and Dias, 2020). Since the size of the area considered also affects the value of predicted extreme wave crest heights due to the different number of waves within such area and the short-crestedness of the sea state (Fedele, 2012), our analysis also traces such dependence.

The paper is organized as follows. In Section 2 we briefly describe the numerical model and setup used for the simulation of nonlinear wave fields carried out in this work and we provide a concise description of the stereo camera system employed. The theoretical framework of our statistical analysis is also outlined. Section 3 first provides details on the main characteristics of the spectra selected within the cyclone Kong-rey field and a preliminary comparison between stereo measurements and numerical simulations is presented. Then, we compare the short-term statistics of extreme wave crest height from our numerical simulations for the single wind sea and swell partitions, identified within three different crossing sea states, with the statistical models currently used to describe extreme waves in unimodal conditions. The comparison between the simulation results for crossing seas and for the constituent partitions is also shown in this section. The accuracy of existing distributions in predicting extreme crest heights in crossing seas is then evaluated in Section 4, where we also propose an alternative formulation for the wave steepness in such complex sea conditions that provides insight into the underlying physics. Conclusions are summarized in Section 5.

2. Methods and data

2.1. High-order spectral numerical model

Spatio-temporal sea surface elevation fields are the most complete source of information for extreme wind wave analysis presently available and they can be produced using phase-resolving numerical models. Indeed, such models allow multiple simulations of the fully nonlinear sea surface elevation field over large physical domains and relatively long time scales, therefore capturing also nonlinear interactions between wave components over long temporal scales. In recent years, one of the most efficient approaches in phase-resolving wave modelling for the fully-nonlinear problem is the so-called High-Order Spectral method (HOS hereinafter), independently proposed by Dommermuth and Yue (1987) and West et al. (1987). HOS is a pseudo-spectral, potential flow method for solving nonlinear free surface boundary conditions up to an arbitrary order of nonlinearity. Since it grants fast convergence, accurate solution and high computational efficiency, it has been widely used to perform long-time nonlinear propagation of arbitrary input wave spectra and investigate the occurrence and generation mechanisms of extreme waves. Many numerical studies focusing on extreme waves under unimodal spectra have been carried out with such phase-resolving models recently (Dysthe et al., 2003; Socquet-Juglard et al., 2005; Toffoli et al., 2006; Ducrozet et al., 2007; Toffoli et al., 2010; Mori et al., 2011; Sergeeva and Slunyaev, 2013; Xiao et al., 2013; Fedele et al., 2016; Slunyaev et al., 2016; Kokorina and Slunyaev, 2019; Liu and Zhang, 2019; Bitner-Gregersen et al., 2021; Kirezci et al., 2021).

In this study, we use the HOS-ocean model developed by Ducrozet et al. (2016) and provided in an open-source code (available at https://github.com/LHEEA/HOS-ocean). This version of the model employs the pseudo-spectral formulation of West et al. (1987), more physically consistent than the one by Dommermuth and Yue (1987) (see Tanaka, 2001; Clamond et al., 2006) and has undergone extensive validation (see Ducrozet et al., 2007; Bonnefoy et al., 2010).

One of the main limitations of this model is that only the propagation of wave fields in non-breaking wave conditions is computed on a periodic domain of constant water depth. Indeed, the HOS solvers are limited to non-breaking (or, equivalently, non-overturning) waves due to the assumption of irrotational flow and inviscid fluid, whereby the free surface position η(x, y, t) must be a single-valued surface function of x and y. When the surface becomes too steep, simulations are terminated due to numerical instability. The method has also been extended to include the effects of energy dissipation due to wave breaking (Wu et al., 2006; Tian et al., 2010; Xiao et al., 2013; Seiffert and Ducrozet, 2018), whose inclusion has shown differences up to 15% compared to the model without breaking (Slunyaev and Kokorina, 2020). However, these additions to the HOS model were not considered in the present study.

Since the phase-resolving model employed does not account for wind input or wave breaking, it might not be fully representative of the extreme conditions investigated herein, so the reliability of the numerical model is investigated by taking advantage of stereo measurements of the 3D sea surface elevation field recorded from a fixed oceanographic platform in the area of interest.

2.1.1. Simulation setup

In the present study, the numerical domain was discretized using N_X·N_Y = 384·384 points free of aliasing errors, which corresponds to the maximum resolved wavenumber k_MAX = 8k_P for the single-peak simulations and k_MAX = 8max(k_Pw; k_Ps) for the bimodal simulations, where k_Pw is the peak wavenumber of the wind sea partition and k_Ps is the peak wavenumber of the swell partition. This wavenumber cut-off has a large influence on the range of applicability of the HOS solver, as shown by Ducrozet et al. (2017), but in general, for common applications such as the propagation of a nonlinear sea state, the choice of k_MAX = [5, 8]k_P is typical.

Since this study aims at investigating the occurrence of high waves during cyclone-driven bimodal sea states due to constructive interference and nonlinear interactions between two wave systems, the nonlinear order in the HOS simulations was set to M = 3. This ensures that all the main nonlinear effects, including four-wave quasi-resonant interactions between free waves, are included in the model simulations (Toffoli et al., 2011) and, at the same time, it grants an accurate solution with limited computational effort.

The HOS models do not employ any atmospheric forcing, so the definition of the initial wave field relies on a directional wave spectrum as input to the model, derived either from measurements (e.g., stereo video or radar), hindcast spectral wave models or analytical formulations, and on random initial phases. For the present study, phase-averaged model spectra and their derived partitions were used to initialize the numerical model. Multiple realizations with different initial random phases were then conducted for each case to limit the role of variability in our estimates and the number of repetitions varies according to the number of individual waves present in the analyzed sea states. Indeed, simulations based on the long-wave swell spectra result in smaller sample size compared to the short-wave wind sea simulations within the same model set-up, so more realizations were required for a consistent statistical comparison of maximum wave crest heights. For the present study, 30 runs were carried out for the wind sea systems and the crossing sea states, whereas 50 runs were considered for the swell. The total duration of the simulations was set to 20 minutes and the solution was taken at 2 Hz. To avoid numerical instabilities, a warm-up period lasting 100s was introduced to allow a smooth transition from the initial (linear) field to fully nonlinear computations (Dommermuth, 2000).

We note that, motivated by ocean applications, we have focused on conditions where the water is deep relative to the wavelength of the carrier wave (i.e., k_Pd > 2, with d representing the water depth).

2.2. Wave model spectra during Kong-rey

The HOS simulations carried out in the present study relied on phase-averaged model directional spectra, which were provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) version (ECWAM, see Janssen, 2008) of the third-generation phase-averaged WAM wave model (Komen et al., 1994), forced by 10-m height neutral wind speeds and two-way coupled to the atmosphere and ocean models. The high-resolution deterministic forecasts produce hourly wind and wave fields at a horizontal resolution of 0.1° (about 9 km × 11 km in the study area) and 0.12° (about 12 km × 14 km), respectively. ECWAM is run on a spectral domain of 36 frequencies (f₁ = 0.0345 Hz with 1.1 geometric progression) and 36 equally spaced directions (from 5° to 355°N). The significant wave height and wave direction fields taken from the hindcast model for the area and dates of interest (see Section 3.1) are shown in Figure 1, as well as the corresponding wind speed and wind direction fields. For further details on the model and its assessment with in-situ measurements the reader is referred to Benetazzo et al. (2021a).

FIGURE 1

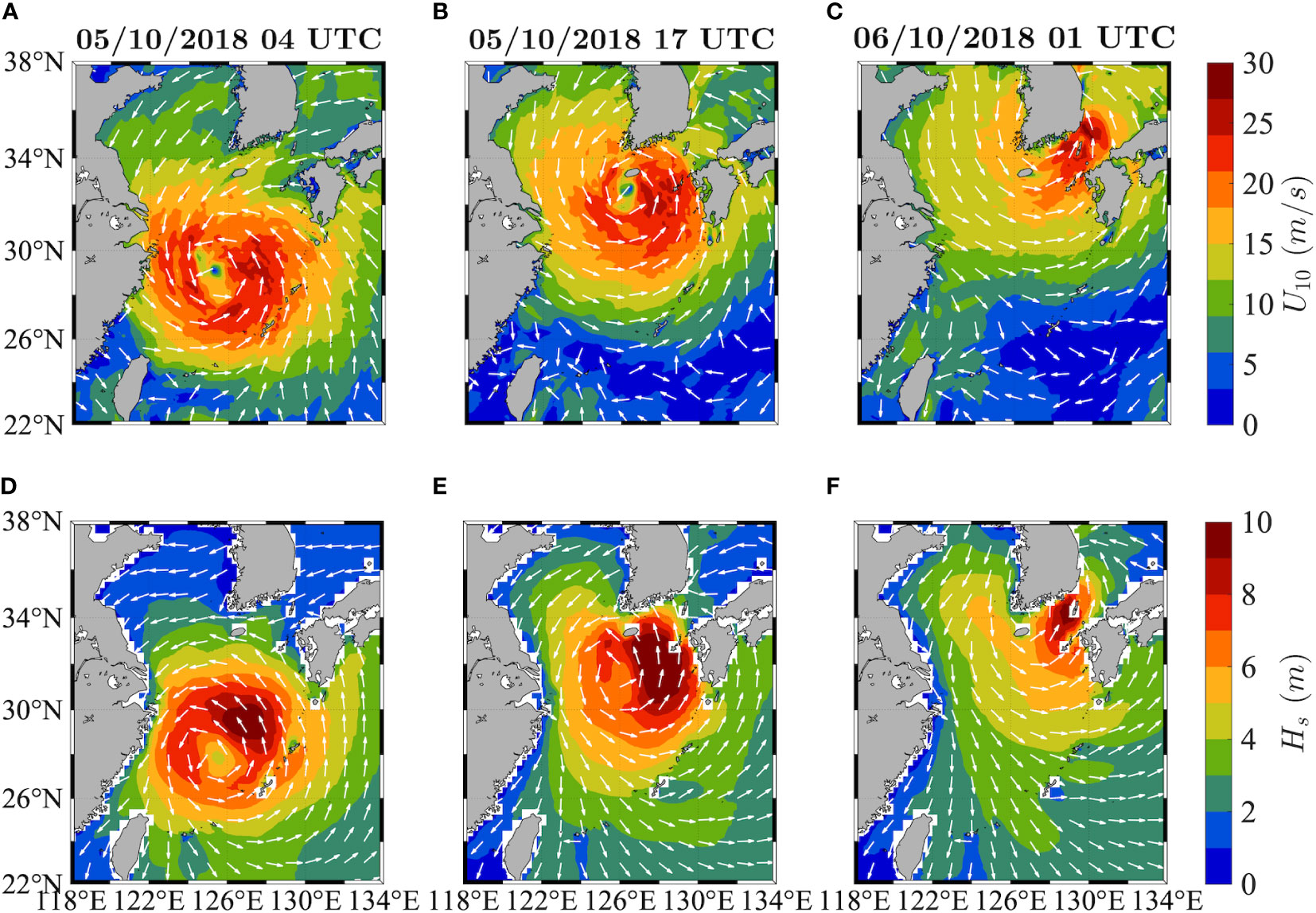
Figure 1 (A–C) Wind speed U₁₀ (coloured shading) and mean wind direction (arrows, decimated for graphical purposes) fields and (D–F) significant wave height Hs (coloured shading) and mean wave direction (arrows, decimated for graphical purposes) fields in the East China Sea and the Yellow Sea during the tropical storm Kong-rey on 5 October 2018 at 04 (left) and 17 UTC (centre) and on 6 October 2018 at 01 UTC (right).

The identification of the different wave systems present within the model spectra was obtained with an automated partitioning procedure of the directional frequency spectrum based on the watershed algorithm of Hasselmann et al. (1996), which treats the wave spectrum as an inverted catchment area, following the implementation of Hanson and Philips (2001).

Although the identification of a wind sea or a swell within the cyclone field is not always straightforward due to the very intense winds (see Portilla et al., 2009), for the selected spectra we have classified the different partitions based on the peak frequency, whereby swells were associated with lower frequency and wind seas with higher values. Given that the focus is on sea states where more than one system is present, regardless of whether they are truly a wind sea or a swell, we consider the adopted classification sufficient for the purpose of this work.

Once the partitions have been identified, to characterize the energy distribution in the bimodal spectra we have adopted the Sea-Swell Energy Ratio (SSER), defined by Rodriguez et al. (2002) and Guedes Soares and Carvalho (2003) as:

$\begin{array}{ll}SSER=\frac{m_{000,w}}{m_{000,s}}& (1)\end{array}$

where m_000,w and m_000,s are the zeroth order moments (m₀₀₀) of wind sea (w) and swell (s) directional spectra S(ω,θ), respectively. In their most general form, the spectral moments can be written as:

$\begin{array}{ll}{m}_{ijl}={\displaystyle \iint k_x^i{k}_y^j{\omega }^{l}S(\omega ,\theta )d\omega d\theta }& (2)\end{array}$

with ω=2πf the angular frequency, θ the wave direction of flow and (k_x,k_y ) the components of the wavenumber vector k.

Wave fields with SSER values smaller than 1.0 represent swell-dominated sea states, while wave conditions with SSER larger than 1.0 represent wind sea-dominated sea states. Similarly, the Intermodal Distance (ID) parameter has been used to describe the peak frequency f_P separation between the two wave systems:

$\begin{array}{ll}ID=\frac{f_{P,w}-f_{P,s}}{f_{P,w}+f_{P,s}}& (3)\end{array}$

When ID approaches 0, the sea state is characterized by a small frequency separation between swell and wind sea, while values of ID above 0.10 correspond to a sea state with clearly separated swell and wind sea peak frequencies. Lastly, to describe the relative crossing angle Δθ between the coexisting wave systems we have used the following definition:

$\begin{array}{ll}\text{Δ}\theta =|{\theta }_{P,W}-{\theta }_{P,S}|& (4)\end{array}$

where θ_P,W and θ_P,S are the peak directions of wind sea and swell, respectively. This way, following the work of Donelan et al. (1997), we define a following condition when the swell travels within 45° of the wind sea, a cross swell when it travels at an angle of 45-135° with respect to the wind sea and an opposing condition when the crossing angle lies in the range 135-180°.

2.3. Stereo wave observations

Within this study, in-situ observations in the Yellow Sea during the cyclone Kong-rey have been considered to assess wave model results. Dedicated data were collected from the offshore platform Gageocho Ocean Research Station (S3 in Figure 2), which is located 150 km east of the southern edge of Korea at an average depth d of 33 m.

FIGURE 2

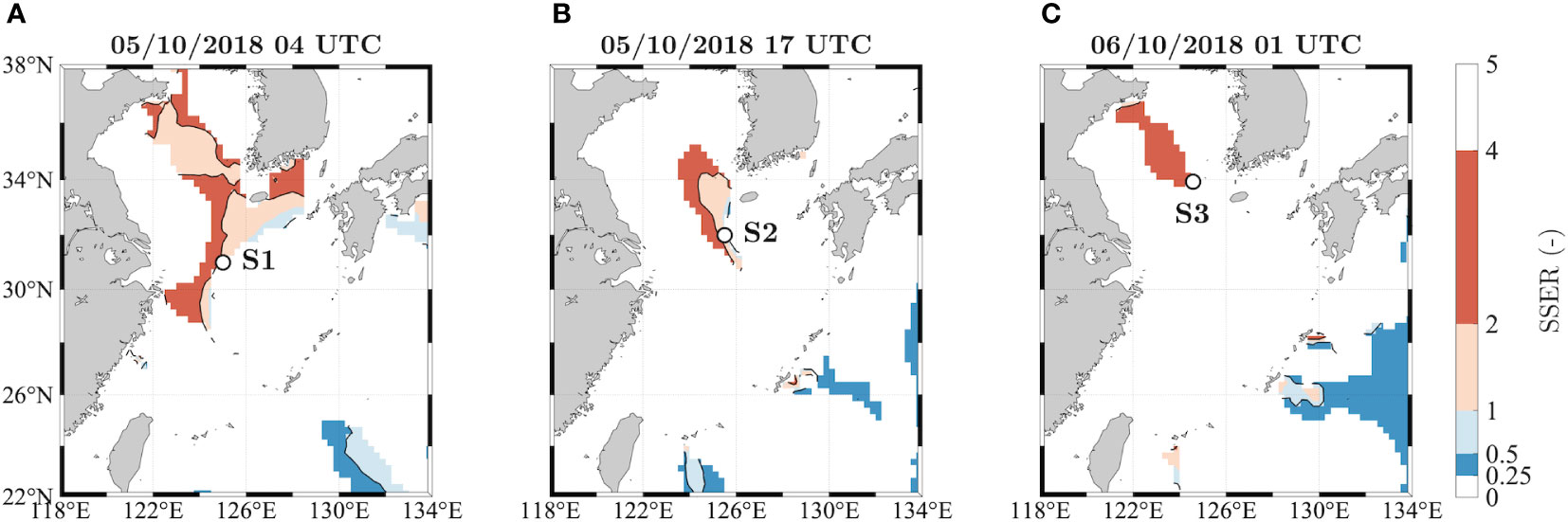
Figure 2 Sea-Swell Energy Ratio (SSER) of the crossing wave fields in the East China Sea and the Yellow Sea during the tropical storm Kong-Rey on 5 October 2018 at 04 (A) and 17 UTC (B) and on 6 October 2018 at 01 UTC (C). Unimodal spectra within the typhoon field and bimodal spectra with one system clearly dominating in terms of energy (i.e. SSER<0.25 or SSER>4) are masked in white. The selected locations where the model spectra used in this study (S1, S2 and S3) were extracted are shown with a white marker.

For the extreme wave characterizations, field data of the spatio-temporal sea surface elevation field η(x,y,t) were recorded using two stereo cameras designed based on the Wave Acquisition Stereo System (WASS) technology (Benetazzo, 2006; Benetazzo et al., 2012) and software (Bergamasco et al., 2017). WASS was mounted facing east at + 26.5 m above the mean sea level, and it had a setup identical to that described in a previous study that focused on sea states at the further north Socheongcho Ocean Research Station (Benetazzo et al., 2018). The stereo processing’s primary result is a temporal sequence (at 7.5 Hz frame rate) of sea surface elevation fields η(x, y). Due to the adopted camera setup and setting, we expect that errors in sea surface vertical displacement η have a maximum absolute value of about 0.1 m and a root-mean-square error of 0.03 m. For processing purposes, 3D scatter points η(x, y) were bi-linearly interpolated onto an Earth-referenced xy-grid with uniform spacing of 0.5 m, spanning the rectangular region x ∈ [-70 m, 70 m] and y ∈ [40 m, 160 m]. To limit the influence of high-frequency noise, independent time series η(t) taken at each xy-position of the gridded elevation were low-pass filtered at 0.9 Hz. For comparison with model data, the 20-minute-long sequence recorded on 6 October 2018 at 01 UTC is considered.

2.4. Extreme wave analysis

In this study, for the characterization of the maximum waves, we consider two different theoretical descriptions of the wave field. Firstly, we consider the sea surface elevation field at a fixed point as a function of time only, which is adequate for the assessment of single-point measured data (e.g., from buoys or wave probes). Then, to account for the 3D geometry of very large waves, we take advantage of the space-time approach, which extends the estimate of wave maxima from a fixed point to a spatial region of a given area larger than zero. It was proven that the values over a sea surface area are generally larger than those found at a single point within the same area, especially for short-crested conditions (Krogstad et al., 2004; Forristall, 2006; Dysthe et al., 2008; Fedele et al., 2013; Barbariol et al., 2015; Benetazzo et al., 2015), so to produce a realistic estimate of maxima that might occur in a mixed sea state it is crucial to consider also the areal effect. This kind of representation is the most appropriate for the comparison, for instance, with data measured by a remote-sensing instrument (e.g., stereo imaging, X-band radar).

Our focus in the present study is on the wave crest heights since they are not affected by crest-trough correlation and are largely influenced by second- and higher-order nonlinearities (Tayfun and Fedele, 2007; Häfner et al., 2021).

2.4.1. Theoretical distributions

For a sea state where the surface elevation η(t) is Gaussian distributed and surface waves are narrow-banded in frequency, the wave crest heights (η_c) normalized with the significant wave height (H_s) at a fixed point in space have a probability of exceedance (or exceedance distribution function; EDF hereinafter) of the level z given by the Rayleigh distribution (Longuet-Higgins, 1952):

$\begin{array}{ll}{\text{P}}_{\text{R}}=\mathrm{Pr}\left\{\frac{{\eta }_c}{H_s}>z\right\}=\exp (-8z^2)& (5)\end{array}$

where H_s = 4σ is significant wave height and σ the standard deviation of η(t). Due to nonlinear effects occurring in realistic active sea states, the above formulation often underpredicts the crest height probability, so other models have been developed to account for nonlinearities. Indeed, realistic, irregular sea states, usually display wave crests that are sharper than their linear counterpart and troughs that are shallower and more rounded. To account for this, a formulation based on a steepness parameter μ was developed by Tayfun (1980), which enhances the tail of the Rayleigh distribution due to the presence of second-order effects:

$\begin{array}{ll}{\text{P}}_{\text{T}}=\mathrm{Pr}\left\{\frac{{\eta }_c}{H_s}>\xi \right\}=\exp (-8z^2)& (6)\end{array}$

where  ξ is the second-order sea surface elevation, satisfying the quadratic equation (also called Tayfun formula) that relates the normalized linear (z) to the second-order nonlinear (ξ ) elevations as follows:

$\begin{array}{ll}\xi =z+2\mu z^2.& (7)\end{array}$

Following Fedele and Tayfun (2009), the wave steepness has been evaluated as a statistically stable estimate from the moments of the directional spectrum and can be written in the following form:

$\begin{array}{ll}\mu ={\mu }_m(1-\mathit{\nu }+{\mathit{\nu }}^2)& (8)\end{array}$

where the spectral bandwidth is defined as $\text{ν}=\sqrt{m_{000}{m}_{002}/m_{001}^2-1}$ (Longuet-Higgins, 1975) and the quantity μ_m represents an integral measure of the wave steepness, defined as μ_m = k_mσ (Fedele and Tayfun, 2009), where the parameter k_m represents the mean wavenumber and is given by:

$\begin{array}{ll}{k}_m=\frac{{\omega }_m^2}{g}=\frac{{\left(\frac{m_{001}}{m_{000}}\right)}^2}{g}& (9)\end{array}$

with ω_m the spectral mean frequency and m₀₀₀ , m₀₀₁ and m₀₀₂ represent the zeroth, first and second-order moments of the directional spectrum. Statistical formulations that account for third-order effects have also been developed namely the Tayfun–Fedele distribution (Tayfun and Fedele, 2007) given by:

$\begin{array}{ll}{P}_{TF}=Pr\left\{\frac{{\eta }_c}{H_s}>\xi \right\}=\exp (-8z^2)\left[1+\Lambda z^2(4z^2-1)\right]& (10)\end{array}$

where the variable Λ is a function of the fourth-order joint cumulants of the sea surface elevation and its conjugate and is often approximated in terms of the excess kurtosis (see Fedele et al., 2017).

The theoretical models shown above are valid for the sea surface elevation recorded in time at a given position in space. However, these models were extended to a space-time framework by generalizing the concept of waves in a multidimensional domain, which in this study spans two spatial dimensions (a sea surface area of sides X and Y) and a time interval D. In this context, then, the reference stochastic formulations of maxima for space-time fields, namely the linear, second-order and third-order space-time extreme asymptotic distributions (STE⁽¹⁾, STE⁽²⁾ and STE⁽³⁾ herein), rely on the distributions (5), (6) and (10) and on the definition of specific spatio-temporal parameters, as shown below:

$\begin{array}{ll}{P}_{STE1}=Pr\left\{\frac{{\eta }_{c,max}}{H_s}>z\text{|(}{N}_{3D},N_{2D},N_{1D})\right\}\approx (16N_{3D}{z}^2+4N_{2D}z+N_{1D})P_R& (11)\end{array}$

$\begin{array}{ll}{P}_{STE2}=Pr\left\{\frac{{\eta }_{c,max}}{H_s}>\xi \text{|(}{N}_{3D},N_{2D},N_{1D})\right\}\approx (16N_{3D}{z}^2+4N_{2D}z+N_{1D})P_T& (12)\end{array}$

$\begin{array}{ll}{P}_{STE3}=Pr\left\{\frac{{\eta }_{c,max}}{H_s}>\xi \text{|(}{N}_{3D},N_{2D},N_{1D})\right\}\approx (16N_{3D}{z}^2+4N_{2D}z+N_{1D})P_{TF}& (13)\end{array}$

where N_3D, N_2D and N_1D, represent the average number of waves within the space-time volume, on the boundary surfaces and along the perimeter, respectively (see Fedele, 2012) and rely on the definition of the mean zero-crossing period (T_z = T_m02), the mean zero-crossing wavelength and wave crest length (L_x = L_xm02 and L_y = L_ym02, respectively), and the irregularity parameters of the sea state (a_xt, a_yt, and a_xy, all ranging between -1 and +1), computed from the moments of the directional spectrum (see Baxevani and Rychlik, 2004; Fedele, 2012). The reader is referred to the work of Fedele (2012) for details on the linear space-time extreme asymptotic distribution, of Benetazzo et al. (2015) for its second-order expansion and of Fedele (2016) (see also Fedele et al., 2017) for the third-order expansion.

In general, provided that the requirements of stationarity in time and homogeneity over space are satisfied, the choice of the time duration and of the spatio-temporal volume over which to compute the space-time extreme statistics is arbitrary and is usually driven only by the purpose of specific applications (e.g., the sea surface footprint of an off-shore platform; Benetazzo et al., 2021b). In this study, rather than choosing a spatial area and time duration of fixed dimensional size, we address the influence of the number of waves considered (viz. the sample size) on the values of the maximum crest heights by selecting a spatio-temporal volume V_ST = XYD which depends on the spectral characteristics. In particular, setting the temporal length at D = 20T_z, we present the results stemming from the space-time extreme analysis for a sea-surface area XY (in this study, taken to be X = Y) of varying size within the numerical domain, from X = 0.5L_x to X = 10L_x (step 0.5L_x), as done by Fedele et al. (2017). This ensures that the extreme value statistics referring to different sea state conditions can be directly compared given that they refer to the same number of waves. For an area of a given size, we compute the expected value (marked with an overbar) of the space-time maximum crest height ${\overline{\eta }}_{\mathit{\text{max}},\text{ST}}$ as the statistical reference measure of comparison. A point worth mentioning is that, since the validity of space-time extreme theoretical distribution only holds for large thresholds, the space-time expected maxima are often estimated from the asymptotic Gumbel limit. The expected value of maximum crest heights can then be described analytically for the linear, second-order and third-order cases. However, in the present work, we found that the asymptotic Gumbel fit space-time extreme distributions tend to overestimate large values of normalized crest heights at low probability levels, whereas it is useful and accurate in providing the expected value in the lower crest height range, where the original asymptotic STE⁽¹⁾ and STE⁽²⁾ asymptotic distributions overestimate maxima (see, for instance, Figure 10 of Benetazzo et al., 2015). For this reason, as reference linear and second-order space-time extreme distributions we have considered the original STE distribution in the upper crest height range, while in the lower range we have resorted to the analytical Gumbel fit formulations. The lower and upper crest height range was arbitrarily defined to the left and the right of the intersection point between the Gumbel fit and the original space-time extreme distribution, respectively, and our estimates of the expected value on the original distributions were taken at the same-probability level of the expected maxima on the Gumbel fit distribution.

2.4.2. Empirical distributions

The empirical wave crest height distributions resulting from the HOS simulations have been computed as follows. For the analysis at a fixed point of the wave field, the time series of the sea-surface elevation were first extracted at the central node of the numerical domain grid for each simulation and the wave crests were identified as the highest point of the sea surface elevation profile between a zero up-crossing and the consecutive zero down-crossing. Then, the wave crests identified for each run were grouped and considered as members of an ordered sample, and their mean and standard deviation were calculated following the definition of Tayfun and Fedele (2007). The same procedure was also used for the analysis of stereo data collected at Gageocho-ORS, with the only evident difference that the in-situ measurements refer to one 20-minute recording and not to multiple 20-minute realizations.

For the space-time analysis, the expected maximum crest heights of HOS and stereo measurements were computed relying on the block maxima approach, an efficient alternative to the peak-over-threshold method (Ferreira and de Haan, 2015) to select extreme values in the measured data. To this end, for each simulation we divide the space-time domain into several non-overlapping space-time subsets (or sub-volumes) V_ST = XYD, whose sides (taken to be X=Y) gradually increase at regular steps (from X = 0.5L_x to X = 10L_x, step 0.5L_x) and whose temporal length was fixed at D = 20T_z. For a given area of width X, then, the maximal surface elevation (η_max,ST) has been pinpointed within each space-time sub-volume and the values of the maximum crest heights thus found were used to draw an empirical distribution both for the HOS and the stereo data. The results of the space-time analysis for an area of increasing size are then presented in terms of the expected value, as for the theoretical estimates.

3. Results

3.1. Crossing sea states during cyclone Kong-rey (2018)

To select different bimodal directional spectra to use as forcings for the HOS simulations, we first analyse the spectral fields over the Yellow Sea during typhoon Kong-rey on the three time instants considered in terms of the crossing sea parameters given in Eqs. (1), (3) and (4). In particular, in Figure 2 we show the values of SSER where two crossing wave systems were found within the cyclone field.

In line with the work by Mori (2012), several crossing sea states can be found within the cyclone wave field, mostly in the left quadrants of the typhoon (west of the eye), where a short fetch due to the Korean peninsula is present and the wind field opposes the direction of the translating cyclone (see Titley et al., 2020 for the full cyclone track). Such crossing sea conditions are likely caused by the particularly intense wind field close to the slow-moving cyclone eye which intercepts the long-crested wave field, generated at an earlier stage, that has overtaken the cyclone eye and is approaching from the S-SE direction. There is a clear dominance of locally generated wind waves (SSER > 1) for all three time instants in the outer parts of the cyclone field, while a narrower area closer to the typhoon eye displays a bimodal spectral shape with approximately the same energy content in both systems (SSER values around 1). Furthermore, in the north-west sector of the cyclone a near-orthogonal crossing angle is present (Δθ around 90°, not shown here), while in the south-west sector an almost opposing crossing condition was found (Δθ around 160°, not shown here). We note that in the south-east side of the eye we are probably underestimating the number of crossing sea states within the wave field, due to the difficulties in identifying the double-peaked structure of the spectra correctly where the spectral peaks are too close together. Interestingly, the bimodal spectra with SSER values around 1 of Figure 2 all lie within a region where particularly high normalized crest heights were found by Benetazzo et al. (2021a), despite a relatively low BFI index.

For our analysis, we have selected different bimodal directional spectra E(f,θ) at specific locations within the cyclone field (S1, S2, and S3, depicted with white markers in Figure 2). In particular, to first investigate the influence of the angular separation Δθ on extreme wave height values, two different bimodal conditions (S1 and S2) were chosen on 05 October 2018, so that the two wave systems have similar energy content and a similar peak frequency separation and only the influence of crossing angle on the statistics of extremes can be analyzed. Then, to test the influence of SSER for a fixed crossing angle and ID value, one bimodal condition (S3) was conveniently taken in a clearly steep, wind sea-dominated location of the cyclone coinciding with the Gageocho-ORS station, so that both hindcast model and stereo data could be inter-compared and the reliability of the HOS model assessed. On the other hand, all the narrow-banded, swell-dominated cases within the typhoon wave field displayed low values of steepness.

In summary, the three bimodal sea states selected for this study are such that the spectra S1 and S2 have similar shape and energy ratio (no dominance of wind sea or swell) but display different crossing angles, while S3 differs mostly from S2 for being wind sea-dominated. The three spectra are shown in Figure 3, as well as their constituent wind sea (solid red line) and swell (solid blue line) partitions, obtained from the aforementioned partitioning procedure.

FIGURE 3

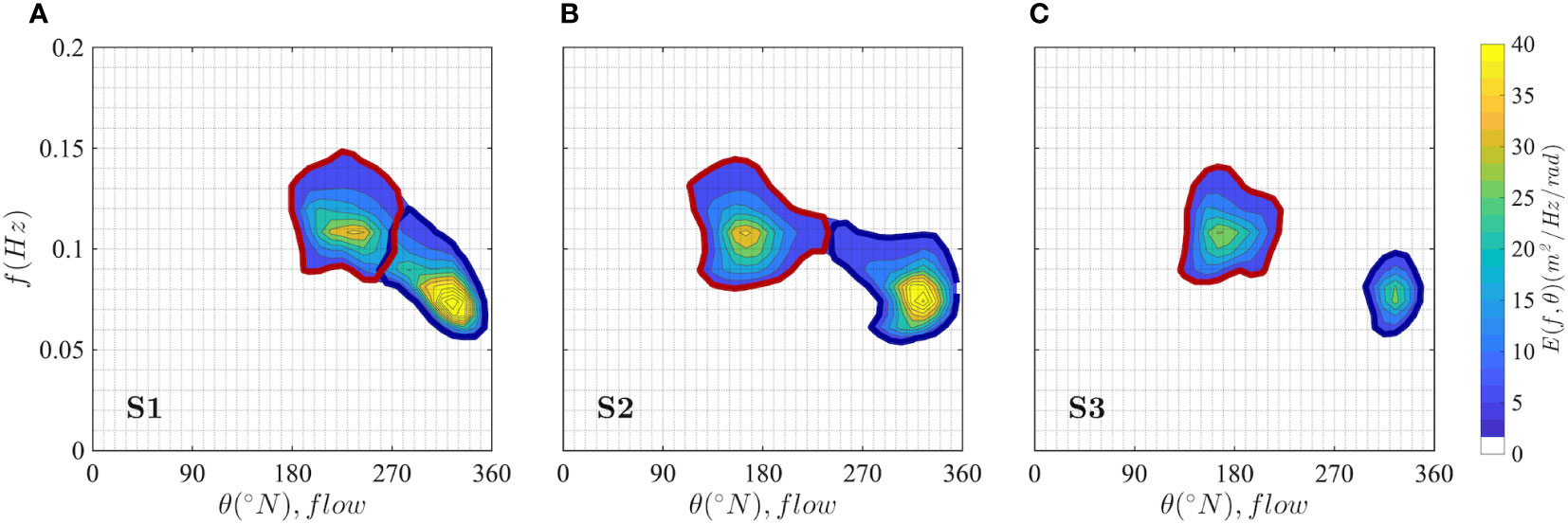
Figure 3 Frequency/direction S(f, θ) wave spectra from ECWAM model at the three selected locations in the Yellow Sea on 5 October 2018 at 04 UTC (S1, A), on 5 October 2018 at 17 UTC (S2, B) and on 6 October 2018 at 01 UTC (S3, C). Wind sea (solid red) and swell (solid blue) partitions are also shown.

The main characteristics of the three conditions S1, S2 and S3 are summarized in Table 1 in terms of the integral parameters (total significant wave height H_s, mean zero-crossing period T_z, peak period T_p), integral wave steepness (μ_m) and of the crossing sea parameters defined above (SSER, ID and Δθ).

TABLE 1

Table 1 Main characteristics of the selected bimodal spectra during typhoon Kong-Rey (2018) in terms of their integral and crossing sea parameters.

The main spectral parameters of the single wind sea and swell systems of each case are shown in Table 2, as well as the peak direction (θ_p), directional spreading (σ_θ), spectral bandwidth (ν). For the directional spreading (σ_θ) we have adopted the formulation implemented in the ECWMF Wave Model Manual (2017). From the data in Table 2, the distinction between wind sea and swell spectra is clear, with the latter displaying steeper (μ_m around 0.09, three times that of swell) and broader (ν around 0.41, twice that of swell) energy distribution over frequencies. Wind sea spectra are also always broader in direction.

TABLE 2

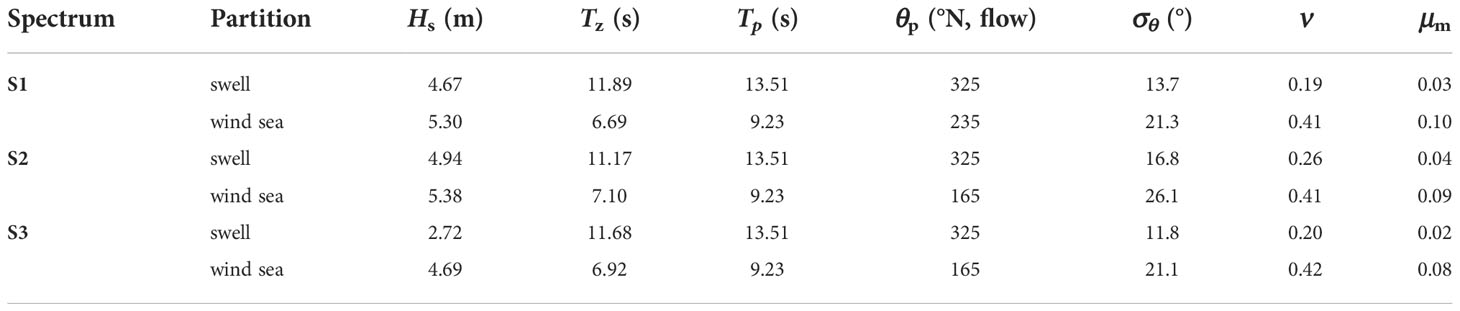
Table 2 Main spectral characteristics of the partitioned wave systems identified within the selected bimodal spectra.

3.2. HOS-ocean assessment using stereo wave observations

A comparison of the sea surface elevation fields obtained from HOS models and those obtained from stereo camera recordings have not yet been carried out to the best of our knowledge, so in this section the two space-time datasets are compared for the first time and jointly used for extreme wave assessment. In particular, one numerical HOS wave field is compared with the 20-minute stereo wave observation set recorded at the Gageocho-ORS on 06 October 2018 at 01 UTC (spectrum S3). For a more complete assessment, the analysis is carried out both at a fixed position of the simulation domain and over a sea surface area of a given size.

The EDF of the dimensionless observed and modelled dimensionless wave crest heights (η_c/H_s) at a fixed point, as well as the corresponding stability bands, are shown in Figure 4A. For reference, we also show the linear Rayleigh distribution.

FIGURE 4

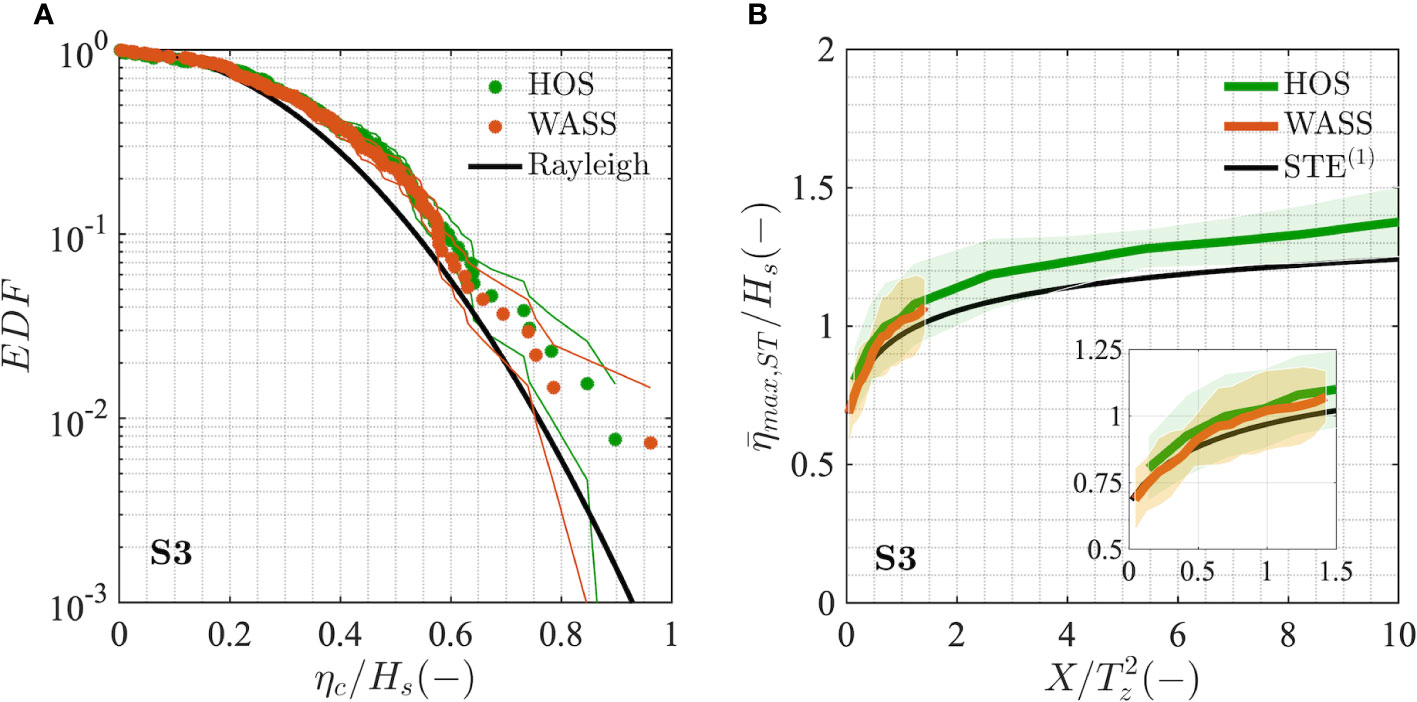
Figure 4 Exceedance distribution function of dimensionless crest heights (η_c/H_s) at a fixed point (A) and space-time extreme distributions of expected normalized maximum wave crest heights ($\overline{\eta }$ _max,ST/H_s) as a function of the normalized sea surface area width $X/T_z^2$(B) from HOS (green circles) and one 20-minute WASS record (orange circles). The stability bands (coloured lines) and the standard deviation (shaded area) are also shown. The inset plot in panel (B) shows an enlargement of the distributions for the overlapping range of sea surface area widths. Reference statistical distributions at a fixed point and for space-time extremes are shown with a black line (Rayleigh and STE⁽¹⁾).

The comparison between the two distributions was then carried out over a sea-surface area of a given size in terms of the mean (or expected) dimensionless crest heights (${\overline{\eta }}_{\max }$_{, ST}/H_s) as a function of the normalized surface area side $X/T_z^2$. The dimensionless space-time expected maxima and the corresponding standard deviation are shown in Figure 4B. We have adopted the dimensionless area width $X/T_z^2$ instead of X/L_x since strong limitations in the estimation of L_x are present for the stereo system under high sea states, such as the ones analyzed herein, due to the limited camera footprint size. Additionally, we note that the wave crest height values resulting from the numerical HOS simulations were corrected to account for the spatial discretization error (see Appendix A), which leads to an underestimation of modelled crest heights compared to the true values.

Minor differences are found between the dimensionless crest heights obtained at a fixed point of the numerical simulations and those obtained from the stereo data for the crossing sea condition S3 (Figure 4A).

As regards the space-time extremes (Figure 4B), crest height values over the smallest sea surface area almost coincide, on average, with those predicted at a given fixed point, whereas the space-time estimates for both datasets increase with the sea-surface area, following the larger number of waves present in the spatio-temporal volume domain. We found a very good match between HOS simulations and stereo data for sea surface areas up to the typical size of the region observed by the stereo system (about 70 x 70 m²), with only a slight overestimation of the model. We note that, since the HOS model does not include wind input and breaking dissipation, and therefore simulations are taken up until the breaking onset, the slightly lower values present in the stereo data compared to the simulations might be caused by a certain amount of active breaking in the highest waves during the stormy conditions analyzed. Conversely, we do not expect the different sea states present at Gageocho-ORS, where stereo data were collected, and at the closest hindcast model grid point, where the wave spectra used for HOS were extracted, to have a significant influence on our results, since their spectral shape and characteristics are very similar (see Benetazzo et al., 2021a).

In the more general context of our study, we note that the above comparison refers to slightly weaker typhoon conditions (see Figure 1), which were downgraded to a tropical storm on 6^th October 2018, compared to those present on 5^th October 2018, so the results of the HOS model under the more extreme and active conditions S1 and S2 might be, to some degree, overestimated compared to real ocean conditions, where we expect a large amount of breaking to limit the growth of very large waves.

3.3. Crest height statistics during crossing seas

3.3.1. Unimodal wind sea and swell

In this study, the statistical distributions presently available for a fixed point and over a spatio-temporal domain are adopted as reference for the analysis of the wave fields under different crossing sea conditions. With this in mind, in this section we verify the empirical distribution of crest heights obtained from the wind sea and swell simulations of each of the three sea states S1, S2, and S3 against the statistical distributions valid for unimodal (single-peaked) conditions. The comparison of the EDFs at a fixed point of the spatial domain is shown in Figure 5.

FIGURE 5

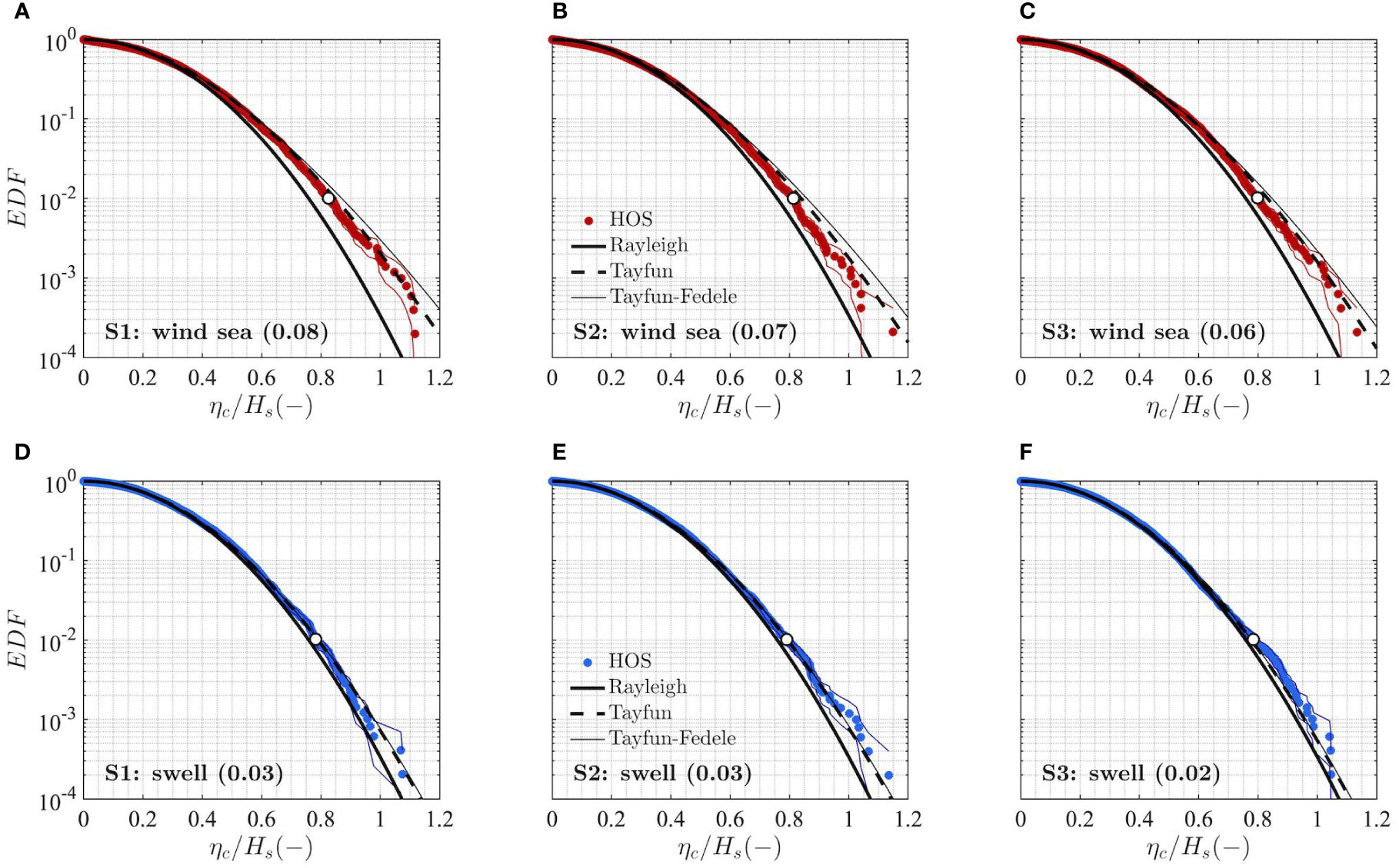
Figure 5 Empirical exceedance distribution functions of dimensionless crest heights (η_c/H_s) at a fixed point of the numerical domain for wind sea (A–C) and swell (D–F) partitions identified within sea conditions S1, S2 and S3. The 99^th percentile (white circle) and the empirical EDF stability band (solid line) are also highlighted. Reference statistical distributions at a fixed point: linear (Rayleigh, solid black), second-order (Tayfun, dashed black) and third-order (Tayfun-Fedele, solid grey). In brackets we display the value of the steepness μ defined in Eq. (8).

The empirical distributions of crest heights for both wind sea and swell show a strong dependence on wave steepness, whereas the influence of directional spreading and spectral bandwidth is somewhat more difficult to assess, also due to the small differences between the three sea states. Indeed, both the broad-banded wind sea (Figures 5A–C) and the narrow-banded swell (Figures 5D–F) from HOS simulations produce higher crests for cases where a high steepness is present (S1 for wind sea and S2 for swell). This behaviour is well described by the Tayfun model, while the third-order contribution, which includes effects related to kurtosis, seems to overpredict the highest crest heights for the wind seas. Although theoretical distributions should be used with care to infer the nature of the nonlinear processes leading to the formation of the highest waves, the analysis of normalized crest heights seems to suggest that second-order bound wave contributions are important in all three sea conditions analyzed, whereas effects related to modulational instability do not seem to be clearly present.

A similar investigation to the one shown above is then carried out in the spatio-temporal domain. For the sake of generalization, we present the results stemming from the space-time extreme analysis for a sea-surface area XY of increasing size within the numerical domain, as was done by Fedele et al. (2017), up to a maximum area width of X = 10 L_x, in order to trace the areal effect on the maximum crest height. The results of the analysis performed on the wind sea and swell systems of the three sea states S1, S2 and S3 for a given normalized sea surface area of side X/L_x are shown in Figure 6.

FIGURE 6

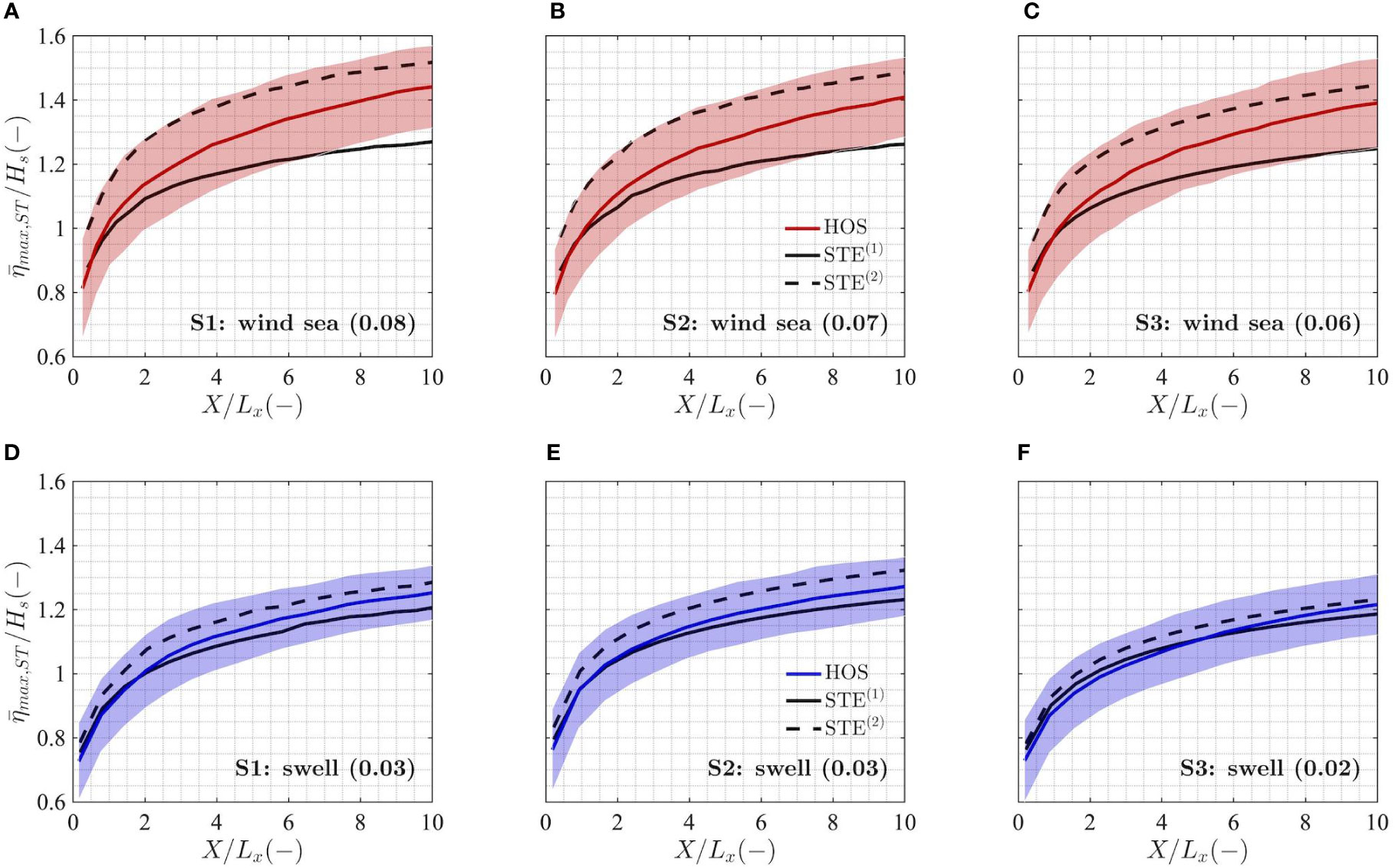
Figure 6 Empirical space-time expected normalized maximum wave crest height ($\overline{\eta }$ _max,ST/H_s) for the wind sea (A–C) and swell (D–F) identified within the sea states S1, S2 and S3 over a space-time volume V_ST=XYD, considering X=Y and a fixed duration of D=20Tm₀₂, and plotted as a function of the normalized sea surface area width (X/L_x). The standard deviation of the empirical distributions (shaded area) is also shown. Reference statistical distributions for space-time extremes: linear space-time extreme (STE⁽¹⁾, solid black) and second-order space-time extreme (STE⁽²⁾, dashed black). In brackets we display the value of the steepness μ.

For the steep, broad-banded, directionally spread wind seas (Figures 6A–C), the empirical maximum crest heights show similar areal statistics for all three conditions, with the value of expected maxima increasing with the sea surface area considered. Overall, extreme crest heights seem marginally higher for sea state S1, characterized by a slightly higher steepness. The empirical distributions match reasonably well (overestimation within 5% of H_s) with the second-order space-time formulation (STE⁽²⁾) for large sea-surface areas, which slightly overestimate maxima for very small sea surface areas. As already mentioned in Section 2.4.1, this is most likely due to the asymptotic nature of the statistical distributions in space-time, whereby their validity holds for particularly large crest height values (and therefore areas), though discrepancies can be also due to the combination of errors from other sources, namely the calculation of the space-time parameters of Eq. (11) and (12) and the spatial discretization error correction of the empirical data (see Appendix A). In general, the swell is much more linear than the wind sea, reflecting the more regular and less sharp wave form.

3.3.2. Crossing wind sea and swell

After having shown the distribution of crest heights derived from the unimodal sea states, in this section we consider the corresponding results from the bimodal sea states. The empirical distribution of dimensionless crest heights for the three crossing sea conditions at a fixed point of the spatial domain is shown in Figure 7. For reference, we also show the empirical distributions from the simulations of the unimodal wind sea and swell partitions described in the previous section.

FIGURE 7

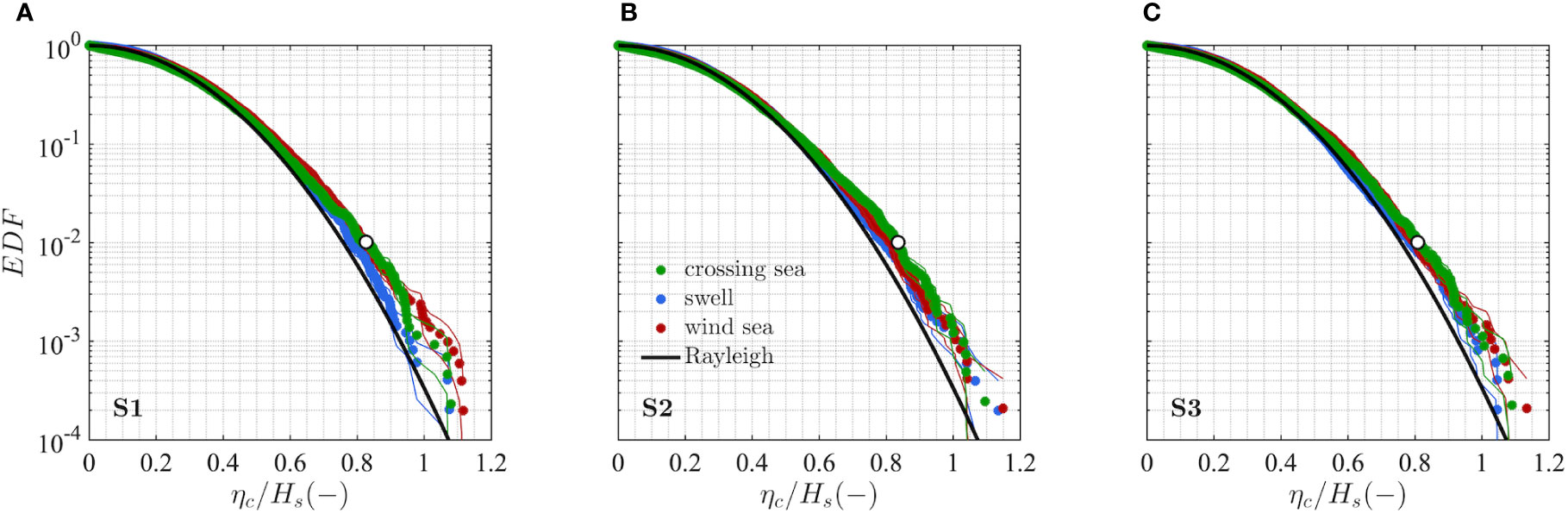
Figure 7 Ensemble exceedance distribution functions of dimensionless crest heights (η_c/H_s) at a fixed point of the numerical domain for sea conditions S1 (A), S2 (B) and S3 (C). Wind sea (solid red line), swell (solid blue line) and total (solid green line) are compared. The 99^th percentile value for the total system (white circle) and the empirical EDF stability band (solid line) are also shown. Reference statistical distributions: linear (Rayleigh, solid black).

For the 90°-separation, wind sea-swell equivalent crossing configuration S1 (Figure 7A), the statistics of the crossing sea are somewhat intermediate between those of its corresponding wind sea and swell partitions for percentiles below the 99^th value (white marker). This is close to what might be expected if the two systems were independent of each other (see Støle-Hentschel et al., 2020), thereby possibly suggesting a weak interaction between the two systems. Conversely, for the 160°-separation, wind sea-swell equivalent crossing configuration S2 (Figure 7B), a higher probability was found, despite the slight increase in both the spectral bandwidth and the directional spreading of the wind sea and the swell partitions (see Table 2). Finally, for the wind sea-dominated case S3 (Figure 7C) differences between the combined system and the two partitions are less clear, though in general crest height values seem to be slightly lower than S2 condition with a similar crossing angle. Conclusions stemming from the comparison at percentiles above the 99^th value are less robust due to their large variability, so they will not be discussed here.

In Figure 8 we present the analysis in terms of the mean values of the maximum crest heights resulting from the space-time analysis of the three crossing sea states for increasing sea surface areas widths up to X = 10L_x.

FIGURE 8

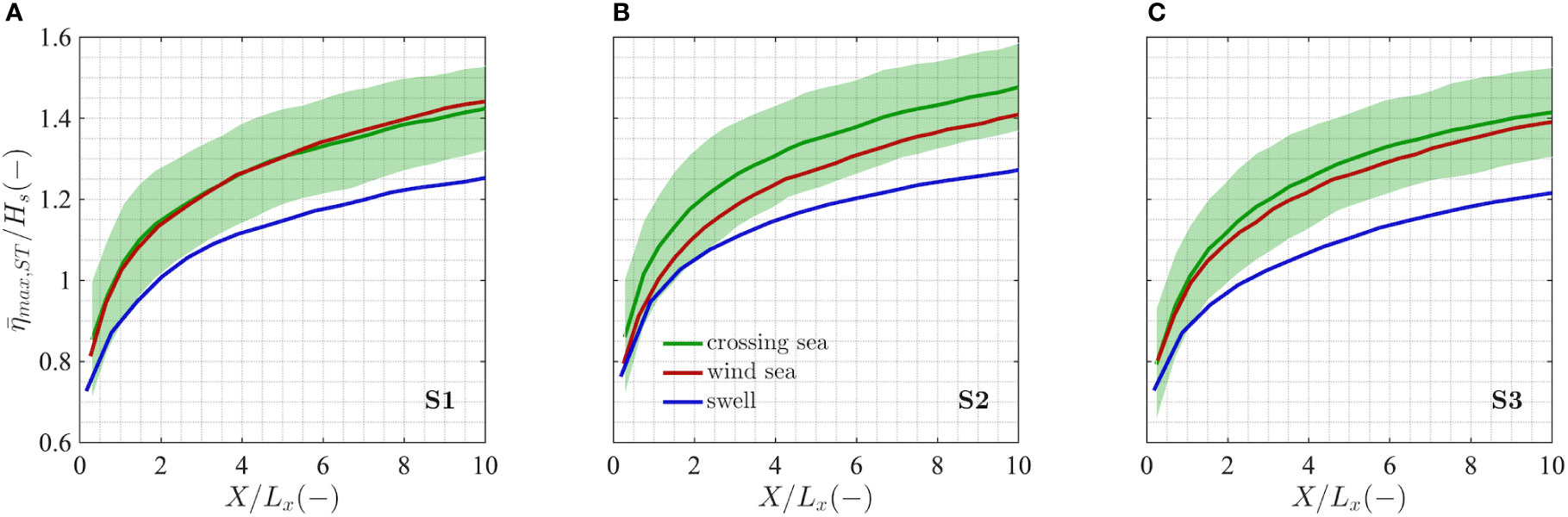
Figure 8 Empirical space-time expected normalized maximum wave crest height ($\overline{\eta }$_max,ST/H_s) for the wind sea (red), swell (blue) and crossing sea (green) conditions of cases S1 (A), S2 (B) and S3 (C) as a function of the normalized sea surface area width (X/L_x). The standard deviation of the crossing seas (shaded area) is also shown.

In line with our findings at a fixed point, the extreme wave crest heights for bimodal conditions S2 (Figure 8B) show increased crest height values compared to the unimodal wind sea and swell and a slight increase in the likelihood of extreme waves was also found for the wind sea-dominated sea state S3 (Figure 8C). On the other hand, the statistics for the crossing sea S1 (Figure 8A) resemble those of its underlying wind sea system.

In general, these results suggest that crossing sea conditions can lead to increased extreme wave probability compared to single wind sea or swell wave systems. Moreover, our results indicate that stronger interactions between the wind sea and swell, which may ultimately raise the wave elevations over those of the generative systems, are present for crossing sea configurations where the relative angle of the two systems approaches an opposing propagation (spectrum S2), and this is particularly evident when the energy between the wind sea and the swell is similar.

Significant differences between S1, S2, and S3 can also be seen if we compare the ensemble-averaged 2D spatial shape of the wave field around the maximum crest heights (Figures 9A–C).

FIGURE 9

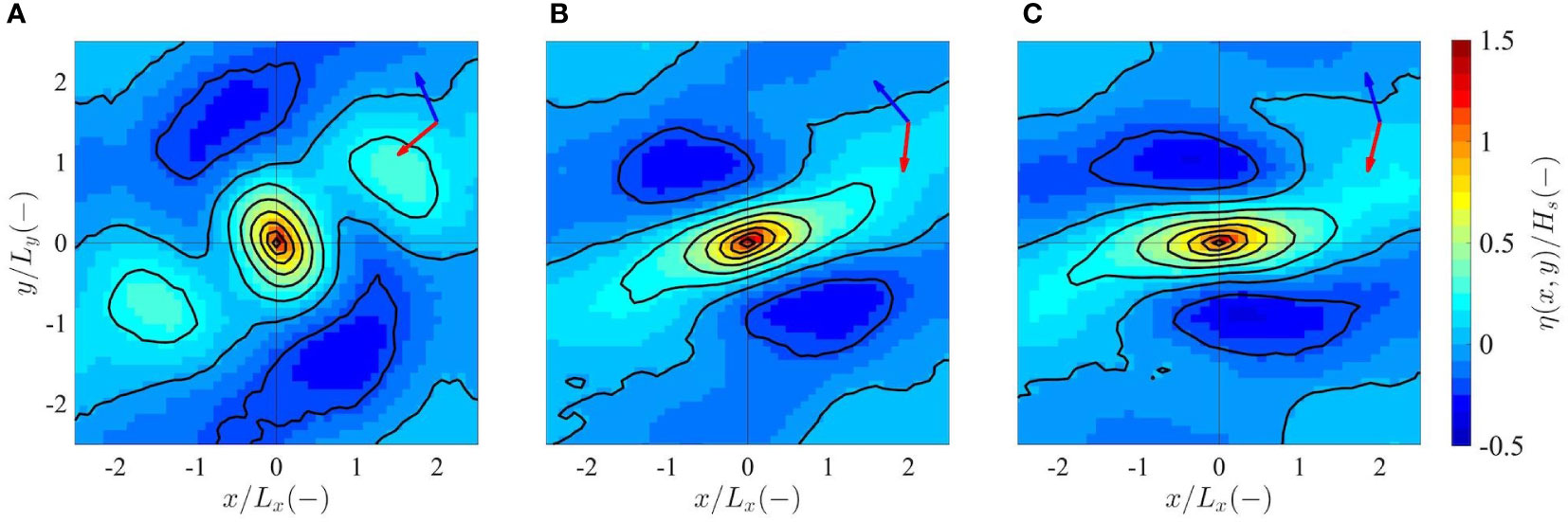
Figure 9 Spatial ensemble-average of the normalized sea surface elevation field (η(x,y)/H_s) around the highest crests for the crossing sea states S1 (A), S2 (B) and S3 (C), identified within an area of width X=10L_x (a smaller sea surface area centred at the focusing point x/L_x=y/L_y=0 is displayed). The corresponding wind sea (solid red) and swell (solid blue) mean directions are plotted in the upper right-hand corner, with the x and y axes representing the zonal and meridional directions, respectively. Sea surface elevation isolines are drawn at 0.2 interval.

Indeed, the spatial shape of the 90° crossing sea condition (Figure 9A) is characterized by multiple troughs along the respective wind sea and swell directions and the highest waves are very short-crested, almost cusp-like. This feature can also be qualitatively appreciated in the case of two wind seas crossing with a near-orthogonal angle, as the one shown in Figure 10. On the other hand, a more typical long-crested wave form alternated by deep troughs is found as the fronts of the two systems travel along similar directions (Figures 9B, C).

FIGURE 10

Figure 10 Example of crossing sea state composed of two wind sea systems travelling at a near-orthogonal angle recorded with stereo cameras from an oceanographic vessel on 28 March 2017 (photo credit: Andrea Bergamasco, CNR-ISP).

In the two cases S2 and S3, sea surface isolines are closer together along the direction of maximum gradient compared to sea state S1, possibly suggesting increased local steepness values. However, the local steepness is difficult to quantify in a crossing sea, since the direction of propagation in the physical xy-space is not clear. Similarly, difficulties arise in the definition of the spectral wave steepness in a crossing sea and, as a consequence, a unified wave steepness computed directly from the bimodal wave spectrum is often used instead. In the following section, we address the issue by introducing a novel wave steepness parametrization suitable in the case of two crossing wave groups.

4. Wave steepness in crossing seas

For unimodal wave spectra, integral parameters, such as the spectral wave steepness μ, can be directly associated with the sea state characteristics and are therefore suited to the Tayfun model for crest heights. The steepness defined from the total spectrum, however, fails to represent wave geometry accurately in complex situations such as crossing sea states. Indeed, the physical meaning of this parameter does not provide information on the various systems that make up the crossing sea state (Portilla-Yandun et al., 2015; Støle-Hentschel et al., 2018) and does not explicitly account for their interactions. With this in mind, in Figure 11 we analyze the second-order nonlinear space-time extreme distribution using such a unified steepness, computed directly from the moments of the total bimodal spectrum.

FIGURE 11

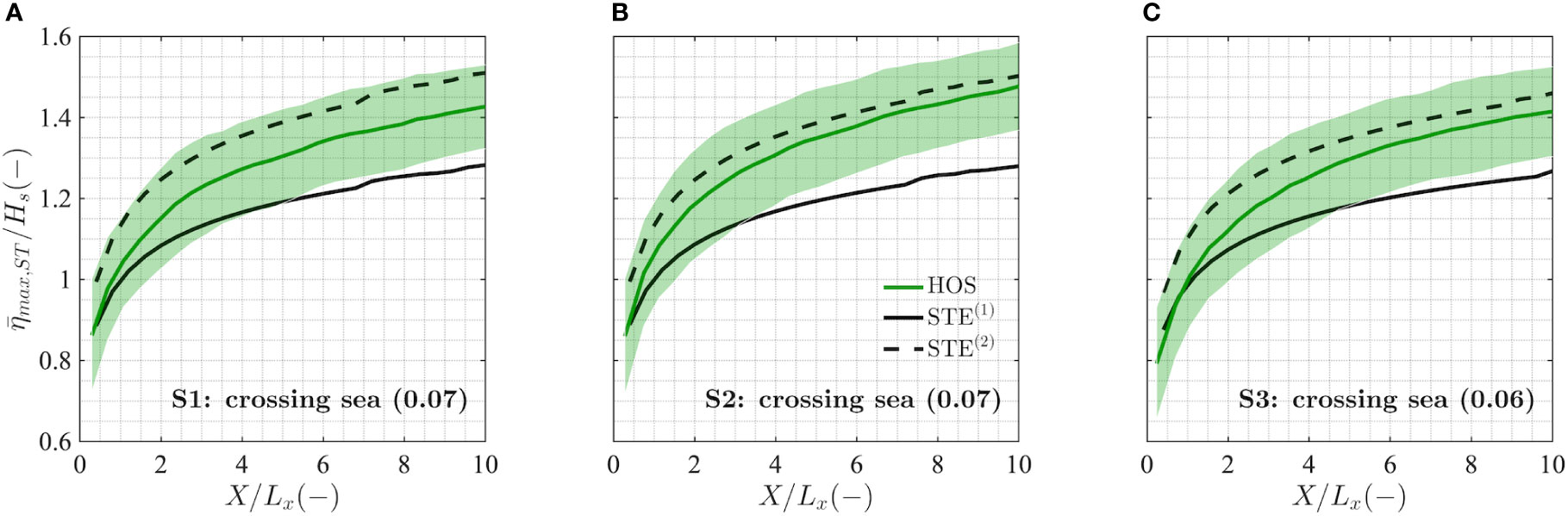
Figure 11 Empirical space-time mean values of normalized maximum wave crest height ($\overline{\eta }$ _max,ST/H_s) as a function of the normalized sea surface area width (X/L_x) for crossing sea conditions S1 (A), S2 (B), and S3 (C). The standard deviation of the empirical distributions (shaded area) is also shown. Reference statistical distributions for space-time extremes: linear (STE⁽¹⁾, thick solid black) and second-order nonlinear (STE⁽²⁾, dashed black). In brackets we display the value of the steepness μ .

Interestingly, the second-order nonlinear distribution STE⁽²⁾ with a unified steepness seems to predict the maximum crest heights fairly well for all three cases (the HOS underestimation is below 5% of H_s). Despite the consistent accuracy of the predictions based on the unified steepness, the above results do not allow an interpretation of the underlying physics and therefore cannot be adequately judged. For instance, the likelihood of extreme waves was found to increase under particular crossing angle configurations (Figure 8B), while the unified steepness does not seem to vary between S1 and S2 (Figures 11A, B). This suggests that the use of a unified wave steepness in bimodal sea conditions represents a potential limitation in accurately describing the extreme crest heights and that an improved definition of the wave steepness for a bimodal spectrum is needed to ensure its physical consistency for both unimodal and bimodal cases.

The main goal of our investigation in this section is therefore to introduce a parametrization of the steepness parameter in bimodal conditions which accounts for the characteristics of the underlying wave systems and sheds light on which types of interactions are present, verifying how it compares with the numerical simulations. Since crossing waves resulting from wind and swell systems will most likely be of different carrier frequencies and energies, which will affect the strength of their interaction, we aim at generalizing the formulation of the steepness in order to include all possible combinations. To this end, we follow two distinct approaches, as explained below.

First, we define a wave steepness by assuming linear interference between the wind sea and the swell waves, which are taken as two uncorrelated and statistically independent systems. Given that the steepness is related to the third-order moment skewness (Tayfun, 2006), one can calculate a weighted steepness parameter (μ_weighted ) using the formulation proposed by Støle-Hentschel et al. (2020). In this context, the condition of independence is assured by setting the covariance between the two systems equal to zero. The weighted steepness can therefore be written as:

$\begin{array}{ll}{\mu }_{weighted}=\frac{{\mu }_W{\sigma }_W^3+{\mu }_S{\sigma }_S^3}{{\left({\sigma }_W^2+{\sigma }_S^2\right)}^{3/2}}& (14)\end{array}$

where μ_W and μ_S represent the steepness parameters of the wind sea and of the swell, respectively, defined in Eq. (8), while the weights σ_W and σ_S are the standard deviations of the wave elevations of the two systems. Operatively, the weighted steepness was used in the STE⁽²⁾ distribution for space-time extremes and will be referred to as STE^(2,w) henceforth. The comparison between the empirical values and the theoretical probabilities derived using the weighted parameter is shown in Figure 12.

FIGURE 12

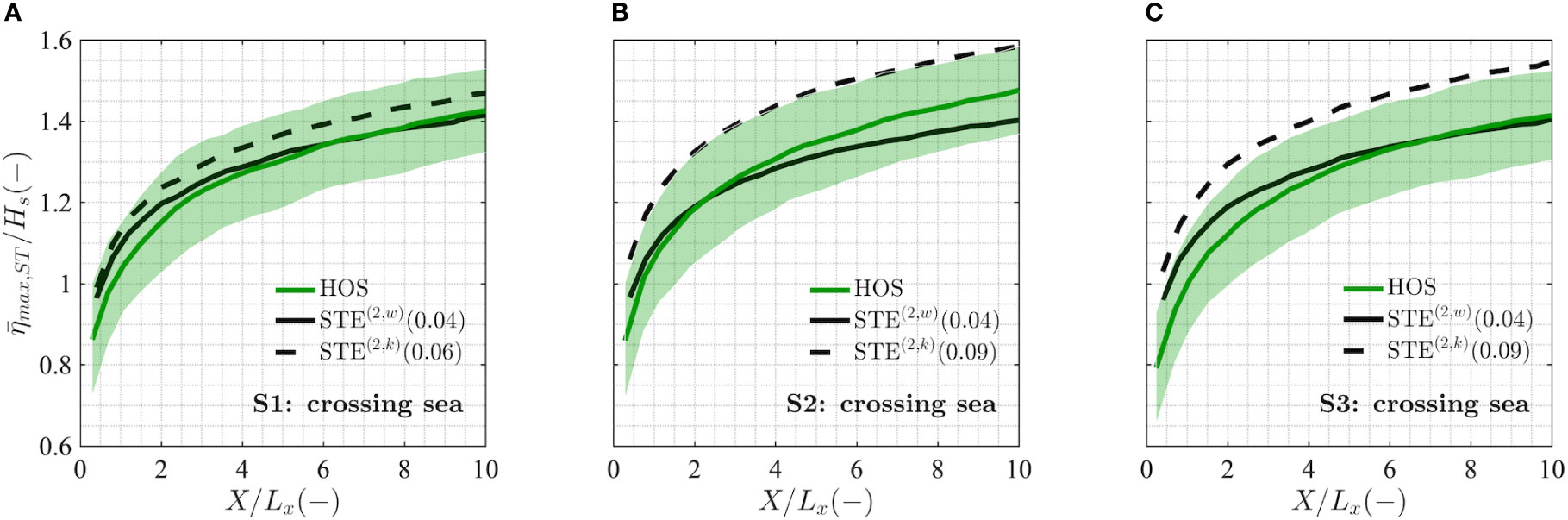
Figure 12 Empirical space-time mean values of normalized maximum wave crest height ($\overline{\eta }$ _max,ST/H_s) as a function of the normalized sea surface area width (X/L_x) for crossing sea conditions S1 (A), S2 (B) and S3 (C). The standard deviation of the empirical distributions (shaded area) is also shown. Reference statistical distributions for space-time extremes: second-order weighted (STE^(2,w), solid black) and second-order including interaction kernels (STE^(2,k), dashed black). In brackets we display the value of the respective steepnesses parameters.

For the wind sea-swell equivalent case S1 and the wind sea- dominated case S3 of Figure 12, the STE^(2,w) formulation tends to slightly underestimate the empirical maxima for large sea surface areas, though it can nevertheless be considered quite a good approximation for the prediction of space-time extreme elevations. However, for the opposing configuration S2 that triggers an increased likelihood of extreme waves, the underestimation using the STE^(2,w) distribution is more significant (Figure 12B) and is most likely because Eq. (14) neglects any contribution arising from the nonlinear wave-wave interaction between the wind sea and the swell.

To include the effects of nonlinear interactions in the steepness parameter, we resort to the multicomponent second-order theory for wave elevations. In this context, the second-order free surface elevation of a crossing sea may be described using a simplified expression for the case of two quasi-monochromatic crossing wave groups in deep water, where each wave group can be described as a carrier wave slowly modulated by the envelope (see Longuet-Higgins, 1962; Dalzell, 1999; McAllister et al., 2018):

$\begin{array}{ll}\eta ={\displaystyle \sum _{j=1}^2{A}_j\cos ({\psi }_j)}+{\displaystyle \sum _{j=1}^2\frac{A_j^2{k}_j}{2}\cos (2{\psi }_j)}+A_1{A}_2{B}^{+}\cos ({\psi }_1+{\psi }_2)+A_1{A}_2{B}^{-}\cos ({\psi }_1-{\psi }_2)& (15)\end{array}$

where A_j is the envelope of wave system j, k_j a characteristic wavenumber (to be specified more in detail in the following) of the j-th carrier wave, while ψ_j is a phase function given by:

$\begin{array}{ll}{\psi }_j=k_j\mathit{\text{X}}-{\omega }_{j}t+{\varphi }_j& (16)\end{array}$

where X is a position vector in the xy-plane, ω_j = ω_m,j is the mean frequency which follows the dispersion relation and ϕ_j is a random phase uniformly distributed between [0 2π]. The coefficients B⁺ and B⁻ represent the second-order sum and difference interaction kernels for the nonlinear bound harmonics, respectively, first introduced by Longuet-Higgins (1963) for deep water and then extended by Sharma and Dean (1981) and Dalzell (1999) to any depth. In the general case, both kernels are functions of the first-order frequencies of the two interacting wave pairs (f₁ and f₂), as well as their relative propagation angle (i.e. the mean crossing angle, which in the analyzed cases coincides with Δθ) and the water depth d. Figures 13A–C shows an example of the second-order sum and difference interaction kernels for deep water.

FIGURE 13

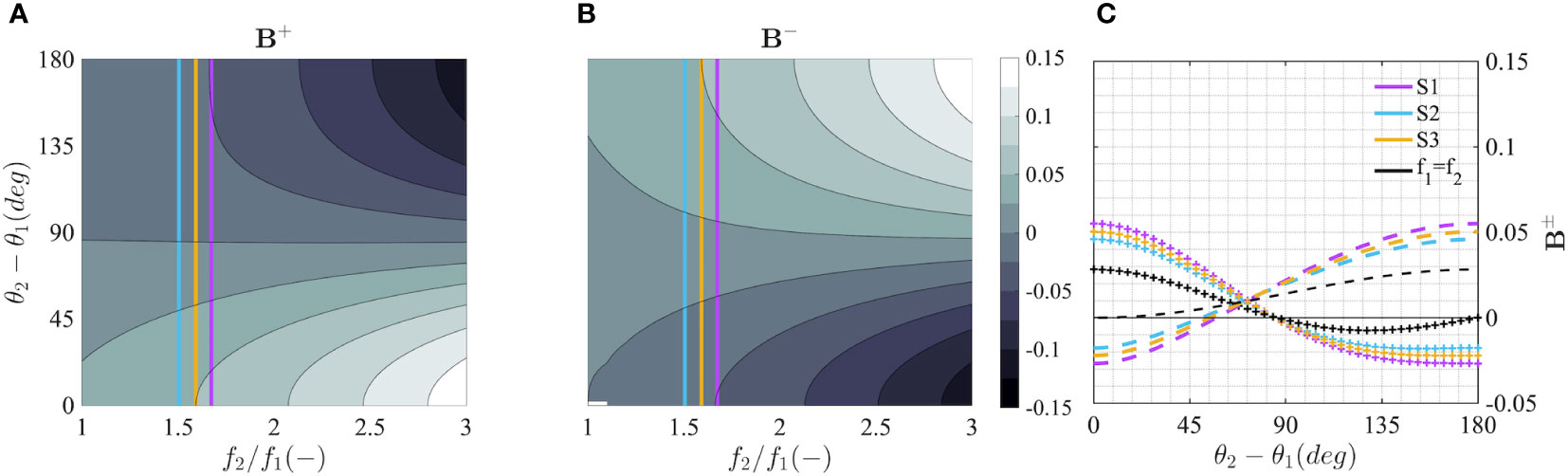
Figure 13 (A, B) Second-order sum (B+) and difference (B-) interaction kernels. The value of the ratio between wind sea (system 2) and swell (system 1) mean frequencies for sea states S1 (purple), S2 (cyan) and S3 (yellow) is also shown. (C) Section of the sum (crossed lines) and difference (dashed lines) interaction kernels taken at the mean frequency ratio value for the three sea states and for the simple case of f₁=f₂.

For a single, weakly spread wave group, the superharmonic term is responsible for the sharpness of the crests and the flatness of the troughs, while the subharmonic term expresses the setdown of the water level beneath the group. Although the setdown may be significant in intermediate and shallow waters, in this study we have neglected its contribution given that it is generally very small in deep water (McAllister and van den Bremer, 2019). When two wave groups cross at a given angle, additional sum and difference terms arise and are expressed in Eq. (15) via the two interaction kernels, with the latter term giving rise to a partial standing-wave pattern that can lead to a set-up (the so-called crossing wave contribution η_CW; see McAllister et al., 2018) in the case of perfect or near-perfect focusing. As we may notice for the theoretical case of a wind sea with the same mean frequency as the swell (f₁ = f₂), the second-order difference interaction kernel B⁻ (dashed black line in Figure 13C) is zero for two co-propagating systems (Δθ = 0°) and the solution of Eq. (15) reduces to that of a single wave group. Conversely, the maximum of the crossing wave contribution is reached when two wave groups travel in the opposite direction (Δθ = 180°) and have the same phases (ϕ₁ = ϕ₂) at the point and time of focus (x = 0, y = 0 and t = 0 , where the second-order elevations reach their maxima). As the difference in frequency of the linear waves increases, the value of B⁻ becomes larger. The sum interaction kernel B⁺ (crossed black line in Figure 13C) reaches its maximum for two co-propagating systems (Δθ = 0°) with the same phases (ϕ₁ = ϕ₂) and remains positive for crossing angles up to Δθ = 90°, after which it approaches zero again for the case of two opposing waves, where the solution coincides with that of a standing wave (McAllister and van den Bremer, 2019). We note that, while the difference term at the point and time of focus cos(ϕ₁−ϕ₂) is always positive, the sum term cos(ϕ₁+ϕ₂) depends on the phases of the two systems and can be negative. Since our interest is in the largest crest heights, following the approach of Tayfun (1980) we can derive the approximation for the maxima associated with the nonlinear wave process up to the second order described in Eq. (15) as follows:

$\begin{array}{ll}{\eta }_c={\displaystyle \sum _{j=1}^2{a}_j}+{\displaystyle \sum _{j=1}^2\frac{a_j^2{k}_j}{2}+a_1{a}_2\left(\left|B^{+}\right|+B^{-}\right)}& (17)\end{array}$

where α_j = A_j (x_j = 0, y_j = 0, t = 0) is the amplitude of each group at the point and time of focus and the particular case of equal phases where the crossing wave contribution is maximized (i.e. cos(ϕ₁+ϕ₂)B⁺= |B⁺|) was considered as an upper bound. However, for a spatially and temporally limited wave field the likelihood of satisfying such condition at the point and time of focus is relatively low, so we expect the numerical simulations to display somewhat lower crest height values compared to the ones given by Eq. (17).

At this point, we can assume that the ratio of the two amplitudes a₁ = a_S (swell) and a₂ = a_W (wind sea) is given by τ = a_W/a_S , and that the linear amplitude of the crossing sea state at the point of focus is given by the simple superposition a_W+a_S = a. Moreover, since the two amplitudes scale with the square of the energy of the respective systems, the ratio can be computed as $\tau =\sqrt[4]{SSER}$.

Then, we may write Eq. (17) in its most general form as:

$\begin{array}{ll}{\eta }_c=a+\frac{1}{2}{a}^2\frac{k_S}{{(1+\tau )}^2}+\frac{1}{2}{a}^2\frac{k_W}{{\left(1+\frac{1}{\tau }\right)}^2}+a^2\frac{\left(\left|B^{+}\right|+B^{-}\right)}{(1+\tau )\left(1+\frac{1}{\tau }\right)}& (18)\end{array}$

If we divide both sides of Eq. (17) by the significant wave height H_s = 4σ of the crossing sea state, we can write the expression of the normalized crest heights for the crossing sea as:

$\begin{array}{ll}\frac{{\eta }_c}{H_s}=\frac{a}{H_s}+2{\left(\frac{a}{H_s}\right)}^2\left(\frac{k_S}{{(1+\tau )}^2}+\frac{k_W}{{\left(1+\frac{1}{\tau }\right)}^2}+\frac{2\left(\left|B^{+}\right|+B^{-}\right)}{(1+\tau )\left(1+\frac{1}{\tau }\right)}\right)\sigma & (19)\end{array}$

This yields a first-order, free-wave term and a second-order nonlinear correction which includes additional terms arising from the interaction between two wave groups, and has the same functional form as (7). As a particular case of (19), one may consider a_W = a_S = a/2 and f₁ = f₂ , obtaining the same expression as the one found by McAllister and van den Bremer (2019).

We note that this simplified functional form represents an upper bound of wave crest heights for two quasi-monochromatic crossing wave groups and represents a relatively simple, though physically consistent, predictor of maximum crest heights. We can therefore conveniently define a crossing sea steepness parameter (μ_kernel), which relies solely on the wavenumbers of the single wave partitions and on the crossing sea state parameters, via the second-order interaction kernels. The equivalent, Tayfun-like steepness is in this case given by:

$\begin{array}{ll}{\mu }_{kernel}=\left(\frac{k_S}{{(1+\tau )}^2}+\frac{k_W}{{\left(1+\frac{1}{\tau }\right)}^2}+\frac{2\left(\left|B^{+}\right|+B^{-}\right)}{(1+\tau )\left(1+\frac{1}{\tau }\right)}\right)\sigma & (20)\end{array}$

The formulations seen above depend, to some extent, on the definition of the characteristic wavenumber k_j , which can be taken as the mean wavenumber of the j-th wave group in the case of narrow-banded seas or it can be defined in several other ways (Tayfun and Al-Humoud, 2002). For consistency with the unimodal distributions used so far, also in the case of crossing seas we have relied on the more general definition of steepness given in Eq. (8), which also includes effects related to the spectral bandwidth. Therefore, since the steepness is defined as μ=kσ, we have considered $k_j=\frac{{\omega }_{m,j}^2}{g}(1-\nu +{\nu }^2)$ as the characteristic wavenumber for each wave group in the bimodal sea state. The steepness defined in Eq. (20) can then be used in the second-order statistical distributions for space-time extremes (referred to as STE^(2,k)). The results stemming from such analysis are shown in Figure 12.

In agreement with the qualitative results of Figure 9, the wave steepness calculated with Eq. (20) yields a lower value for crossing sea condition S1 (0.06) compared to conditions S2 and S3 (0.09 for both cases), due to the enhanced second-order interactions for large crossing angles (see Figure 13C). Moreover, since the positive and negative interaction terms for crossing sea condition S1 are very small, the wave steepness for this case approaches the value of the weighted steepness (0.04), while for sea states S2 and S3 the wave steepness parameters are higher than the weighted steepness (0.04 for both cases). We note that, as anticipated before, the absolute value of the sum interaction kernel employed in the theoretical steepness of Eq. (20) leads to an overestimation of the highest crest height values compared to the empirical data obtained herein. However, we expect that for a very large number of simulated waves the proposed upper bounded formulation provides a reliable prediction of extreme crest heights.

In general, for the moderately steep, broad-banded wind seas and weakly nonlinear, narrow-banded swells considered in this study, extreme crest height values were accurately predicted without considering nonlinear third-order effects in the statistical distributions and, rather, they seem to be well explained by constructive interference enhanced by second-order bound nonlinearities, as suggested by Fedele et al. (2016) and Brennan et al. (2018). This is also supported by the analysis of Benetazzo et al. (2021a), where the role of nonlinear four-wave focusing was found to be limited in the typhoon regions where the directional spectra used in this study were extracted. We note, however, that the wave steepness obtained herein does not include effects related to wave breaking, which have so far only been included indirectly in the upper-bounded distribution of Benetazzo et al. (2020), so further work is still needed.

5. Discussion and conclusions

In this paper, we have analyzed the amplitude of maximum waves that can occur in sea states where crossing wind sea and swell wave systems are present. The subject has been discussed in previous studies using laboratory and numerical data, though mostly under simplified conditions and relying on statistics derived at a fixed point. To date, a firm conclusion on the conditions that trigger high waves in realistic crossing seas is still under debate.

In this context, we have simulated crossing sea conditions during typhoon Kong-Rey (2018) in the Northwestern Pacific (Yellow Sea) using a nonlinear HOS wave model that provides phase-resolved information from initial conditions defined by hindcast model spectra. In particular, three types of crossing sea states and their constituent wind sea and swell partitions within the wave field produced by the cyclone have been simulated and analyzed, to investigate the effects of crossing angle and energy ratio between the two wave systems on the probability of extremes under realistic ocean conditions. To limit the role of variability in our estimates, multiple numerical realizations with random phases have been carried out for each sea state. For completeness, the statistical analysis was performed both at a fixed point (time statistics) and over a sea surface region (space-time statistics).

The HOS-ocean model was validated for the first time by direct comparison with space-time wave measurements acquired from a stereo camera system mounted on a fixed oceanographic platform in the region of interest, showing good agreement between the two sources of wave data. Although the HOS model used in this study does not include wave breaking, the simulated wave fields do not seem to be significantly affected by such effects, since the steepnesses considered are moderate and no sign of numerical instability due to breaking onset was recorded. Our findings provide a preliminary cross-validation of both products and highlight the advantages of the combined use of stereo observations and HOS numerical data for extreme wave assessment at different scales, namely the possibility to extend the space-time analysis to domain sizes far larger than those available from space-time measurements with the HOS model. To strengthen the validation carried out in this study, future work should investigate the performance of the model under sea states with different characteristics.

The time and space-time analysis of the simulated wind sea and swell partitions proved that, in both unimodal conditions, extreme crest heights are well predicted by the existing second-order statistical distributions. On the other hand, the space-time extreme analysis of the three simulated crossing sea conditions showed increased crest height probability for wind sea and swell systems crossing with a relative angle of 160°, especially in the case of two systems with the same energy content. Our results suggest that, under this particular configuration, crossing seas can lead to higher waves compared to their underlying wind sea or swell systems and should therefore be regarded as a particularly dangerous condition for operations at sea. In the case of a slow-moving typhoon in the Northern Hemisphere, we therefore expect particularly high waves in the south-west sector of the cyclone field, where the aforementioned crossing sea conditions can be found.

We show that the main reason for such increased occurrence probabilities is that second-order non-resonant interactions between the two wave systems are present for both very small and very large crossing angles, while their effect becomes less noticeable when the two systems cross at a near-orthogonal angle. In the latter case, then, the likelihood of high waves can be accurately described by only considering linear superposition as the main driving mechanism.

As a first step toward a more accurate statistical prediction of extremes where more than one wave system is present, we propose a relatively simple, though physically consistent, formulation for the upper bound of the wave steepness, which accounts for linear and second-order bound wave interactions between the two systems and relies on the spectral characteristics of the two constituent partitions (mean wavenumber and spectral bandwidth) and on their crossing conditions (mean frequency difference, crossing angle and energy ratio). Given the functional form of the new steepness parameter, it can be easily implemented in operational spectral wave models for the statistical prediction of the single highest waves that might occur in a given crossing sea state. We point out that our results stem from a limited sample of crossing conditions, so additional comparisons against model and observed data are necessary to firmly assess the quality of the new formulations.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SD contributed to the conception and design of the study and produced the model datasets and performed the analyses. SD, AB performed the model assessment with stereo data. JY provided technical support with the observational dataset. GD provided technical support and developed the numerical model. SD, AB, FB and GD contributed to the final version of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by Korea Institute of Marine Science & Technology Promotion (KIMST) funded by the Ministry of Oceans and Fisheries (20210607) and was conducted as part of the bilateral project EOLO-1 (Extreme Oceanic waves during tropical, tropical-like and bomb cyclones) between CNR-ISMAR and the University of Tokyo (Japan; Prof. Takuji Waseda). This work was also partly supported by the WASANO project, funded by the French National Research Agency (ANR) as part of the "Investissements d'Avenir" Programme (ANR-16-IDEX-0007) and by the Interreg project AdriaClim (Climate change information, monitoring and management tools for adaptation strategies in Adriatic coastal areas; Project ID 10252001) funded by the European Union under the V A Interreg Italy-Croatia CBC program.

Acknowledgments

We are grateful to Øyvind Breivik (Norwegian Meteorological Institute), Karsten Trulsen (University of Oslo), Odin Gramstad (Det Norske Veritas), Mark McAllister and Ton van den Bremer (University of Oxford) and Luigi Cavaleri (CNR-ISMAR) for the stimulating and useful discussions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alber (1978). The effects of randomness on the stability of two-dimensional surface wavetrains. Proc. R. Soc. London. A. Math. Phys. Sci. 363, 525–546. doi: 10.1098/rspa.1978.0181

CrossRef Full Text | Google Scholar

Barbariol F., Benetazzo A., Carniel S., Sclavo M. (2015). Space-time wave extremes: The role of metocean forcings. J. Phys. Oceanography 45, 1897–1916. doi: 10.1175/JPO-D-14-0232.1

CrossRef Full Text | Google Scholar

Baxevani A., Rychlik I. (2004). Maxima for Gaussian seas. Ocean Eng. 33, 895–911. doi: 10.1016/j.oceaneng.2005.06.006

CrossRef Full Text | Google Scholar

Benetazzo A. (2006). Measurements of short water waves using stereo matched image sequences. Coast. Eng. 53, 1013–1032. doi: 10.1016/j.coastaleng.2006.06.012

CrossRef Full Text | Google Scholar

Benetazzo A., Barbariol F., Bergamasco F., Bertotti L., Yoo J., Shim J.-S., et al. (2021a). On the extreme value statistics of spatio-temporal maximum sea waves under cyclone winds. Prog. Oceanography 197, 102642. doi: 10.1016/j.pocean.2021.102642

CrossRef Full Text | Google Scholar

Benetazzo A., Barbariol F., Bergamasco F., Torsello A., Carniel S., Sclavo M. (2015). Observation of extreme sea waves in a space-time ensemble. J. Phys. Oceanography 45, 2261–2275. doi: 10.1175/JPO-D-15-0017.1

CrossRef Full Text | Google Scholar

Benetazzo A., Barbariol F., Davison S. (2020). Short-Term/Range extreme-value probability distributions of upper bounded space-time maximum ocean waves. J. Mar. Sci. Eng. 8, 1–14. doi: 10.3390/JMSE8090679

CrossRef Full Text | Google Scholar

Benetazzo A., Barbariol F., Pezzutto P., Staneva J., Behrens A., Davison S., et al. (2021b). Towards a unified framework for extreme sea waves from spectral models: rationale and applications. Ocean Eng. 219, 108263. doi: 10.1016/j.oceaneng.2020.108263

CrossRef Full Text | Google Scholar

Benetazzo A., Bergamasco F., Yoo J., Cavaleri L., Kim S. S., Bertotti L., et al. (2018). Characterizing the signature of a spatio-temporal wind wave field. Ocean Model. 129, 104–123. doi: 10.1016/j.ocemod.2018.06.007

CrossRef Full Text | Google Scholar

Benetazzo A., Fedele F., Gallego G., Shih P.-C., Yezzi A. (2012). Offshore stereo measurements of gravity waves. Coast. Eng. 64, 127–138. doi: 10.1016/j.coastaleng.2012.01.007

CrossRef Full Text | Google Scholar

Benjamin T. B., Feir J. E. (1967). The disintegration of wave trains on deep water part 1. theory. J. Fluid Mechanics 27, 417–430. doi: 10.1017/S002211206700045X

CrossRef Full Text | Google Scholar

Bergamasco F., Torsello A., Sclavo M., Barbariol F., Benetazzo A. (2017). WASS: An open-source pipeline for 3D stereo reconstruction of ocean waves. Comput. Geosciences 107, 28–36. doi: 10.1016/j.cageo.2017.07.001

CrossRef Full Text | Google Scholar

Bitner-Gregersen E. M., Gramstad O., Magnusson A. K., Malila M. P. (2021). Extreme wave events and sampling variability. Ocean Dynamics 71, 81–95. doi: 10.1007/s10236-020-01422-z

CrossRef Full Text | Google Scholar

Bitner-Gregersen E. M., Toffoli A. (2014). Occurrence of rogue sea states and consequences for marine structures. Ocean Dynamics 64, 1457–1468. doi: 10.1007/s10236-014-0753-2

CrossRef Full Text | Google Scholar

Black P. G., D’Asaro E. A., Drennan W. M., French J. R., Niiler P. P., Sanford T. B., et al. (2007). Air–Sea exchange in hurricanes: Synthesis of observations from the coupled boundary layer air–Sea transfer experiment. Bull. Am. Meteorol Soc. 88, 357–374. doi: 10.1175/BAMS-88-3-357

CrossRef Full Text | Google Scholar

Bonnefoy F., Ducrozet G., le Touzé D., Ferrant P. (2010). Time domain simulation of nonlinear water waves using spectral methods. Advances in Numerical Simulation of Nonlinear Water Waves 129–164. doi: 10.1142/9789812836502_0004

CrossRef Full Text | Google Scholar

Boukhanovsky A., Lopatoukhin L. J., Guedes Soares C. (2007). Spectral wave climate of the north Sea. Appl. Ocean Res. 29, 146–154. doi: 10.1016/j.apor.2007.08.004

CrossRef Full Text | Google Scholar

Brennan J., Dudley J. M., Dias F. (2018). Extreme waves in crossing Sea states. Int. J. Ocean Coast. Eng. 01, 1850001. doi: 10.1142/S252980701850001X

CrossRef Full Text | Google Scholar

Clamond D., Francius M., Grue J., Kharif C. (2006). Long time interaction of envelope solitons and freak wave formations. Eur. J. Mechanics - B/Fluids 25, 536–553. doi: 10.1016/j.euromechflu.2006.02.007

CrossRef Full Text | Google Scholar

Dalzell J. F. (1999). A note on finite depth second-order wave–wave interactions. Appl. Ocean Res. 21, 105–111. doi: 10.1016/S0141-1187(99)00008-5

CrossRef Full Text | Google Scholar

Dommermuth D. (2000). The initialization of nonlinear waves using an adjustment scheme. Wave Motion 32, 307–317. doi: 10.1016/S0165-2125(00)00047-0

CrossRef Full Text | Google Scholar

Dommermuth D. G., Yue D. K. P. (1987). A high-order spectral method for the study of nonlinear gravity waves. J. Fluid Mechanics 184, 267–288. doi: 10.1017/S002211208700288X

CrossRef Full Text | Google Scholar

Donelan M. A., Drennan W. M., Katsaros K. B. (1997). The air–Sea momentum flux in conditions of wind Sea and swell. J. Phys. Oceanography 27, 2087–2099. doi: 10.1175/1520-0485(1997)027<2087:TASMFI>2.0.CO;2

CrossRef Full Text | Google Scholar

Ducrozet G., Bonnefoy F., le Touzé D., Ferrant P. (2007). 3-d HOS simulations of extreme waves in open seas. Natural Hazards Earth System Sci. 7, 109–122. doi: 10.5194/nhess-7-109-2007

CrossRef Full Text | Google Scholar

Ducrozet G., Bonnefoy F., Perignon Y. (2017). Applicability and limitations of highly non-linear potential flow solvers in the context of water waves. Ocean Engineering 142, 233–244. doi: 10.1016/j.oceaneng.2017.07.003

CrossRef Full Text | Google Scholar

Ducrozet G., Bonnefoy F., le Touzé D., Ferrant P. (2016). HOS-ocean: Open-source solver for nonlinear waves in open ocean based on high-order spectral method. Comput. Phys. Commun. 203, 245–254. doi: 10.1016/j.cpc.2016.02.017

CrossRef Full Text | Google Scholar

Dysthe K., Krogstad H. E., Müller P. (2008). Oceanic rogue waves. Annu. Rev. Fluid Mechanics 40, 287–310. doi: 10.1146/annurev.fluid.40.111406.102203

CrossRef Full Text | Google Scholar

Dysthe K. B., Trulsen K., Krogstad H. E., Socquet-Juglard H. (2003). Evolution of a narrow-band spectrum of random surface gravity waves. J. Fluid Mechanics 478, 1–10. doi: 10.1017/S0022112002002616

CrossRef Full Text | Google Scholar

Fedele F. (2012). Space–time extremes in short-crested storm seas. J. Phys. Oceanography 42, 1601–1615. doi: 10.1175/JPO-D-11-0179.1

CrossRef Full Text | Google Scholar

Fedele F. (2015). On the kurtosis of deep-water gravity waves. J. Fluid Mechanics 782, 25–36. doi: 10.1017/jfm.2015.538

CrossRef Full Text | Google Scholar

Fedele F., Benetazzo A., Gallego G., Shih P.-C., Yezzi A., Barbariol F., et al. (2013). Space–time measurements of oceanic sea states. Ocean Model. 70, 103–115. doi: 10.1016/j.ocemod.2013.01.001

CrossRef Full Text | Google Scholar

Fedele F., Brennan J., Ponce de Leoín S., Dudley J., Dias F. (2016). Real world ocean rogue waves explained without the modulational instability. Sci. Rep. 6, 1–11. doi: 10.1038/srep27715

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedele F., Lugni C., Chawla A. (2017). The sinking of the El Faro : predicting real world rogue waves during hurricane Joaquin. Sci. Rep. 7 (11188), 1–15. doi: 10.1038/s41598-017-11505-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Fedele F., Tayfun M. A. (2009). On nonlinear wave groups and crest statistics. J. Fluid Mechanics 620, 221–239. doi: 10.1017/S0022112008004424

CrossRef Full Text | Google Scholar

Forristall G. Z. (2000). Wave crest distributions: Observations and second-order theory. J. Phys. Oceanography 30, 1931–1943. doi: 10.1175/1520-0485(2000)030<1931:WCDOAS>2.0.CO;2

CrossRef Full Text | Google Scholar

Forristall G. Z. (2006). “Maximum wave heights over an area and the air gap problem,” in Proceedings of OMAE06, 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, June 4-9. 1–5. doi: 10.1115/OMAE2006-92022

CrossRef Full Text | Google Scholar

Gramstad O., Bitner-Gregersen E., Trulsen K., Borge J. C. N. (2018). Modulational instability and rogue waves in crossing Sea states. J. Phys. Oceanography 48, 1317–1331. doi: 10.1175/JPO-D-18-0006.1

CrossRef Full Text | Google Scholar

Guedes Soares C. (1984). Representation of double-peaked sea wave spectra. Ocean Eng. 11, 185–207. doi: 10.1016/0029-8018(84)90019-2

CrossRef Full Text | Google Scholar

Guedes Soares C. (1991). On the occurence of double peaked wave spectra. Ocean Eng. 18, 167–171. doi: 10.1016/0029-8018(91)90040-W

CrossRef Full Text | Google Scholar

Guedes Soares C., Carvalho A. N. (2003). Probability Distributions of Wave Heights and Periods in Measured Combined Sea-States from the Portuguese Coast. J. Offshore Mech. Arct. Eng. 125, 198–204. doi: 10.1115/1.1576816

CrossRef Full Text | Google Scholar

Häfner D., Gemmrich J., Jochum M. (2021). Real-world rogue wave probabilities. Sci. Rep. 11, 10084. doi: 10.1038/s41598-021-89359-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanson J. L., Phillips O. M. (2001). Automated analysis of ocean surface directional wave spectra. J Atmos Ocean Technol 18, 277–293. doi: 10.1175/1520-0426(2001)018<0277:AAOOSD>2.0.CO;2

CrossRef Full Text | Google Scholar

Hasselmann S., Bruning C., Hasselmann K., Heimbach P. (1996). An improved algorithm for the retrieval of ocean wave spectra from synthetic aperture radar image spectra. J Geophys Res 101(16), 615–616. doi: 10.1029/96JC00798

CrossRef Full Text | Google Scholar

Holthuijsen L. H., Powell M. D., Pietrzak J. D. (2012). Wind and waves in extreme hurricanes. J. Geophysical Research: Oceans 117 (C09003), 10–15. doi: 10.1029/2012JC007983

CrossRef Full Text | Google Scholar

Hu K., Chen Q. (2011). Directional spectra of hurricane-generated waves in the gulf of Mexico. Geophysical Res. Letters. 38, L19608 doi: 10.1029/2011GL049145

CrossRef Full Text | Google Scholar

Janssen P. A. E. M. (2003). Nonlinear four-wave interactions and freak waves. J. Phys. Oceanography 33, 863–884. doi: 10.1175/1520-0485(2003)33<863:NFIAFW>2.0.CO;2

CrossRef Full Text | Google Scholar

Kirezci C., Babanin A. V., Chalikov D. (2021). Probabilistic assessment of rogue wave occurrence in directional wave fields. Ocean Dynamics 71, 1141–1166. doi: 10.1007/s10236-021-01487-4

CrossRef Full Text | Google Scholar

Kokina T., Dias F. (2020). Influence of computed wave spectra on statistical wave properties. J. Mar. Sci. Eng. 8, 1023. doi: 10.3390/jmse8121023

CrossRef Full Text | Google Scholar

Kokorina A., Slunyaev A. (2019). Lifetimes of rogue wave events in direct numerical simulations of deep-water irregular Sea waves. Fluids 4, 70. doi: 10.3390/fluids4020070

CrossRef Full Text | Google Scholar

Krogstad H. E., Liu J., Socquet-Juglard H., Dysthe K., Trulsen K. (2004). “Spatial extreme value analysis of nonlinear simulations of random surface waves,” in Proceedings of OMAE04 23rd International Conference on Offshore Mechanics and Arctic Engineering 285–295.

Google Scholar

Liu Q., Babanin A., Fan Y., Zieger S., Guan C., Moon I.-J. (2017). Numerical simulations of ocean surface waves under hurricane conditions: Assessment of existing model performance. Ocean Model. 118, 73–93. doi: 10.1016/j.ocemod.2017.08.005

CrossRef Full Text | Google Scholar

Liu S., Zhang X. (2019). Extreme wave crest distribution by direct numerical simulations of long-crested nonlinear wave fields. Appl. Ocean Res. 86, 141–153. doi: 10.1016/j.apor.2019.01.018

CrossRef Full Text | Google Scholar

Longuet-Higgins M. S. (1952). On the statistical distribution of the heights of sea waves. J. Mar. Res. 11, 245–265.

Google Scholar

Longuet-Higgins M. S. (1962). Resonant interactions between two trains of gravity waves. J. Fluid Mechanics 12, 321–332. doi: 10.1017/S0022112062000233

CrossRef Full Text | Google Scholar

Longuet-Higgins M. S. (1963). The effect of nonlinearities on statistical distribution in the theory of sea waves. J. Fluid Mechanics 17, 459–480. doi: 10.1017/S0022112063001452

CrossRef Full Text | Google Scholar

Longuet-Higgins M. S. (1975). On the joint distribution of the periods and amplitudes of sea waves. J. Geophysical Res. 80, 2688–2694. doi: 10.1029/JC080i018p02688

CrossRef Full Text | Google Scholar

Luxmoore J. F., Ilic S., Mori N. (2019). On kurtosis and extreme waves in crossing directional seas: a laboratory experiment. J. Fluid Mechanics 876, 792–817. doi: 10.1017/jfm.2019.575

CrossRef Full Text | Google Scholar

McAllister M. L., Adcock T. A. A., Taylor P. H., van den Bremer T. S. (2018). The set-down and set-up of directionally spread and crossing surface gravity wave groups. J. Fluid Mechanics 835, 131–169. doi: 10.1017/jfm.2017.774

CrossRef Full Text | Google Scholar

McAllister M. L., van den Bremer T. S. (2019). Lagrangian Measurement of steep directionally spread ocean waves: Second-order motion of a wave-following measurement buoy. J. Phys. Oceanography 49, 3087–3108. doi: 10.1175/JPO-D-19-0170.1

CrossRef Full Text | Google Scholar

Mori N. (2012). Freak waves under typhoon conditions. J. Geophysical Research: Oceans 117, 1–12. doi: 10.1029/2011JC007788

CrossRef Full Text | Google Scholar

Mori N., Onorato M., Janssen P. A. E. M. (2011). On the estimation of the kurtosis in directional Sea states for freak wave forecasting. J. Phys. Oceanography 41, 1484–1497. doi: 10.1175/2011JPO4542.1

CrossRef Full Text | Google Scholar

Onorato M., Osborne A. R., Serio M., Cavaleri L., Brandini C., Stansberg C. T. (2004). Observation of strongly non-Gaussian statistics for random sea surface gravity waves in wave flume experiments. Phys. Rev. E 70, 67302. doi: 10.1103/PhysRevE.70.067302

CrossRef Full Text | Google Scholar

Onorato M., Proment D., Toffoli A. (2010). Freak waves in crossing seas. Eur. Phys. J. Special Topics 185, 45–55. doi: 10.1140/epjst/e2010-01237-8

CrossRef Full Text | Google Scholar

Onorato M., Waseda T., Toffoli A., Cavaleri L., Gramstad O., Janssen P. A. E. M., et al. (2009). Statistical properties of directional ocean waves: The role of the modulational instability in the formation of extreme events. Phys. Rev. Lett. 102, 114502. doi: 10.1103/PhysRevLett.102.114502

PubMed Abstract | CrossRef Full Text | Google Scholar

Portilla J., Ocampo-Torres F. J., Monbaliu J. (2009). Spectral Partitioning and Identification of Wind Sea and Swell. J Atmos Ocean Technol 26, 107–122. doi: 10.1175/2008JTECHO609.1

CrossRef Full Text | Google Scholar

Portilla-Yandun J., Caicedo A. L., Padilla-Hernández R., Cavaleri L. (2015). Spectral wave conditions in the Colombian pacific ocean. Ocean Model. 92, 149–168. doi: 10.1016/j.ocemod.2015.06.005

CrossRef Full Text | Google Scholar

Rapizo H., Babanin, A. V., Schulz E., Hemer M. A., Durrant T. H. (2015). Observation of wind-waves from a moored buoy in the southern ocean. Ocean Dynamics 65, 1275–1288. doi: 10.1007/s10236-015-0873-3

CrossRef Full Text | Google Scholar

Rodriguez G., Soares C. G., Pacheco M., Pe´rez-Martell E. (2002). Wave Height Distribution in Mixed Sea States. Journal of Offshore Mechanics and Arctic Engineering 124, 34–40. doi: 10.1115/1.1445794

CrossRef Full Text | Google Scholar

Seiffert B. R., Ducrozet G. (2018). Simulation of breaking waves using the high-order spectral method with laboratory experiments: wave-breaking energy dissipation. Ocean Dynamics 68, 65–89. doi: 10.1007/s10236-017-1119-3

CrossRef Full Text | Google Scholar

Sergeeva A., Slunyaev A. (2013). Rogue waves, rogue events and extreme wave kinematics in spatio-temporal fields of simulated sea states. Natural Hazards Earth System Sci. 13, 1759–1771. doi: 10.5194/nhess-13-1759-2013

CrossRef Full Text | Google Scholar

Sharma J. N., Dean R. G. (1981). Second-Order Directional Seas and Associated Wave Forces. Society of Petroleum Engineers Journal 21, 129–140. doi: 10.2118/8584-PA

CrossRef Full Text | Google Scholar

Slunyaev A., Kokorina A. (2020). Account of occasional wave breaking in numerical simulations of irregular water waves in the focus of the rogue wave problem. Water Waves 2, 243–262. doi: 10.1007/s42286-019-00014-9

CrossRef Full Text | Google Scholar

Slunyaev A., Sergeeva A., Didenkulova I. (2016). Rogue events in spatiotemporal numerical simulations of unidirectional waves in basins of different depth. Natural Hazards 84, 549–565. doi: 10.1007/s11069-016-2430-x

CrossRef Full Text | Google Scholar

Socquet-Juglard H., Dysthe K., Trulsen K., Krogstad H. E., Liu J. (2005). Probability distributions of surface gravity waves during spectral changes. J. Fluid Mechanics 542, 195–216. doi: 10.1017/S0022112005006312

CrossRef Full Text | Google Scholar

Støle-Hentschel S., Trulsen K., Nieto Borge J. C., Olluri S. (2020). Extreme wave statistics in combined and partitioned windsea and swell. Water Waves 2, 169–184. doi: 10.1007/s42286-020-00026-w

CrossRef Full Text | Google Scholar

Støle-Hentschel S., Trulsen K., Rye L. B., Raustøl A. (2018). Extreme wave statistics of counter-propagating, irregular, long-crested sea states. Phys. Fluids 30, 67102. doi: 10.1063/1.5034212

CrossRef Full Text | Google Scholar

Tanaka M. (2001). A method of studying nonlinear random field of surface gravity waves by direct numerical simulation. Fluid Dynamics Res. 28, 41–60. doi: 10.1016/S0169-5983(00)00011-3

CrossRef Full Text | Google Scholar

Tayfun M. A. (1980). Narrow-band nonlinear sea waves. J. Geophysical Res. 85, 1548–1552. doi: 10.1029/JC085iC03p01548

CrossRef Full Text | Google Scholar

Tayfun M. A. (1993). Sampling-rate errors in statistics of wave heights and periods. J. Waterway Port Coast. Ocean Engineering 119, 172–192. doi: 10.1061/(ASCE)0733-950X(1993)119:2(172

CrossRef Full Text | Google Scholar

Tayfun M. A. (2006). Statistics of nonlinear wave crests and groups. Ocean Eng. 33, 1589–1622. doi: 10.1016/j.oceaneng.2005.10.007

CrossRef Full Text | Google Scholar

Tayfun M. A. (2008). Distributions of envelope and phase in wind waves. J. Phys. Oceanogr. 38, 2784–2800. doi: 10.1175/2008JPO4008.1

CrossRef Full Text | Google Scholar

Tayfun M. A., Al-Humoud J. (2002). Least upper bound distribution for nonlinear wave crests. J. Waterway Port Coastal Ocean Eng. 128, 144–151. doi: 10.1061/(ASCE)0733-950X(2002)128:4(144

CrossRef Full Text | Google Scholar

Tayfun M. A., Fedele F. (2007). Wave-height distributions and nonlinear effects. Ocean Eng. 34, 1631–1649. doi: 10.1016/j.oceaneng.2006.11.006

CrossRef Full Text | Google Scholar

Tian Z., Perlin M., Choi W. (2010). Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J. Fluid Mechanics 655, 217–257. doi: 10.1017/S0022112010000832

CrossRef Full Text | Google Scholar

Titley H. A., Bowyer R. L., Cloke H. L. (2020). A global evaluation of multi-model ensemble tropical cyclone track probability forecasts. Q. J. R. Meteorological Soc. 146, 531–545. doi: 10.1002/qj.3712

CrossRef Full Text | Google Scholar

Toffoli A., Bitner-Gregersen E. M., Osborne A. R., Serio M., Monbaliu J., Onorato M. (2011). Extreme waves in random crossing seas: Laboratory experiments and numerical simulations. Geophysical Res. Lett. 38. doi: 10.1029/2011GL046827

CrossRef Full Text | Google Scholar

Toffoli A., Gramstad O., Trulsen K., Monbaliu J., Bitner-Gregersen E., Onorato M. (2010). Evolution of weakly nonlinear random directional waves: laboratory experiments and numerical simulations. J. Fluid Mechanics 664, 313–336. doi: 10.1017/S002211201000385X

CrossRef Full Text | Google Scholar

Toffoli A., Onorato M., Monbaliu J. (2006). Wave statistics in unimodal and bimodal seas from a second-order model. Eur. J. Mechanics - B/Fluids 25, 649–661. doi: 10.1016/j.euromechflu.2006.01.003

CrossRef Full Text | Google Scholar

Trulsen K., Nieto Borge J. C., Gramstad O., Aouf L., Lefèvre J. (2015). Crossing sea state and rogue wave probability during the prestige accident. J. Geophysical Research: Oceans 120, 7113–7136. doi: 10.1002/2015JC011161

CrossRef Full Text | Google Scholar

Wang L., Li J., Liu S., Ducrozet G. (2021). Statistics of long-crested extreme waves in single and mixed sea states. Ocean Dynamics 71, 21–42. doi: 10.1007/s10236-020-01418-9

CrossRef Full Text | Google Scholar

Waseda T., Hallerstig M., Ozaki K., Tomita H. (2011). Enhanced freak wave occurrence with narrow directional spectrum in the north Sea. Geophysical Res. Lett. 38. doi: 10.1029/2011GL047779

CrossRef Full Text | Google Scholar

Waseda T., Kinoshita T., Tamura H. (2009). Evolution of a random directional wave and freak wave occurrence. J. Phys. Oceanography 39, 621–639. doi: 10.1175/2008JPO4031.1

CrossRef Full Text | Google Scholar

West B. J., Brueckner K. A., Janda R. S., Milder D. M., Milton R. L. (1987). A new numerical method for surface hydrodynamics. J. Geophysical Res. 92, 11803. doi: 10.1029/JC092iC11p11803

CrossRef Full Text | Google Scholar

Wright C. W., Walsh E. J., Vandemark D., Krabill W. B., Garcia A. W., Houston S. H., et al. (2001). Hurricane directional wave spectrum spatial variation in the open ocean. J. Phys. Oceanography 31, 2472–2488. doi: 10.1175/1520-0485(2001)031<2472:HDWSSV>2.0.CO;2

CrossRef Full Text | Google Scholar

Wu G., Liu Y., Yue D. K. P. (2006). A note on stabilizing the Benjamin–feir instability. J. Fluid Mechanics 556, 45. doi: 10.1017/S0022112005008293

CrossRef Full Text | Google Scholar

Xiao W., Liu Y., Wu G., Yue D. K. P. (2013). Rogue wave occurrence and dynamics by direct simulations of nonlinear wave-field evolution. J. Fluid Mechanics 720, 357–392. doi: 10.1017/jfm.2013.37

CrossRef Full Text | Google Scholar

Zakharov V. E., Filonenko N. N. (1967). Energy spectrum for stochastic oscillations of the surface of a liquid. Sov. Phys. Dokl. 11, 881–883.

Google Scholar

Appendix

Appendix A: numerical discretization errors

The HOS numerical simulation surface elevation fields used in this study are provided at discrete time steps and grid points (see Section 2.1.1), whose resolution depends on the characteristics of the directional wave spectra. When the model sampling rate or the spatial discretization becomes too coarse, we expect errors to be present in the modelled maximum crest height values compared to the true crest height values observed in the ocean. Indeed, sampling-rate errors are known to cause discrepancies in the statistics of crest heights, so that one most likely observes a smaller value than the true one in any zero up-crossing cycle (Tayfun, 1993). To account for this, a sampling-rate error correction was introduced by Tayfun (1993) for the linear sea surface elevation recorded at a fixed point as a function of time η(t) = Acos(ωt+ϕ), where A = A(t) is the Rayleigh-distributed random amplitude function, ω is the spectral frequency and ϕ = ϕ(t) is the random phase with uniform distribution over the interval (0, 2π). The mean of the highest apparent wave crest heights $\tilde{\eta }=\tilde{\eta }\left(t\right)$ can therefore be written as a function of the true mean η = η(t) :

$\begin{array}{ll}\tilde{\eta }=(1-E_t)\eta & (21)\end{array}$

where E_t is the sampling-rate error, given by:

$\begin{array}{ll}{E}_t=\frac{{\pi }^2}{6}{\left(\frac{\Delta t}{T_m}\right)}^2& (22)\end{array}$

with T_m = T_m01 = 2π/ω_m representing the spectral mean period. Similarly, to correct the underestimation of the sharper large crests, a derivation based on the second-order nonlinear model was also introduced (see Tayfun and Al-Humoud, 2002). In this case, the sampling-rate error can be computed as:

$\begin{array}{ll}{E}_t=\frac{{\pi }^2}{6}{\left(\frac{\Delta t}{T_m}\right)}^2\left(1+\frac{3}{2}\alpha \tilde{\eta }\right)& (23)\end{array}$

where α = (2m₀₀₀)^1/2k_z is a measure of the RMS surface steepness, with k_z = m₀₀₂/m₀₀₀g the mean zero-crossing wavenumber.

However, since the temporal sampling rate of the HOS simulations in the present study is small (Δt = 0.5 s) compared to the mean wave periods of the analyzed sea states, the corresponding error is somewhat negligible in the resulting crest height values (E_t generally below 1% for both wind sea and swell). Conversely, the spatial discretization step for the simulated sea states is relatively large with respect to the mean wavelengths in the case of the wind sea (Δx = 8 m), so we expect the spatial discretization to be a non-negligible source of error in the estimation of crest heights. Therefore, given the similar representation of the sea surface elevation either in time or as a function of the linear spatial coordinate η(x) = Acos(kx+ϕ) , the wave crest height correction in Eq. (22) can be extended to the spatial dimension for the linear case as follows:

$\begin{array}{ll}{E}_s=\frac{{\pi }^2}{6}{\left(\frac{\Delta x}{L_x}\right)}^2& (24)\end{array}$

And, similarly, for the second-order nonlinear correction:

$\begin{array}{ll}{E}_s=\frac{{\pi }^2}{6}{\left(\frac{\Delta x}{L_x}\right)}^2\left(1+\frac{3}{2}\alpha \tilde{\eta }\right)& (25)\end{array}$

Although this correction is directly applicable to the case of 1D wave simulations, it might not be accurate in the case of 2D simulations such as the ones discussed in this work. However, we assume this correction to hold for the case of long-crested sea states, where there is little variation of the wave profile along the crest length. In this sense, we assume the correction given in Eq. (25) to be conservative correction in the case of 2D simulations. For the sea states analyzed in the present work, the resulting linear spatial error E_s was 3% in the case of the wind sea and only 1% for the swell, while the second-order error correction in Eq. (25) yielded spatial discretization errors up to 8% for the wind sea and around 1% for the swell. This is somewhat consistent with the errors found in the estimation of the kurtosis due to the discretization of the domain by Toffoli et al. (2010).