Variable-Density Flow and Solute Transport in Stratified Salt Marshes

Subsurface hydrodynamics underpin the eco-functions of salt marshes. Many studies have investigated these processes under various conditions. However, the impact of soil stratification (a low-permeability mud layer overlying a high-permeability sand layer) on the variable-density groundwater flow (particularly unstable flow) and solute transport in regularly tide-flooded marshes remains poorly understood. The present study numerically explored this question based on a 2D cross-creek section of salt marshes, by comparing cases with and without stratification. Results show that, the low-permeability mud layer delays the initiation of unstable flow and leads to smaller and denser salt fingers. Consequently, solute plume stays in the marsh soil for a longer time and spreads more widely than that in the homogeneous case. Also, soil stratigraphy extends the duration and shrinks the zone of solute discharge across the tidal creek. Sensitivity analysis was conducted based on three key controlling variables: hydraulic conductivity contrast between mud layer and sand layer (K_mud/K_sand), salinity contrast between surface water and groundwater (C_sea/C_pore), and mud layer thickness (D_mud). The results demonstrate that the residence time of solute plume in a two-layered salt marsh is less sensitive to C_sea/C_pore than to K_mud/K_sand and D_mud. Moreover, the commencement and duration of solute discharge are more sensitive to K_mud/K_sand and D_mud than to C_sea/C_pore. While the location of solute discharge zone is highly sensitive to D_mud and slightly influenced by K_mud/K_sand and C_sea/C_pore. Findings from this study would facilitate a deeper understanding of the eco-functions of salt marshes.

Highlights

- The impact of soil stratification on unstable flow and solute transport in tidal marshes was numerically investigated.

- Soil stratigraphy considerably postpones the formation of unstable flow in marsh soils.

- Soil stratigraphy increases the residence time and spreading area of solute plume in the marsh aquifer.

- Solute discharges over a longer period and a narrower zone in layered marsh aquifer.

Introduction

Salt marshes distributed at the ocean-land interface are one of the most productive ecosystems that maintain coastal biodiversity, moderate global warming, and buffer deleterious storm impacts (Chapman, 1974; Vernberg, 1993; Valiela et al., 2000; Artigas et al., 2021). However, under the threat of sea level rise due to global climate change, an increasingly larger area of salt marshes worldwide is on the edge of vanishing (Campbell and Wang, 2020). Given the enormous ecological values of the marshes, it is imperative to take actions to reverse the declining trend. A precursor to developing effective measures for marsh restoration and preservation is to understand the eco-functions of marsh systems.

The ecology of salt marshes is closely linked to the hydrological process (Guimond and Tamborski, 2021). The subsurface hydrology of marshes is primarily affected by tidal fluctuations (Wilson and Gardner, 2006; Xin et al., 2010a; Wilson and Morris, 2012; Wilson et al., 2015) and soil structure (Gardner, 2007; Xin et al., 2009; Xiao et al., 2019b). As the rising tide inundates the marsh platform, surface water infiltrates into the unsaturated soil. While during an ebbing tide, the pore water seeps out from the creek bank and bottom. The asymmetrical pore water dynamics at the two stages lead to a net circulation toward the creek over one tidal cycle (Xin et al., 2012). The tidally averaged near-creek circulation is ecologically significant for salt marshes, as it underpins the “nutrient outwelling” hypothesis, which refers to the net export of nutrients from salt marshes to the sea (Teal, 1962). Subsurface flow affects nutrient cycling between marsh sediments and adjacent surface water, because pore water draining out of salt marsh sediments at low tide is enriched in nutrients compared to surface water (Whiting et al., 1985; Velinsky et al., 2017; Schiebel et al., 2018). The net circulation provides a rapid exchange between the marsh sediments and tidal creeks, thereby supporting the observed nutrient outwelling (Gardner, 2005; Wilson and Gardner, 2006; Peterson et al., 2019).

Subsurface hydrology of salt marshes also affects plant zonation, namely the spatial distribution patterns of marsh plants (Silvestri et al., 2005; Xiao et al., 2017; Xie et al., 2020). Salinity distribution (degree of marsh plants’ tolerance to salinity is species-dependent) (Pennings and Callaway, 1992; Rogel et al., 2000; Silvestri et al., 2005; Veldhuis et al., 2019) and aeration condition (for plant root aerobic respiration) (Ursino et al., 2004; Marani et al., 2006; Xin et al., 2009; Xin et al., 2017; Feng et al., 2018) are the two important factors that determine plant zonation. Groundwater flow largely controls the spatial distribution of soil salinity. The rapid tide-driven near-creek circulation can help to limit the buildup of salt in the root zone caused by evapotranspiration, favoring the growth of less salt-tolerant plants (Gardner, 2007). For marsh areas dominated by downward hydraulic gradients, infiltration, and evapoconcentration of tidal water is promoted to create hypersaline conditions suitable for more salt-tolerant species (Thibodeau et al., 1998; Xu et al., 2021). Spatiotemporal variations in the height of the water table below the sediment surface alter the saturation and redox state of subsurface sediments (Howes et al., 1981; Feng et al., 2018). Previous studies have shown that the optimal aeration condition tends to occur near the creek (Ursino et al., 2004; Xin et al., 2009), being consistent with the observation of Dacey and Howes (1984) that plants grow better near the creek.

The hydrology-ecology linkage of salt marshes mentioned above is further tightened by soil stratigraphy, typically with a less permeable mud or silt loam layer overlying sands or sandy loam deposits that are more permeable (Hughes et al., 2012). Soil stratigraphy commonly exists in salt marshes all over the world and has been found to greatly affect the hydrological processes in many ways. Based on the stratified salt marshes in southern United States, Gardner (2007) discovered great enhancement of groundwater seepage flux (from marsh sediments to tidal creeks) due to the presence of the high-permeability sand layer, thereby further underpinning the nutrient outwelling hypothesis. The stratigraphic controls on fluid and solute exchange between marsh sediments and tidal water were confirmed by Sawyer et al. (2014). The more permeable soil layer also lowers the water table height, thereby improving the local aeration conditions in the shallow soil layer to favor the growth of marsh plants (Xin et al., 2012). In addition, marsh stratigraphy has been shown to alter the overall groundwater circulation pattern and discharge locations that could, in turn, affect the pore water conditions (e.g., salinity) in areas of weak flow (Sawyer et al., 2014).

Research on subsurface hydrology in salt marshes mediated by soil stratigraphy has mostly neglected the variable-density flow, which may arise from the salinity contrasts between surface water and groundwater. Many field measurements have reported such salinity contrast (Burdick et al., 2001; Cao et al., 2012; Hughes et al., 2012; McKinney et al., 2019). For example, McKinney et al. (2019) discovered that the mean monthly soil salinity was 25.8 ± 5.5 ppt at the Narrow River marsh near the mouth of the Narragansett Bay, and 17.7 ± 5.3 ppt at the Passeonkquis marsh located in the upper Bay. By contrast, the salinity of surface water is usually higher, leading to an upward salinity gradient. Such upward salinity gradients have been confirmed by Kuhn and Zedler (1997), who showed that the soil salinity in a California marsh was very high at the surface but dropped rapidly with depth. The distribution of decreasing salinity with soil depth was also found by Mahall and Park (1976) in another two California marshes. Generally, the formation of upward salinity gradients is due to that the evaporation period during the exposure of the marsh platform is much longer at high elevation, where salt on the surface soil is likely to become highly concentrated (Adam, 1993). Subsequently, as the marsh surface is inundated, the concentrated salt dissolves in tidal water, leading to an increase in the salinity of surface water.

When an upward salinity gradient exists in marshes, unstable flow may occur in the form of salt fingers, which enhances drainage flux from marsh sediments into tidal creeks, further supporting the nutrient outwelling hypothesis (Shen et al., 2015). Meanwhile, the unstable flow provides a new mechanism for solute removal from the marsh sediments by allowing the solute in the marsh interior to transport upward and exit from the marsh platform instead of the tidal creek (Shen et al., 2016). The interplay of soil stratigraphy and salinity contrasts has been rarely investigated. One exception is the recent work of Xiao et al. (2019a), which examined the combined effects of tidally varying salinity and soil heterogeneity on subsurface hydrology in salt marshes. However, the findings of Xiao et al. (2019a) are applicable to micro-tidal marshes only, because they did not consider tidal inundation. When the marsh platform is not flooded, the exchange between tidal water and pore water is driven only by the filling and draining through the tidal creek. While in the case where the marsh platform is tidally submerged, flow occurs across the entire marsh platform, leading to more significant water exchanges and prolonging the residence time (Wilson and Gardner, 2006; Marois and Stecher, 2020). Given the common existence and significance of tidal inundation, further research targeting the effects of soil stratification on variable-density flow and solute transport in tide-submerged marshes is needed.

Based on the above review, this study aims to numerically explore the unstable flow and solute transport pattern in tidally inundated and layered salt marshes. In particular, two questions are addressed: (1) How will the unstable flow pattern (e.g., initiation, intensity) and solute transport characteristics (e.g., trajectory, spreading, and discharge) be modified by soil stratigraphy in comparison to a homogeneous situation? (2) How sensitive are the effects of soil stratigraphy to the key controlling variables, e.g., the hydraulic conductivity contrast between upper mud layer and deeper sand layer, the salinity contrast between surface water and groundwater, and the thickness of the upper mud layer? Answers to these questions are important as they would provide a deeper insight into the subsurface hydrology and its connection to the ecological functions of salt marshes, thereby guiding the preservation and restoration of these valuable ecosystems.

Numerical Modeling

Governing Equations

The numerical model SUTRA-MS developed by Hughes and Sanford (2004) was used to simulate solute transport associated with the variable-density, variable-saturation pore water flow in salt marshes (Figure 1). This model has been validated against laboratory experiments that explored unstable flow effect on solute transport in homogeneous marsh sediments (Shen et al., 2016) and the influence of aquifer-ocean temperature contrasts on salinity distributions in coastal unconfined aquifers (Nguyen et al., 2020).

FIGURE 1

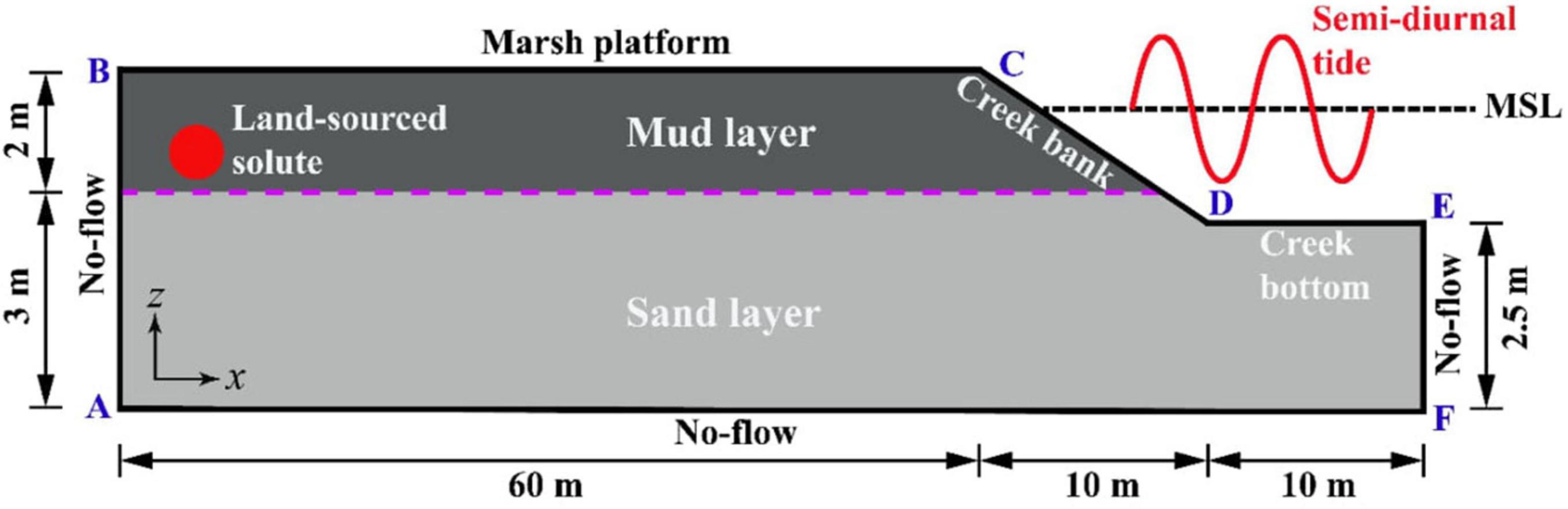
Figure 1. Schematic diagram of the numerical model domain representing a 2D creek-normal transect and corresponding boundary conditions.

Without considering evapotranspiration, precipitation and inland freshwater input, the groundwater flow in marsh soil can be described by:

$\begin{array}{c}\mathrm{\varphi }\rho \frac{\partial S_{\text{W}}}{\partial t}+\varphi S_{\text{W}}\left(\sum _{i=1}^{NS}\frac{\partial \rho }{\partial C_i}\frac{\partial C_i}{\partial t}\right)\hfill \\ =\nabla \cdot \left[\rho K\left(\psi \right)\nabla \mathrm{\Phi }\right]with\mathrm{\Phi }=\frac{P}{\rho g}+z\hfill \end{array}(1)$

where ϕ [-] is the soil porosity; S_W [-] is the soil water saturation; t [-] is the time; C_i [ML^–3] is the concentration of the ith dissolved solute; NS [-] is the total number of dissolved solute (NS = 2 in this study, including salt solute and land-sourced conservative solute, and solute or solute plume hereinafter refers to the latter); K(ψ) [LT^–1] is the hydraulic conductivity depending on capillary pressure head ψ [L] (equals to the saturated hydraulic conductivity K_s [LT^–1] in the saturated zone); Φ [L] is the hydraulic head; P [ML^–1T^–2] is the fluid pressure; z [L] is the elevation; ρ [ML^–3] is the fluid density that varies with salt and solute concentrations according to:

$\rho ={\rho }_0+\sum _i^{NS}{\mathrm{\lambda }}_i{C}_i(2)$

where ρ₀ [ML^–3] is the freshwater density, and λ_i [-] is the coefficient that describes the relationship between fluid density and the concentration of the ith solute (set to 0.7143 and 0 for salt solute and land-sourced conservative solute, respectively). This study does not follow the approach of Reeves et al. (2000) and Wilson and Gardner (2006) to consider the tidal loading effect by including an additional source/sink term in Eq. 1. Instead, meeting the criteria of K_s ≥ 10^–6m s^–1, as suggested by Xin et al. (2012), the sediment storativity is neglected. Readers may refer to these papers for more details.

Coupled with the subsurface flow, the salt and solute transport in marsh sediments is governed by the transport equation:

$\frac{\partial \left(\rho \varphi S_{\text{W}}{C}_i\right)}{\partial t}=\nabla \cdot \left[\rho C_{i}K\left(\psi \right)\nabla \mathrm{\Phi }\right]+\nabla \cdot \left(\rho \varphi S_{\text{W}}\mathbf{\text{D}}\nabla C_i\right)(3)$

where D [L²T^–1] is the hydrodynamic dispersion tensor. Moreover, the Van Genuchten (1980) formulas were used to describe the relationships between K(ψ), S_W, and ψ:

${}_{S_{\text{W}}=S_{\text{Wres}}+\left(1-S_{\text{Wres}}\right){\left[\frac{1}{1+{\left|a\psi \right|}^n}\right]}^{\left(\frac{n-1}{n}\right)}}(\mathrm{4a})$

${}_{K\left(\mathrm{\psi }\right)=K_{\text{s}}{S}_{\text{W}}^{{}^{*}1/2}{\left\{1-{\left[1-S_{\text{W}}^{{}^{*}\left(\frac{n}{n-1}\right)}\right]}^{\left(\frac{n-1}{n}\right)}\right\}}^2\text{with}{S}_{\text{W}}^{{}^{*}}=\frac{S_{\text{W}}-S_{\text{Wres}}}{1-S_{\text{Wres}}}}(\mathrm{4b})$

where K_s [-] is the relative hydraulic conductivity; S_Wres [-] is the residual water saturation; a [L^–1] and n [-] are the Van Genuchten (1980) constants.

Model Setup

The model shown in Figure 1 represents a 2D cross-creek transect that was assumed to be layered (a low-permeability mud layer overlying a high-permeability sandy layer) (Gardner, 2007). The dimensions of the model are based on previous numerical studies of the subsurface hydrodynamics in salt marshes (Gardner, 2005; Wilson and Gardner, 2006). This study neglected the fresh groundwater input from the upland, so the numerical model was representative of salt marshes during dry seasons. Corresponding, the inland boundary AB was set as no-flow. The right vertical boundary EF, which represents the hydraulic divide, and the marsh bottom AF, were also assigned a no-flow boundary. The marsh platform BC and tidal creek CDE, which combine to form the sediment-water interface (SWI), were set as pressure-specified boundaries according to a semidiurnal tidal signal described as H_tide(t) = H_msl + Asin(ωt), with H_tide(t) [L] being the time-varying creek water level, H_msl [L] being the mean sea level (MSL, set to 4.2 m), A [L] being the tidal amplitude (set as 1 m), and ω [T^–1] being the angular frequency (0.5326 rad h^–1 based on a tidal period of 12 h). Note that the tidal signals in some salt marshes fluctuate over a longer period (e.g., spring-neap tides) and lead to more complex pore water flow dynamics (Xin et al., 2010a). Moreover, evaporation and precipitation, which would alter the salinity contrast between surface and subsurface water, was also ignored in this study. Nevertheless, the neglection of these factors allowed us to better focus on the role of soil stratigraphy.

The marsh platform was inundated when the tidal level was higher than its elevation. During falling tide, a seepage face was allowed to form along the creek bank (CD in Figure 1), following the approach of Wilson and Gardner (2006) and Xin et al. (2010b). Specifically, exposed boundary nodes were treated as seepage face nodes with an atmospheric pressure if they were saturated at the previous time step, whereas they were assigned to be no-flow if unsaturated previously. For salt transport, boundary nodes with inflow (to marsh sediments) were assigned a seawater concentration (C_sea) of 35 ppt (parts per thousand), while those with outflow (from marsh sediments) were assigned with a zero-concentration gradient.

Simulation Cases and Parameters

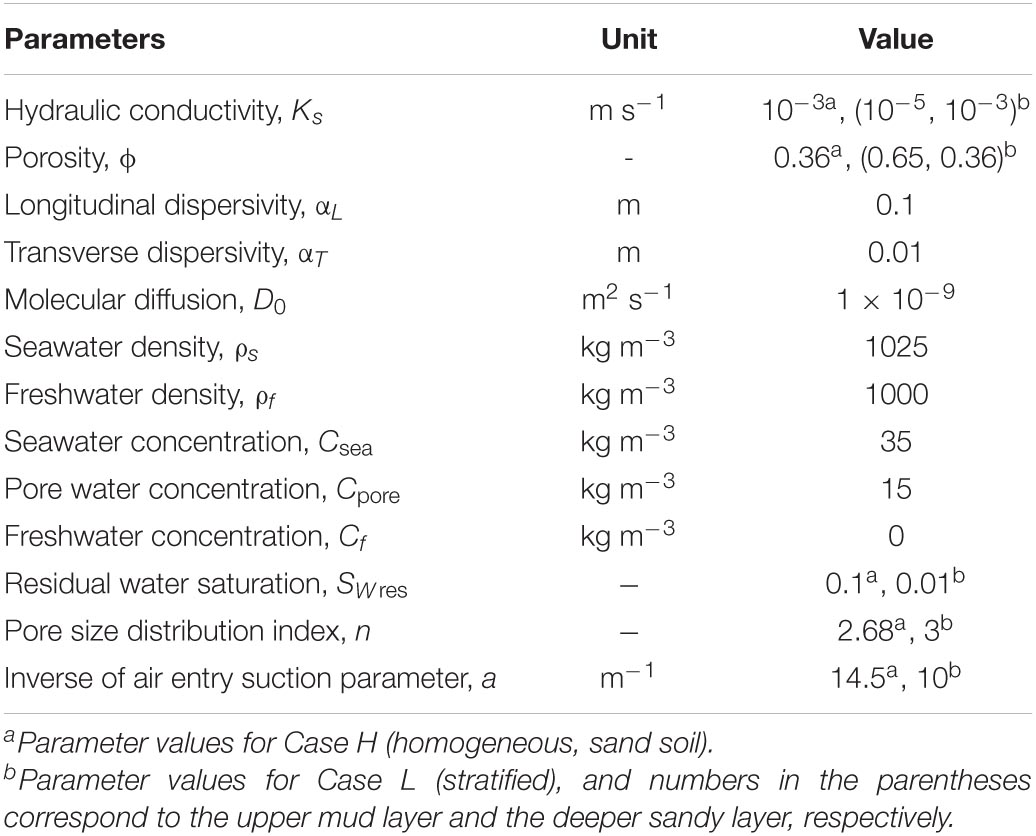
To understand how soil stratigraphy would affect the variable-density flow and solute movement in salt marshes, the current study set up Case H without soil stratigraphy and Case L with a mud layer overlying a sand layer. Following Xiao et al. (2019a), who established the numerical model based on investigations of the Crabhaul creek in North inlet-Winyah Bay National Estuarine Research Reserve system, Case H considers homogeneous sandy marsh sediments, with the K_s and ϕ set to 1 × 10^–3m s^–1 and 0.36. Case L uses a layered soil structure of a 2-m mud layer overlying a 3-m sand layer, with K_s and ϕ being 1 × 10^–5m s^–1 and 0.65 for mud. Xia and Li (2012) observed the high K_s of sand in the mangrove marshes in Dongzhaigang National Nature Reserve, Hainan, China. The longitudinal dispersivity α_L and transverse dispersivity α_T were set to 0.1 and 0.01 m, respectively. S_Wres and the Van Genuchten (1980) constants a and n were set as 0.1, 14.5 m^–1 and 2.68 for sand, and 0.01, 10 m^–1, and 3 for mud. For Cases L and H, the surface water salinity was set as that of seawater (35 ppt), and the initial salinity of pore water was set to 15 ppt. These parameter values have been adopted in previous salt marsh groundwater modeling studies (Xin et al., 2012; Shen et al., 2016). Table 1 provides more details of the parameter values used in the two cases.

TABLE 1

Table 1. Parameter values used for simulations.

The initial pore water salinity was based on the field measurements of Cao et al. (2012), which observed salinities between 9 and 17 ppt across different transects in the marsh soil at the Chongming Dongtan wetland, China. The lower salinity in marsh sediments is mainly diluted by freshwater input from the inland boundary, which, however, was prescribed as no-flow in this study. Such a setup is possible when there is little freshwater input after dilution of pore water salinity and the inundation period is relatively short. Correspondingly, upward salinity/density gradients in the marsh soil may persist for a long period. Note that in the current study, a constant tidal water salinity was used for all cases, since the focus was on the effects of soil stratigraphy. Tidal salinity fluctuations, as revealed by Xiao et al. (2019a), would further complicate the entire groundwater flow and solute transport processes.

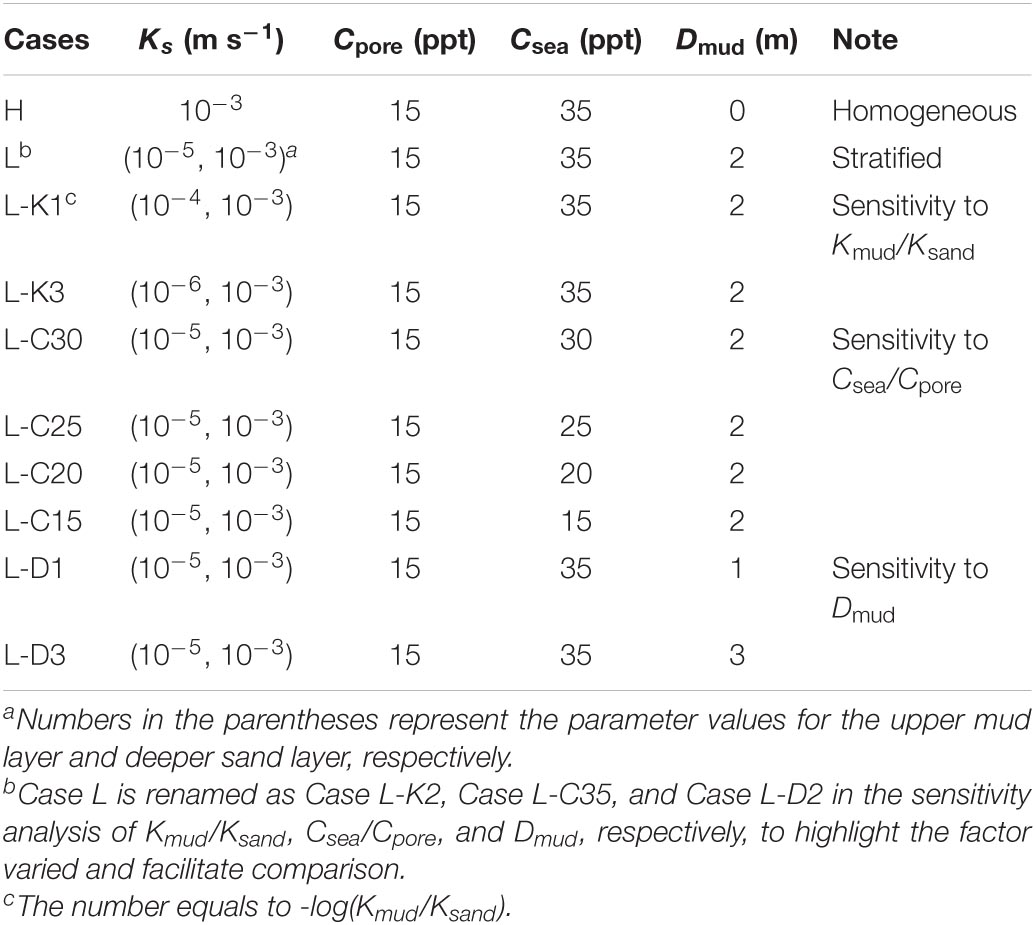
Based on Case L, a sensitivity analysis was conducted by altering three controlling variables: (1) the hydraulic conductivity contrast between mud and sand layers (K_mud/K_sand), (2) the tidal water salinity (C_sea, and hence the salinity contrast C_sea/C_pore), and (3) the thickness of upper mud layer (D_mud). Changes of these variables are within the value ranges used by other researchers. For example, in the study of Gardner (2007) based on southeastern United States marsh, the smallest K_mud/K_sand is 0.001, while D_mud is between 2.5 and 5 m. More information on the sensitivity analysis is given in Table 2. Note that there are other factors that would modify the extent to which soil stratigraphy may affect the unstable flow pattern and solute transport in salt marshes. For example, spring-neap tides fluctuating over a longer period may complicate the unstable flow regime, evaporation tends to increase pore water salinity and thus enhances flow instability. While inland fresh groundwater recharge is expected to decrease the salinity contrast between infiltration surface water and pore water, thereby reducing the likelihood of unstable flow formation. However, this study focused primarily on the three controlling variables since they are more relevant to the soil stratigraphy and unstable flow, which are the major research subject.

TABLE 2

Table 2. Simulated cases with model parameter values.

All the simulations began with an initial condition of hydrostatic pressure distribution based on the MSL and a uniform subsurface water salinity of 15 ppt. Note that the formation of salt fingers is sensitive to the initial concentration. For the same surface water salinity, a higher/lower initial concentration will decrease/increase the salinity contrast between surface and subsurface water, thereby impeding/promoting the salt fingers formation. The land-sourced conservative solute was introduced by applying an initial concentration (C₀) of 100 ppt, a value that has been used by Robinson et al. (2007), to all nodes within a circle centered at x = 10 m and z = 4 m underneath the water table, with a radius of 0.5 m (Figure 1). No concentrations were further prescribed for the solute plume after the simulations started. Therefore, the same initial solute mass (M₀) was applied to all the cases. Simulations stopped when the solute plume had completely exited the marsh sediments. The same mesh discretization scheme (as described below) was applied to all simulations to ensure an identical amount of initial solute mass in all cases. Also, the solute was passive without density effect, so a different value of C₀ would not alter the transport characteristics of the solute plume in marsh soil.

All the simulations were run with a time step size of 60 s. The mesh discretization consists of 40,501 nodes and 40,000 elements. This scheme ensured numerical stability, which was evaluated by the grid Péclet number P_e ≈ ΔL/α_L, with ΔL [L] being the transport distance between two sides of an element along the subsurface flow direction and α_L [L] being the longitudinal dispersivity (Hughes and Sanford, 2004). The largest P_e under the mesh discretization scheme was 2, satisfying the criterion of P_e ≤ 4 for avoiding numerical oscillations. To ensure the numerical convergence of results presented in this paper, we tested four grid resolutions: 10,251 nodes, 22,876 nodes, 40,501 nodes, and 90,751 nodes. Results under the two highest resolutions were found to be almost identical, so the scheme of 40,501 nodes was used for all the simulations.

Measurable Diagnostics

To quantify the influence of soil stratigraphy on unstable flow and solute transport in salt marshes, several measurable diagnostics were used, e.g., residual solute mass remaining in the marsh sediments, centroids (x_c, z_c) and variances (${\sigma }_{\text{xx}}^2$ and ${\sigma }_{\text{zz}}^2$) of the solute plume. These diagnostics were obtained using the zero-order (M₀₀), first-order (M₁₀, M₀₁), and second-order (M₂₀, M₀₂) spatial moments, following the approach of Freyberg (1986):

${}_{M_{00}=\int \int \varphi C(x,z,t)\text{d}x\text{d}z}(\mathrm{5a})$

${}_{M_{10}=\int \int \varphi C(x,z,t)x\text{d}x\text{d}z,M_{01}=\int \int \varphi C(x,z,t)z\text{d}x\text{d}z}(\mathrm{5b})$

${}_{x_{\text{c}}=\frac{M_{10}}{M_{00}},z_{\text{c}}=\frac{M_{01}}{M_{00}}}(\mathrm{5c})$

${}_{M_{20}=\int \int \varphi C(x,z,t){(x-x_c)}^2\text{d}x\text{d}z,M_{02}=\int \int \varphi C(x,z,t){(z-z_c)}^2\text{d}x\text{d}z}(\mathrm{5d})$

${}_{{\mathrm{\sigma }}_{xx}^2=\frac{M_{20}}{M_{00}},{\mathrm{\sigma }}_{zz}^2=\frac{M_{02}}{M_{00}}}(5e)$

Also, the residence time (T_res) and spreading area (A_spr) of the solute plume, time-varying total solute efflux (integrated along the SWI) and spatial distribution of net solute efflux (integrated over time) were calculated. The criterion of C/C₀ = 0.0001 was applied to determining the solute plume edge. The intensity of unstable flow was quantified using the initiation time, T_ini, which was determined based on the aspect ratio of salt fingers: r_fin = L_fin/W_fin ≥ 4, with L_fin [L] and W_fin [L] being the length and width, respectively. Once r_fin exceeds 4, the salt fingers have “formally” formed, indicating the occurrence of unstable flow. A different threshold of r_fin may lead to a different T_ini, but the trend of comparison among the simulated cases would be similar.

Results

Unstable Flow Regime and Solute Transport

The simulated salinity distributions, solute transport path and flow field in Cases 1–2 are shown in Figure 2. Unstable flow occurs in both cases, with salt fingers initially forming near the inland boundary, where density effect is dominant and the advection process is much weaker. The formation of unstable flow is early in Case H and considerably delayed in Case L. For example, by Day 30, the flow instability has been quite fully developed in Case H, whereas there are only a few small salt fingers forming near the inland boundary in Case L. The comparison indicates that the low-permeability mud layer delays the formation of unstable flow in marsh sediments. Moreover, it is noteworthy that, in Case L, the unstable flow does not occur until the infiltrating surface water has entered the lower high-permeability sand layer, as reflected by the result of Day 30. Furthermore, in Case H, the sizes of salt fingers near the tidal creek are larger than those in the marsh interior, due to the stronger tide-induced near-creek circulation and hence a weaker role of density-dependent flow. By contrast, the salt finger sizes in Case L are more evenly distributed across the marsh aquifer. This is because the low permeability of the mud layer weakens the tidally driven near-creek circulation, thereby enhancing the role of density effect.

FIGURE 2

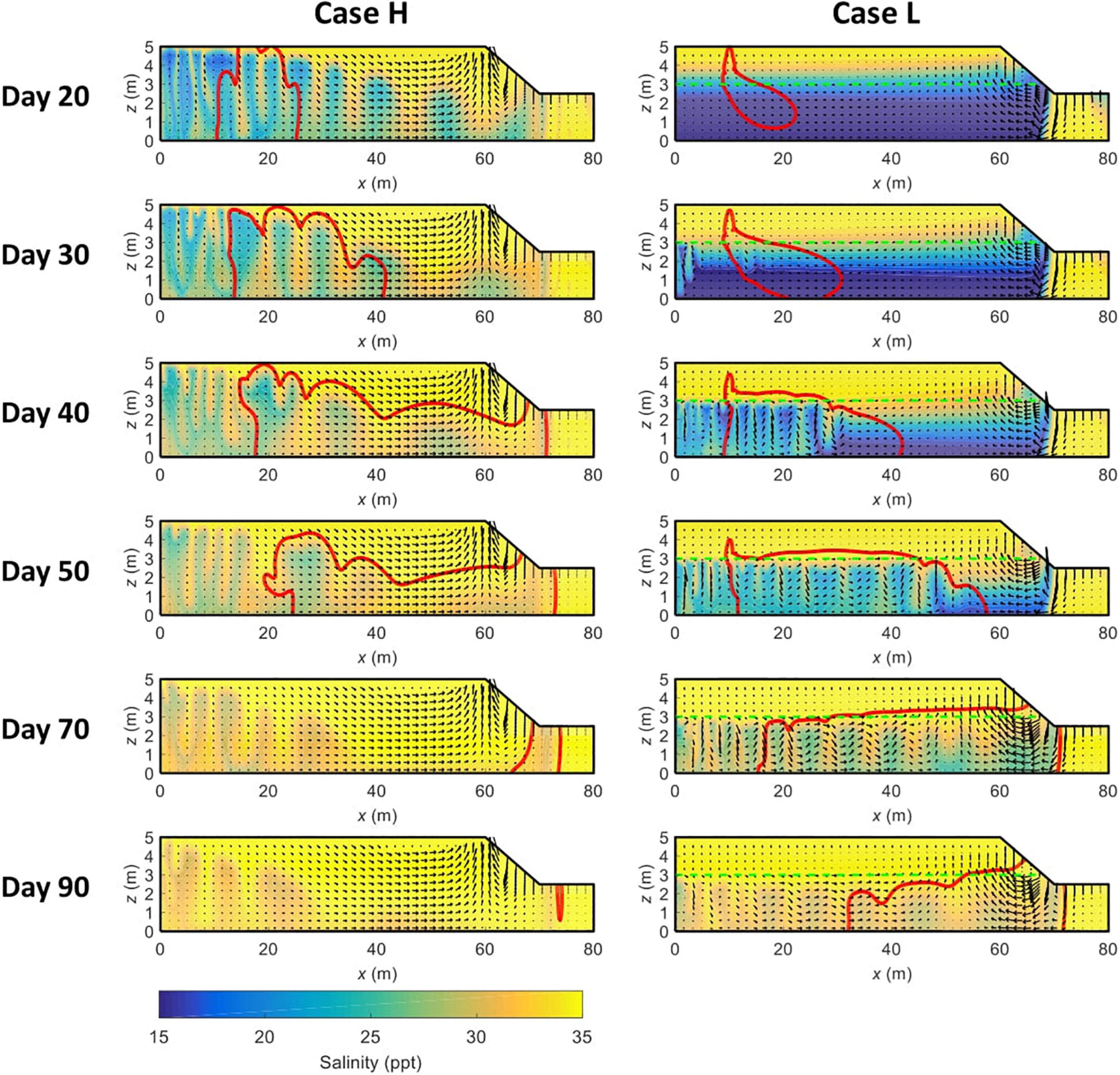
Figure 2. Temporal variations of solute distribution contour line (in red, 0.0001C₀) and pore water salinity distributions in Cases H and L. The green dashed line represents the boundary between the mud (upper) and sand (deeper) layers. All the plots show conditions at the mid-rising tide, with the arrows indicating the corresponding pore water flow field.

Without the low-permeability mud layer (Case H), the solute plume is stretched upward by salt fingers and partially exits the marsh sediments from the marsh platform (e.g., Day 20, Figure 2). As salt fingers develop, solute plume in Case H becomes more meandering, eventually discharging into tidal water from the creek bank (e.g., Day 50, Figure 2). In comparison, solute plume in Case L exhibits different transport characteristics, owning to the modified unstable flow regime by soil stratigraphy. After the initial release, solute plume in the mud layer is primarily pushed downward by the infiltration of surface water. The part of the solute plume that enters the sand layer starts to be affected by the unstable flow and so becomes irregularly shaped. As time goes by, the majority of the solute plume is in the sand layer, with a small fraction staying in the mud layer and moving toward the tidal creek. While the solute plume in Case H is vertically stretched almost from the marsh platform to the marsh bottom, the stretch of the solute plume in Case L mainly occurs in the sand layer, attributed to the constraint of the mud layer. Besides, the smaller and denser salt fingers in Case L play a stronger role in trapping the solute plume and so prolong the duration of solute discharge. For example, by Day 90, solute plume in Case H has almost been completely removed while a large proportion remains in the marsh soil in Case L.

Spatiotemporal Variations of Solute Efflux

Figure 3 compares the time-varying total solute efflux between Cases 1–2. Notably, without the constrain of the mud layer, there is a very early episode of solute discharge in Case H, corresponding to the solute discharge from the marsh platform shown in Figure 2. Except for this episode, the remaining solute plume in Case H still starts to discharge into creek water much earlier than that in Case L, e.g., commencement on Day 38 and Day 58 in Cases 1 and 2, respectively, differing by 52.6%. Also, the solute discharge takes a shorter time in Case H than in Case L (37 versus 47 days), leading to more intensive solute efflux, i.e., a higher peak value.

FIGURE 3

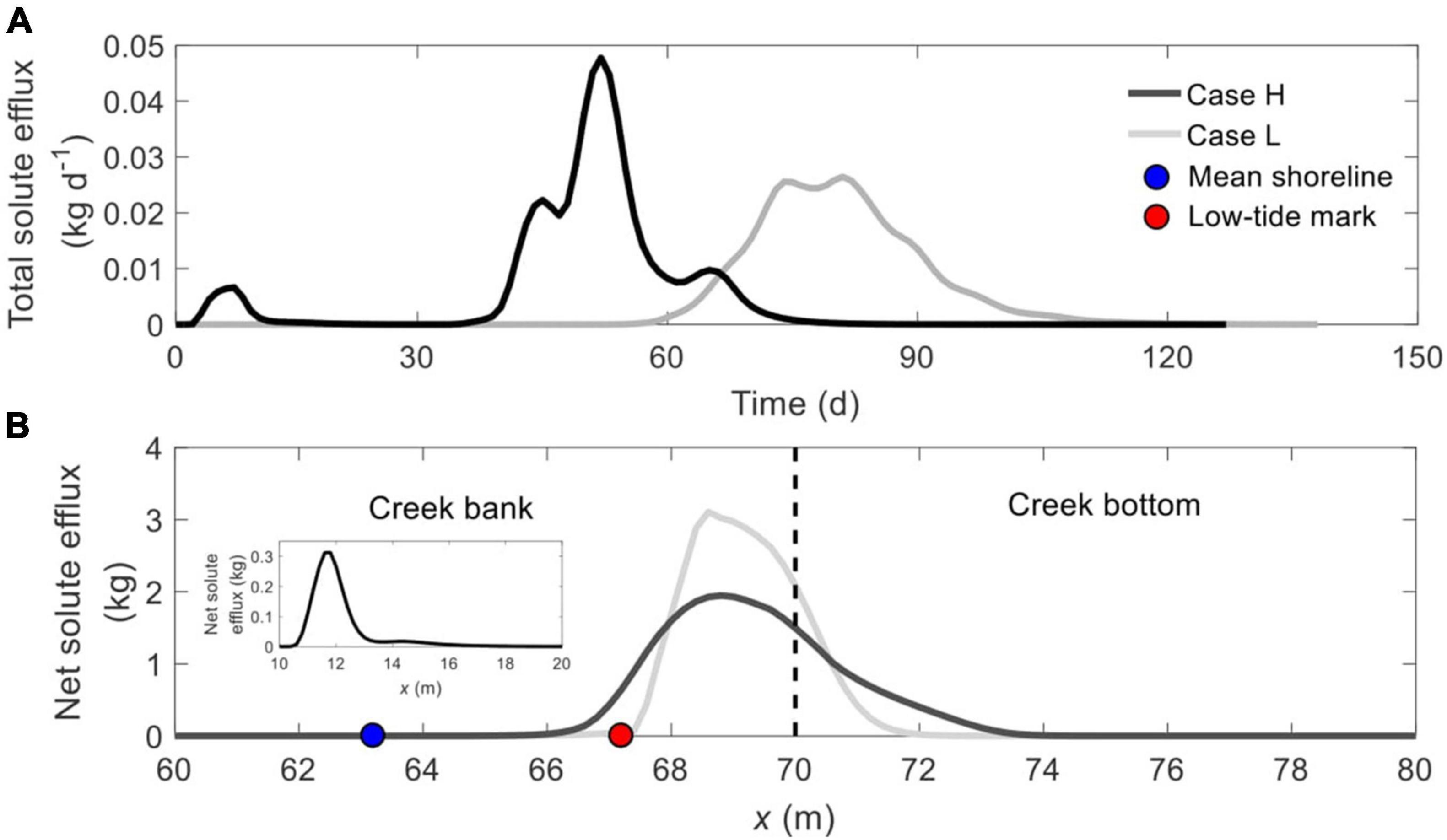
Figure 3. Comparison of (A) time-dependent total solute efflux and (B) spatial distribution of net solute efflux across the SWI (BCDE in Figure 1) between Cases H and L. The blue and red nodes in panel (B) represent the mean shoreline and low-tide mark, respectively, while the vertical dashed line separates creek bank (left) and creek bottom (right). The subplot in panel (B) shows the location of the first discharge episode from the marsh platform in Case H.

The early episode of solute discharge (from the marsh platform) in Case H occurs between x = 10.6 m and x = 15.6 m, one landward segment of the marsh platform (subplot in Figure 3B). Meanwhile, soil stratification narrows down the solute discharge zone along the tidal creek, reducing the width from 7.2 m (x = 66.4 ∼ 73.6 m) in Case H to 4.6 m in Case L (x = 67.2 ∼ 71.8 m), a reduction of 36%. Correspondingly, the maximum spatial solute efflux in Case L is much higher than that in Case H. In addition, solute plume in Case H discharges across both intertidal zone (left side of the cyan node) and subtidal zone (right side of the cyan node), but the discharge zone is shifted to be entirely in the subtidal zone in Case L.

This study further compares the spatial distribution of daily solute efflux across the sediment-water interface at different times (Figure 4). Consistent with the results in Figure 3A, due to the earlier discharge, the solute efflux in Case H is quite large on Day 30, while that in Case L is zero. Later on, the solute plume in Case L starts to discharge into the tidal water (e.g., on Day 50 and Day 70), whereas the solute efflux in Case H has almost declined to zero.

FIGURE 4

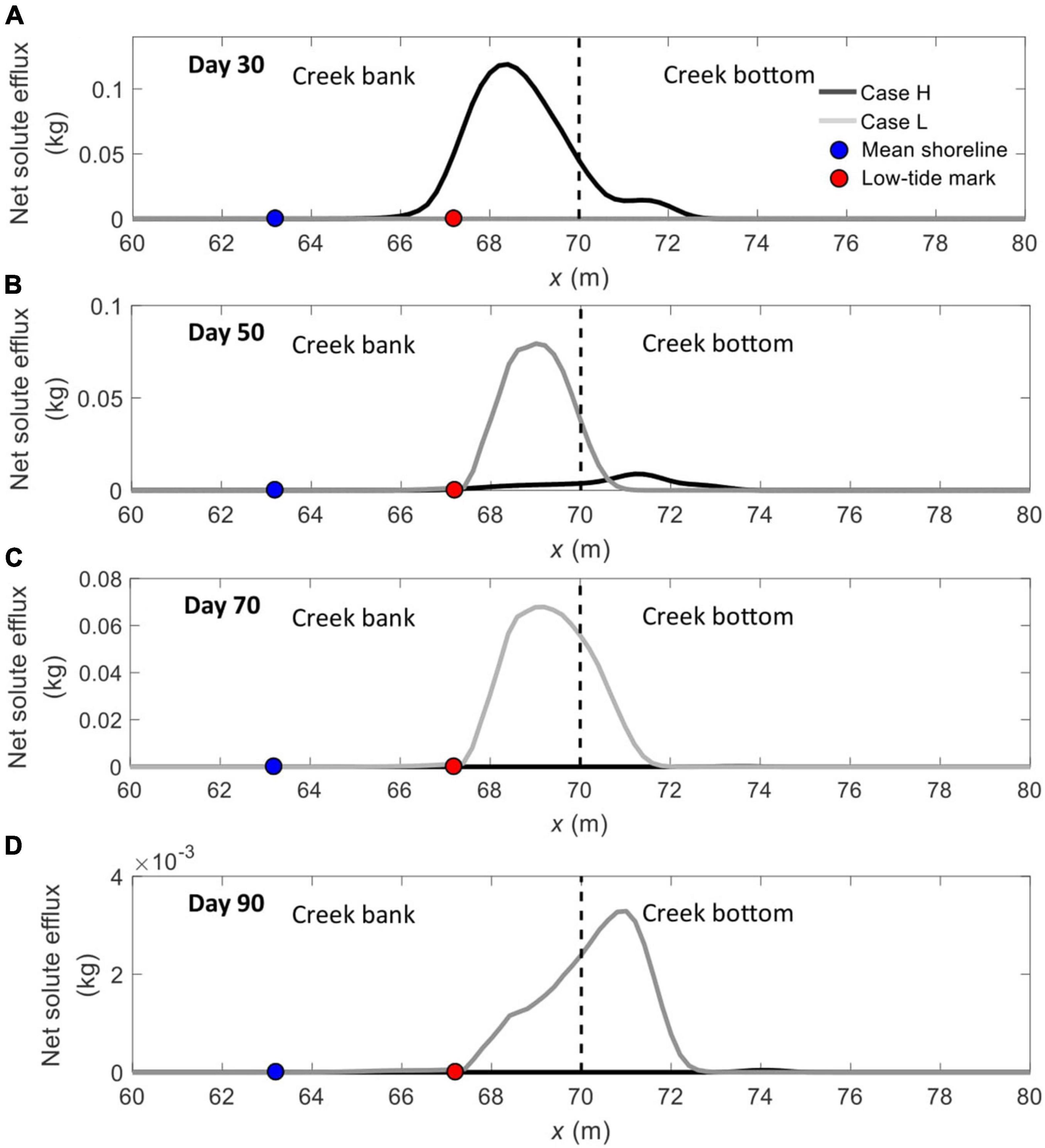
Figure 4. Temporal variations of daily integrated solute effluxes across the sediment–water interface (BCDE in Figure 1) between Cases H and L on (A) Day 30, (B) Day 50, (C) Day 70, and (D) Day 90. The blue and red nodes represent the mean shoreline and low-tide mark, respectively, while the vertical dashed line separates creek bank (left) and creek bottom (right).

Flow Instability Initiation, Solute Residence, and Spatial Moments

T_inc and T_res are highly sensitive to soil stratigraphy, with the former increasing from 5 days in Case H to 26 days in Case L (an increase of 420%), and the latter rising by 26% (104 days in Case H versus 131 days in Case L) (Figure 5A). The variations of normalized residual solute mass in the marsh soil (M_f = M₀₀/M₀) in Cases 1 and 2 exhibit the same trend, namely that M_f remains at one before solute discharge, followed by a rapid decrease as the solute plume exits the marsh soils (Figure 5B). In accordance with the results in Figure 2, M_f in Case H falls below one and to zero much earlier than in Case L, revealing the impediment of soil stratigraphy on solute discharge again. Also, corresponding to the early discharge episode shown in Figure 3A, M_f in Case H decreases slightly and maintains at the level for a certain period before rapidly falling.

FIGURE 5

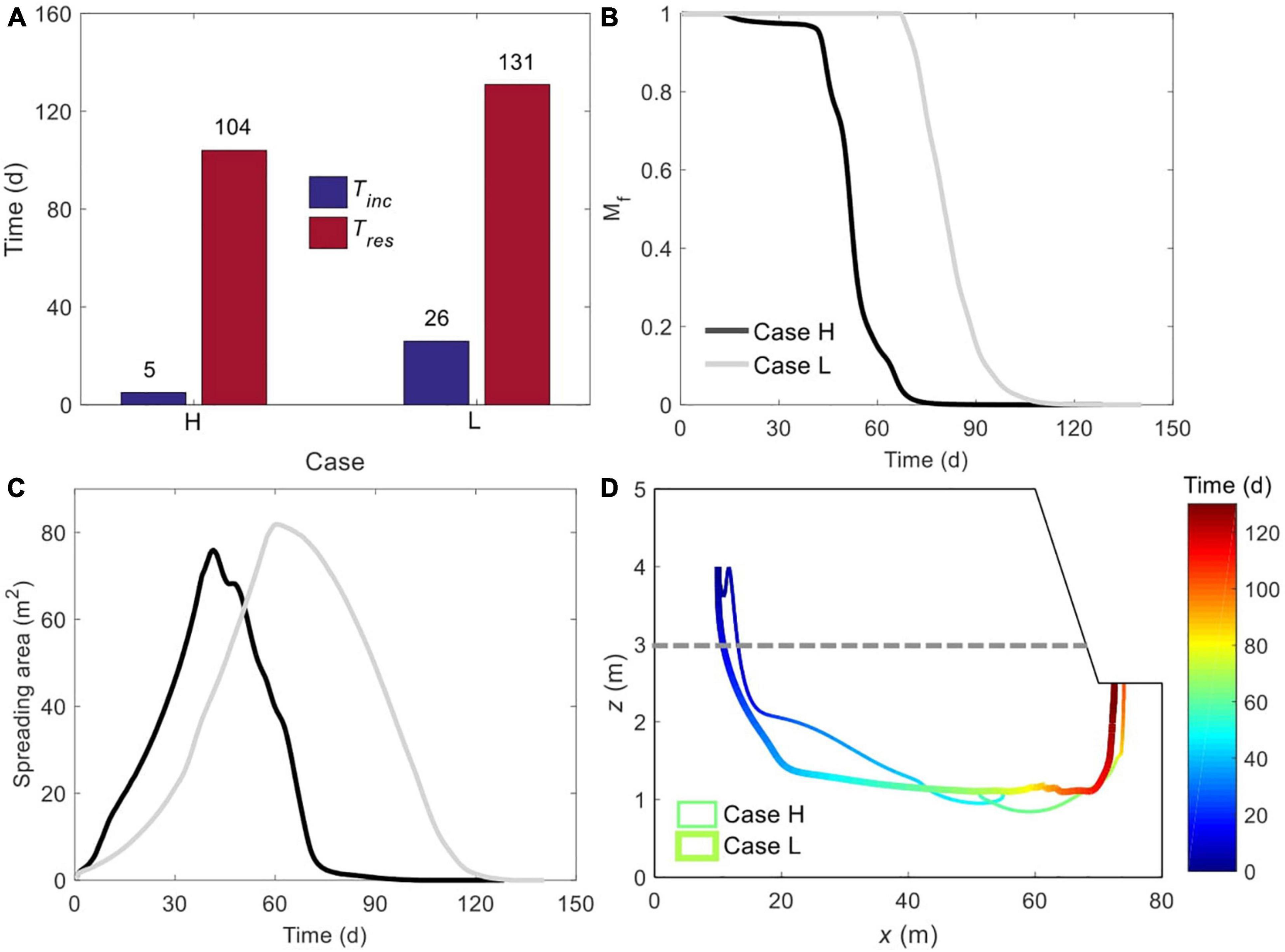
Figure 5. Comparison of (A) initiation time of unstable flow and residence time of solute plume, (B) time-dependent, normalized amount of solute mass remaining in marsh soil, (C) plume spreading area, and (D) spatiotemporal variation of plume centroid between Cases H and L. The plume edge was determined based on the concentration of 0.0001C₀. The gray dashed line in panel (D) represents the boundary between mud layer (upper) and sand layer (deeper).

The solute plume in layered marsh sediments not only stays for a longer time but also spreads to a broader scale (Figure 5C). The maximum A_pre is 75.6 m² in Case H and 81.87 m² in Case L, differing by 8.3%. Also note that the A_pre in Case H has dropped to zero while that in Case L has not even reached the maxima, and this is consistent with the T_res.

The movements of solute plume centroids in Cases 1 and 2 are shown in Figure 5D. After the initial release, the centroid in Case H fluctuates up and down instead of keeping moving downward as that in Case L. The fluctuations may be because that the solute plume is pushed up associated with the upward pore water flow resulting from the downward penetration of salt fingers. It is also noteworthy that, as the centroid sinks to a certain depth in Case L, its further downward movement is relatively limited (i.e., the trajectory between x = 20 ∼ 68 m) before rising to exit from the creek bottom. In comparison, the centroid in Case H moves to a greater depth. Such a difference is attributed to the different unstable flow patterns in the two cases. As Figure 2 shows, salt fingers are confined to the sand layer in Case L. Consequently, the vertical stretch of the solute plume is limited to the sand layer only, leaving little space for the centroid to further move down. While in Case H, without the mud layer, salt fingers can stretch the solute plume to a greater extent.

The extents to which the solute plume spreads along the horizontal (x) and vertical (z) directions are indicated by the variances shown in Figures 6A,B, respectively. The variations of plume spreading in Cases 1 and 2 exhibit similarly a rising phase followed by a decreasing phase. Notably, limited by the mud layer, the solute plume in Case L is stretched to a lower degree than that in Case H, along both x- and z-direction. For example, the maximum horizontal variance in Case H is 272.95 m², more than doubled of the 119.44 m² in Case L (Figure 6A). Moreover, the oscillations of variances along x- and z-direction in both cases reflect how the dynamic salt fingers associated with the unstable flow may split the solute plume into parts.

FIGURE 6

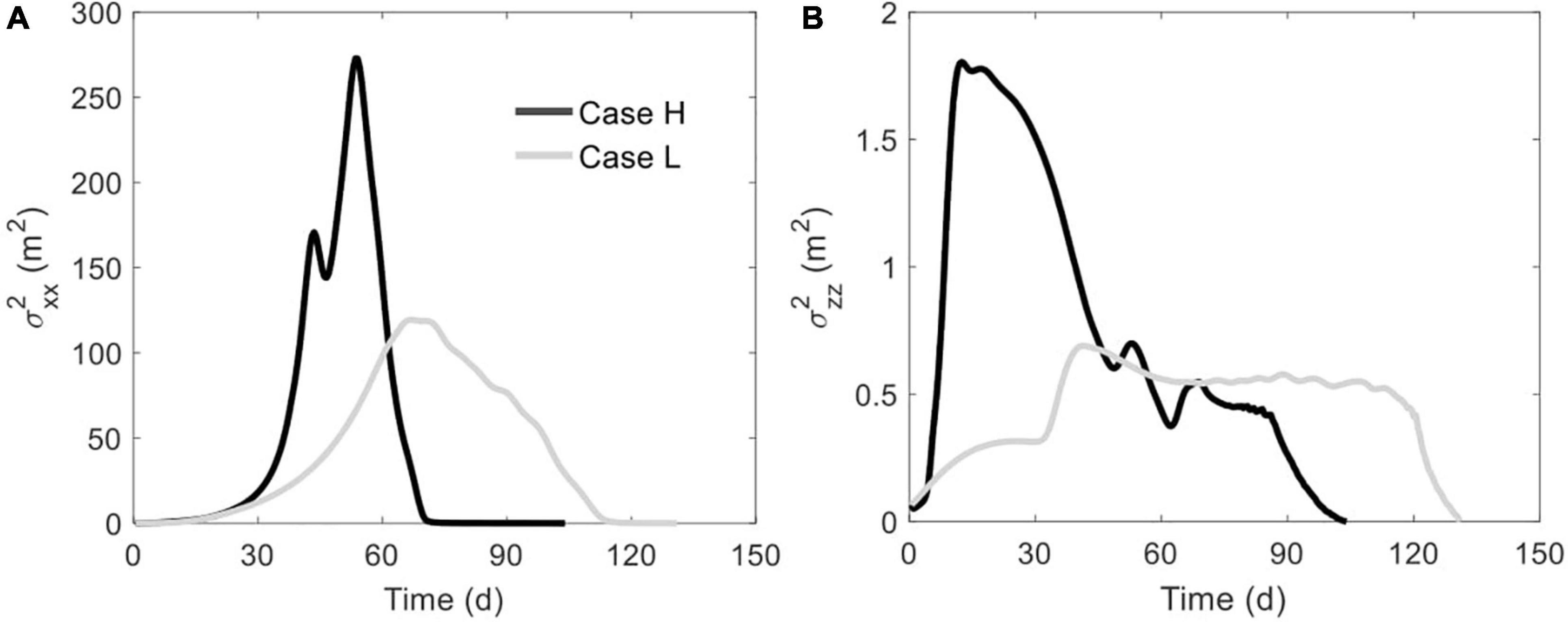
Figure 6. Comparison of (A) horizontal variance and (B) vertical variance between Cases H and L. The plume edge was determined based on the concentration of 0.0001C₀.

Sensitivity Analysis

This section further examines how the variations of K_mud/K_sand, C_sea/C_pore, and D_mud would impact the unstable flow and solute transport pattern in a stratified salt marsh. Note that, to facilitate the comparison, the above-mentioned Case L is renamed as Case L-K2, Case L-C35, and Case L-D2 in the sensitivity analysis of K_mud/K_sand, C_sea/C_pore, and D_mud, respectively.

Sensitivity to K_mud/K_sand

The comparison in Supplementary Figure 1 shows the delayed formation of unstable flow as K_mud/K_sand decreases. For example, salt fingers are visible on Day 40 in Case L-K1 (K_mud/K_sand = 0.1) and on Day 80 in Case L-K3 (K_mud/K_sand = 0.001). Also, the lower the contrast is, the smaller and denser the salt fingers are, owing to the increased impediment on advection by the reduced hydraulic conductivity of the mud layer. In addition, it is apparent from Supplementary Figure 1 that a smaller K_mud/K_sand leads to a longer residence time of solute plume in the marsh soil, because of more local water circulations resulting from the smaller salt fingers.

A different K_mud/K_sand value leads to largely different time-varying total solute efflux and spatial distribution of net solute efflux (Figure 7). When the contrast reduces (Cases L-K1 → L-K2 → L-K3), the solute plume discharges into tidal water later and over a more extended period, hence with lower peak values (Figure 7A). For example, the discharge starts on Day 44 in Case L-K1 and on Day 176 in Case L-K3, with the start time increase by 300%. Meanwhile, the discharge in Case L-K1 lasts for 32 days, but continues for 201 days in Case L-K3, an increase of 528%. Besides, the reduced K_mud/K_sand complicates the pattern of temporal solute efflux, e.g., unimodal in Case L-K1, bimodal in Case L-K2, and multimodal in Case L-K3. Such a trend may be explained by the fact that the solute plume is split into multiple parts in the situation of a smaller K_mud/K_sand.

FIGURE 7

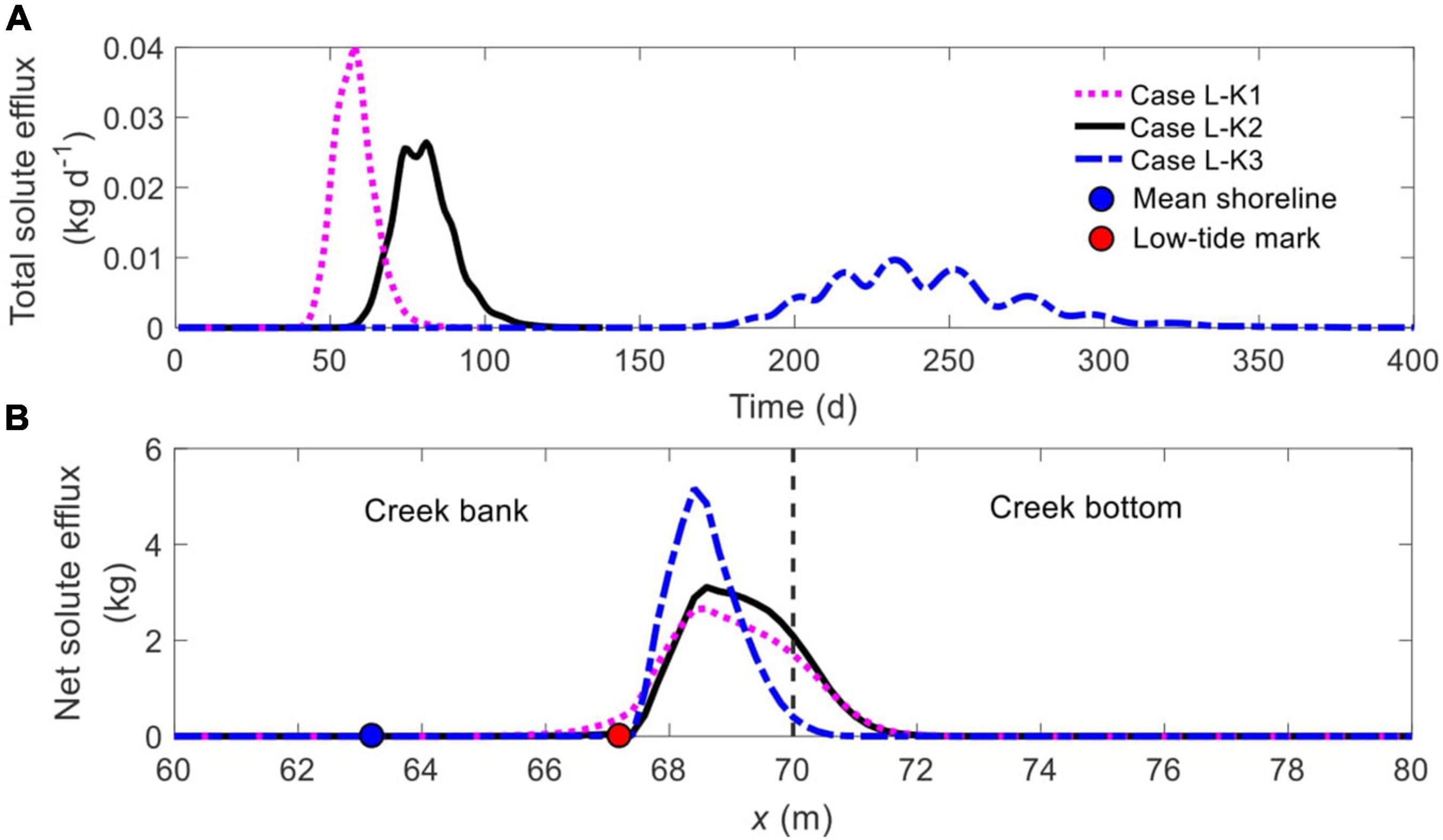
Figure 7. Comparison of (A) time-dependent total solute efflux and (B) spatial distribution of net solute efflux across the SWI (BCDE in Figure 1) for different ratios of K_mud/K_sand. The blue and red nodes in panel (B) represent the mean shoreline and low-tide mark, respectively, while the vertical dashed line separates creek bank (left) and creek bottom (right).

The spatial distributions of solute efflux across the SWI are quite similar by all exhibiting a unimodal pattern, with a majority of the solute plume discharging from the creek bank below the low-tide mark (cyan node in Figure 7B). Despite the similarity, a reduction in K_mud/K_sand narrows down the discharge area along the SWI. For example, the width of solute discharge zone is 4.6 m (between x = 67.2 ∼ 71.8 m) in Case L-K2 (black line, Figure 7B) but shrinks to 3.0 m (from x = 67.6 ∼ 70.6 m) in Case L-K3 (blue dash-dotted line, Figure 7B), a reduction of 34.8%.

Both T_ini and T_res are highly sensitive to the change of K_mud/K_sand (Figure 8A). As the contrast decreases from 0.1 (Case L-K1) to 0.01 (Case L-K2), T_ini rises from 16 to 26 days (an increase of 62.5%) while T_res increases by 33.7% from 98 to 131 days. With a further reduction in K_mud/K_sand (to 0.001, Case L-K3), it takes 63 days for unstable flow to form and 393 days for the solute plume to completely exit the marsh soil, more than doubled and almost tripled in comparison to that in Case L-K2, respectively. The comparison of M_f variations between Cases L-K1, L-K2, and L-K3, as shown in Figure 8B, demonstrates that a reduced K_mud/K_sand does decelerate the decrease of M_f, particularly when the contrast falls from 0.01 (Case L-K2, black line, Figure 8B) to 0.001 (Case L-K3, blue dash-dotted line, Figure 8B).

FIGURE 8

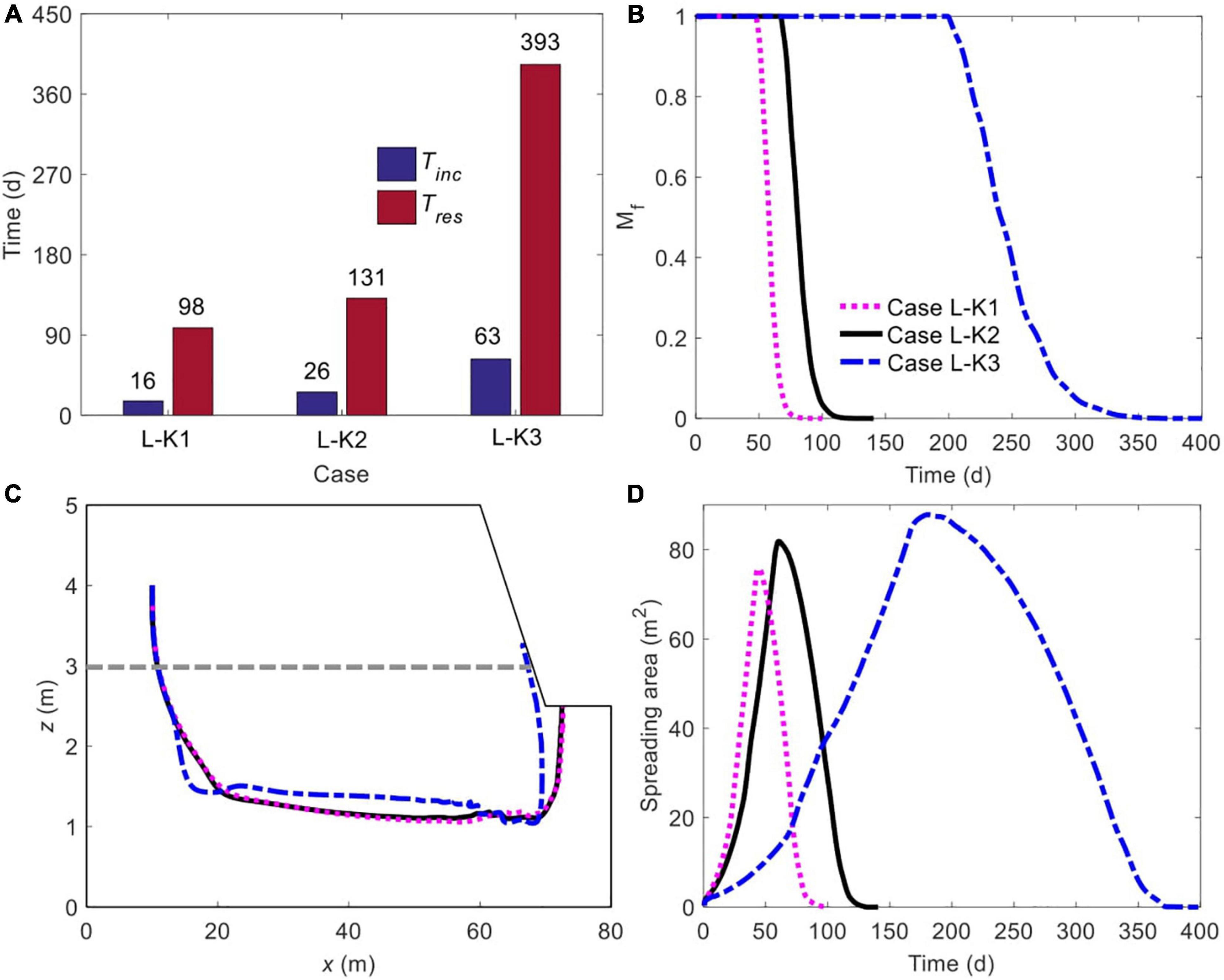
Figure 8. Comparison of (A) initiation time of unstable flow and residence time of solute plume, (B) time-dependent, normalized amount of solute mass remaining in marsh soil, (C) spatiotemporal variation of plume centroid, and (D) plume spreading area for different ratios of K_mud/K_sand. The plume edge was determined based on the concentration of 0.0001C₀. The gray dashed line in panel (C) represents the boundary between mud layer (upper) and sand layer (deeper).

The movement of solute plume centroid is quite insensitive to K_mud/K_sand as the value decreases from 0.1 (Case L-K1) to 0.01 (Case L-K2), indicated by the rather overlapped trajectories (black solid and purple dashed lines, Figure 8C). With a further reduced K_mud/K_sand (to 0.001, Case L-K3), the traveling path is notably different (blue dash-dotted line, Figure 8C). Note that the centroid in Case L-K3 travels to a depth shallower than that in Cases L-K1 and L-K2. As mentioned above, the lower hydraulic conductivity of the mud layer enhances the strength of unstable flow in the sand layer by weakening tide-induced advection to a greater extent. Therefore, the most intense flow instability in Case L-K3 plays a more significant role in trapping the solute plume in marsh sediments and allowing it to be fully stretched vertically, particularly along the upward direction. In addition, it is noteworthy that the centroids in Cases L-K1 and L-K2 exit the marsh soil from the creek bottom while that in Case L-K3 leaves via the lower part of the creek bank.

The patterns of A_spr in Cases L-K1, L-K2, and L-K3 demonstrate the same trend: a rapid increase before falling to zero (Figure 8D). The comparison further shows that as K_mud/K_sand reduces, the solute plume tends to spread more widely over a longer period, due to the more intense unstable flow. The maximum spreading area in Case L-K1 is 75.73 m², and increases to 81.87 and 87.84 m² in Cases L-K2 and L-K3, rising by 8.1 and 15.9%, respectively.

Sensitivity to C_sea/C_pore

The solute transport trajectories for Cases L-C30 (C_sea = 30 ppt), L-C25 (C_sea = 25 ppt), L-C20 (C_sea = 20 ppt), and L-C15 (C_sea = 15 ppt, without unstable flow) are shown in Supplementary Figure 2. As the surface water salinity decreases, it takes a longer time for the unstable flow to form in the marsh soil. For example, by Day 40, salt fingers have evolved from the inland boundary (x = 0 m) to beyond x = 20 m in Case L-C30 and to approximately x = 5 m in Case L-C25, but are hardly visible in Case L-C20 (Supplementary Figure 2). Moreover, despite the formation of unstable flow in Case L-C20, the solute plume is barely affected by it, due to the rather late initiation. Unlike the solute plume that is considerably stretched in Cases L-C30 and L-C25, the solute plume in Case L-C20 is quite regularly shaped, similar to that in Case L-C15, which does not involve unstable flow. However, the combined effects of tides and density-dependent flow still remove solute from the marsh soil faster in Case L-C20 than in Case L-C15, as reflected by the results of Day 120 in Supplementary Figure 2.

The comparison of time-dependent total solute efflux between all the cases, as shown in Figure 9A, indicates that the change of C_sea/C_pore does not significantly modify the start time and duration of solute discharge. Nonetheless, as C_sea/C_pore decreases, the pattern of temporal solute discharge shifts from a bimodal mode (Cases L-C35, L-C30 and L-C25) to a unimodal mode (Cases L-C20 and L-C15). Also, without salinity contrast, the solute discharges over a longer period (Case L-C15).

FIGURE 9

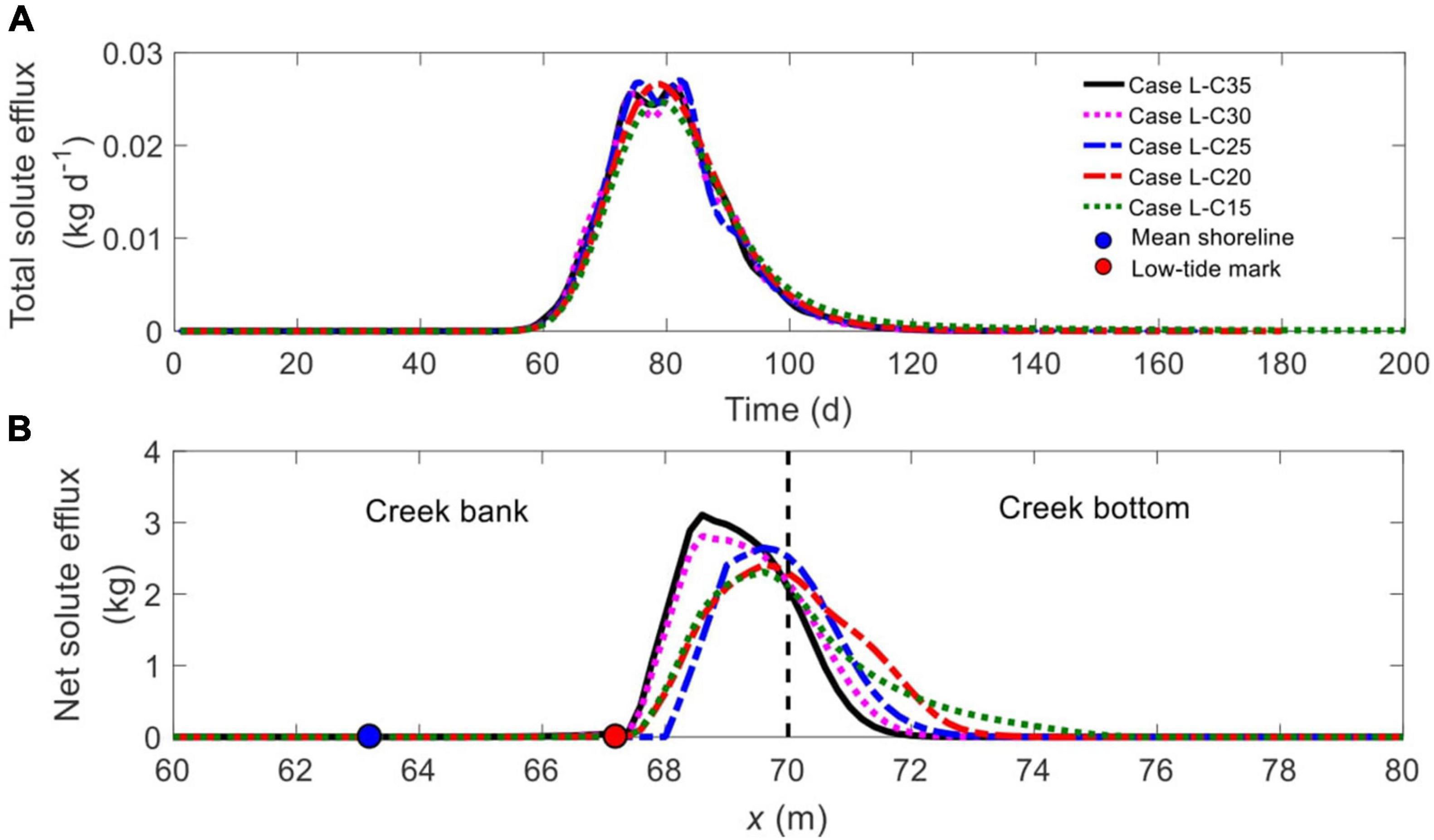
Figure 9. Comparison of (A) time-dependent total solute efflux and (B) spatial distribution of net solute efflux across the SWI (BCDE in Figure 1) for different ratios of C_sea/C_pore. The blue and red nodes in panel (B) represent the mean shoreline and low-tide mark, respectively, while the vertical dashed line separates creek bank (left) and creek bottom (right).

By comparing the spatial distribution of net solute efflux along the SWI (Figure 9B), it is found that a reduction in C_sea/C_pore tends to widen the discharge zone, as manifested in the further landward extension of the right end of the discharge zone. For example, solute discharges between x = 67.2 m and x = 71.8 m in Case L-C35, between x = 68.0 m and x = 71.0 m in Case L-C25, and between x = 67.2 m and x = 75.6 m in Case L-C15. Moreover, the reduced C_sea/C_pore increases the amount of solute discharge from the creek bottom relative to that from the creek bank, with the ratio being 0.17, 0.26, 0.45, 0.68, and 0.72 in Cases L-C35, L-C30, L-C25, L-C20, and L-C15, respectively.

Both T_ini and T_res increase monotonically with the reduction of C_sea/C_pore, but they are less sensitive to C_sea/C_pore than to K_mud/K_sand, as witnessed by the rather close values in all the cases (Figure 10A). As the salinity contrast vanishes (C_sea/C_pore = 1, Case L-C15), T_res becomes the longest, rising from 174 days (in Case L-C20) to 192 days, an increase of 10.3% (Figure 10A). Again, the prolonged T_res in Case L-C15 is attributed to the more stagnant groundwater flow underneath the tidal creek in the absence of density effect.

FIGURE 10

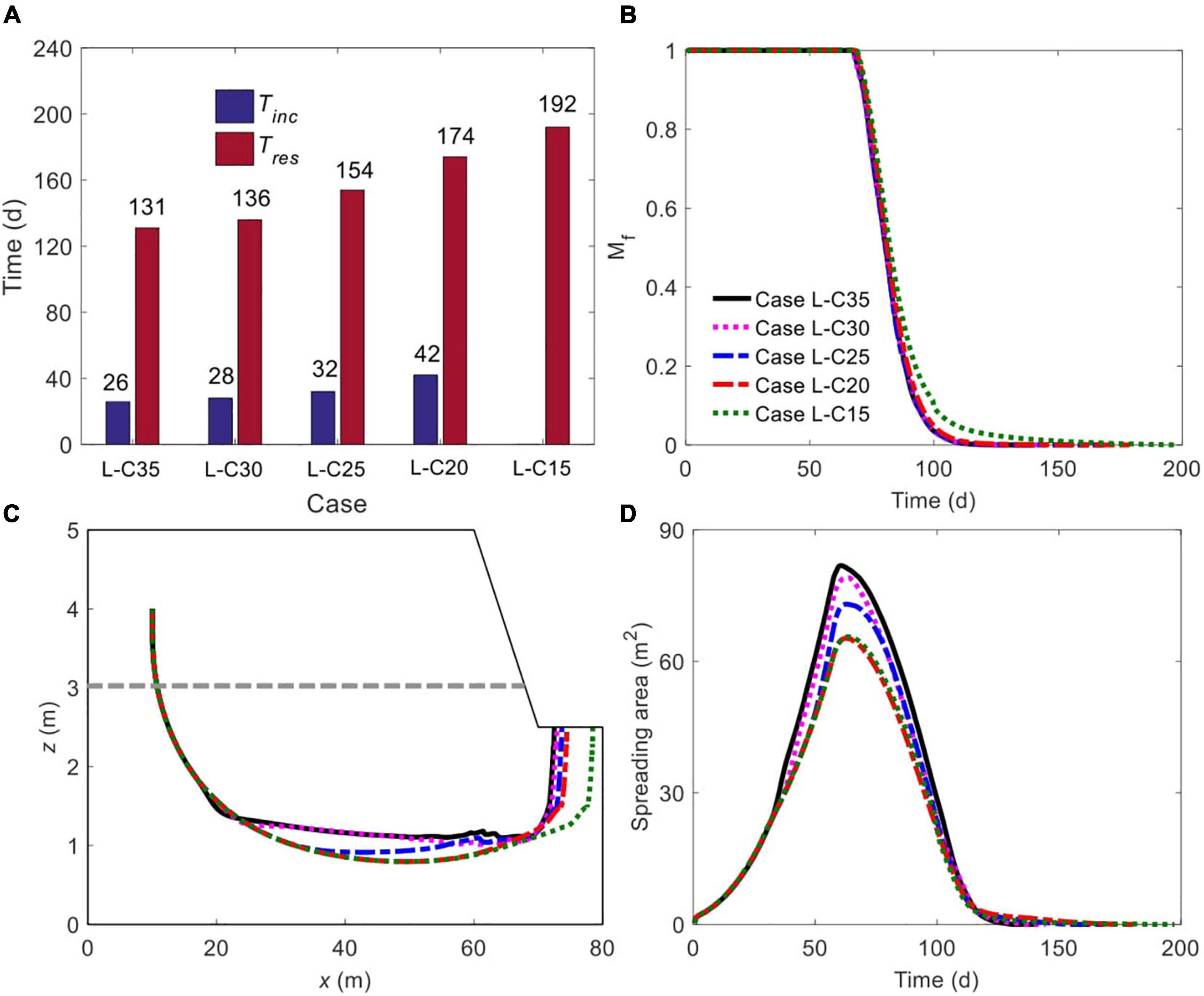
Figure 10. Comparison of (A) initiation time of unstable flow and residence time of solute plume, (B) time-dependent, normalized amount of solute mass remaining in marsh soil, (C) spatiotemporal variation of plume centroid, and (D) plume spreading area for different ratios of C_sea/C_pore. The plume edge was determined based on the concentration of 0.0001C₀. The gray dashed line in panel (C) represents the boundary between mud layer (upper) and sand layer (deeper).

As long as unstable flow occurs, the decline of C_sea/C_pore monotonically slows down the decreasing rate of M_f, but the effect is quite slight (Figure 10B). Notably, for Case L-C15 without flow instability, the decline of M_f (green dotted line, Figure 10B) is almost identical to that in Case L-C20 (red dash-dotted line, Figure 10B) at the early stage (e.g., by Day 90), and becomes slower afterward (i.e., after Day 90), when the solute plume has approached and discharged from the creek bottom, where the groundwater is more stagnant.

The variation of C_sea/C_pore also modifies the trajectory of plume centroid movement. As Figure 10C shows, at the initial stage, when unstable flow has not yet exerted influence, the centroids in all cases travel along the same path. Subsequently, the centroid affected by a smaller C_sea/C_pore moves deeper into the marsh soil (e.g., Case L-C35 versus Case L-C25) before gradually traveling upward to exit from the creek bottom. Also, the exit location of the centroid is further landward as C_sea/C_pore reduces. Moreover, as discussed above, the solute plume in Case L-C20 is not affected by unstable flow until it approaches the tidal creek. Therefore, before the involvement of the flow instability effect, the centroid in Case L-C20 travels along a path almost the same as that in Case L-C15, which does not involve unstable flow.

Associated with the reduction of C_sea/C_pore, the maximum A_spr decreases monotonically as a result of weaker flow instability (Figure 10D). Moreover, when C_sea/C_pore is greater than one but small enough (Case L-C20), even though unstable flow occurs, the maximum A_spr is almost identical to that in Case L-C15 without flow instability formation.

Sensitivity to D_mud

The time-varying groundwater flow field, salinity distributions and solute transport with 1-m (Case L-D1) and 3-m (Case L-D3) thick mud layer are shown in Supplementary Figure 3. As expected, a thinner (Case L-D1) and a thicker (Case L-D3) upper mud layer (relative to the 2-m thickness in Case L-D2) brings forward and delays the formation of unstable flow, respectively. Meanwhile, the solute plume in Case 9 tends to discharge primarily from the creek bank while that in Case L-D3 exits the marsh soil via both the creek bank and creek bottom.

The comparison of time-dependent total solute efflux between Cases L-D1, L-D2, and L-D3 (Figure 11A) indicates that a thicker mud layer tends to delay the commencement and increase the duration of solute discharge and hence reduce the peak value, particularly when D_mud increases from 2 m (Case L-D2, black line) to 3 m (Case L-D3, blue dash-dotted line). Also, the location of solute discharge zone is rather sensitive to D_mud (Figure 12B). In Case L-D1 (1-m thickness), the majority of the solute enters creek water from the creek bank, with quite a part discharging via the intertidal zone (between the black and cyan nodes). When D_mud increases to 2 m (Case L-D2), the discharge zone shifts seaward to be entirely in the subtidal area, while a large proportion of solute still exits via the creek bank. A further increase of D_mud (to 3 m, Case L-D3) leads to more even solute discharge across the entire subtidal zone (blue dash-dotted line, Figure 11B).

FIGURE 11

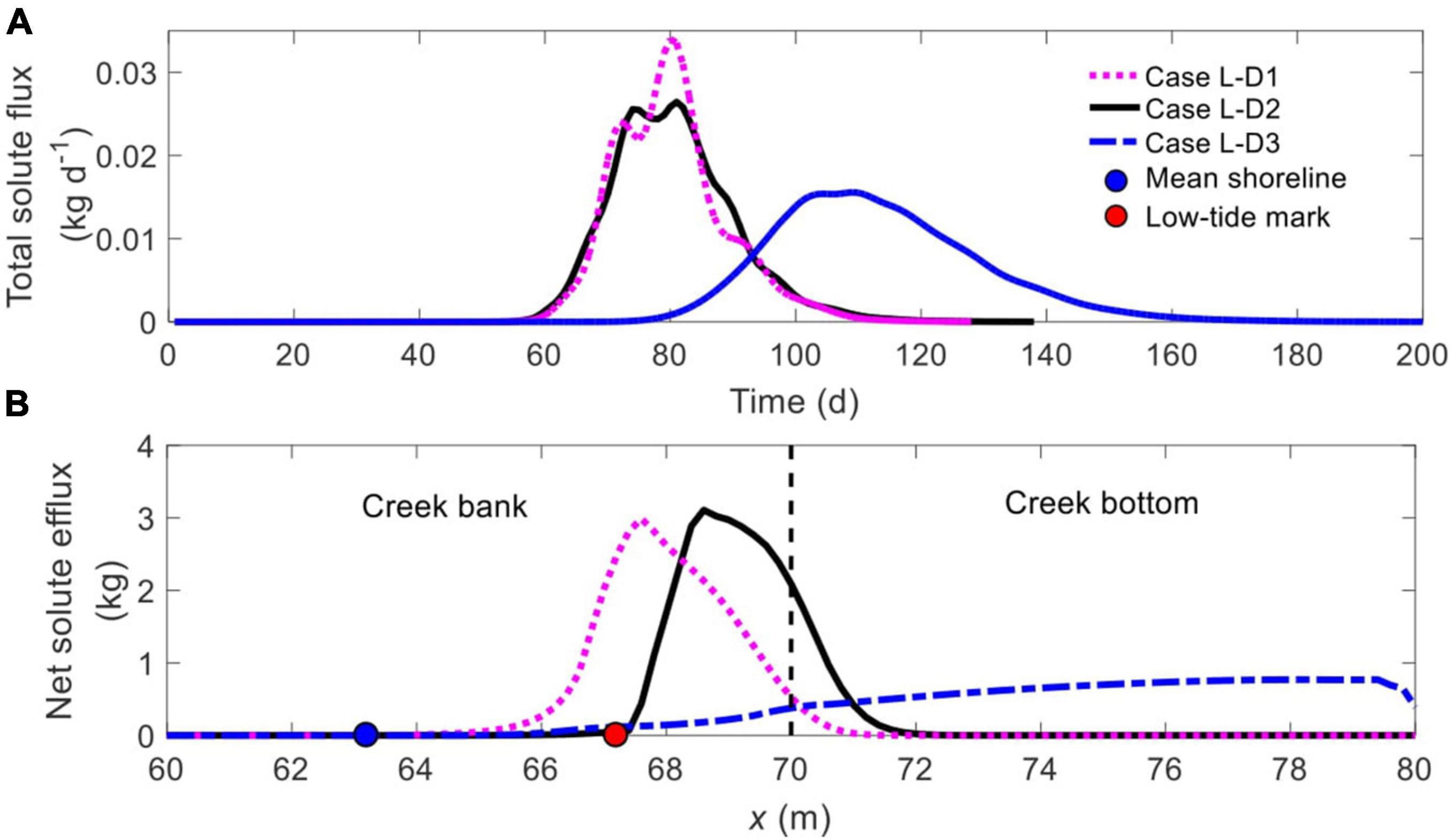
Figure 11. Comparison of (A) time-dependent total solute efflux and (B) spatial distribution of net solute efflux across the SWI (BCDE in Figure 1) for different D_mud. The blue and red nodes in panel (B) represent the mean shoreline and low-tide mark, respectively, while the vertical dashed line separates creek bank (left) and creek bottom (right).

FIGURE 12

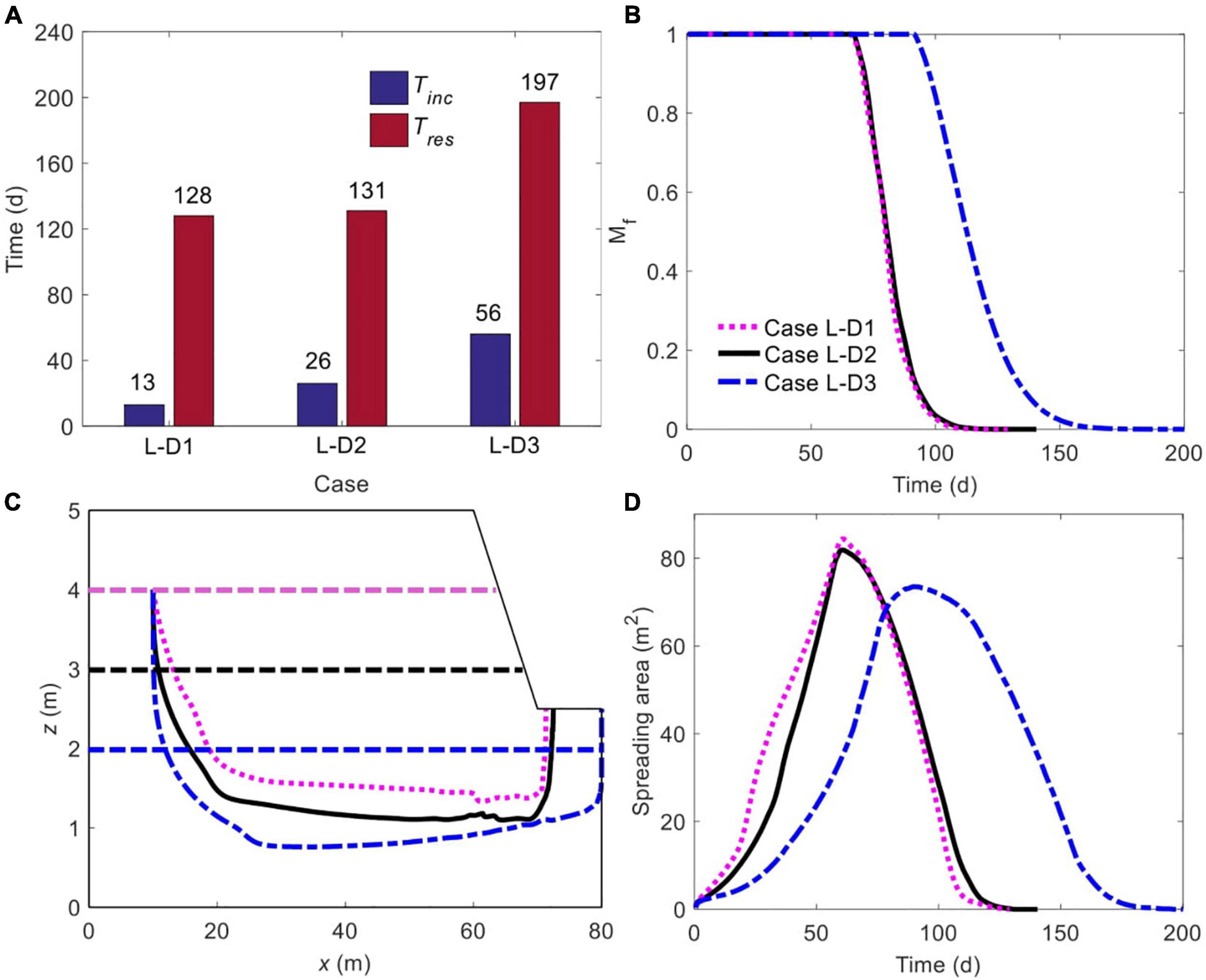
Figure 12. Comparison of (A) initiation time of unstable flow and residence time of solute plume, (B) time-dependent, normalized amount of solute mass remaining in marsh soil, (C) spatiotemporal variation of plume centroid, and (D) plume spreading area for different D_mud. The plume edge was determined based on the concentration of 0.0001C₀. The horizontal purple, black and blue dashed lines in panel (C) represent the boundary between mud layer (upper) and sand layer (deeper) in Cases L-D1, L-D2, and L-D3, respectively.

T_ini and T_res are sensitive to D_mud, particularly for T_ini (Figure 12A). Interestingly, although a 2-m thick mud layer (Case L-D2) extends T_ini by 13 days in comparison to the 1-m thickness (Case L-D1), the residence time is almost unchanged, increasing by merely 3 days (Figure 12A). With a further increase of D_mud (to 3 m, Case L-D3), values of both T_ini and T_res become much larger. It is clear from Figure 12B that a greater value of D_mud mere slightly slow down the decrease of M_f when increasing from 1 m (Case L-D1) to 2 m (Case L-D2), but the effect becomes much more significant as D_mud increases from 2 m (Case L-D2) to 3 m (Case L-D3). Also, for a larger D_mud, the plume centroid moves down to a greater depth and the exit point of the centroid is closer to the right vertical boundary (Figure 12C). Figure 12D demonstrates an almost monotonically decreasing trend of maximum A_spr as the mud layer becomes thicker. This may be due to that the increase of D_mud compresses the area of the sand layer, in which the solute plume can spread.

Discussion

Sediment stratification, as a common feature of salt marshes, exerts great influences on soil conditions, subsurface flow (constant- or variable-density), water exchange across the SWI, and seepage flux (Gardner, 2007; Wilson and Morris, 2012; Xin et al., 2012; Xiao et al., 2019a). However, little research has considered the impact of soil stratigraphy on the density-dependent groundwater flow and solute transport in periodically flooded salt marches. As evident from the simulation results presented (e.g., Figures 2–5), a two-layered soil structure can lead to a more complex behavior of pore water flow and solute transport.

Previous research of Shen et al. (2015) based on the homogeneous condition revealed a more dominant role of unstable flow in the marsh interior (adjacent to the inland boundary) than near the tidal creek, where tide-induced advection is stronger. Shen et al. (2016) found that solute released in the marsh interior may, under the effect of unstable flow, move upward and eventually discharge from the marsh platform (BC in Figure 1) with a concentration up to two orders of magnitude higher than exit solute concentrations via the tidal creek (CDE in Figure 1). Subsequently, they divided a salt marsh spatially into fingering flow-dominated and circulation-dominated zones, with the former occupying a relatively large area in a poorly channelized marsh. However, this paradigm would be greatly different in stratified salt marshes, since the less permeable mud layer acts as a barrier to constrain the movement of solute plume in the bottom sand layer, thereby disabling solute discharge from the marsh platform (e.g., Figure 2).

The findings of current study have certain ecological implications. Drainage from marsh sediments into tidal creeks has long been regarded as a contributor to the degradation of estuarine water quality (Grant et al., 2001; Koch and Gobler, 2009), yet there lacks a thorough understanding of the various geochemical processes in salt marshes. Xiao et al. (2019a), for the first time, quantified the distribution of nitrification and denitrification rates in marsh systems. They discovered that, in comparison to a constant salinity condition, tidally varying salinity would modify the rates and locations of nitrification and denitrification, thereby removing more nitrogen and lowering nitrogen loads into creek water. However, without tidal flooding, these reactive processes are restricted to the near-creek zone. For macro-tidal marshes, the inundation of the marsh platform leads to a much larger scale of geochemical reactions. As revealed in this study, solute affected by unstable flow in stratified, tide-submerged salt marshes resides for a longer period and spreads to a wider range (e.g., results in Figures 10, 12B). This is likely to prolong the duration and enlarge the spatial scale of geochemical reactions if the solutes are reactive (i.e., nutrients), ultimately modifying the cycling pattern. The longer residence time and broader spreading of solute may imply more significant modifications to the geochemical conditions in marsh sediments. In particular, the lower sand layer is constantly saturated, favoring anaerobic reactions, e.g., denitrification. Nonetheless, in this study, we considered a constant tidal water salinity, given the significance of tidally varying salinity unveiled by Xiao et al. (2019a), the salinity oscillations may further alter the geochemical conditions in layered salt marshes frequently flooded by tides.

Analysis based on the three controlling variables shows a high-degree sensitivity of solute discharge zone (along the SWI) to D_mud and less sensitivity to K_mud/K_sand and C_sea/C_pore, while the discharge duration is more sensitive to K_mud/K_sand and D_mud than to C_sea/C_pore. These different patterns of spatial and temporal solute efflux across the tidal creek indicate that field investigations of salt marshes need to carefully evaluate these variables to more accurately measure the exchange fluxes by properly deploying instruments and setting the monitoring duration. Attention should be paid to the soil structure (e.g., the thickness of the upper mud layer) and hydraulic parameters (e.g., hydraulic conductivity) of different sediment compositions.

Despite the findings, there are limitations of current study due to the neglect of several factors, such as spring-neap tidal cycle (Jeng et al., 2005; Xin et al., 2010a), evaporation, precipitation, freshwater input from the inland boundary (Michael et al., 2005; Kuan et al., 2019), topography, and macro pores (e.g., crab burrows) (Xin et al., 2009; Xu et al., 2021). All these factors may, in combination with soil stratification, increase the complexity of variable-density flow and solute transport and so further modify the geochemical conditions in salt marshes. For example, salt affected by evaporation can accumulate on the marsh surface in concentrations of over 200 ppt (Shen et al., 2018), and its dissolution during tidal inundation will increase surface water salinity to favor the formation of unstable flow. While the existence of crab burrows may facilitate preferential flow even in a layered salt marsh without salinity contrasts (Xin et al., 2009). Future studies should aim to investigate these additional factors to better understand the complex groundwater flow and solute transport processes in marsh ecosystems.

Previous studies linking soil stratigraphy to subsurface hydrology in salt marshes have mostly ignored the impact of the variable-density flow (Gardner, 2007; Wilson and Morris, 2012; Xin et al., 2012). In addition, other studies that detected the salinity contrasts between surface and subsurface water did not investigate how such contrasts would affect the groundwater flow and solute transport patterns in salt marshes (Cao et al., 2012). While more recent research focusing on the salinity contrasts-induced unstable flow either assumed a homogeneous marsh aquifer (Shen et al., 2015, 2016) or ignored tidal inundation (Xiao et al., 2019a). The present study extends to these early studies by systematically investigating the unstable flow and solute transport processes in a stratified salt marsh regularly inundated by tides. The results from this study further reveal the complex subsurface hydrology in tide-inundated salt marshes where the soil structure is two-layered and the salinity contrasts between surface and subsurface water are sufficiently high to induce flow instability. However, as discussed above, this study considered simplified conditions by neglecting other factors, such as spring-neap tides, macro pores, and inland freshwater input. Inclusion of these factors would further complicate the characteristics of unstable flow and solute transport in tide-submerged, stratified salt marshes.

Conclusion

Soil stratigraphy with a low-permeability mud layer overlying a high-permeability sand layer is a common soil structure of salt marshes. In this study, we numerically explored the impact of such soil stratigraphy on variable-density flow and solute transport in a 2D creek-normal transect with regular tidal inundations. The results show that, compared to the homogeneous condition, soil stratigraphy postpones the formation of unstable flow, leading to smaller and denser salt fingers. The less permeable mud layer confines the movement of the solute plume in the sand layer, and it takes a longer time for complete solute removal. Also, soil stratigraphy delays the start time and extends the duration of solute discharge into creek water, and narrows down the width of solute discharge zone along the SWI. In addition, solute plume spreads to a broader range in a layered marsh.

The sensitivity analysis based on the stratified case further demonstrates that, when unstable flow occurs, the initiation time of unstable flow and residence time of solute is quite insensitive to salinity contrast between surface and subsurface water. By contrast, the hydraulic conductivity contrast between mud and sand layers and the thickness of the mud layer exert greater influences on these two time scales. Moreover, the spatial location of the solute discharge zone along the SWI is sensitive to mud layer thickness and less affected by the variation of hydraulic conductivity contrast and salinity contrast. In contrast, the start time and duration of the solute discharge are more sensitive to hydraulic conductivity contrast and hydraulic conductivity contrast than to salinity contrast. These findings have implications for the geochemical conditions in marsh soils. For example, the longer residence time and larger spreading area indicate a vaster spatiotemporal scale of geochemical reactions if the solutes are reactive (i.e., nutrients), ultimately modifying the cycling pattern.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CS and ZZ: conceptualization, writing—review and editing, and supervision. XW: methodology. YW: software. XW and YW: formal analysis, investigation, writing—original draft preparation, and visualization. All authors contributed to the article and approved the submitted version.

Funding

This study was financially supported by National Natural Science Foundation of China (41807178), Fundamental Research Funds for the Central Universities (B200202065), Jiangsu Planned Projects for Postdoctoral Research Funds (2018K129C), and China Postdoctoral Science Foundation Funded Project (2018M642150 and 2019T120381).

Conflict of Interest

XW and YW were employed by Jiangsu Taihu Planning and Design Institute of Water Resources Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.804526/full#supplementary-material

References

Adam, P. (1993). Saltmarsh Ecology. Cambridge: Cambridge University Press.

Google Scholar

Artigas, F. J., Grzyb, J., and Yao, Y. (2021). Sea level rise and marsh surface elevation change in the Meadowlands of New Jersey. Wetl. Ecol. Manag. 29, 181–192. doi: 10.1007/s11273-020-09777-2

CrossRef Full Text | Google Scholar

Burdick, D. M., Buchsbaum, R., and Holt, E. (2001). Variation in soil salinity associated with expansion of Phragmites australis in salt marshes. Environ. Exp. Bot. 46, 247–261. doi: 10.1016/S0098-8472(01)00099-5

CrossRef Full Text | Google Scholar

Campbell, A. D., and Wang, Y. (2020). Salt marsh monitoring along the mid-Atlantic coast by google earth engine enabled time series. PLoS One 15:e0229605. doi: 10.1371/journal.pone.0229605

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, M., Xin, P., Jin, G., and Li, L. (2012). A field study on groundwater dynamics in a salt marsh – Chongming Dongtan wetland. Ecol. Eng. 40, 61–69. doi: 10.1016/j.ecoleng.2011.12.018

CrossRef Full Text | Google Scholar

Chapman, V. J. (1974). Salt Marshes and Salt Deserts of the World. Cramer. Available online at: https://books.google.com.au/books?id=dKUKAQAAIAAJ (accessed September 16, 2020).

Google Scholar

Dacey, J. W., and Howes, B. L. (1984). Water uptake by roots controls water table movement and sediment oxidation in short spartina marsh. Science 224, 487–489. doi: 10.1126/science.224.4648.487

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, Y., Sun, T., Zhu, M. S., Qi, M., Yang, W., and Shao, D. D. (2018). Salt marsh vegetation distribution patterns along groundwater table and salinity gradients in yellow river estuary under the influence of land reclamation. Ecol. Indic. 92, 82–90. doi: 10.1016/j.ecolind.2017.09.027

CrossRef Full Text | Google Scholar

Freyberg, D. L. (1986). A natural gradient experiment on solute transport in a sand aquifer: 2. Spatial moments and the advection and dispersion of nonreactive tracers. Water Resour. Res. 22, 2031–2046. doi: 10.1029/WR022i013p02031

CrossRef Full Text | Google Scholar

Gardner, L. R. (2005). Role of geomorphic and hydraulic parameters in governing pore water seepage from salt marsh sediments. Water Resour. Res. 41:W07010. doi: 10.1029/2004WR003671

CrossRef Full Text | Google Scholar

Gardner, L. R. (2007). Role of stratigraphy in governing pore water seepage from salt marsh sediments. Water Resour. Res. 43:W07502. doi: 10.1029/2006WR005338

CrossRef Full Text | Google Scholar

Grant, S. B., Sanders, B. F., Boehm, A. B., Redman, J. A., Kim, J. H., Mrše, R. D., et al. (2001). Generation of enterococci bacteria in a coastal saltwater marsh and its impact on surf zone water quality. Environ. Sci. Technol. 35, 2407–2416. doi: 10.1021/es0018163

PubMed Abstract | CrossRef Full Text | Google Scholar

Guimond, J., and Tamborski, J. (2021). Salt marsh hydrogeology: a review. Water 13:543. doi: 10.3390/w13040543

CrossRef Full Text | Google Scholar

Howes, B. L., Howarth, R. W., Teal, J. M., and Valiela, I. (1981). Oxidation-reduction potentials in a salt marsh: spatial patterns and interactions with primary production. Limnol. Oceanogr. 26, 350–360.

Google Scholar

Hughes, A. L. H., Wilson, A. M., and Morris, J. T. (2012). Hydrologic variability in a salt marsh: assessing the links between drought and acute marsh dieback. Estuar. Coast. Shelf Sci. 111, 95–106. doi: 10.1016/j.ecss.2012.06.016

CrossRef Full Text | Google Scholar

Hughes, J. D., and Sanford, W. E. (2004). SUTRA-MS, a Version of SUTRA Modified to Simulate Heat and Multiple-Solute Transport (Open-File Report 2004-1207, Issue. Available online at: https://water.usgs.gov/nrp/gwsoftware/SutraMS/OFR2004-1207.pdf (accessed December 21, 2020).

Google Scholar

Jeng, D. S., Mao, X., Enot, P., Barry, D. A., and Li, L. (2005). Spring-neap tide-induced beach water table fluctuations in a sloping coastal aquifer. Water Resour. Res. 41, 1–4. doi: 10.1029/2005WR003945

CrossRef Full Text | Google Scholar

Koch, F., and Gobler, C. J. (2009). The effects of tidal export from salt marsh ditches on estuarine water quality and plankton communities. Estuar. Coasts 32, 261–275. doi: 10.1007/s12237-008-9123-y

CrossRef Full Text | Google Scholar

Kuan, W. K., Xin, P., Jin, G., Robinson, C. E., Gibbes, B., and Li, L. (2019). Combined effect of tides and varying inland groundwater input on flow and salinity distribution in unconfined coastal aquifers. Water Resour. Res. 55, 8864–8880. doi: 10.1029/2018wr024492

CrossRef Full Text | Google Scholar

Kuhn, N. L., and Zedler, J. B. (1997). Differential effects of salinity and soil saturation on native and exotic plants of a coastal salt marsh. Estuaries 20, 391–403. doi: 10.2307/1352352

CrossRef Full Text | Google Scholar

Mahall, B. E., and Park, R. B. (1976). The ecotone between Spartina foliosa Trin and Salicornia virginica L in salt marshes of Northern San Francisco Bay: II. Soil water and salinity. J. Ecol. 64, 793–809. doi: 10.2307/2258809

CrossRef Full Text | Google Scholar

Marani, M., Silvestri, S., Belluco, E., Ursino, N., Comerlati, A., Tosatto, O., et al. (2006). Spatial organization and ecohydrological interactions in oxygen-limited vegetation ecosystems. Water Resour. Res. 42:W06D06. doi: 10.1029/2005WR004582

CrossRef Full Text | Google Scholar

Marois, D. E., and Stecher, H. A. (2020). A simple, dynamic, hydrological model for mesotidal salt marshes. Estuar. Coast. Shelf Sci. 233:106486. doi: 10.1016/j.ecss.2019.106486

PubMed Abstract | CrossRef Full Text | Google Scholar

McKinney, R., Hanson, A., Johnson, R., and Charpentier, M. (2019). Seasonal variation in apparent conductivity and soil salinity at two Narragansett Bay, RI salt marshes. PeerJ 7:e8074. doi: 10.7717/peerj.8074

PubMed Abstract | CrossRef Full Text | Google Scholar

Michael, H., Mulligan, A., and Harvey, C. (2005). Seasonal oscillations in water exchange between aquifers and the coastal ocean. Nature 436, 1145–1148. doi: 10.1038/nature03935

PubMed Abstract | CrossRef Full Text | Google Scholar

Nguyen, T. T. M., Yu, X., Pu, L., Xin, P., Zhang, C., Barry, D. A., et al. (2020). Effects of temperature on tidally influenced coastal unconfined aquifers. Water Resour. Res. 56:e2019WR026660. doi: 10.1029/2019wr026660

CrossRef Full Text | Google Scholar

Pennings, S. C., and Callaway, R. M. (1992). Salt marsh plant zonation: the relative importance of competition and physical factors. Ecology 73, 681–690. doi: 10.2307/1940774

CrossRef Full Text | Google Scholar

Peterson, R. N., Meile, C., Peterson, L. E., Carter, M., and Miklesh, D. (2019). Groundwater discharge dynamics into a salt marsh tidal river. Estuar. Coast. Shelf Sci. 218, 324–333. doi: 10.1016/j.ecss.2019.01.007

CrossRef Full Text | Google Scholar

Reeves, H. W., Thibodeau, P. M., Underwood, R. G., and Gardner, L. R. (2000). Incorporation of total stress changes into the ground water model SUTRA. Ground Water 38, 89–98. doi: 10.1111/j.1745-6584.2000.tb00205.x

CrossRef Full Text | Google Scholar

Robinson, C., Li, L., and Barry, D. A. (2007). Effect of tidal forcing on a subterranean estuary. Adv. Water Resour. 30, 851–865. doi: 10.1016/j.advwatres.2006.07.006

CrossRef Full Text | Google Scholar

Rogel, J. A., Ariza, F. A., and Silla, R. O. (2000). Soil salinity and moisture gradients and plant zonation in Mediterranean salt marshes of Southeast Spain. Wetlands 20, 357–372.

Google Scholar

Sawyer, A. H., Lazareva, O., Kroeger, K. D., Crespo, K., Chan, C. S., Stieglitz, T., et al. (2014). Stratigraphic controls on fluid and solute fluxes across the sediment—water interface of an estuary. Limnol. Oceanogr. 59, 997–1010. doi: 10.4319/lo.2014.59.3.0997

CrossRef Full Text | Google Scholar

Schiebel, H. N., Gardner, G. B., Wang, X., Peri, F., and Chen, R. F. (2018). Seasonal export of dissolved organic matter from a new England salt marsh. J. Coast. Res. 34, 939–954. doi: 10.2112/JCOASTRES-D-16-00196.1

CrossRef Full Text | Google Scholar

Shen, C., Jin, G., Xin, P., Kong, J., and Li, L. (2015). Effects of salinity variations on pore water flow in salt marshes. Water Resour. Res. 51, 4301–4319. doi: 10.1002/2015WR016911

CrossRef Full Text | Google Scholar

Shen, C., Zhang, C., Jin, G., Kong, J., and Li, L. (2016). Effects of unstable flow on solute transport in the marsh soil and exchange with coastal water. Geophys. Res. Lett. 43, 12,091–12,101. doi: 10.1002/2016GL070576

CrossRef Full Text | Google Scholar

Shen, C., Zhang, C., Xin, P., Kong, J., and Li, L. (2018). Salt dynamics in coastal marshes: formation of hypersaline zones. Water Resour. Res. 54, 3259–3276. doi: 10.1029/2017wr022021

CrossRef Full Text | Google Scholar

Silvestri, S., Defina, A., and Marani, M. (2005). Tidal regime, salinity and salt marsh plant zonation. Estuar. Coast. Shelf Sci. 62, 119–130. doi: 10.1016/j.ecss.2004.08.010

CrossRef Full Text | Google Scholar

Teal, J. M. (1962). Energy flow in the salt marsh ecosystem of Georgia. Ecology 43, 614–624. doi: 10.2307/1933451

CrossRef Full Text | Google Scholar

Thibodeau, P. M., Gardner, L. R., and Reeves, H. W. (1998). The role of groundwater flow in controlling the spatial distribution of soil salinity and rooted macrophytes in a southeastern salt marsh, USA. Mangroves Salt Marshes 2, 1–13. doi: 10.1023/A:1009910712539

CrossRef Full Text | Google Scholar

Ursino, N., Silvestri, S., and Marani, M. (2004). Subsurface flow and vegetation patterns in tidal environments. Water Resour. Res. 40:W05115. doi: 10.1029/2003WR002702

CrossRef Full Text | Google Scholar

Valiela, I., Cole, M. L., McClelland, J., Hauxwell, J., Cebrian, J., and Joye, S. B. (2000). “Role of salt marshes as part of coastal landscapes,” in Concepts and Controversies in Tidal Marsh Ecology, eds M. P. Weinstein and D. A. Kreeger (Dordrecht: Springer Netherlands), 23–36. doi: 10.1007/0-306-47534-0_3

CrossRef Full Text | Google Scholar

Van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898. doi: 10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Veldhuis, E. R., Schrama, M., Staal, M., and Elzenga, J. T. M. (2019). Plant stress-tolerance traits predict salt marsh vegetation patterning. Front. Mar. Sci. 5:501. doi: 10.3389/fmars.2018.00501

CrossRef Full Text | Google Scholar

Velinsky, D. J., Paudel, B., Belton, T. J., and Sommerfield, C. K. (2017). Tidal marsh record of nutrient loadings in Barnegat Bay, New Jersey. J. Coast. Res. 78, 79–88. doi: 10.2112/SI78-008.1

CrossRef Full Text | Google Scholar

Vernberg, F. J. (1993). Salt-marsh processes–a review. Environ. Toxicol. Chem. 12, 2167–2195. doi: 10.1002/etc.5620121203

CrossRef Full Text | Google Scholar

Whiting, G. J., McKellar, H. N. Jr., Kjerfve, B., and Spurrier, J. D. (1985). Sampling and computational design of nutrient flux from a southeastern U.S. saltmarsh. Estuar. Coast. Shelf Sci. 21, 273–286. doi: 10.1016/0272-7714(85)90102-7

CrossRef Full Text | Google Scholar

Wilson, A. M., Evans, T., Moore, W., Schutte, C. A., Joye, S. B., Hughes, A. H., et al. (2015). Groundwater controls ecological zonation of salt marsh macrophytes. Ecology 96, 840–849. doi: 10.1890/13-2183.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, A. M., and Gardner, L. R. (2006). Tidally driven groundwater flow and solute exchange in a marsh: numerical simulations. Water Resour. Res. 42:W01405. doi: 10.1029/2005WR004302

CrossRef Full Text | Google Scholar

Wilson, A. M., and Morris, J. T. (2012). The influence of tidal forcing on groundwater flow and nutrient exchange in a salt marsh-dominated estuary. Biogeochemistry 108, 27–38. doi: 10.1007/s10533-010-9570-y

CrossRef Full Text | Google Scholar

Xia, Y. Q., and Li, H. L. (2012). A combined field and modeling study of groundwater flow in a tidal marsh. Hydrol. Earth Syst. Sci. 16, 741–759. doi: 10.5194/hess-16-741-2012

CrossRef Full Text | Google Scholar

Xiao, K., Li, H., Wilson, A. M., Xia, Y., Wan, L., Zheng, C., et al. (2017). Tidal groundwater flow and its ecological effects in a brackish marsh at the mouth of a large sub-tropical river. J. Hydrol. 555, 198–212. doi: 10.1016/j.jhydrol.2017.10.025

CrossRef Full Text | Google Scholar

Xiao, K., Wilson, A. M., Li, H., and Ryan, C. (2019b). Crab burrows as preferential flow conduits for groundwater flow and transport in salt marshes: a modeling study. Adv. Water Resour. 132:103408. doi: 10.1016/j.advwatres.2019.103408

CrossRef Full Text | Google Scholar

Xiao, K., Li, H., Xia, Y., Yang, J., Wilson, A. M., Michael, H. A., et al. (2019a). Effects of tidally varying salinity on groundwater flow and solute transport: insights from modelling an idealized creek marsh aquifer. Water Resour. Res. 55, 9656–9672. doi: 10.1029/2018WR024671

CrossRef Full Text | Google Scholar

Xie, H., Yi, Y., Hou, C., and Yang, Z. (2020). In situ experiment on groundwater control of the ecological zonation of salt marsh macrophytes in an estuarine area. J. Hydrol. 585:124844. doi: 10.1016/j.jhydrol.2020.124844

CrossRef Full Text | Google Scholar

Xin, P., Gibbes, B., Li, L., Song, Z., and Lockington, D. (2010a). Soil saturation index of salt marshes subjected to spring-neap tides: a new variable for describing marsh soil aeration condition. Hydrol. Process. 24, 2564–2577. doi: 10.1002/hyp.7670

CrossRef Full Text | Google Scholar

Xin, P., Robinson, C., Li, L., Barry, D. A., and Bakhtyar, R. (2010b). Effects of wave forcing on a subterranean estuary. Water Resour. Res. 46:W12505. doi: 10.1029/2010WR009632

CrossRef Full Text | Google Scholar

Xin, P., Jin, G., Li, L., and Barry, D. A. (2009). Effects of crab burrows on pore water flows in salt marshes. Adv. Water Resour. 32, 439–449. doi: 10.1016/j.advwatres.2008.12.008

CrossRef Full Text | Google Scholar

Xin, P., Kong, J., Li, L., and Barry, D. A. (2012). Effects of soil stratigraphy on pore-water flow in a creek-marsh system. J. Hydrol. 475, 175–187. doi: 10.1016/j.jhydrol.2012.09.047

CrossRef Full Text | Google Scholar

Xin, P., Zhou, T., Lu, C., Shen, C., Zhang, C., D’Alpaos, A., et al. (2017). Combined effects of tides, evaporation and rainfall on the soil conditions in an intertidal creek-marsh system. Adv. Water Resour. 103, 1–15. doi: 10.1016/j.advwatres.2017.02.014

CrossRef Full Text | Google Scholar

Xu, X., Xin, P., Zhou, T., and Xiao, K. (2021). Effect of macropores on pore-water flow and soil conditions in salt marshes subject to evaporation and tides. Estuar. Coast. Shelf Sci. 261:107558. doi: 10.1016/j.ecss.2021.107558

CrossRef Full Text | Google Scholar