Rene-Marcel Plonus
Stefanie Vogl
Jens Floeter- 1Institute of Marine Ecosystem and Fishery Science, University of Hamburg, Hamburg, Germany
- 2Department of Informatics and Mathematics, Hochschule für Angewandte Wissenschaften München, Munich, Germany
It remains difficult to segregate pelagic habitats since structuring processes are dynamic on a wide range of scales and clear boundaries in the open ocean are non-existent. However, to improve our knowledge about existing ecological niches and the processes shaping the enormous diversity of marine plankton, we need a better understanding of the driving forces behind plankton patchiness. Here we describe a new machine-learning method to detect and quantify pelagic habitats based on hydrographic measurements. An Autoencoder learns two-dimensional, meaningful representations of higher-dimensional micro-habitats, which are characterized by a variety of biotic and abiotic measurements from a high-speed ROTV. Subsequently, we apply a density-based clustering algorithm to group similar micro-habitats into associated pelagic macro-habitats in the German Bight of the North Sea. Three distinct macro-habitats, a “surface mixed layer,” a “bottom layer,” and an exceptionally “productive layer” are consistently identified, each with its distinct plankton community. We provide evidence that the model detects relevant features like the doming of the thermocline within an Offshore Wind Farm or the presence of a tidal mixing front.
Introduction
Submesoscale features like eddies, fronts or filaments structure the pelagic realm at spatial scales of order (1–10 km) (Lévy et al., 2012; Shulman et al., 2015; Buckingham et al., 2016) and temporal scales that range from several hours to a few days (Baschek and Maarten Molemaker, 2010; Thompson et al., 2016). Associated processes determine nutrient fluxes (Omand et al., 2015; Thompson et al., 2016) as well as plankton patchiness (Levy and Martin, 2013; Shulman et al., 2015; Lévy et al., 2018) and thereby even shape the seascape for top predators like sea birds (Bertrand et al., 2014).
Recent advances in marine remote sensing technology (Wedding et al., 2011) enabled scientists to separate benthic structures into mosaic-like patterns of different habitat classes (Hinchey et al., 2008; Pittman et al., 2011) following the role model of terrestrial ecosystems. However, what is well known and trivial in landscape ecology can be quite challenging in seascape ecology. While it remains difficult to segregate pelagic habitats, which exhibit no clear boundaries (Hinchey et al., 2008; Pittman et al., 2011; Wedding et al., 2011) and can be quite dynamic on a wide range of scales, benthic habitat maps can give an impression of physically distinct areas that consistently occur together with particular species communities (Harris and Baker, 2012). Some effort has been undertaken to characterize fish habitats (e.g., Bellido et al., 2008; Giannoulaki et al., 2011; Tugores et al., 2011; Laman et al., 2017; Amorim et al., 2018; Friedland et al., 2020; Funk et al., 2020), but fewer studies focused on zooplankton (e.g., Labat et al., 2009; Alvarez-Berastegui et al., 2014; Espinasse et al., 2014). Thus, mechanisms contributing to the enormous diversity of plankton, a fundamental component of pelagic food webs, are still not fully understood (Sano et al., 2013; North et al., 2016). Understanding the processes shaping plankton communities is essential to improve our knowledge of existing ecological niches (Houliez et al., 2021). Despite the growing awareness of the importance of spatial structure for ecology and management (Pittman et al., 2011; Wedding et al., 2011), there is still a lack of concepts and techniques applicable to characterize the spatial structure of the seascape in pelagic environments (Alvarez-Berastegui et al., 2014). Mainly, because traditional oceanographic methods are inadequate for observing the submesoscale (Baschek and Maarten Molemaker, 2010) due to insufficient resolution and range (Marmorino et al., 2018). Recent advances in instrumentation partially closed this gap, but there still is a need for novel analysis methods to take advantage of the existing data (North et al., 2016). Some machine learning techniques are specifically designed to identify and characterize features in a “sea of data,” which makes it very promising to apply them also in this challenging field of research.
Autoencoders (AE) are a common tool in the machine learning community which consist of an encoding and a decoding part (Hinton, 2006). Initially devised to reduce (Encoder) and recover (Decoder) the dimensionality of their inputs (Hinton, 2006), they have been soon applied to a wide range of tasks like denoising (e.g., Vincent et al., 2010) or anomaly detection (e.g., Zhao et al., 2017; Chen et al., 2018).
Autoencoders do not classify or detect specific elements or objects in their inputs, but learn meaningful low dimensional representations, i.e., relevant high-level abstractions, of their inputs (Bengio et al., 2006) so that the original data can be reconstructed as similar as possible by the decoder part. The input data don’t need any pre-processing, e.g., labeling of subsets, by humans, since the target the network aims to reconstruct is basically the original input. The compressed representations of the encoder can also be used as input for subsequent modeling, e.g., in a Convolutional Neural Network (CNN) application. In that case the unsupervised pre-training of a CNN embedded in an AE can help to capture more intricate dependencies (Erhan et al., 2009) and better initialize the weights of the extended model (Bengio et al., 2006). Thus, the (local) minimum in the loss surface of the AE corresponds to a good transformation of a high dimensional input to a lower dimensional intermediate output (output of the Encoder-part) (Bengio et al., 2006), which would become the input for the classifier in a CNN. In this setting, the final output of the AE, the reconstructions, are secondary. However, a low reconstruction error of the AE ensures that the compressed signal incorporates the important features of the original high dimensional input data.
In this study we take advantage of this specific application of AEs. Instead of substituting the decoder part with a classification or regression network we use the compressed signal of the encoder as input for a subsequent clustering algorithm. We use a fully connected AE to reduce a high dimensional input consisting of a variety of abiotic and biotic oceanographic measurements to a lower dimensional meaningful representation (intermediate output), skip the decoding part after the training is completed and cluster the encoded features to macro-habitats. Similar micro-habitats lead to similar representations and therefore regions with different characteristics are segregated as different macro-habitats. These macro-habitats correspond to distinct pelagic habitats in the southern North Sea, whose plankton communities are compared and analyzed.
Materials and Procedures
Data Acquisition and Preparation
Physical and biological oceanographic measurements were recorded on a North Sea summer cruise with the RV Heincke (HE429, July 19–24, 2014) with a MacArtney TRIAXUS Remotely Operated Towed Vehicle (ROTV). For a detailed description of the device see Plonus et al. (2021). The ROTV transects were located in the direct vicinity of two Offshore Wind Farms (OWF) BARD Offshore 1 (BARD) and Global Tech I (GTI; Figure 1). The map was generated using QGIS v3.18 (QGIS, 2021) with bathymetric metadata and Digital Terrain Model data products from the EMODnet Bathymetry portal (15.7.21)1. The ROTV was towed at a speed of 8 knots (4.1 m s–1) with a three-degree lateral offset to lessen any disturbance from the vessels wake. During most transects the ROTV was undulating with a vertical speed of 0.1 m s–1 from ∼ 4 m below the sea surface to ∼ 8 m above the sea floor. The horizontal resolution between two surface peaks was ∼ 560 m, while the vertical resolution was ∼ 0.3 m. The ROTV measured water temperature, salinity, oxygen, and chlorophyll-a at a frequency of 1 Hz and was equipped with a Video Plankton Recorder (VPR, Seascan Inc., Falmouth, MA, United States) which provided zoo- and phytoplankton densities on the taxonomic family-, and sometimes even genus-level. For a detailed description of the VPR plankton image classification see Floeter et al. (2017). We used a similar summer cruise with the RV Heincke 5 years later (HE534, June 16–21, 2019) as a test data set. For our analyses we selected the following variables: temperature (°C), salinity (PSU), oxygen (μmol l–1), density (kg × m–1), and chlorophyll-a (RFU). For each of the variables, we calculated the horizontal (grid cell to the left, i.e., ∼ 25 m) and vertical (grid cell above, i.e., 1 m) gradient. Furthermore, we had sufficient density data (N l–1) available for the taxa “Appendicularia,” “Copepoda,” “Dinoflagellates,” “Gastropoda,” “Jelly,” “Marine snow,” “Nauplii,” “Ophiuroida,” “Pilidium,” “Pluteus,” and “Polychaeta.”
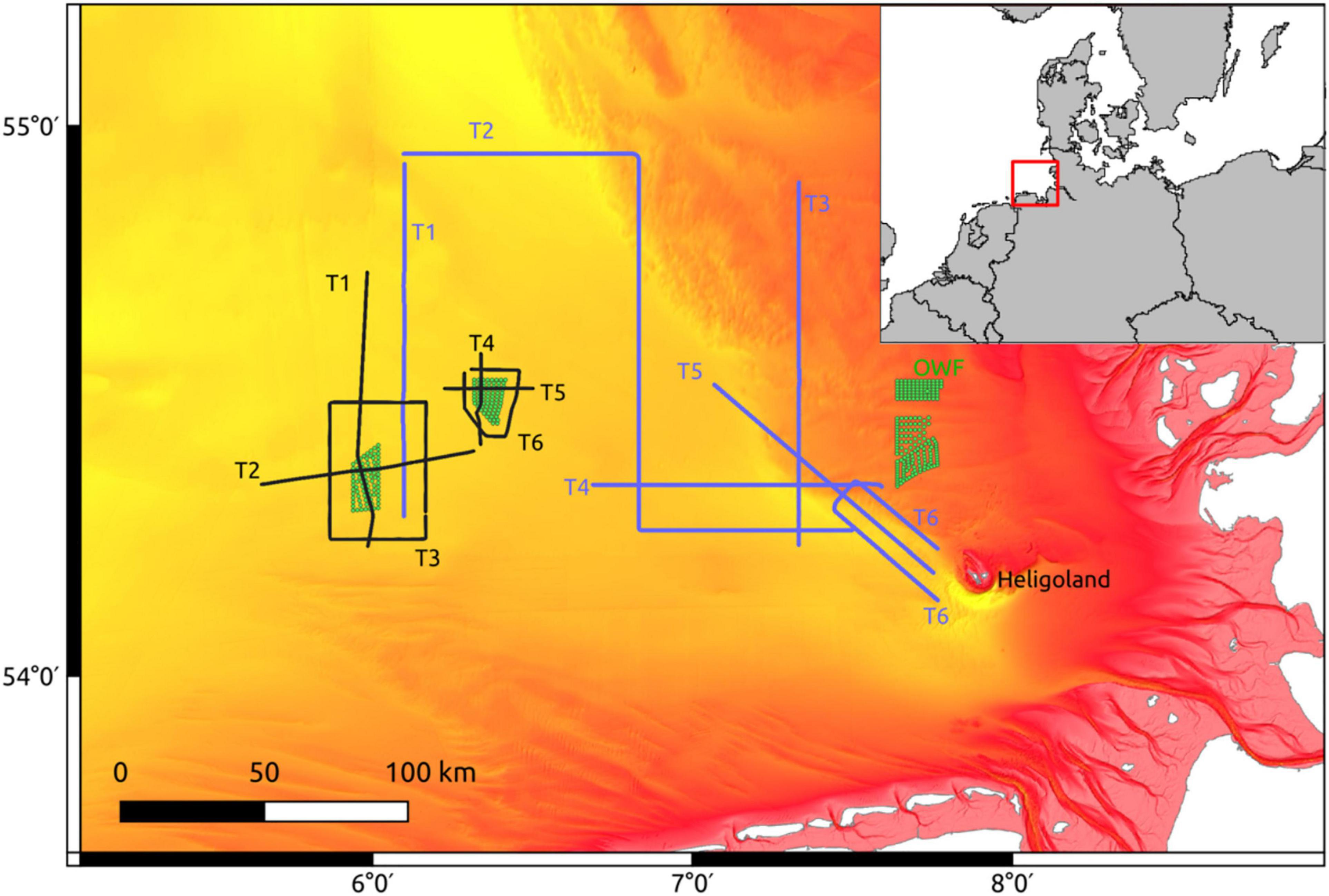
Figure 1. Sampling transects from HE429 (black) and HE534 (blue) in the German Bight of the North Sea. Green dots: Wind turbines. Depth ranges from 10 m (red) to 50 m (yellow). The red box marks the location of the bigger map.
Transect diagrams were generated using Ocean Data View (ODV, Schlitzer, 2020) with the embedded spatial interpolation software DIVA (Troupin et al., 2012) and exported as grids with a resolution of ∼ 25 m length × 1 m depth. Abiotic measurements as well as density values were normalized and rescaled to range from −1 to 1. This was necessary since deep learning models generally perform better with homogeneous, small values (Bishop, 1995).
To check for multicollinearity between our variables we calculated the variance inflation factor (VIF) in R (R Core Team, 2020) using functions provided by Zuur et al. (2009). A threshold of VIF > 3 was applied to identify highly collinear variables and exclude them from further analyses (Zuur et al., 2010). The exported grids for each selected parameter were stacked and transformed into feature-vectors where each grid cell became one vector with four features (1 parameter = 1 feature). In our definition, a pelagic micro-habitat with a spatial extent of ∼25 m × 1 m corresponds to one of those feature-vectors (Figure 2).
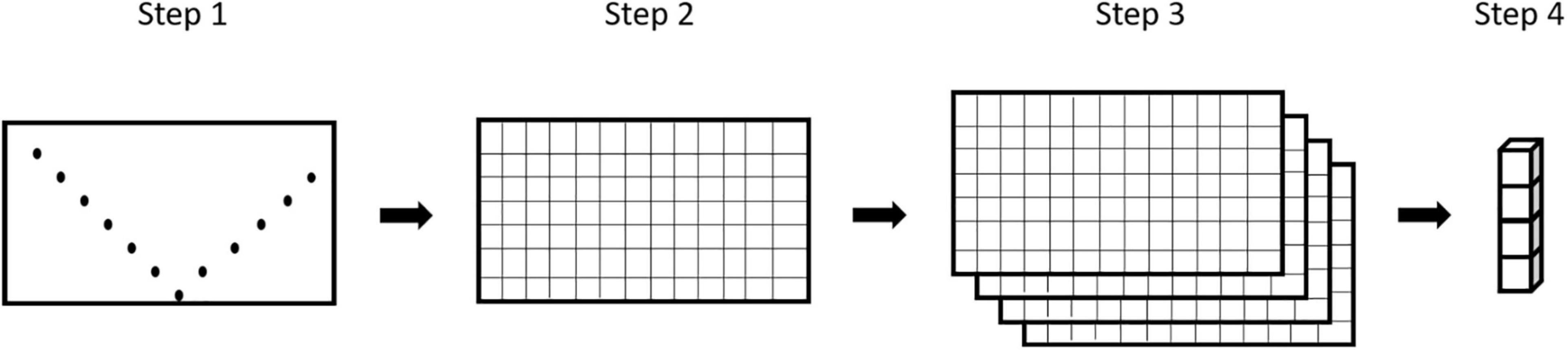
Figure 2. Schematic data processing from measurements to feature-vector. Step 1: original measurements; Step 2: gridded parameter table; Step 3: stacked grids; Step 4: feature-vector for 1 of the 91 grid-cells.
Based on these feature-vectors the AE was trained to reconstruct the original micro-habitats and thereby learn relevant abstractions that represent important patterns in the pelagic environment. We used a GPU supported TensorFlow backend (Abadi et al., 2015) for Keras (Chollet, 2015) under Python 3.7 (Van Rossum and Drake, 2009) to build and train our AE.
Model Description
The AE consisted of two fully connected layers in the Encoder and Decoder, respectively. The Decoder used the transposed weights of the Encoder in reversed order, e.g., the weights of the first Encoder-Layer were shared with the last Decoder-Layer. The first layer of the Encoder inflated the 4-dimensional feature-vector to a 100-dimensional feature-vector, which was reduced to a 2-dimensional feature-vector by the second layer (4 – 100 – 2). The Decoder did the same in reverse (2 – 100 – 4). The batch size (number of inputs that are processed simultaneously) was set to 38 and the learning rate followed a sawtooth-like scheme, initialized at 5e–8. Each input feature-vector corresponds to one micro-habitat and includes 1 measurement of each parameter selected for the analyses. The model was trained using the data from HE429 exclusively. Approximately ∼ 13% of the data was separated to validate the training process based on the remaining 87%. Data from HE534 was used as a final test set. As an AE is a gradient-based method, the chosen starting point may be crucial for the final fit of the model (Hinton, 2006), and one way of assessing and reducing the effect of start conditions are multi-start approaches (Subbey, 2018). Therefore, we trained multiple models and selected the one with the smallest final validation RMSE.
Habitat Segregation
By applying the trained Encoder only, we projected all micro-habitats into a xy-coordinate system using the 2-dimensional intermediate output. We will refer to the encoded outputs as “Encoded Components” in the following. Micro-habitats with similar characteristics were projected closer to each other than micro-habitats with different characteristics. We used the Euclidean distance to calculate the dissimilarity matrix for the Encoded Components of the micro-habitats, which was clustered by the HDBSCAN algorithm (McInnes et al., 2017). HDBSCAN uses a density-based linkage function, defining clusters by the size of the area in which a certain number of neighbors is found. Micro-habitats in “sufficiently dense” regions were assigned to a macro-habitat. Obviously, the parameters “size of the neighborhood” (Epsilon) and the “critical number of neighbors” (min_samples) are determining the resulting clusters (dense areas) with HDBSCAN. Thus, we checked the resulting macro-habitats for multiple different combinations of these two parameters as well as “min_cluster_size.” The parameter “min_cluster_size” is the threshold that separates “sufficiently dense” regions (clusters) from the random background noise. All micro-habitats that were not assigned to a specific macro-habitat by HDBSCAN got the label “−1.” Homogeneous regions in the transect produced more dense regions in the 2-dimensional surface that were more likely to trespass the “min_cluster_size” threshold and were separated from other homogeneous water masses by less dense regions. We used the silhouette method (Rousseeuw, 1987) to select the best segregation of micro-habitats. The silhouette score ranges from “−1” to “1” and indicates how well each point fits into the assigned cluster (macro-habitat) and is one of the best performing indices available (Arbelaitz et al., 2013). “−1” is probably wrong labeled, “0” is close to the decision boundary of two clusters and “1” means this specific point is far away from points of other clusters. The silhouette scores were calculated using the scikit-learn module (Pedregosa et al., 2011) for python.
Analyses
We used ODV to add a transect plot of the identified macro-habitats to the original measurements and plankton densities. Isolines of selected parameter measurements were overlayed on the macro-habitat plots to investigate which feature characteristics contributed to the segregation and to assess the associated plankton communities.
We furthermore described the macro-habitat plankton communities by modified Species-Abundance-Plots (SAP). We calculated the relative number of micro-habitats by plankton density and taxonomic group for each cluster. As is common for SAPs we used a log2 scale for density. That way we visualized the shift in specific species densities between the macro-habitats of different segregations of the same ROTV survey transect.
Pelagic submesoscale features often are highly productive areas and aggregate particles (Levy and Martin, 2013; Lévy et al., 2018). Therefore, we calculated Lloyd’s mean crowding (Lloyd’s MC) and Lloyd’s index of patchiness (Lloyd’s IP) with the R-function “agg_index” from the “epiphy” package (Gigot, 2018) and compared the results for different segregations of the same transects. Lloyd’s index is >1 if species were aggregated, 1 if the distribution is random and <1 indicates an overdispersed distribution compared to a homogeneous distribution. The Index of aggregation proposed by Bez (2000) (Bez’s IoA) was calculated in addition to Lloyd’s IP.
Data handling was done with R (R Core Team, 2020) and some tidyverse packages (Wickham et al., 2019), namely purrr, tibble, dplyr, ggplot2, and tidyr.
Results
In the initial VIF analysis with the full dataset a couple of parameters had VIF > 3. After removing “density” which had the highest score, no further parameter exceeded this threshold (Supplementary Table 1). After a detailed analysis of model sensitivities and reconstruction quality we decided to limit the final parameter selection to (1) vertical temperature difference to the grid cell above, (2) salinity, (3) oxygen, and (4) chlorophyll-a concentration.
Model Training
The root mean squared error (RMSE) after the first epoch ranged roughly between 0.7 and 1.0. Each training epoch took 10–15 s using a graphic card with 768 gpu-cores and we trained each model for 15 epochs until a plateau was reached (Supplementary Figure 1). The final training and validation RMSE of our selected model were RMSETr ∼ 0.33 and RMSEVal ∼ 0.35 (Figure 3).
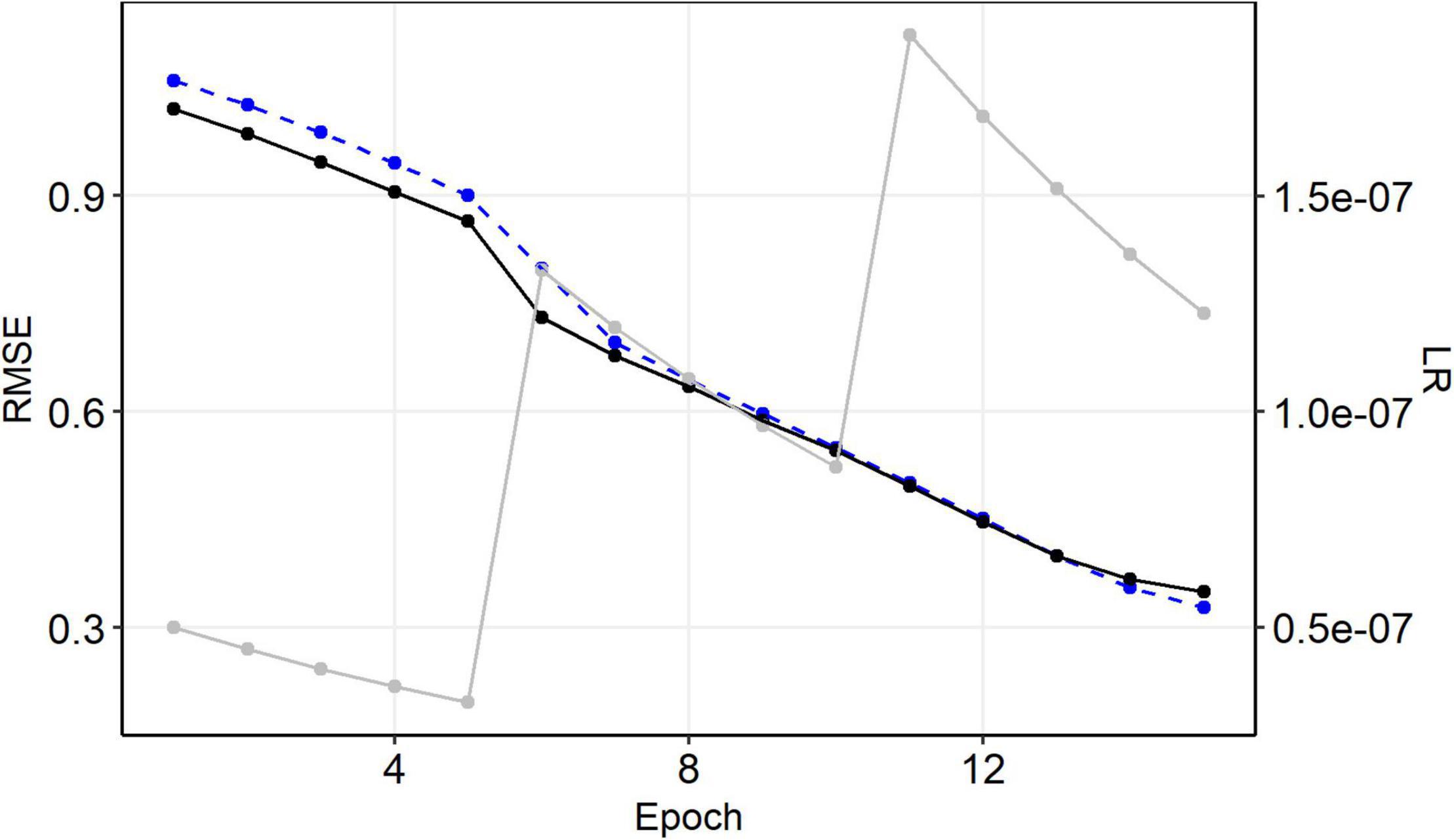
Figure 3. History of model training. Black: validation, blue: training, gray: learning rate (sec. axis).
Clustering
Depending on the HDBSCAN parameter selection, micro-habitats were grouped into 2–20 macro-habitats that ranged in size from <0.1 to 97% of all micro-habitats in a transect. We present exemplary the results for the segregation of T3 into different numbers of macro-habitats. Different parameter combinations could lead to an identical number of segregations. We chose an inverse size-cluster-relationship in the figure since more macro-habitats were usually ecologically less plausible (Figure 4). Mostly, “epsilon” had a great impact on the segregation with specific combinations of “min_cluster_size” and “min_samples” but less influence with other tested combinations of those two parameters, indicating that segregations changed discontinuously with slopes and plateaus (Supplementary Figure 2).
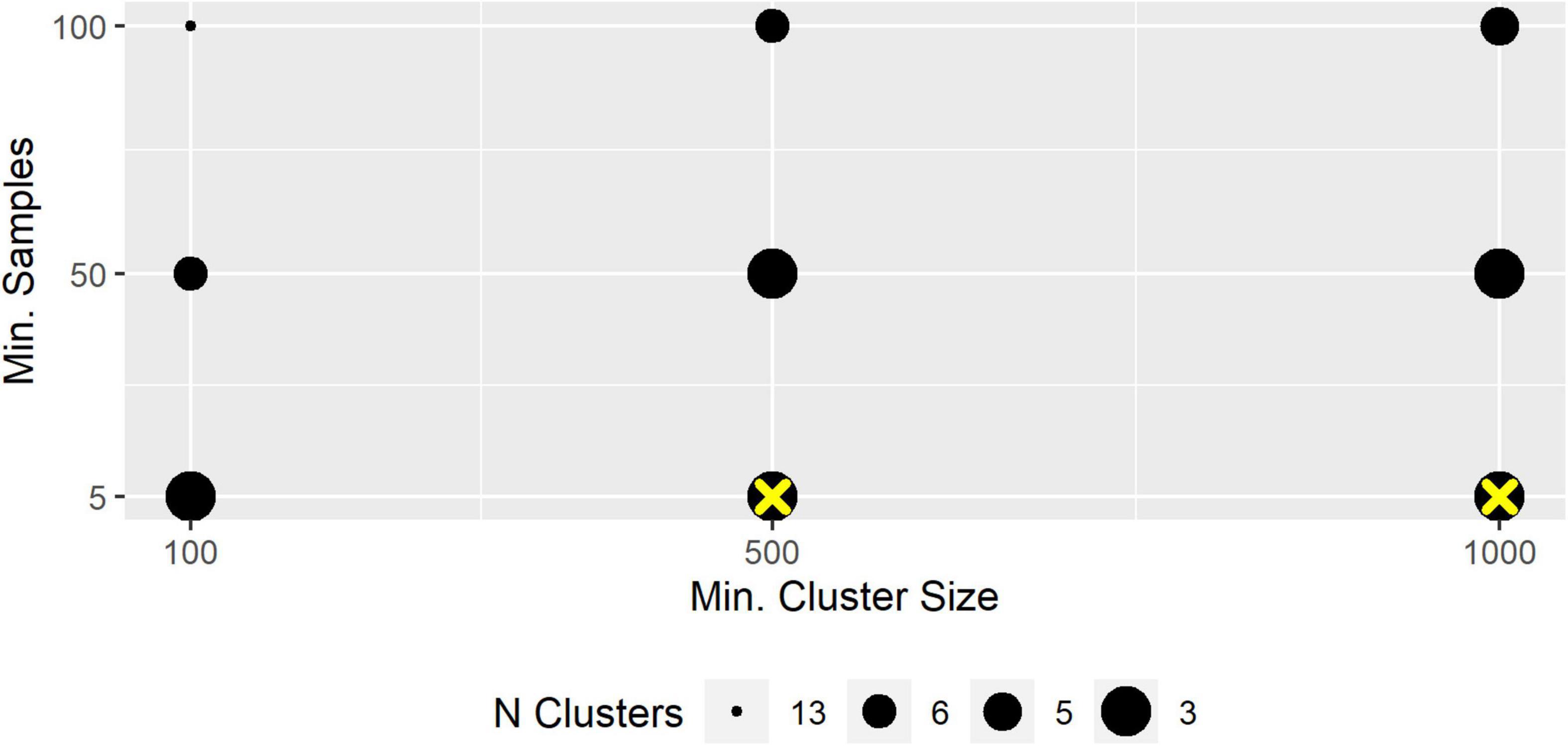
Figure 4. Number of segregated macro-habitats. The Figure was produced with Epsilon = 0.32. Yellow cross: selected segregation.
Even though the label “−1” is used by HDBSCAN to indicate the lack of belonging to a specific cluster, we observed a close relationship between micro-habitats labeled “−1” and exceptionally strong chlorophyll-peaks throughout all transects. Therefore, we decided to treat “−1” as a macro-habitat of its own instead of unclassified micro-habitats. Micro-habitats labeled as “−1” were also frequently located between the BL and the SL.
Projections
While cluster-labeling was not consistent in that cluster “0” always referred to, e.g., the “surface mixed layer,” the projections of the “surface mixed layer” micro-habitats were always located in a similar position throughout all projection plots. Thus, while the cluster denotations related to a macro-habitat were not consistent, the position indicated the affiliation to a specific macro-habitat (Figure 5).
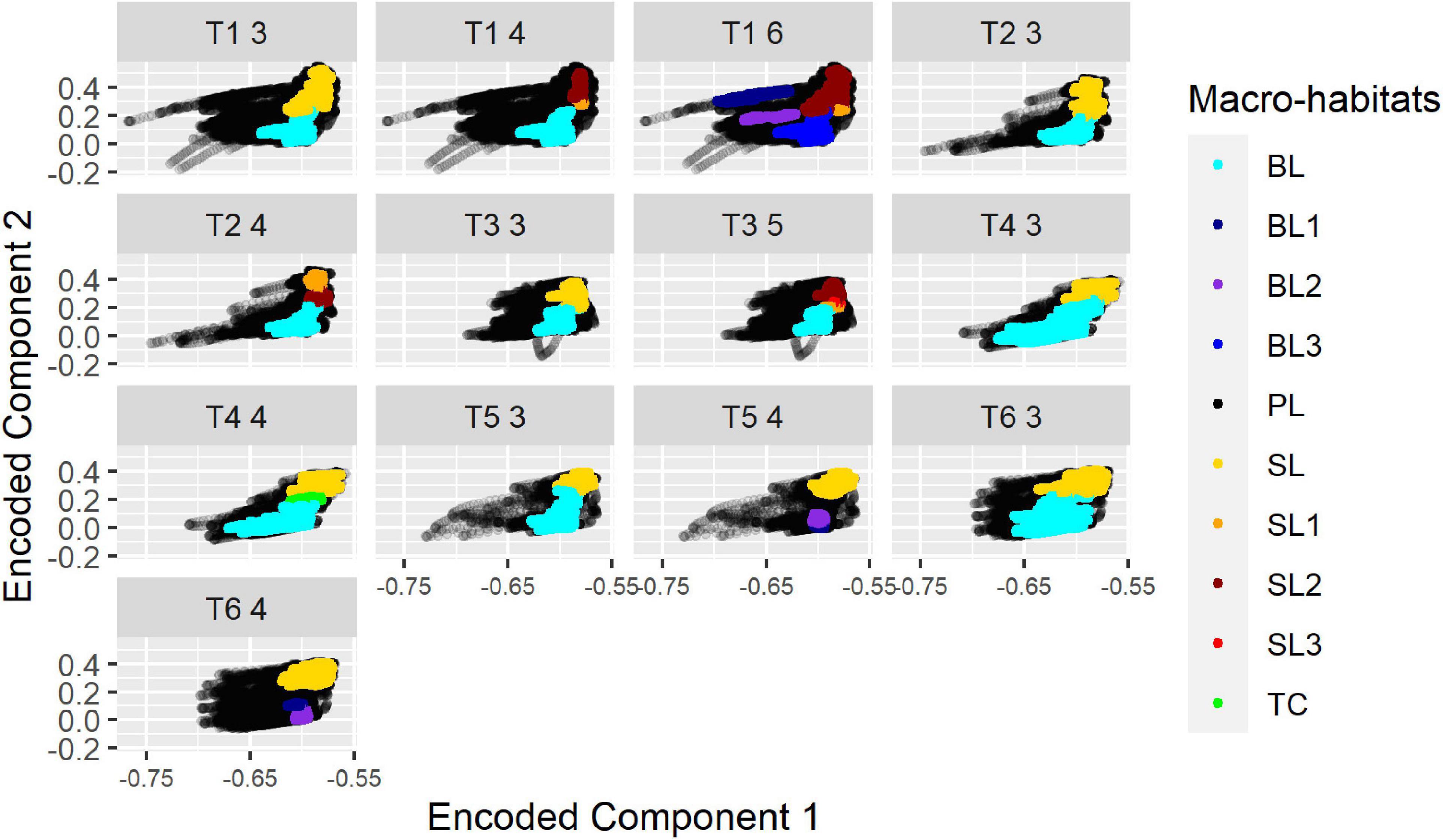
Figure 5. Projections for different segregations of all transects from HE429. The number of segregated macro-habitats is indicated by the last digit in the panel header. BL, Bottom layer (blue); SL, Surface mixed layer (yellow-red); TC, Thermocline Layer; PL, Productive layer (black). Numbers were used to indicate that, e.g., more than 1 “Bottom layer” was segregated (e.g., B1/B2 instead of BL).
Silhouette Method
The segregation into three macro-habitats gave the highest average silhouette-scores in most cases: notably high chlorophyll-peaks were merged into one macro-habitat (1) and two further macro-habitats were separated at around 17°C in an upper surface mixed layer (2) and a lower bottom layer (3). There was only one exception from this rule in T1 where in the northern, deeper area the bottom layer (3) was replaced with the layer including the chlorophyll-peaks (1). Another anomaly occurred in T2, where one of the basic macro-habitats was further separated into two “sublayers” so that a total of four macro-habitats were segregated. The highest silhouette-scores ranged from 0.35 (T1) to 0.59 (T5) (Table 1).
Table 1. Silhouette method to select the best clustering.
In the following we will use abbreviations for the three main layers and their sublayers, namely “PL” for the productive layer with the high chlorophyll values, “BL” for the bottom layer and “SL” for the surface mixed layer. A segregation into more than one layer is indicated using numbers, e.g., “SL1”/“SL2” instead of “SL.”
Habitat Maps
We present T2 exemplarily for all transects of HE429 (Figure 6). Segregating the output of the Encoder into 3 macro-habitats, we got the typical scheme of a SL with temperatures above 17°C, a macro-habitat which was strongly associated with extraordinary high chlorophyll-peaks (PL) and a BL as a third macro-habitat. The average silhouette-score for the entire transect was 0.54 (Table 1). However, this clustering did not account, e.g., for the intrusion of marine snow particles into the SL in the eastern half of the transect. When accepting 4 different macro-habitats, the BL and PL macro-habitats were mostly unaffected, while the SL was further separated into 2 different macro-habitats. One corresponded to the area where marine snow particles were predominant while the second macro-habitat corresponded to the area where pluteus larvae were observed in high densities. Segregating characteristics of the two macro-habitats were a salinity difference of 0.2 and a shallowing of the thermocline from 10 m to 5 m water depth. Notably, this change around section distance 18–20 km was located at the entry point of the transect into the Offshore Wind Farm BARD. This segregation increased the average silhouette-score for the entire transect to 0.56 (Table 1).
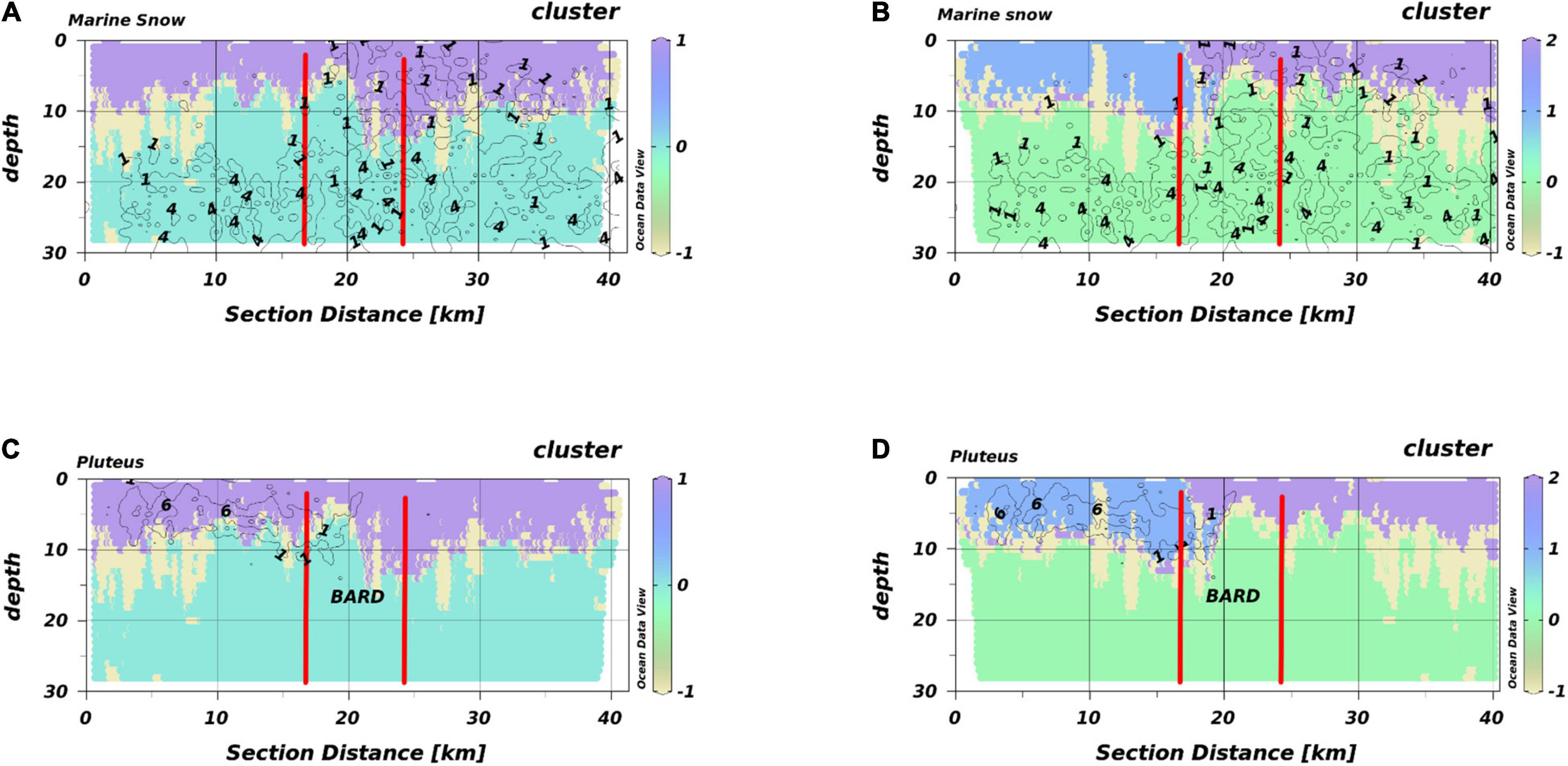
Figure 6. HabitatMap of T2 (HE429) with marine snow density (A,B) and pluteus density (C,D) as isolines. The OWF BARD is located between the vertical red lines. (A,C) 3 segregated macro-habitats, (B,D) 4 segregated macro-habitats. Different colors represent different macro-habitats. Different numbers are the respective densities indicated by the isolines.
Species Abundance Plots
The segregation into four macro-habitats was further supported by the modified SAPs. The relative amounts of PL and BL did not change much between 3 and 4 macro-habitats. However, SL1 included all micro-habitats with copepod densities >8 N l–1 and basically all micro-habitats where pluteus larvae occurred. SL2 instead included micro-habitats with copepod densities <8 N l–1 and generally less chlorophyll, but most micro-habitats where Appendicularia occurred. Thus, the SL1 and SL2 plankton communities were clearly distinct (Figure 7).
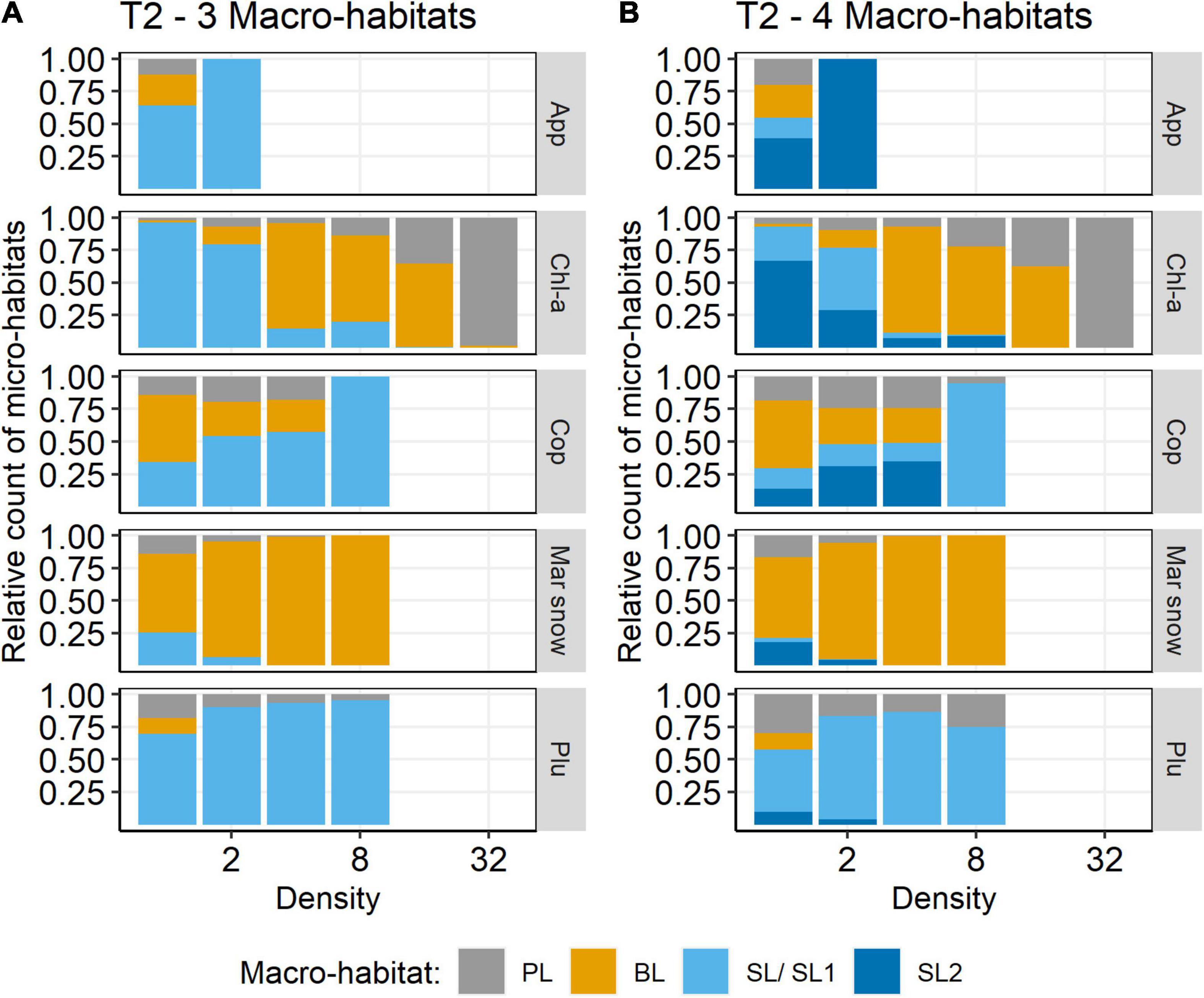
Figure 7. Relative count of density by macro-habitat for selected species on transect T2 (HE429). (A) 3 macro-habitats, (B) 4 macro-habitats. App, Appendicularia (N l–1); Chl-a, chlorophyll-a (RFU); Cop, Copepoda (N l–1); Mar snow, marine snow (N l–1); Plu, pluteus (N l–1).
Lloyd
Lloyd’s mean crowding underpinned the SAP results. Patchiness in PL and BL did not change for “marine snow” and “pluteus” but differed clearly between SL1 and SL2, indicating a higher pluteus aggregation in SL1 and a higher aggregation of marine snow in SL2 (Table 2).
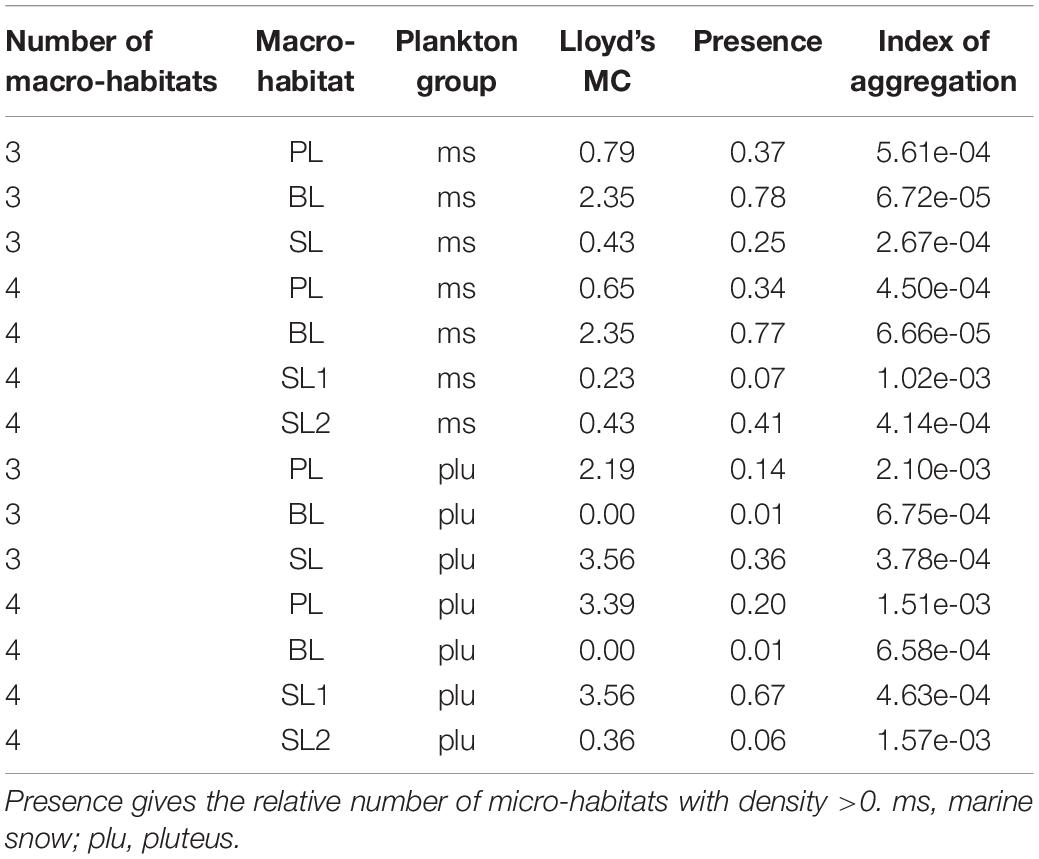
Table 2. Lloyd’s mean crowding and Bez’s Index of aggregation for 3 and 4 segregated macro-habitats for transect T2 (HE429).
Test Dataset HE534
The temperature maximum during HE534 was around 15°C, i.e., 2°C lower than the threshold that separated SL and BL in HE429. Consequently, no thermal stratification was detected by the Encoder trained with HE429 measurements. However, this model segregated an oxygen-rich layer that, based on the projections of the Encoder, resembled a similar habitat as the SL in HE429. This oxygen driven stratifications were not consistent over the entire range of a transect and in some areas the macro-habitat with projections similar to BL in HE429 comprised the entire water column, indicating a mixed water column closer toward the coast. Notably, plankton aggregations were commonly located at the border between oxygen-stratified and mixed water columns (Figure 8). The highest average silhouette-scores were reached with three segregated macro-habitats. However, the scores were much lower compared to HE429 with a maximum between 0.26 and 0.40.
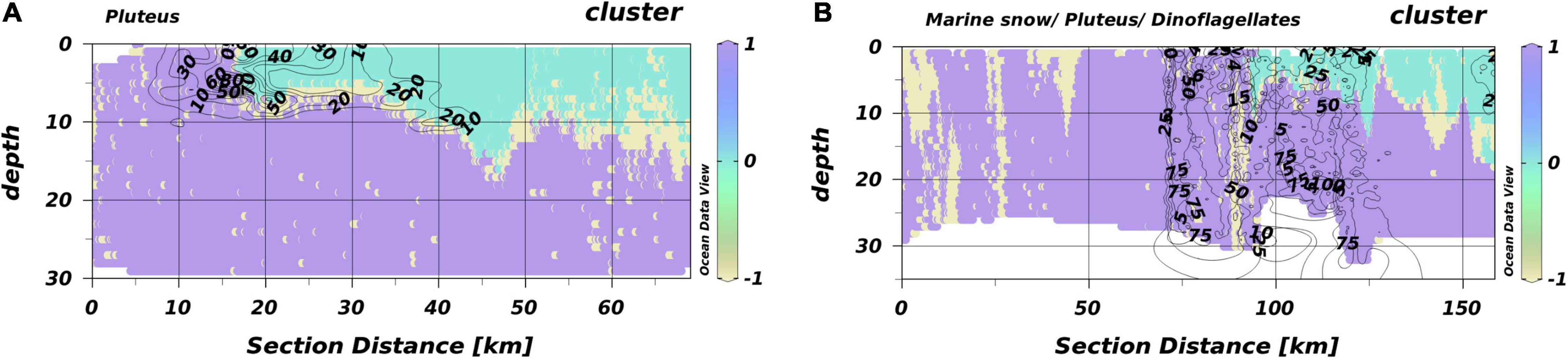
Figure 8. Habitat maps for T1 and T2 from HE534. The isolines give the densities (N l–1) of pluteus for T1. Isolines in the figure of T2 include pluteus, marine snow, and dinoflagellates (all in N l–1). (A) T1 and (B) T2. Different colors represent different macro-habitats. Different numbers are the respective densities indicated by the isolines.
Discussion
Selection of Parameters
When training the model, we got the best results with a limited selection of parameters compared to the entire set of available data. The selected parameters are, however, in accordance with previous findings that physical properties contribute most to differences in habitat utilization by plankton organisms (Schulz et al., 2012; Friedland et al., 2020). In contrast to Alvarez-Berastegui et al. (2014), we did not benefit from the combination of gradients with the original measurements. However, a prior wavelet analysis as in North et al. (2016) could help to identify relevant spatial scales for the derivation of gradients. It is also possible, that the architecture of the model limited the amount of compressed information accessible to the clustering algorithm. In convolutional AEs, the size of the bottleneck (intermediate output) limits the generalization of the model (Manakov et al., 2019). This is also true for the fully connected AE architecture of this model and might limit the potential of including more variables like species densities and environmental gradients.
Reconstruction Loss
The loss for the optimization of an AE is based on the difference between the reconstruction and the original input. However, driving forces behind habitat partitioning vary with study region and season and specific parameters have a higher contribution than others (Schulz et al., 2012; Espinasse et al., 2014; Friedland et al., 2020). Thus, we deemed it more important to accurately reconstruct specific features (parameters) compared to entire vectors (micro-habitats). Accordingly, we calculated the sum of the batchwise RMSE between the specific feature-values (e.g., temperature) of each input and the corresponding feature-values of the reconstructions and not the RMSE of an entire feature-vector (micro-habitat) and its reconstruction. This forced the AE to learn all parameters individually and furthermore made it possible to give specific parameters a higher priority if appropriate.
Aggregation
Lloyd’s IP is an area-related quality measure for Lloyd’s MC and thus sensitive to zeros. As can be seen in our example (Table 2), the “spillover” from a crowded to an empty macro-habitat in the area of the decision boundary leads to misleadingly high Lloyd’s IP, and to a lesser degree, misleadingly high Bez’s IoA, even though this Index is supposedly insensitive to zeros. In accordance with the recommendation by Bez (2000) we therefore suggest Lloyd’s MC as a measure of aggregation within a macro-habitat. Lloyd’s IP and Bez’s IoA might still be informative if the overall colonialization of the macro-habitat is considered.
Pelagic Habitats
The model segregated three (four) distinct pelagic habitats in HE429: (1) a SL (SL1/SL2) mainly characterized by temperatures >17°C, (2) a BL on the other side of that threshold, and (3) a PL dominated by high chlorophyll concentrations. In contrast to SL and BL, PL was not a true cluster by the definition of HDBSCAN, which indicates a great variability within the micro-habitats belonging to PL. That makes them “special” or at least “different” from common micro-habitats in SL and BL. Micro-habitats of PL were usually located around the 17°C isoline and at the occurrence of exceptionally strong chlorophyll-peaks.
In the North Sea, peaks of primary production following the spring bloom were observed in subsurface layers (Richardson et al., 1998, 2000). The PL most likely resembles such areas of subsurface productivity.
Furthermore, the model detected an upward doming of the thermocline within an OWF, probably caused by enhanced vertical mixing (Segtnan and Christakos, 2015; Floeter et al., 2017; Schultze et al., 2020). The upward doming and the resulting temperature differences are comparable to those observed within cyclonic eddies (Dong and McWilliams, 2007; Marmorino et al., 2018), indicating that OWF’s can influence the pelagic realm in the same order of magnitude as natural (sub-) mesoscale processes like eddies. The doming of colder, nutrient-rich water can produce chlorophyll peaks (Munk et al., 1999), indicating the potential for an enhanced primary production in this area.
Cumulative effects of single foundations might lead to a blocking effect around OWF’s, similar as observed for islands (Simpson et al., 1982), which has the potential to produce submesoscale eddies (Dong and McWilliams, 2007) in addition to local upwelling fronts (Floeter et al., 2017). Common properties that are used to describe hydrographic eddies and fronts include water velocity, vorticity and the Rossby number (e.g., Lévy et al., 2012; Marmorino et al., 2018), all of which were not available to us, which makes it less likely to detect such features.
The situation during HE534 was fundamentally different from HE429, most likely due to the weather conditions prior to the cruise that dispersed a thermal stratification. However, the projections indicated that similar SL and BL as in HE429 were detected. In case of HE534, segregations occurred along an oxygen isoline (>235 μmol l–1) instead of temperature (>17°C) as during HE429. This is in accordance with findings of Friedland et al. (2020) and references within that the predictive power of variables might change. This variable nature inherently present in pelagic data (Hinchey et al., 2008; Thompson et al., 2016) makes it so challenging to accurately predict pelagic habitats. The temperature isolines in T1 and T2 (Supplementary Figure 3) clearly indicate the presence of a tidal mixing front (see Hill et al., 1993). A convergence slick, which is typically associated with such tidal mixing fronts (Hill et al., 1993), would also explain the observed aggregation of plankton particles at the intersection of the two macro-habitats (Figure 8).
There exists plenty of evidence that physical properties also structure the marine plankton communities (e.g., Swalethorp et al., 2015; Van Leeuwen et al., 2015; Lindegren et al., 2020). However, the generated habitat maps have only limited explanatory power considering the observed plankton communities. This is not unexpected since physical properties are merely incomplete predictors for the community structure which is most likely further shaped by niche-based processes and interactions (Houliez et al., 2021).
Top predators aggregate in areas with the highest prey-patch densities (not to be confused with the area of highest prey densities!) (Benoit-Bird et al., 2013) and peak abundances of zooplankton and fish larvae are frequently observed in the direct vicinity of frontal convergence zones (Munk et al., 1995, 2002; Höffle et al., 2013; Munk, 2014; Swalethorp et al., 2015). In addition to the horizontal agglomerations, thermo-, and haloclines can produce further vertical structuring (Höffle et al., 2013; Lindegren et al., 2020). Thereby, more pronounced differences lead to a stronger niche separation and less overlap between different species (Lindegren et al., 2020). Changes in nitrate (Scharfe and Wiltshire, 2019) and silicate (Wiltshire et al., 2015) availability produce a temporal succession of different dominant taxa in the tidal advected phytoplankton community. Especially the plankton community is thus shaped by complex spatio-temporal dynamics and local prey patches have the potential to shape the distribution of higher trophic levels (Pope et al., 1994; Burkhard et al., 2011; Benoit-Bird et al., 2013; Defriez et al., 2016), even though this might be of less importance for ecosystem services in a highly diverse and partly functionally redundant plankton communities like that of the North Sea (Atkinson et al., 2015).
Comments and Recommendations
Future work should aim to include species densities and water current related measurements in order to accurately predict not only physical habitats but also realized ecological niches and hopefully improve our understanding of the complex dynamics shaping the pelagic realm.
Our approach offers beneficial properties to solve this challenge: the AE is a highly non-linear tool to reduce the dimensionality of a nearly unlimited amount of data that can be extended as needed. Additionally, HDBSCAN is a cluster algorithm that makes as few assumptions as possible, i.e., regarding number or shape of clusters. HDBSCAN can also handle outliers on it’s own in opposite to, e.g., k-means, and even enables to treat them in our case as an own macro-habitat. While machine learning might not give insight into the underlying mechanistic, it can give a starting point from which to begin future investigations (Friedland et al., 2020).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SV and R-MP constructed the Autoencoder used to process the data. R-MP was responsible for the data analyses. JF and R-MP wrote the submitted manuscript. All authors contributed to the article and approved the submitted version.
Funding
The RV Heincke Research Cruises were supported by grant numbers AWI_HE429_00 and AWI_HE534_00.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.754375/full#supplementary-material
Footnotes
References
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: Large-scale Machine Learning on Heterogeneous Distributed Systems. Available Online at: https://www.tensorflow.org/ (accessed March 30, 2020).
Alvarez-Berastegui, D., Ciannelli, L., Aparicio-Gonzalez, A., Reglero, P., Hidalgo, M., López-Jurado, J. L., et al. (2014). Spatial scale, means and gradients of hydrographic variables define pelagic seascapes of bluefin and bullet tuna spawning distribution. PLoS One 9:e109338. doi: 10.1371/journal.pone.0109338
Amorim, E., Ramos, S., Elliott, M., and Bordalo, A. A. (2018). ‘Dynamic habitat use of an estuarine nursery seascape: ontogenetic shifts in habitat suitability of the european flounder (platichthys flesus)’. J. Exp. Mar. Biol. Ecol. 506, 49–60. doi: 10.1016/j.jembe.2018.05.011
Arbelaitz, O., Gurrutxaga, I., Muguerza, J., Pérez, J. M., and Perona, I. (2013). An extensive comparative study of cluster validity indices. Patt. Recogn. 46, 243–256. doi: 10.1016/J.PATCOG.2012.07.021
Atkinson, A., Harmer, R. A., Widdicombe, C. E., McEvoy, A. J., Smyth, T. J., Cummings, D. G., et al. (2015). ‘Questioning the role of phenology shifts and trophic mismatching in a planktonic food web’. Progr. Oceanogr. 137, 498–512. doi: 10.1016/j.pocean.2015.04.023
Baschek, B., and Maarten Molemaker, J. (2010). Aerial and In Situ Measurements of Submesoscale Eddies, Fronts, and Filaments. Available Online at: https://ui.adsabs.harvard.edu/abs/2010EGUGA..12.1106B/abstract (accessed April 26, 2021).
Bellido, J. M., Brown, A. M., Valavanis, V. D., Giráldez, A., Pierce, G. J., Iglesias, M., et al. (2008). “Identifying essential fish habitat for small pelagic species in spanish mediterranean waters,” in Essential Fish Habitat Mapping in the Mediterranean, ed. V. D. Valavanis (Dordrecht: Springer), 171–184.
Bengio, Y., Lamblin, P., Popovici, D., and Larochelle, H. (2006). “Greedy layer-wise training of deep networks,” in Proceedings of the 19th International Conference on Neural Information Processing Systems, (Cambridge: MIT Press), 153–160.
Benoit-Bird, K. J., Battaile, B. C., Heppell, S. A., Hoover, B., Irons, D., Jones, N., et al. (2013). Prey patch patterns predict habitat use by top marine predators with diverse foraging strategies. PLoS One 8:e53348. doi: 10.1371/journal.pone.0053348
Bertrand, A., Grados, D., Colas, F., Bertrand, S., Capet, X., Chaigneau, A., et al. (2014). Broad impacts of fine-scale dynamics on seascape structure from zooplankton to seabirds’. Nat. Commun. 5:5239. doi: 10.1038/ncomms6239
Bez, N. (2000). On the use of lloyd’s index of patchiness. Fish. Oceanogr. 9, 372–376. doi: 10.1046/j.1365-2419.2000.00148.x
Buckingham, C. E., Garabato, A. C. N., Thompson, A. F., Brannigan, L., Lazar, A., Marshall, D. P., et al. (2016). Seasonality of submesoscale flows in the ocean surface boundary layer. Geophys. Res. Lett. 43, 2118–2126. doi: 10.1002/2016GL068009
Burkhard, B., Opitz, S., Lenhart, H., Ahrendt, K., Garthe, S., Mendel, B., et al. (2011). Ecosystem based modeling and indication of ecological integrity in the german north sea—case study offshore wind parks. Ecol. Indic. 11, 168–174. doi: 10.1016/j.ecolind.2009.07.004
Chen, Z., Yeo, C. K., Lee, B. S., and Lau, C. T. (2018). Autoencoder-based network anomaly detection. Wireless Telecommun. Symp. 2018, 1–5. doi: 10.1109/WTS.2018.8363930
Chollet, F. (2015). Keras. GitHub. Available Online at: https://github.com/fchollet/keras (accessed March 30, 2020).
Defriez, E. J., Sheppard, L. W., Reid, C., and Reuman, D. C. (2016). Climate change-related regime shifts have altered spatial synchrony of plankton dynamics in the north sea. Global Change Biol. 22, 2069–2080. doi: 10.1111/gcb.13229
Dong, C., and McWilliams, J. C. (2007). A numerical study of island wakes in the southern california bight. Cont. Shelf Res. 27, 1233–1248. doi: 10.1016/j.csr.2007.01.016
Erhan, D., Manzagol, P.-A., Bengio, Y., Bengio, S., and Vincent. (2009). The difficulty of training deep architectures and the effect of unsupervised pre-training. Artif. Intell. Stat. 5, 153–160.
Espinasse, B., Carlotti, F., Zhou, M., and Devenon, J. L. (2014). Defining zooplankton habitats in the gulf of lion (NW mediterranean sea) using size structure and environmental conditions. Mar. Ecol. Progr. Ser. 506, 31–46. doi: 10.3354/meps10803
Floeter, J., Beusekom, J. E. E., van, Auch, D., Callies, U., Carpenter, J., et al. (2017). Pelagic effects of offshore wind farm foundations in the stratified north sea. Progr. Oceanogr. 156, 154–173. doi: 10.1016/j.pocean.2017.07.003
Friedland, K. D., Bachman, M., Davies, A., Frelat, R., McManus, M. C., Morse, R., et al. (2020). Machine learning highlights the importance of primary and secondary production in determining habitat for marine fish and macroinvertebrates. Aquat. Conserv. 13, 1482–1498. doi: 10.1002/aqc.3527
Funk, S., Krumme, U., Temming, A., and Möllmann, C. (2020). ‘Gillnet fishers’ knowledge reveals seasonality in depth and habitat use of cod (gadus morhua) in the western baltic sea’. ICES J. Mar. Sci. 77, 1816–1829. doi: 10.1093/icesjms/fsaa071
Giannoulaki, M., Pyrounaki, M. M., Liorzou, B., Leonori, I., Valavanis, V. D., Tsagarakis, K., et al. (2011). Habitat suitability modelling for sardine juveniles (sardina pilchardus) in the mediterranean sea. Fish. Oceanogr. 20, 367–382. doi: 10.1111/j.1365-2419.2011.00590.x
Gigot, C. (2018). Epiphy: Analysis of Plant Disease Epidemics. Available Online at: https://CRAN.R-project.org/package=epiphy (accessed May 14, 2020).
Harris, T., and Baker, E. K. (2012). “1 - Why map benthic habitats?” in Seafloor Geomorphology as Benthic Habitat, eds T. Harris and E. K. Baker (London: Elsevier), 3–22.
Hill, A. E., James, I., Linden, P., Matthews, J., Prandle, D., Simpson, J., et al. (1993). Dynamics of tidal mixing fronts in the north sea. Philos. Trans. R. Soc. B Biol. Sci. 343, 431–446. doi: 10.1098/rsta.1993.0057
Hinchey, E. K., Nicholson, M. C., Zajac, R. N., and Irlandi, E. A. (2008). Preface: marine and coastal applications in landscape ecology. Landscape Ecol. 23, 1–5. doi: 10.1007/s10980-007-9141-3
Hinton, G. E. (2006). Reducing the dimensionality of data with neural networks. Science 313, 504–507. doi: 10.1126/science.1127647
Höffle, H., Nash, R. D. M., Falkenhaug, T., and Munk, P. (2013). Differences in vertical and horizontal distribution of fish larvae and zooplankton, related to hydrography. Mar. Biol. Research 9, 629–644. doi: 10.1080/17451000.2013.765576
Houliez, E., Lefebvre, S., Dessier, A., Huret, M., Marquis, E., Bréret, M., et al. (2021). Spatio-temporal drivers of microphytoplankton community in the bay of biscay: do species ecological niches matter? Progr. Oceanogr. 194:102558. doi: 10.1016/j.pocean.2021.102558
Labat, J.-P., Gasparini, S., Mousseau, L., Prieur, L., Boutoute, M., and Mayzaud, P. (2009). Mesoscale distribution of zooplankton biomass in the northeast atlantic ocean determined with an optical plankton counter: relationships with environmental structures. Deep Sea Res. I Oceanogr. Res. Pap. 56, 1742–1756. doi: 10.1016/j.dsr.2009.05.013
Laman, E. A., Rooper, C. N., Turner, K., Rooney, S., Cooper, D. W., and Zimmermann, M. (2017). Using species distribution models to describe essential fish habitat in alaska. Can. J. Fish. Aquat. Sci. 75, 1230–1255. doi: 10.1139/cjfas-2017-0181
Lévy, M., Ferrari, R., Franks, J. S., Martin, A. P., and Rivière, P. (2012). Bringing physics to life at the submesoscale. Geophys. Res. Lett. 39:L14602. doi: 10.1029/2012GL052756
Lévy, M., Franks, J. S., and Smith, K. S. (2018). The role of submesoscale currents in structuring marine ecosystems. Nat. Commun. 9:4758. doi: 10.1038/s41467-018-07059-3
Levy, M., and Martin, A. P. (2013). The influence of mesoscale and submesoscale heterogeneity on ocean biogeochemical reactions. Global Biogeochem. Cyc. 27, 1139–1150. doi: 10.1002/2012GB004518
Lindegren, M., Thomas, M. K., Jónasdóttir, S. H., Nielsen, T. G., and Munk, P. (2020). Environmental niche separation promotes coexistence among ecologically similar zooplankton species—north sea copepods as a case study. Limnol. Oceanogr. 65, 545–556. doi: 10.1002/lno.11322
Manakov, I., Rohm, M., and Tresp, V. (2019). Walking the Tightrope: An Investigation of the Convolutional Autoencoder Bottleneck. Available Online at: https://openreview.net/forum?id=ryguP1BFwr [accessed Sep 23, 2020].
Marmorino, G. O., Smith, G. B., North, R. P., and Baschek, B. (2018). Application of airborne infrared remote sensing to the study of ocean submesoscale eddies. Front. Mech. Eng. 4:10. doi: 10.3389/fmech.2018.00010
McInnes, L., Healy, J., and Astels, S. (2017). Hdbscan: hierarchical density based clustering. J. Open Source Softw. 2:205. doi: 10.21105/joss.00205
Munk, P. (2014). Fish larvae at fronts: horizontal and vertical distributions of gadoid fish larvae across a frontal zone at the norwegian trench. Deep Sea Res. II Top. Stud. Oceanogr. 107, 3–14. doi: 10.1016/j.dsr2.2014.01.016
Munk, P., Larsson, P., Danielsen, D., and Moksness, E. (1995). Larval and small juvenile cod gadus morhua concentrated in the highly productive areas of a shelf break front. Mar. Ecol. Progr. Ser. 125, 21–30. doi: 10.3354/meps125021
Munk, P., Larsson, P., Danielssen, D., and Moksness, E. (1999). Variability in frontal zone formation and distribution of gadoid fish larvae at the shelf break in the northeastern north sea. Mar. Ecol. Progr. Ser. 177, 221–233. doi: 10.3354/meps177221
Munk, P., Wright, J., and Pihl, N. J. (2002). Distribution of the early larval stages of cod, plaice and lesser sandeel across haline fronts in the north sea. Estuar. Coast. Shelf Sci. 55, 139–149. doi: 10.1006/ecss.2001.0892
North, R. P., Riethmüller, R., and Baschek, B. (2016). Detecting small–scale horizontal gradients in the upper ocean using wavelet analysis. Estuar. Coast. Shelf Sci. 180, 221–229. doi: 10.1016/j.ecss.2016.06.031
Omand, M. M., D’Asaro, E. A., Lee, C. M., Perry, M. J., Briggs, N., Cetinić, I., et al. (2015). Eddy-driven subduction exports particulate organic carbon from the spring bloom. Science 348, 222–225. doi: 10.1126/science.1260062
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12, 2825–2830.
Pittman, S. J., Kneib, R. T., and Simenstad, C. A. (2011). Practicing coastal seascape ecology. Mar. Ecol. Progr. Ser. 427, 187–190. doi: 10.3354/meps09139
Plonus, R.-M., Conradt, J., Harmer, A., Janßen, S., and Floeter, J. (2021). Automatic plankton image classification—can capsules and filters help cope with data set shift? Limnol. Oceanogr. 19, 176–195. doi: 10.1002/lom3.10413
Pope, J. G., Shepherd, J. G., Webb, J., Stebbing, A. R. D., Mangel, M., Beverton, R. J. H., et al. (1994). Successful surf-riding on size spectra: the secret of survival in the sea. Philos. Trans. R. Soc. Lond. B Biol. Sci. 343, 41–49. doi: 10.1098/rstb.1994.0006
R Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Richardson, K., Nielsen, T., Pedersen, F., Heilmann, J., Løkkegaard, B., and Kaas, H. (1998). Spatial heterogeneity in the structure of the planktonic food web in the north sea. Mar. Ecol. Progr.Ser. 168, 197–211. doi: 10.3354/meps168197
Richardson, K., Visser, A. W., and Pedersen, F. B. (2000). Subsurface phytoplankton blooms fuel pelagic production in the north sea. J. Plankton Res. 22, 1663–1671. doi: 10.1093/plankt/22.9.1663
Rousseeuw, J. (1987). Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 20, 53–65. doi: 10.1016/0377-0427(87)90125-7
Sano, M., Maki, K., Nishibe, Y., Nagata, T., and Nishida, S. (2013). Feeding habits of mesopelagic copepods in sagami bay: insights from integrative analysis. Progr. Oceanogr. 110, 11–26. doi: 10.1016/j.pocean.2013.01.004
Scharfe, M., and Wiltshire, K. H. (2019). Modeling of intra-annual abundance distributions: constancy and variation in the phenology of marine phytoplankton species over five decades at helgoland roads (north sea). Ecol. Model. 404, 46–60. doi: 10.1016/j.ecolmodel.2019.01.001
Schlitzer, R. (2020). Ocean Data View. Available Online at: https://odv.awi.de/ [accessed March 30, 2021].
Schultze, L. K. P., Merckelbach, L. M., Horstmann, J., Raasch, S., and Carpenter, J. R. (2020). Increased mixing and turbulence in the wake of offshore wind farm foundations. J. Geophys. Res. Oceans 125:e2019JC015858. doi: 10.1029/2019JC015858
Schulz, J., Peck, M. A., Barz, K., Schmidt, J. O., Hansen, F. C., Peters, J., et al. (2012). Spatial and temporal habitat partitioning by zooplankton in the bornholm basin (central baltic sea). Progr. Oceanogr. 107, 3–30. doi: 10.1016/j.pocean.2012.07.002
Segtnan, O. H., and Christakos, K. (2015). ‘Effect of offshore wind farm design on the vertical motion of the ocean. Energy Procedia 80, 213–222. doi: 10.1016/j.egypro.2015.11.424
Shulman, I., Penta, B., Richman, J., Jacobs, G., Anderson, S., and Sakalaukus, P. (2015). Impact of submesoscale processes on dynamics of phytoplankton filaments. J. Geophys. Res. Oceans 120, 2050–2062. doi: 10.1002/2014JC010326
Simpson, J. H., Tett, B., Argote-Espinoza, M. L., Edwards, A., Jones, K. J., and Savidge, G. (1982). Mixing and phytoplankton growth around an island in a stratified sea. Cont. Shelf Res. 1, 15–31. doi: 10.1016/0278-4343(82)90030-9
Subbey, S. (2018). Parameter estimation in stock assessment modelling: caveats with gradient-based algorithms. ICES J. Mar. Sci. 75, 1511–1511. doi: 10.1093/icesjms/fsy060
Swalethorp, R., Malanski, E., Dalgaard Agersted, M., Gissel Nielsen, T., and Munk, P. (2015). Structuring of zooplankton and fish larvae assemblages in a freshwater-influenced greenlandic fjord: influence from hydrography and prey availability. J. Plankton Res. 37, 102–119. doi: 10.1093/plankt/fbu099
Thompson, A. F., Lazar, A., Buckingham, C., Naveira Garabato, A. C., Damerell, G. M., and Heywood, K. J. (2016). Open-ocean submesoscale motions: a full seasonal cycle of mixed layer instabilities from gliders. J. Phys. Oceanogr. 46, 1285–1307. doi: 10.1175/JPO-D-15-0170.1
Troupin, C., Barth, A., Sirjacobs, D., Ouberdous, M., Brankart, J. M., Brasseur, P., et al. (2012). Generation of analysis and consistent error fields using the data interpolating variational analysis (DIVA). Ocean Model. 52-53, 90–101. doi: 10.1016/j.ocemod.2012.05.002
Tugores, M. P., Giannoulaki, M., Iglesias, M., Bonanno, A., Tičina, V., Leonori, I., et al. (2011). Habitat suitability modelling for sardine sardina pilchardus in a highly diverse ecosystem: the mediterranean sea. Mar. Ecol. Progr. Ser. 443, 181–205. doi: 10.3354/meps09366
Van Leeuwen, S., Tett, P., Mills, D., and van der Molen, J. (2015). Stratified and nonstratified areas in the north sea: long-term variability and biological and policy implications. J. Geophys. Res. Oceans 120, 4670–4686. doi: 10.1002/2014JC010485
Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., and Manzagol, P.-A. (2010). Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 11, 3371–3408.
Wedding, L. M., Lepczyk, C. A., Pittman, S. J., Friedlander, A. M., and Jorgensen, S. (2011). Quantifying seascape structure: extending terrestrial spatial pattern metrics to the marine realm. Mar. Ecol. Progr. Ser. 427, 219–232. doi: 10.3354/meps09119
Wickham, H., Averick, M., Bryan, J., Chang, W., McGowan, L. D., François, R., et al. (2019). Welcome to the tidyverse. J. Open Source Softw. 4:1686. doi: 10.21105/joss.01686
Wiltshire, K. H., Boersma, M., Carstens, K., Kraberg, A. C., Peters, S., and Scharfe, M. (2015). Control of phytoplankton in a shelf sea: determination of the main drivers based on the helgoland roads time series. J. Sea Res. 105, 42–52. doi: 10.1016/j.seares.2015.06.022
Zhao, Y., Deng, B., Shen, C., Liu, Y., Lu, H., and Hua, X.-S. (2017). “Spatio-temporal AutoEncoder for video anomaly detection,” in Proceedings of the 25th ACM International Conference on Multimedia, (New York: Association for Computing Machinery (MM ’17)), 1933–1941.
Zuur, A., Ieno, E. N., Walker, N., Saveliev, A. A., and Smith, G. M. (2009). Mixed Effects Models and Extensions in Ecology with R. New York: Springer-Verlag.
Keywords: machine learning, North Sea, submesoscale, pelagic habitats, plankton patchiness
Citation: Plonus R-M, Vogl S and Floeter J (2021) Automatic Segregation of Pelagic Habitats. Front. Mar. Sci. 8:754375. doi: 10.3389/fmars.2021.754375
Received: 06 August 2021; Accepted: 15 September 2021;
Published: 04 October 2021.
Edited by:
Tracey T. Sutton, Nova Southeastern University, United StatesReviewed by:
Adolf Konrad Stips, European Commission, ItalyMarco Uttieri, Anton Dohrn Zoological Station, Italy
Copyright © 2021 Plonus, Vogl and Floeter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rene-Marcel Plonus, cmVuZS1tYXJjZWwucGxvbnVzQHVuaS1oYW1idXJnLmRl; ci5wbG9udXNAd2ViLmRl