Freshwater Composition and Connectivity of the Connecticut River Plume During Ambient Flood Tides

Introduction

Rivers deliver terrestrial freshwater, nutrients, sediments, and contaminants to the marine environment (Meybeck, 2003). River plumes influence the physical dynamics, biogeochemistry, ecosystems and fisheries in coastal and open-ocean waters (e.g., Dittmar and Kattner, 2003; Hickey et al., 2010; Grimes, 2001). Due to these manifold effects on the marine environment, it is critically important to continue studying and improving the understanding of river plumes. The structure, mixing, and transport of river plumes has been studied extensively, as described in several research reviews (O’Donnell, 2010; Chant, 2011; Hetland and Hsu, 2013; Horner-Devine et al., 2015). Particular attention has been devoted to the main plume front, a region characterized by strong surface convergence, downwelling, and mixing of the plume with ambient waters (e.g., Garvine, 1974a; Garvine and Munk, 1974; O’Donnell et al., 1998; Marmorino and Trump, 2000; Orton and Jay, 2005). Flow within the plume can overtake the propagating plume front, thereby creating a large intake region of plume waters that interacts with the front (e.g., Garvine, 1974a; Mazzini and Chant, 2016). This connectivity with the front can extend all the way back to the river mouth, can be short-circuited by developing interior fronts, or can be limited by many other processes including tides, winds, ambient currents, and changing source conditions (e.g., McClimans, 1978; Garvine, 1984; O’Donnell, 2010; Chant, 2011; Huguenard et al., 2016; Cole et al., 2020). The degree of connectivity between river source waters and bounding fronts merits further study. The degree of source-front connectivity likely varies considerably for different plumes and forcing situations. The approach of Cole et al. (2020) provides guidance for plume connectivity studies. The transport, mixing, and trapping of pollutants, sediments, nutrients, and plankton within the plume is influenced by when and where source waters reach the plume front. Thus, identifying times and locations of particularly strong or weak source-front connectivity within plumes is important for understanding coastal biogeochemical distributions.

Tides modulate many river plumes. Strong tidal currents within rivers can reverse flow, preventing freshwater from exiting the mouth during river flood tides and intensifying freshwater outflow during ebbs. Two well-studied examples of ebb-pulsed plumes entering ambient environments with weaker tides are the Columbia River (e.g., Cudaback and Jay, 1996; Hickey et al., 1998; Horner-Devine et al., 2009; Nash et al., 2009; Kilcher and Nash, 2010; Akan et al., 2018) and the Merrimack River (e.g., MacDonald et al., 2007; Hetland and MacDonald, 2008; Chen et al., 2009; Kakoulaki et al., 2014; Cole et al., 2020). Ebb-pulse outflows also have been studied for smaller plumes (e.g., Luketina and Imberger, 1987; Pritchard and Huntley, 2006). Other tidal plumes are swept back and forth by strong ambient tidal currents in the receiving waters of the adjacent estuary, sea, or continental shelf (e.g., Spicer et al., 2021). The combination of tidally pulsed outflows through the mouth and swift ambient tidal currents along the coast can cut off plume waters from the river source and create a series of discrete tidal plume pulses (de Ruijter et al., 1997). Two formative examples are the Connecticut River plume (e.g., Garvine, 1974b; Garvine and Munk, 1974; Garvine, 1977; O’Donnell et al., 1998; Ackelson and O’Donnell, 2011; Jia and Whitney, 2019) and the Rhine region of freshwater influence (e.g., van Alphen et al., 1988; Simpson and Souza, 1995; de Ruijter et al., 1997; Hessner et al., 2001). Flow reversals and mixing by strong ambient tides also have been studied for smaller plumes (e.g., Bricker et al., 2006; Basdurak et al., 2020). Plume connectivity and overall behavior in these situations depends on the relative magnitudes of the subtidal mouth outflow velocity, plume propagation speed (scaled by the internal wave speed), and river and ambient tidal current amplitudes as well as the relative phasing of river and ambient tides. These factors influence which portions of the tidal cycle have a plume fed by source waters, a plume starved or cut off from the source, or no plume at all.

The present study investigates the composition of and connectivity within the Connecticut River plume, an important example of plumes influences by strong ambient tides. The Connecticut, named after a Native American word meaning ‘on the long tidal river’ (Trumbull, 1881), is the largest freshwater source flowing into Long Island Sound (LIS, Figure 1A). Average annual discharge (from 2009 to 2019) is 600 m³/s and average monthly discharge ranges from 1294 m³/s in April down to 304 m³/s in September (USGS 01193050, Middle Haddam, CT). The Connecticut River has a tidal salt-wedge estuary with a salinity intrusion that typically extends 5–15 km from the mouth (Meade, 1966; Garvine, 1975; Ralston et al., 2017). The navigational channel is bounded by two jetties (collectively referred to as the Saybrook Jetty) extending beyond the mouth (Figure 1B). Planetary vorticity (f = 9.6 × 10^–5 s^–1) does not exert a strong influence on the mouth outflow, indicated by a large Rossby number associated with the relatively fast outflow velocities O(0.1–1 m/s) through the 1 km wide mouth. Plume waters enter into the ambient macrotidal environment of eastern LIS, where tidal currents are O(1 m/s) with substantial spring-neap variability (O’Donnell et al., 2014). Ambient tides are predominantly rectilinear and shore-parallel near the coast, but have more ellipticity in the deeper waters farther offshore within the Sound (Bennett et al., 2010). Tides advect plume waters eastward during ambient ebbs and westward during flood tides (Garvine, 1974b; Garvine and Munk, 1974). The present study focuses on the plume that forms during ambient flood tides. During this tidal stage, the plume can pass over Long Sand Shoal, which is within 5 km from shore and stretches 10 km westward from the river mouth (Figure 1B; Ellis and Gen, 1874; Poppe et al., 2000). Higher river discharge decreases salinities and increases the extent of the plume (Figures 2A,B; Garvine, 1974b). After high discharge events (e.g., tropical storm Irene flooding), coherent plumes formed during prior tidal cycles are evident farther offshore (Figure 2C; Whitney et al., 2014). Connecticut River water persists in LIS after it is no longer part of a dynamically distinct tidal river plume. Some of its freshwater joins the LIS estuarine outflow and progresses through Block Island Sound onto the continental shelf within several days (Jia and Whitney, 2019). The rest of the Connecticut River water takes longer months-long routes through LIS, where it comprises most of the freshwater residing in the large estuary (Deignan-Schmidt and Whitney, 2018; Jia and Whitney, 2019). Despite the many studies on the Connecticut River plume, the degree of connectivity between the front and the rest of the plume is still unknown. Early models imply connectivity extending from the front all the way back to the river source (Garvine, 1974a; 1984). This high connectivity may be representative of frontal areas near the mouth, such as the upstream front. As the front travels farther from the mouth, however, increasingly large velocities within the plume would be necessary for water to travel from the mouth to the leading edge front before ambient tidal conditions switch from flood to ebb (or vice versa). Thus it is probable that less plume water interacts with the downstream front as the plume grows during a tidal cycle, resulting in relatively weak plume-front connectivity as seen for the Merrimack plume (Cole et al., 2020).

FIGURE 1

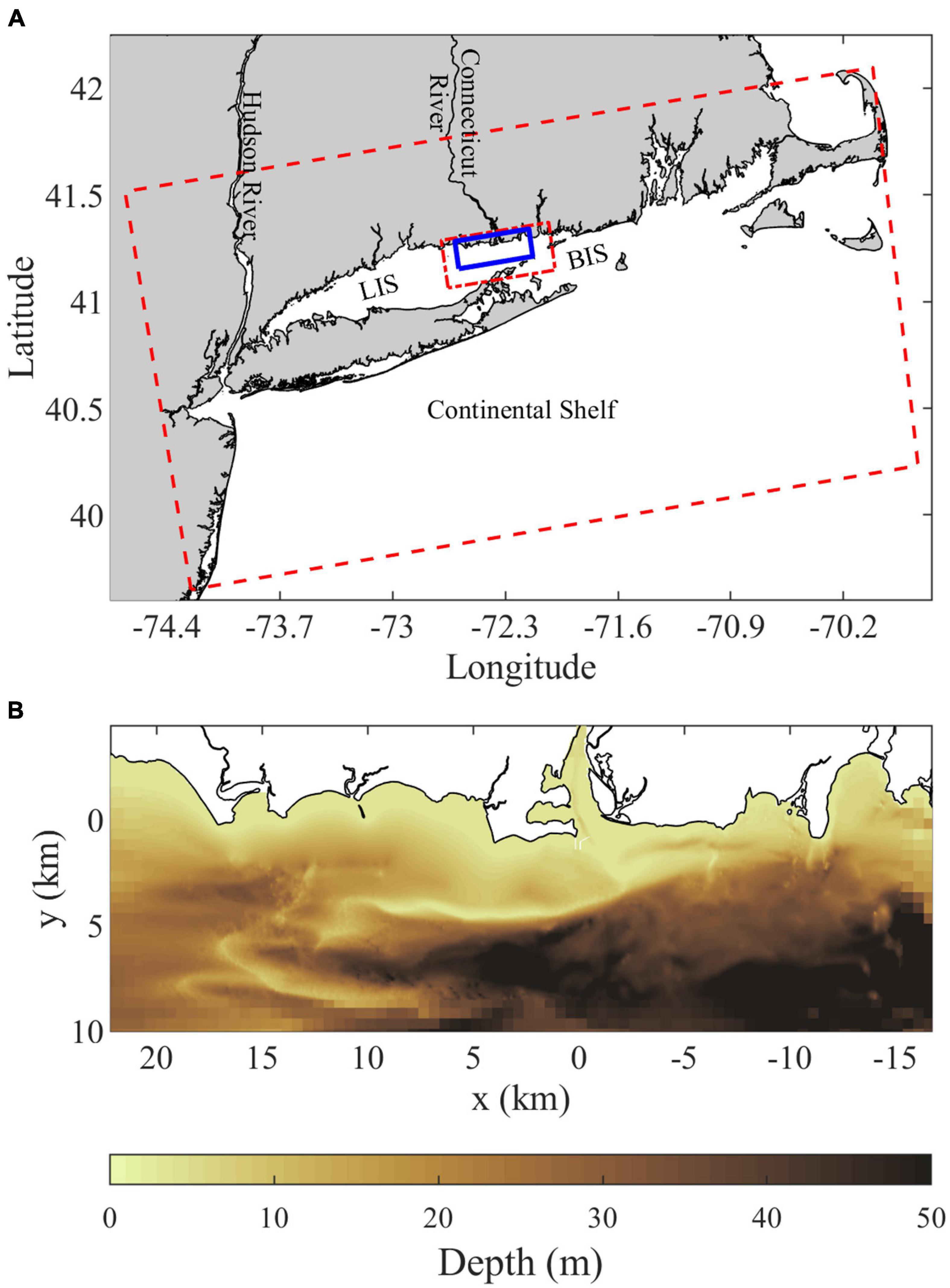
Figure 1. (A) Location map showing the Connecticut River, Long Island Sound (LIS), Block Island Sound (BIS), and the continental shelf along with the outer (dashed red), intermediate (short-long dashed red), and inner highest-resolution (solid blue) grid domains. (B) Bathymetry within the inner grid domain, the Saybrook Jetties immediately outside the Connecticut River mouth show as thin white lines and are land points in the model.

FIGURE 2

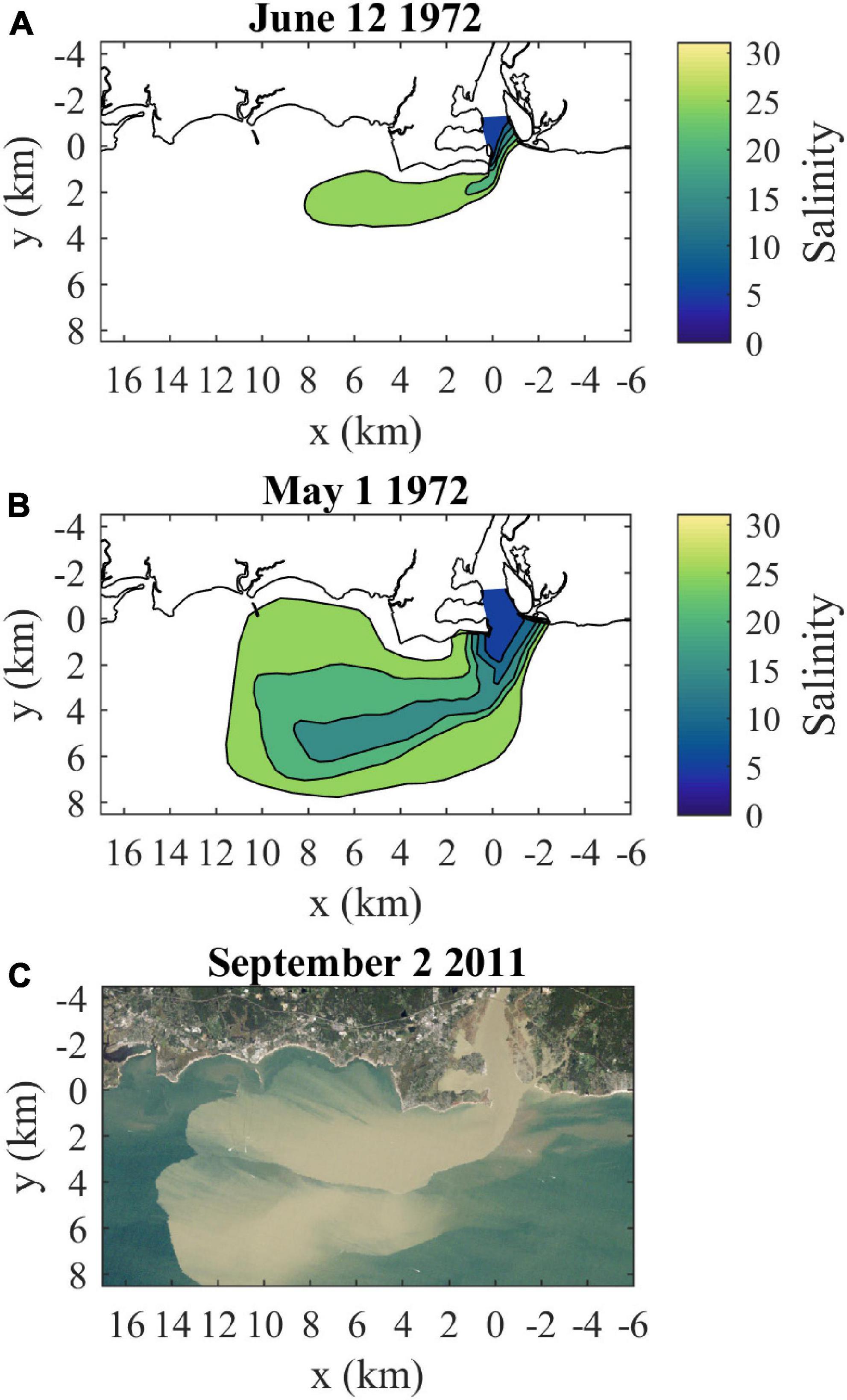
Figure 2. Connecticut River plume observations: (A) surface salinities at high slack (near spring tide) for moderate discharge (720 m³/s) conditions (from Figure 15 in Garvine, 1974b), (B) surface salinities at high slack (near neap tide) for high discharge (1580 m³/s) conditions (from Figure 13b in Garvine, 1974b), and (C) a true-color Landsat 5 satellite image coincident with max ambient flood tide (near spring tide) during high discharge (1633 m³/s) and sediment load from tropical storm Irene (from Figure 2 in Whitney et al., 2014). Discharges in parentheses are daily data from USGS station 01184000 (Thompsonville, CT) multiplied by 1.086 to represent total Connecticut River discharge. The salinity contour interval is 5, as in Garvine (1974b).

The main objectives of this study on the Connecticut River plume formed during ambient flood tidal conditions are: 1) determining the contributions of river source waters from different parts of the tidal cycle and 2) quantifying the degree and spatial distribution of connectivity of these source waters with the bounding plume fronts. A high-resolution numerical modeling approach is taken. The character of the tidal plume will be described to provide context for the subsequent analysis. Conservative passive freshwater tracers are employed as a key tool for studying plume composition and connectivity. A tracer variance budget also is applied to describe how the plume entrains waters and is mixed during the tidal cycle. The main case with low discharge during neap tides is compared to other cases with higher discharge and/or spring tides. Results are discussed relative to other plumes in weaker ambient tidal environments to emphasize how strong ambient tides can reshape the plume and patterns of source-front connectivity.

Materials and Methods

Model Setup

The Regional Ocean Modeling System (ROMS, Haidvogel et al., 2000, 2008) is applied to model the Connecticut River plume and surrounding waters. ROMS is a free-surface, hydrostatic, primitive-equation model that evolves the governing momentum, mass, and tracer conservation equations in finite-differenced form. The applied advection schemes are 3rd-order upstream for 3D momentum, 4th-order centered for 2D (depth-averaged) and vertical momentum, and the Wu and Zho (2010) 3rd-order scheme for salinity, temperature, and passive tracers. Vertical turbulent viscosity and diffusivity are parameterized with the generic length scale method k-epsilon closure scheme. Note that salinity is calculated with the Practical Salinity Scale, thus reported salinities are dimensionless.

The outer (mother) grid domain includes the tidal extent of the Connecticut River (and other rivers), LIS, Block Island Sound, and a large portion of the adjacent continental shelf (Figure 1A). Full details of the outer model configuration are included in Jia and Whitney (2019). The horizontal resolution is 500 m within LIS and vertical resolution is supplied by 30 sigma levels evenly distributed through the water column. Outer model bathymetry is derived from the NOAA 3 arc-second United States Coastal Relief Model. The outer model is forced along the open ocean boundaries with eight semi-diurnal and diurnal tidal coefficients from the OSU TOPEX/Poseidon Global Inverse Solution (Egbert and Erofeeva, 2002) and subtidal velocities, temperatures, and salinities from the Hybrid Coordinate Ocean Model (Chassignet et al., 2008). Chapman (1985) and Flather (1976) boundary conditions are applied for surface elevation and 2D velocities along the open boundaries. Radiation with nudging open boundary conditions are applied for 3D velocities, temperature, and salinity. Surface winds, humidity, air temperature, surface pressure, net shortwave radiation, and downward longwave radiation are supplied by the North American Regional Reanalysis (NARR, Mesinger et al., 2006). Bulk flux formulae (Fairall et al., 2003) are applied within ROMS to compute surface fluxes of momentum and sensible, latent, and longwave heat. Jia and Whitney (2019) describe how the NARR temperatures were modified to better align with NOAA buoy observations. Daily river discharge for the Connecticut and 78 other rivers are derived from USGS streamgage records. Jia and Whitney (2019) validated tidal performance with tidal harmonic analysis at NOAA coastal stations along LIS and with depth-averaged tidal current observations throughout LIS (Bennett et al., 2010).

This study adds a nested intermediate grid with 100 m resolution and an inner grid with 20 m horizontal resolution covering the lower Connecticut River estuary and the tidal plume region (Figure 1A). The nested runs are initialized with a mother grid simulation that spans at least 2.5 years prior to nesting. The nested runs each are evolved for only 1.5 days, these short runs are sufficient to capture the intratidal evolution of the plume. Light wind periods are selected and then wind stress is set to zero to remove all immediate wind influence during the short nested runs. Four cases are analyzed that are combinations of low and high discharge and neap and spring tides. Connecticut River discharge (Q_R) is set at 250 and 1500 m³/s for low and high discharge cases, respectively. The dates and details of these cases are summarized in Table 1. The low discharge and neap tide case is analyzed in greatest detail as it produces the most compact plume and pairs with new observational efforts. Instantaneous fields (in ROMS ‘history’ files) output at 20-min intervals are analyzed. Results are mapped on an x-y grid with the origin at center channel of the river mouth, the positive x axis is oriented along the coast in the direction of LIS flood tides (approximately west-southwestward), and the positive y axis is pointed down-river and offshore (approximately south-southeastward) (Figure 1).

TABLE 1

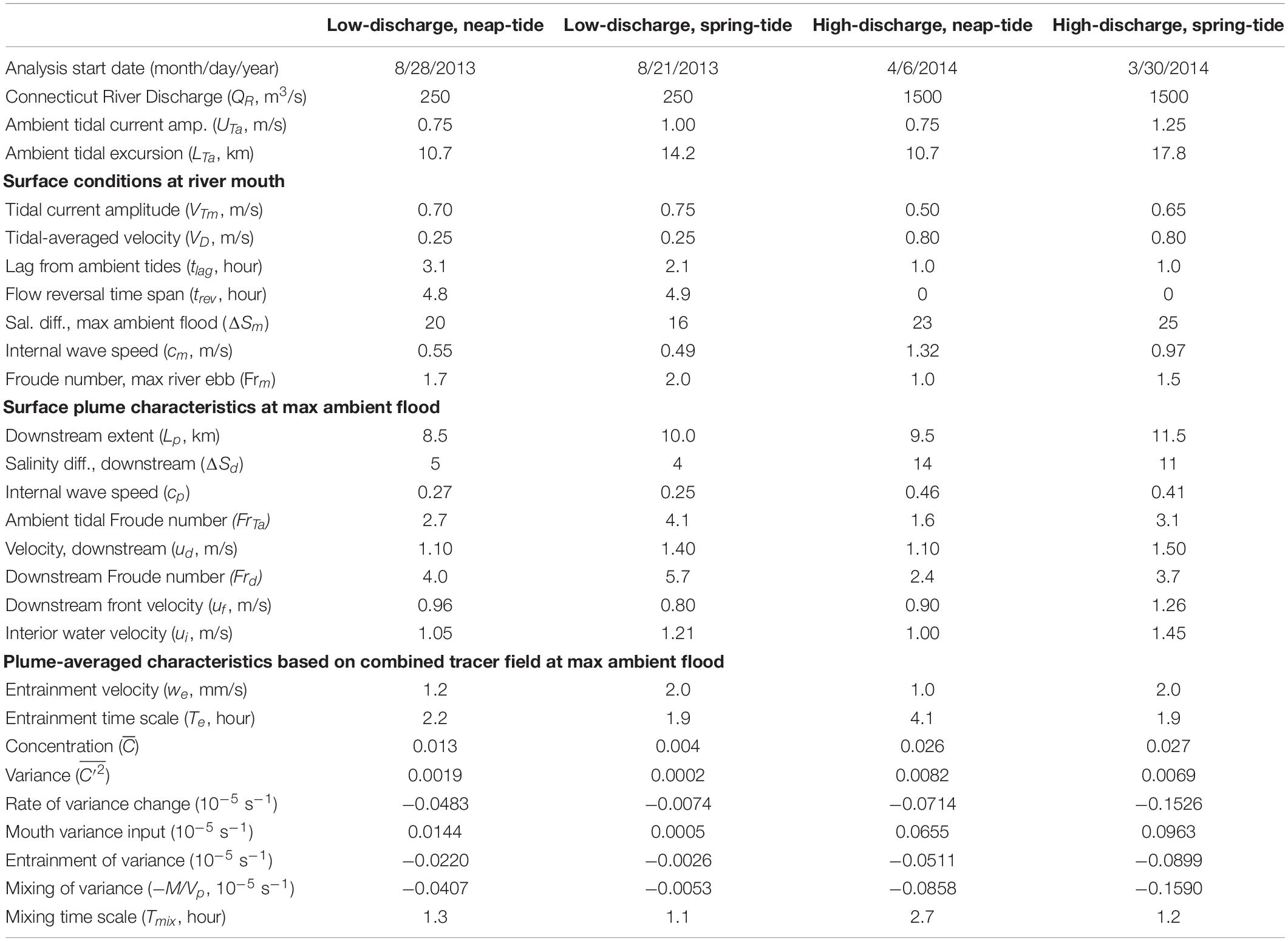
Table 1. Comparison of nested model runs: forcing, surface mouth and plume characteristics, and plume-averaged quantities.

Freshwater Tracers and Plume Characteristics

Freshwaters from the Connecticut River are tracked with conservative passive tracers using the tracer routines included within ROMS. The passive tracers are evolved in the Eulerian framework and are akin to continuous dye fields. Tracer concentrations are normalized so that they represent the fraction of the tracked freshwater. Individual freshwater tracers are released at an hourly interval spanning a tidal cycle. Each tracer is imposed as an hour-long release at the up-river boundary of the inner grid (4 km up-river from the mouth) with the same volume flux and freshwater fraction of the Connecticut River waters flowing through the boundary over the release time interval. There are no other interior or boundary tracer sources. There are no tracer sinks; therefore, concentrations of these conservative passive tracers decrease only through dilution. The hourly tracers are summed to create a combined tracer that tracks all the recently discharged Connecticut River freshwater within the plume. Plume waters are identified as including all locations (both horizontal and vertical) outside of the Connecticut River mouth where the combined freshwater tracer concentration exceeds a low threshold value (C₀) set to 10^–6 for standard analysis. In practice, the plume boundaries change little with an order of magnitude increase or decrease of C₀ because of typically sharp concentration gradients at plume fronts. Plume volume (V_p) and area at the surface (A_p) are calculated within the plume boundaries. The average plume depth (H_p) can be calculated as V_p/A_p. Plume length (L_p) is calculated as the farthest downstream extent of the tracer plume. The plume width (W_p) is reported as the farthest offshore extent of the main plume marked by a sharp surface front and does not include more diffuse tracer waters farther offshore that are included within V_p. Plume perimeter (P_p) is calculated as the total length of the plume boundary at the surface. The composition of plume boundary points in terms of individual freshwater tracers is used to quantify connectivity between the plume fronts and source waters released at different times of the tidal cycle.

Plume volume changes due to the volume flux through the mouth (Q_m, with positive into the plume) and entrainment volume flux into the plume (Q_e, positive into the plume):

$$\frac{d{V}_p}{dt}=Q_m+Q_e(1)$$

Q_m is calculated as the section integral of the v velocity component through the mouth where there is tracer (with higher concentration than C₀), operationally v is multiplied by a binary coefficient that is set to one if the tracer is present above the concentration threshold and zero otherwise. The instantaneous Q_m can either be into or out of the plume, but represents a net source to the plume overall. The entrainment flux adds water with zero tracer concentration to the plume. V_p, its rate of change dV_p/dt, and Q_m are calculated directly from model output fields and Q_e is solved for as the unknown in (1). The plume-averaged entrainment velocity (w_e) is calculated by dividing Q_e by the plume surface area:

$$w_e=\frac{1}{A_p}\left(\frac{d{V}_p}{dt}-Q_m\right)(2)$$

Note that, despite the suggestive notation, entrainment does not have to occur exclusively through vertical velocities; entrainment velocities are locally normal to plume boundaries. The analysis is completed with the combined tracer to represent conditions for the entire plume. Individual hourly tracer fields identify the plume regions associated with source waters distinguished by river release time. Thus, corresponding analysis of individual hourly tracers indicates the entrainment within different parts of the plume.

Freshwater Tracer Variance Budgets

Analysis of salinity variance has been applied to studying mixing in estuaries and coastal waters (e.g., Burchard and Rennau, 2008; Li et al., 2018; MacCready et al., 2018; Wang and Geyer, 2018; Burchard, 2020; Warner et al., 2020). Analogous tracer variance analysis is applied to the freshwater tracers described above. The first step is decomposing tracer concentration (C) into a spatial-mean value ($\overline{C}$) and deviations from the mean (C′) such that $C=\overline{C}+C^{\prime }$. The tracer variance is defined as ${\left(C-\overline{C}\right)}^2$ which equals $C^{\prime }{}^2$. The spatial mean may be taken over a fixed volume (e.g., an estuary or part of a continental shelf) or a time-varying volume tracking a water mass (e.g., a river plume). Most prior published examples analyze fixed volumes extending throughout the water column, whereas the present analysis considers expanding control volumes encompassing river plumes. In this application, the plume control volume (V_p) is the region with freshwater tracer concentrations above the threshold value (C₀ = 10^–6, as described above). The control volume only extends throughout the water column where the plume interacts with the bottom, otherwise there is a sub-surface interface between plume and ambient waters. The plume-averaged concentration ($\overline{C}$) is calculated as:

$$\overline{C}=\frac{1}{V_p}\int C\mathit{d}{V}_p(3)$$

Following MacCready et al. (2018), the volume-integrated tracer variance budget is:

$$\frac{d}{dt}\int C^{\prime }{}^2\mathit{d}{V}_p=-\int u_n{C}^{{}^{\prime }2}\mathit{d}{A}_b-\int 2K{(\nabla {\text{C}}^{{}^{\prime }})}^2\mathit{d}{V}_p(4)$$

where, u_n is the outward normal velocity through the bounding area (A_b) of the control volume, K is the eddy diffusivity, and ∇⁡C′ is the concentration gradient. K is written as a scalar in (4) for simplicity (as in MacCready et al., 2018), but a more detailed representation involves a diagonal diffusivity tensor with different horizontal and vertical eddy diffusivities (e.g., Li et al., 2018). Alternately, horizontal diffusion is sometimes considered negligible and only vertical diffusion is included (e.g., Warner et al., 2020). The final integrand in (4) represents the tracer mixing per unit volume; it is symbolized with χ in some prior studies (e.g., Wang and Geyer, 2018; Burchard, 2020). The term on the left-hand side of (4) can change both because of tracer variance changes and plume volume changes. The first term on the right-hand side of (4) is the advective transport of variance through the control volume boundaries. Note that (4), does not include a term representing diffusive transport of tracer variance across the boundary between the plume and ambient waters. This diffusive transport is implicitly considered negligible relative to advective transport in (4), but the diffusive transport of tracer variance is considered in other studies (e.g., Burchard, 2020; Wang et al., 2021). The final term in (4) is the dissipation of variance by mixing inside the control volume; it can be symbolized as –M for ‘mixing’; M is positive definite. The M notation follows MacCready et al. (2018) except in that study M is a tidal-averaged quantity, whereas here it is tidally varying. In the present application, M is calculated (as described below) such that it includes vertical and horizontal physical mixing as well as numerical diffusion arising from discretization errors associated with the advection scheme (Burchard and Rennau, 2008).

For the plume control volume, transport through the plume boundaries can be partitioned into contributions through the river mouth and by plume entrainment. The mouth will tend to have higher concentrations than the plume and therefore have a strong tracer variance signature. With an outflow through the mouth cross-sectional area (A_m) and into the tracer plume, the velocity through the mouth (v_m) is positive and adds both volume and tracer variance to the plume. Entrained water comes from outside the tracer plume and its tracer concentration equals the low threshold value (C₀). The corresponding variance of entrained water is $C^{\prime }{}_e{}^2={\left(C_0-\overline{C}\right)}^2$ and the entrainment tracer variance flux is $C^{\prime }{}_e{}^2{Q}_e$, a positive flux. Substituting this information into (4), the volume-integrated tracer budget for the tracer plume is:

$$\frac{d}{dt}\int C^{\prime }{}^2\mathit{d}{V}_p=+\int v_m{C}^{{}^{\prime }2}\mathit{d}{A}_m+C^{\prime }{}_e{}^2{Q}_e-M(5)$$

Note that, $C_0\ll \overline{C}$ since an exceedingly small C₀ has been selected (i.e., the entrained water has nearly zero tracer concentration) and $C^{\prime }{}_e{}^2\approx {\overline{C}}^2$. Therefore, the entrainment tracer variance flux is approximately ${\overline{C}}^2{Q}_e$. This approximation is used when describing results and discussing generalization of tracer variance budgets for other plumes. In summary, (5) indicates that river inputs and entrainment both increase volume-integrated variance, while mixing within the plume reduces it.

Analyzing the volume-averaged (rather than volume-integrated) budget provides a different perspective that isolates changes in tracer variance and facilitates intercomparison of results for different plumes. A first step is defining the volume-averaged variance:

$$\overline{C^{\prime }{}^2}=\frac{1}{V_p}\int C^{\prime }{}^2\mathit{d}{V}_p(6)$$

With this definition, the term on the left-hand side of (5) can be expressed as the time derivative of the product of the volume-averaged variance and plume volume (7, the intermediate step). Then the product rule for derivatives can be applied and the plume volume budget (1) can be substituted to separately show the contributions associated with changing volume-averaged tracer variance, mouth volume inputs, and entrained volume flux (7).

$$\frac{d}{dt}\int C^{\prime }{}^2\mathit{d}{V}_p=\frac{d}{dt}\left(\overline{C^{\prime }{}^2}{V}_p\right)=V_p\frac{d}{dt}\overline{C^{\prime }{}^2}+\overline{C^{\prime }{}^2}{Q}_m+\overline{C^{\prime }{}^2}{Q}_e(7)$$

It also is useful to define the flux-weighted average tracer variance at the mouth:

$$C^{\prime }{}_m{}^2=\frac{1}{Q_m}\int v_{m}C^{\prime }{}^2\mathit{d}{A}_m(8)$$

With this definition, the first term on the right-hand side of (5) can be expressed as:

$$\int v_m{C}^{{}^{\prime }2}\mathit{d}{A}_m=C^{\prime }{}_m{}^2{Q}_m(9)$$

Dividing the volume-integrated tracer variance budget (5) by V_p and substituting in expressions from (6), (7), (8), and (9) yields the volume-averaged tracer variance budget:

$$\frac{d}{dt}\overline{C^{\prime }{}^2}=+\left(C^{\prime }{}_m{}^2-\overline{C^{\prime }{}^2}\right)\frac{Q_m}{V_p}+\left(C^{\prime }{}_e{}^2-\overline{C^{\prime }{}^2}\right)\frac{Q_e}{V_p}-\frac{M}{V_p}(10)$$

It can be seen from this balance that a volume source from the mouth tends to increase plume-averaged tracer variance as long as there is higher variance at the mouth ($C^{\prime }{}_m{}^2/\overline{C^{\prime }{}^2}$ >1), as would be the case for high-concentration source waters. Since $C^{\prime }{}_e{}^2$ is approximately ${\overline{C}}^2$ for small C₀, entrainment will tend to increase plume-averaged tracer variance when the variance is smaller than plume-averaged concentration squared ($\overline{C^{\prime }{}^2}/{\overline{C}}^2$ <1); otherwise $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ >1 and the entrainment term is negative and tends to decrease $\overline{C^{\prime }{}^2}$. The mixing term is simply divided by V_p and remains negative as it represents the internal destruction of tracer variance. The relationship between (5) and (10) is similar to the relationship between heat and temperature budgets in the sense that any net advective inflow will increase heat and volume-integrated tracer variance yet the same inflow can either increase or decrease temperature and volume-averaged tracer variance depending on whether the inflow has higher or lower scalar values than the control-volume average. Both perspectives are useful, but the volume-averaged budget (10) is analyzed in this study to focus on tracer variance changes.

The model provides the information to directly calculate all terms in tracer variance balances (5) and (10). The computational approach in this study applies model results to directly calculate all but the final term in (5) and (10). Then M is solved as the unknown in (5) and divided by V_p for the final term in (10). This calculation method for M ensures that the tracer variance budget closes exactly and that M represents the total mixing in the model, which includes physical mixing and numerical mixing from advection scheme discretization errors. Analyzing the combined tracer fields provides the tracer variance budget associated with the entire active plume. Analyzing individual hourly tracers indicates the tracer variance budgets of plume regions associated with different source waters, distinguished by river release time.

Results

Salinity and Velocity

For the standard case with low discharge and neap tides, the along-estuary currents in LIS (2 km east of the river mouth within 4 km from shore) indicate the ambient LIS tidal amplitude (U_Ta) is 0.75 m/s (Figure 3A). With the time origin at the onset of ambient flood tide the time-varying ambient velocity (u_a) can be approximated as:

FIGURE 3

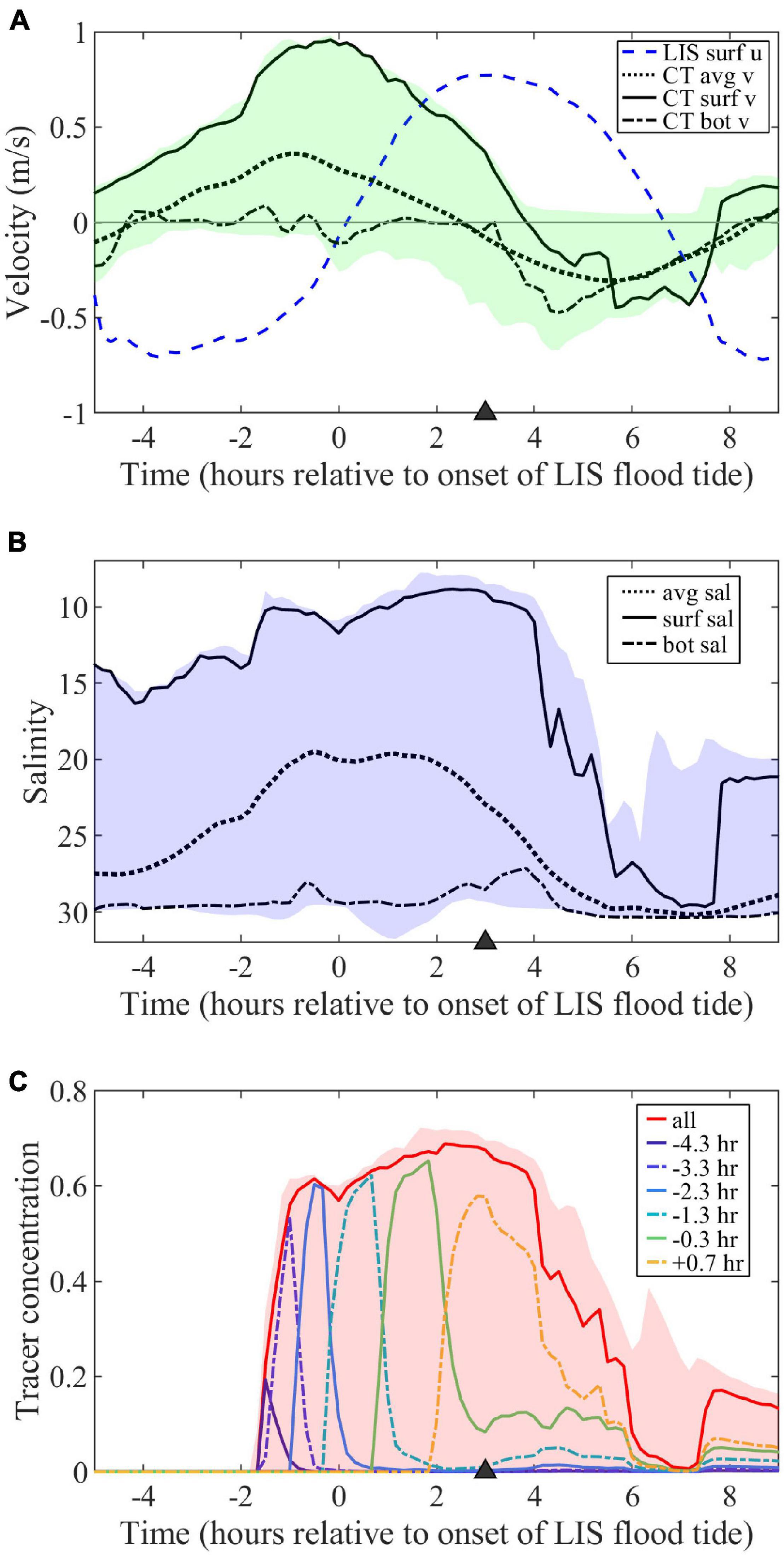
Figure 3. (A) Time series of along-estuary velocity (u, positive for LIS flood tides) at surface in LIS and depth- (avg), surface- (surf), and near-bottom- (bot) averaged across-estuary velocities (v, positive out of mouth) through the Connecticut (CT) River mouth. Shading indicates the v range over the mouth cross-section. (B) Depth-, surface-, and near-bottom-averaged salinities at the mouth with shading indicating the mouth salinity range. (C) Surface freshwater tracer concentrations at the mouth for hourly tracers (labeled according to first release times) and the combination of all hourly tracers (labeled ‘all’) along with the combined tracer range. The triangle (here and in other figures with time series) marks the timing of the max ambient flood surface maps and sections in subsequent figures.

$$u_a=U_{Ta}\text{sin}(\frac{2\mathrm{\pi }}{T}t)(11)$$

where, t is time, T is the tidal period (12.42 h for the dominant semidiurnal lunar tides), and u_a is positive during flood tide. The corresponding ambient tidal excursion (L_Ta = U_TaT/π) is 10.7 km.

The surface flow is outward through the mouth for much of the tidal cycle (Figure 3A). The tidal-averaged surface velocity at the mouth (V_D, following the notation in de Ruijter et al., 1997) is 0.25 m/s and the mouth tidal amplitude (V_Tm) is 0.70 m/s. The V_D/V_Tm ratio is 0.36 and meets the V_D/V_Tm < 1 ‘pinching off criterion’ for flow reversal at the mouth and shutoff of plume source waters (de Ruijter et al., 1997). The surface velocity at the mouth (v_m) can be approximated as the combination of the steady flow and sinusoidal tidal variations:

$$v_m=V_D-V_{Tm}\text{sin}(\frac{2\mathrm{\pi }}{T}(t-t_{lag}))(12)$$

where, t_lag it the lag time of the mouth tides relative to ambient tides, such that a positive lag indicates ambient flood leads the mouth flood tide. Note that v_m is negative while the flood tide reverses the flow to inward through the mouth. The ambient flood tides lead mouth flood tides by approximately $\frac{1}{4}$ of the tidal cycle for this model run (Figure 3A, t_lag = 3.1 h). As found in de Ruijter et al. (1997), trigonometric investigation of (12) indicates the mouth flow reversal time span (t_rev) is:

$$t_{rev}=\frac{T}{\mathrm{\pi }}\text{acos}(V_D/V_{Tm})(13)$$

For this low-discharge neap-tide case, t_rev is 4.8 h; indicating the plume is cut off from source waters for at least 38% of the tidal cycle. Since this study focuses on plumes during ambient flood tides, it is useful to express the time interval when there is a mouth reversal during ambient flood tides. With equations (11), (12), and (13), this mouth-reversal during ambient-flood time interval can be expressed as:

$$\text{max}(0,\frac{T}{4}+t_{lag}-\frac{t_{rev}}{2})<t<\text{min}(\frac{T}{2},\frac{T}{4}+t_{lag}+\frac{t_{rev}}{2})(14)$$

For this model run, flow at the mouth is reversed throughout late ambient flood beginning at t = (T-t_rev)/2 (t = 3.8 h). This indicates the plume is fed by source waters during early and max ambient flood tides, but is cut off from the source during late flood.

Mouth surface-averaged salinity falls from 14.0 to 8.8 throughout mouth ebb tides, then increases to 29.6 near the end of mouth flood (Figure 3B). Bottom-averaged salinities at the mouth remain salty throughout the tidal cycle (27.2–30.4). By the end of mouth ebb, which corresponds to max ambient flood, the bulk vertical salinity difference (ΔS_m, between surface- and bottom-averaged values) is 19.5. The corresponding bulk density difference (Δρ_m) can be approximated as ρ_oβΔS_m (with reference density ρ_o and haline-contraction coefficient β = 7.7 × 10^–4) using a salinity-based linear equation of state. The scale for the first-mode internal wave speed at the mouth (c_m) is (g’h_m)^1/2, where g’ = gΔρ_m/ρ_o, g is gravitational acceleration (9.8 m/s²), and h_m is the upper-layer thickness scale. With the Δρ_m expression, c_m = (gβΔS_mh_m)^1/2. For ΔS_m = 20.0 and h_m = 2 m (representative of mouth conditions), c_m = 0.55 m/s. The internal Froude number associated with the mouth surface outflow is Fr_m = v_m/c_m. The outflow is supercritical during most of mouth ebb with Fr_m reaching 1.7 at max ebb, which is coincident with the onset of ambient flood tide. During early ambient flood tide, Fr_m transitions from supercritical to subcritical prior to mouth flow reversal near max ambient flood.

Near the start of ambient flood tide, the plume has expanded 6 km outward from the mouth with a western (downstream, relative to ambient flood tidal flow) bias in lower salinities, higher velocities, and sharper boundaries (Figure 4A). The flow of low-salinity source waters is bifurcated by Saybrook Jetty outside the mouth and bifurcation effects are evident out to the plume boundary. The lowest salinities on the eastern (upstream) side are within 2 km from the mouth, but more diffuse plume waters associated with the prior ambient ebb extend to 5 km eastward along the coast. The sharp boundary on the downstream side bends around farther offshore and the highest velocities (0.9 m/s) and lowest salinities (20) are near the middle of this front. The Froude number in the downstream frontal zone (Fr_d) exceeds two, for ΔS_d = 8.5 and h_d = 2 m, indicating supercritical flow. Two hours later at max ambient flood (Figure 4B), the plume stretches 8 km downstream (L_p > L_Ta/2), extends 4.5 km offshore, has higher salinities than before, and remains connected to source waters. Velocities within the plume increase downstream from 0.7 to 1.1 m/s and are predominantly westward except the offshore flow near the mouth. The plume is supercritical, the plume internal wave speed (c_p) is 0.27 m/s and Fr_d = 4.0 with ΔS_d = 5.0 and h_d = 2 m. The sum of c_p and U_Ta is consistent with the total plume velocity near the downstream front, indicating plume propagation is superimposed on the ambient currents. The upstream front near the mouth has the sharpest salinity contrast and the ambient flood flow (0.75 m/s) converges with the offshore plume flow. The propagation of the upstream front has been arrested by the opposing tidal flow because the Froude number associated with ambient tides (Fr_Ta = U_Ta/c_p) exceeds one. Plume salinities increase downstream along the offshore boundary, but remain lower than inshore. The downstream front is clearly defined and the plume overtakes the slower ambient waters. Two hours later during late ambient flood (Figure 4C), the plume has extended to 14 km from the mouth (farther than L_Ta) and is bending toward the coast. Flow is reversed at the mouth and velocities increase along the plume to 0.9 m/s near the downstream front, approximately double the weakening ambient tidal flow. The plume, now cut off from source waters, has higher salinities than before and the lowest salinities are in a partially disconnected area (7–14 km downstream), where the minimum salinity is 24.2. The plume remains supercritical, with Fr_d exceeding three for ΔS_d = 4.5 and h_d = 2 m. Two hours later as ambient tides switch to ebb (Figure 4D), the freshwater supply still is cut off and the remnants of the plume are evident. In the plume area, the salinity difference has diminished (ΔS_d < 2.0) and velocities have reversed with the tides.

FIGURE 4

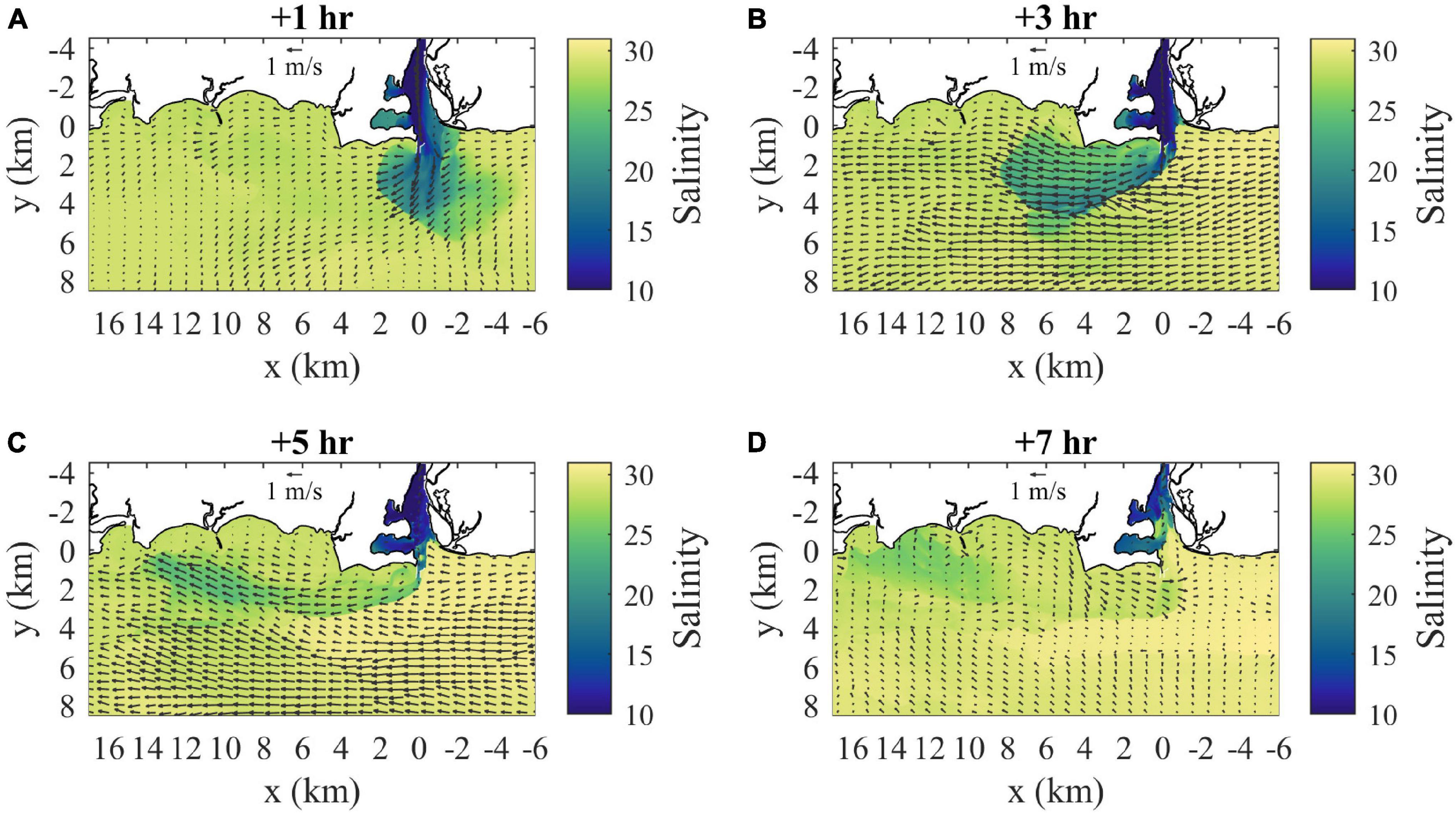
Figure 4. Surface velocity (arrows) and salinity (shaded) maps for (A) 1 h, (B) 3 h, (C) 5 h, and (D) 7 h after the onset of ambient flood tide. Velocity arrows are shown for every 40th point (800 m spacing) and every 20th point (400 m spacing) in x and y, respectively.

Velocities and salinities at max ambient flood tide are examined in further detail in Figures 5, 6, respectively. With a closer view of surface conditions (Figures 5A, 6A), the main plume and ambient flow features can still be seen and a secondary more diffuse plume farther offshore (from y = 4.5 to 8 km) with a convergent downstream front is evident. The mouth velocity field (Figure 6B) indicates the outflow is within 1–2 m from the surface where salinities are lowest (Figure 5B). There is stratification throughout the channel water column. The nearfield section shows the sharp offshore salinity front (Figure 5C) which has strong convergence of the cross-shore flow (Figure 6C). The surface-intensified freshwater layer increases thickness from the coast out to the offshore front, contrary to large-scale buoyancy-driven plumes (e.g., Yankovsky and Chapman, 1997). The salinity front is farther offshore and not as sharp in the farfield section (Figure 5D), but there is still strong flow convergence (Figure 6D). The freshwater layer plunges deeper just inshore of Long Sand Shoal, likely due to plume interaction with bathymetry along the shoal.

FIGURE 5

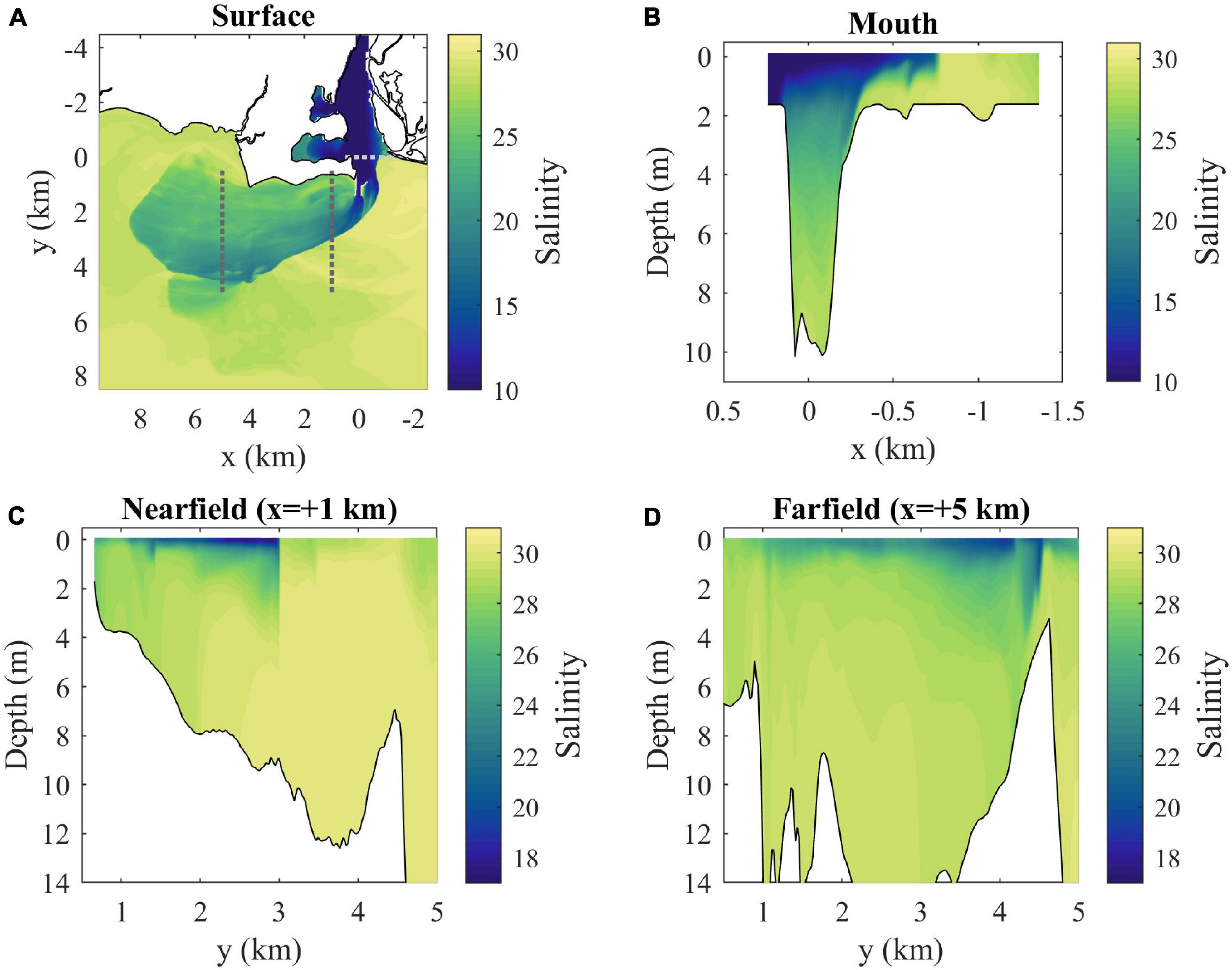
Figure 5. (A) Surface salinity map with locations of cross-sections (dotted lines) and (B) mouth, (C) nearfield, and (D) farfield salinity sections at max ambient flood (3 h after onset of LIS flood tide).

FIGURE 6

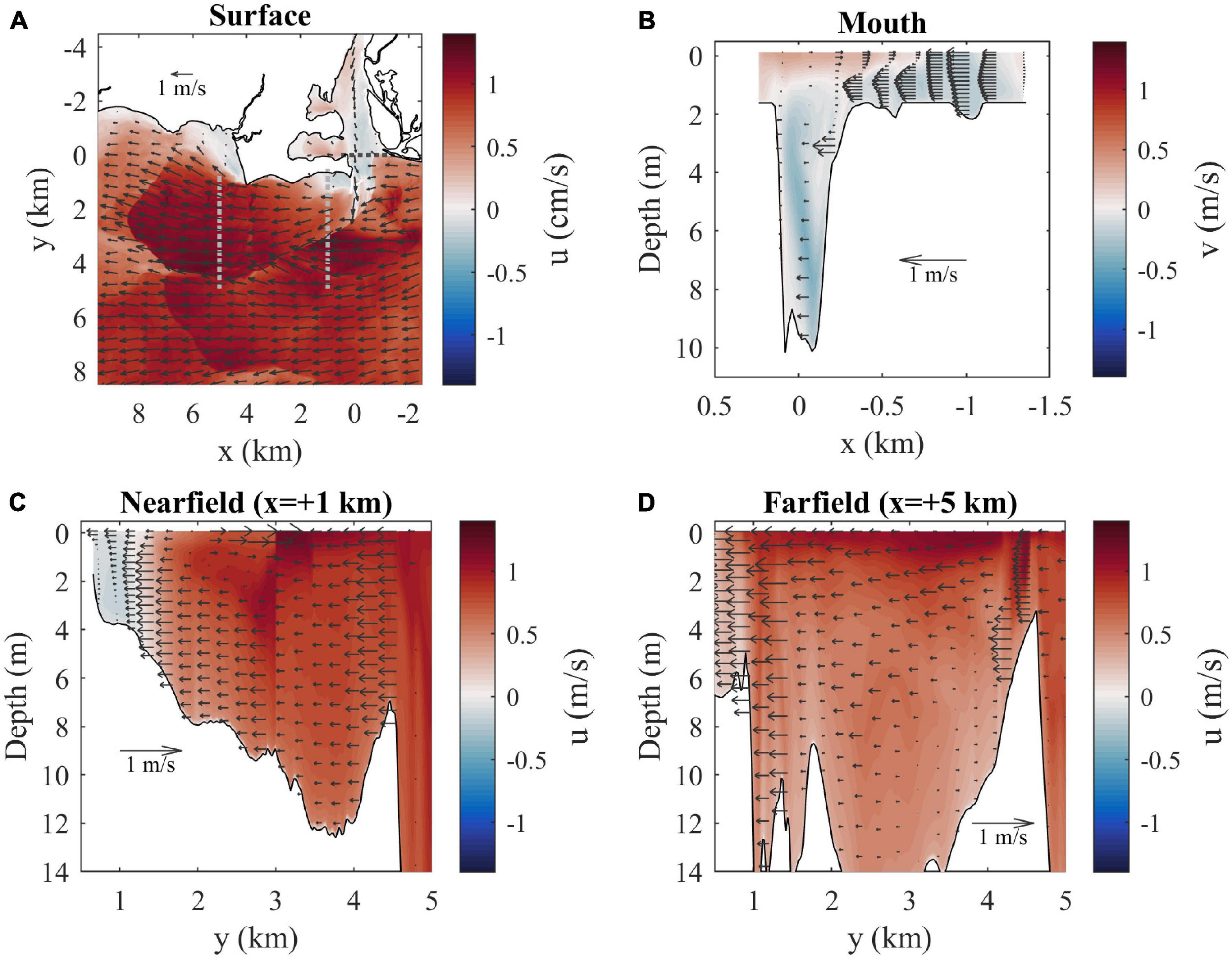
Figure 6. (A) Surface velocity map (u is shaded and arrows indicate horizontal velocity vectors) with locations of cross-sections (dotted lines). Velocity arrows are shown for every 40th point (800 m spacing) and every 20th point (400 m spacing) in x and y, respectively. (B) Mouth, (C) nearfield, and (D) farfield velocity sections (flow through sections is shaded and arrows indicate the horizontal velocity component across sections) at max ambient flood. Horizontal spacing for velocity arrows is every 8th point (160 m) across the mouth and every 12th point (240 m) across the other sections. Vertical spacing for arrows is every other vertical grid point.

Freshwater Tracers

Surface concentrations of freshwater tracers at the mouth (Figure 3C) show the pulses associated with hourly tracer releases. Peak concentrations range from 0.20 to 0.65; the hourly tracers with the highest peak concentrations (>0.60) are mixed less within the river estuary before reaching the mouth. The tracers that first appear at the mouth during early mouth ebb (late ambient ebb) were released during late river flood. Concentrations peak at the mouth about an hour after peaking at the release point 4 km upriver. The final tracer appearing at the mouth was released during late river ebb (early ambient flood). Despite all being imposed as hour-long pulses, the time interval of elevated concentrations at the mouth increases substantially for each subsequent tracer. The combined tracer increases during late ambient ebb, remains high through max ambient flood, and drops through late ebb.

By max ambient flood the plume is composed of a variety of source waters, mostly originally released in the river during ambient ebb tide (Figure 7A). Average freshwater ages are calculated as the time interval between the average tracer release time at each location (determined by the concentration-weighted average of all tracers) and the mapped time (3 h into ambient flood). Freshwater age increases along the plume, with the oldest water (with earliest release time) at the downstream tip. The offshore secondary plume has the oldest waters, indicating it is a relic of the prior ebb plume. Overall, the upstream plume boundary has the youngest freshwater, the downstream boundary has the oldest, and the offshore and inshore boundaries have a downstream progression from younger to older waters. The mouth section (Figure 7B) indicates the outflowing surface layer has the youngest waters. The nearfield section (Figure 7C) shows age decreases toward the offshore front with some vertical variability, whereas the farfield section (Figure 7D) shows less spatial variability in water age.

FIGURE 7

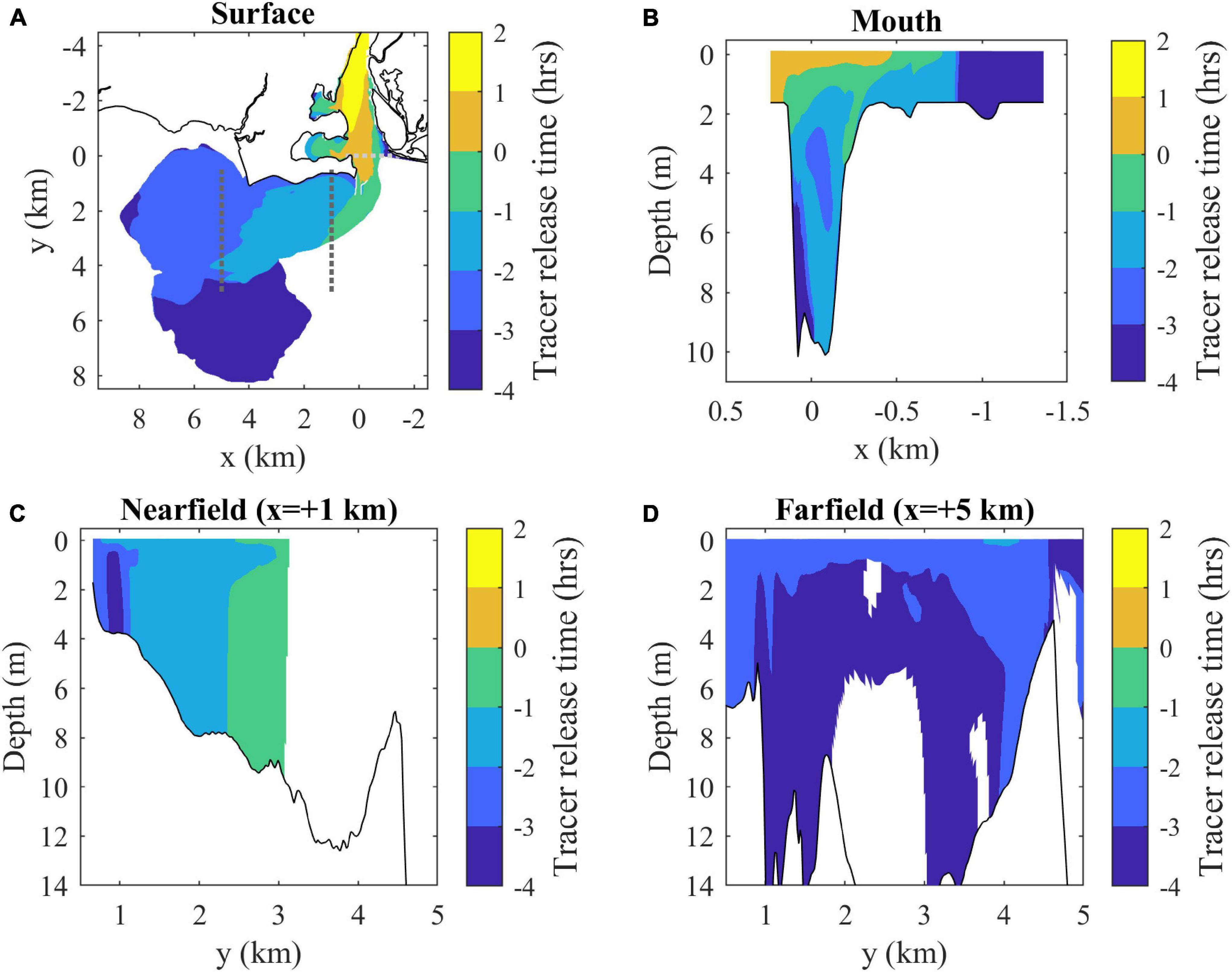
Figure 7. (A) Surface map and (B) mouth, (C) nearfield, and (D) farfield sections of average freshwater composition indicated by average release times of tracers present in each location at max ambient flood. Tracer release times are expressed relative to the onset of ambient flood tides (as in Figure 3). Average freshwater age can be calculated by subtracting the average release times from 3 h (the mapped time). Shaded contouring only includes locations where the combined tracer concentration is above the C₀ = 10^{– 6} threshold.

Higher combined tracer concentrations correspond to lower salinity, so surface concentrations highlight the same plume patterns (Figure 8A) as the surface salinity field (Figure 5A). The texture of plume composition is better seen with maps of the hourly tracers. By max ambient flood, the two tracers introduced during late river flood and exiting the mouth in late ambient ebb (Figure 8B) either are in the secondary offshore plume (a relic of the prior ebb plume) or have been incorporated in the new flood plume. Concentrations increase from <0.001 at the mouth to 0.05 toward the downstream front. These source waters are mostly disconnected from the mouth at this time, but some tracer remains trapped in coves along the river. The two early river ebb tracers, exiting the mouth from late ambient ebb into early ambient flood, (Figure 8C) are distributed throughout the plume and tend to increase in concentration from 0.02 along the coast to 0.12 toward the offshore front. The tracers introduced later in river ebb (Figure 8D) enter the plume later in ambient flood. These tracers are present in highest concentrations (>0.30) near the mouth, particularly along the arrested upstream front, and extend only halfway downstream into the plume. Overall, the downstream half of the plume only includes source waters introduced from late river flood to early river ebb, while the upstream half is composed of a greater variety of source waters with the late river ebb waters at highest concentrations. It is evident that all tracers interact with some portions of the plume boundaries, but the downstream front only sees older waters.

FIGURE 8

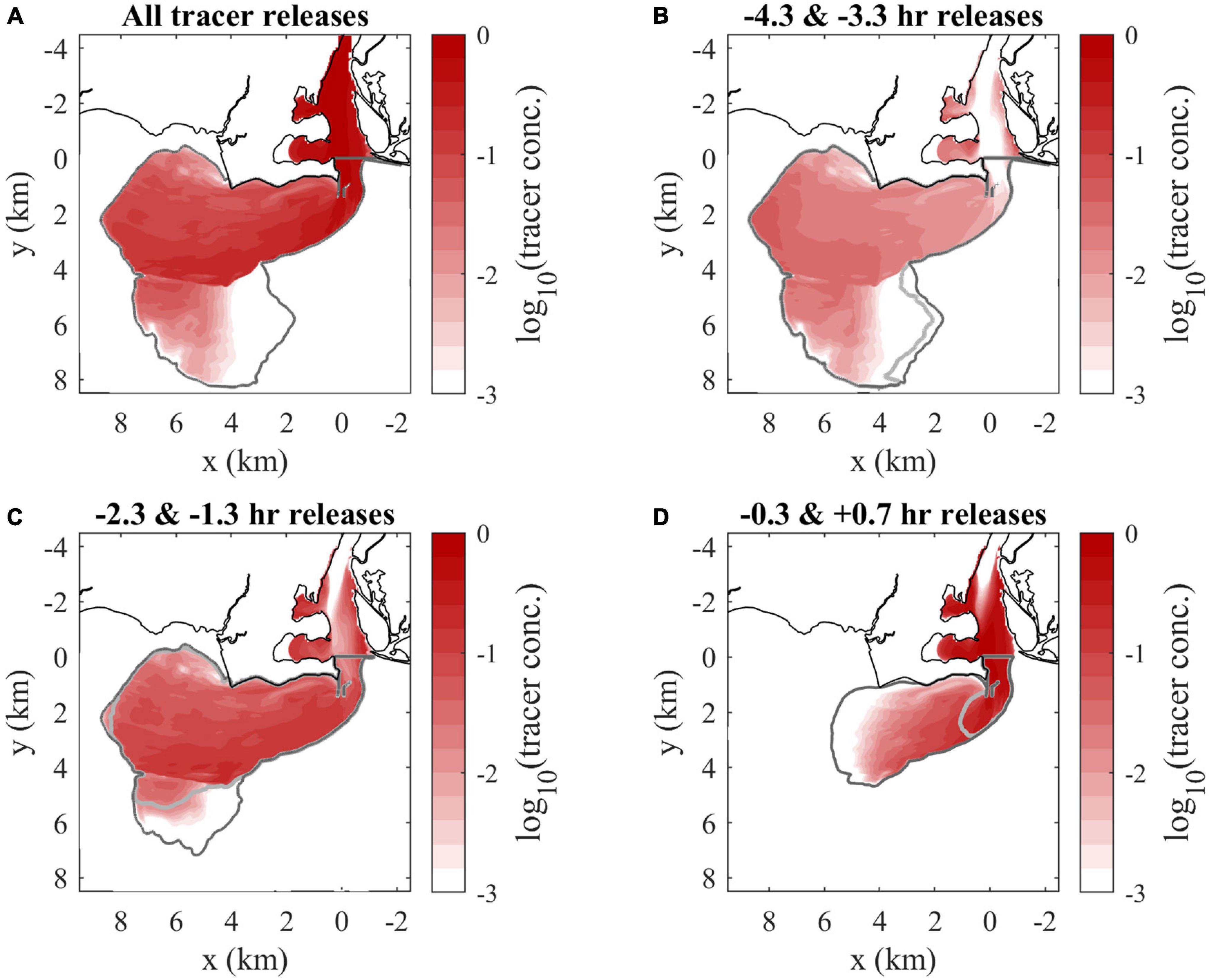
Figure 8. Surface tracer concentration maps at max ambient flood of (A) the combination of all hourly tracers, (B) late river flood releases, (C) early river ebb releases, and (D) max and late river ebb releases. Tracers are designated by first release times (relative to the onset of ambient flood tide). The darker and lighter gray lines indicate the boundaries (the C₀ = 10^{– 6} tracer concentration contour, outside of the river) of the earlier and later releases included in each panel, respectively. Tracer concentrations are shown on a logarithmic scale.

The plume perimeter grows linearly over the ambient flood tidal cycle (Figure 9A). The perimeter of each individual tracer field also approximately grows linearly with time, but the growth rate decreases for later tracers. How much each tracer interacts with plume fronts is quantified by the percent of the plume boundary with each hourly tracer present (Figure 9B). Each tracer goes through an initial period (lasting 1.5 to 3 h) of increasing interaction with plume boundaries. Frontal connectivity is highest for the oldest waters (present when the early ambient flood plume forms), with prevalence at the front exceeding 80%. Frontal connectivity is lowest for the youngest waters (entering as the ambient flood progresses), which interact with only 20% of the plume front. Overall, frontal connectivity is proportional to water age.

FIGURE 9

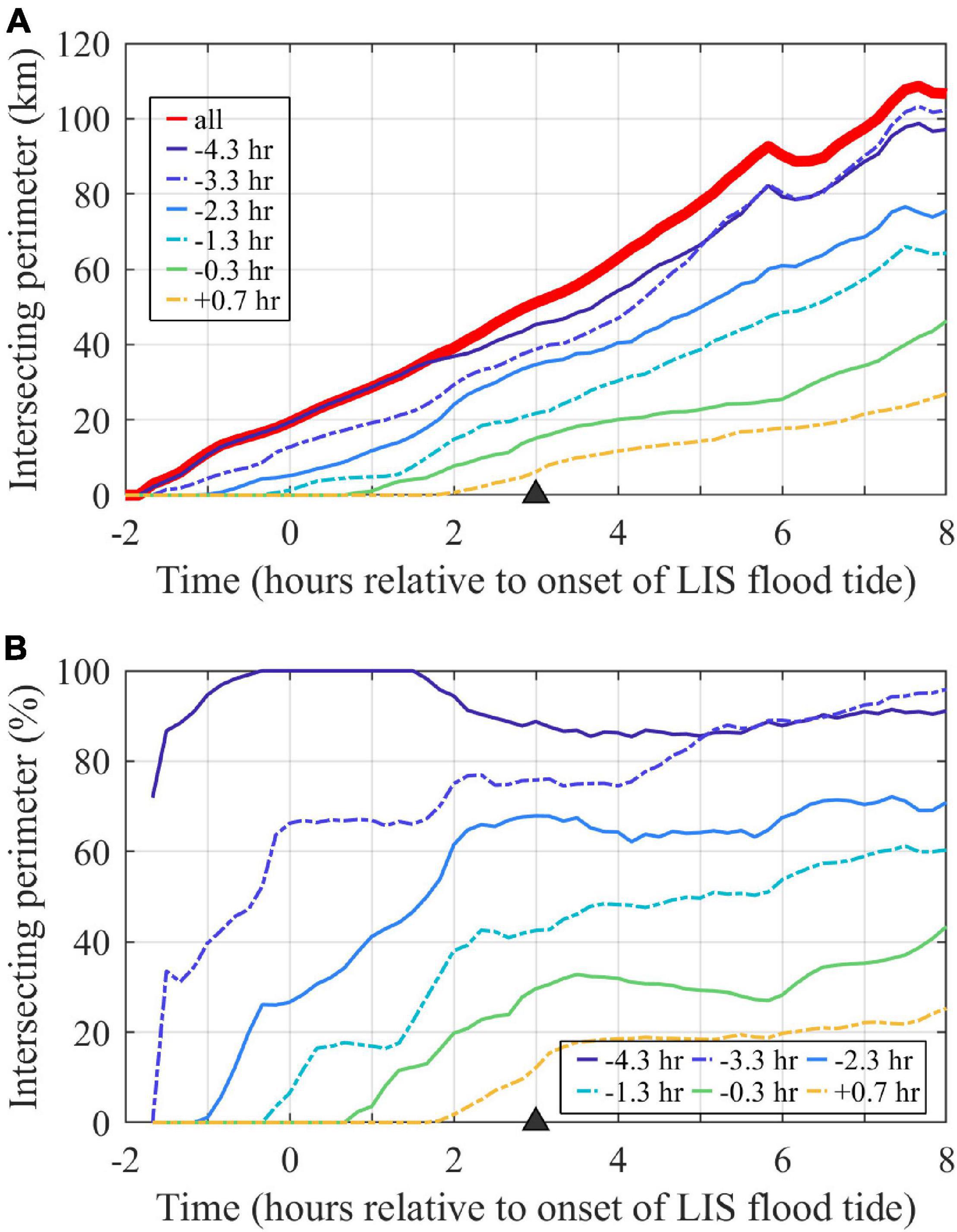
Figure 9. Time series of tracers at the surface plume boundary. (A) The entire plume perimeter is indicated by the perimeter of the combined tracer (labeled ‘all’), as contoured in Figure 8A at the max ambient flood time (marked with a triangle), and each other line shows the portion of the plume perimeter with an hourly tracer present (at least at 10^{– 7} concentration). (B) The percent of the plume perimeter with each hourly tracer present, calculated by dividing time series for each hourly tracer in the upper panel by the plume perimeter time series. Tracers are labeled by first release times.

Tracking the perimeter allows for analysis of downstream front advancement relative to ambient and interior plume waters. At max ambient flood, the downstream front advance velocity (u_f) is 0.96 m/s, which is 0.21 m/s faster than U_Ta and is 94% of U_Ta+c_p. The interior water (the leading edge of the −0.3 h tracer release, Figure 8D) advance velocity (u_i) is 1.05 m/s, which is 0.09 m/s faster than the downstream plume front is advancing. Thus, the plume front is overtaking ambient water while interior waters are more gradually closing the gap at relative velocity u_i -u_f. The interior waters, however, are not traveling quickly enough to reach the downstream plume front by the end of ambient flood.

Plume volume (Figure 10A) grows at an increasing rate over time throughout ambient flood tide, reflecting a combination of plume lengthening, widening, and deepening. As for perimeters, the volumes and increase rates of individual tracers are higher for earlier tracer releases than later ones. Following (1), plume volumes increase only due to entering source waters and entraining ambient waters. After source inputs are shutoff (when Q_m = 0), plume volume exponentially increases due only to entrainment with an e-folding time scale (T_e) equal to the average plume depth divided by the entrainment velocity:

FIGURE 10

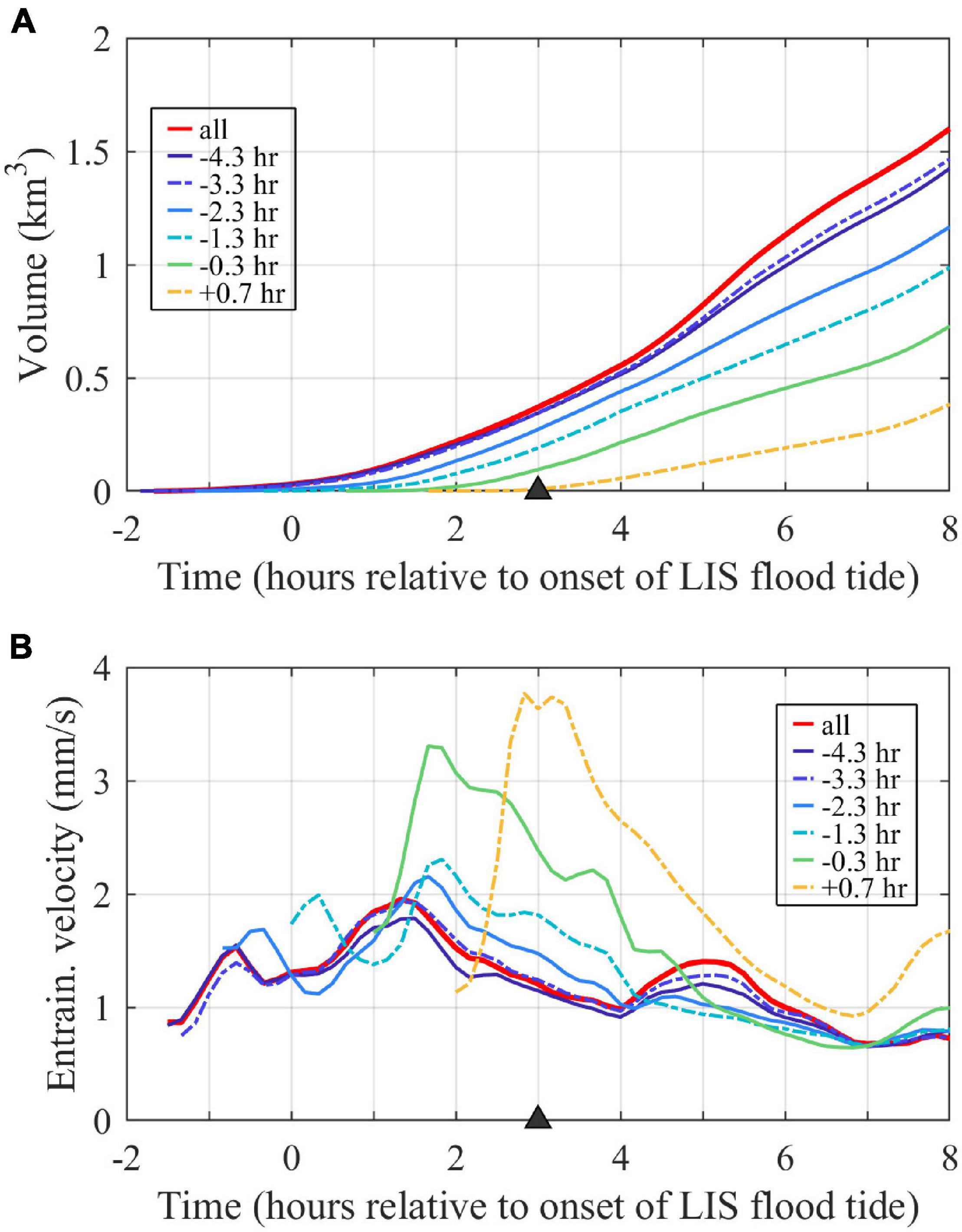
Figure 10. Time series of (A) plume volume (assessed with the combined tracer, labeled ‘all’) and volumes associated with individual tracer waters and (B) spatial-averaged entrainment velocities for the entire plume (labeled ‘all’) and plume regions associated with individual tracers. Tracers are labeled by first release times.

$$T_e=H_p/w_e(15)$$

Since H_p = V_p/A_p and w_e = Q_e/A_p, T_e also can be expressed as V_p/Q_e. Note that T_e can be time variable, as both the entrainment velocity and plume depth can vary. Plume-averaged entrainment velocities, calculated with (2), are 0.7–2.0 mm/s with variability during the tidal cycle (Figure 10B). Most of the tracers have entrainment velocities within about the same range (0.7–2.3 mm/s), indicating a similar entrainment efficiency to each other and the plume as a whole. The younger waters included in the latest two tracer releases have notably higher peak entrainment velocities (3.3–3.8 mm/s). Since these younger waters are concentrated in the upstream half of the plume (Figure 8D), the result indicates more vigorous entrainment in the nearfield plume. The linear increase in average plume depth over time (not shown) results in a linear increase in plume entrainment time scale (T_e) from 1 to 6 h from the onset to the end of ambient flood tides, so plume volume exponentially increases at a slower rate over time.

Volume-averaged tracer concentrations within the plume ($\overline{C}$, Figure 11A), calculated with (3), initially increase (for 0.5–1 h) due to source water supply and then decrease due to dilution by continued entrainment of ambient waters. Peak plume-averaged concentrations range from 0.035 to 0.085, with a 0.060 peak for the combined tracer. Concentrations exponentially decay at the same rate (set by T_e) at which plume volume increases. Note that the decay in concentrations is only due to dilution, as the conservative nature of these tracers precludes imposed exponential tracer loss or other interior tracer sinks. By the end of ambient flood, average tracer concentrations decrease to <0.004, which are <5% of their peak average concentrations and <0.4% of the undiluted unit concentration. Thus, entrainment leads to a voluminous but highly diluted plume by the end of ambient flood tide.

FIGURE 11

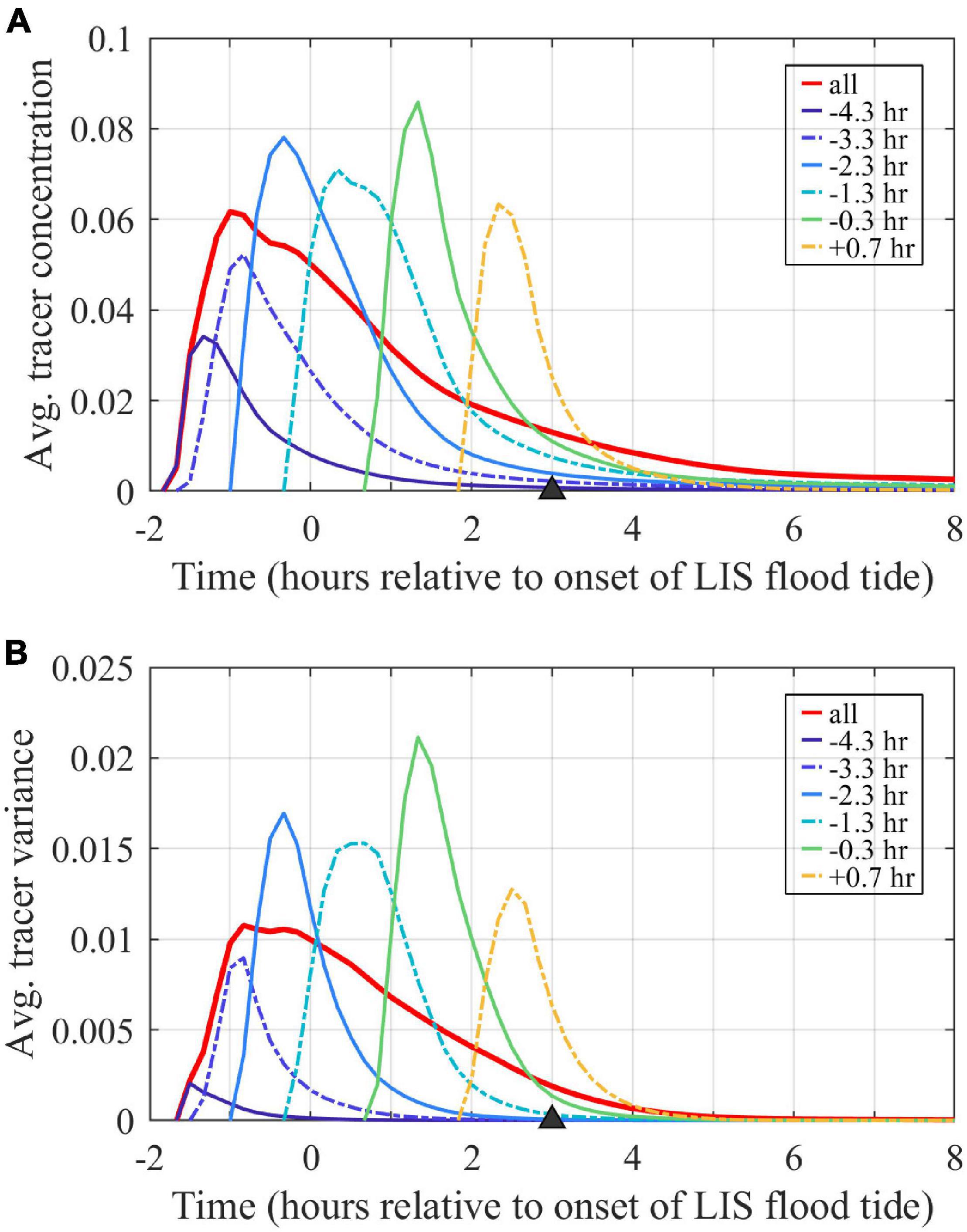
Figure 11. Time series of volume-averaged (A) tracer concentrations and (B) tracer variances. Values for the entire plume volume are calculated with the combined tracer (labeled ‘all’). Averages are associated with the volumes bounded by each tracer outside of the river. Tracers are labeled by first release times.

Freshwater Tracer Variance Budgets

The freshwater tracer variance budgets assess how source water inputs, entrainment, and mixing affect plume evolution over time. The analysis is completed over the expanding plume control volume, defined as the region where the combined freshwater tracer concentrations exceed the threshold value (C₀ = 10^–6). The plume control volume boundaries are shown in Figures 7, 8A. At the mouth (Figure 7B) and in the nearfield (Figure 7C), the control volume extends throughout the water column. Farther downstream (Figure 7D), the plume does not reach the bottom in all locations. Volume-averaged tracer variances ($\overline{C^{\prime }{}^2}$, Figure 11B) follow patterns similar to volume-averaged tracer concentrations (Figure 11A), with an initial increase pattern and a long decay period through the rest of the tidal cycle. Peak tracer variances range from 0.002 to 0.021 and are two to three times larger than the corresponding squared peak concentration values (i.e., $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ >1). By the end of ambient flood tide, tracer variances decrease to <10^–4, which are <1% their peak concentrations.

The volume-averaged tracer variance budgets (10) track how $\overline{C^{\prime }{}^2}$ changes. The rate of change for the combined tracer variance (Figure 12A) is positive with a peak during the initial period of concentration and variance increase (Figure 11) and then is negative with smaller magnitude during the longer decay period. Mouth input (Figure 12B) is the single largest term and the only one that acts to increase $\overline{C^{\prime }{}^2}$, as it adds high concentration water with higher tracer variance than the plume average. Entrainment (Figure 12C) brings in low concentration water (at the C₀ threshold value) and tends to decrease $\overline{C^{\prime }{}^2}$. The entrainment term in (10) is negative because $\overline{C^{\prime }{}^2}/C^{\prime }{}_e{}^2$ >1. As described earlier, an approximately equivalent condition is $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ >1 because $C^{\prime }{}_e{}^2$ is approximately ${\overline{C}}^2$ for small C₀. The $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ >1 condition is met for this plume, but this does not have to be the case in general. The internal mixing term (Figure 12D) always acts to destroy tracer variance; the term grows smaller while $\overline{C^{\prime }{}^2}$ decreases and V_p increases. This mixing within the plume control volume reflects vertical and/or horizontal mixing that tends to homogenize tracer concentrations within the plume. Dividing the tracer variance by the absolute value of the mixing term in (10) yields a mixing time scale:

FIGURE 12

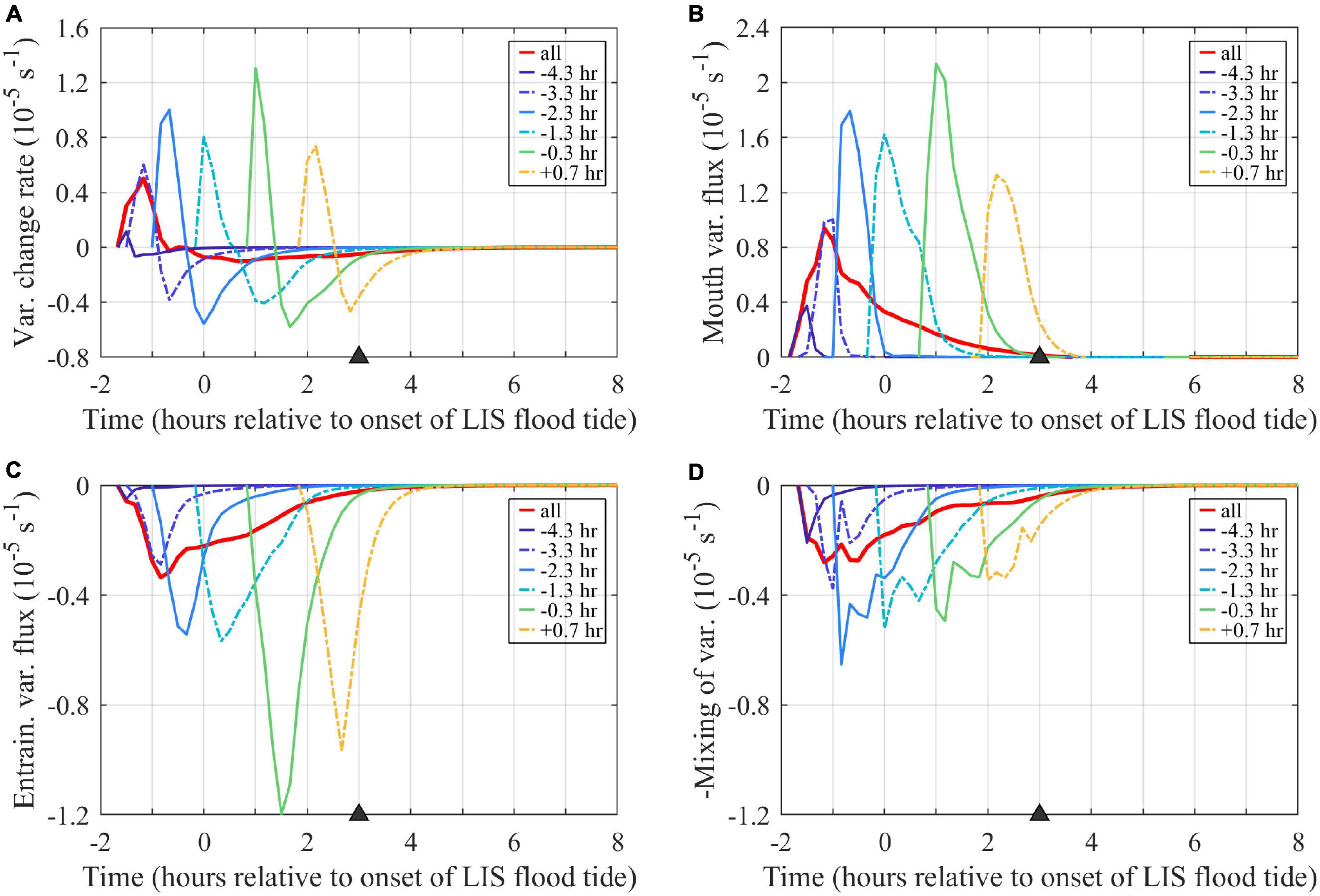
Figure 12. Time series of terms in the volume-averaged tracer variance budget (10): (A) rate of change, (B) mouth flux, (C) entrainment, and (D) mixing (–M/V_p). The entrainment and mixing terms are graphed with half the y-axis range of the rate of change and mouth terms. Term units are (concentration units)² (10^{– 5} s^{– 1}), where the concentration units are non-dimensional because tracers are source water fractions. Volume averages include the entire region bounded by each tracer outside the river. The combined tracer (labeled ‘all’) includes the entire plume. Tracers are labeled by first release times.

$$T_{mix}=\overline{C^{\prime }{}^2}{V}_p/M(16)$$

T_mix is 1.3 h and T_e is 2.2 h at max ambient flood, indicating mixing (Figure 12D) is about twice as powerful as entrainment (Figure 12C) in reducing tracer variance at this stage of plume evolution. Sensitivity testing indicates tracer variance budgets at max ambient flood are similar when higher concentration threshold values (up to C₀ = 10^–3) are applied, but the term magnitudes approximately double (increasing by a factor of 2.1–2.2) from the original C₀ = 10^–6 to the C₀ = 10^–3 results. For all tested C₀, mixing is approximately twice (1.8 to 1.9 times) the entrainment at max ambient flood. During early ambient flood (1 h after the onset of flood tide), however, sensitivity testing indicates the mixing to entrainment ratio increases from 0.6 to 1.5 from the C₀ = 10^–6 to the C₀ = 10^–3 results. The volume-averaged variance budgets for the hourly tracer are broadly similar (Figure 12). The entrainment and mixing terms contribute about equally to reducing variance for the combined tracer and most hourly tracers. Entrainment is more than double the mixing term for the two latest tracer releases; this is consistent with the higher associated entrainment velocities (Figure 10B, described above) for younger waters in the nearfield plume. Overall, tracer variance inputs from the mouth exceed reductions via entrainment and mixing only during an initial 0.5- to 1-h period; tracer variance is eroded throughout the rest of the ambient flood tide.

Other Discharge and Tide Conditions

The standard case is representative of summer low discharge conditions during neap tides. By comparison, the low-discharge spring-tide case increases ambient tidal currents by 33% (Table 1). Tides through the river mouth increase by a smaller amount (7%) and t_lag is shorter (Table 1). Surface flow reverses an hour earlier during spring tides; therefore, the plume is cut off from source waters prior to max ambient flood. Consistent with stronger river tides, the bulk vertical salinity difference at the mouth is smaller (ΔS_m = 16.0) and the Froude number at the mouth is larger (Fr_m = 2.0) (Table 1). The plume is somewhat longer (10 km length), narrower (3.5 km width), and has a lower downstream salinity anomaly (ΔS_d = 4.0) during spring tides (Figure 13 and Table 1), but the dimensions and salinity anomaly are within 30% of the neap plume characteristics. The spring-tide plume is supercritical with Fr_d exceeding five. Comparing the high-discharge neap-tide case to the standard case indicates how river mouth and plume conditions change with six times stronger discharge (Table 1). Even though ambient tides are the same, river tides are weaker with a shorter t_lag (Table 1). The tidal-averaged flow exceeds the river tidal amplitude (V_D/V_Tm < 1), so currents do not reverse and the ‘pinching off criterion’ (de Ruijter et al., 1997) is not met. Consequently, the plume is fed by source waters throughout the tidal cycle. Completely freshwater reaches the mouth (Table 1) and low-salinity water occupies the entire water column in the channel (not shown). The fresher and thicker mouth outflow (ΔS_m = 23.0, h_m = 10 m) has a faster c_m (1.32 m/s), but source conditions are still at least critical at max ambient flood (Table 1). The main plume is somewhat longer (9.5 km length) and wider (5.5 km width), but the much higher salinity anomaly (ΔS_d = 14.0) and the more apparent offshore relic plume are the most conspicuous changes relative to the low-discharge plume (Figure 13 and Table 1). The stronger salinity anomaly increases c_p to 0.46 m/s and decreases Fr_d to 2.4, but the plume still is supercritical at max ambient flood. Even with a stronger c_p, ambient tides still arrest the upstream front (Fr_Ta > 1). Comparing the high-discharge runs with neap and spring tides indicates a qualitatively similar spring-neap tidal dependence as shown for the two low-discharge runs.

FIGURE 13

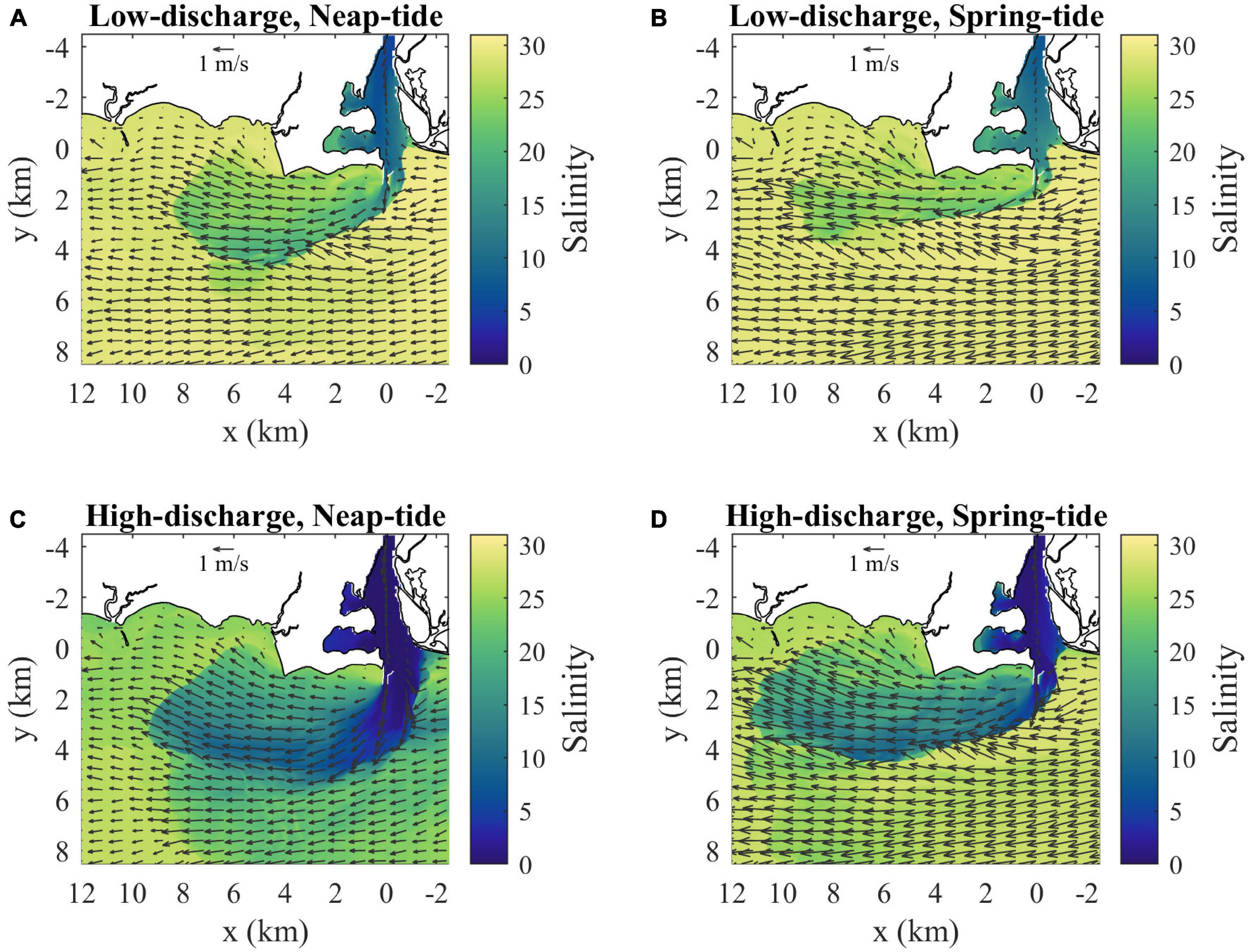
Figure 13. Surface velocity (arrows) and salinity (shaded) maps at max ambient flood for (A) low discharge during neap tides (as in Figure 4B), (B) low discharge during spring tides, (C) high discharge during neap tides and (D) high discharge during spring tides. Velocity arrows are shown for every 40th point (800 m spacing) and every 20th point (400 m spacing) in x and y, respectively.

Intercomparison of the four model runs at max ambient flood (Figure 13 and Table 1) indicates the mouth outflow and plume velocities always become supercritical during part of the tidal cycle. Under low-discharge conditions, the tidal plume is fed by source waters until max ambient flood, when flow reversal at the mouth cuts off the source water supply. During high-discharge, the plume maintains a connection with source waters because the mouth surface flow always is outward. The plume at max ambient flood is always faster than ambient tidal currents (i.e., u_d > U_Ta), and longer than the time-integral of the tidal flow (i.e., L_p > L_Ta/2). Plume salinities decrease with weaker tides and particularly with higher discharge. Plume dimensions, however, are less sensitive to changing tidal and discharge forcing. The upstream extent is limited because ambient tidal currents arrest the opposing plume propagation, as Fr_Ta > 1 in all runs. The downstream extent of the tidal plume always is within 20 km from the mouth, which is less than twice the ambient tidal excursion.

The hourly freshwater tracers released within each run indicate the composition and connectivity within the plume under various forcing conditions. In all cases, water age increases downstream and offshore to a lesser degree (Figure 14). The downstream front has older waters, the upstream front has younger waters, and the main offshore front and more gradual inshore boundary span young to old waters. The oldest waters are found in the relic offshore plume (Figure 14). At max ambient flood, the plumes are chiefly composed of source waters released in the river during the preceding ambient ebb. The oldest water ages are detected during neap tides, particularly within the relic plume that persists under high-discharge conditions. The low-discharge spring-tide plume has the narrowest age range because the oldest waters have been mixed away and the youngest waters are cut off from the plume by the mouth flow reversal (Figure 14). The plume front advances downstream faster than ambient tidal currents in all runs, but the u_f advancement velocity is somewhat less than (64–94%) U_Ta+c_p. Interior waters in all runs, assessed with the hourly tracer closest to but not at the downstream front, approach the downstream front with a relative velocity (0.09 < u_i < 0.19 m/s) at max ambient flood (Table 1). The interior waters, however, are not traveling quickly enough to reach the downstream plume front by the end of ambient flood. Thus, the downstream front always has the lowest overall connectivity with source waters, as interaction is limited to waters that exited the mouth by early ambient ebb. In stark contrast, the arrested upstream front has high connectivity, as all freshwaters exiting the mouth immediately interact with this boundary. Thus, energetic ambient tides lead to a strong upstream-to-downstream asymmetry in source-front connectivity.

FIGURE 14

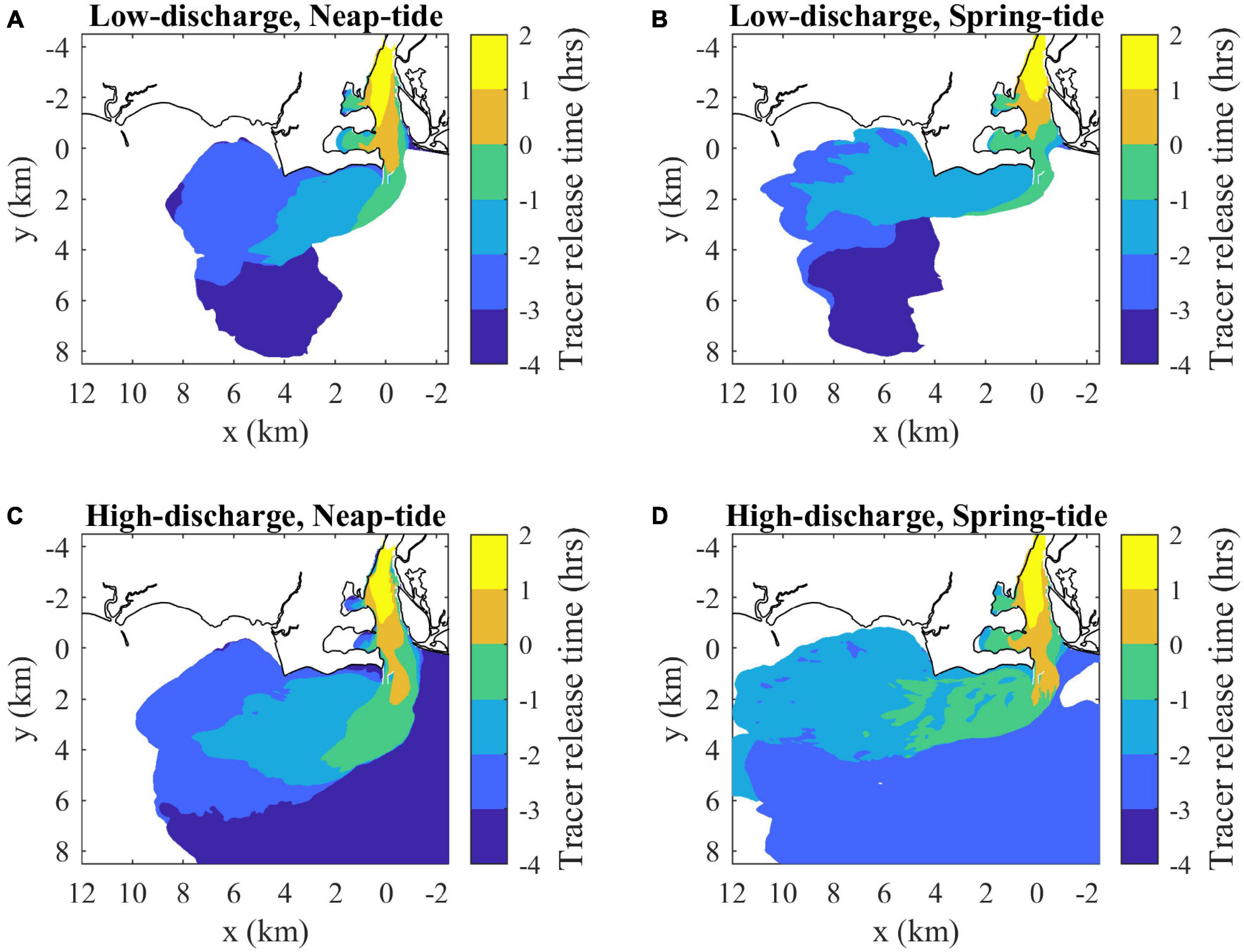
Figure 14. Surface maps of average freshwater composition (indicated by average release times of tracers present in each location at max ambient flood) for (A) low discharge during neap tides (as in Figure 7A), (B) low discharge during spring tides, (C) high discharge during neap tides and (D) high discharge during spring tides. Tracer release times are expressed relative to the onset of ambient flood tides (as in Figure 7). Average freshwater age can be calculated by subtracting the average release times from 3 h (the mapped time).

Analysis of the plume volume budgets, identified with the combined tracer fields, indicates how the entrainment velocity and the associated e-folding time scale vary among runs. The w_e values for both spring-tide cases (1.0–1.2 mm/s) are approximately the same and are about twice the w_e values for neap-tide cases (2.0 mm/s) (Table 1). The w_e tidal dependence, and lack of sensitivity to discharge, point to entrainment driven by tidal shear. The entrainment time scale (T_e) at max ambient flood is about the same (2 h) for all but the high-discharge neap-tide plume, which has double the T_e. For the combined tracer at max ambient flood, $\overline{C}\ge 0.026$ in both high discharge runs; these values are at least double the concentration in the standard low-discharge neap-tide run ($\overline{C}=0.013$) and several times greater than in the low-discharge spring-tide run ($\overline{C}=0.004$) (Table 1). Note that the higher concentration values in the high-discharge cases correspond to lower plume salinities. Both high discharge runs also have much higher variance at max ambient flood ($\overline{C^{\prime }{}^2}\ge 0.0069$) than the low-discharge neap-tide run ($\overline{C^{\prime }{}^2}=0.0019$) and the low-discharge spring-tide run ($\overline{C^{\prime }{}^2}=0.0002$) (Table 1). The ratio $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ at max ambient flood ranges from 9.5 to 12.5 (Table 1) and $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ > 1 during the entire ambient flood tide in all cases.

Tracer variance budgets are qualitatively similar, but term magnitudes vary by orders of magnitude among runs. In all runs, $\overline{C^{\prime }{}^2}$ is increased only by mouth inputs and is decreased both by entrainment and mixing (Table 1). Entrainment decreases tracer variance because $C^{\prime }{}_e{}^2$ is approximately ${\overline{C}}^2$ and $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ >1 for all tidal and discharge conditions explored; indicating that the plume remains in the same regime in this regard. By max ambient flood, mixing is about twice as strong as entrainment and T_mix (1–2 h) is shorter than T_e. Both time scales are less than half the tidal cycle, indicating mixing and entrainment are vigorous enough to rapidly diminish tracer variance within the plume.

Discussion

This study investigates the Connecticut River plume formed during ambient flood tides. Observations (e.g., Garvine, 1974b; Figure 2) and model results indicate strong plume salinity variability with forcing conditions, but the downstream extent of the tidal plume always is within 20 km from the mouth. The plume length is strikingly short in comparison to plumes exiting other estuaries with similar river discharge ranges. For comparison, the buoyant outflow from the Delaware Bay can stretch over 100 km along the coast during buoyancy driven conditions (e.g., Whitney and Garvine, 2006). The key difference is the Connecticut River plume forms in a much stronger ambient tidal environment. Tidal advection during flood increases downstream transport and extent, but plume length ultimately is limited by ebb currents strong enough to arrest and then reverse the plume. Simple estimates are useful for characterizing plume length generally for other tidally reversing plumes. The frontal advancement velocity is approximated as the internal wave speed superimposed on the ambient tidal velocity: u_f≈c_p+u_a, where u_a can be expressed in terms of a sinusoidal tide as in (11). Integrating over half a tidal cycle (either flood or ebb) yields L_p≈(T/2)(c_p+2U_Ta/π), where 2U_Ta/π is the mean tidal current during one phase (flood or ebb) of the tide. Writing c_p in terms of the salinity anomaly as before, the ratio of the plume length to the tidal excursion (L_Ta, as defined earlier) is approximately:

$$\frac{L_p}{L_{Ta}}\approx \left(\frac{\sqrt{g\beta \mathrm{\Delta }{S}_p{H}_p}}{2U_{Ta}/\pi }+1\right)(17)$$

Plumes experiencing substantial tidal reversals are expected to be approximately within two tidal excursions from the mouth (L_p < 2L_Ta) because c_p should be less than 2U_Ta/π in these strong tidal regimes. For the Connecticut River, 2L_Ta ranges from 22 km during neap tides up to 36 km during spring tides. The actual plume extent is smaller mostly because c_p typically is much less than 2U_Ta/π, particularly during spring tides.

Results indicate the downstream front has very limited connectivity with interior waters. These waters are approaching the front with an overtake velocity equaling the difference between the interior water velocity and the frontal advancement velocity: Δu = u_i-u_f. This overtake velocity does not depend on the ambient tidal velocity. The time available for interior waters to travel from the mouth to the advancing front position (x_f) is at most the time between when the interior water first exits the mouth (t_i) and when the ambient tidal phase (in this case flood) ends at T/2. The downstream extent of the interior water (x_i) is less than x_f while approaching the front and equals x_f after reaching the front, if that occurs. Assuming constant u_i and u_f for simplicity, the condition for reaching the front by the end of the tidal phase is u_i(T/2-t_i) ≥ u_fT/2. Expressed as a velocity ratio, the condition for interior water interacting with the downstream front is:

$$\frac{u_i}{u_f}\ge \frac{1}{1-2t_i/T}(18)$$

Note that u_f and u_i, respectively can be scaled as c_p+u_a and Δu+u_f, so there is an implicit dependence on ambient tidal currents that tends to reduce u_i/u_f with stronger tides. Late-flood interior water exits the mouth with t_i ≥ T/4 and (18) indicates that these waters can only reach the downstream front if u_i/u_f ≥ 2. This is a difficult threshold to meet, so it is unlikely that late-stage waters interact with the downstream front of tidally reversing plumes. For the Connecticut River plume, three of the runs have u_i/u_f ≤ 1.2 (Table 1), so t_i ≤ 1 h to reach the downstream front. For the low-discharge spring-tide case, u_i/u_f = 1.5 and t_i ≤ 2 h to overtake the front. Thus, interaction with the downstream front is limited to source waters exiting the mouth by early ambient flood. The tracers are identified by the first time they are released within the river, which can be several hours earlier than when they exit the mouth. For the standard low-discharge neap-tide case, the tracer released at −1.3 h is the youngest tracer with t_i ≤ 1 h (Figure 3C) and, consistent with the u_i/u_f value and (18), it is the youngest water to interact with the downstream front (Figure 8C).

The present results are most directly comparable to the Cole et al. (2020) plume connectivity study. Cole et al. (2020) studies the Merrimack River plume, which is fed by a river-ebb pulse of fresh source waters and evolves in a much lower-energy ambient tidal environment than the Connecticut River plume experiences. Simulated tracers injected at the Merrimack River mouth indicate that only source waters released within the first 2 h (t_i ≤ 2 h) overtake the front within a half tidal cycle after plume formation. This limited frontal connectivity is similar to results for the downstream front of the Connecticut River plume. A key difference between the plumes is weak ambient tides allow the Merrimack plume to spread almost radially outward from the mouth, while strong ambient tides arrest the upstream front (Fr_Ta > 1) in the Connecticut plume and elongate it in the tidally downstream direction. The Connecticut’s arrested upstream front has strong and immediate connectivity with all source waters exiting the mouth. There is no part of the Merrimack plume front that has such strong connectivity. The strong connectivity is not guaranteed for all plumes with an arrested upstream front, as it is possible for later source waters to slip past in the plume interior without interacting with the bounding front. For the Connecticut plume, energetic ambient tides lead to large differences in connectivity and source-water composition along the bounding plume front. It is likely other plumes with a tidally arrested upstream front (where Fr_Ta > 1) exhibit a similar transition from youngest to oldest waters progressing from the upstream front, along the offshore and onshore fronts, and to the downstream front. Consequently, such plumes will have more source-front connectivity than plumes in weaker ambient tidal environments, but the downstream front still will have very limited connectivity. Relative to plumes in weak ambient tidal regimes, the Connecticut River plume and other tidally reversing plumes should have key differences with respect to the fate and transport of pollutants, sediments, and biogeochemical substances. The relatively short length of tidally reversing plumes should tend to keep the highest concentrations close to the mouth. Spatial gradients of substances along the river can result in large differences in transport pathways. Material passing through the mouth in late ambient ebb or early flood will tend to be transported the farthest in plumes formed during ambient flood tides; this material can be processed at the downstream front. Substances in late-flood source waters would tend to remain closer to the mouth and only interact with the arrested upstream front. The strong connectivity of the arrested upstream front and its constrained location make it a good location for studying the frontal processing of pollutants, sediments, and biogeochemical substances. Future research incorporating plume biogeochemistry and source-front connectivity characteristics would help advance the understanding of plume effects on coastal ecosystem dynamics. It is also important to connect processes acting within the tidally reversing active plume to tracking substances over longer time scales (e.g., days to months), after plume waters have been extensively mixed with ambient waters.

Entrainment and mixing occur throughout the Connecticut River plume; as indicated by the results that concentrations and variances for all hourly tracers diminish quickly (Figure 11). The plume-averaged tracer variance budgets (10) for the combined tracer are qualitatively similar for all runs: tracer variance is increased by mouth inputs, decreased by entrainment, and destroyed by internal mixing. Mouth inputs increase tracer variance because source waters have higher concentrations than the plume (leading to $C^{\prime }{}_m{}^2/\overline{C^{\prime }{}^2}$ >1), a common situation for plumes. Entrainment decreases tracer variance because $\overline{C^{\prime }{}^2}/C^{\prime }{}_e{}^2$ >1; this condition is approximately $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ >1 because $C^{\prime }{}_e{}^2$ is approximately ${\overline{C}}^2$ for small C₀. The $\overline{C^{\prime }{}^2}/{\overline{C}}^2$>1 condition should be met by other strongly mixed low-concentration plumes. The tracer variance budget terms vary by orders of magnitude among runs (Table 1). It is useful to simplify and scale the budget in a way that collapses results for the investigated range of tidal and discharge conditions. For $C^{\prime }{}_m{}^2/\overline{C^{\prime }{}^2}\gg$ 1 and $\overline{C^{\prime }{}^2}/{\overline{C}}^2\gg$1, the mouth input term and entrainment term in (10) are approximately $C^{\prime }{}_m{}^2{Q}_m/V_p$ and $-\overline{C^{\prime }{}^2}{Q}_e/V_p$, respectively. These simplifications are reasonable approximations for the Connecticut River plume results. Analysis of tracer variance budgets of other plumes should include evaluating the $C^{\prime }{}_m{}^2/\overline{C^{\prime }{}^2}$ and $\overline{C^{\prime }{}^2}/{\overline{C}}^2$ ratios. The latter ratio is larger for strongly mixed low-concentration (low freshwater fraction) plumes, while the former ratio will be greater than one for any case with much higher concentration (fresher) source waters than the plume. The estimated mouth input term ($C^{\prime }{}_m{}^2{Q}_m/V_p$) at t = 0 h (onset of ambient floods) can be used to scale the time-varying terms in (10). This mouth-based scaling reduces term magnitude differences among runs from orders of magnitude to approximately a factor of two. The successful collapsing of budget results indicates a dose-response relationship, whereby stronger tracer variance inputs by source waters have correspondingly larger variance decreases by entrainment and destruction via internal mixing.

Plume-averaged tracer budgets are valuable for analyzing plume evolution as a whole, but combine together horizontal and vertical processes as well as processes occurring in different regions of the plume. Future analysis of the Connecticut River plume should explore the decomposition of tracer variance into its horizontal and vertical parts, as introduced in Li et al. (2018) and applied in other studies (e.g., Wang and Geyer, 2018; Warner et al., 2020). The vertical tracer variance is particularly useful since it is directly related to stratification and it may be more readily applied to understanding biogeochemical processes in plumes. Analyzing spatial variations of tracer variance and budget terms as in Li et al. (2018) and other works (e.g., Warner et al., 2020) would help highlight important areas for variance advection and dissipation. The multiple tracer approach applied in the present study already allows for distinguishing between near-field and far-field plume regions. The mixing term in the tracer budgets for the present study includes the total mixing acting in the model, which includes physical mixing and numerical mixing associated with the advection scheme. Several studies have shown that numerical mixing can be comparable to physical mixing (e.g., Burchard and Rennau, 2008; Li et al., 2018; Burchard et al., 2021; Wang et al., 2021) and the ratio of numerical to physical diffusivities can have pronounced spatial variability within estuaries and plumes (Burchard et al., 2021).

Mixing in idealized tidal plumes representative of the Connecticut River plume and other situations has been studied in more detail in Spicer et al. (2021), following the turbulent buoyancy flux approach of Pritchard and Huntley (2006). Spicer et al. (2021) finds that bottom-generated tidal mixing dominates over mixing associated with buoyant plume shear if the estuarine Richardson number (Ri_E = c_m²V_D/U_Ta³; modified from Fischer (1972) to use ambient tides) divided by the mouth Rossby number (Ro_m = V_D/(fW_m), where W_m is mouth width) is less than one (Ri_E/Ro_m < 1). Provided that c_p ≤ c_m, this condition is satisfied when the product of the ambient tidal Froude number squared and the corresponding Rossby number exceeds one (Fr_Ta²Ro_Ta > 1, where Ro_Ta = U_Ta/(fW_m)), which is true for all model runs in this study. Thus, the Connecticut River plume belongs in the class of plumes strongly influenced by tidal mixing (Spicer et al., 2021).

Other plumes in energetic ambient tidal environments, whether generated during flood or ebb, are expected to share similarities with the Connecticut River plume. These tidally reversing plumes should be within two tidal excursions from the mouth, be cut off from source waters while flow reverses at the mouth, have limited connectivity at the downstream front, strong connectivity along the arrested upstream front, and rapid entrainment and mixing that reduces the plume buoyancy signature over intratidal time scales. Follow-up work should compare the present results to connectivity within the Connecticut’s ambient ebb plume. Future research should extend the connectivity and tracer analysis approach to the transport and processing of pollutants, sediments, and biogeochemical material by the Connecticut River plume and other plumes in energetic ambient tidal environments.

Data Availability Statement

The original contributions presented in the study are publicly available. This data can be found here: https://opencommons.uconn.edu/marine_sci/12.

Author Contributions

MW led this research, completed analysis, constructed figures, and wrote this manuscript with input from co-authors. YJ completed the hydrodynamic model runs, contributed to analysis, and edited and suggested improvements to the manuscript. KC, DM, and KH contributed to the ideas underpinning this research, helped set the scope of this manuscript, and improved the manuscript through their suggestions. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the NSF Ocean Sciences Physical Oceanography grant 1756578.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The manuscript was improved by the helpful suggestions of the reviewers and editor.

References

Ackelson, S. G., and O’Donnell, J. (2011). Small-scale variability in suspended matter associated with the Connecticut River plume front. J. Geophys. Res. 116:C10013. doi: 10.1029/2011JC007053

CrossRef Full Text | Google Scholar

Akan, Ç, McWilliams, J. C., Moghimi, S., and Özkan-Haller, H. T. (2018). Frontal dynamics at the edge of the Columbia River plume. Ocean Modell. 122, 1–12. doi: 10.1016/j.ocemod.2017.12.001

CrossRef Full Text | Google Scholar

Basdurak, N. B., Largier, J. L., and Nidzieko, N. J. (2020). Modeling the dynamics of small-scale river and creek plumes in tidal waters. J. Geophys. Res. 125:e2019JC015737. doi: 10.1029/2019JC015737

CrossRef Full Text | Google Scholar

Bennett, D. C., O’Donnell, J., Bohlen, W. F., and Houk, A. (2010). Tides and overtides in long Island Sound. J. Mar. Res. 68, 1–35. doi: 10.1357/002224010793079031

CrossRef Full Text | Google Scholar

Bricker, J. D., Okabe, I., and Nakayama, A. (2006). Behavior of a small pulsed river plume in a strong tidal cross-flow in the Akashi strait. Environ. Fluid. Mech. 6, 203–225. doi: 10.1007/s10652-005-3480-x

CrossRef Full Text | Google Scholar

Burchard, H. (2020). A universal law of estuarine mixing. J. Phys. Oceanogr. 50, 81–93. doi: 10.1175/JPO-D-19-0014.1

CrossRef Full Text | Google Scholar

Burchard, H., Gräwe, U., Klingbeil, K., Koganti, N., Lange, X., and Lorenz, M. (2021). Effective diahaline diffusivities in estuaries. J. Adv. Model. Earth Sys. 13. doi: 10.1029/2020MS002307

CrossRef Full Text | Google Scholar

Burchard, H., and Rennau, H. (2008). Comparative quantification of physically and numerically induced mixing in ocean models. Ocean Modell. 20, 293–311. doi: 10.1016/j.ocemod.2007.10.003

CrossRef Full Text | Google Scholar

Chant, R. J. (2011). “Interactions between estuaries and coasts: river plumestheir formation transport and dispersal,” in Treatise on Estuarine and Coastal Science, Vol. 2, eds E. Wolanski and D. McLusky (Amsterdam: Elsevier), 213–235. doi: 10.1016/B978-0-12-374711-2.00209-6

CrossRef Full Text | Google Scholar

Chapman, D. C. (1985). Numerical treatment of cross-shelf open boundaries in a barotropic coastal ocean model. J. Phys. Oceanogr. 15, 1060–1075. doi: 10.1175/1520-04851985015<1060:NTOCSO<2.0.CO;2

CrossRef Full Text | Google Scholar

Chassignet, E. P., Hurlburt, H. E., Smedstad, O. M., Halliwell, G. R., Hogan, P. J., Wallcraft, A. J., et al. (2008). The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 65, 60–83. doi: 10.1016/j.jmarsys.2005.09.016

CrossRef Full Text | Google Scholar

Chen, F., MacDonald, D. G., and Hetland, R. D. (2009). Lateral spreading of a near-field river plume: observations and numerical simulations. J. Geophys. Res. 114:C07013. doi: 10.1029/2008JC004893

CrossRef Full Text | Google Scholar

Cole, K. L., MacDonald, D. G., Kakoulaki, G., and Hetland, R. D. (2020). River plume source-front connectivity. Ocean Modell. 150:101571. doi: 10.1016/j.ocemod.2020.101571

CrossRef Full Text | Google Scholar

Cudaback, C. N., and Jay, D. A. (1996). “Formation of the columbia river plume-hydraulic,” in Buoyancy Effects on Coastal and Estuarine Dynamics, Vol. 53, eds D. G. Aubrey and C. T. Friedrichs (Washington, DC: American Geophysical Union), 139–154. doi: 10.1029/CE053p0139

CrossRef Full Text | Google Scholar

de Ruijter, W. P., Visser, A. W., and Bos, W. G. (1997). The Rhine outflow: a prototypical pulsed discharge plume in a high energy shallow sea. J. Mar. Systems 12, 263–276. doi: 10.1016/S0924-7963(96)00102-9

CrossRef Full Text | Google Scholar

Deignan-Schmidt, S. R., and Whitney, M. M. (2018). A model study on the summertime distribution of river waters in long island sound. Estuaries Coasts 41, 1002–1020. doi: 10.1007/s12237-017-0348-5

CrossRef Full Text | Google Scholar

Dittmar, T., and Kattner, G. (2003). The biogeochemistry of the river and shelf ecosystem of the Arctic Ocean: a review. Mari. Chem. 83, 103–120. doi: 10.1016/S0304-4203(03)00105-1

CrossRef Full Text | Google Scholar

Egbert, G. D., and Erofeeva, S. Y. (2002). Efficient inverse modeling of barotropic ocean tides. J. Atmosph. Oceanic Tech. 19, 183–204. doi: 10.1175/1520-04262002019<0183:EIMOBO<2.0.CO;2

CrossRef Full Text | Google Scholar

Ellis, and Gen, T. G. (1874). The Causes of the Formation of Bars at the Mouths of Rivers, as Shown in An Examination of the Connecticut River, Van Nostrand’s Eclectic Engineering Magazine. Available online at: https://search.proquest.com/docview/357141998 (accessed October 1, 1874).

Google Scholar

Fairall, C. W., Bradley, E. F., Hare, J. E., Grachev, A. A., and Edson, J. B. (2003). Bulk parameterization of air–sea fluxes: updates and verification for the COARE algorithm. J. Climate 16, 571–591. doi: 10.1175/1520-04422003016<0571:BPOASF<2.0.CO;2

CrossRef Full Text | Google Scholar

Fischer, H. (1972). Mass transport mechanisms in partially stratified estuaries. J. Fluid Mech. 53, 671–687. doi: 10.1017/S0022112072000412

CrossRef Full Text | Google Scholar

Flather, R. A. (1976). A tidal model of the northwest European continental shelf. Memoires de la Soc. R. des Sci. de Liege 10, 141–164.

Google Scholar

Garvine, R. W. (1974a). Dynamics of small-scale oceanic fronts. J. Phys. Oceanogr. 4, 557–569. doi: 10.1175/1520-04851974004<0557:DOSSOF<2.0.CO;2

CrossRef Full Text | Google Scholar

Garvine, R. W. (1974b). Physical features of the Connecticut River outflow during high discharge. J. Geophys. Res. 79, 831–846.

Google Scholar

Garvine, R. W. (1975). The distribution of salinity and temperature in the Connecticut River estuary. J. Geophys. Res. 80, 1176–1183. doi: 10.1029/JC080i009p01176

CrossRef Full Text | Google Scholar

Garvine, R. W. (1977). Observations of the motion field of the Connecticut River plume. J. Geophys. Res. 82, 441–454. doi: 10.1029/JC082i003p00441

CrossRef Full Text | Google Scholar

Garvine, R. W. (1984). Radial spreading of buoyant, surface plumes in coastal waters. J. Geophys. Res. 89, 1989–1996. doi: 10.1029/JC089iC02p01989

CrossRef Full Text | Google Scholar

Garvine, R. W., and Munk, J. D. (1974). Frontal structure of a river plume. J. Geophys. Res. 79, 2251–2259. doi: 10.1029/JC079i015p02251

CrossRef Full Text | Google Scholar

Grimes, C. B. (2001). Fishery production and the Mississippi River discharge. Fisheries 26, 17–26. doi: 10.1577/1548-84462001026<0017:FPATMR<2.0.CO;2

CrossRef Full Text | Google Scholar

Haidvogel, D. B., Arango, H., Budgell, W. P., Cornuelle, B. D., Curchitser, E., Di Lorenzo, E., et al. (2008). Ocean forecasting in terrain-following coordinates: formulation and skill assessment of the Regional Ocean modeling system. J. Comput. Phys. 227, 3595–3624. doi: 10.1016/j.jcp.2007.06.016

CrossRef Full Text | Google Scholar

Haidvogel, D. B., Arango, H. G., Hedstrom, K., Beckmann, A., Malanotte-Rizzoli, P., and Shchepetkin, A. F. (2000). Model evaluation experiments in the North Atlantic basin: simulations in nonlinear terrain-following coordinates. Dynam. Atmos. Oceans 32, 239–281.

Google Scholar

Hessner, K., Rubino, A., Brandt, P., and Alpers, W. (2001). The Rhine outflow plume studied by the analysis of synthetic aperture radar data and numerical simulations. J. Phys. Oceanogr. 31, 3030–3044. doi: 10.1175/1520-04852001031<3030:TROPSB<2.0.CO;2

CrossRef Full Text | Google Scholar

Hetland, R., and MacDonald, D. (2008). Spreading in the near-field Merrimack River plume. Ocean Modell. 21, 12–21. doi: 10.1016/j.ocemod.2007.11.001

CrossRef Full Text | Google Scholar

Hetland, R. D., and Hsu, T.-J. (2013). “Freshwater and sediment dispersal in large river plumes,” in Biogeochemical Dynamics at Large River-Coastal Interfaces: Linkages With Global Climate Change, eds T. S. Bianchi, M. A. Allison, and Cai W-J (New York: Springer), 55–85. doi: 10.1017/CBO9781139136853

CrossRef Full Text | Google Scholar

Hickey, B. M., Kudela, R. M., Nash, J. D., Bruland, K. W., Peterson, W. T., MacCready, P., et al. (2010). River influences on shelf ecosystems: introduction and synthesis. J. Geophys. Res. 115:112. doi: 10.1029/2009JC005452

CrossRef Full Text | Google Scholar

Hickey, B. M., Pietrafesa, L. J., Jay, D. A., and Boicourt, W. C. (1998). The Columbia River plume study: subtidal variability in the velocity and salinity fields. J. Geophys. Res: Oceans 103, 339–368.

Google Scholar

Horner-Devine, A. R., Hetland, R. D., and MacDonald, D. G. (2015). Mixing and transport in coastal river plumes. Ann. Rev. Fluid Mech. 47, 569–594. doi: 10.1146/annurev-fluid-010313-141408

CrossRef Full Text | Google Scholar

Horner-Devine, A. R., Jay, D. A., Orton, P. M., and Spahn, E. Y. (2009). A conceptual model of the strongly tidal Columbia River plume. J. Mar. Sys. 78, 460–475. doi: 10.1016/j.jmarsys.2008.11.025

CrossRef Full Text | Google Scholar

Huguenard, K. D., Bogucki, D. J., Ortiz-Suslow, D. G., Laxague, N. J. M., MacMahan, J. H., Özgökmen, T. M., et al. (2016). On the nature of the frontal zone of the Choctawhatchee bay plume in the Gulf of Mexico. J. Geophys. Res. 121, 1322–1345. doi: 10.1002/2015JC010988

CrossRef Full Text | Google Scholar

Jia, Y., and Whitney, M. M. (2019). Summertime Connecticut River water pathways and wind impacts. J. Geophys. Res. 124, 1897–1914. doi: 10.1029/2018JC014486

CrossRef Full Text | Google Scholar

Kakoulaki, G., MacDonald, D., and Horner-Devine, A. R. (2014). The role of wind in the near field and midfield of a river plume. Geophys. Res. Lett. 41, 5132–5138. doi: 10.1002/2014GL060606

CrossRef Full Text | Google Scholar

Kilcher, L. F., and Nash, J. D. (2010). Structure and dynamics of the Columbia River tidal plume front. J. Geophys. Res. 115:58. doi: 10.1029/2009JC006066

CrossRef Full Text | Google Scholar

Li, X., Geyer, W. R., Zhu, J., and Wu, H. (2018). The transformation of salinity variance: a new approach to quantifying the influence of straining and mixing on estuarine stratification. J. Phys. Oceanogr. 48, 607–623. doi: 10.1175/JPO-D-17-0189.1

CrossRef Full Text | Google Scholar

Luketina, D. A., and Imberger, J. (1987). Characteristics of a surface buoyant jet. J. Geophys. Res. 92, 5435–5447. doi: 10.1029/JC092iC05p05435

CrossRef Full Text | Google Scholar

MacCready, P., Geyer, W. R., and Burchard, H. (2018). Estuarine exchange flow is related to mixing through the salinity variance budget. J. Phys. Oceanogr. 48, 1375–1384. doi: 10.1175/JPO-D-17-0266.1

CrossRef Full Text | Google Scholar

MacDonald, D. G., Goodman, L., and Hetland, R. D. (2007). Turbulent dissipation in a near-field river plume: a comparison of control volume and microstructure observations with a numerical model. J. Geophys. Res. 112:51. doi: 10.1029/2006JC004075

CrossRef Full Text | Google Scholar

Marmorino, G. O., and Trump, C. L. (2000). Gravity current structure of the Chesapeake Bay outflow plume. J. Geophys. Res. 105, 28847–28861. doi: 10.1029/2000JC000225

CrossRef Full Text | Google Scholar

Mazzini, P. L. F., and Chant, R. J. (2016). Two-dimensional circulation and mixing in the far field of a surface advected river plume. J. Geophys. Res. Oceans 121, 3757–3776. doi: 10.1002/2015JC011059

CrossRef Full Text | Google Scholar

McClimans, T. A. (1978). Fronts in fjords. Geophys. Astrophys. Fluid Dynam. 11, 23–34. doi: 10.1080/03091927808242649

CrossRef Full Text | Google Scholar

Meade, R. H. (1966). Salinity variations in the Connecticut River. Water Resour. Res. 2, 567–579. doi: 10.1029/WR002i003p00567

CrossRef Full Text | Google Scholar

Mesinger, F., DiMego, G., Kalnay, E., Mitchell, K., Shafran, P. C., Ebisuzaki, W., et al. (2006). North American regional reanalysis. Bull. Am. Meteorolog. Soc. 87, 343–360.

Google Scholar

Meybeck, M. (2003). Global analysis of river systems: from Earth system controls to Anthropocene syndromes. Philosoph. Trans. R. Soc. London B Biol. Sci. 358, 1935–1955. doi: 10.1098/rstb.2003.1379

PubMed Abstract | CrossRef Full Text | Google Scholar

Nash, J. D., Kilcher, L. F., and Moum, J. N. (2009). Structure and composition of a strongly stratified, tidally pulsed river plume. J. Geophys. Res. 114:42. doi: 10.1029/2008JC005036

CrossRef Full Text | Google Scholar

O’Donnell, J. (2010). “The dynamics of estuary plumes and fronts,” in Contemporary Issues in Estuarine Physics, ed. A. Valle Levinson (Cambridge: Cambridge Univ. Press), 186–246. doi: 10.1017/CBO9780511676567

CrossRef Full Text | Google Scholar

O’Donnell, J., Marmorino, G. O., and Trump, C. L. (1998). Convergence and downwelling at a river plume front. J. Phys. Oceanogr. 28, 1481–1495. doi: 10.1175/1520-04851998028<1481:CADAAR<2.0.CO;2

CrossRef Full Text | Google Scholar

O’Donnell, J., Wilson, R. E., Lwiza, K., Whitney, M. M., Bohlen, W. F., Codiga, D., et al. (2014). “The physical oceanography of long island sound,” in Long Island Sound: Prospects for the Urban Sea, ed. J. S. Latimer (Springer), 79–158. doi: 10.1007/978-1-4614-6126-5_3

CrossRef Full Text | Google Scholar

Orton, P. M., and Jay, D. A. (2005). Observations at the tidal plume front of a high-volume river outflow. Geophys. Res. Lett. 32:L11605. doi: 10.1029/2005GL022372

CrossRef Full Text | Google Scholar

Poppe, L. J., Knebel, H. J., Mlodzinska, Z. J., Hastings, M. E., and Seekins, B. A. (2000). Distribution of surficial sediment in Long Island Sound and adjacent waters: texture and total organic carbon. J. Coast. Res. 16, 567–574.

Google Scholar

Pritchard, M., and Huntley, D. (2006). A simplified energy and mixing budget for a small river plume discharge. J. Geophys. Res. Oceans 111:C03019. doi: 10.1029/2005JC002984

CrossRef Full Text | Google Scholar

Ralston, D. K., Cowles, G. W., Geyer, W. R., and Holleman, R. C. (2017). Turbulent and numerical mixing in a salt wedge estuary: Dependence on grid resolution, bottom roughness, and turbulence closure. J. Geophys. Res. Oceans 122, 692–712. doi: 10.1002/2016JC011738

CrossRef Full Text | Google Scholar

Simpson, J. H., and Souza, A. J. (1995). Semidiurnal switching of stratification in the region of freshwater influence of the Rhine. J. Geophys. Res. 100, 7037–7044. doi: 10.1029/95JC00067

CrossRef Full Text | Google Scholar

Spicer, P., Cole, K. L., Huguenard, K., MacDonald, D. G., and Whitney, M. M. (2021). The effect of bottom – generated tidal mixing on tidally pulsed river plume. J. Phys. Oceanogr. 51, 2223–2241.

Google Scholar

Trumbull, J. H. (1881). Indian Names of Places Etc., in and On the Borders of Connecticut: With Interpretations of Some of Them. Available online at: https://books.google.com/books?id=JS8TAAAAYAAJ&num=10. (accessed July 1, 2021)

Google Scholar

van Alphen, J. S. L. J., de Ruijter, W. P. M., and Borst, J. C. (1988). “Outflow and three-dimensional spreading of rhine river water in the netherlands coastal zone,” in Physical Processes in Estuaries, eds J. Dronkers and W. van Leussen (Berlin: Springer), doi: 10.1007/978-3-642-73691-9_5

CrossRef Full Text | Google Scholar

Wang, T., and Geyer, W. R. (2018). The balance of salinity variance in a partially stratified estuary: implications for exchange flow, mixing, and stratification. J. Phys. Oceanogr. 48, 2887–2899. doi: 10.1175/JPO-D-18-0032.1

CrossRef Full Text | Google Scholar

Wang, T., Wei, Z., Jiang, W., Xu, T., Chen, J., and Bian, C. (2021). Quantification of numerical mixing in coastal ocean models through an offline method. Ocean Eng. 222:108588. doi: 10.1016/j.oceaneng.2021.108588

CrossRef Full Text | Google Scholar

Warner, J. C., Geyer, W. R., Ralston, D. K., and Kalra, T. (2020). Using tracer variance decay to quantify variability of salinity mixing in the hudson river estuary. J. Geophys. Res. 125:e2020JC016096. doi: 10.1029/2020JC016096

CrossRef Full Text | Google Scholar

Whitney, M. M., and Garvine, R. W. (2006). Simulating the delaware bay buoyant outflow: comparison with observations. J. Phys. Oceanogr. 36, 3–21. doi: 10.1175/JPO2805.1

CrossRef Full Text | Google Scholar

Whitney, M. M., Jia, Y., McManus, P. M., and Kunz, C. J. (2014). Sill effects on physical dynamics in eastern long Island sound. Ocean Dynam. 64, 443–458. doi: 10.1007/s10236-013-0681-6

CrossRef Full Text | Google Scholar

Wu, H., and Zho, J. (2010). Advection scheme with 3rd high-order spatial interpolation at the middle temporal level and its application to saltwater intrusion in the Changjiang Estuary. Ocean Modell. 33, 33–51. doi: 10.1016/j.ocemod.2009.12.001

CrossRef Full Text | Google Scholar

Yankovsky, A. E., and Chapman, D. C. (1997). A simple theory for the fate of buoyant coastal discharges. J. Phys. Oceanogr. 27, 1386–1401. doi: 10.1175/1520-04851997027<1386:ASTFTF<2.0.CO;2

CrossRef Full Text | Google Scholar