Investigating the Prevailing Hydrodynamics Around a Cold-Water Coral Colony Using a Physical and a Numerical Approach

Framework-forming cold-water corals provide a refuge for numerous organisms and, consequently, the ecosystems formed by these corals can be considered as impressive deep-sea biodiversity hotspots. If suitable environmental conditions for coral growth persist over sufficiently long periods of time in equilibrium with continuous sediment input, substantial accumulations of coral mound deposits consisting of coral fragments and baffled sediments can form. Although this conceptual approach is widely accepted, little is known about the prevailing hydrodynamics in their close proximity, which potentially affect sedimentation patterns. In order to refine the current understanding about the hydrodynamic mechanisms in the direct vicinity of a model cold-water coral colony, a twofold approach of a laboratory flume experiment and a numerical model was set up. In both approaches the flow dynamics around a simplified cold-water coral colony used as current obstacle were investigated. The flow measurements of the flume provided a dataset that served as the basis for validation of the numerical model. The numerical model revealed data from the vicinity of the simplified cold-water coral, such as the pressure field, velocity field, or the turbulent kinetic energy (TKE) in high resolution. Features of the flow like the turbulent wake and streamlines were also processed to provide a more complete picture of the flow that passes the simplified cold-water coral colony. The results show that a cold-water coral colony strongly affects the flow field and eventually the sediment dynamics. The observed decrease in flow velocities around the cold water-coral hints to a decrease in the sediment carrying potential of the flowing water with consequences for sediment deposition.

Introduction

Cold-water corals are abundant in all oceans and occupy latitudes from the Barents Sea (71°N) in the north to the Ross Sea (75°S) in the Antarctic (Roberts et al., 2009). So far, more than 700 species are known and these can be found in various water depths ranging from a few meters to over 6,000 m (Roberts et al., 2009). In contrast to tropical corals, cold-water corals are azooxanthellate, i.e., do not carry symbionts, and favor colder water temperatures. Among the cold-water corals the framework-forming scleractinian species, also referred to as constructional, habitat-, reef-, or structure-forming corals, are of special importance (see Roberts et al., 2009). So far, most framework-forming scleractinian corals have been discovered in the North Atlantic, including the Gulf of Mexico, the Caribbean Sea, as well as the Mediterranean Sea (Wienberg and Titschack, 2015). By forming reef-like structures, the framework-forming cold-water corals provide a refuge for a large number of organisms and, consequently, the ecosystems formed by these corals can be considered as impressive deep-sea biodiversity hotspots (e.g., Marshall, 1954; Henry and Roberts, 2015; Orejas and Jiménez, 2017).

Over geological time scales, millennia and longer, such reef-like structures can develop into coral mounds, three-dimensional seafloor obstacles reaching heights from a few to >300 m (Hebbeln et al., 2016). Consisting of fragments of the aragonitic coral skeleton and hemipelagic sediments, such coral mounds are widely distributed along the continental margins of the Atlantic Ocean (Hebbeln and Samankassou, 2015). They are found in shelf environments down to the upper and middle slopes and are mostly arranged in large provinces that comprise hundreds of individual mounds and cover extensive areas of several tens of square kilometers (e.g., Paull et al., 2000; Wheeler et al., 2007; Hebbeln et al., 2014, 2019; Vandorpe et al., 2014; Glogowski et al., 2015). Mound development is controlled by sustained coral growth and sediment supply (Hebbeln et al., 2016). The corals are controlled by a set of environmental boundary conditions, which include (i) physical and chemical properties of the surrounding water masses (e.g., temperature, dissolved oxygen concentration, pH); (ii) food supply, which can be either phytodetritus or zooplankton; and (iii) the local hydrodynamic regime providing food particles to the sessile suspension-feeding cold-water corals (e.g., White et al., 2005; Mienis et al., 2007; Davies et al., 2009; Davies and Guinotte, 2011; Flögel et al., 2014). The needed strong hydrodynamics are well-documented, by actual field surveys on living cold-water coral settings. For example, at various sites in the Atlantic current speeds in the range of several 10 s of cm s^–1 have been measured in situ at and around coral mounds (e.g., Dorschel et al., 2007a; Mienis et al., 2007; Guihen et al., 2013; Hebbeln et al., 2014) with maximum speeds of ∼1 m s^–1 (de Clippele et al., 2018; Lim et al., 2020). Laboratory experiments revealed that flow speed affects the feeding behavior of cold-water corals where Zooplankton is best captured at flow speeds below 2 cm s^–1, while phytodetritus is captured at higher flow speeds (Orejas et al., 2016).

In addition to the proliferation of the corals, the development toward coral mounds is further dependent on the capacity of the coral framework to entrap (baffle) bypassing sediment and thereby significantly increase sediment accumulation. For example, from sediment cores collected from various cold-water coral mounds it was shown that the amount of accumulated sediment, contributes >50% to the mound material (e.g., Dorschel et al., 2007b; Titschack et al., 2009, 2015, 2016). Thus, the capability of the coral framework to baffle current-transported sediments plays a crucial role as the entrapped sediments stabilize the biogenic construction, and hence, favor mound aggradation (Huvenne et al., 2007; Thierens et al., 2013; Titschack et al., 2015).

The interplay between bottom current strength and the coral framework influences the amount of sediments baffled by the corals. Hence, if suitable environmental conditions for corals persist over sufficiently long periods of time, and coral growth is faster than sediment accumulation, substantial deposits of coral mound material consisting of coral fragments and baffled sediments can form. Although this conceptual approach is widely accepted (e.g., Wienberg and Titschack, 2015), little is known about the prevailing sediment and fluid dynamical mechanisms in the direct vicinity of the corals.

In this context, the question is to which extent the flow and the sediment dynamics are affected by the presence of corals? To answer this question, the interplay of the prevailing hydrodynamics and sediment transport with corals should be investigated on a high spatial and temporal scale. Many successful in situ surveys have been done over the last decades using various devices, such as landers or moorings (e.g., Guihen et al., 2013; Mohn et al., 2014; Cyr et al., 2016). However, the data acquired with such investigations provides information about the general flow patterns near the reefs, but does not resolve the flow characteristics in the direct vicinity of the cold-water coral colonies. In order to assess to which amount a cold-water coral colony affects the flow, it is essential to measure close to the seafloor next to a colony, particularly on the centimeter to meter scale.

Here, laboratory-based investigations may foster our process understanding. As highlighted by Mienis et al. (2019), literature broadly reports about flume studies with a background in geoengineering where the focus was set on research, such as the flow alteration induced by underwater vegetation (e.g., Chen et al., 2012) and their consequences for sedimentation with regard to the turbulent wake. From research about the nutrient supply of tropical corals, Chang et al. (2009) impressively showed the prevailing hydrodynamics that occur within the branches of a tropical coral (Stylophora pistillata) by using a flume experiment. Also, from research about a tropical coral canopy (Porites compressa) Reidenbach et al. (2007) were able to resolve hydrodynamic processes that occur near a coral canopy, such as the turbulences on the small scale by a flume experiment. With regard to cold-water corals, Mienis et al. (2019) investigated in a flume experiment the prevailing hydrodynamics in the upstream and downstream reach of a cold-water coral patch, but did not map flows within the interior, i.e., between the branches. Consequently, little is known about the hydrodynamic conditions within the direct vicinity of a cold water coral and specifically within or behind the branches and about the development of the turbulent wake, which are important factors affecting food supply and sediment transport.

Numerical models can help to overcome such limitations. Even though, these models are simplifications of reality, they can provide remarkably useful approximations (aphorism attributed to George Box, 1978) and hence can be treated as a supplementary tool for field or laboratory-based investigations in order to refine the current understanding of the complex processes related to the effect of coral colonies on the flow and therefore sedimentation processes. Nonetheless, numerical simulation results are often challenged in the scientific community onto the accuracy of the simulation results. In order to overcome this challenge and to demonstrate the capability of numerical simulations, we performed a set of hydraulic laboratory flume experiments to investigate the effects of a simplified cold-water coral colony used as current obstacle on the prevailing hydrodynamics. The acquired data is used to validate a 3D numerical model. The cold-water coral structure used in the experiments mimics the shape of a cold-water coral colony that grew on a hard substrate at the bottom of the ocean. Notice, our attempt was not to replicate nature but to focus on the main flow features that are to be expected as the flow passes a simplified cold-water coral colony. Moreover, we aimed on the quantification to which extent a colony is capable to alter the flow field and to reduce flow velocities.

Materials and Methods

Physical Experiment Description

The hydraulic laboratory flume experiments were conducted in a unidirectional tilting flume at the Leichtweiß-Institute for Hydraulic Engineering and Water Resources, TU Braunschweig (see Figure 1 for the experimental flume setup). The dimensions of the rectangular flume were X = 32.0 m in the downstream direction, Y = 0.6 m in the across stream direction and Z = 0.3 m for the mean water depth in the channel and it was filled with freshwater with a temperature of 20°C, and a kinematic viscosity of 10–6 m² s^–1. Notice that focus of this study is on the main flow characteristics that occur in the case of a cold-water colony in general. Therefore, slightly higher density values, as found in the ocean, would have a neglectable impact in the main flow characteristics. The discharge was controlled by a valve and measured by a Krohne Aquaflux inductive flow meter, which had a resolution of 0.01 l/s. Point gauges were installed to measure the water depth. The tilting slope, discharge and water depth were adapted in accordance to ensure stationary, uniform flow conditions. The water depth was kept constant by a tailgate positioned at X = 25.5 m. In addition, to suppress the disturbance of the flow field by wave generation at the inlet flow straighteners made of honeycomb perforated bricks were installed in the direct vicinity of the inlet. The test section for the experiments was located at 16.0 m downstream of the inlet and was 1.5 m in length. For the experiment a flow velocity of 0.73 m s^–1 was selected, which is at the higher end of what is found at thriving cold-water coral sites in the ocean. Nevertheless, current speeds of several decimeters per second are a common feature in various regions (e.g., Porcupine Seabight: Dorschel et al., 2007b; Rockall Bank: Mienis et al., 2007; Campeche margin: Hebbeln et al., 2014; Cape Lookout: Mienis et al., 2014) with peak values of 1 m s^–1 (Tisler Reef, de Clippele et al., 2018) to 1.1 m/s (Porcupine Bank; Lim et al., 2020). As the corals depend on the lateral food supply provided by bottom currents, we suppose that the above average current speeds are the most favorable for the corals. For this reason, we use a current speed of 0.73 m s^–1 for this experiment. In order to achieve these maximum flow speeds of 0.73 m s^–1, in the free stream, at the beginning of the test section toward the downstream direction under steady uniform flow conditions, the slope of the flume was set to 4%.

FIGURE 1

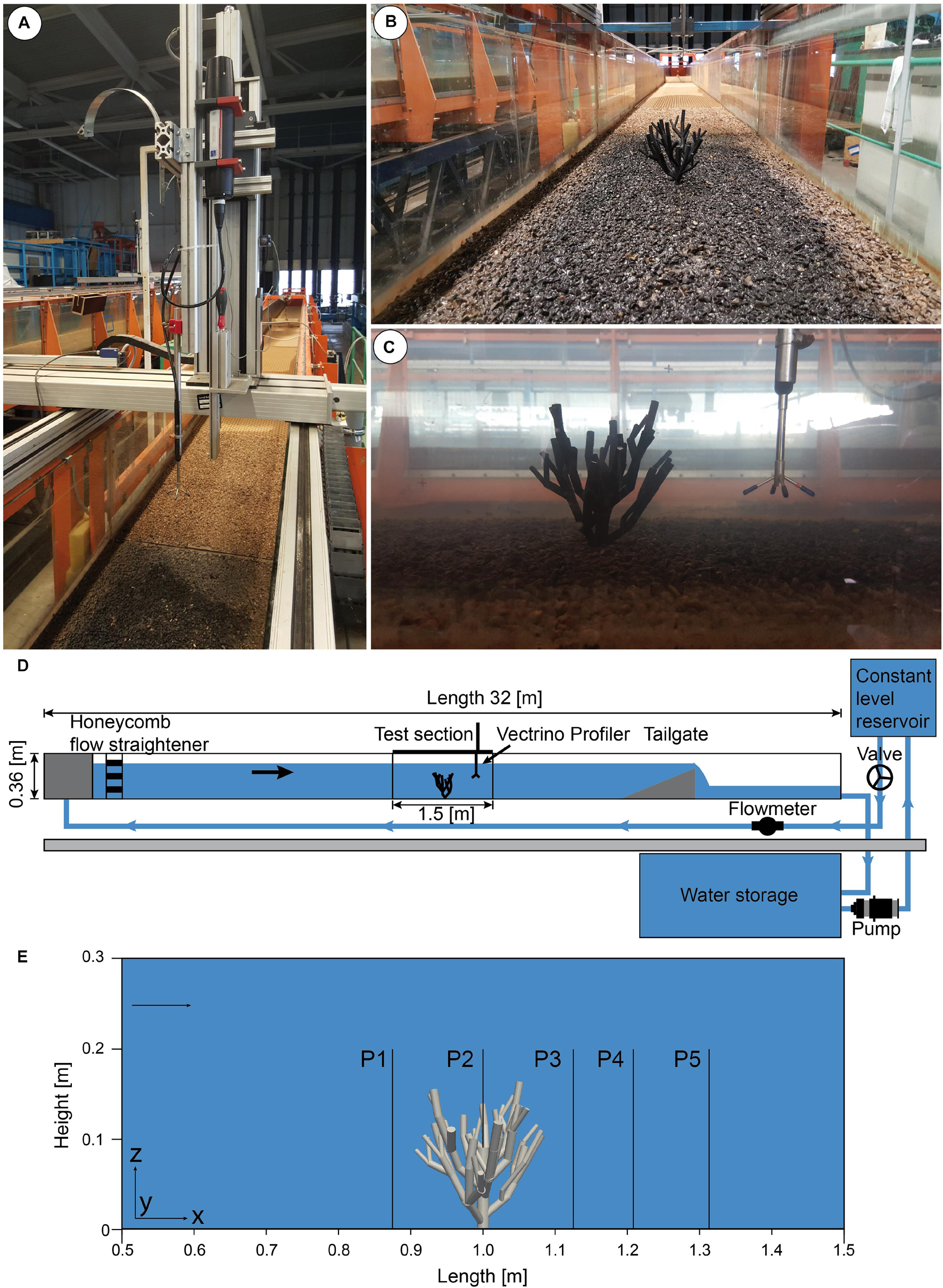
Figure 1. Summary of the laboratory-based flume experiment. (A) Traversing unit mounted above the drained flume with installed Vectrino profiler. (B) View into the downstream direction of the drained flume with the mounted cold-water coral model and roughness elements. (C) Sideview of the experiment showing the cold-water coral model as well as the Vectrino profiler. (D) Schematic of the setup of the flume experiment. (E) Positions of the reference profiles in the test section.

For the exact positioning of the measurement devices within the flume with respect to the desired measurement coordinates, a traversing unit (Isel Automation KG) was installed above the test section and was connected to a control unit. An artificial seabed with a surface roughness (D50 = 4 mm) that mimics the hardground that is typical for environments onto which cold-water corals may grow was installed at the bottom of the flume. It is anticipated that this configuration resembles the hard substrate e.g., small coral fragments in sediment or a rocky seafloor, needed for larvae settlement. Therefore, gravel in a grainsize ranging between 2 and 8 mm was glued on a plate that is installed on the bottom wall over the entire test section. Furthermore, nubby PVC mats were placed at the bottom of the flume ranging from the inlet to the test section.

The cold-water coral model (Figure 1) was designed to mimic a Lophelia pertusa colony, the most common framework-forming cold-water coral in the Atlantic Ocean, in a simplified manner. Please notice that in our experimental setup we decided to use a simplified structure that served as a shape model to capture the main flow features within and in the rear of a cold water colony, which allows for a better comparison of the results of the flume experiment and the numerical model. The structure of the coral was generated using a computer aided graphics design (CAD) program (AutoCAD) and was designed with cylinders. The virtual structure was then printed using an Ultimaker UM2 3D-printer. The filament used to print the structure was a polylactide polyester (PLA), with a building strength of 103,0 MPa, produced by the company Dremel. The final spatial dimensions of the simplified coral resulted in an average height of 0.14 m and an average horizontal diameter of 0.12 m. The cylindrical stem in the center of the simplified coral colony has a height of 0.07 m. In order to fix the structure at the bottom of the flume, a screw thread was milled and glued with a two-component glue into the bottom cylinder of the coral model. In order to ensure a solid stance also at relatively high flow speeds, the cold-water coral colony was positioned and fixated in the center of the test section. The exact location as well as the orientation of the cold-water coral facing the flow were recorded as this information was needed for the three-dimensional reconstruction of the exact same orientation and position of the coral in the numerical experiment.

An Acoustic Doppler Velocimeter (ADV) Vectrino II with a 3D down looking probe was used to measure the time average of the downstream velocity component (Ux) (Figures 1A,C). The device was mounted on the automatic traverse, which enabled an accurate positioning of the probe. The velocity components could be measured with a sampling rate of 1–100 Hz. The diameter of the sampling volume was 6.5 mm and its height could be changed between 1 and 9 mm. In the present study, each point was sampled with 100 Hz for 60 s. This ensured a representative time averaged mean value of the flow velocity. The sampling (or measuring) volume of the ADV is 5 cm below the probe, thus, it is not affected by the presence of the measuring device. The quality of the measurements was ensured by two parameters: signal to noise ratio above 25%, and correlation parameter. The correlation parameter serves as an indicator of the relative consistency of the behavior of the scatterers in the sampling volume during the sampling period, which was at least above 85%. In total five profiles arranged in a line were acquired using the Vectrino II for the validation of the numerical simulation results.

All profiles ranged from Z = 0.0 m to Z = 0.2 m in height, except Profile 2, which ranges from Z = 0.07 m to Z = 0.2 m due to its position above the coral colony. The profiles were laterally spaced 0.1 m apart with Profile 1 being located at X = 0.9 m downstream from the inlet, Profile 2 at X = 1.0 m, Profile 3 at X = 1.1 m, Profile 4 at X = 1.2 m, and Profile 5 at X = 1.3 m (Figure 2). The respective Y coordinate was located at the center of the flume at Y = 0.3 m. For each profile 51 points were acquired, whereby the vertical distance between the measurement points was Δz = 0.4 cm. Due to the structure of the coral, Profile 2 which is located above the major coral trunk only had 34 measurement points. Measurements close to the water surface were not obtained to exclude bias from potential surface water movements.

FIGURE 2

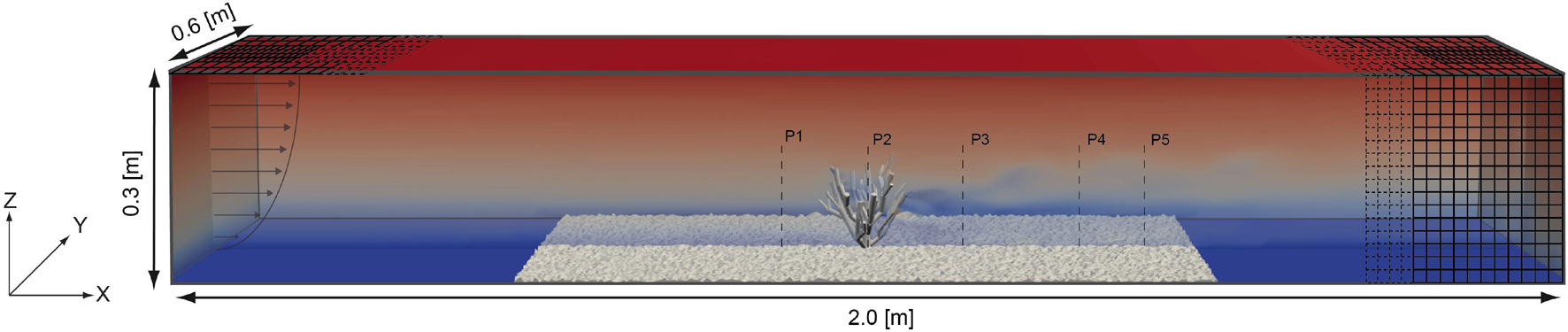
Figure 2. Setup of the numerical model domain showing the position of the roughness elements and the cold-water coral model as well as the exact locations of the processed fluid profiles. The profile on the left indicates the flow distribution at the inlet. The mesh at the right side indicates the used resolution levels used in the numerical model.

In order to reconstruct the surface roughness for the numerical model the gravel bed was scanned over the entire length of the test section after the flume was drained. This was done by defining a raster of measurement points over the test section in a Δx = 1.6 mm and Δy = 2 mm spacing. The resulting point cloud was then filtered, interpolated, and meshed into a STL file (STereoLithography file). The point cloud was interpolated using the Matlab function gridfit. By the combination of the coral model and the surface roughness files a single STL file was generated that was imported into a numerical Computational-Fluid-Dynamics (CFD) environment for further treatment.

Numerical Model Description

To investigate the flow within the test section of the hydraulic laboratory flume channel and in the direct vicinity, as well as, in the rear of the cold-water colony and hence that is used as a shape model to capture the main flow features, a numerical CFD model was used based on the open source toolbox OpenFOAM (Open Field Operation and Manipulation). This C++ based software package provides a wide range of solvers that are readily compiled, but also may be personalized by the user for individual purposes (Schmeeckle, 2014; Bartzke et al., 2018). In order to resolve the flow equations OpenFOAM uses the Finite Volume Method (FVM). The study domain is discretized into a grid of three-dimensional hexagonal elements, over which volume integral formulations of conservation equations are applied. Variables, such as the pressure scalar, and velocity vector are stored at the center of each control volume i.e., cell of the mesh. In the present study OpenFOAM version 1706 was used.¹

For the simulation of turbulence in the numerical model, a Detached Eddy Simulation model (DES) was used. The choice of this model type was inspired by industrial CFD simulations that rely on Scale-Resolving Simulation (SRS) models, which resolve the turbulence spectrum in at least a part of the flow domain and are computational cost efficient (Gritskevich et al., 2012). This technique has been broadly used in aerospace engineering (Viswanathan et al., 2007; Keylock et al., 2011; Shur et al., 2011), and geophysics (Alvarez et al., 2017). A DES simulation is a hybrid technique for turbulence modeling combining RANS (Reynolds-averaged Navier–Stokes equations) near the bed and the coral and a LES (Large Eddy Simulation) for the simulation of the flow interior, aiming to alleviate the costly near-wall meshing requirements imposed by the LES. According to Gritskevich et al. (2012) the original intent of DES was to be run in RANS mode for attached boundary layers and to switch to LES mode in large separated (detached) flow regions. Regions near solid boundaries and where the turbulent length scale is less than the maximum grid dimension are assigned the RANS mode of the solution. As the turbulent length scale exceeds the grid dimension, the regions are solved using the LES mode. Therefore, the grid resolution is not as demanding as in the case of a pure LES, and is thereby considerably cutting down the cost of the computation. This strategy allowed for the computation of the model results on a standard workstation on 12 cores.

The LES equations are derived by applying a spatial filtering operation. These equations are shown below in terms of the LES decomposition:

$$\text{Continuity}\frac{\mathrm{\delta }\overline{u_i}}{\mathrm{\delta }{x}_i}=0(1)$$

$$\text{Momentum}\frac{\mathrm{\delta }\overline{u_i}}{\mathrm{\delta }t}+\frac{\mathrm{\delta }(\overline{u_i{u}_j})}{\mathrm{\delta }{x}_j}=-\frac{1}{\mathrm{\rho }}\frac{\mathrm{\delta }\overline{p}}{\mathrm{\delta }{x}_i}+\frac{\mathrm{\delta }}{\mathrm{\delta }{x}_i}(({\mathrm{\nu }}^{\prime }+{\mathrm{\nu }}_t^{\prime })\frac{\mathrm{\delta }\overline{u_i}}{\mathrm{\delta }{x}_i})(2)$$

where $\overline{u}$ and p are the velocity and pressure components, ϱ is the density, ν is the kinematic viscosity, and ν_t is the turbulent eddy viscosity. The term on the right hand side of the momentum equation containing the kinematic viscosity and the eddy viscosity $({\mathrm{\nu }}^{\prime }+{\mathrm{\nu }}_t^{\prime })$ represents the unresolved subgrid (SGS) stress tensor, and is modeled using the Spalart-Allmaras (S-A) turbulence closure. The S-A model has the advantage of being a non-zonal technique, implying that one single momentum Eq. (2) can be used with no a priori declaration of the RANS vs. LES zones. The length scale of the S-A model is equal to the minimum of the distance to the bed and the coral, and the length scale proportional to the local grid spacing(C_DESΔ_G). Thus, $\tilde{d}=\min (d,C_{DES}{\mathrm{\Delta }}_G)$ provides a way to make a transition between RANS and LES by retaining RANS within the boundary layer when $\tilde{d}<d$ and applying LES to the zone away from the bed or the coral when $\tilde{d}\ge C_{DES}{\mathrm{\Delta }}_G$. In more detail a Spalart-Allmaras IDDES (Improved Delayed Detached Eddy Simulation) was used. The IDDES is based on original formulation Spalart-Allmaras DES model (Spalart et al., 2006) but uses a modified improved formulation of the length scale to solve the unresolved subgrid (SGS) stress tensor (Gritskevich et al., 2012). The performance of this model has been extensively tested and verified on a large set of test cases (Gritskevich et al., 2012). In the present study, the standard OpenFOAM solver pisoFoam was used for velocity pressure coupling for time dependent flows. The PISO (Pressure-Implicit with Splitting of Operators) algorithm (Issa, 1986) is a pressure correction scheme used to calculate the pressure distribution correction to derive the local velocity field toward a result that satisfies both momentum and continuity (Ferziger and Perić, 2002). Please note, to interpret the results from this incompressible solver, the kinematic pressure was multiplied by the density (ϱ) value (OpenFoam User Guide).

Numerical Model Setup

The numerical model domain was setup to replicate the test section of the laboratory-based flume experiment with dimensions of 2.0 × 0.6 × 0.3 m (Figure 2). The coral was positioned in the center of the domain at X = 1.0 m and Y = 0.3 m. The coral in the numerical simulation as well as in the flume experiment had the same orientation. The computational mesh of the domain was constructed from a background mesh (mesh level 0; 400 × 60 × 30 cells). This background mesh was refined using a refinement box ranging from X = 0.0 to 2.0 m, from Y = 0.2 to 0.4 m, and from Z = 0.0 to 0.3 m. The cell dimensions in the refinement box were 50 percent smaller as compared to the background mesh (mesh level 1, 800 × 80 × 60 cells). In order to resolve the fluid dynamical processes in the vicinity of the coral colony as well as near the pebble bottom in highest resolution a surface wise refinement was applied. The surface refinement was defined to cover all cells located at a maximum of 0.05 m apart from the coral colony or the bottom (mesh level 1–3). This procedure resulted in 12,746,939 cells in total. The meshing of the coral colony and the bottom was performed with the OpenFOAM inbuild utility snappyHexMesh that allows to mesh structures into the background mesh.

An inlet boundary condition was imposed at the left sidewall and an inlet/outlet boundary condition was assigned at the right sidewall. No-slip boundary conditions were assigned to the front, bottom, and back walls of the domain. The same applies for the gravel as well as for the coral structure located in the center of the domain. The boundary condition chosen at the top wall was a slip boundary condition, so no flux could pass through this wall. In order to force the flow in a comparable manner to the flume experiment, a velocity profile from the beginning of the test section of the flume experiment was mapped and applied as inlet boundary condition. The maximum flow speed was U = 0.73 m s^–1. Notice that this velocity value was chosen to reflect the relative strong current speeds reported by Lim et al. (2020). As a result, the flow became unidirectional by entering the domain on the left side of the domain (upstream) and leaving it on the right (downstream). Notice that the mapped profile of the flume experiment was time averaged and did not exhibit any fluctuations over the entire simulation time, but ensured a constant flow into the model domain. Physical properties in the numerical model were chosen to mimic an incompressible fluid. The kinematic viscosity ν was set to 1e-6 m²/s implying a density (ρ) of 1,000 kg/m³. In order to ensure the comparability of the model results with those of the flume experiment the same physical parameters were chosen, which represent the physical properties of freshwater. Each calculation run simulated a total time of 30 s with a time step of 0.0025 s. The simulation was numerically stable showing Courant numbers smaller than 0.2. The numerical simulation was run in parallel on a single workstation (Intel Xeon CPU E5-2650 v4 @ 2.20 GHz) on 12 processors, whereby the entire computation time lasted for 16 days.

Data Analysis

Please note that only the data after 20.0 s of simulation time was considered for further evaluation to ensure that the flow traveled once through the entire domain but also to avoid backward flow at the outlet. All data processing was either performed with Matlab or with the inbuilt utility paraFoam, a customized version of Kiteware’s ParaView that comes with the OpenFOAM software environment.

Flow velocity profiles from the numerical model were taken at the same positions as in the experimental flume with the goal of comparing the two approaches. The velocity profiles obtained by the flume experiment were acquired as a time average. In order to provide additional information about the instantaneous flow behavior, we also plotted the corresponding instantaneous velocity components. Each profile consisted of 200 datapoints in the vertical direction with increments of 1.0 mm. The time average profiles were processed for comparison with the profiles obtained by the flume experiment by averaging the instantaneous flow speed values over time. The time average of the instantaneous profiles was computed over 10 s with increments of 0.1 s. In order to highlight the effect of flow speed changes by the presence of the cold-water coral, the downstream velocity component (Ux) was processed. The same procedure was applied for the transversal (Uy) and vertical (Uz) velocity components. In order to aid visualization a set of slices was cut through the domain facing in the Y normal and the Z normal of the model domain. The slices indicate the instantaneous as well as the mean flow conditions without the velocity fluctuations. On the contrary, the velocity fluctuations are highlighted by the instantaneous velocities. The same approach was done to highlight the distribution of the pressure field as well as for the turbulent kinetic energy (TKE) values.

All profiles were extracted from a time averaged Y normal slice at Y = 0.3 m and Z normal slice at Z = 0.05 m. The downstream positions of the solid lines represent profiles that were extracted in the rear of the coral. In total 37 individual profiles were extracted from the numerical model between 1.1 and 2.0 m.

To compare the velocity data of the numerical model to the data of the flume experiment the coefficient of determination R² = 1 − SS_reg/SS_tot was computed. Therefore, the sum of squares of the regression (SS_reg), where SS_reg = ∑(y_i − f_i)² of the time averaged velocity values (Ux) from the model (y_i) and the corresponding experimental data (f_i) and the sum of squares total (SS_tot), where SS_tot = ∑(y_i − y)² of the model (y_i) and the mean values of the model (y) were calculated.

In order to visualize typical features that can be processed from a CFD model, such as the streamlines and the drag distribution (Figure 3A), the flow velocity contour (Figure 3B), and the Q-criterion (Figure 3C) in three-dimensions the software paraview (Kiteware) was used.

FIGURE 3

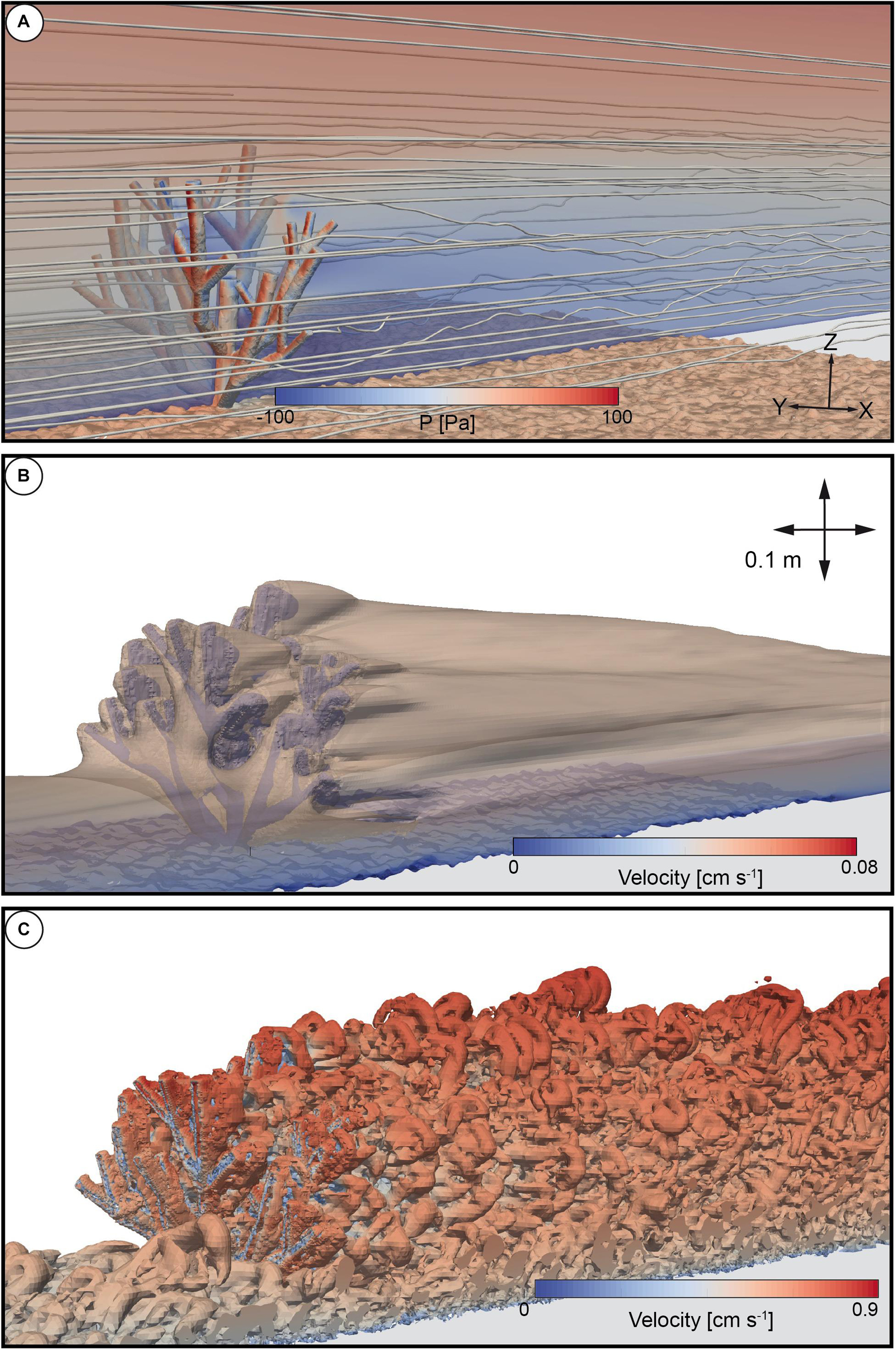
Figure 3. (A) Rendered 3D image of the streamlines and pressure drag values affecting the cold-water coral model as well as roughness elements at the bottom of the domain. The transparent 2D slice in the center of the domain indicates the flow field. (B) Rendered isosurface, indicating flow velocity values of 0.08 m s^{– 1}. (C) Rendered isosurface indicating the Q-criterion.

Please note that the results shown in Figure 3 were all derived from the same timeframe at 25.0 s. The streamlines are shown as an example case in three dimensions. The same applies for the isosurfaces to highlight the flow shading zone using a velocity contour of 0.08 m s^–1. In addition, the Q-criterion as well as the drag forces were processed with the inbuilt filters of paraFoam (Kiteware). The Q-criterion [Q = 0.5 (²−S²)] is a vortex identification method and was used to visualize the development of turbulences as isosurfaces. Here, S and Omega are the symmetric and antisymmetric components of the velocity gradient tensor, where S is the rate of strain tensor and Omega the vorticity tensor. By definition, a vortex is located where Q > 0. Notice that the Q-criterium can be post-processed within paraview (Kiteware) or with the postprocessing toolbox that comes with the OpenFoam environment.

Based on the pressure field values, the drag force was computed to show the impact of the hydrodynamic forces acting on the coral. Therefore, the surface planes of the coral were extracted. The corresponding pressure values were then multiplied by the surface normal values with respect to their direction. For example, the surface normals facing in the downstream direction were multiplied with the pressure values. This resulted in the drag force vectors acting on the individual branches of the coral. Subsequently, all values were integrated to gain the desired drag force. Notice that this value was the result of averaging over 10.0 s of model time. After computing the drag force, the drag coefficient (CD) can be computed as CD = Drag/(V²A/2). Drag refers to the dragforce, refers to the fluid density, V refers to the far field flow velocity, and A refers to the surface area.

This led to a computed drag coefficient CD of 0.71 by taking an averaged velocity value (Ux) of 0.55 m s^–1, a surface area of 0.041 m², a density of 1,000 kg/m³, and a Reynolds number of 77000, into account. Notice that also the Drag coefficient can be post-processed within paraview (Kiteware) or with the postprocessing toolbox of OpenFoam.

Results

Flow Velocity Profiles Obtained With the Laboratory Flume

In total five-time averaged velocity profiles indicating the vertical distribution of the downstream velocity component Ux were processed from the flume experiment (Figure 4). In order to capture changes in the horizontal flow component with respect to the presence of the coral all profiles were located in the center of the test section traversing in a line from the upstream to the downstream reach of the test section. Profile 1 served as a reference profile to measure the flow speed values upstream of the coral. From the bottom of the bed to a height of 0.04 m the shape of the Profile 1 indicates a curved pattern of the flow velocity value distribution due to the roughness of the hardground at the bed. Velocity values in that area range from 0.0 to 0.4 m s^–1. Toward the top the velocity values of profile 1 increase to 0.72 m s^–1. In the case of Profile 2 that was extracted right above the central stem of the coral colony a clear deflection with respect to the reference profile can be observed. The maximal change of the velocity values is indicated between the top of the coral stem to 0.12 m. The velocity values here increased from 0.0 to 0.6 m s^–1. Above 0.12 m toward 0.2 m the pattern of profile 2 seems to reattach the shape of the reference profile 1. This is indicated by a linear increase of the flow speeds values from 0.12 to 0.72 m s^–1 toward the top. Profile 3 is characterized by an oscillating pattern of velocity values, ranging from the bottom at 0.0 m toward 0.14 m. In this region the flow velocity values increase from 0.0 m s^–1 at the bottom to 0.5 m s^–1 at 0.14 m. Similar to profile 2 but with an offset of 0.02 m, a trend of linearly increasing velocity values can be observed. This distribution appears also to match with the shape of the reference profile. The corresponding velocity values ranged between 0.5 m s^–1 at 0.12 m to 0.72 m s^–1 at the top. In comparison to the two prior profiles the pattern of Profile 4 appeared smoother in shape. Similar to profile 3, between 0.0 and 0.06 m a velocity increase to 0.18 m s^–1 can be observed. Up to a height of 0.14 m the velocity increase is more pronounced as compared to the section below, where the velocity values increase toward 0.5 m s^–1. Above, in the region from 0.14 m to the top, a similar distribution compared to the reference profile can be observed. Here a maximal velocity value of 0.72 m s^–1 was measured similar to the other profiles. Profile 5, indicates a smoother pattern as compared to profile 4. However, in the lower part of profile 5 between 0.0 and 0.09 m, in average 0.01 m s^–1 higher velocity values were measured as compared to profile 4. Similar to the prior cases the upperpart of profile 5, between 0.15 and 0.2 m in height, the velocity values appeared to reattach, showing a similar pattern as compared to profile 1.

FIGURE 4

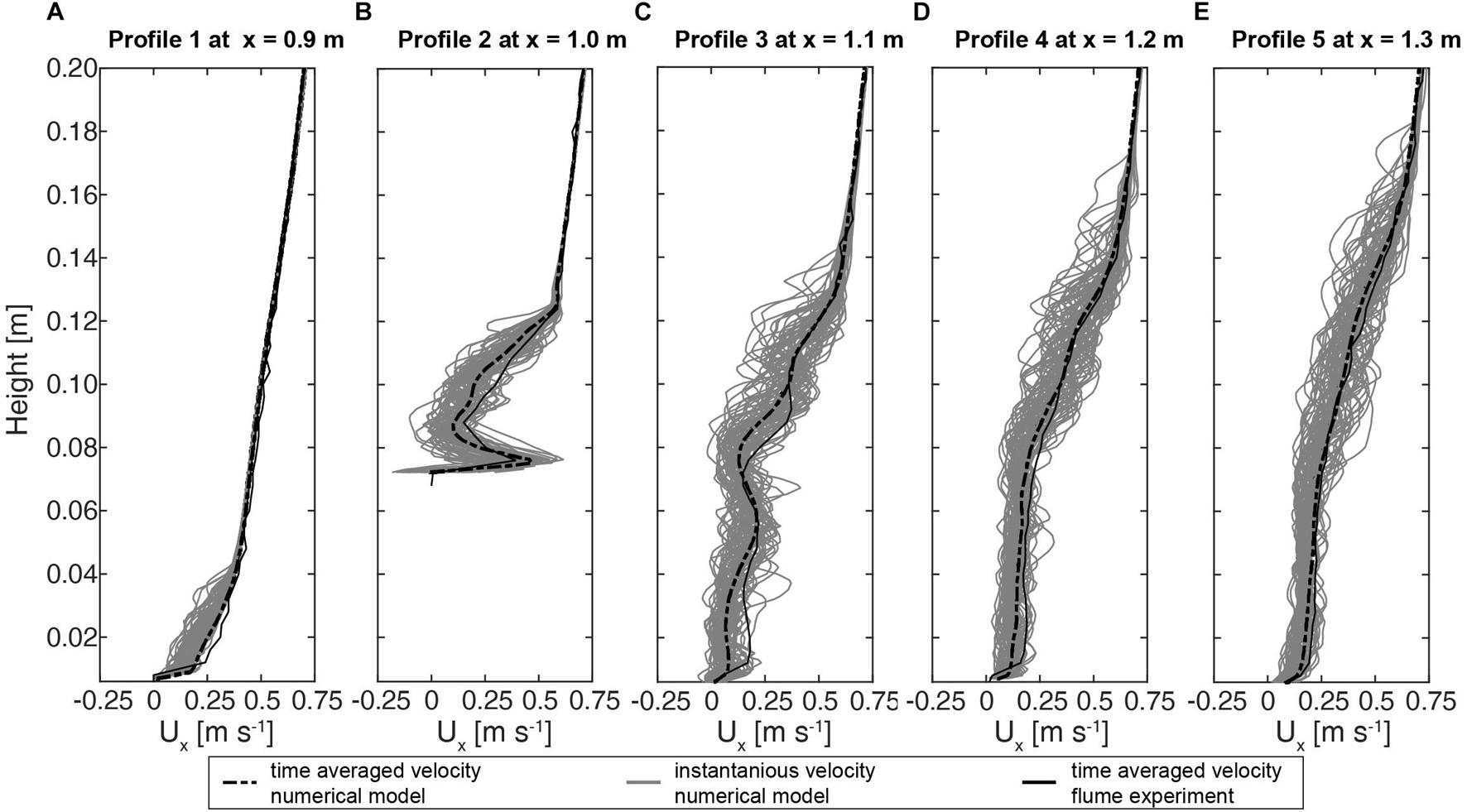
Figure 4. (A–E) Fluid profiles processed from the laboratory-based flume experiment as well as from the numerical model.

Flow Velocity Profiles Obtained With the Numerical Model

For the validation of the numerical model the downstream facing flow velocity values were plotted against those obtained by the flume experiment. Moreover, for a better representation of the model results both the instantaneous velocity values as well as the time averaged values were plotted (Figures 4A–E). For all measuring points, the time averaged profiles of both the numerical and the flume channel experiment are in excellent agreement. Particularly the shape of the velocity distributions (Ux) of profile 1 (R² = 0.99), profile 4 (R² = 0.98), profile 3 (R² = 0.98), and profile 5 (R² = 0.99) indicated a nearly perfect match. A slight underestimation of the flow speeds with respect to the time averaged velocity component is present in the case of profile 2 (R² = 0.77). Nonetheless, the goodness of the results is further supported by the distribution of the instantaneous velocity profiles, which clearly indicate that the overall velocity fluctuations match the pattern of the profiles measured by the flume experiment.

Flow Field Derived With the Numerical Model

Two slices were cut through the domain facing in the Y normal and Z normal direction in order to highlight velocity field patterns (Figure 5). In addition to the instantaneous (Figures 5A,C), also the time averaged values are shown as mean velocity magnitude (Figures 5B,D). The flow velocities observed between the inlet of the domain and the coral exhibit an almost homogenous flow field with a logarithmic gradient from the bottom to the top indicating a mean velocity value of 0.58 m s^–1 (Figures 5A,C). Slight fluctuations within the flow field can be observed in the case of the instantaneous flow field near the bottom indicating the deflection of the flow velocity values near the roughness elements (Figures 5A,C). In general, velocity magnitude changes were largest in the regions where the branches touched the freestream, exhibiting values of 0.7 m s^–1, whereas the lowest values were derived in within the coral and ranged between 0.0 to 0.05 m s^–1 (Figures 5A,C). Both minimum and maximum values are concentrated in patches located in the direct vicinity of the coral branches forming alternating regions of low and high velocity fields. Detailed observation of the slices both in the vertical and horizontal directions indicates that the flow separates as it encounters the branches of the corals. In particular, the instantaneous velocity fields (Figures 5A,C) showed that the flow values are generally higher in front of the branches and lower in their rear, where the fields are disturbed. The flow field above the coral appeared unaltered (Figures 5A,B). In contrast to the homogeneous distribution of the flow velocity field in the upstream reach, a pattern of fluctuating velocity values becomes visible downstream from the coral toward the end of the domain. The fluctuations within the flow field can be directly observed in the case of the instantaneous flow field in the direct rear of the coral, where a reduction of the flow velocity values can be observed. For example, at a height of 0.05 m, from the upstream reach at (X = 0.9 m) toward the direct rear of the coral colony (X = 1.1 m) the decrease of the flow speeds was 0.3 m s^–1. This reduction is indicated in both the side and top views in Figure 5. The height of this zone is successively thickening from 0.12 m at 1.1 m toward 0.16 m at 2.0 m (Figures 5A,B). The shape of this zone appears to form a curved region that is characterized by patches of fluctuating velocity values that are lower as compared to the upstream reach, and is defined here as the low velocity zone.

FIGURE 5

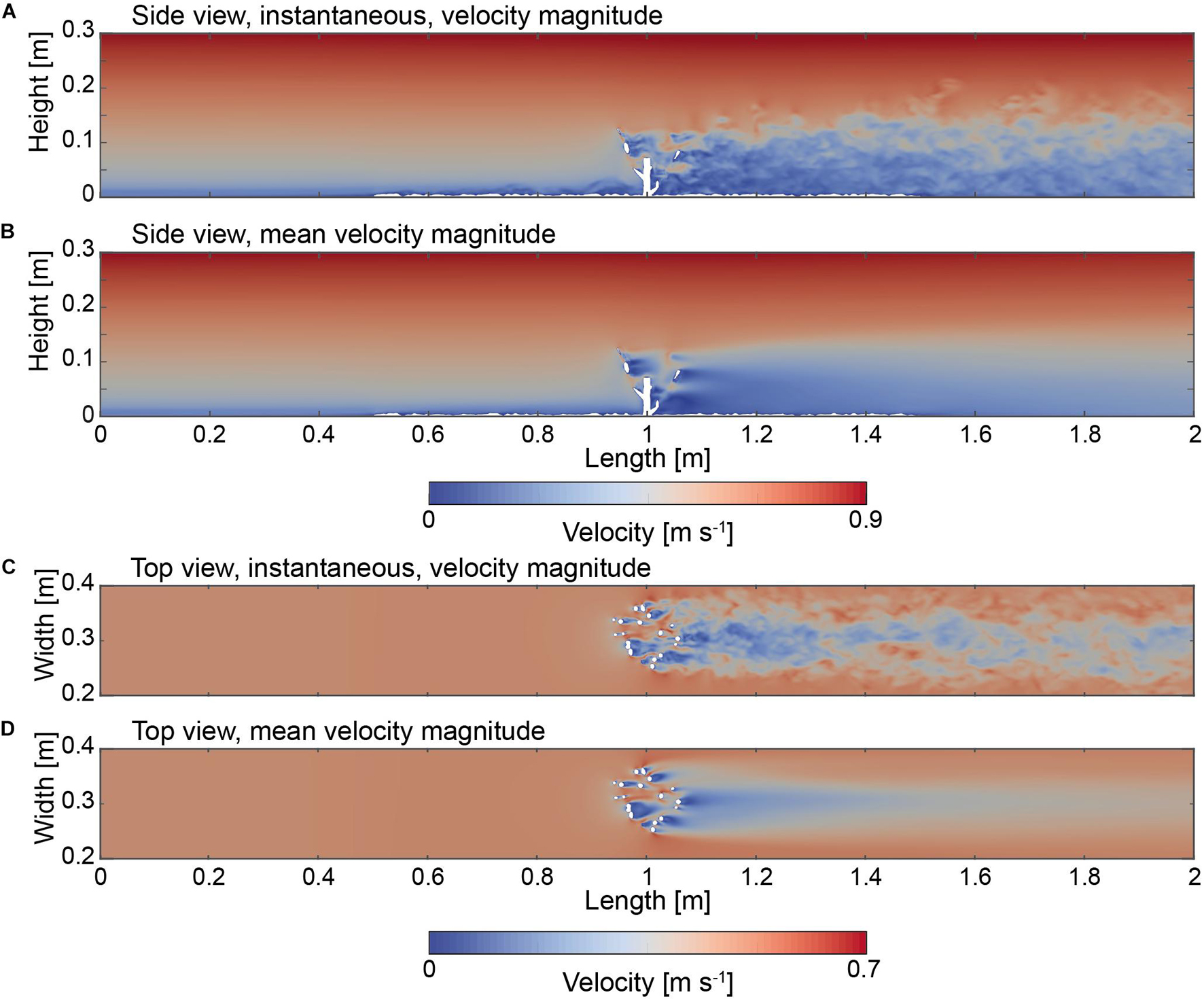
Figure 5. (A) Side view (Y = 0.15 m) indicating the instantaneous flow field at 25.0 s. (B) Side view (Y = 0.15 m) of the time averaged flow field. (C) Top view (Z = 0.05 m) indicating the instantaneous flow field at 25.0 s. (D) Top view (Z = 0.05 m) of the time averaged flow field.

Downstream Evolution of the Flow Velocity Profiles Obtained With the Numerical Model

In order to aid visualization of the flow velocity distribution, the time averaged flow speeds facing into downstream direction that were derived from the numerical model are shown in Figure 6. All flow profiles are characterized by relatively low flow velocity values close to the bottom of the domain and increase with respect to height (Figure 6A). In the case of the reference profile indicating the undisturbed flow speed values upstream of the coral (dashed lines in Figure 6) the velocity values increase from 0.0 m s^–1 at the bottom toward 0.4 m s^–1 at 0.06 m. In this region the profile is characterized by a parabolic shape. Further toward the top of the profile the velocity values increase in a linear pattern to 0.7 m s^–1. The profiles extracted in the vicinity of the coral (white colored profiles in Figure 6A) differ from the pattern of the reference profile and are characterized by an undulated distribution of the flow velocity values. For example, the profile that was extracted directly from the rear of the coral appeared disturbed in shape. Toward the top of the profile, in the range between 0.12 to 0.18 m the pattern of the profile appears to reattach to the original shape of the reference profile. With further distance into the downstream direction the shapes of the profiles appeared smoother and tend to transform into a linear pattern with height. In addition, a shift of the velocity value distribution with respect to the distance further in the downstream direction becomes evident. For example, all values that were extracted in the range between 0.0 and 0.12 m close to the rear of the coral are characterized by relatively low flow speeds. i.e., low velocity zone. However, those profiles that were extracted further downstream indicate a trend of successively increasing values (black colored profiles in Figure 6A). For example, the profile that was extracted in the far region of the domain is characterized by a straight pattern showing a velocity increase ranging between 0.3 m s^–1 at 0.01 m and 0.45 m s^–1 at 0.12 m. The velocity increase in this region averaged 0.22 m s^–1 with respect to the distance into the downstream direction. An opposing trend of decreasing velocity values that is indicated by the position of the profiles with respect to their distance into the downstream direction, can be observed in the region above 0.12 m. The flow profiles that were extracted in the vicinity of the coral initially appear to match with the velocity distribution of the reference profile ranging between 0.55 m s^–1 at 0.12 m toward 0.7 m s^–1 at 0.2 m. However, with increasing distance into the downstream direction the flow speed values successively decrease, whereas a transformation from an initially parabolic shape into a linear shape becomes obvious. The velocity decrease in this region averaged at 0.2 m s^–1 with respect to distance of the profiles facing into the downstream direction.

FIGURE 6

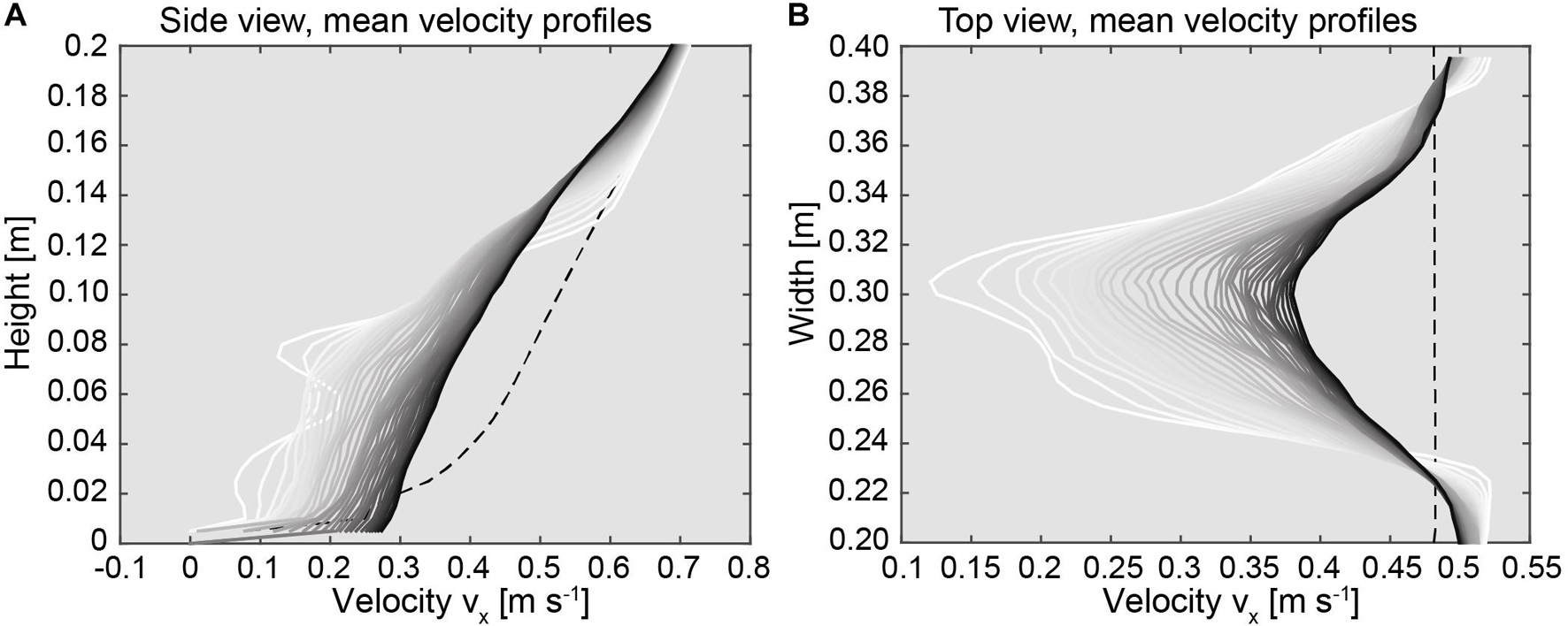
Figure 6. (A) Profiles indicating the downstream velocity component with respect to model height (Z = 0.05 m). (B) Profiles indicating the downstream velocity component with respect to model width (Y = 0.15 m). The 37 individual profiles were extracted from the model between 1.1 and 2.0 m. The white color refers to profiles that were extracted close to the coral, whereas the black colors references to profiles that were located further downstream of the coral. The dashed line indicates the profile that was extracted before the coral. For comparison, the dashed lines refer to an undisturbed reference profile measured at 0.9 m in the upstream reach of the coral.

For the profiles extracted over the width of the model (Figure 6B) a similar trend of increasing flow speed values into the downstream direction can be observed. The velocity ranges of the reference profile indicated a uniform velocity distribution over the entire width of the domain of 0.48 m s^–1 at 0.08 m. All flow velocity profiles in the downstream region of the coral are characterized by a parabolic distribution of the flow velocity values. Highest values were measured further away from the coral toward the side walls of the domain at 0.2 and 0.4 m. Lowest values were obtained from the center of the domain in the range between 0.28 and 0.32 m (Figure 6B). For example, the minimal values of the profile that was located in the direct vicinity of the coral (white colored profiles in Figure 6B) were 0.13 m s^–1 and increased to a flow speed of 0.55 m s^–1 toward the sides, indicating a decrease of the flow speeds by 0.42 m s^–1 over the entire model width. However, with increasing distance further into the downstream direction, the pattern of the velocity values appear to smooth out, which is indicated by an almost perfectly shaped parabolic distribution of the velocity values with respect to width (black colored profiles in Figure 6B). For example, in the case of the profile located at 1.9 m, the velocities were lowest within the center of the domain, which is indicated by a velocity value of 0.4 m s^–1, whereas the flow speeds at the sides of the domain appeared to reattach to the shape of the reference profile to 0.5 m s^–1. Comparing the differences of the flow velocity values of the profiles close to the coral to those from the end of the domain taken in the range of the centerline, a difference of 0.32 m s^–1 over a distance of 1.0 m into the downstream direction was derived.

Pressure Field and Turbulent Kinetic Energy Field

The pressure fields of the instantaneous as well as the time averaged flow field are shown in a side and top view that was sliced through the model domain (Figure 7). The pressure distribution between the inlet of the domain and the coral colony exhibit an almost homogenous pressure field in the water column as well as in the regions close to the bottom. The pattern of the pressure field in the vicinity of the coral colony appeared highly diverse. Highest pressure values were observed in the range where the branches faced the flow, which is indicated by values peaking at 80 Pa. In the region within the center of the coral, the pattern of the pressure values changed, which is indicated by negative values in the range of –90 Pa. The pressure values within the center region as well as in the direct rear of the coral appeared concentrated into patches in the rear of the respective branches. Similar to the pattern indicated by velocity magnitudes (Figure 6), the instantaneous values in the range from the rear of the coral toward the end of the domain indicated a thickening pattern of fluctuating pressure values ranging between –50 and 50 Pa. The same trend can be observed with respect to the top view (Figure 7B) by which a conical narrowing out toward the end of the domain of the pressure fluctuations can be observed.

FIGURE 7

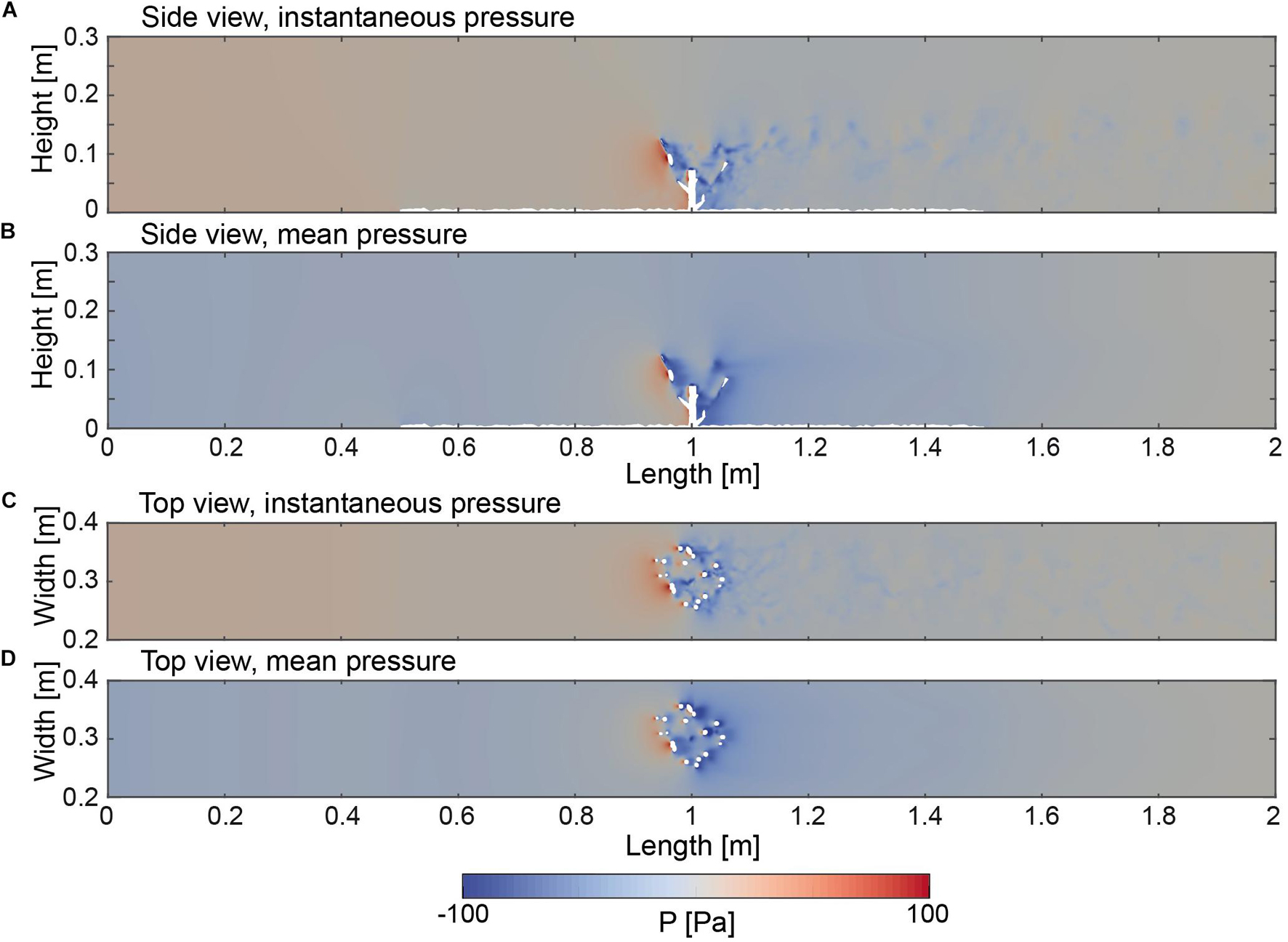
Figure 7. (A) Side view (Y = 0.15 m) indicating the instantaneous pressure field at 25.0 s. (B) Side view (Y = 0.15 m) of the time averaged pressure field. (C) Top view (Z = 0.05 m) indicating the instantaneous pressure field at 25.0 s. (D) Top view (Z = 0.05 m) of the time averaged pressure field.

The TKE values were derived as an additional field to characterize the mean kinetic energy per unit mass that is associated with eddies that form in a turbulent flow (Figure 8). The side view indicates TKE values in the range of zero within the region from the inlet toward the front of the coral. Increased values can be observed in the vicinity of the rough bottom. In the center region of the coral from 0.9 to 1.1 m, the TKE values increased to a maximum of 0.05 m²/s², and averaged at 0.02 m²/s². This indicates that the highest amount of TKE is distributed in the direct vicinity of the coral branches. From the rear of the coral toward the end of the domain the TKE values remained in the similar range of 0.02 m²/s² but successively deceased to 0.03 m²/s² toward the downstream end of the domain. The width of the TKE field remained relatively constant from the rear of the coral colony toward the end of the domain and ranged between 0.22 and 0.38 m.

FIGURE 8

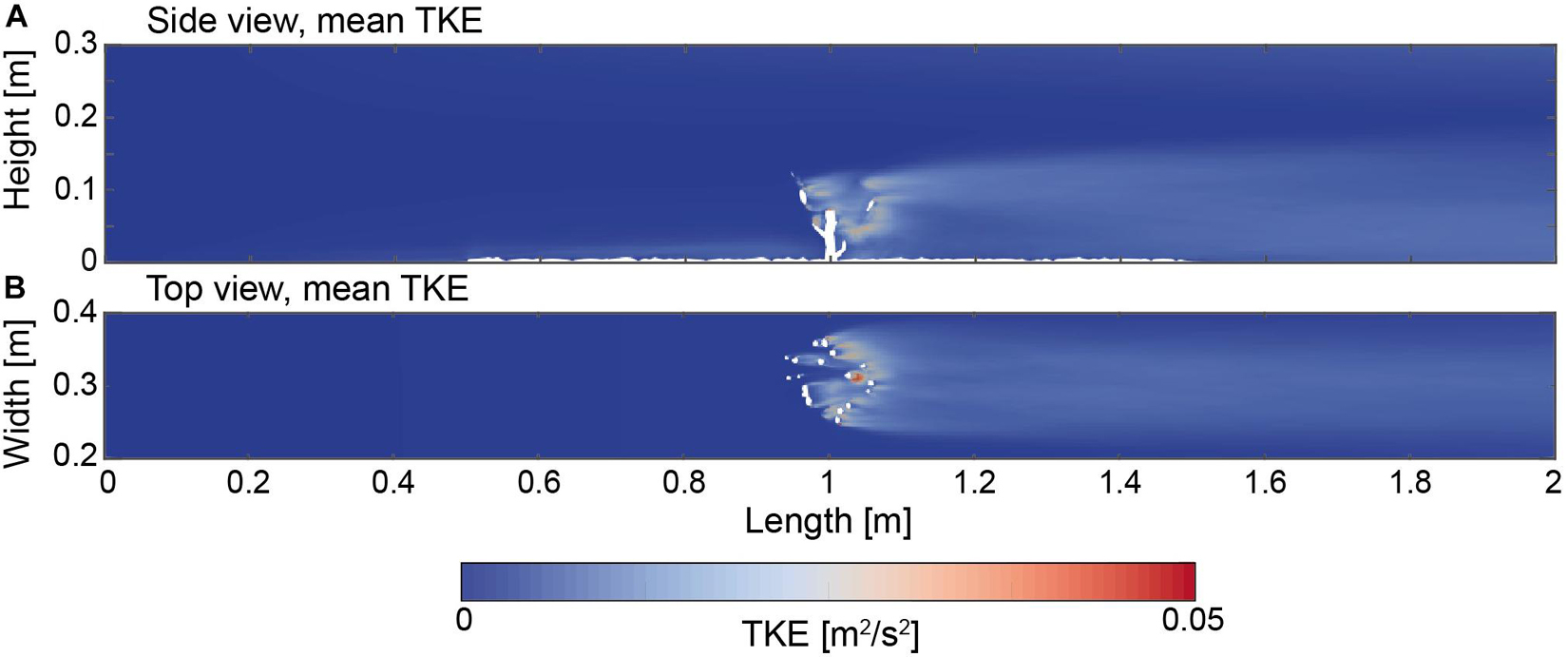
Figure 8. (A) Side view (Y = 0.15 m) indicating the turbulent kinetic energy (TKE) field as a time average. (B) Top view (Z = 0.05 m) indicating the turbulent kinetic energy field as a time average.

Streamlines, Pressure Drag, Velocity Deflection, and Q-Criterion

In order to demonstrate additional capabilities of the numerical model, and hence, to improve the understanding of the flow with respect to the presence of a cold-water coral colony a set of analysis tools that are common in the field of Computational-Fluid-Dynamics were summarized for an overview: (i) 3D-visualization of streamlines and the pressure drag distribution affecting the coral (Figure 3A); (ii) the flow velocity contour (Figure 3B), and (iii) the Q-criterion (Figure 3C), with all data are derived from the same timeframe at 25.0 s. This graph aids the visual representation of the hydrodynamics and ultimately will implicate a basis to derive information on the impact of changing hydrodynamics on sediment dynamics in a future study.

All streamlines located upstream of the coral colony were oriented in a parallel pattern indicating a homogeneous flow (Figure 3A). A transition toward a chaotic arrangement of the streamlines becomes evident in the rear of the coral colony and is also evident further into the downstream direction ranging over a height of Z = 0.0 m to Z = 0.12 m. The streamlines above the coral in the range of 0.12 and 0.3 m appear to resume parallel pattern. The pressure values affecting the coral colony were highest in the regions of the branches of the coral that faced the flow. Negative pressure values were observed in the regions where the branches opposed the flow direction. The respective drag forces revealed a value of 0.971 N. The deflection of the flow field with respect to the coral colony is shown in Figure 3B. The three-dimensional representation shows an isosurface that was processed to indicate a three-dimensional surface that represents the distribution of all velocity values lower than 0.08 m s^–1 as an example case. The hull appears as a conical shaped shadow indicating the low velocity zone that ranges from the rear toward the end of the domain. Moreover, the isosurface indicates that this hull was lower in height in the upstream direction and appeared lower in height in the rear of the coral as well. This highlights the effect of a reduction of the flow velocity values with respect to height. For example, the height of the isosurface was at 0.05 m in the upstream region, and at 0.14 m in height in the downstream region. This indicates a deflection of the initial flow field by 9 cm in terms of height and corresponds to a factor of 2.8 with respect to the measured height difference. Furthermore, as an indicator for turbulent flow structures, the Q-criterion was processed as an isosurface (Figure 3C). Coherent structures can be observed near the bottom of the upstream region before the flow reached the coral. In the area where the branches of the coral faced the flow for the first-time, coherent structures also appeared to form. A similar trend can be observed within the center of the coral. In the region ranging from the rear of the coral toward the end of the domain the pattern of the isosurfaces is characterized by a large number of alternating vortexes that appear to migrate in a staggered pattern toward the end of the domain.

Discussion

Flume Channel and the Numerical Experiment Data

The velocity profiles obtained from the flume and the numerical experiment show excellent agreement, and hence demonstrate the predictive capabilities of the DES model with respect to the chosen parameters. The instantaneous profiles as well as the time averaged profiles obtained with the numerical model are in agreement with the flume experiments as shown by the coefficient of determination values. Nonetheless, one might argue that the model might slightly tend to underestimate the flow conditions of the flume experiment in the cases of profiles 2 and 3 (Figure 4) by a maximum of 0.08 m s^–1 in the bottom region. However, this offset can be related to the sampling rate and hence is dependent on the amount of instantaneous profiles available to compute the time average. The sampling rate of the Vectrino profiler was set to 100 Hz to produce the time averaged flow velocity profiles, whereas the sampling rate to produce the profiles of the numerical model was 10 Hz. Nonetheless a higher sampling frequency would have exceeded our storage capacities. Nonetheless, the pattern of the instantaneous and time averaged profiles reflects an excellent agreement with the velocities obtained by the flume experiment, which greatly demonstrates the fidelity of the numerical model results.

With respect to the evolution of the flow field, the instantaneous velocity profiles indicated velocity fluctuations at the bottom and in the direct vicinity as well as in the rear of the cold-water coral colony. These fluctuations can be related to turbulences generated due to the rough bottom as well as due to the presence of the coral opposing the flow as an obstacle. Main flow features observed in the range of the coral include the presence of flow separation zones along the individual branches of the cold-water coral mixing up into turbulent zones. This is indicated by alternating patches of flow speed values, pressure values, as well as, TKE values (Figure 8). Downstream from the coral the vortices form into a lee-wake vortex shed. The shape of the vortex shed behind the coral corresponds well to the appearance of the low velocity zones as indicated by the flow speed measurements (Figures 4–6). It is also comparable to the distribution of the enhanced TKE values (Figure 8) extending from the rear of the coral downstream. This indicates that the presence of the coral causes a reduction in the flow speeds, but also initializes turbulences. The pattern of the flow field changes as the flow encounters the individual coral branches and separates in the regions where the pressure is highest (Figures 5, 6). Regions of low pressure appear in the rear of the branches, resulting from the interaction between the unidirectional flow and the coral branches. The interplay of developing flow separation zones and producing a pressure gradient from the front toward the rear of the branches favors the generation of downstream wakes. These can be compared to flows around cylinders as shown, for example, by Graf and Istiarto (2002) or Chen et al. (2012). According to Roulund et al. (2005) these vortices are caused by the rotation in the boundary layer over the surface of the pile, or in this case the branches of the coral. The shear layers emanating from the side edges of the pile roll up to form these vortices in the lee wake of the pile. This flow pattern is also evident in the rear of the coral branches and called vortex shedding or a turbulent wake. Further downstream the vortices initialized by the branches contain eddying motions. Because a large part of the mechanical energy in the flow goes into the formation of these eddies, low velocity regions can be observed in this area and in the turbulent wake. This becomes especially evident in the TKE increase in regions where the flow velocity values appear to decrease, e.g., within the coral and toward the downstream direction, These observations are further supported by the results of other flume experiments of a trailing vortex-system in which high turbulences established in the rear of a vertical cylinder (Graf and Istiarto, 2002; Chen et al., 2012).

When comparing the results of the present study to the findings obtained from research on tropical corals, similarities of the flow features described above become evident. Chang et al. (2009) obtained direct measurements of the velocity field throughout the entire volume of a single coral colony of the scleractinian species S. pistillata with a flume experiment. Their presented velocity fields indicate similar patterns as observed in the numerical model presented here (Figure 5) as e.g., (a) flow patterns indicating alternating patches of relatively high and low velocity zones among the branches, (b) the development of flow separation and a conical shaped flow shadow indicating the low velocity zone, and (c) the streamlines indicating the development of turbulences as shown by the disordered appearance of the streamlines in the rear of the cold-water coral colony, i.e., vortex shedding (Figure 3). Moreover, Reidenbach et al. (2007) impressively showed by a flume experiment, the effects of dye transfer from a tropical coral canopy P. compressa under an unidirectional flow, which visualized the associated turbulences that developed at the branches of the coral canopies. Such micro turbulences at the surface of the coral are also evident in our data and indicated by the Q-criterion in Figure 3. However, in order to cover these features, a higher resolution would be required, which exceeds our computational resources. Nonetheless, the findings presented here are well supported by studies on tropical corals, which further proofs the high fidelity of the experimental, as well as, numerically obtained results, and ultimately reveals a holistic picture of the general flow features that are to be expected with regard to a cold-water coral colony.

Flow Past a Cold-Water Coral Colony With Potential Implications on Food Supply and Sediment Transport

Upstream of the coral the undisturbed flow reached an average velocity of 0.5 m s^–1, whereas the flow on the downstream side of the coral averaged at 0.15 m s^–1. This indicates that the presence of the cold-water coral over a distance of 0.2 m caused an average velocity decrease by 0.35 m s^–1, and hence reduced the flow speed by 70%. Obviously, such a reduction in flow speed also would affect the sediment carrying capacity of the water and result in the partial deposition of the sediment carried in suspension.

With respect to food supply, such a large reduction underlines the need for a strong hydrodynamic forcing to allow for sufficient food supply. This would become also the case for the coral polyps on the lee side of the coral (cf. Orejas et al., 2016), especially keeping in mind coral colony sizes of up to 1 m arranged in larger clusters of colonies (Fanelli et al., 2017; Vad et al., 2017). In addition, as indicated by the drag force (Figure 3), the orientation of the branches and potentially their shape have an additional effect on the flow that may enhance the potential to catch food particles from suspension. From the perspective of the interior of a large coral colony or of a cluster of coral colonies, according to Chang et al. (2009), this behavior would imply a reduced access to food particles carried in suspension within the branches as well as in the flow shadow. Moreover, if the flow would not reattach as in the presented case, but would travel further downstream encountering other cold-water coral colonies, further reduced current strengths would affect the prevailing sediment dynamics as well as the food supply to these corals, similar to cases of flow passing an array of cylinders (Yagci et al., 2017). This agrees with the findings of Mienis et al. (2019) who found that increasing sizes of corals/colonies would cause steadily decreasing current strengths toward the downstream direction. In the case of lower flow speeds this effect would become even more dominant (Mienis et al., 2019). The resulting increasing deposition of suspended sediments finally plays a crucial role in stabilizing the biogenic construction (Huvenne et al., 2007; Thierens et al., 2013; Titschack et al., 2015). Ultimately, due to the reduced current strength, at least temporarily relatively strong currents flowing with several decimeters per second through cold-water corals as frequently observed in nature (e.g., Dorschel et al., 2007b; Mienis et al., 2007; Hebbeln et al., 2014; Mienis et al., 2014; de Clippele et al., 2018; Lim et al., 2020) are needed to bring food (and sediment) toward an increasing number of corals to eventually enable the construction of an entire reef (mound). This would fit observations pointing to enhanced mound formation in the past driven by above-average strong hydrodynamic forcing (e.g., Dorschel et al., 2005; Matos et al., 2015; Wang et al., 2019). Finally, considering the fact that cold water coral growth requires any kind of hard substrate allowing larvae settlement, the reduced flow speeds may also increase the potential of favoring larvae settlement within the shadowing zone further enhancing reef and eventually mound formation (Wilson, 1979; Correa et al., 2012; van der Kaaden et al., 2020). Additionally, budding as a way to reproduce or keeping the coral fragments in place, could further enhance this process due to the resulting reduced flow conditions.

The formation of coral mounds is dependent on the complex interplay between cold-water coral growth and sediment input, which both are largely controlled by the prevailing hydrodynamics triggering the lateral sediment supply. The present study provides an initial step to investigate the impact of a cold-water coral on the hydrodynamics and it demonstrates the capabilities of a numerical model for developing a small-scale process understanding. This is further confirmed when comparing the model results with the flow patterns shown by Reidenbach et al. (2007) or Chang et al. (2009). In particular, the flow observations within the corals in-between the branches, as well as in their rear, appear to match with the flow patterns produced by the numerical model.

In follow-up studies on larger objects, such a numerical model should be used to investigate the prevailing sediment and hydrodynamics of CWC reefs, patches, or even small mounds, which would allow a further upscaling toward coral mound formation. For instance, the simplified coral, as presented here, could be replaced by a natural shaped coral digitalized by photo stereometry as it has been done for mangrove seedlings by Le Minor et al. (2019). Also, other model configurations as, e.g., the simulation of multiple arrays of cold-water corals facing the flow and their effects on the prevailing hydrodynamics could be tested. The cumulative effects of multiple corals or even entire reefs on the hydrodynamics are assumed to be critical for mound formation, especially with respect to sediment deposition. This could be addressed by implementing a sediment transport solver into the presented model (e.g., Le Minor et al., 2019), which eventually could provide a much more quantitative understanding of coral mound formation processes.

Conclusion

The presented approach of a combined laboratory flume experiment and a numerical model allows to refine the current understanding to which extend the flow dynamics are affected by the presence of a simplified cold-water coral colony. It reveals the impact of a cold-water coral colony on the hydrodynamics and it demonstrates the capabilities of a numerical model for developing a small-scale process understanding. In particular measurements obtained from the interior of the coral colony in-between the individual branches are a valuable result produced by the numerical model as these values are difficult to measure from the laboratory flume experiment. Moreover, it was demonstrated that the presence of a single cold-water coral colony has an effect on the overall hydrodynamics by building up turbulences as well as reducing the flow speed. This observed decrease in flow velocities around the coral’s hints to a decrease in the sediment carrying potential of the flowing water with consequences for sediment deposition. Due to the validation of the numerical model with a dataset of a fume channel experiment, the model approach can be used in future studies as a basis for more complex arranged corals, with the potential to upscale even to coral mound formation.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work has been funded through the Cluster of Excellence “The Ocean Floor – Earth’s Uncharted Interface”.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We gratefully acknowledge the constructive help by J. Titschack, C. Wienberg, and L. Höhnehopp. We thank the editor A. Hilário, and F. Mienis and A. Rüggeberg for reviewing this manuscript.

Footnotes

1. ^ www.openfoam.com

References

Alvarez, L. V., Schmeeckle, M. W., and Grams, P. E. (2017). A detached eddy simulation model for the study of lateral separation zones along a large canyon-bound river. J. Geophys. Res. Earth Surf. 122, 25–49. doi: 10.1002/2016jf003895

CrossRef Full Text | Google Scholar

Bartzke, G., Schmeeckle, M. W., and Huhn, K. (2018). Understanding heavy mineral enrichment using a three-dimensional numerical model. Sedimentology 65, 561–581. doi: 10.1111/sed.12392

CrossRef Full Text | Google Scholar

Chang, S., Elkins, C., Alley, M., Eaton, J., and Monismith, S. (2009). Flow inside a coral colony measured using magnetic resonance velocimetry. Limnol. Oceanogr. 54, 1819–1827. doi: 10.4319/lo.2009.54.5.1819

CrossRef Full Text | Google Scholar

Chen, Z., Ortiz, A., Zong, L., and Nepf, H. (2012). The wake structure behind a porous obstruction and its implications for deposition near a finite patch of emergent vegetation. Water Resour. Res. 48, 9517. doi: 10.1029/2012WR012224

CrossRef Full Text | Google Scholar

Correa, T. B. S., Eberli, G. P., Grasmueck, M., Reed, J. K., and Correa, A. M. S. (2012). Genesis and morphology of cold-water coral ridges in a unidirectional current regime. Mar. Geol. 326, 14–27. doi: 10.1016/j.margeo.2012.06.008

CrossRef Full Text | Google Scholar

Cyr, F., van Haren, H., Mienis, F., Duineveld, G., and Bourgault, D. (2016). On the influence of cold-water coral mound size on flow hydrodynamics, and vice versa. Geophys. Res. Lett. 43, 775–783. doi: 10.1002/2015gl067038

CrossRef Full Text | Google Scholar

Davies, A. J., and Guinotte, J. M. (2011). Global habitat suitability for framework-forming cold-water corals. PLoS One 6:1–15. doi: 10.1007/978-3-319-17001-5_32-1

CrossRef Full Text | Google Scholar

Davies, A. J., Duineveld, G. C. A., Lavaleye, M. S. S., Bergman, M. J. N., and Van Haren, H. (2009). Downwelling and deep-water bottom currents as food supply mechanisms to the cold-water coral Lophelia pertusa (Scleractinia) at the mingulay reef complex. Limnol. Oceanogr. 54, 620–629. doi: 10.4319/lo.2009.54.2.0620

CrossRef Full Text | Google Scholar

de Clippele, L. H., Huvenne, V. A. I., Orejas, C., Lundälv, T., Fox, A., Hennige, S. J., et al. (2018). The effect of local hydrodynamics on the spatial extent and morphology of cold-water coral habitats at Tisler Reef, Norway. Coral. Reefs 37, 253–266. doi: 10.1007/s00338-017-1653-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Dorschel, B., Hebbeln, D., Foubert, A., White, M., and Wheeler, A. J. (2007a). Hydrodynamics and cold-water coral facies distribution related to recent sedimentary processes at galway mound west of ireland. Mar. Geol. 244, 184–195. doi: 10.1016/j.margeo.2007.06.010

CrossRef Full Text | Google Scholar

Dorschel, B., Hebbeln, D., Rüggeberg, A., and Dullo, C. (2007b). Carbonate budget of a cold-water coral carbonate mound: propeller mound, porcupine seabight. Int. J. Earth Sci. 96, 73–83. doi: 10.1007/s00531-005-0493-0

CrossRef Full Text | Google Scholar

Dorschel, B., Hebbeln, D., Rüggeberg, A., Dullo, W.-C., and Freiwald, A. (2005). Growth and erosion of a cold-water coral covered carbonate mound in the northeast atlantic during the late pleistocene and holocene. Earth Planet. Sci. Lett. 233, 33–44. doi: 10.1016/j.epsl.2005.01.035

CrossRef Full Text | Google Scholar

Fanelli, E., Delbono, I., Ivaldi, R., Pratellesi, M., Cocito, S., and Peirano, A. (2017). Cold-water coral Madrepora oculata in the eastern Ligurian Sea (NW Mediterranean): historical and recent findings. Aquat. Conserv. Mar. Freshw. Ecosyst. 27, 965–975. doi: 10.1002/aqc.2751

CrossRef Full Text | Google Scholar

Ferziger, J. H., and Perić, M. (2002). Computational Methods for Fluid Dynamics. Berlin: Springer, 200.

Google Scholar

Flögel, S., Dullo, W.-C., Pfannkuche, O., Kiriakoulakis, K., and Rüggeberg, A. (2014). Geochemical and physical constraints for the occurrence of living cold-water corals. Deep Sea Res. Part II Top. Stud. Oceanogr. 99, 19–26. doi: 10.1016/j.dsr2.2013.06.006

CrossRef Full Text | Google Scholar

Glogowski, S., Dullo, W.-C., Feldens, P., Liebetrau, V., von Reumont, J., Hühnerbach, V., et al. (2015). The Eugen Seibold coral mounds offshore western Morocco: oceanographic and bathymetric boundary conditions of a newly discovered cold-water coral province. Geo Mari. Lett. 35, 257–269. doi: 10.1007/s00367-015-0405-7

CrossRef Full Text | Google Scholar

Graf, W. H., and Istiarto, I. (2002). Flow pattern in the scour hole around a cylinder. J. Hydraul. Res. 40, 13–20. doi: 10.1080/00221680209499869

CrossRef Full Text | Google Scholar

Gritskevich, M. S., Garbaruk, A. V., Schütze, J., and Menter, F. R. (2012). Development of DDES and IDDES formulations for the k-ω shear stress transport model. Flow Turbul. Combust. 88, 431–449. doi: 10.1007/s10494-011-9378-4

CrossRef Full Text | Google Scholar

Guihen, D., White, M., and Lundälv, T. (2013). Boundary layer flow dynamics at a cold-water coral reef. J. Sea Res. 78, 36–44. doi: 10.1016/j.seares.2012.12.007

CrossRef Full Text | Google Scholar

Hebbeln, D., Portilho-Ramos, RdC., Wienberg, C., and Titschack J. (2019). The fate of cold-water corals in a changing world: A geological perspective. Front. Mar. Sci. 6:119. doi: 10.3389/fmars.2019.00119

CrossRef Full Text | Google Scholar

Hebbeln, D., and Samankassou, E. (2015). Where did ancient carbonate mounds growin bathyal depths or in shallow shelf waters? Earth Sci. Rev. 145, 56–65. doi: 10.1016/j.earscirev.2015.03.001

CrossRef Full Text | Google Scholar

Hebbeln, D., Van Rooij, D., and Wienberg, C. (2016). Good neighbours shaped by vigorous currents: cold-water coral mounds and contourites in the North Atlantic. Mar. Geol. 378, 171–185. doi: 10.1016/j.margeo.2016.01.014

CrossRef Full Text | Google Scholar

Hebbeln, D., Wienberg, C., Wintersteller, P., Freiwald, A., Becker, M., Beuck, L., et al. (2014). Environmental forcing of the Campeche cold-water coral province, southern Gulf of Mexico. Biogeosciences 11, 1799–1815. doi: 10.5194/bg-11-1799-2014

CrossRef Full Text | Google Scholar

Henry, L.-A., and Roberts, J. M. (2015). “Global biodiversity in cold-water coral reef ecosystems,” in Marine Animal Forests: The Ecology of Benthic Biodiversity Hotspots, eds S. Rossi, L. Bramanti, A. Gori, and C. del Valle (Cham: Springer International Publishing), 1–21. doi: 10.1007/978-3-319-17001-5_6-1

CrossRef Full Text | Google Scholar

Huvenne, V. A. I., Bailey, W. R., Shannon, P. M., Naeth, J., di Primio, R., Henriet, J. P., et al. (2007). The magellan mound province in the porcupine basin. Int. J. Earth Sci. 96:85. doi: 10.1007/s00531-005-0494-z

CrossRef Full Text | Google Scholar

Issa, R. I. (1986). Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65. doi: 10.1016/0021-9991(86)90099-9

CrossRef Full Text | Google Scholar

Keylock, C. J., Tokyay, T. E., and Constantinescu, G. (2011). A method for characterising the sensitivity of turbulent flow fields to the structure of inlet turbulence. J. Turbul. 12:N45.

Google Scholar

Le Minor, M., Bartzke, G., Zimmer, M., Gillis, L., Helfer, V., and Huhn, K. (2019). Numerical modelling of hydraulics and sediment dynamics around mangrove seedlings: implications for mangrove establishment and reforestation. Estuar. Coast. Shelf Sci. 217, 81–95. doi: 10.1016/j.ecss.2018.10.019

CrossRef Full Text | Google Scholar

Lim, A., Wheeler, A. J., Price, D. M., O’Reilly, L., Harris, K., and Conti, L. (2020). Influence of benthic currents on cold-water coral habitats: a combined benthic monitoring and 3D photogrammetric investigation. Sci. Rep. 10:19433.

Google Scholar

Marshall, N. B. (1954). Aspects of Deep Sea Biology. New York: Philosophical Library, 230.

Google Scholar

Matos, L., Mienis, F., Wienberg, C., Frank, N., Kwiatkowski, C., Groeneveld, J., et al. (2015). Interglacial occurrence of cold-water corals off cape lookout (NW Atlantic): first evidence of the gulf stream influence. Deep Sea Res. Part I Oceanogr. Res. Pap. 105, 158–170. doi: 10.1016/j.dsr.2015.09.003

CrossRef Full Text | Google Scholar

Mienis, F., de Stigter, H. C., White, M., Duineveld, G., de Haas, H., and van Weering, T. C. E. (2007). Hydrodynamic controls on cold-water coral growth and carbonate-mound development at the SW and SE rockall trough margin, NE Atlantic Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 54, 1655–1674.

Google Scholar

Mienis, F., Duineveld, G. C. A., Davies, A. J., Lavaleye, M. M. S., Ross, S. W., Seim, H., et al. (2014). Cold-water coral growth under extreme environmental conditions, the cape lookout area, NW Atlantic. Biogeosciences 11, 2543–2560. doi: 10.5194/bg-11-2543-2014

CrossRef Full Text | Google Scholar

Mienis, F., Tj, B., Witbaard, R. D., van, O., and Duineveld, G. C. A. (2019). Experimental assessment of the effects of coldwater coral patches on water flow. Mar. Ecol. Prog. Ser. 609, 101–117. doi: 10.3354/meps12815

CrossRef Full Text | Google Scholar

Mohn, C., Rengstorf, A., White, M., Duineveld, G., Mienis, F., Soetaert, K., et al. (2014). Linking benthic hydrodynamics and cold-water coral occurrences: a high-resolution model study at three cold-water coral provinces in the NE Atlantic. Prog. Oceanogr. 122, 92–104. doi: 10.1016/j.pocean.2013.12.003

CrossRef Full Text | Google Scholar

Orejas, C., and Jiménez, C. (2017). “The builders of the oceanspart I: Coral architecture from the tropics to the poles, from the shallow to the deep,” in Marine Animal Forests: The Ecology of Benthic Biodiversity Hotspots, eds S. Rossi, L. Bramanti, A. Gori, and O. Covadonga (Cham: Springer International Publishing), 1–30. doi: 10.1007/978-3-319-17001-5_10-2

CrossRef Full Text | Google Scholar

Orejas, C., Gori, A., Rad-Menéndez, C., Last, K. S., Davies, A. J., Beveridge, C. M., et al. (2016). The effect of flow speed and food size on the capture efficiency and feeding behaviour of the cold-water coral Lophelia pertusa. J. Exp. Mar. Bio. Ecol. 481, 34–40. doi: 10.1016/j.jembe.2016.04.002

CrossRef Full Text | Google Scholar

Paull, C. K., Neumann, A. C., am Ende, B. A., Ussler, W. III, and Rodriguez, N. M. (2000). Lithoherms on the florida–hatteras slope. Mar. Geol. 166, 83–101. doi: 10.1016/s0025-3227(00)00003-7

CrossRef Full Text | Google Scholar

Reidenbach, M. A., Koseff, J. R., and Monismith, S. G. (2007). Laboratory experiments of fine-scale mixing and mass transport within a coral canopy. Phys. Fluids 19:75107.

Google Scholar

Roberts, M. J., Wheeler, A. J., Freiwald, A., and Cairns, S. D. (2009). Cold-Water Corals: The Biology and Geology of Deep-Sea Coral Habitats. Cambridge: Cambridge University Press, 1–336.

Google Scholar

Roulund, A., Sumer, B. M., Fredsøe, J., and Michelsen, J. (2005). Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 534, 351–401. doi: 10.1017/s0022112005004507

CrossRef Full Text | Google Scholar

Schmeeckle, M. W. (2014). Numerical simulation of turbulence and sediment transport of medium sand. J. Geophys. Res. Earth Surf. 119, 1240–1262. doi: 10.1002/2013jf002911

CrossRef Full Text | Google Scholar

Shur, M., Spalart, P. R., Strelets, M., and Travin, A. (2011). A rapid and accurate switch from RANS to LES in boundary layers using an overlap region. Flow Turbul. Combust. 86, 179–206. doi: 10.1007/s10494-010-9309-9

CrossRef Full Text | Google Scholar

Spalart, P. R., Deck, S., Shur, M. L., Squires, K. D., Strelets, M. K., and Travin, A. (2006). A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 20:181. doi: 10.1007/s00162-006-0015-0

CrossRef Full Text | Google Scholar

Thierens, M., Browning, E., Pirlet, H., Loutre, M.-F., Dorschel, B., Huvenne, V. A. I., et al. (2013). Cold-water coral carbonate mounds as unique palaeo-archives: the plio-pleistocene challenger mound record (NE Atlantic). Quat. Sci. Rev. 73, 14–30. doi: 10.1016/j.quascirev.2013.05.006

CrossRef Full Text | Google Scholar

Titschack, J., Baum, D., De Pol-Holz, R., López Correa, M., Forster, N., Flögel, S., et al. (2015). Aggradation and carbonate accumulation of holocene norwegian cold-water coral reefs. Sedimentology 62, 1873–1898. doi: 10.1111/sed.12206

CrossRef Full Text | Google Scholar

Titschack, J., Fink, H. G., Baum, D., Wienberg, C., Hebbeln, D., and Freiwald, A. (2016). Mediterranean cold-water coralsan important regional carbonate factory? Depos. Rec. 2, 74–96. doi: 10.1002/dep2.14

CrossRef Full Text | Google Scholar

Titschack, J., Thierens, M., Dorschel, B., Schulbert, C., Freiwald, A., Kano, A., et al. (2009). Carbonate budget of a cold-water coral mound (challenger mound, IODP Exp. 307). Mar. Geol. 259, 36–46. doi: 10.1016/j.margeo.2008.12.007

CrossRef Full Text | Google Scholar

Vad, J., Orejas, C., Moreno-Navas, J., Findlay, H. S., and Roberts, J. M. (2017). Assessing the living and dead proportions of cold-water coral colonies: implications for deep-water marine protected area monitoring in a changing ocean. PeerJ 5:e3705. doi: 10.7717/peerj.3705

PubMed Abstract | CrossRef Full Text | Google Scholar

van der Kaaden, A.-S., van Oevelen, D., Rietkerk, M., Soetaert, K., and van de Koppel, J. (2020). Spatial self-organization as a new perspective on cold-water coral mound development. Front. Mar. Sci. 7:631.

Google Scholar

Vandorpe, T., Van Rooij, D., and de Haas, H. (2014). Stratigraphy and paleoceanography of a topography-controlled contourite drift in the Pen Duick area, southern Gulf of Cádiz. Mar. Geol. 349, 136–151. doi: 10.1016/j.margeo.2014.01.007

CrossRef Full Text | Google Scholar

Viswanathan, K., Shur, M. L., Spalart, P. R., and Strelets, M. K. (2007). Comparisons between experiment and large-eddy simulation for jet noise. AIAA J. 45, 1952–1966. doi: 10.2514/1.25892

CrossRef Full Text | Google Scholar

Wang, H., Lo Iacono, C., Wienberg, C., Titschack, J., and Hebbeln, D. (2019). Cold-water coral mounds in the southern Alboran Sea (western Mediterranean Sea): internal waves as an important driver for mound formation since the last deglaciation. Mar. Geol. 412, 1–18. doi: 10.1016/j.margeo.2019.02.007

CrossRef Full Text | Google Scholar

Wheeler, A. J., Beyer, A., Freiwald, A., de Haas, H., Huvenne, V. A. I., Kozachenko, M., et al. (2007). Morphology and environment of cold-water coral carbonate mounds on the NW European margin. Int. J. Earth Sci. 96, 37–56. doi: 10.1007/s00531-006-0130-6

CrossRef Full Text | Google Scholar

White, M., Mohn, C., de Stigter, H., and Mottram, G. (2005). “Deep-water coral development as a function of hydrodynamics and surface productivity around the submarine banks of the rockall trough, NE Atlantic,” in Cold-Water Corals and Ecosystems, eds A. Freiwald and J. M. Roberts (Berlin: Springer), 503–514. doi: 10.1007/3-540-27673-4_25

CrossRef Full Text | Google Scholar

Wienberg, C., and Titschack, J. (2015). “Framework-forming scleractinian cold-water corals through space and time: a late quaternary north atlantic perspective,” in Marine Animal Forests, eds S. Rossi, L. Bramanti, A. Gori, and C. del Valle (Cham: Springer International Publishing), 1–34. doi: 10.1007/978-3-319-17001-5_16-1

CrossRef Full Text | Google Scholar

Wilson, J. B. (1979). ‘Patch’ development of the deep-water coral lophelia pertusa (L.) on rockall bank. J. Mar. Biol. Assoc. U. K. 59, 165–177. doi: 10.1017/s0025315400046257

CrossRef Full Text | Google Scholar

Yagci, O., Yildirim, I., Celik, M. F., Kitsikoudis, V., Duran, Z., and Kirca, V. S. O. (2017). Clear water scour around a finite array of cylinders. Appl. Ocean Res. 68, 114–129. doi: 10.1016/j.apor.2017.08.014

CrossRef Full Text | Google Scholar