Sea-Air Exchange of Methane in Shallow Inshore Areas of the Baltic Sea

We report sea-air fluxes of methane in physically and biologically distinct inshore habitats of the Baltic Sea with the goal to establish empirical relationships that allow upscaling of local site-specific flux measurements. Flux measurements were conducted using floating chambers with and without bubble shields, and by using a boundary layer gas transfer model before, during, and after an annually occurring algal bloom from June to October 2019. Water and air temperature, salinity, wind, sediment organic content, and organic content of floating algal biomass were found to successfully discriminate the different habitats in terms of methane flux, both over periods of days and over a season. Multivariate statistical analysis was used to establish the relative environmental forcing of methane emissions over one growth season for each flux method. Floating algal biomass carbon and sediment organic content were identified as the most important controlling factors for methane emissions based on flux chamber measurements over a period of days to weeks, whereas water and air temperature and wind velocity were the most important factors based on the gas transfer model on these time scales. Over the season, water and air temperature were the most important controlling factors with both methods. We present a first attempt how our observations can be extrapolated to determine the coastal methane emission along the coastline.

Introduction

The trace gas methane contributes about 23% to the radiative balance of Earth’s atmosphere and its increasing emissions contribute significantly to ongoing global warming (Mende et al., 2019). Atmospheric methane burdens have increased over pre-industrial levels 2.5 times making present and future methane levels highly relevant in discussions about climate forcing and effective mitigation measures (Nisbet et al., 2019). Aquatic ecosystems are responsible for about 53% of the total global methane emissions from anthropogenic and natural sources (Rosentreter et al., 2021). Methane has anthropogenic sources from fertilizer application, animal food stocks, industrial and agricultural emissions, and fossil fuel combustion (Seitzinger et al., 2006; Saunois et al., 2016), but also natural sources such as thawing permafrost, wetlands, natural gas seeps, and emissions from lakes and the coastal ocean that react sensitively to climate change and human activities (Nisbet et al., 2019). A fundamental concern in budgeting these different sources are the discrepancies that arise between top-down or bottom-up approaches (Nisbet and Weiss, 2010; Crill and Thornton, 2017), and in the large range of global estimates for bottom-up approaches that vary between 594 and 880 Tg y^–1. Although emissions from lakes and terrestrial wetlands comprise the bulk of the global aquatic methane emissions, shallow-water coastal environments dominate the emissions from aquatic marine environments by area (Weber et al., 2019; Bižić et al., 2020; Rosentreter et al., 2021). Coastal ecosystems, and in particular the inshore habitats, are of interest for global methane emissions, because they are most directly affected by anthropogenic disturbances of the land-ocean interface (Smith and Hollibaugh, 1993; Gattuso et al., 1998; Battin et al., 2008; Torres-Pulliza et al., 2020). Inshore coastal habitats have also been identified as potentially important blue carbon repositories to mitigate CO₂ accumulation in the atmosphere (Macreadie et al., 2019), but the efficiency of this carbon sink is partially offset by methane emissions (Rosentreter et al., 2018).

Part of the problem with inshore bottom-up estimates of methane emissions lies in the challenge to scale emissions in habitats that vary strongly over both spatial and temporal scales. Inshore coastal habitats worldwide are very diverse and range from highly productive coastal ecosystems such as coastal wetlands to bare rocky cliffs largely devoid of significant sediment organic carbon accumulation or dense vegetation coverage. In inshore habitats, environmental factors that lead to large spatial and temporal variations in methane production and emission include vegetation density, organic richness of the bottom substrate, air and water temperature, wind velocity and direction relative to the coastline, and wave activity (Jeffrey et al., 2019). An additional factor is the release of methane as bubbles from the sediment, which can escape to the atmosphere before significant oxidation (Keller and Stallard, 1994; Joyce and Jewell, 2003; Jeffrey et al., 2019; Weber et al., 2019). Bubble emissions comprising up to 95% of methane emissions have been suggested (Casper et al., 2000; Walter et al., 2006; Bastviken et al., 2011; Delwiche et al., 2015), but these emissions are highly localized. Lastly, inshore methane emission also takes place via plant vascular tissue transport, but the impact from plants varies by season (Jeffrey et al., 2019) and life cycle phase (Van Der Nat and Middelburg, 1998; Van der Nat and Middelburg, 2000). For example, hornbeam (Typha albida) and reed (Phragmites australis) can reduce methane emissions by oxidation during their growth phase, but when the plants have matured the oxidation is significantly reduced.

A combination of biological, chemical, and physical properties of the inshore coastal environment can be used to evaluate correlations that weigh in the different environmental forcing factors for methane emission. Quantification of methane emissions from coastal habitats in which such steering variables are analyzed may also allow testing which parameters exert a dominating influence on methane fluxes in different coastal habitats. This parametric approach could ultimately be used for empirical scaling approaches in which the geographic and temporal variability of the steering parameters are used as guiding variables to estimate methane emissions over larger coastal areas. At present, however, we do not know the methane emissions of many coastal ecotypes and the variation of these emissions throughout the year – data that are key for a more accurate bottom-up upscaling of the coastal methane emission.

The Baltic Sea coastline has a large diversity of inshore ecotypes such as rocky shorelines, shallow bays, small fjärds, wetlands, small deltas, and coastal lagoons with bottom types ranging from organic-rich soft muds to unvegetated bare rocks (Bartley et al., 2001; Niemelä et al., 2015). Baltic Sea coastal wetlands have some of the highest methane emissions in the Baltic Sea (Heyer and Berger, 2000), but are most directly affected by land-side anthropogenic perturbances. Inshore water temperatures range from up to 27°C in the summer to below freezing in the winter, along with air temperature variations of over 40°C during the year. Light and temperature variability make productivity of the coastal habitat highly seasonal and locally variable. In addition, algal blooms increase the amount of organic matter transferred to sediment, which cause hypoxia and enhanced methanogenesis at shallow sediment depth (Bange et al., 2010; Maltby et al., 2018). The current work had as its purpose to evaluate the forcing of trace CH₄ gas emission rates by different environmental factors and to contribute directly measured near-shore trace gas exchange rates. This is a new approach for establishing scaled-up CH₄ fluxes in the littoral coastal zone that explicitly takes near-shore vegetation variations, bubble emissions, and seasonal variability of physical environmental forcing factors in these inshore habitats of the Baltic Sea into account. As the main objective the present study therefore lays the ground for scaling scenarios to arrive at empirically constrained trace gas emissions from inshore habitats that can be incorporated into comparisons of bottom-up and top-down emission budgets.

Materials and Methods

Study Location and General Approach

The island of Askö is located in the Trosa archipelago on the east coast of Sweden in the central Baltic Sea (Figure 1). Askö extends in NW-SE direction and is about 10 km long and 1 km wide and covers an area of 272 ha. The whole island is a nature reserve, covered by forest and open land and managed by a resident landholder, with cows and sheep who graze the land to help maintain the open landscape. The SW facing side of the island is dominated rocky cliffs and shallow embayments and is relatively open to the Baltic Sea, whereas the NE side of the island faces the archipelago sea with calmer wave conditions. The dominant wind directions in the area are S to SW and secondarily NW to NE (Station Landsort A¹).

FIGURE 1

Figure 1. Map of Askö island and the locations of the five sampling areas.

We categorized five sampling areas of the island shoreline based on salinity, wind velocity, water temperature, air temperature, water depth, organic content of floating algal biomass, shore vegetation, and sediment organic carbon content into four different habitats (Table 1). Discriminators were indicator species for eutrophication (see descriptions for habitats A and B below), algal mat occurrence, occurrence of bubbles during sampling, indicators of human activities such as cut reeds, and the occurrence of hydrogen sulfide.

TABLE 1

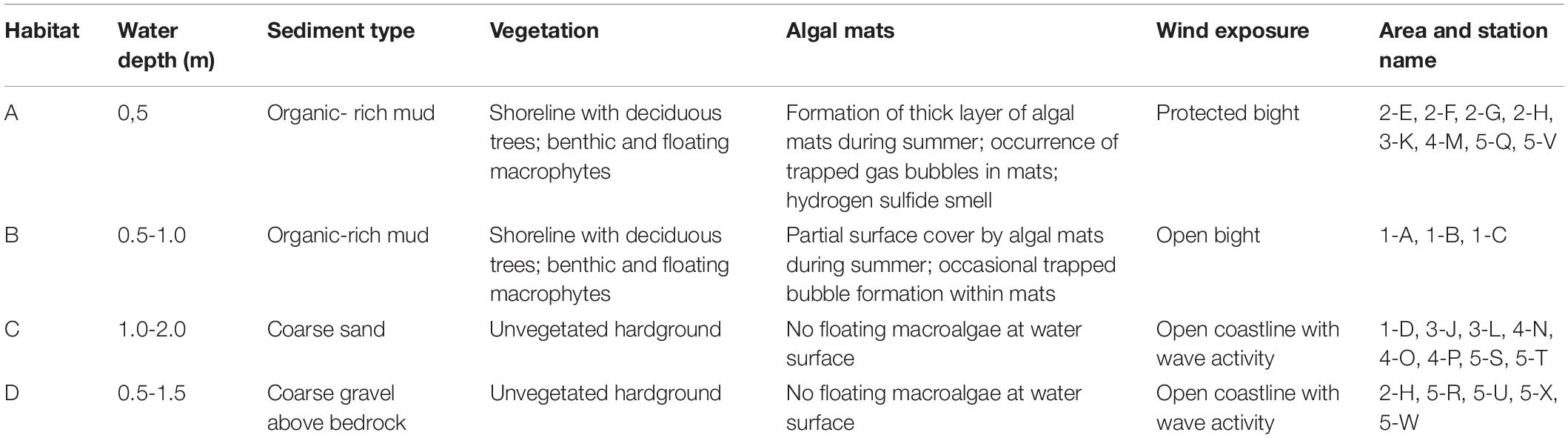
Table 1. Habitat with corresponding sampling stations in the respective habitats and sampling areas.

Habitat A was characterized by reeds and soft organic-rich clays with a water depth up to 0.5 m in small, relatively wind-protected bights. Deciduous tree shorelines characterize this habitat. The shoreline has dense reed areas (P. australis), hornbeam (T. albida), seagrasses (Carex pendula and Sagittaria sagittifolia), and is covered by thick layers of algae mats (Archaeplastida or Cyanophyceae) during July and August, when water lilies (Nymphaea alba) also occupy the surface. Visible bubble emissions appear between June and August in combination with a strong smell of hydrogen sulfide. Human activities such as reed cutting and agriculture affect this habitat.

Habitat B also has soft, organic-rich sediment, a generally vegetated shoreline with deciduous trees and water depths between 0.5 and 1.0 m. There are dense areas of sessile aquatic vegetation with different species of brown algae (Phaeophyceae) and reed (P. australis), hornbeam (T. albida) and dense summer coverage of bladder wrack (Fucus vesiculosus). Benthic algae cover about half of the area. Visible bubble emissions appear in July and August, but hydrogen sulfide is generally absent. Human activities and agriculture generally do not affect this habitat.

In habitat C the sea bottom consists of sandy sediment and unvegetated rocky hard ground. It is located in more open areas with higher currents and wave activity and water depth-up to 2.0 m. There is generally no sessile aquatic vegetation, algal blooms, or any significantly smell of hydrogen sulfide.

Habitat D is characterized by its unvegetated hard ground and strong water currents. The surrounding area of this habitat has rocky cliffs with sparse plants, sessile aquatic vegetation, and summer algal accumulations, and water depths between 0.5 and 1.5 m. There is also no smell of hydrogen sulfide in this habitat.

Field Methods

Methane fluxes were determined using round, anchored, ca. 8 L large floating chambers with and without bubble shield between June and October 2019 following the design described in Schilder et al. (2016). Chamber fluxes were determined with and without a bubble shield at the same station in order to quantify the contribution of ebullition to the total flux. The bubble shield consisted of a 0.12 m² large transparent PVC plate that was mounted underneath the chamber such that it was positioned 15 cm below the floating chamber. Time intervals for the flux measurements varied between 15 and 78 h, with 89% of the measurements were conducted with less than 32 h intervals. Only sampling intervals with linear increase in CH₄ concentration with r² above 0.78 were considered as significant gradients, and 85% had r² above 0.90. At stations, where intermittent bubbling rapidly increased the methane concentration over an interval of less than 15 h, only that time interval was used in the final calculation and the other time intervals were ignored. At several stations, the flux measurement was reset to conduct multiple flux measurements over a period of up to 6 days per monthly measuring campaign. Air samples were collected from the chamber headspace every 24 h over a period of 3–6 days. Example time series evolution of concentrations in Supplementary Figures 3, 4. Sampling was done according to the method of Keller and Stallard (1994). To collect samples, the sampling syringe was connected via a three-way stopcock to the chamber and was flushed at least 10 times before filling the syringe with 60 ml of air from the chamber. The first 20 ml of the air sample was emptied to the atmosphere to flush the transfer needle. Subsequently, the remaining air in the syringe was transferred through a butyl rubber stopper into a 20 ml glass vial filled, without headspace, with saturated salt solution.

Dissolved methane was collected with the headspace equilibration method described in Bastviken et al. (2003). A 60 ml syringe was filled, flushed and re-filled with seawater three times. A total of 40 ml of the water was equilibrated in the syringe with 20 ml air for 1 min and exactly 20 ml air was then transferred to a glass vial filled, without headspace, with saturated salt solution by replacing the salt solution with the sample air. The glass vials were kept upside-down until all vials were analyzed.

Three to five locations were selected in each habitat totaling 23 sampling stations. On each sampling occasion and before collecting each sample the following data were recorded: air and water concentration of CH₄, date, time, salinity in water, air temperature, O₂ concentration in water, water temperature and GPS location. Wind data and air temperature were obtained from the database of the Swedish Meteorological and Hydrological Institute (SMHI) (SMHI, 2010). O₂, water temperature, and salinity data were obtained with a handheld WTW Salinometer.

Laboratory CH₄ Analysis

Water and air samples were analyzed by gas chromatography on a Shimadzu GC-8A with FID detector and a 1 ml loop injection system. The instrument was calibrated using the average of multiple gas standards that were analyzed during each analysis session with concentrations of 11, 100, and 10,000 ppmv. Replicate standard analyses were performed with a coefficient of variation between 1 and 3%. For the analysis of air and air-equilibrated water samples, 2 ml of a sample were injected on the loop of the Gas Chromatograph (GC) compensating for the withdrawn volume in the air-equilibrated samples with an equivalent volume of salt solution of the same salinity as the sample (6‰). Gas concentrations in (ppm) were converted to (nmol/L) according to Johnson et al. (1990)

$$C_W^{\circ }=\frac{n_g+n_w}{V_w}(1)$$

where $C_W^{\circ }$ is the concentration of the dissolved gas in the sample (mol/L), n_g are the moles in headspace after equilibration, n_w are the moles in the aqueous phase after equilibration, and V_w is the volume of the water sample. To calculate ng, the ideal gas was used

$$n_g=\frac{P\times p^{\prime }\times V_g}{R{T}_a}(2)$$

where P is the air pressure in Pa, p′ is the partial pressure of the gas in Pa, V_g is the volume of the headspace (L), T_a is air temperature (K) and R is the universal gas constant 8314.46 (L Pa mol⁻¹K⁻¹).

n_w was calculated using Henry’s law constant and the volume of water V_w according to Johnson et al. (1990)

$$n_w=\frac{\beta \times P\times p^{\prime }\times K_H\times V_w}{RT}(3)$$

Flux Calculations

The flux calculations reported in this study are explained and discussed in detail in Supplementary Material and are briefly summarized here: The flux (F) of methane in the floating chambers, henceforth described as the “chamber method” was calculated according to:

$$F=(\frac{C_{t_{n+1}}-C_{t_n}}{\mathrm{\Delta }{t}_{n+1-n}}\times \frac{V_{ch}}{A_{ch}})(M\times {10}^3)\times {10}^{-9}\times 24(4)$$

where F is the flux (mg/m²/day), M is the molar mass for the component CH₄ (g/mol), C_{tn + 1}, C_tn are concentrations (nmol/L) of component in air sample at sampling times t_n+1 and t_n, respectively, Δt_{n + 1−n} is the time difference between sampling times t_n+1 and t_n in hours. V_ch is the volume of the flux chamber (L) and A_ch is the water surface area of the flux chamber (m²). The volume of the floating flux chamber was 7.5 L with a surface area of 0.08 m² and followed the general design described by Schilder et al. (2016). Fluxes determined from dissolved methane concentrations and wind velocity, henceforth termed “gas transfer model” were calculated according to the general boundary layer flux equation:

$$F=k\left(C_w-\alpha C_a\right)M\times 2.4\times {10}^{-4}(5)$$

where F is the flux (mg/m²/day), M is the molar mass for the component CH₄ (g/mol), k is the gas transfer velocity (cm/h), C_w is the concentration of the dissolved gas in surface water (nmol/L), C_a is the concentration of the gas in the air at the surface (nmol/L), α is the Ostwald solubility coefficient (dimensionless).

From the Ostwald solubility coefficient (α) for methane from the Bunsen solubility coefficient (β) and water temperature (T_w) (Battino, 1984) according to

$$\alpha =\frac{\beta T_w}{273.15}(6)$$

where β is the dimensionless Bunsen solubility coefficient of the dry mole fraction

$$\begin{array}{c}\hfill ln\beta =A_1+A_2(100/T_w)+A_{3}ln(T_w/100)+\hfill \\ \hfill S[B_1+B_2(T_w/100)+B_3{(T_w/100)}^2]\hfill \end{array}(7)$$

where T_w is the water temperature (K), S is the salinity (‰). A₁, A₂, A₃, B₁, B₂, B₃ are constants specific for CH₄ (Wanninkhof, 2014)). A number of different models are used to determine the gas transfer velocity k and for this context the equation used by Wanninkhof (2014) was used:

$$\text{k}=0.251U_{10}{}^2\times {(\frac{Sch}{660})}^{-0.5}(8)$$

where k is the gas transfer velocity (cm/hour), U₁₀ is the wind velocity at 10 m height(m/s), andSch is the Schmidt number for the gas component (dimensionless). We have also used the k models of Ho et al. (2006); Nightingale et al. (2000b), Wanninkhof et al. (2009), and Wanninkhof (1992) and calculated averages from the different k models (Figure 2). The average k-values were close to those of the Wanninkhof (2014) relationship for the range of wind velocities encountered in our study and we have therefore decided to use this relationship. The k model for CH₄ used by Rosentreter et al. (2017) and Jeffrey et al. (2018) for estuaries (mangroves) was considered, and in these studies, tidal currents were a significant factor. However, the central Baltic Sea region in the study does not have any significant permanent or tidal currents, and estuarine models may not provide better results for the setting of this study.²

FIGURE 2

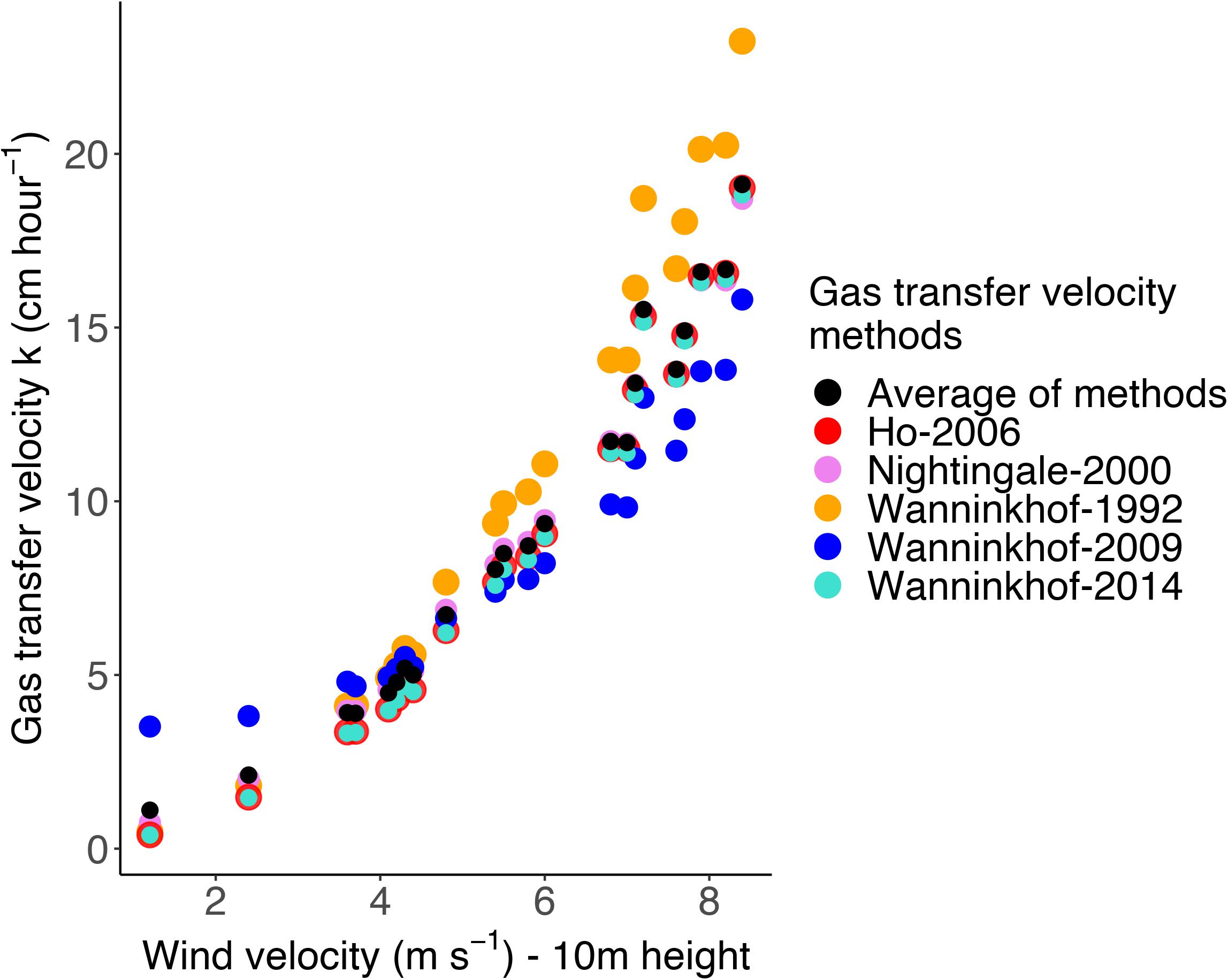
Figure 2. Relationship between gas transfer velocity and wind velocity at 10 m height for five different gas transfer models and the corresponding mean. The relationship by Wanninkhof (2014) was used in this study.

Wind velocity measurements were taken from the coastal measuring buoy at Askö (Askö Kustmätsystem). Wind velocity was adjusted by using measurements at 1.5 m height to get the corresponding wind velocity at 10 m height according to Amorocho and DeVries (1980).

$$U_{10}=\frac{U_z}{(1-(\frac{\sqrt{c_{10}}}{\kappa })ln(\frac{10}{z}))}(9)$$

U_z is the wind velocity at z meters height (m/s), U₁₀ is the wind velocity at 10 m height (m/s), c₁₀ is the surface drag coefficient for shallow water depth c₁₀ = 1.3×10⁻³, κ is the von Kármán constant κ = 0.41.

The Schmidt number for Baltic Sea brackish water (salinity ∼ 6‰) with measured salinity (S_balticsea) was calculated by interpolation of the Schmidt number for fresh water (salinity 0‰) and sea water (salinity 35‰) following (Gülzow et al., 2013) and (Jähne et al., 1987).

$$Sc{h}_{balticsea}=\frac{(Sc{h}_{seawater}-Sc{h}_{freshwater})\times S_{balticsea}}{35}+Sc{h}_{freshwater}(10)$$

$$Sch=A+B{t}_w+Ct_w{}^2+Dt_w{}^3+Et_w{}^4(11)$$

where t_w is the water temperature (°C), A, B, C, D, and E are constants which depends on the gas component (Wanninkhof, 2014). The constants A,B,C, D, and E in Equation 9 to calculate the Schmidt number were used for fresh water and sea water (Wanninkhof, 2014). A detailed description with examples for the flux calculations can be found in Supplementary Material.

Organic Matter

The concentration of organic carbon in sediment and in algal mats was determined by the loss on ignition method (LOI) according to Hoogsteen et al. (2015). About 3–5 g of surface sediment (top 2 cm) or floating algal biomass covering approximately 20–30 cm² was oven-dried at 105°C and subsequently combusted at 450°C. Water and organic matter content were determined by difference and expressed in weight %. The analytical uncertainty of the method is about 1–2%.

Statistical Analysis

Hierarchical Clustering Analysis

The parameters CH₄ flux, water and air temperature, salinity, wind velocity, sediment organic content, and algal biomass carbon were used in a hierarchical cluster analysis (Wilks, 2011) to determine the relative influence of the measured environmental forcing factors on CH₄ fluxes for either the gas transfer model or the chamber method. The different forcing parameters have different units and value ranges. To ensure that parameters had equal weight in the cluster analysis (unweighted), the value range for each parameter was scaled to a value between 0 and 1, where 0 represents the minimum value of that parameter and 1 the maximum value. For flux and sediment organic content parameters, a log transformation was applied prior to this normalization to reduce skewness. All parameters were applied to each flux result and each parameter was given equal weight in the analysis. The parameter water depth was categorized into three depth ranges. The first range was up to 0.5 m, the next range was between 0.5 and 1.0 m and the last range was between 1.0 and 2.0 m, which were then represented by the numbers 2, 1, and 0, respectively. If a parameter had identical values for all observations, the chosen value was 0.5 to represent the middle range. This was used in some exceptional cases in an analyzed sampling period with few values for a particular parameter. The hierarchical cluster analysis used Euclidian distance to calculate distance between observations and a bottom-up method to determine which clusters were closest to each other at each stage, using unweighted pair group method with arithmetic mean (UPGMA). Two types of clustering categories were used – category one used grouping of stations based on flux and environmental forcing factors and category two used grouping of flux and environmental forcing factors across all stations. The hierarchical cluster analysis was performed to the point where only a single cluster remained for each analyzed data set. Dendrograms were used for graphical representation of the cluster analysis results, with hierarchical clustering distance representing the calculated distance between two clusters, using UPGMA at the junction point for a pairwise grouping of clusters. Correlation between different parameters are shown by early clustering (low distance) if there was a strong correlation between parameters, while weak correlation make the clusters late (high distance) in different groups. Dendrograms only show proximity (hierarchical clustering distance) between the clusters that are closest to each other at each clustering stage – not between arbitrary data points. Nodes in a dendrograms can be rotated at its junction points without changing the topology and meaning.

Pairwise Correlation Coefficients (Kendall)

Given the limitations of dendrograms in terms of indicating correlations between all of the different parameters, we extended the analysis to include pairwise correlation calculation (Felipe-Lucia et al., 2020) of environmental forcing factors and flux. Pairwise correlations between CH₄ flux gas transfer model and environmental forcing factors were calculated for all stations for all sampling periods, using Kendall rank correlation coefficient. Possible value range is between −1 and 1. Using Cohen’s standard (Sawilowsky, 2009; Chen et al., 2010) for evaluation of the relationships, a weak association is between 0.10 and 0.29, medium association between 0.30 and 0.49 and strong association for 0.50–1.00. The Kendall rank correlation coefficient was chosen as it does not impose any requirements on distribution of analyzed parameter values, other than they can be ranked and provided more robust values than a Spearman rank correlation coefficient or the Pearson correlation coefficient (Croux and Dehon, 2010), since these required that values adhered to normal distribution, a linear relationship between variables, and equal distribution along a regression line. This was not true for all parameters and hence Pearson was not used.

Multiple Factor Analysis

Our data consists primarily of quantitative data, but also qualitative data such as water depth categories. We applied multiple factor analysis (MFA) in order to combine all these data series in the analysis and to allow for grouping of different variables to compress and simplify the data set and explore the structure of the observations. MFA (de Tayrac et al., 2009; Abdi et al., 2013) is a generalization of principal component analysis (Abdi and Williams, 2010; Kherif and Latypova, 2019), which allows grouping of data sets in terms of weight and also can combine quantitative and qualitative data in the analysis. We used this method to get a better understanding of the variances of fluxes and environmental forcing factors and their correlations.

Multiple factor analysis calculates new variables referred to as principal components, which are calculated as linear combinations of the original variables. The contribution to the total variance for the principal components was investigated for all data for chamber method, and gas transfer model, as well as different groupings per sampling period and habitat. The variance for all different combinations was explained to 68–96% with the first four principal components, which we considered to explain the variance good enough. Thus our analysis focused on these four components. The contribution of the original variables to the different principal components was then used to study correlation between these variables. In our analysis, we focused on the two to three principal component dimensions. As a graphical depiction of the analysis, the variables are represented by the length and direction of an arrow in a plot of the principal components. Arrows close to each other in the same quadrant are correlated in both dimensions. If variables have similar values on one axis they are correlated for that principal component. Variables in opposing quadrants are negatively correlated in one or two dimensions.

Results

Variability in Dissolved Methane Concentrations

The concentration of dissolved methane differed widely between the studied seasons (spring–summer and fall) and the four investigated habitats (Figures 3A–E). Considering all sampling periods, methane concentrations ranged between 26 and 6596 nmol/L in habitat A, between 42 and 1167 nmol/L in habitat B, 47 and 1201 nmol/L in habitat C, and 69 and 874 nmol/L in habitat D. All methane samples were oversaturated between 908% and 83,865% relative to the dissolved equilibrium concentrations of 2.7–3.6 nM for salinities between 5.4 and 6.7‰ and temperatures between 8.5 and 28.6°C at the respective ambient air pressures for the different sampling periods. A Wilcoxon-Mann–Whitney test of all habitats showed that the concentration ranges were significantly different between the habitats except C and D (Supplementary Table 1). Habitat A had the largest proportion of high CH₄ concentrations, likely due to the location of the sampling stations in protected bays, which had significantly more inshore and floating vegetation compared to the other habitats. Average concentrations were calculated by excluding major outliers, thus defining a valid concentration range as

$$\begin{array}{c}\hfill \left(25\mathrm{t}\mathrm{h}\mathrm{percentile}-3\times \text{IQR}\right)\le \text{C}\le \hfill \\ \hfill (75\mathrm{t}\mathrm{h}\mathrm{percentile}+3\times \text{IQR})\hfill \end{array}(12)$$

FIGURE 3

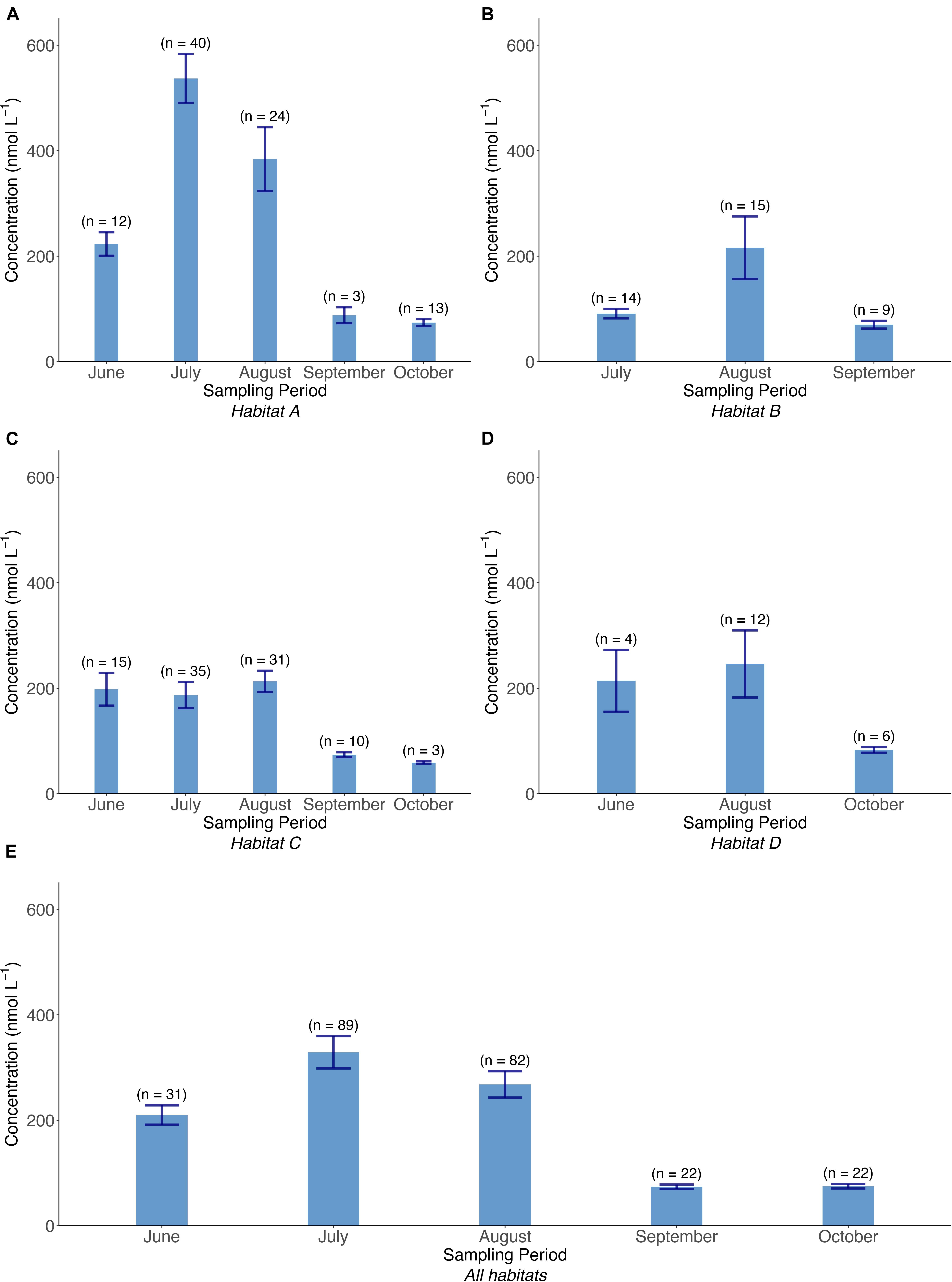
Figure 3. (A–E) Average of water concentration of CH₄ (without outliers) in each habitat and the average of all habitats together during all sampling periods. The standard error of the mean is shown on each bar.

where IQR is the interquartile range, defined as IQR = (75th percentile − 25th percentile). The averaged dissolved CH₄ concentrations during all sampling periods in all habitats showed a clear seasonal trend and increased from 210 nmol/L (n = 31) in June through the summer to highest concentrations of 329 nmol/L (n = 89) in July, from where they decreased in the fall to the lowest seasonal concentrations of 75 nmol/L (n = 22) in October (Supplementary Table 2). Median values were in almost all cases lower than average values, indicating that the concentration distribution was skewed toward the high end.

CH₄ Fluxes

Methane fluxes calculated with the gas transfer model ranged from 0.6 to 8.3 mg m^–2 d^–1 in habitat A, 1.5–5.6 mg m^–2 d^–1 in habitat B, 0.4–6.6 mg m^–2 d^–1 in habitat C, and 0.6–6.6 mg m^–2 d^–1 in habitat D (Figure 4A). Monthly averaged methane fluxes were calculated by excluding outliers in analogy to the procedure used for dissolved methane. There was a good first order relationship between methane fluxes calculated with the gas transfer model and gas transfer velocity k for all habitats during all whole sampling periods, but the data show significant variability of the fluxes for a given gas transfer velocity (Figure 5). This variability is best explained by high variability in methane concentrations and their influence on the calculated flux. It cannot be excluded that some of the variability is due to the presence of microbubbles in some of the samples. High fluxes in June and August were observed during periods with high wind speeds when rising gas bubbles were observed at the water surface, indicating destabilization of trapped shallow gas in sediments of the near-shore area.

FIGURE 4

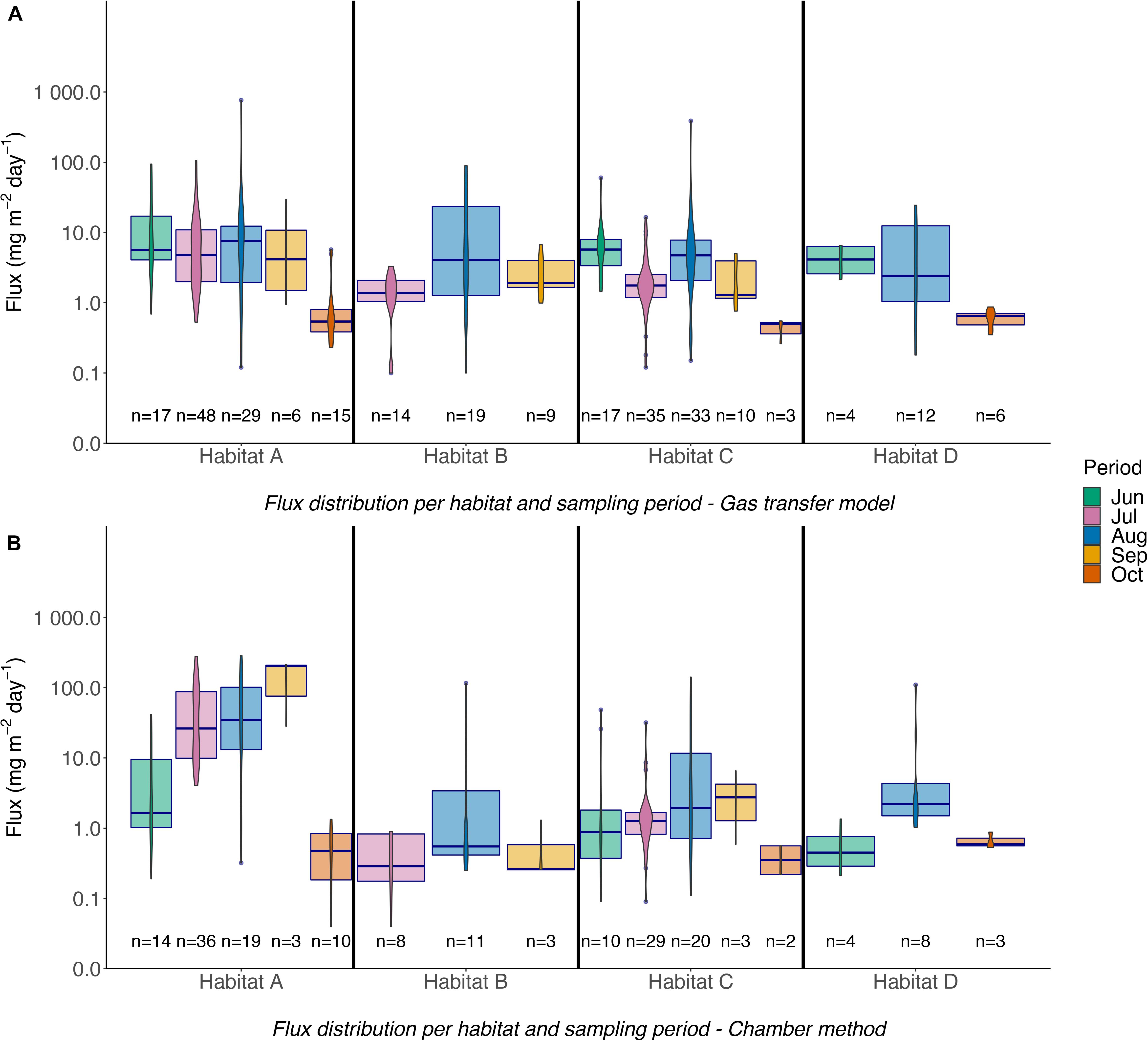
Figure 4. (A,B) Flux variation in different habitats and sampling periods based on the gas transfer model and the chamber method.

FIGURE 5

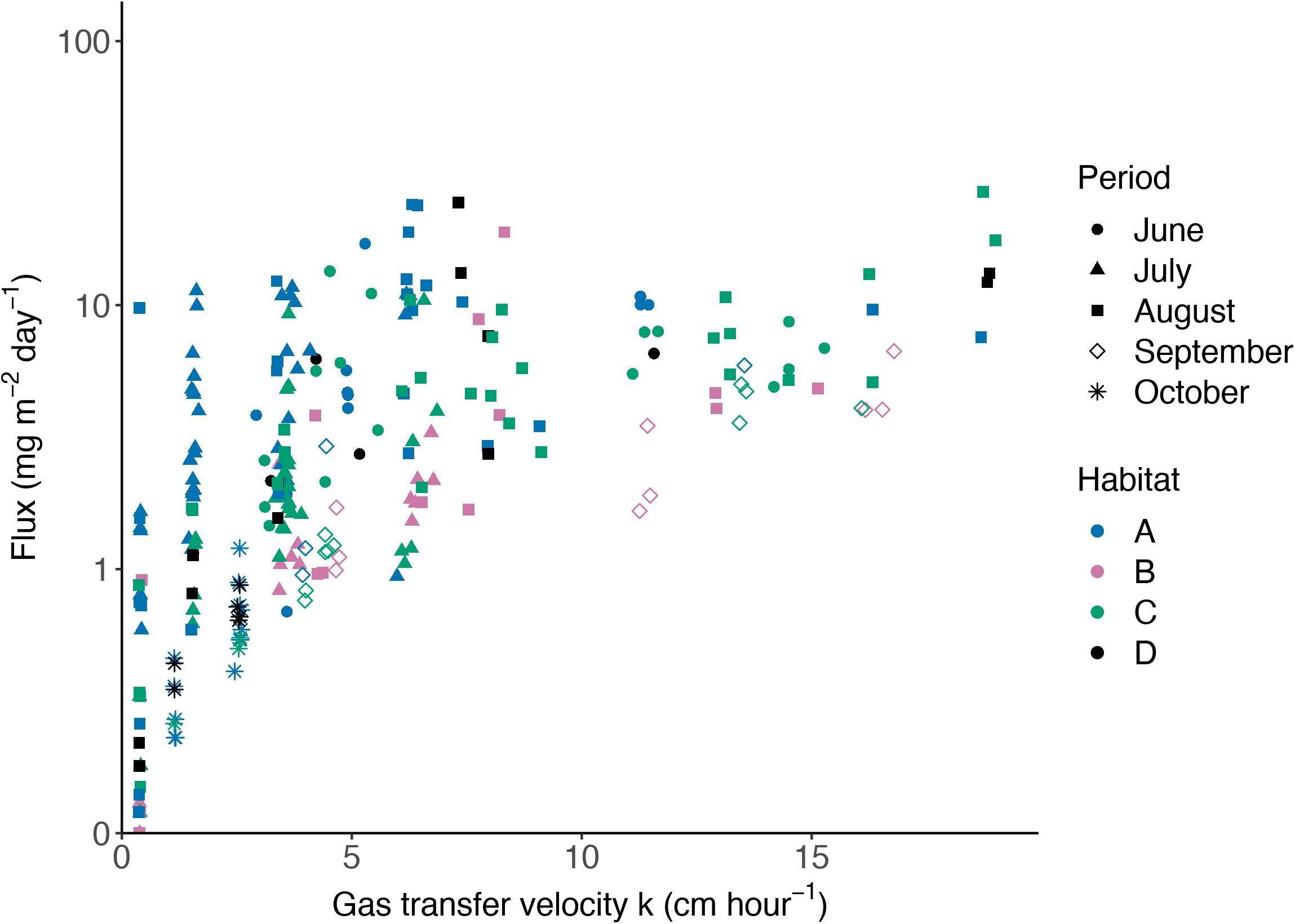
Figure 5. Relationship between gas transfer velocity k and CH₄ flux calculated with the gas transfer velocity model. The variability in flux for a given k-value indicates the strong water-side CH₄ concentration dependence of the flux. The concentration variability may include captured microbubbles of CH₄.

Fluxes calculated with the chamber method in habitat A were in the range 0.6–162.6 mg m^–2 d^–1, 0.3–22.9 mg m^–2 d^–1 in habitat B, 0.4–10.4 mg m^–2 d^–1 in habitat C, and 0.7–2.0 mg m^–2 d^–1 in habitat D (Figure 4B). Figures 6A,B show CH₄ concentrations and fluxes for those sites, at which chambers were deployed with and without bubble shields covering the whole sampling period. From June to August, unshielded fluxes in habitats A, B, and C were higher by factor 5–10 compared to shielded fluxes indicating that bubbles accounted for the majority of the total flux to the atmosphere at all stations. In October, there were no significant difference between fluxes from chambers with and without bubble shields indicating that diffusive fluxes dominated the transport to the atmosphere (Additional variance and mean flux data in Supplementary Table 3). The Wilcoxon-Mann–Whitney test (Fay and Proschan, 2010) indicated that habitat A was significantly different from habitats B, C, and D. On the other hand, based on the chamber method measurements, only habitats B and C were significantly different from each other (p < 0.01; Supplementary Table 1).

FIGURE 6

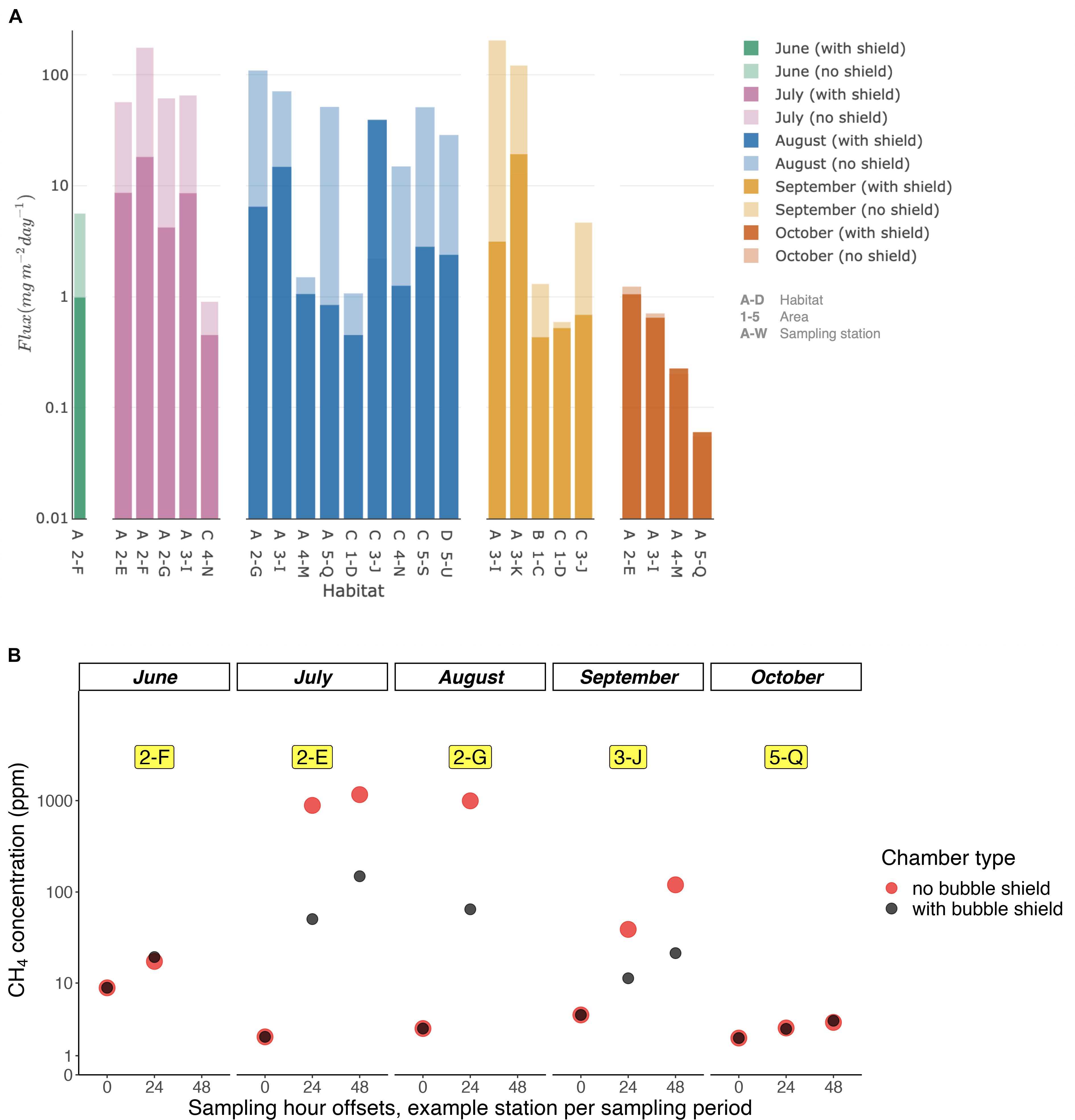
Figure 6. Comparison between CH₄ flux with and without bubble shield for different habitats (A) and during the different sampling periods (B).

Habitat Categorization of Methane Fluxes and Their Environmental Forcing

Water temperatures less than 15°C generally showed fluxes lower than 5 mg m^–2 d^–1. Wind velocities varied between 1 and 8 m/s during all sampling periods, but there were large variations between sampling periods with low winds in July and October and during periods with higher winds in June, August, and September. There was an expected significant positive relationship between methane flux and wind velocity due to the dependency of k on wind velocity, and a slightly negative relationship between flux and salinity for fluxes calculated with the gas transfer model. There was no correlation between flux and wind velocity for the floating chamber method, likely due to contribution from ebullition for CH₄, but the correlation between CH₄ flux and water and air temperature was weak, but positive (Kendall’s τ < 0.29). Algal biomass and sediment organic contents also showed a significant positive correlation with fluxes, when each habitat was considered individually, but the overall correlation, when all habitats were combined, was weak. The biomass of algae including floating algal mats varied seasonally with highest accumulations in August and a virtual absence of floating algal mats in October. Accumulation in the inshore water also depended on the prevailing wind direction relative to the shoreline orientation, where south to southwesterly winds pushed algal mats into the shore region. Both algal biomass carbon and sediment organic content have a similar correlation with flux for the chamber method and gas transfer model.

Flux Variation in Different Habitats

Flux data from our different sampling stations and environmental parameters were used to test the statistical significance of our station classification scheme into four different habitats. This classification was then used to identify relationships between flux and environmental forcing factors in different habitats and their habitat-specific and seasonal variation. Objective hierarchical statistical clustering was used to determine whether the chosen environmental forcing factors and gas transfer mode-derived methane fluxes discriminated between the four habitat types (Figure 7A). The analysis showed that the statistics-based grouping reproduced the a priori choice of different habitats for the different stations relatively well. For the fluxes determined with the gas transfer model, habitats A and B group closely together because they have similarities in several environmental parameters. It should be noted that stations in area 5 only had two observations for two sampling periods, compared to stations from the other areas that were sampled 4–5 times, which may have affected the results of the cluster analysis. Habitat C and D are grouped together in the cluster analysis because they have more similarity with each other than the other two habitats. Habitat C is the most distant because it has deeper water than the other habitats.

FIGURE 7

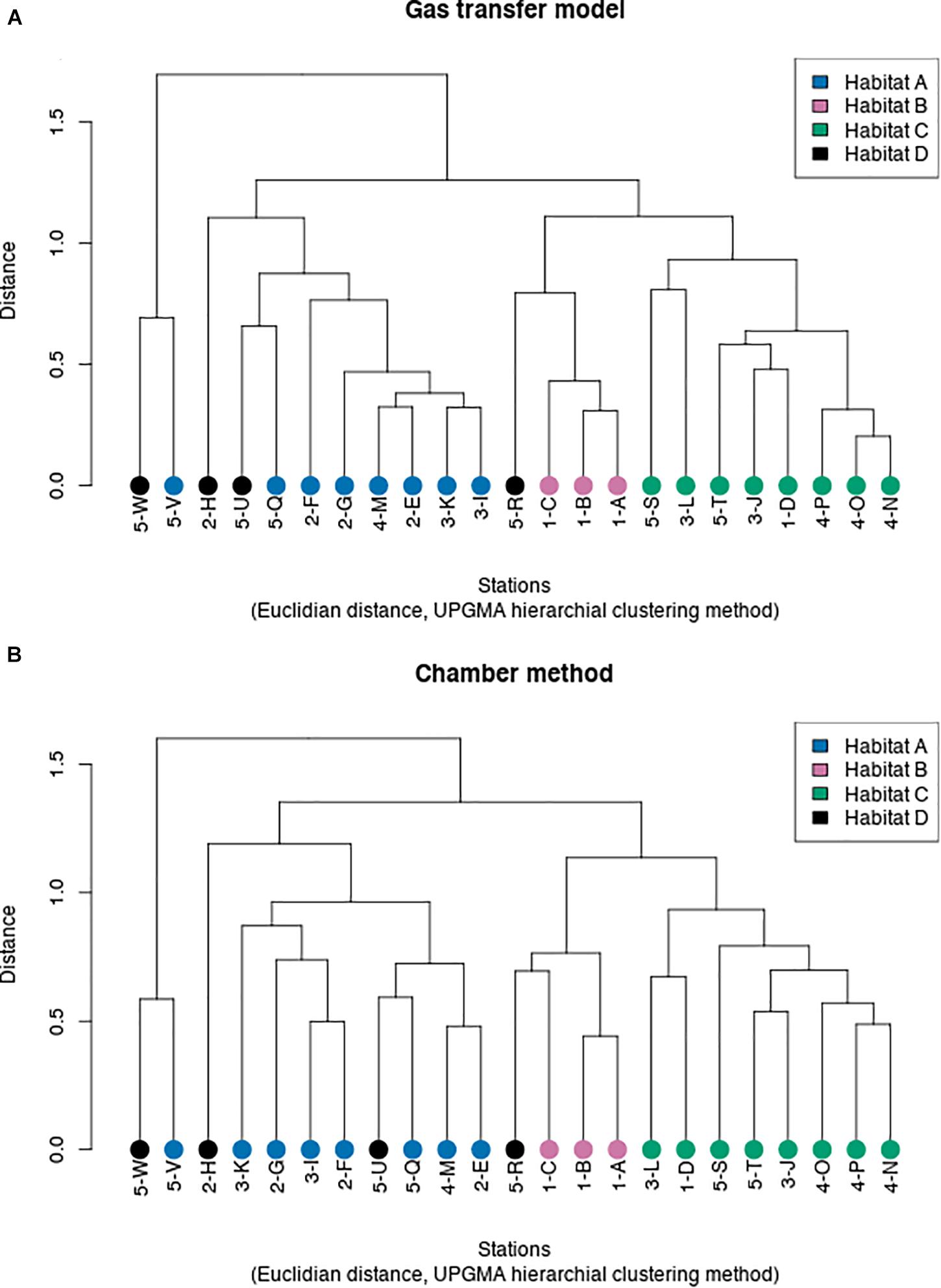
Figure 7. Hierarchical clustering of habitats as a function of CH₄ flux relative to environmental forcing factors for the gas transfer model (A) and the unshielded chamber method (B).

Hierarchical clustering was also performed with the fluxes determined with the floating chamber method (Figure 7B). These results differed somewhat from the gas transfer model-based results because the calculated fluxes represent the integral of a 12–72-h time interval, and the values for water and air temperature, wind velocity, and salinity were taken at the end of the flux calculation interval, whereas the values used for the gas transfer model were taken at the beginning of each flux experiment. In addition, only fluxes from chambers without bubble shield were used in this analysis. The chamber fluxes include both the diffusive and ebullitive flux, whereas the gas transfer model, at least nominally, only accounts for the diffusive flux. The hierarchical cluster distance of stations according to habitats based on the floating chamber method was larger than for the gas transfer model, likely reflecting the temporal asynchroneity between the flux calculation and some of the environmental parameters, foremost wind velocity and air temperature, suggesting that the analysis for the gas transfer model was statistically more reliable than the floating chamber-based cluster analysis.

The cluster analysis for the four different habitats indicated early clustering between fluxes, organic content of floating algal biomass, and sediment organic content on timescale of a few days and between fluxes, wind velocity, and water temperature on timescale covering the whole sampling period of this study. A relatively late clustering was found between flux, salinity, and water depth, likely because all our sampling areas had about the same water depth and only small variations in salinity (Figures 8A,B). Both dendrograms in Figures 8A,B form clusters with flux, algal biomass, sediment organic content, salinity, and wind velocity, although with slightly different ordering of individual elements. The main difference was a tighter clustering between flux and sediment organic content instead of algal mats for the chamber method, which may indicate the added contribution of sediment gas ebullition. Water and air temperature are expected to have a more significant impact across longer time periods (seasonal time ranges). When the hierarchical cluster analysis was broken down for each month in the different habitats, the same pattern resulted for habitats A, C, and D with exception of the months of July and October, but the clustering results were different for Habitat B, likely because of the small number of observations for this habitat.

FIGURE 8

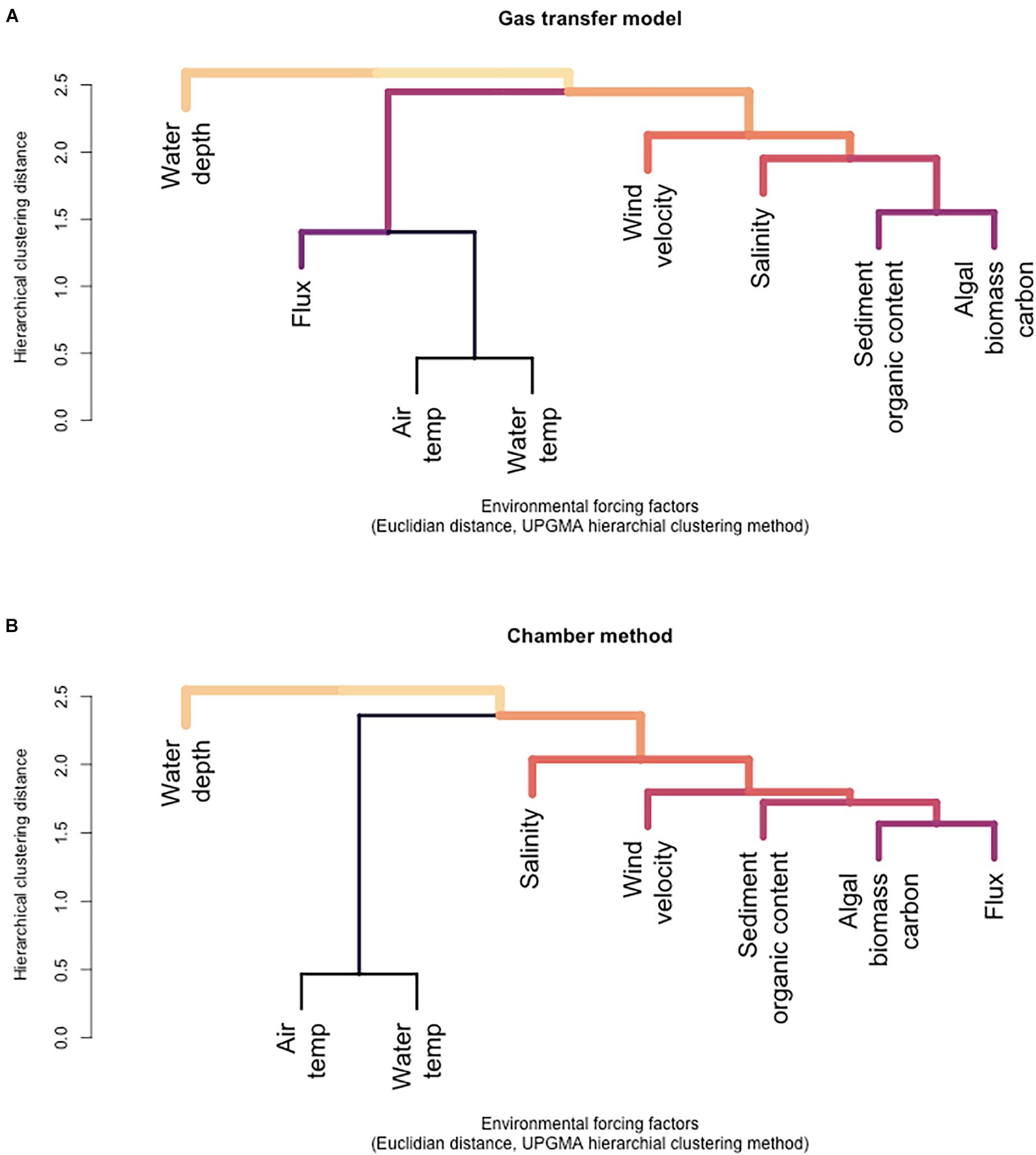
Figure 8. Hierarchical clustering of environmental forcing factors and CH₄ flux calculated with the gas transfer model (A) and hierarchical clustering of environmental forcing factors and CH₄ flux calculated with the unshielded flux chamber method (B).

In order to further evaluate the strength of the correlation between individual parameters and methane fluxes, we used Kendall rank correlation coefficient for each pair of flux and environmental forcing factors (Table 2). For the gas transfer model, the strongest association was found between flux and wind velocity. For the chamber method, sediment organic content and algal biomass carbon provided the strongest associations with methane flux. Overall, with the exception of salinity, most correlations were positive. The associations between parameters other than flux were similar for both gas transfer model and chamber method, with strong positive associations between air and water temperature and medium negative associations for both wind velocity and temperatures (air and water) with salinity. Most other associations were weaker. When the analysis was broken down into individual habitats focusing on correlations with methane flux, wind velocity still had the strongest correlation in the gas transfer model, in particular for habitats B, C, and D, and a medium correlation for habitat A. For the chamber method, methane flux showed medium correlations in individual habitats with air and water temperature and a weak correlation between methane flux and air and water temperature when all habitats were pooled together.

TABLE 2

Table 2. Pairwise correlation coefficients between CH₄ flux and environmental forcing factors for all habitats and sampling periods.

Variations and correlation between flux and environmental forcing factors in the different habitats were further analyzed using MFA by reducing the multiple environmental variables into smaller sets of dimensions. Figures 9A,B shows the quantitative variable correlation in all habitats and sampling periods for the two primary principal components (dimensions) of the MFA for fluxes derived with the gas transfer model and chamber method. Altogether, the MFA confirmed the results of the pairwise correlation and the hierarchical cluster analysis indicating wind velocity as the major driving factor for the CH₄ flux in the gas transfer model and sediment organic content and algal biomass carbon as the main drivers for the CH₄ flux in the chamber method. There was no association between flux and wind velocity in the chamber method and only a weak negative correlation between flux and salinity. The secondary factor for both methods were air and water temperature. The MFA analysis showed variable association patterns between flux and environmental forcing factors when conducted for individual habitats, which is probably due to the different number of observations for some of the habitats; habitats B and D have less than one third of the number of observations compared to habitats A and B. The contribution from the two primary principal components varied between 41 and 71%. The inclusion of a third dimension increased the total contribution from the three primary principal components to between 56 and 93%. For the gas transfer model in habitats B, C, and D the methane flux showed the strongest correlation with wind velocity in dimension 3, while in habitat A the strongest correlation existed between CH₄ flux and temperature. In the chamber method a strong correlation was found between CH₄ flux and sediment organic content in habitat A, while habitat B and D had stronger correlations between flux and wind velocity. In habitat C, dimension 3 did not enhance the correlation indicated in dimensions 1 and 2. The flux correlation deviated during July sampling period for gas transfer model and in June sampling period for chamber method. The supplementary material contains additional quantitative variable correlation for the two primary principal components (dimensions) of the MFA per habitat (Supplementary Figure 1) and per sampling period (Supplementary Figure 2).

FIGURE 9

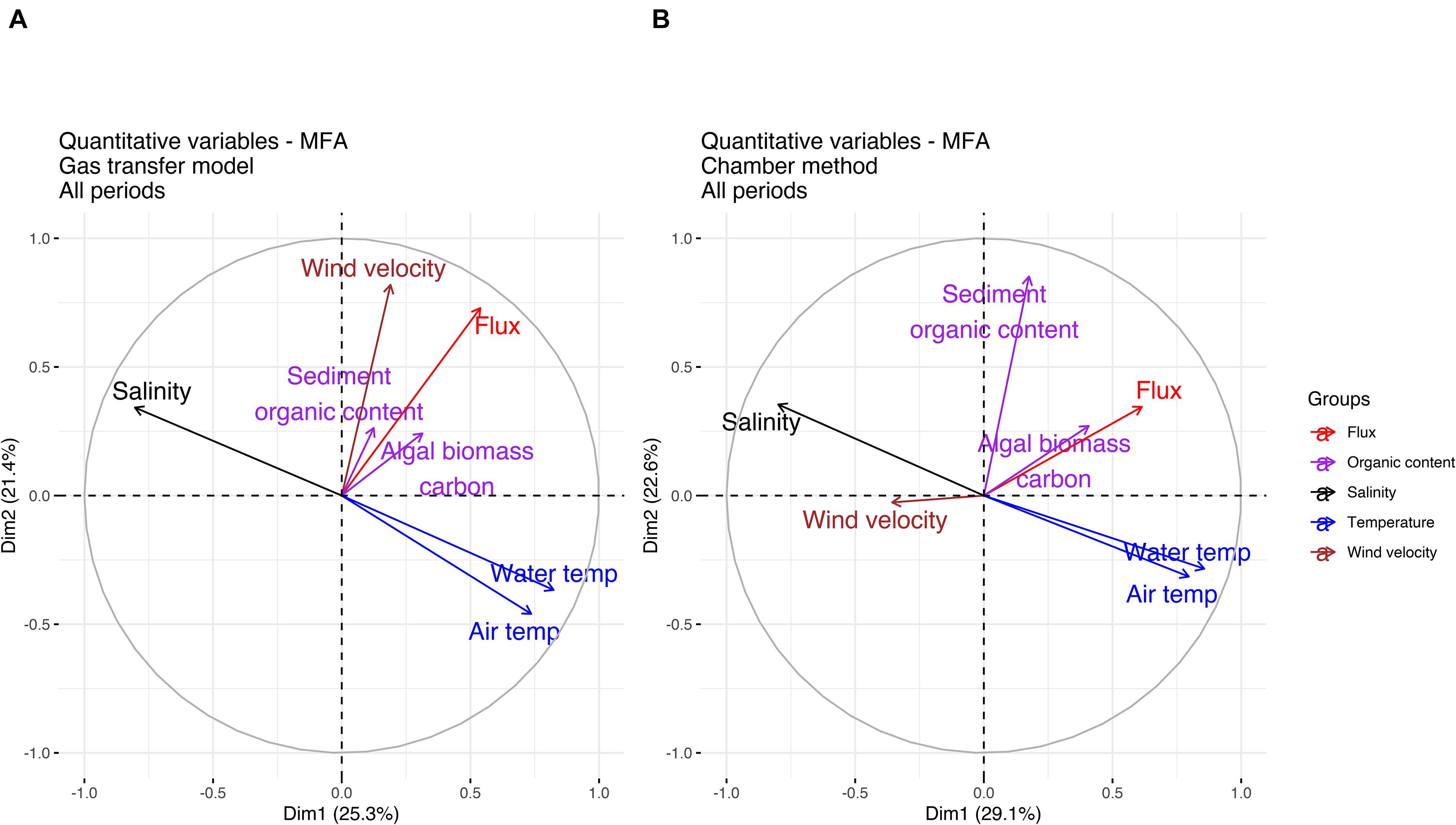
Figure 9. Multiple factor analysis (MFA) for all sampling periods showing weighted correlations between CH₄ flux and environmental forcing factors for the gas transfer model (A) and the chamber method (B).

Discussion

Method Comparison and Implications for Environmental Forcings

An important observation of this study has been that the statistical associations of the environmental forcing factors varied with the flux method. Other studies that compared a gas transfer model-derived with chamber-based flux measurements including day- and nighttime measurements found higher methane emissions with the chamber method than the gas transfer model (Erkkilä et al., 2018). Our measurements with the chamber method generally occurred over a 12–24-h period several times over a week thereby integrating diurnal flux variations over this time period. This is not the case for the gas transfer model, which represents daytime methane measurements and air temperature and wind velocity measurements that were retrieved from measurements from nearby weather stations and do not consider local and short-term temporal variations.

The underlying assumption of the gas transfer model is that transport through the sea surface boundary layer takes place via diffusion of methane in one phase. It cannot be said with certainty that the high concentrations of the water samples represent truly dissolved methane, a precondition for the application of the gas transfer model. It is possible that some of the water samples contained microbubbles that were not detected visually and interpreted as dissolved methane due to high concentration of methane in water. This raises the question whether the gas transfer model represented the best suited equation for all sampling periods. In addition, as expected, the gas transfer model fluxes were most closely related to variations in wind velocity, however, the strong correlation does not reflect the overall importance of wind as regulating factor considering the dominance of bubble transport in the shallow inshore areas. The chamber-based fluxes make no assumptions about the transport mechanisms diffusion, ebullition and plant-mediated transport, but here shielding effects of the chamber regarding wind can have affected the forcing by wind.

In addition, the seasonally varying presence of algal biofilms at the water surface may have affected the gas transfer velocity and thus the flux of methane when using a gas transfer model. In July and August, thick algal mats covered the water surface of most of the sampling stations of habitats A and B. The algal mat thickness was between 0.5 and 2 cm. Goldman et al. (1988) noted that natural surfactant films in algal mats can affect the oxygen exchange coefficient and reduced gas transfer velocity to 63–85% of a control value for gas transfer for distilled water. This is due to changes in the oxygen exchange coefficient that is sensitive to small changes in carbohydrate concentration, since they affect the viscosity and thereby the Schmidt number (Frew et al., 1990). Reductions of k by up to 50% were reported in near coastal estuarine areas (Goldman et al., 1988) contrary to open ocean water (Nightingale et al., 2000a). Cyanobacterial biofilms can have high concentrations of organic calcium and magnesium complexes (Arp et al., 2001; Dupraz et al., 2009). These may also cause a decrease in k by up to a factor 2 (Frew et al., 1990). Due to the variability in the presence and thickness of the biofilms at different stations and during the different sampling periods, we would only have been able to make qualitative adjustments to the gas exchange coefficient, but we note that the gas transfer flux calculations in our study at certain times and in areas with thick biofilms may have overestimated the actual gas transfer model flux. A surface algal biofilm can also increase the retention of rising bubbles in the viscous biofilm and may therefore reduce the bubble flux released to the overlying chamber. This would imply that methane fluxes determined with the chamber method in areas of thick algal mats may actually be lowered due to the biofilm presence.

In summary, the chamber-based flux method appeared to be superior in capturing variations in flux as a function of the different environmental forcing factors. The chamber method also provided a more stable environmental forcing pattern across the different habitats during the whole season. We therefore conclude that this approach may be more useful than the gas transfer model for spatial scaling of flux measurements provided that a good categorization of different habitats and their prevalence can be performed. Practically, however, the chamber method presents greater technical challenges in comparison to the gas transfer model, with which measurements generally are easier to obtain. Thus, in practice a combination of methods will be needed and also compared to eddy correlation-based flux methods.

Magnitude of Methane Fluxes

The monthly averaged fluxes of our study were in the same order of magnitude as fjord-type environments and coastal lagoons, whereas fluxes in estuarine waters tend to be up to an order of magnitude lower (Borges and Abril, 2012). Our highest fluxes also compare well with those reported by Heyer and Berger (2000) for coastal wetlands of the southwestern Baltic Sea. Shallow inshore areas generally have well-mixed waters compared to the more stratified offshore areas in deeper water. Compared to fluxes in the offshore Baltic Sea, the range of the spatial and temporal variability of fluxes in our study was almost two orders of magnitude higher. The lowest fluxes in our study were 0.1 mg m^–2 d^–1, which is similar to the lowest fluxes reported in Gülzow et al. (2013), but the highest values in our study were 162.6 mg m^–2 d^–1, compared to the highest fluxes of 1.5 mg m^–2 d^–1 reported by Gülzow et al. (2013). A similar distinct onshore-offshore difference was observed by Borges et al. (2016), who also observed the highest inshore fluxes in the summer season and attributed these to a positive feedback from marine seepage in near-shore shallow areas with gassy sediment. However, the combined effects of seasonal variability and onshore-offshore patterns were different from our study, since Borges et al. (2016) found the lowest fluxes in the offshore areas in late spring and summer, and the highest fluxes in late winter, whereas our study observed the highest fluxes in the summer and the lowest in autumn. Borges et al. (2016) observed similar trends in relation to salinity, where higher fluxes correlated with lower salinity, although the range of salinity was an order of magnitude larger than in our study and also related to greater range in water depth. These comparisons indicate that the environmental effects of the forcing parameters are different for inshore and offshore areas, which make simple extrapolations of our study to greater water depths difficult.

Environmental Forcing

Three main paths have been identified for atmospheric methane emissions from inshore shallow areas: ebullition, diffusion, and plant mediated transport (Jeffrey et al., 2019). In shallow, littoral waters, most methane is produced in the underlying sediment by methanogenic archaea and methylotrophs, from where it diffuses to the atmosphere by diffusion or is emitted as gas bubbles (Crill and Martens, 1986; Chanton et al., 1989; Madigan et al., 2003). The formation of methane bubbles in sediment or floating algal mats reflects the prevailing physicochemical conditions that determine its solubility at a given hydrostatic pressure and temperature, the rate of methane production and oxidation (Martens et al., 1998; Wever et al., 2006; Mogollón et al., 2011). Methane bubble fluxes between 1.6 and 277 mg m^–2 d^–1 have been reported in various coastal settings (Chanton et al., 1989; Chanton and Dacey, 1991; Leifer and Patro, 2002; Borges et al., 2011), which agrees well with measurements in our study.

Transport of methane through plants (Van der Nat and Middelburg, 2000) and the shallow water depth favor direct transfer of gas bubbles to the atmosphere minimizing oxidation (Van der Nat and Middelburg, 2000). In certain types of habitats, plant-mediated methane transport may account for the majority of methane emissions of these three paths annually (Jeffrey et al., 2019).

In addition, sudden air pressure changes and periods with high winds also enhance the release of methane (Lohrberg et al., 2020). It has been suggested that at least 45% of the initial methane gas content in sediment may escape to the atmosphere during a storm event (McGinnis et al., 2006; Lohrberg et al., 2020). Our study was conducted the sampling over a period of 5 months, with samples taken during a period of a few days each calendar month. Although the weather was relatively stable during this period, there were periods with high winds and heavy rain, which occurred both between and on sampling days during June and August, when it was not practically possible to obtain sampling data. Weather data for the region during our sampling season indicate high-wind events during eight occasions with wind velocities higher than 10 m/s. The effects of these high-wind events in the middle of July and end of August/beginning of September can be noted in Figure 4 and show higher fluxes than those measured during the other sampling months. It is also important to note that these events improve the correlations between methane fluxes and wind velocities in the statistical analyses.

Our data show that ebullition was related to habitat type and season. Wind- and wave-protected embayments with organic-rich fine-grained sediment covered by dense mats of floating algae (habitats A and B) had the highest ebullition rates, but this mode of transport only dominated during the late spring and summer, and ceased in the fall. Both temperature and salinity affect the solubility of methane, but the observed salinity in our study (5.4–6.7‰) had a negligible effect on the solubility itself. Temperatures measured during the sampling days in each period were generally considered representative of each sampling period representing a whole month with the exception of July 2019, which had an unusually large temperature range from 9°C in the beginning to 33°C at the end of the month. The full consequences of this large temperature increase are insufficiently captured with the discrete week-long measurements of our study. Taking these considerations into account, the most significant environmental forcing factor on seasonal timescales were temperature and organic content. This is in line with other studies in the Baltic Sea, which found that the primary ecological driver for methane emission was the seasonal variation of the sediment organic matter content, while temperature controlled daytime and nighttime as well as long-term seasonal long-term variability (Heyer and Berger, 2000; Gülzow et al., 2013).

Habitats A and B with their dense reed beds and floating algal cover in only 0.5 m water depth had the highest fluxes in our study emphasizing the role of plant-mediated methane transport as additional contribution. This was also concluded by Van der Nat and Middelburg (2000), who found that transport through reed and bulrush represented over 85% of the total net methane emission from such habitats. In situ production in floating algal mats contributes additional methane, but has generally been considered secondary compared to the sediment source. However, the high fluxes in habitat C, where boulders covered the seafloor and methanogenic sediment was absent, indicate that in certain habitats floating algal mats are the sole source of the methane flux to the atmosphere during the summer.

Hierarchical clustering analysis helped to validate the categorization of our sampling stations into the four different habitats, but the clustering results showed different group constellations of parameters depending on whether methane fluxes were calculated with the gas transfer model or using floating chambers. There were also different forcing constellations depending on habitat. These results suggest that the calculated hierarchy of forcing parameters for methane fluxes was dependent on the field method and habitat. In the case of the chamber method, this is due to the fact that the methane flux was more strongly forced by methane bubble transport than by wind velocity. Since the bubble-mediated flux far exceeded the diffusive flux for all months except October, we conclude that the environmental forcing constellations associated with the chamber measurements are more realistic for habitats A and B, whereas for the vegetation-poor and open areas habitats C and D, where wind forcing plays the dominant role, the forcing constellations of either gas transfer model or chamber-based measurements yield realistic constellations.

The basic forcing constellations derived from the hierarchical clustering were confirmed by the pairwise correlation analysis using Kendall correlation coefficients for each of the flux measurement methods. As expected, the Kendall correlation coefficients provided very good correlation coefficients between wind velocity and methane flux for gas transfer model-derived data, but very weak correlations of the same parameters for the chamber-based measurements. However, since wind velocity only had a minor influence on the actual fluxes in habitats A and B, where vegetation density and organic richness played a much stronger role, these high correlation coefficients can be misleading for understanding the environmental multi-parameter forcing. These problems were overcome with the MFA, which provided a measure of the correlation quality and the relative weight of different forcing parameters in the different habitats. The primary control of vegetation and sediment organic content followed by air/water temperature as secondary and, finally, wind velocity as tertiary control provided a realistic assessment of the hierarchy of environmental forcing factors in habitat A. The weighting shifted in the more open habitat B, with the primary control parameters to be the same as in habitat A, but with wind velocity and air/water temperature switching positions as secondary and tertiary controls. Finally, the statistical selection of wind velocity as the primary control followed by water depth as secondary, and air/water temperature as tertiary control, for the barer and deeper habitats C and D is a realistic reflection of the environmental drivers in these more open and rocky bottom habitats.

Spatial Extrapolation

Multiple factor analysis provided the first steps toward a scaling approach to predict the methane fluxes in areas represented by our four habitats, for which no direct measurements were taken. At present, the flux database per habitat is too limited to develop algorithms based on algal biomass density, sediment organic content, temperature, and wind velocity for these shallow-water habitats. As an alternative, we chose to use the monthly averages for our habitats as guideline values and partitioned the coastline of the island of Askö into the habitat groups by calculating areas extending 10 m from the shore using aerial photographs. This made it possible to extrapolate the methane emissions of our investigated areas with known habitats to the coast line of the entire island (Table 3). The total length of the Askö coastline was estimated to be 34 km, and the total calculated coastal area within 10 m of the shore is 0.34 km². Habitat A comprises 0.08 km², habitat B 0.05 km², habitat C 0.13 km², and habitat D 0.09 km², representing 24, 14, 37, and 25% of the total area (Figure 10), and the presence of habitat categories that were not included in our study such as a sandy beach, which covers 500 m of the northern shoreline of the island. Here, habitat D was selected as the closest analog. The estimated emission of methane from the inshore habitat of the island of Askö varied from 8.8 kg/day in August to 0.17 kg/day in October for the chamber-based flux. Notably, habitat A- and B-type areas contributed 89% to the total flux in August, but no more than 50% in October, when ebullition had ceased and the emissions were more evenly distributed across the habitats. Extrapolation of the emission over a full year assuming similar emissions for October, the winter, and early spring months yielded a very high estimate of 594 kg per year for the whole coast of the island. Based on the seasonal trend in emissions, we estimate that about 90% of the emission flux occurred during July and August and dominated by habitats A (72%) and B (7%). These daily emissions only provide first-order estimates of emissions and probably overestimate the actual emission. Uncertainties of our approach arise from the resolution of published aerial photographs and small-scale variability of fluxes within a defined habitat area, the local inshore wind field on the seaward and landward side of the island, and the variable shoreline shape and geographic orientation.

TABLE 3

Table 3. Scaled methane emissions for August 2019 for the total coastline of the island of Askö.

FIGURE 10

Figure 10. Habitat (A–D) distribution along the Askö coastline.

The data require comparisons from ongoing, supplemental, continuous eddy correlation, and continuous water sampling measurement campaigns.

Conclusion

The current study demonstrates that a habitat-based approach to upscale local, time-limited sea-air exchange measurements of methane fluxes can only be successful, if a weighting of the multiple primary drivers for methane emissions in shallow water coastal habitats is carried out, because no single environmental driver dominates fluxes. In addition, the forcing mechanisms between environmental drivers and methane flux are not linear, because the onset of ebullition is characterized by the passing of temperature and primary productivity thresholds above which the emission type switches from diffusion to ebullition thereby increasing the emission rates more than tenfold. It is likely that such ‘switches’ in the dominant transport process do not occur synchronously along shorelines. In rocky bottom habitats that lack sufficient organic richness or surface algal accumulations, transport mode changes likely do not occur at all and the exchanges are likely controlled by wind forcing and temperature only. The study also demonstrates that apparent good correlations between environmental forcing variables such as wind velocity and temperature only provide good correlations for boundary layer models, but not when ebullition is explicitly accounted for in the measurement. There is a need for complementary approaches to determine the exchange fluxes, because the spatial and temporal extrapolations have many uncertainties. One possible approach may be to use flux measurements carried with eddy correlation towers in the different habitats. This would overcome the problem of discontinuous measurements and could account for the habitat-specific variability in fluxes within an eddy footprint.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) are: Bolin Centre Database, https://doi.org/10.17043/lundevall-zara-2021-asko-methane-1.

Author Contributions

ML-Z: main researcher, planning and execution of fieldwork, collection of samples, laboratory analysis of samples, dataanalysis, and visualization of data. EL-Z: software development for statistical analysis and visualization of data. VB: supervisor and scientific review and editing. All authors contributed to the article and approved the submitted version.

Funding

The research was made with support from the Research School for Teachers on Climate and the Environment, Swedish Research Council Grant 2017-06037, project support from the Bolin Centre for Climate Research at Stockholm University, and a donation stipendium from Sandström.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to thank the editors and two reviewers of this manuscript for their comments, Eva Lindahl and the staff at Askö Laboratory for support during sampling, David Bastviken for suggestions about the chamber design, Hildred Crill for language and academic writing discussions and encouragement, Julia Steinbach for technical assistance in the laboratory, John Prytherch, and Florian Roth for discussions about gas transfer flux calculations, and Alasdair Skelton for the coordination of the Research School for Teachers on Climate and the Environment.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2021.657459/full#supplementary-material

Footnotes

1. ^ https://www.smhi.se/data
2. ^ https://www.smhi.se/en/theme/tides-1.11272

References

Abdi, H., and Williams, L. J. (2010). Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2, 433–459. doi: 10.1002/wics.101

CrossRef Full Text | Google Scholar

Abdi, H., Williams, L. J., and Valentin, D. (2013). Multiple factor analysis: principal component analysis for multitable and multiblock data sets. Wiley Interdiscip. Rev. Comput. Stat. 5, 149–179. doi: 10.1002/wics.1246

CrossRef Full Text | Google Scholar

Amorocho, J., and DeVries, J. J. (1980). A new evaluation of the wind stress coefficient over water surfaces. J. Geophys. Res. 85, 433–442. doi: 10.1029/jc085ic01p00433

CrossRef Full Text | Google Scholar

Arp, G., Reimer, A., and Reitner, J. (2001). Photosynthesis-induced biofilm calcification and calcium concentrations in phanerozoic oceans. Science 292, 1701–1704. doi: 10.1126/science.1057204

PubMed Abstract | CrossRef Full Text | Google Scholar

Bange, H. W., Bergmann, K., Hansen, H. P., Kock, A., Koppe, R., Malien, F., et al. (2010). Dissolved methane during hypoxic events at the Boknis Eck time series station (Eckernförde Bay, SW Baltic Sea). Biogeosciences 7, 1279–1284. doi: 10.5194/bg-7-1279-2010

CrossRef Full Text | Google Scholar

Bartley, J. D., Buddemeier, R. W., and Bennett, D. A. (2001). Coastline complexity: a parameter for functional classification of coastal environments. J. Sea Res. 46, 87–97. doi: 10.1016/S1385-1101(01)00073-9

CrossRef Full Text | Google Scholar

Bastviken, D., Ejlertsson, J., Sundh, I., and Tranvik, L. (2003). Methane as a source of carbon and energy for lake pelagic food webs. Ecology 84, 969–981. doi: 10.1890/0012-9658(2003)084[0969:maasoc]2.0.co;2

CrossRef Full Text | Google Scholar

Bastviken, D., Tranvik, L. J., Downing, J. A., Crill, P. M., and Enrich-Prast, A. (2011). Freshwater methane emissions offset the continental carbon sink. Science 331:50. doi: 10.1126/science.1196808

PubMed Abstract | CrossRef Full Text | Google Scholar

Battin, T. J., Kaplan, L. A., Findlay, S., Hopkinson, C. S., Marti, E., Packman, A. I., et al. (2008). Biophysical controls on organic carbon fluxes in fluvial networks. Nat. Geosci. 1, 95–100. doi: 10.1038/ngeo101

CrossRef Full Text | Google Scholar

Battino, R. (1984). The Ostwald coefficient of gas solubility. Fluid Phase Equilib. 15, 231–240. doi: 10.1016/0378-3812(84)87009-0

CrossRef Full Text | Google Scholar

Bižić, M., Klintzsch, T., Ionescu, D., Hindiyeh, M. Y., Günthel, M., Muro-Pastor, A. M., et al. (2020). Aquatic and terrestrial cyanobacteria produce methane. Sci. Adv. 6:eaax5343. doi: 10.1126/sciadv.aax5343

PubMed Abstract | CrossRef Full Text | Google Scholar

Borges, A. V., and Abril, G. (2012). “Carbon dioxide and methane dynamics in estuaries,” in Treatise on Estuarine and Coastal Science, eds E. Wolanski and D. S. McLusky (Waltham, MA: Academic Press), doi: 10.1016/B978-0-12-374711-2.00504-0

CrossRef Full Text | Google Scholar

Borges, A. V., Abril, G., Delille, B., Descy, J. P., and Darchambeau, F. (2011). Diffusive methane emissions to the atmosphere from Lake Kivu (Eastern Africa). J. Geophys. Res. Biogeosci. 116:G03032. doi: 10.1029/2011JG001673

CrossRef Full Text | Google Scholar

Borges, A. V., Champenois, W., Gypens, N., Delille, B., and Harlay, J. (2016). Massive marine methane emissions from near-shore shallow coastal areas. Sci. Rep. 6:27908. doi: 10.1038/srep27908

PubMed Abstract | CrossRef Full Text | Google Scholar

Casper, P., Maberly, S. C., Hall, G. H., and Finlay, B. J. (2000). Fluxes of methane and carbon dioxide from a small productive lake to the atmosphere. Biogeochemistry 49, 1–19. doi: 10.1023/A:1006269900174

CrossRef Full Text | Google Scholar

Chanton, J. P., and Dacey, J. W. H. (1991). “Effects of Vegetation on Methane Flux, Reservoirs, and Carbon Isotopic Composition,” in Trace Gas Emissions by Plants, eds T. D. Sharkey, E. A. Holland, and H. A. Mooney (San Diego, CA: Academic Press), doi: 10.1016/b978-0-12-639010-0.50008-x

CrossRef Full Text | Google Scholar

Chanton, J. P., Martens, C. S., and Kelley, C. A. (1989). Gas transport from methane−saturated, tidal freshwater and wetland sediments. Limnol. Oceanogr. 34, 807–819. doi: 10.4319/lo.1989.34.5.0807

CrossRef Full Text | Google Scholar

Chen, H., Cohen, P., and Chen, S. (2010). How big is a big odds ratio? Interpreting the magnitudes of odds ratios in epidemiological studies. Commun. Stat. Simul. Comput. 39, 860–864. doi: 10.1080/03610911003650383

CrossRef Full Text | Google Scholar

Crill, P. M., and Martens, C. S. (1986). Methane production from bicarbonate and acetate in an anoxic marine sediment. Geochim. Cosmochim. Acta 50, 2089–2097. doi: 10.1016/0016-7037(86)90262-0

CrossRef Full Text | Google Scholar

Crill, P. M., and Thornton, B. F. (2017). Whither methane in the IPCC process? Nat. Clim. Chang. 7, 678–680. doi: 10.1038/nclimate3403

CrossRef Full Text | Google Scholar

Croux, C., and Dehon, C. (2010). Influence functions of the Spearman and Kendall correlation measures. Stat. Methods Appl. 19, 497–515. doi: 10.1007/s10260-010-0142-z

CrossRef Full Text | Google Scholar

de Tayrac, M., Lê, S., Aubry, M., Mosser, J., and Husson, F. (2009). Simultaneous analysis of distinct omics data sets with integration of biological knowledge: multiple factor analysis approach. BMC Genomics 10:32. doi: 10.1186/1471-2164-10-32

PubMed Abstract | CrossRef Full Text | Google Scholar

Delwiche, K., Senft-Grupp, S., and Hemond, H. (2015). A novel optical sensor designed to measure methane bubble sizes in situ. Limnol. Oceanogr. Methods 13, 712–721. doi: 10.1002/lom3.10060

CrossRef Full Text | Google Scholar

Dupraz, C., Reid, R. P., Braissant, O., Decho, A. W., Norman, R. S., and Visscher, P. T. (2009). Processes of carbonate precipitation in modern microbial mats. Earth Sci. Rev. 96, 141–162. doi: 10.1016/j.earscirev.2008.10.005

CrossRef Full Text | Google Scholar

Erkkilä, K. M., Ojala, A., Bastviken, D., Biermann, T., Heiskanen, J., Lindroth, A., et al. (2018). Methane and carbon dioxide fluxes over a lake: comparison between eddy covariance, floating chambers and boundary layer method. Biogeosciences 15, 429–445. doi: 10.5194/bg-15-429-2018

CrossRef Full Text | Google Scholar

Fay, M. P., and Proschan, M. A. (2010). Wilcoxon-Mann-Whitney or T-test? on assumptions for hypothesis tests and multiple interpretations of decision rules. Stat. Surv. 4, 1–39. doi: 10.1214/09-SS051

CrossRef Full Text | Google Scholar

Felipe-Lucia, M. R., Soliveres, S., Penone, C., Fischer, M., Ammer, C., Boch, S., et al. (2020). Land-use intensity alters networks between biodiversity, ecosystem functions, and services. Proc. Natl. Acad. Sci. U.S.A. 117, 28140–28149. doi: 10.1073/pnas.2016210117

PubMed Abstract | CrossRef Full Text | Google Scholar

Frew, N. M., Goldman, J. C., Dennett, M. R., and Johnson, A. S. (1990). Impact of phytoplankton-generated surfactants on air-sea gas exchange. J. Geophys. Res. 95:3337. doi: 10.1029/jc095ic03p03337

CrossRef Full Text | Google Scholar

Gattuso, J. P., Frankignoulle, M., and Wollast, R. (1998). Carbon and carbonate metabolism in coastal aquatic ecosystems. Annu. Rev. Ecol. Syst. 29, 405–434. doi: 10.1146/annurev.ecolsys.29.1.405

CrossRef Full Text | Google Scholar

Goldman, J. C., Dennett, M. R., and Frew, N. M. (1988). Surfactant effects on air-sea gas exchange under turbulent conditions. Deep Sea Res. A Oceanogr. Res. Pap. 35, 1953–1970. doi: 10.1016/0198-0149(88)90119-7

CrossRef Full Text | Google Scholar

Gülzow, W., Rehder, G., Deimling, J. S. V., Seifert, T., and Tóth, Z. (2013). One year of continuous measurements constraining methane emissions from the Baltic Sea to the atmosphere using a ship of opportunity. Biogeosciences 10, 81–99. doi: 10.5194/bg-10-81-2013

CrossRef Full Text | Google Scholar

Heyer, J., and Berger, U. (2000). Methane emission from the coastal area in the Southern Baltic Sea. Estuar. Coast. Shelf Sci. 51, 13–30. doi: 10.1006/ecss.2000.0616

CrossRef Full Text | Google Scholar

Ho, D. T., Law, C. S., Smith, M. J., Schlosser, P., Harvey, M., and Hill, P. (2006). Measurements of air-sea gas exchange at high wind speeds in the Southern Ocean: implications for global parameterizations. Geophys. Res. Lett. 33:L16611. doi: 10.1029/2006GL026817

CrossRef Full Text | Google Scholar

Hoogsteen, M. J. J., Lantinga, E. A., Bakker, E. J., Groot, J. C. J., and Tittonell, P. A. (2015). Estimating soil organic carbon through loss on ignition: effects of ignition conditions and structural water loss. Eur. J. Soil Sci. 66, 320–328. doi: 10.1111/ejss.12224

CrossRef Full Text | Google Scholar

Jähne, B., Münnich, K. O., Bösinger, R., Dutzi, A., Huber, W., and Libner, P. (1987). On the parameters influencing air-water gas exchange. J. Geophys. Res. Ocean 92, 1937–1949. doi: 10.1029/JC092iC02p01937

CrossRef Full Text | Google Scholar

Jeffrey, L. C., Maher, D. T., Johnston, S. G., Kelaher, B. P., Steven, A., and Tait, D. R. (2019). Wetland methane emissions dominated by plant-mediated fluxes: contrasting emissions pathways and seasons within a shallow freshwater subtropical wetland. Limnol. Oceanogr. 64, 1895–1912. doi: 10.1002/lno.11158

CrossRef Full Text | Google Scholar

Jeffrey, L. C., Maher, D. T., Santos, I. R., Call, M., Reading, M. J., Holloway, C., et al. (2018). The spatial and temporal drivers of pCO2, pCH4 and gas transfer velocity within a subtropical estuary. Estuar. Coast. Shelf Sci. 208, 83–95. doi: 10.1016/j.ecss.2018.04.022

CrossRef Full Text | Google Scholar

Johnson, K. M., Hughes, J. E., Donaghay, P. L., and Sieburth, J. M. N. (1990). Bottle-calibration static head space method for the determination of methane dissolved in seawater. Anal. Chem. 62, 2408–2412. doi: 10.1021/ac00220a030.0

CrossRef Full Text | Google Scholar

Joyce, J., and Jewell, P. W. (2003). Physical controls on methane ebullition from reservoirs and lakes. Environ. Eng. Geosci. 9, 167–178. doi: 10.2113/9.2.167

CrossRef Full Text | Google Scholar

Keller, M., and Stallard, R. F. (1994). Methane emission by bubbling from Gatun Lake, Panama. J. Geophys. Res. 99, 8307–8319. doi: 10.1029/92JD02170

CrossRef Full Text | Google Scholar

Kherif, F., and Latypova, A. (2019). “Principal component analysis,” in Machine Learning: Methods and Applications to Brain Disorders, eds A. Mechelli and S. Vieira (London: Academic Press. doi: 10.1016/B978-0-12-815739-8.00012-2

CrossRef Full Text | Google Scholar

Leifer, I., and Patro, R. K. (2002). The bubble mechanism for methane transport from the shallow sea bed to the surface: a review and sensitivity study. Cont. Shelf Res. 22, 2409–2428. doi: 10.1016/S0278-4343(02)00065-1

CrossRef Full Text | Google Scholar

Lohrberg, A., Schmale, O., Ostrovsky, I., Niemann, H., Held, P., and Schneider von Deimling, J. (2020). Discovery and quantification of a widespread methane ebullition event in a coastal inlet (Baltic Sea) using a novel sonar strategy. Sci. Rep. 10:4393. doi: 10.1038/s41598-020-60283-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Macreadie, P. I., Anton, A., Raven, J. A., Beaumont, N., Connolly, R. M., Friess, D. A., et al. (2019). Author correction: the future of blue carbon science (nature communications, (2019), 10, 1, (3998), 10.1038/s41467-019-11693-w). Nat. Commun. 10:5145. doi: 10.1038/s41467-019-13126-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Madigan, M. T., Martinko, J. M., and Parker, J. (2003). Brock Biology of Microorganisms, 10th Edn. Upper Saddle River, NJ: Prentice Hall/Pearson Education.

Google Scholar

Maltby, J., Steinle, L., Löscher, C. R., Bange, H. W., Fischer, M. A., Schmidt, M., et al. (2018). Microbial methanogenesis in the sulfate-reducing zone of sediments in the Eckernförde Bay, SW Baltic Sea. Biogeosciences 15, 137–157. doi: 10.5194/bg-15-137-2018

CrossRef Full Text | Google Scholar

Martens, C. S., Albert, D. B., and Alperin, M. J. (1998). Biogeochemical processes controlling methane in gassy coastal sediments–Part 1. A model coupling organic matter flux to gas production, oxidation and transport. Cont. Shelf Res. 18, 1741–1770. doi: 10.1016/S0278-4343(98)00056-9

CrossRef Full Text | Google Scholar

McGinnis, D. F., Greinert, J., Artemov, Y., Beaubien, S. E., and Wüest, A. (2006). Fate of rising methane bubbles in stratified waters: how much methane reaches the atmosphere? J. Geophys. Res. Ocean. 111:C09007. doi: 10.1029/2005JC003183

CrossRef Full Text | Google Scholar

Mende, S. B., Harding, B. J., and Turner, C. (2019). Subauroral green STEVE arcs: evidence for low-energy excitation. Geophys. Res. Lett. 46, 14256–14262. doi: 10.1029/2019GL086145

CrossRef Full Text | Google Scholar

Mogollón, J. M., Dale, A. W., L’Heureux, I., and Regnier, P. (2011). Impact of seasonal temperature and pressure changes on methane gas production, dissolution, and transport in unfractured sediments. J. Geophys. Res. Biogeosci. 116:03031. doi: 10.1029/2010JG001592

CrossRef Full Text | Google Scholar

Niemelä, P., Tolvanen, H., Rönkä, M., Kellomäki, S., Krug, J., Schurgers, G., et al. (2015). “Environmental Impacts—Coastal Ecosystems, Birds and Forests,” in Second Assessment of Climate Change for the Baltic Sea Basin. Regional Climate Studies, ed. The BACC II Author Team (Cham: Springer), doi: 10.1007/978-3-319-16006-1_16

CrossRef Full Text | Google Scholar

Nightingale, P. D., Liss, P. S., and Schlosser, P. (2000a). Measurements of air-sea gas transfer during an open ocean algal bloom. Geophys. Res. Lett. 27, 2117–2120. doi: 10.1029/2000GL011541

CrossRef Full Text | Google Scholar

Nightingale, P. D., Malin, G., Law, C. S., Watson, A. J., Liss, P. S., Liddicoat, M. I., et al. (2000b). In situ evaluation of air-sea gas exchange parameterizations using novel conservative and volatile tracers. Glob. Biogeochem. Cycles 14, 373–387. doi: 10.1029/1999GB900091

CrossRef Full Text | Google Scholar

Nisbet, E., and Weiss, R. (2010). Top-down versus bottom-up. Science 328, 1241–1243. doi: 10.1126/science.1189936

PubMed Abstract | CrossRef Full Text | Google Scholar

Nisbet, E. G., Manning, M. R., Dlugokencky, E. J., Fisher, R. E., Lowry, D., Michel, S. E., et al. (2019). Very strong atmospheric methane growth in the 4 years 2014–2017: implications for the Paris agreement. Glob. Biogeochem. Cycles 33, 318–342. doi: 10.1029/2018GB006009

CrossRef Full Text | Google Scholar

Rosentreter, J. A., Borges, A. V., Deemer, B. R., Holgerson, M. A., Liu, S., Song, C., et al. (2021). Half of global methane emissions come from highly variable aquatic ecosystem sources. Nat. Geosci. 14, 225–230. doi: 10.1038/s41561-021-00715-2

CrossRef Full Text | Google Scholar

Rosentreter, J. A., Maher, D. T., Erler, D. V., Murray, R. H., and Eyre, B. D. (2018). METHANE Emissions Partially Offset “Blue Carbon” Burial in Mangroves. Available online at: http://advances.sciencemag.org/ (accessed June 2, 2021)

Google Scholar

Rosentreter, J. A., Maher, D. T., Ho, D. T., Call, M., Barr, J. G., and Eyre, B. D. (2017). Spatial and temporal variability of CO2 and CH4 gas transfer velocities and quantification of the CH4 microbubble flux in mangrove dominated estuaries. Limnol. Oceanogr. 62, 561–578. doi: 10.1002/lno.10444

CrossRef Full Text | Google Scholar

Saunois, M., Jackson, R. B., Bousquet, P., Poulter, B., and Canadell, J. G. (2016). The growing role of methane in anthropogenic climate change. Environ. Res. Lett. 11:120207. doi: 10.1088/1748-9326/11/12/120207

CrossRef Full Text | Google Scholar

Sawilowsky, S. S. (2009). New effect size rules of thumb. J. Mod. Appl. Stat. Methods 8, 597–599. doi: 10.22237/jmasm/1257035100

CrossRef Full Text | Google Scholar

Schilder, J., Bastviken, D., van Hardenbroek, M., and Heiri, O. (2016). Spatiotemporal patterns in methane flux and gas transfer velocity at low wind speeds: implications for upscaling studies on small lakes. J. Geophys. Res. Biogeosci. 121, 1456–1467. doi: 10.1002/2016JG003346

CrossRef Full Text | Google Scholar

Seitzinger, S., Harrison, J. A., Böhlke, J. K., Bouwman, A. F., Lowrance, R., Peterson, B., et al. (2006). Denitrification across landscapes and waterscapes: a synthesis. Ecol. Appl. 16, 2064–2090. doi: 10.1890/1051-0761(2006)016[2064:dalawa]2.0.co;2

CrossRef Full Text | Google Scholar

SMHI (2010). Tides. Available online at: https://www.smhi.se/en/theme/tides-1.11272 (accessed July 11, 2021)

Google Scholar

Smith, S. V., and Hollibaugh, J. T. (1993). Coastal metabolism and the oceanic organic carbon balance. Rev. Geophys. 31, 75–89. doi: 10.1029/92RG02584

CrossRef Full Text | Google Scholar

Torres-Pulliza, D., Dornelas, M. A., Pizarro, O., Bewley, M., Blowes, S. A., Boutros, N., et al. (2020). A geometric basis for surface habitat complexity and biodiversity. Nat. Ecol. Evol. 4, 1495–1501. doi: 10.1038/s41559-020-1281-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Van der Nat, F. J., and Middelburg, J. J. (2000). Methane emission from tidal freshwater marshes. Biogeochemistry 49, 103–121. doi: 10.1023/A:1006333225100

CrossRef Full Text | Google Scholar

Van Der Nat, F. J. W. A., and Middelburg, J. J. (1998). Seasonal variation in methane oxidation by the rhizosphere of Phragmites australis and Scirpus lacustris. Aquat. Bot. 61, 95–110. doi: 10.1016/S0304-3770(98)00072-2

CrossRef Full Text | Google Scholar

Walter, K. M., Zimov, S. A., Chanton, J. P., Verbyla, D., and Chapin, F. S. (2006). Methane bubbling from Siberian thaw lakes as a positive feedback to climate warming. Nature 443, 71–75. doi: 10.1038/nature05040

PubMed Abstract | CrossRef Full Text | Google Scholar

Wanninkhof, R. (1992). Relationship between wind speed and gas exchange over the ocean. J. Geophys. Res. 97, 7373–7382. doi: 10.1029/92JC00188

CrossRef Full Text | Google Scholar

Wanninkhof, R. (2014). Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 12, 351–362. doi: 10.4319/lom.2014.12.351

CrossRef Full Text | Google Scholar

Wanninkhof, R., Asher, W. E., Ho, D. T., Sweeney, C., and McGillis, W. R. (2009). Advances in quantifying air-sea gas exchange and environmental forcing. Ann. Rev. Mar. Sci. 1, 213–244. doi: 10.1146/annurev.marine.010908.163742

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, T., Wiseman, N. A., and Kock, A. (2019). Global ocean methane emissions dominated by shallow coastal waters. Nat. Commun. 10:4584. doi: 10.1038/s41467-019-12541-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Wever, T. F., Lühder, R., Voß, H., and Knispel, U. (2006). Potential environmental control of free shallow gas in the seafloor of Eckernförde Bay, Germany. Mar. Geol. 225, 1–4. doi: 10.1016/j.margeo.2005.08.005

CrossRef Full Text | Google Scholar

Wilks, D. S. (2011). Cluster analysis. Int. Geophys. 100, 603–616. doi: 10.1016/B978-0-12-385022-5.00015-4

CrossRef Full Text | Google Scholar