- Application Laboratory (APL), Research Institute for Value-Added-Information Generation (VAiG), Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Yokohama, Japan
Extreme sea level rise seriously impacts habitation and is indicative of changes in primary production in the North Pacific. Because of its rising trend associated with global warming, skillful seasonal-to-interannual predictions have become increasingly valuable to guide the introduction of suitable adaptation measures that help us reduce the risks of socioeconomic losses. Here, we have used a dynamical coupled ocean–atmosphere model called “SINTEX-F” to revisit the potential predictability of sea level anomalies at a lead of up to about 2 years. Skillful prediction is found mainly in the tropical Pacific as shown in previous work. Here, we found a new skillful prediction region in the North Pacific (30°–40°N, 180°–150°W) at about 2 years’ lead time. We also analyzed the co-variability among ensemble members and found the long-lasting ENSO/ENSO-Modoki in the tropical Pacific seems to contribute to the predictability source. The result may be useful to develop systematic and synergistic attempts to predict marine ecosystem responses to regional and global climate variations.
Introduction
The North Pacific marine ecosystems are primary sources of ecosystem services (e.g., fishing, shipping, and recreation) for its surrounding countries including Canada, U.S., China, Russia, Korea, and Japan. Coastlines of the North Pacific are seriously damaged by extreme sea level rise (Nicholls et al., 2007). In particular, the coastal zones are immediately affected by submergence and increased flooding of coastal land, as well as saltwater intrusion of surface waters (Nicholls and Cazenave, 2010).
In addition to the rising sea level trend associated with the global warming, extreme sea level events occur in association with natural climate variability such as the Pacific Decadal Oscillation (PDO), the Interdecadal Pacific Oscillation (IPO), the North Pacific Gyre Oscillation (NPGO), and the El Niño-Southern Oscillation (ENSO) in the North Pacific (Mantua et al., 1997; Zhang et al., 1997; McGowan et al., 1998; Lombard et al., 2005; Di Lorenzo et al., 2008; Hamlington et al., 2019; Han et al., 2019). To address relatively short-term risks, stakeholders desire a forecast of monthly/seasonal rising or falling sea levels caused by those climate variabilities. Hinkel et al. (2019) analyzed user needs for sea level rise information, and how they are able to be met given the state-of-the-art of sea level forecast science. Jacox et al. (2020) reviewed statistical and dynamical marine ecosystem forecasting methods and highlighted examples of their application along U.S. coastlines for seasonal-to-interannual prediction. Payne et al. (2017) also reviewed the state of the art marine ecological forecasts and suggested forecasts ranging from seasonal to decadal time scales are now a reality. Tommasi et al. (2017a) evaluated the multi-annual SST predictions over Large Marine Ecosystems (LMEs), a coastal scale relevant to managed fisheries stocks. Tommasi et al. (2017b) also highlighted advances in seasonal to decadal prediction of managing living marine resources in a dynamic environment. Those previous studies provide information relevant for supporting coastal adaptation decision making.
Although skillful predictions of SST have already proven useful for a number of marine resource applications (e.g., Hobday et al., 2014; Stock et al., 2015), further studies about sea level anomaly are necessary. Rebert et al. (1985) showed that the oceanic Kelvin and Rossby waves have a direct relation between thermocline depth and sea level, while they have only an indirect relation to SST. These ocean dynamics are responsible for the relatively high skill of sea level prediction relative to SST prediction (Miles et al., 2014). Zainuddin et al. (2017) found that SST was an important variable for detecting hotspots of skipjack tuna distribution, as they are sensitive to the changes in temperature. Sea level anomaly is related to the changes in the depth of the thermocline and mesoscale variability. They combined these variables to improve detection of potential pelagic hotspots for skipjack tuna.
To expand prediction of large-scale sea level anomalies into coastal areas and to further the understanding of its potential predictability, it is necessary to evaluate the lead-time and locations in which a dynamical, physics-based prediction system performs well. It might allow coastal communities to better adapt for the impacts of severe flooding and erosion driven by high sea levels.
Although decadal climate variation is more predictable than previously thought, it is still challenging (Meehl et al., 2014; Smith et al., 2019). Here, our focus is on seasonal-to-interannual prediction. Generally speaking, the most important potential source of seasonal-to-interannual predictability is often from ENSO events, which develop via air-sea coupled feedback. Therefore, application of an ocean-atmosphere coupled general circulation model (GCM) is naturally a proven approach to overcome shortcomings of stand-alone atmospheric/oceanic models. Miles et al. (2014) initially attempted to apply a coupled GCM to predict seasonal sea level anomalies, and assessed the skill globally for up to 7 months in advance. McIntosh et al. (2015) showed the prediction skill by dynamical GCMs is better relative to statistical approaches for coastal sea level. Polkova et al. (2015) used the decadal prediction system and found predictability in the subtropics. Roberts et al. (2016) assessed the predictability of large-scale dynamic sea level anomalies up to 15 months using a climate model and found that prediction of seasonal-to-interannual sea level variability in the extratropics will be governed by the predictability of surface wind stress and modes of atmospheric variability.
This study is a follow-up study of those pioneering studies. Here, we have revisited the predictability of sea level up to about 2 years in advance by analyzing results of a coupled ocean–atmosphere general circulation model “SINTEX-F.” Such a long lead time retrospective forecast is beyond most current operational capabilities, and hence a skill assessment of the model results is conducted here as a first attempt. We believe that the obtained result is useful to attempt systematic and synergistic prediction of marine ecosystem responses to regional and global climate variations.
Materials and Methods
Dynamical Prediction System
The Scale Interaction Experiment-Frontier ver. 1 (SINTEX-F1) prediction system was used here, which is based on a fully coupled global ocean–atmosphere circulation model (CGCM) developed under the EU-Japan collaborative framework (Luo et al., 2003; Luo et al., 2005; Masson et al., 2005). The atmospheric component has a horizontal resolution of 1.125° (T106) with 19 vertical levels. The oceanic component has a horizontal resolution of about 2° × 2° but with meridional refinement to 0.58° in the tropics. It has 31 vertical levels from the surface to the bottom with a relatively finer resolution of 10 m from the sea surface to 110 m depth. This system adopts a relatively simple initialization scheme based only on the nudging of observed SST. In consideration of uncertainties of both initial conditions and model physics, it has nine ensemble members. More details about the prediction system are available in Luo et al. (2005). This system has demonstrated high performance for prediction of ENSO (Jin et al., 2008). In particular, Luo et al. (2008) showed that several ENSO events can be predicted at lead times of up to 2 years by this system, which can be a strong advantage in this study. The quasi real-time predictions are updated every month and made publicly available from 2005 (see http://www.jamstec.go.jp/aplinfo/sintexf/e/seasonal/outlook.html).
We have analyzed the reforecasting experiments for the 1993–2018 period issued on the first day of March, June, September, and December with about 2-year lead time. The prediction anomalies were determined by removing the model mean climatology at each lead-time over the same period. To evaluate the prediction results, we have used the multi-mission altimeter satellite gridded sea surface heights (SEALEVEL_GLO_PHY_L4_REP_ OBSERVATIONS_008_047; available from http://marine.copernicus.eu/services-portfolio/access-to-products/?option=com_csw&view=details&product_id=SEALEVEL_GLO_PHY_L4_REP_OBSERVATIONS_008_047) for sea level, the NOAA OISSTv2 (Reynolds et al., 2002) for SST, and the NCEP/NCAR reanalysis data (Kalnay et al., 1996) for atmospheric variables anomalies. The monthly climatologies of these datasets are also calculated by averaging monthly data over the same period, and then anomalies are derived through deviations from those mean climatologies. All anomalies are linearly detrended, which can prevent long time scale changes from artificially increasing correlation analysis.
Results
Skill Assessment up to 2-Year Lead
The correlation coefficient (Pearson’s “r”) between two time series of observed and predicted anomalies for each grid points is used as a deterministic prediction skill score of the phase variation. The persistence method is the simplest way of producing a forecast; it assumes that the conditions will not change. The persistence method works well when anomalies vary very slowly. Therefore, the correlation of the persistence is generally used to assess the advantage of prediction models. Skillful prediction of sea level is found mainly in the tropical Pacific (Figure 1). It drops outside of the oceanic Kelvin, Rossby, and coastally trapped waveguides in the tropical Pacific region. The correlation often exceeds the skill of persistence and 0.6 in many regions within 20° of the equator at the first season (0–2 months lead). The correlation decreases at longer lead times but generally remaining above 0.5 in the waveguides up to 11 months lead times. The advantage of the SINTEX-F prediction relative to the persistence increases at longer lead times. This suggests that the skill is mainly derived from the ability to predict ENSO accurately as expected from the previous works (Miles et al., 2014). It is also found skillful prediction regions off the west coast of Australia and California, which may be related to the successful predictions of the Ningaloo Niño/Niña (Doi et al., 2013, 2015a) and the California Niño/Niña (Doi et al., 2015b); some of those events are strongly linked with coastally trapped ocean waves forced by ENSO events.
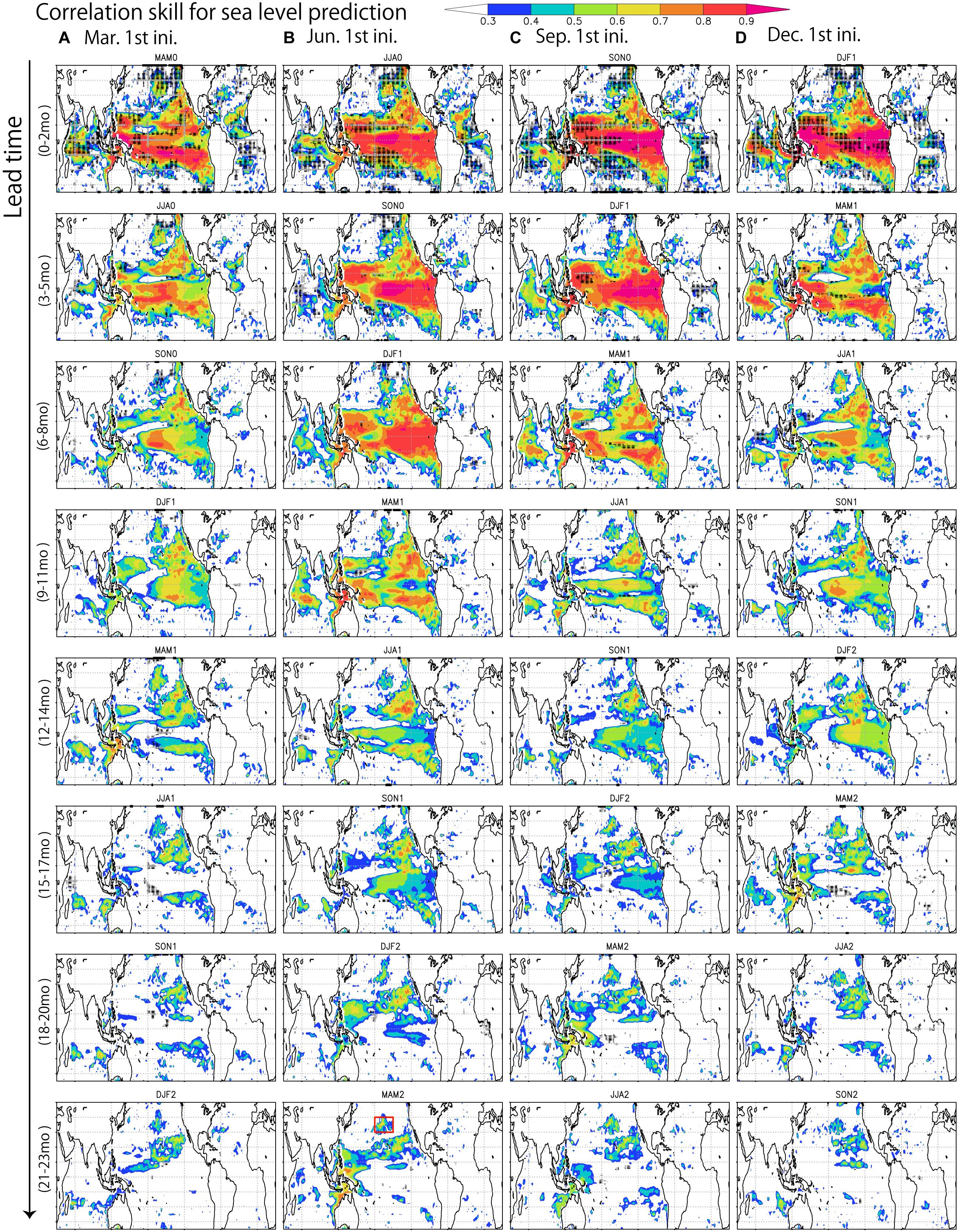
Figure 1. (A) The correlation coefficient for seasonal-to-interannual prediction for sea level anomalies (ensemble mean) from the 0–2 months lead average up to the 21–23 months lead average issued on March 1, 1993–2018. Black dots indicate regions where the correlation is below the persistence (lag autocorrelation of observation). Considering that the degree of freedom based on the sample size, the correlation beyond 0.3 is statistically significant at a 90% level. So, the correlation greater than 0.3 is masked out. (B–D) Same as (A), but for the prediction issued on June 1, September 1, and December 1. The target area in the North Pacific (30°–40°N, 180°–150°W) is shown by a red box in MAM2 prediction issued on June 1.
We can also find the seasonal dependence of the correlation, likely because of the so-called spring predictability barrier in forecasting the development of ENSO (e.g., Latif et al., 1998). Prediction of sea level anomalies in the 3–5 months lead average issued on March 1 shows low correlation in many regions relative to that issued on other seasons. Also, we see a quick decrease in the correlation from prediction of the December-January-February (DJF) average into that of the March-April-May (MAM) average.
At the extratropical latitudes in 20°–30°N, the skill still remains in some regions in the North Pacific up to about 2-year lead. This is likely due to the slowly propagating Rossby wave features and some stationary anomalies. In the extratropics of the North Pacific, which is often defined the latitude bands of 30°–60°N, interestingly, we found the predictability of a region in the North Pacific (30°–40°N, 180°–150°W) to be skillful up to 2 years ahead. This is not yet discussed by the previous work. Figure 2 shows its time series for the MAM seasonal average. The time series at first glance shows the presence of a decadal variability. The correlation of the 2-year lead prediction is 0.67 for 26 samples (1993–2018 years). After removing the 5-years running mean, it is 0.65 for 22 samples (1995–2016 years). The spread of the ensemble of prediction provides information about the uncertainty inherent. The large uncertainty suggests low potential predictability of sea level anomalies here. Interestingly, however, the sea level anomaly in 2000 exhibits relatively high predictability. We will discuss the details later.
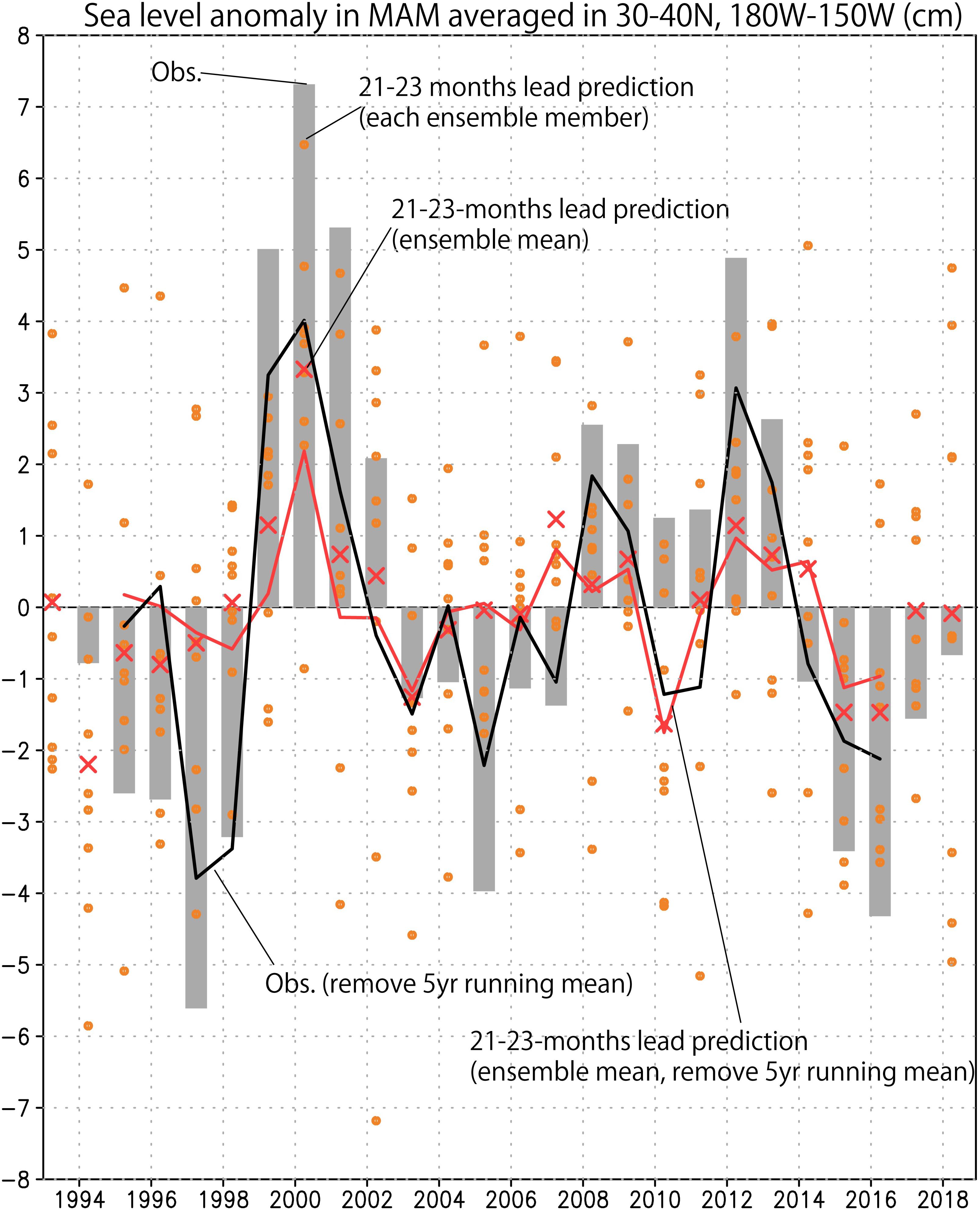
Figure 2. Time series of sea level anomaly averaged over 30°–40°N, 180°–150°W during March-April-May (cm). Gray column: observation, Red cross: ensemble mean prediction issued on June 1, 2-year before (21–23 months lead average), orange dot: each ensemble member prediction, black line: observation after removing 5-years running mean, red line: ensemble mean prediction after removing 5-years running mean.
How about the other oceans? We can find some skillful prediction regions in the southern Indian Ocean beyond 1-year lead (Figure 1). This may be related to the successful prediction of the Subtropical Indian Ocean Dipole (Beherea and Yamagata, 2001; Yuan et al., 2014). In the Atlantic, prediction beyond 1-year lead is relatively challenging. For example, the pattern associated with the North Atlantic Oscillation, which is the dominant climate mode in the Atlantic Ocean, is not represented well by the model. We need further analysis to understand similarities and differences among the ocean basins.
Inter-Ensemble Members Relationship
Why is the skillful prediction found about 2-year lead in a region in the North Pacific (30°–40°N, 180°–150°W)? Investigating co-variability of inter-member anomalies (defined as deviations from the ensemble mean) may provide useful insights into possible precursors and teleconnection patterns related to a climate event considering the intrinsic variability (Ma et al., 2017; Ogata et al., 2019; Doi et al., 2020a,b). Figure 3A shows the correlation coefficients among the inter-ensemble members of the reforecast for the March–May average of 1995–2016 (198 sample: 9 members times 22 years after removing 5-years running mean) at 2-year lead. In this analysis, the conventional time dimension could be enlarged by the ensemble dimension. The co-variability between the sea level anomaly in that region and the tropical Pacific condition shows a pattern resembling a mixture of the Modoki-type and the canonical-type of ENSO (Ashok et al., 2007; Karnauskas, 2013). Also, a similar co-variability is seen between the sea level and local wind-induced Ekman downwelling in that region (Figure 3B). Since the similar features are able to be captured by liner regression analysis to ENSO (Vimont, 2005; Zhang and Church, 2012; Han et al., 2019), the successful prediction of ENSO and/or ENSO-Modoki in the tropical Pacific may be related to the success in predicting sea level anomaly in that region at about 2-year lead. Note that a corresponding co-variability with the surface heat flux was not found in that region (Figure 3C). This may suggest that the dynamic process is more important in that region than the thermodynamic process.
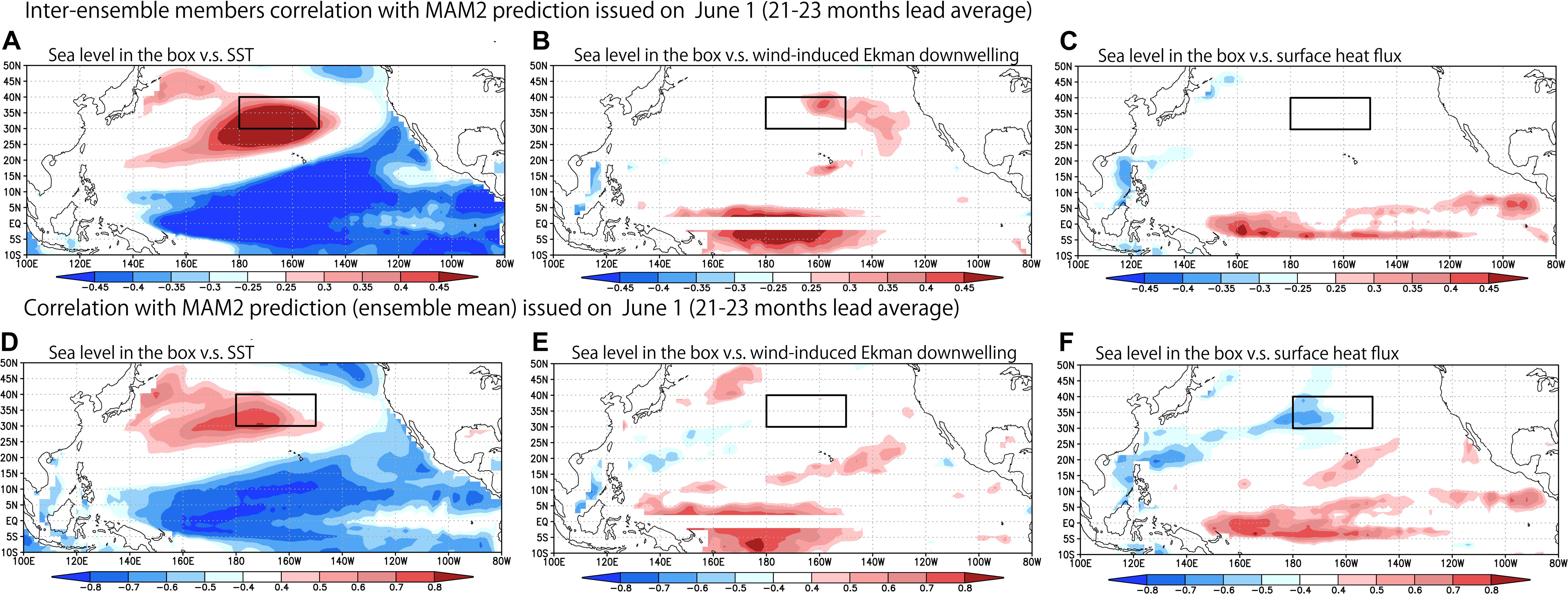
Figure 3. (A) Inter-ensemble member correlation between sea level anomaly averaged in 30°–40°N, 180°–150°W (shown by a box) and a horizontal distribution of SST anomaly in a nine-member ensemble reforecast for the 21–23 months lead average issued on June 1. (B) Same as (A), but for regional wind-induced Ekman downwelling. (C) Same as (A), but for surface heat flux. (D–F) Same as (A–C), but for correlation using the ensemble mean prediction. The color scale is different from that in (A–C) because the sample size is different (198 and 22). Considering the degree of freedom based on the sample size, the correlation below 0.25 (0.40) is masked out in the upper (lower) panel.
We see a similar relation with SST anomalies when an ensemble mean of the prediction was considered (Figure 3D), which shows the horizontal map of the correlation coefficients between the ensemble mean of the sea level anomalies averaged in the box and the ensemble mean of the SST fields (22 sample: 22 years of the reforecast). However, the correlation with local wind-induced Ekman downwelling does not show a clear relation (Figure 3E). Since the signal-to-noise ratio is relatively low in the mid-latitude atmosphere (Scaife and Smith, 2018), the sample size of 22 may not be enough to capture the signal reasonably in the ensemble mean.
Case Study for the 2000 Event
The successful prediction of the high sea level in 2000 (Figure 2) demonstrates the model’s high skill to predict such events. As in the observations, the sea level anomaly developed from boreal summer of 1998 and reached about 7 cm during March–May 2000. The prediction issued on June 1, 1998, captured the subsequent development in the tropical Pacific and the target region (30°–40°N, 180°W–150°W), albeit a bit weaker than in observations (Figures 4A,B). This is supported by the pattern correlations shown in the upper right corner of each panel of Figure 4B, which are calculated after interpolating the horizontal distributions of the observational data to those of the prediction output. At 3–5 months lead, the pattern correlation for the sea level prediction is 0.70. At this time, a La Niña Modoki was observed (Figures 4C,D) in the tropical Pacific. Then, the pattern correlation reduced at longer lead time, however it is still 0.47 at 21–23 months lead time. Local processes seem to contribute to the variability in 30°–40°N, 180°–150°W relative to remote processes such as a propagation of Rossby waves. Dynamic process associated with the local wind-driven Ekman downwelling may be responsible for that (Figures 5A,C), while the heat flux anomaly acted as the damping of the anomaly in the reanalysis (Figure 5B) and showed very weak values in the model (Figure 5D). Those features are consistent with the results shown by the previous subsection. We note that the signal in the Kuroshio Extension region was not represented well in this prediction system. Nonaka et al. (2016) revealed that stochastic variability in that region limits deterministic potential predictability of its interannual variability through three-member ensemble simulations with an eddy-resolving ocean model. Even if the spatial resolution of the SINTEX-F is enhanced, it might be intrinsically difficult to improve the prediction skill in that region.
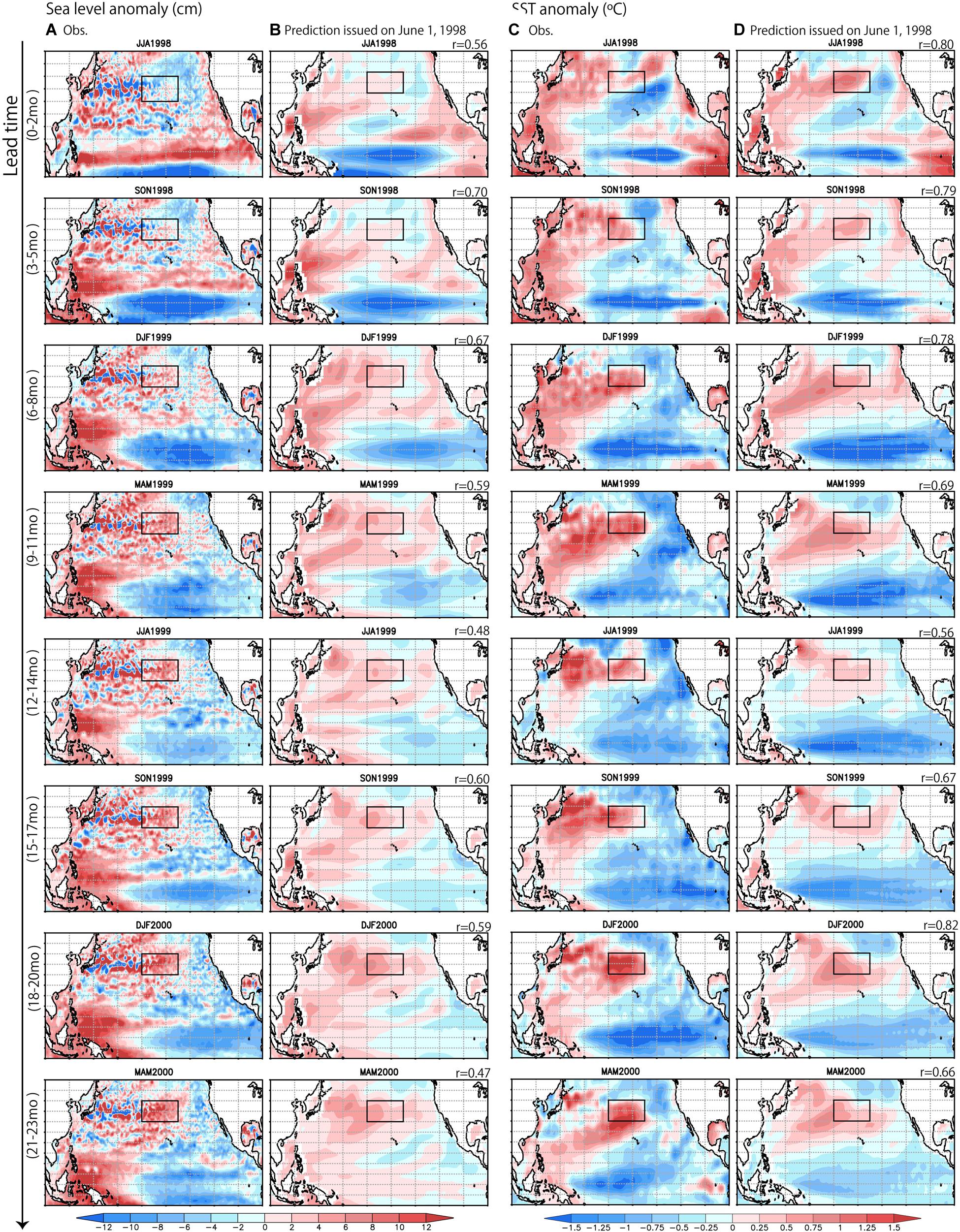
Figure 4. (A) Three-month averaged variations of sea level anomaly (cm) from June–August 1998 (upper) through March–May 2000 (bottom). The box shows the study region of 30°–40°N, 180°–150°W based on observation. (B) Same as (A), but for prediction issued on June 1, 1998 (ensemble mean). Pattern correlation is shown in the upper right corner. (C,D) Same as (A,B), but for SST (°C).
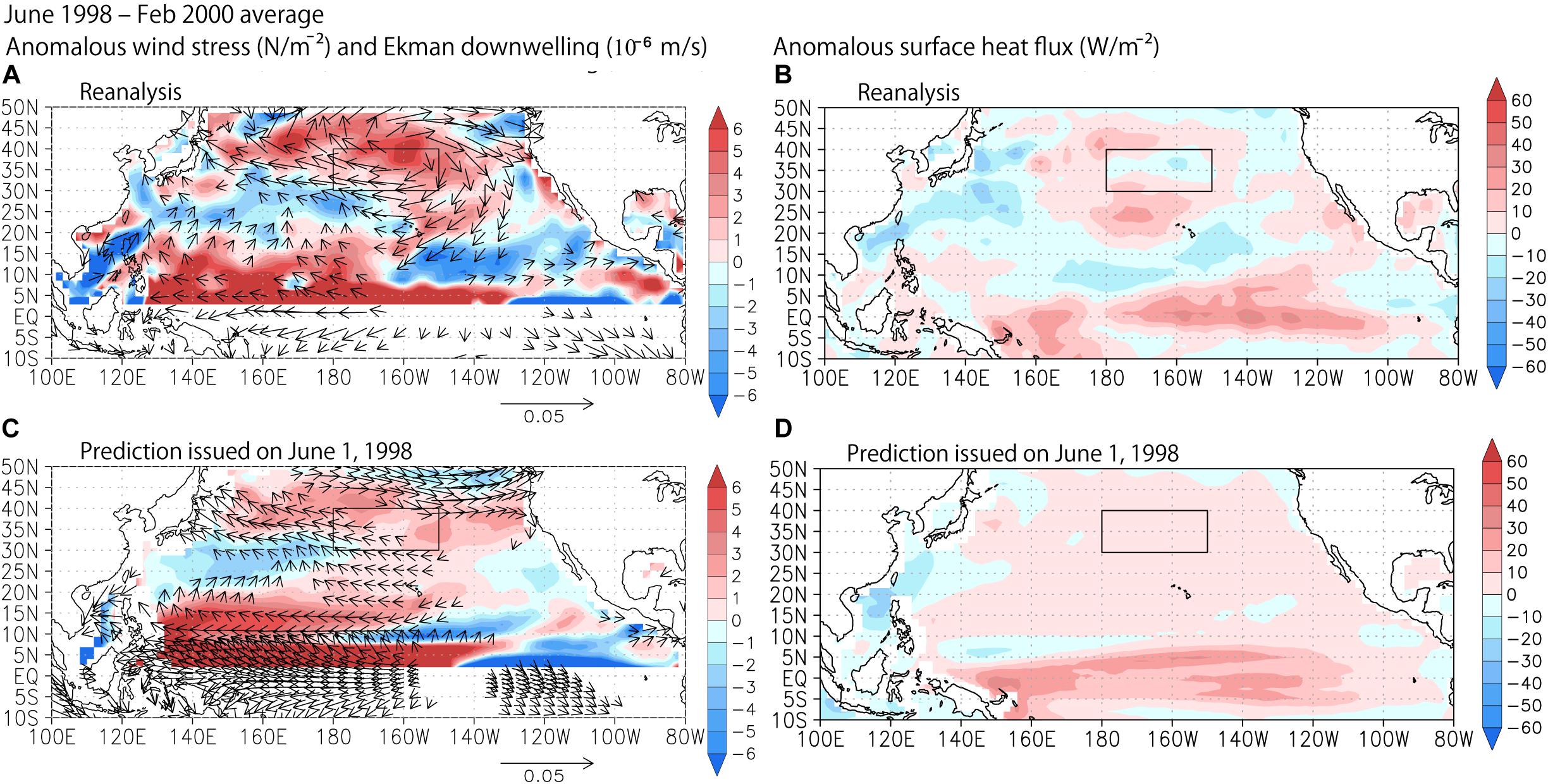
Figure 5. (A) Anomalous surface wind stress (vector: N m–2) and its induced-Ekman vertical velocity (shaded: 10–6 m s–1) averaged in June 1998–February 2000 based on the reanalysis data. Positive values show downwelling. The rectangle box demarcates the region of 30°–40°N, 180°–150°W. (B) Same as (A), but for surface heat flux (W m–2). Positive values show that it warms ocean. (C,D) Same as (A,B), but for prediction issued on June 1, 1998 (ensemble mean).
Discussion
Sea level anomalies in the region of (30°–40°N, 180°–150°W) may be related to the PDO. The PDO is now interpreted as an empirical mode, which includes teleconnection from ENSO and stochastic atmospheric/oceanic fluctuations (Schneider and Cornuelle, 2005; Newman et al., 2016). Decadal or longer timescale signals appear also to be important for the 2000 event. About 50% of the sea level anomaly averaged over 30°–40°N, 180°–150°W during March-April-May 2000 is due to the decadal signal in the prediction (Figure 2). Actually, 2000 is an extreme year for decadal variations in the IPO index and also basin-wide sea level in the Pacific (see Figure 3 in Lyu et al., 2017), which is closely related to the ENSO-like low-frequency variability. Although low-frequency sea level variations with periods longer than interannual time scales are interesting, it might be difficult to clearly separate the interannual variations from the decadal and longer timescale variations mainly due to limitation of the sample size and the lead time of the reforecast experiments. Although the focus of this study is on seasonal-to-interannual scale prediction, in the future, we may need to develop skillful seamless prediction abilities from seasonal-to-decadal (S2D) timescale.
Tropical and North Pacific processes are interlinked, which means that the North Pacific processes might also contribute to ENSO predictability (e.g., Ogata et al., 2019). The build-up of subsurface ocean heat content in the tropical western Pacific as well as the northeastern subtropical Pacific is identified as ENSO precursors (Capotondi et al., 2015; Yu and Paek, 2015). Chikamoto et al. (2015) also showed that the low-frequency trans-basin tropical climate variations between the Pacific and the other two adjacent ocean basins can be predicted up to 3 years ahead. Further studies are necessary to estimate the role of the inter-basin coupling on multi-year predictability of the tropical and North Pacific using partial assimilation reforecast experiments.
Since our results are based on a single-model system, we need to check them by a multi-model ensemble system (e.g., Kirtman et al., 2014; Tompkins et al., 2017; Widlansky et al., 2017).
A noble path to systematic and synergistic prediction of marine ecosystem variations may be to develop an earth system model, to incorporate biogeochemical processes into a climate model to represent the interacting physical, chemical, and biological processes. It can provide outlooks for marine-resource–relevant changes beyond physical variables. Along this line, Park et al. (2019) showed that an earth system model can skillfully predict seasonal to multiannual chlorophyll fluctuations in many regions.
Although predictability of open-ocean anomalies was the focus in this study, its connection to coastal sea level is also important. However, it is still challenging to resolve the complicated topography near the coastal regions for the resolution used in current climate models. Therefore, downscaling techniques are helpful to capture the open-ocean and coastal region connections (e.g., Jacox et al., 2020) in a manner similar to successful examples for atmospheric downscaling (e.g., Ratnam et al., 2016, 2017).
Enhancement of the relatively coarse ocean model grid will help to resolve more accurately some islands and narrow upwelling regions. Higher resolution in the atmospheric model may also help to improve winds that are an important component of the ENSO teleconnection. In addition, the accuracy should be improved by better initial conditions by explicit use of altimeter data and in situ subsurface ocean temperature and salinity observation from the expendable bathythermographs (XBTs), mooring buoys, sea stations, Argo floats, etc. Increasing the ensemble size may be beneficial for improving prediction of the extratropics, where the signal-to-noise ratio is relatively low. Actually, we have been developing the new version of the SINTEX-F prediction system called as SINTEX-F2 based on a high-resolution model by updating the initialization scheme and increasing the ensemble size (Doi et al., 2016, 2017, 2019, 2020a; Morioka et al., 2019). However, because the computational cost is expensive, the SINTEX-F2 mainly targets for prediction up to 11-month lead time at this stage. We are now extending the lead time up to 23 months because its benefit was shown in this paper.
Conclusion
We assessed the prediction skill of sea level anomaly up to 23 months in advance by the SINTEX-F system and found a skillful prediction region in the North Pacific (30–40 N, 180–150 W) at about 2-year lead. The successful prediction of the long-lasting ENSO/ENSO-Modoki in the tropical Pacific seems to contribute to that sea level predictability. The result may be useful to attempt systematic and synergistic prediction of marine ecosystem responses to regional and global climate variations.
Data Availability Statement
The datasets generated for this study can be found in the online repositories. The names of the repository/repositories and accession number(s) can be found below: https://fbox.jamstec.go.jp/public/3vnQgARS2EDAjpEBzL10R3qP8jcy2W-xWLfXy5mE7u8Z/m/3x5AD2lA.
Author Contributions
TD performed the seasonal prediction experiments, and analyzed the observation data and model prediction outputs. All authors contributed to designing the research, interpreting results, and writing the manuscript.
Funding
This research was supported by the JSPS KAKENHI Grant 20K04074.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The SINTEX-F seasonal climate prediction system was run by the Earth Simulator at JAMSTEC (see http://www.jamstec.go.jp/es/en/index.html, for the system overview). We are grateful to Wataru Sasaki, Jing-Jia Luo, Sebastian Masson, Antonio Navarra, and Toshio Yamagata and our European colleagues of INGV/CMCC, L’OCEAN, and MPI for their valuable contributions in developing the prototypes of the systems. We would also like to thank Shoshiro Minobe for his helpful comments and suggestions. The GrADS software was used to create the figures and maps.
References
Ashok, K., Behera, S. K., Rao, S. A., Weng, H., and Yamagata, T. (2007). El Niño Modoki and its possible teleconnection. J. Geophys. Res. Ocean. 112, 1–27. doi: 10.1029/2006JC003798
Beherea, S. K., and Yamagata, T. (2001). Subtropical SST dipole events in the southern Indian ocean. Geophys. Res. Lett. 28, 327–330. doi: 10.1029/2000GL011451
Capotondi, A., Wittenberg, A. T., Newman, M., Di Lorenzo, E., Yu, J. Y., Braconnot, P., et al. (2015). Understanding ENSO diversity. Bull. Am. Meteorol. Soc. 96, 921–938. doi: 10.1175/BAMS-D-13-00117.1
Chikamoto, Y., Timmermann, A., Luo, J.-J., Mochizuki, T., Kimoto, M., Watanabe, M., et al. (2015). Skilful multi-year predictions of tropical trans-basin climate variability. Nat. Commun. 6:6869. doi: 10.1038/ncomms7869
Di Lorenzo, E., Schneider, N., Cobb, K. M., Franks, P. J. S., Chhak, K., Miller, A. J., et al. (2008). North Pacific Gyre Oscillation links ocean climate and ecosystem change. Geophys. Res. Lett. 35, 2–7. doi: 10.1029/2007GL032838
Doi, T., Behera, S. K., and Yamagata, T. (2013). Predictability of the Ningaloo Niño/Niña. Sci. Rep. 3:2892. doi: 10.1038/srep02892
Doi, T., Behera, S. K., and Yamagata, T. (2015a). An interdecadal regime shift in rainfall predictability related to the Ningaloo Niño in the late 1990s. J. Geophys. Res. Ocean. 120, 1388–1396. doi: 10.1002/2014JC010562
Doi, T., Yuan, C., Behera, S. K., and Yamagata, T. (2015b). Predictability of the California Niño/Niña. J. Clim. 28, 7237–7249. doi: 10.1175/JCLI-D-15-0112.1
Doi, T., Behera, S. K., and Yamagata, T. (2016). Improved seasonal prediction using the SINTEX-F2 coupled model. J. Adv. Model. Earth Syst. 8, 1847–1867. doi: 10.1002/2016MS000744
Doi, T., Behera, S. K., and Yamagata, T. (2019). Merits of a 108-member ensemble system in ENSO and IOD predictions. J. Clim. 32, 957–972. doi: 10.1175/jcli-d-18-0193.1
Doi, T., Behera, S. K., and Yamagata, T. (2020a). Predictability of the super IOD event in 2019 and its link with El Niño Modoki. Geophys. Res. Lett. 47:e2019GL086713. doi: 10.1029/2019gl086713
Doi, T., Behera, S. K., and Yamagata, T. (2020b). Wintertime impacts of the 2019 super IOD on East Asia. Geophys. Res. Lett. 47:e2020GL089456. doi: 10.1029/2020GL089456
Doi, T., Storto, A., Behera, S. K., Navarra, A., and Yamagata, T. (2017). Improved prediction of the Indian Ocean Dipole Mode by use of subsurface ocean observations. J. Clim. 30, 7953–7970. doi: 10.1175/JCLI-D-16-0915.1
Hamlington, B. D., Cheon, S. H., Piecuch, C. G., Karnauskas, K. B., Thompson, P. R., Kim, K. Y., et al. (2019). The dominant global modes of recent internal sea level variability. J. Geophys. Res. Ocean. 124, 2750–2768. doi: 10.1029/2018JC014635
Han, W., Stammer, D., Thompson, P., Ezer, T., Palanisamy, H., Zhang, X., et al. (2019). Impacts of basin-scale climate modes on coastal sea level: a review. Surv. Geophys. 40, 1493–1541. doi: 10.1007/s10712-019-09562-9568
Hinkel, J., Church, J. A., Gregory, J. M., Lambert, E., Le Cozannet, G., Lowe, J., et al. (2019). Meeting user needs for sea level rise information: a decision analysis perspective. Earth’s Futur. 7, 320–337. doi: 10.1029/2018EF001071
Hobday, A. J., Maxwell, S. M., Forgie, J., McDonald, J., Darby, M., et al. (2014). Dynamic ocean management: integrating scientific and technological capacity with law, policy and management. Stanford Environ. Law J. 33, 125–165.
Jacox, M. G., Alexander, M. A., Siedlecki, S., Chen, K., Kwon, Y., Brodie, S., et al. (2020). Seasonal-to-interannual prediction of U.S. coastal marine ecosystems: forecast methods, mechanisms of predictability, and priority developments. Prog. Oceanogr. 183:102307. doi: 10.1016/j.pocean.2020.102307
Jin, E. K., Kinter, J. L., Wang, B., Park, C. K., Kang, I. S., Kirtman, B. P., et al. (2008). Current status of ENSO prediction skill in coupled ocean-atmosphere models. Clim. Dyn. 31, 647–664. doi: 10.1007/s00382-008-0397-393
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., et al. (1996). The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 77, 437–471.
Karnauskas, K. B. (2013). Can we distinguish canonical El Niño from Modoki? Geophys. Res. Lett. 40, 5246–5251. doi: 10.1002/grl.51007
Kirtman, B. P., Min, D., Infanti, J. M., Kinter, J. L., Paolino, D. A., Zhang, Q., et al. (2014). The North American multimodel ensemble: phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull. Am. Meteorol. Soc. 95, 585–601. doi: 10.1175/BAMS-D-12-00050.1
Latif, M., Anderson, D., Barnett, T., Cane, M., Kleeman, R., Leetmaa, A., et al. (1998). A review of the predictability and prediction of ENSO. J. Geophys. Res. 103, 14375–14393. doi: 10.1029/97JC03413
Lombard, A., Cazenave, A., Le Traon, P. Y., and Ishii, M. (2005). Contribution of thermal expansion to present-day sea-level change revisited. Glob. Planet. Change 47, 1–16. doi: 10.1016/j.gloplacha.2004.11.016
Luo, J. J., Masson, S., Behera, S., Delecluse, P., Gualdi, S., Navarra, A., et al. (2003). South Pacific origin of the decadal ENSO-like variation as simulated by a coupled GCM. Geophys. Res. Lett. 30, 4–7. doi: 10.1029/2003GL018649
Luo, J. J., Masson, S., Behera, S., Shingu, S., and Yamagata, T. (2005). Seasonal climate predictability in a coupled OAGCM using a different approach for ensemble forecasts. J. Clim. 18, 4474–4497. doi: 10.1175/JCLI3526.1
Luo, J. J., Masson, S., Behera, S. K., and Yamagata, T. (2008). Extended ENSO predictions using a fully coupled ocean-atmosphere model. J. Clim. 21, 84–93. doi: 10.1175/2007JCLI1412.1
Lyu, K., Zhang, X., Church, J. A., Hu, J., and Yu, J. Y. (2017). Distinguishing the Quasi-decadal and multidecadal sea level and climate variations in the pacific: implications for the ENSO-like low-frequency variability. J. Clim. 30, 5097–5117. doi: 10.1175/JCLI-D-17-0004.1
Ma, J., Xie, S. P., and Xu, H. (2017). Contributions of the North Pacific meridional mode to ensemble spread of ENSO prediction. J. Clim. 30, 9167–9181. doi: 10.1175/JCLI-D-17-0182.1
Mantua, N. J., Hare, S. R., Zhang, Y., Wallace, J. M., and Francis, R. C. (1997). A pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 78, 1069–1079. doi: 10.1175/1520-0477(1997)078<1069:apicow>2.0.co;2
Masson, S., Luo, J. J., Madec, G., Vialard, J., Durand, F., Gualdi, S., et al. (2005). Impact of barrier layer on winter-spring variability of the southeastern Arabian Sea. Geophys. Res. Lett. 32, 1–4. doi: 10.1029/2004GL021980
McGowan, J. A., Cayan, D. R., and Dorman, L. R. M. (1998). Climate-ocean variability and ecosystem response in the Northeast Pacific. Science 281, 210–217. doi: 10.1126/science.281.5374.210
McIntosh, P. C., Church, J. A., Miles, E. R., Ridgway, K., and Spillman, C. M. (2015). Seasonal coastal sea level prediction using a dynamical model. Geophys. Res. Lett. 42, 6747–6753. doi: 10.1002/2015GL065091
Meehl, G. A., Goddard, L., Boer, G., Burgman, R., Branstator, G., Cassou, C., et al. (2014). Decadal climate prediction an update from the trenches. Bull. Am. Meteorol. Soc. 95, 243–267. doi: 10.1175/BAMS-D-12-00241.1
Miles, E. R., Spillman, C. M., Church, J. A., and McIntosh, P. C. (2014). Seasonal prediction of global sea level anomalies using an ocean–atmosphere dynamical model. Clim. Dyn. 43, 2131–2145. doi: 10.1007/s00382-013-2039-2037
Morioka, Y., Doi, T., Iovino, D., Masina, S., and Behera, S. K. (2019). Role of sea-ice initialization in climate predictability over the Weddell Sea. Sci. Rep. 9, 1–11. doi: 10.1038/s41598-019-39421-w
Newman, M., Alexander, M. A., Ault, T. R., Cobb, K. M., Deser, C., Di Lorenzo, E., et al. (2016). The pacific decadal oscillation, revisited. J. Clim. 29, 4399–4427. doi: 10.1175/JCLI-D-15-0508.1
Nicholls, R. J., and Cazenave, A. (2010). Sea-level rise and its impact on coastal zones. Science 328, 1517–1520. doi: 10.1126/science.1185782
Nicholls, R. J., Wong, P. P., Burkett, V. R., Codignotto, J. O., Hay, J. E., and McLean, R. F. (2007). “Coastal systems and low-lying areas,” in Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, eds M. L. Parry, O. F. Canziani, J. P. Palutikof, P. J. van der Linden, and C. E. Hanson (Cambridge: Cambridge University Press), 315–356.
Nonaka, M., Sasai, Y., Sasaki, H., Taguchi, B., and Nakamura, H. (2016). How potentially predictable are midlatitude ocean currents? Sci. Rep. 6:20153. doi: 10.1038/srep20153
Ogata, T., Doi, T., Morioka, Y., and Behera, S. (2019). Mid-latitude source of the ENSO-spread in SINTEX-F ensemble predictions. Clim. Dyn. 52, 2613–2630. doi: 10.1007/s00382-018-4280-4286
Park, J., Stock, C. A., Dunne, J. P., Yang, X., and Rosati, A. (2019). Seasonal to multiannual marine ecosystem prediction with a global Earth system model. Science 288, 284–288. doi: 10.1126/science.aav6634
Payne, M. R., Hobday, A. J., MacKenzie, B. R., Tommasi, D., Dempsey, D. P., Fässler, S. M. M., et al. (2017). Lessons from the first generation of marine ecological forecast products. Front. Mar. Sci. 4:289. doi: 10.3389/fmars.2017.00289
Polkova, I., Köhl, A., and Stammer, D. (2015). Predictive skill for regional interannual steric sea level and mechanisms for predictability. J. Clim. 28, 7407–7419. doi: 10.1175/JCLI-D-14-00811.1
Ratnam, J. V., Behera, S. K., Doi, T., Ratna, S. B., and Landman, W. A. (2016). Improvements to the WRF seasonal hindcasts over South Africa by bias correcting the driving sintex-F2v CGCM fields. J. Clim. 29, 2815–2829. doi: 10.1175/JCLI-D-15-0435.1
Ratnam, J. V., Doi, T., and Behera, S. K. (2017). Dynamical downscaling of SINTEX-F2v CGCM seasonal retrospective austral summer forecasts over Australia. J. Clim. 30, 3219–3235. doi: 10.1175/JCLI-D-16-0585.1
Rebert, J. P., Donguy, J. R., Eldin, G., and Wyrtki, K. (1985). Relations between sea level, thermocline depth, heat content, and dynamic height in the tropical Pacific Ocean. J. Geophys. Res. 90, 11719–11725. doi: 10.1029/jc090ic06p11719
Reynolds, R. W., Rayner, N. A., Smith, T. M., Stokes, D. C., and Wang, W. (2002). An improved in situ and satellite SST analysis for climate. J. Clim. 15, 1609–1625. doi: 10.1175/1520-0442(2002)015<1609:aiisas>2.0.co;2
Roberts, C. D., Calvert, D., Dunstone, N., Hermanson, L., Palmer, M. D., and Smith, D. (2016). On the drivers and predictability of seasonal-to-interannual variations in regional sea level. J. Clim. 29, 7565–7585. doi: 10.1175/JCLI-D-15-0886.1
Scaife, A. A., and Smith, D. (2018). A signal-to-noise paradox in climate science. npj Clim. Atmos. Sci. 1:28. doi: 10.1038/s41612-018-0038-34
Schneider, N., and Cornuelle, B. D. (2005). The forcing of the Pacific Decadal Oscillation. J. Clim. 18, 4355–4373. doi: 10.1175/JCLI3527.1
Smith, D. M., Eade, R., Scaife, A. A., Caron, L.-P., Danabasoglu, G., DelSole, T. M., et al. (2019). Robust skill of decadal climate predictions. npj Clim. Atmos. Sci. 2, 1–10. doi: 10.1038/s41612-019-0071-y
Stock, C. A., Pegion, K., Vecchi, G. A., Alexander, M. A., Tommasi, D., Bond, N. A., et al. (2015). Seasonal sea surface temperature anomaly prediction for coastal ecosystems. Prog. Oceanogr. 137, 219–236. doi: 10.1016/j.pocean.2015.06.007
Tommasi, D., Stock, C. A., Alexander, M. A., Yang, X., Rosati, A., and Vecchi, G. A. (2017a). Multi-annual Climate predictions for fisheries: an assessment of skill of sea surface temperature forecasts for large marine ecosystems. Front. Mar. Sci. 4:201. doi: 10.3389/fmars.2017.00201
Tommasi, D., Stock, C. A., Hobday, A. J., Methot, R., Kaplan, I. C., Eveson, J. P., et al. (2017b). Managing living marine resources in a dynamic environment: the role of seasonal to decadal climate forecasts. Prog. Oceanogr. 152, 15–49. doi: 10.1016/j.pocean.2016.12.011
Tompkins, A. M., Ortiz, de Zárate, M. I., Saurral, R. I., Vera, C., Saulo, C., et al. (2017). The climate-system historical forecast project: providing open access to seasonal forecast ensembles from centers around the globe. Bull. Am. Meteorol. Soc. 98, 2293–2301. doi: 10.1175/BAMS-D-16-0209.1
Vimont, D. J. (2005). The contribution of the interannual ENSO cycle to the spatial pattern of decadal ENSO-like variability. J. Clim. 18, 2080–2092. doi: 10.1175/JCLI3365.1
Widlansky, M. J., Marra, J. J., Chowdhury, M. R., Stephens, S. A., Miles, E. R., Fauchereau, N., et al. (2017). Multimodel ensemble sea level forecasts for tropical Pacific Islands. J. Appl. Meteorol. Climatol. 56, 849–862. doi: 10.1175/JAMC-D-16-0284.1
Yu, J.-Y., and Paek, H. (2015). Precursors of ENSO beyond the tropical Pacific. US CLIVAR Var. 13, 15–20.
Yuan, C., Tozuka, T., Luo, J. J., and Yamagata, T. (2014). Predictability of the subtropical dipole modes in a coupled ocean-atmosphere model. Clim. Dyn. 42, 1291–1308. doi: 10.1007/s00382-013-1704-1701
Zainuddin, M., Farhum, A., Safruddin, S., Selamat, M. B., Sudirman, S., Nurdin, N., et al. (2017). Detection of pelagic habitat hotspots for skipjack tuna in the gulf of bone-flores sea, southwestern Coral Triangle tuna. Indonesia. PLoS One 12:e0185601. doi: 10.1371/journal.pone.0185601
Zhang, X., and Church, J. A. (2012). Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 39, 1–8. doi: 10.1029/2012GL053240
Keywords: seasonal-interannual prediction, sea level, climate model, dynamical system, skill assessment
Citation: Doi T, Nonaka M and Behera S (2020) Skill Assessment of Seasonal-to-Interannual Prediction of Sea Level Anomaly in the North Pacific Based on the SINTEX-F Climate Model. Front. Mar. Sci. 7:546587. doi: 10.3389/fmars.2020.546587
Received: 29 March 2020; Accepted: 22 September 2020;
Published: 20 October 2020.
Edited by:
Zhiyu Liu, Xiamen University, ChinaReviewed by:
Debora Bellafiore, National Research Council (CNR), ItalyRu Chen, Tianjin University, China
Soo-Jin Sohn, APEC Climate Center, South Korea
Kewei Lyu, Oceans and Atmosphere (CSIRO), Australia
Copyright © 2020 Doi, Nonaka and Behera. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Takeshi Doi, dGFrZXNoaS5kb2lAamFtc3RlYy5nby5qcA==; orcid.org/0000-0002-7342-9145
 Takeshi Doi
Takeshi Doi Masami Nonaka
Masami Nonaka Swadhin Behera
Swadhin Behera