- 1National Institute of Oceanography and Applied Geophysics (OGS), Trieste, Italy
- 2Institute of Polar Sciences, National Research Council, Lecce, Italy
- 3Center for Marine Research, Rudjer Boskovic Institute, Rovinj, Croatia
- 4ENEA-CLIMOSS, Palermo, Italy
Coastal ecosystems are subject to multiple processes that drive pH change over time. Therefore, efforts to understand the variability in the coastal carbonate system are crucial to assess the marine system vulnerability to acidification. The variations of the carbon dioxide (CO2) system were studied, from December 2014 to January 2017, on 6 stations along a transect latitudinally crossing the northern Adriatic, from the Po River delta to the Istrian Peninsula. The study aims to evaluate the influence of riverine inputs and other environmental drivers, such as temperature, air-sea CO2 exchanges and biological processes, on the carbonate system. Riverine discharges significantly affected the carbonate system, as they are an input of total alkalinity and nutrients. High alkalinity concentrations were measured in low salinity waters and a significant negative correlation between salinity and alkalinity was found. The influence of biological processes was underscored by the significant inverse correlation between pHT at a constant temperature (pHT25^°C) and apparent oxygen utilization, and by the positive correlation between chlorophyll a and pHT25^°C in samplings close to flood events. Moreover, thermic and non-thermic partial pressure (p) of CO2 in surface waters was evaluated. pCO2 was more strongly influenced by the thermal effect during summer, while the biological effect prevailed in the other seasons. The analysis of air-sea CO2 fluxes highlighted that the area acts as a sink of CO2 during winter, spring and autumn and as a source during summer. A biogeochemical simulation was used for bottom and surface waters to estimate future changes in northern Adriatic carbonate chemistry with the increase of anthropogenic CO2 and temperature, and to understand how biological processes could affect the expected trends. By 2100, under the IPCC scenario of business as usual and without the effect of biological processes, pHT is expected to decrease by ∼0.3 and the aragonite saturation is expected to decline by ∼1.3, yet not reach undersaturation values. Even though the northern Adriatic is characterized by high alkalinity buffering, pH seasonal variability will likely be more pronounced, due to the strong decoupling of production and respiration processes driven by stratification of the water column.
Introduction
Atmospheric carbon dioxide (CO2) levels increased over 40% passing from 280 ppm (parts per million volume), before the Industrial Revolution, to 415 ppm in 2019, as is shown by the Keeling Curve1. This is mainly due to fossil fuel combustion, deforestation, cement production and land use change. The increasing concentration surpassed the highest level in the last 800.000 years (Lüthi et al., 2008) and the rate of increase is an order of magnitude faster than has occurred for millions of years (Doney and Schimel, 2007). The oceanic uptake of CO2 has resulted in the acidification of the ocean (OA), since the beginning of the industrial era; the pH of ocean surface water has decreased by 0.1 units corresponding to a 26% increase in acidity, measured as hydrogen ion concentration (IPCC, 2014) and a further decrease of 0.4 is expected for the end of the century (Orr, 2011). Together with the change in pH, the whole carbonate system is changing rapidly (IPCC, 2013). As a consequence of CO2 addition to the ocean: the concentration of bicarbonate ions (HCO3–) and the concentration of dissolved inorganic carbon (TCO2) increases, whereas pH, the concentration of carbonate ions (CO32–) and the saturation state of the carbonate minerals present in the seawater decreases. These changes can have negative effects on the marine biota, especially on calcifying organisms (Kleypas et al., 1999). Long-term pH reduction due to the anthropogenic CO2 in the open ocean has been demonstrated in the long-term records acquired in the last decades. However, the effects of acidification processes in coastal areas are still difficult to assess and predict. Coastal ecosystems are more complex and dynamic than that of the open ocean (Borges and Gypens, 2010; Cai et al., 2011; Ingrosso et al., 2016a), thus pH changes and long-term trends in coastal seas are usually considerably more complex (Duarte et al., 2013; Carstensen et al., 2018). These characteristics do not allow a direct transport of OA patterns from open oceans to coastal areas, leaving a remarkable lack in projections about acidification effects. How ocean acidification will affect marine organisms depends on changes in both the long-term, mean and short-term temporal variability of carbonate chemistry (Kwiatkowski and Orr, 2018). The duration of very low pH periods can be relevant for marine organisms both at seasonal or interannual level. The duration of seasonal events with very low pH could increase in the next future and can have long-term consequences. Moreover, the cumulation with other stressors as oxygen depletion and temperature increase (Wallace et al., 2014; Bednaršek et al., 2016), that are becoming more common in the last years, could worsen the impacts on marine organisms in the future.
The analysis of long-term changes in pH across 83 coastal ecosystems showed that these ecosystems present a much broader range (∼20 times larger) of rates of change in pH than the open ocean does (Carstensen and Duarte, 2019). Metabolic effects, represented by net community production and respiration rates, tend to be greater in coastal and estuarine ecosystems (Duarte and Cerbrian, 1996; Gattuso et al., 1998; Anthony et al., 2011). Observations of pH in a variety of coastal habitats indicate site-specific variability at scale ranging from diel to seasonal oscillations (Hofmann et al., 2011). Regional scale processes such as phytoplankton blooms (Kapsenberg and Hofmann, 2016), upwelling (Chan et al., 2017), and freshwater inputs (Fassbender et al., 2016) further modify CO2 exposures, thus the negative impact of acidification could be enhanced in some coastal ecosystems subject to changes in the eutrophication pressure (Provoost et al., 2010; Wallace et al., 2014). Coastal phytoplankton blooms can increase pH up to 8.6–9.0 (Brussaard et al., 1996). Metabolic-intense ecosystems, such as seagrass meadows, mangroves, salt marshes, coral reefs and macroalgal beds, can support diel changes in pH as high as 1.0 unit. Consequently, long-term trends are difficult to separate from interannual and decadal oscillations.
In the Mediterranean Sea the acidification process seems more rapid than in the Atlantic Ocean, where the decrease range is from −0.0013 to −0.0026 yr–1 (Bates et al., 2014). A pHT decrease of 0.0028 yr–1 has been observed in the NW Mediterranean Sea (Kapsenberg et al., 2017) while one of 0.0025 pHT units yr–1 was estimated in the Adriatic Sea (Luchetta et al., 2010) and of 0.009 units yr–1 in the Levantine sea (Hassoun et al., 2019). The northern Adriatic (NAd) is a shallow semi-enclosed system strongly influenced by the Po River freshwater discharge, the second largest river in the Mediterranean Sea (Cozzi et al., 2019). Moreover, NAd is one of the few sites in the Mediterranean Sea where dense waters are formed (Font et al., 2009). Winter cooling determines heat loss and evaporation which induce the formation of dense waters (Supič and Vilibic, 2006) which flow southwards partially filling the meso- and south Adriatic pits and partially flowing along the western coast toward the Ionian Sea, contributing to the Mediterranean deep waters (Russo and Artegiani, 1996). Depending on the formation rate, dense water formation in NAd could potentially sequester high levels of anthropogenic carbon dioxide and contribute to acidification of deep waters (Ingrosso et al., 2017). The aim of this work is to investigate the spatial and temporal variability of the carbonate system in a Mediterranean system strongly influenced by riverine discharges, as the NAd, and to determine the main physical and biogeochemical drivers influencing it.
Description of the Area
The study area is the shallow northern Adriatic, with an average bottom depth of about 35 m. The area is a part of the Adriatic Sea (Figure 1) and represents the largest shelf area of the entire Mediterranean region (Gačič et al., 2001).
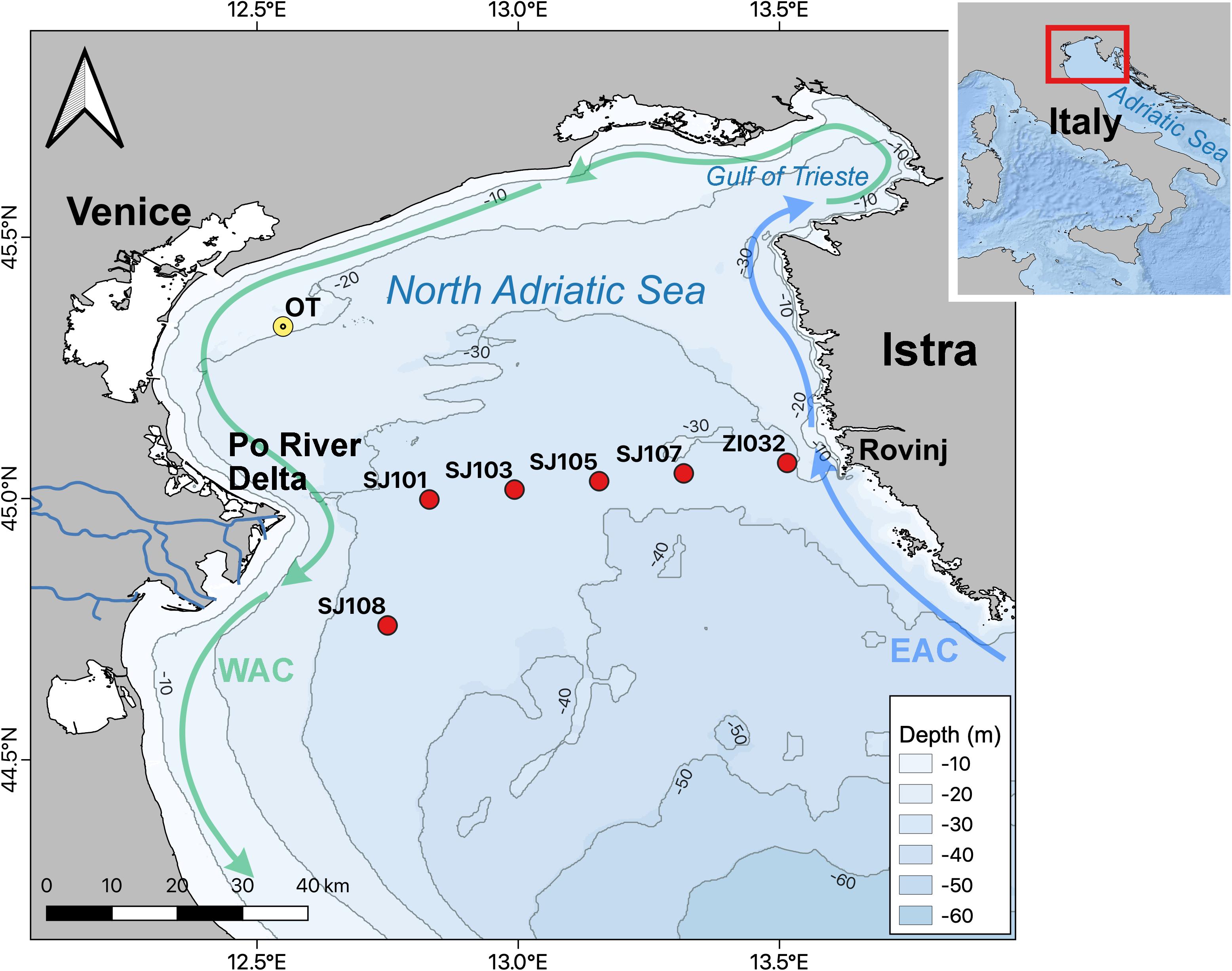
Figure 1. Map of the sampling stations along a transect from Po River delta to Istra, and of the oceanographic tower (OT) Acqua Alta.
River runoff is particularly strong in the northern basin and it affects circulation by altering the buoyancy of water masses, and the ecosystem by introducing large amounts of nutrients (Zavatarelli et al., 1998), making the northern Adriatic a highly productive area (Pugnetti et al., 2006). Po River flow rates amount to around 45 km3 yr–1 (70% of the total freshwater discharge in the region) with spring and autumn floods up to 10000 m3 s–1 (Cozzi and Giani, 2011).
The Adriatic mean surface circulation is generally cyclonic, with the Eastern Adriatic Current (EAC) flowing northward along the eastern side from the Strait of Otranto to as far north as the Istrian Peninsula, and the return flow, referred to as the Western Adriatic Current (WAC), that runs along the Italian coast (Poulain, 2001). The WAC between the Po River delta and the Gargano Promontory is more concentrated near the Italian coast in winter and spring, while during the other seasons its core is found farther offshore (about 20–30 km from the coast in fall). The WAC and EAC are generally stronger in summer/fall than in winter/spring (Poulain, 2001).
During winter in the NAd the northern Adriatic dense water (NAdDW), the densest water of the entire Mediterranean, is generated (Bensi et al., 2013; Raicich et al., 2013). This water is characterized by low temperature, high salinity and density, usually: T 11.35 ± 1.4°C, S 38.3 ± 0.28 and σt > 29.2 kg m–3 (Artegiani et al., 1997). In general, NAdDW is formed on the central eastern side of the NAd, whereas the western part of the northern shelf, which is affected by the WAC, is characterized by lower-density water masses (Querin et al., 2013). Additionally, this area is characterized by the occurrence of the northern Adriatic surface water (NAdSW), which corresponds to low salinities and relatively high temperature in summer (Artegiani et al., 1997). Flow of this water is cyclonic due to its mixed positive–negative estuarine circulation (Hopkins et al., 1999) forced by buoyant freshwater from the rivers (mainly the Po River) and by strong air–sea fluxes resulting in loss of buoyancy and dense water formation. Along the eastern side of the basin, an occasional inflow of the modified Levantine intermediate water (MLIW) may occur (Zavatarelli et al., 1998; Manca and Giorgetti, 1999).
Materials and Methods
Sampling Scheme
Data were sampled along a transect from the mouth of the Po River to the area of Rovinj in the northern Adriatic basin (Figure 1) from December 2014 to January 2017 in 16 oceanographic cruises. During cruises 6 stations (SJ108; SJ101; SJ103; SJ105; SJ107; and ZI032) were sampled. These stations were selected based on circulation patterns to obtain a river-sea gradient and were made to potentially match a seasonal trophic gradient. Water samples for temperature, salinity, pH on total scale (pHT) AT, dissolved oxygen (DO), dissolved inorganic nutrients and chlorophyll a (Chl-a) were collected and analyzed.
All parameters were sampled at 4 depths (0.5, 10, 20, and 2 m above the bottom). DO, pHT and AT samples were the first to be drawn from Niskin bottles. pHT samples were drawn into 120 mL borosilicate glass bottles, with a 1% headspace, poisoned with 50 μL of saturated mercuric chloride (HgCl2), and stored at 4°C in the dark, until analysis. Samples for AT were filtered on pre-combusted (450°C for 4 h) Whatman GF/F filters to remove phytoplankton cells and particles of CaCO3 derived from calcifying organisms (Gattuso et al., 2010; Bockmon and Dickson, 2014), collected into borosilicate flasks (250 mL) with 1% headspace, poisoned with 100 μL of saturated HgCl2, and stored in the dark at a 4°C temperature until analysis. For both parameters, analyses were performed by the National Institute of Oceanography and Applied Geophysics (OGS) in Trieste, Italy. DO, nutrients and Chl-a instead, have been analyzed by the Center of Marine Research (CMR) of Rudjer Boskovic Institute (RBI) in Rovinj, Croatia, Istrian Peninsula.
Analytical Measurements of Temperature, Salinity, Dissolved Oxygen, Inorganic Nutrients and Chlorophyll a
Temperature was measured by protected reversing thermometers (digital thermometers SIS RTM 4002, precision ± 0.003°C, accuracy ± 0.005°C) attached to the Niskin bottles. Salinity from Niskin bottles samples was determined by high precision salinometer (RBR Precision Instruments MS-310) as the ratio of the value of conductivity of sample and standard (IAPSO standard seawater) using algorithms recommended by UNESCO (1983) with accuracy of ±0.002.
DO and inorganic nutrients were analyzed directly on-board by the CMR/RBI research group, according to methods widely used in oceanography (Parsons et al., 1984). DO was determined by the Winkler titration method, while the saturation percentage was calculated following the Benson and Krause equation (UNESCO, 1986). The method accuracy was ±0.5% with a detection limit of 0.9 μmol kg–1 (Parsons et al., 1984). The apparent oxygen utilization (AOU) was determined as the difference between the equilibrium saturation of oxygen’s concentration in seawater with the same physical and chemical properties and the measured oxygen concentration. AOU represents an estimate of the oxygen utilized due to biochemical processes, providing an approximation of the balance between biological processes of primary production and respiration.
Dissolved inorganic nutrients concentrations [nitrite N-NO2, nitrate N-NO3, phosphate P-PO4, and silicate Si-Si (OH)4] were analyzed spectrophotometrically (Parsons et al., 1984), moreover, ammonia (N-NH4) concentrations were determined by a modified technique of the indophenol blue method (Ivančič and Degobbis, 1984). Dissolved inorganic nitrogen (DIN) was obtained as a sum of ammonia, nitrite and nitrate. The absorbance readings for all nutrients were made on Shimadzu UV-Mini 1240 double-beam spectrophotometer using 10 and 5 cm quartz cuvettes. Method accuracies for NO2, NO3, NH4, PO4 and Si(OH)4 were ±3%, ±3%, ±5%, ±3%, and ±6%, respectively, and detection limits were 0.05, 0.01, 0.1, 0.02, and 0.05 μmol L–1, respectively.
The samples for Chl-a measurement were prefiltered through 290 μm Nybolt net, and then filtered through Whatman GF/C filters (1 μm pore size) on-board, immediately after collection. The filters were stored at −20°C until analyses, which were performed fluorometrically after a 3 h extraction in 90% acetone (in the dark, with grinding after addition of acetone) by using Turner Designs, TD-700 fluorometer at the inland CMR/RBI laboratories. Method accuracy of 78%, and detection limit of 0.02 μg L–1 were calculated according to equations of Parsons et al. (1984).
Analytical Determination of Seawater pHT and Total Alkalinity
pHT determination was performed at OGS using a double wavelength spectrophotometer (Cary 100 Scan UV-visible) and employing purified dye m-cresol purple 4 mM as indicator, as described in SOP 6b of Dickson et al. (2007). The results were expressed on the ‘pH total hydrogen ion scale’ (pHT) at 25°C, with a reproducibility of ±0.001, determined by replicates from the same Niskin bottles. The day of the analysis samples were brought to 25°C and subsampled by siphoning with a tygon tube, avoiding gas exchange, in a 10 cm path-length cylindrical quartz cell; no head-space was left. pHT was measured within a few hours from the sub-sampling. During the whole analysis, the temperature of the samples was controlled through thermostatic cell holders inside the spectrophotometer, connected to a circulation criothermostat (LAUDA RE415) and monitored with a digital thermometer (VWR Traceable).
The accuracy of pHT (±0.004) spectrophotometric measurements was assessed through the analysis of Tris buffers supplied by Prof. A.G. Dickson, Scripps Institute of Oceanography, United States. Tris buffer reference value was calculated, at the temperature of the measurements, following DelValls and Dickson (1998).
AT was analyzed in the laboratory by an open cell potentiometric titration, using a Mettler Toledo G20, at 25°C; ∼100 g of sample were weighed and titrated with HCl 0.1 mol kg–1 in NaCl 35‰ as defined by the SOP 3b (Dickson et al., 2007), using a non-linear least squares approach. The HCl was calibrated against seawater certified reference materials (CRMs) for TCO2 and AT supplied by Prof. A.G. Dickson, Scripps Institute of Oceanography, USA (Batch numbers #107, #133, #153). AT calculations were run by Alka Open Cell 2.0, a computer program developed by OGS according to programs listed in SOP 3 of Dickson and Goyet (1994); the program was adapted to work in association with the Mettler Toledo LabX software. AT reproducibility was <2 μmol kg–1 and the accuracy ±4 μmol kg–1, they were assessed by analyzing both CRMs and local reference materials (LRM) of natural seawater; moreover, the OGS laboratory participated in the Inter-laboratory Comparison of Seawater CO2 Measurements organized by the Scripps Institution of Oceanography in 2013 and 2017. The differences for AT and pHT measurements were < 4 μmol kg–1 and <0.0004 respectively.
All other carbonate system parameters, including pHT at in situ temperature, seawater partial pressure of CO2 (pCO2), TCO2, and aragonite saturation state (Ωar), were calculated using the CO2Sys program (Pierrot et al., 2006) through AT concentration, pHT (25°C), temperature, salinity, phosphate, and silicate concentration data. Carbonic acid dissociation constants (i.e., pK1 and pK2) proposed by Lueker et al. (2000) as well as the Dickson constant for the ion HSO4 (Dickson, 1990) and borate dissociation constant of Uppström (1974) were used. Uncertainties for the derived carbonate system parameters have been calculated using CO2Sys, following Orr et al. (2018). The estimated uncertainties were: ±0.006 for pHT at in situ temperature, ±8 μatm for pCO2, ±9 μmol kg–1 for TCO2 and ±0.2 for aragonite saturation state.
Thermic (T) and non-thermic (B) pCO2 in surface waters has been calculated following the procedure described by Takahashi et al. (2002) to distinguish the effect of temperature change from the effect of other processes (i.e., biological processes, advection of water masses..). For each station seasonal T was calculated as the difference between the maximum and the minimum thermic pCO2 and B as the difference between the maximum and the minimum non-thermic pCO2. Thermic pCO2 was calculated as described in equation 1:
Where pCO2mean is the mean surface pCO2 of the investigated period, Tobs is the measured temperature and Tmean is the mean surface temperature of the investigated period.
While non-thermic pCO2 was computed as described in equation 2:
where pCO2obs is the measured surface pCO2.
In order to remove the variations due to freshwater input, mixing and evaporation/precipitation influence, AT and TCO2 were normalized (nAT and nTCO2) to a different salinity for every year using a traditional normalization style. We are aware that the tradition approach (Millero et al., 1998) could create artificial variance in distributions (Friis et al., 2003), but we chose the classical normalization since we do not have a stable endmember.
For the contour plots the advanced DIVA gridding of the software Ocean Data View (Schlitzer, 2018) was used. Since we are aware of the limitations of this gridding method, we checked the representativeness of the interpolations with the discrete data points.
Air-Sea CO2 Flux Calculations
The daily air-sea CO2 flux (FCO2, mmol m–2 day–1) has been calculated following the equation:
where:
K0 is the solubility coefficient of CO2 at in situ temperature and salinity of seawater (Weiss, 1974; Zeebe and Wolf-Gladrow, 2001);
k is the gas transfer velocity (m day–1) and pCO2 – pCO2atm is the difference between pCO2 at sea surface and daily mean pCO2 in atmosphere.
Since several algorithms for k calculation exists, two different parameterizations were used to compute k: the one described by Wanninkhof (2014) in equation 4, hereafter referred to as W14, and the parameterization described by Nightingale et al. (2000) in equation 5, hereafter referred to as N00:
where u is the daily mean wind speed recorded at the oceanographic tower (OT) Acqua Alta (Figure 1) and Sc the Schmidt number for CO2.
If the FCO2 is < 0 the flux is from air to seawater, on the contrary if FCO2 is > 0 the flux is from the seawater to the atmosphere.
CO2 monitoring in air was run with continuous measurements at ENEA Station for Climate Observations on the island of Lampedusa (Italy). CO2 measurements were made with a Picarro G2401 gas analyzer. Ambient air was taken from a tower at a height of 8 m above the surface, about 50 m above sea level. Water vapor was removed from the sampled air by means of a cryogenic trap at about −60°C. The gas analyzer was calibrated biweekly, using 4 cylinders which concentration is traceable to the WMO CO2-X2007 reference scale (provided by the Max Planck Institute in Jena, Germany, as part of the InGOS European Union Project). Gas from an additional cylinder was injected in the instrument every 6 h as an additional quality control check. Data were subsequently verified by means of standard quality control procedures, the accuracy on 5-min average CO2 measurements was better than 0.02 ppm.
pCO2atm data of Lampedusa were used because there were no pCO2atm daily measurements available in the offshore NAd for the investigated period.
Buffer Factors and Carbonate Saturation State
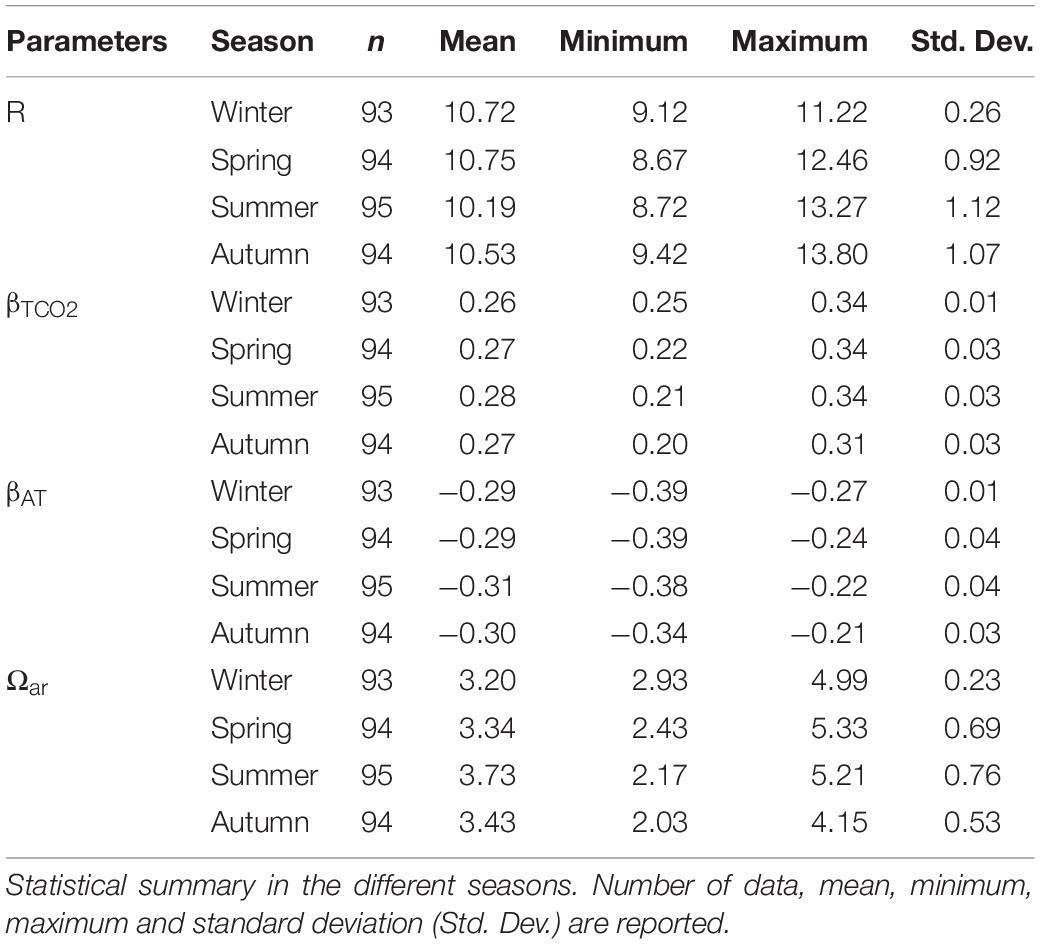
The fractional change in concentration of CO2 over the fractional change in TCO2 has been referred to as the Revelle factor, or R (Revelle and Suess, 1957; Broecker et al., 1979):
This quantifies the ocean’s sensitivity to an increase in atmospheric CO2. Moreover, we considered two other buffer factors, βTCO2 and βAT, as defined by Egleston et al. (2010):
The parameter βAT, defined as:
measures the resistance to change of the hydrogen ion concentration (or activity) when alkalinity changes at constant TCO2, i.e., upon addition of a strong base, directly related to the traditional buffer capacity of the system.
The parameter βTCO2, defined as:
measures the resistance to change of the hydrogen ion concentration (or activity) when TCO2 changes at constant AT.
Where
as revised in the Appendix B of Orr et al. (2018), and
We performed the calculations with the routine buffesm of the Seacarb (Gattuso et al., 2015) package in R (R Core Team, 2016) employing the same constants used in CO2Sys to calculate the other carbonate system parameters (see section “Analytical Determination of Seawater pHT and Total Alkalinity”).
Seawater CO2 Chemistry Simulations
In order to estimate future changes in the northern Adriatic Sea carbonate chemistry with the increase of anthropogenic CO2, and to estimate how biological processes could affect the expected trends, we set up a biogeochemical simulation following Sunda and Cai (2012). In our simulation, we considered how a high level of atmospheric CO2 could affect the carbonate system of NAd in two water types that usually have pronounced metabolic activity: the bottom waters and NAdSW. The initial carbonate chemistry conditions for these two water types were calculated using their AT and CO2 at air-sea equilibrium as a function of their specific temperature and salinity. Atmospheric pCO2 was set at two levels (400 and 910 ppm) corresponding to present-day and year 2100 Representative Concentration Pathway for high emission scenario (RCP 8.5, van Vuuren et al., 2011; IPCC, 2013). A seawater temperature increase of +2.58°C for the 2100 was also considered in our simulation, as projected by IPCC (2019) for global sea surface under RCP 8.5 scenario. The adopted trend implies a +0.03°C yr–1, which is intermediate between the NAd warming rate reported by Raicich and Colucci (2019) of 0.013 ± 0.005°C yr–1 and that of 0.01–0.06°C yr–1 reported by Vilibič et al. (2019). The biogeochemical model for respiratory increases or photosynthetic decrease in CO2 concentration is based on AOU calculations as described by Redfield et al. (1963). Once the initial surface conditions were calculated, aerobic respiration or photosynthetic activity were assumed to increase or decrease TCO2 respectively, due to respiration or primary production at the Redfield ratio of 106 CO2 to 138 O2. Then the resulting TCO2 was used to calculate the other carbonate chemistry parameters for 2100, assuming reference AT, salinity and temperature (sea surface temperature in 2100 = present day temperature +2.58°C) specific for each water mass and using the same equilibrium constants as previously described for the carbonate system. AT was considered constant because in the organic matter, the aerobic oxidation of amine nitrogen to nitric acid has only a small decrease in alkalinity, but this effect is essentially canceled by denitrification under hypoxic conditions, which converts HNO3 to N2. All calculations were performed with the Seacarb (Gattuso et al., 2015) and Marelac (Soetaert et al., 2015) packages in R (R Core Team, 2016).
Statistical Analysis
The Shapiro–Wilk test (Shapiro and Wilk, 1965) was used to check the normality of the data. Due to their non-normal distribution a non-parametric approach was adopted. Spearman’s coefficient was used for correlations. The Kruskal–Wallis rank sum test (Kruskal and Wallis, 1952) was used to test statistically significant differences between seasons for each parameter whereas the multiple comparison test (Siegel and Castellan, 1988) was used to determine which pair of seasons were different. Analyses were performed with R program and the package pgirmess. Seasons were considered as follows: winter (January–March), spring (April–June), summer (July–September), and autumn (October–December). Seasons were defined based on the climatological work of Zavatarelli et al. (1998).
Results
Riverine Influence
Po River discharges strongly influence the NAd, particularly after the freshets; daily variations of Po river flow rate (Q) measured at Pontelagoscuro station (Ferrara, Italy) and discrete sampling days are presented in Figure 2.
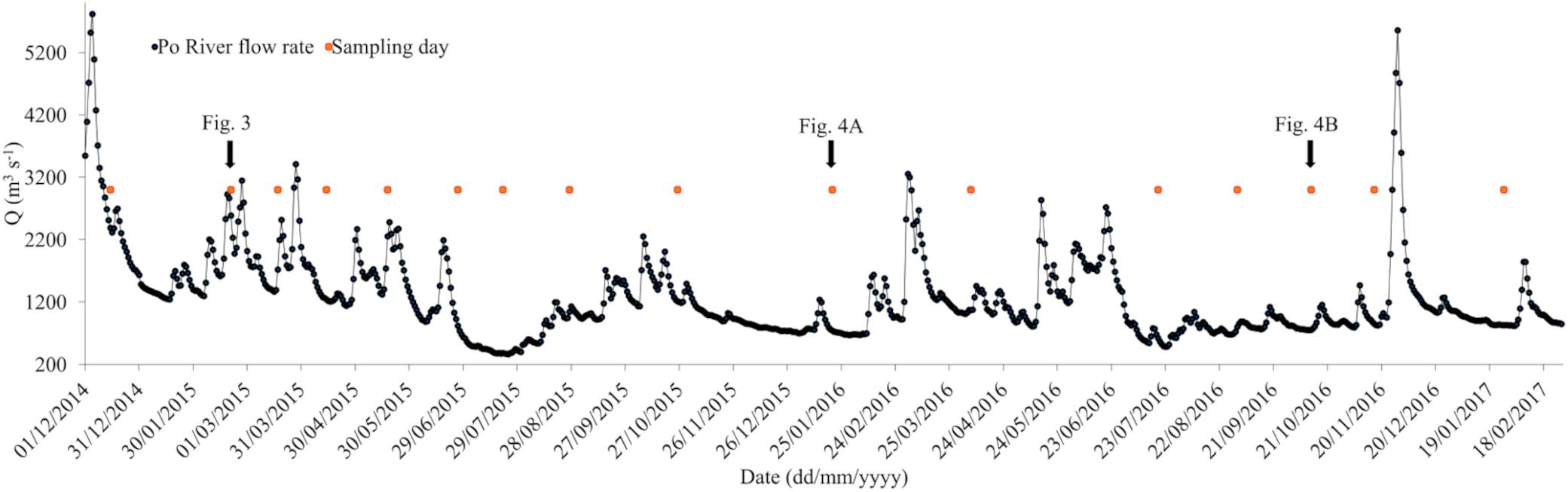
Figure 2. Daily variations of Po river flow rate (Q) measured at Pontelagoscuro station (Ferrara, Italy) and sampling days from December 2014 to January 2017 (red square symbols).
The mean Po flow rate decreased between 2015 and 2017; in 2015 (from December 2014 to December 2015) was of 1421 m3 s–1, while in 2016 (from January 2016 to January 2017) was of 1148 m3 s–1.
The strong effect of the freshwater discharge was observed on the majority of the parameters along the section, highlighted by (i) their seasonal variability, strongly connected to Po River discharges and (ii) the formation of a gradient from the western toward the eastern sector of the basin.
The formation of a horizontal gradient along the transect, is evident from the spatial distribution of salinity, AT, pHT and TCO2 in February 2015 (Figure 3), sampled close to a flood event, with values of AT and TCO2 higher in the WAC, decreasing eastwards, and values of salinity and pHT increasing eastwards.
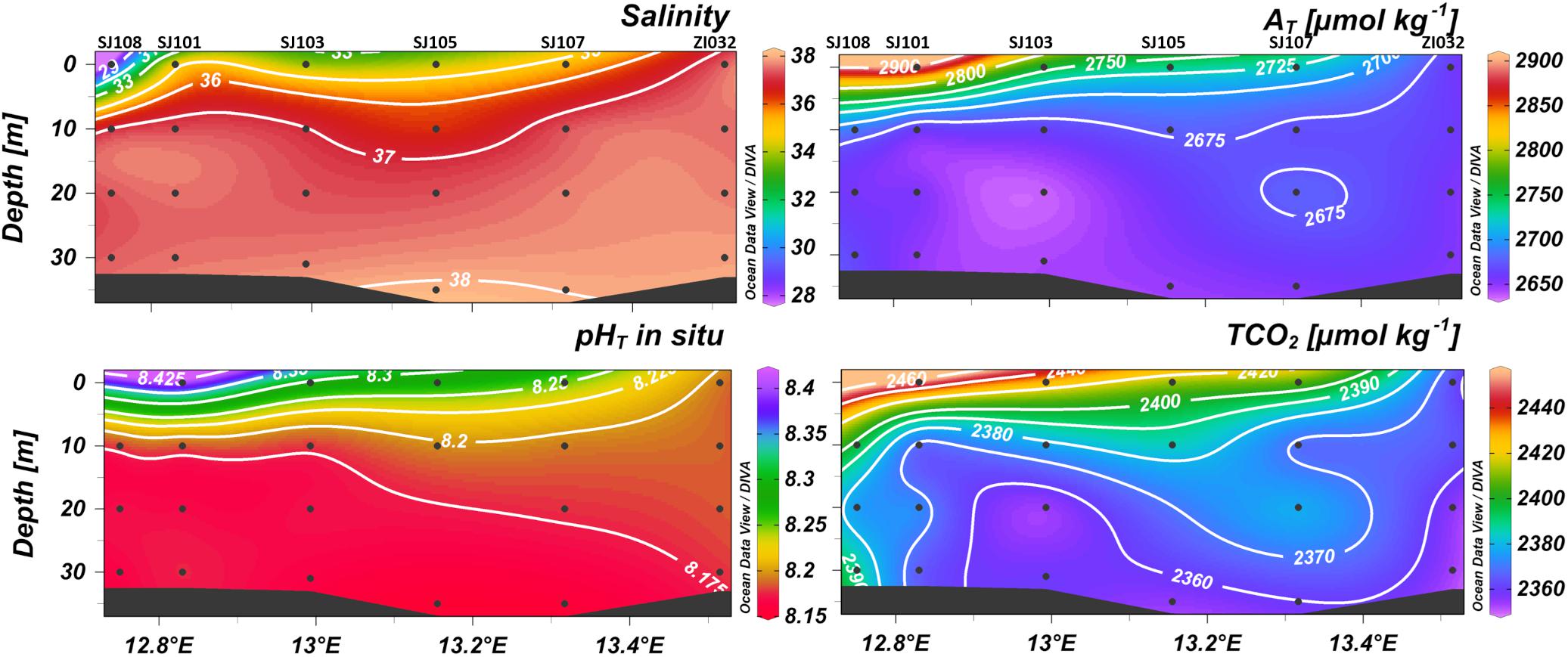
Figure 3. Contour plots of salinity, total alkalinity (AT), pHT and dissolved inorganic carbon (TCO2) versus depth in February 2015 along the transect from Po River (left) to Rovinj (right).
The effect of riverine inputs on the concentration of AT is also highlighted by its negative correlation with salinity. The most significant correlations were found in surface waters during the period of high freshwater discharges: high concentrations of AT (2668 ± 51 μmol kg–1) were measured in February, March and April 2015 (late winter-spring) when also the strongest correlation with salinity was found (r = −0.66; p < 0.0001; n = 69). However, even considering all the data, the correlation was still significant (r = −0.50; p < 0.0001; n = 377) (Supplementary Figures 1, 2).
Beside the effects of temperature, riverine inputs influenced pHT values mainly due to the fertilization effect. In fact, higher pHT values were measured at surface during winter/spring period, characterized by higher freshwater discharges that brings inorganic nutrients to support primary production.
The TCO2 concentration resulted influenced by freshwater discharges, as it is underlined by its negative correlation (r = −0.79; p < 0.001; n = 17) in surface waters with salinity in February, March and April 2015 (Supplementary Figure 3).
The effect of riverine inputs on inorganic nutrient concentrations was highlighted by the highly significant negative correlation between salinity in surface waters and nitrate (r = −0.96; p < 0.0001; n = 18), nitrite (r = −0.90; p < 0.0001; n = 18), phosphate (r = −0.79; p < 0.001; n = 18) and silicate (r = −0.66; p < 0.01; n = 18) in samplings close to flood events. The highest concentrations of nitrate (74.42 μmol L–1), silicate (65.35 μmol L–1), phosphate (1.31 μmol L–1), and ammonium (7.38 μmol L–1) have been measured in February 2015 in surface waters close to the Po River delta (Supplementary Figure 4).
Influence of Biological Processes
The biological processes in the water column which affect the CO2 system in the NAd are strongly related to the seasonality, as evidenced by the difference between the winter homogeneity (Figure 4A) and the autumn thermohaline stratification (Figure 4B).
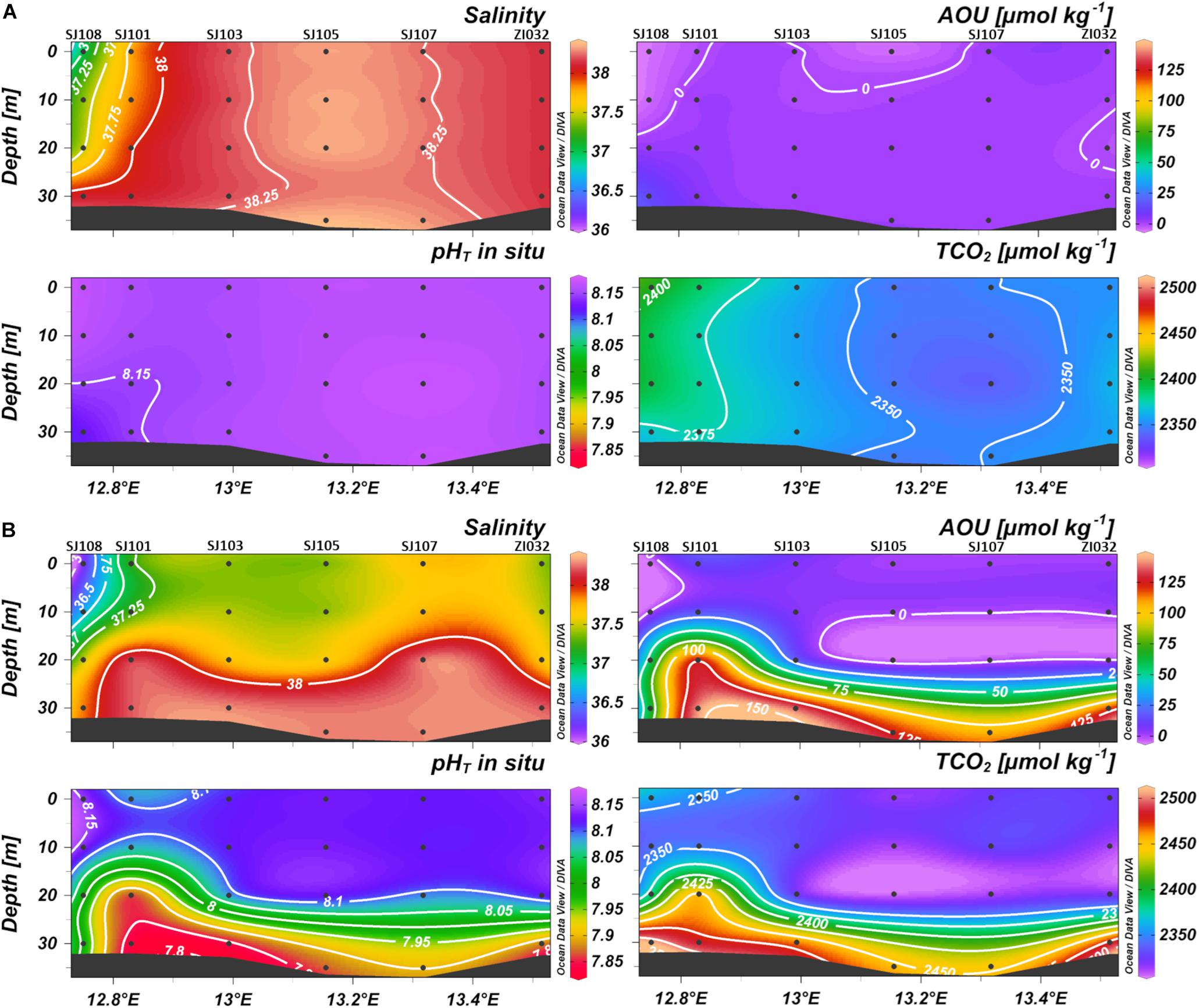
Figure 4. Contour plots of salinity, apparent oxygen utilization (AOU), pHT and dissolved inorganic carbon (TCO2) versus depth along the transect in (A) January 2016 and (B) October 2016, from Po River (left) to Rovinj (right).
During winter (Figure 4A) the water column was homogenous for all the parameters, with a weak horizontal gradient of salinity that increased eastwards from the Po River delta. AOU was uniform along the section, with an average value of 1 ± 4 μmol kg–1, indicating that DO was near to saturation. pHT was high and homogeneous in the whole water column (8.160 ± 0.010 on average), TCO2 instead followed the weak horizontal gradient of salinity decreasing toward the offshore waters.
During the seasonal stratification (Figure 4B), a marked oxygen depletion occurred under the pycnocline, where, due to respiration and organic matter remineralization, carbon dioxide was produced, lowering pHT and increasing the concentration of TCO2.
The influence of biological processes on pHT variations, removing the effect of temperature, is evidenced by the correlation between AOU and pHT25^°C, which was significant for all the data (r = −0.59; p < 0.0001; n = 383). Considering just the layer below 20 m depth, where respiration processes prevail, the correlation resulted more significant (r = −0.76; p < 0.0001; n = 95) (Supplementary Figures 5, 6). Moreover, in bottom waters, the influence of biological processes is underlined by the slope of the regression line between AOU and nTCO2, that had a value of 0.799 (Supplementary Figure 7), close to the Redfield ratio of 0.768 (C: AOU = 106: 138).
The relative importance of biology and temperature effects on pCO2 is expressed by the thermic/non thermic ratio (T/B; Figure 5). If the biological effect exceeds the temperature changes, ratio varies from 0 to 1, if the temperature effect is stronger than the biological processes the ratio is greater than 1, the two effects have the same influence if the ratio is 1. During winter, the biological effect on pCO2 prevailed on the temperature effect in all stations of the transect, but mostly in the two stations closer to the Po River delta (Figure 5). During spring the biological processes still exceeded temperature changes, but less intensively than in winter (Figure 5). In summer the thermic effect was stronger in all the stations except the most eastern one, where the ratio was 1. The two stations near the Po River delta were the ones where the temperature effects were stronger. In autumn, the biological effect prevailed in all the stations (Figure 5).
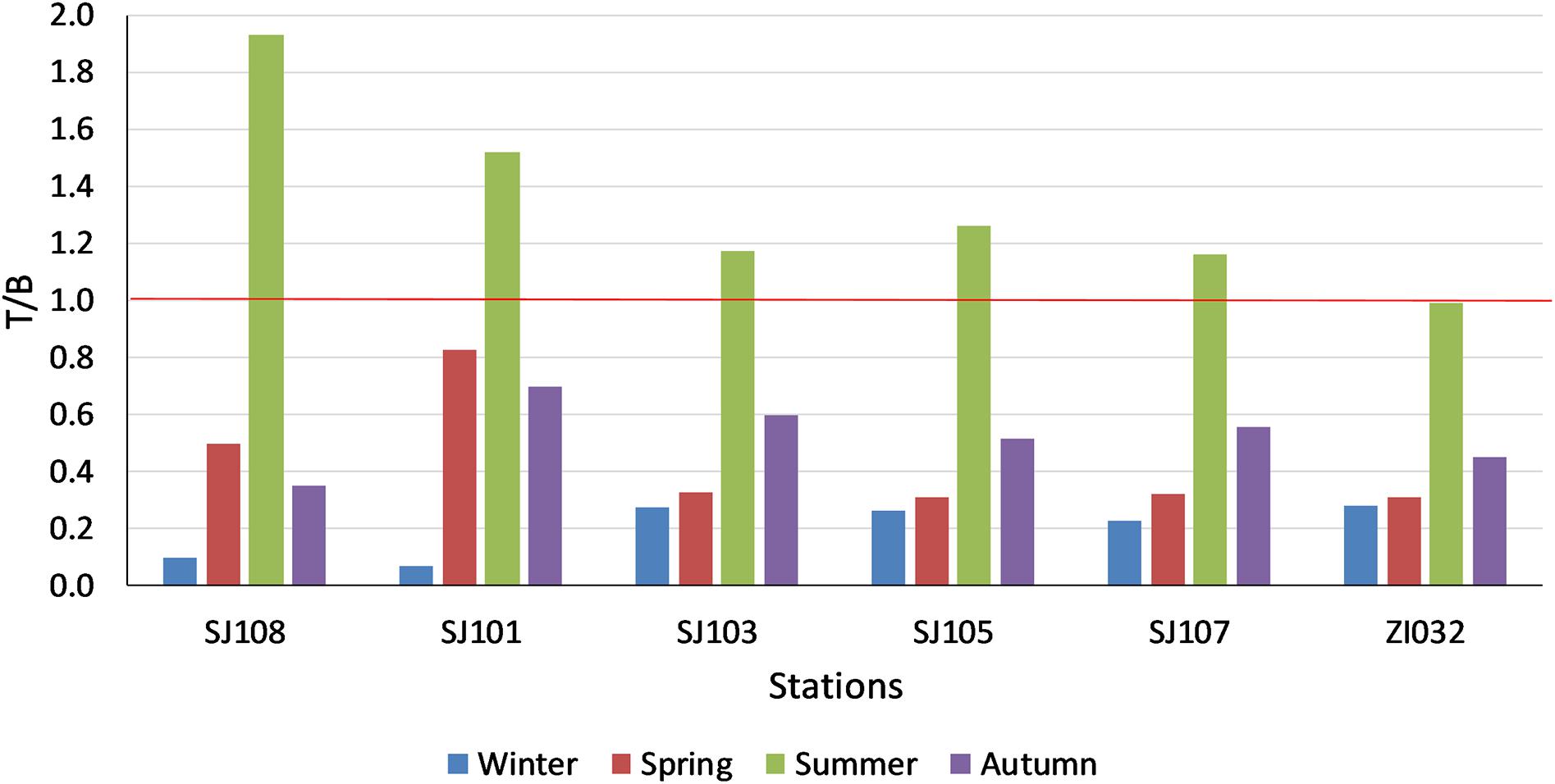
Figure 5. Thermic/not thermic pCO2 ratio (T/B) in surface waters in the stations of the transect in the different seasons.
A horizontal gradient of Chl-a concentration, decreasing from the western to the eastern waters, was found, more marked in winter-spring 2015 and autumn 2016 (Supplementary Figure 8). The biological effect of the trophic gradient is supported by the positive correlation (r = 0.36; p < 0.05; n = 71) between pHT25^°C, and Chl-a in samplings close to flood events. Moreover, the significant inverse relationship (r = −0.35; p < 0.001; n = 95) in the waters above the pycnocline of pCO2 and Chl-a points out the possible effects of the CO2 drawdown by phytoplankton.
Seasonal and Interannual Variations
The wide variation of both the physical and chemical properties observed during the two years, strongly influenced the marine carbonate system. Seasonal average values of temperature, salinity, density anomaly (σt), AOU, TCO2 and pHT are summarized in Table 1. Three stations (SJ101, SJ105, and ZI032) were selected to represent the time evolution in the western, central, and eastern NAd (Figures 6, 7). For the western side of the basin, station SJ101 was selected, as it is strongly influenced by riverine discharges and it is representative for the coastal area; similar thermohaline conditions between station SJ108 and SJ101 were found, but a stronger variability characterized SJ101. Station SJ105 was selected to represent the central area of the transect, while station ZI032 was chosen to represent the eastern side of the basin, where southern waters enter into the NAd. The differences between seasons for each parameter were tested with the non-parametric Kruskal–Wallis rank sum test and the results are presented in Table 2. Seawater temperature in the water column varied between 8.10 and 29.58°C during the investigated period (Table 1), with the surface layer minimum measured in winter (January 2017), and the surface layer maximum reached in summer (July 2015). Seawater temperature resulted significantly different (p < 0.001) among each season (Table 2). Salinity ranged between 26.36 and 38.53, while σt varied between 18.85 and 29.85 kg m–3 (Table 1). For both parameters the minimum was measured in spring and the maximum in winter. The highest variability along the transect was detected in spring (36.96 ± 1.86 and 27.60 ± 2.10, respectively). Salinity was significantly different (p < 0.001) only among spring and winter and among summer and winter (Table 2). The variation of observed AOU was consistent with the typical seasonal cycle; during all the investigated period it ranged between −180 and 144 μmol kg–1, with the maximum reached in autumn 2016 at surface and the minimum measured in winter 2015 at bottom. During winter, when the biological activity is usually low, the mean AOU along the whole water column was close to zero (Table 1). In spring, primary production was the predominant process, as shown by the negative mean AOU (−10 ± 31 μmol kg–1). In summer the effect of primary production was still evident in the upper layer (−17 ± 11 μmol kg–1), while below 10 m depth, due to stratification, oxygen consumption prevailed (13 ± 38 μmol kg–1). In autumn the water column was oxygen undersaturated, the mean AOU was 25 ± 40 μmol kg–1, due to the prevalence of respiration processes. The concentration of TCO2 ranged between 2234 and 2582 μmol kg–1, both recorded during spring. In winter and spring high and comparable TCO2 concentrations were detected. In winter low temperatures enhance the solubility of CO2 in seawater and TCO2 increases (physical pump), even if this is a slow process it lasts for a long period. In spring these concentrations are due to freshwater inputs increase. The average TCO2 value decreased in summer and increased again in autumn, with the seawater cooling. As for AOU, there was a clear difference due the proximity to the Po River delta: higher values of TCO2 at the bottom, under the pycnocline in the most western stations, and a decrease at the bottom toward the eastern waters.
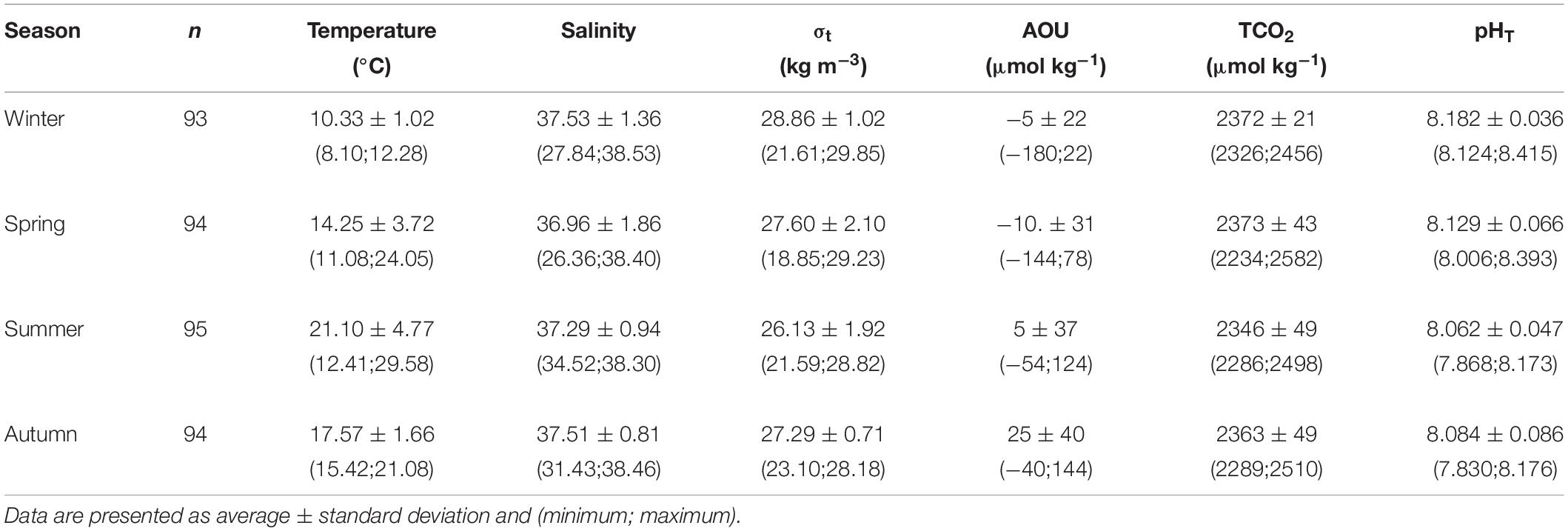
Table 1. Summary statistics for temperature, salinity, density anomaly (σt), apparent oxygen utilization (AOU), dissolved inorganic carbon (TCO2), and pHT at in situ temperature along the transect during the four seasons.
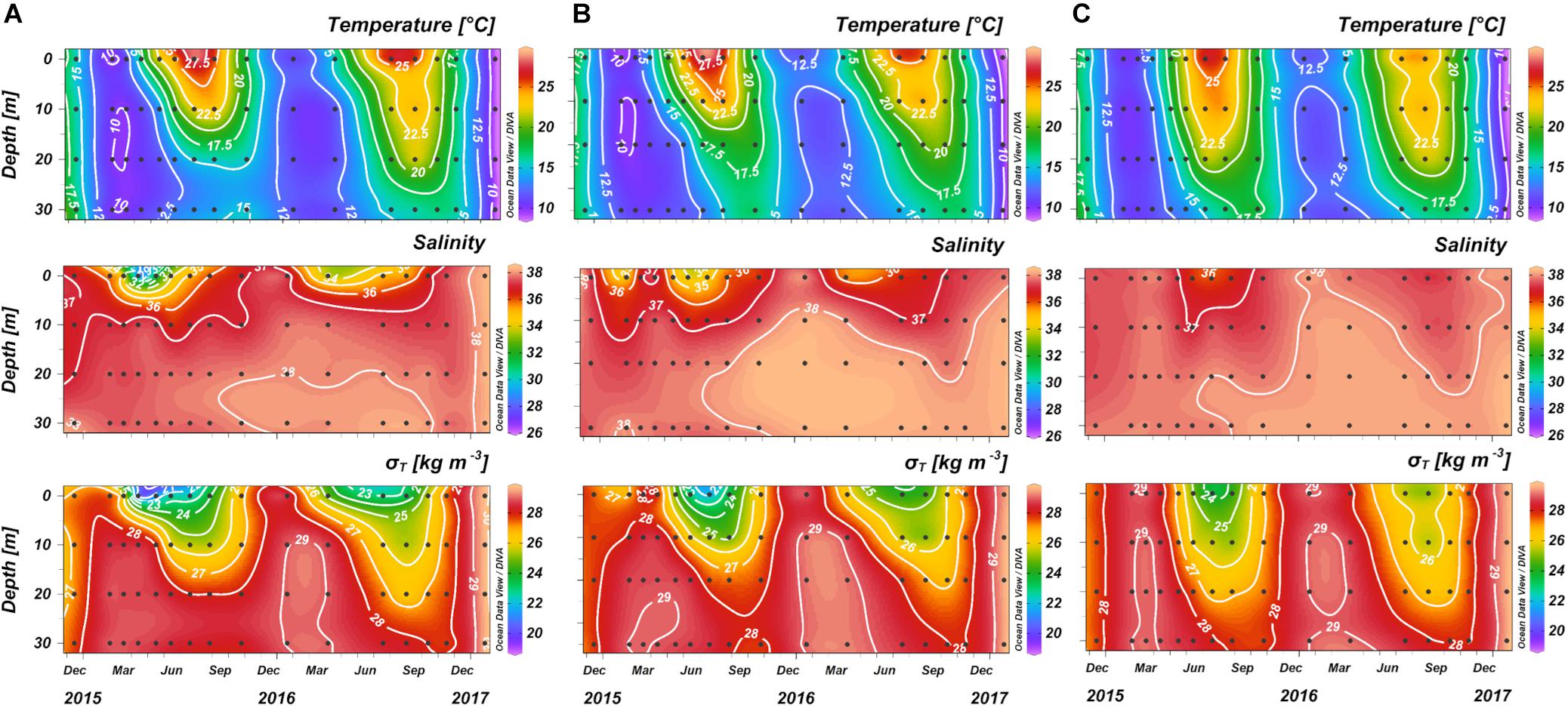
Figure 6. Temporal variations of temperature, salinity, and density anomaly (σt) in the stations: (A) SJ101, (B) SJ105, and (C) ZI032.
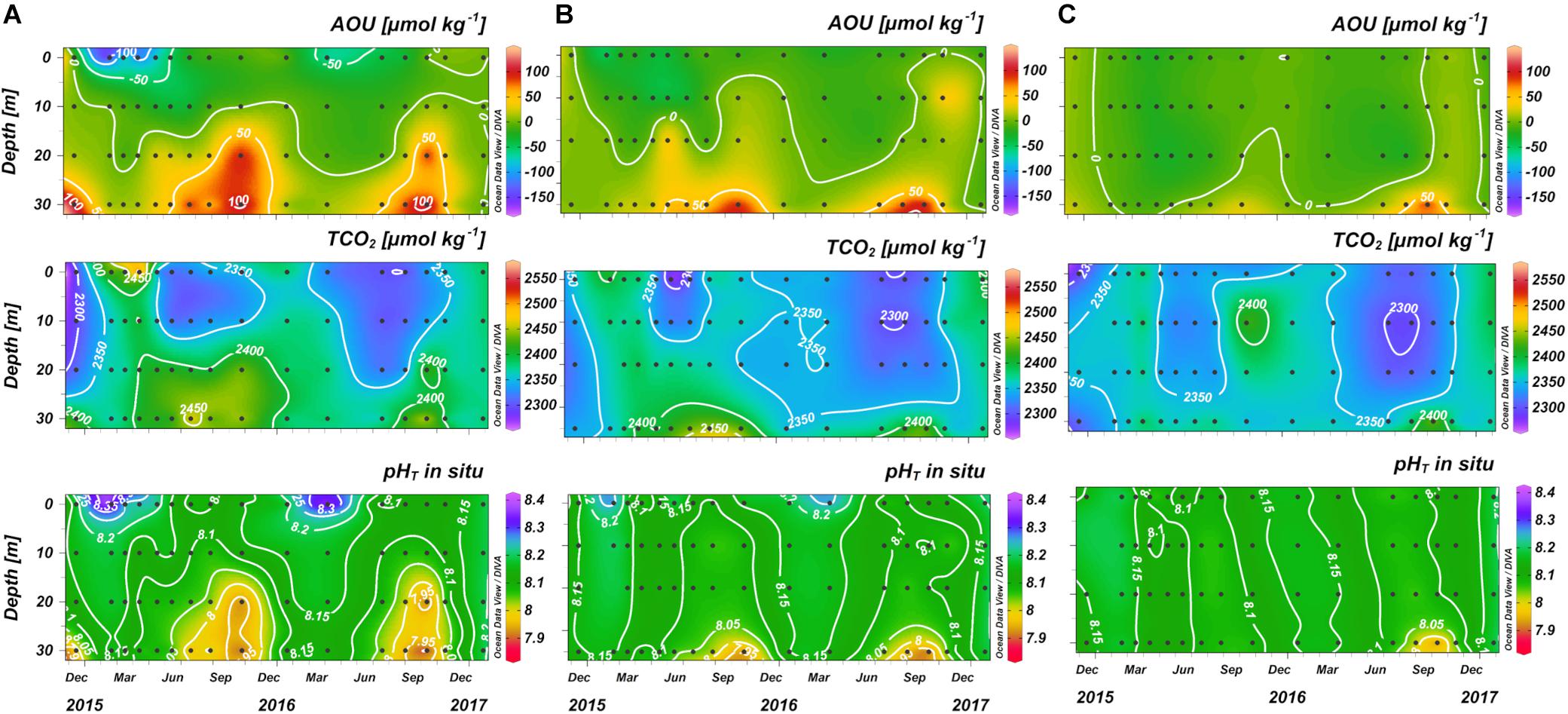
Figure 7. Temporal variations of apparent oxygen utilization (AOU), dissolved inorganic carbon (TCO2) and pHT in the stations: (A) SJ101, (B) SJ105, and (C) ZI032.
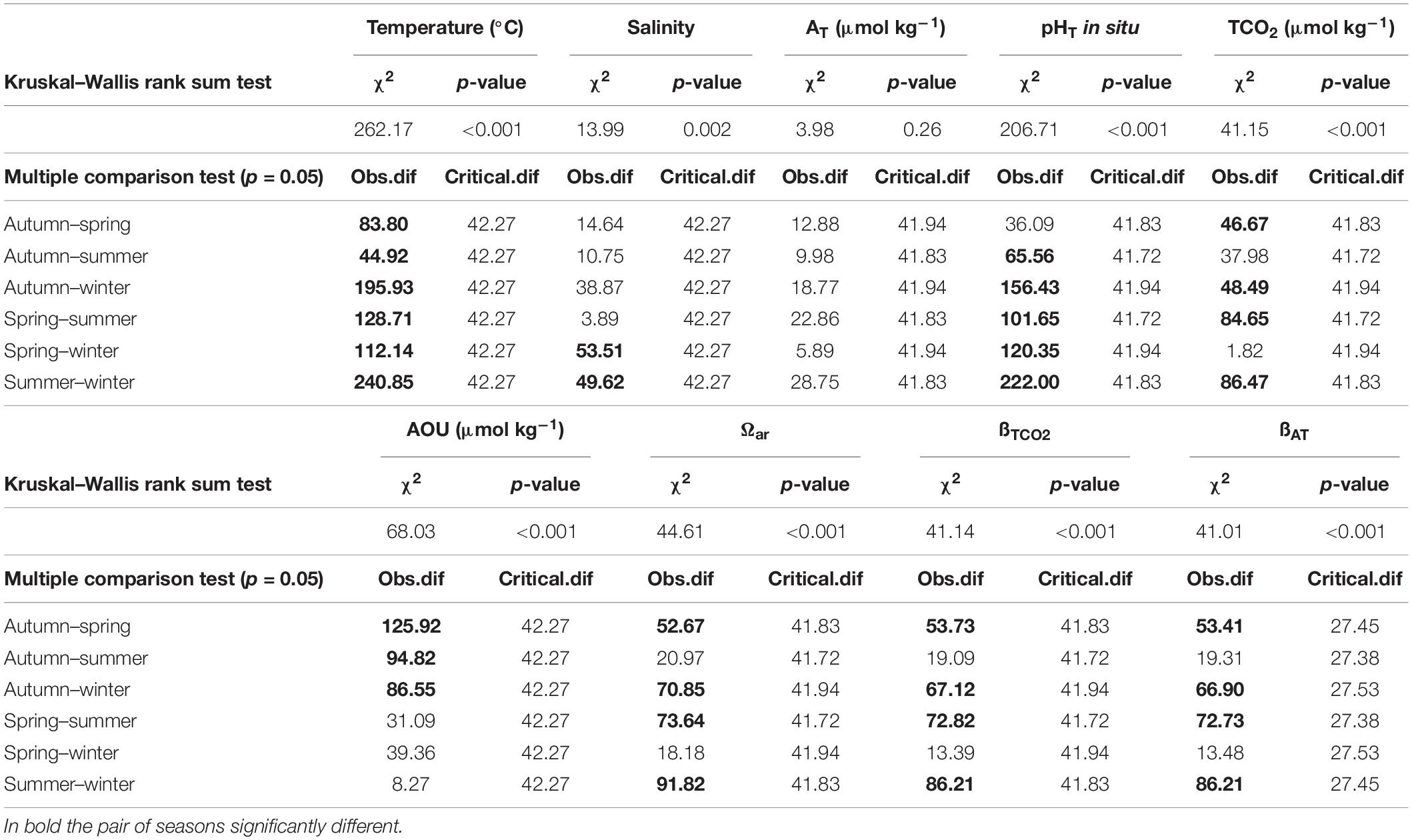
Table 2. Results of Kruskal–Wallis rank sum test and multiple comparison test among seasons on different physico-chemical parameters.
pHT seasonal variation strongly depended on thermal seasonal variation of seawater. During all the study period, the variation was of 0.585, with the maximum (8.415) reached in winter and the minimum (7.830) measured in autumn. pHT values were high in winter (8.182 ± 0.036), when the average temperature was 10.33 ± 1.02°C and gradually decreased with seawater warming in spring (8.129 ± 0.066) and summer (8.062 ± 0.086), The seawater cooling in autumn caused an increase in pHT (8.084 ± 0.086). pHT was significantly different (p < 0.001) among each season (Table 2), with the only exception of spring and autumn. The buffer capacity showed marked seasonal variations (Table 3): it was lower in winter and higher in summer. The highest values were observed in summer surface waters, due to the riverine inputs of total alkalinity and high seawater temperature that causes shifts in acid-base dissociation constants. All the buffer factors were significantly correlated (p < 0.0001) with temperature, βTCO2 directly and βAT and R inversely. In the surface waters, freshwater inputs increased the buffer factors (p < 0.005). Interestingly in bottom waters the buffer capacity was higher in winter and lower in summer (the opposite with respect to the upper water column). The saturation state also showed a marked seasonality, with the lowest values during winter and highest during summer, similarly to the buffer factors, in the bottom waters it was the opposite.
The CO2 System in the Different Water Types
Density, salinity and temperature were used to identify the main water types that characterize the northern Adriatic (Figure 8):
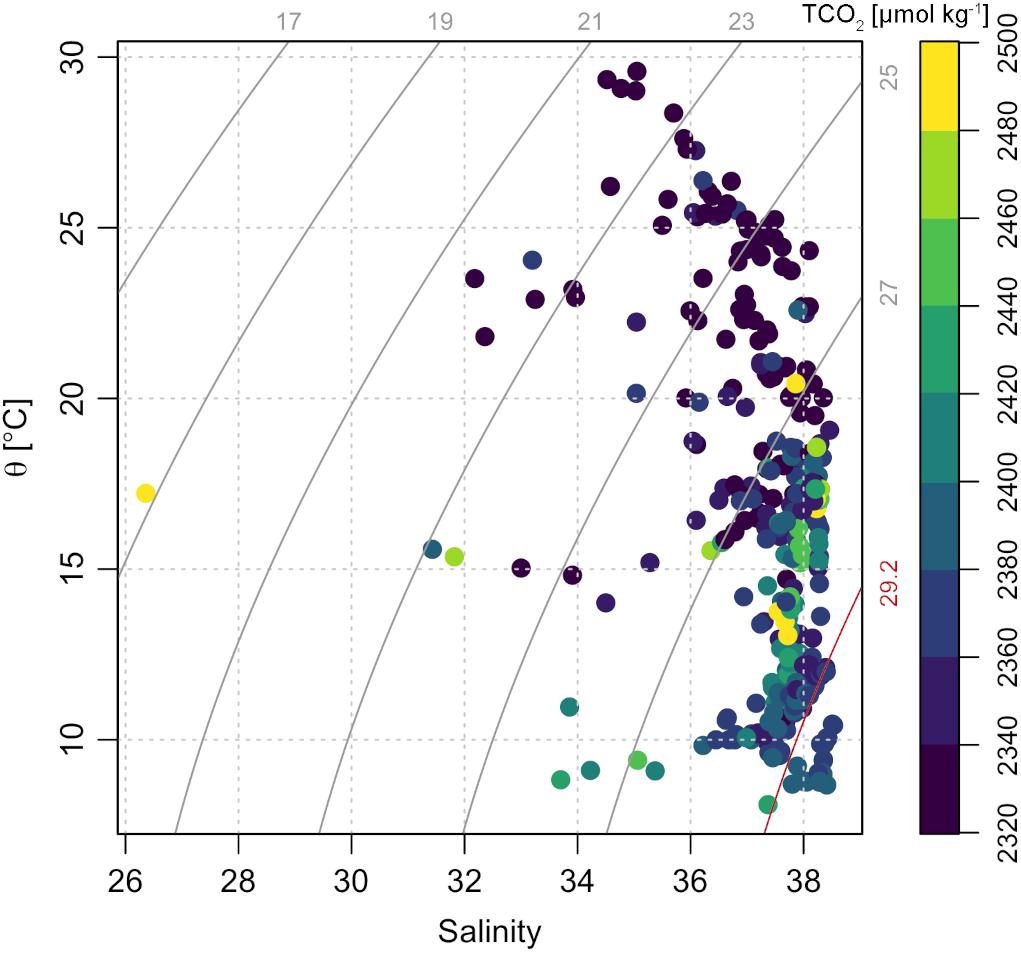
Figure 8. Potential temperature – salinity plot with isopycnes. The color scale represents dissolved inorganic carbon (TCO2) concentration. The plot was made using the R package oce (Kelley, 2018).
(1) the NAdDW: dense and cold water mass formed in winter;
(2) dense and relatively warm bottom waters present from late spring to autumn: they derive from NAdDW which, with warming and partial mixing, becomes progressively less dense;
(3) the NAdSW: surface waters diluted by the Po River, occurring throughout the entire year.
The NAdDW, characterized by σt values higher than 29.2 kg m–3 (Figure 8 and Table 4), was identified along the transect in January 2016 and 2017. In both periods the seawater temperatures were lower than 13°C and the salinity ranged from 37.80 to 38.53. In January 2016 the newly formed dense water filled the intermediate and bottom layers only in the central area of the transect. A remain of NAdDW was still present in April 2016, at the bottom of the central station (σt = 29.23 kg m–3). In winter 2017 lower temperature characterized the water column, reaching the minimum of 8.68°C. The dense waters formed as a result of the intense cooling combined with high salinity (37.80 – 38.53) and reached the maximum σt of 29.85 kg m–3. The relatively high salinity bottom waters with temperatures above 13°C, were typically present from spring through autumn during the investigated period (Table 4). In 2015 the mean salinity was 37.81 ± 0.27, with a mean temperature of 15.56 ± 1.77°C, while in 2016 the mean salinity was 38.17 ± 0.20, with a mean temperature of 16.46 ± 1.28°C. NAdSW, occupied the surface layer reaching the 10 m depth. The dilution was more marked in the western waters, especially during spring. The influence of fresh waters affected the water column differently throughout the seasons. This affect, was evident even in the eastern stations of the transect. Spring months showed the minimum salinity values throughout the year, ranging from 26.36 to 37.46. Salinity increased in summer and was more homogeneous (36.60 ± 0.87), and in autumn increased slightly (37.18 ± 0.97). Salinity values were lower in 2015 for all the seasons. In 2015 Po River discharges were higher (mean discharges: 1421 ± 765 m3 s–1 in 2015 and 1148 ± 615 m3 s–1 in 2016). The carbonate system showed different features in the identified water types: the concentration of AT was higher in NAdSW, where the absolute maximum and minimum were measured (Table 4). Average pHT values were lower in warm bottom waters, due to respiration process that occur under the pycnocline, as confirmed by AOU values above 0. In contrast, NAdDW were characterized by higher pHT and mean AOU concentrations close to 0 (Table 4). Warm bottom waters were characterized also by the highest average TCO2 concentration, while the lowest average TCO2 concentration was recorded in NAdSW (Table 4).
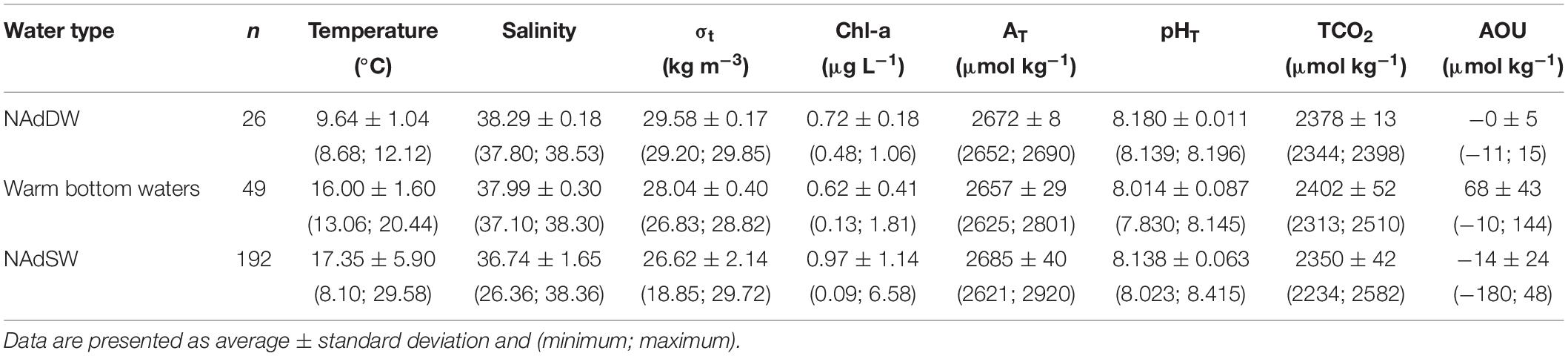
Table 4. Summary of temperature, salinity, density anomaly (σt), chlorophyll a (Chl-a), total alkalinity (AT), pHT at in situ temperature, dissolved inorganic carbon (TCO2) and apparent oxygen utilization (AOU) in the different water types.
Fluxes of CO2 at Seawater-Atmosphere Interface
The air-sea CO2 fluxes in the different seasons computed using W14 and N00 gas transfer velocity are presented in Table 5.
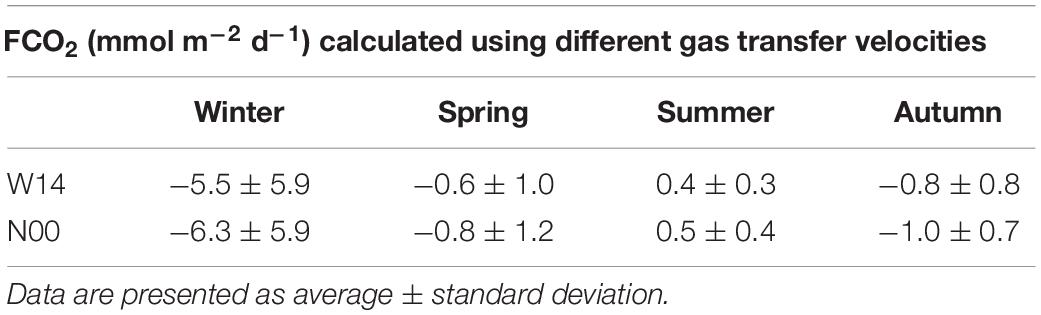
Table 5. Seasonal air-sea CO2 fluxes (FCO2) calculated using different gas transfer velocities: Wanninkhof (2014)-W14 and Nightingale et al. (2000)-N00.
The absolute difference between the two parameterizations ranged between 0.5 and 2.3 mmol m–2 day–1. During the investigated period FCO2 ranged from −14.9 mmol m–2 day–1 to 2.5 mmol m–2 day–1 adopting W14 parameterization, or from −15.2 mmol m–2 day–1 to 3.0 mmol m–2 day–1 according to N00 parameterization. FCO2 were strongly influenced by riverine inputs, temperature and wind speed. The study area acted as a sink of carbon dioxide during winter, spring and autumn; and as a source of CO2 during summer (Table 5). A clear influx of CO2 toward the sea was detected in January 2017 in all the stations of the transect (average FCO2 = −14.2 ± 0.5 mmol m–2 day–1 −W14 or −14.8 ± 0.5 mmol m–2 day–1 -N00). This condition was driven by the low seawater temperature, which led to pCO2 undersaturation in surface waters with respect to the atmosphere, in synergy with a wind speed 8.2 m s–1, more than the double of the mean wind speed of all the other months. The months with the most relevant flux of CO2 from the sea to the atmosphere were April 2015, just in the offshore stations (mean FCO2 = 2.3 ± 0.2 mmol m–2 day–1-W14; or 2.8 ± 0.2 mmol m–2 day–1-N00), and July 2016, except station SJ108 (mean FCO2 = 0.8 ± 0.4 mmol m–2 day–1-W14; or 1.2 ± 0.5 mmol m–2 day–1-N00). A different seasonal pattern between stations located close to the Po River mouth and offshore stations was evident. In March 2015 all the stations acted as a sink, whereas in April 2015 the two stations closer to the river acted as a CO2 sink, with an average FCO2 of −2.3 ± 1.2 mmol m–2 day–1-W14; or −2.8 ± 1.5 mmol m–2 day–1-N00, and the other stations of the transect acted as a CO2 source. This was probably due to an increase of Chl-a and nutrients in the stations inside the river plume, and to an increase of 4°C and a decrease of Chl-a 0.9 μg L–1 in the offshore stations, with respect to the previous month. In October 2016 on the contrary, all the stations of the transect acted as a CO2 sink (mean FCO2 = −2.7 ± 0.9 mmol m–2 day–1-W14; or −2.9 ± 1.0 mmol m–2 day–1-N00) except SJ101 that acted as a source of carbon dioxide (1.92.0 mmol m–2 day–1-W14; or mmol m–2 day–1-N00) due to higher temperature with respect to the adjacent stations.
Future Coastal Acidification
Considering the IPCC RCP 8.5 scenario, business as usual for the year 2100, the atmospheric pCO2 is projected to reach the value of 910 μatm and global mean sea surface temperature is expected to increase by 2.58°C. Under this scenario and without the effect of biological processes (Figure 9, air-equilibrated CO2 condition) the pHT is expected to decrease by approximately 0.3 in the northern Adriatic (warm bottom water pHT = 7.798, NAdSW pHT = 7.806). In the same way, the Ωar is expected to decline by about 1.3 units, reaching the value of 2.02 in the warm bottom waters and 2.15 in NAdSW. Respiration of organic matter leads to carbon dioxide production, which results in a greater reduction of pHT and Ωar. By considering the warm bottom waters with a mean AOU equal to that measured in our study (AOU = 68 μmol kg–1), pHT and Ωar are expected to reach the mean value of 7.679 and 1.58 respectively for the year 2100. The pHT and Ωar levels could be further reduced by stronger respiration events, as detected in warm bottom waters during autumn (AOU = 144 μmol kg–1), which could determine strong acidification conditions (pHT = 7.529) and Ωar very close to saturation level (Ωar = 1.15). In the NAdSW the future decline of pH and Ωar is less extreme, thanks to the predominance of photosynthetic activity that reduces the anthropogenic CO2 levels at the surface. Therefore, with average AOU levels detected for the NAdSW (−14 μmol kg–1) the acidification in the 2100 could be less marked: pHT = 7.829 and Ωar = 2.25. This trend could be further enhanced during events of high primary production (AOU = −181 μmol kg–1) which would rise the pH and carbonate saturation level far away from critical acidification conditions (pHT = 8.060 and Ωar = 3.51).
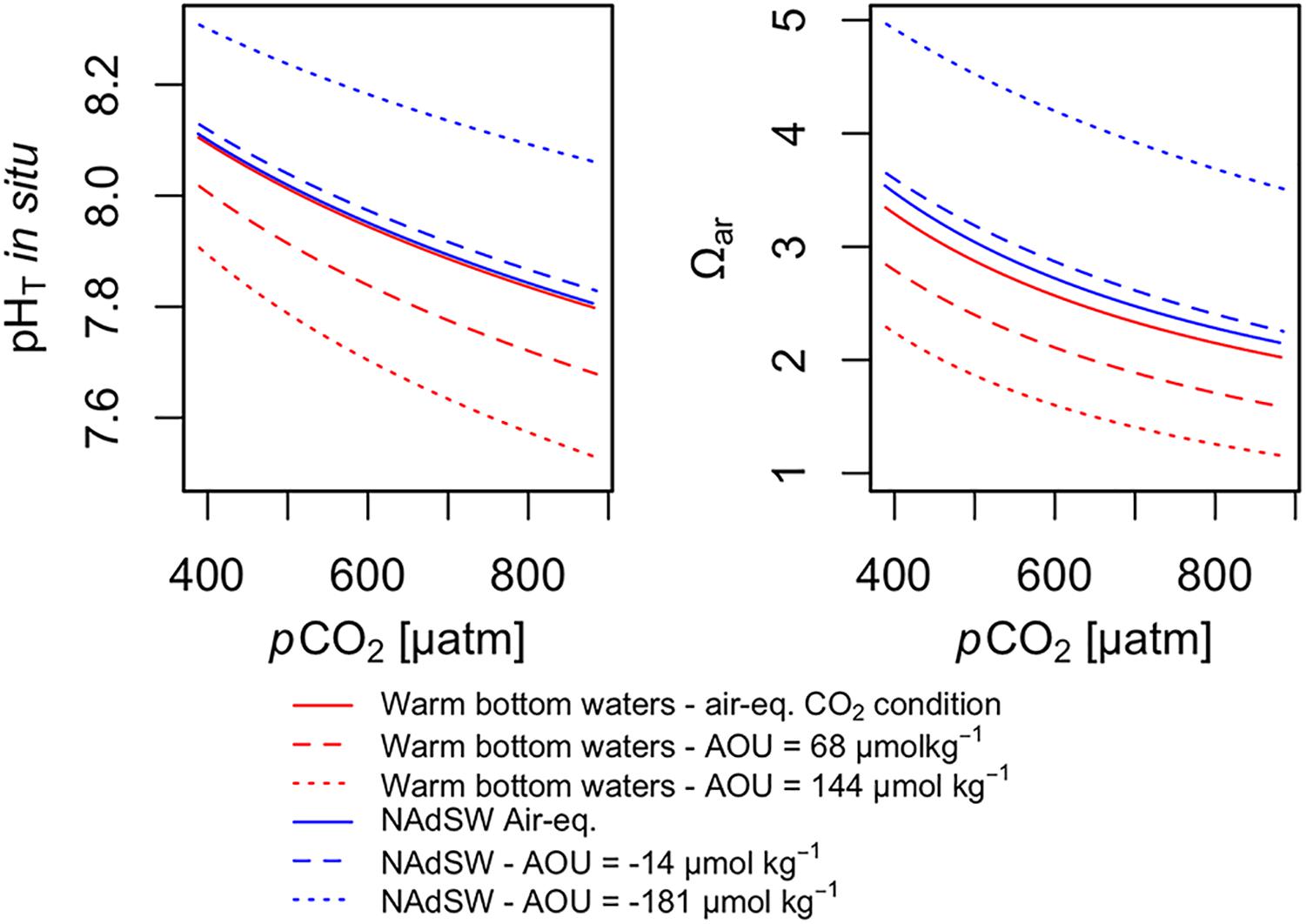
Figure 9. Simulated effect of atmospheric pCO2 increase on pHT and Ωar considering: (1) warm bottom waters and NAdSW at air-equilibrated CO2 conditions (without biological effect), (2) warm bottom waters with medium AOU (68 μmol kg–1) and high AOU (144 μmol kg–1) (3) NAdSW with medium AOU (–14 μmol kg–1) and high AOU (–181 μmol kg–1). All the modeled future changes in carbonate chemistry were calculated assuming a mean sea surface warming of 2.58°C for the year 2100 under the RCP 8.5 scenario.
Biogeochemical Processes Driving Carbonate System Seasonal Variation
Analysis of the relationship between nTCO2 and nAT can provide useful insights into the dominant biogeochemical processes that drive the carbonate system seasonal variation (Borges et al., 2003; Krumins et al., 2013; Sippo et al., 2016; Saderne et al., 2019). The slope of the regression between nAT and nTCO2 follows a stoichiometric relationship that is informative of a specific metabolic pathway (Figure 10). Assuming that organic matter has the Redfield Ratio C: N: P, the slopes for the main biogeochemical processes that occur in the water column or at the sediment-water interface are: aerobic respiration = −0.2, primary production = +0.2, denitrification = 0.8, nitrification = −1, calcium carbonate dissolution = 2.0, calcium carbonate precipitation = −2.0 (Krumins et al., 2013).
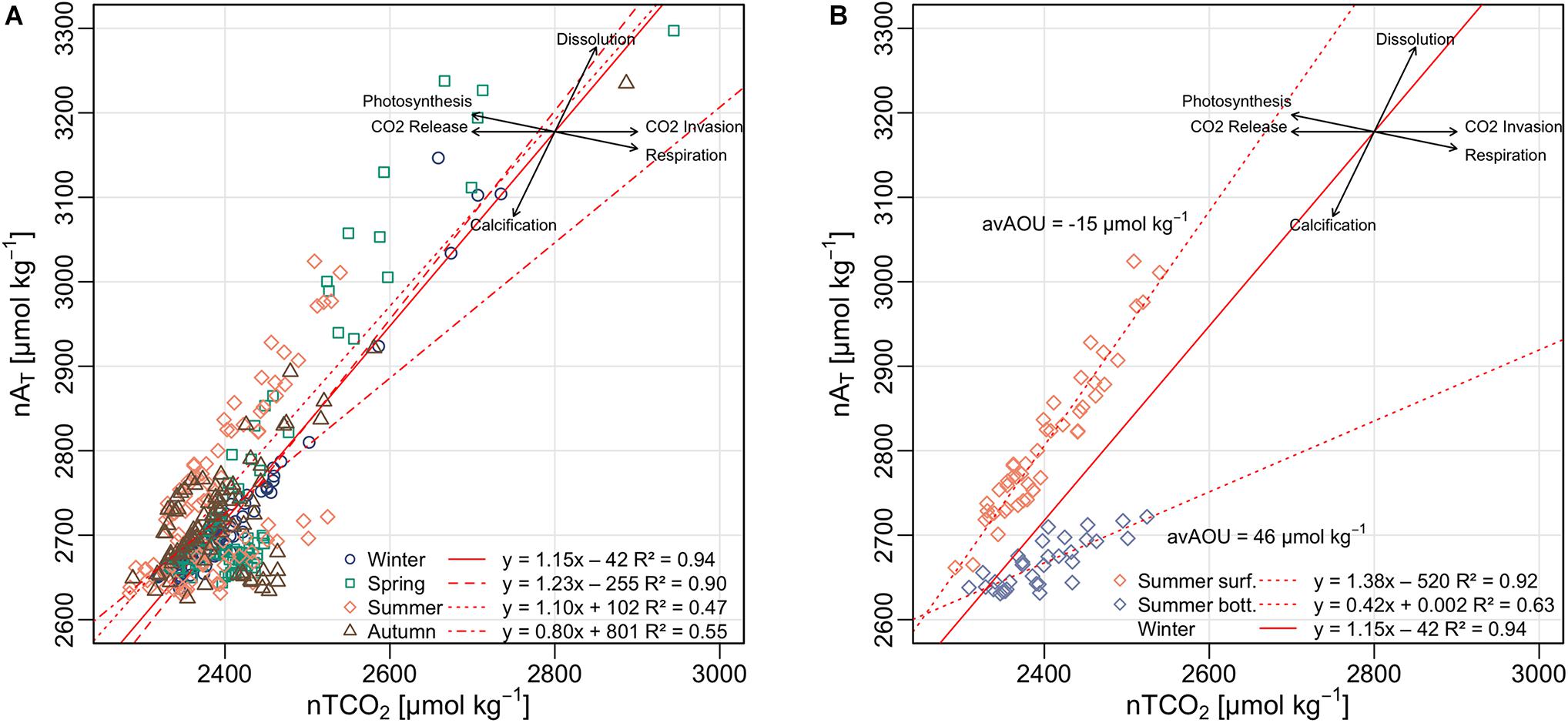
Figure 10. (A) nAT – nTCO2 relationship in the NAd and linear regressions of the different seasons. (B) Summer nAT – nTCO2 relationship of the surface and bottom waters. The vectors are represented following the stoichiometric ratios of the main biogeochemical processes in order to visualize the dominant processes driving the CO2 system.
In the northern Adriatic, the nAT-nTCO2 regression was statistically significant for all the seasons (F-statistic > 81.93, p < 0.001, R2 > 0.47) and the slopes ranged from 0.80 to 1.23, indicating a combination of biogeochemical processes that affect the carbonate system of the study area. The influence of biological activity on the carbonate system was very clear during summer (Figure 10B). By assuming winter as a reference period (slope = 1.15), due to its very low biological activity, and considering water column as a two layer system (i.e., surface and bottom waters), in summer the nAT-nTCO2 slope of the surface (1.38) was greater than the winter one by about 0.23, which indicate a relevant influence of the primary production (+0.2). On the other hand, the nAT-nTCO2 slope of the bottom waters (0.42) was 0.73 lower with respect to the winter reference. This could be interpreted as a combined effect of aerobic respiration (−0.2) and nitrification (−1.0), due to high concentration of AOU (46 μmol kg–1) and nitrate close to the bottom (Supplementary Figure 9). Therefore, nitrification could be considered a relevant metabolic pathway in this system. The correlation between pHT and Chl-a, was positive in autumn (p < 0.01) and negative in summer (p < 0.0001). The negative correlation in summer was probably due to remineralization processes under the pycnocline. Indeed, considering just the upper layer (down to 10 m depth) the correlation was positive (p < 0.01) while below 20 m it is still significantly negative (p < 0.001). The predominance of remineralization is also confirmed by the negative correlations (p < 0.01) between pHT and inorganic nutrients. This underscores the strong decoupling of production and respiration processes driven by seasonal stratification of water column in the area.
Discussion
Po River Role on Carbonate System Variability
Po River discharges are the major source of freshwater (47.17 km3 yr–1) and nutrients in the northern Adriatic basin (Cozzi and Giani, 2011), and, in concurrence with meteorological forcing, they drive a seasonal stratification regime and circulation pattern (Spillman et al., 2007). The distribution of land nutrients discharged by the river, follows the structure of the haline fronts, spreading, in particular conditions, along the entire basin (Russo and Artegiani, 1996) and showing a complex patchiness characterized by horizontal and vertical gradients (Cozzi et al., 2002). This patchiness strongly influences the distribution of the carbonate system parameters in all seasons and was also subject to the strength of the WAC and the EAC, which influences the spreading of riverine discharges.
The salinity seasonal average along the transect was low during spring–summer and high during autumn–winter (Table 1), following the same seasonal pattern of other riverine influenced areas of the NAd (e.g., Gulf of Trieste, Ingrosso et al., 2016a). The general negative relationship between AT and salinity is consistent with the findings of Cantoni et al. (2012) and Ingrosso et al.(2016a; 2016b), highlighting that the NAd acts as a source of alkalinity for the Mediterranean Sea. The AT-salinity correlation in the surface layer differed between seasons. AT values extrapolated at S = 0 varied from 2892 μmol kg–1 in autumn to 3616 μmol kg–1 in winter, while the TCO2 values at S = 0 varied from 2242.79 μmol kg–1 in summer to 2889.11 μmol kg–1 in winter, indicating a potential high temporal variability of riverine AT and TCO2 end-member. The supply of nutrients sustains the large productivity of the coastal zone especially during winter and spring, triggering intense phytoplankton blooms. This biological effect is underscored by the correlation between Chl-a and pCO2.
Buffer Capacity and Saturation State
Despite the marked seasonal “acidification,” the carbonate system never reached the undersaturation state: even with the lowest pHT value (7.830) the saturation state of aragonite (Ωar) was 2.04. This was probably due to the freshwater discharges, which increases the ratio alkalinity dissolved inorganic carbon and thus the buffering capacity of the system, as demonstrated by the lower Revelle factors at lower salinities. As the ratio AT/TCO2 in the oceans decreases in response to the uptake of atmospheric CO2, the buffer factors will decrease consequently. The net result will be a less efficient absorption of CO2 from the atmosphere and a greater sensitivity of [CO2], [H+], and Ω to environmental changes (Egleston et al., 2010). NAd was supersaturated with respect to both calcite and aragonite along the whole water column. Interestingly an opposite trend was found in bottom waters with respect to the upper water column. The buffer capacity and the saturation state were higher in winter and lower in summer in bottom waters, yet in surface they were lower in winter and higher in summer. This difference is due to the influence of riverine inputs and temperature at surface, which causes shifts in acid-base dissociation constants and a consequent increase of the buffering capacity. At the bottom, however, the segregation of seawater under the pycnocline causes an increase of respiration and organic matter remineralization processes, that lowers pHT and increases the concentration of TCO2, decreasing the saturation state of aragonite and the buffering capacity of the system. The 2-year average of the Revelle factor that we found (10.5 ± 0.9) is in agreement with previous studies for the Adriatic Sea (Luchetta et al., 2010; Álvarez et al., 2014; Ingrosso et al., 2016a). This underscores the high uptake capacity for the anthropogenic CO2 of the NAd (Ingrosso et al., 2017).
Air-Sea CO2 Fluxes Spatial and Temporal Variations
According to the “continental shelf pump” hypothesis (Tsunogai et al., 1999), winter cooling depresses seawater pCO2 below saturation, whereas nutrients inputs and biological CO2 drawdown in summer and the vertical export of organic matter and horizontal export of CO2, maintain the CO2 sink of the continental shelf throughout the year (Bates, 2006). On the basis of data available from 87 continental shelves, Chen et al. (2013) stated that most of the temperate regions are CO2-undersaturated and absorb CO2 from the atmosphere during most of the year. Summer is an exception as seawater warming increases pCO2 and surface water becomes a weak CO2 source (Chen et al., 2012). Our data show that the NAd acts prevalently as CO2 sink with higher influxes during the winter cooling, as found in specific areas of NAd (i.e., the Gulf of Trieste, Cantoni et al., 2012; Turk et al., 2013; Ingrosso et al., 2016a) and in the modeling study which considered the whole sub-basin (Cossarini et al., 2015b). In agreement with the findings of Chen et al. (2013), the CO2 effluxes are limited to the stratified period, mainly in spring or summer, as also found in the Gulf of Trieste by Ingrosso et al. (2016b). CO2 fluxes were directly correlated with the sea surface temperature (W14: r = 0.62; p < 0.0001; n = 96 – N00: r = 0.64; p < 0.0001; n = 96), this highlights the importance of the thermodynamic driver, that leads to effluxes at high temperatures, and influxes when temperatures are lower.
If we consider an increase in temperature of 21.5°C (measured between winter and summer) and we keep all other factors constant, the mean pCO2 of the shelf changes from 318 to 762 μatm. This demonstrates that temperature causes an increase of 21 μatm °C–1, pCO2 increases by 6.6% for an increase of 1°C, slightly higher than the 4.3% for an increase of 1°C reported by Takahashi et al. (1993), for a salinity range of 34–36 and a temperature range of 2–20°C. This emphasizes that the thermodynamic effect is relevant to determine the supersaturation in summer, and thus causing the system to be a source of carbon dioxide, if the heterotrophic processes prevail. The strongest influxes were observed near the Po River delta, at station SJ108 (mean of all the investigated period in station SJ108: FCO2 = −2.4 ± 3.9 mmol m–2 day–1-W14; or −2.8 ± 4.3 mmol m–2 day–1-N00), in agreement with the “continental shelf pump” hypothesis, whereas the effluxes occurred mostly in the central eastern waters. The observed spatial variations are attributable to a higher drawdown due to higher phytoplankton biomass in the western waters, influenced by riverine inputs. Measurements performed in the northernmost part of the NAd, the Gulf of Trieste, showed that Bora wind, a typical cold ENE wind, can determine higher daily inflows of the CO2 from the atmosphere (−22.6/−24.2 mmol m–2 day–1, Turk et al., 2013). Moreover, during winter a significant correlation between TCO2 and temperature was found (r = −0.69; p < 0.0001; n = 93) in surface waters, evidencing the role of the dense water formation in the CO2 absorption and transport southwards. Our average efflux in summer was 0.4 ± 0.34 mmol m–2 day–1-W14; or 0.5 ± 0.4 mmol m–2 day–1-N00, with a peak of 1.4 mmol m–2 day–1-W14; or 2.0 mmol m–2 day–1-N00 observed in July 2016 in station SJ101, but higher values, up to 11.4 ± 7.6 mmol m–2 day–1 where reported for the Gulf of Trieste (Turk et al., 2013). The strongest efflux was measured in April 2015, in the offshore waters, while the waters in the river plume acted as a sink. This difference was probably due to a prevalence of the biological processes in stations SJ108 and SJ101, inside the plume, where the input of Chl-a and nutrients supported primary production, and a predominance of the thermodynamic effect in the offshore waters, where temperature increased by 4°C with respect to the previous month. This hypothesis is supported by the T/B ratio analysis, that resulted higher than 1 (temperature effect stronger than the biological processes) in the central-eastern waters and below 1 in the coastal waters near the Po delta.
Future Trends
Estimating the long-term trend and variability of pH and saturation state in coastal areas is challenging and different modeling approaches have been used. Sunda and Cai (2012) showed that in waters like the Gulf of Mexico hypoxic zone, the combined effects of increasing anthropogenic pCO2 and respiratory increases in TCO2 on pH will be more than additive and will exert a synergistic interaction. While in areas like the Baltic Sea hypoxic zone there will be no synergism, but the effect of both processes together in lowering pH will still be worse than from either process alone (Sunda and Cai, 2012). With a similar methodological approach, Feely et al. (2018) demonstrated that pH and Ωar decrease related to the future anthropogenic CO2 emissions will be more severe in coastal waters affected by respiration-induced hypoxia. Shen et al. (2020), by using a retrospective coupled hydrodynamic-biogeochemical model simulations, demonstrated that pH variability in the mid Chesapeake Bay was primarily influenced by acidification and biological process, while river basification along with acidification played a key role in regulating the long-term Ωar variability. Our parameterization is in good agreement with these previous works, since we found a strong influence of biological processes on the future acidification in the northern Adriatic. Following the RCP 8.5 scenario, in warm bottom waters respiration could reach the mean value of 7.679 and 1.58 for pHT and Ωar, respectively. This acidification could be magnified by stronger respiration events, as detected during autumn, leading to lower pHT values and to a Ωar very close to the saturation level. This could be enhanced by the increase in hypoxic events and may cause significant negative impacts on ecosystems that are already stressed. On the other hand, in the NAdSW the future decline of pH and Ωar is less extreme, due to the predominance of photosynthetic activity, which reduces the anthropogenic CO2 levels at the surface. In this case, acidification in 2100 could be less marked and such condition could be further enhanced during events of high primary production that serve to raise the pH and carbonate saturation level far away from acidification conditions. However, it is important to consider our simulation as a simple estimation of the future CO2 system in the NAd based on physical-chemical constraints and considering different biological thresholds. Ocean acidification, warming and increased stratification will drive changes in marine microbial community (Dutkiewicz et al., 2015) and in their metabolic processes. We did not consider this aspect into our simulation since it is not yet known how these changes will alter global ecosystem functions, such as net primary production/respiration and export or air-sea gas exchange (Doney et al., 2020).
Comparison With Other Areas
CO2 Exchanges With the Atmosphere
Our CO2 influxes measured during winter 2017 (−14.2 ± 0.4 mmol m–2 day–1 -W14 or −14.8 ± 0.5 mmol m–2 day–1 -N00), when north-easterly Bora wind was blowing in the Gulf of Trieste, are comparable with the estimates of other temperate regions under freshwater influence. The Aegean Sea as a whole absorbs CO2 during winter at a rate ranging from −6.2 to −11.8 mmol m–2 day–1 (Krasakopoulou et al., 2009), while in the East China Sea in winter a −13.7 ± 5.7 mmol m–2 day–1 was measured (Chou et al., 2011). Estimating a mean annual flux based on the mean values for each season, we would get −0.4 mol m–2 y–1-W14 or −0.5 mol m–2 y–1-N00 for the year 2014/2015 and −0.8 mol m–2 y–1-W14 or −0.9 mol m–2 y–1-N00 for the year 2016/2017 which ranges from 35 to 85% (W14) or from 44 to 94% (N00)of the previous estimates of −1.0 and −1.06 mol m–2 y–1 made by Catalano et al. (2014) and by Cossarini et al. (2015b), respectively. This CO2 absorption from the atmosphere is of the same order of magnitude as the −1.8 mol m–2 y–1 estimated for the north-west European shelf by Kitidis et al. (2019) and as the −0.8 mol m–2 y–1 estimated for the Biscay Bay (Borges et al., 2006). Similar annual fluxes were reported also in the Otaru Bay (Sakamoto et al., 2008), in the New Jersey coast (Boehme et al., 1998) and in the East China Sea (Wang et al., 2000). Our results also underline that in NAd, as in other temperate areas as East China Sea, west European continental shelves (Tsunogai et al., 1999; Thomas et al., 2004; Borges, 2005; Bozec et al., 2005; Prowe et al., 2009), lower estuary of Guadalquivir Estuary and the Bay of Cádiz (Ribas-Ribas et al., 2011a), seawater pCO2 remains below atmospheric CO2 values for most of the year and these shelves are net CO2 sinks.
Our fluxes are, however, about five folds lower than the annual estimate of the Chukchi Sea shelf (Bates, 2006). This is due to the lower temperature and higher productivity of the Arctic region.
Carbonate System
Coastal ecosystems display a complex set of interacting processes that drive high pH variability over time.
An analysis of long-term pH measured in coastal waters around the world showed that seasonal variability could be as high as 1.4 pH units (Carstensen and Duarte, 2019). High-latitudes sites with low alkalinity buffering display largest seasonal ranges in pH, typically up to 1 unit as found in Baltic Sea and Danish straits (Carstensen et al., 2018; Carstensen and Duarte, 2019). Whereas pH in low- mid-latitude sites and with high alkalinity buffering typically vary less than 0.4 over the year. In our study despite high total alkalinity, the seasonal variability in pH was 0.59, which is a variation comparable with the one found in the gulf of Trieste by Cantoni et al. (2012). High seasonal change in temperature (ranging from 8.10 to 29.58°C) and strong decoupling of production and respiration processes likely explain this result. Effect of mixing on observed pH variability is, however, expected to be low, because coastal ecosystems receiving freshwater with AT > 1200 μmol kg–1 have modest variation in pH across a salinity gradient (Carstensen and Duarte, 2019). The effect of mixing on pH is typically more pronounced in sites with low and medium buffering, such as Northern Baltic Sea (Beldowski et al., 2010) and Chesapeake Bay (Brodeur et al., 2019) respectively, where changing salinity overall controls the mean pH levels.
Metabolic imbalance between production and respiration processes, which remove or add dissolved inorganic carbon respectively, is a key driver of pH change in this coastal ecosystem. Under present day conditions, biological metabolism results in a pH change of 0.59 in NAd (from 8.415 at the surface to 7.830 at the bottom waters). The metabolic-driven chemistry change of the carbonate system expected for 2100 (under RCP 8.5 scenario) is similar to present day condition, with pH variability range of 0.53 (8.060 to 7.529). This pH range is more pronounced than the one observed in the Gulf of Mexico, where oxidation-driven increases in CO2 result in pHT decreases of 0.46 under present day condition, and 0.51 under for 2100 under RCP 8.5 scenario (Feely et al., 2018).
In our study area a negative correlation between AT and salinity was found, especially in samplings close to flood events, showing that riverine inputs increase seawater total alkalinity. Negative AT-salinity correlations were also found in coastal areas of the Mediterranean Sea (Schneider et al., 2007; Cossarini et al., 2015a), in the North Aegean Sea (Krasakopoulou et al., 2017) and in the study of Ribas-Ribas et al. (2011b) near the mouth of the Guadalquivir River, Bay of Càdiz.
Thanks to the high AT and TCO2 riverine inputs the NAd was supersaturated, during all the seasons, with respect to both calcite and aragonite throughout the whole water column, in contrast to other coastal area where strong undersaturation (<0.6) is reached, as found in the Baltic Sea (Tyrrell et al., 2008), Long Island Sound (Wallace et al., 2014), and the lower St. Lawrence estuary (Mucci et al., 2011). In Chesapeake Bay for example Ωca is <1 in the bottom waters of the upper bay, but it is >1 in the lower bay (Brodeur et al., 2019). In the northern Gulf of Mexico indeed, notwithstanding a high acidification with pH in bottom waters of 7.85 or less, the Ωar is 2.63 ± 0.25 (Laurent et al., 2017) due to high alkalinity brought by Mississippi River (Wang et al., 2013).
Conclusion
This work presents temporal and seasonal variability of the CO2 system in the waters of the NAd based 16 cruises.
Po River influence contributes to maintain a gradient from coast to offshore. The freshwater discharges in NAd increase total alkalinity and total inorganic carbon, changing the buffer capacity of the system. In surface waters the riverine contribution enhances the buffer capacity, which is also positively correlated to temperature and reaches the higher values in summer.
Phytoplankton blooms triggered by river-borne nutrients fertilization, contribute to increase the pH in the upper part of the water column. The riverine discharges contribute also to enhance the saturation state in surface waters. With the progression of the sea warming and the formation of a marked pycnocline, in bottom waters the respiration and degradation of organic matter decrease pH, that reaches the minimum values in autumn.
The strong seasonal variability of the saturation state between winter and summer is mainly driven by the effect of temperature on the carbonate solubility, however, due to the CO2 increase under the pycnocline, the lowest values are reached during summer and autumn.
It is remarkable that in NAd, notwithstanding the high buffer capacity of the system, there is a high seasonal variability of pH (0.59) and also within the same season the pH variation between surface and bottom waters is of a similar amplitude. This finding highlight that the system could be very sensitive to changes in the balance between primary productivity and respiration processes.
The analysis of CO2 fluxes emphasized that the NAd acts overall as a sink of CO2, but with marked seasonal and spatial variations driven by wind strength, riverine inputs, temperature and biological processes. The CO2 absorbed from the atmosphere in the NAd contributes to the transport of anthropogenic CO2 in the deeper layers of the Mediterranean Sea through the dense waters formed in the area. The estimated annual influxes of CO2 are comparable to the fluxes measured in other temperate continental shelves.
The estimation of the future seawater CO2 chemistry for the end of the century highlights that, under business-as-usual scenario and without the effect of biological processes, pHT could decline by 0.3 and aragonite saturation by 1.3. Moreover, in the warm bottom waters during high respiration events Ωar could reach the value of 1.15. This value is very close to the saturation level and could negatively affect the marine biota, especially calcifying organisms, and subsequently lead to repercussions on the marine ecosystem.
Our results are important to advance the knowledge and the understanding of the global carbon cycle and will likely be of use for future studies to address potential changes in the NAd coastal acidification.
Data Availability Statement
Data are available at PANGAEA®. doi: https://doi.pangaea.de/10.1594/PANGAEA.916129.
Author Contributions
LU, MG, and GI wrote the draft. MG and TD conceived the study and the experimental design. LU performed the CO2 system analyses. TD collected the data from the field survey. SP performed the analyses of the pCO2 in air. All the authors interpreted all data, revised and approved the final version of the manuscript.
Funding
This research was carried out in the framework of Acid.It project financially supported by the Italian Ministry of Education, University and Research, and to other projects supported by Croatian Ministry of Science, Education and Sports.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank the crew of R/V Vila Velebita, and all the other CMR-RBI colleagues who contributed to sampling and analysis. Mauro Bastianini of CNR-ISMAR for the meteorological data measured at the oceanographic tower “Acqua Alta”, Damiano Sferlazzo, Alcide di Sarra, Tatiana Di Iorio, and Francesco Monteleone of ENEA for their contributions, Giulia Cataluffi who contributed to the CO2 system analyses, Erin Cox for the assistance and support during the writing. Measurements at Lampedusa contribute to the Integrated Carbon Observation System (ICOS), European Multidisciplinary Seafloor and water-column Observatory (EMSO), and Aerosols, Clouds and Trace Gases (ACTRIS) Research Infrastructures. We are in debt to Gianpiero Cossarini and Giorgio Bolzon of OGS for the Alka Open Cell 2.0 software development. We kindly acknowledge the three reviewers for the constructive comments that improved the quality of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.00679/full#supplementary-material
Footnotes
References
Álvarez, M., Sanleón-Bartolomé, H., Tanhua, T., Mintrop, L., Luchetta, A., and Cantoni, C. (2014). The CO2 system in the Mediterranean Sea: a basin wide perspective. Ocean Sci. 10, 69–92. doi: 10.5194/os-10-69-2014
Anthony, K. R. N., Kleypas, J. A., and Gattuso, J. P. (2011). Coral reefs modify their seawater carbon chemistry–implications for impacts of ocean acidification. Glob, Chan. Biol. 17, 3655–3666. doi: 10.1111/j.1365-2486.2011.02510.x
Artegiani, A., Bregant, D., Paschini, E., Pinardi, N., Raicich, F., and Russo, A. (1997). The adriatic sea general circulation: part I. Air-sea interaction and water mass structure; Part II. Baroclinic circulation structure. J. Phys. Oceanogr. 27, 1492–1532.
Bates, N. R. (2006). Air-sea CO2 fluxes and the continental shelf pump of carbon in the Chukchi Sea adjacent to the Arctic Ocean. J. Geophys. Res. 111, 1–21. doi: 10.1029/2005JC003083
Bates, N. R., Astor, Y. M., Church, M. J., Currie, K., Dore, J. E., and González-Dávila, M. (2014). A time-series view of changing ocean chemistry due to ocean uptake of anthropogenic CO2 and ocean acidification. Oceanogr. 27, 126–141. doi: 10.5670/oceanog.2014.16
Bednaršek, N., Harvey, C. J., Kaplan, I. C., Feely, R. A., and Mozina, J. (2016). Pteropods on the edge: cumulative effects of ocean acidification, warming, and deoxygenation progress. Oceanography 145, 1–24. doi: 10.1016/j.pocean.2016.04.002
Beldowski, J., Löffler, A., Schneider, B., and Joensuu, L. (2010). Distribution and biogeochemical control of total CO2 and total alkalinity in the Baltic Sea. J. Mar, Syst. 81, 252–259. doi: 10.1016/j.jmarsys.2009.12.020
Bensi, M., Cardin, V., Rubino, A., Notarstefano, G., and Poulain, P. M. (2013). Effects of winter convection on the deep layer of the Southern Adriatic Sea in 2012. J. Geophys. Res. 118, 6064–6075. doi: 10.1002/2013JC009432
Bockmon, E. E., and Dickson, A. G. (2014). A seawater filtration method suitable for total dissolved inorganic carbon and pH analyses. Limnol. Oceanogr. Methods 12, 191–195. doi: 10.4319/lom.2014.12.191
Boehme, S. E., Sabine, C. L., and Reimers, C. E. (1998). CO2 fluxes from a coastal transect: a time-series approach. Mar. Chem. 63, 49–67. doi: 10.1016/s0304-4203(98)00050-4
Borges, A. V. (2005). Do we have enough pieces of the jigsaw to integrate CO2 fluxes in the coastal ocean? Estuaries 28, 3–27. doi: 10.1007/bf02732750
Borges, A. V., Djenidi, S., Lacroix, G., Théate, J., Delille, B., and Frankignoulle, M. (2003). Atmospheric CO2 flux from mangrove surrounding waters. Geophys. Res. Lett. 30:1558. doi: 10.1029/2003GL017143
Borges, A. V., and Gypens, N. (2010). Carbonate chemistry in the coastal zone responds more strongly to eutrophication than ocean acidification. Limnol. Oceanogr. 55, 346–353. doi: 10.4319/lo.2010.55.1.0346
Borges, A. V., Schiettecatte, L. S., Abril, G., Delille, B., and Gazeau, F. (2006). Carbon dioxide in European coastal waters. Estuar. Coast. Shelf Sci. 70, 375–387. doi: 10.1016/j.ecss.2006.05.046
Bozec, Y., Thomas, H., Elkalay, K., and de Baar, H. J. W. (2005). The continental shelf pump for CO2 in the North Sea—evidence from summer observation. Mar. Chem. 93, 131–147. doi: 10.1016/j.marchem.2004.07.006
Brodeur, J. R., Chen, B., Su, J., Xu, Y.-Y., Hussain, N., and Scaboo, K. M. (2019). Chesapeake bay inorganic carbon: spatial distribution and seasonal variability. Front. Mar. Sci. 6:99. doi: 10.3389/fmars.2019.00099
Broecker, W. S., Takahashi, T., Simpson, H. J., and Peng, T. H. (1979). Fate of fossil fuel carbon dioxide and the global carbon budget. Science 206, 409–418. doi: 10.1126/science.206.4417.409
Brussaard, C. P. D., Gast, G. J., van Duyl, F. C., and Riegman, R. (1996). Impact of phytoplankton bloom magnitude on a pelagic microbial food web. Mar, Ecol. Prog. Ser. 144, 211–221. doi: 10.3354/meps144211
Cai, W.-J., Hu, X., Huang, W.-J., Murrell, M. C., Lehrter, J. C., and Lohrenz, S. E. (2011). Acidification of subsurface coastal waters enhanced by eutrophication. Nat. Geosci. 4, 766–770. doi: 10.1038/ngeo1297
Cantoni, C., Luchetta, A., Celio, M., Cozzi, S., Raicich, F., and Catalano, G. (2012). Carbonate system variability in the Gulf of Trieste (North Adriatic Sea). Estuar. Coast. Shelf Sci. 115, 51–62. doi: 10.1016/j.ecss.2012.07.006
Carstensen, J., Chierici, M., Gustafsson, B. G., and Gustafsson, E. (2018). Long-term and seasonal trends in estuarine and coastal carbonate systems. Glob. Biogeochem. Cycles 32, 497–513. doi: 10.1002/2017gb005781
Carstensen, J., and Duarte, C. M. (2019). Drivers of pH Variability in Coastal Ecosystems. Environ. Sci. Technol. 53, 4020–4029. doi: 10.1021/acs.est.8b03655
Catalano, G., Azzaro, M., Bastianini, M., Bellucci, L. G., Bernardi Aubry, F., and Bianchi, F. (2014). The Carbon budget in the northern Adriatic Sea, a winter case study. J. Geophys. Res 119, 1399–1417. doi: 10.1002/2013JG002559
Chan, F., Barth, J. A., Blanchette, C. A., Byrne, R. H., Chavez, F., and Cheriton, O. (2017). Persistent spatial structuring of coastal ocean acidification in the California Current System. Sci. Rep. 7:2526. doi: 10.1038/s41598-017-02777
Chen, C.-T. A., Huang, T.-H., Chen, Y.-C., Bai, Y., He, X., and Kang, Y. (2013). Air–sea exchanges of CO2 in the world’s coastal seas. Biogeosciences 10, 6509–6544. doi: 10.5194/bg-10-6509-2013
Chen, C. T. A., Huang, T. H., Fu, Y. H., Bai, Y., and He, X. (2012). Strong sources of CO2 in upper estuaries become sinks of CO2 in large river plumes. Curr. Opin. Env. Sust. 4, 179–185. doi: 10.1016/j.cosust.2012.02.003
Chou, W.-C., Gong, G.-C., Tseng, C.-M., Sheu, D. D., Hung, C.-C., and Chang, L.-P. (2011). The carbonate system in the East China Sea in winter. Mar. Chem. 123, 44–55. doi: 10.1016/j.marchem.2010.09.004
Cossarini, G., Lazzari, P., and Solidoro, C. (2015a). Spatiotemporal variability of alkalinity in the Mediterranean Sea. Biogeosciences 12, 1647–1658. doi: 10.5194/bg-12-1647-2015
Cossarini, G., Querin, S., and Solidoro, C. (2015b). The continental shelf carbon pump in the northern Adriatic Sea (Mediterranean Sea): influence of wintertime variability. Ecol. Modelling 314, 118–134. doi: 10.1016/j.ecolmodel.2015.07.024
Cozzi, S., and Giani, M. (2011). River water and nutrient discharges in the Northern Adriatic Sea: current importance and long term changes. Cont. Shelf Res. 31, 1881–1893. doi: 10.1016/j.csr.2011.08.010
Cozzi, S., Ibáñez, C., Lazar, L., Raimbault, P., and Giani, M. (2019). Flow regime and nutrient-loading trends from the largest south european watersheds: implications for the productivity of mediterranean and Black Sea’s Coastal Areas. Water 11:1. doi: 10.3390/w11010001
Cozzi, S., Lipizer, M., Cantoni, C., and Catalano, G. (2002). Nutrient balance in the ecosystem of the north western Adriatic Sea. Chem. Ecol. 18, 1–12. doi: 10.1080/02757540212685
DelValls, T. A., and Dickson, A. G. (1998). The pH of buffers based on 2-amino-2-hydroxymethyl-1,3-propanediol (‘tris’) in synthetic sea water. Deep Sea Res Part I 45, 1541–1554. doi: 10.1016/s0967-0637(98)00019-3
Dickson, A. G. (1990). Standard potential of the reaction – AgCl(S) +1/2h-2(g)=Ag(S) + HCl(Aq) and the standard acidity constant of the ion HSO4- in synthetic sea water from 273.15 to 318.15 K. J. Chem. Thermodyn. 22, 113–127. doi: 10.1016/0021-9614(90)90074-z
Dickson, A. G., and Goyet, C. (1994). Handbook of Methods for the Analysis of the Various Parameters of the Carbon dioxide System of Sea Water. Version 2. DOE (No. ORNL/CDIAC-74. Oak Ridge, TN: Oak Ridge National Lab.
Dickson, A. G., Sabine, C. L., and Christian, J. R. (eds) (2007). Guide to Best Practices for Ocean CO2 Measurements, Vol. 3. Sidney: North Pacific Marine Science Organization.
Doney, S. C., Busch, D. S., Cooley, S. R., and Kroeker, K. J. (2020). The impacts of ocean acidification on marine ecosystems and reliant human communities. Annu. Rev. Environ. Resour. 45, 11.1–11.30.
Doney, S. C., and Schimel, D. (2007). Carbon and climate system coupling on timescales from the precambrian to the anthropocene. Annu. Rev. Environ. Resour. 32, 31–66. doi: 10.1146/annurev.energy.32.041706.124700
Duarte, C. M., and Cerbrian, J. (1996). The fate of marine autotrophic production. Limnol. Oceanogr. 41, 1758–1766. doi: 10.4319/lo.1996.41.8.1758
Duarte, C. M., Hendriks, I. E., Moore, T. S., Olsen, Y. S., Steckbauer, A., and Ramajo, L. (2013). Is ocean acidification an open ocean syndrome? understanding anthropogenic impacts on seawater pH. Estuar. Coast. 36, 221–236. doi: 10.1007/s12237-013-9594-3
Dutkiewicz, S., Morris, J. J., Follows, M. J., Scott, J., Levitan, O., Dyhrman, S. T., et al. (2015). Impact of ocean acidification on the structure of future phytoplankton communities. Nature Climate Change 5, 1002–1006. doi: 10.1038/nclimate2722
Egleston, E. S., Sabine, C. L., and Morel, F. M. M. (2010). Revelle revisited: buffer factors that quantify the response of ocean chemistry to changes in DIC and alkalinity. Glob. Biogeochem. Cycles 24:GB1002. doi: 10.1029/2008GB003407
Fassbender, A. J., Sabine, C. L., and Feifel, K. M. (2016). Consideration of coastal, carbonate chemistry in understanding biological calcification. Geophys. Res. Lett. 43, 4467–4476. doi: 10.1002/2016GL068860
Feely, R. A., Okazaki, R. R., Cai, W. J., Bednaršek, N., Alin, S. R., and Byrne, R. H. (2018). The combined effects of acidification and hypoxia on pH and aragonite saturation in the coastal waters of the California current ecosystem and the northern Gulf of Mexico. Cont. Shelf Res. 152, 50–60. doi: 10.1016/j.csr.2017.11.002
Font, J., Béranger, K., Bryden, H., Budillon, G., Fuda, J. L., and Gačič, M. (2009). Executive Summary of CIESM Workshop 38 “Dynamics of Mediterranean Deep Waters. Monaco: CIESM Workshop Monographs.
Friis, K., Körtzinger, A., and Wallace, D. W. R. (2003). The salinity normalization of marine inorganic carbon chemistry data. Geophys. Res. Lett. 30:1085. doi: 10.1029/2002GL015898
Gačič, M., Lascaratos, A., Manca, B. B., and Mantziafou, A. (2001). “Adriatic deep water and interaction with the eastern mediterranean Sea,” in Physical Oceanography of the Adriatic Sea, eds B. Cushman-Roisin, M. Gačič, P. M. Poulain, and A. Artegiani, (Dordrecht: Springer), doi: 10.1007/978-94-015-9819-4_4
Gattuso, J.-P., Epitalon, J.-M., and Lavigne, H. (2015). Seacarb: Seawater Carbonate Chemistry. R Package Version 3.0.14. Available online at: https://cran.r-project.org/web/packages/seacarb/index.html
Gattuso, J.-P., Frankignoulle, M., and Wollast, R. (1998). Carbon and carbonate metabolism in coastal aquatic ecosystems. Annu. Rev, Ecol. Syst. 29, 405–434. doi: 10.1146/annurev.ecolsys.29.1.405
Gattuso, J.-P., Lee, K., Rost, B., and Schulz, K. (2010). “Approaches and tools to manipulate the carbonate chemistry,” in Guide for Best Practices in Ocean Acidification Research and Data Reporting, eds U. Riebesell, V. J. Fabry, L. Hansson, and J.-P. Gattuso, (Luxembourg: Office for Official Publications of the European Union).
Hassoun, A. E. R., Raad, N., Fakhri, M., Abboud-Abi Saab, M., Gemayel, E., and De Carlo, E. (2019). The carbonate system of the eastern-most mediterranean sea, levantine sub-basin: variations and drivers. Deep Sea Res. II 164, 54–73. doi: 10.1016/j.dsr2.2019.03.008
Hofmann, A. F., Peltzer, E. T., Walz, P. M., and Brewer, P. G. (2011). Hypoxia by degrees: establishing definitions for a changing ocean. Deep Sea Res. I 58, 1212–1226. doi: 10.1016/j.dsr.2011.09.004
Hopkins, T. S., Artegiani, A., Kinder, C., and Pariante, R. (1999). “A discussion of the northern Adriatic circulation and flushing as determined from the ELNA hydrography,” in The Adriatic Sea, Vol. 32, eds T. S. Hopkins, A. Artegiani, G. Cauwet, D. Degobbis, and A. Malej, (Brussel: European Commission), 85–106.
Ingrosso, G., Bensi, M., Cardin, V., and Giani, M. (2017). Anthropogenic CO2 in a dense water formation area of the Mediterranean Sea. Deep Sea Res. I 123, 118–128. doi: 10.1016/j.dsr.2017.04.004
Ingrosso, G., Giani, M., Comici, C., Kralj, M., Piacentino, S., and De Vittor, C. (2016a). Drivers of the carbonate system seasonal variations in a Mediterranean gulf. Estuar. Coast. Shelf Sci. 168, 58–70. doi: 10.1016/j.ecss.2015.11.001
Ingrosso, G., Giani, M., Cibic, T., Karuza, A., Kralj, M., and Del Negro, P. (2016b). Carbonate chemistry dynamics and biological processes along a river–sea gradient (Gulf of Trieste, northern Adriatic Sea). J. Mar. Syst. 155, 35–49. doi: 10.1016/j.jmarsys.2015.10.013
IPCC (2013). “The physical science basis,” in Contribution of Working Group I the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds T. F. Stocker, D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, et al. (Cambridge: Cambridge University Press), 1535.
IPCC (2014). “Climate change 2014: synthesis report,” in Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, eds R. K. Pachauri, and L. A. Meyer, (Geneva: IPCC), 151.
IPCC (2019). “Technical Summary,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate, eds H.-O. Pörtner, D. C. Roberts, V. Masson-Delmotte, P. Zhai, M. Tignor, E. Poloczanska, et al. (Geneva: IPCC).
Ivančič, I., and Degobbis, D. (1984). An optimal manual procedure for ammonia analysis in natural waters by the indophenol blue method. Water Res. 18, 1143–1147. doi: 10.1016/0043-1354(84)90230-6
Kapsenberg, L., Alliouane, S., Gazeau, F., Mousseau, L., and Gattuso, J.-P. (2017). Coastal ocean acidification and increasing total alkalinity in the northwestern Mediterranean Sea. Ocean Science 13, 411–426. doi: 10.5194/os-13-411-2017
Kapsenberg, L., and Hofmann, G. E. (2016). Ocean pH time-series and drivers of variability along the northern Channel Islands. California, USA. Limnol. Oceanogr. 61, 953–968. doi: 10.1002/lno.10264
Kelley, D. E. (2018). The OCE Package. In Oceanographic Analysis With R. New York, NY: Springer, 91–101.
Kitidis, V., Shutler, J. D., Ashton, I., Warren, M., Brown, I., and Findlay, H. (2019). Winter weather controls net influx of atmospheric CO2 on the northwest European shelf. Sci. Rep. 9:20153. doi: 10.1038/s41598-019-56363-5
Kleypas, J. A., Buddemeier, R. W., Archer, D., Gattuso, J.-P., Langdon, C., and Opdyke, B. N. (1999). Geochemical consequences of increased atmospheric carbon dioxide on coral reefs. Science 284, 118–120. doi: 10.1126/science.284.5411.118
Krasakopoulou, E., Rapsomanikis, S., Papadopoulos, A., and Papathanassiou, E. (2009). Partial pressureand air–sea CO2 flux in the aegean sea during February 2006. Cont. Shelf Res. 29, 1477–1488. doi: 10.1016/j.csr.2009.03.015
Krasakopoulou, E., Souvermezoglou, E., Giannoudi, L., and Goyet, C. (2017). Carbonate system parameters and anthropogenic CO2 in the North Aegean Sea during October 2013. Cont. Shelf Res. 147, 69–81. doi: 10.1016/j.csr.2017.04.002
Krumins, V., Gehlen, M., Arndt, S., Van Cappellen, P., and Regnier, P. (2013). Dissolved inorganic carbon and alkalinity fluxes from coastal marine sediments: model estimates for different shelf environments and sensitivity to global change. Biogeosciences 10, 371–398. doi: 10.5194/bg-10-371-2013
Kruskal, W. H., and Wallis, W. A. (1952). Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 47, 583–621. doi: 10.1080/01621459.1952.10483441
Kwiatkowski, L., and Orr, J. C. (2018). Diverging seasonal extremes for ocean acidification during the twenty-first century. Nat. Clim. Change 8, 141–145. doi: 10.1038/s41558-017-0054-0
Laurent, A., Fennel, K., Cai, W. -J., Huang, W. -J., Barbero, L., and Wanninkhof, R. (2017). Eutrophication-induced acidification of coastal waters in the northern Gulf of Mexico: insights into origin and processes from a coupled physical-biogeochemical model. Geophys. Res. Lett. 44, 946–956. doi: 10.1002/2016GL071881
Luchetta, A., Cantoni, C., and Catalano, G. (2010). New observations of CO2 induced acidification in the Northern Adriatic Sea, over the last quarter century. Chem. Ecol. 26, 1–17. doi: 10.1080/02757541003627688
Lueker, T., Dickson, A. G., and Keeling, C. D. (2000). Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: validation based on laboratory measurements of CO2 in gas and seawater at equilibrium. Mar. Chem. 70, 105–119. doi: 10.1016/s0304-4203(00)00022-0
Lüthi, D., Le Floch, M., Bereiter, B., Blunier, T., Barnola, J.-M., and Siegenthaler, U. (2008). High-resolution carbon dioxide concentration record 650,000–800,000?years before present. Nature 453, 379–382. doi: 10.1038/nature06949
Manca, B., and Giorgetti, A. (1999). “Flow patterns of the main water masses across transversal areas in the Southern Adriatic Sea: seasonal variability,” in The Eastern Mediterranean as a Laboratory Basin for the Assessment of Contrasting Ecosystems, eds P. Malanotte-Rizzoli, and V. N. Eremeev, (Netherlands: Kluwer Acad), 495–506. doi: 10.1007/978-94-011-4796-5_37
Millero, F. J., Lee, K., and Roche, M. (1998). Distribution of alkalinity in the surface waters of the major oceans. Mar. Chem. 60, 111–130. doi: 10.1016/s0304-4203(97)00084-4
Mucci, A., Starr, M., Gilbert, D., and Sundby, B. (2011). Acidification of Lower Sy. Lawrence Estuary Bottom Waters. Atmos. Ocean 49, 206–218. doi: 10.1080/07055900.2011.599265
Nightingale, P. D., Malin, G., Law, C. S., Watson, A. J., Liss, P. S., and Liddicoat, M. I et al. (2000). In situ evaluation of air-sea exchange parametrizations using novel conservative and volatile tracers. Global Biogeochem. Cycles 14, 373–387. doi: 10.1029/1999gb900091
Orr, J. C. (2011). “Recent and future changes in ocean carbonate chemistry,” in Ocean Acidification, eds J. P. Gattuso, and L. Hansson, (Oxford: Oxford Univ. Press), 41–66.
Orr, J. C., Epitalon, J.-M., Dickson, A. G., and Gattuso, J.-P. (2018). Routine uncertainty propagation for the marine carbon dioxide system. Mar. Chem. 207, 84–107. doi: 10.1016/j.marchem.2018.10.006
Parsons, T. R., Maita, Y., and Lalli, C. M. (1984). A Manual of Chemical and Biological Methods for Seawater Analysis. Oxford: Pergamon Press.
Pierrot, D., Lewis, E., and Wallace, D. W. R. (2006). MS Excel Program Developed for CO2 System Calculations. Technical Report. Oak Ridge, TN: U.S. Department of Energy.
Poulain, P. M. (2001). Adriatic Sea surface circulation as derived from drifter data between 1990 and 1999. J. Mar. Syst. 29, 3–32. doi: 10.1016/s0924-7963(01)00007-0
Provoost, P., van Heuven, S., Soetaert, K., Laane, R. W. P. M., and Middleburg, J. J. (2010). Seasonal and long term changes in pH in the Dutch coastal zone. Biogeosciences 7, 3869–3878. doi: 10.5194/bg-7-3869-2010
Prowe, A. E. F., Thomas, H., Pätsch, J., Kühn, W., Bozec, Y., Schiettecatte, L.-S., et al. (2009). Mechanisms controlling the air–sea CO2 flux in the North Sea. Cont. Shelf Res. 29, 1801–1808. doi: 10.1016/j.csr.2009.06.003
Pugnetti, A., Camatti, E., Mangini, O., Morabito, G., Oggioni, A., and Saggiomo, V. (2006). Phytoplankton production in Italian freshwater and marine ecosystems: state of the art and perspectives. Chem. Ecol. 22(Suppl. 1), S49–S69.
Querin, S., Cossarini, G., and Solidoro, C. (2013). Simulating the formation and fate of dense water in a midlatitude marginal sea during normal and warm winter conditions. J. Geophys. Res.: Oceans 118, 1–16. doi: 10.1002/jgrc.20092
R Core Team (2016). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Raicich, F., and Colucci, R. R. (2019). A near-surface sea temperature time series from Trieste, northern Adriatic Sea (1899–2015). Earth Syst. Sci. Data 11, 761–768. doi: 10.5194/essd-11-761-2019
Raicich, F., Malacic, V., Celio, M., Giaiotti, D., Cantoni, C., and Colucci, R. R. (2013). Extreme air-sea interactions in the Gulf of Trieste (North Adriatic) during the strong Bora event in winter 2012. J. Geophys. Res. 118, 5238–5250. doi: 10.1002/jgrc.20398
Redfield, A. C., Ketchum, B. H., and Richards, F. A. (1963). “The influence of organisms on the chemical composition of seawater,” in The Sea, ed. M. N. Hill, (New York, NY: Interscience), 26–77.
Revelle, R., and Suess, H. E. (1957). Carbon dioxide exchange between atmosphere and ocean and the question of an increase of atmospheric CO2 during the past decades. Tellus 9, 18–27. doi: 10.3402/tellusa.v9i1.9075
Ribas-Ribas, M., Gómez-Parra, A., and Forja, J. M. (2011a). Air–sea CO2 fluxes in the north-eastern shelf of the Gulf of Cádiz (southwest Iberian Peninsula). Mar. Chem. 123, 56–66. doi: 10.1016/j.marchem.2010.09.005
Ribas-Ribas, M., Gómez-Parra, A., and Forja, J. M. (2011b). Seasonal distribution of the inorganic carbon system and net ecosystem production in the north eastern shelf of the Gulf of Cadiz (Southwest Iberian Peninsula). Cont. Shelf Res. 31, 1931–1942. doi: 10.1016/j.csr.2011.09.003
Saderne, V., Baldry, K., Anton, A., Agustí, S., and Duarte, C. M. (2019). Characterization of the CO2 system in a coral reef, a seagrass meadow, and a mangrove forest in the central Red Sea. J. Geophys. Res. 124, 7513–7528. doi: 10.1029/2019JC015266
Sakamoto, A., Watanabe, Y. W., Osawa, M., Kido, K., and Noriki, S. (2008). Time series of carbonate system variables off Otaru coast in Hokkaido, Japan. Estuar. Coast. Shelf Sci. 79, 377–386. doi: 10.1016/j.ecss.2008.04.013
Schlitzer, R. (2018). Ocean Data View, Version 5.1.5. Available at http://odv.awi.de (accessed June 03, 2020).
Schneider, A., Wallace, D. W. R., and Kortzinger, A. (2007). Alkalinity of the Mediterranean Sea. Geophys. Res. Lett. 34:L15608. doi: 10.1029/2006GL028842
Shapiro, S. S., and Wilk, M. B. (1965). An analysis of variance test for normality (complete samples). Biometrika 52, 591–611. doi: 10.1093/biomet/52.3-4.591
Shen, C., Testa, J. M., Li, M., and Cai, W. J. (2020). Understanding anthropogenic impacts on pH and aragonite saturation in Chesapeake Bay: insights from a 30-year model study. J. Geophys. Res.: Biogeosciences 125:e2019JG005620. doi: 10.1029/2019JG005620
Siegel, S., and Castellan, N. J.Jr. (1988). Nonparametric Statistics for the Behavioral Sciences. New York, NY: McGraw-Hill Int, 213–214.
Sippo, J. Z., Maher, D. T., Tait, D. R., Holloway, C., and Santos, I. R. (2016). Are mangroves drivers or buffers of coastal acidification? Insights from alkalinity and dissolved inorganic carbon export estimates across a latitudinal transect. Global Biogeochem. Cycles 30, 753–766. doi: 10.1002/2015GB005324
Soetaert, K., Petzoldt, T., and Meysman, F. (2015). Marelac: Tools for Aquatic Sciences. R Package Version 2.1.5.
Spillman, C. M., Imberger, J., Hamilton, D. P., Hipsey, M. R., and Romero, J. R. (2007). Modelling the effects of Po River discharge, internal nutrient cycling and hydrodynamics on biogeochemistry of the Northern Adriatic Sea. J. Mar. Syst. 68, 167–200. doi: 10.1016/j.jmarsys.2006.11.006
Sunda, W. G., and Cai, W.-J. (2012). Eutrophication induced CO2-acidification of subsurface coastal waters: interactive effects of temperature, salinity, and atmospheric pCO2. Environ. Sci. Technol. 46, 10651–10659. doi: 10.1021/es300626f
Supič, N., and Vilibic, I. (2006). Dense water characteristics in the northern Adriatic in the 1967-2000 interval with respect to surface fluxes and Po river discharge rates. Estuar. Coast. Shelf Sci. 66, 580–593. doi: 10.1016/j.ecss.2005.11.003
Takahashi, T., Olafsson, J., Goddard, J. G., Chipman, D. W., and Sutherland, S. C. (1993). Seasonal variation of CO2 and nutrients in the high-latitude surface oceans: a comparative study. Global Biogeochem.Cycles 7, 843–847.
Takahashi, T., Sutherlan, S. C., Sweeney, C., Poisson, A., Metzl, N., and Tilbrook, B. (2002). Global sea–air CO2 flux based on climatological surface ocean pCO2, and seasonal biological and temperature effects. Deep-Sea Res. II 49, 1601–1622. doi: 10.1016/s0967-0645(02)00003-6
Thomas, H., Bozec, Y., Elkalay, K., and De Baar, H. J. W. (2004). Enhanced open ocean storage of CO2 from shelf sea pumping. Science 304, 1005–1008. doi: 10.1126/science.1095491
Tsunogai, S., Watanabe, S., and Sato, T. (1999). Is there a “continental shelf pump” for the absorption of atmospheric CO2? Tellus 51B, 701–712. doi: 10.3402/tellusb.v51i3.16468
Turk, D., Book, J. W., and McGills, W. R. (2013). pCO2 and CO2 exchange during high bora winds in the Northern Adriatic. J. Mar. Syst. 11, 65–71. doi: 10.1016/j.jmarsys.2013.02.010
Tyrrell, T., Schneider, B., Charalampopoulou, A., and Riebesel, U. (2008). Coccolithophores and calcite saturation state in the Baltic and Black Seas. Biogeosciences 5, 485–494. doi: 10.5194/bg-5-485-2008
UNESCO (1983). “Algorithms for computation of fundamental properties of seawater,” in UNESCO Technical Papers in Marine Science, (Paris: UNESCO).
UNESCO (1986). “Progress on oceanographic tables and standards 1983 e 1986, Work and recommendations of the Unesco/SCOR/ICES/IAPSO Joint Panel,” in UNESCO Technical Papers in Marine Science, (Paris: UNESCO).
Uppström, L. R. (1974). The boron/chlorinity ratio of deep-sea water from the Pacific Ocean. Deep Sea Res. 21, 161–162. doi: 10.1016/0011-7471(74)90074-6
van Vuuren, D., Edmonds, J., Kainuma, M., Riahi, K., Thomson, A., and Hibbard, K. (2011). The representative concentration pathways: an overview. Clim. Change 109, 5–31. doi: 10.1007/s10584-011-0148-z
Vilibič, I., Zemunik, P., Šepič, J., Dunič, N., Marzouk, O., Mihanovič, H., et al. (2019). Present climate trends and variability in thermohaline properties of the northern Adriatic shelf. Ocean Sci. 15, 1351–1362. doi: 10.5194/os-15-1351-2019
Wallace, R. B., Baumann, H., Grear, J. S., Aller, R. C., and Gobler, C. J. (2014). Coastal ocean acidification: the other eutrophication problem. Estuar. Coast. Shelf Sci. 148, 1–13. doi: 10.1016/j.ecss.2014.05.027
Wang, S. L., Chen, C. T. A., Hong, G. H., and Chung, C. S. (2000). Carbon dioxide and related parameters in the East China Sea. Cont. Shelf Res. 20, 525–544. doi: 10.1016/s0278-4343(99)00084-9
Wang, Z. A., Wanninkhof, R., Cai, W.-J., Byrne, R. H., Hu, X., and Peng, T.-H. (2013). The marine inorganic carbon system along the Gulf of Mexico and Atlantic coasts of the United States: insights from a transregional coastal carbon study. Limnol. Oceanogr. 58, 325–342. doi: 10.4319/lo.2013.58.1.0325
Wanninkhof, R. (2014). Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 12, 351–362. doi: 10.4319/lom.2014.12.351
Weiss, R. F. (1974). Carbon dioxide in water and seawater: the solubility of a non-ideal gas. Mar. Chem. 2, 203–215. doi: 10.1016/0304-4203(74)90015-2
Zavatarelli, M., Raicich, F., Artegiani, A., Bregant, D., and Russo, A. (1998). Climatological Biogeochemical characteristics of the Adriatic Sea. J. Mar. Syst. 18, 227–263. doi: 10.1016/s0924-7963(98)00014-1
Keywords: CO2 system, pH, Adriatic, river, fluxes, nutrients
Citation: Urbini L, Ingrosso G, Djakovac T, Piacentino S and Giani M (2020) Temporal and Spatial Variability of the CO2 System in a Riverine Influenced Area of the Mediterranean Sea, the Northern Adriatic. Front. Mar. Sci. 7:679. doi: 10.3389/fmars.2020.00679
Received: 11 May 2020; Accepted: 27 July 2020;
Published: 13 August 2020.
Edited by:
Nina Bednarsek, Southern California Coastal Water Research Project, United StatesReviewed by:
Mariana Ribas Ribas, University of Oldenburg, GermanyMatthew Paul Humphreys, Royal Netherlands Institute for Sea Research (NIOZ), Netherlands
Leif Anderson, University of Gothenburg, Sweden
Copyright © 2020 Urbini, Ingrosso, Djakovac, Piacentino and Giani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lidia Urbini, bHVyYmluaUBpbm9ncy5pdA==; Michele Giani, bWdpYW5pQGlub2dzLml0
 Lidia Urbini
Lidia Urbini Gianmarco Ingrosso
Gianmarco Ingrosso Tamara Djakovac
Tamara Djakovac Salvatore Piacentino
Salvatore Piacentino Michele Giani
Michele Giani