Understanding Environmental Changes in Temperate Coastal Seas: Linking Models of Benthic Fauna to Carbon and Nutrient Fluxes

Introduction

Coastal marine ecosystems have high ecological and societal values. They provide a range of services to society, such as fish and shellfish as livelihoods and recreational opportunities. Coastal systems also contribute to the regulation of climate and nutrient cycles, by efficiently processing anthropogenic emissions from land before they reach the ocean (Tappin, 2002; Laruelle et al., 2009; Regnier et al., 2013a, b; Ramesh et al., 2015). The high value of these ecosystem services is obvious considering that a large proportion of the world population lives close to the coast (Costanza et al., 1997, 2014).

Currently, coastal seas around the world are undergoing major ecological changes driven by human-induced pressures, such as climate change, anthropogenic nutrient inputs, overfishing and the spread of invasive species (Halpern et al., 2008; Cloern et al., 2016). In many cases, the changes alter underlying ecological functions to such an extent that new states are achieved and that baselines are shifted (Lotze et al., 2006; Duarte et al., 2009; Kemp et al., 2009). Globally, eutrophication is one of the major environmental problems in coastal ecosystems. Over the last century riverine inputs of nitrogen (N) and phosphorus (P) to the oceans have increased from 19 to 37 Tg N yr^–1 and from 2 to 4 Tg P yr^–1 (Beusen et al., 2016). Regionally, these increases were even more substantial as observed in the United States, Europe and China; in the Baltic Sea N and P loads increased by roughly a factor of three and six, respectively (Gustafsson et al., 2012). The riverine N flux has increased by an order of magnitude to coastal waters of China within thirty years, while P export has tripled between 1970 and 2000 (Qu and Kroeze, 2012; Cui et al., 2013).

Efforts to mitigate eutrophication through nutrient load reductions are hampered by the effects of climate change (Cloern et al., 2016). Changes in precipitation increase the runoff of N, P and carbon (C) from land, which together with warming and increased CO₂ dissolution alter the coupled marine nutrient and carbon cycles (Falkowski et al., 2000; Gruber and Galloway, 2008).

In contrast to the open ocean where biogeochemical cycling is largely dominated by pelagic processes driven primarily by ocean circulation, in the coastal zone, pelagic and benthic processes interact strongly and are driven by a complex and dynamic physical environment (Statham, 2012). Eutrophication in coastal areas leads to shifts toward rapidly growing opportunistic algae, and generally to a decline in benthic macrovegetation because of decreased light penetration, substrate change and more reducing sediments (Sand-Jensen and Borum, 1991; Cloern, 2001; Grall and Chauvaud, 2002). Increased production and warming waters have caused expanding hypoxia at the seafloor with a consequent loss of benthic fauna (Diaz and Rosenberg, 2008; Breitburg et al., 2018). Hypoxic systems tend to lose many long-lived higher organisms and biogeochemical cycles typically become dominated by benthic bacterial processes and rapid pelagic turnover (Griffiths et al., 2017). However, if hypoxia does not occur, benthic fauna tends to increase in biomass with eutrophication (Cederwall and Elmgren, 1980; Pearson and Rosenberg, 1987; Josefson and Rasmussen, 2000).

Changes in benthic biota have far-reaching impacts on biogeochemical cycles in the coastal zone and beyond. In the illuminated zone, benthic micro- and macrophytes mediate biogeochemical fluxes through primary production, nutrient storage and sediment stabilization and act as a habitat and food source for a variety of animals (Figure 1). Benthic animals contribute to biogeochemical transformations and fluxes between water and sediments both directly through their metabolism and indirectly by physically reworking the sediments and their porewaters and stimulating bacterial processes (Figure 1). Grazing on pelagic organic matter and biodeposition of feces and pseudofeces by suspension-feeding fauna increases organic matter sedimentation rates (Kautsky and Evans, 1987; Newell, 2004). In addition, nutrients and carbon are retained in biomass and transformed from organic to inorganic forms through metabolic processes (Herman et al., 1999; Josefson and Rasmussen, 2000; Ehrnsten et al., 2019b). Bioturbation, including sediment reworking and burrow ventilation activities (bioirrigation), redistributes particles and solutes within the sediment and enhances sediment-water fluxes of solutes (Kristensen et al., 2012; Villnäs et al., 2013). Bioturbation can also enhance resuspension of particles, a phenomenon termed ‘bioresuspension’ (Graf and Rosenberg, 1997; Le Hir et al., 2007). Together, all these processes affect physical and chemical conditions at the sediment-water interface (Rhoads, 1974; Aller, 1982; Lohrer et al., 2004; Stief, 2013), and strongly influence organic matter degradation (Aller, 1982; Furukawa, 2001; Canuel and Hardison, 2016). When up-scaled to the ecosystem level, such modified conditions can significantly alter the functioning of coastal ecosystems and ultimately, the role of the coastal zone in filtering and transforming nutrients and carbon.

FIGURE 1

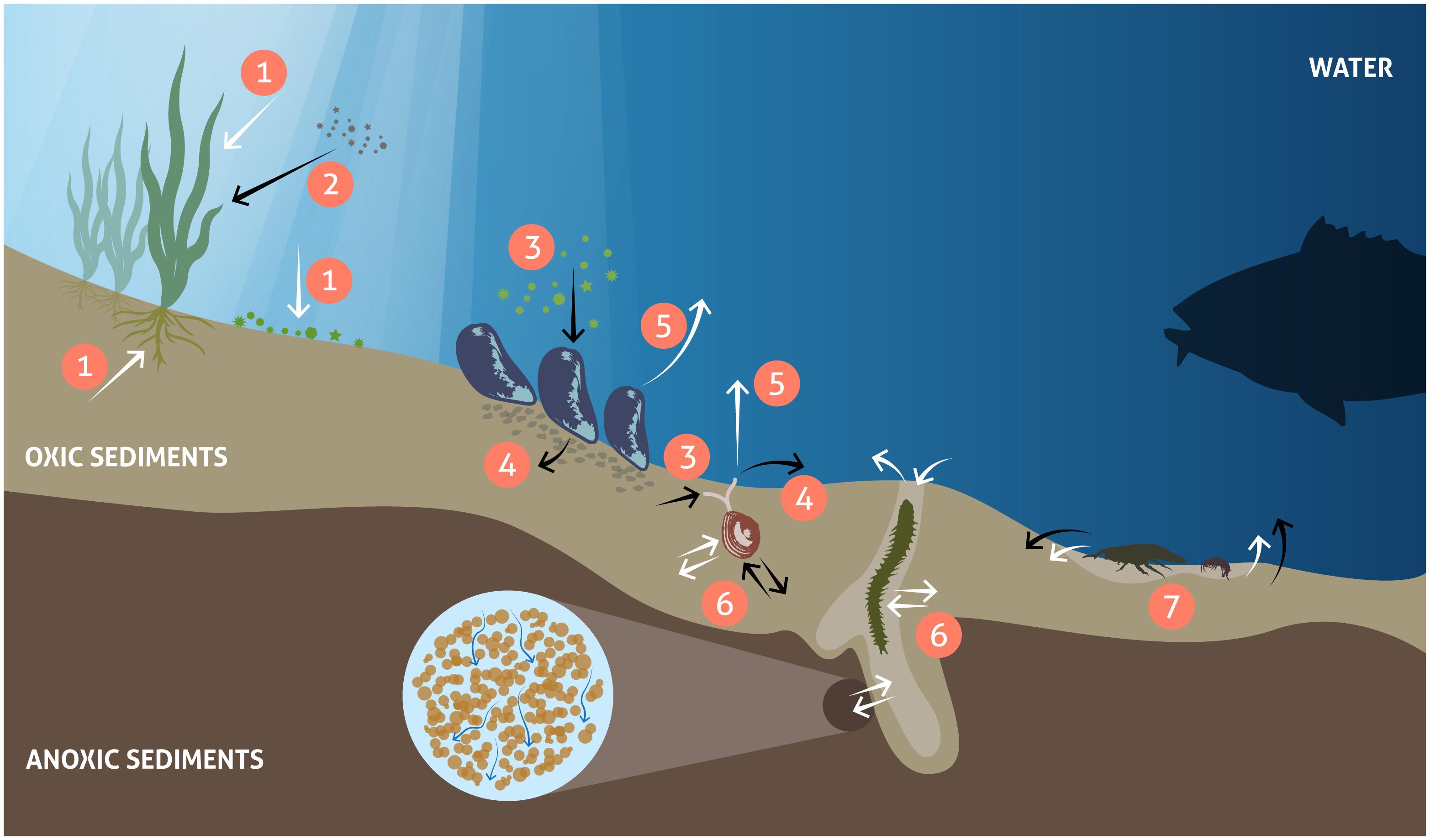
Figure 1. Major processes related to vegetation and fauna controlling benthic biogeochemical fluxes. White arrows: solute fluxes, black arrows: particulate fluxes. Primary production: nutrient and CO₂ uptake and oxygen release (1), enhanced sedimentation and sediment stabilization by benthic primary producers (2), food uptake (3), egestion/biodeposition of feces (4), nutrient excretion and respiration (5), and bioturbation, including bioirrigation (6) and mixing of sediments (7).

Accordingly, quantitative insight in the presence and activities of benthic biota and the tight and complex mechanisms controlling benthic ecosystem functioning at various spatial and temporal scales is of primary importance for unraveling nutrient and carbon cycles in coastal areas. Globally, numerous studies have measured bioturbation processes (Wheatcroft et al., 1990; Maire et al., 2010) and assessed the relation between benthic fauna and biogeochemical cycling through manipulative experiments (Michaud et al., 2005; Gilbertson et al., 2012; Renz and Forster, 2013, 2014; Braeckman et al., 2014). However, the results of such observations and experiments are generally not fully up-scaled to field situations. Especially in dynamic and heterogeneous coastal seas, lab-controlled experiments only consider limited parts of natural systems (Snelgrove et al., 2014). One way to circumvent lack of system knowledge is to use empirical models (i.e., models that are built solely on empirical observations without explicit descriptions of the underlying mechanisms) to analyze the response of a system to environmental changes. These may provide realistic system-level integrated information based on large-scale in situ observations of e.g., biogeochemical fluxes. However, as empirical models do not describe the underlying mechanisms, their predictive power beyond the observations is uncertain. Therefore, mechanistic models, i.e., models that mathematically describe the individual processes within the modeled system, are needed to elucidate the effects of environmental change on ecosystem functioning.

However, in existing mechanistic models of marine ecosystems, the sediment is often simplified to a reactive boundary layer (Soetaert et al., 2000; Savchuk, 2002; Lessin et al., 2018), while models focusing on sediment biogeochemistry (early diagenesis) have traditionally considered the role of fauna in mixing and transport processes (Aller, 1980; Boudreau, 1984), but not its metabolism and biomass dynamics (Middelburg, 2018; Snelgrove et al., 2018). While these approaches may be adequate in deep basins where biogeochemistry is dominated by pelagic processes and sediment biological dynamics are relatively stable, these assumptions do not hold in shallow coastal ecosystems where the coupling between benthic and pelagic systems is strong and highly dynamic over time. For example, studies from a long-term monitoring station in the North Sea suggest that the majority of sinking organic matter is processed by benthic macrofauna before it reaches the microbial community (Tait et al., 2015; Zhang et al., 2015; Lessin et al., 2019). Moreover, macrofaunal respiration has been estimated to account for up to 45–70% of benthic carbon mineralization in coastal areas of the Baltic Sea and Black Sea, with seasonal variations spanning one order of magnitude (Wenzhofer et al., 2002; Rodil et al., 2019).

Evidently, in order to represent both the current state of coastal ecosystems and, especially possible future developments, there is a clear need to include benthic biological processes in mechanistic models. Several authors have reviewed the effects of benthic primary producers (Nielsen et al., 2004; Duarte et al., 2005; McGlathery et al., 2007; Krause-Jensen and Duarte, 2016) and bioturbating fauna (Meysman et al., 2006b; Mermillod-Blondin, 2011; Norkko and Shumway, 2011; Kristensen et al., 2012; Stief, 2013) on nutrient and carbon processing, but the effects of biomass production and metabolism of benthic fauna, and especially mechanistic models thereof, have received relatively little attention.

In this review, we discuss current approaches that are used to model benthic fauna and their role as drivers of biogeochemical processes in the coastal zone, with a focus on fluxes of carbon (C), nitrogen (N) and phosphorus (P). First, we provide an overview of existing mechanistic models of biomass and metabolism that can be used to simulate the quantity of benthic fauna and its direct effects on biogeochemical fluxes in the coastal zone. We then discuss how these models can be used to quantify physical effects on the sediment, including bioturbation and bioresuspension, which require a coupling between benthic biology and physical transport models. In the third section, we provide examples of ecosystem models that allow these processes to be combined and up-scaled. We also examine the capabilities and limitations of current models for simulating changes in the benthos and associated nutrient fluxes in coastal areas under environmental change, and give suggestions for future research directions. The opportunities and challenges for modeling nutrient and carbon cycling in estuaries and marine sediments in general have recently been reviewed (Arndt et al., 2013; Regnier et al., 2013a; Ganju et al., 2016; Lessin et al., 2018). To avoid repetition, we only focus on the opportunities and challenges when integrating models of benthic fauna and the biogeochemistry of coastal ecosystems. We do not attempt an extensive review of all the relevant literature, but rather discuss current capabilities and future challenges through representative examples. Most of the modeling studies to date focus on temperate systems, and this region is also the focus of the current review.

Modeling the Effects of Benthic Fauna on Biogeochemical Fluxes

The impact of benthic fauna on nutrient and carbon cycling depends on e.g., density, biomass and the functional traits of individual species in the benthic community (Mermillod-Blondin et al., 2005; Norkko et al., 2013; Gammal et al., 2019), as well as on sediment structure (Braeckman et al., 2014; Bernard et al., 2019). Benthic animals process organic matter by consuming particulate organic matter (POM) and transforming a fraction of the ingested food into inorganic components that are respired and excreted (Figure 2). Organic matter is also incorporated in the biomass, transferred in the food web through predation and reproduction, and released back to the inanimate POM pool by egestion of feces and mortality. Detailed knowledge on the biomass and activity of benthic fauna is thus needed in order to quantify their effects on benthic nutrient fluxes. Below we go through different modeling approaches that couple biomass and metabolism of benthic fauna to biogeochemical processes in marine ecosystems.

FIGURE 2

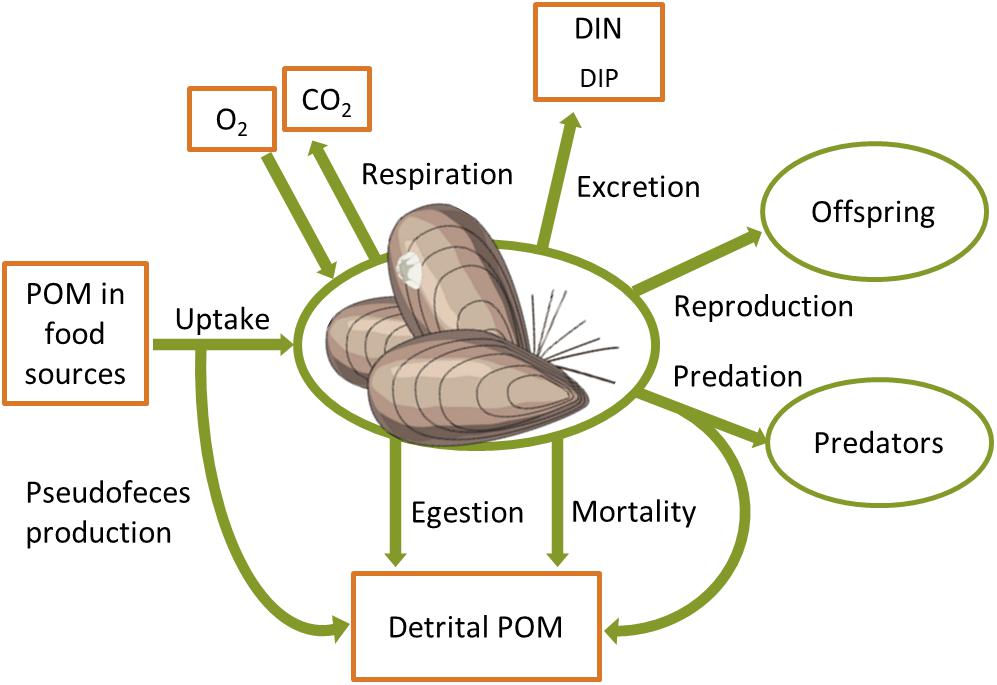
Figure 2. Biomass source and sink processes of a typical benthic animal with links to C, N, P and O cycles. POM, particulate organic matter; DIN, DIP, dissolved inorganic N and P, respectively.

Biomass Model Types and State Variables

The main sources and sinks of faunal biomass can be seen in Figure 2. The level of detail or aggregation of these source and sink processes varies among models, as seen in the examples in Table 1. The simplest models describe biomass of benthic fauna as a function of growth rate, mortality rate and environmental constraints, similar to conventional zooplankton formulations in pelagic biogeochemical models (Murray and Parslow, 1999; Fulton et al., 2004a; Kim and Montagna, 2009; Montagna and Li, 2010). For example, Murray and Parslow (1997, 1999) model the change in biomass of benthic suspension-feeders (B, in mg N m^–2) over time (t) as:

TABLE 1

Table 1. Examples of benthic fauna biomass models of different complexity.

$\frac{dB}{dt}=growth-mortality(1)$

where growth is a function of food uptake and a growth efficiency constant, and mortality is a function of biomass. While these kinds of models may include carbon and nutrient fluxes out of the organisms (cf. Figure 2) as derived variables, a more detailed and mechanistic approach is to model the metabolic fluxes explicitly. For example, in the benthic biological submodule of the European Regional Seas Ecosystem Model (ERSEM) (Baretta et al., 1995; Ebenhöh et al., 1995), the dynamics of a standard benthic organism representing a functional group (in units of C, N and P concentration) is expressed as a function of food uptake (U), egestion of feces (F), respiration of carbon (R) or excretion of nutrients (E), predation (P) and other mortality (M):

$\frac{dB}{dt}=U-F-R-E-P-M(2)$

This formulation is closely related to the ecological bioenergetics concepts developed in the International Biological Programme (Holme and McIntyre, 1971; Grodzinski et al., 1975), which also produced practical advice for the measurement of the component processes in benthic invertebrates (Holme and McIntyre, 1971; van der Meer et al., 2013). Similar formulations can also be found in Soetaert and Herman (1995), Cerco and Noel (2007), Maar and Hansen (2011), Timmermann et al. (2012) and Ehrnsten et al. (2019b).

In large-scale models like ERSEM, the macrofaunal biomass is often described by functional groups, representing feeding mode (e.g., suspension-feeders, deposit-feeders, predators), size (e.g., meiofauna, macrofauna) and/or position in relation to the sediment (e.g., infauna, epibenthos, hyperbenthos) (Soetaert and Herman, 1995; Murray and Parslow, 1999; HydroQual, 2000; Sohma et al., 2000, 2018; Fulton et al., 2004a, b; Maar and Hansen, 2011; Heath, 2012). Even though the dominant species belonging to a functional group may change over time and space, the rate of functional processes are generally more stable, making the functional group approach attractive when modeling systems on large scales (Vichi, 2002). However, the parameterization of such a model is not straightforward, as process rates are generally species and life-stage specific (Ebenhöh et al., 1995; Norkko et al., 2013).

More detailed models follow the biomass or energy dynamics of different life-stages of a population. For example, the Scope for Growth-model (Winberg, 1960) describes physiological processes of a standard organism similar to Eq. 2, but applies an allometric scaling function to the processes for different size classes. Spillman et al. (2008) use this approach to model the biomass dynamics of three size classes j of the infaunal clam Tapes philippinarum as:

$\frac{d{B}_j}{dt}=U_j-F_j-R_j-E_j-M_j-H_j+S{d}_j-T{r}_j+T{r}_{j-1}(3)$

where H is harvesting, Sd is seeding and Tr is recruitment between the size classes. Such structured population models avoid the error introduced by aggregating species and life-stages, and often include further processes, such as reproduction, which is usually omitted in functional group-based models. Structured population models are often used to study growth of farmed bivalves, but can also include feedbacks to biogeochemical cycles through ingestion of phytoplankton and detritus, excretion of dissolved nutrients and carbon, biodeposition of feces, and CO₂ production (Cranford et al., 2007; Grant et al., 2008; Spillman et al., 2008).

A simpler model type based on the universal allometric relationship between organism size and metabolic rate (Gillooly et al., 2001; Brown et al., 2004b) are size-based models, where diverse communities can be aggregated into size classes. This type of model has been used to simulate present and future C biomass of benthic meio- and macrofauna on a global scale (Yool et al., 2017).

Probably the most detailed and mechanistic approach to simulate faunal biomass is that used in Dynamic Energy Budget (DEB) models (Kooijman, 2000; van der Meer, 2006; Augustine and Kooijman, 2019). DEB models describe the processes that distribute energy through individual organisms from the uptake and assimilation of food to the utilization for maintenance, growth, development and reproduction. The models include energy reserves and structural tissue (e.g., shells) as separate state variables, allowing for a mechanistic description of energy distribution and conservation and varying C:N:P ratios within the individual. There are a few examples of DEB models integrated into in biogeochemical-hydrodynamic models used to study the effects of bivalves on nutrient cycles in coastal areas (Maar et al., 2009; Grangeré et al., 2010; Ren et al., 2010; Saraiva et al., 2017), but their more extensive use in this context is probably hampered by their complexity (Brown et al., 2004a; Filgueira et al., 2011), and because they require parameters that are difficult to derive from commonly measured rates (van der Meer, 2006).

A part of biomass dynamics rarely resolved is the migration and recruitment of pelagic life-stages. This requires a coupling between benthic biology and pelagic hydrodynamics, as well resolving different life-stages, including continued post-larval dispersal that may dominate dispersal and hence the maintenance of several benthic species (Pilditch et al., 2015). Supply and successful establishment of pelagic larvae may be an important factor limiting species occurrence and biomass especially in enclosed coastal areas (Barnes, 1994; Palmer et al., 1996). Saraiva et al. (2017) showed the importance of larval recruitment and survival for blue mussels Mytilus edulis in the Wadden Sea using a DEB model coupled to a 3D hydrodynamic-biogeochemical model.

Particulate Fluxes: Food Uptake, Egestion and Mortality

Benthic fauna redistributes and transforms POM in the sediment through its feeding and metabolic processes. Additionally, suspension-feeders increase pelagic-benthic fluxes of POM by grazing on plankton and detritus in the water column and biodepositing unassimilated particles on the sediment surface (Graf and Rosenberg, 1997). Biodeposition can have substantial effects on benthic nutrient cycles, especially in bivalve farming areas (Chapelle et al., 2000; Cranford et al., 2007; Mesnage et al., 2007). The high organic carbon and nitrogen content in biodeposits stimulate deposit-feeding and bacterial remineralization in the sediment, leading to accelerated removal of nitrogen through denitrification and recycling due to dissimilatory nitrate reduction to ammonium (DNRA) (Henriksen et al., 1983; Kautsky and Evans, 1987; Norkko et al., 2001).

When linking models of faunal metabolism to organic matter fluxes, it is important not only to quantify the amount of organic matter that is ingested, retained in biomass and released back through egestion and mortality, but also to determine how the composition of this organic matter changes along the way. Organic matter degradability (lability/bio-availability) is one of the most important parameters when quantifying nutrient and carbon cycling, but constraining this parameter in sediment models is challenging (Middelburg et al., 1996; Holstein and Wirtz, 2009; Lessin et al., 2018).

In models, food uptake is generally related to food concentration, and can be limited by various environmental variables such as temperature, salinity (Cerco and Noel, 2007; Spillman et al., 2008) and bottom water oxygen concentration (Blackford, 1997; Sohma et al., 2001; Maar et al., 2010; Timmermann et al., 2012) and, especially in the case of suspension-feeders, by crowding (Blackford, 1997; Fulton et al., 2004a). The Michaelis-Menten or type II functional response of asymptotic saturation (Holling, 1966) is a common expression for food uptake (or growth rate), but for suspension-feeders a linear type I response is often used (Dowd, 2005; see Jeschke et al., 2004 for a review). There are also various other functions in the literature, including type III sigmoid expressions (Fulton et al., 2003b), that are less frequently used.

The choice of response function is especially important to consider when models are used to extrapolate beyond present states. What may look like a linear or exponentially increasing response in the present ecosystem state (e.g., food uptake in relation to food availability or respiration in relation to temperature), may in fact reach saturation or even a decline at higher levels (e.g., as a consequence of eutrophication or climate change). Thus, choosing the appropriate parameterization requires knowledge of the shape of response curves for the whole range of simulated environmental conditions (Sharpe and DeMichele, 1977; van der Veer et al., 2006).

Only part of ingested food is assimilated, while the rest is egested as feces, adding to the pool of detrital POM. The production of feces (F) is often inversely related to an assimilation factor (AF), that reflects the assumed nutritional quality of the food (Soetaert et al., 1992; Ebenhöh et al., 1995; Timmermann et al., 2012):

$F=U(1-AF)(4)$

Although crucial, the assimilability of dead organic matter (detrital POM) is poorly restrained, with values for AF spanning from 0.15 (Blackford, 1997) to 0.8 (Heymans et al., 2016) used in different models. In a model of a deep-sea benthic food-web, van Oevelen et al. (2011) divided detrital organic carbon (POC) into labile, semi-labile and refractory fractions, with AFs depending both on the lability class of detritus and the group of fauna, based on an extensive literature review. They also assumed that egested POC ‘moves down’ one category, e.g., unassimilated labile detritus becomes semi-labile. A similar approach with two sediment food banks of different quality was used by Ehrnsten et al. (2019b), while Butenschön et al. (2016) used a dilution coefficient to account for the reduced nutrient content of feces compared to ingested material. In some DEB models, the assimilated food is assumed to have the same chemical composition as the reserve tissues in the animal, and thus the amount and composition of feces is dynamically modeled as the difference between ingested food composition and reserve composition (Saraiva et al., 2011).

Some suspension-feeding bivalves, primarily epifaunal mussels and oysters (Hawkins et al., 1998; Gallardi, 2014), have the capability to sort out nutrient-poor particles before ingestion and deposit them as mucus-bound pseudofeces. Pseudofeces production can be formulated as a simple threshold function: if food uptake exceeds a threshold value, the excess is released as pseudofeces (Klepper, 1989; Soetaert et al., 1992; Soetaert and Herman, 1995). More mechanistic approaches relate pseudofeces production to the amount of inorganic matter (Thomas and Bacher, 2018) or size and chemical composition of filtered particles (Saraiva et al., 2011).

In models where food assimilation is not explicitly modeled, the production of POM waste, including feces, pseudeofeces and loss through ‘messy feeding’ can be derived from uptake (U) and growth efficiency (GE) assuming a constant fraction (W_POM). Thus, for example, Murray and Parslow (1997) model the production of POM waste as:

$PO{M}_{waste}=U\left(1-GE\right)W_{POM}(5)$

The formulation of biomass removal terms depend on the aims of the study, and can include predation from benthos or a coupled pelagic food-web (Ebenhöh et al., 1995; Fulton et al., 2004b), harvest by humans (Fulton et al., 2004a; Spillman et al., 2007; Bossier et al., 2018) and ‘natural mortality.’ Additionally, cannibalism is not uncommon among the benthos, and especially in models where several species are aggregated into a functional group, a cannibalism term may be appropriate to represent predation within the group. This term also stabilizes the biomass dynamics in simple systems (Blackford, 1997), as does wide-spread omnivory. While predation and harvest generally remove biomass from a system, natural mortality, like feces, adds to the pool of POM that is readily available for bacterial decomposition. The different forces causing natural mortality are seldom modeled explicitly, but generally represented as a fixed fraction (M_nat) of biomass (B). Thus, the flux from mortality to POM (POM_mort) can be expressed as:

$PO{M}_{mort}=M_{nat}B(6)$

A fraction of the dead tissue can be assumed to be directed to a pool of dissolved organic matter (Butenschön et al., 2016). In seasonally hypoxic environments, hypoxia-induced mortality can be an important structuring factor of benthic populations and included as a separate mortality term (Blackford, 1997; Bossier et al., 2018; HydroQual, 2000; Maar et al., 2010; Soetaert and Herman, 1995; Sohma et al., 2001, 2018; Timmermann et al., 2012). In estuarine areas, mortality due to salinity variations can also be important (Spillman et al., 2008). DEB models can also include starvation mortality when catabolic needs exceed reserve density (Maar et al., 2009; Saraiva et al., 2017).

Some predators or other mortality inducing factors may act outside the model boundaries. In such cases, model closure by mortality is commonly achieved through either a linear or quadratic loss term (Fulton et al., 2003b). In cases where different kinds of biomass removal are aggregated into one mortality term (M_unresolved), it is not straightforward to link this to production of detrital POM, as part of the flow may be directed to sinks outside the model system. In such cases, an additional term is needed, describing the fraction of mortality directed to detrital POM (M_POM):

$PO{M}_{mort}=M_{unresolved}B{M}_{POM}(7)$

Solute Fluxes: Respiration and Nutrient Excretion

Respiration by benthic fauna consumes oxygen and thereby affects the redox conditions of sediments and bottom water. This, in turn, can alter the pathways of microbial degradation and recycling of carbon and nutrients. The mineralization of organic carbon through food uptake and subsequent respiration can also have major effects on the carbon cycle. Macrofaunal respiration has been estimated to account for ca 10-60% of annual benthic carbon mineralization in the Baltic Sea area (Elmgren, 1984; Hansen and Bendtsen, 2013; Ehrnsten et al., 2019b; Rodil et al., 2019). In a mussel-dominated area on the northwestern shelf of the Black Sea, up to 70% of carbon mineralization was attributed to macrofaunal respiration (Wenzhofer et al., 2002).

Respiration is commonly modeled as release of dissolved inorganic carbon, and oxygen consumption may then be calculated using a fixed stochiometric ratio (Ebenhöh et al., 1995; Fulton et al., 2004b; Spillman et al., 2008; Butenschön et al., 2016). However, oxygen consumption can also be modeled explicitly (Ichikawa et al., 2007; Maar et al., 2009). Respiration is commonly divided into a basal rate (R_b) dependent on biomass and active respiration as a fraction of food uptake (R_a), as feeding can be expected to correlate to some degree with activity. For example, Maar and Hansen (2011) model respiration (R) as a function of functional group biomass (B) and assimilated uptake (U x AF):

$R=R_{b}B+R_{a}UAF(8)$

In structured population models, respiration is usually allometrically scaled to individual biomass (Grant et al., 2008; Spillman et al., 2008), while in DEB models respiration is related to structural volume and reserve density (van der Meer, 2006). DEB models also specifically resolve the respiration related to the breakdown and assimilation of food. In all types of models, (basal) respiration is generally dependent on temperature, and might also be related to other environmental constraints such as oxygen concentration (Blackford, 1997) and salinity (Spillman et al., 2008).

The metabolic processes of animals lead to waste products that are released through excretion. Excretion of dissolved nutrients by dense bivalve populations can increase pelagic concentrations of nitrogen and promote phytoplankton production (Asmus and Asmus, 1991; Dame and Libes, 1993; Prins and Smaal, 1994), but the balance between effects of grazing, denitrification and DNRA in biodeposits and nitrogen excretion on the total N budget is highly dependent on the local hydrological and biological setting (Smyth et al., 2018). A depleting effect on phytoplankton can generally be expected when the clearance time is approximately equal to phytoplankton turnover time and shorter than water residence time (Dame and Prins, 1998; Grall and Chauvaud, 2002).

The effect of infaunal excretion on benthic nutrient fluxes has been suggested to be negligible compared to microbial processes (Aller, 1978; Tuominen et al., 1999) and is often omitted in sediment diagenetic models. It is difficult to accurately measure infaunal excretion in situ, but several studies estimate considerable contributions to sediment-water fluxes. For example, Kristensen (1984) estimated that a third of sediment-water NH₄ flux originated from excretion by the polychaete worm Nereis virens in a fjord system in the Baltic Sea, while Magni et al. (2000) estimated excretion rates of NH₄ and PO₄ by infaunal bivalves one order of magnitude higher than fluxes from defaunated sediments in a sandy tidal flat environment in Japan. They also estimated 10- to 100-fold seasonal variations in excretion fluxes, highlighting the importance of temporal variations in biologically mediated fluxes in coastal areas. In another study from the Baltic Sea, Norkko et al. (2013) showed that the outflux of NH₄ and PO₄ from shallow sandy sediments was directly proportional to the biomass of infaunal bivalves.

The chemical composition of an animal is generally fixed within certain limits. In models including both carbon and nutrient components in the biomass, a fixed carbon to nutrient ratio is often assumed and maintained through excretion of excess nutrients as dissolved ammonium NH₄ (Ebenhöh et al., 1995; Maar and Hansen, 2011) or, more rarely, phosphate PO₄ (Vichi, 2002; Spillman et al., 2008). When food is poor in nutrients, excess carbon can instead be respired (Ebenhöh et al., 1995). Some models also assume that a proportion of ingested food is excreted as dissolved organic carbon (Spillman et al., 2008). In simpler model formulations where stoichiometry is not resolved, nutrient release cannot be dynamically modeled in this way. However, nutrient release can be formulated as a constant proportion of uptake or growth rate similar to Eq. 5 (Murray and Parslow, 1997; Fulton et al., 2004a).

Physical Effects on the Sediment

Bioturbation

Benthic animals physically disturb the sediments in different ways (Figure 1). Their activities can alter the distribution of chemical substances and microorganisms and change redox conditions, and thus play a dominant role in biogeochemical fluxes across the sediment-water interface. The physical mixing of sediments by burrowing and by ingestion and defecation is generally referred to ‘biodiffusion’, a random, diffusive-like process (Goldberg and Koide, 1962; Aller, 1982; Boudreau, 2000; Meysman et al., 2003). Mixing between non-adjacent parts of the sediments is called ‘non-local mixing,’ but in the case of a diverse benthic community, this is commonly overshadowed by biodiffusion. Another activity is water exchange between the sediment and the overlying water through burrows or tubes built by benthic macrofauna, which is termed ‘bioirrigation.’ Bioirrigation can alter benthic fluxes by expanding the area of the sediment-water interface (Rhoads, 1974; Aller, 1988, 2001; Kristensen, 1988, 2001; Robbins, 1986; Boudreau, 1998). Bioturbation is defined as an umbrella term covering the physical effects and transport processes carried out by faunal activities, including biodiffusion and bioirrigation (Meysman et al., 2006b; Kristensen et al., 2012). However, it should be noted that the definitions of these terms vary between studies and fields.

Biodiffusion is widely modeled by assuming a single mixed surface layer of sediment with a biodiffusion coefficient (D_b) describing the intensity of biological mixing, and that below this layer, bioturbation is absent (D_b = 0) (Sanford, 2008; Rooze et al., 2016). The mixed layer depth varies from site to site in marine sediments and the average depth is around 5 – 10 cm, while the shallowest mixed layers in oxic coastal systems are found in the Baltic Sea, about 0.2 – 2 cm (Boudreau, 1998; Teal et al., 2008). Also D_b varies across marine sediments, with much higher values in coastal sediments (often on the order of 10-100 cm² yr^–1), while in deep-sea sediments D_b is as low as 0.01-1 cm² yr^–1 (Boudreau, 1994; Tromp et al., 1995; Middelburg et al., 1997). Furthermore, Berg et al. (2001) concluded that the effects of bioturbation on solutes are up to 20 times stronger than that on solids in coastal sediments, suggesting that the D_b for solutes and solids should be different. In general, biodiffusion is defined in reactive-transport models (RTMs) for simulating distributions of solutes and solids over time and depth in sediments as follows, Eq. 9 for solids and Eq. 10 for solutes:

$\frac{\partial C_{solid}}{\partial t}=\frac{\partial }{\partial z}\left((1-\text{φ})D_b\frac{\partial C_{solid}}{\partial z}\right)-(1-\text{φ})\text{ω}\frac{\partial C_{solid}}{\partial z}+(1-\text{φ}){\displaystyle \sum R_{solid}}(9)$

$\frac{\partial C_{solute}}{\partial t}=\frac{\partial }{\partial z}\left(\text{φ}(D_b+D_s)\frac{\partial C_{solute}}{\partial z}\right)-\text{φ\hspace{0.17em}ω}\frac{\partial C_{solute}}{\partial z}+\text{φ}{\displaystyle \sum R_{solute}}(10)$

where C_solid and C_solute stand for the concentration of a solid and a solute, respectively, t is time, z is depth, φ is porosity, ω is sedimentation rate, D_b is the biodiffusion coefficient, D_s is the molecular diffusion coefficient and R_solid and R_solute are the reactions for a solid and a solute, respectively.

The biodiffusion coefficient (D_b) is the predominant parameter in RTMs to represent biological activities in marine sediments. In most cases, the magnitude of D_b is difficult to constrain, as the abundance and activity of benthic fauna are variable in time and space, particularly in coastal areas. To account for this variation without explicitly including fauna in the model, D_b has been scaled with functions of various natural conditions as proxies for faunal activities. One common way is to scale D_b with oxygen concentration in the sediment (Wang et al., 2003; Reed et al., 2011) or bottom water (Fossing et al., 2004), as benthic animals are aerobic. D_b has also been scaled with temperature and with labile organic matter concentration as an indicator of food availability (Boudreau, 1998; Wang et al., 2003; Reed et al., 2011).

There are some examples of an explicit coupling of models of benthic fauna and RTMs. In the ERSEM model, the benthic system is modeled in three submodules dealing with (1) benthic biology, (2) bioturbation and (3) nutrient profiles in a multi-layer reactive-transport model (Ebenhöh et al., 1995; Ruardij and Van Raaphorst, 1995). The submodules exchange information, for example the biomass of macrofauna affects the distribution of oxygen and detritus in the sediments through bioturbation, which in turn affects the growth of benthic fauna. Each functional group is assigned a coefficient of contribution to bioturbation, and D_b is then defined as the weighted sum of the contribution of each functional group according to a Michaelis-Menten function (Supplementary Eq. S1). The same approach has been adopted in the ecosystem models IGBEM, Bay Model 2 and Atlantis (Fulton et al., 2004a, b; Audzijonyte et al., 2017). Several coastal ecosystem models developed for Japanese waters use a similar formulation, but without the weighing coefficients (Sohma et al., 2001, 2004, 2008, 2018). As the bioturbation activity is more strongly related to the activity of fauna than to its biomass, D_b has also been related to the net carbon uptake flux in other versions of ERSEM, as feeding can be assumed to correlate with the general activity of the animals (Blackford, 1997; Butenschön et al., 2016). See Supplementary Material for a comparison of different ways to couple fauna to bioturbation in RTMs.

The first model formulation for bioirrigation was provided by Aller’s radial-diffusion tube model (Aller, 1980), which approximates the bioirrigated zone in sediments as a series of evenly distributed and closely packed hollow cylinders of equal length, with burrows represented by the hollow portion of the cylinders. For such bioirrigated sediments, Eq. 10 is rewritten as:

$\frac{\partial C_{solute}}{\partial t}=\frac{\partial }{\partial z}\left(\text{φ}(D_b+D_s)\frac{\partial C_{solute}}{\partial z}\right)+\text{φ\hspace{0.17em}}\frac{D_s}{r}\frac{\partial }{\partial r}\left(r\frac{\partial C_{solute}}{\partial r}\right)+\text{φ}{\displaystyle \sum R_{solute}}(11)$

where r is the radial distance between cylinders. The boundary conditions are time-dependent, as the animals ventilate their burrows periodically, not constantly. This approach has been shown to reproduce porewater profiles in the bioirrigated zone well (Aller, 1982; Boudreau and Marinelli, 1994; Boudreau, 2000; Gilbert et al., 2003). Shull et al. (2009) extended the model to include burrow ventilation by benthic fauna through injection of bottom waters, suggesting that burrow ventilation strongly influences the vertical profiles of porewater and fluxes. In permeable (sandy) sediments where irrigation flows penetrate the surrounding sediments, advection and not diffusion can be the dominant mode of transport. In order to quantify the advective transport induced by bioirrigation, 1D and 2D advection models have been developed and used to study the effects of advective transport on e.g., inert tracers and oxygen (Timmermann et al., 2002, 2006; Meysman et al., 2006a).

Another way to model bioirrigation was developed by Boudreau (1984) and Emerson et al. (1984). Here, bioirrigation is expressed by a bioirrigation coefficient (α_s), which describes the exchange rate between bottom water and porewater at a certain depth in the irrigated sediments. Eq. 11 can be reformulated as:

$\frac{\partial C_{solute}}{\partial t}=\frac{\partial }{\partial z}\left(\text{φ\hspace{0.17em}}(D_b+D_s)\frac{\partial C_{solute}}{\partial z}\right)+\text{φ\hspace{0.17em}}{\text{α}}_s(C_{solute}-C_0){\displaystyle \sum R_{solute}}(12)$

where C₀ is the concentration at the sediment surface. Although bioirrigation actually occurs by a complex network of sediment burrows and their 3D geometrical sources, Eq. 12 parameterizes the process by assuming exchange between bottom waters and the average porewater at any given sediment depth. Nowadays, this model has become the most common way to express bioirrigation intensity, and thus how to define α_s is crucial for modeling bioirrigation properly. Studies have shown that α_s depends on the depth distribution of burrows both in laboratory (Furukawa, 2001) and field conditions (Schlüter et al., 2000; Norkko et al., 2012; Dale et al., 2013). Meile et al. (2005) have reported that α_s is highly chemical species-dependent, i.e., different solutes should be assigned their own α_s rather than sharing the same value. Studies sometimes use 3D models to represent explicitly the burrow networks that are constructed by resident macrofauna populations, but also in these models the bioirrigation intensity is based on α_s as a function of depth and the total burrow volume (Koretsky et al., 2002). Isaev et al. (2017) also considered burrows as an expansion of the sediment surface area and made bioirrigation effects dependent on the total surface area and on oxygen concentrations as they decrease over sediment depth. So far, dynamic models of the distribution or activities of bioirrigating animals have not been coupled to these models, and the number and shape of tubes are generally fixed parameters.

Bioresuspension

In addition to effects on processes within the sediment, the activities of benthic fauna can have major impacts on sediment stability and resuspension (Graf and Rosenberg, 1997; Le Hir et al., 2007; Joensuu et al., 2018). Burrows, mounds and tracks produced by benthic fauna affect bottom roughness and erodibility of sediments. The increased sediment resuspension caused directly by faunal activities and indirectly by alteration of sediment properties has been termed ‘bioresuspension’ (Graf and Rosenberg, 1997).

As erosion is fundamentally linked to lateral hydrodynamic processes, it is rarely included in one-dimensional (vertical) sediment reactive-transport models. Additionally, the same animal can have both stabilizing and destabilizing effects on the sediment, making it difficult to include such effects in models (Le Hir et al., 2007; Cozzoli et al., 2019). However, there are several examples of models coupling resuspension of sediment and benthic microalgae to fauna, including effects of infaunal bivalves (Willows et al., 1998; Wood and Widdows, 2002; Orvain et al., 2012; Rakotomalala et al., 2015) and epifaunal snail tracks (Orvain et al., 2003, 2012). For example, Wood and Widdows (2002) simulated effects of Limecola balthica on sediment erosion in an intertidal area of the Humber estuary, United Kingdom, and showed that bioresuspension by the clam was of the same order of magnitude as effects of tidal currents. This clearly shows that there is a need to account for biological effects in sediment transport modeling, especially in intertidal areas with dense biological communities.

The studies mentioned above have all used semi-empirical formulations for the relationship between animal density and sediment erosion based on flume studies. van Prooijen et al. (2011) developed a more process-based model for cohesive (muddy) sediment resuspension by deposit-feeding activities of L. balthica based on the individual rate, area and maximum depth of feeding and density of individuals. A recent study by Cozzoli et al. (2019) proposed another process-based model for cohesive sediment resuspension mediated by a variety of bioturbators and demonstrated metabolic rate as a general indicator of impacts of biological activities on sediment resuspension. They concluded that the overall metabolic rate of the bioturbators was well correlated with changes in hydrodynamic energy gradients of suspended cohesive sediments, and a better predictor than size, density or biomass of the fauna. However, the metabolic rates were not dynamically modeled, but derived from species identity and size of the animals based on an empirical model (Brey, 2001).

The presence of live and dead bivalves increases the structural heterogeneity of the sediment surface (Norkko and Shumway, 2011), affecting the near-bottom flow regime and providing an extended, hard surface area for colonization of nitrifying and denitrifying microbes as well as algae (Commito and Dankers, 2001; Stief, 2013). However, these processes have not been well quantified and to our knowledge there are no models of their effects on biogeochemical fluxes.

Discussion

Scaling Up to the Ecosystem

As shown by the examples above, there is a large array of models simulating the effects of benthic fauna on biogeochemistry. The main processes and model formulations discussed are summarized in Table 2. A major challenge is the combination and upscaling of these individual processes to understand system-level effects. Ecosystem models can be used to evaluate the joint dynamics of biological, chemical and physical processes of coastal systems and their response to environmental change. To capture and be able to predict effects of these often non-linear changes (Cloern, 2001; Kemp et al., 2005; Hewitt et al., 2016) is a major challenge in mechanistic modeling. Below we go through illustrative examples of ecosystem models used to simulate interactions between nutrient loading and benthic ecology and geochemistry in coastal areas. We include examples of both natural assemblages of benthic fauna and assemblages influenced by human intervention (e.g., restoration, artificial habitats), but exclude a wealth of models dealing with seafood farming (see section “Biomass Model Types and State Variables” for some examples).

TABLE 2

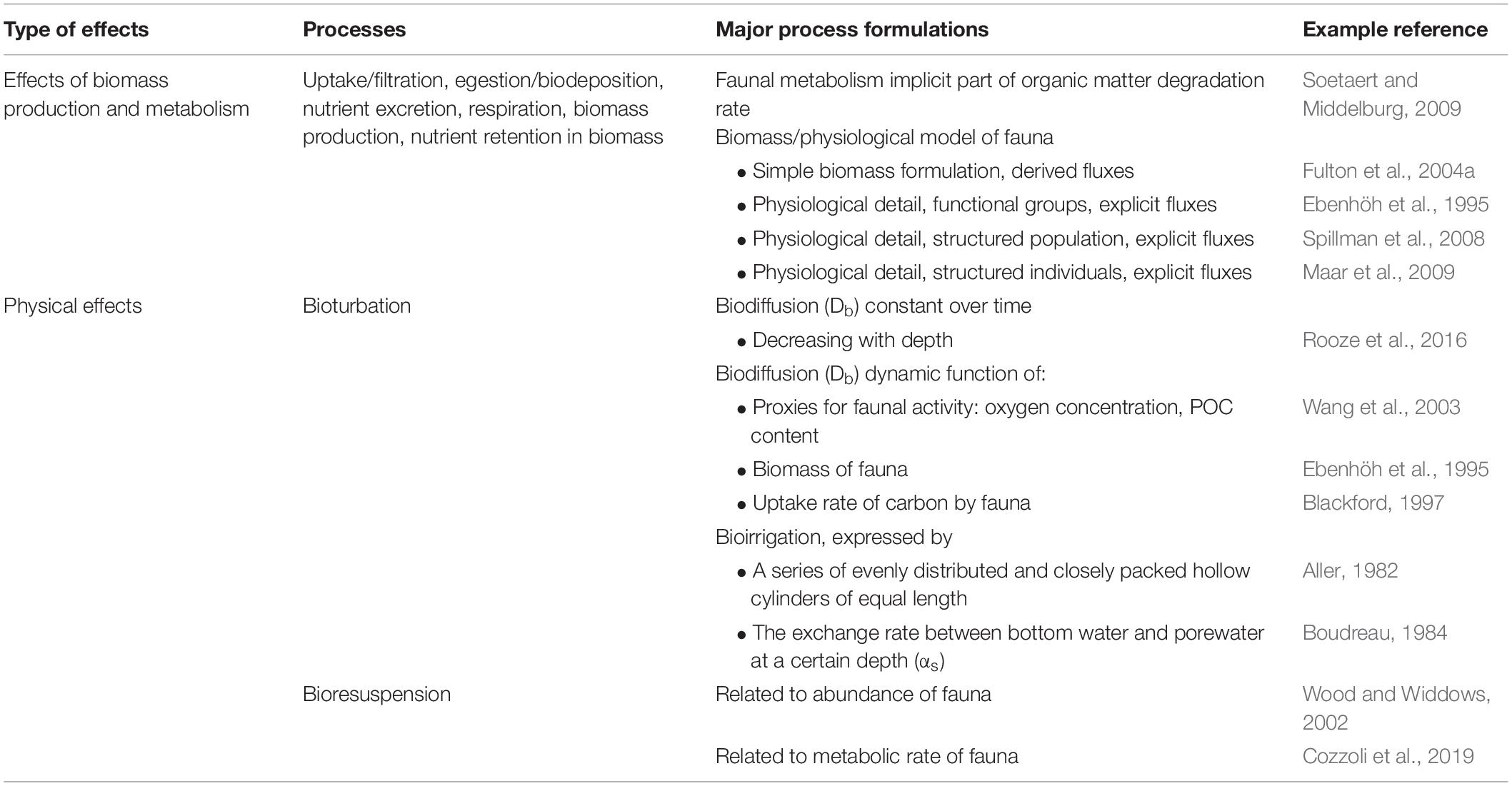
Table 2. Summary of the main approaches to model benthic faunal processes affecting benthic carbon and nutrient fluxes discussed.

The development of marine ecosystem models stems from Riley’s simple nutrient-phytoplankton-zooplankton model (Riley, 1946; Riley et al., 1949). The Ems estuary model was the first to include carbon dynamics of benthic functional groups about four decades later (Baretta and Ruardij, 1988). In the three decades since, ecosystem models have developed to include e.g., nutrient and oxygen dynamics of benthic fauna and vegetation in a range of coastal ecosystems from shelf seas (Ebenhöh et al., 1995) to shallow lagoons (Plus et al., 2003) and tidal flats (Sohma et al., 2000, 2008), and these models vary in complexity from simple box models (Triantafyllou et al., 2000; Kim and Montagna, 2009) to 3D-applications with tens of state variables, such as the Chesapeake Bay Environmental Model Package (Cerco et al., 2010; Cerco and Noel, 2013) and Atlantis (Fulton et al., 2011; Bossier et al., 2018).

A prominent example of a comprehensive model coupling benthic biology to biogeochemistry is ERSEM (Baretta et al., 1995; Butenschön et al., 2016). It explicitly simulates the dynamics of several chemical elements (C, N, P, Si, Fe and O) and living functional groups in the pelagic and benthic subsystems and can be coupled to different hydrodynamic transport models. Recent versions include the options to use either a single- or a multi-layer benthic component. The feeding and feces egestion depth is defined separately for each group of fauna, while faunal mineralization products (CO₂, NH₄ and PO₄) are assumed to be released in the uppermost oxic layer (Ruardij and Van Raaphorst, 1995). The model has been applied to study carbon and nutrient fluxes in coastal areas, including the effects of benthic fauna and bacteria (Petihakis et al., 1999, 2005; Triantafyllou et al., 2000; Mussap and Zavatarelli, 2017), benthic microalgae (Blackford, 2002), as well as seagrasses and macroalgae (Aveytua-Alcázar et al., 2008).

Triantafyllou et al. (2000) used ERSEM to simulate the effects of increased nutrient input to the shallow, temperate Gialova lagoon in the Mediterranean and showed a significant increase in suspension-feeders leading to increased biodeposition and a switch from nutrient limitation to grazing control for phytoplankton. While the model could capture the main characteristics of the changing system as observed in the field, it failed to match the great variability in measured biomass and nutrient fluxes (Petihakis et al., 1999; Triantafyllou et al., 2000), illustrating the difficulty of modeling shallow, dynamic systems. The authors mention the inclusion of benthic primary producers and effects of hypoxia as major future development needs.

Blackford (2002) illustrated the advantages of coupling dynamics of benthic vegetation and fauna for a more realistic representation of shallow productive systems. A simulation of benthic and pelagic processes along a depth gradient in the Adriatic Sea showed significant interactions between benthic primary producers and consumers: the presence of benthic microalgae increased the biomass of bacteria and fauna by increasing sediment oxygenation and providing a food source to grazers, which in turn formed an important limiting factor for microalgal biomass. Together these processes enhanced nitrogen regeneration in the photic zone. The study is also a good example of extensive model validation of several important aspects, including annual means and seasonal cycles of biomass stocks, biogeochemical fluxes as well as measures of net ecosystem metabolism (i.e., the relation between primary production and ecosystem respiration). In general, model outputs were within the range of observed values.

The coupling of physical, chemical and biological processes and detailed descriptions of several benthic functional groups in ERSEM allows for comprehensive testing of the joint effects of benthic biological dynamics on biogeochemical processes. Yet, the model requires estimations of a large number of parameters, which are usually site-specific and laborious to measure. The advantages of model simplification are many including lower computational needs, fewer uncertain parameters and increased interpretability (Fulton et al., 2003a; Fulton, 2010; Ganju et al., 2016). Therefore, many ecosystem models use simpler approaches to describe the biota. For example, Bay Model 2 (Fulton et al., 2004a), a predecessor of Atlantis (Fulton et al., 2011; Bossier et al., 2018), explicitly includes only dynamics of the main limiting nutrient, N, and uses a simple formulation for biomass dynamics of functional groups (see section “Biomass Model Types and State Variables”, Table 1).

Fulton et al. (2004a) applied Bay Model 2 to Port Phillip Bay, Australia including six functional groups of benthic fauna and three groups of benthic primary producers. Despite the simple description of benthic biology, the model was able to predict emergent complex biological interactions such as competitive exclusion of benthic microalgae by macrophytes and predator-prey interactions, leading to a spatial differentiation of biological communities within the bay. However, the predicted biomasses of benthic microalgae and macrofauna for a range of temperate bays were significantly different from measured values, showing that some constraints were missing or inaccurate in the benthic compartment. The model was also used to study the effects of differing nutrient loads on the ecosystem by applying two nitrogen load scenarios to the same model bay, one corresponding to the eutrophic Chesapeake Bay and the other to the mesotrophic Port Phillip Bay (Fulton et al., 2004a). The model did remarkably well in predicting biological changes due to eutrophication, such as simplification of communities, extinction of seagrasses, a shift from a primary producer-based to a more detritus-based food chain and an increase in small-sized functional groups, corresponding to general theory and field observations from the two bays. Unfortunately, the feedbacks from changing benthic communities on nutrient cycles were not discussed.

Eutrophication and effects of benthic biology on nutrient cycles in Chesapeake Bay were simulated in several studies using the Chesapeake Bay Environmental Model Package, which couples pelagic biogeochemistry and hydrodynamics in 3D with a sediment diagenetic model and several biological components including two functional groups of benthic fauna (HydroQual, 2000; Cerco and Noel, 2007, 2013; Cerco et al., 2010, 2013). Cerco and Noel (2007) explored the potential of oyster restoration as a means to reduce eutrophication effects in the bay. Even though increased suspension-feeder biomass led to increased respiration, DIN excretion and biodeposition, the grazing on plankton simultaneously decreased sedimentation rates, leading to overall lower sediment oxygen consumption. Decreased water turbidity increased biomass of seagrasses and benthic microalgae, further increasing sediment oxygenation. The overall result was decreased sediment-water ammonium fluxes and increased N loss through denitrification. Although this hypothetical simulation cannot be validated against measured data, it shows the potential of complex models to explore large-scale, non-linear changes on the coastal ecosystem level.

Also Rasmussen et al. (2009) simulated positive effects of filter-feeding bivalves on restoration of the eutrophied Ghar el Melh lagoon in the southern Mediterranean using a nutrient-plankton-detritus model including benthic vegetation and 2D transport of sediments and suspended matter. Simulations with up to 75% reductions in nutrient loads showed a decrease in macroalgae, but only marginal effects on rooted vegetation (Ruppia spp.), which were still limited by shading from resuspended sediments. Introducing filter-feeding by bivalves as a forcing function increased water clarity and allowed for re-establishment of Ruppia spp., but also increased the accumulation of N, P and organic C in the sediments due to biodeposition. The study also nicely illustrates how ecosystem models can be used to build nutrient budgets of coastal ecosystems to elucidate their overall role as a source or sink for nutrient inputs to the open sea.

Similar effects of suspension-feeders were simulated ‘the other way around’ in the northern Mediterranean Gulf of Trieste using a 1D version of ERSEM (BFM-POM), including five groups of benthic fauna and two groups of bacteria (Mussap and Zavatarelli, 2017). Removal of suspension-feeders increased dissolved P outflux from sediments, fueling increased phytoplankton production and increasing POM content in the water column, while less POM entered the sediments in the absence of suspension-feeders. In another application of ERSEM in the North Sea, Lessin et al. (2016) concluded that increased benthic nutrient outfluxes following a reduction in benthic macrofauna were due to increased activity of bacteria and meiobenthos.

Maar et al. (2009) coupled a DEB model of blue mussels to a small-scale 3D hydrodynamic-biogeochemical model to study the effects of mussel beds on a wind farm foundation in a shallow coastal ecosystem in Limfjorden in northern Denmark. Simulations showed that although bivalves increased organic carbon sedimentation rates in the immediate surrounding, the overall effect was reduced sedimentation due to depletion of phyto- and zooplankton by grazing. Another example of a DEB model coupled to a pelagic ecosystem model is given by Saraiva et al. (2017), who simulated the detailed distribution and population dynamics of blue mussels in the shallow Balgzand area of the Wadden Sea. They concluded that the area acts as a sink for phytoplankton due to filtration by the bivalves, and as a source of ammonia, exporting about 40% more than the input flux from land and surrounding waters.

The diverse effects of suspension-feeders on sedimentation fluxes simulated in the different studies may stem from differences in model formulations and assumptions, such as the representation of physical transport in one, two or three dimensions, but it is also highly likely that the results reflect the true complexity and context-dependency of coastal biological and biogeochemical dynamics.

Evidently, mechanistic models are useful tools to quantitatively study the biogeochemistry of coastal ecosystems and to tackle managements questions such as the relationships between nutrient inputs, human interventions (e.g., restoration, constructions, shellfish farming) and the nutrient filtering capacity or ecological state of the ecosystem. Such models also have great potential to investigate the influence of climate change on coastal benthos (Thomas and Bacher, 2018; Ehrnsten et al., 2019a) and the role of coastal ecosystems as sources or sinks for greenhouse gases (Sohma et al., 2018). Isaev et al. (2017) also demonstrate how an ecosystem model can be used to study the combined impact of climate change and invasion of a bioturbating species on coastal nutrient fluxes. In a rapidly changing world, mechanistic models will become increasingly important for management, through their capacity to explore outcomes of different environmental change scenarios. They may also help pin-point variables that can indicate when an ecosystem is nearing a tipping point to an alternate state.

Opportunities and Challenges

Coupling Benthic Fauna and Benthic Biogeochemistry

Models focusing on benthic biology on the one hand and benthic biogeochemistry on the other, have been developed in parallel in different scientific communities with largely diverging foci and assumptions that may be difficult to reconcile (Meysman et al., 2005; Middelburg, 2018; Snelgrove et al., 2018). However, there is a growing number of model studies coupling benthic fauna and biogeochemistry, although so far primarily focusing on coupling bivalve models to pelagic processes (e.g., nutrient-plankton-detritus dynamics) while the coupling of benthic biogeochemistry to biology is less mature.

Many sediment biogeochemical models simplify benthic biology by omitting fauna and vegetation as state variables, and only model their effects implicitly, e.g., as a bioturbation and/or bioirrigation coefficient in reactive-transport models (RTMs). This implicit approach has been successfully applied to systems with relatively simple and stable benthic communities (e.g., Soetaert et al., 1996, 2000; Paraska et al., 2014), but has been insufficient to explain nutrient fluxes in some shallow, near-shore areas (Murray and Parslow, 1997; Holstein and Wirtz, 2009), suggesting that the temporal variability in fauna and flora and associated processes typical for many shallow coastal areas needs to be accounted for by dynamic state variables. However, linking biodiffusion (D_b) to biomass dynamics of functional groups (Ebenhöh et al., 1995; Sohma et al., 2001, 2004, 2008, 2018; Vichi, 2002; Fulton et al., 2004a, b; Audzijonyte et al., 2017) may not be enough to account for the great variability in reworking rates measured between coastal areas (Boudreau, 1994; Tromp et al., 1995; Middelburg et al., 1997), and even between replicates from the same site (Morys et al., 2016).

Ecological studies have developed indices of bioturbation and bioirrigation potential based on abundance and traits such as size, mobility and feeding type of the individual animals observed in natural communities (Solan et al., 2004; Wrede et al., 2018), which correlate to some degree with reworking rates, mixing depth, oxygen penetration depth and ammonium efflux (Braeckman et al., 2014; Gogina et al., 2017). Even though this kind of detail is not feasible in mechanistic modeling, these studies may aid improved model parameterizations. Trait-based descriptions of pelagic groups are emerging in ecosystem models (Follows et al., 2007; Andersen et al., 2015). In general, metabolism seems to be a better predictor of biogenic mixing and resuspension than biomass, advocating the modeling approaches of Blackford (1997) and Cozzoli et al. (2019). As metabolic rate is increasingly recognized as master parameter for the ‘pace of life’ (Gillooly et al., 2001; Brown et al., 2004b; McClain et al., 2012), this provides a promising avenue for parameterization of the ‘pace of bioturbation’. However, there is a clear need to develop and test the generality of metabolism-based model formulations.

Despite decades of bioturbation research, there still seems to be a lack of mechanistic understanding of the complex processes that determine bioturbation rates in natural settings, as well as the diverse effects of bioturbation on physical, chemical and biological processes in the sediment, especially in heterogeneous coastal areas. On top of the effects of individual traits, the environmental surroundings of those individuals also modify their behavior and metabolism, leading to different effects on biogeochemical fluxes, as shown for example in a series of recent studies of a coastal gradient in the Baltic Sea (Joensuu et al., 2018; Bernard et al., 2019; Gammal et al., 2019).

Another long-lasting paradigm in RTMs has been the assumption that animal metabolism is unimportant compared to microbial degradation of organic matter, and can be omitted or implicitly included in a first-order organic matter degradation rate (Soetaert and Middelburg, 2009). As discussed in section “Solute Fluxes: Respiration and Nutrient Excretion”, accumulating evidence suggests that faunal metabolisms can contribute significantly to the mineralization of organic carbon (Elmgren, 1984; Wenzhofer et al., 2002; Hansen and Bendtsen, 2013; Ehrnsten et al., 2019b) and nitrogen (Kristensen, 1984; Prins and Smaal, 1994; Magni et al., 2000). How can the metabolism of fauna then be coupled to organic matter degradation in RTMs? In theory, a straightforward way is to include the respiration and excretion of fauna in the sum of reactions affecting solids and solutes in the general diagenetic equations (Eqs. 9-10). In practice, this is not so straightforward. Sediment models generally resolve small-scale 1D processes with a fine depth resolution in mm to cm. Ecological or ecosystem models often focus on large-scale processes on m to km scales, and reduce the sediment depth resolution to a single layer, e.g., because of computational constraints (Soetaert et al., 2000). Additionally, even when sediments are resolved into several layers, the benthic fauna is usually represented as vertically integrated variables (i.e., mass area^–1, e.g., Fulton et al., 2004b; Butenschön et al., 2016), making it challenging to link biological and chemical processes in the vertical dimension. Thus, combining these scales is a major challenge for coupled modeling to understand benthic and pelagic processes, as also pointed out by Lessin et al. (2018).

Another challenge is the representation of organic matter. RTMs usually model the degradation of organic matter as a continuous process over depth, while ecological models generally include sediment organic matter as food for the benthos as a single depth-integrated variable. A good ‘compromise’ could be to divide the organic matter into a finite number of lability classes with different bio-availability for both faunal assimilation and microbial degradation, as in van Oevelen et al. (2011). Sohma et al. (2004, 2018) took this approach one step further by also dividing the benthic functional groups into lability classes. While this formulation can help keep track of organic matter classes in a coupled RTM, it is hard to validate against observations.

Choosing the ‘Right’ Processes and Formulations

When modeling benthic nutrient and carbon cycling, there is a need to carefully consider which processes to include and how they are formulated to best answer the specific questions of the study. There are always trade-offs between realism, precision and generality of any given model (Levins, 1966). It is not possible to construct comprehensive guidelines for model combinations and formulations to be used in different circumstances, but here we try to provide some general advice.

The role of benthic fauna in coastal systems could be broadly categorized into three cases: (1) systems dominated by direct effects on pelagic processes, such as the effects of dense bivalve beds on pelagic N cycles and plankton dynamics; (2) systems dominated by direct and/or indirect effects in the sediment, such as effects of metabolism and bioturbation on microbial processes; and (3) systems where benthic fauna has a minor effect on biogeochemical fluxes. Modeling case 1 requires a good representation of the pelagic systems in terms of resolution, hydrodynamic transport and biological dynamics of plankton and suspension-feeders, but may not need a detailed description of sediment reactive-transport. In case 2, there may be a strong need to couple detailed sediment processes with a dynamic description of fauna, but pelagic processes may be simplified, while in case 3, benthic fauna could be omitted from the model.

It has been argued that benthic fauna generally is of minor importance for sediment processes in advection-dominated systems as opposed to diffusion-dominated ones, as hydrological forces override the effects of bioturbation and biodeposition (Mermillod-Blondin, 2011). Also, the effects of suspension-feeders on pelagic processes (case 1) generally decrease with decreasing water residence time, which is strongly related to hydrodynamic flow speed (Dame and Prins, 1998; Grall and Chauvaud, 2002). Thus, as a general rule, one may expect the importance of benthic fauna to increase with decreasing flow speed and increasing water residence time. However, there are exceptions from this general rule, such as intertidal areas where bioturbation and grazing on microphytobenthos can have large effects on sediment resuspension and transport despite a dominance of advective tidal currents (Wood and Widdows, 2002; Le Hir et al., 2007; Rakotomalala et al., 2015).

In addition to the main types of impact, another important consideration when choosing a modeling approach is the main research question. Understanding responses to major environmental changes that may lead to completely new system states and shifted baselines requires an explicit description of mechanisms that determine the biological and biogeochemical dynamics of the system (e.g., complex mechanistic ecosystem-level models). In contrast, studies focusing on biogeochemical fluxes in systems with little ecological change may work better with empirical formulations for benthic activities that emphasize precision over generality (e.g., as is done in RTMs tuned to a specific site).

A related consideration is in what detail is desired in ecological aspects. Sophisticated individual-level models such as Dynamic Energy Budget models add more realism to the simulation of biomass, reproductive constraints and physiological fluxes compared to simpler functional group approaches, but so far, they have only been applied to single, well-studied species, as they require a large number of species-specific parameter values and several state variables for each individual. If the interest is in the effects of a diverse benthic community on biogeochemical fluxes (case 2), a functional group approach is probably the best option while structured population models and (sub)individual-level models are better suited for systems dominated by single species, e.g., bivalves (case 1). Simplifying, while more physiological detail leads to a more accurate description of biology, there is no clear proof that this automatically improves the description of biogeochemical fluxes at the ecosystem scale. A meta-analysis of pelagic biogeochemical models also concluded that increased complexity did not improve the ability of models to predict spatial and temporal patterns of plankton dynamics (Arhonditsis and Brett, 2004).

Can We Model the Future Biogeochemical Cycles in Coastal Ecosystems?

In principle, mechanistic models can be used to understand the dynamics of a system outside the boundaries of observations as long as the generic mechanisms of the model are validated. However, coastal ecosystems are extremely complex and our understanding of the different mechanisms determining the dynamics of these systems is far from complete. Additionally, accurate spatiotemporal information to force and initialize the models is largely lacking. Therefore, models describing processes in coastal systems all contain a large degree of empiricism. For example, diagenetic models (RTMs) are usually tuned to fit observational datasets of the distribution of sediment components from specific sites (Arndt et al., 2013). Attempts to find globally valid (empirical) relationship for parameterizations have been marginally successful (Boudreau, 1994; Middelburg et al., 1997). Similarly, models of biomass and metabolism of fauna generally contain environment-specific rate constants (such as ingestion half-saturation constants or mortality rates) that are used as tuning parameters. These empirical formulations limit the predictive capacity of models in a changing environment.

However, despite large uncertainties, models are still the most cost-effective tools available to simulate plausible future states of coastal ecosystems and may provide valuable management advice by examining future nutrient and carbon cycling in coastal areas, as long as the uncertainties are properly recognized. The use of model ensembles to quantify uncertainty in model projections has become increasingly popular in climate and marine hydrodynamic-biogeochemical sciences (Murphy et al., 2004; Meier et al., 2012, 2018). When moving up in complexity to biological process modeling, this approach would increase model utility considerably both for scientific and applied purposes.

An important part of model development is the validation against observations. For this purpose, long-term and consistent monitoring of benthic fauna and biogeochemical properties are invaluable. Only when we know that we can simulate past changes with reasonable accuracy, may we endeavor into projections of the future. We also acknowledge that the methods and extent of validation in published studies vary and call for more rigorous validation of benthic model dynamics in future modeling studies.

In addition, to increase the mechanistic understanding of complex coastal dynamics we suggest that model development should concentrate on well-studied coastal systems where process understanding and data availability are good. Increased interdisciplinary collaboration and understanding between e.g., benthic ecologists and biogeochemical modelers is a prerequisite to be able to plan experiments and monitoring that support modeling efforts and vice versa. A prime example is Port Phillip Bay in Australia where large field campaigns supported the development of several coupled hydrodynamic-biogeochemical ecosystem models (Murray and Parslow, 1997, 1999; Fulton et al., 2004a, b). Another area with large potential for future model development is the Baltic Sea, because of its long research and monitoring tradition focusing on benthic fauna, its responses to environmental change and its role in coupled benthic-pelagic processes (Remane, 1934; Karlson et al., 2007; Griffiths et al., 2017; Ehrnsten et al., 2019b; Rodil et al., 2019). Additionally, the Baltic Sea has been affected by multiple anthropogenic pressures, such as eutrophication, climate change and overfishing, far longer and more severely than most other coastal seas. It also has a long history of management of these pressures, making it a good test case for the study of management challenges in the future coastal ocean under multiple pressures and shifting baselines (Villnäs and Norkko, 2011; Reusch et al., 2018).

To understand the carbon and nutrient cycles and constrain their budgets in coastal systems, it is important to recognize that coastal areas constitute a continuum from land to sea rather than only from the water surface to the bottom. In general, the variability in scales and complexity of coastal areas require models that are carefully built to answer specific questions in the study system. Some ecosystem modeling packages recognize this need for flexibility in their design, enabling the user to combine modules of different complexity, e.g. choosing between a single- or multi-layer benthic component (DHI, 2007; Butenschön et al., 2016).

Another major challenge is to incorporate the role of stochastic events, such as storms, upwelling and heavy precipitation, which may significantly impact biogeochemical cycling and the retention capacity of coastal systems (Canuel and Hardison, 2016; Malta et al., 2017). As some of the examples discussed in this study demonstrate, models are generally better at predicting the average conditions and potential distributions of biota than the large and somewhat stochastic variability often present in real coastal ecosystems (Triantafyllou et al., 2000; Fulton et al., 2004a). As climate change is expected to lead to changing extremes in the future (Easterling et al., 2000; Alexander et al., 2018), being able to incorporate the effects of extreme stochastic events becomes increasingly important when simulating future ecosystem states and biogeochemical fluxes.

Conclusions

Benthic fauna is an important component of nutrient and carbon cycles in coastal seas. There is a clear need to include and improve the description of benthic fauna in models of coastal nutrient and carbon cycling in order to properly describe the coupled benthic and pelagic processes, especially in the light of environmental change. We have summarized existing model formulations of different complexity to help implement descriptions of relevant zoobenthic processes in a variety of coastal habitats. In general, metabolism appears to be a good descriptor of both direct and indirect effects of benthic fauna on nutrient and carbon fluxes, offering a promising avenue for future developments in model formulations. Although numerical models can capture a large number of processes in a system, a full mechanistic description of the ecosystem dynamics will never be possible; therefore, it is important to clearly delineate the scope of each model with its purpose in terms of scales and complexity.

Major challenges and research priorities identified in this article are (1) to couple the dynamics of zoobenthic biomass and metabolism to sediment reactive-transport in models, (2) to test and validate model formulations against real-world data to better incorporate the context-dependency of processes in heterogeneous coastal areas in models, and (3) to capture the role of stochastic events. To understand coastal carbon and nutrient cycling in the present and future, lateral thinking is needed, recognizing that coastal biogeochemical cycles are heavily influenced by processes acting along the gradient from land to sea, and that the role of physics, chemistry and biology should all be considered.

Author Contributions

EE, XS, AN, KT, and BG designed the review. EE, XS, and KT were mainly responsible for collecting the literature. All authors contributed to writing the manuscript, with XS mainly responsible for section “Bioturbation” and EE mainly responsible for all other sections. All listed authors have made significant intellectual contributions to the study.

Funding

This study received funding from the EU, the Academy of Finland and Formas through BONUS (Art 185) as part of the BONUS BALTICAPP and BONUS COCOA projects, and from the Swedish Agency for Marine and Water Management through their grant 1.11 – Measure for Marine and Water environment. Further funding was provided by research grants from The Academy of Finland (Project ID 294853 to AN) and the University of Helsinki and Stockholm University strategic fund for collaborative research (the Baltic Bridge initiative; AN, CH, and BG).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank the participants in the BONUS COCOA project Elin Almroth-Rosell, Moa Edman, Tatjana Eremina, Jacob Carstensen, Joanna Norkko, and Artūras Razinkovas-Baziukas for ideas and input to earlier versions of the review. The authors also wish to thank Prof. Ragnar Elmgren for comments improving the manuscript. Figure 1 illustrated by J. Lokranz/Azote. Mussel symbol in Figure 2 courtesy of the Integration and Application Network, University of Maryland Center for Environmental Science (http://ian.umces.edu/symbols/).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.00450/full#supplementary-material

Abbreviations

D_b, Biodiffusion coefficient; DEB, Dynamic Energy Budget; DIN, Dissolved inorganic nitrogen; DIP, Dissolved inorganic phosphorus; DNRA, Dissimilatory nitrate reduction to ammonium; ERSEM, European Regional Seas Ecosystem Model; POC, Particulate organic carbon; POM, Particulate organic matter; RTM, Reactive-Transport Model.

References

Alexander, M. A., Scott, J. D., Friedland, K. D., Mills, K. E., Nye, J. A., Pershing, A. J., et al. (2018). Projected sea surface temperatures over the 21st century: changes in the mean, variability and extremes for large marine ecosystem regions of Northern Oceans. Elem. Sci. Anth. 6:9. doi: 10.1525/elementa.191

CrossRef Full Text | Google Scholar

Aller, R. C. (1978). Experimental studies of changes produced by deposit feeders on pore water, sediment, and overlying water chemistry. Am. J. Sci. 278, 1185–1234. doi: 10.2475/ajs.278.9.1185

PubMed Abstract | CrossRef Full Text | Google Scholar

Aller, R. C. (1980). Quantifying solute distributions in the bioturbated zone of marine sediments by defining an average microenvironment. Geochim. Cosmochim. Acta 45, 1955–1965. doi: 10.1016/0016-7037(81)90155-90151

CrossRef Full Text | Google Scholar

Aller, R. C. (1982). Carbonate dissolution in nearshore terrigenous muds: The role of physical and biological reworking. J. Geol. 90, 79–95. doi: 10.1086/628652

CrossRef Full Text | Google Scholar

Aller, R. C. (1988). “Benthic fauna and biogeochemical processes in marine sediments: the role of burrow structures,” in Nitrogen Cycling in Coastal Marine Environments, eds T. H. Blackburn and J. Sorensen (Hoboken, NJ: John Wiley & Sons), 301–338.

Google Scholar

Aller, R. C. (2001). “Transport and reactions in the bioirrigated zone,” in The Benthic Boundary Layer, eds B. P. Boudreau and B. B. Jørgensen (Oxford: Oxford University Press), 269–301.

Google Scholar

Andersen, K. H., Aksnes, D. L., Berge, T., and Fiksen, Ø, and Visser, A. (2015). Modelling emergent trophic strategies in plankton. J. Plankton Res. 37, 862–868. doi: 10.1093/plankt/fbv054

CrossRef Full Text | Google Scholar

Arhonditsis, G., and Brett, M. (2004). Evaluation of the current state of mechanistic aquatic biogeochemical modeling. Mar. Ecol. Prog. Ser. 271, 13–26. doi: 10.3354/meps271013

CrossRef Full Text | Google Scholar

Arndt, S., Jørgensen, B. B., LaRowe, D. E., Middelburg, J. J., Pancost, R. D., and Regnier, P. (2013). Quantifying the degradation of organic matter in marine sediments: A review and synthesis. Earth Sci. Rev. 123, 53–86. doi: 10.1016/j.earscirev.2013.02.008

CrossRef Full Text | Google Scholar

Asmus, R. M., and Asmus, H. (1991). Mussel beds: limiting or promoting phytoplankton? J. Exp. Mar. Biol. Ecol. 148, 215–232. doi: 10.1016/0022-0981(91)90083-9

CrossRef Full Text | Google Scholar

Audzijonyte, A., Gorton, R., Kaplan, I., and Fulton, E. A. (2017). Atlantis User’s Guide Part I: general overview. Phys. Ecol. 223. Available online at: https://research.csiro.au/atlantis/home/useful-references/ (accessed October 10, 2019).

Google Scholar

Augustine, S., and Kooijman, S. A. L. M. (2019). A new phase in DEB research. J. Sea Res. 143, 1–7. doi: 10.1016/j.seares.2018.06.003

CrossRef Full Text | Google Scholar

Aveytua-Alcázar, L., Camacho-Ibar, V. F., Souza, A. J., Allen, J. I., and Torres, R. (2008). Modelling Zostera marina and Ulva spp. in a coastal lagoon. Ecol. Modell. 218, 354–366. doi: 10.1016/j.ecolmodel.2008.07.019

CrossRef Full Text | Google Scholar

Baretta, J., Ebenhöh, W., and Ruardij, P. (1995). The European regional seas ecosystem model, a complex marine ecosystem model. Neth. J. Sea Res. 33, 233–246. doi: 10.1016/0077-7579(95)90047-90040

CrossRef Full Text | Google Scholar

Baretta, J., and Ruardij, P. (1988). Tidal Flat Estuaries, eds J. Baretta and P. Ruardij (Berlin: Springer Berlin Heidelberg), doi: 10.1007/978-3-642-73753-4

CrossRef Full Text | Google Scholar

Barnes, R. S. K. (1994). “Macrofaunal community structure and life histories in coastal lagoons,” in Coastal Lagoon Processes Elsevier Oceanography Series, ed. B. Kjerfve (Amsterdam: Elsevier), 311–362. doi: 10.1016/S0422-9894(08)70016-3

CrossRef Full Text | Google Scholar

Berg, P., Rysgaard, S., Funch, P., and Sejr, M. K. (2001). Effects of bioturbation on solutes and solids in marine sediments. Aquat. Microb. Ecol. 26, 81–94. doi: 10.3354/ame026081

CrossRef Full Text | Google Scholar

Bernard, G., Gammal, J., Järnström, M., Norkko, J., and Norkko, A. (2019). Quantifying bioturbation across coastal seascapes: Habitat characteristics modify effects of macrofaunal communities. J. Sea Res. 152, 101766. doi: 10.1016/j.seares.2019.101766

CrossRef Full Text | Google Scholar

Beusen, A. H. W., Bouwman, A. F., Van Beek, L. P. H., Mogollón, J. M., and Middelburg, J. J. (2016). Global riverine N and P transport to ocean increased during the 20th century despite increased retention along the aquatic continuum. Biogeosciences 13, 2441–2451. doi: 10.5194/bg-13-2441-2016

CrossRef Full Text | Google Scholar

Blackford, J. C. (1997). An analysis of benthic biological dynamics in a North Sea ecosystem model. J. Sea Res. 38, 213–230. doi: 10.1016/S1385-1101(97)00044-40

CrossRef Full Text | Google Scholar

Blackford, J. C. (2002). The influence of microphytobenthos on the Northern Adriatic ecosystem: a modelling study. Estuar. Coast. Shelf Sci. 55, 109–123. doi: 10.1006/ecss.2001.0890

CrossRef Full Text | Google Scholar

Bossier, S., Palacz, A. P., Nielsen, J. R., Christensen, A., Hoff, A., Maar, M., et al. (2018). The Baltic sea Atlantis: An integrated end-to-end modelling framework evaluating ecosystem-wide effects of human-induced pressures. PLoS One 13:e0199168. doi: 10.1371/journal.pone.0199168

PubMed Abstract | CrossRef Full Text | Google Scholar

Boudreau, B. P. (1984). On the equivalence of nonlocal and radial-diffusion models for porewater irrigation. J. Mar. Res. 42, 731–735. doi: 10.1357/002224084788505924

CrossRef Full Text | Google Scholar

Boudreau, B. P. (1994). Is burial velocity a master parameter for bioturbation? Geochim. Cosmochim. Acta 58, 1243–1249. doi: 10.1016/0016-7037(94)90378-6

CrossRef Full Text | Google Scholar

Boudreau, B. P. (1998). Mean mixed depth of sediments: The wherefore and the why. Limnol. Oceanogr. 43, 524–526. doi: 10.4319/lo.1998.43.3.0524

CrossRef Full Text | Google Scholar

Boudreau, B. P. (2000). The mathematics of early diagenesis: From worms to waves. Rev. Geophys. 38, 389–416. doi: 10.1029/2000rg000081

CrossRef Full Text | Google Scholar

Boudreau, B. P., and Marinelli, R. L. (1994). A modelling study of discontinuous biological irrigation. J. Mar. Res. 52, 947–968. doi: 10.1357/0022240943076902

CrossRef Full Text | Google Scholar

Braeckman, U., Foshtomi, M. Y., Van Gansbeke, D., Meysman, F., Soetaert, K., Vincx, M., et al. (2014). Variable importance of macrofaunal functional biodiversity for biogeochemical cycling in temperate coastal sediments. Ecosystems 17, 720–737.

Google Scholar

Breitburg, D., Levin, L. A., Oschlies, A., Grégoire, M., Chavez, F. P., Conley, D. J., et al. (2018). Declining oxygen in the global ocean and coastal waters. Science 359:eaam7240. doi: 10.1126/science.aam7240

PubMed Abstract | CrossRef Full Text | Google Scholar

Brey, T. (2001). Population Dynamics in Benthic Invertebrates. A Virtual Handbook. Version 01.2. Available online at: http://www.thomas-brey.de/science/virtualhandbook (accessed June 24, 2019).

Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004a). Response to Forum Commentary on “Toward a Metabolic Theory of Ecology.”. Ecology 85, 1818–1821. doi: 10.1890/03-0800

CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004b). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Butenschön, M., Clark, J., Aldridge, J. N., Icarus Allen, J., Artioli, Y., Blackford, J., et al. (2016). ERSEM 15.06: A generic model for marine biogeochemistry and the ecosystem dynamics of the lower trophic levels. Geosci. Model Dev. 9, 1293–1339. doi: 10.5194/gmd-9-1293-2016

CrossRef Full Text | Google Scholar

Canuel, E. A., and Hardison, A. K. (2016). Sources, ages, and alteration of organic matter in estuaries. Ann. Rev. Mar. Sci. 8, 409–434. doi: 10.1146/annurev-marine-122414-134058

CrossRef Full Text | Google Scholar

Cederwall, H., and Elmgren, R. (1980). Biomass increase of benthic macrofauna demonstrates eutrophication of the Baltic Sea. Ophelia Suppl. 1, 287–304.

Google Scholar

Cerco, C. F., Kim, S.-C., and Noel, M. R. (2010). The 2010 Chesapeake Bay Eutrophication Model. A report to the US Environmental Protection Agency Chesapeake Bay Program and to the US Army Engineer Baltimore District. Vicksburg MS: US Army Engineer Research and Development Center.

Google Scholar

Cerco, C. F., and Noel, M. R. (2007). Can oyster restoration reverse cultural eutrophication in Chesapeake Bay? Estuar. Coasts 30, 331–343. doi: 10.1007/BF02700175

CrossRef Full Text | Google Scholar

Cerco, C. F., and Noel, M. R. (2013). Twenty-one-year simulation of Chesapeake Bay water quality using the CE-QUAL-ICM eutrophication model. J. Am. Water Resour. Assoc. 49, 1119–1133. doi: 10.1111/jawr.12107

CrossRef Full Text | Google Scholar

Cerco, C. F., Noel, M. R., and Wang, P. (2013). The shallow-water component of the Chesapeake Bay Environmental Model Package. J. Am. Water Resour. Ass. 49, 1091–1102. doi: 10.1111/jawr.12106

CrossRef Full Text | Google Scholar

Chapelle, A., Ménesguen, A., Deslous-Paoli, J. M., Souchu, P., Mazouni, N., Vaquer, A., et al. (2000). Modelling nitrogen, primary production and oxygen in a Mediterranean lagoon. Impact of oysters farming and inputs from the watershed. Ecol. Model. 127, 161–181. doi: 10.1016/S0304-3800(99)00206-9

CrossRef Full Text | Google Scholar

Cloern, J. E. (2001). Our evolving conceptual model of the coastal eutrophication problem. Mar. Ecol. Prog. Ser. 210, 223–253. doi: 10.3354/meps210223

CrossRef Full Text | Google Scholar

Cloern, J. E., Abreu, P. C., Carstensen, J., Chauvaud, L., Elmgren, R., Grall, J., et al. (2016). Human activities and climate variability drive fast-paced change across the world’s estuarine–coastal ecosystems. Glob. Chang. Biol. 22, 513–529. doi: 10.1111/gcb.13059

PubMed Abstract | CrossRef Full Text | Google Scholar

Commito, J. A., and Dankers, N. M. J. A. (2001). “Dynamics of Spatial and Temporal Complexity in European and North American Soft-Bottom Mussel Beds,” in Ecological Comparisons of Sedimentary Shores, ed. K. Reise (Berlin: Springer Berlin Heidelberg), 39–59. doi: 10.1007/978-3-642-56557-1_3

CrossRef Full Text | Google Scholar

Costanza, R., D’Arge, R., de Groot, R., Farber, S., Grasso, M., Hannon, B., et al. (1997). The value of the world’s ecosystem services and natural capital. Nature 387, 253–260. doi: 10.1038/387253a0

CrossRef Full Text | Google Scholar

Costanza, R., de Groot, R., Sutton, P., van der Ploeg, S., Anderson, S. J., Kubiszewski, I., et al. (2014). Changes in the global value of ecosystem services. Glob. Environ. Chang. 26, 152–158. doi: 10.1016/j.gloenvcha.2014.04.002

CrossRef Full Text | Google Scholar

Cozzoli, F., Gjoni, V., Del Pasqua, M., Hu, Z., Ysebaert, T., Herman, P. M. J., et al. (2019). A process based model of cohesive sediment resuspension under bioturbators’ influence. Sci. Total Environ. 670, 18–30. doi: 10.1016/j.scitotenv.2019.03.085

PubMed Abstract | CrossRef Full Text | Google Scholar

Cranford, P. J., Strain, P. M., Dowd, M., Hargrave, B. T., Grant, J., and Archambault, M. C. (2007). Influence of mussel aquaculture on nitrogen dynamics in a nutrient enriched coastal embayment. Mar. Ecol. Prog. Ser. 347, 61–78. doi: 10.3354/meps06997

CrossRef Full Text | Google Scholar

Cui, S., Shi, Y., Groffman, P. M., Schlesinger, W. H., and Zhu, Y.-G. (2013). Centennial-scale analysis of the creation and fate of reactive nitrogen in China (1910-2010). Proc. Natl. Acad. Sci. U.S.A. 110, 2052–2057. doi: 10.1073/pnas.1221638110

PubMed Abstract | CrossRef Full Text | Google Scholar

Dale, A. W., Bertics, V. J., Treude, T., Sommer, S., and Wallmann, K. (2013). Modeling benthic–pelagic nutrient exchange processes and porewater distributions in a seasonally hypoxic sediment: evidence for massive phosphate release by Beggiatoa? Biogeosciences 10, 629–651. doi: 10.5194/bg-10-629-2013

CrossRef Full Text | Google Scholar

Dame, R., and Libes, S. (1993). Oyster reefs and nutrient retention in tidal creeks. J. Exp. Mar. Bio. Ecol. 171, 251–258. doi: 10.1016/0022-0981(93)90007-B

CrossRef Full Text | Google Scholar

Dame, R. F., and Prins, T. C. (1998). Bivalve carrying capacity in coastal ecosystems. Aquat. Ecol. 31, 409–421. doi: 10.1023/A:1009997011583

CrossRef Full Text | Google Scholar

DHI (2007). DHI Eutrophication Model 1 – Including Sediment and Benthic Vegetation. Saint Paul: ECO Lab.

Google Scholar

Diaz, R. J., and Rosenberg, R. (2008). Spreading dead zones and consequences for marine ecosystems. Science 321, 926–929. doi: 10.1126/science.1156401

PubMed Abstract | CrossRef Full Text | Google Scholar

Dowd, M. (2005). A bio-physical coastal ecosystem model for assessing environmental effects of marine bivalve aquaculture. Ecol. Model. 183, 323–346. doi: 10.1016/j.ecolmodel.2004.08.018

CrossRef Full Text | Google Scholar

Duarte, C. M., Conley, D. J., Carstensen, J., and Sánchez-Camacho, M. (2009). Return to Neverland: Shifting baselines affect eutrophication restoration targets. Estuar. Coasts 32, 29–36. doi: 10.1007/s12237-008-9111-9112

CrossRef Full Text | Google Scholar

Duarte, C. M., Middelburg, J. J., and Caraco, N. (2005). Major role of marine vegetation on the oceanic carbon cycle. Biogeosciences 2, 1–8. doi: 10.5194/bg-2-1-2005

CrossRef Full Text | Google Scholar

Easterling, D. R., Meehl, G. A., Parmesan, C., Changnon, S. A., Karl, T. R., and Mearns, L. O. (2000). Climate extremes: observations. modeling, and impacts. Science 289, 2068–2074. doi: 10.1126/science.289.5487.2068

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebenhöh, W., Kohlmeier, C., and Radford, P. J. (1995). The benthic biological submodel in the European Regional Seas Ecosystem Model. Neth. J. Sea Res. 33, 423–452. doi: 10.1016/0077-7579(95)90056-X

CrossRef Full Text | Google Scholar

Ehrnsten, E., Bauer, B., and Gustafsson, B. G. (2019a). Combined effects of environmental drivers on marine trophic groups – A systematic model comparison. Front. Mar. Sci. 6:492. doi: 10.3389/fmars.2019.00492

CrossRef Full Text | Google Scholar

Ehrnsten, E., Norkko, A., Timmermann, K., and Gustafsson, B. G. (2019b). Benthic-pelagic coupling in coastal seas – Modelling macrofaunal biomass and carbon processing in response to organic matter supply. J. Mar. Syst. 196, 36–47. doi: 10.1016/j.jmarsys.2019.04.003

CrossRef Full Text | Google Scholar

Elmgren, R. (1984). Trophic dynamics in the enclosed, brackish Baltic Sea. Rapp. Proces-verbaux des Réunions. Cons. Int. pour l’Éxploration la Mer. 183, 152–169.

Google Scholar

Emerson, S., Jahnke, R., and Heggie, D. (1984). Sediment-water exchange in shallow water estuarine sediments. J. Mar. Res. 42, 709–730. doi: 10.1357/002224084788505942

CrossRef Full Text | Google Scholar

Falkowski, P., Scholes, R. J., Boyle, E., Canadell, J., Canfield, D., Elser, J., et al. (2000). The global carbon cycle: A test of our knowledge of earth as a system. Science 290, 291–296. doi: 10.1126/science.290.5490.291

PubMed Abstract | CrossRef Full Text | Google Scholar

Filgueira, R., Rosland, R., and Grant, J. (2011). A comparison of scope for growth (SFG) and dynamic energy budget (DEB) models applied to the blue mussel (Mytilus edulis). J. Sea Res. 66, 403–410. doi: 10.1016/j.seares.2011.04.006

CrossRef Full Text | Google Scholar

Follows, M. J., Dutkiewicz, S., Grant, S., and Chisholm, S. W. (2007). Emergent biogeography of microbial communities in a model ocean. Science 315, 1843–1846. doi: 10.1126/science.1138544

PubMed Abstract | CrossRef Full Text | Google Scholar

Fossing, H., Berg, P., Thamdrup, B., Rysgaard, S., and Munk, H. (2004). A Model Set-Up for An Oxygen and Nutrient Flux Model for Aarhus Bay (Denmark). Nagpur: National Environmental Research Institute.

Google Scholar

Fulton, E. A. (2010). Approaches to end-to-end ecosystem models. J. Mar. Syst. 81, 171–183. doi: 10.1016/j.jmarsys.2009.12.012

CrossRef Full Text | Google Scholar

Fulton, E. A., Link, J. S., Kaplan, I. C., Savina-Rolland, M., Johnson, P., Ainsworth, C., et al. (2011). Lessons in modelling and management of marine ecosystems: the Atlantis experience. Fish Fish. 12, 171–188. doi: 10.1111/j.1467-2979.2011.00412.x

CrossRef Full Text | Google Scholar

Fulton, E. A., Parslow, J. S., Smith, A. D. M., and Johnson, C. R. (2004a). Biogeochemical marine ecosystem models II: The effect of physiological detail on model performance. Ecol. Model. 173, 371–406. doi: 10.1016/j.ecolmodel.2003.09.024

CrossRef Full Text | Google Scholar

Fulton, E. A., Smith, A. D. M., and Johnson, C. R. (2004b). Biogeochemical marine ecosystem models I: IGBEM - A model of marine bay ecosystems. Ecol. Model. 174, 267–307. doi: 10.1016/j.ecolmodel.2003.09.027

CrossRef Full Text | Google Scholar

Fulton, E. A., Smith, A. D. M., and Johnson, C. R. (2003a). Effect of complexity on marine ecosystem models. Mar. Ecol. Prog. Ser. 253, 1–16. doi: 10.3354/meps253001

CrossRef Full Text | Google Scholar

Fulton, E. A., Smith, A. D. M. M., and Johnson, C. R. (2003b). Mortality and predation in ecosystem models: Is it important how these are expressed? Ecol. Model. 169, 157–178. doi: 10.1016/S0304-3800(03)00268-260

CrossRef Full Text | Google Scholar

Furukawa, Y. (2001). Biogeochemical consequences of macrofauna burrow ventilation. Geochem. Trans. 2:83. doi: 10.1186/1467-4866-2-83

PubMed Abstract | CrossRef Full Text | Google Scholar

Gallardi, D. (2014). Effects of Bivalve aquaculture on the environment and their possible mitigation: a review. Fish. Aquac. J. 05:105. doi: 10.4172/2150-3508.1000105

CrossRef Full Text | Google Scholar

Gammal, J., Järnström, M., Bernard, G., Norkko, J., and Norkko, A. (2019). Environmental context mediates biodiversity-ecosystem functioning relationships in coastal soft-sediment habitats. Ecosystems 22, 137–151. doi: 10.1007/s10021-018-0258-259

CrossRef Full Text | Google Scholar

Ganju, N. K., Brush, M. J., Rashleigh, B., Aretxabaleta, A. L., del Barrio, P., Grear, J. S., et al. (2016). Progress and challenges in coupled hydrodynamic-ecological estuarine modeling. Estuar. Coasts 39, 311–332. doi: 10.1007/s12237-015-0011-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Gilbert, F., Aller, R. C., and Hulth, S. (2003). The influence of macrofaunal burrow spacing and diffusive scaling on sedimentary nitrification and denitrification: An experimental simulation and model approach. J. Mar. Res. 61, 101–125. doi: 10.1357/002224003321586426

CrossRef Full Text | Google Scholar

Gilbertson, W. W., Solan, M., and Prosser, J. I. (2012). Differential effects of microorganism-invertebrate interactions on benthic nitrogen cycling. FEMS Microbiol. Ecol. 82, 11–22. doi: 10.1111/j.1574-6941.2012.01400.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M., and Charnov, E. L. (2001). Effects of size and temperature on metabolic rate. Science 293, 2248–2251. doi: 10.1126/science.1061967

PubMed Abstract | CrossRef Full Text | Google Scholar

Gogina, M., Morys, C., Forster, S., Gräwe, U., Friedland, R., and Zettler, M. L. (2017). Towards benthic ecosystem functioning maps: Quantifying bioturbation potential in the German part of the Baltic Sea. Ecol. Indic. 73, 574–588. doi: 10.1016/j.ecolind.2016.10.025

CrossRef Full Text | Google Scholar

Goldberg, E. D., and Koide, M. (1962). Geochronological studies of deep sea sediments by the ionium/thorium method. Geochim. Cosmochim. Acta 26, 417–450. doi: 10.1016/0016-7037(62)90112-6

CrossRef Full Text | Google Scholar

Graf, G., and Rosenberg, R. (1997). Bioresuspension and biodeposition: A review. J. Mar. Syst. 11, 269–278. doi: 10.1016/S0924-7963(96)00126-121

CrossRef Full Text | Google Scholar

Grall, J., and Chauvaud, L. (2002). Marine eutrophication and benthos: The need for new approaches and concepts. Glob. Chang. Biol. 8, 813–830. doi: 10.1046/j.1365-2486.2002.00519.x

CrossRef Full Text | Google Scholar

Grangeré, K., Lefebvre, S., Bacher, C., Cugier, P., and Ménesguen, A. (2010). Modelling the spatial heterogeneity of ecological processes in an intertidal estuarine bay: dynamic interactions between bivalves and phytoplankton. Mar. Ecol. Prog. Ser. 415, 141–158. doi: 10.3354/meps08659

CrossRef Full Text | Google Scholar

Grant, J., Bacher, C., Cranford, P. J., Guyondet, T., and Carreau, M. (2008). A spatially explicit ecosystem model of seston depletion in dense mussel culture. J. Mar. Syst. 73, 155–168. doi: 10.1016/j.jmarsys.2007.10.007

CrossRef Full Text | Google Scholar

Griffiths, J. R., Kadin, M., Nascimento, F. J. A., Tamelander, T., Törnroos, A., Bonaglia, S., et al. (2017). The importance of benthic-pelagic coupling for marine ecosystem functioning in a changing world. Glob. Chang. Biol. 23, 2179–2196. doi: 10.1111/gcb.13642

PubMed Abstract | CrossRef Full Text | Google Scholar

Grodzinski, W., Klekowski, R. Z., and Duncan, A. (eds) (1975). Methos for Ecological Bioenergetics. Hoboken, NJ: Blackwell Scientific Publications.

Google Scholar

Gruber, N., and Galloway, J. N. (2008). An Earth-system perspective of the global nitrogen cycle. Nature 451, 293–296. doi: 10.1038/nature06592

PubMed Abstract | CrossRef Full Text | Google Scholar

Gustafsson, B. G., Schenk, F., Blenckner, T., Eilola, K., Meier, H. E. M., Müller-Karulis, B., et al. (2012). Reconstructing the development of Baltic Sea eutrophication 1850-2006. Ambio 41, 534–548. doi: 10.1007/s13280-012-0318-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Halpern, B. S., Walbridge, S., Selkoe, K. A., Kappel, C. V., Micheli, F., D’Agrosa, C., et al. (2008). A global map of human impact on marine ecosystems. Science 319, 948–952. doi: 10.1126/science.1149345

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, J. L. S., and Bendtsen, J. (2013). Parameterisation of oxygen dynamics in the bottom water of the Baltic Sea-North Sea transition zone. Mar. Ecol. Prog. Ser. 481, 25–29. doi: 10.3354/meps10220

CrossRef Full Text | Google Scholar

Hawkins, A. J. S., Bayne, B. L., Bougrier, S., Héral, M., Iglesias, J. I. P., Navarro, E., et al. (1998). Some general relationships in comparing the feeding physiology of suspension-feeding bivalve molluscs. J. Exp. Mar. Bio. Ecol. 219, 87–103. doi: 10.1016/S0022-0981(97)00176-177

CrossRef Full Text | Google Scholar

Heath, M. R. (2012). Ecosystem limits to food web fluxes and fisheries yields in the North Sea simulated with an end-to-end food web model. Prog. Oceanogr. 102, 42–66. doi: 10.1016/j.pocean.2012.03.004

CrossRef Full Text | Google Scholar

Henriksen, K., Ramussen, M. B., and Jensen, A. (1983). Effect of bioturbation on microbial nitrogen transformations in the sediment and fluxes of ammonium and nitrate to the overlaying water. Ecol. Bull. 35, 193–205.

Google Scholar

Herman, P. M. J., Middelburg, J. J., van de Koppel, J., and Heip, C. H. R. (1999). “Ecology of estuarine macrobenthos,” in Advances in Ecological Research, eds D. B. Nedwell and D. G. Raffaelli (Cambridge, MA: Academic Press), 195–240. doi: 10.1016/S0065-2504(08)60194-4

CrossRef Full Text | Google Scholar

Hewitt, J. E., Ellis, J. I., and Thrush, S. F. (2016). Multiple stressors, nonlinear effects and the implications of climate change impacts on marine coastal ecosystems. Glob. Chang. Biol. 22, 2665–2675. doi: 10.1111/gcb.13176

PubMed Abstract | CrossRef Full Text | Google Scholar

Heymans, J. J., Coll, M., Link, J. S., Mackinson, S., Steenbeek, J., Walters, C., et al. (2016). Best practice in Ecopath with Ecosim food-web models for ecosystem-based management. Ecol. Model. 331, 173–184. doi: 10.1016/j.ecolmodel.2015.12.007

CrossRef Full Text | Google Scholar

Holling, C. S. (1966). The functional response of invertebrate predators to prey density. Mem. Entomol. Soc. Canada 98, 5–86. doi: 10.4039/entm9848fv

CrossRef Full Text | Google Scholar

Holme, N. A., and McIntyre, A. D. (eds) (1971). Methods for the Study of Marine Benthos. Hoboken, NJ: Blackwell Scientific Publications.

Google Scholar

Holstein, J. M., and Wirtz, K. W. (2009). Sensitivity analysis of nitrogen and carbon cycling in marine sediments. Estuar. Coast. Shelf Sci. 82, 632–644. doi: 10.1016/j.ecss.2009.02.008

CrossRef Full Text | Google Scholar

HydroQual (2000). Development of a Suspension Feeding and Deposit Feeding Benthos Model for Chesapeake Bay. Mahwah, NJ: HydroQual.

Google Scholar

Ichikawa, T., Aizaki, M., and Takeshita, M. (2007). Numerical study on amelioration of water quality in Lakes Shinji and Nakaumi: A coastal brackish lagoon system. Limnology 8, 281–294. doi: 10.1007/s10201-007-0222-224

CrossRef Full Text | Google Scholar

Isaev, A. V., Eremina, T. R., Ryabchenko, V. A., and Savchuk, O. P. (2017). Model estimates of the impact of bioirrigation activity of Marenzelleria spp. on the Gulf of Finland ecosystem in a changing climate. J. Mar. Syst. 171, 81–88. doi: 10.1016/j.jmarsys.2016.08.005

CrossRef Full Text | Google Scholar

Jeschke, J. M., Kopp, M., and Tollrian, R. (2004). Consumer-food systems: why type I functional responses are exclusive to filter feeders. Biol. Rev. Camb. Philos. Soc. 79, 337–349. doi: 10.1017/S1464793103006286

PubMed Abstract | CrossRef Full Text | Google Scholar

Joensuu, M., Pilditch, C. A., Harris, R., Hietanen, S., Pettersson, H., and Norkko, A. (2018). Sediment properties, biota, and local habitat structure explain variation in the erodibility of coastal sediments. Limnol. Oceanogr. 63, 173–186. doi: 10.1002/lno.10622

CrossRef Full Text | Google Scholar

Josefson, A. B., and Rasmussen, B. (2000). Nutrient retention by benthic macrofaunal biomass of Danish estuaries: importance of nutrient load and residence time. Estuar. Coast. Shelf Sci. 50, 205–216. doi: 10.1006/ecss.1999.0562

CrossRef Full Text | Google Scholar

Karlson, K., Bonsdorff, E., and Rosenberg, R. (2007). The impact of benthic macrofauna for nutrient fluxes from Baltic Sea sediments. Ambio 36, 161–167. doi: 10.1579/0044-7447200736

PubMed Abstract | CrossRef Full Text | Google Scholar

Kautsky, N., and Evans, S. (1987). Role of biodepostion by Mytilus edulis in the circulation of matter and nutrients in a Baltic coastal ecosystem. Mar. Ecol. Prog. Ser. 38, 201–212. doi: 10.3354/meps038201

CrossRef Full Text | Google Scholar

Kemp, W. M., Boynton, W. R., Adolf, J. E., Boesch, D. F., Boicourt, W. C., Brush, G., et al. (2005). Eutrophication of Chesapeake Bay: historical trends and ecological interactions. Mar. Ecol. Prog. Ser. 303, 1–29. doi: 10.3354/meps303001

CrossRef Full Text | Google Scholar

Kemp, W. M., Testa, J. M., Conley, D. J., Gilbert, D., and Hagy, J. D. (2009). Temporal responses of coastal hypoxia to nutrient loading and physical controls. Biogeosciences 6, 2985–3008. doi: 10.5194/bg-6-2985-2009

CrossRef Full Text | Google Scholar

Kim, H. C., and Montagna, P. A. (2009). Implications of Colorado river (Texas, USA) freshwater inflow to benthic ecosystem dynamics: A modeling study. Estuar. Coast. Shelf Sci. 83, 491–504. doi: 10.1016/j.ecss.2009.04.033

CrossRef Full Text | Google Scholar

Klepper, O. (1989). A Model of Carbon Flows in Relation to Macrobenthic Food Supply in the Oosterschelde Estuary (S.W. Netherlands). Dissertation thesis, University of Waeningen, Waeningen.

Google Scholar

Kooijman, S. A. L. M. (2000). Dynamic Energy and Mass Budgets in Biological Systems, 2nd Edn. Cambridge: Cambridge University Press, doi: 10.1017/CBO9780511565403

CrossRef Full Text | Google Scholar

Koretsky, C. M., Meile, C., and Van Cappellen, P. (2002). Quantifying bioirrigation using ecological parameters: a stochastic approach. Geochem. Trans. 3, 17–30. doi: 10.1039/b110459d

CrossRef Full Text | Google Scholar

Krause-Jensen, D., and Duarte, C. M. (2016). Substantial role of macroalgae in marine carbon sequestration. Nat. Geosci. 9, 737–742. doi: 10.1038/ngeo2790

CrossRef Full Text | Google Scholar

Kristensen, E. (1984). Effect of natural concentrations on nutrient exchange between a polychaete burrow in estuarine sediment and the overlying water. J. Exp. Mar. Bio. Ecol. 75, 171–190. doi: 10.1016/0022-0981(84)90179-90175

CrossRef Full Text | Google Scholar

Kristensen, E. (1988). “Benthic fauna and biogeochemical processes in marine sediments:Microbial activities and fluxes, in Nitrogen Cycling in Coastal Marine Environments, T. H. Blackburn, and J. Sørensen (New York, NY: John Wiley and Sons) 301–341.

Google Scholar

Kristensen, E. (2001). Impact of polychaetes (Nereis spp. and Arenicola marina) on carbon biogeochemistry in coastal marine sediments†. Geochem. Trans. 2:92. doi: 10.1186/1467-4866-2-92

PubMed Abstract | CrossRef Full Text | Google Scholar

Kristensen, E., Penha-Lopes, G., Delefosse, M., Valdemarsen, T., Quintana, C. O., and Banta, G. T. (2012). What is bioturbation? the need for a precise definition for fauna in aquatic sciences. Mar. Ecol. Prog. Ser. 446, 285–302. doi: 10.3354/meps09506

CrossRef Full Text | Google Scholar

Laruelle, G. G., Roubeix, V., Sferratore, A., Brodherr, B., Ciuffa, D., Conley, D. J., et al. (2009). Anthropogenic perturbations of the silicon cycle at the global scale: Key role of the land-ocean transition. Global Biogeochem. Cycles 23:GB4031. doi: 10.1029/2008GB003267

CrossRef Full Text | Google Scholar

Le Hir, P., Monbet, Y., and Orvain, F. (2007). Sediment erodability in sediment transport modelling: Can we account for biota effects? Cont. Shelf Res. 27, 1116–1142. doi: 10.1016/j.csr.2005.11.016

CrossRef Full Text | Google Scholar

Lessin, G., Artioli, Y., Almroth-Rosell, E., Blackford, J. C., Dale, A. W., Glud, R. N., et al. (2018). Modelling marine sediment biogeochemistry: Current knowledge gaps, challenges, and some methodological advice for advancement. Front. Mar. Sci. 5:19. doi: 10.3389/fmars.2018.00019

CrossRef Full Text | Google Scholar

Lessin, G., Artioli, Y., Queirós, A. M., Widdicombe, S., and Blackford, J. C. (2016). Modelling impacts and recovery in benthic communities exposed to localised high CO2. Mar. Pollut. Bull. 109, 267–280. doi: 10.1016/j.marpolbul.2016.05.071

PubMed Abstract | CrossRef Full Text | Google Scholar

Lessin, G., Bruggeman, J., McNeill, C. L., and Widdicombe, S. (2019). Time scales of benthic macrofaunal response to pelagic production differ between major feeding groups. Front. Mar. Sci. 6:15. doi: 10.3389/fmars.2019.00015

CrossRef Full Text | Google Scholar

Levins, R. (1966). The strategy of model building in population biology. Am. Sci. 54, 421–431.

Google Scholar

Lohrer, A. M., Thrush, S. F., and Gibbs, M. M. (2004). Bioturbators enhance ecosystem function through complex biogeochemical interactions. Nature 431, 1092–1095. doi: 10.1038/nature03042

PubMed Abstract | CrossRef Full Text | Google Scholar

Lotze, H. K., Lenihan, H. S., Bourque, B. J., Bradbury, R. H., Cooke, R. G., Kay, M. C., et al. (2006). Depletion, degradation, and recovery potential of estuaries and coastal seas. Science 312, 1806–1809. doi: 10.1126/science.1128035

PubMed Abstract | CrossRef Full Text | Google Scholar

Maar, M., Bolding, K., Petersen, J. K., Hansen, J. L. S., and Timmermann, K. (2009). Local effects of blue mussels around turbine foundations in an ecosystem model of Nysted off-shore wind farm. Denmark. J. Sea Res. 62, 159–174. doi: 10.1016/j.seares.2009.01.008

CrossRef Full Text | Google Scholar

Maar, M., and Hansen, J. L. S. (2011). Increasing temperatures change pelagic trophodynamics and the balance between pelagic and benthic secondary production in a water column model of the Kattegat. J. Mar. Syst. 85, 57–70. doi: 10.1016/j.jmarsys.2010.11.006

CrossRef Full Text | Google Scholar

Maar, M., Timmermann, K., Petersen, J. K., Gustafsson, K. E., and Storm, L. M. (2010). A model study of the regulation of blue mussels by nutrient loadings and water column stability in a shallow estuary, the Limfjorden. J. Sea Res. 64, 322–333. doi: 10.1016/j.seares.2010.04.007

CrossRef Full Text | Google Scholar

Magni, P., Montani, S., Takada, C., and Tsutsumi, H. (2000). Temporal scaling and relevance of bivalve nutrient excretion on a tidal flat of the Seto Inland Sea. Japan. Mar. Ecol. Prog. Ser. 198, 139–155. doi: 10.3354/meps198139

CrossRef Full Text | Google Scholar

Maire, O., Lecroart, P., Meysman, F., Rosenberg, R., Duchêne, J., and Grémare, A. (2010). Quantification of sediment reworking rates in bioturbation research: a review. Aquat. Biol. 2, 219–238. doi: 10.3354/ab00053

CrossRef Full Text | Google Scholar

Malta, E., Stigter, T. Y., Pacheco, A., Dill, A. C., Tavares, D., and Santos, R. (2017). Effects of external nutrient sources and extreme weather events on the nutrient budget of a southern European coastal lagoon. Estuar. Coasts 40, 419–436. doi: 10.1007/s12237-016-0150-159

CrossRef Full Text | Google Scholar

McClain, C. R., Allen, A. P., Tittensor, D. P., and Rex, M. A. (2012). Energetics of life on the deep seafloor. Proc. Natl. Acad. Sci. U.S.A. 109, 15366–15371. doi: 10.1073/pnas.1208976109

PubMed Abstract | CrossRef Full Text | Google Scholar

McGlathery, K. J. K., Sundbäck, K., and Anderson, I. C. I. C. (2007). Eutrophication in shallow coastal bays and lagoons: the role of plants in the coastal filter. Mar. Ecol. Prog. Ser. 348, 1–18. doi: 10.3354/meps07132

CrossRef Full Text | Google Scholar

Meier, H. E. M., Edman, M. K., Eilola, K. J., Placke, M., Neumann, T., Andersson, H. C., et al. (2018). Assessment of Eutrophication abatement scenarios for the baltic sea by multi-model ensemble simulations. Front. Mar. Sci. 5:440. doi: 10.3389/fmars.2018.00440

CrossRef Full Text | Google Scholar

Meier, H. E. M., Müller-Karulis, B., Andersson, H. C., Dieterich, C., Eilola, K., Gustafsson, B. G., et al. (2012). Impact of climate change on ecological quality indicators and biogeochemical fluxes in the Baltic Sea: A multi-model ensemble study. Ambio 41, 558–573. doi: 10.1007/s13280-012-0320-323

CrossRef Full Text | Google Scholar

Meile, C., Berg, P., Van Cappellen, P., and Tuncay, K. (2005). Solute-specific pore water irrigation: Implications for chemical cycling in early diagenesis. J. Mar. Res. 63, 601–621. doi: 10.1357/0022240054307885

CrossRef Full Text | Google Scholar

Mermillod-Blondin, F. (2011). The functional significance of bioturbation and biodeposition on biogeochemical processes at the water–sediment interface in freshwater and marine ecosystems. J. North Am. Benthol. Soc. 30, 770–778. doi: 10.1899/10-121.1

CrossRef Full Text | Google Scholar

Mermillod-Blondin, F., François-Carcaillet, F., and Rosenberg, R. (2005). Biodiversity of benthic invertebrates and organic matter processing in shallow marine sediments: an experimental study. J. Exp. Mar. Bio. Ecol. 315, 187–209. doi: 10.1016/j.jembe.2004.09.013

CrossRef Full Text | Google Scholar

Mesnage, V., Ogier, S., Bally, G., Disnar, J. R., Lottier, N., Dedieu, K., et al. (2007). Nutrient dynamics at the sediment-water interface in a Mediterranean lagoon (Thau, France): Influence of biodeposition by shellfish farming activities. Mar. Environ. Res. 63, 257–277. doi: 10.1016/j.marenvres.2006.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Meysman, F. J. R., Boudreau, B. P., and Middelburg, J. J. (2003). Relations between local, nonlocal, discrete and continuous models of bioturbation. J. Mar. Res. 61, 391–410. doi: 10.1357/002224003322201241

CrossRef Full Text | Google Scholar

Meysman, F. J. R., Galaktionov, O. S., Gribsholt, B., and Middelburg, J. J. (2006a). Bioirrigation in permeable sediments: advective pore-water transport induced by burrow ventilation. Limnol. Oceanogr. 51, 142–156. doi: 10.4319/lo.2006.51.1.0142

CrossRef Full Text | Google Scholar

Meysman, F. J. R., Middelburg, J. J., and Heip, C. H. R. (2006b). Bioturbation: a fresh look at Darwin’s last idea. Trends Ecol. Evol. 21, 688–695. doi: 10.1016/j.tree.2006.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Meysman, F. J. R., Galaktionov, O. S., Madani, S., and Middelburg, J. J. (2005). “Modelling Biological Interactions in Aquatic Sediments as Coupled Reactive Transport,” in Interactions Between Macro- and Microorganisms in Marine Sediments, eds E. Kristensen, R. R. Haese, and J. E. Kostka (Washington, DC: American Geophysical Union (AGU)), 359–388. doi: 10.1029/CE060p0359

CrossRef Full Text | Google Scholar

Michaud, E., Desrosiers, G., Mermillod-Blondin, F., Sundby, B., and Stora, G. (2005). The functional group approach to bioturbation: The effects of biodiffusers and gallery-diffusers of the Macoma balthica community on sediment oxygen uptake. J. Exp. Mar. Bio. Ecol. 326, 77–88. doi: 10.1016/j.jembe.2005.05.016

CrossRef Full Text | Google Scholar

Middelburg, J. J. (2018). Reviews and syntheses: to the bottom of carbon processing at the seafloor. Biogeosciences 15, 413–427. doi: 10.5194/bg-15-413-2018

CrossRef Full Text | Google Scholar

Middelburg, J. J., Klaver, G., Nieuwenhuize, J., Wielemaker, A., de Hass, W., Vlug, T., et al. (1996). Organic matter mineralization in intertidal sediments along an estuarine gradient. Mar. Ecol. Prog. Ser. 132, 157–168. doi: 10.3354/meps132157

CrossRef Full Text | Google Scholar

Middelburg, J. J., Soetaert, K., and Herman, P. M. J. (1997). Empirical relationships for use in global diagenetic models. Deep-Sea Res. Pt I. 44, 327–344. doi: 10.1016/S0967-0637(96)00101-X

CrossRef Full Text | Google Scholar

Montagna, P. A., and Li, J. (2010). “Effect of freshwater inflow on nutrient loading and macrobenthos secondary production in texas lagoons,” in Coastal Lagoons: Critical Habitats of Environmental Change, eds M. J. Kennish and H. W. Paerl (Boca Raton, FL: CRC Press), 513–539. doi: 10.1201/ebk1420088304-c20

CrossRef Full Text | Google Scholar

Morys, C., Forster, S., and Graf, G. (2016). Variability of bioturbation in various sediment types and on different spatial scales in the southwestern Baltic Sea. Mar. Ecol. Prog. Ser. 557, 31–49. doi: 10.3354/meps11837

CrossRef Full Text | Google Scholar

Murphy, J. M., Sexton, D. M. H., Barnett, D. N., Jones, G. S., Webb, M. J., Collins, M., et al. (2004). Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature 430, 768–772. doi: 10.1038/nature02771

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, A., and Parslow, J. (1997). Port Phillip Bay Integrated Model: Final Report. CSIRO Division of Marine Research Technical Report No. 44, Canberra: CSIRO.

Google Scholar

Murray, A. G., and Parslow, J. S. (1999). Modelling of nutrient impacts in Port Phillip Bay - a semi-enclosed Australian ecosystem. Mar. Freshw. Res. 50, 567–611. doi: 10.1071/mf98087

CrossRef Full Text | Google Scholar

Mussap, G., and Zavatarelli, M. (2017). A numerical study of the benthic–pelagic coupling in a shallow shelf sea (Gulf of Trieste). Reg. Stud. Mar. Sci. 9, 24–34. doi: 10.1016/j.rsma.2016.11.002

CrossRef Full Text | Google Scholar

Newell, R. I. E. (2004). Ecosystem influences of natural and cultivated populations of suspension-feeding bivalve molluscs: a review. J. Shellfish Res. 23, 51–61.

Google Scholar

Nielsen, S. L., Banta, G. T., and Pedersen, M. F. (2004). Estuarine Nutrient Cycling: The Influence of Primary Producers, eds S. L. Nielsen, G. T. Banta, and M. F. Pedersen (Dordrecht: Springer Netherlands), doi: 10.1007/978-1-4020-3021-5

CrossRef Full Text | Google Scholar

Norkko, A., Hewitt, J. E., Thrush, S. F., and Funnell, T. (2001). Benthic-pelagic coupling and suspension-feeding bivalves: Linking site-specific sediment flux and biodeposition to benthic community structure. Limnol. Oceanogr. 46, 2067–2072. doi: 10.4319/lo.2001.46.8.2067

CrossRef Full Text | Google Scholar

Norkko, A., Villnäs, A., Norkko, J., Valanko, S., and Pilditch, C. (2013). Size matters: implications of the loss of large individuals for ecosystem function. Sci. Rep. 3:2646. doi: 10.1038/srep02646

PubMed Abstract | CrossRef Full Text | Google Scholar

Norkko, J., Reed, D. C., Timmermann, K., Norkko, A., Gustafsson, B. G., Bonsdorff, E., et al. (2012). A welcome can of worms? Hypoxia mitigation by an invasive species. Glob. Chang. Biol. 18, 422–434. doi: 10.1111/j.1365-2486.2011.02513.x

CrossRef Full Text | Google Scholar

Norkko, J., and Shumway, S. E. (2011). “Bivalves as bioturbators and bioirrigators,” in Shellfish Aquaculture and the Environment, ed. S. E. Shumway (Oxford: Wiley-Blackwell), 297–317. doi: 10.1002/9780470960967.ch10

CrossRef Full Text | Google Scholar

Orvain, F., Hir, P. L., Sauriau, P.-G., and Lefebvre, S. (2012). Modelling the effects of macrofauna on sediment transport and bed elevation: Application over a cross-shore mudflat profile and model validation. Estuar. Coast. Shelf Sci. 108, 64–75. doi: 10.1016/j.ecss.2011.12.036

CrossRef Full Text | Google Scholar

Orvain, F., Le Hir, P., and Sauriau, P.-G. (2003). A model of fluff layer erosion and subsequent bed erosion in the presence of the bioturbator, Hydrobia ulvae. J. Mar. Res. 61, 821–849. doi: 10.1357/002224003322981165

CrossRef Full Text | Google Scholar

Palmer, M. A., Allan, J. D., and Butman, C. A. (1996). Dispersal as a regional process affecting the local dynamics of marine and stream benthic invertebrates. Trends Ecol. Evol. 11, 322–326. doi: 10.1016/0169-5347(96)10038-10030

CrossRef Full Text | Google Scholar

Paraska, D. W., Hipsey, M. R., and Ursula Salmon, S. (2014). Sediment diagenesis models: review of approaches, challenges and opportunities. Environ. Model. Softw. 61, 297–325. doi: 10.1016/j.envsoft.2014.05.011

CrossRef Full Text | Google Scholar

Pearson, T. H., and Rosenberg, R. (1987). “Feast and famine: Stucturing factors in marine benthic communities,” in Organization Of Communities:The 27th Symposium of the British Ecological Society, Aberystwyth 1986, eds P. S. Giller and J. H. R. Gee (Oxford: Blackwell), 373–395.

Google Scholar

Petihakis, G., Triantafyllou, G., Koutsoubas, D., Allen, I., and Dounas, C. (1999). Modelling the annual cycles of nutrients and phytoplankton in a Mediterranean lagoon (Gialova. Greece). Mar. Environ. Res. 48, 37–58. doi: 10.1016/S0141-1136(99)00031-38

CrossRef Full Text | Google Scholar

Petihakis, G., Triantafyllou, G., Pollani, A., Koliou, A., and Theodorou, A. (2005). Field data analysis and application of a complex water column biogeochemical model in different areas of a semi-enclosed basin: Towards the development of an ecosystem management tool. Mar. Environ. Res. 59, 493–518. doi: 10.1016/j.marenvres.2004.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Pilditch, C. A., Valanko, S., Norkko, J., and Norkko, A. (2015). Post-settlement dispersal: the neglected link in maintenance of soft-sediment biodiversity. Biol. Lett. 11:20140795. doi: 10.1098/rsbl.2014.0795

PubMed Abstract | CrossRef Full Text | Google Scholar

Plus, M., Chapelle, A., Ménesguen, A., Deslous-Paoli, J.-M., and Auby, I. (2003). Modelling seasonal dynamics of biomasses and nitrogen contents in a seagrass meadow (Zostera noltii Hornem.): application to the Thau lagoon (French Mediterranean coast). Ecol. Model. 161, 213–238. doi: 10.1016/S0304-3800(02)00350-352

CrossRef Full Text | Google Scholar

Prins, T. C., and Smaal, A. C. (1994). The role of the blue mussel Mytilus edulis in the cycling of nutrients in the Oosterschelde estuary (The Netherlands). Hydrobiologia 282, 413–429. doi: 10.1007/BF00024645

CrossRef Full Text | Google Scholar

Qu, H. J., and Kroeze, C. (2012). Nutrient export by rivers to the coastal waters of China: management strategies and future trends. Reg. Environ. Change 12, 153–167. doi: 10.1007/s10113-011-0248-243

CrossRef Full Text | Google Scholar

Rakotomalala, C., Grangeré, K., Ubertini, M., Forêt, M., and Orvain, F. (2015). Modelling the effect of Cerastoderma edule bioturbation on microphytobenthos resuspension towards the planktonic food web of estuarine ecosystem. Ecol. Model. 316, 155–167. doi: 10.1016/j.ecolmodel.2015.08.010

CrossRef Full Text | Google Scholar

Ramesh, R., Chen, Z., Cummins, V., Day, J., D’Elia, C., Dennison, B., et al. (2015). Land-ocean interactions in the coastal zone: Past, present & future. Anthropocene 12, 85–98. doi: 10.1016/j.ancene.2016.01.005

CrossRef Full Text | Google Scholar

Rasmussen, E. K., Petersen, O. S., Thompson, J. R., Flower, R. J., Ayache, F., Kraiem, M., et al. (2009). Model analyses of the future water quality of the eutrophicated Ghar El Melh lagoon (Northern Tunisia). Hydrobiologia 622, 173–193. doi: 10.1007/s10750-008-9681-9689

CrossRef Full Text | Google Scholar

Reed, D. C., Slomp, C. P., and Gustafsson, B. G. (2011). Sedimentary phosphorus dynamics and the evolution of bottom-water hypoxia: a coupled benthic-pelagic model of a coastal system. Limnol. Oceanogr. 56, 1075–1092. doi: 10.4319/lo.2011.56.3.1075

CrossRef Full Text | Google Scholar

Regnier, P., Arndt, S., Goossens, N., Volta, C., Laruelle, G. G., Lauerwald, R., et al. (2013a). Modelling estuarine biogeochemical dynamics: From the local to the global scale. Aquat. Geochem. 19, 591–626. doi: 10.1007/s10498-013-9218-9213

CrossRef Full Text | Google Scholar

Regnier, P., Friedlingstein, P., Ciais, P., Mackenzie, F. T., Gruber, N., Janssens, I. A., et al. (2013b). Anthropogenic perturbation of the carbon fluxes from land to ocean. Nat. Geosci. 6, 597–607. doi: 10.1038/ngeo1830

CrossRef Full Text | Google Scholar

Remane, A. (1934). Die Brackwasserfauna. Verhandlungen der Dtsch. Zool. Gesellschaft 36, 34–74.

Google Scholar

Ren, J. S., Ross, A. H., Hadfield, M. G., and Hayden, B. J. (2010). An ecosystem model for estimating potential shellfish culture production in sheltered coastal waters. Ecol. Model. 221, 527–539. doi: 10.1016/j.ecolmodel.2009.11.003

CrossRef Full Text | Google Scholar

Renz, J. R., and Forster, S. (2013). Are similar worms different? a comparative tracer study on bioturbation in the three sibling species Marenzelleria arctia, M. viridis, and M. neglecta from the baltic sea. Limnol. Oceanogr. 58, 2046–2058. doi: 10.4319/lo.2013.58.6.2046

CrossRef Full Text | Google Scholar

Renz, J. R., and Forster, S. (2014). Effects of bioirrigation by the three sibling species of Marenzelleria spp. on solute fluxes and porewater nutrient profiles. Mar. Ecol. Prog. Ser. 505, 145–159. doi: 10.3354/meps10756

CrossRef Full Text | Google Scholar

Reusch, T. B. H., Dierking, J., Andersson, H. C., Bonsdorff, E., Carstensen, J., Casini, M., et al. (2018). The Baltic Sea as a time machine for the future coastal ocean. Sci. Adv. 4:eaar8195. doi: 10.1126/sciadv.aar8195

PubMed Abstract | CrossRef Full Text | Google Scholar

Rhoads, D. C. (1974). Organism-sediment relations on the muddy sea floor. Oceanogr. Mar. Biol. An Annu. Rev. 12, 263–300.

Google Scholar

Riley, G. A. (1946). Factors controlling phytoplankton populations on the Georges bank. J. Mar. Res. 6, 54–73.

Google Scholar

Riley, G. A., Stommel, H., and Bumpus, D. F. (1949). Quantitative ecology of the plankton of the Western North Atlantic. Bull. Bingham Oceanogr. Collect. 12, 1–169.

Google Scholar

Robbins, J. A. (1986). A model for particle-selective transport of tracers in sediments with conveyor belt deposit feeders. J. Geophys. Res. 91, 8542–8558. doi: 10.1029/JC091iC07p08542

CrossRef Full Text | Google Scholar

Rodil, I. F., Attard, K. M., Norkko, J., Glud, R. N., and Norkko, A. (2019). Estimating respiration rates and secondary production of macrobenthic communities across coastal habitats with contrasting structural biodiversity. Ecosystems 23, 630–647. doi: 10.1007/s10021-019-00427-420

CrossRef Full Text | Google Scholar

Rooze, J., Egger, M., Tsandev, I., and Slomp, C. P. (2016). Iron-dependent anaerobic oxidation of methane in coastal surface sediments: Potential controls and impact. Limnol. Oceanogr. 61, S267–S282. doi: 10.1002/lno.10275

CrossRef Full Text | Google Scholar

Ruardij, P., and Van Raaphorst, W. (1995). Benthic nutrient regeneration in the ERSEM ecosystem model of the North Sea. Neth. J. Sea Res. 33, 453–483. doi: 10.1016/0077-7579(95)90057-90058

CrossRef Full Text | Google Scholar

Sand-Jensen, K., and Borum, J. (1991). Interactions among phytoplankton, periphyton, and macrophytes in temperate freshwaters and estuaries. Aquat. Bot. 41, 137–175. doi: 10.1016/0304-3770(91)90042-90044

CrossRef Full Text | Google Scholar

Sanford, L. P. (2008). Modeling a dynamically varying mixed sediment bed with erosion, deposition, bioturbation, consolidation, and armoring. Comput. Geosci. 34, 1263–1283. doi: 10.1016/j.cageo.2008.02.011

CrossRef Full Text | Google Scholar

Saraiva, S., Fernandes, L., van der Meer, J., Neves, R., and Kooijman, S. A. L. M. (2017). The role of bivalves in the Balgzand: First steps on an integrated modelling approach. Ecol. Modell. 359, 34–48. doi: 10.1016/j.ecolmodel.2017.04.018

CrossRef Full Text | Google Scholar

Saraiva, S., van der Meer, J., Kooijman, S. A. L. M., and Sousa, T. (2011). Modelling feeding processes in bivalves: a mechanistic approach. Ecol. Model. 222, 514–523. doi: 10.1016/j.ecolmodel.2010.09.031

CrossRef Full Text | Google Scholar

Savchuk, O. P. (2002). Nutrient biogeochemical cycles in the Gulf of Riga: scaling up field studies with a mathematical model. J. Mar. Syst. 32, 253–280. doi: 10.1016/S0924-7963(02)00039-38

CrossRef Full Text | Google Scholar

Schlüter, M., Sauter, E., Hansen, H. P., and Suess, E. (2000). Seasonal variations of bioirrigation in coastal sediments: Modelling of field data. Geochim. Cosmochim. Acta 64, 821–834. doi: 10.1016/S0016-7037(99)00375-370

CrossRef Full Text | Google Scholar

Sharpe, P. J. H., and DeMichele, D. W. (1977). Reaction kinetics of poikilotherm development. J. Theor. Biol. 64, 649–670. doi: 10.1016/0022-5193(77)90265-X

CrossRef Full Text | Google Scholar

Shull, D. H., Benoit, J. M., Wojcik, C., and Senning, J. R. (2009). Infaunal burrow ventilation and pore-water transport in muddy sediments. Estuar. Coast. Shelf Sci. 83, 277–286. doi: 10.1016/j.ecss.2009.04.005

CrossRef Full Text | Google Scholar

Smyth, A. R., Murphy, A. E., Anderson, I. C., and Song, B. (2018). Differential effects of bivalves on sediment nitrogen cycling in a shallow coastal bay. Estuar. Coasts 41, 1147–1163. doi: 10.1007/s12237-017-0344-349

CrossRef Full Text | Google Scholar

Snelgrove, P. V. R., Soetaert, K., Solan, M., Thrush, S., Wei, C.-L., Danovaro, R., et al. (2018). Global carbon cycling on a heterogeneous seafloor. Trends Ecol. Evol. 33, 96–105. doi: 10.1016/j.tree.2017.11.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Snelgrove, P. V. R., Thrush, S. F., Wall, D. H., and Norkko, A. (2014). Real world biodiversity-ecosystem functioning: A seafloor perspective. Trends Ecol. Evol. 29, 398–405. doi: 10.1016/j.tree.2014.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Soetaert, K., and Herman, P. M. J. (1995). Carbon flows in the Westerschelde estuary (The Netherlands) evaluated by means of an ecosystem model (MOSES). Hydrobiologia 311, 247–266. doi: 10.1007/BF00008584

CrossRef Full Text | Google Scholar

Soetaert, K., Herman, P. M. J., and Middelburg, J. J. (1996). A model of early diagenetic processes from the shelf to abyssal depths. Geochim. Cosmochim. Acta 60, 1019–1040. doi: 10.1016/0016-7037(96)00013-0

CrossRef Full Text | Google Scholar

Soetaert, K., Herman, P. M. J., and Scholten, H. (1992). MOSES: Model of the Scheldt estuary. Ecolmod rapport EM-3 66.

Google Scholar

Soetaert, K., and Middelburg, J. J. (2009). Modeling eutrophication and oligotrophication of shallow-water marine systems: the importance of sediments under stratified and well-mixed conditions. Hydrobiologia 629, 239–254. doi: 10.1007/s10750-009-9777-x

CrossRef Full Text | Google Scholar

Soetaert, K., Middelburg, J. J., Herman, P. M. J., and Buis, K. (2000). On the coupling of benthic and pelagic biogeochemical models. Earth Sci. Rev. 51, 173–201. doi: 10.1016/S0012-8252(00)00004-0

CrossRef Full Text | Google Scholar

Sohma, A., Sato, T., and Nakata, K. (2000). New numerical model study on a tidal flat system - Seasonal, daily and tidal variations. Spill Sci. Technol. Bull. 6, 173–185. doi: 10.1016/S1353-2561(00)00070-70

CrossRef Full Text | Google Scholar

Sohma, A., Sekiguchi, Y., Kuwae, T., and Nakamura, Y. (2008). A benthic-pelagic coupled ecosystem model to estimate the hypoxic estuary including tidal flat - Model description and validation of seasonal/daily dynamics. Ecol. Model. 215, 10–39. doi: 10.1016/j.ecolmodel.2008.02.027

CrossRef Full Text | Google Scholar

Sohma, A., Sekiguchi, Y., and Nakata, K. (2004). Modeling and evaluating the ecosystem of sea-grass beds, shallow waters without sea-grass, and an oxygen-depleted offshore area. J. Mar. Syst. 45, 105–142. doi: 10.1016/j.jmarsys.2003.11.011

CrossRef Full Text | Google Scholar

Sohma, A., Sekiguchi, Y., Yamada, H., Sato, T., and Nakata, K. (2001). A new coastal marine ecosystem model study coupled with hydrodynamics and tidal flat ecosystem effect. Mar. Pollut. Bull. 43, 187–208. doi: 10.1016/S0025-326X(01)00083-82

CrossRef Full Text | Google Scholar

Sohma, A., Shibuki, H., Nakajima, F., Kubo, A., and Kuwae, T. (2018). Modeling a coastal ecosystem to estimate climate change mitigation and a model demonstration in Tokyo Bay. Ecol. Model. 384, 261–289. doi: 10.1016/j.ecolmodel.2018.04.019

CrossRef Full Text | Google Scholar

Solan, M., Cardinale, B. J., Downing, A. L., Engelhardt, K. A. M., Ruesink, J. L., and Srivastava, D. S. (2004). Extinction and ecosystem function in the marine benthos. Science 306, 1177–1180. doi: 10.1126/science.1103960

PubMed Abstract | CrossRef Full Text | Google Scholar

Spillman, C. M., Hamilton, D. P., Hipsey, M. R., and Imberger, J. (2008). A spatially resolved model of seasonal variations in phytoplankton and clam (Tapes philippinarum) biomass in Barbamarco Lagoon. Italy. Estuar. Coast. Shelf Sci. 79, 187–203. doi: 10.1016/j.ecss.2008.03.020

CrossRef Full Text | Google Scholar

Spillman, C. M., Imberger, J., Hamilton, D. P., Hipsey, M. R., and Romero, J. R. (2007). Modelling the effects of Po River discharge, internal nutrient cycling and hydrodynamics on biogeochemistry of the Northern Adriatic Sea. J. Mar. Syst. 68, 167–200. doi: 10.1016/j.jmarsys.2006.11.006

CrossRef Full Text | Google Scholar

Statham, P. J. (2012). Nutrients in estuaries — An overview and the potential impacts of climate change. Sci. Total Environ. 434, 213–227. doi: 10.1016/j.scitotenv.2011.09.088

PubMed Abstract | CrossRef Full Text | Google Scholar

Stief, P. (2013). Stimulation of microbial nitrogen cycling in aquatic ecosystems by benthic macrofauna: mechanisms and environmental implications. Biogeosciences 10, 7829–7846. doi: 10.5194/bg-10-7829-2013

CrossRef Full Text | Google Scholar

Tait, K., Airs, R. L., Widdicombe, C. E., Tarran, G. A., Jones, M. R., and Widdicombe, S. (2015). Dynamic responses of the benthic bacterial community at the Western English Channel observatory site L4 are driven by deposition of fresh phytodetritus. Prog. Oceanogr. 137, 546–558. doi: 10.1016/j.pocean.2015.04.020

CrossRef Full Text | Google Scholar

Tappin, A. D. (2002). An examination of the fluxes of nitrogen and phosphorus in temperate and tropical estuaries: current estimates and uncertainties. Estuar. Coast. Shelf Sci. 55, 885–901. doi: 10.1006/ecss.2002.1034

CrossRef Full Text | Google Scholar

Teal, L. R., Bulling, M. T., Parker, E. R., and Solan, M. (2008). Global patterns of bioturbation intensity and mixed depth of marine soft sediments. Aquat. Biol. 2, 207–218. doi: 10.3354/ab00052

CrossRef Full Text | Google Scholar

Thomas, Y., and Bacher, C. (2018). Assessing the sensitivity of bivalve populations to global warming using an individual-based modelling approach. Glob. Chang. Biol. 24, 4581–4597. doi: 10.1111/gcb.14402

PubMed Abstract | CrossRef Full Text | Google Scholar

Timmermann, K., Banta, G. T., and Glud, R. N. (2006). Linking Arenicola marina irrigation behavior to oxygen transport and dynamics in sandy sediments. J. Mar. Res. 64, 915–938. doi: 10.1357/002224006779698378

CrossRef Full Text | Google Scholar

Timmermann, K., Christensen, J. H., and Banta, G. T. (2002). Modeling of advective solute transport in sandy sediments inhabited by the lugworm Arenicola marina. J. Mar. Res. 60, 151–169. doi: 10.1357/002224002762341285

CrossRef Full Text | Google Scholar

Timmermann, K., Norkko, J., Janas, U., Norkko, A., Gustafsson, B. G., and Bonsdorff, E. (2012). Modelling macrofaunal biomass in relation to hypoxia and nutrient loading. J. Mar. Syst. 105–108, 60–69. doi: 10.1016/j.jmarsys.2012.06.001

CrossRef Full Text | Google Scholar

Triantafyllou, G., Petihakis, G., Dounas, C., Koutsoubas, D., Arvanitidis, C., and Eleftheriou, S. (2000). Temporal variations in benthic communities and their response to physicochemical forcing: a numerical approach. ICES J. Mar. Sci. 57, 1507–1516. doi: 10.1006/jmsc.2000.0923

CrossRef Full Text | Google Scholar

Tromp, T. K., Cappellen, P., and Van, and Key, R. M. (1995). A global model for the early diagenesis of organic carbon and organic phosphorus in marine sediments. Geochim. Cosmochim. Acta 59, 1259–1284. doi: 10.1016/0016-7037(95)00042-X

CrossRef Full Text | Google Scholar

Tuominen, L., Mäkelä, K., Lehtonen, K. K., Haahti, H., Hietanen, S., and Kuparinen, J. (1999). Nutrient fluxes, porewater profiles and denitrification in sediment influenced by algal sedimentation and bioturbation by Monoporeia affinis. Estuar. Coast. Shelf Sci. 49, 83–97. doi: 10.1006/ecss.1999.0492

CrossRef Full Text | Google Scholar

van der Meer, J. (2006). An introduction to Dynamic Energy Budget (DEB) models with special emphasis on parameter estimation. J. Sea Res. 56, 85–102. doi: 10.1016/j.seares.2006.03.001

CrossRef Full Text | Google Scholar

van der Meer, J., Brey, T., Heip, C. H. R., Herman, P. M. J., Moens, T., and van Oevelen, D. (2013). “Measuring the flow of energy and matter in marine benthic animal populations,” in Methods for the Study of Marine Benthos, ed. A. Eleftheriou (Hoboken, NJ: John Wiley & Sons, Ltd), 349–425. doi: 10.1002/9781118542392.ch8

CrossRef Full Text | Google Scholar

van der Veer, H. W., Cardoso, J. F. M. F., and van der Meer, J. (2006). The estimation of DEB parameters for various Northeast Atlantic bivalve species. J. Sea Res. 56, 107–124. doi: 10.1016/j.seares.2006.03.005

CrossRef Full Text | Google Scholar

van Oevelen, D., Bergmann, M., Soetaert, K., Bauerfeind, E., Hasemann, C., Klages, M., et al. (2011). Carbon flows in the benthic food web at the deep-sea observatory HAUSGARTEN (Fram Strait). Deep-Sea Res. Pt I. 58, 1069–1083. doi: 10.1016/j.dsr.2011.08.002

CrossRef Full Text | Google Scholar

van Prooijen, B. C., Montserrat, F., and Herman, P. M. J. (2011). A process-based model for erosion of Macoma balthica-affected mud beds. Cont. Shelf Res. 31, 527–538. doi: 10.1016/j.csr.2010.12.008

CrossRef Full Text | Google Scholar

Vichi, M. (2002). Predictability Studies of Coastal Marine Ecosystem Behavior. Dissertation thesis, Carl von Ossietzky Universität Oldenburg, Oldenburg.

Google Scholar

Villnäs, A., and Norkko, A. (2011). Benthic diversity gradients and shifting baselines: implications for assessing environmental status. Ecol. Appl. 21, 2172–2186. doi: 10.1890/10-1473.1

CrossRef Full Text | Google Scholar

Villnäs, A., Norkko, J., Hietanen, S., Josefson, A. B., Lukkari, K., and Norkko, A. (2013). The role of recurrent disturbances for ecosystem multifunctionality. Ecology 94, 2275–2287. doi: 10.1890/12-1716.1

CrossRef Full Text | Google Scholar

Wang, H., Appan, A., and Gulliver, J. S. (2003). Modeling of phosphorus dynamics in aquatic sediments: I - Model development. Water Res. 37, 3928–3938. doi: 10.1016/S0043-1354(03)00304-X

CrossRef Full Text | Google Scholar

Wenzhofer, F., Riess, W., and Luth, U. (2002). In situ macrofaunal respiration rates and their importance for benthic carbon mineralization on the northwestern Black Sea shelf. Ophelia 56, 87–100. doi: 10.1080/00785236.2002.10409492

CrossRef Full Text | Google Scholar

Wheatcroft, R. A., Jumars, P. R., Smith, C. R., and Nowell, A. R. M. (1990). A mechanistic view of the particulate biodiffusion coefficient: Step lengths, rest periods and transport directions. J. Mar. Res. 48, 177–207. doi: 10.1357/002224090784984560

CrossRef Full Text | Google Scholar

Willows, R. I., Widdows, J., and Wood, R. G. (1998). Influence of an infaunal bivalve on the erosion of an intertidal cohesive sediment: A flume and modeling study. Limnol. Oceanogr. 43, 1332–1343. doi: 10.4319/lo.1998.43.6.1332

CrossRef Full Text | Google Scholar

Winberg, G. G. (1960). Rate of metabolism and food requirements of fishes. Transl. Ser. Fish. Res. Board Can. 194, 1–202.

Google Scholar

Wood, R., and Widdows, J. (2002). A model of sediment transport over an intertidal transect, comparing the influences of biological and physical factors. Limnol. Oceanogr. 47, 848–855. doi: 10.4319/lo.2002.47.3.0848

CrossRef Full Text | Google Scholar

Wrede, A., Beermann, J., Dannheim, J., Gutow, L., and Brey, T. (2018). Organism functional traits and ecosystem supporting services – A novel approach to predict bioirrigation. Ecol. Indic. 91, 737–743. doi: 10.1016/j.ecolind.2018.04.026

CrossRef Full Text | Google Scholar

Yool, A., Martin, A. P., Anderson, T. R., Bett, B. J., Jones, D. O. B., and Ruhl, H. A. (2017). Big in the benthos: Future change of seafloor community biomass in a global, body size-resolved model. Glob. Chang. Biol. 23, 3554–3566. doi: 10.1111/gcb.13680

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Q., Warwick, R. M., McNeill, C. L., Widdicombe, C. E., Sheehan, A., and Widdicombe, S. (2015). An unusually large phytoplankton spring bloom drives rapid changes in benthic diversity and ecosystem function. Prog. Oceanogr. 137, 533–545. doi: 10.1016/j.pocean.2015.04.029

CrossRef Full Text | Google Scholar