The Interaction Between Stock Dynamics, Fishing and Climate Caused the Collapse of the Jack Mackerel Stock at Humboldt Current Ecosystem

The collapse of marine fisheries had caused a cascade of ecological, social and economic consequences. Recognizing the complex nature of the fisheries collapses is essential for understanding the impact of human activities on natural systems. The rapid and abrupt shifts in abundance exhibited by some marine fish populations can be driven by the fishing fleet behaving like generalist predators. Here, we propose that fishing fleet has a s-shaped functional predator function that, combined with economic factors and ENSO variability could cause rapid and abrupt transitions in the of jack mackerel (Trachurus murphyi) fishery in the south-eastern Pacific. Our results showed that fishing fleet predator functional response is well described by a s-shaped function, where ENSO variability (El Niño/La Niña years) appears to decrease/increase the fishing rate. Our model predictions were able to accurately forecast independent data of jack-mackerel acoustic survey estimates. We show that the population trend and collapse of jack mackerel stock at the Humboldt Current Ecosystem (HCE) can be explained by the changes in fishing effort, which seem to be driven by economic forces and El Niño climatic variability. Our simple model allows us to explore some management responses in a heuristic manner. The most critical element seems to be the combination of an n-shaped isocline for fish stock growth, modulated by ENSO variability, and a horizontal isocline of fishing effort which is highly sensitive to changes in the profitability of the fishery. Therefore, the implementation of management policies based on simple theoretical models will be increasingly required to harvest fish stocks in these times of growing demographic demands and climate change.

Introduction

Many global marine fisheries have collapsed during the last decades (Hutchings, 2000; Jackson et al., 2001), often causing severe ecological and socio-economic consequences (Hilborn, 2007). Although collapses of fish stocks are generally caused by overfishing (Myers et al., 1995; Hutchings, 2000), other factors may also interact with human exploitation, such as, the inherent climate variability of marine ecosystems (Alheit and Niquen, 2004; Ottersen et al., 2005) and the complex web of ecological interactions where the exploited stocks are embedded (Pitcher, 2001; Pikitch et al., 2004; Lindegren et al., 2009). Determining the relative effect of these factors is one of the major challenges for the sustainability of marine fisheries.

The jack mackerel (Trachurus murphyi) is one of the most important commercial species inhabiting the Humboldt Current Ecosystem (HCE) at the south-eastern Pacific Ocean. The stock biomass has declined abruptly after 2005 and still remains at historically low levels despite the reduction of fishing mortality (Quiroz, 2019). Some studies suggest that a combination of low recruitment, overfishing and climate may explain the collapse of the stock (Arcos et al., 2001; Gang et al., 2013; Quiroz, 2019), but the relative influence of these factors is still controversial. In fact, at HCE, the jack-mackerel fishery had been subjected to both factors, high fishing pressure (Quiroz, 2019) and ENSO driven inter-annual variability.

The jack-mackerel pelagic catches had been driven by the high demand for fishmeal directly related to the growth of the world population and the feed requirements of poultry, aquaculture and derivatives, triggering the acceleration in the prices during the last 10 years (Figure 1A). The determination of the harvest quotas determined by economic forces seem to have induced the abrupt change in the stock (Figure 1A). Changes in fishing effort not only depend on the stock abundance, but also they are largely determined by socio-economic factors, such as, the difference between the income and the costs of the fishery (Gordon, 1954; Grafton et al., 2007; Fryxell et al., 2010, 2017; Sethi et al., 2010). In fact, some studies showed how the sustained increases in consumer demand coupled with the dynamics of the fish stock can generate a rapid and surprising transition from high-yield/low-price to low-yield/high-price fisheries, generating severe disruptions in socio-economic and ecological systems (Fryxell et al., 2010, 2017).

FIGURE 1

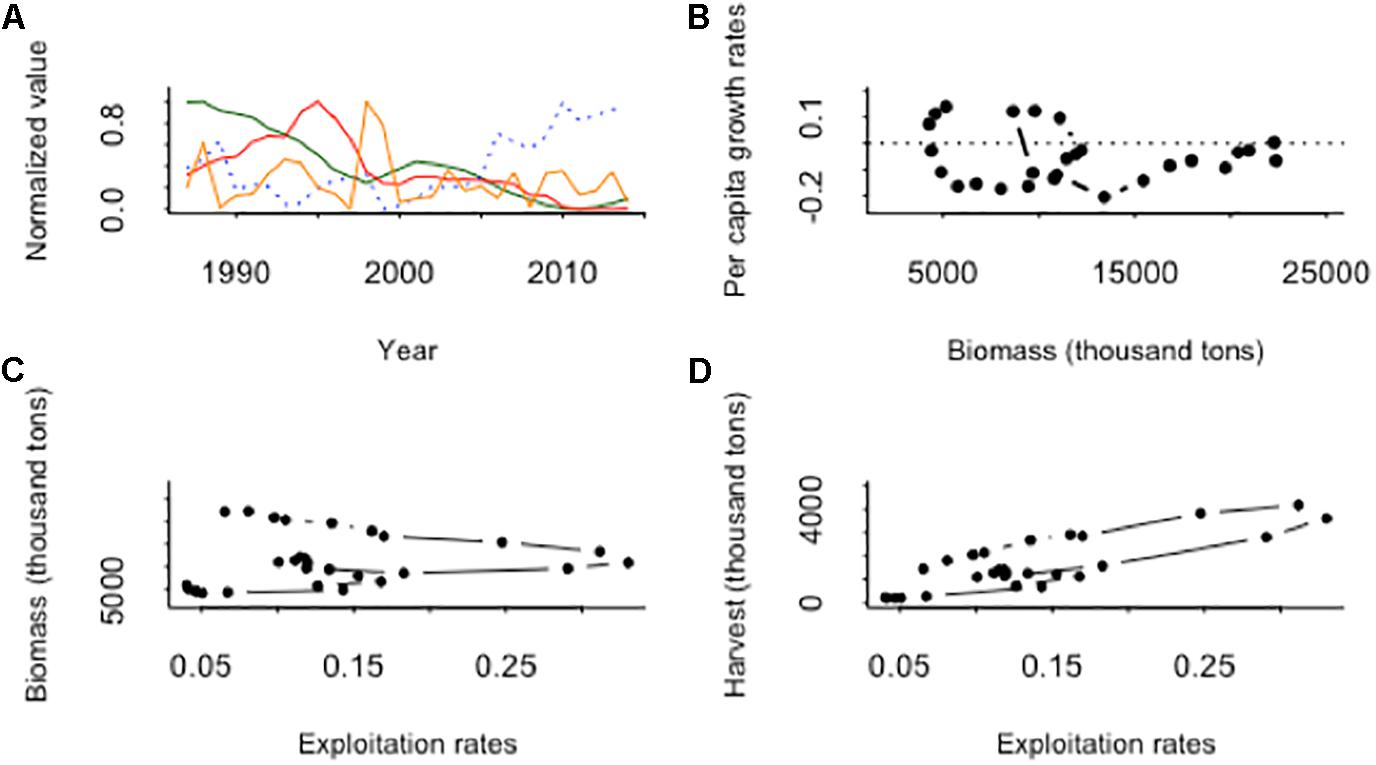
Figure 1. (A) Observed dynamics of the jack-mackerel fish stock biomass (green solid line), harvest (red solid line) and inflation-corrected price (blue dotted line), and the Niño 3.4 anomalies (orange solid line) for the period 1986–2015. (B) The phase plot of the per capita population growth rates against biomass showed a low-frequency oscillatory pattern in the jack mackerel dynamics toward low biomass. (C) The relationship between stock biomass (thousand tons) and exploitation rates (fishing mortality) for the period 1986–2015, stock biomass declined with exploitation rates, but the reduction in exploitation rates did not caused a recovery of the stock, during the late period much lower stock biomass are observed for the same range of exploitation rates. (D) The observed relationship between stock yield and exploitation rates for the period 1986–2014.

On the other hand, ENSO variability seems to influence the spatial distribution of jack-mackerel, hence, affecting the catchability to the fishery (Yañez et al., 1996; Arcos et al., 2001; Naranjo et al., 2015). A similar finding was described for another jack mackerel species at New Zealand coasts, where ENSO variability has strong effects on krill distribution at coastal waters and introduce changes in the jack mackerel school behavior leading to fishery failures (Harris et al., 1992). These lines of evidence suggest climatic effects on the spatial distribution of jack mackerel schools may have consequences on catchability which is a combination of fishing efficiency and availability. Such combination of economic and climatic forces on the fishery dynamics may cause rapid and abrupt shifts in abundance, sometimes in responses to small changes in external factors (Jones and Walters, 1976; May, 1977; Steele and Henderson, 1984; Scheffer and van Nes, 2004). The notion of abrupt shifts in the state of a dynamical system derives from catastrophe theory (Thom, 1972), which is a topological approach for analyzing complex dynamical systems (Thom, 1972; Zeeman, 1976). In fact, catastrophe theory was first applied to fisheries by Jones and Walters (1976) in a heuristic manner relating the stock dynamics, the fishing effort and technological efficiency. This idea was applied in the salmon fishery of British Columbia by Peterman (1977), who proposed that stable alternative states in the fish stock may emerge as a consequence of including mechanisms of depensatory predation mortality (Neave, 1953) in Ricker’s production models (Peterman, 1977). The same author (Peterman, 1980) determined that the mortality of these salmon stocks emerges as a consequence of the operations of the fishery that behaves similarly to the functional responses of natural predators (Holling, 1959, 1965). In fact, processes such as fleet aggregation and changes in search efficiency in response to certain thresholds of stock sizes are similar to those observed in generalist predators.

Here, using time series data of fish biomass, fishing effort and climate, we develop a model of fishery dynamics based on the relationships between fish stock abundance, effort exerted by the fishing fleet and ENSO variability. Our model is based on a logistic population dynamic growth of fish stock combined with a functional predator response of the fishery (Jones and Walters, 1976). We assumed that the rate of change in effort from year to year is a positive function of fishery revenue, but is negatively influenced by fishing costs which are proportional to the fishing effort (Grafton et al., 2007; Fryxell et al., 2010). We use this model to test the effects of ENSO variability and consider how changes in the fishing effort can generate the observed large abrupt shifts in the abundance of the jack mackerel (T. murphyi) stock at south-eastern Pacific.

Materials and Methods

Data

Jack Mackerel Biomass

We used model-based estimates of total biomass available in Canales et al. (2015). The model used corresponded to the one part of the assessment method for the Jack mackerel fishery adopted in the Scientific Committee of the South Pacific Regional Fishery Management Organization¹ in 2010 (JMSWG-Report, 2014). The model is an integrated statistical catch-at-age analysis implemented in AD Model Builder (ADMB) for the jack mackerel fisheries and population in the South Eastern Pacific area covering the period from 1970 to 2014 (Canales, 2014; JMSWG-Report, 2014). Several population-structure hypotheses have been proposed for jack mackerel in the South Pacific, the model used here corresponded to the one that assumes that jack mackerel conforms one single population in the South Eastern Pacific.

A detailed summary about the stock assessment of jack mackerel in the South Eastern Pacific is provide in the Supplementary Material as well as the sources of information (Supplementary Table S1) and the time series of biomass and their interval of confidence (Supplementary Figure S1).

Fishing Effort

Data were obtained from the logbooks of the Chilean purse seine commercial fleet requested to the Instituto de Fomento Pesquero of Chile². Fishing effort was estimated as the product of the annual number of trips with positives catches to jack mackerel and the proportion of days off port. We used the product of these two effort variables because as the jack mackerel stock declined in biomass, the days off port have increased significantly (Supplementary Figure S2). Thus, we accounted for the change in the availability of jack mackerel to the fishery by weighting the fishing trips with positive catches by the days off port. Although, jack mackerel is caught by different fleets such as the Far North fleet (Peru) and Offshore Trawl (China, European Union, Faroe Islands, South Korea, Japan, Russian Federation, Ukraine, and Vanuatu countries) the majority of the catches has been taken by the Chilean fleets and the largest fraction of the estimated total allowed catch is assigned to Chile. Supplementary Figure S3 shows that the Chilean fleets (North and Central-South) accounted for an average of a 73% of the total annual catches of jack mackerel in the South Eastern Pacific over the period 1985–2014, and a 70% for the period 1970–2014. Therefore, we assume that the Chilean fishing effort is a good proxy of total fishing effort of the jack mackerel fishery in the South Eastern Pacific.

Climatic Data

Fluctuations in tropical Pacific Sea Surface Temperature (SST) are related to the occurrence of El Niño (EN), during which equatorial surface waters warm considerably from the International Date Line to the western coast of South America. The atmospheric phenomenon linked to EN is termed Southern Oscillation (SO), which involves exchanges of air between the eastern and western hemispheres mainly in tropical and subtropical latitudes. EN and SO are linked so closely that the term ENSO is used to describe the atmosphere ocean interactions throughout the tropical Pacific. Various EN indices exist, for example the El Niño 3.4 index (5N-5S, 170W-120W): The Niño 3.4 anomalies may be thought of as representing the average equatorial SSTs across the Pacific from about the dateline to the South American coast. The Niño 3.4 index typically uses a 5-month running mean, and El Niño or La Niña events are defined when the Niño 3.4 SSTs exceed ±0.4C for a period of 6 months or more. Annual average of the Niño 3.4 index was obtained from https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, for the period 1986–2015.

The Model

We started modeling the stock biomass annual changes of the jack mackerel according a simple Ricker logistic function minus annual harvest as it had been proposed in recent studies (Fryxell et al., 2010, 2017);

$$B_t=B_{t-1}\cdot e^{\left[R_{\text{max}}\cdot \left(1-\frac{B_{t-1}}{K}\right)\right]-b\left(B_{t-1}\right)\cdot E_{t-1}},(1)$$

where R_max is the exponential rate of growth, K is the carrying capacity of the jack mackerel stock, b is the catchability function, B is the stock biomass and E is the fishing effort. Our first hypothesis was based in the basic type of functional responses of predators (Holling, 1959, 1965). Because any fishing operation imply at least two time-consuming activities, searching and handling the fish, the basic functional response equation of the catches is an asymptotic function of fish biomass (Holling, 1959). Therefore, we examined the type of functional response of the fishery by fitting the following equation;

$$y=w\cdot \frac{B}{h+B}(\mathrm{2a})$$

where y is the harvested biomass per unit of fishing effort and B is the jack-mackerel biomass, parameters w is the maximum fishery catch rate and h is the fish biomass where the fishing rate is half saturated. Our second hypothesis was that the functional response of fishing was s-shaped as it has been proposed earlier in the literature (Jones and Walters, 1976);

$$y=w\cdot \frac{B^2}{h^2+B^2}(\mathrm{2b})$$

Dividing the behavioral fishing responses (density-dependent catchability functions) y by the fish biomass, we obtain the per capita (or per biomass unit) exploitation rates z = y/B, in the case of a type II behavioral response the fishing mortality rates are negatively related to fish biomass;

$$z=\frac{w}{h+B},(\mathrm{3a})$$

while in the case of the sigmoid behavioral response, per capita fishing mortality is a humped function of fish biomass;

$$z=w\cdot \frac{B}{h^2+B^2}.(\mathrm{3b})$$

Therefore, the function b (B_t–1) in Eq. 1 can be represented as the two types of functional responses of Eqs 2a,b as:

$$B_t=B_{t-1}\cdot e^{\left[R_{\text{max}}\cdot \left(1-\frac{B_{t-1}}{K}\right)\right]-w\cdot \frac{B_{t-1}\cdot E_{t-1}}{h+B_{t-1}}},(\mathrm{4a})$$

$$B_t=B_{t-1}\cdot e^{\left[R_{\text{max}}\cdot \left(1-\frac{B_{t-1}}{K}\right)\right]-w\cdot \frac{B_{t-1}\cdot E_{t-1}}{h^2+B_{t-1}^2}},(\mathrm{4b})$$

where w and h are the same parameters that Eqs 2a,b.

The following step is to include climatic forces (ENSO-El Niño) to the model, we included the effects of ENSO variability on the carrying capacity of the fish biomass (K), and also on the maximum catch rate (w) and on the fish biomass where the fishing rate is half saturated (h).

On the other hand, because the jack-mackerel fishery is regulated by quotas, we assumed that fishing effort changes at a rate proportional to the difference between revenue, calculated by harvest quota (H), price (P), and cost per unit effort (c) multiplied by effort (E) (Bjørndal and Conrad, 1987; Fryxell et al., 2010).

$$E_t=E_{t-1}\cdot e^{\left[a\cdot \left(P_{t-1}\cdot H_{t-1}-c\cdot E_{t-1}\right)\right]},(5)$$

where a is the scale parameter fort the response in effort and c is the cost per unit of effort.

Statistical Analyses

Parameters were estimated using maximum likelihood approach via nls library in the R program (R Core Team, 2015³) and ranked according to the corrected Akaike information criterion for small samples (AIC_c). For clarity, AIC_c weights also figure in the results. Minimum AIC_c was selected to determine the most parsimonious (best) model.

Simulations were conducted to elucidate the capacity of the models to describe real dynamics. Models were fitted with data from 1987 to 2015 jack-mackerel biomass estimated from the assessment model (Canales et al., 2015) and the simulations were conducted using independent data by using the acoustic biomass surveys (Canales et al., 2015) for the period 1997–2009. Uncertainty on biomass estimates was incorporated by resampling a joint multivariate normal distribution of the estimated parameters considering the asymptotic distribution of maximum likelihood estimates. 95% confidence intervals (CIs) of biomass time series were obtained by the percentile method (Efron and Tibshirani, 1993) based on 10,000 realizations. Furthermore, values of the root-mean-square prediction error (rmse; Sheiner and Beal, 1981) were calculated to evaluate the predictive performance of the models. Smallest rmse values represent better predictive performance.

Results

Jack-mackerel biomass, fishing effort and harvest showed a fivefold magnitude variation over time (Figure 1A). During the late 1980s population peaked, then declined severely along the 1990s, showed a small recovery during the first years of the 2000, and declined toward low biomass during the last 10 years (Figure 1A). On the other hand, fishing effort and catches showed an increasing trend until they peaked around the late 1990s and a subsequent decline (Figure 1A). Inflation-corrected price was unresponsive as jack-mackerel fishery went through the phase of increase, but after the collapse in catches around the year 2000 inflation-corrected prices started to increase (Figure 1A). In fact, the jack-mackerel stock experienced fourfold variations in total biomass, harvest and real price over time (Figure 1A). The phase plot of the per capita population growth rates against biomass showed a low-frequency oscillatory pattern in the jack mackerel dynamics toward low biomass (Figure 1B), suggesting the existence of population cycles in the declining trend of the stock. The relationship between stock biomass and fishing mortality, showed also a low-frequency oscillatory pattern, stock biomass declined with exploitation rates, but the reduction in exploitation rates did not cause a recovery of the stock (Figure 1C), during the late period much lower stock biomass are observed for the same range of exploitation rates. A similar trend is observed for the relationship between stock yield and exploitation rates (Figure 1D).

The functional response function is better described by a type III response (sigmoid or s-shaped) (Table 1 and Figure 2A). A type III functional response model was 17 times more plausible than a type II response (w₂/w₁ = 17.03; Table 1). This response is typical of predators that switch from one prey to another (generalist) and/or concentrate in areas where preys are more abundant (spatial density-dependence). Dividing behavioral responses by fish stock biomass, we obtain an estimate of the per capita fishing death rate, sigmoid functional predator responses produces a humped-mortality rate function in its preys with higher mortality rates at intermediate stock abundances (Figure 2B). In fact, this model of fishing per capita mortality rates was almost 34 times better than a simple exponential negative model (w₂/w₁ = 33.74; Table 1).

TABLE 1

Table 1. The behavioral responses of the fishery to changes in jack-mackerel stock biomass.

FIGURE 2

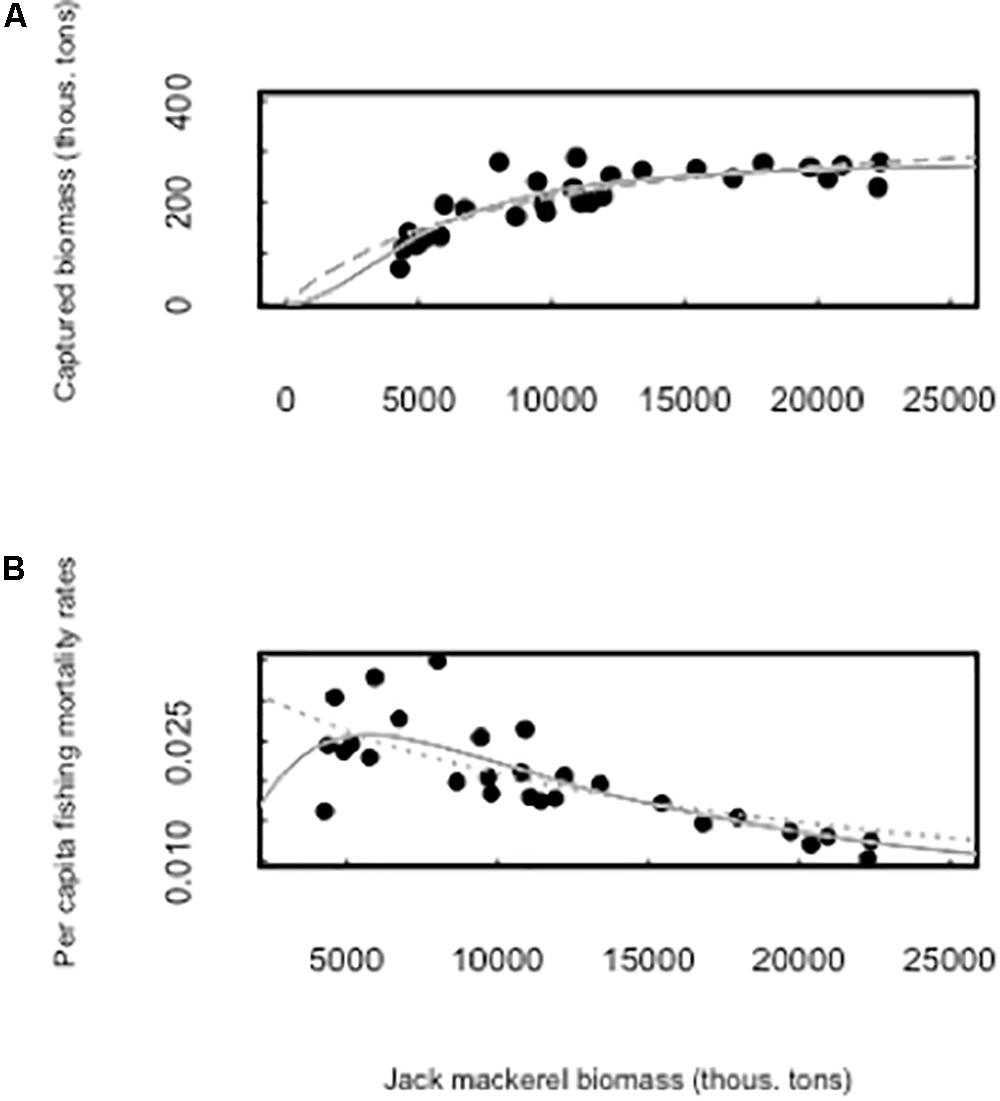
Figure 2. (A) The behavioral responses of the fishery catch per effort unit to changes in jack-mackerel stock biomass, the gray dotted line is the type II behavioral response model while the gray solid line is the type III functional response model. (B) Resulting per capita fishing death rates from the type II (dotted line) and III (solid line) behavioral responses of the fishery.

According to our results, the best model structure for the jack-mackerel dynamics is one including intraspecific competition and a functional predator response type III of the fishery as is described in Eq. 4b (Table 2; model 1).

TABLE 2

Table 2. Population dynamic models for the Jake mackerel biomass, the fishing effort and prices.

Comparing the basic model versus the models that include ENSO effects on the carrying capacity of the jack-mackerel population (model 1 versus models 6 and 7), our results show that ENSO did not influence limiting factors of jack-mackerel dynamics (w₁/w₆ = 3.25; w₁/w₇ = 3.25; Table 2). In the same vein, our results did not account for the ENSO effects on the maximum fishery catch rate (model 1 versus models 2 and 3; w₁/w₂ = 6.50; w₁/w₃ = 1.08; Table 2). However, the best model was one including the 2-year lagged ENSO effects on the parameter h, the fish biomass where the fishing rate is half saturated (model 1 versus model 5; w₅/w₁ = 48.46; Table 2). In fact, our basic and best models (Table 2; models 1 and 5) were able to predict quite well independent data as the acoustic survey estimates from Chilean fishery (Figure 3B). An interesting result is that ENSO variability (El Niño/La Niña years) may decrease/increase the half-saturated fishing rate (Figure 3C).

FIGURE 3

Figure 3. Comparison of the observed jack-mackerel biomass extracted from the acoustic estimates (red dots) for the period 1997–2009 with predictions from models fit to the 1986–2014 estimated biomass from the stock assessment model (gray lines) and the 95% confidence band. (A) predictions from model 1, (B) model 5 from Table 2, (C) hypothesized ENSO effects on the parameter h (the fish biomass where the fishing rate is half saturated) of the functional response of fishing suggesting that ENSO variability (El Niño/La Niña years) decrease/increase the half-saturated fishing rate. For the same jack-mackerel biomass during the El Niño years the captures biomass is lower than La Niña or normal conditions.

The dynamics of the fishing effort was captured by the model from Eq. 5 (Figure 4 and Table 2). In fact, the model where fishing costs are proportional to the fishing effort is a good description of fishing effort annual changes (Figure 4 and Table 2). Setting the fish stock and the fishing effort at equilibrium in the Eqs 4 and 5 and solving these equations for B^∗ and E^∗, we can obtain the fish stock and fishing effort isoclines and the phase space plot determining the system dynamics and equilibrium (Figure 5). In the case of a fish population exploited by a fleet with s-shaped behavioral responses, the stock isoclines are humped and the isoclines of the fishing effort are horizontal (Figure 5), because the fishing effort is determined by quotas. When the fishing fleet behave as a generalist predator with sigmoid functional responses, the fish stock isocline is now n-shaped with the possibility of multiple equilibrium points (Figure 5), the fishery can change from a situation from high fish biomass, low harvest toward an intermedium harvest scenario generating alternative stable states in the fish stock (Figure 5).

FIGURE 4

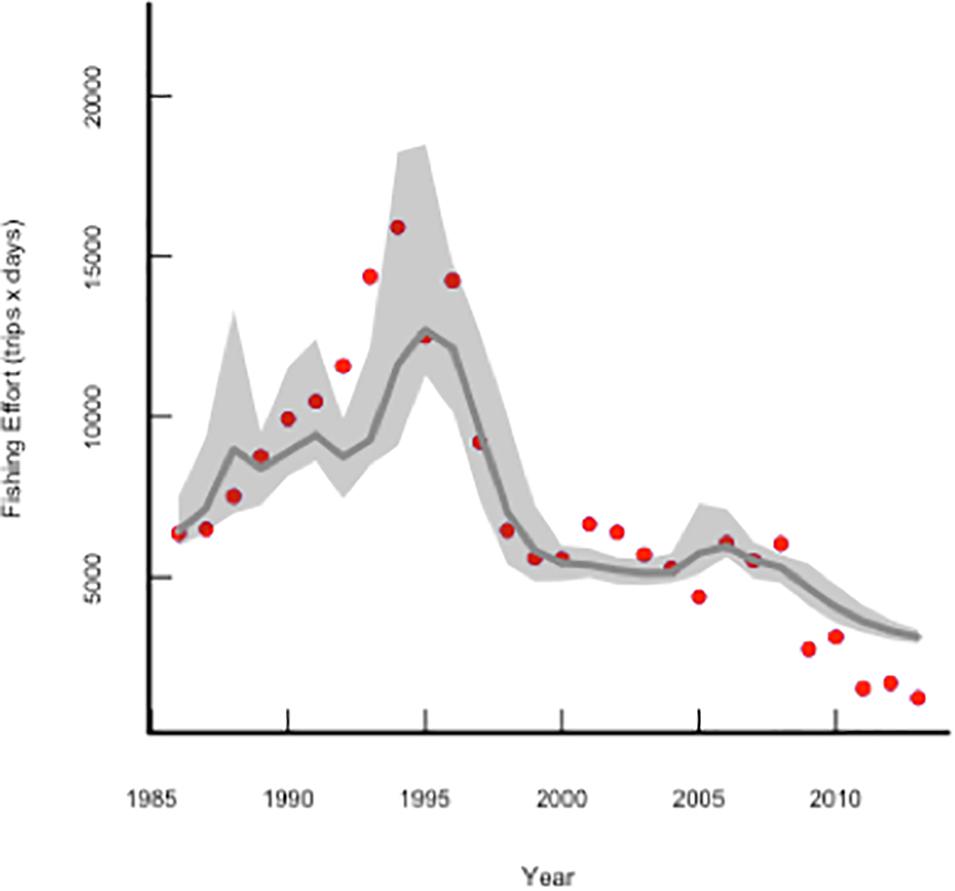
Figure 4. Comparison of the observed changes in fishing effort (number of trips × days out of port, red dots) with the predictions from models (gray line) (Table 2).

FIGURE 5

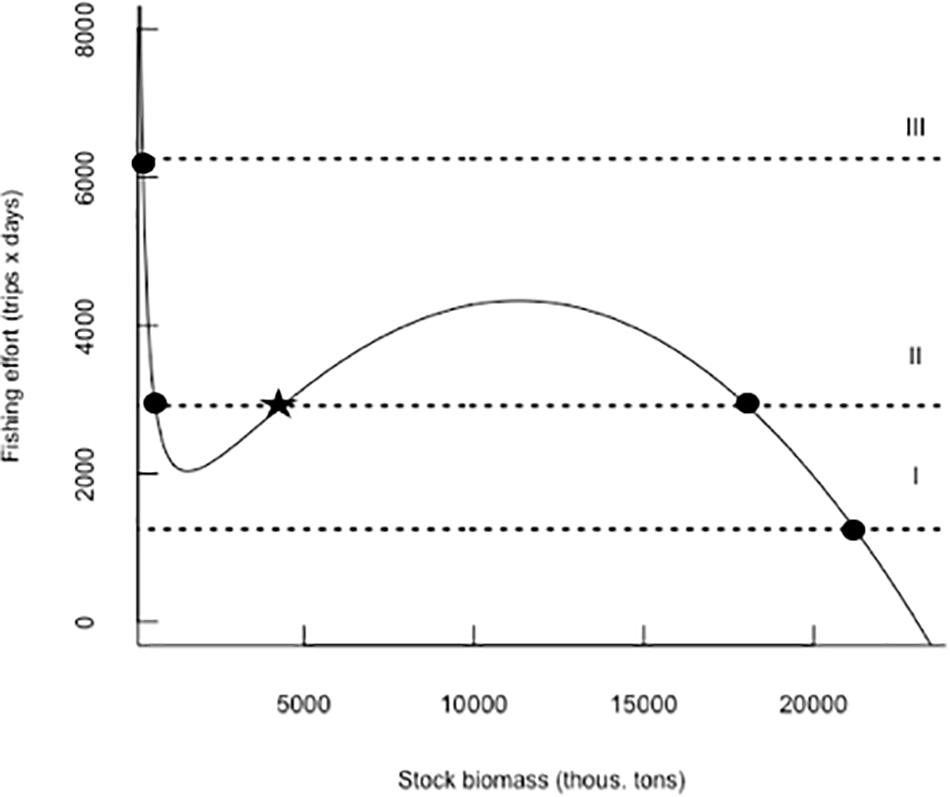
Figure 5. Equilibrium isoclines from model 1 (Table 2) for fish stock (solid line) and model 1 for fishing effort dynamics (Table 2), the system can be stabilized toward a high fish biomass equilibrium (Isocline I), but increases in harvest or fish prices can lead the system rapidly toward a low fish biomass equilibrium with complex oscillatory transient dynamics (Isocline II) (Berryman, 1999). Closed dots are stable equilibrium points and the star represents an unstable equilibrium point.

Discussion

Our results provide evidence that the collapse of the jack-mackerel stock at the HCE can be explained by the changes in fishing effort, which seem to be driven by economic forces and El Niño climatic variability. Our model predict that jack-mackerel stock dynamics can have alternate stable states. In particular, the fishing dynamics is described by a harvest characterized as a generalist predator with a type III sigmoid functional response able to generate a complex n-shaped stock fish isocline, which is modulated by the presence of ENSO variability. The combination of these ecological, economic, and climatic factors has the potential to explain the large and abrupt changes exhibited by the jack-mackerel stock size at the Humboldt current ecosystem during the last decades.

Abrupt and persistent changes in the size of the populations can be caused by the existence of multiple points of equilibrium or meta-stability (Berryman, 1999). It is well established that generalist predators with a sigmoid (s-shaped) functional responses are capable of generate a prey per capita mortality function that increases to intermediate prey abundances generating three equilibrium points, a low and high abundance stable equilibrium points an unstable equilibrium at intermediate abundances (Holling, 1965; Berryman, 1999). In fact, sigmoid behavioral responses of predators usually result from the action of generalist predators that switch to and/or aggregate on dense prey populations (Holling, 1965; Murdoch, 1969). This theory has been previously applied for explaining the fishery development and collapse (Jones and Walters, 1976).

Pelagic fishing operations may behave as generalist predators by searching the high-densities fish schools. This pattern may be the result of density-dependent catchability because at low school densities, the CPUE and the economic revenues are also very low in pelagic fisheries. As a consequence, there is a non-linear increase in catch per unit of effort with fish biomass, a process described as hyperstability of CPUE (Harley et al., 2001). Therefore, the sigmoid generalist of functional response of the jack-mackerel fishery may be consequence of density-dependent catchability. In the jack-mackerel, we determined a type III functional response of the fishery where the per capita fishing mortality is a humped function of the fish abundance, generating negative feedbacks in sparse fish populations (Berryman, 1999). This property give rise to n-shaped isocline for the fish stock suggesting that meta-stable dynamics can arise depending on the shape of the fishing effort isoclines (Jones and Walters, 1976). Horizontal fishing effort isoclines generate important changes in the dynamics of the system (Figure 5), because the determination of the harvest quotas can generate alternative states in the dynamic of the system. Therefore, under low harvest scenarios, the system can be stabilized toward a high fish biomass equilibrium (Isocline I, Figure 5) but increases in harvest can led the system toward a low fish biomass equilibrium (Isocline III, Figure 5; Berryman, 1999). The most interesting situation occurs at intermediate harvest quotas, under these conditions the isoclines can cross at three locations giving rise to a metastable dynamic with a high and low biomass stable equilibriums and intermediate unstable equilibrium or threshold at intermediate fish stock biomass. In fact, a severe reduction in quotas during the last years seem to be necessary for the recovery of the stock biomass.

Our analyses highlight that ENSO variability may have important effects on the availability of fish in the fishing grounds and the efficiency of the fishing gear to catch the available fish (catchability). This is to our knowledge the first study that included the effects of the ENSO variability in a predator response function model of fishing (Figure 3) and its consequences on catchability. Although, catchability is associated with fish availability, is also influenced by fish behavioral responses to the fishing gear and environmental factors (Arreguín-Sánchez, 1996). Climate variability could affect the spatial and depth distribution of fishes and hence their availability to a particular fishing fleet (Rijnsdorp et al., 2009). In theHCE, the pattern of ENSO variability modifies the range of the favorable habitat conditions of pelagic species such as, anchovy, sardine, mackerel, and jack mackerel (Alheit and Niquen, 2004). Migrations inshore, shallow or bottom waters, can increase or decrease fish availability and therefore catchability to the purse seine fleets (Bertrand et al., 2004). The jack mackerel population at HCE is characterized by large horizontal/vertical displacements due to change in ENSO variability (Arcos et al., 2001; Bertrand et al., 2004). Strong changes in acoustic biomass were observed at the end of El Niño event because the jack-mackerel followed the offshore flow of oceanic water when the warm waters (El Niño) started to disappearing (Bertrand et al., 2004). Our predator functional response model seems to capture the ENSO effects on the jack-mackerel catchability proposing a mechanism for the interaction between climate variability and fishing (Figure 3C).

The hypothesis that climatic variability influence catchability has not been formally tested on fish stocks. Indeed, Yañez et al. (1996) reported that strong thermal gradients associated with the intrusion of oceanic waters off the Chilean coast increases the probability of catching jack mackerel, hence, influencing the operations of fishing vessels. For example, Chilean fishing fleet increased it capacity (larger vessels), the duration of the fishing trips and number of hauls per trip in response to changes in jack mackerel spatial distribution (Naranjo et al., 2015).

Management Implications

In the case of jack mackerel, the high demand for fishmeal is directly related to the growth of the world population and the feed requirements of poultry, aquaculture, and derivatives, triggering the acceleration in the prices during the last 10 years. The determination of the harvest quotas over time seems to have induced the abrupt change in the stock, but mediated by a sigmoid functional response of the fishing fleet. These two elements seem to be key to explaining the abrupt decline of the stock in the south-eastern Pacific.

Our simple model allows us to explore some management responses in a heuristic manner. The most critical element seems to be the combination of an n-shaped isocline for fish stock growth, modulated by ENSO variability, and a horizontal isocline of fishing effort which is highly sensitive to changes in the profitability of the fishery (harvest quotas and fishing costs). This complex dynamic system can take the stock from a situation of high abundance and stability to a metastable dynamic at intermediate fishing effort levels (Figure 5). Using this approach for management purposes, some counter-intuitive policies from an economic point of view may be applied. For example, given that the annual changes in fishing effort are driven by the difference between harvest (H) and fishing costs c × (E), in order to apply tariffs to increase fishing costs in situations of high abundance (B), high harvests (H) could be used as a measure capable of keeping the fishery away from equilibrium point II (Figure 5). Undoubtedly, the current challenges related to the management of fisheries require a more integrated view of the growing demand for marine food products and the dynamic changes that fishing induces in the exploited stocks. Therefore, the implementation of management policies based on simple theoretical models, such as those applied in this article, will be increasingly required to restore the feedback processes that maintain natural systems in these times of growing demographic demands and climate change.

Data Availability Statement

All datasets generated for this study are included in the article/Supplementary Material.

Ethics Statement

Ethical review and approval was not required for the animal study because we used fishery data.

Author Contributions

ML, TC, RW, and JM: conceptualization, investigation, validation, and writing – original draft. ML and JM: formal analysis and visualization. ML: methodology, and writing – review and editing.

Funding

We acknowledge the financial support from the Center of Applied Ecology and Sustainability (CAPES; CONICYT FB 0002-2014).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful for Liesbeth van der Meer from OCEANA for helpful data and discussion. We thank Antonio Aranis from the Instituto de Fomento Pesquero (IFOP, Chile) for providing the fishing effort information used in this work. We appreciate the comments from the reviewers of this paper that helped to improve the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2020.00123/full#supplementary-material

Footnotes

1. ^ www.sprfmo.int
2. ^ www.ifop.cl
3. ^ http://www.r-project.org

References

Alheit, J., and Niquen, M. (2004). Regime shifts in the humboldt ecosystem. Prog. Oceanogr. 60, 201–222. doi: 10.1111/gcb.13991

PubMed Abstract | CrossRef Full Text | Google Scholar

Arcos, D., Cubillos, L., and Núñez, S. (2001). The jack mackerel fishery and El Niño 1997-98 effects off Chile. Prog. Oceanogr. 49, 597–617. doi: 10.1016/s0079-6611(01)00043-x

CrossRef Full Text | Google Scholar

Arreguín-Sánchez, F. (1996). Catchability: a key parameter for fish stock assessment. Rev. Fish Biol. Fish. 6, 221–242.

Google Scholar

Berryman, A. A. (1999). Principles of Population Dynamics and their Application. Cheltenham: Stanley Thornes.

Google Scholar

Bertrand, A., Segura, M., Gutiérrez, M., and Vásquez, L. (2004). From small-scale habitat loopholes to decadal cycles: a habitat-based hypothesis explaining fluctuations in pelagic fish populations off Peru. Fish Fish. 5, 296–316. doi: 10.1111/j.1467-2679.2004.00165.x

CrossRef Full Text | Google Scholar

Bjørndal, T., and Conrad, J. M. (1987). The dynamics of an open access fishery. Can. J. Econ. 20, 74–85. doi: 10.2307/135232

CrossRef Full Text | Google Scholar

Canales, C. (2014). Informe de Estatus y Cuota Jurel 2015. Convenio de Desempeño 2014: Estatus y Posibilidades de Explotacion Biologicamente Sustentables de los Principales Recursos Pesqueros Nacionales Año 2015. Valparaíso: Instituto de Fomento Pesquera.

Google Scholar

Canales, T. M., Wiff, R., Lima, M., Serra, R., and Montero, J. (2015). Jack Mackerel (Trachurus murphyi) Status in the South Eastern Pacific and Exploitation Management Strategies. Wellington: South Pacific Regional Fisheries Management Organisation.

Google Scholar

Efron, B., and Tibshirani, R. J. (1993). An Introduction to Bootstrap. London: Chapman and Hall.

Google Scholar

Fryxell, J. M., Hilborn, R., Bieg, C., Turgeon, K., Caskenette, A., and McCann, K. S. (2017). Supply and demand drive a critical transition to dysfunctional fisheries. PNAS 114, 12333–12337. doi: 10.1073/pnas.1705525114

PubMed Abstract | CrossRef Full Text | Google Scholar

Fryxell, J. M., Packer, C., McCann, K., Solberg, E. J., and Saether, B. E. (2010). Resource management cycles and the sustainability of harvested wildlife populations. Science 328, 903–906. doi: 10.1126/science.1185802

PubMed Abstract | CrossRef Full Text | Google Scholar

Gang, L., Xiaorong, Z., Xinjun, C., Yinqi, Z., and Zhang, M. (2013). Standardization of CPUE for chilean jack mackerel (Trachurus murphyi) from chines trawls fleets in the high seas of the Southeast Pacific Ocean. J. Ocean Univ. China 12, 441–451. doi: 10.1007/s11802-013-1987-1

CrossRef Full Text | Google Scholar

Gordon, H. S. (1954). The economic theory of a common-property resource: the fishery. J. Polit. Econ. 62, 124–142. doi: 10.1086/257497

CrossRef Full Text | Google Scholar

Grafton, R. Q., Kompas, T., and Hilborn, R. W. (2007). Economics of overexploitation revisited. Science 318:1601. doi: 10.1126/science.1146017

PubMed Abstract | CrossRef Full Text | Google Scholar

Harley, S. J., Myers, R. A., and Dunn, A. (2001). Is catch-per-unit-effort proportional to abundance? Can. J. Fish. Aquat. Sci. 58, 1760–1772. doi: 10.1139/f01-112

CrossRef Full Text | Google Scholar

Harris, G. P., Griffiths, F. B., and Clementson, L. A. (1992). Climate and the fisheries off Tasmania – interactions of physics, food chains and fish. S. Afr. J. Mar. Sci. 12, 585–597. doi: 10.2989/02577619209504726

CrossRef Full Text | Google Scholar

Hilborn, R. (2007). Managing fisheries is managing people: what has been learned? Fish Fish. 8, 285–296. doi: 10.1111/jfb.13546

PubMed Abstract | CrossRef Full Text | Google Scholar

Holling, C. S. (1959). The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320. doi: 10.4039/ent91293-5

CrossRef Full Text | Google Scholar

Holling, C. S. (1965). The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 97, 5–60.

Google Scholar

Hutchings, J. A. (2000). Collapse and recovery of marine fishes. Nature 406, 882–885. doi: 10.1038/35022565

PubMed Abstract | CrossRef Full Text | Google Scholar

Jackson, J. B. C., Kirby, M. X., Berger, W. H., Bjorndal, K. A., Botsford, L. W., Bourque, B. J., et al. (2001). Historical overfishing and the recent collapse of coastal ecosystems. Science 293, 629–638.

PubMed Abstract | Google Scholar

JMSWG-Report (2014). “Report of the Jack Mackerel Subgroup,” in Report of the 2th Scientific Committee Meeting (Honolulu, HI: Report of the Science Working Group IX). Available at: https://www.sprfmo.int/assets/Meetings/Meetings-2013-plus/SC-Meetings/2nd-SC-Meeting-2014/Report/SC-02-Annex-4-Assessment-final3Nov.pdf

Google Scholar

Jones, D. D., and Walters, C. J. (1976). Catastrophe theory and fisheries regulation. J. Fish. Res. Board Can. 33, 2829–2833. doi: 10.1139/f76-338

CrossRef Full Text | Google Scholar

Lindegren, M., Möllmann, C., Nielsen, A., and Stenseth, N. C. (2009). Preventing the collapse of the Baltic cod stock through an ecosystem-based management approach. Proc. Natl. Acad. Sci. U.S.A. 106, 14722–14727. doi: 10.1073/pnas.0906620106

PubMed Abstract | CrossRef Full Text | Google Scholar

May, R. M. (1977). Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 269, 471–477. doi: 10.1038/269471a0

CrossRef Full Text | Google Scholar

Murdoch, W. W. (1969). Switching in general predators: experiments on predator specificity and stability of prey populations. Ecology 39, 335–354. doi: 10.2307/1942352

CrossRef Full Text | Google Scholar

Myers, R. A., Barrowman, N. J., Hutchings, J. A., and Rosenberg, A. A. (1995). Population dynamics of exploited fish stocks at low population levels. Science 269, 1106–1108. doi: 10.1126/science.269.5227.1106

PubMed Abstract | CrossRef Full Text | Google Scholar

Naranjo, L., Plaza, F., Yáñez, E., Barbieri, M. A., and Sánchez, F. (2015). Forecasting of jack mackerel landings (Trachurus murphyi) in central-southern Chile through neural networks. Fish. Oceanogr. 24, 219–228. doi: 10.1111/fog.12105

CrossRef Full Text | Google Scholar

Neave, F. (1953). Principles affecting the size of pink and chum salmon populations in British Columbia. J. Fish. Board Can. 9, 450–491. doi: 10.1139/f52-023

CrossRef Full Text | Google Scholar

Ottersen, G., Alheit, J., Drinkwater, K., Friedland, K., Hagen, E., and Stenseth, N. C. (2005). “The response of fish populations to climatic fluctuations,” in Marine Ecosystems and Climate Variation. The North Atlantic a Comparative Perspective, eds N. C. Stenseth, G. Ottersen, J. W. Hurrell, and A. Belgrano (Oxford: Oxford University Press), 73–94.

Google Scholar

Peterman, R. M. (1977). A simple mechanism that causes collapsing stability regions in exploited salmonid populations. J. Fish. Res. Board Can. 34, 1130–1142. doi: 10.1139/f77-170

CrossRef Full Text | Google Scholar

Peterman, R. M. (1980). Dynamics of native indian food fisheries on salmon in British Columbia. Can. J. Fish. Aquat. Sci. 37, 561–566. doi: 10.1139/f80-071

CrossRef Full Text | Google Scholar

Pikitch, E. K., Santora, C., Babcock, E. A., Bakun, A., Bonfil, R., Conover, D. O., et al. (2004). Ecosystem-based fishery management. Science 305, 346–347. doi: 10.1126/science.1098222

PubMed Abstract | CrossRef Full Text | Google Scholar

Pitcher, T. J. (2001). Fisheries managed to rebuild ecosystems? Reconstructing the past to salvage the future. Ecol. Appl. 11, 601–617. doi: 10.1016/j.cub.2014.05.070

PubMed Abstract | CrossRef Full Text | Google Scholar

Quiroz, J. C. (2019). Consolidado Estatus y CBA Jurel, 2019. Valparaíso: Instituto de Fomento Pesquero.

Google Scholar

R Core Team (2015). R: A Language and Environment for Statistical Computing [Internet]. Vienna: R Foundation for Statistical Computing.

Google Scholar

Rijnsdorp, A. D., Peck, M. A., Engelhard, G. H., Mollmann, C., and Pinnegar, J. (2009). Resolving the effect of climate change on fish populations. ICES J. Mar. Sci. 66, 1570–1583. doi: 10.1111/gcb.14551

PubMed Abstract | CrossRef Full Text | Google Scholar

Scheffer, M., and van Nes, E. H. (2004). Mechanisms for marine regime shifts: can we use lakes as microcosms for oceans? Prog. Oceanogr. 60, 303–319. doi: 10.1016/j.pocean.2004.02.008

CrossRef Full Text | Google Scholar

Sethi, S. A., Branch, T. A., and Watson, R. (2010). Global fishery development patterns are driven by profit but not trophic level. Proc. Natl. Acad. Sci. U.S.A. 107, 12163–12167. doi: 10.1073/pnas.1003236107

PubMed Abstract | CrossRef Full Text | Google Scholar

Sheiner, L., and Beal, S. (1981). Some suggestions for measuring predictive performance. J. Pharmacokinet. Phar. 9, 503–512. doi: 10.1007/bf01060893

PubMed Abstract | CrossRef Full Text | Google Scholar

Steele, J. H., and Henderson, E. W. (1984). Modeling long-term fluctuations in fish stocks. Science 224, 985–987. doi: 10.1126/science.224.4652.985

PubMed Abstract | CrossRef Full Text | Google Scholar

Thom, R. (1972). Stabilité Structurelle et Morphogénèse–Essai d’une Théorie Générale des Modèles. Reading: CRC Press.

Google Scholar

Yañez, E., Catasti, V., Barbieri, M. A., and Bohm, G. (1996). Relaciones entre la distribución de recursos pelágicos pequeños y la temperatura superficial del mar registrada con satélites NOAA en la zona central de Chile. Invest. Mar. 24, 107–122.

Google Scholar

Zeeman, E. C. (1976). Catastrophe theory. Sci. Am. 234, 65–83.

Google Scholar