Trawling in the Mediterranean: An Exploration of Empirical Relations Connecting Fishing Gears, Otterboards and Propulsive Characteristics of Fishing Vessels

Fishing pressure is often expressed in terms of a vessels physical attributes, like tonnage and engine power, while a common definition of fishing capacity identifies vessel size as a convenient proxy for the size of the gear used. Nevertheless, these definitions remain arguable, and the refinement of these fishing descriptors is increasingly being considered. A stronger understanding of the relationship between the standard measures of effort and capacity and fishing mortality remains a primary objective, followed by the need to overcome a traditional approach that simply describes effort, capacity and mortality as linearly related, conferring a greater fishing power to larger vessels. In this perspective, the analysis of trawlers’ technical features in relation to the size and power of the vessel might constitute an essential step. This study specifically investigated a collection of trawling gears’ technical specifications collected by CNR-IRBIM, Ancona. The dataset used includes records from several Mediterranean fisheries, and involves three trawling techniques, including single trawling, twin trawling and pair trawling, and diverse trawling gear categories, comprising demersal/bottom 2-panel trawls (OTB2), demersal/bottom 4-panel trawls (OTB4), pelagic 4-panel trawls (PTM4), semi-pelagic 2-panel trawls (OTM2), semi-pelagic 4-panel trawls (OTM4), and a Mediterranean bottom beam trawl (TBB). We analyzed and described the relationships between vessels’ technical features (LOA, towing force, and engine power), some among the main trawl-metrics (headline length, footrope length, trawl length, square width; fishing circle) and the otterboard’s technical features (height, width, and projected area) in an attempt to enhance fishing capacity definition through the inclusion of the fishing gear deployed. Self-organizing maps (SOM) were used to explore the empirical relationships among different parts of the fishing trawl gears, as well as between some of these parts, the otterboard size and the engine power of the vessel.

Introduction

Fishing activity regulation is aimed at the management of exploited fish populations while ensuring maximum sustainable yield and maximum economic yield. Mortality management is generally achieved through a couple of competing and alternative approaches, the input control, regulating the extent at which fishing activity is performed, and the output control, with a core concept that revolves around limitations in catches of one or more selected species. The former approach finds its management tools in restrictions in fleet capacity, fishing gears used and the number of licenses, limitations on technological updates and on the spatial and temporal distribution of fishing activity. These may involve the institution of ad hoc area closures, MPAs, zoning schemes and the rotation of areas (Veiga et al., 2016; McLachlan and Defeo, 2018). The output control approach instead relies on the definition of total allowable catches per season, daily catch limits, allowance of the capture and retention of a maximum amount (threshold values), and the establishment of minimum legal landing sizes and Individual transferable or non-transferable quotas. In general, fisheries targeting a limited number of species lean toward an output control scheme, while for mixed fisheries, characterized by multiple species and multiple gear types deployed in the same area, the input control strategy represents a more viable solution (Pope, 2009; McLachlan and Defeo, 2018). Management redundancy, namely the simultaneous application of measures pertaining to both strategies, is also sometimes a possibility (Caddy and Defeo, 2003; Gutiérrez et al., 2011; Santiago et al., 2015) in the pursue of profitable, sustainable and long-lasting fishing activity.

Spatial and temporal limitations of activity are strongly related to the concepts of fishing capacity and fishing effort. Fishing capacity can be either measured in number of vessels or in terms of engine power, size and gross tonnage (FAO, 2008). These vessel-metrics are normally used to cluster together all the exponents of a fleet falling within the same category and thus far represents an indirect method of measuring a vessels harvesting potential. Accordingly, the simple association between vessel size and the size of the fishing gear deployed may be used to estimate harvesting potential, and restrictions to a vessels temporal activity may be applied based on the fleet segment it belongs to. The greater the vessel and the larger its engine power is, the fewer the times a year it can practice fishing.

Fishing effort, on the other hand, can be defined as the product of capacity and activity (European Commission [EC], 2002). It represents a vessels time span of activity and can be measured as numbers of days at sea or number of hours fishing. With the recent establishment of VMS (Vessel monitoring System) and AIS (Automatic Identification System) technologies, the ability to gage fishing effort has indefinitely increased. Where needed, the estimate of both capacity and effort is now relatively simple. What remains to be clarified is how these two standard measures are related and how they affect the fishing mortality of different target species. The traditional association between fishing capacity and gear size, remains questionable, since it has already been demonstrated that no simple and clear relationship between a fishing vessels power and the size of the net it tows exists (Reid et al., 2011). Furthermore, the connection between horsepower, gear size (fishing circle) and swept area was found to be non-uniform across vessels, gear types and species targeted (Fiorentini et al., 2004; Eigaard et al., 2011). Furthermore, several studies have described the relationship between the effort deployed, fishing capacity and fishing mortality as weak and variable, underlining the need to include other effects (“skipper effect”) to explain the variance observed (Squires and Kirkley, 1999; Marchal et al., 2006, 2007). These knowledge gaps still interfere with a more accurate modulation of fishing pressure and with the achievement of a sustainable fishing mortality level. The outcome is often faulty management restrictions and a general imbalance between the fleets ability to harvest resources and their ability to regenerate.

Fishing gears, with all their intrinsic variability, represent the physical link between a fishing management strategy and the target populations directly affected by its application. Gear type and trawl size do not represent the only measures that affect catch-efficiency. Other gear components may also be of equal importance such as gear geometry, door spread and ground gear. Furthermore, the horizontal and vertical opening of the mouth may also play a significant role in affecting the gear catchability (Eigaard et al., 2011). In this perspective, better knowledge of the geometries and the technical characteristics of fishing gears is an important aspect to consider on par with fishing effort, size class and engine power, while also assessing the fishing mortality induced by a vessel or a fleet belonging to a specific fleet segment. In this paper we specifically investigated a collection of trawling gears’ technical specifications collected by CNR-IRBIM, Ancona. The dataset used includes records collected from eight Mediterranean fisheries, and involves three trawling techniques, including single trawling, twin trawling and pair trawling, and diverse trawling gear categories, comprising demersal/bottom 2-panel trawls (OTB2), demersal/bottom 4-panel trawls (OTB4), pelagic 4-panel trawls (PTM4), semi-pelagic 2-panel trawls (OTM2), semi-pelagic 4-panel trawls (OTM4), and a Mediterranean bottom beam trawl (TBB). We analyzed and described the relationships between vessels’ technical features, some among the main trawl-metrics and otterboards technical specifications in an attempt to enhance the definition of fishing capacity through the inclusion of the fishing gear deployed. These aspects were explored using Kohonen self-organizing maps (SOM) (Kohonen, 1997) and model-based clustering, based on finite Gaussian mixture modeling. Finally, we tested the predictive capabilities of the trained SOM, observing its ability to predict the size of different trawling gear components, as well as of the otterboards. These parameters were estimated, providing the map with quantitative variables (vessel-metrics) and qualitative descriptors (vessel provenance and gear type), for the observations contained in a test dataset.

Materials and Methods

Data Collection

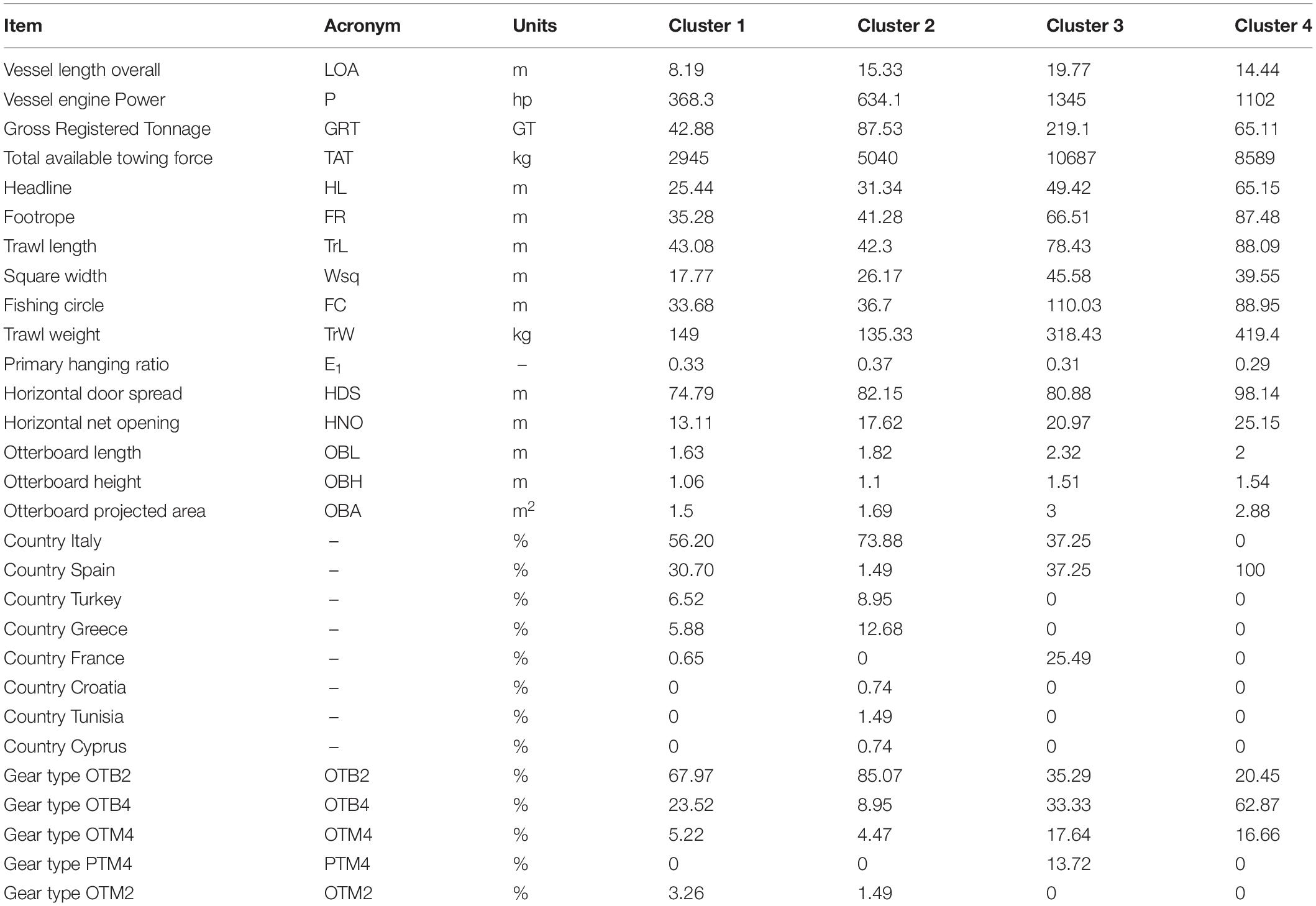
In this paper we analyzed a collection of trawling gears’ technical specifications collected by CNR-IRBIM Ancona. The information collected includes technical specifications of trawling nets (headline length, footrope length, square width, codend circumference and extension, etc.), doors (length, height, and weight) and general fishing vessel features (engine power, LOA, GRT, fleet registry number, bollard pull, base harbor, etc.) collected from eight Mediterranean fisheries, including Italy, France, Spain, Greece, Turkey, Croatia, Tunisia, and Cyprus. Data collection involved a first critical review of diverse literature sources (technical and scientific papers), followed by direct in situ measurements of vessels and fishing gears, performed with the help of fishermen, net makers and door manufacturers. The analysis of literature sources proved invaluable in establishing the main gear characteristics required for the evaluation of the overall gear size, while field technical measurements helped in completing the information obtained through literature research, filling the emergent knowledge gaps in all the inspected trawling techniques. The collected data can be subdivided by trawling techniques and gear typologies. Three trawling techniques were described, including single trawling, twin trawling and pair trawling techniques, performed with diverse trawling gear categories, comprising demersal/bottom 2-panel trawls (OTB2), demersal/bottom 4-panel trawls (OTB4), pelagic 4-panel trawls (PTM4), semi-pelagic 2-panel trawls (OTM2), semi-pelagic 4-panel trawls (OTM4), and a Mediterranean bottom beam trawl (TBB). Among the available technical specifications, Vessel Length Overall (LOA), Gross Registered Tonnage (GRT), Engine Power (P) and Total Available Towing force (TAT) were chosen as indicators of vessel size; headline and footrope length (HL, FL), trawl length (TrL), trawl weight (TrW), square width (Wsq), fishing circle (FC) and the primary hanging ratio (E1), were chosen as indicators of gear magnitude; and door height (OBH), length (OBL) and projected area (OBA) were selected as descriptors of the otterboard size. As additional information, vessel and gear provenance (country and base harbor) were also considered in the analysis.

Definition of Vessel Size, Gear-Metrics and Otterboard’s Descriptors

The adopted vessel-metrics (LOA, GRT, and P) defined the size of a fishing vessel in terms of the maximum length of its hull (in meters), its internal volume (registered tons), and the power of the main propulsion engine installed onboard (hp). TAT represents an alternative vessel descriptor proposed to overcome the lack of information regarding a vessel’s bollard pull, rarely available. The indicator considers installed engine power, propulsion system (nozzle and propeller) and trawling speed, and it was used as an alternative metric of the vessel’s actual power in operation. A more extensive description of this indicator can be found in Notti et al. (2013).

Among gear metrics, the headline and the footrope respectively represent the upper frame rope to which netting and floats are attached, and the lower combination rope, carrying the sinkers. Both their lengths are measured in meters. Fishing circle and square width, also measured in meters, are two additional gear descriptors. The fishing circle indicates the perimeter of the net measured at the footrope bosom, while the square width describes the width of the square, the first section of the gear netting, placed in the top panel right behind the wings. Trawl length and weight respectively describe the length of the trawl, codend excluded, along its longitudinal axis (in meters), and the overall trawl weight, expressed in kilograms. The primary hanging ratio indicates the ratio between the length of the rope frame on which a net panel is attached, and the length of the attached net panel stretched. This ratio affects the ability of a net to change shape and area in water, consequently increasing or reducing a trawl’s fishing efficiency. Finally, the collection of gear descriptors was completed by two additional calculated indicators, the Horizontal Net Opening (HNO) and the Horizontal Door Spread (HDS), also measured in meters.

As for the otterboards, OBL and OBH respectively represent the length and height of the otterboard, while the projected area indicates the area of its surface, corrected by an otterboard-specific factor to consider the otterboard’s shape. A schematic representation of the gear descriptors considered, is reported in Figure 1.

FIGURE 1

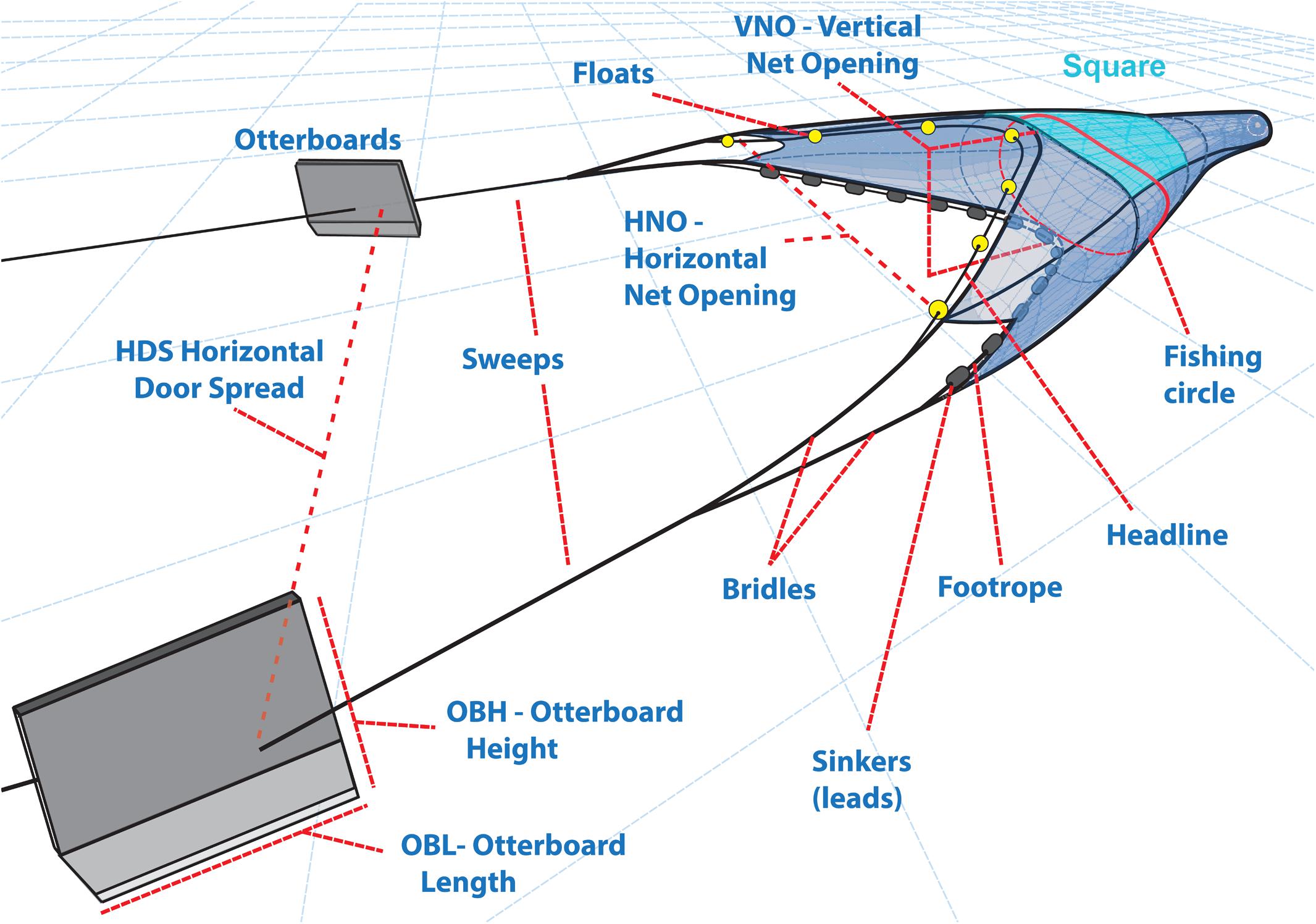
Figure 1. Schematic representation of the main gear-metrics and otterboard’s descriptors considered.

Trawling Techniques and Gear Typologies

Each record analyzed was assigned to one of the five gear typologies, based on a classification first described in Eigaard et al. (2011) broadened by the addition of a sixth category, the Mediterranean “Rapido” trawl. A brief description of the observed gear categories is provided below, while a short summary of the described gears is available in Table 1.

TABLE 1

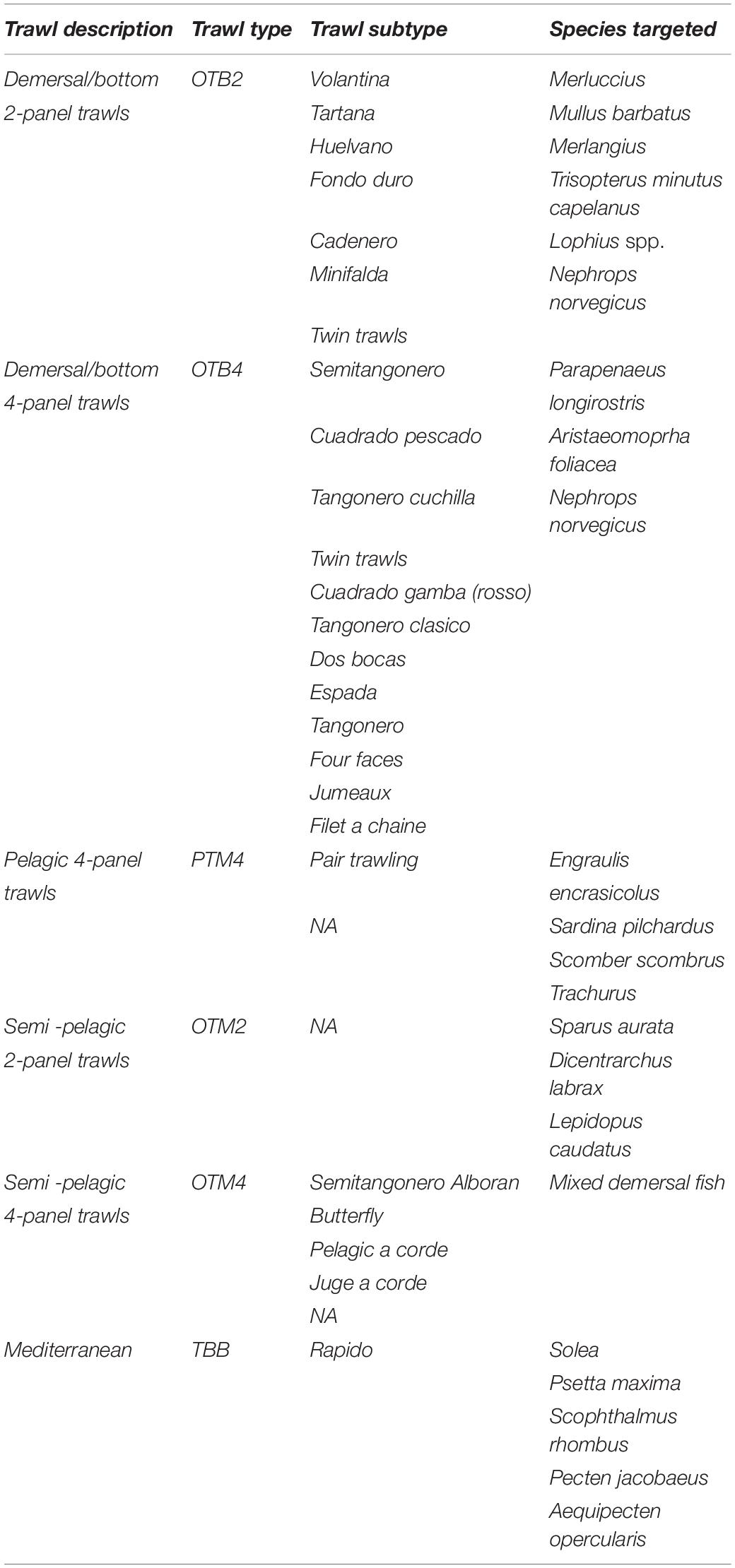
Table 1. Summary table of the observed gear types and subtypes followed by an indication of the major species targeted.

Demersal/Bottom 2-Panel Trawls (OTB2)

Often made entirely of knotless PA netting, the OTB2 trawls present a wide winghead opening attached to long sweeps and bridles, coupled with a narrow vertical opening. Target species of these gears include Merluccius merluccius, Mullus barbatus, Merlangius merlangius, Trisopterus minutus capellanus, Lophius spp., Nephrops norvegicus.

Demersal/Bottom 4-Panel Trawls (OTB4)

These trawls are made by 4 panels, the upper and lower panel and two side panels, which are usually made entirely of knotless polyethylene netting, though sometimes a portion of knotless polyamide netting may appear in the lower panel. The vertical opening of these trawls can reach up to 2 to 4 m in height, increased by a couple of long bridles whose length can easily reach 10 to 15 m. This gear category usually mainly targets crustaceans like Parapenaeus longirostris, Aristaeomoprha foliacea and Nephrops norvegicus.

Pelagic 4-Panel Trawls (PTM4)

Large pelagic gears built with four connected panels, characterized by a wide vertical opening made with very wide meshes or ropes, specifically constructed to flock target species toward the center of the net, where a smaller mesh size collects the catch. These fishing gears are used to mostly target pelagic species like Sardina pilchardus, Engraulis encrasicolus, Scomber scombrus, and Trachurus trachurus.

Semi-Pelagic 2-Panel Trawls (OTM2)

This fishing gear type is typically used near the seabed in Tyrrhenian fisheries to catch demersal species living a semi-pelagic lifestyle, characterized by frequent ascending displacements. Lepidopus caudatus, Sparus aurata and Dicentrarchus labrax are among the major representatives of these trawls’ target species. Their main features include relatively large meshes (up to 1600 mm), a mean vertical opening of 3 to 4 m, and a four-cable rigging. In semi-pelagic 2-panel trawls, catching efficiency is determined mainly by the gear’s volume.

Semi-Pelagic 4-Panel Trawls (OTM4)

These trawls are similar to semi-pelagic 2-panel trawls but characterized by a wider vertical opening usually ranging within 4 to 10 m. Although this trawl typology mainly targets demersal species, the increased vertical opening also improves their catch efficiency for pelagic species.

Mediterranean Bottom Beam Trawl Typology (“Rapido” – TBB)

This peculiar gear type, mostly used in Northern Adriatic fisheries, is constituted by a cone-shaped net with a mouth opening that attaches itself to a metallic frame, up to 4 m wide, that slides on the sea floor aided by sledges. The trawl uses a rake-like structure, equipped with iron teeth, to dig through the upper layers of sediment and to forcefully displace its target species, herding them toward its body. The Rapido trawl primarily targets flatfish species like Solea solea, Psetta maxima, Scophthalmus rhombus, and bivalve mollusks like Pecten jacobeus and Aequipecten opercularis.

Data Analysis – Self Organizing Maps

Data analysis was performed using the R language¹. The collection of technical gears was examined using SOM (Kohonen, 1982, 2001), an unsupervised neural network-based approach, commonly used for classification and association, suitable for non-linear data mining, exploration, clustering and summarization of the variability in a dataset (Park et al., 2018). The SOM were applied as an explorative method to examine and classify vessels and gear records according to similarities in their technical features. Their predictive power was also evaluated observing the map’s capability to estimate the major descriptors of gear and otterboards’ magnitude on the basis of information regarding the size of the vessel, its geographical provenance and type of trawling gear used.

Self-Organizing Maps algorithms learn from complex multidimensional data and project the multi-dimensional data space onto a regular lower-dimensional grid, usually a two-dimensional space map. The visualization of more than two dimensions is possible, but a bidimensional map is usually preferred since it is closer to human perception. The projection is made preserving the topology (or neighborhood) of the original dataset, with similar records creating neighboring clusters on the grid, and distant records expected to be distant on the map. The distance between sample units and virtual units is calculated by applying a user-defined distance measure, selected to provide an accurate data representation on the map (Brosse et al., 2001). A SOM neural network uses two layers of nodes, an input layer, connected to the original dataset, and an output layer (the Kohonen layer). The output layer, made by n neurons, is a two-dimensional array of virtual units used to represent in an ordered way the distribution of the original dataset. The projection of the sample units of the input layer onto the output layer is achieved through an unsupervised learning algorithm that calculates the components (W_ik) of each virtual unit during the training phase. The algorithm starts the learning process, assigning random weights w to the output units, then calculating the distance between each input vector x_ij and the weight vectors, identifying the best matching unit (BMU) for every input vector; the unit showing minimum distance from the input vector. A neighborhood is defined around the BMU by the units whose distance from the BMU is less than or equal to the neighbor radius r. The units’ weights w are then updated following the rule:

$$w_{ik}\left(t+1\right)=w_{ik}\left(t\right)+\mathrm{\alpha }\left(t\right)h_{ck}\left(t\right)\left[x_{ij}\left(t\right)-w_{ik}\left(t\right)\right]$$

where w_ik is the weight vector of the BMU, x_ij is the input vector and α(t) is the learning rate at the time step (t). The function in charge of this update is the Neighborhood function, identified in the equation as h_ck(t). During the learning process, the BMU is not the only updated unit, since the units falling within its neighborhood range are updated as well, in inverse proportion of their distance from the BMU. The learning rate and the radius are progressively decreased at each iteration, and the process is iteratively repeated until an ending criterion is met. A more complete descriptions of SOM algorithms can be found in Kohonen (1982, 2001, 2012), Park et al. (2018).

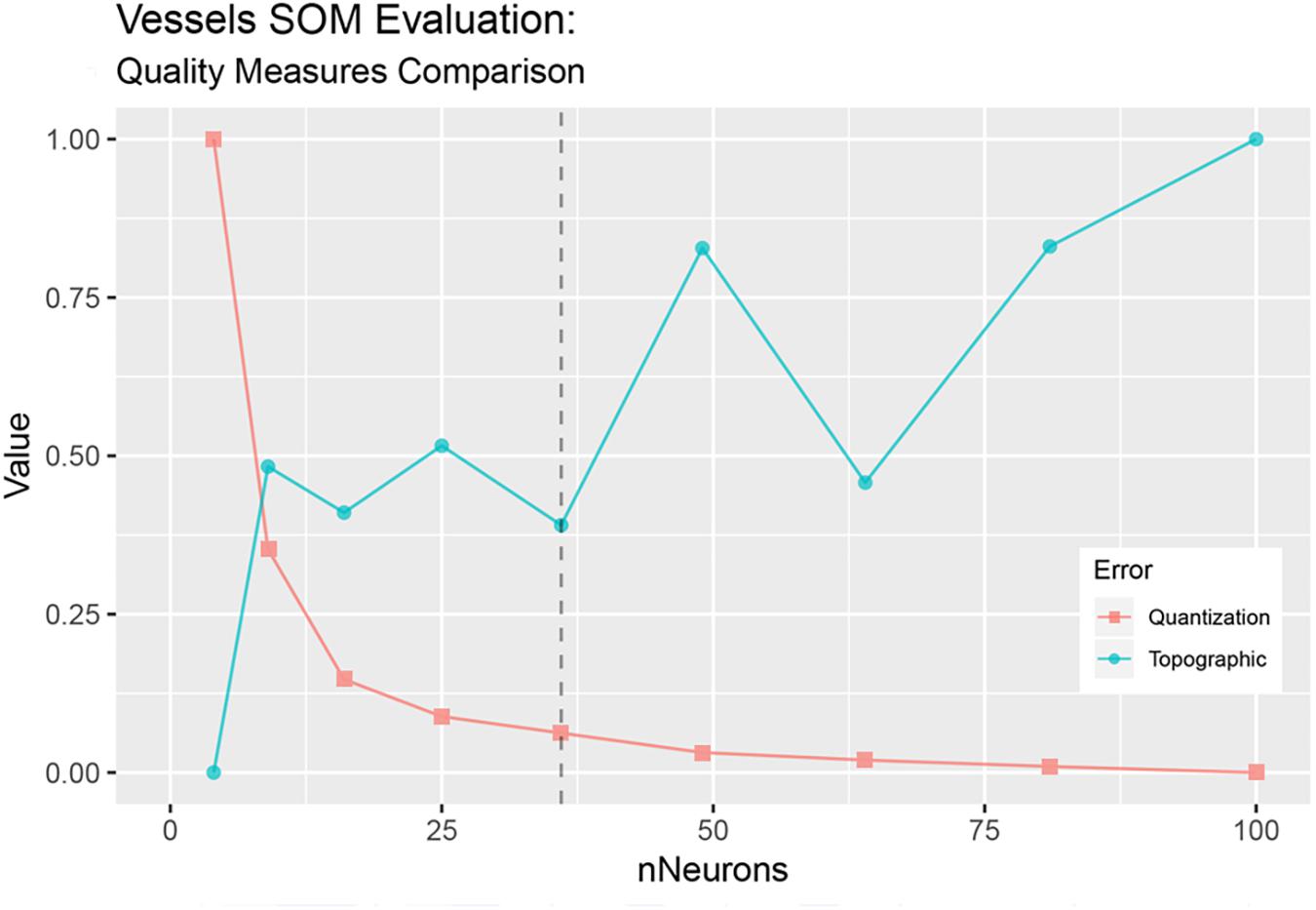
We used two different SOMs, the first for data recovery and the second for the actual exploration of the dataset. The first step of the analysis involved dealing with missing data which, to different degrees, affected the variables describing vessels’ characteristics. Missing data can be treated with three possible approaches, they can either be deleted, skipped or replaced by estimated values (Park et al., 2018). SOMs’ ability to cluster together in the output space data points showing similar characteristics makes them reliable candidates for data mining and recovery, as outliers and gaps in the original dataset can be replaced by their features in the map (Adeloye et al., 2012). Strictly speaking, when a vector containing gaps is presented to the SOM, its BMU can still be identified according to the other variables available. An estimate of the values for the missing variables can then be obtained as their corresponding values in the BMU (Adeloye et al., 2012). Several studies have already used this approach to recover gaps in datasets with positive results (Kalteh and Hjorth, 2009; Adeloye et al., 2012; Mwale et al., 2012, 2014; Kim et al., 2015; Nkiaka et al., 2016). Following this method, a first SOM was trained to estimate gaps in vessels’ description where present, using all the observations available in the dataset (591 records), but keeping only the variables that concern the characteristics of the fishing vessels. A 6 × 6 virtual unit map was trained using the “supersom” function from the R package “Kohonen” (Wehrens and Kruisselbrink, 2018). Map size was decided on the observation and comparison of two SOM quality measures, the quantization error and the topographic error. The quantization error (Kohonen, 2001) represents the average distance between the nodes and the training data points, while the topographic error (Kiviluoto, 1996) was calculated as the mean distance in map coordinates between the BMU and the second BMU for all data vectors. Both measures were repeatedly calculated while testing different map sizes with an increasing number of output neurons. The optimal map size was then defined aimed at the best tradeoff that minimizes both quantization and topographic error, as shown in Figure 2. SOM Training was performed on two separate data layers, the first containing continuous variables (LOA, GRT, and P) and the second with categorical data (vessels’ provenance), coded as a binary variable. The adoption of two separate layers was motivated by the need to select two different distance measures, each one appropriate to the specific data typology. For the first layer the SOM algorithm used Euclidean distance applied to a transformed dataset, normalized between zero and one, in the range of the minimum and maximum values of each variable. Range normalization represented a necessary step to provide the same weight to all variables, otherwise spanning very different ranges. For the second layer, distances were calculated using the Tanimoto distance, which is more suitable for data with binary-valued features. The outcome of the first SOM enabled the completion of vessel data, achieved through the replacement of missing values with their corresponding values in the BMUs. A second SOM was then trained, this time using the updated gapless vessels dataset, joined with the remaining portion of selected variables of interest, describing fishing gears’ technical features and otterboards’ metrics. The second map, a 10 × 10 unit map, was trained using the same algorithm applied to three layers of data, one for vessel metrics, one for gears and otterboard specifications and a third one carrying categorical data (reporting vessel provenance and trawl type). Euclidean distance was used for the first two layers, along with Tanimoto distance for the third layer. The SOM algorithm was applied to 80% of the collected net observations, from a random 80/20 split of the data, into training and test sets specifically devised to test the map predictive capabilities on a new dataset and to evaluate its ability to infer the dimensions of the gear and otterboards used. The size of the map was decided based on the same optimization method of topographic and quantization errors previously used for the first SOM.

FIGURE 2

Figure 2. SOM quality evaluation through the optimization of quantization and topographic error.

SOM and Clustering

Model-based clustering, based on finite Gaussian mixture modeling, was performed on the trained map to identify groups of observations with similar metrics. Clustering was obtained using the Mclust function from the R “Mclust” package (Scrucca et al., 2016). This function estimates the optimal number of clusters and defines the best partition according to the Bayesian Information Criterion (BIC) for expectation-maximization, initialized by hierarchical clustering for parameterized Gaussian mixture models. The function runs several competing models and identifies the best one as the one with the highest BIC. The optimal number of clusters is defined as the point at which adding additional clusters no longer increases the BIC value. This clustering technique is described extensively in Scrucca et al. (2016). Clustering results were optimized excluding the cluster analysis variables that did not show recognizable patterns, therefore contributing less to the final distribution of the variables on the map. Clusters were compared, and between-cluster vessels and gear parameters where further examined with the purpose to improve the description of the relationships between various gear components, gear-metrics and vessel sizes.

Predictive Power and Performance

After the SOM training, the distribution of the variables on the created map remains fixed and can be used to predict values for new observations. This process is very similar to a linear regression, where the parameters of a function are estimated first, then the defined function is used to predict the value of the dependent variable of interest for new observations. A SOM can be considered as a form of non-linear regression without a presupposed form of a defined function. Given the non-linearity of the model, defining the exact contribution to the estimated values could be trivial, but its performance can still be measured using common statistical techniques. The trained SOM was used to infer the dimensions of gears and otterboards used, estimated on the basis of quantitative variables (vessel metrics), and qualitative descriptors (vessel provenance and gear type), for the observations contained in the test dataset. The performance of the obtained predictions was assessed comparing predicted estimates with real observed values. A common measure of the performance of a linear regression model is the coefficient of determination. Given the non-linearity of SOMs, in this case the R² coefficient was not the appropriate method of model performance assessment, but still a simulated R² coefficient was calculated assuming that the predicted results constituted the outcome of a linear model. We created several scatterplots of predicted vs. observed values, then calculated a linear regression through these values, calculating the associated R² measure. The simulated coefficient is not comparable to the R² measure in a linear regression model but could still be used to explore model performance and to approximate a description of the fit of predicted values to the observed values. This procedure is described in Tan et al. (2002).

Results

Database Description

The original database contained more than 600 trawling gear records, 589 of which were effectively analyzed during this research study. A few records were excluded from the analysis due to too much missing data, resulting in the inability of the SOM to classify them correctly and properly assigning them to a BMU. Beam trawl data were also omitted due to the small number of records (less than 10) associated with trawl gear metrics that were too different from the rest of the dataset. Their presence, taken into consideration at first, was finally ruled out as they generated anomalous peaks in the trained map. The analyzed dataset is then composed of 55.68% of OTB2, 32.25% of OTB4, 9% of OTM4, 1.69% of PTM4 and 1.32% to OTM2. Trawling gear records belong to eight different countries, with approximately 44% of the records belonging to Italy, 40.77% coming from Spain, 6.26% from Greece, 4.56% from Turkey and 3.55% from France. Croatia, Tunisia and Cyprus are represented in the dataset with less than 1% of the data. Table 2 shows a summary of the descriptive statistics of gear and vessel metrics observed, without a subdivision per trawl typology.

TABLE 2

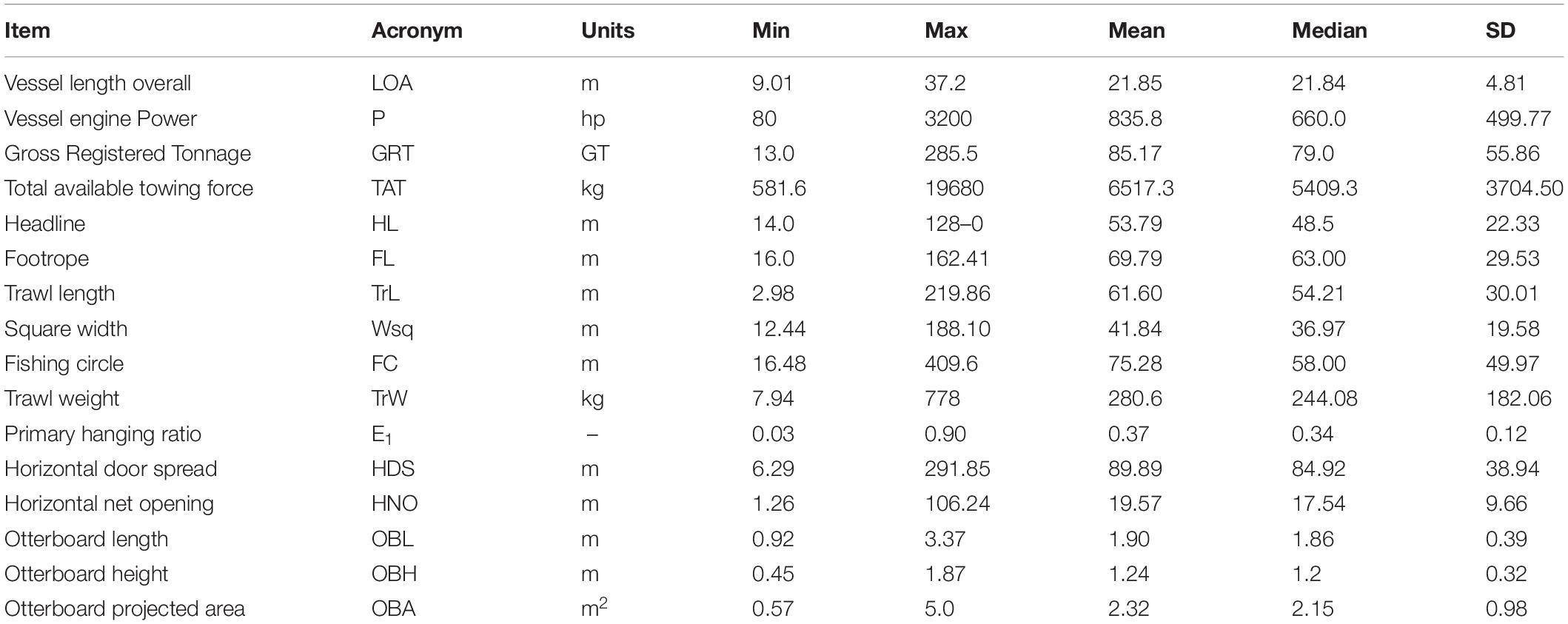
Table 2. Summary table of the descriptive statistics of gear, vessel and otterboard’s metrics observed.

Self-Organizing Maps and Data Recovery

The first SOM is represented by a map of 36 output units, generated from two information layers, the first one containing normalized vessel metrics (LOA, GRT, and Engine Power) and the second one containing geographical information such as the vessel’s nationality and port of origin, coded as binary variables. The map training process went through 18,000 iterations, following the suggestion of Kohonen (2001), which recommends that the number of iterations in the training process should be at least 500 times the number of network units. All output units were associated with input records in the training dataset, with no empty units emerging at the end of the training process. The number of input records associated with each unit ranged between one and 30 with an average of 14.72 records associated per unit. The main results of the SOM are reported in Figure 3. The trained SOM revealed very similar distribution patterns for the continuous variables observed, showing a diagonal gradient that places smaller vessels, characterized by minor LOA, GRT and P, in the upper left corner of the map, and larger vessels in the lower right corner, with values gradually increasing along the diagonal connecting the two corners. According to the gradient shown, vessels characterized by average tonnage, length and engine power are distributed in the central area of the map, following the diagonal connecting the two opposite corners. Although the patterns returned by the map agree in the general distribution of the vessels, the observed gradients diverge slightly from one another in the positioning of the extreme peaks in the units of the map (near but not necessarily overlapping) and for the smoothness in the transition from smaller to higher values, indicating the non-linear nature of the correlation between the observed variables. No further analysis was carried out on the first trained map, which represented only an intermediate step. The estimates delivered by the SOM output units, based on the similarity of the weight vectors, were used as a replacement of the gaps in the original dataset.

FIGURE 3

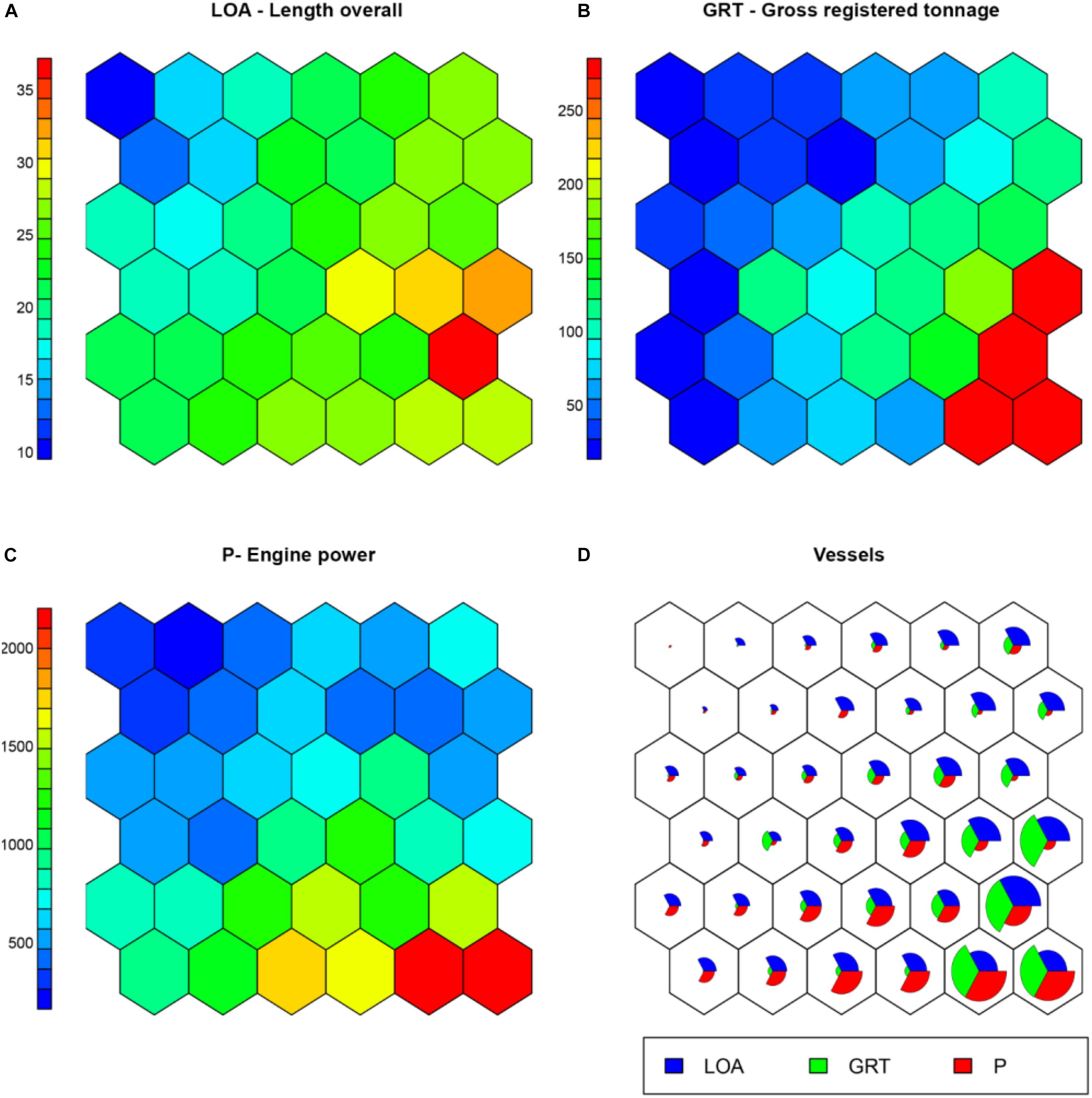
Figure 3. Results of the first trained SOM. From (A–C) the patterns of the considered unscaled vessel metrics are represented in a color scale; (D) shows the “codes plot,” representing the magnitude of each variable per output unit.

Second Map - Analysis of the Observed Patterns

The final trained SOM is a map of 10 × 10 output units, generated from three information layers, the first two containing normalized vessel metrics (LOA, GRT, TAT, and P) and normalized gear and otterboard measurements (HL, FL, TrL, Wsq, FC, TrW, E1, HDS, HNO, OBH, OBL, OBA), and a third one containing categorical variables such as trawl type and gear’s nationality, coded as binary variables. The map training process went through 50000 iterations, a number determined following the same procedure adopted during the training of the first SOM. Only four out of 100 units were not associated with input records in the training dataset at the end of the training process. The number of input records associated with each output unit ranged between one and 17 with an average of 4.89 records associated per unit. Figure 4 shows how the different variables relate to each other within the trained map. A first observation of the patterns delivered by the SOM shows a distribution of the highest values in the upper half of the map, followed by a concentration of the lower values in the lower half. A finer observation highlights a general distribution trend of the highest values in the upper right corner for vessel metrics such as engine power and TAT, gear metrics such as HL, FL, gear length and gear weight, and otterboard descriptors such as otterboard height and the projected area. Associated with the distributions of gear type and country of origin, these higher values can be ascribed to the Spanish gear types OTB2, OTB4 and OTM4 and to the French gear type OTM4.

FIGURE 4

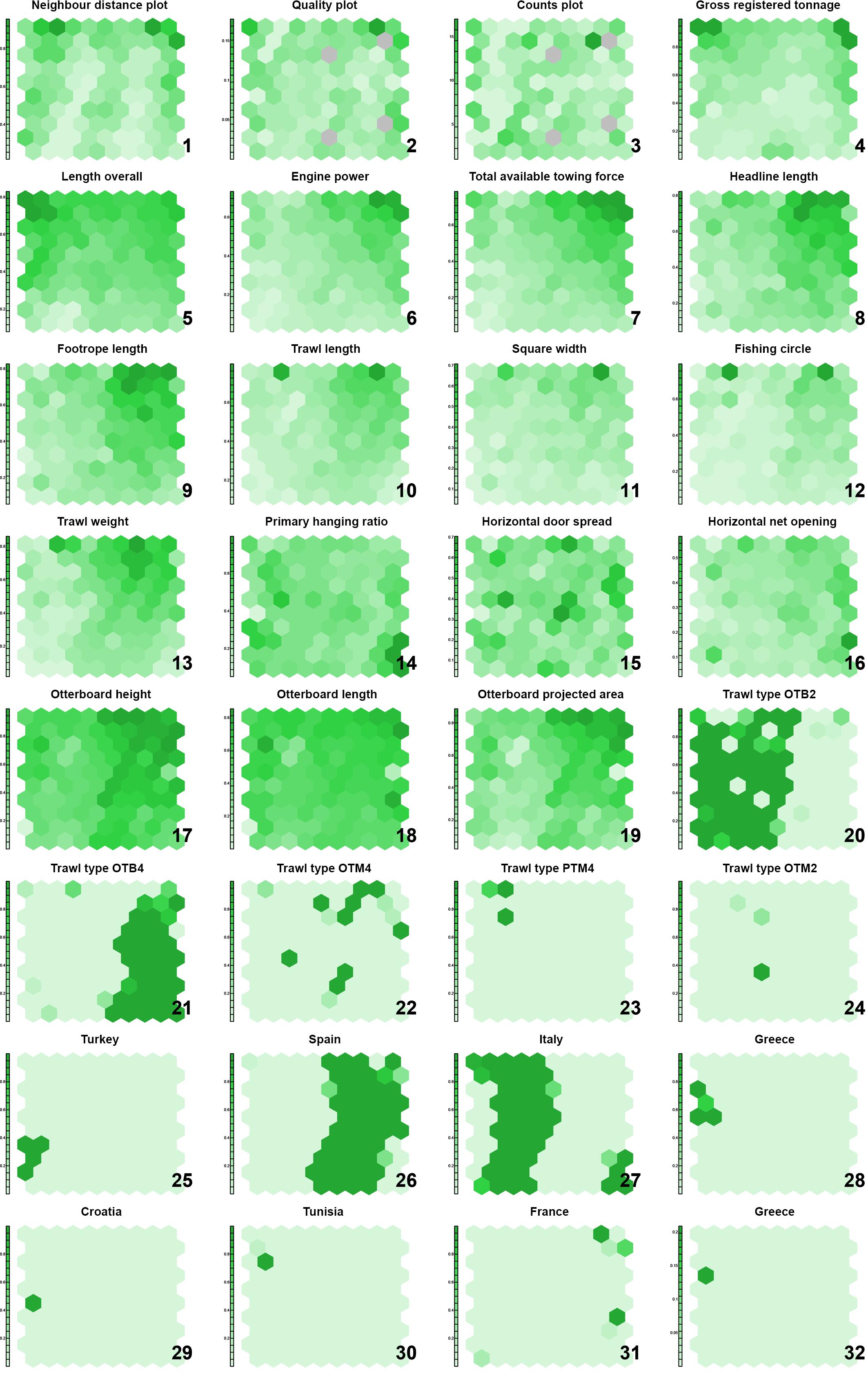
Figure 4. Trained SOM. The distribution pattern of the observed variables, normalized between 0 and 1, is expressed in the SOM using a color scale. Darker areas correspond to the higher values of each variable.

The vessel variables LOA and GRT showed a second peak in the upper left corner of the map, which however, are associated average values in terms of trawl size, belonging to the fishing gear types OTB2, PTM4, and OTM4, all of Italian origin. The variables HL, TrL, Wsq, FC, TrW showed two evident peaks of maximum values in two units positioned on the left and right of the first line of hexagons in the upper portion of the map. Those units correspond to the larger size category of Italian PTM4 trawls, and to the larger size category of French OTM4 fishing gears, respectively. The minimum values in terms of size of the vessel and the size of the gear used are displayed on the map in the lower left corner, dominated by OTB2 gears of Italian origin. It was not possible to identify any recognizable pattern for the variables HDS and HNO, while the hanging ratio E1 displayed a rather homogeneous distribution gradient, with slightly higher values displayed by gears of a smaller size class (lower right corner of the map). Regarding the distribution patterns of gear types and geographical provenance, the gear type OTB2 clustered on the left side of the map, while the right side of the map was dominated by the OTB4 gear type. Italian and Spanish trawls almost followed the same distribution pattern with a small degree of overlap. The OTM4 trawl type was almost entirely positioned in the upper right portion of the map, among gears belonging to a larger size class, with a second cluster of three units placed in the central-lower portion of the map. Pelagic 4-panel trawls clustered in the upper left corner, in the larger vessel and gear class, while OTM2 records did not show any recognizable pattern. Greek and Turkish trawls clustered on the left side of the map, among the OTB2 gear type and the average and average-to-small vessels and gear classes, respectively. Finally, Tunisia, Croatia and Cyprus had concentrated values within single output units, scattered in the OTB2 portion of the SOM.

Cluster Analysis

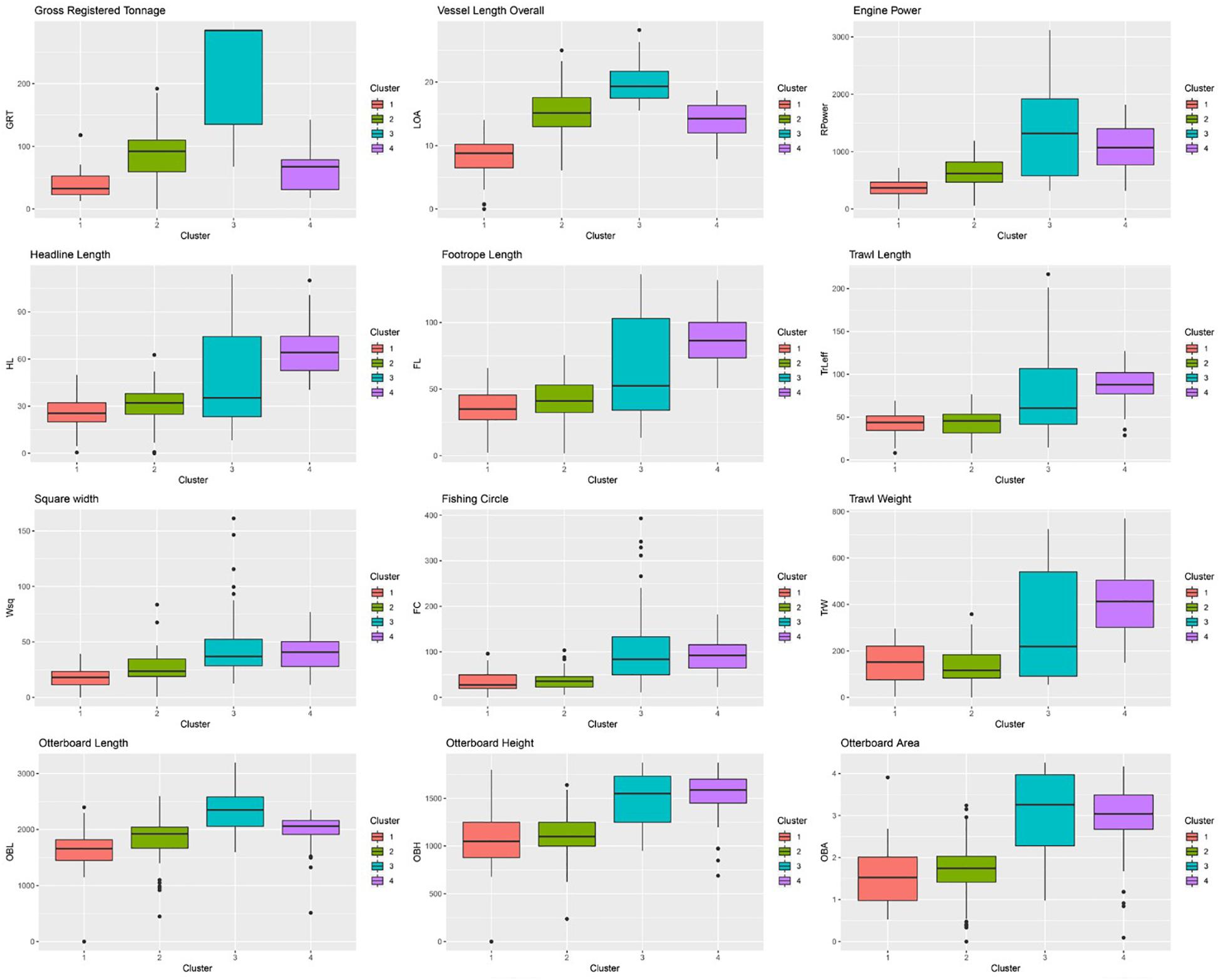
The model-based clustering approach based on finite Gaussian mixture modeling evaluated 14 competing models, choosing an ellipsoidal, equal shape and orientation (VEE) model with four components as the best model, indicating an optimal partition of the trained map in four clusters. The HDS and HNO variables were excluded from the cluster analysis as they did not show recognizable patterns, but an approximately homogeneous distribution of values instead, evenly spread all over the map. The outcome of the clustering algorithm and the resulting partition transposed on the trained map are shown in Figure 5. The clustering algorithm partitioned the trained map into four subgroups, one for the smaller vessel/gear/otterboard combinations (Cluster 1), another for the heavyweight class (Cluster 3), and two clusters for the average sized vessels (Clusters 2 and 4), which did not necessarily correspond to medium sized gears. Cluster 1, was placed at the bottom of the map, gathering smaller vessels with an average 8.19 m LOA, 368.3 hp and 42.88 GRT; corresponding to the average trawl length of 43.08 m, a square width of 17.77 m, FC of 33.68 and trawl weight of 149.0 kg. Cluster 3, was placed at the top of the map, collecting observations pertaining to the larger LOA and GRT vessels, but characterized by a wide variability in terms of engine power. Vessels belonging to this cluster share an average 19.77 m LOA, 1345.0 hp and 219.1 GRT; corresponding to the average trawl length of 78.43 m, square width of 45.58 m, FC of 110.03 and trawl weight of 318.43 kg. Clusters 2 and 4 represented the average size class vessels and shared very similar characteristics in terms of LOA and GRT. These two clusters were instead very different in terms of engine power, with Cluster 2 vessels characterized by an average 634.1 hp and Cluster 4 vessels characterized by an average 1102 hp. In this case the observed differences in engine power translated into marked differences in the size of the gears deployed. Cluster 2 vessels operated trawls characterized by an average length of 42.3 m, square width of 26.17 m, FC of 36.7 and trawl weight of 135.3 kg. Cluster 4 vessels, on the other hand, deployed trawls characterized by an average length of 88.09 m, square width of 39.55 m, FC of 88.95 and trawl weight of 419.4 kg. A summary of the reported average value for each cluster is reported Table 3, while a description of each variable range, median and interquartile ranges divided by cluster is available in Figure 6.

FIGURE 5

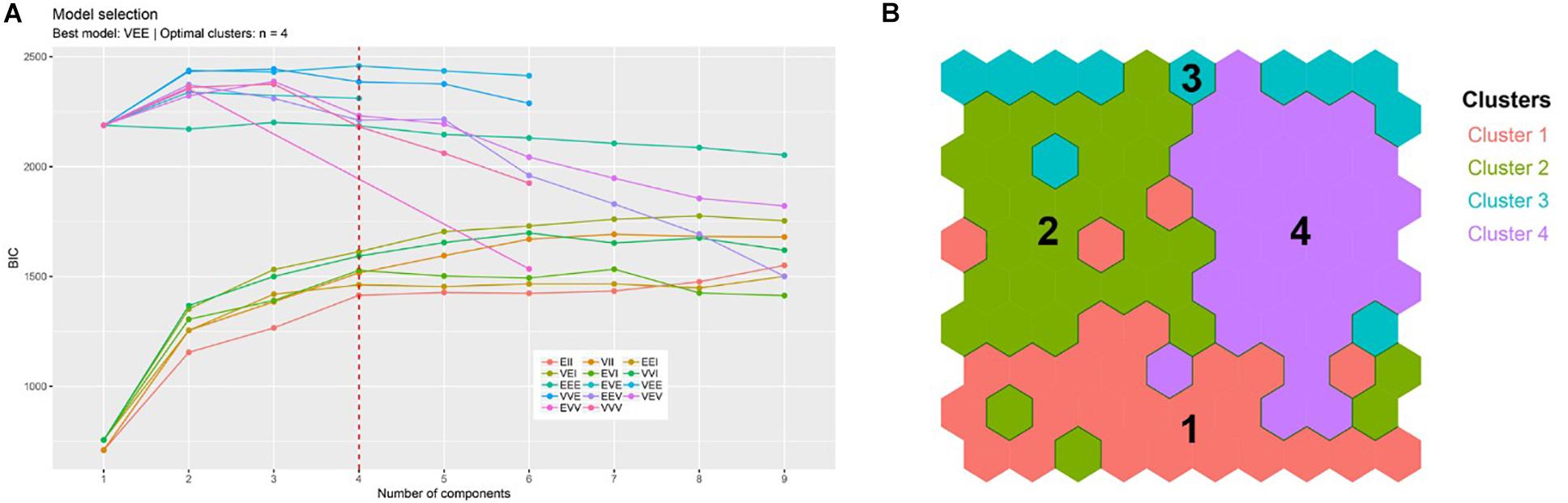
Figure 5. (A) Outcome of the clustering algorithm and (B) the resulting partition transposed on the trained map.

TABLE 3

Table 3. Summary table of the observed statistics for the identified clusters.

FIGURE 6

Figure 6. Description of each variable range, median and interquartile ranges divided by cluster.

SOM Predictive Performance Evaluation

The analysis of 472 observations, corresponding to 80% of the dataset, allowed the investigation of the SOM’s ability to predict gears and otterboard sizes for the remaining 20% of the dataset, with a total number of 119 observations. The prediction was based on independent variables describing vessel size and the categorical factors indicating gear type and vessel provenance. A simulated R² coefficient was calculated assuming that the predicted results constituted the outcome of a linear model. It was then used to explore model performance and to approximate a description of the fit of the predicted values to the observed values. The SOM predictive ability performed differently depending on the variable considered, obtaining the best results in the prediction of trawl length, headline length, footrope length and otterboard area variables. A summary of the evaluation of the SOM predictive performance is available in Figure 7.

FIGURE 7

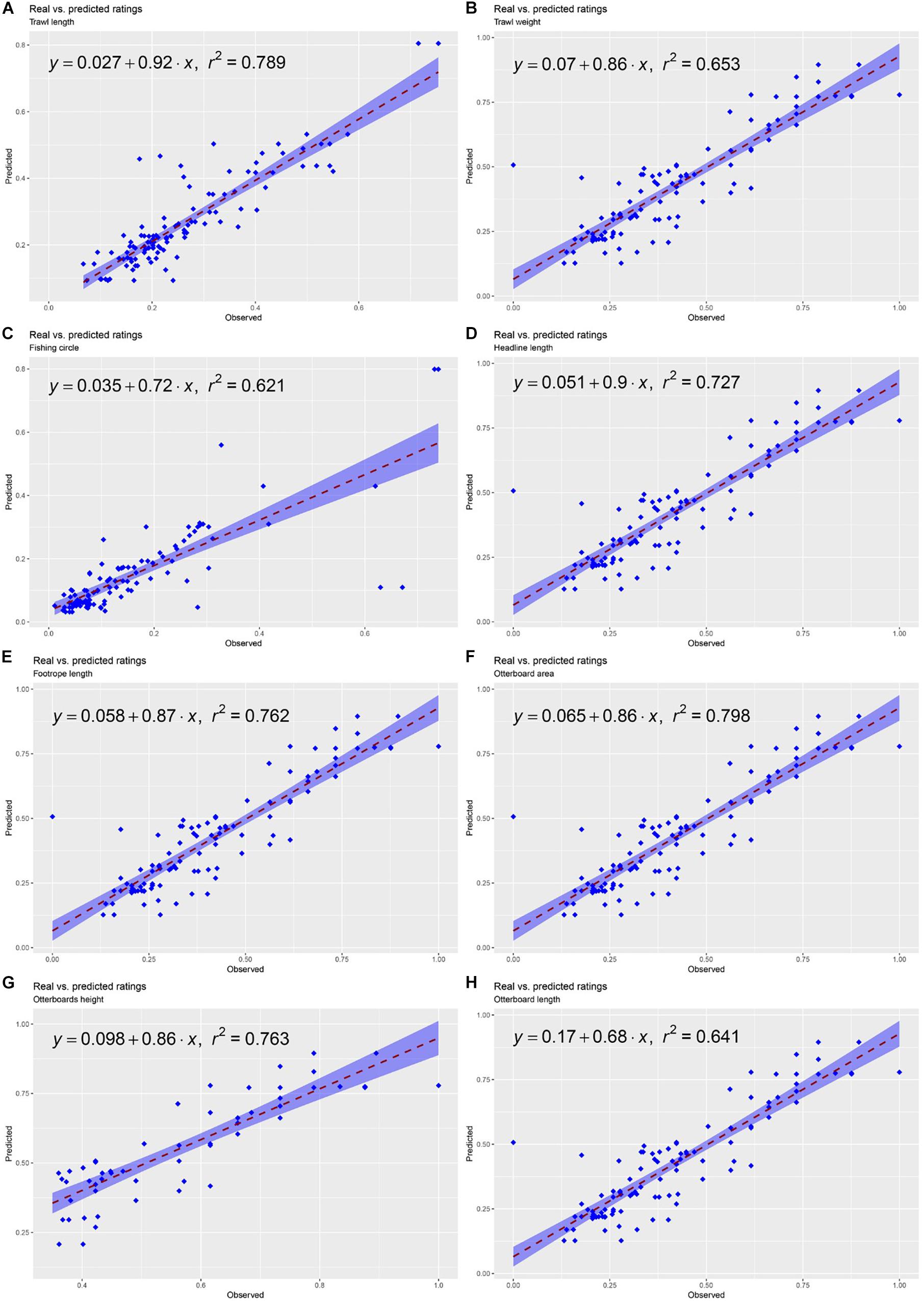
Figure 7. Summary of the evaluation of the SOM predictive performance. (A) Trawl length, (B) Trawl weight (C) Fishing circle, (D) Headline length, (E) Footrope length, (F) Otterboard area, (G) Otterboard height, (H) Otterboard length.

Discussion

The continuous improvement of fishing efforts and capacity descriptors is an essential element for the adoption of reliable management measures, aimed at the optimization of fishing activity revenues and the concurrent maintenance of sustainable exploitation levels. The purpose of this work was to explore the relationship that connects vessel size to the size of the fishing gear deployed, to facilitate tracing the dimensions of the trawl from readily available information like LOA, tonnage and the engine power of the vessel. If such a relationship were accurately described, it would be extremely useful to tailor specific management measures for specific fleet segments, improving the estimate of the impact exerted on the populations of target species. To the best of our knowledge, this is the first study using SOM applied to the exploration of these technical aspects of fishing activity, taking advantage of the capability of neural networks to perform non-linear data mining, clustering and summarization of the multidimensional variability of a dataset.

The main outcome of the study is that a simple relationship connecting vessels’ magnitude and gear size could not be described, confirming the findings produced by other authors in previous studies (Reid et al., 2011). Certainly, the patterns described by the SOM suggests the existence of a general trend that associates the increasing dimensions of the vessel with an increasing size of gears and its components, but the great amount of variability observed in the dataset, reflected in the heatmaps delivered by the SOM, suggests the interaction of multiple factors in determining the size of the fishing gear. A first variable to consider is the distribution of vessel-metrics within the fleet, displayed by the first map, trained using only vessel size descriptors and their geographical origin. Although the first map was only devised for the estimation of missing data in the dataset, it proved useful to observe the distribution of vessel-metrics within the fleet that are not influenced by any additional factor. The patterns displayed by the first SOM suggests a general trend that indicates a correlation between the length of a vessel, its tonnage and the power of the engine. At the same time, however, the positioning of the extreme values in near but non-overlapping units of the map, better defined the nature of this correlation, characterizing it as non-linear. Vessel-metrics per se cannot be described by a simple linear relationship, even without the intervention of any additional factor, and this evidence already sets a first level of complexity to consider while studying the relationship between vessels and gears used.

The complexity of the analysis increased with the addition of the parameters pertaining to fishing gears, which complicated the distribution of the patterns in the map. The length of the vessel and gross registered tonnage, described by a unique gradient when only vessel-metrics are considered, resulted divided by the addition of descriptive parameters of the fishing gear, and showed patterns of distribution that associated large-sized boats with different gear sizes, depending on the type of gear, nationality and geographical origin of the vessels. The subdivision of the map into clusters facilitated the identification of extremes in the fleet in terms of vessel and gear size (Clusters 1 and 3), as well as the definition of the intermediate clusters (Clusters 2 and 4), where important differences could be highlighted. In Clusters 2 and 4 vessels characterized by very similar LOA and GRT reported marked differences in terms of engine power. This difference allowed the vessels belonging to cluster 4 (Spanish vessels using gears of the OTB4 type) to operate with much larger trawls, often equal in size to the gears used by the heavyweight class of the analyzed fleet. Among vessel descriptors, engine power was the only variable showing a unique gradient on the map, that associated higher hp values to a larger size gear. This association is visible when comparing the engine power gradient with the distribution patterns of gear descriptors like headline length, footrope length, trawl length, trawl weight, square width, fishing circle and the size of the otterboards used. This result suggests that the engine power, more than the size of the vessel (GRT or LOA), has the greatest influence on the size of the gear deployed. Given two vessels of similar magnitude, a greater engine power grants much more freedom in the choice of the size of the trawl and consequently in the type of fishing that can be practiced. This parameter, more than vessel size, should certainly have a greater relevance when formulating management indications.

The size of the gear used is also dependent on gear type, and varies with the geographical origin of the vessel. In fact, gear type and geographical origin were important variables used by the SOM when estimating gear-metrics and otterboard magnitudes. The inclusion of these factors has indeed contributed to improving the SOM’s predictive performance. In many cases the map was able to infer gear and otterboard metrics properly, but its performance can certainly be enhanced through a training phase performed on a larger dataset, and via the inclusion of additional descriptors that might be still missing. The geographical variability observed could probably be traced back to a similarity which characterizes vessels belonging to the same local fleet, which usually share similar characteristics and adopt similar solutions in the implementation of a peculiar type of fishing. This speculation, if confirmed, would discourage the adoption of fleet management measures applied on an international scale, in favor of solutions that give greater relevance to local homogeneity/variability.

Future Steps

From this analysis, an excessive variability in the description of the vessels/gears of greater size has emerged, indicating that the dataset should be expanded to provide a more accurate description of this fleet component. Furthermore, the dataset considered provided an adequate description of a portion of the fleet pertaining to two countries (Italy and Spain) but did not allow an equally adequate characterization of the intrinsic variability of other fleets operating in the Mediterranean Sea. Geographical variability has greatly contributed to improving the predictive capabilities of the trained map, suggesting that the dataset should be enriched to consider the regional variability characteristic of Mediterranean fleets even more. A step forward in this direction would also be the inclusion of the species targeted by each fishery/gear combination. The incorporation of these variables, and others to be evaluated, would certainly allow the improvement of descriptive and forecasting models, and will be considered in a future work.

Data Availability

The authors do not have permission to share dataset used.

Author Contributions

AC and AS and EN developed research described in the manuscript, curated and maintained the historical dataset, and wrote the manuscript with inputs from SB and JP. AC performed the statistical analyses.

Funding

This work was supported by the Italian National Research Council (CNR), Institute of Marine Biological Resources and Biotechnologies (IRBIM), Ancona, Italy.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful to all independent researchers and fishermen involved in the scientific data collection. We would like to thank the reviewers for their constructive comments and criticism.

Footnotes

1. ^ http://cran.R-project.org/

References

Adeloye, A. J., Rustum, R., and Kariyama, I. D. (2012). Neural computing modeling of the reference crop evapotranspiration. Environ. Model. Softw. 29, 61–73. doi: 10.1016/j.envsoft.2011.10.012

CrossRef Full Text | Google Scholar

Brosse, S., Giraudel, J. L., and Lek, S. (2001). Utilisation of non-supervised neural networks and principal component analysis to study fish assemblages. Ecol. Model. 146, 159–166. doi: 10.1016/S0304-3800(01)00303-9

CrossRef Full Text | Google Scholar

Caddy, J. F., and Defeo, O. (2003). Enhancing or Restoring the Productivity of Natural Populations of Shellfish and Other Marine Invertebrate Resources. FAO Fish. Tech. Paper 448. Rome: FAO.

Google Scholar

Eigaard, O. R., Rihan, D., Graham, N., Sala, A., and Zachariassen, K. (2011). Improving fishing effort descriptors: modelling engine power and gear-size relations of five European trawl fleets. Fish. Res. 110, 39–46. doi: 10.1016/j.fishres.2011.03.010

CrossRef Full Text | Google Scholar

European Commission [EC] (2002). European Commission Regulation (EC) no. 2371/2002 of 20 December 2002. On the conservation sustainable exploitation of fisheries resources under the Common Fisheries Policy. Official J. Eur. Union L358, 59–80.

Google Scholar

FAO, (ed.) (2008). Managing Fishing Capacity, Fisheries Management. Rome: Food and Agriculture Organization of the United Nations.

Google Scholar

Fiorentini, L., Sala, A., Hansen, K., Cosimi, G., and Palumbo, V. (2004). Comparison between model testing and full-scale trials of new trawl design for Italian bottom fisheries. Fish. Sci. 70, 349–359. doi: 10.1111/j.1444-2906.2004.00813.x

CrossRef Full Text | Google Scholar

Gutiérrez, N. L., Hilborn, R., and Defeo, O. (2011). Leadership, social capital and incentives promote successful fisheries. Nature 470, 386–389. doi: 10.1038/nature09689

PubMed Abstract | CrossRef Full Text | Google Scholar

Kalteh, A. M., and Hjorth, P. (2009). Imputation of missing values in a precipitation–runoff process database. Hydrol. Res. 40, 420–432. doi: 10.2166/nh.2009.001

CrossRef Full Text | Google Scholar

Kim, M., Baek, S., Ligaray, M., Pyo, J., Park, M., and Cho, K. H. (2015). Comparative studies of different imputation methods for recovering streamflow observation. Water 7, 6847–6860. doi: 10.3390/w7126663

CrossRef Full Text | Google Scholar

Kiviluoto, K. (1996). “Topology preservation in self-organizing maps,” in Presented at the Proceedings of International Conference on Neural Networks (ICNN’96), Washington, DC, 294–299. doi: 10.1109/ICNN.1996.548907

CrossRef Full Text | Google Scholar

Kohonen, T. (1982). Self-organized formation of topologically correct feature maps. Biol. Cybern. 43, 59–69. doi: 10.1007/BF00337288

CrossRef Full Text | Google Scholar

Kohonen, T. (1997). Self-Organizing Maps, Springer Series in Information Sciences, 2nd Edn. Heidelberg: Springer-Verlag.

Google Scholar

Kohonen, T. (2001). Self-Organizing Maps, Springer Series in Information Sciences, 3rd Edn. Heidelberg: Springer-Verlag.

Google Scholar

Kohonen, T. (2012). Self-Organization and Associative Memory. Berlin: Springer Science & Business Media.

Google Scholar

Marchal, P., Andersen, B., Bromley, D., Iriondo, A., Mahevas, S., Quirijns, F., et al. (2006). Improving the definition of fishing effort for important European fleets by accounting for the skipper effect. Can. J. Fish. Aquat. Sci. 63, 510–533.

Google Scholar

Marchal, P., Andersen, B., Caillart, B., Eigaard, O., Guyader, O., Hovgaard, H., et al. (2007). Impact of technological creep on fishing effort and fishing mortality, for a selection of European fleets. ICES J. Mar. Sci. 64, 192–209. doi: 10.1093/icesjms/fsl014

CrossRef Full Text | Google Scholar

McLachlan, A., and Defeo, O. (2018). Fisheries, in: The Ecology of Sandy Shores. Amsterdam: Elsevier, 331–374. doi: 10.1016/B978-0-12-809467-9.00014-X

CrossRef Full Text | Google Scholar

Mwale, F. D., Adeloye, A., and Rustum, R. (2012). Infilling of missing rainfall and streamflow data in the Shire River basin, Malawi – A self organizing map approach. Phys. Chem. Earth 50–52, 34–43. doi: 10.1016/j.pce.2012.09.006

CrossRef Full Text | Google Scholar

Mwale, F. D., Adeloye, A. J., and Rustum, R. (2014). Application of self-organising maps and multi-layer perceptron-artificial neural networks for streamflow and water level forecasting in data-poor catchments: the case of the Lower Shire floodplain, Malawi. Nord. Hydrol. 45, 838–854. doi: 10.2166/nh.2014.168

CrossRef Full Text | Google Scholar

Nkiaka, E., Nawaz, N. R., and Lovett, J. C. (2016). Using self-organizing maps to infill missing data in hydro-meteorological time series from the Logone catchment, Lake Chad basin. Environ. Monit. Assess. 188, 400. doi: 10.1007/s10661-016-5385-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Notti, E., De Carlo, F., Brčić, J., and Sala, A. (2013). “Technical specifications of Mediterranean trawl gears,” in Proceedings of the 11th International Workshop on Methods for the Development and Evaluation of Maritime Technologies (DeMaT’13), Rostock, doi: 10.13140/2.1.3147.1687

CrossRef Full Text | Google Scholar

Park, Y.-S., Chon, T.-S., Bae, M.-J., Kim, D.-H., and Lek, S. (2018). “Multivariate Data Analysis by Means of Self-Organizing Maps,” in Ecological Informatics, eds F. Recknagel and W. K. Michener (Cham: Springer International Publishing), 251–272. doi: 10.1007/978-3-319-59928-1_12

CrossRef Full Text | Google Scholar

Pope, J. G. (2009). “Input and output controls: the practice of fishing effort and catch management in responsible fisheries,” in A Fishery Manager’s Guidebook, eds K. L. Cochrane and S. M. Garcia (Oxford: Blackwell), 220–252. doi: 10.1002/9781444316315.ch9

CrossRef Full Text | Google Scholar

Reid, D. G., Graham, N., Rihan, D. J., Kelly, E., Gatt, I. R., Griffin, F., et al. (2011). Do big boats tow big nets? ICES J. Mar. Sci. 68, 1663–1669. doi: 10.1093/icesjms/fsr130

CrossRef Full Text | Google Scholar

Santiago, J. L., Ballesteros, M. A., Chapela, R., Silva, C., Nielsen, K. N., Rangel, M., et al. (2015). Is Europe ready for a results-based approach to fisheries management? The voice of stakeholders. Mar. Policy 56, 86–97. doi: 10.1016/j.marpol.2015.02.006

CrossRef Full Text | Google Scholar

Scrucca, L., Fop, M., Murphy, T. B., and Raftery, A. E. (2016). mclust 5: clustering, classification and density estimation using gaussian finite mixture models. R J. 8:289. doi: 10.32614/rj-2016-021

CrossRef Full Text | Google Scholar

Squires, D., and Kirkley, J. (1999). Skipper skill and panel data in fishing industries. Can. J. Fish. Aquat. Sci. 56, 2011–2018. doi: 10.1139/f99-135

CrossRef Full Text | Google Scholar

Tan, R. P. G. H., van den Berg, J., and van den Bergh, W.-M. (2002). “Credit rating classification using self-organizing maps,” in Neural Networks in Business: Techniques and Applications, eds K. Smith and J. Gupta (Pennsylvania, PA: IGI Global), 140–153. doi: 10.4018/978-1-930708-31-0.ch009

CrossRef Full Text | Google Scholar

Veiga, P., Pita, C., Rangel, M., Gonçalves, J. M. S., Campos, A., Fernandes, P. G., et al. (2016). The EU landing obligation and European small-scale fisheries: what are the odds for success? Mar. Policy 64, 64–71. doi: 10.1016/j.marpol.2015.11.008

CrossRef Full Text | Google Scholar

Wehrens, R., and Kruisselbrink, J. (2018). Flexible self-organizing maps in kohonen 3.0. J. Stat. Softw. 87, 1–18. doi: 10.18637/jss.v087.i07

CrossRef Full Text | Google Scholar