Metrology for pH Measurements in Brackish Waters—Part 1: Extending Electrochemical pHT Measurements of TRIS Buffers to Salinities 5–20

Harned cell pH_T measurements were performed on 2-amino-2-hydroxymethyl-1,3-propanediol (TRIS) buffered artificial seawater solutions in the salinity range 5–20, at three equimolal buffer concentrations (0.01, 0.025, 0.04 mol·kg-H₂O⁻¹), and in the temperature range 278.15–318.15 K. Measurement uncertainties were assigned to the pH_T values of the buffer solutions and ranged from 0.002 to 0.004 over the investigated salinity and temperature ranges. The pH_T values were combined with previous results from literature covering salinities from 20 to 40. A model function expressing pH_T as a function of salinity, temperature and TRIS/TRIS·H⁺ molality was fitted to the combined data set. The results can be used to reliably calibrate pH instruments traceable to primary standards and over the salinity range 5–40, in particular, covering the low salinity range of brackish water for the first time. At salinities 5–20 and 35, the measured dependence of pH_T on the TRIS/TRIS·H⁺ molality enables extrapolation of quantities calibrated against the pH_T values, e.g., the dissociation constants of pH indicator dyes, to be extrapolated to zero TRIS molality. Extrapolated quantities then refer to pure synthetic seawater conditions and define a true hydrogen ion concentration scale in seawater media.

Introduction

Changes in seawater pH are linked to changes in the concentration of dissolved inorganic carbon and alkalinity. Precise and accurate pH measurements are therefore an ideal tool to investigate two processes of global importance: (i) Ocean acidification, caused by the uptake of anthropogenic carbon dioxide (CO₂) from the atmosphere (Le Quéré et al., 2016), can be directly traced by pH measurements in open ocean environments (Byrne et al., 2010). (ii) The investigation of biogeochemical transformations can be supported by pH measurements, as any production or mineralization of organic matter is inevitably coupled to the uptake and release of CO₂.

In many brackish water systems, intense biogeochemical transformations cause pronounced pH fluctuations superimposed on long-term pH trends due to the uptake of anthropogenic CO₂ (Hofmann et al., 2011). Accurate traceable and direct pH measurements are essential in deciphering the impact of both drivers. Furthermore, open ocean and brackish waters differ with respect to two characteristics of alkalinity, which underlines the need for accurate and traceable pH measurements in the latter waters. Firstly, alkalinity levels in brackish waters can change on time scales of ocean acidification. For example, Müller et al. (2016) reported an increase in alkalinity over the past two decades for the Baltic Sea, one of the world's largest estuarine systems, that significantly buffered the acidification caused by anthropogenic CO₂ uptake. Consequently, acidification trends cannot reliably be predicted from changes in pCO₂ as is the case in open ocean waters with stable alkalinity levels (Doney et al., 2009), but require direct pH measurements. Secondly, brackish waters are typically characterized by high loads of dissolved organic matter that contribute significantly to alkalinity, which results in erroneous results if alkalinity is used as an input parameter for CO₂ system calculations (Kulinski et al., 2014). Under such conditions, accurate and precise pH measurements are extremely valuable for a complete determination of the CO₂ system. It was shown that this can in principle be achieved by spectrophotometric pH measurements, because the methods work reliably even in the presence of high amounts of dissolved organic matter (Müller et al., 2018).

According to its definition on the activity scale, pH $=-{\text{log}}_{10}(a_{{\text{H}}^{+}})$, pH involves a single ion quantity and is as such immeasurable by any thermodynamically valid method (Buck et al., 2002). pH measurements according to the IUPAC recommendation require conventions which are only valid for ionic strength ≤ 0.1 mol·kg⁻¹. For measurements in seawater with a higher ionic strength it is convenient to measure pH on scales that refer to the hydrogen ion concentration. The definition of such concentration scales requires the definition of a standard composition of seawater, because hydrogen ions are in equilibrium with other acid base components in seawater. pH_T, where the index T denotes the total pH scale, has become a widely accepted convention within the scientific community (Dickson et al., 2015). According to its definition, ${\text{p}\text{H}}_{\text{T}}=-{\text{log}}_{10}\left\{\left[H^{+}\right]\left(1+\frac{{\left[{\text{SO}}_4^{2-}\right]}_T}{K_{{\text{HSO}}_4^{-}}}\right)\right\}$, it accounts for the concentrations of both, the free hydrogen ions, [H⁺], and hydrogen sulfate ions, expressed as the total sulfate concentration ${\left[{\text{S}\text{O}}_4^{2-}\right]}_T$ divided by the dissociation constant of hydrogen sulfate $K_{{\text{HSO}}_4^{-}}$. The latter contribute to the acidity of the solution by the potential to transfer further hydrogen ions to other proton acceptors.

In order to assure comparability of pH_T measurement results, internationally accepted primary pH_T standards are essential. Currently the de facto standards are TRIS (2-amino-2-hydroxymethyl-1,3-propanediol) buffered artificial seawater (ASW) solutions (DelValls and Dickson, 1998; Pratt, 2014) in the salinity (S) range 20–40, where pH_T values have been measured using an electrochemical setup comprising Harned cells. This setup represents a primary method for pH measurements (Buck et al., 2002). In oceanographic practice, pH_T is typically measured by other methods such as spectrophotometry (Clayton and Byrne, 1993; Liu et al., 2011) and Ion Selective Field Effect Transistor (ISFET) (Martz et al., 2010). The spectrophotometric pH_T measurement relies on pH indicator dyes such as m-Cresol Purple (mCP). Standard buffer solutions with well-defined, traceable pH_T values are required for the physico-chemical characterization of the purified dyes. This characterization was previously achieved for the indicator mCP in the salinity range 20–40 and temperatures from 273.15 to 308.15 K (Liu et al., 2011), based on the TRIS buffer characterization by DelValls and Dickson (1998). Recently, similar standards were achieved for sea-ice brines with temperatures as low as the freezing point by a successive characterization of hypersaline TRIS buffers (Papadimitriou et al., 2016) and–based on those buffer solutions—the extended characterization of mCP (Loucaides et al., 2017).

Up to now, Harned cell measurements on TRIS buffered ASW solutions in the lower salinity range (S < 20) have not been made. Consequently, spectrophotometrically obtained pH_T values in this salinity range were not traceable to a primary pH_T standard. Mosley et al. (2004) provided an interim solution by interpolating the pH_T values of TRIS buffered ASW solutions for the salinity range 0–20. The interpolation was based on the results for S = 20–40 of DelValls and Dickson (1998) and for TRIS in pure water by Bates and Hetzer (1961). Although the solutions of Bates and Hetzer (1961) contained no other salts, (Mosley et al., 2004) interpreted the buffer ionic strength as salinity, leading to questionable accuracy. Moreover, non-purified dye was used for the mCP characterization and measurements were conducted only at 298.15 K (Mosley et al., 2004). Consequently, spectrophotometric pH_T measurements in brackish waters with salinity below 20 were not traceable to a primary pH_T standard and results were subject to an unknown degree of measurement uncertainty.

To fill this gap, we present Harned cell pH_T measurement results in the salinity range 5–20 and, in addition, at 35 for assessment of consistency with the previous results of DelValls and Dickson (1998) and Pratt (2014). In particular, we discuss issues of buffer solution preparation in the low salinity range, which differs significantly from that in the upper salinity range and affects pH_T measurements. Measurements were performed in the temperature range 278.15 to 318.15 K. All buffer solutions were prepared at three equimolal concentrations of TRIS/TRIS·H⁺, which allows extrapolation of calibration parameters determined in these solutions to pure artificial seawater conditions as recommended by Nemzer and Dickson (2005). We combined our results with those of DelValls and Dickson (1998) to derive a consistent pH_T model for the salinity range 5–40, which is a prerequisite to comparing pH_T values measured in ocean and brackish waters.

Materials and Methods

Scope and Concept

We prepared and analyzed TRIS buffered ASW solutions (ASW/TRIS-HCl) with salinities S = 5, 10, 15, 20, and 35. Preparing low-saline buffer solutions for subsequent calibration of pH instruments includes a general problem: HCl added contribute significantly to the ionic strength of the buffer solution. An equivalent amount of salt components of the ASW matrix has to be removed to ensure constant ionic strength. Consequently, the solution composition used for the calibration of any pH instrument differs from the seawater to be analyzed. For a classical equimolal TRIS/TRIS·H⁺ buffer with a molality of 0.04 mol·kg-H₂O⁻¹ (DelValls and Dickson, 1998), the ionic strength contribution ranges from 5 to 10% for salinities of 40–20. The impact of this ionic strength contribution on the determination of the dissociation constant of mCP has not yet been assessed. Even though it might be negligible within the overall uncertainty of seawater pH_T measurements at salinities above 20, this assumption is critical at lower salinities since the contribution of the buffer substance increases with decreasing salinity. This problem is inevitable and counteracting it by reducing the concentration of the buffer component comes at the cost of reduced buffer stability. To account for this problem, equimolal buffer consisting of TRIS and protonated TRIS (TRIS·H⁺) each at molalities of 0.04, 0.025, and 0.01 mol·kg-H₂O⁻¹ were prepared and individual pH_T values measured. This allows extrapolation of the measured quantities to zero TRIS/TRIS·H⁺ molality (Müller and Rehder, 2018).

The relative composition of the salts (NaCl, MgCl₂, Na₂SO₄, CaCl₂, and KCl) that form the ASW matrix is an associated problem. DelValls and Dickson (1998) computed the salt composition by first scaling a TRIS-free reference composition from S = 35 to the target salinity. Afterwards, the amount of NaCl was reduced by the amount of HCl added to maintain the nominal ionic strength. If a specific HCl concentration, e.g., 0.04 mol·kg-H₂O⁻¹, is adjusted, this approach implies changing the ratios between Na⁺ and other cations at different salinities. For salinities of 20–40 those changes are small (Figure 1A). However, toward lower salinities the differences in the cation ratios become more pronounced. At a salinity of ~4, NaCl would be entirely replaced by HCl when preparing solutions according to DelValls and Dickson (1998). Therefore, only our buffers at S = 35 and the buffer at S = 20 with equimolal TRIS/TRIS·H⁺ molality of 0.04 mol·kg-H₂O⁻¹ have been prepared according to the recipe of DelValls and Dickson (1998) in order to achieve best comparability to previous studies. The recipe was modified to achieve constant ratios between the ASW salts for all other buffer solutions.

FIGURE 1

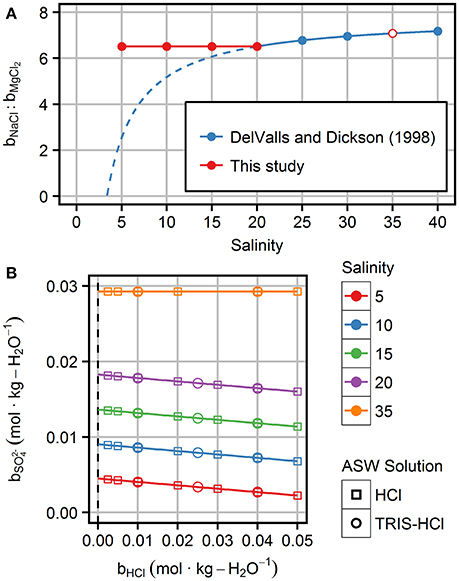
Figure 1. Characteristics of artificial seawater solutions prepared in this study: (A) Cation composition represented by b_NaCl: b_MgCl2 molality ratios for ASW solutions with a HCl molality of 0.04 mol·kg-H₂O⁻¹. The cation ratios as prepared in this study (red) are compared to those proposed by DelValls and Dickson (1998)—actually prepared: blue circles and solid line; recipe hypothetically applied for lower salinities: dashed blue line. (B) Sulfate molality, $b_{{\text{SO}}_4^{2-}}$, as a function of HCl molality and salinity. Squares represent HCl solutions in ASW to measure the standard potential of the Harned cell, E*°. Circles indicate the three investigated TRIS/TRIS·H⁺ molalities.

Preparation of the TRIS-HCL and HCL Solutions in Artificial Seawater

We have chosen the composition proposed by DelValls and Dickson (1998) for S = 20 and HCl molality b_HCl = 0.04 mol·kg-H₂O⁻¹ as the reference composition of ASW (Table 1). Based on the reference composition at S = 20, the concentrations of all ASW salts were varied proportionally to compensate for the HCl ionic strength contribution and achieve target salinities. This proportional variation of the molality b of any salt component x (NaCl, MgCl₂, Na₂SO₄, CaCl₂, and KCl) was computed as a function of S and b_HCl according to:

$\begin{array}{l}{b}_{\text{x}}(S,b_{\text{HCl}})=\\ \frac{I\left(S\right)-b_{\text{HCl}}}{I\left(20\right)-0.04\text{ mol}·{\text{kg-H}}_{\text{2}}{\text{O}}^{-1}}·b_{\text{x}}(20,0.04\text{ mol}·{\text{kg}-\text{H}}_2{\text{O}}^{-1})& (1)\end{array}$

where b_HCl is the target molality of HCl in mol·kg-H₂O⁻¹ (which is identical to $b_{{TRIS/TRIS·H}^{+}}$), 0.04 mol·kg-H₂O⁻¹ refers to b_HCl in the reference solution, b_x (20, 0.04 mol·kg-H₂O⁻¹) is the molality of salt x in the reference solution summarized in Table 1, and I is the ionic strength calculated from the target salinity S by:

$\begin{array}{cc}I\left(S\right)=\frac{19.919·S}{1000-1.00192·S}& (2)\end{array}$

Based on the reference composition of ASW according to DelValls and Dickson (1998), Equation (2) achieves proportional scaling of ionic strength in moles per kg solution with salinity (nominator) and conversion to ionic strength in moles per kg water (denominator). Coefficients in Equation (2) are based on IUPAC 2013 atomic weights (Meija et al., 2016).

TABLE 1

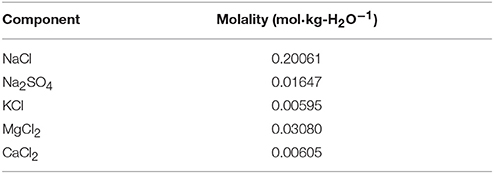
Table 1. Reference solution composition computed according to DelValls and Dickson (1998) for S = 20 and b_HCl = 0.04 mol·kg-H₂O⁻¹.

For measurements of pH_T with Harned cells it is necessary to determine the standard potential of the silver-silver chloride (Ag|AgCl) electrodes. This can be achieved by measurements of a serial dilution of HCl in the respective solution (see chapter “Determination of pH_T” below). Therefore, HCl solutions were prepared in ASW (ASW/HCl) at b_HCl of 0.0025, 0.005, 0.01, 0.02, 0.03, 0.04, and 0.05 mol·kg-H₂O⁻¹ at each target salinity according to Equations (1) and (2) and Table 1.

Our preparation method of ASW/TRIS-HCl and ASW/HCl solutions has the following implications at salinities ≤ 20:

• Constant ratios of the ASW salt components at all salinities and HCl molalities, which is reflected in the b_NaCl: b_MgCl2 ratio (Figure 1A).

• Variable chloride and sulfate molality at a given salinity, because more sulfate is removed at higher HCl (Figure 1B). This change in sulfate molality requires corrections (see “Sulfate correction for effective E^*° values” below).

All solutions were prepared from stock solutions of NaCl, KCl, CaCl₂, MgCl₂, Na₂SO₄, TRIS and HCl that have been gravimetrically prepared with ultrapure water (see supplement). All weighings were performed using an analytical balance (Sartorius Genius) and were buoyancy corrected. The air density for buoyancy correction was calculated from the atmospheric conditions measured with a combined humidity and temperature sensor (Almemo) as well as a barometer (Setra Systems).

The various salts, NaCl, KCl, CaCl₂, MgCl₂ (originating from MV laboratories Inc., Frenchtown, NJ, USA and kindly supplied from METAS, Switzerland), and Na₂SO₄ (originating from Merck), were characterized by coulometric measurements (see supplement: Tables S1, S2.1). NaCl and KCl were dried at 383 K for 2 h before use. CaCl₂ and MgCl₂ are hygroscopic. Hence, stock solutions were prepared and characterized using ion chromatography (see supplement: Table S2.1). TRIS was purchased from NIST (SRM 723e). No losses of TRIS weight on drying over magnesium perchlorate could be detected in the range of weighing uncertainty. The HCl stock solution was prepared from Titrisol ampoules (Merck). The HCl stock solution molality was assayed by potentiometric titration against the stock solution of TRIS SRM 723e (see supplement). The titration of the HCl against the TRIS stock solution ensures equimolal TRIS/TRIS·H⁺ ratios in the produced buffer solutions. All dilutions were carried out with ultrapure water obtained from a Milli-Q system. Actual salinities of the ASW/TRIS-HCl solutions were calculated from the actual ionic strength based on weighings according to Equation (2).

Harned Cell Measurements

The pH_T values of the ASW/TRIS-HCl solutions were calculated from measured potentials using Harned cells (Harned and Owen, 1958), which consist of a platinum hydrogen electrode and an Ag|AgCl reference electrode. Both electrodes are placed into a U-tube measurement cell. Both electrodes are in direct contact with the solution measured, i.e., there is no electrolyte bridge or a similar junction necessary to connect the electrodes electrically. The cells also comprise a unit for humidification of the hydrogen gas (see picture of the Harned measurement cell in Figure S1). The cell voltage was measured after temperature stabilization using a digital voltmeter (Agilent A3458) and corrected for the actual partial pressure of the hydrogen gas p_H2 (Hills and Ives, 1951). Details of the Harned cell setup and the cell voltage correction are given in the supplement.

Measurements of the artificial seawater solutions containing TRIS-HCl were always measured in triplicate while artificial seawater solutions containing different HCl molalities were measured only once in most of the cases (see Tables S5.1, S5.2 in the Supplement).

Determination of pH_T

pH_T is defined on an amount content basis (moles per kilogram solution). However, the electrochemical measurement of pH_T is established via the molality-based expression of pH_b (DelValls and Dickson, 1998) according to:

$\begin{array}{cc}{\text{pH}}_{\text{b}}=\frac{E_{\text{ASW/TRIS}-\text{HCl}}-E^{\ast °}}{\frac{RT\text{ln10}}{F}}+{\text{log}}_{10}\left(\frac{b_{{\text{Cl}}^{-}}^{°}}{b}\right)& (3)\end{array}$

with the electric Harned cell potential E_{ASW/TRIS−HCl} of the buffered artificial seawater solution, the standard potential E^*° of the Ag|AgCl electrode in pure ASW of the same nominal salinity, the molality $b_{{\text{Cl}}^{-}}$ of chloride in the solution and the standard molality b° = 1 mol·kg-H₂O⁻¹. The expression of pH_b in Equation (3) assumes that the activity coefficient of HCl in the buffer solution is the same as its trace value in the pure artificial seawater (see section Discussion).

E^*° was determined at each salinity and temperature from measured potentials E_ASW/HCl of 7 ASW solutions with HCl molalities ranging from 0.0025 to 0.05 mol·kg-H₂O⁻¹. Therefore, E′ values were calculated from measured E_ASW/HCl according to Equation (4):

$\begin{array}{cc}{E}^{\prime }=E_{\text{ASW/HCl}}+\frac{RT\text{ln10}}{F}·{\text{log}}_{10}\left(\frac{b_{\text{HCl}}·b_{{\text{Cl}}^{-}}}{{\left(b^{°}\right)}^2}\right)& (4)\end{array}$

with b_HCl the molality of HCl. E^*° was determined as the intercept at zero HCl molality of a second order polynomial fitted to E′ as a function of b_HCl.

The pH_b value derived from Equation (3) is molality-based, while pH_T is defined in terms of the amount content (moles per kg solution). Therefore, pH_T has to be calculated from pH_b (DelValls and Dickson, 1998) according to:

$\begin{array}{cc}{\text{pH}}_{\text{T}}={\text{pH}}_{\text{b}}-{\text{log}}_{10}\left(1-0.00106·S\right)& (5)\end{array}$

where the term 1 – 0.00106·S expresses the relation between salinity and the water content of the pure ASW solution, ω_H2O. The latter is defined as mass water per mass solution (see section Discussion).

Twelve Harned cells have been used to measure the potential of 12 solutions simultaneously to reduce measurement time. Measurements of ASW/HCl solution to determine E^*° were not carried out in the same measurement run as the potential measurements of the ASW/TRIS-HCl solutions for practical reasons. To ensure that the electrochemical properties of the Ag|AgCl electrodes is, within the uncertainty limits, the same for all solutions, the potentials of these electrodes were measured against a master Ag|AgCl electrode. The master electrode was always stored in 0.005 M hydrochloric acid and was considered to be stable in potential with time. The comparison measurements of all electrodes against the master electrode were performed in the same HCl solution before each measurement run and found to differ not more than 85 μV, corresponding to around 0.0015 in terms of pH.

The uncertainties of the measured pH_T values were determined for all temperatures, salinities and TRIS/TRIS·H⁺ molalities according to the Guide to the expression of uncertainty in measurement (https://www.bipm.org/en/publications/guides/) using a Monte Carlo method in Mathematica (for details see Supplement) (ISO/IEC, 2008).

Sulfate Correction for Effective E^*° Values

E^*° of an Ag|AgCl electrode that is immersed in artificial seawater containing sulfate can be expressed as (DelValls and Dickson, 1998):

$\begin{array}{cc}{E}^{\ast °}=E^{°}-\frac{2RT}{F}\ln {\gamma }_{\pm }\left(\text{HCl}\right)+\frac{RT}{F}\ln \left(1+\frac{b_{{\text{SO}}_{\text{4}}^{\text{2}-},\text{T}}}{K_{{\text{HSO}}_{\text{4}}^{-}}}\right)& (6)\end{array}$

where E° is the potential of the Harned cell under standard conditions, γ_±(HCl) is the trace activity coefficient of HCl in ASW, $b_{{\text{SO}}_4^{2-},\text{T}}$ is the total sulfate molality and $K_{{\text{HSO}}_4^{-}}$ is the limiting molality quotient for hydrogen sulfate in artificial seawater medium.

It is assumed that E^*°, determined at a particular salinity and temperature, remains unchanged if some of the artificial seawater salts are replaced with TRIS-HCl such that the ionic strength is unchanged. However, in this study the TRIS-HCl addition was compensated by a proportional reduction of all ASW salts to keep the ratios of cations constant. Consequently, the sulfate concentration was also reduced. The change in sulfate concentration requires a correction so that the effective E^*° corresponds to the respective ASW/TRIS-HCl solutions (E^*°(ASW/TRIS-HCl)) and not to the infinite dilution of HCl solutions to pure ASW condition (E*(ASW)). According to Equation (3) the required correction can be expressed as:

$\begin{array}{cc}\Delta {\text{pH}}_{\text{T}}=\frac{F}{RT\ln 10}\left(E^{\ast °}\left(\text{ASW}\right)-E^{\ast °}\left(\text{ASW/TRIS - HCl}\right)\right)& (7)\end{array}$

E^*°(ASW) and E^*°(ASW/TRIS-HCl) in Equation (7) can be expressed by applying Equation (6), where $b_{{\text{SO}}_4^{2-},\text{T}}$ is replaced by $b_{{\text{SO}}_4^{2-},\text{T}}(ASW)$ and $b_{{\text{SO}}_4^{2-},\text{T}}$(ASW/TRIS-HCl), respectively. The former describes the sulfate molality in pure ASW and the latter describes the sulfate molality in ASW containing TRIS-HCl. $K_{{\text{HSO}}_4^{-}}$ is assumed constant for a given temperature and salinity according to Dickson (1990). Thus,

$\begin{array}{l}\Delta {\text{pH}}_{\text{T}}={\text{log}}_{\text{10}}\left(1+\frac{b_{{\text{SO}}_4^{2-},\text{T}}(\text{ASW})}{K_{{\text{HSO}}_4^{-}}}\right)-{\text{log}}_{\text{10}}\left(1+\frac{b_{{\text{SO}}_{\text{4}}^{\text{2-}},\text{T}}(\text{ASW/TRIS-HCl})}{K_{{\text{HSO}}_4^{-}}}\right)\hfill \\ -{\text{log}}_{\text{10}}\left(1+\frac{b_{{\text{SO}}_4^{2-},\text{T}}(\text{ASW/TRIS-HCl})}{K_{{\text{HSO}}_4^{-}}}\right)\hfill & (8)\end{array}$

The values of ΔpH_T calculated for the solution compositions of this study are displayed in Figure 2 and referred to as sulfate corrections hereafter. This correction does not account for any changes in the activity coefficients implicit in Equation 6 (see section Discussion).

FIGURE 2

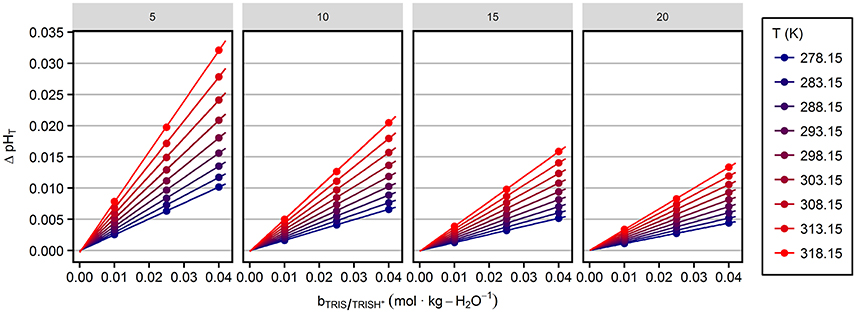
Figure 2. Correction of pH_T terms due to changes in the total sulfate concentration as a function of TRIS/TRIS·H⁺ molality. Panels represent the four investigated salinities indicated at the top. Lines indicate the linear behavior at various temperatures.

Fitting Combined pH_T Results for the Salinity Range 5–40

In order to derive a common expression of pH_T as a function of salinity, temperature and TRIS/TRIS·H⁺ molality over the largest range of conditions, the sulfate-corrected pH_T data from this study in the salinity range 5–20 were combined with previous pH_T data in the salinity range 20–40. The latter were calculated from potentials given in Table 2 of DelValls and Dickson (1998) and corresponding E^*° values from Dickson (1990) according to Equations (3) and (5). Only measurements in the temperature range investigated in this study (278.15–318.15 K) were included in the combined data set.

TABLE 2

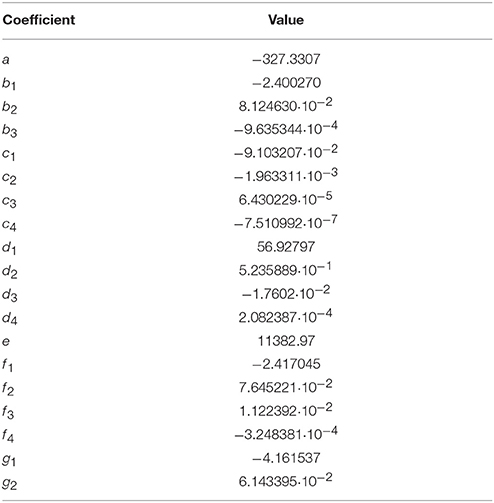
Table 2. Coefficients for the pH_T model (Equation 10). Test value: pH_T = 8.0703 at S = 20, T = 298.15 K, and $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}$ = mol·kg-H₂O⁻¹.

The following expression of pH_T as a function (f) of S, T and $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}$was specified as a full model and fitted to the combined data set:

$\begin{array}{l}{\text{pH}}_{\text{T}}=f\{\left[\left(1+S+S^2+S^3\right)·\left(1+T+\ln \text{}\left(T\right)+\frac{1}{T}\right)\right]\text{ }\\ \text{ }+\left[(b_{\text{TRIS/TRIS}·{\text{H}}^{+}}+b_{\text{TRIS/TRIS}·{\text{H}}^{+}}^2)·\left(1+S+T+S·T\right)\right]\}& (9)\end{array}$

The first part of this full model includes all combinations of the terms of a third order salinity polynomial with the terms of the physico-chemical expression of the temperature dependence of dissociation constants. This first part of Equation (9) deviates from the model fitted by DelValls and Dickson in their Equation (18) only by the higher order of the salinity polynomial. The second part of Equation (9) accounts for the dependence of pH_T on the TRIS/TRIS·H⁺ molality. The total number of terms of the full model given in Equation (9) is 24.

The fit of the full model was obtained by generalized linear modeling with the “stats” package of the statistical programming language “R” (R Core Team, 2014). The model was fitted to the mean pH_T values at each combination of target salinity, temperature, and TRIS/TRIS·H⁺ molality. Mean pH_T values were weighted by the respective standard measurement uncertainty (Table S6) as 1/u(pH_T)². The temperature dependency of measurement uncertainty found in this study at salinities 20 and 35 was fitted with a linear model and the same uncertainty was assigned to the data of DelValls and Dickson (1998). After fitting the full model (Equation 9), insignificant terms were removed by stepwise variable selection in both directions based on the Akaike information criterion. The removal of insignificant terms was performed with the “stepAIC” function from the R package “MASS,” and resulted in an expression with 19 terms given below in Equation (10).

Results

pH_T of TRIS Buffers

The pH_T values of the equimolal TRIS buffered ASW solutions at salinities 5, 10, 15, 20, and 35, temperatures from 278.15 to 318.15 K in intervals of 5 K, as well as equimolal TRIS/TRIS·H⁺ molalities 0.04, 0.025, and 0.01 mol·kg-H₂O⁻¹ are given in Table S6, the corresponding electric potentials of all solutions measured are given in Table S5.1 in the Supplemental Material.

Figure 3 shows mean pH_T values (triplicate measurements) of ASW/TRIS-HCl solutions as a function of temperature (278.15 – 318.15 K), for salinities 5, 10, 15, and 20 and at equimolal TRIS/TRIS·H⁺ molality 0.04 mol·kg-H₂O⁻¹. pH_T decreased almost linearly from around 8.7 to 7.5 with increasing temperature (around −0.03 K⁻¹). The investigation of the pH_T dependence on temperature at other TRIS/TRIS·H⁺ molalities showed no significant difference from the results shown in Figure 3.

FIGURE 3

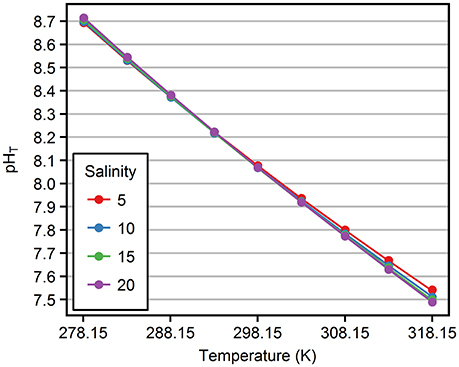
Figure 3. pH_T values as a function of temperature. Circles represent mean measured pH_T for $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}=0.04$ mol·kg-H₂O⁻¹ and salinities 5–20 (color). Lines indicate the fitted pH_T model at respective conditions. Measurement uncertainties are < 0.005 and cannot be visualized due to the scaling of the y-axis.

Figure 4 displays in more detail the dependence of pH_T on salinity and TRIS/TRIS·H⁺ molality, including previous results from DelValls and Dickson (1998). pH_T values shown in Figure 4 were corrected for minor difference (< 0.06 K) between the actual measurement temperature (Table S6) and the target temperature indicated at the top of the panels to achieve a consistent presentation with the model results. At low temperatures pH_T decreased with decreasing salinity. Toward higher temperatures, the lowest pH_T values were found at intermediate salinities.

FIGURE 4

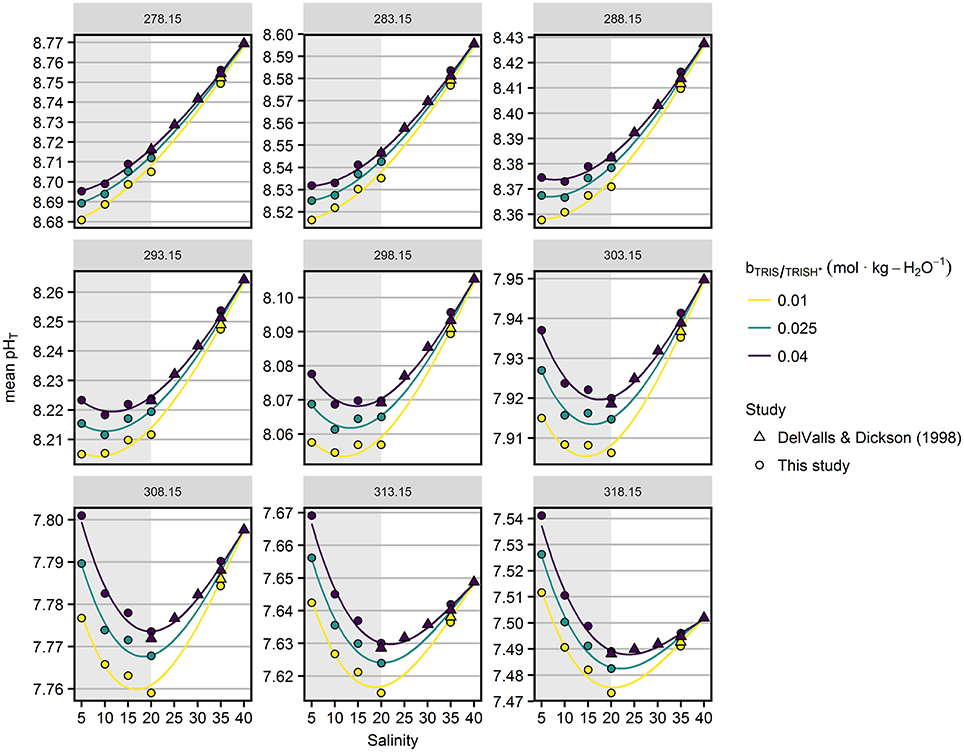
Figure 4. Mean pH_T values as a function of salinity (x-axis), temperatures (in K, indicated at the top of the panels) and TRIS/TRIS·H⁺ molalities (color). Circles represent results from this study highlighted by the gray area, triangles refer to DelValls and Dickson (1998). Lines represent the pH_T model (Equation 10) fitted to the combined data set.

The expanded measurement uncertainty (coverage factor k = 2) of pH_T was found to range between 0.002 and 0.004, with the highest uncertainties at salinity 5 and 15 (Figure S3). The uncertainty of pH_T significantly increased with temperature at salinity 5 (Figure S3), whereas the temperature dependence of the measurement uncertainty was much less pronounced at higher salinities.

It was found that the uncertainty of the pH_T values was dominated by the uncertainty contributions of the standard potential of the silver-silver chloride electrodes, E^*°, with relative contributions of 55–95% (Figure S4). The determination of E^*° was found to be sensitive to the extrapolation to zero HCl molality. The highest uncertainties of E^*° were found at salinities 5 and 15 (Figure S4) resulting in the highest pH_T uncertainties being found at these salinities (Figure S3).

The second most important uncertainty contribution was that of the cell potential measured in the buffer solutions, E_{ASW/TRIS−HCl}, ranging between 5 and 35% (Figure S4). The uncertainty of the measurement temperature T contributed 1–4% and the molalities of the NaCl, and MgCl₂ stock solutions contributed in sum 1–7% to the pH_T measurement uncertainty. All other contributions to the measurement uncertainty were < 1%.

pH_T Model

The pH_T model fitted to the combined data set including results from this study and DelValls and Dickson (1998) is expressed in Equation (10). The parameters T and $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}$ in Equation (10) were multiplied with 1/K and 1/mol·kg-H₂O⁻¹, respectively, to derive dimensionless quantities. The corresponding dimensionless coefficients are given in Table 2.

pH_T values predicted by this model are displayed along with mean pH_T values in Figures 3 and 4. Residuals of triplicate pH_T measurements from the model are shown in Figure 5, along with expanded measurement uncertainties (coverage factor k = 2). No uncertainties are available for the results of DelValls and Dickson (1998). Therefore, we interpolated our uncertainties determined at salinity 20 and 35 to provide a rough estimate of the consistency between measurement results and residuals in the salinity range 20–40. The dependency of the measurement uncertainty on $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}$ is negligible (Figure S3) and therefore not displayed in Figure 5. The residuals are within the range of the expanded measurement uncertainty, except for a few results at lowest TRIS/TRIS·H⁺ molality and salinities 15 and 20 (Figure 5).

$\begin{array}{l}{\text{pH}}_{\text{T}}=a+\left(b_1·S+b_2·S^2+b_3·S^3\right)\\ +\left(c_1·T+c_2·S·T+c_3·S^2·T+c_4·S^3·T\right)\\ +(d_1·\ln \left(T\right)+d_2·S·\ln \left(T\right)+d_3·S^2·\ln \left(T\right)\\ +d_4·S^3·\ln \left(T\right))+\left(e·\frac{1}{T}\right)\\ +(f_1·b_{TRIS/TRIS·H^{+}}+f_2·b_{TRIS/TRIS·H^{+}}·S\\ +f_3·b_{TRIS/TRIS·H^{+}}·T+f_4·b_{TRIS/TRIS·H^{+}}·S·T)\\ +\left(g_1·b_{TRIS/TRIS·H^{+}}^2+g_2·b_{TRIS/TRIS·H^{+}}^2·S\right)& (10)\end{array}$

Discussion

Measurement Uncertainty and pH_T Model

The deviations of measured pH_T values from the pH_T model (Equation 10, Table 2) agree well with the range of the expanded measurement uncertainty (Figure 5), i.e., they are not significantly higher or lower. This indicates that the model represents the experimental results well, and does not overfit the data.

FIGURE 5

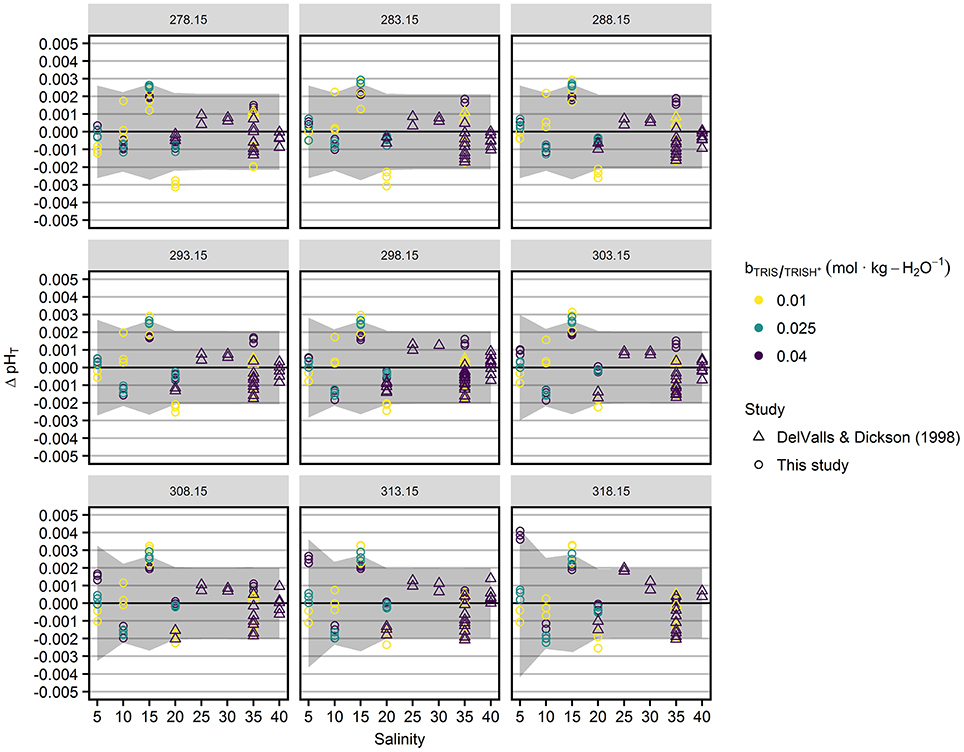
Figure 5. Residuals of pH_T values from the model (Equation 10, Table 2, Figure 4), ΔpH_T = pH_{T, measured} – pH_{T, model}, as a function of salinity (x-axis), temperatures (in K, indicated at the top of the panels), and TRIS/TRIS·H⁺ molalities (color). Circles represent results from this study, triangles refer to DelValls and Dickson (1998). The gray areas indicate the expanded (coverage factor k = 2) measurement uncertainty of pH_T.

The deviations from the model reveal a minor salinity-dependent pattern. In the salinity range 5–20, there is a tendency toward positive offsets at S = 15 and negative offsets at S = 20. As this tendency exists for the pH_T of all TRIS/TRIS·H⁺ molalities and replicates, the patterns must have a common cause, which is likely to be the determination of the standard potential of the silver-silver chloride electrodes, E^*°. The determination of E^*° represents the major contribution to the measurement uncertainty (55–95%, Figure S4) and was only performed once for each combination of temperature and salinity. The uncertainty in the E^*° determination is presumably related to the extrapolation to pure ASW conditions, which is especially sensitive to the E′ measurements (Equation 4) at lowest HCl molalities. The model deviations reveal slightly positive offsets at S = 25 and 30, which is very similar to the patterns displayed in Figure 2B of DelValls and Dickson (1998).

No pronounced temperature-dependence of the residuals exists, except at salinity 5 and $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}$ = 0.04 mol·kg-H₂O⁻¹, where a positive offset increases to a maximum of 0.004 at highest temperatures.

Comparison to Previous Studies

The highest deviation between pH_T values measured in this study and by DelValls and Dickson (1998) across all temperatures, at salinities 20 and 35, and $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}=$ 0.04 mol·kg-H₂O⁻¹ is 0.0025 at S = 35 and T = 288.15 K. The deviations are therefore within the extended measurement uncertainty of the method.

At salinities ≥ 20, excellent agreement was found between our pH_T model at $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}=$ 0.04 mol·kg-H₂O⁻¹ and the model defined in Equation (18) of DelValls and Dickson (1998). Differences are < 0.001 for the entire salinity range 20–40 and the temperature range 278.15–318.15 K (Figure S5). Within the range of the extended measurement uncertainty both models do not differ. The residuals from the model fitted in this study are larger than those presented in Figure 2 of DelValls and Dickson (1998), presumably a result of the larger range of salinities and the included dependency of pH_T on TRIS/TRIS·H+ molality in our model.

Our pH_T model at $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}=$ 0.04 mol·kg-H₂O⁻¹ and 298.15 K and the model by Mosley et al. (2004) agree within 0.002 in the salinity range 20–40 (Figure S5), which is not surprising, because both models are based on the same results of DelValls and Dickson (1998). However, in the salinity range 5–20, where Mosley et al. (2004) interpolated the pH_T of TRIS buffer solutions between the results of DelValls and Dickson (1998) for S>20 and the results of Bates and Hetzer (1961) in pure water, deviations increase up to 0.009 (Figure S5) and highlight the shortcomings of the interim solution.

Correction of E^*° for Changes in Sulfate Concentration and Activity Coefficients

Changes in the sulfate concentration between pure ASW and ASW/TRIS-HCl solutions were corrected in this study according to Equation (8) (Figure 2). However, determined E^*° values do not exactly correspond to the values required for pH_T calculation in Equation (3), because changes in activity coefficients between pure ASW and ASW/TRIS-HCl solutions remain unaccounted for, namely:

(1) Changes in the value of $K_{{\text{HSO}}_4^{-}}$ arising from changes in the activity coefficients of H⁺, ${\text{SO}}_4^{2-}$ and ${\text{HSO}}_4^{-}$

(2) Changes in the activity coefficients of H⁺ and Cl⁻

This limitation was previously discussed (e.g., Nemzer and Dickson, 2005; Dickson et al., 2015) and applies to all currently available experimental pH_T measurements of TRIS buffered ASW solutions. The activity changes can only be corrected with estimates from a speciation model. Gallego-Urrea and Turner (2017) have recently developed optimized Pitzer coefficients for TRIS in artificial seawater at 298.15 K, using the artificial seawater model of Waters and Millero (2013). According to Gallego-Urrea and Turner (2017), pH_T correction terms, addressing the above mentioned effects (1) and (2), were calculated for the results of this study at 298.15 K. Those ΔpH_T values from the speciation model differed from the applied sulfate corrections shown in Figure 2 by < 0.002, indicating that changes in sulfate concentration dominate over the effect of changes in the activity coefficient.

However, the Pitzer coefficients for TRIS buffered ASW solutions are restricted to 298.15 K (Gallego-Urrea and Turner, 2017) due to scarcity of experimental data for other temperatures and can therefore not be applied consistently to the full temperature range covered in this study. The development of accurate Pitzer models for TRIS in artificial seawater over an extended temperature range is a main focus of the SCOR Working Group 145 “Modelling Chemical Speciation in Seawater to Meet Twenty first Century Needs” (http://marchemspec.org/).

It should be noted that the neglected effect of changes in activity coefficients does not impact the calibration of pH instruments, if those are performed at variable TRIS/TRIS·H⁺ molality and extrapolated to zero TRIS (see section: Calibration of pH instruments).

Conversion Between pH_b and pH_T

The conversion of pH from the molality to the amount content scale (from pH_b to pH_T) was calculated as the negative decadic logarithm of

$\begin{array}{cc}{\omega }_{{\text{H}}_2\text{O}}=1-0.00106·S& (11)\end{array}$

according to DelValls and Dickson (1998). ω_H2O represents the mass of water per mass solution and the given relationship between ω_H2O and salinity refers to the composition of pure ASW. As pointed out by Pratt (2014), ω_H2O in pure ASW is not exactly identical to ω_H2O of the corresponding ASW/TRIS-HCl solution, due to the difference of the total mass of solution per amount of water after replacing some of the ASW salts with TRIS/HCl. As a result, for solutions with a TRIS molality of 0.04 mol·kg-H₂O⁻¹, the pH conversion based on the actually weighed buffer composition gives 0.003 and 0.004 higher pH_T values at salinity 35 and 5, respectively, compared to those using Equation (4). Obviously, the conversion error decreases toward lower TRIS molality. To be consistent with the pH_T results measured previously and to perform the pH_T-fit on a consistent database we have also used Equation (4) for the correction, even though we deem the conversion based on the actually weighed buffer composition more appropriate.

It should be noted that preliminary results obtained with the speciation model by Gallego-Urrea and Turner (2017) indicate that the correction of changes in activity coefficients between pure ASW and ASW/TRIS-HCl solutions, which has been neglected in this study due to the restriction of model results to 298.15 K, is around −0.005 at S = 35 and $b_{{\text{TRIS}/\text{TRIS}·H}^{+}}$ = 0.04 mol·kg-H₂O⁻¹. This is in a similar order of magnitude, but with opposite sign compared to the effect of pH scale conversion according to Equation (11). Therefore, if adequate activity coefficients were available, superposition of the pH scale conversion using the actual buffer composition and the correction of changes in activity coefficients would be expected to provide pH_T values that are within the range of uncertainties of the pH_T value we have presented here.

In any case, the choice of the scale conversion does not impact the calibration of pH instruments, if they are performed at variable TRIS/TRIS·H⁺ molality and extrapolated to zero TRIS (see chapter: Calibration of pH instruments).

Calibration of pH Instruments

We recommend the use of TRIS buffered ASW solutions as prepared in this study as pH_T-standards for future calibration of pH instruments in the salinity range 5–20, with assigned pH_T values according to Equation (10) and Table 2. Moreover, this approach also allows for a consistent assignment of pH_T values without discontinuity or significant differences to previous results in the salinity range 20–40 when buffer solutions are prepared according to DelValls and Dickson (1998).

As discussed in the previous two chapters, the composition of TRIS buffer solutions differs from that of pure ASW. The contribution of TRIS-HCl to the total ionic strength increases toward lower salinities and:

(1) affects the pH_T values of the buffer solutions (Figure 4),

(2) requires corrections of the E^*° differences between pure ASW and ASW/TRIS-HCl,

(3) affects ω_H2O and therefore the scale conversion between pH_b and pH_T, and

(4) impacts the calibration quantity of any pH instrument, such as the determination of dissociation constants of pH indicator dyes.

Uncertainties in (2) and (3) result in uncertainties of the assigned pH_T values of the buffer solutions. However, it must be emphasized that effects (1)–(4) do not affect the calibration of pH instruments, if they include the extrapolation of calibrated parameters, e.g., the dissociation constant of mCP (Müller and Rehder, 2018), to pure ASW conditions. The extrapolated quantity refers to an exact definition of the total hydrogen ion concentration scale without constraints (Nemzer and Dickson, 2005; Dickson et al., 2015). Therefore, we recommend calibration of pH instruments in the salinity range 5–20 at the three TRIS/TRIS·H⁺ molalities reported in this study and extrapolation of the results to zero TRIS/TRIS·H⁺ molality. However, the dependence of pH_T on TRIS/TRIS·H⁺ in Equation (10) is strictly valid only for salinities 5–20 and 35, due to the lack of experimental data at other salinities. It must also be noted that no uncertainties have been calculated for the coefficients listed in Table 2, since no uncertainties have been available for the results of DelValls and Dickson (1998). We recommend assigning uncertainties to pH_T values corresponding to those given Table S6 if Equation (10) is used to calculate pH_T values.

Recommendations for the Preparation of TRIS Buffer Solutions

To replicate the TRIS buffer solutions characterized in this study, we recommend production of stock solutions for the salt components of the ASW matrix. The impact of salt impurities on buffer pH_T has not yet been systematically studied. Therefore, we recommend using salts of the highest purity grade, although the contribution of ASW composition to the measurement uncertainty budget is assumed to be small. The stock solution of HCl should be titrated against the TRIS stock solution with potentiometric or colorimetric (e.g., methyl red) endpoint detection. This ensures an exact equimolal TRIS:TRIS·H⁺ ratio, which is essential for reproducing the correct pH_T value. Finally, all TRIS containing solutions should be handled so as to avoid uptake of atmospheric CO₂. Ideally, the headspace of the containers should be flushed with humidified argon.

Solution Composition Concept and Relevance to Natural Waters

Alternative strategies for the solution composition applied in this study would result in pronounced changes in cation ratios at low salinity (Figure 1). Based on current knowledge it is impossible to quantify the effect of such changes of cation ratios on TRIS buffer pH_T, because information is lacking on the sensitivity of the TRIS·H⁺ dissociation constant on the ionic composition of the matrix. As a future experimental approach to this open question it would be informative to perform electrochemical pH_T measurement of TRIS buffered solutions in variable ASW matrices.

Characterized buffer solutions in various ASW matrices would enable studies of the impact of solution composition on the measurement signals of other pH instruments, including the dissociation behavior of mCP. Such experiments could shed light on the ultimate question of how representative pH_T measurements are for various natural brackish and freshwaters that differ in ionic composition (Feistel et al., 2010). Currently, it remains impossible to estimate the uncertainty of pH measurements arising from differences in the ionic composition of natural brackish water samples and the simplified composition of buffer solutions prepared in ASW matrix based on experimental data. A more detailed discussion of this issue is given in “Metrology for pH Measurements in Brackish Waters—Part 2: Experimental Characterization of Purified meta-Cresol Purple for Spectrophotometric pH_T Measurements” by Müller and Rehder (2018).

Conclusion

This study extends the characterization of TRIS buffer solutions by Harned cell measurements to brackish waters and provides a consistent pH_T model for the salinity range 5–40. It is emphasized that minor assumptions and uncertainties remain in the pH_T assignment and restrict the accuracy of all currently available TRIS buffer characterizations. However, these limitations do not affect the calibration of other pH instruments, if calibration results are extrapolated to zero buffer molality, which is especially important at low salinities. This study provides the required characterization of buffer solutions with variable TRIS molality in the salinity range 5–20. Measurements with pH instruments that have been calibrated against the buffer concentration represent currently the only access to the total hydrogen ion concentration without constraints.

Data Availability Statement

All datasets [GENERATED/ANALYZED] for this study are included in the manuscript and the supplementary files.

Author Contributions

JM: contributed to the research idea and plan, participated in the characterization of chemicals used, analyzed and interpreted the results and is first main author (shared authorship with FB) of the manuscript; FB: contributed to the research plan, analyzed and interpreted the measurement results and is the second main author (shared authorship with JM) of the manuscript; BS: contributed to the research plan, performed the measurements and revised the manuscript; SS: contributed to the research plan, analyzed and interpreted the measurement results and revised the manuscript; DT: contributed in performing the research activities, in the interpretation of the results and revision of the manuscript; AD: contributed to the research plan, interpreted the results and revised the manuscript; GR: contributed to the research plan and revised the manuscript.

Funding

AD was supported by the US National Science Foundation, Grant No. OCE-1657799. Physikalisch-Technische Bundesanstalt (PTB). The research leading to this manuscript has received funding from BONUS, the joint Baltic Sea research and development program (Art 185), funded jointly from the European Union's Seventh Program for research, technological development and demonstration and from the German Federal Ministry of Education and Research through Grant No. 03F0689A (BONUS PINBAL).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the Swiss Federal Institute of Metrology (METAS) for providing characterized salts. The quality of this paper gained from scientific discussions with Bernd Schneider, Robert H. Byrne, Kenneth W. Pratt, Regina Easley, and Michael DeGrandpre. We thank Franko Schmähling for valuable recommendations concerning appropriate fitting procedures.

Supplementary Material

The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fmars.2018.00176/full#supplementary-material

References

Bates, R. G., and Hetzer, H. B. (1961). Dissociation constant of the protonated acid form of 2-amino-(hydroxymethyl)-1,3-propanediol [trishydroxymethyl)-aminomethane] and related thermodynamic quantities from 0 to 50°. J. Phys. Chem. 65, 667–671. doi: 10.1021/j100822a017

CrossRef Full Text | Google Scholar

Buck, R. P., Rondinini, S., Covington, A. K., Baucke, F. G. K., Brett, C. M. A., Camoes, M. F., et al. (2002). Measurement of pH. Definition, standards, and procedures (IUPAC recommendations 2002). Pure Appl. Chem. 74, 2169–2200. doi: 10.1351/pac200274112169

CrossRef Full Text | Google Scholar

Byrne, R. H., Mecking, S., Feely, R. A., and Liu, X. (2010). Direct observations of basin-wide acidification of the North Pacific Ocean. Geophys. Res. Lett. 37:L0260. doi: 10.1029/2009GL040999

CrossRef Full Text | Google Scholar

Clayton, T. D., and Byrne, R. H. (1993). Spectrophotometric seawater pH measurements — total hydrogen-ion concentration scale calibration of m-cresol purple and at-sea results. Deep Sea Res. Part I Oceanogr. Res. Pap. 40, 2115–2129. doi: 10.1016/0967-0637(93)90048-8

CrossRef Full Text | Google Scholar

DelValls, T. A., and Dickson, A. G. (1998). The pH of buffers based on 2-amino-2-hydroxymethyl-1,3-propanediol (‘tris') in synthetic sea water. Deep Sea Res. Part I Oceanogr. Res. Pap. 45, 1541–1554. doi: 10.1016/S0967-0637(98)00019-3

CrossRef Full Text | Google Scholar

Dickson, A. G. (1990). Standard potential of the reaction: AgCl(s) + ½H₂(g) = Ag(s) + HCl(aq), and the standard acidity constant of the ion ${\text{HSO}}_4^{-}$ in synthetic sea water from 273.15 to 318.15 K. J. Chem. Thermodynamics 22, 113–127. doi: 10.1016/0021-961490074-Z

CrossRef Full Text | Google Scholar

Dickson, A. G., Camões, M. F., Spitzer, P., Fisicaro, P., Stoica, D., Pawlowicz, R., et al. (2015). Metrological challenges for measurements of key climatological observables. Part 3: seawater pH. Metrologica 53, R26–R39. doi: 10.1088/0026-1394/53/1/R26

CrossRef Full Text | Google Scholar

Doney, S. C., Fabry, V. J., Feely, R. A., and Kleypas, J. A. (2009). Ocean acidification: the other CO₂ problem. Ann. Rev. Mar. Sci. 1, 169–192. doi: 10.1146/annurev.marine.010908.163834

PubMed Abstract | CrossRef Full Text | Google Scholar

Feistel, R., Weinreben, S., Wolf, H., Seitz, S., Spitzer, P., Adel, B., et al. (2010). Density and absolute salinity of the Baltic Sea 2006–2009. Ocean Sci. 6, 3–24. doi: 10.5194/os-6-3-2010

CrossRef Full Text | Google Scholar

Gallego-Urrea, J. A., and Turner, D. R. (2017). Determination of pH in estuarine and brackish waters: Pitzer parameters for Tris buffers and dissociation constants for m-cresol purple at 298.15 K. Mar. Chem. 195, 84–89. doi: 10.1016/j.marchem.2017.07.004

CrossRef Full Text | Google Scholar

Hills, G. J., and Ives, D. J. G. (1951). 69. The hydrogen-calomel cell. Part I. The hydrogen electrode. J. Chem. Soc. 318, 305–310. doi: 10.1039/JR9510000305

CrossRef Full Text | Google Scholar

Hofmann, G. E., Smith, J. E., Johnson, K. S., Send, U., Levin, L. A., Micheli, F., et al. (2011). High-frequency dynamics of ocean pH: a multi-ecosystem comparison. PLoS ONE 6:e28983. doi: 10.1371/journal.pone.0028983

PubMed Abstract | CrossRef Full Text | Google Scholar

Harned, H. S., and Owen, B. B. (1958). The Physical Chemistry of Electrolytic Solutions, Chap. 14. New York, NY: Reinhold.

Google Scholar

ISO/IEC (2008). Guide to the expression of uncertainty in measurement (2008), Guide 98-3, Geneva, Switzerland

Kulinski, K., Schneider, B., Hammer, K., Machulik, U., and Schulz-Bull, D. (2014). The influence of dissolved organic matter on the acid–base system of the Baltic Sea. J. Mar. Syst.. 132, 106–115. doi: 10.1016/j.jmarsys.2014.01.011

CrossRef Full Text | Google Scholar

Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Peters, G. P., et al. (2016). Global carbon budget 2016. Earth Syst. Sci. Data 8, 605–649. doi: 10.5194/essd-8-605-2016

CrossRef Full Text | Google Scholar

Liu, X., Patsavas, M. C., and Byrne, R. H. (2011). Purification and characterization of meta-cresol purple for spectrophotometric seawater pH measurements. Environ. Sci. Technol.. 45, 4862–4868. doi: 10.1021/es200665d

PubMed Abstract | CrossRef Full Text | Google Scholar

Loucaides, S., Rèrolle, V. M. C., Papadimitriou, S., Kennedy, H., Mowlem, M. C., Dickson, A. G., et al. (2017). Characterization of meta-Cresol Purple for spectrophotometric pH measurements in saline and hypersaline media at sub-zero temperatures. Sci. Rep. 7, 1–11. doi: 10.1038/s41598-017-02624-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Martz, T. R., Connery, J. G., and Johnson, K. S. (2010). Testing the Honeywell Durafet for seawater pH applications. Limnol. Oceanogr. Methods 8, 172–184. doi: 10.4319/lom.2010.8.172

CrossRef Full Text | Google Scholar

Meija, J., Coplen, T. B., Berglund, M., Brand, W. A., De Bièvre, P., Gröning, M., et al. (2016). Atomic weights of the elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 88, 265–291. doi: 10.1515/pac-2015-0305

CrossRef Full Text | Google Scholar

Mosley, L. M., Husheer, S. L. G., and Hunter, K. A. (2004). Spectrophotometric pH measurement in estuaries using thymol blue and m-cresol purple. Mar. Chem. 91, 175–186. doi: 10.1016/j.marchem.2004.06.008

CrossRef Full Text | Google Scholar

Müller, J. D., and Rehder, G (2018) Metrology for pH measurements in brackish waters - part 2: experimental characterization of purified m-Cresol Purple for spectrophotometric pHT measurements. Front. Mar. Sci. 5:177. doi: 10.3389/fmars.2018.00177

CrossRef Full Text | Google Scholar

Müller, J. D., Schneider, B., Aßmann, S., and Rehder, G. (2018). Spectrophotometric pH measurements in the presence of dissolved organic matter and hydrogen sulfide. Limnol. Oceanogr. Methods 16, 68–82. doi: 10.1002/lom3.10227

CrossRef Full Text | Google Scholar

Müller, J. D., Schneider, B., and Rehder, G. (2016). Long-term alkalinity trends in the Baltic Sea and their implications for CO₂-induced acidification. Limnol. Oceanogr. 61, 1984–2002. doi: 10.1002/lno.10349

CrossRef Full Text | Google Scholar

Nemzer, B. V., and Dickson, A. G. (2005). The stability and reproducibility of Tris buffers in synthetic seawater. Mar. Chem. 96, 237–242. doi: 10.1016/j.marchem.2005.01.004

CrossRef Full Text | Google Scholar

Papadimitriou, S., Loucaides, S., Rérolle, V., Achterberg, E. P., Dickson, A. G., Mowlem, M., et al. (2016). The measurement of pH in saline and hypersaline media at sub-zero temperatures: characterization of Tris buffers. Mar. Chem. 184, 11–20. doi: 10.1016/j.marchem.2016.06.002

CrossRef Full Text | Google Scholar

Pratt, K. (2014). Measurement of pH_T values of Tris buffers in artificial seawater at varying mole ratios of Tris:Tris·HCl. Mar. Chem. 162, 89–95. doi: 10.1016/j.marchem.2014.03.003

CrossRef Full Text | Google Scholar

R Core Team (2014). R: A Language and Environment for Statistical Computing. Available online at: http://www.r-project.org/

Waters, J. F., and Millero, F. J. (2013). The free proton concentration scale for seawater pH. Mar. Chem. 149, 8–22. doi: 10.1016/j.marchem.2012.11.003

CrossRef Full Text | Google Scholar