Navigating benefit transfer for salmon improvements in the Western US

Introduction

In the Western US, migratory salmon are iconic symbols of nature's strength and bounty. However, wild salmon stocks have precipitously declined in the last century (Nehlsen et al., 1991). Some populations may be on the brink of extinction, already the fate of hundreds of West Coast evolutionarily significant units (Gustafson et al., 2007). Numerous anthropogenic stressors have played a role, such as dams, overfishing, hatchery practices, and multiple forms of habitat degradation (Stouder et al., 1997; Lackey et al., 2006). More recently, negative impacts from climate change have also been recognized (Doney et al., 2012).

As salmon losses continue, policymakers are increasingly called upon to consider ways of mitigating impacts and/or promoting salmon recovery. Indeed, numerous state and federal policies are oriented toward this goal, such as Total Maximum Daily Loads for pollutants such as temperature, and critical habitat designations under the Endangered Species Act. However, regulations do not guarantee a given salmon stock will persist, nor is simple survival necessarily the sole objective. Often the debate over different options involves economic questions—i.e., benefits and costs. For example, an entity responsible for dam operations may be making tradeoffs between flood control, hydropower generation, water availability for agriculture, reservoir recreation, and migratory fish. Similarly, planning agencies confront tradeoffs between development proposals and environmental mitigation strategies of various costs. While not every decision context requires monetized environmental impacts, it does allow resource management options to be compared in a common unit. This can be helpful at multiple levels of governance, with established use of such information at the US federal level (Weber, 2010; Lipton et al., 2014). The direct interpretability of benefit and cost information also facilitates public discussion on issues such as salmon recovery, rather than simply “leaving it to the experts,” or special-interest lobbyists. Typically, costs of environmental protection are better characterized than benefits. If benefits are not represented, there is cause for concern that protection efforts will be sub-optimal.

How can the benefits of salmon be estimated? This difficult problem is the focus of the paper. First, the case study literature on the “total economic value” of changes in abundance of Western US salmon will be synthesized, including particularities of each study. Second, challenges in utilizing these data (in conjunction with other available literature) will be illustrated in the course of conducting “benefit transfer” for a new Western US example context. Several benefit transfer methods are applied, insights and pitfalls that arise are documented, and the range of results is discussed. While the paper revolves around a single policy case, the discussion is designed to make benefit transfer techniques more accessible for those seeking to apply or develop the tools more generally. Finally, based on lessons learned, suggestions are made for future salmon valuation studies, both for more robust case studies and improved benefit transfer capacity from them.

Valuing societal impacts from changes in salmon proceeds from recognizing various pathways of human benefit. Some benefits are relatively obvious, such as resource use and extraction in the market economy, e.g., commercial fish harvest, and revenue from fishing-related expenditures. A less recognized but important dimension are nonmarket benefits, such as the recreational enjoyment of a fishing experience. An angler may contribute only minimally to a local economy through the act of fishing—yet the opportunity to engage in this pastime may be of extraordinarily high value to that individual. By studying recreation behavior analysts can construct a demand curve for recreational fishing for a given site or a site network, and estimate the monetary value per day of the enjoyment associated with an angler-day, as well as monetary impacts from site closures or fish abundance changes. Such nonmarket environmental amenities are an important dimension of natural resources management, and have been referred to as a “second-paycheck.” For example, a person may be willing to accept less income in order to live near particular environmental amenities (Power and Barrett, 2001).

Yet human appreciation of natural resources such as salmon goes deeper still. For decades environmental economists have recognized an important category of benefits known as non-use values (e.g., Krutilla, 1967; Johnston et al., 2003). Essentially, resources may be valued without the necessity of direct experience. Notions of value predicated on resource extraction, harvest, and even nonconsumptive recreational use are overly limiting. Categorically neglecting non-use values can lead to significant underestimates of public welfare (Freeman, 2003: p. 138). The evidence for non-use values comes from survey research, in which respondents have consistently demonstrated a “willingness-to-pay” (WTP) to protect or increase environmental amenities even when there are essentially no resource use opportunities. Non-use values have enormous potential importance for managing environmental resources for the best benefit of society. The total economic value (TEV) conceptual framework helps maintain attention on the diverse components of value potentially associated with changes in a natural resource: market as well as nonmarket values are included, with nonmarket values including both use and non-use (US National Research Council of the National Academy of Sciences, 2004).

The survey-based methods that allow insight into both the use and non-use components of TEV are known as contingent valuation and choice experiments (Mitchell and Carson, 1989; Louviere et al., 2000). Numerous such “stated preference” valuation survey studies exist (e.g., tallied by Carson, 2000). However, only a few feature Western US salmon, despite their high-profile role in historical and contemporary culture. To address this problem, methodologies of benefit transfer can be employed to apply valuation results from prior relevant studies to a new context. Benefit transfer has received substantial academic attention. Notable milestones are edited compendiums: Brookshire and Neill (1992); Florax et al. (2002); Wilson and Hoehn (2006); and Navrud and Ready (2007). For a summary of the recent literature, see Johnston and Rosenberger (2010). Compared with an original study, benefit transfer is usually viewed as second best or even a last resort. This is tempered by acknowledgment that environmental decisions need guidance more often than valuation studies can be marshaled. Furthermore, methodological idiosyncrasies and biases associated with any single study are dampened when placed in context of additional observations. Benefit transfer will continue; more awareness of the techniques including their weaknesses will aid both analysts and those interpreting the resulting monetized estimates.

Methods

While there is no single way to conduct benefit transfer, counsel is found in multiple sources, e.g., Brouwer and Spaninks (1999), Nelson and Kennedy (2009), Johnston and Rosenberger (2010), and US Environmental Protection Agency (2010). A general three-step outline for benefit transfer follows: describe the policy case; select study cases; and transfer values (US Environmental Protection Agency, 2010). To satisfy the first step, in the next section we describe an illustrative policy case of the Willamette Valley, Oregon, although certainly many more policy cases are possible. Regarding step two, we review the context and background for various available study cases to gauge similarities with the policy case, and to address any potential study quality or bias issues. For step three, several benefit transfer methods will be explored in turn:

• Transfer a point value from a single study,

• Transfer with the aid of a study's valuation function,

• Apply an existing meta-regression,

• New meta-regression, and

• New structural benefit transfer.

An Illustrative Policy Case

To illustrate benefit transfer methods, as well as provide management insight in a specific case, this paper will estimate the TEV of an increase in Spring Chinook for the Willamette Valley, Oregon. The valley is an 11,704 sqmi watershed in northwest Oregon, draining a north-trending valley between the Coast Range to the west, and the Cascades to the east. The basin has a rapidly growing population, currently home for nearly three million people. This encompasses most of Oregon's population, despite the valley representing only about 10% of the state's total area. Significant tourism occurs in the region, attracted by recreational, scenic, and cultural amenities. Urban and exurban areas in the river valley share space with agricultural lands, timberland, and natural areas. With the watershed size, human population, and diverse land use, environmental policymaking processes are complex, similar to multi-use contexts found in many other watersheds.

The wild salmon run of the entire Columbia River of the late 1990s was estimated to be less than 2% of runs in the late 1800s (Gresh et al., 2000), allowing some inference as to the decline for the Willamette as a Columbia subwatershed. Sheer and Steel (2006) estimate over 40% of salmon habitat in the Willamette and lower Columbia watersheds has been lost due to dams alone, the majority of which was higher-quality upland habitat. Spring Chinook comprise by far the largest salmon run in the Willamette, although there are Coho and Winter Steelhead runs as well. All three are threatened under the US Endangered Species Act [US National Oceanic and Atmospheric Administration (NOAA), 2010]. Recovery plans are in process by the Oregon Department of Fish and Wildlife (ODFW) for Spring Chinook and Winter Steelhead, and critical habitat for Coho has been proposed by NOAA as of 2013. These listings do not guarantee recovery, and proposed goals go beyond simply preventing extinction. For example, ODFW describe both minimum viability and “broad sense” recovery options with different associated salmon abundance levels (ODFW, 2011).

Spring Chinook are the state fish of Oregon and salmon are a conspicuous symbol in the US Pacific Northwest in general. Given their cultural importance, a significant TEV for increasing salmon abundance in the Willamette seems likely¹. As of this writing, no empirical studies are known estimating the TEV of changes in abundance specifically for Willamette salmon. However, Olsen et al. (1990) and Layton et al. (1999) implicitly include the Willamette watershed as a portion of the change they consider for the entire Columbia River watershed. In addition, Wallmo and Lew (2012) query a national sample to estimate the value of a change in status for Willamette Spring Chinook from threatened to recovered (not explicitly tied to a change in abundance) as one of eight listed marine species included their study.

To constrain the benefit transfer, a specific salmon population change for the Willamette must be cited. At Willamette Falls on the Willamette River, the ODFW has counted returning Spring Chinook since 1946: the most recent ten-year average (up through 2014) is 35,115 fish. Not all spawning habitat is upstream of the Falls, and there is significant attrition before they reach that point, e.g., anglers in the popular Lower Willamette fishery. ODFW also reports an estimated entire Willamette Run, which was 64% higher than counts at the Falls in 2014. Thus, for the purposes of this paper, the status quo Willamette Spring Chinook run is estimated to be 164% of the 10-year average, rounded to the nearest 100 fish, or 57,600 fish. The majority of returns are hatchery fish. The specific commodity valued in this paper is a doubling in the average annual Willamette Spring Chinook run, from the estimated status quo average of 57,600 fish per year, to 115,200 fish per year. Note that this is not the only possible fish-related commodity. Also note that the change does not specify whether increases pertain to hatchery or wild fish. This decision was forced mainly by most available studies neglecting to specify for survey respondents whether hatchery or wild fish were impacted. It seems likely that preserving wild fish in particular would matter mainly for the non-use component of TEV, but perhaps also for angling use value.

The market extent—which households will be considered in the analysis—must also be specified. This judgment determines how values will be aggregated, and the outcome can be especially sensitive when non-use values are involved. Defining market extent also aids selection of study cases (and their market extents) most relevant for the policy case. Salmon recovery within a relatively small watershed has been found to be valuable to households across the nation (Loomis, 1996). Thus Pate and Loomis (1997) caution against artificially limiting market extent specifically for changes in salmon, due to the underestimates of public welfare that could result. However this paper takes a relatively conservative stance, defining the market extent as just the households within the Willamette watershed. While values for increases in Willamette salmon abundance may well extend more broadly, the author believes it preferable to err on the conservative side when relying on secondary estimates. Furthermore, substitute salmon resources do not appear to have been well characterized within available studies. This leads to somewhat more caution than usual when applying such values at market extents beyond which households could be reasonably expected to have familiarity with the range of substitute salmon resources available in the Western US. However, the value estimates derived in this paper will be on a per household basis to facilitate comparison with other valuation work, and will not actually be presented in aggregate form.

To provide an example of how monetizing the societal benefits of salmon could assist regional decision-making, consider the long-running debate in Oregon over the appropriate distance buffer for logging on private timberlands near streams. The issue was recently reignited with a study finding that the current buffer set by the Oregon Board of Forestry does not do enough for small and middle-sized streams to maintain shading and temperature requirements set by the Oregon Environmental Quality Commission (Barnard, 2015a,b). Costs to private timberland owners of larger buffers are relatively easy to estimate, and are readily available. Missing from the debate is an estimate of the TEV of increased salmon associated with cooler streamwater (although this value would certainly not be the only consideration).

The above forest practices example raises the interconnectedness of estimating TEV with biophysical predictions of salmon populations. Such predictions are extraordinarily challenging—models quantifying salmon response to changing conditions and restoration strategies contain significant uncertainty (e.g., ODFW, 2011). Interconnected freshwater factors must be further combined with ocean conditions, one of which is the Pacific Decadal Oscillation (Mantua et al., 1997). Limiting factors for salmonids in the freshwater environment that have been identified by regional research, in addition to elevated water temperature (see also McCullough et al., 2009), are lack of large wood in the channel (Oregon Department of Environmental Quality, 2009), and increased silt (Honea et al., 2009).

Data

In assembling case study data, criteria were that the study must supply at least one estimate in WTP format to preserve, increase, or avoid the loss of a given number of Western US salmon; sample the general population in one or more regions of the US; and be intended to capture TEV. A broad internet-based search was conducted including the “Environmental Valuation Resource Inventory” of Environment Canada, and inquiries were made with other valuation researchers. Ultimately, only six relatively well-known studies were located: Jones and Stokes Associates (1990); Olsen et al. (1990); Loomis (1996); Layton et al. (1999); Bell et al. (2003); and Mansfield et al. (2012). A summary of these studies is given in the Appendix.

Qualitative and quantitative metadata from the six studies and corresponding 29 observations are summarized in Table 1. Publication dates range from 1990 to 2012. Since the studies occur in different years, have varying payment plans, and reference different salmon changes, TEV results are not directly comparable. Raw values were adjusted to 2015 dollars using an inflation calculator based on the national Consumer Price Index (CPI) (US Bureau of Labor Statistics, 2015). To account for different payment plans ranging from 10 years to perpetuity, net present value (NPV) was calculated with a 7% yearly discount rate, a common base-case rate (US Office of Management and Budget, 2003). However, the reader should be aware that the discount rate is a sensitive and controversial variable (Weitzman, 1998). Furthermore, it is not clear how survey respondents themselves discount a stream of payments into the future when responding to a WTP questionnaire. Since each observation values a different change in fish population from a different baseline scarcity, Table 1 provides additional context for value interpretation. Figure 1 plots the NPV of salmon abundance against the scope of the salmon population increase. Both axes are on a logarithmic scale to make it easier to differentiate clustered observations. Data labels in Figure 1 match the observation numbers in Table 1. Note that observation 28 is dropped from the figure (and from later analyses) since it is negative, an anomaly in the dataset.

TABLE 1

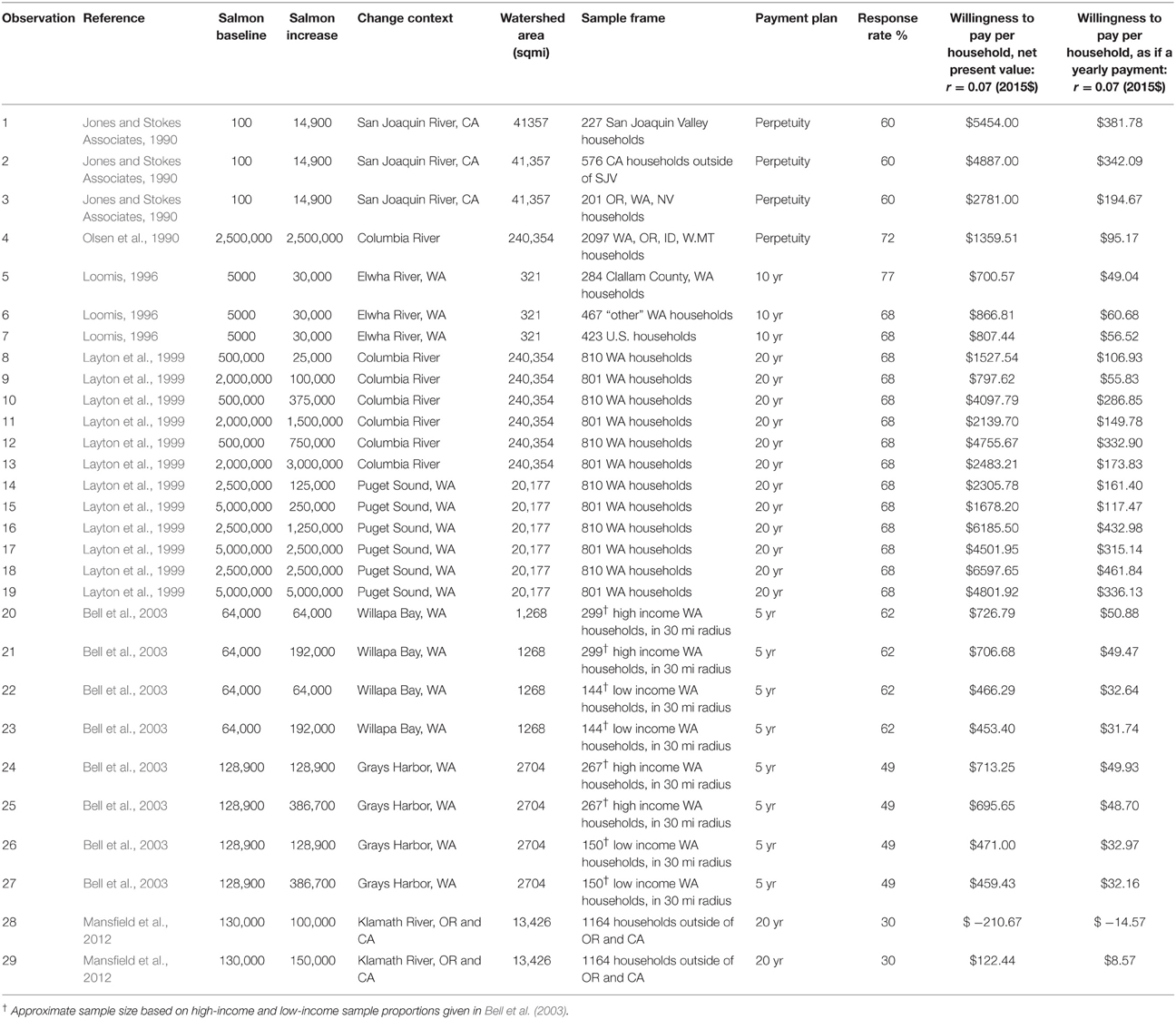
Table 1. Studies estimating the total economic value of migratory pacific salmon abundance changes in the US.

FIGURE 1

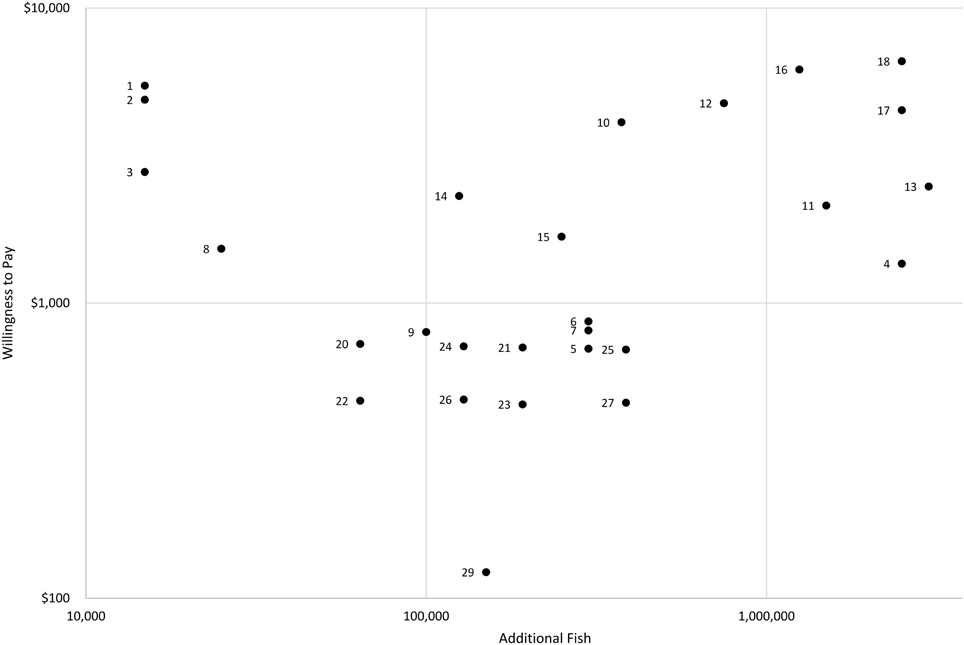
Figure 1. Total economic value of Western US salmon increases vs. size of salmon increase (Net Present Value per household 2015$, r = 7%).

Although all the studies in Table 1 meet selection criteria, they have numerous differences, such as examining different salmon populations (although they occasionally overlap), and surveying different market extents. The early studies by Jones and Stokes Associates (1990) and Olsen et al. (1990) are fully or partially conducted by telephone, in contrast to later studies which rely almost exclusively on mail surveys, with the most recent study combining mail and internet modes. The elicitation format is contingent valuation for all but Layton et al. (1999) and Mansfield et al. (2012). Explanation within the survey regarding how improvements would occur varies, with Jones and Stokes Associates (1990) and Loomis (1996) providing the most detail. In the author's opinion, all of the surveys could have included more information on substitute migratory fish resources in the Western US. None of the studies included information on salmon resources outside of the watersheds that were the topic of the survey. That said, the Olsen et al. and Layton et al. studies considered large systems, e.g., the entire Columbia River watershed, which implicitly captures regional substitutes.

What then can be gleaned from Table 1 regarding the TEV of changes in Western US salmon abundance for the policy case and other applications? The studies consistently indicate that households in the Pacific Northwest and beyond have a high WTP for increased salmon, yet they do not cover all of the areas in the Western US that currently provide salmon habitat. If the parameters of a given study in Table 1 happen to match a context of interest, perhaps no further analysis is required. More often, there is interest in estimating a value for an “out of sample” context. Furthermore, insights drawn from a group of observations are arguably stronger even if the parameters of a single study are well matched to a given policy scenario. Benefit transfer tools developed for these situations will be reviewed in the next several sections.

Before proceeding, it should be noted that studies in Table 1 do not include all of the available insight on salmon values in the Western US. Notably, some survey studies have elicited a WTP for recovery of salmon listed under the Endangered Species Act, rather than specifying population changes. This focuses specifically on wild fish, and the values would seem to be more associated with non-users than an equivalent study citing abundance changes. For examples see Bell et al. (2003), Lew and Wallmo (2011), Wallmo and Lew (2011, 2012), and Mansfield et al. (2012). Other survey studies have treated habitat improvements for salmon, without specifying the impact on salmon either in terms of listing status or in terms of abundance (e.g., Garber-Yonts et al., 2004). At least one study has elicited values for changes in salmon abundance as a commodity lumped with other environmental attributes, Douglas and Taylor (1999). Still more studies have focused on just recreational or commercial benefits of salmon.

Point Estimate Transfer

The simplest form of benefit transfer is transferring a point estimate. The value for the most similar context should serve as a reference, but this is challenging to identify since there are multiple dimensions of applicability. There are no obvious reasons to suspect quality issues with estimates in Table 1 except observations 28 and 29 from Mansfield et al. (2012), which as described in the Appendix have broad confidence intervals; the response rate for this study is also the lowest in Table 1. Survey response rates are quite high for the other five studies, from 49% (Bell et al., 2003: Grays Harbor) to 77% (Loomis, 1996, Clallam Co.). No two studies were conducted by exactly the same protocol, and there remains active debate about best practices in valuation. One of the debates concerns contingent valuation vs. alternative stated preference formats. Layton et al. (1999) and Mansfield et al. (2012) are the only studies that do not use contingent valuation. On one hand, alternatives to contingent valuation are gaining in popularity and choice experiments seem to have become the new standard. On the other hand, value estimates can be higher (Stevens et al., 2000; Bateman et al., 2006), and consensus protocols are still emerging (e.g., Hanley et al., 2001; Louviere et al., 2010; Boyd and Krupnick, 2013). However, to be sure, a variety of application styles is possible within either contingent valuation or choice experiments that may eclipse the effect of methodology alone.

In addition to study methodology, other obvious differences between studies in Table 1 are the size of fish change, regional scarcity, and market extent. It is tempting to utilize the survey results of Olsen et al. (1990) since some of the respondents would have been Willamette valley households, but the scale of change is the entire Columbia, an area about 20 times as large as the Willamette, and features a salmon abundance change measured in millions rather than tens of thousands of fish. Jones and Stokes Associates (1990) offer an estimate for San Joaquin Valley households, a watershed similar in size to the Willamette, but the baseline fish population is extremely low. The change would essentially create a Chinook fishery rather than supplement an existing one. The Bell et al. (2003) estimate for a 100% improvement in Coho salmon in Willapa Bay, WA is the most similar in terms of baseline and final fish population, even though the extent of market surveyed and the watershed itself are relatively small. Since no prior studies match the Willamette context in all dimensions, a judgment was made to match closest available baseline and final fish population. Comparing US Census household income for the Willapa Bay and Willamette valley regions indicates that of the two possible Bell et al. models, the high income (observation 20) more closely matches Willamette valley demographics. The corresponding estimate is $726.97 NPV, or $50.89 per household as if a yearly payment (2015$).

Functional Transfer

The next step in complexity is functional transfer, which uses a model offered by the study case, and adjusts context variables to estimate the policy case value (Loomis, 1992). By elimination, Layton et al. (1999) is best suited for functional transfer; other studies either did not include a model or used highly specialized information available only through their survey instrument. The Layton et al. models are scaled by the context variable of percentage change in fish population. There are different models for different fish category, and either high or low baseline fish population. The Layton et al. functions were developed for a much larger area and much larger absolute numbers of fish, however there are a few to choose from. Of the two migratory fish models, Columbia River and Puget Sound, the former was chosen since the Willamette is at least a tributary of this system. The Columbia models also have lower status quo fish populations than the Puget Sound models, although even the low baseline option is still higher than the Willamette Spring Chinook status quo by an order of magnitude. An alternative possibility is choosing the high baseline model in an attempt to harness diminishing returns to offset the larger scope of the Columbia system, but here the low baseline option is employed as a more logical usage of the functional transfer method. The Layton et al. (1999) formula for monthly WTP when the increase in fish is greater than 5% is:

$\text{WTP}={\beta }_{\text{fish}}(0-\text{ln}(\text{fish}\%\text{change}))/{\beta }_{\text{cost}}$

Solving the function for a 100% change using their regression parameters, converting the monthly value to a yearly value, and then converting this to a NPV using a 7% discount rate yields $4,370.83 per household; if expressed as a yearly payment the value is $305.96. Both values are converted to 2015$ using the CPI.

Existing Meta-regressions

With both point transfer and functional transfer, the analyst must choose a single study. In contrast, meta-analysis uses observations from multiple studies to gain insight, and may use statistical techniques such as meta-regression to isolate sources of influence on a dependent variable (Stanley, 2001). Three published meta-regressions were found that could be applied to the policy case of doubling Willamette Spring Chinook. Johnston et al. (2005) estimated a meta-regression of TEV for changes in US water bodies that provide fishing or other recreational improvements, using 81 observations. Richardson and Loomis (2009) supply a meta-regression of TEV for US Threatened and Endangered species using 67 observations, as an update to Loomis and White (1996). Last, Loomis and Richardson (2007) provide a meta-analysis specifically for Western US Salmon, using 20 observations from five of the six studies earlier described.

While meta-regressions supply predictive relationships, applying them is not necessarily straightforward. Context variables can reflect both household preferences and study methodology. For methodological variables, it is usually recommended that the analyst employ sample means, yet one may also wish to select particular “favorite” methodologies for a given transfer, e.g., a method known to be relatively conservative. Preference variables may be straightforward, but can also be specialized and difficult to generate for the policy case. Meta-regressions may also present multiple functional forms, leaving the analyst uncertain regarding which to utilize.

To illustrate how these factors can affect the benefit transfer for the selected policy case, limited sensitivity analyses are presented based on the three existing meta-regressions. Table 2 shows choices used in applying Johnston et al. (2005). Of their three models, the weighted semi-log specification is used since it had the best fit as published [the functional form is not reproduced here, but parameters and estimates can be viewed in (Johnston et al., 2005): Table 3]. Only eight of the 34 regressors are adjusted here, chosen for relevance to the application and for their influence. Variables not shown were constant throughout². The first two adjusted variables are based on the well-known water quality index, mathematically determined from numeric values of fecal coliform, dissolved oxygen, biological oxygen demand, turbidity, and pH (Vaughan, 1986). The index has been used to define rungs on a water quality “ladder”: boatable; fishable; swimmable; and drinkable, that has had a legacy influence on water quality valuation studies (Carson and Mitchell, 1993). A primary limiting water quality factor for salmon in the Willamette is thought to be elevated stream temperature, with migration barriers posed by dams being another major factor. Yet there is no defined “rung” for increased fish abundance per se. Thus, different changes in the water index are shown as part of the sensitivity analysis.

TABLE 2

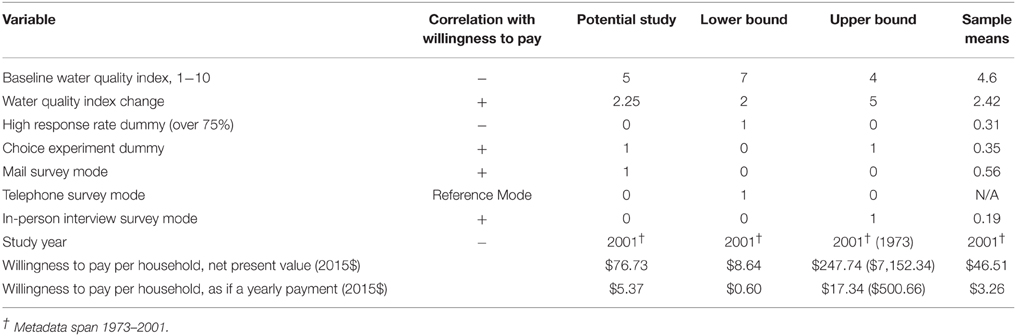
Table 2. Meta-regression results applying Johnston et al. (2005).

In applying the Johnston et al. (2005) meta-regression, the first column of Table 2 shows a potential study, i.e., one that might be designed if pursuing an original survey for the case study. For the water quality index, a baseline corresponding to “game fishing” is entered with a change halfway to the next rung of “drinking without treatment” (Vaughan, 1986). A choice experiment would allow direct inclusion of potential substitutes, an attractive feature in valuation, thus discrete choice methodology is selected. Mail survey mode is selected due to its low cost, and high response rate is not selected since achieving rates above the 75% threshold is uncommon. The second and third columns adjust eight selected variables within reasonable bounds to explore lower and upper bounds, respectively. The fourth column utilizes Johnston et al. (2005) sample means. For year, the most recent study year is used as typically recommended for benefit transfer. The impact of study year is shown by providing an additional upper bound value using the earliest meta-data date instead. The function returns estimates in 2002$, which were adjusted to 2015$ using the CPI. Using sample means, the estimate is $46.51 per household NPV, or $3.26 per household as if a yearly payment in perpetuity.

The meta-regression by Richardson and Loomis (2009) for endangered species values is applied in Table 3, again comparing four columns. The authors recommend their reduced double log model 3 for benefit transfer, which includes 10 regressors (the functional form is not reproduced here but a calculation example showing parameters and estimates is provided by Richardson and Loomis, 2009: Section 3.5). The key preference variable is the percentage change in population of the endangered species; this is set to 100%. There is no adjustment for the baseline level of fish, although one would expect that a lower baseline would mean a higher marginal value for each additional fish as compared with a location where fish are already plentiful. As with using Layton et al. (1999) for functional transfer above, percentage increase must be used rather than absolute increase in fish numbers. Selections in the function were made to indicate that the endangered species was a fish. The “visitor” variable was not selected to indicate that value beyond recreation was desired. For a potential study scenario in column 1, selections were made to parallel those in column 1 of Table 2. Study year again has a large impact, but in the opposite direction. Thus, an additional lower bound value is shown using the earliest meta-data date. The function returns values in 2006$, which were adjusted to 2015$ using the CPI. The estimate based on sample means is $185.84 per household. The payment schedule is unspecified since the observations had various payment plans that did not appear to be adjusted to a NPV.

TABLE 3

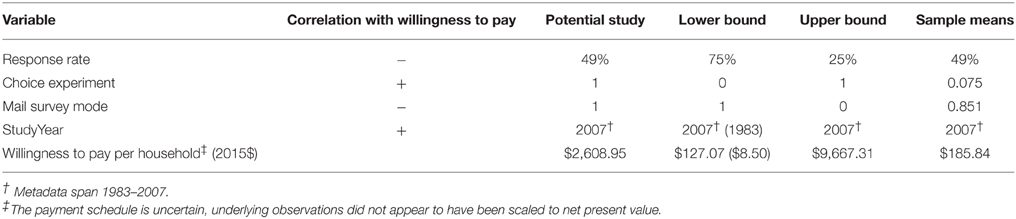
Table 3. Meta-regression results applying Richardson and Loomis (2009).

The third meta-regression, utilizing Loomis and Richardson (2007), only requires input on percentage change in fish run, with the meta-regression utilizing percentage change and percentage change squared (with no constant term). This function has a strong advantage in simplicity of application, particularly given the online calculator provided by the authors. However again there is no adjustment possible for baseline fish populations, and percentage change must be used instead of absolute fish numbers. The calculator provides estimates in 2006$. Using the CPI to adjust to 2015$, the resulting estimate for a 100% increase in salmon population is $89.23 per household. The payment schedule is unspecified since the observations had various payment plans that did not appear to be adjusted to a NPV.

New Meta-regression

Taken together, the three meta-regressions represent five of the six studies in Table 1, but not all of the observations that can be extracted from those five studies. For example, Loomis and Richardson (2007) represent the various Layton et al. (1999) models at only the 50% fish increase levels. In addition, there are two new observations from Mansfield et al. (2012). As noted earlier, observation 28 is the only negative value in Table 1 and thus appears to be an outlier. This leaves 28 observations with which to explore a new meta-regression. The dependent variable was defined as NPV of household TEV elicited as WTP in 2015$.

As seen earlier, meta-regressions typically include methodological regressors to control for study differences. Here, this has not been explored due to there being few studies, which often vary in more than one methodological respect from each other, leading to confounding effects. This meta-regression is limited to preference variables. Different hypotheses were considered regarding conversion of before and after fish abundance into one or more resource quality variables. As discussed above it was desired to incorporate not only the scope of change, but also the baseline level of fish. However, change in fish and baseline fish have a correlation coefficient of 0.7, signaling multicollinearity issues in a regression model using both variables. The problem is that when researchers have elicited WTP for large increases in salmon, this has tended to occur when the baseline levels of salmon were also large. Thus, there is limited independent variation in added fish and baseline fish. Transforming the variables by centering data (subtracting the mean from each observation) was ineffectual in reducing this high correlation. A different transformation is possible by dividing baseline fish by watershed area, under the rationale that when gauging scarcity a household might consider overall watershed size. Although numeric watershed areas were not specified in the study cases, a map was typically provided, except when telephone sampling. Transforming the scarcity variable in this manner substantially reduced correlation (correlation coefficient reduced to 0.4). Note that both variables cannot be transformed or the high correlation reappears. Watershed areas were found using publicly available national hydrography data (Horizon Systems Corporation, 2015; US Geological Survey, 2015) and are shown in Table 1. Constructing the independent variables in this way hypothesizes that survey respondents viewed scarcity in context of the watershed, but instead reacted directly to the added number of fish. This is questionable, thus the transformation is only employed in one of the regression models presented below.

All models use a log form for both the baseline fish and added fish variables. For baseline fish, this means that as baseline level decreases, the (expected) influence on increasing WTP would accelerate per unit decrease. For added fish, a log form is one way of instituting the common assumption of diminishing returns: as added fish goes up, added WTP also goes up but at a decreasing rate. All models also use a cluster adjustment for standard errors, to control for non-independence of observations from the same study. Results from four models are shown in Table 4. Model 1 has the expected positive sign for added fish and expected negative sign for baseline fish. However, Model 1 has several weaknesses. Only the added fish variable is significant, the model has a low r-squared, the two regressors are highly correlated, and examination of standardized residuals shows two outliers (exceeding positive or negative two). Model 2 utilizes the transformed baseline fish variable as described above to reduce correlation between variables. This improves r-squared, both variables retain expected sign, and both variables are now significant. Model 3 repeats Model 1, dropping the two outliers (observations 16 and 18). This only minimally affects the model. However, the model is sensitive to dropping certain observations and/or studies, since there are only 28 observations total from six studies. To illustrate this, the study contributing the most observations (Layton et al., 1999) is dropped for Model 4. Now only the baseline fish variable is significant, and interestingly the r-squared improves dramatically. Model 4 also shows a dramatic reduction in predicted TEV for the policy site.

TABLE 4

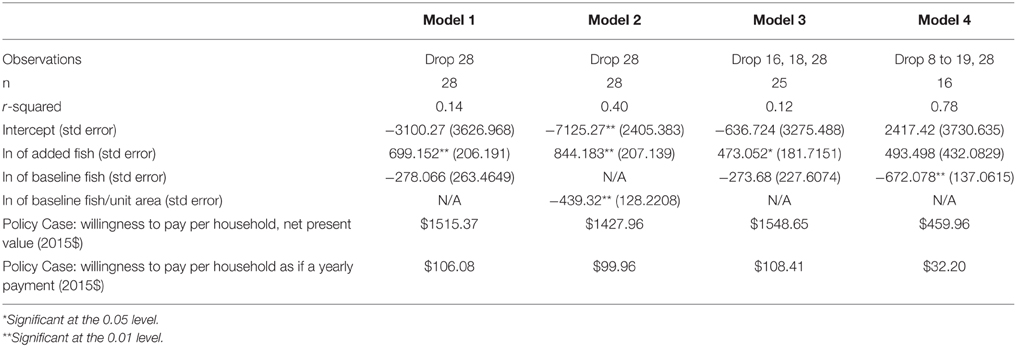
Table 4. New meta-regression of the total economic value of migratory pacific salmon abundance changes in the US.

Further development of the meta-regression is certainly possible. Despite potentially confounding effects with so few studies, methodological variables could be attempted. A treatment for heteroskedasticity would be desirable, however variance was not uniformly available from the study cases. Observations could be weighted by sample-size, a second-best solution for benefit-transfer (Nelson and Kennedy, 2009). However, given the known efficiency of some valuation methodologies relative to others, and development of valuation techniques across the span of years in the sample, weighting on sample size would seem a dubious approach. There are also few observations overall, limiting the ability to include additional context variables due to the danger of overfitting. Overall the investigation of a new meta-regression is less than satisfying. Parameters do show the theoretically expected sign, but parameter significance and overall model performance are low or unstable.

Structural Benefit Transfer

Meta-regression reanalyzes valuation estimates along with other meta-data from original studies in search of statistical predictors for WTP. However the resulting equation cannot be viewed as a utility function when there are variables (i.e., methodological) not theoretically linked to preferences. A separate form of meta-analysis known as structural benefit transfer (aka preference calibration) uses a different approach. A utility function for a representative agent is defined, and outcomes of valuation studies are used to calibrate preference coefficients. From that point, application is similar to functional benefit transfer. Advantages of this technique are its explicit connections to economic theory (for example WTP can be bounded by household income), consistency, and its ability to integrate value estimates from different techniques and welfare measures, such as recreational value from travel-cost techniques, and TEV from a survey. A weakness is subjective identification of the underlying utility function, and as typically employed, use of relatively few observations to calibrate parameters. Studies used for calibration should reasonably apply to representative households for the policy case. In contrast to the relatively large number of environmental valuation meta-analysis studies, there are relatively few for structural benefit transfer.

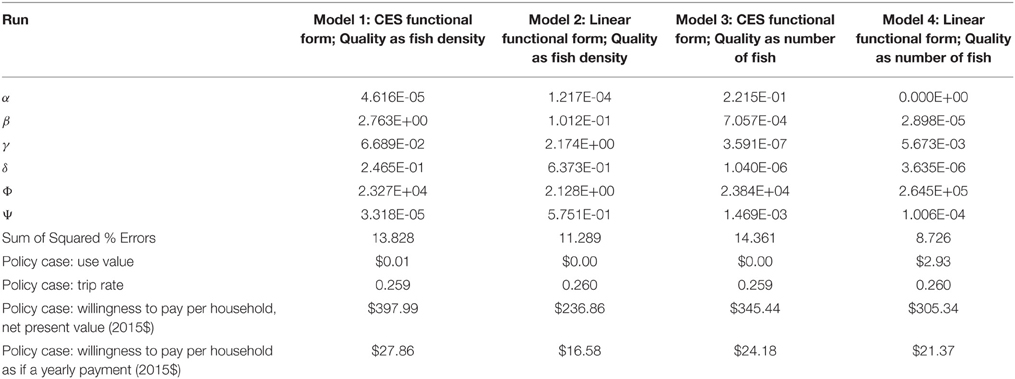
For references developing structural benefit transfer, see Smith and Pattanayak (2002), Smith et al. (2002), Van Houtven et al. (2011), and Van Houtven and Poulos (2009). Only Van Houtven et al. include treatment of non-use values, a crucial concern for the policy case. Here we include two of the five functional forms they considered, a modified constant elasticity of substitution (CES) functional form (Equation group 1), and a linear functional form (Equation group 2), both of which performed reasonably well for their case study. It should be plainly stated that multiple functional forms are possible other than the two tested here. Both functional forms predict indirect utility “V,” with changes in the resource quality from “Q.” Also included are the price of visiting the resource “P” (i.e., travel cost), and income “Y.” Subscripts “0” and “1” correspond to initial and final resource quality levels. Each equation has five parameters to calibrate, alpha α, beta β, gamma γ, delta δ, phi φ, and psi ψ. Income less WTP for improved quality (or WTP to avoid degraded quality) that equilibrates initial and final indirect utility corresponds to a Hicksian welfare change expressed in dollars. Via Roy's Identity the functions can be re-expressed in terms of number of trips demanded per household per year (X) which can in turn be related to a Marshallian welfare change (ΔMCS) in dollars typical in travel cost studies. Based on these algebraic manipulations the following formulas are taken from Van Houtven et al. (2011):

(1) Modified Constant Elasticity of Substitution (CES) Functional Form:

$\begin{array}{l}\text{ V}=\phi {\text{Q}}^{\psi }+{({\left(P-{\text{Q}}^{\gamma }\right)}^{-\alpha }\text{}{\text{Y}}^{\delta })}^{\beta }\hfill \\ \text{ WTP}=\text{Y}-(((\phi {\text{Q}}_0^{\psi })-(\phi {\text{Q}}_1^{\psi })\hfill \\ +{({(\text{P}-{\text{Q}}_0^{\gamma })}^{-\alpha }{{\text{Y}}^{\delta })}^{\beta })}^{1/\beta \delta })/{(\text{P}-{\text{Q}}_1^{\gamma })}^{-\alpha /\delta }\hfill \\ \text{ X}=(\alpha /\delta ){}^{\ast }(\text{Y}/(\text{P}-{\text{Q}}^{\gamma })\hfill \\ \Delta \text{MCS}=(\alpha /\delta ){}^{\ast }\text{Y}{}^{\ast }(\text{ln}(\text{P}-{\text{Q}}_0^{\gamma })-\text{ln}(\text{P}-{\text{Q}}_1^{\gamma }))\hfill \end{array}$

(2) Linear Functional Form:

$\begin{array}{l}\text{V}=\phi {\text{Q}}^{\psi }+{\left(\text{Y}+1/\delta (\alpha -\beta \text{P}+\gamma \text{Q}-\beta /\delta )\right)}^{\ast }\\ \text{exp}(\delta /\beta (\gamma \text{Q}-\beta P))\\ \text{WTP}=1/\delta (({\text{X}}_1-\beta /\delta )\\ -{\left({\text{X}}_0-\beta /\delta \right)}^{\ast }\text{exp}\left(({\delta }_{\gamma }/\beta ){}^{\ast }({\text{Q}}_0-{\text{Q}}_1)\right)\\ +\phi {({\text{Q}}_1^{\psi }-{\text{Q}}_0^{\psi })}^{\ast }\text{exp}\left((\delta /\beta ){}^{\ast }(\beta \text{P}-\gamma {\text{Q}}_1)\right)\\ \text{X}=\alpha -\beta \text{P}+\delta \text{Y}+\gamma \text{Q}\\ \Delta \text{MCS}=({\text{X}}_1^2-{\text{X}}_0^2)/2\beta \end{array}$

In both cases the first term on the right-hand-side of “V” is a simple means of expressing non-use value, while the second more complicated term represents use value. Only preference variables are included: income (Y); trip price (P); the quality variable (Q); and the six parameters (greater than or equal to 0) to be calibrated. Changes in utility are effected by changing from the initial to a final quality state, Q₀ to Q₁. Increases in quality increase the non-use component directly, and reduce the effective price of the trip within the use value term. For example, all else equal, people are less likely to incur a high travel cost P to visit a site with low Q. Hicksian and Marshallian welfare estimates, an average income estimate, an average trip price, and recreational demand statistics can all be used to calibrate parameters.

In addition to testing two functional forms, we also test two ways of calculating quality, resulting in four models total in Table 5. The first method of calculating quality is based on amount of fish per watershed area. To rescale the variable to have an upper limit of 10, observed fish density was multiplied by 10 and divided by the in-sample maximum density post-increase (observations 5, 6, and 7 all have this maximum density). The second method of calculating quality is based on the number of fish without regard to watershed area. In this latter case, scaling from 0 to 10 was done based on the upper limit being the maximum in-sample total number of fish post-increase (observation 19).

TABLE 5

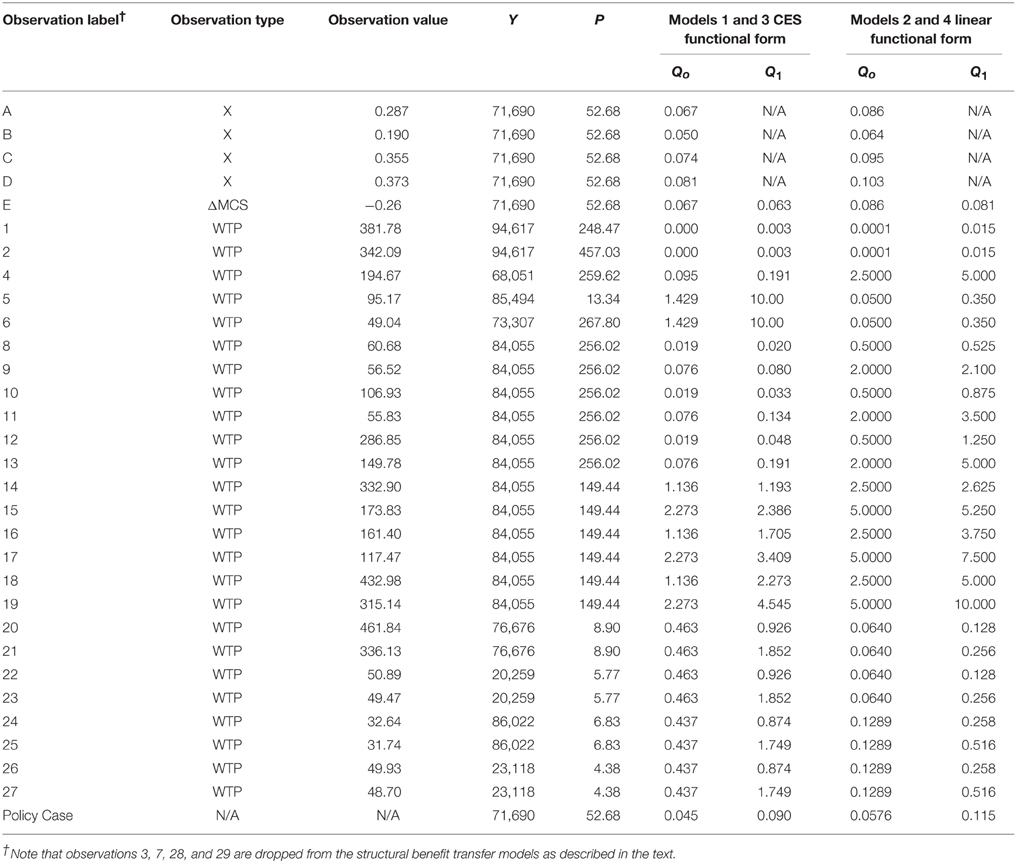
Table 5. Structural benefit transfer of the total economic value of migratory pacific salmon abundance changes in the US.

For recreational statistics and recreational angling use-value, we utilize angler survey results for Spring Chinook in the Lower Willamette River. The Research Group (1989) conducted the survey and Lin et al. (1996) provide additional analysis by leveraging data on site characteristics during 1988 from ODFW. Four observations, A, B, C, and D of angler trips per household per season are possible from the data, corresponding to different Spring Chinook run sizes (these receive letter labels in Table 5 to avoid confusing these observation with the numbered observations in Table 1). First, overall angler-day effort for the fishery was estimated at 222,457 days in 1988 while the average run size for 1986–1993 was 86,000 fish (as cited in Lin et al., 1996). The interception-mode survey conducted in the 1988 season asked anglers about their current average trip frequency (11.6 trips/season), their expected trip frequency with a 10% increase in the run (2.3 additional trips/season), and with a 20% increase in the run (3.0 additional trips/season). A fourth estimate of how fishing trips change with fishing quality is possible using an estimated average angler-day effort in 1974–1979 being 147,000 and average run size during a similar timeframe 1976–1985 being 63,500 fish (as cited in Lin et al., 1996). All four of these observations are scaled to represent trip frequency for a representative household by dividing by the approximate number of households in the Willamette valley based on Census data. Note that observations A, B, C, and D assume the Willamette valley is a feasible market extent for the Willamette Spring Chinook fishery. Observations B and C based directly on the angler survey assume no influx of new anglers with run size: the stated change number of trips by those who are already anglers is used to estimate total change in angler effort. All four are “X” observations, i.e., average trips per household per season.

Loss in Marshallian consumer's surplus based on change in Willamette Spring Chinook run size is also available from Lin et al. (1996). Based on a random utility model they calculate welfare loss at $0.4657 per trip with a reduction in run size of 5000 fish, or $-0.92 in 2015$ using the CPI. This calculation relies on the more conservative formulation of the travel cost variable presented by Lin et al. with opportunity cost of time valued at 1/3 of the average wage rate rather than at 100%. Adjusting the welfare loss by the average number of trips per household from the first observation results in observation E; loss in use value for the given quality decrease.

Remaining observations in Table 5 used for the four calibrations are Hicksian WTP estimates from Table 1. In an effort to have the calibrated utility function more reasonably match relatively limited market extents, given that the policy case is limited to the Willamette valley, observations were dropped in which the WTP was associated with out-of-state respondents (observations 3, 7, 28, and 29).

Estimates for average household income and average travel cost are also needed to calibrate the utility functions. For average household income, Jones and Stokes Associates (1990) was the only study that provided sample information. For other observations average income was calculated from Census estimates corresponding to the sampled geography. When more than one geography was sampled (e.g., Olsen et al. included more than one state), a weighted average based on population was calculated. For the Bell et al. (2003) models distinguished by above and below median income respondents, an estimate of average household income given the condition of being above or below the median was interpolated based on Census county level income quintiles (Census table b19081). In all cases average income estimates were adjusted to 2015$ using the CPI.

The average cost of salmon angling “P” relevant for each observation in Table 1 is the travel cost facing a representative household within the market extent, not just the price paid by households that regularly fish. An average travel cost depends on the opportunity cost of time, vehicular depreciation and fuel cost per mile, the distribution of population for a given market extent, and the distribution of places to fish. The last two factors are particularly difficult to assess precisely, and this study relies on simplifying assumptions as follows. Salmon fishing is often considered preferable closer to a river's mouth, due to fish attrition and lower meat quality upstream. Thus a single angling location was researched for each fishery, as a point close to the river mouth with public boat ramp facilities³. For each observation's market extent, the top five population centers were used as starting point “hubs,” with roundtrip travel times and distances calculated with Google Maps. For small county-level market extents, the single top population center in that county was used. Travel cost was then calculated from the hubs to the angling site and weighted based on hub population. Round trip travel cost for a given hub was:

$\begin{array}{l}1/3{}^{\ast }(\text{Y}/2,000){}^{\ast }(\text{round}-\text{trip}\text{driving}\text{time})\\ \text{ +}0.58{}^{\ast }(\text{round}-\text{trip}\text{driving}\text{distance})\end{array}$

The calculation assumes 2000 h worked per year, counts the opportunity cost of time at 1/3 of the average wage rate (Parsons, 2003; p. 285), and uses a national average of $0.58/mile for driving cost (American Automobile Association, 2015).

For the four models tested, preference parameters were calibrated by minimizing the sum of errors between observed and predicted values (with error calculated as percent difference between observed and predicted). Observed and predicted values correspond to WTP (25 observations per model), X (four observations per model), and ΔMCS (one observation per model) associated with the quality changes from Q₀ to Q₁. Calibrations were achieved by crosschecking an evolutionary algorithm with a generalized reduced gradient algorithm, using a multi-start option to avoid local optima. The calibrated parameters, associated minimized errors, WTP, X, and ΔMCS data for the four models are shown in Table 6.

TABLE 6

Table 6. Structural benefit transfer calibrated parameters and predicted values.

Discussion

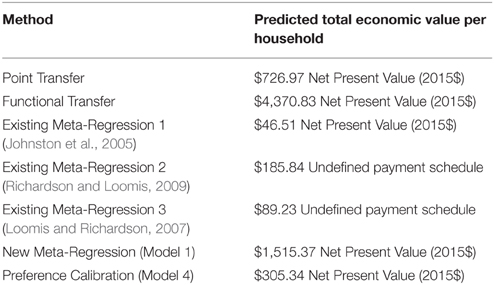
The TEV estimates of doubling Willamette Spring Chinook using each benefit transfer method are summarized in Table 7. There is a remarkable order of magnitude range in values, from $46.41 to $4,370.83 per household. The lowest estimates are from prior meta-regressions. For comparison, Table 1 values (excluding observation 28) range from $122.44 from Mansfield et al. (2012) to $6,597.65 from Layton et al. (1999).

TABLE 7

Table 7. Comparing estimates of the total economic value of doubling willamette salmon.

Point transfer is the most straightforward benefit transfer technique, with a strong underlying study having similar baseline and final salmon populations to the policy case. However, as compared with the Willamette policy case the Willapa study case is about one-tenth the area, with about one-hundredth the human population. Furthermore, it is possible that TEV would reflect more angling use value in the Willapa watershed than in the Willamette watershed, due to a close proximity of the population surveyed to the fishery. Functional transfer, a technique slightly more complex than point transfer, returns an extreme high value prediction. This is attributable to a 100% change for Layton et al. (1999) representing an order of magnitude more fish than the policy case, even using the low baseline model option. In other words, there remains a context mismatch.

Prior meta-regressions revealed both insights and difficulties. Estimates based on both Johnston et al. (2005) and Richardson and Loomis (2009) were sensitive to selections in key methodological and preference variables. Study year in particular stands out for having a large impact in each study but in opposite directions, and thus may be proxying for other unobserved variables. All else equal, the two studies find that higher response rates and use of choice experiments boost values. Estimates utilizing sample means and most recent study year in the meta-data provide the least extreme estimates from Tables 2 and 3, and represent best-practices estimates utilizing the meta-regressions. If meta-data for both studies could be recovered, discrepancies between observed and predicted values for the salmon-related observations could be gauged as a further test of how the regressions performed in those instances.

Comparing all three existing meta-regressions, values for increasing abundance for threatened and endangered species appear to be highest, followed by values for increasing salmon abundance, followed by values for aquatic resource improvements in general. However existing meta-regression results are difficult to interpret and compare since the underlying observations mix payment plans, without calculating a NPV using a defined discount rate. Modeled outputs thus also reflect a mix of payment schedules, not strictly yearly payments in perpetuity nor NPVs. Johnston et al. (2005) provide a separate “lump-sum” dummy variable regressor, set to 1 for this paper for clarity in calculating NPV, but this does not actually adjust underlying observations to NPV using a defined discount rate.

A simplistic new meta-regression using two variables has only limited success, but does include more salmon-oriented TEV observations than any other available regression. Of the four models, Model 1 employs the fewest adjustments regarding dropping observations or transforming underlying variables, and has the theoretically expected signs on both variables. The salmon fish change is expressed in absolute numbers, retaining raw information rather than rescaling to percentage. The log format of the salmon change variable conforms with diminishing returns; WTP per additional fish decreases the larger the increase in fish. Modeled WTP is explicitly NPV; underlying observations were discounted to NPV using a discount rate of 7%. If a rapid, rough estimate is needed, the model could be applied to other Western US salmon contexts, with awareness of model sensitivity to relatively few observations and even fewer studies. In particular there is the disclaimer that the model does not accommodate important methodological differences between studies. For example, extent of market is not a regressor and thus the function implicitly assumes no distance-decay effect. It would be possible to re-estimate the function by dropping observations with especially large market extents, if desired. For the policy case, the function returns a relatively large NPV similar to Layton et al. observations associated with much larger fish increases. Dropping Layton et al. observations returns a value about 1/3 as large. It seems that even when controlling for the relatively high baseline and high fish changes considered in Layton et al. within a meta-regression, the Layton et al. observations still represent high TEV estimates.

Structural benefit transfer was the most time intensive method employed for this paper, even testing just two functional forms. An obvious weakness of functional forms as they were tested is that quality must be summarized in a single variable. Furthermore, the quality scale was tied to a maximum observed number rather than a theoretic number. Testing two representations of quality showed the scale based on absolute number of fish to be superior to fish per unit area for both the CES and linear functional forms, based on lower error as reported in Table 6. Exploration of combining variables into a quality index, or functional forms with different quality variables, would be possible with future research. Certain observations could also be weighted as more important for the optimization, e.g., use value observations. The linear functional form with quality scaled as absolute number of fish has the lowest error overall, and predicts a use-value that appears to be the most realistic. As compared with the new meta-regression, structural benefit transfer predicts lower estimates. This may be due to the meta-regression explicitly accounting for a separate impact of scarcity on WTP. There may also be some effect of the meta-regression and structural benefit transfer minimizing different calculations of error: sum of squared errors and sum of percentage errors respectively. However, re-running the calibration to minimize sum of squared errors yielded only a slighter higher value, still far less than the new meta-regression models. The structural benefit transfer also has more stable estimates than the meta-regression, despite much variability in the six optimized parameters.

Any of the estimates aggregated over time and over the approximately 1 million households in the basin (as a possible market extent) supports substantial recovery efforts for Willamette Spring Chinook⁴. Since it is already listed under the Endangered Species Act, such quantifications may seem moot. Yet the decision space for recovery is broad and estimates of TEV can inform policy decisions. Economic criteria figure directly into critical habitat designation by 16 U.S.C. § 1533(b)(2). This often reduces designated habitat since costs are easier to estimate than benefits (Duane et al., 2007).

Conclusions

The hypothetical context of doubling a salmon run in the Western US is used to guide passage through the analytic procedures of benefit transfer techniques. Compiling observations from several studies surveying several thousand Western US households, there is a consistently high WTP for increased salmon abundance. Applying benefit transfer tools to these results requires that the analyst consider numerous factors that influence value, which offers perspective beyond what can be learned from a single estimate. With the illustrative policy case as a vehicle, challenges of applying each benefit transfer technique were discussed.

Simplistic benefit transfer methods and previous meta-regressions displayed a variety of weaknesses for the application. The new meta-regression and structural benefit transfer also required a number of judgments. These are detailed in the paper for transparency, and to facilitate further tailoring best suiting future applications. Each method returns vastly different TEV estimates for the policy case as seen in Table 7. The new meta-regression is simpler to estimate and includes two separate gauges of resource quality, yet is highly sensitive to modeling decisions. The structural benefit transfer allows inclusion of more data, produces separate use value and trip rate estimates, and yields more stable estimates over the sensitivity analysis. However structural benefit transfer required more assumptions to execute and was more time consuming. In this paper both methods are utilized solely with preference variables, but meta-regression has the ability to include methodological factors if desired.

Ultimately both forms of meta-analysis are useful for crosschecking values, and the wide variety in estimates of the “true” value should be kept in mind. For the selected policy case the author would recommend use of structural benefit transfer for two reasons. First, the meta-regression was unstable, at least partially due to relatively few studies and observations. Second, the structural benefit transfer allows portraying TEV in the context of use value. According to available data, use value appears to be much less than non-use value. This has potentially important policy implications for fishery management, since commercial and recreational anglers are typically thought of as the main stakeholders. For different policy scenarios, it is possible that a different benefit transfer approach would be preferred—for example if the fishery had dwindled to extremely low numbers as in Jones and Stokes Associates (1990), a point transfer from that study could be justifiable since it is the only one dealing with a highly scarce situation.

For conducting TEV benefit transfer for other marine resources, it would not be obvious which technique would be preferred until a literature review of available studies, as compared with the intended application, is complete. Meta-regression and structural benefit transfer are both sophisticated techniques, and are likely to receive continued development. Their intention is to make benefit transfer more reliable; however both techniques of meta-analysis require a series of judgments which this paper attempts to make clear to facilitate use of the tools and interpretation of their results. Of the two techniques, structural benefit transfer is relatively less developed in terms of potential functional forms and other best practice details. There would seem to be opportunities to combine meta-regression with structural benefit transfer, to leverage the benefits of each and offset respective weaknesses. For example, the empirical behavior of preference variables from numerous studies (e.g., linear or exponential relationship with WTP) could be integrated into development of theoretically consistent utility functions, to provide more reliable guidance on functional form for both techniques.

One of the surprising outcomes of this study is the advantage of proactively applying benefit transfer to glean contextual factors explicit or implicit in prior research. These help plan an original valuation effort to address holes in meta-data. During this journey through benefit transfer, several suggestions emerge for future salmon TEV studies:

• Distinguish between wild and hatchery fish. It is currently unclear whether values are sensitive to the distinction. This is important due to controversies regarding hatcheries. Complicating the issue is that angler harvests are sometimes limited to hatchery fish.

• Differentiate between abundance changes and species loss/recovery in the survey. ODFW recommend population increases in wild Willamette Spring Chinook simply to guard against extinction. Surveys do not appear to have represented the concept of a biologically viable population, thus it is unclear whether value estimates apply solely to increased abundance, with a separate, yet undiscovered value applying to avoid a species loss. None of the studies in Table 1 includes discussion of threatened or endangered species status for the salmon values in Table 1, although Mansfield et al. (2012) do mention such status for other species treated in their choice experiment.

• Include information on substitutes, perhaps in a split sample approach, to test Pate and Loomis' (1997) result (which used external data) that substitutes were of low importance. Optimally, relevant information on substitutes would be discovered through focus group and/or interview research with case study residents, but could include presence of or numbers of other salmon species in the watershed or neighboring watersheds. Salmon density per unit watershed area is another possibility.

• Further test the impact of scarcity and salmon baseline. There is evidence from the new meta-regression that low baseline populations have a positive influence on value, but isolating this was hampered by the correlation of fish baseline with fish change.

• Conduct complementary new use value studies. Despite established econometric methods and widespread interest in the recreational and commercial salmon fishery, relatively few recent studies have quantified these for the Willamette or other areas.

Disclaimer

This manuscript has been subjected to Agency review and has been approved for publication. The views expressed in this paper are those of the authors and do not necessarily reflect the views or policies of the U.S. Environmental Protection Agency. Mention of trade names or commercial products does not constitute endorsement or recommendation for use.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

In addition to the editor and two reviewers, the author is grateful for the assistance (in some cases occurring long ago) of the following persons: B. Barnhart; K. Bell; J. Ebersole; R. Johnston; J. Loomis; C. Mansfield; M. Papenfus; M. Plummer; G. Van Houtven, P. Walsh, and M. H. Weber. Their aid does not necessarily indicate endorsement of the manuscript. All errors and faults remain with the author.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/article/10.3389/fmars.2015.00074

Footnotes

1. ^Describing the policy case helps define the appropriate scope of the benefit analysis, such as whether relevant values are exclusively ecological in character or if human health concerns are an issue; unequal distributive impacts of an environmental change may also be important to consider (US Environmental Protection Agency, 2010). This application focuses on ecological values. Adverse health impacts seem unlikely since contamination advisories in the region focus on resident (non-migratory) fish. Distributional analysis would require additional social and biological data, including a model of fish distribution at baseline and improved levels.

2. ^Methodological variables not in Table 2 were set to sample means. Sample means were not used for preference variables; settings constant throughout were that the value represents a lump-sum payment, the geographic context is the Pacific Mountain USDA region, the population includes the non-user community, water quality improvements only benefit fin fish, the improvement is more than a 50% increase, and mean household income is $71,690 (weighted average based on Census data for the 10 counties most closely corresponding with the watershed boundary, adjusted to 2015$ with the Consumer Price Index).

3. ^The angling sites used for the observations are as follows: 1 and 2 = Buckley Cove Park, CA; 4 and 8 to 13 = Rainier City Park, OR; 5 and 6 = Lake Aldwell, WA; 14 to 19 = Port of Edmonds, WA; 20 to 23 = Town of Willapa, WA; 24 to 27 = Morrisson Riverfront Park, WA. Last, for the Willamette policy case, Cathedral Peak Park, OR.

4. ^Ideally, survey studies in Table 1 that provided the foundation for benefit transfer have captured both use and non-use values, in the correct proportions that they exist across households. However, there are relatively few commercial salmon anglers, thus their values may not be well represented by a sample, or observations could have been removed as outliers. Thus, for additional context on this issue, salmon constituted 8% of onshore landed value across all coastal Oregon commercial fisheries in 2013, amounting to about $12.4 million in gross revenue (The Research Group, 2014). The year 2013 was abnormally high compared to the several prior years. There are no known estimates of how Willamette Spring Chinook contribute to the coastal Oregon commercial salmon fishery overall, since the fishery has many other sources, such as the rest of the Columbia system and Oregon's Coast Range. For these reasons welfare impacts on commercial anglers from doubling Willamette Spring Chinook would appear to be relatively small, especially given that costs of fishing would need to be subtracted from gross revenue. Hanna et al. (2006) citing Huppert et al. (2004) discuss the possibility that net profit may even approach zero for Columbia Spring Chinook (one factor noted is the rise of farmed salmon, potentially offset by the popularity of wild-caught brands).

References

American Automobile Association. (2015). Your Driving Costs: How Much are You Really Paying to Drive? Available online at: http://exchange.aaa.com/wp-content/uploads/2015/04/Your-Driving-Costs-2015.pdf

Barnard, J. (2015a). “Private land logging buffers considered by Oregon forestry board,” in OREGONLIVE. Available online at: http://www.oregonlive.com/environment/index.ssf/2015/07/private_land_logging_buffers_c.html

Barnard, J. (2015b, July 23). “Board postpones decision on logging buffers to cool streams,” in MMC-NEWS. Available online at: http://mmc-news.com/news-board-postpones-decision-on-logging-buffers-to-cool-streams-40834.dbv

Bateman, I. J., Colec, M. A., Georgiou, S., and Hadley, D. J. (2006). Comparing contingent valuation and contingent ranking: a case study considering the benefits of urban river water quality improvements. J. Environ. Manage. 79, 221–231. doi: 10.1016/j.jenvman.2005.06.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bell, K. P., Huppert, D., and Johnson, R. L. (2003). Willingness to pay for local coho salmon enhancement in coastal communities. Mar. Resour. Econ. 18, 15–31.

Google Scholar

Boyd, J., and Krupnick, A. (2013). Using ecological production theory to define and select environmental commodities for nonmarket valuation. Agric. Resour. Econ. Rev. 42, 1–32.

Google Scholar

Brookshire, D. S., and Neill, H. R. (1992). Problems and issues in the validity of benefit transfer methodologies. Special Sect. Water Resour. Res. 28, 651–722. doi: 10.1029/91WR02590

CrossRef Full Text

Brouwer, R., and Spaninks, F. A. (1999). The validity of environmental benefits transfer: further empirical testing. Environ. Resour. Econ. 14, 95–117. doi: 10.1023/A:1008377604893

CrossRef Full Text | Google Scholar

Carson, R. T., and Mitchell, R. C. (1993). The value of clean water: the public's willingness to pay for boatable, fishable, and swimmable quality water. Water Resour. Res. 29, 2445–2454. doi: 10.1029/93WR00495

CrossRef Full Text | Google Scholar

Carson, R. T. (2000). Contingent valuation: a user's guide. Environ. Sci. Technol. 34, 1413–1418. doi: 10.1021/es990728j

CrossRef Full Text | Google Scholar

Doney, S. C., Ruckelshaus, M., Duffy, J. E., Barry, J. P., Chan, F., English, C. A., et al. (2012). Climate change impacts on marine ecosystems. Mar. Sci. 4, 11–37. doi: 10.1146/annurev-marine-041911-111611

CrossRef Full Text | Google Scholar

Douglas, A. J., and Taylor, J. G. (1999). The economic value of trinity river water. Water Resour. Dev. 15, 309–322. doi: 10.1080/07900629948835

CrossRef Full Text | Google Scholar

Duane, T. P., Carnefix, G., Chattopadhyay, S., Davidson, C., DellaSala, D. A., Duffield, J., et al. (2007). Economics of Critical Habitat Designation and Species Recovery: Consensus Statement of a Workshop Sponsored by the Pacific Rivers Council. Environmental Studies Program at San Francisco State University, Ecotrust, and the National Center for Conservation Science and Policy. Available online at: http://pacificrivers.org/science-research/resources-publications/economics

Florax, R. J. G. M., Nijkamp, P., and Willis, K. G. (2002). Comparative Environmental Assessment. Northampton, MA: Edward Elgar.

Google Scholar

Freeman, A. M. (2003). The Measurement of Environmental and Resource Values: Theory and Methods. 2nd Edn. Washington DC: Resources for the Future.

Google Scholar

Garber-Yonts, B., Kerkvliet, J., and Johnson, R. (2004). Public values for biodiversity conservation policies in the Oregon Coast Range. For. Sci. 50, 589–602.

Google Scholar

Gresh, T., Lichatowich, J. A., and Schoonmaker, P. (2000). An estimation of historic and current levels of salmon production in the Northeast Pacific ecosystem: evidence of a nutrient deficit in the freshwater systems of the Pacific Northwest. Fisheries 25, 15–21. doi: 10.1577/1548-8446(2000)025<0015:AEOHAC>2.0.CO;2

CrossRef Full Text | Google Scholar

Gustafson, R. G., Waples, R. S., Myers, J. M., Weitkamp, L. A., Bryant, G. J., Johnson, O. W., et al. (2007). Pacific salmon extinctions: quantifying lost and remaining diversity. Conserv. Biol. 21, 1009–1020. doi: 10.1111/j.1523-1739.2007.00693.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanemann, M., Loomis, J., and Kanninen, B. (1991). Statistical efficiency of double-bounded dichotomous choice contingent valuation. Am. J. Agric. Econ. 73, 1255–1263. doi: 10.2307/1242453

CrossRef Full Text | Google Scholar

Hanley, N., Mourato, S., and Wright, R. E. (2001). Choice modelling approaches: a superior alternative for environmental valuation? J. Econ. Surv. 15, 435–462. doi: 10.1111/1467-6419.00145

CrossRef Full Text | Google Scholar

Hanna, S., Gilbert, S., Harte, M., and Achterman, G. (2006). Review of Economic Literature and Recommendations for Improving Economic Data and Analysis for Managing Columbia River Spring Chinook. A Report to Oregon Department of Fish and Wildlife in Fulfillment of ODFW Agreement No. 005-4132S-Wild. Available online at: http://www.ecy.wa.gov/programs/wr/hq/pdf/elried_osu.pdf

Honea, J. M., Jorgensen, J. C., McClure, M. M., Cooney, T. D., Engie, K., Holzer, D. M., et al. (2009). Evaluating habitat effects on population status: influence of habitat restoration on spring-run Chinook salmon. Freshw. Biol. 54, 1576–1592. doi: 10.1111/j.1365-2427.2009.02208.x

CrossRef Full Text | Google Scholar

Horizon Systems Corporation. (2015). NHDPlus. Available online at: http://www.horizon-systems.com/nhdplus/

Huppert, D., Green, G., Beyers, W., Subkoviak, A., and Wenzel, A. (2004). Economics of Columbia River Initiative. Final Report to the Washington Department of Ecology and CRI Economics Advisory Committee.

Johnston, R. J., Besedin, E. Y., and Wardwell, R. F. (2003). Modeling relationships between use and nonuse values for surface water quality: a meta-analysis. Water Resour. Res. 39, 1363–1372. doi: 10.1029/2003WR002649

CrossRef Full Text | Google Scholar

Johnston, R. J., Besedin, E. Y., Iovanna, R., Miller, C. J., Wardwell, R. F., and Ranson, M. H. (2005). Systematic variation in willingness to pay for aquatic resource improvements and implications for benefit transfer: a meta-analysis. Can. J. Agric. Econ. 53, 221–248. doi: 10.1111/j.1744-7976.2005.04018.x

CrossRef Full Text | Google Scholar

Johnston, R. J., and Rosenberger, R. S. (2010). Methods, trends and controversies in contemporary benefit transfer. J. Econ. Surv. 24, 479–510. doi: 10.1111/j.1467-6419.2009.00592.x

CrossRef Full Text | Google Scholar

Jones and Stokes Associates. (1990). Environmental Benefits Study of San Joaquin Valley's Fish and Wildlife Resources. JSA 87-150, Final Report. Prepared by J. B. Loomis, W. M. Hanemann, and T. C. Wegge. Sacramento, CA.

Knetsch, J. L. (2007). Biased valuations, damage assessments, and policy choices: the choice of measure matters. Ecol. Econ. 63, 684–689. doi: 10.1016/j.ecolecon.2007.02.012

CrossRef Full Text | Google Scholar

Krutilla, J. V. (1967). Conservation reconsidered. Am. Econ. Rev. 57, 777–786.

Google Scholar

Lackey, R. T., Lach, D. H., and Duncan, S. L. (eds.) (2006). Salmon 2100: The Future of Wild Pacific Salmon. American Fisheries Society: Bethesda, MD.

Google Scholar

Layton, D. F., Brown, G. M., and Plummer, M. L. (1999). Valuing Multiple Programs to Improve Fish Populations.

Lew, D. K., and Wallmo, K. (2011). External tests of scope and embedding in stated preference choice experiments: an application to endangered species valuation. Environ. Resour. Econ. 48, 1–23. doi: 10.1007/s10640-010-9394-1

CrossRef Full Text | Google Scholar

Lin, P., Adams, R. M., and Berrens, R. P. (1996). Welfare effects of fishery policies: Native American Treaty Rights and Recreational Salmon Fishing. J. Agric. Resour. Econ. 21, 263–276.

Google Scholar

Lipton, D., Lew, D. K., Wallmo, K., Wiley, P., and Dvarskas, A. (2014). The Evolution of Non-Market Valuation of Coastal, U. S., and Marine Resources. J. Ocean Coast. Econ. 2014, 6. doi: 10.15351/2373-8456.1011

CrossRef Full Text

Loomis, J. (1992). The evolution of a more rigorous approach to benefit transfer: benefit function transfer. Water Resour. Res. 28, 701–705. doi: 10.1029/91WR02596

CrossRef Full Text | Google Scholar

Loomis, J. (1996). Measuring the economic benefits of removing dams and restoring the elwha river: results of a contingent valuation survey. Water Resour. Res. 32, 441–447. doi: 10.1029/95WR03243

CrossRef Full Text | Google Scholar

Loomis, J. B., and White, D. S. (1996). Economic benefits of rare and endangered species: summary and meta-analysis. Ecol. Econ. 18, 197–206. doi: 10.1016/0921-8009(96)00029-8

CrossRef Full Text | Google Scholar

Loomis, J., and Richardson, L. (2007). Benefit Transfer and Visitor Use Estimating Models of Wildlife. Fort Collins, CO: Department of Agricultural and Resource Economics, Colorado State University. Available online at: http://dare.agsci.colostate.edu/outreach/tools/

Louviere, J. J., Hensher, D. A., and Swait, J. D. (2000). Stated Choice Methods: Analysis and Application. Cambridge, UK: Cambridge University Press.

Louviere, J. J., Flynn, T. N., and Carson, R. T. (2010). Discrete choice experiments are not conjoint analysis. J. Choice Model. 3, 57–72. doi: 10.1016/S1755-5345(13)70014-9

CrossRef Full Text | Google Scholar

Mansfield, C., Van Houtven, G., Hendershott, A., Chen, P., Porter, J., Nourani, V., et al. (2012). Klamath River Basin Restoration Nonuse Value Survey Final Report. Research Triangle Park, NC: RTI International, prepared for the US Bureau of Reclamation.

Google Scholar

Mantua, N. J., Hare, S. R., Zhang, Y., Wallace, J. M., and Francis, R. C. (1997). A pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 78, 1069–1079.

Google Scholar

McCullough, D. A., Bartholow, J. M., Jager, H. I., Beschta, R. L., Cheslak, E. F., Deas, M. L., et al. (2009). Research in thermal biology: burning questions for coldwater stream fishes. Rev. Fish. Sci. 17, 90–115. doi: 10.1080/10641260802590152

CrossRef Full Text | Google Scholar

Mitchell, R. C., and Carson, R. T. (1989). Using Surveys to Value Public Goods: The Contingent Valuation Method. New York, NY: Resources for the Future.

Google Scholar

Navrud, S., and Ready, R., (eds.) (2007). Environmental Value Transfer: Issues and Methods. Dordrecht: Springer.

Google Scholar

Nehlsen, W., Williams, J. E., and Lichatowich, J. A. (1991). Pacific salmon at the crossroads: stocks at risk from California, Oregon, Idaho, and Washington. Fisheries 16, 4–21.

Google Scholar

Nelson, J. P., and Kennedy, P. E. (2009). The use (and abuse) of meta-analysis in environmental and natural resource economics: an assessment. Environ. Resour. Econ. 42, 345–377. doi: 10.1007/s10640-008-9253-5

CrossRef Full Text | Google Scholar

Olsen, D., Richards, J., and Scott, R. D. (1990). Columbia River and Tributaries Study CRT 73: A Study of Existence and Sport Values for Doubling the Size of the Columbia River Basin Salmon and Steelhead Runs. US Army Corps of Engineers North Pacific Division.

Olsen, D., Richards, J., and Scott, R. D. (1991). Existence and sport values for doubling the size of Columbia River Basin salmon and Steelhead runs. Rivers 2, 44–56.

Oregon Department of Environmental Quality. (2009). Willamette Rivers & Streams Assessment. An Oregon Plan for Salmon & Watersheds report funded through Oregon Watershed Enhancement Board grant # 206–932. Available online at: http://www.deq.state.or.us/about/eqc/agendas/attachments/2009oct/F-WillametteBasinAssessmentRpt.pdf

Oregon Department of Fish and Wildlife (ODFW). (2011). Upper Willamette River Conservation and Recovery Plan for Chinook Salmon and Steelhead. Available online at: http://www.dfw.state.or.us/fish/CRP/upper_willamette_river_plan.asp

Parsons, G. R. (2003). “The travel cost model. Chapter 9,” in A Primer on Nonmarket Valuation eds P. A. Champ, K. J. Boyle, and T. C. Brown (Dordrecht: Kluwer), 269–329. doi: 10.1007/978-94-007-0826-6_9

CrossRef Full Text

Pate, J., and Loomis, J. (1997). The effect of distance on WTP values: a case study of wetlands and salmon in California. Ecol. Econ. 20, 199–207. doi: 10.1016/S0921-8009(96)00080-8

CrossRef Full Text | Google Scholar

Power, T. M., and Barrett, R. N. (2001). Post-cowboy economics: pay and prosperity in the New American West. Island Press: Washington, DC.

Google Scholar

Richardson, L., and Loomis, J. (2009). The total economic value of threatened, endangered and rare species: an updated meta-analysis. Ecol. Econ. 68, 1535–1548. doi: 10.1016/j.ecolecon.2008.10.016

CrossRef Full Text | Google Scholar

Sheer, M. B., and Steel, E. A. (2006). Lost watersheds: barriers, aquatic habitat connectivity, and salmon persistence in the Willamette and Lower Columbia Rivers Basins. Trans. Am. Fish. Soc. 135, 1654–1669. doi: 10.1577/T05-221.1

CrossRef Full Text | Google Scholar

Smith, V. K., and Pattanayak, S. K. (2002). Is Meta-Analysis a Noah's Ark for non-market valuation? Environ. Resour. Econ. 22, 271–296. doi: 10.1023/A:1015567316109

CrossRef Full Text | Google Scholar

Smith, V. K., Van Houtven, G., and Pattanayak, S. K. (2002). Benefit transfer via preference calibration: “prudential algebra” for policy. Land Econ. 78, 132–152. doi: 10.2307/3146928

CrossRef Full Text | Google Scholar

Stanley, T. (2001). Wheat from chaff: meta-analysis as quantitative literature review. J. Econ. Perspect. 15, 131–150. doi: 10.1257/jep.15.3.131

CrossRef Full Text | Google Scholar

Stevens, T. H., Belkner, R., Dennis, D., Kittredge, D., and Willis, C. (2000). Comparison of contingent valuation and conjoint analysis in ecosystem management. Ecol. Econ. 32, 63–74. doi: 10.1016/S0921-8009(99)00071-3

CrossRef Full Text | Google Scholar

Stouder, D. J., Peter Bisson, A., and, Naiman, R. (eds.) (1997). Pacific Salmon & Their Ecosystems: Status and Future Options. Dordrecht: Springer Science & Business Media. doi: 10.1007/978-1-4615-6375-4

CrossRef Full Text | Google Scholar

The Research Group. (1989). Final Report: Survey and Economic Impact Analysis of the 1988 Willamette Run Spring Chinook Sports Fishery. Corvallis, OR: Prepared for the Oregon Department of Fish and Wildlife.

The Research Group. (2014). “LLC, with assistance from the Coastal Oregon Marine Experiment Station,” Oregon Commercial Fishing Industry in 2013, Briefing Report. Prepared for Oregon Department of Fish and Wildlife and Oregon Coastal Zone Management Association. Available online at: http://www.dfw.state.or.us/agency/economic_impact.asp

US Geological Survey. (2015). National Hydrography Dataset, Watershed Boundary Dataset. Available online at: http://nhd.usgs.gov/wbd.html

US Bureau of Labor Statistics. (2015). Consumer Price Index Inflation Calculator. Available online at: http://www.bls.gov/data/inflation_calculator.htm

US Environmental Protection Agency. (2010). Guidelines for Preparing Economic Analyses. Available online at: http://yosemite.epa.gov/ee/epa/eerm.nsf/vwAN/EE-0568-50.pdf/\protect\T1\textdollarfile/EE-0568-50.pdf

US National Oceanic and Atmospheric Administration (NOAA). (2010). ESA Salmon Listings. Available online at: http://www.nwr.noaa.gov/ESA-Salmon-Listings,/

US National Research Council of the National Academy of Sciences. (2004). Toward Better Environmental Decision-Making. Committee on Assessing and Valuing the Services of Aquatic and Related Terrestrial Ecosystems. The National Academies Press: Washington, DC.

US Office of Management and Budget. (2003). Regulatory Analysis. Available online at: http://www.whitehouse.gov/omb/circulars_a004_a-4/

Van Houtven, G., and Poulos, C. (2009). Valuing welfare impacts of beach erosion: an application of the structural benefit transfer method. Am. J. Agric. Econ. 91, 1343–1350. doi: 10.1111/j.1467-8276.2009.01345.x

CrossRef Full Text | Google Scholar

Van Houtven, G. L., Pattanayak, S. K., and Depro, B. M. (2011). “Benefits transfer of a third kind: an examination of structural benefits transfer,” in Preference Data for Environmental Valuation (Explorations in Environmental Economics Series) Routledge eds J. Whitehead, J. C. Huang, and T. Haab. Available online at: http://yosemite.epa.gov/ee/epa/eerm.nsf/vwAN/EE-0505-01.pdf/\protect\T1\textdollarfile/EE-0505-01.pdf

Vaughan, W. J. (1986). The Water Quality Ladder, included as “Appendix B” in The Use of Contingent Valuation Data for Benefit/Cost Analysis in Water Pollution Control CR-810224-02, eds R. C. Mitchell and R. T. Carson (Washington, DC: U.S. Environmental Protection Agency).

Wallmo, K., and Lew, D. K. (2011). Valuing improvements to threatened and endangered marine species: an application of stated preference choice experiments. J. Environ. Manage. 92, 1793–1801. doi: 10.1016/j.jenvman.2011.02.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Wallmo, K., and Lew, D. K. (2012). Public willingness to pay for recovering and downlisting threatened and endangered marine species. Conserv. Biol. 26, 830–839. doi: 10.1111/j.1523-1739.2012.01899.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Weber, M. A. (May, 2010). EPA use of ecological nonmarket valuation. Assoc. Environ. Resour. Econ. Newsl. 30, 26–35.

Weitzman, M. L. (1998). Why the far-distant future should be discounted at its lowest possible rate. J. Environ. Econ. Manage. 36, 201–208. doi: 10.1006/jeem.1998.1052

CrossRef Full Text | Google Scholar

Wilson, M. A., and Hoehn, J. (2006). Valuing environmental goods and services using benefit transfer: the state-of-the art and science. Ecol. Econ. 60, 335–342. doi: 10.1016/j.ecolecon.2006.08.015

CrossRef Full Text | Google Scholar