
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
HYPOTHESIS AND THEORY article
Front. Lang. Sci. , 21 February 2023
Sec. Neurobiology of Language
Volume 2 - 2023 | https://doi.org/10.3389/flang.2023.1107584
This article is part of the Research Topic Syntax, the brain, and linguistic theory: a critical reassessment View all 11 articles
Classical syntactic features are revisited from an algebraic perspective, recalling a traditional argument that the ±N vs. ±V distinction involves correlated, conceptually orthogonal, features, which can be represented in the algebraic format of ±1 vs. ±i complementary elements in a vectorial space. Coupled with natural assumptions about shared information (semiotic) systems, such a space, when presumed within a labeling algorithm, allows us to deduce fundamental properties of the syntax that do not follow from the presumed computation, like core selectional restrictions for lexical categories or their very presupposition in the context of a system of grammatical categories. This article suggests how that fundamental distinction can be coupled with neurophysiological realities, some of which (represented as mathematically real) can be pinpointed into punctual representations, while others (represented as mathematically complex) are, instead, fundamentally distributed. The postulated matrix mechanics amounts to a novel perspective on how to analyze syntactic neurophysiological signals.
Syntax has profited from the Computational Theory of Mind (CTM, Fodor, 1975), which sustains recursion—a hypothesis that Generative Grammar was central in establishing. In the current Minimalist Program (MP), the recursive operation Merge (M) is foundational, as is the presumption of a computational system of human language: CHL. The force of this assumption has taken some to seek M in neurophysiology. Frederici (2017), for instance, asserts that “Merge has a well-defined localization in the human brain,” in “the most ventral anterior portion of the BA 44”—within Broca's area, the premise being that “neural activation reflects the mental construction of hierarchical linguistic structures.” Many are interested in grounding the categories M relates1, correlating the presumed symbols to brain events. Friederici herself suggests that different neuronal networks, bound by fiber tracts, support the presumed syntactic processes, as well as a functional language network (FLN) at the molecular level, inferring information to flow “from the inferior frontal gyrus back to the posterior temporal cortex via the dorsal pathway” (p. 129).
Other researchers are more guarded. Emphasizing how theories of the brain, TB, and theories of the mind, TM, appear orthogonal to one another, Embick and Poeppel (2015) stress how “although cognitive theories and [neurobiology] theories are advancing in their own terms, there are few (if any) substantive linking hypotheses connecting these domains.” Two reasons underlie that incommensurability: (i) “computational/ representational and [neurobiological] theories have… distinct ontologies” and also (ii) there appears to be a granularity mismatch at the level of analysis. TM deals with formal devices and their interactions, while TB deals with waves and how they overlap in time sequences, across brain regions. Correlation questions then arise: are TM and TB elementarily equivalent? Is one an extension of the other? Do they share a common model or at least a mapping? Poeppel and Embick (2005) plead that the computational/representational theories of language can be used to investigate its foundations. It is worth asking how such hopes can materialize, also for two reasons.
One reason has to do with what appears to gear neuroscience. It is useful to check, for example, its Wikipedia entry2, where the discipline is described as “a multidisciplinary science” that is taken to range from biophysics to statistics, including medicine, chemistry, psychology, or computer science. Linguistics is only briefly mentioned via neurolinguistics, described as “the study of the neural mechanisms in the human brain that control the comprehension, production, and acquisition of language.” The relevant entry for that subdiscipline3, in turn, has relatively little bearing on the theoretical issues that concerned Embick and Poeppel (2015). While this is meant as a mere sociological indicator, it can be distressing, particularly when approaches that have emerged as self-perceived opponents of the CTM are seen as a priori more relevant, inasmuch as they deal with so-called neural networks, whose relative success mesmerize much of the general public4.
The second reason for caution stems from the realities of MP as it stands, as reviewed in Lasnik and Uriagereka (2022). It is easy to show that the CTM is tangential to whether the phenomena we model should exhibit, for instance, selectional restrictions or separate into lexical and functional interactions. It seems at right angles with the computational aspects of the CTM, its finitistic nature, and its properties of systematicity, productivity, or transparency, whether computations are bottom-up or left-to-right, splitting into form and interpretation, or even when lexicalization happens. More generally, it is unclear whether relevant units—a syllable or a verb phrase—are categories, interactions, or whether it may all depend. It seems unlikely that future empirical research will demonstrate that vowels and consonants actually do not organize into syllables or that languages do not universally distinguish nouns and verbs. But “associationist” alternatives to the CTM are quick to presume that relevant conditions “emerge” from the communicative strictures taken to affect language, the idea being that hallmarks of the system are effective stabilities within an interconnected ensemble. While that may be hard to ascertain, there is nothing much that the CTM has to offer about substantive realities, or why the system is not carried on other modes of expression. It is all summarily blamed “on the interfaces,” except those too tend to say little as to why that is, as opposed to some reasonable alternative.
The call for the present volume probes “Which brain regions support syntax, what are [its] temporal dynamics …; and is [its] processing separable from lexical and semantic processing?” We ask because we do not know. We have a consensus that Broca's area is key, which we get glimmerings of in deficits like Broca's aphasia. We know this remarkable system manipulates and carries a particular kind of information forward in time—in Gallistel and King's (2010) memorable characterization of memory—but we lack an understanding, yet, as to what even a symbolic unit is, whether it is consonants/vowels or their interactions into syllables, nouns, verb phrases, and long-range correlations. In what follows, I delve into these matters from the perspective of correlated categorial features, as reviewed in section 3, after assessing the syntactic problem of types, tokens, and crucially (long-range) occurrences in section 2. The technical solution I have proposed elsewhere is discussed in section 4 and the proposal for a neurophysiological approach is introduced in section 5.
The CTM generally presumes Marr's (1982) Tri-Level Hypothesis in treating vision as an information processing system—with three levels of analysis: (i) computational (what problems the system solves), (ii) algorithmic/representational (what representations it uses), and (iii) implementational (how it is physically realized). Pylyshyn (1984) interpreted these as intentional, symbolic, and biophysical. We do not have a good understanding yet of how even the more abstract intentional level connects to the symbolic one. The relationship (between expression and meaning) is philosophically taken to be a representation between a subject and a theory of a formal language, correlating a symbol and what it stands for. Arguing that there is no simple referent in the natural language examples this hypothesis presupposes, Chomsky (1993) has been consistently critical of our understanding of this particular relationship. Bringing this to formatives of grammar, elements manipulated in syntactic computations include sentences, phrases, words, all the way “down” to features. The question is what the putative representational relationship is between feature F, word W, phrase P, sentence S, etc., and whatever F, W, P, or S, ultimately signifies for the linguistic system.
In these terms, we tell ourselves that, for instance, the feature voiced in phonology (separating the first phoneme in bit vs. pit) represents something in neurophysiology (e.g., voice onset time, VOT, see Poeppel, 2003)5. It is, however, unclear whether the “representational” claim helps us understand what the phenomenon boils down to, let alone more abstract notions like phrases and the like. Are we to seek a literal representation for the projection of what syntacticians call (little) v, so that we can expect to (eventually find) vP within the FLN? This can get quite abstract when considering long-range correlations presumed for bound-variable bindings. To date, a fair amount is understood about the intentional/computational level and speculations exist about the “lower” symbolic (for Pylyshyn) or algorithmic (for Marr) level; some are even willing to consider a Tractable Cognition Thesis [van Rooij (2008), see Balari and Lorenzo (2012) for a minimalist view], taking human computational capacities to be constrained by computational tractability. All of that seems relevant to neurophysiology, even if one can independently measure brain activity with whatever technology or technique may become available.
In between the computational and implementational levels, conditions on the algorithmic level, and in particular computational tractability, may actually vary depending on the biophysical support of the presumed algorithm, for example depending on how much parallel computation they allow [see Rieffel and Polak's (2011) introductory chapter on this, for a broader perspective]. The syntax is often likened to “Lego rules”: smaller and smaller pieces combine to yield structures within some aggregative architecture (Baker, 2001). Cognition from this perspective translates into systematically manipulating symbols in combination with the internal states of some Turing machine, its details (whether carried by neurons or silicon chips) being irrelevant if computational inputs are arbitrarily represented. It is at that foundational assumption that alternative foundations bottom out - less “legos” than separable states in entangled networks. While classical computations build the system constructively from bits, from the parts to the whole (including the difficult emergence of long-range correlations), computations may also work restrictively, with long-range correlations in the nature of the ensemble itself; the issue then being under what circumstances these separate into classical units.
To be candid, no one could seriously affirm that the mind phenomenon, at least with regards to language as we experience it, is not classical in some fundamental sense, since obviously we remember words and they are different from one another (even if related in intricate ways). We know not just that the word pet is different from the word charming, but also from the word bet. At the same time, is the feature separating bet from pet (intuitively relating to VOT) exactly the same as the feature separating bit from pit? If this identity of features indeed obtains, how does the brain store feature types like F that get distributed over token uses as the need emerges—e.g., VOT for bet, bit, “the same” for each relevant word?
Color perception may be a relevant model (see Palmer, 1999). This starts with activating light-sensitive (retinal) cones, the types of which allow for various nuances (selectively deactivated in “color-blindness”). In this view, there would be some locus for VOT that gets invoked when pronouncing a voiced phoneme. But it could also be that, as they get more abstract, features are somehow distributed over a network of words like pit and bit, in which case we need to think about what it means to have information thus dispersed. The identity of token uses of a word like bit need not be the same as the identity implied by the VOT associated with given features. While folks seem aware of their knowledge of words—being able to comment on (never) having heard them—only language scientists care about feature uses, the ultimate repository of relevant features still being debated. In short, classical memory concerns seem rather more relevant to words than to their underlying features.
Only the most abstract features may enter into entangled ensembles of the sort relevant to long-range correlations. For instance, so-called φ-features surface via the phenomenon of agreement, across domains and under tight strictures (c-command or locality), none of which matters to VOT triggering. If a feature does not participate in long-range Agree specifications, why should one think of it in computational terms that presume such a correlation? In contrast, though, for features where said correlations are manifest, assuming the correlations in the ensemble does simplify our analysis.
Bear in mind how syntactic ontologies really go well beyond type and token distinctions, into occurrences in the general sense of Quine (1940):
(1) Some politician seems to hate every reporter after meeting them.
(2) a. ∃x politician(x) [∀y reporter(x) [x seems [x to hate y [after x meeting y]]]]
b. ∀y reporter(y) [∃x politician(x) [x seems [x to hate y [after x meeting y]]]]
Sentence (1) is structurally ambiguous, as in (2), with each representation of variables x, y as occurrences thereof, whose denotation happens to be distributed over the quantifier-variable dependency, thus simultaneously expressed over various configurations. This leads to many formal complications6. The problem boils down to what it means for the system to copy the relevant information and how that differs from bonafide repetitions of that information. Compare7:
(3) a. Some seem some to hate problems.
b. Some seem as if some hate problems.
In most minimalist proposals, (3a) involves two occurrences of (copied) some, while in (3b) some is fully repeated, not copied—each repetition bearing independent and autonomous reference. However, the English lexicon only has one lexical type some, “tapped” twice in (3b) but only once in (3a).
The theory also presumes that there is a full copy of some as in the strikeout representation in (3a), because of “reconstructed” examples as in (4), which presuppose anaphoric licensing:
(4) a. Some pictures of himself seemed to Trump some pictures of himself to create problems.
b. Some pictures of himself seemed to Trumpi some pictures of himselfi to create problems.
The gist of Chomsky (1995) analysis is simple. Whereas the representation yielding the overt PF is of the sort in (4a), the one covertly leading to LF is as in (4b), the anaphor “reconstructed” (interpreted) in the structurally lower site, under the scope of the co-indexed antecedent. This, note, implies that copied tokens are interpreted at one of their occurrences. While a well-characterized phenomenon, this is a difficult outcome to obtain beyond stipulating the result itself, for unclear reasons.
The same issues arise for features, in languages exhibiting the relevant concord:
(5) Terminadas las tareas, parecían
finished.FM.PL the.FM.PL work.FM.PL seemed.PL
las cinco ya dadas,
the.FM.PL five already given.FM.PL
a. … que puede que sea<(n)> hora<(s)> de ir a casa.
which may.SG that be(PL) hour.FM(.PL) of to.go to home
b. … que pued<(en)> ser hora<(s)> de ir a casa.
which may(.PL) to.be hour.FM(.PL) of to.go to home
“With the work finished, it seemed to be past five, which is likely
that it is time to be home already/to be time to go home already.”
In Spanish (5), the copied or repeated item in this instance is the abstract bundle corresponding to plural and possibly also gender marking. Note that there are co-occurrence restrictions at stake: the sets of features within the sentential portions contained within the commas can be argued to be occurrences, while those across—although also identical in observed shape—are nonetheless repetitions with fully separate import, not mere copies that somehow spread within a domain.
The case of agreement repetition/copy is interesting on two counts. First, it is unclear what it would mean to copy anything in these agreement instances. The idea behind copies stems from generalizing the M operation—which assembles syntactic objects α, β (heads or their phrasal projections) into a set {α, β}—to conditions in which β is contained within α (i.e., [α … β … α]). Then the system creates a separate occurrence of β at the root of the phrasemaker: [β [α … β … α]]. But if this is how the syntax obtains copies through M, how could the copies presume, for instance, in the main sentence in (5) be obtained? Observe the relevant portion of the structure:
(6) [T′ T[VPparecían[SClas cinco [PredP ya dadas PredP]SC]VP]T′]
seemed.PL the.FM.PL five already given.FM.PL
“It seemed to be past five.” (Five seemed to have been struck.)
It is impossible to reproduce this sentence in English, where subjects must be preverbal. In Spanish, though, one can leave the subject behind8, but the concord still shows up in the verb parecían, literally “(they) seemed”, with a mark of plurality, in agreement with the subject in point. Now the key here is that, in that representation, the subject has not actually been copied (via “internal” M, IM) at the beginning of the sentence: it appears in situ instead. So the agreement occurrences that one observes in said verb must have gotten there some other way.
One may be tempted to open some semantic file to deal with such agreement occurrences, which after all show up in quantificational instances as in (3) and (4), where the presumed co-variations led Quine to his 1940 proposal about variable occurrences. Then again, there is not much of a reference at stake in the occurrences in (6): here they are purely formal, accessing indications of time that, thus, get spread over the sentence. While one may speak of reference to politicians and reporters, it is less obvious what that might mean for five o'clock, which in Spanish happens to be the feminine plural, arbitrarily so. Indeed, in an acceptable variant of (6) without concord, the morphological features that still show up (third person singular) do so “by default”—which absolutely lack referentiality. In sum, something allows these features to spread throughout syntactic domains, sometimes as occurrences, others being lexically accessed as separate token features, which happen to be identical (e.g., FM.PL) to other features independently occurring in the structure [as boldfaced in (5)]. The question is whether these instantiations of feature types are tokens or, instead, occurrences.
Here is the punchline then: while classical computational systems are generally quite good at building interactions of the token sort, by accessing types within some long-term repository (a lexicon) and treating them as building blocks, they are less apt to create these immaterial occurrences, only the collective of which end up amounting to a token, in some aggregative fashion. In contrast, computations building on correlations do just that, by their very design: the (relatively) easy part is to model the interaction in abstract space, while the hard job is actually to have any of that collapse into observables that behave classically enough to get pronounced, obtain concrete interpretations9, and to crucially be stored in some reliable way that makes future access straightforward. Then again, the linguistic system seems to be telling us, also, that the task is performed so delicately that it can be mediated by long-range correlations allowing such nuanced expressions as those discussed in this section, which no classical computation has been able to state without resorting to arbitrary codings.
Supposing a neurophysiological FLN, what sort of information does it manipulate? The theory an FLN presumes computationally rests on underlying features. This was the case for Chomsky since his transformational 1955 manuscript. In the appendix to chapter 4 of the unpublished version10, the reader is reminded that the “analysis into Nouns, Verbs, and Adjectives is a fundamental one… into four categories N, V, A, and X (everything else), with heavy overlaps.” By 1981, Chomsky was taking the overlaps to be “based on two categories of traditional grammar: substantive … and predicate.” Indeed, Varro had spoken of a similar intuition in De Lingua Latina11, when reminding us how “… the Greeks have divided speech into four parts, one in which the words have cases, a second in which they have indications of time, a third in which they have neither, a fourth in which they have both.”
That idea resurfaced in Chomsky (1974), where it was taken as a working hypothesis that:
… the structures of formal grammar are generated independently and … associated with semantic interpretations by… semiotic theory… Under this hypothesis one would expect to find systematic relations between form and context [sic] … [T]he organism has the theory of formal grammar… as a basis for language learning that will allow certain grammars… [p. 21]
Since the manuscript was never edited for publishing, it is unclear whether Chomsky meant “form and content,” but either way it is clear that he was arguing for the autonomy of syntax while exploring how it may relate to meaning, which relates to the Projection Problem12. In 1974, Chomsky was already pursuing a restrictive theory (for explanatory adequacy), hypothesizing a grammar to be “a system of constraints on derivations,” so as “to restrict the class of possible systems” (p. 23, lecture 1). He had already signaled there (albeit as a “secondary consideration”) the minimalist desideratum that “the restrictions that we impose on the theory [should] be in some poorly understood sense natural.”
Chomsky's more technical discussion in 1974 is as follows:
As far as the categorial component is concerned, it seems to me plausible to suggest that it is a kind of projection from basic lexical features through a certain system of schemata as roughly indicated in [7] and [8]:
(7) [±N, ±V]: [+N, –V] = N[oun]; [+N, +V] = A[djective]; [–N, +V] = V[erb], [–N, –V] = everything else;
(8) Xn → … Xn − 1…, where xi = [a = ±N, b = ±V ]i and X1 = X. Let us assume that there are two basic lexical features N and V (±N, ±V). Where the language has rules that refer to the categories nouns and adjectives… they will be framed in terms of the feature +N and where there are rules that apply to the category nouns and adjectives, … in terms of the feature +V. [Chomsky, 1974: Lecture 3, p. 2]
This is Chomsky's way of addressing the “heavy overlaps” from Chomsky (1955)—the features representing relevant correlations. It is worth exploring those more thoroughly.
Note that the “else” category category from Chomsky (1955) remains in Chomsky (1974), over combinations of the [–N, –V] type. The fact that it is both features that entail the elsewhere case suggests they are correlated. More generally, in Lecture 3 of 1974, Chomsky spoke of “rules that refer to the categories nouns and adjectives [+N] … and … rules that apply to the category of verbs and adjectives… framed in terms of the feature +V.” He also considered “lexical categories” as those with “feature complexes that give N, A, and V” (with some positive values in the pair), once again suggesting a correlation between the features themselves. By 1981, Chomsky was explicit about –N elements, which he took to assign Case (an idea that he was willing to extend to the functional category INFL) vs. +N elements that were taken to receive Case13. It is less obvious what feature ±V amounts to, beyond its being “predicative” (p. 46) for +V.
In 1981, Chomsky took “the Base component of the grammar” to consist of “the categorial component and… the lexicon, to which [he] assigned a central role in the syntax by virtue of the projection principle… [taking] the lexicon to be a set of lexical entries, each specified as to category and complement structure, with further idiosyncrasies” (p. 92). For Chomsky, the primary way to address the problem of projection from data to grammar is to take “the categorial component of the core grammar of a particular language… [to] be just a specification of parameters … with regard to ordering and internal structure of major categories… [T]he class of well-formed base structures for the language is determined by properties of lexical entries under the projection principle, and by… Case theory, perhaps also parametrized. Many potential grammars are excluded by these assumptions [within the] guiding principle of restrictiveness for linguistic theory.” (p. 95)
In that context, Chomsky considered language-specific selectional restrictions, with auxiliary have rejecting [+N] complements, as compared to be, which takes [+V] complements (p. 55). The idea of “rejecting a class of complements” implies a disjunction14, again a correlation between the relevant features. Chomsky discussed several other feature correlations; e.g., in terms of government and proper government (p. 50, 52, and 163; see fn. 16). On page 252, he considered the possibility that only “categories with the features [+N] or [+V]” are proper governors—this being closer to the notion of “lexical category” in lecture 3 of 197415, emphasizing attribute correlation within the features.
There are further passages in 1981 where Chomsky concentrates on feature attributes, neutralizing corresponding values (p. 52, pp. 117–118). One such is deployed for syntactic passives (treated as “neutralized verb-adjectives with the [sole] feature [+V]”). One must then surmise either a free-standing N attribute (instead of a pair (attribute, value), as presumed for any full feature) or else a ±N feature, with dual value. According to Chomsky, this is because “syntactic passive participles are sometimes treated as adjectival and sometimes as verbal”—again suggesting a correlation between feature values, which can thus be targeted in unison. On pages 127 and 142, fn. 49, Chomsky considered parameterizing such nuances, to distinguish English from Hebrew passives.
In 1974, lecture 3, page 3, Chomsky asserted that basic phrase-markers are “projected from the lexical categories uniformally,” for “in a fundamental way the expansion of major categories like NP, VP, AP is independent of categorial choice of the head … [as] instantiations of the same general schemata.” This is the origin of X'-theory, later to morph into the minimalist Bare Phrase Structure in chapter 3 of Chomsky 1995—instantiating M and presuming not just learnability considerations, but also economy/symmetry criteria. In that lecture, Chomsky seemed interested already in “subsidiary features” relating to “higher order endocentric categories.” At that time, only INFL and COMP had been explored, and Chomsly in 1981 took the “S-system [not to be] a projection of V but rather of INFL,” this category containing “the element AGR … when … [+Tense], where AGR… [stems from] a feature complex including [+N, –V] (p. 164).” The categorial system is, thus, not restricted to the lexical categories, but it extends to functional categories. Similar considerations apply to small clauses on page 169, as projections of an [+N, +V] element. Other authors within that theoretical framework raised similar questions about COMP (treated as adpositional in Kayne, 1994) or DET, once it became isolated as its own category (as relationally analyzed in Szabolcsi, 1983).
It is also interesting that A-chains were characterized in Chomsky 1981 (to distinguish them from A'-chains of Wh-movement) and restricted to [+N, –V] projections (see, e.g., p. 224, fn. 23). This raises the question of why A-chains should be thus restricted or why the Case/Agr system should target nominal projections only. If it were to target the +N elements it should extend to adjectives, and if –V elements, also to adpositions. But neither is the case, only the combination [+N, –V] is targeted for the transformational process in point, again emphasizing a correlation among those categorial features.
The foundational matters we have been sketching have not disappeared. Thus, languages:
(9) a. … distinguish lexical and functional categories, the latter being (relatively) structurally higher.
b. … separate the major syntax-articulating categories of nouns and verbs (even abstract ones).
c. … exhibit abstract features from nouns/verbs, arguably playing syntactic roles elsewhere.
d. … display sub-categorization and selection restrictions that are specific to a particular language.
In addition, after decades of studying how to constrain grammar, we continue to wonder:
(10) a. Why there are so many grammatical sub-theories about (extended) noun projections.
b. Why the grammar exhibits A vs. A' movement—and how it can be characterized.
c. Why A is movement restricted to (extended) NP projections.
d. Why A-chains “collapse” into a single occurrence (of many derivationally generated).
e. Why all long-range correlations are not clearly reducible to local correlations.
The list is neither meant as exhaustive nor is it clear that any available theoretical framework provides simple (let alone unified) answers to such questions.
In order to continue with a (biolinguistic) research program that should be able to directly address—or at least be guarded about—these foundational matters, it is instructive to explore ways in which to continue to formulate and constrain our theories, based on traditional considerations of feasibility. The following proposal is made in that spirit, noting how Smolensky and Legendre (2005) could be interpreted as a step in this general direction. While that work comes from a connectionist tradition that opposes the CTM (see Joe Pater's blog entries: https://blogs.umass.edu/brain-wars/the-debates/smolensky-vs-fodor-and-pylyshkyn/), it is not difficult to show how many of the basic presuppositions in this Integrated connectionist/symbolic (ICS) cognitive architecture can be achieved by one possible interpretation of Chomsky's 1974/1981 system of categorial features.
Without going into the ICS model, I will say this approach presumes two levels of description for cognition (as compared to the Marr/Pylyshyn classical approach). As Smolenksy (2006) puts it:
Parallel distributed processing (PDP) characterizes mental processing; this PDP system has special organization in virtue of which it can be characterized at the macrolevel as a kind of symbolic computational system. The symbolic system inherits certain properties from its PDP substrate; the symbolic functions computed constitute optimization of a well-formedness measure called Harmony. The most important outgrowth of the ICS research program is optimality theory… Linguistically, Harmony maximization corresponds to minimization of markedness or structural ill-formedness. Cognitive explanation in ICS requires the collaboration of symbolic and connectionist principles.
The development of this architecture rests on the compositional embedding of symbolic structures in a vector space, via tensor product operations. While the approach has been applied to linguistic and psycholinguistic problems not reviewed here—let alone its ramifications into so-called deep learning—I acknowledge this connection while showing how one can get there from symbolic presuppositions.
Chomsky 1974 worked from the traditional idea that N and V dimensions are conceptually orthogonal—as different as can be, being comparable to whatever distinguishes consonants and vowels. When facing such differences in a substantive way, one pulls from binary cognitive dualities to maximize interpretive differences. It is interesting how those can be addressed when dealing with matrices presenting specific eigenvalues that correspond to subspaces—as labels for measurement outcomes. While such labels can be used to represent any given property (like energy in a corresponding eigenspace), this assignment is not crucial, any distinct set of eigenvalues sufficing (see Rieffel and Polak, 2011, p. 54). Taking that idea as formal inspiration, Martin et al. (2019) express the implicit “conceptual orthogonality” (between the N and V dimensions) through mathematical orthogonality16:
(11) Fundamental Assumption
The V dimension is a transformation over an orthogonal N dimension.
Instantiating (11) in the complex plane, we can then conclude:
(12) Fundamental Corollary
The N dimension has unit value 1; the V dimension, unit value i; [±N, ±V] = [±1, ±i].
The Fundamental Corollary thus allows for algebraic operation with these features, as we see momentarily. In the Appendix to Chapter 4, Chomsky in 1955 attempted to derive the four major categories his formal features covered on information theoretic grounds, suggesting that this view of the relevant features was distributional. Here too, so far, all we are presuming is that the N and V features are formally as distinct as possible—in other words, nothing much about their “meaning.”
Chomsky (1981) did not seem to care about the order of the features he discussed. Although he normally listed them as the customary [±N, ±V], on page 48 [example (1)], he offers [V, ±N] as a possibility, which again surfaces on page 142, fn. 49, where he discusses [+V, –N] combinations. There is nothing wrong with this if the features are meant as substantive—the equivalent of advertising an item as “cheap, valuable” or “valuable, cheap.” Then again, if the features are meant to be correlated, the order could matter, just as it is not the same to put a golf ball on a tee to then hit it than to hit a tee to then put a ball on it… The complex expression (±1, ±i) expresses a different scalar from (±i, ±1), which can also be said about related vectors. This is relevant in that, as noted, in 1981, Chomsky wanted AGR in INFL (one of several subsidiary categories) to be [+N, –V], small clauses corresponding to [+N, +V] projections. If an order does matter, these decisions can be immediately separated by describing them as [–V, +N] and [+V, +N], respectively—similar possibilities obtaining for a relational DET with verbal characteristics [+V, –N] or an adpositional COMP assumed as [–V, –N].
It is hard to see how to operate with lists of substantive features (like “cheap” or “valuable”), but quite easy to imagine how to do so with formally orthogonal features like [±1, ±i] or [±i, ±1], since the following equivalences hold when presuming an entry-wise—also known as Hadamard—multiplication (remembering that i = √−1, so (±i)2 = −1 and i (–i) = –i i = 1)17:
(13) [±i, ±i] = [±i, ±1]
Note, in turn, that [±i, ±i] emerges from [±1, ±i] [±i, ±1] and [±i, ±1] [±1, ±i] products, while self-products (squares) of these very elements are as follows, with [1, 1] never emerging as a product:
(14) a. [±1, ±i]2 = [1, −1]; b. [±i, ±1]2 = [−1, 1];
c: [±i, ±i]2 = [−1, −1]
That [1, 1] category, however, does arise in many combinations. For instance:
(15) a. [1, i] [1, –i] = [1, 1]; [1, –i] [1, i] = [1, 1];
[−1, i] [−1, –i] = [1, 1]; [−1, –i] [−1, i] = [1, 1].
b. [i, 1] [–i, 1] = [1, 1]; [–i, 1] [i, 1] = [1, 1];
[i, −1] [–i, −1] = [1, 1]; [–i, −1] [i, −1] = [1, 1].
An entry-wise product by [1, 1], in turn, leaves any results unchanged, signaling an identity element:
(16) a. [±1, ±i] [1, 1] = [±1, ±i]; b. [±i, ±1] [1, 1] = [±i, ±1].
This, together with a simple examination of any other comparable products, easily shows the emergence of a group for Hadamard multiplication from these interactions, of the following general shape:
(17) a. [±1, ±i]; b. [±i, ±1]; c. [±1, ±1]; [±i, ±i].
While elements as in (17a) correspond to the Chomsky objects (per the Fundamental Assumption and its corollary), and those in (17b) may model functional categories associated with N, V, A, and elsewhere (e.g., P) projections, we need to consider what the other elements in the group correspond to.
Martin et al. (2019) model labeling in M (bare phrase) projections in such terms, for which they first consider a comprehensive characterization of M. The relation is often assumed to be asymmetrical, between a head (selected from the lexicon) and a phrasal projection (assembled in a syntactic derivation). That said, such an asymmetry is impossible when a derivational space is initiated, and we only have two heads from the lexicon. To keep M unified, though, one can presume it is anti-symmetrical, allowing reflexivity and otherwise forcing asymmetry in its terms. If M is to be thus interpreted, such a base condition—presuming reflexivity or asymmetry pertain to “level of projection” (whether the category projects)—entails that labeling in self-M (of the Chomsky objects) is equivalent to the squaring operations in (14a). This results in a trivial phrase, but a phrase nonetheless18.
However, note that all the powers in (14a) result in the very same [1, −1] category, which seems senseless for a semiotic system. We may thus assume the following, for now as an axiom:
(18) Anchoring Axiom: Only N categories [1, –i]N self-M (with labeling [1, –i]2 = [1, −1]).
There are some other reasonable assumptions one could make about the emerging algebraic system if it is to describe a semiotic/information algorithmic, recursive system; for example:
(19) a. All four category types within the group are deployed.
b. A given category must be included regardless of whether it falls into an equivalence class.
c. Categorial operators Ô maximize value diversity.
Maximizing said conditions, a labeling algorithm emerges. The system starts self-multiplying [1, –i] Chomsky's noun signaled by subscript N. The square of that category (where it is taken to act as an operator, represented with a hat “∧”, on itself) results in the N projection [1, −1]. The rest proceeds in like fashion, with the other categorial operators (the other three Chomsky categories). There are always “twin” results, an equivalent class in that the product of their values is the same −1 for the noun projections, i for the verb projections, –i for the adposition (elsewhere) projections, and 1 for the adjective projections. This equivalence leads to a refinement I return to momentarily. The graph in (18) carries a labeling algorithm with a START state and two possible END states, as well as presumed internal recursion. Although I will not prove this here, of all the possible multiplications the ensuing group allows, only those in the Jarret graph and those in a graph involving the mirror image of these categories (associated with functional categories, see fn. 25) satisfy the restrictive desiderata in (20).
(20) Original Jarret Graph19:
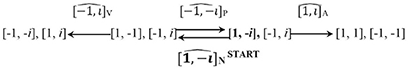
(21) It is also not hard to associate the Jarret graph with elementary “subcategorization restrictions”20:
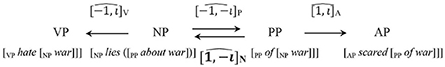
Importantly, these restrictions are not imposed here because of external (interface) conditions: they follow, instead, from the system's algebra, under the circumstances we have been examining. They would be different, for instance, if we were to change the Anchoring Axiom in (17), or we did not impose the information/semiotic conditions in (18). The take-home message: projections (“vertical”) and selection (“horizontal”) restrictions, which the Projection Problem encourages us to seek, follow from the “restrictivist” (labeling) theory, regardless of considerations of language use.
I mentioned a way to improve on the system: while the internal multiplication of the entries is of no obvious algebraic significance, it would be if, instead of just listing the features, we were to place them as diagonals in 2 × 2 square matrices (those being the simplest possible such matrices)21:
(22) a. NP: ; b. VP: ;
c. PP: ; d. AP: .
Now the subindices associated with the “twin” matrices are a well-known independent scalar: the matrix determinant, in this instance the product of the elements in the diagonal (the matrix eigenvalues)22. The twin matrices are, then, equivalent in that they have the very same eigenvalues, whose products result in the syntactic labeling without reference to the system's interfaces23. It is easy to show how the objects in (20) constitute an Abelian (commutative) group for matrix multiplication, directly satisfying the desiderata in (18) for a recursive semiotic/information algorithm, again with a START state at the object 24. I will not show this here, but once this matrix format is assumed, it can also be shown that the Anchoring Axiom becomes a theorem. This is because any anchoring of the system (via self-M, with labeling from a matrix square) in any other Chomsky matrix does not result in a semiotic/system satisfying the desiderata in (18)—so the Jarret graph is improved via 2 × 2 matrices25.
Orús et al. (2017) show how a direct extension of the Abelian group in (20) also covers all other standard Pauli matrices (X and Y). It is also easy to prove how the Pauli group can be expressed by way of the Chomsky matrices, none of which is crucial now. It is noteworthy that the ensuring system can express relevant correlations in superposed conditions that I will not review now, but which have a direct bearing on the questions in (10), rationally modeling chain labeling as in (10d). I will set this central motivation aside now though, to focus on neurophysiological matters instead.
Important for our purposes is to gain some insight into what the Fundamental Corollary in (12) amounts to while equating N to 1 and V to i. If meant seriously, this will have an immediate consequence for Euler's identity relating i to −1, via the base e of the natural logarithms:
(23) a. Euler's Identity: eiπ = −1 b. Linguistic version: evπ + N = 0
While that may seem arcane, bear in mind the trigonometric expression in (22), also extended:
(24) eix = cos x + i sin x; for x = π, eiπ = cos π + i sin π;
cos π + V sin π = –N
Euler's formula establishes a basic relation between complex exponential functions and trigonometric functions26. In the context of signal analysis, it is well-known from the Fourier series that any signal can be approximated to sums of sinusoidal functions, whose expression can be reduced to sines and cosines (Fourier analysis). Euler's formula allows us to express this algebraically. Thus, the Fourier Transform can be expressed indistinctly in terms of sines and cosines or in the boldfaced form in (25), the latter with implications now in that it gives a geometrical meaning to the fundamental assumption that the V dimension is a transformation over an orthogonal N dimension27.
(25) Feature Fourier Transform (FFT)
F(w) = ∫f(x)[cos(wx) − i sin(wx)] dx = iwx dx
Unpacking (25): the relation between the V and N dimensions can be seen as a Fourier transform F(w) between two correlated variables, w and x, such that w corresponds to some wave expression and x to some measurable—those variables then being complementary. Given the logic of this FFT, the more accurate representation we obtain of x, the less we can ascertain the details of w, and vice-versa28.
That formal complementarity can surface in a variety of linguistic contexts, just as it does in real-life situations (from acoustics to quantum mechanics). Lasnik and Uriagereka (2022), chapters 4 and 5, show how linguistic categories/interactions come in two guises: they may be punctual within the computation of a representation or, rather, distributed. In the realm of phonology, this is seen when comparing vowels (or continuant phonemes) to consonants (particularly stops). The phenomenon of alliteration banks on the repetition of the punctual stuff, while rhyme, instead, repeats the distributed information; a rhyme is distributed also in that, unlike alliteration, it can run across sentences. In terms of an equation as in (25), all we have to do is plug in the “consonant qualities” into N and the vowel “qualities” into V, and we have the presumed complementarity. We could think of it as a way to regulate articulators so that the more punctual they are, the less distributed, and vice-versa—but the complementarity remains as two aspects of the same FFT. The question is how to generalize that.
I lack the space here to go into various syntactic domains in which we arguably also obtain the complementarity the formal system allows, so I will discuss just one:
(26) a. Verbs constitute examples, in this sentence.
b. [TP Verbs [VP [ constitute examples] in-this-sentence]]]
c. ∃e {Cause (e, Verbs) ∃e' [Theme (e, e') & Present-constitute (e') & Theme (e', examples) & in-this-sentence(e')]}
The issue is not lexical access to the encyclopedic knowledge coded in the items verbs or constitute, associated with the pronunciations /vǝrbz/ and /'känstǝt(y)t/. The point is that the interpretation of verbs as in (26)—more accurately, verb, without the plural marker—is essentially indexical with regards to the meaning of that root, whatever it happens to be (in this instance an abstract entity, but it could be the concrete this verb, a more concrete entity associated to a verb name, or an actual pointing by the speaker). For the purposes of that logical form, verbs are a constant that can be replaced by any other29. This is not the case for constitute, which goes together with sub-event and quantificational paraphernalia as in (26c) that can be changed (if the verb is intransitive, ditransitive, introducing a clause, etc.) and be further modified by aspect nuances, modals, perspective shifts, and more. Again, it does not matter that the encyclopedic information of this particular transitive verb is constitute (as opposed to establish, comprise, represent…), but the verb must have the particular thematic structure in (26c), which could be further enriched into structural nuances too numerous to go into.
Just as we saw for the consonants and vowels, the formula in (25) provides us with features in the relevant categories whose effect is to secure the verb gets distributed over an expression like (26), unlike the argument nouns. Of course, this will necessarily have to be more abstract than in the phonemic case, but it is mathematically comparable. We could thus conceptualize verbs as modeling classes of eventualities obtaining of given kinds with some probability30, with the verb itself being a superposition of said probabilities. If so, the verb amounts to a probability ensemble (a wave of some sort), which can obtain a given realization through its subject in whatever context happens to be relevant. Usually, we presume phrasal axioms mapping syntactic objects to semantic representations. This is all fine, but also fairly arbitrary. The present system suggests that there are key features within the relevant categories that limit those mappings, so that, for instance, a noun phrase cannot be taken as the main event—unless, of course, there is a circumstance (e.g., an identification) in which this is actually plausible, relying on the fact that the relevant features are still complementary31.
The linguistic version of Euler's identity tells us why, if the verbal label is the imaginary i, then the corresponding nominal label has to be the real −132, or in matrix terms why the verbal matrix is the negative of the nominal one. Once that is, the verbal matrix has the elsewhere one as its conjugate, just as the nominal matrix has the adjectival as its conjugate (and those conjugates are negatives of one another). In terms of projections, moreover, any matrix in the Chomsky/Pauli group associated with determinant i will be a verbal extension in the functional domain, the same generalization holding for any other matrices within the group associated with −1 for nominal extensions, 1 for adjectival ones, and –i for the elsewhere case33, thus covering a wider grammatical space without going outside the overall algebraic system, in principle allowing us to extend the Jarret graph to grammatical categories.
Several other such examples of the same sorts of correlations can be provided, for instance, Vendler's (1957) classification of verbal aspect, as refined in Rothstein (2016) to separate achievements and accomplishments that involve a punctual endpoint (the telos), unlike states or activities that are open-ended. Transformational representations in syntax, too, have to be distributed through the reach of their scope, which is at the core of the problem of distributed occurrences that were discussed above. Once again, the suggestion is that the labeling situation arising in transformational instances involving voice (among several others: questions, relativization, ellipses, and more) is in some fundamental sense akin to the distributed interpretation of a verbal expression as in (26c), per the FFT in (25).
One could treat each such instance in a piecemeal fashion, with different substantive assumptions and separate mappings to relevant representations. But the more daring consideration is that for some features (establishing basic scaffoldings) there is a deeper correlation that Chomsky hinted at in 1981. This labeling matter can be resolved internally to feature systems without altering what syntacticians, phonologists, or semanticists, do with their representation thereafter. The proposal presupposes all of that, suggesting that the way to address the odd behavior of occurrences—together with some systemic symmetries, like the sub-categorization generalizations the Jarret graph presumes—is by assuming a correlation between relevant scaffolding features as strong as in (25): a complementarity.
If nothing else, the claim is testable, indeed beyond grammatical considerations, which moves us into neurophysiology. The intuition is that, just as we encounter syllables articulated around vowels and bounded by consonants or aspectualities for telic expressions bounded by the end point of the event, we also confront sentences articulated around verbs and bounded by entities normally expressed through nouns. Moreover, in syntax we can turn categories into interactions by way of transformational procedures, in which case we invoke long-range correlations that typically make our representations grow in size, getting us into distributed instantiations of tokens into variable occurrences. In all these instances, the Fourier transform expects complementary variables w and x correlating in corresponding labels; we have sketched this for behavioral systemic outputs in phonology, syntax, or semantics, but in principle, one should see whether any such correlations obtain for brain signals themselves, at whatever level we manage to read. There may not, or we may not be able to unearth anything from the noise, but this should be the first thing to attempt, from two opposing foundational approaches.
From a conservative perspective, consistent with various theories, we expect “punctual” brain events to correlate with more definite indicators, spatially or temporally; in contrast, the “distributed” situations should be more dispersed and just harder to isolate. If any of this is on track, one should also see some putative correlation between those two types of observations. But a more radical approach is also mathematically possible; we may be able to pinpoint only the “punctual” indicators. This would be if, in fact, the brain wetware is, in any serious sense, obeying quantum mechanical conditions, where only certain outcomes correspond to measurable observables. I raise this point only to bear in mind a spectrum of possibilities, even if that option may raise more questions than it addresses.
More mundanely, we already distinguish (distributed) phenomena like muscle tetanization vs. ballistic gestures, which would seem relevant to phonological distinctions, among others involving muscle (groups) in animal activities. This is less obvious for the more abstract notions that pertain to syntax or semantics, but there too one may consider active maintenance of perceived categories vis-a-vis more punctual perception modes, presupposing, for instance, neural responses from visuospatial working memory (of some entity in space), which conjunctively track the entity's features and spatial coordinates. Each such conjunction requires a sustained neural response. While tetanization does seem relevant in sustaining tense (stressed) vowels, for instance as compared to ballistic phonemic gestures, a more nuanced matter is whether active maintenance is relevant in keeping a verb active as in (26c), distributed agreement occurrences of the sort in the Spanish (5), or a displaced noun phrase with the range of occurrences presupposed in (4). Moreover, one ought to worry about whether tetanization and active maintenance correlate, as implied if these phenomena instantiate the same underlying FFT34.
The presumed lexicon that syntax operates on in this general approach is of the sort in Smolensky and Legendre (2005)—albeit with the non-trivial addition of complex scalars. It is a network of multiplicative (scalar) relations, covering a vector space that projects into Hermitian territory (±Z/NP within the recursive core of the graph, possibly terminating into ±I/AP) or otherwise (±C1/PP within the recursive core of the graph, possibly terminating into ±C2/VP). Needless to say, assigning categorial features [+N, –V] or a corresponding Chomsky matrix does not distinguish all possible nouns there could be. But the implied algebra is meant to combine with other cognitive systems (vision, audition, motoric, etc.) for nuances arising in the vector space—still by way of matrix operations (structure-preserving tensor products). If this is the case, the syntactic scaffolding should still be what it is: the algebraic foundation of the vector space where syntax lives, no more—but no less either. The objects in our group are useful in relating to the derivational workspace where syntactic operations are understood vectorially. The issue is how that space corresponds to neurophysiological observables.
Suppose we presume a Hebbian approach to real quantities, as customary in connectionist models summarized in Smolensky and Legendre (2005)—which numerical weights purport to reflect. This is straightforward for a class of matrices in (20) of a sort called Hermitian, all of whose eigenvalues are real35.
Rieffel and Polak (2011) chapter 4.3 reminds us how Hermitian operators define unique orthogonal subspace decomposition, understood as their own eigenspace decomposition, which stands in a bijective correlation with that particular operator. As a consequence, Hermitian operators describe measurements in the system. The intention is to presume the same underlying notions, then relate complex entries in a transition matrix to these dynamics, given the FFT.
Such a transform is relevant to some temporal slice x of a wave w, for instance carrying a vowel for which we want to process vowel formants. The wave function describing w has solutions involving trigonometric expressions with complex variables. Again, the smaller x gets, the harder it gets to identify w, as we are making the wave package smaller, hence it gets harder to understand its aggregative nuances (w being approximated by integrating a sum of sinusoidal waves, less accurately as x shrinks). That uncertainty directly underlies a variable correlation, which can be interpreted conservatively (in cognitive models sensitive to these), or radically, if the brain's wetware is somehow sensitive to quantum effects. While in the classical view, w's states simply evolve in time, in a vector (Hilbert) space, w's time evolution is abstractly expressed via the matrices crucially involving complex entries, in that respect differing slightly from those in Smolensky and Legendre (2005)36.
In either interpretation of the FFT, decoupling a wave state from a measurable state boils down to the idea that the Hermitian projections in the Jarret graph (NPs, APs) are the observable entities; but while the other projections (VPs, PPs) still exist for the architecture to make sense, they either are harder to pin down (in the conservative interpretation) or do not materialize (in the radical view).
That, of course, can be the wrong assumption to make—just as the entire algebraic translation of Chomsky (1974) via the Fundamental Assumption, or even the Varro/Chomsky generalizations, could be wrong. But if on track, the hypothesis has a direct consequence for the neurophysiological tracking of punctual vs. distributed features, only Hermitian categories like ±Z/NP or ±I/AP can be punctual in the desired sense and identifiable in brain events, while others like ±C1/PP and ±C2/VP should correspond to distributed interactions. Right or wrong, the purported differences should be (relatively) simple to spot, starting with the identification of rigid ±Z/NP entity-types as punctual (measurable) as compared to the descriptive types associated with ±C2/VP, or similar considerations for other domains (consonants/vowels, aspect, etc.). If the program is on track, the distributed pattern should show up, more generally, in A-movement transformations (like passives) and similar interactions.
Another way of stating the overarching goal of this program is that, beyond formal virtues that one may argue for in the computational/representational part of the EEF equation of the present hypothesis, regarding the labeling algorithm, its neurobiological consequences are a complementary duality for which we expect different neurophysiological signatures. By the system's postulates, only phrases like NP (or other Hermitian projections) correspond to a primitive semantic type; VP (or the Varro/Chomsky lexical items, understood as operators) do not correspond to one such observable, regardless of algebraic reality. This is the spirit of the account, which has consequences in terms of the ways to identify each category type. Only those with real determinant labels are expected to correspond to ballistic gestures in any way one can characterize the notion, when appropriately generalized beyond phonetics to other levels of representation. In turn, categories with complex determinant labels correspond to distributed realities, in the realm of tetanization, active maintenance, and like-notions.
The interest in tetanization thus seems two-fold. Descriptively, because it involves an engaged eventuality that lasts for so long as the process is involved, which may be arbitrarily large and suddenly ceases, once the engaged muscle groups discontinue their engagement. Second, at a more explanatory level, forms of tetanization would seem to involve nuanced synaptic mechanisms beyond the familiar local ones. If we are modeling Hebbian plasticity through a representation involving real quantities in the matrices that we are exploring, are the complex quantities to be related to heterosynaptic dimensions, in particular for tetanization or putative extensions/correlations into active maintenance?
As Smolensky and Legendre (2005) emphasize, the beauty of linear algebra is its ability to express both differential equations and a certain symbolic representation in underlying eigenfunctions. In that program, as in the present variant with MP presuppositions about labeling algorithms, this could constitute a translation between the abstract(er) computational/representation formulation and its neurobiological consequence in terms of familiar oscillators. It may be worth isolating neurophysiological signals for global wave-states associated with tetanization and active maintenance, in contrast to less dynamic counterparts that may collapse into punctual gestures and identified categories, among which one hopes to be able to fix rigid designators. This may give us an achievable way to seek a testable correlation between formal theories of the mind and in principle measurable theories of the brain.
This volume invited contributors to think about whether theoretical syntax can effectively guide neuroscience research, in the context of what linking theories are necessary to facilitate the prospect. I believe it can, if we are ready to analyze existing syntactic theories at an abstract enough level, with the help of linear algebra. Standard systems, based on classical information theory, have mappings between syntactic representations and semantic correlates that are as easy to state as they are hard to map to identifiable neurophysiological correlates (mapping is cheap and one arbitrary decision as good as any other). The present system has examined formal properties for underlying features, involving complex scalars correlated with real ones. It seems to me an empirical question whether the language faculty presents such scaffolding features; but if it does, the task of identifying the brain correlates may be slightly less daunting, presuming they correspond to observables of the punctual vs. distributed sort. The syntactic model presented here presumes M and a corresponding labeling algorithm, which one can state in the algebraic fashion sketched above. The jury of time will decide whether the translation analyzed here is fanciful or, instead, relevant to our quest for a mapping hypothesis between TM and TB, the old chestnut of mind and body from a perspective aided by a math lens. The fact that Pauli's group is the foundation of quantum computation adds a curious dimension to this enterprise, with consequences well-beyond anything I could possibly reflect on in this context. But without even presuming anything at all in that realm, it seems worth exploring whether this hypothesis helps us constrain the search. For that is its main goal, beyond deducing some syntactic phenomena. If the theory is right, the familiar (growing) “particle Zoo” of syntactic cartographies and feature ontologies may need to be rationalized within algebraic projections as discussed here, only a handful of which (the Hermitian ones) are measurable in any punctual sense, the remaining categories then predicted to be as distributed as any corresponding wave would be. That would seem to be in the spirit of the remarkable Chomsky (1974), by attempting a rigorous instantiation of some of its presuppositions.
The author confirms being the sole contributor of this work and has approved it for publication.
The author appreciates William Matchin's interest in this piece, as well as various comments from the reviewers. In addition, the author thanks Drew Baden, D.J. Bolger, Naomi Feldman, Bill Idsardi, Michael Jarret, Diego Krivochen, Ellen Lau, Steve Marcus, Román Orús, Doug Saddy, and Jonathan Simon for the help of various sorts. All errors remain the author's responsibility.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. ^This is regardless of whether one assumes a “meaningful” or a “fee” variant of M, which one of the reviewers asks about. As discussed below, the issue is presented from a different perspective in present terms, where to the extent that any M is meaningful, this is because of the free operation of the algebraic labeling system, with its own formal constraints.
2. ^https://en.wikipedia.org/wiki/Neuroscience
3. ^https://en.wikipedia.org/wiki/Neurolinguistics
4. ^See for instance https://openai.com/.
5. ^See Idsardi (2022) for mental maps regarding phonemes generally along these lines.
6. ^For example, as shown in the formulation in Collins and Stabler (2016), as also noted in Collins and Groat (2018).
7. ^I am attempting to show a minimal pair here, presuming raising in the first instance but not the second. Some minimalist theories have argued that non-standard movements also happen in the second instance, but I will set that aside now.
8. ^Although one could also say las cinco parecían ya dadas, literally “five seemed to have been struck”.
9. ^Often of a referential sort, such that one could point at something or single it out in some model.
10. ^This was co-authored with Peter Elias and circulated in mimeographed version, chapter 5 of the 1975 published version, which unfortunately does not include the Appendix.
11. ^Vol 2: Book IX, XXIV-31, translated by Kent (1938).
12. ^As formulated in Peters (1972) and Baker (1979), this amounts to determining some mapping from primary linguistic data to an acquired grammar, under conditions presuming the poverty of the stimulus that underdetermines data for the acquisition task (see chapter 2 of Lasnik and Uriagereka, 2022).
13. ^Obviously noun projections, but also adjectival ones in relevant languages.
14. ^Here, of implicitly permitting [–N, +V] and [–N, –V] complements, which cannot be stated as a generalization over V.
15. ^Proper government was seen as a form of restricting long-range correlations involving traces (Lasnik and Saito, 1992).
16. ^Both reviewers ask for a comparison of the theory I am assuming with Adger (2013) and Panagiotidis (2014). Adger's monograph is a paradigmatic example of the opposite of what the present theory attempts: a syntax of form, not substance. Panagiotidis's is tangential, in that it questions the classical distinction the Chomskyan divide presumes; if the system in point is taken to follow from algebraic considerations, the putative correctness of that challenge would disprove the theory.
17. ^To execute these multiplications, readers need only multiply the corresponding entries between themselves. The vector schemata with multiple values represent separate vector types, one per value. The reason the 16 possible outcomes reduce to only four after the multiplication is because many of these multiplications are equivalent.
18. ^Building on an insight in Guimarães (2000), we take the problematic merger of sail boats to result into something like sail boats-boats, with two occurrences boats-boats that linearize as the token boats (the occurrences then collapsing).
19. ^This graph is so-called because it was suggested by quantum information theorist Michael Jarret. It takes a first step of self-M (matrix power) restricted by the Anchoring Axiom, yielding NPs, while restricting the identity element to adjectival projections resulting from an adjective taking a PP complement; in turn, the system presumes the two Chomsky objects involving identical values correspond to VP projections, while the two Chomsky matrices involving alternating values correspond to PP projections, in both instances by taking NP complements.
20. ^, operators take projections hypothetically associated NP, while , Â operators take those hypothetically associated to PP. Empirically this is true (for nouns, adjectives, and adpositions) or statistically dominant (for verbs, in the more prevalent transitive condition—although that system extends to bi-clausality, di-transitivity, and their interrelations, which I cannot go into in the present context, where we have not thoroughly discussed corresponding functional categories).
21. ^Readers may check https://en.wikipedia.org/wiki/Linear_algebra or any introduction to linear algebra, as well as the helpful tutorials Essence of Linear Algebra: https://www.youtube.com/watch?v=fNk_zzaMoSs.
22. ^The Chomsky matrices stand in an eight-matrix Abelian group for matrix multiplication, where each has a negative, a conjugate, and a negative conjugate within other Chomsky matrices, as well as projections, each of which is its own conjugate. Those elements can be arranged into the Jarret graph, with which it is easy to define a simple Hilbert space.
23. ^So, the labeling algorithm is based on said determinants, more so than the matrices they are the eigenvalue products of. This, thus, is a direct way in which the present theory (postulating matrix determinants as formal labels) is the opposite of what Adger (2013) (or any theory presuming feature substance as foundational) presumes about syntactic labels.
24. ^This first Chomsky matrix, or C1, is categorially ambiguous between a noun and one of the “twin” PP projections. As a noun it can act as a categorial operator on itself, yielding self-M.
25. ^One can also state an “anti-Jarret” graph starting in the “flipped” version of C1 that also satisfies (20), so deriving (18) as a theorem requires a stochastic decision: the grammar could have also been represented in a different vectorial basis. This is expected of systems expressed within vector spaces.
26. ^For a tutorial on the significance of Euler's formula, see https://www.youtube.com/watch?v=mvmuCPvRoWQ.
27. ^Calling these dimensions V and N, i and 1, or anything else is less important than recognizing the orthogonality. This is to say that Euler's formula could equally apply to, for instance, the relation between a vowel and a consonant space.
28. ^This fact about the Fourier transform (https://www.youtube.com/watch?v=MBnnXbOM5S4) underlies Heisenberg's Uncertainty Principle—the correlation underlying the basis for quantum entanglement.
29. ^This is said largely for concreteness, not to go into the semantics of kinds. Obviously, individual variables too can discharge relevant thematic roles and be bound by their own quantifiers, leading to various occurrences as in (2) above.
30. ^For any conceptualized kind k that a speaker can conceive of, we could, in fact, consider what the relative probability is for k to be [e.g., for (26)] constituted (of such-and-such)—and similarly for other eventualities.
31. ^Mutatis mutandis, nothing prevents certain consonants from appearing as syllabic nuclei; it is a matter of perspective, which the correlation of features allows. This is because, in effect, we are presuming a (wave, particle) duality. This bears on an issue one of the reviewer's raises, regarding categorial gradience. As it turns out, in principle any gradiance could be expressed in terms of the correlated variables, so long as they are correlated. But the topic is too broad to explore here.
32. ^1 goes to the other side of the equation as −1, but the basis of the system could change, and so long as the four categories preserve their algebraic interrelations, nothing would (see footnote 26). Note also that aside from eiπ = −1 (= ei3π = einπ, where n is odd), we also have e−i2π = 1 (= e−i4π = e−inπ, where n is even), which makes sense if we think of this formula as corresponding to a unit circle, completed (and thus repeated) every two or any even number of π occurrences, and half completed at π, 3π, and so on, in the odd sequence. Linguistically, in that unit circle, eVπ = –N, e−V2π = N, which amounts to saying that the ideal nominal representation is the conjugate of the ideal verbal representation, while the ideal adjectival representation is the conjugate of the ideal elsewhere (adpositional) representation, and that all four lexical categories correlate in the relevant underlying group. Moreover, “going in circles” amounts to representing the periodicity of some (aggregation of) sinusoidal waves, which may lead to characteristic complexity for each complex subcase within this general format.
33. ^Bear in mind that the determinant is the label for the “twin” projections, which are categorial arguments of the projecting categories, the operators (e.g., the Chomsky matrices). The operators do not have a meaningful twin and, if they have a label at all, this is intrinsic to the assumptions about the Euler identity, for instance stipulating that, say, V will be i by a choice of basis for the system. That is, in effect, the (unavoidable) anchoring step, that can also be stated from the point of view of N or, more generally, as the linguistic version of the equality: eiπ + 1 = 0.
34. ^I thank Ellen Lau for useful discussion of these matters, regarding the possible relevance of active maintenance.
35. ^The Hermitian matrices in (20) are easy to identify by noticing how their entries (corresponding to eigenvalues) are all real. Readers can verify the following simple formal facts:
(i) The trace (sum of diagonal elements) of a Chomsky matrix falls within ±1±i,
while it is zero for Pauli's Z and its negative –Z.
(ii) The determinant (product of the eigenvalues) of a Chomsky matrix is ±i;
while it is −1 for Z and its negative –Z (here seen as twin projections of C1/N.
(iii) The characteristic polynomial of both Z and -Z is x2 – 1; for the Chomsky matrices we have:
nouns: x2 – (1 – i) x – i; verbs: x2 + (1 – i) x – i; adjectives: x2 – (1 + i) x + i; adpositions: x2 + (1 + i) x +i.
36. ^This can describe the fundamentals of the wave behavior in a system involving quantization, with relevant states being eigenstates of relevant operators, as presumed in quantum computation.
Adger, D. (2013). A Syntax of Substance. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/9780262018616.001.0001
Balari, S., and Lorenzo, G. (2012). Computational Phenotypes: Towards an Evolutionary Developmental Biolinguistics. Oxford: Oxford University Press. doi: 10.1093/acprof:oso/9780199665464.001.0001
Chomsky, N. (1955). The Logical Structure of Linguistic Theory [Ph.D. Thesis]. Harvard/MIT. [Published in part, 1975, New York: Plenum].
Collins, C., and Groat, E. (2018). Copies and Repetitions. Available online at: https://ling.auf.net/lingbuzz/003809 (accessed January 28, 2023).
Collins, C., and Stabler, E. (2016). A formalization of minimalist syntax. Syntax 19, 43–78. doi: 10.1111/synt.12117
Embick, D., and Poeppel, D. (2015). Towards a computationalist neurobiology of language. Lang. Cogn. Neurosci. 30, 357–366. doi: 10.1080/23273798.2014.980750
Frederici, A. (2017). Language in Our Brain. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/9780262036924.001.0001
Guimarães, M. (2000). “In defense of vacuous projections in bare phrase structure,” in University of Maryland Working Papers in Linguistics, College Park, MD, Vol. 9.
Idsardi, W. (2022). Underspecification in time. Can. J. Linguist. 67, 1–13. doi: 10.1017/cnj.2022.36
Lasnik, H., and Uriagereka, J. (2022). Structure: Concepts, Consequences, Interactions. Cambridge, MA: MIT Press. doi: 10.7551/mitpress/11276.001.0001
Marr, D. (1982). Vision: A Computational Investigation Into the Human Representation and Processing of Visual Information. Cambridge, MA: MIT Press.
Martin, R., Orús, R., and Uriagereka, J. (2019). “Towards matrix syntax,” in Generative Syntax: Questions, Crossroads and Challenges, special issue of the Catalan Journal of Linguistics. Barcelona.
Orús, R., Martin, R., and Uriagereka, J. (2017). Mathematical foundations of matrix syntax. arXiv. doi: 10.48550/arXiv.1710.00372
Panagiotidis, P. (2014). Categorial Features. Cambridge, MA: Cambridge University Press. doi: 10.1017/CBO9781139811927
Peters, S. (1972). “The projection problem: how is a grammar to be selected?” in Goals of Linguistic Theory, ed S. Peters (Englewood Cliffs, NJ: Prentice-Hall), 171–188.
Poeppel, D. (2003). The analysis of speech in different temporal integration windows: cerebral lateralization as ‘asymmetric sampling in time'. Speech Commun. 41, 245–255. doi: 10.1016/S0167-6393(02)00107-3
Poeppel, D., and Embick, D. (2005). “Defining the relation between linguistics and neuroscience,” Twenty-First Century Psycholinguistics: Four Cornerstones, ed A. Cutler (Mahwah: Lawrence Erlbaum Associates), 103–118.
Rieffel, E., and Polak, W. (2011). Quantum Computing: A Gentle Introduction. Cambridge, MA: MIT Press.
Rothstein, S. (2016). “Aspect,” in Cambridge Handbook of Formal Semantics, eds M. Aloni and P. Dekker (Cambridge: Cambridge University Press), pp. 342–368. doi: 10.1017/CBO9781139236157.013
Szabolcsi, A. (1983). The possessor that ran away from home. Linguist. Rev. 3, 89–102. doi: 10.1515/tlir.1983.3.1.89
van Rooij, I. (2008). The tractable cognition thesis. Cogn. Sci. 32–6, 939–984. doi: 10.1080/03640210801897856
Keywords: categorial features, merge, punctual vs. distributed, matrices, real vs. complex entries
Citation: Uriagereka J (2023) Correlated attributes: Toward a labeling algorithm of complementary categorial features. Front. Lang. Sci. 2:1107584. doi: 10.3389/flang.2023.1107584
Received: 25 November 2022; Accepted: 09 January 2023;
Published: 21 February 2023.
Edited by:
William Matchin, University of South Carolina, United StatesReviewed by:
Elliot Murphy, University of Texas Health Science Center at Houston, United StatesCopyright © 2023 Uriagereka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan Uriagereka,  anVhbkB1bWQuZWR1
anVhbkB1bWQuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.