Mathematical modeling of the synergistic interplay of radiotherapy and immunotherapy in anti-cancer treatments

Introduction: While radiotherapy has long been recognized for its ability to directly ablate cancer cells through necrosis or apoptosis, radiotherapy-induced abscopal effect suggests that its impact extends beyond local tumor destruction thanks to immune response. Cellular proliferation and necrosis have been extensively studied using mathematical models that simulate tumor growth, such as Gompertz law, and the radiation effects, such as the linear-quadratic model. However, the effectiveness of radiotherapy-induced immune responses may vary among patients due to individual differences in radiation sensitivity and other factors.

Methods: We present a novel macroscopic approach designed to quantitatively analyze the intricate dynamics governing the interactions among the immune system, radiotherapy, and tumor progression. Building upon previous research demonstrating the synergistic effects of radiotherapy and immunotherapy in cancer treatment, we provide a comprehensive mathematical framework for understanding the underlying mechanisms driving these interactions.

Results: Our method leverages macroscopic observations and mathematical modeling to capture the overarching dynamics of this interplay, offering valuable insights for optimizing cancer treatment strategies. One shows that Gompertz law can describe therapy effects with two effective parameters. This result permits quantitative data analyses, which give useful indications for the disease progression and clinical decisions.

Discussion: Through validation against diverse data sets from the literature, we demonstrate the reliability and versatility of our approach in predicting the time evolution of the disease and assessing the potential efficacy of radiotherapy-immunotherapy combinations. This further supports the promising potential of the abscopal effect, suggesting that in select cases, depending on tumor size, it may confer full efficacy to radiotherapy.

1 Introduction

Immunological experiments during the last two decades have answered many important questions related to the causal relationship between chronic inflammation and carcinogenesis. The presence of inflammatory cells in the cancer milieu raises the question of the tumor progression despite a likely immune system reaction to tumor antigens. This aspect is particularly important since untreated tumors grow according to non-linear, macroscopic, laws as the Gompertz law (GL) Gompertz (1); Norton (2); Vaghi et al. (3) or the logistic one (LL) Verhulst (4); Vaghi et al. (3). Therefore those growth patterns emerge, at a larger level of magnification, from many microscopic biological factors, which turn out to be summarized by simple mathematical descriptions.

Since prolonged inflammation is a hallmark of cancer Hiam-Galvez et al. (5), initiating tumor genesis or supporting tumor growth, and the global immune response is significantly altered during tumor progression, immunotherapy is becoming a valid option in cancer treatment. However, the immune response can be detrimental rather than helpful [see, for example, Lin et al. (6)]: individual auto-antibodies play an antagonist role in cancer, but the agonist auto-antibody in some cancer patients turned out to be deleterious and harmful.

Some preclinical and clinical evidence confirm the synergistic action of radiotherapy (RT) and immunotherapy against the tumor cells Zhao and Shao (7). Although The intrinsic sensitivity to radiation is patient-specific Puglisi et al. (8); Puglisi et al. (9) and may depend on different factors, RT is able to ablate cancer cells not only by directly induced necrosis or apoptosis but also by triggering an immune response that actively recruits immune cells within the tumor microenvironment. For example, RT promotes the release of tumor-associated antigens, which, once processed by antigen-presenting cells (APCs), prime CD8⁺ and CD4⁺ T cells in the draining lymph nodes. These lymphocytes attack both primary tumor and metastatic sites, posing the biological basis of the in situ vaccination driving the so-called abscopal effect Ngwa et al. (10); Mole (11); Demaria et al. (12): RT induces a systemic behavior that can activate the immune response against metastasis, i.e., in locations that are far from the RT-treated primary tumor.

The involvement of the immune system has been demonstrated in different experimental models such as melanoma Twyman-Saint Victor et al. (13), colorectal Dovedi et al. (14) and breast cancers Demaria et al. (15), but the clinical presentation where considered anecdotal or at least rare.

Its rarity in clinical practice is likely due to the simultaneous engagement of immune escape mechanisms, such as the recruitment of regulatory CD4⁺ (Treg) and myeloid-derived suppressor cells counterbalancing the anti-tumor CD8⁺ T cell-mediated effects, and the tumor release of hypoxia-inducible factors with pro-survival activity Ji et al. (16).

More generally, susceptibility to the abscopal effect has been associated with several biological factors, such as tumor size or oxygen levels in tumor tissues. Indeed, the presence of hypoxic regions results in both increased resistance to the lethal effect of radiation mediated by reactive oxygen species (ROS) production and an immune suppressive tumor landscape ruled by Treg-recruiting chemokines and impaired APC function McNamee et al. (17); Castorina et al. (18)

Mathematical modeling approaches have become increasingly abundant in describing immunotherapy and its synergy with RT Dewan et al. (19) Agur and Vuk-PavlovićCheck that all equations and special characters are displayed correctly. (20) Walker and Enderling (21); Ng and Dai (22); Serre et al. (23) Gong et al. (24) Marconi et al. (25); Vanpouille-Box et al. (26); Chakwizira et al. (27); Kosinsky et al. (28); Liu et al. (29); Valentinuzzi et al. (30); Friedrich et al. (31); Malinzi et al. (32); Bekker et al. (33). Indeed, the complexity of cancer provides challenges and opportunities for new developments, and mathematical formulations contribute by helping to elucidate mechanisms and by quantitative predictions that can be validated experimentally Agur and Vuk-Pavlović (20); Altrock et al. (34); Brady and Enderling (35) .

A large part of mathematical models on tumor growth and therapies are based on sets of coupled differential equations. The number of equations increases together with the details of the biological description and this implies a large number of parameters and initial conditions to be specified. The detailed analyses are often so complex to require surrogate models for a reliable determination of the parameters Browning and Simpson (36).

On the other hand, more economical models introduce a macroscopic evolution of tumor growth and therapy with fewer parameters and a coarse-grain dynamical evolution Norton (2); Wheldon (37); Vaghi et al. (3); Guiot et al. (38); Castorina et al. (39); Castorina et al. (40).

This is the key point to obtain an effective quantitative control of the tumor progression. Indeed, microscopic models, which have the advantage of a deep understanding of the biological dynamics, of the physiologically-based pharmacokinetic [see for example Maaß et al. (41)] and of the possible translation to different populations/diseases, require many parameters and, although some of them can be determined by previous analyses, the parametric error propagation will produce a large band of fluctuation in the prediction of the quantitative evolution of the disease. Therefore we prefer to apply macroscopic growth laws of the sigmoid family with two parameters. Our choice of the GL is due to the result that untreated tumor growth has been better described by it (see Vaghi et al. (3) for a recent study). Moreover, in a transplantable rat tumor, it was shown that control and regrowth curves after radiotherapy could be fitted by the same Gompertzian law, provided adjustments for the initial lag and the estimated number of clonogens immediately after irradiation were performed [Jung et al. (42)]. Gompertzian growth has been assumed to describe human tumor repopulation during fractional radiotherapy also in Hansen et al. (43) and by O’Donoghue (44).

The main motivation of the proposed approach is, in our opinion, its complementary role in the clinical evaluation of disease progression, often based on macroscopic variables, and the better parameter identification, thus increasing model verifiability Braakman et al. (45).

Finally, this method offers a clear description of the complex interplay between radiotherapy, immunotherapy, and tumor progression, providing insights for advancing cancer treatment strategies that harness the abscopal effect.

The paper is structured as follows: the mathematical model, based on the GL and on the definition of the effective GL parameters, is recalled in the next section (Appendices A, B and C contain the corresponding calculations). Different macroscopic growth laws (as the LL) can be applied, without changing the underlying method. The emerging phenomenological approach, based on the suitable redefinition of the two GL parameters to describe the data, is reported in Section 3. The final sections are devoted to discussion and to the possible clinical use of the phenomenological model.

2 Methods

The proposed method is based on the mathematical model reported in detail in Appendices A, B and C in the Supplementary Materials. In what follows, the assumptions and some exact results are reported. Then, the phenomenological model is discussed.

2.1 Mathematical modeling

A general classification of macroscopic growth laws is reported in Castorina et al. (39) Castorina and Blanchard (46). For a population N(t) they are solutions of a general differential equation that can be written as

$\begin{array}{ll}\frac{1}{N\left(t\right)}\frac{dN\left(t\right)}{dt}=f\left[N\right(t\left)\right],& (1)\end{array}$

where f(N) is the specific growth rate and its N dependence describes the feedback effects during the time evolution. If in Equation 1 f(N) becomes constant, the growth follows an exponential pattern.

The untreated tumor progression is described by the GL Norton (2); Vaghi et al. (3), solution of the previous equation (see Data Sheet 1) with

$\begin{array}{ll}f\left[N\right(t\left)\right]=a-k \text{ln }\frac{N(t)}{N_0}=k \text{ln }\frac{N_{\infty }}{N\left(t\right)}& (2)\end{array}$

where a,k,N₀ are constants that respectively indicate the exponential growth, the limiting factor, the initial cell number and N_∞ is the carrying capacity (N_∞ = N(0)exp(a/k)).

For untreated tumors, the GL emerges from microscopic, biological mechanisms where natural/adaptive immunity is taken into account Berendt and North (47); Gonzalez et al. (48); Castorina and Carco’ (49) The further effects of immune therapy, I(t), can be described by a modification of the previous Equation 2 as follows (see for example Wheldon (37))

$\begin{array}{ll}\frac{1}{N\left(t\right)}\frac{dN\left(t\right)}{dt}=k\text{ ln }\frac{N\infty }{N\left(t\right)}-\gamma \text{I}\left(t\right)& (3)\end{array}$

where γ is a constant.Notice that the sign of γ indicates the agonist or antagonist effect of the immune response: a negative γ increases the specific growth rate. The variable I(t) generically refers to the passive immunity resulting from the injection of anti-cancer-specific monoclonal antibodies i.e., the drug effects. However, it is, in general, unknown and requires a specific model. An example is the model of immunotherapeutic drug T11 target structure in the progression of malignant gliomas Khajanchi and Ghosh (50)Khajanchi and Banerjee (51).

The general solution of the previous equation and the IT effects on the tumor progression are discussed in Mathematical Formalism. For illustrative purposes, two specific cases are analyzed: I(t) = I(0) = constant and I(t) = I(0)exp(−ρt). The role of the therapy can be assimilated to a redefinition of an effective carrying capacity (in the first of the two cases) and, in general, in the introduction of effective, time and therapy dependent, parameters $a_{eff},k_{eff}\text{\hspace{0.17em}or\hspace{0.17em}}{N}_{\infty }^{eff},k_{eff}$, whose quantitative relation with I(t) is given in Mathematical Formalism. The introduction of an effective carrying capacity is well-known in population dynamics Royama (52). For example, the invention and diffusion of technologies lift the growth limit. Its possible time dependence is usually included by (at least) another differential equation, coupled with the growth equation. This will increase the number of parameters and initial conditions and, therefore, in our computational method the two effective parameters will be determined by data fits, giving a phenomenological indication about the disease progression.

There are different outcomes following an immune response to cancer Lin et al. (6): i) a surveillance role that inhibits the initiation and progression of the cancer; ii) the possibility that under certain conditions the immune response may nourish rather than curtail tumor growth. In other terms, monoclonal antibodies can exert antagonistic as well as sympathetic effects on tumor growth Lin et al. (6).

This possibility translates into a direct comparison among the parameters that describe the immunotherapy effects in Equation 3 and its solutions and the available data. For example, the determination of the crucial sign of the constant γ.

Let us now consider the combination of immune therapy (IT) and radiotherapy (RT). As a first step, we study the case of independent effects, i.e. no synergy between IT and RT.

The effect of radiotherapy is described by the linear quadratic model (LQM). Denoting by $N\left(t^{-}\right),N\left(t^{+}\right)$ respectively the cell number before and after the single dose d at time t, the RT effect is given by

$\begin{array}{ll}N\left(t^{+}\right)=N\left(t^{-}\right)e^{-D}=N\left(t^{-}\right)e^{-\alpha d-\beta d^2}& (4)\end{array}$

where α and β are constants (numerically β ≃ α/10) and d is the dose, Van Leeuwen et al. (53). The result in Equation 4 assumes an instantaneous effect of the RT, which could be, in general, not strictly applicable. Also, In this case, the therapy and immune response effects can be translated in the definition of effective parameters of the GL (see Mathematical Formulation).

The number of tumor cells after n_f treatments at time t_n,t_n+1,t_n+2,…t_nf turns out to be (see Mathematical Formalism)

$\begin{array}{ll}N\left(t_{n_f}^{+}\right)=N\left(t_0\right)e^{ln\frac{N_{\infty }}{N\left(t_0\right)}\left[1-e^{-k\left(t_{n_f}-t_0\right)}\right]-\overline{W}\left(t_{n_f},t_0\right)-D_{n_f}}& (5)\end{array}$

with the functions $D_{n_f}$ and $\overline{W}\left(t_{n_f},t_0\right)$ as described in Mathematical Formalism.

According to Equation 5, if

$\begin{array}{ll}ln\frac{N_{\infty }}{N\left(t_0\right)}\left[1-e^{-k\left(t_{n_f}-t_0\right)}\right]-\overline{W}\left(t_{n_f},t_0\right)-D_{n_f}<0& (6)\end{array}$

the tumor cell number decreases and the time evolution of the diseases moves toward complete recovery.

Therefore, although RT and IT are considered independent, if the effects of RT are such that

$\begin{array}{ll}ln\frac{N_{\infty }}{N\left(t_0\right)}\left[1-e^{-k\left(t_{n_f}-t_0\right)}\right]\simeq D_{n_f}& (7)\end{array}$

then, a small impact of the immunotherapy, $\overline{W}$, can produce a tumor volume regression. Moreover, the critical conditions in Equations (6, 7) depend on the fractioning of the radiotherapy, since different schedules give different values of $D_{n_f}$ and $\overline{W}\left(t_{n_f},t_0\right)$. Therefore, the previous conditions correspond to optimal control of the therapy effects, Khajanchi and Banerjee (54); Khajanchi (55); Khajanchi and Banerjee (56).

2.2 The synergy between immune and radio therapies

In the macroscopic framework, the description of the synergy between RT and IT requires a new term in the specific rate, which takes into account the immune response activated by RT, i.e.

$\begin{array}{ll}\frac{1}{N}\frac{dN}{dt}=kln\left(\frac{N_{\infty }}{N}\right)-\gamma I\left(t\right)-\delta Y\left(t\right)F\left(d,t\right)& (8)\end{array}$

where δ is a constant, F(d,t) is a function of the dose d and of the time series of the treatments on the tumor, quantifying the cell-killing effect of the adaptive immune response Y (t), triggered by the RT. Y (t) is different from I(t) as it represents the outcome of the active immunization due to antigenic peptides coming from the disintegration of tissues hit by radiotherapy, and following the inflammation. To be more specific, Y (t) represents the immune response to tumor-associated antigens, promoted by the inflammation context due to the damage perpetrated by RT. Also, it must be specified that this immune response has a chance to exert an effect only before evasion mechanisms are established by the tumor (factors that are not counted in the present model).

If d = 0, F(d,t) = 0 there is no synergy. The specific form of the function F(d,t) requires a microscopic model, however one expects that the coupling Y (t)F(d,t), i.e. the immune activation due to RT, has a typical time decay, τ, after the single dose radiotherapy described by the LQM. For the primary tumor, the parameter δ is small, i.e., δ << 1 and the synergy is small. The abscopal effect is described by considering a finite value of δ for metastases that are far away from the primary tumor location. The result for the time evolution of the abscopal effect is given in Mathematical Formalism.

3 Results

According to the mathematical approach in the previous section a phenomenological, simplified, method of analysis of the experimental data emerges. Indeed, a large part of the therapy and immune response effects can be assimilated to a redefinition of the GL parameters, with time and treatment dependence, which turns out to be detailed enough to compare with data. This phenomenological, simpler, procedure facilitates the validation of the model [Braakman et al. (45)] with respect to more complex analytical approaches, as discussed later.

Moreover, the function I(t),W(t),Y (t) in the previous differential equations are largely unknown, therefore the data fits of the effective GL parameters (see the general formulas in Mathematical Formalism) give model-independent information about the role of IT and RT.

3.1 Analysis of experimental data - immune therapy

In ref. Lin et al. (6) the different immune responses to cancer have been described. The authors highlight the agonist and antagonist effects of, respectively, AB93 and AB641 autoantibodies for the growth factor receptor TrkB in patients with breast cancer. After injection of MDA-MB-231 cells in immunodeficient mice they show the response to treatment, for different dosages of autoantibodies, measuring tumor growth. In particular, the data on the effects of AB641 and AB93 on tumor progression can be analyzed in the proposed macroscopic approach by Equation 3, by redefining GL parameters. Initially, one has to fit the untreated tumor progression data by GL to determine the corresponding parameters. Then, one repeats the analysis with immunotherapy. The results are shown in Figure 1, which clearly reveal the agonist or antagonist role of the different antibodies.

Figure 1

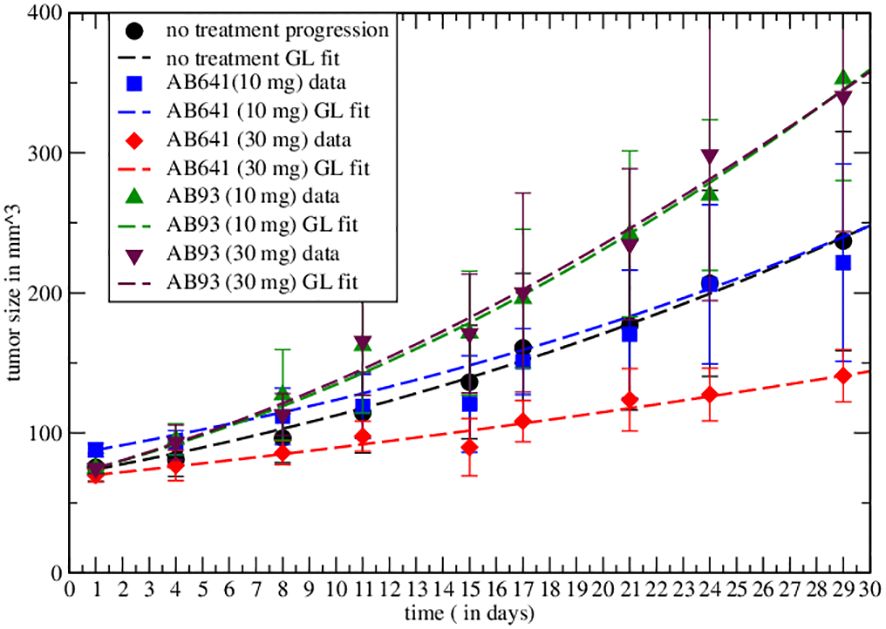
Figure 1 Comparison of the effective GL with data from the literature for untreated tumor and immunotherapy results. In the graph the symbols represent real data recorded and the dashed curves represent the Gompertzian fit, the colors are paired for both results. Fitted parameters are reported in Table 1.

The experimental result in the case of therapy can be fitted by redefining the GL parameters with respect to the untreated ones (see Equation S2, Equation S23 and Mathematical Formalism in Supplementary Material). The values are reported in Table 1. The agonist effects increase both parameters, producing faster growth, corresponding to a negative γ  in Equation 3, whereas the antagonistic effect induces tumor depletion. Notice that the change in the GL parameters, i.e. of the therapy, implies a modification of the exponential rate and the carrying capacity with respect to the untreated tumor.

Table 1

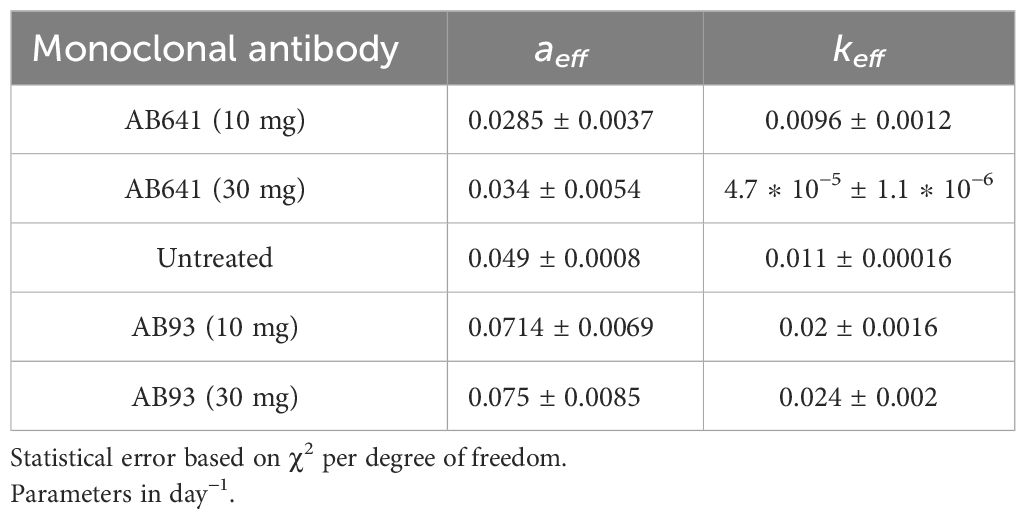
Table 1 GL effective parameters of the comparison in Figure 1 (see Equation S23 in Supplementary Material.

Non-linear curve fitting was made using Grace (version 5.1.25) Dataset Grace (57), data fitted by GL effective parameters are promising. The correlation coefficients and the root mean squared relative errors are respectively given by (0.982,0.062),(0.977,0.052),(0.995,0.051),(0.992,0.058),(0.996,0.04) for AB641/30 (red curve in Figure 1), AB641/10 (blue), AB93/10 (green), AB93/30 (black triangle) and untreated case.

3.2 Analysis of experimental data - RT and abscopal effect

The abscopal effect has been experimentally studied in Nesseler et al. (58) by inoculation of undifferentiated fibrosarcoma cells (FSA1) into immunocompetent mice to simulate primary and metastatic conditions, successively divided in four treatment groups: no treatment, anti-PD-1 monoclonal antibody alone, RT alone, and combination of anti-PD-1 with RT.

Initially, only the effect of RT on the primary has been detected, showing a critical dose administration for tumor regression [Figure 2A of ref. Nesseler et al. (58)]. The limited role of anti-PD-1 on the untreated primary tumor has been observed [Figure 2B of ref. Nesseler et al. (58)] and it has been checked that the RT on the primary has no direct effect on the implanted secondary. Finally, the synergy between IT and RT has been verified by the regression of the metastasis.

Figure 2

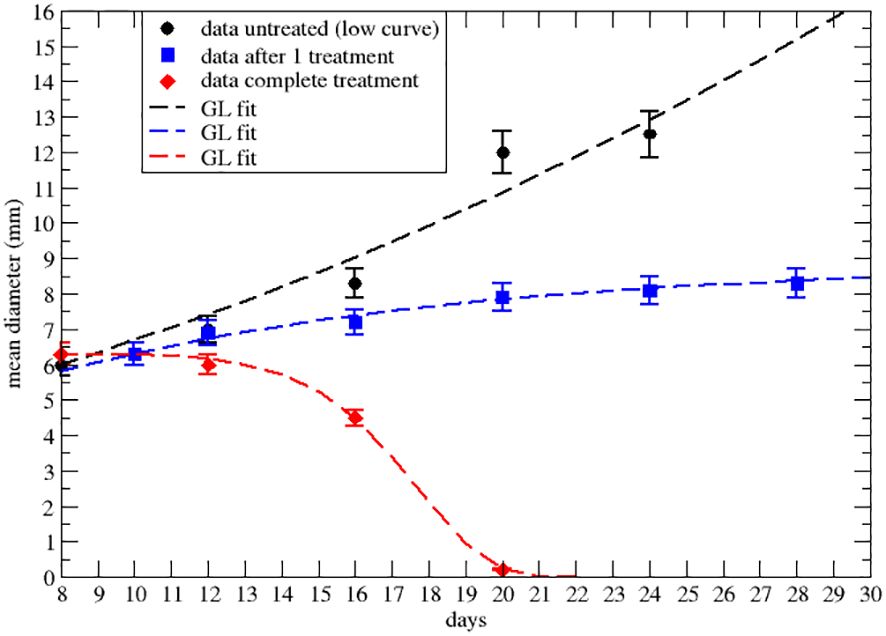
Figure 2 Effective GL fit of literature data with effective parameters of the lower data set of Figure 2A of ref.Nesseler et al. (58). Black point and the dashed line represent respectively real data and Gompertzian fitting. Blue squares and curve are data and GL fit after the first 8Gy RT treatment. The red rhombus and curve are data and GL after three treatments of 8Gy each. Parameters reported in Table 2.

Let us first consider the data on the primary tumor, treated by RT only, with three treatments of 8 Gy on days 9,10 and 11 after the injection of the cancer cells. The qualitative analysis [Figure 2A of ref. Nesseler et al. (58)] clearly indicates that the LQM with instantaneous cell killing effect is not able to reproduce the observed effect, due to a delay between the treatments (on days 9,10 and 11) and the regression behavior (i.e., a negative specific rate), starting on day 15, Lim et al. (59); McMahon (60). Therefore, more complex dynamics are in place, which, however, can still be described by a GL pattern. As discussed, the effective parameters can be time-dependent (see Equation S23-S30 in Mathematical Formalism) due to the therapy and the results are reported in Figures 2, 3 respectively for the lower and upper data sets of Figure 2A of ref. Nesseler et al. (58). The corresponding fitted effective parameter values are given in Tables 2, 3. The (∗) indicates that the fitted parameter a_eff has a linear time dependence a_eff → a_eff (t − t₀). This time dependence and the sign change of k_eff, compared to the untreated case, signal that the therapy produces a complete depletion of the tumor size, analogously to the extinction in population dynamics.

Figure 3

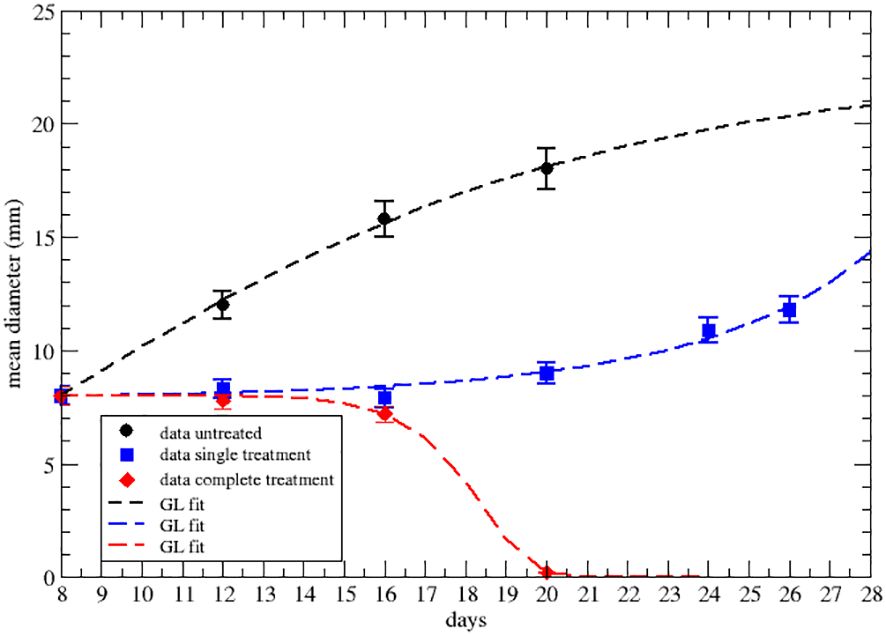
Figure 3 GL fit of literature data with effective parameters of the upper data set of Figure 2A of ref.Nesseler et al. (58), where the untreated data are in black, blue for one shot of 8Gy of irradiation and red for three 8Gy shots. Parameter reported in Table 3.

Table 2

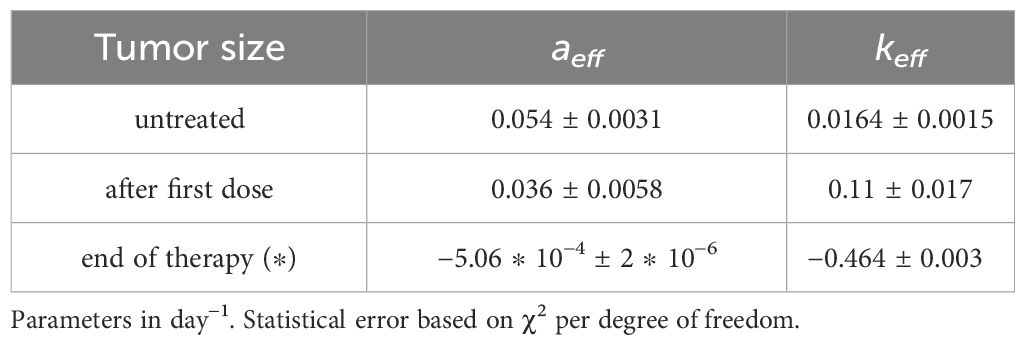
Table 2 GL effective parameters of the comparison in Figure 2 (see Equation S23 in Supplementary Material).

Table 3

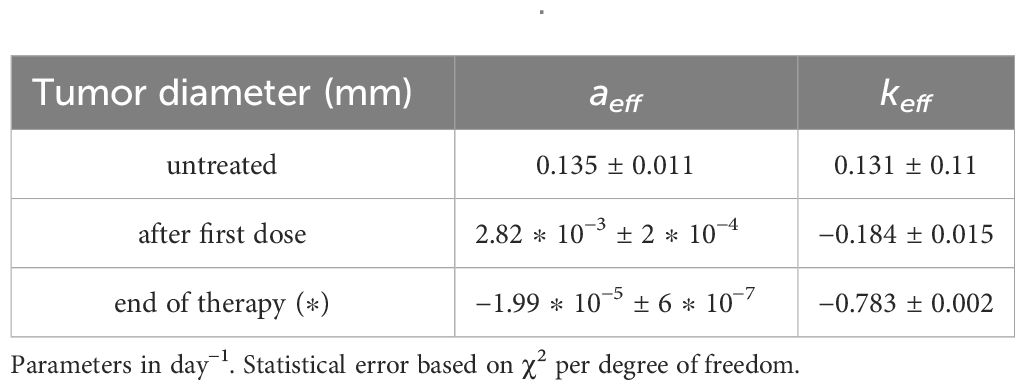
Table 3 GL effective parameters of the comparison in Figure 3 (see Equation S23 in Supplementary Material.

The strong signal of the change of sign in the effective parameters can also be summarized by plotting the specific rate (1/NdN/dt), in Figures 4, 5, where its negative value indicates the complete tumor regression trend.

Figure 4

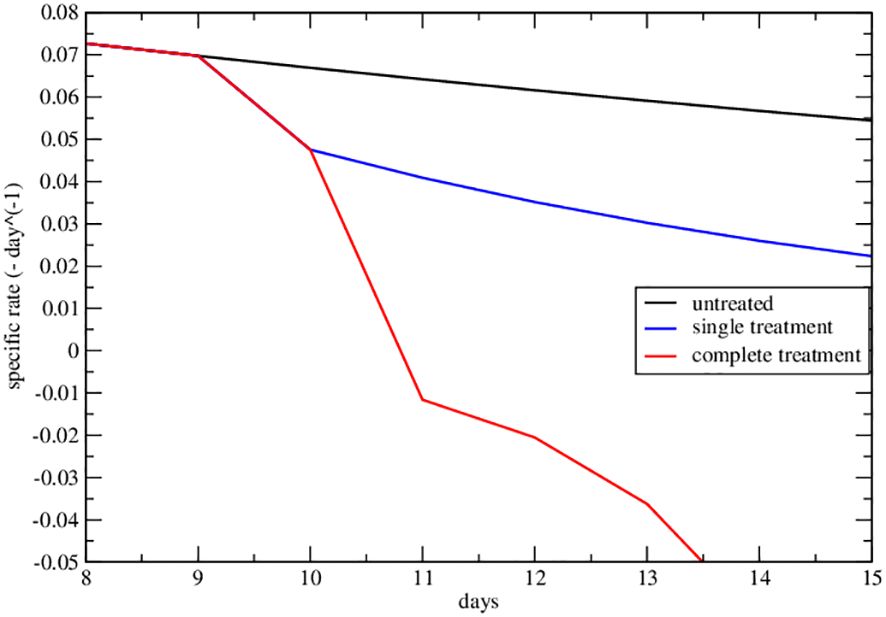
Figure 4 Specific rate of the lower data set of Figure 2A of ref. Nesseler et al. (58). The curves represent the specific growth rate day by day, the response to therapy is highlighted by a negative trend.

Figure 5

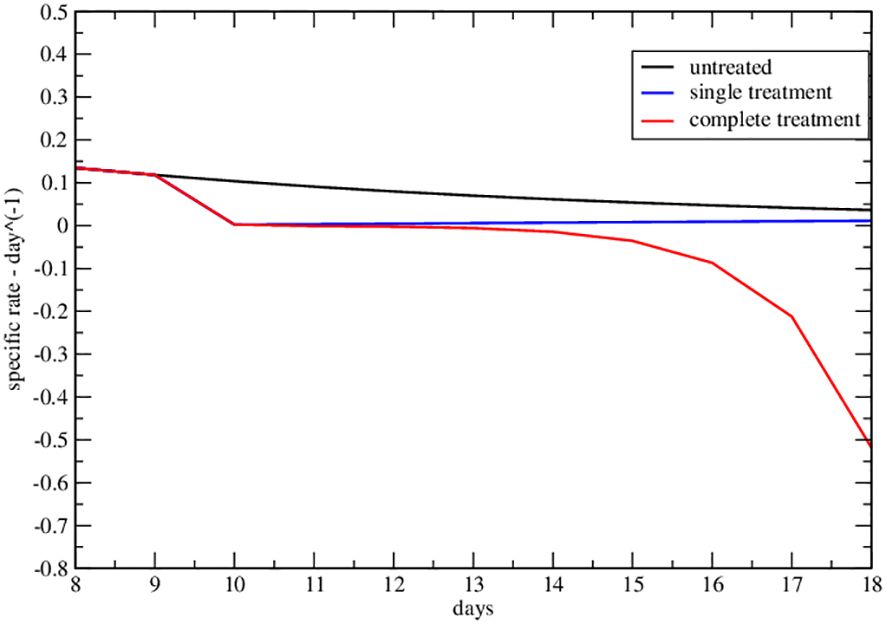
Figure 5 Specific rate of the upper data set of Figure 2A of ref. Nesseler et al. (58). The curves represent the specific growth rate day by day, the response to therapy is highlighted by a negative trend.

It should be stressed that the approach with GL effective parameters, suggested by the more rigorous previous mathematical model (see Mathematical Formalism), is a phenomenological one with the aim of a simplified clinical, but quantitative, understanding of the tumor progression at a more personalized level (see next discussion section).

The final analysis concerns the abscopal effect, according to Equation 8 with γ = 0. Let us assume: a) an exponential decay of the immune response with a time delay τ between the RT on the primary and the immunological effect on the secondary; b) the activated immune system continues its effect on the secondary with an exponential rate corresponding to the specific rate obtained at the end of the RT.

In other words, if t_in is the starting day of RT on the primary, for t < t_in the metastatic site evolves according to the GL progression with the untreated parameters. At t_in the RT starts and the immune system targets the secondary (see Equation 8 and its solution reported in Mathematical Formalism). At the end of the RT, the immunity response continues to reduce the metastasis with an exponential behavior if the specific rate turns out to be negative.

In Figure 6 the result is depicted, i.e., the abscopal effect, according to the previous approach, for different values of the parameter I(0), determining the response of the immune system on the secondary induced by RT (see Mathematical Formalism).

Figure 6

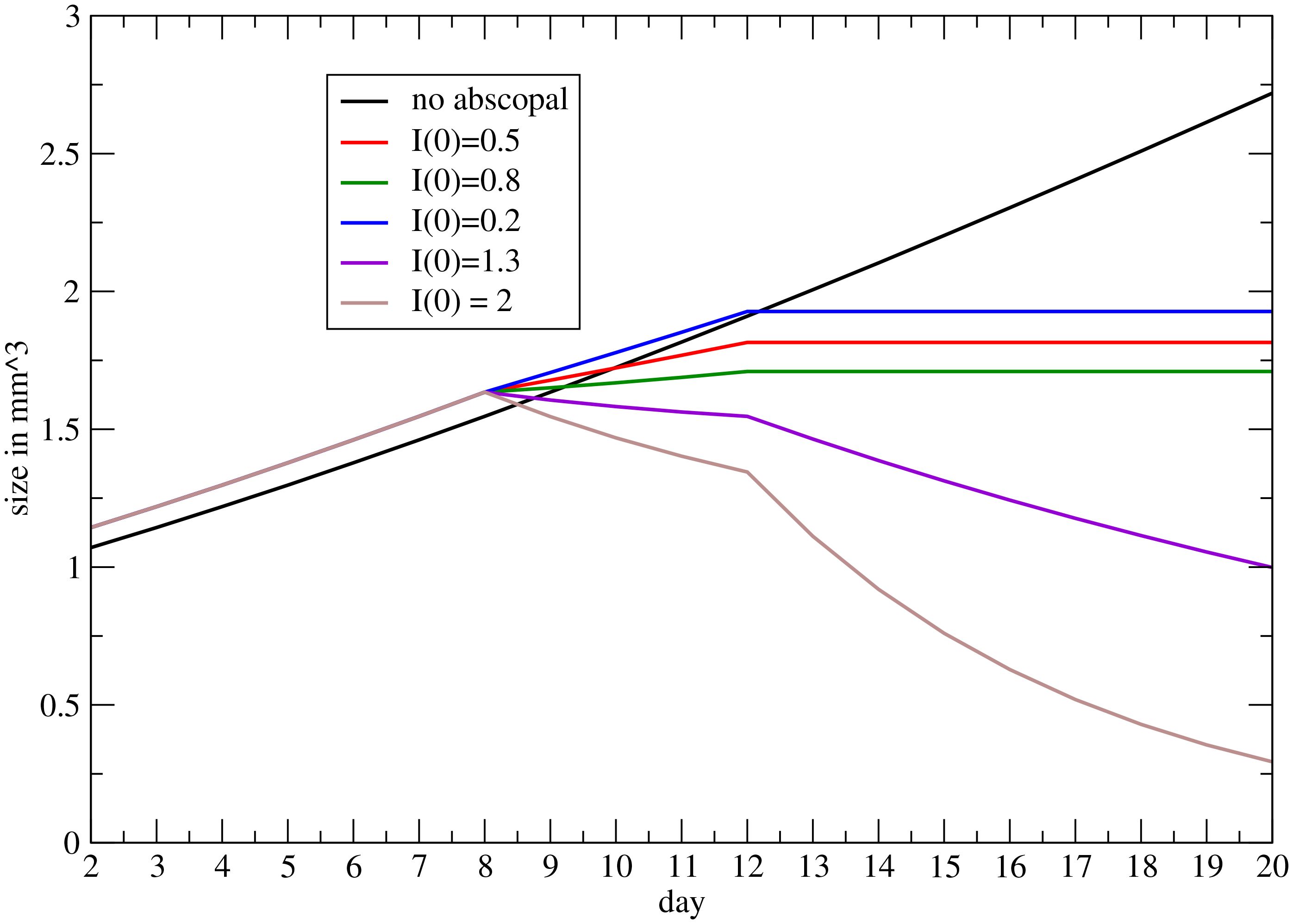
Figure 6 Progression on the metastatic volume, triggered by RT on the primary, for different values of the coupling between the immune system and RT (see Mathematical Formalism).

4 Discussion

The phenomenological approach, based on the previous mathematical formulation, consists in fitting the specific rate data by GL with effective parameters. Let us recall that the specific rate is much more reliable than the volume tumor variation, in determining its progression and the phase of growth or decrease.

We are aware that the coarse-grain proposed approach misses the detailed dynamics and can be considered an oversimplified description since the underlying pathways, Ng and Dai (22); Serre et al. (23); Marconi et al. (25); Liu et al. (29); Valentinuzzi et al. (30); Friedrich et al. (31); Bekker et al. (33) are summarized by the macroscopic Equation 8. However, one has to recall that, independently of the microscopic conditions, a large part of untreated tumors follow the GL (see Vaghi et al. (3) for a recent review) and that with a small number of parameters, one gets quantitative clinical indications for personalized treatments. If, for example, a patient gets a small specific rate by RT on the primary tumor, then a small contribution of IT might be able to result in a complete recovery.

The abscopal effect has been described by a macroscopic coupling between RT and immune system response, where the initial progression of the metastasis follows the GL with untreated primary tumor parameters. This is a reasonable assumption although the in-situ conditions can produce different results.

According to the specific conditions recalled in the introduction, choosing the best dose fractionation and timing with respect to immunotherapy is difficult. Notoriously, the use of protracted RT schedules (standard fractionation or slight hypofractionation) is discouraged since radiosensitive lymphocytes are cleared out from tumor tissues at each fraction delivery, thus preventing their anti-tumor function, Filatenkov et al. (61). Conversely, large doses per fraction are effectively immunogenic, Muraro et al. (62). In particular, doses below 12 Gy are the most suitable for enhancing the anti-tumor immune response as over such a threshold there is the degradation of immunogenic cytosolic DNA by an exonuclease, Trex, whose expression, as evaluated in preclinical experiments, is cell line-dependent and increases with increasing radiation dose Dewan et al. (19); Vanpouille-Box et al. (26). On the other side, even very low doses per fraction (< 1 Gy) seem to activate macrophages against cancer cells and stimulate T-cell immunity Klug et al. (63). Doses over 12 Gy are involved in the damage of tumor vasculature by activation of acid sphingomyelinase and production of ceramides, which culminate in vessel obliteration with subsequent tumor regression for insufficient nutrient and oxygen supply Song et al. (64). Therefore, the entire dose range used in clinical practice may be useful to control tumors and all RT fractionations combined with immunotherapy deserve clinical investigations.

Recently, old RT techniques simultaneously combining very different doses within the tumor, namely spatially fractionated radiation therapy (SFRT), are gaining new interest because of the assumption that tumor tissues spanning a wide dose range may benefit from multiple immune activation mechanisms, which eventually could be further boosted by ICI administration Ferini et al. (65); Tubin et al. (66). Given the ability of new instrumental exams to “map” tumor areas with different metabolisms, there is the possibility of modulating the dose distribution according to the oxygenation patterns inside the tumor to maximize both direct and indirect (immune-mediated) lethal effects of radiation Ferini et al. (67); Ferini et al. (68). With the latter approach, complete responses have been documented earlier than with classic homogeneously-delivered stereotactic RT doses and before ICI administration, likely implying rapid immune intervention enhanced and maintained by the addition of IT Ferini et al. (69).

All of the above considerations require the modeling of tumor response to RT and IT to help predict the best combination strategy, also given the inadequacy of current radiobiological mathematical models to comprehensively explain the results deriving from this association Ferini et al. (69).

In the proposed mathematical and computational approach, the fractionization effects are taken into account by the functions $D_{n_f}$ and $\overline{W}\left(t_{n_f},t_0\right)$ and a spatially non-homogeneous behavior can be easily implemented. However, a complete discussion requires a forthcoming devoted analysis.

5 Conclusions

A comprehensive scope of the combined impact of radiotherapy and immunotherapy is vital for clinical decision-making. Yet, numerous mathematical models in existing literature prove overly complex, characterized by an abundance of differential equations, parameters, and initial conditions, rendering their practical implementation quite challenging.

In this study, we use a macroscopic mathematical approach that does not rely on the underlying microscopic dynamics. Instead, we propose a simplified model of the tumor progression using a Gompertz law, which involves just two parameters. Moreover, utilizing numerical solvers of the equations provided in the appendices is a straightforward process.

Examining how control influences system dynamics under radiation and/or drug therapy sheds light on the disease’s temporal progression. This approach holds promise in assisting clinicians to make informed decisions by providing a clearer understanding of treatment outcomes, namely, assessing whether the therapy administered results in full recovery.

Besides its clinical relevance, our approach shows potential for additional experimental validation of the synergistic impact of the abscopal phenomenon on treatment outcomes.

We recognize the importance of conducting rigorous experimental investigations to solidify the theoretical basis of our approach. By performing targeted studies and gathering more empirical data, we aim to validate the approach in different conditions and the significance of the abscopal effect in influencing therapy outcomes. This experimental validation will provide a deeper understanding of the interplay between the administered treatment, tumor response, and the abscopal effect.

Moreover, our future research endeavors will focus on elucidating the mechanisms underlying the abscopal effect and quantifying its impact on treatment efficacy. By combining computational modeling with comprehensive experimental studies, we strive to enhance our understanding of this phenomenon and optimize therapeutic strategies accordingly. Ultimately, we aim to improve patient-oriented outcomes by harnessing the full potential of the abscopal effect in cancer therapy.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://figshare.com/articles/dataset/autoantibody_discovery/10302227; data on AB93 and AB641, platform figshare.

Author contributions

PC: Conceptualization, Formal analysis, Methodology, Writing – original draft. FC: Conceptualization, Data curation, Investigation, Validation, Writing – review & editing. GF: Methodology, Validation, Writing – original draft. SF: Funding acquisition, Methodology, Resources, Validation, Writing – review & editing. EM: Data curation, Investigation, Software, Validation, Writing – review & editing. DG: Funding acquisition, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was totally funded by the department for productive activities of the Sicilian Region, project title: “DiOncoGen Diagnostica innovativa”, PO FESR (grant number: G89J18000700007). This work is partially funded by the Italian Ministry of University and Research (MUR, grant “Heal Italia (Health Extended Alliance for Innovative Therapies, Advanced Lab-research, and Integrated Approaches of Precision Medicine, grant n. B83D22001050004).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fimmu.2024.1373738/full#supplementary-material

Mathematical Formalism | Mathematical model for untreated tumor growth with GL, immune therapy, immune and radiotherapies, critical behavior, and abscopal effect.

References

1. Gompertz B. Xxiv. on the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. in a letter to francis baily, esq. frs &c. Philos Trans R Soc London. (1825) 115:513–83. doi: 10.1098/rstl.1825.0026

CrossRef Full Text | Google Scholar

2. Norton L. A gompertzian model of human breast cancer growth. Cancer Res. (1988) 48:7067–71.

PubMed Abstract | Google Scholar

3. Vaghi C, Rodallec A, Fanciullino R, Ciccolini J, Mochel JP, Mastri M, et al. Population modeling of tumor growth curves and the reduced gompertz model improve prediction of the age of experimental tumors. PLoS Comput Biol. (2020) 16:e1007178. doi: 10.1371/journal.pcbi.1007178

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Verhulst P-F. Notice sur la loi que la population poursuit dans son accroissement. Correspondance Mathématique Physique. (1838) 10:113–21. doi: 10.4000/msh.2893

CrossRef Full Text | Google Scholar

5. Hiam-Galvez KJ, Allen BM, Spitzer MH. Systemic immunity in cancer. Nat Rev Cancer. (2021) 21:345–59. doi: 10.1038/s41568-021-00347-z

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lin C-W, Xie J, Zhang D, Han KH, Grande G, Wu NC, et al. Immunity against cancer cells may promote their proliferation and metastasis. Proc Natl Acad Sci. (2020) 117:426–31. doi: 10.1073/pnas.1916833117

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhao X, Shao C. Radiotherapy-mediated immunomodulation and anti-tumor abscopal effect combining immune checkpoint blockade. Cancers (Basel). (2020) 12:2762. doi: 10.3390/cancers12102762

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Puglisi C, Giuffrida R, Borzì G, Di Mattia P, Costa A, Colarossi C, et al. Radiosensitivity of cancer stem cells has potential predictive value for individual responses to radiotherapy in locally advanced rectal cancer. Cancers (Basel). (2020) 12:2072–6694. doi: 10.3390/cancers12123672

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Puglisi C, Giuffrida R, Borzì G, Illari S, Caronia F, Di Mattia P, et al. Ex vivo irradiation of lung cancer stem cells identifies the lowest therapeutic dose needed for tumor growth arrest and mass reduction in vivo. Front Oncol. (2022) 12:837400. doi: 10.3389/fonc.2022.837400

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ngwa W, Irabor O, Schoenfeld J, Hesser J, Demaria S, Formenti S. Using immunotherapy to boost the abscopal effect. Nat Rev Cancer. (2018) 18:313–22. doi: 10.1038/nrc.2018.6

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Mole R. Whole body irradiation; radiobiology or medicine? Br J Radiol. (1953) 26:234–41. doi: 10.1259/0007-1285-26-305-234

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Demaria S, Ng B, Devitt M, Babb J, Kawashima N, Liebes L, et al. Ionizing radiation inhibition of distant untreated tumors (abscopal effect) is immune mediated. Int J Radiat Oncology Biology Phys. (2004) 58:862–70. doi: 10.1016/j.ijrobp.2003.09.012

CrossRef Full Text | Google Scholar

13. Twyman-Saint Victor C, Rech A, Maity A, Rengan R, Pauken K, Stelekati E, et al. Radiation and dual checkpoint blockade activate non-redundant immune mechanisms in cancer. Nature. (2015) 520:373–7. doi: 10.1038/nature14292

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Dovedi S, Cheadle E, Popple A, Poon E, Morrow M, Stewart R, et al. Fractionated radiation therapy stimulates anti-tumor immunity mediated by both resident and infiltrating polyclonal t-cell populations when combined with pd1 blockade. Clin Cancer Res. (2017) 23:5514–26. doi: 10.1158/1078-0432.CCR-16-1673

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Demaria S, Kawashima N, Yang A, Devitt M, Babb J, Allison J, et al. Immune-mediated inhibition of metastases after treatment with local radiation and ctla-4 blockade in a mouse model of breast cancer. Clin Cancer Res. (2005) 11:728–34. doi: 10.1158/1078-0432.728.11.2

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ji D, Song C, Li Y, Xia J, Wu Y, Jia J, et al. Combination of radiotherapy and suppression of tregs enhances abscopal antitumor effect and inhibits metastasis in rectal cancer. J ImmunoTherapy Cancer. (2018) 8:313–22. doi: 10.1136/jitc-2020-000826

CrossRef Full Text | Google Scholar

17. McNamee E, Korns Johnson D, Homann D, Clambey E. Hypoxia and hypoxia-inducible factors as regulators of t cell development, differentiation, and function. Immunol Res. (2013) 55:58–70. doi: 10.1007/s12026-012-8349-8

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Castorina P, Castorina L, Ferini G. Non-homogeneous tumor growth and its implications for radiotherapy: A phenomenological approach. J Personalized Med. (2021) 11:527. doi: 10.3390/jpm11060527

CrossRef Full Text | Google Scholar

19. Dewan MZ, Galloway AE, Kawashima N, Dewyngaert JK, Babb JS, Formenti SC, et al. Fractionated but not single-dose radiotherapy induces an immune-mediated abscopal effect when combined with anti–ctla-4 antibodyfractionated radiation synergizes with immunotherapy. Clin Cancer Res. (2009) 15:5379–88. doi: 10.1158/1078-0432.CCR-09-0265

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Agur Z, Vuk-Pavlović S. Mathematical modeling in immunotherapy of cancer: personalizing clinical trials. Mol Ther. (2012) 20:1–2. doi: 10.1038/mt.2011.272

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Walker R, Enderling H. From concept to clinic: Mathematically informed immunotherapy. Curr Probl Cancer. (2016) 40(1):68–83. doi: 10.1016/j.currproblcancer.2015.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Ng J, Dai T. Radiation therapy and the abscopal effect: a concept comes of age. Ann Transl Med. (2016) 4(6):118–20. doi: 10.21037/atm.2016.01.32

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Serre R, Benzekry S, Padovani L, Meille C, André N, Ciccolini J, et al. Mathematical modeling of cancer immunotherapy and its synergy with radiotherapymodeling of radioimmunotherapy. Cancer Res. (2016) 76:4931–40. doi: 10.1158/0008-5472.CAN-15-3567

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Gong C, Milberg O, Wang B, Vicini P, Narwal R, Roskos L, et al. A computational multiscale agent-based model for simulating spatio-temporal tumour immune response to pd1 and pdl1 inhibition. J R Soc Interface. (2017) 14:20170320. doi: 10.1098/rsif.2017.0320

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Marconi R, Strolin S, Bossi G, Strigari L. A meta-analysis of the abscopal effect in preclinical models: Is the biologically effective dose a relevant physical trigger? PLoS One. (2017) 12:e0171559. doi: 10.1371/journal.pone.0171559

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Vanpouille-Box C, Alard A, Aryankalayil MJ, Sarfraz Y, Diamond JM, Schneider RJ, et al. Dna exonuclease trex1 regulates radiotherapy-induced tumour immunogenicity. Nat Commun. (2017) 8:15618. doi: 10.1038/ncomms15618

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chakwizira A, Ahlstedt J, Nittby Redebrandt H, Ceberg C. Mathematical modelling of the synergistic combination of radiotherapy and indoleamine-2, 3-dioxygenase (ido) inhibitory immunotherapy against glioblastoma. Br J Radiol. (2018) 91:20170857. doi: 10.1259/bjr.20170857

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kosinsky Y, Dovedi SJ, Peskov K, Voronova V, Chu L, Tomkinson H, et al. Radiation and pd-(l) 1 treatment combinations: immune response and dose optimization via a predictive systems model. J immunotherapy Cancer. (2018) 6:1–15. doi: 10.1186/s40425-018-0327-9

CrossRef Full Text | Google Scholar

29. Liu Y, Dong Y, Kong L, Shi F, Zhu H, Yu J. Abscopal effect of radiotherapy combined with immune checkpoint inhibitors. J Hematol Oncol. (2018) 11:1–15. doi: 10.1186/s13045-018-0647-8

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Valentinuzzi D, Simončič U, Uršič K, Vrankar M, Turk M, Jeraj R. Predicting tumour response to anti-pd-1 immunotherapy with computational modelling. Phys Med Biol. (2019) 64:025017. doi: 10.1088/1361-6560/aaf96c

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Friedrich T, Henthorn N, Durante M. Modeling radioimmune response—current status and perspectives. Front Oncol. (2021) 11:647272. doi: 10.3389/fonc.2021.647272

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Malinzi J, Basita KB, Padidar S, Adeola HA. Prospect for application of mathematical models in combination cancer treatments. Inf Med Unlocked. (2021) 23:100534. doi: 10.1016/j.imu.2021.100534

CrossRef Full Text | Google Scholar

33. Bekker RA, Kim S, Pilon-Thomas S, Enderling H. Mathematical modeling of radiotherapy and its impact on tumor interactions with the immune system. Neoplasia. (2022) 28:100796. doi: 10.1016/j.neo.2022.100796

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Altrock PM, Liu LL, Michor F. The mathematics of cancer: integrating quantitative models. Nat Rev Cancer. (2015) 15:730–45. doi: 10.1038/nrc4029

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Brady R, Enderling H. Mathematical models of cancer: when to predict novel therapies, and when not to. Bull Math Biol. (2019) 81:3722–31. doi: 10.1007/s11538-019-00640-x

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Browning AP, Simpson MJ. Geometric analysis enables biological insight from complex non-identifiable models using simple surrogates. PLoS Comput Biol. (2023) 19:e1010844. doi: 10.1371/journal.pcbi.1010844

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wheldon TE. Mathematical models in cancer research. Adam Hilger Publisher. (1988).

Google Scholar

38. Guiot C, Degiorgis PG, Delsanto PP, Gabriele P, Deisboeck TS. Does tumor growth follow a “universal law”? J Theor Biol. (2003) 225:147–51. doi: 10.1016/S0022-5193(03)00221-2

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Castorina P, Delsanto P, Guiot C. Classification scheme for phenomenological universalities in growth problems in physics and other sciences. Phys Rev Lett. (2006) 96:188701. doi: 10.1103/PhysRevLett.96.188701

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Castorina P, Carcò D, Guiot C, Deisboeck TS. Tumor growth instability and its implications for chemotherapy. Cancer Res. (2009) 69:8507–15. doi: 10.1158/0008-5472.CAN-09-0653

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Maaß C, Sachs JP, Hardiansyah D, Mottaghy FM, Kletting P, Glatting G. Dependence of treatment planning accuracy in peptide receptor radionuclide therapy on the sampling schedule. EJNMMI Res. (2016) 6:1–9. doi: 10.1186/s13550-016-0185-8

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Jung H, Krüger H-J, Brammer I, Zywietz F, Beck-Bornholdt H-P. Cell population kinetics of the rhabdomyosarcoma r1h of the rat after single doses of x-rays. Int J Radiat Biol. (1990) 57:567–89. doi: 10.1080/09553009014552701

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Hansen O, Grau C, Bentzen SM, Overgaard J. Repopulation in the sccvii squamous cell carcinoma assessed by an in vivo-in vitro excision assay. Radiotherapy Oncol. (1996) 39:137–44. doi: 10.1016/0167-8140(96)01728-8

CrossRef Full Text | Google Scholar

44. O’Donoghue JA. The response of tumours with gompertzian growth characteristics to fractionated radiotherapy. Int J Radiat Biol. (1997) 72:325–39. doi: 10.1080/095530097143329

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Braakman S, Pathmanathan P, Moore H. Evaluation framework for systems models. CPT Pharmacometrics Syst Pharmacol. (2022) 11:264–289. doi: 10.1002/psp4.12755

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Castorina P, Blanchard P. Unified approach to growth and aging in biological, technical and biotechnical systems. SpringerPlus. (2012) 1:1–5. doi: 10.1186/2193-1801-1-7

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Berendt MJ, North RJ. T-cell-mediated suppression of anti-tumor immunity. an explanation for progressive growth of an immunogenic tumor. J Exp Med. (1980) 151:69–80. doi: 10.1084/jem.151.1.69

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Gonzalez H, Hagerling C, Werb Z. Roles of the immune system in cancer: from tumor initiation to metastatic progression. Genes Dev. (2018) 32:1267–84. doi: 10.1101/gad.314617.118

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Castorina P, Carco’ D. Nutrient supply, cell spatial correlation and gompertzian tumor growth. Theory Biosci. (2021) 140:197–203. doi: 10.1007/s12064-021-00344-8

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Khajanchi S, Ghosh D. The combined effects of optimal control in cancer remission. Appl Mathematics Comput. (2015) 271:375–88. doi: 10.1016/j.amc.2015.09.012

CrossRef Full Text | Google Scholar

51. Khajanchi S, Banerjee S. Quantifying the role of immunotherapeutic drug t11 target structure in progression of Malignant gliomas: Mathematical modeling and dynamical perspective. Math Biosci. (2017) 289:69–77. doi: 10.1016/j.mbs.2017.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Royama T. Analytical population dynamics Vol. 10. UK: Springer Science & Business Media (2012).

Google Scholar

53. Van Leeuwen C, Oei A, Crezee J, Bel A, Franken N, Stalpers L, et al. The alfa and beta of tumours: a review of parameters of the linear-quadratic model, derived from clinical radiotherapy studies. Radiat Oncol. (2018) 13:1–11. doi: 10.1186/s13014-018-1040-z

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Khajanchi S, Banerjee S. Influence of multiple delays in brain tumor and immune system interaction with t11 target structure as a potent stimulator. Math Biosci. (2018) 302:116–30. doi: 10.1016/j.mbs.2018.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Khajanchi S. Stability analysis of a mathematical model for glioma-immune interaction under optimal therapy. Int J Nonlinear Sci Numerical Simulation. (2019) 20:269–85. doi: 10.1515/ijnsns-2017-0206

CrossRef Full Text | Google Scholar

56. Khajanchi S, Banerjee S. A strategy of optimal efficacy of t11 target structure in the treatment of brain tumor. J Biol Syst. (2019) 27:225–55. doi: 10.1142/S0218339019500104

CrossRef Full Text | Google Scholar

57. Dataset Grace. (2008). Available at: https://plasma-gate.weizmann.ac.il/Grace/.

Google Scholar

58. Nesseler JP, Lee M-H, Nguyen C, Kalbasi A, Sayre JW, Romero T, et al. Tumor size matters—understanding concomitant tumor immunity in the context of hypofractionated radiotherapy with immunotherapy. Cancers. (2020) 12:714. doi: 10.3390/cancers12030714

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Lim K, Chan P, Dinniwell R, Fyles A, Haider M, Cho Y-B, et al. Cervical cancer regression measured using weekly magnetic resonance imaging during fractionated radiotherapy: radiobiologic modeling and correlation with tumor hypoxia. Int J Radiat Oncol Biol Phys. (2008) 70:126–33. doi: 10.1016/j.ijrobp.2007.06.033

PubMed Abstract | CrossRef Full Text | Google Scholar

60. McMahon SJ. The linear quadratic model: usage, interpretation and challenges. Phys Med Biol. (2018) 64:01TR01. doi: 10.1088/1361-6560/aaf26a

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Filatenkov A, Baker J, Mueller A, Kenkel J, Ahn G, Dutt S, et al. Ablative tumor radiation can change the tumor immune cell microenvironment to induce durable complete remissions. Clin Cancer Res. (2015) 21:3727. doi: 10.1158/1078-0432.CCR-14-2824

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Muraro E, Furlan C, Avanzo M, Martorelli D, Comaro E, Rizzo A, et al. Local highdose radiotherapy induces systemic immunomodulating effects of potential therapeutic relevance in oligometastatic breast cancer. Front Immunol. (2017) 8:1476. doi: 10.3389/fimmu.2017.01476

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Klug F, Prakash H, Huber P, Seibel T, Bender N, Halama N, et al. Low-dose irradiation programs macrophage differentiation to an inos+/m1 phenotype that orchestrates effective t cell immunotherapy. Cancer Cell. (2013) 24:589. doi: 10.1016/j.ccr.2013.09.014

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Song C, Glatstein E, Marks L, Emami B, Grimm J, Sperduto P, et al. Biological principles of stereotactic body radiation therapy (sbrt) and stereotactic radiation surgery (srs): Indirect cell death. Int J Radiat Oncology Biology Phys. (2021) 110:21. doi: 10.1016/j.ijrobp.2019.02.047

CrossRef Full Text | Google Scholar

65. Ferini G, Valenti V, Tripoli A, Illari S, Molino L, Parisi S, et al. Lattice or oxygen-guided radiotherapy: What if they converge? possible future directions in the era of immunotherapy. Cancers (Basel). (2021) 13:3290. doi: 10.3390/cancers13133290

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Tubin S, Vozenin M, Prezado Y, Durante M, Prise K, Lara P, et al. Novel unconventional radiotherapy techniques: Current status and future perspectives - report from the 2nd international radiation oncology online seminar. Clin Trans Radiat Oncol. (2023) 40:100605. doi: 10.1016/j.ctro.2023.100605

CrossRef Full Text | Google Scholar

67. Ferini G, Parisi S, Lillo S, Viola A, Minutoli F, Critelli P, et al. Impressive results after ”metabolism-guided“ lattice irradiation in patients submitted to palliative radiation therapy: Preliminary results of lattice₀₁ multicenter study. Cancers (Basel). (2022) 14:3909. doi: 10.3390/cancers14163909

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Ferini G, Valenti V, Viola A, Umana G, Illari S, Parisi S, et al. First-ever clinical experience with magnetic resonance-based lattice radiotherapy for treating bulky gynecological tumors. Anticancer Res. (2022) 42:4641. doi: 10.21873/anticanres.15968

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Ferini G, Castorina P, Valenti V, Illari S, Sachpazidis I, Castorina L, et al. A novel radiotherapeutic approach to treat bulky metastases even from cutaneous squamous cell carcinoma: Its rationale and a look at the reliability of the linear-quadratic model to explain its radiobiological effects. Front Oncol. (2022) 12:809279. doi: 10.3389/fonc.2022.809279

PubMed Abstract | CrossRef Full Text | Google Scholar