
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Immunol. , 14 March 2024
Sec. Autoimmune and Autoinflammatory Disorders: Autoinflammatory Disorders
Volume 15 - 2024 | https://doi.org/10.3389/fimmu.2024.1371620
This article is part of the Research Topic New Approach Methods in Immunology View all 20 articles
A correction has been applied to this article in:
Corrigendum: Mathematical modeling in autoimmune diseases: from theory to clinical application
 Yaroslav Ugolkov1,2,3
Yaroslav Ugolkov1,2,3 Antonina Nikitich1,2
Antonina Nikitich1,2 Cristina Leon4
Cristina Leon4 Gabriel Helmlinger5
Gabriel Helmlinger5 Kirill Peskov1,2,4,6
Kirill Peskov1,2,4,6 Victor Sokolov2,4
Victor Sokolov2,4 Alina Volkova2,4*
Alina Volkova2,4*The research & development (R&D) of novel therapeutic agents for the treatment of autoimmune diseases is challenged by highly complex pathogenesis and multiple etiologies of these conditions. The number of targeted therapies available on the market is limited, whereas the prevalence of autoimmune conditions in the global population continues to rise. Mathematical modeling of biological systems is an essential tool which may be applied in support of decision-making across R&D drug programs to improve the probability of success in the development of novel medicines. Over the past decades, multiple models of autoimmune diseases have been developed. Models differ in the spectra of quantitative data used in their development and mathematical methods, as well as in the level of “mechanistic granularity” chosen to describe the underlying biology. Yet, all models strive towards the same goal: to quantitatively describe various aspects of the immune response. The aim of this review was to conduct a systematic review and analysis of mathematical models of autoimmune diseases focused on the mechanistic description of the immune system, to consolidate existing quantitative knowledge on autoimmune processes, and to outline potential directions of interest for future model-based analyses. Following a systematic literature review, 38 models describing the onset, progression, and/or the effect of treatment in 13 systemic and organ-specific autoimmune conditions were identified, most models developed for inflammatory bowel disease, multiple sclerosis, and lupus (5 models each). ≥70% of the models were developed as nonlinear systems of ordinary differential equations, others – as partial differential equations, integro-differential equations, Boolean networks, or probabilistic models. Despite covering a relatively wide range of diseases, most models described the same components of the immune system, such as T-cell response, cytokine influence, or the involvement of macrophages in autoimmune processes. All models were thoroughly analyzed with an emphasis on assumptions, limitations, and their potential applications in the development of novel medicines.
Autoimmune diseases (ADs) are a group of diverse disorders that occur widely and affect approximately 12.5% of the global population, with a greater prevalence among childbearing women (1). A landmark feature in ADs can be found in immune disturbances causing autoreactivity of lymphocytes against normal cells of the organism (2). Even though all ADs share a common pathophysiological basis of development, their clinical manifestations could vary from mild abnormalities in laboratory measurements to life-threatening conditions such as organ failure following serious tissue damage (3). Depending on the origin of their manifestation, ADs could be restricted to a single organ (organ-specific ADs) such as the thyroid gland in Hashimoto’s thyroiditis (HT) or the pancreas in type 1 diabetes mellitus (T1DM) or, on the other hand, affect multiple organs and tissues within the body, such as systemic lupus erythematosus (SLE) or rheumatoid arthritis (RA). Both types of ADs may exhibit a wide range of symptoms and can be challenging to diagnose and treat (4).
The exact causes of autoimmunity are not fully understood. Despite the presence of known genetic and epigenetic predisposing factors, environmental factors are believed to be an essential trigger of autoimmune response (5). The most well-studied example of such an external stimulus are pathogenic microorganisms or dysbiosis in commensal organisms, initiating either a non-specific immune response, or an immune response specific to self-antigens through molecular mimicry, like in the cases of the Epstein–Barr virus (6) or the group A streptococcus (7). Other well-known environmental factors leading to autoimmunity include smoking, diet, and drug administration (e.g., immune checkpoint inhibitors therapy); and more such factors remain to be defined (3, 8).
ADs exhibit multi-phase dynamics and complex pathogenesis, including dysregulation in both adaptive and innate immune systems (9). At preclinical stages of the disease, autoantibodies – the hallmark of ADs – are expressed, in the absence of clinical signs and symptoms of autoimmune disorders such as fever, rash, and fatigue (10). A gradual involvement of functional elements of the immune system over time, such as aberrant B- and T-cells, leads to an eventual diversification of clinical phenotypes. However, despite the evolving understanding of the autoimmunity mechanisms, there are still numerous gaps in our knowledge regarding the role of specific immune components within a tangled network with multiple feedback loops in the pathophysiology of ADs, further complicating the management of disease progression (11).
The first-line therapy to control ADs include conventional immunosuppressive or anti-inflammatory therapies, such as corticosteroids and methotrexate, which dampen the overactivated immune system (12, 13). However, non-selective immunomodulators do not always provide sufficient benefit in a heterogeneous population of patients; also, their long-term administration leads to the appearance of side effects, the most common ones being an increased risk of infections and malignancies (14). Eventually, the accumulated knowledge on the pathophysiology of ADs has contributed to the development of targeted drugs with notably higher benefit-risk ratios. These selective immunotherapies are designed to suppress major pro-inflammatory signaling pathways by blocking inflammatory cytokines (e.g., anti-interleukin (IL)-17 in psoriasis), target immune cells (e.g., anti-B-cell activating factor (BAFF) in SLE), or intracellular kinases (e.g., Janus kinase (JAK) inhibitors in RA). Despite the tremendous success of targeted therapies in ADs, unmet medical needs remain, in terms of long-term safety as well as overall efficacy, since many patients do not achieve disease remission (15). A deeper understanding of mechanisms and of their corresponding heterogeneity in the development of ADs would provide opportunities to overcome these limitations, ultimately leading to a more personalized and, therefore, a more efficient approach to treatment.
Mechanistic, physiologically-based mathematical modeling is widely accepted as a supportive tool for better understanding and interrogating diseases pathophysiology, given its ability to integrate biological and pharmacological knowledge with a quantitative description of the underlying processes, therefore making such modeling essential in enhancing decision-making at all stages of drug development (16, 17). For example, by reconstructing biochemical or signaling cascades in silico, a researcher may formulate and challenge theoretical hypotheses regarding the contribution of certain signaling components, to support the rational identification and validation of new drug targets (18, 19). Mechanistic modeling can also be employed to explore the impact of patient-specific factors, such as demographic characteristics and comorbidities, on drug action, potentially explaining the heterogeneity in treatment responses and providing options for adjustments or changes in treatment strategies. Modeling may further help in rationalizing the selection and application of drug combinations, in optimizing dosing schedule, and more (16). In summary, mechanistic mathematical modeling represents a tool to support the targeting of the right molecular pathway in a given disease context, with the right dose, and in the right patient population or phenotype (20).
The aim of this work was to conduct a systematic review and analysis of mathematical models of ADs focused on the mechanistic description of the immune system, to shape and consolidate the current landscape of quantitative knowledge on autoimmune processes, to outline most promising directions for further model developments, and to perform model-informed analyses aimed at supporting drug discovery and development against autoimmune pathologies.
A systematic literature search was performed in the PubMed database, to identify all mechanistic mathematical models with relevance to ADs. The search query consisted of two semantic components. The first one involved keywords related to autoimmunity, specifically, 184 disease-specific terms from the list of ADs (21) and general descriptors of autoimmune-related processes (e.g., “autoimmune disease”, “autoinflammatory”, etc.). The second one was used to seek out studies on mechanistic, physiologically-based, or quantitative systems pharmacology (QSP) models. Additional search conditions were implemented, to eliminate records in non-English language and those focused on clinical trial results, reviews, or meta-analyses. To derive and compare the number of publications available in the PubMed database on mechanistic models versus empirical ones, another search was performed, with the second semantic component replaced with terms related to pharmacokinetics (PK) and pharmacodynamics (PD) analyses. The exact queries used are listed in the Supplementary Methods.
The search resulted in 500 potentially relevant publications (last accessed: 20 October 2023). Two authors (Y.U., A.V.) independently screened the articles for duplication and eligibility. Disagreements were resolved through discussion with independent reviewers (V.S., K.P.). A prerequisite for transferring an article into further analysis was the description of autoimmune-related processes at any level of generalization and organization (e.g., molecular, cellular, tissue-level), including antigen presentation, cytokine production, immune complex (IC) formation, etc., using a mathematical framework such as ordinary differential equations (ODEs), partial differential equations (PDEs), and others. A model with any number of variables or parameters was considered mechanism-based as long as it included more than one of the above-mentioned components. In addition, articles featuring minor modifications vs. previously published models within a single AD were grouped and analyzed together.
Several classifications were used to categorize the models: by target organ or system, by indication, by mathematical method, and by associated data. The following criteria were applied to define the latter: if only clinical vs. preclinical data were used for calibration, fine-tuning of parameters, or model validation, the model was tagged to the respective group (i.e., “Clinical” or “Preclinical”). If both types of data, preclinical and clinical, were used, or the parametrization was not within the scope of the research, “Combined” or “Not specified” tags were assigned.
Visualization and statistical analyses of the gathered data were carried out using reproducible scripts in the R Statistics software (version 4.0.2), using the R “tidyverse” package (version 1.3.0) (22). A network diagram of immune components was prepared using the R “igraph” package (version 1.2.7) (23).
To illustrate the growing body of publications related to mathematical modeling in ADs, the numbers of articles appearing in the PubMed database following the search queries for either PK/PD models or mechanistic models were visualized against years of publication (Figure 1A). According to the search results, the first papers matching the specifications date back to the 1970s. Since then, the number of relevant articles increased exponentially, reaching more than 200 publications per year by 2024. The ratio of studies appearing in the search for mechanistic models vs. empirical ones was small (~1-to-5).
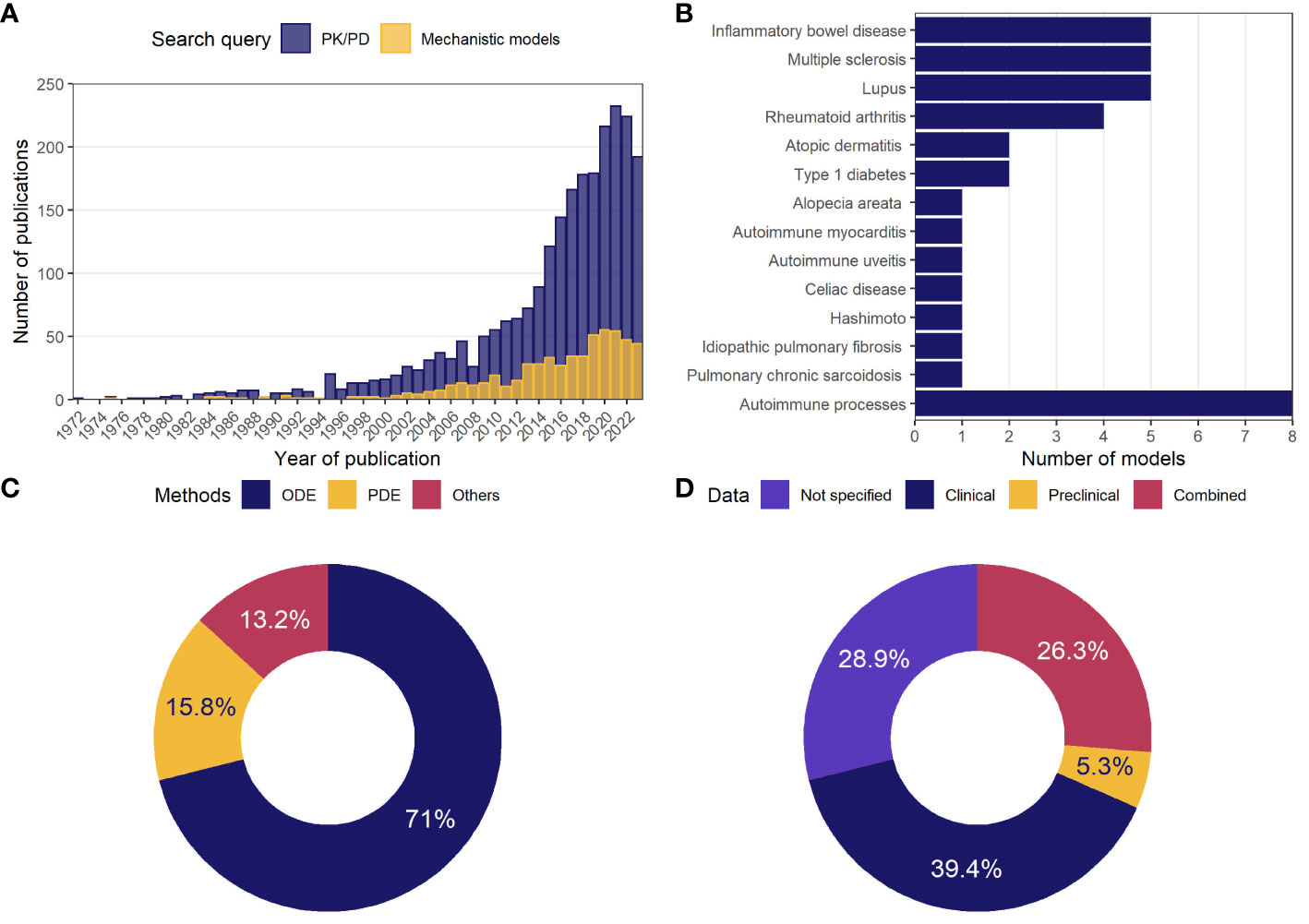
Figure 1 General statistics on model-based analyses in autoimmune diseases. (A) Number of publications in the PubMed database per year, following a search for mechanistic or PK/PD models of ADs; (B) number of mechanistic models identified through a systematic review and classified by indication; (C) percentage of mechanistic models using the described methodology; (D) percentage of mechanistic models by type of data used in model development or validation. AD, autoimmune disease; ODE, ordinary differential equations; PD, pharmacodynamics; PDE, partial differential equations; PK, pharmacokinetics.
Following a detailed investigation of these 500 publications potentially associated with mechanistic models, 47 studies were identified, which described the development, analysis, and application of 38 unique physiologically-based models. These 38 models were categorized according to 13 related AD indications, including alopecia areata, atopic dermatitis, autoimmune myocarditis, experimental autoimmune uveitis (EAU), celiac disease, HT, idiopathic pulmonary fibrosis (IPF), inflammatory bowel disease (IBD), multiple sclerosis (MS), pulmonary sarcoidosis, RA, SLE, T1DM, or classified into “Autoimmune processes” category if the model investigated autoimmunity in a more generic context rather than according to a specific AD (Figure 1B). The most frequently featured pathologies were IBD, MS, and lupus (5 models per disease), followed by RA (4 models), atopic dermatitis and T1DM (2 models each).
These models predominantly employed nonlinear systems of ODEs (71%) (Figure 1C). Some models were built using PDEs (15.8%); others featured integro-differential equations, Boolean networks, or Markov jump processes (13.2%). The models were developed primarily based on clinical data (39.4%); a small proportion of models made use of preclinical data only (5.3%), while 26.3% of model used a combination of clinical and preclinical data; 28.9% of models did not rely on quantitative data (Figure 1D).
Given the multitude of ramifications found in the immune system, the mechanistic models we evaluated typically focused on specific aspects of autoimmune conditions and the related pathophysiology, and often at various levels of “mechanistic granularity”. To identify those components and interactions which occurred most frequently in the mathematical systems, we extracted all variables from the modeling papers – except for the Boolean network models – i.e., 214 variables from 36 models; we then unified these variables into 60 terms and counted the incidence of terms occurring simultaneously within a single model (Supplementary Material; Table 1). If a term was encountered together with another term for at least 3 times, the corresponding interaction was added to the network diagram (Figure 2). The 31 nodes which appeared on the diagram were next divided into 3 categories, by biological origin (i.e., cellular, or molecular) or effect (e.g., fibrosis, inflammation, tissue damage). The most frequently occurring terms were antigen and regulatory T-cells (Treg) (12 cases), followed by interferon (IFN)-γ and macrophages (Mφ) (9 cases each), tumor necrosis factor-α (TNF-α), T-helper cells (Th) and Th1, (8 cases each), and Th17, inflammation, fibrosis (7 cases each). Consequently, most frequent interactions (at least 5 per edge) were observed between T-cells (Tregs, Th1, Th17) and related cytokines (IFN-γ, IL-2, IL-4, IL-6, IL-17).
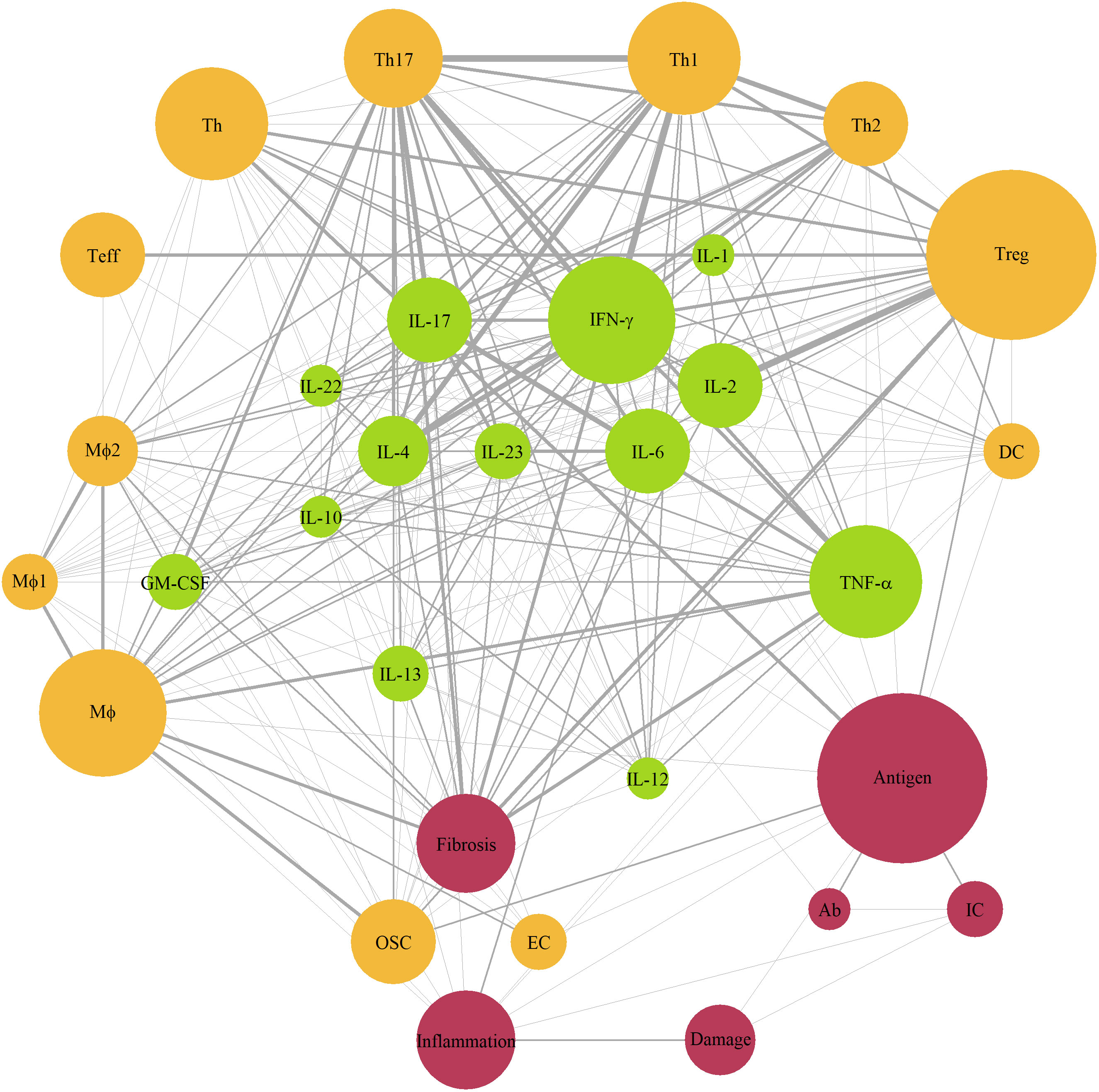
Figure 2 Network diagram of immune components represented in mechanistic models of autoimmune diseases. Green color – cytokines; yellow color – cells; red color – other components; size of a node – number of models with the component (3 to 11); edge width – number of interaction (3 to 6). Ab, antibody; APC, antigen-presenting cells, DC, dendritic cells; EC, epithelial cells; GM-CSF, granulocyte-macrophage colony-stimulating factor; IC, immune complex; IFN, interferon; IL, interleukin; Mφ, macrophages; OSC, organ-specific cells; Teff, effector T-cells; Th, T-helper cells; TNF-α, tumor necrosis factor-α; Treg, regulatory T-cells.
Next, the 30 models associated with specific diseases (see Figure 1B) were categorized into 2 groups: systemic- and organ-specific. The latter category was, in turn, separated into 6 subgroups: endocrine, lungs, skin, nervous system and eyes, cardiovascular, and gastrointestinal (GI) tract (Figure 3). Mathematical systems describing autoimmune processes in a more generic sense (8 models) were kept in a separate category. All 38 models were subjected to a comprehensive evaluation encompassing their description, applications, and limitations, summarized in Table 1 and in the text below.
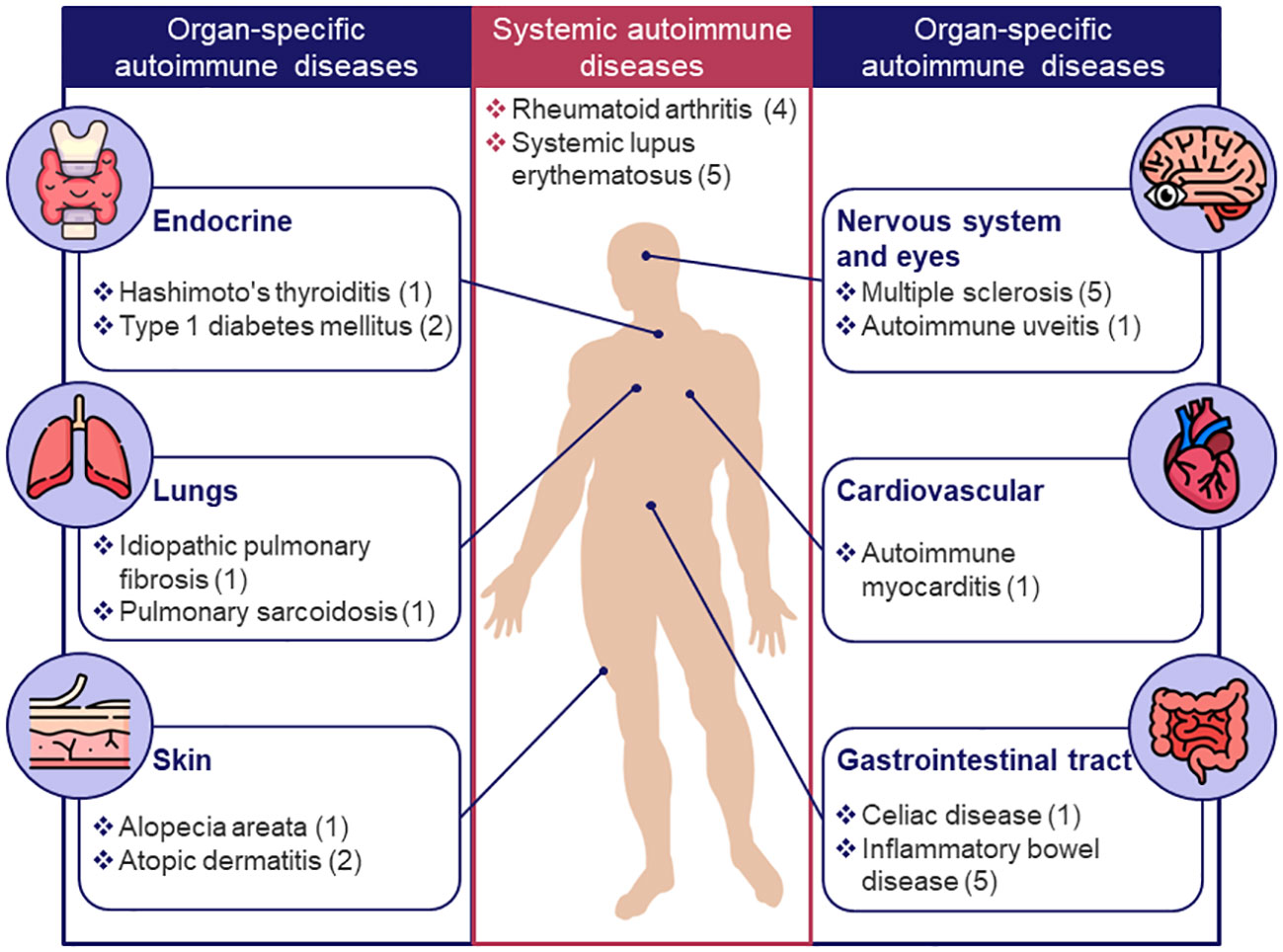
Figure 3 Classification of existing models for autoimmune diseases by target organ or system. Only diseases for which mechanistic models were identified are shown; the number of models for a given disease is indicated in brackets.
Lupus is a chronic systemic AD with heterogeneous clinical manifestations, ranging from mild joint and skin abnormalities to life-threatening kidney, cardiac, or central nervous system (CNS) impairment (71). The etiology and pathophysiology of this AD is complex and is still poorly understood. Multiple genetic, immunological, and environmental factors may influence the loss of immunological tolerance against self-antigens, leading to the activation of autoreactive T- and B-cells. Dysregulation in T-cell response results in an imbalance in cytokine production, attracting an increasing number of immune cells to the affected tissue and provoking further inflammation. Moreover, pathological B-cells produce autoantibodies that cause organ damage by IC deposition and complement system activation (72, 73).
The first endeavor in providing a comprehensive depiction of systemic inflammation in SLE was a Boolean network model developed by Ruiz-Cerdá and colleagues (24). This model employed 52 nodes, to represent components of antigen presentation by antigen-presenting cells (APC) to T-cells, with 254 interactions describing activation, inhibition, upregulation, or downregulation processes between nodes. By knocking out or overstimulating isolated nodes, the authors identified and classified perturbations leading to a “lupus-like” phenotype in a virtual subject.
A recent example of another self-contained SLE model, built upon ODEs, is the work by Yazdani et al. (25). These authors created a system that delineates various stages of SLE progression, encompassing the entire immune response in 13 variables: 8 of these are generic (e.g., “proinflammatory mediators”, “damaged tissue”), and the other 5 reflect specific immune response components: autoantibodies, antigens, IC, and mesenchymal stem cells, as a potential approach for SLE treatment. Model parameters were manually tuned to reproduce key immunological patterns at different phases of SLE, such as tolerance breach, the onset of systemic inflammation, the development of clinical signs, and the occurrence of flares and remissions.
Subsequently, this model underwent modifications through the incorporation of a tissue inflammation submodule, which, in turn, was adopted from another model developed by Budu-Grajdeanu and colleagues for lupus nephritis (LN) (26). This model describes changes over time for 4 variables: IC, anti-inflammatory mediators, pro-inflammatory mediators, and damaged tissue. The first two variables are generic (i.e., not associated with specific biological entities), whereas the last two variables represent urine biomarkers measured in routine clinical practice: urine monocyte chemotactic protein-1 (uMCP-1) and urine protein-to-urine creatinine ratio, respectively. 4 sets of individual parameters were derived from the model calibration procedure, based on individual data from 4 subjects with SLE – a first step towards the quantification of inter-individual variability.
The pathophysiology of LN, specifically in relation to the progression of renal fibrosis, is also the focus of another series of articles published by Hao and colleagues (27, 28). The publications describe the system as a set of 11 PDEs depicting the dispersion of various types of cells involved in fibrosis, across rectangular cross-section of the renal cortex, and regulated by a network of cytokines and growth factors, including uMCP-1, platelet-derived growth factor (PDGF), transforming growth factor-beta (TGF-β), matrix metalloproteinase (MMP), and tissue inhibitor of metalloproteinases (TIMP). Through a sensitivity analysis, two parameters were identified as most influential for the formation of interstitial fibrosis and were estimated based on uMCP-1 time profiles measured in 84 subjects. Between-subject variability was taken into account by dividing the subjects according to their severity of fibrosis (low, intermediate, or high). The estimated two parameters affect the production of TGF-β by tubular epithelial cells (EC) and uMCP-1 synthesis by Mφ; modulating these has been shown to provide a potentially beneficial therapeutic strategy for mitigating renal fibrosis.
As opposed to a rather qualitative assessment of drug effects in the aforementioned models, another model considered in this section was specifically designed to quantify the treatment effect of exogenous IL-2 therapy in patients with SLE (29). The model by Gao et al. consists of 10 ODEs and focuses on a limited number of immune components directly associated with the therapeutic effect of IL-2, including conventional T-cells (Tcon), Treg, and natural killer (NK) cells – also taking into account differences in IL-2 receptor densities on each cell type and the formation of receptor-ligand complexes. The model was applied to select an effective range of IL-2 concentrations for treating SLE patients based on their Tcon/Treg ratio. Furthermore, factors affecting the exposure-response relationship were identified, and a new prognostic biomarker (Treg/CD4+ T-cells ratio) was proposed to separate responders and non-responders prior to treatment initiation.
RA is a chronic, systemic AD characterized by joint inflammation, synovial hyperplasia, and the progressive destruction of cartilage and bone, leading to disability and impaired quality of life. The disease pathophysiology is complex and involves a wide array of elements of the innate and adaptive immune responses, including Mφ, dendritic cells (DC), NK cells, T- and B-cells, fibroblast-like synoviocytes, as well as cytokines such as TNF-α and IL-6, along with others: IL-7, IL-15, IL-17, IL-21, IL-23, and granulocyte-macrophage colony-stimulating factor (GM-CSF) (74–77). Similarly to other ADs, the heterogeneity in RA pathophysiology represents a major confounding factor for the development of targeted RA therapies. Despite several drugs available on the market, including anti-TNF-α (infliximab, etanercept), anti-IL-6 (tocilizumab), anti-JAK (tofacitinib), and anti-CD20 (rituximab), their effectiveness is limited to subgroups of patients, while their administration is associated with serious side effects such as ulcers, fatigue, reduced immunity to infections, and osteoporosis (78, 79).
In our search, we identified 4 diverse examples of mechanistic models applied to study RA disease and associated treatments. The first study by Rullmann, published in 2005, describes the application of the Entelos® (80) RA PhysioLab® platform to validate potential biological targets as well as to predict the effect of hypothetical anti-IL-15 and anti-IL-12 treatments on synovial cell density and cartilage degradation rate (30). The model consists of ODEs, is claimed to include several dozens of soluble factors, cell surface molecules, and numerous types of cells in rheumatoid joint, and can simulate virtual patients with various properties; the lack of the source code, however, prevents a further detailed evaluation.
In 2018, Moise and Friedman developed their own model of a rheumatic joint in a chronic RA state, using PDEs (31). The system describes the dynamics, distribution, and cross-influence of Th17 cells, fibroblasts, Mφ, and associated cytokines and chemokines (e.g., IL-17, GM-CSF, IL-6, fibroblast growth factors, TNF-α, etc.) across cartilage, synovial membrane, and synovial fluid compartments. In addition to an evaluation of model behavior over time without treatment (i.e., disease progression), the model was used to test theoretical effects of conventional therapies (methotrexate, infliximab, tocilizumab), and hypothetical ones (anti-IL-23 and anti-IL-17), including their combinations. Cartilage degradation was used as a surrogate measure of disease status.
One of the more recent works published by Nakada and Mager (2022) describes a mechanistic ODE model focused on the interplay between several key cytokines associated with RA pathophysiology: IL-6, IL-17, TNF-α and IL-1 – complemented with the PK of therapeutic agents such as tocilizumab, secukinumab, infliximab, canakinumab, and anakinra (32). The dynamics of each cytokine and respective antagonist(s) were described by a target-mediated drug disposition module. Modules were connected through a network of feedback mechanisms, with, at the top, C-reactive protein (CRP) turnover as a marker of inflammation. The model is highly quantitative, being informed by data from multiple clinical trials based on the above-mentioned compounds and validated using external datasets not used for model calibration. From a drug development perspective, the model was applied to identify covariates (primarily baseline cytokine concentrations) explaining inter-patient variability in anti-inflammatory effects of the considered anti-cytokine therapies.
The fourth and final model in this section does not focus on inflammatory components but rather on circadian variations of cortisol, noradrenaline, and TNF-α as key players, respectively, of the endocrine, nervous, and immune system, in healthy subjects and patients with RA (33). As such, the characterization of daily oscillations of these markers under anti-TNF-α treatment can be considered as the main output of this model-based research. In addition, the authors demonstrated, via simulations, that glucocorticoid treatment between midnight and 2:00 AM would result in the strongest inhibitory effect on TNF-α secretion.
The GI tract is a chain of interconnected organs that consists of the oral cavity, pharynx, esophagus, stomach, small intestine, large intestine, and anal canal. It is a system constantly exposed to the elements of the environment, simultaneously providing an organism with nutrition while keeping numerous pathogens at bay. Multiple ADs (e.g., autoimmune hepatitis, autoimmune pancreatitis, SLE) exhibit symptoms associated with the GI tract (81), while others are directly caused by abnormal immune reactions within the organ system. Most common examples of the latter are IBD, which includes Crohn’s disease (CD) and ulcerative colitis (UC), and celiac disease (82). A large volume of empirical knowledge has accumulated over the years, allowing us to define the pathogenesis of these conditions with relative certainty. Firstly, the right balance between a proper immune response to disease agents and the lack of such for food-related antigens can be challenged by an increased permeability in the gut and a loss of immune tolerance to self-antigens (83). Secondly, inflammation may be provoked by the dysregulation of Th processes, e.g., an increased activation of Th1/Th17 or deactivation of the Th2/Treg pathway (84).
One of the first mechanistic models of IBD by Wendelsdorf and colleagues attempts to quantify these processes across three physiological compartments: the lumen, the lamina propria, and the mesenteric lymph node (34). The model describes the amplification of innate and adaptive immune responses in response to bacteria stimuli which may cause depletion of the epithelial lining. The model operates with 30 variables which can be roughly divided between Mφ (M0, M1, M2), DC, and T-cells (both pro- and anti-inflammatory), as well as cytokines (activating and deactivating). The model allows for a comprehensive sensitivity analysis and a high-level hypothesis evaluation related to general interactions between immune cells. For example, the model was applied to propose rescue strategies that remove M1 from the site of infection, which explains the mechanisms of proliferator-activated receptor-γ-mediated IBD prevention; the model also describes effects of chemokine and cytokine deprivation that allow for Mφ to remain activated. However, the price for the large scale of the model is a rather abstract description of mechanisms, a limitation which has been partially compensated for by subsequent modeling research.
For example, Lo and colleagues focused on aspects of T-cell polarization during the initial steps of the inflammatory processes in IBD, by modeling Th1, Th2 and Treg population densities as a function of concentrations of transcription factors (T-bet, Gata3 and Foxp3) and four cytokines (IFN-γ, IL-4, TGF-β and IL-2) (35). The system was explored primarily along two scenarios: bacterial infection and protozoan infection - under normal and abnormal immune responses, through the modulation of model parameters. It provides a better understanding of the delicate balance between cytokine and transcription factors required for proper T-cell immune response in the gut and the consequences of its disruption. At the same time, the model lacks several essential mechanistic components, including the polarizing effect of cytokines produced by activated Mφ. This limitation was addressed in subsequent work by the same authors, where they expanded on the developed model and added several additional immune components, including Th17, M1 and M2 Mφ, along with IL-6, IL-10, IL-12, IL-21 and TNF-α (36). The model was applied to characterize 4 subgroups of patients with CD, as defined by the ratio of Th1 and Th2 transcription factors, relative to values in healthy volunteers, based on biopsy data. A hypothetical anti-TNF-α therapy was then tested in each subgroup, to find the population most sensitive to the treatment. The article by Park et al. capitalizes on the work by Lo and colleagues and explores the effect of anti-IL-12 and pro-IL-10 treatment along with TNF-α suppression in the same system, with 4 cohorts of patients differing in their quantities of Th1 and Th2 (37).
The model by Dwivedi et al. is another example of a systems model focused on cytokine effects, IL-6 in particular (38), which contribute to Th17 differentiation (85). This network of ODEs is based on a previously developed model of IL-6-mediated immune signaling, includes 3 compartments (liver, GI tract and circulation), and describes IL-6 binding with its IL-6 receptor (IL-6R) and gp130. The model was validated based on tocilizumab (an anti-IL-6R antibody) data and used to benchmark different targets for IL-6 signaling disruption using circulating levels of CRP, a well-established marker of inflammation, as the primary pharmacodynamic measurement.
The most ambitious attempt to quantify and integrate all pathways and processes described above and beyond can be attributed to a series of papers by Rogers and colleagues, who describe a model with 116 reactions and 334 parameters (39, 40). This model includes multiple cell types associated with innate (DC, Mφ, NK cells, and neutrophils) and adaptive immunity (Th1, Th2, Th17, and Tregs), more than 10 cytokines, CRP and fecal calprotectin as dependent variables, and was parameterized for three types of subjects (healthy, CD, UC), using a technique proposed by Allen et al. (86) to generate virtual populations with baseline biomarker levels corresponding to actual observations. Moreover, the model includes PK models of anti-TNF-α (infliximab), anti-IL-12p40 (ustekinumab), anti-IL-23 (risankizumab and brazikumab), and anti-IL-6 (PF-04236921) compounds. In the first part of their work, the authors performed a sensitivity analysis to identify key mechanisms affecting fecal calprotectin and CRP; they then applied the model to understand mechanisms underlying the worsening of CD, in the case of IL-17 inhibition. In the second part, the model was thoroughly validated against data on multiple existing compounds and was used to predict responder rates based on biomarker cutoffs as well as the effect of combined anti-TNF-α and anti-IL-12p40 treatments.
Another example of a comprehensive, yet qualitative model of IBD is based on a Boolean network, rather than ODEs, created by Balbas-Martines et al. (41). It consists of 43 nodes spread across lymph node, blood, lymph circulatory system, and gut lumen, with MMP being the main marker of tissue damage in the system. The model was shown to correctly reflect the lack of response in MMPs under IL-10 overexpression, IL-17 or IFN-γ knockout and, in turn, demonstrates marked improvement in disease condition mediated by TNF-α suppression or granulocyte and monocyte apheresis. Subsequently the system was ameliorated to a hybrid model of ODEs and Boolean processes, to allow for the characterization of the magnitude and dynamics of IL response, to predict the effect of recombinant human IL-10 administration on 14 cytokines involved in CD pathogenesis (42).
Aside from IBD, which holds the central place as the subject of multiple model-based research, other GI tract-related ADs, such as celiac disease, have been represented by a single model (43). It is similar in principle to the model by Wendelsdorf et al. (34) and attempts to describe the dynamics of several key immune components and disease progression elements, including gluten deamidation, antigen presentation, T-cell activation, and the formation of auto-antibodies, in the lamina propria. The model was applied to evaluate potential targets for the treatment of celiac disease, among which gluten-peptide analogues showed the strongest effect on antibodies and the villous area, although the clinical efficacy of DQ2 or DQ8 gene analogues remains, to date, unknown (87).
Various ADs, including RA, SLE, and MS, might have devastating effects on vision (88–90). However, the eyes themselves can be the target of an autoimmune condition such as, for example, EAU, which has been explored via the means of mathematical modeling by Nicholson et al. (44). Similarly to many other organ-specific autoimmune disorders, EAU is caused by an abnormal influx of effector cells into the target organ. A distinctive feature of EAU, however, is the presence of the blood-retina barrier. Thus, Nicholson et al. developed a minimalistic model of 10 ODEs that describes essential processes of antigen presentation and T-cell activation on both sides of the blood-retina barrier, with corresponding transitions. This allowed the authors to evaluate the impact of permeability on disease state and highlight other factors (i.e., APC production) which may contribute significantly to abnormal inflammation.
The nervous system, comprised of the CNS and the peripheral nervous system, regulates the functionality of organs through the processing of internal and external information conveyed via electrical impulses along an extensive network of nerve endings. MS, a prevalent autoimmune neurological disorder, manifests itself as demyelinating lesions in the CNS (91, 92). From a clinical perspective, MS displays notable heterogeneity, divided among a primarily progressive multiple sclerosis (PPMS) type, which is characterized by a gradual accumulation of clinical disabilities, and a relapsing-remitting multiple sclerosis (RRMS) type, which is characterized by disease exacerbations followed by periods of remission – although often switching to a secondary progressive multiple sclerosis (SPMS) type in the long-term (93, 94). The immune pathophysiology of MS involves bidirectional interactions among peripheral immune cells (T-cells, B-cells, myeloid cells) and resident CNS cells (microglia, astrocytes). For the RRMS type, focal inflammatory demyelination caused by peripheral immune cells infiltrating the CNS is believed to be the cause of relapses, whereas for the progressive type, diffuse tissue damage of white and gray matter is predominant (95).
In their model, Moise and Friedman focused on delineating immune and inflammatory interactions within the focal plaque, quantifying their impact on plaque growth (45). The authors proposed a model based on 23 PDEs encompassing the dynamics of Th, cytotoxic T-cells, Mφ, astrocytes, oligodendrocytes, chemokines, and 8 pro- and anti-inflammatory cytokines. Additionally, 4 PDEs defined the PK of immunomodulators such as IFN-β, glatiramer acetate, natalizumab, and dimethyl fumarate, which have all been evaluated in the treatment of MS. The authors used the model to explore the effects of these drugs and their combinations; the combination of the first three aforementioned drugs resulted in a decrease in initial plaque volume under specific dose combinations, emphasizing the potential efficacy of drug combinations in MS treatment.
Other modeling studies have adopted a more generalized approach to immune response dynamics (46–48). Vélez de Mendizabal et al., using a system of 6 ODEs, postulated that recurrent dynamics in autoimmunity could arise from failures in cross-regulation mechanisms between regulatory and effector T-cells (Teff), alongside stochastic events triggering the immune response (46). Their model incorporated concepts such as cross-regulation between regulatory and Teff and tissue damage. By introducing reversible and irreversible tissue damage, the model aimed at linking autoimmune activity with clinical relapses in MS patients. Simulations suggested that weakened negative feedback between effector and Treg enabled the immune system to generate characteristic RRMS dynamics without additional environmental triggers.
Another example of a generalized model has been proposed by Kannan et al. (47). It includes 4 ODEs, reflecting inflammatory and anti-inflammatory components, demyelination, and neuronal death in MS. By embedding complex control mechanisms into the equations, the authors were able to identify two key thresholds – one in the immune components and another one in the CNS – that separate distinct dynamical behaviors in the model, classifying disease subtypes in silico as RRMS or progressive SPMS/PPMS, based on these thresholds, once exceeded.
Expanding the ways in using mathematical tools to model detailed biological processes, Gross et al. proposed a probabilistic model to predict the differentiation and migration of lymphocyte subsets in the CNS under homeostatic and neuroinflammatory conditions (48). The 7-equation model aimed at reproducing the acquired data on the location and differentiation states of lymphocyte subsets, to provide quantitative assessments of differentiation and transmigration rates and to predict the qualitative behavior of immune-modulating therapies – thereby enabling simulation-based predictions of lymphocyte subset distributions. Validated based on data from patients with somatoform disorders, RRMS patients, and patients undergoing specific treatments, the model demonstrated accuracy in predicting differentiation stages and distribution of lymphocyte subsets under both steady-state conditions and neuroinflammatory diseases such as MS.
Finally, Broome and colleagues attempted to describe MS pathophysiology from a biochemical perspective, using a complex model capable of predicting: interactions between reactive oxygen and nitrogen species; the permeability transition pore; apoptotic factors; and eventual cell death in oligodendrocytes (49). Immune components within the model were represented only at a high level by Mφ, T-cells and several cytokines (IFN-γ, TNF-α, and IL-1), while the main focus of the model was on intracellular molecular processes. The system reflects healthy, diseased, and treated states, and allows for the identification of trigger points for disease onset and the exploration of potential drug therapies.
The skin is an organ constantly exposed to external factors such as injuries and infections that can disrupt the barrier function and initiate a dysregulated immune response, which may, in turn, cause chronic inflammation and autoimmunity. Despite the prevalence of autoimmune skin diseases, only two of them – alopecia areata and atopic dermatitis – have been studied using mechanistic mathematical models (50–55). Although the autoimmune nature of the latter is a matter of debate, the well-known association with multiple ADs and the presence of autoreactive T-cells and autoantibodies provide sufficient evidence for including this atopic dermatitis disorder to this review (96–99).
Atopic dermatitis (also known as eczema) is a chronic disease affecting the upper level of the skin and characterized by persistent skin inflammation. The pathogenesis of dermatitis involves epidermal barriers abnormalities, leading to heterogeneous immunological dysregulations predominantly in type 2 immunity (Th2, IL-4, IL-13, IL-31), but also including varying degrees of upregulation of the Th1 (IFN-γ), Th17 (IL-17), and Th22 axes (IL-22) (100). Tanaka and colleagues published several articles focused on the interplay between the pathogen load, immune response, and the degree of skin barrier integrity to describe recurrent dermatitis flares associated with pathogen levels surpassing certain thresholds (52–55). The model reproduces 4 types of dynamical phenotypes typically observed in patients – recovery, chronic damage, oscillations, and bi-stability – mirroring different stages of dermatitis severity. The model was applied to evaluate the effects of first-line nonspecific therapies (topical antibiotics, emollients, corticosteroids) on the transition from pathologic to healthy state. The model gradually evolved over time, for example, by introducing multiple subtypes of Th and their effector ILs (IL-4, IL-13, etc.) (55). Another significant augmentation of the modified model was the inclusion of clinical efficacy endpoints – eczema area and severity index (EASI) – which enabled a comparison of the efficacy of multiple anti-IL drugs.
Alopecia areata is an AD that causes the formation of distinct hairless patterns on the scalp or other parts of the body. According to a widely accepted hypothesis, hair loss occurs due to the collapse of the immune privilege of hair follicles under environmental factors, with subsequent migration of autoreactive lymphocytes into the hair bulb (101). A set of modeling studies by Atanaska Dobreva et al. describes the dynamics of autoreactive CD4+ and CD8+ T-cells, immune privilege guardians and IFN-γ involved in the development of alopecia, and the hair follicle growth cycles (50, 51). The developed model succeeds in capturing healthy and pathological states of a subject, highlighting the key role of IFN-γ and immune privilege guardians in disease progression. However, the uniqueness of the triggers and localness of the disease challenges the applicability of this model to other autoimmune disorders.
The endocrine system is a vital regulator of biological processes, responsible for the development of the nervous system, growth, reproductive function, metabolism, and more (102). As such, autoimmune conditions associated with it usually lead to severe health complications (103).
T1DM is one such disease known from ancient times and considered fatal until the invention of recombinant insulin in the early XXth century (104). The autoimmune response in T1DM is directed primarily towards β-cells in the islets of Langerhans in the pancreas, thereby depriving the organism of insulin hormone, which in turn regulates glucose uptake by tissues. Since recombinant insulin is the primary method of controlling the disease, the majority of mathematical models for this indication are focused on short- and long-term glycemic controls (105, 106). However, two models stand out, in terms of characterizing autoimmune processes relevant for the disease, and beyond insulin-glucose cross-talks (56, 57). Both models contain 5 to 6 ODEs of a highly theoretical nature, which capture the quantities of β-cells, Teff, Tregs, antigen, and other components (either Mφ or IL-2), and they allow for the exploration of the fundamental systems behavior rather than addressing questions specific to drug development. Jaberi-Douraki and colleagues highlight the impact of T-cell avidity on disease outcomes in T1DM, whereas Magombedze et al. emphasize the crucial role of the balance between Treg and auto-reactive T-cells in diabetes progression.
HT is another example of a relatively common chronic autoimmune condition, affecting the thyroid gland through an infiltration of T- and B-cells (107). Excessively stimulated Th1 cells, Th17 cells, and Tregs play important roles in the pathogenesis of HT (108). Thus, in their work, Salazar-Viedma et al. investigated the immune response mediated by Th1 and Th17 on thyrocytes (3 ODEs) (58). Interestingly, the authors also included gut microbiota into the model (a 4th ODE), thereby linking autoimmunity with the function of the microbiome. Results of the modeling suggest that an imbalance in the intestinal microbiota could lead to an increase in Th17 lymphocyte activity, contributing to the development of HT.
There are two mechanistic models describing autoimmune-related lung diseases, namely pulmonary sarcoidosis and IPF (59–61). It should be noted that the etiology and role of autoimmunity in the development and progression of these diseases are still unknown. However, genetic predisposition and external triggers such as infection, inorganic materials, and environmental factors are likely to lead to the development of an autoimmune response (109–112). Mφ and lymphocytes are key players involved in the initiation of the immune response in the lung, in both indications: Mφ, serving as scavenger cells, ingesting and degrading the inhaled antigenic load, initiate a typical Th1 immune response. Interestingly, both diseases are characterized by a shift from the M1 (pro-inflammatory) to the M2 (anti-inflammatory) Mφ phenotype, which is considered responsible for the progression from inflammation to interstitial fibrosis in IPF and formation of granulomas in sarcoidosis.
The first model by Hao et al. considers the progression of sarcoidosis in terms of a granuloma radius represented as a conglomerate of Mφ, Th1, Treg and Th17 cells, which affect each other through a network of cytokines and chemokines (IL-2, IL-10, IL-12, IL-13, chemokine ligand 20, IFN-γ, TNF-α and TGF-β) (59, 60). The model shows the beneficial effect of infliximab (anti-TNF-α) and other potential anti-cytokine therapies on the granuloma radius. In subsequent work, the authors investigated the progression of fibrosis in IPF by adding features unique to pulmonary tissue fibrosis, based on their previous model of kidney fibrosis (27, 61). This second model includes two Mφ phenotypes and takes into account the complex geometry of lungs through a system of PDEs, to calculate the effective interactions among model species: Mφ, epithelial and mesenchymal cells, extracellular matrix and molecular pro-fibrotic mediators (TNF-α, TGF-β, PDGF, TIMP). The authors explored the efficacy of four therapies (anti-TNF-α, anti-PDGF, anti-IL13, anti-TGF-β) and showed that only targeting TGF-β should result in a beneficial effect on pulmonary fibrosis.
The heart muscle, just like any other part of the body, is no exception in terms of self-stimulated inflammation and tissue damage. While rare, autoimmune myocarditis can be caused as a side effect incurred by treatment using immune checkpoint inhibitors – a large and effective class of anti-cancer therapies (113, 114). Building up on the historical research of the immune system, Van der Vegt and colleagues pioneered the modeling of checkpoint-induced autoimmune reaction, in an effort to provide an instrument that helps in balancing the benefits and risks of this type of treatment (62). The core of the developed system consists of 4 ODEs, complemented with the pharmacodynamic effects of PD-1 and CTLA-4 inhibitors as explicit functions. The model was subjected to stability and sensitivity analyses. Most importantly, model evaluation results demonstrate that the development of autoimmune myocarditis under treatment with high doses of nivolumab or ipilimumab is practically inevitable, depending on individual patient characteristics reflected in the values of several key model parameters.
Mathematical modeling, by implication, is a transformation of empirical knowledge into a system of cause-consequence relationships using the universal language of mathematics, theoretically applicable to any object or phenomenon. As such, not all models are necessarily associated with specific diseases but rather focus on the general behavior of immune response components potentially leading to autoimmune disorders. Although mostly qualitative, inferences derived from these models significantly broaden our understanding of interactions within the system of interest and provide a companion tool for further experimental research.
A notable early example of such a mathematical system is the ICMODEL developed by Martha Head et al. (63). This model represents a theoretical interpretation of a mechanism for IC formation, opsonization, and clearance. It consists of 3 sub-modules: (1) production of antibodies and their interaction with antigen (i.e., IC formation); (2) opsonization and clearance of IC; (3) tissue damage and antigen release. The model was explored for consistency with the known behavior of the immune system, evaluated for stability, and then applied to identify processes leading to a substantial rise or oscillations in pathogenic IC concentrations (e.g., impaired antigen efflux, Fc-γ-mediated phagocytosis, complement synthesis). Such a model may be beneficial in understanding the cyclical course of various autoimmune disorders.
Later, Arazi and Neumann developed a more parsimonious model focused on the same spectrum of processes as the ICMODEL; it consists of 3 ODEs reflecting the quantities of autoreactive B-cells, autoantigen, and IC (64). Thorough steady-state, hysteresis, and parameter sensitivity analyses, as well as an evaluation of the different functional relationships was performed, to demonstrate that a positive feedback loop between IC and tissue damage would not be sufficient to drive the system to a pathological state - thereby confirming that the clearance rates of ICs and self-antigens are one of the key factors triggering a clinically impactful autoimmune response.
Another example, similar in principle to the work by Arazi and Neumann, is a minimalistic ODE model by Iwami and colleagues that includes 3 dependent variables: population size of target cells, damaged cells, and immune cells (65). The authors proposed several functional relationships (linear and non-linear) of target cell growth and immune response followed by a stability analysis, to describe mathematically different states of immune tolerance/dormancy and repeated flare-ups.
Further modeling work can be found in a generalized model by Khailaie et al., in a series of studies dedicated to the investigation of T-cell activation (66). However, this paper is centered around disturbances in the delicate balance between Tcon and Tregs leading to autoimmunity. The authors methodically tested different models, starting from the simplest structure with 2 ODEs describing the dynamics of activated T-cells and IL-2 and ending with pathways of Tregs and Tcon renewal rates, activation, proliferation, and reciprocal influences. They derived an antigen-stimulation threshold (i.e., the proliferation rate of activated T-cells depending on the avidity to an antigen) that defines three scenarios of immune response: a complete lack of a response; a first peak followed by complete clearance of the antigen; or the failure of such, which would result in chronic persistence of the antigen, and is primarily defined by the renewal rate of naïve T-cells and resting Tregs.
The balance of T-cells, although Th1 and Th2 instead of Tcon and Tregs, is the subject of another model-based analysis, performed by Louzoun et al. (67). This work, published in 2001, thoroughly explores mathematical system that includes 5 cell types (Th1, Th2, Mφ, naïve T-cells, and pooled Teff and Treg) and 3 types of cytokines, aggregated by associated cells (Th1, Th2, or Mφ), to characterize the transition from healthy condition (designated as Th2 steady-state) to autoimmunity (designated as Th1 steady-state). Although the rationale behind the model is based on the preclinical observations (i.e., insulin-dependent diabetes and experimental autoimmune encephalomyelitis mouse models), proposed model is positioned as qualitative investigation of Th1-mediated autoimmune diseases.
Another aspect of autoimmune disease onset, namely immune response to self-antigen caused by cross-reactivity to viral antigen, was investigated by Hara and Iwasa using a model in 4 ODEs, which reflects the kinetics of Th-cells (reactive to self-antigen or viral infection), viral antigen, and memory T-cells (68). As in the case of previous qualitative model, characterization of general patterns in the dynamics of the system through sensitivity analysis, including the evaluation of autoimmune response relative to the different modes of cross-immunity, rather than qualitative predictions of the treatment-related effects was the focus of this research.
Continuing the thread of qualitative models, the study by Machado Ramos et al. considers three cell populations associated with autoimmune response – self-APCs, self-reactive T-cells, and immunosuppressive cells (69). The model was developed using a combination of integro-differential equations and ODEs to track the total number of cells within each population and their respective functional states and tested for robustness. Sensitivity analysis of the model highlights the critical roles of proliferation of immunosuppressive cell, destruction of self-APC and self-reactive T-cell, and the tolerance of self-reactive T-cells to self-antigens in regulating autoimmune responses effectively.
The last piece of modeling work evaluated in this section is devoted to the mathematical description of two generic, inter-dependent immune cell populations, mutually regulating one another via cytokine production (70). The interactions between the two cytokine production profiles reflect the point of a synergistic balance, where both cell populations reach equilibrium. An exhaustive screening of possible parameter values revealed that an AD may occur when the alteration of the feedback between immune cells results in hyper-induced homeostasis or a loss of stability in the system, leading to oscillations or trigger-based inflammatory disease phenotypes.
Mathematical modeling in drug development is an essential tool necessary to transform heterogeneous experimental data from numerous sources into a system of quantitative knowledge, with an ultimate goal of facilitating the delivery of innovative therapies to patients. The indispensability of this tool is especially noticeable in therapeutic areas such as ADs, with non-trivial diversity in pathogenesis, etiology, manifestations, and the associated plethora of unanswered questions related to drug development. Among modeling methods, empirical PK/PD models first introduced in the 1970s and focused on the direct assessment of the dose-concentration-effect relationship can be considered as the most established and frequently used models (115, 116). In ADs, this type of research has been pioneered by Brooks et al., with a model-based investigation of the clinical effects of concomitant use of indomethacin and furosemide in RA patients (117). Since then, the number of publications that could be attributed towards PK/PD modeling in ADs grew almost exponentially (Figure 1A). However, the utility of empirical models can be limited by their simplicity, whereas multiple drug R&D questions, such as target selection, animal-to-human translation, and others, require an in-depth analysis of the underlying biological mechanisms (16, 17).
This is where mechanistic models may come into play. These models represent a slice of knowledge in selected disease areas, and, therefore, first understanding the scope of a given endeavor in this field is important, to focus the efforts of subsequent research – which is the main purpose of this review. In our systematic search and curation, we identified 38 mechanistic models of ADs across 47 publications. While it is challenging to define the fine line between mechanistic and non-mechanistic models, in this paper, we attributed models to the former category if they contained a description of autoimmune processes at any level of generalization, regardless of the mathematical method used or the number of equations featured. It is worth noting that the majority of the identified models (>70%) are expressed as ODEs, similarly to most systems pharmacology models, with a minimum of 3 equations being featured in their structure (Figure 1C) (118). In addition to ODE models, two groups of models featuring PDEs were found, with a distinct focus on tissue remodeling: a set of publications by Wenrui Hao and colleagues (27, 28, 60, 61), examining kidney and lung fibrosis, and models of plaque growth in MS and cartilage degradation in RA, by Moise and Friedman (31, 45). A Boolean model was developed by Ruiz-Cerdá and colleagues, to describe the antigen presentation process in lupus (24), and another Boolean model with subsequent ODE extensions, by Balbas-Martinez et al., was identified for IBD (41, 42). Finally, a unique probabilistic (Markov jump processes) model by Catharina Gross and colleagues was developed, to capture the differentiation and migration of lymphocyte subsets to CNS (48).
The number of publications related to mechanistic modeling is overall markedly smaller as compared to PK/PD modeling studies, with a slower and shallower increase over time (Figure 1A), which could be explained by the time and efforts, as well as the high expertise in immunology required, to build such models. Interestingly, while the search contained more than 180 terms for different ADs (see Supplementary Materials), only models for 13 disease-specific were identified by the search, with models for 2 systemic conditions (SLE and RA) and 11 for organ-specific indications (Figure 1B). Hence, the mechanisms for more than 150 other ADs, such as psoriasis, systemic sclerosis, involvement of the urinary system and Sjogren’s syndrome, are not covered by the currently available mathematical modeling literature, and thus present a high opportunity for further research. However, the biological entities embedded in the identified models are all linked to the immune response and are thus expected to overlap in these other ADs. Indeed, the analysis of variables and their interactions among currently available models revealed several common clusters (Figure 2).
Approximately 1/3 of the models included antigens, in a broad sense (e.g., pathogen load, commensal bacteria, damaged tissue), as a dependent variable, which is not surprising considering ADs are characterized by responses to self-antigen or may be triggered via external microorganisms. A similar frequency of occurrence in the models was observed for Tregs, important gatekeepers of the immune system that inhibit the activation and expansion of Th, cytotoxic T-cells and B-cells. Their role has been extensively described in SLE, RA and MS (119). Overall, most of the models explored T-cell-mediated immune response with an emphasis on Th, with a different degree of generalization (i.e., either by pooling different subtypes of cells into generic variables or by considering them individually). In contrast, autoreactive cytotoxic T lymphocytes characterized by cytolytic activities against target cells are under-represented in the models and are often lumped together into effector T-cell variables. Other types of lymphocytes are modeled only in isolated cases, even in ADs classified as B-cell-mediated or antibody-driven pathologies, such as SLE (120).
In addition to featuring immune cells, the models cover a wide range of pro- and anti-inflammatory ILs as a critical part of cross-regulation, proliferation, and polarization of Th subtypes. For example, 6 out of 36 models incorporate the connection between IL-2 and Tregs, as well as IFN-γ and Th1. Furthermore, cytokines with well-established roles in AD progression (e.g., TNF-α, IL-6, IL-23, etc.) and respective therapeutic interventions are also frequently included in the models. Despite this, none of them contain type I IFN (e.g., IFN-α or IFN-β), although its substantial role has been highlighted in several ADs, including SLE, where multiple approved or developing therapies are designed to block the type I IFN-inducible pathway of inflammation.
Lastly, tissue damage or fibrosis is also frequently modeled, as a final outcome of AD progression. In Figure 2, tissue scarring is associated with a cluster of Mφ, GM-CSF, and a lumped term “fibrosis” that includes MMPs, elements of the extracellular matrix, fibroblasts, and several growth factors (e.g., TGF-β, FGF, PDGF). Tissue damage is either modeled as a generic variable or through a number of organ-specific cells, e.g., thyrocytes in HT. It is worth noting that the main mechanisms of tissue damage, consisting of cytotoxic activity of autoreactive CD8+ T-cells and IC-related activation of complement system, are missing in these models, with few exceptions that link IC to cell death.
While mathematical modeling is an essential tool to support decision-making, the practical value of a particular model for drug development is defined by the adherence to good modeling practices and is inherently limited by the underlying assumptions (121). The latter is directly tied to the data used for model development and calibration. About 40% of the identified models were built around clinical data only, whereas practically 29% of models additionally involved animal data, when information in human was lacking or scarce (Figure 1D). Mixing such different types of data may be a sensitive subject to perform model inference, and it calls for further verification of the similarities in immune mechanisms across species, as a distinct direction for future analyses (122, 123). Among good modeling practices, several key components could be named, e.g., extensive model calibration and evaluation, including identifiability analyses, external validation, sensitivity analyses, and more (124). Several models, e.g., the works of Gao et al. (29), Nakada and Mager (32), Rogers et al. (39, 40), and Miyano et al. (55) feature a broad array of these technical model-based analyses. Furthermore, these models attempt to incorporate subject inter-individual variability through the means of generating realistic virtual populations; they also consider realistic PK models of the compounds, driving the effects, which greatly expands the applicability of such models to real-world scenarios. These models may be considered as an exception, since the remaining models discussed here do not rely on parameter identifiability, extensive model diagnostics or advanced simulations. In fact, nearly a quarter of all models considered in this review operate as a system without a direct link to the observed time series of laboratory measurements (Figure 1D) and do not make use of external validation techniques (Table 1). This may be explained by differences in the relevant questions that motivate the development of such models. For example, modeling studies classified as describing general autoimmune reactions as well as several others are built to explore mathematical systems with specific behaviors, through an analysis of stability and phase portraits (e.g., to describe periodical nature of flares) (64, 66). Likewise, many models are primarily developed to perform a sensitivity analysis, with parameter values assumed or fine-tuned manually (65, 70). As a result, the potential impact of such models can be limited to mechanistic hypothesis generation and target validation. Because of that reason, our search was restricted to the PubMed database, which specifically indexes biomedical and life sciences journals. As such, it should be mentioned that the total number of published model-based analyses of autoimmune processes exceeds those discussed in detail in this review e.g., (125–131). However, the focus of these studies lies primarily in the analysis of specific patterns of mathematical systems, their phase trajectories, steady-states, etc., rarely informed by the large quantities of clinical data and thereby, while providing important insights into theoretical behavior of the immune system, have limited practical applicability in model-informed drug development.
In summary, the applicability of current mechanistic models of ADs in drug development could be limited by several factors. Firstly, the lack of evaluation of model performance against the observed clinical data, including the assessment of uncertainty in model parameters and the validation against independent data, results in qualitative predictions of system behavior rather than quantitative ones. Secondly, most existing models do not incorporate PK submodules to describe drug exposure in target compartments over time. Furthermore, some components of the immune system are under-represented or simply are lacking in the available models. For instance, current treatment options for SLE are focused primarily in three areas: disrupting type I IFN-mediated inflammation, targeting B-cell response, and inhibiting intracellular signaling; none of which are among the modeled immune components (15). Finally, to provide insight into an actual clinical benefit, the models should strive to incorporate clinical endpoints. Currently available models are built upon inferences around surrogate biomarkers or generic variables (e.g., tissue damage or fibrosis), with a single exception by Miyano et al. (55), where the EASI endpoint was described as a function of skin barrier integrity and infiltrated pathogens.
This analysis follows the requirements of a robust systematic review, with documented sources and search queries, and, to our knowledge, is a unique venture to comprehensively identify and categorize existing mechanistic models of ADs. It should not be viewed as an objective effort to qualify the formidable effort that each of the analyzed models represents, as the value of modeling is always relative to its aim. Rather, it is an attempt to draw a landscape of the ever-evolving quantitative knowledge on ADs in the form of mathematical models to define the most desirable paths of moving forward in relation to drug development. In this context, the amount of robust QSP models, with extensive model calibration and evaluation and built on clinical data, while maintaining a delicate balance between the available data and model complexity, is significantly lacking in the considered disease domain. This gap is further broadened by the emergence of new therapeutic modalities (e.g., chimeric antigen receptor T-cell), not yet covered by these existing models (132). Taken together, these results highlight the necessity and aspiration to enhance proactiveness and efforts in mechanistic quantitative analyses in the intricate therapeutic area of ADs, to facilitate the development of novel therapeutics.
YU: Data curation, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing – original draft. AN: Formal Analysis, Investigation, Writing – original draft. CL: Formal Analysis, Investigation, Methodology, Visualization, Writing – original draft. GH: Writing – review & editing. KP: Funding acquisition, Resources, Writing – review & editing. VS: Conceptualization, Methodology, Project administration, Supervision, Writing – review & editing. AV: Conceptualization, Funding acquisition, Methodology, Project administration, Supervision, Validation, Writing – original draft, Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Academic leadership program Priority 2030 proposed by the Federal State Autonomous Educational Institution of Higher Education I.M. Sechenov First Moscow State Medical University of the Ministry of Health of the Russian Federation (Sechenov University), the Ministry of Science and Higher Education of the Russian Federation (Agreement 075-10-2021-093, Project MMD-RND-2266), Russian Science Foundation (Grant Number 23-71-10051) and Modeling & Simulation Decisions FZ -LLC, Dubai, UAE.
Author GH was employed by the company Biorchestra Co., Ltd. Authors CL, KP, VS, and AV were employed by the company Modeling and Simulation Decisions FZ-LLC.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fimmu.2024.1371620/full#supplementary-material
Ab, Antibody; AD, Autoimmune disease; APC, Antigen-presenting cells; BAFF, B-cell activating factor; CD, Crohn’s disease; CNS, Central nervous system; CRP, C-reactive protein; DC, Dendritic cells; EASI, Eczema Area and Severity Index; EAU, Experimental autoimmune uveitis; EC, Epithelial cells; GI, Gastrointestinal; GM-CSF, Granulocyte-macrophage colony-stimulating factor; HT, Hashimoto’s thyroiditis; IBD, Inflammatory bowel disease; IC, Immune complex; IFN, Interferon; IL, Interleukin; IL-6R, IL-6 receptor; IPF, Idiopathic pulmonary fibrosis; JAK, Janus kinase; LN, Lupus nephritis; MMP, Matrix metalloproteinase; MS, Multiple sclerosis; Mφ, Macrophages; NK, Natural killer; ODE, Ordinary differential equation; OSC, Organ-specific cells; PD, Pharmacodynamics; PDE, Partial differential equation; PDGF, Platelet-derived growth factor; PK, Pharmacokinetics; PPMS, Primarily progressive multiple sclerosis; QSP, Quantitative systems pharmacology; R&D, Research & development; RA, Rheumatoid arthritis; RRMS, Relapsing-remitting multiple sclerosis; SLE, Systemic lupus erythematosus; SPMS, Secondary progressive multiple sclerosis; T1DM, Type 1 diabetes mellitus; Tcon, Conventional T-cells; Teff, Effector T-cells; TGF, Transforming growth factor; Th, T-helper cells; TIMP, Tissue inhibitor of metalloproteinases; TNF-α, Tumor necrosis factor-α; Treg, Regulatory T-cells; UC, Ulcerative colitis; uMCP-1, Urine monocyte chemotactic protein-1.
1. Lerner A, Jeremias P, Matthias T. The world incidence and prevalence of autoimmune diseases is increasing. Int J Celiac Dis. (2015) 3:151–5. doi: 10.12691/ijcd-3-4-8
2. Pisetsky DS. Pathogenesis of autoimmune disease. Nat Rev Nephrol. (2023) 19:509–24. doi: 10.1038/s41581-023-00720-1
3. Wang L, Wang F-S, Gershwin ME. Human autoimmune diseases: a comprehensive update. J Intern Med. (2015) 278:369–95. doi: 10.1111/joim.12395
4. Fugger L, Jensen LT, Rossjohn J. Challenges, progress, and prospects of developing therapies to treat autoimmune diseases. Cell. (2020) 181:63–80. doi: 10.1016/j.cell.2020.03.007
5. Villalta D, Tozzoli R, Tonutti E, Bizzaro N. The laboratory approach to the diagnosis of autoimmune diseases: is it time to change? Autoimmun Rev. (2007) 6:359–65. doi: 10.1016/j.autrev.2007.01.009
6. Ascherio A, Munger KL. EBV and autoimmunity. Curr Top Microbiol Immunol. (2015) 390:365–85. doi: 10.1007/978-3-319-22822-8_15
7. Cunningham MW. Molecular mimicry, autoimmunity, and infection: the cross-reactive antigens of group A streptococci and their sequelae. Microbiol Spectr. (2019) 7(4). doi: 10.1128/microbiolspec.GPP3-0045-2018
8. Trier NH, Houen G. Antibody cross-reactivity in auto-immune diseases. Int J Mol Sci. (2023) 24:13609. doi: 10.3390/ijms241713609
9. Lang KS, Burow A, Kurrer M, Lang PA, Recher M. The role of the innate immune response in autoimmune disease. J Autoimmun. (2007) 29:206–12. doi: 10.1016/j.jaut.2007.07.018
10. Deane KD. Preclinical rheumatoid arthritis (Autoantibodies): an updated review. Curr Rheumatol Rep. (2014) 16:419. doi: 10.1007/s11926-014-0419-6
11. Rosenblum MD, Remedios KA, Abbas AK. Mechanisms of human autoimmunity. J Clin Invest. (2015) 125:2228–33. doi: 10.1172/JCI78088
12. Bach JF. Immunosuppressive therapy of autoimmune diseases. Immunol Today. (1993) 14:322–6. doi: 10.1016/0167-5699(93)90053-N
13. Cipriani P, Ruscitti P, Carubbi F, Liakouli V, Giacomelli R. Methotrexate: an old new drug in autoimmune disease. Expert Rev Clin Immunol. (2014) 10:1519–30. doi: 10.1586/1744666X.2014.962996
14. Dropulic LK, Lederman HM. Overview of infections in the immunocompromised host. Microbiol Spectr. (2016) 4(4). doi: 10.1128/microbiolspec.dmih2-0026-2016
15. Jung SM, Kim W-U. Targeted immunotherapy for autoimmune disease. Immune Netw. (2022) 22:e9. doi: 10.4110/in.2022.22.e9
16. Bradshaw EL, Spilker ME, Zang R, Bansal L, He H, Jones RDO, et al. Applications of quantitative systems pharmacology in model-informed drug discovery: perspective on impact and opportunities. CPT Pharmacomet Syst Pharmacol. (2019) 8:777–91. doi: 10.1002/psp4.12463
17. Felmlee MA, Morris ME, Mager DE. Mechanism-based pharmacodynamic modeling. Methods Mol Biol Clifton NJ. (2012) 929:583–600. doi: 10.1007/978-1-62703-050-2_21
18. Zhang L, Pfister M, Meibohm B. Concepts and challenges in quantitative pharmacology and model-based drug development. AAPS J. (2008) 10:552–9. doi: 10.1208/s12248-008-9062-3
19. Madabushi R, Seo P, Zhao L, Tegenge M, Zhu H. Review: role of model-informed drug development approaches in the lifecycle of drug development and regulatory decision-making. Pharm Res. (2022) 39:1669–80. doi: 10.1007/s11095-022-03288-w
20. Morgan P, Brown DG, Lennard S, Anderton MJ, Barrett JC, Eriksson U, et al. Impact of a five-dimensional framework on R&D productivity at AstraZeneca. Nat Rev Drug Discovery. (2018) 17:167–81. doi: 10.1038/nrd.2017.244
21. Autoimmune Disease List. Glob Autoimmune Inst . Available online at: https://www.autoimmuneinstitute.org/resources/autoimmune-disease-list/ (Accessed December 13, 2023).
22. R: The R Project for Statistical Computing . Available online at: https://www.r-project.org/ (Accessed December 13, 2023).
23. igraph – Network analysis software . Available online at: https://igraph.org/ (Accessed December 25, 2023).
24. Ruiz-Cerdá ML, Irurzun-Arana I, González-Garcia I, Hu C, Zhou H, Vermeulen A, et al. Towards patient stratification and treatment in the autoimmune disease lupus erythematosus using a systems pharmacology approach. Eur J Pharm Sci Off J Eur Fed Pharm Sci. (2016) 94:46–58. doi: 10.1016/j.ejps.2016.04.010
25. Yazdani A, Bahrami F, Pourgholaminejad A, Moghadasali R. A biological and a mathematical model of SLE treated by mesenchymal stem cells covering all the stages of the disease. Theory Biosci Theor Den Biowissenschaften. (2023) 142:167–79. doi: 10.1007/s12064-023-00390-4
26. Budu-Grajdeanu P, Schugart RC, Friedman A, Birmingham DJ, Rovin BH. Mathematical framework for human SLE Nephritis: disease dynamics and urine biomarkers. Theor Biol Med Model. (2010) 7:14. doi: 10.1186/1742-4682-7-14
27. Hao W, Rovin BH, Friedman A. Mathematical model of renal interstitial fibrosis. Proc Natl Acad Sci. (2014) 111:14193–8. doi: 10.1073/pnas.1413970111
28. Karagiannis G, Hao W, Lin G. Calibrations and validations of biological models with an application on the renal fibrosis. Int J Numer Methods BioMed Eng. (2020) 36:e3329. doi: 10.1002/cnm.3329
29. Gao X, He J, Sun X, Li F. Dynamically modeling the effective range of IL-2 dosage in the treatment of systemic lupus erythematosus. iScience. (2022) 25:104911. doi: 10.1016/j.isci.2022.104911
30. Rullmann J a. C, Struemper H, Defranoux NA, Ramanujan S, Meeuwisse CML, van Elsas A. Systems biology for battling rheumatoid arthritis: application of the Entelos PhysioLab platform. Syst Biol. (2005) 152:256–62. doi: 10.1049/ip-syb:20050053
31. Moise N, Friedman A. Rheumatoid arthritis - a mathematical model. J Theor Biol. (2019) 461:17–33. doi: 10.1016/j.jtbi.2018.10.039
32. Nakada T, Mager DE. Systems model identifies baseline cytokine concentrations as potential predictors of rheumatoid arthritis inflammatory response to biologics. Br J Pharmacol. (2022) 179:4063–77. doi: 10.1111/bph.15845
33. Meyer-Hermann M, Figge MT, Straub RH. Mathematical modeling of the circadian rhythm of key neuroendocrine-immune system players in rheumatoid arthritis: a systems biology approach. Arthritis Rheum. (2009) 60:2585–94. doi: 10.1002/art.24797
34. Wendelsdorf K, Bassaganya-Riera J, Hontecillas R, Eubank S. Model of colonic inflammation: immune modulatory mechanisms in inflammatory bowel disease. J Theor Biol. (2010) 264:1225–39. doi: 10.1016/j.jtbi.2010.03.027
35. Lo W-C, Arsenescu RI, Friedman A. Mathematical model of the roles of T cells in inflammatory bowel disease. Bull Math Biol. (2013) 75:1417–33. doi: 10.1007/s11538-013-9853-2
36. Lo W-C, Arsenescu V, Arsenescu RI, Friedman A. Inflammatory bowel disease: how effective is TNF-α Suppression? PloS One. (2016) 11:e0165782. doi: 10.1371/journal.pone.0165782
37. Park A, Kim S, Jung IH, Byun JH. An immune therapy model for effective treatment on inflammatory bowel disease. PloS One. (2020) 15:e0238918. doi: 10.1371/journal.pone.0238918
38. Dwivedi G, Fitz L, Hegen M, Martin SW, Harrold J, Heatherington A, et al. A multiscale model of interleukin-6-mediated immune regulation in Crohn’s disease and its application in drug discovery and development. CPT Pharmacomet Syst Pharmacol. (2014) 3:e89. doi: 10.1038/psp.2013.64
39. Rogers KV, Martin SW, Bhattacharya I, Singh RSP, Nayak S. A dynamic quantitative systems pharmacology model of inflammatory bowel disease: part 1 - model framework. Clin Transl Sci. (2021) 14:239–48. doi: 10.1111/cts.12849
40. Rogers KV, Martin SW, Bhattacharya I, Singh RSP, Nayak S. A dynamic quantitative systems pharmacology model of inflammatory bowel disease: part 2 - application to current therapies in crohn’s disease. Clin Transl Sci. (2021) 14:249–59. doi: 10.1111/cts.12850
41. Balbas-Martinez V, Ruiz-Cerdá L, Irurzun-Arana I, González-García I, Vermeulen A, Gómez-Mantilla JD, et al. A systems pharmacology model for inflammatory bowel disease. PloS One. (2018) 13:e0192949. doi: 10.1371/journal.pone.0192949
42. Balbas-Martinez V, Asin-Prieto E, Parra-Guillen ZP, Troconiz IF. A quantitative systems pharmacology model for the key interleukins involved in crohn’s disease. J Pharmacol Exp Ther. (2020) 372:299–307. doi: 10.1124/jpet.119.260539
43. Demin OO, Smirnov SV, Sokolov VV, Cucurull-Sanchez L, Pichardo-Almarza C, Flores MV, et al. Modeling of celiac disease immune response and the therapeutic effect of potential drugs. BMC Syst Biol. (2013) 7:56. doi: 10.1186/1752-0509-7-56
44. Nicholson D, Kerr EC, Jepps OG, Nicholson LB. Modelling experimental uveitis: barrier effects in autoimmune disease. Inflammation Res Off J Eur Histamine Res Soc Al. (2012) 61:759–73. doi: 10.1007/s00011-012-0469-z
45. Moise N, Friedman A. A mathematical model of the multiple sclerosis plaque. J Theor Biol. (2021) 512:110532. doi: 10.1016/j.jtbi.2020.110532
46. Vélez de Mendizábal N, Carneiro J, Solé RV, Goñi J, Bragard J, Martinez-Forero I, et al. Modeling the effector - regulatory T cell cross-regulation reveals the intrinsic character of relapses in Multiple Sclerosis. BMC Syst Biol. (2011) 5:114. doi: 10.1186/1752-0509-5-114
47. Kannan V, Kiani NA, Piehl F, Tegner J. A minimal unified model of disease trajectories captures hallmarks of multiple sclerosis. Math Biosci. (2017) 289:1–8. doi: 10.1016/j.mbs.2017.03.006
48. Gross CC, Pawlitzki M, Schulte-Mecklenbeck A, Rolfes L, Ruck T, Hundehege P, et al. Generation of a model to predict differentiation and migration of lymphocyte subsets under homeostatic and CNS autoinflammatory conditions. Int J Mol Sci. (2020) 21:2046. doi: 10.3390/ijms21062046
49. Broome TM, Coleman RA. A mathematical model of cell death in multiple sclerosis. J Neurosci Methods. (2011) 201:420–5. doi: 10.1016/j.jneumeth.2011.08.008
50. Dobreva A, Paus R, Cogan NG. Mathematical model for alopecia areata. J Theor Biol. (2015) 380:332–45. doi: 10.1016/j.jtbi.2015.05.033
51. Dobreva A, Paus R, Cogan NG. Analysing the dynamics of a model for alopecia areata as an autoimmune disorder of hair follicle cycling. Math Med Biol J IMA. (2018) 35:387–407. doi: 10.1093/imammb/dqx009
52. Tanaka G, Domínguez-Hüttinger E, Christodoulides P, Aihara K, Tanaka RJ. Bifurcation analysis of a mathematical model of atopic dermatitis to determine patient-specific effects of treatments on dynamic phenotypes. J Theor Biol. (2018) 448:66–79. doi: 10.1016/j.jtbi.2018.04.002
53. Domínguez-Hüttinger E, Christodoulides P, Miyauchi K, Irvine AD, Okada-Hatakeyama M, Kubo M, et al. Mathematical modeling of atopic dermatitis reveals “double-switch” mechanisms underlying 4 common disease phenotypes. J Allergy Clin Immunol. (2017) 139:1861–1872.e7. doi: 10.1016/j.jaci.2016.10.026
54. Christodoulides P, Hirata Y, Domínguez-Hüttinger E, Danby SG, Cork MJ, Williams HC, et al. Computational design of treatment strategies for proactive therapy on atopic dermatitis using optimal control theory. Philos Transact A Math Phys Eng Sci. (2017) 375:20160285. doi: 10.1098/rsta.2016.0285
55. Miyano T, Irvine AD, Tanaka RJ. A mathematical model to identify optimal combinations of drug targets for dupilumab poor responders in atopic dermatitis. Allergy. (2022) 77:582–94. doi: 10.1111/all.14870
56. Magombedze G, Nduru P, Bhunu CP, Mushayabasa S. Mathematical modelling of immune regulation of type 1 diabetes. Biosystems. (2010) 102:88–98. doi: 10.1016/j.biosystems.2010.07.018
57. Jaberi-Douraki M, Pietropaolo M, Khadra A. Continuum model of T-cell avidity: Understanding autoreactive and regulatory T-cell responses in type 1 diabetes. J Theor Biol. (2015) 383:93–105. doi: 10.1016/j.jtbi.2015.07.032
58. Salazar-Viedma M, Vergaño-Salazar JG, Pastenes L, D’Afonseca V. Simulation model for hashimoto autoimmune thyroiditis disease. Endocrinology. (2021) 162:bqab190. doi: 10.1210/endocr/bqab190
59. Aguda BD, Marsh CB, Thacker M, Crouser ED. An in silico modeling approach to understanding the dynamics of sarcoidosis. PloS One. (2011) 6:e19544. doi: 10.1371/journal.pone.0019544
60. Hao W, Crouser ED, Friedman A. Mathematical model of sarcoidosis. Proc Natl Acad Sci U.S.A. (2014) 111:16065–70. doi: 10.1073/pnas.1417789111
61. Hao W, Marsh C, Friedman A. A mathematical model of idiopathic pulmonary fibrosis. PloS One. (2015) 10:e0135097. doi: 10.1371/journal.pone.0135097
62. van der Vegt SA, Polonchuk L, Wang K, Waters SL, Baker RE. Mathematical modelling of autoimmune myocarditis and the effects of immune checkpoint inhibitors. J Theor Biol. (2022) 537:111002. doi: 10.1016/j.jtbi.2021.111002
63. Head M, Meryhew N, Runquist O. Mechanism and computer simulation of immune complex formation, opsonization, and clearance. J Lab Clin Med. (1996) 128:61–74. doi: 10.1016/s0022-2143(96)90114-6
64. Arazi A, Neumann AU. Modeling immune complex-mediated autoimmune inflammation. J Theor Biol. (2010) 267:426–36. doi: 10.1016/j.jtbi.2010.08.033
65. Iwami S, Takeuchi Y, Miura Y, Sasaki T, Kajiwara T. Dynamical properties of autoimmune disease models: tolerance, flare-up, dormancy. J Theor Biol. (2007) 246:646–59. doi: 10.1016/j.jtbi.2007.01.020
66. Khailaie S, Bahrami F, Janahmadi M, Milanez-Almeida P, Huehn J, Meyer-Hermann M. A mathematical model of immune activation with a unified self-nonself concept. Front Immunol. (2013) 4:474. doi: 10.3389/fimmu.2013.00474
67. Louzoun Y, Atlan H, Cohen IR. Modeling the influence of TH1- and TH2-type cells in autoimmune diseases. J Autoimmun. (2001) 17:311–21. doi: 10.1006/jaut.2001.0548
68. Hara A, Iwasa Y. Autoimmune diseases initiated by pathogen infection: Mathematical modeling. J Theor Biol. (2020) 498:110296. doi: 10.1016/j.jtbi.2020.110296
69. Ramos MPM, Ribeiro C, Soares AJ. A kinetic model of T cell autoreactivity in autoimmune diseases. J Math Biol. (2019) 79:2005–31. doi: 10.1007/s00285-019-01418-4
70. Valeyev NV, Hundhausen C, Umezawa Y, Kotov NV, Williams G, Clop A, et al. A systems model for immune cell interactions unravels the mechanism of inflammation in human skin. PloS Comput Biol. (2010) 6:e1001024. doi: 10.1371/journal.pcbi.1001024
71. Lisnevskaia L, Murphy G, Isenberg D. Systemic lupus erythematosus. Lancet Lond Engl. (2014) 384:1878–88. doi: 10.1016/S0140-6736(14)60128-8
72. Tsokos GC. Systemic lupus erythematosus. N Engl J Med. (2011) 365:2110–21. doi: 10.1056/NEJMra1100359
73. Mok CC, Lau CS. Pathogenesis of systemic lupus erythematosus. J Clin Pathol. (2003) 56:481–90. doi: 10.1136/jcp.56.7.481
74. Smolen JS, Aletaha D, McInnes IB. Rheumatoid arthritis. Lancet Lond Engl. (2016) 388:2023–38. doi: 10.1016/S0140-6736(16)30173-8
75. Angelotti F, Parma A, Cafaro G, Capecchi R, Alunno A, Puxeddu I. One year in review 2017: pathogenesis of rheumatoid arthritis. Clin Exp Rheumatol. (2017) 35:368–78.
76. Edilova MI, Akram A, Abdul-Sater AA. Innate immunity drives pathogenesis of rheumatoid arthritis. BioMed J. (2021) 44:172–82. doi: 10.1016/j.bj.2020.06.010
77. Kondo N, Kuroda T, Kobayashi D. Cytokine networks in the pathogenesis of rheumatoid arthritis. Int J Mol Sci. (2021) 22:10922. doi: 10.3390/ijms222010922
78. Ben Mrid R, Bouchmaa N, Ainani H, El Fatimy R, Malka G, Mazini L. Anti-rheumatoid drugs advancements: New insights into the molecular treatment of rheumatoid arthritis. BioMed Pharmacother. (2022) 151:113126. doi: 10.1016/j.biopha.2022.113126
79. Polmar SH. New drugs for rheumatoid arthritis: The industry point of view. Reumatol Clínica. (2010) 6:3–4. doi: 10.1016/j.reuma.2009.10.002
80. Entelos Inc. - CMOCRO. Domain Name . Available online at: http://www.cmocro.com/ (Accessed December 25, 2023)
81. Cojocaru M, Cojocaru IM, Silosi I, Vrabie CD. Gastrointestinal manifestations in systemic autoimmune diseases. Mædica. (2011) 6:45–51.
82. Kunovsky L, Dite P, Jabandziev P, Kala Z, Vaculova J, Andrasina T, et al. Autoimmune diseases of digestive organs—A multidisciplinary challenge: A focus on hepatopancreatobiliary manifestation. J Clin Med. (2021) 10:5796. doi: 10.3390/jcm10245796
83. An J, Liu Y, Wang Y, Fan R, Hu X, Zhang F, et al. The role of intestinal mucosal barrier in autoimmune disease: A potential target. Front Immunol. (2022) 13:871713. doi: 10.3389/fimmu.2022.871713
84. Xu X-R, Liu C-Q, Feng B-S, Liu Z-J. Dysregulation of mucosal immune response in pathogenesis of inflammatory bowel disease. World J Gastroenterol. (2014) 20:3255–64. doi: 10.3748/wjg.v20.i12.3255
85. Shahini A, Shahini A. Role of interleukin-6-mediated inflammation in the pathogenesis of inflammatory bowel disease: focus on the available therapeutic approaches and gut microbiome. J Cell Commun Signal. (2023) 17:55–74. doi: 10.1007/s12079-022-00695-x
86. Allen RJ, Rieger TR, Musante CJ. Efficient generation and selection of virtual populations in quantitative systems pharmacology models. CPT Pharmacomet Syst Pharmacol. (2016) 5:140–6. doi: 10.1002/psp4.12063
87. Alhassan E, Yadav A, Kelly CP, Mukherjee R. Novel nondietary therapies for celiac disease. Cell Mol Gastroenterol Hepatol. (2019) 8:335–45. doi: 10.1016/j.jcmgh.2019.04.017
88. Petzold A, Balcer LJ, Calabresi PA, Costello F, Frohman TC, Frohman EM, et al. Retinal layer segmentation in multiple sclerosis: a systematic review and meta-analysis. Lancet Neurol. (2017) 16:797–812. doi: 10.1016/S1474-4422(17)30278-8
89. Conigliaro P, Cesareo M, Chimenti MS, Triggianese P, Canofari C, Barbato C, et al. Take a look at the eyes in Systemic Lupus Erythematosus: A novel point of view. Autoimmun Rev. (2019) 18:247–54. doi: 10.1016/j.autrev.2018.09.011
90. Reddy AK, Kolfenbach JR, Palestine AG. Ocular manifestations of rheumatoid arthritis. Curr Opin Ophthalmol. (2022) 33:551–6. doi: 10.1097/ICU.0000000000000890
91. Compston A, Coles A. Multiple sclerosis. Lancet. (2008) 372:1502–17. doi: 10.1016/S0140-6736(08)61620-7
92. Barkhane Z, Elmadi J, Satish Kumar L, Pugalenthi LS, Ahmad M, Reddy S. Multiple sclerosis and autoimmunity: A veiled relationship. Cureus. (2022) 14:e24294. doi: 10.7759/cureus.24294
93. Filippi M, Bar-Or A, Piehl F, Preziosa P, Solari A, Vukusic S, et al. Multiple sclerosis. Nat Rev Dis Primer. (2018) 4:43. doi: 10.1038/s41572-018-0041-4
94. Bennett JL, Stüve O. Update on inflammation, neurodegeneration, and immunoregulation in multiple sclerosis: therapeutic implications. Clin Neuropharmacol. (2009) 32:121–32. doi: 10.1097/WNF.0b013e3181880359
95. Greiner T, Kipp M. What guides peripheral immune cells into the central nervous system? Cells. (2021) 10:2041. doi: 10.3390/cells10082041
96. Mothes N, Niggemann B, Jenneck C, Hagemann T, Weidinger S, Bieber T, et al. The cradle of IgE autoreactivity in atopic eczema lies in early infancy. J Allergy Clin Immunol. (2005) 116:706–9. doi: 10.1016/j.jaci.2005.06.025
97. Roesner LM, Werfel T. Autoimmunity (or not) in atopic dermatitis. Front Immunol. (2019) 10:2128. doi: 10.3389/fimmu.2019.02128
98. Tang TS, Bieber T, Williams HC. Does “autoreactivity” play a role in atopic dermatitis? J Allergy Clin Immunol. (2012) 129:1209–1215.e2. doi: 10.1016/j.jaci.2012.02.002
99. Badloe FMS, De Vriese S, Coolens K, Schmidt-Weber CB, Ring J, Gutermuth J, et al. IgE autoantibodies and autoreactive T cells and their role in children and adults with atopic dermatitis. Clin Transl Allergy. (2020) 10:34. doi: 10.1186/s13601-020-00338-7
100. Orciani M, Campanati A, Caffarini M, Ganzetti G, Consales V, Lucarini G, et al. T helper (Th)1, Th17 and Th2 imbalance in mesenchymal stem cells of adult patients with atopic dermatitis: at the origin of the problem. Br J Dermatol. (2017) 176:1569–76. doi: 10.1111/bjd.15078
101. Bertolini M, McElwee K, Gilhar A, Bulfone-Paus S, Paus R. Hair follicle immune privilege and its collapse in alopecia areata. Exp Dermatol. (2020) 29:703–25. doi: 10.1111/exd.14155
102. Hiller-Sturmhöfel S, Bartke A. The endocrine system. Alcohol Health Res World. (1998) 22:153–64.
104. Polonsky KS. The past 200 years in diabetes. N Engl J Med. (2012) 367:1332–40. doi: 10.1056/NEJMra1110560
105. Ajmera I, Swat M, Laibe C, Le Novère N, Chelliah V. The impact of mathematical modeling on the understanding of diabetes and related complications. CPT Pharmacomet Syst Pharmacol. (2013) 2:e54. doi: 10.1038/psp.2013.30
106. Fritzen K, Heinemann L, Schnell O. Modeling of diabetes and its clinical impact. J Diabetes Sci Technol. (2018) 12:976–84. doi: 10.1177/1932296818785642
107. Ralli M, Angeletti D, Fiore M, D’Aguanno V, Lambiase A, Artico M, et al. Hashimoto’s thyroiditis: An update on pathogenic mechanisms, diagnostic protocols, therapeutic strategies, and potential Malignant transformation. Autoimmun Rev. (2020) 19:102649. doi: 10.1016/j.autrev.2020.102649
108. Pyzik A, Grywalska E, Matyjaszek-Matuszek B, Roliński J. Immune disorders in Hashimoto’s thyroiditis: what do we know so far? J Immunol Res. (2015) 2015:979167. doi: 10.1155/2015/979167
109. Kaiser Y, Eklund A, Grunewald J. Moving target: shifting the focus to pulmonary sarcoidosis as an autoimmune spectrum disorder. Eur Respir J. (2019) 54:1802153. doi: 10.1183/13993003.021532018
110. Starshinova AA, Malkova AM, Basantsova NY, Zinchenko YS, Kudryavtsev IV, Ershov GA, et al. Sarcoidosis as an autoimmune disease. Front Immunol. (2019) 10:2933. doi: 10.3389/fimmu.2019.02933
111. Koether K, Besnard V, Sandig H, Carruthers A, Miranda E, Grootenboer-Mignot S, et al. Autoantibodies are associated with disease progression in idiopathic pulmonary fibrosis. Eur Respir J. (2023) 61:2102381. doi: 10.1183/13993003.02381-2021
112. Leuschner G, Semenova A, Mayr CH, Kapellos TS, Ansari M, Seeliger B, et al. Mass spectrometry-based autoimmune profiling reveals predictive autoantigens in idiopathic pulmonary fibrosis. iScience. (2023) 26:108345. doi: 10.1016/j.isci.2023.108345
113. Bracamonte-Baran W, Čiháková D. Cardiac autoimmunity: myocarditis. Adv Exp Med Biol. (2017) 1003:187–221. doi: 10.1007/978-3-319-57613-8_10
114. Tsuruoka K, Wakabayashi S, Morihara H, Matsunaga N, Fujisaka Y, Goto I, et al. Exacerbation of autoimmune myocarditis by an immune checkpoint inhibitor is dependent on its time of administration in mice. Int J Cardiol. (2020) 313:67–75. doi: 10.1016/j.ijcard.2020.04.033
115. Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther. (1979) 25:358–71. doi: 10.1002/cpt1979253358
116. Holford NH, Sheiner LB. Understanding the dose-effect relationship: clinical application of pharmacokinetic-pharmacodynamic models. Clin Pharmacokinet. (1981) 6:429–53. doi: 10.2165/00003088-198106060-00002
117. Brooks PM, Bell MA, Lee P, Rooney PJ, Dick WC. THE EFFECT OF FRUSEMIDE ON INDOMETHACIN PLASMA LEVELS. Br J Clin Pharmacol. (1974) 1:485–9. doi: 10.1111/j.1365-2125.1974.tb01698.x
118. Nijsen MJMA, Wu F, Bansal L, Bradshaw-Pierce E, Chan JR, Liederer BM, et al. Preclinical QSP modeling in the pharmaceutical industry: an IQ consortium survey examining the current landscape: preclinical QSP in pharmaceutical industry. CPT Pharmacomet Syst Pharmacol. (2018) 7:135–46. doi: 10.1002/psp4.12282
119. Zhang X-M, Liu C-Y, Shao Z-H. Advances in the role of helper T cells in autoimmune diseases. Chin Med J (Engl). (2020) 133:968–74. doi: 10.1097/CM9.0000000000000748
120. Foreman AL, Van de Water J, Gougeon M-L, Gershwin ME. B cells in autoimmune diseases: Insights from analyses of immunoglobulin variable (Ig V) gene usage. Autoimmun Rev. (2007) 6:387–401. doi: 10.1016/j.autrev.2006.12.005
121. Mould DR, Upton RN. Basic concepts in population modeling, simulation, and model-based drug development. CPT Pharmacomet Syst Pharmacol. (2012) 1:e6. doi: 10.1038/psp.2012.4
122. Bolton C. The translation of drug efficacy from in vivo models to human disease with special reference to experimental autoimmune encephalomyelitis and multiple sclerosis. Inflammopharmacology. (2007) 15:183–7. doi: 10.1007/s10787-007-1607-z
123. Zhu AZ. Quantitative translational modeling to facilitate preclinical to clinical efficacy & toxicity translation in oncology. Future Sci OA. (2018) 4:5. doi: 10.4155/fsoa-2017-0152
124. Caro JJ, Briggs AH, Siebert U, Kuntz KM, ISPOR-SMDM Modeling Good Research Practices Task Force. Modeling good research practices–overview: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force-1. Med Decis Mak Int J Soc Med Decis Mak. (2012) 32:667–77. doi: 10.1177/0272989X12454577
125. Delitala M, Dianzani U, Lorenzi T, Melensi M. A mathematical model for immune and autoimmune response mediated by T -cells. Comput Math Appl. (2013) 66:1010–23. doi: 10.1016/j.camwa.2013.06.026
126. Zhang W, Wahl LM, Yu P. Modeling and analysis of recurrent autoimmune disease. SIAM J Appl Math. (2014) 74:1998–2025. doi: 10.1137/140955823
127. Zhang W, Yu P. Hopf and generalized hopf bifurcations in a recurrent autoimmune disease model. Int J Bifurc Chaos. (2016) 26:1650079. doi: 10.1142/S0218127416500796
128. Zhang W, Yu P. Revealing the role of the effector-regulatory t cell loop on autoimmune disease symptoms via nonlinear analysis. Commun Nonlinear Sci Numer Simul. (2021) 93:105529. doi: 10.1016/j.cnsns.2020.105529
129. Kolev M. Mathematical modeling of autoimmune diseases. Symmetry. (2020) 12:1457. doi: 10.3390/sym12091457
130. Costa MFP, Ramos MP, Ribeiro C, Soares AJ. Optimal control model of immunotherapy for autoimmune diseases. Math Methods Appl Sci. (2021) 44:8883–902. doi: 10.1002/mma.7318
131. Della Marca R, MaChado Ramos M da P, Ribeiro C, Soares AJ. Mathematical modelling of oscillating patterns for chronic autoimmune diseases. Math Methods Appl Sci. (2022) 45:7144–61. doi: 10.1002/mma.8229
Keywords: autoimmune diseases, mathematical modeling, quantitative systems pharmacology, model-informed drug development, immune system modeling
Citation: Ugolkov Y, Nikitich A, Leon C, Helmlinger G, Peskov K, Sokolov V and Volkova A (2024) Mathematical modeling in autoimmune diseases: from theory to clinical application. Front. Immunol. 15:1371620. doi: 10.3389/fimmu.2024.1371620
Received: 16 January 2024; Accepted: 29 February 2024;
Published: 14 March 2024.
Edited by:
Thomas Hartung, Johns Hopkins University, United StatesReviewed by:
Maria Ramos, University of Minho, PortugalCopyright © 2024 Ugolkov, Nikitich, Leon, Helmlinger, Peskov, Sokolov and Volkova. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alina Volkova, YWxpbmEudm9sa292YUBtc2RlY2lzaW9ucy50ZWNo
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.