The Role of Multiscale Protein Dynamics in Antigen Presentation and T Lymphocyte Recognition

T lymphocytes are stimulated when they recognize short peptides bound to class I proteins of the major histocompatibility complex (MHC) protein, as peptide–MHC complexes. Due to the diversity in T-cell receptor (TCR) molecules together with both the peptides and MHC proteins they bind to, it has been difficult to design vaccines and treatments based on these interactions. Machine learning has made some progress in trying to predict the immunogenicity of peptide sequences in the context of specific MHC class I alleles but, as such approaches cannot integrate temporal information and lack explanatory power, their scope will always be limited. Here, we advocate a mechanistic description of antigen presentation and TCR activation which is explanatory, predictive, and quantitative, drawing on modeling approaches that collectively span several length and time scales, being capable of furnishing reliable biological descriptions that are difficult for experimentalists to provide. It is a form of multiscale systems biology. We propose the use of chemical rate equations to describe the time evolution of the foreign and host proteins to explain how the original proteins end up being presented on the cell surface as peptide fragments, while we invoke molecular dynamics to describe the key binding processes on the molecular level, including those of peptide–MHC complexes with TCRs which lie at the heart of the immune response. On each level, complementary methods based on machine learning are available, and we discuss the relationship between these divergent approaches. The pursuit of predictive mechanistic modeling approaches requires experimentalists to adapt their work so as to acquire, store, and expose data that can be used to verify and validate such models.

Introduction

The immune system’s ability to fight against pathogens such as viruses and bacteria varies between individuals and is influenced by an area of the human genome known as the major histocompatibility complex (MHC). MHC class I (MHCI) complexes present small fragments of proteins, known as peptides, on the cell surface, which allows cytotoxic T-cells to recognize intracellular pathogens.

The MHCI antigen presentation pathway is a multistage process, which essentially hijacks the waste disposal system of cells (Figure 1). The proteasomal degradation of cytoplasmic proteins generates peptides that bind to the transporter associated with antigen processing (TAP), thereby shipping them to the endoplasmic reticulum (ER). Once in the ER, peptides may be loaded on to MHCI molecules, which are then transported through the Golgi apparatus to the cell surface. The abundance of specific peptides on the cell surface therefore depends on several factors. First, 99% of all cytoplasmic peptides are degraded before encountering TAP (1) so a high cytoplasmic peptide concentration is key to eventual peptide presentation. The outcome depends upon a trade-off between protein synthesis and degradation including the probability of cleavage of a peptide from the protein. The rate of transport of a peptide to the ER depends upon the sequence-specific affinity of the peptide with TAP. Once in the ER, peptides will compete for loading onto the MHC molecules via the peptide loading complex. Chaperone molecules, such as tapasin, facilitate the formation of peptide–MHC (pMHC) complexes with high affinity, which then egress to the cell surface. The cell surface pMHC complexes bind with T-cell receptors (TCRs), initiating a signal cascade resulting in T-cell activation and the killing of target cells. pMHC affinity to TCR (2) and cell surface peptide abundance are correlated with T-cell immunodominance (3), the dominant clonal expansion of T-cells that respond to specific peptides, or epitopes.

FIGURE 1

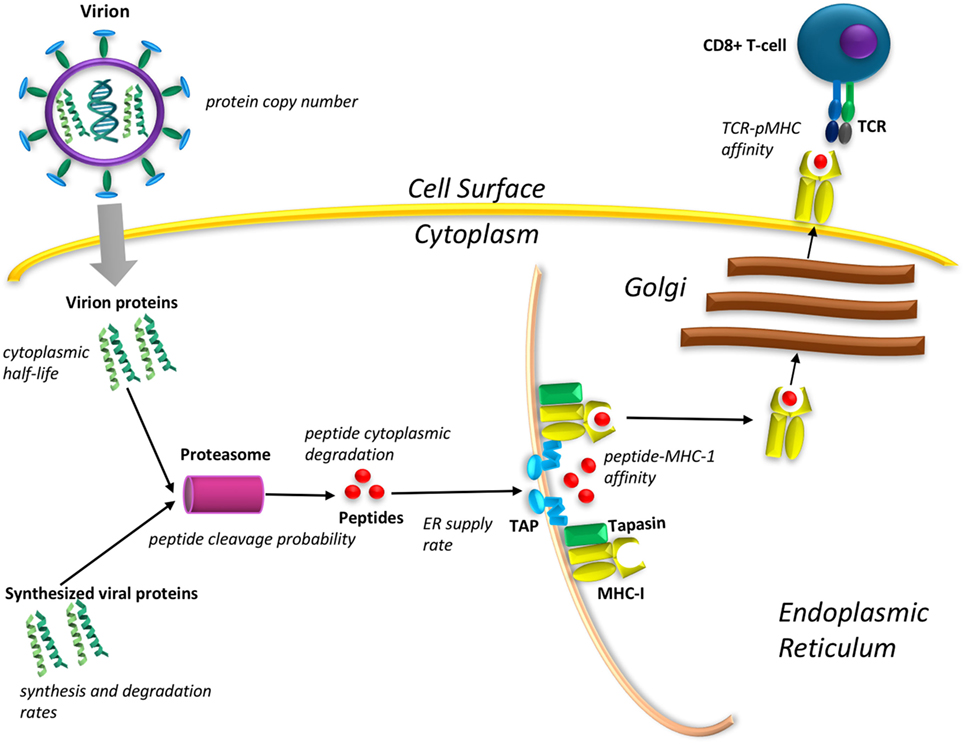
Figure 1. Diagrammatic representation of the major steps in the major histocompatibility complex (MHC) antigen presentation pathway that need to be included in a mechanistic model of viral peptide cell surface presentation. The measurable quantities required for such a model are mentioned in italics next to each step.

Knowledge of the hierarchy and timing of presentation of such epitopes by MHC is key to the development of peptide vaccines and immunotherapy for a myriad of diseases including viral infections and cancer. This requires measurements of T-cell recognition and/or the pMHC cell surface abundance. T-cell epitopes can be mapped using high-throughput experimental methods. However, the number of proteins and MHC alleles that can be scanned at any given time is limited. Croft et al. (4) made temporal measurements of the cell surface abundance of eight vaccinia peptides using mass spectrometry, demonstrating how the abundance of viral peptides relates to the timing of T-cell responses. However, it is infeasible at present to perform such an experiment over the full potential peptidome of viral peptides for any MHC allele. To obtain a more comprehensive view of the dynamics of viral peptide presentation, quantitative models are required to generate predictions of cell surface presentation of viral or cancerous peptides.

It is desirable to predict which peptides are immunogenic, that is those which evoke an immune response. Several epitope prediction algorithms have been produced using machine learning methods, such as the MHC peptide processing tool from the immune epitope database (IEDB) (5). This algorithm is built upon datasets of in vitro experiments characterizing proteasomal cleavage rates, TAP affinity, and MHC binding of thousands of different peptides, combining the three metrics to produce a total “score” for each possible peptide from an input protein amino acid sequence. The higher the score, the greater the probability of the peptide being presented.

Machine learning algorithms are thought to be able to predict the efficiency of peptide processing for MHC presentation accurately when comparing peptides originating from a single protein. However, their predictions provide a static view of immunogenicity based upon sequence-specificity; they cannot account for protein abundance kinetics, which has a substantial impact on the hierarchy of peptide abundance at the cell surface (4). This is a general limitation of data-driven, as opposed to theory-led, approaches in biomedical research (6). Predicting the timing and hierarchy of peptide presentation following pathogen infection requires mechanistic models that integrate pathogen kinetics throughout infection and replication. It is, however, possible to include machine learning methods within mechanistic pathway prediction models by incorporating sequence-specific distinctions between peptides via their kinetic behavior.

A Motivating Example: HIV Infection and Long-Term Control

HIV-infected individuals usually progress to AIDS within 10 years, with 10−15% of people progressing rapidly within 3 years of infection, whereas 5−10% remain asymptomatic for over 10 years (7). These widely differing rates of progression are linked to the differing expression of specific MHC alleles, which in humans are known as human leukocyte antigen (HLA) proteins, and the peptides they present. Experimental evidence suggests an association between T-cell recognition of Gag epitopes presented by a subsection of MHC alleles known as long-term non-progressors (LTNPs) and control of HIV progression; however, this is far from a solved issue.

The MHC alleles HLA-B*58, -B*57, -B*27, and -B*44 are overrepresented among LTNPs and are associated with Gag-specific T-cell responses (8). Conversely, the alleles HLA-B*35 and -B*18 have been found to be associated with rapid progression to AIDS with T-cell responses against non-Gag epitopes, such as those from the Nef and Env proteins (9).

The Env and Nef proteins are both highly variable, with Env being the most variable sequence in the HIV genome (8) and mutations in these epitopes are fitness neutral (10). The Gag protein amino acid sequence, however, is highly conserved, and escape mutations in its epitopes negatively impact viral fitness. For example, the T242N escape mutation in the HLA-B*57/B*58:01 restricted Gag epitope TW10 (TSTLQEQIGW) leads to diminished viral replication capacity, as does the A163G mutation of the similarly restricted Gag KF11 (KAFSPEVIPMF) epitope (11). However, other highly conserved proteins, such as Pol, are not as strongly associated with HIV control. Therefore, sequence conservation may not be the only important factor in immune control. Gag is the most abundant protein in both the HIV virion and in the cytoplasm following the nuclear export of full-length mRNA during replication. The kinetics of the Gag protein could also be very important in shaping the resulting abundance of derived peptides. As existing analyses considering several different factors separately have yet to elucidate a coherent picture of HIV control, we propose analyzing this question in an integrated manner. Specifically, a dynamic, mechanistic model could help to determine the relative importance of protein abundance and sequence variability, and help to explain Gag’s role in the control of HIV.

Mechanistic Pathway Models, Their Construction, and the Data Required

To create a mechanistic model to predict peptide cell surface presentation following viral infection, each step in the pathway from viral protein synthesis to pMHC binding and presentation (Figure 1) can be represented in the form of an ordinary differential equation based on the law of mass action. The rate coefficients in such equations require collection of experimental data pertaining to the viral intracellular dynamics. When a virion enters a cell, viral proteins and the viral genome are dumped into the cytoplasm. The viral proteins are degraded into peptides that can potentially lead to host recognition of the infected cell soon after infection. Therefore, determining the copy number of the viral proteins contained within a virion and their cytoplasmic half-lives are required to predict the production of virion-derived peptides prior to the onset of viral replication. Detecting infected cells before viral replication begins would prevent the spread of the virus to other cells in the body.

As mentioned above, an ideal candidate pathogen to test this method is HIV-1, as there is a wealth of experimental data available characterizing many of the important steps in viral replication within a single infected cell. Furthermore, several models of HIV-1 intracellular kinetics exist describing the dynamics of viral mRNA production together with synthesis and degradation of many of the important HIV-1 proteins, as well as steps in assembly of virion particles.

Reddy and Yin (12) modeled HIV-1 intracellular kinetics from reverse transcription and integration of the viral genome into the host genome, transcription of full-length viral mRNA, subsequent splicing, and export into the cytoplasm, followed by the translation of the proteins Gag, GagPol, and Env. Several steps in the creation of new virions are also modeled, including posttranslation protein modifications, transport to the cell membrane, and the budding and assembly of viral particles. The majority of the kinetic rate parameters used in this model have been experimentally measured, and its predictions agree well with available experimental measurements of HIV DNA, mRNA, protein, and virion concentrations.

Kim and Yin (13) also described the translation and splicing of HIV mRNA, and nuclear export; furthermore, their model includes the translation of the regulatory proteins Tat and Rev as well as their regulation of transcription and export of viral mRNA. Wang and Lai (14) modeled the transcription of viral mRNA, translation of Gag, Tat, and the accessory protein Vif, the creation of Vif-Gag, Vif-APO, and Gag-APO complexes, where APO is a cellular antiviral protein, together with incorporation of these complexes into budding virions. The model was verified using several experimental data sets. The combination of these models may be expected to result in a quantitative description of intracellular HIV-1 kinetics from viral genome integration to budding of new virions. Missing parameters could be taken from publications where available, or otherwise chosen to have plausible values.

The steps of the peptide processing pathway would also need to be converted to a kinetic pathway model. Dalchau et al. (15) presented such a model of peptide–MHC binding in the ER and subsequent egression to the cell surface while also accounting for the effect of the chaperone molecule tapasin, which enhances the preferential selection of peptides that form stable complexes with MHC. In this model, a peptide P_i is supplied to the ER with rate coefficient g_i where it can bind to empty MHC with rate coefficient b or to tapasin-bound MHC with a higher value c. The values for b and c are assumed to be similar for all peptides binding to the same MHC allele. The peptide can unbind from the MHC or MHC–tapasin complexes with rate coefficient u_i or u_i⋅q respectively, where q is the increase in the peptide–MHC unbinding rate coefficient u_i in the presence of tapasin.

To combine a model of viral intracellular kinetics with a peptide processing model and simulate such a model for a large set of possible peptides requires sequence-specific parameters describing the rate of proteasomal cleavage, TAP transport and peptide–MHC binding and unbinding. The IEDB MHC processing tool (5) may be used to infer relative parameters for each peptide sequence in the model. The proteasomal cleavage prediction is a relative score proportional to the logarithm of the amount of peptide generated from the cleavage of the peptides C-terminal. The TAP transport prediction is given in terms of the IC₅₀ of the interaction between TAP and a peptide. Similarly, the MHC binding prediction is given as an IC₅₀ value. The proteasomal cleavage score from the IEDB machine learning tool can be converted to a relative probability of peptide production each time a protein degrades by scaling the scores so that they lie within a reasonable range of probabilities.

The predicted peptide–MHC IC₅₀ can be used to approximate the dissociation constant K_D=u_i/b of the peptide when bound to MHC. As peptide off-rates are known to vary more than peptide on-rates (16), we suggest making the assumption that the variation in predicted IC₅₀ values is accounted for purely in terms of variation in the peptide off-rates. Accordingly, the on-rate would be non-peptide-specific and can be assigned a value in the middle of what has been measured experimentally. In this way, peptide off-rates can be calculated from predicted IC₅₀ values as k_off = k_on × IC₅₀. For example, by using k_on = 10⁴ M⁻¹ s⁻¹ [in the middle of values measured for peptides at 26°C and 32°C in the study by Garstka et al. (16)], a tight binding peptide with affinity 1 nM would translate into an off-rate of k_off = 10⁻⁵ s⁻¹.

However, not all presented peptides will become T-cell epitopes. Calis et al. (17) used a large dataset of immunogenic and non-immunogenic pMHC complexes to determine the important amino acid properties associated with immunogenic pMHCs, and trained a predictive model to classify new pMHCs as either immunogenic or non-immunogenic. Therefore, a final step in the large mechanistic predictive model would be to use predictions of pMHC immunogenicity to filter for those peptides that are predicted to be presented that will actually result in a T-cell response. A further step involves combining existing models of T-cell signaling in response to pMHC complexes—the most recent being Lever et al. (2)—to further investigate the differences in predicted T-cell response to different pMHC complexes.

Molecular Dynamics Studies of TCR–pMHC Interactions

A signal cascade involves a series of communications among a number of proteins and small molecules which establish many interactions within and between signaling networks. The interactions induce conformational changes that are important to many aspects of protein function. TCR interacting with antigenic peptides bound to MHC molecules, for example, changes the conformations of both pMHC and TCR, and initiates a signal cascade. There is a huge gap between the atomic-resolution molecule–molecule interactions and the cellular or intercellular level of signaling, which is both spatial and temporal (18). A large number of parameters are required in the pathway models (these are primarily rate coefficients) and for the most part they are difficult, if not impossible, to measure, or infer from data. Molecular dynamics (MD) simulations (19), along with multiscale modeling, provide a way to estimate the kinetic parameters for the pathway modeling (18, 20).

T-cell receptor–pMHC recognition involves two steps: a peptide binds to an MHC molecule to create a peptide–MHC complex, the complex being presented to TCRs. X-ray crystallographic structures provide detailed insights into the TCR–pMHC interactions, the number of structures having increased significantly in recent years. However, there are two major limitations: (i) they provide static pictures of “snapshots” from a vast ensemble of dynamic conformations; (ii) they reveal a partial representation of a full complex, usually its extracellular domain, due to the problem of crystallizing the membrane-associated proteins. Experimental methods have been used to characterize TCR–pMHC interactions, including surface plasmon resonance, IC₅₀, micropipette adhesion frequency, and atomic force microscopy.

A range of immunoinformatics (i.e., machine learning)-based binding affinity prediction methods have also been developed, of which sequence-based and structure-based methods are two main classes with variable accuracies, usually depending on the size and quality of training sets (5, 6, 21, 22). As in the context of pathway modeling, a mechanistic, and quantitative approach exists for obtaining predictions of pMHC or TCR–pMHC binding affinities, based on MD simulation (23–25). It has the advantage that it provides de novo prediction of all relevant properties based on certain prior information.

The MD approach (19), and molecular modeling in general, is valuable to elucidate the molecular structures, dynamics, and function of biological molecules. Indeed, the Nobel Prize for Chemistry was awarded to Karplus, Levitt, and Warshel in 2013 for their work on multiscale modeling of biological systems (26). MD is a computer simulation technique wherein the time evolution of a set of interacting atoms is followed by integrating their Newtonian equations of motion. MD simulations can, in principle, provide “an unsurpassed and unsurpassable level of detail” (23) of dynamic phenomena, one that can greatly enhance our understanding of biological function. Today, MD is feasible for very complex macromolecules, such as multi-protein complexes in a heterogeneous environment which can consist of water molecules, ions, lipid bilayers, etc.

Since the first simulation of a protein was published in 1977 (27), the MD methodology and its applications have progressed substantially. Applications in immunology have been summarized in a few review papers (23–25). Here, we mention some of our studies in the area, in the order of publication and the complexity of the systems investigated: (i) truncated pMHC (α1–α2 domains of MHC) (28); (ii) pMHC with entire extracellular domain of MHC (α1, α2, α3, and β2m domains of MHC) (28, 29) (Figure 2A); (iii) TCR–pMHC (entire extracellular domains of TCR and MHC) (30, 31) (Figure 2B); and (iv) TCR–pMHC–CD4 (cluster of differentiation 4) embedded in a lipid bilayer (32) (Figure 2C). These studies demonstrate that structural and energetic properties can be accurately predicted using molecular systems in realistic settings through the introduction of physiological details. In the TCR–pMHC–CD4 study (32), the tri-molecular system was constructed based on available X-ray structures with missing regions modeled by homology, including transmembrane domains, adjoining regions, and loops. The entire model was embedded in a membrane environment likely to influence the interactions of these membrane-associated proteins with each other. The computed structural and thermodynamic properties from the simulation are in good agreement with limited experimental data, including the binding free energies of CD4 to pMHC and pMHC to TCR. As we have demonstrated recently in small molecule–protein systems (33, 34), the simulations could provide insight into the interactions of individual molecule–molecule complexes. The overall free energy change upon binding, along with the kinetic properties such as the on- and off-rates, is critical for the recognition and discrimination process. The binding of pMHC to TCR is, in terms of underlying physico-chemical principles, identical to binding of small molecule inhibitors to protein receptors, although the models and simulations need to be carefully designed because of the complexity of the protein–protein complexes.

FIGURE 2

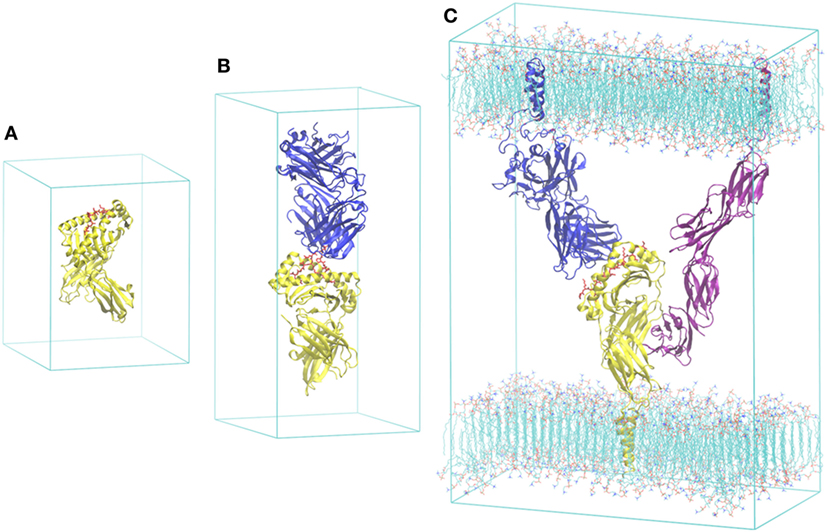
Figure 2. The escalating scale necessary to simulate large-scale immunological phenomenon: (A) model of the peptide-–MHC (pMHC) (28, 29), (B) pMHC bound to T-cell receptor (TCR) (30, 31), and (C) a viable unit of the immune synapse, comprising pMHC, TCR, CD4, and two opposing sections of membrane (32). Major histocompatibility complex (MHC) is colored yellow, TCR blue, the peptide red, and the CD4 purple. All of the models are simulated with explicit water molecules and 3D periodic boundary conditions. Water molecules are omitted for clarity.

It should be noted that while the current paper focuses on MHC I-based recognition, the model of the TCR–pMHC–CD4 (32) is a CD4 T cell that interacts with peptides on MHC class II. There are no crystallographic structures reported for a TCR–pMHC–CD8 ternary complex. A hypothetical model of TCR–pMHC–CD8 was assembled based on the available structures of the components, which demonstrated remarkable similarities in the overall topology with the TCR–pMHC–CD4 complex (35). The TCR–pMHC–CD4 or TCR–pMHC–CD8 tri-molecular complex, which is a key unit for the immune synapse, provides the minimum complexity needed to trigger transient calcium signaling. The simulation of the TCR–pMHC–CD4 model (32) therefore provided a basis for understanding how the CD4 and CD8 act as co-receptors during the process of T lymphocyte recognition. The immune synapse involves the formation of a highly organized pattern of proteins in the intercellular junction, of which the pattern is spontaneous evolving. This is another aspect in the multiscale process, resulting from self-assembly processes and active feedback mechanisms. Coarse-grained descriptions, such as a mathematical representation using reaction–diffusion equations (36), can be used to model the synapse formation.

Molecular dynamics methods have been developed for the improvement of configurational sampling, of which replica-exchange (37) and biased potential (38) methods are among the more promising. Our recent work shows that ensemble-based methods are capable of producing rapid, accurate, precise, and reliable binding free energies (33, 34, 39, 40). In these studies, we have used these approaches, termed “enhanced sampling of molecular dynamics with approximation of continuum solvent” (ESMACS) (40) and “thermodynamic integration with enhanced sampling” (TIES) (39). Even for peptide–MHC molecular systems where peptides are much larger, more flexible, and diverse than most small molecules used in drug discovery, ESMACS produces precise and reproducible free energy estimates, which correlate well with experimental data (40). Using standard protocols as established in our publications (33, 34, 39, 40), reproducible results can be generated with MD for molecular systems as complicated as the multi-protein complexes implicated in the immune response.

Recent models of MHCI presentation have predicted a beneficial role for conformational flexibility in shaping the dynamics of peptide loading (29). This work demonstrated that pathway models explicitly describing an encounter complex during peptide–MHC loading were most predictive of experimental observations. In the same study, MD analysis showed evidence of multiple conformations in some but not all MHC alleles. The hierarchy of conformational flexibility observed by MD was the same as the ordering of rate constants in the pathway model, demonstrating consistency in the two modeling approaches, despite the analyses being aimed at timescales differing by many orders of magnitude. Moreover, there is scope to use MD to generate estimates for key missing parameters, most notably peptide–MHCI off-rates, as experimental measurements are only available for a very small subset of the peptidome, to complement or extend immunoinformatics methods.

Agent-Based Models Can Integrate Intracellular and Intercellular Interactions

For a long time now, there have been attempts to model and simulate the interactions of the multiple cell types that contribute to immune responses (41). However, only more recently have truly multiscale models emerged, where both the intracellular biochemistry and cell–cell interactions can be analyzed simultaneously (42). This is due, in part, to advances in computer hardware. However, simulation of such models remains cumbersome, as each cell requires a set of sizeable differential equations to be numerically integrated, leading to a very large number of such equations overall. Accordingly, parameter inference of agent-based models is normally impractical. Instead, the intracellular biochemistry can be modeled in isolation first, and calibrated against data from isogenic cultures. Furthermore, such isolation would enable the intracellular models to be simplified, making their embedding in agent-based simulations less computationally demanding.

Applied to HIV, agent-based modeling could be instrumental in understanding the contributions of direct- and cross-presentation to T-cells, which has been the subject of much debate (43). Many of the components required to build such a model already exist, but would need to be adapted and calibrated to experimental data. In Section “A Motivating Example: HIV Infection and Long-term Control,” we described how direct-presentation in HIV-infected cells can be modeled at the cellular level. Adapting the model of MHCI presentation to dendritic cells could be achieved by redefining the peptide supply terms (g_i) to reflect internalization and processing of extracellular antigen. How the new values of g_i are to be specified would require further work, but relevant data are already available [e.g., Ref. (44)]. Finally, interactions between dendritic cells and T-cells have already been modeled in multicellular simulations (45), offering a starting point for creating an integrated model of direct- and cross-presentation.

Concluding Remarks

As we have discussed elsewhere, biology and medicine are dominated by the primacy of experimental observations, where theory is essentially a form of rationalization invoked to explain observations post hoc (6). Scientific progress, based in part on the increasing acquisition of all forms of data, and the pressing need to make sense of it, has now reached a stage wherein predictive, mechanistic, and quantitative modeling methods are emerging and could transform the future of these disciplines. The accessibility and accuracy of the theoretical predictions, for example, in clinically relevant HIV drug ranking (46, 47) and in pharmaceutical compound evaluation (33, 34), support our perspective about predictive computational modeling in pharmaceutical drug discovery and personalized medicine. In order that these methods realize their full potential, especially for personalized medicine, it is imperative that biologists design their experiments to facilitate the construction and exploitation of quantitative models (48). Immunology, with its intrinsically multiscale nature, is a field which stands to benefit greatly from this new approach.

Author Contributions

All authors designed the research and contributed in the writing of the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past coauthorship with one of the authors, ND, and states that the process nevertheless met the standards of a fair and objective review.

Acknowledgments

We acknowledge the Leibniz Supercomputing Centre for providing access to SuperMUC and the very able assistance of its scientific support staff. We made use of ARCHER, the UK’s national High Performance Computing Service, funded by the Office of Science and Technology through EPSRC’s High-End Computing Programme. Access to ARCHER was provided through the 2020 Science programme. We acknowledge use of Hartree Centre computer BlueWonder2 in this work and assistance from its scientific support staff. The STFC Hartree Centre is a research collaboratory in association with IBM providing High Performance Computing platforms funded by the UK’s investment in e-Infrastructure. This work was also supported by the PLGrid Infrastructure through which access to Prometheus, located at ACK Cyfronet AGH in Krakow, was provided.

Funding

RE was funded by CoMPLEX, UCL’s Centre for Mathematics and Physics in the Life Sciences and Experimental Biology, with support from EPSRC, BBSRC, MRC, and the British Heart Foundation. Our work was supported by EPSRC via the 2020 Science programme (EP/I017909/1), the Qatar National Research Fund (7-1083-1-191), the MRC Medical Bioinformatics project (MR/L016311/1), the EU H2020 CompBioMed (675451) and ComPat (671564) projects, and funding from the UCL Provost.

References

1. Yewdell JW, Reits E, Neefjes J. Making sense of mass destruction: quantitating MHC class I antigen presentation. Nat Rev Immunol (2003) 3:952–61. doi:10.1038/nri1250

CrossRef Full Text | Google Scholar

2. Lever M, Lim HS, Kruger P, Nguyen J, Trendel N, Abu-Shah E, et al. Architecture of a minimal signaling pathway explains the T-cell response to a 1 million-fold variation in antigen affinity and dose. Proc Natl Acad Sci U S A (2016) 113:E6630–8. doi:10.1073/pnas.1608820113

CrossRef Full Text | Google Scholar

3. Tenzer S, Wee E, Burgevin A, Stewart-Jones G, Friis L, Lamberth K, et al. Antigen processing influences HIV-specific cytotoxic T lymphocyte immunodominance. Nat Immunol (2009) 10:636–46. doi:10.1038/ni.1728

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Croft NP, Smith SA, Wong YC, Tan CT, Dudek NL, Flesch IEA, et al. Kinetics of antigen expression and epitope presentation during virus infection. PLoS Pathog (2013) 9:e1003129. doi:10.1371/journal.ppat.1003129

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Tenzer S, Peters B, Bulik S, Schoor O, Lemmel C, Schatz MM, et al. Modeling the MHC class I pathway by combining predictions of proteasomal cleavage, TAP transport and MHC class I binding. Cell Mol Life Sci (2005) 62:1025–37. doi:10.1007/s00018-005-4528-2

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Coveney PV, Dougherty ER, Highfield RR. Big data need big theory too. Philos Transact A Math Phys Eng Sci (2016) 374:20160153. doi:10.1098/rsta.2016.0153

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Poropatich K, Sullivan DJ Jr. Human immunodeficiency virus type 1 long-term non-progressors: the viral, genetic and immunological basis for disease non-progression. J Gen Virol (2011) 92:247–68. doi:10.1099/vir.0.027102-0

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Goulder PJ, Watkins DI. Impact of MHC class I diversity on immune control of immunodeficiency virus replication. Nat Rev Immunol (2008) 8:619–30. doi:10.1038/nri2357

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Streeck H, Lichterfeld M, Alter G, Meier A, Teigen N, Yassine-Diab B, et al. Recognition of a defined region within p24 gag by CD8+ T cells during primary human immunodeficiency virus type 1 infection in individuals expressing protective HLA class I alleles. J Virol (2007) 81:7725–31. doi:10.1128/JVI.00708-07

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Troyer RM, McNevin J, Liu Y, Zhang SC, Krizan RW, Abraha A, et al. Variable fitness impact of HIV-1 escape mutations to cytotoxic T lymphocyte (CTL) response. PLoS Pathog (2009) 5:e1000365. doi:10.1371/journal.ppat.1000365

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Goulder PJ, Bunce M, Krausa P, McIntyre K, Crowley S, Morgan B, et al. Novel, cross-restricted, conserved, and immunodominant cytotoxic T lymphocyte epitopes in slow progressors in HIV type 1 infection. AIDS Res Hum Retroviruses (1996) 12:1691–8. doi:10.1089/aid.1996.12.1691

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Reddy B, Yin J. Quantitative intracellular kinetics of HIV type 1. AIDS Res Hum Retroviruses (1999) 15:273–83. doi:10.1089/088922299311457

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kim H, Yin J. Effects of RNA splicing and post-transcriptional regulation on HIV-1 growth: a quantitative and integrated perspective. Syst Biol (Stevenage) (2005) 152:138–52. doi:10.1049/ip-syb:20050004

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang Y, Lai LH. Modeling the intracellular dynamics for Vif-APO mediated HIV-1 virus infection. Chin Sci Bull (2010) 55:2329–40. doi:10.1007/s11434-010-3103-x

CrossRef Full Text | Google Scholar

15. Dalchau N, Phillips A, Goldstein LD, Howarth M, Cardelli L, Emmott S, et al. A peptide filtering relation quantifies MHC class I peptide optimization. PLoS Comput Biol (2011) 7:e1002144. doi:10.1371/journal.pcbi.1002144

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Garstka MA, Fish A, Celie PH, Joosten RP, Janssen GM, Berlin I, et al. The first step of peptide selection in antigen presentation by MHC class I molecules. Proc Natl Acad Sci U S A (2015) 112:1505–10. doi:10.1073/pnas.1416543112

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Calis JJA, Maybeno M, Greenbaum JA, Weiskopf D, De Silva AD, Sette A, et al. Properties of MHC class i presented peptides that enhance immunogenicity. PLoS Comput Biol (2013) 9:e1003266. doi:10.1371/journal.pcbi.1003266

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Smock RG, Gierasch LM. Sending signals dynamically. Science (2009) 324:198–203. doi:10.1126/science.1169377

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat Struct Biol (2002) 9:646–52. doi:10.1038/nsb0902-646

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Stein M, Gabdoulline RR, Wade RC. Bridging from molecular simulation to biochemical networks. Curr Opin Struct Biol (2007) 17:166–72. doi:10.1016/j.sbi.2007.03.014

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Parker KC, Bednarek MA, Coligan JE. Scheme for ranking potential HLA-A2 binding peptides based on independent binding of individual peptide side-chains. J Immunol (1994) 152:163–75.

PubMed Abstract | Google Scholar

22. Rammensee H, Bachmann J, Emmerich NP, Bachor OA, Stevanovic S. SYFPEITHI: database for MHC ligands and peptide motifs. Immunogenetics (1999) 50:213–9. doi:10.1007/s002510050595

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Flower DR, Phadwal K, Macdonald IK, Coveney PV, Davies MN, Wan S. T-cell epitope prediction and immune complex simulation using molecular dynamics: state of the art and persisting challenges. Immunome Res (2010) 6:S4. doi:10.1186/1745-7580-6-s2-s4

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kass I, Buckle AM, Borg NA. Understanding the structural dynamics of TCR-pMHC complex interactions. Trends Immunol (2014) 35:604–12. doi:10.1016/j.it.2014.10.005

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Knapp B, Demharter S, Esmaielbeiki R, Deane CM. Current status and future challenges in T-cell receptor/peptide/MHC molecular dynamics simulations. Brief Bioinform (2015) 16:1035–44. doi:10.1093/bib/bbv005

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Thiel W, Hummer G. Nobel 2013 chemistry: methods for computational chemistry. Nature (2013) 504:96–7. doi:10.1038/504096a

CrossRef Full Text | Google Scholar

27. McCammon JA, Gelin BR, Karplus M. Dynamics of folded proteins. Nature (1977) 267:585–90. doi:10.1038/267585a0

CrossRef Full Text | Google Scholar

28. Wan S, Coveney P, Flower DR. Large-scale molecular dynamics simulations of HLA-A*0201 complexed with a tumor-specific antigenic peptide: can the alpha3 and beta2m domains be neglected? J Comput Chem (2004) 25:1803–13. doi:10.1002/jcc.20100

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Bailey A, Dalchau N, Carter R, Emmott S, Phillips A, Werner JM, et al. Selector function of MHC I molecules is determined by protein plasticity. Sci Rep (2015) 5:14928. doi:10.1038/srep14928

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Wan S, Coveney PV, Flower DR. Peptide recognition by the T cell receptor: comparison of binding free energies from thermodynamic integration, Poisson-Boltzmann and linear interaction energy approximations. Philos Trans A Math Phys Eng Sci (2005) 363:2037–53. doi:10.1098/rsta.2005.1627

CrossRef Full Text | Google Scholar

31. Wan S, Coveney PV, Flower DR. Molecular basis of peptide recognition by the TCR: affinity differences calculated using large scale computing. J Immunol (2005) 175:1715–23. doi:10.4049/jimmunol.175.3.1715

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Wan S, Flower DR, Coveney PV. Toward an atomistic understanding of the immune synapse: large-scale molecular dynamics simulation of a membrane-embedded TCR-pMHC-CD4 complex. Mol Immunol (2008) 45:1221–30. doi:10.1016/j.molimm.2007.09.022

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Wan S, Bhati AP, Skerratt S, Omoto K, Shanmugasundaram V, Bagal SK, et al. Evaluation and characterization of Trk kinase inhibitors for the treatment of pain: reliable binding affinity predictions from theory and computation. J Chem Inf Model (2017) 57:897–909. doi:10.1021/acs.jcim.6b00780

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Wan S, Bhati AP, Zasada SJ, Wall I, Green D, Bamborough P, et al. Rapid and reliable binding affinity prediction of bromodomain inhibitors: a computational study. J Chem Theory Comput (2017) 13:784–95. doi:10.1021/acs.jctc.6b00794

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Li YL, Yin YY, Mariuzza RA. Structural and biophysical insights into the role of CD4 and CD8 in T cell activation. Front Immunol (2013) 4:206. doi:10.3389/fimmu.2013.00206

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Qi SY, Groves JT, Chakraborty AK. Synaptic pattern formation during cellular recognition. Proc Natl Acad Sci U S A (2001) 98:6548–53. doi:10.1073/pnas.111536798

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem Phys Lett (1999) 314:141–51. doi:10.1016/S0009-2614(99)01123-9

CrossRef Full Text | Google Scholar

38. Hamelberg D, Mongan J, McCammon JA. Accelerated molecular dynamics: a promising and efficient simulation method for biomolecules. J Chem Phys (2004) 120:11919–29. doi:10.1063/1.1755656

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Bhati AP, Wan S, Wright DW, Coveney PV. Rapid, accurate, precise, and reliable relative free energy prediction using ensemble based thermodynamic integration. J Chem Theory Comput (2017) 13:210–22. doi:10.1021/acs.jctc.6b00979

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wan S, Knapp B, Wright DW, Deane CM, Coveney PV. Rapid, precise, and reproducible prediction of peptide-MHC binding affinities from molecular dynamics that correlate well with experiment. J Chem Theory Comput (2015) 11:3346–56. doi:10.1021/acs.jctc.5b00179

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Celada F, Seiden PE. A computer-model of cellular interactions in the immune-system. Immunol Today (1992) 13:56–62. doi:10.1016/0167-5699(92)90135-T

CrossRef Full Text | Google Scholar

42. Prokopiou S, Barbarroux L, Bernard S, Mafille J, Leverrier Y, Arpin C, et al. Multiscale modeling of the early CD8 T-cell immune response in lymph nodes: an integrative study. Computation (2014) 2:159. doi:10.3390/computation2040159

CrossRef Full Text | Google Scholar

43. Gutierrez-Martinez E, Planes R, Anselmi G, Reynolds M, Menezes S, Adiko AC, et al. Cross-presentation of cell-associated antigens by MHC class I in dendritic cell subsets. Front Immunol (2015) 6:363. doi:10.3389/fimmu.2015.00363

CrossRef Full Text | Google Scholar

44. Dinter J, Duong E, Lai NY, Berberich MJ, Kourjian G, Bracho-Sanchez E, et al. Variable processing and cross-presentation of HIV by dendritic cells and macrophages shapes CTL immunodominance and immune escape. PLoS Pathog (2015) 11:e1004725. doi:10.1371/journal.ppat.1004725

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Celli S, Day M, Muller AJ, Molina-Paris C, Lythe G, Bousso P. How many dendritic cells are required to initiate a T-cell response? Blood (2012) 120:3945–8. doi:10.1182/blood-2012-01-408260

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Wright DW, Hall BA, Kenway OA, Jha S, Coveney PV. Computing clinically relevant binding free energies of HIV-1 protease inhibitors. J Chem Theory Comput (2014) 10:1228–41. doi:10.1021/ct4007037

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Wright DW, Wan S, Shublaq N, Zasada SJ, Coveney PV. From base pair to bedside: molecular simulation and the translation of genomics to personalized medicine. Wiley Interdiscip Rev Syst Biol Med (2012) 4:585–98. doi:10.1002/wsbm.1186

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Tegnér J, Zenil H, Kiani NA, Ball G, Gomez-Cabrero D. A perspective on bridging scales and design of models using low-dimensional manifolds and data-driven model inference. Philos Transact A Math Phys Eng Sci (2016) 374:20160144. doi:10.1098/rsta.2016.0144

PubMed Abstract | CrossRef Full Text | Google Scholar