- 1School of Business, Social and Decision Sciences, Constructor University, Bremen, Germany
- 2Accenture GmbH, Kronberg, Germany
- 3Laboratoire de Physique Théorique de la Matière Condensée (LPTMC), Centre National de la Recherche Scientifique, (CNRS), Sorbonne Université, Paris, France
- 4School of Science, Constructor University, Bremen, Germany
Introduction: Production systems are bound to operate in stochastic conditions. Prominent sources of performance-reducing uncertainty are constituted by machine failures, decision errors, and fluctuating supplies. This article offers a novel approach to uncertainty through modelling and simulation of nonlinear production systems. In particular, the authors consider production systems where the output is drastically reduced when a resource of fluctuating input values reaches an upper threshold.
Methods: The article introduces minimal models of such hreshold-impeded stochastic production (TISP) systems and the system performance (i.e., the output) is analyzed as a function of system parameters (e.g., the type of nonlinearity) and noise input features (e.g., the distribution width or time correlations). Applications to steel manufacturing via continuous casting and power generation through wind turbines are discussed in detail.
Results and Discussion: The simulation experiments illustrate that especially the extent of the input fluctuations affects the output performance which is why the authors recommend that TISP system operators counterbalance such fluctuations if possible.
1 Introduction
1.1 Context
Uncertainty and stochasticity compromise real-life production systems in many ways. For instance, customer demand, customer order changes, operator absences (Merten et al., 2022a), machine breakdowns, or supply delays are very difficult to predict, and, thus, they pose a difficult challenge for the managers and operators of such production systems (Koh et al., 2002). Failure to cope with uncertainty might result in reduced customer order punctuality (Koh and Saad, 2002), quality issues, increased production costs, and diminished performance in general. Additionally, production systems often entail nonlinear transformations or correlations. One nonlinear transformation of this sort (Pervozvanskii, 1965) is portrayed by a system that has a precisely defined upper threshold on the input, above which production is forced to stop and stays idle for a fixed amount of time. The disruptive interplay of a threshold and uncertain inputs described here is also of relevance in the context of predictable production (Cho and Erkoc, 2009).
While the threshold value is usually beyond the system operator’s control, the average production level (i.e., the input) can frequently be selected at will. Therefore, such systems display a fundamental optimization problem that covers the interface of production planning and control as well process design: How to choose the average input level of threshold-impeded stochastic production (TISP) systems–given the input fluctuation type, the threshold value or the duration of the idle time–so that the system’s output is maximized? Figure 1 offers an intuitive graphical representation of this question: By altering the mean of the input stochastic distribution (e.g.,
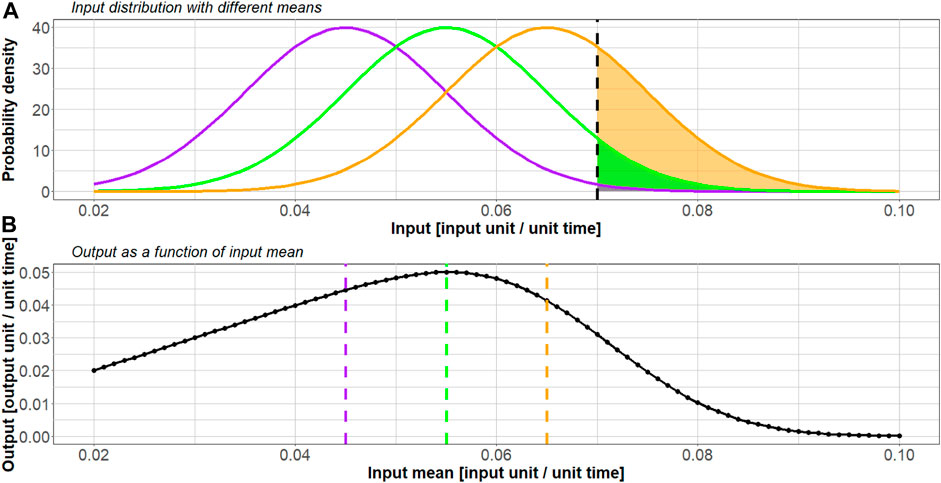
Figure 1. (A) Gaussian input distributions for three different means (0.045, 0.055, and 0.065 input units per unit time, respectively) and a cut-off threshold of 0.070 input units per unit time; (B) output as a function of the input mean (i.e., average production level) given a Gaussian input distribution with a standard deviation of 0.01 input units per unit time.
1.2 Research goals
The goals of this investigation are: 1) The authors introduce the basic notion of threshold-impeded stochastic production systems. 2) The authors show that these systems display a non-monotonous relationship between the production output and the average input level (representing the resource load at which the production system is run). This relationship is a universal feature of such TISP systems. 3) The authors offer a method to assess the output sensitivity of TISP systems in response to varying system and input parameters. 4) The authors illustrate applicability of this theoretical concept to real-life systems through two application scenarios which both fall into the category of TISP systems.
1.3 Application scenarios
TISP systems can be found in diverse industrial contexts such as the continuous casting of steel and the generation of electric power through wind turbines. For example, if a continuous caster operates so fast that the mass flow of manufactured steel outruns the supply of liquid steel, the entire casting procedure needs to be interrupted for maintenance (Merten et al., 2022b). Analogously, wind turbines have to be switched off during stormy weather, or else they will possibly suffer structural damages (Klimstra and Hotakainen, 2011). The idea behind choosing two vastly different application scenarios is to emphasise the wide-ranging applicability of TISP concepts.
1.4 Approach
The authors intend to approach the TISP-inherent optimization problem by abstracting real-life nonlinear systems into minimal models (Batterman and Rice, 2014), capturing the “stylized facts” of the production mechanisms and then revealing, via careful numerical analysis, the influencing factors that allow an accurate control of the system. The study of nonlinear dynamics has a long tradition of contributing to a better understanding of phenomena in industrial production, assembly and supply systems (Chankov et al., 2016; Alkan et al., 2018; Chankov et al., 2018; Lin and Naim, 2019).
The stylized representation of TISP systems allows one to define TISP subtypes, which lead to various input-output relationships and sensitivities with respect to noise types. To this end, the authors consider the output of TISP systems that exhibit typical nonlinear transformations, as sketched in Figure 2. Depending on the application scenario, three TISP subtypes are distinguished (i) standard TISP: The nonlinearity of the system (i.e., the threshold): brings excess input values down to zero (see Figure 2B); (ii) penalized TISP: The nonlinearity brings excess input values to a value below zero (see Figure 2C); (iii) lagged recovery TISP: After excess input values are reduced, the system is unable to produce further output for a certain number of time steps (see Figure 2D).
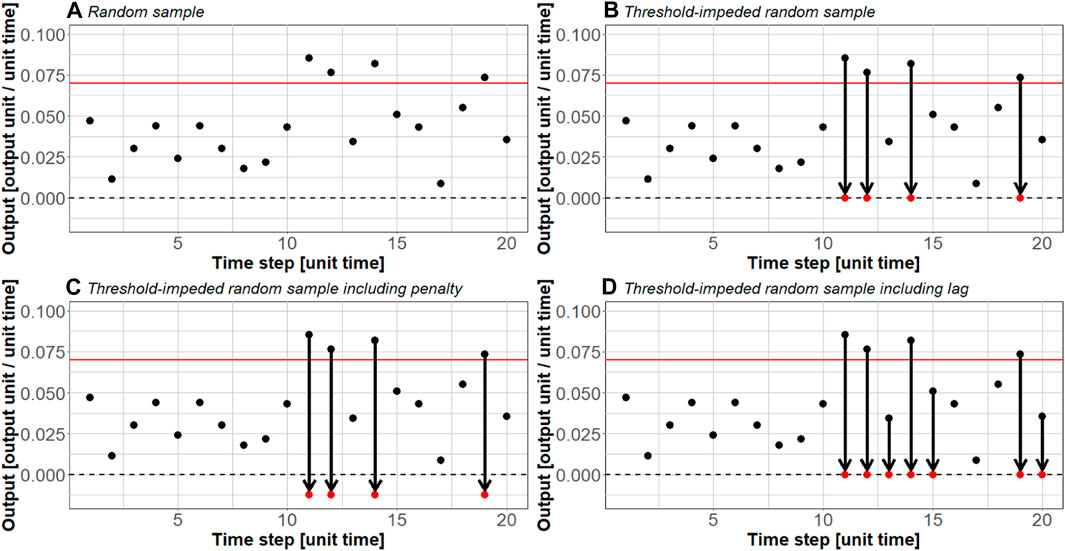
Figure 2. Examples of generic TISP subtypes; (A) 20 time steps of uniformly distributed random input values; the input values are processed by a threshold device acting as a nonlinear transformation (i.e., (B) standard TISP, (C) penalized TISP, or (D) lagged recovery TISP).
In order to provide a quantitative relationship between the generic TISP systems (i.e., standard, penalized, or lagged recovery) and the application scenarios outlined above, the authors estimate the systems’ output (i.e., steel mass flow and electric power) by simulating and transforming random input values from several probability models (e.g., uniform or Weibull noise) as well as computing expected values numerically. Since these expected values originate in output integrals of the minimal models, it is shown how the models compare against the simulated outputs. Then, varying the average input level enables one to determine the maximally achievable output and its corresponding parameter values. This procedure is repeated numerous times subject to changing statistical features of the noisy input (e.g., distribution width) and other experimental parameters (e.g., penalty and lag size) which reveals how sensitive the system output is to such adjustments. For the continuous casting application, the authors also examined time-correlated input from an Ornstein-Uhlenbeck process that experiences a lagged recovery nonlinearity (see Figure 2D). Contrasting the mean-reversing behavior of an Ornstein-Uhlenbeck process with uncorrelated Gaussian input will demonstrate the impact of noise correlations on the production performance.
1.5 Novelty
To the authors’ best knowledge, the category of TISP systems has not been described before. Understanding such high-level categories can be helpful for production planning and control, where the resource load either can be selected or the system can be set up to perform optimally at typical input levels, and for a more detailed modeling of specific systems. For such modeling efforts, the authors argue that in any TISP system, non-monotonous input-output relationships will be encountered independent of the intricacies of the mathematical or computational model.
1.6 Outline
The remainder of this article is organized in the following way: First, the authors present selected works revolving around uncertainty in production systems and they point out in what sense this study fits into the research landscape (Section 2). Section 3 (“Application scenarios”) explains the production mechanisms and input distributions behind the two scenarios, i.e., steel continuous casting and wind power generation. Once the underlying production mechanism has been understood, the authors establish the expected value integrals that describe the output of the various TISP system subtypes (see Section 4 “Minimal models”). In Section 5, the Ornstein-Uhlenbeck process for time-correlated input values is introduced which becomes useful in the case of the lagged recorvery TISP system (see Figure 2D). Section 6 (“Methods”) discloses the simulation framework and it reveals how the minimal models as well as the respective system or input parameters are deployed to assess the output sensitivity of TISP systems. Throughout Section 7, the numeric and simulation results are presented and discussed before, finally, in Section 8 the authors conclude the findings and give an outlook on promising future research directions.
2 Related work
2.1 Control and flexibility
In response to uncertainty, Correa (1992) offers two remedies, namely, control and flexibility. “Control” includes all efforts that aim at proactively reducing uncertainty before it arises, whereas “flexibility” stands for reactively coping with uncertainty after it has arisen. Angkiriwang et al. (2014) compare the usage of reactive uncertainty strategies such as buffering and proactive uncertainty strategies such as redesigning. However, buffering will not have the desired effect if the interplay between uncertain production inputs and TISP thresholds complicates the determination of appropriate buffer strategies. Similarly, redesigning the production process will not reduce uncertainty if the production process cannot be redesigned further due to technology and cost restrictions or saturation effects.
Sreedevi & Saranga, (2017) state that flexibility helps “in reducing […] supply and manufacturing process risks” but the “effect is context-dependent.” As a solution to this, the authors offer a generalized description of uncertainty in threshold-impeded production systems that can be adapted to different contexts (the only condition being that the production mechanism itself is understood and can be modelled mathematically). Regardless of whether common control or flexibility strategies are applicable, this description deepens the understanding of production outputs and their sensitivity to uncertain inputs.
2.2 Rescheduling
Production uncertainty can be combatted reactively through rescheduling (Vieira et al., 2003; Psarommatis et al., 2021). Rescheduling has a long history in the steel industry; especially multi-agent systems were often used for this purpose (Cowling et al., 2003; Cowling et al., 2004; Ouelhadj et al., 2004). More recently, evolutionary algorithms (Guo and Tang, 2019; Merten et al., 2024) and machine learning (Iglesias-Escudero et al., 2019; Li et al., 2020) have become the preferred solutions. However, all of these solutions are extremely context-dependent and they are invalid with respect to other application scenarios such as wind turbines. As stated above, this is something the authors try to avoid with the TISP approach.
2.3 Buffering and diversification
In the context of wind turbines, a common “buffering” strategy comprises changing the orientation of the wind turbine rotor blades with respect to the direction from which the wind is blowing. So, one can either harness more energy by aligning the rotor blades with the wind or protect the wind turbine from strong winds by turning the rotor blades away from the wind input direction (Castellani et al., 2015; Yan, 2015). Nevertheless, this is only feasible for rather small variations in the wind speed and, again, this strategy is highly context-dependent.
On top of that, to reduce the power output variability of wind farms, diversification methods could be applied. For instance, spatially distributing wind turbines over a given area (Cassola et al., 2008) or combining different types of wind turbines (e.g., smaller turbines for weaker winds and larger turbines for stronger winds) helps to reduce variability. One a higher level, it is even feasible to interconnect entire wind farms (Archer and Jacobson, 2007; Katzenstein et al., 2010). While these diversification methods are to some extent adaptable to other application scenarios such as steel continuous casting, they primarily aim at only reducing the output variability but not at maximizing the overall output. Nevertheless, output maximization is “usually one of the most important objectives for any [wind farm] designer” because it is closely linked to the revenue of a wind farm company (Feng and Shen, 2017). On the contrary, maximizing the overall output is the central purpose of the TISP approach as explained in the introduction of this article.
In steel continuous casting, the tundish (which is a reservoir of molten steel; see Section 3) may serve as a buffer containment. Therefore, it can be used to slightly slow down or ramp up the production process. Yet, the tundish’s ability to combat uncertainty is limited because changing the flow pattern of the molten steel has profound effects on the steel quality (Zhong et al., 2007). Besides, one has to consider a multitude of constraints when adjusting the casting speed or else the resulting steel strand might be torn apart or it might not be sufficiently solidified before leaving the production machine (Merten et al., 2022b). Both these occurrences would cause the production to halt for cost- and time-intensive maintenances.
2.4 Modernization
A proactive way to reduce uncertainty is to modernize the production environment (Gerwin and Tarondeau, 1982; Ettlie, 1990; Groover, 2006; Bertsimas and Thiele, 2014; Dotoli, et al., 2019; Ghobakhloo, 2020). For this purpose, Industry 4.0 technologies such as cyber-physical systems (CPS), internet of things (IoT), artificial intelligence (AI), and cloud computing (Zhong et al., 2017; Xu et al., 2018; Oztemel and Gursev, 2020) are routinely implemented. In particular, AI applications have proven valuable as means to combat production uncertainty (Iglesias-Escudero et al., 2019; Arinez et al., 2020). For example, Roy et al. (2004) describe an inference model that is capable of handling schedule disturbances in steel production. With respect to wind turbine control and optimization, neural networks are frequently utilized (Chatterjee and Dethlefs, 2021). But what is to be done in production environments where access to advanced technologies is limited or the necessary input data does not exist (Lee et al., 2013)? In fact, many steel factories still fall under this category. For these situations, the authors offer a technique that, instead of focusing on individual input events or threshold violations, yields universal recommendations which work very well on average.
2.5 Analytical models and simulation
On a more theoretical level, Peidro et al. (2009) suggested analytical models and simulations (Aouam et al., 2018; Jamalnia et al., 2019; Gupta and Maravelias, 2020; Tordecilla et al., 2021). Simulation tools have been successfully deployed to tackle uncertainty in production systems (Negahban and Smith, 2014; Jeon and Kim, 2016; Zhang et al., 2019) because “due to [their] low cost, quick analysis, low risk and meaningful insight that [they] may provide” (Mourtzis, 2020) simulation tools allow “for the experimentation and validation of […] process and system design” (Mourtzis et al., 2014) and show “unique advantages in solving practical problems” (Zhang et al., 2019). Nevertheless, a few research gaps concerning state-of-the-art simulation tools have been identified: (i) Capable tools only exist for a selective subset of application scenarios (Mourtzis et al., 2014) and (ii) “unified approaches and terminology” are missing (Mourtzis, 2020). As a solution to this, the methodology can be viewed as a simulation toolbox that is adaptable to diverse application scenarios and, regardless of the scenario, always follows the same underlying recipe or approach.
3 Application scenarios
3.1 Steel continuous casting
Over the past 70 years, continuous casting has widely replaced ingot casting as the primary fabrication method for steel slabs (Santos et al., 2003). The working principle of a continuous caster is shown in Figure 3. First, the steel alloy is poured into the tundish from which it passes through a mold. Here, the tundish serves as a funnel and buffer containment that ideally ensures a constant delivery of liquid metal. The design of the mold basically dictates the shape and proportions of the emerging steel slabs, while the amount of steel flowing across the mold can be modified with the help of a nozzle. At the mold exit, the nascent steel slabs are still largely molten, and secondary cooling in the form of water sprays has to be carried out for further shell solidification (Irving, 1993).
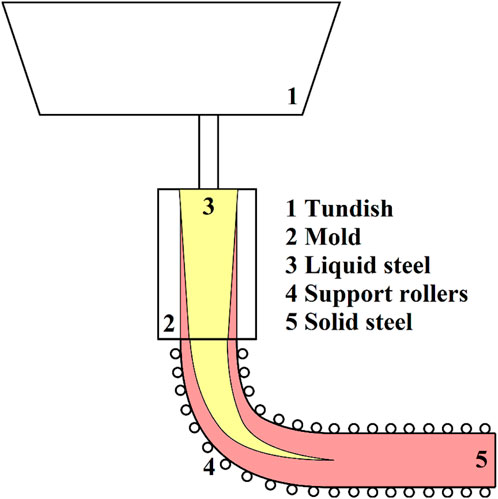
Figure 3. Steel slab production through continuous casting; the liquid (solid) steel is colored yellow (red); abstracted from Louhenkilpi, 2014.
Extensive attempts have been made to increase the operating speed of casters and, therefore, their output. Faced with the ubiquitous compromise between output maximization (Li and Thomas, 2000) and process quality/steadiness, numerous researchers have examined likely limitations of the operating speed (Merten et al., 2022b) which, among others, encompass several customer-dependent slab properties (e.g., slab dimensions). For instance, to ensure sufficient shell solidification the operating speed has to be chosen so that the slabs have enough time to solidify. This solidification time is tightly linked to one of the most important planning parameters in steel production (Özgür et al., 2021), namely, the slab thickness (Thomas, 2002). In practice, it is often not possible to maintain a constant operating speed which would be beneficial for the slab quality (Zhang et al., 2006; Wang and Zhang, 2010; Zhang and Wang, 2010) since subsequently manufactured customer orders typically exhibit divergent thickness values.
Another example shedding light onto the output maximization trade-off is discussed in Merten et al. (2022b). The authors inspected historical production data from an industrial casting machine which revealed an abrupt adjustment of the casting speed strategy and, subsequently, they traced this regime transition back to the existence of a theoretical limit for the maximum achievable steel mass flow. In essence, this maximum achievable steel mass flow is motivated by the fact that the tundish (see Figure 3) must not run out of liquid steel. As soon as the steel mass flow (and, hence, the operating speed) exceeds this maximum limit, the continuous casting process has to be stopped for cost-intensive and time-consuming maintenance during which no output can be generated.
In this application scenario, the system’s input uncertainty originates from complex planning constraints (Merten et al., 2022a) as well as unstable customer demand entailing fluctuations of the casting speed-relevant variables. At the same time, a threshold/nonlinear transformation is imposed by the maximum achievable steel mass flow beyond which the steel slab might be torn apart (Merten et al., 2022b). These systemic features turn the continuous casting of steel into a TISP device.
3.2 Wind turbines
Wind turbines play an important role in today’s renewable energy market (Liu et al., 2013; Wood et al., 2013). By means of rotor blades and an electric generator, they convert wind kinetic energy into electric energy, where the relationship of the wind speed
where
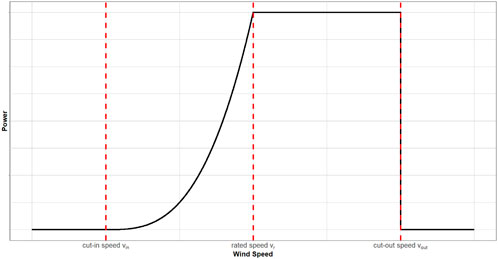
Figure 4. Typical power curve relating the wind speed to the power output of a wind turbine (Salameh and Safari, 1992); it exhibits three thresholds: cut-in, rated and cut-out speeds.
From the principles of fluid flow, Lanchester and Betz have deduced a physical boundary for the maximum energy that can be obtained through wind turbines (Bergey, 1979). More recently, the literature concerning wind energy mainly addressed two distinct research topics—(i) the fitting of stochastic distributions to wind speed data (Morgan et al., 2011) and (ii) the analysis of technical details of wind turbines (Carrillo et al., 2013)—with some articles considering both jointly (Kwon, 2010; Liu et al., 2013). While Morgan et al. (2011) explore the suitability of theoretical wind speed models with regards to offshore wind measurements, Carillo et al. (2013) evaluate a series of generic equations to approximate the conversion of wind to energy via wind turbines. Stevens and Smoulders (1979) observe the energy production as a function of the Weibull distribution shape parameter (whereby the Weibull distribution is the most commonly used distribution to characterize wind speeds). Furthermore, frameworks that enable one to match wind turbines to wind speed distributions/wind sites are provided by Salameh and Safari (1992)/Ritter and Deckert (2017). Here, the authors intend to expand previous methodologies through additional TISP features such as penalties and lagged recoveries.
4 Minimal models
In order to assess the parameter sensitivity of a TISP system on the output performance
Standard TISP system (uncorrelated noisy input; both application scenarios): In the case of standard TISP systems, the predicted average outcome per unit time Y can be computed via the expected value
In the case of steel continuous casting, there is only one upper threshold T, corresponding to the maximum mass flow (i.e., mass per unit time) above which the machine must stop (Merten et al., 2022b). When the system operates below the threshold, the output is equal to the input, therefore
In the case of a wind turbine, the power curve depicted on Figure 4 leads to:
where
Note that in both application scenarios (steel continuous casting and wind power generation), the simulation of the TISP system amounts to computing
Penalized TISP system (uncorrelated noisy input, both application scenarios): In penalized TISP systems, overshooting the upper threshold (T or
Similarly, for the wind power application scenario, a term
Lagged recovery TISP system (uncorrelated noisy input, both application scenarios): The authors also consider the possibility that resetting the TISP system after overshooting the upper threshold takes some time, say,
The authors denote
Note that in this case, the output
Combination of penalized and lagged recovery TISP system (uncorrelated noisy input; both application scenarios): Barring any time-correlated inputs, the lagged recovery TISP system can adopt penalized TISP features through (i) the addition of a term
Lagged recovery TISP system (correlated noisy input; steel continuous casting only): Time-correlated inputs only matter when some integration over multiple time steps occurs in the production process. In lagged recovery TISP systems, the sequence of input values during
The average output for the continuous casting application scenario can then be expressed as
where the contribution
5 Ornstein-Uhlenbeck (OU) process
A standard framework for modeling the noisy input of TISP systems is that of stochastic processes, in particular the Ornstein-Uhlenbeck process for the case of a time-correlated input. The latter is a stochastic process
Ornstein and Uhlenbeck (1930) have proven that the motion of OU-particles is normally distributed; Hence, expressions for the mean and covariance function of an OU-process are easily derived (Maller et al., 2009). An OU-process
Besides, Gillespie (1996) contributes an efficient algorithm for the simulation of the position and velocity of OU-particles. Special interest was shown in the question at what time an OU-particle exceeds a given distance
During the numerical experiments of output performance, the authors use this mean hitting time as the simulation length for the OU-process (see Sections 6 and 7).
Note that such time-correlated input processes only impact the output productivity in the case of a lagged recovery TISP system (see Figure 2; Section 4). Apart from an OU-process, the authors could have chosen any other type of time-correlated input but they wanted to deploy a stochastic process for which the probability density can be written in terms of elementary functions. This will be helpful with regards to the minimal models presented in Section 4.
6 Methods
As stated earlier, the goal is to investigate the output sensitivity of TISP systems to changing process parameters through minimal models (see Section 4) and simulations. The output simulations are achieved by creating input samples with the desired type/extent of randomness and subsequently transforming them through the TISP system. For comparison reasons, the output integrals from Section 4 are numerically integrated and held against these output simulations.
Based on regression methods, the authors then investigate the optimal output’s dependence on tunable process parameters. Here, the distribution width
6.1 Uncorrelated noisy input (both application scenarios)
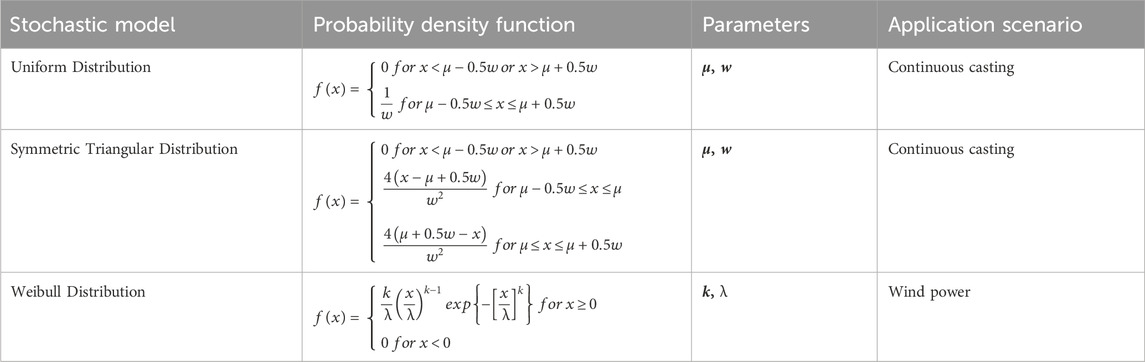
For both application scenarios–the continuous casting of steel and the generation of power via wind turbines–the authors choose the input probability distributions according to the pertaining literature and industrial data. A summary of all distributions is presented in Table 1 and an explanation for their parameters is enclosed in Table 2. Moreover, Table 2 indicates the range of the noise parameter values in the numerical experiments.
As can be seen in Table 1, the authors characterize the mass flow data (Merten et al., 2022b) by uniform and symmetric triangular distributions, while wind speeds are most commonly reproduced by Weibull distributions (Stevens and Smulders, 1979). The mean steel mass flow as well as the scale of the wind speed distribution are varied between
After studying the discrepancy between the numerical integration and the simulations, the authors determine, by means of regression, the position of the performance maximum as a function of the noise parameters
6.2 Time-correlated noisy input (steel continuous casting only)
Next, the effects of input correlations on the output productivity of a lagged recovery TISP system (lag
For the simulation of the OU-process starting at a start value
7 Results and discussion
7.1 Uncorrelated noisy input (both application scenarios)
7.1.1 Steel continuous casting
As can be seen in the quantile-quantile plots shown in Figure A.1 (see Supplementary Material A), the fluctuations of the input mass flow in Merten et al. (2022b) are described by uniform and symmetric triangular distributions to an adequate extent. Figure 5 and A.2 demonstrate the perfect agreement of the minimal model and the simulations for these two distributions. While the size of the penalty or the lag do not seem to affect the position of the maximum output with respect to the distribution mean (see Supplementary Material A: Figure A.2), the distribution width does have a substantial effect. In the selected parameter ranges, the relationship between the value of the distribution mean at which the maximum performance occurs and the distribution width turns out to be linear (see Supplementary Material A: Figure A.3). Once an optimum has been reached, the output curve drops off more sharply for the uniform distribution than for the symmetric triangular distribution. This happens since, for uniformly distributed input samples, a much larger part of the area under the probability density curve is located beyond the threshold compared to the symmetric triangular distribution (given the same distribution mean
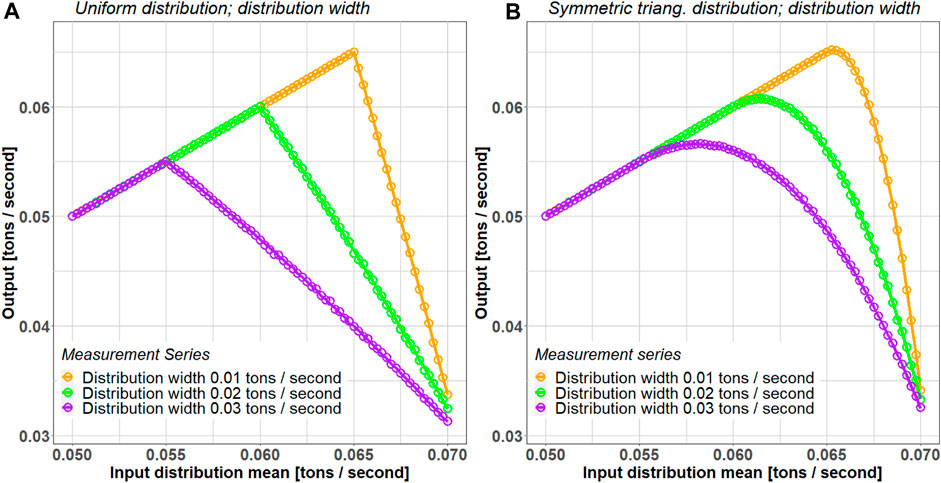
Figure 5. Output mass flow as a function of the mean of the mass flow input distribution for various input distribution widths for the (A) uniform distribution (distribution width
7.1.2 Wind turbines
In Figure 6, the authors describe the wind power production as a function of the Weibull distribution scale
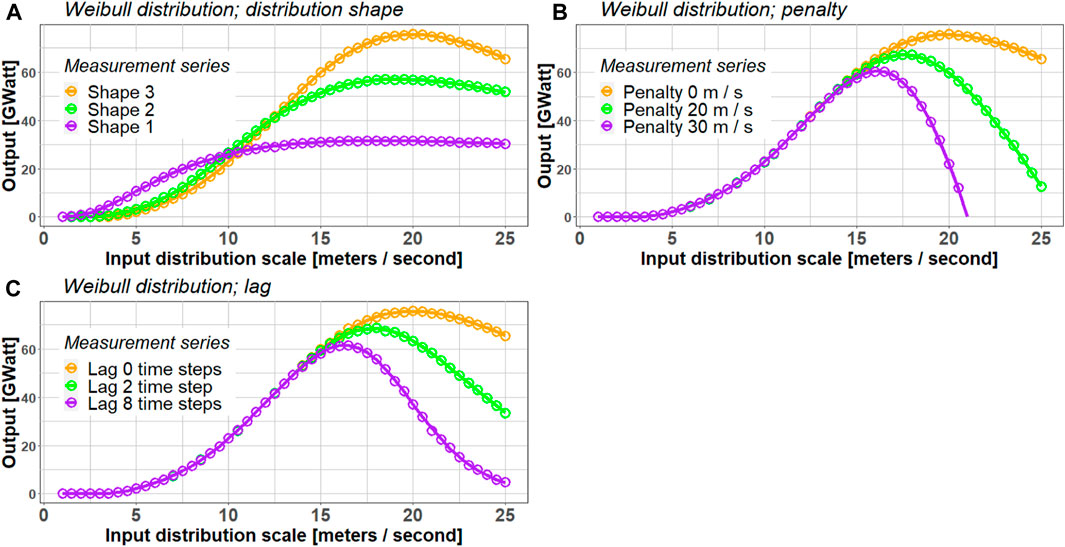
Figure 6. Output wind power as a function of the scale of the wind speed input distribution under changing (A) distribution shape (distribution shape
7.2 Time-correlated noisy input (steel continuous casting only)
Earlier, the authors have established the mean hitting time of an Ornstein-Uhlenbeck process (see Section 5). In Figure 7, the analytical formula from Cerbone et al. (1981) is compared with the average time span that a simulated OU-process needs to surpass a given threshold, by looking at how much the simulation deviates from the analytical hitting time. If the cut-off threshold is chosen to be
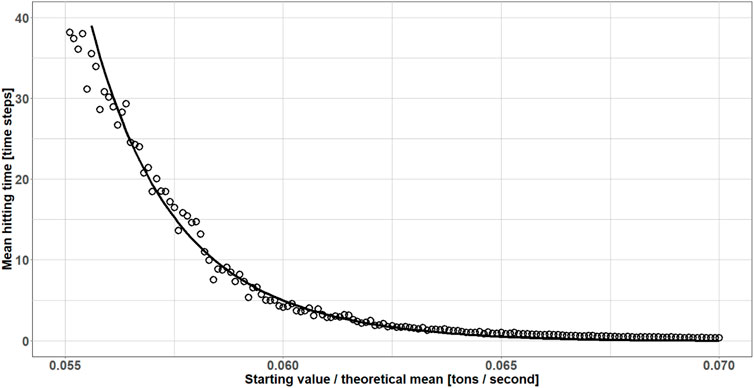
Figure 7. Mean hitting time of an Ornstein-Uhlenbeck process as a function of the starting value
Figure 8 displays the comparison between the minimal models and the output simulations for the lagged recovery TISP model (lag
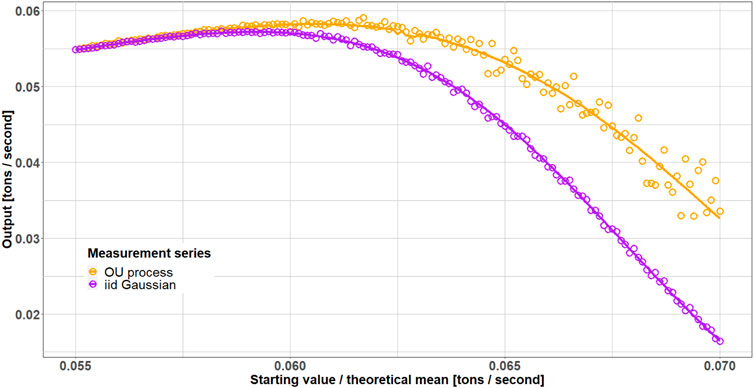
Figure 8. Output mass flow as a function of the starting value
Apart from this, Figure 8 also suggests that a production device powered by OU-noise input could be less susceptible to the disruptive threshold, as the curve associated with the uncorrelated Gaussian noise sinks much quicker. For a starting value/theoretical mean equal to the size of the disruptive threshold, the curves differ by already 50 percent. This is due to the mean-reverting behavior of the OU-process or the system operator that meticulously attempts to counterbalance performance fluctuations. Lastly, the authors monitored what consequences a change in the input distribution standard deviation or stiffness has on the location of the maximum performance. The position of the maximum appears to move logarithmically with the stiffness and inversely proportional with the standard deviation (see Supplementary Material A: Figure A.7). Thus, the larger the stiffness (or the more the input fluctuations are regulated by the system operator), the better the performance.
8 Conclusion
8.1 Summary
In this article, the authors have examined the output characteristics of several threshold-impeded stochastic production (TISP) systems using minimal models and simulations. The output experiments differ in terms of their input fluctuations (e.g., Gaussian or Weibull noise), application scenarios (i.e., steel continuous casting and wind turbines), and nonlinear features of the transformation (e.g., number of thresholds, magnitude of the penalties/lags). The influence of multiple input characteristics (e.g., noise distribution width) on the position of the maximum output performance in the parameter space has been explored. It turns out that for the continuous casting application scenario, neither the size of the penalty nor the duration of the lag have a significant effect on the maximum output, while they are essential for the calculation of the maximum power that can be generated by wind turbines. Ultimately, time-correlated and time-uncorrelated inputs have been compared by applying a simple nonlinear transformation to a mean-reversing Ornstein-Uhlenbeck process and uncorrelated Gaussian noise. The authors showed that a hypothetical production apparatus fuelled by OU-noise input would be superior to an equivalent apparatus fuelled by uncorrelated Gaussian noise (provided with the same system and noise parameters). Hence, a machine operator that constantly tries to dampen the input fluctuations of a TISP-type system improves the output performance.
8.2 Impact and practical relevance
Our work has further highlighted and developed the work of Merten et al. (2022b) as they essentially describe the existence of a TISP system in the continuous casting of steel (see Section 3). Clearly, in the case of a maximum possible steel flow around
8.3 Future outlook
With this work the authors want to draw attention to production situations, where a balance is required between the process stability and the strive for increased production–due to both input stochasticity and the presence of disruptive thresholds. Often such a balance is hidden within the intricacies of the production process (e.g., disruptive thresholds masked as load-dependent errors or sudden declines in product quality when reaching critical load levels in the production system). Identification of such situations requires a dialog between different divisions of a production facility that are responsible for maximizing production (e.g., operations management) or surveying the occurrence of component failures and errors, as well as quality standards (e.g., quality control). The authors believe that the procedure can contribute to this dialog as it is applicable to any production system that a) relies on stochastic inputs and b) is subject to nonlinear transformations involving disruptive thresholds. Accordingly, the authors would like to encourage researchers to test this methodology with regards to a wider range of applications scenarios and extra technical details such as different noise correlations and flavors. One potential scenario for this endeavour is portrayed by a situation where a company wants to sell a product through its website. Obviously, more website visitors should lead to greater sales; however, once a critical number of visitors is reached the website server might crash resulting in extended downtimes. The respective company should adjust its marketing activities to account for this possibility.
In earlier publications (Merten et al., 2022a; Merten et al., 2022b) we have studied the technical details and algorithmic challenges of steel production in some detail. Hence, the description here has a stronger emphasis on this example. With our second example, wind farms, we wish to emphasize that the TISP systems are not just confined to this one application domain. We hope that other researchers are encouraged to think about their production systems from a TISP perspective.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
DM: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. AL: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Validation, Writing–review and editing. YU: Funding acquisition, Project administration, Resources, Supervision, Writing–review and editing. M-TH: Conceptualization, Funding acquisition, Methodology, Project administration, Resources, Supervision, Validation, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
Author DM was employed by Accenture GmbH at the time of submission.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fieng.2024.1353531/full#supplementary-material
References
Alili, L. P., Patie, P., and Pedersen, J. L. (2005). Representations of the first hitting time density of an Ornstein-Uhlenbeck process. Stoch. Models 21 (4), 967–980. doi:10.1080/15326340500294702
Alkan, B., Vera, D. A., Ahmad, M., Ahmad, B., and Harrison, R. (2018). Complexity in manufacturing systems and its measures: a literature review. Eur. J. Industrial Eng. 12 (1), 116–150. doi:10.1504/ejie.2018.089883
Angkiriwang, R., Pujawan, I. N., and Santosa, B. (2014). Managing uncertainty through supply chain flexibility: reactive vs. proactive approaches. Prod. Manuf. Res. 2 (1), 50–70. doi:10.1080/21693277.2014.882804
Aouam, T., Geryl, K., Kumar, K., and Brahimi, N. (2018). Production planning with order acceptance and demand uncertainty. Comput. Operations Res. 91, 145–159. doi:10.1016/j.cor.2017.11.013
Archer, C. L., and Jacobson, M. Z. (2007). Supplying baseload power and reducing transmission requirements by interconnecting wind farms. J. Appl. meteorology Climatol. 46 (11), 1701–1717. doi:10.1175/2007jamc1538.1
Arinez, J. F., Chang, Q., Gao, R. X., Xu, C., and Zhang, J. (2020). Artificial intelligence in advanced manufacturing: current status and future outlook. J. Manuf. Sci. Eng. 142 (11), 110804. doi:10.1115/1.4047855
Batterman, R. W., and Rice, C. C. (2014). Minimal model explanations. Philosophy Sci. 81 (3), 349–376. doi:10.1086/676677
Bendat, J. S., and Piersol, A. G. (2011). Random data: analysis and measurement procedures. New Jersey, United States: John Wiley and Sons.
Bergey, K. H. (1979). The Lanchester-Betz limit (energy conversion efficiency factor for windmills). J. Energy 3 (6), 382–384. doi:10.2514/3.48013
Bertsimas, D., and Thiele, A. (2014). “Robust and data-driven optimization: modern decision making under uncertainty,” in Models, methods, and applications for innovative decision making. Editor P. Grey (Catonsville, MD, United States: INFORMS), 95–122.
Carrillo, C., Obando Montaño, A., Cidrás, J., and Díaz-Dorado, E. (2013). Review of power curve modelling for wind turbines. Renew. Sustain. Energy Rev. 21, 572–581. doi:10.1016/j.rser.2013.01.012
Cassola, F., Burlando, M., Antonelli, M., and Ratto, C. F. (2008). Optimization of the regional spatial distribution of wind power plants to minimize the variability of wind energy input into power supply systems. J. Appl. Meteorology Climatol. 47 (12), 3099–3116. doi:10.1175/2008jamc1886.1
Castellani, F., Astolfi, D., Garinei, A., Proietti, S., Sdringola, P., Terzi, L., et al. (2015). How wind turbines alignment to wind direction affects efficiency? A case study through SCADA data mining. Energy Procedia 75, 697–703. doi:10.1016/j.egypro.2015.07.495
Cerbone, G., Ricciardi, L. M., and Sacerdote, L. (1981). Mean variance and skewness of the first passage time for the Ornstein-Uhlenbeck process. Cybern. Syst. 12 (4), 395–429. doi:10.1080/01969728108927683
Chankov, S., Hütt, M. T., and Bendul, J. (2016). Synchronization in manufacturing systems: quantification and relation to logistics performance. Int. J. Prod. Res. 54 (20), 6033–6051. doi:10.1080/00207543.2016.1165876
Chankov, S., Hütt, M. T., and Bendul, J. (2018). Influencing factors of synchronization in manufacturing systems. Int. J. Prod. Res. 56 (14), 4781–4801. doi:10.1080/00207543.2017.1400707
Chatterjee, J., and Dethlefs, N. (2021). Scientometric review of artificial intelligence for operations and maintenance of wind turbines: the past, present and future. Renew. Sustain. Energy Rev. 144, 111051. doi:10.1016/j.rser.2021.111051
Cho, S., and Erkoc, M. (2009). Design of predictable production scheduling model using control theoretic approach. Int. J. Prod. Res. 47 (11), 2975–2993. doi:10.1080/00207540701749281
Correa, H. L. (1992). The links between uncertainty, variability of outputs and flexibility in manufacturing systems. Coventry, England: University of Warwick. Doctoral dissertation.
Cowling, P. I., Ouelhadj, D., and Petrovic, S. (2003). A multi-agent architecture for dynamic scheduling of steel hot rolling. J. intelligent Manuf. 14, 457–470. doi:10.1023/a:1025701325275
Cowling, P. I., Ouelhadj, D., and Petrovic, S. (2004). Dynamic scheduling of steel casting and milling using multi-agents. Prod. Plan. Control 15 (2), 178–188. doi:10.1080/09537280410001662466
Dotoli, M., Fay, A. M., Miśkowicz, M., and Seatzu, C. (2019). An overview of current technologies and emerging trends in factory automation. Int. J. Prod. Res. 57, 5047–5067. doi:10.1080/00207543.2018.1510558
Ettlie, J. E. (1990). What makes a manufacturing firm innovative? Acad. Manag. Perspect. 4 (4), 7–20. doi:10.5465/ame.1990.4277195
Feng, J., and Shen, W. Z. (2017). Wind farm power production in the changing wind: robustness quantification and layout optimization. Energy Convers. Manag. 148, 905–914. doi:10.1016/j.enconman.2017.06.005
Gerwin, D., and Tarondeau, J. C. (1982). Case studies of computer integrated manufacturing systems: a view of uncertainty and innovation processes. J. Operations Manag. 2 (2), 87–99. doi:10.1016/0272-6963(82)90025-0
Ghobakhloo, M. (2020). Industry 4.0, digitization, and opportunities for sustainability. J. Clean. Prod. 252, 119869. doi:10.1016/j.jclepro.2019.119869
Gillespie, D. T. (1996). Exact numerical simulation of the Ornstein-Uhlenbeck process and its integral. Phys. Rev. E 54 (2), 2084–2091. doi:10.1103/physreve.54.2084
Groover, M. P. (2006). Fundamentals of modern manufacturing: materials, processes, and systems. New Jersey, United States: John Wiley and Sons.
Guo, Q., and Tang, L. (2019). Modelling and discrete differential evolution algorithm for order rescheduling problem in steel industry. Comput. Industrial Eng. 130, 586–596. doi:10.1016/j.cie.2019.03.011
Gupta, D., and Maravelias, C. T. (2020). Framework for studying online production scheduling under endogenous uncertainty. Comput. Chem. Eng. 135, 106670. doi:10.1016/j.compchemeng.2019.106670
Hau, E. (2013). Wind turbines: fundamentals, technologies, application, economics. Springer Science and Business Media.
Iglesias-Escudero, M., Villanueva-Balsera, J., Ortega-Fernandez, F., and Rodriguez-Montequín, V. (2019). Planning and scheduling with uncertainty in the steel sector: a review. Appl. Sci. 9 (13), 2692. doi:10.3390/app9132692
Jamalnia, A., Yang, J. B., Feili, A., Xu, D. L., and Jamali, G. (2019). Aggregate production planning under uncertainty: a comprehensive literature survey and future research directions. Int. J. Adv. Manuf. Technol. 102 (1), 159–181. doi:10.1007/s00170-018-3151-y
Jeon, S. M., and Kim, G. (2016). A survey of simulation modeling techniques in production planning and control (PPC). Prod. Plan. Control 27 (5), 360–377. doi:10.1080/09537287.2015.1128010
Katzenstein, W., Fertig, E., and Apt, J. (2010). The variability of interconnected wind plants. Energy policy 38 (8), 4400–4410. doi:10.1016/j.enpol.2010.03.069
Koh, S. C., and Saad, S. M. (2002). Development of a business model for diagnosing uncertainty in ERP environments. Int. J. Prod. Res. 40 (13), 3015–3039. doi:10.1080/00207540210140077
Koh, S. C., Saad, S. M., and Jones, M. H. (2002). Uncertainty under MRP-planned manufacture: review and categorization. Int. J. Prod. Res. 40 (10), 2399–2421. doi:10.1080/00207540210136487
Kwon, S. D. (2010). Uncertainty analysis of wind energy potential assessment. Appl. Energy 87 (3), 856–865. doi:10.1016/j.apenergy.2009.08.038
Laing, C., and Lord, G. J. (2010). Stochastic methods in neuroscience. Oxford, United Kingdom: Oxford University Press.
Lee, J., Lapira, E., Bagheri, B., and Kao, H. A. (2013). Recent advances and trends in predictive manufacturing systems in big data environment. Manuf. Lett. 1 (1), 38–41. doi:10.1016/j.mfglet.2013.09.005
Li, C., and Thomas, B. G. (2000). “Analysis of the potential productivity of continuous cast molds,” in The Brimacombe Memorial Symposium, Vancouver, October 1-4, 2000, 595–611.
Li, Y., Carabelli, S., Fadda, E., Manerba, D., Tadei, R., and Terzo, O. (2020). Machine learning and optimization for production rescheduling in Industry 4.0. Int. J. Adv. Manuf. Technol. 110, 2445–2463. doi:10.1007/s00170-020-05850-5
Lin, J., and Naim, M. M. (2019). Why do nonlinearities matter? The repercussions of linear assumptions on the dynamic behaviour of assemble-to-order systems. Int. J. Prod. Res. 57 (20), 6424–6451. doi:10.1080/00207543.2019.1566669
Liu, H., Shi, J., and Qu, X. (2013). Empirical investigation on using wind speed volatility to estimate the operation probability and power output of wind turbines. Energy Convers. Manag. 67, 8–17. doi:10.1016/j.enconman.2012.10.016
Louhenkilpi, S. (2014). “Chapter 1.8 - continuous casting of steel,” in Treatise on process metallurgy. Editor S. Seetharaman (Amsterdam, Netherlands: Elsevier), 373–434.
Maller, R. A., Müller, G., and Szimayer, A. (2009). “Ornstein–Uhlenbeck processes and extensions,” in Handbook of financial time series. Editors T. G. Andersen, R. A. Davis, J. P. Kreiß, and T. V. Mikosch (Cham: Springer Science and Business Media), 421–437.
Manwell, J. F., McGowan, J. G., and Rogers, A. L. (2010). Wind energy explained: theory, design and application. New Jersey, United States: John Wiley and Sons.
Martin Bland, J., and Altman, D. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 327 (8476), 307–310. doi:10.1016/s0140-6736(86)90837-8
Merten, D., Hütt, M., Uygun, Y., Özgür, A., and Klein, C. (2024). “Comparative study of two genetic algorithms for steel production planning under different order,” in Steel 4.0: digitalization in steel industry. Editors Y. Uygun, A. Özgür, and M. Hütt (Cham: Springer Nature).
Merten, D., Hütt, M.-T., and Uygun, Y. (2022a). A network analysis of decision strategies of human experts in steel production. Submitt. Comput. Industrial Eng. doi:10.1016/j.cie.2022.108120
Merten, D., Hütt, M.-T., and Uygun, Y. (2022b). The effect of the slab width on the choice of the appropriate casting. J. Iron Steel Res. Int., 71–79. doi:10.1007/s42243-021-00729-5
Morgan, E. C., Lackner, M., Vogel, R. M., and Baise, L. G. (2011). Probability distributions for offshore wind speeds. Energy Convers. Manag. 52 (1), 15–26. doi:10.1016/j.enconman.2010.06.015
Mourtzis, D. (2020). Simulation in the design and operation of manufacturing systems: state of the art and new trends. Int. J. Prod. Res. 58 (7), 1927–1949. doi:10.1080/00207543.2019.1636321
Mourtzis, D., Doukas, M., and Bernidaki, D. (2014). Simulation in manufacturing: review and challenges. Procedia Cirp 25, 213–229. doi:10.1016/j.procir.2014.10.032
Negahban, A., and Smith, J. S. (2014). Simulation for manufacturing system design and operation: literature review and analysis. J. Manuf. Syst. 33 (2), 241–261. doi:10.1016/j.jmsy.2013.12.007
Ouelhadj, D., Petrovic, S., Cowling, P. I., and Meisels, A. (2004). Inter-agent cooperation and communication for agent-based robust dynamic scheduling in steel production. Adv. Eng. Inf. 18 (3), 161–172. doi:10.1016/j.aei.2004.10.003
Özgür, A., Uygun, Y., and Hütt, M.-T. (2021). A review of planning and scheduling methods for hot rolling mills in steel production. Comput. Industrial Eng. 151, 106606. doi:10.1016/j.cie.2020.106606
Oztemel, E., and Gursev, S. (2020). Literature review of Industry 4.0 and related technologies. J. Intelligent Manuf. 31 (1), 127–182. doi:10.1007/s10845-018-1433-8
Peidro, D., Mula, J., Poler, R., and Lario, F. C. (2009). Quantitative models for supply chain planning under uncertainty: a review. Int. J. Adv. Manuf. Technol. 43 (3-4), 400–420. doi:10.1007/s00170-008-1715-y
Pervozvanskii, A. A. (1965). “Random processes,” in Nonlinear control systems. Editor A. A. Pervozvanskii (New Jersey, United States: Elsevier).
Psarommatis, F., Martiriggiano, G., Zheng, X., and Kiritsis, D. (2021). A generic methodology for calculating rescheduling time for multiple unexpected events in the era of zero defect manufacturing. Front. Mech. Eng. 7, 646507. doi:10.3389/fmech.2021.646507
Ricciardi, L. M., and Sacerdote, L. (1979). The Ornstein-Uhlenbeck process as a model for neuronal activity. Biol. Cybern. 35 (1), 1–9. doi:10.1007/bf01845839
Ritter, M., and Deckert, L. (2017). Site assessment, turbine selection, and local feed-in tariffs through the wind energy index. Appl. energy 185, 1087–1099. doi:10.1016/j.apenergy.2015.11.081
Roy *, R., Adesola, B. A., and Thornton, S. (2004). Development of a knowledge model for managing schedule disturbance in steel-making. Int. J. Prod. Res. 42 (18), 3975–3994. doi:10.1080/00207540410001716453
Salameh, Z. M., and Safari, I. (1992). Optimum windmill-site matching. IEEE Trans. Energy Convers. 7 (4), 669–676. doi:10.1109/60.182649
Santos, C. A., Spim, J. A., and Garcia, A. (2003). Mathematical modeling and optimization strategies (genetic algorithm and knowledge base) applied to the continuous casting of steel. Eng. Appl. Artif. Intell. 16 (5-6), 511–527. doi:10.1016/s0952-1976(03)00072-1
Sreedevi, R., and Saranga, H. (2017). Uncertainty and supply chain risk: the moderating role of supply chain flexibility in risk mitigation. Int. J. Prod. Econ. 193, 332–342. doi:10.1016/j.ijpe.2017.07.024
Stevens, M. J., and Smulders, P. T. (1979). The estimation of the parameters of the Weibull wind speed distribution for wind energy utilization purposes. Wind Eng., 132–145.
Thomas, B. G. (2002). Modeling of the continuous casting of steel—past, present, and future. Metallurgical Mater. Trans. B 33 (6), 795–812. doi:10.1007/s11663-002-0063-9
Thomas, M. (1975). Some mean first-passage time approximations for the Ornstein-Uhlenbeck process. J. Appl. Probab. 12 (3), 600–604. doi:10.1017/s0021900200048439
Tordecilla, R. D., Juan, A. A., Montoya-Torres, J. R., Quintero-Araujo, C. L., and Panadero, J. (2021). Simulation-optimization methods for designing and assessing resilient supply chain networks under uncertainty scenarios: a review. Simul. Model. Pract. theory 106, 102166. doi:10.1016/j.simpat.2020.102166
Uhlenbeck, G. E., and Ornstein, L. S. (1930). On the theory of the Brownian motion. Phys. Rev. 36 (5), 823–841. doi:10.1103/physrev.36.823
Vasicek, O. (1977). An equilibrium characterization of the term structure. J. Financial Econ. 5 (2), 177–188. doi:10.1016/0304-405x(77)90016-2
Vieira, G. E., Herrmann, J. W., and Lin, E. (2003). Rescheduling manufacturing systems: a framework of strategies, policies, and methods. J. Sched. 6, 39–62. doi:10.1023/a:1022235519958
Wang, Y., and Zhang, L. (2010). Transient fluid flow phenomena during continuous casting: Part II—cast speed change, temperature fluctuation, and steel grade mixing. ISIJ Int. 50 (12), 1783–1791. doi:10.2355/isijinternational.50.1783
Wood, A. J., Wollenberg, B. F., and Sheblé, G. B. (2013). Power generation, operation, and control. New Jersey, United States: John Wiley and Sons.
Xu, L. D., Xu, E. L., and Li, L. (2018). Industry 4.0: state of the art and future trends. Int. J. Prod. Res. 56 (8), 2941–2962. doi:10.1080/00207543.2018.1444806
Yan, Y. (2015). “Nacelle orientation based health indicator for wind turbines,” in IEEE Conference on Prognostics and Health Management (PHM), Austin, TX, USA, June 22-25, 2015 (IEEE), 1–7.
Zhang, L., Zhou, L., Ren, L., and Laili, Y. (2019). Modeling and simulation in intelligent manufacturing. Comput. Industry 112, 103123. doi:10.1016/j.compind.2019.08.004
Zhang, Q., Wang, L., and Wang, X. (2006). Influence of casting speed variation during unsteady continuous casting on non-metallic inclusions in IF steel slabs. ISIJ Int. 46 (10), 1421–1426. doi:10.2355/isijinternational.46.1421
Zhang, Q., and Wang, X. (2010). Numerical simulation of influence of casting speed variation on surface fluctuation of molten steel in mold. J. Iron Steel Res. Int. 17 (8), 15–19. doi:10.1016/s1006-706x(10)60121-5
Zhong, L., Li, B., Zhu, Y., Wang, R., Wang, W., and Zhang, X. (2007). Fluid flow in a four-strand bloom continuous casting tundish with different flow modifiers. ISIJ Int. 47 (1), 88–94. doi:10.2355/isijinternational.47.88
Keywords: production systems, uncertainty, minimal model, simulation, optimization, Ornstein-Uhlenbeck process
Citation: Merten DC, Lesne A, Uygun Y and Hütt M-T (2024) Threshold-impeded stochastic production: how noise interacts with disruptive thresholds to affect the production output in fluctuating environments. Front. Ind. Eng. 2:1353531. doi: 10.3389/fieng.2024.1353531
Received: 10 December 2023; Accepted: 10 April 2024;
Published: 15 May 2024.
Edited by:
Francisco J. G. Silva, Polytechnic Institute of porto, PortugalReviewed by:
Foivos Psarommatis, University of Oslo, NorwayGustavo Pinto, Instituto Superior de Engenharia do Porto (ISEP), Portugal
Paolo Salini, University of L’Aquila, Italy
Milton Borsato, Federal Technological University of Paraná, Brazil
Copyright © 2024 Merten, Lesne, Uygun and Hütt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Daniel Christopher Merten, ZGFuaWVsLm1lcnRlbjFAZ214LmRl
 Daniel Christopher Merten
Daniel Christopher Merten Annick Lesne
Annick Lesne Yilmaz Uygun
Yilmaz Uygun Marc-Thorsten Hütt
Marc-Thorsten Hütt