- 1School of Electrical Engineering and Telecommunications, University of New South Wales, Sydney, NSW, Australia
- 2Data61, The Commonwealth Scientific and Industrial Research Organisation (CSIRO), Canberra, ACT, Australia
The fact that emotions are dynamic in nature and evolve across time has been explored relatively less often in automatic emotion recognition systems to date. Although within-utterance information about emotion changes recently has received some attention, there remain open questions unresolved, such as how to approach delta emotion ground truth, how to predict the extent of emotion change from speech, and how well change can be predicted relative to absolute emotion ratings. In this article, we investigate speech-based automatic systems for continuous prediction of the extent of emotion changes in arousal/valence. We propose the use of regression (smoothed) deltas as ground truth for emotion change, which yielded considerably higher inter-rater reliability than first-order deltas, a commonly used approach in previous research, and represent a more appropriate approach to derive annotations for emotion change research, findings which are applicable beyond speech-based systems. In addition, the first system design for continuous emotion change prediction from speech is explored. Experimental results under the Output-Associative Relevance Vector Machine framework interestingly show that changes in emotion ratings may be better predicted than absolute emotion ratings on the RECOLA database, achieving 0.74 vs. 0.71 for arousal and 0.41 vs. 0.37 for valence in concordance correlation coefficients. However, further work is needed to achieve effective emotion change prediction performances on the SEMAINE database, due to the large number of non-change frames in the absolute emotion ratings.
Introduction
Capacity to recognize a person's emotions is considered an important step toward intelligent machines, motivated by which, speech based emotion recognition has emerged as a key area of research during the last decade. The majority of studies in this field focus on either classifying several basic emotion categories (classification) or predicting emotion dimensions (classification/regression) (Sethu et al., 2015). The divergence in the problem setting is because emotions can be represented by not only using basic categories (e.g., fear, happiness, anger, etc.) to cover common emotions, but also numerical affect dimensions (e.g., arousal and valence) to describe a person's feeling. Although emotion recognition systems based on the categorical representation are straightforward from an engineering perspective and have been widely studied, they are, however, problematic due to the ambiguous nature of emotions (Mower et al., 2009). In addition, emotion categories are considered less capable of representing complex emotions and capturing subtle changes in emotions, especially for naturalistic data (Gunes and Schuller, 2013). In spite of some work done toward resolving this problem (Steidl et al., 2005; Mower and Narayanan, 2011), this drawback has led to an increasing number of studies using the dimensional representation (Cowie and Cornelius, 2003; Cowie et al., 2012; Gunes and Schuller, 2013). Among the most widely used affect dimensions are arousal (i.e., activated vs. deactivated) and valence (i.e., positive vs. negative), constituting a so-called arousal-valence space. Other dimensions such as potency and unpredictability have also been proposed to complement the two-dimensional space for a better representation of emotions (Jin and Wang, 2005; Fontaine et al., 2007).
Regardless of representation methods, emotion recognition in most studies is conducted on a per-speech segment basis. That is, speech sequences are pre-segmented into small emotional utterances with one global category or dimension label for each. However, this per-utterance labeling is based on an implicit assumption that emotions are in steady-state across the whole utterance, while emotions are dynamic in nature and change over time (Scherer, 2005; Kuppens, 2015). With growing awareness of this, there has been an increasing number of groups considering the time course of emotions by employing continuously annotated corpora (Gunes and Schuller, 2013). Examples of this kind of corpora are SEMAINE (McKeown et al., 2012), CreativeIT (Metallinou et al., 2015), RECOLA (Ringeval et al., 2013) and Belfast Naturalistic Database (Sneddon et al., 2012), where emotional ratings (e.g., arousal and valence) are evaluated continuously using real-time annotation tools such as Feeltrace (Cowie and Douglas-Cowie, 2000), Gtrace (Cowie et al., 2013), and ANNEMO (Ringeval et al., 2013), based on audio and video signals. Based on continuous annotation, a number of systems have been built with the intention of predicting the ratings at a fine temporal granularity, for example, the Audio-visual Emotion Challenge (AVEC) (Schuller et al., 2011; Ringeval et al., 2015b), but overall performances are not always satisfactory. Moreover, patterns, regularities and trajectories of how emotions evolve over time, which are known as affect (or emotion) dynamics, remain relatively less investigated, certainly from an automatic system perspective.
In affective science, emotion dynamics have attracted increasing interest. Back in 1998, Davidson introduced the term “affective chronometry” to describe temporal dynamics of emotions (Davidson, 1998). Affective chronometry includes rise time to peak, amplitudes and recovery time of affective responses. After about 20 years, Davidson has reemphasized their crucial role in understanding emotions (Davidson, 2015), in a special issue of the journal Emotion Review on advancing research into affect dynamics (Kuppens, 2015). Additionally, it has been shown in the literature that emotion transitions carry a great deal of valuable information for social interactions (Filipowicz et al., 2011; Mesquita and Boiger, 2014; Hareli et al., 2015), marital relationships, emotional intelligence (Gross, 2001; Kuppens and Verduyn, 2015) and psychological well-being (Kuppens et al., 2010; Choi et al., 2015; Houben et al., 2015). For instance, emotional transitions during conversations have a great impact on conversational outcomes (Filipowicz et al., 2011) and the final impression/perception of how dominant a person is (Hareli et al., 2015). A psychological sociodynamic model of emotions in context was proposed, and many interesting aspects of emotions were discussed, one of which is that emotions do not occur or change simply in response to social events, but are also an integral part of determining how social interactions proceed (Mesquita and Boiger, 2014). Recently, emotion regulation and emotion dynamics were associated using several parameters describing trajectories of emotion changes (Kuppens and Verduyn, 2015). Regulating emotions is more often than not associated with knowing the timings of emotional transitions, so that people react to change in the course of emotions (Gross, 2001). As an example, if a person is detected to be increasingly sad, people or machines may apply deliberate intervention such as telling a joke to please them (Devillers et al., 2015). Moreover, it has been found that emotion instability (Houben et al., 2015), which refers to emotion changes between previous and current emotional states, carries a great deal of information about psychological well-being. A measure of emotion instability is the Mean Squared Successive Difference (MSSD), and this relates to the likelihood that a patient is suffering from disease, anxiety and depression. It is also found that people with low self-esteem or depression tend to exhibit a lower frequency of changes in their emotional states, which is quantified by a term called emotional inertia (Kuppens et al., 2010). Accordingly, studies have shown that considering emotion change is useful for treatment of self-criticism associated with depression (Choi et al., 2015). Taken together, these findings suggest that research of emotion dynamics plays a crucial role in understanding emotions as well as contributing to interactions, emotion intelligence and psychological healthiness.
Compared with the increasing popularity of emotion dynamics in affective science, automatic systems for emotion dynamics in speech have been explored less. A recent experiment designed to analyze emotion dynamics computationally based on facial expression using a statistical model, was reported in Hakim et al. (2013). In the study, emotion categories were mapped frame-by-frame into the arousal-valence space to visualize trajectories of emotion dynamics, and emotion changes were observed to follow smooth common paths. That is, emotion transitions between two uncorrelated or negatively correlated emotions (e.g., excitement and frustration) tend to pass through the neutral state, whilst those between two positively correlated emotions (e.g., excitement or happiness) do not. These smooth paths are reasonable because they are frame-level (25 frames per second) emotion dynamics without considering external stimulus. On a larger scale, utterance-level emotion dynamics for classifying emotions was exploited based on a hypothesis that there exist emotion-specific dynamical patterns that may repeat within the same emotion class (Kim and Provost, 2013). A different way to capture emotion dynamics is the dynamic influence model proposed in Stolar et al. (2013), where Markov models were used to capture long-term conditional dependencies of emotion. Similarly to the above studies, employing dynamic information, either from emotion-related features or emotions themselves, to facilitate emotion recognition is not uncommon (Han and Eyben, 2012; Nicolle et al., 2012; Wei et al., 2014). For instance, spectra of temporal signals can be used to generate dynamic features (Nicolle et al., 2012). An utterance-level emotion prediction system was built based on the trade-off between conventional mean square error and a proposed rank-based trend loss to successfully preserve the overall dynamic trend of emotion dimensions (Han and Eyben, 2012). In Wei et al. (2014), an HMM-based language model was used to capture the temporal patterns of emotional states via a predefined grammar, achieving an accuracy of 87.5% for classifying the four quadrants of the arousal-valence space on the SEMAINE dataset. However, there are few systems aiming to understand and interpret emotion dynamics. This is in part due to difficulties in describing emotion dynamics and “a lack of databases for emotion dynamics” (e.g., duration, ramp-up rate and decay rate) (Hudlicka, 2008). Continuously annotated corpora such as RECOLA, SEMAINE and CreativeIT are helpful in investigating emotion dynamics, but still have the limitation that they are annotated in an absolute manner, rather than annotators being explicitly directed to rate emotion changes.
It is also worth noting that studies on emotion dynamics are often placed in context, where emotion transitions take place and are influenced by events (Niedenthal et al., 2001) as well as other speakers (Stolar et al., 2013). During conversations, an agreeable trajectory of emotion dynamics would be an onset-apex-offset path (Davidson, 1998; Waugh et al., 2015). There exists an emotion-arousing process between events (or situations) and people's emotional responses (Gross, 1998) and these responses tend to fade across time (Ritchie et al., 2009). Based on this, an affective scene framework to investigate emotion unfolding across time during call-center conversations was proposed (Danieli and Riccardi, 2015). In their study, continuous emotional unfolding was converted into several discrete emotional episodes (e.g., one of the episodes is that an Agent first expresses emotions, and the customer ends up experiencing positive emotions). The fading phenomenon was also observed in Böck and Siegert (2015), in which it is shown that emotional evolution in speech is detectable based on an emotion recognition system.
While the above studies related to emotion dynamics involve a broad spectrum of topics, there is a need for more systematic insights into emotion dynamics that can be used to facilitate applications of affective computing and Human Computer Interaction (HCI). In this paper, we provide insights into emotion changes, from an engineering perspective, by addressing the questions: what is required to construct delta emotion ground truth from continuous absolute ratings, how can the “extent” of emotion change be predicted from speech and can it be predicted as reliably as absolute emotion ratings? The latter questions we refer to herein as Emotion Change Prediction (ECP).
Related Work
For emotion change research, most previous literature has focused on detecting emotion change points in time, which we refer to as Emotion Change Detection (ECD). Recently, it is found in Böck and Siegert (2015) that emotional evolution both inter- and intra-speaker is detectable using per-file emotion recognition methods. Also, there have been some studies explicitly attempting to localize the time when emotion changes occur, among different emotion categories using audio features (Xu and Xu, 2009; Pao et al., 2010; Fan et al., 2014) or psychological measures (Leon et al., 2004). For instance, an approach was proposed to detect emotion evolution based on intersections of the two most prominent smoothed emotional scores within a sliding window framework (Xu and Xu, 2009). In Fan et al. (2014), the authors tried to detect boundaries of different emotions (neutral-anger and neutral-happiness) continuously using multi-timescaled sliding windows where decisions of emotion recognition from each scale collectively contribute to a final decision. Using several psychological measures, emotion change detection in a user's environment was investigated (Leon et al., 2004). Specifically, the presence of emotion changes was detected via a large residual between measured emotion and estimated emotion. Different from the aforementioned studies aiming to detect changes among emotion categories, an adaptive temporal topic model was proposed to detect huge changes in emotion dimensions, i.e., arousal and valence using audiovisual features (Lade et al., 2013). In our previous work (Huang et al., 2015b), a sliding window framework was proposed to detect emotion changes among four emotion categories with and without prior knowledge of emotions. Later, an introduction of martingale framework yielded further improvements (Huang and Epps, 2016a).
Nevertheless, systems developed in the aforementioned studies do not provide information regarding how emotions evolve such as the “extent” of emotion change, which we term ECP. ECP herein is treated as a regression problem, which aims to predict the extent of a change in affect dimension(s) between two consecutive utterances or frames. In this paper, we only consider ECP at frame level, because this is in line with the increasing popularity of studies adopting continuous affect ratings.
There are two motivations behind the study. Firstly, an analysis in a continuously annotated database showed that evaluators tend to agree more on relative emotions (e.g., an increase in arousal) than on absolute emotions (e.g., arousal) (Metallinou and Narayanan, 2013). Indeed, this has been shown elsewhere in the literature (Yang and Chen, 2011; Han et al., 2012; Yannakakis and Martínez, 2015a; Parthasarathy et al., 2016), where rank-based annotations of affect dimensions yield higher inter-rater reliability than conventional absolute ratings. In Yannakakis and Martínez (2015a), evaluators only rank (i.e., increase or decrease their rating) when they perceive changes in affect dimensions. This facilitates the annotation process in terms of inter-rater agreement and reduction of cognitive load, because the ranking scheme allows simplification of annotation as well as being robust to different personal scales in affect dimension of evaluators. That is, each evaluator has his/her own understanding of the arousal and valence scales, which may differ from others'. From an emotion perception perspective, conventional ratings based on these various scales may lead to misrepresentation of speakers' original emotions, especially when we simply average them across different evaluators (Martinez et al., 2014; Yannakakis and Martínez, 2015b). Performing evaluator-specific z-normalization to mitigate the difference in the scales could be effective, however, it also carries a risk of possible misinterpretation.
Rank-based annotations, where emotions are treated in relative way, can potentially do better in emotion perception. Given the advantages of relative emotions over absolute emotions, one wonders whether changes in emotion ratings can be better predicted than absolute ratings. Secondly, despite the increasing popularity of predicting emotion dimensions either at utterance level (Grimm et al., 2007; Bone et al., 2014) or at frame level (Gunes et al., 2011; Metallinou et al., 2011; Nicolaou et al., 2011), all of the studies focus on prediction of absolute emotions across time. From these studies, it seems that predicting absolute emotion dimension remains challenging, and predicting absolute emotion alone may not provide insight into dynamic components, properties and regularities of emotion changes.
Given the motivations, the purpose of ECP study herein is two-fold: (1) investigate emotion change annotation and prediction system design, providing a different perspective for understanding emotions; and (2) compare ECP and conventional absolute emotion prediction, understanding how well emotion dynamics can be predicted, in comparison with absolute emotions.
Overview and Possibilities for Emotion Change Systems
This section presents an overview and envisions several possibilities for developing systems that take advantage of emotion dynamics, depending on the application context. As shown in Figure 1, we proposed two main possibilities for emotion change research, namely, Emotion Change Detection and Emotion Change Assessment. Emotion Change Detection aims to localize the time of emotion changes such as changes in emotional categories (e.g., neutral to anger) and large changes in affect dimensions (e.g., arousal and valence). Emotion Change Assessment can be used directly (without ECD) or in conjunction with ECD to characterize how emotions change across time.
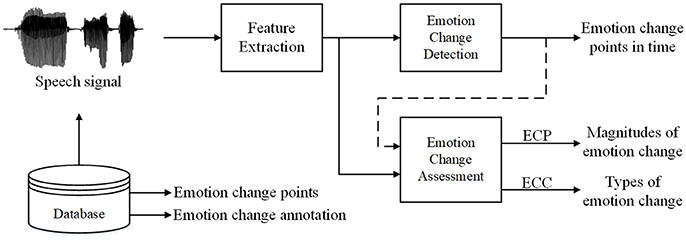
Figure 1. General overview of emotion change based systems. ECP refers to predicting the extent of emotion change, while ECC represents classifying different type of emotion change, e.g., increase/decrease in arousal.
ECD itself may have significant research potential and application possibilities. An intuitive application is HCI, where ECD can be an integral part of a real-time emotion recognition system. ECD can operate in real-time, and trigger emotion recognition algorithms once a change in emotions is detected, in place of continuous recognition of emotions, which may be more applicable and computationally efficient in HCI (Lade et al., 2013). These advantages are more pronounced in spontaneous data, where the majority of emotions tend to be neutral. Furthermore, emotion changes may somehow reflect changes in the external environment, such as events that trigger emotions, e.g., changes in task difficulty have been found to be associated with changes in arousal (Chen and Epps, 2013). In addition, emotion change points in time can be referred to as boundaries of different salient emotional segments, obviating the need for manual segmentation prior to emotional signal processing. The need for ECD also arises for detecting outbursts of emotion changes within a larger group of people for security applications, as well as monitoring emotional changes in patients for medical purposes (Choi et al., 2015). Methods for automatic ECD from speech have been investigated previously (Huang et al., 2015b; Huang and Epps, 2016a) and are not the focus of this paper.
A variation of ECD is emotion segmentation (Schuller and Rigoll, 2006; Kim and Mower Provost, 2014; Huang and Epps, 2016b), which aims to select speech or facial segments with salient emotional information for improved emotion recognition system performances. Different segmentation schemes, normally fixed-length or variable-length segmentation, were employed to effectively exploit segment-level features (Schuller and Rigoll, 2006; Huang and Epps, 2016b) or models (Kim and Mower Provost, 2014). Nevertheless, this type of system typically produces little explicit information about the timing of emotion boundaries or the extent of changes in emotion between segments.
Emotion change assessment involves either predicting the extent or classifying the direction/type of emotion changes. The “extent” could be quantitative measures of changes in emotional intensity or emotional dimensions, whereas the “direction” could be qualitative categories describing emotion changes such as increase, decrease or non-change. One can easily envisage an emotion change system that detects emotion changes, and then for each emotion change, tries to determine what type of change it is. Such a system may be well suited to speech that is predominantly neutral, but occasionally becomes emotional. Both approaches enable investigation of emotions from a change perspective. In some cases, emotion changes may be more informative and meaningful in practice, e.g., knowing that a person is becoming less or more aroused compared to simple recognition of arousal.
Data
In this study, two corpora were considered: SEMAINE (McKeown et al., 2012) and RECOLA (Ringeval et al., 2013). These two corpora have annotations of arousal and valence at frame-level. For frame-level ECP, we considered SEMAINE and RECOLA. However, for both tasks, these corpora were not originally designed for studying emotion changes, so there is no explicit ground truth provided, i.e., extent of emotion dynamics. To resolve this, we constructed delta emotion ground truth for ECP on RECOLA and SEMAINE, which are discussed below.
The SEMAINE corpus1 is a widely used and reasonably large English spontaneous audiovisual database collected in the Sensitive Artificial Listener (SAL) scenario where a person engages in emotionally colored interactions with one of four emotional operators. They are angry Spike, happy Poppy, gloomy Obadiah and sensible Prudence who try to make people experience the same emotions. Recordings on the database were continuously evaluated by 2–8 annotators in terms of five core affect dimensions (i.e., arousal, valence, power, expectation and intensity), as well as other optional descriptors (e.g., agreeing, happiness, and interests) via Feeltrace. Within SEMAINE, we considered only Solid SAL sessions with transcriptions and annotations from R1, R2, R3, R4, R5, and R6 for consistency, which leads to 57 sessions from 14 speakers. Within each session, since lengths of annotations from six annotators may vary during data collection, all ratings were shortened to the minimum length of annotations from the six annotators by removing the trailing redundant annotations. Accordingly, the session with ID number 60 was further discarded because of insufficient valence ratings from one of the annotators. In total, this study used audio recordings of 56 sessions from 14 speakers (users).
The RECOLA corpus2 is a spontaneous multimodal database collected in settings where two French speakers remotely collaborate to complete a survival task via a video conference. During the collaborative interactions, multimodal signals, including audio, video and physiological signals such as ECG and EDA, were collected from 46 participants (data from 23 participants are publically available). For each participant, each recording is 5 min long and continuously annotated for arousal and valence by six annotators. The AV+EC 2015 challenge (Ringeval et al., 2013) employed this database for a continuous emotion prediction task. A subset of the database from 18 speakers were partitioned into training and development set for this challenge. In this study, we considered the same partitions used in AV+EC 2015 for ECP.
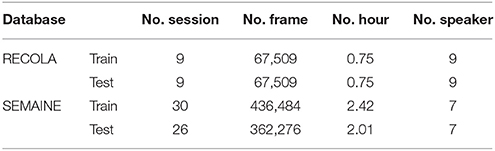
For ECP, we considered SEMAINE (56 sessions from 14 speakers) and RECOLA (18 sessions from 18 speakers), which have frame-level emotional annotation. To allow comparisons with published studies where commonly the RECOLA dataset was divided into training (9 speakers) and testing (9 speakers) partitions, we kept the same partitions on RECOLA. Similarly, the SEMAINE dataset was divided into training (30 speakers) and testing (26 speaker) sets for consistency. In this task, we constructed “delta” emotion ground truth, which captures emotion dynamics, i.e., the extent of emotion changes across time, from the original absolute ratings (section Delta Emotion Ground Truth). We evaluated inter-rater reliability of the delta emotion ground truth before exploring system design for ECP (section Delta Emotion Ground Truth). The process used to construct the “delta” emotion ground truth is elaborated in section Delta Emotion Ground Truth. Regression deltas were calculated within a certain window size before being averaged across all annotators to form “delta” (emotion change) ground truth.
Delta Emotion Ground Truth
Despite a trend toward evaluators being encouraged to rate when changes in affect dimensions occur (Yannakakis and Martínez, 2015a; Celiktutan and Gunes, 2016), to the best of our knowledge, there are no studies introducing annotation of emotion changes in dimension ratings apart from Yannakakis and Martínez (2015a). Ordinal or ranked-based annotations such as increase and decrease of arousal and valence ratings have shown improved inter-rater reliability over conventional absolute ratings (Yannakakis and Martínez, 2015a). An alternative way to attain the rank-based annotations is to derive relative labels from original absolute ratings using Qualitative Analysis (Parthasarathy et al., 2016). The study (Parthasarathy et al., 2016) highlights the importance of annotator agreement for reliable rank-based labels and emotion recognition accuracies. Another possible approach is to fit linear curves to absolute ratings to calculate the slopes, and then categorize them into increase, decrease and non-change (Metallinou et al., 2011). However, from either the ordinal annotations or the slopes, we know only the directions of changes but do not know their extent. An alternative investigation applied herein to speech with continuous dimensional ratings is to calculate “deltas” from existing “absolute” ratings, where “absolute” refers to the original ground truth provided by the databases. By computing deltas, changes in emotion dimensions can be characterized and then be used as a reference for modeling.
A naïve approach to calculating delta emotion ground truth is to use the first-order temporal difference of the absolute ground truth, referred to as first-order delta emotion ground truth. However, this is problematic: (i) it assumes the possibility of extremely rapid emotion changes (in the order of 0.04 s and 0.02 s in RECOLA and SEMAINE, respectively—the sampling interval between ratings), which are unrealistic; (ii) because raters tend not to move their cursor continuously, it tends to result in a very large proportion of zero first-order delta emotion ground truth, which in consequence leads to unreliable ground truth with low inter-rater reliability and less effective regression models; (iii) there is annotation noise caused by annotator tremble, especially when they are uncertain about the emotions being evaluated (Martinez et al., 2014).
Observation (iii) was borne out in previous experimental work (Metallinou et al., 2011). In addition, preliminary experiments on the RECOLA database demonstrated that first-order differences of frame-level absolute ratings have a very low inter-rater agreement, which is sensible because the ratings are originally annotated in an absolute manner and conversion from absolute to first-order delta may not be straightforward (Yannakakis and Martínez, 2015a). More specifically, several problems manifested in absolute ratings such as sensitivity to the range, anchor point and sequential effects (Parthasarathy et al., 2016) among different annotators would cause noise in the first-order delta. Inter-rater agreement refers to agreement on categorical or numeric annotations among annotators, which is normally measured by Cronbach's α (McKeown et al., 2012; Ringeval et al., 2013; Metallinou et al., 2015).
In psychology, emotion response is cohesively formed by a number of components which unfold at different time scales from milliseconds to minutes (Waugh et al., 2015). It is difficult to identify the temporal resolution of emotion change, that is, how fast emotions can change. However, an empirical analysis of continuous annotations suggests that affect dimensions are generally slowly varying and detailed annotations might capture annotation noise irrelevant to emotions (Metallinou and Narayanan, 2013). In Metallinou and Narayanan (2013), window-level ratings, which is an average over a certain length of window (3 s), were compared with frame-level ratings in terms of Cronbach's α, yielding slight improvements. This may be because the window-level ratings are smooth and reduce the effect of annotation noise. In light of this, it is reasonable to speculate that annotation noise also exists in first-order delta emotion ground truth and smoothed delta emotion ground truth is more reasonable and has a higher inter-rater agreement. Hence, we calculated a smoother version of the deltas for the SEMAINE database and for RECOLA.
Proposed Regression Delta Emotion Ground Truth
In this study, we propose the calculation of regression delta emotion ground truth GD = {d1, …, dt} from absolute ground truth GA = {a1, …, at} as delta emotion ground truth using the following equation (Young et al., 1997):
where K denotes the number of absolute ratings taken into account on each side of frame t for calculating the regression deltas. Accordingly, we define a regression delta window as NS = 2K + 1, containing the current frame plus K frames on each side. The larger the K is, the smoother the GD, which however gives rise to information loss in GA. More specifically, if a set of reconstructed absolute ratings Gr = {r1, …, rt} are determined from the regression delta emotion ground truth GD by accumulating (integrating) them, the Gr becomes a smoother version of GA.
Then we measure the information loss by comparing Gr and GA using Concordance Correlation Coefficient (CCC) ρc (Equation 3) (Ringeval et al., 2015a), which takes into account correlation and square of mean error. If K = 1, GD is an approximation to the first-order differences of GA, and accumulating GD provides an identical set of absolute ratings Gr as GA, which means no information loss and ρc = 1. As K increases, the information loss increases, i.e., ρc declines. A similar way to compute information loss can be seen in Ringeval et al. (2015a), where information loss was evaluated by comparing original ratings and mean-filtered versions of the ratings using ρc.
where is the reconstructed absolute emotion ratings Gr, whilst Yi is the original absolute emotion ground truth GA. Note that ρc (i.e., CCC) is also used as a measure of prediction accuracy in the following experiments in sections Design of Emotion Change Prediction Systems and Emotion Change Prediction Using SVR, RVM, and OA RVM, where is predictions, whilst Yi is the ground truth.
Apart from the information loss, another important criterion to evaluate the reliability of the ground truth is inter-rater reliability or agreement, which is commonly measured using Cronbach's α (Cronbach, 1951) among all annotators. Our hypothesis is that as NS gets larger, the inter-rater agreement would increase, since the delta emotion ground truth gets smoother.
Evaluation of Window Size for Regression Deltas: A Trade-Off Between Inter-Rater Agreement and Information Loss
The window size choice NS for calculating regression delta emotion ground truth seems to have impacts on both inter-rater agreement and information loss, which is investigated in this section.
For inter-rater agreement, we compared GA (i.e., absolute emotion ground truth) and GD (i.e., delta emotion ground truth) with respect to mean correlation ρ and Cronbach's α (Cronbach, 1951) among six annotators on RECOLA and SEMAINE. GD was calculated from GA using Equation (1) for each annotator per session, denoted as , where l ≤ L represents the l-th rater and s ≤ S means the s-th session. was then concatenated for all sessions for each annotator , prior to calculating the mean correlation ρ and Cronbach's α among six annotators using Equation (4) and (5) (Cronbach, 1951).
where corr(•) denotes correlation and var(•) denotes variance. Following the same scheme, we calculated GD using different regression delta window lengths NS, each of which has corresponding mean correlation ρ and Cronbach's α. Note that a Cronbach's α = 0.6 is considered the minimum acceptable internal agreement among annotators, whereas 0.7 < α < 0.9 is considered good (McKeown et al., 2012).
For information loss, we calculated ρc between GA (i.e., the original absolute emotion ground truth) and Gr (i.e., the reconstructed absolute emotion ground truth). Within each session, regression deltas for each annotator were integrated into reconstructed absolute ratings to compare with the original ones in terms of ρc using Equation (3). Then the final ρc was obtained by averaging all the across six annotators and all sessions as in Equation (6).
Figure 2 depicts various regression delta window sizes NS = 2K + 1 for regression delta calculation, which lead to different inter-rater agreement and information loss.
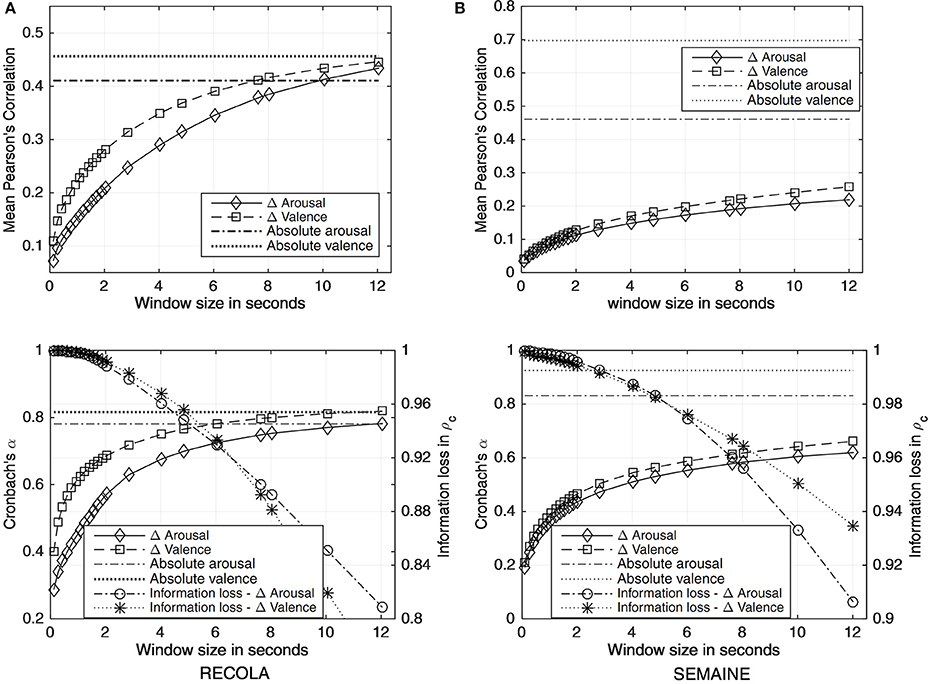
Figure 2. Mean Pearson's correlation and Cronbach's α of regression delta emotion ground truth and absolute ground truth for (A) RECOLA and (B) SEMAINE, as a function of the regression delta window sizes NS = 2K + 1: longer regression delta window for calculating delta ratings from absolute ratings resulted in increased inter-rater reliability. Information loss in ρc for the regression delta emotion ground truth calculated under various regression delta window sizes is also shown on the second y-axes in the lower figure: longer window sizes result in more information loss.
Overall, Figure 2 offers a guide toward making choices of suitable window sizes for calculating regression delta emotion ground truth based on the trade-offs between inter-rater reliability and information loss. More specifically, we selected a regression delta window length of 4 s for RECOLA, since its corresponding deltas have acceptable inter-rater agreement (α = 0.677 for arousal and α = 0.750 for valence) while preserving enough detailed information (i.e., a reduction of 0.04 ρc for arousal and for valence). For constructing regression delta emotion ground truth GD, we also tried mean filtering of first-order derivatives of absolute ratings with different window lengths. However, this method was found to lose more information than regression deltas (0.05 ρc for arousal and valence).
For SEMAINE, absolute ground truth has much higher mean correlation and inter-rater reliability than the regression delta emotion ground truth. To account for this large contrast, we observed that differences between adjacent SEMAINE annotated frames are mostly zeros, 92.33% (±2.95%) for arousal and 93.19% (±2.09%) for valence. Since mean correlation measures a linear relationship rather than comparing exact values between annotations among different evaluators, the high correlation of absolute ground truth might be attributed to the large proportion of non-change frames. Accordingly, the Cronbach's α, calculated from mean correlation, is correspondingly high for the absolute ground truth. This is also supported by the argument in Siegert et al. (2014) that Cronbach's α might not be suitable in some cases since it measures the internal consistency among annotators, which in this case is that annotators tend not to change their ratings, resulting in the large proportion of non-change frames (seen clearly in Figure 3). On the contrary, regression delta emotion ground truth, calculated using NS ∈ {4, 8} s, is smooth but results in Cronbach's α around 0.6. This reflects the low inter-rater agreements on the extent of emotion changes, which may further partially reveal the challenging nature of SEMAINE from an emotion change perspective.
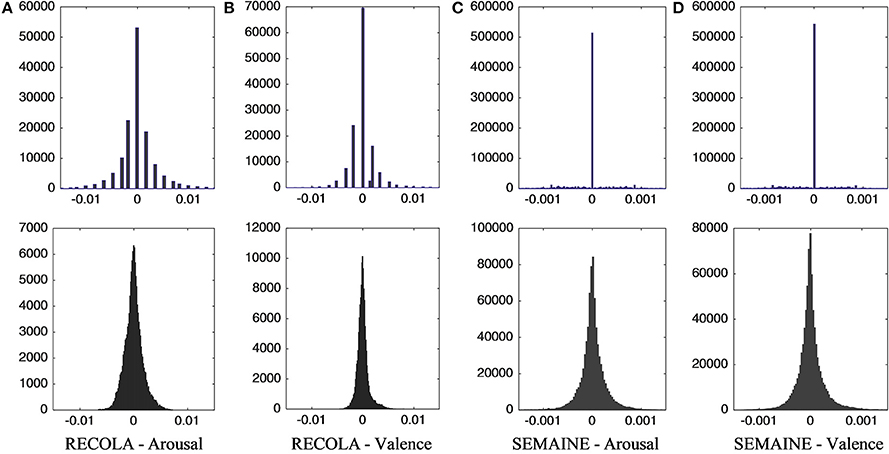
Figure 3. Histograms of delta emotion ratings for arousal and valence on RECOLA and SEMAINE datasets. The x-axes represents the value of delta emotion ratings, while y-axes represents the frequency (counts) for each certain delta emotion value. The upper figures represents first-order differences of absolute emotion ratings, which have a significantly larger proportion of zero for both arousal and valence. The lower figures represents regression delta emotion ground truth (using NS is Table 2), which offer reasonable distributions for emotion change.
In terms of information loss, SEMAINE has lower loss than RECOLA, and the reason observed behind this is that SEMAINE has smoother annotations than RECOLA. According to Figure 2 for SEMAINE, a choice between 6 and 8 s seems acceptable, so we empirically considered a regression delta window length of 6 seconds (with α = 0.554 for arousal and α = 0.588 for valence and information loss of 0.03 ρc for arousal and valence). According to Figure 2, the choices for sizes of sliding windows were summarized as in Table 2 based on trade-offs between inter-rater agreement α and information loss 1-ρc.
Comparisons Between Regression Delta and First-Order Delta Emotion Ground Truth
There are multiple ways of determining delta emotion ground truth from continuous absolute ratings, and all of these are approximations to the derivative. We considered two in particular, the first-order difference and a regression-based approach, whose effects on the distributions of delta emotion are compared in this section, as seen in the histograms shown in Figure 3.
The trade-offs in Figure 2 favor selection of a regression delta window of 4 seconds and 6 seconds for RECOLA and SEMAINE, respectively. These choices could be reasonable for two reasons. Firstly, the Equation (1), which was used to calculate regression deltas, incorporates emotion changes (at+k − at−k) at different time scales controlled by k, with further emotion changes being weighted more heavily, i.e., a large k. To this end, the regression deltas can represent sub-utterance emotion changes with reasonably distributed values (Figure 3). Secondly, a suitable time scale to investigate emotion changes remains controversial in both engineering systems and affective science fields. For instance, it is suggested that it takes several seconds to spot different emotion categories, which may be the same case for emotion changes (Kim and Provost, 2016).
The finding that attaining regression delta emotion ground truth using a sliding window can yield drastically improved inter-rater agreement while preserving detailed emotion change information as shown in Figure 2 underlies one of the key contributions for ECP. This is, to the best of our knowledge, the first time that continuous delta emotion ground truth has been investigated, showing that a sliding window regression delta is a better way to represent and evaluate sub-utterance emotion changes with high inter-rater reliability, small information loss (Figure 2) and meaningful representations (Figure 3).
For convenience, the delta emotion ground truth can be equivalently obtained by calculating the regression delta of absolute ground truth ratings, namely the mean of six raters in SEMAINE and the gold standard used in RECOLA. Based on the delta emotion ground truth, we then performed extensive comparisons between absolute emotion prediction and delta emotion prediction in terms of delay compensation and prediction performances.
Emotion Change Prediction (ECP)
The regression delta emotion ground truth proposed in section Proposed Regression Delta Emotion Ground Truth offers a nice characterization and representation of sub-utterance emotion change across time. Given the numerical nature of the regression delta emotion ground truth, ECP herein can be formulated as a regression problem as per continuous emotion prediction, where the target is to learn from informative features using machine learning algorithms to continuously predict the extent of emotion change. Since continuous emotion prediction is also treated as a regression problem, it may be intuitive to compare it with ECP. The aim of this section is to explore system design and maximized system performance for a robust ECP, based on empirical experience in dealing with the emotion prediction problem. One may be interested in using emotion changes to facilitate absolute emotion predictions, such as Huang and Epps (2017) and Oveneke et al. (2017) in which Kalman filtering was used. However, an important premise could be accurate predictions of emotion change, which is the only focus of this study. Note that investigating absolute emotion prediction is not in the scope of this study.
Experimental System Settings
Experiments were evaluated on the RECOLA and SEMAINE datasets. For RECOLA, we used recordings from 9 speakers for training and recordings from other 9 speakers for testing, as shown in Table 1. On SEMAINE, among 14 speakers, we used the first 7 speakers for training and another 7 speakers for testing.
Initial investigations were carried out to evaluate two potentially important parameters, i.e., feature window size and annotation delay (section Design of Emotion Change Prediction Systems). This was then followed by evaluations of three commonly used regression models, i.e., Support Vector Regression (SVR), Relevance Vector Machine (RVM)3 and Output-Associative RVM (OA-RVM), which are effective affective regression models (section Emotion Change Prediction Using SVR, RVM, and OA RVM).
SVR's solid theoretical framework ensures global solutions, sparsity in weights and good generalization ability. During training, SVR searches for an optimal hyperplane by minimizing its geometric margins whose width equals to ε, where ε is called the slack coefficient. The tube-like hyperplane itself is supported by only a small number of training samples (support vectors) with non-zero weights. In contrast, the remaining training instances within the hyperplane are assigned as zero weights and contribute nothing to the SVR model. In prediction, testing instances are then transformed linearly (inner product) or nonlinearly (so-called “kernel trick”) to perform prediction. RVM is a probabilistic framework that is advantageous in terms of sparsity in features. RVM enforces a zero-mean Gaussian prior distribution to the feature weights whose variances become mostly zeros as training, which introduces sparsity. Within the OA-RVM framework, input features are used to perform initial predictions using a first-stage RVM for arousal and valence. The initial arousal and valence predictions within a temporal window are stacked and then combined with the input features to perform final predictions using a second stage RVM. This enables the framework to take advantage of the following dependencies: (1) between arousal and valence predictions; (2) between previous and future predictions; and (3) between output predictions and input features. In addition, it is robust for different system configurations while providing state-of-the-art performances (Huang et al., 2015a). Detailed descriptions of SVR, RVM and OA RVM can be referred to in Grimm and Kroschel (2007), Tipping (2001) and Nicolaou et al. (2012).
We considered linear kernel for SVR and RVM. The libsvm toolkit (Chang and Lin, 2011) was used to implement SVR, where the complexity C was optimized from among {10−6, 10−5,…, 10−0, 101} on the testing partition; during training, only 1 out of 20 frames was used, similarly to Ringeval et al. (2015b); For RVM4, only the number of iterations needs to be tuned, this was optimized from among {30, 50, 70, 90, 110, 150, 200, 250} on the testing partition. For OA-RVM, the size of the temporal window used to construct output-associative matrices (OA matrices) was set to 6 seconds, namely 151 frames for RECOLA and 301 frames for SEMAINE.
We evaluated the performances of the two systems using three measures, namely: Relative Root Mean Square Error (RRMSE) (Equation 7), Pearson's Correlation Coefficients (ρ), and Concordance Correlation Coefficients (ρc) (Equation 3). The RRMSE calculates Root Mean Square Error (RMSE) between predictions and ground truths, which is further divided by the Root Mean Square (RMS) of the ground truth to eliminate the effect of various ranges for absolute and delta emotions.
where is predictions, whilst Yi is the ground truth.
Design of Emotion Change Prediction Systems
Feature Window
Functionals, global statistics of short-term acoustic features extracted on a larger time span, have been successfully applied to emotion recognition, because they capture distribution characteristics of short-term features while being insensitive to fluctuations in short-term features.
From RECOLA and SEMAINE, 88-dimensional eGeMAPS functionals (Eyben et al., 2016), which are an expert-based, interpretable and effective feature set for affective computing, were extracted using the Open-SMILE toolkit at window level with frame steps equivalent to the time interval of ground truth, namely 0.04 s for RECOLA and 0.02 s for SEMAINE. The 88-dim eGeMAPS features were used for absolute emotion prediction, whilst 176-dim features (two adjacent functionals, i.e., from the previous window n−1 and the current window n, are concatenated) were used for delta emotion prediction. This was because the 176-dim features performed more poorly than the 88-dim features for absolute emotion prediction, while they performed slightly more accurately for delta emotion prediction. Precisely, with a 2-s feature window and no delay compensation, the 176-dim and 88-dim features achieved 0.365 and 0.340 for delta arousal, 0.195 and 0.184 for delta valence in CCC on RECOLA while there was no significant difference on SEMAINE. This is sensible since the concatenation potentially allows the “difference” of the two functionals to be calculated when regression model weights that are negative relative to each other for the same features within two functionals. All the features were scaled to {0, 1} for training and the scaled coefficients were used to normalize testing features.
It is important to know the best feature extraction window size NF for absolute and delta emotions. From Figure 4, a 2 s feature window was selected for delta emotions on RECOLA and SEMAINE because it yielded the best or second-best performance. For absolute emotion prediction, 2 s feature windows yielded reasonably good performances on RECOLA, while larger feature windows contributed to better performances on SEMAINE. However, 8 s feature windows might be too large, and lose detailed changes in emotions (Ringeval et al., 2015a). Accordingly, 2 s and 4 s feature windows were used for absolute emotion prediction respectively on RECOLA and SEMAINE. These feature windows were fixed for different tasks throughout the following experiments.
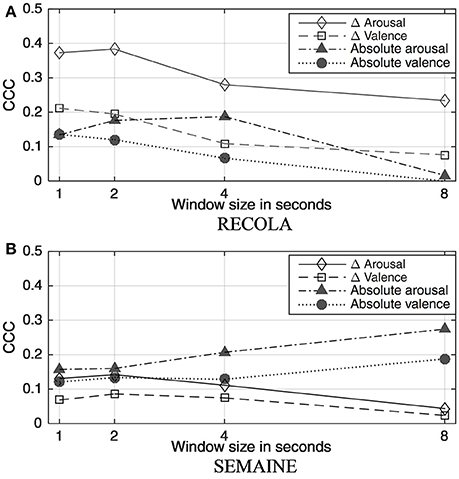
Figure 4. Performances were evaluated and compared under different window length that are used to extract the eGeMAPS functionals between the (A) RECOLA and (B) SEMAINE corpora. CCC represents system performances for prediction using RVM. Consistent trends of declining performances for delta arousal and delta valence were observed for both databases as feature window increased. By contrast, this was not the case for absolute emotions, where with larger feature window, performances degraded for (A) RECOLA and improved for (B) SEMAINE.
Delay Compensation
An important issue in continuously annotated emotional corpora such as RECOLA and SEMAINE is the synchronization issue with the continuous annotations. This is largely caused by the inherent annotation delay between evaluators' perceptual observations and their decision-making. We hypothesize that people tend to notice changes in emotion easily, which may result in lower annotation delays for emotion change than those for emotion. This hypothesis may be somewhat undermined herein because the delta emotion ground truth is calculated from absolute emotion ground truth. However, the assumption behind investigation of delay compensation is that absolute emotion ground truth represents how annotators perceive absolute emotion, whilst the proposed delta emotion ground truth represents how annotators perceive changes in emotion.
Attempts to resolve this issue can be seen in some literature (Cowie et al., 2012; Nicolle et al., 2012; Mariooryad and Busso, 2014), where this synchronization issue is compensated via temporal shifts of the features and ground truth ratings, and the best delay value in time can be optimized using a number of measures such as information gain and average correlation (Nicolle et al., 2012; Mariooryad and Busso, 2014). Dynamic Time Warping (DTW) was also been found effective to eliminate inter-rater delays and outliers (Katsimerou et al., 2015). Another method proposed in Huang et al. (2015a) for compensating delays is to apply temporal shifts of features and ratings to build reliable models in the training phase. Delays introduced in predictions were further compensated via a binomial filter, which, in addition, smooths predicted affect dimensions. Applying the same technique herein, we estimated the best delay values for absolute and delta emotion ground truth on both RECOLA and SEMAINE, as seen in Figure 5.
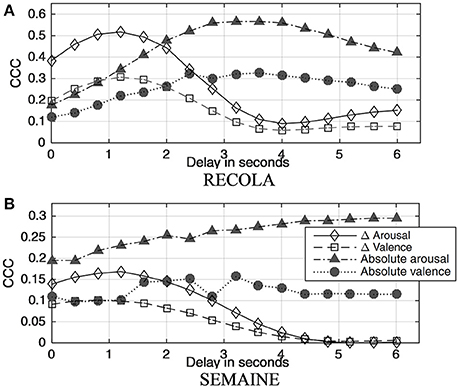
Figure 5. Annotation delays were evaluated and compensated for both absolute and delta emotions for the (A) RECOLA and (B) SEMAINA database via temporal shift and smoothing. CCC represents system performances for prediction using RVM. The optimal delays for delta arousal and delta valence were smaller than absolute emotions, around 1.2 s across both databases, whilst best delays for absolute emotions vary for arousal and valence as well as for different corpora.
It is seen from Figure 5 that without delay compensation, delta arousal and valence prediction achieve considerably higher CCCs than their absolute counterparts on RECOLA. This shows encouraging results for predicting emotion changes. On SEMAINE, however, delta arousal has similar CCCs to that of absolute, while delta valence has much lower CCCs than absolute valence. This may be due to the relatively low inter-rater agreement of delta emotion ground truth, which misled the regression model. With delay compensation, on one hand, consistent delays for delta arousal and delta valence can be observed on the two databases, around 1.2 s. This was expected, because raters tend to notice changes. On the other hand, delays for absolute emotions vary for arousal and valence as well as for different databases. The delays for absolute affect dimensions yielded similar results as previous studies on RECOLA (Huang et al., 2015a) and SEMAINE (Nicolle et al., 2012; Mariooryad and Busso, 2014).
Even though studies (Yannakakis and Martínez, 2015a) have shown that instructing annotators to rank provides higher inter-rater reliability as well as effort-saving, to the best of our knowledge, there is no study that has aimed to quantify delays for emotion changes.
Overall, the feature window and annotation delay have been reported to have a huge impact on predicting emotion change. An interesting finding shown in Table 2 is that, unlike continuous emotion prediction systems where the optimal values for the two factors tend to vary across datasets, cross-corpus consistency was found for both, i.e., a 2 s feature window and 1.2 s delay were used for both delta arousal and delta valence across RECOLA and SEMAINE. This is potentially interesting to the affective computing context, since datasets tend to vary significantly.
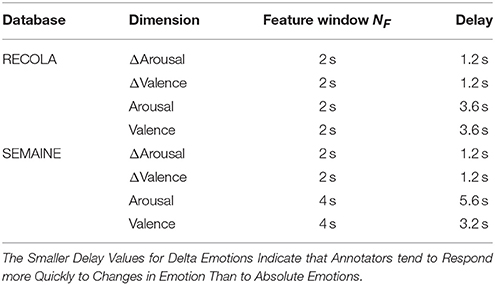
Table 2. Summary of feature window size and annotation delay compensation for absolute and delta emotions.
With the best feature window sizes in Figure 4 and delay values estimated in Figure 5, we further conducted experiments comparing absolute and delta emotion prediction using SVR and RVM.
Emotion Change Prediction Using SVR, RVM, and OA RVM
The aim of this section is to investigate whether predicting emotion change may be possible using three regression approaches, namely SVR, RVM, and OA RVM. The performance of absolute emotion prediction was also presented herein as a reference (i.e., the goal here was not to outperform absolute emotion prediction but to learn how well delta emotion prediction can be achieved), since there is no existing benchmark for emotion change prediction. Comparison of this kind has not been conducted before, in part because the ground truths are different for absolute and delta emotion prediction. However, to ensure reasonable comparability between delta emotion prediction and conventional emotion prediction, we have empirically selected the feature window sizes and delay values that provide approximately the best performances for arousal and valence for both two tasks (absolute vs. delta) on both two databases (RECOLA and SEMAINE) in Table 2.
Baseline performances for absolute and delta emotion prediction using SVR and RVM are shown in Table 35. It is suggested that the relative RMSEs for delta emotion prediction is slightly larger than that for absolute emotion on RECOLA, which also holds true for arousal on SEMAINE when SVR was used. On the other hand, when RVM was used, predicting delta emotions attained marginally lower relative RMSEs. The comparisons of relative RMSEs imply roughly similar error ranges for predicting both absolute and delta emotions. In addition to this, RVM achieved better performances for delta emotion prediction than SVR, whilst there is not an evident impact on absolute emotion prediction.

Table 3. Comparison of absolute and delta emotion prediction using SVR, RVM, and OA-RVM on RECOLA and SEMAINE databases.
On RECOLA, when predicting absolute emotions, SVR provided better arousal prediction, whilst RVM performed better in terms of valence prediction. Using both approaches, delta emotion prediction is in general slightly more challenging than absolute emotion prediction, except that employing SVR worked better for predicting delta valence than predicting absolute valence. This was the same on SEMAINE. However, CCCs for predicting absolute and delta dimensions were similar on RECOLA but differed notably on SEMAINE.
We suspected that the performance degradation for delta emotion on SEMAINE might be due to the low inter-rater agreement of delta emotion ground truth in SEMAINE, because it may undermine regression models, as shown in Figure 2. However, experimental results using only annotations from one individual rater did not narrow the gap. In section Delta Emotion Ground Truth, we attributed the low inter-rater reliability of delta emotion ground truth to the large proportion of non-change between adjacent frames observed on SEMAINE. This may also be associated with the gaps in performances for predicting absolute and delta emotions. Accordingly, further experiments for analyzing percentages of non-changes in the first-order differences of absolute ratings for RECOLA and SEMAINE were conducted but not shown due to the space limit. Briefly, the experiments confirmed our hypothesis that a large proportion of non-change frames complicates delta emotion prediction and causes the performance gaps on the SEMAINE dataset, because as non-change frames were gradually dropped, the gaps narrowed (Huang, 2018).
Furthermore, the OA-RVM framework improves system performances for all the tasks on both datasets, suggesting that predicting delta emotions even provides slightly higher performances than predicting absolute emotions on RECOLA.
The result that the newly developed delta emotion prediction system can produce higher CCC than absolute emotion prediction taken alone is significant, since the field of absolute emotion prediction has been researched for many years. Moreover, the proposed delta emotion prediction is able to explicitly predict the extent of emotion change.
However, delta systems had poorer CCC than the absolute systems for both arousal and valence on SEMAINE. Moreover, there are large gaps between absolute and delta systems in SEMAINE, and we speculate that the most likely reason behind this is once again the large proportion of non-changes frame in the first-order differences of the absolute ground truth on SEMAINE. Despite these results, Table 3 partly answers our question of how well we can predict the extent of emotion changes, in comparison to absolute emotion prediction.
In terms of the reference performances of absolute emotion prediction, OA-RVM outperformed SVR and RVM on both datasets. The OA-RVM performances in ρc were higher than the audio-only results but somewhat lower than the multimodal results in Huang et al. (2015a) on the RECOLA dataset. For SEMAINE, the OA-RVM performances were much lower in Pearson's correlation ρ when compared with the winners of the AVEC 2012 challenge (Nicolle et al., 2012), who achieve 0.65 (arousal) and 0.33 (valence) on development set, 0.61(arousal), and 0.34 (valence) on test set. However, it is worth noting that we are comparing our audio-only system with the multimodal systems of Nicolle et al. (2012). The audio-only results in Nicolle et al. (2012) were 0.45 for arousal and −0.06 for valence on the development set and not reported on the test set, compared with which we achieved similar performance for arousal and much improved performance for valence.
However, it is worth noting that the focus of this work is not to improve absolute emotion prediction but to evaluate how well emotion change can be automatically predicted. It is acknowledged that the absolute and delta predicting results are not strictly directly comparable, because each is evaluated on a different ground truth, i.e., absolute (original) ground truth and regression delta ground truth. However, the comparison signals the promise of delta emotion prediction.
Limitations
Some limitations to the experiments in this section should be noted. Firstly, since the aim of the section, instead of demonstrating state-of-the-art performance, was to investigate delta emotion prediction systems and to invoke comparisons with absolute emotion prediction systems, the SVR and RVM parameter sweeps were performed over the test set, as indicated in Table 1. Although this might result in slightly optimistic results for both absolute and delta emotion prediction, the comparisons between these two tasks are still fair because we optimized the two systems in the same ways. Secondly, another concern was deriving delta emotion ground truth from the absolute ratings, as raised in Nicolaou et al. (2011). Although the delta emotion ground truth achieved acceptable inter-rater agreement, it should instead be ideally annotated in a relative manner for preserving more characteristics of emotion dynamics, as discussed in Nicolaou et al. (2011) and Oveneke et al. (2017). However, where annotations of emotion changes are not available, and re-annotating data in a relative way could be labor-demanding and time-consuming, deriving relative labels from the absolutes as we proposed herein could be a reasonable compromise. The matter of annotating specifically for emotion change is an interesting research challenge which definitely deserves some deeper investigation, but this is beyond the scope of this paper. Also, more work on additional widely used datasets may be needed to further validate and extend the investigations of emotion change prediction.
Conclusions
This article has investigated emotion changes, from an automatic system design perspective, by looking at continuous Emotion Change Prediction (ECP). We firstly investigated how to construct delta emotion ground truth from continuous absolute emotion ratings by calculating the regression deltas from the absolute ratings, while trading off their inter-rater reliability and information loss for two databases. This approach yielded considerably higher inter-rater reliability than first-order difference deltas used in previous research, and is more appropriate for deriving annotations for emotion change research. These findings are applicable to non-speech based affective computing research.
Moreover, to the best of our knowledge, we investigated the first system design for continuously predicting the extent of emotion change from speech, including appropriate features, delay compensation and feature window sizes. An analysis of annotation delays suggested that evaluators respond quickly to changes in emotions, which was consistent across databases.
Comparison of the best system configurations for arousal and valence using the OA-RVM framework showed a very interesting result that we can achieve higher CCCs for emotion change prediction than conventional (absolute) emotion prediction on the RECOLA database (0.74 vs. 0.71 for arousal and 0.41 vs. 0.37 for valence). This presents the research community with an exciting new perspective on the problem and strongly suggests the promise of investigating emotion changes further.
Overall, we showed in this study how to build an automatic system that predicts changes in emotion, what are the important factors to be considered during development, and how well the newly proposed task can be achieved in comparison with conventional absolute emotion prediction. These aspects potentially offer practical guidelines for emotion change prediction. More broadly, the question of whether it is interesting to build systems that predict emotion change has been answered in the affirmative, at least from a qualitative point of view.
One limitation of this work was employing delta emotion ground truth constructed from absolute ratings. Since the absolute ratings are originally annotated in an absolute manner, directly converting them to delta emotion ground truth suffers from low inter-rater reliability, especially on the SEMAINE database. Despite this, ECP is worth more investigation and perhaps may be further improved with annotation directly produced in delta manner. After all, literature has shown higher inter-rater reliability for relative emotions.
Indeed, emotion change research can be studied further and possibilities for investigating emotion changes are definitely not confined to ECP studied herein or ECD (Emotion Change Detection) and ECA (Emotion Change Assessment) mentioned in section Overview and Possibilities for Emotion Change Systems. Yet, there are still some inevitable issues. One of them is the unavailability of emotion change databases, but this can be alleviated by constructing suitable databases from the existing ones. The other issue is that definition and description for emotion changes are not as well-founded in psychology literature, which leads to rather empirical-oriented studies in practice.
Author Contributions
ZH did the literature survey, conducted experiments, and engaged in paper writing. JE advised ideas, provided insightful analysis, offered inspiring guidance, and engaged in paper writing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was partly funded by the US Army International Technology Center (Pacific) under Contract No. FA5209-17-P-0154.
Footnotes
2. ^https://diuf.unifr.ch/diva/recola/download.html
3. ^http://www.miketipping.com/downloads.htm
4. ^SparseBayes MATLAB Toolbox.
5. ^Note that the ground truths for absolute emotion prediction and delta emotion prediction are different.
References
Böck, R., and Siegert, I. (2015). “Recognising emotional evolution from speech,” in ERM4CT'15 (Seattle, WA), 13–18.
Bone, D., Lee, C., C., and Narayanan, S. (2014). Robust unsupervised arousal rating: A rule-based framework withknowledge-inspired vocal features. IEEE Trans. Affect. Comput. 5, 201–213. doi: 10.1109/TAFFC.2014.2326393
Celiktutan, O., and Gunes, H. (2016). Automatic prediction of impressions in time and across varying context: personality, attractiveness and likeability in IEEE Trans. Affect. Comput. 8, 29–42. doi: 10.1109/TAFFC.2015.2513401
Chang, C.-C., and Lin, C. J. (2011). “LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2, 1–27. doi: 10.1145/1961189.1961199
Chen, S., and Epps, J. (2013). Automatic classification of eye activity for cognitive load measurement with emotion interference. Comput. Methods Programs Biomed. 110, 111–124. doi: 10.1016/j.cmpb.2012.10.021
Choi, B. H., Pos, A. E., and Magnusson, M. S. (2015). Emotional change process in resolving self-criticism during experiential treatment of depression. Psychother. Res. 26, 484–499. doi: 10.1080/10503307.2015.1041433
Cowie, R., and Cornelius, R. R. (2003). Describing the emotional states that are expressed in speech. Speech Commun. 40, 5–32. doi: 10.1016/S0167-6393(02)00071-7
Cowie, R., and Douglas-Cowie, E. (2000). “FEELTRACE': An instrument for recording perceived emotion in real time,” in ISCA Tutorial and Research Workshop (ITRW) on Speech and Emotion (Belfast), 1–6.
Cowie, R., McKeown, G., and Douglas-Cowie, E. (2012). Tracing emotion. Int. J. Synth. Emot. 3, 1–17. doi: 10.4018/jse.2012010101
Cowie, R., Sawey, M., Doherty, C., Jaimovich, J., Fyans, C., and Stapleton, P. (2013). “Gtrace: general trace program compatible with emotionML,” in 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction (ACII) (Geneva), 709–710.
Cronbach, L. (1951). Coefficient alpha and the internal structure of tests. Psychometrika 16, 297–334. doi: 10.1007/BF02310555
Danieli, M., and Riccardi, G. (2015). ”Emotion unfolding and affective scenes: a case study in spoken conversations,“ in Proceedings of the International Workshop on Emotion Representations and Modelling for Companion Technologies (Seattle, WA), 5–11.
Davidson, R. J. (1998). Affective style and affective disorders: perspectives from affective neuroscience. Cogn. Emot. 12, 307–330. doi: 10.1080/026999398379628
Davidson, R. J. (2015). Comment: affective chronometry has come of age. Emot. Rev. 7, 368–370. doi: 10.1177/1754073915590844
Devillers, L., Rosset, S., Duplessis, G. D., Sehili, M. A., Bechade, L., Delaborde, A., et al. (2015). “Multimodal data collection of human-robot humorous interactions in the joker project,” in ACII (Xi'an), 348–354.
Eyben, F., Scherer, K., Schuller, B., Sundberg, J., André, E., Busso, C., et al. (2016). The Geneva Minimalistic Acoustic Parameter Set (GeMAPS) for voice research and affective computing. IEEE Trans. Affect. Comput. 7, 190–202. doi: 10.1109/TAFFC.2015.2457417
Fan, Y., Xu, M., Wu, Z., and Cai, L. (2014). “Automatic emotion variation detection in continuous speech,” in APSIPA (Siem Reap).
Filipowicz, A., Barsade, S., and Melwani, S. (2011). Understanding emotional transitions: the interpersonal consequences of changing emotions in negotiations. J. Pers. Soc. Psychol. 101, 541–556. doi: 10.1037/a0023545
Fontaine, J. R. J., Scherer, K., R., Roesch, E. B, and Ellsworth, P. C. (2007). The world of emotions is not two-dimensional. Psychol. Sci. 18, 1050–1057. doi: 10.1111/j.1467-9280.2007.02024.x
Grimm, M., and Kroschel, K. (Eds). (2007). “Emotion estimation in speech using a 3D emotion space concept,” in Robust Speech Rcognition Underst (Vienna: IntechOpen), 281–300.
Grimm, M., Kroschel, K., and Narayanan, S. (2007). “Support vector regression for automatic recognition of spontaneous emotions in speech,” in IEEE International Conference on Acoustics, Speech and Signal Processing, 4, 1085–1088.
Gross, J. (1998). The emerging field of emotion regulation: an integrative review. Rev. Gen. Psychol. 2, 271–299. doi: 10.1037/1089-2680.2.3.271
Gross, J. J. (2001). Emotion regulation in adulthood: timing is everything. Curr. Dir. Psychol. Sci. 10, 214–219. doi: 10.1111/1467-8721.00152
Gunes, H., Nicolaou, M., A., and Pantic, M. (2011). “Continuous analysis of affect from voice and face,” in Computer Analysis of Human Behavior, eds A. A. Salah and T. Gevers (London: Springer), 255–291.
Gunes, H., and Schuller, B. (2013). Categorical and dimensional affect analysis in continuous input: Current trends and future directions. Image Vis. Comput. 31, 120–136. doi: 10.1016/j.imavis.2012.06.016
Hakim, A., Marsland, S., and Guesgen, H. W. (2013). “Computational analysis of emotion dynamics,” in Human Association Conference Affective Computing and Intelligent Interaction (Geneva), 185–190.
Han, W., and Eyben, F. (2012). “Preserving actual dynamic trend of emotion in dimensional speech emotion recognition categories and subject descriptors,” in Proceedings of the 14th ACM International Conference on Multimodal Interaction (Santa Monica, CA), 523–528.
Han, W., Li, H., Ma, L., Zhang, X., and Schuller, B. (2012). “A ranking-based emotion annotation scheme and real-life speech database,“ in the 4th International Workshop on Emotion, Sentiment $ Social Signals (Istanbul), 67–71.
Hareli, S., David, S., and Hess, U. (2015). The role of emotion transition for the perception of social dominance and affiliation. Cogn. Emot. 30, 1260–1270 doi: 10.1080/02699931.2015.1056107
Houben, M., Van Den Noortgate, W., and Kuppens, P. (2015). The relation between short-term emotion dynamics and psychological well-being: a meta-analysis. Psychol. Bull. 141, 901–930. doi: 10.1037/a0038822
Huang, Z. (2018). Speech Based Emotion and Emotion Change in Continuous Automatic Systems. PhD Thesis, UNSW Australia.
Huang, Z., Dang, T., Cummins, N., Stasak, B., Phu, L., Sethu, V., et al. (2015a). “An investigation of annotation delay compensation and output-associative fusion for multimodal continuous emotion prediction,” in Proceedings of the 5th International Workshop on AVEC, ACM MM (Brisbane).
Huang, Z., and Epps, J. (2016a). “Detecting the instant of emotion change from speech using a martingale framework,“ in ICASSP (Shanghai).
Huang, Z., and Epps, J. (2016b). “Time to embrace emotion change: selecting emotionally salient segments for speech-based emotion prediction,” in 16th Australasian International Conference on Speech Science and Technology (SST2016) (Parramatta, NSW).
Huang, Z., and Epps, J. (2017). “An investigation of emotion dynamics and kalman filtering for speech-based emotion prediction,” in INTERSPEECH (Stockholm), 3301–3305.
Huang, Z., Epps, J., and Ambikairajah, E. (2015b). “An investigation of emotion change detection from speech,” in INTERSPEECH (Dresden).
Hudlicka, E. (2008). “What are we modeling when we model emotion?,” in Proceedings of the AAAI Spring Symposium on “Emotion, Personality and Social Behavior (Standford, CA).
Jin, X., and Wang, Z. (2005). ”An emotion space model for recognition of emotions in spoken chinese,“ in Proceedings of International Conference on Affective Computing and Intelligent Interaction (ACII) (Beijing), 397–402.
Katsimerou, C., Heynderickx, I., and Redi, J. (2015). Predicting mood from punctual emotion annotations on videos. IEEE Trans. Affect. Comput. 6, 179–192. doi: 10.1109/TAFFC.2015.2397454
Kim, Y., and Mower Provost, E. (2014). “Say cheese vs. smile: reducing speech-related variability for facial emotion recognition,” in Proceedings of the ACM International Conference on Multimedia - MM'14 (Orlando, FL), 27–36.
Kim, Y., and Provost, E. M. (2013). “Emotion classification via utterance-level dynamics: a pattern-based approach to characterizing affective expressions,” in ICASSP (Vancouver, BC), 3677–3681.
Kim, Y., and Provost, E. (2016). “Emotion spotting: discovering regions of evidence in audio-visual emotion expressions,” in Proceedings of the 18th ACM International Conference on Multimodal Interaction. ACM (Tokyo).
Kuppens, P. (2015). It's about time: a special section on affect dynamics. Emot. Rev. 7, 297–300. doi: 10.1177/1754073915590947
Kuppens, P., Allen, N. B., and Sheeber, L. B. (2010). Emotional inertia and psychological maladjustment. Psychol. Sci. 21, 984–991. doi: 10.1177/0956797610372634
Kuppens, P., and Verduyn, P. (2015). Looking at emotion regulation through the window of emotion dynamics. Psychol. Inq. 26, 72–79. doi: 10.1080/1047840X.2015.960505
Lade, P., Balasubramanian, V., N, Venkateswara, H., and Panchanathan, S. (2013). “Detection of changes in human affect dimensions using an adaptive temporal topic model,” in 2013 IEEE International Conference on Multimedia and Expo (ICME) (San Jose, CA), 1–6.
Leon, E., Clarke, G., Leon, E., Clarke, G., Callaghan, V., and Sepulveda, F. (2004). Real-time detection of emotional changes for inhabited environments. Comput. Graph. 28, 635–642. doi: 10.1016/j.cag.2004.06.002
Mariooryad, S., and Busso, C. (2014). Correcting time-continuous emotional labels by modeling the reaction lag of evaluators. IEEE Trans. Affect. Comput. 6, 97–108. doi: 10.1109/TAFFC.2014.2334294
Martinez, H. P., Yannakakis, G., N., and Hallam, J. (2014). Don't classify ratings of affect; rank them!. IEEE Trans. Affect. Comput. 5, 314–326. doi: 10.1109/TAFFC.2014.2352268
McKeown, G., Valstar, M., Cowie, R., Pantic, M., and Schröder, M. (2012). The SEMAINE database: annotated multimodal records of emotionally colored conversations between a person and a limited agent. IEEE Trans. Affect. Comput. 3, 5–17. doi: 10.1109/T-AFFC.2011.20
Mesquita, B., and Boiger, M. (2014). Emotions in context: a sociodynamic model of emotions. Emot. Rev. 6, 298–302. doi: 10.1177/1754073914534480
Metallinou, A., Katsamanis, A., Wang, Y., and Narayanan, S. (2011). “Tracking changes in continuous emotion states using body language and prosodic cues,” in ICASSP (Prague), 2288–2291.
Metallinou, A., and Narayanan, S. (2013). “Annotation and processing of continuous emotional attributes: Challenges and opportunities,” in 10th IEEE Int. Conf. Work. Autom. Face Gesture Recognit (Shanghai), 1–8.
Metallinou, A., Yang, Z., Lee, C., Busso, C., Carnicke, S., and Narayanan, S. (2015). The USC CreativeIT database of multimodal dyadic interactions: from speech and full body motion capture to continuous emotional annotations. Lang. Resour. Eval 50, 497–521. doi: 10.1007/s10579-015-9300-0
Mower, E., Metallinou, A., Lee, C. C., Kazemzadeh, A., Busso, C., Lee, S., et al. (2009). “Interpreting ambiguous emotional expressions,” in The 3rd International Conference on Affective Computing and Intelligent Interaction (Amsterdam), 1–8.
Mower, E., and Narayanan, S. (2011). “A hierarchical static-dynamic framework for emotion classification,” in ICASSP (Prague), 2372–2375.
Nicolaou, M. A., Member, S., Gunes, H., Pantic, M., and Member, S. (2011). Continuous prediction of spontaneous affect from multiple cues and modalities in valence – arousal space. IEEE Trans. Affect. Comput. 2, 92–105. doi: 10.1109/T-AFFC.2011.9
Nicolaou, M. A., Gunes, H., and Pantic, M. (2012). Output-associative RVM regression for dimensional and continuous emotion prediction. Image Vis. Comput. 30, 186–196. doi: 10.1016/j.imavis.2011.12.005
Nicolle, J., Rapp, V., Bailly, K., Prevost, L., and Chetouani, M. (2012). “Robust continuous prediction of human emotions using multiscale dynamic cues,” in Proceedings of the 14th ACM international conference on Multimodal Interaction (Santa Monica, CA), 501–508.
Niedenthal, P. M., Brauer, M., Halberstadt, J., B., and Innes-Ker, Å. H (2001). When did her smile drop? Facial mimicry and the influences of emotional state on the detection of change in emotional expression. Cogn. Emot. 15, 853–864. doi: 10.1080/02699930143000194
Oveneke, M., Gonzalez, I., Enescu, V., Jiang, D., and Sahli, H. (2017). Leveraging the bayesian filtering paradigm for vision-based facial affective state estimation. IEEE Trans. Affect. Comput. 14, 1. doi: 10.1109/TAFFC.2016.2643661
Pao, T., Yeh, J., and Tsai, Y. (2010). “Recognition and analysis of emotion transition in mandarin speech signal,” in 2010 IEEE International Conference on Systems Man and Cybernetics (SMC) (Istanbul), 3326–3332.
Parthasarathy, S., Cowie, R., and Busso, C. (2016). Using agreement on direction of change to build rank-based emotion classifiers in IEEE/ACM Trans. Audio, Speech Lang. Process. 24, 2108–2121. doi: 10.1109/TASLP.2016.2593944
Ringeval, F., Eyben, F., Kroupi, E., Yuce, A., Thiran, J. P., Ebrahimi, T., et al. (2015a). Prediction of asynchronous dimensional emotion ratings from audiovisual and physiological data. Pattern Recognit. Lett. 66, 22–30. doi: 10.1016/j.patrec.2014.11.007
Ringeval, F., Schuller, B., Jaiswal, S., Valstar, M., Marchi, E., Lalanne, D., et al. (2015b). “AV+EC 2015 – The first affect recognition challenge bridging across audio, video, and physiological data,” in Proceedings of the 5th International Workshop on AVEC, ACM MM (Brisbane, QLD), 3–8.
Ringeval, F., Sonderegger, A., Sauser, J., and Lalanne, D. (2013). “Introducing the RECOLA multimodal corpus of remote collaborative and affective interactions,” in 10th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG) (Shanghai), 1–8.
Ritchie, T., Skowronski, J., J., Hartnett, J., Wells, B., and Walker, W. R. (2009). The fading affect bias in the context of emotion activation level, mood, and personal theories of emotion change. Memory 17, 428–444. doi: 10.1080/09658210902791665
Scherer, K. R. (2005). What are emotions? And how can they be measured?. Soc. Sci. Inf. 44, 695–729. doi: 10.1177/0539018405058216
Schuller, B., and Rigoll, G. (2006). “Timing levels in segment-based speech emotion recognition,” in INTERSPEECH (Pittsburgh, PA).
Schuller, B., Valstar, M., Eyben, F., McKeown, G., Cowie, R., and Pantic, M. (2011). “AVEC 2011 - The first international audio/visual emotion challenge,” in Affective Computing and Intelligent Interaction (Memphis, TN), 415–424.
Sethu, V., Epps, J., and Ambikairajah, E. (2015). Speech based emotion recognition,“ in Speech and Audio Processing for Coding, Enhancement and Recognition (New York, NY: Springer). 197–228.
Siegert, I., Böck, R., and Wendemuth, A. (2014). Inter-rater reliability for emotion annotation in human-computer interaction: comparison and methodological improvements. J. Multimodal User Inter. 8, 17–28. doi: 10.1007/s12193-013-0129-9
Sneddon, I., McRorie, M., McKeown, G., and Hanratty, J. (2012). The belfast induced natural emotion database. IEEE Trans. Affect. Comput. 3, 32–41. doi: 10.1109/T-AFFC.2011.26
Steidl, S., Levit, M., Batliner, A., Noth, E., and Niemann, H. (2005). “Of all things the measure is Man' automatic classification of emotions and inter-labeler consistency,” in ICASSP (Philadelphia, PA), 317–320.
Stolar, M. N., Lech, M., Sheeber, L., B., Burnett, I. S., and Allen, N. B. (2013). Introducing emotions to the modeling of intra-and inter-personal influences in parent-adolescent conversations. IEEE Trans. Affect. Comput. 4, 372–385. doi: 10.1109/TAFFC.2013.2297099
Tipping, M. E. (2001). Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 1, 211–244.
Waugh, C. E., Shing, E., Z., and Avery, B. M. (2015). Temporal dynamics of emotional processing in the brain. Emot. Rev. 7, 323–329. doi: 10.1177/1754073915590615
Wei, W., Wu, C., Lin, J., and Li, H. (2014). Exploiting psychological factors for interaction style recognition in spoken conversation. IEEE/ACM Trans. Audio Speech Lang. Process. 22, 659–671. doi: 10.1109/TASLP.2014.2300339
Xu, L., and Xu, M. (2009). “Shift window based framework for emotional change detection of speech,” in 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery (Tianjin), 458–462.
Yang, Y., and Chen, H. (2011). Ranking-based emotion recognition for music organization and retrieval,” in IEEE Trans. Audio. Speech. Lang. Process. 19, 762–774. doi: 10.1109/TASL.2010.2064164
Yannakakis, G. N., and Martínez, H., P. (2015a). “Grounding truth via ordinal annotation,” in ACII (Xi'an), 574–580.
Yannakakis, G. N., and Martínez, H., P. (2015b). Ratings are overrated !. Front. ICT 2:13. doi: 10.3389/fict.2015.00013
Keywords: emotion change, continuous emotion prediction, emotion change prediction, speech based affective computing, emotion change ground truth, emotion dynamics, relevance vector machine, inter-rater agreement
Citation: Huang Z and Epps J (2018) Prediction of Emotion Change From Speech. Front. ICT 5:11. doi: 10.3389/fict.2018.00011
Received: 06 March 2018; Accepted: 02 May 2018;
Published: 05 June 2018.
Edited by:
Mohamed Chetouani, Université Pierre et Marie Curie, FranceReviewed by:
Eric Bolo, Batvoice Technologies, FranceJiri Pribil, Institute of Measurement Science, Slovak Academy of Sciences, Slovakia
Copyright © 2018 Huang and Epps. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhaocheng Huang, emhhb2NoZW5nLmh1YW5nQHVuc3cuZWR1LmF1
Julien Epps, ai5lcHBzQHVuc3cuZWR1LmF1
 Zhaocheng Huang
Zhaocheng Huang Julien Epps
Julien Epps