Evaluation of work distribution schedulers for heterogeneous architectures and scientific applications

This article explores and evaluates variants of state-of-the-art work distribution schemes adapted for scientific applications running on hybrid systems. A hybrid implementation (multi-GPU and multi-CPU) of the NASA Parallel Benchmarks - MutiZone (NPB-MZ) benchmarks is described to study the different elements that condition the execution of this suite of applications when parallelism is spread over a set of computing units (CUs) of different computational power (e.g., GPUs and CPUs). This article studies the influence of the work distribution schemes on the data placement across the devices and the host, which in turn determine the communications between the CUs, and evaluates how the schedulers are affected by the relationship between data placement and communications. We show that only the schedulers aware of the different computational power of the CUs and minimize communications are able to achieve an appropriate work balance and high performance levels. Only then does the combination of GPUs and CPUs result in an effective parallel implementation that boosts the performance of a non-hybrid multi-GPU implementation. The article describes and evaluates the schedulers static-pcf, Guided, and Clustered Guided to solve the previously mentioned limitations that appear in hybrid systems. We compare them against state-of-the-art static and memorizing dynamic schedulers. Finally, on a system with an AMD EPYC 7742 at 2.250GHz (64 cores, 2 threads per core, 128 threads) and two AMD Radeon Instinct MI50 GPUs with 32GB, we have observed that hybrid executions speed up from 1.1× up to 3.5× with respect to a non-hybrid GPU implementation.

1 Introduction

Hybrid computing systems have become ubiquitous in the high-performance computing (HPC) domain. These systems are composed of computational nodes where CPUs and accelerators coexist, defining a hybrid architecture. The most widely accepted solution uses nodes that combine CPUs and GPUs, and given the impressive computing power delivered by these architectures, significant efforts have been devoted in many computing domains for port applications to this type of HPC systems. For instance, machine learning, bioinformatics, scientific computing, and others, have clear examples of representative applications, such as TensorFlow (Abadi et al., 2016), Caffe (NVIDIA, 2020), Smith-Waterman (Manavski and Valle, 2008), and Alya (Giuntoli et al., 2019), have recently been developed to support GPU-based systems.

Current technologies for programming hybrid systems are based on language extensions to general-purpose programming languages such as C/C++ and Fortran. Nvidia CUDA, OpenCL, and OpenACC are reference programming models for heterogeneous computing that follow this approach. In general, all these programming frameworks focus on the essential actions for porting an application to a hybrid architecture. This includes memory allocation, data transfers between the host and devices that now operate within a shared distributed memory address space, and the specification of computations to be offloaded to devices, as well as those to be executed by the host.

A hybrid parallelization simultaneously exploits fine and coarse levels of parallelism. This parallelism, orchestrated from one or more CPUs (e.g., one CPU to control one GPU), requires defining memory allocation strategies for each device. It also involves work distribution schemes that are aware of the different natures of the host and devices to balance work execution, along with communication phases whenever exchanging values between the host and devices residing in different address spaces is necessary.

Current programming frameworks include almost no support for enabling such parallel strategies. As a result, programmers have to manually code the exploitation of the two levels of parallelism. This is usually implemented by mixing two programming models (e.g., OpenMP and CUDA). However, the available work distribution schemes do not provide the necessary support and adaptability for hybrid systems.

Moreover, communications always depend on the memory footprint induced by the work distribution schemes, as communication patterns arise according to where the data has been placed. A trade-off exists between the work distribution schemes and their impact on communication phases. Therefore, work distribution is conditioned not only by the need for balanced execution but also by the necessity to minimize communications between the host and devices. All of this has been observed in previous work in which specific work distribution mechanisms have been described for hybrid architectures (Belviranli et al., 2013; Choi et al., 2013; Mittal and Vetter, 2015; Zhong et al., 2012).

The challenge of simultaneously balancing both CPUs and GPUs in a hybrid execution is essentially limited by the missing support to deploy an appropriate work distribution. This article addresses this challenge and builds from the previous work developed by González and Morancho (2021a,b, 2023, 2024). The main contributions of this paper are that

• the study of different state-of-the-art work distribution schemes and the proposal of variants of the static and dynamic task schedulers, based on a performance conversion factor (pcf; the Static-pcf scheduler; scheduler Augonnet et al., 2011; Beaumont et al., 2019) and based on task execution times collected at runtime (the Guided and Clustered Guided schedulers Duran et al., 2005).

• the evaluation of the proposed schedulers is done using the NPB-MZ benchmark suite, implemented to execute a hybrid and multilevel parallel strategy mixing OpenMP and HIP (C++ Heterogeneous-Compute Interface for Portability). In particular, the article studies the impact of the work distribution in both the communication and computation phases of this benchmark suite.

On a system composed by an AMD EPYC 7742 at 2.250 GHz (64 cores, 2 threads per core, 128 threads) and 2 AMD Radeon Instinct MI50 GPUs with 32GB, our hybrid executions speed up from 1.1 × up to 3.5 × with respect to a pure GPU implementation, depending on the number of activated CPUs and GPUs.

This article is organized as follows: Section 2 describes the NPB-MZ benchmark suite used to perform the study and evaluation of the new proposed scheduler for hybrid systems. Section 3 defines the concept of compute unit (CU). Section 4 describes the implementation of the schedulers. Section 5 evaluates our proposal. Section 6 discusses related work, and finally, Section 7 presents our conclusions.

2 Benchmark characterization

2.1 NAS Parallel Benchmarks

The NAS Parallel Benchmarks suite (NPB; Bailey et al., 1991) has been used to evaluate parallel computer systems since 1991. The suite includes five kernels and three pseudo-applications. Because the kernels are not suitable for evaluating the performance of highly parallel systems, we focus solely on the three pseudo-applications. These applications are designed to represent a broad range of computational fluid dynamics problems and can adapt to the increasing memory capacities of the new parallel systems.

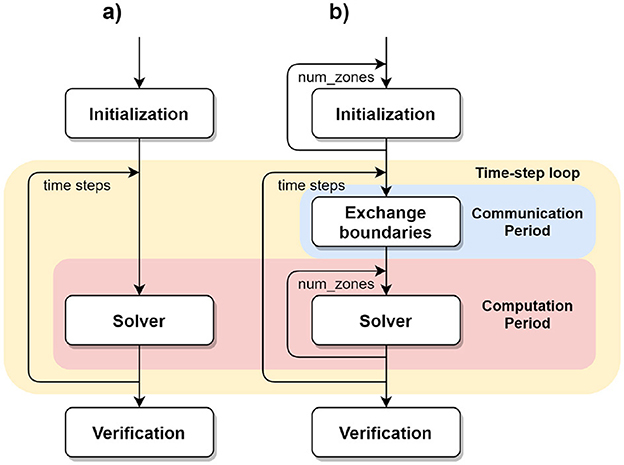
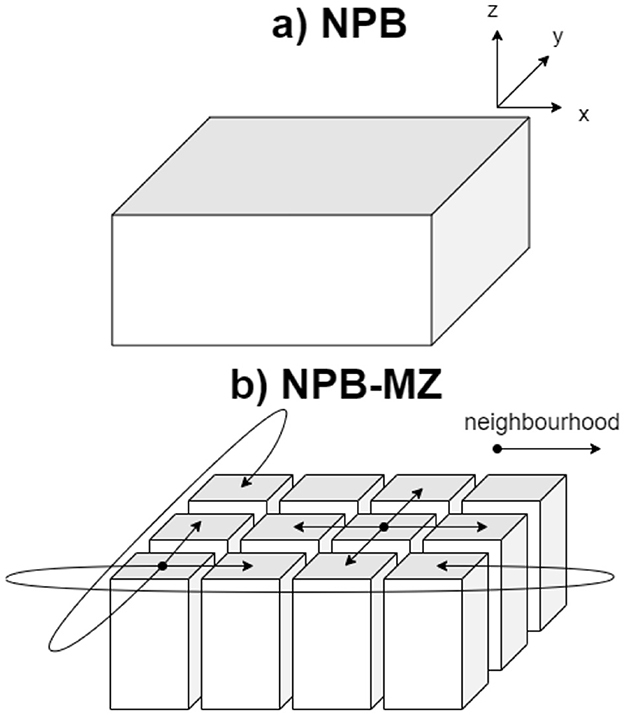
Each of the three applications features a main loop known as the time-step loop, which executes a fixed number of iterations. During each iteration, a three-dimensional (3D) volume is traversed to compute discrete solutions to the Navier–Stokes equation (Figure 1A). However, the applications differ in their equation solvers: block tridiagonal (BT), lower-upper Gauss-Seidel (LU), and scalar pentadiagonal (SP). Each application is named after its corresponding solver.

Figure 1

Figure 1. Flow diagrams of (A) NPB and (B) NPB-MZ.

The multizone NPB suite (NPB-MZ; der Wijngaart and Jin, 2003) re-implements the NPB to expose a coarse level of parallelism. By dividing the 3D volume into tiles along both the x- and y-dimensions (Figure 2), a grid of prisms, referred to as zones, is formed. While these zones can be processed in parallel, the values of their lateral faces depend on the values of the lateral faces of its neighbor zones. As a result, an exchange-boundaries procedure is required between iterations of the time-step loop to update the lateral faces of all zones (Figures 1B, 3A1). Thus, each time-step iteration consists of two phases: the communication period, for transferring zone faces, and the computation period, for updating zones.

Figure 2

Figure 2. (A) Unizone (NPB) vs. (B) multizone (NPB-MZ) three-dimensional volumes.

Figure 3

Figure 3. Code snippets of (A) interzone parallelism in the computation period and (B) intrazone parallelism in the computation period. (A1) Fortran 90 code skeleton of NPB-MZ's time-step loop. Its body traverses the zones to apply the computational phases to all zones. (A2) OpenMP and C++ implementation that distributes the zones to the GPUs. An OpenMP parallel region is defined, and one thread controls one GPU, executing the body of the parallel region. The while loop invokes the runtime system to acquire work. (B1) C++ code skeleton of the Pth computation phase. Several loop nests traverse the three-dimensional volume that represents the zone. (B2) C++ implementation of the Kth loop nest of the Pth computation phase as a CUDA kernel (Kernel Definition). Each kernel operates over a single zone.

Table 1 summarizes the input classes (B, C, …) of the NPB-MZ, detailing the overall 3D volume size (in terms of points and memory usage), as well as specific information for each application, including the number of zones, zone size, and the number of time steps.

Table 1

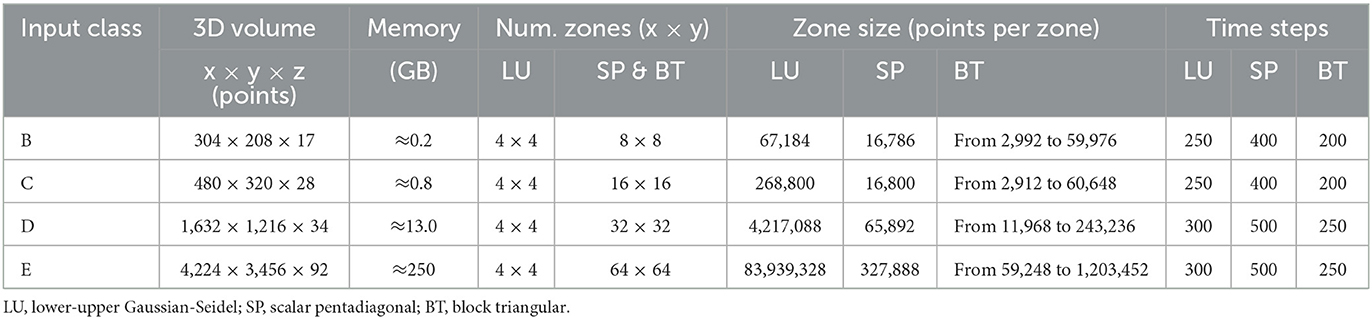
Table 1. Input classes of NPB-MZ: overall size (number of points and memory usage) and, for each application, number of zones, zone size, and number of time steps.

Notice that each application exposes the multizone parallelism in distinct ways:

• LU: The number of zones is 16, independently on the input class. Zone sizes are uniform.

• SP: The larger the input class, the larger the number of zones. Like LU, the zone sizes are uniform; however the SP zones are smaller than the LU zones.

• BT: Like SP, the larger the input class, the larger the number of zones. However, the zone sizes are not uniform; for each input class, the ratio between the size of the largest zone and the size of the smallest zone is about 20 × .

2.2 Sources of parallelism

The NPB-MZ suite exposes several levels of parallelism. Its key distinction from the original NPB is the introduction of a new parallelism level known as interzone parallelism. This type of parallelism can be exploited during the computational period by the parallel processing of zones across several CUs (i.e., CPUs and GPUs). In addition to interzone parallelism, NPB-MZ also exposes intra-zone parallelism during both periods while processing each individual zone. It can be exploited through several parallelization techniques (i.e., multi-threading, vectorization, and porting to GPU).

The following subsections detail these levels of parallelism and how they are exploited by our implementation.

2.2.1 Computation period: interzone parallelism

Figure 3A1 presents the structure of the time-step loop for the NPB-MZ applications. The computation period is implemented by a loop that traverses the zones and processes them. Because the processing of a zone is independent of the others, interzone parallelism can be exploited by parallelizing this loop.

Figure 3A2 illustrates the OpenMP implementation of this parallel strategy. The parallel region is executed using as many threads as there are CUs in the hybrid multi-CPU and multi-GPU setup. CUs are defined in Section 3; for simplicity we can assume that a CPU-based CU corresponds to one CPU core, while a GPU-based CU corresponds to one GPU. For each GPU-based CU, an OpenMP thread manages both the computation and the communication associated with that GPU. Similarly, each CPU-based CU has an OpenMP thread dedicated to executing zone computations on a CPU core. The body of the parallel region (Figure 3A2) consists of a while loop statement where at each iteration the runtime checks for work availability to be offloaded to a GPU. Based on the applied scheduling, the iterations of the zone-phase loop are distributed among the threads. Each OpenMP thread translates the assigned iterations to zones. Zones assigned to a particular thread will be executed on the GPU the thread is responsible for. The runtime invocations to get-task and commit-task track whether a zone has already been processed.

2.2.2 Computation period: intrazone Parallelism

Figure 3B1 shows that each computational phase calls a subroutine containing several loop nests that implement the computation for one zone and a computational phase. The intra-zone parallelism is derived from exploiting the parallelism exposed by these loop nests.

For GPU-based CU, we adopt the approach outlined by Dümmler and Rünger (2013), where a single-GPU implementation is developed for the NPB-MZ benchmark suite. Figure 3B2 depicts the transformation from a loop nest to a CUDA kernel definition and its invocation. We code each loop body as a CUDA kernel, and we translate, at kernel invocation time, the iteration space into a CUDA < grid, block> definition; this translation requires the definition of functions that map CUDA threads to actual elements in the data structures (e.g., matrices) representing the zones. In general, each computational phase contains multiple loop nests; therefore, each phase is coded with as many CUDA kernels as parallelized nests. All kernel invocations target the default CUDA stream and, whenever feasible, we use shared memory.

For CPU-based CUs, the loop nests have been parallelized using OpenMP directives, taking their implementation from the Fortran version of the NPB-MZ. In all cases, a STATIC scheduling has been selected as implemented by der Wijngaart and Jin (2003).

2.2.3 Communication period: intrazone parallelism

The algorithm for exchanging boundary values is applied over all zones sequentially (Figure 4A). Since zones must be processed sequentially, interzone parallelism can not be exploited. However, there is still potential for parallelism within the computations of each individual zone.

Figure 4

Figure 4. Code snippets for exchanging boundaries. Zones are processed sequentially. No interzone parallelism exists; only intra-zone parallelism can be exploited. (A) Shows the sequential host version. (B) Shows the single-GPU version where intra-zone parallelism is coded in the form of a kernel invocation. (C) Shows the hybrid version with zone-transfer statements.

This interzone parallelism can be exploited by kernels that implement the border computation. In single-GPU execution, this approach resembles the phase parallelization described in Section 2.2.2 (Figure 4B). Each loop iteration processes one zone and updates the boundaries with only two adjacent zones (east and north zones). The boundaries with the other adjacent zones (west and south) will be updated in the loop iterations that process those respective zones.

A hybrid execution that combines GPUs and CPUs requires the introduction of data-transfer statements for the boundary-exchange computations. For a zone located on a device, the boundary computation must check if all adjacent zones are also on that device; if any are not, those missing zones need to be transferred. Similarly, this applies when the zone is stored in the host memory.

Because the boundary computation updates both the zone and its adjacent zones, any replicated zones must be copied back to their original locations. Figure 4C presents the pseudocode for the hybrid boundary-exchange algorithm. Note the communication statements (e.g., the CUDA::copy-zone function) used between kernels. These statements perform memory copy operations between the host and the device address spaces that store adjacent zones. Only the border data are exchanged, not the entire adjacent zones, with the border data temporarily stored in buffers. This process is implemented using nested loops to gather border elements and place them in the temporary buffers. The buffers are then transferred between the CUs where the adjacent zones reside. It is important to note that, depending on how zones are distributed, some copy statements may be unnecessary. These statements are required only when adjacent zones are mapped to different memory spaces. For simplicity, we have omitted the code and data structures related to zone placement management, assuming that this is handled within the copy statement call. The impact of these communication processes is a critical aspect of our study, as is understanding the relationship between work distribution schemes (the mapping of zones to hosts/devices) and their effects on the execution of the boundary-value exchange algorithm.

3 Tasks and compute units

For scheduling purposes, we treat zones as the smallest unit of work. As such, a task encompasses the entire processing of a zone, including the execution of all its phases in sequence. The task scheduling approach presented in this article maps tasks to CUs to exploit interzone parallelism. Intra-zone parallelism, by comparison, is exploited by each individual CU.

CUs can be either CPU-based or GPU-based. In the case of CPU-based CUs, they consist of one or more aggregated CPUs. For example, a CU can be formed by pairing two CPUs, which we denote as a 1 × 2 configuration: “1” represents one CU, and “2” indicates the number of CPUs in that CU. Similarly, a 4 × 8 configuration represents four CUs, each consisting of eight CPUs.

GPU-based CUs are structured as a single thread that manages all operations on a single GPU, including memory allocation, data transfers, and computation offloading.

In this work, the most common use cases are addressed with hybrid configurations of the form N×M+G CPUs, where N represents the number of CPU-based CUs, each utilizing M CPUs, and G denotes the number of GPU-based CUs. All CPU-based CUs consist of the same number of CPUs. For these configurations, a total of N×M+G threads are required for execution.

Threads are created using OpenMP directives. For thread-to-CU association, we leverage the thread affinity features available in OpenMP, specifically the environment variables OMP_PROC_BIND and OMP_PLACES. Our CU runtime support depends on properly configuring these variables to establish the correct thread-to-CU mapping, enabling the simultaneous activation of both CPUs and GPUs.

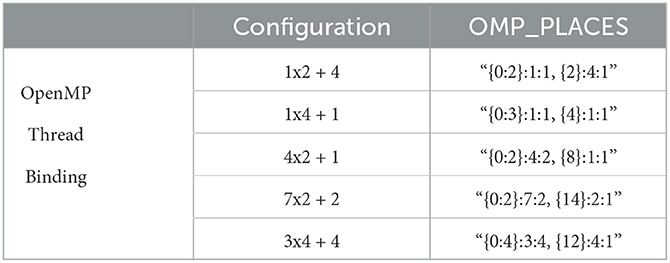
Figure 5 illustrates an 8-CU hybrid system, consisting of 4 CPU-based CUs, each with 4 CPUs, and 4 GPU-based CUs, each with 1 CPU and 1 GPU. This configuration requires a total of 20 physical CPUs. The CPU aggregation is achieved by configuring the OpenMP environment variables that control affinity and thread binding to the CPUs. OMP_PLACES specifies the aggregation of physical CPU identifiers, referred to as places, to which threads are bound. OMP_PROC_BIND defines how the content of OMP_PLACES is interpreted across nested levels of parallelism. Table 2 presents the appropriate values for OMP_PLACES variable in compact OpenMP form for specific CU configurations.

Figure 5

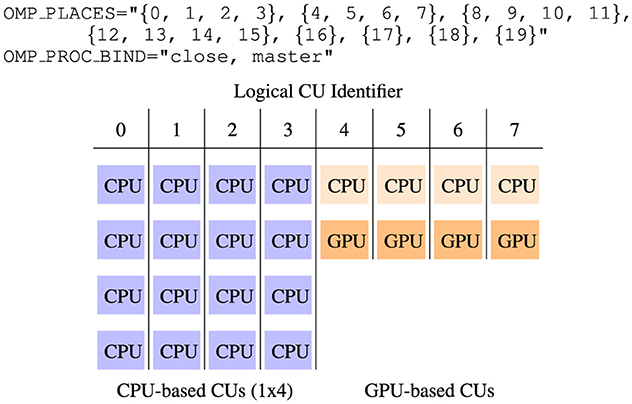
Figure 5. Example of an 8-CU organization: 4 CPU-based CUs composed each one of 4 CPUs, 4 GPU-based CUs composed of 1 CPU and 1 GPU. This configuration needs 20 physical CPUs. OpenMP thread binding is used to configure the thread-CU association. OpenMP variables OMP_PLACES and OMP_PROC_BIND are set to achieve the desired configuration.

Table 2

Table 2. Value of the OpenMP OMP_PLACES environment variable for various hybrid configurations.

For the reader reference, a proposal for OpenMP extensions with compute unit semantics is presented in “Compute units in OpenMP: Extensions for heterogeneous parallel programming” (González and Morancho, 2024). The proposal in this paper builds upon the extensions proposed in the mentioned publication.

4 Schedulers

This section provides an overview of all the schedulers studied in this work. Two of these are state-of-the-art schedulers: the Static and Dynamic task schedulers, as implemented in their OpenMP versions (OpenMP Architecture Review Board, 2021). The remaining schedulers are variants of these two, specifically adapted to address heterogeneity and computation within the NPB-MZ suite. In this section, we define a CU as either a group of CPUs (i.e., a CPU-based CU) or a single CPU that manages a GPU (i.e., a GPU-based CU).

4.1 Static

This scheduling distributes zones uniformly across the CUs, ensuring that each CU processes an equal number of zones.The scheduler assigns to each CU consecutive zones based on the iteration space defined in the computation period loop (Figure 3A1). It is important to note that, due to zone adjacency (as discussed in Section 2), each CU is assigned a group of contiguous zones along the x-dimension. Consequently, communications are primarily influenced by y-dimension adjacencies, while x-dimension adjacencies lead to inter-CU communications only for the first and last zones in each group.

Figure 3A2 illustrates that SCHEDULING::schedTasks preassigns a group of zones to each CU. The accompanying while statement iterates through the zones mapped to a CU.

This scheduler does not attempt to address any work imbalance that may arise. However, it limits data transfers to the y-dimension, which can help minimize the total number of communications during the communication period. Additionally, because the mapping of zones to CUs remains invariant throughout the computation period, the volume of zone transfers during the communication period will also remain invariant.

4.2 Dynamic

This scheduler partitions the iteration space of the computation period loop into blocks of consecutive zones, with the size of each block determined by the chunk parameter. The scheduler assigns a block of zones to each CU, and once a block is processed, a new one is immediately assigned.

In Figure 3A2, zones are not preassigned to CUs. Instead, each iteration of the while loop allocates a block of chunk consecutive zones to a CU. This dynamic scheduling approach helps balance execution time when zone sizes vary, regardless of the zone adjacency in both dimensions. However, this may result in data transfers between adjacent zones in both dimensions, potentially increasing the total execution time of the communication period.

The chunk parameter can smooth the impact of data transfers. The minimal work unit to be distributed is a block of chunk adjacent zones along the x-dimension. Consequently, there is a compromise between the chunk size, the number of communications, and the work unbalance.

Because this scheduler may change the zone-to-CU mapping on each iteration of the computation period, the number of zone transfers will also vary.

Balancing the computation period, while simultaneously keeping constant and low the amount of zone transfers is achieved by implementing a memorizing variant of the feedback dynamic loop scheduler (Bull, 1998), a state-of-the-art dynamic scheduler. After a few iterations of the time-step loop, the scheduler locks the zone-to-CU mapping for the remaining iterations to prevent zone migrations between CUs. This transforms the scheduler into an affinity-oriented one, where the chunk parameter determines the task granularity.

4.3 Static-pcf

This scheduler is a variant of the Static scheduler, previously described for heterogeneous architectures (Augonnet et al., 2011; Beaumont et al., 2019). In this article we develop a new variant designed to maximize zone adjacency for each execution flow.

Our variant relies on determining, at profile time, the performance conversion factor (PCF). Given a hybrid configuration and a task, the PCF is defined as the ratio between the execution time required by a CPU-based CU and that required by a GPU-based CU to process the same task. For instance, a PCF_1x2 equal to 3 means that the execution time required by a 2-CPU CU to process a task triples the time needed by one GPU-based CU (e.g., 1 GPU). Similarly, PCF_2x8 is the ratio between the execution times of a 8-CPU CU and a 2-GPU CU processing the same task.

The Static-pcf scheduler splits the task set into two subsets, to be processed by the CPU-based CUs and the GPU-based CUs respectively, according to the PCF value. Static scheduling is then applied within each subset. The goal is balancing the execution time of both kinds of CUs.

Given T tasks, N_cpu CPU-based CUs, and N_gpu GPU-based CUs, this scheduler assigns T_gpu tasks to the GPU-based CUs:

$T_{gpu}=\lfloor \frac{T}{N_{gpu}·PCF+N_{cpu}}\rfloor ·N_{gpu}·PCF.$

Additionally, T_gpu is increased by the remainder of the integer division (but only up to N_gpu·PCF tasks). The remaining tasks are assigned to the CPU-based CUs, that is, T_cpu = T−T_gpu.

Note that the integer division of T by N_gpu·PCF+N_cpu gives the number of task groups that can be formed with enough work to distribute the tasks among both kinds of CUs in a balanced way. For instance, if T = 40, N_gpu = 1, N_cpu = 1, and PCF = 4, then we want to form groups of five tasks (N_gpu·PCF+N_cpu = 5), where four of them will be mapped to the GPU and one will to the CPU. As PCF = 4, this distribution is balanced.

After determining T_gpu and T_cpu, the Static-pcf applies a static scheduling within each subset.

4.4 Guided

Similar to the Static scheduler, this scheduler partitions the zones in number of CUs chunks of consecutive zones. However, the chunks may vary in size. The zone-phase loops traverse chunks of consecutive iterations (i.e., zones). The starting and ending points of the chunks depend on the workload of each chunk. We have developed two versions of the Guided scheduler: Guided-Sizes and Guided-Runtime. Both variants rely on approximating the workload of the chunks.

Guided-Sizes approximates the workload of a chunk by summing its zone sizes. Like the Static scheduler, this scheduler assigns to each CU zones adjacent along the x-dimension (except for the first and last zones of the chunk). The workload is balanced based on the sum of the zone sizes.

Guided-Runtime approximates the workload of a chunk by summing the execution time of its zones. This scheduler collects, at runtime, the execution time of each zone (excluding communications and boundary computations). This information guides balancing the execution time among CUs. Like the Guided-Sizes scheduler, communications appear just in the y-dimension.

Figures 6, 7 depict the structure and pseudocode for both Guided schedulers. The algorithm takes two input vectors: WorkPerZone, which represents the workload of each zone, and WorkDonePerCU, which represents the workload processed by each CU during the previous iteration of the computation period. These input vectors define the workload in terms of either zone sizes (Guided-Sizes) or execution time (Guided-Runtime). The total workload, TotalWork, is just the accumulation of the workload processed by each CU; the ideal balanced workload per CU, WorkPerCU, is computed by dividing the total work by the number of CUs (Figure 7 from line 1 to 3, corresponding to step 1 in Figure 6).

Figure 6

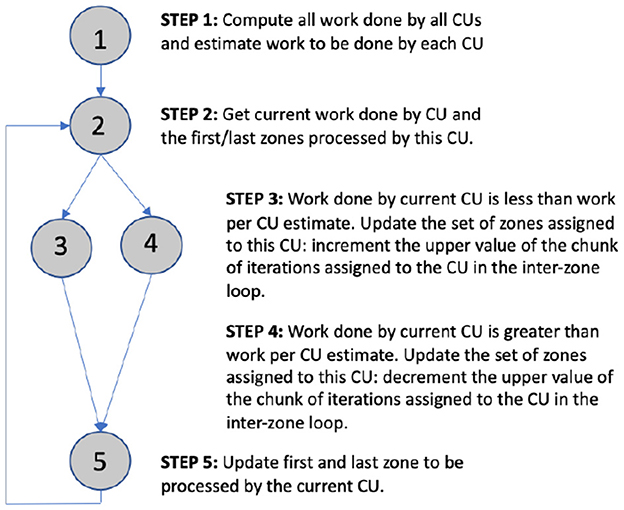
Figure 6. Steps for Guided scheduling. Step 1 calculates the total workload and estimates the work assigned to each CU. Step 2 enters in an iterative process where per each CU steps 3, 4, and 5 are performed. Steps 3 and 4 increment and decrement, respectively, the chunk of iterations assigned to current CU. Step 5 sets the exact first and last zones to be processed by the current CU.

Figure 7

Figure 7. Algorithm for the Guided schedulers. Input vectors: the work done by each compute unit (WorkDonePerCU) and the zone sizes (WorkPerZone). Input/output vectors: indexes that define chunks of consecutive zones along the global numbering of zones (IndexFirstZone and IndexLastZone).

The algorithm also takes two input/output vectors, IndexFirstZone and IndexLastZone, which indicate the current starting and ending points of each chunk (the first and last zones in the chunk of consecutive zones). The remainder of the algorithm explores how to adjust the current chunk limits to improve the work balance. For each CU, if its work done is smaller than the ideal WorkPerCU (line 8) the algorithm tries to add new zones at the end of its chunk (lines 9–17), step 3 in Figure 6. The while loop (line 9) increases Last as long as the workload assigned to the CU gets closer to WorkPerCU. However, if the workload of the CU exceeds WorkPerCU, the algorithm tries to detach zones at the end of its chunk (lines 19–27). Similarly, the while loop (line 19) decreases Last as long as the assigned workload to the CU gets closer to WorkPerCU (step 4 in Figure 6). Finally, lines 28–31 set the new assignment of zones to the current CU (step 5 in Figure 6).

4.5 Clustered Guided

The Clustered Guided scheduler partitions the zones into two clusters: one for CPUs and one for GPUs. For each cluster, likewise the Static scheduler, zones are distributed in as many chunks of consecutive zones as the number of CUs in the cluster. However, chunk sizes may vary to balance the execution time across CUs.

Figure 8D depicts the zone set, represented as a segment ranging from zone 1 to zone N_zones. The partition point, labeled Pivot, divides the zones: Those from zone 1 up to the Pivot are assigned to CPUs, while zones beyond the pivot are assigned to GPUs. The chunks are represented as the pairs T_first and T_last. The convenient value for the Pivot is determined using a dichotomic search.

Figure 8

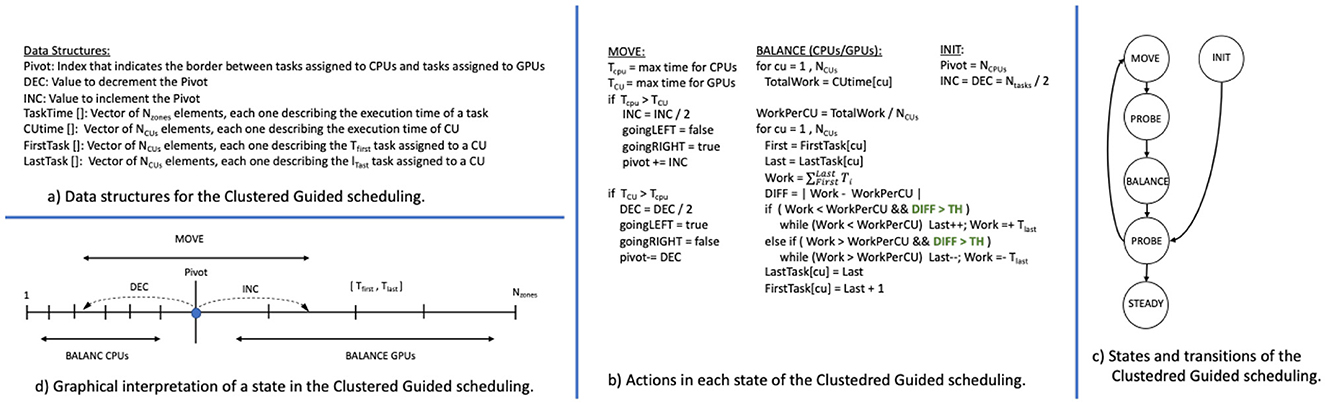
Figure 8. Data structures (A), states and computation (B), state transitions (C), and graphical interpretation (D) of the Clustered Guided scheduling.

Clustered Guided maintains several data structures (Figure 8A). The Pivot marks the partition point. Integers DEC and INC indicate the current steps applied by the dichotomic search. Vector TaskTime[N_zones] records the execution time of each zone. Vector CUtime[N_CUs] tracks the total execution time of each CU. Vectors FirstTask[N_CUs] and LastTask[N_CUs] store the T_first and T_last values that describe the zone assignment per each CU.

Figure 8C shows the state diagram of the scheduler. Figure 8B describes the actions performed by the scheduler in each state and which data structures are updated.

• The INIT state assigns one zone to each CPU; thus, Pivot = N_CPUS and sets the initial value for both INC/DEC as N_zones /2. Finally, one time-step iteration is performed.

• The PROBE state also performs a time-step iteration, keeping constant the latest zone distribution, with the purpose of collecting accurate timings.

• The MOVE state computes which cluster is executing slower. If CPUs take longer, then the Pivot moves left. If GPUs take longer, the Pivot moves right. The scheduling uses the timing information kept in CUtime. At his point, the INC/DEC increment/decrement is halved. This makes smaller the step the scheduling follows to find the work balancing point. Then, within each cluster, a Static scheduler is applied among the CUs that belong to the cluster. Then, a time-step iteration is executed under the new scheduling (PROBE state).

• The BALANCE state balances the execution within each cluster (pseudocode in Figure 8 is applied to each cluster separately). It calculates TotalWork, the cumulative execution time for each cluster, by summing each CU's time from CUtime. Then, the ideal balanced workload per CU (WorkPerCU) is obtained by dividing the total work by the number of CUs in the cluster. Given a CU, if the work done is less than the estimated WorkPerCU the scheduling adds new zones at the end of the chunk. This is performed by the while loop that increases Last as long as the assigned workload to the CU approaches to WorkPerCU. If the workload is greater than WorkPerCU, then the state discards zones at the end of the chunk: The while loop decreases Last as long as the assigned workload to the CU approaches WorkPerCU. After the reassignment, one time-step is executed.

• The STEADY state is reached once INC/DEC value is 1 and the scheduling detects a switch from moving left/right to right/left. After that, the scheduling remains constant for the remaining time steps.

Corner cases have been deliberately omitted to simplify the description. For instance, the Pivot may define an empty cluster (e.g., the CPUs are too slow to compute any zone). Additionally, the BALANCE state for a zero-zone cluster is not included. Also, when the number of zones in a cluster is smaller than the number of CUs in the cluster, then the BALANCE state assigns a single zone per each CU.

Note that the scheduler requires four time-step iterations to get closer to the balanced work distribution (states MOVE, PROBE, BALANCE, and PROBE). Then, less than 4·log₂(N_zones) iterations are needed to reach the STEADY state. The effect of this aspect of the scheduler is analyzed in Section 5.

To sum up, Figure 9 shows possible schedulings of eight zones among two CPUs and two GPUs. Static scheduler maps adjacent zones to each CU regardless work balance. Dynamic balances work regardless zone adjacencies. Clustered Guided gets the best of both strategies, balancing workload while preserving adjacency where possible.

Figure 9

Figure 9. Possible schedulings of 8 zones on 2 CPUs & 2 GPUs.

5 Evaluation

This section evaluates the schedulers for a hybrid implementation of the NPB-MZ benchmark suite. We have used the ROCm-3.5.0 framework and llvm 12 compiler with -O3 and -openmp flags. The hybrid code has been compiled combining a C++ NPB-MZ implementation (Dümmler and Rünger, 2013) and the original NPB-MZ Fortran implementation (der Wijngaart and Jin, 2003) to generate a version compatible with the ROCm implementation of the applications. All experiments have been performed in a system composed of an AMD EPYC 7742 at 2.250GHz (64 cores, 2 threads per core, 128 threads) and two AMD Radeon Instinct MI50 GPUs with 32GB. We run class D NPB-MZ benchmarks (Table 1), so the input mesh is composed by 16 zones (LU-MZ) or 1024 zones (BT-MZ and SP-MZ); memory usage is 13 GB.

The evaluation is organized in a first section where we analyze the effect of the schedulers in the execution times for the computation period and communication period. A second part describes the overall performance of the applications under all of the schedulers. Along the evaluation, we refer to a CU as defined in Section 3.

5.1 Performance analysis

Along this section we analyze the effect of the work scheduling in both the computation period and the communication period. We have taken 50 samples of execution time for both and computed the average and standard deviation of the samples. As all the NPB-MZ applications perform a first initial iteration where memory allocation happen, the samples do not include this event. In all cases, with a 99% confidence interval, the margin of error for the average values is from ±0.02% to ±0.53%. Consequently, the average execution times are significant. For the Clustered Guided scheduling, we have taken the samples after reaching the steady state. The effect of the search process of this scheduling is addressed in Section 5.2 where we study the overall performance.

5.1.1 BT-MZ

Figure 10 shows the performance of the BT-MZ and class D application under several configurations and Static, Dynamic, Static-pcf, Guided, and Clustered Guided schedulers. The charts expose the performance of the computation period and the communication period (execution time in ms). The right-side part of the charts shows the speedup observed in the computation period with respect the non-hybrid CPU-based execution. Also, the bottom-right chart exposes the speedup observed in the communication period with respect the 1-CPU serial version to understand the effects of the schedulers on this phase on the overall performance. For CPU-only execution with several CPU-cores, the computation period speedups range from 8 × and 19 × . The modest scalability is related to two main aspects. The last level of cache memory has a small capacity compared to the input data size: 256 MB in contrast to 13 GB (Figure 1). The time it takes to compute one zone when executing with 16, 32, 48, and 64 CUs is not constant (see Table 3). This is essential for understanding the effects of the schedulers in the computation period. We refer to the data in Table 3 several times along the scheduler analysis. Moreover, BT-MZ computes over a mesh composed of 1,024 unequally sized zones. The input set defines an scenario of many tasks combining small, medium, and large tasks. These increments in the average task execution time limit the effectiveness of the schedulers. The following paragraphs describe the performance for each one.

Figure 10

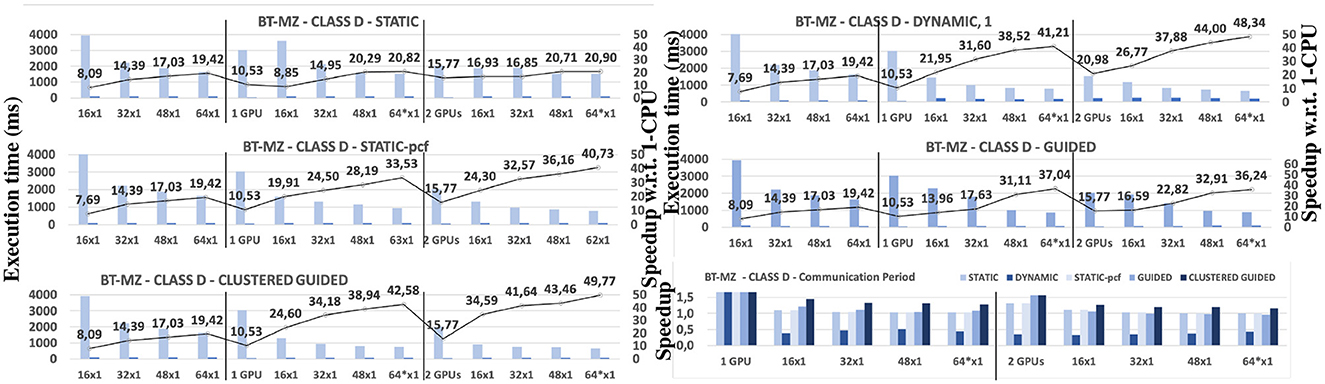
Figure 10. Benchmark BT-MZ. computation period (light gray) and communication period (dark gray) execution times (left axis) and speedup (right axis) for the computation period with respect to 1-CPU configuration. From left to right, CPU-only, 1-GPU, and 2-GPU hybrid configurations (for 1 GPU, version 16 × 1 corresponds to 1 + 16 × 1 configuration). BT, block triangular. ^*For configurations with 1 and 2 GPUs, one CPU thread is dedicated to manage a GPU. Therefore, configurations with 64 CPU threads actually use 63 and 62 CPU threads for actual computation, respectively.

Table 3

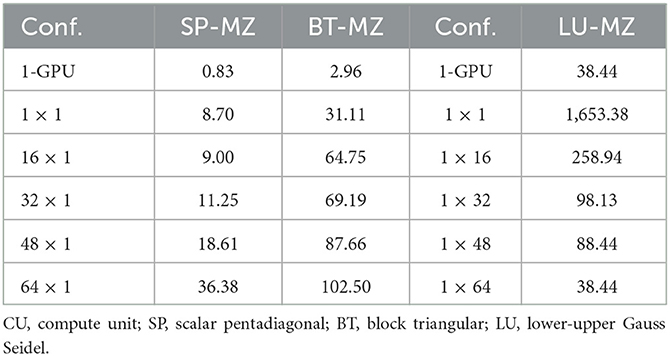
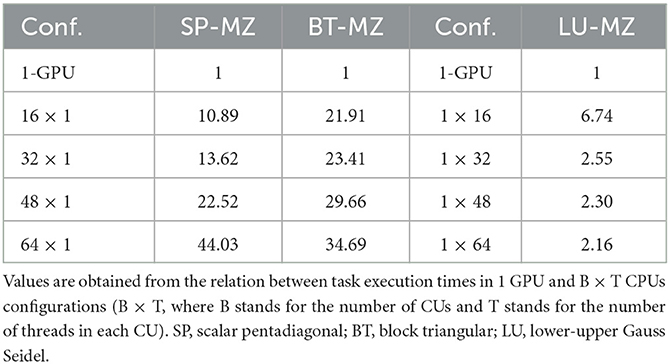
Table 3. Average task time (ms) for all NPB-MZ applications with different CU configurations: B×T, where B stands for the number of CUs and T stands for the number of threads in each CU, no-hybrid 1-GPU, and 2-GPU configurations (B = 0).

Static: Hybrid configurations show poor performance as the scheduler fails to balance the work distribution (speedup factors from 8 × to 20 × ). In addition to the combination of GPUs and CPUs, the zones are not equally sized, which complicates the definition of a well-balanced work distribution. In none of the hybrid configurations did the scheduler exposes more than a speedup of 20 × , compared to non-hybrid configurations with 1-GPU (10 × ) and 2-GPU (15 × ) configurations (notice how this corresponds to poor scaling, essentially caused by the the degree of work unbalance in the input mesh). The lower rightmost chart in Figure 10 shows the observed speedup for the communication period: 1.10 × –1.20 × across all hybrid configurations. This implies that the work distribution is not negatively impacting on the communication period. The main reason for that is that zone adjacency is maintained when zones are assigned to CUs. If adjacency is maintained, then data locality is improved with respect the border computation. This will become an important issue for Dynamic-based schedulers where zone adjacency is no longer kept, leading to data transfers associated to border elements.

Dynamic: Speedups for the computation period range from 21 × to 48 × , improving the Static performance. This scheduler responds well work unbalance due to the differences in the zone sizes and the compute power of the CUs. But this scheduler causes that adjacent zones are assigned to different CUs, which requires additional data transfers to compute border values. Therefore, the communication period is affected by an increment in its execution time. We have observed that for CPU-only configurations, the communication period takes approximately 80 ms, while for hybrid configurations, it takes approximately 200 ms. The lower rightmost chart in Figure 10 shows the observed slowdowns for the communication period: 0.3 × –0.5 × across all hybrid configurations. This corresponds to data transfers of border elements of adjacent zones that have been executed by different CUs. This effect will justify the overall performance levels for this scheduler. One particular observation for the BT-MZ benchmark is that the zones in its input mesh are not equally sized. This results that for a scheduling that balances the work across the CUs, the balancing effect generates speedup values much greater than would be expected. For instance, the 1-GPU configuration is approximately 2 times slower than the 64 × 1 CPU configuration. One would expect that the 64 × 1+1 hybrid configuration be at most 3 times faster than the 1-GPU configuration. But because of the work balance induced by the scheduling, we observe a greater speedup of 4 × . The same happens with the case of 2-GPU and hybrid configurations, where the baseline performance value is a STATIC scheduling and when switching to hybrid configurations, the scheduling balances not only according to the nature of the CUs but also in terms of the zone sizes and the total amount of work assigned to a CU. In general, this phenomenon appears in any of the studied schedulings for the BT-MZ benchmark.

Static-pcf: The Static-pcf scheduler uses a PCF between the GPUs and the CPUs. PCF values are computed from the data in Table 3: Divide the average task execution time under a CPU and non-hybrid configuration by the average task execution time when executed in one GPU. Table 4 shows the PCF values for each configuration and application, calculated from Table 3. The performance of this scheduler is lower than the Dynamic scheduler. The speedup for the computation period ranges between 20 × and 40 × depending on the number of CUs. The Static-pcf only adapts to the difference in compute power of the CUs but not to the work unbalance generated by the differences in the zone sizes. The computation period dominates the total execution time over the communication period, in contrast to the Dynamic scheduling. The Static-pcf does not increase its execution time (the lower rightmost chart in Figure 10 shows the observed speedup for the communication period: 1.1 × –1.2 × across all hybrid configurations). This effect will be essential for understanding later the overall performance differences between Static-pcf and Dynamic. Zone adjacency is only kept with he Static-pcf schedule, not the Dynamic. Therefore, the scheduler impact on the communication period will determine which scheduler performs better in terms of overall performance.

Table 4

Table 4. PFC values used per each application and configuration.

Guided: Speedups for the computation period range from 14 × to 37 × for 1-GPU hybrid configurations, and from 15.5 × to 36 × for 2-GPU hybrid configurations. This scheduler is below the Dynamic performance, mainly for two reasons. First, the resulting work distribution is limited by the fact that the assigned zones to CUs have to be consecutive (e.g., adjacent) following the order in the loop that traverses the set of zones. In contrast, Dynamic is able to map zones to CUs with no restriction according on the compute speed of each CU. Second, the schedule starts assigning zones to first CU (e.g., the one with id = 0, up to NCU-1) and then continues for all CUs. At some point, zones move from and to CPU-based and GPU-based CUs. And when this happens, the scheduler takes the current execution time of the moving zone as reference for its total contribution to the work scheduling. Therefore, the scheduler moves the zones not having the actual execution time for them when run on the selected CU. With the two mentioned restrictions, the solution found by this scheduler is not as good as the one of the Dynamic scheduler. To address this limitation, the Clustered Guided scheduler clusters the zones per CPU-based and GPU-based CUs and measures the execution times before changing the zone-CU mapping (whose performance is analyzed in the next). Regarding the communication period, the Guided scheduling does not cause any slowdown, in contrast to the Dynamic scheduler. Therefore, the impact on the overall performance will be conditioned by the fact the schedulers define an appropriate trade-off between the two phases.

Clustered Guided: Speedups for the computation period range from 24 × to 42 × for 1-GPU hybrid configurations, and from 34 × to 49 × for 2-GPU hybrid configurations. This scheduler outperforms both the Static-pcf and Guided schedulers and exposes similar performance levels as the Dynamic scheduler. Also, it exposes good performance for the communication period, with speedups that range from 1.10 × to 1.45 × . Therefore, this scheduler succeeds in having the best execution time for the computation period with a very good trade-off between the execution of the computation period and the communication period. Compared to Guided, the scheduler overcomes one main observed limitation of this schedule: Never does the zone assignment moves the zones between CPU-based and GPU-based CUs. Instead, two clusters are defined, and the Guided scheduler is applied in each cluster moving zones between CUs of the same type. One main aspect of this scheduler is the induced overheads due to the time it takes to reach a steady work distribution and how this affects the overall performance. The speedup numbers in Figure 10 refer to the speedup after the steady state is reached. Before that, the scheduler traverses several configurations in search of the appropriate zone-CU mapping. Figure 11 exposes the evolution of the Clustered Guided scheduler for a configuration of 32 × 1 + 2 CUs. The x-axis shows average execution time of each CPU, while the left y-axis shows average execution time per GPU. The right y-axis shows the time step where the average times have been computed. It is clear how after few application time steps, both clusters are balanced and remain in a configuration where GPUs do about 900ms of computation and CPUs do about 600ms of computation. For other configurations (e.g., 16 × 1+1, 16 × 1+2, …) the charts expose very similar behaviors as what has been described in Figure 11.

Figure 11

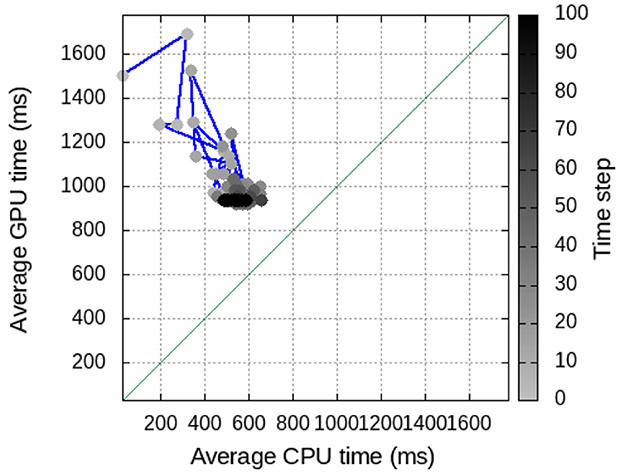
Figure 11. Evolution of the Clustered Guided scheduler for the BT-MZ application under the 32 × 1 + 2 configuration. The x-axis shows average execution time of each CPU, while the left y-axis shows average execution time per GPU. The right y-axis shows the time step where the average times have been computed.

In conclusion, the best schedulers for the computation period are the Dynamic and Clustered Guided. Dynamic exposes speedup factor between 21 × and 48 × depending on the number of activated CUs, while Clustered Guided exposes speedup factors of 24 × and 49 × . For the communication period, the schedulers that assign adjacent zones to the same CUs improve the execution time of this phase. Between the two, only the Clustered Guided maximizes adjacency, therefore it achieves improvements in both phases and overcomes the performance of the Dynamic scheduler. The Dynamic scheduling presents speedup factors of 0.3 × –0.5 × in the communication period, while the Clustered Guided scheduling exposes speedup factors between 1.2 × –1.5 × in the communication period. Section 5.2 quantifies this effect on the overall performance.

5.1.2 SP-MZ

As SP-MZ behaves similarly to BT-MZ, we do not show the performance analysis for SP-MZ. However, in Section 5.2, we discuss its overall performance.

5.1.3 LU-MZ

Figure 12 shows the performance of the LU-MZ and class D application under several configurations and Static, Dynamic, Static-pcf, Guided, and Clustered Guided schedulers. The charts expose the performance of the computation period and the communication period (execution time in ms). The leftmost part of the chart shows the performance respect the CPU-only execution in terms of speedup. For the computation period, expose a moderate scalability (speedups range from 6 × and 19 × with just one single CPU-based CU, composed of 16, 32, 48, and 64 CPUs). The performance increments show that the innermost loops in the computational stages respond moderately well to the increment of threads.

Figure 12

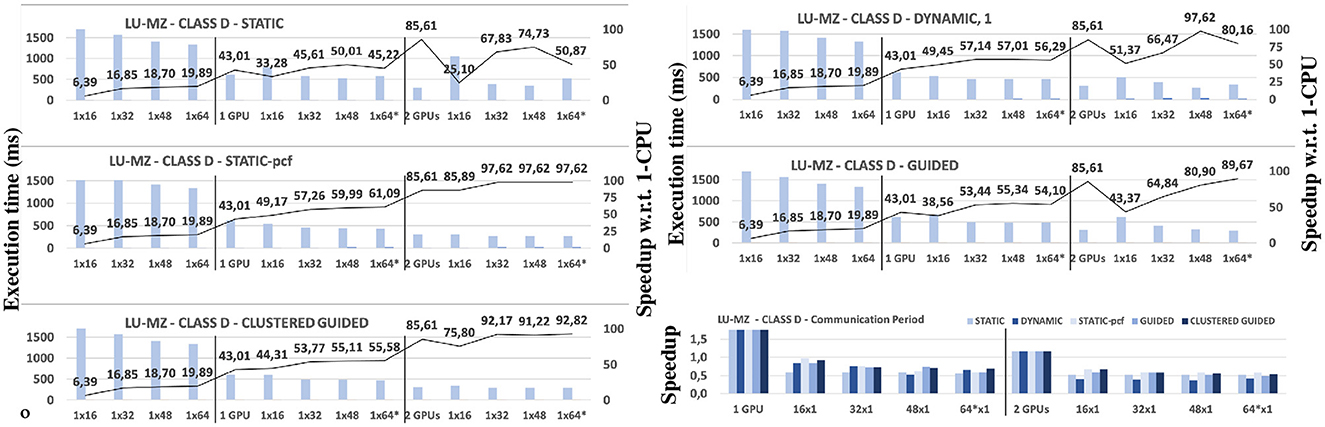
Figure 12. Benchmark LU-MZ. Computation period (light gray) and communication period (dark gray) execution times (left axis) and speedup (right axis) for Computation Period with respect to 1-CPU configuration. From left to right, CPU only, 1-GPU and 2-GPU hybrid configurations (for 1 GPU, version 16 × 1 corresponds to 1 + 16 × 1 configuration). ^*For configurations with 1 and 2 GPUs, one CPU thread is dedicated to manage a GPU. Therefore, configurations with 64 CPU threads actually use 63 and 62 CPU threads for actual computation, respectively.

Static: We observe a very poor response to the increment on the total count of CUs: The speedups for 1-GPU hybrid configurations range between 30 × and 50 × , far below from the speedup value observed for non-hybrid 1-GPU configuration (speedup of 43 × ). Similarly, the 2-GPU configuration for 2-GPU hybrid configurations, speedups range between 25 × and 74 × , again far below the 2-GPU configuration with speedup of 85 × . The resulting work distribution fails to balance the assignment between CPU-based and GPU-based CUs.

Dynamic: For 1-GPU configurations, we observe a maximum speedup of 57 × with 1-GPU and 48 CPU threads. This version solves the work balance problem. This is not the case for 2-GPU configurations. The optimal work distribution corresponds to just assign one task to the CU-based CU. But in 1 × 16, 1 × 32, and 1 × 64 configurations, two or more tasks are assigned to the CPU-based CU. This explains the poor performance.

Static-pcf: Speedups range from 57 × and 61 × for 1-GPU configurations, and between 85 × and 97 × for 2-GPU configurations. In this case, the problem observed in the Dynamic scheduling is solved as for this scheduler, just one task is assigned to the CPU-based CU.

Guided: For the 1-GPU hybrid configurations, the speedups for the computation period range between 38 × and 55 × . This scheduler only improves the performance with respect the Static scheduler. It is below the Dynamic and Static-pcf schedulers. Two factors determine this trend. On one side, the LU-MZ application operates with a mesh with very few zones, only 16. In addition, Tables 3, 4 expose that the performance factors between the execution time for one zone between 1-GPU and CPU-based configurations are in the range of 2 × –6 × clearly exposing that one GPU process one zone much faster than 16, 32, 48, or 64 CPUs. The Guided scheduler relies on actual measurements of execution time, but at the moment of making, the zone-CU mapping cannot predict the impact on the overall execution time of the computation period. And for the LU-MZ application, moving one zone from GPU execution to CPU execution has a very significant impact. Thus, the Static-pcf and Dynamic result in a better work distribution. We observe the same trends for 2-GPU hybrid configurations, where the Guided scheduler exposes speedup factors that range from 43 × to 89 × on the computation period.

Clustered Guided: For the 1-GPU hybrid configurations, the improvement for the computation period ranges between 44 × and 55 × speedup factors. This scheduler clearly improves the performance seen for the Static, Dynamic and Guided schedulers, but it is below the performance levels exposed by the Static-pcf scheduler. We observe the same trends for 2-GPU hybrid configurations, where the computation period exposes speedup factors that range from 75 × to 92 × . For these configurations, this scheduler outperforms Static and Dynamic schedulers but not the Static-pcf . Respect the communication period, this scheduler maximizes adjacency when zones are distributed across the CUs. We observe speedups of the communication period in the range of 1.10 × and 1.20 × . Regarding the overheads of this schedule, we have observed far below overhead levels as those observed with the BT-MZ and SP-MZ applications. The main reason is the number of zones: 16 for LU-MZ. Thus, with very few iterations, the scheduler captures the appropriate configuration. Figure 13 exposes the evolution of the scheduler for a configuration of 63 × 1 + 1 CUs. The x-axis shows average execution time of each CPU, while the left y-axis shows average execution time per GPU. The right y-axis shows the time step where the average times have been computed. It is clear how after very few application time steps, both clusters are balanced and remain in a configuration where both CPUs and GPUs do about 400ms of computation. As with all of the previous schedulers, the computation period experiments increments of performance as long as the number of active CUs is also increased but only up to 32 CUs. Then we observe a drop in performance for 48 and 63 CUs. Again, the reason is related to the average processing time of one zone. When using different 32, 48, or 64 CPU-based CUs, the zone processing time suffers from a significant slowdown (see Tables 3, 4).

Figure 13

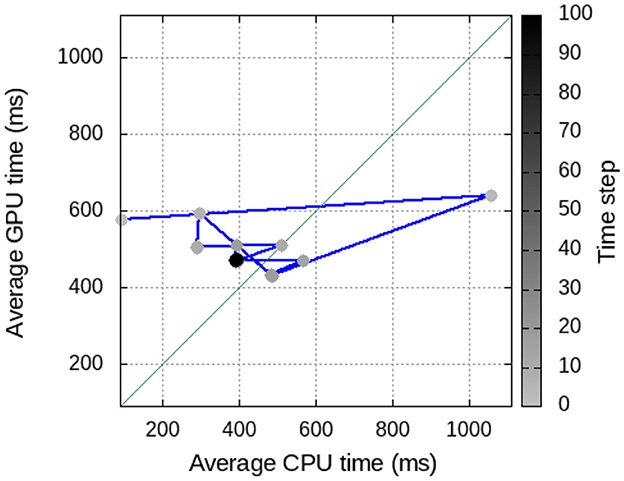
Figure 13. Evolution of the Clustered Guided scheduler for the LU-MZ application under the 63 × 1 + 1 configuration. The x-axis shows the average execution time of each CPU, while the left Y-axis shows average execution time per GPU. The right y-axis shows the time step where the average times have been computed. LU, Upper-lower Gauss-Seidel.

In conclusion, the best schedulers for the Computation Period are the Static-pcf and Clustered Guided. Static-pcf demonstrates a speedup factor between 49 × and 97 × , depending on the number of activated CUs, while Clustered Guided demonstrates a speedup factor of 44 × and 97 × . For the communication period, both schedulers assign adjacent zones to the same CUs, so both improve the execution time of this phase, exposing similar speedup factor of the communication period, in the range of 1.1 × −1.2 × .

5.2 Overall performance

This section describes the overall performance of each scheduler. The performance numbers are explained by the effect of the three main limiting factors observed in the previous sections: number of zones and differences in their sizes, the zone adjacency, and whether the scheduler obtains runtime information or not. Figures 14–16 include the evaluation data for each application in the NPB-MZ suite.

Figure 14

Figure 14. Overall performance of the BT-MZ application under the Static, Dynamic, Static-pcf, Guided, and Clustered Guided schedulers. The x-axis describes the CU configuration: from left to right, only CPU execution, 1-GPU execution, hybrid 1-GPU executions, 2-GPU executions, and hybrid 2-GPU executions. The y-axis shows the speedup with respect the 1-CPU execution. BT, block triangular.

Figure 15

Figure 15. Overall performance of the SP-MZ application under the Static, Dynamic, Static-pcf, Guided, and Clustered Guided schedulers. The x-axis describes the CU configuration: from left to right, only CPU execution, 1-GPU execution, hybrid 1-GPU executions, 2-GPU executions, and hybrid 2-GPU executions. The y-axis shows the speedup with respect the 1-CPU execution. ^*For configurations with 1 and 2 GPUs, one CPU thread is dedicated to manage a GPU. Therefore, configurations with 64 CPU threads actually use 63 and 62 CPU threads for actual computation, respectively.

Figure 16

Figure 16. Overall performance of the LU-MZ application under the Static, Dynamic, Static-pcf, Guided, and Clustered Guided schedulers. The x-axis describes the CU configuration: from left to right, only CPU execution, 1-GPU execution, hybrid 1-GPU executions, 2-GPU executions, and hybrid 2-GPU executions. The y-axis shows the speedup with respect the 1-CPU execution. ^*For configurations with 1 and 2 GPUs, one CPU thread is dedicated to manage a GPU. Therefore, configurations with 64 CPU threads actually use 63 and 62 CPU threads for actual computation, respectively.

BT-MZ: This application operates on a mesh with many zones (1,024) combining small, medium, and big sizes. For 1-GPU configuration, initial speedup is 10 × with respect the serial version. For Static, as the CU count is increased, the response is very poor: Speedups range between 8 × and 19 × . The reason for this trend is related to two factors: the difference between CUs and the fact that the zones are not equally sized. Dynamic and Static-pcf schedulers solve both issues with performance factors from 19 × to 33 × , having the maximum values for the Dynamic scheduler. In this case, the Dynamic assignment of zones to CUs, balances the load across the CUs in a much more effective manner than a profile-based mapping. Static-pcf is guided by average task time (see Tables 3, 4), while Dynamic is guided by actual execution time of tasks (e.g., the speed of each CU determines the work assignment). The work unbalance caused by the differences in the zone sizes has more impact that the different compute power of GPUs and CPUs. But one main limitation of the Dynamic scheduler is its effect on the communication period. If we compare the speedup factors for the Computation Period, with those achieved in the overall performance, Dynamic presents much better results than any of the other schedulers (e.g., 21 × −41 × speedup factors; see Figure 10). But the combination with its effects on the communication period lowers its overall performance. This explains that when compared to the Clustered Guided schedule, this one presents better overall performance factors. The Guided scheduler is led by runtime information, but it does not have a mechanism to predict what will be the execution time of a zone when moved from/to a CPU/GPU. Thus, both Static-pcf and Dynamic outperform this scheduler. In contrast, Clustered Guided scheduler is the one exposing the best performance. It collects runtime information and besides observes what are the actual changes in the zone execution time to guide the evolution of the work distribution. For 1-GPU configurations, this scheduler presents speedup factors from 23 × to 39 × , and for 2-GPU configurations, 32 × to 49 × . Notice that although the overheads related to the search period of this schedule, these do not hinder to achieve the best performance levels.

SP-MZ: This application operates on a mesh with many zones (1,024) all of them equally sized and of small sizes. For 1-GPU executions, speedup is 10 × . As more CUs are added, the response is different in each scheduler. Static fails to adapt the work distribution according to the different type of CUs. The maximum speedup is 18 × with 32 additional CUs but dropping with 48 and 63 CUs. This drop is explained by data in Table 3, with average zone execution time comparing 1-GPU executions with CPU executions (e.g., 16, 32, 48, and 64 CPUs). Basically, the more zones are computed in parallel, the more CPU cores execute simultaneously putting more pressure to the cache hierarchy, resulting in an clear lack of scalability. Dynamic performs better for 32 or fewer additional CUs, with speedups of 14 × and 20 × for 16 CUs and 32 CUs configurations, respectively. But, as we have already seen, this scheduler tends to map adjacent zones to different CUs, thus causing additional overheads in the communication period. The Static-pcf scheduler solves this but presents again a similar drop in performance with more than 32 CUs. The maximum speedup for 1-GPU hybrid configurations is 25 × and 32 additional CUs. For 2-GPU configurations, we observe speedup factors in the from 18 × to 30 × , maximum factor of speedup. The Guided scheduler is below the Static-pcf mainly because its inability to predict what is the effect when moving one zone from/to CPU/GPU-based CUs. Clustered Guided solves this and clearly exposes much higher levels of performance, as similar to Static-pcf .

LU-MZ: For 1-GPU non-hybrid executions, speedup is 42 × . With additional CUs, speedups range between 44 × and 48 × showing a drop for the 1 GPU and 63 CPUs. Both the Dynamic and Static-pcf schedulers outperform with 55 × −59 × factors, having a maximum value for the Static-pcf scheduler with 1-GPU and 63 CPUs. For 2-GPU executions, the base speedup is 83 × and the trends are similar to those observed previously. In this case, maximum speedup is 92 × and corresponds to Static-pcf with 62 additional CUs. The Guided and Clustered Guided schedulers perform similarly but below the Static-pcf performance. In this case, we have seen that the small number of zones and the fact that zones a large enough so that the effects on the communication period are almost negligible, Static-pcf is sufficient to capture an effective work distribution with no need of tracking execution times at runtime. However, needing the a precomputed value obtained through the profiling of non-hybrid CPU executions.

6 Related works

6.1 NPB-MZ studies

Dümmler (2013) and Dümmler and Rünger (2013) evaluated NPB-MZ benchmarks on hybrid CPU+GPU architectures. They decompose the workloads and, using a static scheduling, distribute them among the CPUs or the GPU. Their evaluations show a significant performance improvement with respect to both pure GPU and pure CPU implementations. González and Morancho (2021a) develop a multi-GPU CUDA version of the NPB-MZ suite, including a study of basic state-of-the-art schedulings but without combining GPUs and CPUs in the evaluation study. Pennycook et al. (2011) detail their implementation of the LU-NPB application on CUDA. Moreover, they develop an analytical model to estimate the execution time of the benchmark on a range of architectures. They validate the model using evaluation environments that range from a single GPU to a cluster of GPUs. Xu et al. (2014) focused on directive-based parallelization of NPB benchmarks. After analyzing and profiling the OpenMP version of NPB, they annotated the source code with OpenACC directives to automatically generate GPU versions of the benchmarks.

Heterogeneous Work Scheduling: The porting of applications to heterogeneous architectures has generated previous proposal for work scheduling. Works from different domains describe the adaptation of specific frameworks to execute on multi-GPU systems, where CPUs take the role of orchestrating the parallelism execution and GPUs act as accelerators (Hermann et al., 2010; Nere et al., 2013; Toharia et al., 2012; Chen et al., 2012; Yang et al., 2013). Other works describe a cooperative heterogeneous computing frameworks that enable the efficient utilization of available computing resources of host CPU cores for CUDA kernels (Scogland et al., 2012, 2014; Yang et al., 2010). For work distribution, performance models have been proposed guide the schedulers (Choi et al., 2013; Zhong et al., 2012). Ogata et al. (2008) present a library for 2D fast Fourier transform (FFT) that automatically uses both CPUs and GPUs to achieve optimal performance. Using a performance model, it evaluates the respective contributions of each computing unit and then makes an estimation of total execution times. Other recent works introduce application specific work distributions between CPUs and GPUs. Zhang et al. (2021) describe a cooperative framework to acces a database, showing the benefits of the hybrid execution in terms of total throughput. Similarly, Gowanlock (2021) implements a hybrid knn-joins algorithm with a CPU/GPU approach for low-dimensional KNN-joins, where the GPU is not yielding substantial performance gains over parallel CPU algorithms. The paper introduces priority work queues that enable the computation over data points in high-density regions on the GPU, and low-density regions on the CPU.

With respect the schedulers described in this article, the static-pcf corresponds to a variant of the scheduler strategies described in Beaumont et al. (2019), Augonnet et al. (2011), and Khaleghzadeh et al. (2018). We have adapted this scheduler so that the zones in the input mesh get assigned maximizing adjacency, not only the work balance. Similarly, the guide and clustered guided schedulers correspond to strategies that originate from the schedulers described in Duran et al. (2005). But the work in Duran et al. (2005) only studied CPU-based shared memory architecture, not heterogeneous. In Gautier et al. (2013), similar work is presented by focusing on linear algebra kernels like matrix product and Cholesky factorization.

7 Conclusion

In this article, we have described and evaluated variants of state-of-the-art work distribution schemes adapted for scientific applications running on hybrid systems. We have implemented a hybrid (multi-GPU and multi-CPU) version of the NPB-MZ benchmarks to study the different elements that condition the execution of this suite of applications when parallelism is spread over a set of computational units of different nature (GPUs and CPUs). We have shown that the combination of the GPUs and CPUs results in an effective parallel implementation that speeds up the execution of a strict non-hybrid multi-GPU implementation. We have evaluated how the work distribution schemes determine the data placement across the devices and the host, which in turn has a direct impact over the communications between the host/devices. Only the schedules that expose a good trade-off between the work balance and the communication overheads succeed in effectively using all available compute resources. In particular, the state-of-the-art Static and Dynamic schedulers are not effective and need variants based on precomputed performance-modeling parameters (Static-pcf scheduler) or runtime collected execution times to guide the work distribution (Guided and Clustered Guided schedulers). For these variants and on a system composed by an AMD EPYC 7742 at 2.250GHz (64 cores, 2 threads per core, 128 threads) and two AMD Radeon Instinct MI50 GPUs with 32GB, hybrid executions speedup from 1.1 × to 3.5 × with respect to a non-hybrid GPU implementation, depending on the number of activated CPUs/GPUs.

Data availability statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Author contributions

MG: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. EM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Spanish Ministry of Science and Technology under the grant no. PID2019-107255GB.

Acknowledgments

All authors confirm that the following manuscript is a transparent and honest account of the reported research. This research is related to a previous study by González and Morancho (2024). The previous study was focused on programming while this study focuses on scheduling.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2016). Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv preprint arXiv:1603.04467.

Google Scholar

Augonnet, C., Thibault, S., Namyst, R., and Wacrenier, P.-A. (2011). Starpu: A unified platform for task scheduling on heterogeneous multicore architectures. Concurr. Comput. 23, 187–198. doi: 10.1002/cpe.1631

Crossref Full Text | Google Scholar

Bailey, D., Barszcz, E., Barton, J., Browning, D., Carter, R., Dagum, L., et al. (1991). The NAS parallel benchmarks. Int. J. High Perform. Comput. Appl. 5, 63–73. doi: 10.1177/109434209100500306

Crossref Full Text | Google Scholar

Beaumont, O., Becker, B. A., DeFlumere, A., Eyraud-Dubois, L., Lambert, T., and Lastovetsky, A. (2019). Recent advances in matrix partitioning for parallel computing on heterogeneous platforms. IEEE Trans. Parallel Distr. Syst. 30, 218–229. doi: 10.1109/TPDS.2018.2853151

Crossref Full Text | Google Scholar

Belviranli, M. E., Bhuyan, L. N., and Gupta, R. (2013). A dynamic self-scheduling scheme for heterogeneous multiprocessor architectures. ACM Trans. Archit. Code Optim. 9, 1–20. doi: 10.1145/2400682.2400716

Crossref Full Text | Google Scholar

Bull, J. M. (1998). “Feedback guided dynamic loop scheduling: algorithms and experiments,” in Euro-Par'98 Parallel Processing, eds. D. Pritchard, and J. Reeve (Berlin, Heidelberg: Springer), 377–382. doi: 10.1007/BFb0057877

Crossref Full Text | Google Scholar

Chen, L., Huo, X., and Agrawal, G. (2012). “Accelerating MapReduce on a coupled CPU-GPU architecture,” in Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, SC '12 (Washington, DC, USA: IEEE Computer Society Press). doi: 10.1109/SC.2012.16

Crossref Full Text | Google Scholar

Choi, H. J., Son, D. O., Kang, S. G., Kim, J. M., Lee, H.-H., and Kim, C. H. (2013). An efficient scheduling scheme using estimated execution time for heterogeneous computing systems. J. Supercomput. 65, 886–902. doi: 10.1007/s11227-013-0870-6

Crossref Full Text | Google Scholar

der Wijngaart, R. F. V., and Jin, H. (2003). NAS parallel benchmarks, multi-zone versions. Technical Report NAS-03–010, NASA Ames Research Center.

Google Scholar

Dümmler, J. (2013). NPB-CUDA, an Implementation of the NAS Parallel Benchmarks (NPB) for NVIDIA GPUs in CUDA. Available at: https://www.tu-chemnitz.de/informatik/PI/sonstiges/downloads/npb-gpu/index.php.en

Google Scholar

Dümmler, J., and Rünger, G. (2013). “Execution schemes for the NPB-MZ benchmarks on hybrid architectures: a comparative study,” in Proceedings of the International Conference on Parallel Computing, ParCo 2013, 733–742.

Google Scholar

Duran, A., Gonzàlez, M., and Corbalán, J. (2005). “Automatic thread distribution for nested parallelism in OpenMP,” in Proceedings of the 19th Annual International Conference on Supercomputing (New York, NY, USA: Association for Computing Machinery), 121–130. doi: 10.1145/1088149.1088166

Crossref Full Text | Google Scholar

Gautier, T., Lima, J. V., Maillard, N., and Raffin, B. (2013). “Xkaapi: a runtime system for data-flow task programming on heterogeneous architectures,” in 2013 IEEE 27th International Symposium on Parallel and Distributed Processing, 1299–1308. doi: 10.1109/IPDPS.2013.66

Crossref Full Text | Google Scholar

Giuntoli, G., Grasset, J., Figueroa, A., Moulinec, C., Vázquez, M., Houzeaux, G., et al. (2019). “Hybrid CPU/GPU FE2 multi-scale implementation coupling Alya and micropp,” in Supercomputing Conference.

Google Scholar

González, M., and Morancho, E. (2021a). Multi-GPU parallelization of the NAS multi-zone parallel benchmarks. IEEE Trans. Parallel Distr. Syst. 32, 229–241. doi: 10.1109/TPDS.2020.3015148

Crossref Full Text | Google Scholar

González, M., and Morancho, E. (2021b). Multi-GPU systems and unified virtual memory for scientific applications: the case of the NAS multi-zone parallel benchmarks. J. Parallel Distrib. Comput. 158, 138–150. doi: 10.1016/j.jpdc.2021.08.001

Crossref Full Text | Google Scholar

González, M., and Morancho, E. (2023). Heterogeneous programming using OpenMP and CUDA/HIP for hybrid CPU-GPU scientific applications. Int. J. High Perform. Comput. Appl. 37, 626–646. doi: 10.1177/10943420231188079

Crossref Full Text | Google Scholar

González, M., and Morancho, E. (2024). Compute units in openMP: extensions for heterogeneous parallel programming. Concurr. Comput. 36:e7885. doi: 10.1002/cpe.7885

Crossref Full Text | Google Scholar

Gowanlock, M. (2021). Hybrid KNN-join: parallel nearest neighbor searches exploiting CPU and GPU architectural features. J. Parallel Distrib. Comput. 149, 119–137. doi: 10.1016/j.jpdc.2020.11.004

Crossref Full Text | Google Scholar

Hermann, E., Raffin, B., Faure, F., Gautier, T., and Allard, J. (2010). “Multi-GPU and Multi-CPU parallelization for interactive physics simulations,” in Euro-Par 2010 - Parallel Processing (Berlin, Heidelberg: Springer), 235–246. doi: 10.1007/978-3-642-15291-7_23

Crossref Full Text | Google Scholar

Khaleghzadeh, H., Manumachu, R. R., and Lastovetsky, A. (2018). A novel data-partitioning algorithm for performance optimization of data-parallel applications on heterogeneous HPC platforms. IEEE Trans. Paral. Distr. Syst. 29, 2176–2190. doi: 10.1109/TPDS.2018.2827055

Crossref Full Text | Google Scholar

Manavski, S., and Valle, G. (2008). CUDA compatible GPU cards as efficient hardware accelerators for Smith-Waterman string alignment. BMC Bioinfor. 9:S10. doi: 10.1186/1471-2105-9-S2-S10

PubMed Abstract | Crossref Full Text | Google Scholar

Mittal, S., and Vetter, J. S. (2015). A survey of CPU-GPU heterogeneous computing techniques. ACM Comput. Surv. 47, 1–35. doi: 10.1145/2788396

Crossref Full Text | Google Scholar

Nere, A., Franey, S., Hashmi, A., and Lipasti, M. (2013). Simulating cortical networks on heterogeneous multi-GPU systems. J. Paral. Distr. Comput. 73, 953–971. doi: 10.1016/j.jpdc.2012.02.006

Crossref Full Text | Google Scholar

NVIDIA (2020). GPU-accelerated Caffe. Available at: https://www.nvidia.com/en-au/data-center/gpuaccelerated-applications/caffe/

Google Scholar

Ogata, Y., Endo, T., Maruyama, N., and Matsuoka, S. (2008). “An efficient, model-based CPU-GPU heterogeneous FFT library,” in 2008 International Symposium on Parallel and Distributed Processing, 1–10. doi: 10.1109/IPDPS.2008.4536163

Crossref Full Text | Google Scholar

OpenMP Architecture Review Board (2021). OpenMP Application Program Interface Version 5.2. Available at: https://www.openmp.org/wp-content/uploads/OpenMP-API-Specification-5-2.pdf

Google Scholar

Pennycook, S. J., Hammond, S. D., Jarvis, S. A., and Mudalige, G. R. (2011). Performance analysis of a hybrid MPI/CUDA implementation of the NASLU benchmark. SIGMETRICS Perform. Eval. Rev. 38, 23–29. doi: 10.1145/1964218.1964223

Crossref Full Text | Google Scholar

Scogland, T. R., Rountree, B., Feng, W.-c., and de Supinski, B. R. (2012). “Heterogeneous task scheduling for accelerated OpenMP,” in International Parallel and Distributed Processing Symposium, 144–155. doi: 10.1109/IPDPS.2012.23

Crossref Full Text | Google Scholar

Scogland, T. R. W., Feng, W. C., Rountree, B., and de Supinski, B. R. (2014). “CoreTSAR: adaptive worksharing for heterogeneous systems,” in Supercomputing (Cham. Springer International Publishing), 172–186. doi: 10.1007/978-3-319-07518-1_11

Crossref Full Text | Google Scholar

Toharia, P., Robles, O. D., Suárez, R., Bosque, J. L., and Pastor, L. (2012). Shot boundary detection using zernike moments in multi-GPU multi-CPU architectures. J. Parallel Distrib. Comput. 72, 1127–1133. doi: 10.1016/j.jpdc.2011.10.011

Crossref Full Text | Google Scholar

Xu, R., Tian, X., Chandrasekaran, S., Yan, Y., and Chapman, B. M. (2014). “NAS parallel benchmarks for gpgpus using a directive-based programming model,” in Languages and Compilers for Parallel Computing, eds. J. C. Brodman, and P. Tu (Cham: Springer International Publishing), 67–81. doi: 10.1007/978-3-319-17473-0_5

Crossref Full Text | Google Scholar

Yang, C., Wang, F., Du, Y., Chen, J., Liu, J., Yi, H., et al. (2010). “Adaptive optimization for petascale heterogeneous CPU/GPU Computing,” in 2010 IEEE International Conference on Cluster Computing, 19–28. doi: 10.1109/CLUSTER.2010.12

Crossref Full Text | Google Scholar

Yang, C., Xue, W., Fu, H., Gan, L., Li, L., Xu, Y., et al. (2013). A peta-scalable CPU-GPU algorithm for global atmospheric simulations. SIGPLAN Not. 48, 1–12. doi: 10.1145/2517327.2442518

Crossref Full Text | Google Scholar

Zhang, F., Zhang, C., Yang, L., Zhang, S., He, B., Lu, W., et al. (2021). Fine-grained multi-query stream processing on integrated architectures. IEEE Trans. Paral. Distr. Syst. 32, 2303–2320. doi: 10.1109/TPDS.2021.3066407

Crossref Full Text | Google Scholar

Zhong, Z., Rychkov, V., and Lastovetsky, A. (2012). “Data partitioning on heterogeneous multicore and multi-GPU systems using functional performance models of data-parallel applications,” in IEEE International Conference on Cluster Computing, 191–199. doi: 10.1109/CLUSTER.2012.34

Crossref Full Text | Google Scholar