- 1Department of Bioinformatics and Biostatistics, School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, Shanghai, China
- 2SJTU-Yale Joint Center for Biostatistics, Shanghai Jiao Tong University, Shanghai, China
- 3Jinmai Community Service Center, Guiyang, China
- 4Clinical Research Institute, Shanghai Jiao Tong University School of Medicine, Shanghai, China
High-dimensional mediation analysis has been developed to study whether epigenetic phenotype in a high-dimensional data form would mediate the causal pathway of exposure to disease. However, most existing models are designed based on the assumption that there are no confounders between the exposure, the mediators, and the outcome. In practice, this assumption may not be feasible since high-dimensional mediation analysis (HIMA) tends to be observational where a randomized controlled trial (RCT) cannot be conducted for some economic or ethical reasons. Thus, to deal with the confounders in HIMA cases, we proposed three propensity score-related approaches named PSR (propensity score regression), PSW (propensity score weighting), and PSU (propensity score union) to adjust for the confounder bias in HIMA, and compared them with the traditional covariate regression method. The procedures mainly include four parts: calculating the propensity score, sure independence screening, MCP (minimax concave penalty) variable selection, and joint-significance testing. Simulation results show that the PSU model is the most recommended. Applying our models to the TCGA lung cancer dataset, we find that smoking may lead to lung disease through the mediation effect of some specific DNA-methylation sites, including site Cg24480765 in gene RP11-347H15.2 and site Cg22051776 in gene KLF3.
1 Introduction
Mediation analysis was proposed by Baron and Kenny (1986). It has been widely used in sociological, psychological, and medical research (MacKinnon et al., 2007; Lockhart et al., 2011; Wen and Ye, 2014), aiming to study how a primary exposure
Nevertheless, the premise of an unbiased inference in mediation analysis is the no-confounding assumption: there are no confounders between the exposure, the mediators, and the outcome (VanderWeele, 2009). Imai et al. (2010) modified it as a sequential ignorability assumption: 1) given the confounders, the treatment assignment is assumed to be ignorable (independent of outcomes and mediators); 2) given the confounders and exposure, the mediator is ignorable. Part 1) can be satisfied by RCT, while part 2) is often considered to be irrefutable (Manski, 2007), which is hard to guarantee even in RCT. Thus, in this study, we assume by default that part 2) holds and mainly focus on the confounding problem caused by non-randomization. In most high-dimensional mediation cases, RCT is not feasible because of the economic cost or ethical issues. This results in an uneven distribution of confounders between exposure groups. For example, when exploring the relationship among smoking
To adjust for the confounders in observational studies, regression analyses (e.g., linear and logistic regression) are the most popular due to their simplicity (Normand et al., 2005). Nonetheless, when there are a large number of variables, regression may work inefficiently and another helpful tool, propensity score (PS), would be more powerful (Lu, 2009). A propensity score represents the probability for an individual to have been assigned to an exposure (or treatment), conditional on a host of potential confounders (Lanza et al., 2013). By controlling the propensity score in a proper way like matching, regression, or inverse probability weighting, the confounders could be adjusted, which helps to create a theoretical randomized controlled trial (RCT) (Rosenbaum and Rubin, 1983; D'Agostino, 1998) and satisfy the ignorability assumption. Compared with the regression adjustments, propensity score concentrates all covariates into a single “score” variable, which is more flexible and adequate to eliminate confounding bias (Austin, 2011; Yu et al., 2021). Previous studies have already applied PS in mediation analysis (Coffman, 2011; Jo et al., 2011; Yu et al., 2021). However, there is still a lack of insights into the appropriate utilization of PS for adjusting confounders in HIMA under continuous (or binary) outcomes.
Therefore, in this article, we proposed three propensity score-related approaches to adjust for confounders in HIMA with continuous outcomes. The first two methods are inspired, respectively, by viewing PS as a covariate or using PS to conduct weighted estimation. The third method is a hybrid of the former two. Our results show that the hybrid model performs the best, with the most accurate inference result.
The structure of this article is as follows. The following section introduces the proposed high-dimensional mediation models, adjusting for confounders based on the propensity score. Then, we show the simulation results to illustrate the performance of the models. Additionally, we apply our models to the lung dataset in TCGA, identifying the true DNA methylation sites that mediate the causal pathway of smoking in lung disease. Lastly, we summarize and list prospects of future research.
2 Methods
2.1 The model
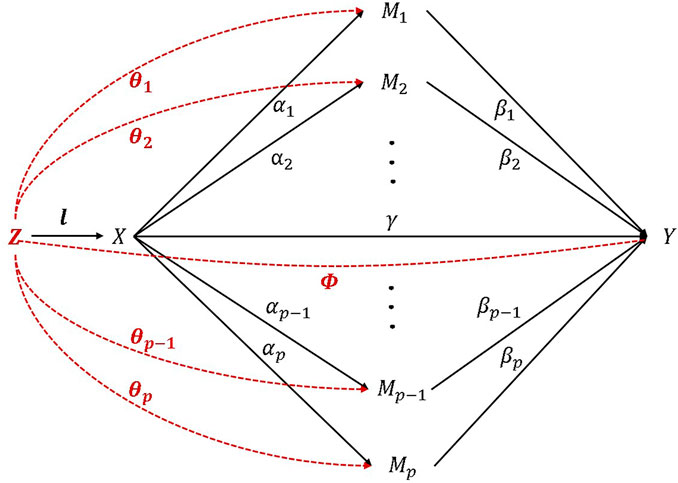
In typical observational HIMA research with a sample size of
Note that
2.2 Methodology
2.2.1 Adjusting confounders using propensity score
Since there are baseline confounders, we integrate a propensity score (PS) into the model. Rosenbaum and Rubin (Rubin, 1983) defined propensity score as the probability of treatment assignment according to the baseline covariates
The propensity score represents the probability of an individual
In consideration of the baseline confounders, the actual high-dimensional mediation analysis model is shown in (1). Therefore, we adopt propensity score regression (PSR) and propensity score weighting (PSW) to reduce the bias.
The main idea of PSR is adding the PS variable into regression. The propensity score can be regarded as the “coarsest function” of the confounding covariates (D’Agostino, 1998). Therefore, controlling the propensity score in regression works similar to taking all the confounders as covariates when estimating. We can use a linear regression model, if the outcome variable is continuous, and a logistic regression model, if the outcome variable is binary (Austin, 2011). We estimate the effect of the model (2):
In contrast, PSW first constructs inverse probability weights from the propensity score for individual
The weighted sample satisfies the condition that exposure (or treatment) assignment is independent of the baseline covariates (Austin and Stuart, 2015), and meets the ignorability assumption. Consequently, by weighted estimation, we can get an unbiased estimation of the coefficient related to
In the above formula,
In the preliminary Monte Carlo simulation, we found that PSM performs better in the estimation of
We apply these three model ideas to steps 2–4 in the following procedure.
2.2.2 Procedure
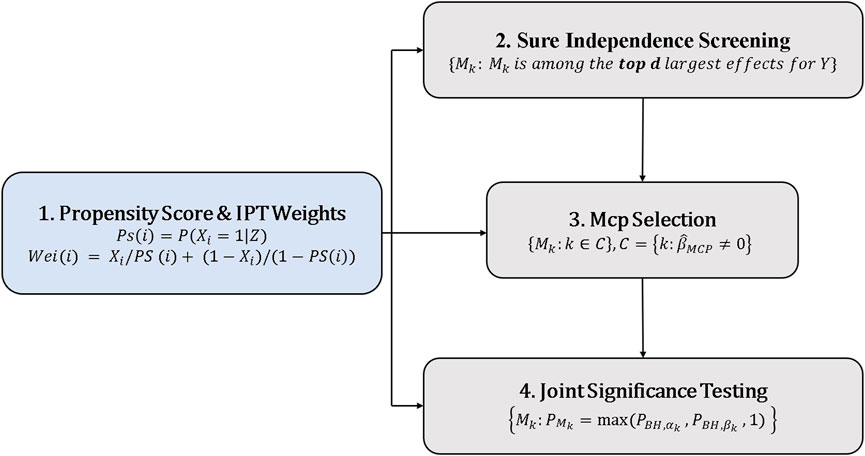
We take the analysis procedure used by Zhang et al. (2016) as HIMA and propose to use the propensity score to adjust for confounders in the HIMA procedure. The detailed procedure is as follows:
1. The propensity score and inverse probability weight were calculated.
First,
Then, we calculated the weight. The weight of the group was given as
2. The dimension was reduced by sure independence screening (SIS).
Penalty estimation methods such as MCP and SCAD may not perform ideally in accuracy and computational cost under an ultra-high-dimensional variable space (Fan and Lv, 2008). Thus, we first adopted the sure independence screening (SIS) (Fan and Lv, 2008) method to reduce dimension
For PSR and PSU methods,
where the maximum likelihood function
For the PSW method, since the confounders indirectly affect
where the maximum likelihood function
After obtaining
Then
The purpose of SIS is to filter out most of the mediators that are irrelevant or weakly related to the response.
3. Candidate mediators for testing through MCP-penalized estimation were selected.
Through SIS, we obtained a set of potential mediators with
Then, we employed MCP-penalized estimation to further select mediators. For PSR method, we minimized the sum of squared residuals including propensity score term
For PSW and PSU, we minimized the sum of squared residuals:
We selected the MCP penalty function:
where
4. Joint-significance test.
For
where
Here, we chose to control FDR instead of family-wise error rate (FWER) because FDR gave a less conservative way than FWER to detect mediators in HIMA. Similarly, the
The effect
Finally, the joint-significance
We set the type I error rate
3 Simulation
In this section, we will evaluate our models by simulation studies. The simulation data are generated according to the true model (1):
Ten confounders
Exposure
Mediators
In order to cover most scenarios in practical application, two sample size levels (
(1) Mode 1: Let
(2) Mode 2: Let
(3) Mode 3: Let
It should be noted that in our settings, only the first eight mediators are non-zero, which satisfy the condition
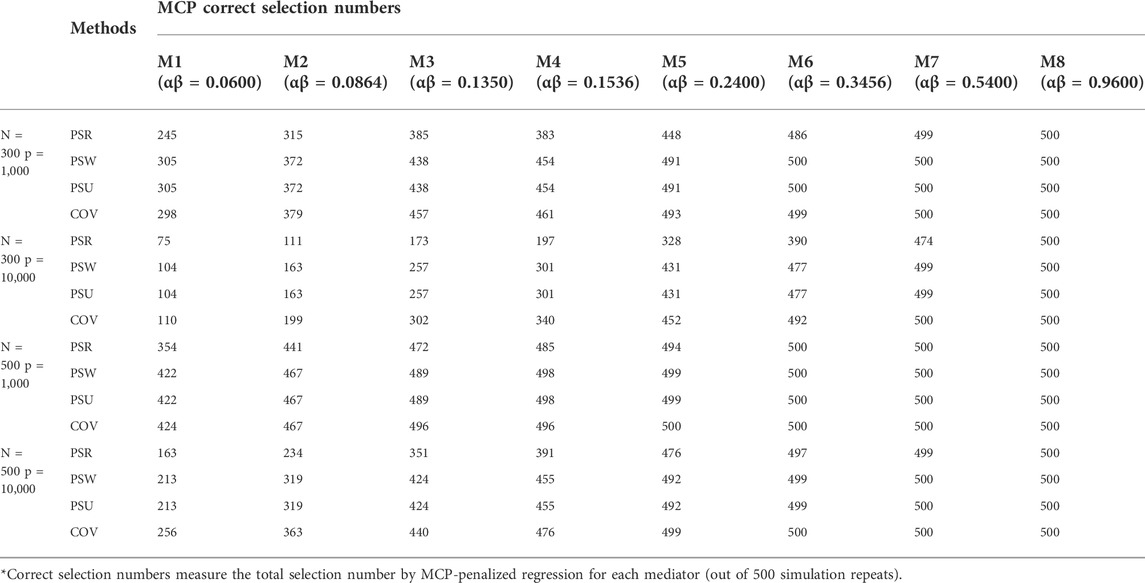
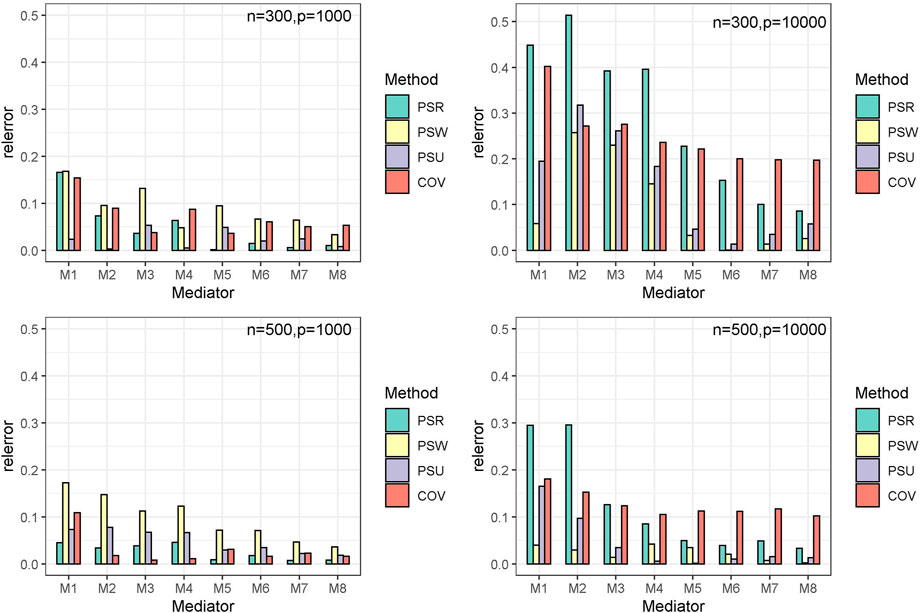
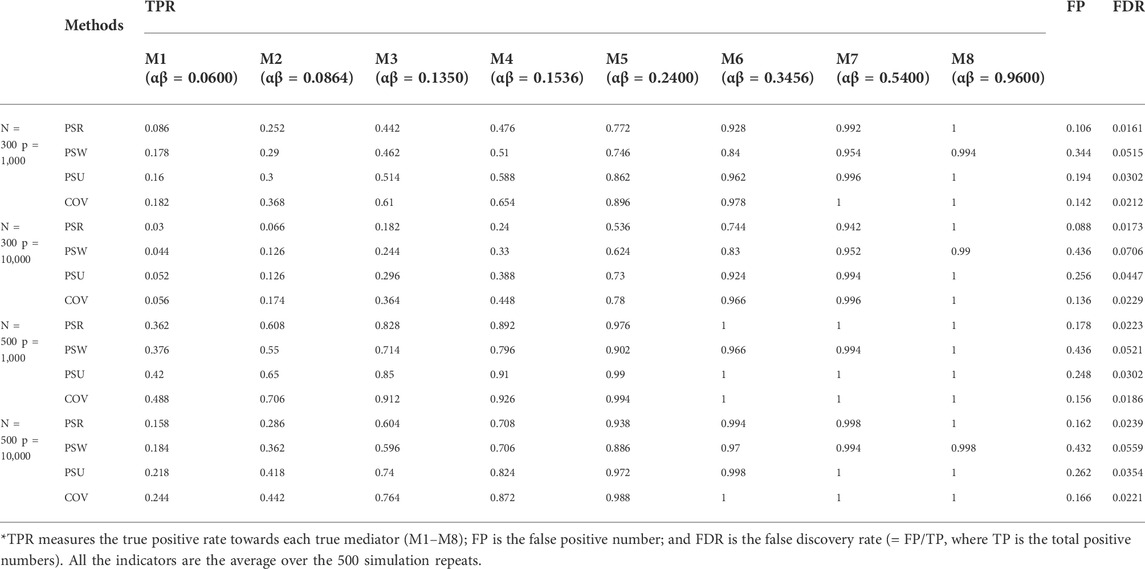
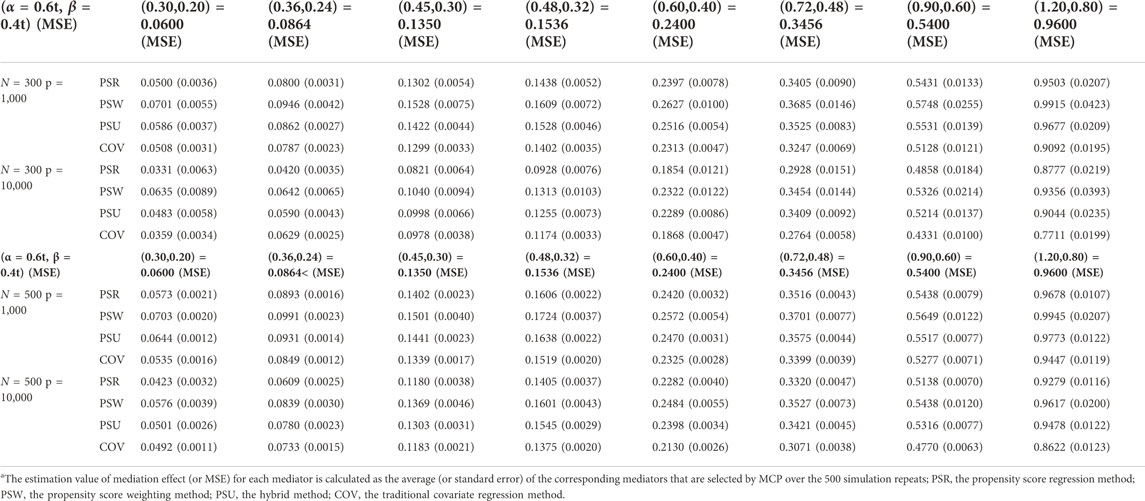
The simulation results are similar among the three modes. Only results of mode 1 are shown in Tables 1–3 and Figure 3. The other results are provided in Supplementary Material S1.
Tables 1 describes the mediator correct selection numbers by MCP out of 500 repeats, and Table 2 describes the testing performance by measuring the truth positive rate (TPR), the false positive rate (FP), and the false discovery rate (FDR). Under most settings, both the correct select numbers and TPR are ranked consistently as COV > PSU > PSR > PSW, and the FP is ranked as PSW > PSU > COV > PSR. For example, when detecting the mediator
Table 3 presents the estimate and mean square error (MSE) for the indirect effects
Overall, although the COV model has the highest TPR, it shows a large bias when estimating the mediation effects. The PSU model is the most recommended, which performs best in estimating and is only second to the COV model in testing.
4 Data application
Smoking is a major environmental hazard promoting lung disease development. Previous studies have demonstrated that smoking can lead to some abnormal expression of CpG islands (DNA methylation sites) in lung-related genes, which may be the immediate cause of lung disease (Toyooka et al., 2003; Harlid et al., 2014). Generally, DNA methylation data can be obtained by the technology Infinium HumanMethylation450, resulting in a dataset of more than 480,000 CpG sites over the whole genome (Dedeurwaerder et al., 2011). Hence, we conducted high-dimensional mediation analysis to further discover the specific functional CpG sites that mediate the relationship between smoking and lung disease.
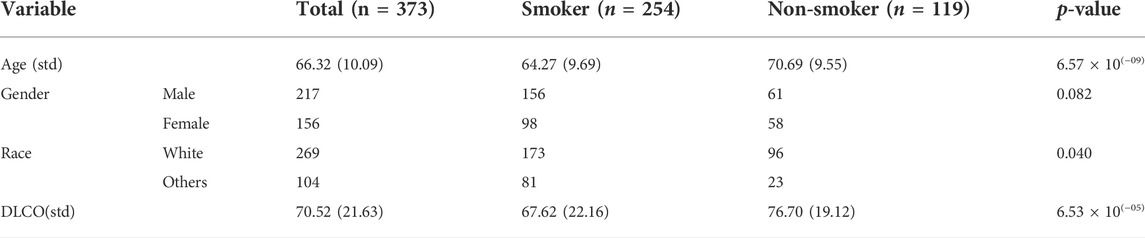
Clinical and methylation data from the cohorts of lung squamous cell carcinoma (LUSC) and lung adenocarcinoma (LUAD) were used for analysis. The clinical datasets included 626 and 706 samples, respectively, and the methylation dataset included 485,577 probes. Baseline information such as age, sex, and race were collected, and DLCO (diffusing capacity of the lung for carbon monoxide) was measured to characterize the lung function of every individual. Subjects were categorized into the non-smoker group and smoker group according to their smoking status.
After removing the subjects with “not available,” there were 254 samples in the smoker group and 119 samples in the non-smoker group. As shown in Table 4, the baseline variables such as age, race, gender, and the outcome variable DLCO show marginally significant differences between the smoking groups, indicating the necessity to adjust for confounders in the following analysis.
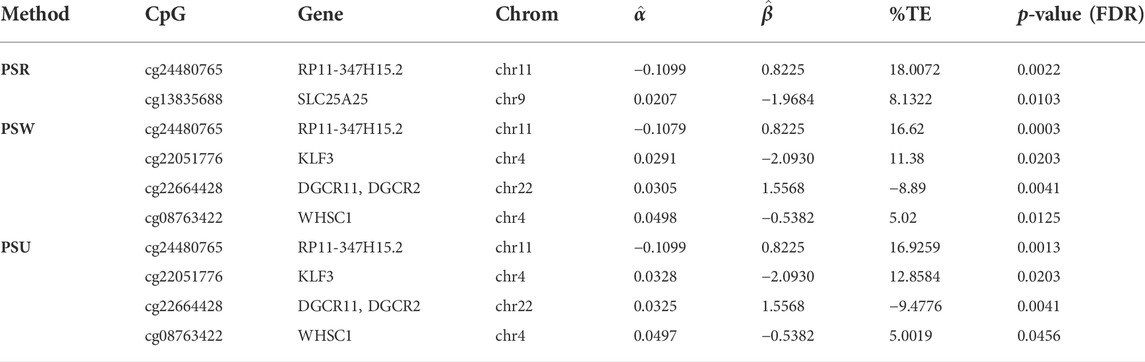
Table 5 summarizes the analysis results. We focused on methylation sites with a %TE (total effect proportion) greater than 10. Cg24480765 in the gene RP11-347H15.2 was a significant mediation site detected by all models, whose mediation effect
We identified another site, Cg22051776, in the KLF3 gene by models PSU and PSW. The indirect mediation effect
5 Discussion
The unbiased high-dimensional mediation inference needs to satisfy the no-confounding assumption. However, confounding is almost inevitable in observational HIMA cases because of the non-randomization of the baseline covariates. To solve the problem, we adopted the HIMA framework of SIS, MCP, and joint-significance testing, and combined it with three propensity score utilization methods to adjust for confounders. We compared them to the regression adjustment method (COV model) that takes all confounders as covariates. Simulation results show that our proposed model PSU performs the best from the overall perspective of estimation accuracy, TPR, FP, FDR, and model simplicity. Finally, we applied our models to the TCGA lung cancer dataset and found the important DNA methylation mediators, cg24480765 and cg22051776. Particularly, our utilization of propensity scores is not just limited to HIMA. It gives an idea of adjusting for confounders under other causal inference cases.
Still, there are some improvements worth discussion in the future. First, the HIMA framework we adopted can be developed in some aspects. For example, Gao et al. (2019) used a de-biased lasso estimator in the variable selection part, and developed a new model called HDMA, which can deal with the correlation between methylation sites better. In addition, applying other weighting methods such as the stable weights proposed by Zubizarreta (2015) in the PSW and PSU models might help to enhance the model robustness. As for the significance testing part, the joint-significance testing we used may be conservative (Dai et al., 2022) and other testing methods such as bootstrapping would be more powerful. MacKinnon et al. revealed that the bias-corrected bootstrap is the best method for testing indirect effects (MacKinnon et al., 2004); Benjamini and Yekutieli. (2005) introduced a procedure of getting FDR-adjusted multiple confidence intervals for selected parameters. Yet our research did not focus much on the testing part. Moreover, the exposure variable in our model is set to be binary. Continuous variables or discrete variables with more than two groups need further expansion.
Data availability statement
Our numerical analysis is implemented by R and the corresponding code is available in https://github.com/linghaoluo/PS_HIMA_CON.
Author contributions
LL, YY, and ZY proposed and implemented the method. LL and ZY drafted the manuscript, conceived the idea, and designed the study. LL and YC implemented the code. LL, YY, and XY participated in data analysis. All authors read and approved the final manuscript.
Funding
This study was supported by the National Natural Science Foundation of China (ID:12171318) and the Shanghai Science and Technology Development Fund (ID: 21ZR1436300). Shanghai Commission Science and Technology (ID:21ZR1436300), Shanghai Jiao Tong University, Star Grant (ID: 20190102), Medical Engineering Cross Fund of Shanghai Jiao Tong University (ID:YG2021QN50).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2022.961148/full#supplementary-material
References
Austin, P. C. (2011). An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivar. Behav. Res. 46 (3), 399–424. doi:10.1080/00273171.2011.568786
Austin, P. C., and Stuart, E. A. (2015). Moving towards best practice when using inverse probability of treatment weighting (IPTW) using the propensity score to estimate causal treatment effects in observational studies. Stat. Med. 34 (28), 3661–3679. doi:10.1002/sim.6607
Baron, R. M., and Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. J. Pers. Soc. Psychol. 51 (6), 1173–1182. doi:10.1037/0022-3514.51.6.1173
Benjamini, Y., and Yekutieli, D. (2005). False discovery rate-adjusted multiple confidence intervals for selected parameters. J. Am. Stat. Assoc. 100 (469), 71–81. doi:10.1198/016214504000001907
Breheny, P., and Huang, J. (2011). Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Ann. Appl. Stat. 5 (1), 232–253. doi:10.1214/10-aoas388
Coffman, D. L. (2011). Estimating causal effects in mediation analysis using propensity scores. Struct. Equ. Model. 18 (3), 357–369. doi:10.1080/10705511.2011.582001
Cortessis, V. K., Thomas, D. C., Levine, A. J., Breton, C. V., Mack, T. M., Siegmund, K. D., et al. (2012). Environmental epigenetics: Prospects for studying epigenetic mediation of exposure-response relationships. Hum. Genet. 131 (10), 1565–1589. doi:10.1007/s00439-012-1189-8
Cui, Y., Luo, C., Luo, L., and Yu, Z. (2021). High-dimensional mediation analysis based on additive hazards model for survival data. Front. Genet. 12, 771932. doi:10.3389/fgene.2021.771932
D'Agostino, R. B. (1998). Propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Stat. Med. 17 (19), 2265–2281. doi:10.1002/(sici)1097-0258(19981015)17:19<2265::Aid-sim918>3.0.Co;2-b
Dai, J. Y., Stanford, J. L., and LeBlanc, M. (2022). A multiple-testing procedure for high-dimensional mediation hypotheses. J. Am. Stat. Assoc. 117, 198–213. doi:10.1080/01621459.2020.1765785
Dedeurwaerder, S., Defrance, M., Calonne, E., Denis, H., Sotiriou, C., and Fuks, F. (2011). Evaluation of the Infinium methylation 450K technology. Epigenomics 3 (6), 771–784. doi:10.2217/epi.11.105
Djordjilovic, V., Page, C. M., Gran, J. M., Nost, T. H., Sandanger, T. M., Veierod, M. B., et al. (2019). Global test for high-dimensional mediation: Testing groups of potential mediators. Stat. Med. 38 (18), 3346–3360. doi:10.1002/sim.8199
Fan, J. Q., and Lv, J. C. (2008). Discussion of "sure independence screening for ultra-high dimensional feature space. J. R. Stat. Soc. Ser. B Stat. Methodol. 70, 903–883. doi:10.1111/j.1467-9868.2008.00674.x
Fujii, R., Sato, S., Tsuboi, Y., Cardenas, A., and Suzuki, K. (2021). DNA methylation as a mediator of associations between the environment and chronic diseases: A scoping review on application of mediation analysis. Epigenetics 17, 759–785. doi:10.1080/15592294.2021.1959736
Gao, Y., Yang, H., Fang, R., Zhang, Y., Goode, E. L., and Cui, Y. (2019). Testing mediation effects in high-dimensional epigenetic studies. Front. Genet. 10, 1195. doi:10.3389/fgene.2019.01195
Harlid, S., Xu, Z. L., Panduri, V., Sandler, D. P., and Taylor, J. A. (2014). CpG sites associated with cigarette smoking: Analysis of epigenome-wide data from the sister study. Environ. Health Perspect. 122 (7), 673–678. doi:10.1289/ehp.1307480
Hirano, K., and Imbens, G. W. (2001). Estimation of causal effects using propensity score weighting: An application to data on right heart catheterization. Health Serv. Outcomes Res. Methodol. 2 (3), 259–278. doi:10.1023/A:1020371312283
Huang, Y.-T., and Pan, W.-C. (2016). Hypothesis test of mediation effect in causal mediation model with high-dimensional continuous mediators. Biometrics 72 (2), 402–413. doi:10.1111/biom.12421
Huarte, M. (2015). The emerging role of lncRNAs in cancer. Nat. Med. 21 (11), 1253–1261. doi:10.1038/nm.3981
Imai, K., Keele, L., and Tingley, D. (2010). A general approach to causal mediation analysis. Psychol. Methods 15 (4), 309–334. doi:10.1037/a0020761
Jo, B., Stuart, E. A., MacKinnon, D. P., and Vinokur, A. D. (2011). The use of propensity scores in mediation analysis. Multivar. Behav. Res. 46 (3), 425–452. doi:10.1080/00273171.2011.576624
Lanza, S. T., Moore, J. E., and Butera, N. M. (2013). Drawing causal inferences using propensity scores: A practical guide for community psychologists. Am. J. Community Psychol. 52 (3-4), 380–392. doi:10.1007/s10464-013-9604-4
Lockhart, G., Mackinnon, D. P., and Ohlrich, V. (2011). Mediation analysis in psychosomatic medicine research. Psychosom. Med. 73 (1), 29–43. doi:10.1097/PSY.0b013e318200a54b
Loh, W. W., Moerkerke, B., Loeys, T., and Vansteelandt, S. (2020). Nonlinear mediation analysis with high-dimensional mediators whose causal structure is unknown. Biometrics 78, 46–59. doi:10.1111/biom.13402
Lu, C. Y. (2009). Observational studies: A review of study designs, challenges and strategies to reduce confounding. Int. J. Clin. Pract. 63 (5), 691–697. doi:10.1111/j.1742-1241.2009.02056.x
Luo, C., Fa, B., Yan, Y., Wang, Y., Zhou, Y., Zhang, Y., et al. (2020). High-dimensional mediation analysis in survival models. PLoS Comput. Biol. 16 (4), e1007768. doi:10.1371/journal.pcbi.1007768
MacKinnon, D. P., Fairchild, A. J., and Fritz, M. S. (2007). Mediation analysis. Annu. Rev. Psychol. 58, 593–614. (Palo Alto: Annual Reviews). doi:10.1146/annurev.psych.58.110405.085542
MacKinnon, D. P., Lockwood, C. M., and Williams, J. (2004). Confidence limits for the indirect effect: Distribution of the product and resampling methods. Multivar. Behav. Res. 39 (1), 99–128. doi:10.1207/s15327906mbr3901_4
Manski, C. F. (2007). Identification for prediction and decision. Cambridge, MA and London, England: Harvard University Press. doi:10.4159/9780674033665
Normand, S. L. T., Sykora, K., Li, P., Mamdani, M., Rochon, P. A., and Anderson, G. M. (2005). Readers guide to critical appraisal of cohort studies: 3. Analytical strategies to reduce confounding. Bmj-British Med. J. 330 (7498), 1021–1023. doi:10.1136/bmj.330.7498.1021
Rosenbaum, P. R., and Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika 70 (1), 41–55. doi:10.1093/biomet/70.1.41
Rubin, P. R. R. B., and Rubin, D. B. (1983). Assessing sensitivity to an unobserved binary covariate in an observational study with binary outcome. J. R. Stat. Soc. Ser. B 45 (2), 212–218. doi:10.1111/j.2517-6161.1983.tb01242.x
Schmitt, A. M., and Chang, H. Y. (2016). Long noncoding RNAs in cancer pathways. Cancer Cell. 29 (4), 452–463. doi:10.1016/j.ccell.2016.03.010
Sun, W., Hu, S., Zu, Y., and Deng, Y. (2019). KLF3 is a crucial regulator of metastasis by controlling STAT3 expression in lung cancer. Mol. Carcinog. 58 (11), 1933–1945. doi:10.1002/mc.23072
Toyooka, S., Maruyama, R., Toyooka, K. O., McLerran, D., Feng, Z. D., Fukuyama, Y., et al. (2003). Smoke exposure, histologic type and geography-related differences in the methylation profiles of non-small cell lung cancer. Int. J. Cancer 103 (2), 153–160. doi:10.1002/ijc.10787
Valeri, L., Reese, S. L., Zhao, S. S., Page, C. M., Nystad, W., Coull, B. A., et al. (2017). Misclassified exposure in epigenetic mediation analyses. Does DNA methylation mediate effects of smoking on birthweight? Epigenomics 9 (3), 253–265. doi:10.2217/epi-2016-0145
VanderWeele, T. J. (2009). Marginal structural models for the estimation of direct and indirect effects. Epidemiology 20 (1), 18–26. doi:10.1097/EDE.0b013e31818f69ce
Wen, Z., and Ye, B. (2014). Analyses of mediating effects: The development of methods and models. Adv. Psychol. Sci. 22 (5), 731–745. doi:10.3724/SP.J.1042.2014.00731
Yu, Z., Cui, Y., Wei, T., Ma, Y., and Luo, C. (2021). High-dimensional mediation analysis with confounders in survival models. Front. Genet. 12, 688871. Article No.: 688871. doi:10.3389/fgene.2021.688871
Zhang, C. H. (2010). Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38 (2), 894–942. doi:10.1214/09-aos729
Zhang, H., Zheng, Y., Hou, L., Zheng, C., and Liu, L. (2021). Mediation analysis for survival data with high-dimensional mediators. Bioinformatics 37 (21), 3815–3821. doi:10.1093/bioinformatics/btab564
Zhang, H., Zheng, Y., Zhang, Z., Gao, T., Joyce, B., Yoon, G., et al. (2016). Estimating and testing high-dimensional mediation effects in epigenetic studies. Bioinformatics 32 (20), 3150–3154. doi:10.1093/bioinformatics/btw351
Zhu, Y., Zhu, J., Yang, X., and Xiao, M. (2012). Significance of kruppel-like factor 3 expression in lung adenocarcinoma. Chin. J. Clin. Oncol. 39 (15), 1087–1090. doi:10.3969/j.issn.1000-8179.2012.15.023
Keywords: high-dimensional mediation model, confounders, propensity score, inverse probability weighting, SIS, MCP, joint-significance test
Citation: Luo L, Yan Y, Cui Y, Yuan X and Yu Z (2022) Linear high-dimensional mediation models adjusting for confounders using propensity score method. Front. Genet. 13:961148. doi: 10.3389/fgene.2022.961148
Received: 04 June 2022; Accepted: 14 September 2022;
Published: 10 October 2022.
Edited by:
Zhigang Li, University of Florida, United StatesReviewed by:
Heining Cham, Fordham University, United StatesLihong Huang, Zhongshan Hospital, Fudan University, China
Copyright © 2022 Luo, Yan, Cui, Yuan and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhangsheng Yu, eXV6aGFuZ3NoZW5nQHNqdHUuZWR1LmNu
 Linghao Luo
Linghao Luo Yuting Yan
Yuting Yan Yidan Cui
Yidan Cui Xin Yuan
Xin Yuan Zhangsheng Yu
Zhangsheng Yu