- 1Department of Crop and Soil Sciences, Washington State University, Pullman, WA, United States
- 2School of Electrical Engineering and Computer Science, Washington State University, Pullman, WA, United States1
Soft white wheat is a wheat class used in foreign and domestic markets to make various end products requiring specific quality attributes. Due to associated cost, time, and amount of seed needed, phenotyping for the end-use quality trait is delayed until later generations. Previously, we explored the potential of using genomic selection (GS) for selecting superior genotypes earlier in the breeding program. Breeders typically measure multiple traits across various locations, and it opens up the avenue for exploring multi-trait–based GS models. This study’s main objective was to explore the potential of using multi-trait GS models for predicting seven different end-use quality traits using cross-validation, independent prediction, and across-location predictions in a wheat breeding program. The population used consisted of 666 soft white wheat genotypes planted for 5 years at two locations in Washington, United States. We optimized and compared the performances of four uni-trait– and multi-trait–based GS models, namely, Bayes B, genomic best linear unbiased prediction (GBLUP), multilayer perceptron (MLP), and random forests. The prediction accuracies for multi-trait GS models were 5.5 and 7.9% superior to uni-trait models for the within-environment and across-location predictions. Multi-trait machine and deep learning models performed superior to GBLUP and Bayes B for across-location predictions, but their advantages diminished when the genotype by environment component was included in the model. The highest improvement in prediction accuracy, that is, 35% was obtained for flour protein content with the multi-trait MLP model. This study showed the potential of using multi-trait–based GS models to enhance prediction accuracy by using information from previously phenotyped traits. It would assist in speeding up the breeding cycle time in a cost-friendly manner.
Introduction
Wheat (Triticum aestivum L.) is one of the most important staple crops worldwide, providing 18% of the caloric intake (Awika, 2011; Saini et al., 2022). Hexaploid wheat is categorized into soft and hard wheat classes based on protein strength, kernel texture, water absorption, and milling quality (Kiszonas et al., 2013). In the United States, six major classes of wheat, namely, hard white wheat, hard red spring wheat, hard red winter wheat, soft white wheat, soft red winter wheat, and durum, are grown in different regions. Soft white wheat (SWW) is a predominant class in eastern Washington and the inland Pacific Northwest (Kiszonas and Morris, 2018). SWW is one of the wheat classes with high demands from overseas markets in countries like the Philippines, Korea, Japan, and Indonesia, due to its high end-use quality. Soft wheat is mainly used for making cakes, cookies, pastries, Asian-style noodles, crackers, and pretzels (Morris et al., 2008). In addition to having high grain yield, disease and insect resistance, wide adaptability, and cold tolerance, the released wheat cultivar needs to maintain high end-use quality attributes required by millers, bakers, and grain markets (Morris et al., 2009; Carter et al., 2012; Guzman et al., 2016; Sandhu et al., 2021d).
Phenotyping for end-use quality traits is usually delayed until advanced generations in wheat breeding owing to the associated cost, labor, and amount of seed required (Battenfield et al., 2016). Delayed phenotyping usually results in hindrance of releasing promising cultivars due to lack of end-use quality data to make decisions. Important end-use quality traits in wheat include cookie diameter, flour sedimentation value, flour yield, grain protein content, and milling score (Campbell et al., 2007; Kiszonas et al., 2015). Linkage and association mapping have been used to identify the genomic loci controlling end-use quality traits, and most of the major effect genes are now fixed into the breeding programs for different market classes (Jernigan et al., 2018; Yang et al., 2020). Marker-assisted selection has been used to screen for some major effect end-use quality genes in wheat classes based on granule-based starch synthase 1, low and high molecular weight glutenins, and kernel texture (Aoun et al., 2021b). These major effect loci only assist in differentiating between different classes but do not provide the complete profile (Kumar et al., 2019). Association mapping studies in wheat have shown that more than 300 small effect QTLs control these end-use quality traits and suggest the quantitative nature of these traits, requiring appropriate strategies to be adopted in breeding programs for selection (Breseghello and Sorrells, 2006; Bhave and Morris, 2008; Jernigan et al., 2018; Yang et al., 2020).
The ultimate interest of a plant breeding program is to enhance the long-term genetic gain, and in modern terms, genetic gain is defined as
Most genomic selection studies use the uni-trait model, where a single trait is predicted (Qin et al., 2019; Pérez-Rodríguez et al., 2020; Sandhu et al., 2022). However, plant breeders have shifted to multi-trait (MT) GS models that simultaneously predict two or more traits and demonstrate improved accuracy (Calus and Veerkamp, 2011; Sandhu et al., 2021a). MT models use the shared genetic information between the traits using the same set of predictors with the assumption of some structure in the captured output. MT models leverage the correlation between different traits and show a considerable advantage in other domains, such as ecological modeling, weather forecasting, forest management, and data mining (Voyant et al., 2017). MT models using shared genetic information are important for hard/expensive to phenotype traits having low heritability (Juliana et al., 2019). Several studies have demonstrated the improvement of prediction accuracy for a primary trait with the inclusion of a secondary trait into the MT models in wheat. Sandhu et al. (2021a) showed an improvement of 20 and 12% prediction accuracies for grain yield and grain protein content in wheat, respectively, by including correlated spectral reflectance indices into the model as secondary traits in the MT approach. Similarly, Hayes et al. (2017), Lado et al. (2018), and Bhatta et al. (2020) observed the improvement of prediction abilities with MT models over the uni-trait models for end-use quality traits in cereals.
A previous study from our group showed that GS accuracies varied from 0.27 to 0.81 for 14 end-use quality traits using nine different uni-trait models (Sandhu et al., 2021c). Statistical models used for training the uni- or multi-trait GS models play an important role in evaluating performance (Jia and Jannink, 2012). Ridge regression best linear unbiased prediction (rrBLUP) is one of the most frequently used models for quantitative traits assuming normal distribution of marker effects with constant variances (Endelman, 2011). Bayes Cpi uses variable selection, scaled-t distribution to estimate marker effects and assumes different variances for adjusting to the different genetic architecture of the trait (Pérez and De Los Campos, 2014; Montesinos-López et al., 2019a). rrBLUP and Bayes Cpi are known as parametric models as they assume a prior relationship between features and predictors, and this opens up the avenue for the nonparametric machine and deep learning algorithms. Machine learning models such as random forest, ensemble learning, and support vector machines use algorithms that progressively learn the pattern from sample data to make final predictions (Hastie et al., 2009). Deep learning is one of the branches of machine learning focusing on the artificial neural network for model training and predictions. Deep learning models such as generative neural networks, convolutional neural networks, and recurrent neural networks use different combinations of layers and nonlinear activation functions to transform the data at each layer to obtain a better fit for each trait by considering genetic architecture (Lecun et al., 2015).
In previous studies, we have shown the advantages of multi-trait GS models (Sandhu et al., 2021e) and machine and deep learning models for predicting complex traits in wheat (Sandhu et al., 2021b; Sandhu et al., 2021c). Building upon the findings of previous studies, this study’s objectives were to 1) optimize the uni- and multi-trait GS models for seven end-use quality traits, 2) compare the performances of four uni- and multi-trait GS models using cross-validation and independent predictions, and 3) assess the potential of across-location prediction using multi-trait models and with the inclusion of genotype by environment interaction component.
Materials and Methods
Plant material: A total of 666 SWW genotypes from the Washington State University winter wheat breeding program were screened at two locations, namely, Lind and Pullman, WA, United States, from 2015 to 2019. These genotypes consist of preliminary and advanced yield lines, doubled haploid lines, and F3:5 lines screened as part of the breeding program. Genotypes in the advanced and preliminary yield trials were screened for yield, and superior lines were later evaluated for end-use quality traits. Double haploid lines and F3:5 derived lines were screened for disease resistance and agronomic traits, and the selected genotypes were screened for quality traits and not for yield traits. As the dataset was from a breeding program, some lines were continuously removed each year with new genotypes in the subsequent year, resulting in an unbalanced dataset. More information about the dataset is referred to Aoun et al., 2021a and Sandhu et al., 2021b. End-use quality data were collected separately at both locations for all the genotypes.
Phenotyping for the end-use quality traits: These genotypes were tested for seven end-use quality traits, namely, cookie diameter (CODI), grain protein content (GPC), flour yield (FYELD), flour SDS sedimentation (FSDS), flour ash (FASH), flour protein (FPROT), and milling score (MSCOR). Complete information about all these traits and their summary is provided in Table 1. To evaluate grain characteristics, GPC was measured following AACC Approved Method 39–10.01 using an NIR analyzer (Perten Elmer, Sweden). Flour parameters, namely, FASH, FPROT, and FSD were measured using the extracted flour. FASH and FPROT were measured using Approved methods 08–01.01 and 39–11.01. The milling traits, that is, FYELD and MSCOR were measured using the sample obtained from the modified Quadrumat Senior Experimental Milling System. FYELD was estimated as a ratio of total flour by weight (reduction rolls and break). MSCOR was obtained using FYELD and FASH. CODI is one of the baking parameters and is estimated by following the AACC Approved Method 10–52.02. More information about the phenotyping is referred to Aoun et al., 2021a and Sandhu et al., 2021b.
Genotyping: Genotyping by sequencing (GBS) was used for genotyping the complete population using the facilities from Genomics Sciences Laboratory, Raleigh, NC (Poland et al., 2012). The complete details about the genotyping and SNP calling was reported in Aoun et al. (2021a) and Sandhu et al. (2021a). Initial SNP data consisted of 216,392 markers anchored to the T. aestivum RefSeq v1.0 reference genome. Markers were removed based on the minor allele frequency less than 5%, heterozygosity more than 15%, and markers missing more than 20% of data, and the whole pipeline was implemented in R (R Development Core Team, 2020). At the end of the filtering, we were left with 40,518 SNPs used for further analysis.
Phenotypic data analysis: To account for the unbalanced dataset in this study, adjusted means were extracted using residuals obtained from the unreplicated genotypes in individual environments using the augmented complete block design model implemented in the R statistical program. Adjusted means were obtained according to the method implemented in Sandhu et al. (2021b), and the model equation is given as follows:
where Yij is the raw phenotype, Blocki corresponds to the fixed block effect, Checkj is the replicated check cultivar effect; Blocki is the fixed block effect, and eij is the residuals.
Adjusted means across the environments were obtained using the models and are given as follows:
where Yijk is the raw phenotype value; Checkj, Blocki, and Envk are the fixed effect of the ith check, jth block, and kth environment, respectively; and eijk is the residuals.
Heritability of each trait was calculated using the model as follows:
where
Genetic correlation among traits was obtained using the multivariate models as follows:
where yA and yB are the BLUPs of the two traits, X and Z denote the design matrix, g is the random genetic effects, and e is the residual for each trait. Variance components were calculated assuming
where cov(A, B) is the covariance between two traits, Var(A) and Var(B) represent variances of two traits individually, and the analysis was performed using JMP genomics (SAS Institute Inc, 2011).
Genomic selection models: We evaluated the performances of four uni-trait and multi-trait GS models for predicting seven end-use quality traits, and prediction accuracy was compared under different validation scenarios to mimic the breeding program. These four models were GBLUP, Bayes B, RF, and MLP and were tried under both uni-trait and multi-trait scenarios. Complete information about the model structure and optimization is provided below:
Genomic best linear unbiased predictor: The uni-trait GBLUP model was used to train each trait individually, and the model is represented as follows:
where y is the vector of end-use quality phenotype for each genotype,
where n is the number of traits,
Bayesian B: The uni-trait Bayes B model was used to train each trait individually, and the model is represented as follows:
where
which is a mixture of distribution with mass at zero and same prior for all remaining markers, that is, χ−2 (dfβ, Sβ) where Sβ is a scaling parameter and dfβ is the degree of freedom (Pérez and De Los Campos, 2014).
The MT Bayes B model is represented as follows:
where y represents the vector of phenotypes of the end-use quality traits,
Bayesian multi-trait multi-environment model (BMTME): Montesinos-López et al., 2016, Montesinos-López et al., 2019b provided a BMTME model for predictions which is represented as follows:
where
Random forests: RF is a tree-based machine learning model where output is predicted from the collection of identically distributed trees. Input features are split at each node of the tree to create a new branch, and splitting is performed by lowering the loss function. Bootstrap sampling was performed over the training set to select the best set of features for tree building (Ramzan et al., 2020). The model equation is given as follows:
where
1) Bootstrap sampling was performed to select the plants from the training set with replacement and was repeated for b = (1,…, B) times.
2) Max feature (max_feature) function from the random forest regressor library was used to identify the best set of features (SNP) by lowering the loss function while building new trees.
3) Splitting at each node of the tree was performed using genotypic data to lower the mean square error
4) The aforementioned three steps were repeated until a minimum node or maximum depth was reached. The set of these trees were used to predict the output of a genotype
The hyperparameter space was explored using the grid search cross-validation (CV) function to optimize the hyperparameters for each trait by lowering the mean squared error. The important hyperparameters used for RF training were number and depth of trees, feature importance, and number of features sampled for each iteration. Hyperparameters tried were number of trees (200, 300, 500, and 1,000), max features (auto and sqrt), and max depth (40, 60, 80, and 100) using random forest regression and Scikit learn libraries.
Multilayer perceptron (MLP): MLP is a special type of neural network where information flows in one direction, starting from input layer through different hidden (processing) layers to the output layer. The output from the last hidden layer is used to predict output and is represented as follows:
where Yj is the output from the jth hidden layer,
The hyperparameter space was explored using the Keras inner grid search cross-validation (CV) function to optimize the hyperparameters for each trait by lowering the mean squared error. For hyperparameter optimization, 80% of the training data were used, where 80% of this dataset was used for exploring the hyperparameter space and the remaining 20% for validation. Scikit learn and Keras libraries were used to optimize the model in Python (Gulli and Pal 2017). A full-factor design was implemented using grid search CV to explore parameters, that is, solvers, dropout, learning rate, number of filters, activation function, number of hidden layers and neurons, and regularizations. Overfitting in the model was controlled using early stopping, regularization, and dropout (Srivastava et al., 2014). More information about the MLP models, hyperparameter optimization, and overfitting control is used in Sandhu et al., 2021c, Sandhu et al., 2021a.
Assessing the model’s prediction abilities: The genomic selection model performance was evaluated as prediction accuracy, which is the correlation between GEBVs and the observed phenotype. The correlate function from the “corrr” R package was used to assess prediction accuracy (Max et al., 2020). Cross-validation approach, that is, a five-fold CV was used to evaluate the prediction accuracies where each fold was used separately as a testing fold, and this process was repeated two hundred times. For each location, that is, Pullman and Lind, performances of both uni- and multi-trait models were evaluated separately using five-fold CV, and the results were reported separately for each trait and model.
Across-location prediction scenarios were also tested where the dataset from one location was used to predict the performances of genotypes at another location and environment. In our case, the complete data set from one location, that is, Lind was used to train the model, and predictions were made for 2019 Pullman environment and vice versa. Genotype by environment components was also included during across-location predictions.
Results
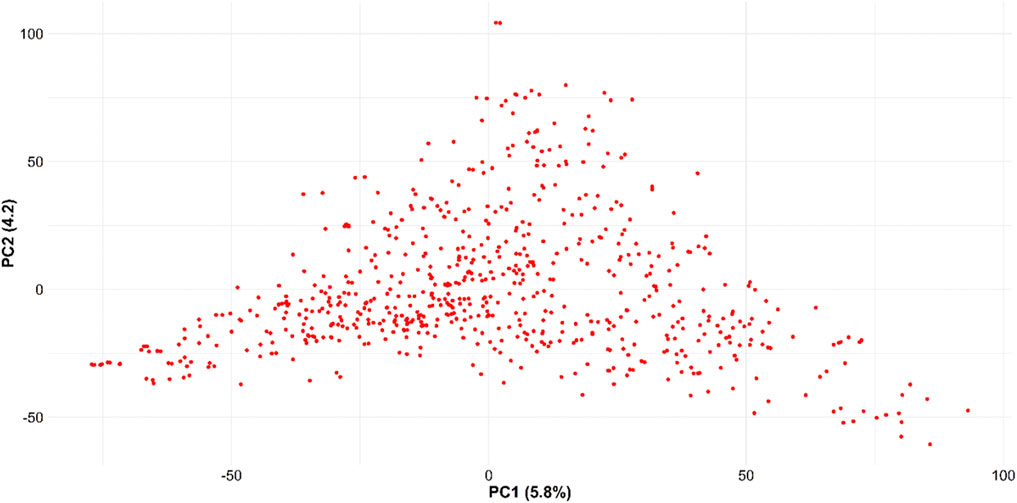
Trait summary, heritability, and correlation: Table 1 provides the summary and broad-sense heritability of seven end-use quality traits evaluated from the SWW population planted at two locations in this study. Most of the traits had moderate to high heritability, except grain protein content and flour protein. Heritability of FSDS and FYELD was 0.92 and 0.91, respectively, highest among all the traits. Phenotypic and genetic correlation results provided evidence that few traits were correlated (Figures 1, 2). The highest phenotypic and genetic correlations were observed between GPC and FPROT, which was 0.93 and 0.91, respectively (Figures 1, 2). Some traits were negatively correlated with each other. Principal component analysis showed the absence of structure in the population, where first and second PCs only explained the 5.8 and 4.2% variation, respectively (Figure 3), and this was expected as the population was from the same breeding program. Frequency distribution for all the traits at both locations is shown in Supplementary Figure S1. Furthermore, ANOVA results showed that all the traits, except CODI, have significant GXE interaction (Supplementary Table S1).
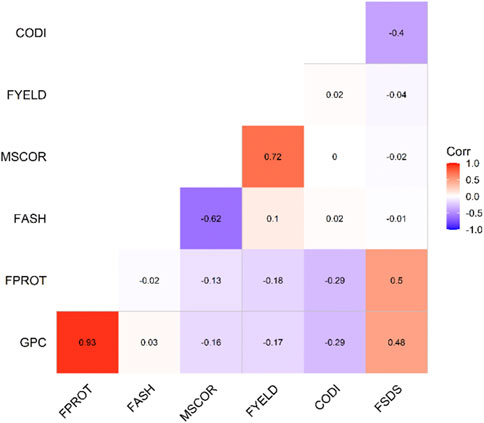
FIGURE 1. Phenotypic correlation among the seven end-use quality traits evaluated from the SWW population.

FIGURE 2. Genetic correlation among the seven end-use quality traits evaluated from the SWW population.
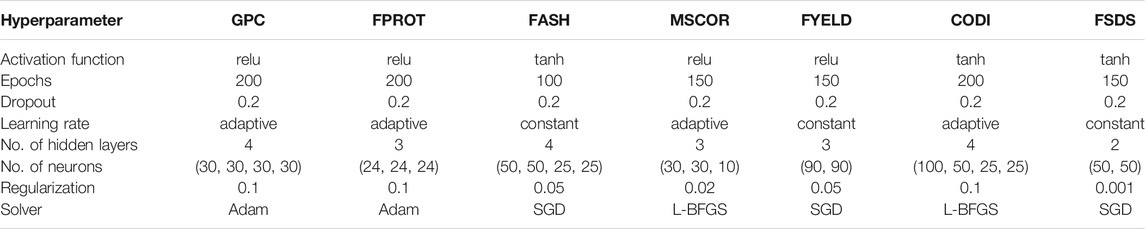
Hyperparameter optimization for the MLP model: Two hundred iterations were performed for the MLP model using Keras inner grid search CV function to optimize the hyperparameters for each trait by lowering the mean squared error. The hyperparameters optimized for each trait were later used for predicting traits in the testing set. Tables 2, 3 provide the set of hyperparameters optimized for each trait under the uni- and multi-trait MLP model. Regularization and dropout were used in the model to control the overfitting following Srivastava et al. (2014). The number of hidden layers and neurons played a critical role during model optimization compared to other hyperparameters. For the uni-trait MLP model, some traits required different activation functions other than relu, while for multi-trait MLP, all the traits gave the lowest MSE with a relu activation function. Information about the hyperparameters is provided separately for each trait, demonstrating that different genetic architecture required specific combinations of hyperparameters for best performance (Tables 2, 3).

TABLE 3. Hyperparameters optimized for seven end-use quality traits using the multi-trait MLP model.
Prediction accuracies within the location using cross-validation: We compared the performance of four uni- and multi-trait models using a five-fold CV approach to predict seven quality traits. Average results for each trait in the multi-trait GS were used to compare its performance with uni-trait GS models. Figures 4, 5 show the uni- and multi-trait prediction accuracies for the two locations, namely, Pullman and Lind, respectively. Multi-trait prediction accuracies were higher for all the traits, except CODI, for both locations (Table 4). Prediction accuracies varied from 0.44 to 0.76 and from 0.40 to 0.79 for uni- and multi-trait models, respectively, for seven traits evaluated in this study (Figures 4, 5). The Bayes B uni-trait model obtained the lowest prediction accuracies, while the MLP multi-trait model obtained the highest prediction accuracies. On average, multi-trait GS models gave 5.5% higher prediction accuracies than uni-trait GS models (Table 4). There was no difference in the uni- and multi-trait Bayes B model’s performance for most traits. In summary, multi-trait GBLUP, Bayes B, RF, and MLP performed 6.9, 1.8, 6.6, and 6.5% superior to their uni-trait counterparts, respectively (Table 4).
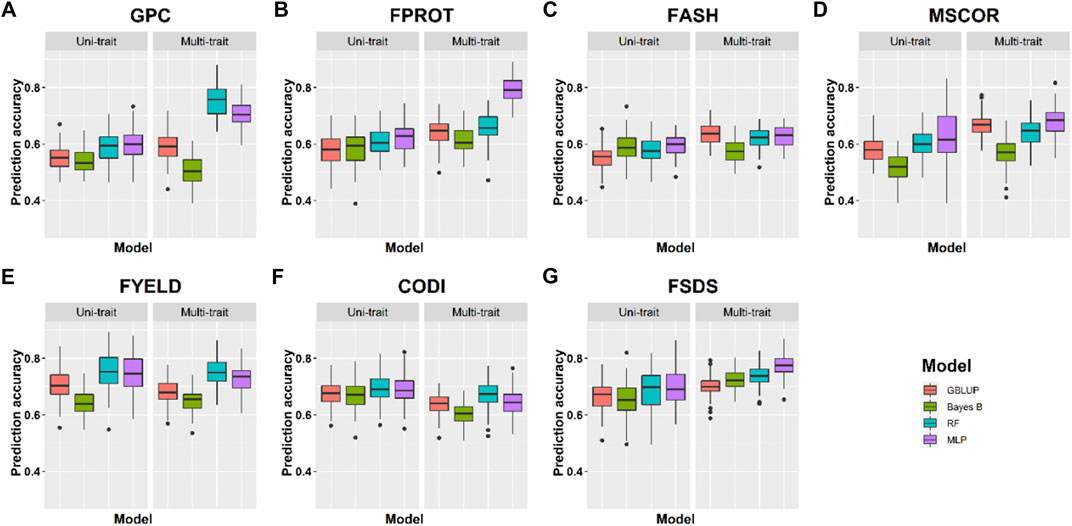
FIGURE 4. Prediction accuracies for seven end-use quality traits using four different uni- and multi-trait genomic selection models for the Pullman location.
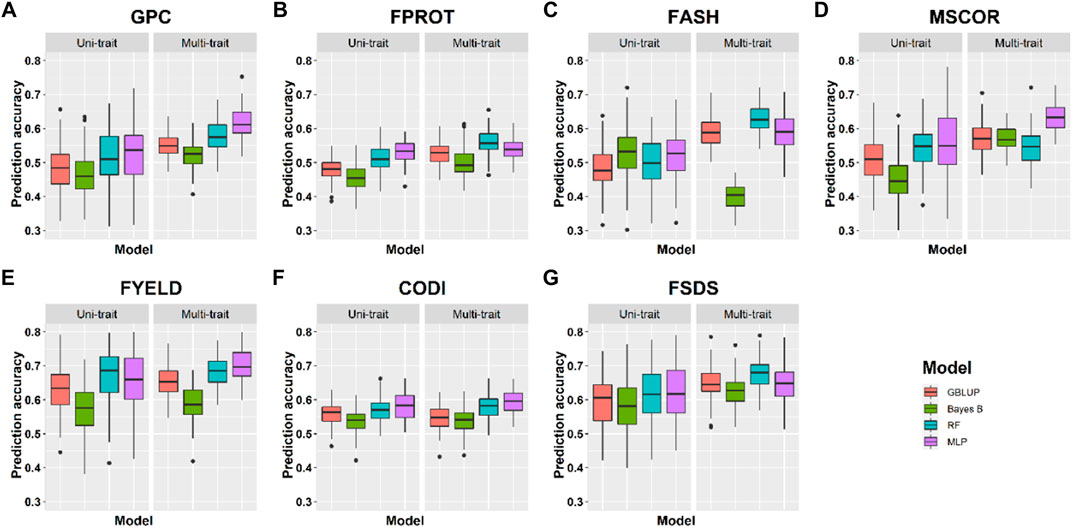
FIGURE 5. Prediction accuracies for seven end-use quality traits using four different uni- and multi-trait genomic selection models for the Lind location.
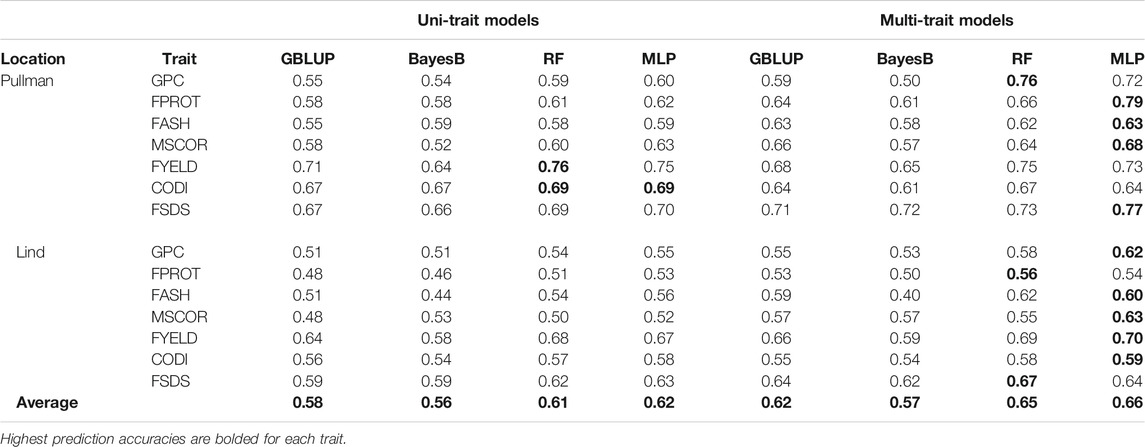
TABLE 4. Prediction accuracies for seven end-use quality traits using four different uni- and multi-trait genomic selection models for the two locations across the years, namely, Pullman and Lind using the cross-validation approach.
The highest prediction accuracies were obtained using a multi-trait MLP model for five of the seven traits evaluated in this study, closely followed by the multi-trait–based RF and GBLUP model. FPROT showed the greatest improvement in prediction accuracy, that is, 36%, with the multi-trait model compared to uni-trait GS models, while CODI showed the lowest improvement in prediction accuracy, that is, -2.9%. Prediction accuracies for the Pullman and Lind locations varied from 0.52 to 0.79 and from 0.40 to 0.70, respectively, with higher accuracy for all the traits at the Pullman location. Improvement in prediction accuracies for GPC, FASH, MSCOR, FYELD, and FSDS with multi-trait models was -0.1–31.6%, 5.4–15.4%, 9.6–31.6%, 1.5–2.3%, and 7.6–16.7%, respectively (Figures 4, 5).
Prediction accuracies across the environments: Across-location predictions were performed where data from the Pullman environment was used for model training and predictions were made for the Lind environment, and vice versa. Across-location prediction accuracies were lower than prediction accuracies within the environment using cross-validation (Tables 4, 5). Figure 6 and Table 5 show the prediction accuracies for 2019_Pullman when the model was trained on Lind data, and predictions were made for seven end-use quality traits with four different uni- and multi-trait GS and one multi-trait multi-environment model. Similarly, Figure 7 and Table 5 show the prediction accuracies for 2019_Lind when the model was trained using the Pullman dataset. Across-location prediction accuracies varied from 0.25–0.50, 0.28–0.48, to 0.31–0.56 for uni-trait, multi-trait, and multi-trait multi-environment models, respectively, for seven traits evaluated in this study. Similar to cross-validation results, Bayes B models performed inferior compared to all other models.
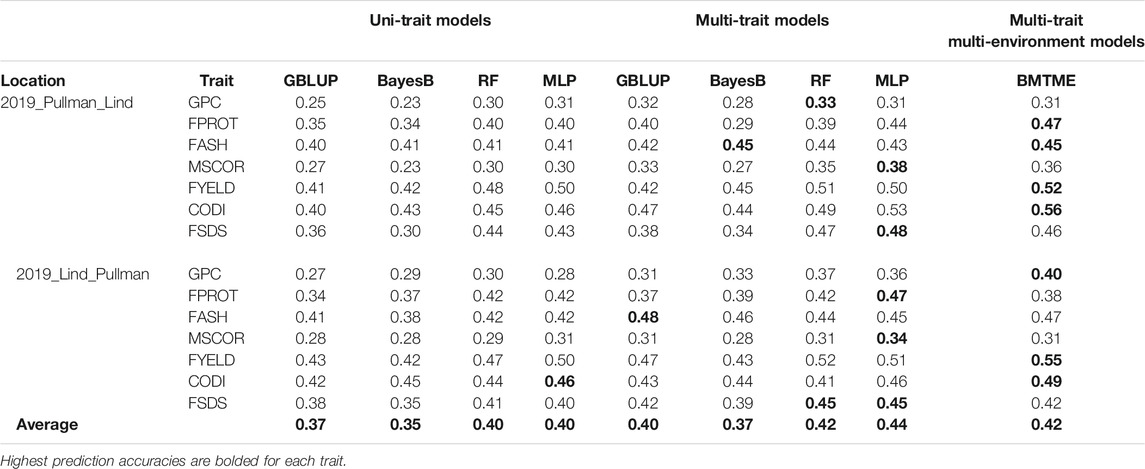
TABLE 5. Prediction accuracies for seven end-use quality traits using four different uni- and multi-trait genomic prediction models for the across-location predictions. 2019_Pullman_Lind represents the scenario where predictions were made on 2019_Pullman by training models on the Lind dataset.
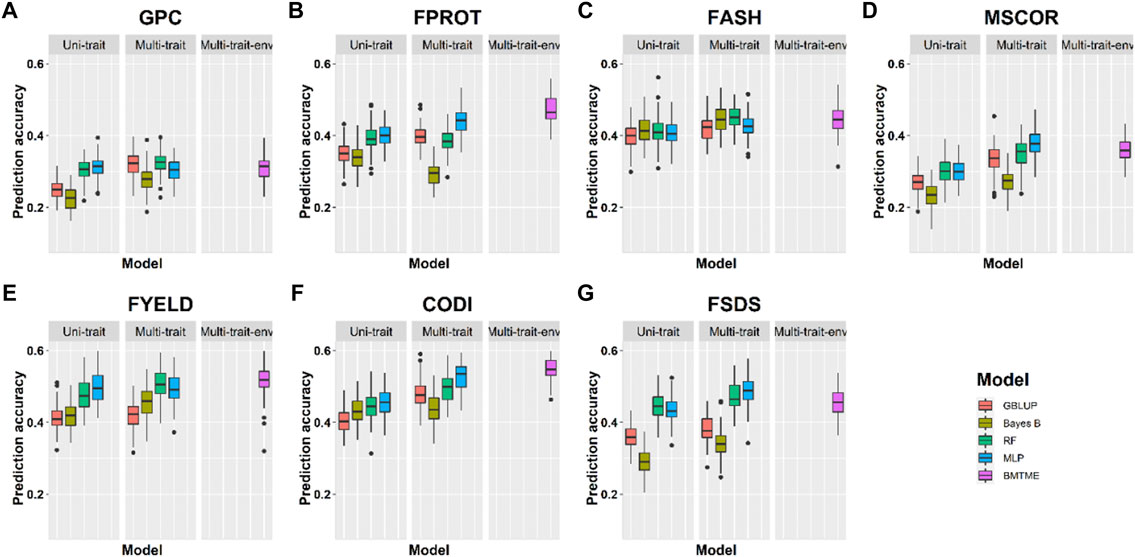
FIGURE 6. Prediction accuracies across environment Pullman with training on the Lind dataset for seven end-use quality traits using four different uni- and multi-trait and one Bayesian multi-trait multi-environment genomic prediction models.
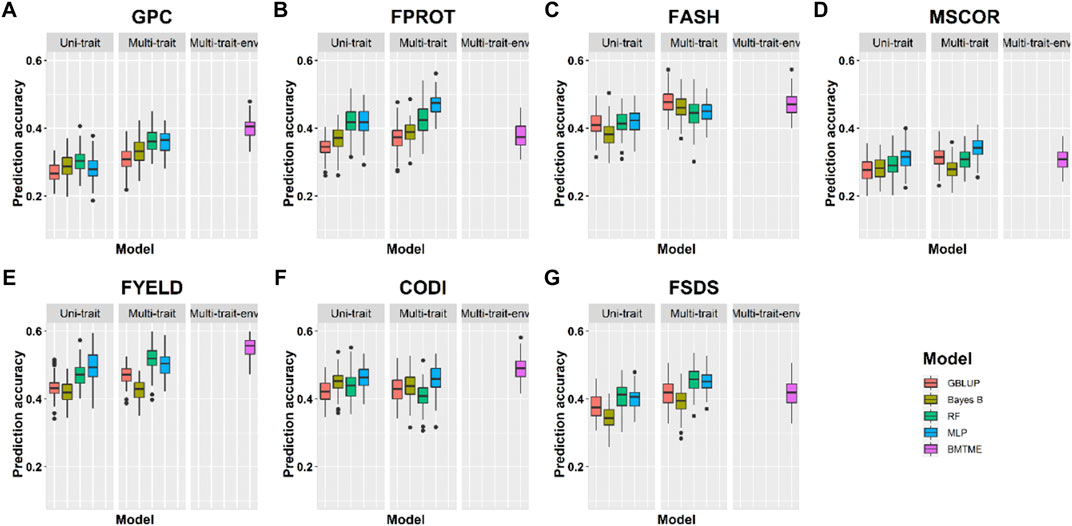
FIGURE 7. Prediction accuracies across environment Lind with training on the Pullman dataset for seven end-use quality traits using four different uni- and multi-trait and one Bayesian multi-trait multi-environment genomic prediction models.
We observed that multi-trait GS models performed 7.9% superior compared to uni-trait GS models, and it further strengthens the results obtained for within the environment scenario that multi-trait GS models are better for predicting end-use quality traits. Multi-trait GBLUP, Bayes B, RF, and MLP performed 8.1, 5.7, 5.0, and 10.0% superior to their uni-trait counterparts, respectively (Table 5). Improvement in prediction accuracies for GPC, FPROT, FASH, MSCOR, FYELD, CODI, and FSDS with multi-trait models was 21.7–43.4%, -14.7–29.4%, 5.0–12.5%, -17.4–65.2%, 2.4–24.4%, 10.0–32.5%, and 13.3–60.0%, respectively, over the uni-trait models (Figures 4, 5). There was no difference in the performance of multi-trait machine and deep learning models from the multi-trait multi-environment model which consisted of genotype by environmental interaction in the model (Table 5).
Discussion
Plant breeders routinely collect data for multiple traits from multiple environments before making final selections. Genomic selection is becoming popular to predict GEBVs due to robust next-generation sequencing technologies and its cost-effectiveness. However, few studies have utilized the multi-trait and multi-environment prediction models due to the model’s complexity, huge computational burden, and lack of good quality phenotyping data (Cuevas et al., 2017). Multi-environment prediction represents a perfect scenario to reduce the number of locations or plots needed in subsequent selection trials (Tolhurst et al., 2019; de Oliveira et al., 2020). Multi-trait GS models showed improved prediction accuracy in previous studies when traits are correlated and have low heritability; these models provide an opportunity to predict traits simultaneously by borrowing information from each other (Gill et al., 2021; Larkin et al., 2021). This study explored the potential of using multi-trait–based GS models to predict seven end-use quality traits in soft white wheat population planted at two locations in Washington, United States, from 2015 to 2019. Prediction accuracies for individual traits varied from 0.23 to 0.79 using different models, with multi-trait models performing superior to uni-trait models for the majority of the traits and validation scenarios.
Seven out of the 14 end-use quality traits from our previous study were selected for multi-trait and multi-environment predictions, which showed lower prediction accuracies and higher genotype by environment interactions (Aoun et al., 2021a; Sandhu et al., 2021c). These higher values of the genotype by environment interactions demonstrated the potential of using multi-trait multi-location models in the breeding programs. We observed a change in genotypes ranking across the multiple environments for these seven traits due to high genotype by environment interactions and negative correlation among the environments. Multi-trait models performed 5.5 and 7.9% superior to uni-trait GS models for within-environment and across-location predictions, while multi-trait multi-environment models performed 10.5% superior to uni-trait GS models. Across-location prediction accuracies for the seven traits varied from 0.23 to 0.53, which were higher than those of previous studies for across-location predictions for end-use quality traits (Lado et al., 2013; Hayes et al., 2017). This was attributed to the reference population, which included the progeny of different lines from the same breeding program. Likewise, Heffner et al. (2011) showed higher across-location prediction for end-use quality by using the same set of biparental populations across the locations. The high prediction accuracy in their study was reflected from a biparental population where training and testing sets must have a relationship and with little variation (Heffner et al., 2011). Furthermore, we observed that genotype by environment interaction components could improve across-location prediction accuracies in the models. Similar work was shown by Ward et al. (2019) and Monteverde et al. (2019) that describe the advantage of including genotype by environment and marker by environment interaction components into the models when correlation among environments is lower.
Predicting breeding values of un-phenotyped individuals is always a daunting task, but different strategies have been employed in recent years for predictions under different circumstances. Inclusion of correlated traits into multi-trait models has been effective to increase predictions for primary traits with low heritability when the secondary trait is highly correlated with high heritability. However, some studies have shown no improvement of prediction accuracies when secondary correlated traits were included into the models for predicting traits in rice (Oryza sativa L.) (Schulthess et al., 2016), avocado (He et al., 2016), and mice (Jiang et al., 2015), which could be attributed to some environmental changes or interactions not captured by the associated models. Similarly, Jia and Jannink (2012) showed no advantage of using multi-trait GS models even when traits have high heritability differences. However, in our study, we observed that even though traits have moderate to high heritability, they still showed an increase in prediction accuracies using multi-trait models when the traits have moderate to high correlation. Highest improvement was observed for traits like GPC, FPROT, and FSDS due to their high correlation, whereas CODI showed lowest improvement due to low correlation with other traits. Correlated traits help predict correlated responses when traits of interest are not phenotyped; this will also help predict expensive to phenotype traits. Previous works have shown that prediction accuracies increase when traits have high correlation, but not with low to intermediate correlation among traits (Rutkoski et al., 2012; Jiang et al., 2015).
Our study showed that uni-trait– and multi-trait–based machine and deep learning models performed superior to traditional GS models. We observed that machine and deep learning models performed 5–11% superior to Bayes B and GBLUP under cross-validation and across-location predictions. Liu et al. (2019), Sandhu et al. (2021a) and Zingaretti et al. (2020) also demonstrated the advantage of using deep learning models in soybean (Glycine max L.), wheat, and strawberries (Fragaris ananassa) over the traditional mixed model–based approaches and supported our findings. Similarly, Montesinos-López et al. (2018) demonstrated the multi-trait–based deep learning model’s superiority over the multi-trait Bayesian models for predicting four different traits in wheat and maize (Zea mays L.). These machine learning models are highly flexible for understanding complex interactions present in these datasets, thus inferring the current trends in the datasets compared to parametric models like GBLUP and Bayes B. Furthermore, multi-trait machine learning models are more suitable as they could further explore relationships between traits and sets of predictors with the removal of redundant information from the models with explicit programming. Due to these characteristics of machine and deep learning models, we observed their better performances under uni- and multi-trait scenarios than under Bayes B and GBLUP.
As discussed, multi-trait machine and deep learning models performed better than multi-trait Bayes B and GBLUP models; however, the advantage of machine and deep learning models diminishes when the genotype by environment interaction component was included in the BMTME model. The inclusion of genotype by environment components perfectly models the environmental effects and correlation among the traits for different environments, resulting in improvement of prediction accuracy. Similarly, Guo et al. (2020) and Ibba et al. (2020) showed an increase in prediction accuracies for yield-related traits in U.S. soft wheat and end-use quality traits using multi-trait multi-environment models over the uni-trait models. The comparable performance of multi-trait machine learning models and BMTME models could be attributed to the capacity of BMTME models to provide separate penalization for the genotypes, environment, and genotype by environmental interaction, while working of the machine and deep learning models follow the black-box nature, creating problem for biological understanding of the process.
Conclusion
We explored the potential of using multi-trait–based genomic selection models for predicting seven end-use quality traits in soft white wheat population. Uni-trait– and multi-trait–based genomic selection models were optimized separately for each trait, and optimized hyperparameters were used for testing. Different cross-validation, independent, and across-location prediction scenarios were applied to compare the model’s performance. Multi-trait genomic selection models performed superior to uni-trait models when traits were correlated with each other. The inclusion of genotype by environment interaction components further improves the across-location prediction accuracies, a typical advantage shown by machine and deep learning models. Prediction accuracies obtained in this study using multi-trait models for within-environment and across-location predictions open up the avenue to explore the use of genomic selection to select for end-use quality traits in wheat. The prediction accuracies obtained in this study further provide evidence of the usefulness of genomic selection in wheat breeding and will enhance the confidence of the breeder to utilize this tool when making selections.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author Contributions
KS and AC contributed to conceptualization; KS and SP helped with data analysis; MA assissted with genotyping and curation; KS wrote the original draft; KS, SP, MA, and AC involved in review and editing; AC acquired resources; and AC contributed to supervision and funding. All authors approved the final document for submission.
Funding
This project was supported by the Washington Grain Commission, the O.A. Vogel Wheat Research Fund from Washington State University, the Agriculture and Food Research Initiative Competitive Grant 2017-67007-25939 (WheatCAP), USDA ARS CRIS Project 2090-43440008-00D, and Hatch project 1014919.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
This work was highly supported by the late Craig Morris, who until his passing was the director of the USDA-ARS Western Wheat and Pulse Quality Laboratory. Morris was instrumental in the advancement of soft white wheat quality efforts, and his insights were invaluable as we prepared this manuscript. His collaborative efforts would have had him listed as a co-author on this publication had it not been for his unexpected and untimely passing, and thus, we acknowledge here his efforts in memoriam.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2022.831020/full#supplementary-material
References
Aoun, M., Carter, A. H., Ward, B. P., and Morris, C. F. (2021a). Genome-wide Association Mapping of the 'super-Soft' Kernel Texture in white winter Wheat. Theor. Appl. Genet. 134, 2547–2559. doi:10.1007/S00122-021-03841-Y
Aoun, M., Carter, A., Thompson, Y. A., Ward, B., and Morris, C. F. (2021b). Environment Characterization and Genomic Prediction for End-Use Quality Traits in Soft white winter Wheat. Plant Genome 14, e20128. doi:10.1002/TPG2.20128
Awika, J. M. (2011). Major Cereal Grains Production and Use Around the World. ACS Symp. Ser. 1089, 1–13. doi:10.1021/BK-2011-1089.CH001
Battenfield, S. D., Guzmán, C., Gaynor, R. C., Singh, R. P., Peña, R. J., Dreisigacker, S., et al. (2016). Genomic Selection for Processing and End-Use Quality Traits in the CIMMYT Spring Bread Wheat Breeding Program. Plant Genome 9. doi:10.3835/plantgenome2016.01.0005
Bernardo, R. (2016). Bandwagons I, Too, Have Known. Theor. Appl. Genet. 129, 2323–2332. doi:10.1007/s00122-016-2772-5
Bhatta, M., Gutierrez, L., Cammarota, L., Cardozo, F., Germán, S., Gómez-Guerrero, B., et al. (2020). Multi-trait Genomic Prediction Model Increased the Predictive Ability for Agronomic and Malting Quality Traits in Barley (Hordeum Vulgare L.). G3 Genes, Genomes, Genet. 10, 1113–1124. doi:10.1534/g3.119.400968
Bhave, M., and Morris, C. F. (2008). Molecular Genetics of Puroindolines and Related Genes: Allelic Diversity in Wheat and Other Grasses. Plant Mol. Biol. 66, 205–219. doi:10.1007/s11103-007-9263-7
Breseghello, F., and Sorrells, M. E. (2006). Association Mapping of Kernel Size and Milling Quality in Wheat (Triticum aestivum L.) Cultivars. Genetics 172, 1165–1177. doi:10.1534/genetics.105.044586
Calus, M. P., and Veerkamp, R. F. (2011). Accuracy of Multi-Trait Genomic Selection Using Different Methods. Genet. Sel. Evol. 43, 1–14. doi:10.1186/1297-9686-43-26
Campbell, G. M., Fang, C., and Muhamad, I. I. (2007). On Predicting Roller Milling Performance VI. Food Bioproducts Process. 85, 7–23. doi:10.1205/fbp06005
Carter, A. H., Garland-Campbell, K., Morris, C. F., and Kidwell, K. K. (2012). Chromosomes 3B and 4D Are Associated with Several Milling and Baking Quality Traits in a Soft white spring Wheat (Triticum aestivum L.) Population. Theor. Appl. Genet. 124, 1079–1096. doi:10.1007/s00122-011-1770-x
Cobb, J. N., Biswas, P. S., and Platten, J. D. (2019a). Back to the Future: Revisiting MAS as a Tool for Modern Plant Breeding. Theor. Appl. Genet. 132, 647–667. doi:10.1007/s00122-018-3266-4
Cobb, J. N., Juma, R. U., Biswas, P. S., Arbelaez, J. D., Rutkoski, J., Atlin, G., et al. (2019b). Enhancing the Rate of Genetic Gain in Public-Sector Plant Breeding Programs: Lessons from the Breeder's Equation. Theor. Appl. Genet. 132, 627–645. doi:10.1007/s00122-019-03317-0
Cuevas, J., Crossa, J., Montesinos-López, O. A., Burgueño, J., Pérez-Rodríguez, P., and de los Campos, G. (2017). Bayesian Genomic Prediction with Genotype × Environment Interaction Kernel Models. G3 Genes, Genomes, Genet. 7, 41–53. doi:10.1534/G3.116.035584
de los Campos, G., and Grüneberg, A. (2016). MTM Package. Available at: http://quantgen.github.io/MTM/vignette.html.
de Oliveira, A. A., Resende, M. F. R., Ferrão, L. F. V., Amadeu, R. R., Guimarães, L. J. M., Guimarães, C. T., et al. (2020). Genomic Prediction Applied to Multiple Traits and Environments in Second Season maize Hybrids. Heredity 125, 60–72. doi:10.1038/s41437-020-0321-0
Endelman, J. B. (2011). Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. The Plant Genome 4, 250–255. doi:10.3835/plantgenome2011.08.0024
Gill, H. S., Halder, J., Zhang, J., Brar, N. K., Rai, T. S., Hall, C., et al. (2021). Multi-trait Multi-Environment Genomic Prediction of Agronomic Traits in Advanced Breeding Lines of winter Wheat. Front. Plant Sci. 12, 1619. doi:10.3389/FPLS.2021.709545
Guo, J., Khan, J., Pradhan, S., Shahi, D., Khan, N., Avci, M., et al. (2020). Multi-trait Genomic Prediction of Yield-Related Traits in US Soft Wheat under Variable Water Regimes. Genes 11, 1270–1326. doi:10.3390/genes11111270
Guzman, C., Peña, R. J., Singh, R., Autrique, E., Dreisigacker, S., Crossa, J., et al. (2016). Wheat Quality Improvement at CIMMYT and the Use of Genomic Selection on it. Appl. Translational Genomics 11, 3–8. doi:10.1016/j.atg.2016.10.004
Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction.
Hayes, B. J., Panozzo, J., Walker, C. K., Choy, A. L., Kant, S., Wong, D., et al. (2017). Accelerating Wheat Breeding for End-Use Quality with Multi-Trait Genomic Predictions Incorporating Near Infrared and Nuclear Magnetic Resonance-Derived Phenotypes. Theor. Appl. Genet. 130, 2505–2519. doi:10.1007/s00122-017-2972-7
He, D., Kuhn, D., and Parida, L. (2016). Novel Applications of Multitask Learning and Multiple Output Regression to Multiple Genetic Trait Prediction. Bioinformatics 32, i37–i43. doi:10.1093/BIOINFORMATICS/BTW249
Heffner, E. L., Jannink, J.-L., Iwata, H., Souza, E., and Sorrells, M. E. (2011). Genomic Selection Accuracy for Grain Quality Traits in Biparental Wheat Populations. Crop Sci. 51, 2597–2606. doi:10.2135/cropsci2011.05.0253
Herter, C. P., Ebmeyer, E., Kollers, S., Korzun, V., and Miedaner, T. (2019). An Experimental Approach for Estimating the Genomic Selection Advantage for Fusarium Head Blight and Septoria Tritici Blotch in winter Wheat. Theor. Appl. Genet. 132, 2425–2437. doi:10.1007/s00122-019-03364-7
Ibba, M. I., Crossa, J., Montesinos-López, O. A., Montesinos-López, A., Juliana, P., Guzman, C., et al. (2020). Genome-based Prediction of Multiple Wheat Quality Traits in Multiple Years. Plant Genome 13, e20034. doi:10.1002/TPG2.20034
Jernigan, K. L., Godoy, J. V., Huang, M., Zhou, Y., Morris, C. F., Garland-Campbell, K. A., et al. (2018). Genetic Dissection of End-Use Quality Traits in Adapted Soft white winter Wheat. Front. Plant Sci. 9, 1–15. doi:10.3389/fpls.2018.00271
Jia, Y., and Jannink, J.-L. (2012). Multiple-trait Genomic Selection Methods Increase Genetic Value Prediction Accuracy. Genetics 192, 1513–1522. doi:10.1534/genetics.112.144246
Jiang, J., Zhang, Q., Ma, L., Li, J., Wang, Z., and Liu, J.-F. (2015). Joint Prediction of Multiple Quantitative Traits Using a Bayesian Multivariate Antedependence Model. Heredity 115, 29–36. doi:10.1038/hdy.2015.9
Juliana, P., Montesinos-López, O. A., Crossa, J., Mondal, S., González Pérez, L., Poland, J., et al. (2019). Integrating Genomic-Enabled Prediction and High-Throughput Phenotyping in Breeding for Climate-Resilient Bread Wheat. Theor. Appl. Genet. 132, 177–194. doi:10.1007/s00122-018-3206-3
Kaur, B., Sandhu, K. S., Kamal, R., Kaur, K., Singh, J., Röder, M. S., et al. (2021). Omics for the Improvement of Abiotic, Biotic, and Agronomic Traits in Major Cereal Crops: Applications, Challenges, and Prospects. Plants 10, 1989. doi:10.3390/plants10101989
Kiszonas, A. M., Fuerst, E. P., and Morris, C. F. (2013). A Comprehensive Survey of Soft Wheat Grain Quality in U.S. Germplasm. Cereal Chem. J. 90, 47–57. doi:10.1094/CCHEM-06-12-0073-R
Kiszonas, A. M., Fuerst, E. P., and Morris, C. F. (2015). Modeling End-Use Quality in u.S. Soft Wheat Germplasm. Cereal Chem. J. 92, 57–64. doi:10.1094/CCHEM-06-14-0135-R
Kiszonas, A. M., and Morris, C. F. (2018). Wheat Breeding for Quality: A Historical Review. Cereal Chem. J. 95, 17–34. doi:10.1094/CCHEM-05-17-0103-FI
Kumar, N., Kiszonas, A. M., Ibba, M. I., and Morris, C. F. (2019). Identification of Loci and Molecular Markers Associated with Super Soft Kernel Texture in Wheat. J. Cereal Sci. 87, 286–291. doi:10.1016/J.JCS.2019.04.014
Lado, B., Matus, I., Rodríguez, A., Inostroza, L., Poland, J., Belzile, F., et al. (2013). Increased Genomic Prediction Accuracy in Wheat Breeding through Spatial Adjustment of Field Trial Data. G3 Genes, Genomes, Genet. 3, 2105–2114. doi:10.1534/G3.113.007807
Lado, B., Vázquez, D., Quincke, M., Silva, P., Aguilar, I., and Gutiérrez, L. (2018). Resource Allocation Optimization with Multi-Trait Genomic Prediction for Bread Wheat (Triticum aestivum L.) Baking Quality. Theor. Appl. Genet. 131, 2719–2731. doi:10.1007/s00122-018-3186-3
Larkin, D. L., Mason, R. E., Moon, D. E., Holder, A. L., Ward, B. P., and Brown-Guedira, G. (2021). Predicting fusarium Head Blight Resistance for Advanced Trials in a Soft Red winter Wheat Breeding Program with Genomic Selection. Front. Plant Sci. 12, 2342. doi:10.3389/FPLS.2021.715314
Lecun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539
Liu, Y., Wang, D., He, F., Wang, J., Joshi, T., and Xu, D. (2019). Phenotype Prediction and Genome-wide Association Study Using Deep Convolutional Neural Network of Soybean. Front. Genet. 10, 1091. doi:10.3389/fgene.2019.01091
Lorenz, A. J., Chao, S., Asoro, F. G., Heffner, E. L., Hayashi, T., Iwata, H., et al. (2011). Genomic Selection in Plant Breeding, 77–123. doi:10.1016/B9780123855312.000025
Lorenz, A. J. (2013). Resource Allocation for Maximizing Prediction Accuracy and Genetic Gain of Genomic Selection in Plant Breeding: A Simulation experiment. G3 Genes, Genomes, Genet. 3, 481–491. doi:10.1534/g3.112.004911
Meuwissen, T. H. E., Hayes, B. J., and Goddard, M. E. (2001). Prediction of Total Genetic Value Using Genome-wide Dense Marker Maps. Genetics 157, 1819–1829. doi:10.1093/genetics/157.4.1819
Montesinos-López, O. A., Martín-Vallejo, J., Crossa, J., Gianola, D., Hernández-Suárez, C. M., Montesinos-López, A., et al. (2019a). A Benchmarking between Deep Learning, Support Vector Machine and Bayesian Threshold Best Linear Unbiased Prediction for Predicting Ordinal Traits in Plant Breeding. G3 Genes, Genomes, Genet. 9, 601–618. doi:10.1534/g3.118.200998
Montesinos-López, O. A., Montesinos-López, A., Crossa, J., Gianola, D., Hernández-Suárez, C. M., and Martín-Vallejo, J. (2018). Multi-trait, Multi-Environment Deep Learning Modeling for Genomic-Enabled Prediction of Plant Traits. G3 Genes, Genomes, Genet. 8, 3829–3840. doi:10.1534/g3.118.200728
Montesinos-López, O. A., Montesinos-López, A., Crossa, J., Toledo, F. H., Pérez-Hernández, O., Eskridge, K. M., et al. (2016). A Genomic Bayesian Multi-Trait and Multi-Environment Model. G3 Genes, Genomes, Genet. 6, 2725–2744. doi:10.1534/g3.116.032359
Montesinos-López, O. A., Montesinos-López, A., Luna-Vázquez, F. J., Toledo, F. H., Pérez-Rodríguez, P., Lillemo, M., et al. (2019b). An R Package for Bayesian Analysis of Multi-Environment and Multi-Trait Multi-Environment Data for Genome-Based Prediction. G3 Genes, Genomes, Genet. 9, 1355–1369. doi:10.1534/G3.119.400126
Monteverde, E., Gutierrez, L., Blanco, P., Pérez de Vida, F., Rosas, J. E., Bonnecarrère, V., et al. (2019). Integrating Molecular Markers and Environmental Covariates to Interpret Genotype by Environment Interaction in rice (Oryza Sativa L.) Grown in Subtropical Areas. G3 Genes, Genomes, Genet. 9, 1519–1531. doi:10.1534/g3.119.400064
Morris, C. F., Bettge, A. D., Pitts, M. J., King, G. E., Pecka, K., and McCluskey, P. J. (2008). Compressive Strength of Wheat Endosperm: Comparison of Endosperm Bricks to the Single Kernel Characterization System. Cereal Chem. J. 85, 359–365. doi:10.1094/CCHEM-85-3-0359
Morris, C. F., Li, S., King, G. E., Engle, D. A., Burns, J. W., and Ross, A. S. (2009). A Comprehensive Genotype and Environment Assessment of Wheat Grain Ash Content in oregon and washington: Analysis of Variation. Cereal Chem. J. 86, 307–312. doi:10.1094/CCHEM-86-3-0307
Pérez-Rodríguez, P., Flores-Galarza, S., Vaquera-Huerta, H., del Valle-Paniagua, D. H., Montesinos-López, O. A., and Crossa, J. (2020). Genome-based Prediction of Bayesian Linear and Non-linear Regression Models for Ordinal Data. Plant Genome 13, e20021. doi:10.1002/tpg2.20021
Pérez, P., and De Los Campos, G. (2014). Genome-wide Regression and Prediction with the BGLR Statistical Package. Genetics 198, 483–495. doi:10.1534/genetics.114.164442
Poland, J., Endelman, J., Dawson, J., Rutkoski, J., Wu, S., Manes, Y., et al. (2012). Genomic Selection in Wheat Breeding Using Genotyping-By-Sequencing. Plant Genome 5, 103–113. doi:10.3835/plantgenome2012.06.0006
Qin, J., Shi, A., Song, Q., Li, S., Wang, F., Cao, Y., et al. (2019). Genome Wide Association Study and Genomic Selection of Amino Acid Concentrations in Soybean Seeds. Front. Plant Sci. 10, 1445. doi:10.3389/fpls.2019.01445
R Development Core Team (2020). R: A Language and Environment for Statistical Computing. Vienna, Austria: R foundation for statistical computing.
Ramzan, F., Gültas, M., Bertram, H., Cavero, D., and Schmitt, A. O. (2020). Combining Random Forests and a Signal Detection Method Leads to the Robust Detection of Genotype-Phenotype Associations. Genes 11, 892. doi:10.3390/GENES11080892
Rutkoski, J., Benson, J., Jia, Y., Brown-Guedira, G., Jannink, J.-L., and Sorrells, M. (2012). Evaluation of Genomic Prediction Methods for fusarium Head Blight Resistance in Wheat. The Plant Genome 5, 51–61. doi:10.3835/plantgenome2012.02.0001
Saini, D. K., Chopra, Y., Singh, J., Sandhu, K. S., Kumar, A., Bazzer, S., et al. (2022). Comprehensive Evaluation of Mapping Complex Traits in Wheat Using Genome-wide Association Studies. Mol. Breed. 42, 1. doi:10.1007/s11032-021-01272-7
Sandhu, K., Aoun, M., Morris, C., and Carter, A. (2021c). Genomic Selection for End-Use Quality and Processing Traits in Soft white winter Wheat Breeding Program with Machine and Deep Learning Models. Biology 202110, 689. doi:10.3390/BIOLOGY10070689
Sandhu, K., Patil, S. S., Pumphrey, M., and Carter, A. (2021a). Multitrait Machine- and Deep-Learning Models for Genomic Selection Using Spectral Information in a Wheat Breeding Program. Plant Genome 14, e20119. doi:10.1002/TPG2.20119
Sandhu, K. S., Lozada, D. N., Zhang, Z., Pumphrey, M. O., and Carter, A. H. (2021d). Deep Learning for Predicting Complex Traits in spring Wheat Breeding Program. Front. Plant Sci. 11, 613325. doi:10.3389/fpls.2020.613325
Sandhu, K. S., Mihalyov, P. D., Lewien, M. J., Pumphrey, M. O., and Carter, A. H. (2021e). Combining Genomic and Phenomic Information for Predicting Grain Protein Content and Grain Yield in spring Wheat. Front. Plant Sci. 12, 170. doi:10.3389/fpls.2021.613300
Sandhu, K. S., Mihalyov, P. D., Lewien, M. J., Pumphrey, M. O., and Carter, A. H. (2021b). Genomic Selection and Genome-wide Association Studies for Grain Protein Content Stability in a Nested Association Mapping Population of Wheat. Agronomy 11, 2528. doi:10.3390/agronomy11122528
Sandhu, K. S., Merrick, L. F., Sankaran, S., Zhang, Z., and Carter, A. H., (2022). Prospectus of Genomic Selection and Phenomics in Cereal, Legume and Oilseed Breeding Programs. Front. Genet. 12, 829131. doi:10.3389/fgene.2021.829131
Schulthess, A. W., Wang, Y., Miedaner, T., Wilde, P., Reif, J. C., and Zhao, Y. (2016). Multiple-trait- and Selection Indices-Genomic Predictions for Grain Yield and Protein Content in rye for Feeding Purposes. Theor. Appl. Genet. 129, 273–287. doi:10.1007/s00122-015-2626-6
Srivastava, N., Hinton, G., Krizhevsky, A., and Salakhutdinov, R. (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. doi:10.5555/2627435.2670313
Tolhurst, D. J., Mathews, K. L., Smith, A. B., and Cullis, B. R. (2019). Genomic Selection in Multi-Environment Plant Breeding Trials Using a Factor Analytic Linear Mixed Model. J. Anim. Breed. Genet. 136, 279–300. doi:10.1111/JBG.12404
Voyant, C., Notton, G., Kalogirou, S., Nivet, M.-L., Paoli, C., Motte, F., et al. (2017). Machine Learning Methods for Solar Radiation Forecasting: A Review. Renew. Energ. 105, 569–582. doi:10.1016/j.renene.2016.12.095
Ward, B. P., Brown-Guedira, G., Tyagi, P., Kolb, F. L., van Sanford, D. A., Sneller, C. H., et al. (2019). Multienvironment and Multitrait Genomic Selection Models in Unbalanced Early-Generation Wheat Yield Trials. Crop Sci. 59, 491–507. doi:10.2135/cropsci2018.03.0189
Yang, Y., Chai, Y., Zhang, X., Lu, S., Zhao, Z., Wei, D., et al. (2020). Multi-locus GWAS of Quality Traits in Bread Wheat: Mining More Candidate Genes and Possible Regulatory Network. Front. Plant Sci. 11, 1091. doi:10.3389/fpls.2020.01091
Keywords: end-use quality, genomic prediction, heritability, machine learning, multi-trait, secondary traits, wheat
Citation: Sandhu KS, Patil SS, Aoun M and Carter AH (2022) Multi-Trait Multi-Environment Genomic Prediction for End-Use Quality Traits in Winter Wheat. Front. Genet. 13:831020. doi: 10.3389/fgene.2022.831020
Received: 07 December 2021; Accepted: 06 January 2022;
Published: 31 January 2022.
Edited by:
Muhammad Sajjad, COMSATS University, PakistanReviewed by:
Dinesh Saini, Punjab Agricultural University, IndiaAhmed Sallam, Assiut University, Egypt
Copyright © 2022 Sandhu, Patil, Aoun and Carter. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Arron H. Carter, YWhjYXJ0ZXJAd3N1LmVkdQ==
 Karansher S. Sandhu
Karansher S. Sandhu Shruti Sunil Patil2
Shruti Sunil Patil2 Meriem Aoun
Meriem Aoun Arron H. Carter
Arron H. Carter