Testing Gene-Gene Interactions Based on a Neighborhood Perspective in Genome-wide Association Studies

Unexplained genetic variation that causes complex diseases is often induced by gene-gene interactions (GGIs). Gene-based methods are one of the current statistical methodologies for discovering GGIs in case-control genome-wide association studies that are not only powerful statistically, but also interpretable biologically. However, most approaches include assumptions about the form of GGIs, which results in poor statistical performance. As a result, we propose gene-based testing based on the maximal neighborhood coefficient (MNC) called gene-based gene-gene interaction through a maximal neighborhood coefficient (GBMNC). MNC is a metric for capturing a wide range of relationships between two random vectors with arbitrary, but not necessarily equal, dimensions. We established a statistic that leverages the difference in MNC in case and in control samples as an indication of the existence of GGIs, based on the assumption that the joint distribution of two genes in cases and controls should not be substantially different if there is no interaction between them. We then used a permutation-based statistical test to evaluate this statistic and calculate a statistical p-value to represent the significance of the interaction. Experimental results using both simulation and real data showed that our approach outperformed earlier methods for detecting GGIs.

1 Introduction

Genome-wide association studies (GWAS) has been used to investigate the associations between genetic variants and complex disorders with great success. Researchers have discovered more than 71,000 unique single nucleotide polymorphisms (SNPs) associated to diseases throughout the last decade (Hindorff et al., 2009; Zhang et al., 2016; Zeng et al., 2017; Guo et al., 2018; Buniello et al., 2019; Loos, 2020; Li et al., 2021). Traditional GWAS, on the other hand, concentrated on the independent, additive, and cumulative effects of individual SNPs on specific diseases. The majority of associated SNPs are common genetic variants with small effects that only explain a portion of complex disease heritability. Many genes, environmental variables, and interactions play a crucial role in the underlying genetic architecture of complex diseases (Cordell, 2009; Moore et al., 2010; Jiang et al., 2018; Liu et al., 2018; Liu et al., 2019a; Zhang et al., 2019; Chen et al., 2020; Luo et al., 2020; Liu et al., 2021; Shao et al., 2021; Su et al., 2021; Wang et al., 2021). As a result, genetic interactions are thought to enlighten studies into “missing heritability” (Manolio et al., 2009; Fang et al., 2019; Young, 2019; Tang et al., 2020; Song et al., 2021) and give important knowledge for constructing topologies for complex disease-related pathway.

Genetic interaction was originally explored at the SNP level, named epistasis. Methods (Li et al., 2015a; Ritchie and Van Steen, 2018; Lyu et al., 2020) can be classified into three categories based on their search strategy: exhaustive methods, searching methods, and machine learning-based methods, such as statistics based on entropy (Dong et al., 2008) and odds-ratios (Emily, 2012); MDR (Ritchie et al., 2003), BEAM (Zhang and Liu, 2007), BOOST (Wan et al., 2010), Epi-GTBN (Guo et al., 2019), GenEpi (Chang et al., 2020), and some accelerate methods (Nobre et al., 2021). For example, a logistic regression analysis revealed a significant interaction between the genes ERAP1 (rs27524) and HLA-C (rs10484554) in psoriasis ($p=6.95\times {10}^{-6}$), indicating that ERAP1 SNP was effective only in individuals who had at least one copy of the HLA-C SNP risk allele (Képíró et al., 2021). The statistical weakness of high-order or pairwise tests, which come from enormous multiple testing corrections over all pairs of SNPs, is one of the general problems of these marker-based approaches. Instead, we explored the interaction of two genes in a single gene-based interaction detection by treating SNPs inside a gene as a group.

The effectiveness of gene-based methods in GWAS marginal association studies should be extended to the study of gene-gene interaction (GGIs) (Emily, 2018; Emily et al., 2020). This strategy offers a number of possible benefits. For starters, it often has substantially fewer genes than SNPs, which dramatically decreases the number of pairwise testing. To discover GGIs in pair of 20,000 genes, for example, $\sim 2\times {10}^8$ tests are necessary. However, for three million SNPs in a marker-based interaction, more than $5\times {10}^{12}$ tests are required. Second, gene-based methods are more powerful statistically because a gene carries more information than individual SNP and genes interact in a variety of ways (Liu et al., 2010; Li et al., 2011; Jiang et al., 2017; Su et al., 2019; Hu et al., 2020; Hu et al., 2021a; Hu et al., 2021b; Guo et al., 2021). Furthermore, these methods can include biological prior knowledge (e.g., information about known gene association within protein-protein interactions (PPIs) or pathways) (Wei et al., 2017a; Wei et al., 2017b; Wei et al., 2018; Liu et al., 2019b; Wei et al., 2019; Zeng et al., 2019; Cai et al., 2020; Zhai et al., 2020; Zhu et al., 2020). Finally, gene-based outcomes stand out for their better interpretability and crucial biological consequences.

Many statistical and computational approaches for detecting gene-based GGIs have been established. Peng et al.(Peng et al., 2010) introduced the canonical correlation-based U statistic (CCU). They calculated canonical correlation of two genes in both cases and controls. They next used CCU to calculate the difference in correlation, which revealed the presence of GGIs between the two genes. However, this strategy only considered linear correlation in the study. CCU was then expanded to Kernelized CCU (KCCU) (Yuan et al., 2012; Larson et al., 2013), where the kernel discovered a nonlinear relationship. Emily (Emily, 2016) recently introduced AGGrGATOr, a method that combines p-values of interaction tests at the marker-level to assess how a pair of genes interacted, which was a strategy that Ma et al. (Ma et al., 2013) previously utilized to discover interactions under quantitative traits. GBIGM is a non-parametric entropy-based approach suggested by Li et al. (Li et al., 2015b).

In this paper, we propose a new approach called gene-based, gene-gene interaction through a maximal neighborhood coefficient (GBMNC), which uses the maximal neighborhood coefficient (MNC) (Cheng et al., 2020) to identify gene-gene interaction of complex diseases at the gene-level in case-control studies. MNC measures a wide variety of dependence with no bias toward relationship types between two random vectors of arbitrary, but not necessarily equal, dimensions; this is superior to Pearson’s correlation, which only consider linear correlations. We introduced a statistic that uses the difference of MIC in cases and controls as an indicator of occurrence of GGIs, bases on the assumption that the joint distribution of two genes should not be significantly different in case and in control samples if there is no interaction between them (i.e. independent) under complex diseases. In simulation studies, our method exhibited an outstanding performance in recognizing the underlying GGIs at the gene level under a variety of conditions. Its application using real data sets showed accurate identification of GGIs.

2 Materials and Methods

The statistical procedure for GBMNC is described in depth in this section. We give different parameter settings for simulation studies to evaluate the power to identify GGIs and the ability to control type-I error. Then, we adopted a real-world Rheumatoid Arthritis data set from the WTCCC (Wellcome Trust case Control Consortium) database to evaluate out method’s effectiveness in a real situation.

2.1 GBMNC

2.1.1 Preliminaries and Notation

Here, we take genes, a couple of SNPs, as the basic unit. Suppose that we have $n$ random samples:

$\left(G_{1,i},G_{2,i}\right)\in {\mathrm{ℛ}}^{p+q},i=\mathrm{1,2},\dots ,n(1)$

where

$G_{1,i}=\left(g_{1,i,1},g_{1,i,2},\dots ,g_{1,i,p}\right),G_{2,i}=\left(g_{2,i,1},g_{2,i,2},\dots ,g_{2,i,q}\right), i=\mathrm{1,2},\dots ,n$

and $G_1$ and $G_2$ represent two genes each with $p$ and $q$ SNPs, independently. In the case-control studies, $y_i\in \left\{\mathrm{0,1}\right\}$ is a categorical label where 0 is a control subject and one is a case subject. $g_{k,i,j}\in \left\{\mathrm{0,1,2}\right\}$ represents the copy number of the minor alleles of SNP $j$ in gene $k$ for sample $i$.

In this work, to investigate whether there is a statistical interaction between two genes in a qualitative phenotype, we designed a statistic based on the maximal neighborhood coefficient to characterize the GGI intensity. We applied a permutation strategy to estimate the distribution of the statistic. Our approach was based on the intuition that, if there was no interaction between two genes, then, if they were independent of the case set, they should be independent of the control set; if they were dependent on the case set, they should be dependent on the control set as well, and the “strength” of such dependence should be the same for the case and control sets. Pearson’s correlation coefficient measures the degree of dependence between two random variables. However, it can only measure linear dependency and not nonlinear dependency, and it is not very convenient for random variables that take a value in ${\mathrm{ℛ}}^n$. Therefore, we proposed to measure dependency between random variables by the maximal neighborhood coefficient (MNC) instead.

2.1.2 Maximal Neighborhood Coefficient

MNC is an association measure that decipher the potential complex associations from neighborhood insight. It assumes that if a relationship exists between two variables, the samples of each variable will appear to have a similar neighborhood tendency to approximate that relationship, and MNC can find those common neighborhood structures by exploring the possible neighborhoods of each variable. By introducing a $k$-NN granule to reconstruct samples, and a novel neighborhood mutual information (NMI) to measure the certainty information of one variable from another under a fixed $\left(k_x,k_y\right)$ neighborhood combination, MNC enables us to detect more complex associations.

Let $S=\{\left(x_1,y_1\right),\dots ,(x_n,y_n)\}\in {\mathrm{ℛ}}^2$ be a finite set that is sampled from a joint distribution $(X,Y)$, and $S_X=\left\{x_1,\dots ,x_n\right\}$ and $S_Y=\left\{y_1,\dots ,y_n\right\}$ represents samples from marginal variables $X$ and $Y$, respectively. Given a designated neighborhood combination $\left(k_x,k_y\right)$ (a pairwise positive integer), $N_X^{k_x}\left(x\right)=\{x_{j_1},\dots ,x_{j_{k_x}}\}$ designed as the $k_x$-NN granule of $x$, where the subscript sequence $j_1<j_2<\dots <j_{k_x}$ is obtained by $d\left(x,x_{j_i}\right)={\Vert x-x_{ji}\Vert }_2$. All samples of $k_x$-NN granules form a cover of $S_X$, that is ${\cup }_{i=1}^n{N}_X^{k_x}\left(x_i\right)=U{S}_X$. At the same time, there exists a cover for $S_Y$, ${\cup }_{i=1}^n{N}_Y^{k_y}\left(y_i\right)=S_Y$. The cover of samples $S$ under $\left(k_x,k_y\right)$ is recorded as $C_{k_x,k_y}$. Let $S{|}_{C_{k_x,k_y}}$ represents the distribution of $S$ on the cover $C_{k_x,k_y}$, and different neighborhood combinations produce different distributions.

MNC is defined based on the neighborhood characteristic matrix (NM) of a sample set $S$. Given a finite data set $S$ and a neighborhood combination $\left(k_x,k_y\right)$, the element of NM of $S$ is:

$NM{\left(S\right)}_{k_x,k_y}=\frac{NMI\left(S{|}_{C_{k_x,k_y}}\right)}{log\frac{n}{\text{max}\left(k_x,k_y\right)}}(2)$

$NMI\left(S{|}_{C_{k_x,k_y}}\right)$ denotes the neighborhood mutual information of distribution $S{|}_{C_{k_x,k_y}}$. The neighborhood mutual information of ($x_i,y_i$) is defined as follow:

$NM{I}_{C_{k_x,k_y}}\left(x_i,y_i\right)=-log\frac{n|N_X^{k_x}\left(x_i\right)\cap N_Y^{k_y}\left(y_i\right)|}{k_x{k}_y}(3)$

Based on the equation above, the neighborhood mutual information of $\left(X,Y\right)$ is defined as:

$NM{I}_{C_{k_x,k_y}}\left(X,Y\right)=-\frac{1}{n}{\displaystyle \sum }_{i=1}^{n}log\frac{n|N_X^{k_x}\left(x_i\right)\cap N_Y^{k_y}\left(y_i\right)|}{k_x{k}_y}(4)$

With the definition of $NM\left(S\right)$ in Eq. 2, NMC is defined as:

$NMC\left(S\right)=\underset{1\le k_x{k}_y\le NB\left(n\right)}{\max }\left\{NM{\left(S\right)}_{k_x,k_y}\right\}(5)$

where $NB\left(n\right)$ is the search range, and $1\le k_x{k}_y\le O\left(n^{\alpha }\right)$ for some $0<\alpha <1$. It also naturally extends to the case of two random vectors with arbitrary, but not necessarily equal, dimensions.

MNC Satisfies the Following Properties

1) Symmertry: $MNC\left(X,Y\right)=MNC(Y,X)$;

2) Comparability: $MNC\in \left[\mathrm{0,1}\right]$, $MNC=0$ denotes that two variables are statistically independent; $MNC=1$ implies a strong association between two variables.

3) Generality: $MNC$ captures comprehensive range relationships.

4) Equitability: $MNC$ is robust to noisy relationships. It provides similar scores to the equally noisy relationships of different types.

2.1.3 Illustration of the GBMNC Workflow

Assume there are $n_1$ control samples and $n_2$ case samples in a case-control study for a pair of genes such that $G_1$ has $p$ SNPs and $G_2$ has $q$ SNPs. Let $MN{C}_n(G_1,G_2)$ be the sample association score between $G_1$ and $G_2$. First, we calculate the $MN{C}_{n_1}^C(G_1,G_2)$ for control samples and $MN{C}_{n_2}^D(G_1,G_2)$ for case samples. Second, we design a statistic $\Delta MNC= \frac{|MN{C}_{n_1}^C\left(G_1,G_2\right)-MN{C}_{n_2}^D(G_1,G_2)|}{MN{C}_{n_2}^D(G_1,G_2)}$ to measure the difference in $MNC$ between cases and controls. $\Delta MNC$ represents how different the two joint distributions $(G_1^C,G_2^C)$ and $(G_1^D,G_2^D)$ are. The larger the $\Delta MNC$, the higher the probability that $G_1$ and $G_2$ interact.

To get a p-value, we needed to estimate the distribution of $\Delta MN{C}^0$ under the null hypothesis. Here, we used a non-parametric strategy based on permutation: we shuffled the label y randomly $m$ times, calculated $\Delta MNC$ using the same procedure above, and used the resulting empirical distribution as an estimate for the distribution of $\Delta MNC$ under the null hypothesis. Let the result of these $m$ permutations be $\Delta MN{C}^1,\dots ,\Delta MN{C}^m$, then an estimated p-value for the null hypothesis is

$p=\frac{\left|\{i:\Delta MN{C}^i\ge \Delta MN{C}^0\}\right|}{m}(6)$

We summarized the process of GBMNC in the algorithm below (Algorithm 1) and presented the overall workflow (Figure 1).

FIGURE 1

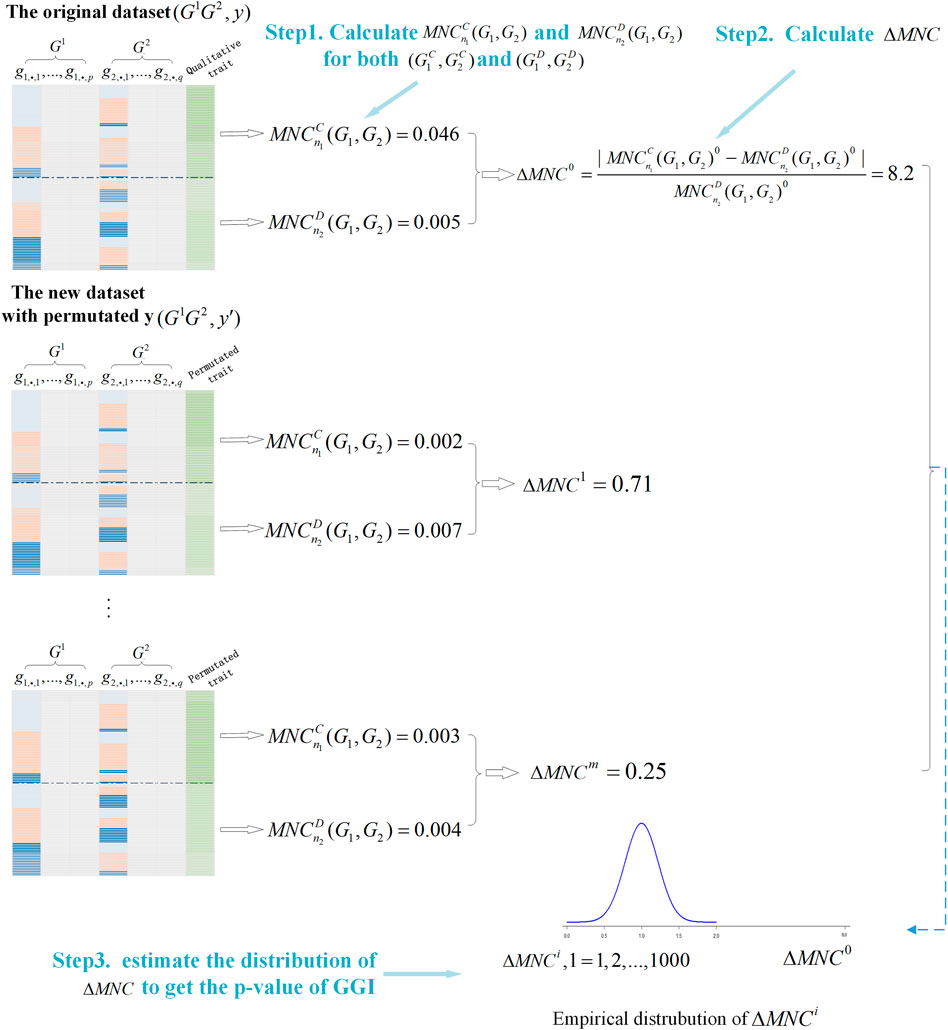
FIGURE 1. Illustration of the Gene-Based gene-gene interaction through a Maximal Neighborhood Coefficient (GBMNC) workflow for detection of gene-based, gene-gene interaction.

Algorithm 1 GBMNC

Data: Genotype $G_1,G_2$, Phenotype $y$, permutation times $m$

Result: significant p-value for interaction between $G_1,G_2$

1  Calculate $MN{C}_{n_1}^C(G_1,G_2)$ and $MN{C}_{n_2}^D\left(G_1,G_2\right)$ for both $(G_1^C,G_2^C)$ and $\left(G_1^D,G_2^D\right)$ by Eq. 5;

2  Calculate the difference $\Delta MN{C}^0$ between $MN{C}_{n_1}^C(G_1,G_2)$ and $MN{C}_{n_2}^D(G_1,G_2)$;

 3 for $i=1$ to $m$ do

  4 Randomly permute label $y$, and generate the new data set;

  5 Repeat Steps 1 and 2;

  6 end

  7 Estimated p-value of $\Delta MN{C}^0$ is the number of $\Delta MN{C}^i$, $i=1,\dots ,m$, which are larger than $\Delta MN{C}^0$, divided by $m$.

2.2 Simulation Study

To assess the performance of GBMNC to control type I error and the power to detect GGIs, we compared GBMNC with KCCA (Larson et al., 2013), GBIGM (Li et al., 2015b), and AGGrEGATOr (Emily, 2016).

2.2.1 Simulation With GAMETES

The goal of this simulation study was to evaluate the performance of the GBMNC procedure to detect gene-gene interaction. We set all simulated datasets to have 50 SNPs. Among them, two SNPs were functional, and the remaining 48 SNPs were non-functional. The 50 SNPs formed five genes, and each had 10 SNPs. The two functional SNPs were put into the first and second genes. We chose the publicly available tool GAMETES (Urbanowicz et al., 2012) to generate the simulated genotype data. This tool was designed to generate pure and strict epistasis models. Pure and strict epistasis models are the most difficult disease-related patterns to identify. Such associations can only be observed if all n-loci are included in the disease model. This requirement makes these types of models an attractive gold standard for simulation studies of complex multi-locus effects.

Evaluation of Type-I error: The type-I error indicates the ability of a method to reject the null hypothesis when it is true (i.e., the false positive rate). We used GAMETES to generate the custom disease model (Table 1) with one causal SNP pair. $\gamma$ characterizes the baseline odds (i.e., the odds conditional on genotype pair $AABB$). We ran the simulation 100 times with each sample size $n\in \{1k,2k,3k,4k,5k\}$ and $\gamma =1$. The significance level $\alpha$ was set to be 0.05.

TABLE 1

TABLE 1. Table of odds for the no effect model without interaction between a pair of SNPs.

Evaluation of power of the test: The power of a test indicates the probability that the method rejects the null hypothesis correctly when the alternative hypothesis is true. In this simulation study, we generated 100 data sets for each parameter settings. The power under each parameter setting was expressed by the frequency, and the null hypothesis of the data set was rejected correctly at the significance level of $\alpha =0.05$.

1) To assess the impact of heritability $h$, which measured the intensity of correlation between genotype and phenotype, we chose $h\in \{0.01,0.025,0.05,0.1,0.2\}$ and two different minor allele frequencies MAF $\in \{0.2,0.4\}$ with population prevalence set to 0.2 and sample size set at 4,000. Under each parameter combination, five models were generated so that we had a total of 100 models that followed Hardy-Weinberg proportions. For a specified genetic constrain combination, the 10 models were sorted roughly by the ascending customized odds ratio (COR) using GAMETES and labeled M1 to M5. COR is a metric of detectability that was calculated directly from the genetic model. The higher it is, the easier it is to detect GGIs. GAMETES generated the penetrance tables for these 100 models in the absence of the main effect. One hundred replicated data sets were generated from each model with balanced cases and controls, which resulted in 5,000 data sets in total in this scenario.

2) To evaluate the influence of sample size, we set heritability to be 0.025, MAF $\in$ {0.2,0.4} and prevalence to be 0.2 with a sample size of 10,000. Then, 100 data sets were generated by random sampling from this large dataset for each of the sample sizes $n\in \{1k,2k,3k,4k,5k\}$. In this scenario, we had 1,000 datasets in total.

For GBMNC, KCCU, AGGrEGATOr, and GBIGM, if the number of data sets with a significance level less than $\alpha$ is $m_1$, then the power can be calculated by the following formula:

$power= \frac{m_1}{100}(7)$

GBIGM and AGGrEGATOr methods are nonparametric methods, so no parameters need to be specific. We only set the ratio of the trimmed jackknife to 0.05 ($\omega =0.05$) for KCCU.

2.3 Experiments Using Rheumatoid Arthritis Data

To evaluate GBMNC’s ability to process real GGIs in a qualitative data set, we analyzed the susceptibility of a series of pairs of genes in Rheumatoid Arthritis (RA). RA is a chronic autoimmune disease that causes pannus development and cartilage and bone loss in synovial joints. It leads to progressive bone deterioration and interferes with bone repair. In this work, we used the WTCCC (2007) data set, which includes genotype data from the British population obtained by the Affymetrix GeneGhip 500 k. Our dataset was pre-processed in the following ways:

1) We used pathway hsa05323 from the KEGG pathway database to validate the GGIs in the RA. The WTCCC data set’s genotyping coordinates can be found in UCSC hg18/NCBI Build36. This pathway contained 90genes. Many of the genes belonged to the protein combinations MHCII and V-ATPase. Because numerous GGIs happened on their own, we only chose representative genes from each protein combination and then remove the others. Finally, 48genes remained, resulting in a total of $C_{48}^2=1128$ pairs of genes to be analyzed.

2) We collected the detailed gene information from the NCBI Build36 annotation file, and for each gene, we inserted a 10 kb buffer region both downstream and upstream of the originally defined gene location. For each gene, all SNPs within the area were chosen.

3) According to the quality control of GWAS, samples that included gender that did not match the chromosome X heterozygote rates were removed. SNPs were also removed if any of the following requirements were met: the missing rate in the sample was $\ge 10\%$, MAF was $\le 0.05$, or the frequency of control violated Hardy-Weinberg equilibrium ($p<0.0001$). Finally, 385 SNPs remained in 4,966 samples, which included 2,993 control subjects and 1973 case subjects.

3 Results and Discussion

The experimental environment for all the following results was a workstation with an Intel Xeon CPU E5-2,620 v2 at 2.10GHz, 96 GB of DDR3, and python3.6.

3.1 Simulation Study

3.1.1 Evaluation of Type-I Error

For type-I error, we varied the sample size from 1,000 to 5,000. Except for GBIGM with $n=\mathrm{1,000}$, all methods tested had a type-I error comparable to a significance level $\text{α}=0.05$ (Table 2), which implied that these methods controlled for type-I error for various sample sizes quite well.

TABLE 2

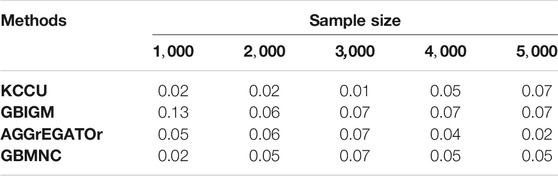
TABLE 2. Type-I error for KCCU, GBIGM, AGGrEGATOr, and GBMNC when varying the sample size from 1,000 to 5,000.

3.1.2 Evaluation of the Power of GBMNC

Impact of heritability: To evaluate the statistical power of our GBMNC and the other three methods, we used 10 heritability-MAF combinations, with a population prevalence of 0.2, a sample size of 4,000, and heritability that varied from 0.01 to 0.2 (Table 3). The bold in Table 3 shows the best-performed method in each model under a given heritability-MAF combination. Notice that a larger value indicates better performance. On average, GBMNC was the best performing algorithm in this comparison. It largely outperformed the other methods, but not for all the data sets; it was inferior to AGGrEGATOr for some data sets. However, its performance was remarkably consistent, and it was the top performer for most data sets. AGGrEGATOr achieved the same performance when MAF was 0.2 and heritability was >0.05.

TABLE 3

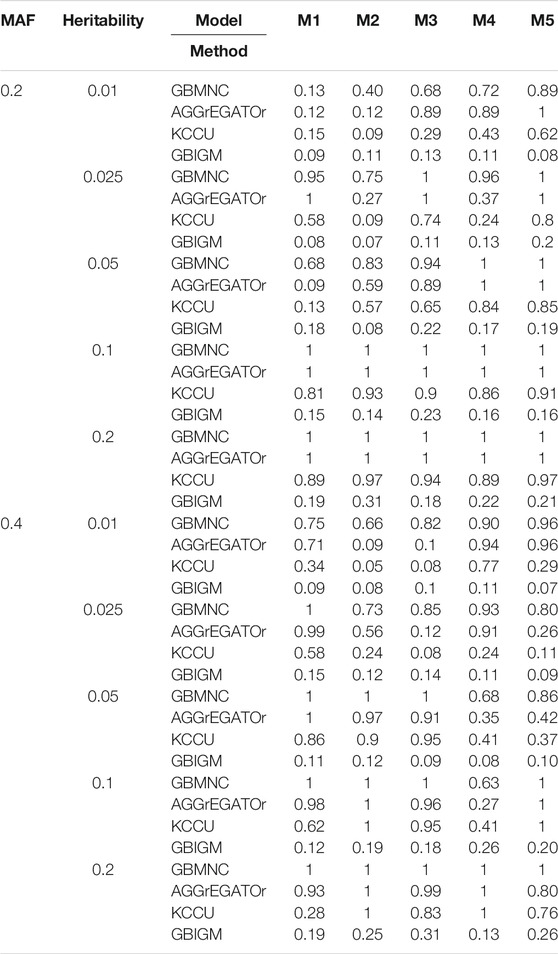
TABLE 3. The statistical power of simulation studies for GBMNC, AGGrEGATOr, KCCU and GBIGM under 10 heritability-MAF combinations, with $h\in \{0.01,0.025,0.05,0.1,0.2\}$ and MAF $\in \{0.2,0.4\}$. Each heritability-MAF combination has five models. Bold font indicates the method that performed best under each model.

The power of all the methods was significantly affected by heritability (i.e., the effect size of interaction) (Table 4). A larger heritability led to better performance for all methods under a specific MAF. When heritability varied from 0.01 to 0.025, GBMNC almost doubled its power for a given sample size of 4,000 with MAF $=0.2$. Other methods also show a steady upward trend (Table 4). The power also depended on the MAF of the interacting SNPs (e.g., for the cases of $h=0.01$, the power of GBMNC under model M1-M5 ranged between 0.13–0.89 for MAF $=0.2$, but it ranged between 0.66–0.96 for MAF $=0.4$ (Table 3)). The average power was 0.564 for MAF $=0.2$, which was much lower than 0.818 for MAF $=0.4$ (Table 4).

TABLE 4

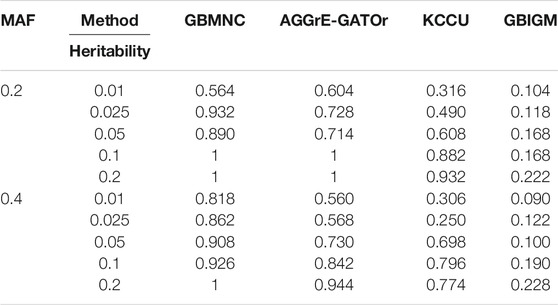
TABLE 4. Average power for GBMNC, AGGrEGATOr, KCCU, and GBIGM under 10 heritability-MAF combinations, with heritability $\in \{0.01,0.025,0.05,0.1,0.2\}$ and MAF. $\in \{0.2,0.4\}$

It is worth noting that under the same combination of habitability and MAF, GBMNC was more stable under models with different COR compared with AGGrEGATOr (Figure 2). KCCU detected the interaction of some simulated disease models in our study, and it had a similar performance pattern with AGGrEGATOr. However, AGGrEGATOr was much more powerful in most of the simulated scenarios. GBIGM had little power to detecting pure gene-gene interaction,. This result replicated Emily's (Emily, 2016) result of the simulation.

FIGURE 2

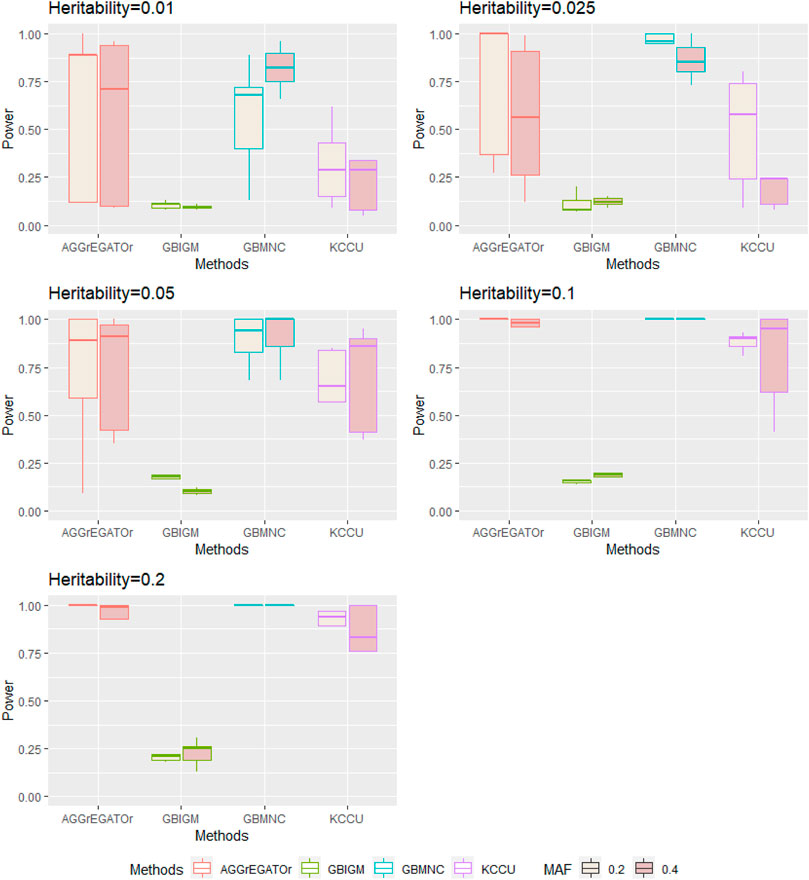
FIGURE 2. Illustration of the distribution of power of each method in each heritability-MAF combination with $h\in \{0.01,0.025,0.05,0.1,0.2\}$ and MAF $\in \{0.2,0.4\}$.

Impact of sample size: The sample size of the data set had a considerable effect on power. Let the sample size be $n\in \{1k,2k,3k,4k,5k\}$, $h=0.025$, and MAF $\in \{0.2,0.4\}$ (Table 5). As the sample size increased, the power of all methods increased almost monotonically under different MAF settings. With all methods, a larger sample size corresponded to better performance.

TABLE 5

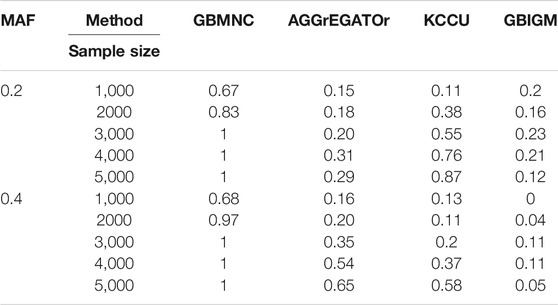
TABLE 5. The statistical power of simulation studies for GBMNC, AGGrEGATOr, KCCU, and GBIGM under models with $h=0.025$, MAF $\in \{0.2,0.4\}$, and sample sizes that varied from $1k$ to $5k$.

In conclusion, in simulated studies, our results showed that GBMNC detected gene-gene interaction effectively, in which a pair of SNPs was a causal factor by the purely and strictly epistasis model without main effect, which can only be observed if all 2-loci are included in the disease model. Compared with other methods, GBMNC identified a broad range of epistatic signals accurately.

3.2 Experiments Using Rheumatoid Arthritis Data

RA is a chronic autoimmune disease where HLA genes, TNF family, and TRAF1 are important genetic risk factors in the development. Each unique gene pair of the hsa05323 pathway was evaluated in the RA study, which resulted in $C_{48}^2=1128$ total pairs for 48 genes. With a significance level $\alpha =0.01$ and multiple testing adjustment, for KCCU and GIGBM, we obtained 159 and 134 significant GGIs, respectively. Among them, 30 and 65 had p-values equal to 0; hence we were unable to rank them in the order of significance. AGGrGETOr did not show any significant results. Following Emily (Emily, 2016), and after removing the multiple testing correction, AGGrGETOr exhibited 17 significant GGIs, which we ranked by their p-values. We chose the top 10 gene pairs obtained by GBMNC and by AGGrGETOr to analyze, which comprised approximately 1% of the total interactions (Table 6).

TABLE 6

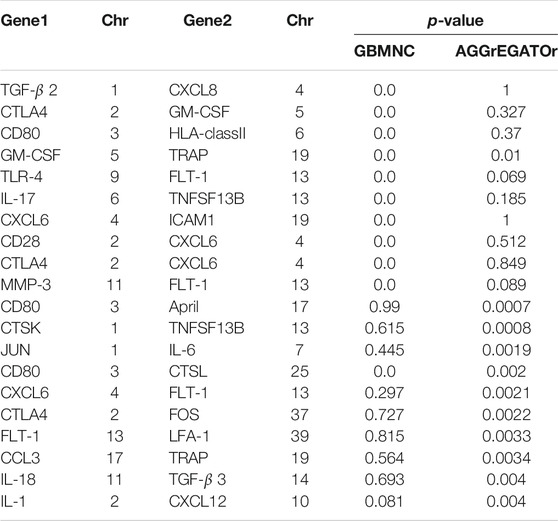
TABLE 6. The calculated p-value for the 20 gene pairs using GBMNC and AGGrEGATOr. p-values in bold font indicate that they are significant. The “Chr” column indicates the chromosome number of the human genome where the gene is located.

We found that some of our findings were supported by prior research (Xiao et al., 2008; Klocke et al., 2016; Cen et al., 2019). For instance, our method detected a significant interaction between IL17 and TNFSF13B. Studies (Xiao et al., 2008) show that both B cells and T cells formed aggregates in the synovium of inflamed joints and mediated the pathogenesis of RA, and B-cell-activating factor (BAFF, also named TNFSF13B, BLys) played a vital role in B-cell survival and maturation. After activation and expansion, CD4⁺ T cells developed into different T helper cell subsets with different cytokine profiles and distinct effector functions. In addition to Th1 and Th2 cells, Th17 cells were a third T helper cell and produce IL-17. Th17 cells can recruit and activate inflammatory cells and they have been recognized as a primary cause of bone destruction and inflammation in autoimmune diseases. BAFF promoted Th17 cell proliferation and expansion preferentially (Lai Kwan Lam et al., 2008). IL-17 was a key cytokine for BAFF-mediated proinflammatory effects during collagen-induced arthritis pathogenesis. Only one pair of potential interactions between CD80 and CTSL was captured by both methods within the top 10 GGIs. However, there is not yet direct evidence to show the interaction between CD80 and CTSL.

4 Conclusion

The study of detecting GGIs is of great importance in understanding the pathogenesis of complex human diseases. In this paper, we proposed a gene-based GGI detection method called GBMNC based on a maximal neighborhood coefficient and a permutation strategy for case-control studies in GWAS. The method not only benefited from the ability of a maximal neighborhood coefficient, which considered the neighborhood structure of each sample and captured a wide range of associations, but also from the robustness of our permutation-based hypothesis testing scheme.

We designed a statistic to capture the different intensities of interaction between two genes in both cases and controls, then transformed the problem of GGI detection into a form of hypothesis testing; our null hypothesis was there was no significant difference in the relationship between the two genes in the disease data and the control data. This hypothesis did not limit the form of interaction between genes, and it enhanced the method’s ability to detect different types of interactions. We demonstrated the effectiveness of our method through a simulation study and retrospective analysis of rheumatoid arthritis. Under a large range of settings, GBMNC outperformed previous methods in the power to detect GGIs. The statistical power of our method increased monotonically with the increase in the heritability and the MAF. The method was also stable to sample size based on a test of false positive rates. MNC did not restrict the dimension of two random vectors. Therefore, it is possible to generalize the method for marker-based detection of gene pairs that are identified as interactive. Investigating the mechanism of gene-based interaction at the marker level might point the way for further research. In summary, GBMNC is a helpful addition to the current toolbox of statistical models to elucidate GGIs in case-control studies.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.wtccc.org.uk/info/access_to_data_samples.html.

Author Contributions

YG: Conceptualization, Methodology, Investigation, Funding acquisition, Writing-Original Draft. HC: Methodology, Formal analysis, Writing-Original Draft. ZY: Software, Formal analysis. ZL: Resources, Data Curation. YW: Formal analysis, Writing-Review and Editing. DD: Conceptualization, Project administration.

Funding

The work was supported by the National Natural Science Foundation of China (No. 62002243, No. 31900306), the Post-doctoral Foundation Project of Shenzhen Polytechnic China (6020330004K), the Post-doctoral Foundation Project of Shenzhen Polytechnic China (6020330004K). Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (2021L286).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Buniello, A., MacArthur, J. A. L., Cerezo, M., Harris, L. W., Hayhurst, J., Malangone, C., et al. (2019). The NHGRI-EBI GWAS Catalog of Published Genome-wide Association Studies, Targeted Arrays and Summary Statistics 2019. Nucleic Acids Res. 47 (D1), D1005–D1012. doi:10.1093/nar/gky1120

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, L., Wang, L., Fu, X., Xia, C., Zeng, X., and Zou, Q. (2020). ITP-pred: an Interpretable Method for Predicting, Therapeutic Peptides with Fused Features Low-Dimension Representation. Brief. Bioinform. 22 (4), bbaa367. doi:10.1093/bib/bbaa367

CrossRef Full Text | Google Scholar

Cen, S., Wang, P., Xie, Z., Yang, R., Li, J., Liu, Z., et al. (2019). Autophagy Enhances Mesenchymal Stem Cell-Mediated CD4+ T Cell Migration and Differentiation through CXCL8 and TGF-Β1. Stem Cel Res Ther. 10 (1), 265. doi:10.1186/s13287-019-1380-0

CrossRef Full Text | Google Scholar

Chang, Y.-C., Wu, J.-T., Hong, M.-Y., Tung, Y.-A., Hsieh, P.-H., Yee, S. W., et al. (2020). GenEpi: Gene-Based Epistasis Discovery Using Machine Learning. BMC Bioinformatics 21 (1), 68. doi:10.1186/s12859-020-3368-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Li, J., and Chang, M. (2020). Cancer Diagnosis and Disease Gene Identification via Statistical Machine Learning. Curr. Bioinformatics 15 (9), 956–962. doi:10.2174/1574893615666200207094947

CrossRef Full Text | Google Scholar

Cheng, H., Liang, J., Qian, Y., and Hu, Z. (2020). Association Mining Method Based on Neighborhood Perspective. Sci. Sin.-Inf. 50 (6), 824–844. doi:10.1360/ssi-2020-0009

CrossRef Full Text | Google Scholar

Cordell, H. J. (2009). Detecting Gene-Gene Interactions that Underlie Human Diseases. Nat. Rev. Genet. 10 (6), 392–404. doi:10.1038/nrg2579

PubMed Abstract | CrossRef Full Text | Google Scholar

Dong, C., Chu, X., Wang, Y., Wang, Y., Jin, L., Shi, T., et al. (2008). Exploration of Gene-Gene Interaction Effects Using Entropy-Based Methods. Eur. J. Hum. Genet. 16 (2), 229–235. doi:10.1038/sj.ejhg.5201921

CrossRef Full Text | Google Scholar

Emily, M. (2016). AGGrEGATOr: A Gene-Based GEne-Gene interActTiOn Test for Case-Control Association Studies. Stat. Appl. Genet. Mol. Biol. 15 (2), 151–171. doi:10.1515/sagmb-2015-0074

PubMed Abstract | CrossRef Full Text | Google Scholar

Emily, M. (2018). A Survey of Statistical Methods for Gene-Gene Interaction in Case-Control Genome-wide Association Studies. Journal de la société française de statistique. 159 (1), 27–67.

Google Scholar

Emily, M. (2012). IndOR: a New Statistical Procedure to Test for SNP-SNP Epistasis in Genome-wide Association Studies. Statist. Med. 31 (21), 2359–2373. doi:10.1002/sim.5364

PubMed Abstract | CrossRef Full Text | Google Scholar

Emily, M., Sounac, N., Kroell, F., and Houée-Bigot, M. (2020). Gene-Based Methods to Detect Gene-Gene Interaction in R: The GeneGeneInteR Package. J. Stat. Softw. 95 (12), 1–32. doi:10.18637/jss.v095.i12

CrossRef Full Text | Google Scholar

Fang, G., Wang, W., Paunic, V., Heydari, H., Costanzo, M., Liu, X., et al. (2019). Discovering Genetic Interactions Bridging Pathways in Genome-wide Association Studies. Nat. Commun. 10 (1), 4274. doi:10.1038/s41467-019-12131-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, F., Wang, D., and Wang, L. (2018). Progressive Approach for SNP Calling and Haplotype Assembly Using Single Molecular Sequencing Data. Bioinformatics 34 (12), 2012–2018. doi:10.1093/bioinformatics/bty059

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Yan, K., Lv, H., and Liu, B. (2021). PreTP-EL: Prediction of Therapeutic Peptides Based on Ensemble Learning. Brief. Bioinform. 22 (6), bbab358. doi:10.1093/bib/bbab358

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Zhong, Z., Yang, C., Hu, J., Jiang, Y., Liang, Z., et al. (2019). Epi-GTBN: an Approach of Epistasis Mining Based on Genetic Tabu Algorithm and Bayesian Network. BMC Bioinformatics 20 (1), 444. doi:10.1186/s12859-019-3022-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Hindorff, L. A., Sethupathy, P., Junkins, H. A., Ramos, E. M., Mehta, J. P., Collins, F. S., et al. (2009). Potential Etiologic and Functional Implications of Genome-wide Association Loci for Human Diseases and Traits. Proc. Natl. Acad. Sci. 106 (23), 9362–9367. doi:10.1073/pnas.0903103106

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Qiu, S., and Cheng, L. (2021). Integration of Multiple-Omics Data to Analyze the Population-specific Differences for Coronary Artery Disease. Comput. Math. Methods Med. 2021, 7036592. doi:10.1155/2021/7036592

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Sun, J. Y., Zhang, Y., Zhang, H., Gao, S., Wang, T., et al. (2021). rs1990622 Variant Associates with Alzheimer's Disease and Regulates TMEM106B Expression in Human Brain Tissues. BMC Med. 19 (1), 11. doi:10.1186/s12916-020-01883-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, Y., Zhang, H., Liu, B., Gao, S., Wang, T., Han, Z., et al. (2020). rs34331204 Regulates TSPAN13 Expression and Contributes to Alzheimer's Disease with Sex Differences. Brain 143 (11), e95. doi:10.1093/brain/awaa302

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, L., Xiao, Y., Ding, Y., Tang, J., and Guo, F. (2018). FKL-Spa-LapRLS: an Accurate Method for Identifying Human microRNA-Disease Association. Bmc Genomics 19, 911. doi:10.1186/s12864-018-5273-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Q., Jin, S., Jiang, Y., Liao, M., Feng, R., Zhang, L., et al. (2017). Alzheimer's Disease Variants with the Genome-wide Significance Are Significantly Enriched in Immune Pathways and Active in Immune Cells. Mol. Neurobiol. 54 (1), 594–600. doi:10.1007/s12035-015-9670-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Képíró, L., Széll, M., Kovács, L., Keszthelyi, P., Kemény, L., and Gyulai, R. (2021). The Association of HLA-C and ERAP1 Polymorphisms in Early and Late Onset Psoriasis and Psoriatic Arthritis Patients of Hungary. Postepy Dermatol. Alergol. 38 (2), 43–51. doi:10.5114/ada.2021.104277

PubMed Abstract | CrossRef Full Text | Google Scholar

Klocke, K., Sakaguchi, S., Holmdahl, R., and Wing, K. (2016). Induction of Autoimmune Disease by Deletion of CTLA-4 in Mice in Adulthood. Proc. Natl. Acad. Sci. USA 113 (17), E2383–E2392. doi:10.1073/pnas.1603892113

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai Kwan Lam, Q., King Hung Ko, O., Zheng, B.-J., and Lu, L. (2008). Local BAFF Gene Silencing Suppresses Th17-Cell Generation and Ameliorates Autoimmune Arthritis. Proc. Natl. Acad. Sci. 105 (39), 14993–14998. doi:10.1073/pnas.0806044105

PubMed Abstract | CrossRef Full Text | Google Scholar

Larson, N. B., Jenkins, G. D., Larson, M. C., Vierkant, R. A., Sellers, T. A., Phelan, C. M., et al. (2013). Kernel Canonical Correlation Analysis for Assessing Gene-Gene Interactions and Application to Ovarian Cancer. Eur. J. Hum. Genet. 22 (1), 126–131. doi:10.1038/ejhg.2013.69

CrossRef Full Text | Google Scholar

Li, H.-L., Pang, Y.-H., and Liu, B. (2021). BioSeq-BLM: a Platform for Analyzing DNA, RNA and Protein Sequences Based on Biological Language Models. Nucleic Acids Res. gkab829. doi:10.1093/nar/gkab829

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Huang, D., Guo, M., Liu, X., Wang, C., Teng, Z., et al. (2015). A Gene-Based Information Gain Method for Detecting Gene-Gene Interactions in Case-Control Studies. Eur. J. Hum. Genet. 23 (11), 1566–1572. doi:10.1038/ejhg.2015.16

CrossRef Full Text | Google Scholar

Li, M.-X., Gui, H.-S., Kwan, J. S. H., and Sham, P. C. (2011). GATES: a Rapid and Powerful Gene-Based Association Test Using Extended Simes Procedure. Am. J. Hum. Genet. 88 (3), 283–293. doi:10.1016/j.ajhg.2011.01.019

CrossRef Full Text | Google Scholar

Li, P., Guo, M., Wang, C., Liu, X., and Zou, Q. (2015). An Overview of SNP Interactions in Genome-wide Association Studies. Brief. Funct. Genomics 14 (2), 143–155. doi:10.1093/bfgp/elu036

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., Gao, X., and Zhang, H. (2019). BioSeq-Analysis2.0: an Updated Platform for Analyzing DNA, RNA and Protein Sequences at Sequence Level and Residue Level Based on Machine Learning Approaches. Nucleic Acids Res. 47 (20), e127. doi:10.1093/nar/gkz740

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, G., Hu, Y., Han, Z., Jin, S., and Jiang, Q. (2019). Genetic Variant Rs17185536 Regulates SIM1 Gene Expression in Human Brain Hypothalamus. Proc. Natl. Acad. Sci. USA 116 (9), 3347–3348. doi:10.1073/pnas.1821550116

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, G., Jin, S., Hu, Y., and Jiang, Q. (2018). Disease Status Affects the Association between Rs4813620 and the Expression of Alzheimer's Disease Susceptibility geneTRIB3. Proc. Natl. Acad. Sci. USA 115 (45), E10519–E10520. doi:10.1073/pnas.1812975115

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J., Su, R., Zhang, J., and Wei, L. (2021). Classification and Gene Selection of Triple-Negative Breast Cancer Subtype Embedding Gene Connectivity Matrix in Deep Neural Network. Brief. Bioinform. 22, 1477–4054. (Electronic). doi:10.1093/bib/bbaa395

CrossRef Full Text | Google Scholar

Liu, J. Z., Mcrae, A. F., Nyholt, D. R., Medland, S. E., Wray, N. R., Brown, K. M., et al. (2010). A Versatile Gene-Based Test for Genome-wide Association Studies. Am. J. Hum. Genet. 87 (1), 139–145. doi:10.1016/j.ajhg.2010.06.009

CrossRef Full Text | Google Scholar

Loos, R. J. F. (2020). 15 Years of Genome-wide Association Studies and No Signs of Slowing Down. Nat. Commun. 11 (1), 5900. doi:10.1038/s41467-020-19653-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Luo, J., Meng, Y., Zhai, J., Zhu, Y., Li, Y., and Wu, Y. (2020). Screening of SLE-Susceptible SNPs in One Chinese Family with Systemic Lupus Erythematosus. Cbio 15 (7), 778–787. doi:10.2174/1574893615666200120105153

CrossRef Full Text | Google Scholar

Lyu, P., Hou, J., Yu, H., and Shi, H. (2020). High-density Genetic Linkage Map Construction in Sunflower (Helianthus Annuus L.) Using SNP and SSR Markers. Curr. Bioinformatics 15 (8), 889–897. doi:10.2174/1574893615666200324134725

CrossRef Full Text | Google Scholar

Ma, L., Clark, A. G., and Keinan, A. (2013). Gene-based Testing of Interactions in Association Studies of Quantitative Traits. Plos Genet. 9 (2), e1003321. doi:10.1371/journal.pgen.1003321

PubMed Abstract | CrossRef Full Text | Google Scholar

Manolio, T. A., Collins, F. S., Cox, N. J., Goldstein, D. B., Hindorff, L. A., Hunter, D. J., et al. (2009). Finding the Missing Heritability of Complex Diseases. Nature 461 (7265), 747–753. doi:10.1038/nature08494

PubMed Abstract | CrossRef Full Text | Google Scholar

Moore, J. H., Asselbergs, F. W., and Williams, S. M. (2010). Bioinformatics Challenges for Genome-wide Association Studies. Bioinformatics 26 (4), 445–455. doi:10.1093/bioinformatics/btp713

PubMed Abstract | CrossRef Full Text | Google Scholar

Nobre, R., Ilic, A., Santander-Jimenez, S., and Sousa, L. (2021). Retargeting Tensor Accelerators for Epistasis Detection. IEEE Trans. Parallel Distrib. Syst. 32 (9), 2160–2174. doi:10.1109/tpds.2021.3060322

CrossRef Full Text | Google Scholar

Peng, Q., Zhao, J., and Xue, F. (2010). A Gene-Based Method for Detecting Gene-Gene Co-association in a Case-Control Association Study. Eur. J. Hum. Genet. 18 (5), 582–587. doi:10.1038/ejhg.2009.223

CrossRef Full Text | Google Scholar

Ritchie, M. D., Hahn, L. W., and Moore, J. H. (2003). Power of Multifactor Dimensionality Reduction for Detecting Gene-Gene Interactions in the Presence of Genotyping Error, Missing Data, Phenocopy, and Genetic Heterogeneity. Genet. Epidemiol. 24 (2), 150–157. doi:10.1002/gepi.10218

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritchie, M. D., and Van Steen, K. (2018). The Search for Gene-Gene Interactions in Genome-wide Association Studies: Challenges in Abundance of Methods, Practical Considerations, and Biological Interpretation. Ann. Transl. Med. 6 (8), 157. doi:10.21037/atm.2018.04.05

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao, J., Yan, K., and Liu, B. (2021). FoldRec-C2C: Protein Fold Recognition by Combining Cluster-To-Cluster Model and Protein Similarity Network. Brief Bioinform 22 (3), bbaa144. doi:10.1093/bib/bbaa144

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, B., Li, F., Liu, Y., and Zeng, X. (2021). Deep Learning Methods for Biomedical Named Entity Recognition: a Survey and Qualitative Comparison. Brief. Bioinform. 22 (6), bbab282. doi:10.1093/bib/bbab282

PubMed Abstract | CrossRef Full Text | Google Scholar

Su, R., Liu, X., Jin, Q., Liu, X., and Wei, L. (2021). Identification of Glioblastoma Molecular Subtype and Prognosis Based on Deep MRI Features. Knowledge-Based Syst. 232, 107490. doi:10.1016/j.knosys.2021.107490

CrossRef Full Text | Google Scholar

Su, R., Liu, X., Wei, L., and Zou, Q. (2019). Deep-Resp-Forest: A Deep forest Model to Predict Anti-cancer Drug Response. Methods 166, 91–102. doi:10.1016/j.ymeth.2019.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, Y.-J., Pang, Y.-H., and Liu, B. (2020). IDP-Seq2Seq: Identification of Intrinsically Disordered Regions Based on Sequence to Sequence Learning. Bioinformaitcs 36 (21), 5177–5186. doi:10.1093/bioinformatics/btaa667

PubMed Abstract | CrossRef Full Text | Google Scholar

Urbanowicz, R. J., Kiralis, J., Sinnott-Armstrong, N. A., Heberling, T., Fisher, J. M., and Moore, J. H. (2012). GAMETES: a Fast, Direct Algorithm for Generating Pure, Strict, Epistatic Models with Random Architectures. BioData Mining 5 (1), 16. doi:10.1186/1756-0381-5-16

PubMed Abstract | CrossRef Full Text | Google Scholar

Wan, X., Yang, C., Yang, Q., Xue, H., Fan, X., Tang, N. L. S., et al. (2010). BOOST: A Fast Approach to Detecting Gene-Gene Interactions in Genome-wide Case-Control Studies. Am. J. Hum. Genet. 87 (3), 325–340. doi:10.1016/j.ajhg.2010.07.021

CrossRef Full Text | Google Scholar

Wang, H. T., Tang, J., Ding, Y., and Guo, F. (2021). Exploring Associations of Non-Coding RNAs in Human Diseases via Three-Matrix Factorization with Hypergraph-Regular Terms on Center Kernel Alignment. Brief. Bioinform. 22 (5), bbaa409. doi:10.1093/bib/bbaa409

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, L., Chen, H., and Su, R. (2018). M6APred-EL: A Sequence-Based Predictor for Identifying N6-Methyladenosine Sites Using Ensemble Learning. Mol. Ther. - Nucleic Acids 12, 635–644. doi:10.1016/j.omtn.2018.07.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, L., Luan, S., Nagai, L. A. E., Su, R., and Zou, Q. (2019). Exploring Sequence-Based Features for the Improved Prediction of DNA N4-Methylcytosine Sites in Multiple Species. Bioinformatics 35 (8), 1326–1333. doi:10.1093/bioinformatics/bty824

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, L., Wan, S., Guo, J., and Wong, K. K. (2017). A Novel Hierarchical Selective Ensemble Classifier with Bioinformatics Application. Artif. Intelligence Med. 83, 82–90. doi:10.1016/j.artmed.2017.02.005

CrossRef Full Text | Google Scholar

Wei, L., Xing, P., Zeng, J., Chen, J., Su, R., and Guo, F. (2017). Improved Prediction of Protein-Protein Interactions Using Novel Negative Samples, Features, and an Ensemble Classifier. Artif. Intelligence Med. 83, 67–74. doi:10.1016/j.artmed.2017.03.001

CrossRef Full Text | Google Scholar

Xiao, Y., Motomura, S., and Podack, E. R. (2008). APRIL (TNFSF13) Regulates Collagen-Induced Arthritis, IL-17 Production and Th2 Response. Eur. J. Immunol. 38 (12), 3450–3458. doi:10.1002/eji.200838640

PubMed Abstract | CrossRef Full Text | Google Scholar

Young, A. I. (2019). Solving the Missing Heritability Problem. Plos Genet. 15 (6), e1008222. doi:10.1371/journal.pgen.1008222

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, Z., Gao, Q., He, Y., Zhang, X., Li, F., Zhao, J., et al. (2012). Detection for Gene-Gene Co-association via Kernel Canonical Correlation Analysis. BMC Genet. 13, 83. doi:10.1186/1471-2156-13-83

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, X., Liao, Y., Liu, Y., and Zou, Q. (2017). Prediction and Validation of Disease Genes Using HeteSim Scores. Ieee/acm Trans. Comput. Biol. Bioinf. 14 (3), 687–695. doi:10.1109/tcbb.2016.2520947

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, X., Zhu, S., Liu, X., Zhou, Y., Nussinov, R., and Cheng, F. (2019). deepDR: a Network-Based Deep Learning Approach to In Silico Drug Repositioning. Bioinformatics 35 (24), 5191–5198. doi:10.1093/bioinformatics/btz418

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhai, Y., Chen, Y., Teng, Z., and Zhao, Y. (2020). Identifying Antioxidant Proteins by Using Amino Acid Composition and Protein-Protein Interactions. Front. Cel Dev. Biol. 8, 591487. doi:10.3389/fcell.2020.591487

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, T., Hu, Y., Wu, X., Ma, R., Jiang, Q., and Wang, Y. (2016). Identifying Liver Cancer-Related Enhancer SNPs by Integrating GWAS and Histone Modification ChIP-Seq Data. Biomed. Res. Int. 2016, 2395341. doi:10.1155/2016/2395341

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Zou, Q., Rodriguez-Paton, A., and Zeng, X. (2019). Meta-path Methods for Prioritizing Candidate Disease miRNAs. Ieee/acm Trans. Comput. Biol. Bioinf. 16 (1), 283–291. doi:10.1109/tcbb.2017.2776280

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., and Liu, J. S. (2007). Bayesian Inference of Epistatic Interactions in Case-Control Studies. Nat. Genet. 39 (9), 1167–1173. doi:10.1038/ng2110

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, H., Du, X., and Yao, Y. (2020). ConvsPPIS: Identifying Protein-Protein Interaction Sites by an Ensemble Convolutional Neural Network with Feature Graph. Cbio 15 (4), 368–378. doi:10.2174/1574893614666191105155713

CrossRef Full Text | Google Scholar