An Information-Entropy Position-Weighted K-Mer Relative Measure for Whole Genome Phylogeny Reconstruction

Alignment methods have faced disadvantages in sequence comparison and phylogeny reconstruction due to their high computational costs in handling time and space complexity. On the other hand, alignment-free methods incur low computational costs and have recently gained popularity in the field of bioinformatics. Here we propose a new alignment-free method for phylogenetic tree reconstruction based on whole genome sequences. A key component is a measure called information-entropy position-weighted k-mer relative measure (IEPWRMkmer), which combines the position-weighted measure of k-mers proposed by our group and the information entropy of frequency of k-mers. The Manhattan distance is used to calculate the pairwise distance between species. Finally, we use the Neighbor-Joining method to construct the phylogenetic tree. To evaluate the performance of this method, we perform phylogenetic analysis on two datasets used by other researchers. The results demonstrate that the IEPWRMkmer method is efficient and reliable. The source codes of our method are provided at https://github.com/ wuyaoqun37/IEPWRMkmer.

Introduction

The reconstruction of a phylogenetic tree is a primary problem in evolutionary biology. Sequence alignment is a key step in the reconstruction, aiming to identify the homology of sequences and uncover phylogenetic relationships in sequences. Traditional sequence comparison is based on pairwise or multiple sequence alignment (Felsenstein and Felenstein, 2004; Morrison, 2006) and was implemented by software packages such as BLAST (Altschul et al., 1990), ClustalW (Thompson et al., 1994), and MrBayes (Ronquist et al., 2012). However, the methods based on sequence alignment have some disadvantages, including high computational cost in handling the time and space complexity of the algorithm. Therefore, alignment-free methods have been proposed to overcome these problems (Zielezinski et al., 2017). The computational cost of alignment-free methods is low because they are generally of linear complexity (Fox et al., 1977).

Several alignment-free methods for sequence comparison are based on word counts (Blaisdell, 1986; Höhl et al., 2006; Wang et al., 2016). A key idea is to use the close distribution of k-mers to imply the high correlation degree, hence the similarity of the sequences. The methods have been implemented in software tools, such as FFP (Sims et al., 2009), kWIP (Murray et al., 2017), CVtree (Qi et al., 2004), and DLtree (Wu et al., 2017). Many k-mer methods transform the input sequence into a frequency vector of k-mers, then define the distance of the sequences by that of the frequency vector of k-mers (Qi et al., 2004; Wu et al., 2017). To reduce the statistical dependence between adjacent word matches, Spaced-Words (Leimeister and Boden, 2014) proposed to use spaced words, which are defined by patterns of matches without reference to positions. Some alignment-free methods are based on match length, which defines the distance between sequences based on the length of substring matches between two sequences. These include the shortest unique substring method (Haubold et al., 2005), ACS (Ulitsky et al. 2006), UA (Comin and Verzotto, 2012), and ALFRED (Thankachan et al. 2016). In addition, graphical representation was used to construct the probability distribution of a DNA sequence (Yu et al., 2011). The chaos game representation transforms the distribution of characters in a DNA sequence into the distribution of nodes in a graph (Hoang et al. 2016; Yin, 2017; Mendizabal-Ruiz et al., 2018). Many researchers considered extracting the position information of a k-mer (Huang and Wang, 2011; Ding et al., 2013; Tang et al., 2014). Ding et al. (2013) used the average interval distance of normalized k-mers to capture evolutionary information for sequence comparison. Tang et al. (2014) presented the average relative distance of normalized k-mers to improve the method of Ding et al. (2013). Ma et al. (2020) proposed the PWKmer method, which combines the k-mer counts and k-mer position distributions for phylogenetic analysis.

In this work, we propose a new alignment-free method which combines the position-weighted measure of k-mers proposed by Ma et al. (2020) and the information entropy of frequency of k-mers to obtain phylogenetic information for sequence comparison. It is named information-entropy position-weighted k-mer relative measure (IEPWRMkmer). To evaluate the performance of this method, we carry out phylogenetic analysis on two data sets used by other researchers.

Materials and Methods

Genomic Datasets

Dataset 1

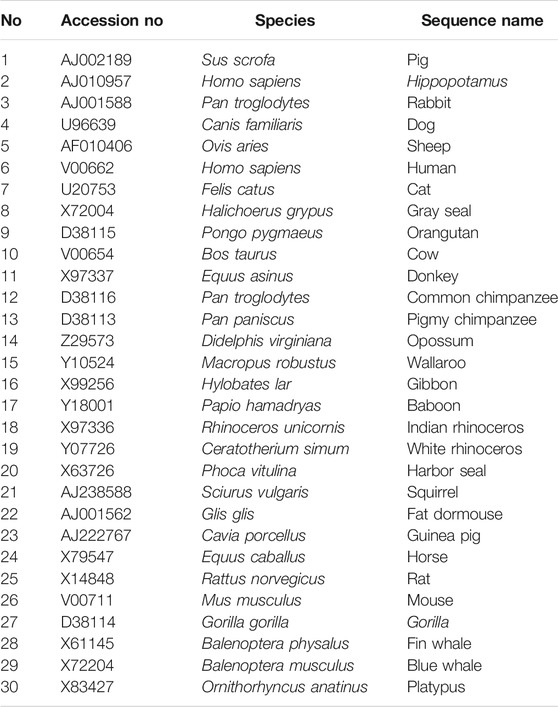
The first dataset for analysis consists of the same whole genome DNA sequences of 30 mammalian species studied in Li et al. (2001), Otu and Sayood (2003), and Tang et al. (2014). The accession numbers, species, and species name are listed in Table 1. All sequences were downloaded from NCBI GenBank.

TABLE 1

TABLE 1. Names, species, and accession numbers for mitochondrial genomes of 30 mammalian species.

Dataset 2

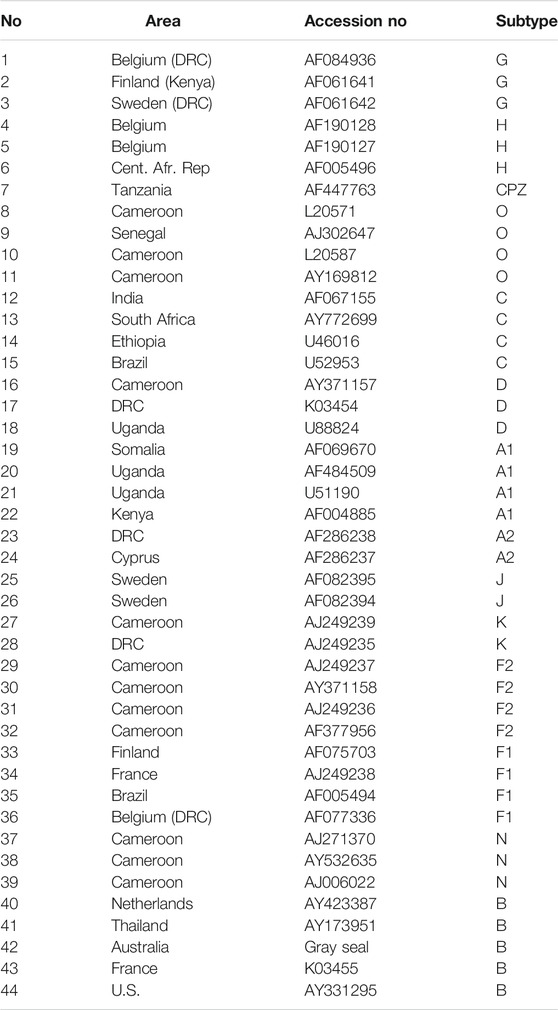
The second dataset for analysis is the HIV-1 dataset studied in Ma et al. (2020). This dataset contains 43 HIV genome sequences used in Wu et al. (2007) and a controversial taxonomic sequence used in Chang et al. (2014). The dataset includes subtypes A, B, C, D, F, G, J, K, and H of the HIV-1 M, O, N groups and the CPZ sequence. The area, accession numbers, and subtypes are listed in Table 2. All these sequences were downloaded from NCBI GenBank.

TABLE 2

TABLE 2. Accession numbers, subtype, and area for 44 HIV-1.

We use two approaches to validate the method. First, we use the Robinson-Foulds (RF) distance to compare our method with other alignment-free methods. Second, we use the bootstrap method to construct consensus trees and show the stability of the trees obtained by our method.

Methods

Let S = $s_1{s}_2\cdots s_L$ be a DNA sequence with length L, $a_1{a}_2\cdots a_k$is a k-mer, where $a_i$∈(A,T,C,G). If the k-mer $a_1{a}_2\cdots a_k$ occurs in S, we denote by $p_{a_1{a}_2\cdots a_k}$ the vector composed of the positions of $a_1{a}_2\cdots a_k$ in this given sequence and by $p_{a_1{a}_2\cdots a_k }\left(i\right)$ its ith element. If the k-mer $a_1{a}_2\cdots a_k$ does not occur in S,$\text{ we set }{p}_{a_1{a}_2\cdots a_k}$=(0). For example, for the DNA sequence GTA​ACC​TGA​ACG​TAC​TTG​GA with length 20, we list all 2-mer position vectors:

P_AA=(3,9); P_AC=(4,10,14); P_AG= (0); P_AT= (0); P_CA=(0); P_CC=(5); P_CG=(11); P_CT=(6,15); P_GA=(8,19); P_GC=(0); P_GG=(18); P_GT=(1,12); P_TA=(2,13); P_TC = 0; P_TG=(7,17); P_TT=(16).

In this example, the 2-mers AG, AT, CA, GC, and TC do not appear. For each k-mer, its position vector provides its position distribution information in the sequence. One can use the k-mer position vectors to reconstruct the DNA sequence (Ma et al., 2020).

Ma et al. (2020) defined the position-weighted measure $D\left(a_1{a}_2\cdots a_k\right)$ of $a_1{a}_2\cdots a_k$ based on its position in the sequence as

$D\left(a_1{a}_2\cdots a_k\right)=\{\begin{array}{cc}\frac{{\displaystyle {\sum }_{i=1}^n{p}_{a_1{a}_2\cdots a_k}}\left(i\right)}{L\left(L-k+1\right)},& n\ne 0,\\ 0,& n=0,\end{array}(1)$

where n is the length of the vector $p_{a_1{a}_2\cdots a_k}$. Actually $p_{a_1{a}_2\cdots a_k }\left(i\right)/L$ means the position weight of $a_1{a}_2\cdots a_k$ in the given sequence with length L.

We denote by N the number of sequences in a dataset. In order to characterize the importance of k-mers in the whole dataset, we count the number m of the sequences that contain a k-mer $a_1{a}_2\cdots a_k$. Then the occurrence frequency F$\left(a_1{a}_2\cdots a_k\right)$ of this k-mer in the whole dataset is defined as m/N. We introduce the Shannon entropy H($a_1{a}_2\cdots a_k$) of frequency F($a_1{a}_2\cdots a_k$) defined by Murray et al. (2017) as

$H\left(a_1{a}_2\cdots a_k\right)=-\left(F{\log }_2\left(F\right)+\left(1-F\right){\log }_2\left(1-F\right)\right),(2)$

where F stands for F ($a_1{a}_2\cdots a_k$).

In this study, we aim to get more DNA phylogenetic information by combining the above two methods and defining

$E\left(a_1{a}_2\cdots a_k\right)=D\left(a_1{a}_2\cdots a_k\right)\times H\left(a_1{a}_2\cdots a_k\right)(3)$

Here, we regard Shannon entropy H ($a_1{a}_2\cdots a_k$) as another weight.

For a fixed K, there are 4^K k-mers. For each k-mer $a_1{a}_2\cdots a_k$, we can calculate the corresponding $E\left(a_1{a}_2\cdots a_k\right)$, then arrange 4^K of these $E\left(a_1{a}_2\cdots a_k\right)$ to get a feature representation vector ($E_1,E_2,\cdots ,E_{4^K}$) according to the alphabet order of the 4^K k-mers for each genome.

For two given genome sequences A and B, we can obtain $E_{\text{A}}$ = $\left(E_1^A,E_2^A,\cdots ,E_{4^K}^A\right)$ and $E_{\text{B}}=\left(E_1^B,E_2^B,\cdots ,E_{4^K}^B\right)$ by the method. We use the Manhattan distance to calculate the pairwise distance between these two genome sequences:

$D\left(A,B\right)={\displaystyle {\sum }_i^{4^K}\left|\left(E_i^A-E_i^B\right)\right|}(4)$

For a given dataset, we can derive a distance matrix by Eq. 4. This distance matrix contains the sequence similarity information. After obtaining the distance matrix, we insert it into the mega 7.0 software (Sudhir et al., 2016) and use Neighbor-Joining (NJ) program (Saitou et al. 1987) to construct the phylogenetic tree.

Robinson-Foulds Distance and the Bootstrap Method

We use the Robinson-Foulds (RF) distance (Robinson and Foulds 1981) to judge the quality of the method. A smaller RF value means a closer distance between the phylogenetic tree and the reference tree.

(Yu et al., 2010) proposed a modified version of the bootstrap method to evaluate the reliability of the constructed phylogenetic tree. We also use this method in the present work. Its workflow is as follows: Each row is the feature vector ($E_1,E_2,\cdots ,E_{4^K})$ of a species, and each column is the feature value of all genome sequences based on the same k-mer. Through random sampling of all columns, in which some columns may be selected many times, while some columns may not be selected at all, we randomly select one column. After 4^K times of selection, a new N$\times$4^K feature matrix is constructed. Using the new feature matrix, the Manhattan distance of any two rows is calculated to get a new distance matrix. Then we use the NJ method to construct a phylogenetic tree and repeat the above steps 100 times. Finally, a consensus tree is drawn by using consense. exe in the Phylip package. The frequency of a particular branch of a phylogenetic tree can be used as a measure of the stability of this branch.

Results

Experiment 1

We use the genomes of 30 mammalian species in dataset 1 to construct a phylogenetic tree using ClustalX (Larkin et al. 2007) as the reference tree. ClustalX is one of the widely used multiple alignment programs. The result is shown in Figure 1A. It is seen that rabbit, fat dormouse, squirrel, guinea pig, mouse, rat, platypus, opossum, and wallaroo belong to the rodents group; human, baboon, orangutan, gibbon, gorilla, pigmy chimpanzee, and common chimpanzee belong to the primates group; blue whale, fin whale, hippopotamus, cow, sheep, pig, donkey, horse, Indian-rhinoceros, white rhinoceros, cat, dog, gray seal, and harbor seal belong to the ferungulates group. When K < 5, it is not feasible to construct a phylogenetic tree using our method. When K = 5, 6, the 30 mammals cannot be divided into three groups in our tree. When K = 7, it can be divided into three groups, but the relationship between guinea pig and fat dormouse is not correct. When K = 8, 9, the branches of the tree become correct. We list the RF distances between the phylogenetic tree constructed by our method at K = 5, 6, 7, 8, 9 and the reference tree constructed by ClustalX in Table 3. From Table 3, we can see that the RF distance reaches the minimum when K = 8. We show the phylogenetic tree of K = 8 constructed by our method in Figure 1B. From Figure 1B, we can see that the species in the three main categories are grouped correctly. Primates and ferungulates are closer, and this relationship is consistent with that in Figure 1A. In terms of branches, monotremes (platypus), marsupials (wallaroo, opossum), murid rodents (mouse, rat), non-murid rodents (guinea pig, squirrel, fat dormouse, rabbit), perissodactyls (white rhinoceros, horse, Indian rhinoceros, donkey), carnivores (harbor seal, dog, gray seal, cat), artiodactyls (sheep, cow, hippopotamus, pig), primates (human, pigmy chimpanzee, common chimpanzee, gorilla, baboon, gibbon, orangutan), and cetaceans (blue whale, fin whale) are grouped into respective taxonomic classes accurately.

FIGURE 1

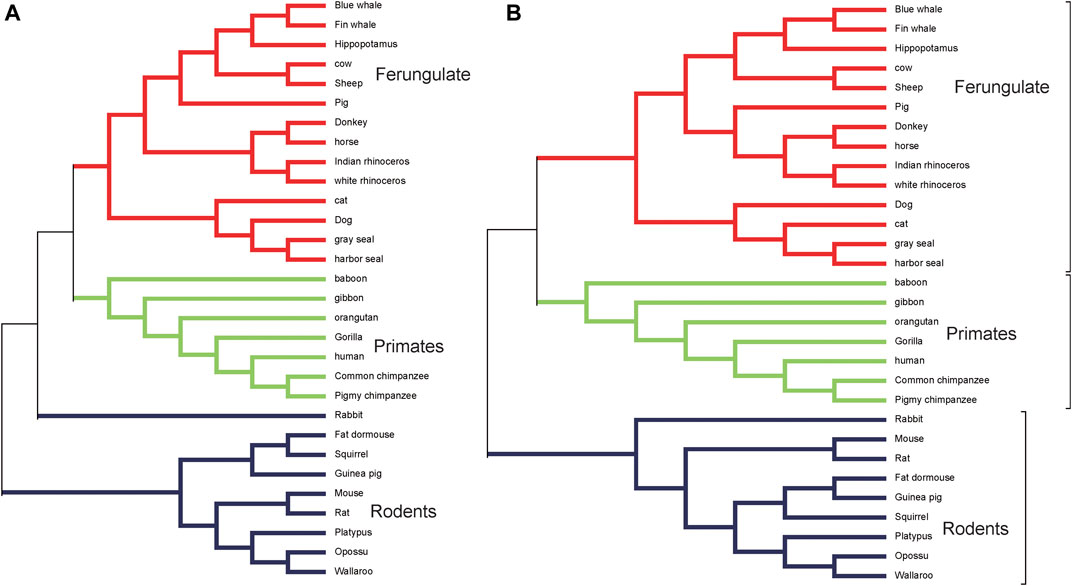
FIGURE 1. (A) The phylogenetic tree of 30 mammalian species reconstructed by ClustalX. (B) The phylogenetic tree of 30 mammalian species at K = 8 based on our method.

TABLE 3

TABLE 3. The RF distance between the phylogenetic tree conducted by our method at K = 5,6,7,8,9 and the reference tree conducted by ClustalX.

Figure 2 shows the RF distance between the reference tree constructed by ClustalX and the phylogenetic tree constructed by our method, Tang’s method, PWKmer, DLtree, and CVtree on dataset 1. Using our method, when K = 8, the RF distance is 8. The shortest RF distance of DLtree (K = 9) is 10, the shortest distance of CVtree (K = 9) is 16, the shortest distance of Tang’s method (K = 7) is 16, and the shortest distance of PWKmer (K = 9) is 10. Therefore, the results of our method are closer to those of ClustalX than those of the other methods, which indicates that our method is effective.

FIGURE 2

FIGURE 2. The Robinson–Foulds distance between the tree reconstructed by ClustalX method and the phylogenetic trees reconstructed by our method (IEPWRMkmer K = 8), the CVTree method, the DLTree method, Tang’s method (K = 7), and the PWKmer method (K = 9) on dataset 1 (we used the optimal tree by CVTree and DLTree).

Figure 3 shows the consensus tree of 30 mammalian species based on our method. Compared with Figure 1B, 30 mammalian species are divided into the rodents group, the ferungulates group, and the primates group correctly. The support rate is 80% for the rodents group and 100% for both ferungulates and primates groups. Among the branches, marsupials (opossum, wallaroo), carnivores (dog, cat, harbor seal, gray seal), murid roots (rat, mouse), and cetaceans (fin whale, blue whale) are all supported by a 100% rate. In the artiodactyls group (cow, sheep, pig, hippopotamus), pig is separated out of the artiodactyls group, but the support rate is low at 43%. It indicates that the phylogenetic tree constructed by our method is quite robust.

FIGURE 3

FIGURE 3. The modified bootstrap consensus tree for Figure 1B based on 100 replicates.

Experiment 2

The human immunodeficiency viruses (HIV) represent a group of retroviruses, which are not presumed to have originated from human cellular DNA sequences, hence are distinct from endogenous retroviruses (Wu et al., 2007). HIV-1 can be classified into three major phylogenetic groups, namely M (major), N (new), and O (others). Group M is responsible for the HIV pandemic, it is divided into nine subtypes, namely A, B, C, D, F, G, J, K, and H. Based on differential phylogenetic clustering, the subtypes A and F are further divided into sub-subtypes (A1, A2) and (F1, F2), respectively. Groups N and O are derived from other primates and then infect humans. CPZ is a non-human primate virus isolated from chimpanzees, which is closest to human-to-human transmission of HIV.

We performed the phylogenetic analysis of 44 HIV-1 complete genome sequences in dataset 2 using ClustalX and our method. The phylogenetic trees reconstructed by ClustalX and our method (K = 7) are shown in Figure 4A and Figure 4B, respectively. From Figure 4B, we can see that the species from all subtypes can be correctly classified into their groups (A, B, C, D, F, G, J, K, H, O, and M), and CPZ as the reference sequence is separated into the outermost. From the internal branches, both F and A contain two subtypes (F1 and F2) and (A1 and A2), respectively. Our method can separate the two subtypes, and in the branches, both F and A subtypes can be closely grouped together.

FIGURE 4

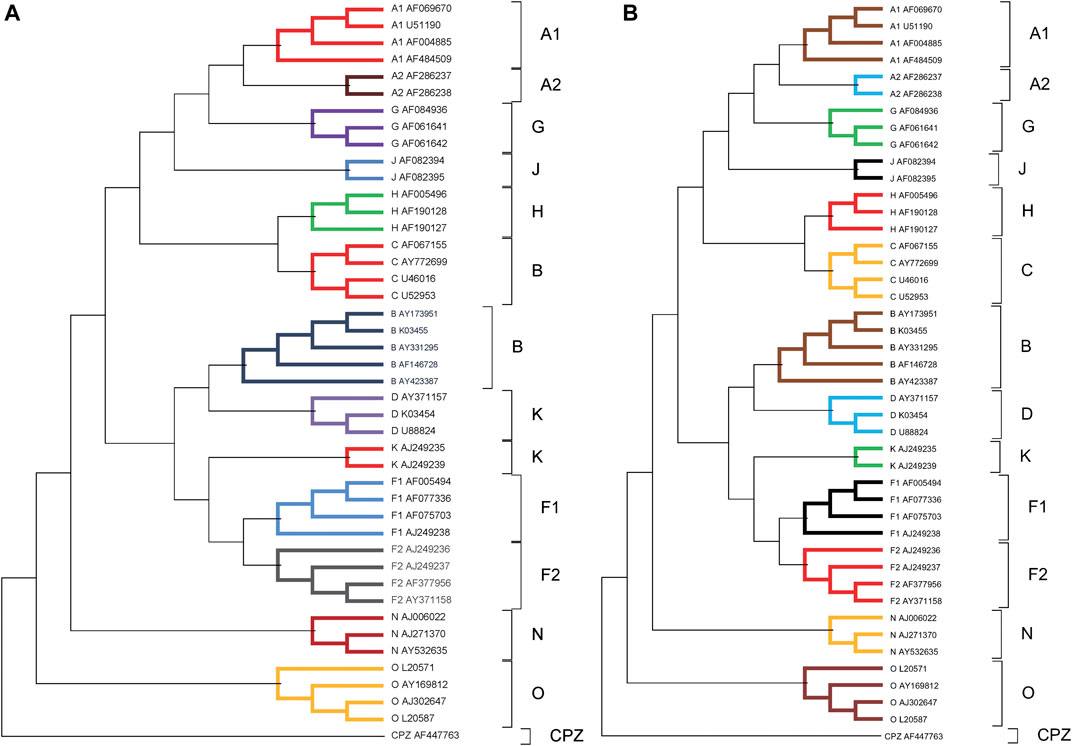
FIGURE 4. (A) The phylogenetic tree of 44 HIV-1 genomes reconstructed by ClustalX. (B) The phylogenetic tree of 44 HIV-1 genomes reconstructed by our method (K = 7).

Figure 5 shows the RF distances between the reference tree constructed by ClustalX and the phylogenetic trees constructed by our method, Tang’s method, PWKmer, DLtree, and CVtree. Using our method, when K = 7, the RF distance is 10. The shortest RF distance of the DLtree (K = 11) is 12, the shortest distance of the CVtree (K = 9) is 16, the shortest distance of the PWKmer (K =9) is 10, and the shortest distance of Tang’s method (K = 9) is 10. Therefore, our method performs better than the DLtree and the CVtree on dataset 2 and has the same performance as Tang’s method and PWKmer. The results indicate that our method is quite effective again.

FIGURE 5

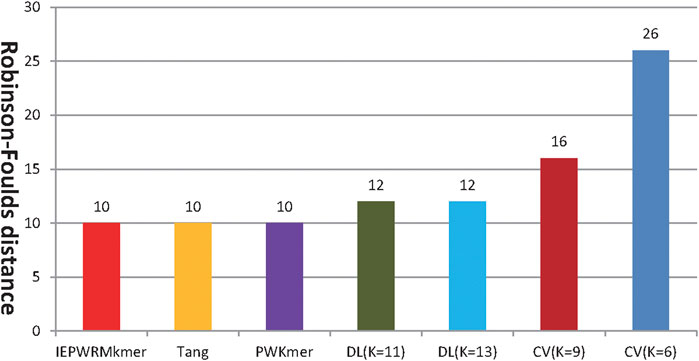
FIGURE 5. The RF distance between the reference tree constructed by Clustalx and the phylogenetic trees constructed by our method (IEPWRMkmer, K = 7), Tang’s method (K = 8), the PWKmer method (K = 9), the DLtree method, and the CVtree method. (For the PWKmer method, the DLtree method, and the CVtree method, we chose their optimal classification tree).

Figure 6 shows the consensus tree of 44 HIV-1 based on our method. Comparing with Figure 4B, all HIV-1 sequences are divided into the M, N, O, and CPZ groups, whose support rate is 100%. From the branch point of view, in group M, the branch support rate of all subtypes is 100%. For subtypes A and F, the subtypes (A1, A2) and (F1 and F2) are clustered with 100% support. It again indicates that the phylogenetic tree constructed by our method is quite robust.

FIGURE 6

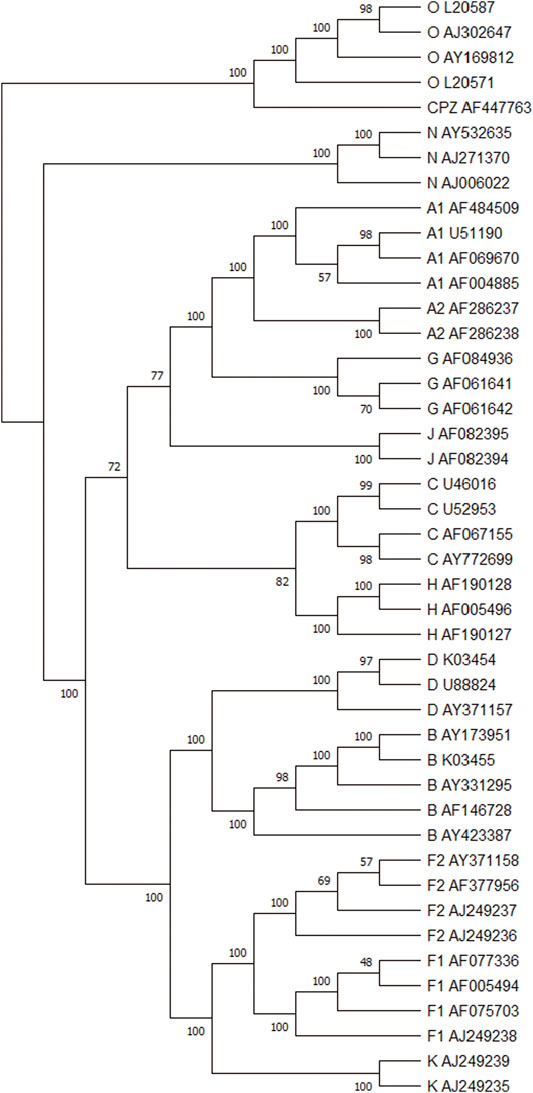
FIGURE 6. The modified bootstrap consensus tree for Figure 4B based on 100 replicates.

Estimate of the Optimal Parameter K

Different lengths of k-mers contain different phylogenetic information. Short k-mers may not contain sufficient DNA sequence information. Long k-mers contain sufficient phylogenetic information, but it needs large memory and takes a long time to calculate the distance based on information on long k-mers. Therefore, it is also very important to estimate an optimal value of K as heralded in (Yu et al., 2010) for the DLTree method and (Qi et al., 2004) for the CVTree method.

In this paper, we propose to use the Shannon entropy of the feature matrix to determine the optimal value of K. Using Eq. 3, we can obtain an N $\times$4^K feature matrix for a dataset with N genomes. Then, we propose to define a scoring strategy as

$\text{score}\left(K\right)=-\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{\displaystyle {\sum }_{i=1}^{4^K}\left(E_{ij}{\log }_2{E}_{ij}+\left(1-E_{ij}\right){\log }_2\left(1-E_{ij}\right)\right)}}.(5)$

The optimal K is the value at which $\text{score}\left(K\right)$ reaches its maximum.

We use Eq. 5 to calculate $\text{score}\left(K\right)$ on datasets 1 and 2 for different K. The relationship between $\text{score}\left(K\right)$ and K is shown in Figure 7 for these two datasets. It is seen that $\text{score}\left(K\right)$ reaches the largest value when K = 8 on the two datasets. Considering that the larger K is, the more memory resources are consumed, we only consider the values near K = 8 (e.g., K = 7, 8, 9). For the 30 mammalian species dataset, we have seen that the phylogenetic tree for K = 8 constructed by our method is closest to the reference tree. The same happened for the HIV-1 dataset with K = 7. The outcomes indicate that $\text{score}\left(K\right)$ can provide an effective means to estimate the optimal value of K.

FIGURE 7

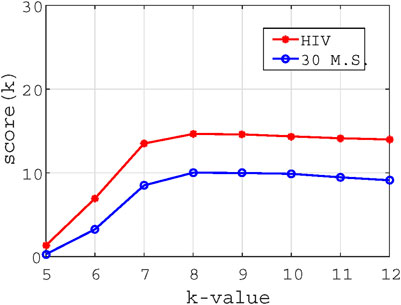
FIGURE 7. The trend chart of K value vs scoring measure $\text{score}\left(K\right)$. The red circles represent the scores of the dataset of 30 mammalian species for different K values, and the blue dots represent the scores of the HIV dataset for different K values.

Conclusion

In this paper, a new alignment-free method is proposed for phylogenetic analysis and sequence comparison based on whole genome sequences. Our method combines the position-weighted measure of k-mers and the information entropy of frequency of k-mers. We used the Manhattan metric to measure the distance between a pair of sequences and the NJ method to construct the phylogenetic tree. In order to test the effectiveness and reliability of our method, we applied it on two datasets of 30 mammalian species and 44 HIV-1 genomes. The results demonstrated that the present method is efficient and reliable. A suitable K value is important to capture rich phylogenetic information of DNA sequences. In order to choose an optimal K value, we proposed a scoring measure based on the information entropy. The obtained results on two real datasets support that the method can capture the k-mer distribution information and is effective for whole genome sequence comparison and phylogenetic analysis.

Remark: The method of this paper is derived from the two studies Ma et al. (2020) and Murray et al. (2017). There are differences between this work and previous works: Tang et al. presented the average relative distance for normalized k-mers. PWKmer uses the counts and position distributions of k-mers to capture more evolutionary information. KWIP (Murray et al. 2017) uses information entropy to weight the inner product (Si$\ast$Sj), while we use information entropy to weight the relative positions of k-mers. KWIP uses a kernel function to calculate the distance, while we use the Manhattan metric to calculate the pairwise distance between species. Here, we claimed that the results obtained by the IEPWRMkmer method are close to those by ClustalX and the IEPWRMkmer is superior to the other distance metrics. We used the phylogenetic tree constructed by ClustalX as the reference tree or standard tree, hence we cannot claim that our method is superior to the ClustalX method.

Data Availability Statement

The genome datasets analyzed for this study can be found in the GenBank https://www.ncbi.nlm.nih.gov/

Author Contributions

Y-QW contributed to the conception and design of the study, developed the method, and wrote the manuscript. Z-GY gave the ideas and supervised the project. All authors discussed the results and reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by funds from the National Natural Science Foundation of China (grant numbers: 11871061 and 12026213); The National Key Research and Development Program of China (grant number: 2020YFC0832405); Innovation Foundation of Qian Xuesen Laboratory of Space Technology.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altschul, S. F., Gish, W., Miller, W., Myers, E. W., and Lipman, D. J. (1990). Basic Local Alignment Search Tool. J. Mol. Biol. 215 (3), 403–410. doi:10.1016/S0022-2836(05)80360-2

CrossRef Full Text | Google Scholar

Blaisdell, B. E. (1986). A Measure of the Similarity of Sets of Sequences Not Requiring Sequence Alignment. Proc. Natl. Acad. Sci. 83 (14), 5155–5159. doi:10.1073/pnas.83.14.5155

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, G., Wang, H., and Zhang, T. (2014). A Novel Alignment-free Method for Whole Genome Analysis: Application to HIV-1 Subtyping and HEV Genotyping. Inf. Sci. 279, 776–784. doi:10.1016/j.ins.2014.04.029

CrossRef Full Text | Google Scholar

Comin, M., and Verzotto, D. (2012). Alignment-free Phylogeny of Whole Genomes Using Underlying Subwords. Algorithms Mol. Biol. 7 (1), 1–12. doi:10.1186/1748-7188-7-34

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, S., Li, Y., Yang, X., and Wang, T. (2013). A Simple K-word Interval Method for Phylogenetic Analysis of DNA Sequences. J. Theor. Biol. 317, 192–199. doi:10.1016/j.jtbi.2012.10.010

CrossRef Full Text | Google Scholar

Felsenstein, J., and Felenstein, J. (2004). Inferring Phylogenies. (Sunderland, MA: Sinauer Associates). doi:10.1086/383584

CrossRef Full Text | Google Scholar

Fox, G. E., Magrum, L. J., Balch, W. E., Wolfe, R. S., and Woese, C. R. (1977). Classification of Methanogenic Bacteria by 16S Ribosomal RNA Characterization. Proc. Natl. Acad. Sci. 74 (10), 4537–4541. doi:10.1073/pnas.74.10.4537

PubMed Abstract | CrossRef Full Text | Google Scholar

Haubold, B., Pierstorff, N., Möller, F., and Wiehe, T. (2005). Genome Comparison without Alignment Using Shortest Unique Substrings. BMC Bioinformatics 6 (1), 123–211. doi:10.1186/1471-2105-6-123

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoang, T., Yin, C., and Yau, S. S.-T. (2016). Numerical Encoding of DNA Sequences by Chaos Game Representation with Application in Similarity Comparison. Genomics 108, 134–142. doi:10.1016/j.ygeno.2016.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Höhl, M., Rigoutsos, I., and Ragan, M. A. (2006). Pattern-based Phylogenetic Distance Estimation and Tree Reconstruction. Evol. Bioinformatics 2, 359–375. doi:10.2174/157489306775330570

CrossRef Full Text | Google Scholar

Huang, Y., and Wang, T. (2011). Phylogenetic Analysis of DNA Sequences with a Novel Characteristic Vector. J. Math. Chem. 49 (8), 1479–1492. doi:10.1007/s10910-011-9811-x

CrossRef Full Text | Google Scholar

Kumar, S., Stecher, G., and Tamura, K. (2016). MEGA7: Molecular Evolutionary Genetics Analysis Version 7.0 for Bigger Datasets. Mol. Biol. Evol. 33 (7), 1870–1874. doi:10.1093/molbev/msw054

PubMed Abstract | CrossRef Full Text | Google Scholar

Larkin, M. A., Blackshields, G., Brown, N. P., Chenna, R., McGettigan, P. A., McWilliam, H., et al. (2007). Clustal W and Clustal X Version 2.0. Bioinformatics 23 (21), 2947–2948. doi:10.1093/bioinformatics/btm404

PubMed Abstract | CrossRef Full Text | Google Scholar

Leimeister, C.-A., Boden, M., Horwege, S., Lindner, S., and Morgenstern, B. (2014). Fast Alignment-free Sequence Comparison Using Spaced-word Frequencies. Bioinformatics 30, 1991–1999. doi:10.1093/bioinformatics/btu177

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M., Badger, J. H., Chen, X., Kwong, S., Kearney, P., and Zhang, H. (2001). An Information-Based Sequence Distance and its Application to Whole Mitochondrial Genome Phylogeny. Bioinformatics 17 (2), 149–154. doi:10.1093/bioinformatics/17.2.149

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Y., Yu, Z., Tang, R., Xie, X., Han, G., and Anh, V. V. (2020). Phylogenetic Analysis of HIV-1 Genomes Based on the Position-Weighted K-Mers Method. Entropy 22 (2), 255. doi:10.3390/e22020255

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendizabal-Ruiz, G., Román-Godínez, I., Torres-Ramos, S., Salido-Ruiz, R. A., Vélez-Pérez, H., and Morales, J. A. (2018). Genomic Signal Processing for DNA Sequence Clustering. PeerJ 6 (3), e4264. doi:10.7717/peerj.4264

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrison, D. A. (2006). Multiple Sequence Alignment for Phylogenetic Purposes. Aust. Syst. Bot. 19 (6), 479–539. doi:10.1071/sb06020

CrossRef Full Text | Google Scholar

Murray, K. D., Webers, C., Ong, C. S., Borevitz, J., and Warthmann, N. (2017). KWIP: The K-Mer Weighted Inner Product, a De Novo Estimator of Genetic Similarity. Plos Comput. Biol. 13 (9), e1005727. doi:10.1371/journal.pcbi.1005727

PubMed Abstract | CrossRef Full Text | Google Scholar

Otu, H. H., and Sayood, K. (2003). A New Sequence Distance Measure for Phylogenetic Tree Construction. Bioinformatics 19 (16), 2122–2130. doi:10.1093/bioinformatics/btg295

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, J., Luo, H., and Hao, B. (2004). CVTree: a Phylogenetic Tree Reconstruction Tool Based on Whole Genomes. Nucleic Acids Res. 32 (Suppl. l_2), W45–W47. doi:10.1093/nar/gkh362

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, D. F., and Foulds, L. R. (1981). Comparison of Phylogenetic Trees. Math. Biosciences 53 (1-2), 131–147. doi:10.1016/0025-5564(81)90043-2

CrossRef Full Text | Google Scholar

Ronquist, F., Teslenko, M., Van Der Mark, P., Ayres, D. L., Darling, A., Höhna, S., et al. (2012). MrBayes 3.2: Efficient Bayesian Phylogenetic Inference and Model Choice across a Large Model Space. Syst. Biol. 61 (3), 539–542. doi:10.1093/sysbio/sys029

PubMed Abstract | CrossRef Full Text | Google Scholar

Saitou, N., and Nei, M. (1987). The Neighbor-Joining Method: a New Method for Reconstructing Phylogenetic Trees. Mol. Biol. Evol. 4 (4), 406–425. doi:10.1093/oxfordjournals.molbev.a040454

PubMed Abstract | CrossRef Full Text | Google Scholar

Sims, G. E., Jun, S.-R., Wu, G. A., and Kim, S.-H. (2009). Alignment-free Genome Comparison with Feature Frequency Profiles (FFP) and Optimal Resolutions. Pnas 106 (8), 2677–2682. doi:10.1073/pnas.0813249106

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, J., Hua, K., Chen, M., Zhang, R., and Xie, X. (2014). A Novel K-word Relative Measure for Sequence Comparison. Comput. Biol. Chem. 53, 331–338. doi:10.1016/j.compbiolchem.2014.10.007

CrossRef Full Text | Google Scholar

Thankachan, S. V., Chockalingam, S. P., Liu, Y., Apostolico, A., and Aluru, S. (2016). ALFRED: a Practical Method for Alignment-free Distance Computation. J. Comput. Biol. 23 (6), 452–460. doi:10.1089/cmb.2015.0217

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, J. D., Higgins, D. G., and Gibson, T. J. (1994). CLUSTAL W: Improving the Sensitivity of Progressive Multiple Sequence Alignment through Sequence Weighting, Position-specific gap Penalties and Weight Matrix Choice. Nucl. Acids Res. 22 (22), 4673–4680. doi:10.1093/nar/22.22.4673

PubMed Abstract | CrossRef Full Text | Google Scholar

Ulitsky, I., Burstein, D., Tuller, T., and Chor, B. (2006). The Average Common Substring Approach to Phylogenomic Reconstruction. J. Comput. Biol. 13 (2), 336–350. doi:10.1089/cmb.2006.13.336

CrossRef Full Text | Google Scholar

Wang, Y., Lei, X., Wang, S., Wang, Z., Song, N., Zeng, F., et al. (2016). Effect of K-Tuple Length on Sample-Comparison with High-Throughput Sequencing Data. Biochem. Biophysical Res. Commun. 469 (4), 1021–1027. doi:10.1016/j.bbrc.2015.11.094

CrossRef Full Text | Google Scholar

Wu, Q., Yu, Z.-G., and Yang, J. (2017). DLTree: Efficient and Accurate Phylogeny Reconstruction Using the Dynamical Language Method. Bioinformatics 33 (14), 2214–2215. doi:10.1093/bioinformatics/btx158

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X., Cai, Z., Wan, X.-F., Hoang, T., Goebel, R., and Lin, G. (2007). Nucleotide Composition String Selection in HIV-1 Subtyping Using Whole Genomes. Bioinformatics 23 (14), 1744–1752. doi:10.1093/bioinformatics/btm248

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, C. (2019). Encoding and Decoding DNA Sequences by Integer Chaos Game Representation. J. Comput. Biol. 26 (2), 143–151. doi:10.1089/cmb.2018.0173

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, C., Deng, M., and Yau, S. S.-T. (2011). DNA Sequence Comparison by a Novel Probabilistic Method. Inf. Sci. 181 (8), 1484–1492. doi:10.1016/j.ins.2010.12.010

CrossRef Full Text | Google Scholar

Yu, Z.-G., Chu, K. H., Li, C. P., Anh, V., Zhou, L.-Q., and Wang, R. W. (2010). Whole-proteome Phylogeny of Large dsDNA Viruses and Parvoviruses through a Composition Vector Method Related to Dynamical Language Model. BMC Evol. Biol. 10 (1), 1–11. doi:10.1186/1471-2148-10-192

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Z.-G., Zhan, X.-W., Han, G.-S., Wang, R. W., Anh, V., and Chu, K. H. (2010). Proper Distance Metrics for Phylogenetic Analysis Using Complete Genomes without Sequence Alignment. Ijms 11 (3), 1141–1154. doi:10.3390/ijms11031141

PubMed Abstract | CrossRef Full Text | Google Scholar

Zielezinski, A., Vinga, S., Almeida, J., and Karlowski, W. M. (2017). Alignment-free Sequence Comparison: Benefits, Applications, and Tools. Genome Biol. 18 (1), 1–17. doi:10.1186/s13059-017-1319-7

PubMed Abstract | CrossRef Full Text | Google Scholar