Inferring Functional Epigenetic Modules by Integrative Analysis of Multiple Heterogeneous Networks

Gene expression and methylation are critical biological processes for cells, and how to integrate these heterogeneous data has been extensively investigated, which is the foundation for revealing the underlying patterns of cancers. The vast majority of the current algorithms fuse gene methylation and expression into a network, failing to fully explore the relations and heterogeneity of them. To resolve these problems, in this study we define the epigenetic modules as a gene set whose members are co-methylated and co-expressed. To address the heterogeneity of data, we construct gene co-expression and co-methylation networks, respectively. In this case, the epigenetic module is characterized as a common module in multiple networks. Then, a non-negative matrix factorization-based algorithm that jointly clusters the co-expression and co-methylation networks is proposed for discovering the epigenetic modules (called Ep-jNMF). Ep-jNMF is more accurate than the baselines on the artificial data. Moreover, Ep-jNMF identifies more biologically meaningful modules. And the modules can predict the subtypes of cancers. These results indicate that Ep-jNMF is efficient for the integration of expression and methylation data.

1. Introduction

DNA methylation modifies the cytosine base associating with cellular differentiation and cell development (Suzuki and Bird, 2008; Deaton and Bird, 2011; Teschendorff et al., 2012; Ziller et al., 2013). For example, DNA methylation regulates the expression of genes by decreasing the affinity of transcription factors (Bird and Wolffe, 1999). Furthermore, abberations of methylation directly result in oncogenesis of cancers (Varley et al., 2013). For instance, the methylation of CpG islands (CGIs) plays a critical role in renal cell cancers (Herman et al., 1994), breast cancer (Fleischer et al., 2014), and colorectal cancer (Hinoue et al., 2012).

Thus, it is promising to mine methylation patterns, such as the methylated CpG islands and epigenetic modules, because they are the foundation for revealing the mechanisms of cancers. For instance, dynamics of methylation of tissues is critical for the development of cells. The methylation patterns of genes closely associate with survival time of patients (Fleischer et al., 2014), and similarity of methylation profiles is also associated with cancer subtypes (West et al., 2013; Gavaert et al., 2015).

These efforts are insufficient to fully exploit the methylation patters because they only make use of methylation data, ignoring the regulation of methylation (Teschendorff and Relton, 2018; West et al., 2018). Since methylation directly regulates the expression of genes, it is natural to identify the epigenetic modules by integrating them. However, it is non-trivial for this issues largely due to two reasons. First, the pre-requisite of the integration of methylation and expression is the matched samples. Second, no cut-off definition of epigenetic modules is available because the regulation strategies vary. For instance, in most case, methylation in promoters negatively regulates the expression, whereas the positive regulation also exists (Varley et al., 2013).

For the first concern, the world consortia make use of the next-generation sequencing technologies to generate sample-matched data for cancers, which enables the possibility to exploit epigenetic modules. For instance, The Cancer Genome Atlas (TCGA)¹ produces genomic data for various cancers, covering mutation, transcription, methylation, etc. Furthermore, Encyclopedia of DNA Elements (ENCODE)² generate matched samples for cell lines and tissues.

For the second concern, even though it is intuitive to define epigenetic module for methylation profiles and networks by simply extending the traditional clustering problem, it is difficult to present a satisfied definition with heterogeneous data. The available algorithms for the integration of methylation and expression by either using a integrated network and multiple networks. Algorithms in the first class construct an integrated network, where the correlation between methylation and expression are integrate edge weight. Then, the epigenetic module in the integrated network is defined as a dense subgraph. For example, the FEM algorithm (Jiao et al., 2014) addresses this problem with the assumption that DNA methylation and expression is anti-correlated, where hot-spot and methylated modules are successfully identified. However, the recent evidence indicates that the correlation between methylation and expression could be both positive and negative (Varley et al., 2013), implying that the integrated network-based approaches are not precise enough to characterize the epigenetic modules.

To attack this issue, efforts have been devoted by using multiple networks to identify graph patterns. For example, in our previous study (Ma et al., 2014), dynamic modules are extracted from multiple networks by exploiting the temporality of cancer progression. Driver genes of cancers can be identified by exploiting the relations of various layers (Cantini et al., 2015), implying the importance and effectiveness of multiple networks. Clustering multiple networks aims to identify modules in networks, which can be achieved by extending measurement for single networks (Didier et al., 2015). These results demonstrate that multiple networks are more accurate and generalized than single networks in terms of characterizing biological patterns. In our previous study (Ma et al., 2017), the epigenetic module is a group of co-methylated and co-expressed genes in multiple networks, and then the epigenetic modules are discovered by using the M-Module algorithm (Ma et al., 2014). The success of the multiple network-based approaches demonstrates that the multiple networks model is much better than the integrated network base method.

Even though multiple network-based algorithms have been devoted to the epigenetic module discovery, many unsolved problems exit. Particularly, the quantification of modules in multiple networks is fundamental, and how to further improve performance of algorithms for epigenetic modules. In the present study, we discuss these two issues. To identify the epigenetic modules in the co-methylation and co-expression networks, the key problem is how to characterize the topological structure of modules in multiple networks. Then, we define the epigenetic module as the common module in multiple networks. To discover the functional epigenetic modules in multiple networks, a novel non-negative matrix factorization algorithm for epigenetic module (Ep-jNMF) is proposed, which jointly analyzes the gene co-expression and co-methylation networks (Figure 1). It first constructs the two layer networks, and extracts features using matrix factorization, where the topological structure is regularized into the objective function. Extensive experiments are performed, where Ep-jNMF achieves the best performance on the artificial networks. Moreover, it identifies more biological meaningful modules than the baselines, and some of obtained modules precisely predict the survival time of patients.

FIGURE 1

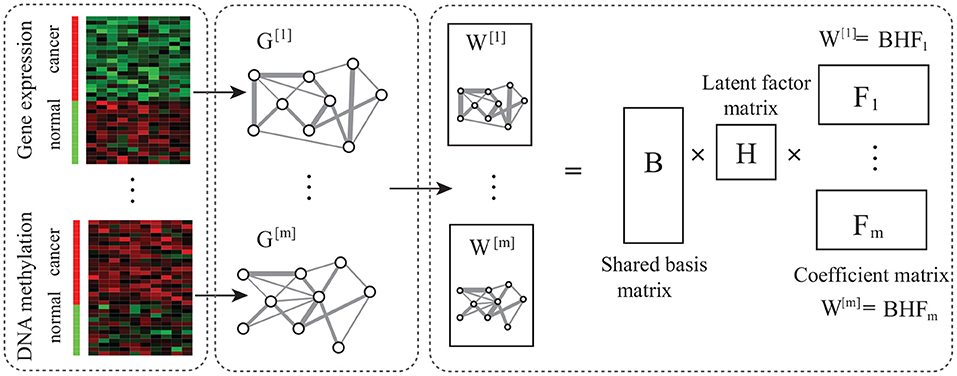
Figure 1. Overview of Ep-jNMF. It is composed of network construction, matrix factorization, and module discovery, where network construction obtains the gene co-expression and co-methylation networks, and the matrix decomposition extracts features.

The rest of this study is organized as follows: section 2 presents the mathematical model and algorithm. The experiments and conclusion are depicted in sections 3 and 4, respectively.

2. Methods

The model and procedure of Ep-jNMF are depicted in this section.

2.1. Notations

A network (graph) is denoted by G = (V, E) with vertex set V and edge set E. Multiple network ${G}=\left\{G_1,G_2,\dots ,G_M\right\}$ is a sequence of networks, where G_m is the m-th snapshot. In this study, the vertex set of ${G}$ is fixed, i.e., G_m = (V, E_m). The adjacent matrix of ${G}$ is a tensor W = (_wijm)n×n×M, where n = |V| and w_ijm is the weight on the edge (v_i, v_j) in G_m. Actually, W = [W₁, W₂, …, W_M], where W_m = (_wijm)n×n is the adjacency matrix of G_m. In this study, the attached subscript m represents the value of the variable at condition m.

Vertex degree is the sum of weights on the incident edges, i.e., $d_{im}=\sum _j{w}_{ijm}$. Betweenness is a typical centrality (Freeman, 1979; Brandes, 2001), which is defined as

$\begin{array}{l}betweennes{s}_m(v)={\displaystyle \sum _{v_i\ne v_j,v_i\ne v,v_j\ne v}}\frac{g_{ivj}}{g_{ij}},\end{array}$

where g_ivj and g_ij are the number of the shortest paths between v_i and v_j passing, and without passing v, respectively. Given a group of genes, denoted by C, the density of C in network G_m is defined as

$\begin{array}{l}Densit{y}_m(C)=\frac{2|E_m(C)|}{|C|(|C|-1)},\end{array}$

where E_m(C) is the edge set of the subgraph induced by C in network G_m, i.e., E_m(C) = {(v_i, v_j)|v_i∈C, v_j∈C, (v_i, v_j)∈E_m}.

In G, a module is a group of vertices with more edges within it, and fewer ones outside it. In ${G}$, the common module is a group of vertices whose connectivity is strong in all snapshots. For example, the module consisting of {1, 2, …, 6} in Figure 2 is well-connected in both networks. In this study, we aim to obtain the common modules in the co-expression and co-methylation networks. The common module detection corresponds to a hard partitioning {C₁, C₂, …, C_k} (denoted by ${\left\{C_l\right\}}_{l=1}^k$) such that C_l1∩C_l2 = ∅ if l₁≠l₂ and $V=\sum _l{C}_l$, where k is the number of modules.

FIGURE 2

Figure 2. A schematic example of common module, which is well-connected in both networks.

2.2. Mathematical Model

The quantification of connectivity of common modules in multiple networks is fundamental. Typical measurements, including the entropy function (Ma et al., 2014), modularity (Newman and Girvan, 2004), and modularity density (Li et al., 2008), are proposed. However, these strategies are inapplicable for the multiple networks. Here, we extend the modularity density D (Li et al., 2008) since it tolerates the resolution limit problem at some extent. Specifically, connectivity of module C_l in G_m is defined as

$\begin{array}{ll}{D}_m(C_l)=\frac{1}{{\displaystyle {\sum }_{v_i\in C_l}}{d}_{im}}L(C_l,C_l)-L(C_l,{\overline{C}}_l),& (1)\end{array}$

where $L(C_l,C_l)=\sum _{v_i\in C_l,v_j\in C_l}{w}_{ijm}$ and ${\overline{C}}_l=V\backslash C_l$. Ideally, we maximize the connectivity of module C_l in all snapshots, i.e.,

$\begin{array}{ll}\{\begin{array}{l}\max D_1(\{C_l\}),\\ \cdots \\ \max D_M(\{C_l\}).\end{array}& (2)\end{array}$

However, it is difficult to reach maximal value for each network. Therefore, we transform the multi-objective function in Equation (2) into a single objective function using the geometric mean of the connectivity, i.e.,

$\begin{array}{ll}D(C_l)={({\displaystyle \prod _m}{D}_m(C_l))}^{1/M}.& (3)\end{array}$

The underlying assumption is that a group of genes form a common module if and only if they are well-connected in all networks.

The partitioning ${\left\{C_l\right\}}_{l=1}^k$ is represented by X_n×k with x_ij =1 if v_i∈C_j, 0 otherwise. The overall function is the connectivity of all modules, i.e.,

$\begin{array}{ll}{\displaystyle \sum _l}maxD(C_l)& (4)\end{array}$

$s.t.\{\begin{array}{l}{x}_{ij}\in \{0,1\},\\ {\displaystyle {\sum }_{j=1}^k{x}_{ij}=1,}\\ {\displaystyle {\sum }_{i=1}^n{x}_{ij}\ge 1,}\end{array}$

where the second constraint enable the hard partitioning, and the last one ensures non-empty of modules. To avoid multi-objectives in Equation (4), we relax it as

$\begin{array}{ll}max{\displaystyle \sum _l}D(C_l)& (5)\end{array}$

$s.t.\{\begin{array}{l}{x}_{ij}\in \{0,1\},\\ {\displaystyle {\sum }_{j=1}^k{x}_{ij}=1,}\\ {\displaystyle {\sum }_{i=1}^n{x}_{ij}\ge 1,}\end{array}$

2.3. The Ep-jNMF Algorithm

The algorithm consists of three components, which are introduced in turn (Figure 1). Networks are constructed using the Pearson correlation of gene profiles, and the PCIT package (Reverter and Chan, 2008) is adopted to remove noise.

NMF (Lee and Seung, 1999) approximates the target matrix using the product of two low-rank matrices as

$\begin{array}{ll}W\approx BF& (6)\end{array}$

$s.t.\{\begin{array}{l}B\ge 0,\\ F\ge 0,\end{array}$

where B_n×k and F_k×n are the basis and coefficient matrix, respectively, and k is the number of features. Usually, k≪n indicates that BF represents a compressed form of the original data W. Not allowing negative entries in B and F enables a non-subtractive combination of parts to form a whole. Equation (6) is solved by minimizing the approximation error as

$\begin{array}{ll}e(B,F)=||W-BF|{|}^2,& (7)\end{array}$

where ||W|| is the Frobenius Norm of matrix W. Tri-factorization is more efficient than NMF (Yoo and Choi, 2010), where Equation (8) is formulated as

$\begin{array}{ll}e(B,F)=||W-BHF|{|}^2,& (8)\end{array}$

where H is the factor matrix.

For each snapshot, Ep-jNMF jointly factorizes W_m as

$\begin{array}{ll}{W}_m\approx BH{F}_m.& (9)\end{array}$

Intuitively, we can minimize the approximation error for each snapshot as

$\begin{array}{ll}{\displaystyle \sum _m}min||W_m-BH{F}_m|{|}^2& (10)\end{array}$

$\text{s.t.}\{\begin{array}{l}B\ge 0,\\ F_m\ge 0\end{array}$

However, it is difficult to reach minimization for each snapshot. Similar to Equation (5), we reformulate Equation (11)

$\begin{array}{ll}min{\displaystyle \sum _m}||W_m-B{F}_m|{|}^2& (11)\end{array}$

$\text{s.t.}\{\begin{array}{l}B\ge 0,\\ F_m\ge 0.\end{array}$

The algorithm iteratively updates B and F_m by following the multiplicative rules (Lee and Seung, 1999), where the update rules are formulated as

$\begin{array}{ll}B=B\frac{{\displaystyle {\sum }_m}{W}_m{F}_m^T}{B{\displaystyle {\sum }_m}{F}_m{F}_m^T},& (12)\end{array}$

$\begin{array}{ll}H=H\frac{{\displaystyle {\sum }_m}{B}^T{F}_m^T{W}_m}{B^{T}B{F}_m{F}_m^T},& (13)\end{array}$

and

$\begin{array}{ll}{F}_m=F_m\frac{B^T{W}_m}{B^T{W}_{m}B}.& (14)\end{array}$

Ep-jNMF (Algorithm 1) updates rules until termination is reached. For example, the approximation error threshold is set as 10⁻², or the maximum iteration number is 10³. Because the initial solution is random, we repeat the procedure 50 runs with different initial solution matrices. The modules are extracted based on B, i.e., $x_{i{j}^{*}}=1$ where $j^{*}=argma{x}_j{B}_{ij}$, 0 otherwise. The Ep-jNMF algorithm involves one parameter k, which is the number of features to obtain the coefficient matrices. We select it using the instability of matrix factorization (Wu et al., 2016).

ALGORITHM 1

Algorithm 1. Ep-jNMF.

2.4. Algorithm Analysis

On the space complexity, ${G}$ requires space O(n²M). The basis matrix requires space O(nk) and the coefficient matrices need space O(knm). The space of the index matrix X is the same as the basis matrix B. In all, Ep-jNMF takes space O(n²m)+2O(nk)+O(nkm) = O(n²M) since k≪n.

On the time complexity, for each F_m, Ep-jNMF needs time O(rkn²), where r is the number of iterations. And the running time for coefficient matrices in Ep-jNMF is O(rkn²M). Therefore, the total time complexity of Ep-jNMF is O(rkn²M).

3. Experiments

To validate the performance of Ep-jNMF, we select sixe state-of-the-art methods for a comparison, including M-Module (Ma et al., 2014), consensus clustering (CSC) (Cantini et al., 2015), multiple-modularity method (MolTi) (Didier et al., 2015), stability NMF (sNMF) (Wu et al., 2016), FEM (Jiao et al., 2014) and spectral clustering (SPEC) (Newman, 2006a), covering single-network- and multiple-network-based approaches. The former ones are extended using the consensus strategy (Cantini et al., 2015).

3.1. Data and Criteria

The artificial networks are derived from GN benchmark (Newman, 2006b), where each snapshot consists of 4 equal size communities with 32 vertices, and the degree of vertices is fixed as 16. Parameter Z_out controls the noise level of networks, and Z_out increases from 1 to 8. By manipulating parameter Z_out, two types of multiple networks are generated, where in the homogeneous networks (HomoNet) the noise levels in snapshots are the same, and in heterogeneous networks (Heter-Net) it varies in different snapshots. Specifically, Z_out is fixed as 4 in the first snapshot, and it varies from 1 to 8 in the others. We downloaded the sample-matched gene expression and methylation profiles of breast cancer from TCGA. Specifically, the gene expression level is quantified using RPKM values and methylation level is measured by β signal, which are imputed using PCIT (Tibshirani et al., 2002).

The normalized mutual information (NMI) (Danon et al., 2005) measures the closeness of two partitioning: standard partition P^* and obtained partitioning P. NMI generates matrix N with the element N_ij as the size of vertices overlapped by $C_i^{*}$ and C_j, which is formulated as

$\begin{array}{l}NMI(P,P^{*})=\frac{-2{\displaystyle {\sum }_{i=1}^{|P|}}{\displaystyle {\sum }_{j=1}^{|P^{*}|}}{N}_{ij}log(\frac{N_{ij}N}{N_{i.}{N}_{.j}})}{{\displaystyle {\sum }_{i=1}^{|P|}}{N}_{i.}log(\frac{N_{i.}}{N})+{\displaystyle {\sum }_{i=1}^{|P^{*}|}}{N}_{.j}log(\frac{N_{.j}}{N})},\end{array}$

where |P| is the cardinality of P and $N_{i.}={\sum }_j{N}_{ij}$.

To check whether the predicted epigenetic modules are biological meaningful, various annotation databases are selected as gold standards for the enrichment analysis, where the significance is obtained by using the hypergeometric test (corrected by Benjamini–Hochberg test) with a cutoff of 0.05.

3.2. Performance on Simulated Networks

Each simulated snapshot contains 128 vertices and 4 modules of equal size with fixed degree 16. Parameter Z_out controls the noise level of networks. As Z_out increases from 1 to 8, the module structure is obscure. In this study, we generate two types of simulated networks with M = 2: Homo-Net and Heter-Net. Specifically, the parameter Z_out of both networks of Homo-Net is the same, while the Z_out of one network of Heter-Net is fixed as 4 and the parameter of the other network varies from 1 to 8. Figure 3A is the heatmap of the Homo-Net networks with Z_out = 1, where the common modules locate at the diagonal.

FIGURE 3

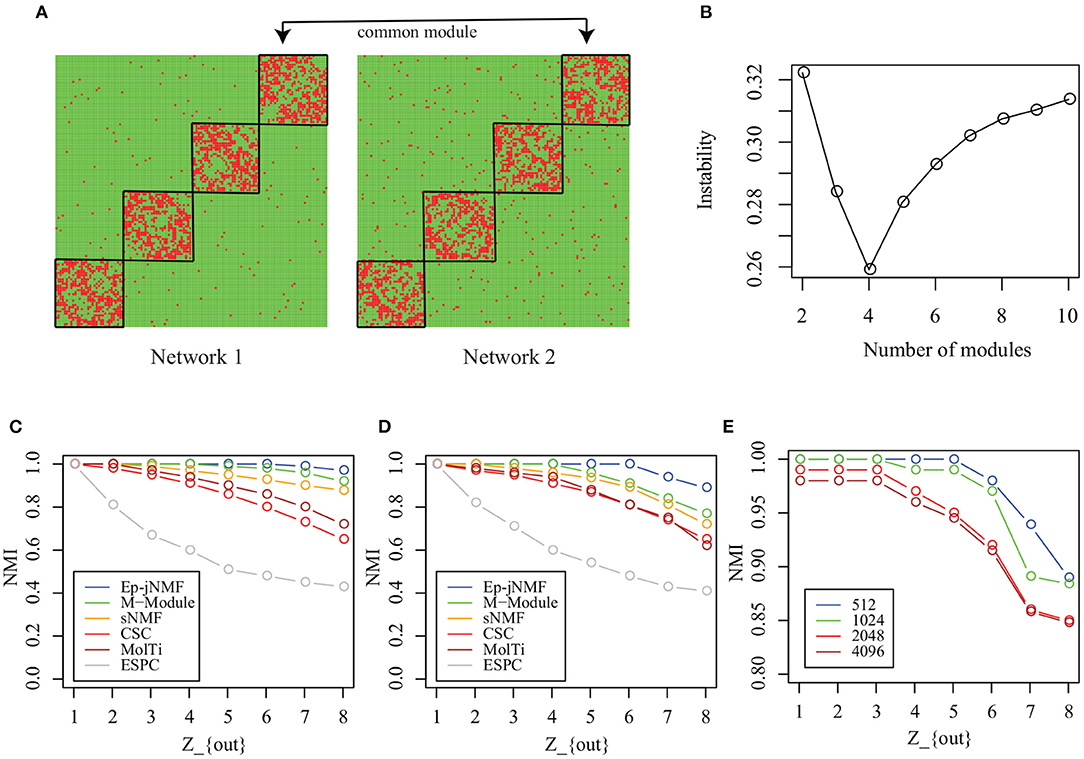
Figure 3. Performance on artificial networks: (A) Heatmap of common modules in Homo-Net (Z_out = 1); (B) selection of the number of modules using instability of matrix factorization with various noise levels; (C) NMIs of algorithms on Homo-Net; (D) NMI of algorithms on Heter-Net; and (E) scalability analysis of Ep-jNMF.

First, how the Ep-jNMF algorithm selects the parameter k, i.e., the number of modules, is studied. How the instability of Ep-jNMF changes as k increases from 2 to 10 for Homo-Net is shown in Figure 3B, where it chooses the optimal value 4 because the minimal is reached at 4. The similar pattern repeats for Heter-Net, which is not shown because of redundancy. The result demonstrates that the strategy is promising in selecting the number of modules.

Then, we compare M-Module, CSC, MolTi, sNMF, and SPEC on the simulated networks. Figure 3C shows the accuracy of various algorithms for Homo-Net, while Figure 3D shows the accuracy of various algorithms for Heter-Net. The performance of all these algorithms decreases as the parameter Z_out increases from 1 to 8 because the module structure is difficult to detect as Z_out increases. M-Module and Ep-jNMF outperform the rest of algorithms because the CSC, MolTi, and SPEC are based on the consensus clustering, which ignores the connection among multiple networks. However, M-Module and Ep-jNMF make use the multiple networks simultaneously during the module search procedure, which improves the accuracy of detecting the common modules. In all, the Ep-jNMF algorithm is better than the M-Module algorithm. More specifically, when Z_out is less than or equal to 5 in Homo-Net, the Ep-jNMF and M-Module algorithms have a similar performance. When Z_out is greater than or equal to 6, Ep-jNMF outperforms M-Module, indicating the superiority of Ep-jNMF. The similar tendency also repeats in Heter-Net (Figure 3D).

Finally, we investigate the accuracy of Ep-jNMF by increasing the number of vertices from 512 to 4096. The performance of Ep-jNMF is shown in Figure 3E, suggesting that the algorithm is robust. These results demonstrate that Ep-jNMF is promising to identify common modules in artificial networks.

3.3. Performance on Cancer Networks

For cancer networks, we select the Ep-jNMF, M-Module, MolTi, sNMF, and FEM algorithms for a comparison since they significantly outperform CSC and SPEC. The Ep-jNMF, M-Module, MolTi, sNMF, and FEM algorithms identify 17, 26, 94, 26, and 460 modules, respectively.

Figure 4A presents a functional epigenetic module obtained by Ep-jNMF with cell proliferation (p = 3.8E-4), which is critical for breast cancer metastasis (Loayza-Puch et al., 2016; Thienpont et al., 2016). Interestingly, the epigenetic module contains the HAND2 sub-module, which is validated by the biological experiments (Jones et al., 2013). The HAND2 module has been used as the benchmark for the algorithms for the methylated module (Jiao et al., 2014). Furthermore, we find that only FEM and Ep-jNMF can discover the HAND2 module, whereas the others cannot. These results imply that Ep-jNMF is effective for the identification of critical epigenetic modules. To check whether the genes within the obtained common module are well-connected in both networks, the density of the module in different snapshots is shown in Figure 4B. Clearly, the connectivity is strong in both snapshots because the density is 0.47 and 0.22, which is significantly higher than that in random networks. The possible reason why the module is much denser in the co-expressed network than that in the co-methylated network is that methylation is more specific than expression.

FIGURE 4

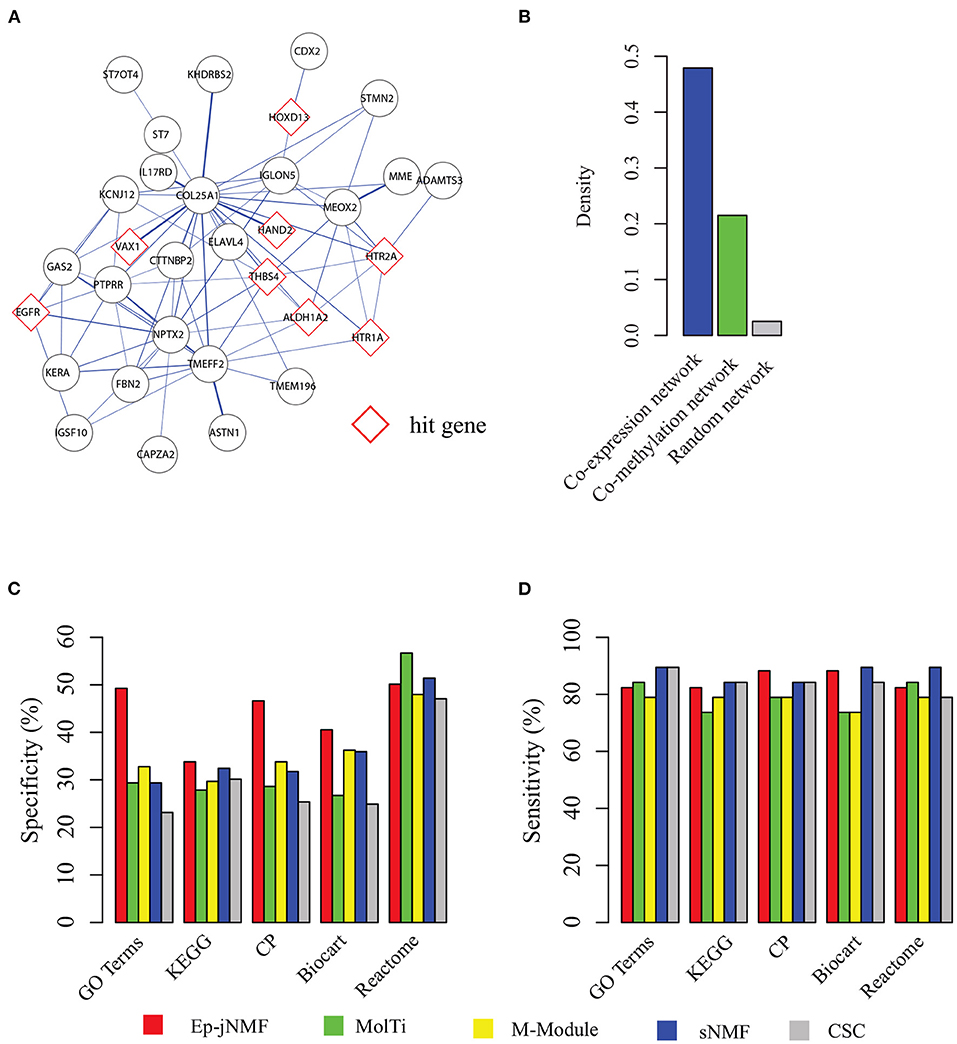
Figure 4. Performance on the cancer networks: (A) a typical epigenetic module predicted by Ep-jNMF with red border color as hit genes; (B) the density of the modules in the co-methylation and co-expression network; (C) percentage of predicted modules enriched by one reference pathways or functions (specificity); and (D) percentage of reference pathways or functions enriched by a predicted module.

To fully validate the performance of Ep-jNMF, Gene Ontology (Ashburner et al., 2000), KEGG (Kanehisa et al., 2012), Reactome (Croft et al., 2014), Biocart (Nishimura, 2001), and Canonical pathways (Subramanian et al., 2005) are selected as reference annotation. To evaluate the performance, we first check the percentage of predicted modules that significantly enriched by at least one reference annotation, and then we calculate the percentage of the reference pathways that significantly overlaps with at least one predicted module. Figures 4C,D show that Ep-jNMF achieves higher specificity with comparable sensitivity, implying that the predicted modules are more meaningful in terms of the biological background.

3.4. Performance on Predicting Cancer Subtypes

Evidence proves that hub genes facilitate the prognosis of cancers (Taylor et al., 2009). Therefore, we check whether epigenetic modules also serve as biomarkers to discriminate cancer subtypes by using the methylation profiles. We select modules predicted by Ep-jNMF, FEM, sNMF, M-Module, and MolTi. Furthermore, we also include size-matched set of randomly modules to validate the performance of different features. Support vector machine is selected as classifier to calculate the percentage of patient samples that are classified correctly (accuracy). The fivefold cross-validation is used for SVM, which is shown in Figure 5A, indicating that modules obtained by Ep-jNMF are more discriminative than the others. Specifically, the accuracy of Ep-jNMF is 82.4%, whereas that of M-Module is 75.1% (p = 4.9E-6, Wilcoxon test), showing that modules in multiple networks are more accurate to capture the structure and functions of cancers. The external dataset is also performed (GSE5874), which is shown Figure 5B. Specifically, Ep-jNMF is also superior to the baselines (i.e., 74.6% for Ep-jNMF vs. 62.9% for M-Module, p = 2.1E-4, Wilcoxon test).

FIGURE 5

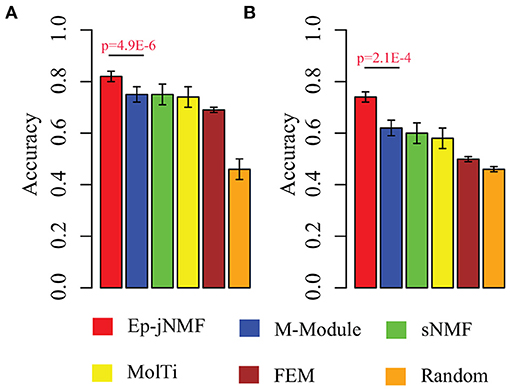
Figure 5. Performance on the prediction of subtypes with various validation in terms of accuracy: (A) internal validation with the error bar as for the standard deviation and (B) external validation.

4. Conclusion

Epigenetic modification is a critical biological process, and mining the patterns is promising for the understanding of cancers. The advances in the next-generation sequencing technologies facilitate the generation of genomic data for cancers, which enables the integrative analysis of omic data. How to integrate gene methylation and expression data is the fundamental step for revealing the mechanisms of cancers. The traditional methods fuse them into a single network by assuming the positive and negative correlation between expression and methylation. However, these strategies are criticized for the undesirable performance since the underlying assumption is not consistent with the biological principle.

In this study, we use the multiple networks model to characterize functional epigenetic modules, which corresponds to the common modules detection in multiple networks. Finally, we present a matrix factorization algorithm for extracting the common modules from heterogeneous networks. Overall, the contributions are summarized as follows: (i) it provides a mathematical model for the functional epigenetic modules, which overcomes the limitation of the current approaches, i.e., the correlation specification between methylation and expression is not required; (ii) a joint learning method is proposed to identify the epigenetic modules in multiple networks, which avoids the structure preservation of single network-based method, which can be easily extended for other data, such as Chip-seq and mutation data; and (iii) the experiments show the superiority of Ep-jNMF.

In further research, we will investigate how to integrate heterogeneous entities, such as microRNAs, to extract the regulation programming based on multiple heterogeneous networks.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: TCGA.

Author Contributions

ZD and XM designed the method and coded the algorithm. XM wrote the paper. Both authors contributed to the article and approved the submitted version.

Funding

This work was supported by the open funding of Key Laboratory of China's Ethnic Languages and Information Technology of Ministry of Education (Grant Nos. KFKT202009 and KFKT202010).

Conflict of Interest

ZD is employed by China Electronics Technology Group Corporation.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors appreciate the reviewers for their suggestions.

Footnotes

1. ^https://cancergenome.nih.gov/

2. ^https://www.encodeproject.org/

References

Ashburner, M., Ball, C., Blake, J., Botstein, D., Butler, H., Cherry, J. M., et al. (2000). Gene ontology: tool for the unification of biology. Nat. Genet. 25, 25–29. doi: 10.1038/75556

PubMed Abstract | CrossRef Full Text | Google Scholar

Bird, A., and Wolffe, A. (1999). Methylation-induced repression-belts, braces, and chromatin. Cell 99, 451–454. doi: 10.1016/S0092-8674(00)81532-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandes, U. (2001). A faster algorithm for betweenness centrality. J. Math. Sociol. 25, 163–177. doi: 10.1080/0022250X.2001.9990249

CrossRef Full Text | Google Scholar

Cantini, L., Medico, E., Fortunato, S., and Caselle, M. (2015). Detection of gene communities in multi-networks reveals cancer drivers. Sci. Rep. 5:17386. doi: 10.1038/srep17386

PubMed Abstract | CrossRef Full Text | Google Scholar

Croft, D., Mundo, A., Haw, R., Milacic, M., Joel, W., Wu, G., et al. (2014). The reactome module knowledgebase. Nucleic Acids Res. 42, D472–D477. doi: 10.1093/nar/gkt1102

PubMed Abstract | CrossRef Full Text | Google Scholar

Danon, L., Duch, J., Diaz-Guileram, A., and Arenas, A. (2005). Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005:P09008. doi: 10.1088/1742-5468/2005/09/P09008

CrossRef Full Text | Google Scholar

Deaton, A., and Bird, A. (2011). Cpg islands and the regulation of transcription. Genes Dev. 25, 1010–1022. doi: 10.1101/gad.2037511

PubMed Abstract | CrossRef Full Text | Google Scholar

Didier, G., Brun, C., and Baudot, A. (2015). Identifying communities from multiplex biological networks. Peer J 3:e1525. doi: 10.7717/peerj.1525

PubMed Abstract | CrossRef Full Text | Google Scholar

Fleischer, T., Frigessi, A., Johnson, K., Edvardsen, H., Touleimat, N., Klajic, J., et al. (2014). Genome-wide dna methylation profiles in progression to in situ and invasive carcinoma of the breast with impact on gene transcription and prognosis. Genome Biol. 15:435. doi: 10.1186/s13059-014-0435-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Freeman, L. (1979). Centrality in social networks I: conceptual clarification. Soc. Netw. 1, 215–239. doi: 10.1016/0378-8733(78)90021-7

CrossRef Full Text | Google Scholar

Gavaert, O., Tibshirani, R., and Plevritis, S. (2015). Pancancer analysis of DNA methylation-driven genes using methylmix. Genome Biol. 16:17. doi: 10.1186/s13059-014-0579-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Herman, J., Latif, F., Weng, Y., Lerman, M., Zbar, B., Samid, D., et al. (1994). Silencing of the vhl tumor-suppressor gene by DNA methylation in renal carcinoma. Proc. Natl. Acad. Sci. U.S.A. 91, 9700–9704. doi: 10.1073/pnas.91.21.9700

PubMed Abstract | CrossRef Full Text | Google Scholar

Hinoue, T., Weisenberger, D., Lange, C., Shen, H., Byun, H. M., Van, D. B. D., et al. (2012). Genome-scale analysis of aberrant dna methylation in colorectal cancer. Genome Res. 22, 271–282. doi: 10.1101/gr.117523.110

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, Y., Widschwendter, M., and Teschendorff, A. (2014). A systems-level integrative framework for genome-wide dna methylation and gene expression data identifies differential gene expression modules under epigenetic control. Bioinformatics 30, 2360–2366. doi: 10.1093/bioinformatics/btu316

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, A., Teschendorff, A., Li, Q., Hayward, J. D., Kannan, A., Mould, T., et al. (2013). Role of DNA methylation and epigenetic silencing of hand2 in endometrial cancer development. PLoS Med. 10:e1001551. doi: 10.1371/journal.pmed.1001551

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanehisa, M., Goto, M., Sato, Y., Furumichi, M., and Tanabe, M. (2012). Kegg for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 40, D109–D114. doi: 10.1093/nar/gkr988

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, D., and Seung, H. (1999). Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791. doi: 10.1038/44565

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Zhang, S., and Wang, R. (2008). Quantative function for community detection. Phys. Rev. E 77:036109. doi: 10.1103/PhysRevE.77.036109

PubMed Abstract | CrossRef Full Text | Google Scholar

Loayza-Puch, F., Rooijers, K., Buil, L., Zijlstra, J., Vrielink, J., Lopes, R., et al. (2016). Tumour-specific proline vulnerability uncovered by differential ribosome codon reading. Nature 530, 490–494. doi: 10.1038/nature16982

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, X., Gao, L., and Tan, K. (2014). Modeling disease progression using dynamics of pathway connectivity. Bioinformatics 30, 2343–2350. doi: 10.1093/bioinformatics/btu298

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, X., Liu, Z., Zhang, Z., Huang, X., and Tang, W. (2017). Multiple network algorithm for epigenetic modules via the integration of genome-wide DNA methylation and gene expression data. BMC Bioinformatics 1:18. doi: 10.1186/s12859-017-1490-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, M. (2006a). Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 74:036104. doi: 10.1103/PhysRevE.74.036104

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, M. (2006b). Modularity and community structure in networks. Proc. Natl. Acad. Sci. U.S.A. 103, 8577–8582. doi: 10.1073/pnas.0601602103

PubMed Abstract | CrossRef Full Text | Google Scholar

Newman, M., and Girvan, M. (2004). Finding and evaluating community structure in networks. Phys. Rev. E 69:026113. doi: 10.1103/PhysRevE.69.026113

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishimura, D. (2001). Biocarta. Biotech. Softw. Internet Rep. 2, 117–120. doi: 10.1089/152791601750294344

CrossRef Full Text | Google Scholar

Reverter, A., and Chan, E. (2008). Combining partial correlation and an information theory approach to the reverse engineering of gene co-expression networks. Bioinformatics 24, 2491–2497. doi: 10.1093/bioinformatics/btn482

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramanian, A., Tamayo, P., Mootha, V., Mukherjee, S., Ebert, B. L., Gillette, M. A., et al. (2005). Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. U.S.A. 102, 15545–15550. doi: 10.1073/pnas.0506580102

PubMed Abstract | CrossRef Full Text | Google Scholar

Suzuki, M., and Bird, A. (2008). DNA methylation landscapes: provocative insights from epigenomics. Nat. Rev. Genet. 9, 465–476. doi: 10.1038/nrg2341

PubMed Abstract | CrossRef Full Text | Google Scholar

Taylor, I., Linding, R., Warde-Farley, D., Liu, Y., Pesquita, C., Faria, D., et al. (2009). Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat. Biotechnol. 27, 199–204. doi: 10.1038/nbt.1522

PubMed Abstract | CrossRef Full Text | Google Scholar

Teschendorff, A., Jones, A., Fiegl, H., Sargent, A., Zhuang, J., Kitchener, H., et al. (2012). Epigenetic variability in cells of normal cytology is associated with the risk of future morphological transformation. Genome Med. 4:24. doi: 10.1186/gm323

PubMed Abstract | CrossRef Full Text | Google Scholar

Teschendorff, A., and Relton, C. (2018). Statistical and integrative system-level analysis of dna methylation data. Nat. Rev. Genet. 19, 129–147. doi: 10.1038/nrg.2017.86

PubMed Abstract | CrossRef Full Text | Google Scholar

Thienpont, B., Steinbacher, J., Zhao, H., D'Anna, F., Kuchnio, A., Ploumakis, A., et al. (2016). Tumour hypoxia causes dna hypermethylation by reducing tet activity. Nature 537, 63–68. doi: 10.1038/nature19081

PubMed Abstract | CrossRef Full Text | Google Scholar

Tibshirani, R., Hastie, T., Narasimhan, B., and Chu, B. (2002). Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proc. Natl. Acad. Sci. U.S.A. 99, 6567–6572. doi: 10.1073/pnas.082099299

PubMed Abstract | CrossRef Full Text | Google Scholar

Varley, K., Gertz, J., Bowling, K., Parker, S., Reddy, T. E., Pauli-Behn, F., et al. (2013). Dynamic DNA methylation across diverse human cell lines and tissues. Genome Res. 23, 555–567. doi: 10.1101/gr.147942.112

PubMed Abstract | CrossRef Full Text | Google Scholar

West, J., Beck, S., Wang, X., and Teschendorff, A. (2013). An integrative network algorithm identifies age-associated differential methylation interactome hotspots targeting stem-cell differentiation pathways. Sci. Rep. 3:1630. doi: 10.1038/srep01630

PubMed Abstract | CrossRef Full Text | Google Scholar

West, J., Beck, S., Wang, X., and Teschendorff, A. (2018). Epigenome-based cancer risk prediction: rationale, opportunities and challenges. Nat. Rev. Clin. Oncol. 15, 292–309. doi: 10.1038/nrclinonc.2018.30

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, S., Joseph, A., Hammonds, A., Celniker, S., Yu, B., and Frise, E. (2016). Stability-driven nonnegative matrix factorization to interpret spatial gene expression and build local gene networks. Proc. Natl. Acad. Sci. U.S.A. 113, 4290–4295. doi: 10.1073/pnas.1521171113

PubMed Abstract | CrossRef Full Text | Google Scholar

Yoo, J., and Choi, S. (2010). Orthogonal nonnegative matrix tri-factorization for co-clustering: Multiplicative updates on stiefel manifolds. Inform. Process. Manage. 46, 559–570. doi: 10.1016/j.ipm.2009.12.007

CrossRef Full Text | Google Scholar

Ziller, M., Gu, H., Muller, F., Donaghey, J., Tsai, L., Kohlbacher, O., et al. (2013). Charting a dynamic dna methylation landscape of the human genome. Nature 500, 477–481. doi: 10.1038/nature12433

PubMed Abstract | CrossRef Full Text | Google Scholar