A Single-Step Genome Wide Association Study on Body Size Traits Using Imputation-Based Whole-Genome Sequence Data in Yorkshire Pigs

The body shape of a pig is the most direct production index, which can fully reflect the pig’s growth status and is closely related to important economic traits. In this study, a genome-wide association study on seven body size traits, the body length (BL), height (BH), chest circumference (CC), abdominal circumference (AC), cannon bone circumference (CBC), rump width (RW), and chest width (CW), were conducted in Yorkshire pigs. Illumina Porcine 80K SNP chips were used to genotype 589 of 5,572 Yorkshire pigs with body size records, and then the chip data was imputed to sequencing data. After quality control of imputed sequencing data, 784,267 SNPs were obtained, and the averaged linkage disequilibrium (r²) was 0.191. We used the single-trait model and the two-trait model to conduct single-step genome wide association study (ssGWAS) on seven body size traits; a total of 198 significant SNPS were finally identified according to the P-value and the contribution to the genetic variance of individual SNP. 11 candidate genes (CDH13, SIL1, CDC14A, TMRPSS15, TRAPPC9, CTNND2, KDM6B, CHD3, MUC13, MAPK4, and HMGA1) were found to be associated with body size traits in pigs; KDM6B and CHD3 jointly affect AC and CC, and MUC13 jointly affect RW and CW. These genes are involved in the regulation of bone growth and development as well as the absorption of nutrients and are associated with obesity. HMGA1 is proposed as a strong candidate gene for body size traits because of its important function and high consistency with other studies regarding the regulation of body size traits. Our results could provide valuable information for pig breeding based on molecular breeding.

Introduction

Pork is widely used as an important animal protein resource and has become one of the main sources of human protein. Commercial pigs (e.g., Duroc, Yorkshire, and Landrace pigs) have the characteristics of fast growth, high feed utilization rate, high lean meat rate, and obvious economic benefits. Therefore, it is not only used for a large number of breeding production, but also has been the focus of research. The body size trait is an important phenotypic trait that can reflect the overall appearance of animals. Compared with the description of physical appearance, body size traits can objectively reflect the response of pigs to their environment and other aspects (Ohnishi and Satoh, 2018). In pig breeding, the body shape character index is often used as the most direct production index of a pig. Body size is a typical quantitative (or complex) trait; understanding the genetic mechanism of body size differences among individuals can effectively help control the growth and production of animals (Niu et al., 2013). At present, there is a large amount of research on genetic parameters of pig external traits, which accelerate the process of genetic improvement of related traits. With the development of molecular biotechnology, many studies have been carried out to clarify the genetic basis of pig body size traits.

So far, 1172 QTLs have been found related to body size traits in pigs according to PigQTLdb database¹. Although a range of research has been done in QTL mapping, wide confidence intervals (covering more than 20 CM) for the positions of QTL remain that have rarely been replicated (Schreiweis et al., 2005; Soller et al., 2006). A new research era was initiated with advances in single nucleotide polymorphism (SNP) chip and sequencing technology, and genome wide association study (GWAS) has become one of the most efficient methods to detect genetic variation in livestock (Mackay et al., 2009). Compared with traditional QTL localization, GWAS has more advantages in mining the intensity of medium-potency variation sites and defining the accuracy of genome segments containing variation sites (Risch, 1996; Hirschhorn and Daly, 2005; Klein et al., 2005; Simon-Sanchez et al., 2009). Although a large number of genome-wide association studies have been carried out in pigs, only a few GWAS focused on identifying genes related to external traits. In particular, the investigation on body height, cannon bone circumference, rump width, and other important body size traits are still lacking.

Marker density is one key factor affecting the efficiency of GWAS as gene mapping mainly relies on the linkage disequilibrium between causal mutation and markers (Brondum et al., 2012). Whole genome sequence data can definitely meet such requirements. In recent years, with the rapid development of the new generation of sequencing technology, the cost of sequencing has been reduced rapidly. On one hand, the large number of samples and the subsequent processing of sequence data are still time-consuming and costly, limiting its utilization in genetic analysis. On the other hand, genotype imputation provides an efficient tool to improve the marker density of SNP chips based on sequence data. It can accurately predict the genotypes of polymorphic sites not covered by the widely used SNP chip, allowing more genetic loci to be applied to association analysis and improving the possibility of discovering new pathogenic genes (Marchini and Howie, 2010; van Leeuwen et al., 2015). In this study, we used imputation-based whole genome sequence data to carry out GWAS on seven body size traits in pigs.

Materials and Methods

Ethics Statement

The whole recording procedure of ear tissue samples was carried out in strict accordance with the protocol approved by the Institutional Animal Care and Use Committee (IACUC) at the China Agricultural University. The IACUC of the China Agricultural University approved this study (permit number DK996).

Animals and Phenotypes

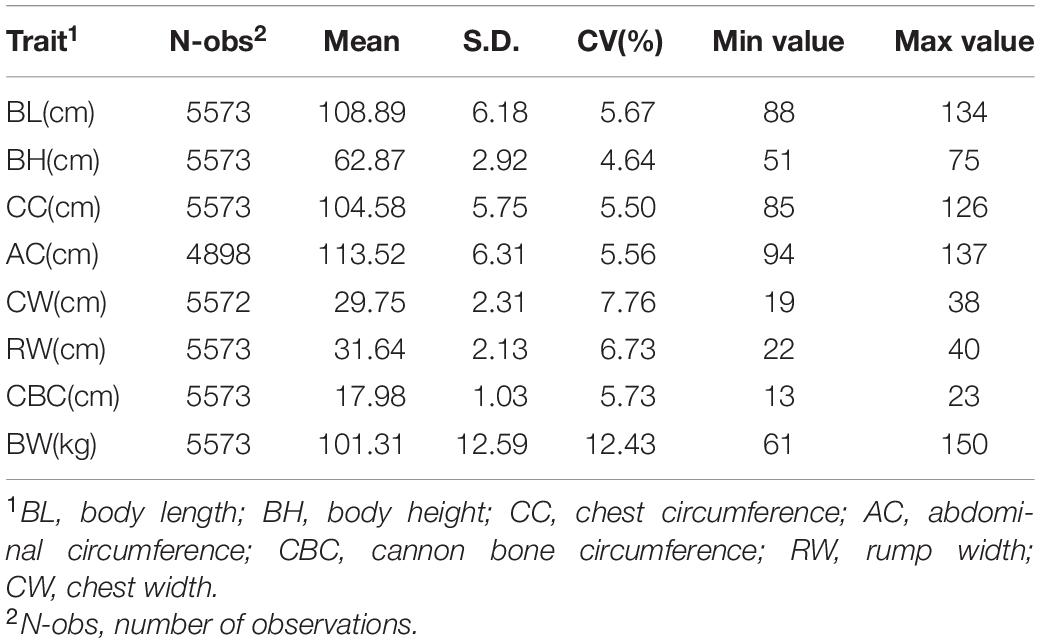
Yorkshire pigs born from 2013-2016 from one pig breeding farm in Beijing were collected in this study. A performance test on seven body size traits were carried out at the body weight of about 100 kg for pigs. In total, 5,572 Yorkshire pigs with phenotypic records and pedigree information were selected. The seven body size traits included body length (BL), body height (BH), chest circumference (CC), abdominal circumference (AC), cannon bone circumference (CBC), chest width (CW), and rump width (RW). Table 1 presents the descriptive statistics of body weight and seven body size traits. There were 4898 records for AC and 5572 records for the other six body size traits and body weight. The Shapiro test function in the Stats package of R language was used to test if the phenotypic values of the seven body size traits followed normal distribution, and the results showed that all traits followed normal distribution. Body weight had the largest standard deviation of 12.59 kg and coefficient of variation of 12.43%; it was used as a covariate considering its influence on the body size traits in further analysis.

TABLE 1

Table 1. Descriptive statistics for body weight and seven body size traits.

Genotype Data and Imputation

In this study, 589 out of 5572 Yorkshire pigs with body size records were genotyped using the PorcineSNP80 Bead Chip (Illumina, San Diego, CA, United States), which includes 68,528 SNPs across the whole pig genome. In order to improve the marker density, the genotyped animals with another 6103 pigs genotyped with PorcineSNP80 (Song et al., 2019) were imputed to whole genome sequence data using Beagle 4.1 (Browning and Browning, 2009). A wide collection of 289 sequenced pigs all with average sequencing depths of ∼25X from six different pig breeds were used as reference data for imputation and each breed contained 24 to 94 pigs. The composition of reference data and the SNP calling of these individuals were described by Yan et al. (2017). After SNP calling, 46,766,110 SNPs were retained as the reference panel for imputation. On average, the genotype concordance rate across all variants was 92%, which is sufficient for further analysis (Song et al., 2019). After imputation, in this study, the following genotype quality control procedure was carried out using the PLINK software (v1.90) (Purcell et al., 2007). SNPs with minor allele frequency (MAF) lower than 0.01 and that deviated from the Hardy - Weinberg equilibrium (P < 10^–6) were excluded and only variants located on autosomes were used for further analysis. SNP with call rates less than 0.95 were removed. Individuals with call rates less than 0.90 were excluded. In addition, in order to decrease the influence of the dependence of adjacent markers on the high false positive of GWAS analysis, the SNP were further pruned, and the SNP with linkage disequilibrium (r²) in slide window of 50 SNPs less than 0.9 were selected. Finally, all the genotyped animals and 784267 SNPs were retained.

Statistical Models

Genetic Correlation

According to the information of 5,572 pigs in this study, the restricted maximum likelihood method (AI-REML) in DMU v6.0 software (Jensen and Madsen, 2000) was used to estimate the genetic correlations of seven body size traits.

The animal model was used to estimate the genetic parameters:

$\text{y}=\mathrm{\mu }+\mathrm{X}\text{b}+{\text{Z}}_{\mathbf{1}}\text{a}+{\text{Z}}_{\mathbf{2}}\text{t}+\mathbf{\text{e}},$

with

$\text{E}\left\{\begin{array}{c}\text{y}\hfill \\ \mathbf{\text{a}}\hfill \\ \text{t}\hfill \\ e\hfill \end{array}\right\}={\left\{\begin{array}{c}\text{Xb}\hfill \\ \mathbf{0}\hfill \\ \mathbf{0}\hfill \\ \mathbf{0}\hfill \end{array}\right\}}_{,}Var\left\{\begin{array}{c}\text{a}\hfill \\ t\hfill \\ \text{e}\hfill \end{array}\right\}=\{\begin{array}{c}\mathbf{\text{A}}{\mathrm{\sigma }}_{\mathbf{a}}^{\mathbf{2}}\hfill \\ \end{array}\begin{array}{c}\hfill \mathbf{0}\hfill \\ \hfill \mathbf{\text{I}}{\mathrm{\sigma }}_{\mathbf{t}}^{\mathbf{2}}\hfill \end{array}\begin{array}{c}\mathbf{0}\hfill \\ \mathbf{0}\hfill \\ \mathbf{\text{I}}{\mathrm{\sigma }}_{\mathbf{e}}^2\hfill \end{array}\}$

where, y is the vector of phenotypic values of each body size trait; μ is the population mean; b is the fixed effect of herd-year-season; a is the vector of additive genetic effects; t is the covariate vector of body weight effects; and e is a vector of residual error effects. X, Z₁, and Z₂ are incidence matrices associating b, a, and t with y, respectively. A is the genetic relationship matrix, five generations of pedigree were traced back to construct A, and σ_a² is the additive genetic variance. I is the identity matrix of appropriate dimension, σ_t² is the variance of body weight effect, and σ_e² is the residual variance.

As the following two-trait model was constructed, the same designs and similar methods were used to combine seven body size traits to construct a matrix equation to form a seven-trait model, which was mainly used to calculate the genetic correlation

$\begin{array}{l}\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=\left[\begin{array}{cc}{X}_1& 0\\ 0& X_2\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]+\left[\begin{array}{cc}{Z}_{11}& 0\\ 0& Z_{12}\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]\\ +\left[\begin{array}{cc}{Z}_{21}& 0\\ 0& Z_{22}\end{array}\right]\left[\begin{array}{c}{t}_1\\ t_2\end{array}\right]+\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right],\end{array}$

where all letter representations are the same as the single trait model above and the subscript numbers 1 and 2 represent the two body size traits.

Subsequently, genetic correlations were calculated based on the variance components as follows:

${\text{r}}_{\mathbf{A}}=\frac{\text{cov}({\mathbf{\text{a}}}_{\mathbf{1}},{\mathbf{\text{a}}}_{\mathbf{2}})}{{\mathrm{\sigma }}_{{\mathbf{a}}_{\mathbf{1}}}{\mathrm{\sigma }}_{{\mathbf{a}}_{\mathbf{2}}}}$

where, r_A is the genetic correlation between trait 1 and trait 2, a₁ and a₂ represent the additive genetic values of trait 1 and trait 2 for the same individuals, cov (a1, a2) and σ_a1, σ_a2 refer to the genetic covariance of two traits and the genetic standard deviation of trait 1 and trait 2, respectively.

Genome-Wide Association Study

In this study, single-step GWAS (ssGWAS), which can simultaneously use all the SNP information and utilize the ungenotyped animals with phenotypic records (Wang et al., 2012), was implemented to identify significant SNPs associated with body size traits. Considering the genetic correlations between body size traits, the two-trait model is used for the traits with high genetic correlation, while the single-trait model is used for the rest of the traits.

Single-trait ssGWAS

The single-trait ssGWAS model was used for three body size traits: BL, BH, and CBC.

$\mathbf{\text{y}}=\mathbf{Xb}+\mathrm{\gamma }\mathbf{W}+\mathbf{Zg}+\mathbf{\text{e}}$

where y is the vector of phenotypic values, b is the vector of fixed effects including herd-year-season-sex, W is the covariate of body weight, γ is the regression coefficient associating W, g is the vector of additive genetic effects, following a normal distribution of $N(\mathbf{0},\mathbf{\text{H}}{\mathrm{\sigma }}_g^2)$, in which H is the matrix of additive genetic relationships incorporating both pedigree and genomic information, ${\mathrm{\sigma }}_g^2$ is the additive genetic variance and estimated from the pedigree-based BLUP (PBLUP), e is the vector of random residuals with distribution of N(0, $\text{I}{\mathrm{\sigma }}_e^2$), in which I is the identity and ${\mathrm{\sigma }}_e^2$ is the residual variance. X, W, and Z are the incidence matrixes associating b, w, and g with y, respectively.

The genotyped and ungenotyped animals were considered simultaneously based on a H matrix (Aguilar et al., 2010). The inverse of the H matrix was written as follows:

${\mathbf{\text{H}}}^{-\mathbf{1}}=\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{\text{G}}}_{\mathbf{w}}^{-\mathbf{1}}-{\mathbf{\text{A}}}_{\mathbf{22}}^{-\mathbf{1}}\hfill \end{array}\right]+{\mathbf{\text{A}}}^{-\mathbf{1}}$

where A⁻¹ is the inverse of the numerator relationship matrix, ${\mathbf{\text{A}}}_{\mathbf{22}}^{-\mathbf{1}}$ is the inverse of the pedigree-based relationship matrix for the genotyped animals, and ${\mathbf{\text{G}}}_{\mathbf{w}}^{-\mathbf{1}}$ is the inverse of the genomic relationship matrix;, G weight markers were obtained by reciprocals of expected marker variance (VanRaden, 2008).

The SNP effects could be estimated by ssGWAS. The proportion of genetic variance explained by single SNP was calculated as follows:

$\frac{\mathbf{\text{Var}}\left({\mathbf{\text{Z}}}_{\mathbf{j}}{\widehat{u}}_j\right)}{{\mathrm{\sigma }}_{\mathbf{a}}^{\mathbf{2}}}\times \mathbf{100}\%$

where ${\mathrm{\sigma }}_{\mathbf{a}}^{\mathbf{2}}$ is the total genetic variance, Z_j is a vector of the gene content of the jth SNP for all animals, and ${\widehat{u}}_j$ is the estimated marker effect of the jth SNP.

Two-trait ssGWAS

According to the genetic correlation estimations, four body size traits with high genetic correlations (CC, AC, RW, and CW) were carried out using two-trait ssGWAS model.

$\begin{array}{l}\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=\left[\begin{array}{cc}{X}_1& 0\\ 0& X_2\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\end{array}\right]+\left[\begin{array}{c}{\gamma }_1\\ {\gamma }_2\end{array}\right]\left[\begin{array}{c}{W}_1\\ W_2\end{array}\right]+\left[\begin{array}{cc}{Z}_1& 0\\ 0& Z_2\end{array}\right]\left[\begin{array}{c}{g}_1\\ g_2\end{array}\right]\\ +\left[\begin{array}{c}{e}_1\\ e_2\end{array}\right]\end{array}$

where $\left[\begin{array}{c}{\mathbf{\text{y}}}_1\\ {\mathbf{\text{y}}}_2\end{array}\right]$ is the vector of observation values of trait I and II, b₁ and b₂ are the vector of fixed effects of herd-year-season-sex of trait I and II, X₁ and X₂ are the incidence matrix associating b₁ and b₂> with y₁ and y₂, $\left[\begin{array}{c}{\mathbf{\text{W}}}_1\\ {\mathbf{\text{W}}}_2\end{array}\right]$ is the vector of covariate of body weight of trait I and II, γ₁ and γ₂ are the regression coefficient associating W₁ and W₂, $\left[\begin{array}{c}{\mathbf{\text{g}}}_1\\ {\mathbf{\text{g}}}_2\end{array}\right]$ is the vector of additive genetic effects of the two traits, following a normal distribution of N(0,H⊗M), where M = $\left[\begin{array}{cc}\hfill {\mathrm{\sigma }}_{\mathbf{g1}}^{\mathbf{2}}\hfill & \hfill {\mathrm{\sigma }}_{\mathbf{g12}}^{\mathbf{2}}\hfill \\ \hfill {\mathrm{\sigma }}_{\mathbf{g12}}^{\mathbf{2}}\hfill & \hfill {\mathrm{\sigma }}_{\mathbf{g2}}^{\mathbf{2}}\hfill \end{array}\right]$ is the additive genetic variance and covariance matrix of the two traits, Z₁ and Z₂ are the incidence matrix associating g₁ and g₂ with y₁ and y₂, and $\left[\begin{array}{c}{\mathbf{\text{e}}}_1\\ {\mathbf{\text{e}}}_2\end{array}\right]$ is the vector of random errors with distribution of N(0,I⊗R), where I is the identity matrix and R = $\left[\begin{array}{cc}\hfill {\mathrm{\sigma }}_{\mathbf{e1}}^{\mathbf{2}}\hfill & \hfill {\mathrm{\sigma }}_{\mathbf{e12}}^2\hfill \\ \hfill {\mathrm{\sigma }}_{\mathbf{e12}}^{\mathbf{2}}\hfill & \hfill {\mathrm{\sigma }}_{\mathbf{e2}}^{\mathbf{2}}\hfill \end{array}\right]$ is the residual variance and covariance matrix of the two traits.

In this study, for both the single-trait model and two-trait model of ssGWAS, blupf90 (Aguilar et al., 2011)was implemented to estimate genomic breeding values (GEBV), and afterwards, based on GEBV, SNP effects and P-values were estimated via postGSf90. The significance test of SNP effects was performed using two-sided t-test and the P-value of each marker was calculated as follows (Aguilar et al., 2019):

${\mathbf{\text{P}}}_{\mathbf{i}}={\mathbf{\text{P}}}_{\mathbf{t}}(\frac{{\widehat{u}}_i}{\sqrt{{\widehat{\mathrm{\sigma }}}_i^2\mathrm{/}n}},\mathbf{\text{n}}-\mathbf{1}),$

where P_i is the distribution function of t distribution, ${\widehat{u}}_i$ is ith SNP effect, ${\widehat{\mathrm{\sigma }}}_i^2$ is the genetic variance of ith SNP, and n is the number of animals with ith SNP. In addition, the proportion of genetic variance explained by the ith SNP could also be calculated as ${\widehat{\mathrm{\sigma }}}_i^{\mathbf{2}}\mathrm{/}{\mathrm{\sigma }}_{\mathbf{g}}^{\mathbf{2}}$. Manhattan plots of SNP variance were obtained by the “qqman” R package(D. Turner, 2018).

In order to control false positives, the False Discovery Rate (FDR) (Benjamini and Hochberg, 1995; Weller et al., 1998) method for multiple testing was used as follows:

$\mathrm{FDR}={\mathrm{m}}^{*}{\mathrm{P}}_{\mathrm{Max}}/\mathrm{n}$

where m is the number of times to be tested and n is the number of significant SNPs at assigned FDR level, e.g., 0.05. P_Max is the genome-wide significance level empirical P-value of FDR adjusted. Based on the P-values of SNPs obtained by ssGWAS, the empirical P-value of FDR adjusted at the genome-wide significance level of 0.05 was calculated on each trait in this study.

Identification of Candidate Genes

After identifying significant SNPs by ssGWAS, the genes located in the 50Kb downstream and 50 Kb upstream region of the significant SNPs were determined using BedTools (Quinlan and Hall, 2010) and pig reference gene annotation (² Sus scrofa 11.1 genome version). The R package bioconductor³ was used to identify the related pathways and perform functional annotation. QTLdb⁴ was used to annotate significant SNPs located in previously mapped QTLs in pigs. R package ‘Cluster Profiler’ (Yu et al., 2012) was used to carry out Gene Ontology (GO) and Kyoto research on annotated candidate genes from the Encyclopedia of Genes and Genomes(KEGG) enrichment analysis.

Results

Genetic Correlations of Body Size Traits

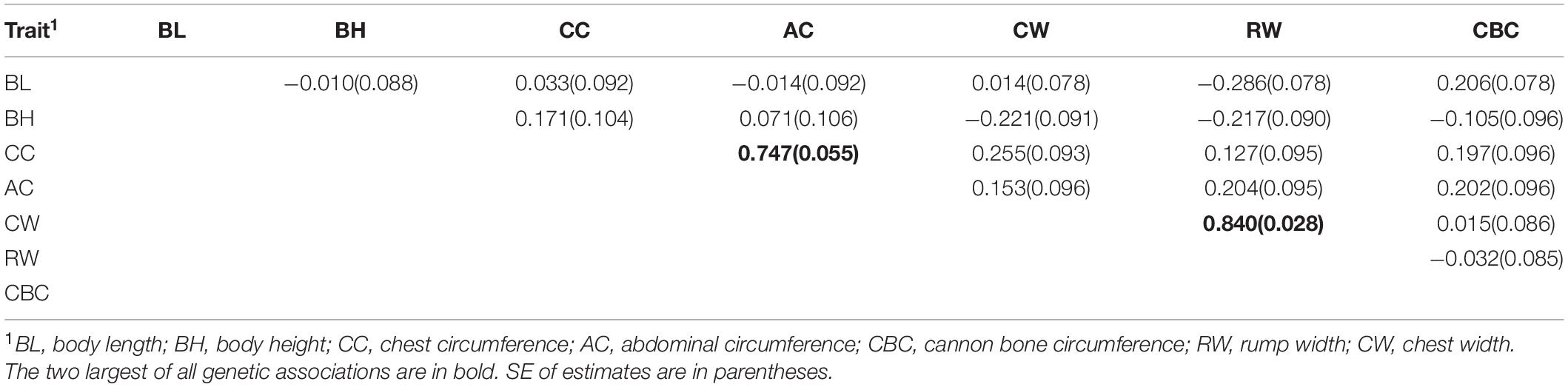
Table 2 shows the genetic correlations of seven body size traits. The genetic correlations ranged from −0.286 to 0.840 with standard errors ranging from 0.028 to 0.106. Among the seven body size traits, chest circumference (CC) and abdominal circumference (AC), and chest width (CW) and rump width (RW) had the higher genetic correlations of 0.747 and 0.840 with standard errors of 0.055 and 0.028, respectively. The genetic correlations between other traits were lower than 0.3, and some traits were almost not genetically correlated with other traits, e.g., body length (BL) had a very low genetic correlation of −0.010, 0.03, −0.01, and 0.01 with body height (BH), CC, AC, and CW, respectively.

TABLE 2

Table 2. Genetic correlations between seven body size traits.

Identification of Significant SNPs Associated With Body Size Traits

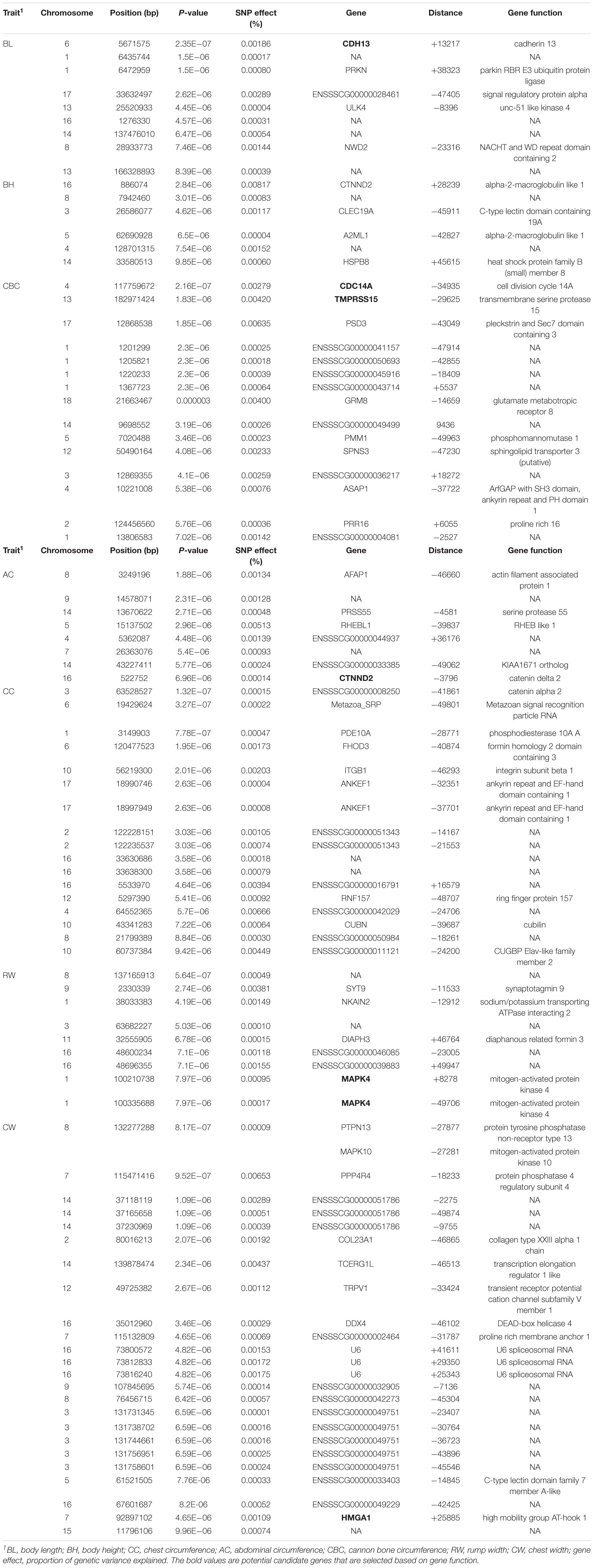
Two criteria of P-value and SNP effect were respectively used to determine the SNPs associated with body size traits. As for the P-value, after the 0.05 significance level of the whole genome was adjusted, the P_Max-values of FDR-based multiple tests were 9.26E−06 for BL, 1.08E−05 for BH, 1.02E−05 for CBC, 9.74E-06 for AC, 1.05E−05 for CC, 9.60E−06 for RW, and 1.01E−05 for CW. As shown in Table 3, a total of 88 significant SNPs was identified for seven body size traits. The Manhattan plots of the three traits BL, BH, and CBC using the single trait model are shown in Figure 1. For BL, a total of nine significant SNPs reached the genome-wide significance level, accounting for 0.0085% of the genetic variance in total. These significant SNPS were located on SSC1, SSC6, SSC8, SSC13, SSC14, SSC16, and SSC17. The SNP at SSC17:33632497 explained the largest genetic variance (0.0029%). For BH, only six SNPs were genome-wide significant, accounting for a total of 0.0123% of genetic variance. They were located on SSC3, SSC5, SSC14, and SSC16. The interpretation of ssc16: 886074 has the largest genetic variance (0.0082%). For CBC, there were 15 significant SNPs at the genome-wide level, which explained 0.0267% of the genetic variance, and the most significant SNPs were closely located on SSC1. For the two pairs of genetically correlated traits using the two-trait model, the Manhattan plots of AC and CC, and RW and CW are shown in Figure 2. In total, eight, 17, nine, and 24 SNPs were identified associated with AC, CC, RW, and CW, respectively, and these SNPs explained 0.0109, 0.0242, 0.0099, and 0.0281% of genetic variances for the corresponding traits. For each trait, the genetic variance explained by a single significant SNP was very small, the largest of which for each trait were 0.0051% (SSC5:15137502), 0.0067% (SSC4:64552365), 0.0038% (SSC9:2330339), and 0.0065% (SSC7:115471416), respectively. Although the genetic correlations existed among seven body size traits, no common significant SNPs were found.

TABLE 3

Table 3. Significant SNPs and associated genes for seven body size traits.

FIGURE 1

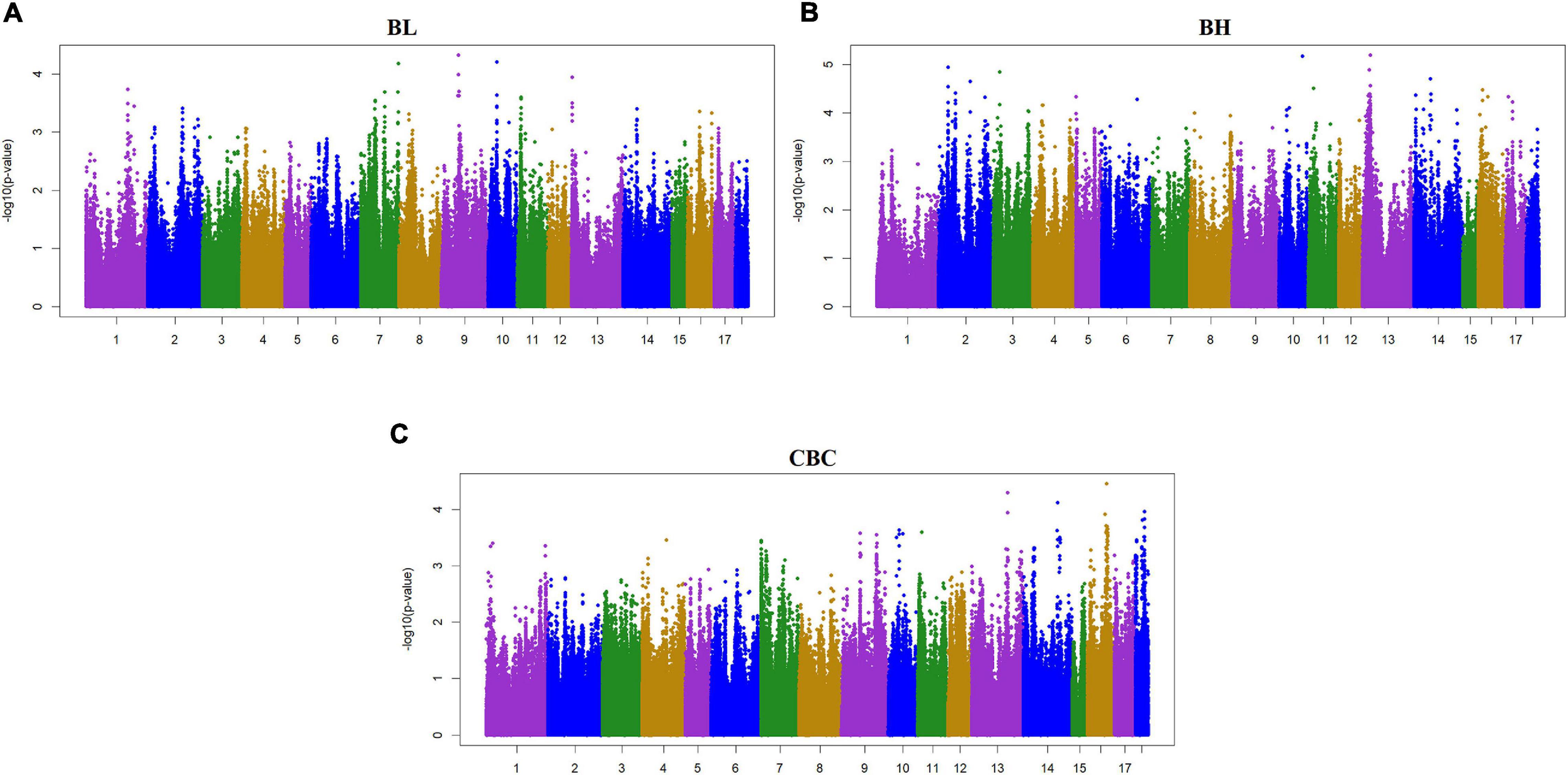
Figure 1. Manhattan plot of the genome-wide association study on three body size traits by using single-trait model ssGWAS. BL, Body length; BH, Body height; CBC, Cannon bone circumference. In the Manhattan plots, negative log10 P-values of the quantified SNPs were plotted against their genomic positions. The x-axis represents the chromosomes and the y-axis represents the observed −log10(P-value). Different colors indicate various chromosomes. Each trait has a significant threshold of FDR adjusted, for (A) BL, it was 9.26 × 10^–6. Similarly, (B) BH was 1.08 × 10^–5, and (C) CBC was 1.02 × 10^–5.

FIGURE 2

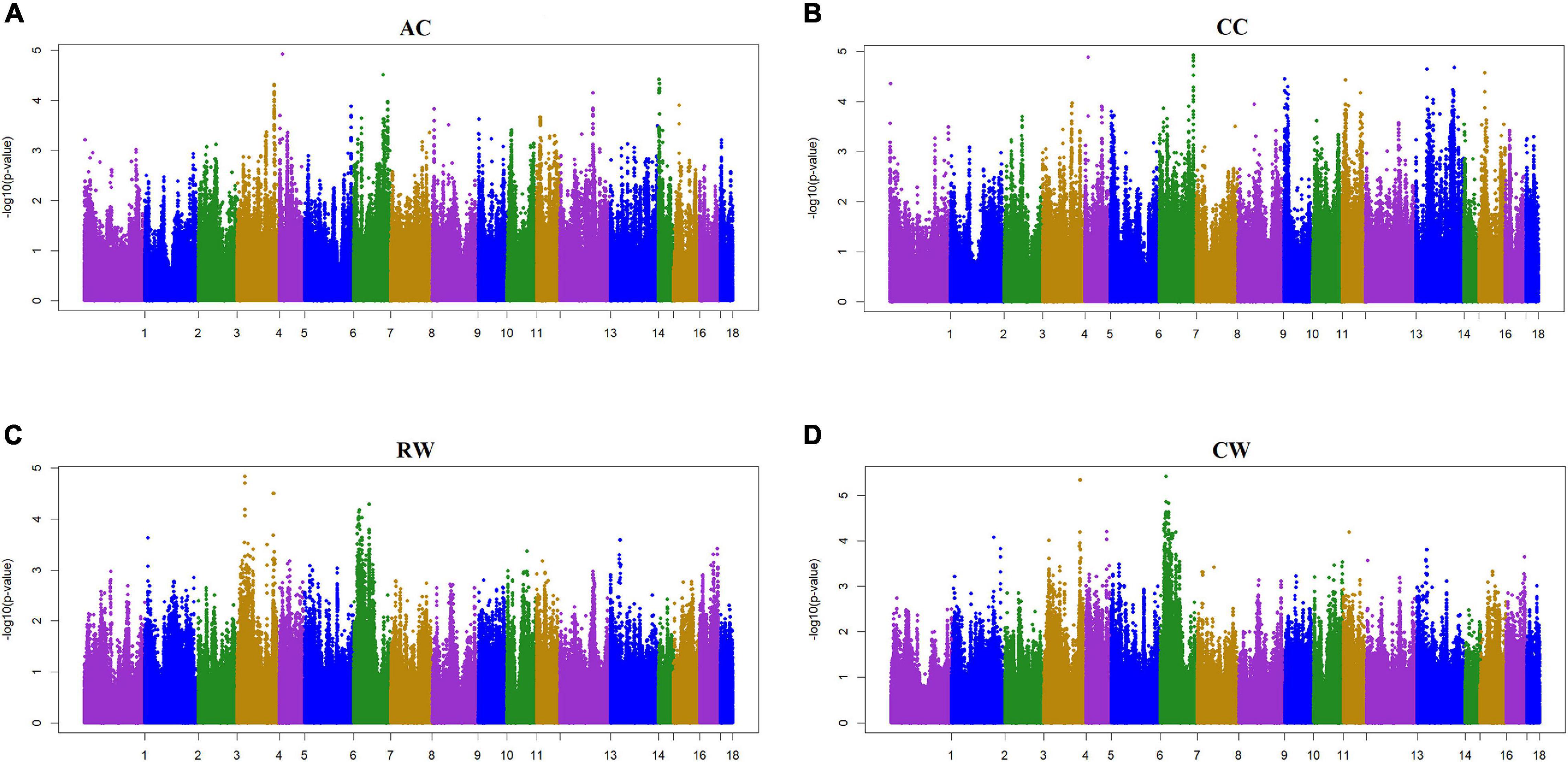
Figure 2. Manhattan plot of the genome-wide association study on four body size traits by using two-trait model ssGWAS. AC, Abdominal circumference; CC, Chest circumference; RW, Rump width; CW, Chest width. AC and CC are a pair of traits, RW and CW are a pair of traits. In the Manhattan plots, negative log10 P-values of the quantified SNPs were plotted against their genomic positions. The x-axis represents the chromosomes and the y-axis represents the observed –log10(P-value). Different colors indicate various chromosomes. Each trait has a significant threshold of FDR adjusted, for (A) AC, it was 9.74 × 10^–6. Similarly, (B) CC was 1.05 × 10^–5, (C) RW was 9.60 × 10^–6, and (D) CW was 1.01 × 10^–5.

Considering the small contribution of the above significant SNPs to the genetic variance, the proportion of genetic variance explained by each SNP were also illustrated as shown in Figure 3 in this study. Top 20 SNPs with the largest genetic variance were selected for each trait (Table 4); SNPs for BL were located on SSC17, BH on SSC2, SSC5 and SSC16, and CBC on SSC7 and SSC4. SNPs with the largest genetic variance for AC and CC are located on SSC12, while those for RW and CW were on SSC6 SSC7, SSC13 and SSC17. For each body size trait, BL, BH, CBC, AC, CC, RW, and CW, the top 20 SNPs explained 2.01%, 1.56%, 1.63%, 2.39%, 2.32%, 1.54%, and 1.23% of the genetic variance, respectively. Interestingly, the top 20 SNPs for AC and CC were the same, while RW and CW shared half of the 20 SNPs. In total, 110 SNPs with a larger proportion of explanatory genetic variance were retained for further analysis (Supplementary Table 1).

FIGURE 3

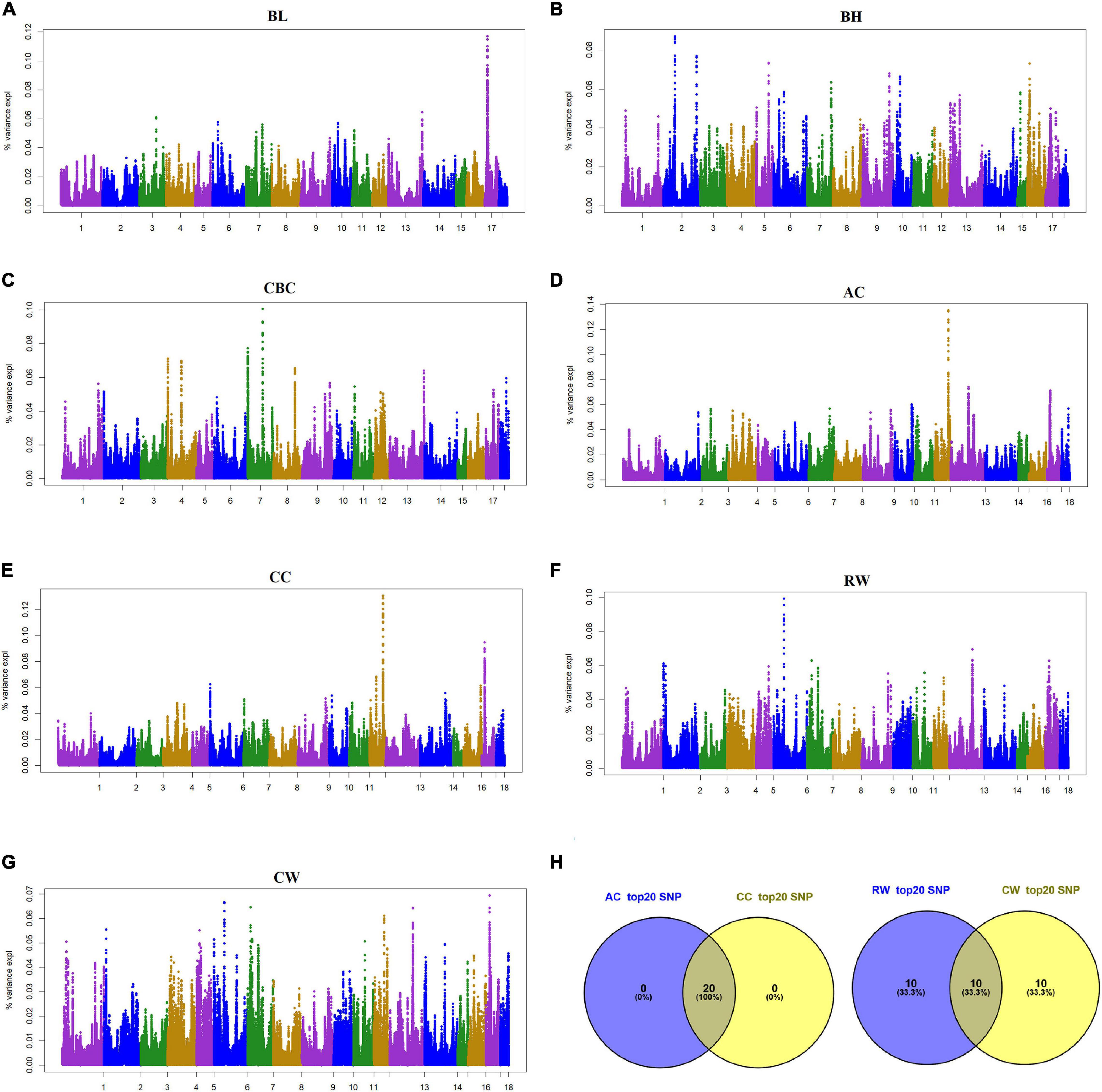
Figure 3. Manhattan plot of the genome-wide association study on seven body size traits and Venn plot of SNPs according to the contribution of SNP to genetic variance by using ssGWAS. BL, Body length; BH, Body height; CBC, Cannon bone circumference; AC, Abdominal circumference; CC, Chest circumference; RW, Rump width; CW, Chest width. BL, BH, and CBC were single-trait models, AC, CC, RW, and CW were two-trait models. AC and CC are a pair of traits, RW and CW are a pair of traits. In the Manhattan plots (A–G), the proportion of genetic variance of the quantified SNPs were plotted against their genomic positions. The x-axis represents the chromosomes and the y-axis represents the percentage of SNP explaining the genetic variance. Different colors indicate different chromosomes. Venn plot (H) of SNPs for the two pairs of body size traits, AC and CC, RW, and CW are a pair of traits, respectively.

TABLE 4

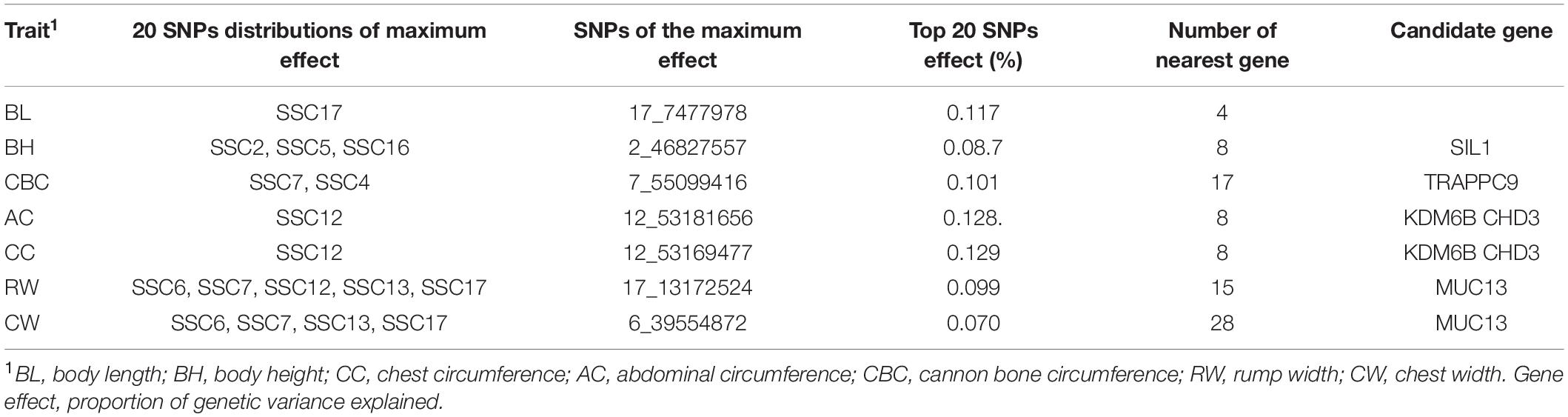
Table 4. Overview of ssGWAS location for the percentage that explains the proportion of genetic variance.

Identification of Candidate Genes

All the significant SNPs identified by the two methods were annotated within the 50 Kb downstream and upstream region with reference to the Sus scrofa 11.1 genome assembly. According to the two methods of SNP significance and explained genetic variance, 88 and 110 SNPs were identified without overlapping, and 64 and 40 genes were found near these SNPs, with only two of them in common (Tables 1, 3). Six (CDH13, CDC14A, TMRPSS15, CTNND2, MAPK4, and HMGA1) and five (SIL1, TRAPPC9, KDM6B, CHD3, and MUC13) genes were found to be related to the corresponding body size traits by the two methods. The biological processes and pathways involved in these genes include calcium channel proteins, lipid metabolism, and cell proliferation.

Discussion

The Superiority of Imputation-Based WGS Data

Genotype marker density is one important factor affecting the efficiency of GWAS (Brondum et al., 2012). With the increase of marker density, the linkage disequilibrium between markers and the target trait QTL is increased, which is helpful for QTL detection. In previous studies, the advantages of whole genome sequencing data have been demonstrated (Wang L. et al., 2017). However, its high cost hampered the wide application of sequencing data. Genotype imputation proved efficient at imputing the SNP chip data to sequencing data with high accuracy (Hoze et al., 2013). Our results indicated that imputation-based WGS data dramatically improved the power of GWAS; among the significant SNPs identified in this study, only three out of the 88 significant SNPs were located in the PorcineSNP80 SNP chip, the remaining 85 loci were identified in the sequencing data. Moreover, among the 110 non-repeating loci screened by interpretation variance, 101 are new loci after imputation, which indicates that imputed WGS data adds a lot of useful information.

Increasing marker density could lead to high linkage disequilibrium (LD) to improve the resolution of gene mapping, although it may also be a burden (Joiret et al., 2019). Too high LD between markers will cause noise and increase false positive rates (Wang et al., 2010). One of the strategies to deal with such a dilemma is to pre-select SNP, which can be done via SNP selection, to only keep a set of SNPs that are mutually uncorrelated (Hazelett et al., 2016; Calus and Vandenplas, 2018). Therefore, we pruned SNPs according to the genome-wide sequence data to reduce the LD degree between SNPs, and retained the loci in the original 80K chip. In this study, 44003 out of the qualified 50179 SNPs in PorcineSNP80 chip according to the genotype quality control were retained, and the average linkage disequilibrium of the finally used 784, 267 SNPs is similar to that of the chip data. The average r² was 0.191 and 0.195, respectively. This not only retains the original SNPs but also increases a large number of SNPS, and does not cause an increase of LD.

The Advantage of ssGWAS

The single SNP regression model is widely used in GWAS to identify the association of SNP with traits of interest, although it usually yields a high false-positive rate due to ignoring the linkage disequilibrium between adjacent SNPs. Wang et al. (2012) proposed Single-step GWAS (ssGWAS) that combines all the data (genotype, phenotype, and pedigree information) in one step. It can simultaneously utilize all the markers compared with the single-marker regression genome-wide association analysis, resulting in higher power and accuracy (Wang et al., 2014). In addition, ssGWAS is able to use sliding windows to simultaneously analyze multiple SNPs to reduce errors (Braz et al., 2019; Guerra et al., 2019). Wang et al. (2012) reported that ssGWAS achieved an accuracy of 0.81 ± 0.02 using 1500 genotype animals, which was more accurate than single SNP regression model (Wang et al., 2012). Moreover, ssGWAS can utilize more individuals; the sample size in this study is not very large, but has a large amount of phenotypic data of ungenotyped animals. Compared with traditional GWAS, ssGWAS can make full use of this information, expand the sample size to a certain extent, improve the accuracy of SNP effect estimation, and further improve the efficiency of SNP identification.

In this study, different analysis models were used for body size traits. Two-trait GWAS model was used for traits with high genetic correlation, which can simultaneously use SNPs affecting two traits, resulting in reducing the false positives and improving the statistical power to detect genes (Chesler et al., 2005; Xu et al., 2009; Korte et al., 2012). However, for traits with low genetic correlation, the multi-trait model can easily lead to error information sharing across traits, reducing the lower accuracy of gene mapping as pointed out by Wang C. et al. (2017). We therefore used two traits with high genetic correlation in this study. In addition, we also conducted four-trait model for the GWAS on CC, AC, CW, and RW, in which the genetic correlation between CC and AC, and CW and RW was above 0.7, and the correlation between the other two traits were all lower than 0.3. The results showed that only 40% of significant SNPs (P-value) and 60% of large effects SNPs obtained by the four-trait model on average overlapped with those from the two-trait model for each trait. Moreover, the computation of the multi-trait model is demanding and difficult to converge.

The Determination of Significant SNP Using P-value or SNP Effect

Theoretically, the SNPs with the smallest P-values were supposed to explain relatively high proportions of genetic variance. Likewise, the SNPs with large effects should be significantly associated with the trait of interest. However, our results indicated that the SNPs with the smallest P-values did not have large effects, and there was no overlap between the top 20 SNPs with the smallest P-values and with the largest SNPs effects for each trait. Spearman correlation of P-values and effects of all SNPs showed that the rank correlations of seven body size traits were low (ranging 0.38–0.4), although they were significant. As pointed out by Aguilar et al. (2019), P-value explains whether markers have apparent effects that are seemingly different from 0 with statistical assessment, while SNP effect mainly explains part of the genetic variance, with no statistical assessment. The consistence of SNPs fitting well these two criteria could not be high due to the linkage disequilibrium of SNP, the impact of environment, and the interaction of SNPs. However, it provides an efficient way to determine the SNPs related to traits of interest. Therefore, in order to locate QTLs related to traits more accurately and comprehensively, this study identified significant SNPs from both P-value and SNP effect. The proportion of genetic variance explained by most of the significant SNPs was small (0.00004–0.00653%) for all traits, and the maximum genetic variance of all SNPs was also not large (0.0557–0.1205%), perhaps because too many SNPs were used in the sequencing data in this study, leading to a small effect of each related SNP for each trait. It also indicates that SNPs controlling body size traits are widely distributed on the genome, fitting the infinitesimal model well. It was reported that for complex traits such as height, action sites are widely distributed across the entire genome, indicating that almost all genes are involved in the regulation of height (Boyle et al., 2017).

Pleiotropic effects can lead to genetic correlation between traits. From the aspect of P-value, no overlap of significant SNPs associated with two genetic related trait pairs, AC and CC, and RW and CW, were detected in this study. However, more common SNPs with the largest effects (not statistically significant) were found in each pair of genetic related traits, e.g., the top 20 SNPs with largest effects for AC and CC were completely overlapped, and these SNPs were adjacent to each other and located near SSC12:53132997. Therefore, it is speculated that these SNPs constitute an important QTL and jointly affect AC and CC. Similarly, there may be QTLs associated with RW and CW around SSC6:39553559 and SSC13:135373704. In addition, we took 20 SNPs as a sliding window, and found that the top 20 windows with the largest genetic effects, respectively, for AC and CC were overlapped, as well as for RW and CW. The above results further reflect ‘one factor produces multiple effects’, suggesting that highly genetically related traits are probably regulated by the same QTL.

Potential Candidate Genes for BL, BH, and CBC

The body length (BL) is an important index to investigate the breeding performance of animals. According to bioinformatics analysis, CDH13 near SSC6:5671575 could be used as a candidate gene affecting body length. CDH13 is a unique cadherin (Takeuchi et al., 2002) that regulates cell adhesion, signal transduction, and cell growth (Liu et al., 2016), and plays an important role in the formation of tissues and organs (Iotzova-Weiss et al., 2017). The ingestion and transfer of Ca will affect the bone development of the body for a long time (Kovacs, 2016), therefore, CDH13 has a certain influence on the growth and development of the body. For BH, SIL1 was found to be associated with this trait near SSC2:46827557. Proteomic studies showed that SIL1 elevation alters the expression of proteins including crucial players in neurodegeneration, and abnormal expression of SIL1 has an impact on the morphology of the body, which can reduce the body size (Labisch et al., 2018). CBC reflects the physical quality of the animal, whether it is strong or not. There are three candidate genes associated with CBC: CDC14A, TMPRSS15, and TRAPPC9. CDC14A is widely expressed in eukaryotic cell biology of a special kind of highly conservative dual specificity phosphatase; a variety of studies from yeast to human somatic cells have shown that CDC14 plays numerous roles, including in embryonic development and body size. TMPRSS15 has an impact on the digestive efficiency of animals, and has been found to be associated with the formation of cholesterol in humans and with the development of fat and body weight in mice (Wang et al., 2016). TMPRSS15 also has a higher variance ranking based on the SNP effect. The gene mutation of transporter particle complex 9 (TRAPPC9), a protein subunit of transporter particle II (TRAPPII), can lead to abnormal embryonic development and abnormal dietary behavior, and is associated with body mass index (Abbasi et al., 2017; Mbimba et al., 2018).

Potential Candidate Genes for AC and CC

Abdominal circumference and CC are a pair of highly genetically related body size traits, which determine the body size of animals and are indicators of fatness and thinness. CTNND2 was closely related to AC according to the P-value. Studies have shown that CTNND2 participates in the regulation of cell proliferation and affects the body node number of zebrafish (Zhang et al., 2018). It is found that KDM6B and CHD3 jointly affect AC and CC. KDM subfamily 6 enzymes B (KAM6B) plays an important role in the repression of developmental genes(Jones et al., 2018), and has a regulatory effect on chondrocyte differentiation, thus affecting bone growth and development (Dai et al., 2017). CDH3 is a calcium-binding protein that is involved in calcium ion binding and protein binding and is associated with diseases such as malnutrition and developmental malformations. Studies have shown that CHD3 regulates the developmental morphology of zebrafish heart, thereby affecting the abdominal circumference and body shape of zebrafish (Cho et al., 2018).

Potential Candidate Genes for RW and CW

For RW and CW, MUC13 was detected to affect both RW and CW. MUC13 promotes cell proliferation and migration, inhibits apoptosis, reduces adhesion through a number of signaling pathways (Sheng et al., 2013), and has a certain effect on the absorption of intestinal nutrients, thus affecting the growth and development of bone and the organism. It was found that MAPK4 and HMGA1 affect RW and CW of pigs, respectively. MAPK4 is mitogen-activated protein kinase 4, which is involved in the absorption and decomposition of sugars and the formation of fat, so it is related to obesity traits (Wu et al., 2016). HMGA1 affects the expression of two IGFBP (insulin-like growth factor binding protein) protein species and plays an important role in cell growth and differentiation (Cleynen and Van de Ven, 2008; Hristov et al., 2010). Studies have shown that the deletion of HMGA1 gene results in a significant decrease in the body size of mice (Federico et al., 2014). Moreover, a large number of studies have shown that HMGA1 is related to the body size character of pigs. Ji et al. (2017) found HMGA1 was a candidate gene affecting the body size of pigs through genome-wide association analysis. Zhang et al. (2014) found that HMGA1 is expressed in pig limb cells and affects the growth and differentiation of chondrocytes. Because of the functional importance of HMGA1 and several studies having shown that it is highly associated with body size traits, it is worth being verified in the future.

Conclusion

In this study, among seven body size traits in pigs, CC and AC, and CW and RW were highly genetically correlated with correlations of 0.747 and 0.840, respectively. We implemented ssGWAS to identify SNPs associated with body size traits based on two aspects of P-value and the proportion of explanatory genetic variance of SNP. In total, 198 SNPs were identified associated with seven body size traits in Yorkshire pigs, correspondingly, 11 genes were related to body size traits, among which HMGA1 could be worth being validated in further studies.

Data Availability Statement

The data analyzed in this study is subject to the following licenses/restrictions: The ped and the map are not publicly available because the genotyped animals belong to commercial breeding companies, but are available from the corresponding author on reasonable request. Requests to access these datasets should be directed to XD, xding@cau.edu.cn.

Ethics Statement

The animal study was reviewed and approved by the Institutional Animal Care and Use Committee (IACUC) of the China Agricultural University.

Author Contributions

XD and CW conceived and supervised the study. HL, HS, and YL helped complete the imputation of the chip data and provide technical guidance. HL, YaJ, HS, and YiJ collected the samples and recorded the phenotypes. YaJ and YL extracted the DNA for genotyping. HL, FZ, YL, and YS contributed to the visualization of data. HL and XD wrote and revised the manuscript. All authors read and approved the manuscript.

Funding

We are grateful to all the funding agencies. This work was supported by grants for the National Key Research and Development Project (2019YFE0106800), the National Key R&D Program of China (2018YFD0501000), the Beijing Innovation Consortium of Agriculture Research System (BAIC02-2020), China Agriculture Research System (CARS-35), Modern Agriculture Science and Technology Key Project of Hebei Province (19226376D), and the National Natural Science Foundation of China (31671327).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge the colleagues in the molecular quantitative genetics team of China Agricultural University for their helpful comments on the manuscript and Beijing Liuma Pig Breeding Co., Ltd., for providing blood samples.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2021.629049/full#supplementary-material

Footnotes

1. ^ https://www.animalgenome.org/cgi-bin/QTLdb/SS/index
2. ^ http://www.ensembl.org/Sus_scrofa/Info/Index/
3. ^ http://www.bioconductor.org/
4. ^ http://www.animalgenome.org/cgi-bin/QTLdb/SS/download?file=gbpSS_11.1

References

Abbasi, A. A., Blaesius, K., Hu, H., Latif, Z., Picker-Minh, S., Khan, M. N., et al. (2017). Identification of a novel homozygous TRAPPC9 gene mutation causing non-syndromic intellectual disability, speech disorder, and secondary microcephaly. Am. J. Med. Genet. B Neuropsychiatr. Genet. 174, 839–845. doi: 10.1002/ajmg.b.32602

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguilar, I., Legarra, A., Cardoso, F., Masuda, Y., Lourenco, D., and Misztal, I. (2019). Frequentist p-values for large-scale-single step genome-wide association, with an application to birth weight in American Angus cattle. Genet. Sel. Evol. 51:28. doi: 10.1186/s12711-019-0469-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguilar, I., Misztal, I., Johnson, D. L., Legarra, A., Tsuruta, S., and Lawlor, T. J. (2010). Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 93, 743–752. doi: 10.3168/jds.2009-2730

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguilar, I., Misztal, I., Legarra, A., and Tsuruta, S. (2011). Efficient computation of the genomic relationship matrix and other matrices used in single-step evaluation. J. Anim. Breed. Genet. 128, 422–428. doi: 10.1111/j.1439-0388.2010.00912.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Benjamini, Y., and Hochberg, Y. (1995). Controlling the false discovery rate–a practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Stat. Methodol. 57, 289–300. doi: 10.1111/j.2517-6161.1995.tb02031.x

CrossRef Full Text | Google Scholar

Boyle, E. A., Li, Y. I., and Pritchard, J. K. (2017). An expanded view of complex traits: from polygenic to omnigenic. Cell 169, 1177–1186. doi: 10.1016/j.cell.2017.05.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Braz, C. U., Taylor, J. F., Bresolin, T., Espigolan, R., Feitosa, F., Carvalheiro, R., et al. (2019). Sliding window haplotype approaches overcome single SNP analysis limitations in identifying genes for meat tenderness in Nelore cattle. BMC Genet. 20:8. doi: 10.1186/s12863-019-0713-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Brondum, R. F., Ma, P., Lund, M. S., and Su, G. (2012). Short communication: genotype imputation within and across Nordic cattle breeds. J. Dairy Sci. 95, 6795–6800. doi: 10.3168/jds.2012-5585

PubMed Abstract | CrossRef Full Text | Google Scholar

Browning, B. L., and Browning, S. R. (2009). A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am. J. Hum. Genet. 84, 210–223. doi: 10.1016/j.ajhg.2009.01.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Calus, M., and Vandenplas, J. (2018). SNPrune: an efficient algorithm to prune large SNP array and sequence datasets based on high linkage disequilibrium. Genet. Sel. Evol. 50:34. doi: 10.1186/s12711-018-0404-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Chesler, E. J., Lu, L., Shou, S. M., Qu, Y. H., Gu, J., Wang, J. T., et al. (2005). Complex trait analysis of gene expression uncovers polygenic and pleiotropic networks that modulate nervous system function. Nat. Genet. 37, 233–242. doi: 10.1038/ng1518

PubMed Abstract | CrossRef Full Text | Google Scholar

Cho, S. H., Lee, C. H., Gi, E., Yim, Y., Koh, H. J., Kang, K., et al. (2018). The rice rolled fine striped (RFS) CHD3/Mi-2 chromatin remodeling factor epigenetically regulates genes involved in oxidative stress responses during leaf development. Front. Plant Sci. 9:364. doi: 10.3389/fpls.2018.00364

PubMed Abstract | CrossRef Full Text | Google Scholar

Cleynen, I., and Van de Ven, W. J. (2008). The HMGA proteins: a myriad of functions (Review). Int. J. Oncol. 32, 289–305.

Google Scholar

Dai, J., Yu, D., Wang, Y., Chen, Y., Sun, H., Zhang, X., et al. (2017). Kdm6b regulates cartilage development and homeostasis through anabolic metabolism. Ann. Rheum. Dis. 76, 1295–1303. doi: 10.1136/annrheumdis-2016-210407

PubMed Abstract | CrossRef Full Text | Google Scholar

Federico, A., Forzati, F., Esposito, F., Arra, C., Palma, G., Barbieri, A., et al. (2014). Hmga1/Hmga2 double knock-out mice display a “superpygmy” phenotype. Biol. Open 3, 372–378. doi: 10.1242/bio.20146759

PubMed Abstract | CrossRef Full Text | Google Scholar

Guerra, F. P., Suren, H., Holliday, J., Richards, J. H., Fiehn, O., Famula, R., et al. (2019). Exome resequencing and GWAS for growth, ecophysiology, and chemical and metabolomic composition of wood of Populus trichocarpa. BMC Genomics 20:875. doi: 10.1186/s12864-019-6160-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hazelett, D. J., Conti, D. V., Han, Y., Al, O. A., Easton, D., Eeles, R. A., et al. (2016). Reducing GWAS complexity. Cell Cycle 15, 22–24. doi: 10.1080/15384101.2015.1120928

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirschhorn, J. N., and Daly, M. J. (2005). Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 6, 95–108. doi: 10.1038/nrg1521

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoze, C., Fouilloux, M. N., Venot, E., Guillaume, F., Dassonneville, R., Fritz, S., et al. (2013). High-density marker imputation accuracy in sixteen French cattle breeds. Genet. Sel. Evol. 45:33. doi: 10.1186/1297-9686-45-33

PubMed Abstract | CrossRef Full Text | Google Scholar

Hristov, A. C., Cope, L., Di Cello, F., Reyes, M. D., Singh, M., Hillion, J. A., et al. (2010). HMGA1 correlates with advanced tumor grade and decreased survival in pancreatic ductal adenocarcinoma. Mod. Pathol. 23, 98–104. doi: 10.1038/modpathol.2009.139

PubMed Abstract | CrossRef Full Text | Google Scholar

Iotzova-Weiss, G., Freiberger, S. N., Johansen, P., Kamarachev, J., Guenova, E., Dziunycz, P. J., et al. (2017). TLR4 as a negative regulator of keratinocyte proliferation. PLoS One 12:e185668. doi: 10.1371/journal.pone.0185668

PubMed Abstract | CrossRef Full Text | Google Scholar

Jensen, J., and Madsen, P. (2000). “A user’s guide to DMU,” in A Package for Analyzing Multivariate Mixed Models, Tjele: Research Center Foulum, Danish Institute of Animal Science.

Google Scholar

Ji, J., Zhou, L., Guo, Y., Huang, L., and Ma, J. (2017). Genome-wide association study identifies 22 new loci for body dimension and body weight traits in a White DurocxErhualian F2 intercross population. Asian-Australas. J. Anim. Sci. 30, 1066–1073. doi: 10.5713/ajas.16.0679

PubMed Abstract | CrossRef Full Text | Google Scholar

Joiret, M., Mahachie, J. J., Gusareva, E. S., and Van Steen, K. (2019). Confounding of linkage disequilibrium patterns in large scale DNA based gene-gene interaction studies. BioData Min. 12:11. doi: 10.1186/s13040-019-0199-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, S. E., Olsen, L., and Gajhede, M. (2018). Structural basis of histone demethylase KDM6B Histone 3 Lysine 27 specificity. Biochemistry 57, 585–592. doi: 10.1021/acs.biochem.7b01152

PubMed Abstract | CrossRef Full Text | Google Scholar

Klein, R. J., Zeiss, C., Chew, E. Y., Tsai, J. Y., Sackler, R. S., and Haynes, C. (2005). Complement factor H polymorphism in age-related macular degeneration. Science 308, 385–389.

Google Scholar

Korte, A., Vilhjálmsson, B. J., Segura, V., Platt, A., Long, Q., and Nordborg, M. (2012). A mixed-model approach for genome-wide association studies of correlated traits in structured populations. Nat. Genet. 44:1066.

Google Scholar

Kovacs, C. S. (2016). Maternal mineral and bone metabolism during pregnancy, lactation, and post-weaning recovery. Physiol. Rev. 96, 449–547. doi: 10.1152/physrev.00027.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Labisch, T., Buchkremer, S., Phan, V., Kollipara, L., Gatz, C., Lentz, C., et al. (2018). Tracking effects of SIL1 increase: taking a closer look beyond the consequences of elevated expression level. Mol. Neurobiol. 55, 2524–2546. doi: 10.1007/s12035-017-0494-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., Song, J., Luan, J., Sun, X., Bai, J., Wang, H., et al. (2016). Promoter methylation status of tumor suppressor genes and inhibition of expression of DNA methyltransferase 1 in non-small cell lung cancer. Exp. Biol. Med. (Maywood) 241, 1531–1539. doi: 10.1177/1535370216645211

PubMed Abstract | CrossRef Full Text | Google Scholar

Mackay, T. F. C., Stone, E. A., and Ayroles, J. F. (2009). The genetics of quantitative traits: challenges and prospects. Nat. Rev. Genet. 10, 565–577. doi: 10.1038/nrg2612

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchini, J., and Howie, B. (2010). Genotype imputation for genome-wide association studies. Nat. Rev. Genet. 11, 499–511. doi: 10.1038/nrg2796

PubMed Abstract | CrossRef Full Text | Google Scholar

Mbimba, T., Hussein, N. J., Najeed, A., and Safadi, F. F. (2018). TRAPPC9: Novel insights into its trafficking and signaling pathways in health and disease (Review). Int. J. Mol. Med. 42, 2991–2997. doi: 10.3892/ijmm.2018.3889

PubMed Abstract | CrossRef Full Text | Google Scholar

Niu, P., Kim, S., Choi, B., Kim, T., Kim, J., and Kim, K. (2013). Porcine insulin-like growth factor 1 (IGF1) gene polymorphisms are associated with body size variation. Genes Genomics 35, 523–528. doi: 10.1007/s13258-013-0098-0

CrossRef Full Text | Google Scholar

Ohnishi, C., and Satoh, M. (2018). Estimation of genetic parameters for performance and body measurement traits in Duroc pigs selected for average daily gain, loin muscle area, and backfat thickness. Livest. Sci. 214, 161–166. doi: 10.1016/j.livsci.2018.05.022

CrossRef Full Text | Google Scholar

Purcell, S., Neale, B., Todd-Brown, K., Thomas, L., Ferreira, M. A. R., Bender, D., et al. (2007). PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575. doi: 10.1086/519795

PubMed Abstract | CrossRef Full Text | Google Scholar

Quinlan, A. R., and Hall, I. M. (2010). BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26, 841–842. doi: 10.1093/bioinformatics/btq033

PubMed Abstract | CrossRef Full Text | Google Scholar

Risch, N. M. K. (1996). The future of genetic studies of complex human diseases. Epidemiology 9, 350–354.

Google Scholar

Schreiweis, M. A., Hester, P. Y., and Moody, D. E. (2005). Identification of quantitative trait loci associated with bone traits and body weight in an F2 resource population of chickens. Genet. Sel. Evol. 37, 677–698. doi: 10.1051/gse:2005023

CrossRef Full Text | Google Scholar

Sheng, Y. H., Triyana, S., Wang, R., Das, I., Gerloff, K., Florin, T. H., et al. (2013). MUC1 and MUC13 differentially regulate epithelial inflammation in response to inflammatory and infectious stimuli. Mucosal Immunol. 6, 557–568. doi: 10.1038/mi.2012.98

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon-Sanchez, J., Schulte, C., Bras, J. M., Sharma, M., Gibbs, J. R., Berg, D., et al. (2009). Genome-wide association study reveals genetic risk underlying Parkinson’s disease. Nat. Genet. 41, 1308–1312. doi: 10.1038/ng.487

PubMed Abstract | CrossRef Full Text | Google Scholar

Soller, M., Weigend, S., Romanov, M. N., Dekkers, J. C. M., and Lamont, S. J. (2006). Strategies to assess structural variation in the chicken genome and its associations with biodiversity and biological performance. Poult. Sci. 85, 2061–2078. doi: 10.1093/ps/85.12.2061

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, H., Ye, S., Jiang, Y., Zhang, Z., Zhang, Q., and Ding, X. (2019). Using imputation-based whole-genome sequencing data to improve the accuracy of genomic prediction for combined populations in pigs. Genet. Sel. Evol. 51:58. doi: 10.1186/s12711-019-0500-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Takeuchi, T., Liang, S. B., Matsuyoshi, N., Zhou, S., Miyachi, Y., Sonobe, H., et al. (2002). Loss of T-cadherin (CDH13, H-cadherin) expression in cutaneous squamous cell carcinoma. Lab. Invest. 82, 1023–1029. doi: 10.1097/01

CrossRef Full Text | Google Scholar

Turner, S. D. (2018). qqman: an R package for visualizing GWAS results using Q-Q and manhattan plots. J. Open Source. Softw. 3:731. doi: 10.21105/joss.00731

CrossRef Full Text | Google Scholar

van Leeuwen, E. M., Kanterakis, A., Deelen, P., Kattenberg, M. V., Slagboom, P. E., de Bakker, P. I. W., et al. (2015). Population-specific genotype imputations using minimac or IMPUTE2. Nat. Protoc. 10, 1285–1296. doi: 10.1038/nprot.2015.077

PubMed Abstract | CrossRef Full Text | Google Scholar

VanRaden, P. M. (2008). Efficient methods to compute genomic predictions. J. Dairy Sci. 91, 4414–4423. doi: 10.3168/jds.2007-0980

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Li, X., Qian, R., Su, G., Zhang, Q., and Ding, X. (2017). Bayesian methods for jointly estimating genomic breeding values of one continuous and one threshold trait. PLoS One 12:e0175448. doi: 10.1371/journal.pone.0175448

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Misztal, I., Aguilar, I., Legarra, A., Fernando, R. L., Vitezica, Z., et al. (2014). Genome-wide association mapping including phenotypes from relatives without genotypes in a single-step (ssGWAS) for 6-week body weight in broiler chickens. Front. Genet. 5:134. doi: 10.3389/fgene.2014.00134

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, H., Misztal, I., Aguilar, I., Legarra, A., and Muir, W. M. (2012). Genome-wide association mapping including phenotypes from relatives without genotypes. Genet. Res. (Camb.) 94, 73–83. doi: 10.1017/S0016672312000274

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Zhang, Y., Zhang, T., Zhang, L., Yan, H., Liu, X., et al. (2017). Genotyping by sequencing reveals a new locus for pig teat number. Anim. Genet. 48, 470–472. doi: 10.1111/age.12547

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Elston, R. C., and Zhu, X. (2010). The meaning of interaction. Hum. Hered. 70, 269–277. doi: 10.1159/000321967

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Xu, S., Du, K., Huang, F., Chen, Z., Zhou, K., et al. (2016). Evolution of digestive enzymes and RNASE1 provides insights into dietary switch of cetaceans. Mol. Biol. Evol. 33, 3144–3157. doi: 10.1093/molbev/msw191

PubMed Abstract | CrossRef Full Text | Google Scholar

Weller, J. I., Song, J. Z., Heyen, D. W., Lewin, H. A., and Ron, M. (1998). A new approach to the problem of multiple comparisons in the genetic dissection of complex traits. Genetics 150, 1699–1706.

Google Scholar

Wu, Y. S., Chen, Y. T., Bao, Y. T., Li, Z. M., Zhou, X. J., He, J. N., et al. (2016). Identification and verification of potential therapeutic target genes in berberine-treated zucker diabetic fatty rats through bioinformatics analysis. PLoS One 11:e166378. doi: 10.1371/journal.pone.0166378

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, C. W., Wang, X. F., Li, Z. K., and Xu, S. Z. (2009). Mapping QTL for multiple traits using Bayesian statistics. Genet. Res. 91, 23–37. doi: 10.1017/S0016672308009956

PubMed Abstract | CrossRef Full Text | Google Scholar

Yan, G., Qiao, R., Zhang, F., Xin, W., Xiao, S., Huang, T., et al. (2017). Imputation-based whole-genome sequence association study rediscovered the missing QTL for lumbar number in sutai pigs. Sci. Rep. 7:615. doi: 10.1038/s41598-017-00729-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, G., Wang, L. G., Han, Y., and He, Q. Y. (2012). clusterProfiler: an R package for comparing biological themes among gene clusters. OMICS 16, 284–287. doi: 10.1089/omi.2011.0118

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, L. C., Li, N., Liu, X., Liang, J., Yan, H., Zhao, K. B., et al. (2014). A genome-wide association study of limb bone length using a large white x minzhu intercross population. Genet. Sel. Evol. 46:56. doi: 10.1186/s12711-014-0056-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, R., Ding, X., and Ai, K. (2018). EFNB2 acts as the target of miR-557 to facilitate cell proliferation, migration and invasion in pancreatic ductal adenocarcinoma by bioinformatics analysis and verification. Am. J. Transl. Res. 10, 3514–3528.

Google Scholar