Quantifying the Stability of Coupled Genetic and Epigenetic Switches With Variational Methods

The Waddington landscape provides an intuitive metaphor to view development as a ball rolling down the hill, with distinct phenotypes as basins and differentiation pathways as valleys. Since, at a molecular level, cell differentiation arises from interactions among the genes, a mathematical definition for the Waddington landscape can, in principle, be obtained by studying the gene regulatory networks. For eukaryotes, gene regulation is inextricably and intimately linked to histone modifications. However, the impact of such modifications on both landscape topography and stability of attractor states is not fully understood. In this work, we introduced a minimal kinetic model for gene regulation that combines the impact of both histone modifications and transcription factors. We further developed an approximation scheme based on variational principles to solve the corresponding master equation in a second quantized framework. By analyzing the steady-state solutions at various parameter regimes, we found that histone modification kinetics can significantly alter the behavior of a genetic network, resulting in qualitative changes in gene expression profiles. The emerging epigenetic landscape captures the delicate interplay between transcription factors and histone modifications in driving cell-fate decisions.

1. Introduction

A little more than five decades ago, Waddington introduced the metaphor to view cellular differentiation into distinct lineages and cell types as a sequence of transitions among basins in a landscape, wherein basins indicate stable phenotypes (Waddington and Kacser, 1957). The appeal of this metaphor to intuition has inspired efforts of theoretical formulation at the molecular level by studying genetic networks formed by transcription factors (TF) (Sasai and Wolynes, 2003; Hornos et al., 2005; Kærn et al., 2005; Walczak et al., 2005a,b; Xu and Tao, 2006; Goldberg et al., 2007; Kim and Wang, 2007; Shahrezaei and Swain, 2008; Cao et al., 2010; Venegas-Ortiz and Evans, 2011; Wang et al., 2011, 2014; Zhang et al., 2013; Zhang and Wolynes, 2014; Lv et al., 2015; Chen et al., 2016; Qiu et al., 2020). These studies highlighted the importance of gene expression noise in driving the transition among steady states. Noise is a manifestation of the inherent stochasticity of chemical reactions and arises in gene regulatory networks as a result of protein production/degradation and TF binding/unbinding. Noise, or fluctuation, is non-negligible due to the finite number of protein molecules and the single molecule nature of DNA. Stochastic noise and network topology together define the epigenetic landscape, much like the one envisioned by Waddington, that quantifies the stability of various cell-defining gene expression levels or patterns.

For eukaryotic organisms, in addition to transcription factors, epigenetic marks such as DNA methylation and histone modifications also play essential roles in regulating gene expression (Lister et al., 2009; Lu et al., 2009; Artyomov et al., 2010; Krishnakumar and Kraus, 2010; Margueron and Reinberg, 2010; Mariani et al., 2010; Andrew Angel, 2011; Miller-Jensen et al., 2011; Furey and Sethupathy, 2013). They are known to affect local chromatin packaging and global genome organization (Zhou et al., 2011; Schlick et al., 2012; Rowley and Corces, 2018; Parsons and Zhang, 2019; Qi et al., 2020; Xie et al., 2020), which in turn can regulate DNA accessibility to regulatory proteins. Furthermore, DNA methylation directly impacts the DNA binding affinity of transcription factors (Tate and Bird, 1993; Zhou et al., 2016; Flavahan et al., 2019). Importantly, the chemical modifications themselves may give rise to steady states independent of the TF-centric genetic network. For example, modification of nucleosomes recruits enzymes affecting the neighboring nucleosomes, causing them to be similarly modified (Bannister and Kouzarides, 2011). Many elegant theoretical attempts have demonstrated how such interactions can bring about collective changes of many nucleosomes and allow them to exhibit distinct multistable states (Dodd et al., 2007; Sedighi and Sengupta, 2007; David-Rus et al., 2009; Micheelsen et al., 2010; Sneppen and Mitarai, 2012; Dayarian and Sengupta, 2013; Jost, 2014; Sood and Zhang, 2020). Therefore, it is crucial to account for the dynamics and regulation of epigenetic modifications when constructing the landscape for cellular differentiation in eukaryotes.

Many research groups have studied the interplay between genetic and epigenetic switches in regulating gene expression. For instance, generalized genetic networks that couple each gene to a binary or ternary variable representing the collective histone states have been used as models for stem cells to account for epigenetic degrees of freedom, albeit in a coarse grained fashion (Artyomov et al., 2010; Binder et al., 2013; Sasai et al., 2013; Ashwin and Sasai, 2015; Huang and Lei, 2018; Folguera-Blasco et al., 2019). These studies found a significant dependence of the probability landscape of protein expression computed from stochastic simulations on chromatin state dynamics. Similarly coarse-grained treatment of epigenetic switches was shown to introduce hysteresis (Bhattacharyya et al., 2020) and homeorhesis (Matsushita and Kaneko, 2020) to the dynamics of gene regulatory networks. Notably, Zhang et al. (2019) explicitly considered the modification of individual nucleosomes and studied the impact of such modifications on the probability landscape of a single self-activating gene and a pair of mutually repressive genes. However, the lack of analytical results has made the sensitivity analysis of the computed landscape with respect to parameter values, which may vary along cell differentiation, numerically challenging.

In this work, we investigate the combined impact of TF binding and epigenetic modifications in regulating the expression of a self-activating gene. Rather than coarse-graining the epigenetic switch into a binary or ternary variable, we explicitly account for the dynamical modification of individual nucleosomes. The variational approach (Eyink, 1996; Sasai and Wolynes, 2003) was used to compute steady-state probability distributions from deterministic equations and avoid computationally intensive stochastic simulations. Moreover, we generalize the typically used Poisson ansatz to better treat systems with particle conservation constraints, such as our epigenetic switch, that are more naturally described using SU(2) than Bosonic operators (Sood and Zhang, 2020). The approach enabled a convenient exploration of the model's steady-state behavior across a wide range of parameters. Our study suggests that fast, random perturbations to individual histone modifications lead to the formation of a poised, uncommitted chromatin state, which in turn can drive noisy gene expression seen in stem cells. As the rate of such random perturbations decreases and the role of cooperative modifications of nucleosome prevails, the system transitions to a bistable regime resembling a differentiated state. The transition goes through an activated state with high gene expression, highlighting the robustness of the network in activating gene expression due to the feedback between genetic and epigenetic switches. We further compared variational results with stochastic simulations and discussed potential improvements in the accuracy of the variational method.

2. Model

We consider a simplified model of eukaryotic gene regulation that accounts for TF binding/unbinding as well as histone modifications. The model couples the regulatory network of a self-activating gene with an epigenetic switch that can lead to active and repressive chromatin states.

For self-activating genes, their protein products bind with the promoter to upregulate the transcription rate. As illustrated in Figure 1, proteins are produced and destroyed with rates of g and k, respectively. The protein production rate is further dependent on whether the gene's promoter is bound by TF (state 0) or not (state 1), and we have g₁ < g₀ since the proteins are activators. Here TFs correspond to gene transcription products, and they bind to the promoter with rate h as dimers. The corresponding unbinding rate is f. Binding rate depends on protein copy number n_p as well as the number of modified nucleosomes n_x as detailed in Equation (3) below. Self-activating genes are known to occur both as isolated entities (Ptashne et al., 1980; Johnson et al., 1981; Hasty et al., 2000; Rosenfeld et al., 2002) and as common motifs of larger interacting networks (Ralston and Rossant, 2005; Loh et al., 2008; Orkin and Zon, 2008). They have been the subject of extensive theoretical study as models of cellular differentiation (Sasai and Wolynes, 2003; Hornos et al., 2005; Walczak et al., 2005a,b; Xu and Tao, 2006; Goldberg et al., 2007; Kim and Wang, 2007; Shahrezaei and Swain, 2008; Venegas-Ortiz and Evans, 2011; Wang et al., 2011; Zhang et al., 2013; Zhang and Wolynes, 2014). The epigenetic switch concerns a cluster of N = 60 nucleosomes, each of which can exist in a modified (X) or unmodified (Y) state. The kinetics of chromatin system can be described with the non-linear dynamics given below

$\begin{array}{ll}X+X+Y\stackrel{s_1,s_0}{\to }3X,Y+Y+X\stackrel{z}{\to }3Y,& (1)\end{array}$

$\begin{array}{ll}X\stackrel{q}{\to }Y,Y\stackrel{q}{\to }X.& (2)\end{array}$

The inter-conversion between modified and unmodified nucleosomes can either proceed via Equation (1) that requires a pair of similarly modified nucleosomes to alter the state of a nucleosome, or via noisy conversion (Equation 2) with first-order kinetics. The former is meant to account for nucleosomes being actively interconverted by modifying and removing enzymes recruited by the similarly modified nucleosomes in their vicinity. It is this recruitment that forms the positive feedback in the system (Dodd et al., 2007; Micheelsen et al., 2010; Xie and Zhang, 2019; Sood and Zhang, 2020). s, z, and q are the rate constants of the corresponding reactions.

FIGURE 1

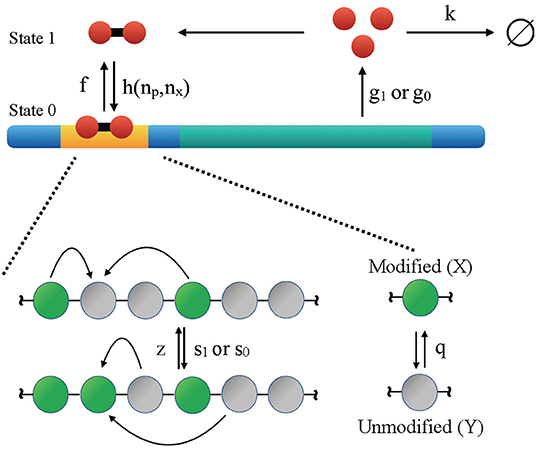
Figure 1. Illustration of the kinetic model that couples the regulatory network of a self-activating gene with the reaction network of histone modifications. The gene is auto-regulatory as the protein produced by the gene (red circles) binds to the promoter region (yellow) with rate h and unbinds with rate f. Depending on whether the regulatory protein is bound (State 0) or unbound (State 1), the rate of protein production is g₀ or g₁. Proteins degrade with rate k. Conversions between modified (X) and unmodified (Y) nucleosomes can occur “randomly” (irrespective to the status of other nucleosomes) with a basal rate q. Nucleosome modifications can also occur more cooperatively with rate of z and s.

The coupling between the genetic and epigenetic switch is achieved by introducing a dependence of protein binding rate on the number of modified nucleosomes, i.e.,

$\begin{array}{ll}h(n_p,n_x)=h_o\frac{n_p(n_p-1)}{1+\text{exp}\left(-0.5(n_x-35)\right)}.& (3)\end{array}$

This dependence is motivated by the realization that actively modified chromatin (n_x > 35) exists in a more open state that is more accessible to regulatory proteins. The particular expression [1 + exp(−0.5(n_x − 35))]⁻¹ as the probability for chromatin being open is typical of a two state system, assuming that the energetic difference between open and closed chromatin depends linearly on the number of modified nucleosomes. Furthermore, the recruited conversion rate of unmodified to modified nucleosomes depends on TF binding with s₀ > s₁, assuming that TFs can attract modification enzymes to chromatin. The values for the kinetic parameters were set relative to the degradation rate k as g₁ = 4, g₀ = 65, h_o = 1, f = 100, s₁ = 8, s₀ = 10s₁, z = 8. The random histone modification rate, q, was varied over a wide range of values as detailed below. We used k = 1s⁻¹, though changing this value will not affect the steady state distributions and only renormalizes the timescale in the model.

We carried out stochastic simulations of the kinetic model using the Gillespie algorithm (Gillespie, 1977). Each plot shown in Figure 2 was obtained from averaging over 100 independent 10⁵-second-long simulations. These trajectories were initialized with random configurations, and the number of modified nucleosomes and protein molecules along each trajectory was recorded at every second. We then combined the values from all trajectories to estimate the steady state probability distributions, P_ss. For the plots shown in Figure 3 we used q = 10 and set n_x = 40 and n_p = 20 at t = 0. 200 independent trajectories were performed to produce the average numbers recorded at every 0.5 s.

FIGURE 2

Figure 2. Comparison between the probability distributions obtained from the variational approach and from stochastic simulations. (A–C) Steady state probability distributions for the number of modified nucleosomes computed using the variational method (black solid line) and from stochastic simulations (red dots) for q = 100 (A), 10 (B), and 0.5 (C). (D–F) Steady state probability distributions for the number of protein molecules computed using the variational method (black solid line) and from stochastic simulations (red dots) for q = 100 (D), 10 (E), and 0.5 (F). (G–I) Steady state probability distributions as a function of both number of proteins and modified nucleosomes computed using the variational method for q = 100 (G), 10 (H), and 0.5 (I), showing two, one and two fixed points, respectively.

FIGURE 3

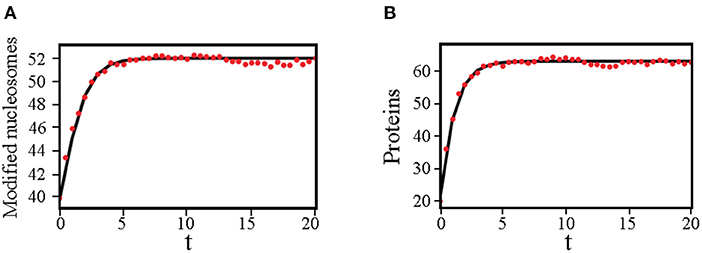
Figure 3. Dynamical trajectories determined from the variational approach agree well with stochastic simulations in favorable regimes. (A) Time evolution of the average number of modified nucleosomes computed using the variational method (black solid line) and stochastic simulations (red dots). (B) Time evolution of the average number of modified nucleosomes computed using the variational method (black solid line) and stochastic simulation (red dots). We used q = 10, M = 60, and set c₁p₁ = 0, c₀p₀ = 20, c₁t₁ = 0, c₁t₀ = 0.66 as the initial values when solving the deterministic equations (Equation 11).

3. Theory

We reformulated the master equation describing the dynamical evolution of the kinetic network as an imaginary time Schrödinger equation

$\begin{array}{ll}\begin{array}{l}{\partial }_t|\Psi (t)\rangle =\Omega |\Psi (t)\rangle .\hfill \end{array}& (4)\end{array}$

The state vector $|\Psi (t)\rangle =\left(\begin{array}{c}{\Psi }_1(t)\\ {\Psi }_0(t)\end{array}\right)$ is a superposition of all possible configurations weighted with their corresponding probabilities such that ${\Psi }_i(t)={\displaystyle {\sum }_{n_p,n_x}{P}_i(\{n_p,n_x\};t)|n_p,n_x\rangle }$ for i = 0, 1. The two components correspond to the DNA state with regulatory proteins unbound (state 1) or bound (state 0), respectively. This reformulation makes use of a second quantization based method (the Doi-Peliti approach), which has been successfully employed in the study of reaction-diffusion processes (Lee and Cardy, 1995), gene switches (Sasai and Wolynes, 2003; Zhang and Wolynes, 2014), and other systems (Täuber, 2014). In previous work, we applied the Doi-Peliti approach to the epigenetic switch using operators that are a representation of the SU(2) algebra (Sood and Zhang, 2020). The SU(2) algebra allows us to treat the constraint of conservation of particle in number in a mathematically elegant and convenient way. When coupled to the self-activating gene, the stochastic Hamiltonian for the system described in Figure 1 is given by

$\begin{array}{l}\Omega =g(a_p^{†}-1)+k(a_p-a_p^{†}{a}_p)+s[J_{+}{\widehat{n}}_x^{\underset{\_}{2}}-{\widehat{n}}_x^{\underset{\_}{2}}{\widehat{n}}_y]\\ +z[J_{-}{\widehat{n}}_y^{\underset{\_}{2}}-{\widehat{n}}_y^{\underset{\_}{2}}{\widehat{n}}_x]+q[J_{-}-{\widehat{n}}_x]+q[J_{+}-{\widehat{n}}_y]\\ +\left(\begin{array}{cc}-h({\widehat{n}}_p,{\widehat{n}}_x)& f\\ h({\widehat{n}}_p,{\widehat{n}}_x)& -f\end{array}\right),& (5)\end{array}$

where $g=\left(\begin{array}{cc}{g}_1& 0\\ 0& g_0\end{array}\right),s=\left(\begin{array}{cc}{s}_1/N^3& 0\\ 0& s_0/N^3\end{array}\right),z=\left(\begin{array}{cc}z/N^3& 0\\ 0& z/N^3\end{array}\right),k=\left(\begin{array}{cc}k& 0\\ 0& k\end{array}\right),q=\left(\begin{array}{cc}q/N& 0\\ 0& q/N\end{array}\right)$, and $h({\widehat{n}}_p,{\widehat{n}}_x)=\frac{{\widehat{n}}_p({\widehat{n}}_p-1)}{1+\text{exp}(-0.5({\widehat{n}}_x-35))}.$ The operator $a_p^{†}$ creates a protein molecule when it acts on a state, $a_p^{†}|n_p,n_x\rangle =|n_p+1,n_x\rangle$, whereas a_p serves to remove a protein molecule when acting on the same state, a_p |n_p, n_x〉 = n_p |n_p − 1, n_x〉. J₊ converts an unmodified nucleosome to a modified one by acting on a state, J₊ |n_p, n_x〉 = (N − n_x) |n_p, n_x + 1〉, while J₋ acts to convert a modified nucleosome to an unmodified one, J₋ |n_p, n_x〉 = n_x |n_p, n_x − 1〉. ${\widehat{n}}_p$ denotes the number operator, as its action on a ket gives the number of protein molecules, ${\widehat{n}}_p|n_p,n_x\rangle =n_p|n_p,n_x\rangle$. In a similar fashion, ${\widehat{n}}_x$ gives the number of modified nucleosomes when it acts on a ket, ${\widehat{n}}_x|n_p,n_x\rangle =n_x|n_p,n_x\rangle$, and ${\widehat{n}}_y$ gives the number of unmodified nucleosomes, ${\widehat{n}}_y|n_p,n_x\rangle =(N-n_x)|n_p,n_x\rangle$. n² = n(n − 1) denotes the falling factorial.

Exact solutions to Equation (4) are difficult to obtain. Instead, we make use of an approximate, yet succinct and powerful, variational approach originally introduced by Eyink (Eyink, 1996; Alexander and Eyink, 1997). First, we realize that the imaginary time Schrödinger equation is equivalent to the functional variation of the following action Γ with respect to Φ, i.e., $\frac{\delta \Gamma }{\delta \Phi }=0$ for

$\begin{array}{ll}\Gamma ={\displaystyle \int }\text{d}t\langle \Phi |{\partial }_t-\Omega |\Psi \rangle .& (6)\end{array}$

By designing trial functions for Φ and Ψ parameterized with ${\alpha }_L={\alpha }_L^1,{\alpha }_L^2,\cdots ,{\alpha }_L^K$ and ${\alpha }_R={\alpha }_R^1,{\alpha }_R^2,\cdots ,{\alpha }_R^K$, minimizing the action leads to a set of ordinary differential equations,

$\begin{array}{ll}{{\displaystyle \sum _{l=1}^K{\displaystyle \left[\langle \frac{\partial \Phi }{\partial {\alpha }_L^m}\rangle \frac{\partial \Psi }{\partial {\alpha }_R^l}\frac{\text{d}{\alpha }_R^l}{\text{d}t}-\langle \frac{\partial \Phi }{\partial {\alpha }_L^m}|\Omega |\Psi \rangle \right]}}}_{{\alpha }_L^m=0}=0,& (7)\end{array}$

$\begin{array}{ll}\text{for }m=1,\cdots ,K.& (8)\end{array}$

Also, we demand (to stay true to the probabilistic interpretation) 〈Φ(α_L = 0)〉Ψ(α_R) = 1. The variational approach was first applied with great success to stochastic gene regulatory networks by Sasai and Wolynes (2003). In its original formulation, Poisson distributions were used as trial functions, with the Poisson mean being the variational parameter. Since protein molecules can be approximately treated as products of a birth-death process, the probability distribution to find n_p molecules should be Poisson at large t (Sasai and Wolynes, 2003). Furthermore, the stochastic Hamiltonian for genetic networks consists of only Bosonic operators, the coherent states of which correspond to Poisson distributions. In this work, we exploit the symmetry imposed on the system by particle number constraints to derive a new variational trial function for the chromatin switch. As shown in the Supplementary Material, an excellent candidate is the binomial distribution function since the coherent states for the SU(2) operators in our stochastic Hamiltonian are binomial (Fu and Sasaki, 1997, 1998). Taken together, we can thus use the following ansatz as variational functions for the coupled genetic and epigenetic switch

$\begin{array}{ll}\begin{array}{l}|\Psi \rangle =\left(\begin{array}{c}{c}_1\exp \left(p_1(a_p^{†}-1)\right){(1-{\theta }_1)}^N\exp \left(\frac{{\theta }_1}{1-{\theta }_1}{J}_{+}\right)|0,0\rangle \\ c_0\exp \left(p_0(a_p^{†}-1)\right){(1-{\theta }_0)}^N\exp \left(\frac{{\theta }_0}{1-{\theta }_0}{J}_{+}\right)|0,0\rangle \end{array}\right),\hfill \end{array}& (9)\end{array}$

and

$\begin{array}{l}\langle \Phi |=(\langle 0,0|e^{a_p}{e}^{J_{-}}\exp \left({\alpha }_1+{\lambda }_1^{(p)}{a}_p+{\lambda }_1^{(x)}{J}_{-}\right)\\ \langle 0,0|e^{a_p}{e}^{J_{-}}\exp \left({\alpha }_0+{\lambda }_0^{(p)}{a}_p+{\lambda }_0^{(x)}{J}_{-}\right)).& (10)\end{array}$

The set of variational parameters is α_R = {c₁, c₀, p₁, p₀, θ₁, θ₀}. Here c₁(c₀) represents the probability of the DNA being in state 1 (state 0), while p₁(p₀) and Nθ₁(Nθ₀) represent the mean number of proteins and modified nucleosomes when DNA is in state 1 (state 0). ${\alpha }_L=\{{\alpha }_1,{\alpha }_0,{\lambda }_1^{(p)},{\lambda }_0^{(p)}{\lambda }_1^{(x)},{\lambda }_0^{(x)}\}$ are the corresponding conjugate variables.

Plugging (10) and (9) into (7), we obtain the following set of variational equations

$\begin{array}{ll}\frac{\text{d}{c}_1}{\text{d}t}=c_{0}f-c_1{\langle h(n_p,n_x)\rangle }_1& (\mathrm{11a})\end{array}$

$\begin{array}{ll}\frac{\text{d}{c}_0}{\text{d}t}=-c_{0}f+c_1{\langle h(n_p,n_x)\rangle }_1& (\mathrm{11b})\end{array}$

$\begin{array}{lll}{c}_1\frac{\text{d}{p}_1}{\text{d}t}+p_1\frac{\text{d}{c}_1}{\text{d}t}& =c_1{g}_1-c_{1}k{p}_1+c_{0}f{p}_0-c_1{\langle n_{p}h(n_p,n_x)\rangle }_1& (\mathrm{11c})\end{array}$

$\begin{array}{lll}{c}_0\frac{\text{d}{p}_0}{\text{d}t}+p_0\frac{\text{d}{c}_0}{\text{d}t}& =c_0{g}_0-c_{0}k{p}_0-c_{0}f{p}_0+c_1{\langle n_{p}h(n_p,n_x)\rangle }_1& (\mathrm{11d})\end{array}$

$\begin{array}{l}N{\theta }_1\frac{\text{d}{c}_1}{\text{d}t}+N{c}_1\frac{\text{d}{\theta }_1}{\text{d}t}=c_1\left(\frac{s_1}{N^3}\right){\langle n_x^{\underset{\_}{2}}(N-n_x)\rangle }_1\\ -c_1\left(\frac{z_1}{N^3}\right){\langle {(N-n_x)}^{\underset{\_}{2}}(n_x)\rangle }_1\\ +c_1\frac{q}{N}(-{\langle n_x\rangle }_1+{\langle N-n_x\rangle }_1)\\ +c_{0}fN{\theta }_0-c_1{\langle n_{x}h(n_p,n_x)\rangle }_1& (11e)\end{array}$

$\begin{array}{l}N{\theta }_0\frac{\text{d}{c}_0}{\text{d}t}+N{c}_0\frac{\text{d}{\theta }_0}{\text{d}t}=c_0\left(\frac{s_0}{N^3}\right){\langle n_x^{\underset{\_}{2}}(N-n_x)\rangle }_0\\ -c_0\left(\frac{z_0}{N^3}\right){\langle {(N-n_x)}^{\underset{\_}{2}}(n_x)\rangle }_0\\ +c_0\frac{q}{N}(-{\langle n_x\rangle }_0+{\langle N-n_x\rangle }_0)-c_{0}fN{\theta }_0\\ +c_1{\langle n_{x}h(n_p,n_x)\rangle }_1.& (\mathrm{11f})\end{array}$

The angular brackets represent ensemble averaging over protein numbers and modified nucleosomes, i.e., ${\langle ·\rangle }_i=\sum _{n_p,n_x}·\frac{e^{-p_i}}{n_p!}{p}_i^{n_p}\left(\begin{array}{c}N\\ n_x\end{array}\right){\theta }_k^{n_x}{(1-{\theta }_k)}^{N-n_x}$. We also make the simplifying approximation for the average binding rate as $\langle h(n_p,n_x)\rangle =\langle \frac{n_p(n_p-1)}{1+\text{exp}(0.5(n_x-35))}\rangle \approx \frac{{\langle n}_p(n_p-1)\rangle }{1+\text{exp}(0.5({\langle n}_x\rangle -35))}$. Numerical integration of Equation (11) yields the time evolution of the variational parameters α_R, from which the probability distributions can be determined using Equation (9).

We solved Equation (11) using scipy.integrate.odeint() module in python with a time step of 0.01 s. The initial conditions were varied and individual trajectories were integrated for 10⁵ s till convergence to obtain the steady state results.

4. Results

Using the variational equations, we studied the dependence of steady-state solutions on the rate of noisy histone mark modification, q. For comparison, we carried out stochastic simulations of the kinetic network using the Gillespie algorithm (Gillespie, 1977) at selected q-values. The noisy modification rate and, in particular, its relative value to the rate for recruited conversions is an important parameter for cell differentiation. For example, recruited conversions arise due to the diffusion of histone-modifying enzymes from modified nucleosomes to the nearby unmodified ones. The more open chromatin conformation seen in stem cells with larger inter-nucleosome distances (Gaspar-Maia et al., 2011; Mas et al., 2018) will, therefore, suppress recruited conversions in favor of the noisy ones. As cells differentiate, chromatin will become more compact, and the importance of noisy conversions will decline. Previous studies of isolated epigenetic switches (Dodd et al., 2007; Micheelsen et al., 2010; Sood and Zhang, 2020) also found q as an important parameter that controls the onset and maintenance of bistability in the epigenetic switch.

In Figure 2, we show the probability distributions obtained from stochastic simulations and from the variational approach at q = 100, 10, and 0.5. We notice that the Binomial ansatz introduced in the Theory section captures the distribution for the number of modified nucleosomes with quantitative accuracy (Figures 2A–C). The Poissonian ansatz also performs well for the distribution of protein numbers at small and medium q values, though deviations from stochastic simulations are apparent at large q (Figures 2D–F). The inconsistency between the two distributions in that regime is mainly due to underestimating the population of intermediate states that bridge the high and low gene expression values by the variation method.

In addition to steady-state solutions, the time evolution of observables, such as the mean number of proteins and modified nucleosomes, can be determined using the variational approach as well. As shown in Figure 3, in parameter regimes where the effect of fluctuations is not too drastic, the dynamical trajectories determined using Equation (11) are in quantitative agreements with those computed using stochastic simulations.

Given its reasonable performance, we next applied the variational approach to study the network model's steady-state behavior at a broader range of q-values. As already mentioned, q is an important variable that might be tuned along the developmental axis for cell differentiation. For large q values, chromatin stabilizes in an undecided state with roughly half the nucleosomes modified (active) and the other half carrying no modification (repressive). The corresponding protein expression is noisy with a broad probability distribution. Stochastic simulations further support a significant mixing between “on” and “off” gene states, and an unambiguous assignment of either state is not warranted (Figure 2D). When the value for q is quenched, we observe the emergence of a coherent epigenetic state along with coherent gene expression. Therefore, both switches are turned on and the combined system exhibits a single attractor. At even lower values of q, both the epigenetic and gene switch exhibit bistability.

We note that the chromatin state changes described above differs from that of an isolated epigenetic switch studied previously (Sood and Zhang, 2020). There, we saw a shift from a unimodal probability distribution indicating an equal admixture of modified and unmodified nucleosomes to a symmetric bimodal probability distribution as the value for q is quenched. The appearance of a single coherent epigenetic state in Figure 4 is a result of the coupling with the gene switch in our model, which breaks the symmetry between active and repressive chromatin states. The coupling works both ways. In an isolated gene switch, a single state with high gene expression is not expected either. Modulating the kinetics of TF binding to the promoter only resolves a broad probability distribution exhibiting no coherent gene expression to a bistable state with high and low levels of gene expression (Walczak et al., 2005a).

FIGURE 4

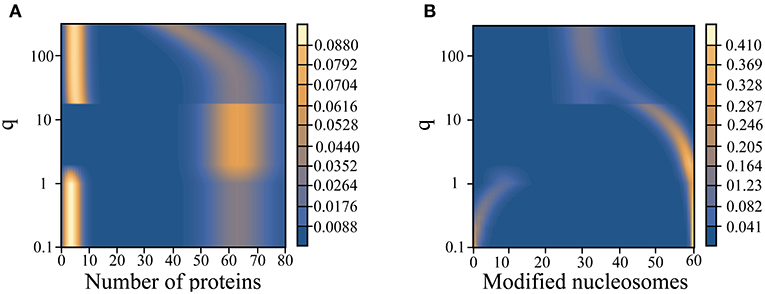
Figure 4. Variation of the steady state probability distribution for the number of proteins (A) and modified nucleosomes (B) as a function of the noisy histone modification rate, q.

5. Discussion

We introduced a kinetic model that couples a genetic network with an epigenetic switch to study the combined role of transcription factors and histone modifications in regulating gene expression. An approximation scheme based on the variational approach was further developed to obtain steady-state solutions. This method is unencumbered by the complexity associated with numerical simulations and more detailed analytical calculations. It would be a useful tool for exploratory studies of the parameter space and identifying regions of interest. While we focused our analysis on a single gene, the variational method can be relatively easily generalized to networks with multiple interacting genetic and epigenetic switches that provide more realistic modeling of stem cell differentiation (Zhang and Wolynes, 2014).

We explored the behavior of the network model across a wide range of parameters. Our model exhibits a poised state for the gene switch at high q, where the chromatin system contains an equal admixture of modified and unmodified nucleosomes. The network in this parameter regime appears to qualitatively capture the behavior of chromatin and gene expression in undifferentiated stem cells. In particular, stem cells are known to exhibit bivalent chromatin with both activating and repressive marks (Bernstein et al., 2006; Vastenhouw and Schier, 2012) and noisy gene expression profiles (Kar et al., 2017). We point out that the exact definition of bivalent chromatin remains controversial, and multiple mechanisms have been proposed for its formation (Azuara et al., 2006; Sneppen and Ringrose, 2019; Lim and Meshorer, 2020). Additional studies are needed to determine whether the stochastic conversion observed here is the key driver for the observed chromatin bivalency.

Upon quenching q, the gene is activated along with a concomitant resolution of the chromatin state. The coupling between the two switches reinforces the stability of the active state and can lead to more robust upregulation of gene expression upon cell differentiation. It also ensures that the genetic and epigenetic switches are always in sync. We observe at most two steady states representing active chromatin with high gene expression and repressive chromatin with low gene expression. We note that the inactive state only becomes stable at minimal q values, arguing for strong noise suppression for gene silencing. Its limited stability may explain the presence of DNA methylation on top of histone modifications to safeguard the silent state against perturbations that might arise from fluctuation in protein concentration or histone marks during cell division.

The strong dependence of the landscape tomography on q shown in Figure 4 suggests that the histone modification rate may act like a knob to be tuned along the developmental axis to facilitate cellular differentiation. Of course, the presented landscape is probably too crude a simplification to be termed the Waddington landscape since many additional factors that contribute to the stability of gene expression patterns could be varied along the developmental axis as well.

In favorable regimes, the variational approach produces results of quantitative accuracy. The discrepancy between the probability distribution obtained from stochastic simulations and the variational method in the high q region can be attributed to the fact that the Poisson ansatz does not sufficiently account for the variance and the effect of fluctuations which become increasingly important as the value for q increases. This situation can be remedied by going beyond the Poisson ansatz, and utilizing the superposition ansatz as described in Ohkubo (2008). Mathematically, this would mean to modify our ansatz as follows,

$\begin{array}{l}|\Psi \rangle \\ =\left(\begin{array}{c}{\int }_0^{\infty }\text{d}{p}_1{F}(p_1;\{{\lambda }_j^{(1)}\})c_1\exp \left(p_1(a_p^{†}-1)\right){(1-{\theta }_1)}^N\exp \left(\frac{{\theta }_1}{1-{\theta }_1}{J}_{+}\right)|0,0\rangle \\ {\int }_0^{\infty }\text{d}{p}_0{F}(p_0;\{{\lambda }_j^{(0)}\})c_0\exp \left(p_0(a_p^{†}-1)\right){(1-{\theta }_0)}^N\exp \left(\frac{{\theta }_0}{1-{\theta }_0}{J}_{+}\right)|0,0\rangle \end{array}\right).& (12)\end{array}$

This new “superposition ansatz” is constructed by the superposition of the coherent states (i.e., Poisson distribution) as defined in (12), where now ${F}$ serves as the variational function. Hence, the real probability distribution is obtained by the superposition of the Poisson distributions of mean p_i weighed by the distribution ${F}$ with parameters $\{{\lambda }_j^{(i)}\}$. We anticipate that doing so can not only improve the agreement between theory and simulation but can in principle allow for the computation of time evolution of other interesting quantities such as variance, and covariance in addition to means. However, in general the choice of an appropriate ${F}$ is a non-trivial problem, and thus has been avoided in this text in favor of a clearer exposition. The choice of appropriate variational functions can be guided by the work done on exact solutions of the master equations of genetic switches (Hornos et al., 2005; Shahrezaei and Swain, 2008; Ramos et al., 2011).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.

Author Contributions

AS and BZ conceived and designed the work, interpreted the results, and wrote the manuscript. AS carried out computer implementation and data analysis. BZ supervised the project. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the National Institutes of Health (Grant 1R35GM133580).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2020.636724/full#supplementary-material

References

Alexander, F. J., and Eyink, G. L. (1997). Rayleigh-ritz calculation of effective potential far from equilibrium. Phys. Rev. Lett. 78, 1–4. doi: 10.1103/PhysRevLett.78.1

CrossRef Full Text | Google Scholar

Angel, A., Song, J., Dean, C., and Howard, M. (2011). A polycomb-based switch underlying quantitative epigenetic memory. Nature 476, 105–108. doi: 10.1038/nature10241

PubMed Abstract | CrossRef Full Text | Google Scholar

Artyomov, M. N., Meissner, A., and Chakraborty, A. K. (2010). A model for genetic and epigenetic regulatory networks identifies rare pathways for transcription factor induced pluripotency. PLoS Comput. Biol. 6:e1000785. doi: 10.1371/journal.pcbi.1000785

PubMed Abstract | CrossRef Full Text | Google Scholar

Ashwin, S. S., and Sasai, M. (2015). Effects of collective histone state dynamics on epigenetic landscape and kinetics of cell reprogramming. Sci. Rep. 5, 1–12. doi: 10.1038/srep16746

PubMed Abstract | CrossRef Full Text | Google Scholar

Azuara, V., Perry, P., Sauer, S., Spivakov, M., Jörgensen, H. F., John, R. M., et al. (2006). Chromatin signatures of pluripotent cell lines. Nat. Cell Biol. 8, 532–538. doi: 10.1038/ncb1403

PubMed Abstract | CrossRef Full Text | Google Scholar

Bannister, A. J., and Kouzarides, T. (2011). Regulation of chromatin by histone modifications. Cell Res. 21, 381–395. doi: 10.1038/cr.2011.22

PubMed Abstract | CrossRef Full Text | Google Scholar

Bernstein, B. E., Mikkelsen, T. S., Xie, X., Kamal, M., Huebert, D. J., Cuff, J., et al. (2006). A bivalent chromatin structure marks key developmental genes in embryonic stem cells. Cell 125, 315–326. doi: 10.1016/j.cell.2006.02.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhattacharyya, B., Wang, J., and Sasai, M. (2020). Stochastic epigenetic dynamics of gene switching. Phys. Rev. E 102:042408. doi: 10.1103/PhysRevE.102.042408

PubMed Abstract | CrossRef Full Text | Google Scholar

Binder, H., Steiner, L., Przybilla, J., Rohlf, T., Prohaska, S., and Galle, J. (2013). Transcriptional regulation by histone modifications: towards a theory of chromatin re-organization during stem cell differentiation. Phys. Biol. 10:026006. doi: 10.1088/1478-3975/10/2/026006

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, Y., Lu, H.-M., and Liang, J. (2010). Probability landscape of heritable and robust epigenetic state of lysogeny in phage lambda. Proc. Natl. Acad. Sci. U.S.A. 107, 18445–18450. doi: 10.1073/pnas.1001455107

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, H., Thill, P., and Cao, J. (2016). Transitions in genetic toggle switches driven by dynamic disorder in rate coefficients. J. Chem. Phys. 144:175104. doi: 10.1063/1.4948461

PubMed Abstract | CrossRef Full Text | Google Scholar

David-Rus, D., Mukhopadhyay, S., Lebowitz, J. L., and Sengupta, A. M. (2009). Inheritance of epigenetic chromatin silencing. J. Theor. Biol. 258, 112–120. doi: 10.1016/j.jtbi.2008.12.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Dayarian, A., and Sengupta, A. M. (2013). Titration and hysteresis in epigenetic chromatin silencing. Phys. Biol. 10:036005. doi: 10.1088/1478-3975/10/3/036005

PubMed Abstract | CrossRef Full Text | Google Scholar

Dodd, I. B., Micheelsen, M. A., Sneppen, K., and Thon, G. (2007). Theoretical analysis of epigenetic cell memory by nucleosome modification. Cell 129:813. doi: 10.1016/j.cell.2007.02.053

PubMed Abstract | CrossRef Full Text | Google Scholar

Eyink, G. L. (1996). Action principle in nonequilibrium statistical dynamics. Phys. Rev. E 54, 3419–3435. doi: 10.1103/PhysRevE.54.3419

PubMed Abstract | CrossRef Full Text | Google Scholar

Flavahan, W. A., Drier, Y., Johnstone, S. E., Hemming, M. L., Tarjan, D. R., Hegazi, E., et al. (2019). Altered chromosomal topology drives oncogenic programs in SDH-deficient gists. Nature 575, 229–233. doi: 10.1038/s41586-019-1668-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Folguera-Blasco, N., Pérez-Carrasco, R., Cuyàs, E., Menendez, J. A., and Alarcón, T. (2019). A multiscale model of epigenetic heterogeneity-driven cell fate decision-making. PLoS Comput. Biol. 15:e1006592. doi: 10.1371/journal.pcbi.1006592

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, H.-C., and Sasaki, R. (1997). Negative binomial and multinomial states: probability distributions and coherent states. J. Math. Phys. 38, 3968–3987. doi: 10.1063/1.532102

CrossRef Full Text | Google Scholar

Fu, H.-C., and Sasaki, R. (1998). Probability distributions and coherent states of, and algebras. J. Phys. A 31, 901–925. doi: 10.1088/0305-4470/31/3/006

CrossRef Full Text | Google Scholar

Furey, T. S., and Sethupathy, P. (2013). Genetics driving epigenetics. Science 342, 705–706. doi: 10.1126/science.1246755

PubMed Abstract | CrossRef Full Text | Google Scholar

Gaspar-Maia, A., Alajem, A., Meshorer, E., and Ramalho-Santos, M. (2011). Open chromatin in pluripotency and reprogramming. Nat. Rev. Mol. Cell Biol. 12, 36–47. doi: 10.1038/nrm3036

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillespie, D. T. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361. doi: 10.1021/j100540a008

CrossRef Full Text | Google Scholar

Goldberg, A. D., Allis, C. D., and Bernstein, E. (2007). Epigenetics: a landscape takes shape. Cell 128, 635–638. doi: 10.1016/j.cell.2007.02.006

CrossRef Full Text | Google Scholar

Hasty, J., Pradines, J., Dolnik, M., and Collins, J. J. (2000). Noise-based switches and amplifiers for gene expression. Proc. Natl. Acad. Sci. U.S.A. 97, 2075–2080. doi: 10.1073/pnas.040411297

PubMed Abstract | CrossRef Full Text | Google Scholar

Hornos, J. E. M., Schultz, D., Innocentini, G. C. P., Wang, J., Walczak, A. M., Onuchic, J. N., et al. (2005). Self-regulating gene: An exact solution. Phys. Rev. E 72:051907. doi: 10.1103/PhysRevE.72.051907

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, R., and Lei, J. (2018). Dynamics of gene expression with positive feedback to histone modifications at bivalent domains. Int. J. Modern Phys. B 32:1850075. doi: 10.1142/S0217979218500753

CrossRef Full Text | Google Scholar

Johnson, A. D., Poteete, A. R., Lauer, G., Sauer, R. T., Ackers, G. K., and Ptashne, M. (1981). λ repressor and cro–components of an efficient molecular switch. Nature 294, 217–223. doi: 10.1038/294217a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Jost, D. (2014). Bifurcation in epigenetics: Implications in development, proliferation, and diseases. Phys. Rev. E 89:010701. doi: 10.1103/PhysRevE.89.010701

PubMed Abstract | CrossRef Full Text | Google Scholar

Kærn, M., Elston, T. C., Blake, W. J., and Collins, J. J. (2005). Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 6, 451–464. doi: 10.1038/nrg1615

PubMed Abstract | CrossRef Full Text | Google Scholar

Kar, G., Kim, J. K., Kolodziejczyk, A. A., Natarajan, K. N., Triglia, E. T., Mifsud, B., et al. (2017). Flipping between Polycomb repressed and active transcriptional states introduces noise in gene expression. Nat. Commun. 8, 1–13. doi: 10.1038/s41467-017-00052-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, K.-Y., and Wang, J. (2007). Potential energy landscape and robustness of a gene regulatory network: toggle switch. PLoS Comput. Biol. 3:e30060. doi: 10.1371/journal.pcbi.0030060

PubMed Abstract | CrossRef Full Text | Google Scholar

Krishnakumar, R., and Kraus, W. L. (2010). Parp-1 regulates chromatin structure and transcription through a kdm5b-dependent pathway. Mol. Cell 39, 736–749. doi: 10.1016/j.molcel.2010.08.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, B. P., and Cardy, J. (1995). Renormalization group study of the a+b->0 diffusion-limited reaction. J. Stat. Phys. 80, 971–1007. doi: 10.1007/BF02179861

CrossRef Full Text | Google Scholar

Lim, P. S. L., and Meshorer, E. (2020). Dppa2 and dppa4 safeguard bivalent chromatin in order to establish a pluripotent epigenome. Nat. Struct. Mol. Biol. 27, 685–686. doi: 10.1038/s41594-020-0453-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lister, R., Pelizzola, M., Dowen, R. H., Hawkins, R. D., Hon, G., Tonti-Filippini, J., et al. (2009). Human DNA methylomes at base resolution show widespread epigenomic differences. Nature 462, 315–322. doi: 10.1038/nature08514

PubMed Abstract | CrossRef Full Text | Google Scholar

Loh, Y.-H., Ng, J.-H., and Ng, H.-H. (2008). Molecular framework underlying pluripotency. Cell Cycle 7, 885–891. doi: 10.4161/cc.7.7.5636

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, R., Markowetz, F., Unwin, R. D., Leek, J. T., Airoldi, E. M., MacArthur, B. D., et al. (2009). Systems-level dynamic analyses of fate change in murine embryonic stem cells. Nature 462, 358–362. doi: 10.1038/nature08575

PubMed Abstract | CrossRef Full Text | Google Scholar

Lv, C., Li, X., Li, F., and Li, T. (2015). Energy landscape reveals that the budding yeast cell cycle is a robust and adaptive multi-stage process. PLoS Comput. Biol. 11:e1004156. doi: 10.1371/journal.pcbi.1004156

CrossRef Full Text | Google Scholar

Margueron, R., and Reinberg, D. (2010). Chromatin structure and the inheritance of epigenetic information. Nat. Rev. Genet. 11, 285–296. doi: 10.1038/nrg2752

PubMed Abstract | CrossRef Full Text | Google Scholar

Mariani, L., Schulz, E. G., Lexberg, M. H., Helmstetter, C., Radbruch, A., Löhning, M., et al. (2010). Short-term memory in gene induction reveals the regulatory principle behind stochastic il-4 expression. Mol. Syst. Biol. 6:359. doi: 10.1038/msb.2010.13

PubMed Abstract | CrossRef Full Text | Google Scholar

Mas, G., Blanco, E., Ballaré, C., Sansó, M., Spill, Y. G., Hu, D., et al. (2018). Promoter bivalency favors: an open chromatin architecture in embryonic stem cells. Nat. Genet. 50, 1452–1462. doi: 10.1038/s41588-018-0218-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Matsushita, Y., and Kaneko, K. (2020). Homeorhesis in waddington's landscape by epigenetic feedback regulation. Phys. Rev. Res. 2:023083. doi: 10.1103/PhysRevResearch.2.023083

CrossRef Full Text | Google Scholar

Micheelsen, M. A., Mitarai, N., Sneppen, K., and Dodd, I. B. (2010). Theory for the stability and regulation of epigenetic landscapes. Phys. Biol. 7:026010. doi: 10.1088/1478-3975/7/2/026010

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller-Jensen, K., Dey, S. S., Schaffer, D. V., and Arkin, A. P. (2011). Varying virulence: epigenetic control of expression noise and disease processes. Trends Biotechnol. 29, 517–525. doi: 10.1016/j.tibtech.2011.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Ohkubo, J. (2008). Approximation scheme for master equations: variational approach to multivariate case. J. Chem. Phys. 129:044108. doi: 10.1063/1.2957462

PubMed Abstract | CrossRef Full Text | Google Scholar

Orkin, S. H., and Zon, L. I. (2008). Hematopoiesis: an evolving paradigm for stem cell biology. Cell 132, 631–644. doi: 10.1016/j.cell.2008.01.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsons, T., and Zhang, B. (2019). Critical role of histone tail entropy in nucleosome unwinding. J. Chem. Phys. 150:185103. doi: 10.1063/1.5085663

PubMed Abstract | CrossRef Full Text | Google Scholar

Ptashne, M., Jeffrey, A., Johnson, A., Maurer, R., Meyer, B., Pabo, C., et al. (1980). How the λ repressor and CRO work. Cell 19, 1–11. doi: 10.1016/0092-8674(80)90383-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, Y., Reyes, A., Johnstone, S. E., Aryee, M. J., Bernstein, B. E., and Zhang, B. (2020). Data-driven polymer model for mechanistic exploration of diploid genome organization. Biophys. J. 119, 1905–1916. doi: 10.1016/j.bpj.2020.09.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiu, B., Zhou, T., and Zhang, J. (2020). Molecular-memory-driven phenotypic switching in a genetic toggle switch without cooperative binding. Phys. Rev. E 101:022409. doi: 10.1103/PhysRevE.101.022409

PubMed Abstract | CrossRef Full Text | Google Scholar

Ralston, A., and Rossant, J. (2005). Genetic regulation of stem cell origins in the mouse embryo. Clin. Genet. 68, 106–112. doi: 10.1111/j.1399-0004.2005.00478.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramos, A. F., Innocentini, G. C. P., and Hornos, J. E. M. (2011). Exact time-dependent solutions for a self-regulating gene. Phys. Rev. E 83:062902. doi: 10.1103/PhysRevE.83.062902

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenfeld, N., Elowitz, M. B., and Alon, U. (2002). Negative autoregulation speeds the response times of transcription networks. J. Mol. Biol. 323, 785–793. doi: 10.1016/S0022-2836(02)00994-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Rowley, M. J., and Corces, V. G. (2018). Organizational principles of 3D genome architecture. Nat. Rev. Genet. 19, 789–800. doi: 10.1038/s41576-018-0060-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Sasai, M., Kawabata, Y., Makishi, K., Itoh, K., and Terada, T. P. (2013). Time scales in epigenetic dynamics and phenotypic heterogeneity of embryonic stem cells. PLoS Comput. Biol. 9:e1003380. doi: 10.1371/journal.pcbi.1003380

PubMed Abstract | CrossRef Full Text | Google Scholar

Sasai, M., and Wolynes, P. G. (2003). Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. U.S.A. 100, 2374–2379. doi: 10.1073/pnas.2627987100

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlick, T., Hayes, J., and Grigoryev, S. (2012). Toward convergence of experimental studies and theoretical modeling of the chromatin fiber. J. Biol. Chem. 287, 5183–5191. doi: 10.1074/jbc.R111.305763

PubMed Abstract | CrossRef Full Text

Sedighi, M., and Sengupta, A. M. (2007). Epigenetic chromatin silencing: bistability and front propagation. Phys. Biol. 4, 246–255. doi: 10.1088/1478-3975/4/4/002

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahrezaei, V., and Swain, P. S. (2008). Analytical distributions for stochastic gene expression. Proc. Natl. Acad. Sci. U.S.A. 105, 17256–17261. doi: 10.1073/pnas.0803850105

PubMed Abstract | CrossRef Full Text | Google Scholar

Sneppen, K., and Mitarai, N. (2012). Multistability with a metastable mixed state. Phys. Rev. Lett. 109:100602. doi: 10.1103/PhysRevLett.109.100602

PubMed Abstract | CrossRef Full Text | Google Scholar

Sneppen, K., and Ringrose, L. (2019). Theoretical analysis of polycomb-trithorax systems predicts that poised chromatin is bistable and not bivalent. Nat. Commun. 10:2133. doi: 10.1038/s41467-019-10130-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sood, A., and Zhang, B. (2020). Quantifying epigenetic stability with minimum action paths. Phys. Rev. E 101:062409. doi: 10.1103/PhysRevE.101.062409

PubMed Abstract | CrossRef Full Text | Google Scholar

Tate, P. H., and Bird, A. P. (1993). Effects of DNA methylation on DNA-binding proteins and gene expression. Curr. Opin. Genet. Dev. 3, 226–231. doi: 10.1016/0959-437X(93)90027-M

PubMed Abstract | CrossRef Full Text | Google Scholar

Täuber, U. C. (2014). Critical Dynamics A Field Theory Approach to Equilibrium and Non-Equilibrium Scaling Behavior. Cambridge: Cambridge University Press.

Google Scholar

Vastenhouw, N. L., and Schier, A. F. (2012). Bivalent histone modifications in early embryogenesis. Curr. Opin. Cell Biol. 24, 374–386. doi: 10.1016/j.ceb.2012.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Venegas-Ortiz, J., and Evans, M. R. (2011). Analytical study of an exclusive genetic switch. J. Phys. A 44:355001. doi: 10.1088/1751-8113/44/35/355001

CrossRef Full Text | Google Scholar

Waddington, C., and Kacser, H. (1957). The Strategy of the Genes: A Discussion of Some Aspects of Theoretical Biology. London: Allen & Unwin.

Google Scholar

Walczak, A. M., Onuchic, J. N., and Wolynes, P. G. (2005a). Absolute rate theories of epigenetic stability. Proc. Natl. Acad. Sci. U.S.A. 102, 18926–18931. doi: 10.1073/pnas.0509547102

PubMed Abstract | CrossRef Full Text | Google Scholar

Walczak, A. M., Sasai, M., and Wolynes, P. G. (2005b). Self-consistent proteomic field theory of stochastic gene switches. Biophys. J. 88, 828–850. doi: 10.1529/biophysj.104.050666

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Zhang, K., Xu, L., and Wang, E. (2011). Quantifying the Waddington landscape and biological paths for development and differentiation. Proc. Natl. Acad. Sci. U.S.A. 108, 8257–8262. doi: 10.1073/pnas.1017017108

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Song, C., Zhang, H., Wu, Z., Tian, X.-J., and Xing, J. (2014). Epigenetic state network approach for describing cell phenotypic transitions. Interface Focus 4:20130068. doi: 10.1098/rsfs.2013.0068

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, W. J., Qi, Y., and Zhang, B. (2020). Characterizing chromatin folding coordinate and landscape with deep learning. PLoS Comput. Biol. 16:e1008262. doi: 10.1371/journal.pcbi.1008262

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, W. J., and Zhang, B. (2019). Learning the formation mechanism of domain-level chromatin states with epigenomics data. Biophys. J. 116, 2047–2056. doi: 10.1016/j.bpj.2019.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, B.-L., and Tao, Y. (2006). External noise and feedback regulation: Steady-state statistics of auto-regulatory genetic network. J. Theor. Biol. 243, 214–221. doi: 10.1016/j.jtbi.2006.06.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, B., and Wolynes, P. G. (2014). Stem cell differentiation as a many-body problem. Proc. Natl. Acad. Sci. U.S.A. 111, 10185–10190. doi: 10.1073/pnas.1408561111

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, K., Sasai, M., and Wang, J. (2013). Eddy current and coupled landscapes for nonadiabatic and nonequilibrium complex system dynamics. Proc. Natl. Acad. Sci. U.S.A. 110, 14930–14935. doi: 10.1073/pnas.1305604110

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Liu, N., Lin, W., and Li, C. (2019). Quantifying the interplay between genetic and epigenetic regulations in stem cell development. New J. Phys. 21:103042. doi: 10.1088/1367-2630/ab4c82

CrossRef Full Text | Google Scholar

Zhou, V. W., Goren, A., and Bernstein, B. E. (2011). Charting histone modifications and the functional organization of mammalian genomes. Nat. Rev. Genet. 12, 7–18. doi: 10.1038/nrg2905

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, H., Wang, G., and Qian, J. (2016). Transcription factors as readers and effectors of dna methylation. Nature Reviews Genetics. 17, 551–565. doi: 10.1038/nrg.2016.83

PubMed Abstract | CrossRef Full Text | Google Scholar