- 1Department of Human Genetics, KU Leuven, Leuven, Belgium
- 2Medical Imaging Research Center, University Hospitals Leuven, Leuven, Belgium
- 3Department of Electrical Engineering, ESAT/PSI, KU Leuven, Leuven, Belgium
- 4Research Group Experimental Otorhinolaryngology, Department of Neurosciences, KU Leuven, Leuven, Belgium
- 5Forensic Biomedical Sciences, Department of Imaging and Pathology, KU Leuven, Leuven, Belgium
- 6Applied Clinical Research and Public Health, School of Dentistry, College of Biomedical and Life Sciences, Cardiff University, Cardiff, United Kingdom
- 7Murdoch Childrens Research Institute, Melbourne, VIC, Australia
Introduction: The human face is a complex trait displaying a strong genetic component as illustrated by various studies on facial heritability. Most of these start from sparse descriptions of facial shape using a limited set of landmarks. Subsequently, facial features are preselected as univariate measurements or principal components and the heritability is estimated for each of these features separately. However, none of these studies investigated multivariate facial features, nor the co-heritability between different facial features. Here we report a spatially dense multivariate analysis of facial heritability and co-heritability starting from data from fathers and their children available within ALSPAC. Additionally, we provide an elaborate overview of related craniofacial heritability studies.
Methods: In total, 3D facial images of 762 father-offspring pairs were retained after quality control. An anthropometric mask was applied to these images to establish spatially dense quasi-landmark configurations. Partial least squares regression was performed and the (co-)heritability for all quasi-landmarks (∼7160) was computed as twice the regression coefficient. Subsequently, these were used as input to a hierarchical facial segmentation, resulting in the definition of facial modules that are internally integrated through the biological mechanisms of inheritance. Finally, multivariate heritability estimates were obtained for each of the resulting modules.
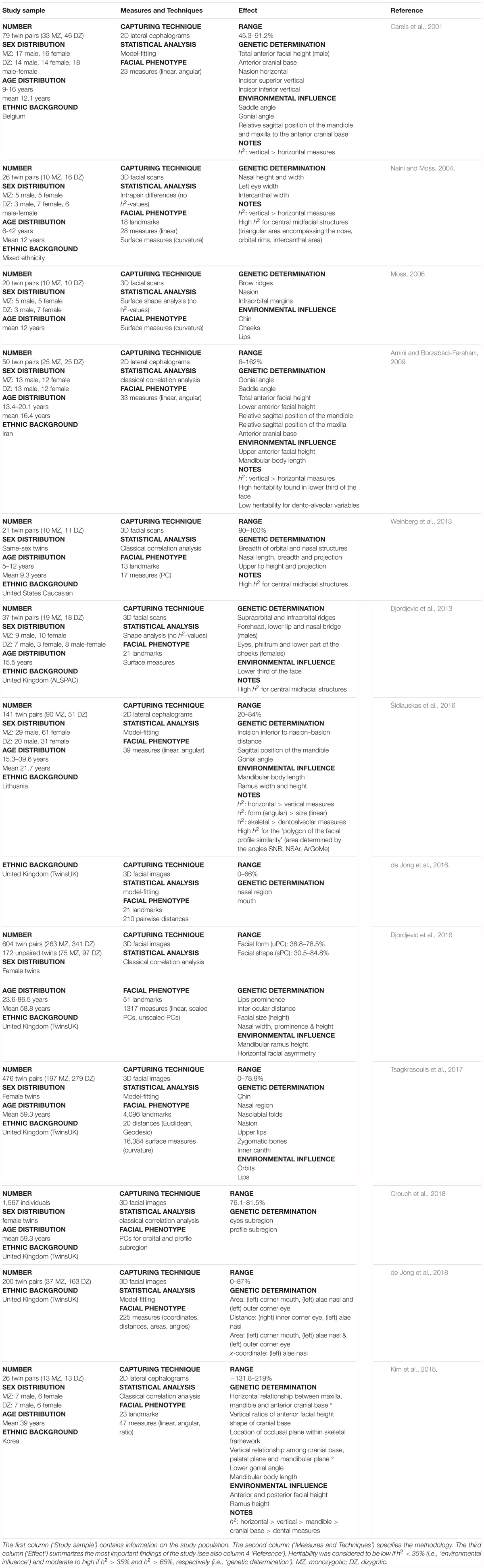
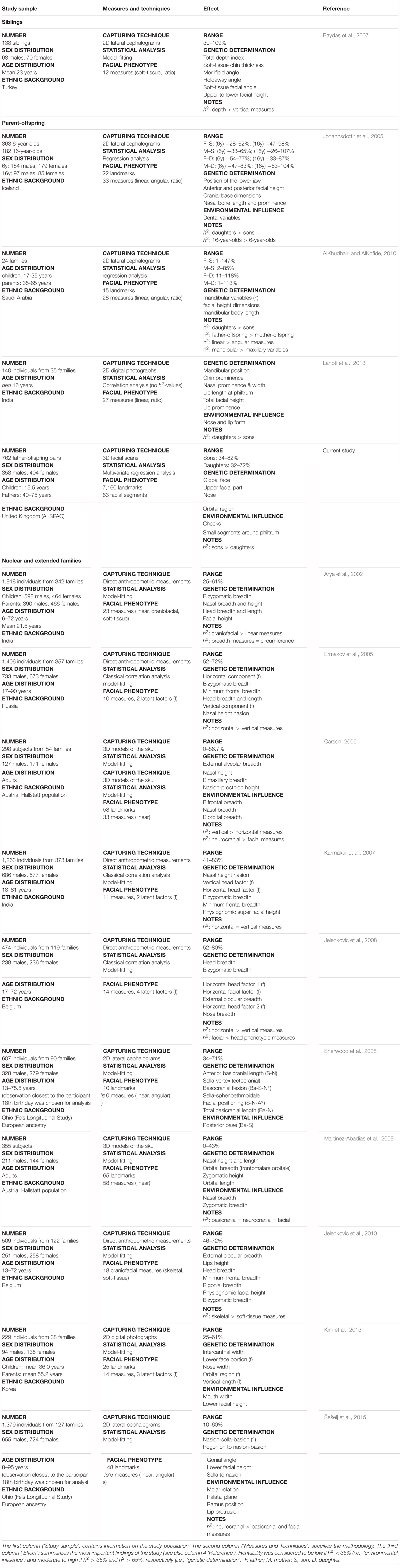
Results: Nearly all modular estimates reached statistical significance under 1,000,000 permutations and after multiple testing correction (p ≤ 1.3889 × 10-3), displaying low to high heritability scores. Particular facial areas showing the greatest heritability were similar for both sons and daughters. However, higher estimates were obtained in the former. These areas included the global face, upper facial part (encompassing the nasion, zygomas and forehead) and nose, with values reaching 82% in boys and 72% in girls. The lower parts of the face only showed low to moderate levels of heritability.
Conclusion: In this work, we refrain from reducing facial variation to a series of individual measurements and analyze the heritability and co-heritability from spatially dense landmark configurations at multiple levels of organization. Finally, a multivariate estimation of heritability for global-to-local facial segments is reported. Knowledge of the genetic determination of facial shape is useful in the identification of genetic variants that underlie normal-range facial variation.
Introduction
The human face is a complex trait displaying a strong genetic component (Kohn, 1991), as evidenced by remarkable facial similarity between identical twins, clear facial resemblances within families, geographic populations (Hopman et al., 2014) and the sexes (Claes et al., 2012b), and finally the distinctive facial features associated with particular genetic conditions (Hammond, 2007; Baynam et al., 2013). This suggests that inter-individual variation in craniofacial morphology is largely determined by genetic variation, most likely in combination with diverse environmental influences.
Studies on craniofacial heritability provide insight into the relative contribution of genetic versus environmental effects on craniofacial parameters. These studies highlight similarities as well as differences in patterns of inheritance, resulting from differences in the study population (sample size, age of assessment, sex, ethnicity), in the capturing technique (2D or 3D), in the way facial shape is measured and finally in the statistical methods yielded. Most craniofacial heritability studies are performed on twin and family (siblings or parent-offspring) databases and many of these apply 2D imaging techniques, limiting their results due to the loss of information when quantifying the facial phenotype in two dimensions only (Tables 1, 2). More recently, 3D imaging techniques are being used to characterize facial morphology (Tables 1–3). All studies, 2D as well as 3D, start from sparse descriptions of facial shape using a limited set of landmarks, with one recent exception that uses spatially dense landmarking instead (Tsagkrasoulis et al., 2017). Variation in these landmarks is simplified by the projection of multivariate landmark configurations onto principal components (PC) or by measuring geometric features such as distances, curvature, ratios and/or angles from the landmarks. Subsequently, a heritability score is computed for each individual PC or geometric feature separately. However, any preselection of individual PCs or geometric features fails to capture the full-range of facial variations as combinations of these measurements are not considered. Finally, heritability studies today do not investigate co-inheritance between different facial features.
In this work, we present a global-to-local analysis of heritability and co-heritability of multivariate facial modules in a father-offspring design. First, we establish spatially dense quasi-landmarks representing complete facial shape and compute 3D landmark heritability as well as 3D pairwise landmark co-heritability. Subsequently, we apply hierarchical spectral clustering to these values and define 63 modules (multiple 3D landmarks grouped together) of co-inheritance, which when analyzed as groups, provide a multivariate estimation of heritability for various facial segments, ranging from the full face (global) to smaller facial regions (local). Finally, in the discussion we embed our results in an elaborate overview of related craniofacial heritability studies published from the year 2000 and onward (Tables 1–3).
Materials and Methods
Sample and Recruitment
Data were collected from the Avon Longitudinal Study of Parents and Children (ALSPAC), a UK-based birth cohort study designed to explore genetic and environmental influences on child health and development. In brief, all pregnant women with an expected delivery date between 1 April 1991 and 31 December 1992 inclusive, were eligible to participate in ALSPAC. A total of 14,541 pregnant women were recruited as part of Phase I (Boyd et al., 2013; Fraser et al., 2013). Detailed information and biological samples have been collected from these women and their offspring at various time points. The study website contains details of all the data that is available through a fully searchable data dictionary1.
3D facial surface scans were obtained for 4,731 adolescents at the 15-year-old follow-up clinic. A total of 3,663 fathers, from the ALSPAC cohort, were also invited to take part in the study. Additional phenotypic measures included demographic descriptors (e.g., sex, age, self-reported ethnicity), basic physical characteristics (e.g., height, weight) and information regarding the pregnancy. Children and their corresponding fathers could be linked by a unique pregnancy identifier, which resulted in 992 pairs (979 first and 13 second born). Participants with missing information on sex, age, height, weight (N = 21) and self-reported ethnic background (N = 45) were excluded from this study.
The current study (B2409: “Exploring the heritability of facial features in fathers and offspring using spatially dense geometric morphometrics”) was approved by the ALSPAC Ethics and Law Committee and the Local Research Ethics Committees. Written informed consent was obtained from all children and their fathers in accordance with the Declaration of Helsinki.
3D Facial Imaging and Preprocessing
3D facial images were captured with two high-resolution Konica Minolta Vivid (VI900) laser scanners (Konica Minolta Sensing Europe Company, Milton Keynes, United Kingdom). The set of left and right facial images of each scanned subject were processed, registered and merged to generate 3D images of the face (Toma et al., 2008). Prior to the scanning procedure, participants were asked to remain still and present a neutral facial expression.
3D images were imported into an in-house scan cleaning program and hair, ears and any dissociated polygons were removed. Rough facial orientation was established by indicating five crude positioning landmarks, followed by non-rigidly mapping2 an anthropometric mask (AM) onto the images (Snyders et al., 2014; Claes et al., 2018). The AM is a predefined surface template covering the facial area of interest and its mapping results in the standardization of image data from all individuals by creating homologous spatially dense (∼7,160) quasi-landmark configurations (Claes et al., 2012a). Subsequently, generalized Procrustes analysis (GPA) was performed to eliminate differences in position, orientation and size of both original and reflected configurations combined, where the latter could be constructed by changing the sign of the x-coordinate (Claes et al., 2011). The average of an original and its reflected configuration constitutes the symmetric component, while the difference between the two constitutes the asymmetric component. Because faces display bilateral symmetry, aspects of symmetry and asymmetry are preferably considered separately when examining facial shape (Claes et al., 2012b). Although patterns of asymmetry may be informative, in this work we concentrate on the symmetric component only.
Facial Quality Control
Outlier faces were detected by establishing z-scores for each face as described by Claes et al. (2018). Manual inspection of faces with a z-score equal to or larger than 2 led to the removal of imaging and mapping errors (N = 24) and participants displaying non-neutral facial expressions (N = 19) or whose images were obstructed by facial hair (N = 85). A further reduction was done by excluding participants with self-reported non-European ancestry (N = 28) and by randomly selecting one sibling from each multiple pregnancy (N = 8), so that only one child per family was included. A total of 762 father-child pairs were retained for analysis, including 358 sons and 404 daughters. Distribution statistics for age and BMI can be found in Supplementary Table S1 for all three cohorts (sons, daughters, and fathers). Lastly, GPA was applied to superimpose and symmetrize the facial shapes.
Regression-Based Heritability Estimation
Patterns of heritability can be explored from the regression of offspring on parents (Falconer and Mackay, 1996). A multivariate generalization was proposed by Monteiro et al. (2002) based on the Procrustes distance. The Procrustes distance serves as a measure of shape difference and was used to compute a multivariate shape coefficient of determination (R2), which could then be transformed to a regression coefficient, reflecting the shape heritability. An extension for the use of high-dimensional data is provided here. Partial least squares regression (PLSR; function plsregress from Matlab 2017b) was performed to predict facial variation in children given the father’s facial variation. PLSR was preferred for this task because it allows to work with two blocks of multivariate and high-dimensional data. Furthermore, PLSR, in contrast to an ordinary multiple regression, is not constrained by collinearity in the data, which for 3D landmarks is practically always present (Zelditch et al., 2004; Tøndel et al., 2011). In essence, PLSR decomposes the dependent and independent variables into pairs of (unobserved) latent variables by maximizing the covariance between the two, which makes it a better prediction model (Zelditch et al., 2004; Shrimpton et al., 2014). Transformation of the variance explained by the regression model (R2) to a multivariate regression coefficient was done according to Monteiro et al. (2002). Given a one-parent one-offspring design, the heritability can directly be estimated by multiplying the regression coefficient by two (Falconer and Mackay, 1996). Note that the reported R2-coefficient was equal to the multivariate shape coefficient of determination defined in terms of the Procrustes distance.
Facial Segmentation and Modules of Co-inheritance
First, the symmetrized facial shapes were adjusted for the confounding effects of age, sex, and BMI using PLSR (Claes et al., 2018). This was done for fathers and children separately. Next, each quasi-landmark was used as a 3D shape variable [x,y,z] and multivariate heritability estimates were obtained as described in Section “Regression-Based Heritability Estimation.” For both sons and daughters combined, a quasi-landmark of the offspring was regressed on the corresponding as well as all other quasi-landmarks of the father. This was done for all the quasi-landmarks in the offspring and the result was a squared similarity matrix (N × N, with N the number of quasi-landmarks). The heritability of each quasi-landmark was located on the diagonal of this matrix, while the co-inheritance between different quasi-landmarks was located in the off-diagonal elements. The mean squared error (MSE), generated by the function plsregress, was used to evaluate the quality of the PLSR model.
The symmetrized similarity matrix was used as input to perform a hierarchical spectral clustering with five levels. A detailed description of the clustering technique is provided by Claes et al. (2018). Quasi-landmarks with strong co-inheritance were grouped together into a series of facial segments or modules, rather than the clustering of highly correlated quasi-landmarks as observed in the structural segmentation (Claes et al., 2018). In order to assess whether differences existed between both segmentations, we computed the normalized mutual information (NMI). NMI values range from 0 to 1, with high values indicating a substantial overlap between two alternative segmentations (Claes et al., 2018).
All quasi-landmarks of the resulting 63 modules were subjected to a new GPA for both children and fathers combined, thereby creating a shape space for each of the facial modules. These shape spaces were constructed independently of the other modules and their relative positioning within the full face, so that only shape information was retained. Yet, integration of the modules was preserved through the hierarchical construction. Subsequently, each shape space was spanned by an orthogonal basis of PCs and parallel analysis was applied to determine the number of significant PCs contributing to facial shape. In contrast to related work using PCs, the resulting PCs are always used together and never individually, to provide a single multivariate description of modular shape variations.
Facial Heritability Per Module
Sons and daughters were treated separately to estimate the heritability and co-heritability for all facial modules (cf. Regression-Based Heritability Estimation). The multidimensional nature of shape was preserved by performing PLSR on all PCs simultaneously and the quality of the regression model was assessed through the MSE. Labels between fathers and children were randomized and 1,000,000-fold permutation tests were undertaken for all 63 modules to determine any significant differences. The significance threshold correcting for the multiple-testing burden was determined at α = 1.3889 × 10-3 (i.e., 0.05/36), corresponding to an adjustment for the number of effective independent tests. The effective number was computed from the eigenvalues of the correlation matrix containing pairwise multivariate correlations of all 63 modules (Li and Ji, 2005). The reduction in effective tests was expected because of the dependency between neighboring quasi-landmarks and the hierarchical and overlapping construction of the facial modules (Claes et al., 2018). Finally, we experimentally determined the extent to which the heritability estimation is affected by the sample size in our multivariate approach by computing the heritability of randomly generated subsamples of different sizes.
The construction of the modular shape spaces on data of children and fathers altogether allowed us to evaluate whether similar patterns of variation in fathers and children were correlated, e.g., does variation in the nasal breadth of children reflect the same pattern of variation in fathers. When corresponding modules in children–father pairs were considered, shape variations encoded by the extracted latent variables each represented a particular direction within the same shape space. Both directions could be depicted graphically by creating morphs and by plotting the normal displacement map between the upper and lower extremes.
Results
3D Landmark (Co-)heritability and Modules of Co-inheritance
Facial heritability maps of both sons and daughters are shown in Figure 1. As expected, these maps were symmetric and coherent, without abrupt changes in the estimates of neighboring quasi-landmarks. Regions in the face with the greatest heritability included the areas encompassing the nasion and zygomas, as well as the nose and forehead. Differences between both cohorts were found in the lower part of the face. For example, higher estimates were obtained in the chin area for daughters compared with sons, while the latter showed higher heritability estimates in the philtrum area. All MSE values were close to zero (Supplementary Figure S1), yet slightly more variation was observed around the chin, nose and forehead.
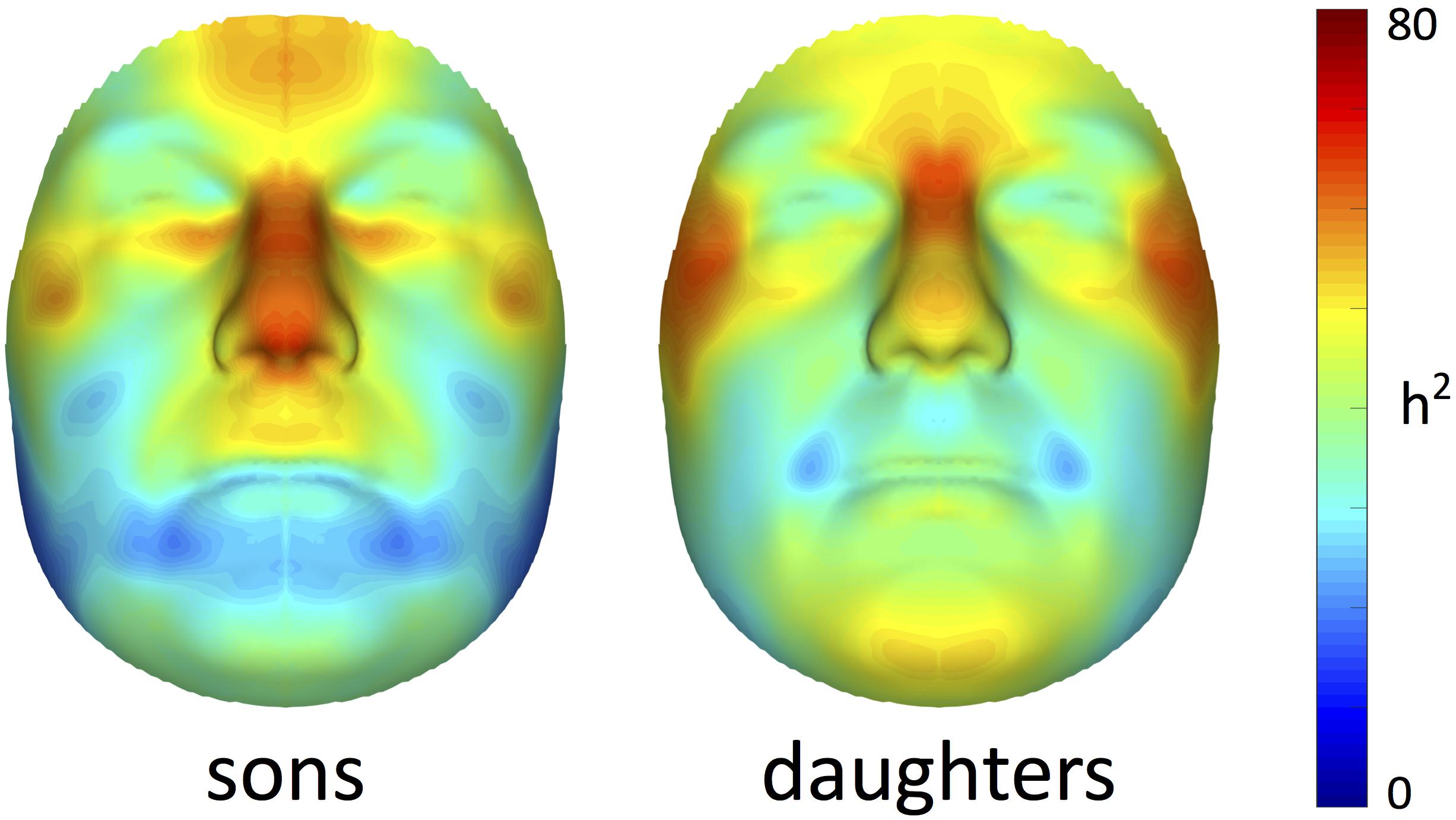
FIGURE 1. Facial heritability maps. 3D landmark heritability (%) for sons and daughters as obtained from the regression on fathers. The red-blue spectrum represents regions of high and low heritability, respectively. The maximum value was set to 80% for visualization purposes.
Starting from 3D landmark heritability and 3D pairwise landmark co-heritability (Figure 2) in children, we subdivided facial shape into 63 modules of co-inheritance (Figure 3). First, the midface was separated from the rest of the face and was further partitioned into the philtrum area (quadrant 3, starting at segment 6) and nose (quadrant 4, starting at segment 7). The same was supported by the facial maps of co-heritability (Figures 2A,B,E) in which the nose is presented as an autonomous feature. The remainder of the face was decomposed into the lower facial area (quadrant 1, starting at segment 4) and upper facial area (quadrant 2, starting at segment 5), also promoted by the co-heritability maps in Figures 2A,H. Each segment was repeatedly partitioned into two toward the next level, increasingly focusing on local shape variations. The structural modules are depicted in Supplementary Figure S2 and a substantial overlap between the two alternative segmentations was proven by the high NMI scores (NMIL0 = 1, NMIL1 = 0.76, NMIL2 = 0.84, NMIL3 = 0.77, NMIL4 = 0.76, NMIL5 = 0.73).
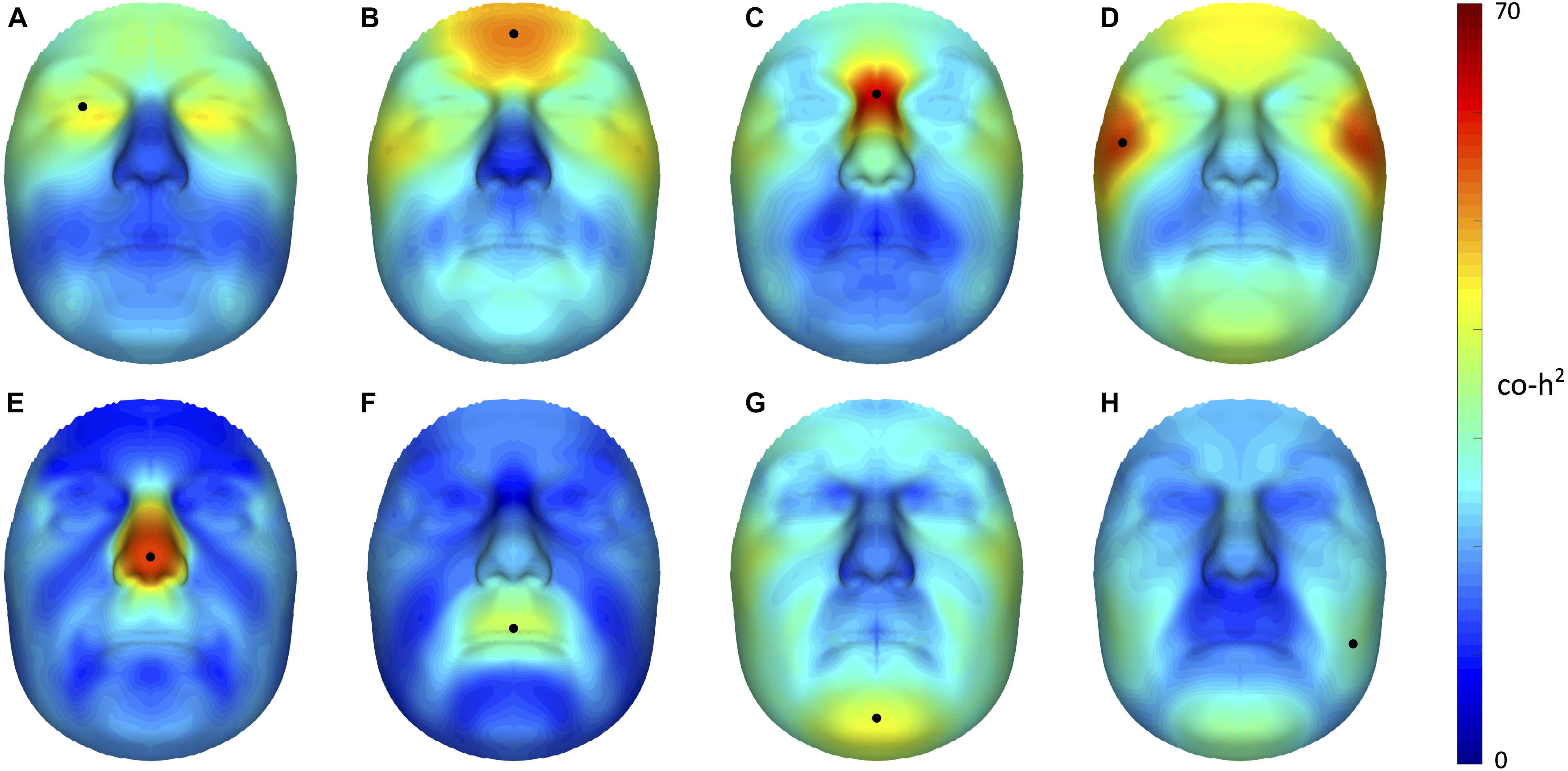
FIGURE 2. Facial maps of co-heritability. 3D pairwise landmark co-heritability (%) of the (A) orbital region, (B) forehead, (C) nasion, (D) zygomas, (E) nasal tip (F) upper lip, (G) chin and (H) cheeks. Landmarks of interest are indicated by a black dot, each representing the quasi-landmark in fathers that was used to predict facial variation in children for the corresponding as well as all other quasi-landmarks. The red-blue spectrum represents regions of high and low co-heritability, respectively. The maximum value was set to 70% for visualization purposes.
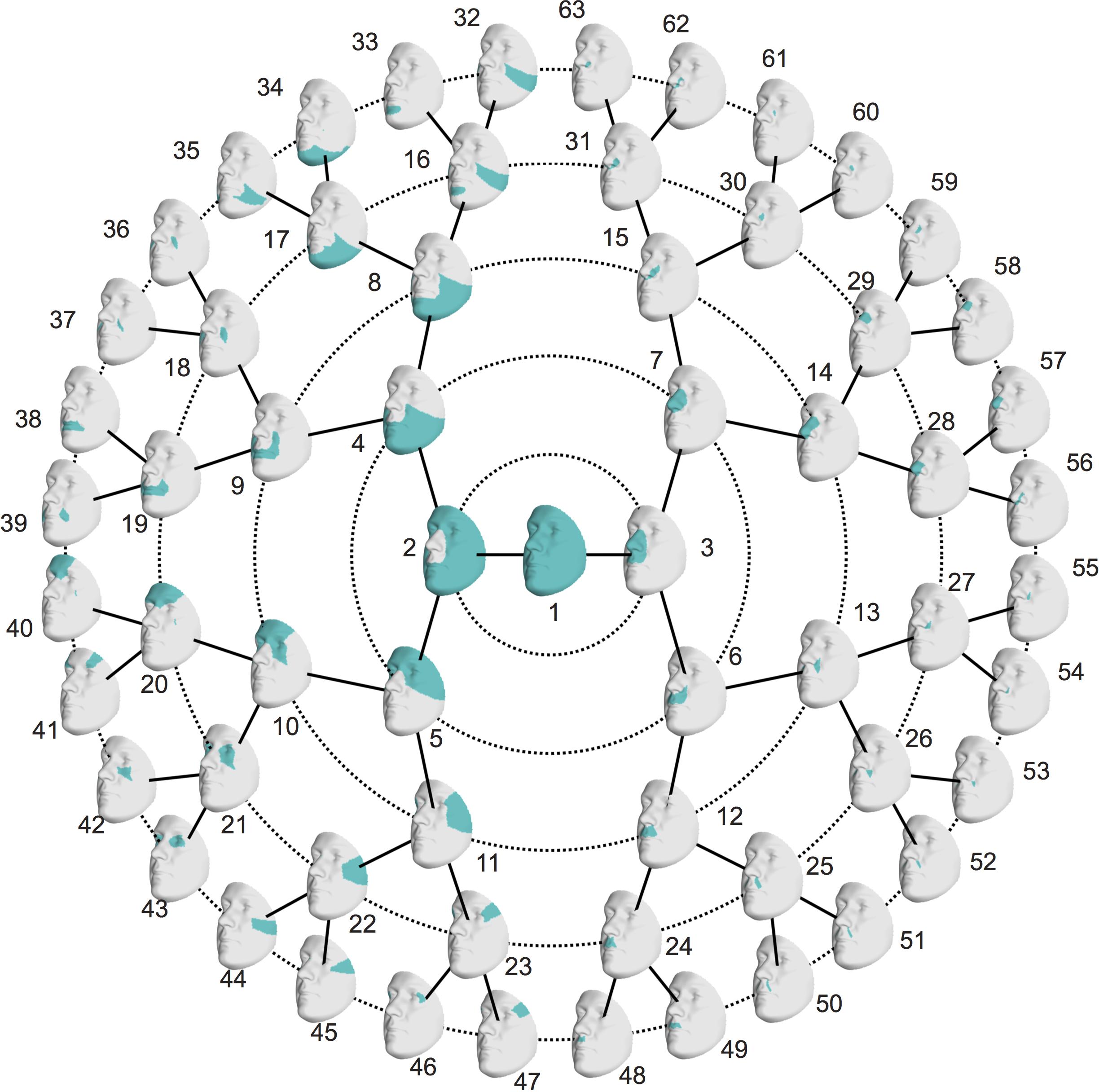
FIGURE 3. Modules of co-inheritance. Hierarchical facial segmentation of the study cohort, resulting from the grouping of quasi-landmarks with strong co-inheritance (N = 762 father-offspring pairs). Segments are colored in blue. Facial shape variation is covered at five different levels of detail, with global shape variations located in the center (L0) and local shape variations located towards the outer circle (L5).
Modular Heritability
Multivariate estimates of heritability were obtained for all 63 modules in sons and daughters separately (Figure 4). Nearly all modules reached statistical significance (Figure 4 and Supplementary Figure S3), displaying low (<35%) to high (>65%) heritability estimates. The corresponding MSE values are listed in Supplementary Table S2 and stabilization of the estimates is demonstrated in Supplementary Figure S4. Modules of high heritability covered well known facial areas in both cohorts, including the nose, orbital area and upper facial parts. However, higher estimates were obtained in sons compared with daughters. The lower part of the face only showed low to moderate levels of heritability, whether or not reaching the significance threshold (quadrants 1, 3). The highest level of heritability was found for the global face (segment 1), followed by the facial area encompassing the nasion, zygomas and forehead (segment 5). Heritability of the nose was also high, with the nasal bridge being more heritable than the nasal tip and alae nasi. Similar to the landmark-based approach (Figure 1), heritability of the philtrum (segments 6, 12, 24) was lower in daughters compared with sons, whereas modular estimates of the chin (segments 33, 34) were roughly the same in both cohorts.
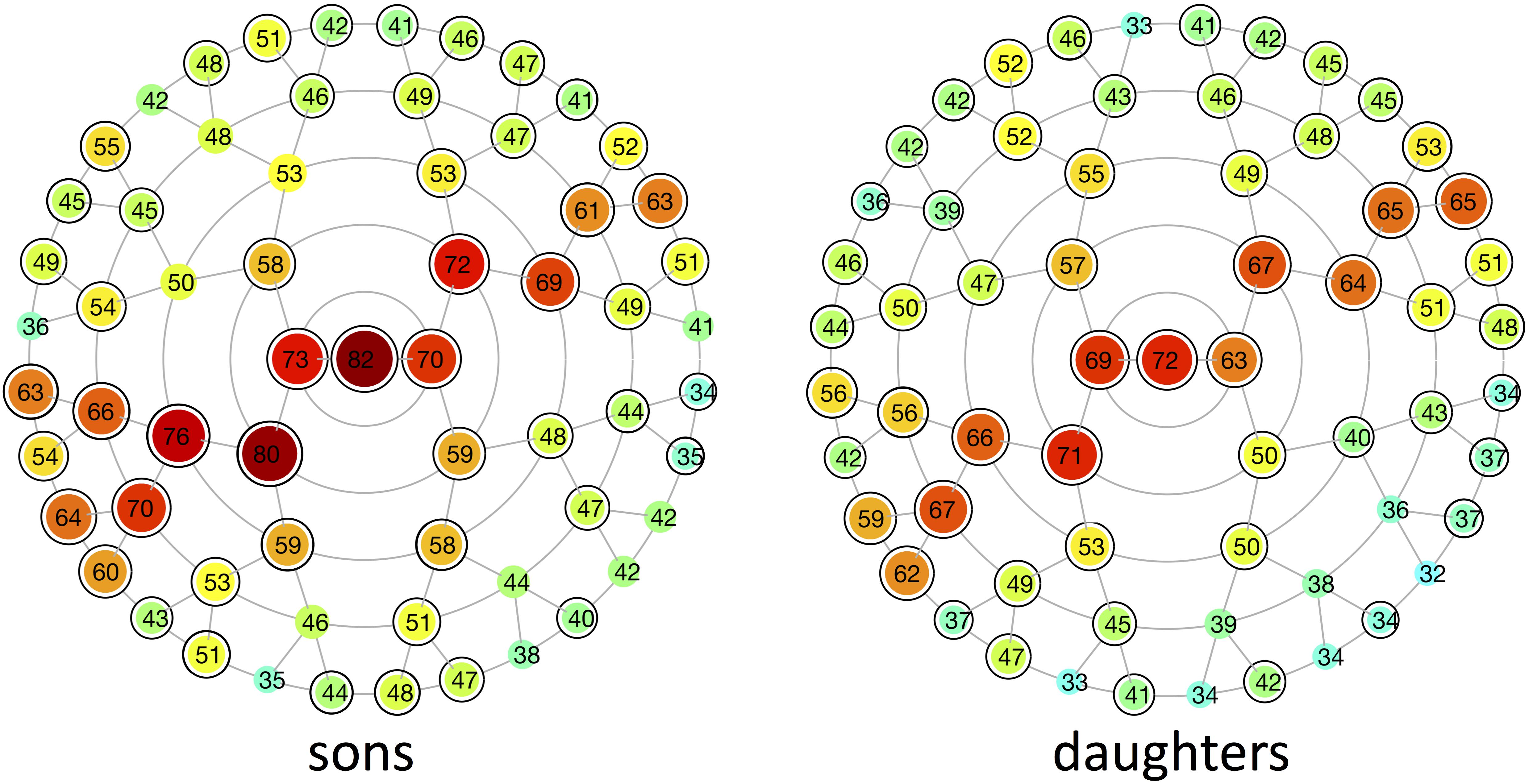
FIGURE 4. Heritability of different global-to-local parts in the face. Modular heritability estimates (%) for sons and daughters, as obtained from the regression on fathers. Each node corresponds to the facial segments depicted in Figure 3. The red-blue spectrum represents levels of high and low heritability, respectively, and the corresponding values are plotted on top of each node. Black-encircled facial segments had p-values below the significance threshold correcting for the multiple-testing burden (α = 1.3889 × 10-3). All significance tests were based on 1,000,000 permutations.
The first three pairs of latent variables were visualized at the global level in sons (Figure 5), ordered according to the percentage covariation explained. Additional figures representing the corresponding directions in daughters and fathers can be found in Supplementary Figure S5. The first pair included aspects related to facial roundness in both fathers and children (Figure 5A and Supplementary Figure S5A), e.g., a short and round face versus an elongated face. The second and third latent pairs represented variation in the prominence of the midfacial area (Figure 5B and Supplementary Figure S5B), e.g., protrusion versus retrusion, and the angle of the nasal tip and prominence of the chin (Figure 5C and Supplementary Figure S5C), respectively.
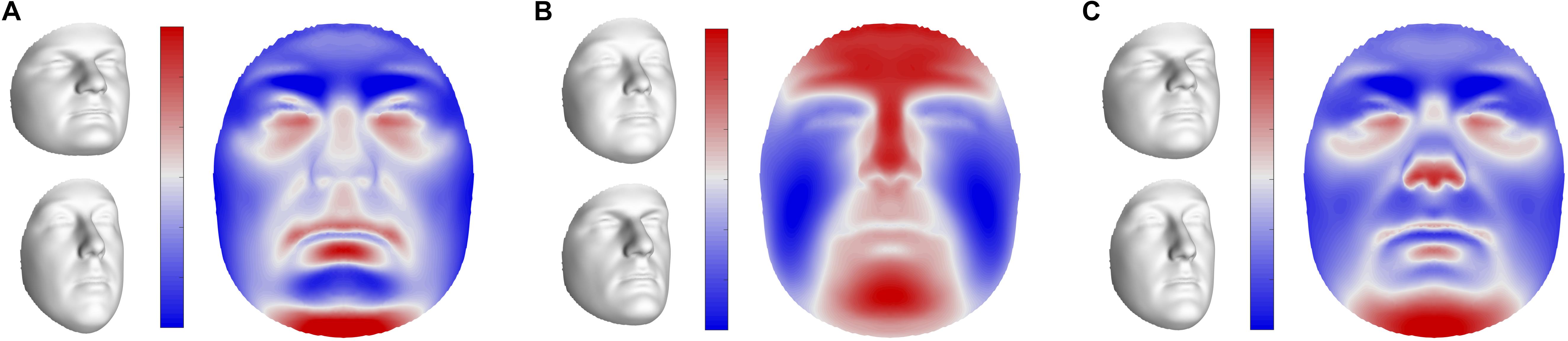
FIGURE 5. Global shape variations in offspring. Visualizations of the first three extracted latent variables at the global level in sons. Shape variations in daughters and fathers can be found in Supplementary Figure S5. (A) PLS component 1, (B) PLS component 2, (C) PLS component 3. In gray, illustrations of shape transformation or morph images (±4 standard deviations of the median), representing the direction in shape space encoded by the latent variables. In color, the normal displacement in each quasi-landmark, going from the lower (top) to the upper (bottom) extreme. Blue, inward repression; red, outward protrusion.
Discussion
In this study, we present a novel approach to determine facial heritability and co-heritability in fathers and offspring, starting from 3D spatially dense descriptions of the human face. By combining the co-heritability of neighboring quasi-landmarks, novel phenotypes with particular heritabilities were generated based on the biological mechanisms of inheritance. In addition to the analysis of co-inheritance, a second novel aspect of this work is the multivariate investigation of facial shape at multiple levels of organization. In general, similar patterns of facial features were inherited from the fathers to their 15-year-old offspring, including the global face, upper facial parts (forehead, orbital region, nasion) and the nose. Interestingly, sons showed stronger heritability to their fathers than daughters did at the age of 15.
Multivariate Analysis of Facial Shape
In contrast to previous work where facial shape is only represented using a sparse set of anatomical landmarks (Tables 1–3), spatially dense representations provide detailed information on the entire geometry of the facial surface (Claes et al., 2012a; Tsagkrasoulis et al., 2017). Moreover, the modularization approach allows focusing on more local shape variations in PCA space. Some previous studies also used PCA (Tables 1–3), but heritability scores were computed for each of these PCs separately. However, orthogonality in the PCs typically overlooks the underlying covariance structure. By contrast, the full-range of facial variations was retained throughout our analyses by considering all PCs simultaneously in a multivariate regression approach. Furthermore, preselection of facial traits as univariate measurements may introduce artifacts and results need to be interpreted with care. Analysis of heritability in the x-dimension consistently showed higher values of heritability at the midline (Supplementary Figure S6), which were erroneously introduced by aligning the faces at x = 0 during GPA, leading to an almost absence of variation in this region (i.e., order of 10-22). The same can be observed in the work of Tsagkrasoulis et al. (2017), where high levels of heritability seem to overlap with regions of zero-curvature, for example at the nasolabial folds.
Novel Facial Phenotypes Determined From the Patterns of Inheritance
A limitation of the AM mapping in combination with GPA to establish spatially dense configurations, is that quasi-landmarks are positioned in the context of all other quasi-landmarks. Facial areas comprising of densely sampled points, e.g., the cheeks, will hence drive the superimposition. This will also affect the heritability estimates obtained in Figure 1, although highlighted regions in our study still coincided with genetically determined facial traits as previously reported in literature (Tables 1–3). The modularization approach surpasses this limitation because all modules are subjected to a separate GPA. In this way, only biological shape was captured, independent from its integration within the full face. Yet, information on the integration of facial parts at higher levels was preserved through the hierarchical construction.
The hierarchical clustering approach is data-driven and segmentation of the face was performed on data of sons and daughters combined to increase the number of individuals (N = 762), although differences in patterns of inheritance were observed between the two cohorts. As expected, the degree of overlap between the co-heritability-based and structural segmentation was high because genetic and functional mechanisms are likely to be linked. Interestingly, modules of co-inheritance seem to reflect differences in tissue types. To illustrate, segment 9 coincided with the maxillary bone (Figure 3), whereas the same segment represented the mouth in the structural approach (Supplementary Figure S2). The nasal tip and bridge (segments 57 and 58, respectively) also formed distinct modules, reflecting the underlying bone-cartilage framework. This result is consistent with the one depicted in Figure 2E and imposes well-known difficulties in forensic applications such as craniofacial reconstruction (Claes et al., 2010).
Estimating Different Components of Variance
It is important to realize that heritability is only a descriptive statistic, referring to a particular population under particular conditions (Falconer and Mackay, 1996; AlKhudhairi and AlKofide, 2010). The reported heritability estimates were based on a European cohort and may not generalize to other populations. Various methods have been used to quantify facial heritability and as with other designs based on relatives, genetic contributions computed here are likely to be biased upward due to the environmental sources of covariance, i.e., common environment, providing an upper bound for the heritability. In essence, heritability is always a variable and never an absolute value, hence findings across studies should be interpreted in terms of low, moderate and high heritability only.
Mixed models provide an alternative method to estimate variance components, allowing for interactions between genotype and environment (Visscher et al., 2008; Lange et al., 2016; Mayhew and Meyre, 2017). Moreover, they can handle different types of (genetic) relationships as well. Moving toward the post-GWAS era, heritability studies will likely shift from the classical twin and family designs toward approaches estimating phenotypic variance from genome-wide SNP (i.e., single nucleotide polymorphism) data, as in the recent population study of Cole et al. (2017). In the context of ‘global’ shape heritability, Klingenberg (2003) states that only the GP-1 matrix (where G and P are the genetic and phenotypic covariance matrices, respectively) can be regarded as the multivariate equivalent of the otherwise univariate heritability measure because the spatial structure of variation is ignored when Procrustes distances are used (cf. Monteiro et al., 2002). The latter is only justified if the assumption of model isotropy holds or if the P and G matrices are proportional (Klingenberg and Monteiro, 2005). However, variance component analyses using mixed models are currently difficult to implement for high-dimensional data due to the computational burden. Moreover, patterns of shape variations in fathers correlated well with those predicted in children (Figure 5 and Supplementary Figure S5).
Facial Heritability and Co-heritability of Different Global-to-Local Segments
Low (<35%) to high (>65%) heritability estimates were obtained for different global-to-local parts in the face, ranging from 32 to 82%. As it is difficult to compute the appropriate sample size in our multivariate approach, we ran an analysis to experimentally determine the effect of sample size on the estimates. From Supplementary Figure S4 we can conclude that, for all segments, the heritability converges toward the tail end of the curve and stable estimates are generated.
In contrast to previous parent-offspring studies on craniofacial heritability, higher estimates were obtained in sons compared with daughters for the majority of the facial segments (Table 2). Heritability of the global face was maximal and equal to 82 and 72% in sons and daughters, respectively, higher than the global estimate observed by Cole et al. (2017) (Table 3). Given the remarkable facial similarity between first-degree relatives, such high values are expected. Consistent with the literature, genetic determination was found for midfacial parameters (Tables 1–3). High heritability was observed for nasal structures in both 3D landmark- and modular-based approaches (Figures 1, 4), as confirmed by previous heritability studies (Tables 1–3). In particular, there is general agreement on the high heritability of the position of the nasion, which is strongly linked to the PAX3 gene (Liu et al., 2012; Paternoster et al., 2012; Adhikari et al., 2016; Claes et al., 2018). Similar to previous studies who reported high heritability of intercanthal width and other traits related to the orbital region (Tables 1–3), we also observed high heritability of the corresponding segments (segments 21, 43). Strong genetic control was found for the upper facial part in general (segment 5), encompassing the zygomas and forehead in addition to the nasion and orbital structures. There have been very few studies investigating the heritability of the forehead, mainly because measurements in this region are lacking due to the definition of anatomical landmarks in the midface only. Surface shape analysis in twins revealed intrapair similarities in the region of the forehead (Naini and Moss, 2004; Djordjevic et al., 2013), consistent with the present results and the study of Tsagkrasoulis et al. (2017) (Table 1).
As expected, heritability of the lower parts of the face only ranged from low to moderate. The effect of BMI or facial fatness is mainly located in the areas around the cheek, chin and neck, reflecting the greater environmental component (Shrimpton et al., 2014). Moreover, there is a greater chance of movement of the jaw as well as a greater risk of trauma. The mandible is also influenced by function, e.g., breathing and eating habits (Al Ali et al., 2014a,b, 2015), and possible middle ear infections might interfere with the growth of the mandible (Kaneyama et al., 2008). In this study, low heritability was specifically observed in the small segments around the philtrum (segments 48–55) and cheeks (segment 32), whether or not significant. A number of genes associated with lip morphology have previously been identified (Wilson-Nagrani, 2016), yet differing levels of heritability were reported in literature (Tables 1–3). Moderate heritability of the mouth (segment 38) was found in this study. Facial segments around the chin area displayed similar levels of moderate heritability in both cohorts (cf. Lahoti et al., 2013; Tsagkrasoulis et al., 2017; Tables 1, 2), whereas 3D landmark heritability in the same region was higher in daughters compared with sons. This inconsistency between the two approaches may be related to the superimposition step as mentioned before, because integration-effects may still be present in the landmark-based approach. In addition, differences in our 15-year-old study cohort can partly be explained by gender-related differences in facial maturation. It is acknowledged that facial maturity develops in women between 12 and 14 years and 2 years later for men, hence male subjects may still be in puberty (Amini and Borzabadi-Farahani, 2009; Šidlauskas et al., 2016). Similarly, facial shape in boys continues to change between ages 12 and 16, mainly involving changes in the area of the chin, nose and supraorbital ridges (Kau and Richmond, 2008; Matthews et al., 2018). Furthermore, contributions of the mothers to the facial features of the offspring would also yield additional information enabling relative parental contributions to the facial shape in their offspring.
The regression approach of Monteiro et al. (2002) is limited in that comparison between modules of different dimensions is not straightforward, even though variation in parental and offspring phenotypes is corrected for. Therefore, multivariate correlation coefficients instead of regression coefficients were used to compute modular co-heritability (Supplementary Figure S7). Given a one-parent one-offspring design, the correlation is the same as the regression when variances in parental and offspring values are equal (Falconer and Mackay, 1996). However, this assumption is often not met. In our example, the moderate to high levels of correlation between the four quadrants (Supplementary Figure S7, level 2) further supported the high level of heritability of the global face.
Heritability Perspective on 3D Facial Shape in Practice
In sharp contrast with the high heritability, little is known on the genetic determinants of particular facial features (Roosenboom et al., 2016). Knowledge of which part of the facial surface is under strong genetic control and which part is mostly influenced by other factors like environmental influences or gene-environment interactions is useful in genetic association studies and allows focusing on those facial parameters displaying a strong genetic component. This can be confirmed by the association study of Claes et al. (2018), where global and local facial patterns of the discovered loci involved modules that are reported here as moderate to highly heritable, e.g., the nose, chin and forehead. Information on modular co-heritability is also useful in the definition of facial phenotypes. The hierarchical clustering approach forces the decomposition of modules into two more localized segments, but preservation of the original segment might be favorable when co-heritability is high. In addition to the use in association studies, the heritability perspective on 3D facial shape is also relevant for a variety of other scientific disciplines, such as anthropology, dysmorphology, ophthalmology, otolaryngology (ENT), orthodontics, craniofacial surgery and forensics.
Conclusion
In conclusion, we here propose a multivariate framework to explore genetic and environmental contributions to facial shape in families (grandparents, parents, and their offspring), which is of interest in a number of fields that deal with craniofacial morphology. Segmentation of the face into modules of co-inheritance allows focusing on global and local aspects of facial variation, demonstrating evidence of high heritability for the global face and for midfacial structures, such as the nasal and orbital region, in both sons and daughters.
Data Availability Statement
The dataset analyzed for this study (B2409: “Exploring the heritability of facial features in fathers and offspring using spatially-dense geometric morphometrics”) can be requested through the ALSPAC website. Please refer to the ALSPAC access policy for further details: https://www.bristol.ac.uk/alspac/researchers/data-access/.
Author Contributions
HH drafted the manuscript and performed all analyses under the supervision of PC, HP, and GH. PC and SR were involved in the initial project design and SR with AZ coordinated the collection of the children’s images. PC, JL, and KI provided input on the application of the analyses. DG conceptualized and implemented the connectome plot containing modular heritability and co-heritability. PC, HP, GH, SR, and ML aided in the interpretation of the data and revised the manuscript. All authors contributed to read and approved the final manuscript.
Funding
This work was supported by the Research Program of the Fund for Scientific Research – Flanders (Belgium) (FWO, G078518N), the National Institutes of Health (1-RO1-DE027023), and the Research Fund KU Leuven (BOF-C1, C14/15/081). The UK Medical Research Council (MRC) and Wellcome Trust (102215/2/13/2) and the University of Bristol provide core support for ALSPAC. A comprehensive list of grants funding is available on the ALSPAC website. Funding for the collection of 3D face shape scans was specifically provided by the MRC and Wellcome Trust (092731) and the University of Cardiff. HP is a Senior Clinical Investigator of The Research Foundation – Flanders (FWO). This publication is the work of the authors and they will serve as guarantors for the contents of this paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are extremely grateful to all the families who took part in this study, the midwives for their help in recruiting them, and the whole ALSPAC team, which includes interviewers, computer and laboratory technicians, clerical workers, research scientists, volunteers, managers, receptionists, and nurses.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2018.00554/full#supplementary-material
Footnotes
- ^ http://www.bris.ac.uk/alspac/researchers/data-access/data-dictionary/
- ^ The facial mapping software is available at https://github.com/TheWebMonks/meshmonk, free to use for academic purposes.
References
Adhikari, K., Fuentes-Guajardo, M., Quinto-Sánchez, M., Mendoza-Revilla, J., Camilo Chacón-Duque, J., Acuña-Alonzo, V., et al. (2016). A genome-wide association scan implicates DCHS2, RUNX2, GLI3, PAX1 and EDAR in human facial variation. Nat. Commun. 7:11616. doi: 10.1038/ncomms11616
Al Ali, A., Richmond, S., Popat, H., Playle, R., Pickles, T., Zhurov, A. I., et al. (2015). The influence of snoring, mouth breathing and apnoea on facial morphology in late childhood: a three-dimensional study. BMJ Open 5:e009027. doi: 10.1136/bmjopen-2015-009027
Al Ali, A., Richmond, S., Popat, H., Toma, A. M., Playle, R., Pickles, T., et al. (2014a). A three-dimensional analysis of the effect of atopy on face shape. Eur. J. Orthod. 36, 506–511. doi: 10.1093/ejo/cjs107
Al Ali, A., Richmond, S., Popat, H., Toma, A. M., Playle, R., Zhurov, A. I., et al. (2014b). The influence of asthma on face shape: a three-dimensional study. Eur. J. Orthod. 36, 373–380. doi: 10.1093/ejo/cjs067
AlKhudhairi, T. D., and AlKofide, E. A. (2010). Cephalometric craniofacial features in Saudi parents and their offspring. Angle Orthod. 80, 1010–1017. doi: 10.2319/050410-66
Amini, F., and Borzabadi-Farahani, A. (2009). Heritability of dental and skeletal cephalometric variables in monozygous and dizygous Iranian twins. Orthod. Waves 68, 72–79. doi: 10.1016/j.odw.2009.01.001
Arya, R., Duggirala, R., Comuzzie, A. G., Puppala, S., Modem, S., Busi, B. R., et al. (2002). Heritability of anthropometric phenotypes in caste populations of visakhapatnam, India. Hum. Biol. 74, 325–344.
Baydaş, B., Erdem, A., Yavuz,İ., and Ceylan, İ. (2007). Heritability of facial proportions and soft-tissue profile characteristics in Turkish Anatolian siblings. Am. J. Orthod. Dentofacial Orthop. 131, 504–509. doi: 10.1016/j.ajodo.2005.05.055
Baynam, G., Walters, M., Claes, P., Kung, S., LeSouef, P., Dawkins, H., et al. (2013). The facial evolution: looking backward and moving forward. Hum. Mutat. 34, 14–22. doi: 10.1002/humu.22219
Boyd, A., Golding, J., Macleod, J., Lawlor, D. A., Fraser, A., Henderson, J., et al. (2013). Cohort profile: the ‘children of the 90s’—the index offspring of the avon longitudinal study of parents and children. Int. J. Epidemiol. 42, 111–127. doi: 10.1093/ije/dys064
Carels, C., Van Cauwenberghe, N., Savoye, I., Willems, G., Loos, R., Derom, C., et al. (2001). A quantitative genetic study of cephalometric variables in twins. Clin. Orthod. Res. 4, 130–140. doi: 10.1034/j.1600-0544.2001.040303.x
Carson, E. A. (2006). Maximum likelihood estimation of human craniometric heritabilities. Am. J. Phys. Anthropol. 131, 169–180. doi: 10.1002/ajpa.20424
Claes, P., Roosenboom, J., White, J. D., Swigut, T., Sero, D., Li, J., et al. (2018). Genome-wide mapping of global-to-local genetic effects on human facial shape. Nat. Genet. 50, 414–423. doi: 10.1038/s41588-018-0057-4
Claes, P., Vandermeulen, D., De Greef, S., Willems, G., Clement, J. G., and Suetens, P. (2010). Bayesian estimation of optimal craniofacial reconstructions. Forensic Sci. Int. 201, 146–152. doi: 10.1016/j.forsciint.2010.03.009
Claes, P., Walters, M., and Clement, J. (2012a). Improved facial outcome assessment using a 3D anthropometric mask. Int. J. Oral Maxillofac. Surg. 41, 324–330. doi: 10.1016/j.ijom.2011.10.019
Claes, P., Walters, M., Shriver, M. D., Puts, D., Gibson, G., Clement, J., et al. (2012b). Sexual dimorphism in multiple aspects of 3D facial symmetry and asymmetry defined by spatially dense geometric morphometrics. J. Anat. 221, 97–114. doi: 10.1111/j.1469-7580.2012.01528.x
Claes, P., Walters, M., Vandermeulen, D., and Clement, J. G. (2011). Spatially-dense 3D facial asymmetry assessment in both typical and disordered growth. J. Anat. 219, 444–455. doi: 10.1111/j.1469-7580.2011.01411.x
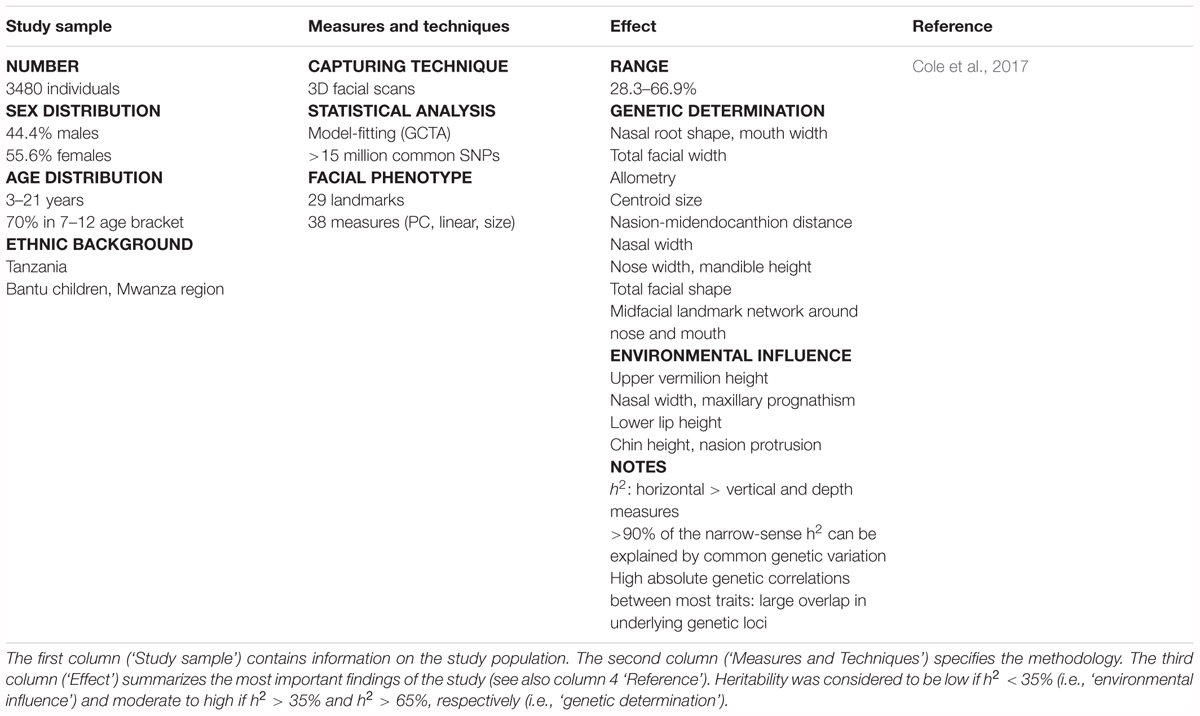
Cole, J. B., Manyama, M., Larson, J. R., Liberton, D. K., Ferrara, T. M., Riccardi, S. L., et al. (2017). Human facial shape and size heritability and genetic correlations. Genetics 205, 967–978. doi: 10.1534/genetics.116.193185
Crouch, D. J. M., Winney, B., Koppen, W. P., Christmas, W. J., Hutnik, K., Day, T., et al. (2018). Genetics of the human face: identification of large-effect single gene variants. Proc. Natl. Acad. Sci. U.S.A. 115, E676–E685. doi: 10.1073/pnas.1708207114
de Jong, M. A., Hysi, P., Spector, T., Niessen, W., Koudstaal, M. J., Wolvius, E. B., et al. (2018). Ensemble landmarking of 3D facial surface scans. Sci. Rep. 8:12. doi: 10.1038/s41598-017-18294-x
de Jong, M. A., Wollstein, A., Ruff, C., Dunaway, D., Hysi, P., Spector, T., et al. (2016). An automatic 3d facial landmarking algorithm using 2d gabor wavelets. IEEE Trans. Image Process. 25, 580–588. doi: 10.1109/TIP.2015.2496183
Djordjevic, J., Jadallah, M., Zhurov, A. I., Toma, A. M., and Richmond, S. (2013). Three-dimensional analysis of facial shape and symmetry in twins using laser surface scanning. Orthod. Craniofac. Res. 16, 146–160. doi: 10.1111/ocr.12012
Djordjevic, J., Zhurov, A. I., and Richmond, S. (2016). Genetic and environmental contributions to facial morphological variation: a 3d population-based twin study. PLoS One 11:e0162250. doi: 10.1371/journal.pone.016225
Ermakov, S., Kobyliansky, E., and Livshits, G. (2005). Quantitative genetic study of head size related phenotypes in ethnically homogeneous Chuvasha pedigrees. Ann. Hum. Biol. 32, 585–598. doi: 10.1080/03014460500247972
Falconer, D. S., and Mackay, T. F. C. (1996). Introduction to Quantitative Genetics, 4th Edn. Harlow: Longman Group Ltd.
Fraser, A., Macdonald-Wallis, C., Tilling, K., Boyd, A., Golding, J., Davey Smith, G., et al. (2013). Cohort profile: the avon longitudinal study of parents and children: ALSPAC mothers cohort. Int. J. Epidemiol. 42, 97–110. doi: 10.1093/ije/dys066
Hammond, P. (2007). The use of 3D face shape modelling in dysmorphology. Arch. Dis. Child. 92, 1120–1126. doi: 10.1136/adc.2006.103507
Hopman, S. M. J., Merks, J. H. M., Suttie, M., Hennekam, R. C. M., and Hammond, P. (2014). Face shape differs in phylogenetically related populations. Eur. J. Hum. Genet. 22, 1268–1271. doi: 10.1038/ejhg.2013.289
Jelenkovic, A., Poveda, A., Susanne, C., and Rebato, E. (2008). Contribution of genetics and environment to craniofacial anthropometric phenotypes in belgian nuclear families. Hum. Biol. 80, 637–654. doi: 10.3378/1534-6617-80.6.637
Jelenkovic, A., Poveda, A., Susanne, C., and Rebato, E. (2010). Common genetic and environmental factors among craniofacial traits in Belgian nuclear families: comparing skeletal and soft-tissue related phenotypes. J. Comp. Hum. Biol. 61, 191–203. doi: 10.1016/j.jchb.2009.10.003
Johannsdottir, B., Thorarinsson, F., Thordarson, A., and Magnusson, T. E. (2005). Heritability of craniofacial characteristics between parents and offspring estimated from lateral cephalograms. Am. J. Orthod. Dentofacial Orthop. 127, 200–207. doi: 10.1016/j.ajodo.2004.07.033
Kaneyama, K., Segami, N., and Hatta, T. (2008). Congenital deformities and developmental abnormalities of the mandibular condyle in the temporomandibular joint. Congenit. Anom. 48, 118–125. doi: 10.1111/j.1741-4520.2008.00191.x
Karmakar, B., Ermakov, S., Yakovenko, K., and Kobyliansky, E. (2007). Genetic determination of head-size-related anthropometric traits in an ethnically homogeneous sample of 373 indian pedigrees of West Bengal. Hum. Biol. 79, 501–514. doi: 10.1353/hub.2008.0007
Kau, C. H., and Richmond, S. (2008). Three-dimensional analysis of facial morphology surface changes in untreated children from 12 to 14 years of age. Am. J. Orthod. Dentofacial Orthop. 134, 751–760. doi: 10.1016/j.ajodo.2007.01.037
Kim, E., Sung, J., Song, Y.-M., Chae, H. S., Mo, S.-S., Kim, Y. H., et al. (2018). Heritability of facial skeletal and dental characteristics of monozygotic and dizygotic twins using cephalometric analysis and falconer’s method. J. Craniofac. Surg. 29, e274–e279. doi: 10.1097/SCS.0000000000004313
Kim, H.-J., Im, S.-W., Jargal, G., Lee, S., Yi, J.-H., Park, J.-Y., et al. (2013). Heritabilities of facial measurements and their latent factors in korean families. Genomics Inform. 11:83. doi: 10.5808/GI.2013.11.2.83
Klingenberg, C. P. (2003). Quantitative genetics of geometric shape: heritability and the pitfalls of the univariate approach. Evolution 57, 191–195.
Klingenberg, C. P., and Monteiro, L. R. (2005). Distances and directions in multidimensional shape spaces: implications for morphometric applications. Syst. Biol. 54, 678–688. doi: 10.1080/10635150590947258
Kohn, L. A. P. (1991). The role of genetics in craniofacial morphology and growth. Annu. Rev. Anthropol. 20, 261–278.
Lahoti, S. K., Karia, A. M., and Lahoti, K. B. (2013). Heritability of facial characteristics between parents and offsprings: a photographic study. J. Indian Orthod. Soc. 47, 419–425. doi: 10.5005/jp-journals-10021-1199
Lange, K., Cantor, R., Horvath, S., Papp, J. C., Sabatti, C., Sinsheimer, J. S., et al. (2016). Analysis option 19: variance components (Polygenic and QTL Mapping) in Mendel 16.0 Documentation. 209–218.
Li, J., and Ji, L. (2005). Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity 95, 221–227. doi: 10.1038/sj.hdy.6800717
Liu, F., Lijn, F., van der, Schurmann, C., Zhu, G., Chakravarty, M. M., Hysi, P. G., et al. (2012). A genome-wide association study identifies five loci influencing facial morphology in Europeans. PLoS Genet 8:e1002932. doi: 10.1371/journal.pgen.1002932
Martínez-Abadías, N., Esparza, M., Sjøvold, T., González-José, R., Santos, M., and Hernández, M. (2009). Heritability of human cranial dimensions: comparing the evolvability of different cranial regions. J. Anat. 214, 19–35. doi: 10.1111/j.1469-7580.2008.01015.x
Matthews, H. S., Penington, A. J., Hardiman, R., Fan, Y., Clement, J. G., Kilpatrick, N. M., et al. (2018). Modelling 3D craniofacial growth trajectories for population comparison and classification illustrated using sex-differences. Sci. Rep. 8:4771. doi: 10.1038/s41598-018-22752-5
Mayhew, A. J., and Meyre, D. (2017). Assessing the heritability of complex traits in humans: methodological challenges and opportunities. Curr. Genomics 18, 332–340. doi: 10.2174/1389202918666170307161450
Monteiro, L. R., Diniz-Filho, J. A., dos Reis, S. F., and Araújo, E. D. (2002). Geometric estimates of heritability in biological shape. Evolution 56, 563–572.
Moss, J. (2006). The use of three-dimensional imaging in orthodontics. Eur. J. Orthod. 28, 416–425. doi: 10.1093/ejo/cjl025
Naini, F. B., and Moss, J. P. (2004). Three-dimensional assessment of the relative contribution of genetics and environment to various facial parameters with the twin method. Am. J. Orthod. Dentofacial Orthop. 126, 655–665. doi: 10.1016/j.ajodo.2003.08.034
Paternoster, L., Zhurov, I., Toma, A. M., Kemp, J. P., St. Pourcain, B., Timpson, N. J., et al. (2012). Genome-wide association study of three-dimensional facial morphology identifies a variant in PAX3 associated with nasion position. Am. J. Hum. Genet 90, 478–485. doi: 10.1016/j.ajhg.2011.12.021
Roosenboom, J., Hens, G., Mattern, B. C., Shriver, M. D., and Claes, P. (2016). Exploring the underlying genetics of craniofacial morphology through various sources of knowledge. Biomed. Res. Int. 2016:3054578. doi: 10.1155/2016/3054578
Šešelj, M., Duren, D. L., and Sherwood, R. J. (2015). Heritability of the human craniofacial complex. Anat. Rec. 298, 1535–1547. doi: 10.1002/ar.23186
Sherwood, R. J., Duren, D. L., Demerath, E. W., Czerwinski, S. A., Siervogel, R. M., and Towne, B. (2008). Quantitative genetics of modern human cranial variation. J. Hum. Evol. 54, 909–914. doi: 10.1016/j.jhevol.2008.02.009
Shrimpton, S., Daniels, K., de Greef, S., Tilotta, F., Willems, G., Vandermeulen, D., et al. (2014). A spatially-dense regression study of facial form and tissue depth: towards an interactive tool for craniofacial reconstruction. Forensic Sci. Int. 234, 103–110. doi: 10.1016/j.forsciint.2013.10.021
Šidlauskas, M., Šalomskienė, L., Andriuškevičiûtė, I., Šidlauskienė, M., Labanauskas,Ž, Vasiliauskas, A., et al. (2016). Heritability of mandibular cephalometric variables in twins with completed craniofacial growth. Eur. J. Orthod. 38, 493–502. doi: 10.1093/ejo/cjv062
Snyders, J., Claes, P., Vandermeulen, D., and Suetens, P. (2014). Development and Comparison of Non-Rigid Surface Registration Algorithms and Extensions. Leuven: ESAT.
Toma, A. M., Zhurov, A., Playle, R., and Richmond, S. (2008). A three-dimensional look for facial differences between males and females in a British-Caucasian sample aged 15½years old. Orthod. Craniofac. Res. 11, 180–185. doi: 10.1111/j.1601-6343.2008.00428.x
Tøndel, K., Indahl, U. G., Gjuvsland, A. B., Vik, J., Hunter, P., Omholt, S. W., et al. (2011). Hierarchical Cluster-based Partial Least Squares Regression (HC-PLSR) is an efficient tool for metamodelling of nonlinear dynamic models. BMC Syst. Biol. 5:90. doi: 10.1186/1752-0509-5-90
Tsagkrasoulis, D., Hysi, P., Spector, T., and Montana, G. (2017). Heritability maps of human face morphology through large-scale automated three-dimensional phenotyping. Sci. Rep. 7:45885. doi: 10.1038/srep45885
Visscher, P. M., Hill, W. G., and Wray, N. R. (2008). Heritability in the genomics era – concepts and misconceptions. Nat. Rev. Genet. 9, 255–266. doi: 10.1038/nrg2322
Weinberg, S. M., Parsons, T. E., Marazita, M. L., and Maher, B. S. (2013). Heritability of face shape in twins: a preliminary study using 3D stereophotogrammetry and geometric morphometrics. Dent 3000, 7–11. doi: 10.5195/D3000.2013.14
Wilson-Nagrani, C. E. (2016). Matching Genotype to Phenotype in a Detailed Assessment of Lip Morphology. Ph.D. thesis, Cardiff University, Wales
Keywords: 3D imaging, (co-)heritability, face, ALSPAC, geometric morphometrics, spatially dense, modularity
Citation: Hoskens H, Li J, Indencleef K, Gors D, Larmuseau MHD, Richmond S, Zhurov AI, Hens G, Peeters H and Claes P (2018) Spatially Dense 3D Facial Heritability and Modules of Co-heritability in a Father-Offspring Design. Front. Genet. 9:554. doi: 10.3389/fgene.2018.00554
Received: 01 June 2018; Accepted: 29 October 2018;
Published: 19 November 2018.
Edited by:
Karen T. Cuenco, Genentech, Inc., United StatesReviewed by:
Jing Hua Zhao, University of Cambridge, United KingdomMarie-Hélène Roy-Gagnon, University of Ottawa, Canada
Copyright © 2018 Hoskens, Li, Indencleef, Gors, Larmuseau, Richmond, Zhurov, Hens, Peeters and Claes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hanne Hoskens, aGFubmUuaG9za2Vuc0BrdWxldXZlbi5iZQ== Peter Claes, cGV0ZXIuY2xhZXNAa3VsZXV2ZW4uYmU=
 Hanne Hoskens
Hanne Hoskens Jiarui Li
Jiarui Li Karlijne Indencleef
Karlijne Indencleef Dorothy Gors2,3
Dorothy Gors2,3 Maarten H. D. Larmuseau
Maarten H. D. Larmuseau Stephen Richmond
Stephen Richmond Alexei I. Zhurov
Alexei I. Zhurov Greet Hens
Greet Hens Peter Claes
Peter Claes