Mappability and read length

Power-law distributions are the main functional form for the distribution of repeat size and repeat copy number in the human genome. When the genome is broken into fragments for sequencing, the limited size of fragments and reads may prevent an unique alignment of repeat sequences to the reference sequence. Repeats in the human genome can be as long as 10⁴ bases, or 10⁵ − 10⁶ bases when allowing for mismatches between repeat units. Sequence reads from these regions are therefore unmappable when the read length is in the range of 10³ bases. With a read length of 1000 bases, slightly more than 1% of the assembled genome, and slightly less than 1% of the 1 kb reads, are unmappable, excluding the unassembled portion of the human genome (8% in GRCh37/hg19). The slow decay (long tail) of the power-law function implies a diminishing return in converting unmappable regions/reads to become mappable with the increase of the read length, with the understanding that increasing read length will always move toward the direction of 100% mappability.

1. Introduction

Shotgun and next-generation sequencing (NGS) involve shredding the genome into smaller fragments, and sequence either full or part of the fragments. The sequenced fragments are called reads. Overlapping of sequences between reads are the basis of de novo assembly (Scheibye-Alsing et al., 2009). Reference assembly is based on mapping reads to a reference genome. The task of reference assembly is straightforward when the read length is long enough. Despite the theoretical possibility that a sequence can be free of any repeats at a specific length scale k (the De Bruijn sequence, Ralston, 1982), real genomes such as the human genome contain many repetitive sequences. Therefore, length-k reads may not be mapped uniquely. The regions where these reads are originally derived are defined as the “unmappable regions” at the read length k, and these reads are defined as “unmappable reads.”

Figure 1 illustrates various factors which influence mappability. (1) The distribution of fragment size F (P_F). This distribution clearly depends on the way fragments are sheared. (2) The distribution of the size of reads R (P_R), which does not contain the pairing information between the two reads from the same fragment. (3) The distribution of repeats, in both the repeat length (D) and the number of copies (C). Note that for read-alignment purpose, both the direct and the reverse complement strands should be considered, e.g., aaagg and ccttt are repeats. There are two approaches in counting repeats: (3a) Only “maximal repeats” are considered (Gusfield, 1997). In this definition, if the length is increased by one to D+1 (extending either to left or right), there is no longer a repeat. (3b) Fixed length (D₀) repeats may or may not be “maximal.” For example, a D₀-length repeat may be part of a larger repeating unit. This definition is more relevant to the situation where the read length is fixed. The two distributions are P_D,C and P_D0,C.

FIGURE 1

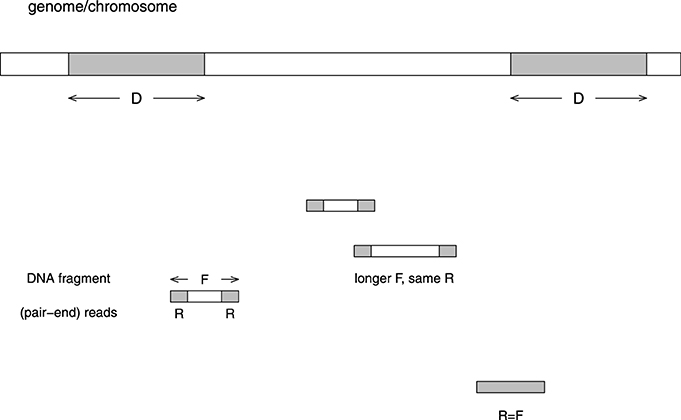
Figure 1. Illustration of the problem caused by repeats in the reads alignment to a reference genome. The length of the repeat unit is D basepairs, the length of a (typical) DNA fragment is F, and the length of a read in the paired-end sequencing is R. If D < R, the fragment can be mapped to the genome uniquely. On the other hand, if D > F, the fragment is unmappable. If R < D < F, the fragment may or may not be mappable. When the whole fragment is sequenced, we consider R = F. Usually the fragment size is not fixed, whereas the read length is fixed. The distribution of fragment sizes and read lengths are P_F = P(x = F) and P_R = P(x = R). The distribution of maximum repeat length and copy number is P_D,C = P(x = D,y = C). The distribution of fixed repeat length and copy number is P_D0,C = P(x = D₀, y = C).

Other considerations further complicate the situation: (4) Given P_F, R, P_D,C, the zero-mismatch mappability problem might be discussed rigorously. However, most of the alignment programs allow mismatches, and we have a new distribution P_D,C,M = P(x = D, y = C, z ≤ M), where M is the maximum number of mismatches allowed. Take M = 1 for example, the appearance of aaagg and cctat, for example, contributes to the distribution at D = 5, C = 2, and M = 1. (5) The existence of copy number variations (CNV) (Pinkel et al., 1998) implies that the person's genome may not be the same as the reference genome, which is used by everybody for alignments. In a sense, the reference genome is not unique: there are many versions corresponding to different forms of CNV.

Obtaining empirically the redundancy distribution P_D,C,M is computationally difficult for a large genome. Our previous work is limited to the situation of zero-mismatch (M = 0) and fixed repeat length D₀ (Li et al., 2014). We also assume that whole fragments are sequenced (F = R). Using the k-mer from the sequenced/assembled portion of the human genome (GRCh37/hg19) as surrogate of reads with length R = D₀, we obtain the fixed-length distribution P(x = D₀, y = C, z = 0) (Li et al., 2014). P(C = 1) is the proportion of uniquely mapped reads. We will review the results obtained in the analysis and discuss various results.

2. Unassembled Portions of the Human Reference Genome

We first examine the unsequenced/unassembled region of the human genome. Because reads from these regions are often available, these are unassembled rather than “unsequenced” (Rudd and Willard, 2004). There are four types of unassembled regions: (1) telomeres; (2) centromeres; (3) short-arms of acrocentric chromosomes (chr13,14,15,21,22, Y); and (4) large heterochromatic regions (in chr1,9,16, Y). All these regions involve repeat sequences.

The telomere regions contain simple repeats of the hexamer ttaggg/ccctaa (Moyzis et al., 1988). This motif is closely related to the telomeric sequence in other genomes (Blackburn et al., 2006). Specifying telomere sequence in a reference genome is difficult because repeat length varies with the age (Blasco, 2005). The G+C content of the above hexamer is 50%, which is higher than the genome-wide value of 40% (Li, 2013). The subtelomeric sequence is also highly repetitive (Riethman et al., 2004), with more varieties in repeat length and pattern, which result from ancestral duplications (Ambrosini et al., 2007; Churikov and Price, 2008).

The centromere region (Willard, 1990; Aldrup-MacDonald and Sullivan, 2014) consists of alpha satellite DNA with 171 basepairs (Manuelidis, 1976, 1978; Vissel and Choo, 1987). In the alpha satellite, the strand symmetry (see e.g., Li, 1997) is reasonably preserved for C% (18.8%) ≈ G% (19.4%), though less so for T% (32.9%) and A% (28.8%). The dimers AG/CT, TT/AA, CA/TG, GA/TC are over-represented in the alpha satellite, and AT, TA, CC/GG, CG, GT/AC under-represented. These dimer frequencies can also be modeled by a Markov chain (Cocho et al., 2014). New computational efforts to fill the assembled centromeres led to a great reduction of N's in GRCh38 (Miga et al., 2014).

The short-arms of acrocentric chromosomes consist of four well partitioned cytogenetic features (from p-term toward the centromere): satellite, stalk, short-arm, and centromere (Wyandt and Tonk, 2011). The repeat composition in these arms are more complicated, with some mainly consisting of HSat2,HSat3, other consisting of HSat1, beta, and gamma satellites. The large heterochromatin regions, such as those on chromosomes 1,9,16, contain similar satellite repeat sequences (Jones, 1973; Jones and Prosser, 1973). These regions are mainly composed of HSat2 and HSat3 evolving from the ancestral pentamer cattc/gaatg (which can also be written as attcc/ggaat, Gredy et al., 1992). In a renewed effort, subfamilies of HSat2/HSat3 are identified and cataloged into a database (Altemose et al., 2014).

The amount and proportion of N's (unassembled bases) in the human reference genome (GRCh37 and GRCh38, from Genome Reference Consortium) is 234 Mb or 7.6% and 151 Mb or 4.9%. There is a contrasting difference of the proportion between metacentric and acrocentric chromosomes (4.3 vs. 25.3% in GRCh37, and 2.0 vs. 20.8% in GRCh38). If we exclude chromosomes 1, 9, and 16 with the large heterochromatin regions, the rest of 14 metacentric autosomes achieve a rather low unsequenced rate of 2.6% in GRCh37 and 0.3% in GRCh38.

Since most unassembled regions contain short tandem repeats, the chance for a read from other regions to be aligned to these regions is relatively small. In fact, reads from unassembled regions can be identified as being distinct by their k-mer composition (Macas et al., 2010; Koch et al., 2014). However, this does not prevent mis-alignments within these regions. The better understanding of the sequence of these regions may subsequently help to develop methods that can determine repeat length variations, such as telomere length, from the read data.

3. Length Distribution of DNA Fragments and Reads

Long DNA sequences are broken into smaller DNA fragments by various means (Quail, 2010), such as sonication and nebulization. Whatever the fragmentation method, the sizes of the fragments in the DNA library is an important parameter (Head et al., 2014). The fragment size distribution is usually single-peaked with the typical size appropriate for the subsequent sequencing methods.

Unlike the fragment size, read size is precisely specified for most sequencing methods. Many companies use pair-end sequencing of relatively short read lengths (2 × 35 bp for Complete Genomics, 2 × 50 for SOLiD of Life Technology/Applied Biosystems, up to 2 × 300 for Illumina). The Ion Torrent of Life Technologies and 454 of Rouche have longer read lengths, up to 400 and 1000 bases, respectively. In comparison, Sanger sequencing can handle up to 1000 bases DNA fragments.

The Pacific Biosciences' single-molecule real-time (SMRT) sequencing (Eid et al., 2009; Roberts et al., 2013) is not equivalent to the highly parallel NGS. However, it is an approach that can produce much longer reads and it may not even need a library preparation (Coupland et al., 2012). For SMRT, P_R instead of P_F is more relevant. Sequences produced by the different technologies are still not 100% identical due to sequencing errors (Huddleston et al., 2014).

4. Distribution of Exact Repeats in the Human Reference Genome

Let's use a simple sequence to illustrate the difference between P_D,C where D is the length of maximal repeats, and P_{D0, C} where D₀ is a fixed length: atcgaaatatccatcc (reverse complement ggatggatatatttcgat). There is one maximal repeating tetramer, atcc/ggat (D = 4, C = 2), and one maximal repeating trimer, atc (D = 3, C = 3). We include atc but not tcc as another repeat unit because there is an extra copy of atc which is not part of atcc. For the same reason, at, tc are independent repeating dimers (D = 2, C = 4), but not cc. On the other hand, with the fixed length D₀ = 3, there are four repeating trimers, atc/gat (C = 3), cga/tcg, ata/tat, and tcc/gga (C = 2). Three of them are part of larger repeat unit of length D₀ = 4.

Obtaining P_D,C for the reference genome needs a pre-processing of the sequence by a suffix array (Manber and Myers, 1993; Crochemore et al., 2007) or other similar data structures (Berger et al., 2013), such as Burrows-Wheeler transform (Burrows and Wheeler, 1994) or FM-index (Ferragina and Manzini, 2005). It is of crucial importance to have a memory(space)-efficient algorithm, as the human genome size is 3 Gbase (or 6 Gbase considering reverse complement) and a typical computer nowadays has only a few Gbyte memory. Compared to suffix tree (Gusfield, 1997), suffix array is known to be more space-efficient. Thus, for genome scale repeat analysis, suffix array is preferred over suffix tree (Sadakane and Shibuya, 2001; Hon et al., 2004; Becher et al., 2009; Barenbaum et al., 2013).

The P_D0,C distribution is more relevant to the read set, and comparatively easier to obtain. However, the relationship between P_D,C and P_D0,C may not be trivial. From P_D0,C to P_D,C, one may first determine the histogram P_D0,C at D₀ and D₀ + 1, then remove the type counts at D₀ that are part of repeating (D₀ + 1)-mer type. In practice, the situation can be complicated as one (D₀ + 1)-mer may contribute two D₀-mer types. Without more detailed information of the repeating pattern, subtracting N_{D0 + 1} from N_D0 is the least one could do, as it provides an upper limit to P_D.

The number of repeat unit types at fixed D₀ in the assembled human reference genome has been obtained at various D₀'s (Li et al., 2014). Most of these repeat types only occur in the genome twice (C = 2). The number of repeat types for C = 2, C = 3, and C > 2 is plotted as a function of D₀ in Figure 2A (in log-log scale). The fact that it is almost a straight line indicates that the decay is a power-law, which is a widespread distribution in nature (Sornette, 2006). We extrapolate N_D0 at all D₀'s between 20 and 1000, using a power-law relationship between two neighboring points in Figure 2A (or linear relationship in log-log scale). Subtracting N_{D0 + 1} from N_D0, we infer the upper limit of P_D in Figure 2B.

FIGURE 2

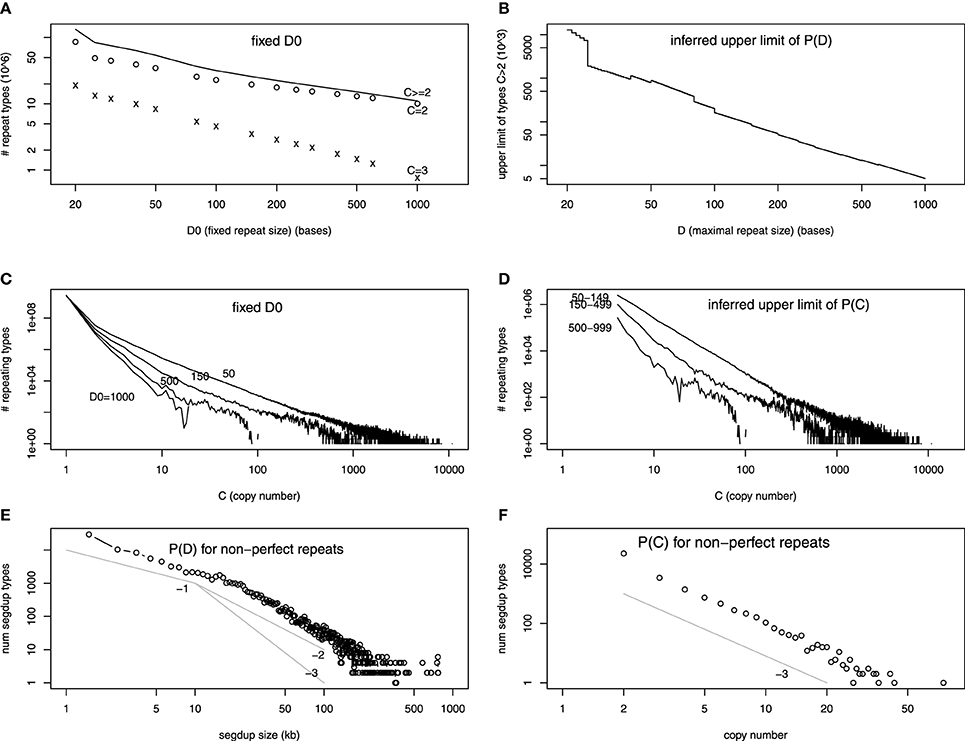
Figure 2. (A–D) are on exact repeats and (E–F) on approximate repeats, all in log-log scale. (A) The number of repeat types as a function of the fixed repeat unit length D₀. The number of repeat types with exact two (three) copies in the genome, C = 2 (C = 3), are shown separately. (B) The difference of number of repeat types at D₀ and D₀ + 1. This is an upper limit of the number of maximal repeat types at D. (C) The number of repeat types at fixed repeat unit lengths (D₀ = 50, 150, 500, 1000, as a function of copy number C). (D) The difference between the number of repeat types at different D₀'s (e.g., between D₀ = 50 and D₀ = 150). This represents the sum of upper limits of number of maximal repeat types at length D, summing over all D's between the two values (e.g., 50 and 150). (E) Number of appearence in the segmental duplication track from the UCSC Genome Browser with certain size D as a function of D. The three power-law functions, 1/D, 1/D², 1/D³ are drawn for a comparison. (F) Number of segmental duplication names as a function of copy number C (number of pairwise alignment lines plus one). The power-law function 1/C³ is drawn for a comparison.

The copy number information is ignored in Figure 2B. The P_C when D₀ is fixed is shown in Li et al. (2014) which is reproduced in Figure 2C. If we subtract N_{D0 = 150,C} from N_{D0 = 50,C}, it will sum up the upper limit of all N_D for 50 < D < 150. It is done in Figure 2D. Figures 2B,D provide evidence that P_D,C is a power-law function in both repeat unit length and copy number.

5. Distribution of Approximate Repeats in the Human Reference Genome

The distribution P_D,C,M or P_D0,C,M allowing up to M mismatches is much harder to obtain due to computational constraints (Derrien et al., 2012). Take our toy sequence for example: atcgaaatatccatcc/ggatggatatatttcgat: with mismatch M = 1, there are three clusters of pentamers (D = 5) that repeat, with 3, 2, and 4 pentamer types, respectively. A pentamer in a cluster should be less than or equal to M mutation away from pentamers in other clusters. But it is not necessary that any two pentamers should be M or less mutations away. Since one-mutation path can link all D₀-mers, they consist of one huge cluster. In a real sequence with limited length, however, the genome cannot sample all possible D₀-mers, breaking the path to separate D₀-mer types into clusters.

We use the segmental duplication track (SegDup) in the UCSC Genome Browser to examine the length and copy number distribution for approximate repeats. SegDup was obtained by aligning RepeatMasker (http://www.repeatmasker.org) filtered 400 kb fragments to the reference genome by BLAST (http://blast.ncbi.nlm.nih.gov) (Bailey et al., 2001). The BLAST alignment result is extended to obtain approximate maximal repeats. The minimum length of the SegDup is 1 kb, and the condition of >90% identity in the pairwise alignment is imposed.

Figure 2E shows the frequency of SegDup with certain sizes appear in the track, as a function of the size. Figure 2F is the frequency of SegDup labels, as a function of C. Since Figures 2E,F are in log-log scale, we have shown that repeats with mismatches have power-law distribution for both D and C. This power-law distribution for size is consistent with other studies: the self-alignment for smaller genomes shows similar power-law like distribution in Gao and Miller (2011, 2014). We also draw power-law functions with the known exponents: 1/D, 1/D², and 1/D³ for size distribution, and 1/C³ for copy number distribution. The size distribution seems to follow 1/D for smaller sizes, whereas 1/D^a (2 < a < 3) for larger SegDup regions. The copy number distribution is clearly 1/C³. Interestingly, the 1/D³ function is predicted by a neutral duplication dynamics model (Massip and Arndt, 2013).

6. Proportion of Unmappable Reads as a Function of Read Length

The unmappability rate depends on whether it is viewed from the reads or the reference sequence perspective. Take the example of our toy sequence, atcgaaatatccatcc: of the 13 tetramer counts, two are copies of atcc. The proportion of reads counts that are unmappable at k = 4 is then 2/13 = 15%. However, the two copies of atcc cover 8 base positions, so the proportion of unmappable regions is 8/16 = 50%.

With k-mer count information but no locations, only the first proportion can be calculated. The number of read counts which are unmappable in the assembled portion of the human genome is shown in Figure 1 of Li et al. (2014). The proportion of reads that are unmappable to the assembled portion of the human genome is 28.4, 20, 16.2, 11.3, 8.2, 4.3, 3.4, 2.4, 2, 1.7, 1.5, 1.3, 1.2, 1.1, and 0.8% at read lengths of 20, 25, 30, 40, 50, 80, 100, 150, 200, 250, 300, 400, 500, 600, and 1000. The fall of these proportions is faster (judged by the slope of the straight line in log-log scale) when the read length is shorter than 80–100, slower when the read length is longer. This led to the “diminishing return” with the read length in Li et al. (2014).

To evaluate unmappable regions in the genome, the location of the unmappable reads should be known. We have carried out an alignment for the length-1000 unmappable reads (Li and Freudenberg, 2014). The unmappable regions at the 1000-bp level cover a size of 35 Mb, or around 1.2% of the assembled portion of the human genome, larger than the 0.8% from the perspective of read population.

7. Discussion

The central thesis of this paper is that if the sequencing produces shorter reads, the length of any repeat unit in the genome sets an upper limit on mappability (a concept applicable to both the read and to the chromosome region). The distribution of repeat lengths, of fragment sizes (if a paired-end method is used), and of read length, together determine the proportion of genome that can be aligned/mapped.

In an analysis (Becher et al., 2009), a repeat of 67632 bases (C = 2) is identified in the human genome, with both copies in chromosome 1. The longest repeat that appears in two different chromosomes has length 21864, appearing in chromosomes 1 and 5. This study did not consider the reverse complement strand, thus it leaves the possibility of finding even longer repeat lengths. For other genomes, long repeat lengths have been reported, such as a 41 kb repeat in E. coli (Haubold and Wiehe, 2006).

If mismatch is introduced, the repeat (duplication) size can be even larger. Tandem repeats of 38.8 kb (chr1), 23.6 kb (chrY), 22.9 kb (chr17), are listed in Warburton et al. (2008). Up to 200 kb segmentally duplicated regions are examined in Zhang et al. (2005). On Y chromosome, the largest duplication length is 1.5 Mb (Sainz et al., 2006). A 106 kb tandem repeat and CNV within the repeat is reported to be associated with male infertility (Avidan et al., 2003). In the SegDup track from the UCSC Genome Browser, duplications of sizes of 400 kb appear on chromosomes 9 and 10.

The repeat-caused unmappable regions are not only problematic for achieving 100% sequencing, but also, by their tendency to cause genomic instability, casts doubt on the concept of a reference genome. Even the simplest tandem repeats are shown to be under-counted in the reference genome, exhibit high level of CNV (Sharp et al., 2005), affect related gene expression (Stranger et al., 2007), and introduce heterochromatin, which silences nearby genes (Brahmachary et al., 2014). Typing CNVs is the goal of many NGS applications in human complex diseases study, forensics, disease markers (Budowle et al., 2009; Zhang et al., 2009; Bassett et al., 2010; Girirajan et al., 2011), but one should keep in mind the uncertainty of the repeat regions in the reference genome, which are prone to CNV.

Can we equate unmappability to being biologically less important? First, short repeats, which are well known to be disease-causing (La Spada and Taylor, 2010), may expand to longer enough repeat segments that are unmappable. Secondly, genes do exist in repeat regions. The gene TPTE was found on the acrocentric arm of chromosome 21 (Chen et al., 1999; Guipponi et al., 2000; Eichler et al., 2004). Many RefGenes are located in the 1 kb-unmappable regions in the assembled reference human genome (Li and Freudenberg, 2014; Li et al., 2014). Thirdly, repeats or duplications are the raw material for evolution (Ohno, 1970). As an anecdotal evidence, all immunoglobulin genes are located near centromeres or telomeres which are full of repeats. To summarize, we have enough facts to conclude that repeats and unmappable regions should not be ignored for a comprehensive analysis of the human genome.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aldrup-MacDonald, M. E., and Sullivan, B. A. (2014). The past, present, and future of human centromere genomics. Genes (Basel) 5, 33–50. doi: 10.3390/genes5010033

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Altemoswe, N., Miga, K. H., Maggioni, M., and Willard, H. F. (2014). Genomic characterization of large heterochromatic gaps in the human genome assembly. PLoS Comput. Biol. 10:e1003628. doi: 10.1371/journal.pcbi.1003628

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ambrosini, A., Paul, S., Hu, S., and Riethman, H. (2007). Human subtelomeric duplicon structure and organization. Genome Biol. 8:R151. doi: 10.1186/gb-2007-8-7-r151

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Avidan, N., Tamary, H., Dgany, O., Cattan, D., Pariente, A., Thulliez, M., et al. (2003). CATSPER2, a human autosomal nonsyndromic male infertility gene. Eur. J. Hum. Genet. 11, 497–502. doi: 10.1038/sj.ejhg.5200991

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bailey, J. A., Yavor, A. M., Massa, H. F., Trask, B. J., and Eichler, E. E. (2001). Segmental duplications: organization and impact within the current human genome project assembly. Genome Res. 11, 1005–1017. doi: 10.1101/gr.GR-1871R

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Barenbaum, P., Becher, V., Deymonnaz, A., Halsband, M., and Heiber, P. (2013). Efficient repeat finding in sets of strings via suffix arrays. Discrete Math. Theor. Comput. Sci. 15, 59–70. Available online at: www.dmtcs.org/dmtcs-ojs/index.php/dmtcs/article/view/2130

Bassett, A. S., Scherer, S. W., and Brzustowicz, L. M. (2010). Copy number variations in Schizophrenia: critical review and new perspectives on concepts of genetics and disease. Am. J. Psychiatry 167, 899–914. doi: 10.1176/appi.ajp.2009.09071016

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Becher, V., Deymonnaz, A., and Heiber, P. (2009). Efficient computation of all perfect repeats in genomic sequences of up to half a gigabyte, with a case study on the human genome. Bioinformatics 25, 1746–1753. doi: 10.1093/bioinformatics/btp321

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Berger, B., Peng, J., and Singh, M. (2013). Computational solutions for omics data. Nat. Rev. Genet. 14, 333–346. doi: 10.1038/nrg3433

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Blackburn, E., Greider, C. W., and Szostak, J. W. (2006). Telomeres and telomerase: the path from maize, Tetrahymena and yeast to human cancer and aging. Nat. Med. 12, 1133–1138. doi: 10.1038/nm1006-1133

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Blasco, M. A. (2005). Telomeres and human disease: ageing, cancer and beyond. Nat. Rev. Genet. 6, 611–622. doi: 10.1038/nrg1656

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Brahmachary, M., Guilmatre, A., Quilez, J., Hasson, D., Borel, C., Warburton, P., et al. (2014). Digital genotyping of macrosatellites and multicopy genes reveals novel biological functions associated with copy number variation of slarge tandem repeats. PLoS Genet. 10:e1004418. doi: 10.1371/journal.pgen.1004418

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Budowle, B., Eisenberg, A. J., and van Daal, A. (2009). Validity of low copy number typing and applications to forensic science. Croatian Med. J. 50, 207–217. doi: 10.3325/cmj.2009.50.207

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Burrows, M., and Wheeler, D. J. (1994). A Block Sorting Lossless Data Compression Algorithm, System Research Center Research Report 124, Digital Equipment Corporation. Palo Alto, CA.

Chen, H., Rossier, C., Morris, M. A., Scott, H. S., Gos, A., Bairoch, A., et al. (1999). A testis-specific gene, TPTE, encodes a putative transmembrane tyrosine phosphatase and maps to the pericentromeric region of human chromosomes 21 and 13, and to chromosomes 15, 22, and Y. Hum. Genet. 105, 399–409. doi: 10.1007/s004390051122

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Churikov, D., and Price, C. M. (2008). Telomeric and subtelomeric repeat sequences. eLS. doi: 10.1002/9780470015902.a0005065.pub3

CrossRef Full Text | Google Scholar

Cocho, G., Miramontes, P., Mansilla, R., and Li, W. (2014). Bacterial genomes lacking long-range correlations may not be modeled by low-order Markov chains: the role of mixing statistics and frame shift of neighboring genes. Comput. Biol. Chem. 53(A), 15–25. doi: 10.1016/j.compbiolchem.2014.08.005

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Coupland, P., Chandra, T., Quail, M., Reik, W., and Swerdlow, H. (2012). Direct sequencing of small genomes on the Pacific Biosciences RS without library preparation. Biotechniques 53, 365–372. doi: 10.2144/000113962

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Crochemore, M., Hancart, C., and Lecrog, T. (2007). Algorithms on Strings. Cambridge, UK: Cambridge University Press. doi: 10.1017/CBO9780511546853

CrossRef Full Text | Google Scholar

Derrien, T., Estellé, J., Sola, S. M., Knowles, D. G., Raineri, E., Guigó, R., et al. (2012). Fast computation and applications of genome mappability. PLoS ONE 7:e30377. doi: 10.1371/journal.pone.0030377

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Eichler, E. E., Clark, R. A., and She, X. (2004). An assessment of the sequence gaps: unfinished business in a finished human genome. Nat. Rev. Genet. 5, 345–354. doi: 10.1038/nrg1322

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Eid, J., Fehr, A., Gray, J., Luong, K., Lyle, J., Otto, G., et al. (2009). Real-time DNA sequencing from single polymerase molecules. Science 323, 133–138. doi: 10.1126/science.1162986

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ferragina, P., and Manzini, G. (2005). Indexing compressed texts, J. ACM 52, 552–581. doi: 10.1145/1082036.1082039

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gao, K., and Miller, J. (2011). Algebraic distribution of segmental duplication lengths in whole-genome sequence self-alignments. PLoS ONE 6:e18464. doi: 10.1371/journal.pone.0018464

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gao, K., and Miller, J. (2014). Human-chimpanzee alignment: ortholog exponentials and paralog power-laws. Comp. Biol. Chem. 53(A), 59–70. doi: 10.1016/j.compbiolchem.2014.08.010

CrossRef Full Text | Google Scholar

Girirajan, S., Campbell, C. D., and Eichler, E. E. (2011). Human copy number variation and complex genetic disease. Ann. Rev. genet. 45, 203–226. doi: 10.1146/annurev-genet-102209-163544

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gready, D. L., Ratliff, R. L., Robinson, D. L., McCanlies, E. C., Meyne, J., and Moyzis, R. K. (1992). Highly conserved repetitive DNA sequences are present at human centromeres. Proc. Natl. Acad. Sci. U.S.A. 89, 1695–1699. doi: 10.1073/pnas.89.5.1695

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Guipponi, M., Yaspo, M. L., Riesselman, L., Chen, H., de Sario, A., Roizés, G., et al. (2000). Genomic structure of a copy of the human TPTE gene which encompases 87 kb on the short arm of chromosome 21. Hum. Genet. 107, 127–131. doi: 10.1007/s004390000343

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gusfield, D. (1997). Algorithms on Strings, Trees, and Sequences. Cambridge, UK: Cambridge University Press. doi: 10.1017/CBO9780511574931

CrossRef Full Text | Google Scholar

Haubold, B., and Wiehe, T. (2006). How repetitive are genomes? BMC Bioinformatics 7:541. doi: 10.1186/1471-2105-7-541

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Head, S. R., Komori, H. K., LaMere, S. A., Whisenant, T., Van Nieuwerburgh, F., Salomon, D. R., et al. (2014). Library construction for next-generation sequencing: overviews and challenges. Biotechniques 56, 61–77. doi: 10.2144/000114133

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hon, W. K., Lam, T. W., Sung, W. K., Tse, W. L., Wong, C. K., and Yu, S. M. (2004). “Practical aspects of compressed suffix arrays and FM-index in searching DNA sequences,” in Proceedings the Sixth Workshop on Algorithm Engineering and Experiments (ALENEX) and the First Workshop On Analytic Algorithms and Combinatorics (ANALC), eds L. Arge, G. F. Italiano, and R. Sedgewick (New Orleans, LA: SIAM), 31–38.

Google Scholar

Huddleston, J., Ranade, S., Malig, M., Antonacci, F., Chaisson, M., Hon, L., et al. (2014). Reconstructing complex regions of genomes using long-read sequencing technology. Genome Res. 24, 688–696. doi: 10.1101/gr.168450.113

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jones, K. W. (1973). Satellite DNA. J. Med. Genet. 10, 273–281. doi: 10.1136/jmg.10.3.273

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jones, K. W., and Prosser, J. (1973). The chromosomal location of human satellite DNA III. Chromosoma 42, 445–451. doi: 10.1007/BF00399411

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Koch, P., Platzer, M., and Downie, B. R. (2014). RepARK – de novo creation of repeat libraries from whole-genome NGS reads. Nucl. Acids Res. 42:e80. doi: 10.1093/nar/gku210

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

La Spada, A. R., and Taylor, J. P. (2010). Repeat expansion disease: progress and puzzles in disease pathogenesis. Nat. Rev. Genet. 11, 247–258. doi: 10.1038/nrg2748

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Li, W. (1997). Study of correlation structure in DNA sequences: a critical review. Comp. Chem. 21, 257–272. doi: 10.1016/S0097-8485(97)00022-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Li, W. (2013). G+C content evolution in the human genome. eLS. doi: 10.1002/9780470015902.a0021751

CrossRef Full Text | Google Scholar

Li, W., and Freudenberg, J. (2014). Characterizing regions in the human genome unmappable by next-generation-sequencing at the read length of 1000 bases. Comput. Biol. Chem. 53(A), 108–117. doi: 10.1016/j.compbiolchem.2014.08.015

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Li, W., Freudenberg, J., and Miramontes, P. (2014). Diminishing return for increased mappability with longer sequencing reads: implications of the k-mer distributions in the human genome, BMC Bioinformatics 15:2. doi: 10.1186/1471-2105-15-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Macas, J., Neumann, P., Novák, P., and Jiang, J. (2010). Global sequence characterization of rice centromeric satellite based on oligomer frequency analysis in large-scale sequencing data. Bioinformatics 26, 2101–2108. doi: 10.1093/bioinformatics/btq343

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Manber, U., and Myers, G. (1993). Suffix arrays: a new method for on-line string searches. SIAM J. Comp. 22, 935–948. doi: 10.1137/0222058

CrossRef Full Text | Google Scholar

Manuelidis, L. (1976). Repeating restriction fragments of human DNA. Nucl. Acids Res. 3, 3063–3076. doi: 10.1093/nar/3.11.3063

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Manuelidis, L. (1978). Chromosomal localization of complex and simple repeated human DNAs. Chromosoma 66, 23–32. doi: 10.1007/BF00285813

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Massip, F., and Arndt, P. (2013). Neutral evolution of duplicated DNA: an evolutionary stick-breaking process causes scale-invariant behavior. Phys. Rev. Lett. 110:148101. doi: 10.1103/PhysRevLett.110.148101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Miga, K. H., Newton, Y., Jain, M., Altemose, N., Willard, H. F., and Kent, W. J. (2014). Centromere reference models for human chromosomes X and Y satellite arrays. Genome Res. 24, 697–707. doi: 10.1101/gr.159624.113

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moyzis, R. K., Buckingham, J. M., Cram, L. S., Dani, M., Deaven, L. L., Jones, M. D., et al. (1988). A highly conserved repetitive DNA sequence (TTAGGG)_n, present at the telomeres of human chromosomes. Proc. Natl. Acad. Sci. U.S.A. 85, 6622–6626. doi: 10.1073/pnas.85.18.6622

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ohno, S. (1970). Evolution By Gene Duplication. New York, NY: Springer. doi: 10.1007/978-3-642-86659-3

CrossRef Full Text | Google Scholar

Pinkel, D., Segraves, R., Sudar, D., Clark, S., Poole, I., Kowbel, D., et al. (1998). High resolution analysis of DNA copy number variation using comparative genomic hybridization to microarrays. Nat. Genet. 20, 207–211. doi: 10.1038/2524

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Quail, M. A. (2010). DNA mechanical breakage. eLS. doi: 10.1002/9780470015902.a0005333

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ralston, A. (1982). De Bruijn sequences – a model example of the interaction of discrete mathematics and computer science. Math. Magn. 55, 131–143. doi: 10.2307/2690079

CrossRef Full Text | Google Scholar

Riethman, H., Ambrosini, A., Castaneda, C., Finklestein, J., Hu, X. L., Mudunuri, U., et al. (2004). Mapping and initial analysis of human subtelomeric sequence assemblies. Genome Res. 14, 18–28. doi: 10.1101/gr.1245004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Roberts, R. J., Carneiro, M. O., and Schatz, M. C. (2013). The advantages of SMRT sequencing. Genome Biol. 14:405. doi: 10.1186/gb-2013-14-6-405

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rudd, M. K., and Willard, H. F. (2004). Analysis of the centrometic regions of the human genome assembly. Trends Genet. 20, 529–533. doi: 10.1016/j.tig.2004.08.008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sadakane, K., and Shibuya, T. (2001). Indexing huge genome sequences for solving various problems. Genome Infor. 12, 175–183. Available online at: www.jsbi.org/pdfs/journal1/GIW01/GIW01F18.html

Sainz, J., Rovensky, P., Gudjonsson, S. A., Thorleifsson, G., Stefansson, K., and Gulcher, J. R. (2006). Segmental duplication density decrease with distance to human-mouse breaks of synteny. Eur. J. Hum. Genet. 14, 216–221. doi: 10.1038/sj.ejhg.5201534

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Scheibye-Alsing, K., Hoffmann, S., Frankel, A., Jensen, P., Stadler, P. F., Mang, Y., et al. (2009). Sequence assembly. Comp. Biol. Chem. 33, 121–136. doi: 10.1016/j.compbiolchem.2008.11.003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sharp, A. J., Locke, D. P., McGrath, S. D., Cheng, Z., Bailey, J. A., Vallente, R. U., et al. (2005). Segmental duplications and copy-number variation in the human genome. Am. J. Hum. Genet. 77, 78–88. doi: 10.1086/431652

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sornette, D. (2006). Critical Phenomena in Natural Sciences: Chaos, Fractals, Selforganization and Disorder: Concepts and Tools. Berlin: Springer.

Google Scholar

Stranger, B. E., Forrest, M. S., Dunning, M., Ingle, C. E., Beazley, C., Thorne, N., et al. (2007). Relative impact of nucleotide and copy number variation on gene expression phenotypes. Science 315, 848–853. doi: 10.1126/science.1136678

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Vissel, B., and Choo, K. H. (1987). Human alpha satellite DNA – consensus sequence and conserved regions. Nucl. Acids Res. 15, 6751–6752. doi: 10.1093/nar/15.16.6751

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Warburton, P. E., Hasson, D., Guillem, F., Lescale, C., Jin, X., and Abrusan, G. (2008). Analysis of the largest tandemly repeated DNA families in the human genome. BMC Genomics 9:533. doi: 10.1186/1471-2164-9-533

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Willard, H. F. (1990). Centromeres of mammalian chromosomes. Trends Genet. 6, 410–416. doi: 10.1016/0168-9525(90)90302-M

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wyandt, H. E., and Tonk, V. S. (eds.). (2011). Human Chromosome Variation: Heteromorphism and Polymorphism. Dordrecht: Springer Science+Business Media.

Google Scholar

Zhang, F., Gu, W., Hurles, M. E., and Lupski, J. R. (2009). Copy number variation in human health, disease, and evolution. Ann. Rev. Genom. Hum. Genet. 10, 451–481. doi: 10.1146/annurev.genom.9.081307.164217

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zhang, L., Lu, H. H., Chung, W. Y., Yang, J., and Li, W. H. (2005). Patterns of segmental duplication in the human genome. Mol. Biol. Evol. 22, 135–141. doi: 10.1093/molbev/msh262

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar