
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Genet., 24 April 2012
Sec. Evolutionary and Population Genetics
Volume 3 - 2012 | https://doi.org/10.3389/fgene.2012.00066
Next-generation sequencing (NGS) technologies have made it possible to address population genetic questions in almost any system, but high error rates associated with such data can introduce significant biases into downstream analyses, necessitating careful experimental design and interpretation in studies based on short-read sequencing. Exploration of population genetic analyses based on NGS has revealed some of the potential biases, but previous work has emphasized parameters relevant to human population genetics and further examination of parameters relevant to other systems is necessary, including situations where sample sizes are small and genetic variation is high. To assess experimental power to address several principal objectives of population genetic studies under these conditions, we simulated population samples under selective sweep, population growth, and population subdivision models and tested the power to accurately infer population genetic parameters from sequence polymorphism data obtained through simulated 4×, 8×, and 15× read depth sequence data. We found that estimates of population genetic differentiation and population growth parameters were systematically biased when inference was based on 4× sequencing, but biases were markedly reduced at even 8× read depth. We also found that the power to identify footprints of positive selection depends on an interaction between read depth and the strength of selection, with strong selection being recovered consistently at all read depths, but weak selection requiring deeper read depths for reliable detection. Although we have explored only a small subset of the many possible experimental designs and population genetic models, using only one SNP-calling approach, our results reveal some general patterns and provide some assessment of what biases could be expected under similar experimental structures.
Principal objectives in population genetics are to identify targets of natural selection, infer historical shifts in demography, and define genetic differentiation among groups. Over the past four decades, the power to address these questions has improved markedly with the increase in scale and availability of genetic markers. The recent arrival of next-generation sequencing (NGS) marks another shift on multiple scales (Pool et al., 2010). The relative low cost and high throughput nature of NGS technologies has made it possible to collect full genome sequence data on population samples, providing the opportunity to address population genetic questions at the genomic scale, sometimes across multiple populations (e.g., Xia et al., 2009; Durbin et al., 2010; Magwene et al., 2011). For example, NGS makes possible unbiased scans of the genome for signatures of positive selection (Durbin et al., 2010), tests of demography and population structure that include rare (<5%) variants (Henn et al., 2010; Gravel et al., 2011), as well as genomic mapping of population parameters such as nucleotide diversity or fine-scale linkage disequilibrium (e.g., Branca et al., 2011; Magwene et al., 2011).
While NGS has expanded the realm of possible experiments, NGS-based population genomic analyses and experimental designs are not yet standard and free of complications. The main challenges to population genomic analysis using NGS data stem from the substantially higher error rates in NGS relative to traditional Sanger sequencing, which complicates identification of low-frequency variants in populations (Johnson and Slatkin, 2006, 2008; Hellmann et al., 2008; Lynch, 2008, 2009; Jiang et al., 2009), uneven sequencing of the homologous chromosomes in a diploid individual, which may compromise accuracy in detecting heterozygotes (Hellmann et al., 2008; Johnson and Slatkin, 2008; Lynch, 2008, 2009; Jiang et al., 2009), and a higher false-negative SNP detection rate due to the Poisson read sampling, which can result in some regions not being sequenced at all (Durbin et al., 2010). One approach to mitigating these challenges is to sequence each sampled individual to substantially greater coverage depth or to obtain larger sample sizes of individuals. However, current experimental designs typically consist of either small, deeply sequenced samples (Xia et al., 2009; Branca et al., 2011; Magwene et al., 2011) or large samples sequenced to low read depths (Durbin et al., 2010), reflecting a common, and practical trade-off between sample size and sequencing depth. In general practice, population genomic experiments in ecological and other non-model systems will likely have to compromise on both sample size and read depth, possibly resulting in losses in power and biases not incurred with larger experimental designs.
In addition to modifying experimental design to mitigate challenges related to NGS data analysis, statistical corrections may also provide a means for accommodating uncertainty in the data. Most current methods for conducting population genetic analysis are based on allele frequencies (reviewed in Nielsen, 2005) or a summary of allele frequencies (e.g., Gutenkunst et al., 2009; but see Yi et al., 2010), and, broadly speaking, two statistical approaches have been proposed to estimate this information from NGS data. The first approach entails calling genotypes of each individual using either a Bayesian or Likelihood framework (Hoberman et al., 2009; Li et al., 2009b; Bansal et al., 2010; DePristo et al., 2011). The other approach attempts to estimate allele frequencies directly from the data without first inferring individual genotypes (Lynch, 2009; Kim et al., 2010, 2011; Martin et al., 2010). In some cases, a posterior probability is generated that provides a quantification of the uncertainty of each genotype call (e.g., Martin et al., 2010; DePristo et al., 2011) that could be directly incorporated into population genetic analyses (e.g., Yi et al., 2010). However, until population genetic analyses are further adapted to incorporate posterior probabilities, standard population genetic analyses must be applied directly to genotype calls. The number of applications of such statistical approaches to empirical data is thus far relatively small with a bias toward human-based studies (e.g., Hellmann et al., 2008; Durbin et al., 2010; Yi et al., 2010), but some examples in non-human systems exist as well (e.g., Williams et al., 2010; Ahmad et al., 2011). More importantly, the biases introduced when population genetic analyses are applied to genotypes inferred from NGS data have not been well characterized, particularly in systems other than humans.
The aim of the present study is to determine how variation in the structure of NGS experiments and inaccuracies inherent to NGS-based genotype calling impact the ability to address several common population genetic questions in non-model or ecological systems. In particular, we sought to provide some assessment of what can be accomplished with NGS data when genetic variation is high, sample sizes, and sequencing budgets are small and independent datasets are not available for calibration. We simulated population genetic samples under Wright–Fisher equilibrium, selective sweep, population growth, and population subdivision models. Short-read datasets were generated in silico and processed through a read-mapping and multi-sample-genotyping-based SNP-calling pipeline similar to that used by the human 1000 Genomes Project (Durbin et al., 2010). We determined the power to infer population genetic parameters and conduct population genetic tests using NGS data of varying depths. Our results demonstrate that very low sequencing depth introduces systematic biases under some, but not all, inference frameworks, yet significant power and accuracy is recovered with as little as 8× sequencing depth.
A graphical flowchart presentation of our analysis pipeline can be found in Figure A1 in Appendix.
We conducted coalescent simulations to generate population samples under a variety of equilibrium and non-equilibrium population models. Our null model is at Wright–Fisher equilibrium with no natural selection, constant population size, and complete random mating. Our alterative models included selective sweeps, exponential population growth, and subdivided populations. The general structure of our simulation approach was to simulate 100 population samples comprised of 30 haplotypes that were 30-kb in length per sample under each set of measured parameters. The departures from this structure were that we conducted 500 simulations under the growth model, and for the subdivided population, we simulated two subpopulations with 30 haplotypes each (total of 60 haplotypes per iteration). Because we wanted to consider levels of genetic variation seen in many organisms with naturally large population sizes, we modeled a population with an effective population size (N) of 106, a per base mutation of 3.5 × 10−9 (Keightley et al., 2009), and a recombination rate of 10−8 per base per generation. These parameters correspond to levels of genetic variation of þeta = 0.011 per site for the Wright–Fisher model and þeta = 0.027 per site for population structure model, and are similar to what one might expect from abundant insects with large geographic ranges such as Drosophila (e.g., Charlesworth, 2009) or Anopheles mosquitoes (e.g., Michel et al., 2006).
We used the coalescent simulation program ssw to simulate population samples under the selective sweep model of Kim and Stephan (2002). We conducted two rounds of simulations for each parameterization of the sweep model. In the first round, we conducted simulations under a rejection framework in which we kept the simulation result only if the likelihood ratio obtained using the program SweepFinder (Nielsen et al., 2005) was deemed significant (described below). As such, this round of simulations contains only datasets that contain patterns of polymorphism that reject in favor of selection with true genotypes, thereby providing a direct contrast when the simulations are processed through the sequencing pipeline and re-tested for selection. In a second round of simulations, we conducted a set of sweep simulations that were retained without regard to whether the null hypothesis of no selection could be rejected with the complete data set. This round of simulations provides a more complete power curve reflecting both the inherent power of the test implemented in Sweepfinder as well as the loss of power due to sequencing. For both rounds, we generated population samples under 6 parameterizations of the sweep model, including three strengths of selection (α = 2Ns) varying from weak (α = 50) to moderate (α = 200) to strong (α = 1000). For each value of selection strength, we also varied the time since completion of the sweep [τ (in units of 2NCURR generations) = 0.01 and 0.005] to reflect a variety of plausible recent selective sweep events. In addition, we simulated population samples under the null Wright–Fisher equilibrium model with ssw. ssw allows for both coding and non-coding sequences to be modeled, and we included six coding regions (covering approximately 21% of the 30-kb simulated) where the mutation rate was reduced by a factor of 0.3, the default value in ssw.
To simulate population samples under growth and structure models, we used the coalescent simulation program ms (Hudson, 2002). The growth model included exponential growth resulting in a doubling of the population size (NANC/NCURR = 0.5) over the last 1NCURR generations. We also simulated paired samples from diverging populations. These models were based on the island model in which, going backward in time, two subpopulations exchanged migrants at a rate of 4NCURRm = 0.05, and at either 2NCURR, 1NCURR, 0.025NCURR generations ago began exchanging migrants at a much greater rate (4NCURRm = 10 or 100) meant to reflect near panmixia. These models generated paired subpopulations with current FST values of approximately 0.54, 0.37, 0.15, and 0.01. Chromosomes were sampled evenly from each current sub-population and population assignment was maintained throughout the analysis.
Short-read sequence libraries were computationally generated and mapped to a reference sequence. A reference sequence of randomly chosen nucleotides was generated and used as the starting material for each simulated chromosome. To generate chromosomes, simulated polymorphism data from above was used as a guide for applying nucleotide changes resulting in a population sample of nucleotide sequences that reflects the simulated sample. Nucleotide changes, or SNPs, were applied to reflect the presence of derived alleles in the simulated polymorphism data. Diploid “individuals” were generated by randomly pairing simulated chromosomes. These diploid sequences were then computationally fragmented and sampled to generate short-reads that emulate Illumina’s HiSeq 2000 platform using the short-read simulation program SimSeq (Earl et al., 2011). One hundred base-pair (bp) paired-end reads were sampled with an average insert size of 500bp (SD = 50) and a duplicate probability of 0.01. SimSeq adds a fixed rate and distribution of “sequencing” errors using an error profile trained on alignments of human-derived HiSeq 2000 reads. Indels were not included in this model. While human data was used to train the error model, patterns of sequencing errors are largely based on sequencing platform and are likely to be similar between experimental systems. We converted BAM alignment files generated by SimSeq into SAM format using SAMtools (Li et al., 2009a), and ultimately into FastQ short-read libraries using the BAMtoFastQ program in the Picard Tools (v1.48) package1. Paired-end short-read libraries were aligned to the reference sequence generated above using BWA (Li and Durbin, 2009) allowing for an edit distance of 4 between each read and the reference, except for samples from the population structure models which we mapped with an edit distance of 5 to accommodate the higher number of SNPs in these samples. Reads with duplicate mapping positions were removed with the rmdup function in SAMtools (Li et al., 2009a). Cleaned BAM files from each of 15 diploids per population were used in subsequent steps for SNP calling. To determine how the power of inference is affected by read depth, we generated short-read libraries for each diploid such that the resulting alignments would achieve an average of 4×, 8×, and 15× read depth. Thus, for each individual diploid, we generated BAM alignments at each of the three read depths resulting in a total of 45 BAM alignment files per population sample.
We used the Genome Analysis Toolkit (GATK v. 1.1-30) to recalibrate FastQ quality scores and call candidate SNPs. The GATK implements a FastQ quality score re-calibration step that is designed to recalibrate reported quality scores by accounting for technology and sequence features that are known to co-vary with the reported quality score (DePristo et al., 2011). The GATK builds a recalibration model by ignoring all sites in a dbSNP database file provided by the user, correlating sequence and technology features with reported quality scores at remaining sites that differ from the reference, and calculating a recalibrated score based on residuals from this model (DePristo et al., 2011). This approach is designed for human genetic analysis, and relies heavily on the well-populated human dbSNP database. It is less ideal for systems with fewer independent SNP datasets. Although, it may be possible in a full genome re-sequencing study to use high-confidence SNPs as the “known” set, this step is likely to be project-specific so we opted not to model SNP ascertainment in this way. Instead, we circumvented the issue by training the re-calibration model on a sample of 15 diploid alignments that are 20 Mb in length and entirely lack “true” SNPs, but that have been processed using SimSeq to introduce “sequencing” error. We confirmed the validity of the re-calibration model and its effectiveness by analyzing the covariates and quality scores before and after re-calibration using the GATK. All BAM alignments in the primary study were recalibrated with this model, and recalibrated BAMs were used for subsequent SNP calling.
We tested the GATK’s Unified Genotyper (UG) for calling SNPs in our simulated population samples. The UG considers all individuals simultaneously to make genotype calls in a technology-aware fashion and uses a Bayesian genotype likelihood model to calculate genotypes for each individual and estimate the allele frequency at each variant site. We submitted each batch of 15 BAMs to the UG with default settings except the expected heterozygosity was set equal to the scaled mutation rate used in the simulations. The UG generates a Phred-scaled Quality score (Q) for each variant indicating the probability that a SNP exists at each site, where Q of 20 indicates a 1 in 100 chance that the call is incorrect. These Q scores are calculated without regard to the surrounding sequence context so the GATK implements a sophisticated variant quality score re-calibration method that has been shown to be more effective at sorting true from false positives than hard filtering based on un-calibrated Q scores or other parameters (DePristo et al., 2011). However, despite efforts to simulate larger SNPs datasets for training, we did not find that re-calibration led to better distinction between true and false positives under our simulation framework (data not shown). Therefore, we opted to use hard filtering based on the Q score and use all SNPs with a score of at least 5. Although this is a quite liberal threshold compared to the standard of Q20, preliminary analyses indicated that, even at 4× read depth, many true positives had Q values on this scale (data not shown). We found a threshold of 5 struck a good balance of minimizing false negatives while permitting a small number of false positives (8.4 false negatives for each false positive for 4× read depth). SNP calls were made for each population sample, converted into appropriate input formats and used in subsequent population genetic analyses.
The goal of this study was to determine the impact of the short-read sequencing, alignment, and SNP-calling process on the inference of population genetic patterns. Therefore, for each simulation under a specific model and sequence read depth, we quantified the difference between the population genetic model inferred using complete, pre-sequencing data, and the model inferred from post-sequencing data to directly measure the effect of sequencing.
To infer selective sweeps, we scanned SNP sets from the sweep simulations as well as the Wright–Fisher simulations using the Parametric version of the Composite Likelihood Ratio Test implemented in the program SweepFinder (Nielsen et al., 2005), which compares the likelihood of a selective sweep under the model of Kim and Stephan (2002) to the likelihood of a model without selection based on background allele frequencies. We used a grid size of 25, which corresponds to 1250 bp. For this part of the study, we aimed to compare the power to infer selection before and after sequencing as well as to specifically quantify the false-negative rate after sequencing. To quantify the difference in power to infer selection before and after sequencing, we searched for selective sweeps in the pre-sequencing data and then searched the SNP set inferred from the post-sequencing alignments. To determine significance, we established a null distribution of the likelihood ratio by conducting 104 simulations under the neutral Wright–Fisher equilibrium model, and collecting the maximum likelihood ratio from each simulation. The simulated “experimental” sweep datasets were considered significant if their likelihood ratio was greater than the 95% threshold from this null distribution. Simulations from both the significance-naïve set and the significance-enriched set (see Coalescent Simulations) were analyzed in this way. The proportions of significant CLRT results were compared between read depths and sweep models.
To infer the population growth parameters, we searched a grid of population growth models using a Poisson log-likelihood approach to determine the fit of the complete and inferred data to each simulated dataset. We used the program PRFREQ (Boyko et al., 2008) to calculate the expected site-frequency spectrum (SFS) across the grid and find the model within the grid with the maximum likelihood for each SNP set. We used the Poisson likelihood function in PRFREQ to determine the best-fit between the data and the models, first using the full pre-sequencing data and then with the SFS inferred from each post-sequencing SNP set. We used the scaled mutation rate and effective population size used in the simulations above, the instantaneous population growth model (two epochs), and the neutral distribution of selective effects (2Ns = 0). The grid consisted of 16 grid points for the timing of growth (τ), varying from 0.05 to 0.9, in units of 2NCURR and 16 points for the ratio of ancestral to current population size (ω), again varying from 0.05 to 0.9, for a total of 256 models. Since SNPs from the same population sample were used for inference before and after sequencing, we compared the pre-sequencing model to the post-sequencing model by subtracting the post-sequencing parameter values from the pre-sequencing values and plotting the difference.
To determine the effect of short-read sequencing on inference of genetic divergence between populations, we calculated FST between the two simulated subpopulations before and after short-read sequencing. We estimated global genetic differentiation between the two subpopulations across the 30-kb fragment using Weir and Cockerham’s unbiased estimator (Weir and Cockerham, 1984) implemented in an R script written by Eva Chan2. We compared the differences between pre- and post-sequencing FST values between read depths using a Paired Student’s t-test (t.test function in R; R Development Core Team, 2011) to determine whether increasing read depth resulted in significantly better inference of population differentiation. We also fit a loess curve to the data using the scatter.smooth function in R (R Development Core Team, 2011).
To quantify the effect of short-read sequencing on the power to infer population genetic models, we simulated a typical empirical re-sequencing pipeline including sequencing and SNP-calling errors inherent to such experimental frameworks. For all population genetic models, short-read datasets were generated at three read depths, aligned to a simulated reference, and queried for SNPs. We found that, under the parameterization of this simulation pipeline, read depth had a significant effect on the rate of true SNP recovery as well as on the rate of false-positive SNP ascertainment. The rate of true SNP recovery was high, increasing as a function of read depth, with average recovery rates across population genetic models of 86.7% at 4× read depth (SD, σ = 0.0134), 95.7% at 8× (σ = 0.0067), and 99.2% at 15× (σ = 0.0025). Furthermore, even without using the false-positive SNP culling steps in the GATK, the false-positive rates across all models were reasonably low with 4.1% (σ = 0.0206) of called SNPs being spurious at 4×, 0.95% (σ = 0.0047) at 8×, and 0.39% (σ = 0.0025) at 15×, highlighting the effect of read depth on the false-positive rate. Importantly, false negative and false-positive rates differed among population genetic models and disproportionately affected low (<0.1) frequency SNPs (Table 1). For example, at 4× read depth, the rates of true SNP recovery (or 1 minus the false-negative rates) differed among population genetic models, with the rate under the selective sweep model being significantly lower than that under the Wright–Fisher equilibrium model (tdf=170 = 2.17, p = 0.0314; Figure 1), and the rate under the growth model being significantly lower than the sweep model (tdf=165 = 8.02, p = 1.85 × 10−13; Figure 1). On the other hand, the rate of false positives was highest under the selection model at 6.1%, which was significantly greater than the rate under the growth model (tdf=195 = 5.67, p = 5.09 × 10−8), and the rate under the growth model (5.2%) was significantly greater than that under the equilibrium model (4.4%; tdf=195 = 7.93, p = 1.7 × 10−13). Since rare variants are disproportionately missed at low read depths (Figure 2; Table 1), the lower rate of recovery under the selective sweep and growth models can likely be attributed to the proportionally greater number of low-frequency variants under these models relative to the Wright–Fisher model (Figure A2 in Appendix). The structure model showed a lower true SNP recover rate relative to Wright–Fisher (Figure 1) and a substantially lower rate of false-positive SNPs (Table 1), but these are not a fair comparison since the structure model is a different genotyping environment as it is comprised of twice as many chromosomes and approximately three times as many true SNPs as the other models.
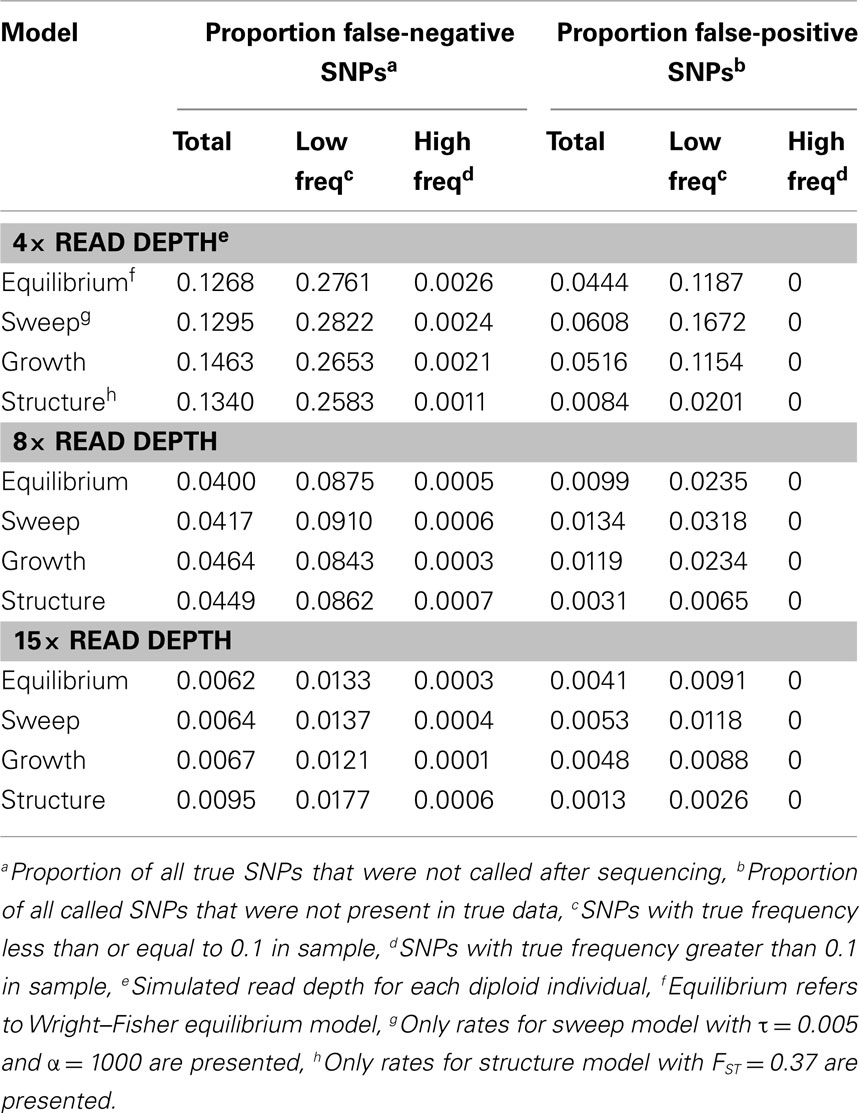
Table 1. Effect of read depth and population genetic model on false negative and false-positive SNP rates.
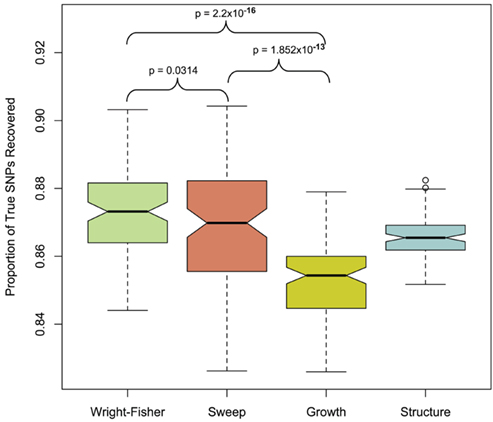
Figure 1. Proportion of true SNPs recovered with 4× sequencing. Data from 100 simulations is presented for each population model (only the selection model with τ = 0.005 and α = 1000 and structure model with FST ≈ 0.37 is presented in each case, see Materials and Methods). Models were compared with paired t-test at a significance threshold of 5%. Note that the y-axis scale is limited from 0.84 to 0.92. The population structure model was not included in this particular statistical contrast (see Materials and Methods).
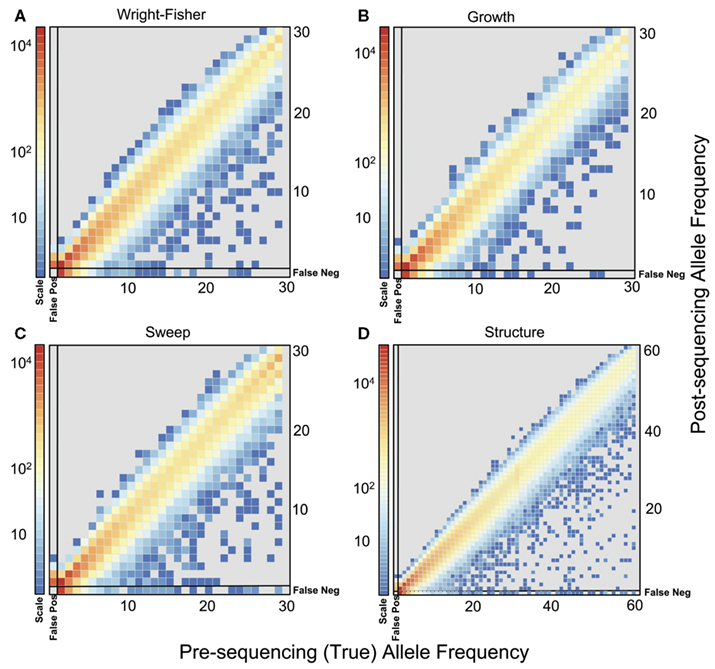
Figure 2. Comparison of allele frequencies before and after sequencing at 4x. Frequencies for SNPs, including false positives and false negatives, from population samples simulated under (A) Wright–Fisher model, (B) Population Growth model, (C) Selective Sweep model (α = 1000, τ = 0.005), and (D) Population Structure (FST ≈ 0.37). The frequencies of false-positive SNPs are found in the left most column of each plot. The frequencies of true SNPs that were missed after sequencing (false negatives) are plotted in the bottom row of each plot. For the population structure model, frequency was calculated as average frequency across both subpopulations. Colors indicate the total number of SNPs (on a log scale) in each bin from 100 simulations for each model.
We assessed the effect of short-read sequencing on the power to infer a selective sweep by testing for selection in patterns of variation in simulated population samples before and after simulated NGS. When we tested a set of random sweep simulations under each sweep model parameterization, we found that power curves are quite comparable before and after simulated sequencing, with only minor loss in power to identify the signature of a selective sweep at lower read depths (Figure A3 in Appendix), although further losses might be incurred under different parameterizations of the selection model, including modeling of older sweeps. To more directly quantify the loss in power of inference at lower read depths, we conducted a second set of genealogical simulations in which we required that the simulation give a significant result prior to simulated sequencing. In this case, we found that the power to infer selection depended on both the strength of selection and the depth of sequencing (Figure 3). Depth of sequencing did not have a strong effect on the power to identify the signature of selection after sequencing when selection was strong (2Ns = 1000; Figure 3). But, when the strength of selection is weak (2Ns = 50), we found a 29.9% reduction in power to infer selection with 8× sequencing relative to 15×, and an additional 29.1% reduction with 4× relative to 8× read depth (Figure 3). Interestingly, a small but noteworthy number of simulated samples that did not give a significant test based on full sequence data yielded a significant result after simulated NGS (data not shown). Inspection of these test results indicated that many of the pre-sequencing likelihood ratios were nearly significant in their rejection of the null hypothesis. We suspect that the higher rate of undetected SNPs in low-pass sequencing datasets altered inference of the background (no selection) model just enough to result in a significant likelihood ratio supporting selection. Collectively, our results indicate that strong and recent selective sweeps can be detected reliably even with low read depths, but that deeper sequencing will be required for consistent detection of weak selective sweeps and, by extrapolation, older sweeps. Although not directly assessed here, we suspect that the shift in power we observe would not apply to the detection of incomplete sweeps since the such sweeps are most reliably detected with statistical tests based on haplotype structure (Sabeti et al., 2002), a feature of the data not likely to be greatly affected by the SNP recovery patterns observed here.
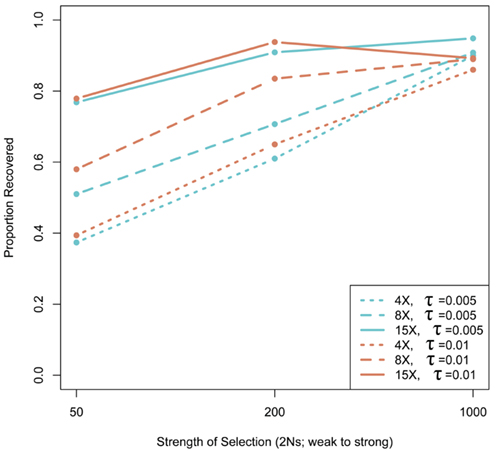
Figure 3. The effect of next-generation sequencing on the power to infer selective sweeps. The proportion of simulated samples that rejected the null hypothesis with complete, pre-sequencing data and also rejected after sequencing is plotted as a function of the strength of selection. Thirty kilobase regions of 30 chromosomes with one selective sweep (n = 100 for each α − τ) were simulated. Simulations were compared to a null distribution generated by neutral simulations and considered significant at 0.05 cutoff.
We simulated population samples under a simplistic model of population size expansion in which the population doubled in effective size 1NCURR generations ago, where NCURR equals the effective population size at the time of sampling. To determine the effect of short-read sequencing on the accuracy of demographic inference, we used a Poisson log-likelihood approach to infer growth parameters from each simulation dataset before and after sequencing. Comparison of inferred values before and after simulated sequencing showed that SNP data inferred from 15× sequencing recovers the demographic signal extremely well (Figure 4). At 8× sequencing depth, a large proportion of simulations returned post-sequencing parameter values that differed slightly from the pre-sequencing values. Sequencing depths of only 4× introduce a systematic downward bias in the inferred timing of expansion, resulting in conclusion of more recent growth (by an approximate difference of 0.17* NCURR generations, under our simulation framework).
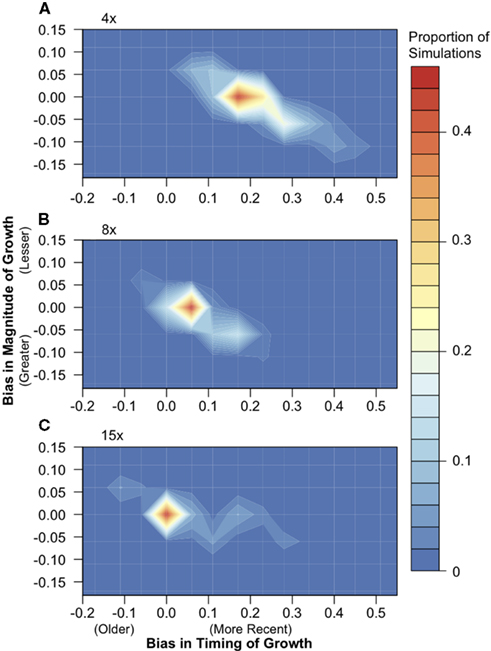
Figure 4. The effect of 4×, 8×, and 15× sequencing on demographic inference. Population samples of 30 chromosomes were simulated under a population expansion model (n = 500), and the timing and magnitude of growth were inferred using a likelihood approach both from full sequence data and after simulated (A) 4×, (B) 8×, and (C) 15× next-generation sequencing. The difference in the timing of growth, or bias, was calculated by subtracting the parameter value inferred post-sequencing from the pre-sequencing inferred value. The same calculation was used for the magnitude of growth. Colors indicate the proportion of simulations in each region of the parameter space.
We simulated structured population samples with four levels of current genetic differentiation between the two subpopulations. The four groups of simulated subdivided populations have mean FST values of 0.54, 0.37, 0.15, and 0.01 as estimated from the simulated samples. Analysis of these same samples after they had been processed through the simulated NGS pipeline revealed a systematic downward bias in FST values (Figure 5). Although, the bias was most severe at 4× read depth with a mean reduction of 0.0147, higher read depths also suffer the downward bias (mean diff at 8× = 0.0069, and 0.0018 at 15×), albeit significantly less so (4× vs. 8× tdf=299 = 39.34, p < 2.2 × 10−16; 8× vs. 15× tdf=299 = 46.41, p < 2.2 × 10−16). Interestingly, the bias increases with the degree of differentiation (Figure 5). While this suggests that the bias is minimized when differentiation is low, it is in systems with low differentiation that such a bias would have the greatest effect on biological interpretation. Therefore, the significant improvements in precision achieved with greater read depths would prove particularly valuable when differentiation is being estimated between closely related subpopulations.
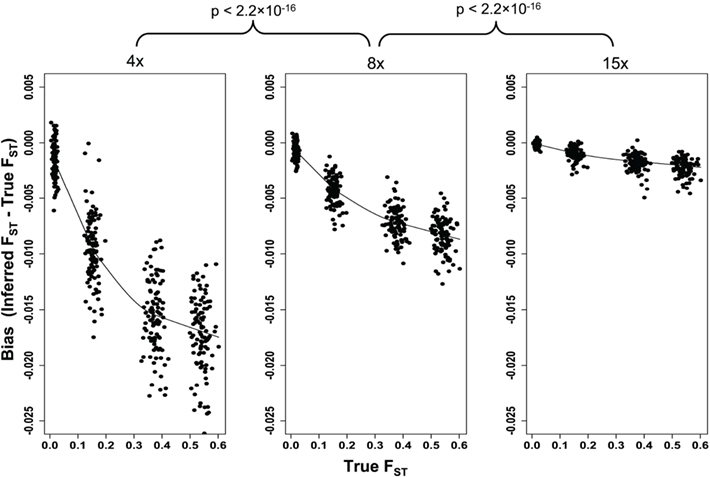
Figure 5. The effect of 4×, 8×, and 15× sequencing on inference of genetic differentiation. FST was calculated with full sequence data (“True FST”) and after simulated next-generation sequencing using Weir and Cockerham’s unbiased estimator (Weir and Cockerham, 1984), and the post-sequencing bias is plotted. A loess curve was fit to the data for each sequencing depth to illustrate both the effect of increasing FST as well as read depth. The difference between pre- and post-sequencing FST was calculated for all simulations (n = 100 for each value of FST) and these differences were compared between sequencing depths using a paired t-test.
Next-generation sequencing technologies hold promise for expanding the field of population genomics into a diverse array of biological and ecological systems (Pool et al., 2010). However, careful consideration of experimental structure and statistical analysis is essential to avoid compounding data-related uncertainty and biases in downstream analyses. Multiple statistical approaches have been proposed to accommodate the limitations of NGS, many specifically designed to handle low (<5×) read depth data (e.g., Lynch, 2009; Martin et al., 2010; DePristo et al., 2011; Kim et al., 2011). A preferred standard approach that performs well in population genetic analyses under a variety of experimental structures has not surfaced, perhaps due to the limited number of applications to empirical data. While these approaches result in improved ability to call SNPs and estimate their population frequencies, particularly for human data or data simulated to resemble human data, the effect of sampling error in low-coverage sequencing data on the capacity to address population genetic questions has not been previously addressed in a broad sense. It is important to note that our study is not meant to be an evaluation of any particular SNP-calling approach, but instead is intended to provide an evaluation of how using NGS data processed through a typical SNP-calling pipeline can affect the power to address population genomic questions, recognizing that both the sequencing technologies and related statistical approaches are likely to change and improve over time. Moreover, we chose to address population genetic models that are most vulnerable to NGS related errors, but other models such as population bottlenecks and incomplete sweeps are also of interest and should be explored.
We evaluated the effect of sequence coverage on the ability to detect three common population genetic scenarios: directional selection, population growth, and partial subdivision. The primary source of variation among read depths is the rate of true SNP recovery, or the false-negative rate. Consistent with previous observations (e.g., Jiang et al., 2009; Lynch, 2009), rare variants are disproportionately missed (Figure 2) due to sparse read sampling, and the rate of SNP recovery increased substantially with read depth (Table 1). Contrary to previous reports that showed an excess of rare variants when the SFS is inferred from short-read data (e.g., Kim et al., 2011), we inferred a deficit of rare variants after computational elimination of putative sequencing errors (Figure 2), underlining how the ability to distinguish between errors and true SNPs in a system with high genetic variation differs from the ability in systems where variation is rare. Another possible explanation for this discrepancy is the fact that in our study the sequencing quality scores were recalibrated in a way that may have lead to an unrealistically accurate estimate of error rates, perhaps resulting in false negative and false-positive SNP-calling rates unachievable in empirical studies. Comparison of recalibration performance in our study to that achieved using human data from the 1000 genomes (DePristo et al., 2011) suggests that our approach resulted in comparable improvements in base quality distributions with this empirical example. Interestingly, we also observed significantly lower rates of SNP recovery from simulations under the growth and sweep models compared to those under the equilibrium model (Figure 1), a difference we attribute to the rare-skewed SFS under the growth and sweep models (Figure A2 in Appendix). While this result may be specific to the models and simulation framework used here, the broader implications is that the dependence of the SNP recovery rate on the SFS itself could lead to heterogeneous error in SFS inference, even among regions of the same genome. Genomic regions of low recombination exhibiting low diversity may experience further complications in SNP recovery since SNP detection is also sensitive to the diversity-to-error ratio (Lynch, 2009). However, in humans and possibly other systems with sufficient external data, improvements in rare-variant recovery can be made through imputation from haplotype information or statistical tuning modeled on independent deep sequencing data from the same diploid individuals have been employed (Durbin et al., 2010; Gravel et al., 2011).
How do the differences in SNP recovery across depths of sequencing affect the ability to address population genetic questions? We compared the power to detect selective sweeps, infer demographic shifts, and estimate genetic differentiation among populations from “true” complete sequence information to the power when sequences inferred from NGS data at 4×, 8×, and 15× read depths are used. Interpretation of our findings follows below, but it is important to recall throughout that our results are specific in their detail to our particular simulated experimental structure. General conclusions can be drawn from our results, but numerical details, such as exact power curves, will depend on experimental parameters such as sample size, levels of genetic variation, and SNP calling approach.
The rapid fixation of a newly arising beneficial mutation leaves a distinct pattern of diversity in flanking chromosomal segments, including an excess of rare variants and high frequency derived alleles. Multiple statistical tests have been developed to detect such selective sweeps (reviewed in Nielsen, 2005). We used the composite likelihood ratio test (Nielsen et al., 2005) to detect sweeps among population samples simulated under a selective sweep model (Kim and Stephan, 2002). We found that, overall, the strength of selection had a larger effect on the power to detect selective sweeps than that of the sequencing process and changes in sequencing coverage (Figure A3 in Appendix). Since the effects of NGS on genotyping accuracy are physically diffuse but the genomic footprint of positive selection is genomically local (reviewed in Nielsen, 2005), it stands to reason that the selection footprint can be inferred with relative accuracy provided that the data is not riddled with false-positive SNPs that will both obscure the selection footprint and alter the neutral background model based on data genomic patterns of variation. However, when we addressed the reduction in power related to read depth with greater resolution, we found an interaction between the strength of selection and read depth (Figure 3), suggesting that strong selective sweeps, leaving large and dramatic selection footprints, can be detected with very low read depths, but weaker selective events will only be detected with greater genotyping and allele frequency accuracy. It should be noted, however, that weak selective events are difficult to detect even with complete true data (Figure A3 in Appendix; Nielsen et al., 2005). Incomplete sweeps (e.g., Sabeti et al., 2002; Juneja and Lazzaro, 2010) and sweeps from standing genetic variation (Przeworski et al., 2005) are also likely to be difficult to detect with low read depth sequencing.
Many systems show genomic patterns of genetic variation that are inconsistent with expectations under canonical equilibrium models, making inference of demography a standard component of genomic analyses, both for its own sake and to inform accompanying tests of other hypotheses (Boyko et al., 2008; e.g., Crawford and Lazzaro, 2010; Gravel et al., 2011; Locke et al., 2011). Demographic inference is typically accomplished by testing the fit of one or several summaries of polymorphism data that include information about both the number of SNPs and their frequency in the sample to expectations under demographic models (e.g., Crawford and Lazzaro, 2010; Gravel et al., 2011; Locke et al., 2011). Thus, accurate inference of polymorphism from NGS is essential for avoiding biases in demographic inference. We simulated a population growth model and quantified the difference in parameter estimates between models inferred from complete sequence data and models inferred from simulated short-read sequence data. Population growth has been shown to result in a negative skew in the SFS owing to an enrichment of external branches in geological structures of populations that have experienced growth (Tajima, 1989; Slatkin and Hudson, 1991; Rogers and Harpending, 1992), suggesting that the lower recovery rate for rare SNPs in low-pass sequencing will obscure the signal of growth. We found that the high genotyping accuracy at 15× read depth results in near perfect recovery of the demographic signal (Figure 4). However, at lower depths, we found a systematic bias toward inference that growth was more recent than it truly was, without any bias in the inferred magnitude of growth. These results suggest that accurately inferring demographic parameters will hinge on full recovery across the SFS, most likely via sequencing depths of at least 8×. This need may be somewhat mitigated in systems that allow alternative approaches for recovery of rare variants such as haplotype imputation (Durbin et al., 2010) or statistical tuning based on reduced-representation deep sequencing data (Gravel et al., 2011). It should be noted that we have tested only one, argruably simplistic, population growth model here. Further study will be required to extend these results to more complex models.
When a panmictic ancestral population is divided into two predominantly reproductively isolated populations, allele frequencies of shared polymorphisms diverge over time via neutral genetic drift at a rate that depends on the amount of gene flow between the populations and the effective population size of the nascent populations (reviewed in Holsinger and Weir, 2009). The signature of this process can be summarized using, among other statistics, FST, which directly compares the partitioning of genetic variance among populations (Weir and Cockerham, 1984; Holsinger and Weir, 2009). Rare variants contribute less to estimates of FST than do intermediate frequency variants (Weir and Cockerham, 1984), suggesting that the missing rare-variant issue inherent to low-pass sequencing may not have a large impact on estimates of genetic differentiation. We compared the accuracy of FST estimates of genetic differentiation between two partially isolated populations inferred from NGS data of various depths and found a systematic underestimation of FST, even at 15× read depth (Figure 5). Inspection of Figure 2 suggests that underestimation of allele frequency is more common than overestimation. A systematic reduction in perceived diversity as well as a tendency to underestimate allele frequencies both result in reduced estimates of differentiation. Interestingly, the bias we inferred here varied across a range of FST values (Figure 5), suggesting that sequencing depths should be tailored according to expected levels of differentiation. When population differentiation is substantial, even short-read data as shallow as 4× is sufficient to detect substantial differences in allele frequencies, suggesting significant progress can be made toward measuring genetic differentiation with minimal investment in sequencing.
In summary, we assessed the power to address population genetic questions using NGS, providing quantification of both the power and accuracy of population inference under experimental conditions typical of many ecological systems with large population sizes. We found that the prospect of identifying strong selective sweeps is good even at low sequencing depths, while inferring weak selection, non-equilibrium population demographics and population structure may suffer significant biases without higher coverage. While our results improve our understanding of the dependencies between read depth, SNP calling and allele frequency estimates, and population genetic inference using NGS, further investigation is warranted to explore how biases and power-loss changes across a broader set of population genetic models and experimental parameterizations.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We are grateful to Matteo Fumagalli and Zhen Wang for helpful discussions and comments on earlier versions of the manuscript. We are also thankful to two anonymous reviewers for their helpful comments. This work was supported by NIH grant AI062995. Jacob E. Crawford is supported by a Cornell Center for Comparative and Population Genomics fellowship.
Ahmad, R., Parfitt, D. E., Fass, J., Ogundiwin, E., Dhingra, A., Gradziel, T. M., Lin, D., Joshi, N. A., and Crisosto1, C. H. (2011). Whole genome sequencing of peach (Prunus persica L.) for SNP identification and selection. BMC Genomics 12, 569. doi: 10.1186/1471-2164-12-569
Bansal, V., Harismendy, O., Tewhey, R., Murray, S. S., Schork, N. J., Topol, E. J., and Frazer, K. A. (2010). Accurate detection and genotyping of SNPs utilizing population sequencing data. Genome Res. 20, 537–545.
Boyko, A. R., Williamson, S. H., Indap, A. R., Degenhardt, J. D., Hernandez, R. D., Lohmueller, K. E., Adams, M. D., Schmidt, S., Sninsky, J. J., Sunyaev, S. R., White, T. J., Nielsen, R., Clark, A. G., and Bustamante, C. D. (2008). Assessing the evolutionary impact of amino acid mutations in the human genome. PLoS Genet. 4, e1000083. doi: 10.1371/journal.pgen.1000083
Branca, A., Paape, T. D., Zhou, P., Briskine, R., Farmer, A. D., Mudge, J., Bharti, A. K., Woodward, J. E., May, G. D., Gentzbittel, L., Ben, C., Denny, R., Sadowsky, M. J., Ronfort, J., Bataillon, T., Young, N. D., and Tiffin, P. (2011). Whole-genome nucleotide diversity, recombination, and linkage disequilibrium in the model legume Medicago truncatula. Proc. Natl. Acad. Sci. U.S.A. 108, E864–E870.
Charlesworth, B. (2009). Effective population size and patterns of molecular evolution and variation. Nat. Rev. Genet. 10, 195–205.
Crawford, J. E., and Lazzaro, B. P. (2010). The demographic histories of the M and S molecular forms of Anopheles gambiae s.s. Mol. Biol. Evol. 27, 1739–1744.
DePristo, M. A., Banks, E., Poplin, R., Garimella, K. V., Maguire, J. R., Hartl, C., Philippakis, A. A., del Angel, G., Rivas, M. A., Hanna, M., McKenna, A., Fennell, T. J., Kernytsky, A. M., Sivachenko, A. Y., Cibulskis, K., Gabriel, S. B., Altshuler, D., and Daly, M. J. (2011). A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat. Genet. 43, 491–498.
Durbin, R., Abecasis, G., Altshuler, D., Auton, A., Brooks, L., and Gibbs, R. (2010). A map of human genome variation from population-scale sequencing. Nature 467, 1061–1073.
Earl, D. A., Bradnam, K., St John, J., Darling, A., Lin, D., Faas, J., Yu, H. O. K., Buffalo, V., Zerbino, D. R., Diekhans, M., Nguyen, N., Ariyaratne, P. N., Sung, W.-K., Ning, Z., Haimel, M., Simpson, J. T., Fonseca, N. A., Birol, I., Docking, T. R., Ho, I. Y., Rokhsar, D. S., Chikhi, R., Lavenier, D., Chapuis, G., Naquin, D., Maillet, N., Schatz, M. C., Kelley, D. R., Phillippy, A. M., Koren, S., Yang, S.-P., Wu, W., Chou, W.-C., Srivastava, A., Shaw, T. I., Ruby, J. G., Skewes-Cox, P., Betegon, M., Dimon, M. T., Solovyev, V., Seledtsov, I., Kosarev, P., Vorobyev, D., Ramirez-Gonzalez, R., Leggett, R., MacLean, D., Xia, F., Luo, R., Li, Z., Xie, Y., Liu, B., Gnerre, S., MacCallum, I., Przybylski, D., Ribeiro, F. J., Yin, S., Sharpe, T., Hall, G., Kersey, P. J., Durbin, R., Jackman, S. D., Chapman, J. A., Huang, X., DeRisi, J. L., Caccamo, M., Li, Y., Jaffe, D. B., Green, R. E., Haussler, D., Korf, I., and Paten, B. (2011). Assemblathon 1: A competitive assessment of de novo short read assembly methods. Genome Res. 21, 2224–2241.
Gravel, S., Henn, B. M., Gutenkunst, R. N., Indap, A. R., Marth, G. T., Clark, A. G., Yu, F., Gibbs, R. A., 1000 Genomes Project, and Bustamante, C. D. (2011). Demographic history and rare allele sharing among human populations. Proc. Natl. Acad. Sci. U.S.A. 108, 11983–11988.
Gutenkunst, R. N., Hernandez, R. D., Williamson, S. H., and Bustamante, C. D. (2009). Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 5, e1000695. doi: 10.1371/journal.pgen.1000695
Hellmann, I., Mang, Y., Gu, Z., Li, P., de la Vega, F. M., Clark, A. G., and Nielsen, R. (2008). Population genetic analysis of shotgun assemblies of genomic sequences from multiple individuals. Genome Res. 18, 1020–1029.
Henn, B. M., Gravel, S., Moreno-Estrada, A., Acevedo-Acevedo, S., and Bustamante, C. D. (2010). Fine-scale population structure and the era of next-generation sequencing. Hum. Mol. Genet. 19, R221–R226.
Hoberman, R., Dias, J., Ge, B., Harmsen, E., Mayhew, M., Verlaan, D. J., Kwan, T., Dewar, K., Blanchette, M., and Pastinen, T. (2009). A probabilistic approach for SNP discovery in high-throughput human resequencing data. Genome Res. 19, 1542–1552.
Holsinger, K. E., and Weir, B. S. (2009). Genetics in geographically structured populations: defining, estimating and interpreting FST. Nat. Rev. Genet. 10, 639–650.
Hudson, R. R. (2002). Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18, 337–338.
Jiang, R., Tavaré, S., and Marjoram, P. (2009). Population genetic inference from resequencing data. Genetics 181, 187–197.
Johnson, P. L. F., and Slatkin, M. (2006). Inference of population genetic parameters in metagenomics: a clean look at messy data. Genome Res. 16, 1320–1327.
Johnson, P. L. F., and Slatkin, M. (2008). Accounting for bias from sequencing error in population genetic estimates. Mol. Biol. Evol. 25, 199–206.
Juneja, P., and Lazzaro, B. P. (2010). Haplotype structure and expression divergence at the Drosophila cellular immune gene eater. Mol. Biol. Evol. 27, 2284–2299.
Keightley, P. D., Trivedi, U., Thomson, M., Oliver, F., Kumar, S., and Blaxter, M. L. (2009). Analysis of the genome sequences of three Drosophila melanogaster spontaneous mutation accumulation lines. Genome Res. 19, 1195–1201.
Kim, S. Y., Li, Y., Guo, Y., Li, R., Holmkvist, J., Hansen, T., Pedersen, O., Wang, J., and Nielsen, R. (2010). Design of association studies with pooled or un-pooled next-generation sequencing data. Genet. Epidemiol. 34, 479–491.
Kim, S. Y., Lohmueller, K. E., Albrechtsen, A., Li, Y., Korneliussen, T., Tian, G., Grarup, N., Jiang, T., Andersen, G., Witte, D., Jorgensen, T., Hansen, T., Pedersen, O., Wang, J., and Nielsen, R. (2011). Estimation of allele frequency and association mapping using next-generation sequencing data. BMC Bioinformatics 12, 231. doi: 10.1186/1471-2105-12-231
Kim, Y., and Stephan, W. (2002). Detecting a local signature of genetic hitchhiking along a recombining chromosome. Genetics 160, 765.
Li, H., and Durbin, R. (2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25, 1754–1760.
Li, H., Handsaker, B., Wysoker, A., Fennell, T., Ruan, J., Homer, N., Marth, G., Abecasis, G., Durbin, R., 1000 Genome Project Data Processing Subgroup. (2009a). The sequence alignment/map format and SAMtools. Bioinformatics 25, 2078–2079.
Li, R., Li, Y., Fang, X., Yang, H., Wang, J., Kristiansen, K., and Wang, J. (2009b). SNP detection for massively parallel whole-genome resequencing. Genome Res. 19, 1124–1132.
Locke, D. P., Hillier, L. W., Warren, W. C., Worley, K. C., Nazareth, L. V., Muzny, D. M., Yang, S.-P., Wang, Z., Chinwalla, A. T., Minx, P., Mitreva, M., Cook, L., Delehaunty, K. D., Fronick, C., Schmidt, H., Fulton, L. A., Fulton, R. S., Nelson, J. O., Magrini, V., Pohl, C., Graves, T. A., Markovic, C., Cree, A., Dinh, H. H., Hume, J., Kovar, C. L., Fowler, G. R., Lunter, G., Meader, S., Heger, A., Ponting, C. P., Marques-Bonet, T., Alkan, C., Chen, L., Cheng, Z., Kidd, J. M., Eichler, E. E., White, S., Searle, S., Vilella, A. J., Chen, Y., Flicek, P., Ma, J., Raney, B., Suh, B., Burhans, R., Herrero, J., Haussler, D., Faria, R., Fernando, O., Darré, F., Farré, D., Gazave, E., Oliva, M., Navarro, A., Roberto, R., Capozzi, O., Archidiacono, N., Valle, G. D., Purgato, S., Rocchi, M., Konkel, M. K., Walker, J. A., Ullmer, B., Batzer, M. A., Arian, F. A. Smit, Hubley, R., Casola, C., Schrider, D. R., Hahn, M. W., Quesada, V., Puente, X. S., Ordoñez, G. R., López-Otín, C., Vinar, T., Brejova, B., Ratan, A., Harris, R. S., Miller, W., Kosiol, C., Lawson, H. A., Taliwal, V., Martins, A. L., Siepel, A., RoyChoudhury, A., Ma, X., Degenhardt, J., Bustamante, C. D., Gutenkunst, R. N., Mailund, T., Dutheil, J. Y., Hobolth, A., Schierup, M. H., Ryder, O. A., Yoshinaga, Y., de Jong, P. J., Weinstock, G. M., Rogers, J., Mardis, E. R., Gibbs, R. A., and Wilson, R. K. (2011). Comparative and demographic analysis of orang-utan genomes. Nature 469, 529–533.
Lynch, M. (2008). Estimation of nucleotide diversity, disequilibrium coefficients, and mutation rates from high-coverage genome-sequencing projects. Mol. Biol. Evol. 25, 2409–2419.
Lynch, M. (2009). Estimation of allele frequencies from high-coverage genome-sequencing projects. Genetics 182, 295–301.
Magwene, P. M., Kayikçi, Ö., Granek, J. A., Reininga, J. M., Scholl, Z., and Murray, D. (2011). Outcrossing, mitotic recombination, and life-history trade-offs shape genome evolution in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. U.S.A. 108, 1987–1992.
Martin, E. R., Kinnamon, D. D., Schmidt, M. A., Powell, E. H., Zuchner, S., and Morris, R. W. (2010). SeqEM: an adaptive genotype-calling approach for next-generation sequencing studies. Bioinformatics 26, 2803–2810.
Michel, A. P., Grushko, O., Guelbeogo, W. M., Sagnon, N., Costantini, C., and Besansky, N. J. (2006). Effective population size of Anopheles funestus chromosomal forms in Burkina Faso. Malar. J. 5, 115.
Nielsen, R., Williamson, S., Kim, Y., Hubisz, M. J., Clark, A. G., and Bustamante, C. (2005). Genomic scans for selective sweeps using SNP data. Genome Res. 15, 1566.
Pool, J. E., Hellmann, I., Jensen, J. D., and Nielsen, R. (2010). Population genetic inference from genomic sequence variation. Genome Res. 20, 291–300.
Przeworski, M., Coop, G., and Wall, J. D. (2005). The signature of positive selection on standing genetic variation. Evolution 59, 2312–2323.
R Development Core Team. (2011). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Rogers, A. R., and Harpending, H. (1992). Population growth makes waves in the distribution of pairwise genetic differences. Mol. Biol. Evol. 9, 552.
Sabeti, P. C., Reich, D. E., Higgins, J. M., Levine, H. Z. P., Richter, D. J., Schaffner, S. F., Gabriel, S. B., Platko, J. V., Patterson, N. J., McDonald, G. J., Ackerman, H. C., Campbell, S. J., Altshuler, D., Cooper, R., Kwiatkowski, D., Ward, R., and Lander, E. S. (2002). Detecting recent positive selection in the human genome from haplotype structure. Nature 419, 832–837.
Slatkin, M., and Hudson, R. R. (1991). Pairwise comparisons of mitochondrial DNA sequences in stable and exponentially growing populations. Genetics 129, 555–562.
Weir, B., and Cockerham, C. C. (1984). Estimating F-statistics for the analysis of population structure. Evolution 1358–1370.
Williams, L. M., Ma, X., Boyko, A. R., Bustamante, C. D., and Oleksiak, M. F. (2010). SNP identification, verification, and utility for population genetics in a non-model genus. BMC Genet. 11, 32. doi: 10.1186/1471-2156-11-32
Xia, Q., Guo, Y., Zhang, Z., Li, D., Xuan, Z., Li, Z., Dai, F., Li, Y., Cheng, D., Li, R., Cheng, T., Jiang, T., Becquet, C., Xu, X., Liu, C., Zha, X., Fan, W., Lin, Y., Shen, Y., Jiang, L., Jensen, J., Hellmann, I., Tang, S., Zhao, P., Xu, H., Yu, C., Zhang, G., Li, J., Cao, J., Liu, S., He, N., Zhou, Y., Liu, H., Zhao, J., Ye, C., Du, Z., Pan, G., Zhao, A., Shao, H., Zeng, W., Wu, P., Li, C., Pan, M., Li, J., Yin, X., Li, D., Wang, J., Zheng, H., Wang, W., Zhang, X., Li, S., Yang, H., Lu, C., Nielsen, R., Zhou, Z., Wang, J., Xiang, Z., and Wang, J. (2009). Complete resequencing of 40 genomes reveals domestication events and genes in silkworm (Bombyx). Science 326, 433–436.
Yi, X., Liang, Y., Huerta-Sanchez, E., Jin, X., Cuo, Z. X. P., Pool, J. E., Xu, X., Jiang, H., Vinckenbosch, N., Korneliussen, T. S., Zheng, H., Liu, T., He, W., Li, K., Luo, R., Nie, X., Wu, H., Zhao, M., Cao, H., Zou, J., Shan, Y., Li, S., Yang, Q., Asan, Ni, P., Tian, G., Xu, J., Liu, X., Jiang, T., Wu, R., Zhou, G., Tang, M., Qin, J., Wang, T., Feng, S., Li, G., Huasang, , Luosang, J., Wang, W., Chen, F., Wang, Y., Zheng, X., Li, Z., Bianba, Z., Yang, G., Wang, X., Tang, S., Gao, G., Chen, Y., Luo, Z., Gusang, L., Cao, Z., Zhang, Q., Ouyang, W., Ren, X., Liang, H., Zheng, H., Huang, Y., Li, J., Bolund, L., Kristiansen, K., Li, Y., Zhang, Y., Zhang, X., Li, R., Li, S., Yang, H., Nielsen, R., Wang, J., and Wang, J. (2010). Sequencing of 50 human exomes reveals adaptation to high altitude. Science 329, 75–78.
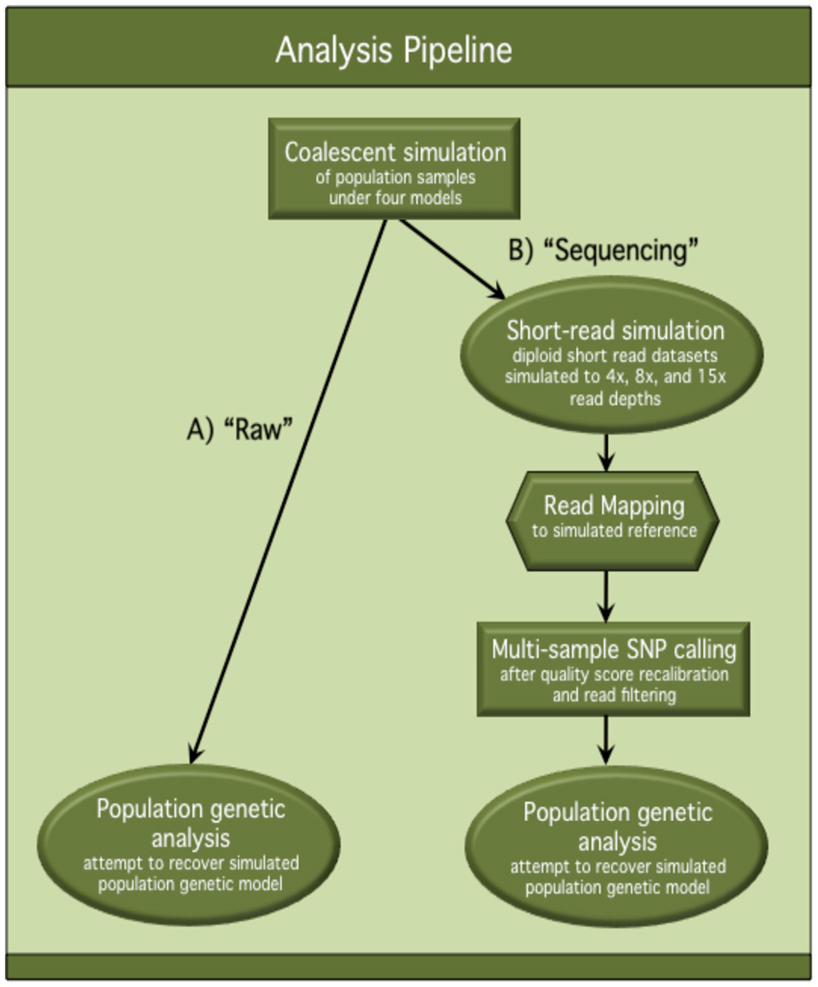
Figure A1. Flowchart of analysis pipeline. This flowchart describes the analysis pipeline used to assess the effects of NGS on population genetic inference and hypothesis testing. Population samples were simulated under four population genetic models and processed through both (A) the “Raw” track of the pipeline and (B) the “Sequencing” track of the pipeline. In the “Raw” track, unmodified, simulated polymorphism datasets were used for population genetic analysis. In the “Sequencing” track, simulated polymorphism datasets were processed through an in silico sequencing pipeline, and polymorphisms inferred from the “sequence” data were used for population genetic analysis. Comparisons were made between population genetic analysis results from the “Raw” track and the “Sequencing” track to quantify the differences in accuracy and power of inference after “Sequencing.”
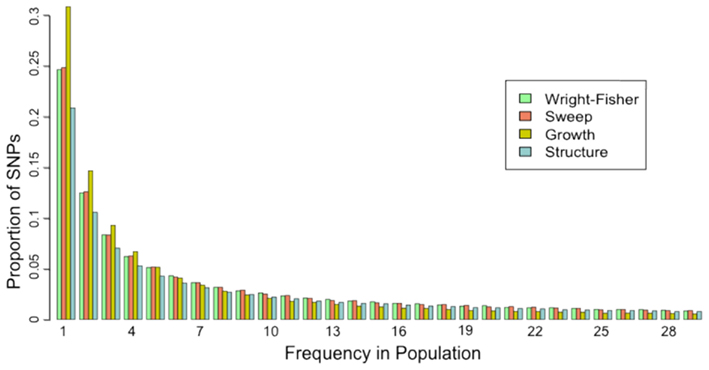
Figure A2. Site-frequency spectrum from “complete” data for each population genetic model. The proportion of all true SNPs at various frequencies in the population is presented. For the structure model, frequency was calculated across both subpopulations (60 chromosomes) and proportions calculated according to that distribution, but only SNPs with frequencies less than 30 are presented here. Data from only one selective sweep model (α = 1000, τ = 0.005) and one structure model (FST = 0.38) are presented here.
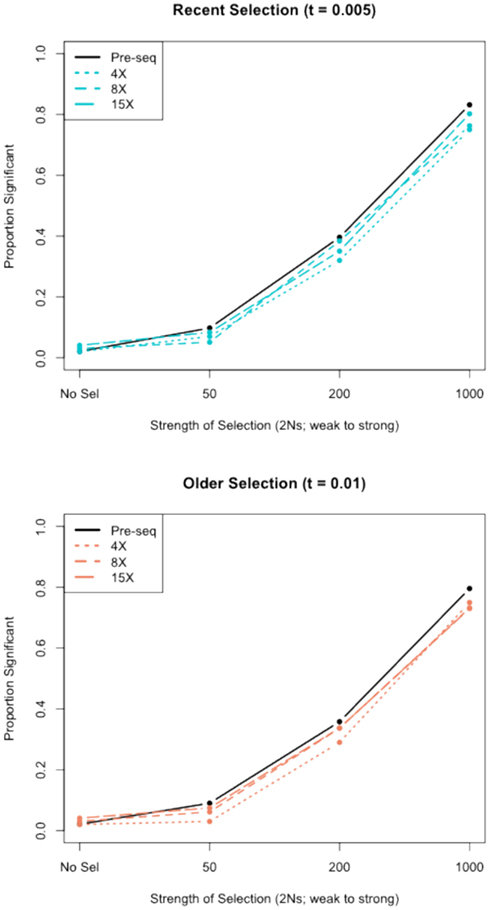
Figure A3. The power to detect selective sweeps before and after simulated next-generation sequencing. The proportion of statistically significant detections of positive selection was calculated from simulations of a 30-kb region of 30 chromosomes with one selective sweep. Simulations were compared to a null distribution generated by neutral simulations and considered significant at 0.05 cutoff. The top panel shows the results for recent selective sweep models (τ = 0.005) and the bottom panel shows results for models with relatively older selective sweeps (τ = 0.01). “Pre-seq” refers to the complete sequence information, without simulated next-generation sequencing and SNP calling.
Keywords: next-generation sequencing, population genetics, population genomics, natural selection, demography, population structure
Citation: Crawford JE and Lazzaro BP (2012) Assessing the accuracy and power of population genetic inference from low-pass next-generation sequencing data. Front. Gene. 3:66. doi: 10.3389/fgene.2012.00066
Received: 26 January 2012; Accepted: 05 April 2012;
Published online: 24 April 2012.
Edited by:
Jeffrey Jensen, École Polytechnique Fédérale de Lausanne, SwitzerlandReviewed by:
Daniel Wegmann, École Polytechnique Fédérale de Lausanne, SwitzerlandCopyright: © 2012 Crawford and Lazzaro. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Brian P. Lazzaro, Department of Entomology, Cornell University, Ithaca, NY 14853, USA. e-mail:YnBsYXp6YXJvQGNvcm5lbGwuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.