Urban freight distribution with electric vehicles: comparing some solution procedures

Polimeni, Antonio; Donato, Alessia; Belcore, Orlando M.

doi:10.3389/ffutr.2024.1491799

ORIGINAL RESEARCH article

Front. Future Transp., 18 October 2024

Sec. Transportation Systems Modeling

Volume 5 - 2024 | https://doi.org/10.3389/ffutr.2024.1491799

Urban freight distribution with electric vehicles: comparing some solution procedures

Antonio Polimeni*

Alessia Donato

Orlando M. Belcore

Department of Engineering, University of Messina, Messina, Italy

The Vehicle Routing Problem (VRP) is a well-known discrete optimization problem that has an impact on theoretical and practical applications. In this paper, a freight distribution model that includes a charging system located at the depot, making it feasible for real world-implementation, is proposed. Two different solution methods are proposed and compared: a genetic algorithm (GA) and a population-based simulated annealing (PBSA) with the number of moves increasing during the iterations. Among the variety of algorithm used to solve the VRP, population-based search methods are the most useful, due to the ability to update the memory at each iteration. To demonstrate the practical aspects of the proposed solution a case study is solved using travel time on a real network to evaluate the potentiality for a real-world application.

1 Introduction

In order to counteract the effect of the global warming, the United Nations has established the Sustainable Development Goals (SDGs). Specifically, a systemic effort has been addressed to the greenhouse gas (GHG) emissions, whose main goals consists in reducing the emission level to a zero net by the 2050.

The transport sector is one of the heavy demands for energy consumption; it requires a large amount of natural resources that traditionally come from non-renewable sources. For such reason, traditional vehicles (e.g., cars, and commercial vehicles) largely contribute to greenhouse emissions and air pollution, thus affecting both the environment and the health. In an attempt to reduce these impacts, several scholars and public administration encouraged new polices and solutions to favor the modal shift for both commuters (Comi and Polimeni, 2024; Nigro et al., 2024) and freight (Comi et al., 2024; Comi and Russo, 2022; Russo and Comi, 2023).

The introduction for digitalization and information communication technology (ICT) enabled the possibility to integrate the classical delivery problems thorough a new dynamic paradigm (Comi and Russo, 2022) and to introduce novel solutions towards a sustainable urban logistic (Knapskog and Browne, 2022). Of course the problem requires adequate models and methods (Cattaruzza et al., 2017; Crainic et al., 2023). Among the wide range of opportunity offered by innovation technology, the electric autonomous delivery robots represent a promising alternative in last-mile delivery (Arntz et al., 2023; Khoufi et al., 2019; Thibbotuwawa et al., 2020). Also, cooperative solutions, such as the integration between traditional vehicles and drones, have been evaluated in order to perform last-mile delivery to customers (Kyriakakis et al., 2023; Marinelli et al., 2018; Ren et al., 2023; Sacramento et al., 2019; Xiao et al., 2024). Although there are notable advantages in terms of efficiency and environmental sustainability compared to the performance offered by fossil fuel fleets, coordination between the two vectors still represents an open problem (Macrina et al., 2020).

The studies that dealt with the transition from fossil fuel-powered vehicles to electric vehicles (EVs) highlighted, first, the possibility of significantly reducing the current dependence on non-renewable energy sources (Jones et al., 2021; Napoli et al., 2021). As a matter of fact, in general, the EVs are responsible for the emission of fewer greenhouse gases (compared to traditional vehicles), especially in those cases where charging energy comes from renewable sources (such as solar or wind power).

In this paper, according to environmental sustainability issues, a freight distribution model based on the use of EVs, with charging system located at the depot, is proposed. The delivery plan represents the most critical phase in delivery operations; thus, customer visit scheduling is at the core of planning activities to minimize travel times, travel costs, and environmental impacts of freight delivery. This problem is well-known in literature as vehicle routing problem (VRP). Since its first formulation (truck dispatching problem, Dantzig and Ramser, 1959) this topic has been enriched with various formulations and solution procedures. In terms of formulation, a big efforts has been underpinned by focusing on the objective functions and problem constraints (e.g., Toth and Vigo, 2002). Concerning the objective function, the mathematical expression contains the components to be optimized (the travel time, the cost, and so on) and the decision variable(s). Regarding the constraints, alongside the classical ones (e.g., on variables, on size/capacity of the vehicle, on the route length), it is also relevant to mention other more specific formulations such as the VRP with time window (VRPTW, e.g., Bräysy et al., 2004) or the vehicle routing problem with delivery and backhaul options (VRPDB, e.g., Koç and Laporte, 2018). Concerning the solution procedures, as first, it is possible to share between the exacts and heuristics ones. An exact procedure provides an optimal solution of the problem, but often with a high computational effort and an unacceptable computation time, therefore the possibility to recur to an exact procedure is deeply connected the problem dimensions. However, over the years, thanks to the new powerful computer computing capacity, the analysts have extended the exact procedures to larger case studies. Likewise, the computational efforts pushed the development for the heuristic procedures, ranging from constructive algorithms (e.g., Clark and Wright algorithm) to more sophisticated ones (e.g., tabu search, simulated annealing, swarm optimization, and genetic algorithm). In this sense, formalizing a problem requires a careful analysis between solution accuracy and computational times (processing time) needed to obtain it. Within the set of heuristic procedures, a particular class is constituted by the metaheuristics, approximated procedures designed both for discrete and continuous variables (Dreo et al., 2006). Among these metaheuristics:

• Tabu search (Glover and Laguna, 1997) is an adaptive procedure; it is based on local search procedures that implement principles to avoid falling into local optimal solutions;

• Simulated annealing is a procedure based on the analogy with the annealing of a material, it can be seen as a sequence of Metropolis algorithms (van Laarhoven and Aarts, 1987; Metropolis et al., 1953) in correspondence of different values of a control parameter; its evolution is the quantum annealing algorithm (Syrichas and Crispin, 2017);

• Ant colony is a bio-inspired algorithm based on the analogy with the movements of ants in food search (Dorigo and Gambardella, 1997) that was successfully applied to resolve the VRP;

• Genetic Algorithm (Goldberg, 1989) a bio-inspired algorithm based on the processes that drive the evolution of biological forms.

The model presented in this work is part of a more general framework, conceived as a two-level service: the first level is the urban freight delivery as usual; the second level consists of a service procedure to provide installation services or collect packaging. Solving this joint problem brings benefits both to the company (which can thus separate the delivery of the installation, thus being able to better employ the operators) and to the consumers (who, for example, no longer have the problem of getting rid of bulky packaging). In both cases, the problem can be formalized as a vehicle routing problem. In particular, in this work, a VRP with soft time windows (VRPSTW, Balakrishnan, 1993; Taillard et al., 1997) is formulated. Thus, each customer is associated with a time window, and the formulation allows a penalty into the vehicle cost function when the time window is not violated. In such a way, taking into account the delivery window, the formulation is not just a one-size-fits-all solution, and it makes the solving solution adaptable to different delivery scenarios, making it applicable in the field of urban freight delivery. Particularly, in the calculation of the objective function, the travel time, the service time (e.g., the time to carry out the parking, to make the delivery and/or provide the installation), and the penalty time (which is greater than zero if the freight vehicle arrives at the user before/after the time window opens/closes) are considered. This study also considers a constraint linked to battery capacity. In fact, the vehicles that make deliveries are fully electric, and it is assumed that each route can be operated without recharging the vehicle and that each vehicle starts from the depot with a full battery charge.

Therefore, this work offers some insights into the use of GA and a particular type/class of population-based SA (named PBSA) to solve the problem. A version of GA and PBSA, where a certain percentage of the initial population is generated by the Clarke and Wright (CW) algorithm, is proposed, and different combinations of algorithms parameters are tested. So, this paper is focused on testing these procedures, and provides a case study/toy model by considering only the first level of the framework. The twofold objective to test a procedure that allows finding a good solution (even if it may not be the optimal one) and that allows for minimizing energy consumption, thus improving vehicle performance and contributing to sustainable development.

The paper is structured as follows: Section 2 reports a concise literature review; Section 3 contains the formulation of the problem, while Section 4 relies on algorithms; Section 5 reports the results of a case study with the associated discussion; and, finally, Section 6 draws conclusions.

2 Literature review

In the last 60 years, many variants of the VRP have been formulated and different procedures have been designed to solve them (Laporte, 2009). The success of this research topic also depends on the fact that it deals with the real and ever-present problem of urban goods distribution. Over the years, variants have been created not only to consider specific constraints (e.g., time windows) of the problem, but also to integrate new technologies (electric vehicles, drones).

In the context of the use of electric vehicles, in literature are provided formulations ad approaches to consider the peculiarity of the problem (Froger et al., 2019). Schneider et al. (2014) introduced the electric vehicle routing problem (EVRP) with time windows developing a heuristic approach to solve it. This problem can be extended by considering a fleet of heterogeneous electric vehicles, varying the capacity and the range (Hiermann et al., 2016). In more detailed models, energy consumption is a function of vehicle load (Lin et al., 2016; Goeke and Schneider, 2015). An aspect of the EVRP is the limited range of the vehicles respect to the traditional fueled vehicles. This implies that the vehicle may be charged during service, and the recharge can be full or partial (Desaulniers et al., 2016; Erdelić et al., 2019; Felipe et al., 2014; Keskin and Çatay, 2016). Other solutions explored in literature, alternative to recharge, are the battery swapping (Qian et al., 2024; Ren et al., 2023; Verma, 2018) and the use of the range as a constraint (Napoli et al., 2021). The current literature on EVRP and its variants is explored in depth by Kucukoglu et al. (2021).

In the context of the city logistics, the problem variants are formulated to consider specific aspects of the urban freight distribution. As an example, more cities impose restriction in accessing some areas (e.g., historical centers), in this case a suitable formulation of the problem is the VRP with Access Time Windows (Grosso et al., 2018; Zhou et al., 2024). Another problem formulation arise from the use of one (or more) urban distribution center(s) (Browne et al., 2005). Some authors formulated this problem considering two aspects: the location of the distribution center (Muñoz Villamizar et al., 2014) and the optimization of the routes (Cepolina and Farina, 2016; Musolino et al., 2019). In general, in this case, the vehicles are often eco-friendly vehicles with restrictive constraints on capacity and range (Díaz-Ramírez et al., 2023). A further aspect to consider in urban areas is that the travel time is not constant during the day, in this case the formulation of the problem takes into consideration this aspect (Ando and Taniguchi, 2006; Musolino et al., 2018). A recent challenge in VRP formulation is the use of unmanned vehicles in performing the service. Such vehicles can be ground robot (Chen et al., 2021; Chirala et al., 2023) or aerial drones (Huang et al., 2022; Kyriakakis et al., 2022). The use of unmanned vehicles imposes further constraints respect to the classical VRP. As an example, aerial drones can deliver the parcels up to a certain weight, there are limits due to the technology (e.g., the weight of the batteries), their (often limited) range depends on the load (this also applies to ground robots). Besides, aerial drones can be affected by weather, ground robots by congestion (Khoufi et al., 2019).

The solution procedures used to solve the VRP (and its variants) range from exact to heuristic algorithms. The following review skips the topic of exact algorithms and focuses only on heuristics and metaheuristics (without the presumption of being exhaustive).

Concerning constructive procedures, a first heuristic that can be cited is the Clarke and Wright (CW) algorithm, a procedure designed to produce a solution that maximizes a variable called saving: The aim is to put customers in the solution to maximize the ‘saved’ cost due to the aggregation of customers. Proposed by Clarke and Wright (1964), this algorithm was improved by introducing a parametric approach (Gaskell, 1967; Yellow, 1970) and is often used in combination with other procedures. As an example, Caccetta et al. (2013) hybridized the algorithm with a domain reduction procedure, demonstrating that the hybrid procedure significantly improves the results obtained. Robbins and Turner (1979) combined the CW algorithm with a 2-opt procedure: the objective is to update the solution provided by CW (the CW procedure individuates the solution rigidly, without further updates). Other examples of constructive heuristics are the sweep algorithm (Gillett and Miller, 1974) and the petal algorithm (Foster and Ryan, 1976; Renaud et al., 1996).

Regarding the improvement proposed in the domain of heuristic procedures, local search (intended as an approach that can explore the search space starting from an initial solution and trying to improve it) and its variations are often used to solve the VRP (e.g., Erdoğan, 2017). Mladenović and Hansen (1997) introduced the concept of variable local search, in this case the idea is to change the neighborhood during the search operations. Toth and Tramontani (2008) proposed a local search algorithm in which the neighborhood of the solution is explored using an integer linear programming procedure. Brandão (2020) defined an iterated local search procedure capable of remembering previous moves, memory use allows for more efficient exploration of the solution space and can prevent falling into local optima. Ropke and Pisinger (2006) and Pisinger and Ropke (2019) proposed an adaptive large neighborhood search heuristic that uses some methods for removing/inserting customers in the solution until a stopping criterion is met. This procedure can be used to solve different variants of the VRP (Pisinger and Ropke, 2007).

The Tabu Search (TS) (Glover, 1989) is an iterative algorithm with memory that allows us to improve an initial solution by applying a certain number of moves that cause local changes in the current solution (Cordeau and Laporte, 2005; Brandão, 2009). Cordeau et al. (1997) and Cordeau et al. (2001) proposed a TS algorithm capable of solving the VRP and some variants, the aim being to have a simple procedure that reduces the number of parameters to consider. Jia et al. (2013) proposed an improved form of TS by adding some local search strategies and a mutation operator. A further possible improvement of the TS consisted in the introduction of a parallel approach, which allows one to simultaneously consider more than one neighborhood of the solution (Badeau et al., 1997; Caricato et al., 2003; Cordeau and Maischberger, 2012; Garcia et al., 1994).

Ant Colony Optimization (ACO) simulates the movements of a set of artificial ants; each ant is independent from the others and exchanges information using a trail of pheromones. The generic ant chooses which node to reach next, depending on the amount of pheromones. The solution is thus built incrementally, each time adding an element to a partial solution. Donati et al. (2008) proposed a parallel approach in which two colonies of ants operate in parallel, optimizing two different aspects of the problem. Yu et al. (2009) introduced a mutation operator in construction to move users from one solution to another.

Simulated Annealing (SA) was originally proposed by van Laarhoven and Aarts (1987), the aim is to minimize a function that makes changes to an initial solution (the results of the algorithm are based on a set of operators used to modify the solutions). A new solution is accepted as the current solution with a certain probability (derived from the Boltzmann distribution): this implies that it is possible to choose a worse solution than the best one found (this mechanism allows us to better explore the space of solutions). Some authors (e.g., Bräysy et al., 2008) used a deterministic approach, with the aim of speeding up the procedure by eliminating randomity due to the probabilistic choice. Osman (1993) proposed a SA procedure in which the generation of new solutions is based on the swap/shift of users from one route to another. Yu et al. (2009) proposed an SA with a random choice of operators used in the search for solutions, a better solution than the current is automatically chosen as the current solution, and a worse one is chosen with a probability obtained from a Boltzmann distribution (that is, the solution is chosen if the probability is higher than a threshold value). However, simulated annealing (SA) is a solo-search algorithm, and the results found by SA depend on the selection of the starting point and the decisions to move to the new solution or not SA makes. To overcome the drawbacks of being trapped in local minima and taking a long computational time to find a reasonable solution, Askarzadeh et al. (2016) proposed a population-based simulated annealing algorithm (PBSA), in which each solution memorizes its best experience and stores it in the population memory. Additionally, Shaabani & Kamalabadi (2016) used a PBSA algorithm compared to genetic algorithms and simulated annealing, which shows the superiority of the PBSA algorithm.

The Genetic Algorithm (GA) simulates, in a simplified manner, the evolution of life forms employing three main operators: selection, crossover, and mutation (Goldberg, 1989). Thus, the basis of the GA is the idea of evolving a population of solutions until a stopping test (for example, the number of iterations) has been satisfied. This algorithm, given its flexibility, is suitable for solving the VRP and different implementations (in terms of operators) have been proposed so far. As an example, Baker and Ayechew (2003) proposed a basic genetic approach demonstrating that GA is competitive (in terms of computation time and solution quality) with other solution procedures. Alba and Dorronsoro (2006) developed a cellular GA (a form of genetic algorithm in which the solutions are placed on a grid and each of them can interact only with those in his neighborhood) to solve the VRP. Yusuf et al. (2014) tested the use of a rank-based operator for selection and a different crossover operator to solve VRP. Nazif and Lee (2012) implemented an improved crossover operator capable of generating two children at the same time. Berger and Barkaoui (2003) proposed a hybrid form of GA to solve the VRP, the basic idea is to develop two populations simultaneously (swap of solutions from one population to another is possible) to minimize the total distance traveled. Ho et al. (Ho et al., 2008) also proposed a hybrid form of the algorithm, combining GA with some heuristics to improve convergence. Vidal et al. (2012) hybridized GA with the introduction of the education operator: it is a form of mutation that uses local search to improve the solution. Ochelska-Mierzejewska et al. (2021) performed experiments to determine the best combination of genetic operators to solve the VRP. The recent lines of research tend to improve the solutions and find better individuals combining the genetic algorithms with deterministic or heuristic methods or combining the work of the genetic algorithm with other metaheuristics, such as Deterministic Annealing or Tabu Search. For example, Xu et al. (2011) proposed an improved GA to solve the classical VRP, incorporating SA into GA. Zhu et al. (2021) proposed an improved neighbor routing initialization method for the adaptive elitist genetic algorithm. Mrad et al. (2021), instead, proposed a two-step procedure that uses GA to find the assignment of companies to depots and CW algorithm to determine the routes from each depot to customers.

3 Model

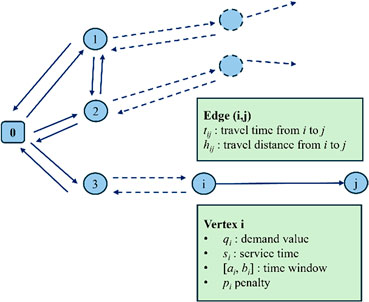
Let G (N, A) be a directed graph, where N = 0, 1,…n, is the set of vertex and A = {(i, j): i ≠ j; i, j ∈ N} the set of edges (an edge represents the path connecting two vertex). At each edge (i, j), there is an associated travel time t_ij. The set N contains the customers and the depot d (labeled vertex 0). At each vertex there are associated (Figure 1):

• a service time (s_i),

• a quantity to deliver (q_i),

• a time window ([a_i,b_i]),

• a penalty time (p_i).

Figure 1

Figure 1. A simplified representation of the graph.

A fleet V of vehicles, with homogeneous capacity Q^v is involved in the process. The problem consists of designing a set of vehicle routes where each costumer is reached only once by a single vehicle. A soft constrained time windows are assumed, and a vehicle pays a penalty p_i for late/early arrival at vertex i.

The formulation is provided in Equation 1, where it is defined as a minimization problem, the objective being to minimize the sum of the time components introduced above:

F = \sum_{i \in N} \sum_{j \in N} \sum_{v \in V} (t_{i j}^{v} + s_{i}^{v} + p_{i}^{v}) \cdot x_{i j}^{v} (1)

subject to:

\sum_{v \in V} \sum_{j \in N} x_{i j}^{v} = 1 \forall i \in N_{c}; i, j \neq d (2)

\sum_{v \in V} \sum_{j \in N} x_{d j}^{v} = |V| j \neq d (3)

\sum_{v \in V} \sum_{j \in N} x_{j d}^{v} = |V| j \neq d (4)

\sum_{i \in N} \sum_{j \in N} q_{j} \cdot x_{i j}^{v} \leq Q^{v} \forall v \in V; i \neq j (5)

\sum_{i \in N} \sum_{j \in N} h_{i j} \cdot x_{i j}^{v} \leq R^{v} \forall v \in V; i \neq j (6)

\sum_{i \in N} \sum_{j \in N} (t_{i j}^{v} + s_{i}^{v} + p_{i}^{v}) \cdot x_{i j}^{v} \leq D^{v} \forall v \in V; i \neq j (7)

τ^{v} \leq τ_{0} \forall v \in V (8)

p_{i}^{v} = \{\begin{array}{l} a_{i} - t_{i}^{v} i f t_{i}^{v} \leq a_{i} \\ t_{i}^{v} - b_{i} i f t_{i}^{v} > b_{i} \end{array} \forall i \in N, i \neq d (9)

x_{i j v} \in [0, 1] (10)

where:

• N is a set including the customers and the depot;

• V is the set of vehicles;

• t^v_ij is the travel time from customer i to customer j;

• s^v_i is the service time at customer i;

• p^v_i is the penalty time at customer i;

• x_ijv is the problem variable, equal to 1 if the vehicles v moves from i to j, 0 otherwise;

• q_i is the demand at customer i;

• Q^v is the vehicle capacity;

• h_ij is the travel distance from customer i to customer j;

• R^v is the range of the vehicle v;

• D^v is a threshold value for the time of a solution.

Equation (1) defines the objective function, whose purpose is to minimize the cost of all routes. Constraint Equation 2 requires that a user must be reached by only one vehicle. Constraint Equation 3 imposes that all vehicles start from the depot, while constraint Equation 4 imposes that all vehicles return to the depot. Constraint Equation 5 is on the vehicle capacity and indicates the total quantity delivered is less than the vehicle capacity. Constraint Equation 6 indicates that the maximum length of a route is less than the vehicle range, while constraint Equation 7 indicated the maximum duration of a route. Constraint Equation 8 is on the departure time from the depot and indicates that all vehicles can start the service after a certain time. Constraint Equation 9 refers the penalty associated to a vehicle for an early or late by arrival to the user location. Finally, constraint Equation 10 defines the domain of decision variables.

4 Methodology

The optimization procedure uses two different algorithms: a genetic algorithm (GA) and a population-based simulated annealing (PBSA), both methods based on the creation of an adaptive population. This characteristic is essential to maintain the best solutions of the previous population along with the subsequent generations. In general, a SA algorithm, if not based on population, is not useful to the scope of the procedure because of it does not update the memory with the best experiences and simply returns the best fitness value (of different solutions) based on the randomly selected initial solution.

The route first cluster second (Beasley, 1983) principle is adopted to determine the vehicle route: as starting solution the classical is adopted by relaxing all the constraints of the problem. This solution can be generated randomly or optimized with standard (heuristic or metaheuristic) procedures such as Clark and Wright savings or tabu search.

The various routes are then obtained by breaking the entire solution into “unique” routes to satisfy the constraint conditions for each of them. Furtherly, the solution must necessarily be decoded after the operators who create the new populations work because of the modifications on the positions of consumers to find better solutions; the values of capacity, distance, and time also change and, therefore, must be recreated groups of consumers that respect the constraints.

In addition, in order to check the quality of the obtained solutions, a tool from literature, based on ALNS algorithm, is used to solve the problem (Erdoğan, 2017). To apply this tool, it was necessary to relax one of the problem constraints. Two test applications will be presented in the following: first, comparing the results from the ALNS, GA and PBSA (this also allowed to calibrate the parameters of the algorithms) and a second assuming that constraints have been restored (in this case it is not possible to compare the results with ALNS).

4.1 Algorithms

In the following, the procedures implemented to solve the problem are presented in their general structure.

4.1.1 Genetic algorithm

The GAs search for the minimum of an objective function (Equation 1), thus representing the total delivery time. The algorithm starts with a population of solutions and then, through the selection, mutation, and crossover operators, improves the solutions while keeping the memory of the analyzed search space. The algorithm runs until a stopping test (for example, the maximum number of iterations) has been satisfied. Figure 2 shows the main steps and the workflow of the algorithm. After initializing the algorithm with the definition of the parameters and stopping criteria, the second step consist in generating the population (each solution is coded), in (Step 3) the population is decoded with respect to the constraints, and the fitness value is calculated (Step 4) for each solution. Selection (Step 5) allows us to individuate the elements in the population to be subjected to crossover and mutation. Specifically, the algorithm:

• selects the parents in relation on their fitness value,

• produces children from the parents,

• replaces the current population with the children to create the next-generation.

Figure 2

Figure 2. Steps of genetic algorithms.

Finally (Step 6) a test on stall generation limit (a number of generations during which there was no improvement in the objective function) and as a control criterium maximum generation number is performed to stop (or not) the procedure.

4.1.2 Population-based simulated annealing

The PBSA also searches for the minimum of the fitness function. The algorithm starts with an initial population of solutions and then, through the swap, reversion, and insertion operators, modify the solutions by updating the memory of the analyzed search space. For each member of the population, a certain number of moves (neighbors) are tested, where these moves usually result in minimal alterations of the last state to progressively improve the solution through iterations. PBSA allows maintaining (through the process) also the worst solutions, with probabilities p depending on the temperature T in the current iteration and on the rate ΔE of the difference between the fitness value of eligible members of the new population with respect to each initial population member (p = exp (-ΔE/T)). This mechanism allows us to better explore the space of solutions. The temperature decreases during the process according to a temperature reduction rate α. The selection method is based on the roulette wheel; in it, the area of the wheel corresponding to a solution is proportional to the probability p. Figure 3 shows the steps followed by the algorithm and the related workflow.

Figure 3

Figure 3. Steps of PBSA procedure.

At Step 1 the parameters of the algorithm are defined, while at Step 2 the population is generated. Each solution in population (Step 3) is decoded and the related fitness value is calculated. In Step 4 the memory is set with the best solution. In Step 5 new solution candidates are generated by means of swap, reversion, and inversion operators (see Section 4.2.2 for details). Each new solution is decoded, the fitness is calculated (Step 6), the eligible members are compared with the other members of the population (Step 7) and some new solutions are accepted (Step 8). The best solution is updated (Step 9), and the temperature decreases (Step 10). Finally, (Step 11), a test is performed to stop the procedure based on the maximum number of iterations.

4.2 Algorithm operators

Solving the VRP by GA or SA does not represent a novelty itself; the novelty consists of how the algorithm operators are used. As stated in the literature review (see also Section 2), previous works differ in how the operators are defined and employed: there are always the operators of selection, crossover, and mutation (in GA) and of insertion, reversion, and swap (in SA), but it is different how such operators are conceived and applied. As an example, the selection could be a roulette wheel or a universal stochastic sampling; the crossover could be a random change of elements or a procedure aimed at preserving segments in the solution, whereas the mutation could be a simple swap of two customers or an optimal swap, and so on. In the following subsections, the operators applied in the present paper are reported.

4.2.1 Selection, crossover and mutation in GA

The method of selection of the population for the next-generation is a stochastic uniform sampling, and each parent corresponds to a stretch of a line of length proportional to its scaled value. The scaled value of each solution is based on its rank, i.e., on the position of the fitness value of the solution in the ascendingly sorted fitness values. A solution with rank r has a scaled value equal to 1/√r. So, the scaled value of the best solution (that with the lowest fitness value) is 1, the scaled value of the next most fit solution is 1/√2, and so on. The algorithm moves in equal-sized steps (starting from an offset, that is, a random number smaller than the step size) and selects a parent based on the section it stops on.

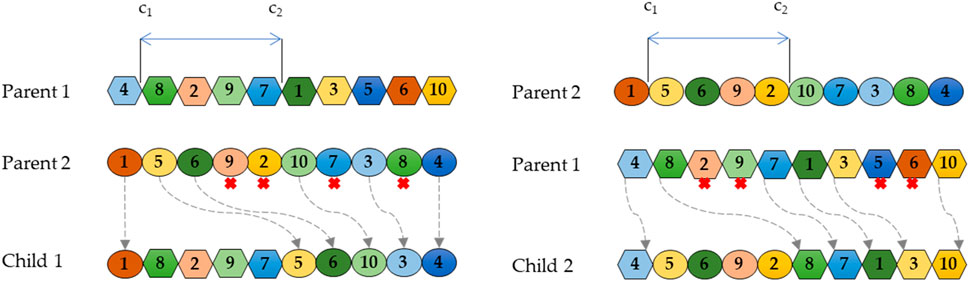
The crossover operator uses two parents to obtain two children (Figure 4). The order crossover operator is tested; a stretch of the first parent is copied to the child, and the remaining values are placed in the child according to the order by which they appear in the second parent (Puljic and Manger, 2013).

Figure 4

Figure 4. Crossover operator.

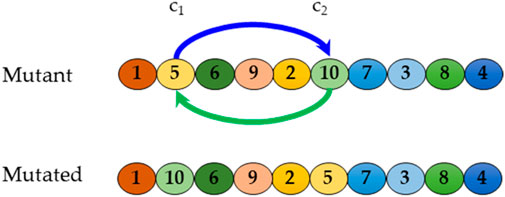
The mutation function simply mutually exchanges the two customers of the two randomly selected points c₁ and c₂ (see Figure 5).

Figure 5

Figure 5. Mutation operator.

4.2.2 Swap, reversion, insertion operators in PBSA

The swap operator works like the mutation in genetic algorithms (Figure 5).

The reversion operator creates the child by randomly selecting 2 cut points c₁ and c₂ within the customers constituting the parent and reversing the order of customers between these two points (Figure 6).

Figure 6

Figure 6. Reversion operator.

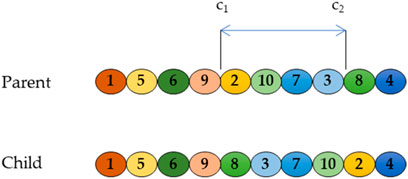
The insertion operator (Figure 7), instead, moves the consumer of the point c₁ and inserts it before the point c₂ (c₁ and c₂ randomly selected).

Figure 7

Figure 7. Insertion operator.

5 Application

5.1 Test problem

The case study consists of a set of 75 customers randomly located in Rome (Italy), that need to be served by freight vehicles departing from the depot and returning to the depot (Figure 8). Each consumer i is associated with a quantity q_i of goods and a delivery time window [a_i b_i]. The cost matrix contains the average travel time between all pairs (user-depot). Considering the symbology introduced in Section 3, this matrix has a number of elements equal to |N |x |N |.

Figure 8

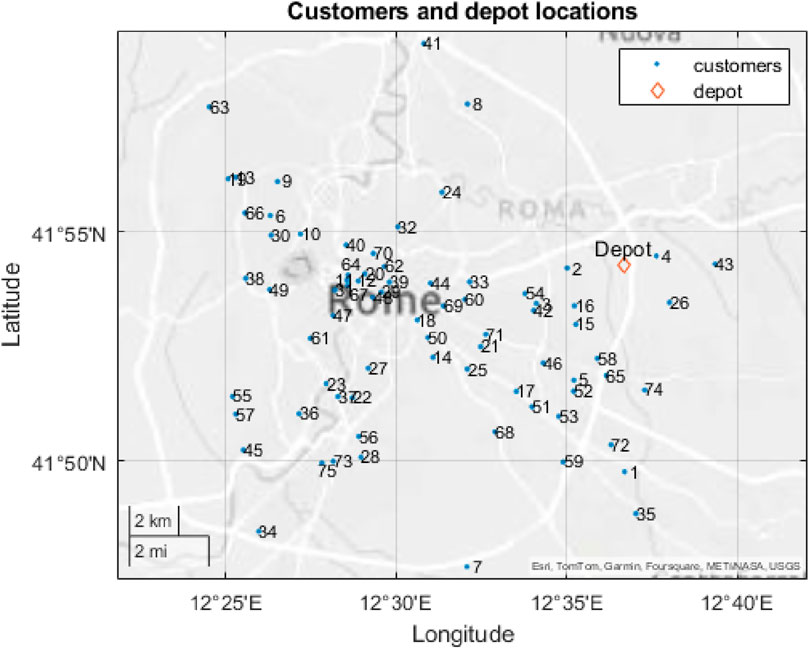
Figure 8. Distribution of the customers across the study area (Source: own elaboration from Garmin, Tomtom Canvas).

A small capable of, easily, moving within the city was considered to perform the delivery operations during the test. Besides, it is assumed that the vehicle characteristics are as follows:

• The vehicle range is of 120 km,

• The maximum delivery time is of 420 min,

• The vehicle load capacity is 150 kg.

Both methods search the best solution starting from the initial population. Thus, the first step is the generation of an initial population: in this work, a method based on the Clarke and Wright algorithm and random generation is used. Then, the solution is decoded to find a set of routes that respect the specific constraints of the problem.

Several analyses were conducted, aimed at establishing which combination of parameters has the most effect in obtaining a better result.

To test the proposed algorithms, the following tests have been performed:

• PBSA: through varying the number of moves (from 8 to 100), the population size (from 2 to 16), and testing different combinations of the parameters;

• GA: through varying the population size (from 30 to 500), the crossover rate (from 0.5 to 0.8), and the mutation rate (from 0.2 to 0.5).

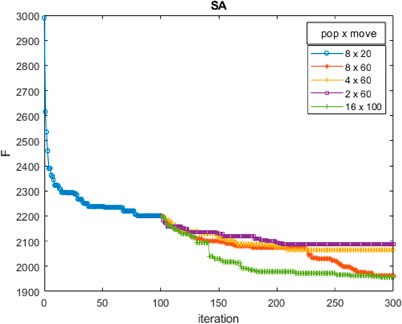
Figure 9 shows the results of the PBSA analyzes, with an increase in the number of moves from 20 to 60 or 100 at iteration 100. The incidence of population size is also shown. At iteration 100 the increased number of moves determines a rapid change in the descending curve of the fitness value, passing from an almost stationary situation (perhaps a local optimum) to a new descending trend. Moreover, it is found that only the two analyses with population and moves 8 × 60 and 16 × 100 manage to obtain a cost value quite below 2,100.

Figure 9

Figure 9. Comparison of PBSAs best fitness value with different parameters.

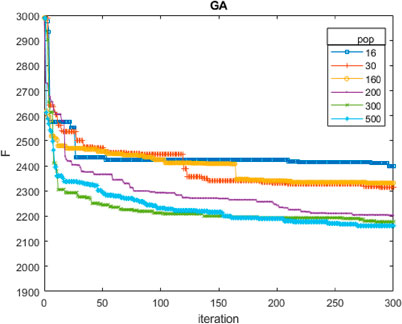
Figure 10 shows the descending curves of the fitness value obtained with the GA, varying the population size. The crossover and mutation rates are fixed as 0.8 and 0.2 respectively. These two rates were considered the best based on previous calibration tests.

Figure 10

Figure 10. Comparison of GA best fitness value with different population size.

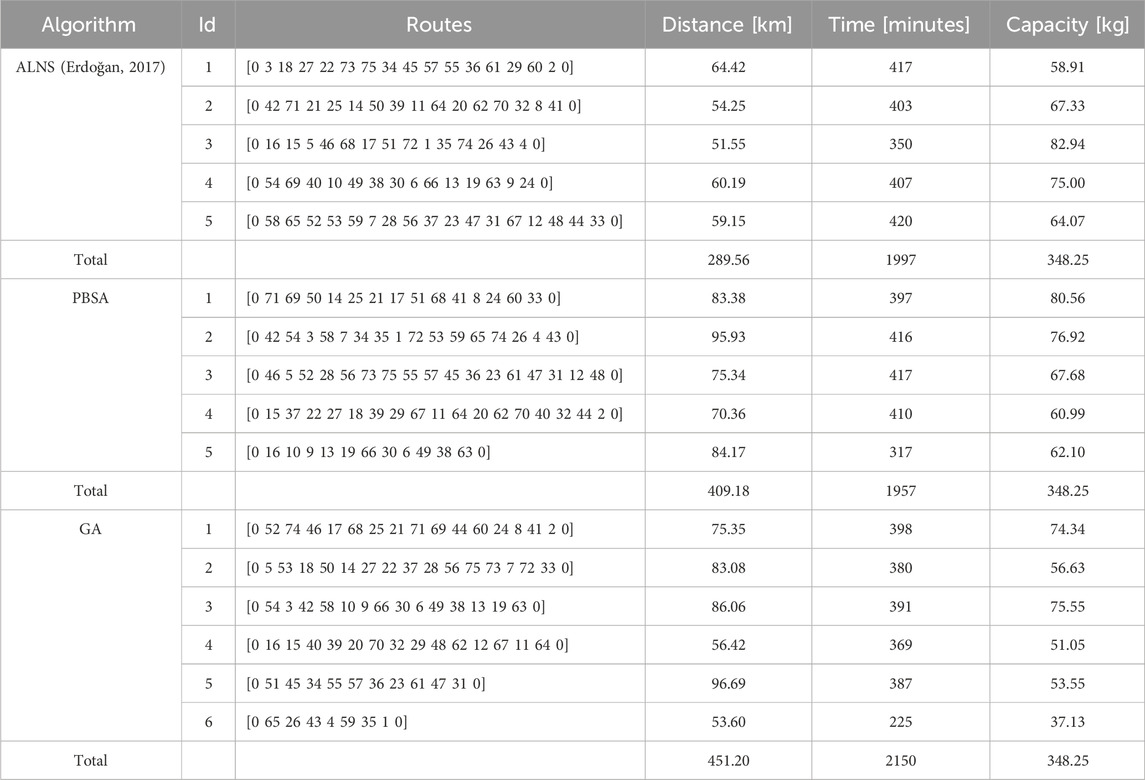
In Table 1, the best solutions are reported and compared to the Adaptive Large Neighborhood Search (ALNS) implemented by Erdoğan (2017). In this test, to make the procedures comparable, the constraint formalized with Equation (7) on the start time of the service is only considered as equality.

Table 1

Table 1. Best results with different optimization methods.

GA is set up has follows:

• Population size: 500 elements,

• Crossover rate: 0.80,

• Mutation rate: 0.20.

SA is set up has follows:

• Population size: 16 elements,

• Number of moves: 100,

• Swap, reversion and insertion rate: 0.2, 0.5, 0.3,

• Initial temperature: 30°C,

• Temperature reduction rate: 0.99.

The solution provided by SA (with population 16 and moves 100) is the best. Instead, our algorithm based on GA reached a solution of 2,150 min, worst of the tool provided by (Erdoğan, 2017).

It is noted that, if for low population size the GA reaches a better solution with respect to a PBSA, when the population (and moves) increase, the PBSA achieve better results.

The literature on the use of population-based algorithms highlights that increasing certain parameters of algorithms should help improve the solution, with an associated increase in computation time. However, after several calibration proofs, it emerged that while increasing the number of moves in the PBSA determines a substantial improvement of the solution, increasing the population both in the PBSA and GA does not determine the same expected effect. Therefore, a fundamental characteristic of the PBSA algorithm is a big number of moves. In conclusion, these considerations are aligned with Shaabani and Kamalabadi (2016), which finds a better result of PBSAs compared to GAs and with Askarzadeh et al. (2016) on the possibility of getting stuck in local optima when using genetic algorithms.

Since the aim is to maintain an acceptable computational effort together with the precision of the result, the proposed procedure for the PBSA is based on two steps, with an increase of the number of moves after certain conditions are reached (for instance, a certain fixed number of iterations or a stall in the improvement of the solution after a fixed number of iterations).

Figures 11, 12 show the routes obtained by the ALNS and PBSA procedures, that are in both cases five.

Figure 11

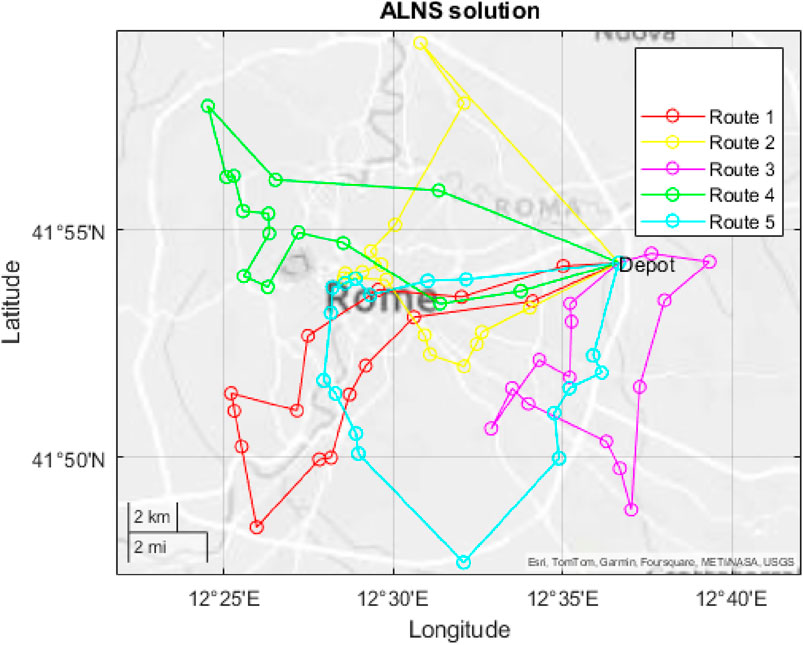
Figure 11. Solution of the ALNS procedure (time 1997 min). (Source: own elaboration from Garmin, Tomtom Canvas).

Figure 12

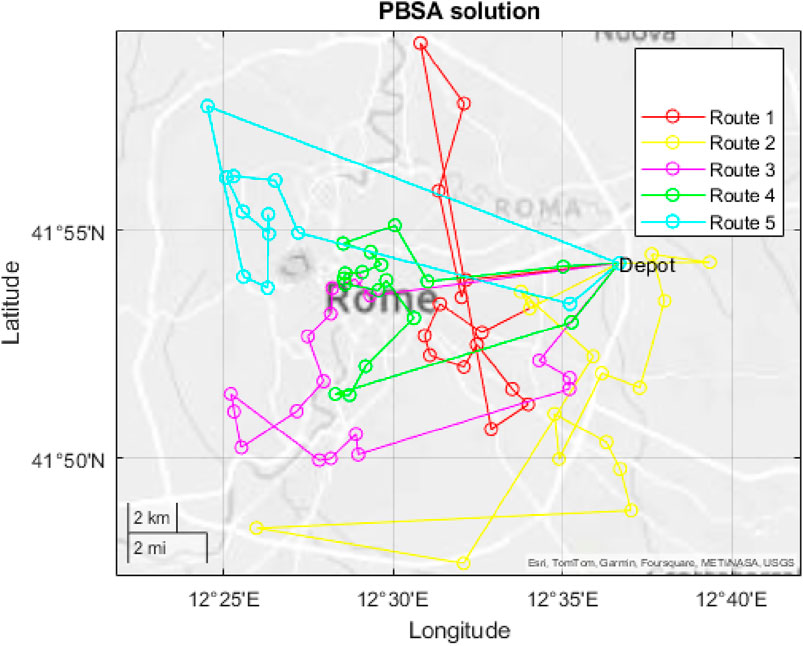
Figure 12. Solution of the PBSA procedure (time 1957 min) (Source: own elaboration from Garmin, Tomtom Canvas).

5.2 Further improvements

In this section, constraint Equation 8 is considered as inequality: this allows every vehicle to adapt the starting time of the route by eliminating first consumer waiting time (if possible).

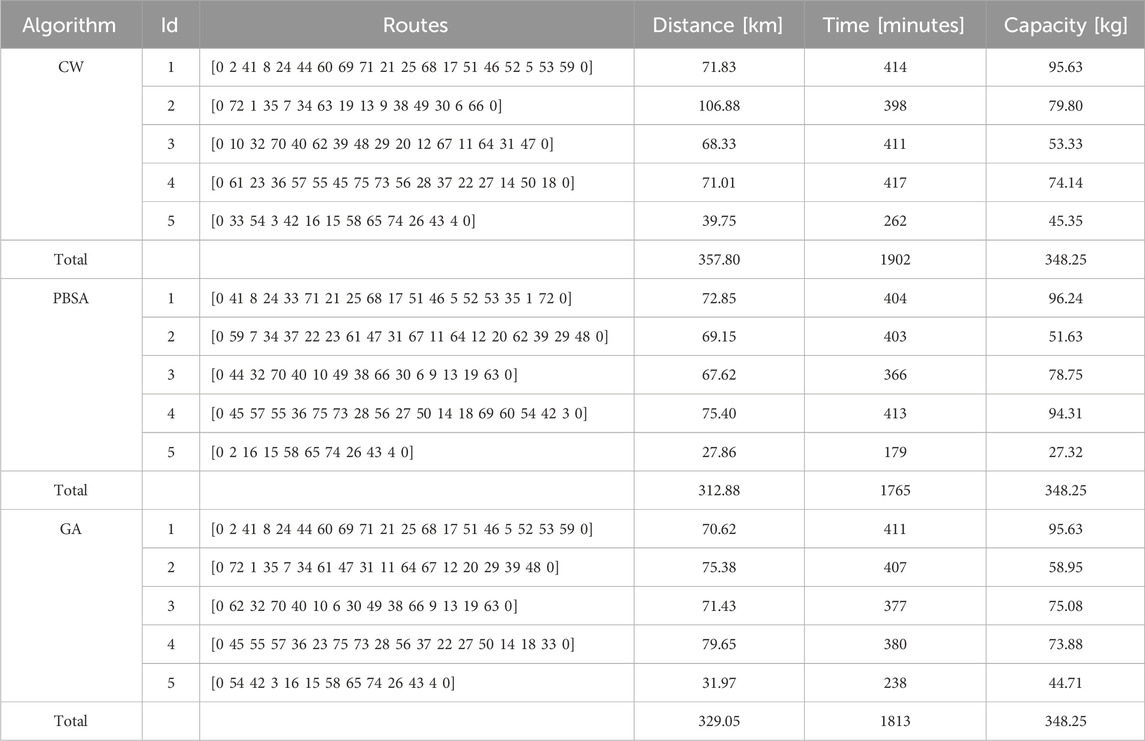
Table 2 reports the best solution found by the CW method, the PBSA algorithm and the GA, also showing the composition of the routes and, for each route, the travel times, the distances, and the demands. The parameters are those that, in the test from Section 5.1, provided the best results.

Table 2

Table 2. Best results with different optimization methods.

GA is set up has follows:

• Population size: 500 elements,

• Crossover rate: 0.80,

• Mutation rate: 0.20,

• Maximum iterations: 300.

PBSA is set up has follows:

• Population size: 16 elements,

• Number of moves: 100,

• Swap, reversion and insertion rate: 0.2, 0.5, 0.3,

• Initial temperature: 30°C,

• Temperature reduction rate:0.99,

• Maximum iterations: 300.

Resuming from Table 2 it’s possible to highlight how travel time severely affects the solution more than maximum length thus indicating that the battery capacity for the electric vehicle is sufficient for the whole tour and no additional charging operation are necessary.

Figures 13, 14 shows the routes obtained by the PBSA and GA procedures.

Figure 13

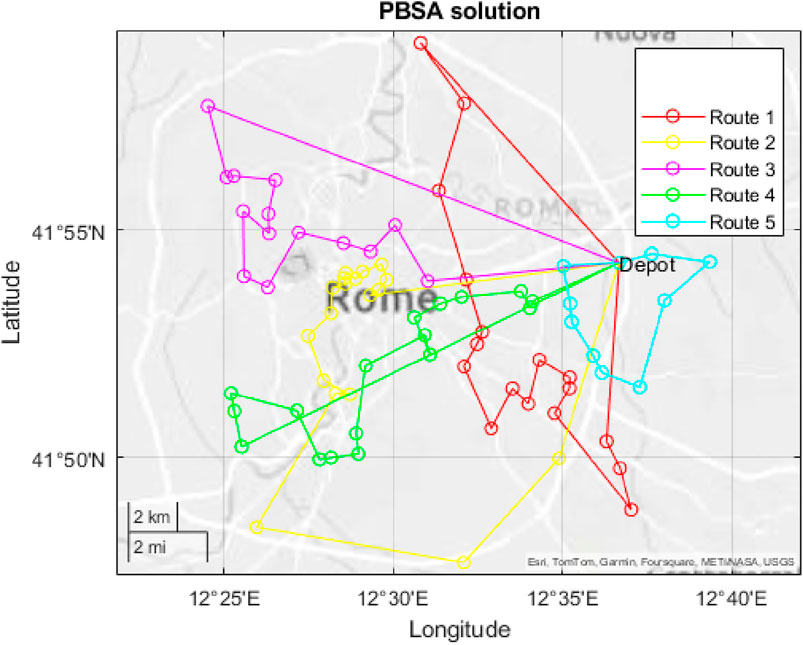
Figure 13. Solution of the PBSA procedure (time 1765 min). (Source: own elaboration from Garmin, Tomtom Canvas).

Figure 14

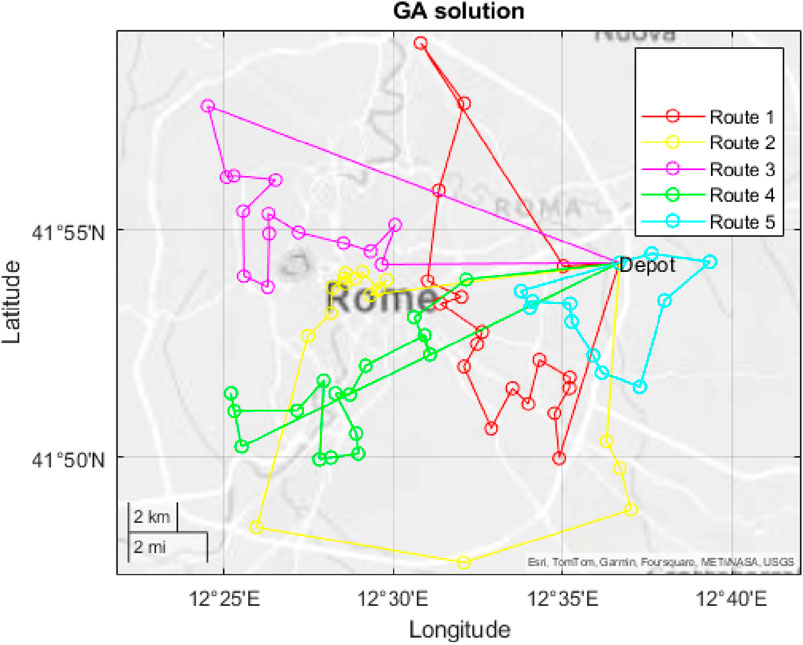
Figure 14. Solution of the GA procedure (time 1813 min). (Source: own elaboration from Garmin, Tomtom Canvas).

6 Conclusion

Freight delivery in urban areas is at the core of the political agenda of many countries and municipalities, and new technologies offer more appealing solutions to develop novels and more sustainable strategies. Thus, urban freight distribution is undertaking the path to a radical transition, thus switching from traditional vehicles with internal combustion engines to electric vehicles (this also to accomplish the Sustainable Development Goals defined by the United Nations). These electric vehicles have limited range, and it is therefore essential to optimize their routes to minimize time and energy consumption.

A general algorithm considering the problem of vehicle routing with electric vehicles (EVRP) has been proposed to support the transition to zero emissions vehicles in urban freight distribution and explore the possibility enabled by these means of transport. This paper has tested two procedures (GA and PBSA) to solve, in an urban context, a VRPSTW with EVs with the aim to minimize the total time with a constraint on the tour distance, due to the restricted battery capacity of electric vehicles; the objective function is based on some time components (travel time, delivery time and a possible penalty). Both the procedures are population-based, which allowed one to update more than one solution over the iterations. The procedures are tested on a small problem, compared with each other and with a literature procedure. It is underlined that both procedures manage to find the solutions due to the ability to maintain and/or modify the best solutions of each iteration in the following iterations. For both GA and PBSA, the route-first cluster-second principle is used, and a decoding procedure (with respect the problem constraints) is implemented to obtain the routes for each vehicle With the aim of reducing the number of iterations, good-quality solutions are introduced in the population by using the CW algorithm.

To test the proposed procedures, two cases on the same test problem are considered. In the first case, a procedure from the literature is used to solve the problem. However, to do this, it was necessary to relax one of the constraints of the problem. This allowed us to obtain: an initial evaluation of the performance of the procedures, and a calibration of the GA and PBSA parameters to obtain good results in acceptable times. In the second case, the problem (without any relaxation) is solved with the parameters determined previously. From this test, the PBSA demonstrated the best performances, but further analyses are required (as an example, improving the GA operators).

The obtained output show that when solving a problem by relaxing the constrained starting time, the total time and the total trip length are reduced, even if the number of vehicles used is the same. Thus, also reflecting the possibility to reduce the environmental costs associated with deliveries. Nevertheless, more specific analyses and further developments that concern improving the proposed procedures (e.g., developing new operators) and the exploring the micro-hub cooperation services are necessary.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AP: Conceptualization, Data curation, Formal Analysis, Methodology, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. AD: Conceptualization, Formal Analysis, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. OB: Conceptualization, Validation, Visualization, Writing–original draft.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by PNRR—Missione 4, Componente 2, Investimento 1.1—Prin 2022—Decreto Direttoriale n. 104 del 02-02-2022 Project: PULSe: Pre-feasibility analysis for Urban Logistics Solutions based on Eco-friendly vehicles. CUP Master: F53D23005490006; Identification Code: PRIN_20225YY2HL_004. Funded by the European Union—Next Generation EU.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alba, E., and Dorronsoro, B. (2006). Computing nine new best-so-far solutions for Capacitated VRP with a cellular Genetic Algorithm. Inf. Process. Lett. 98 (6), 225–230. doi:10.1016/j.ipl.2006.02.006