- Department of Civil Engineering, National Institute of Technology, Warangal, Telangana, India
Earlier studies acknowledged that the design speed does not principally assure consistency in the design of highway geometric elements. Methodologies for estimating operating speeds are limited to specific or local traffic conditions and design standards, as in various studies conducted on two-lane and multi-lane highways. The present study develops operating speed models of the vehicle types observed on horizontal curves and tangent sections on two-lane highways in southern parts of India. Geometric features of the curve section and adjacent tangent sections, such as the radius of the curve, curve length, deflection angle, degree of curvature, gradient, carriageway width, and shoulder width, are obtained from the field. The speed data collected at 24 locations on the highway, including curved and tangent gradient sections, are used to analyze and model operating speed. The results indicate that the inverse of the square root of the radius appears to be an influencing parameter for modeling the operating speed of vehicles. The operating speed is sensitive for a curve radius of up to 600 m; thereafter, the operating speed appears insignificant. On tangent sections, the gradient has a larger influence on the operating speeds of all vehicle types. The operating speed models are validated and compared with models available in the literature. The proposed models developed in the present study are helpful to traffic engineers for predicting the operating speed on two-lane highways.
1 Introduction
According to World Health Organization (WHO) data, approximately 1.35 million people die each year as a result of road traffic accidents (WHO, 2018). The situation is even more concerning for low- and middle-income countries, which account for 93% of global road fatalities despite possessing roughly 60% of the world’s vehicles. With one of the world’s largest road networks, the issue of road safety becomes even more vital for India. The Ministry of Road Transport and Highways (MoRTH) reported a total number of road accidents in India of 4,61,312 in 2022. Of these, 309,247 accidents were reported on a tangent section (MoRTH, 2022). The number of accidents, fatalities, and injuries on a tangent road section increased by 11.2% from 2021 to 2022. Vehicle speed tends to be high on straight roads in an open area, and a high percentage of accidents occur on these road segments. Similarly, 54,593 accidents were reported on curved road sections in 2022 in India (MoRTH, 2022). The number of accidents, fatalities, and injuries that occurred on a curved road section increased to 10% from 2021 to 2022. The main reasons for horizontal curve accidents are improper driver behavior and poor coordination between geometric elements. Horizontal curves are usually analyzed based on the design speed concept with an assumption about the design speed of a vehicle attaining maximum speed on the curve.
In reality, the vehicles may move on the curve with the same or at more or less than the design speed. Fitzpatrick et al. (1995) reported that drivers choose their speeds based on the availability of road features rather than the posted speed limit. This selected speed under free-flow conditions is the operating speed (Tottadi and Mehar, 2022). Moreover, approximately 80% of accidents occurred on tangent and curved sections. Hence, curve and tangent sections have been recognized as important geometric features of highways that affect road safety.
One of the main reasons for road accidents on the highway is high speed. Speed accounts for 71.2% of road accidents during 2022 in India. Therefore, speed is considered the most important parameter defining the convenience, comfort, and safety of road users. Among several other factors associated with travel time and cost, vehicle speeds are directly affected by the decisions made by the drivers when selecting alternative routes. In India, highways have a design speed, and the traffic conditions comprise various vehicles with different static and dynamic characteristics (Karuppanagounder and Arasan, 2008). The speeds of vehicles range as low as 10 kmph in the case of hand-drawn and animal-drawn vehicles and as high as 100 kmph in the case of passenger cars. Road geometry is considered one of the main factors controlling vehicle speed on both curved and tangent highways. The design speed is selected to determine the roadway’s geometric features (AASHO, 2011). The main limitation of the design speed concept is that it uses the design speed of the most restricted geometric feature in the highway segment.
Thus, while using this design speed concept, the speeds at which a vehicle travels on curved or tangent sections have not been considered. This gap could lead to possible inconsistencies between successive elements of a roadway system. Operating speed is observed under free-flow roadway conditions (AASHO, 2011). Highway geometry compatible with driver’s expectancy is a basic and important requirement for highway design (Nicholson, 1999). Most studies examining the relationship between design speed and operating speed have shown a disparity between them (Malaghan et al., 2021; Jacob and Anjaneyulu, 2012; Bella, 2007; Lamm et al., 1998). The geometric design consistency is evaluated using the driver workload, alignment indices, and operating speed. Among these variables, the operating speed-based approach is commonly used for assessing geometric design consistency as it is a visible safety indicator. Therefore, designing a highway without considering the operating speed may lead to numerous road accidents.
Traffic flows in developing countries like India comprise different classes of vehicles with different static and dynamic characteristics that occupy the common road space. The diversity in vehicle classes makes a greater difference in these vehicles’ free speed, which challenges designers and planners to keep updating the speed limits at sections at frequent intervals. Moreover, the operating speed of vehicles does not match the geometry due to inconsistency in highway alignment design. Therefore, the present study analyzes the speed characteristics of different vehicle types to develop operating speed models on two-lane roads with varying geometric conditions.
2 Literature review
The literature review addresses all significant studies performed on the operating speed of vehicles on horizontal curves and tangent sections separately.
2.1 Horizontal curves
Since the 1950s, several studies conducted to estimate operating speed on two-lane rural highways have resulted in various methods for estimating the operating speed on horizontal curve sections of two-lane highways (Taragin and Leisch, 1954; Fitzpatrick and Collins, 2000; Schurr et al., 2002; Misaghi and Hassan, 2005; Malaghan et al., 2020; Shallam and Ahmed, 2016; Mirzahossein et al., 2023). The radius of the curve is considered the most important parameter for estimating operating speed at a horizontal curve (Ottesen and Krammes, 2000; Abbas et al., 2011; Jacob and Anjaneyulu, 2013; Malaghan et al., 2020; Tottadi and Mehar, 2022). The previous studies confirmed that the greatest impact on operating speed is found with a radius of less than 250 m. As per the National Cooperative Highway Research Program (NCHRP) 785 report, curve radius greatly influences the operating speed if it is less than 1000 ft (Ray et al., 2014). Some studies reported that vehicles’ operating speed showed sensitivity at a radius of 400 m (Schurr et al., 2002; Jacob and Anjaneyulu, 2013). In a study by McLean (1978), curve radii greater than 850 m no longer affect the operating speed of vehicles. Researchers found that vehicle operating speeds with curve radii greater than 800 m remain the same as in preceding tangent sections (Fitzpatrick et al., 1995; Misaghi and Hassan, 2005; Jacob and Anjaneyulu, 2013). Many authors recognized that the different forms of radius (√R, 1/√R, 1/R), curvature change rate (CCR), degree of curvature, and deflection angle have a significant impact on operating speed of vehicles on highways (McLean, 1978; Lamm and Choueiri, 1987; Ottesen and Krammes, 2000; Memon et al., 2008; Perco, 2008; Jacob and Anjaneyulu, 2013; Malaghan et al., 2022). A CCR of less than 180 gon/km is designated as “good design.” A CCR between 180 gon/km and 360 gon/km is designated as “fair design,” and a CCR larger than 360 gon/km is designated as “poor design” (Lamm and Choueiri, 1987).
The study used the degree of curvature as an explanatory variable ranging from 4° to 28°. They revealed that a degree of curvature less than 4° may not affect the operating speed of cars on highways (Ottesen and Krammes, 2000). Voigt (1996) considered the rate of super-elevation and degree of curvature when estimating the 85th percentile operating speed on the mid-point of a horizontal curve. They reported that the super-elevation is statistically significant, accounting for 1%–2% more variability in the data. Schurr et al. (2002) revealed that the 50th percentile, 85th percentile, and 98th percentile speeds decrease due to an increase in the deflection angle of a horizontal curve.
Misaghi and Hassan (2005) found no significant difference between the speeds of cars and light commercial vehicles and combined them into a single vehicle type for estimating operating speed on curves and tangent-to-curve transitions. Zuriaga et al. (2010) used curve radius and curvature change rate as independent variables for calibrating a model for the horizontal curve. They reported that the radius has a greater impact on vehicle operating speed when it is less than 400 m. Jacob and Anjaneyulu (2013) developed 85th percentile operating speed models for several vehicle types: car, two-wheeler, bus, and truck. The study found that the radius of the curve affects vehicle operating speeds less than the curve length. Montella et al. (2014) concluded that the speed of drivers is not constant on a horizontal curve from the point of curvature to the point of tangency. The individual drivers reported significantly greater deceleration and acceleration rates than those needed to make operating speed profiles. Wang and Wang (2018) proposed a log-linear relationship between curve radius and 85th percentile operating speed. The authors found that the speeds are significantly decreased for a curve radius of less than 305 m. Malaghan et al. (2020) and Malaghan et al. (2022) proposed a model for predicting the operating speed of heavy vehicles using continuous speed profiles. They found that the curve radius, curve length, and approach tangent length greatly influenced the operating speed of heavy vehicles. Moreover, the authors suggested a relationship between operating speed differential (∆85V) and differential 85th percentile speed (∆V85) and described the merits of the continuous speed profiles method over spot speed measurements. Goyani et al. (2022) developed models for predicting the operating speed of vehicle types car, two-wheelers (2Ws), and heavy commercial vehicles (HCVs) on hilly terrains in India. The authors revealed that the HCVs were more susceptible to geometric variables than cars. However, geometric variables do not significantly affect the speed of 2Ws.
2.2 Tangent section
Several studies have been performed to predict operating speed on horizontal curves, and only a few have been performed on tangent sections. Lamm et al. (1988) suggested a few recommendations while designing rural highways. They found the minimum tangent length between successive elements (viz., curve to curve and tangent to curve) for establishing consistency rating. Polus et al. (2000) divided field data collected at 162 sites into four groups based on the radius of curves and the length of the tangent from small to large. The authors found that the short radii and intermediate tangent length fit the model well. As per earlier studies, tangent length and curve radius of preceding and succeeding sections are significant explanatory variables for predicting operating speed. Fitzpatrick et al. (2005) collected speed data at the mid-point of a long tangent. They stated that the posted speed limit and access point density are significant variables for predicting operating speed on tangent sections.
Other variables, such as median type, parking, and pedestrian activity, number of lanes, the density of objects along the road, and the presence of curbs and sidewalks, also influence the operating speed on a tangent (Fitzpatrick et al., 2005; Wang et al., 2006). Dell’Acqua et al. (2007) revealed that the operating speed on a tangent depends on the tangent length and the average speed measured on the preceding curve. Moreover, the pavement distress and the presence of an intersection nearer to selected sites also influenced the operating speed (Dell’acqua and Russo, 2011). Semeida (2013) reported that the posted speed limit had less effect on operating speed than other variables such as carriageway width, median width, and access point density. Similarly, variables like shoulder width and roadside hazard rating greatly influence the operating speed (Rao and Chandra, 2022). Jacob and Anjaneyulu (2013) stated that the operating speeds of different vehicles on tangents depend on the preceding tangent length. The study also found that trucks move at a lower speed than buses when the tangent length is less than 400 m. Maji et al. (2018) considered geometric variables, pavement characteristics, and traffic parameters for developing operating speed models. They found that the posted speed limit and skid number affect operating speed on tangent sections of highways. Malaghan et al. (2020) and Malaghan et al. (2022) found that the preceding and succeeding tangent lengths significantly influenced the operating speed of heavy passenger vehicles on the tangent section.
Most earlier studies were done to predict the speed of passenger cars, and only a few have been developed for heavy trucks or light commercial vehicles. Few studies have been done in India that consider different types of vehicles such as cars, two-wheelers, light commercial vehicles, and heavy commercial vehicles. In this study, different vehicle types, such as small cars (CSs), big cars (CBs), two-wheelers (2Ws), three-wheelers (3Ws), light commercial vehicles (LCVs), multi-axle vehicles (MAVs), and buses, are considered. The present study determines the operating speed of different vehicle types on various sections of two-lane highways by considering various geometric characteristics. This study aims to analyze the speed characteristics of different vehicle types to develop operating speed models on two-lane roads with various geometric conditions. In addition, the present study performed validation and compared the developed models with the existing models in the literature.
3 Site selection
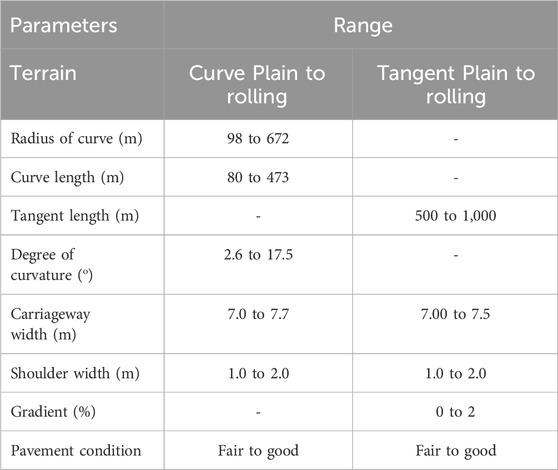
The study identified 48 sites, including 24 tangent grades and 24 curved sections, on rural two-lane highways. The selected horizontal curve radius ranges from 98 m to 672 m. The selected sites are free from the influence of intersections on access points, physical obstructions, and narrow bridges, and all have pavement and shoulders in good condition. Moreover, these sites have proper lane markings, sufficient sight distance, and low average annual daily traffic (AADT) to ensure free-flow conditions. A Google Earth image of a selected location where data collection was performed is shown in Figure 1.
4 Data collection
The data collected for the study include the roadway and geometric data and free-flow speed data. The various geometric features such as the radius of curve (R), length of curve (LC), deflection angle (Δ), degree of curvature (D), and roadway gradients are collected using a total station instrument. The characteristics of the site, such as roadway type, number of lanes, carriageway width (CW), shoulder width (SW), and shoulder type (ST), are measured at the sites. The width of the carriageway on a tangent varies from 7.0 m to 7.7 m on the curve, and the width measured at the mid-point ranges from 7.0 m to 7.5 m. The shoulder width at selected locations varies from 1.0 m to 2.0 m. The parameter values and their ranges of overall data are presented in Table 1.
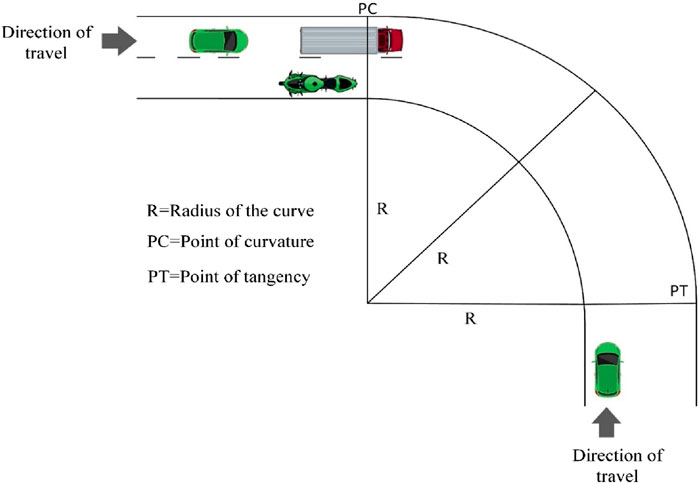
The free-flow speeds of vehicles are measured with a radar gun machine at the mid-point of the curve. The video of the traffic operation is recorded from 08:30 AM to 12:30 PM in good weather conditions for measurement of traffic flow. The schematic diagram of the selected site is given in Figure 2. The traffic volume data are collected using the video-graphic method. A trap length of 30 m was used to calculate the speed data. The speeds were collected for cars (Cs), two-wheelers (2Ws), three-wheelers (3Ws), light commercial vehicles (LCVs), heavy commercial vehicles (HCVs), and buses on horizontal curves and tangent sections of the roadway.
5 Estimation of 85th percentile speed
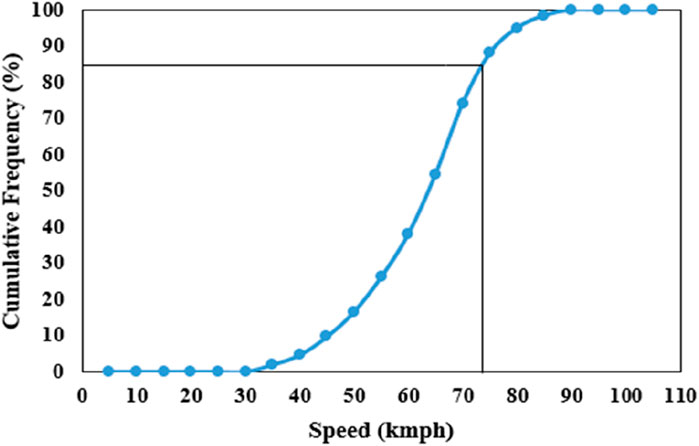
The 85th percentile speed is usually estimated by creating free speed profiles of the traffic stream based on the observed data. The speed frequency and class interval provide an understanding of the speed distributions. The cumulative speed profile explains the speed characteristics and expectations about the 85th percentile speed on a particular highway. The collected data created the speed distribution curve for Section 4 and it is presented in the Figure 3.
6 Field data analysis
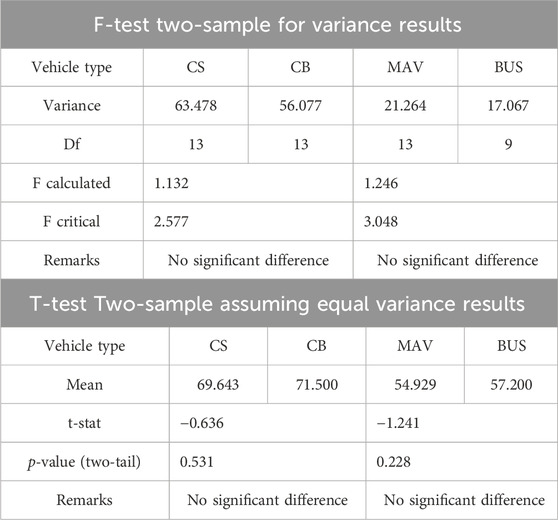
The speed analysis is performed using data obtained from various study locations. The speed distribution analysis is performed for each vehicle type, and mixed traffic speeds are fitted to different distributions. Each vehicle type follows either a normal distribution or a log-normal distribution. However, the mixed traffic speed profile only fits the Beta4 distribution. Statistical tests on the speeds of different types of vehicles are conducted to compare the means and variances between data sets per vehicle type. T-tests and F-tests are performed to compare the mean and variances between speeds of different vehicle types. The results of the statistical tests are shown in Table 2.
The results show no significant difference between the speeds of observed vehicle types CS and CB. Hence, the present study considers them as single vehicle type category, passenger cars, for analyzing operating speeds. Similarly, statistical tests conducted between MAVs and buses showed that the observed speeds between MAVs and buses were not significantly different, and they are combined into a single vehicle type category, HCVs.
6.1 Effect of the radius of the curve on the 85th percentile speed
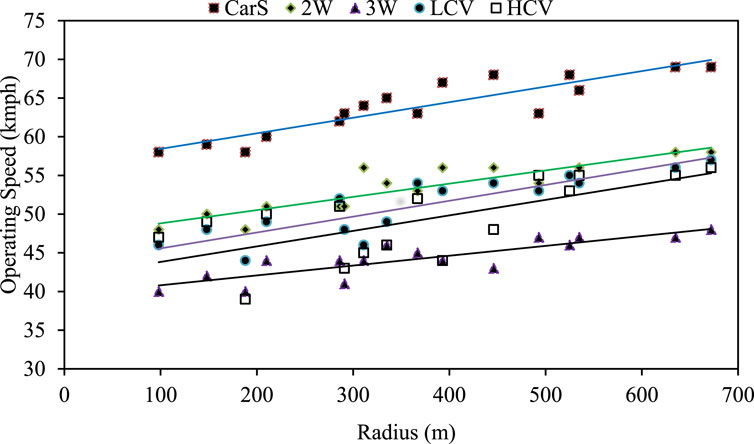
To examine the effect of radius on 85th percentile speed, a relationship is developed between the speeds of different types of vehicles and the radius of the curve (R). The variation of the 85th percentile speed with radius is presented in Figure 4. It can be observed that as the radius (R) increases, the 85th percentile speed also increases. Vehicle types such as 2Ws, LCVs, and HCVs move at similar speeds, whereas cars move at higher speeds, and 3Ws move at slower speeds.
6.2 Effect of grade on the 85th percentile speed
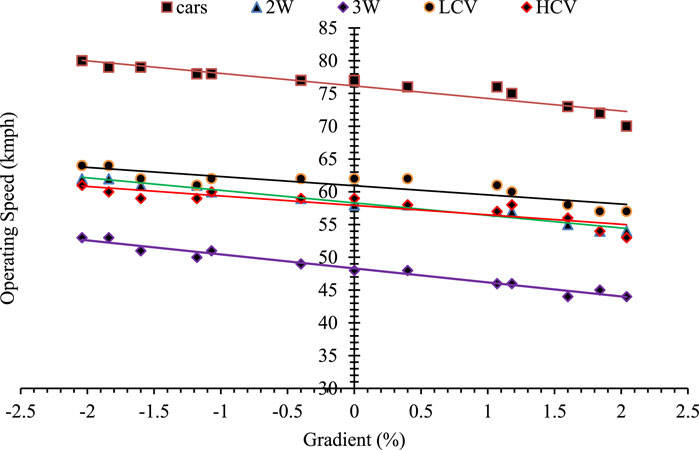
To examine the influence of gradient (both the ascending and descending grade section) on the 85th percentile speeds of different classes of vehicles, the relationship between gradient and speed is plotted and presented in Figure 5. The 85th percentile speed increases with descending grades and decreases with ascending grades. In both Figures 4, 5, the 85th percentile speed of cars was observed to be the fastest, whereas that of 3Ws is the slowest, and the 85th percentile speeds of 2Ws, LCVs, and HCVs were observed to be similar to each other. For every 2% of ascending grade, the observed speeds of cars and 3Ws vary by 4 kmph. In contrast, in the descending grade section, only a 2 kmph variance is observed for 2Ws, LCVs, and HCVs.
7 Model development
Models are developed to estimate the operating speed of vehicles on horizontal curves and tangent sections of two-lane highways. A multiple linear regression method was used to evolve speed prediction models. The independent parameters used for model development are curve radius (R), curve length (CL), degree of curvature (D), gradient (G), carriageway width (CW), and shoulder width (SW).
7.1 Horizontal curve
A preliminary correlation analysis was performed between the 85th percentile speed and various geometric parameters on curves. The radius is transformed into different forms, such as 1/R, LnR, √R, and 1/√R, to check the strongest correlation with the 85th percentile speed. The correlation test was performed between independent variables and 85th percentile speeds of vehicles. The inverse of the square root of the radius (1/√R) was observed as the most significant factor influencing the operating speed. Therefore, the curve radius is used as an independent variable in this study for model development, according to Equation 1:
where V85c = operating speed at the curve (kmph);
R = curve radius (m);
a0 and a1 are the model parameters to be calibrated.
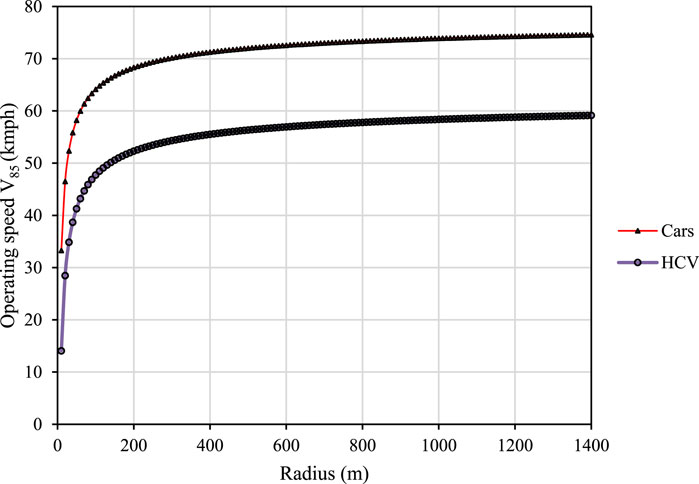
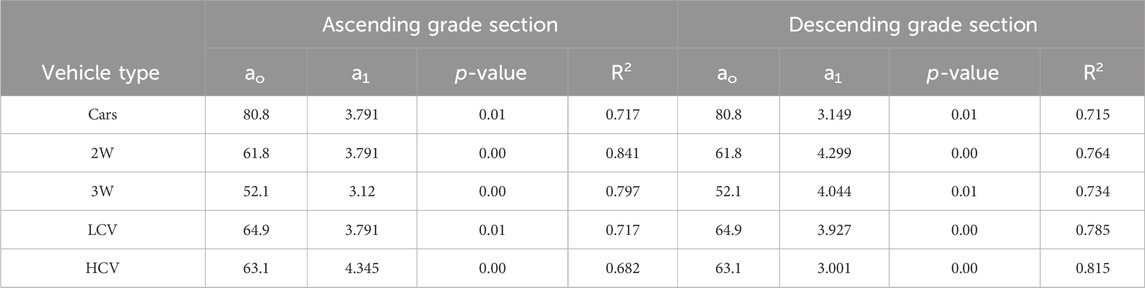
The regression analysis yielded the models for car and HCV vehicle types shown in Figure 6. The model has a steep slope for a small radius and a decreasing slope as the radius increases. It suggests that the radius is less important in speed selection for large-radius curves than for sharp curves. The summary statistics of the developed models are presented in Table 3.
7.2 Operating speed models on tangents
Predicting the operating speed on a tangent road section is complicated. In this study, the tangent section models were developed on ascending and descending grade tangent sections.
7.2.1 Ascending grade section and descending grade section
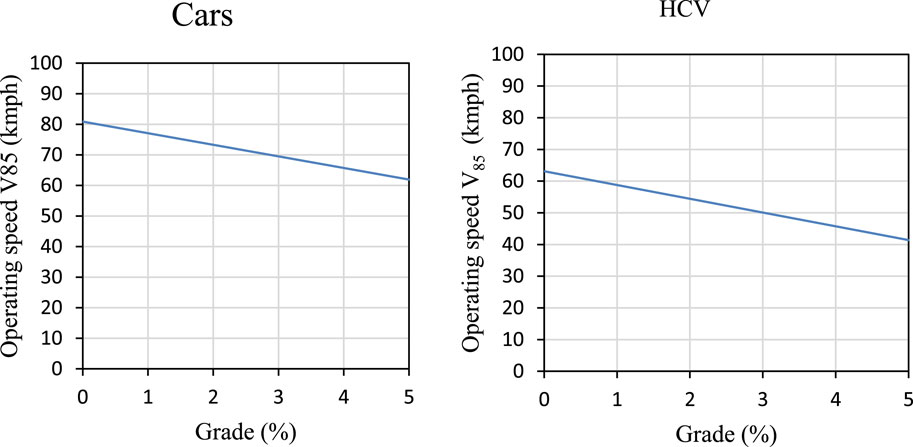
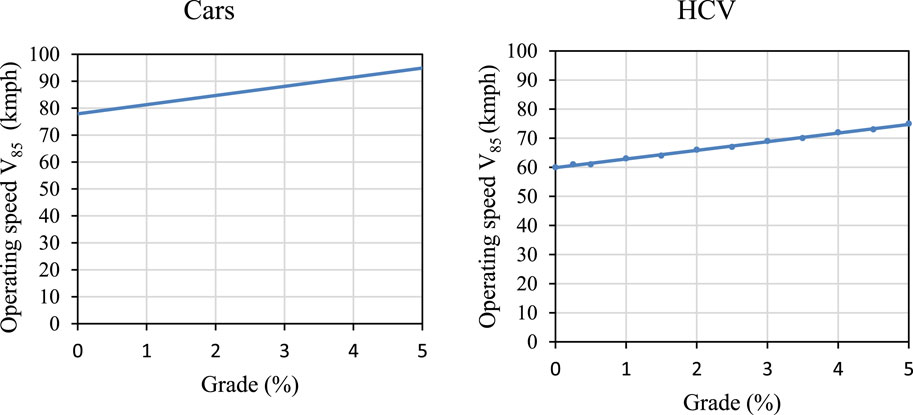
The geometric parameters used for modeling the operating speeds of different vehicle types at ascending grade and descending grade sections on various study locations are gradient (G), carriageway width (CW), and shoulder width (SW). The correlation test was performed between the 85th percentile speed of different vehicle types and geometric parameters to find significant variables. It was observed that only gradient (G) had a significant influence on operating speed in all types of vehicles. All operating speed models of various vehicle types were obtained at 95% confidence levels. The independent variables in the obtained models were significant at the 95% confidence level (i.e., p ≤ 0.05) and are presented in Table 4. When the descending gradient increases, the speed reduction is the same in cars and HCVs. The variations of the predicted operating speed of cars and HCVs with ascending grade and descending grade sections are shown in Figures 7, 8. Therefore, the gradient is used as an independent variable in this study for model development, according to Equation 2:
where V85a&d = operating speed on ascending and descending grade section (kmph), G = gradient (%), and a0 and a1 are the model parameters to be calibrated.
8 Models of operating speed for mixed traffic and comparison
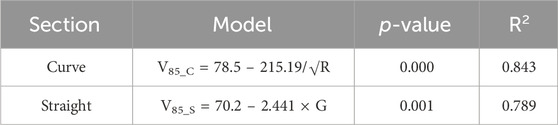
The models are developed to determine the 85th percentile speed on curved and straight sections. A correlation test was conducted among the 85th percentile speeds at the curve section, examining 85th percentile speed parameters such as radius of the curve (R), length of the curve (Lc), deflection angle (Δ), carriageway width (CW), shoulder width (SW), and modified forms of the radius (1/R, Ln R, √R, and 1/√R). It was found that the inverse of the square root of the radius (1/√R) was most significantly correlated with the 85th percentile speed. Therefore, the inverse square root of the radius (1/√R) was considered an independent variable for modeling the operating speed.
A regression model was developed to determine the operating speed of mixed traffic on the curve section, as shown in Table 5. The same procedure was followed to develop the model for the operating speed of mixed traffic on a straight section. Only gradient (G) was found to be correlated with the operating speed of mixed traffic. Therefore, the model was developed for operating speed, considering the gradient as an independent variable, as shown in Table 5.
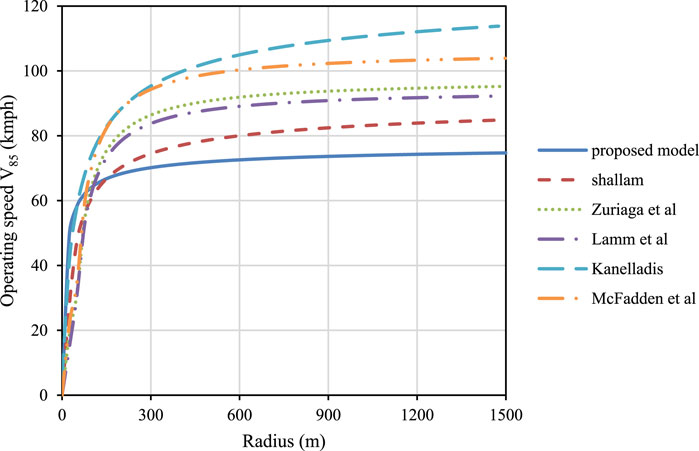
The proposed model for mixed traffic on curved sections was further compared with earlier models. The comparison of the car operating speed model with existing models is shown in Figure 9.
Previous models report higher operating speeds than the proposed model, except the model developed by Shallam et al. (2016), which was proposed under heterogeneous traffic conditions in India. This study helps estimate operating speed under mixed traffic conditions.
9 Model validation
The validation of the developed models used the remaining one-third of the data to compare the observed V85c and predicted V85c values. The accuracies of the developed models are expressed in terms of root-mean-square error (RMSE) and a 45° regression line. A graphical representation was also made among the observed V85c, and V85c was predicted to form the comparative variance shown in Figure 10. The RMSE values were calculated for validation using Equation 3:
where Xi = observed value of ith site observation; Xi’ = predicted value of ith site observation; n = number of observations.
The RMSE value of operating speed on the horizontal curve for mixed traffic conditions is 3.29 kmph. This value is less than previously developed models (Taragin and Leisch, 1954; Kanellaidis and Efstathiads, 1990; Voigt, 1996; Passetti and Fambro, 1998; Zuriaga et al., 2010; Castro et al., 2012; Jacob and Anjaneyulu, 2013; Malaghan et al., 2020), which shows the accuracy of the current model’s prediction of speeds on a horizontal curve in a two-lane highway.
10 Conclusion
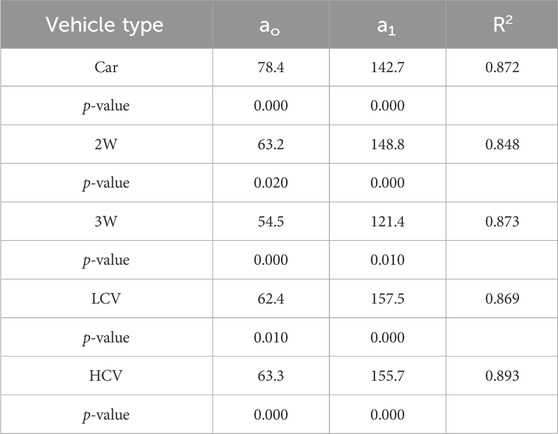
The main objective of this study is to develop operating speed prediction models for horizontal curves and tangent sections of two-lane highways. Seven vehicle types are considered (CB, CS, 2W, 3W, LCV, MAV, and B). The t-test and F-test are performed to compare the mean and variances between different types of vehicle speeds to determine whether any significant difference exists. No significant difference is observed between the speeds of large and small cars or between MAVs and buses. Therefore, CS and CB are combined into a single vehicle type, cars, and MAVs and buses are combined into the category of HCVs. The geometric characteristics such as curve radius (R), curve length (CL), degree of curvature (D), gradient (G), carriageway width (CW), and shoulder width (SW) are used as explanatory variables for model development using the multiple linear regression method. The correlation test was performed between explanatory variables and 85th percentile speeds of different classes of vehicles. It is found that the inverse square root of radius made a strong correlation with 85th percentile speed, and the coefficient of determination (R2) values for predicting operating speed models of cars, 2Ws, 3Ws, LCVs, and HCVs are 0.872, 0.848, 0.823, 0.869 and 0.893, respectively. The curve radius has more impact on operating speed for a radius less than 300 m. The vehicle types of cars, 2Ws, 3Ws, and LCVs were found to be more affected by the radius of the curve.
Operating speed models were developed for both ascending and descending grade sections of tangent sections. The independent variables, which are gradient (G), carriageway width (CW), and shoulder width (SW), and the dependent variable, the 85th percentile speeds of all vehicles, were considered for model development. The gradient was a significant variable for estimating operating speed on ascending and descending grade sections. Passenger cars were found to move at higher speeds than other types of vehicles.
This study also provides a model for mixed traffic conditions on horizontal curves and tangent sections. This curve model is compared with the existing operating speed models. The predicted operating speed is more sensitive at a lower radius as it decreases drastically at a radius smaller than 600 m than previously developed models. The developed models for predicting operating speed on horizontal curves and tangent sections showed high correlation and low error values. These models can evaluate the geometric design consistency and define appropriate posted speed limits on curved and tangent sections. The proposed models make it easier for traffic engineers to anticipate the operating speed on multi-lane highways.
Future studies should incorporate other geometric parameters (such as deflection angle and tangent length) and vehicle characteristics. In addition, pavement characteristics, existing site characteristics, and climatic conditions should be included. A larger number of sites should be considered for better operating speed prediction.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
KT: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, writing–original draft, and writing–review and editing. AM: conceptualization, methodology, supervision, and writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbas, S. K. S., Adnan, M. A., and Endut, I. R. (2011). Exploration of 85th percentile operating speed model on horizontal curve: a case study for two-lane rural highways. Procedia - Soc. Behav. Sci. 16, 352–363. doi:10.1016/j.sbspro.2011.04.456
Castro, M., Sánchez, J. F., and Sánchez, J. A. (2012). Operating speed models for two-lane rural highways. Proc. Inst. Civ. Eng. Transp. 165 (2), 107–118. doi:10.1680/tran.2012.165.2.107
Dell’Acqua, G., Esposito, T., Lamberti, R., and Abate, D. (2007). Operating speed model on tangents of two-lane rural highways. 4th Int. SIIV Congr. – PALERMO, 2848. (September).
Dell’acqua, G., and Russo, F. (2011). Speed factors on low-volume roads for horizontal curves and tangents. Balt. J. Road. Bridg. Eng. 5 (2), 89–97. doi:10.3846/bjrbe.2010.13
Fitzpatrick, K., Blaschke, J. D., Brian, C., Krammes, R. A., and Fambro, D. B. (1995). Compatibility of design speed, operating speed. Transp. Res. Circ. 7, 1–118.
Fitzpatrick, K., and Collins, J. M. (2000). Speed-profile model for two-lane rural highways. Transp. Res. Rec. 1737 (1737), 42–49. doi:10.3141/1737-06
Fitzpatrick, K., Miaou, S. P., Brewer, M., Carlson, P., and Wooldridge, M. D. (2005). Exploration of the relationships between operating speed and roadway features on tangent sections. J. Transp. Eng. 131 (4), 261–269. doi:10.1061/(ASCE)0733-947X(2005)131:4(261)
Goyani, J., Chaudhari, P., Arkatkar, S., Joshi, G., and Easa, S. M. (2022). Operating speed prediction models by vehicle type on two-lane rural highways in Indian hilly terrains. J. Transp. Eng. Part A Syst. 148 (3). doi:10.1061/jtepbs.0000644
Jacob, A., and Anjaneyulu, M. V. L. R. (2013). Operating speed of different classes of vehicles at horizontal curves on two-lane rural highways. J. Transp. Eng. 139 (3), 287–294. doi:10.1061/(ASCE)TE.1943-5436.0000503
Kanellaidis, G. J. G., and Efstathiads, S. (1990). Driver’s speed behaviour on rural road curves. Traffic engg. Control 31 (7–8), 414–415.
Karuppanagounder, K., and Arasan, T. (2008). Effect of traffic volume on PCU of vehicles under heterogeneous traffic conditions. Road. Transp. Res. 17 (1).
Lamm, R., and Choueiri, E. M. (1987). Recommendation for evaluating horizontal design consistency based on investigations in the state of New York. Transp. Res. Rec. (1122), 68–78.
Lamm, R., Choueiri, E. M., and Hayward, J. C. (1988). Tangent as an independent design element. Transp. Res. Rec. (1195), 123–131.
Maji, A., Sil, G., and Tyagi, A. (2018). 85th and 98th percentile speed prediction models of car, light, and heavy commercial vehicles for four-lane divided rural highways. J. Transp. Eng. Part A Syst. 144 (5), 1–8. doi:10.1061/JTEPBS.0000136
Malaghan, V., Pawar, D. S., and Dia, H. (2020). Modeling operating speed using continuous speed profiles on two-lane rural highways in India. J. Transp. Eng. Part A Syst. 146 (11), 04020124–4020211. doi:10.1061/jtepbs.0000447
Malaghan, V., Pawar, D. S., and Dia, H. (2022). Speed prediction models for heavy passenger vehicles on rural highways based on an instrumented vehicle study. Transp. Lett. 14 (1), 39–48. doi:10.1080/19427867.2020.1811005
Memon, R. A., Khaskheli, G. B., and Qureshi, A. S. (2008). Operating speed models for two-lane rural roads in Pakistan. Can. J. Civ. Eng. 35 (5), 443–453. doi:10.1139/L07-126
Mirzahossein, H., Adibi, H., Khishdari, A., Afandizadeh, S., and Severino, A. 2023. “Evaluating geometric design characteristics of two-lane two-way rural roads on crash frequencies occurrences.” Iran. J. Sci. Technol. Trans. Civ. Eng., 47: 2497–2506. doi:10.1007/s40996-023-01072-3
Misaghi, P., and Hassan, Y. (2005). Modeling operating speed and speed differential on two-lane rural roads. J. Transp. Eng. 131 (6), 408–418. doi:10.1061/(ASCE)0733-947X(2005)131:6(408)
Montella, A., Pariota, L., Galante, F., Imbriani, L. L., and Mauriello, F. (2014). Prediction of drivers’ speed behavior on rural motorways based on an instrumented vehicle study. Transp. Res. Rec. 2434 (December 2015), 52–62. doi:10.3141/2434-07
Ottesen, J. L., and Krammes, R. A. (2000). Speed-profile model for a design-consistency evaluation procedure in the United States. Transp. Res. Rec. 1701 (1701), 76–85. doi:10.3141/1701-10
Passetti, K. A., and Fambro, D. B. (1998). Operating speeds on curves with and without spiral transitions. Transp. Res. Rec. 1658 (1658), 9–16. doi:10.3141/1658-02
Perco, P. (2008). Influence of the general character of horizontal alignment on operating speed of two-lane rural roads. Transp. Res. Rec. 2075, 16–23. doi:10.3141/2075-03
Polus, A., Fitzpatrick, K., and Fambro, D. B. (2000). Predicting operating speeds on tangent sections of two-lane rural highways. Transp. Res. Rec. 1737 (1737), 50–57. doi:10.3141/1737-07
Rao, A. M., and Chandra, S. (2022). A close examination of posted speed limits and its compliance on Indian State Highways. Eur. Transp. - Trasp. Eur. (88), 1–16. doi:10.48295/ET.2022.88.4
Ray, B. L., Ferguson, E. M., Knudsen, J. K., Porter, R. J., and Mason, J. (2014). Performance-based analysis of geometric design of highways and streets. Performance-Based Anal. Geom. Des. Highw. Streets.
Schurr, K. S., McCoy, P. T., Pesti, G., and Huff, R. (2002). Relationship of design, operating, and posted speeds on horizontal curves of rural two-lane highways in Nebraska. Transp. Res. Rec. 1796 (1796), 60–71. doi:10.3141/1796-07
Semeida, A. M. (2013). Impact of highway geometry and posted speed on operating speed at multi-lane highways in Egypt. J. Adv. Res. 4 (6), 515–523. doi:10.1016/j.jare.2012.08.014
Taragin, A., and Leisch, L. E. (1954). Driver performance on horizontal curves. Proc. 33rd Annu. Meet. Highw. Res. Board. Wash. D.C. Highw. Res. Board 33.
Tottadi, K. K., and Mehar, A. (2022). Operating speed: review and recommendations for future research. Innov. Infrastruct. Solut. 7 (1), 67. doi:10.1007/s41062-021-00669-9
Voigt, A. (1996). Evaluation of alternative horizontal curve design approaches on rural two-lane highways, 1–103.
Wang, J., Dixon, K., Li, H., and Hunter, M. (2006). Operating-speed model for low-speed urban tangent streets based on in-vehicle global positioning system data. Transp. Res. Rec. 1961, 24–33. doi:10.3141/1961-04
Wang, X., and Wang, X. (2018). Speed change behavior on combined horizontal and vertical curves: driving simulator-based analysis. Accid. Anal. Prev. 119 (February 2017), 215–224. doi:10.1016/j.aap.2018.07.019
Keywords: two-lane highways, operating speed models, curve radius, gradient, multiple linear regression
Citation: Tottadi KK and Mehar A (2024) Influence of horizontal alignment elements on operating speed of vehicles on two-lane highways. Front. Future Transp. 5:1260051. doi: 10.3389/ffutr.2024.1260051
Received: 17 July 2023; Accepted: 05 August 2024;
Published: 23 September 2024.
Edited by:
Uneb Gazder, University of Bahrain, BahrainReviewed by:
Hamid Mirzahossein, Imam Khomeini International University, IranBenedetto Barabino, University of Brescia, Italy
Copyright © 2024 Tottadi and Mehar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kiran Kumar Tottadi, a2lyYW50NjY2NkBzdHVkZW50Lm5pdHcuYWMuaW4=
 Kiran Kumar Tottadi
Kiran Kumar Tottadi Arpan Mehar
Arpan Mehar