Approach for machine learning based design of experiments for occupant simulation

The complexity of crash scenarios in the context of vehicle safety is steadily increasing. This is especially the case on the way to mixed traffic challenges with non-automated and automated driving vehicles. The number of simulations required to design a robust restraint system is thus also increasing. The vast range of possible scenarios here is causing a huge parameter space. Simultaneously biofidelic simulation models are resulting in very high computational costs and therefore the number of simulations should be limited to a feasible operational range. In this study, a machine-learning based design of experiments algorithm is developed, which specifically addresses the issues when designing a safety system with a limited number of simulation samples taking diversity of the occupant and accident scenario into account. In contrast to an optimization task, where the aim is to meet a target function, our job has been to find the critical load case combinations to make sure that these are addressed and not missed. A combination of a space-filling approach and a metamodel has been established to find the critical scenarios in order to improve the system for those cases. It focuses specifically on the areas that are difficult to predict by the metamodel. The developed method was applied to iteratively generate a simulation matrix of a total of 208 simulations with a generic interior model and a detailed FE human body model. Kinematic and strain-based injury metrics were used as simulation output. These were used to train the metamodels after each iteration and derive the simulation matrix for the next iteration. In this paper we present a method that allows the training of a robust metamodel for the prediction of injury criteria, considering both varying load cases and varying restraint system parameters for individual anthropometries and seating postures. Based on that, restraint systems or metamodels can be optimized to achieve the best overall performance for a huge variety of possible scenarios with a specific focus on critical scenarios.

1 Introduction

By means of virtual testing, the assessment of real-world safety instead of the protection in standard load cases is enabled (Freienstein et al., 2019; Luttenberger et al., 2020). The number of scenarios occurring in the real world however, is resulting an enormous parameter space. Furthermore, autonomous driving will enable new seating postures (Poulard et al., 2020) and as a result will therefore increase the overall complexity and the efforts required to safeguard occupant protection even more effectively. At the same time, biofidelic simulation models cause high computational costs and therefore the number of simulations should be limited to a feasible range. To control this increasing number of influencing variables and load cases, methods are needed to understand and scan the complex parameter space in an efficient way.

Adequate design of experiments is playing an increasingly important role in this. If no metamodel is chosen in advance, model-free designs are applied. So-called space-filling experimental designs are model-free designs that are very common for computer simulation. In such approaches, the whole parameter space is covered as uniformly as possible. An important aspect here is that the design is not only space-filling for the entire parameter space but also for subspaces (e.g., when only one parameter or a subset of parameters is being examined). When this is the case, the design is said to have good projection properties. Another point to consider is that the input parameters of the computer simulation can be of different types such as continuous, discrete or categorical and these need to be handled by a DoE algorithm. The points of a design can be chosen all at once, which is termed a one-shot strategy, such as in Joodaki et al. (2021) where a Latin Hypercube sampling was used. If results of experiments are intended to have an influence on the selection of new design points, a sequential strategy can be applied (Gan and Gu, 2019). (Provost et al., 1999; Crombecq et al., 2009; Draguljić et al., 2012; Pronzato and Müller, 2012).

Metamodels, sometimes also referred to as “surrogate models”, are often used to describe the relationship between the input parameters and simulation outputs of interest. They can be used to find correlations between physical inputs and outputs of a given system. Many different metamodels are available for regression such as LASSO, k-nearest neighbors (k-NN), neural nets, support vector machines (Xia et al., 2018), decision trees, random forest (RF), gradient boosting and Gaussian process regression (GPR). It is usually not known in advance which model will be the best for a specific task so different models have to be tested. To evaluate the performance of a metamodel the available data set is split in training and test data. The model is trained with the training data and the performance is measured on the test data. Usually the split is done by randomizing the data and then using a certain percentage as training and the rest as test data. In an iterative approach, a further split into training and test data can also be used. The results of the last iteration of the sequential design can be used as test data and the rest as training data. Metamodels usually have several input parameters, so called hyperparameters, which have to be chosen by the user. In order to find the best set of hyperparameters cross-validation is generally used. Tuning of the machine learning hyperparameters was shown to be essential to achieve a metamodel with high accuracy (Williams, 2006; Watt et al., 2020; Joodaki et al., 2020).

In previous studies in the context of occupant safety and crashworthiness, the aim was to use a combination of metamodels and design of experiments mainly for optimization tasks. For such problems, different types of metamodels are used ranging from support vector regression (Xia et al., 2018) to even combinations of metamodels (Gan and Gu, 2019; Joodaki et al., 2020). Another approach was proposed in Adam and Untaroiu (2011) and Untaroiu and Adam (2013) where first a classification of pre-crash occupant postures was performed and a genetic algorithm was then used to optimize the restraint system for the different classes. In Perez-Rapela et al. (2020) neural networks in combination with Monte Carlo simulations are used to account for occupant response variability in the assessment of safety systems. An overview of design optimization for structural crashworthiness can be found in Fang et al. (2017). Other studies in the field of vehicle safety have tried to use metamodels for on-board prediction. In Bance et al. (2021) a lumped parameter model together with polynomial chaos expansion uncertainty quantification is used for on-board occupant injury risk prediction. Another example is the prediction of an occupant model’s response to time-varying accelerations for applications inside the vehicle for restraint system control units with a metamodel aiming to work in real-time (Kneifl et al., 2022). For this task, a non-intrusive model order reduction with long short-term memory is used (Kneifl et al., 2022).

In summary, metamodels are trained to predict the response for different combinations of input parameters. The accuracy of the metamodel prediction for specific combinations of input-parameters depends to a great extent on the parameter-space covered by the training dataset and testing is only done within the parameter-space covered by the test dataset. Therefore, an appropriate design of experiments for deriving the test and training datasets plays an essential role.

For the development of restraint systems the parameters are usually varied in a defined scenario catalogue. This scenario catalogue tends to be the load cases tested in regulations or consumer information testing. However, ideally these scenario catalogues should cover a wide range of scenarios to finally design a robust restraint system and not to miss potentially critical scenarios, likely to happen in the field (Perez-Rapela et al., 2020).

Since we cannot apply a full factorial design of experiments due to the high computational costs, a smarter method is needed to select the simulation cases. For safety-relevant simulations, it is important to cover especially the critical areas within our parameter space for the development of metamodels or for optimizing the restraint systems. The question arises in this context, of how we can, with a limited number of simulations, focus on the critical areas of the design space if these are unknown when starting the simulation study. This is particularly challenging, as the criticality is determined by a combination of intrinsic and extrinsic factors as well as the applied safety system (Perez-Rapela et al., 2020).

In our study, we have addressed this question and investigated how to select data points in the parameter space that are most useful for training a metamodel and learning about the restraint system performance. Our aim was to gather the maximum quantity of information relevant for occupant protection from a given number of simulations. An intelligent design of experiments for occupant simulation was developed for this purpose, which aims to automatically select simulations in areas that are difficult to control. To demonstrate the methodology, the effect of different loading directions, anthropometries and seating postures for the design of a generic restraint system and the resulting occupant loads was analysed.

2 Materials and methods

2.1 Data generation

2.1.1 Simulation environment

For development and testing of the methodology, an exemplary simulation study was performed. A finite element simulation model was set up, consisting of a generic seat with belt, a simplified airbag load chain representation (SALCR) and the human body model (HBM) THUMS v4.02. The SALCR includes three foam panels, which are attached to a rigid plate, see Figure 1. The characteristics of the generic airbag can be adjusted by changing the stiffness of the beams connected to the head and thorax panels to simulate different stiffnesses (mass flows). Furthermore, by changing the factor of distribution of stiffness between the two panels different loading paths corresponding to different shapes of airbags are simulated. After a maximal deflection of 300 mm, the stiffness of the beams is increased significantly to simulate a contact of the HBM with the vehicle interior. The femur panel consists of a fabric sheet which enables the support of the SALCR on the HBM thighs. This generic setup was chosen in order to represent the same initial conditions for each simulation run by a seat bounded restraint system. Thereby influences of an eventual deviation in airbag deployment are eliminated and the same initial distance between the HBM and the SALCR is provided. In order to check the plausibility of the effects of the SALCR, a comparison of the forces was made with a simulation model based on the vehicle of the oblique THOR Accord model (downloaded on 11.03.2020), that is equipped with a serial driver and passenger airbag model (Singh et al., 2018). A table with adjusted parameters of the airbag model compared to the downloaded version can be found in the Supplementary Material. Since no steering wheel is present in the simulation setup, the comparison is made with the passenger airbag model of the Honda Accord. The plots for the comparison of the forces can be found in the Supplementary Material. Amplitude and shape are comparable for the belt forces as well as the SALCR/airbag contact forces, but a time shift in force between the serial airbag and the conceptual system used in this study is observed, which is caused by the difference in support and deployment. The ISO 18571 (ISO, 2014) scores for the comparison of belt force and airbag forces can be found in the Supplementary Material. Anyhow, no exact replication of one restraint system was targeted. Instead the aim was to enable easy parameter variation over a wide range. Therefore, the developed conceptual SALCR was found to be an appropriate simplification.

FIGURE 1

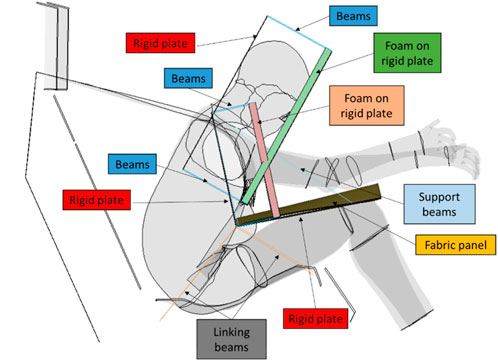
FIGURE 1. Assembly of the simplified airbag load chain representation. Each foam panel contacts only the corresponding body region e.g. head (green), thorax (orange) and femur (yellow). Each panel is connected to a rigid plate (red) via beams (blue). The head and thorax panel are connected to the femur panel via support beams (light blue). The entire construction is connected to the seat structure via linking beams (grey) to keep the generic airbag in place.

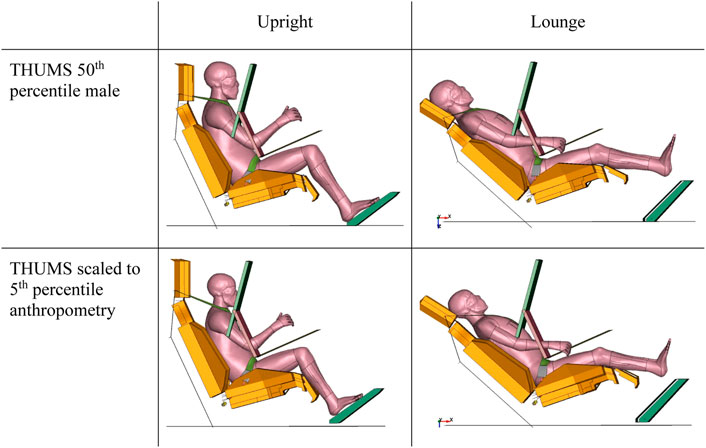
Two different occupant anthropometries were chosen for the investigations. The THUMS v4.02 50th percentile male (AM50) model was utilized as basis. For analysis of anthropometric differences, THUMS was used in its baseline size (height: 1.78 m, mass: 77 kg). Since a consistent THUMS v4.02 model version was not available for the fifth percentile anthropometry, a scaled version of the baseline was used (height: 1.53 m, mass: 46 kg). The model was scaled only, to keep everything else consistent.

An upright and a lounge positioned model were generated for both anthropometries. The upright model equals the available THUMS v4.02 occupant model and the lounge model was generated by positioning the THUMS v4.02 pedestrian model. Figure 2 illustrates the final simulation models. The lounge model basically represents a reclined seating position that allows a relaxed occupant posture. The generic airbag was positioned with the bottom edge aligning with the lap belt. The footrest was transformed to provide adequate foot support for both models in upright position.

FIGURE 2

FIGURE 2. AM50 and AF05 THUMS models in upright and lounge seating position.

2.1.2 Crash pulses

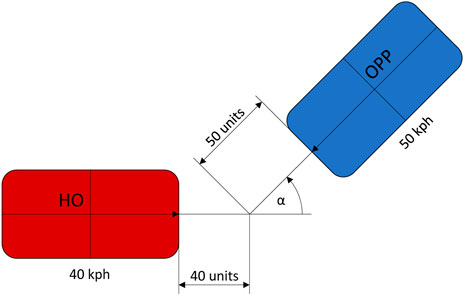
To investigate occupant behaviour for different loading conditions, acceleration-time pulses were generated by finite element simulations (Höschele et al., 2022) with a simulation model based on the vehicle of the oblique THOR Accord model (Singh et al., 2018) (downloaded on 11.03.2020). The description of the crash configuration is based on the “Volvo parametric crash configuration” (Wagström et al., 2019). Table 1 lists the configuration of the simulations by which the four pulses were generated. The values, such as velocity (v), mass (m) and acceleration (acc), of the host vehicle are indicated with HO and the values of the oncoming vehicle or wall encountered are indicated with OPP.

TABLE 1

TABLE 1. Simulation configurations for crash pulse generation.

The full-frontal load case FF56 was generated by a vehicle impact on a rigid wall with 56 km/h. The other pulses were generated by vehicle-to-vehicle impact scenarios with both Honda Accord models of equal mass and vehicle velocities of 40 and 50 km/h respectively. The two oblique impact scenarios Center_m45 and Center_45 were simulated with ±45° impact angle. Figure 3 shows a sketch of the configuration of the Center_45 oblique impact.

FIGURE 3

FIGURE 3. Sketch of the Center_45 oblique impact scenario.

For each simulation, the acceleration was recorded in the centre console of the host vehicle, whereby the accelerations in x- and y-direction as well as the rotational acceleration about the z-axis were output. Plots of the pulses for each axis can be found in the Supplementary Material. These data were used as input for the HBM simulation environment, whereby the acceleration was applied only on the seated HBM model. The load was not applied to the generic airbag model in order to isolate the HBM airbag interaction behaviour and avoid overlaid loadings on the SALCR due to HBM contact and global acceleration.

2.1.3 Simulation and evaluation

The simulation models were parameterised and boundary conditions for the individual parameters were defined. Table 2 summarizes all varied parameters and the corresponding values or thresholds of the baseline occupant simulation model. It contains a combination of categorical and continuous parameters.

TABLE 2

TABLE 2. Parameters to be varied with corresponding values and ranges.

The parameters chosen by the developed DoE method, were automatically inserted in the simulation decks. Simulations were performed on a HPC cluster using LS-Dyna R9.2.1. A single simulation took about 24 h on 80 cores and produced an output of about 5 GB.

The evaluation of the simulation results was conducted with the in-house developed tool “dynasaur”¹ (Klug et al., 2018) from the LS-Dyna binout files. The injury criteria HIC15, Brain 95th percentile strain (Brain 95p), NIC and Rib fracture 1 + risk (Forman et al., 2012) were implemented in the “dynasaur” calculation procedure and evaluated automatically. For the kinematic injury criteria HIC and NIC, accelerometers were positioned in the THUMS model at the head center of gravity, center of C1 and T1 and connected to the bony structure with an interpolation constrained (*CONSTRAINED_INTERPOLATION). Accelerations were filtered with CFC 1000 before further processed. The 95th percentile strain for the brain was calculated from the element time histories. For the rib fracture assessment, the procedure from Forman et al. (2012) and the smoothed risk curve (Larsson et al., 2021) from Forman et al. (2012) for a 45 year old person were applied using the maximum principle strain at the mid-surface per rib to calculate the fracture risk per rib, combined with the probabilistic function to the overall risk of 1 + rib fractures.

2.2 Feedback loop

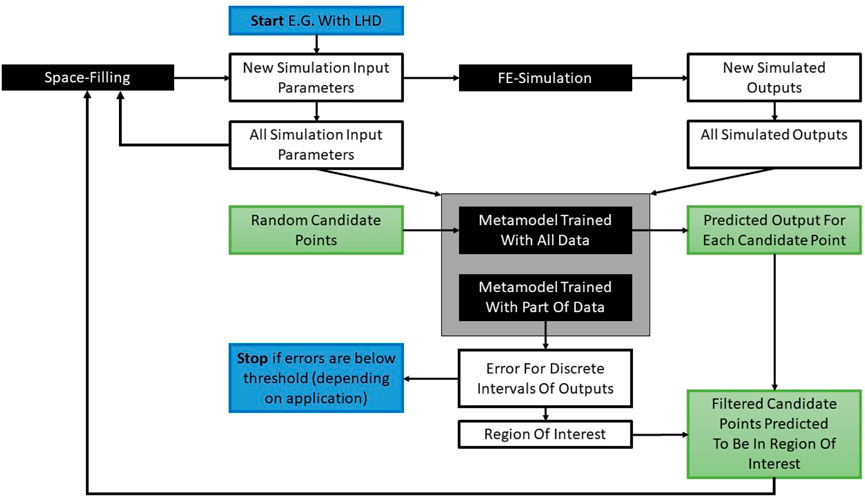
The basic idea of the feedback loop is a combination of a DoE algorithm, which can select a number of points from a set of candidate points, and a metamodel. Any type or combination of metamodels that has good predictive quality can be trained and applied based on the specific problem. Based on the predictions of the metamodel a subset of the set of candidate points is selected. How this subset is chosen can vary, depending on the specific task and goal. This procedure of the feedback loop is illustrated in Figure 4.

FIGURE 4

FIGURE 4. Basic principle of feedback loop combining DoE algorithm and metamodel.

The start and end of the feedback loop are colored blue. The boxes colored black indicate algorithms and boxes related to candidate points are colored green. To start the feedback loop, 64 simulations are selected using a Latin hypercube design (LHD). Finite element simulations are carried out with these input parameters to obtain the simulation results. For further designs, the existing design is augmented with candidate points which are randomly selected points in the design space. The selection of a subset of candidate points is done with the help of metamodels. The goal is to achieve good prediction of the metamodel on the whole parameter space. The following procedure was used:

• For each injury criterion of interest, a metamodel is trained and the performance is measured on the test set.

• The range of predicted values for the whole set (training and testing) is split in ten bins with equal spacing.

• For each of the bins the mean of the absolute error of values from the test set is calculated. However, based on the previous simulations, not all bins contain data points. There can be bins in which there are no predictions for the test set and therefore no error can be calculated. The mean error for such bins is considered zero.

• The bin with the highest mean error is selected as a region of interest.

• The metamodel is retrained with the full data set and predictions are made for the one million candidate points. The subset of these points where the prediction falls into the interval with the highest mean error is used for the augmentation of the design.

• This is done for all the injury criteria of interest.

This method was termed the “highest mean criterion”. A visualization of the steps can be found in the Supplementary Material. From these subsets of candidate points the load cases are selected by a space-filling algorithm. The same number of load cases are selected for each injury criteria (i.e., 8 for iteration 4, which consisted of a total of 32 simulations, considering four injury criteria). The selected parameters are used as input parameters for the simulations of the next iteration.

As space-filling DoE algorithm the MaxPro approach (Joseph et al., 2020) was chosen. It can be seen as an extension to the maximin Latin hypercube design. The maximum projection (MaxPro) criterion ensures that the design is not only space-filling for the entire parameter space but also for subspaces. The MaxPro criterion can also be extended for multiple types of factors. It can create sequential designs and is available as implementation in R.

The selection of a subset of candidate points is done with the help of metamodels. Cross-validation is used for the selection of the metamodel and the hyperparameters of the metamodel. For this the Python machine learning module scikit-learn² (Pedregosa et al., 2011) was used. No scaling of the input parameters was performed since it did not improve the prediction accuracy. Since the k-NN algorithm performed best for the first iterations of data, it was used throughout the study unless stated otherwise.

To show the behaviour of the algorithm using known functions the Styblinski-Tang function as well as Mishra’s bird function (Mishra, 2006) (not constrained) were chosen. These functions are also used in the context of optimization which is not the goal in this work. A Latin hypercube design was used to create the first design. Additional design points were created by augmenting the initial design with candidate points using MaxPro. For the Styblinski-Tang function 32 points were created with LHD and 32 points by augmentation whereas for Mishra’s bird function 16 points were created with LHD and 16 points by augmentation. For the “highest mean criterion” the first design points created by the LHD were used for training a GPR metamodel und the remaining design points were used for testing in the first step. In each iteration 32 new points were created for the Styblinski-Tang function and 16 new points for Mishra’s bird function. For the “highest mean criterion” one-fourth of the points were chosen using the described approach and the remaining points were chosen using the space filling MaxPro algorithm. Choosing the remaining points with MaxPro was done to prevent the “highest mean criterion” from getting stuck in one area. For the MaxPro approach all points in one iteration were created with MaxPro. To compare the two approaches a GPR metamodel was trained using the created design points. The difference of the two functions and the trained metamodels was evaluated on a grid with 1,001 points in x and y direction respectively.

2.3 Sensitivity study

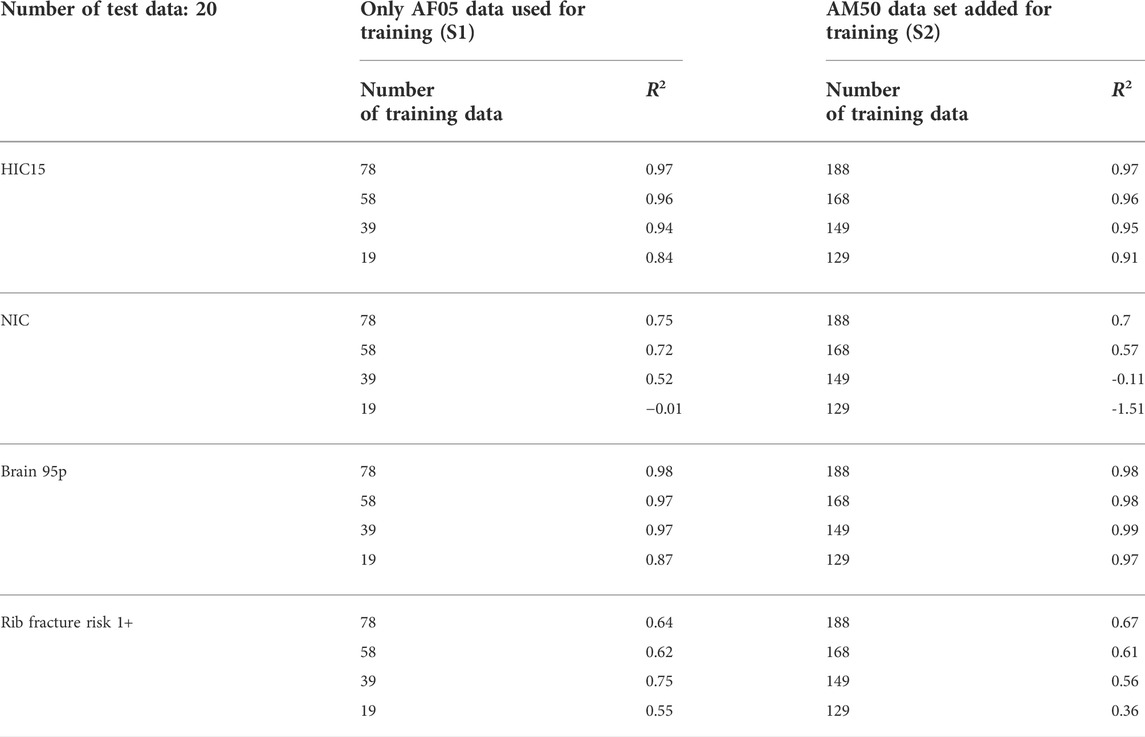
A sensitivity study was performed to investigate if the metamodel is able to learn from the results of different configurations, such as different pulses, anthropometry and seating position. The available data is split into two sets S1 and S2. For the pulses the set S1 comprises all the data with pulse FF56, the second set S2 comprises the rest of the data. For the anthropometry the set S1 comprises the data with the AF05 HBM and for the seating position S1 comprises the data with the HBM in upright position. The first set is randomly split into a set S1_part that contains 80% of the set S1 and a test set S1_test that contains the remaining 20% of the set S1. To investigate different sizes of training data from the set S1, 25%, 50%, 75%, and 100% of the set S1_part are used as training data S1_train. A metamodel is trained, firstly with only the set S1_train and secondly with the union of set S1_train and S2. The test set is both times S1_test. As a metamodel GPR is used since for k-NN the split into the sets is already done inherently.

To quantify the importance of the different input parameters for the metamodel, a score is calculated for each parameter using “permutation feature importance” according to (Breiman, 2001). For this, a trained metamodel with good prediction quality is needed. The values for each feature are permuted one after the other. If the feature is important, the prediction quality decreases. The permutation feature importance is calculated as the prediction score of the metamodel for the original data, minus the prediction score for the permutated data. A mean permutation feature importance can be calculated by repeating the procedure for different permutations. (Breiman, 2001).

3 Results

3.1 Design of experiments

The comparison of the maximum error of the “highest mean criterion” and MaxPro for the Styblinski-Tang function as well as Mishra’s bird function can be seen in Figure 5. For the Styblinski-Tang function the maximum absolute error decreases faster with the exception of the second iteration. After eight iterations the errors for both approaches are approximately the same. The points chosen by the “highest mean criterion” focus on the boundary where there is a steep increase of the Styblinki-Tang function. For Mishra’s bird function again the maximum absolute error decreases faster until the sixth iteration. For the last two iterations the MaxPro approach shows the lower maximum absolute error.

FIGURE 5

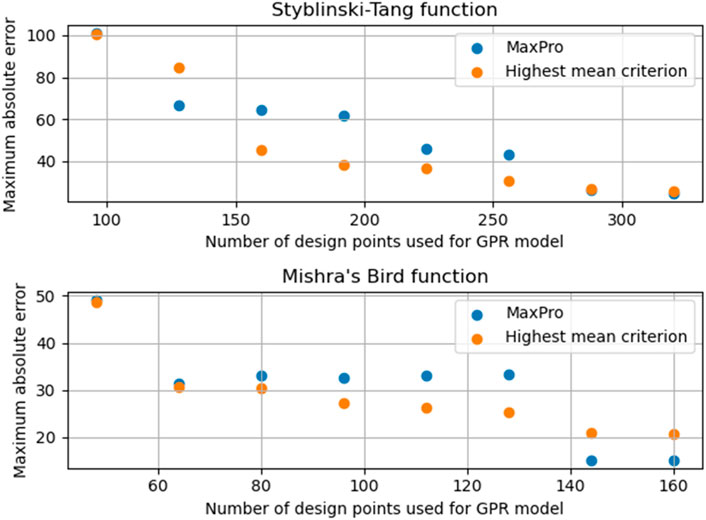
FIGURE 5. Maximum absolute error of the GPR metamodel trainined with the design points created by the MaxPro algorithm and the “highest mean criterion” respectively.

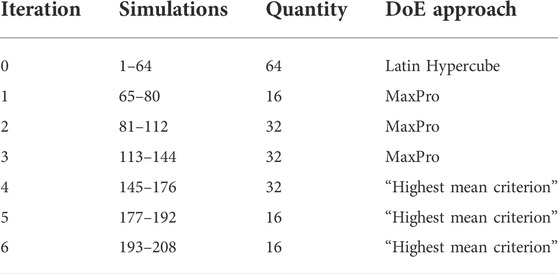
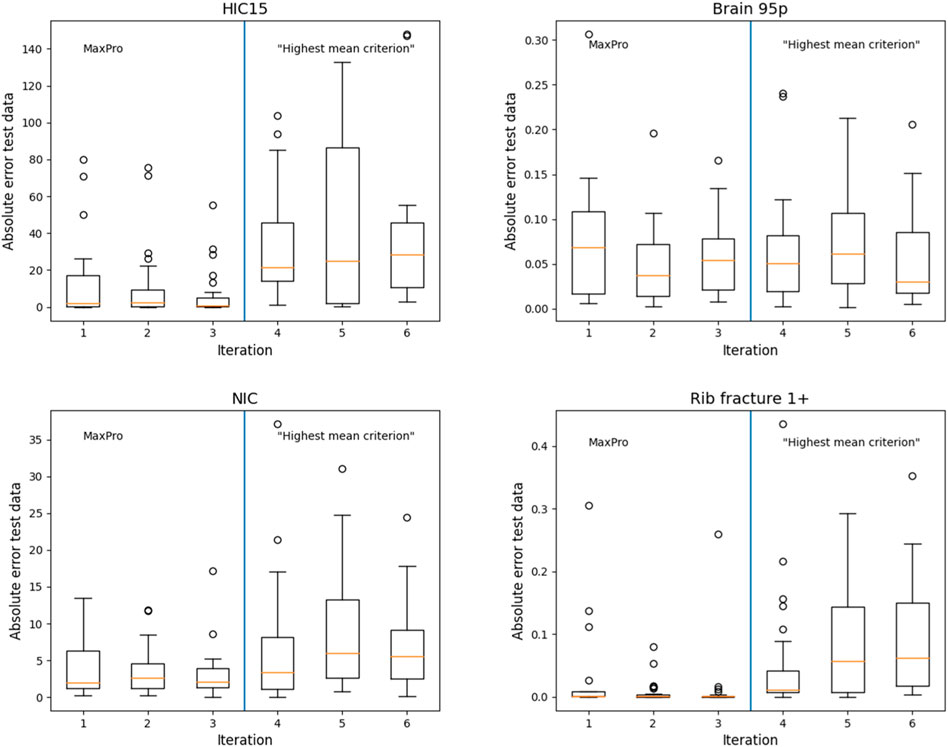
For the finite element simulations the first design was created with Latin Hypercube sampling. Then three iterations were made with no restrictions to the candidate points. Following on from this three iterations were made with the “highest mean criterion”. A summary of all iterations and the applied approach is shown in Table 3.

TABLE 3

TABLE 3. Iterations of simulations with corresponding selection approach.

Figure 6 shows boxplots of the absolute error in the predictions from the test data of the four different injury criteria. The first three iterations are with no restrictions on the set of candidate points, iterations four to six were designed with the “highest mean criterion”. It can be seen that the error increases when switching to the “highest mean criterion” in iteration 4. Only in the case of Brain 95p does it stay roughly the same. This behaviour is intended since the new cases are chosen in areas where the prediction error is highest. The error declines for Brain 95p and NIC in the last iteration but more iterations would be necessary to confirm this trend.

FIGURE 6

FIGURE 6. Boxplots with absolute error of the predictions on the test data for all iterations.

3.2 Prediction quality of the metamodels

The prediction quality of the two metamodels k-NN and GPR is tested with two different splits into training and test data. For the first split the results of the iterations 0 to 5 of the data set are used as training data and the results of iteration six are used as test data. For the second split, the whole data set with all 208 simulations was utilized to also take the data points of the last iteration into account. The k-NN and the GPR metamodels were thus trained with 80% of the randomized whole data set (iteration 0–6). The prediction is then tested on the remaining 20% of the data set. The resulting R² values are summarized in Table 4. Plots with a comparison of simulation results and prediction can be found in the Supplementary Material.

TABLE 4

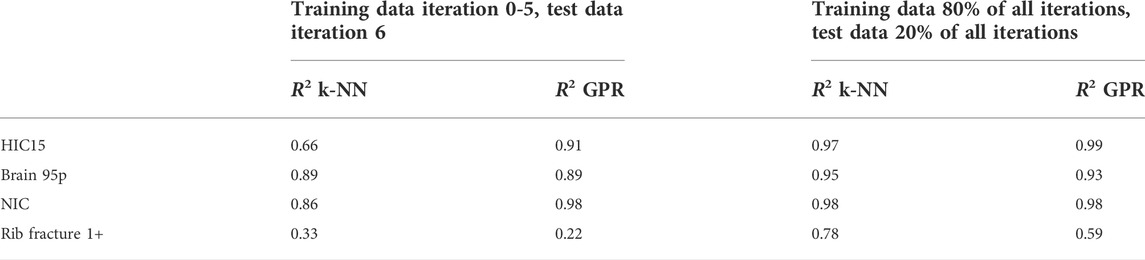
TABLE 4. R² values for predictions with k-NN and GPR metamodels for two different splits into training data and test data.

The predictions for the kinematic-based criteria HIC15 and NIC are very good (R² > 0.9), with the exception of k-NN for the iteration based split. It can be seen, that the prediction is more challenging for strain-based criteria like Brain 95p and especially the rib fracture risk. For HIC15, Brain 95p and NIC GPR shows almost equal or better results compared to k-NN, whereas for Rib fracture 1+ k-NN is more stable. Using 80% of the entire randomized data set as training data increases the accuracy of the metamodels as expected.

3.3 Sensitivity study

One split into two sets S1 and S2 was carried out for the anthropometry. The set S1 comprises all the simulations with the AF05 HBM model and the set S2 comprises the simulations with the AM50 HBM model. The results can be seen in Table 5. As expected, the calculated R² score decreases with a reduced size of the training set. No clear trend emerges for the comparison of the results with and without added data from the set S2. But in most cases adding data from set S2 leads to similar or worse R² values. Similar results can be observed for the split of the data based on pulses and seating position which can be found in the Supplementary Material. This leads to the conclusion that combining simulations with different anthropometries, pulses or seating positions does not help to reduce the necessary number of simulations at least if they are not described by continuous parameters which is the case in this study.

TABLE 5

TABLE 5. Results of sensitivity study for splitting the anthropometry.

To see the influence of the different input parameters on the metamodel the permutation feature importance (Breiman, 2001) for the HIC15 was determined. The GPR metamodel was trained with 80% of the whole data set for this purpose. The permutation feature importance calculation for the test set was repeated ten times, so mean and standard deviation are stated in Table 6. The pulse has the highest feature importance followed by seating position and anthropometry. The feature importance of the parameter stiffness, distribution and belt load limiter are significantly lower.

TABLE 6

TABLE 6. Permutation feature importance for HIC15.

4 Discussion

4.1 Limitations

The focus of this study was the development of a method for a fully automatic design of experiments, enabling to learn as much as possible from a limited number of simulations. The focus was not set on the metamodel and therefore using the metamodel for designing a system, additional simulations would be needed. This becomes evident when looking at the prediction of the rib fracture risk.

The description of the loading scenario was very discontinuous and not described with parameters. In future studies, the pulses should be described in an improved way, using parameters characterising the shape and amplitude. Furthermore, when using more than two anthropometries and more than two seating postures, it might be better to derive a metamodel, which can learn from the different scenarios.

A simplified seat-mounted restraint system was used in order to represent the same initial conditions for each simulation run. Although the comparison with a conventional vehicle shows a similar magnitude and duration of the contact forces, the timing of the applied restraint system is shifted, as it was not deploying. The advantage of the comparable distance is related with a higher distance compared to an airbag which is deploying. Therefore, the results of this study cannot be directly transferred to a real restraint systems.

Two functions were used to show the differences of the proposed “highest mean error” approach and the space-filling MaxPro algorithm. Since the differences depend on the chosen function as well as parameters such as number of design points per iteration a more thorough examination of the proposed algorithm should be conducted in the future. This could lead to a better understanding of the behaviour and to further improvement of the “highest mean error” approach.

The goal of the proposed approach is to achieve good prediction of the metamodel on the whole parameter space and not missing any important regions. The prediction error was increasing for the data from the finite element simulations with our applied procedure. This is an indication that we would have not seen these problems in our metamodel if we would have continued with the space-filling approach. But it is difficult to show that no important regions have been overlooked without being able to simulate every point.

The proposed approach is intended for cases where the number of simulations is limited, e.g., because of limited time or computational resources. If a very large number of simulations can be performed the whole design space could be scanned instead.

4.2 Simulation setup

A parameterised, robust simulation model is needed to train the metamodels. Before starting the parameter variation, the simulation of all extreme load cases should prove the model’s stability. Outliers of simulation results should be always checked manually, as they affect the design of the next iteration. The Human Body Model applied in the current simulations was very robust, but issues in the belt and restraint system interactions (sticky nodes) were observed in single simulations, which required changes of the contact settings such as contact stiffness and search frequency.

It should be checked in advance if the variance in the input parameters leads to significant changes in the results. Originally, it was planned to vary only the angle, but not the collision speed. However, this led to a spread in some of the injury criteria that was too small and therefore did not fulfil the purpose of the study. To achieve a higher range in injury criteria values, the pulse FF56 was added.

4.3 Design of experiments

With the DoE approach of the current study it was not intended to perform a classic optimization approach as in Xia et al. (2018), Gan and Gu (2019) or Joodaki et al. (2021), but to learn as much as possible from a limited number of simulations. Defining the aim of a design of experiments approach is essential. In the concept phase, there was some discussion on whether certain areas of a predicted outcome could be excluded, since the output values were either too high or too low. This was inspired by the approach of Gan and Gu (2019), who developed an algorithm, in which an important region was defined and points that lie within that region were chosen by preference for the next iteration. Ultimately, however, an approach of this kind appeared to be too subjective for our application, since it was found to be difficult to draw a line objectively without running the risk ever and again of missing something essential. Instead of this, the areas of the metamodel with the highest insecurities were defined as the areas, which we should examine more closely as a means of avoiding misleading conclusions. Rooting out the causes of non-stable behaviour is of great importance, especially for safety applications.

On examining the average errors per iteration, it is apparent that the errors in iteration four and five were much higher than those in the previous iterations, but with a decreasing trend for the last iteration. This trend should ideally proceed further. Applying the developed method helps to reveal critical areas. When errors do not increase, even when focusing on those areas with the biggest errors, we were confident that missing important regions would be unlikely.

Metamodels of an entirely acceptable quality within a large parameter space were derived, despite only 208 simulations having been performed. To estimate the number of simulations that would be needed for a full factorial analysis, a discretization of the continuous variable in the current study has to be assumed. A discretization with ten data points each for beam stiffness, distribution of stiffness as well as the belt load limiter would lead to a total of 16,000 simulations for the full parameter space.

4.4 Metamodel

Within the DoE, the metamodel was trained with the k-NN method, although for the final results GPR showed better accuracy. For the first set of iterations, however, k-NN is much more stable and the risk of misleading interpretations is lower. The reason for this might be the small number of data sets at the beginning together with the aforementioned inability to learn from different configurations. For the first training data set with 64 simulations, only eight simulations are with the same pulse, anthropometry and seating position. In the future also combinations of different metamodels could be tested.

Surprisingly the prediction of the metamodel did not seem to improve with data from other configurations. This might be caused by non-continuous and too different configurations. Training the metamodel and performing the DoE for each configuration separately meant that a significantly greater number of simulations would needed. Anthropometry, posture and pulse should be varied in the future more continuous to achieve better learning effects in between the scenarios.

Metamodels were trained to predict four different injury criteria, which were each of a different type. The highest prediction accuracy was achieved for the kinematics-based criteria HIC and NIC, which are mainly applied for dummies and have limited meaningfulness for HBMs. The prediction of the strain-based criteria seemed to be more challenging for the metamodel. The most complex injury criteria applied in this study, the probabilistic rib fracture risk assessment, was the most difficult to predict. To calculate the probabilistic rib fracture risk assessment, the maximum strain of each rib is derived and used as input for the risk calculation per rib which is finally combined to an overall rib fracture risk using a binomial function. In contrast to the brain 95th percentile strain, more complexity layers are thus added, which the metamodel must learn. In future an attempt could be made to predict the strains within the individual rib using metamodels and then to perform the remaining evaluation steps manually.

Ultimately, of course more data is always better. The level of needed accuracy of the metamodel strongly depends on where it should be applied. The metamodel developed in this study can be used to distinguish between critical and non-critical areas for the generic restraint system that was used and prioritize input-parameters for future studies.

5 Conclusion

A DoE approach has been established focusing on those metamodel areas, which are more difficult to predict than others. An approach of this kind is recommended for safety-relevant problems with expensive generation of training data. Instead of optimizing the restraint system to run more and more simulations in “non-critical” areas, the developed algorithm specifically focuses on the more challenging areas to avoid misjudgement in these for the metamodel. This can help engineers to reveal the most critical areas, which should be prioritized to improve the robustness of the study using the individually feasible number of simulations that can be generated as effectively as possible.

Further research is needed in order to also be able to predict more complex injury criteria and further understand the learning effects from the categorical parameters describing the scenarios, such as anthropometry and posture.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

BS carried out the data analysis. BS and CK performed the manuscript preparation. DK designed and carried out the simulations. CK supervised the data analysis and the method development. GD, HF, and MW provided comments, feedback, and edited the manuscript. All authors contributed in continuous discussion on the method, read and approved the final manuscript.

Funding

Open access funding provided by Graz University of Technology Open Access Publishing Fund.

Acknowledgments

The authors would like to acknowledge the use of high-performance computing resources provided by the IT Services (ZID) of Graz University of Technology. We would also like to thank the Toyota Motor Corporation and Toyota Central R&D Labs for providing the academic license of the THUMS v4.02 AM50 occupant model.

Conflict of interest

The authors GD, HF, and MW are employed by Robert Bosch GmbH.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The study was part of the DoSim project that has been funded by the Robert Bosch GmbH within the Mercedes/Bosch Tech Center i-protect. The funder had the following involvement in the study: Problem formulation and discussion of results.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffutr.2022.913852/full#supplementary-material

Footnotes

¹https://gitlab.com/VSI-TUGraz/Dynasaur.

²https://scikit-learn.org/stable/.

References

Adam, T., and Untaroiu, C. D. (2011). Identification of occupant posture using a Bayesian classification methodology to reduce the risk of injury in a collision. Transp. Res. Part C Emerg. Technol. 19, 1078–1094. doi:10.1016/j.trc.2011.06.006

CrossRef Full Text | Google Scholar

Bance, I., Yang, S., Zhou, Q., Li, S., and Nie, B. (2021). A framework for rapid on-board deterministic estimation of occupant injury risk in motor vehicle crashes with quantitative uncertainty evaluation. Sci. China Technol. Sci. 64, 521–534. doi:10.1007/s11431-019-1565-9

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi:10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Crombecq, K., Couckuyt, I., Gorissen, D., and Dhaene, T. (2009). “Space-filling sequential design strategies for adaptive surrogate modelling,” in Proceedings of the first international conference on soft computing Technology in civil, structural and environmental engineering. Editors B. Topping, and Y. Tsompanakis (UK: Civil-Comp Press Stirlingshire).

Google Scholar

Draguljić, D., Santner, T. J., and Dean, A. M. (2012). Noncollapsing space-filling designs for bounded nonrectangular regions. Technometrics 54, 169–178. doi:10.1080/00401706.2012.676951

CrossRef Full Text | Google Scholar

Fang, J., Sun, G., Qiu, N., Kim, N. H., and Li, Q. (2017). On design optimization for structural crashworthiness and its state of the art. Struct. Multidiscipl. Optim. 55, 1091–1119. doi:10.1007/s00158-016-1579-y

CrossRef Full Text | Google Scholar

Forman, J. L., Kent, R. W., Mroz, K., Pipkorn, B., Bostrom, O., and Segui-Gomez, M. (2012). Predicting rib fracture risk with whole-body finite element models: Development and preliminary evaluation of a probabilistic analytical framework. Ann. Adv. Automot. Med. 56, 109–124.

PubMed Abstract | Google Scholar

Freienstein, H., Kolatschek, J., and D‘Addetta, G. A. (2019). Sicherheit zukünftiger hochautomatischer Fahrzeuge im Mischverkehr – anforderungen, Lösungskonzepte und Potenzialabschätzungen. VDI-Tagung Fahrzeugsicherheit, Düsseldorf, Germany 12.

Google Scholar

Gan, N., and Gu, J. (2019). Hybrid meta-model-based design space exploration method for expensive problems. Struct. Multidiscipl. Optim. 59, 907–917. doi:10.1007/s00158-018-2109-x

CrossRef Full Text | Google Scholar

Höschele, P., Smit, S., Tomasch, E., Östling, M., Mroz, K., and Klug, C. (2022). Generic crash pulses representing future accident scenarios of highly automated vehicles. SAE Int. J. Trans. Saf. 10, 1–26. doi:10.4271/09-10-02-0010

CrossRef Full Text | Google Scholar

ISO (2014). Road vehicles - objective rating metric for non-ambiguous signals ISO/TS 18571:2014(E). Geneva, Switzerland: ISO (Accessed January 29, 2020).

Google Scholar

Joodaki, H., Gepner, B., and Kerrigan, J. (2020). Leveraging machine learning for predicting human body model response in restraint design simulations. Comput. Methods Biomech. Biomed. Engin. 24, 597–611. doi:10.1080/10255842.2020.1841754

PubMed Abstract | CrossRef Full Text | Google Scholar

Joodaki, H., Gepner, B., Lee, S.-H., Katagiri, M., Kim, T., and Kerrigan, J. (2021). Is optimized restraint system for an occupant with obesity different than that for a normal BMI occupant? Traffic Inj. Prev. 22, 623–628. doi:10.1080/15389588.2021.1965131

PubMed Abstract | CrossRef Full Text | Google Scholar

Joseph, V. R., Gul, E., and Ba, S. (2020). Designing computer experiments with multiple types of factors: The MaxPro approach. J. Qual. Technol. 52, 343–354. doi:10.1080/00224065.2019.1611351

CrossRef Full Text | Google Scholar

Klug, C., Luttenberger, P., Schachner, M., Micorek, J., Greimel, R., and Sinz, W. (2018). “Postprocessing of human body model results – introduction of the open source tool DYNASAUR,” in Proceedings of the 7th international symposium: Human Modeling and Simulation in automotive engineering (CARHS). Berlin, Germany: CARHS.

Google Scholar

Kneifl, J., Hay, J., and Fehr, J. (2022). Real-time Human Response Prediction Using a Non-intrusive Data-driven Model Reduction Scheme. IFAC-PapersOnLine 55, 283–288. doi:10.1016/j.ifacol.2022.09.109

CrossRef Full Text | Google Scholar

Larsson, K.-J., Blennow, A., Iraeus, J., Pipkorn, B., and Lubbe, N. (2021). Rib cortical bone fracture risk as a function of age and rib strain: Updated injury prediction using finite element human body models. Front. Bioeng. Biotechnol. 9, 677768. doi:10.3389/fbioe.2021.677768

PubMed Abstract | CrossRef Full Text | Google Scholar

Luttenberger, P., Feist, F., Kofler, D., Sinz, W., D‘Addetta, G. A., Freienstein, H., et al. (2020). “Assessment of future occupant restraint principles in autonomous vehicles,” in 2020 IRCOBI Conference Proceedings, Farmington Hills, Michigan, USA: International Research Council on the Biomechanics of Injury IRCOBI 431–455.

Google Scholar

Mishra, S. K. (2006). Some new test functions for global optimization and performance of repulsive particle swarm method. SSRN J, 24. doi:10.2139/ssrn.926132

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830.

Google Scholar

Perez-Rapela, D., Forman, J. L., Huddleston, S. H., and Crandall, J. R. (2020). Methodology for vehicle safety development and assessment accounting for occupant response variability to human and non-human factors. Comput. Methods Biomech. Biomed. Engin. 19, 384–399. doi:10.1080/10255842.2020.1830380

CrossRef Full Text | Google Scholar

Poulard, D., Lin, H., and Panzer, M. B. (2020). Occupant safety in vehicles equipped with automated driving systems, Part 3: Biofidelity evaluation of GHBMC M50-OS against laboratory sled tests. Report No. DOT HS 812 905. National Highway Traffic Safety Administration Washington, D.C., USA.

Google Scholar

Pronzato, L., and Müller, W. G. (2012). Design of computer experiments: Space filling and beyond. Stat. Comput. 22, 681–701. doi:10.1007/s11222-011-9242-3

CrossRef Full Text | Google Scholar

Provost, F., Jensen, D., and Oates, T. (1999). “Efficient progressive sampling”. In Proceedings of the fifth ACM SIGKDD international conference on knowledge discovery and data mining. Editor U. Fayyad (New York, NY, USA: ACM)), 23–32.

CrossRef Full Text | Google Scholar

Singh, H., Ganesan, V., Davies, J., Paramasuwom, M., and Lorenz, G. (2018). Vehicle interior and restraints modeling development of full vehicle finite element model including vehicle interior and occupant restraints systems for occupant safety analysis using THOR dummies. Washington, DC, USA: NHTSA. Report No. DOT HS 812 545.

Google Scholar

Untaroiu, C. D., and Adam, T. J. (2013). Performance-based classification of occupant posture to reduce the risk of injury in a collision. IEEE Trans. Intell. Transp. Syst. 14, 565–573. doi:10.1109/TITS.2012.2223687

CrossRef Full Text | Google Scholar

Wagström, L., Leledakis, A., Östh, J., Lindman, M., and Jakobsson, L. (2019). “Integrated safety: Establishing links for a comprehensive virtual tool chain,” in Proceedings of the 26th ESV conference proceedings. (Washington, DC, USA: NHTSA).

Google Scholar

Watt, J., Borhani, R., and Katsaggelos, A. K. (2020). Machine learning refined: Foundations, algorithms, and applications. New York, NY, USA: Cambridge University Press.

Google Scholar

Williams, C. K. I. (2006). Gaussian processes for machine learning. The MIT Press.Cambridge, MA, USA.

Google Scholar

Xia, L., Liu, W., Lv, X., and Gu, X. (2018). A system methodology for optimization design of the structural crashworthiness of a vehicle subjected to a high-speed frontal crash. Eng. Optim. 50, 634–650. doi:10.1080/0305215X.2017.1334774

CrossRef Full Text | Google Scholar