A Bayesian network model to disentangle the effects of stand and climate factors on tree mortality of Chinese fir plantations

Tree mortality is a complex process that not only be affected by the various factors, such as stand and climate factors, but also the various long-term effects of the factors to each other. In this study, based on the long-term spacing trials of Chinese fir in four regions of southern China, a Bayesian network was used to model tree mortality in response to stand and climate factors, as well as comparing this approach with logistic regression and random forest method. The results showed that the Bayesian network method had the highest accuracy in predicting tree mortality. In addition, the Bayesian network approach could find the dependency in the relationship between data and provide a theoretical framework for modeling uncertainty by using probabilistic calculus and underlying graph structure. Sensitivity analysis showed relative diameter was the most important factor, and temperature was the most important climate factor. Furthermore, climate factors not only directly affected tree mortality, but also indirectly affected tree mortality through affecting relative diameter, stand density and Gini coefficient. We also found that stand competition, structural heterogeneity and age affected tree mortality under climate change, and a moderate level of competition condition and stand structure heterogeneity weakened the negative impact of climate factors on tree mortality. Old trees were more sensitive to climate change than young trees, especially under extreme climate conditions. Besides, we found that tree mortality was negatively correlated with moderate annual precipitation, winter mean minimum temperature, and stand structure (Gini), and low age, but positively correlated with low relative diameter, high density and age. The results will provide adaptive options for effective forest management of Chinese fir plantations under the backdrop of global climate change in the future.

1. Introduction

Tree mortality refers to the process in which the vitality of trees gradually weakens and eventually dies under the combined effects of environmental interference and genetic characteristics (Lee, 1971), which in turn affects resource availability, tree regeneration, stand structure, and stand productivity (Franklin et al., 1987). In the dynamic process of stand development, there are many causes of tree death (Craine and Dybzinski, 2013). Exploring the causes of tree mortality can help us understand stand dynamics and is important for sustainable forest management (Wang et al., 2012; Kweon and Comeau, 2019). Except for a few external factors (such as fires, flash floods, etc.) that can cause trees to die in a short period of time, in most cases, the death of trees is related to the reduction growth productivity; that is, the gradual death of trees is due to their inability to cope with adverse conditions, such as drought, competition and other factors (Camac et al., 2018). Due to the variability and randomness of catastrophic events, the research on the model of tree mortality mainly focuses on endogenous stand characteristics (Crecente-Campo et al., 2009; Zhang et al., 2017).

Stand and climate factors are the main driving factors determining the spatiotemporal patterns of tree mortality (Copenhaver-Parry and Cannon, 2016; Devi et al., 2020); thus, the factors affecting tree mortality are divided into internal factors and external factors correspondingly. Among the stand factors, competition is generally considered to be the most important factor affecting tree growth and death (Ruiz-Benito et al., 2013), and is an important force to promote the dynamic change and succession of stands (Franklin et al., 1987). Due to the different maturity periods of trees, competition for nutrients such as light, water, and nutrients in the forest between large and small trees leads to the gradual death of trees with weaker competitiveness (Zhang et al., 2017). Negrón and Wilson (2003) found a strong relationship between mortality and tree density index, with an increase in mortality in denser stands, which is related to competition among trees. Kweon and Comeau (2019) found that under warmer conditions, competition variables have a stronger impact on tree mortality, and the degree of impact varies among different ages. Zhang et al. (2015a) found that competition, rather than climate, was the main factor leading to tree death in the northern forests of western Canada.

Stand structure (Gini) is the other factor which plays an important role in predicting future growth and death of forests (Cortini et al., 2017; Kweon and Comeau, 2019), and is strongly influenced by a number of factors, which can help in tree mortality modeling and detecting the main drivers of tree mortality (Crecente-Campo et al., 2009). In the process of forest succession, stand structure affects the dynamics of competition by regulating the intensity of competition between trees and their availability of resources, leading to differences in competition intensity and resource use efficiency, ultimately leading to tree death (Luo and Chen, 2013; Forrester, 2019). The other related stand factors including age and site condition can also affect tree mortality (Bennett et al., 2015; Zhang et al., 2015a).

In addition to stand factors, the external factors (hereafter, we refer primarily as climate factors) also have impacts on tree mortality (van Mantgem et al., 2009). Severe droughts, combined with unusually warm temperatures, were thought to be significant drivers of tree death (Jentsch et al., 2007). van Mantgem et al. (2009) studied the causes of death of unmanaged old-growth forest in the western United States and found that the increase in mortality may indicate significant changes in forest structure, composition and function, and regional warming may be the main factor leading to the increase in tree mortality. Allen et al. (2010) found that mortality has increased in some regions as a result of global climate change, due to a combination of higher temperatures and drought.

Extreme droughts caused by higher temperature accompanying climate change have been the main cause of widespread tree death in the southwestern United States in the past decade (Floyd et al., 2009). Furthermore, severe droughts can lead to significant forest death, regardless of tree density (Allen et al., 2010). Gitlin et al. (2006) found tree mortality had a spatially heterogeneous pattern, and drought related climate change can lead to high tree mortality rates along altitudinal gradients. Under drought conditions, rising temperatures not only increases the background rate of tree death, but also increases the physiological pressure related to drought (Trumbore et al., 2015), which affects individual tree resilience and leads to more frequent and widespread death (McDowell et al., 2008; Adams et al., 2009). Luo and Chen (2013) found that climate change led to an increase in mortality, and the increase in the mortality of young forests was significantly higher than that of old forests, possibly because young forests were more sensitive to regional warming and drought (McDowell et al., 2008; Teskey et al., 2014).

Stand and climate factors do not act independently on tree death, but interact with each other (Calama et al., 2019). In recent years, some studies have used different methods to model tree mortality. The main forms of the model are the Weibull distribution function, logistic regression (Yao et al., 2001; Yang et al., 2003; Qiu et al., 2015), and Bayesian model averaging (Lu et al., 2019). Studies mainly focused on the simple linear relationship between the factors affecting mortality, while ignoring the uncertainty in the relationship between factors. However, tree mortality is a complex process that not only needs to consider the impact of various factors on tree mortality, but also consider the uncertainty and linkage of the various long-term interactive effects of the factors (Sevinc et al., 2020).

Bayesian network (BN) and random forest (RF) are both machine learning (ML) models that can learn from input variables. RF models use algorithms to learn and generate predictions directly from data. As a discriminative model, RF models do not assume conditional independence between variables and have a direct mapping from observation to prediction (Wang et al., 2021). BN is a useful technique which utilizes probability calculus together with an underlying graphical structure to provide a theoretical framework for modeling uncertainty (Holmes and Jain, 2008). It expresses conditions and results as probabilities, especially for describing errors of true absence and false absence, which makes BN applicable in risk analysis and management (Fenton and Neil, 2012). In addition, BN can be constructed from a combination of empirical data and prior knowledge (Uusitalo et al., 2005) and can be updated with new information (Pawson et al., 2017). Further, it is reported that given the many interdependencies between variables, BN is better suited to capture the complexity of the underlying decision-making process (Fenton and Neil, 2012). According to the advantages of systematic estimation of occurrence path, causality and probability (Lee et al., 2020), BN has been widely used for effective multi-risk assessment and prediction in different fields, such as clinical medicine (Gevaert et al., 2006; Ducher et al., 2013; Witteveen et al., 2018), transportation (Gret-Regamey and Straub, 2006), education (García et al., 2007; Culbertson, 2016), ecology (Marcot et al., 2001), etc. Although there are some reports on the applications of BN in forestry, especially for forest fire predictions (Dlamini, 2011; Penman et al., 2011; Sevinc et al., 2020), the applications of BN in tree mortality are relatively rare.

Chinese fir [Cunninghamia lanceolata (Lamb.) Hook] is an important fast-growing tree species in China. According to the 9th National Forest Resources Inventory, the area of Chinese fir plantations has reached 10 million hectares, occupying 27.23% of the total plantation area (Zhang et al., 2019). Effective management of this widely distributed tree species needs an accurate understanding of the complex mechanisms of tree mortality. The objectives of this study were to: (1) model tree mortality in relation to stand and climate factors using Bayesian network, random forest and logistic regression methods and find out which method is better; (2) disentangle the effects of stand and climate factors on tree mortality; (3) analyze changes in tree mortality with different climate conditions under a given stand level.

2. Materials and methods

2.1. Study sites and data

The data for this study were obtained from Chinese fir plantations situated in four provinces in southern China. For Jiangxi, the experimental forest was established in 1981, while the remaining three provinces (Fujian, Guangxi, and Sichuan) were all established in 1982. In terms of climate conditions, Fujian, Jiangxi, and Sichuan belong to subtropical climate, while Guangxi belongs to a subtropical climate. The soils in the study areas of Fujian, Guangxi, and Sichuan provinces are mainly red soil developed on parent materials such as granite, while the soils in the study areas of Jiangxi are mainly yellow-brown soil developed on sand shale.

The experiment in each province consisted of five initial planting densities: a density level with a row spacing of 2 × 3 m, 1,667 trees/ha, B density level with a row spacing of 2 × 1.5 m, 3,333 trees/ha, C density level with a row spacing of 2 × 1 m, 5,000 trees/ha, and D density level with a row spacing of 1 × 1.5 m, 6,667 trees/ha, and E density level with a row spacing of 1 × 1 m, 10,000 trees/ha. Each density experiment was repeated three times in each province and the size of each sample plot is 20 m × 30 m. In addition, two rows of trees were set around each plot as a buffer zone to eliminate interference. Plot measurements were all conducted in winter. In Fujian, plot measurements were conducted annually from 1985 to 1990, and every 2 years from 1990 to 2010; in Jiangxi, plot measurements were conducted annually from 1985 to 1989, and every 2 years from 1989 to 2007; in Sichuan, plot measurements were conducted annually from 1985 to 1995, and every 2–3 years from 1995 to 2012; in Guangxi, plot measurements were conducted annually from 1990 to 1995, and every 2 years from 1995 to 2012. In plots, trees above 1.3 m tall were marked and their corresponding diameter at breast height (DBH) were measured. In addition, 50 trees were randomly selected from each plot to measure tree height (H), and the average height of the six tallest trees in a plot was calculated as the stand dominant height (Hd).

2.2. Stand variables

The stand variables that affect tree mortality can be divided into four categories: stand age, competition, site conditions, and stand structure. A total of six stand variables were used in this study, and competition can be represented by stand basal area (BA), number of trees per hectare (N), and relative diameter (RD). The site conditions can be reflected by the stand dominant height (Hd). In terms of stand structure, Gini coefficient was selected to measure the heterogeneity of stand structure. Gini coefficient is a measure of inequality derived from the Lorentz curve (0 ~ 1) and calculated from the DBH of trees in a stand. The closer the value is to 0, the more uniform the stand size. Gini coefficient can be calculated using the software package “ineq” in R (Zeileis, 2014), and the formula is listed as follows:

$\text{Gini}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{j}=1}^{\mathrm{n}}\left|{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{j}}\right|}{2{\mathrm{n}}^2\overline{\mathrm{x}}}$

where n is the number of trees in a sample plot, |x_i -x_j| is the absolute value of the diameter difference between any two trees, and $\overline{x}$ represents the average value of diameter x. The statistics of stand factors are shown in Table 1.

TABLE 1

Table 1. Summary statistics of stand variables by province.

2.3. Climate variables

In order to explore the influence of climate factors on tree mortality of Chinese fir, ClimateAP was used to obtain the climate data of the plots (Wang et al., 2012). The principle of the spatial interpolation is to estimate the climate based on latitude, longitude and elevation of a location. In this study, 10 climate factors, including mean annual temperature (MAT), annual precipitation (AP), annual heat-moisture (AHM), mean warmest month temperature (MWMT), mean coldest month temperature (MCMT), summer mean maximum temperature (SMMT), winter mean minimum temperature (WMMT), and summer mean temperature (SMT), degree-days below 0°C (DD0), degree-days above 5°C (DD5), were selected as candidate variables for model development. The statistics of climate factors are shown in Table 2. Changes in MAT and AP against year are shown in Figure 1.

TABLE 2

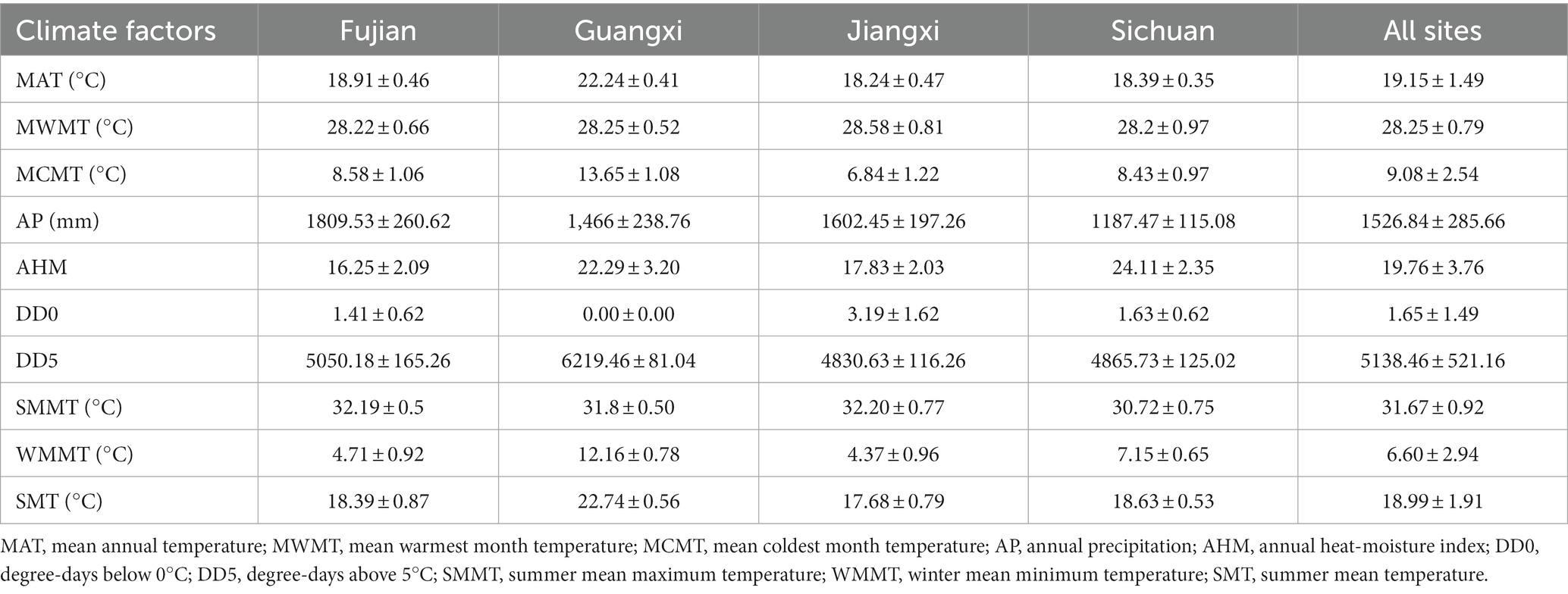
Table 2. Mean values ± standard deviations of 10 climate factors for each provincial site location and an average across all sites.

FIGURE 1

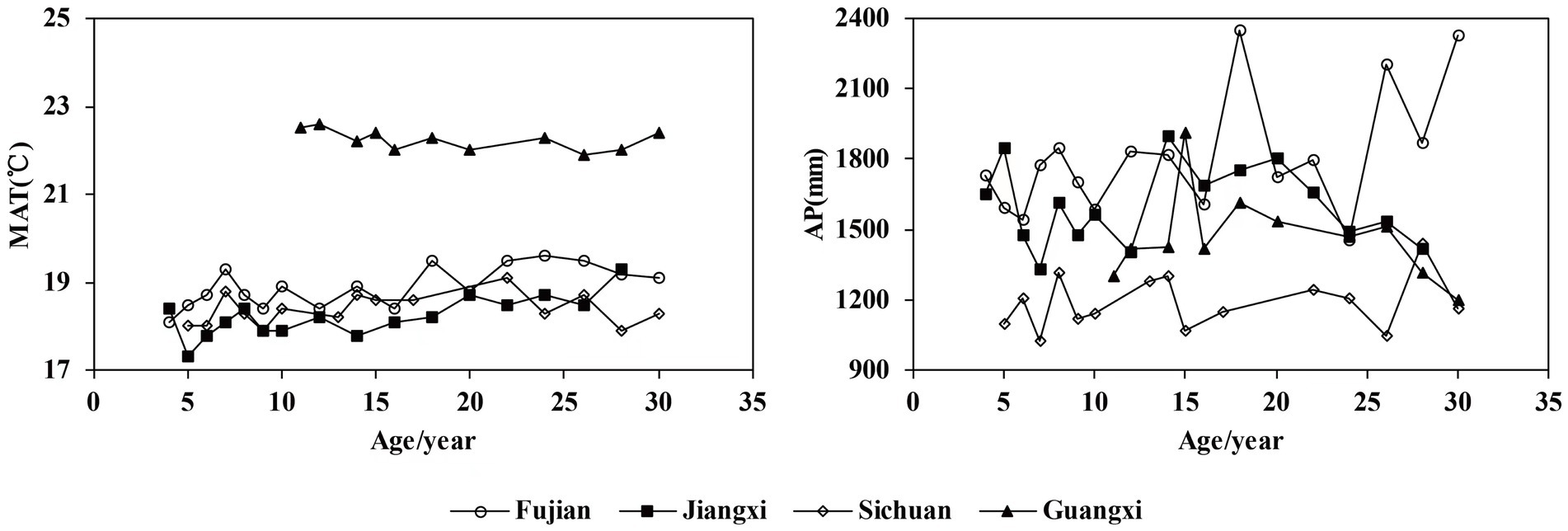
Figure 1. Trends in annual mean temperature (MAT) and precipitation (AP) in relation to age for each site.

2.4. Variable selection

The variance inflation factor (VIF) was used to test the collinearity of the variables. According to the general rule of thumb, there is no collinearity among the variables with VIF test result less than 5, so only the variables with VIF test result less than 5 are retained in this study for model construction development and subsequent analysis. It noted that while independent variables may be discrete or continuous, continuous variables are also divided into discrete ranges for computational reasons when performing the analysis (Nash et al., 2013). In this study, in order to analyze the impact of variables on mortality in high detail, the variables were divided into three groups (Table 3): the low level is the bottom 20% of the value size, the middle level is 20–80%, and the high level is the top 20%.

TABLE 3

Table 3. The three groups of different stand and climate variables.

2.5. Model development

2.5.1. Logistic equation

Tree mortality is a binary classification data set, and the commonly used method for developing a tree mortality model is the logistic equation (Zhang et al., 2017). The model form is as follows:

$P_S={\left\{1+\exp \left[-\left({\alpha }_1+\beta X\right)\right]\right\}}^{-q}$

where Ps is the probability of tree survival, and X is a series of independent variables selected for this study, including stand age, stand dominant height, competition intensity, stand structure, and climate factors. ${\alpha }_1$ is the intercept of the model, β is the parameter vector containing the intercept, and q is the year between two measurements.

2.5.2. Bayesian network

Bayesian network (BN), also known as belief network, is a graphical model that solves problems of uncertain causal relationships in complex systems based on probabilistic graphs (Pearl, 1986). It utilizes existing datasets, process models, and expert knowledge (Penman et al., 2011), integrating qualitative analysis and quantitative research methods, utilizing prior knowledge and objective evidence for effective reasoning, and can uniformly describe multiple causal relationships (Holmes and Jain, 2008).

BN can not only explore the impacts of different variables on tree mortality, but also discover the interrelationship between different variables (Lee et al., 2020). BN model uses boxes to represent the relationship between variables, and arrows to describe the direction of influence (Penman et al., 2011). Among two nodes connected to each, we called the node before the edge as parent node, and called the directed node as child node. The probabilistic relationship between nodes is determined by the following equation:

${\theta }_{X_i|{\pi }_i}=P_{\alpha }\left(X_i|{\pi }_i\right)$

where X represents each variable, and parameter α quantitatively describes this dependency. Assuming that the parent node set of variable X_i in a directed acyclic graph is π_i, then α contains the conditional probability of each variable. P_α represents the specific interdependency values of the target attribute and other variables.

In order to implement the BN approach and disentangle the drivers of tree mortality, we used the Netica modeling environment (Netica, 2019). By selecting the target node in Netica, the degree of influence of other nodes can be sequentially exported. A BN model can be interpreted using what is referred to as The Most Probable Explanation (MPE) (Kwisthout, 2011). The basis of MPE is that it can find the combination of multiple causes (node states) that may lead to a certain result from the combination of multiple causes (node states), and the combination with the greatest possibility is the most possible explanation. The most likely combination of causes can be found through the MPE function available in Netica.

For quantifying the influence of each variable on tree mortality, sensitivity analysis was conducted: this involves the analysis of the influence and degree of multiple reasons (node state) on the result (target node) (Frayer et al., 2014). A BN model can evaluate the sensitivity of the response variable to the probability distribution of other variables (Marcot, 2012). Mutual information refers to the direct or indirect information flow rate, which can indicate whether two nodes are interdependent or not, and measure the degree of dependence between nodes (Zou and Yue, 2017). It not only helps to further verify the validity of the model, but also reveals the most influential and informative variables relative to the target variables of interest (Sun and Müller, 2013). The following formula is used to calculate model sensitivity in Netica:

$I=H\left(Q\right)-H\left(Q|F\right)={\mathrm{\Sigma }}_q{\mathrm{\Sigma }}_f\frac{P\left(q,f\right){\log }_2\left[P\left(q,f\right)\right]}{P\left(q\right)P\left(f\right)}$

where H (Q) is the entropy of Q before any new findings and H (Q|F) is the entropy of Q after new findings from node F. The calculations of model sensitivity were done according to Marcot et al. (2006).

2.5.3. Random forest

Random forest (RF) model is a highly flexible machine learning algorithm based on Bagging integrated learning model. It can generate multiple prediction models and summarize the results of the models to improve the classification accuracy at the same time. Random forest can help prevent overfitting by analyzing large nonparametric data sets with high multicollinearity and nonlinear relationships and creating decision trees by randomly selecting training data to vote out the optimal final model over multiple iterations (Shanley et al., 2021).

In terms of model tuning, RF has two main parameters: mtry (the number of randomly selected split prediction variables at each split) and ntree (the number of decision trees in the random forest) (Zhao et al., 2019). The default value of mtry is usually one-third of all predicted variables, and we set ntree equals 1,000 as a replacement, and set other parameters to default values. The RF model was implemented with the “randomForest” package in the R software (Breiman, 2001).

2.6. Model evaluation

Receiver Operating Characteristic (ROC) curve is a widely accepted indicator used to evaluate the predictive performance of binary models (Kweon and Comeau, 2019). AUC refers to the area under the ROC curve, and the score of AUC ranges from 0 to 1. If a model has a larger AUC value, it indicates that the model is more suitable for data. The widely accepted evaluation rule for an AUC value is: 0.9–1 is excellent, indicating that there can be a good distinction between tree survival and mortality; 0.8–0.9 is good; 0.7–0.8 is average; 0.6–0.7 is poor; 0.5–0.6 is very poor (Zhang et al., 2011).

3. Results

In the study, we used the VIF test to remove the collinear variables and retained 7 non-collinear variables (VIF < 5), including stand age, stand density (N), relative diameter (RD), stand structure (Gini), and climate factors including annual precipitation (AP), winter mean minimum temperature (WMMT), and mean annual temperature (MAT) (Table 3).

3.1. Comparison of the three methods

Based on the 7 variables that passed the VIF test, the three models were constructed to fit the relationship between tree mortality and stand and climate factors. The AUC value of Bayesian network model was 0.9997, and that of random forest model and Logistic regression was 0.9273 and 0.8844, respectively (Table 4), indicating that the three models can effectively fit tree mortality, but Bayesian network model performed the best.

TABLE 4

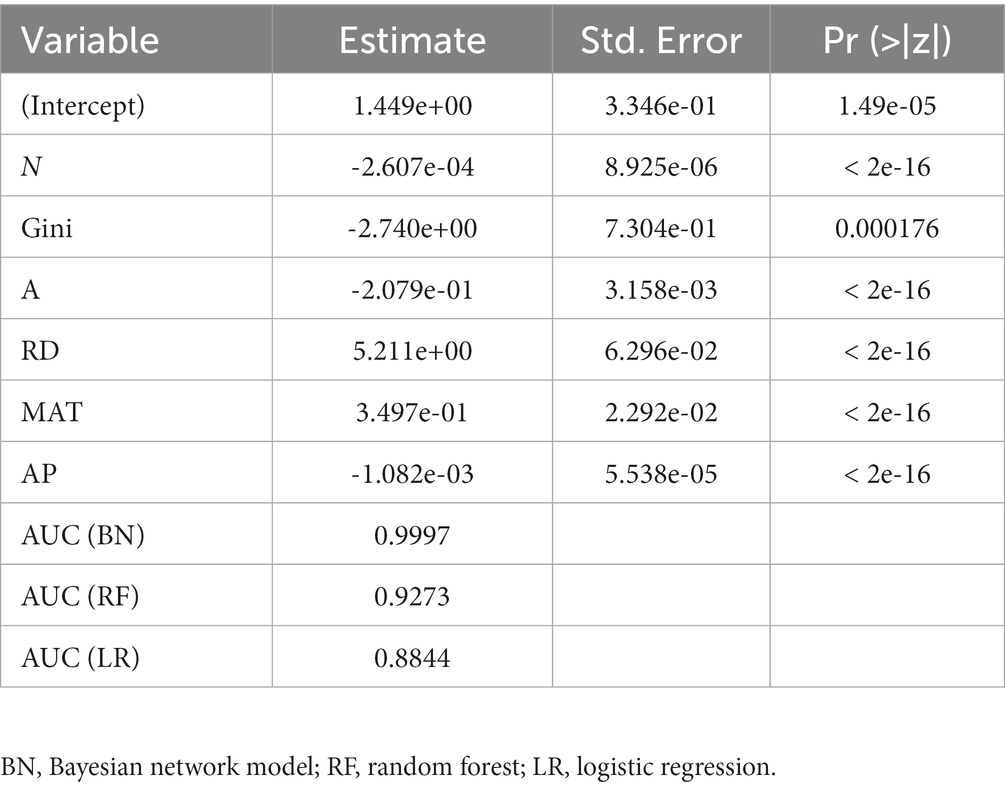
Table 4. Parameter estimates (including mean and standard deviation error) of logistic model and AUC values of three models.

3.2. Effects of stand factors on tree mortality (posterior probability)

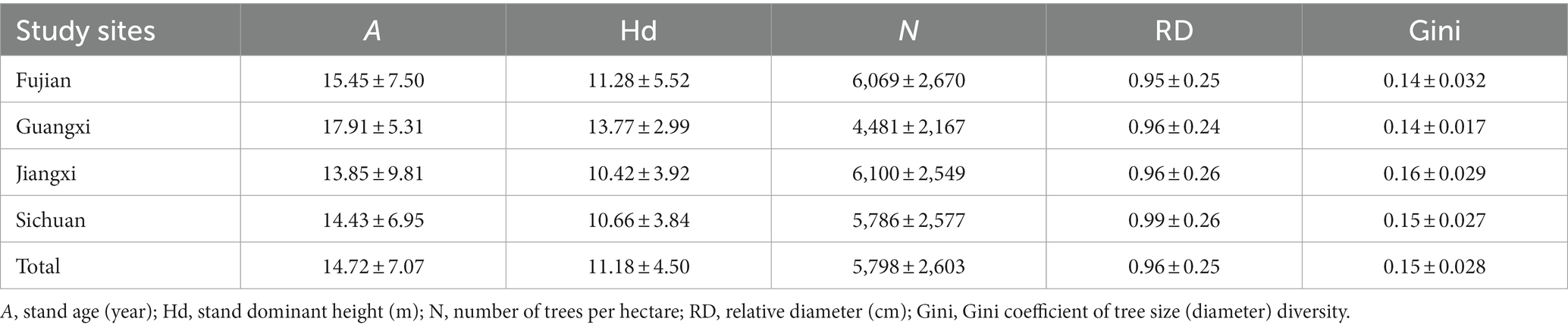
In this study, the Bayesian network model with 8 nodes and 21 directed edges was constructed. Based on Netica software, the response of tree survival to various variables at different levels (low, middle and high) was analyzed. Results showed that under the initial condition of not adjusting any variable, the survival probability was 78% (Figure 2).

FIGURE 2

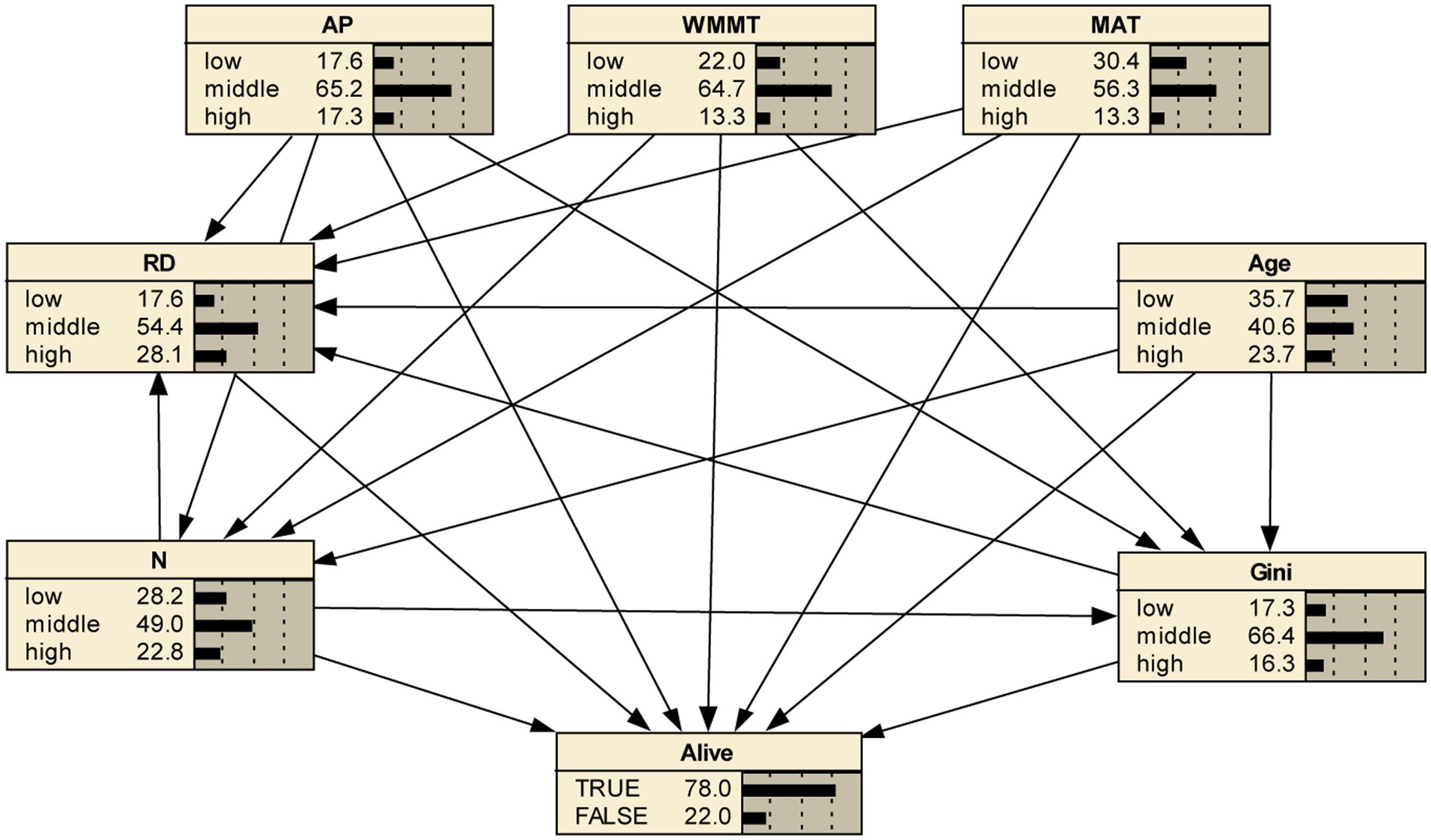
Figure 2. Bayesian network model of tree mortality in the initial case and its posterior probability. RD, relative density; N, number of trees per hectare; Age, plantation age; Gini, coefficient of stand structural heterogeneity; AP, annual precipitation; WMMT, winter mean minimum temperature; MAT, mean annual temperature.

In Netica, we set the statuses of certain levels of factors as 100%, and could also analyze the relationship between different stand factor levels and tree mortality in Figure 3. It could be seen that relative diameter (RD) had the greatest impact on tree mortality. A low level of RD had the greatest impact on mortality compared to middle and high levels, with low levels of RD increasing mortality by 36.9%, and middle (−11.3%) and high (−1.2%) levels of RD reducing tree mortality (Figure 3). N was the other stand variable that had a strong influence on mortality. In contrast to RD, a high level of density had the greatest impact on mortality, resulting in a 23.4% increase in mortality, compared to the low level (−1.4%) and middle level (−10.1%) which reduced tree mortality. Compared with RD and N, age and stand structure (Gini) had less of effects on tree mortality. The high level for age had the greatest impact on mortality with a 5.5% increase, compared to the low level for age (−3.9%) which had a negative effect on mortality, and middle age level had little effect on mortality. The Gini coefficients of low and high levels were positively associated with tree mortality, increasing the mortality rate by 1.4 and 3.4%, respectively, while the Gini coefficients of middle level (−1.2%) decreased tree mortality (Figure 3).

FIGURE 3

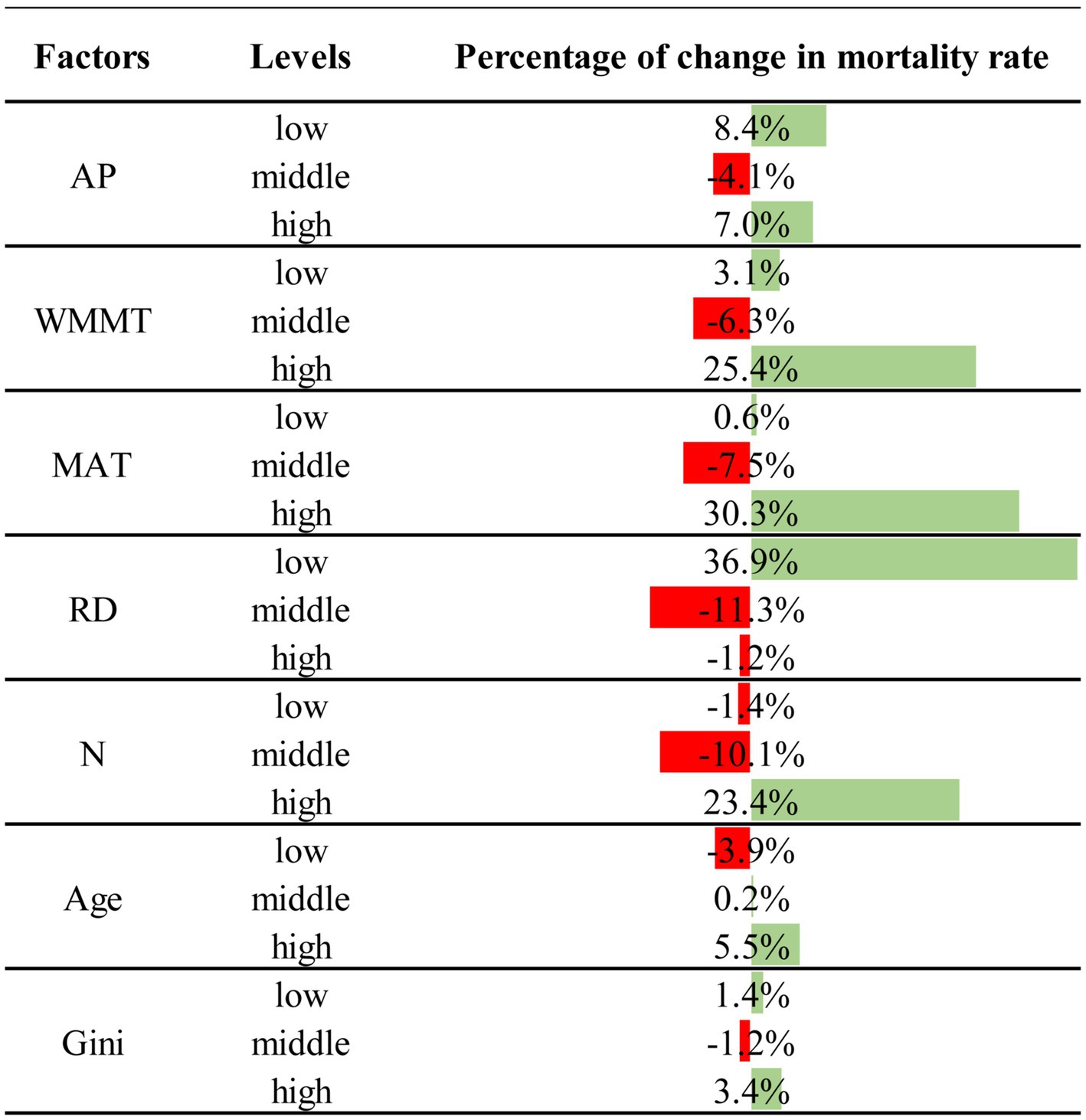
Figure 3. Change in probability of mortality at certain levels of factors. Red shows the decrease in mortality at a certain level of a factor, and green shows the increase in mortality at that level.

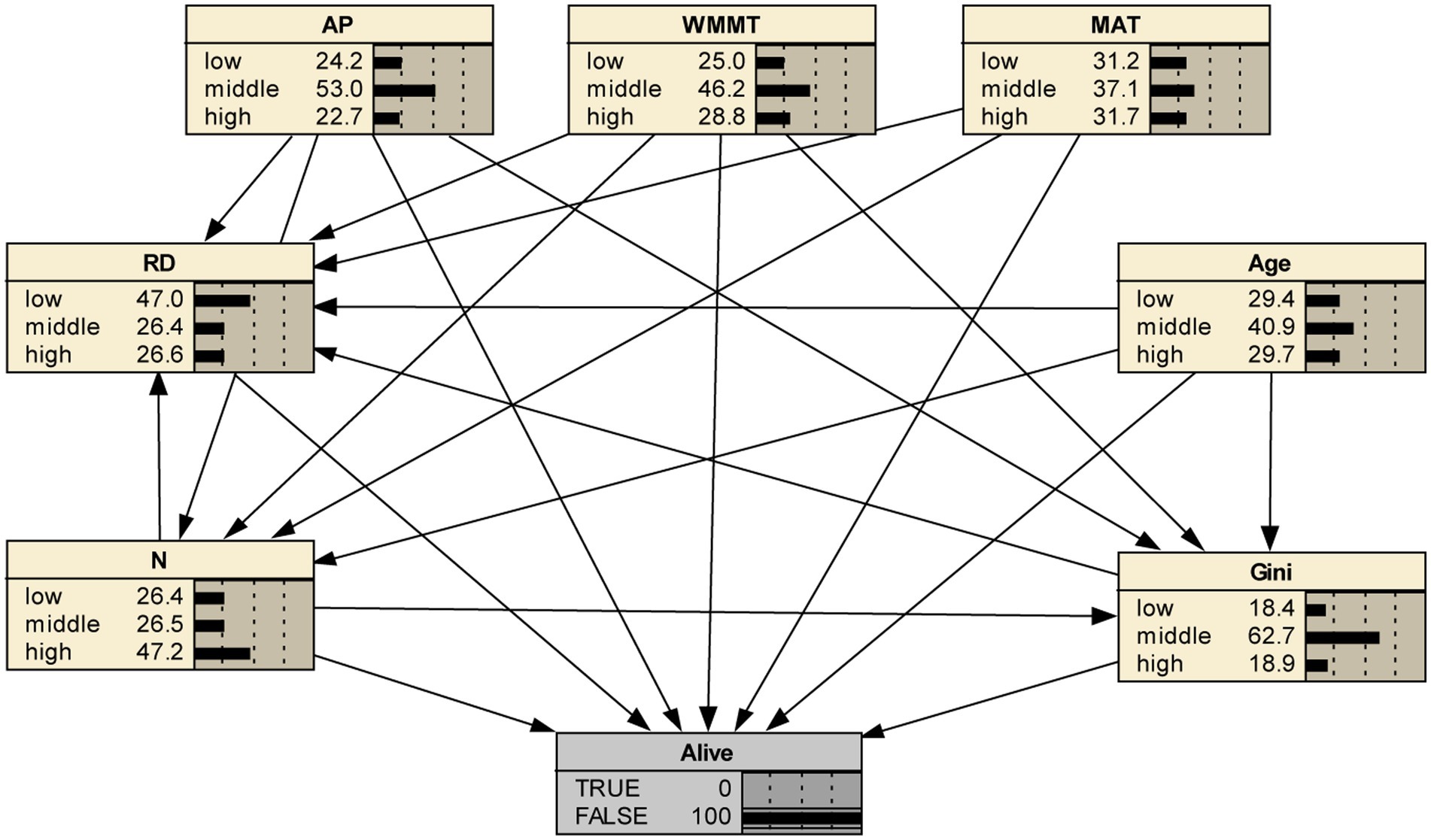
In addition, if we set the status of “alive” to 0, we could further analyze the changes of stand factors at different levels with mortality (Figure 4), thus further verifying our above results. First, RD had the greatest influence on mortality, the probability of low level increased by 29.4%, while the probability of middle and high levels decreased by 28.0 and 1.5%, respectively (Figure 5). It could be seen that with the increase of RD, survival rate showed an increasing trend. The change of N was different from that of RD; i.e., the probability of low and middle levels decreased by 1.8 and 22.5%, respectively, but the probability of the high level increased by 24.4% (Figure 5). It indicated that increases in low and middle stand density were conducive to tree survival, while increases in high stand densities can lead to tree mortality. When the survival rate was adjusted from 78 to 0%, the probability of middle and high level of age increased by 0.3 and 6.0% respectively, while the probability of low age decreased by 6.3%. Stand structure (Gini) had a relatively small impact on tree mortality. As the mortality rate increased, the probability of low and high levels of stand structure increased by 1.1 and 2.6% respectively, while the probability of middle level of stand structure decreased by 3.7% (Figure 5).

FIGURE 4

Figure 4. Bayesian network of tree mortality after adjusting for survival rate.

FIGURE 5

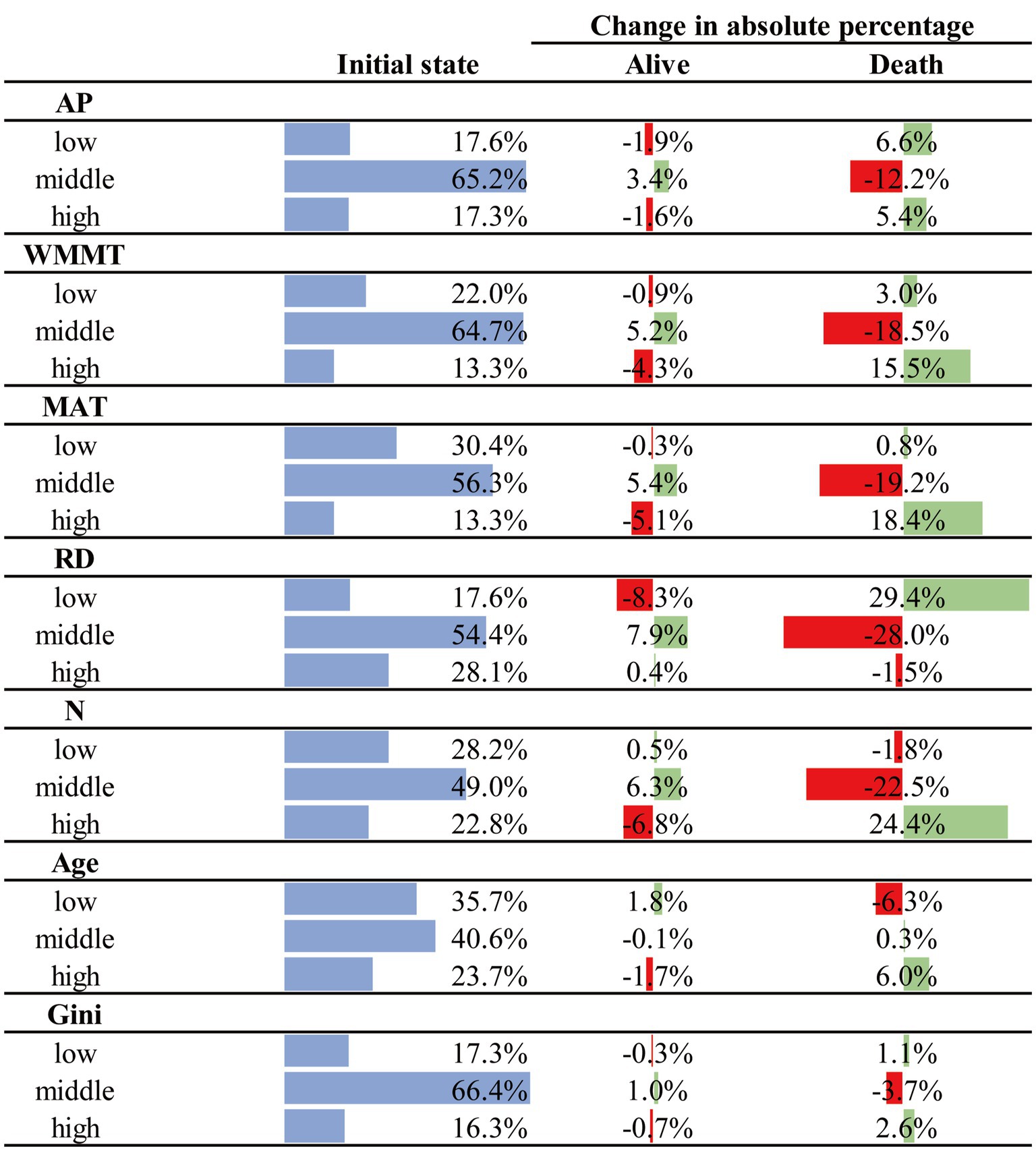
Figure 5. The percentage change of each factor after adjusting the probability of Alive nodes. Red represents the decrease in the probability of a factor at each level after the survival or mortality rate was adjusted to 100%, and green represents the increase in the probability of a factor at each level after the survival or mortality rate was adjusted to 100%.

3.3. Effects of climate factors on tree mortality (posterior probability)

AP, WMMT and MAT not only directly affected tree mortality, but also indirectly affected tree mortality through affecting RD, N, and Gini (Figure 2). It could be seen that with the increase of climate factors, tree mortality rate showed a trend of first decreasing and then increasing, and that the moderate climate condition was the most favorable for tree survival (Figure 3). WMMT and MAT had similar effects on mortality. Low and high levels of WMMT and MAT showed positive effects on tree mortality, while moderate WMMT and MAT reduced tree mortality (Figure 3). The effect of MAT was greater than that of WMMT, and the increase in mortality with high level of the corresponding climate factor was 30.3 and 25.4%, respectively. Furthermore, annual precipitation (AP) of low and high levels were positively associated with tree mortality, increasing the mortality rate by 8.4 and 7.0%, respectively, while the AP of middle level (−4.1%) decreased tree mortality (Figure 3).

In addition, if we set the status of “alive” to 0, we could further analyze the changes of climate factors at different levels with mortality, thus further verifying our above results (Figure 4). First, MAT had the greatest influence on mortality among the climate factors, the probability of middle level decreased by 19.2%, while the probability of low and high levels increased by 0.8 and 18.4%, respectively (Figure 5). The change of WMMT and AP were similar to MAT. The probability of middle level decreased by 18.5 and 12.2%, respectively, but the probability of low levels increased by 3.0 and 6.6%, respectively, and the probability of high levels increased by 15.5 and 5.4%, respectively (Figure 5).

3.4. Combined effects of stand and climate variables on tree mortality (posterior probability)

The correlation among nodes in Bayesian network was relatively complex, and each node influences each other, thereby directly or indirectly affecting tree mortality (Figure 2). Multiple factors can be fixed to analyze their combined effects on tree mortality.

Examples of the combined effects of climate and stand variables on mortality were shown in Table 4. As stand density increased in highest WMMT conditions, tree mortality increased from 48.3 to 49.9%, while the mortality rate of median density was 44.4% (Table 5). Compared with the effects of climate variables alone, the addition of low levels of RD and high levels of N significantly increased tree mortality to a large extent (Figure 6). Middle levels of RD and N reduced the effect of climate change on tree mortality, but this effect was less than the effect of higher levels of increase (Figure 6). Under the effect of only low level of AP, tree mortality was 30.4%, and when considering the effects of age, the high level of age increased tree mortality (36.6%) and the low level of age decreased tree mortality (22.2%), indicating that age modulated the response of tree death to climate change (Table 5). Similar results could be seen at different levels of MAT and AP conditions (Table 5). We could also compare the effects of two variables on tree mortality with one variable. For example, under the influence of the same stand variables, the influence of climate variables also showed that moderate climate variables reduced tree mortality, while low and high climate conditions increased tree mortality, roughly (Figure 7). In addition, high levels of WMMT and MAT had the greatest impact on tree mortality (Figure 7). Besides, we could also analyze the effects of three or more factors on tree mortality. For instance, in the stands with high-density, low relative diameter, and moderate WMMT, tree mortality increased from 22 to 86% compared to the initial state (Figures 2, 8).

TABLE 5

Table 5. Mortality at different levels (low, middle, high) with fixed climate and stand variables.

FIGURE 6

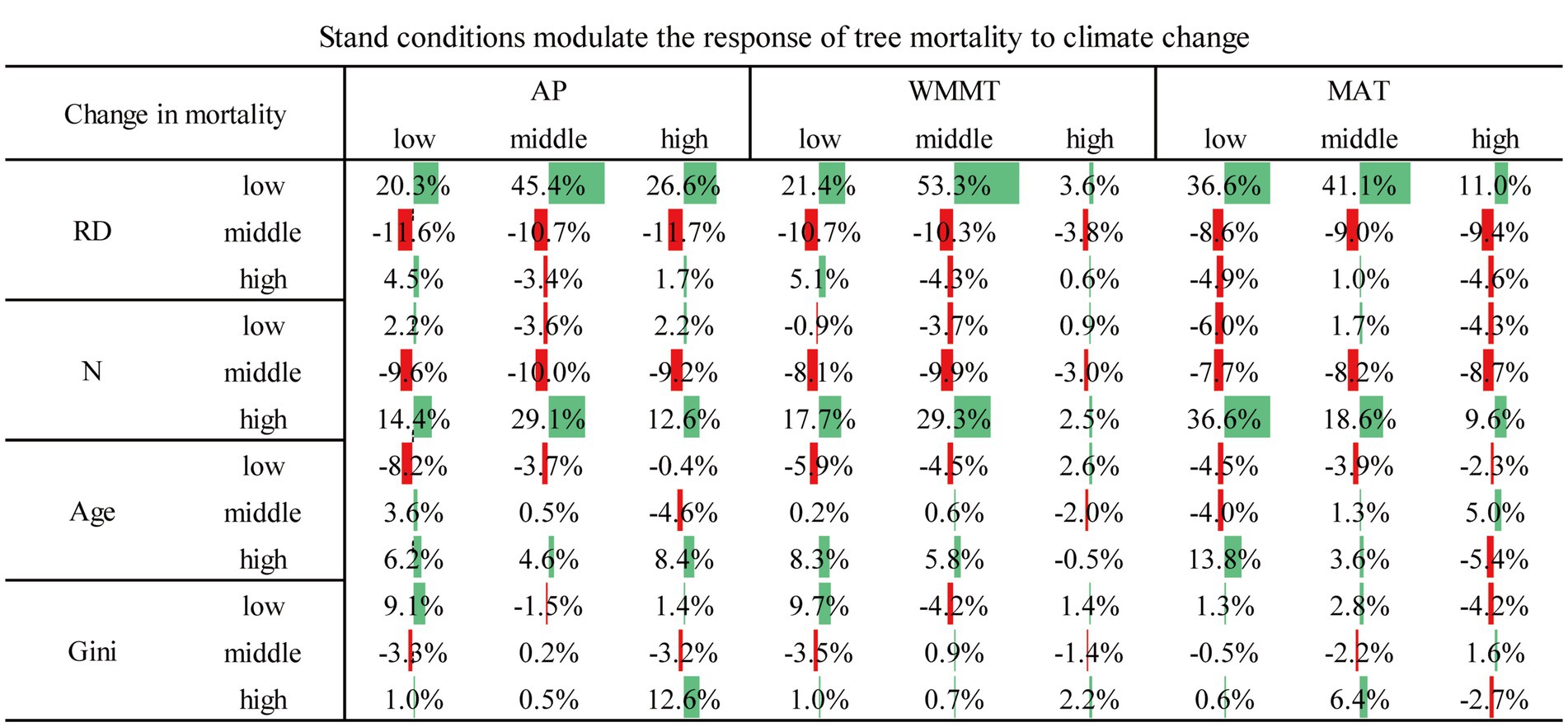
Figure 6. Changes in tree mortality under the combined influence of climate and stand conditions compared to climate conditions only.

FIGURE 7

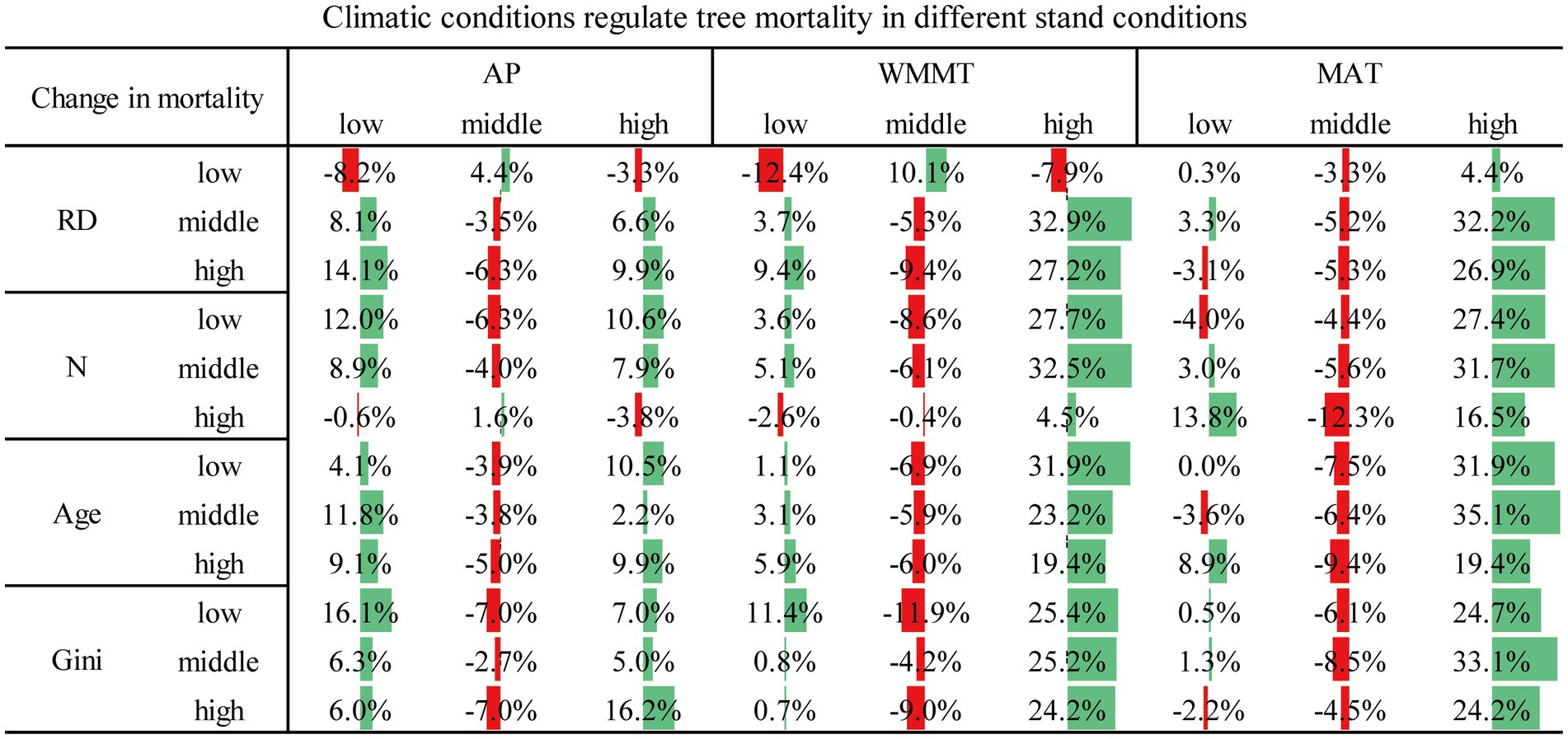
Figure 7. Changes in tree mortality under the combined effects of climate and stand conditions compared to stand conditions only.

FIGURE 8

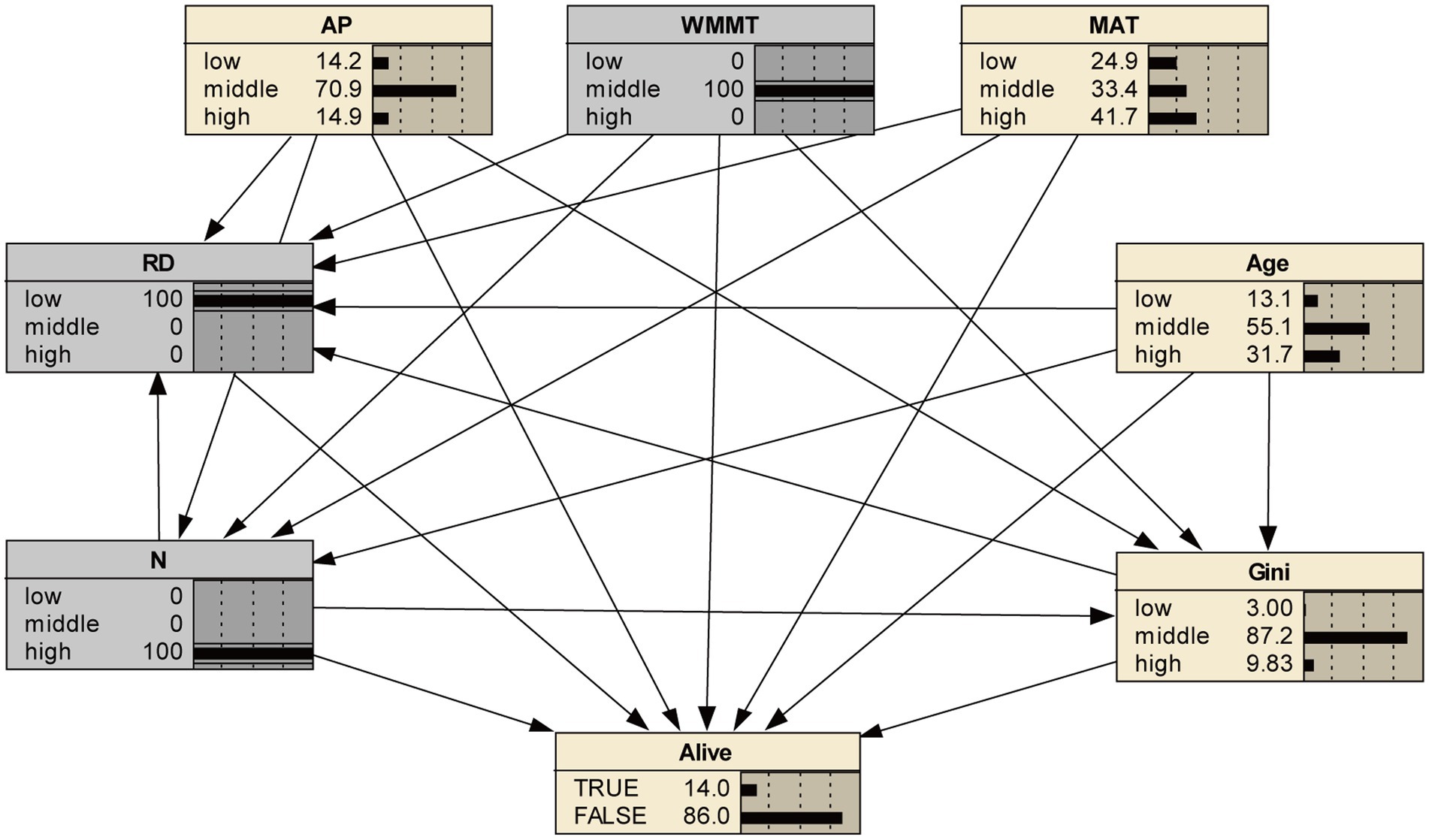
Figure 8. State of the Bayesian network in high-density, low relative diameter stands, and moderate WMMT.

3.5. Model sensitivity analysis

The sensitivity analysis of Netica was able to determine the relative importance of factors to tree mortality. The sensitivity analysis results of this model were presented in Table 6 and the nodes were ranked in according to the degree of influence of their findings on the outcomes of the Alive node calculated as a measure of mutual information or variance reduction (expressed as a percentage).

TABLE 6

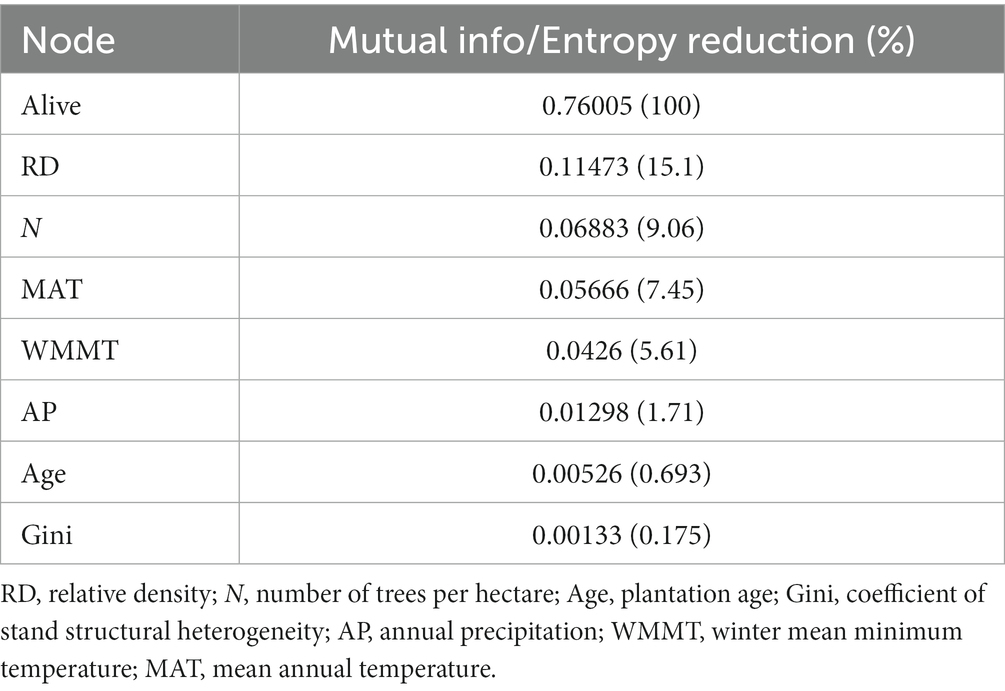
Table 6. Sensitivity analysis results ranked in decreasing order of influence on the Alive variable occurrence based on mutual information (info) or entropy reduction (also expressed as a percentage in brackets).

As shown in Table 6, it can be seen that the mutual information (0.1147) of node “RD” was the largest, which indicated that it had the strongest impact on “Alive,” followed by “N” which had mutual info of 0.0688 and then followed by MAT, WMMT, AP, age and Gini.

3.6. The most probable explanation

In this study, there were 2,187 (3 × 3 × 3 × 3 × 3 × 3 × 3) combinations of causes (node status) that affect tree mortality in the Bayesian network (BN) framework. It can be observed that the combination of the most likely causes (node status) for tree mortality was: low level of RD; middle level of AP, WMMT, age, and Gini; and high level of N and MAT (Figure 9).

FIGURE 9

Figure 9. Most probable explanation of Bayesian network model.

4. Discussion

4.1. Comparison and evaluation of the models

The Bayesian network model (AUC = 0.9997) was superior to the random forest model (AUC = 0.9273) and logistic regression model (AUC = 0.8844) (Table 4). The BN model could overcome the limitations of logistic regression and RF model, and had several major advantages in predictive modeling.

Firstly, BN allows learning causality between variables. When there are many interference factors affecting causality in a problem, BN can also learn. However, when more variables are introduced for a given data set, the interrelationships among the variables become more complex, logistic regression will lead to overfitting (Mazzocco and Hussain, 2012; Witteveen et al., 2018). In addition, unrelated variables may be included after multiple tests, and logistic regression has limited ability to select important variables due to their random effects, leading to inconsistent results (Ottenbacher et al., 2004), whereas BN can manage any inconsistencies in learning databases or applications (Rubin and Schenker, 1991).

Secondly, BN uses graphical methods to describe the relationship between data, which maintains the consistency and integrity of the probability knowledge base and is easy to understand (Ducher et al., 2013). In BN, probability distribution is used to express the strength of the dependency relationship between various variables, and the integration of prior knowledge and data is promoted by combining prior information and sample knowledge (Zhang et al., 2013).

Thirdly, there are several BN calibration and update methods that can be used to better analyze the model, of which the expectation maximization (EM) learning algorithm is a popular method (Watanabe and Yamaguchi, 2003). While RF model uses algorithms to directly learn from data and generate predictions, and requires all input data to generate model output. The development of a RF model is not so transparent. It is like a dark box, and we cannot control its internal calculation operation, which is not as flexible as the Bayesian network approach.

In general, prediction of tree mortality is inherently complex with many factors, e.g., stand competition, age, stand structure, temperature, precipitation, and their interactions affecting tree mortality (Luo and Chen, 2013; Zhang et al., 2020). The interactions are usually excluded from traditional regression models (logistic model) (Zhang et al., 2017; Lu et al., 2019). BN explicitly includes interactions between predictors, and thus it is feasible for modeling complex systems (Aguilera et al., 2011; Hradsky et al., 2017), because it explicitly shows the degree of uncertainty in the prediction, reflected as the distribution of posterior probabilities (Marcot, 2012). We can evaluate the impact of uncertainty and error as they propagate through the network, and we can identify the least understood predictive variables that may have a significant impact on the prediction results. Given the above advantages of the Bayesian network model and its highest accuracy in model performance, the Bayesian network model performed better than logistic regression and random forest in predicting Chinese fir mortality and related problems.

4.2. Effect of stand variables on tree mortality of Chinese fir

Among the stand factors, competition is generally considered to be the most important factors affecting tree growth and death (Ruiz-Benito et al., 2013), as it can affect the trees’ access to resources such as light, water, and mineral elements (Luo and Chen, 2013). Our study showed that competition (including RD and N) was the most important factor affecting tree mortality. As an important manifestation of the interaction between trees, competition can lead to differences in individual growth and development. Stand density (N), as an important indicator of stand competition, is an important driving factor for tree growth and has a promoting effect on tree mortality (Zhang et al., 2015b). The results of this study showed that tree mortality increased with the increase of stand density. Trees that had large RD and were planted in low stand density tend to have lower mortality, which indicated the balance between competition and tree mortality should be paid attention whether through thinning or low-density afforestation. It is generally believed that in a stand with higher stand density, the competition between adjacent trees for limited resources will become more intense, which leads to tree mortality (Calama et al., 2019). Secondly, high stand density will affect resource absorption efficiency of internal trees, reduce the available growth space, and inhibit the growth of tree canopy.

Among all the variables, RD was the most impact factor on tree mortality of Chinese fir, and tree mortality decreased with the increase of RD. Tree size is an important intrinsic attribute and a key factor affecting its growth and death. The relationship between tree death and DBH was usually shown in the form of a U-shaped curve (Coomes and Allen, 2007), that is, as the DBH of trees increases, tree mortality decreases first and then increases, indicating that small trees tend to have higher mortality (Wang et al., 2012). Generally speaking, the larger the tree is, the stronger its ability to resist external environmental pressure is, and compared with the smaller tree, it has an asymmetric competitive advantage for resources (Weiner, 1990; Uriarte et al., 2004).

Age is also a major factor affecting tree mortality (Zhang et al., 2020). The results showed that tree mortality increased with the increase of age, which is consistent with previous findings that old trees were more sensitive to climate change than young trees (Primicia et al., 2015; Chen et al., 2016). Wang et al. (2022) found that tree growth decreased with the increase of tree age, and climate conditions can promote the growth of young trees and inhibit the growth of old trees, which meant that climate change may exacerbate the negative impact of age on tree growth. Research suggested that tree death caused by aging may be due to the decline in physiological vigor of older trees, resulting in carbon starvation or death of trees caused by external interference (Güneralp and Gertner, 2007). At the same time, older trees, affected by size, may have higher mortality due to the restrictions on water and nutrient transport to the canopy (Domec et al., 2008). Stand structure heterogeneity was represented by Gini coefficient, and tree mortality decreased in the middle level values of stand structure (Gini). With the growth and development of the stand, small trees are gradually eliminated due to their inferiority in competition with neighboring trees, which leads to a smaller value of structure in the stand (Soares et al., 2016).

4.3. Effects of climate factors on tree mortality of Chinese fir

4.3.1. Annual precipitation

The impact of climate change on tree mortality has been extensively studied. A suitable climate environment helps to reduce the mortality of trees. Changes in temperature and precipitation alter the climate conditions in which trees grow, leading to maladaptive growth and death of trees, especially dry weather caused by climate change (Zhang et al., 2014).

The annual precipitation (AP) directly affected tree survival. Water condition is the key factor affecting the survival of trees: too dry or too wet is not conducive to the growth of trees (Tei et al., 2019). Peng et al. (2011) estimated tree mortality in natural stands of the Canadian boreal forest and found that water stress caused by regional drought may be the main reason for the general increase in tree mortality, which may be because drought will weaken water uptake and carbon metabolism of trees under the influence of severe drought. At the same time, drought can weaken tree defenses, making trees vulnerable to insect and pathogen attacks (Weed et al., 2013). Besides, if the site has excessive precipitation, it would result in death of fine roots attributed to waterlogging and soil anoxia (Vygodskaya et al., 2002). In areas with enough rainfall, excessive annual rainfall may increase tree mortality by reducing root activity and photosynthetic efficiency, thereby reducing stand density and stand structure (Dannenberg et al., 2019). Over precipitation in some sites might indicate poorer soil condition, due to increasing precipitation and nutrient leaching in the soils (Vizcaíno-Palomar et al., 2016), as well as leading to tree death. Zhang et al. (2020) reported that tree mortality increased with the increase of precipitation. Consistent with these results, it can be foreseen that areas with abundant but excessive rainfall will increase tree mortality of Chinese fir (Figure 3).

In general, under the direct effect of AP on mortality and the indirect effect of AP on stand factors, it was finally shown that moderate annual precipitation had a positive effect on survival, while too high or too low rainfall was detrimental to growth and promoted death.

4.3.2. Temperature

Temperature also plays a crucial role in tree growth and mortality. According to the results of sensitivity analysis, temperature had a greater impact on the survival of Chinese fir than precipitation. It may be because the precipitation in the study area is abundant, such that even an area with relatively little precipitation can satisfy the growth of Chinese fir. In general, increasing temperature can promote tree growth, while insufficient heat is a key factor limiting tree growth (Körner and Paulsen, 2004). Winter mean minimum temperature (WMMT) affected Chinese fir mortality directly and indirectly through RD, N and stand structure (Gini). Some evidence suggests that winter temperatures or pre-growing season temperatures have a positive effect on tree growth (Ols et al., 2018). Elevated winter temperatures can lead to early snow melt, resulting in faster soil drainage and warming, providing suitable conditions for the nutrients required for tree growth in the following growing season (Zheng et al., 2021). A relatively warm winter can increase the length of growing season, therefore increase radial growth in the following year and improving tree vigor and increasing tree survival (Taccoen et al., 2022). Duan et al. (2012) studied the chilling injury dynamics of Pinus massoniana in southeast China and found that lower winter temperatures would have a negative impact on tree growth: i.e., they reported that the decrease of temperature in winter may lead to bud loss, reduce root activity and delay growth, thus inhibiting tree growth and increasing tree mortality. On the one hand, with the increase of WMMT, Chinese fir would be less affected by winter freezing damage and survive, but on the other hand, the increase of temperature may increase the consumption of carbohydrate reserves of Chinese fir due to excessive respiration and thereby inhibit the growth of trees (Chen et al., 2015). Therefore, we believe that a moderate increase in temperature will reduce the frost damage of Chinese fir and reduce the mortality of Chinese fir. With the continuous increase of temperature, the positive effect of temperature increase on trees will be gradually offset by the negative effect of temperature increase, which will lead to tree death (Goulden and Bales, 2019).

Among all the climate factors, MAT had the highest correlation with the mortality of Chinese fir. The effect of MAT on Chinese fir was similar to that of WMMT, but the degree of effect of MAT was stronger than that of WMMT; that is, Chinese fir survival was more sensitive to the change of MAT. MAT directly affected tree mortality, but also indirectly affected mortality through N and RD. Some studies hold the view that tree mortality was positively correlated with MAT (Adams et al., 2009; Yaussy et al., 2012). In our study, tree mortality of Chinese fir was negatively correlated with the middle level of MAT. Chinese fir, as a shade-intolerant species, an increase in temperature within an appropriate range will accelerate its photosynthesis production (Zhang et al., 2019), thereby reducing tree mortality. In addition, it was found that tree mortality of Chinese fir was positive correlated with low and high levels of MAT, and indicates that the climate conditions beyond the appropriate temperature range will lead to lower photosynthetic efficiency, resulting in a decline in productivity (Wang et al., 2021), and ultimately cause tree mortality.

The results of Bayesian Network showed with the increase of mortality, the probability of low and high levels of climate factors increases to varying degrees, while the probability of moderate levels decreases. It indicated that extreme climate change would lead to tree mortality, while the moderate level of climate change would be beneficial for the survival of trees (Figure 5), which was consistent with the findings by Fernández-de-Uña et al. (2015) that the growth of trees increases before reaching the optimal temperature, and then decreases with increasing temperature. Besides, the results of this study found that the impact of precipitation on tree mortality was less than that of other climate factors such as temperature, which was consistent with the results of Fernández-de-Uña et al. (2015) and Wang et al. (2021).

4.4. Stand conditions regulate the response of tree mortality to climate change

The effects of climate variables on tree mortality include direct effects and indirect effects through stand variables. Competition, like a modulator, alters the response of tree growth to climate and regulates the resilience of forests to climate stress (Ford et al., 2017; Wang et al., 2022). Therefore, addressing tree mortality in the context of climate change needs to consider the impact of competition on stand growth and the response of competition to climate variables.

Competition between trees is a chronic stress that affects each tree’s carbon and water balance (Linares et al., 2010). As a medium of interaction between stand variables, the results showed that competition is the most important factor affecting stand growth, and stands with weak competition level tend to obtain higher growth increment (Wang et al., 2022). As a bridge to the impact of climate change on stand growth, competition regulates the adaptability or resistance of tree growth under climate stress, and it may regulate the response of tree growth to climate change. As stand density increased in highest WMMT conditions, tree mortality increased from 48.3 to 49.9%, while the mortality rate of median density was 44.4% (Table 4). Similar results were found at the highest mean annual temperature conditions, which may be explained by the fact that competition also increases the resistance of trees to climate change. For example, a superior carbon balance is required when facing recovery from drought-induced canopy loss (Franklin et al., 1987), and long-term competition may enable trees to overcome the negative effects of drought events. This gives us some inspiration to reduce the impact of climate change by reducing stand density through thinning in forest management (Magruder et al., 2013). Under favorable climatic conditions (e.g., moderate WMMT), tree mortality rate was 15.7%, while with the addition of lower levels of competitive conditions, tree mortality rate dropped to 12% (Table 5). However, under conditions of high competition (e.g., high density), trees were mostly insensitive to climate, such as 42.8, 45, 49.9% of each AP level, with variations of −2.6, −0.4%, and 4.5%, respectively, compared with the original state of 45.4% (Table 5). This was mainly due to high-density crowding, which impinged on a trees’ ability to adapt to a more favorable climate and increase growth (Ford et al., 2017).

In addition, age and stand structure also influence the response of tree mortality to climate change. Under the same climate condition, tree mortality gradually increased with the increase of age (Figure 6), showing that the negative impact of age on tree mortality was greater for old trees than for young trees. This result was in line with Wang et al. (2022) which reported that climate conditions would promote the growth of young trees and inhibit the growth of old trees. Old trees were more vulnerable to extreme weather conditions, such as low and high AP, which increased the mortality rate of old trees by 6.2 and 8.4%, respectively (Figure 6). In addition, at the same age level, the middle level climate conditions had the lowest tree mortality (Table 5), indicating that these moderate climate conditions were the most favorable for tree survival, while the high or low climate conditions would increase tree mortality.

Under the same level of stand structure, the intervention of moderate climate conditions reduced tree mortality (compared with only considering the effect of stand structure). Moderate climate conditions were the most favorable for tree survival, while both high and low levels climate conditions would increase tree mortality (Figure 7). This suggested that low and high levels of climate factors may amplify the negative effects of stand structure heterogeneity on mortality. In addition, combining the effects of stand structure and climate factors, the moderate level of stand structure reduced tree mortality (compared with only considering the effect of climate conditions), while the low and high levels of stand structure increased tree mortality (Figure 6), indicating that the moderate level of stand structure heterogeneity weakened the negative impact of climate variables on tree mortality.

Due to the complex relationship of various variables to tree mortality, the physiological and growth responses of trees to environmental forcing are not linear (Gea-Izquierdo et al., 2013); specifically, the functional responses to specific environmental variables are either sigmoid form or bell-shaped form (Fernández-de-Uña et al., 2015). Fernández-de-Uña et al. (2015) found a nonlinear interaction between climate variables and stand competition, in the Mediterranean ecosystem with limited water resources. Tree growth and mortality are influenced by a combination of climate factors and competition (Panayotov et al., 2016). No matter whether it is climate or stand factors, their effects on tree growth and death are realized through the trees’ own characteristics, such as water use efficiency, resistance and functional traits (Camac et al., 2018). The effects of these variables are not mutually exclusive, but help to reconcile the various mechanisms, or there is some coupling mechanism. Competition modulates the effects of climate change on growth and mortality at the individual and stand scales in important but complex ways (Ford et al., 2017). We found that moderate level of competition condition and stand structure heterogeneity weakened the negative impact of climate variables on tree mortality, and the impact of age on tree mortality was greater for old trees than for young trees.

5. Conclusion

In this study, it showed that Bayesian network could automatically find the dependency relationship between data and provide a theoretical framework for modeling uncertainty by using probabilistic calculus and underlying graph structure. In contrast, Bayesian network has higher estimation accuracy and fitting stability than logistic regression and random forest.

Tree mortality was negatively correlated with moderate AP, WMMT, MAT, and stand structure (Gini) as well as low age, but positively correlated with low RD, high N, and age. According to the Most Probable Explanation, the most likely causes of tree mortality can be determined as low RD, middle AP, WMMT, Age, and Gini, and high N and MAT. Besides, RD was the stand factor with the highest influence on tree mortality, and temperature (including MAT and WMMT) was the climate factor with the highest association with tree mortality, whereas stand structure (Gini coefficient) was less important. There were direct or indirect interactions among the factors affecting tree mortality. Stand conditions modulated the response of tree mortality to climate and regulated the resilience of forests to climate stress. Moderate level of competition condition and stand structure heterogeneity weakened the negative impact of climate variables on tree mortality. The impact of age on tree mortality was greater for old trees than for young trees, which indicated that old trees were more sensitive to extreme weather conditions than young trees. Due to the complex relationship between various variables and tree mortality, as well as the regulatory role of competition, the physiological and growth responses of trees to environmental stress are not linear. This result indicates that we can take different measures according to different stand conditions, such as managing density or adjusting stand structure, while also taking into account stand age and site conditions, so as to mitigate the adverse effects of climate change on tree mortality.

Data availability statement

The datasets presented in this article are not readily available because the authors do not have permission to share this data set. Requests to access the datasets should be directed to eHF6aGFuZzg1QGNhZi5hYy5jbg==.

Author contributions

YJ: Investigation, Data curation, Formal analysis, Methodology, Writing – original draft. ZW: Formal analysis, Writing – review & editing. HC: Investigation, Writing – review & editing. YH: Investigation, Writing – review & editing. YQ: Investigation, Writing – review & editing. SC: Writing – review & editing. JZ: Investigation, Writing – review & editing. XZ: Writing – review & editing, Conceptualization, Funding acquisition, Investigation, Supervision.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The study was supported by the National Natural Science Foundation of China (No. 31971645) and State Administration of Forestry and Grassland of China (2019132605).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adams, H. D., Guardiola-Claramonte, M., Barron-Gafford, G. A., Villegas, J. C., Breshears, D. D., Zou, C. B., et al. (2009). Temperature sensitivity of drought-induced tree mortality portends increased regional die-off under global-change-type drought. Proc. Natl. Acad. Sci. U. S. A. 106, 7063–7066. doi: 10.1073/pnas.0901438106

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguilera, P. A., Fernandez, A., Fernandez, R., Rumi, R., and Salmeron, A. (2011). Bayesian networks in environmental modelling. Environmen. Modell. Softw. 26, 1376–1388. doi: 10.1016/j.envsoft.2011.06.004

CrossRef Full Text | Google Scholar

Allen, C. D., Macalady, A. K., Chenchouni, H., Bachelet, D., McDowell, N., Vennetier, M., et al. (2010). A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 259, 660–684. doi: 10.1016/j.foreco.2009.09.001

CrossRef Full Text | Google Scholar

Bennett, A. C., McDowell, N. G., Allen, C. D., and Anderson-Teixeira, K. J. (2015). Larger trees suffer most during drought in forests worldwide. Nat. Plants 1:15139. doi: 10.1038/nplants.2015.139

PubMed Abstract | CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Mach. Learn. 45, 5–32. doi: 10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

Calama, R., Conde, M., de-Dios-García, J., Madrigal, G., Vázquez-Piqué, J., Gordo, F. J., et al. (2019). Linking climate, annual growth and competition in a Mediterranean forest: Pinus pinea in the Spanish northern plateau. Agric. For. Meteorol. 264, 309–321. doi: 10.1016/j.agrformet.2018.10.017

CrossRef Full Text | Google Scholar

Camac, J. S., Condit, R., FitzJohn, R. G., McCalman, L., Steinberg, D., Westoby, M., et al. (2018). Partitioning mortality into growth-dependent and growth-independent hazards across 203 tropical tree species. Proc. Natl. Acad. Sci. 115, 12459–12464. doi: 10.1073/pnas.1721040115

CrossRef Full Text | Google Scholar

Chen, H. Y. H., Luo, Y., Reich, P. B., Searle, E. B., Biswas, S. R., and Enquist, B. (2016). Climate change-associated trends in net biomass change are age dependent in western boreal forests of Canada. Ecol. Lett. 19, 1150–1158. doi: 10.1111/ele.12653

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, F., Yuan, Y., Yu, S., and Zhang, T. (2015). Influence of climate warming and resin collection on the growth of Masson pine (Pinus massoniana) in a subtropical forest, southern China. Trees 29, 1423–1430. doi: 10.1007/s00468-015-1222-3

CrossRef Full Text | Google Scholar

Coomes, D. A., and Allen, R. B. (2007). Mortality and tree-size distributions in natural mixed-age forests. J. Ecol. 95, 27–40. doi: 10.1111/j.1365-2745.2006.01179.x

CrossRef Full Text | Google Scholar

Copenhaver-Parry, P. E., and Cannon, E. (2016). The relative influences of climate and competition on tree growth along montane ecotones in the Rocky Mountains. Oecologia 182, 13–25. doi: 10.1007/s00442-016-3565-x

CrossRef Full Text | Google Scholar

Cortini, F., Comeau, P. G., Strimbu, V. C., Hogg, E. H. T., Bokalo, M., and Huang, S. (2017). Survival functions for boreal tree species in northwestern North America. For. Ecol. Manag. 402, 177–185. doi: 10.1016/j.foreco.2017.06.036

CrossRef Full Text | Google Scholar

Craine, J. M., and Dybzinski, R. (2013). Mechanisms of plant competition for nutrients, water and light. Funct. Ecol. 27, 833–840. doi: 10.1111/1365-2435.12081

CrossRef Full Text | Google Scholar

Crecente-Campo, F., Marshall, P., and Rodríguez-Soalleiro, R. (2009). Modeling non-catastrophic individual-tree mortality for Pinus radiate plantations in northwestern Spain. For. Ecol. Manag. 257, 1542–1550. doi: 10.1016/j.foreco.2009.01.007

CrossRef Full Text | Google Scholar

Culbertson, M. J. (2016). Bayesian networks in educational assessment: the state of the field. Appl. Psych. Meas. 40, 3–21. doi: 10.1177/0146621615590401

PubMed Abstract | CrossRef Full Text | Google Scholar

Dannenberg, M. P., Wise, E. K., and Smith, W. K. (2019). Reduced tree growth in the semiarid United States due to asymmetric responses to intensifying precipitation extremes. Sci. Adv. 5:eaaw0667. doi: 10.1126/sciadv.aaw0667

PubMed Abstract | CrossRef Full Text | Google Scholar

Devi, N. M., Kukarskih, V. V., Galimova, A. A., Mazepa, V. S., and Grigoriev, A. A. (2020). Change evidence in tree growth and stand productivity at the upper treeline ecotone in the polar Ural Mountains. For. Ecosyst. 7, 1–7. doi: 10.1186/s40663-020-0216-9

CrossRef Full Text | Google Scholar

Dlamini, W. M. (2011). Application of Bayesian networks for fire risk mapping using GIS and remote sensing data. GeoJournal 76, 283–296. doi: 10.1007/s10708-010-9362-x

CrossRef Full Text | Google Scholar

Domec, J. C., Lachenbruch, B., Meinzer, F. C., Woodruff, D. R., Warren, J. M., and McCulloh, K. A. (2008). Maximum height in a conifer is associated with conflicting requirements for xylem design. Proc. Natl. Acad. Sci. U. S. A. 105, 12069–12074. doi: 10.1073/pnas.0710418105

PubMed Abstract | CrossRef Full Text | Google Scholar

Duan, J., Zhang, Q. B., Lv, L., and Zhang, C. (2012). Regional-scale winter-spring temperature variability and chilling damage dynamics over the past two centuries in southeastern China. Clim. Dyn. 39, 919–928. doi: 10.1007/s00382-011-1232-9

CrossRef Full Text | Google Scholar

Ducher, M., Kalbacher, E., Combarnous, F., Finaz de Vilaine, J., McGregor, B., Fouque, D., et al. (2013). Comparison of a Bayesian network with a logistic regression model to forecast IGA nephropathy. Biomed. Res. Int. 2013, 1–6. doi: 10.1155/2013/686150

CrossRef Full Text | Google Scholar

Fenton, N., and Neil, M. (2012). Risk assessment and decision analysis with Bayesian networks. Boca Raton, FL: CRC Press; 524.

Google Scholar

Fernández-de-Uña, L., Cañellas, I., and Gea-Izquierdo, G. (2015). Stand competition determines how different tree species will cope with a warming climate. PLoS One 10:e0122255. doi: 10.1371/journal.pone.0122255

PubMed Abstract | CrossRef Full Text | Google Scholar

Floyd, M. L., Clifford, M., Cobb, N. S., Hanna, D., Delph, R., Ford, P., et al. (2009). Relationship of stand characteristics to drought-induced mortality in three Southwesterns piñon-juniper woodlands. Ecol. Appl. 19, 1223–1230. doi: 10.1890/08-1265.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ford, K. R., Breckheimer, I. K., Franklin, J. F., Freund, J. A., Kroiss, S. J., Larson, A. J., et al. (2017). Competition alters tree growth responses to climate at individual and stand scales. Can. J. For. Res. 47, 53–62. doi: 10.1139/cjfr-2016-0188

CrossRef Full Text | Google Scholar

Forrester, D. I. (2019). Linking forest growth with stand structure: tree size inequality, tree growth or resource partitioning and the asymmetry of competition. For. Ecol. Manag. 447, 139–157. doi: 10.1016/j.foreco.2019.05.053

CrossRef Full Text | Google Scholar

Franklin, J. F., Shugart, H. H., and Harmon, M. E. (1987). Tree death as an ecological process. Bioscience 37, 550–556. doi: 10.2307/1310665

CrossRef Full Text | Google Scholar

Frayer, J., Sun, Z., Müller, D., Munroe, D. K., and Xu, J. (2014). Analyzing the drivers of tree planting in Yunnan, China, with Bayesian networks. Land Use Policy 36, 248–258. doi: 10.1016/j.landusepol.2013.08.005

CrossRef Full Text | Google Scholar

García, P., Amandi, A., Schiaffino, S., and Campo, M. (2007). Evaluating Bayesian networks’ precision for detecting students’ learning styles. Comput. Educ. 49, 794–808. doi: 10.1016/j.compedu.2005.11.017

CrossRef Full Text | Google Scholar

Gea-Izquierdo, G., Fernández-de-Uña, L., and Cañellas, I. (2013). Growth projections reveal local vulnerability of Mediterranean oaks with rising temperatures. For. Ecol. Manag. 305, 282–293. doi: 10.1016/j.foreco.2013.05.058

CrossRef Full Text | Google Scholar

Gevaert, O., Smet, F. D., Timmerman, D., Moreau, Y., and Moor, B. D. (2006). Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks. Bioinformatics 22, e184–e190. doi: 10.1093/bioinformatics/btl230

CrossRef Full Text | Google Scholar

Gitlin, A. R., Sthultz, C. M., Bowker, M. A., Stumpf, S., Paxton, K. L., Kennedy, K., et al. (2006). Mortality gradients within and among dominant plant populations as barometers of ecosystem change during extreme drought. Conserv. Biol. 20, 1477–1486. doi: 10.1111/j.1523-1739.2006.00424.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Goulden, M. L., and Bales, R. C. (2019). California forest die-off linked to multi-year deep soil drying in 2012−2015 drought. Nat. Geosci. 12, 632–637. doi: 10.1038/s41561-019-0388-5

CrossRef Full Text | Google Scholar

Gret-Regamey, A., and Straub, D. (2006). Spatially explicit avalanche risk assessment linking Bayesian networks to a GIS. Nat. Hazards Earth Syst. Sci. 6, 911–926. doi: 10.5194/nhess-6-911-2006

CrossRef Full Text | Google Scholar

Güneralp, B., and Gertner, G. (2007). Feedback loop dominance analysis of two tree mortality models: relationship between structure and behavior. Tree Physiol. 27, 269–280. doi: 10.1093/treephys/27.2.269

PubMed Abstract | CrossRef Full Text | Google Scholar

Holmes, D. E., and Jain, L. C. (2008). Innovations in Bayesian networks: theory and applications, vol. 156. Berlin: Springer.

Google Scholar

Hradsky, B. A., Penman, T. D., Ababei, D., Hanea, A., Ritchie, E. G., York, A., et al. (2017). Bayesian networks elucidate interactions between fire and other drivers of terrestrial fauna distributions. Ecosphere 8:e01926. doi: 10.1002/ecs2.1926

CrossRef Full Text | Google Scholar

Jentsch, A., Kreyling, J., and Beierkuhnlein, C. (2007). A new generation of climate change experiments: events, not trends. Front. Ecol. Environ. 5, 315–324. doi: 10.1890/1540-9295(2007)5[365:ANGOCE]2.0.CO;2

CrossRef Full Text | Google Scholar

Körner, C., and Paulsen, J. (2004). A world-wide study of high altitude treeline temperatures. J. Biogeogr. 31, 713–732. doi: 10.1111/j.1365-2699.2003.01043.x

CrossRef Full Text | Google Scholar

Kweon, D., and Comeau, P. G. (2019). Relationships between tree survival, stand structure and age in trembling aspen dominated stands. For. Ecol. Manag. 438, 114–122. doi: 10.1016/j.foreco.2019.02.003

CrossRef Full Text | Google Scholar

Kwisthout, J. (2011). Most probable explanations in Bayesian networks: complexity and tractability. Int. J. Approx. Reason. 52, 1452–1469. doi: 10.1016/j.ijar.2011.08.003

CrossRef Full Text | Google Scholar

Lee, Y. (1971). Predicting mortality for even-aged stands of lodgepde pine. For. Chron. 47, 29–32. doi: 10.5558/tfc47029-1

CrossRef Full Text | Google Scholar

Lee, S., Kang, J. E., Park, C. S., Yoon, D. K., and Yoon, S. (2020). Multi-risk assessment of heat waves under intensifying climate change using Bayesian networks. Int. J. Disast. Risk. Re. 50:101704. doi: 10.1016/j.ijdrr.2020.101704

CrossRef Full Text | Google Scholar

Linares, J. C., Camarero, J. J., and Carreira, J. A. (2010). Competition modulates the adaptation capacity of forests to climatic stress: insights from recent growth decline and death in relict stands of the Mediterranean fir Abies pinsapo. J. Ecol. 98, 592–603. doi: 10.1111/j.1365-2745.2010.01645.x

CrossRef Full Text | Google Scholar

Lu, L., Wang, H., Chhin, S., Duan, A., Zhang, J., and Zhang, X. (2019). A Bayesian model averaging approach for modelling tree mortality in relation to site, competition and climatic factors for Chinese fir plantations. For. Ecol. Manag. 440, 169–177. doi: 10.1016/j.foreco.2019.03.003

CrossRef Full Text | Google Scholar

Luo, Y., and Chen, H. Y. H. (2013). Observations from old forests underestimate climate change effects on tree mortality. Nat. Commun. 4:1655. doi: 10.1038/ncomms2681

PubMed Abstract | CrossRef Full Text | Google Scholar

Magruder, M., Chhin, S., Palik, B., and Bradford, J. (2013). Thinning increases climatic resilience of red pine. Can. J. For. Res. 43, 878–889. doi: 10.1139/cjfr-2013-0088

CrossRef Full Text | Google Scholar

Marcot, B. G. (2012). Metrics for evaluating performance and uncertainty of Bayesian network models. Ecol. Model. 230, 50–62. doi: 10.1016/j.ecolmodel.2012.01.013

CrossRef Full Text | Google Scholar

Marcot, B. G., Holthausen, R. S., Raphael, M. G., Rowland, M. M., and Wisdom, M. J. (2001). Using Bayesian belief networks to evaluate fish and wildlife population viability under land management alternatives from an environmental impact statement. For. Ecol. Manag. 153, 29–42. doi: 10.1016/S0378-1127(01)00452-2

CrossRef Full Text | Google Scholar

Marcot, B. G., Steventon, J. D., Sutherland, G. D., and McCann, R. K. (2006). Guidelines for developing and updating Bayesian belief networks applied to ecological modeling and conservation. Can. J. For. Res. 36, 3063–3074. doi: 10.1139/x06-135

CrossRef Full Text | Google Scholar

Mazzocco, T., and Hussain, A. (2012). Novel logistic regression models to aid the diagnosis of dementia. Expert Syst. Appl. 39, 3356–3361. doi: 10.1016/j.eswa.2011.09.023

CrossRef Full Text | Google Scholar

McDowell, N., Pockman, W. T., Allen, C. D., Breshears, D. D., Cobb, N., Kolb, T., et al. (2008). Mechanisms of plant survival and mortality during drought: why do some plants survive while others succumb to drought? New Phytol. 178, 719–739. doi: 10.1111/j.1469-8137.2008.02436.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Nash, D., Waters, D., Buldu, A., Wu, Y., Lin, Y., Yang, W., et al. (2013). Using a conceptual Bayesian network to investigate environmental management of vegetable production in the Lake Taihu region of China. Environ. Model. Softw. 46, 170–181. doi: 10.1016/j.envsoft.2013.03.008

CrossRef Full Text | Google Scholar

Negrón, J. F., and Wilson, J. W. (2003). Attributes associated with probability of infestation by the piñon Ips confuses (Coleoptera: Scolytidae), in pinyon pine, Pinus edulis. West. N. Am. Naturalist. 63, 440–451.

Google Scholar

Netica. (2019). Norsys Software Corp. Available at: https://www.norsys.com/netica.html.

Google Scholar

Ols, C., Trouet, V., Girardin, M. P., Hofgaard, A., Bergeron, Y., and Drobyshev, I. (2018). Post-1980 shifts in the sensitivity of boreal tree growth to North Atlantic Ocean dynamics and seasonal climate. Glob. Planet. Chang. 165, 1–12. doi: 10.1016/j.gloplacha.2018.03.006

CrossRef Full Text | Google Scholar

Ottenbacher, K. J., Ottenbacher, H. R., Tooth, L., and Ostir, G. V. (2004). A review of two journals found that articles using multivariable logistic regression frequently did not report commonly recommended assumptions. J. Clin. Epidemiol. 57, 1147–1152. doi: 10.1016/j.jclinepi.2003.05.003

CrossRef Full Text | Google Scholar

Panayotov, M., Kulakowski, D., Tsvetanov, N., Krumm, F., Barbeito, I., and Bebi, P. (2016). Climate extremes during high competition contribute to mortality in unmanaged self-thinning Norway spruce stands in Bulgaria. For. Ecol. Manag. 369, 74–88. doi: 10.1016/j.foreco.2016.02.033

CrossRef Full Text | Google Scholar

Pawson, S. M., Marcot, B. G., and Woodberry, O. G. (2017). Predicting forest insect flight activity: a Bayesian network approach. PLoS One 12:e0183464. doi: 10.1371/journal.pone.0183464

PubMed Abstract | CrossRef Full Text | Google Scholar

Pearl, J. (1986). Fusion, Propagation, and Structuring in Belief Networks. Artif. Intell. 29, 241–288. doi: 10.1016/0004-3702(86)90072-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, C., Ma, Z., Lei, X., Zhu, Q., Chen, H., Wang, W., et al. (2011). A drought-induced pervasive increase in tree mortality across Canada’s boreal forests. Nat. Clim. Chang. 1, 467–471. doi: 10.1038/nclimate1293

CrossRef Full Text | Google Scholar

Penman, T. D., Price, O., and Bradstock, R. A. (2011). Bayes nets as a method for analysing the influence of management actions in fire planning. Int. J. Wildland Fire 20, 909–920. doi: 10.1071/WF10076

CrossRef Full Text | Google Scholar

Primicia, I., Camarero, J. J., Janda, P., Čada, V., Morrissey, R. C., Trotsiuk, V., et al. (2015). Age, competition, disturbance and elevation effects on tree and stand growth response of primary Picea abies forest to climate. For. Ecol. Manag. 354, 77–86. doi: 10.1016/j.foreco.2015.06.034

CrossRef Full Text | Google Scholar

Qiu, S., Xu, M., Li, R., Zheng, Y., Clark, D., Cui, X., et al. (2015). Climatic information improves statistical individual-tree mortality models for three key species of Sichuan Province. China. Ann. For. Sci. 72, 443–455. doi: 10.1007/s13595-014-0449-2

CrossRef Full Text | Google Scholar

Rubin, D. B., and Schenker, N. (1991). Multiple imputation in health-care databases: an overview and some applications. Stat. Med. 10, 585–598. doi: 10.1002/sim.4780100410

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruiz-Benito, P., Lines, E. R., Gómez-Aparicio, L., Zavala, M. A., and Coomes, D. A. (2013). Patterns and drivers of tree mortality in iberian forests: climatic effects are modified by competition. PLoS One 8:e56843. doi: 10.1371/journal.pone.0056843

PubMed Abstract | CrossRef Full Text | Google Scholar

Sevinc, V., Kucuk, O., and Goltas, M. (2020). A Bayesian network model for prediction and analysis of possible forest fire causes. For. Ecol. Manag. 457:117723. doi: 10.1016/j.foreco.2019.117723

CrossRef Full Text | Google Scholar

Shanley, C. S., Eacker, D. R., Reynolds, C. P., Bennetsen, B. M. B., and Gilbert, S. L. (2021). Using LiDAR and random Forest to improve deer habitat models in a managed forest landscape. For. Ecol. Manag. 499:119580. doi: 10.1016/j.foreco.2021.119580

CrossRef Full Text | Google Scholar

Soares, A. A., Leite, H. G., Souza, A. L., Silva, S. R., Lourenço, H. M., and Forrester, D. I. (2016). Increasing stand structural heterogeneity reduces productivity in Brazilian Eucalyptus monoclonal stands. For. Ecol. Manag. 373, 26–32. doi: 10.1016/j.foreco.2016.04.035

CrossRef Full Text | Google Scholar

Sun, Z., and Müller, D. (2013). A framework for modeling payments for ecosystem services with agent-based models, Bayesian belief networks and opinion dynamics models. Environ. Model. Softw. 45, 15–28. doi: 10.1016/j.envsoft.2012.06.007

CrossRef Full Text | Google Scholar

Taccoen, A., Piedallu, C., Seynave, I., Gégout-Petit, A., and Gégout, J. C. (2022). Climate change-induced background tree mortality is exacerbated towards the warm limits of the species ranges. Ann. For. Sci. 79, 1–23. doi: 10.1186/s13595-022-01142-y

CrossRef Full Text | Google Scholar

Tei, S., Sugimoto, A., Yonenobu, H., Kotani, A., and Maximov, T. C. (2019). Effects of extreme drought and wet events for tree mortality: insights from tree-ring width and carbon isotope ratio in a Siberian larch forest. Ecohydrology 12:e2143. doi: 10.1002/eco.2143

CrossRef Full Text | Google Scholar

Teskey, R., Wertin, T., Bauweraerts, I., Ameye, M., Mcguire, M. A., and Steppe, K. (2014). Responses of tree species to heat waves and extreme heat events. Plant Cell Environ. 38, 1699–1712. doi: 10.1111/pce.12417

PubMed Abstract | CrossRef Full Text | Google Scholar

Trumbore, S., Brando, P., and Hartmann, H. (2015). Forest health and global change. Science 349, 814–818. doi: 10.1126/science.aac6759

CrossRef Full Text | Google Scholar

Uriarte, M., Condit, R., Canham, C. D., and Hubbell, S. P. (2004). A spatially explicit model of sapling growth in a tropical forest: does the identity of neighbours matter? J. Ecol. 92, 348–360. doi: 10.1111/j.0022-0477.2004.00867.x

CrossRef Full Text | Google Scholar

Uusitalo, L., Kuikka, S., and Romakkaniemi, A. (2005). Estimation of Atlantic salmon smolt carrying capacity of rivers using expert knowledge. ICES J. Mar. Sci. 62, 708–722. doi: 10.1016/j.icesjms.2005.02.005

CrossRef Full Text | Google Scholar

van Mantgem, P. J., Stephenson, N. L., Byrne, J. C., Daniels, L. D., Franklin, J. F., Fulé, P. Z., et al. (2009). Widespread increase of tree mortality rates in the western United States. Science 323, 521–524. doi: 10.1126/science.1165000

PubMed Abstract | CrossRef Full Text | Google Scholar

Vizcaíno-Palomar, N., Ibáñez, I., González-Martínez, S. C., Zavala, M. A., and Alía, R. (2016). Adaptation and plasticity in aboveground allometry variation of four pine species along environmental gradients. Ecol. Evol. 6, 7561–7573. doi: 10.1002/ece3.2153

PubMed Abstract | CrossRef Full Text | Google Scholar

Vygodskaya, N. N., Schulze, E. D., Tchebakova, N. M., Karpachevskii, L. O., Kozlov, D., Sidorov, K. N., et al. (2002). Climatic control of stand thinning in unmanaged spruce forests of the southern taiga in European Russia. Tellus. B. 54, 443–461. doi: 10.3402/tellusb.v54i5.16680

CrossRef Full Text | Google Scholar

Wang, X., Comita, L. S., Hao, Z., Davies, S. J., Ye, J., Lin, F., et al. (2012). Local-scale drivers of tree survival in a temperate forest. PLoS One 7:e29469. doi: 10.1371/journal.pone.0029469

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Zhang, X., Chhin, S., Zhang, J., and Duan, A. (2021). Disentangling the effects of stand and climatic variables on forest productivity of Chinese fir plantations in subtropical China using a random forest algorithm. Agric. For. Meteorol. 304-305:108412. doi: 10.1016/j.agrformet.2021.108412

CrossRef Full Text | Google Scholar

Wang, Z., Zhang, X., Zhang, J., and Chhin, S. (2022). Effects of stand factors on tree growth of Chinese fir in the subtropics of China depends on climate conditions from predictions of a deep learning algorithm: a long-term spacing trial. For. Ecol. Manag. 520:120363. doi: 10.1016/j.foreco.2022.120363

CrossRef Full Text | Google Scholar

Watanabe, M., and Yamaguchi, K. (2003). The EM algorithm and related statistical models. Marcel Dekker, New York.

Google Scholar

Weed, A. S., Ayres, M. P., and Hicke, J. A. (2013). Consequences of climate change for biotic disturbances in north American forests. Ecol. Monogr. 83, 441–470. doi: 10.1890/13-0160.1

CrossRef Full Text | Google Scholar

Weiner, J. (1990). Asymmetric competition in plant populations. Trends Ecol. Evol. 5, 360–364. doi: 10.1016/0169-5347(90)90095-U

CrossRef Full Text | Google Scholar

Witteveen, A., Nane, G. F., Vliegen, I. M. H., Siesling, S., and IJzerman, M. J. (2018). Comparison of logistic regression and Bayesian networks for risk prediction of breast cancer recurrence. Med. Decis. Mak. 38, 822–833. doi: 10.1177/0272989X18790963

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y. Q., Titus, S. J., and Huang, S. (2003). Modeling individual tree mortality for white spruce in Alberta. Ecol. Model. 163, 209–222. doi: 10.1016/S0304-3800(03)00008-5

CrossRef Full Text | Google Scholar

Yao, X., Titus, S. J., and MacDonald, S. E. (2001). A generalized logistic model of individual tree mortality for aspen, white spruce, and lodgepole pine in Alberta mixedwood forests. Can. J. For. Res. 31, 283–291. doi: 10.1139/x00-162

CrossRef Full Text | Google Scholar

Yaussy, D. A., Iverson, L. R., and Matthews, S. N. (2012). Competition and climate affects US hardwood-forest tree mortality. For. Sci. 59, 416–430. doi: 10.5849/forsci.11-047

CrossRef Full Text | Google Scholar

Zeileis, A. (2014). Ineq: measuring inequality, concentration, and poverty. R package version, 0. 2–13.

Google Scholar

Zhang, J., Huang, S., and He, F. (2015a). Half-century evidence from western Canada shows forest dynamics are primarily driven by competition followed by climate. Proc. Natl. Acad. Sci. U. S. A. 112, 4009–4014. doi: 10.1073/pnas.1420844112

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Lei, Y., and Liu, X. (2015b). Modeling stand mortality using Poisson mixture models with mixed-effects. iForest. 8, 333–338. doi: 10.3832/ifor1022-008

CrossRef Full Text | Google Scholar

Zhang, X., Cao, Q. V., Duan, A., and Zhang, J. (2017). Modeling tree mortality in relation to climate, initial planting density, and competition in Chinese fir plantations using a Bayesian logistic multilevel method. Can. J. For. Res. 47, 1278–1285. doi: 10.1139/cjfr-2017-0215

CrossRef Full Text | Google Scholar

Zhang, X., Chhin, S., Fu, L., Lu, L., Duan, A., and Zhang, J. (2019). Climate-sensitive tree height-diameter allometry for Chinese fir in southern China. Forestry 92, 167–176. doi: 10.1093/forestry/cpy043

CrossRef Full Text | Google Scholar

Zhang, X., Duan, A., Zhang, J., and Muldoon, M. R. (2013). Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method. PLoS One 8:e79868. doi: 10.1371/journal.pone.0079868

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Lei, Y., Cao, Q. V., Chen, X., and Liu, X. (2011). Improving tree survival prediction with forecast combination and disaggregation. Can. J. For. Res. 41, 1928–1935. doi: 10.1139/x11-109

CrossRef Full Text | Google Scholar

Zhang, X., Lei, Y., Ma, Z., Kneeshaw, D., and Peng, C. (2014). Insect-induced tree mortality of boreal forests in eastern Canada under a changing climate. Ecol. Evol. 4, 2384–2394. doi: 10.1002/ece3.988

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Wang, Z., Chhin, S., Wang, H., Duan, A., and Zhang, J. (2020). Relative contributions of competition, stand structure, age, and climate factors to tree mortality of Chinese fir plantations: long-term spacing trials in southern China. For. Ecol. Manag. 465:118103. doi: 10.1016/j.foreco.2020.118103

CrossRef Full Text | Google Scholar

Zhao, Q., Yu, S., Zhao, F., Tian, L., and Zhao, Z. (2019). Comparison of machine learning algorithms for forest parameter estimations and application for forest quality assessments. For. Ecol. Manag. 434, 224–234. doi: 10.1016/j.foreco.2018.12.019

CrossRef Full Text | Google Scholar

Zheng, L., Shi, P., Song, M., Zhou, T., Zong, N., and Zhang, X. (2021). Climate sensitivity of high altitude tree growth across the Hindu Kush Himalaya. For. Ecol. Manag. 486:118963. doi: 10.1016/j.foreco.2021.118963

CrossRef Full Text | Google Scholar

Zou, X., and Yue, W. L. (2017). A Bayesian network approach to causation analysis of road accidents using Netica. J. Adv. Transport. 2017, 1–18. doi: 10.1155/2017/2525481

CrossRef Full Text | Google Scholar