Allometric Models to Estimate Carbon Content in Arecaceae Based on Seven Species of Neotropical Palms

We present allometric models for estimating total carbon content and above ground carbon (AGC) for the Arecaceae family, and for seven abundant neotropical palm species: the canopy species Socratea exorrhiza (n = 10) and Iriartea deltoidea (n = 10), the sub-canopy palm Euterpe precatoria (n = 10), and the understory species Asterogyne martiana (n = 15), Prestoea decurrens (n = 10), Geonoma interrupta (n = 10), and Chamaedorea tepejilote (n = 22). Understanding the allometry of functional groups such as palms is critical for improving carbon stocks estimates in tropical forests and determining how allometric differences affect species functional diversity. The research was carried out in the tropical rainforests of the Caribbean slope of Costa Rica. We harvested 87 palms of a wide range of sizes, and separated them into roots, stems, and leaves, measured their fresh and dry biomass, and calculated their carbon content, tissue density, and dry mass fraction (dmf). Our general palm model estimating total carbon content based on these seven species and 87 samples accounted for 92% of the variation across species. We generated a similar model to estimate AGC and explained 91% of the variation. We compared our AGC model with two models used to estimate palm carbon content: Goodman et al. (2013)’s and Chave et al. (2014)’s models and found that all three converged on the estimation of AGC although our model was the most parsimonious because it achieved the same efficiency with only two variables, stem diameter and stem height. To improve the accuracy of allometric models we need to incorporate more species, a greater diversity of growth forms, a wider range of sizes, a larger sample size, and more diversity of habitats dominated by palms. Estimating carbon content using allometric approaches could benefit from more consistency in data collection across plant groups.

Introduction

Tropical forests are important carbon sinks, influencing the atmospheric concentration of CO₂ and thus playing a significant role in mitigating the consequences of climate change (Houghton, 2007; Saatchi et al., 2011; Goers et al., 2012). However, as logging, land-use changes, droughts, and forest fires reduce their ability to absorb and store carbon, these ecosystems can become net carbon sources (Brando et al., 2019; Friedlingstein et al., 2020). To better understand how different species, ontogenetic stages, and life forms contribute to carbon sequestration in terrestrial ecosystems, we must refine methodologies for quantifying carbon inventories in tropical forests, as well as expand the information on plant groups other than trees (Dewar, 1991; Dewar and Cannell, 1992; Brown, 1997; Achard et al., 2004).

There are several methods for estimating carbon stocks in tropical forests (Zhang et al., 2012). Remote sensing techniques enable low-cost monitoring of large areas (Jucker et al., 2017; Rodríguez-Veiga et al., 2019), but are limited by field validation using ground-based techniques. Traditional allometric methods, on the other hand, are time-consuming and often expensive. These methods are based on regression models that relate morphological measurements to biomass or stored carbon (Hairiah et al., 2001; Chave et al., 2005, 2014; Montero and Montagnini, 2005; Zhang et al., 2012), and can use morphological traits available in extensive databases (Chave et al., 2005; Curtis, 2008; Lal, 2008; Lorenz and Lal, 2010; Kissling et al., 2019). However, most allometric studies were developed for woody dicotyledonous trees, particularly the most common and commercially important species (Brown, 1997; Hairiah et al., 2001; Chave et al., 2005, 2014; Zhang et al., 2012), and typically include only a handful of individuals of a limited size range per species and restricted geographic range, and have excluded life forms such as lianas, hemiepiphytes, ferns, and palms (Clark et al., 2001; Chave et al., 2005, 2014; Jucker et al., 2017). Our understanding of the biomass contribution of different life forms is thus very limited because few studies have considered them in their biomass inventories (Saldarriaga et al., 1988; Hughes et al., 1999; Nascimento and Laurance, 2002; Lima et al., 2012).

With over 2,600 species and 181 genera, palms (Arecaceae) are one of the most diverse and extensively distributed plant families in tropical and subtropical environments (Baker and Dransfield, 2016). They dominate many tropical ecosystems (Mejia and Kahn, 1990; Myers, 2013). Seasonally or permanently inundated wetlands, such as the “aguajales” of the Peruvian Amazon (dominated by Mauritia flexuosa, Sampaio et al., 2008), the “yolillales” of Costa Rica (dominated by Raphia taedigera, Serrano-Sandí et al., 2013; Yaap et al., 2015), and peatlands in tropical swamp forests of the Congo basin (some dominated by R. laurentii and R. hookeri), are important soil carbon reservoirs (Lähteenoja et al., 2009; Dargie et al., 2017). Due to their abundance in the Amazon lowlands, palms have been considered “hyperdominant” elements (ter Steege et al., 2013), with seven out of the 20 most abundant species being palms. In the tropical rainforest of La Selva Biological Station in Costa Rica, palms account for 5.4% of AGB, but make up 25% of stems ≥ 10 cm DBH (Clark and Clark, 2000). Although palms contribute a small percentage of above ground biomass (AGB) in neotropical rainforests (ranging from 0.44% in Manaus, Brazil, DeWalt and Chave, 2004, to 10.9% at the Luquillo tropical rainforest in Puerto Rico, which is dominated by the palm Prestoea montana, Frangi and Lugo, 1985) their high abundance ensures a significant role in forest structure and function (ter Steege et al., 2013; Boukili and Chazdon, 2017). Palms, for example, play an important role in food webs by providing habitat and food for a variety of animal species (Zona and Henderson, 1989; Howard et al., 2001; Onstein et al., 2017). Thus, they provide key resources for seed dispersers, which in turn secure the dispersal of old growth canopy species that store most of the carbon in mature forests (Bello et al., 2015). This is an example of how functional diversity (i.e., the variety and number of species that fulfill different functional roles that influence ecosystem functioning, Petchey and Gaston, 2006) affect carbon sequestration. Palms are also valuable to many human groups who use them as raw materials for construction, food, drink, clothing, fuel, medicine, and fibers (Jones, 1995; Henderson, 2002; Dransfield et al., 2008; Sylvester et al., 2012). To understand the link between carbon stocks and functional diversity it is essential to comprehend how the allometry and carbon sequestration of groups like palms differ from that of dicotyledonous woody plants.

Despite their critical functional roles, palms have been excluded from most tropical forest carbon stock inventories (DeWalt and Chave, 2004; Chave et al., 2005; Lorenz and Lal, 2010), as well as from comprehensive allometric analyses of diameter vs. height relationships (Feldpausch et al., 2011). The few studies that have generated allometric equations to estimate carbon sequestration in tropical forest palms are limited to the nine wetland and terra firme species of Goodman et al. (2013), Euterpe precatoria (Da Silva et al., 2015) and Astrocaryum mexicanum (Hughes et al., 1999), as well as commercially important species, such as peach palm, Bactris gasipaes (Ares et al., 2002), oil palm, Elaeis guineensis (Thenkabail et al., 2004; Syahrinudin., 2005; Leblanc et al., 2006; Ekadinata et al., 2010; Khasanah et al., 2012; Pulhin et al., 2014), the betel nut palm, Areca catechu (i.e., Das et al., 2021), and coconut, Cocos nucifera (Zahabu et al., 2018). These latter studies have been conducted mostly in monocrop plantations. Palms, as monocots, have a different structure, allometry, and strategy of resource use than trees (Tomlinson, 2006, 2011). With a few exceptions, palms are monopodial and lack aerial branching, have only one shoot meristem, and lack dormancy and secondary growth. In palm species where stem diameter and stem height show a significant relationship, diameter increases through sustained primary growth (i.e., through the division, lignification, and expansion of parenchyma cells, which also differentiate into fibers, Tomlinson, 2011). Furthermore, palms show higher leaf longevity and leaf construction costs than dicotyledonous trees (Renninger and Phillips, 2016), which have smaller leaves than palms and may drop leaflets rather than the entire frond to acclimate to new light conditions.

The goals of this research are: (a) to generate allometric models to estimate carbon content in seven species of neotropical palms from different forest strata, (b) to produce general models to estimate above-ground carbon and total carbon for the family Arecaceae based on these species using measurements commonly taken in forest inventories, and (c) to compare our models with two of the most widely used models to estimate the contribution of palms to carbon storage: the Goodman et al. (2013)’s model, developed for a subset of nine species of neotropical palms, and the pantropical model of Chave et al. (2014), developed for dicotyledonous trees.

We expected that the diameter and stem height would be the best predictors of carbon content, because they are related to biomass accumulation (Goodman et al., 2013), are functionally linked to carbon sequestration, determine mechanical support (Avalos et al., 2019), and reflect palm size. We do not expect wood density (or the density of the sclerotized tissue in palms) to be a good predictor of carbon content because palms do not develop wood; instead, they have a sclerotized tissue that is often unevenly distributed along the stem, and which increases in density and mechanical strength from the base and the stem periphery toward the crown (Rich, 1986; Henderson, 2002). We also expected that using the Chave et al. (2014)’s model, which was developed for trees, would lead to an erroneous estimation of carbon storage in palms, due to the significant structural and allometric differences between dicotyledonous trees and palms, and the importance that this model places on wood density.

It is essential to increase the knowledge on the allometry of functional groups like palms, not only for developing more accurate estimates of carbon stocks in tropical forests, but also for understanding the ecological basis of species differences in morphological structure and determining how allometry drives resource allocation and plant responses to environmental gradients, influencing species diversity (Weiner, 2004; Vasseur et al., 2012).

Materials and Methods

Study Site

Palms were harvested in three tropical rain forest sites in the Caribbean lowlands of Costa Rica (Figure 1). The first two were La Selva Biological Station (10°26’N – 83°59’W, 30–150 masl, annual precipitation 4,162 mm) and Tirimbina Biological Reserve (10°24’N – 84°06W, 180–220 masl, annual precipitation 3,833 mm), both situated in Sarapiquí, Heredia. The third site was the lowland forest of the agroecological farm El Progreso (10°30’35” N – 83°44’39” W, 45 masl, annual precipitation of 4,000 to 5,000 mm), located in Pococí, Limón. The three sites present an average daily temperature of 25°C and have a weak climatic seasonality, with November, December and February being the rainiest months (McDade et al., 1994).

FIGURE 1

Figure 1. Location of study sites in the lowland rainforests of the NE Caribbean slope of Costa Rica.

Study Species

We selected four understory and three canopy palm species representing a wide range of growth forms and regeneration strategies. Understory species included Prestoea decurrens (n = 10), Chamaedorea tepejilote (n = 22), Geonoma interrupta (n = 10), and Asterogyne martiana (n = 15). Prestoea decurrens (Nicaragua to Ecuador, 0–900 masl), is a clonal species reaching 10 m in height in the tallest individuals (Grayum, 2003). Chamaedorea tepejilote (S Mexico to Colombia, 0–1,600 masl) is a dioecious species which can grow up to 5 m (Castillo-Mont et al., 1994; Grayum, 2003). Geonoma interrupta (S Mexico to Peru, 0–850 masl) has a solitary stem and may reach 6 m in height (or over 10 m in exceptional cases), being considered as one of the tallest species in the genus (Grayum, 2003). Finally, Asterogyne martiana (Belize to Ecuador, 0–1,000 masl) is shade-tolerant species with a decumbent stem often reaching 2 m in height, and with simple, bifid leaves. The canopy species Socratea exorrhiza (n = 10, S Nicaragua to Brazil, 0–750 masl) and Iriartea deltoidea (n = 10, SE Nicaragua to Brazil, 0–800 masl) can reach 25 and 30 m of stem height, respectively, and are characteristic canopy components of mature forests (Grayum, 2003). Both species have a cone of stilt roots, although roots in I. deltoidea are clustered at the base of the stem and grow up to 1.5 m above ground, and in S. exorrhiza roots are well-separated, covered by spines, and can grow up to 4 m above the ground (Henderson et al., 1995). Both species show plasticity in the diameter vs. height allometry associated with geographic location and terrain slope (Avalos et al., 2019). Euterpe precatoria (n = 10, Belize to Bolivia, 0–1,150 masl) var longevaginata (Henderson, 1995) is often classified as a subcanopy species (Zuidema and Boot, 2000). It is a single-stemmed palm that can reach 26 m in height, developing a stilt root cone that in extreme cases may reach over 2 m above the ground (Avalos and Schneider, 2011). It is a cryptic pioneer since it regenerates under disturbed conditions like canopy gaps but can also withstand shade and regenerates along with the forest as the gap closes (Avalos, 2019).

Palm Harvesting, Morphological Measurements, and Biomass Estimation

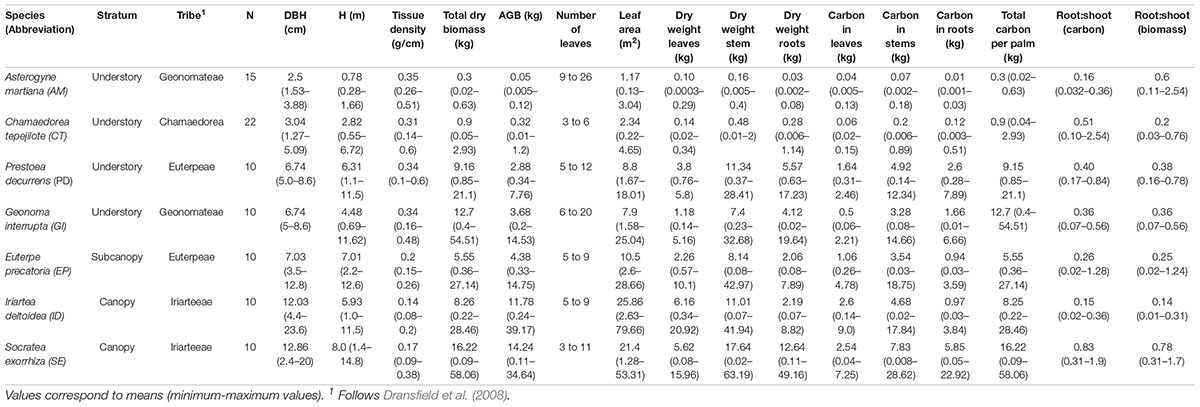
From September 2013 to May 2015, we harvested 87 palms, taking care to represent the full range of size classes representative of the population structure of each species (Appendix Table 1). We selected individual palms to obtain a sufficient spread of the data and reflect the size classes characteristic of the population of each species. We measured stem diameter at 1.3 m above the ground (DBH), at half the stem length in palms less than 1.3 m in height, or immediately above the stilt roots in palms with a stilt root cone higher than 1.3 m. We termed this measurement in all cases as diameter (abbreviated as diam), since strictly DBH was not measured in all cases. Harvested palms were separated into modules (stems, roots, and leaves) and we measured the total fresh biomass of each module using a Pesola^® Macro-Line Spring Scale (30 ± 0.25 kg). We carefully dug out the roots, collected all the root material to the extent that was possible, including fine roots (2–5 mm in diameter). In instances in which it was difficult to extract all the roots, due to their size or depth, a representative section was extracted, and from this, we estimated the total root biomass. We washed out the roots in the field and sun-dried them before weighing them in the laboratory. To determine the dry biomass (and carbon content) we collected 300 mg samples from each module. For leaves, this sample included one young, one intermediate, and one mature frond, determined according to their position from the tip of the apical meristem. In stems, the biomass sample was collected from the base, middle, and upper parts of the stem until reaching the base of the leaf crown. The total stem height of the palm (H_bc) was measured from stem base above the stilt roots (if present) to the base of the crown We also measured the height of the stilt root cone in stilt-rooted palms (S. exorrhiza, I. deltoidea, E. precatoria, and P. decurrens) from the ground to the base of the stem (H_sr). In palms without stilt roots, H_bc corresponded to the total length of the stem, from the connection with the first root to the base of the crown. In A. martiana H_bc also included the section of the subterranean stem from the first root to the insertion of the oldest frond. Finally, to estimate the tissue density of the stem (specific gravity, ρ), we used a Haglof 2-Thread Increment Borer, to collect a tissue sample from the stem, following the methods of Chave et al. (2005). Accordingly, we selected a point of entry for the increment borer near the base of the stem, in the middle, and near the base of the palm crown to place the borer at the center of the internode and carry out the perforation. Once the sclerotized tissue was extracted, the sample was placed in a test tube, sealed, and transferred back to the laboratory for the estimation of tissue density.

Estimation of Carbon Content and Stem Tissue Density

We dried the samples in an oven at 65°C for 48 h or until constant weight. Once dried, we ground the samples and determined their carbon content using an automatic analyzer TruSpec CN, LECO Corporation, at the Department of Systematic Botany at the University of Ulm, Germany, and an automatic elemental carbon and nitrogen analyzer, VarioMacrocube, at the University of Costa Rica. The magnitude of the carbon content in g was calculated by multiplying the total dry weight of each module by the percentage of carbon obtained in the laboratory and adding up all the dry biomass per individual palm. The average carbon fraction for the palms analyzed here was 43.9% ± 1.28 (Cambronero et al., 2018), but for our models we used the average carbon fraction obtained for each species. Stem tissue density (specific gravity, ρ) was calculated as the ratio of dry biomass (g) over volume (cm³). Volume was measured by water displacement. A summary table of all measured morphological characters is shown in (Appendix Table 1).

Calculation of Species-Specific Allometric Models for Estimating Carbon Content

Palms were selected to represent a broad range of sizes characteristic of the species in the field. Thus, our sampling in these regards was not random and corresponded to an ordinary least squares regression (model I) since the magnitude of the predictor variable was selected by the experimenter. As a result, a model II regression with a random predictor variable was not practical.

We developed models including a combination of variables commonly measured under field conditions, such as diameter and stem height, aiming for simplicity. Therefore, only linear (or log-transformed) models were tested, and we did not consider non-linear models even though they could have provided better fits because we consider that linear (and logarithmic) models better represented the mechanistic relationship between the allometric variables.

We included stem tissue density to investigate the significance of this parameter in palms, even though measuring it requires access to instrumentation that may not be readily available in the field. To predict carbon content, we calculated linear and logarithmic backward stepwise regressions between the natural logarithm of the total amount of carbon content in kg per palm (LnC, response variable), and a set of explanatory variables including diameter in cm (diam), total stem height from the base of the stem to the base of the leaf crown (H_bc, m, excluding stilt roots if present), the height of the stilt root cone above the ground (H_sr) if present, the dry mass fraction or tissue moisture (dry mass over fresh mass, dmf), and stem tissue density (g cm^–3). This latter parameter was calculated so that we could compare our family-level models to those of Goodman et al. (2013), who include this variable. The predictor variables were included in the models with their Ln-transformed values as well as in their linear scales. We performed backward stepwise regression analysis for each species, and then chose the most parsimonious general regression models for all seven species based on the magnitudes of the R² value, the mean square of error (MSE), and the Akaike Information Criterion (AIC). The chosen models were listed in decreasing order of R², and the lowest MSE and AIC values. We chose models with at least one size-related variable (i.e., diameter and height). We discarded models that were not statistically significant or had R² values < 0.8 and included models with a single variable only if the model was statistically significant. Because the response variable required a logarithmic transformation, a correction factor was calculated following Sprugel (1983). The correction factor was used to remove the systematic bias introduced by the logarithmic transformation. The predicted value coming from the regression was multiplied by this correction factor, which is calculated as:

$CF=e^{\frac{\left({\left(SEE\right)}^2\right)}{2}}(1)$

Where SEE = standard error of estimate of the regression (the absolute value of lny_i in boldface):

$SEE=\sqrt{\sum {\left(lnyi-\mathbf{\text{lnyi}}\right)}^2/(N-2)}$

Allometric Models for Estimating Total Carbon Content and Above Ground Carbon at the Family Level

We combined all the data from the seven species to generate a series of family-level models to estimate total carbon per palm. The response variable was the natural logarithm of the total amount of carbon content in kg per palm (LnC), and the predictor variables were the set of morphological variables described above (except for Hsr, which was not present in all palms). We applied the same backward stepwise regression protocol to find the most parsimonious models based on the magnitudes of the R² value, MSE, the AIC, and in this case, the Mean Absolute Error (MAE), which is the average absolute difference between predicted and observed values. We compared the saturated model including all the predictor variables, with simpler, more parsimonious models coming from the stepwise regression, using a k-fold cross-validation protocol (James et al., 2013) where k = 8. We randomly divided the data into eight-folds of approximately equal size, one of which served as the test set and the rest as the training set. The resampling process was carried out in R using the library “caret,” which allowed us to estimate the value of MAE, in addition to the R², MSE and AIC values, and obtained the most parsimonious models by considering the number of predictor variables and the magnitude of the selection parameters (R², MSE, AIC). We used a similar cross-validation procedure to generate the AGC models.

Comparison Between Models Estimating Above Ground Carbon for Arecaceae

To compare our Arecaceae AGC family model with those of Goodman et al. (2013) and Chave et al. (2014), we estimated the aboveground carbon content (AGC in kg) by adding the carbon content fractions of stems and leaves without considering the carbon content of roots (AGB). Goodman et al. (2013)’s model estimates AGB for nine species of neotropical palms, including E. precatoria, I. deltoidea and S. exorrhiza, examined here, using AGB^0.25 = 0.56*(dmfD²H_stem)^0.25, where dmf is the dry mass fraction defined above, D is DBH, and H_stem is the height of the palm from the ground to the highest leaf. To determine AGC, we applied the conversion factor of 50% of the dry biomass, which has traditionally been used to determine the carbon accumulated in trees (Chave et al., 2005; Houghton, 2007; Lorenz and Lal, 2010). This model is only valid for individuals with a stem height ≥ 1 m. The pantropical model of Chave et al. (2014) estimates AGB using 0.0673 (ρD²H)^0.976, where ρ corresponds to wood stem density (g cm^–3 or tissue density for palms), D is the DBH (cm), and H is the total height (m); this model is based on data from 4,004 trees ≥ 5 cm DBH. AGC was then calculated by applying the carbon fraction of 50% to AGB as in the case of Goodman et al. (2013)’s model. We did not include other models developed for palms such as the one by Frangi and Lugo (1985), or by Brown (1997) since these had lower performance and lower R² values when applied to our data (0.78 and 0.79, respectively).

We used the actual carbon fraction per palm species measured directly here (Cambronero et al., 2018) for the comparison with Goodman et al. (2013) and Chave et al. (2014) models. In both cases, the accuracy of all models was contrasted against the observed values of AGC using the R² value and the magnitude of their residuals. We used natural logarithmic models for the comparisons. For all regression analyses we used R software (R Core Team, 2022), and the library MASS with the function stepAIC().

Results

Species-Level Allometric Models to Estimate Total Carbon Content

Canopy and Subcanopy Species

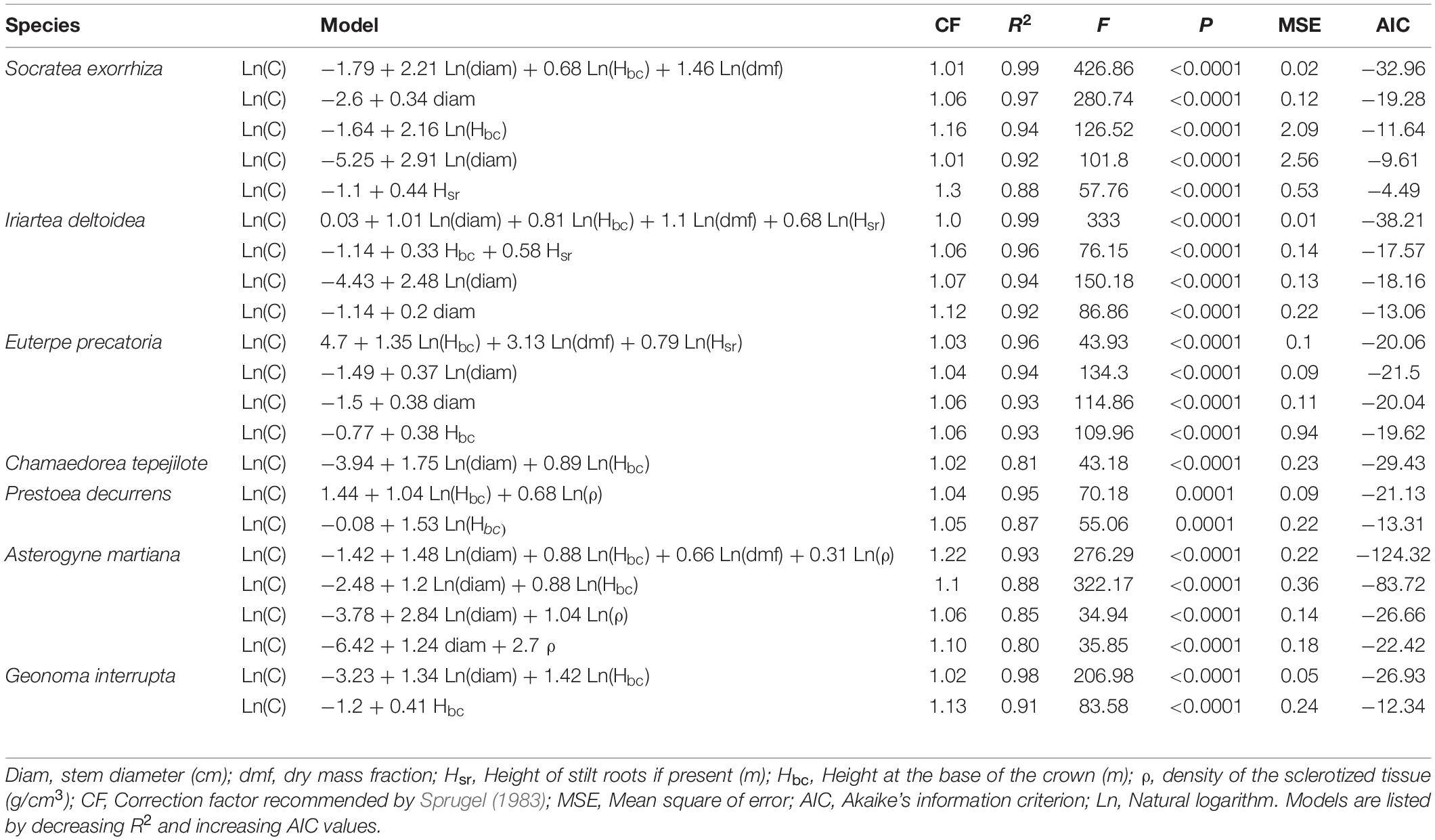
In S. exorrhiza the most parsimonious model for predicting total carbon content had the linear form of diameter. Entering other variables in the model (total height and stem height from the base, in linear and logarithmic forms), in addition to Ln(diam), produced similar R² values but not a lower AIC (Table 1). In I. deltoidea, the most parsimonious model had logarithmic forms of diameter and total height. For the subcanopy palm, E. precatoria, the most parsimonious models had the logarithmic form of total height and diameter. As expected, height and diameter were the most frequent variables in the models to predict carbon content, while tissue density explained the variation in carbon content only in the understory species P. decurrens and A. martiana.

TABLE 1

Table 1. Models to estimate carbon content (C; Ln kg), in seven species of neotropical palms.

Understory Species

In C. tepejilote, we did not find differences in morphological parameters among male and female plants, and thus, the analyses were done for the overall species. In this species, the best-fit model included the logarithmic form of total height and diameter. In P. decurrens, the best-fit model had the logarithmic forms of stem length and tissue density (R² value = 0.95). For A. martiana, the model with the highest R² had the logarithmic forms of the four predictor variables diameter, total height, dmf and tissue density. Finally, G. interrupta showed the highest fit for models including stem height (logarithmic and linear, with a R² of 0.98 and 0.91, respectively).

Family-Level Model to Estimate Total Carbon and Above-Ground Carbon Content (AGC)

To predict total carbon content the saturated model (model 1, Table 2) included all predictor variables and served as a baseline against which the other models were compared. This model had the highest R², and the lowest MSE, AIC and MAE values, but its practical value was low. Models 2 and 3, which included logarithmic values of tissue density, diameter, stem length, and dmf, explained a similar proportion of the variation with fewer variables. From this point of view, model 4 is the most parsimonious since it reached an R² value comparable to that of the previous models with only two variables (diameter and stem height). MAE values for models 2, 3, and 4 were very similar showing that these models were not overfit. Model 5 reached the R² threshold value of 0.8 but its AIC and MAE values were the highest.

TABLE 2

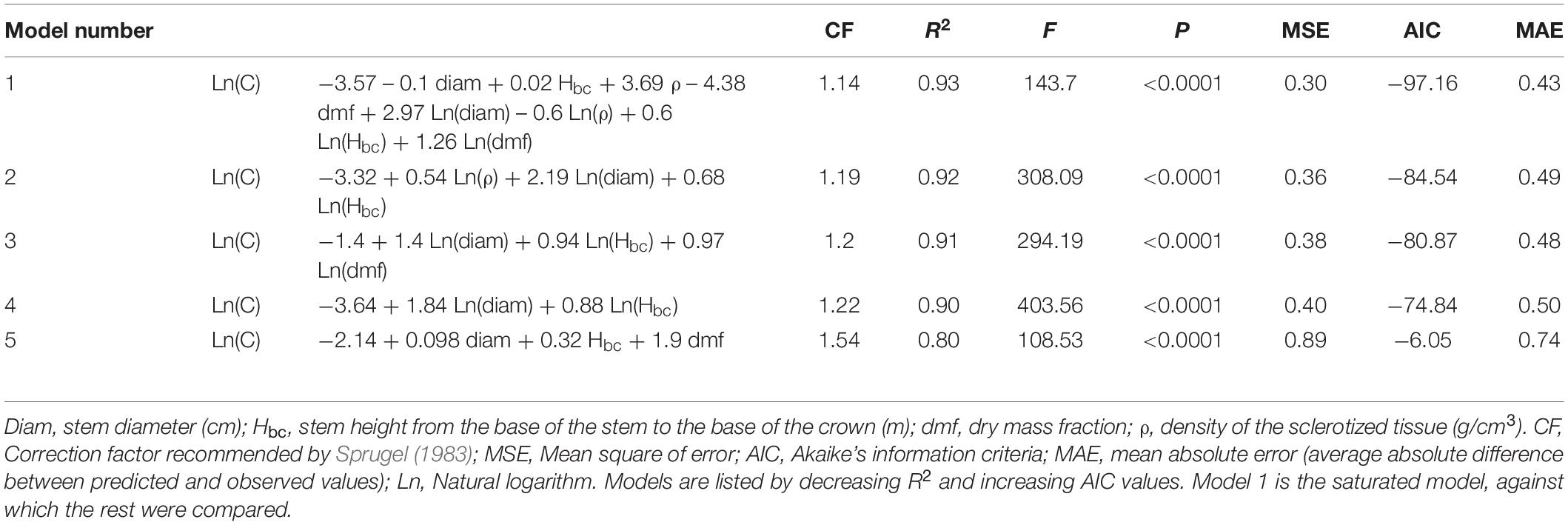
Table 2. General allometric models to estimate total carbon content (C; kg) based on seven species of neotropical palms.

We followed a similar procedure to estimate AGC at the family level (Table 3). As in the previous case, the saturated model (model 1, Table 3) included all the predictor variables, serving as a baseline against which the other models could be compared. Model 2 explained a portion of the variation in Ln (AGC) similar to that of models 1 and 3, with lower MSE, AIC, and MAE values, but with an additional variable [Ln(dmf)] in comparison to model 3. Model 3 was the most parsimonious, since with two variables (Lndiam and LnH_bc) maintained a high R² (0.91) and low AIC and MAE. Model 4 met the threshold value of R² ≥ 0.80, but its efficiency in predicting Ln(AGC) was low.

TABLE 3

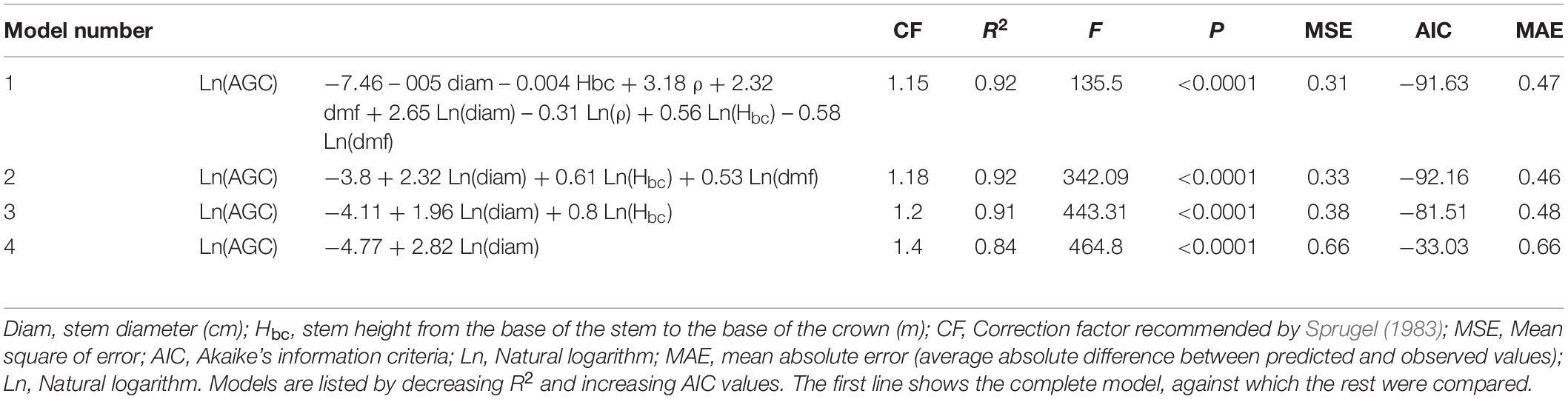
Table 3. General allometric models to estimate above-ground carbon content (AGC; kg) based on seven species of neotropical palms.

We then compared model 3 to the pantropical model proposed by Chave et al. (2014) and the palm model of Goodman et al. (2013) using Ln (AGC). All three models predicted the observed Ln (AGC) with high R² values ranging from 0.89 to 0.913 (Figure 2). Our model had the highest R² value (0.913) followed by Goodman et al. (2013)’s with 0.875 and Chave et al. (2014) with 0.890. We consider all three models have similar ability to predict the AGC of the palm species analyzed here although ours is the most parsimonious because it uses two variables (diameter and stem height) vs. the three variables of Goodman et al. (2013), diameter, stem height and dmf, and the three variables of the Chave et al. (2014) model (diameter, height, and tissue density). Contrary to our prediction, the Chave et al. (2014)’s model satisfactorily predicted the stored AGC of palms despite of being a model generated for dicotyledonous trees.

FIGURE 2

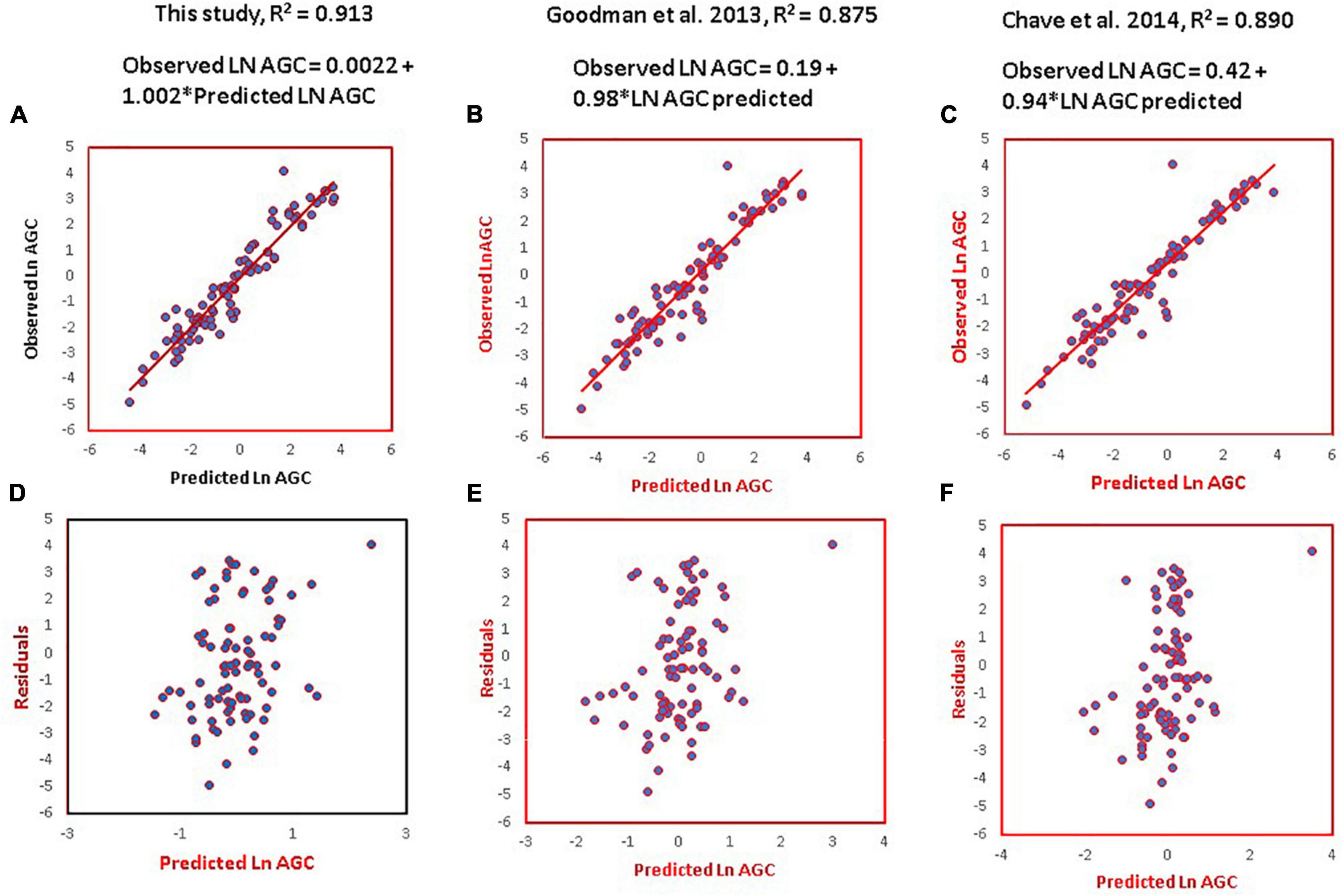
Figure 2. Predicted vs. observed values (A–C) and residuals (D–F) of the Ln of AGC in kg following the general palm model proposed in this study, Goodman et al. (2013)’s model, and the pantropical model of Chave et al. (2014).

Discussion

Developing allometric models specific for palms will improve the accuracy of the estimates of tropical forest carbon stocks, as existing models need to be refined to include this and other life forms (e.g., lianas, epiphytes, tree ferns), that, while not as massive as trees, play essential ecological roles and vary in abundance depending on forest type, elevation, and edaphic factors (Chazdon, 1996). Palms have a major role as keystone plant resources providing food, nesting sites, and habitat for a wide range of vertebrate species (van der Hoek et al., 2019), many of which are seed dispersers and seed predators that regulate plant species diversity and carbon storage (Bello et al., 2015) and contribute to the maintenance of healthy food webs. Palms may account for a higher proportion of AGB in wetlands where they are the dominant group and are established on soils that store large amounts of carbon (Lähteenoja et al., 2009). Therefore, while palms account for a small proportion of neotropical rainforest carbon stocks, they are functionally important by affecting forest succession (Boukili and Chazdon, 2017), food webs (Zona and Henderson, 1989), and varying their abundance according to topography and edaphic conditions, being dominant elements in wetlands (Myers, 2013). Allometric analyses incorporating palm biomass in studies of carbon stocks in tropical forests are still rare (but see Nascimento and Laurance, 2002; Lima et al., 2012); their inclusion would not only improve the accuracy of such models, but would also broaden our understanding of the mechanistic basis of key functional traits, such as the limits of the allometry of the stem diameter versus stem height in palms, and the allocation strategies of plants lacking a vascular cambium in response to wide environmental gradients (Avalos et al., 2019).

Currently, family-level models proposed for Arecaceae are based on a small number of species, a small number of tribes represented, and a limited range of sizes of harvested individuals (i.e., Goodman et al., 2013; and this study). Many canopy palms frequently show heights that exceed the ranges included in these studies. Large individuals are difficult to harvest, and many field sites do not allow it. In addition to sample size bias, allometric relationships may change geographically due to environmental conditions (Avalos et al., 2019), such topography, edaphic factors, successional stage, climate, and nutrient availability (Eiserhardt et al., 2011). The species composition of the palms also affects the accuracy of a family-level allometric model.

The accuracy of allometric models is also limited by an incomplete inventory of functional traits for tropical plants, particularly palms. Tissue density (Rich, 1986, 1987), dmf, slenderness ratio, leaf toughness, and specific leaf area (SLA), as well as stem height and gas exchange parameters, are rarely inventoried for palms as a group or are limited to specific species (i.e., Araus and Hogan, 1994; Da Silva et al., 2015; Renninger and Phillips, 2016). Much less is known about how these traits change depending on environmental and geographic factors, ontogenetic stage, and palm size (but see Chazdon, 1986a,b). Although Kissling et al. (2019) provide a highly comprehensive compilation, functional trait databases still lack data for palms and tropical plants in general. These databases are built using a few individuals per species¹, and frequently lack metadata. It is necessary to incorporate more species, a larger sample size per species, a wider range of sizes, and phylogenetic bias corrections. Finally, many tropical habitats where palms are very abundant and dominant (Myers, 2013) are not regularly inventoried for carbon stocks.

Developing species-specific models has intrinsic value because it increases the level of information at the geographic level and enriches databases, improving the accuracy of carbon inventories in tropical forests, particularly by adding information on a group of plants as abundant as palms. Our first hypothesis was correct because diameter and height were the most common variables in the models and had a significant role in predicting total carbon content as well as AGC. Because these variables reflect the size of the organism it was logical that they would be good predictors of carbon sequestration. Other functional characteristics, such as dmf and tissue density, had a lower predictive value and were more associated with biomass partitioning rather than organismal size. In general, their influence on carbon sequestration was limited across the species studied here. Dmf and tissue density were correlated in Goodman et al. (2013)’s palm assemblage, and ultimately improved their mixed species model estimates of AGB, although they did not measure tissue density directly and instead used data from online databases. Chave et al. (2014)’s model incorporated wood density, and once applied to our subset of palm species, the results were very similar to the general palm family model generated here. The magnitude of the regression slope and degree of residual dispersion for all three models were very similar, but we consider that our model has greater utility value for its application in carbon inventories because it uses diameter and height of the stem, which are commonly measured variables that do not require additional laboratory work, as it is required by the Goodman et al. (2013) and Chave et al. (2014) models that incorporate tissue density and dmf, respectively.

Standardizing data collection to construct family-specific allometric models is difficult due to the variety of palm growth forms (arborescent, acaulescent, and climbing). We measured total stem height from the base of the stem to the base of the leaf crown (H_bc), whereas other studies (e.g., Goodman et al., 2013; Chave et al., 2014) measured total stem height from the ground to the highest point of the plant, which may include the last leaf, with or without stilt roots, if present. We measured AGB from the base of the stem to the apex of the meristem, excluding the cone of stilt roots; this cone is produced above the ground but we considered it part of the below-ground biomass. Similarly, in A. martiana a portion of the stem grows underground, but we considered it as part of AGB. Dioecious palms, such as C. tepejilote, may differ in biomass allocation between sexes, as demonstrated by Oyama and Dirzo (1988), although they harvested 15 individuals, including male and female plants, as well as juveniles. We found no differences in allometric patterns between male and female plants and juveniles. The study by Oyama and Dirzo (1988) was based on the follow-up of 810 individuals in a more comprehensive demographic study. In other cases, stem height is inferred from species descriptions rather than measured directly (de Castilho et al., 2006). Despite efforts to standardize functional trait measurements (e.g., Perez-Harguindeguy et al., 2013), the emphasis remains on woody plants, with little regard for the structural and morphological diversity of other plant groups such as palms.

Estimation of Root Biomass and Carbon Content

Estimating root biomass and carbon content remains a significant challenge in palm allometric analyses. Because the data is still fragmentary and often limited to a few individual species (e.g., Goodman et al., 2013; Da Silva et al., 2015), much of the information focuses on aerial biomass. In general, the functional ecology of roots is still poorly understood, particularly in terms of the integration of above- and below-ground characters. When resources are scarce, for example, leaf life span does not correlate with fine root longevity (Weemstra et al., 2016). Under these conditions, long-lived leaves are preferred, but fine roots, which are responsible for increasing surface area and absorption capacity, have a high turnover rate. Future research should examine the degree of integration between above-ground and below-ground functional traits (Laliberté, 2017). In our case, as in other studies attempting to estimate root biomass (e.g., Da Silva et al., 2015), obtaining all roots, particularly fine roots, was difficult. Many palm species have shallow roots, which may explain their dominance in flooded environments and very wet forests, which are rich in palm species or are dominated by one or two species, because shallow roots perform better in wet environments (Eiserhardt et al., 2011). There have been few studies estimating root biomass for palms in the tropics (Frangi and Lugo, 1985), so comparative data is scarce (but see Da Silva et al., 2015).

Conclusion

This is the only recent study, following Goodman et al. (2013), to propose a family-level model to estimate not only AGC but also total carbon content per individual for Arecaceae. We also provided individual models for seven of the most common and abundant palm species in tropical rainforests, as well as estimates of their below-ground biomass (Appendix Table 1). Allometric models can be very complex because they include a multitude of variables often related non-linearly. The goal of this study was to simplify the selection of allometric models by considering variables of practical importance and easy to measure in forest inventories, as well as to investigate the role of morphological variables on carbon storage without proposing complex variable combinations. The models proposed here had a logarithmic form, which is consistent with the functional relationship between diameter, stem height, and other palm size traits.

To improve the accuracy of allometric models in general, and specifically for palms, more species, a greater diversity of growth forms, a wider range of sizes, and a larger sample size are required. Palm species that dominate wetlands are still lacking in this regard; despite dominating carbon-rich environments, there are few studies that include them, possibly due to the logistical difficulties of conducting research in flooded environments. Finally, progress in estimating carbon content using allometric approaches, which remains a viable and efficient option for estimating carbon stocks, necessitates greater consistency in data collection across plant groups.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

GA conceived and designed the experiments and wrote the manuscript. MC and CA-V conducted the fieldwork with assistance from GA. GA, MC, and CA-V analyzed the data and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by a research grant from the International Palm Society to MC, and scholarships from the Organization for Tropical Studies (MC and CA-V), the University of Costa Rica (MC), and Tirimbina Biological Reserve (CA-V). The School for Field Studies provided logistic support.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Orlando Vargas facilitated fieldwork at La Selva. Juan Manuel Ley facilitated fieldwork at Tirimbina. Nutrient analyses were facilitated by Floria Bertsch at the Centro de Investigaciones Agronómicas, University of Costa Rica, and by Steven Jansen at the Department of Systematic Botany and Ecology, University of Ulm. The Alpízar Chaves family of El Progreso facilitated work in their property.

Footnotes

1. ^ http://db.worldagroforestry.org

References

Achard, F., Eva, H. D., Mayaux, P., Stibig, H. J., and Belward, A. (2004). Improved estimates of net carbon emissions from land cover change in the tropics for the 1990’s. Global Biogeochem. Cycles 18, 1–11. doi: 10.1029/2003GB002142

CrossRef Full Text | Google Scholar

Araus, J. L., and Hogan, K. P. (1994). Leaf structure and patterns of photoinhibition in two neotropical palms in clearings and forest understory during the dry season. Am. J. Bot. 81, 726–738. doi: 10.1002/j.1537-2197.1994.tb15507.x

CrossRef Full Text | Google Scholar

Ares, A., Boniche, J., Quesada, J. P., Yost, R., Molina, E., and Smyth, T. J. (2002). Estimación de biomasa por métodos alométricos, nutrimentos y carbón en plantaciones de palmito en Costa Rica. Agronomía Costarricense 26, 19–30.

Google Scholar

Avalos, G., and Schneider, R. (2011). Quantification of ramet production in the neotropical palm Euterpe precatoria (Arecaceae) in Costa Rica. Ecotropica 17, 95–102.

Google Scholar

Avalos, G. (2019). Shade tolerance within the context of the successional process in tropical rain forests. Rev. Biol. Trop. 67, 53–77. doi: 10.15517/rbt.v67i2supl.37206

CrossRef Full Text | Google Scholar

Avalos, G., Gei, M., Ríos, L. D., Otárola, M. F., Cambronero, M., Alvarez-Vergnani, C., et al. (2019). Scaling of stem diameter and height allometry in 14 neotropical palm species of different forest strata. Oecologia 190, 757–767. doi: 10.1007/s00442-019-04452-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, W. J., and Dransfield, J. (2016). Beyond Genera Palmarum: progress and prospects in palm systematics. Bot. J. Linn. Soc. 182, 207–233. doi: 10.1111/boj.12401

CrossRef Full Text | Google Scholar

Bello, C., Galetti, M., Pizo, M. A., Magnago, L. F. S., Rocha, M. F., Lima, R. A., et al. (2015). Defaunation affects carbon storage in tropical forests. Sci. Adv. 1:e1501105. doi: 10.1126/sciadv.1501105

PubMed Abstract | CrossRef Full Text | Google Scholar

Boukili, V. K., and Chazdon, R. L. (2017). Environmental filtering, local site factors and landscape context drive changes in functional trait composition during tropical forest succession. Perspect. Plant Ecol. Evol. Syst. 24, 37–47. doi: 10.1016/j.ppees.2016.11.003

CrossRef Full Text | Google Scholar

Brando, P. M., Paolucci, L., Ummenhofer, C. C., Ordway, E. M., Hartmann, H., Cattau, M. E., et al. (2019). Droughts, wildfires, and forest carbon cycling: a pantropical synthesis. Annu. Rev. Earth Planet Sci. 47, 555–581. doi: 10.1146/annurev-earth-082517-010235

CrossRef Full Text | Google Scholar

Brown, S. (1997). Estimating Biomass and Biomass change of Tropical Forests: a primer. FAO Forestry Paper –134. Rome: FAO.

Google Scholar

Cambronero, M., Avalos, G., and Alvarez-Vergnani, C. (2018). Variation in the carbon fraction of seven neotropical palm species of different forest strata. Palms 62, 25–34.

Google Scholar

Castillo-Mont, J. J., Gallardo, N. R., and Johnson, D. V. (1994). The pacaya palm (Chamaedorea tepejilote. Arecaceae) and its food use in Guatemala. Econ. Bot. 48, 68–75. doi: 10.1007/BF02901383

CrossRef Full Text | Google Scholar

Chave, J., Andalo, C., Brown, S., Cairns, M. A., Chambers, J. Q., and Yamakura, T. (2005). Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145, 87–99. doi: 10.1007/s00442-005-0100-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Chave, J., Réjou-Méchain, M., Búrquez, A., Chidumayo, E., Colgan, M., Delitti, W., et al. (2014). Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 20, 3177–3190. doi: 10.1111/gcb.12629

PubMed Abstract | CrossRef Full Text | Google Scholar

Chazdon, R. L. (1986a). Light variation and carbon gain in rain forest understorey palms. J. Ecol. 74, 995–1012. doi: 10.2307/2260229

CrossRef Full Text | Google Scholar

Chazdon, R. L. (1986b). Physiological and morphological basis of shade tolerance in rain forest understory palms. Principes 30, 92–99.

Google Scholar

Chazdon, R. L. (1996). Spatial heterogeneity in tropical forest structure: canopy palms as landscape mosaics. Trends Ecol. Evol. 11, 8–9. doi: 10.1016/0169-5347(96)81057-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Clark, D. B., and Clark, D. A. (2000). Landscape-scale variation in forest structure and biomass in a tropical rain forest. For. Ecol. Manage. 137, 185–198. doi: 10.1016/S0378-1127(99)00327-8

CrossRef Full Text | Google Scholar

Clark, D. A., Brown, S., Kicklighter, D. W., Chambers, J. Q., Thomlinson, J. R., and Ni, J. (2001). Measuring net primary production in forests: concepts and field methods. Ecol. Appl. 11, 356–370. doi: 10.1890/1051-07612001011

CrossRef Full Text | Google Scholar

Curtis, P. S. (2008). “Estimating aboveground carbon in live and standing dead trees,” in Field measurements for Forest Carbon Monitoring, a Landscape-Scale Approach, ed. C. M. Hoover (New York, NY: Springer). 39–44. doi: 10.1007/978-1-4020-8506-2_4

CrossRef Full Text | Google Scholar

Da Silva, F., Suwa, R., Kajimoto, T., Ishizuka, M., Higuchi, N., and Kunert, N. (2015). Allometric equations for estimating biomass of Euterpe precatoria, the most abundant palm species in the Amazon. Forests 6, 450–463. doi: 10.3390/f6020450

CrossRef Full Text | Google Scholar

Dargie, G. C., Lewis, S. L., Lawson, I. T., Mitchard, E. T., Page, S. E., Bocko, Y. E., et al. (2017). Age, extent and carbon storage of the central Congo Basin peatland complex. Nature 542, 86–90. doi: 10.1038/nature21048

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, M., Nath, P. C., Sileshi, G. W., Pandey, R., Nath, A. J., and Das, A. K. (2021). Biomass models for estimating carbon storage in Areca palm plantations. Environ. Sust. Indic. 10:100115. doi: 10.1016/j.indic.2021.100115

CrossRef Full Text | Google Scholar

de Castilho, C. V., Magnusson, W. E., de Araújo, R. N. O., Luizao, R. C., Luizao, F. J., Lima, A. P., et al. (2006). Variation in aboveground tree live biomass in a central Amazonian Forest: effects of soil and topography. For. Ecol. Manage. 234, 85–96. doi: 10.1016/j.foreco.2006.06.024

CrossRef Full Text | Google Scholar

DeWalt, S. J., and Chave, J. (2004). Structure and biomass of four lowland Neotropical forests. Biotropica 36, 7–19. doi: 10.1111/j.1744-7429.2004.tb00291.x

CrossRef Full Text | Google Scholar

Dewar, R. C. (1991). Analytical model of carbon storage in the trees, soils and wood products of managed forests. Tree Physiol. 8, 239–258. doi: 10.1111/j.1744-7429.2004.tb00291.x

CrossRef Full Text | Google Scholar

Dewar, R. C., and Cannell, M. G. R. (1992). Carbon sequestration in the trees, products and soils of forest plantations using UK samples. Tree Physioll. 11, 49–71. doi: 10.1093/treephys/11.1.49

PubMed Abstract | CrossRef Full Text | Google Scholar

Dransfield, J., Uhl, N. W., Amussen, C. B., Baker, W. J., Harley, M. M., and Lewis, C. E. (2008). Genera Palmarum: The Evolution and Classification of Palms. Kew: Kew Publishing. 732.

Google Scholar

Eiserhardt, W. L., Svenning, J. C., Kissling, W. D., and Balslev, H. (2011). Geographical ecology of the palms (Arecaceae): determinants of diversity and distributions across spatial scales. Ann. Bot. 108, 1391–1416. doi: 10.1093/aob/mcr146

PubMed Abstract | CrossRef Full Text | Google Scholar

Ekadinata, A. E., Khasanah, N., Rahayu, S., Budidarsono, S., and van Noordwijk, M. (2010). Carbon Footprint of Indonesian Palm Oil Production: Sample Design and Methodology. Nairobi: World Agroforestry Centre.

Google Scholar

Feldpausch, T. R., Banin, L., Phillips, O. L., Baker, T. R., Lewis, S. L., Quesada, C. A., et al. (2011). Height-diameter allometry of tropical forest trees. Biogeosciences 8, 1081–1106. doi: 10.5194/bg-8-1081-2011

CrossRef Full Text | Google Scholar

Frangi, J. L., and Lugo, A. E. (1985). Ecosystem dynamics of a subtropical floodplain forest. Ecol. Monogr. 55, 351–369. doi: 10.2307/1942582

CrossRef Full Text | Google Scholar

Friedlingstein, P., O’Sullivan, M., Jones, M. W., Andrew, R. M., Hauck, J., Olsen, A., et al. (2020). Global carbon budget 2020. Earth Syst. Sci. Data 12, 3269–3340. doi: 10.5194/essd-12-3269-2020

CrossRef Full Text | Google Scholar

James, G., Hastie, T., Tibshirani, R., and Witten, D. (2013). An Introduction to Statistical Learning: With Applications in R. Berlin: Springer. 431. doi: 10.1007/978-1-4614-7138-7

CrossRef Full Text | Google Scholar

Goers, L., Ashton, M. S., and Tyrrell, M. L. (2012). “Introduction,” in Managing Forest Carbon in a Changing Climate, eds M. S. Ashton, M. L. Tyrrell, D. Spalding, and B. Gentry (New York, NY: Springer) 1–4. doi: 10.1007/978-94-007-2232-3_1

CrossRef Full Text | Google Scholar

Goodman, R., Phillips, O. L., Torres, D., Freitas, L., Tapia-Cortese, S., Monteagudo, A., et al. (2013). Amazon palm biomass and allometry. For. Ecol. Manage. 310, 994–1004. doi: 10.1016/j.foreco.2013.09.045

CrossRef Full Text | Google Scholar

Grayum, M. H. (2003). “Arecaceae,” in Manual de Plantas de Costa Rica, Vol. III, eds B. E. Hammel, M. H. Grayum, C. Herrera, and N. Zamora (St. Louis: Missouri Botanical Garden). 201–293.

Google Scholar

Hairiah, K., Sitompul, S. M., van Noordwijk, M., and Palm, C. (2001). Methods for Sampling Carbon Stocks Above and Below Ground. Nairobi: International Centre for Research in Agroforestry.

Google Scholar

Henderson, A. (1995). The Palms of the Amazon. New York: Oxford University Press. 374.

Google Scholar

Henderson, A., Galeano, G., and Bernal, R. (1995). Field Guide to the Palms of the Americas. New York: Princeton University Press. 352.

Google Scholar

Henderson, A. (2002). Evolution and Ecology of Palms. New York, NY: New York Botanical Garden. 259.

Google Scholar

Houghton, R. A. (2007). Balancing the global carbon budget. Ann. Rev. Earth Planet. Sci. 35, 313–347. doi: 10.1146/annurev.earth.35.031306.140057

CrossRef Full Text | Google Scholar

Howard, F. W., Moore, D., Giblin-Davis, R. M., and Abad, R. G. (2001). Insects on Palms. Wallingford: CABI Publishing. 131. doi: 10.1079/9780851993263.0000

CrossRef Full Text | Google Scholar

Hughes, R. F., Kauffman, J. B., and Jaramillo, V. J. (1999). Biomass, carbon, and nutrient dynamics of secondary forests in a humid tropical region of Mexico. Ecology 80, 1892–1907. doi: 10.1890/0012-96581999080[1892:BCANDO]2.0.CO;2

CrossRef Full Text | Google Scholar

Jones, D. L. (1995). Palms throughout the World. Washington DC: Smithsonian Institution Press. 410.

Google Scholar

Jucker, T., Caspersen, J., Chave, J., Antin, C., Barbier, N., Bongers, F., et al. (2017). Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Glob. Change Biol. 23, 177–190. doi: 10.1111/gcb.13388

PubMed Abstract | CrossRef Full Text | Google Scholar

Khasanah, N., van Noordwijk, M., Ekadinata, A., Dewi, S., Rahayu, S., Ningsih, H., et al. (2012). The Carbon Footprint of Indonesian Palm Oil Production. (Technical Brief No 25: Palm oil series). Nairobi: World Agroforestry Centre - ICRAF.

Google Scholar

Kissling, W. D., Balslev, H., Bake, R. W. J., Dransfield, J., Göldel, B., Lim, J. Y., et al. (2019). PalmTraits 1.0, a species-level functional trait database of palms worldwide. Sci. Data 6, 1–13. doi: 10.1038/s41597-019-0189-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Lähteenoja, O., Ruokolainen, K., Schulman, L., and Oinonen, M. (2009). Amazonian peatlands: an ignored C sink and potential source. Glob. Change Biol. 15, 2311–2320. doi: 10.1111/j.1365-2486.2009.01920.x

CrossRef Full Text | Google Scholar

Lal, R. (2008). Carbon sequestration. Philos. Trans. R. Soc. B Biol. Sci. 363, 815–830. doi: 10.1098/rstb.2007.2185

PubMed Abstract | CrossRef Full Text | Google Scholar

Laliberté, E. (2017). Below-ground frontiers in trait-based plant ecology. New Phytol. 213, 1597–1603. doi: 10.1111/nph.14247

PubMed Abstract | CrossRef Full Text | Google Scholar

Leblanc, H., Russo, R., Cueva, J. J., and Subía, E. (2006). Fijación de carbono en palma aceitera en la región tropical húmeda de Costa Rica. Tierra Tropical 2, 197–202.

Google Scholar

Lima, A. J. N., Suwa, R., de Mello Ribeiro, G. H. P., Kajimoto, T., dos Santos, J., da Silva, R. P., et al. (2012). Allometric models for estimating above-and below-ground biomass in Amazonian forests at São Gabriel da Cachoeira in the upper Rio Negro, Brazil. For. Ecol. Manage. 277, 163–172. doi: 10.1016/j.foreco.2012.04.028

CrossRef Full Text | Google Scholar

Lorenz, K., and Lal, R. (2010). Carbon Sequestration in Forest Ecosystems. Berlin: Springer. 279. doi: 10.1007/978-90-481-3266-9

CrossRef Full Text | Google Scholar

McDade, L. A., Bawa, K. S., Hespenheide, H. A., and Hartshorn, G. S. (1994). La Selva: Ecology and Natural History of a Neotropical Rainforest. Chicago: University of Chicago Press. 493.

Google Scholar

Mejia, K., and Kahn, F. (1990). Palm communities in wetland forest ecosystems of Peruvian Amazonia. For. Ecol. Manage. 3, 169–179. doi: 10.1016/0378-1127(90)90191-D

CrossRef Full Text | Google Scholar

Montero, M., and Montagnini, F. (2005). Modelos alométricos para la estimación de biomasa de diez especies nativas en plantaciones en la región Atlántica de Costa Rica. Recursos Naturales Ambiente 45, 112–119.

Google Scholar

Myers, R. L. (2013). Humedales dominados por palmas (Arecaceae) en el Neotrópico: Una introducción. Rev. Biol. Trop. 61, 5–24.

Google Scholar

Nascimento, H. E., and Laurance, W. F. (2002). Total aboveground biomass in central Amazonian rainforests: a landscape-scale study. For. Ecol. Manage. 168, 311–321. doi: 10.1016/S0378-1127(01)00749-6

CrossRef Full Text | Google Scholar

Onstein, R. E., Baker, W. J., Couvreur, T. L., Faurby, S., Svenning, J. C., and Kissling, W. D. (2017). Frugivory-related traits promote speciation of tropical palms. Nat. Ecol. Evol. 1, 1903–1911. doi: 10.1038/s41559-017-0348-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Oyama, K., and Dirzo, R. (1988). Biomass allocation in the dioecious tropical palm Chamaedorea tepejilote and its life history consequences. Plant Species Biol. 3, 27–33. doi: 10.1111/j.1442-1984.1988.tb00168.x

CrossRef Full Text | Google Scholar

Perez-Harguindeguy, N., Diaz, S., Garnier, E., Lavorel, S., Poorter, H., Jaureguiberry, P., et al. (2013). New handbook for standardised measurement of plant functional traits worldwide. Aust. J. Bot. 61, 167–234. doi: 10.1071/BT12225

CrossRef Full Text | Google Scholar

Petchey, O. L., and Gaston, K. J. (2006). Functional diversity: back to basics and looking forward. Ecol. Lett. 9, 741–758. doi: 10.1111/j.1461-0248.2006.00924.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pulhin, F. B., Lasco, R. D., and Urquiola, J. P. (2014). Carbon sequestration potential of oil palm in Bohol. Philippines. Ecosyst. Dev. J. 4, 14–19.

Google Scholar

R Core Team (2022). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Vienna: R Core Team.

Google Scholar

Renninger, H. J., and Phillips, N. G. (2016). “Palm physiology and distribution in response to global environmental change,” in Tropical Tree Physiology, eds G. Goldstein and L. S. Santiago (New York, NY: Springer). 67–101. doi: 10.1007/978-3-319-27422-5_4

CrossRef Full Text | Google Scholar

Rich, P. M. (1986). Mechanical architecture of arborescent rain forest palms. Principes 30, 117–131.

Google Scholar

Rich, P. M. (1987). Mechanical structure of the stem of arborescent palms. Bot. Gazzette 148, 42–50. doi: 10.1098/rsif.2012.0341

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodríguez-Veiga, P., Quegan, S., Carreiras, J., Persson, H. J., Fransson, J. E., and Hoscilo, A. (2019). Forest biomass retrieval approaches from earth observation in different biomes. Int. J. Appl. Earth Obs. Geoinf. 77, 53–68. doi: 10.1016/j.jag.2018.12.008

CrossRef Full Text | Google Scholar

Saatchi, S. S., Harris, N. L., Brown, S., Lefsky, M., Mitchard, E. T., Salas, W., et al. (2011). Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci.U.S.A 108, 9899–9904. doi: 10.1073/pnas.1019576108

PubMed Abstract | CrossRef Full Text | Google Scholar

Saldarriaga, J. G., West, D. C., Tharp, M. L., and Uhl, C. (1988). Long-term chronosequence of forest succession in the upper Rio Negro of Colombia and Venezuela. J. Ecol. 76, 938–958. doi: 10.2307/2260625

CrossRef Full Text | Google Scholar

Sampaio, M. B., Schmidt, I. B., and Figueiredo, I. B. (2008). Harvesting effects and population ecology of the buriti palm (Mauritia flexuosa L. f., Arecaceae) in the Jalapão Region, Central Brazil. Econ. Bot. 62, 171–181. doi: 10.1007/s12231-008-9017-8

CrossRef Full Text | Google Scholar

Serrano-Sandí, J., Bonilla-Murillo, F., and Sasa, M. (2013). Distribución, superficie y área protegida de humedales dominados por pantanos de palmas (Arecaceae) en Costa Rica y Nicaragua. Rev. Biol. Trop. 61, 25–33.

Google Scholar

Sprugel, D. G. (1983). Correcting for bias log-transformed allometric equations. Ecology 64, 209–210. doi: 10.2307/1937343

CrossRef Full Text | Google Scholar

Syahrinudin. (2005). The potential of oil palm and forest plantations for carbon sequestration on degraded land in Indonesia. Ecol. Dev. Series 28, 1–9.

Google Scholar

Sylvester, O., Avalos, G., and Chávez-Fernández, N. (2012). Notes on the ethnobotany of Costa Rica’s palms. Palms 56, 190–201.

Google Scholar

ter Steege, H., Pitman, N. C. A., Sabatier, D., Baraloto, C., Salomão, R. P., Guevara, J. E., et al. (2013). Hyperdominance in the Amazonian tree flora. Science 342, 325–342. doi: 10.1126/science.1243092

PubMed Abstract | CrossRef Full Text | Google Scholar

Thenkabail, P. S., Stucky, N., Griscom, B. W., Ashton, M. S., Diels, J., Van Der Meer, B., et al. (2004). Biomass estimations and carbon stock calculations in the oil palm plantations of African derived savannas using IKONOS data. Int. J. Remote Sens. 25, 5447–5472. doi: 10.1080/01431160412331291279

CrossRef Full Text | Google Scholar

Tomlinson, P. B. (2006). The uniqueness of palms. Bot. J. Linn Soc. 151, 5–14. doi: 10.1111/j.1095-8339.2006.00520.x

CrossRef Full Text | Google Scholar

Tomlinson, P. B. (2011). The anatomy of palms. New York, NY: Oxford University Press, 251. doi: 10.1093/acprof:osobl/9780199558926.001.0001

CrossRef Full Text | Google Scholar

van der Hoek, Y., Álvarez Solas, S., and Peñuela, M. C. (2019). The palm Mauritia flexuosa, a keystone plant resource on multiple fronts. Biodivers. Conserv. 28, 539–551. doi: 10.1007/s10531-018-01686-4

CrossRef Full Text | Google Scholar

Vasseur, F., Violle, C., Enquist, B. J., Granier, C., and Vile, D. (2012). A common genetic basis to the origin of the leaf economics spectrum and metabolic scaling allometry. Ecol. Lett. 15, 1149–1157. doi: 10.1111/j.1461-0248.2012.01839.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Weemstra, M., Mommer, L., Visser, E. J., van Ruijven, J., Kuyper, T. W., Mohren, G. M., et al. (2016). Towards a multidimensional root trait framework: a tree root review. New Phytol. 211, 1159–1169. doi: 10.1111/nph.14003

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiner, J. (2004). Allocation, plasticity and allometry in plants. Perspect. Plant Ecol. Evol. Syst. 6, 207–215. doi: 10.1078/1433-8319-00083

CrossRef Full Text | Google Scholar

Yaap, B., Watson, H., and Laurance, W. F. (2015). Mammal use of Raphia taedigera palm stands in Costa Rica’s Osa Peninsula. Mammalia 79, 357–362. doi: 10.1515/mammalia-2014-0033

CrossRef Full Text | Google Scholar

Zahabu, E., Mugasha, W. A., Malimbwi, R. E., and Katani, J. Z. (2018). Allometric Biomass and Volume Models for Coconut Trees. Dar es Salaam: E&D Vision Publishing Ltd.

Google Scholar

Zhang, X., Zhao, Y., Ashton, M. S., and Lee, X. (2012). “Measuring carbon in forests,” in Managing Forest Carbon in a Changing Climate, eds M. S. Ashton, M. L. Tyrrell, D. Spalding, and B. Gentry (Netherlands: Springer). 139–164. doi: 10.1007/978-94-007-2232-3_7

CrossRef Full Text | Google Scholar

Zona, S., and Henderson, A. (1989). A review of animal-mediated seed dispersal of palms. Selbyana 11, 6–21.

Google Scholar

Zuidema, P. A., and Boot, R. G. (2000). “Demographic constraints to sustainable palm heart extraction from a sub-canopy palm in Bolivia,” in Demography of Exploited Tree Species in the Bolivian Amazon, ed. P. Zuidema (Riberalta: Utrecht Univ). 54–79.

Google Scholar

Appendix

TABLE A1

TABLE A1. Summary of morphological variables of seven palm species harvested in the Caribbean lowlands of Costa Rica to obtain allometric models to estimate carbon content and above ground biomass.