Evaluation of geographically weighted logistic model and mixed effect model in forest fire prediction in northeast China

Introduction: Forest fires seriously threaten the safety of forest resources and human beings. Establishing an accurate forest fire forecasting model is crucial for forest fire management.

Methods: We used different meteorological and vegetation factors as predictors to construct forest fire prediction models for different fire prevention periods in Heilongjiang Province in northeast China. The logistic regression (LR) model, mixed-effect logistic (mixed LR) model, and geographically weighted logistic regression (GWLR) model were developed and evaluated respectively.

Results: The results showed that (1) the validation accuracies of the LR model were 77.25 and 81.76% in spring and autumn fire prevention periods, respectively. Compared with the LR model, both the mixed LR and GWLR models had significantly improved the fit and validated results, and the GWLR model performed best with an increase of 6.27 and 10.98%, respectively. (2) The three models were ranked as LR model < mixed LR model < GWLR model in predicting forest fire occurrence of Heilongjiang Province. The medium-and high-risk areas of forest fire predicted by the GWLR model were distributed in western and eastern parts of Heilongjiang Province in spring, and western part in autumn, which was consistent with the observed data. (3) Driving factors had strong temporal and spatial heterogeneities; different factors had different effects on forest fire occurrence in different time periods. The relationship between driving factors and forest fire occurrence varied from positive to negative correlations, whether it’s spring or autumn fire prevention period.

Discussion: The GWLR model has advantages in explaining the spatial variation of different factors and can provide more reliable forest fire predictions.

Introduction

Forest fires seriously threaten the safety of forest resources, human life, and property (Flannigan et al., 2010; Turetsky et al., 2011). The occurrence of forest fire is a complex process with large spatial heterogeneity, which is not only affected by a variety of environmental factors but also interacts with them (Martinez-Fernandez et al., 2013; Rodrigues et al., 2014). A scientific and accurate forest fire prediction model is conducive to establishing a scientific and efficient forest fire ecological management system to reduce the risk of forest fires, which plays an essential role in sustainable forest management (Curt et al., 2016).

At present, extensive research on forest fire prediction models have been carried out. Among them, the logistic regression (LR) model is most widely used (Liu et al., 2012; Guo et al., 2015; Guo et al., 2016a). The logistic regression global prediction model is simple in form, can apply the fitting parameters to the whole study area. However, the model established has shortages in reflecting the variability and spatial heterogeneity of observed data between different fire points. It is especially obvious when the research area is fair-sized (Boubeta et al., 2015; Nunes et al., 2016).

With the development of the research, the geographical weighted logistic regression (GWLR) model and mixed effects model have been gradually applied in forest fire prediction (Drever et al., 2008). By establishing the GWLR model of forest fire, it has been found that the GWLR model can better predict the spatial relationship between forest fires and their driving factors. For example, a pervious study using the GWLR model has demonstrated that the behavior of the driving factors affecting the occurrence of Spanish forest fires would change with time and space (Rodrigues et al., 2018). Su et al. (2021) found that drivers of wildfire in Leizhou Peninsula (coastal area) had clear spatial variation, and the GWLR model has better prediction ability. The mixed effects model incorporates some factors other than variables into the modelling process through random effects, which can effectively deal with the influence of spatial heterogeneity and individual differences of samples on the model (Groom et al., 2012; Blozis and Harring, 2021). For example, Hegeman et al. (2014) included five management units of the Mojave Desert Network can be used as a subject-level random effect to account for heterogeneity in fire occurrence among management units. Stan et al. (2014) took the stations of Hualapai Tribal lands as a random effect, and used the generalized linear mixed model to model the combustion probability in this area.

These three models have been wildly applied in forest fire prediction (Guo et al., 2015; Rodrigues et al., 2018). However, these studies have varied research areas, research purposes, selections of driving factors and data sources. Chang et al. (2013) selected daily rain fall, mean wind speed, mean temperature, minimum temperature, vegetation type and other factors in Heilongjiang Province of China to predict the probability of forest fire using LR model. Oddi et al. (2019) applied a nonlinear mixed effect method to model the time change of water content of live fuel in Northwestern Patagonia area. Rodrigues et al. (2019) used forest fire data from Spanish fire database, and based on the fire season in Spain, used GWLR model to parameterize the marginal impact of driving factors. And so on. In such a variety of situations, it is difficult to have a clear and comprehensive view of the applicability of the three models in forest fire prediction.

Heilongjiang Province is located in the northeast of China, with its high spatial variability of natural conditions (Guan et al., 2021). It is crucial to understand where wildfires are more likely to occur as well as their drivers in complex landscapes (Wu et al., 2021). Based on the above considerations, we established a prediction model of forest fire occurrence during different forest fire seasons in Heilongjiang Province, based on LR model, mixed LR model, and GWLR model. We aim to understand the applicability of these forest fire prediction models by using the same variables in the same study area, so as to provide a basis for scientific forest fire management.

Materials and methods

Study area

Heilongjiang Province (43°26’-53°33’N, 121°11’-135°05’E) is located in Northeastern China (Figure 1), with a land area of 473,000 square kilometers. The province has a terrestrial monsoon climate, and the climate varies significantly among regions. The forest stock in Heilongjiang Province amounts to 2.24 billion cubic meters. The forest area, total forest volume, and timber production of Heilongjiang Province all rank at the forefront of China. At the same time, Heilongjiang is also a province with a high incidence of forest fire in China. According to the Chinese Forestry Statistical Yearbook (National Forestry and Grassland Administration, 2018), the total area of the fire site in Heilongjiang Province was 18,400 ha, of which the affected forest area was 12,385 ha, from 2010 to 2016. These data have not included forest fires with a small fire area or no casualties. By taking strict actions on wildfire prevention, human-caused forest fires have been greatly limited to occur in Heilongjiang Province over the last decade. As a result, climate and vegetation factors play a crucial role in Heilongjiang’s wildfires (Faivre et al., 2014; Wu et al., 2021).

FIGURE 1

Figure 1. Location of Heilongjiang Province, China.

Data

The data used in this study consists of forest fire data, meteorological data, and vegetation data.

Forest fire data

Forest fire data is derived from the daily forest fire product (including fire coordinates, time, and reliability, etc.) of 1 km-resolution imaging spectrum of MODIS satellite, provided by Geospatial Data Cloud¹ during 2019. This product has been proved to be a suitable and reliable source for monitoring vegetation fires (Justice et al., 2002; Amraoui et al., 2015), and has been widely used in forest fire research (Eskandari et al., 2015). Since there may be multiple fire points in a fire, ArcGIS software was used to eliminate the fire points with a distance of less than 1 km within 24 h. The fire point data in 2019 was superimposed with the 1 km-resolution land use type map of Heilongjiang Province in 2015, which was provided by the multi-temporal 1:100,000 scale land use status database covering the national land area. After eliminating fire points in non-forest areas, 5,226 credible fire points were finally obtained during the fire prevention period (Figure 2). The Logistic regression model requires the response variable data to be in the form of a binomial distribution, so a certain proportion of random points (non-fire points) need to be created (Guo et al., 2016a). The ArcGIS software (10.8) was used to generate random points at a ratio of 1:1. Usually, the number of random points is slightly more than that of fire points, and the distribution of random points is completely random in time and space. A total of 5,523 non-fire points were generated in this study.

FIGURE 2

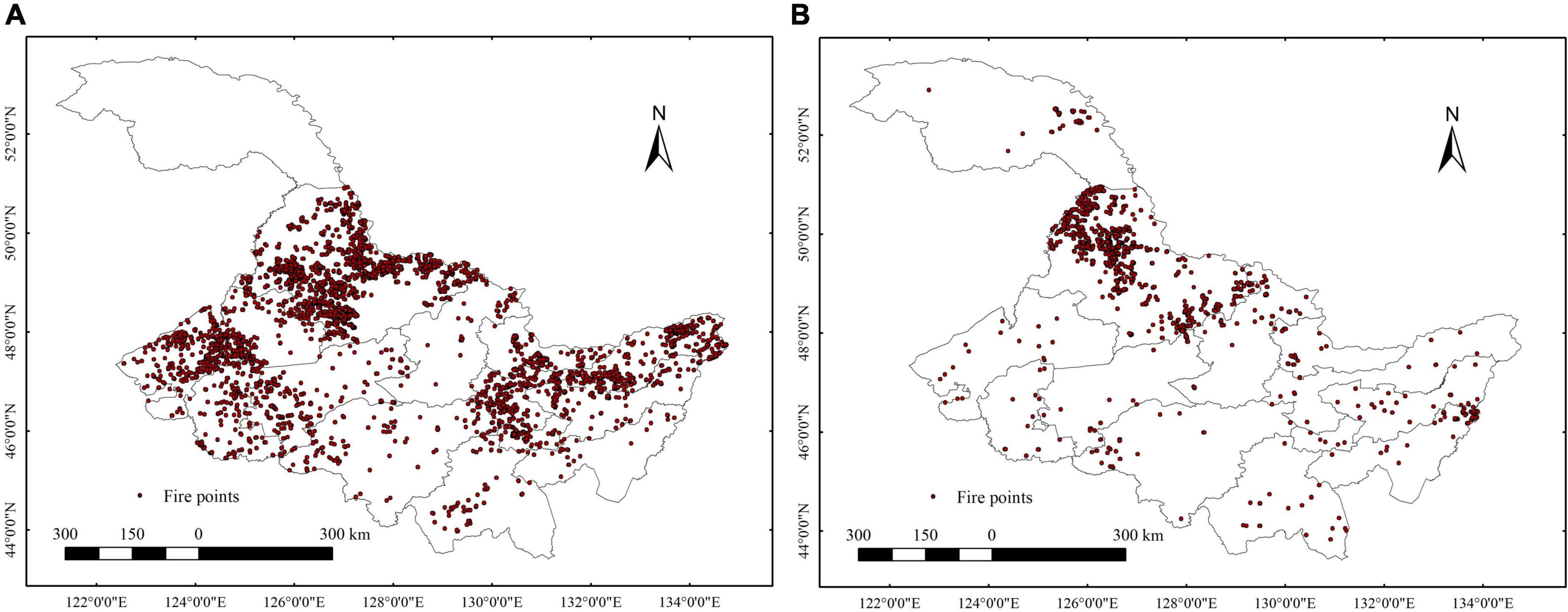
Figure 2. Distribution of fire points in Heilongjiang Province at 2019. (A) Fire points in spring fire prevention period. (B) Fire points in autumn fire prevention period.

Meteorological and vegetation data

Meteorological and vegetation data were derived from the global ERA5-Land database,² from which the daily data of Heilongjiang Province in 2019 was extracted. Among them, the meteorological data included the wind speed, precipitation, and the surface temperature of the day. Vegetation data included leaf area index (LAI) of the day. The meteorological and vegetation data and forest fire data were connected by temporal and spatial information through python to form the complete sample data.

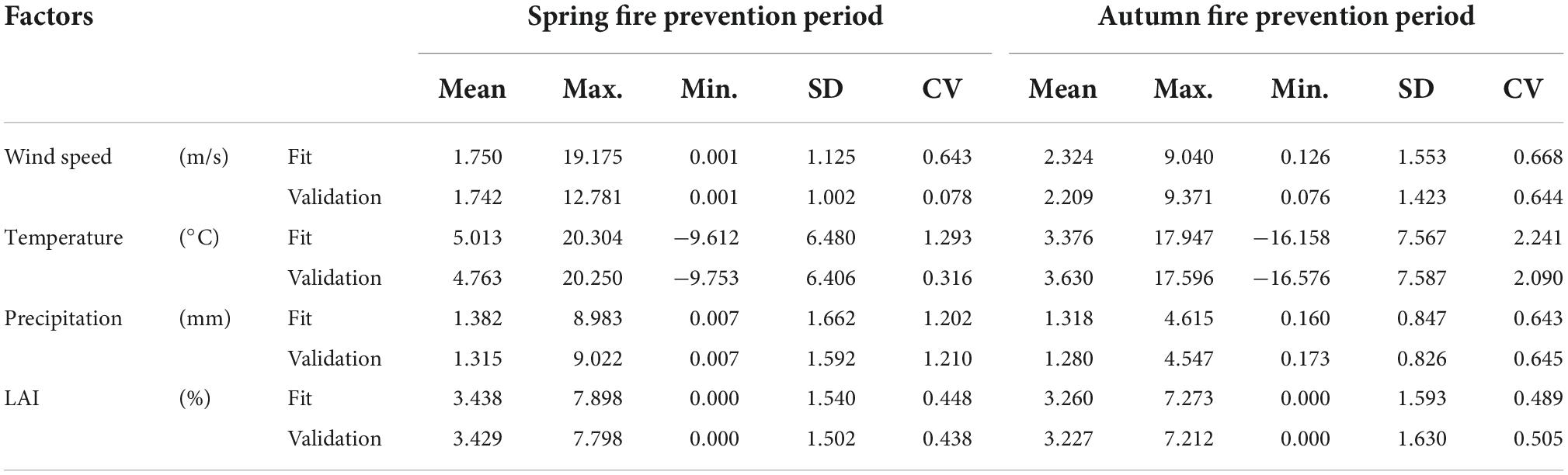
In Heilongjiang Province, there are two primary forest fire prevention periods at spring and autumn every year. The spring fire prevention period ranges from 15 March to 15 June, and the autumn fire prevention period ranges from 15 September to 15 November. In this study, we calculated statistics of the factors for both fire prevention periods, and all data were randomly divided into a fit data set (60%) for estimating regression parameters and a validation data set (40%) for evaluating the models (Table 1).

TABLE 1

Table 1. Statistics of the influencing factors of forest fires.

Methods

Our main research steps are as follows: (1) Variable selection. (2) Establish a base model, namely the logistic regression model in this study. (3) Construct the mixed model by adding random effects to the base model. (4) Build the geographically weighted regression model by use of the base model (5) Model evaluation and application.

Variable selection

In order to avoid the influence of the possible multicollinearity among the meteorological factors on the model prediction, we calculated the Variance Inflation Factor (VIF) for each meteorological factor. According to the thumb rule, if any of the VIF values exceed five or ten, it implies that the associated regression coefficients are poorly estimated because of the multicollinearity (Kennedy, 1992; Parajuli et al., 2020). In this study, we eliminated the variable with a VIF value larger than five. Then, the two-way stepwise regression technique was used to eliminate the variables with no significant difference (p > 0.05). Finally, the variables that had no collinearity and were extremely significant with fire occurrence were retained in the basic model (Rodrigues et al., 2014).

Logistic regression model

In this study, the values of forest fire occurrence or not were taken as follows: Fire y = 1, no fire y = 0. The probability of forest fire (y = 1) was set as P, then the LR model between fire occurrence probability and predictors could be developed. The regression model is expressed as:

$\ln \left(\frac{P}{1-P}\right)=\alpha +\beta \mathbf{\text{X}}(1)$

where P is the probability of forest fire; X is the vector of predictive variables; α is the constant term; β is the parameter vector of the predictive variables.

After logit transformation, the probability formula of forest fire occurrence can be obtained as:

$P=\frac{e^{\alpha +\beta \mathbf{X}}}{1+e^{\alpha +\beta \mathbf{X}}}(2)$

Mixed-effects model

The mixed-effects model is a statistical analysis model composed of fixed effects and random effects. In order to understand the impact of different geographic regions on meteorological conditions and overcome its spatial heterogeneity, we divided the data into 13 groups, corresponding to the 13 prefecture-level cities in Heilongjiang Province (Figure 1). We tested different mixed models that containing random effects on different combinations of parameters based on the LR model to find the optimal parameters that random effects account for. In this way, the error caused by the prediction of the fixed-effect model could be reduced. The mixed-effects model can be expressed as:

$\{\begin{array}{c}\hfill \text{ln}\left(\frac{P}{1-P}\right)=\alpha +\beta \mathbf{\text{X}}+\mathbf{\text{bZ}}+\mathbf{\text{e}}\hfill \\ \hfill \mathbf{\text{b}}\sim \text{N}(0,\mathbf{D})\hfill \\ \hfill e\sim \text{N}(0,{\mathbf{\text{R}}}_{\mathbf{i}})\hfill \end{array}(3)$

where: α is the constant term; β is the parameter vector of the predictors with fixed effects; X is the vector of predictive variables with fixed effects; b is the parameter vector of the predictors with random effects; Z is the vector of predictive variables with random effects;boldsymbole is the error vector; D is the random effect variance-covariance matrix; R_i is the within-group variance-covariance matrix.

The variance-covariance structure matrix of random effects can reflect the difference between forest fire occurrence and various meteorological factors among different groups. Therefore, its structure will change with the number of random parameters. For the simplicity of the model, this study only considers the variance-covariance structure of random effects and assumes that it is a generalized positive definite matrix. Take the variance-covariance structure matrix containing two random parameters as an example; its structure is as follows:

$\text{D}=\left[\begin{array}{cc}\hfill {\sigma }_{b_1}^2\hfill & \hfill {\sigma }_{b_1{b}_2}\hfill \\ \hfill {\sigma }_{b_1{b}_2}\hfill & \hfill {\sigma }_{b_2}^2\hfill \end{array}\right](4)$

where ${\sigma }_{b_1}^2$is the variance of random parameterb₁; ${\sigma }_{b_2}^2$ is the variance of random parameter b_2; σ_b1b2 is the covariance of random parameters b₁ and b₂.

The within-group variance-covariance structure was described by the commonly used error effect variance-covariance structure:

${\mathit{\text{R}}}_{\mathit{i}}={\sigma }^2{I}_i(5)$

where σ² is the error variance of the model; I_i is the variance matrix of within-group errors.

Geographically weighted logistic regression model

The geographically weighted logistic regression model is the extension of the traditional logistic regression model by taking spatial location information into account (Fotheringham et al., 2002). The GWLR model estimates the parameters of each coordinate point by using the weighted least square method. The parameter estimation is local rather than global. Therefore, data in different coordinates have corresponding specific parameters. In the construction of the GWLR model, we used the exponential kernel function and determined the optimal bandwidth according to the corrected Akaike information criterion (AICc). Assume that the probability of fire occurrence (y = 1) at location i is P, then the probability of no forest fire (y = 0) is (1-P). The expression of the GWLR model is:

$\text{ln}(\frac{P}{1-P})={\alpha }_{0(u_i,v_i)}+{\alpha }_{1(u_i,v_i)}{x}_{i1}+{\alpha }_{2(u_i,v_i)}{x}_{i2}+\mathrm{\dots }+{\alpha }_{n(u_i,v_i)}{x}_{in}(6)$

where (u_i,v_i) is the geographic coordinate of location i, α_(ui,vi) is the parameter estimates of predictive variables at location i, and x_in is the predictive variables at location i.

After logit transformation, we have,

$P_{y=1}$

$=\frac{exp({\alpha }_{0(u_i,v_i)}+{\alpha }_{1(u_i,v_i)}{x}_{i1}+{\alpha }_{2(u_i,v_i)}{x}_{i2}+\mathrm{\dots }+{\alpha }_{n(u_i,v_i)}{x}_{in})}{1+exp({\alpha }_{0(u_i,v_i)}+{\alpha }_{1(u_i,v_i)}{x}_{i1}+{\alpha }_{2(u_i,v_i)}{x}_{i2}+\mathrm{\dots }+{\alpha }_{n(u_i,v_i)}{x}_{in})}$

$=\frac{e^z}{1+e^z}(7)$

where z = α_1(ui,vi)x_i1 + α_2(ui,vi)x_i2 + ⋯ + α_n(ui,vi)x_in.

The data structure of the model was first assumed to be spatially non-stationary, then the spatial non-stationarity of the relationship between forest fire occurrence and predictors was evaluated. If the quartile range of the estimated coefficient of an explanatory variable is larger than the coefficient ± standard deviation of the same variable in the LR model, then the explanatory variable will be considered to be significantly spatial non-stationary (Chen et al., 2012).

Model evaluation

For model fitting comparison, Akaike information criterion (AIC), Bayesian information criterion (BIC), and −2* Log-likelihood value (−2LogL) were used in this study (Rawlings et al., 1998; Hastie et al., 2001; Burnham and Anderson, 2002). For each criterion, the best model produced the smallest value. The criteria are computed as follows:

$\text{AIC}=2m-2\text{ln}(L)(8)$

$\text{BIC}=-2\ln \left(L\right)+\text{kln}(n)(9)$

where L is the maximum value of the likelihood function of estimated model, n is the number of samples, and m is the number of parameters.

For model validation, we applied mean absolute error (MAE), root mean squared error (RMSE), and the area under the receiving operating characteristic (ROC) curve. The ROC curve shows the ability of a system to classify binary data at various threshold settings, and the area under the ROC curve (AUC) ranges from 0.5 (poor fit) to 1 (perfect fit) (He et al., 2018). A good model should produce a smaller MAE, smaller RMSE, and larger AUC. The calculations for MAE and RMSE are as follows:

$\text{MAE}=\frac{{\sum }_{\mathrm{i}=1}^{\text{n}}|{\widehat{y}}_i-y_i|}{n}(10)$

$\text{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n{({\widehat{y}}_i-y_i)}^2}{n}}(11)$

where ${\widehat{y}}_i$ and y_i are the predicted and observed values of the i-th point, respectively.

The global Moran’s index (Moran’s I) was used to evaluate the spatial autocorrelation of model residuals (residual = observed value–predicted value). A smaller value of the global Moran’s I indicates lower spatial dependence of residuals, meaning that more spatial information is considered in the model. The calculation for the global Moran’s I is:

$\text{I}={\frac{n}{S}}^{*}\left[\frac{{\sum }_{\mathrm{i}=1}^{\text{n}}{\sum }_{\mathrm{j}=1}^{\text{n}}{\omega }_{ij}(e_{\text{i}}-\overline{e})(e_{\text{j}}-\overline{e})}{{\sum }_{\mathrm{i}=1}^{\text{n}}{\left(e_{\text{i}}-\overline{e}\right)}^2}\right](12)$

where n is the number of spatial units in data, e_i and e_j are residual values of spatial units i and j, respectively, $\overline{e}$ is the average value of the residuals, S is the sum of all spatial weights, and ω_ij represents an element in the spatial weight matrix. If space units i and j are adjacent, then ω_ij = 1; otherwise ω_ij = 0. The values of Moran’s I ranges between [−1, 1]. When the value of Moran’s I index is greater than 0, the residuals in the study area are positively correlated in space, whereas a value less than 0 indicates negative correlate on in space.

In addition, we calculated the accuracy of fitting data and validation data of different models respectively. The model accuracy is computed as follows:

$\text{Accuracy}=\frac{TP+TN}{n}=\frac{TP+TN}{TP+TN+FP+FN}(13)$

where n is number of samples; TP is number of correct predictions of fire points; TN is number of correct predictions of non-fire points; FP is number of wrong predictions of fire points; FN is number of wrong predictions of non-fire points.

In this study, all model fitting and validation were implemented by R. The parameter estimation of the LR model was realized by the glm function in stats package. The parameter estimation of the mixed effect model was realized by the glmer function in lme4 package. The bandwidth selection and parameter estimation of the GWLR model were respectively implemented by the bw.ggwr and ggwr.basic functions in GWmodel package.

Results

Parameter estimation of the logistic regression model

The VIF values of all meteorological and vegetation variables are less than 3, indicating that there are no multicollinearities among these factors. During stepwise regression, all variables are extremely significant (p < 0.01). Table 2 shows parameter estimation of the LR model during both spring and autumn fire prevention periods. Among them, wind speed, surface temperature, and LAI have negative effects on fire occurrence in both seasons, precipitation has negative effect in spring whereas positive effect in autumn.

TABLE 2

Table 2. Parameter estimation based on the logistic regression model.

Parameter estimation of the mixed-effects logistic regression model

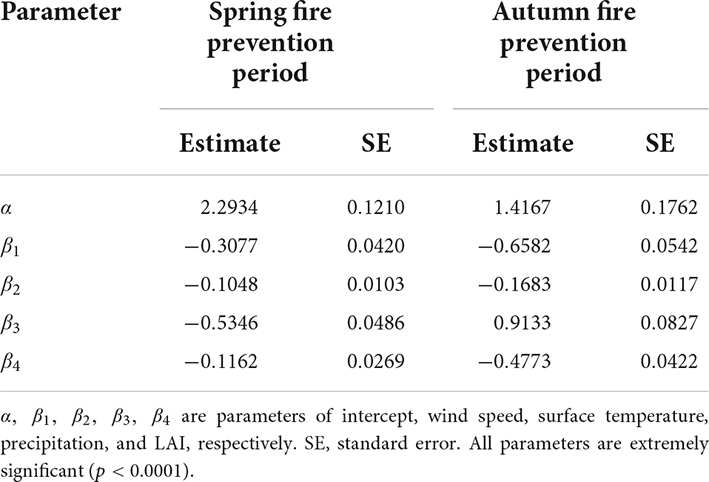
A total of 22 models were received by adding the random effects on different combinations of parameters (Appendix 1). Among them, 11 models were developed for spring fire prevention period and the other 11 models for autumn fire prevention period, in the same order for different models. The mixed-effects model considering random effects on intercept, temperature and precipitation (Model 9) for spring fire prevention period, and the model considering random effects on intercept, temperature and leaf area index (Model 10) for autumn fire prevention period obtained the best evaluation statistics (Appendix 1). Table 3 shows the parameter estimation of the optimal mixed-effects models for spring and autumn fire prevention periods. Surface temperature has negative effect on the fire occurrence in both seasons. Wind speed and LAI have positive effect in spring whereas negative effect in autumn. Precipitation has negative effect in spring whereas positive effect in autumn. Meanwhile, different parameters show varied significance levels (Table 3). Precipitation is significantly related to forest fire in spring fire prevention period, while other variables become insignificant. Wind speed, precipitation and LAI are significantly related to forest fire in autumn prevention period, while temperature is not significant. We conducted ANOVA test on the LR model and the optimal mixed LR model of both seasons, and the results showed that there were significant difference between the two model types (p < 0.0001).

TABLE 3

Table 3. Parameter estimation of the optimal mixed-effects model.

Parameter estimation of the geographically weighted logistic regression model

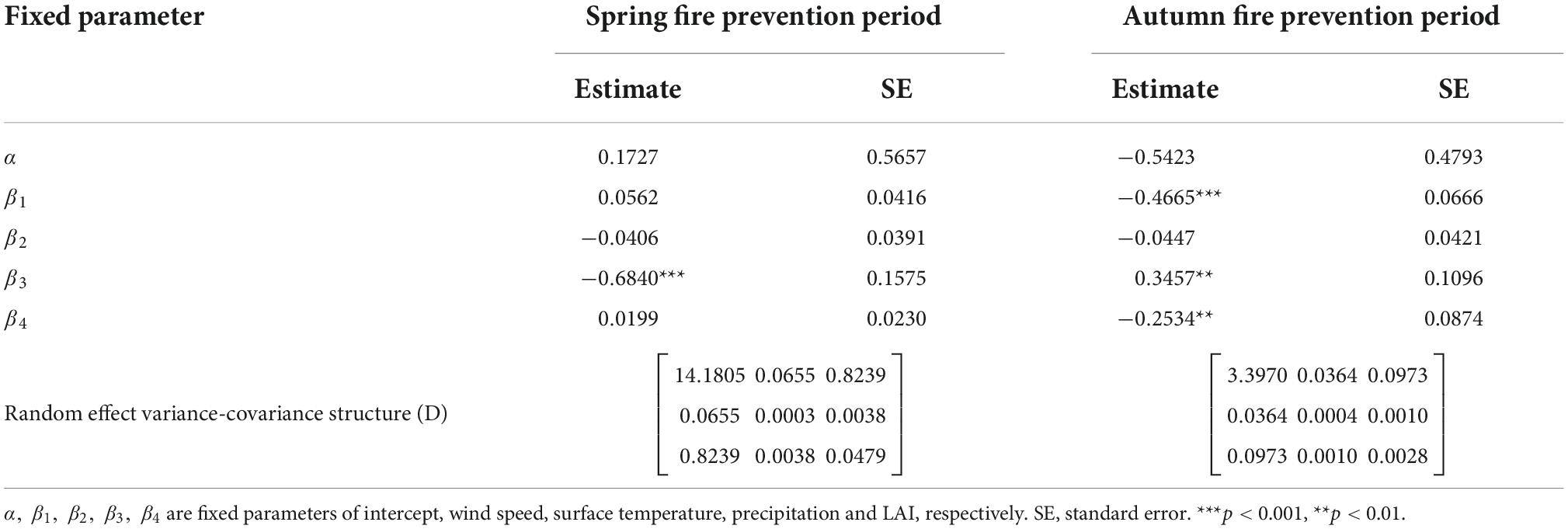
Appendix 2 evaluates the spatial stationarity of parameter estimation for the GWLR model based on the entire data set, intercept, wind speed, surface temperature, precipitation, and leaf area index are all non-stationary spatial variables. The parameters of all meteorological and vegetation factors vary between positive and negative correlations over the entire study area (Table 4). In order to reflect the local variations of the parameters for each variable in the GWLR model, we divided each parameter into 5 intervals based on the Natural Breaks (Jenks) method, and performed spatial interpolation on the parameters using the ArcGIS 10.8 software (Figure 3). The parameters of the GWLR model vary with spatial location, revealing obvious spatial heterogeneity. Meanwhile, there are differences in spatial heterogeneity among different parameters, and spatial heterogeneity within the same parameter has great distinctions during different fire seasons. The distribution maps of t-values for parameter estimations also show that all variables in the GWLR model have locally significant influence on forest fire (Figure 4).

TABLE 4

Table 4. Parameter estimation of the geographically weighted logistic regression (GWLR) model.

FIGURE 3

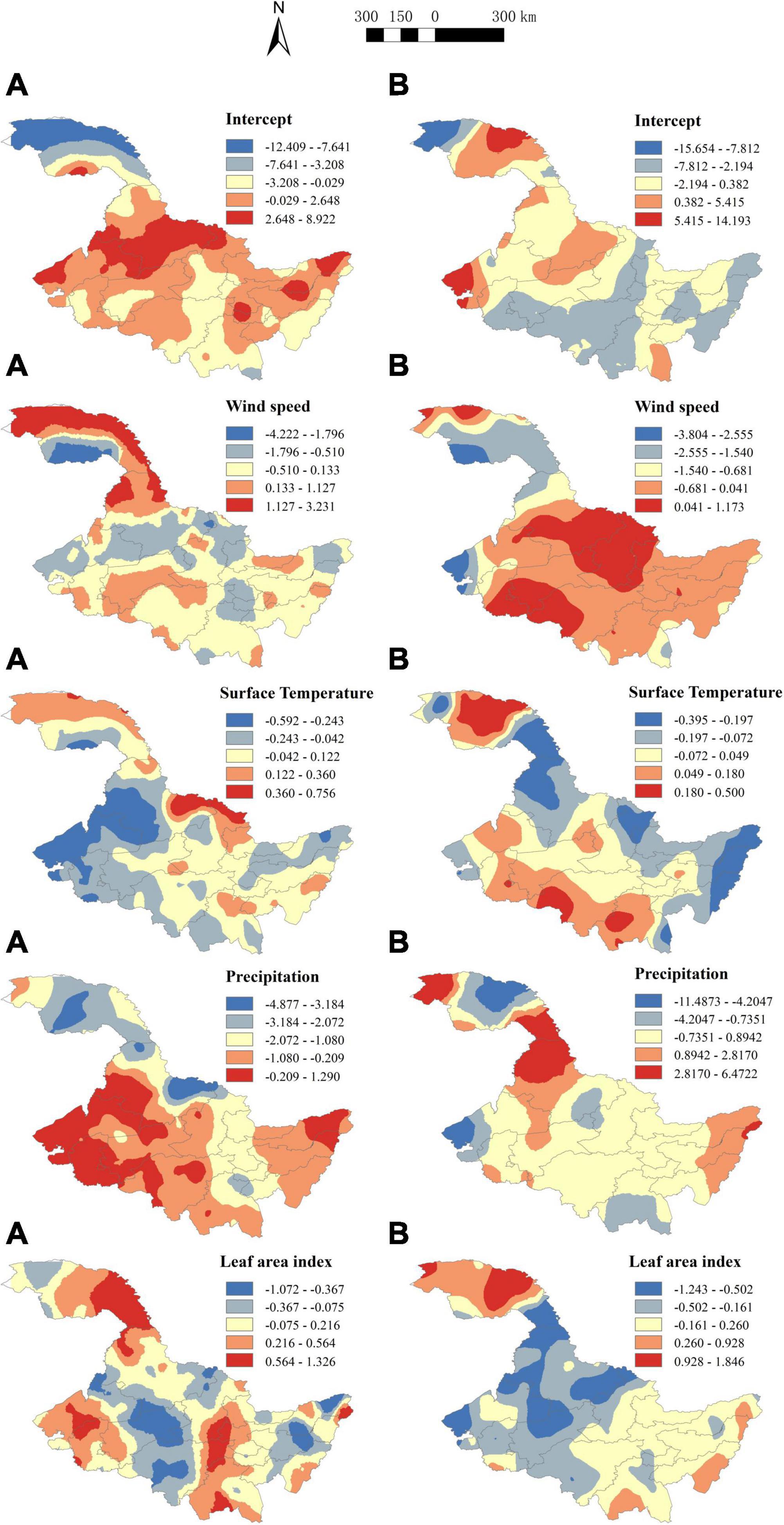
Figure 3. Parameter distribution for each variable of the geographically weighted logistic regression (GWLR) model. (A) Parameter distribution in spring fire prevention period. (B) Parameter distribution in autumn fire prevention period.

FIGURE 4

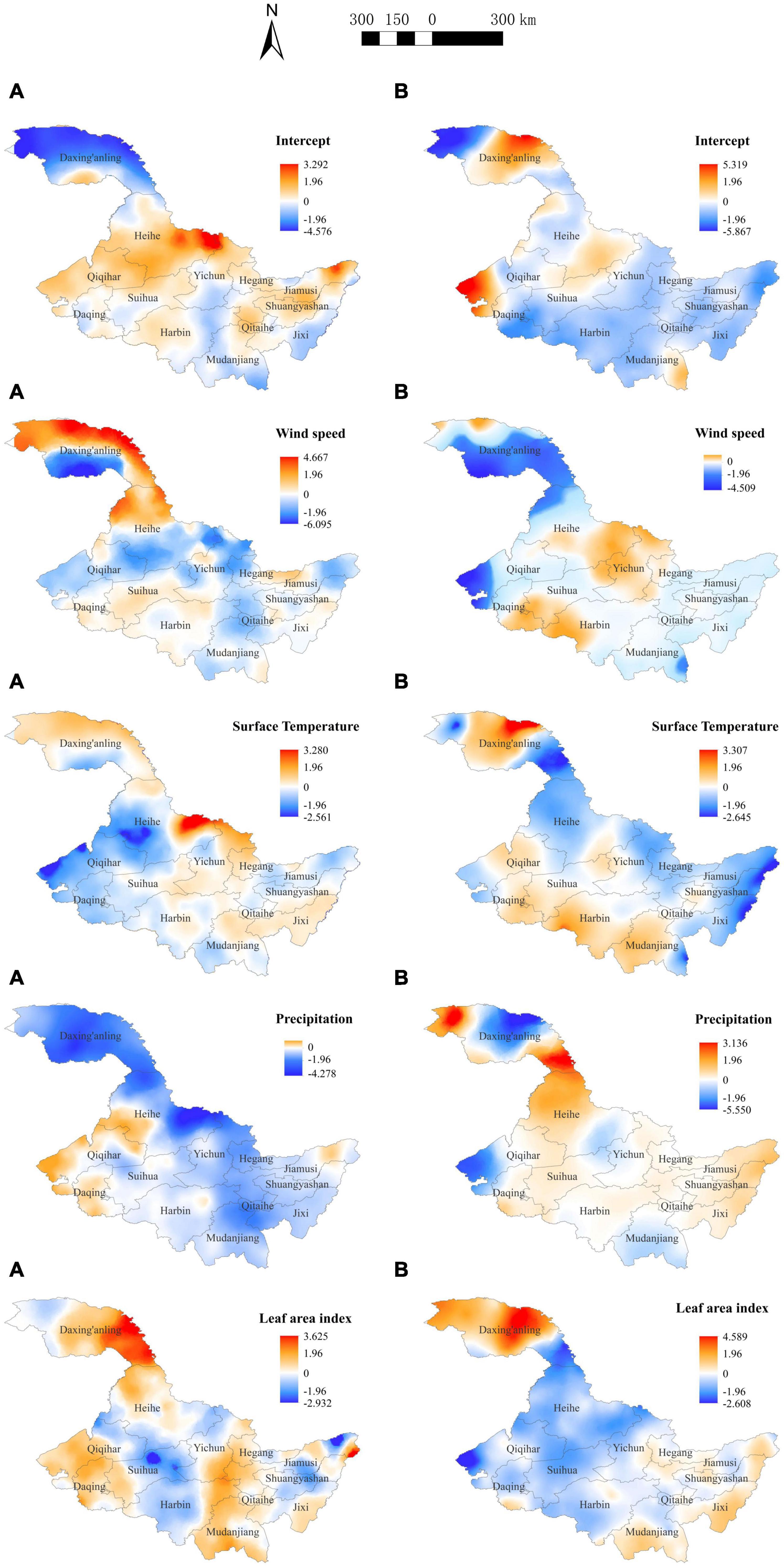
Figure 4. Distribution of t-values for each parameter of the geographically weighted logistic regression (GWLR) model. (A) Distribution of t-values in spring fire prevention period. (B) Distribution of t-values in autumn fire prevention period. If the t-test value is less than –1.96 or greater than 1.96, it means that the estimated coefficient is significant.

Model evaluation

Table 5 shows the fitting and validation statistics of the LR model, the mixed LR model, and the GWLR model. In the fitting process, the AIC (3332.708, 1362.171), BIC (3364.675, 1390.383), and −2LogL (3322.708, 1352.171) values of the GWLR model were the smallest in both spring and autumn fire prevention periods. Those values in the mixed LR model were in the middle, and the LR model received the largest values. Similar in the validation process, the GWLR model obtained the best values of all evaluation statistics (MAE, RMSE, Moran’s I, AUC, Accuracy) during the spring and autumn fire prevention periods, followed by the mixed effect model, and the LR model performed relatively poor (Table 5). Figure 5 shows the ROC curves of the LR model, the mixed LR model and the GWLR model, which presented the same results. The residual distribution of the LR model was relatively scattered, while the residuals of the mixed LR model and the GWLR model were more concentrated around zero (Figure 6). Particularly, the residual distribution of the GWLR model was the most concentrated in the two fire prevention periods. Therefore, the three models showed consistent model performance in both fire prevention periods, that is, the LR model < the mixed LR model < the GWLR model.

TABLE 5

Table 5. Model fitting and validation for two fire prevention periods.

FIGURE 5

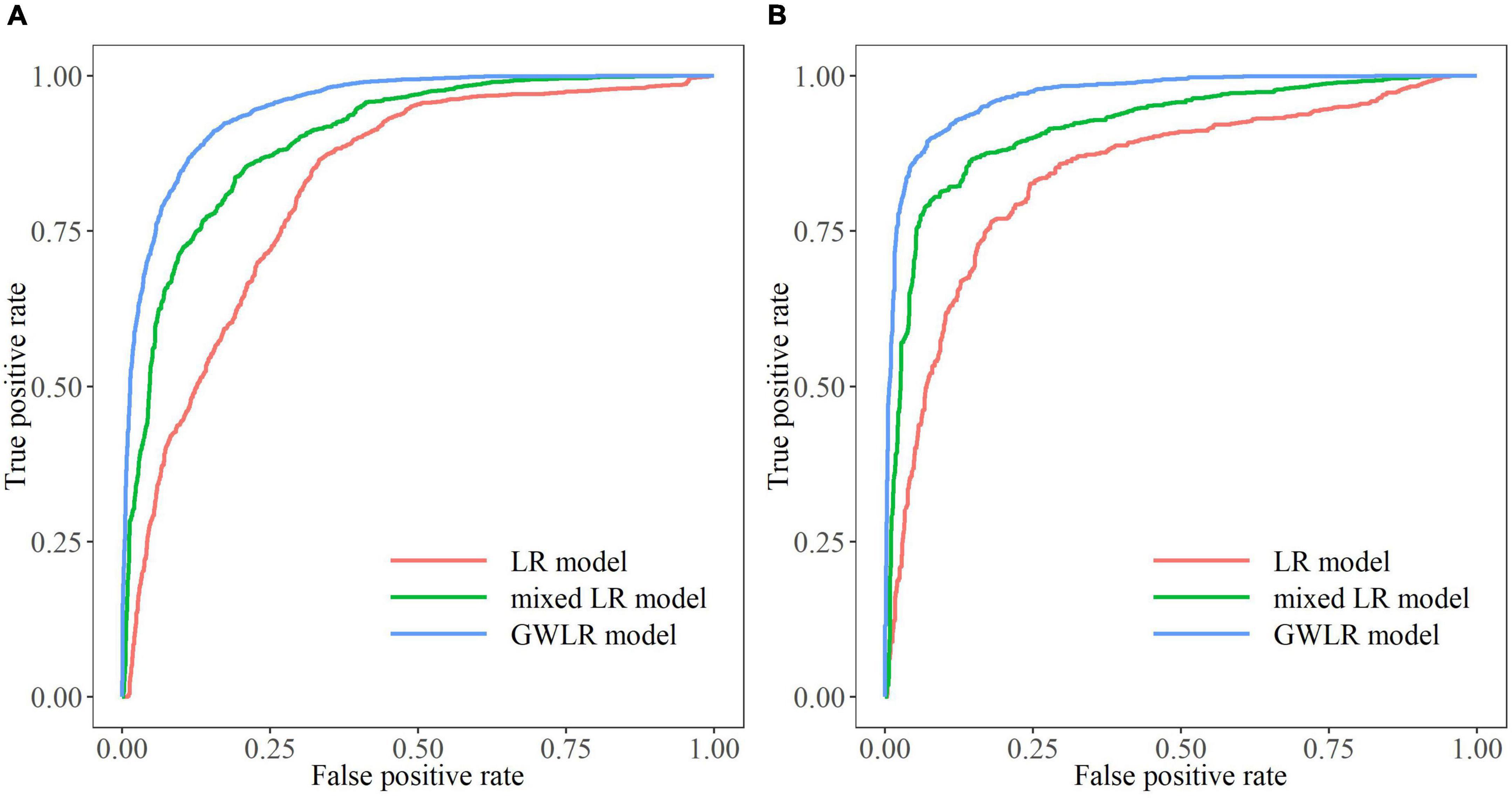
Figure 5. The receiving operating characteristic (ROC) curves of different models. (A) ROC curves in spring fire prevention period. (B) ROC curves in autumn fire prevention period.

FIGURE 6

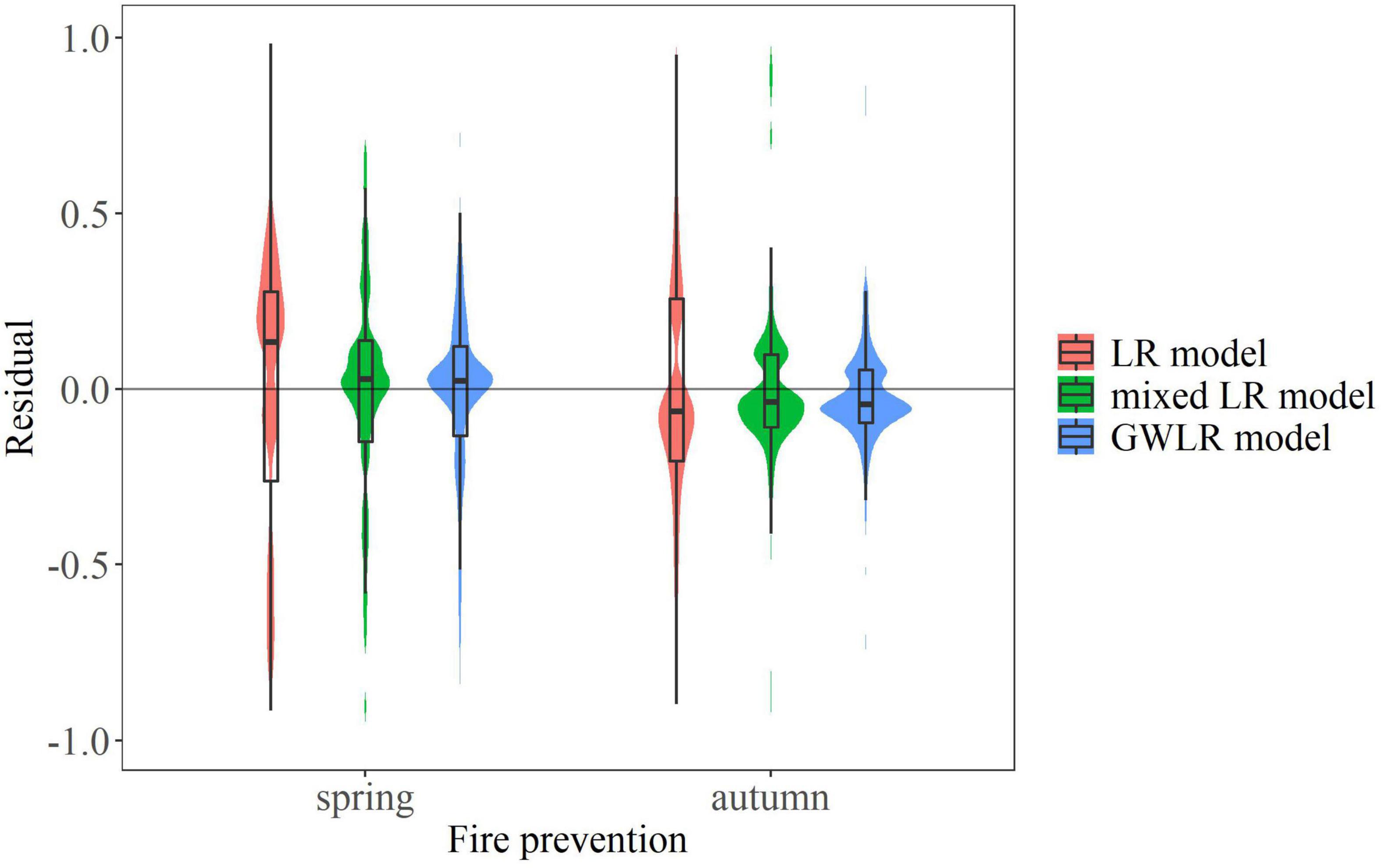
Figure 6. Residual distributions of different models. The violin plots represent the probability densities of residual distributions of different models in spring and autumn fire prevention periods. The box plots display the distributions of residuals, the middle line of the box represents the median of residuals, the two ends of the box represent the upper and lower quartiles respectively, and the two ends of the upper and lower lines outside the box represent the maximum and minimum residuals excluding outliers.

Prediction of forest fire occurrence probability in Heilongjiang Province

The LR model, mixed LR model and GWLR model were used to predict the probability of forest fire occurrence in Heilongjiang Province, and the Kriging interpolation method was applied to analyze its spatial probability. Figure 7 shows the probability distribution of forest fire in two fire prevention periods. In the prediction of the LR model, the probabilities of forest fire occurrence in northern parts of Heilongjiang Province are high, while the probabilities in southern parts are low. The high-probability areas in spring are larger than those in autumn. In the mixed LR model, the regions with higher probability of forest fire in spring are distributed in western and eastern parts of Heilongjiang Province, while those regions in autumn are mainly distributed in western parts. The results of the GWLR model are basically similar to those of the mixed LR model, except that there are sporadic medium-and high-probability areas in northern and southern regions during autumn fire prevention period.

FIGURE 7

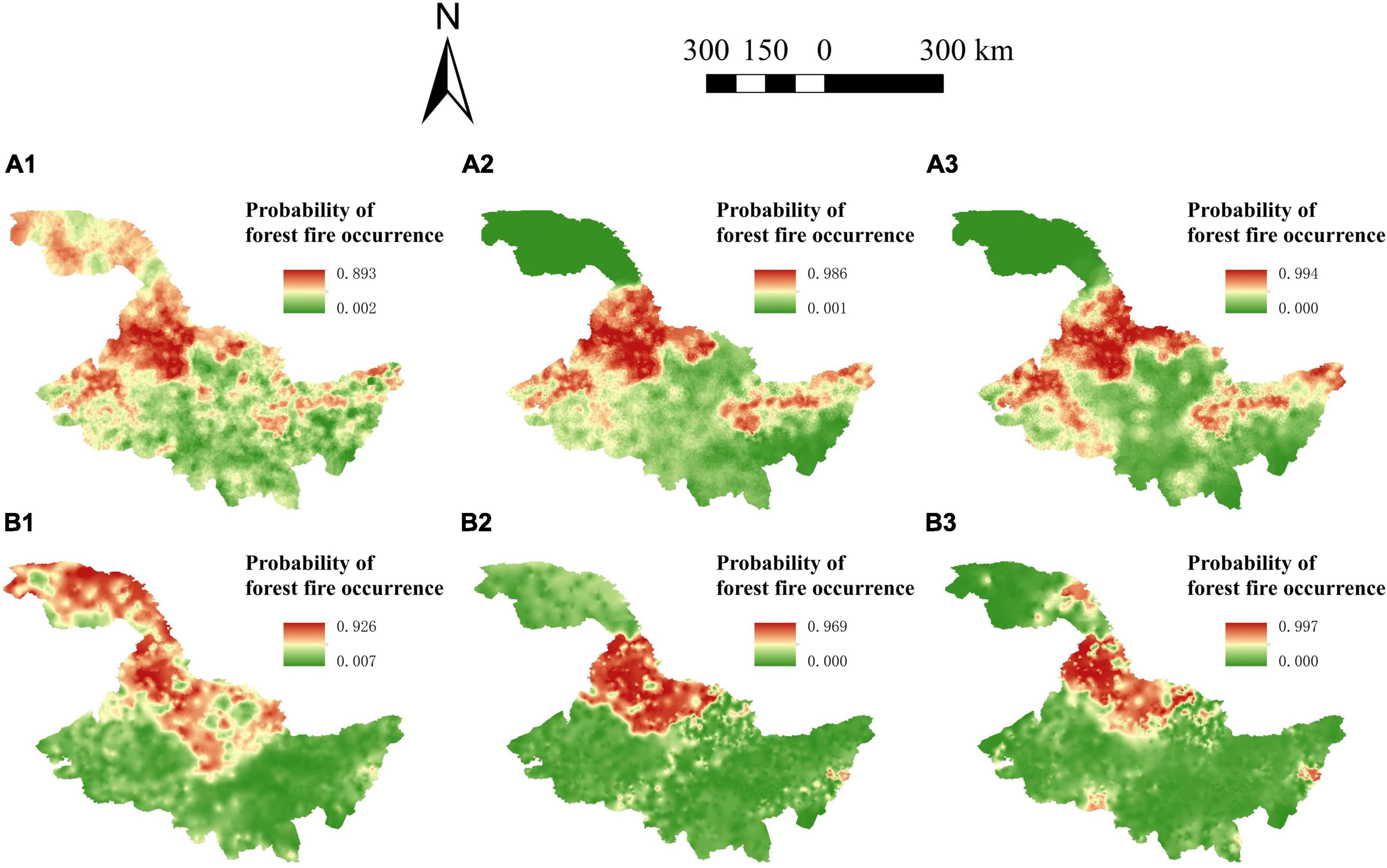
Figure 7. Spatial variation of forest fire probability in Heilongjiang Province, China. (A1) Forest fire probabilities predicted by the logistic regression (LR) model in spring fire prevention period. (A2) Forest fire probabilities predicted by the mixed LR model in spring fire prevention period. (A3) Forest fire probabilities predicted by the geographically weighted logistic regression (GWLR) model in spring fire prevention period. (B1) Forest fire probabilities predicted by the LR model in autumn fire prevention period. (B2) Forest fire probabilities predicted by the mixed LR model in autumn fire prevention period. (B3) Forest fire probabilities predicted by the GWLR model in autumn fire prevention period.

Discussion

Comparison of statistical indicators of different models

Compared with the LR model, the mixed LR model, and GWLR model both improved the fit and validation results significantly. Among them, the GWLR model produced the best accuracy of prediction, followed by the mixed LR model. The ROC curves, Moran’s I index and residual distribution also showed the same results. The superiority of the mixed-effects and GWLR models in forest fire prediction has been demonstrated by many prior research. For example, Oddi et al. (2019) applied a nonlinear mixed-effects model to estimate temporal changes in live fuel moisture content in Northwestern Patagonia area, and the model showed greater goodness of fit and a smaller AIC value than the traditional statistical model. The AIC, BIC, and prediction probability difference of the mixed effect model were also smaller than those of the corresponding fixed effect model in the study of forest fire in Qiannan Autonomous Prefecture, Guizhou Province, China (Xiao et al., 2015). Similarly, In the study of estimating the spatial pattern of forest fire in Korea, it was found that the predictions using the mixed-Poisson model for the validation quadrats showed a remarkably lower RMSE and a higher correlation between predictions and observed values than the estimates using Poisson (Kwak et al., 2012). In the study of modeling human-caused forest fire in north China, the GWLR model performs better than the LR model in terms of model prediction accuracy, model residual reduction, and spatial parameter estimation by considering geospatial information of explanatory variables (Guo et al., 2016b). The GWLR model better described the relationship between wildfire drivers and ignition probability than global LR model in Chinese tropical forest ecosystems (Su et al., 2021). On the basis of these findings, we made a comprehensive comparison among these three models, and highlighted the effectiveness of the GWLR model.

Driving factors of forest fire occurrence in Heilongjiang Province have obvious spatial heterogeneity. The LR base model assumes that all variables are spatially stationary, and establishes a simple regression relationship between the probability of forest fire occurrence and driving factors while ignoring the complex interactions among the meteorological factors and the spatial variations among the fire points. Therefore, the LR model cannot reflect the spatial relationship among variables (Boubeta et al., 2015). For the mixed LR model, we mainly considered the effects of latitude and longitude differences in the horizontal direction, as well as natural environment differences, on the occurrence of forest fires. We added random effects to different influence factors to improve the fitting and predicting effects of the model (Liu et al., 2021). At the same time, because the social economy, human activities, and forest fire prevention policies of different administrative divisions varies, the mixed LR model considering administrative division effects can better meet the needs of practical applications. Although some parameters become insignificant after adding random effects (Table 3), the mixed LR model still highly improved the performance of the LR model. The GWLR model fully considers the influence of spatial location on the dependent variables and estimates parameters for each coordinate point, which has higher prediction accuracy (Koutsias et al., 2005; Saeuddin et al., 2012).

Comparison of different models for forest fire probability prediction

From the perspective of predicted probability, the probability predicted by the LR base model ranges from 0.002 to 0.893, the probability of the mixed LR model ranges from 0.001 to 0.986, and the probability of the GWLR model is between 0.000 and 0.994, during the spring fire prevention period. In the autumn fire prevention period, the ranges of fire occurrence probability predicted by the 3 models are 0.007 to 0.926, 0.000 to 0.969, and 0.000 to 0.997, respectively (Table 5). The 3 models show consistent performance rank regardless of spring or autumn fire prevention period, i.e., LR model < mixed LR model < GWLR model.

During the spring fire prevention period, the areas with medium- and high-probability of forest fire predicted by the LR model basically cover the whole Heilongjiang Province except the southern part. The areas with medium-and high-probability of forest fire predicted by the mixed LR and GWLR models are similar, both concentrating in the western and eastern parts of Heilongjiang Province (Figure 7). However, during the autumn fire prevention period, the areas with medium- and high-probability of forest fire predicted by the mixed LR and GWLR models are concentrated in the northwestern part of Heilongjiang Province, with sporadic areas of the GWLR model scattered in the northern and southern regions (Figure 7).

According to the National Forest Fire Risk Classification of China (NFFRCC), the first-and second-level risk areas are mainly distributed in northwest, east and south Heilongjiang Province, while the third-level risk areas are distributed in the southwest region (National Forestry and Grassland Administration, 2016). Compared with the LR and mixed LR models, the regions with high probability of forest fire predicted by the GWLR model are all included in the first-level fire risk areas in the NFFRCC map. In addition, the GWLR model gave consistent predictions with the actual fire data distribution, indicating that the GWLR model has immense predictive ability. This research is consistent with other studies that showed the best prediction performance of the GWLR model (Wang et al., 2013; Su et al., 2021).

For the accuracy of the prediction probability for forest fire, the prediction accuracy of logistic regression (Table 4) is only 77.25 and 81.76% for spring and autumn fire prevention period, respectively, which are lower than that of the mixed LR and GWLR models. Thus, logistic regression analysis has poorer performance in predicting forest fires in Heilongjiang Province. This is consistent with the results of previous studies. For example, the logistic regression has been found to be less accurate with a prediction accuracy of 64.9% in forest fire prediction of Heilongjiang Province (Chang et al., 2013). The prediction accuracy of the LR model ranged from 58.6 to 70.5%, whereas the prediction accuracy of the GWLR model ranged from 65.2 to 79.9% in modeling human-caused forest fire in north China (Guo et al., 2016b).

Driving factors of forest fire occurrence in fire prevention period

The distributions of parameters (Figure 3) and its t-values (Figure 4) show spatial and temporal variations in Heilongjiang Province. Compared with other regions, the spatial and temporal heterogeneities of the Daxing’anling region in northwest Heilongjiang Province are relatively strong. Different driving factors have different effects in the same fire prevention period (Figure 3). In the spring fire prevention period, the Daxing’anling region has small spatial variations of precipitation and temperature, and large spatial variations of wind speed and LAI; in other regions, the spatial variations of temperature and leaf area index are large, and the spatial variations of wind speed and precipitation are small. In the autumn fire prevention period, the spatial variation of each driving factor in the Daxing’anling region is large, while the spatial variations of factors in other regions are relatively small.

The same driving factor has different effects during different fire prevention periods (Figure 3). Wind speed has positive effects on forest fire occurrence in the Daxing’anling region whereas negative effects in other regions during spring fire prevention period. But the opposite is true during the autumn fire prevention period. This may be due to the temperate continental monsoon climate in Heilongjiang Province. Affected by low pressure in winter and spring, less vapor accelerates the decline of the moisture content of combustibles and increases the possibility of forest fire. On the contrary, southeast monsoon will reduce the probability of forest fire by bringing precipitation in summer and autumn, because of the tropical cyclones. The effect of surface temperature on fire occurrence varies little in different seasons. This may be because Heilongjiang Province is located in the middle and high latitudes of the Northern Hemisphere, and the temperatures in both spring and autumn are low, which has little impact on the occurrence of forest fires. The influence of precipitation on forest fire in autumn is greater than that in spring. Although the dead combustibles increase in autumn, more precipitation can increase the moisture content of combustibles, thus reducing the possibility of fire occurrence. Previous studies have shown that precipitation affects the fuel moisture content, and high precipitation contributes to the moisture of dead combustibles, thus reducing the likelihood of fire ignition (Murthy et al., 2019; Xiong et al., 2020; Su et al., 2021). During the two fire seasons, LAI always shows a positive effect in the Daxing’anling region, but has large spatial variations in other regions of Heilongjiang Province. This may be due to the fact that the Daxing’anling region is mainly covered by deciduous needle-leaved forest, herbaceous species, deciduous broadleaved forest and cultural vegetation, which are the most important natural forest area of China (Zhang et al., 2014). The leaf growth in this area is affected by seasonal changes, resulting in a large change in LAI space in this area.

The occurrence of forest fires is usually determined by the local environmental variables. Heilongjiang Province has a large span of longitude and latitude, and great variations of its topography. Meanwhile, the climate in Heilongjiang Province changes greatly in different seasons because of monsoons. These variations make the driving factors have diverse effects on fire occurrence in different time periods and different spatial environments, resulting in strong spatial and temporal heterogeneities (Wu et al., 2014). The same phenomenon is also shown in Australia (Williamson et al., 2016), where there are strong geographic and seasonal patterns in fire weather. Therefore, the mixed LR model and GWLR model that can express spatial heterogeneity have shown better applicability in regions with variable climate (Guo et al., 2016b; Liu et al., 2021).

Limitations

We applied meteorological and vegetation factors to predict forest fire occurrence in Heilongjiang Province. However, human activities are also important factors in triggering forest fires in many other regions. Therefore, socio-economic variables should be taken into account in these regions when predicting forest fires. We only selected the data of the fire prevention period in 2019 in this study, aiming to evaluate different forest fire prediction models, as well as different influencing factors, in different fire prevention periods. In the context of climate change, drastic changes of climate in different years may affect the predictions of the models in this study. In future research, including multiple regions and long time periods should be carried out to expand the application of the model.

Conclusion

In this study, the LR model, the mixed LR model, and the GWLR model were developed for spring and autumn fire prevention period in Heilongjiang Province in northeast China, and the effects of different driving factors on forest fire occurrence were explored. The driving factors of forest fire occurrence show great spatial heterogeneities in both spring and autumn forest fire seasons. Compared with the LR model, both the mixed LR model and the GWLR model can significantly improve the prediction of forest fire occurrence. Among them, the GWLR model always produced the best predictions. The GWLR models can provide more reliable forest fire prediction and provide useful information for forest fire monitoring and management.

Data availability statement

The original contributions presented in this study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

ZZ, SY, and SS: study conception and design. ZZ and SS: data analysis, interpretation of results, and draft manuscript preparation. ZZ, GW, WW, HX, SS, and FG: critical revision of article. All authors reviewed the results and approved the final version of the manuscript.

Funding

This research was funded by the National Key R&D Plan of Strategic International Scientific and Technological Innovation Cooperation Project (2018YFE0207800).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^ http://www.gscloud.cn/
2. ^ https://cds.climate.copernicus.eu/

References

Amraoui, M., Pereira, M. G., DaCamaram, C. C., and Calado, T. J. (2015). Atmospheric conditions associated with extreme fire activity in the Western Mediterranean region. Sci. Total Environ. 52, 32–39. doi: 10.1016/j.scitotenv.2015.04.032

PubMed Abstract | CrossRef Full Text | Google Scholar

Blozis, S. A., and Harring, J. R. (2021). Fitting nonlinear mixed-effects models with alternative residual covariance structures. Soc. Method Res. 50, 531–566. doi: 10.1177/0049124118789718

CrossRef Full Text | Google Scholar

Boubeta, M., Lombardia, M. J., Marey-Perez, M. F., and Morales, D. (2015). Prediction of forest fires occurrences with area-level poisson mixed models. J. Environ. Manage. 154, 151–158. doi: 10.1016/j.jenvman.2015.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Burnham, K. P., and Anderson, D. R. (2002). Model selection and multi-model inference: A practical information-theoretic approach. New York: Springer.

Google Scholar

Chang, Y., Zhu, Z. L., Bu, R. C., Chen, H. G., Feng, Y. T., Li, Y. H., et al. (2013). Predicting fire occurrence patterns with logistic regression in Heilongjiang province. China. Landsc. Ecol. 28, 1989–2004. doi: 10.1007/s10980-013-9935-4

CrossRef Full Text | Google Scholar

Chen, Y. J., Deng, W. S., Yang, T. C., and Matthews, S. A. (2012). Geographically weighted quantile regression (GWQR): An application to US mortality data. Geogr. Anal. 44, 134–150. doi: 10.1111/j.1538-4632.2012.00841.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Curt, T., Frejaville, T., and Lahaye, S. (2016). Modeling the spatial patterns of ignition causes and fire regime features in south France: Implications for fire prevention policy. Int. J. Wildland Fire 25, 785–796. doi: 10.1071/WF15205

CrossRef Full Text | Google Scholar

Drever, C. R., Drever, M. C., Messier, C., Bergeron, Y., and Flannigan, M. (2008). Fire and the relative roles of weather, climate and landscape characteristics in the great lakes-st. Lawrence forest of Canada. J. Veg. Sci. 19, 57–66. doi: 10.3170/2007-8-18313

CrossRef Full Text | Google Scholar

Eskandari, S., Ghadikolaei, J. O., Jalilvand, H., and Saradjian, M. R. (2015). Evaluation of the MODIS fire-detection product in neka-zalemroud fire-prone forests in Northern Iran. Pol. J. Environ. Stud. 24, 2305–2308.

Google Scholar

Faivre, N., Jin, Y., Goulden, M. L., and Randerson, J. T. (2014). Controls on the spatial pattern of wildfire ignitions in Southern California. Int. J. Wildland Fire 23, 799–811. doi: 10.1071/WF13136

CrossRef Full Text | Google Scholar

Flannigan, M., Stocks, B., Turetsky, M., and Wotton, M. (2010). Impacts of climate change on fire activity and fire management in the circumboreal forest. Global Change Biol. 15, 549–560. doi: 10.1111/j.1365-2486.2008.01660.x

CrossRef Full Text | Google Scholar

Fotheringham, A. S., Brunsdon, C., and Charlton, M. (2002). Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. Hoboken: Wiley.

Google Scholar

Groom, J. D., Hann, D. W., and Temesgen, H. (2012). Evaluation of mixed-effects models for predicting Douglas-fir mortality. For. Ecol. Manag. 276, 139–145. doi: 10.1016/j.foreco.2012.03.029

CrossRef Full Text | Google Scholar

Guan, Y. L., Lu, H. W., Jiang, Y. L., Tian, P. P., Qiu, L. H., Pellikka, P., et al. (2021). Changes in global climate heterogeneity under the 21st century global warming. Ecol. Indic. 130:108075. doi: 10.1016/j.ecolind.2021.108075

CrossRef Full Text | Google Scholar

Guo, F. T., Innes, J. L., Wang, G. Y., Ma, X. Q., Sun, L., Hu, H. Q., et al. (2015). Historical distribution and driving factors of human-caused fires in the Chinese boreal forest between 1972 and 2005. J. Plant Ecol. 8, 480–490. doi: 10.1093/jpe/rtu041

CrossRef Full Text | Google Scholar

Guo, F. T., Wang, G. Y., Su, Z. W., Liang, H. L., Wang, W. H., Lin, F. F., et al. (2016a). What drives forest fire in Fujian. China? Evidence from logistic regression and random forests. Int. J. Wildland Fire 25, 505–519. doi: 10.1071/WF15121

CrossRef Full Text | Google Scholar

Guo, F. T., Selvalakshmi, S., Lin, F. F., Wang, G. Y., Wang, W. H., Su, Z. W., et al. (2016b). Geospatial information on geographical and human factors improved anthropogenic fire occurrence modeling in the Chinese boreal forest. Can. J. For. Res. 46, 582–594. doi: 10.1139/cjfr-2015-0373

CrossRef Full Text | Google Scholar

Hastie, T., Tibshirani, R., and Friedman, J. (2001). The elements of statistical learning: Data mining, inference and prediction. New York: Springer. doi: 10.1007/978-0-387-21606-5

CrossRef Full Text | Google Scholar

He, Z. M., Li, L. Z., Huang, Z. M., and Situ, H. Z. (2018). Quantum-enhanced feature selection with forward selection and backward elimination. Quantum Inf. Process. 17:154. doi: 10.1007/s11128-018-1924-8

CrossRef Full Text | Google Scholar

Hegeman, E. E., Dickson, B. G., and Zachmann, L. J. (2014). Probabilistic models of fire occurrence across National Park Service units within the Mojave Desert Network. USA. Landsc. Ecol. 29, 1587–1600. doi: 10.1007/s10980-014-0078-z

CrossRef Full Text | Google Scholar

Justice, C. O., Giglio, L., Korontzi, S., Owens, J., Morisette, J. T., Roy, D., et al. (2002). The MODIS fire products. Remote Sens. Environ. 83, 244–262. doi: 10.1016/S0034-4257(02)00076-7

CrossRef Full Text | Google Scholar

Kennedy, P. (1992). A Guide to Econometrics. Oxford: Blackwell.

Google Scholar

Koutsias, N., Martinez, J., Chuvieco, E., and Alligwer, B. (2005). Modeling wildland fire occurrence in southern Europe by a geographically weighted regression approach // Proceedings of the 5th International Workshop on Remote Sensing and GIS Applications to Forest Fire Management: Fire Effects Assessment. Spain: Universidad de Zaragoza, 57–60.

Google Scholar

Kwak, H., Lee, W. K., Saborowski, J., Lee, S. Y., Won, M. S., Koo, K. S., et al. (2012). Estimating the spatial pattern of human-caused forest fires using a generalized linear mixed model with spatial autocorrelation in South Korea. Int. J. Geogr. Inf. Sci. 26, 1589–1602. doi: 10.1080/13658816.2011.642799

CrossRef Full Text | Google Scholar

Liu, X., Hao, Y. S., Widagdo, F. R. A., Xie, L. F., Dong, L. H., and Li, F. R. (2021). Predicting height to crown base of Larix olgensis in northeast China using UAV-LiDAR data and nonlinear mixed effects models. Remote Sens-basel 13:1834. doi: 10.3390/rs13091834

CrossRef Full Text | Google Scholar

Liu, Z. H., Yang, J., Chang, Y., Weisberg, P. J., and He, H. S. (2012). Spatial patterns and drivers of fire occurrence and its future trend under climate change in a boreal forest of Northeast China. Global Change Biol. 18, 2041–2056. doi: 10.1111/j.1365-2486.2012.02649.x

CrossRef Full Text | Google Scholar

Martinez-Fernandez, J., Chuvieco, E., and Koutsias, N. (2013). Modelling long-term fire occurrence factors in Spain by accounting for local variations with geographically weighted regression. Nat Hazard Earth Syst. 13, 311–327. doi: 10.5194/nhess-13-311-2013

CrossRef Full Text | Google Scholar

Murthy, K. K., Sinha, S. K., Kaul, R., and Vaidyanathan, S. (2019). A fine-scale state-space model to understand drivers of forest fires in the Himalayan foothills. For. Ecol. Manag. 432, 902–911. doi: 10.1016/j.foreco.2018.10.009

CrossRef Full Text | Google Scholar

National Forestry and Grassland Administration. (2018). National Forestry and Grassland Statistical Yearbook. Beijing: China Forestry Publishing House, 4–5.

Google Scholar

National Forestry and Grassland Administration. (2016). National forest fire prevention program (2016–2025). Beijing: [EB/OL]. (in Chinese)

Google Scholar

Nunes, A. N., Lourenco, L., and Meira, A. C. C. (2016). Exploring spatial patterns and drivers of forest fires in Portugal (1980-2014). Sci. Total Environ. 573, 1190–1202. doi: 10.1016/j.scitotenv.2016.03.121

PubMed Abstract | CrossRef Full Text | Google Scholar

Oddi, F. J., Miguez, F. E., Ghermandi, L., Bianchi, L. O., and Garibaldi, L. A. (2019). A nonlinear mixed-effects modeling approach for ecological data: Using temporal dynamics of vegetation moisture as an example. Ecol. Evol. 9, 10225–10240. doi: 10.1002/ece3.5543

PubMed Abstract | CrossRef Full Text | Google Scholar

Parajuli, A., Gautam, A. P., Sharma, S. P., Bhujel, K. B., Sharma, G., Thapa, P. B., et al. (2020). Forest fire risk mapping using GIS and remote sensing in two major landscapes of Nepal. Geomatics, Nat. Hazards Risk 11, 2569–2586. doi: 10.1080/19475705.2020.1853251

CrossRef Full Text | Google Scholar

Rawlings, J. O., Pantula, S. G., and Dickey, D. A. (1998). Applied regression analysis: A research tool. New York: Springer. doi: 10.1007/b98890

CrossRef Full Text | Google Scholar

Rodrigues, M., Costafreda-Aumedes, S., Comas, C., and Vega-Garcia, C. (2019). Spatial stratification of wildfire drivers towards enhanced definition of large-fire regime zoning and fire seasons. Sci. Total Environ. 689, 634–644. doi: 10.1016/j.scitotenv.2019.06.467

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodrigues, M., de la Riva, J., and Fotheringham, S. (2014). Modeling the spatial variation of the explanatory factors of human-caused wildfires in Spain using geographically weighted logistic regression. Appl. Geogr. 48, 52–63. doi: 10.1016/j.apgeog.2014.01.011

CrossRef Full Text | Google Scholar

Rodrigues, M., Jimenez-Ruano, A., Pena-Angulo, D., and de la Riva, J. (2018). A comprehensive spatial-temporal analysis of driving factors of human-caused wildfires in Spain using Geographically Weighted Logistic Regression. J. Environ. Manag. 255, 177–192. doi: 10.1016/j.jenvman.2018.07.098

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeuddin, A., Setiabudi, N. A., and Fitrianto, A. (2012). On comparison between logistic regression and geographically weighted logistic regression: With application to Indonesian poverty data. World Appl. Sci. J. 19, 205–210.

Google Scholar

Stan, A. B., Fule, P. Z., Ireland, K. B., and Sanderlin, J. S. (2014). Modern fire regime resembles historical fire regime in a ponderosa pine forest on native American lands. Int. J. Wildland Fire 23, 686–697. doi: 10.1071/WF13089

CrossRef Full Text | Google Scholar

Su, Z. W., Zheng, L. J., Luo, S. S., Tigabu, M., and Guo, F. T. (2021). Modeling wildfire drivers in Chinese tropical forest ecosystems using global logistic regression and geographically weighted logistic regression. Nat. Hazards 108, 1317–1345. doi: 10.1007/s11069-021-04733-6

CrossRef Full Text | Google Scholar

Turetsky, M. R., Kane, E. S., Harden, J. W., Ottmar, R. D., Manies, K. L., Hoy, E., et al. (2011). Recent acceleration of biomass burning and carbon losses in Alaskan forests and peatlands. Nat. Geosci. 4, 27–31. doi: 10.1038/ngeo1027

CrossRef Full Text | Google Scholar

Wang, L. T., Zhou, Y., Zhou, W. Q., and Wang, S. X. (2013). Fire danger assessment with remote sensing: A case study in Northern China. Nat. Hazards 65, 819–834. doi: 10.1007/s11069-012-0391-2

CrossRef Full Text | Google Scholar

Williamson, G. J., Prior, L. D., Jolly, W. M., Cochrane, M. A., Murphy, B. P., and Bowman, D. M. J. S. (2016). Measurement of inter- and intra-annual variability of landscape fire activity at a continental scale: The Australian case. Environ. Res. Lett. 11:035003. doi: 10.1088/1748-9326/11/3/035003

CrossRef Full Text | Google Scholar

Wu, Z. C., Li, M. Z., Wang, B., Quan, Y., and Liu, J. Y. (2021). Using artificial intelligence to estimate the probability of forest fires in Heilongjiang. Northeast China. Remote Sens. 13:1813. doi: 10.3390/rs13091813

CrossRef Full Text | Google Scholar

Wu, Z. W., He, H. S., Yang, J., Liu, Z. H., and Liang, Y. (2014). Relative effects of climatic and local factors on fire occurrence in boreal forest landscapes of northeastern China. Sci. Total Environ. 493, 472–480. doi: 10.1016/j.scitotenv.2014.06.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, Y. D., Zhang, X. Q., and Ji, P. (2015). Modeling forest fire occurrences using count-data mixed models in qiannan autonomous prefecture of Guizhou province in China. PLoS One 10:e0120621. doi: 10.1371/journal.pone.0120621

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, Q., Luo, X., Liang, P., Xiao, Y., Xiao, Q., Sun, H., et al. (2020). Fire from policy, human interventions, or biophysical factors? Temporal–spatial patterns of forest fire in southwestern China. For. Ecol. Manag. 474:118381. doi: 10.1016/j.foreco.2020.118381

CrossRef Full Text | Google Scholar

Zhang, H. J., Qi, P. C., and Guo, G. M. (2014). Improvement of fire danger modelling with geographically weighted logistic model. Int. J. Wildland Fire 23, 1130–1146. doi: 10.1071/WF13195

CrossRef Full Text | Google Scholar

Appendix

APPENDIX TABLE 1

Appendix Table 1. Fitting results of the mixed effect model.

APPENDIX TABLE 2

Appendix Table 2. Spatial stationarity evaluation of parameter estimation for the geographically weighted logistic regression (GWLR) model.