- 1Interdisciplinary Centre for Mountain Research, University of Lausanne, Sion, Switzerland
- 2Department of Ecology and Evolution, University of Lausanne, Lausanne, Switzerland
- 3Institute of Earth Surface Dynamics, University of Lausanne, Lausanne, Switzerland
- 4Centre Alpien de Phytogéographie, Champex-Lac, Switzerland
- 5Dynamic Macroecology, Swiss Federal Institute of Forest, Snow and Landscape Research WSL, Birmensdorf, Switzerland
In steep terrain, forests play an important role as natural means of protection against natural hazards, such as rockfall. Due to climate warming, significant changes in the protection service of these forests have to be expected in future. Shifts of current to more drought adapted species may result in temporary or even irreversible losses in the reduction of rockfall risk provided by these forests. In this study, we assessed how the protective capacity against rockfall of a protection forest in the western part of the Valais in the Swiss Alps may change in future, by combining dynamic forest modelling with a quantitative risk analysis. Current and future forest development was modelled with the spatially explicit forest model TreeMig under a moderate (RCP4.5) and an extreme (RCP8.5) climate change scenario. The simulated forest scenarios were compared to ground-truth data from the current forest complex. We quantified the protective effect of the different forest scenarios based on the reduction of rockfall risk for people and infrastructure at the bottom of the slope. Rockfall risk was calculated on the basis of three-dimensional rockfall simulations. The forest simulations predicted a clear decrease in basal area of most of the currently occuring species (Fagus sylvatica, Picea abies, Larix decidua, and Abies alba) in future. The forest turned into a Quercus pubescens dominated forest, for both climate scenarios, mixed with Pinus sylvestris under RCP4.5. With climate warming, a clear increase in risk is expected for both climate change scenarios. In the long-term (>100 years), a stabilization of risk, or even a slight decline may be expected due to an increase in biomass of the trees. The results of this study further indicate that regular forest interventions may promote regeneration and thus accelerate the shift in species distribution. Future research should explore into more details the long-term effect of different adaptive forest management strategies on the protection service of forests under climate change.
Introduction
Forests provide a series of ecosystem services to human beings, such as water filtration, biodiversity, wood production, carbon sequestration, and protection from natural hazards (Costanza et al., 1998; Pagiola et al., 2002). In steep, mountainous terrain, the protective effect of forests against natural hazards is of particular importance (Sakals et al., 2006; Grêt-Regamey et al., 2008). Thanks to this so-called “nature-based solution,” costs for technical structures for the protection of settlements and infrastructure can be reduced or even avoided (Getzner et al., 2017).
Various studies have shown the high effectiveness of forests in reducing the negative effects of natural hazards (see for review, Moos et al., 2018a; Sebald et al., 2019; Ruangpan et al., 2020). These, however, mostly focused on a specific (static) forest state and did not take the temporal evolution of forests into account. The evaluation of the long-term efficacy of protection forests remains complicated since uncertainties in the protective capacity are high (Woltjer et al., 2008). Natural forest dynamics and disturbances can result in temporal variation of the protective effect of forests (Silins et al., 2009; Vacchiano et al., 2015). Furthermore, climate change is expected to induce shifts in the forest structure and extent (e.g., treeline) and in the distribution of their constitutive species (Kulakowski et al., 2010; Lindner et al., 2014; Albrich et al., 2020; Scherrer et al., 2020). This may, on the one hand, increase the protective effect of temperature limited mountain forests and treeline ecotones, where higher temperatures are expected to increase the forest extent (e.g., along altitude) and growth (Bebi et al., 2017; Scherrer et al., 2020). On the other hand, more frequent drought periods at lower elevations lead to a shift of the current species composition to more drought adapted species (Peñuelas and Boada, 2003; Urli et al., 2013). This shift ideally happens gradually. However, abrupt diebacks of contemporary species, followed by a slow reforestation with better adapted species can also be expected in the future (Elkin et al., 2013). This may result in temporary or even irreversible losses in the protective effect of forests due to a reduced stem density and diameters (Bebi et al., 2017; Irauschek et al., 2017).
Dynamic forest landscape models (Schumacher et al., 2004; Lischke et al., 2006; Seidl et al., 2012) enable to both understand and predict (sensu Shmueli, 2010) forest development over larger areas under past or future climate scenarios. They are a promising way to investigate the evolution of the forest structure and composition at broad temporal and spatial scale (Petter et al., 2020). So far, few attempts have been made to assess the future development of the protective effect of forests. Furthermore, previous studies have mostly used simple indicators to estimate the protection efficacy of the forest without calculating the explicit risk reduction provided by the forest (Elkin et al., 2013; Albrich et al., 2020). In contrast, a risk-based approach allows for the translation of the physical effect of trees on the natural hazard process into monetary terms (Teich and Bebi, 2009; Moos et al., 2018b). This can then serve as input for economic evaluation techniques, such as cost-benefit analyses (Olschewski et al., 2012). An economic evaluation, however, can only be realistic if it accounts for the long-term evolution of the protective effect, which becomes increasingly challenging in the face of climate change (Dale et al., 2001; Allen et al., 2010; Elkin et al., 2013).
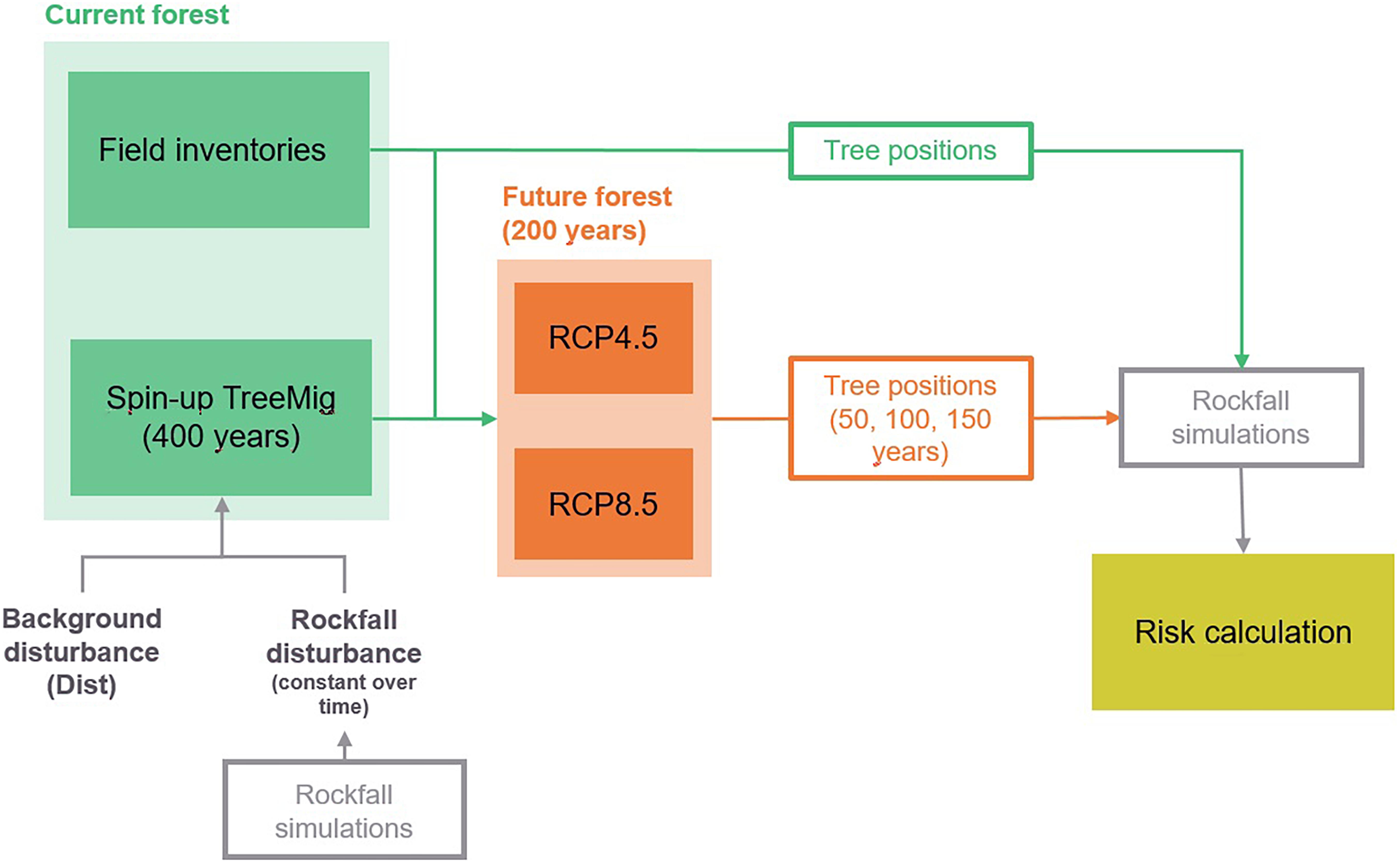
In this study, we used the dynamic forest model TreeMig (Lischke et al., 2006) to project the future forest development of a regularly managed rockfall protection forest complex in the Swiss Alps under two different climate change scenarios. We first compared the model projections to the forest cover under current climatic conditions, including the regeneration in areas where forest interventions have taken place in the past 30 years. We then assessed how the protective effect of the forest against rockfall may change under climate change in the next 150 years based on a quantitative risk analysis. The combined analysis of current data on forest regeneration and future forest simulation then provides a basis to evaluate on the role of management in protection forests under climate change.
Materials and Methods
Study Area
The study area (Figure 1) is located in the east-west oriented main valley of the canton of Valais (Switzerland) in the south of the town Martigny (46°05′32″N/7°04′09″E). It ranges from 500 to 1,000 m a.s.l. and the slope has an inclination between 0° and 70° (0° and 55° in the forested area). The climate of Martigny is dry (one of the driest regions in Switzerland) with an average yearly precipitation of 880 mm and a maximum mean temperature of 14°C (June) and –2°C (January) and minimum mean temperature of 3°C (June) and –10°C (January). Due to already low precipitation, climate change is expected to distinctly influence the forests in this region, and, consequently, also their protective effect against natural hazards. Since the forest above Martigny plays an important role in protecting subjacent infrastructure (road/railway) and houses from rockfall, it is particularly suitable to analyze climate change effects on the protection service. The rockfall area consists of small, dispersed rock cliffs with a total area of ∼2 ha and consists mainly of gneiss and mica slate. The forest is mainly dominated by Fagus sylvatica, Picea abies, Pinus sylvestris, and Abies alba and covers a total area of ∼77 ha. In the past 30 years, regular interventions have been made across forest with cable-based harvesting, where relatively large openings for regeneration were created (information from local forest manager and orthophotos).
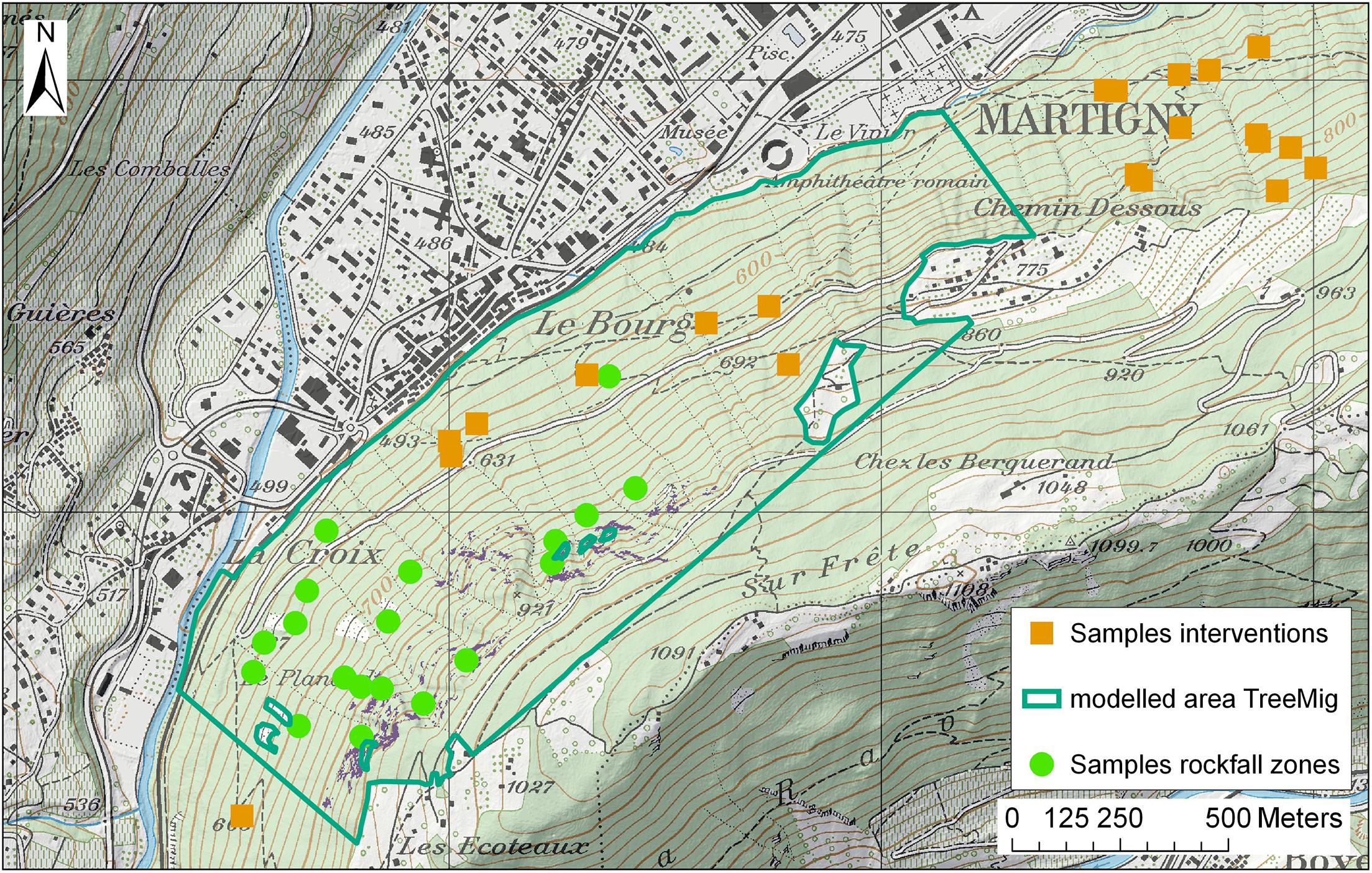
Figure 1. Study area with sample plots in the intervention areas (orange squares), sample plots in the rockfall zone (green dots), and the forest area modelled in TreeMig (dark green).
Forest Scenarios
We modelled current and future forest development with the dynamic, distribution based, spatially explicit forest landscape model TreeMig (Lischke et al., 2006; Lischke, 2020). TreeMig simulates reproduction, tree establishment, growth, competition, and mortality of trees per height class and cells of 25 m × 25 m; the state variables are the numbers of individuals per height class, grid cell and species. These processes are controlled by the yearly bioclimatic drivers day-degree sum (sum of mean daily temperatures above 5.5°C), minimum winter temperature (mean temperature of the coldest month), and a drought stress index (based on monthly precipitation, temperature, and on soil water holding capacity). Because of the yearly resolution, also extreme events of drought or heat are taken into account. Trees of different cells interact spatially through seed dispersal. The tree density and light distribution in a cell is represented by a Poisson distribution, assuming trees to be randomly distributed. Currently, 30 European species are parameterized in TreeMig (Supplementary Tables 1, 2). Because only rarely sufficient area-covering forest data for all height classes and species are available and initializing point data (e.g., NFI data) transformed to such format tends to lead to artefacts in the first simulated years, TreeMig is usually initialized by running a spin-up under different disturbance regimes (also representing simplified management) and then choosing the final output of the scenario which fits best to current forest data. TreeMig is embedded in an R-wrapper which helps to prepare the input files; the model and support thereon can be obtained upon request from bGlzY2hrZUB3c2wuY2g=, and in future on GitHub.
Simulations were run in different steps: (a) spin-up under different disturbance scenarios, (b) choice of simulated current forest at the end of the spin-up period by comparison to the real forest, and (c) future simulations from the simulated current forest under different climate change scenarios. (a) We simulated forest development in a forest mask based on the existing forest cover derived from land cover data (swisstopo, 2020b). The current forest state was modelled based on a simulation from bare ground for a time span of 400 years (“spin-up” simulation). Climate data (Figure 2) were taken from measurements from 1930 to 2016 with randomly sampled values for the years before. Soil water holding capacity (“bucket size”) for the study area was estimated between 11 and 33 cm based on water retention potential and soil wetness data from the Swiss soil suitability map (BFS, 2000; Lischke et al., 2006). The simulations were conducted considering the disturbing effect of rockfall, and with and without a random “background disturbance.” The rockfall disturbance was derived from three-dimensional rockfall simulations on the unforested slope following Moos and Lischke (in revision) and held constant over time (rockfall disturbance does not change over the considered time period). The “background disturbance” (Dist) is a spatially randomly distributed additional mortality that can represent natural disturbances or-very much simplified–forest management, for example. We implemented two scenarios of a low and a high background disturbance (Table 1). In the low disturbance scenario, a cell is on average disturbed once in 1,000 years with an intensity of 0.8 (80% of the cell are destroyed). Under the high disturbance scenario, a cell is on average disturbed once in 20 years with an intensity of 0.8. The latter represents very regular and rather intense forest management and/or natural disturbances. For both disturbance probabilities, we further tested a lower disturbance intensity of 0.3 to get an estimate on the sensitivity of forest development to disturbance intensity. (b) The simulated current forest state was validated based on data from field samples in recent and former forest intervention areas and samples in the rockfall zone (see section “Field Investigations”). Based on this validation, we used the spin-up of the current forest state with low background disturbance as initial state for the simulations with future climate.
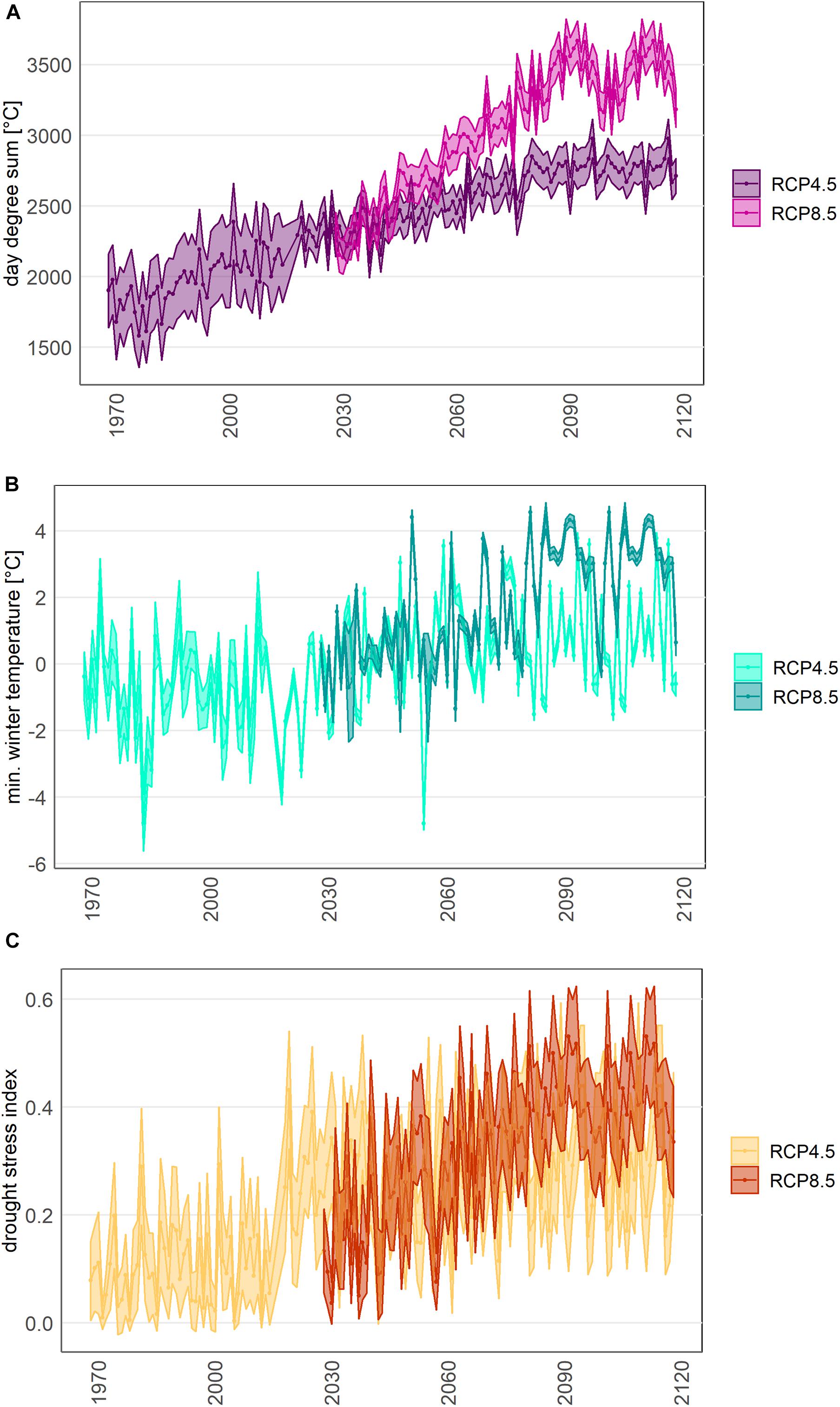
Figure 2. Bioclimatic variables used for the TreeMig simulations: day degree sum (A), mean minimum winter temperature (B), and drought stress index (C) from 1970 to the beginning of the stabilizing period (2120). The spin up of the simulations run from 1616 to 2016, with climate data sampled from interpolated measured data from 1930 to 2016.
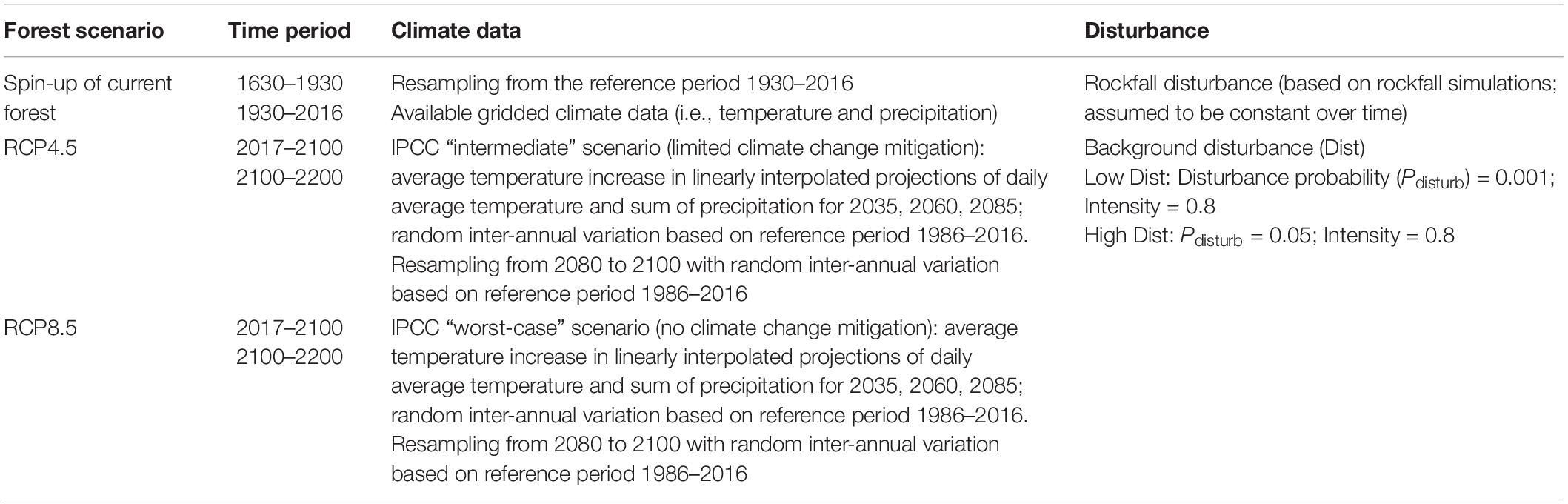
Table 1. Time period, climate data and disturbance regimes [disturbance probability (PDist) and intensity] for the spin-up forest simulation and the future forest scenarios.
(c) From this initial state, future forest development was simulated under warming conditions for 2016–2100 followed by a stabilizing period (2101–2200). Bioclimatic variables were derived from average daily temperature and precipitation data for a moderate (RCP4.5) and an extreme (RCP8.5) climate change scenario (Figure 2; CH2018 Project Team, 2018). The CH2018 scenarios are derived from the EURO-CORDEX ensemble of regional climate simulations. In CH2018, multiple Global Climate Models (GCMs) were dynamically downscaled by different RCMs for three future emissions scenarios (i.e., RCP2.6, RCP4.5, and RCP8.5). We chose RCP4.5 (moderate climate mitigation) and RCP8.5 (no climate mitigation) as the two most likely trajectories. CH2018 scenarios currently provide the best available dataset of future climate change estimates in Switzerland (Sørland et al., 2020). Gridded projections from CH2018 at a 1-km resolution were downscaled to a 25-m resolution based on a lapse rate (Broennimann, 2020). We linearly interpolated temperature and precipitation data from the available projections for 2035, 2060, and 2085 and added a random inter-annual variation based on the reference period of 1986–2016. The climate variables of the stabilizing period were randomly sampled from the last 20 years of the climate projection and complemented with the same random inter-annual variation.
Field Investigations
The simulated forest scenarios after the spin-up were compared to and validated with ground-truth data from the current forest. We measured adult trees and regeneration in 21 sample plots in areas with recent interventions (last intervention ≤ 10 years) and areas that have not been intervened in the past 10 years (Figure 1). The time since the last intervention was estimated based on a series of orthophotos (swisstopo, 2020a) and information from local forest managers. At each sampling site, we measured the diameter at breast height (dbh) and the species of each tree with a dbh ≥ 12 cm in a 20 m × 20 m plot (measured on the slope), and the species, age and height (for plants with a height ≤ 3 m) or dbh (for plants with a height > 3 m) of the regeneration in a 5 m × 5 m subplot. The subplots were selected based on the criteria that they were representative for the regeneration in the large plot. The plots cover the total slope and go beyond the area simulated with TreeMig (Figure 1).
Furthermore, data on species and dbh distribution (trees with dbh ≥ 8 cm) were available from 19 sample plots in the main rockfall zone (simulation area) from a previous study (Moos et al., 2020). Based on the data from these plots, we calculated tree density, species and diameter distribution for homogeneous forest areas (determined based on the orthophoto). We then generated trees with random positions in each area based on the derived tree densities and diameter distributions. This “treefile” served for validation of the rockfall risk assessment based on the simulated forest scenarios (see section “Protective Effect of Forest”).
Protective Effect of Forest
We quantified the protective effect of the different forest scenarios based on the reduction of rockfall risk for people and infrastructure at the bottom of the slope. The risk reduction is the difference between the risk without forest and the risk with forest (i.e., avoided costs). Rockfall risk is defined as the yearly expected damage of all possible damaging events (Agliardi et al., 2009). This is a useful indicator for a long-term perspective, although the damages actually caused can vary strongly from year to year. Rockfall risk for buildings and roads below and along the slope was calculated spatially explicitly following Moos et al. (2018b). The rockfall risk Ri,j of a specific element at risk i and for a rockfall scenario j is defined as the product of the onset probability of rockfall scenario j (Ponset,j), the probability that the block j reaches the element at risk i (propagation probability Pprop,i,j), the value of the element at risk Ei, its presence probability Ppresence,i and its vulnerability V(I)i,j. The latter depends on the intensity I of the rockfall impact (quantified as kinetic energy). The risk is finally averaged over all possible impacts ni,j.
The total risk R is the sum of the risks of all elements at risk e and for all expected rockfall scenarios v:
By stopping or deviating falling blocks, the forest can on the one hand influence their propagation probability, and on the other hand reduce their energy (and thus their intensity). These two effects were quantified based on rockfall simulations.
Rockfall Simulations
Rockfall simulations were conducted with the three-dimensional rockfall module RockyFor3D (Dorren, 2016). This “probabilistic process-based” rockfall model simulates flying, bouncing and rolling blocks depending on terrain characteristics and standing trees. After each impact of a block on a tree, the energy reduction of the block is calculated depending on the tree species, the tree diameter and the impact height (Dorren, 2016). The rockfall release area was determined based on slope inclination and orthophotos. Rock density was set to 2,700 kg m–3. Soil types and roughness were determined for homogenous areas based on land cover data (swisstopo, 2020b), the geological map (swisstopo, 2019) and the slope inclination and verified in the field. We simulated 100 blocks per block volume scenario and start cell (in total 684,000 simulations per block volume). Blocks were simulated with a cubic form with uniform edge length. The simulations were conducted with a digital elevation model with a resolution of 2 m. Buildings were considered as “rockfall nets” in the simulations with an energy absorption capacity of 600 kJ and their actual height. The rockfall simulations were conducted for the current forest cover (based on field samples and based on the forest simulations; see sections “Forest Scenarios” and “Field Investigations”) and for the future forest scenarios (after 50, 100, and 150 years of forest simulations; Figure 3). For this purpose, the cell-based output of the TreeMig simulations was translated into single tree positions by assuming a random tree distribution per 25 m × 25 m cell.
Rockfall Risk Calculation
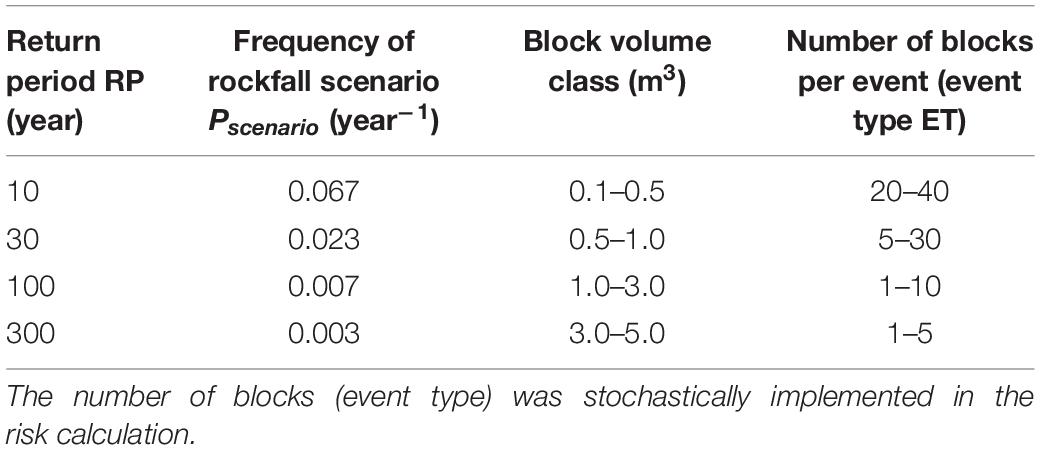
We calculated rockfall risk per forest scenario for four different rockfall release scenarios with return periods of 10, 30, 100, and 300 years (Table 2). The respective block volumes were determined by expert estimation and validated based on rockfall deposits measured in the forest sample plots in the rockfall zone (Moos et al., 2020). For each scenario, we estimated a varying number of blocks potentially releasing per event (“event type” ET, Table 2). An ET > 1 means that multiple blocks of this block volume class release in the time period of the rockfall scenario (e.g., 20 blocks in 10 years). The resulting block volume distribution was generally in good agreement with the distribution of the blocks assessed in the field (power law coefficient of estimated volume-frequency distribution: –1.80; power law coefficient of block deposits: –1.38). We further estimated the overall onset frequency of blocks ≥0.05 m3 based on tree damages below the release area, following Trappmann and Stoffel (2013). We counted all visible fresh tree damages (younger than approximately 1 year) in a strip of 10 m width 20 m below the cliff (Moos et al., 2020). We then used the “conditional impact probability” (CIP) concept (Moya et al., 2010) resulting in a rockfall frequency of blocks ≥0.05 m3 of ∼30 year–1 below the cliff. This is well in line with the derived rockfall release scenarios used in the risk analysis (Ponset (v ≥ 0.05 m3) = 34 year–1 and Ponset (v ≥ 0.1 m3) = 2 year–1).
The varying number of blocks per rockfall scenario was considered probabilistically in the rockfall risk analysis based on a Monte-Carlo simulation. The risk calculation was repeated 50 times and for each repetition, the number of released blocks per scenario was sampled randomly. We finally calculated the mean risk for each rockfall scenario. Varying the number of releasing blocks allows at least for a partial representation of the uncertainty associated with the release frequency.
The propagation probability (Pprop,i,j) of a block j at the element at risk i was determined based on the rockfall simulations (section “Rockfall Simulations”). It is defined as proportion of the potential rockfall trajectories of volume j through i (ni,j), and the total number of simulated trajectories of volume j (nj,tot):
The energy of each block reaching an element at risk in the simulations was registered and classified according to the Swiss risk concept as low (0–30 kJ), medium (30–300 kJ) and high (>300 kJ) intensities (Bründl et al., 2009). We considered roads (with a width > 4 m), buildings and the railway below the slope as elements at risk. Object categories and occupancy were determined based on national dwelling data (FOS, 2020) and values and vulnerabilities of objects and persons were derived for the different intensity classes based on standard values of the Swiss risk concept (FOEN, 2020; Supplementary Tables 3, 4). We calculated risk only for direct impacts and infrastructure damage, and did not consider road/railway closure. Mean daily traffic (MDT) was determined based on census data from the cantonal authorities and estimations based on GoogleMaps.
The risk reduction (in CHFyear–1) provided by a forest was finally calculated as the difference of the risk without forest and the risk with forest. It was evaluated for the current forest cover based on field data and the forest simulations, and for the future forest scenarios after 50, 100, and 150 years of simulated forest development. We only considered changes in forest cover under future climate, and no other potential (climate related) changes in risk, such as a shift in the release frequency and magnitude of rockfall.
Results
Forest Today: Modelling Results Compared to Field Data
The initial forest as generated by the TreeMig model after spin up had a mean basal area of 50.1 m2 ha–1 [standard deviation (sd.) = 15.4 m2 ha–1] with low background disturbance (Dist) and a mean basal area of 43.7 m2 ha–1 (sd. = 15.9 m2 ha–1) with high Dist. For both disturbance scenarios, highest basal area was found in the lower (<700 m a.s.l.) and upper (900–1,100 m a.s.l.) parts of the slope, whereas it was slightly lower at medium elevation. This is well in line with the actual measures of the current forest, which has a mean basal area up to 60 m2 ha–1 in the upper part of the slope and a slightly smaller basal area (45–50 m2 ha–1) at medium altitude, where the stand is generally denser (800–900 trees ha–1) but with lower diameters (dbh) (mean dbh = 25–28 cm). In the upper part of the forest, the current forest has a tree density of 550–600 trees ha–1 and a mean dbh of ∼35 cm. In contrast, TreeMig predicted a slightly denser forest (on average 870 trees ha–1 with low Dist; 1,270 trees ha–1 with high Dist), but with a lower dbh (mean dbh = 23.0 cm with low Dist and 20.5 cm with high Dist). Both the modelled forest and the actual forest are mainly dominated by F. sylvatica, mixed with P. abies, Acer pseudoplatanus, Fraxinus excelsior, and Tilia cordata (Figure 4). However, the model predicted a lower abundance of Larix decidua and A. alba than observed in the sample plots. In contrast, there were more Quercus pubescens in the modelled forest.
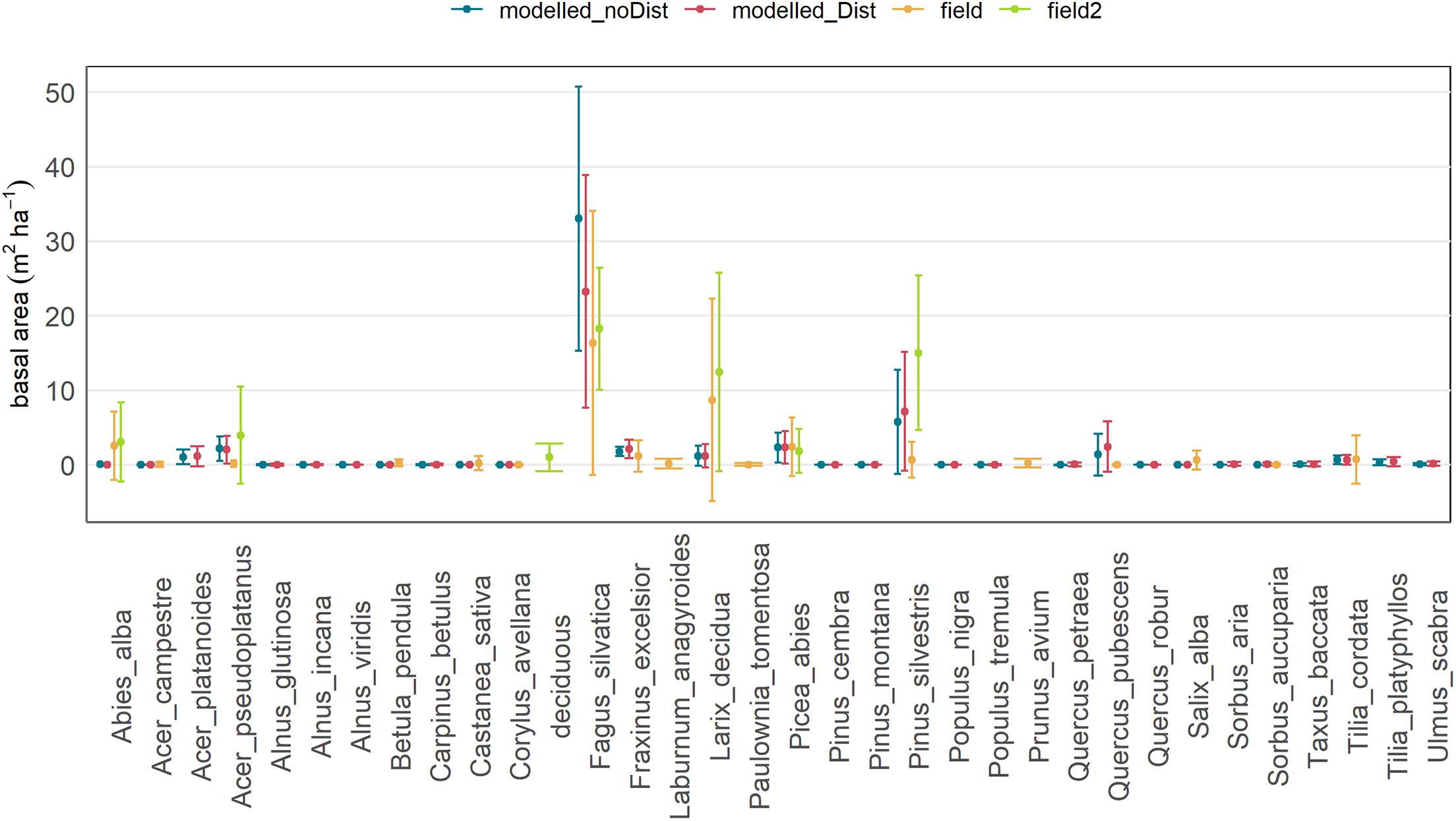
Figure 4. Mean basal area and standard deviation of the species measured throughout the study area and/or modelled by TreeMig for the spin-up simulation with background disturbance (“modelled_Dist”; red), without background disturbance (“modelled_noDist”, blue), and based on field measurements in sample plots in recent and older intervention areas (“field”; orange) and sample plots in the rockfall zone (“field2”; green), where deciduous tree species with a low abundance were summarized as “deciduous”. The standard deviation represents the variation in the basal area between the sample plots (field data) and the cells (modelled data), respectively.
The regeneration in the modelled forest as well as found in the field samples was also clearly dominated by F. sylvatica, followed by F. excelsior (Figure 5). The regeneration density of P. abies, Acer sp., and of P. sylvestris and Q. pubescens (in simulations with Dist) were higher in the simulations than in the field data. The regeneration density in the present forest clearly decreased with increasing age of the intervention and density of mature trees (see Supplementary Figure 2).
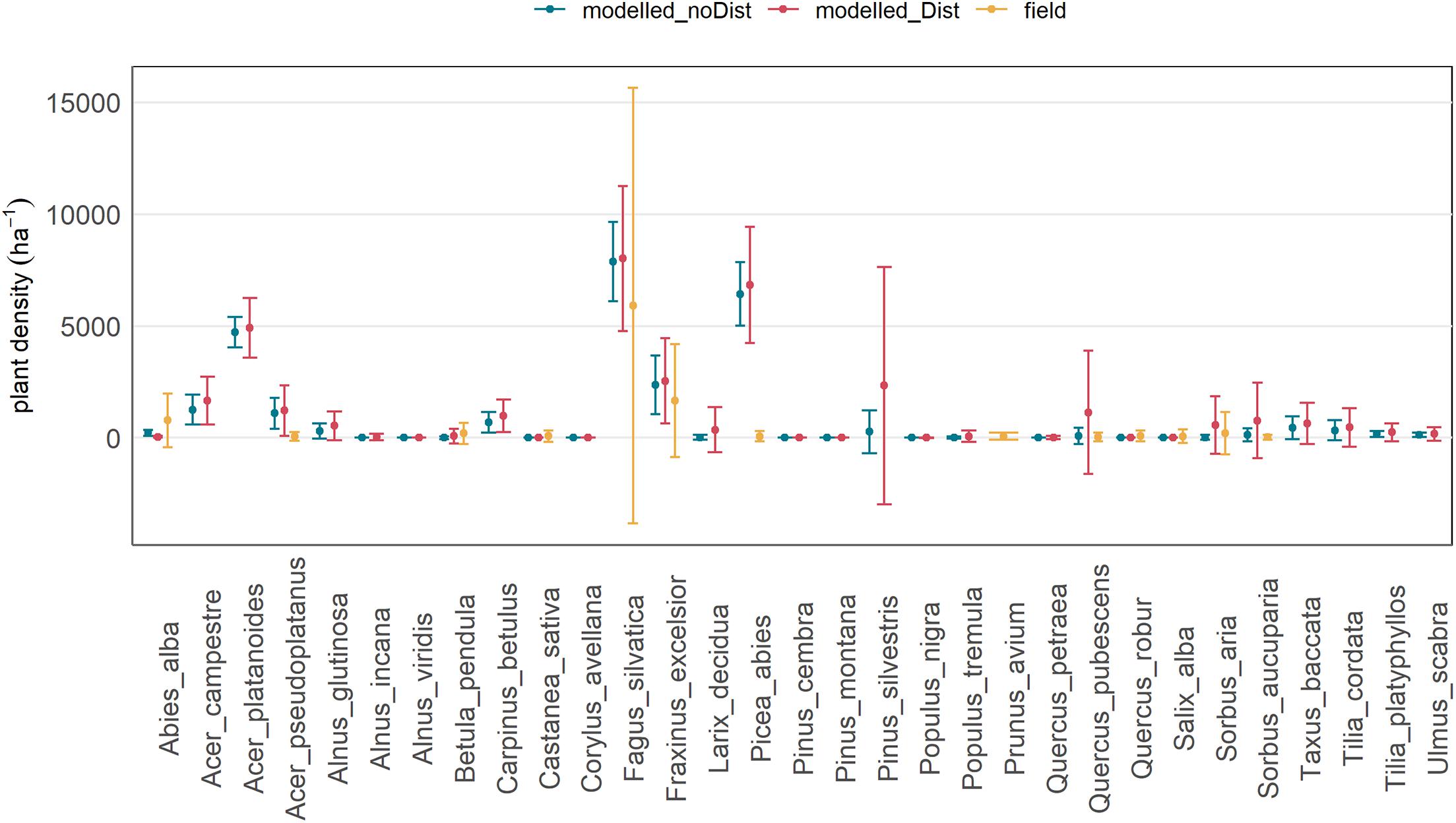
Figure 5. Mean density and standard deviation of the regeneration of the species found in the field samples in recent and older intervention areas (“field”; orange), and modelled in TreeMig with background disturbance (“modelled_Dist”; red) and without background disturbance (“modelled_noDist”; blue).
Forest in Future: Modelling Results
The forest simulations predicted a clear decrease in basal area of most of the currently present species under climate scenario RCP4.5 and RCP8.5 after 150 years (Figure 6). The decline started after ∼20–30 years of simulation (∼2040–2050; Figure 7). The forest finally turned into a Q. pubescens dominated forest, for both scenarios, and mixed with P. sylvestris in RCP4.5 (Figures 6, 8). The total basal area of the forest declined to 20–50 m2 ha–1 (mean BA = 27.5 m2 ha–1) in RCP4.5 and to 10–50 m2 ha–1 (mean BA = 19.8 m2 ha–1) in RCP8.5, whereas the strongest decrease can be observed in the steep part of the slope (500–900 m a.s.l.; Figure 8), where a relatively dense forest of mainly Q. pubescens with low diameters was predicted (Figure 8). F. sylvatica completely disappeared under the extreme climate scenario RCP8.5, whereas the model predicted an average basal area of ∼5 m2 ha–1 for the climate scenario RCP4.5. A. alba and P. abies disappeared in both scenarios. A small abundance of L. decidua remained in RCP8.5, while a slight increase is predicted in RCP4.5. In both scenarios, the basal area of F. sylvatica (RCP4.5) and Q. pubescens is slightly smaller with enhanced disturbance (Figures 6, 7). No difference or even a slight increase was found for P. sylvestris and L. decidua (Figure 6, 7). In contrast, an increase in the regeneration density with increasing disturbance could be observed for Q. pubescens, P. sylvestris, L. decidua, and B. pendula after 50 years of simulation (Figure 9). The comparison to simulations with the same disturbance probabilities, but a low disturbance intensity (0.3) did not reveal a significant difference in the predicted basal area (not shown).
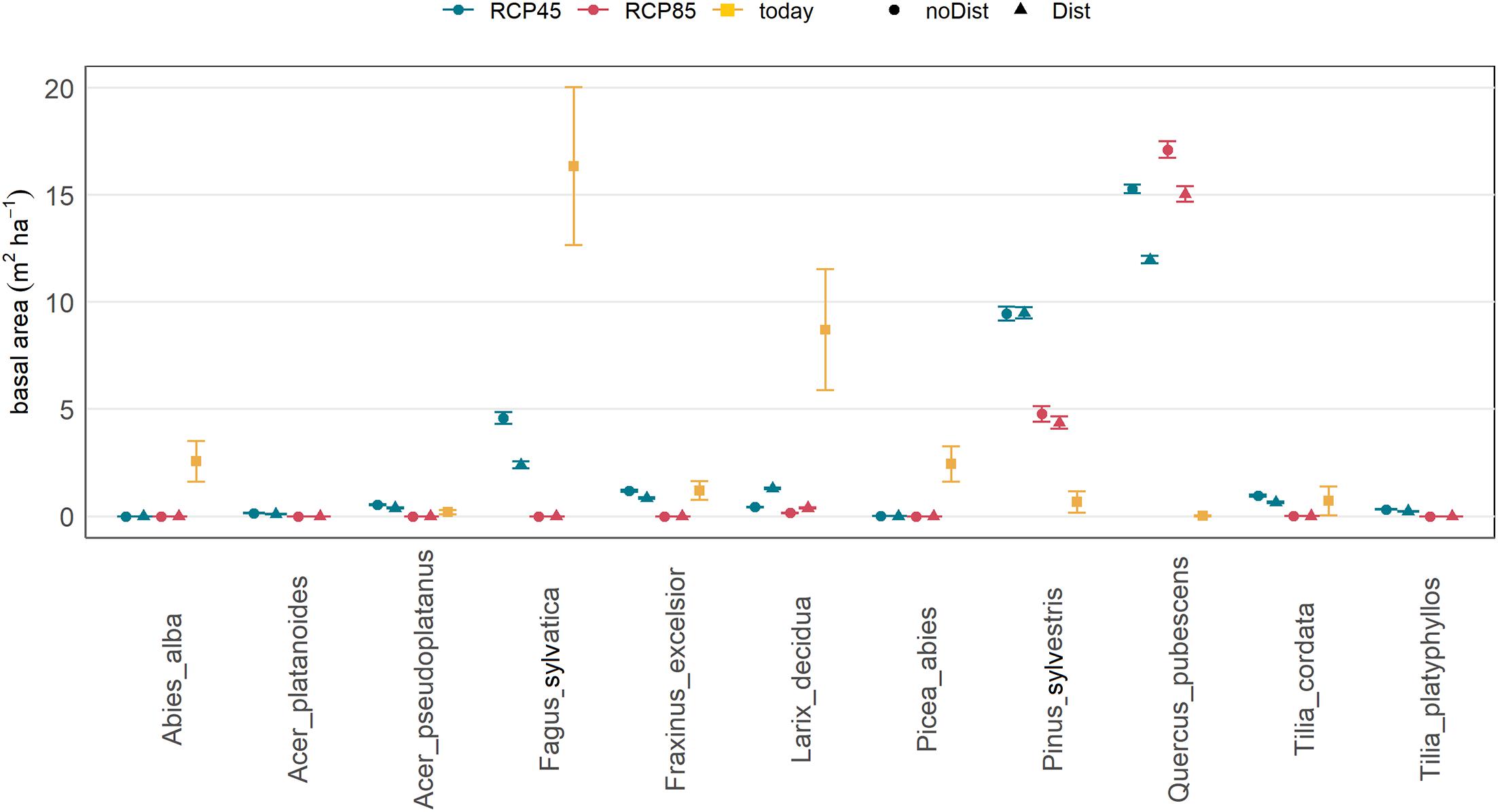
Figure 6. Basal area per main species after 150 years of simulation with climate scenario RCP4.5 (above) and RCP8.5 (below) and for low (blue) and high (red) background disturbance (Dist) as well as the basal area of the current forest (orange).
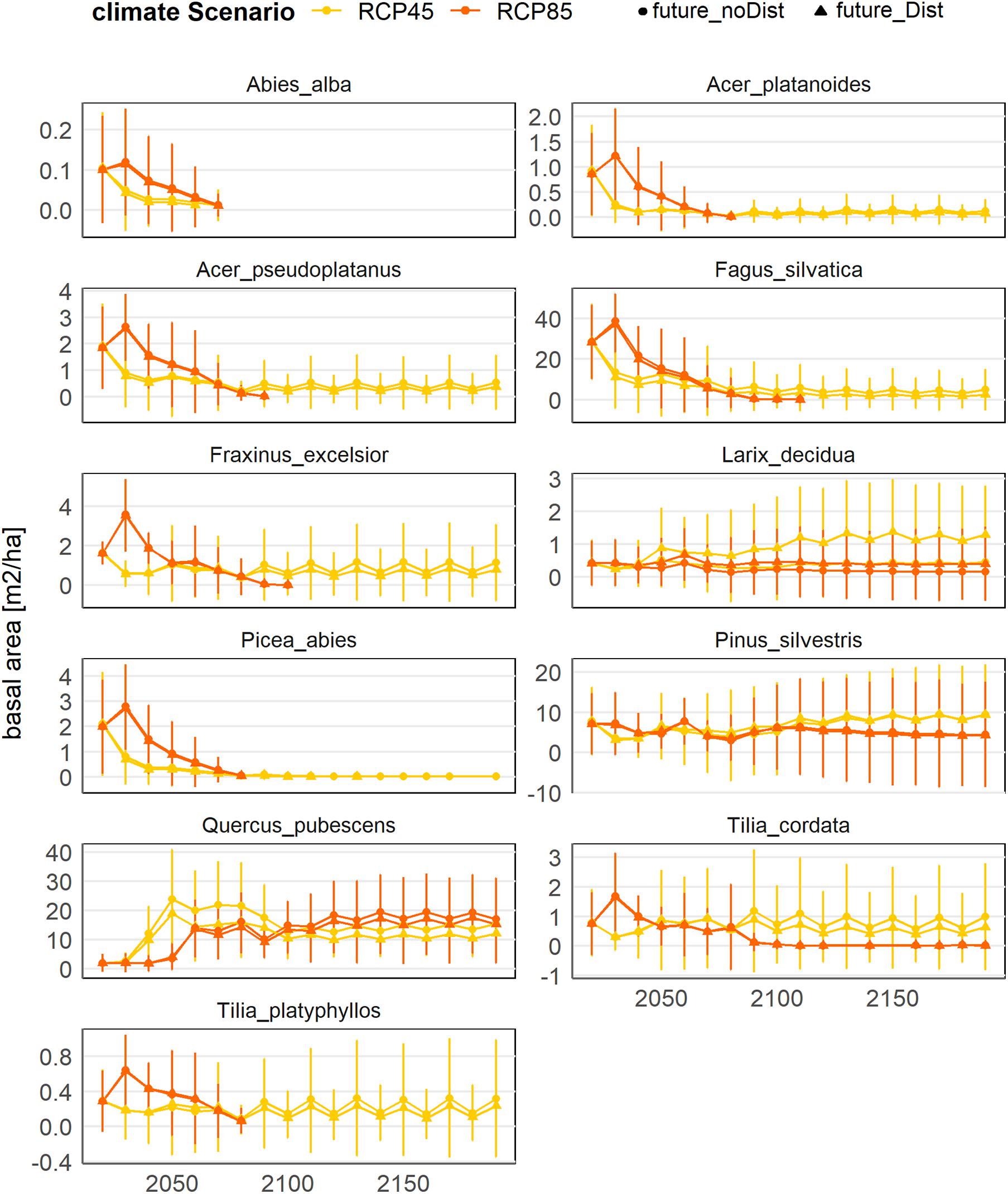
Figure 7. Simulated evolution of the basal area of the main species in Martigny under climate scenario RCP4.5 (yellow) and RCP8.5 (orange) and for low (points) and high (triangle) background disturbance (Dist).
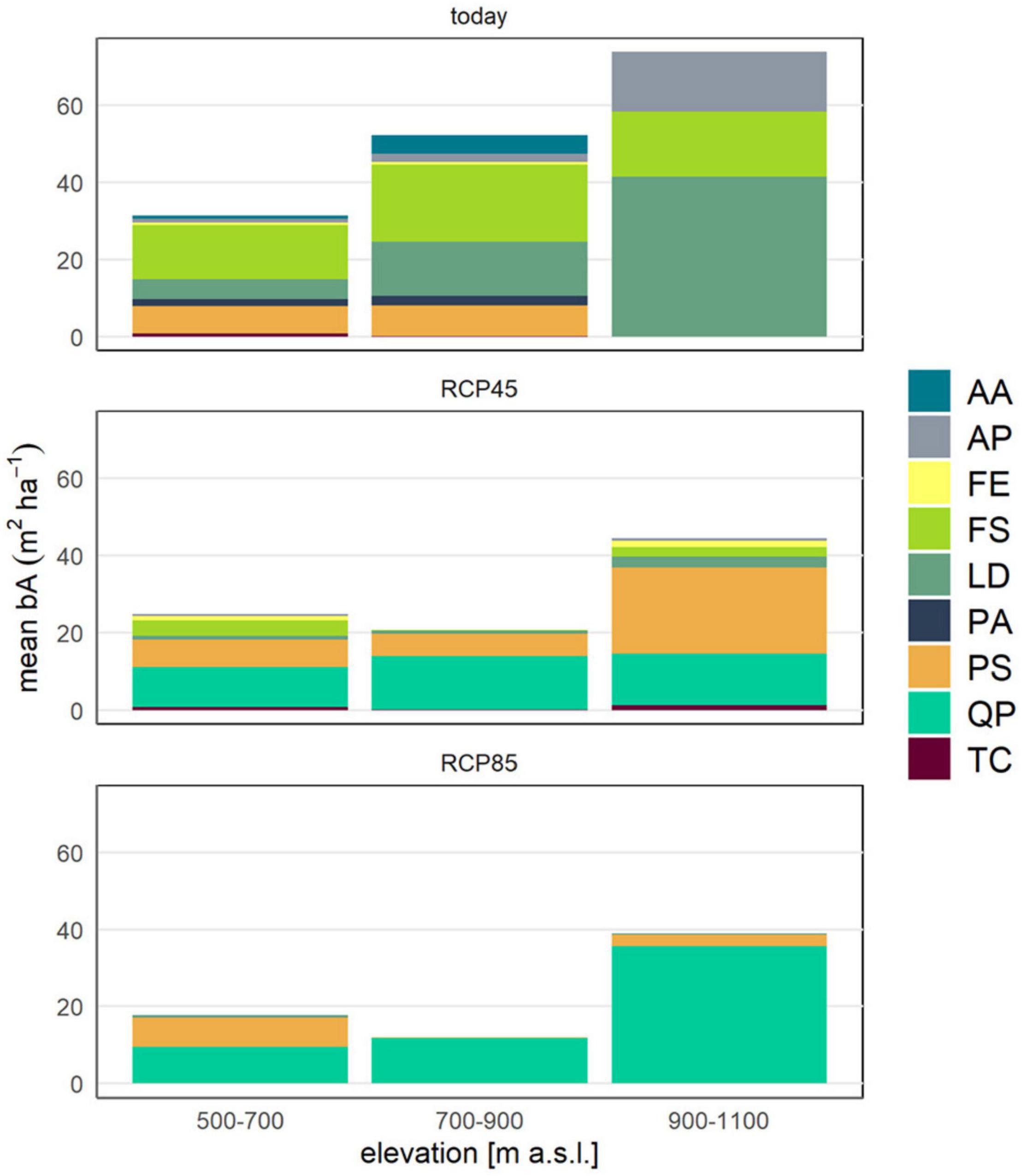
Figure 8. Current (“today”; based on field data) and future (“RCP4.5” and RCP8.5” in 50 years) mean basal area per elevation level and main species. Species abbreviations: AA, Abies alba; AP, Acer pseudoplatanus; FE, Fraxinus excelsior; FS, Fagus sylvatica; LD, Larix decidua; PA, Picea abies; PS, Pinus sylvestris; QP, Quercus pubescens; TC, Tilia cordata.
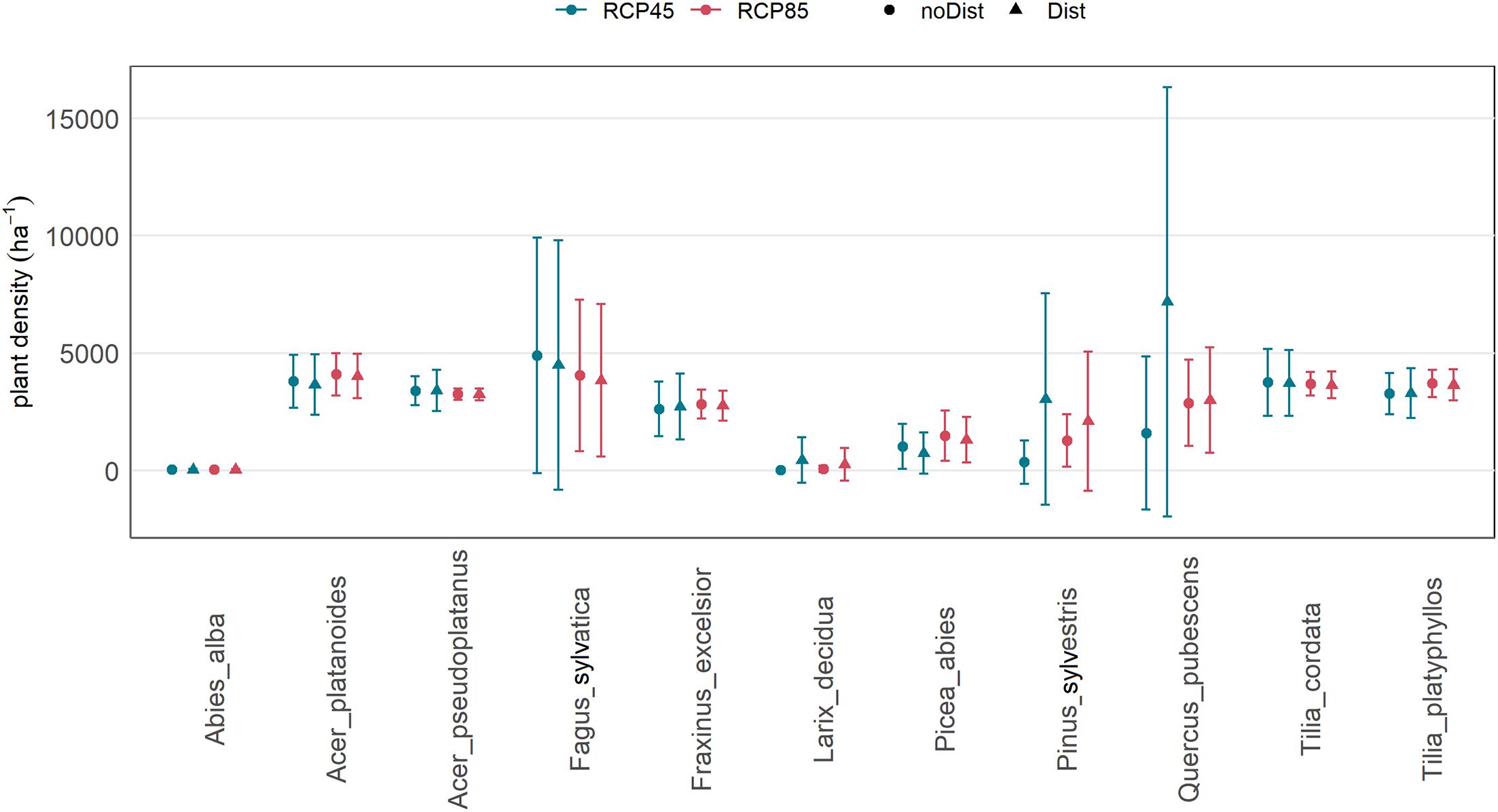
Figure 9. Simulated mean density and standard deviation of the regeneration of the main species under the future climate scenarios RCP4.5 (above) and RCP8.5 (below) in 50 years and for high background disturbance (“future_Dist”; red) and low background disturbance (“future_noDist”; blue).
Protective Effect of Forest
The current forest substantially reduces rockfall risk for subjacent buildings, roads and the railway. Today, a total risk of 19,100 CHFyear–1 is expected for people and infrastructure (current forest based on field samples; Figure 10 left and Supplementary Figure 4). With the current forest simulated with TreeMig, risk was slightly higher. Without forest, the risk would be five times as high. The current forest consequently provides a risk reduction of ∼1,350 CHF per ha forest and year. The strong increase under non-forested conditions was mainly caused by small block volumes (≤1 m3), which are currently stopped by trees and rarely reach the roads or houses (see also Supplementary Figure 3).
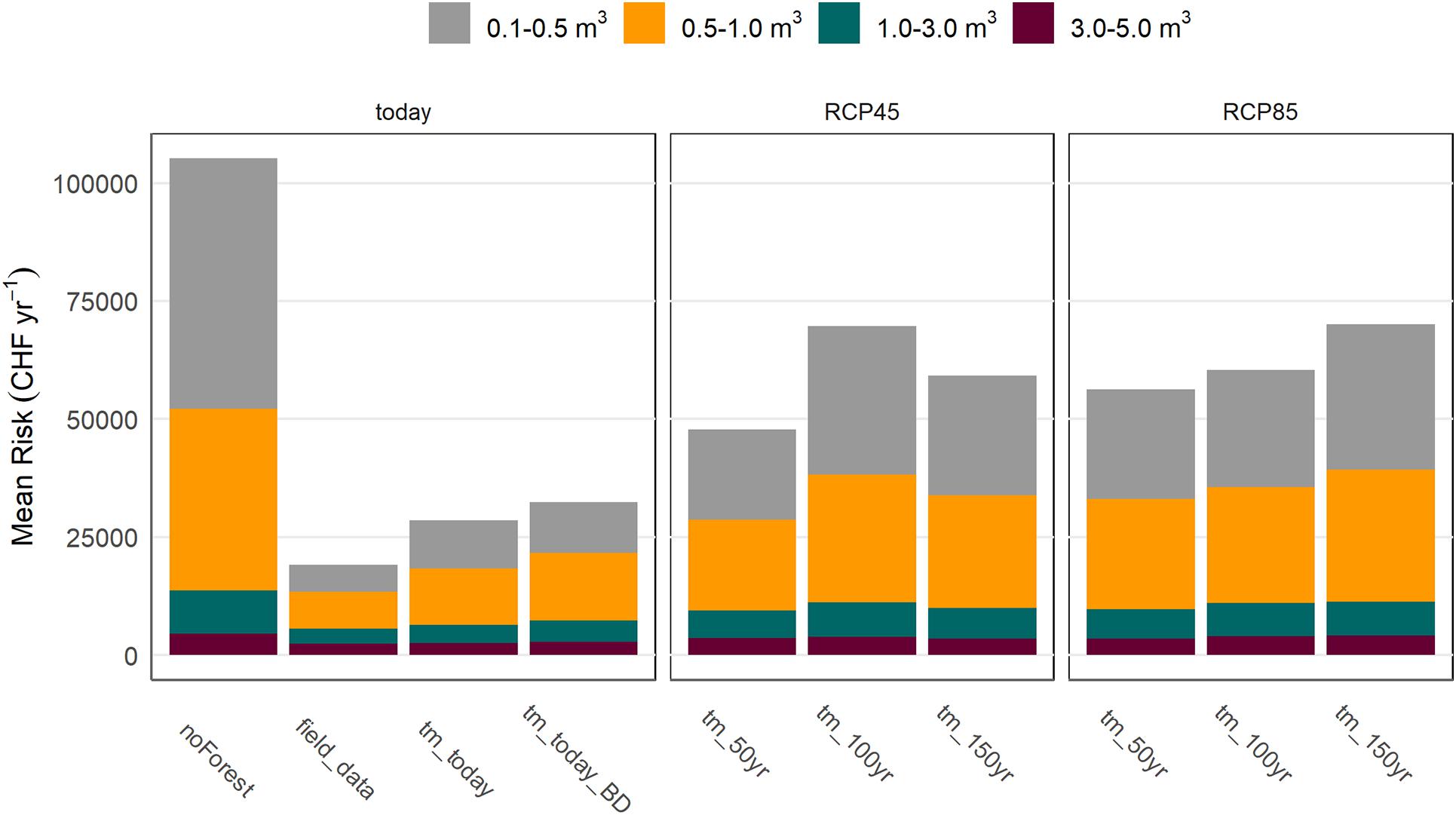
Figure 10. Mean risk for all considered elements at risk for the current forest based on field data (top; “field_data”), based on TreeMig simulations (tm) with (above; “tm_today_Dist”) and without (left, “tm_today”) disturbance, and for future forest scenarios in 50 (tm_50yr), 100 (tm_100yr), and 150 years (tm_150yr) under climate scenario RCP4.5 (middle) and RCP8.5 (right) (only shown with background disturbance).
With climate warming, a clear increase in risk is expected for both climate change scenarios (Figure 10 middle and right). In ∼150 years, an increase in risk to 59,250 CHFyear–1 (two times the risk of the spin-up forest) and 70,100 CHFyear–1 was predicted (2.5 times the risk of the spin-up forest). While highest risk under scenario RCP4.5 was expected after 100 years (69,700 CHFyear–1), followed by a decline, a steady increase in risk could be observed for RCP8.5. The risk increased mainly due to an increase in the occurrence frequency of blocks. Currently, a block with a volume between 0.1 and 0.5 m3 is expected to reach the railway about once in 10 years. In future, its occurrence frequency could increase to once in 3 years (Figure 11).
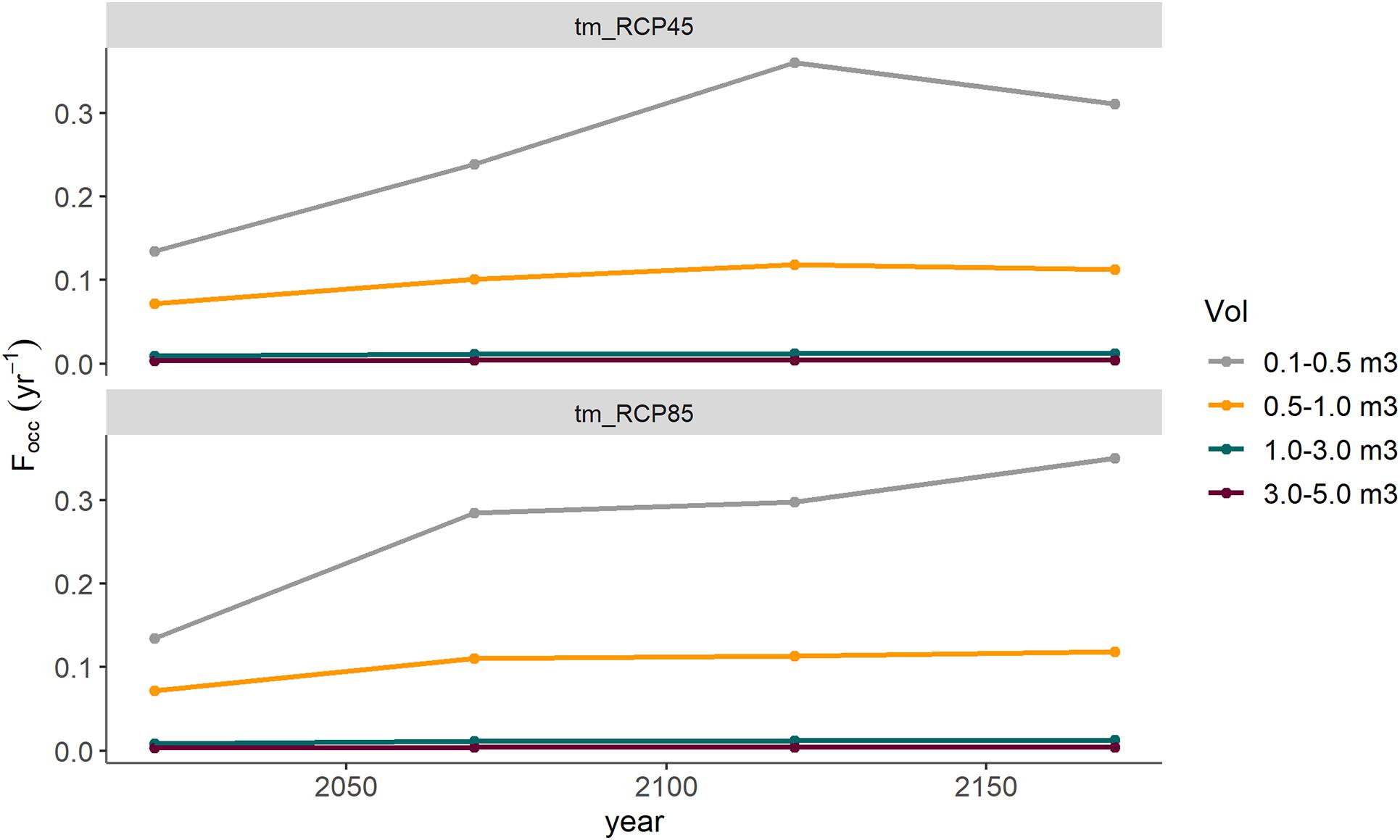
Figure 11. Predicted development of the occurrence frequency of the considered block volume scenarios at the level of the railway until 2200 for the future forest scenarios under climate scenario RCP4.5 (above) and RCP8.5 (below).
Discussion
The results of our case study suggest that the protective effect of forests against rockfall may substantially decrease under future climate change at sites where significant shifts in tree species distribution due to increased drought stress can be expected. The reduced protection effect observed in this study is mainly due to a decrease in the basal area in the middle part of the mountain slopes (at mid-elevations), where drought stress will be particularly pronounced due to the steep slopes with shallow soils. Under both climate scenarios, our simulations predicted a shift towards a Q. pubescens dominated forest, mixed with P. sylvestris, leading to significant decrease in tree diameters, partially also a reduced stem number under the extreme climate scenario. This would result in a substantial increase in risk, and thus in the expected damages due to rockfall for subjacent houses and infrastructure in the next decades. In the medium term (i.e., 50–100 years), the results of this study suggest a stabilization of the risk, or even a slight decline in the long-term (i.e., >100 years) since the Q. pubescens dominated forest would increase in biomass.
The comparison of detailed field data on the species and diameter distribution, the tree density and the regeneration of the current forest with the TreeMig simulations allow concluding that the overall accuracy of the model was satisfactory. The slightly higher abundance of F. sylvatica and the lower abundance of L. decidua and P. sylvestris in the spin-up simulations indicate that the current forest corresponds to an earlier stage in the forest simulations (see Supplementary Figure 1). This is possibly an effect of local forest management, since regular forest interventions in the past decades (or even centuries; Farquet and Métral, 2004) accelerated a continuous regeneration, without reaching the equilibrium state of the forest.
Limitations of the Study
The predictions of future forest cover are, however, subject to several uncertainties. Firstly, while species parameters in the TreeMig model are primarily based on general ecological knowledge, partly they are based on observational data sources, which might be of low precision. For example, in the Swiss NFI, only few plots are located in dry conditions, so that an accurate estimation of the dry distribution limit of the species is difficult. Furthermore, the observed forests might be influenced by other factors (e.g., management history). Secondly, they are based on species behavior under past and current climate, while some species may adapt to changing climatic conditions (Kurparinen et al., 2010; Lefèvre et al., 2013). Thirdly, the soil conditions, strongly affecting the drought experienced by the trees in both model and reality, are spatially variable and hard to cover by measurement based empirical models such as the underlying soil suitability map. Fourthly, the TreeMig model is particularly sensitive to extreme drought events compared to other forest landscape models, due to a different formulation of mortality, whereas it is not clear which formulation is more realistic (Petter et al., 2020). Finally, climate change scenarios used in this study are highly uncertain (CH2018 and 2018) and the downscaling of the data added a potential bias. In general, our simulation results are in line with previous modelling studies, predicting a decline in biomass at lower elevations in the Valais or comparable regions as well as a shift from F. sylvatica to P. sylvestris (Schumacher and Bugmann, 2006; Speich et al., 2020) and/or an expansion of Q. pubescens (Vacchiano and Motta, 2015). The analysis of long-term data further revealed an increasing abundance of Q. pubescens in low-elevation forests in the Valais in the past few years (Weber et al., 2007; Rigling et al., 2012). Finally, observations of the local forest managers confirmed increasing problems particularly of F. sylvatica in drought periods in the past few years (R. Métral, personal communication).
The rockfall risk with the forest simulated in the spin-up (initial state for future simulations) is higher than the risk with the forest based on field samples, since the basal area of the latter is slightly higher than the basal area simulated with TreeMig. This suggests that risk under future scenarios might also be somewhat overestimated due to a potentially general underestimation of the basal area by the model. Additionally, TreeMig is a cell-based forest model and thus remains limited in representing local differences in forest structure potentially relevant for the risk reducing effect of the forest. However, the current forest does not represent true positions of trees, but is constructed based on forest samples. Consequently, its protective effect might also be biased because of local spatial variations in the forest structure (e.g., insufficient representation of gaps). Combining field data with tree positions derived from remote sensing data may increase the accuracy of the representation of the current forest cover (Mathys et al., 2004; Engler et al., 2013). Overall, the calculated rockfall risk of today seems plausible. Based on our risk assessment, a block with a volume between 0.1 and 0.5 m3 reaches the bottom of the slope about once in 10 years. Although hardly any events have been registered in the past few years, this is quite realistic based on the observations of the local forest engineer, as well as our own observation of rockfall deposits at the bottom of the slope, demonstrating that blocks regularly reach the lower part of the slope. Nevertheless, the risk assessment faces several sources of uncertainties, including, among others, the rockfall onset frequency, which was based on a scarce data basis, and the input parameters of the rockfall simulations. Additionally, the parameters for the quantification of the elements at risk are highly disputable due to missing observational data (Agliardi et al., 2009; Daniell et al., 2015). These parameters are also likely to change in future due to changing economic and social dynamics (Fuchs et al., 2013). Moreover, rockfall release frequency and magnitude may be affected by climate warming and thus change in future. Recent observations indicate, however, that climate change will mainly affect high mountain areas, above the permafrost limit, but not significantly alter rockfall frequency at lower elevations (Sass and Oberlechner, 2012). Since these potential additional changes are independent from the evolution of the forest, the relative differences between the forest scenarios do not change and, thus, the simplified assumptions regarding the risk assessment underlying this study remain reasonable.
Generalization of the Results
The results of our study are not only relevant for our case study site, but can provide important information for other sites with similar forest and rockfall conditions in the Alps (i.e., sites with similar species distribution and climate predictions). By combining dynamic forest modelling with rockfall risk assessment, it provides a methodological framework that can be applied at other case study sites, where climate change has not yet been considered in the forest scenarios (Bigot et al., 2009; Moos et al., 2019a) or even be transferred to regional scale (Scheidl et al., 2020b). Our results also indicate that regular disturbances can promote regeneration, and therefore favor the transition of current species to more drought resistant ones, which may positively influence the protective function of the forest in long-term (Scheidl et al., 2020a). Consequently, forest management may play a crucial role in accelerating the regeneration and immigration of drought adapted species and thus increase the resistance and resilience of the protection forest analyzed in this study under a changing climate (Brang, 2001). At the same time, forest interventions as well as natural disturbances can cause temporary declines in the protective effect of a forest due to the removal of trees (Bigot et al., 2009; Irauschek et al., 2017). Temporary measures, such as lying logs in openings, can at least partially bridge such periods of reduced protection. Furthermore, a sudden decline in the protection capacity of a forest can mostly be avoided through well planned and site-adapted management interventions (Woltjer et al., 2008). According to our analysis of current regeneration as a function of intervention age, an intervention interval of ∼30 years is indicated to maintain a constant level of regeneration (see also Supplementary Material 4). This may, however, strongly be influenced by the prevailing browsing pressure (Cailleret et al., 2014; Kupferschmid et al., 2019). Additionally, large disturbances, such as fire, insect outbreaks or wind throw, are likely to become more frequent and/or severe with climate change and might have even more drastic effects on species composition and structure than the direct effects of climate change as analyzed in this study (Bebi et al., 2017; Seidl et al., 2017; Wohlgemuth et al., 2017; Taeroe et al., 2019).
Future Avenues
Future research on the long-term efficacy and efficiency of forest management is needed to finally conclude, under which conditions, where and when, targeted forest interventions are appropriate, and in which form (e.g., planting of drought adapted species, assisted migration), to improve the protection function of forests. Furthermore, future studies should quantify the influence of changing natural disturbance regimes, which was only included as random background disturbance with varying probabilities and intensities in this study. In general, higher frequencies and intensities of large-scale disturbances can be expected (Seidl et al., 2017). In the specific context of our study area, an increasing risk of forest fires has to be reckoned (Schumacher and Bugmann, 2006; Wastl et al., 2012). Furthermore, it is probable that new and invasive species, such as Ailanthus altissima or Paulownia tomentosa (of which single exemplars can already be found on the slope or nearby), will immigrate and maybe even suppress some current tree species. Recent studies, however, indicate that these species should not prevail on larger scales (Knüsel et al., 2017; Wunder et al., 2018), and that the protection capacity of the single tree is comparable to that of other deciduous trees (Moos et al., 2019b). Large-scale modelling of forest development including species’ natural or assisted migration, e.g., with TreeMig, would shed light on the role of immigration of new species.
Conclusion
This case study evidences that climate change may lead to a decline in the protective effect of forests against rockfall. By combining dynamic forest modelling with quantitative rockfall risk assessment, we could show that increased drought at lower and medium elevations in the Swiss Alps potentially could cause critical periods of a decreased protection service of forests due to shifts in species distribution. This means that the risk for subjacent houses and infrastructure may substantially increase in future. Hence the need for engineered protection measures, such as rockfall nets, may arise, and cause additional costs. Our results further indicate that forest management can potentially promote the transition to more drought-adapted species and thus dampen the strong decrease in the protective effect of the forest. However, future research should address the long-term effect of different forest management strategies on the protection service of forests under climate change. The study was conducted on local scale, but the underlying methods as well as the results can be transferred to other sites with similar conditions and serve decision-makers as an important basis in natural hazard and ecosystem management. Upscaling the methods used in this study to a larger scale will further facilitate detecting areas where a particularly strong decrease in the protection service of the forest can be expected and thus facilitate prioritization in forest management.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
All authors contributed to the conception and method of the study. CM organized the field investigations and conducted the data analysis, the simulations and the risk analysis, and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
The funding of this research was provided by the “Interdisciplinary Centre for Mountain Research” (CIRM) of the University of Lausanne as part of a postdoctoral project on the temporal evolution of the protective effect of forests against rockfall.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank R. Métral for the information on local conditions and the valuable discussions about this study, as well as N. Khelidj and Z. Bontognali for helping in the field.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2021.682923/full#supplementary-material
References
Agliardi, F., Crosta, G. B., and Frattini, P. (2009). Integrating rockfall risk assessment and counter-measure desing by 3D modeling techniques. Nat. Hazard Earth Sys. 9, 1059–1073. doi: 10.5194/nhess-9-1059-2009
Albrich, K., Rammer, W., and Seidl, R. (2020). Climate change causes critical transitions and irreversible alterations of mountain forests. Glob. Chang. Biol. 26, 4013–4027. doi: 10.1111/gcb.15118
Allen, C. D., Macalady, A. K., and Chenchouni, H. (2010). A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. Forest Ecol. Manag. 259, 660–668. doi: 10.1016/j.foreco.2009.09.001
Bebi, P., Seidl, R., Motta, R., Fuhr, M., Firm, D., Krumm, F., et al. (2017). Changes of forest cover and disturbance regimes in the mountain forests of the Alps. Forest Ecol. Manag. 388, 43–56. doi: 10.1016/j.foreco.2016.10.028
BFS. (2000). Digital Soil Suitability Map of Switzerland. Neuchâtel: BFS, Federal Statistical Office.
Bigot, C., Dorren, L. K. A., and Berger, F. (2009). Quantifying the protective function of a forest against rockfall for past, present and future scenarios using two modelling approaches. Nat. Hazards 49, 99–111. doi: 10.1007/s11069-008-9280-0
Brang, P. (2001). Resistance and elasticity: promising conecepts for the management of protection forests in the European Alps. Ecol. Manag. 145, 15.
Broennimann, O. (2020). CHclim25 Dataset. Department of Ecology nd Evolution & Institute of Earth Surface Dynamics, University of Lausanne, Switzerland. Available online at: https://www.unil.ch/ecospat/files/live/sites/ecospat/files/shared/PDF_site/chclim25.pdf (accessed December 1, 2020).
Bründl, M., Romang, H. E., Bischof, N., and Rheinberger, C. M. (2009). The risk concept and its application in natural hazard risk management in Switzerland. Nat. Hazard Earth Syst. 9:13. doi: 10.1201/9780203963562-3
Cailleret, M., Heurich, M., and Bugmann, H. (2014). Reduction in browsing intensity may not compensate climate change effects on tree species composition in the Bavarian Forest National Park. Forest Ecol. Manag. 328, 179–192. doi: 10.1016/j.foreco.2014.05.030
CH2018 Project Team (2018). ch2018climate scenarios for Switzerland. Natl. Centre Clim. Servic. doi: 10.18751/Climate/Scenarios/CH2018/1.0
Costanza, R., d’Arge, R., de Groot, R., Farber, S., Grasso, M., Hannon, B., et al. (1998). The value of the world’s ecosystem services and natural capital. Ecol. Econ. 25, 3–15.
Dale, V. H., Joyce, L. A., McNulty, S., Neilson, R. P., Aytes, M. P., Flannigan, M. D., et al. (2001). Climate change and forest disturbances. BioScience 51, 723–734.
Daniell, J. E., Schaefer, A. M., Wenzel, F., and Kunz-Plapp, T. (2015). “The value of life in earthquakes and other natural disasters: historical costs and the benfits of investing in life safety,” in Paper Presented at the Proceedings of the Tenth Pacific Conference on Earthquake Engineering, Building an Earquake-Resilient Pacific, Sydney, Australia.
Dorren, L. (2016). Rockyfor3D (v5.2) Revealed–Transparent Description of the Complete 3D Rockfall Mode. Geneva: Eocrisq. Available online at: www.ecorisq.org.
Elkin, C., Gutierrez, A. G., Leuzinger, S., Manusch, C., Temperli, C., Rasche, L., et al. (2013). A 2 degrees C warmer world is not safe for ecosystem services in the European Alps. Global Change Biol. 19, 1827–1840. doi: 10.1111/gcb.12156
Engler, R., Waser, L. T., Zimmermann, N. E., Schaub, M., Berdos, S., Ginzler, C., et al. (2013). Combining ensemble modeling and remote sensing for mapping individual tree species at high spatial resolution. Forest Ecol. Manag. 310, 64–73. doi: 10.1016/j.foreco.2013.07.059
Farquet, R., and Métral, R. (2004). Les Forêts du Mont Chemin – Un Héritage en Évolution. Bulletin: Patrimoines de Martigny, 14.
FOEN. (2020). EconoMe 5.0. Effectiveness and Efficiency of Protection Measures Against Natural Hazards. Berlin: Federal Office for the Environment, FOEN.
Fuchs, S., Keiler, M., Sokratov, S., and Shnyparkov, A. (2013). Spatiotemporal dynamics: the need for an innovative approach in mountain hazard risk management. Nat. Hazards 68, 1217–1241. doi: 10.1007/s11069-012-0508-7
Getzner, M., Gutheil-Knopp-Kirchwald, G., Kreimer, E., Kirchmeir, H., and Huber, M. (2017). Gravitational natural hazards: valuing the protective function of Alpine forests. Forest Policy Econ. 80, 150–159. doi: 10.1016/j.forpol.2017.03.015
Grêt-Regamey, A., Bebi, P., Bishop, I. D., and Schmid, W. A. (2008). Linking GIS-based models to value ecosystem services in an Alpine region. J. Environ. Manage. 89:11.
Irauschek, F., Rammer, W., and Lexer, M. J. (2017). Evaluating multifunctionality and adaptive capacity of mountain forest management alternatives under climate change in the Eastern Alps. Eur. J. Forest Res. 136, 1051–1069. doi: 10.1007/s10342-017-1051-6
Knüsel, S., de Boni, A., Conedera, M., Schleppi, P., Thormann, J. J., Frehner, M., et al. (2017). Shade tolerance of Ailanthus altissima revisited: novel insights from southern Switzerland. Biol. Invasions 19, 455–461. doi: 10.1007/s10530-016-1301-4
Kulakowski, D., Bebi, P., and Rixen, C. (2010). The interacting effects of land use change, climate change and suppression of natural disturbances on landscape forest structure in the Swiss Alps. Oikos 120:10.
Kupferschmid, A. D., Bütikofer, L., Hothorn, T., Schwyzer, A., and Brang, P. (2019). Quantifying the relative influence of terminal shoot browsing by ungulates on tree regeneration. Forest Ecol. Manag. 446, 331–344. doi: 10.1016/j.foreco.2019.05.009
Kurparinen, A., Savolainen, O., and Schurr, F. M. (2010). Increased mortality can promote evolutionary adaptation of forest trees to climate change. Forest Ecol. Manag. 259, 1003–1008. doi: 10.1016/j.foreco.2009.12.006
Lefèvre, F., Boivin, T., Bontemps, A., Courbet, F., Davi, H., Durand-Gilmmann, M., et al. (2013). Considering evolutionary processes in adaptive forestry. Ann. Forest Sci. 71, 723–739. doi: 10.1007/s13595-013-0272-1
Lindner, M., Fitzgerald, J. B., Zimmermann, N. E., Reyer, C., Delzon, S., van der Maaten, E., et al. (2014). Climate change and European forests: what do we know, what are the uncertainties, and what are the implications for forest management? J. Environ. Manage 146, 69–83. doi: 10.1016/j.jenvman.2014.07.030
Lischke, H. (2020). Simulation der baumartenmigration im klimawandel. Schweizerische Zeitschrift für Forst. 171, 151–157. doi: 10.3188/szf.2020.0151
Lischke, H., Zimmermann, N. E., Bolliger, J., Rickebusch, S., and Löffler, T. J. (2006). TreeMig: a forest-landscape model for simulating spatio-temporal patterns from stand to landscape scale. Ecol. Mod. 199, 409–420. doi: 10.1016/j.ecolmodel.2005.11.046
Mathys, L., Zimmermann, N. E., and Guisan, A. (2004). Spatial pattern of forest resources in a multifunctional landscape. Int. Arch. Photog. Remote Sensing Spatial Inform. Sci. 36, 340–342.
Moos, C., Bebi, P., Schwarz, M., Stoffel, M., Sudmeier-Rieux, K., and Dorren, L. (2018a). Ecosystem-based disaster risk reduction in mountains. Earth Sci. Rev. 177, 497–513.
Moos, C., Fehlmann, M., Trappmann, D., Stoffel, M., and Dorren, L. (2018b). Integrating the mitigating effect of forests into quantitative rockfall risk analysistwo case studies in Switzerland. Int. J. Disaster Risk Reduc. 32, 55–74. doi: 10.1016/j.ijdrr.2017.09.036
Moos, C., Khelidj, N., Guisan, A., Lischke, H., and Randin, C. F. (2020). A quantitative assessment of rockfall influence on forest structure in the Swiss Alps. Eur. J. Forest Res. doi: 10.1007/s10342-020-01317-0
Moos, C., Thomas, M., Pauli, B., Bergkamp, G., Stoffel, M., and Dorren, L. (2019a). Economic valuation of ecosystem-based rockfall risk reduction considering disturbances and comparison to structural measures. Sci. Total Environ. 697:134077. doi: 10.1016/j.scitotenv.2019.134077
Moos, C., Toe, D., Bourrier, F., Knüsel, S., Stoffel, M., and Dorren, L. (2019b). Assessing the effect of invasive tree species on rockfall riskthe case of Ailanthus altissima. Ecol. Eng. 131, 63–72. doi: 10.1016/j.ecoleng.2019.03.001
Moya, J. C., Pérez Arcaz, J., and Baeza, C. (2010). Tree-ring based assessment of rockfall frequency on talus slopes at Solà d’Andorra. East. Pyrenees. Geomorphol. 118:16.
Olschewski, R., Bebi, P., Teich, M., Wissen Hayek, U., and Grêt-Regamey, A. (2012). Avalanche protection by forestsa choice experiment in the Swiss Alps. Forest Policy Econ. 15, 108–113. doi: 10.1016/j.forpol.2011.10.002
Pagiola, S., Bishop, J., and Landell-Mills, N. (2002). Selling Forest Environmental Services: Market-Based Mechanisms For Conservation and Development. London: Earthscan Publications.
Peñuelas, J., and Boada, M. (2003). A global change-induced biome shift in the Montseny mountains (NE Spains). Glob. Chang. Biol. 9, 131–140. doi: 10.1046/j.1365-2486.2003.00566.x
Petter, G., Mairota, P., Albrich, K., Bebi, P., Bruna, J., Bugmann, H., et al. (2020). How robust are future projections of forest landscape dynamics? Insights from a systematic comparison of four forest landscape models. Environ. Mod. Softw. 134:104844. doi: 10.1016/j.envsoft.2020.104844
Rigling, A., Bigler, C., Eilmann, B., Feldmeyer-Christe, E., Gimmi, U., Ginzler, C., et al. (2012). Driving factors of a vegetation shift from Scots pine to pubescent oak in dry Alpine forests. Glob. Chang. Biol. 19, 229–240. doi: 10.1111/gcb.12038
Ruangpan, L., Vojinovic, Z., Di Sabatino, S., Leo, L. S., Capobianco, V., Oen, A. M. P., et al. (2020). Nature-based solutions for hydro-meteorological risk reduction: a state-of-the-art review of the research area. Nat. Hazard Earth Syst. 20, 243–270. doi: 10.5194/nhess-20-243-2020
Sakals, M. E., Innes, J. L., Wilford, D. J., Sidle, R. C., and Grant, G. E. (2006). The role of forests in reducing hydrogeomorphic hazards. Forest Snow Land. Res. 80, 11–22.
Sass, O., and Oberlechner, M. (2012). Is climate change causing increased rockfall frequency in Austria? Nat. Hazard Earth Syst. 12, 3209–3216. doi: 10.5194/nhess-12-3209-2012
Scheidl, C., Heiser, M., Kamper, S., Thaler, T., Klebinder, K., Nagl, F., et al. (2020a). The influence of climate change and canopy disturbances on landslide susceptibility in headwater catchments. Sci. Total Environ. 742:140588. doi: 10.1016/j.scitotenv.2020.140588
Scheidl, C., Heiser, M., Vospernik, S., Lauss, E., Perzl, F., Kofler, A., et al. (2020b). Assessing the protective role of alpine forests against rockfall at regional scale. Eur. J. Forest Res. 139, 969–980. doi: 10.1007/s10342-020-01299-z
Scherrer, D., Vitasse, Y., Guisan, A., Wohlgemuth, T., and Lischke, H. (2020). Competition and demography rather than dispersal limitation slow down upward shifts of trees’ upper limits in the Alps. J. Ecol. 108:14. doi: 10.1111/1365-2745.13451
Schumacher, S., and Bugmann, H. (2006). The relative importance of climatic effects, wildfires and management for future forest landscape dynamics in the Swiss Alps. Glob. Chang. Biol. 12, 1435–1450. doi: 10.1111/j.1365-2486.2006.01188.x
Schumacher, S., Bugmann, H., and Mladenoff, D. J. (2004). Improving the formulation of tree growth and succession in a spatially explicit landscape model. Ecol. Mod. 180:20.
Sebald, J., Senf, C., Heiser, M., Scheidl, C., Pflugmacher, D., and Seidl, R. (2019). The effects of forest cover and disturbance on torrential hazards: large-scale evidence from the Eastern Alps. Environ. Res. Lett. 14. doi: 10.1088/1748-9326/ab4937
Seidl, R., Rammer, W., Scheller, R. M., and Spies, T. A. (2012). An individual-based process model to simulate landscape-scale forest ecosystem dynamics. Ecol. Mod. 231:14. doi: 10.1016/j.ecolmodel.2012.02.015
Seidl, R., Thom, D., Kautz, M., Martin-Benito, D., Peltniemi, M., Vacchiano, G., et al. (2017). Forest disturbances under climate change. Nat. Clim. Chang. 7, 395–402. doi: 10.1038/nclimate3303
Silins, U., Stone, M., Emelko, M. B., and Bladon, K. D. (2009). Sediment production following severe wildfire and post-fire salvage logging in the rocky mountain headwaters of the oldman river basin. Alberta. Catena 79, 189–197. doi: 10.1016/j.catena.2009.04.001
Sørland, S. L., Fischer, A. M., Kotlarski, S., Künsch, H. R., Liniger, M. A., Rajczak, J., et al. (2020). CH2018national climate scenarios for Switzerland: how to construct consistent multi-model projections from ensembles of opportunity. Clim. Serv. 20:100196. doi: 10.1016/j.cliser.2020.100196
Speich, M., Zappa, M., and Lischke, H. (2020). FORests and HYdrology under climate change in Switzerland v1.0: a spatially distributed model combining hydrology and forest dynamics Geoscientific. Model Dev. 13, 537–564. doi: 10.5194/gmd-13-537-2020
swisstopo (2019). GeoCover V3.0. Swiss Federal Office of Topography. Berlin. Available online at: https://www.swisstopo.admin.ch/de/geodata/geology/maps/geocover.html#tabs_copy_copy_copy__1 (accessed December 1, 2020).
swisstopo (2020a). SWISSIMAGE - Das Digitale Orthofotomosaik Der Schweiz. Swiss Federal Office of Topography. Berlin. Available online at: https://www.swisstopo.admin.ch/de/home/products/images/ortho/swissimage.html (accessed December 1, 2020).
swisstopo (2020b). Swisstlm3d. A Large-Scale Topographic Landscape Model, Version 1.8 edn. Federal Office of Topography, Swisstopo, Wabern, Switzerland. Available online at: https://www.swisstopo.admin.ch/de/geodata/landscape/tlm3d.html (accessed December 1, 2020).
Taeroe, A., de Koning, J. H. C., Löf, M., Tolvanen, A., Heidarsson, L., and Raulund-Rasmussen, K. (2019). Recovery of temperate and boreal forests after windthrow and the impacts of salvage logging. a quantitative review. Forest Ecol. Manag. 446, 304–316. doi: 10.1016/j.foreco.2019.03.048
Teich, M., and Bebi, P. (2009). Evaluating the benefit of avalanche protection forest with GIS-based risk analyses-a case study in Switzerland. Forest. Ecol. Manag. 257, 1910–1919. doi: 10.1016/j.foreco.2009.01.046
Trappmann, D., and Stoffel, M. (2013). Counting scars on tree stems to assess rockfall hazards: a low effort approach, but how reliable? Geomorphology 180, 180–186. doi: 10.1016/j.geomorph.2012.10.009
Urli, M., Delzon, S., Eyermann, A., Couallier, V., García-Valdés, R., Zavala, M. A., et al. (2013). Inferring shifts in tree species distribution using asymmetric distribution curves: a case study in the Iberian mountains. J. Veget. Sci. 25, 147–159. doi: 10.1111/jvs.12079
Vacchiano, G., and Motta, R. (2015). An improved species distribution model for scots pine and downy oak under future climate change in the NW Italian Alps. Ann. Forest Sci. 72, 321–334. doi: 10.1007/s13595-014-0439-4
Vacchiano, G., Maggioni, M., Perseghin, G., and Motta, R. (2015). Effect of avalanche frequency on forest ecosystem services in a spruce-fir mountain forest. Cold Reg. Sci. Technol. 115, 9–21. doi: 10.1016/j.coldregions.2015.03.004
Wastl, C., Schunk, C., Leuchner, M., Pezzatti, G. B., and Menzel, A. (2012). Recent climate change: long-term trends in meteorological forest fire danger in the Alps. Agric. Forest Meteorol. 162-163, 1–13. doi: 10.1016/j.agrformet.2012.04.001
Weber, P., Bugmann, H., and Rigling, A. (2007). Radial growth responses to drought of pinus sylvestris and quercus pubescens in an inner-alpine dry valley. J. Veget. Sci. 18, 777–792. doi: 10.1111/j.1654-1103.2007.tb02594.x
Wohlgemuth, T., Schwitter, R., Bebi, P., Sutter, F., and Brang, P. (2017). Post-windthrow management in protection forests of the Swiss Alps. Eur. J. Forest Res. 136, 1029–1040. doi: 10.1007/s10342-017-1031-x
Woltjer, M., Rammer, W., Brauner, M., Seidl, R., Mohren, G. M. J., and Lexer, M. J. (2008). Coupling a 3D patch model and a rockfall module to assess rockfall protection in mountain forests. J. Environ. Manage. 87, 373–388. doi: 10.1016/j.jenvman.2007.01.031
Keywords: rockfall risk, protection forest, climate change, dynamic forest modelling, TreeMig, Eco-DRR
Citation: Moos C, Guisan A, Randin CF and Lischke H (2021) Climate Change Impacts the Protective Effect of Forests: A Case Study in Switzerland. Front. For. Glob. Change 4:682923. doi: 10.3389/ffgc.2021.682923
Received: 19 March 2021; Accepted: 02 June 2021;
Published: 29 June 2021.
Edited by:
Thomas Cordonnier, Institut National de Recherche pour l’Agriculture, l’Alimentation et l’Environnement (INRAE), FranceReviewed by:
Marco Mina, Université du Québec à Montréal, CanadaPaula Soares, University of Lisbon, Portugal
Copyright © 2021 Moos, Guisan, Randin and Lischke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christine Moos, Y2hyaXN0aW5lLm1vb3NAYmZoLmNo
†These authors have contributed equally to this work and share senior authorship
 Christine Moos
Christine Moos Antoine Guisan
Antoine Guisan Christophe F. Randin
Christophe F. Randin Heike Lischke
Heike Lischke