
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Ecol. Evol. , 04 April 2024
Sec. Conservation and Restoration Ecology
Volume 12 - 2024 | https://doi.org/10.3389/fevo.2024.1332985
This article is part of the Research Topic Insect Conservation Behavior View all 11 articles
Plant diversity and productivity, two crucial properties that sustain ecosystem structures, functions, and services, are intrinsically linked to numerous ecological fields, making productivity–richness relationships (PRR) a central ecological concern. Despite extensive research from the Darwinian era to the 21st century, the various shapes of PRR and their underlying theories have sparked ongoing debates. While several processes, theories, and integrative models have been proposed to explain PRR, a comprehensive understanding of the types of PRR, the effects of these processes on plant productivity and richness, and the relationships between PRR shapes remains elusive. This paper proposes a new integrative framework that focuses on these aspects, aiming to elucidate the diverse shapes of PRR and their interconnections. We review recent integrative methods that explain the roles of processes and the varying shapes in PRR to support this new framework. The paper traces the distinct phases in PRR research, including the discovery of PRR shapes, tests of influencing processes, and integrative research. We discuss the application of the Structural Equation Model (SEM), Statistical Dynamical Model (SDM), and Differential Dynamical Model (DDM) in integrative research. This integrative framework can guide theoretical and applied ecologists in identifying, deriving, explaining, and predicting the interconnected but distinct shapes of PRR. The humped, asymptotic, positive, negative, and irregular shapes of PRR are interconnected, with one shape potentially transforming into another. The balance between the positive and negative effects of different processes determines the different shapes of PRR, ultimately leading to a globally positive effect of plant diversity on plant productivity and other ecosystem functions.
Plant diversity and productivity are fundamental for the structure and functioning of ecosystems, including the composition, proportion, interrelation of organisms in the food chain and a variety of ecosystem functions (Humborg et al., 1997; Grace et al., 2016; Laforest-Lapointe et al., 2017). Ecosystems with diverse plant species are essential for achieving sustainable primary productivity and stability, although there are a few counter-examples (Bezemer & van der Putten, 2007). Additionally, diverse ecosystems can provide valuable ecosystem services, such as carbon sequestration, oxygen release, wood production, water resource regeneration, and soil erosion control (Sugden, 2018; Leclère et al., 2020). Consequently, plant productivity and richness relationships (PRR) have become a core issue for ecologists worldwide (Tilman et al., 2001; Chen et al., 2018).
Ecologists have observed various shapes of PRR across different continents and ecosystems, including forests, grasslands, lakes, and seas (Mittelbach et al., 2003; Whittaker and Heegaard, 2003; Adler et al., 2011; Pierce, 2014). However, information on the occurrence of these PRR shapes is scattered and irregular, leading to confusion among ecologists (Gillman and Wright, 2006; Whittaker and Heegaard, 2003; Pierce, 2014). Numerous processes and theories have been proposed to explain the shapes of PRR (Abrams, 1995; Willig, 2011). For instance, intra- and inter-specific competition effects have been proposed to explain PRR, clarifying specific sections or shapes of PRR (Stevens and Carson, 1999; Michalet et al., 2006). The dynamic equilibrium hypothesis has been applied to explain the growth and decline of populations in humped-shaped PRR (Huston, 1979; Chiarucci et al., 2006). Species-pool effect, environmental heterogeneity, and negative density dependence are often considered to regulate species richness, while selection effects, complementary effects, and inter-specific facilitation influence plant productivity in PRR (Zobel et al., 1998; Hector et al., 1999; Loreau et al., 2001; Grossman et al., 2017). Due to the diversity of PRR shapes and corresponding explanations, the general pattern of PRR and its underlying mechanisms have been the subject of debate since the 1950s (Abrams, 1995; Schmid, 2002; Adler et al., 2011; Duffy et al., 2017). However, ecologists have not clearly classified the types of PRR, despite identifying many different shapes and proposing various explanations. Furthermore, the positive and negative effects of each process on plant productivity and richness, as well as the relationships between different shapes of PRR, have rarely been analyzed.
Ecologists have also employed mathematical models to integrate the effects of different processes, aiming for a comprehensive explanation of PRR (Tilman et al., 1997; Loreau, 1998; Grace et al., 2014, Grace et al., 2016; Liang et al., 2016b; Wang et al., 2019). For example, competition models quantify the impact of inter-specific competition influenced by abiotic factors on plant productivity and species richness in PRR (Huston, 1979; Tilman et al., 1997). Mechanistic models, which consider selection effects, complementary effects, resource availability, and species’ functional traits, have been established to reveal the effects of species richness on plant productivity in competition for limiting soil nutrients (Loreau, 1998). Structural equation models, as a form of stochastic process analysis, have been widely used to quantify the roles of different processes in regulating plant diversity, productivity, biomass, and soil organic carbon in PRR (Grace et al., 2016; Chen et al., 2018). However, these integrative methods have been applied independently and have not incorporated actual values of each process contributing to plant species richness and productivity based on sampling analysis, which would enhance the understanding of PRR shapes and their relationships.
In this review, we propose a new integrative framework to explain PRR based on multiple processes or theories and previous integrative studies. The framework incorporates processes or theories proposed by ecologists after extensive research, as well as integrative models and results of PRR. Additionally, we conduct a comprehensive review of the positive and negative effects of processes on PRR, as well as relevant theories. We also examine recent integration analyses that utilize structural equation models to quantify the roles of different processes in shaping PRR, and integration analyses that employ dynamical models to provide insights into the mechanisms underlying PRR shapes. These reviews serve as valuable support for the proposed new integrative framework. Our aim is to promote further research on PRR in the field of biodiversity and ecosystem functions.
The integrative framework comprises three sections:
(1) Definition of the two types of PRR, and multiple processes influencing plant richness and productivity in PRR at the top layer (Figure 1). The two types of PRR encompass: (i) the plant productivity-species richness relationship (PSRR), where plant productivity serves as an independent variable and species richness as a dependent variable, describing the patterns of diversity influenced by productivity and other changing processes; (ii) the species richness-plant productivity relationship (SRPR), which represents the converse relationship to PSRR. In SRPR, species richness acts as the independent variable and plant productivity as the dependent variable, elucidating the effects of plant diversity on productivity and its role in regulating ecosystem functioning, stability, and services (Wang, 2017; Wang et al., 2019; Figure 1). PSRR and SRPR are closely linked to key processes in ecology. However, the classification and definition of these two types of PRR have been vague in previous studies, contributing to the ongoing debate on the shapes of PRR and the underlying mechanisms (Mittelbach et al., 2003; Cardinale et al., 2007; Whittaker, 2010; Grace et al., 2014). In the framework, processes or theories are also classified into two types, affecting or explaining PSRR and SRPR, respectively. However, some processes, such as disturbance, can influence both PSRR and SRPR (Grace et al., 2016). Generally, processes affecting PSRR or SRPR can have either positive or negative effects on species richness, plant productivity, and subsequently on PRR. Some processes may even have both positive and negative effects (Wang, 2017; Wang et al., 2019). However, the explicit definition of the positive or negative effects, or the dual effects of these processes, has been rare. Some processes have not received sufficient attention, and we provide a generalization of them in Box 1.
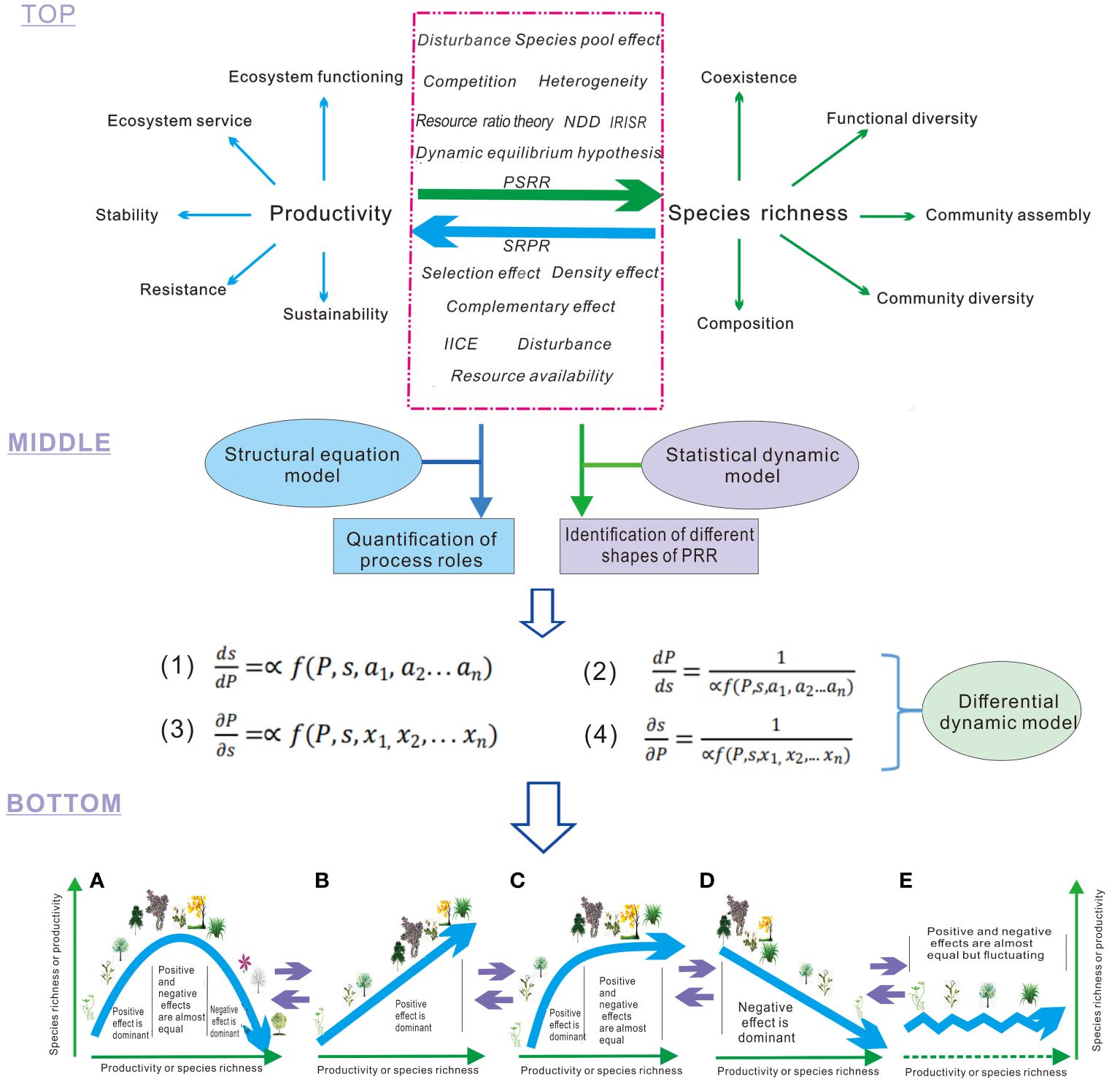
Figure 1 Processes acting on productivity-richness relationship (PRR). Top layer: The green arrow represents productivity as an independent variable that influences species richness and related patterns in conjunction with other processes. The blue arrow indicates species richness as an independent variable that affects productivity and related ecosystem properties in conjunction with other processes. The red dashed box encompasses various processes that directly or indirectly impact productivity or species richness, consequently altering PRR. NDD, Negative Density Dependence; PSRR, Productivity-Richness Relationship with productivity as the independent variable and species richness as the dependent variable; SRPR, Species Richness-Productivity Relationship with species richness as the independent variable and productivity as the dependent variable; IICE, Intra- and Inter-specific Competition Effects. Middle layer: The first and fourth equations represent the rates of change in species richness (S, a dependent variable) with plant productivity (P, an independent variable), respectively. These equations integrate different processes (i.e., variables, a1-an, x1-xn) to derive the shapes of PSRR. The second and third equations reflect the rates of change in plant productivity (a dependent variable) with species richness (an independent variable) and integrate diverse processes to derive the shapes of SRPR. Bottom layer: The results depict the diverse shapes of PRR derived from integrative analysis and dynamic models: (A) Humped; (B) Positive; (C) Asymptotic; (D) Negative; (E) Irregular. These shapes are interconnected, and one shape can transition into another shape with changes in the overall positive and negative effects of processes. A and C represent the dominant shapes of PSRR and SRPR, respectively, in the absence of exclusion of other shapes (Mittelbach et al., 2003; Fraser et al., 2015; Liang et al., 2016b). The purple arrows represent that the different forms (A,B,C,D and E) of PRR can be transformed each other.
Box 1. Integrated ecological processes and theories in the framework.
(1) Intrinsic rate of increase in species richness with productivity (IRISR). IRISR is a positive process to directly increase species richness with increasing plant productivity because high productivity can increase metabolic rate, mutation rate of genes and rapid speciation, resulting in higher species richness in communities (Allen et al., 2002; Stegen et al., 2009). The process has not been explicitly defined before but it exists with a high possibility at a scale of evolutionary time. (+species richness/+/-productivity)*.
(2) Intra- and inter-specific competition effects (IICE). IICE is an effect of competition among individuals of same and different species on species richness and productivity, which include competition stress, competitive exclusion and assemblage-level thinning to decrease species richness and productivity or increase productivity (Goldberg & Miller, 1990; Huston & DeAngelis, 1994). (-species richness/+/-productivity)
(3) Dynamic equilibrium hypothesis. The hypothesis proposes that poor competitors are excluded rapidly in highly productive habitats with rare disturbance, leading to low diversity; a strong disturbance also results in the disappearance of inadaptable species, leading to low species richness; with moderate disturbances, diversity remains relatively high in the habitats of any productivity to form the peak of the humped shape of PSRR (Huston, 1979; Michalet et al., 2006). (+/-species richness/+/-productivity).
(4) Resource ratio theory. Resource ratio theory argues that as the availability of any one resource R1 increases, another resource R2 is likely to become limiting; because different species are superior competitors for different resources, a balanced resource supply between R1 and R2 can help maintain species coexistence (Tilman, 1982; Cardinale et al., 2009). (+species richness).
(5) Species-pool effect. Species pools are a set of plant species with each species of a community, local, or regional flora being a member of any community, local, or regional species pool, with different degrees of probability; species-pool effect is a contribution of species from a species pool to species richness in the community on a certain scale (Zobel et al., 1998; Foster et al., 2004). (+species richness).
(6) Disturbances. Disturbances are some processes such as grazing, fire, severe windstorms, wave damage, land cover alterations, habitat fragmentation, and forest destruction, which often alters plant productivity and species richness, primarily via a negative or positive effect (Hughes et al., 2007; Wu et al., 2019). (-/+species richness and productivity)
(7) Environmental heterogeneity. Environmental heterogeneity is locally diverse configurations in resource types with different availability levels along with more complex configurations in abiotic and biotic resources and more heterogeneities but environmental heterogeneity is the configurations of diverse habitats, i.e., habitat heterogeneity, on a landscape scale (Amarasekare, 2003; Lasky et al., 2014). (+species richness).
(8) Density effects. Density effects are an ecological process resulting in species richness with increasing number of plant individuals in a plant community; plant density increases with increasing species richness also leads to high and low biomass production at low and high inter-specific and intra-specific competition levels, respectively (Marquard et al., 2009). (+species richness/+/-productivity).
(9) Negative density dependence (NDD). NDD is a process by which population growth rates decline at high densities as a result of natural enemies (e.g., predators, pathogens, or herbivores) and/or competition for space and resources to lead to the coexistence of species (Yenni et al., 2012; LaManna et al., 2017a, LaManna et al., 2017b). (+ species richness).
(10) Selective and complementary effects. Selection effect is the standard positive covariance effect, as a diverse community stochastically contains highly productive species (Balvanera et al., 2006; Loreau et al., 2001); complementary effect refers to an effect caused by species`differentiation in resource use and/or inter-specific facilitation at higher levels of species richness (Balvanera et al., 2006; Cardinale et al., 2007). (+productivity).
(11) Resource availability. Resource availability is relatively higher quantities of limited resources which ensures that weaker competitors are able to capture the limited resources for the maintenance of a population leading to the diversity and productivity of coexisting species (Tilman, 1982; Cardinale et al., 2009). (+ productivity/+species richness).
* “+” or “-” represents positive or negative effect on species richness or productivity.
(2) Integrative models in the middle layer. The integrative models encompass the structural equation model, statistical dynamical model, and differential dynamical model within the framework. The structural equation model is a statistical method used to analyze the relationship between variables based on their covariance matrix. It enables the estimation, testing, and quantification of causality (Grace et al., 2016; Chen et al., 2018). The structural equation model has been applied to various practical scenarios, including multi-dependent variable analysis, latent variable analysis, and intermediate variable analysis. It can be viewed as a combination of path analysis and confirmatory factor analysis. The positive or negative effects (i.e., contributions) of multiple processes on plant species richness and productivity in PRR are quantified integrally using the structural equation model. The quantified effects (standardized) are then assigned as coefficients of the integrated processes in the dynamical model to derive the shapes of PRR. This application of the structural equation model to the framework avoids the subjective assignment of coefficients for the process variables and enhances the practicality of the differential equation in the framework.
The statistical dynamical model is a type of dynamic model that describes the occurrence of random processes. It is often employed in meta-analysis and sampling analysis to identify the shapes of PRR (Mittelbach et al., 2003; Liang et al., 2016b). In the framework, statistical dynamical models can determine the occurrence ratios of different-shaped PRR. The differential dynamical model is a type of dynamic model used to describe the continuous change of dependent and independent variables regulated by multiple processes. Ecologists commonly establish such models to derive the shapes of PRR based on assumed parameter values of processes. These models further reveal how the shapes of PRR occur under the regulation of these processes and how they are linked with each other, i.e., underlying mechanisms (Loreau, 1998; Wang, 2017; Wang et al., 2019). In the framework, the actual parameter values of processes from the analysis of structural equation models may be introduced to differential dynamical models for deriving the shapes of PRR which have been identified by statistical dynamic models. Therefore, the three types of models are related to each other.
(3) Integrative results in the bottom layer. As shown in Figure 1, the integrative framework allows for the derivation of five typical shapes of the PRR by applying the three types of models discussed earlier. This approach differs from previous methods that relied on assumed coefficients to determine the shapes of PRR (Loreau, 1998; Liang et al., 2016b; Wang, 2017; Wang et al., 2019). When the positive effects of integrated processes dominate, the PRR shapes exhibit an upward trend. Conversely, when the negative effects of integrated processes dominate, the PRR shapes show a downward trend. When the positive and negative effects of integrated processes are approximately equal, the PRR shapes display a horizontal or fluctuating pattern. Finally, when the positive and negative effects of integrated processes successively dominate, the PRR shapes exhibit a humped pattern. This integrative framework effectively resolves the long-standing debate surrounding the shapes of PRR and their underlying mechanisms (Schmid, 2002; Adler et al., 2011; Duffy et al., 2017).
The integrative framework provides an explanation for the occurrence of different shapes in the productivity-richness relationship observed in the real world, considering the effects of multiple variables. It can specifically demonstrate which processes are strong or weak, and whether they have a positive or negative effect, thereby determining the shapes of the PSRR and SRPR. In contrast, a meta-analysis or statistical dynamical approaches such as P=α(X)SB cannot achieve this level of understanding. While statistical dynamical models can be used to simply identify the shapes of SRPR (Liang et al., 2016b), the integrative framework allows for tracking the dynamics of the interactions among different processes that influence the shapes of PSRR and SRPR. For example, it can capture the dynamics of species-pool effects and inter-specific competition by utilizing differential equations, which offer greater flexibility in dealing with variable dynamics compared to statistical dynamical methods. Ecologists can identify the inflection points at which the shapes of PSRR and SRPR change from one pattern to another, and determine the corresponding processes or integrative processes responsible for these changes (Wang et al., 2019). Consequently, the integrative framework provides a clearer understanding of the underlying mechanisms driving PSRR and SRPR, resolving key debates regarding the drivers of hump-shaped patterns and other patterns. By combining the strengths of structural equation models, statistical dynamical models, and differential dynamical models while avoiding their shortcomings, this framework presents a novel technology roadmap for deriving the shapes of PSRR and SRPR.
The integrative framework has broad applications in the study of diversity patterns, ecosystem functions and services, underlying mechanisms, and ecosystem management. Ecologists can start by conducting field vegetation investigations to collect data on productivity, species richness, and the processes influencing productivity and species richness in a particular research region, either through new data collection or using existing datasets. The interaction relationships among productivity, species richness, and influencing processes can then be analyzed using structural equation modeling, providing factor loadings and determinant coefficients through analysis. Subsequently, the field data can be used to identify the shapes of PSRR and SRPR using statistical dynamical models under specific conditions, thereby determining the shapes of PRR. The differential equation set for PSRR and SRPR can be established by utilizing the factor loadings as coefficients for the variables of productivity, species richness, and processes. Mathematical methods such as Fortran or Python can be employed to solve the equations and obtain solutions for each variable, including productivity, species richness, and processes. The dynamics of these variables can be modeled with changes in other variables such as disturbance and resource availability, and compared with the shapes identified by statistical dynamical models. The differential equations can be further refined to predict PSRR and SRPR for management purposes in similar regions. These methods are also applicable to purely theoretical research.
The following review includes two sections that utilize structural equation models and dynamical models (both statistical and differential) to analyze the integration of processes in PRR and explain the formation of PRR shapes. These sections serve to recapitulate the contributions of previous integration research on PRR while highlighting certain research limitations. These limitations align with the issues that the integration framework proposed in this review aims to address. As a result, these two sections provide valuable support for the proposed new integrative framework.
Previous studies have recognized that individual processes or theories can only explain specific sections or dominant shapes of PRR, although they have contributed to the understanding of PRR (Axmanová et al., 2012; Pierce, 2014). As the dominant shapes of PRR have been challenged by diverse patterns, some researchers have argued that PRR is variable, complex, and scale-dependent, influenced by numerous abiotic and biotic processes (Grace et al., 2007; Willig, 2011). Consequently, ecologists have shifted their focus towards incorporating more processes to explain the shapes of PRR, utilizing structural equation models to integrate different processes within the bivariate relationship of plant richness and productivity (Grace et al., 2014, Grace et al., 2016). The structural equation model approach allows for the calculation of the role values of each process affecting species richness and productivity based on field investigations and meta-analyses of previous studies.
In one specific integration, Grace et al. (2014) established a causal network for the humped shape of PSRR, assuming the hump as the basic shape. Using a structural equation model, the corresponding processes influencing plant richness and productivity in the humped shapes were quantified. Surprisingly, this analysis did not support the assumed humped shape of PSRR but instead revealed alternative shapes and influencing processes. This study demonstrates how causal networks can be established through hypotheses and explicit tests to explain PSRR as an abstracting system, providing powerful predictions beyond bivariate analysis. Building upon this concept, further structural equation modeling was employed to integrate competing theories into a multi-process hypothesis and evaluate it using global data from 1,126 plots in grass-dominated sites (Grace et al., 2016). The variables measured included plant species richness, productivity, total biomass, and various drivers such as soil fertility, climate, heterogeneity, soil suitability, and shading. In contrast to a bivariate species richness-productivity model, this modeling approach explained 61% of the variation in richness at the site and plot levels, quantifying the roles of different processes in regulating PSRR and SRPR (Figure 2).
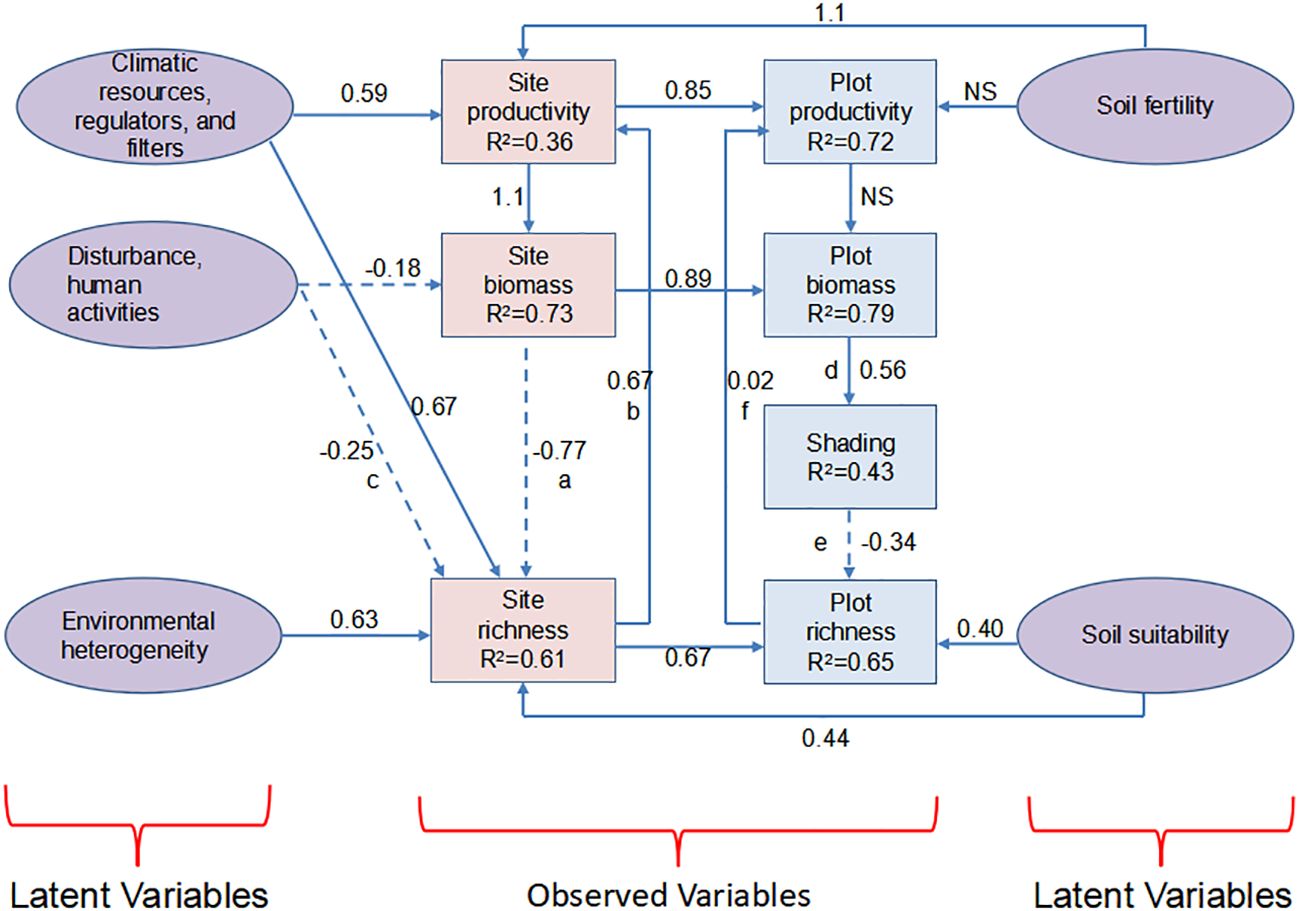
Figure 2 Roles of multiple processes in PRR quantified by a structural equation model. This figure illustrates the roles of multiple processes in PRR as quantified by a structural equation model. Solid arrows indicate positive effects, while dashed arrows represent negative effects. The digits alongside the lines indicate the magnitude of these effects. The lowercase letters represent the different plots for the data of collection. NS, no significance. Adapted from Grace et al. (2016).
In another integration, field observations from 6,098 forest, shrubland, and grassland sites across China were collected to integrally quantify the first-type effects of climate, soils, and human impacts on soil organic carbon (SOC) storage, as well as the second-type effects mediated by species richness, above-ground net primary productivity (ANPP), and below-ground biomass (BB), using a structural equation model (Chen et al., 2018). The analysis revealed a positive SRPR and a positive biomass-SOC relationship. Favorable climates (high temperature and precipitation) consistently had a negative effect on SOC storage but a positive effect on species richness, ANPP, and BB. The positive relationships between species richness and ANPP/BB offset the negative effect of favorable climate on SOC storage. Maintaining high levels of diversity can enhance soil carbon sequestration (Chen et al., 2018). These results are supported by other local studies conducted in China and Canada (Chen et al., 2018; Huang et al., 2018; Chen et al., 2020).
The aforementioned studies by Grace et al. (2014, 2016) primarily focused on PRR influenced by abiotic processes, while the study by Chen et al. (2018) attempted to reveal the underlying mechanisms linking SOC storage with PRR. The results indicated that species richness had positive effects on productivity, biomass, and subsequently SOC storage, highlighting the regulation of PRR by diverse processes. Structural equation modeling represents a significant advancement in the analysis of PRR beyond two-dimensional variables of plant productivity and diversity. However, the data on species richness, productivity, and abiotic and biotic processes used in structural equation models are often collected simultaneously. Abiotic and biotic processes continuously vary and exhibit hysteresis in the regulation of PRR. In other words, the sampled abiotic and biotic processes, such as soil fertility, when plant richness and productivity are measured, will primarily affect plant richness and productivity in the future. Additionally, a single application of a structural equation model cannot identify the shapes of PRR. Therefore, it is necessary to consider dynamic processes when establishing a model network to assess the effects of processes on PRR. Nevertheless, the role values of different processes in regulating plant richness and productivity, quantified by structural equation models, can be used as coefficients for independent and dependent variables in dynamic models. The application of a structural equation model alone cannot derive or model the shapes of PRR or reveal underlying mechanisms. Instead, it encourages us to leverage its advantages in combination with other methods within the integrative framework.
In order to predict the variation of species richness in PRR and elucidate the underlying mechanisms, ecologists have previously developed integrative models such as the CSR strategy, non-equilibrium interaction model, multispecies patch-occupancy model, resource-ratio model, and modified neutral model (Grime, 1974; Huston, 1979; Hastings, 1980; Tilman, 1982; Kadmon and Benjamini, 2001). These models, with their respective differences, aimed to understand the mechanisms of plant diversity and could be integrated to explain the humped shape of PRR, which was widely accepted by many ecologists at that time (Figure 3A). To explain the shapes of SRPR, integrative models were developed to characterize inter-specific competitive interactions among randomly chosen species and a spatially structured ecosystem competing for a limiting soil nutrient. These models were based on complementary effects, inter-specific facilitation, and selection effects, which provided an explanation for why species richness had positive effects on productivity (Tilman et al., 1997; Loreau, 1998; Loreau et al., 2001; Figure 3B). These theoretical approaches represented early integration analyses with dynamical models and significantly contributed to the understanding of the underlying mechanisms of SRPR.

Figure 3 Two dominant shapes of PSRR and SRPR in early integrative studies. (A) Humped shape of PSRR: The figure illustrates the humped shape of PSRR. In this shape, the plant community exists in a non-equilibrium state with multi-species patch occupancy along a gradient of resource availability and environmental severity. On the high environmental severity side, strong environmental stress or disturbance selects for stress-tolerant species adapted to such conditions, resulting in low species richness. Conversely, on the high resource availability side, strong competitive species dominate the competition for limiting resources, such as light, excluding other species that freely immigrate but are not adapted to such competitive habitats, leading to low species richness. Intermediate levels of stress or disturbance between the two sides favor both neutral and stress-tolerant species, and strong competitive species can also thrive with neutral species, allowing for the coexistence of multiple species and maintaining high richness. (B) Relationship among species richness, productivity, and resource-use intensity in SRPR: The figure depicts the relationship among species richness, productivity, and resource-use intensity in SRPR. An ecosystem with high species richness exhibits complementarity in resource use, leading to increased resource absorption by plants and higher productivity. At the same time, inter-specific competition is intense in the ecosystem. Additionally, as species richness increases, more productive and reciprocal species occur in the ecosystem, resulting in high productivity. This phenomenon is attributed to the selection effect and inter-specific facilitation, where more productive species are favored and occur in greater numbers as species richness increases.
However, these early integrative models were primarily designed to integrate the important processes suggested (or excluded) by researchers to explain (or support) the widely accepted shapes of PRR. While these studies made efforts to reveal the mechanisms of PRR, the focused integrative methods weakened the universality of the results regarding the diverse shapes of PRR. Recent integrative analyses using dynamical models have taken a different approach. On one hand, they have moved away from focused studies that only consider a few processes related to the dominant shapes of PRR, such as the effects of environmental heterogeneity, resource availability, plant density, trait variability, etc., to clarify the underlying mechanisms (Hodapp et al., 2016; Wang, 2017; Hodapp et al., 2018; Wang et al., 2019). On the other hand, unlike early integration, these analyses have attempted to incorporate as many processes as possible that have been identified by ecologists as factors influencing plant richness and productivity (Box 1). These integrative analyses focus on two types of methods: using statistical dynamic models to test the shapes of PRR observed in literature and field studies, and using differential dynamic models to integrate multiple processes in order to derive the shapes of PRR and analyze the underlying mechanisms.
To address the limitations of early integrative studies that focused only on dominant shapes of PRR, ecologists have employed statistical dynamic models. These models combine statistical and dynamic methods, originating from weather forecasting models, to test the occurrence ratios of different shapes of PRR in previous species-assembly experiments and field investigations (Cardinale et al., 2007; Adler et al., 2011). One commonly used statistical dynamic model is meta-analysis, which analyzes study cases to determine the shapes of PRR as a function of various dynamic factors such as scales, investigation methods, plant taxa, grains, and regions (Mittelbach et al., 2003; Gillman and Wright, 2006; Cardinale et al., 2007; Whittaker, 2010). Meta-analyses have indicated that, while there is still debate regarding the shapes of PRR, the humped shape is dominant for PSRR in all collected cases, with a relatively lower probability of occurrence for other shapes such as negative, U-shaped, and unrelated forms (Mittelbach et al., 2003; Adler et al., 2011; Fraser et al., 2015; Figure 4A). For SRPR, a positive or asymptotic shape is dominant compared to other shapes (Cardinale et al., 2007; Duffy et al., 2017). It is evident that scales, investigation methods, and plant taxa influence these statistical results. However, meta-analysis fails to capture the changes in PRR and the relationships between different shapes of PPR, as it provides static results without considering the impact of plant productivity, diversity, or other processes affecting PRR. Nevertheless, statistical models are valuable tools for identifying and validating the shapes of PRR in previous study cases within the framework (Figure 1).
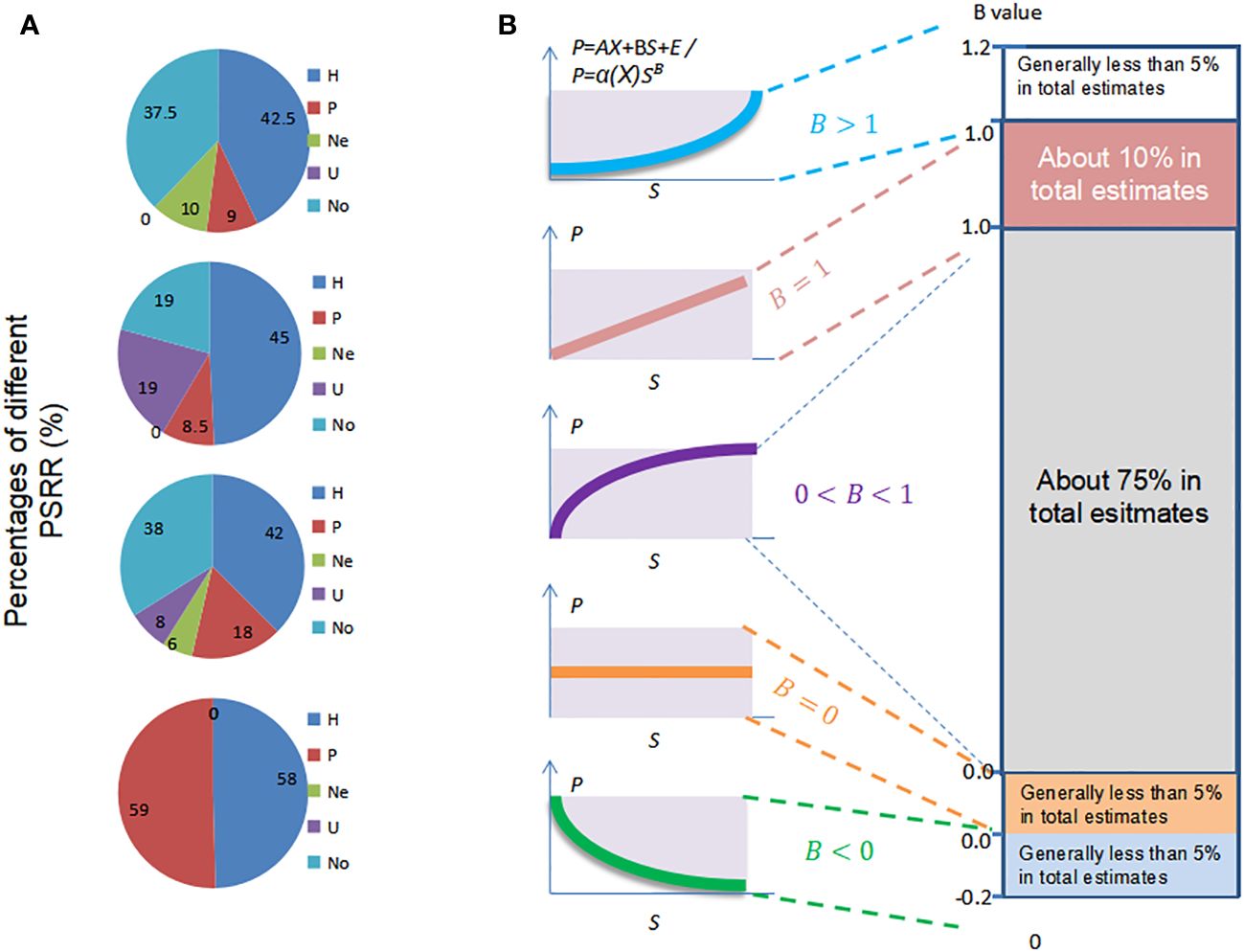
Figure 4 Shapes of PSRR and SRPR based on multiple references cited in the text. (A) Statistical results of the shapes of PSRR observed in study cases at various scales, including local, landscape, regional, and continental to global scales. The shapes are represented by the following abbreviations: H (humped), P (positive), Ne (negative), U (U-shaped), and No (unrelated). (B) Sampling results of the shapes of SRPR based on the coefficient B representing the effect of tree diversity on forest productivity. Left: B values ranging from 0 to 1 correspond to positive and asymptotic shapes, while B ≤ 0 corresponds to level and negative shapes. Right: Dominance of different shapes based on the distribution of the sampling data. Tree diversity is represented by S, and productivity is represented by P. Adapted from Liang et al. (2016b).
Another statistical dynamic model is the use of simple regression with empirical equations or direct regression analysis to demonstrate the different shapes of PRR based on field sampling results (Axmanová et al., 2012; Steudel et al., 2012; Huang et al., 2018). In such models, the coefficient of species richness (independent variable) is utilized to determine the shapes of SRPR corresponding to the sampling results (Figure 4B). For instance, an empirical dynamical model P=α·f(X)·SB(P, productivity; X, environmental factors such as soil and climate; S, species richness; α, coefficient; B, the effects of species richness on productivity) was employed to quantify the dependence of productivity on species richness and measure the marginal productivity, which represents the change in productivity resulting from a one-unit decline in species richness, while accounting for climatic, soil, and plot-specific covariates (Liang et al., 2016b). When B > 1, the shape of SRPR is concave-down; when B = 1, the shape is positive; when 1 > B > 0, the shape is asymptotic; when B = 0, the shape is parallel (no effect); when B < 0, the shape is negative. Direct sampling data from various sources indicated that the average θ was 0.26, suggesting a predominantly positively asymptotic shape. Other forms occupied only a small percentage. A sampling study across the Amazon Basin, involving 90 one-hectare plots, also demonstrated the dominant positively asymptotic effect of taxonomic and evolutionary diversity on productivity, which was separated from environmental factors using generalized least-squares modeling (De Souza et al., 2019). These field sampling results were consistent with meta-analyses of other ecologists’ studies, although meta-analysis represents a secondary form of sampling (Hooper et al., 2005; Grace et al., 2007; Forrester & Bauhus, 2016; Duffy et al., 2017).
The statistical dynamical models based on field sampling are effective and straightforward approaches for identifying the shapes of PRR. Additionally, by utilizing a coefficient known as marginal productivity—the change in productivity resulting from a one-unit decline in species richness—the relationship between different shapes of PRR can be defined in a simple manner. However, these models have limited flexibility in considering variables other than productivity and species richness (represented by variable X). This limitation hinders the ability to reveal the interactions among these processes since X is often quantified using linear methods rather than non-linear ones (Liang et al., 2016b). In reality, the non-linear interactions of other processes significantly impact PRR, as demonstrated by earlier studies examining interactions among disturbance, competition, stress, resource availability, and more (Grime, 1974; Huston, 1979; Hastings, 1980; Tilman, 1982). Unfortunately, the statistical dynamical models fail to adequately quantify these non-linear interactions of other processes, leading to increased errors in explaining the shapes of PRR.
Some ecologists argue that PRR is governed by diverse and complex processes, and to clarify the shapes of PRR, it is necessary to assess the different effects of these processes on plant richness and productivity and simulate their interactions (Willig, 2011; Grace et al., 2014; Wang, 2017). In line with this perspective, a set of differential equations, known as the PSRR model, was established based on the positive and/or negative effects of 21 widely accepted processes on plant productivity and species richness, as identified in the relevant literature (Wang et al., 2019). These equations integrate the effects of these processes into a comprehensive measure of plant productivity, allowing for the derivation of the shapes of PSRR. Each process is assigned a different parameter value to represent its strength, and these parameter values can be adjusted to regulate the strengths of the processes. Plant richness is explicitly defined as a dependent variable, while plant productivity serves as an independent variable in the equations, quantifying the effects of plant productivity on species richness. Subsequently, the PSRR model is transformed into the SRPR model, which represents the feedback relationships to PSRR. In the SRPR model, plant productivity is determined as a dependent variable, and species richness as an independent variable. Using the PSRR model, the five typical shapes of PSRR, the dynamics of IICE (Box 1), and the effects of the species pool on these shapes with increasing productivity were derived and verified using field data (Wang et al., 2019; Figure 5). It was observed that the shapes of PSRR can change from one shape to another by altering the parameter values representing the strengths of the processes. Since the same set of parameters is used in the SRPR model, the diverse shapes of SRPR can also be derived. These derivations indicate that different strengths of processes acting on species richness and productivity give rise to different shapes of PSRR and SRPR. Specifically, when the integrated processes show a dominant positive effect, the shape of PSRR or SRPR is linear or asymptotic; when the integrated processes show a dominant negative effect, the shape of PSRR or SRPR is negative; and when the integrated processes successively show a dominant positive and negative effect, the shape of PSRR or SRPR is humped. These integrative methods can explain the documented PSRR and SRPR patterns observed in empirical studies conducted over several decades on various terrestrial, freshwater, and marine taxa from different regions of the world (Mittelbach et al., 2003; Gillman & Wright, 2006; Whittaker, 2010; Grace et al., 2014; Liang et al., 2016b; Fichtner et al., 2017). Furthermore, these results reveal the connections between the different shapes of PSRR and SRPR and the underlying processes (Wang, 2017; Wang et al., 2019).
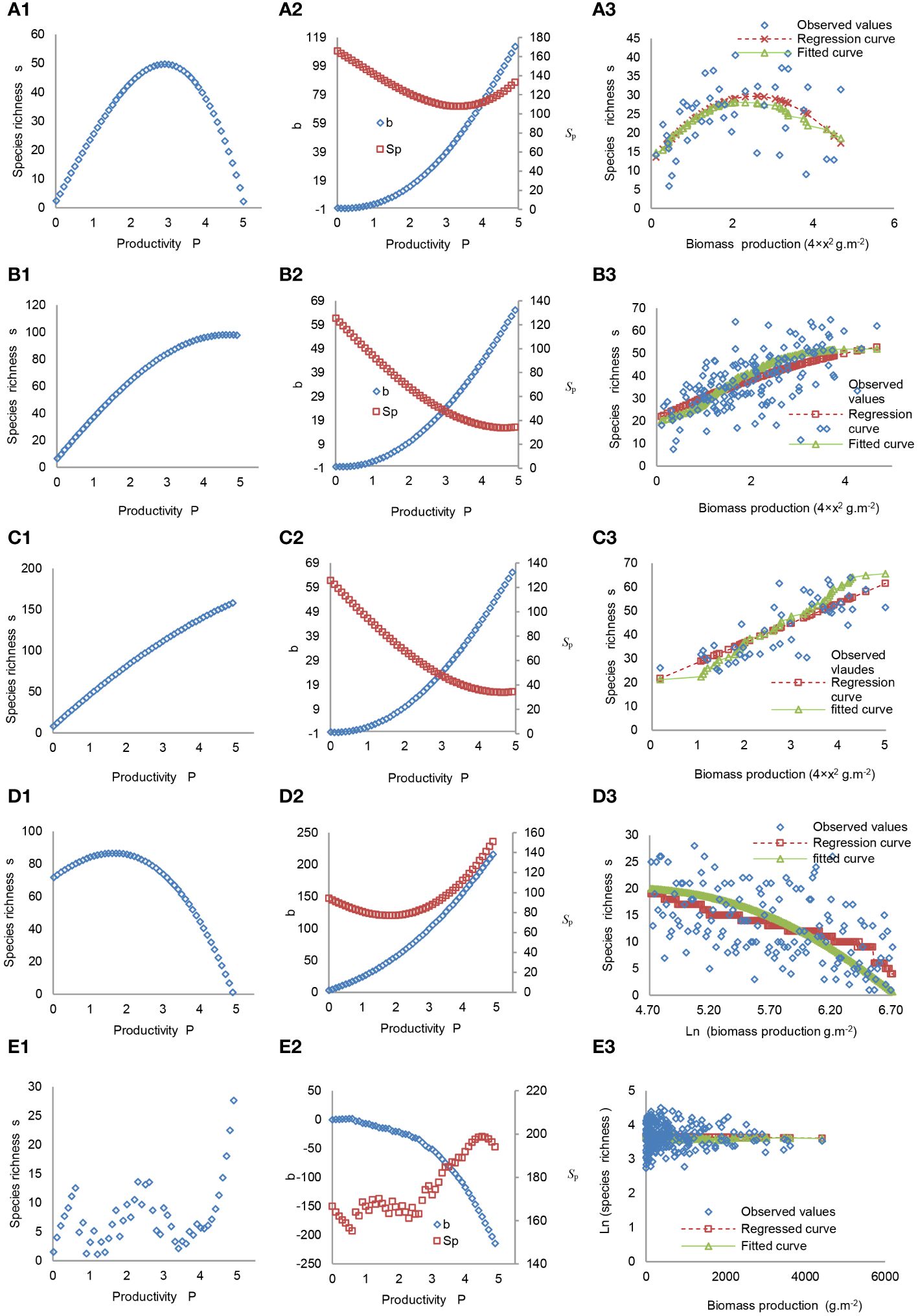
Figure 5 Typical Shapes of PSRR. (A1–E1) These curves represent the humped, asymptotic, positive, negative, and irregular shapes, respectively, derived by the PSRR model, which incorporates almost all processes affecting species richness. Adapted from Wang et al. (2019). (A2–E2) These curves illustrate the dynamics of intra- and inter-specific competition effects (b) and the potential species-pool effect (Sp), which directly influence the shapes of PSRR. (A3–E3) These curves depict the observed species richness along a productivity gradient at a local plot across Germany, Czech Republic, Russia, USA, and Australia, respectively. The regression curves represent the results fitted based on these observed species richness and productivity. The fitted curves correspond to the outcomes obtained by fitting the observed data with the PSRR model. Notably, there was no significant difference between the fitted and observed species richness.
While the differential dynamical model offers a flexible solution for revealing the dynamical interactions of different processes affecting PRR and can elucidate the mechanisms underlying PRR, it is challenging to determine the coefficients of the numerous variables in the model. Moreover, the shapes of PRR derived or modeled using this non-linear differential model are generally diverse and require validation using field sampling data. Therefore, the structural equation model and statistical dynamical model can complement the limitations of the differential dynamical model within an integrative framework.
The recent integrative studies using statistical and differential dynamic models (Cardinale et al., 2007; Liang et al., 2016a, b; Wang et al., 2019) have improved the limited universality of results obtained by earlier studies that primarily integrated only a few processes to explain the accepted dominant shapes of PRR. The differential dynamical model provides insights into why and how the diverse PRR patterns discovered by statistical dynamical models based on meta-analysis and field sampling occur in the real world. Based on the differential dynamic model, it has been found that: (i) ecological processes that have a positive or negative effect on plant richness and productivity in PSRR and SRPR can vary temporally or spatially; (ii) processes that have a strongly positive effect at one productivity or richness level may have a weakly positive or negative effect at another level; and (iii) the integration of all positive and/or negative effects of processes, species richness, and plant productivity into a total effect (which continually changes but may be positive or negative) fundamentally determines the shapes of PSRR and SRPR (Wang et al., 2019; Leclère et al., 2020). However, these integrative methods still require further improvement. Theoretically, integrative methods are based on the analysis of processes affecting plant richness and productivity to establish dynamical models of PRR (Tilman et al., 1997; Loreau, 1998; Wang et al., 2019). The parameter values representing the effects of processes on PRR in dynamical models are often assumed and subjectively determined, although many derived PRR shapes have been validated by field data. Such an approach can influence the reliability of the derived PRR shapes. Therefore, within the framework of explaining PRR, we propose that the parameter values representing the effects of processes on PRR in the PRR dynamical models should be determined by quantifying the roles of different processes in the regulation of PPR in the field using a structural equation model (Figure 1).
PRR has been a subject of extensive debate and research in ecology. Over time, research on PRR has progressed through distinct stages, including the identification of different PRR shapes, investigations of influencing processes, and integrative studies involving vegetation analysis, manipulation experiments, and theoretical analysis. The central focus of the debate has been on determining the dominant shapes of PRR and understanding the underlying mechanisms.
Recent integrative research, which involves analyzing and integrating the effects of respective processes influencing PRR, has revealed that the humped, asymptotic, positive, negative, and irregular shapes of PRR are interconnected. These shapes are not fixed, and one shape of PRR can transition into another. The balance between the positive and negative effects of different processes plays a crucial role in determining the various shapes of PRR. Furthermore, this balance leads to plant diversity having a globally positive effect on plant productivity and other ecosystem functions.
Respective and integrative research represent two types of methods employed to study the ecological processes influencing PRR. Respective research focuses on testing the effects of individual processes on PRR and uncovering the underlying mechanisms. Integrative research, on the other hand, examines the relative roles and interactions of processes in regulating PRR in real-world settings, as well as the relationships between different PRR shapes. PRR is considered a fundamental ecological issue that spans populations, communities, ecosystems, and landscapes. Ecologists have long been interested in PRR and the ecological processes that affect it, which has led to the development of various ecological theories.
Future studies on PRR should emphasize the relationships between metabolic rates related to resource availability and productivity, gene mutation rates, and increasing plant diversity, as these factors are evolutionarily significant. It is essential to identify the relative importance of each process and understand their interactions for the advancement of integrative studies. While significant progress has been made in understanding PRR, it is crucial for ecologists to carefully differentiate between the two types of PRR influenced by respective and integrative processes. Confusion between these types of PRR and different research methods can contribute to additional debates and challenges in the field.
ZW: Conceptualization, Funding acquisition, Methodology, Project administration, Software, Supervision, Validation, Writing – original draft, Writing – review & editing. JA: Software, Validation, Writing – review & editing. TY: Data curation, Methodology, Software, Writing – review & editing. CZ: Data curation, Formal Analysis, Writing – original draft. AC: Conceptualization, Supervision, Validation, Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work was supported by the Fundamental Research Funds for the central Universities (No.300111230018; No. 300102292902).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abrams P. A. (1995). Monotonic or unimodal diversity-productivity gradients: what does competition theory predict? Ecology 76, 2019–2027. doi: 10.2307/1941677
Adler P. B., Seabloom E. W., Borer E. T., Hillebrand H., Hautier Y., Hector A., et al. (2011). Productivity is a poor predictor of plant species richness. Science 333, 1750–1752. doi: 10.1126/science.1204498
Allen A. P., Brown J. H., Gillooly J. F. (2002). Global biodiversity, biochemical kinetics, and the energetic-equivalence rule. Science 297, 1545–1548. doi: 10.1126/science.1072380
Amarasekare P. (2003). Competitive coexistence in spatially structured environments: a synthesis. Ecol. Lett. 6, 1109–1122. doi: 10.1046/j.1461-0248.2003.00530.x
Axmanová I., Chytrý M., Zelený D., Li C. F., Vymazalová M., Danihelka J., et al. (2012). The species richness-productivity relationship in the herb layer of European deciduous forests. Global Ecol. Biogeography 21, 657–667. doi: 10.1111/j.1466-8238.2011.00707.x
Balvanera P., Pfisterer A. B., Buchmann N., He J. S., Raffaelli D., Schmid B. (2006). Quantifying the evidence for biodiversity effects on ecosystem functioning and services. Ecol. Lett. 9, 1146–1156. doi: 10.1111/j.1461-0248.2006.00963.x
Bezemer T. M., van der Putten W. H. (2007). Diversity and stability in plant communities. Nature 446, E6–E7. doi: 10.1038/nature05749
Cardinale B. J., Hillebrand H., Harpole W. S., Gross K., Ptacnik R. (2009). Separating the influence of resource “availability” from resource “imbalance” on productivity-diversity relationships. Ecol. Lett. 12, 475–487. doi: 10.1111/j.1461-0248.2009.01317.x
Cardinale B. J., Wright J. P., Cadotte M. W., Carroll I. T., Hector A., Srivastava D. S., et al. (2007). Impacts of plant diversity on biomass production increase through time because of species complementarity. Proc. Natl. Acad. Sci. 104, 18123–18128. doi: 10.1073/pnas.0709069104
Chen Y., Huang Y. Y., Niklaus P. A., Castro-Izaguirre N., Clark A. T., Bruelheide H., et al. (2020). Directed species loss reduces community productivity in a subtropical forest biodiversity experiment. Nat. Ecol. Evol. 4, 550–559. doi: 10.1038/s41559-020-1127-4
Chen S. P., Wang W. T., Xu W. T., Wang Y., Wan H. W., Chen D. M., et al. (2018). Plant diversity enhances productivity and soil carbon storage. Proc. Natl. Acad. Sci. 115, 4027–4032. doi: 10.1073/pnas.1700298114
Chiarucci A., Viciani D., Winter C., Diekmann M. (2006). Effects of productivity on species area curves in herbaceous vegetation: evidence from experimental and observational data. Oikos 115, 475–483. doi: 10.1111/j.2006.0030-1299.15116.x
De Souza F. C., Dexter K. G., Phillips O. L., Pennington R. T., Neves D., Sullivan M. J. P., et al. (2019). Evolutionary diversity is associated with wood productivity in Amazonian forests. Nat. Ecol. Evol. 3, 1754–1761. doi: 10.1038/s41559-019-1007-y
Duffy J., Godwin C., Cardinale B. (2017). Biodiversity effects in the wild are common and as strong as key drivers of productivity. Nature 549, 261–264. doi: 10.1038/nature23886
Fichtner A., Härdtle W., Li Y., Bruelheide H., Kunz M., von Oheimb G. (2017). From competition to facilitation: how tree species respond to neighborhood diversity. Ecol. Lett. 20, 892–900. doi: 10.1111/ele.12786
Forrester D. I., Bauhus B. J. (2016). A review of processes behind diversity-productivity relationships in Forests. Curr. Forestry Rep. 2, 45–61. doi: 10.1007/s40725-016-0031-2
Foster B. L., Dickson T. L., Murphy C. A., Karel I. S., Smith V. H. (2004). Propagule pools mediate community assembly and diversity-ecosystem regulation along a grassland productivity gradient. J. Ecol. 92, 435–449. doi: 10.1111/j.0022-0477.2004.00882.x
Fraser L. H., Pither J., Jentsch A., Sternberg M., Zobel M., Skarizadeh D., et al. (2015). Worldwide evidence of a unimodal relationship between productivity and plant species richness. Science 349, 302–305. doi: 10.1126/science.aab3916
Gillman L. N., Wright S. D. (2006). The influence of productivity on the species richness of plants: a critical assessment. Ecology 87, 1234–1243. doi: 10.1890/0012-9658(2006)87[1234:TIOPOT]2.0.CO;2
Goldberg D. E., Miller T. E. (1990). Effects of different resource additions on species diversity in an annual plant community. Ecology 71, 213–225. doi: 10.2307/1940261
Grace J. B., Adler P. B., Harpole W. S., Borer E. T., Seabloom E. W. (2014). Causal networks clarify productivity-richness interrelations, bivariate plots do not. Funct. Ecol. 28, 787–798. doi: 10.1111/1365-2435.12269
Grace J. B., Anderson T. M., Seabloom E. W., Borer E. T., Adler P. B., Harpole W. S., et al. (2016). Integrative modeling reveals mechanisms linking productivity and plant species richness. Nature 529, 390–393. doi: 10.1038/nature16524
Grace J. B., Anderson T. M., Smith M. D., Seabloom E., Andelman S. J., Meche G., et al. (2007). Does species diversity limit productivity in natural grassland communities? Ecol. Lett. 10, 680–689. doi: 10.1111/j.1461-0248.2007.01058x
Grime J. P. (1974). Vegetation classification by reference to strategies. Nature 250, 26–31. doi: 10.1038/250026a0
Grossman J. J., Cavender-Bares J., Hobbie S. E., Reich P. B., Montgomery R. A. (2017). Species richness and traits predict overyielding in stem growth in an early-successional tree diversity experiment. Ecology 98, 2601–2614. doi: 10.1002/ecy.1958
Hastings A. (1980). Disturbance, coexistence, history, and competition for space. Theor. Population Biol. 18, 363–373. doi: 10.1016/0040-5809(80)90059-3
Hector A., Schmid B., Beierkuhnlein C., Caldeira M. C., Diemer M., Dimitrakopoulos P. G., et al. (1999). Plant diversity and productivity experiments in European grasslands. Science 286, 1123–1127. doi: 10.1126/science.286.5442.1123
Hodapp D., Borer E. T., Harpole W. S., Lind E. M., Seabloom E. W., Adler P. B., et al. (2018). Spatial heterogeneity in species composition constrains plant community responses to herbivory and fertilization. Ecol. Lett. 21, 1364–1371. doi: 10.1111/ele.13102
Hodapp D., Hillebrand H., Blasius B., Ryabov A. B. (2016). Environmental and trait variability constrain community structure and the biodiversity-productivity relationship. Ecology 97, 1463–1474. doi: 10.1890/15-0730.1
Hooper D. U., Chapin F. S. III, Ewel J. J., Hector A., Inchausti P., Lavorel S., et al. (2005). Effects of biodiversity on ecosystem functioning: a consensus of current knowledge. Ecol. Monogr. 75, 3–35. doi: 10.1890/04-0922
Huang Y. Y., Chen Y. X., Castro-Izaguirre N., Baruffol M., Brezzi M., Lang A., et al. (2018). Impacts of species richness on productivity in a large-scale subtropical forest experiment. Science 362, 80–83. doi: 10.1126/science.aat6405
Hughes A. R., Byrnes J. E., Kimbro D. L., Stachowicz J. J. (2007). Reciprocal relationships and potential feedbacks between biodiversity and disturbance. Ecol. Lett. 10, 849–864. doi: 10.1111/j.1461-0248.2007.01075.x
Humborg C., Ittekkot V., Cociasu A., Bodungen B. V. (1997). Effect of Danube River dam on Black Sea biogeochemistry and ecosystem structure. Nature 386, 385–388. doi: 10.1038/386385a0
Huston M. A. (1979). A general hypothesis of species diversity. Am. Nat. 113, 81–101. doi: 10.1086/283366
Huston M. A., DeAngelis D. L. (1994). Competition and coexistence: the effects of resource transport and supply rates. Am. Nat. 144, 954–977. doi: 10.1086/285720
Kadmon R., Benjamini Y. (2001). Effects of productivity and disturbance on species richness: a neutral model. Am. Nat. 167, 939–946. doi: 10.1086/504602
Laforest-Lapointe I., Paquette A., Messier C., Kembel S. W. (2017). Leaf bacterial diversity mediates plant diversity and ecosystem function relationships. Nature 546, 145–147. doi: 10.1038/nature22399
LaManna J. A., Belote R. T., Burkle L. A., Catano C. P., Myers J. A. (2017a). Negative density dependence mediates biodiversity-productivity relationships across scales. Nat. Ecol. Evol. 1, 1107–1115. doi: 10.1038/s41559-017-0225-4
LaManna J. A., Mangan S. A., Alonso A., Bourg N. A., Brockelman W. Y., Bunyavejchewin S., et al. (2017b). Plant diversity increases with the strength of negative density dependence at the global scale. Science 356, 1389–1392. doi: 10.1126/science.aar3824
Lasky J. R., Uriarte M., Boukili V. K., Erickson D. L., Kress W. J., Chazdon R. L. (2014). The relationship between tree biodiversity and biomass dynamics changes with tropical forest succession. Ecol. Lett. 17, 1158–1167. doi: 10.1111/ele.12322
Leclère D., Obersteiner M., Barrett M., Butchart S. H. M., Chaudhary A., Palma A. D., et al. (2020). Bending the curve of terrestrial biodiversity needs an integrated strategy. Nature 585, 551–556. doi: 10.1038/s41586-020-2705-y
Liang J. J., Crowther T. W., Picard N., Wiser S., Zhou M., Alberti G., et al. (2016b). Positive biodiversity-productivity relationship predominant in global forests. Science 354, 1–12. doi: 10.1126/science.aaf8957
Liang J. J., Watson J. V., Zhou M., Lei X. (2016a). Effects of productivity on biodiversity in forest ecosystems across the United States and China. Conserv. Biol. 30, 308–317. doi: 10.1111/cobi.12636
Loreau M. (1998). Biodiversity and ecosystem functioning: A mechanistic model. Proc. Natl. Acad. Sci. 95, 5632–5636. doi: 10.1073/pnas.95.10.5632
Loreau M., Naeem S., Inchasusti P., Bengtsson J., Grime J. P., Hector A., et al. (2001). Biodiversity and ecosystem functioning: current knowledge and future challenges. Science 294, 804–808. doi: 10.1126/science.1064088
Marquard E., Weigelt A., Roscher C., Gubsch M., Lipowsky A., Schmid B. (2009). Positive biodiversity–productivity relationship due to increased plant density. J. Ecol. 97, 696–704. doi: 10.1111/j.1365-2745.2009.01521.x
Michalet R., Brooker R. W., Cavieres L. A., Kikvidze Z., Lortie C. J., Pugnaire F. I., et al. (2006). Do biotic interactions shape both sides of the humped-back model of species richness in plant communities? Ecol. Lett. 9, 767–773. doi: 10.1111/j.1461-0248.2006.00935.x
Mittelbach G. G., Steiner C. F., Scheiner S. M., Steiner C. H. (2003). What is the observed relationship between species richness and productivity? Reply. Ecol. 84, 3390–3395. doi: 10.1890/03-3077
Pierce S. (2014). Implications for biodiversity conservation of the lack of consensus regarding the humped-back model of species richness and biomass production. Funct. Ecol. 28, 253–257. doi: 10.1111/1365-2435.12147
Schmid B. (2002). The species richness–productivity controversy. Trends Ecol. Evol. 17, 113–114. doi: 10.1016/S0169-5347(01)02422-3
Stegen J. C., Enquist B. J., Ferriere R. (2009). Advancing the metabolic theory of biodiversity. Ecol. Lett. 12, 1001–1015. doi: 10.1111/j.1461-0248.2009.01358.x
Steudel B., Hector A., Friedl T., Löffler C., Lorenz M., Wesche M., et al. (2012). Biodiversity effects on ecosystem functioning change along environmental stress gradients. Ecol. Lett. 15, 1397–1405. doi: 10.1111/j.1461-0248.2012.01863.x
Stevens M. H. H., Carson W. P. (1999). Plant density determines species richness along experimental gradients. Ecology 80, 455–465. doi: 10.1890/0012-9658(1999)080[0455:PDDSRA]2.0.CO;2
Sugden A. M. (2018). Tree diversity improves forest productivity. Science 362, 41–43. doi: 10.1126/science.2018.362.6410.twis
Tilman D. (1982). Resource competition and community structure (New Jersey, USA: Princeton University Press). doi: 10.1515/9780691209654
Tilman D., Lehman C. L., Thomson K. T. (1997). Plant diversity and ecosystem productivity: Theoretical considerations. Proc. Natl. Acad. Sci. 94, 1857–1861. doi: 10.1073/pnas.94.5.1857
Tilman D., Reich P. B., Knops J., Wedin D., Mielke T., Lehman C. (2001). Diversity and productivity in a long-term grassland experiment. Science 294, 843–845. doi: 10.1126/science.1060391
Wang Z. H. (2017). Process strengths determine the forms of the relationship between plant species richness and primary productivity. PloS One 12, e0185884. doi: 10.1371/journal.pone.0185884
Wang Z. H., Chiarucci A., Arratia F. J. (2019). Integrative models explain the relationships between species richness and productivity in plant communities. Sci. Rep. 9, 13730. doi: 10.1038/s41598-019-50016-3
Whittaker R. J. (2010). Meta-analyses and mega-mistakes: calling time on meta-analysis of the species richness-productivity relationship. Ecology 91, 2522–2533. doi: 10.1890/08-0968.1
Whittaker R. J., Heegaard E. (2003). What is the observed relationship between species richness and productivity? Comment. Ecol. 84, 3384–3390. doi: 10.1890/02-3128
Willig M. R. (2011). Biodiversity and productivity. Science 333, 1709–1710. doi: 10.1126/science.1212453
Wu J. H., Li M., Sebastian F., Ma W. L., Wang X. T., Zhang X. Z., et al. (2019). Impacts of grazing exclusion on productivity partitioning along regional plant diversity and climatic gradients in Tibetan alpine grasslands. J. Environ. Manage. 231, 635–645. doi: 10.1016/j.jenvman.2018.10.097
Yenni G., Adler P. B., Ernest S. K. M. (2012). Strong self-limitation promotes the persistence of rare species. Ecology 93, 456–461. doi: 10.1890/11-1087.1
Keywords: plant diversity, productivity, dynamical models, structural equation model, ecological processes, ecosystem functions, integrative research
Citation: Wang Z, Arratia J, Yan T, Zhang C and Chiarucci A (2024) Integrative framework of multiple processes to explain plant productivity–richness relationships. Front. Ecol. Evol. 12:1332985. doi: 10.3389/fevo.2024.1332985
Received: 04 November 2023; Accepted: 15 March 2024;
Published: 04 April 2024.
Edited by:
Darren Norris, Universidade Federal do Amapá, BrazilReviewed by:
Lalasia Bialic-Murphy, ETH Zürich, SwitzerlandCopyright © 2024 Wang, Arratia, Yan, Zhang and Chiarucci. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhenhong Wang, d196aGVuaG9uZ0AxMjYuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.